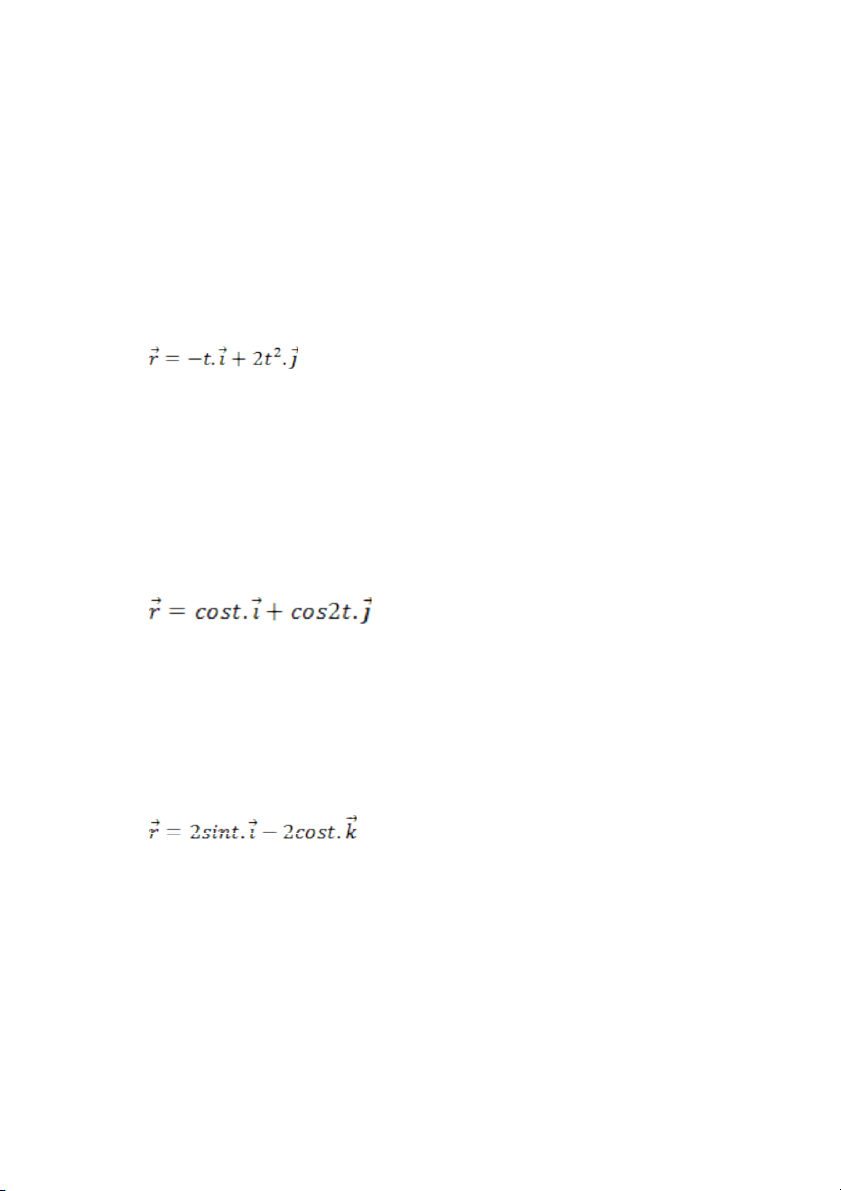
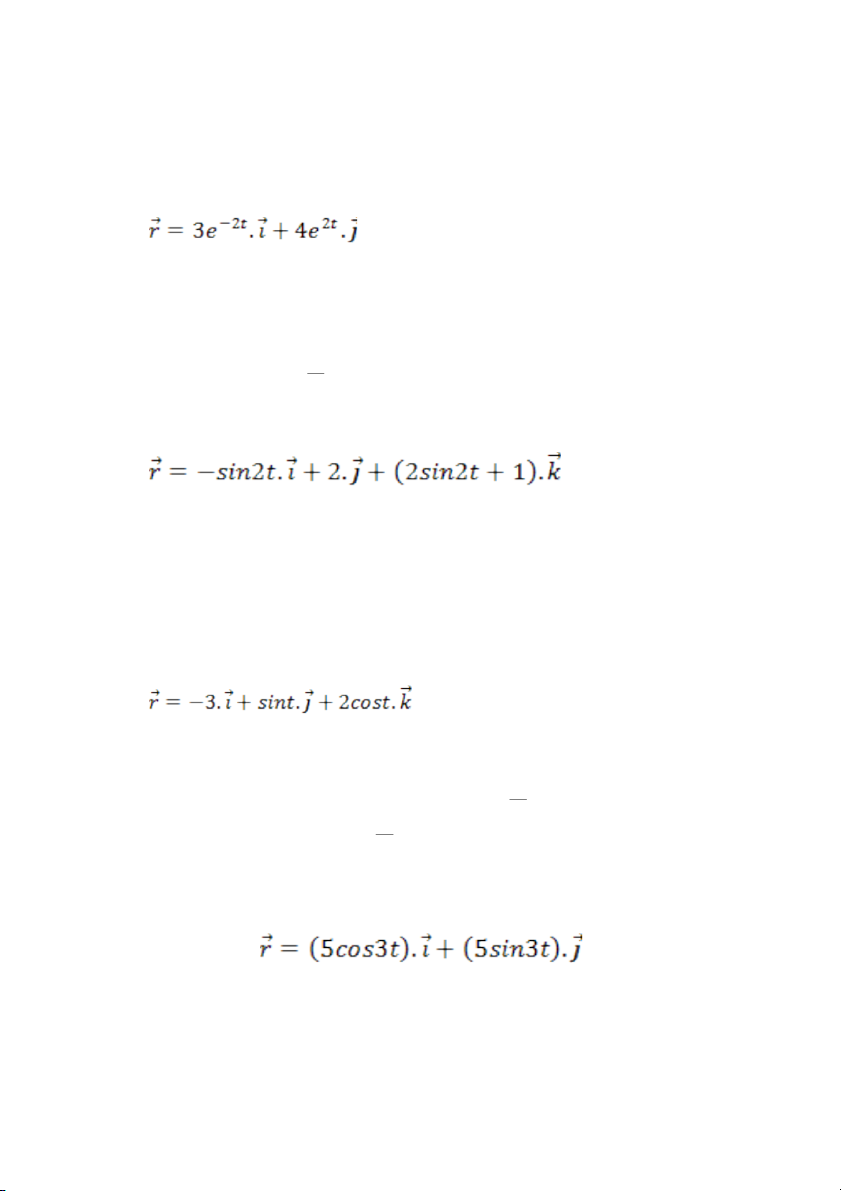

Preview text:
BÀI TẬP VẬT LÝ ĐẠI CƯƠNG PHẦN I: CƠ HỌC
Bài 1) Xác định quỹ đạo chuyển động và viết biểu thức vectơ vận tốc, vectơ gia tốc biết
phương trình chuyển động của chất điểm có dạng sau: a) x t 2 y 2 x 2 y 2 t
Suy ra Quĩ đạo là parabol Vecto v n tốốc ậ v 1.i 4t. j Vecto gia tốốc a 4 . j b) x cos t x cos t y cos 2t 2 y 2 cos t 1 Suy ra 2 Quĩ đ o là parabol ạ y 2 x 1
v sin t.i 2sin 2t. j
a cos t.i 4cos 2t. j c) 2 2 x 2 sin t x ( 2sin t) z 2 2 2 cos t z ( 2cos t) 2 2 2 2 2 x z 4(sin t cos t) 4 2 Quĩ đ o là đ ạ ng tròn t ườ âm O có r=2 v 2 co s t.i 2 sin t.k
a 2 sin t.i 2 cos t.k d) 2t x 3 e 2t y 4e Nhân vế theo vế Hay xy 12 12 y x Quĩ đ o là đ ạ ng Hyperbol ườ 2t 2t v 6e .i 8e . j 2t 2t a 12e .i 16e . j e)
x sin 2t
x sin 2t y 2 y 2
z 2x 1 Đường thẳng z 2 sin 2t 1 z 2x 1
v 2co s 2t.i 4co s 2t.k a 4 sin 2t.i 8sin 2t.k f) x 3 x 3 x 3 2 z y sin t 2 2 y sin t 2 2 y sin t 2 2 2 y sin t cos t 1 Elip 2 2 z 2 cost 2 2 2 z 2 2 cos t z 2 cos t 2 2 v c os t. j 2sin t.k a sin t. j 2co s t.k
Bài 2) Vị trí một chất điểm trong mặt phẳng Oxy được xác định bởi phương trình:
a) Xác định quỹ đạo của chất điểm 2 2 2 x 5 cos3t x 5 cos 3t y 5 2 2 2 sin 3t y 5 sin 3t Cộng vế theo vế : x + y 2 2 = 52 Đường tròn
b) Tìm vectơ vận tốc và vectơ gia tốc, tính độ lớn của chúng. c) Chứng v 15minh rằng sin 3t.i 15vectơ gia cos 3t. j tốc luôn hướng a 4 vào 5cos tâm quỹ 3t.i 45s đạo in 3t. và tính j gia tốc hướng tâm.
Bài 3) Một chất điểm chuyển động trên quỹ đạo tròn có bán kính 50m. Quãng đường đi
được trên quỹ đạo xác định bởi công thức: s = 10t – 0,5t2. Tìm at, a và a toàn n phần lúc t=5s.
Vận tốc của oto lúc t: v=s’= -t+10 Lúc t=5s, v= -5+10 = 5(m/s) Gia tốc tiếp tuyến: a 2 t =v’= -1m/s
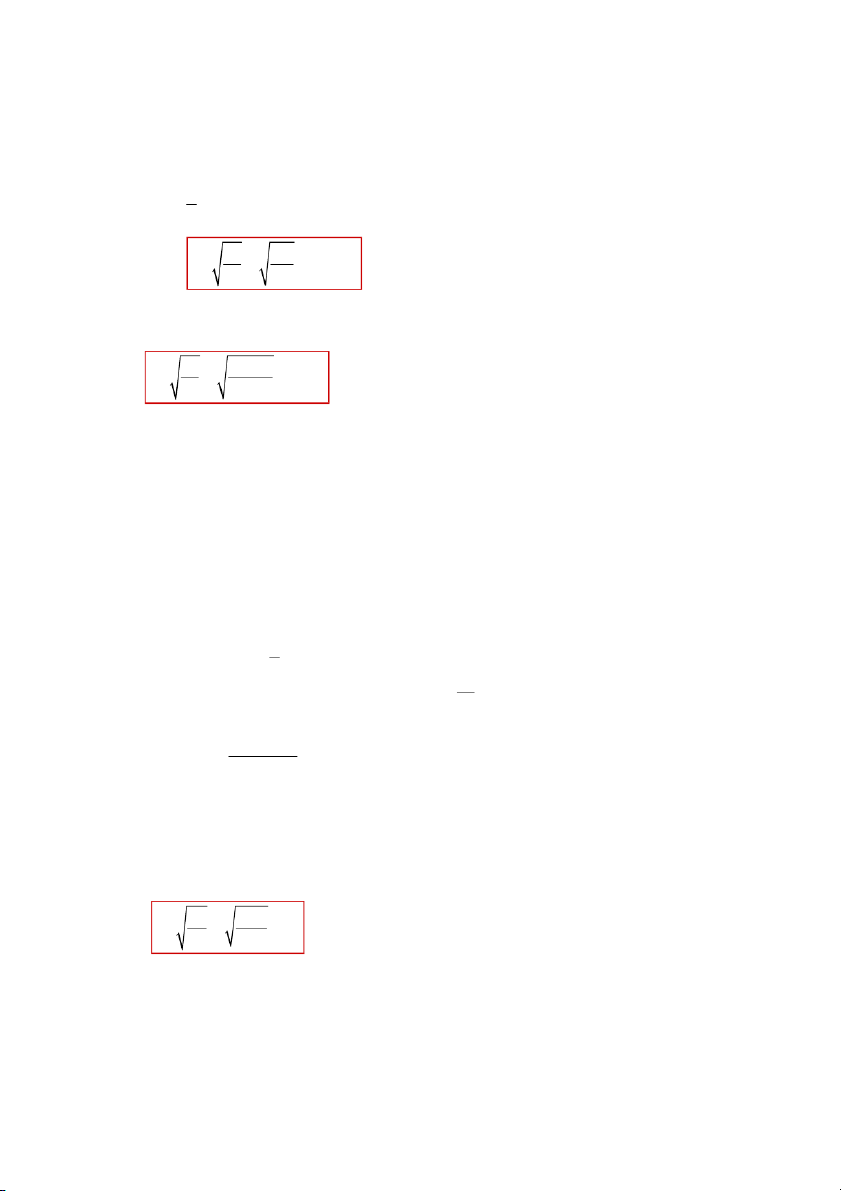
at<0 do đó oto đag chạy chậm dần đều Gia tốc pháp tuyến: a 2 2 2 n =v ÷R =5 ÷50 =0,5 m/s Gia tốc toàn phần : a 2 2 2 2
tp= √at +an = √(-1)2 + 0,5 = 1,12m/s
Bài 4) Một ôtô đang chuyển động với vận tốc 72km/h thì tắt máy, hãm phanh, chuyển
động chậm dần đều, sau 5s thì dừng hẳn.
a) Tìm quãng đường ôtô đi được kể từ lúc hãm phanh đến khi dừng hẳn.
b) Ôtô mất bao lâu để đi được thêm 25m kể từ lúc hãm phanh?
c) Tìm quãng đường ôtô đi được trong giây thứ 3 kể từ lúc hãm phanh.
Bài 5) Thả rơi tự do không vận tốc đầu một vật từ độ cao h=19,6m xuống đất. Cho gia
tốc trọng trường g =9,8m/s . T 2 ính:
a) Quãng đường mà vật rơi được trong 0,1s đầu và 0,1s cuối của thời gian rơi. + trong 0,1s đầu 1 2 1 2
s gt .9,8.0,1 0 ,049m 2 2 + trong 0,1s cuối Thời gian rơi: 2h 2.19,6 t 2 s g 9,8
Quãng đường đi được trong 1,9s đầu: 1 2 1 2
s gt .9,8.1,9 17, 689m 2 2
Quãng đường đi được trong 0,1s cuối : s = 19,6 – 17,689 = 1,911m
b) Tìm thời gian cần thiết để vật rơi 1m đầu và 1m cuối của độ cao h.
vật rơi 1m đầu thì s = 1m 1 2 s gt 2 thì 2s 2.1 t 0, 452 s g 9,8
vật rơi 18,6m đầu thì s = 18,6m 2s 2.18,6 t 1 ,94 s g 9,8
thời gian rơi 1m cuối của độ cao : t = 2 -1,94 = 0.06s
Bài 6) Từ đỉnh một ngọn tháp cao 80m, một quả cầu được ném theo phương ngang với
vận tốc ban đầu V0=20m/s.
a) Xác định phương trình chuyển động, phương trình quỹ đạo của quả cầu và tọa độ
của quả cầu sau khi ném 2s.
Chọn gốc tọa độ tại đỉnh tòa nhà.
PTCĐ : với góc ném = 0 và V0=20m/s. x v
cos .t 20t o r 1 2 2 y v sin . t gt 5t o
PTQĐ : thế t = x/20 vào y ta được : 2 1 2 y x
Hoặc thế = 0 và V0=20m/s vào pt quỹ đạo có sẵn 80 g 2 y . x tg .x 2 2 2v cos o
Tọa độ sau khi ném t = 2s : x 20.2 40 2 y 5.2 20
b) Xác định thời gian rơi và vận tốc của quả cầu sau khi ném 2s.
Thời gian của ném ngang bằng thời gian của bài toán rơi tự do: 2h 2.80 t 4 s g 10
Vận tốc của quả cầu: v r ' v 20 x v v 10t y Độ lớn vận tốc 2 2
v 20 (10t)
Với t = 2s thì v = 28,28 m/s
c) Quả cầu chạm đất cách chân ngọn tháp bao xa?
- thế thời gian rơi t = 4s vào phương trình x = 20.t = 20.4 = 80 m
Bài 7) Từ nóc một tòa nhà cao 45m, người ta ném một hòn đá lên phía trên theo phương
hợp với phương ngang một góc α =300 với vận tốc V0=20m/s. Cho gia tốc trọng
trường g =10m/s2 .Xác định:
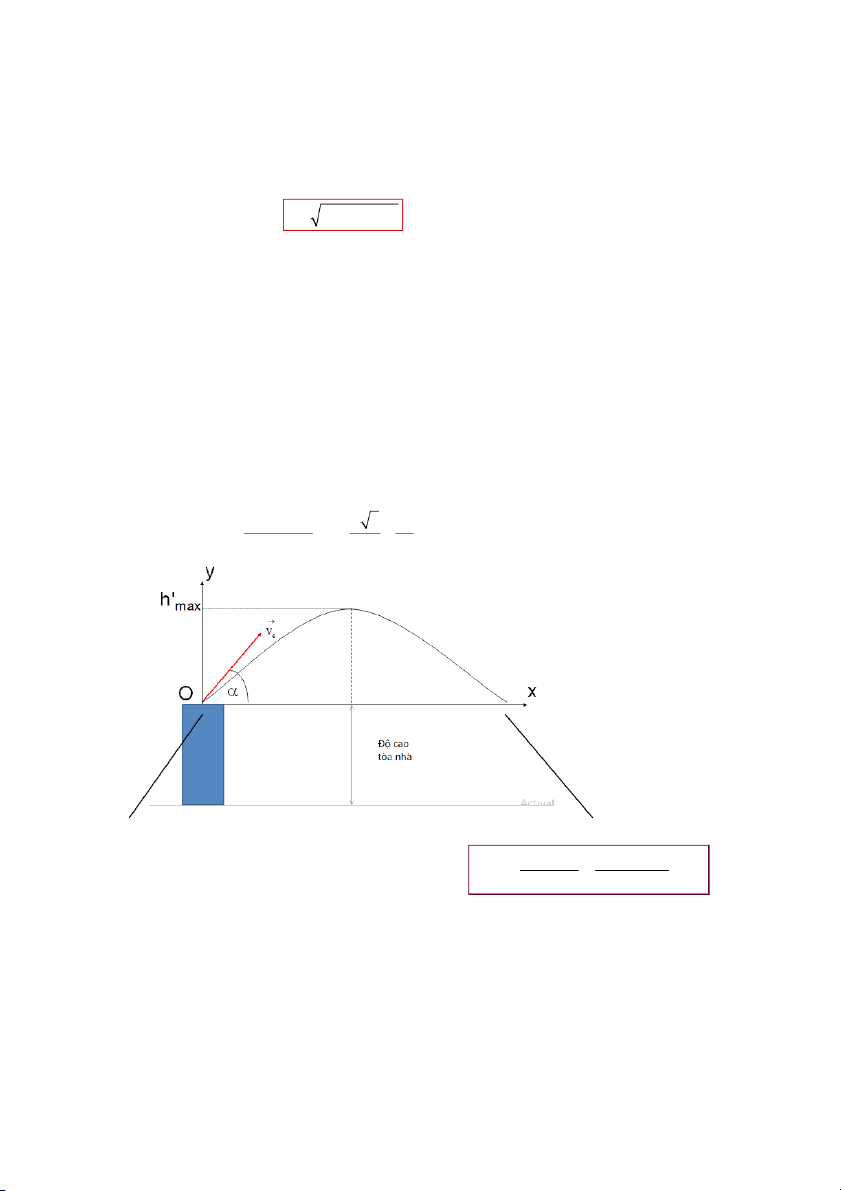
a) Phương trình quỹ đạo của hòn đá và vị trí cao nhất mà hòn đá có thể lên tới.
Chọn gốc tọa độ tại nóc tòa nhà, thế α =300 và v0=20m/s vào g x 3 1 2 2 y . x tg .x x 2 2 2v cos 3 60 o
H(max)=h’(max)+h(độ cao tòa nhà) 2 2 2 2 v o sin 20 .sin 30 h' 5 max m H(max)=5+45=50m 2g 2.10
b) Thời gian chuyển động của hòn đá và vận tốc hòn đá ngay khi chạm đất.
Khi hòn đá chạm đất thì tọa độ y = -45m và thế vào biểu thức tọa độ trên trục y 1 2 y v sin.t gt 2 45 1 0.t 5t o 2
Giải tìm t > 0 : t= 4,16s Vecto vận tốc 0 x v o v cos 20.cos 30 10 3 v 0 v v sin gt 20. sin 30 10t 10 10t y o 2 2 2 2
v v v
(10 3) (10 10.4,16) 3 6,03m / s x y
c) Khoảng cách từ chân tòa nhà đến điểm rơi của hòn đá. x v cos . t 1 0 3.t o Với t = 4,16s thì x = 72 m
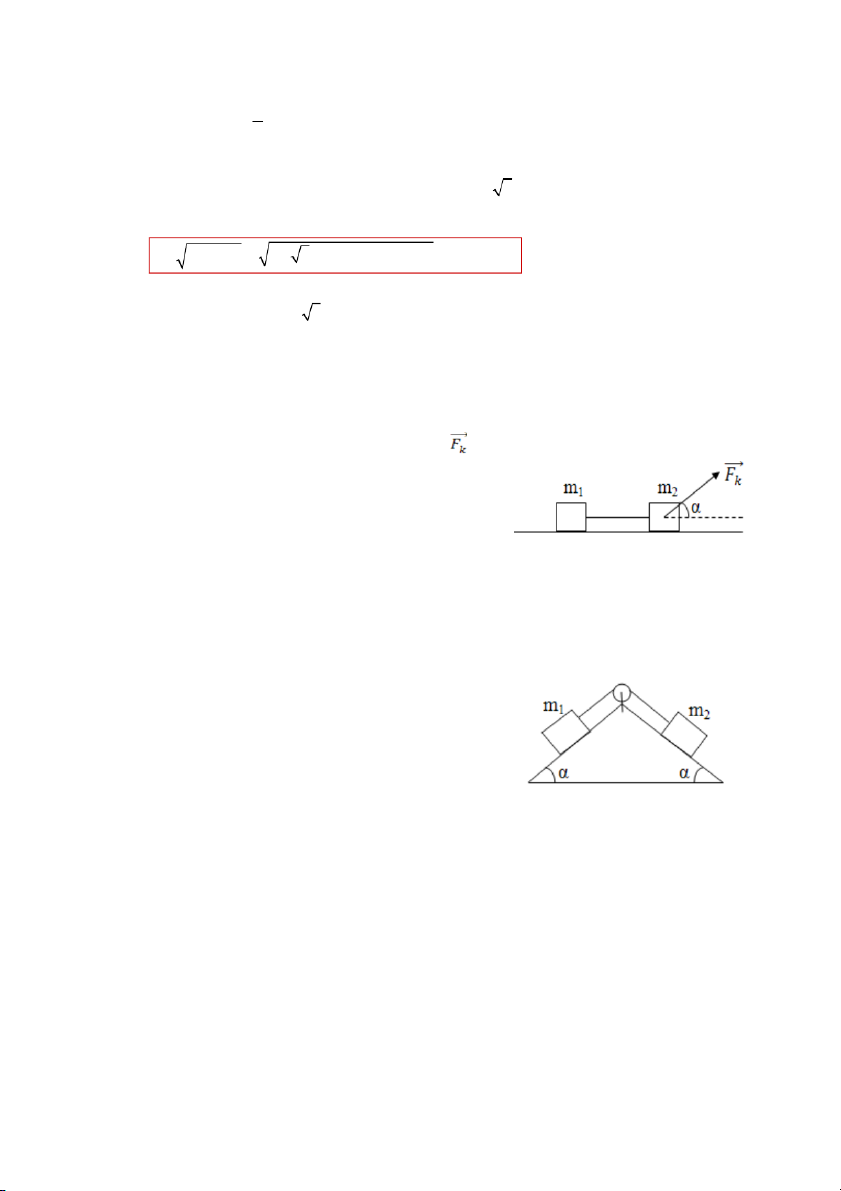
Bài 8) Cho hệ cơ học như hình vẽ. Các vật m1=3kg,
m2=5kg được nối với nhau bằng một sợi dây
nhẹ, không co dãn. Kéo m2 bằng một lực có
độ lớn bằng 20N theo phương hợp với phương
ngang một góc α =300 sao cho cả m1 và m2 đều
chuyển động theo phương ngang. Biết hệ số
ma sát giữa hai vật và mặt phẳng đều bằng
nhau và bằng µ=0,2, gia tốc trọng trường g
=9,8m/s2. Tính gia tốc các vật và độ lớn lực căng dây.
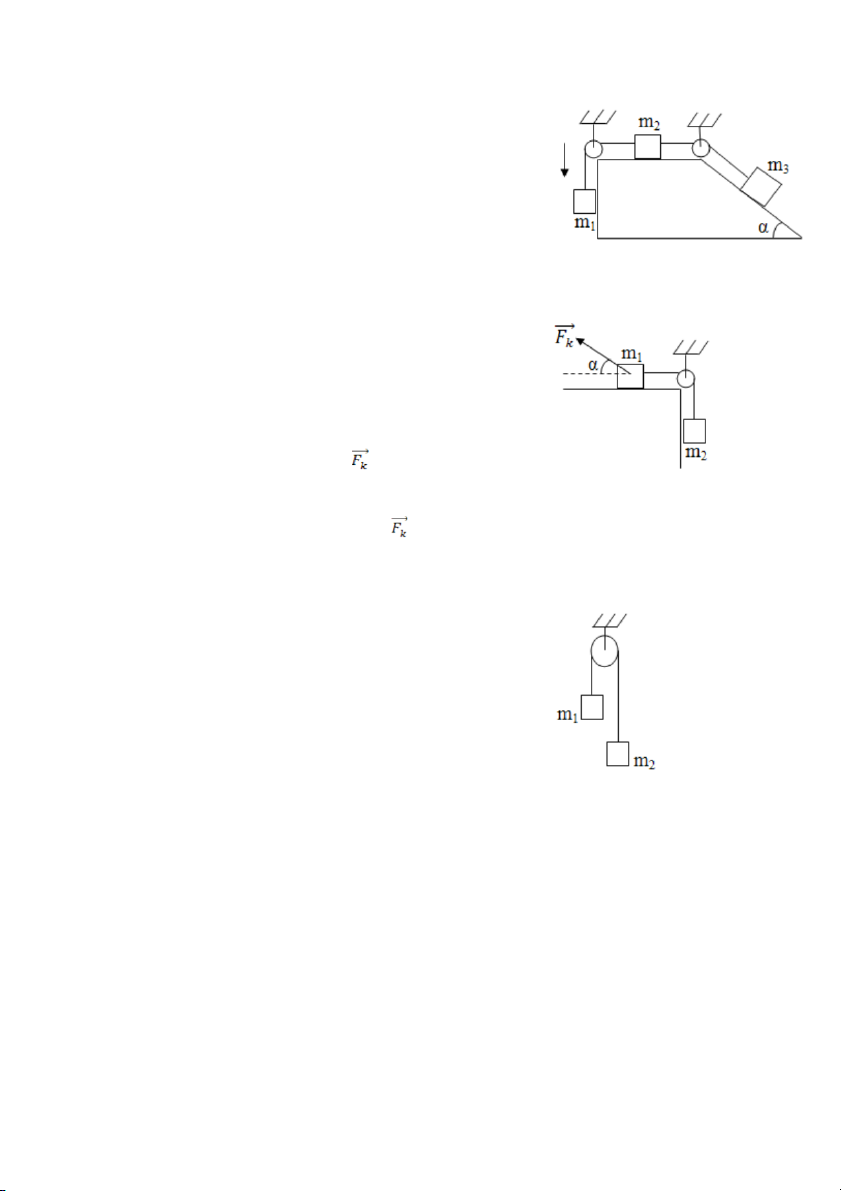
Bài 9) Cho hệ cơ học như hình vẽ. Các vật m1=2kg,
m2=7kg được nối với nhau bằng một sợi dây
nhẹ không co dãn vắt qua một ròng rọc có khối
lượng không đáng kể, góc nghiêng α=30 .0 Hệ
số ma sát giữa hai vật và mặt phẳng nghiêng là
µ, bỏ qua ma sát giữa dây và ròng rọc thì hệ
chuyển động với gia tốc a=1,5m/s . Cho gia tốc 2
trọng trường g=10m/s .2 Tính hệ số ma sát µ và lực căng dây T. Bài 10)
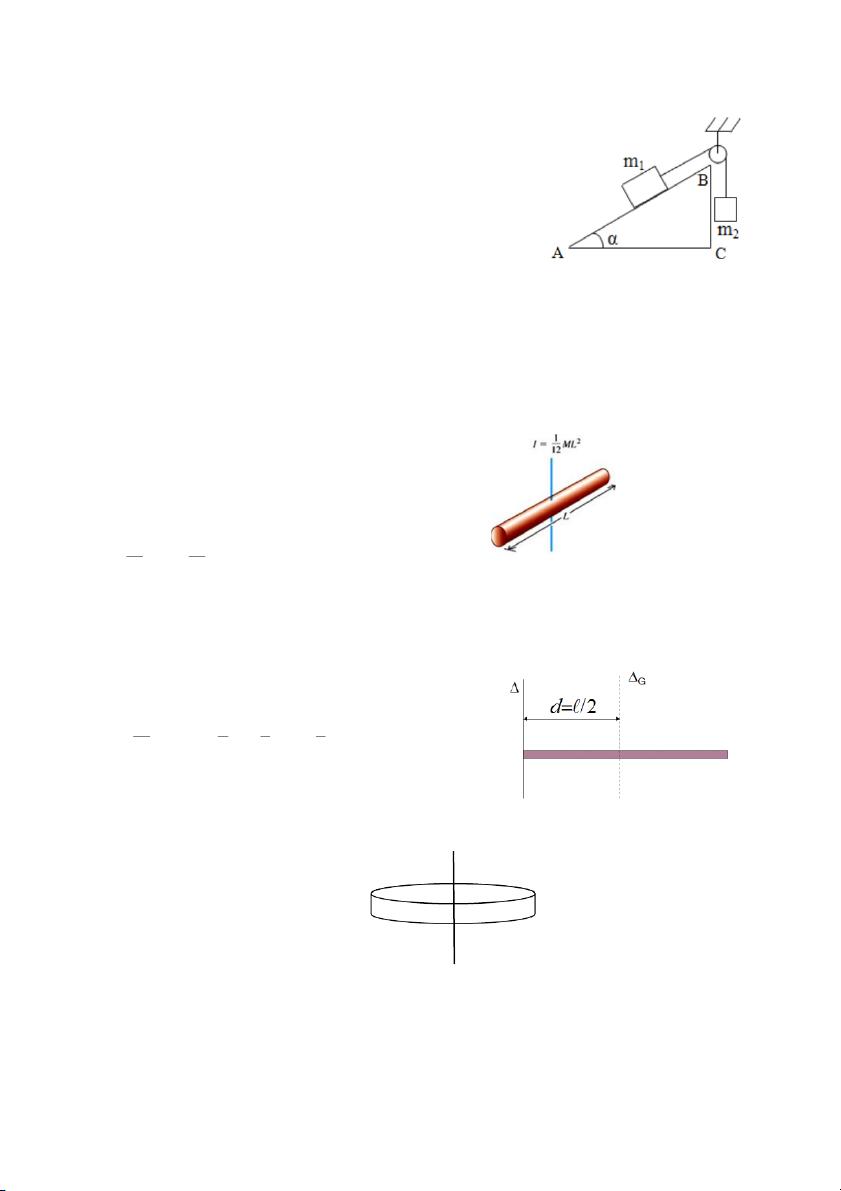
Cho ba vật khối lượng lần lượt là m1=10kg, Biết góc
m2=5kg, m3=3kg được nối với nhau bằng hai sợi dây nghiêng của
nhẹ không co dãn vắt qua hai ròng rọc có khối lượng nêm là α=300,
không đáng kể, bỏ qua ma sát giữa dây và ròng rọc. gia tốc trọng
trường g=10m/s2, m1 chuyển động theo chiều từ trên
xuống dưới với gia tốc a=2m/s2.
a) Độ lớn các lực căng dây.
b) Tính hệ số ma sát giữa m2, m3 với các mặt phẳng, biết
hệ số ma sát giữa chúng với các mặt phẳng là như nhau. Bài 11)
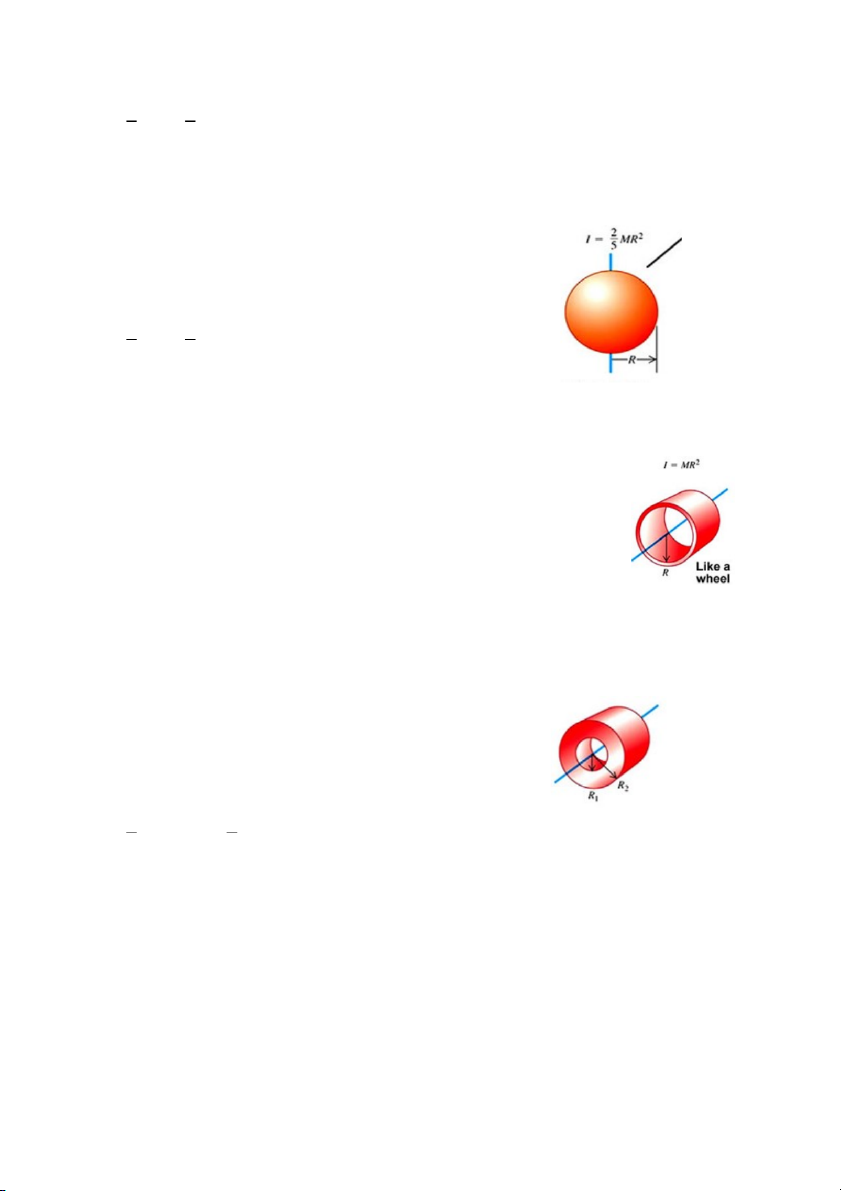
Cho hệ cơ học như hình vẽ. Các vật m1= b) Tính lực căng dây T.
m2= 1kg được nối với nhau bằng một sợi dây
nhẹ không co dãn, vắt qua một ròng rọc có
khối lượng không đáng kể, bỏ qua ma sát giữa
ròng rọc và dây nối. Hệ số ma sát giữa m 1và
mặt phẳng ngang là µ=0,1, gia tốc trọng trường g=10m/s2.
a) Phải kéo m 1 bằng một lực có độ lớn bằng
bao nhiêu để m 1 chuyển động về bên trái với
gia tốc a=1m/s2, biết góc hợp bởi và phương ngang là α=300. Bài 12)
Cho hệ cơ học như hình vẽ. Các vật m1 và m 2 (m2 > m )
1 được nối với nhau bằng một
sợi dây nhẹ không co dãn vắt qua ròng rọc có
khối lượng không đáng kể. Bỏ qua ma sát giữa dây và ròng rọc.
a) Biết quãng đường m2 chuyển động sau 5s là
4m kể từ lúc thả cho các vật bắt đầu chuyển
động. Tính gia tốc và vận tốc các vật sau 5s.
b) Tính lực căng dây và khối lượng m1 biết m2=32kg.
c) Nếu sau 5s dây treo bị đứt thì quãng đường
mỗi vật đi được sau 2s kể từ khi dây bị đứt là bao nhiêu? Bài 13)
Cho hệ cơ học như hình vẽ. Các vật một sợi dây nhẹ m1=4kg, m =1,5kg 2
được nối với nhau bằng không co dãn vắt qua
một ròng rọc có khối lượng không đáng kể.
Góc nghiêng α=300, hệ số ma sát giữa vật và
mặt phẳng nghiêng là µ=0,1 và chiều cao mặt phẳng đứng là BC=h=1m.
a) Tính gia tốc chuyển động của các vật và độ lớn lực căng dây.
b) Lúc bắt đầu chuyển động thì m2 ở ngay sát mặt
đất, tính vận tốc của nó ngay khi lên đến đỉnh mặt phẳng nghiêng B.
Bài 14) 14a. Xác định mômen quán tính của một thanh AB đồng chất có khối lượng m =
200g, chiều dài l = 50 cm đối với trục quay Δ đi qua trung điểm của thanh và vuông góc với thanh. m = 200g = 0,2kg l = 50 cm = 0,5m 1 2 1 2 3 2 I mL
.0,2.0,5 4,16.10 kgm 12 12
14b. Xác định mômen quán tính của một thanh AB đồng chất có khối lượng m =
200g, chiều dài l = 50 cm đối với trục quay Δ đi qua 1 đầu của thanh và vuông góc với thanh. I 2
= I G + md 2 1 2 1 2 1 2 3 2 I m m m .0, 2.0,5 16 ,7.10 kgm 12 2 3 3
Bài 15) Xác định mômen quán tính của một đĩa tròn
đồng chất có khối lượng m = 500g, bán kính R = 40 cm đối với trục quay Δ đi qua
tâm đĩa và vuông góc với mặt phẳng đĩa. m = 500g =0,5kg R = 40 cm = 0,4m 1 2 1 2 2
I mR .0,5.0,4 0, 04kgm 2 2
Bài 16) Xác định mômen quán tính của một khối cầu đặc đồng chất có khối lượng m =
2kg , bán kính R = 30cm đối với trục quay Δ trùng với đường kính bất kỳ của khối cầu. m = 2kg R = 30 cm = 0,3m 2 2 2 2 2
I mR .2.0,3 0, 072kgm 5 5
Bài 17) Xác định mômen quán tính của một vành tròn (hoặc trụ rỗng) đồng chất có khối
lượng m = 100g , bán kính R = 60 cm đối với trục quay Δ trùng với trục của nó. m = 100g = 0,1kg R = 60 cm = 0,6m 2 2 2 I m R 0 ,1.0,6 0 ,036kgm
Bài 18) Xác định mômen quán tính của một vành khăn đồng chất có khối lượng m=500g,
bán kính nhỏ r=20cm, bán kính lớn R=50cm đối với trục quay Δ đi qua tâm của
hình và vuông góc với mặt phẳng hình. m = 500g = 0,5kg r = 20cm = 0,2m R = 50 cm = 0,5m 1 1 2 2 2 2 2 I (
m R r ) .0,5(0,5 0,2 ) 0, 0725kgm 2 2
Bài 19) Xác định mômen quán tính của một hình chữ nhật đồng chất có khối lượng m =
2kg , kích thước (20 x 30cm) đối với trục quay Δ đi qua giao điểm hai đường chéo
và vuông góc với mặt phẳng hình chữ nhật.
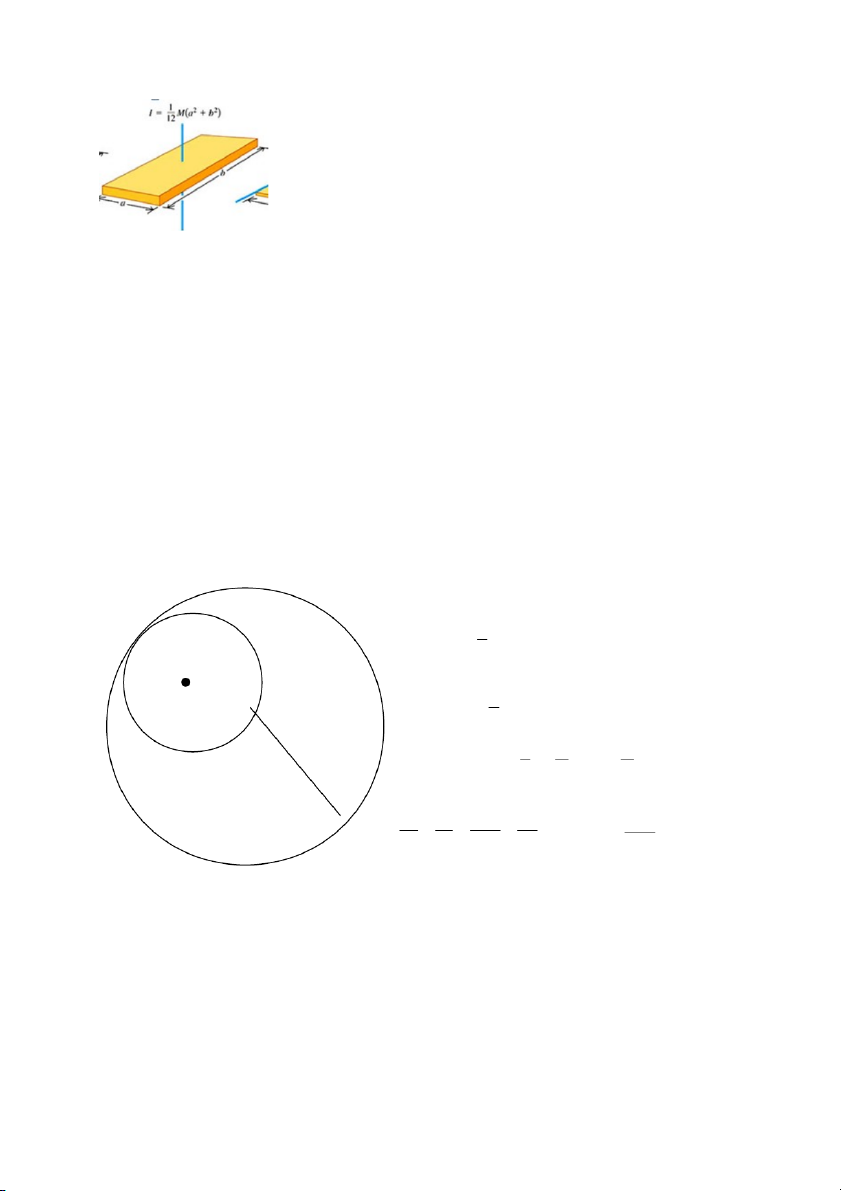
Bài 20) Một đĩa bằng đồng có khối lượng riêng ρ = 8,9 .10 kg/m 3 . Có bề d 3 ày b = 4mm,
bán kính R = 50 cm. Đĩa bị khoét thủng một lỗ tròn bán kính R/2 , tâm O’ của lỗ
khoét cách tâm O của đĩa một khoảng R/2 . Tìm mômen quán tính của đĩa bị khoét
đối với trục vuông góc với đĩa và đi qua tâm O của đĩa. Đĩa khi chưa bị khoét 1 2 I MR 2 O’
Phần đĩa bị khoét: I 2 = I G + md 1 2 2
I ' mr md với r =R/2, d=R/2 O 2 2 2 R 1 ' R R I m m 2 2 2
Phần đĩa còn lại : I’’= I – I’ 2 2 m 2 1 S r r suy ra Mr 2 2 m M 2 2 S R R R
Bài 21) Tính mômen quán tính của một vành tròn đồng chất khối lượng m = 0,01 kg, bán
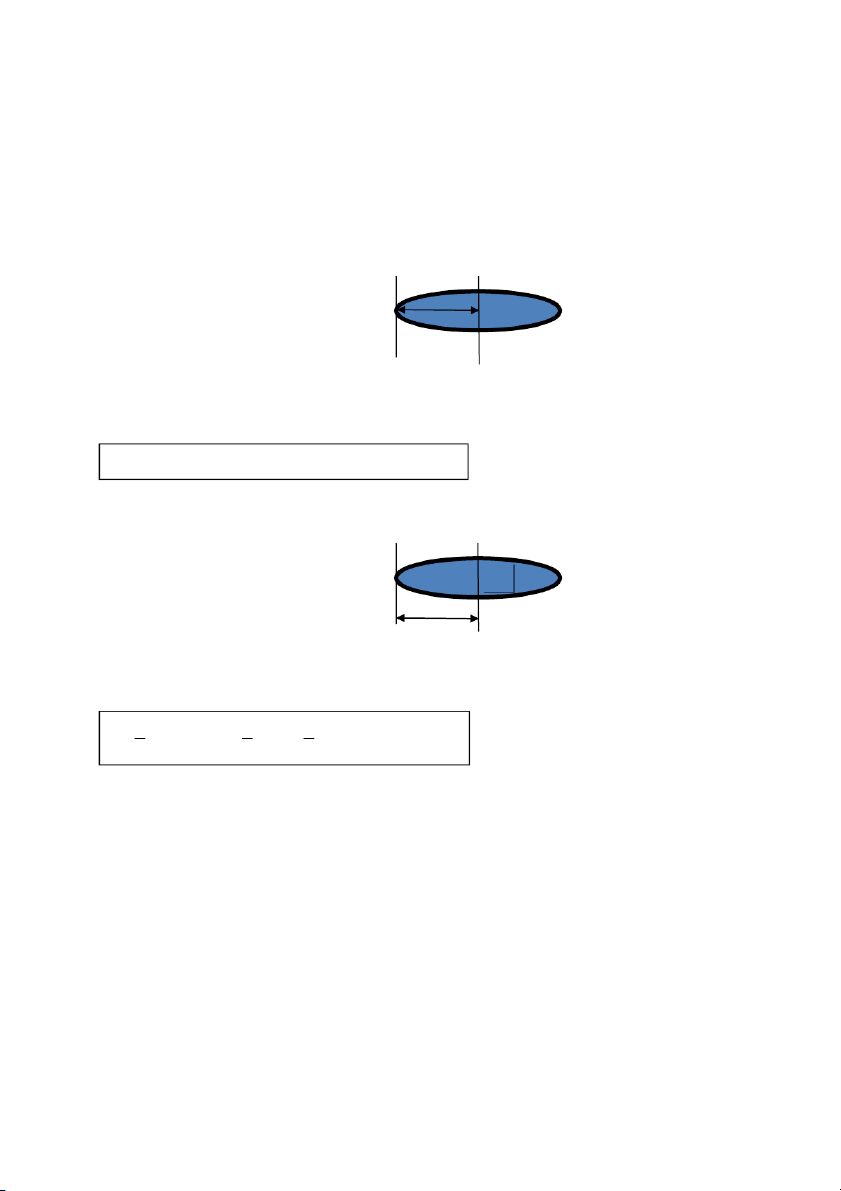
kính R= 20 cm đối với trục qua mép vành và vuông góc với mặt phẳng vành tròn. ∆ d=R ∆G
m = 0,01 kg, bán kính R= 20 cm = 0,2 m I 2 = IG + md Với d = R 2 2 2 2 4 2 I m R mR 2 mR 2 .0,01.0, 2 8 .10 kgm
Bài 22) Tính mômen quán tính của một đĩa tròn đồng chất khối lượng m = 300 g, bán
kính R= 30 cm đối với trục qua mép đĩa và vuông góc với mặt phẳng đĩa. O ∆ d=R ∆G m = 300g= 0,3kg R= 30 cm = 0,3 m I 2
= I∆G + md 1 2 2 3 2 3 2 2
I mR mR mR .0,3.0,3 0, 04kgm 2 2 2
Bài 23) Tính mômen quán tính của trái đất đối với trục quay của nó nếu lấy bán kính quả
đất là R = 6400km và khối lượng riêng trung bình của trái đất ρ = 5,5 .10 kg/m 3 3
Bài 24) Tính mômen quán tính của một khung hình vuông đồng chất tiết diện đều có khối
lượng m =100g, cạnh a= 30cm đối với trục thẳng góc tại tâm với mặt phẳng của hình vuông.




