


Preview text:
BÀI TẬP LẦN 1
1. Có ba SV đi phỏng vấn tìm việc làm. Gọi là biến cố sinh viên thứ i đậu phỏng vấn. Hãy:
a) Biểu diễn các biến cố sau thành phép toán theo
Có ít nhất 1 sinh viên đậu phỏng vấn; A1 + A2 + A3
Có đúng một sinh viên đậu phỏng vấn;
Không có sinh viên nào đậu phỏng vấn; =
Cả 3 sinh viên cùng đậu phỏng vấn; A1.A2.A3
b) Phát biểu thành lời các phép toán sau: - - -
- Có ít nhất 1 sinh viên rớt phỏng vấn
2. Giả sử ta có một không gian mẫu với 5 biến cố sơ cấp có khả năng xuất hiện như nhau . Đặt a) Tính ; P(A) = , P(B) = , P(C) = b) Tính ; = => = => c) Tính , = {E1, E5} = {E1, E5} =
3. Tài khoản séc của Sun Bank được phân loại theo tuổi tài khoản và số dư tài khoản.
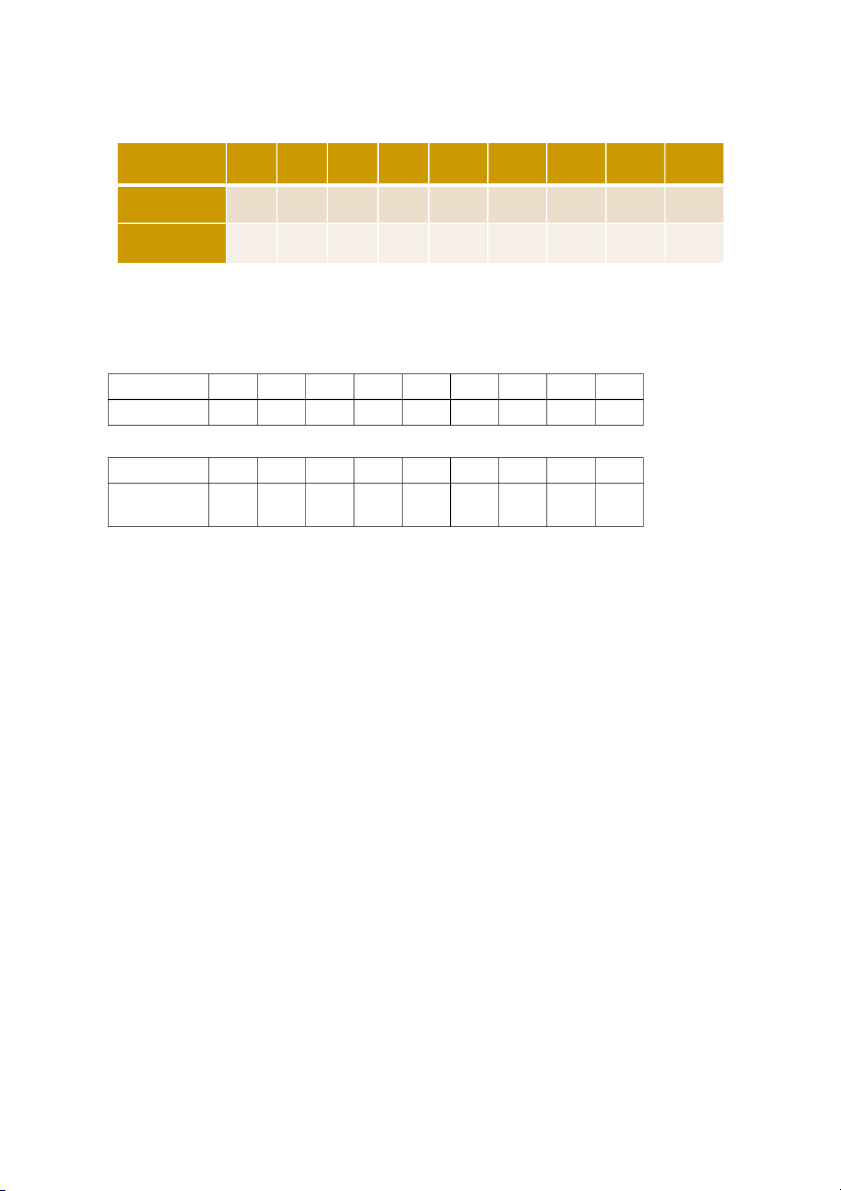
Kiểm toán viên chọn ngẫu nhiên một số tài khoản để thống kê thì thu được bảng số liệu như sau: Số dư tài khoản Tổng Tuổi tài khoản 0 – 499 $ 500 – 999 $ 1000 $ Dưới 2 năm 150 230 110 490 Từ 2 năm trở 90 300 180 570 lên 240 530 290 1060
a) Xác suất một tài khoản ít hơn 2 năm là bao nhiêu?
Gọi A:” Tài khoản ít hơn 2 năm”
b) Xác suất một tài khoản có số dư tối thiểu $ 1000 là bao nhiêu?
Gọi B: “Số dư tối thiểu $1000”
c) Xác suất một tài khoản ít hơn 2 năm có số dư tối thiểu $ 1000 là và bao nhiêu?
Thế A.B “tài khoản ít hơn 2 năm và có số dư tối thiểu $ 1000” P(A.B) =
d) Giả sử chọn 1 tài khoản có số dư $ 500–999, tìm xác suất tuổi tài khoản từ 2 năm trở lên?
Gọi D: “tài khoản có số dư $ 500–999” P() =
e) Xác suất 1 tài khoản có tuổi ít hơn 2 năm
có số dư dưới $ 500 là bao nhiêu? hoặc
Gọi C:” Số dư dưới $500”
Thế thì A+C:” Tài khoản có tuổi ít hơn 2 năm hoặc có số dư dưới $500”
P(A+C) = P(A) + P(C) – P(AC)
f) Giả sử chọn 1 tài khoản có tuổi từ 2 năm trở lên, xác suất số dư tài khoản này nằm
trong khoảng $ 500–999 là bao nhiêu? P() =
4. Xổ số kiến thiết của tỉnh A mỗi lần phát hành có giá là 10 nghìn đồng/vé. Cơ cấu giải
thưởng cho 1 triệu vé như sau: Giải Đặc Nhất Nhì Ba Tư Năm Sáu Bảy Tám Tổng biệt Số tiền 2000 30 15 10 3 1 0,4 0,2 0,1 2059,7 (triệu) Số giải 1 10 10 20 70 100 300 1000 10000 11511 Tổng 2001 40 25 30 73 101 300,4 1000,2 10000, 13570.7 1 X 0 0,1 0,2 0,4 1 3 10 15 30 2000 P 0.988489
0,01 0,001 0,0003 0,0001 0,00007 0,00002 0,00001 0,00001 0,000001
a) Hãy tính số tiền kì vọng nhận được khi mua một vé? Từ đó hãy so sánh với giá vé và cho nhận xét?
Gọi E(X) là số tiền kỳ vọng nhận được khi mua vé
E(X) = 4,28.10-3 (triệu đồng) = 4280 đồng
So với giá vé 10.000đ/1, trung bình mỗi khi mua 1 tờ vé số người mua lỗ: 5720 đồng
b) Mỗi lần phát hành, tỉnh A cung cấp cho thị trường 10 triệu vé. Hãy cho biết, nếu
bán hết số vé này, thì mỗi lần phát hành tỉnh A thu về bao nhiêu tiền lời?
Vậy số tiền lời thu được khi bán hết 10 triệu vé là:
5270*10.000.000 = 57.200.000.000đ = 57,2 (tỷ đồng)
5. Sau kỳ thi, giảng viên thống kê điểm số của sinh viên hai lớp A và B trong bảng sau: Điểm 2 3 4 5 6 7 8 9 10 Số SV lớp A 1 3 5 9 11 8 6 2 2 Số SV lớp B 2 2 4 8 10 9 5 3 1
Gọi tương ứng điểm số của sinh viên lớp A và lớp B
a) Hãy lập bảng phân phối xác suất của . LỚP A X 2 3 4 5 6 7 8 9 10 P 1/47 3/47 5/47 9/47 11/47 8/47 6/47 2/47 2/47 LỚP B X 2 3 4 5 6 7 8 9 10 P 2/44 2/44 4/44 8/44 10/4 9/44 5/44 3/44 1/44 4
b) Làm sao để biết SV lớp nào học tốt hơn? Giải thích.
So sánh E(X) lớp A với E(X) lớp B để biết sinh viên lớp nào học tốt hơn E(XA) = 6.043 E(XB) = 6.045
=> Lớp A và lớp B có năng lực học tập gần như bằng nhau.
c) Lớp nào SV có năng lực học tập đồng đều hơn? Giải thích. σ(XA) = 1.809 σ(XB) = 1.821
Sự đồng đều của 2 lớp cũng gần như giống nhau




