Bài tập ôn tập điện học - Vật lý đại cương | Trường Đại Học Duy Tân

Cho một mạch điện như hình 5-5. Trong đó ống dây có độ tự cảm L = 6H, điện trở R = 200 mắc song song với điện trở R1 = 1000. Hiệu điện thế U = 120V; K là cái ngắt điện. Hiệu điện thế giữa các điểm A và B sau khi mở khoá K một thời gian  = 0,001 giây. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đọc đón xem!

Trường:

Đại học Duy Tân 1.8 K tài liệu

Thông tin:
101 trang 4 tháng trước
Tác giả:
Student
Mai Nguyệt
docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Bài tập ôn tập điện học - Vật lý đại cương | Trường Đại Học Duy Tân

Cho một mạch điện như hình 5-5. Trong đó ống dây có độ tự cảm L = 6H, điện trở R = 200 mắc song song với điện trở R1 = 1000. Hiệu điện thế U = 120V; K là cái ngắt điện. Hiệu điện thế giữa các điểm A và B sau khi mở khoá K một thời gian  = 0,001 giây. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đọc đón xem!

37 19 lượt tải Tải xuống

Môn: Vật lý đại cương (Phy 101) 68 tài liệu

Trường: Đại học Duy Tân 1.8 K tài liệu

Thông tin:

101 trang 4 tháng trước

Tác giả:

Profile Mai Nguyệt
142
ĐIỆN HỌC
CHƯƠNG 1: TRƯỜNG TĨNH ĐIỆN
1-1. Tìm lực hút giữa hạt nhân và electron trong nguyên tử Hyđrô. Biết rằng bán kính nguyên tử
Hyđrô là 0,5.10
-8
cm, điện tích của electron e = -1,6.10
-19
C.
Giải:
Sử dụng công thức lực tương tác giữa hai điện tích của định luật Culông (với điện tích của
electron và h
ạt nhân hyđrô q
e
= - q = -1,6.10 C, kho
p
-19
ảng cách r = 0,5.10
-10
m):
N10.23,9
)10.5,0(
)10.6,1.(10.9
r
qqk
F
8
210
2199
2
21
1-2. Lực đẩy tĩnh điện giữa hai proton sẽ lớn hơn lực hấp dẫn giữa chúng bao nhi ần, cho biết êu l
điện tích của proto
là 1,6.10 C, kh
-19
ối lượng của nó bằng 1,67.10
-27
kg.
Giải:
Theo công thức của định luật Culông và định luật vạn vật hấp dẫn, ta có:
2
2
2
2
2
1
r
Gm
Fvµ;
r
kq
F
)lÇn(10.25,1
)10.67,1.(10.67,6
)10.6,1.(10.9
Gm
kq
F
F
36
22711
2199
2
2
2
1
1-3. Hai qu ùng bán kính và cùng khả cầu đặt trong chân không có c ối lượng được treo ở hai đầu
sợi dây sao cho mặt ngo ủa chúng tiếp xúc với nhau. Sau khi truyền cho các quả cầu một ài c
điện tích q
0
= 4.10
-7
C, chúng đẩy nhau v ữa hai sợi dây bây giờ bằng 60à góc gi
0
. Tính khối
lượng của các quả cầu nếu khoảng cách từ điểm treo đến tâm quả cầu bằng l = 20 cm.
Giải:
Do các qu à giả cầu l ống nhau nên điện tích mỗi quả cầu nhận được là:
143
C10.2
2
q
qq
7
0
21
Hai quả cầu cân bằng khi:
0TFP
d
Khi đó, dễ dàng nhận thấy:
P
F
tg
d
với P = mg và
2
2
0
2
21
sin.24
l
kq
r
qkq
F
d

tgl
kq
tgl
q
P
Pl
q
tg
.sin.16.sin64.sin16.4
22
2
0
22
0
2
0
22
0
2
0
Thay số:
)(157,0
30.30sin.2,0.16
10.4.10.9.1
0022
2
79
N
tg
P
)(16)(016,0
81,9
157,0
gkg
g
P
m
1-4. Tính kh êng c àm quối lượng ri ủa chất l ả cầu trong bài 1-3. Bi u ết rằng khi nhúng các quả cầ
này vào d
ầu hỏa, góc giữa hai sợi dây bây giờ chỉ bằng 54 = 2 đối với dầu hỏa).
0
(
Giải:
Từ kết quả b 3, ta đài 1- ã có đối với quả cầu đặt trong không khí thì:
11
22
01
2
0
.sin64

tgl
q
P (1)
Khi nhúng các quả cầu v ầu hoả, mỗi quả cầu sẽ c ịu th ụng của lực đẩy Acsimét Pào d h êm tác d
1
hướng ngược chiều với trọng lực. Do đó, bằng tính toán tương tự bài trên, ta thu được:
F
đ
T
P
2
144
22
22
02
2
0
1
.sin64

tgl
q
PP (2)
Mặt khác:
VgPVgmgP
01
;
(3)
Từ (1), (2) và (3), ta có:
0
22
2
2
11
2
11
.sin
.sin
tg
tg
P
PP
)(tg.sin.tg.sin
022
2
211
2
1
11
2
122
2
2
22
2
2
0
tg.sin.tg.sin.
tg.sin.
.
Thay s
ố với: )/(800;27;30;2;1
3
0
0
2
0
121
mkg
)/(2550800.
30.30sin27.27sin
27.27sin
3
002002
002
mkg
tgtg
tg


1-5. Hai quả cầu mang điện có bán kính và khối lượng bằng nhau được treo ở hai đầu sợi dây có
chiều d ằng nhau. Người ta nhúng chú ột chất điện môi (dầu) có khối lượng riài b ng vào m êng
1
và hằng số điện môi . Hỏi khối lượng ri ủa quả cầu ( ải bằng bao nhiêu để góc êng c ) ph
giữa các sợi dây trong không khí và trong điện môi là như nhau.
Giải:
Sử dụng các tính toán đ ở bã làm ài 1-4, và thay 1,,
1210
, ta có:
22
2
1
2
1
11
2
22
2
22
2
1
.sin
.sin.sin.sin.
.sin.
.
tg
tgtgtg
tg
Với điều kiện góc lệch giữa các sợi dây trong không khí và chất điện môi là như nhau hay:
22
2
11
2
21
.sin.sin
tgtg
biểu thức trên tr ành: ở th
1
1
145
1-6. Một electron điện tích e, kh ên mối lượng m chuyển động đều tr ột quỹ đạo tròn bán kính r
quanh hạt nhân nguy ử Hyđrô. Xác định vận tốc chuyển động của electron tr ỹ đạo. ên t ên qu
Cho e = -1,6.10
-19
C, m = 9,1.10
-28
kg, khoảng cách trung b ừ electron đến hạt nhân lình t à
r
= 10
-8
cm.
Giải:
Êlêctrôn chuyển động xung quanh hạt nhân theo quỹ đạo tròn dưới tác dụng của lực hướng tâm
chính là lực Culông.
Coulombht
FF
2
0
22
r4
e
r
v
m

mr4
e
r4.m
e.r
v
0
2
2
0
2
2

mr2
e
mr4
e
v
0
0
2


Thay số, ta có:
)/(10.6,1
10.10.1,9.10.86,8.1.2
10.6,1
6
103112
19
smv
1-7. Tại các đỉnh A, B, C của một hình tam giác người ta lần lượt đặt các điện tích điểm: q
1
=
3.10
-8
C; q = 5.10
2
-8 -8
C; q
3
= -10.10
C. Xác định lực tác dụng tổng hợp lên điện tích đặt tại A.
Cho biết AC = 3cm, AB = 4cm, BC = 5cm. Các điện tích đều đặt trong không khí.
Giải:
B
F
2
F
1
F
ỏ
146
Ta có:
+ Lực
1
F
c tác dủa q
2
ụng lên q :
1
)(10.4,8
)10.4.(10.86,8.1.4
10.5.10.3
4
3
2212
88
2
0
21
1
N
r
qq
F
AB

+ Lực
2
F
c tác d ên q : ủa q
3
ụng l
1
)(10.30
)10.3.(10.86,8.1.4
10.10.10.3
4
3
2212
88
2
0
31
2
N
r
qq
F
AC

+ D àng nh
ễ d ận thấy:
222
ACABBC
Vậy, tam giác ABC vuông tại A. Khi đó:
- Lực
F
có phương hợp với cạnh AC một góc ỏ xác định bởi:
'421528,0
10.30
10.4,8
0
3
3
2
1
F
F
tg
- Chiều của
F
như hình v ẽ.
- Độ lớn của lực được tính bằng:
)(10.11,3)10.30()10.4,8(
223232
2
2
1
NFFF
1-8. Có hai điện tích bằng nhau v ấu. Chứng minh rằng tại mọi điểm cách đều hai điện tích à trái d
đó, phương của lực tác dụng lên điện tích thử q ới đường thẳng nối hai điện tích
0
song song v
đó.
Giải:
Gọi là đường trung trực của đoạn thẳng AB nối hai điện tích q ằng nhau v ấu. Xét 
1
và q b
2
à trái d
điện tích thử q
0
(cùng dấu với điện tích đặt tại B) đặt tại C nằm trên . Ta có:
2
2
0
02
2
0
01
1
)(4)(4
F
AC
qq
CB
qq
F

147
Xét thành phần của tổng hợp lực
F
dọc theo :
0cos)(coscos
2121
FFFFF
Vậy,
F
ch ành phỉ có th ần hướng theo phương vuông góc với , hay
song song với đường
thẳng nối hai điện tích q
1
và q .
2
2
0
3
01
2
0
01
21
sin2
sin2
sin
4
2
sinsin
AB
AB
l
qq
l
qq
FFF


1-9.
Tìm l ên mực tác dụng l ột điện tích điểm q = (5/3).10
-9
C đặt ở tâm nửa vòng xuyến bán kính
r
0
= 5cm. tích điện đều với điện tích Q = 3.10
-7
C (đặt trong chân không).
Giải:
Ta chia n òng xuyửa v ến thành những phần tử dl mang điện tích dQ. Chúng tác dụng lên điện tích
q lực dF. áp dụng nguyên lý chồng chất lực, ta có:
x
ỏ
y
q
dF
x
dF
r
o
ỏ
F
1
F
2
F
ỏ
A
B
C
148
cos;sin dFFdFF
yx
(nửa v ửa vòng xuyến) (n òng xuy ến)
Ta có:
2
00
4
.
r
qdQ
dF

v ới
drdldl
r
Q
dQ .;
0
0

d
r
Qq
dF
2
00
2
4
Do tính đối xứng, ta thấy ngay F
y
= 0, nên
2
00
2
2
2
2
00
2
2
.cos
4 r
Qq
d
r
Qq
FF
x


Thay số:
)(10.14,1
)10.5.(10.86,8.1..2
10).3/5.(10.3
3
22122
97
NF
1-10.
Có hai điện tích điểm q
1
= 8.10 C và q = -3.10
-8
2
-8
C đặt cách nhau một khoảng d = 10cm
trong không khí ( ). Tính: hình 1-1
1. Cường độ điện trường gây bởi các điện tích đó tại các điểm A, B, C. Cho biết:
MN = d = 10cm, MA = 4cm, MB = 5cm, MC = 9cm,
NC = 7cm.
2.
Lực tác dụng lên điện tích q = -5.10
-10
C đặt tại C.
Giải:
1. Áp d ên lý chụng nguy ồng chất điện trường:
+ Điện trường do q
1
và q gây ra t
2
ại A cùng phương cùng chiều:
149
2
0
2
2
0
1
)(4)(4
21
AN
q
AM
q
EEE
AAA

)/(10.5,52
)10.6(
10.3
)10.4(
10.8
10.86,8.1.4
1
4
22
8
22
8
12
mV
E
A
+ Điện trường do q
1
và q gây ra t
2
ại B cùng phương ngược chiều:
2
0
2
2
0
1
)(4)(4
21
BN
q
BM
q
EEE
BBB

)/(10.6,27
)10.15(
10.3
)10.5(
10.8
10.86,8.1.4
1
4
22
8
22
8
12
mVE
B
+ Phương, chiều của E
A
và E
B
được xác định như trên hình v ẽ.
Dùng định lý h ố cos, ta thu được:àm s
cos2
2121
22
CCCCC
EEEEE
Ta c ũng có:
23,0
7
.
9
.
2
1079
.
2
coscos..2
222222
222
NC
MC
MNNCMC
NCMCNCMCMN
)m/V(10.87,8
)10.9.(10.86,8.4
10.8
)CM(4
q
E
4
2212
8
2
0
1
C
1

)m/V(10.50,5
)10.7.(10.86,8.4
10.3
)CN(4
q
E
4
2212
8
2
0
2
C
2

Vậy:
)/(10.34,923,0.10.50,5.10.87,8.2)10.50,5()10.87,8(
4442424
mVE
C
Để xác định phương của E , ta xác định góc
C
là góc giữa E
C
và CN theo định lý h ố sin:àm s
C
q
1
B
A
N
q
2
ỏ
E
B
E
A
E
C
E
C1
E
C2
ỏ
150
C
C
C
C
E
sinE
sin
sin
E
sin
E
11
'096792,0
10.34,9
)23,0(1.10.87,8
sin
0
4
24
2. Ta có:
)(10.467,010.34,9.10.5.
4410
NEqF
CC
Chiều của lực F ngược với chiều của điện trường
C
E trên hình v
C
ẽ.
1-11. Cho hai điện tích q và 2q đặt cách nhau 10 cm. Hỏi tại điểm nào trên đường nối hai điện tích
ấy điện trường triệt tiêu.
Giải:
Trên đường nối hai điện tích, điện trường do chúng gây ra luôn cùng phương ngược chiều nên ta
có:
2
2
2
10
2
20
2
10
21
21
44
2
4 rr
q
r
q
r
q
EEE

Giả sử tại điểm M cách điện tích q một khoảng r, điện trường triệt tiêu. Điểm M cách điện tích 2q
một khoảng là (l-r) v à khoới l l ảng cách giữa q và 2q.
0
)rl(
2
r
1
4
q
E
22
0

22
22
r2)rl(0
)rl(
2
r
1
r
2
r
l
)cm(14,4
21
10
21
l
r
Vậy, điện trường giữa hai điện tích q v ệt ti ại điểm M nằm trên đường nối hai điện tích à 2q tri êu t
tại vị trí cách điện tích q là 4,14 (cm).
1-12. Xác định cường độ điện trường ở tâm một lục giác đều cạnh a, biết rằng ở sáu đỉnh của nó có
đặt:
1. 6 điện tích bằng nhau và cùng d ấu.
2. 3 điện tích âm và 3 điện tích dương về trị số đều bằng nhau.
151
Giải:
1. Nếu ta đặt tại sáu đỉnh của lục giác đều các điện tích bằng nhau v ấu, th ặp điện à cùng d ì các c
tích ở các đỉnh đối diện sẽ tạo ra tại tâm các điện trường bằng nhau nhưng ngược chiều, nên chúng
triệt ti ẫn nhau. Do vậy, điện trường tổng cộng tại tâm lục giác bằng không.êu l
E
0
= 0 (do tính đối xứng)
2. Để đặt ba điện tích dương và ba điện tích âm cùng độ lớn vào sáu đỉnh của lục giác đều, ta có ba
cách xếp như sau:
a) Các điện tích âm và dương được đặt xen kẽ với nhau:
Ta nh , E ), (E , E ) và (E , Eận thấy: các cặp điện trường (E
1 4 2 5 3 6
) cùng phương cùng chiều và các
điện trường có cùng độ lớn.
 Các cặp điện tích 1 ạo ra các điện trường bằng -4, 2-5 và 3-6 t
nhau và h
ợp với nhau các góc bằng 120
0
(Hình vẽ).
Do tính đối xứng nên điện trường tổng hợp có giá trị bằng 0.
b) Các điện tích dương và âm đặt liên tiếp:
Các cặp điện tích 1-4, 2-5 và 3-6 tạo ra các điện trường bằng nhau
như hình vẽ:
2
0
2
0
1362514
24
22
a
q
a
q
EEEE

Ta có thể dễ dàng tính được: điện trường tổng cộng E hướng theo
phương của điện trường E và có độ lớn bằng:
14
2
0
14
2
a
q
EE

c) Các điện tích đặt như trên hình bên:
Hai cặp điện tích c ấu đặt tại các đỉnh đối diện tạo ra tại O ùng d
các điện trường có cùng độ lớn nhưng ngược chiều. Do đó, điện
trường do hai cặp điện tích 2 ạo ra tại O l ằng không. -5 và 3-6 t à b
Vậy, điện trường tại O bằng điện trường do cặp điện tích 1-4 tạo ra tại O:
2
0
14
2 a
q
EE

1-13.
Trên hình 1-2, AA’ là một mặt phẳng vô hạn tích điện đều với mật độ điện mặt = 4.10
-
9 2
C/cm và B là m ùng d ên một quả cầu tích điện c ấu với điện tích tr ặt phẳng. Khối lượng của
120
0
E
14
E
25
E
36
1
6
5
4
3 2
O
E
14
E
25
E
36
1
6
5
4
3
2
O
E
14
1
6
5
4
3
2
O
152
qu
ả cầu bằng m = 1g, điện tích của nó bằng q = 10 ỏi sợi dây treo quả cầ ệch đi một
-9
C. H u l
góc bằng bao nhiêu so với phương thẳng đứng.
Giải:
Tại vị trí cân bằng:
0 PFT
Trong đó:
0
2
;

q
EqFmgP
T ình vừ h ẽ ta thấy:
2309,0
81,9.10.10.86,8.1.2
10.10.4
2
312
95
0
mg
q
P
F
tg

0
13
1-14.
Một đĩa tròn bán kính a = 8cm tích điện đều với mật độ điện mặt = 10
-8 2
C/m .
1. Xác định cường độ điện trường tại một điểm tr ục của đĩa và cách tâm đĩa một đoạn b = ên tr
6cm.
2. Ch ứng minh rằng nếu b 0 thì biểu thức thu đượ ẽ chuyển th ểu thức tính cường độ c s ành bi
điện trường gây bởi một mặt phẳng vô hạn mang điện đều.
3. Ch ứng minh rằng nếu b ểu thức thu được chuyển th ểu thức tính cường độ điện  a thì bi ành bi
trường gây bởi một điện tích điểm.
Giải:
1. Chia đĩa th ừng dải vành khăn có bề rộng dr. Xét dải vành khăn có bán kính r (r<a). Vành ành t
khăn có điện tích tổng cộng:
A
F
A’
R
P
T
153
drrdQ .2.
Chia vành khăn thành các điện tích điểm dq. Chúng gây ra điện trường
Ed
tại A. Theo định lý
chồng chất điện trường, điện trường tại A bằng tổng tất cả các giá trị
Ed
đó.
Điện trường
Ed
có thể phân th ần ành hai thành ph
1
Ed
và
2
Ed
. Do tính ên tđối xứng n ổng các
thành phần
1
Ed
bằng không. Vậy:
cos
2
dEdEdE
r
, v à góc giới ỏ l ữa
Ed
và OA
2/3
22
0
2/3
22
0
22
22
0
2
..
.
4
.
4
br
drrb
dQ
br
b
br
b
br
dq
dE
r



Điện trường do cả đĩa gây ra tại A là:
22
0
22
0
0
2/3
22
0
/1
1
1
2
0
1
2
.
2
ba
a
br
b
br
drrb
dEE
a
r



m/V226
10.6/10.81
1
1
10.86,8.2
10
E
2
2
2
2
12
8
2. Nếu cho b 0, ta có:
0
22
0
0
2
/1
1
1
2
lim


ba
E
b
Điện trường khi b 0 có biểu thức giống với điện trường do mặt phẳng tích điện đều gây ra.
3. N a, áp dếu b ụng công thức gần đúng:
2
2
22
2
1
/1
1
b
a
ba
Vậy:
2
0
2
0
2
2
0
2
2
2
0
44
).(
4
.
2
11
2 b
q
b
a
b
a
b
a
E



Điện trường khi b a có biểu thức giống với điện trường do một điện tích điểm gây ra.
1-15.
Một mặt h ầu tích điện đều, mật độ điện mặt . Xác định cường độ điện ình bán c = 10
-9
C/m
2
trường tại tâm O của bán cầu.
154
Giải:
Chia bán cầu th ững đới cầu có bề rộng dh (tính theo phương trục của nó). Đới cầu được tích ành nh
điện tích:
..2
/
.2
cos
.2.
dhR
Rr
dhrdhr
dQ
h
hh


với
là góc giữa mặt đới cầu v ục đối xứng của đới cầu.à tr
Tính tương tự như phần đầu của b 14, ta tính được điện trường dE do đới cầu gây ra tại O có ài 1-
hướng như hình vẽ và có độ lớn bằng:
3
0
2/3
22
0
4
.2.
.
4
R
dhRh
dQ
hr
h
dE
h



Lấy tích phân theo h từ 0 đến R, ta có:
0
2
2
00
2
0
4
0
222
..



R
h
R
dh
R
h
dEE
R
Coi
1
, ta có: )/(2,28
10.86,8.1.4
10
12
9
mVE
1-16.
Một thanh kim loại mảnh mang điện tích q = 2.10 C. Xác định cường độ điện trường tại một
-7
điểm nằm cách hai đầu thanh R = 300cm và cách trung điểm thanh R
0
= 10cm. Coi như điện
tích được phân bố đều trên thanh.
Giải:
Chia thanh thành những đoạn nhỏ dx. Chúng có điện tích là:
dx
RR
q
dx
l
q
dq
2
0
2
2
Xét điện trường
dE
gây ra do đoạn dx gây ra tại điểm đang xét. Ta có thể tách
dE
thành hai thành
phần
1
dE và
2
dE . Điện trường tổng cộng
E
là tổng tất cả các điện trường
dE
đó. Do tính
đối xứng n ổng tất cả các th ần ên t ành ph
1
dE
bằng không. Ta có:
155
dx
xRl
qR
dx
l
q
xR
R
xRr
dq
dE
2/3
22
00
0
22
0
0
22
00
2
0
2
4
..
4
1
cos.
4



0
0
0
d
)tgRR.(cos
R
l4
qR
dx
xRl4
qR
dEE
2/322
0
2
0
2
0
0
0
tgRx
2/l
2/l
2/3
22
00
0
2


000000
0
0
0
0000
RR4
q
R2
l
.
lR2
q
lR4
sinq2
sin
lR4
q
d.cos
lR4
q
0
0



Thay s ố: )/(10.6
1,0.3.10.86,8.1.4
10.2
3
12
7
mVE
1-17. Một mặt phẳng tích điện đều với mật độ . Tại khoảng giữa của mặt có một lỗ hổng bán kính
a nhỏ so với kích thước của mặt. Tính cường độ điện trường tại một điểm nằm trên đường
thẳng vuông góc với mặt phẳng và đi qua tâm lỗ hổng, cách tâm đó một đoạn b.
Giải:
Ta có thể coi mặt phẳng tích điện có lỗ hổng không tích điện như một mặt phẳng tích điện đều
mật độ  và một đĩa bán kính a nằm tại vị trí lỗ tích điện đều với mật độ -.
+ Điện trường do mặt phẳng tích điện đều gây ra tại điểm đang xét là:
0
1
2

E
+ Điện trường do đĩa gây ra tại điểm đang xét là: (xem cách tính trong bài 1-14)
22
0
2
/1
1
1
2
ba
E

+ Điện trường do mặt phẳng và đĩa gây ra c ng phương và ngược chiều nù ên:
22
0
21
/12 ba
EEE

1-18.
Một hạt bụi mang một điện tích q
2
= -1,7.10
-16
C ở cách một dây dẫn thẳng một khoảng 0,4
cm và ở gần đường trung trực của dây dẫn ấy. Đoạn dây dẫn này dài 150cm, mang điện tích
q
1
= 2.10 h l
-7
C. Xác địn ực tác dụng l ạt bụi. Giả thiết rằng q được phân bố đều tr ợi ên h
1
ên s
dây và sự có mặt của q
2
không ảnh hưởng g đến sự phân bố đó.ì
156
Giải:
Xét m à mặt Gaox l ặt trụ đáy tròn bán kính R có tr ùng v
0
ục tr ới sợi dây, chiều cao h (h l)
ở vùng gi y và cách s l, ta có thữa sợi dâ ợi dây một khoảng R
0
 ể coi điện trường tr ặt trụ là đều. ên m
Sử dụng định lý Otxtrôgratxki-Gaox, ta có:
l
hqq
hRE
1
00
0
0
.
1
.2.

lR
q
E
00
1
2

Lực điện tác dụng lên hạt bụi là:
N
lR
qq
EqF
10
312
716
00
21
2
10
5,1.10.4.10.86,8.1.2
10.2.10.7,1
2

1-19. Trong điện trường của một mặt phẳng vô hạn tích điện đều có đặt hai thanh tích điện như
nhau. Hỏi lực tác dụng của điện trường lên hai thanh đó có như nhau không nếu một thanh
nằm song song với mặt phẳng còn thanh kia nằm vuông góc với mặt phẳng.
Giải:
L ng lên thanh nực tác dụ ằm song song là:
ii
EqFF
1
và lực tác dụng lên thanh nằm vuông góc là:
kk
EqFF
2
Do điện trường do mặt phẳng vô hạn tích điện đều gây ra là điện trường đều nên:
21
FFEE
ki
Vậy, lực tác dụng lên hai thanh là như nhau.
1-20.
Một mặt phẳng vô hạn mang điện đều có mật độ điện tích mặt ỏi lực tác =2.10 . H
-9
C/cm
2
dụng l ột đơn vị chiều d ủa một sợi dây d ạn mang điện đều. Cho biết mật độ ên m ài c ài vô h
điện d
ài của dây = 3.10
-8
C/cm.
Giải:
157
Ta th tác dấy, lực ụng lên dây không phụ thuộc vào cách đặt dây trong điện trường. Ta có:
+ Điện trường do mặt phẳng gây ra là:
0
2

E
+ Điện tích của dây là:
Lq
Vậy, lực tác dụng lên mỗi đơn vị chiều dài dây là:
)(4,3
10.86,8.1.2
1.10.3.10.2
2
12
65
0
N
L
EqF


1-21. Xác định vị trí của những điểm ở gần hai điện tích điểm q ại đó điện trường bằng
1
và q t
2
không trong hai trường hợp sau đây: 1) q ấu; 2) q ấu. Cho biết khoảng
1
, q cùng d
2 1
, q khác d
2
cách giữa q
1
và q là .
2
l
Giải:
Véctơ cường độ điện trường tại một điểm M bất kỳ bằng
21
EEE
với
1
E
và
2
E
là các véctơ cường độ điện trường do q
1
, q
2
gây ra.
Để
E
= 0, thì ta phải có:
21
EE
+ Hai điện trường E cùng phương, M phải nằm trên đường thẳng đi qua điểm đặt các điện
1
và E
2
tích.
+ Hai điện trường E cùng độ lớn:
1
và E
2
2
1
2
2
0
2
2
0
1
21
q
q
xl
x
xl4
q
x4
q
EE


xl
q
q
x
q
q
xl
x
2
1
2
1
l
qq
q
q
q
1
q
q
l
x
21
1
2
1
2
1
158
+ Hai điện trường E ngược chiều:
1
và E
2
1. Nếu q
1
, q cùng d
2
ấu th ải nằm giữa hai điì M ph ên tích:
l
qq
q
xlx
21
1
0
2. Nếu q
1
, q khác d ì M ph
2
ấu th ải nằm ngoài hai điện tích:
l
qq
q
xlxhayx
21
1
0
1-22. Giữa hai dây dẫn h ụ song song cách nhau một khoảng = 15cm người ta đặt một hiệu ình tr l
điện thế U = 1500V. Bán kính tiết diện mỗi dây l định cường độ điện à r = 0,1cm. Hãy xác
trường tại trung điểm của khoảng cách giữa hai sợi dây biết rằng các dây dẫn đặt trong
không khí.
Giải:
Ta đi xét trường hợp tổng quát: nếu gọi k ảng cách từ điểm M đến trục dây dẫn thứ nhất lho à x thì
cường độ điện trường tại M là:
)(22
1
00
xlx
l
xlx
E


với  là mật độ điện dài trên dây. Mặt khác:
dU = - Edx
r
rl
r
rl
xlxdx
xlx
EdxU
rl
r
lnlnln
2
11
2
000



r
rl
U
ln
0

Thế vào biểu thức cường độ điện trường và thay x = /2, ta có: l
r
rl
l
U
r
rl
U
l
l
l
l
E
ln.
2
ln
.
2
.
2
2
1
0
0


Thay s ố:
mVE /10.4
001,0
149,0
ln.15,0
1500.2
3
159
1-23.
Cho hai điện tích điểm q
1
= 2.10 C, q = -10
-6
2
-6
C đặt cách nhau 10cm. Tính công của lực tĩnh
điện khi điện tích q ịch chuyển trên đường thẳng nối hai điện tích đó ột đoạn
2
d xa thêm m
90cm.
Giải:
Ta có: Công của lực tĩnh điện khi dịch chuyển điện tích q
2
từ điểm A đến điểm B là:
A = q – V )
2
.(V
A B
Vậy:
)(4
.
)(44
0
21
0
2
0
1
2
rlr
qql
rl
q
r
q
qA

Thay s ố:
JA 162,0
1.1,0.10.86,8.1.4
10.2.10.9,0
12
66
Dấu trừ thể hiện ta cần thực hiện một công để đưa q ra xa điện tích q
2
1
.
1-24.
Tính công cần thiết để dịch chuyển một điện tích q = (1/3).10
-7
C từ một điểm M cách quả
cầu tích điện bán kính r = 1cm một khoảng R = 10cm ra xa vô cực. Biết quả cầu có mật độ
điện mặt
= 10
-11 2
C/cm .
Giải:
Công của lực tĩnh điện ịch chuyển điện tích lkhi d à:
A = q.(V – V )
A B
Vậy:
)(
444
.
2
102010
Rdo
R
qQ
R
Q
R
Q
qA

)()(4
..4.
0
2
0
2
Rr
qr
Rr
rq


Thay s ố:
JA
7
212
2
277
10.42,3
10.11.10.86,8.1
10.10.3/1.10
1-25.
Một vòng dây tròn bán kính 4cm tích điện đều với điện tích Q = (1/9).10 C. Tính điện thế
-8
tại:
1. Tâm vòng dây.
2. M ột điểm M tr ục vên tr òng dây, cách tâm c òng dây mủa v ột đoạn h = 3cm.
160
Giải:
Chia vòng dây thành những đoạn vô c ỏ dl mang điện tích dq. Điện thế do điện tích dq gây ùng nh
ra tại điểm M trên trục vòng dây, cách tâm c òng dây mủa v ột đoạn h là:
22
0
4 hR
dq
dV

Điện thế do cả vòng gây ra t à: ại M l
22
0
22
0
44 hR
Q
hR
dq
dVV

1. Điện thế tại tâm vòng (h =0):
V
R
Q
V
O
250
10.4.10.86,8.1.4
10.9/1
4
212
8
0

2. Điện thế tại M (h = 3cm):
V
hR
Q
V
H
200
10.310.410.86,8.1.4
10.9/1
4
2
2
2
212
8
22
0

1-26.
Một điện tích điểm q = (2/3).10 ằm cách một sợi dây dài tích điện đều một khoảng r
-9
C n
1
=
4cm; dưới tác dụng của điện trường do sợi dây gây ra, điện tích dịch chuyển theo hướng
đường sức điện trường đến khoảng cách r = 2cm, khi đó lực điện trường thực hiện một công
2
A = 50.10
-7
J. Tính mật độ điện dài c y. ủa dâ
Giải:
Ta có: dA = q.dV
dr
r2
.q)Edr.(qdA
0

2
1
0
12
0
r
r
0
r
r
ln
2
q
rlnrln
2
q
r
dr
2
q
dAA
2
1



2
1
0
r
r
ln.q
A2

161
Vậy:
mC /10.6
2
4
ln.10.3/2
10.50.10.86,8.1..2
7
9
712
1-27. Trong chân không liệu có thể có một trường tĩnh điện mà phương của các véctơ cường độ
điện trường trong cả khoảng không gian có điện trường th đổi nhưng giá trị lại thay ì không
đổi, ví dụ như thay đổi theo phương vuông góc với các véctơ điện trường ( ) được hình 1-3
không?
Giải:
Xét đường cong kín h ữ nhật như hình ch ình vẽ, ta có:
dlEdV .
ABCDA
AA
dl.EVV
DACDBCAB
dl.Edl.Edl.Edl.E
0CD.E0AB.E
21
0lEE
12
Vậy: Nếu phương của véctơ cường độ điện trường không đổi thì giá trị của nó cũng phải không đổi
trong toàn bộ không gian. Không có điện trường nào như nêu trong đề bài.
1-28. Tính điện thế gây ra bởi một quả cầu dẫn điện mang điện q bằng cách coi điện thế tại một
điểm A nào đó bằng tổng các điện thế do từng điện tích điểm gây ra, trong các trường hợp
sau:
1. Tại một điểm nằm tr ả cầu.ên qu
2. Tại một điểm nằm trong quả cầu.
3. Tại một điểm nằm ngo ả cầu cách bề mặt của nó một đoạn bằng a.ài qu
E
Hình 1
-
3
| 1/101

Tài liệu khác của Đại học Duy Tân

Preview text:

ĐIỆN HỌC
CHƯƠNG 1: TRƯỜNG TĨNH ĐIỆN 1-1.
Tìm lực hút giữa hạt nhân và electron trong nguyên tử Hyđrô. Biết rằng bán kính nguyên tử
Hyđrô là 0,5.10-8 cm, điện tích của electron e = -1,6.10-19 C. Giải:
Sử dụng công thức lực tương tác giữa hai điện tích của định luật Culông (với điện tích của
electron và hạt nhân hyđrô q -19 e = - qp = -1,6.10
C, khoảng cách r = 0,5.10-10m): k q q 1 . 9 09.( 1 . 6 , 1 0 1  9 )2 F 1 2     , 9 2 . 3 10 8  N r 2 ( . 5 , 0 10 1  0 )2 1-2.
Lực đẩy tĩnh điện giữa hai proton sẽ lớn hơn lực hấp dẫn giữa chúng bao nhiêu lần, cho biết
điện tích của proto là 1,6.10-19C, khối lượng của nó bằng 1,67.10-27 kg. Giải:
Theo công thức của định luật Culông và định luật vạn vật hấp dẫn, ta có: 2 2 kq Gm F   ; vµ F   1 2 2 2 r r F kq2 1 . 9 0 .9( 1 . 6 , 1 0 1 ) 9 2 1     2 , 1 5 1 . 036 (lÇ ) n F   2 Gm2 , 6 67 1 . 0 1 . 1 ( 6 , 1 7 1 . 0 27) 2 1-3.
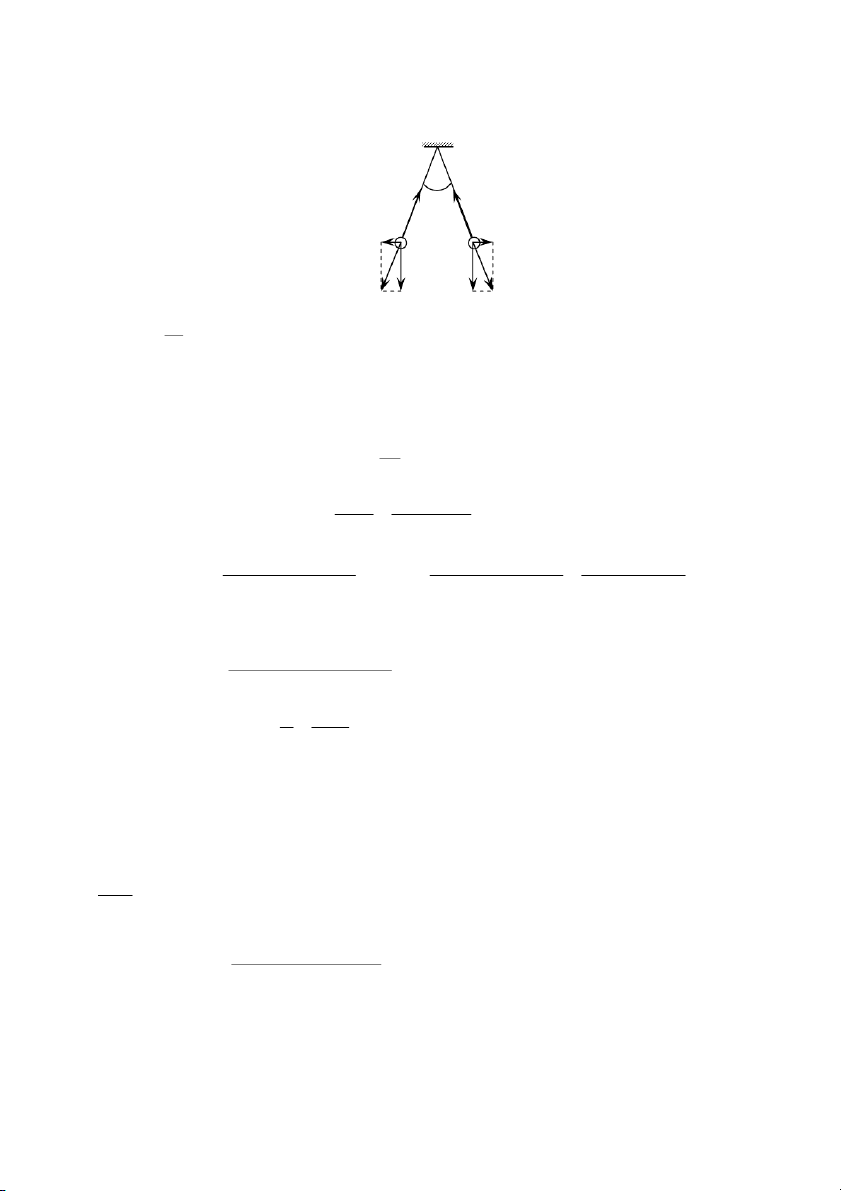
Hai quả cầu đặt trong chân không có cùng bán kính và cùng khối lượng được treo ở hai đầu
sợi dây sao cho mặt ngoài của chúng tiếp xúc với nhau. Sau khi truyền cho các quả cầu một điện tích q 0
0 = 4.10-7C, chúng đẩy nhau và góc giữa hai sợi dây bây giờ bằng 60 . Tính khối
lượng của các quả cầu nếu khoảng cách từ điểm treo đến tâm quả cầu bằng l = 20 cm. Giải:
Do các quả cầu là giống nhau nên điện tích mỗi quả cầu nhận được là: 142 T 2  Fđ P q q  q 0   1 . 2 07 C 1 2 2
Hai quả cầu cân bằng khi:    P  F  T  0 d F
Khi đó, dễ dàng nhận thấy: tg d   P 2 kq q kq với P = mg và 1 2 0 F   d 2 r  4 2l.sin 2 q 2 q2 kq2  t g 0   P 0 0    4  .1 l 6 2 sin 2 0  P . 6  4  l 2 sin 2 0  t .  g 1 l 6 2.sin 2  t.  g Thay số: 2 1 . 9 . 109. . 4 10 7  P   N 16 , 0
. 22.sin2 300 .tg300  1 , 0 5 ( 7 ) P 1 , 0 57  m    , 0 01 ( 6 kg)  16(g) g 8 , 9 1 1-4.
Tính khối lượng riêng của chất làm quả cầu trong bài 1-3. Biết rằng khi nhúng các quả cầu
này vào dầu hỏa, góc giữa hai sợi dây bây giờ chỉ bằng 540 ( = 2 đối với dầu hỏa). Giải:
Từ kết quả bài 1-3, ta đã có đối với quả cầu đặt trong không khí thì: 2 q 0 P  (1) 2 2
64  l sin  .t g 1 0 1 1
Khi nhúng các quả cầu vào dầu hoả, mỗi quả cầu sẽ chịu thêm tác dụng của lực đẩy Acsimét P1
hướng ngược chiều với trọng lực. Do đó, bằng tính toán tương tự bài trên, ta thu được: 143 2 q 0 P   (2) 1 P 2 2
64  l sin  . 2 0 2 t g 2 Mặt khác:
P mg Vg; P   Vg (3) 1 0
Từ (1), (2) và (3), ta có: 2 P P sin .tg  1 1 1 1   0   P  2 sin . 2  2 t g 2    sin 2   1 1 t.g1.  sin 2 2  t . g (  ) 2 2 0 2  .sin  t . g 2 2  2     . 0 2 2  .sin  t . g  .sin  t.g 2 2 2 1 1 1 Thay số với:   ; 1   ;
2   300 ;   270;   80 ( 0 kg / 3 m ) 1 2 1 2 0  sin2 270 .tg 270   .800  255 ( 0 kg / 3 m )
sin2 270.tg 270  sin2 300.tg 300 1-5.
Hai quả cầu mang điện có bán kính và khối lượng bằng nhau được treo ở hai đầu sợi dây có
chiều dài bằng nhau. Người ta nhúng chúng vào một chất điện môi (dầu) có khối lượng riêng
1 và hằng số điện môi . Hỏi khối lượng riêng của quả cầu () phải bằng bao nhiêu để góc
giữa các sợi dây trong không khí và trong điện môi là như nhau. Giải:
Sử dụng các tính toán đã làm ở bài 1-4, và thay    ,   ,   1, ta có: 0 1 2 1 2 .sin  .tg 2  2    .   1  2 2 1 2  .sin  .t g  sin  .t g sin  .t g 2 2 1 1 1   2 sin  . 2 tg 2
Với điều kiện góc lệch giữa các sợi dây trong không khí và chất điện môi là như nhau hay: 2 2   
 sin  .tg  sin  . 1 2 1 1 2 tg  2
biểu thức trên trở thành:    1   1  144 1-6.
Một electron điện tích e, khối lượng m chuyển động đều trên một quỹ đạo tròn bán kính r
quanh hạt nhân nguyên tử Hyđrô. Xác định vận tốc chuyển động của electron trên quỹ đạo.
Cho e = -1,6.10-19C, m = 9,1.10-28kg, khoảng cách trung bình từ electron đến hạt nhân là r = 10-8cm. Giải:
Êlêctrôn chuyển động xung quanh hạt nhân theo quỹ đạo tròn dưới tác dụng của lực hướng tâm chính là lực Culông. F F ht Coulomb 2 2 v e  m  2 r 4 r 0 e . r 2 e 2  v 2   . m 4 r 2 4 0 0mr e2 e  v   4 mr 2  mr 0 0 Thay số, ta có: 1  9 . 6 , 1 10 v   6 , 1 1 . 06 (m / s) 2 . 8 , 8 . 1 6.10 12. . 1 , 9 10 31.10 10 1-7.
Tại các đỉnh A, B, C của một hình tam giác người ta lần lượt đặt các điện tích điểm: q1 = 3.10-8C; q -8 -8
2 = 5.10 C; q3 = -10.10 C. Xác định lực tác dụng tổng hợp lên điện tích đặt tại A.
Cho biết AC = 3cm, AB = 4cm, BC = 5cm. Các điện tích đều đặt trong không khí. F 1 A   ỏ F  2 F C B Giải: 145 Ta có: 
+ Lực của q2 tác dụng lên q1: 1 F q q 3 1 . 0 8 . 5 . 10 8 1 2 F    , 8 . 4 10 3( ) 1 N 4 2  r 4 . 1 . 8 , 8 6.10 . 12 ( . 4 10 2) 2 0 AB  + Lực
của q3 tác dụng lên q1: 2 F q q . 3 10 .810.108 1 3  F   3 . 0 10 ( 3 ) 2 N 4 2    r 4 1 . 8 , 8 . . 6 10 . 12 ( 1 . 3 0 2)2 0 AC + Dễ dàng nhận thấy: 2 2 2
BC AB AC
Vậy, tam giác ABC vuông tại A. Khi đó: 
- Lực F có phương hợp với cạnh AC một góc ỏ xác định bởi:  1 F , 8 . 4 10 3 tg    , 0 28    15042' F 3 . 0 103 2 
- Chiều của F như hình vẽ.
- Độ lớn của lực được tính bằng: 2 2
F F F  4 , 8 ( 1 . 0 3  )2  3 ( 0 1 . 0 3  )2  1 , 3 1 1 . 0 2  ( ) 1 N 2 1-8.
Có hai điện tích bằng nhau và trái dấu. Chứng minh rằng tại mọi điểm cách đều hai điện tích
đó, phương của lực tác dụng lên điện tích thử q0 song song với đường thẳng nối hai điện tích đó. Giải:
Gọi  là đường trung trực của đoạn thẳng AB nối hai điện tích q1 và q2 bằng nhau và trái dấu. Xét
điện tích thử q0 (cùng dấu với điện tích đặt tại B) đặt tại C nằm trên . Ta có: q q q q 1 0 2 0   1 FF 2 2 2 4 (BC) 4 (AC ) 0 0 146 F1  F C ỏ ỏ F2 A B 
Xét thành phần của tổng hợp lực F dọc theo :
F F cos  F cos  (F F ) cos  0  1 2 1 2  
Vậy, F chỉ có thành phần hướng theo phương vuông góc với , hay F song song với đường
thẳng nối hai điện tích q1 và q2. 3 2 q q sin 2 q q sin  1 0 1 0
F F sin  F sin   1 2  2 2 4 0  l   0  lAB AB    2sin   1-9.
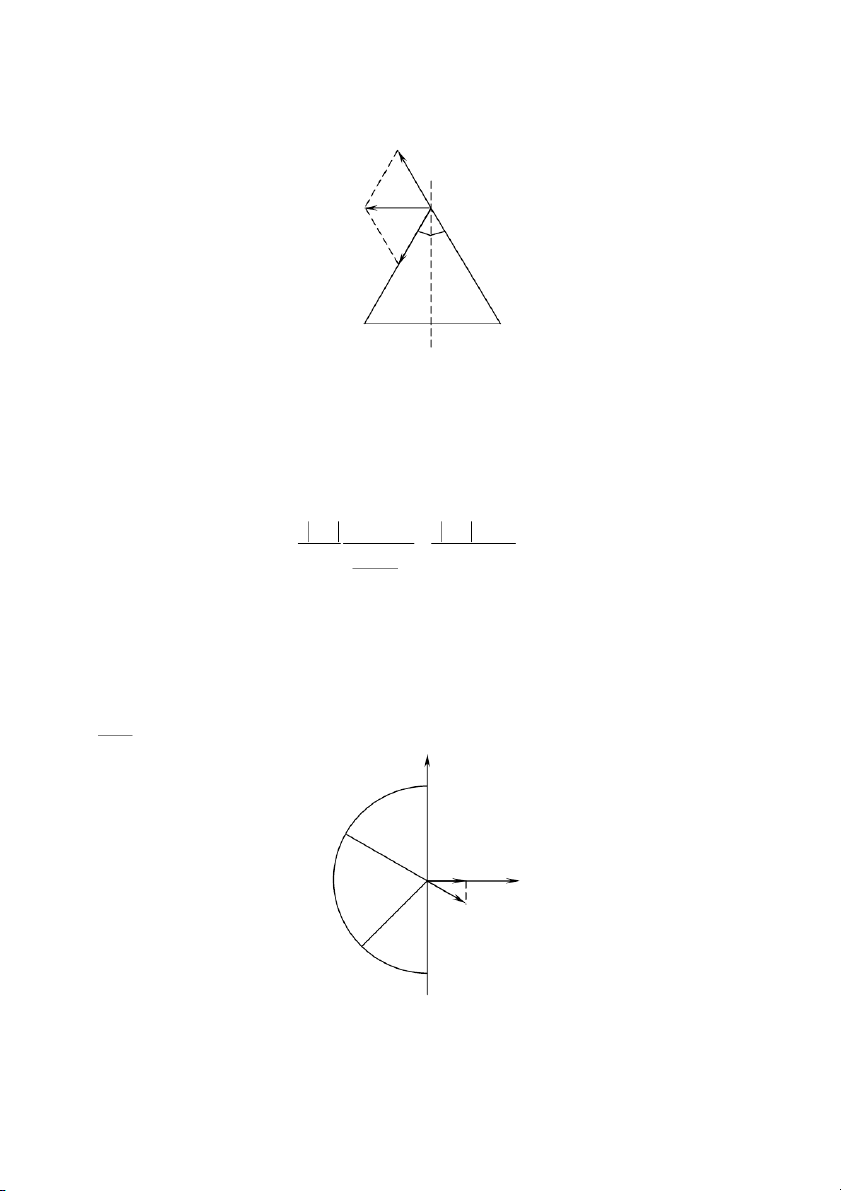
Tìm lực tác dụng lên một điện tích điểm q = (5/3).10-9C đặt ở tâm nửa vòng xuyến bán kính
r0 = 5cm. tích điện đều với điện tích Q = 3.10-7C (đặt trong chân không). Giải: y dl q dFx ỏ ro x dF
Ta chia nửa vòng xuyến thành những phần tử dl mang điện tích dQ. Chúng tác dụng lên điện tích
q lực dF. áp dụng nguyên lý chồng chất lực, ta có: 147 F xdF sin; F ydF cos (nửa vòng xuyến) (nửa vòng xuyến) Ta có: dQ.q dF  2 4 r 0 0 Q với dQ dl ; dl r d .  0 r0 QqdF   d   2 4 r2 0 0
Do tính đối xứng, ta thấy ngay Fy = 0, nên  2 Qq F F  cos . Qqd   x 2 2 2 2  4  r 2 0 0  0 0 r  2 Thay số: 3.107.(5 / ) 3 1 . 09 F   1 , 1 4.10 3  (N ) . 2 2  1 . 8 , 8 . 6 1 . 0 . 12 ( . 5 102)2
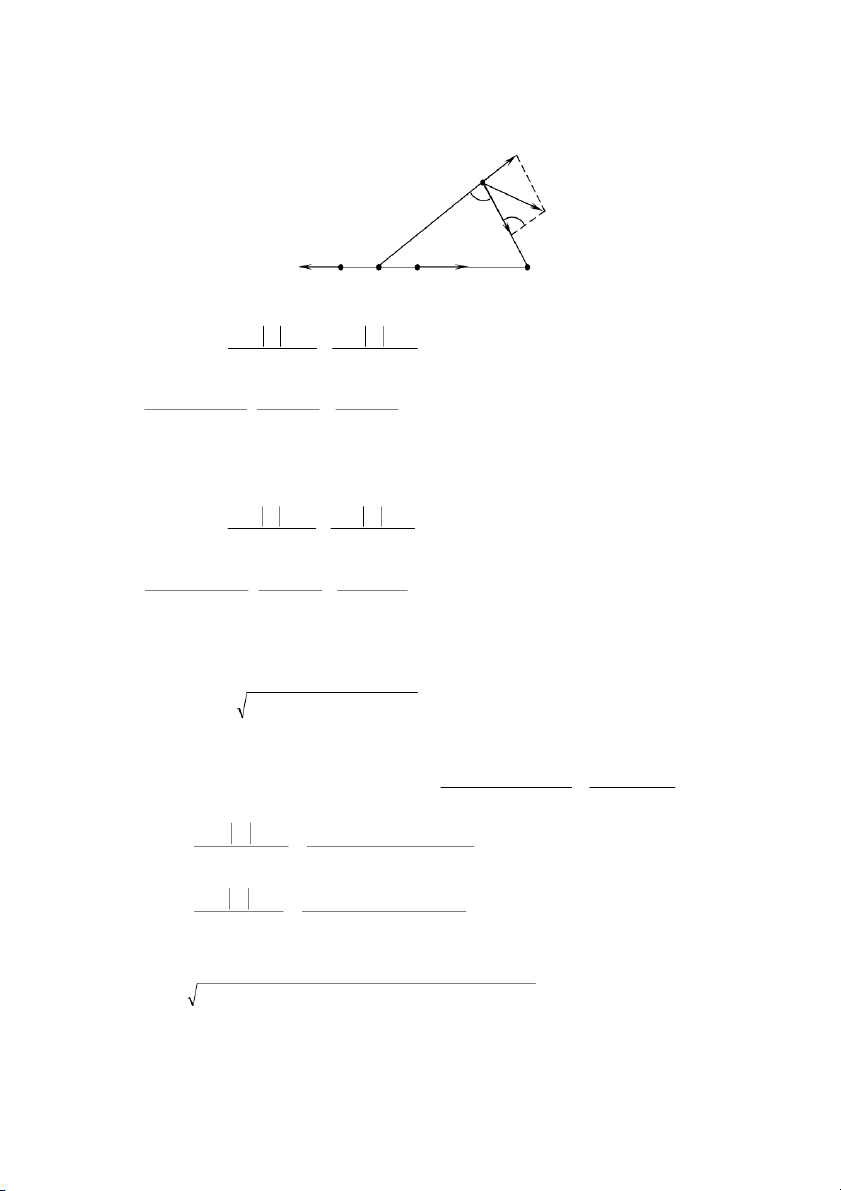
1-10. Có hai điện tích điểm q -8 -8
1 = 8.10 C và q2 = -3.10 C đặt cách nhau một khoảng d = 10cm
trong không khí (hình 1-1). Tính:
1. Cường độ điện trường gây bởi các điện tích đó tại các điểm A, B, C. Cho biết:
MN = d = 10cm, MA = 4cm, MB = 5cm, MC = 9cm, NC = 7cm.
2. Lực tác dụng lên điện tích q = -5.10-10C đặt tại C. Giải:
1. Áp dụng nguyên lý chồng chất điện trường:
+ Điện trường do q1 và q2 gây ra tại A cùng phương cùng chiều: 148 EC1 C ỏ ỏ EC E E C2 B q1 q2 B M A E N A q q 1 2 EE E   A 1 A A2 2 2 4 (AM ) 4 (AN ) 0 0 1  . 8 108 . 3 10 8  E   A 4 . 1 . 8 , 8 6.1012  ( . 4 102 )2 ( . 6 102 )2     52 1 . 5 , 04 (V / m)
+ Điện trường do q1 và q2 gây ra tại B cùng phương ngược chiều: q q 1 2
E E E   B 1 B B2 2 2 4 ( BM) 4 (BN) 0 0 1  . 8 10 8 . 3 10 8  E    27 6 , 1 . 04 (V / m) B 4 . 1 . 8 , 8 6.1012 ( . 5 10 2) 2 1 ( 5.10 2) 2   
+ Phương, chiều của EA và EB được xác định như trên hình vẽ.
Dùng định lý hàm số cos, ta thu được: 2 2 E EE E E C C C 2 C C cos 1 2 1 2 Ta cũng có: 2 2 2
MC NC MN   2 2 2 9 2 7 2 10 2
MN MC NC  2MC.NC.cos  cos    , 0 23 2MC .NC 2.9.7 q  1 8 1 . 0 8 E    8 , 8 . 7 104 (V / m) C1 4 C ( M)2 4 8 , 8 . . 6 10 12.( . 9 102 )2 0 q  2 . 3 10 8 E    5 , 5 0 1 . 04(V / m) C2 4 (CN)2 4 8 , 8 . . 6 101 .2( 1 . 7 02) 2 0 Vậy: E  8 , 8 ( . 7 104)2  ( 5 , 5 . 0 104 )2  . 2 8 , 8 . 7 104 5 , 5 . 0 1 . 04 , 0 . 23  3 , 9 4 1 . 04 (V / m) C
Để xác định phương của EC, ta xác định góc  là góc giữa EC và CN theo định lý hàm số sin: 149 E  1 E E sin C C C   sin 1   sin sin EC , 8 8 . 7 104. 1 , 0 ( 2 ) 3 2 sin   , 0 92    6700 ' 9 , 9 3 . 4 104 2. Ta có:  
F q.E  . 5 10 10 3 , 9 . . 4 104  , 0 46 . 7 10 4 (N ) C C
Chiều của lực FC ngược với chiều của điện trường EC trên hình vẽ.
1-11. Cho hai điện tích q và 2q đặt cách nhau 10 cm. Hỏi tại điểm nào trên đường nối hai điện tích
ấy điện trường triệt tiêu. Giải:
Trên đường nối hai điện tích, điện trường do chúng gây ra luôn cùng phương ngược chiều nên ta có: q 2q q  1 2 
E E E    1 2 2 2   2 2   4 r 4 r 4 r r 0 1 0 2 0  1 2 
Giả sử tại điểm M cách điện tích q một khoảng r, điện trường triệt tiêu. Điểm M cách điện tích 2q
một khoảng là (l-r) với l là khoảng cách giữa q và 2q. q  1 2  E    0 4    r 2 (l  r)2  0  1 2 2 2    0  (l  r)  2r 2 2 r (l  r)  l  r  r 2 l 10  r    1 , 4 ( 4 cm) 1 2 1  2
Vậy, điện trường giữa hai điện tích q và 2q triệt tiêu tại điểm M nằm trên đường nối hai điện tích
tại vị trí cách điện tích q là 4,14 (cm).
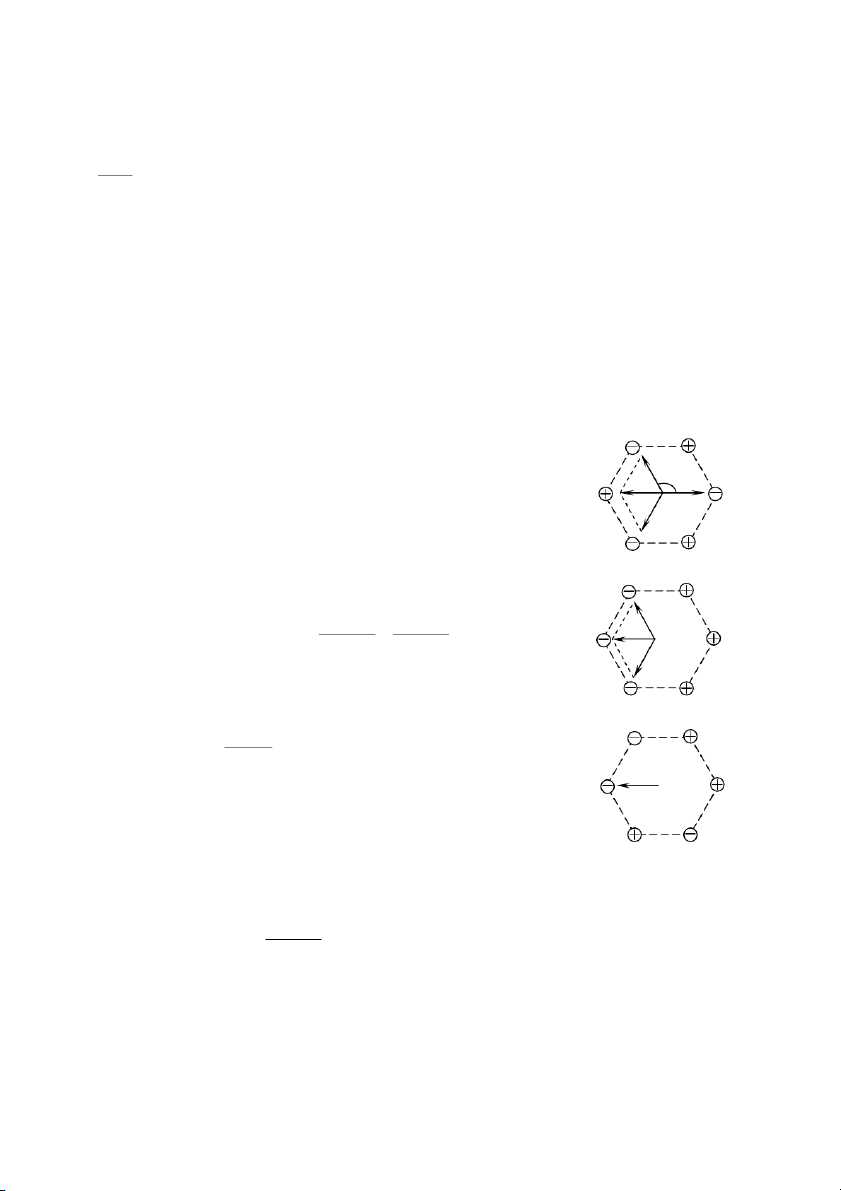
1-12. Xác định cường độ điện trường ở tâm một lục giác đều cạnh a, biết rằng ở sáu đỉnh của nó có đặt:
1. 6 điện tích bằng nhau và cùng dấu.
2. 3 điện tích âm và 3 điện tích dương về trị số đều bằng nhau. 150 Giải:
1. Nếu ta đặt tại sáu đỉnh của lục giác đều các điện tích bằng nhau và cùng dấu, thì các cặp điện
tích ở các đỉnh đối diện sẽ tạo ra tại tâm các điện trường bằng nhau nhưng ngược chiều, nên chúng
triệt tiêu lẫn nhau. Do vậy, điện trường tổng cộng tại tâm lục giác bằng không.
E0 = 0 (do tính đối xứng)
2. Để đặt ba điện tích dương và ba điện tích âm cùng độ lớn vào sáu đỉnh của lục giác đều, ta có ba cách xếp như sau:
a) Các điện tích âm và dương được đặt xen kẽ với nhau:
Ta nhận thấy: các cặp điện trường (E1, E4), (E2, E5) và (E3, E6) cùng phương cùng chiều và các
điện trường có cùng độ lớn. 5  6
Các cặp điện tích 1-4, 2-5 và 3-6 tạo ra các điện trường bằng
nhau và hợp với nhau các góc bằng 1200 (Hình vẽ). E25 1200 4 1
 Do tính đối xứng nên điện trường tổng hợp có giá trị bằng 0. O E14
b) Các điện tích dương và âm đặt liên tiếp: E36 3 2
Các cặp điện tích 1-4, 2-5 và 3-6 tạo ra các điện trường bằng nhau 5 6 như hình vẽ: E25 q q E
E E E  2E  2  14 14 25 36 1 2 2 4 1  a 2 4 O 0  0a
Ta có thể dễ dàng tính được: điện trường tổng cộng E hướng theo E36
phương của điện trường E 2
14 và có độ lớn bằng: 3 5 6 q E  2E  14 2 0a E14
c) Các điện tích đặt như trên hình bên: 4 O 1
Hai cặp điện tích cùng dấu đặt tại các đỉnh đối diện tạo ra tại O
các điện trường có cùng độ lớn nhưng ngược chiều. Do đó, điện 3 2
trường do hai cặp điện tích 2-5 và 3-6 tạo ra tại O là bằng không.
Vậy, điện trường tại O bằng điện trường do cặp điện tích 1-4 tạo ra tại O: q E E  14 2 2 0  a
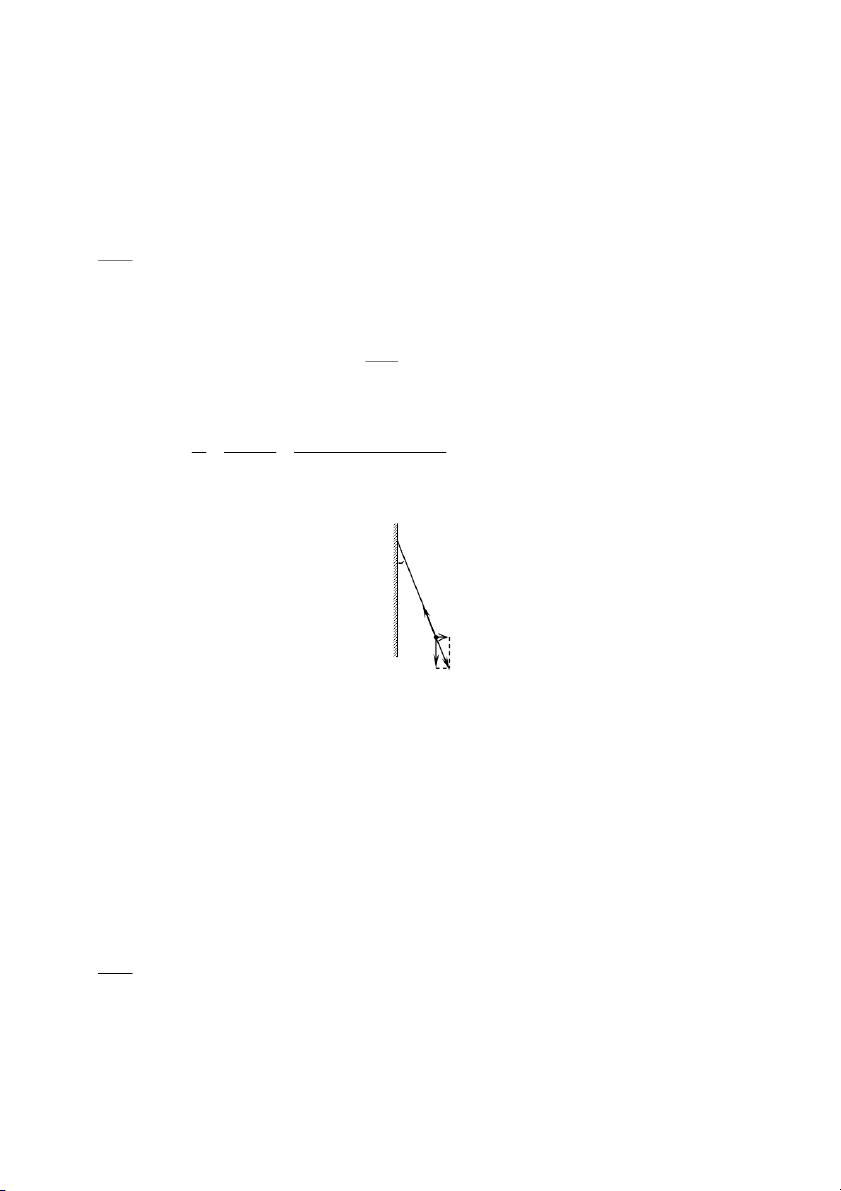
1-13. Trên hình 1-2, AA’ là một mặt phẳng vô hạn tích điện đều với mật độ điện mặt  = 4.10- 9 2
C/cm và B là một quả cầu tích điện cùng dấu với điện tích trên mặt phẳng. Khối lượng của 151
quả cầu bằng m = 1g, điện tích của nó bằng q = 10-9C. Hỏi sợi dây treo quả cầu lệch đi một
góc bằng bao nhiêu so với phương thẳng đứng. Giải: Tại vị trí cân bằng:   
T F P  0 Trong đó: P mg; q F Eq  20 Từ hình vẽ ta thấy: F q  1 . 4 0 .510 9 tg     , 0 2309 P 2 mg 2 . 1 . 8 , 8 . 6 10 . 12 103 8 , 9 . 1 0 0    13 A  T F A’ P R
1-14. Một đĩa tròn bán kính a = 8cm tích điện đều với mật độ điện mặt  = 10-8 2 C/m .
1. Xác định cường độ điện trường tại một điểm trên trục của đĩa và cách tâm đĩa một đoạn b = 6cm.
2. Chứng minh rằng nếu b  0 thì biểu thức thu được sẽ chuyển thành biểu thức tính cường độ
điện trường gây bởi một mặt phẳng vô hạn mang điện đều.
3. Chứng minh rằng nếu b  a thì biểu thức thu được chuyển thành biểu thức tính cường độ điện
trường gây bởi một điện tích điểm. Giải:
1. Chia đĩa thành từng dải vành khăn có bề rộng dr. Xét dải vành khăn có bán kính r (rkhăn có điện tích tổng cộng: 152 dQ  2 . rd . r
Chia vành khăn thành các điện tích điểm dq. Chúng gây ra điện trường dE tại A. Theo định lý 
chồng chất điện trường, điện trường tại A bằng tổng tất cả các giá trị E d đó.    Điện trường E
d có thể phân thành hai thành phần E d và E d
. Do tính đối xứng nên tổng các 1 2  thành phần bằng không. Vậy: 1 E ddE
, với ỏ là góc giữa E d và OA rdE   cos 2 dEdq b b b . . r drdE  .  .dQ r
 4 r b 0 2 2  2 2 r b
4 r b 2  0 2 2 3/2  2 2 0 r b 3/ 2
Điện trường do cả đĩa gây ra tại A là: a b a  . r dr b  1    1  E dE   r  1 3 / 2 2 2 2 2 2 0  0 r b       2 2   2 2   0  r b  0  1  a /b  0 108   1  E  1    226V / m . 2 8 , 8 . 6 10 1  2  1      1 . 8 0 2 2 / .610 2 2   2. Nếu cho b  0, ta có:   1  E  lim 1    b    0 2 2 2  1 a /b 2 0   0
Điện trường khi b  0 có biểu thức giống với điện trường do mặt phẳng tích điện đều gây ra.
3. Nếu b a, áp dụng công thức gần đúng: 2 1 a 1  2 2 2 1 a / 2 b b 2 2 2    a   .a .( a  ) Vậy: q E  1   1     2   2 2 2 2  2b  4 b 4 b 4 0   0 0  0b
Điện trường khi b a có biểu thức giống với điện trường do một điện tích điểm gây ra.
1-15. Một mặt hình bán cầu tích điện đều, mật độ điện mặt  = 10-9C/m2. Xác định cường độ điện
trường tại tâm O của bán cầu. 153 Giải:
Chia bán cầu thành những đới cầu có bề rộng dh (tính theo phương trục của nó). Đới cầu được tích điện tích:  2 . r  .dh 2 r  . dh dQ h h    R  dh cos r / R h  2 . .
với  là góc giữa mặt đới cầu và trục đối xứng của đới cầu.
Tính tương tự như phần đầu của bài 1-14, ta tính được điện trường dE do đới cầu gây ra tại O có
hướng như hình vẽ và có độ lớn bằng: h h 2 .  . dE  . R dh dQ
4 r h 4 R 0 2 2 h 3/2 3 0
Lấy tích phân theo h từ 0 đến R, ta có: R R 2  .h. h    E dE dh     2 2 2    R 2 R 2 4 0 0 0   0 0 10 9 Coi  1, ta có: E   2 , 8 2(V / m) 1 . 4 8 , 8 . 6.10 12
1-16. Một thanh kim loại mảnh mang điện tích q = 2.10-7C. Xác định cường độ điện trường tại một
điểm nằm cách hai đầu thanh R = 300cm và cách trung điểm thanh R0 = 10cm. Coi như điện
tích được phân bố đều trên thanh. Giải:
Chia thanh thành những đoạn nhỏ dx. Chúng có điện tích là: q q dq dx dx l R 2 2  R 20
Xét điện trường dE gây ra do đoạn dx gây ra tại điểm đang xét. Ta có thể tách dE thành hai thành
phần dE1 và dE 2. Điện trường tổng cộng E là tổng tất cả các điện trường dE đó. Do tính
đối xứng nên tổng tất cả các thành phần dE1 bằng không. Ta có: 154 dq 1 R q dE 0  .cos  . . 2 4 r2 4  0 0 R2 x2 0  dx 2 2 l R  0 x qR0  3 / 2 4 l  0 R2 2 0  dx x l / 2  0 qR qR R  E  dE  2  0 dx  0 0 d 3 / 2 2 2 2 2 3 / 2 2 2      l / 2 4 l R  x R0tg 4 l cos .(R  R tg )  0  x 0    0  0 0 0 q  0 q   cos d .   sin  0 2q sin q l q 0   .   4 lR 4 lR  4 lR 2 lR 2R 4 RR 0 0 0 0   0 0 0 0 0 0 0 0 2.10 7 Thay số: E   6 1 . 03 (V / ) m 4 . . 1 8 , 8 6 1 . 0 1  2 3 . 1 , 0 .
1-17. Một mặt phẳng tích điện đều với mật độ . Tại khoảng giữa của mặt có một lỗ hổng bán kính
a nhỏ so với kích thước của mặt. Tính cường độ điện trường tại một điểm nằm trên đường
thẳng vuông góc với mặt phẳng và đi qua tâm lỗ hổng, cách tâm đó một đoạn b. Giải:
Ta có thể coi mặt phẳng tích điện có lỗ hổng không tích điện như một mặt phẳng tích điện đều
mật độ  và một đĩa bán kính a nằm tại vị trí lỗ tích điện đều với mật độ -.
+ Điện trường do mặt phẳng tích điện đều gây ra tại điểm đang xét là:  E  1 2 0
+ Điện trường do đĩa gây ra tại điểm đang xét là: (xem cách tính trong bài 1-14)   1  E  1 2   2 2   2 0  1  a / b
+ Điện trường do mặt phẳng và đĩa gây ra cùng phương và ngược chiều nên: 
E E E  1 2 2 2 2 1  a / 0 b
1-18. Một hạt bụi mang một điện tích q2 = -1,7.10-16C ở cách một dây dẫn thẳng một khoảng 0,4
cm và ở gần đường trung trực của dây dẫn ấy. Đoạn dây dẫn này dài 150cm, mang điện tích q -7
1 = 2.10 C. Xác định lực tác dụng lên hạt bụi. Giả thiết rằng q1 được phân bố đều trên sợi
dây và sự có mặt của q2 không ảnh hưởng gì đến sự phân bố đó. 155 Giải:
Xét mặt Gaox là mặt trụ đáy tròn bán kính R0 có trục trùng với sợi dây, chiều cao h (h l)
ở vùng giữa sợi dây và cách sợi dây một khoảng R0 l, ta có thể coi điện trường trên mặt trụ là đều.
Sử dụng định lý Otxtrôgratxki-Gaox, ta có: q 1 q h E 2 . Rh 0 1 .   . 0   l 0 0 qE 1  2 R l 0 0
Lực điện tác dụng lên hạt bụi là: 16  7 . 7 , 1 10 . . 2 10 q q F Eq 1 2  10    10 2 12  3 N  2 R l 2 1 . 8 , 8 . 6.10 . . 4 10 5 , 1 . 0 0
1-19. Trong điện trường của một mặt phẳng vô hạn tích điện đều có đặt hai thanh tích điện như
nhau. Hỏi lực tác dụng của điện trường lên hai thanh đó có như nhau không nếu một thanh
nằm song song với mặt phẳng còn thanh kia nằm vuông góc với mặt phẳng. Giải:
Lực tác dụng lên thanh nằm song song là: F  1  F qE ii
và lực tác dụng lên thanh nằm vuông góc là: F  2 F qE kk
Do điện trường do mặt phẳng vô hạn tích điện đều gây ra là điện trường đều nên: E E   i k 1 F 2 F
Vậy, lực tác dụng lên hai thanh là như nhau.
1-20. Một mặt phẳng vô hạn mang điện đều có mật độ điện tích mặt  =2.10-9C/cm2. Hỏi lực tác
dụng lên một đơn vị chiều dài của một sợi dây dài vô hạn mang điện đều. Cho biết mật độ
điện dài của dây  = 3.10-8C/cm. Giải: 156
Ta thấy, lực tác dụng lên dây không phụ thuộc vào cách đặt dây trong điện trường. Ta có:
+ Điện trường do mặt phẳng gây ra là:  E  20
+ Điện tích của dây là: q  L
Vậy, lực tác dụng lên mỗi đơn vị chiều dài dây là:  L  2 1 . 0 5 . 3 . 10 .61 F Eq    , 3 4(N) 2 1 . 2 8 , 8 . 6.10 12  0
1-21. Xác định vị trí của những điểm ở gần hai điện tích điểm q1 và q2 tại đó điện trường bằng
không trong hai trường hợp sau đây: 1) q1, q2 cùng dấu; 2) q1, q2 khác dấu. Cho biết khoảng
cách giữa q1 và q2 là l. Giải:
Véctơ cường độ điện trường tại một điểm M bất kỳ bằng    E   1 E E2  
với E và E là các véctơ cường độ điện trường do q 1 2 1, q2 gây ra.   
Để E = 0, thì ta phải có:   1 E E2
+ Hai điện trường E1 và E2 cùng phương, M phải nằm trên đường thẳng đi qua điểm đặt các điện tích.
+ Hai điện trường E1 và E2 cùng độ lớn: E  E 1 2 2 q q  x  q 1 2 1       2 4 x 4 l  x  l  x  q 0  2 0 2 x q q 1     x 1   l  x l x q q 2 2 q  l 1 q q  x 2 1   l q q  q 1 1 2 1  q2 157
+ Hai điện trường E1 và E2 ngược chiều:
1. Nếu q1, q2 cùng dấu thì M phải nằm giữa hai điên tích: qx lx 1 0  l q q 1 2
2. Nếu q1, q2 khác dấu thì M phải nằm ngoài hai điện tích: q x hay x lx 1 0  l q q 1 2
1-22. Giữa hai dây dẫn hình trụ song song cách nhau một khoảng l = 15cm người ta đặt một hiệu
điện thế U = 1500V. Bán kính tiết diện mỗi dây là r = 0,1cm. Hãy xác định cường độ điện
trường tại trung điểm của khoảng cách giữa hai sợi dây biết rằng các dây dẫn đặt trong không khí. Giải:
Ta đi xét trường hợp tổng quát: nếu gọi khoảng cách từ điểm M đến trục dây dẫn thứ nhất là x thì
cường độ điện trường tại M là: 1     lE     
2 x l x  2 x (l x) 0 0
với  là mật độ điện dài trên dây. Mặt khác: dU = - Edx l r   1 1   l rl r
U   Edx     dx
lnx  l nl x      l  n    2 2 0   r
x l x r 0 0  r   U    0  l r  l  n   r
Thế  vào biểu thức cường độ điện trường và thay x = l/2, ta có: 1  2 E l U . 0  U 2 l 0  l   l r   l r  .l   l  n  l.l  n  2  2  r   r  . 2 1500 Thay số: 3 E   1 . 4 0 V / m  1 , 0 49 1 , 0 5.ln   , 0 001 158
1-23. Cho hai điện tích điểm q -6 -6
1 = 2.10 C, q2 = -10 C đặt cách nhau 10cm. Tính công của lực tĩnh
điện khi điện tích q2 dịch chuyển trên đường thẳng nối hai điện tích đó xa thêm một đoạn 90cm. Giải:
Ta có: Công của lực tĩnh điện khi dịch chuyển điện tích q2 từ điểm A đến điểm B là: A = q2.(VA – VB)  q ql. Vậy: 1 2 1 q q2 A q   2  4   r
4 (l r)    0 0 4  0 r (l r ) 9 , 0 . 1  06 . 2 . 106 Thay số: A    1 , 0 62J  4 8 , 8 . 1 . 6 1 . 012. 1 , 0 1 .
Dấu trừ thể hiện ta cần thực hiện một công để đưa q2 ra xa điện tích q1.
1-24. Tính công cần thiết để dịch chuyển một điện tích q = (1/3).10-7C từ một điểm M cách quả
cầu tích điện bán kính r = 1cm một khoảng R = 10cm ra xa vô cực. Biết quả cầu có mật độ điện mặt  = 10-11 2 C/cm . Giải:
Công của lực tĩnh điện khi dịch chuyển điện tích là: A = q.(VA – VB)  Q Q  Vậy: A qQ q.   (do R )   4 R 4   R  4 2  R 0 1 0 2 0 1 q 4 .  . 2 r . 2  qr   4    0 (r R) 0 (r R ) 7 10 .1/  7 3 1 . 0 .10 2 2 Thay số: A 7   , 3 4 . 2 10 J  1  2 2 8 , 8 . 1 . 6 10 .11.10
1-25. Một vòng dây tròn bán kính 4cm tích điện đều với điện tích Q = (1/9).10-8C. Tính điện thế tại: 1. Tâm vòng dây.
2. Một điểm M trên trục vòng dây, cách tâm của vòng dây một đoạn h = 3cm. 159 Giải:
Chia vòng dây thành những đoạn vô cùng nhỏ dl mang điện tích dq. Điện thế do điện tích dq gây
ra tại điểm M trên trục vòng dây, cách tâm của vòng dây một đoạn h là: dq dV  2 2 4  0 R h
Điện thế do cả vòng gây ra tại M là: V     dq dVQ 2 4 R  2 2 h 4 R  2 0 0 h
1. Điện thế tại tâm vòng (h =0): Q 1/9.10 8 V    250V O 4 12  2  0R 4 1 . 8 , 8 . 6 1 . 0 4 . .10
2. Điện thế tại M (h = 3cm):  8 Q 1/91.0 V    200 HV  4 R2  h2    0 4. . 1 8 , 8 6 1 . 0 12  . 4 10 2 2   . 3 10 2 2
1-26. Một điện tích điểm q = (2/3).10-9C nằm cách một sợi dây dài tích điện đều một khoảng r1 =
4cm; dưới tác dụng của điện trường do sợi dây gây ra, điện tích dịch chuyển theo hướng
đường sức điện trường đến khoảng cách r2 = 2cm, khi đó lực điện trường thực hiện một công
A = 50.10-7J. Tính mật độ điện dài của dây. Giải: Ta có: dA = q.dV   dA  . q (Edr)   . q dr 2 r 0 r q 2  dr q q r  A  dA      ln r  ln r  ln   2 1  1 2 r 2 2 r 0 r 0 0 2 1 2 A 0    r1 . q ln r2 160 . 2 8 , 8 . 1 . 6 1 . 012 5 . 0 1 . 07 Vậy:     .
6 10 7C / m 2 /  9 4 3 1 . 0 .ln 2
1-27. Trong chân không liệu có thể có một trường tĩnh điện mà phương của các véctơ cường độ
điện trường trong cả khoảng không gian có điện trường thì không đổi nhưng giá trị lại thay
đổi, ví dụ như thay đổi theo phương vuông góc với các véctơ điện trường (hình 1-3) được không?  E Hình 1 -3 Giải:
Xét đường cong kín hình chữ nhật như hình vẽ, ta có:  dV  E dl .   V V d . E l A  A    ABCDA          d . E l  E d . l  d . E l  d . E l         AB BC CD DA   E .AB 0 E C . D  1 2  0  E E  2 1 l 0
Vậy: Nếu phương của véctơ cường độ điện trường không đổi thì giá trị của nó cũng phải không đổi
trong toàn bộ không gian. Không có điện trường nào như nêu trong đề bài.
1-28. Tính điện thế gây ra bởi một quả cầu dẫn điện mang điện q bằng cách coi điện thế tại một
điểm A nào đó bằng tổng các điện thế do từng điện tích điểm gây ra, trong các trường hợp sau:
1. Tại một điểm nằm trên quả cầu.
2. Tại một điểm nằm trong quả cầu.
3. Tại một điểm nằm ngoài quả cầu cách bề mặt của nó một đoạn bằng a. 161