Bài tập ôn tập Thống kê ứng dụng | Trường Đại học Kinh tế – Luật

lOMoAR cPSD| 46348410
PHẦN ÔN TẬP TRONG GIÁO TRÌNH Câu 1:
a) Tổng thể của khảo sát: 954 khách hàng của Plano
b) Mẫu của khảo sát: 100 khách hàng được phát bảng câu hỏi khảo sát
c) Tham số của tổng thể: Tầm quan trọng tương đối của tính năng sản phẩm
d) Thống kê của mẫu: Thống kê mô tả
Câu 2: Phương pháp lấy mẫu a) Hệ thống b) Ngẫu nhiên đơn giản c) Thuận tiện d) Khối cụm e) Khối cụmCâu 3: Câu Thang đo Kiểu dữ liệu a Rời rạc Khoảng b Rời rạc Tỷ lệ c Rời rạc Tỷ lệ d Định tính Định danh e Liên tục Khoảng f Định tính Khoảng g Định tính Định danh h Rời rạc Tỷ lệ i Liên tục Thứ bậc Câu 4:
a) Trung bình số tuổi là = 19.825
Ý nghĩa: Số tuổi trung bình của sinh viên là 19.825
b, Phương sai số tuổi: = 0.507
Độ lệch chuẩn số tuổi: s = 0.712
Ý nghĩa: Mức độ phân tán số tuổi sinh viên là: 0.507 c) Trung vị: Med X = 20
Ý nghĩa: Số sinh viên có độ tuổi nhỏ hơn 20 bằng số sinh viên có độ tuổi lớn hơn 20 . d) = 20 lOMoAR cPSD| 46348410
Ý nghĩa: Có 25% số sinh viên có độ tuổi nhỏ hơn 20 và có 75% số sinh viên có độ tuổi lớn hơn 20. e) = 20
Ý nghĩa : Có 75% số sinh viên có độ tuổi nhỏ hơn 20 và có 75% số sinh viên có độ tuổi lớn hơn 20. f) IQR = - = 20 – 20 = 0
Ý nghĩa: Sự biến động của dữ liệu về số tuổi của sinh viên trong khoảng giữa Q1 và Q3 là 0.
g) Số yếu vị: Mod X = 20
Ý nghĩa: Số tuổi có số sinh viên nhiều nhất là 20.
h) Tính khoảng tin cậy cho trung bình tổng thể với độ tin cậy 99%Theo đề bài ta có: n =
40; = 19.825; s = 0.712 ĐTC 99% = 0.01 = = 2.704
Theo công thức, khoảng tin cậy của µ là: - < µ < 19.825 - + 19.825 + 19.521 < µ < 20.129
Vậy khoảng tin cậy cho trung bình tuổi sinh viên là (19.521; 20.129)
i) Tính khoảng tin cậy cho phương sai tổng thể với độ tin cậy 95% Ta có: ĐTC 95% = 0.05 = 59.34; = 24.43
Theo công thức, khoảng tin cậy hai phía là: < < 0.333 < < 0.809
Vậy khoảng tin cậy của phương sai tổng thể là: (0.333; 0.809)
j) Tìm khoảng tin cậy cho tỷ lệ sinh viên đang ở độ tuổi 20, với độ tin cậy 90%.
Gọi p là tỉ lệ sinh viên đang ở độ tuổi 20;
Với n = 40 và số sinh viên ở độ tuổi 20 là k = 28
Đặt f là tỉ lệ sinh viên đang ở độ tuổi 20 trong mẫu : f = lOMoAR cPSD| 46348410 Ta có ĐTC 90% = 0.1 = 1.645 Công thức: f - 0.581 < p < 0.819 Vậy khoảng < p < f +
tin cậy cho tỉ lệ sinh viên đang ở độ tuổi 20 là: (0.581; 0.819)
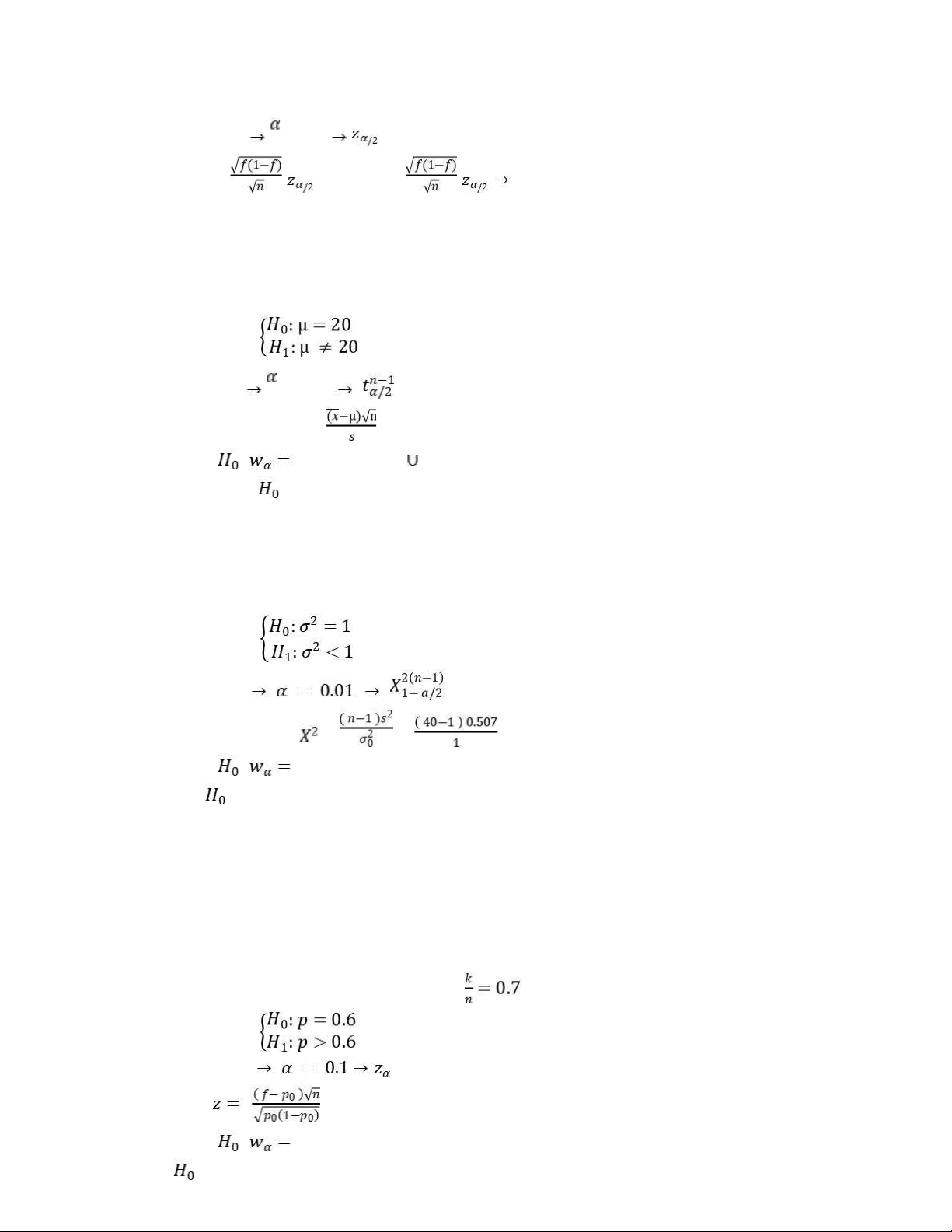
k) Có nhận định cho rằng, trung bình độ tuổi của sinh viên là 20. Với mức ý nghĩa 5%,bạn
hãy kiểm định nhận định trên? Cặp giả thuyết là: Ta có MYN 5% = 0.05 = 1.684
Tiêu chuẩn kiểm định: t = = - 1.5545 Miền bác bỏ : ( - ∞; -1.684) (1.684; ∞)
Từ đó, chấp nhận . Vậy với mức ý nghĩa 5% độ tuổi trung bình của sinh viên là 20.
l) Giả sử tổng thể tuân theo phân phối chuẩn với độ lệch chuẩn bằng 1. Có nhận địnhrằng,
độ phân tán của dữ liệu của độ tuổi đồng đều hơn. Với mức ý nghĩa 1%, bạn hãy kiểm định nhận định trên? Cặp giả thuyết là: Ta có MYN 1% = 20.71
Tiêu chuẩn kiểm định: = = = 19.773 Miền bác bỏ : ( 0; 19.773 )
Chấp nhận . Vậy với mức ý nghĩa 1% độ phân tán của dữ liệu của độ tuổi không đồng đều hơn. m)
Có nhận định cho rằng tỷ lệ sinh viên có độ tuổi 20 tuổi chiếm trên 60%. Hãy
kiểmđịnh nhận định trên với mức ý nghĩa 10%.
Gọi p là tỉ lệ sinh viên đang ở độ tuổi 20;
Với n = 40 và số sinh viên ở độ tuổi 20 là k = 28 Đặt f là tỉ lệ
sinh viên đang ở độ tuổi 20 trong mẫu : f = Cặp giả thuyết là: Ta có MYN 10% = 1.285 lOMoAR cPSD| 46348410 Tiêu chuẩn: = 1.291 Miền bác bỏ : (1.285: + )
Bác bỏ . Vậy tỷ lệ sinh viên có độ tuổi 20 tuổi chiếm trên 60% Câu 5:
- Hình a: Dữ liệu phân phối lệch phải.
Vì dữ liệu tập trung nhiều bên trái, quan sát ta thấy Med < Mean
- Hình b: Dữ liệu phân phối đối xứng.
Vì quan sát ta thấy Mean = Med = Mod = 22,5 - Hình c:
Dữ liệu phân phối lệch trái.
Vì nhìn đồ thị ta có bảng sau: x f 2 2 3 5 4 7 5 11 6 9 7 15 8 20 9 8 10 7 11 7 12 4
Tính được: Mean = 7.34 ; Med = 8 hay Med > Mean dữ liệu phân phối lệch trái. Câu 6:
a. Nhận xét hình dáng của từng đồ thị: - Đồ thị 1 lệch phải - Đồ thị 2 đối xứng
b. So sánh khoảng biến thiên giữa hai đồ thị:
- Khoảng biến thiên của đồ thị 1: 16 - 0 = 16
- Khoảng biến thiên của đồ thị 2: 11.5 - ( -0.5 ) = 12 lOMoAR cPSD| 46348410
=> Khoảng biến thiên của hai đồ thị 1 lớn hơn khoảng biến thiên của đồ thị 2
c. So sánh độ trải giữa giữa hai đồ thị:
- R1 = Q3 - Q1 = 6,5 - 2,5 = 4
- R2 = Q3 - Q1 = 8,5 - 2,5 = 6
=> Độ trải giữa của đồ thị 1 lớn hơn độ trải giữa của đồ thị 2
d. Ý nghĩa trung vị bằng 5 ở đồ thị thứ 2 là: chia 2 phía mỗi phía 50% giá trị
e. So sánh trung bình tổng thể giữa hai đồ thị:
Đồ thị thứ nhất có trung bình tổng thể lớn hơn đồ thị thứ 2
f. So sánh giá trị nhỏ nhất của hai đồ thị: Gía trị nhỏ nhất của đồ thị thứ 2 bé hơn giá
trị nhỏ nhất của đồ thị thứ nhất.
g. So sánh giá trị lớn nhất của hai đồ thị: Gía trị lớn nhất của đồ thị nhứt nhất lớn hơn
giá trị lớn nhất của đồ thị thứ hai. Câu 7:
a. Dạng bài kiểm định:
Kiểm định so sánh trung bình giữa hai nhóm độc lập.
b. Ước lượng điểm tốt nhất cho sự khác biệt của hai trung bình tổng thể:
Ước lượng điểm tốt nhất cho sự khác biệt giữa hai trung bình tổng thể là hiệu giữa hai trung bình mẫu:
d^=X1ˉ−X2ˉ=16−14=2
c. Khoảng ước lượng 99% cho sự khác biệt: X1 – X2 – Zx
< µ1 - µ2 < X1 – X2 + Zx
= 0,39 < µ1 - µ2 < 3,61
d. Kiểm tra nhận định với α=0.01: H0 : µ1 = µ2 H1: µ1 ≠ µ2 Z0= = 3,2 lOMoAR cPSD| 46348410 Bác bỏ H0
với α=0.01, số lần đi ăn ngoài của cư dân ở Raymondville và cư dân Rosenberg là khác nhau. Câu 8:
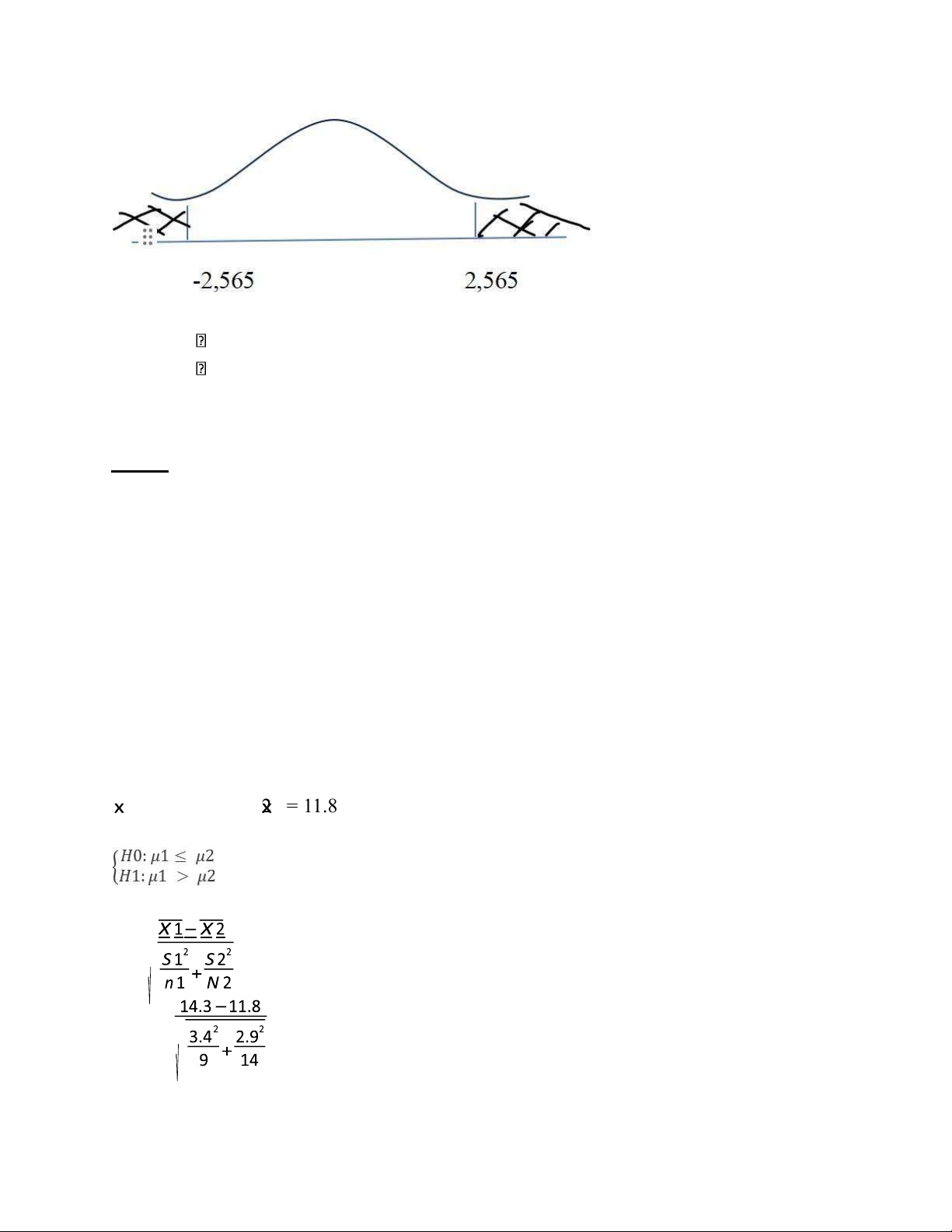
a. Kiểm định so sánh hai giá trị trung bình của hai tổng thể khác nhau.Ước lượng điểm
tốtnhất cho sự khác biệt của hai trung bình tổng thể: Để ước lượng điểm tốt nhất cho sự
khác biệt của hai trung bình tổng thể, chúng ta sử dụng ước lượng điểm.
Giá trị trung bình của tổng thể thứ nhất: μ1 = 14.3
Giá trị trung bình của tổng thể thứ hai: μ2 = 11.8
b. Vậy ước lượng điểm tốt nhất cho sự khác biệt của hai trung bình tổng thể là 14.3 - 11.8 = 2.5. c. với α = 0.05 n1 = 9 n2 = 14 1 = 14.3 2 = 11.8 s1 = 3.4 s2 = 2.9 T = => T = = 1.8208 lOMoAR cPSD| 46348410
=> Bác bỏ H0. Vậy có thể thấy giá trị trung bình của tổng thể thứ nhất lớn hơn giá trị trung
bình của tổng thể thứ hai. Câu 9:
a. Xác định dạng bài cần kiểm định:
Loại kiểm định: Kiểm định giả thuyết về sự chênh lệch giữa hai nhóm.
b. Tìm ước lượng điểm tốt nhất cho bài toán này.
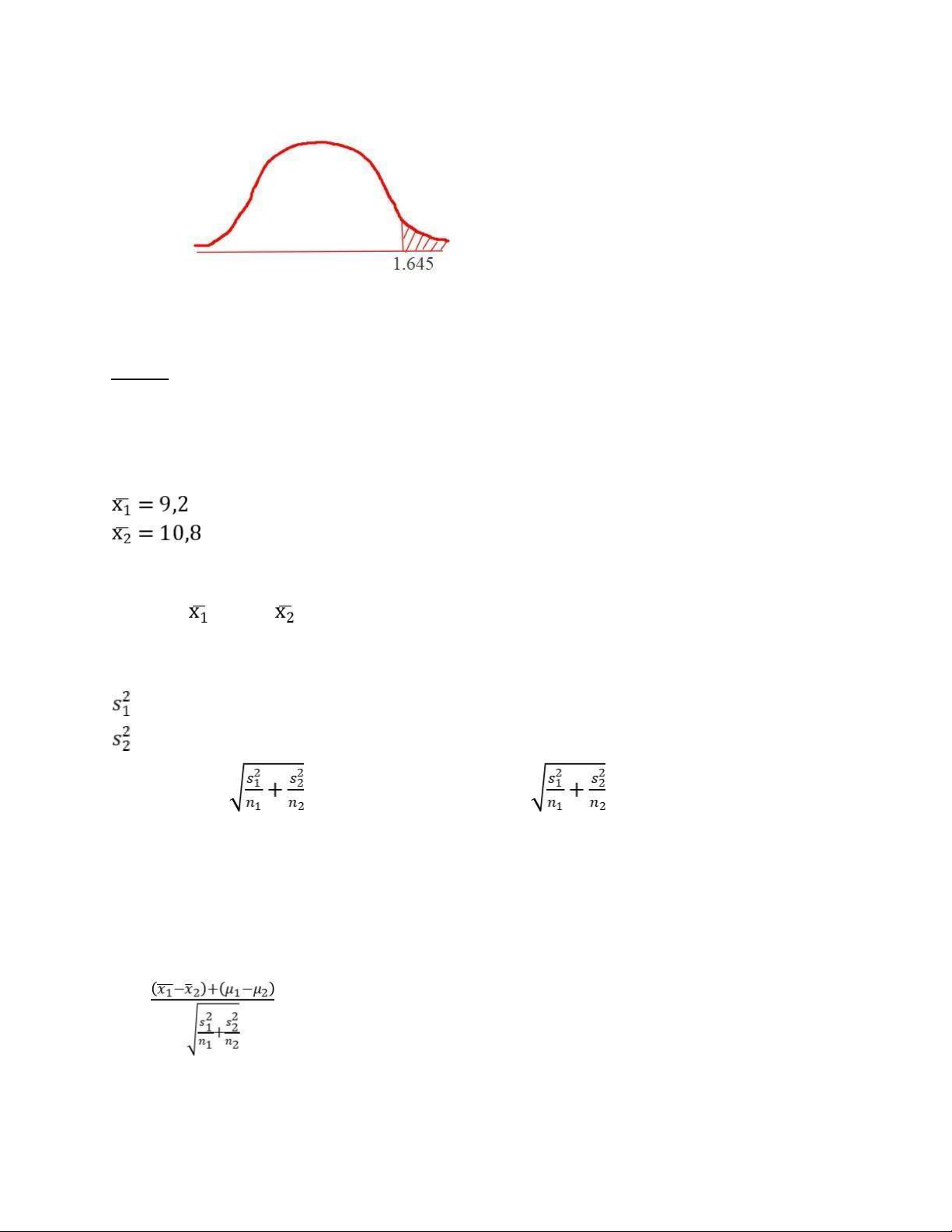
Ước lượng điểm tốt nhất cho sự khác biệt giữa hai trung bình tổng thể là hiệu giữa hai trung bình mẫu: d= − = 9,2 – 10,8 = -1,6
c. Tìm khoảng ước lượng 90% cho sự chênh lệch này. = 1,7 = 1,7 X1 – X2 – Zx
< µ1 - µ2 < X1 – X2 + Zx
= -3,216 < µ1 - µ2 < 0,016
d. Với α = 0.1, hãy kiểm tra nhận định trên. H0 : µ1 = µ2 H1: µ1 ≠ µ2 Z0= = - 1,94 lOMoAR cPSD| 46348410 Chấp nhận H0
Với α = 0.1, có sự chênh lệch giữa hai nhóm này Câu 10:
a. Dạng bài cần kiểm định là so sánh hai tỷ lệ độc lập của hai nhóm là tỷ lệ đơn hàngđược
giao trong vòng 24 giờ của Kho Bờ Tây và Kho Bờ Đông.
b. Ước lượng điểm tốt nhất: Để ước lượng điểm tốt nhất cho tỷ lệ thành công của mỗikho
hàng, chúng ta sử dụng tỷ lệ mẫu.
Tỷ lệ thành công của Kho Bờ Tây (dân số 1) = Số đơn hàng Bờ Tây được giao trong vòng
24 giờ / Tổng số đơn hàng Bờ Tây đã chọn mẫu = 190/200 = 0.95
Tỷ lệ thành công của Kho Bờ Đông (dân số 2) = Số đơn hàng Bờ Đông được giao trong
vòng 24 giờ / Tổng số đơn hàng Bờ Đông đã chọn mẫu = 372/400 = 0.93
Vậy ước lượng điểm tốt nhất cho tỷ lệ thành công của Kho Bờ Tây là 0.95 và tỷ lệ thành
công của Kho Bờ Đông là 0.93.
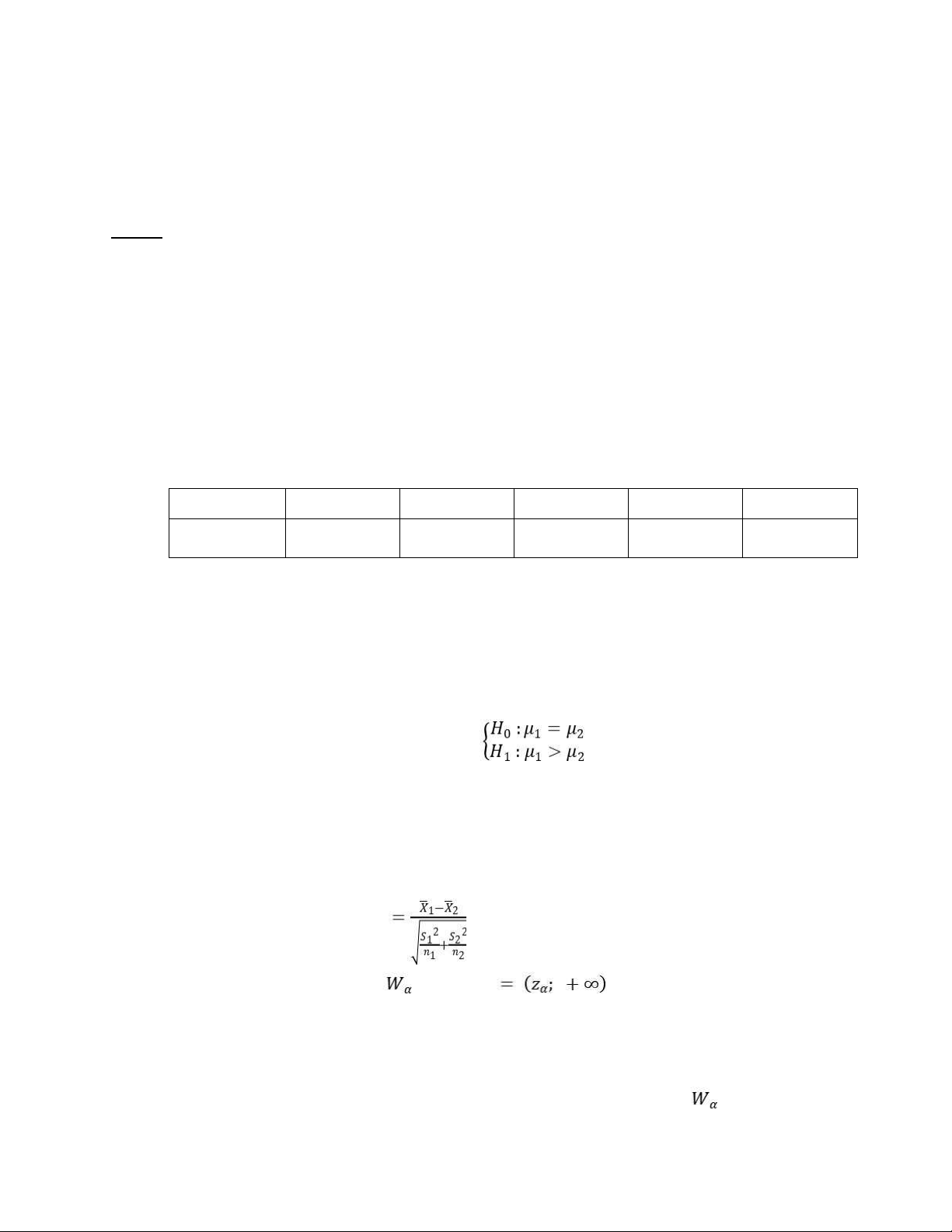
c. Công thức ước lượng hiệu hai tỷ lệ tổng thể: f1 - f2 - < p1 - p2 < f1 - f2 + ɛ ɛ Ɛ = 1.96 × lOMoAR cPSD| 46348410 Từ công thức trên =>
0.95 - 0.93 - 0.0392 < p1 - p2 < 0.95 - 0.93 + 0.0392 ⇔
-0.0192 < p1 - p2 < 0.0592 d. với α = 5%
Gọi p1: Tỷ lệ đơn hàng giao thành công kho bờ Đông Gọi
p2: Tỷ lệ đơn hàng giao thành công kho bờ Tây f1=0.93 f2=0.95 k k = = 0.9367 = n f 1−f 2 Ta có công thức: Z0 = ( 1.645
=> Không bác bỏ H0. Vậy không thể khẳng định tỷ lệ giao hàng thành công trong 24h kho
bờ Đông vượt hơn kho bờ Tây Câu 11:
a. Xác định dạng bài cần kiểm định.
Loại kiểm định: Kiểm định giả thuyết về sự chênh lệch giữa hai phương sai.
b. Tìm khoảng ước lượng 95% cho tỷ lệ hai phương sai này. = 4,197 = 4,899 lOMoAR cPSD| 46348410 =>=> 2,4495 2,0985
Khoảng ước lượng 95% cho tỷ lệ hai phương sai là (2,4495;2,0985)
c. Với α = 5%, hãy kiểm tra nhận định trên. H0 : = H1: ≠ F = = 2 = 4,197 = 0.207 0.207 4.197 Không bác bỏ H0
Chất lượng các thanh thép của Redding và Stockton như nhau.
PHẦN ĐỌC KẾT QUẢ STATA Câu 1:
+ 408802.4 là giá trị lớn nhất của biến gdp
+ 20736.16 là giá trị nhỏ nhất của biến gdp
+ 388066.2 là khoảng biến thiên của biến gdp
+ 126079.1 là độ lệch chuẩn của biến gdp
+ 102572.5 là trung vị của biến gdp
+ 214302.5 là độ trải giữa của biến gdp
+ 150888.6 là giá trị trung bình của biến gdp
+ 33874.65 là tứ phân vị thứ nhất (Q1) của biến gdp
+ 248177.2 là tứ phân vị thứ 3 (Q3) của biến gdp lOMoAR cPSD| 46348410 Câu 2:
Ước lượng tốt nhất cho trung bình GDP = Trung bình mẫu = 150888,6
a) Khoảng tin cậy 95% cho ước lượng trung bình GDP (102000,2; 199776,9)
b) Với mức ý nghĩa 5% tiêu chuẩn kiểm định t = -0,3824
c) i. P-value = 0,7052ii. Vì P-value
Vậy không có đủ bằng chứng kết luận trung bình tổng thể khác 160000
(Bằng chứng mẫu phù hợp với kết luận trung bình tổng thể bằng 160000)
d) i. P-value = 0,6474ii. Vì P-value
Vậy không có đủ bằng chứng kết luận trung bình GDP lớn hơn 160000
(Bằng chứng mẫu phù hợp với kết luận trung bình tổng thể nhỏ hơn hoặc bằng 160000)
e) i. P-value = 0,3526sii. Vì P-value
Vậy không có đủ bằng chứng để kết luận rằng trung bình tổng thể nhỏ hơn 160000.
(Bằng chứng mẫu phù hợp với kết luận trung bình tổng thể lớn hơn hoặc bằng 160000) Câu 3:
a. Đây là dạng bài toán Kiểm định giả thuyết hiệu trung bình 2 tổng thể có phương sai không bằng nhau
b.Tiêu chuẩn kiểm định: t=1.3673
c. Phương sai mẫu gộp: s=1.427976
d. Ước lượng tốt nhất cho trung bình tổng thể 1 : 0.1003556.
Ước lượng tốt nhất cho trung bình tổng thể 2 : -0.1793656
e. Khoảng tin cậy 95% cho trung bình của tổng thể 1 là (-0.1920467 ; 0.3927579) Khoảng
tin cậy 95% cho trung bình của tổng thể 2 là (-0.4611753 ; 0.1024441)
f. Khoảng tin cậy 95% cho sự khác biệt giữa trung bình hai tổng thể (0.1238053 ; 0.6832476) g. i. p-value=0.0866
ii. Với mức ý nghĩa 5%, chấp nhận
. Vậy không thể khẳng định được rằng trung bình
tổng thể 1 lớn hơn trung bình tổng thể 2. lOMoAR cPSD| 46348410 Câu 4:
a) Dạng bài toán: Kiểm định giả thuyết về tỷ lệ tổng thể
b) Tiêu chuẩn kiểm định: z = − 0, 7621
c) Ước lượng tốt nhất tỷ lệ tổng thể: Mean = 0.2164948
d) Khoảng tin cậy 95% của tỷ lệ biến var3: (0. 1345339, 0. 2984558) e) Xét cặp giả thuyết: + p – value = 0.446
+ Nhân xét: Với mức ý nghĩa α = 1%, không có cơ sở bác bỏ giả thuyết vì p – value > α Câu 5:
a) Dạng bài toán: Kiểm định so sánh giá trị trung bình của hai mẫu cặp
b) Tiêu chuẩn kiểm định là: t = -1.3625
c) Ước lượng tốt nhất cho trung bình tổng thể 1 là: - 0.1793656
Ước lượng tốt nhất cho trung bình tổng thể 2 là: 0.1003556
d) Ước lượng tốt nhất cho sự chênh lệch của biến var 1 và biến var 2 theo từng cặp: - 0.2797212
e) Khoảng tin cậy 95% cho trung bình của tổng thể 1 là: ( - 0.4611753; 0.1024441)
Khoảng tin cậy 95% cho trung bình của tổng thể 2 là: ( - 0.1920467; 0.3927579)
f) Khoảng tin cậy 95% cho sự chênh lệch của biến var 1 và biến var 2 theo từng cặp là: (-
0.6872372; 0.1277949) g) i, p – value = 0.0881
ii, Mức ý nghĩa 10% > p – value ( 0.1 > 0.0881 ) à bác bỏ Vậy
sự chênh lệch trung bình của var 1 và var 2 nhỏ hơn 0
PHẦN CÂU HỎI TÌNH HUỐNG Câu 1:
Ta thực hiện những bước sau đây để kiểm định
Bước 1: Xác định đối tượng
Nhân viên làm việc trong công ty Bước
2: Thu thập dữ liệu
Nguồn thu thập dữ liệu thứ cấp •
Lập danh sách nhân viên làm việc tại công ty và mức tiền lương trung bình của nhân
viên thông qua dữ liệu phòng nhân sự công ty cung cấp lOMoAR cPSD| 46348410 •
Kỹ thuật chọn mẫu: Từ danh sách áp dụng phương pháp lấy mẫu xác suất: lấy mẫu
ngẫu nhiên đơn giản, lấy ngẫu nhiên 50 nhân viên từ danh sách
Bước 3: Mô tả dữ liệu
Từ mẫu danh sách đã chọn: do mức lương trung bình của các nhân viên là biến có nhiều
giá trị khác nhau nên sẽ tiến hành phân tổ dữ liệu. •
Có thể áp dụng phân tổ dữ liệu theo khoảng cách đều •
Sau khi đã tiến hành phân tổ, lập bảng tần số theo tổ đã được phân. •
Có thể mô tả dữ liệu của mẫu dựa trên bảng tần số bằng cách vẽ biểu đồ histogram.
Bước 4: Xác định bài toán
Xác định bài toán kiểm định ở đây là kiểm định tiền lương trung bình của nhân viên công
ty nên cần xác định các tham số như độ lệch chuẩn mẫu ( s ) của các nhân viên trong công ty
Đặt là tiền lương trung bình của tất cả nhân viên
µ = 2 là tiền lương tăng gấp đôi sau 3 năm tính từ lúc được tuyển dụng
Bước 5: Xác định các giả định Giả định : µ = 2 Giả định : µ 2
Bước 6: Chọn mức ý nghĩa
Chọn mức ý nghĩa cho bài toán thường là 90%, 95%, 99%,...Tùy vào mức ý nghĩa ta chọn từ đó tính được
Bước 7: Tính tiêu chuẩn kiểm định
Bước 8: So sánh giá trị kiểm định hoặc giá trị kiểm định
Kiểm định bằng cách so sánh | với
. Từ đó đưa ra quyết định chấp nhận hay bác bỏ Bác bỏ khi - hoặc
Bước 9: Kết luận Câu 2:
Ta thực hiện những bước sau đây để kiểm định
Bước 1: Thu thập dữ liệu
- Chọn mẫu ngẫu nhiên gồm 200 sinh viên.
- Thu thập điểm môn TKUD của mẫu 200 sinh viên. lOMoAR cPSD| 46348410
Bước 2: Sắp xếp và trình bày dữ liệu
- Sau khi thu thập được, ta trình bày dữ liệu dưới dạng bảng hoặc biểu đồ phù hợp để
có thể đánh giá khách quan dữ liệu đã có. Ví dụ như
Điểm môn TKUD của sinh viên nữ Điểm Tần số
- Tính các giá trị trung bình, phương sai, độ lệch chuẩn, … rồi lấy chúng để đánh giá và phân tích dữ liệu.
Bước 3: Đánh giá và phân tích dữ liệu
- Cụ thể ở bài toán này có yêu cầu so sánh điểm trung bình của 2 nhóm sinh viên nam
và nữ nên ta lập được bài toán kiểm định có dạng:
- Giả sử một mức ý nghĩa hợp lý cụ thể cho bài toán để thuận tiện trong quá trình tính
toán: Xác định tiêu chuẩn kiểm định
- Vì đây là bài toán kiểm định trung bình tổng thể khi chưa biết phương sai tổng thể và
nên ta áo dụng công thức:
- Kiểm định bằng cách so sánh Z với => Chấp nhận
=> Kết luận: Trung bình
điểm số môn TKUD của sinh viên nam và sinh viên nữ không có sự khác
biệt, do đó nhận xét của giảng viên này không đúng. => Bác bỏ => Kết luận: Trung
bình điểm môn TKUD của sinh viên nam và nữ có sự khác biệt, do đó nhận
xét của giảng viên này đúng. Câu 3:
Ta thực hiện những bước sau đây để kiểm định
Bước 1: Thu thập dữ liệu
Khảo sát, điều tra lợi nhuận của các doanh nghiệp trong hai năm 2019 và 2020. lOMoAR cPSD| 46348410
Ta chọn mẫu phân tầng, chia lợi nhuận theo thang đo thứ bậc, từ đó phân tầng ra để chọn
mẫu và thực hiện bước tiếp theo.
Bước 2: Phân tích và xử lý dữ liệu
Đây là dạng bài toán: Kiểm định giả thuyết về hiệu hai trung bình tổng thể theo phân phối chuẩn.
- Gọi µ1, µ2 lần lượt là lợi nhuận trung bình của doanh nghiệp năm 2019 và 2020.
S1, S2 lần lượt là độ lệch chuẩn mẫu của lợi nhuận trung bình của doanh nghiệp năm 2019 và 2020. ,
lần lượt là trung bình mẫu của lợi nhuận trung bình của doanh nghiệp năm 2019 và 2020. ,
lần lượt là kích thước mẫu của lợi nhuận trung bình của doanh nghiệp năm 2019 và 2020.
- Kiểm định cặp giả thuyết:
- Vì chưa biết phương sai hai tổng thể và chắc chắn cỡ mẫu lớn hơn 30, ta áp dụng công thức:
+ Tiêu chuẩn kiểm định: Z=
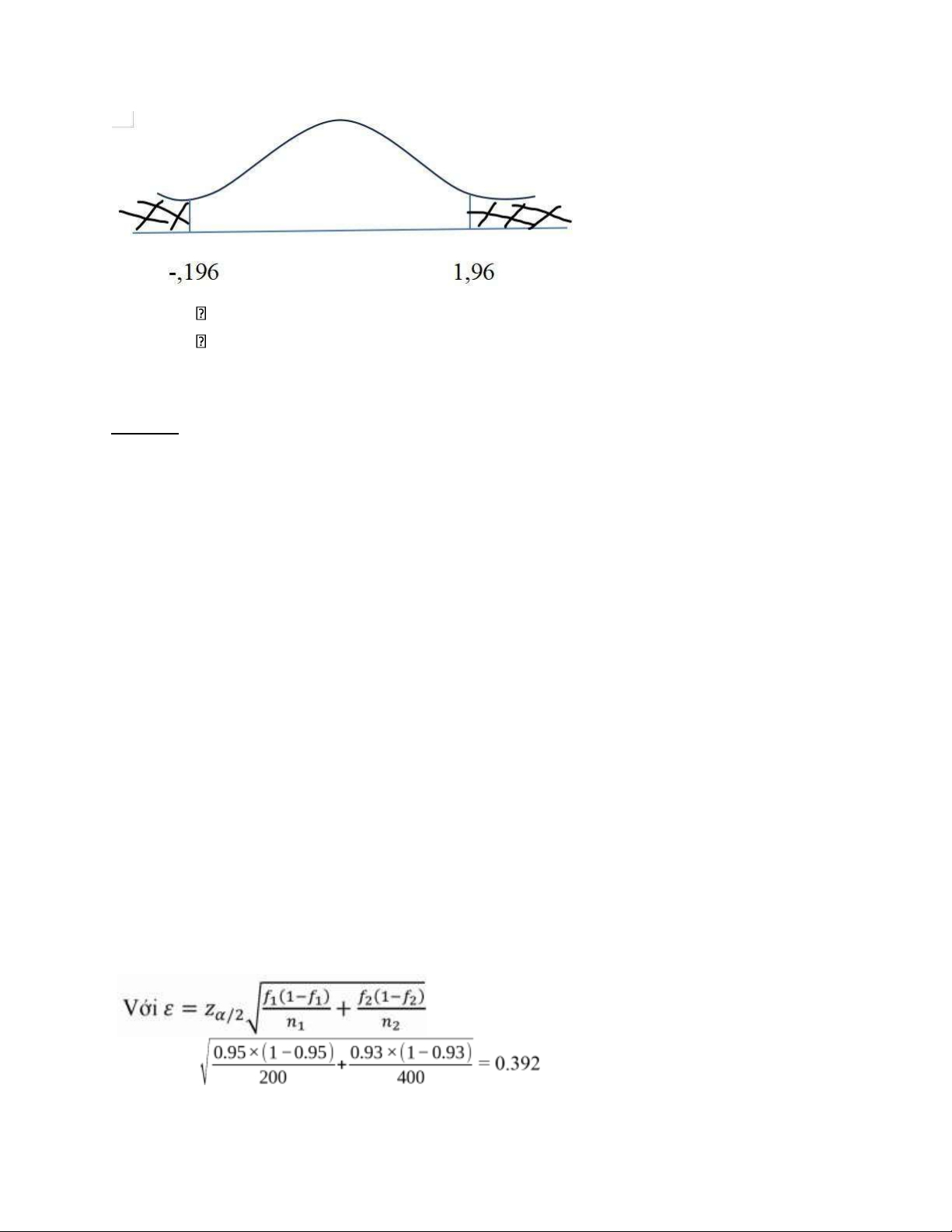
+ Miền bác bỏ H0: Wα = (zα ; +∞) Bước
3: Kết luận, kiểm định
+ Z thuộc Wα , bác bỏ H0
Kết luận: Không thể cho rằng do tác động của dịch bệnh, mà lợi nhuận của các doanh
nghiệp trong năm 2020 bị giảm so với năm 2019.
+ Z không thuộc Wα , không bác bỏ H0 lOMoAR cPSD| 46348410
Kết luận: Có thể cho rằng do tác động của dịch bệnh, mà lợi nhuận của các doanh nghiệp
trong năm 2020 bị giảm so với năm 2019. Câu 4
Ta thực hiện những bước sau đây để kiểm định Bước
1: Thu thập dữ liệu
- Số liệu doanh thu từng ngày của mẫu 34 ngày tại cửa hàng số 1.
- Số liệu doanh thu từng ngày của mẫu 36 ngày tại cửa hàng số 2.
Bước 2: Sắp xếp và trình bày dữ liệu
Sau khi thu thập được, ta trình bày dữ liệu dưới dạng bảng hoặc biểu đồ phù hợp
để có thể đánh giá khách quan dữ liệu đã thu thập được Ví dụ như: Cửa hàng số 1 Ngày 1 2 3 4 ... Doanh thu
Từ bảng ta có thể xác định các giá trị trung bình, phương sai, độ lệch chuẩn,...rồi
lấy chúng làm cơ sở để đánh giá và phân tích dữ liệu
Bước 3: Đánh giá và phân tích dữ liệu
Xây dựng cặp giả thuyết
Giả sử doanh thu phân phối chuẩn với mức ý nghĩa 5%
Ta xác định được đây là bài toán kiểm định giả thuyết về hiệu trung bình của hai
tổng thể phân phối chuẩn mà kích thước 2 mẫu đều lớn hơn 30, do đó tiêu chuẩn
kiểm định sẽ được tính theo công thức: Tiêu chuẩn Z Miền bác bỏ
Bước 4: Kiểm định và đưa ra kết luận
Kiểm định bằng cách xem Z có thuộc miền bác bỏ hay không lOMoAR cPSD| 46348410 Nếu Z , bác bỏ
Nếu Z không thuộc miền bác bỏ
, không đủ điều kiện để bác bỏ Câu 5:
Ta thực hiện những bước sau đây để kiểm định
Bước 1: Xác định đối tượng nghiên cứu: nhân viên công ty A và công ty B
- Thu thập dữ liệu: mức lương của 100 nhân viên công ty A và 100 nhân viên công ty B
Bước 2: Xử lí dữ liệu
- Vì mức lương thu được là biến có nhiều giá trị nên ta tiến hành phân tổ 2 mẫu A, B
+ Có thể áp dụng phân tổ dữ liệu theo khoảng cách đều với công thức h= với n=100
+Sau khi đã tiến hành phân tổ, lập bảng tần số theo tổ đã được phân
+Có thể mô tả dữ liệu của mẫu dựa trên bảng tần số bằng cách vẽ biểu đồ histogram - Từ
bảng tần số lập được tính độ phân tán lương của 100 nhân viên công ty A và độ phân tán
lương của 100 nhân viên công ty B.
Bước 3: Xác định dạng bài toán
- Kiểm định sự khác biệt phương sai 2 tổng thể độc lập
Bước 4: Xây dựng bài toán kiểm định
. Xây dựng cặp giả thuyết:
Với lần lượt là phương sai tổng thể công ty A, B. Từ dữ liệu mẫu thu được trên ta đã tính được
-Tùy theo mức ý nghĩa lựa chọn, ta .
xác định . Giả sử bài toán này với độ tự do (
-Tiến hành tính tiêu chuẩn kiểm định
- Xác định giá trị tới hạn trong bài toán này là lOMoAR cPSD| 46348410
- So sánh giá trị kiểm định với tiêu chuẩn kiểm định, bác bỏ
Bước 5: Kết luận:
- Nếu bác bỏ thì kết luận có sự phân tán lương không đồng đều giữa 2 công ty A và B.
- Nếu không bác bỏ thì kết luận: không có sự phân tán lương không đồng đều giữa 2 công ty A và B.