Bài tập ôn tập Thống kê ứng dụng | Trường Đại học Kinh tế – Luật, Đại học Quốc gia Thành phố Hồ Chí Minh

lOMoAR cPSD| 46348410 XÁC SUẤT
Câu 1. Khả năng lãi suất cổ phiếu của công ty A đạt mức 10% trong năm tới phụ
thuộc vào tỉ lệ lãi suất trên thị trường bất động sản như sau:
Lãi suất trên thị thường BĐS <1% 1% - 5% >5%
Khả năng lãi suất cổ phiếu của công ty A đạt 0.1 0.2 0.7 mức
Dự báo năm tới lãi suất trên thị trường bất động sản như sau:
Lãi suất trên thị trường BĐS <1% 1% - 5% >5% P 0.3 0.5 0.2 a.
Khả năng trong năm tới lãi suất cổ phiếu của công ty A đạt mức 10% và lãi
suất trên thị trường BĐS đạt mức trên 5% là bao nhiêu? b.
Tìm xác suất lãi suất cổ phiếu của công ty A đạt mức 10% trong năm tới. ĐA: a. 0.14, b. 0.27
Câu 2. Một người đầu tư vào 3 loại cổ phiếu A, B, C. Xác suất trong thời gian T các
cổ phiếu tăng giá là 0.6, 0.7, 0.8. Tìm xác suất trong thời gian T a. có cổ phiếu tăng giá.
b. có 1 cổ phiếu tăng giá.
c. Giả sử có hai cổ phiếu tăng giá. Tìm xác suất B không tăng giá.
Biết rằng các cổ phiếu A, B, C hoạt động độc lập.
ĐA: a. 0.976, b. 0.188, c. 0.7021
Câu 3. Để thi hết môn học, mỗi học sinh phải học 30 câu. Đề thi gồm 5 câu trong 30
câu đã cho. Một học sinh chỉ thuộc 20 câu. Tính xác suất để một học sinh dự thi: a.
làm được ít nhất một câu.
b. sẽ đỗ. Biết rằng học sinh sẽ đỗ khi trả lời được ít nhất 3 câu. ĐA: a. 0.9982, b. 0.8088
Câu 4. Một cơ sở sản xuất các bao kẹo. Số kẹo trong mỗi bao là một biến ngãu nhiên
có phân phối xác suất như sau: Số kẹo trong 18 19 20 21 22 bao Xác suất 0.14 0.24 0.32 0.21 0.09
a. Tìm xác suất để một bao kẹo được chọn ngẫu nhiên sẽ chưa từ 19 đến 21 viên kẹo. lOMoAR cPSD| 46348410
b. Hai bao kẹo được chọn ngẫu nhiên. Tính xác suất để ít nhất một trong hai bao chứa ít nhất 20 viên kẹo.
c. Tìm trung bình và phương sai của số viên kẹo trong mỗi bao.
d. Chi phí sản xuất của mỗi bao kẹo là !" # $%, trong đó X là biến ngẫu nhiên chỉ số
kẹo trong bao. Tiền bán mỗi bao kẹo là 100$. Không phân biệt số kẹo trong bao.
Tìm lợi nhuận trung bình và độ lệch chuẩn của lợi nhuận mỗi bao kẹo.
ĐA: a. 0.77; b. 0.8556, c. 19.87, 1.3531, d. 24.39, 3.48969 Câu 5. Cho hàm số , &’() * +(! - ( . $ /- ( 0 $ a. Tìm k.
b. Tìm hàm phân phối xác suất 1’() của X.
c. Tính xác suất 2’/ 3 " 3 !). /- ( 0 $ $
ĐA: a. 2, b. 1’() * 4$ 5 # "! - ( . $, c. %
Câu 6. Một lô hàng có rất nhiều sản phẩm, với tỉ lệ hàng giả là 30%. Lấy ngẫu nhiên
từ lô hàng ra 10 sản phẩm. Tính xác suất để có nhiều nhất 2 sản phẩm giả. Tính trung
bình và độ lệch chuẩn số sản phẩm giả. ĐA: 0.0455, 3, 1.4491
Câu 7. Một thí sinh tên M tham dự một kỳ thi môn XSTK. M phải làm một đề thi
trắc nghiệm khách quan gồm 10 câu; mỗi câu có lời giải khác nhau, trong đó chỉ có
một lời giải đúng. M sẽ được chấm đậu nếu trả lời đúng ít nhất 6 câu.
a. Giả sử M không học bài, mà chỉ chọn ngẫu nhiên lời giải trong cả 10 câu. Tính
xác suất để M thi đậu.
b. Giả sử M chắc chắn trả lời đúng được 2 câu; còn các câu khác, M chọn ngẫu nhiên
một trong 4 lời giải của mỗi câu. Tính xác suất để M thi rớt. ĐA: a. 0.0197, b. 0.8862
Câu 8. Thời gian để sản suất một sản phẩm loại A là một đại lượng ngẫu nhiên tuân
theo phân phối chuẩn với trung bình là 10 phút và độ lệch chuẩn là 1 phút. lOMoAR cPSD| 46348410 a.
Tính xác suất để một sản phẩm loại A nào đó được sản xuất trong khoảng
thời gian từ 9 phút đến 12 phút. b.
Tính thời gian cần thiết để sản xuất một loại sản phẩm loại A bất kỳ. ĐA:
a. 0.88185, b. 7 phút đến 13 phút.
Câu 9. Cho biến ngẫu nhiên X tuân theo phân phối chuẩn với trung bình là 6 và
phương sai là 7&. Biết rằng X lấy giá trị nhỏ hơn 60 với xác suất 0.1003 và lấy giá
trị lớn hơn 90 với xác suất 0.0516. Tìm 6 và 7. ĐA: 73.15 và 10.27
Câu 10. Đường kính của một chi tiết máy do một máy sản suất có phân phối chuẩn
với trung bình là 20mm và phương sai ’/89)&mm. Tính xác suất khi lấy ngẫu nhiên một chi tiết máy
a. Có đường kính trong khoảng 19.9mm đến 20.3mm
b. Có đường kính sai khác với kỳ vọng không quá 0.3mm. ĐA: a. 0.6247, b. 0.8664 lOMoAR cPSD| 46348410 THỐNG KÊ
PHẦN ÔN TẬP TRONG GIÁO TRÌNH.
Câu 1 (Tổng thể - Mẫu): Manuel Banales, Giám đốc Tiếp thị của Bộ phận Điện của
Plano Power Plants, Inc., đang dẫn đầu một nghiên cứu để xác định và đánh giá tầm
quan trọng tương đối của các tính năng sản phẩm. Manuel chỉ đạo nhân viên của
mình thiết kế một bảng câu hỏi khảo sát và phân phát nó cho 100 trong số 954 khách hàng của Plano. a. Xác định tổng thể. b. Xác định mẫu.
c. Tham số của tổng thể. d. Thống kê của mẫu.
Câu 2 (Phương pháp lấy mẫu): Xét xem đây là tình huống lấy mẫu nào?
a. Nhà phân tích tài chính Larry Potts cần một mẫu gồm 100 chứng khoán được
niêm yết trên thị trường chứng khoán New York. Trong số hiện tại của tờ Wall
Street Journal, 2.531 chứng khoán được liệt kê trong "Các giao dịch tổng hợp
của Sàn giao dịch New York", một danh sách theo thứ tự bảng chữ cái của tất
cả các chứng khoán được giao dịch vào ngày làm việc trước đó. Larry chọn
ngẫu nhiên bảo mật thứ 7 làm điểm bắt đầu và chọn mọi bảo mật thứ 25 sau đó (7, 32, 57, v.v.)
b. Nhà phân tích tài chính Larry Potts cần một mẫu gồm 100 chứng khoán được
niêm yết trên thị trường chứng khoán New York. Trong số hiện tại của tờ Wall
Street Journal, 2.531 chứng khoán được liệt kê trong "Các giao dịch tổng hợp
của Sàn giao dịch New York", một danh sách theo thứ tự bảng chữ cái của tất
cả các chứng khoán được giao dịch vào ngày làm việc trước đó. Larry sử dụng
bảng số ngẫu nhiên để chọn 100 số từ 1 đến 2531.
c. Vào các ngày thứ Bảy, ô tô đến tiệm rửa xe David Zebda's Scrub and Shine
với tốc độ 80 ô tô mỗi giờ trong ca làm việc kéo dài 10 giờ. David muốn một
mẫu gồm 40 khách hàng vào thứ Bảy trả lời phiên bản dài của bảng câu hỏi
về chất lượng dịch vụ của anh ấy. Anh ấy hướng dẫn đội thứ bảy chọn 40 khách hàng đầu tiên.
d. Một xe nhôm đúc xếp chồng lên nhau đã đến Nhà sản xuất Ô tô Mansfield.
Xe chứa 1.000 pallet mỗi pallet 100 tấm. Mario Munoz, giám đốc Đảm bảo
Chất lượng, chỉ đạo đội tiếp nhận chuyển pallet thứ 127 và 869 cho đội của
mình để kiểm tra 100%. Mario chọn ngẫu nhiên pallet thứ 127 và 869 từ bảng
số ngẫu nhiên. Mẫu 200 tấm pallet của Mario là _____________. lOMoAR cPSD| 46348410
e. Catherine Chao, Giám đốc Nghiên cứu Tiếp thị, cần một mẫu hộ gia đình tham
gia thử nghiệm gói kem đánh răng mới. Cô chỉ đạo 7 nhân viên của mình, mỗi
người tìm năm hộ gia đình. Mẫu của Catherine là một mẫu _____________.
Câu 3 (Thang đo): Thang đo của các câu sau là gì? Dữ liệu là rời rạc hay liên tục?
a. Đánh giá chất lượng sản phẩm (từ 1 sao đến 5 sao).
b. Mức thu nhập của một người (ghi cụ thể một con số).
c. Giá của cổ phiếu chứng khoán (ghi một số cụ thể). d. Ngành nghề của bạn.
e. Nhiệt độ của một ngày.
f. Kết quả học tập của một sinh viên trên thang điểm A, B, C, D, E, F.
g. Số điện thoại của bạn.
h. Cân nặng của một người (ghi một số cụ thể).
i. Chiều cao của một người được chia theo các khoảng sau: i. Dưới 1,3m ii. Từ 1,3mđến1,5m iii. Từ 1,5m đến 1,7m iv. Trên 1,7m
Câu 4 (Bảng tần số): Cho bảng dữ liệu sau: Tuổi Số sinh viên 18 3 19 5 20 28 21 4
a. Tính trung bình số tuổi. Giải thích ý nghĩa.
b. Tính phương sai, độ lệch chuẩn số tuổi. Giải thích ý nghĩa.
c. Tính trung vị. Giải thích ý nghĩa.
d. Tính Q1. Giải thích ý nghĩa.
e. Tính Q3. Giải thích ý nghĩa.
f. Tính IQR. Giải thích ý nghĩa.
g. Tính yếu vị. Giải thích ý nghĩa.
h. Tìm khoảng tin cậy cho trung bình của tổng thể với độ tin cậy 99%.
i. Tìm khoảng tin cậy cho tỷ lệ sinh viên đang ở độ tuổi 20, với độ tin cậy 90%.
j. Có nhận định cho rằng, trung bình độ tuổi của sinh viên là 20. Với mức ý nghĩa
5%, bạn hãy kiểm định nhận định trên?
k. Có nhận định cho rằng tỷ lệ sinh viên có độ tuổi 20 tuổi chiếm trên 60%. Hãy
kiểm định nhận định trên với mức ý nghĩa 10%. lOMoAR cPSD| 46348410
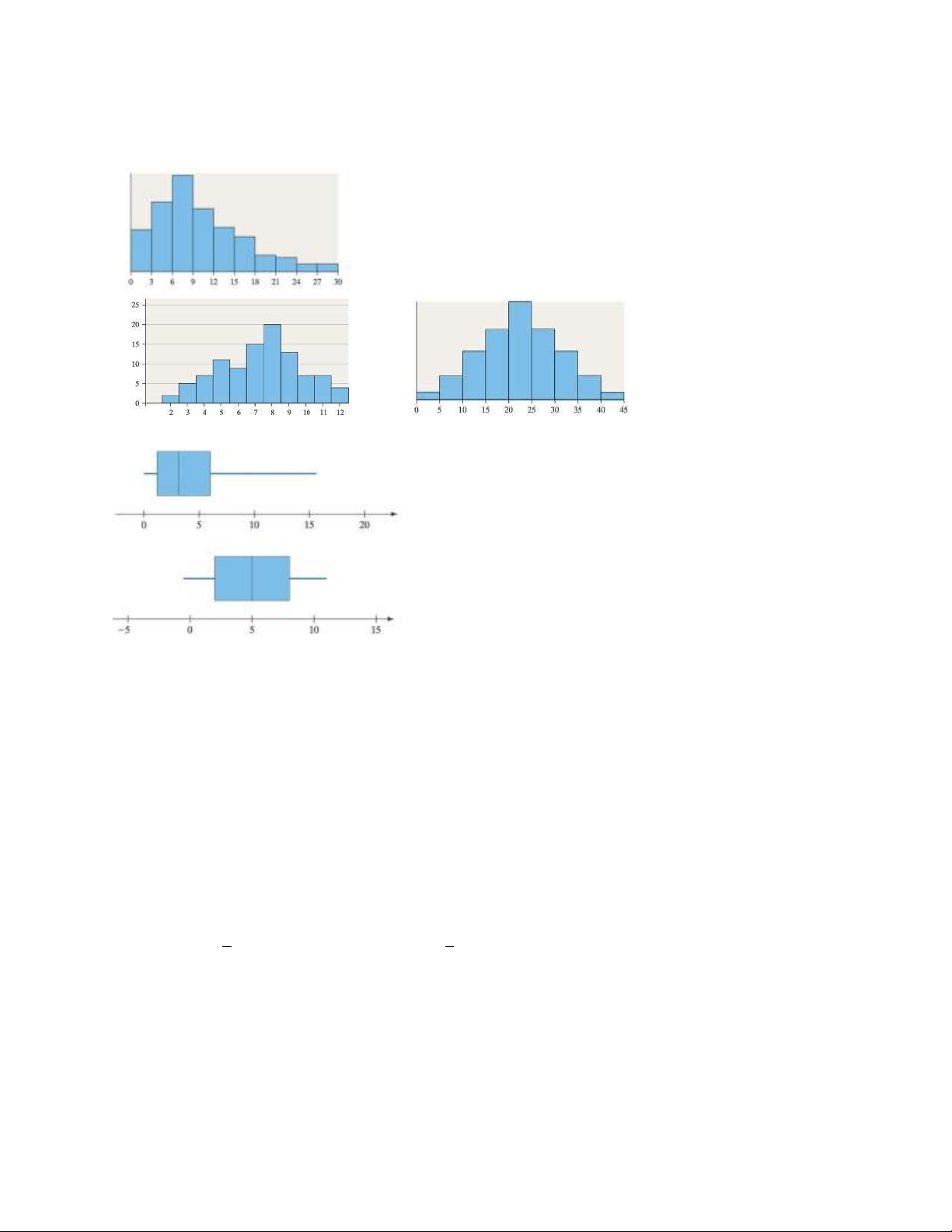
Câu 5 (Mô tả hình ảnh): Mô tả hình dáng của đồ thị a. b. c. Câu 6 (Boxplot):
a. Nhận xét hình dáng của từng đồ thị.
b. So sánh khoảng biến thiên của hai đồ thị.
c. So sánh độ trải giữa giữa hai đồ thị.
d. Nhìn tổng quan, so sánh trung bình tổng thể của hai đồ thị.
e. So sánh giá trị nhỏ nhất của hai đồ thị.
f. So sánh giá trị lớn nhất của hai đồ thị.
Câu 7: Chủ nhà hàng Denny Valentine đang đánh giá hai địa điểm, Raymondville
và Rosenberg, cho nhà hàng tiếp theo của mình. Anh ấy muốn chứng minh rằng cư
dân Raymondville đi ăn ngoài thường xuyên hơn cư dân Rosenberg. Denny thực
hiện một cuộc khảo sát thị trường để kiểm tra giả thuyết này. Nhà nghiên cứu thị
trường đã sử dụng một mẫu ngẫu nhiên gồm 64 gia đình từ mỗi vùng ngoại ô và báo
cáo như sau:(" :* :$% lần mỗi tháng và(& * :$; lần mỗi tháng. Giả sử rằng 7" * :; và 7& * !8
a. Xác định dạng bài cần kiểm định.
b. Tìm ước lượng điểm tốt nhất cho sự khác biệt của hai trung bình tổng thể.
c. Tìm khoảng ước lượng 99% cho sự khác biệt này.
d. Với < = 0.01, hãy kiểm tra nhận định trên. lOMoAR cPSD| 46348410
Câu 8: Một nhà nghiên cứu quan tâm đến việc thử nghiệm để xác định xem giá trị
trung bình của tổng thể thứ nhất có lớn hơn giá trị trung bình của tổng thể thứ hai
hay không. Anh ta chọn ngẫu nhiên một mẫu gồm 9 sản phẩm từ tổng thể thứ nhất
nhận được giá trị trung bình là 14.3 và độ lệch chuẩn là 3.4. Anh ta chọn ngẫu nhiên
một mẫu gồm 14 sản phẩm từ tổng thể thứ hai nhận được giá trị trung bình là 11.8
và độ lệch chuẩn là 2.9.
a. Xác định dạng bài cần kiểm định.
b. Tìm ước lượng điểm tốt nhất cho sự khác biệt của hai trung bình tổng thể.
c. Với < = 0.05, hãy kiểm tra nhận định trên.
Câu 9: Một nhà nghiên cứu đang tiến hành một nghiên cứu bắt cặp và điều tra xem
có sự chênh lệch giữa hai nhóm này hay không. Cô ấy tiến hành thu thập dữ liệu của
từng cặp, kết quả được cho trong bảng sau: Cặp Nhóm 1 Nhóm 2 1 10 12 2 8 9 3 11 11 4 8 10 5 9 12
Giả sử tổng thể tuân theo phân phối chuẩn.
a. Xác định dạng bài cần kiểm định.
b. Tìm ước lượng điểm tốt nhất cho bài toán này.
c. Tìm khoảng ước lượng 90% cho sự chênh lệch này.
d. Với < = 0.1, hãy kiểm tra nhận định trên.
Câu 10: Maureen McIlvoy, chủ sở hữu và Giám đốc điều hành của một doanh nghiệp
đặt hàng qua thư cho thiết bị và vật tư lướt sóng, đang xem xét các hoạt động đặt
hàng tại kho của mình. Mục tiêu của cô là 100% đơn hàng được giao trong vòng 24
giờ. Trong những năm trước, cả hai kho đều không đạt được mục tiêu, nhưng Kho
Bờ Đông đã liên tục vượt qua Kho Bờ Tây. Nhân viên của cô ấy đã chọn ngẫu nhiên
200 đơn đặt hàng từ Kho Bờ Tây (tổng thể 1) và 400 đơn đặt hàng từ Kho Bờ Đông
(tổng thể 2) và báo cáo rằng 190 Đơn đặt hàng Bờ Tây đã được vận chuyển trong
vòng 24 giờ và Kho hàng Bờ Đông đã vận chuyển 372 đơn đặt hàng trong vòng 24 giờ.
a. Xác định dạng bài cần kiểm định.
b. Tìm ước lượng điểm tốt nhất cho bài toán này. lOMoAR cPSD| 46348410
c. Tìm khoảng ước lượng 95% cho sự khác biệt này.
d. Với < = 5%, hãy kiểm tra nhận định trên.
Câu 11: Công ty Xây dựng Collinsville mua thanh thép cho các dự án của mình.
Dựa trên các thử nghiệm trước đó, Claude Carter, Giám đốc đảm bảo chất lượng, đã
khuyến nghị mua các thanh từ Redding Rods, Inc., thay vì Stockton Steel, vì các
thanh của Redding có độ dài ít thay đổi hơn. Gần đây, Stockton đã sửa đổi hoạt động
để cải tiến độ đồng đều của các thanh thép. Claude đã lấy mẫu kết quả đầu ra từ các
quy trình sản xuất thanh của Redding và Stockton. Kết quả đối với Redding là =" *
/8$/với >" * ?và đối với Stockton, kết quả là =& * /8/@:với >& * $/. Giả sử rằng độ
dài của thanh thép tuân theo phân phối chuẩn.
a. Xác định dạng bài cần kiểm định.
b. Tìm khoảng ước lượng 95% cho tỷ lệ hai phương sai này.
c. Với < = 5%, hãy kiểm tra nhận định trên.
PHẦN ĐỌC KẾT QUẢ STATA
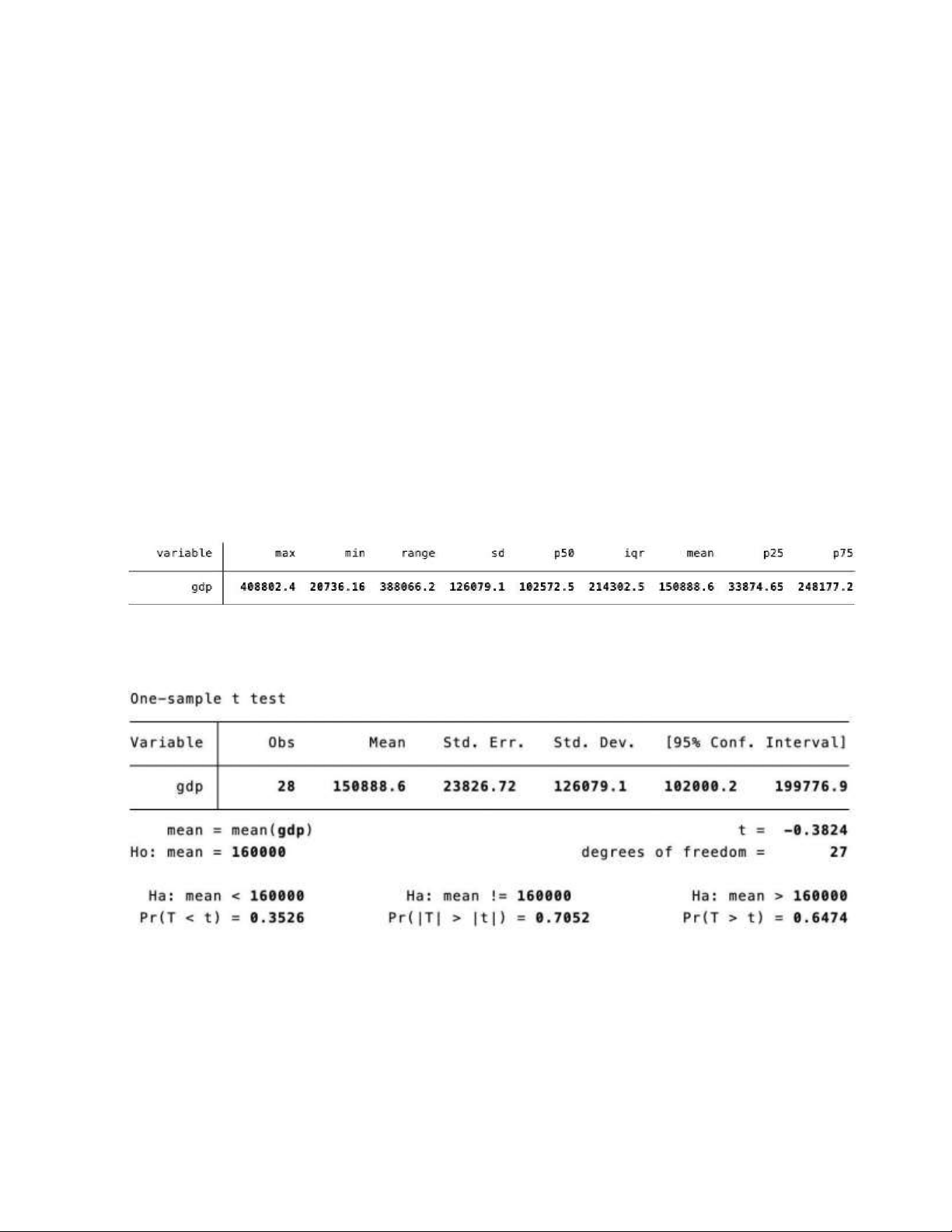
Câu 1: Giải thích ý nghĩa của các con số sau:
Ví dụ: 408802.4 là giá trị lớn nhất của biến gdp.
Câu 2: Cho kết quả sau:
a. Tìm ước lượng tốt nhất cho trung bình của GDP.
b. Tìm khoảng tin cậy 95% cho ước lượng trung bình của GDP.
c. Tiêu chuẩn kiểm định bằng bao nhiêu? Với mức ý nghĩa 5%.
d. Xét cặp giả thuyết ABB(’C 6 * $%///C 6 D $%/// lOMoAR cPSD| 46348410
i. Cho biết p-value bằng bao nhiêu?
ii. Đưa ra nhận xét cho kiểm định này.
e. Xét cặp giả thuyết ABB(’C 6 * $%///C 6 . $%///.
i. Cho biết p-value bằng bao nhiêu? ii. Đưa ra nhận xét cho kiểm định này.
f. Xét cặp giả thuyết ABB(’C 6 * $%///C 6 3 $%///.
i. Cho biết p-value bằng bao nhiêu? ii. Đưa ra nhận xét cho kiểm định này. Câu 3: a. Đây là dạng bài toán gì? b.
Tiêu chuẩn kiểm định bằng bao nhiêu? c.
Phương sai mẫu gộp bằng bao nhiêu? d.
Ước lượng tốt nhất cho trung bình tổng thể 1, tổng thể 2. e.
Ước lượng tốt nhất cho sự khác biệt giữa trung bình hai tổng thể. f.
Khoảng tin cậy 95% cho trung bình của tổng thể 1, tổng thể 2. g.
Khoảng tin cậy 95% cho sự khác biệt giữa trung bình hai tổng thể. h.
Xét cặp giả thuyết AB’C EFG>’HGI$) 5 EFG>’HGI9) * / B(C EFG>’HGI$) 5 EFG>’HGI9) . / i.
Cho biết p-value bằng bao nhiêu? lOMoAR cPSD| 46348410
iii. Đưa ra nhận xét cho kiểm định này với mức ý nghĩa 5%.
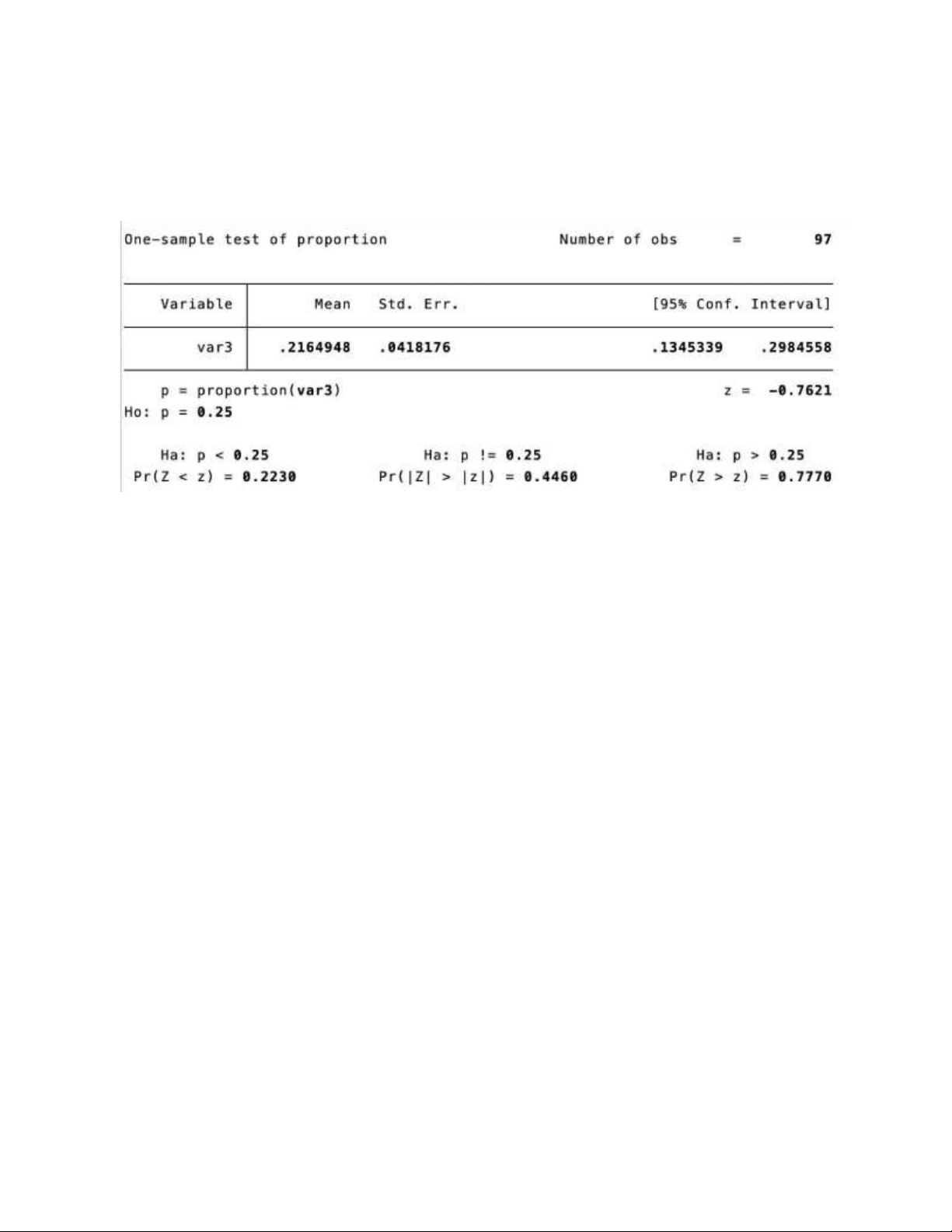
Câu 4: Cho kết quả sau: a.
Đây là dạng bài toán gì?
b. Tiêu chuẩn kiểm định bằng bao nhiêu?
c. Ước lượng tốt nhất cho tỷ lệ tổng thể.
d. Khoảng tin cậy 95% cho tỷ lệ của biến var3.
e. Xét cặp giả thuyết ABB(’C J * /89@C J D /89@.
i. Cho biết p-value bằng bao nhiêu?
ii. Đưa ra nhận xét cho kiểm định này với mức ý nghĩa 1%.
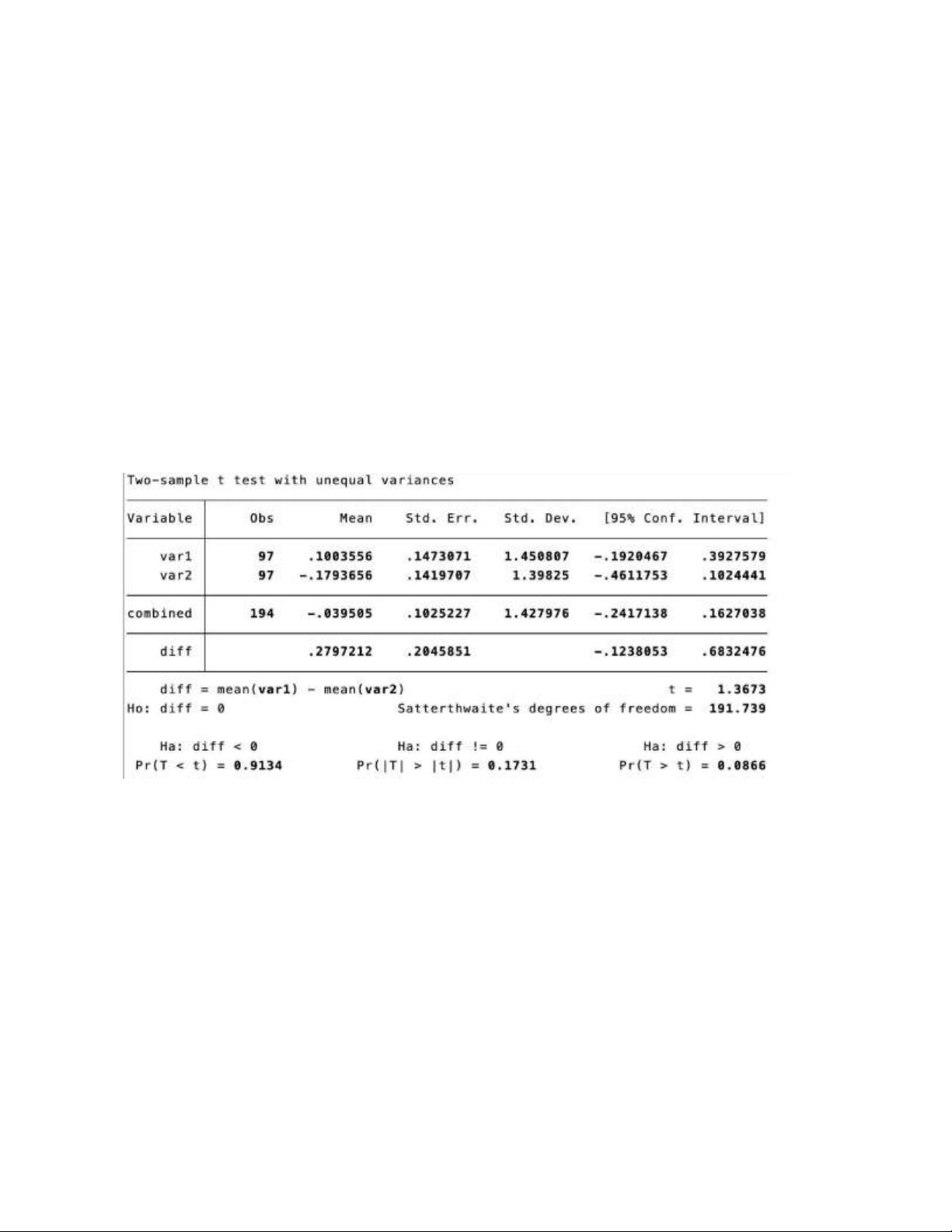
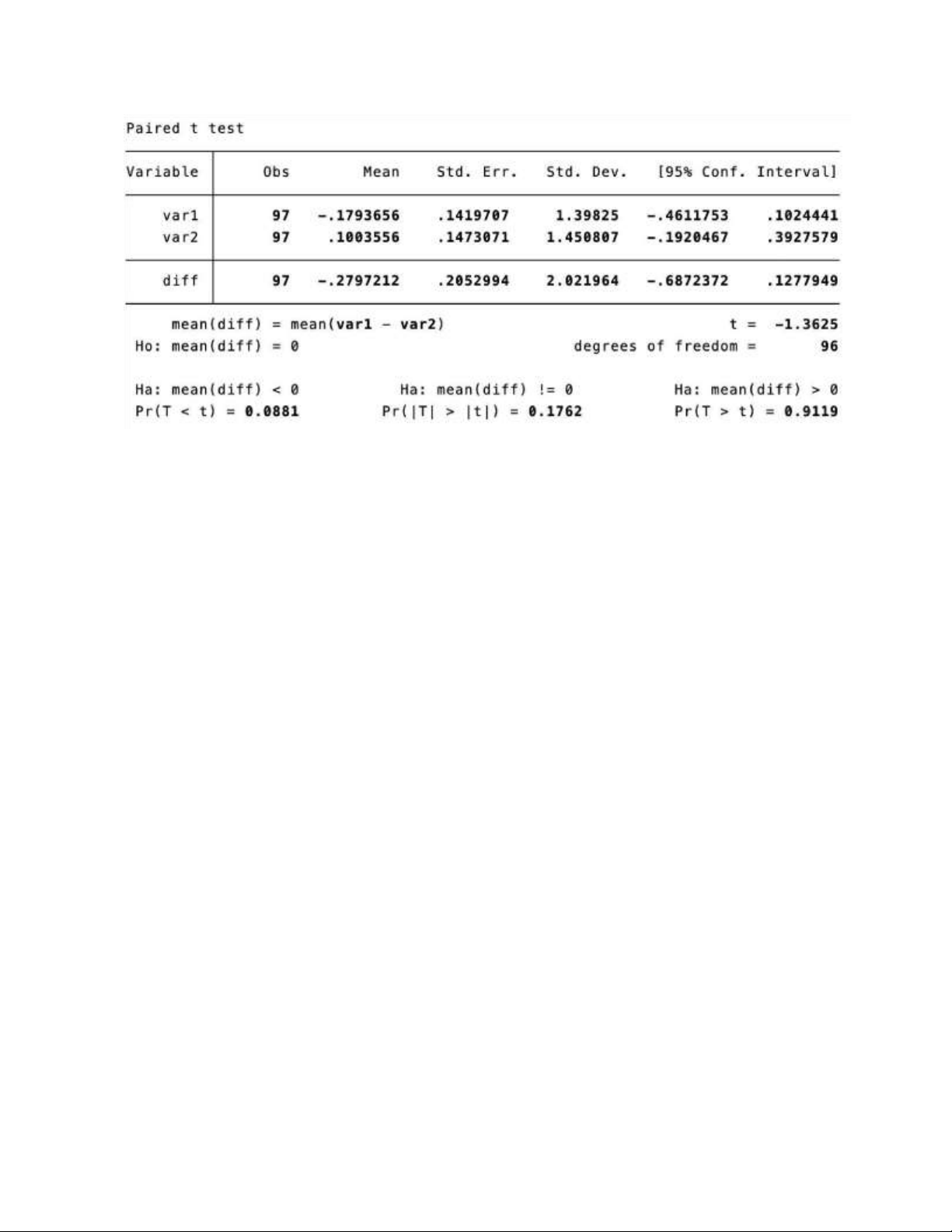
Câu 5: Cho kết quả sau: lOMoAR cPSD| 46348410
a. Đây là dạng bài toán gì?
b. Tiêu chuẩn kiểm định bằng bao nhiêu?
c. Ước lượng tốt nhất cho trung bình tổng thể 1, tổng thể 2.
d. Ước lượng tốt nhất cho sự chênh lệch của biến var1 và biến var2 theo từng cặp.
e. Khoảng tin cậy 95% cho trung bình của tổng thể 1, tổng thể 2.
f. Khoảng tin cậy 95% cho sự chênh lệch của biến var1 và biến var2 theo từng cặp.
g. Xét cặp giả thuyết AB’C EFG>’HGI$) 5 EFG>’HGI9) * /. B(C
EFG>’HGI$) 5 EFG>’HGI9) 3 /
i. Cho biết p-value bằng bao nhiêu?
ii. Đưa ra nhận xét cho kiểm định này với mức ý nghĩa 10%.
PHẦN CÂU HỎI TÌNH HUỐNG
Câu 1: Trưởng phòng nhân sự của một công ty tuyên bố rằng tiền lương trung bình
của tất cả nhân viên làm việc ở công ty này sau 3 năm sẽ tăng gấp đôi so với khi vừa
được tuyển dụng vào công ty? Dựa trên kiến thức đã học, làm thế nào để kiểm tra
xem tuyên bố trên có đáng tin cậy không? Câu 2: Một giảng viên nhận xét rằng kết
qủa môn TKUD phụ vào giới tính của sinh viên. Dựa vào kiến thức đã học, làm thế
nào để kiểm tra xem nhận xét của giảng viên này có đúng hay không? Câu 3: Người
ta cho rằng do tác động của dịch bệnh lợi nhuận của các doanh nghiệp trong năm
2020 bị giảm so với năm 2019. Bạn hãy đề xuất cách thực hiện một kiểm định để đánh giá ý kiến đó. lOMoAR cPSD| 46348410
Câu 4: Một công ty có 2 cửa hàng kinh doanh ở 2 vị trí khác nhau, công ty có số
liệu doanh thu từng ngày của mẫu 34 ngày của cửa hàng số 1 và số liệu doanh thu
từng ngày của một mẫu 36 ngày của cửa hàng số 2. Làm thế nào để so sánh được
doanh thu của 2 cửa hàng trên?
Câu 5: Người ta nghi ngờ về sự phân tán lương không đồng đều của hai công ty A
và công ty B. Dựa vào kiến thức đã học, làm thế nào để kiểm tra nghi ngờ trên.