














Preview text:
lOMoAR cPSD| 46348410 3.11
Ta xác định đây là 2 mẫu độc lập vì mẫu là tiền lãi hàng tháng được lấy từ 100 hộ kinh
doanh mặt hàng K và 100 hộ kinh doanh mặt hàng L
H0:μ1≤μ2
{H1:μ1>μ2
μ1: tiền lãi hàng tháng của 100 hộ kinh doanh mặt hàng L μ2: là tiền lãi
hàng tháng của 100 hộ kinh doanh mặt hàng K
H0: Tiền lãi kinh doanh mặt hàng L không cao hơn tiền lãi khi kinh doanh mặt hàng K
H1: Tiền lãi kinh doanh mặt hàng L cao hơn tiền lãi khi kinh doanh mặt hàng K
Ta có p-value =0.4142 > 0.02 => chấp nhận H0
Kết luận: tiền lãi kinh doanh mặt hàng L không cao hơn tiền lãi khi kinh doanh mặt hàng K 3.16
Ta xác định đây là 2 mẫu độc lập vì 129/516 nam giới Mỹ có hút thuốc và 87/484 nữ giới Mỹ có hút thuốc lOMoAR cPSD| 46348410
{HH01::pp11=>pp22
p1: tỉ lệ nam giới ở Mỹ từ 18 tuổi trở lên có hút thuốc p2: tỉ lệ nữ
giới ở Mỹ từ 18 tuổi trở lên có hút thuốc
H0: tỷ lệ nam giới ở Mỹ có độ tuổi từ 18 trở lên không cao hơn tỷ lệ hút thuốc ở nữ giới
có độ tuổi từ 18 trở lên
H1: tỷ lệ nam giới Mỹ có độ tuổi từ 18 trở lên cao hơn tỷ lệ hút thuốc ở nữ giới có độ tuổi từ 18 trở lên => B 3.17
Ta xác định đây là 2 mẫu độc lập vì được tính theo giá cố phiếu REE và HAP trong 10 phiên giao dịch
{H0:σ212≤σ222
H1:σ1>σ2 𝜎 2
1 là mức độ ổn định của giá cổ phiếu REE 𝜎 2
2 là mức độ ổn định của giá cổ phiếu HAP
H0: giá cổ phiếu HAP không ổn định bằng giá cố phiếu REE
H1: giá cổ phiếu HAP ổn định hơn giá cổ phiếu REE lOMoAR cPSD| 46348410
Ta có p-value=0.99 > 0.05=> chấp nhận H0
Kết luận giá cổ phiếu HAP không ổn định bằng giá cổ phiếu REE 3.18
Ta xác định đây là hai mẫu độc lập vì mức thu nhập được lấy từ các hộ ngoại thành và nội thành
{H0:σ221≥σ222
H1:σ1<σ2
σ21: mức độ ổn định thu nhập của các hộ ngoại thành σ22: mức độ ổn
định thu nhập của các hộ nội thành
H0: thu nhập của các hộ ngoại thành không ổn định bằng mức thu nhập của các hộ nội thành
H1: thu nhập của các hộ ngoại thành ổn định hơn mức thu nhập của các hộ nội thành lOMoAR cPSD| 46348410
Ta có p-value = 0<0.05 => chấp nhận H1
Kết luận: thu nhập của các hộ ngoại thành ổn định hơn thu nhập của các hộ nội thành 4.1
H0: Máy hoạt động bình thường
H1: Máy hoạt động không bình thường
𝜇: trọng lượng sản phẩm thực tế
HH01::μμ≠=1414 { lOMoAR cPSD| 46348410
Ta có p-value =0.0000<0.05 => chấp nhận H1
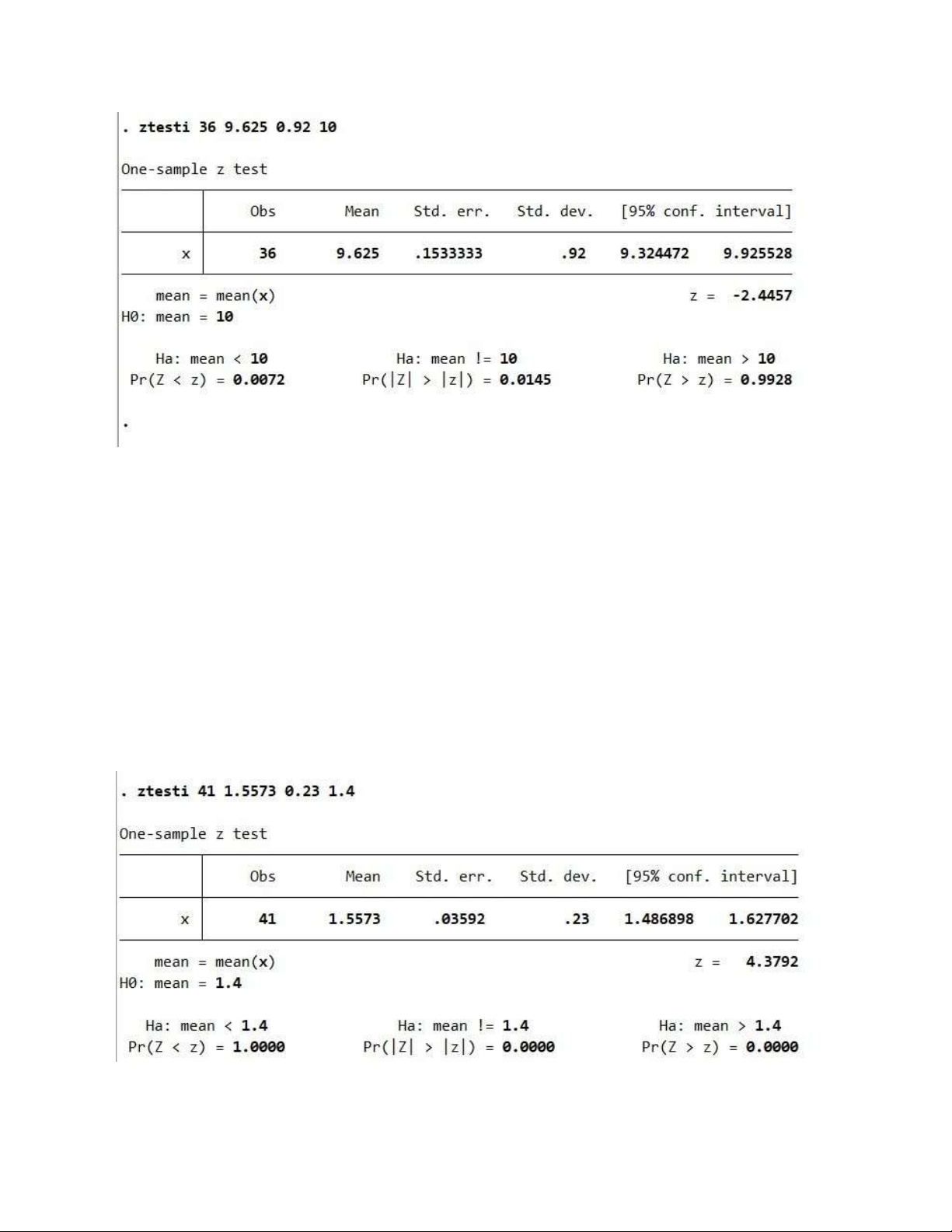
Kết luận: máy hoạt động không bình thường làm trọng lượng của sản phẩm giảm đi 4.2
H0: định mức thời gian hoàn thành một sản phẩm không cần thay đổi H1: định mức thời
gian hoàn thành một sản phẩm cần thay đổi
𝜇: thời gian hoàn thành sản phẩm trong thực tế
HH10::μμ≠=1010 { lOMoAR cPSD| 46348410
Ta có p-value = 0.0145 <0.05 => chấp nhận H1
Kết luận: định mức thời gian hoàn thành một sản phẩm cần thay đổi 4.3
a) H0: mức chi tiêu hằng tháng của sinh viên không tăng lên H1: mức chi tiêu
hằng tháng của sinh viên có tăng lên
𝜇: mức chi tiêu hằng tháng của sinh viên trong thực tế
{HH01::μμ11≤>1.41.4
Ta có p-value =0< 0.05 => chấp nhận H1 lOMoAR cPSD| 46348410
Kết luận: mức chi tiêu hằng tháng của sinh viên có tăng lên b) H0: Độ phân
tán của mức chi tiêu của sinh viên là 300 ngàn đồng
H1: Độ phân tán của mức chi tiêu của sinh viên không phải là 300 ngàn đồng
𝜎2: độ phân tán mức chi tiêu của sinh viên trong thực tế
{H0:σ22=90000 H1:σ ≠90000
Ta có p-value =0.0352<0.05 => chấp nhận H1
Kết luận: độ phân tán của mức chi tiêu của sinh viên không phải là 300 ngàn đồng 4.4
H0: độ đồng đều của trọng lượng các gói mì chính không tăng lên H1: độ đồng đều
của trọng lượng các gói mì chính có tăng lên
𝜎2: độ đồng đều của trọng lượng các gói mì chính lOMoAR cPSD| 46348410
{H0:σ22≤4 H1:σ >4
Ta có p-value=1 > 0.05 => chấp nhận H0
Kết luận: độ đồng đều của trọng lượng các gói mì chính không tăng lên 4.5
a) H0: Định mức mức tiêu hao nhiên liệu của xe không cần thay đổi H1: Định mức
mức tiêu hao nhiên liệu của xe cần thay đổi μ: mức tiêu hao nhiên liệu của xe
{HH10::μμ≠=66 lOMoAR cPSD| 46348410
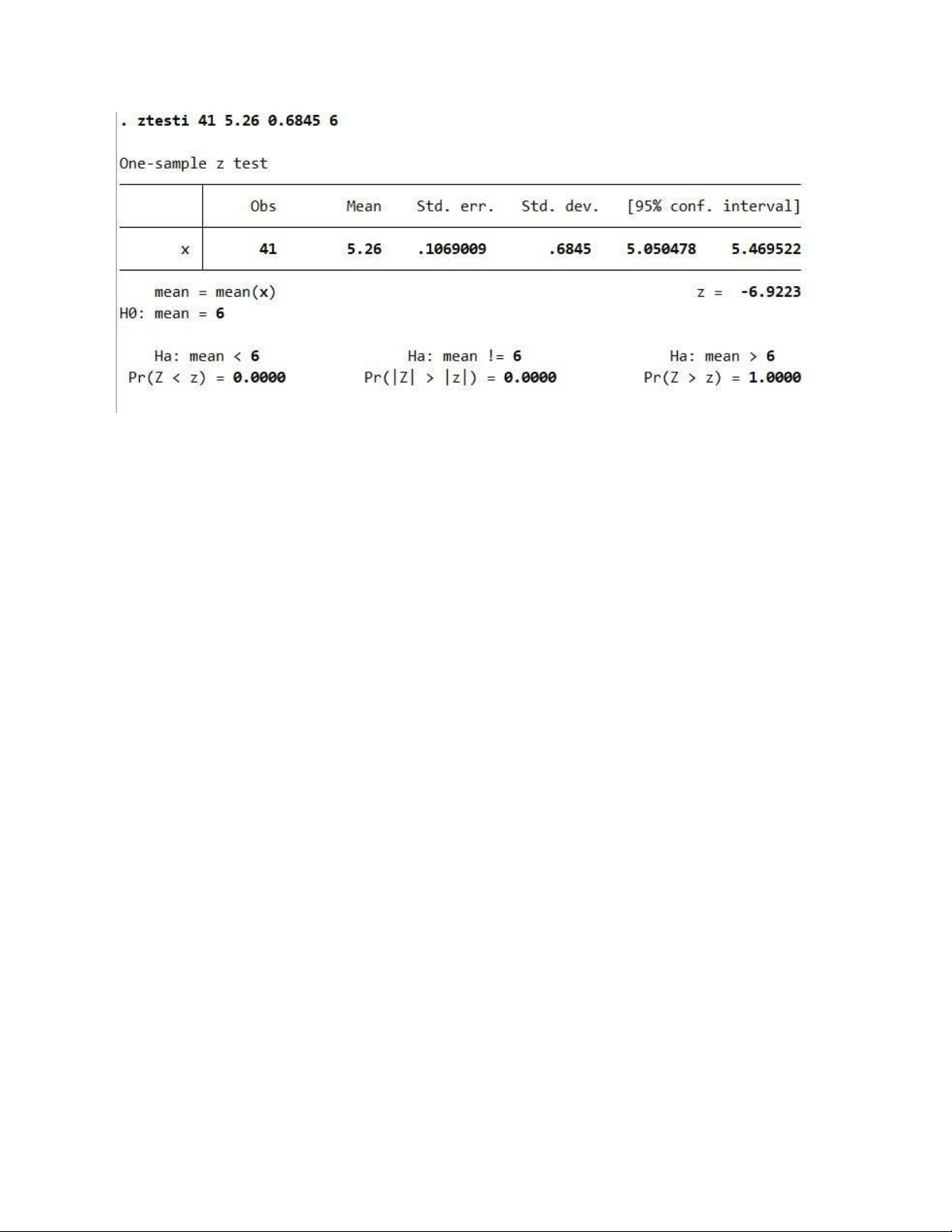
Ta có p-value =0<0.05 => chấp nhận H1
Kết luận: định mức mức tiêu hao nhiên liệu của xe cần thay đổi b)
H0: Độ phân tán của lượng tiêu thụ nhiên liệu là 1.5 lít
H1: Độ phân tán của lượng tiêu thụ nhiên liệu không phải là 1.5 lít
𝜎2 : Độ phân tán của lượng tiêu thụ nhiên liệu {H0:μ=1.522 H1:μ≠1.5 lOMoAR cPSD| 46348410
Ta có p-value = 0.0000 <0.05 => chấp nhận H1
Kết luận: độ phân tán của lượng tiêu thụ nhiên liệu không phải là 1.5 lít 4.6
H0: Sự chênh lệch thu nhập không tăng lên
H1: Sự chênh lệch thu nhập có tăng lên
Với 𝜎2 là sự chênh lệch thu nhập của người dân lao động thành thị
{H0:σ22≤1 H1:σ >1 lOMoAR cPSD| 46348410
Ta có p-value =0.0000 < 0.05 => chấp nhận H1
Kết luận: sự chênh lệch thu nhập của người dân lao động thành thị có tăng lên 4.7
H0: Phương pháp giảng dạy mới không hiệu quả
H1: Phương pháp giảng dạy mới có hiệu quả
Với pA là tỉ lệ sinh viên chính quy thi đạt ở một môn học nào đó trong một trường đại học
{HH01::ppAA≤>0.70.7 lOMoAR cPSD| 46348410
Ta có p-value = 0.0404< 0.05 => chấp nhận H1
Kết luận: phương pháp giảng dạy mới có hiệu quả 4.8
a) {HH10::ppAA=≠0.50.5
H0: Tỷ lệ giới của trường đại học là như nhau
H1: Tỷ lệ giới của trường đại học là khác nhau
Ta có p-value=0.1573 > 0.05, chấp nhận H0 Kết luận: Tỷ lệ giới
của trường đại học là như nhau
b) p1 là tỷ lệ sinh viên nữ đi làm thêm ngoài giờ học
p2 là tỷ lệ sinh viên nam đi làm thêm ngoài giờ học
{HH01::pp11≤p>p22
H0: Tỷ lệ sinh viên nam đi làm thêm ngoài giờ không cao hơn tỉ lệ sinh viên nữ đi làm thêm ngoài giờ
H1: Tỷ lệ sinh viên nam đi làm thêm ngoài giờ cao hơn tỉ lệ sinh viên nữ đi làm thêm ngoài giờ lOMoAR cPSD| 46348410
Ta có p-value =0.3014 >0.05 => chấp nhận H0
Kết luận: tỷ lệ sinh viên nam đi làm thêm ngoài giờ không cao hơn tỉ lệ sinh viên nữ đi làm thêm ngoài giờ
4.9 p1là tỷ lệ phế phẩm ở dây chuyền 1 p2 là
tỷ lệ phế phẩm ở dây chuyền 2
{HH10::pp11=≠pp22
H0: chất lượng hai dây chuyền như nhau
H1: chất lượng hai dây chuyền khác nhau lOMoAR cPSD| 46348410
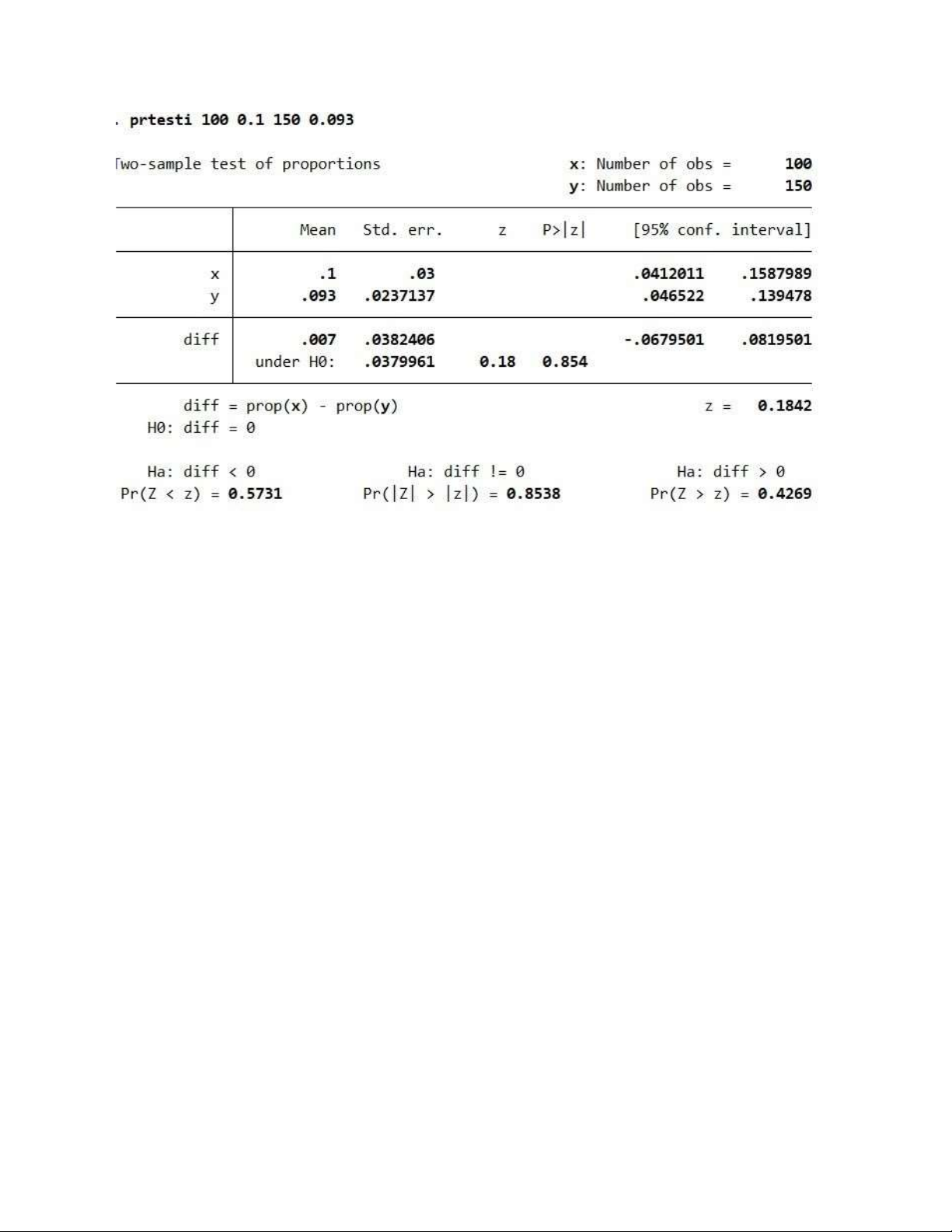
Ta có p-value =0.8538 > 0.05 => chấp nhận H0
Kết luận: chất lượng hai dây chuyền như nhau 4.10
H0: Tỉ lệ phế phẩm của nhà máy 1 không cao hơn 10%
H1: Tỉ lệ phế phẩm của nhà máy 1 cao hơn 10% pA: tỉ lệ phế phẩm của nhà máy 1
{HH01::ppAA≤>0.10.1 lOMoAR cPSD| 46348410
Ta có p-value =0.1007 > 0.05 => chấp nhận H0 Kết luận: Tỉ lệ
phế phẩm của nhà máy 1 không cao hơn 10%
b) p1 là tỷ lệ phế phẩm ở nhà máy 1
p2 là tỷ lệ phế phẩm ở nhà máy 2
H0: tỷ lệ phế phẩm ở 2 nhà máy như nhau
H1: tỷ lệ phế phẩm ở 2 nhà máy khác nhau
{HH01::pp11=≠pp22 lOMoAR cPSD| 46348410
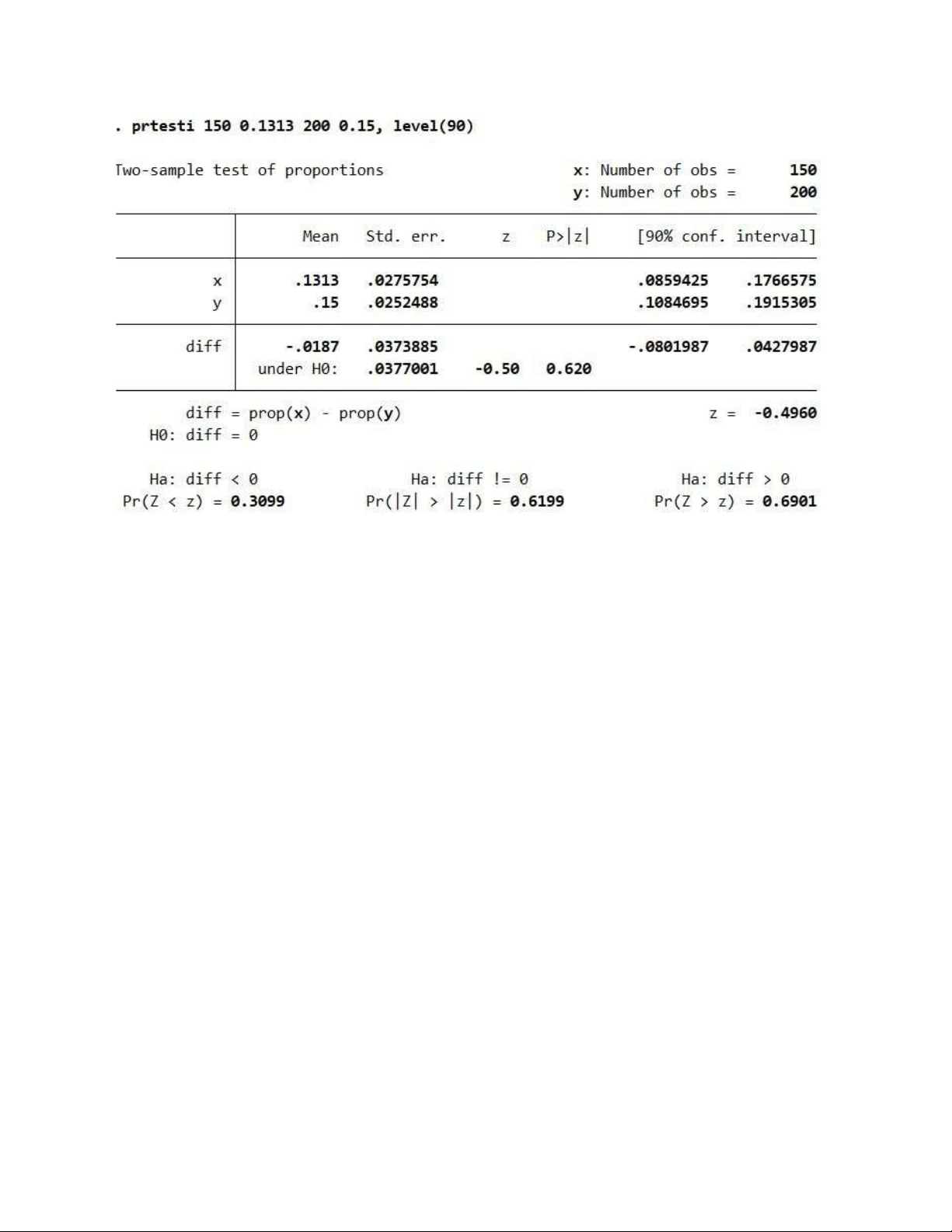
Ta có p-value =0.6199 > 0.1=> chấp nhận H0
Kết luận: tỷ lệ phế phẩm ở 2 nhà máy như nhau 4.11 a)
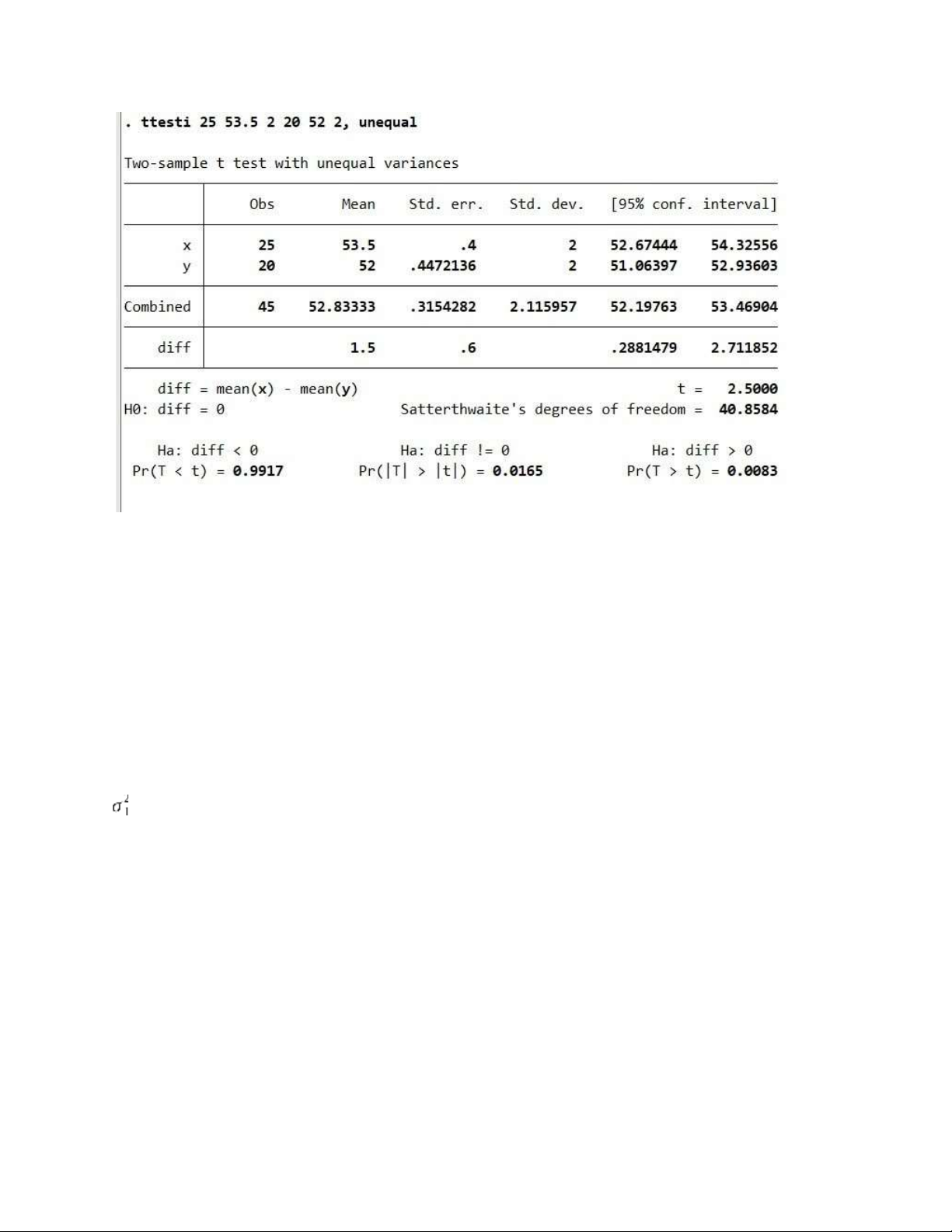
H0: Hai giống lúa năng suất như nhau H1: Hai giống lúa năng suất khác nhau
{HH01::μμ11=≠μμ22
μ1 là năng suất lúa trung bình của giống lúa A μ1 là năng
suất lúa trung bình của giống lúa B lOMoAR cPSD| 46348410
Ta có p-value =0.0165 <0.05 => chấp nhận H1
Kết luận: Hai giống lúa năng suất khác nhau b)
H0: độ ổn định của năng suất 2 giống lúa là như nhau H1:
độ ổn định của năng suất 2 giống lúa là khác nhau
{H0:σ212=σ222
H1:σ1≠σ2
: độ ổn định của năng suất giống lúa A σ22 :độ ổn
định của năng suất giống lúa B lOMoAR cPSD| 46348410
Ta có p-value =0.9865>0.1 => chấp nhận H0 Kết luận: độ ổn định
của năng suất 2 giống lúa là như nhau 4.12
H0: độ phân tán của mức doanh thu hằng ngày của 2 trạm là như nhau
H1: độ phân tán của mức doanh thu hằng ngày của 2 trạm là khác nhau
{H0:σ212=σ222
H1:σ1≠σ2
: độ phân tán của mức doanh thu hằng ngày của trạm A : độ phân
tán của mức doanh thu hằng ngày của trạm B lOMoAR cPSD| 46348410
Ta có p-value =0.4915>0.05 => chấp nhậnH0
Vậy với mức ý nghĩa 0.05 thì độ phân tán của mức doanh thu hằng ngày của 2 trạm là như nhau
b) H0: Doanh thu trạm thu phí B không cao hơn trạm thu phí A H1: Doanh thu
trạm thu phí B không cao hơn trạm thu phí A
{HH01::μμ11≥μ<μ22
μ1 là doanh thu trạm thu phí A
μ2 là doanh thu trạm thu phí B Ta có df= 38
Tra bảng student ta có Z0 < −¿1.304 => chấp nhậnH1 lOMoAR cPSD| 46348410
Kết luận: doanh thu trạm thu phí B cao hơn trạm thu phí A 4.T1
H0: mức lương trung bình hằng năm của nhân viên bán hàng nam và nữ như nhau
H1: mức lương trung bình hằng năm của nhân viên bán hàng nam và nữ khác nhau
{HH01::μμ11=≠μμ22
μ1 là mức lương trung bình hằng năm của nhân viên bán hàng nam μ2 là mức lương
trung bình hằng năm của nhân viên bán hàng nữ
Ta có p-value =0.0145 < 0.05=> chấp nhận H1
Kết luận: mức lương trung bình hằng năm của nhân viên bán hàng nam và nữ là khác nhau => D
4.T2 H0: tỷ lệ trễ hạn thanh toán vượt quá 90 ngày năm nay và năm trước là như nhau
H1: tỷ lệ trễ hạn thanh toán vượt quá 90 ngày năm nay và năm trước là khác nhau




