-
Thông tin
-
Quiz
Bài tập ôn tập - Vật lý đại cương | Trường Đại Học Duy Tân
Bài tập ôn tập - Vật lý đại cương | Trường Đại Học Duy Tân được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn sinh viên cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!
Vật lý đại cương (Phy 101) 68 tài liệu
Đại học Duy Tân 1.8 K tài liệu
Bài tập ôn tập - Vật lý đại cương | Trường Đại Học Duy Tân
Bài tập ôn tập - Vật lý đại cương | Trường Đại Học Duy Tân được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn sinh viên cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!
Môn: Vật lý đại cương (Phy 101) 68 tài liệu
Trường: Đại học Duy Tân 1.8 K tài liệu
Thông tin:
Tác giả:
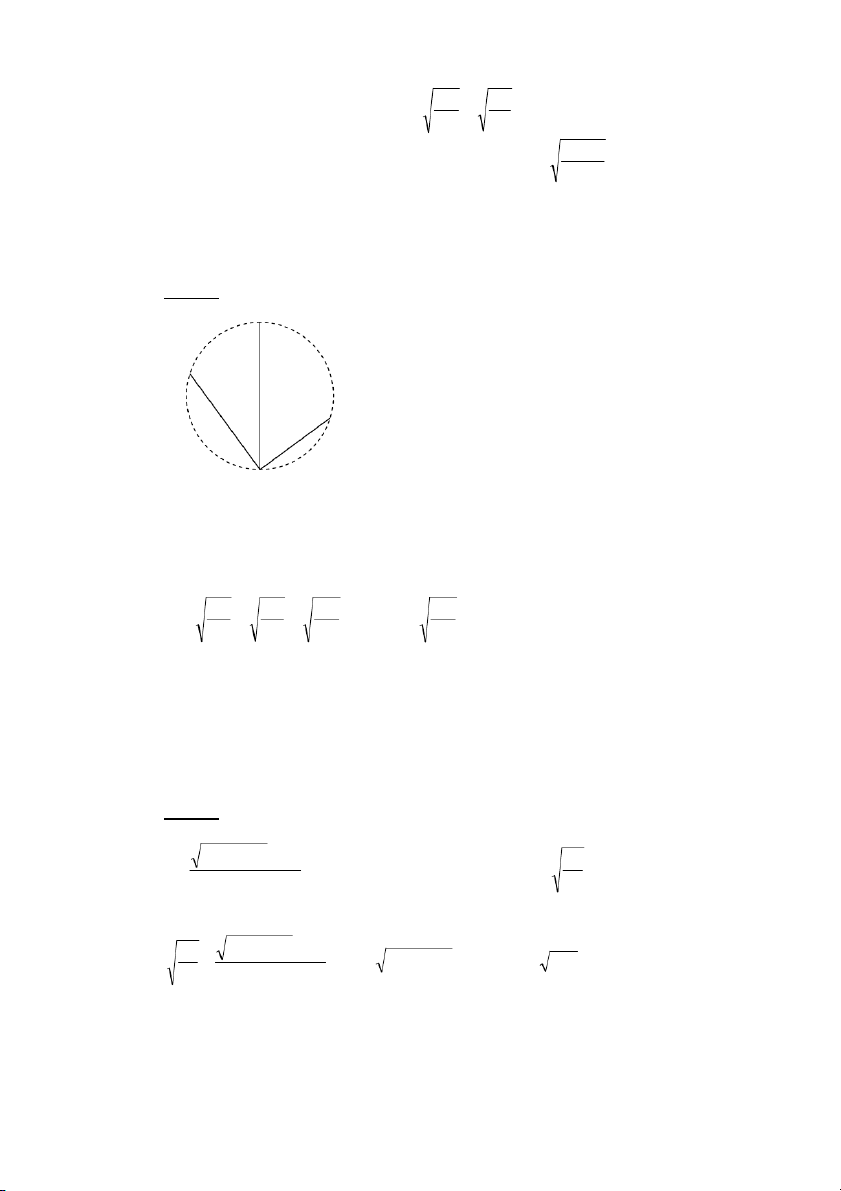
Preview text:
!"ω# $" $ ϕ
!"ω# $"%$ % ϕ%
&'()*+,-! $ϕ . %/ ϕ% π0
/12!345
6$ϕ . "%/# $ ϕ% π5 $ π
ϕ . "%/# $ 5 ϕ% 2
($ϕ . 7'6/8 ϕ%
9:;06<,()*27
-=7>12-6(?3)@
AB07C/D6<+8E7062B-27
12!8
$Fϕ #%/ ϕ%
πA2" $7
!"ω# $ !"ω# #%/π$ !"ω# $0 ϕ ϕ% ϕ%
!"ω# $ % ϕ% FG7 x y a = y 2 = x a a a 1 2 1
H. ≤!"ω#ϕ $≤ 4. ≤≤
HB-I$24J6(?6K a y 2 = x AL . ≤≤ a1
6$92M-I$ !" $ !" #%/ !" $ ω#ϕ ω#ϕ% π#π$. ω#ϕ%
FG7N4J6(?6K a y 2 = − x AL
. ≤≤ a1 $F π
ϕ #"%/# $
(?(2N6> ϕ% 2 x 2 y 2 + = 1 a 2 a 2 1 2
26(?+41O-AP071LA2Q;
48
($=/D-" $A2"%$8R3</2!3!
" $A2"%$
x = cosωt.cosϕ −sinωt.sinϕ "S$ 1 1 a1
y = cosωt.cosϕ − sinωt.sinϕ "T$ 2 2 a 2
UV"S$AL!ϕ A2"T$AL.! WA<ALA< % ϕ
x y cosϕ − cosϕ = sin t
ω .sin(ϕ − ϕ )"X$ 2 1 2 1 a a 1 2
9V"S$AL!ϕ A2"T$AL.! WA<ALA< % ϕ x y sinϕ − ϕ = t ω ϕ − ϕ "Y$ 2 sin 1 cos sin( 2 1 ) a a 1 2
Z-"X$A2"Y$WA<ALA< 2 2 x y 2xy + −
cos( ϕ − ϕ ) = sin2 (ϕ − ϕ ) "[$ 2 2 2 1 2 1 a a a a 1 2 1 2
"[$6(?+41O-8
! "!#$%#$#%&!' ϕ ) ( ϕ*
%&+,-./012#3
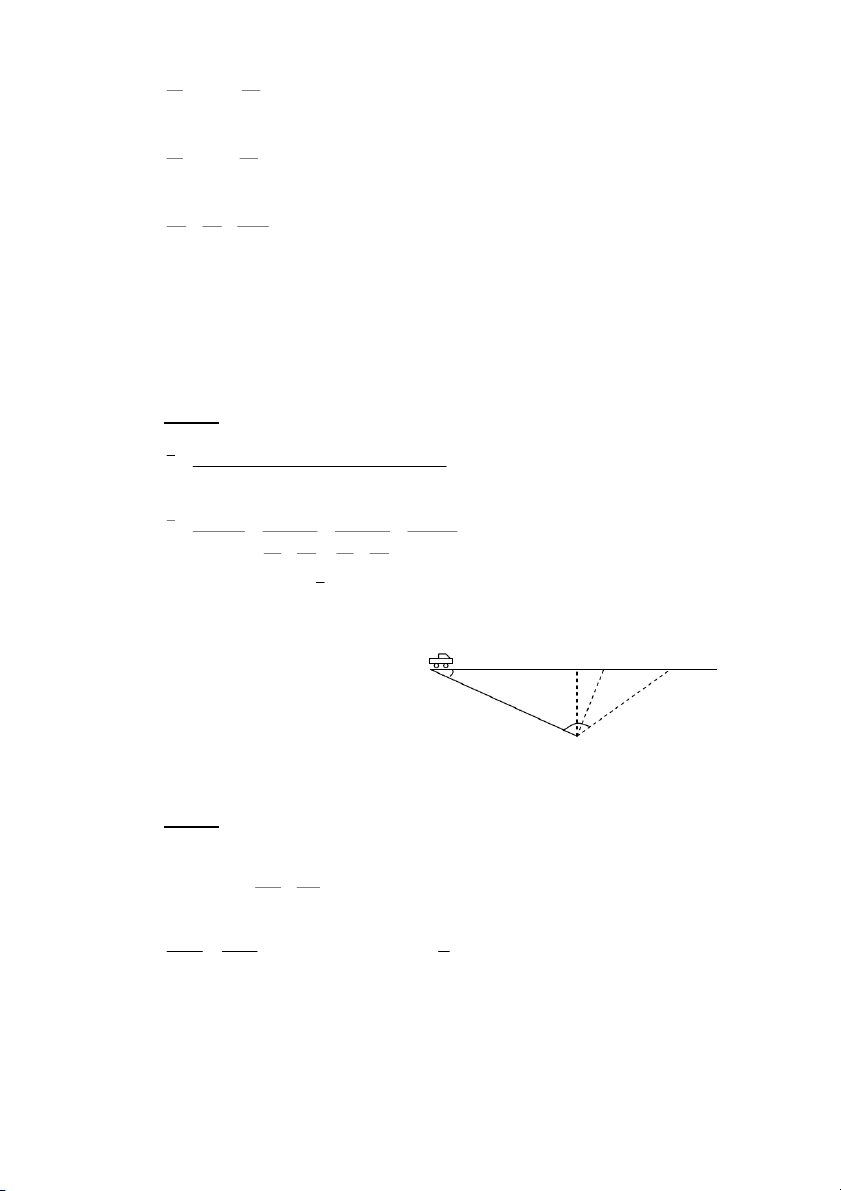
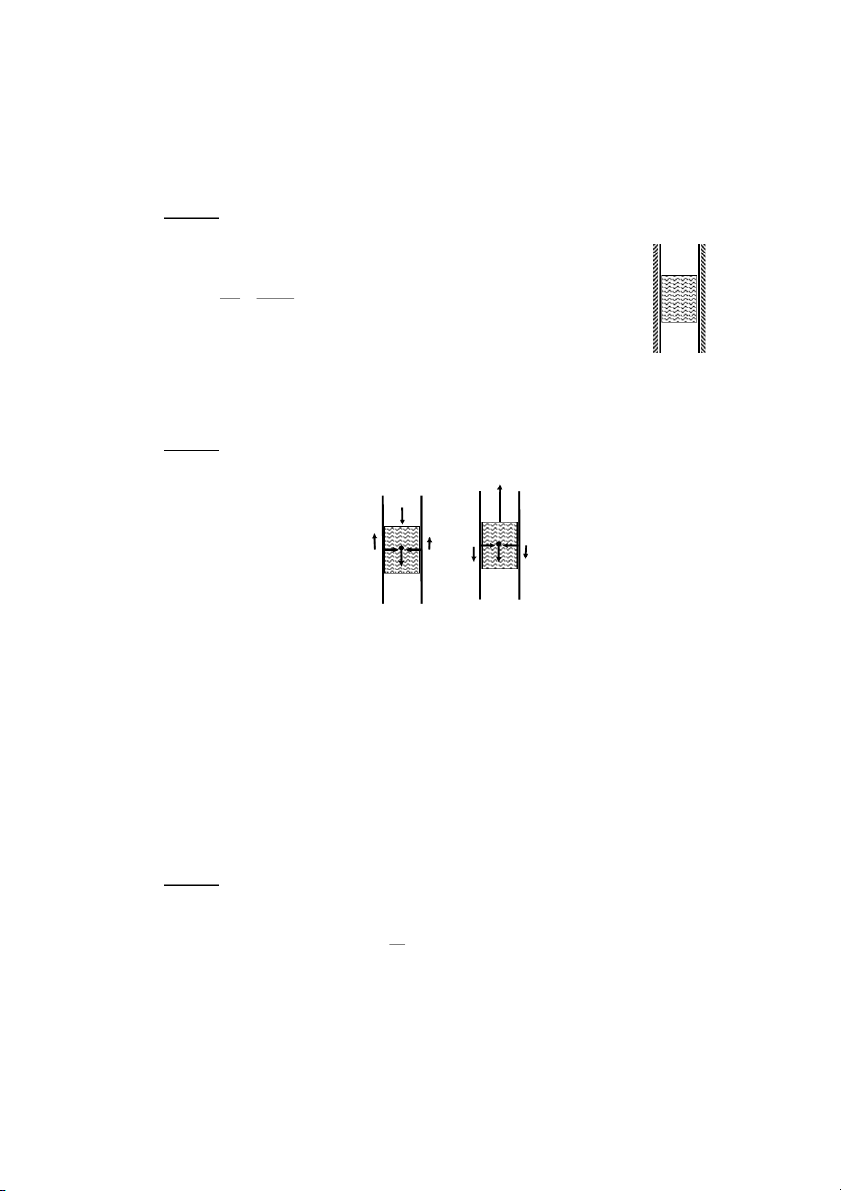
RPPG\]<\ZALAB3A T^/_+W1G\
ZKA\]ALAB3A S^/_+8 %
FAB36PP4+A]Z0Z]7`
a)C+]Z6;!8F!bOAB36cP> 6 . 4 5 4 + v = 6 5 + +! 4 + . 4 5 0' F, s + s s+ s 2 2v v v 1 2 = = = = = 9,5 m 3 / s. t + t s s 1 1 v + v ( A 1 2 + + v v v v 1 2 1 2
F!3, v = 9 ,5 m 3 / s .
R+> R +J /=X^ +
PP5/PPd f i E Z
%^^ + 6e I β
+ a- PP "f .%$8 Z< PP ]
ALAB3SY/_+8
fQ $ U+ -= c α
L 2 a- N PP` Z< ; R
+ALAB3A ^0g/_+5 % f .%
6$ U+ -= ALAB 3 Q
6;647a-,PP`
$R3a-NPPZ++GRLZ-=6;+
PPG]LZ
MB AB = " $ v v 2 1
hD('1:2!3!]ZR7 MB AB h = , AL sin β = "%$ sin β sin α a
FG" $A2"%$N
h v1 sinα = . = 0 8
, 33αXY^S^jaα %S^ S^j8 a v2
775+0''89:;<0
α = >:; ? <. 56 3 0 ' 0 ≤ α ≤ 123 3 0 ' 0 3 @+ 56 3 0 ' 0 < α < 12303 '
0 5+ 0' '
5?++8h v
C/'+?DE5+'+<F?<.+G0' 1 sin α > . 3 a v2 MD AD 1 h v 1 a v :0 = → AD = sinα . M . D > . . A . D 1 = M . D 8 sinβ sinα sinβ a v h v 2 2 AD MD >
1-05++!8'F95++!5+'F#3 v v 1 2
6$7a-,PPALAB3Qk2;1N2+
<+l121NcPPL"+a-NPP2/P-=+,1C-O
+$0AAB0c-I$@LA2AB3+-=7) h v 1 sinα = . a v2 HALm h v h
α!"α$≤ 4 1 . ≤ 1 v ≥ .v 2 1 a v a 2
h hv v 1 = = 2 5
, m / s = 9km / h 8 2 min a
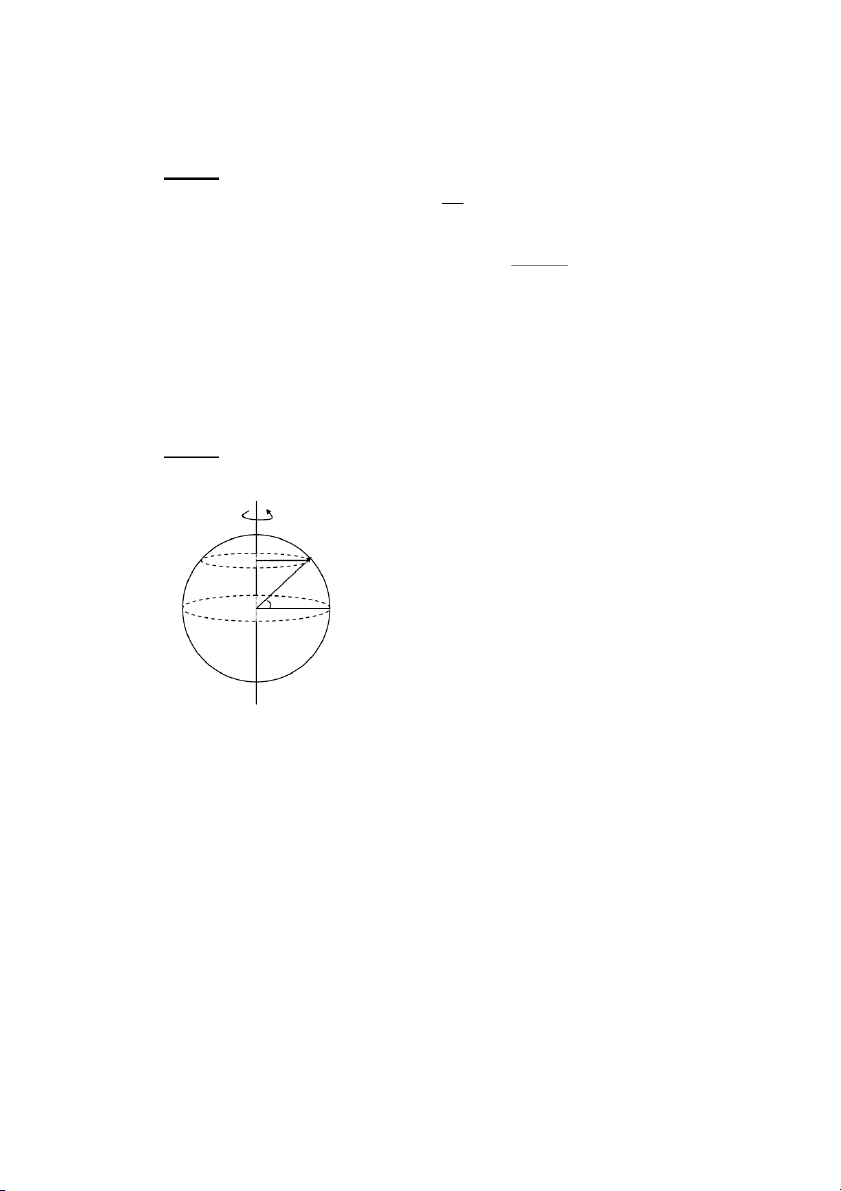
9N20+-=cLRi0ALRi⊥]R8
RAB,=G/OI6KS^^8fQ!61V
ABLa0<
$nOI614"cLJ>$ALAB3X_!5
6$nOI3"c-J>$ALAB3X_!5
$nOI>48
n/OI0ABK4/OIcAB3/OI8U</O
I 3(L ALAB3 A + 2ABL = C ^
-6B+ 1 v .t + g t 2 . = h 8 0 2 v 2 + 2gh − v
om(-27/<)= t 0 0 = 8 g
n/OI14403(La>40-(6>
2ALAB36IA .X_!0A X_!5aA ^A27/<)= ^ ^ ^ $g0T!5 6$[0S!5 $[0g!8
RAB,=Gf#c-J>EEj"Ep12V
f#$8oq1N7AB>,r14GEpc-J>
ALAB3A 8 ^
$fQAB3A -=6;64ABa-K` ^
6$FO/=@ABL1Na-c+`
$U</P7AB>AB>1L6;64`
oIL1P>M(
$ F+ AB G E < a- 12 2H t = l g
6;+AB%GEj<s0(7 E 1 + f 2 h gt H h
h = v .t − g.t → v = + = g 2 H 0 s 2 0 t 2 H 2
6$n=@AB+L/a-,
Oc)C+!A2!jAB,
"f#$."!#!j$8 Ej x = (H + h) 1 2 1 − gt − v .t − .
g t2 = (H + h) − v .t 0 0 2 2 H+ h = ( 2H − g 2 H.t ) H 2
$ hD ( P > ) A0 0 ! J 6< t 2 2 v − v
= 2.a.sALAB3KM6;A^0.0!
!0</P 0
7!M=KAB 0AB%14<M12 v2 ( H + h 2 ) h = = 8 max 2g 4H
F=M(ABG u0Yr8FO
$vC+2AB,^0 VIA2^0 V3+
8 6$F+I<AB< IA2 38
hD(P> A)C+AB,!+ /G 1N6eI ,= 1 2
s = gt !b7P>)cA+AB, 2
+7/GA'O=12 2h t =
8-(P>2!b=1+ g
,VQ62B-2
$vC+2AB,^0 !I 1 2 1 s = g t. = 9 8 , 0 . 12 , = 0 0 , 49m 8 1 2 2
Ft+AB 2h 2 1 . 9 6 , t = = = 2(s)8 g 9 8 ,
vC+AB,^0 !3q0,Oc)C+,
%.^0 0u!I 1 s = h − g(t − 0, )2 1 1 = 19,6− .9 8 , .(2 − 0 1 , )2 = 1 9 , (m )8 2 2 2
6$FM4
F+AB, I 2s 2.1 t 3 = = = 0 4 , s 5 8 3 g 9 8 ,
F+AB< 3 2 1 . 8 6 , t =t −t =2 − = 0,0 s 5 4 6 (I$J < H" 9 8 ,
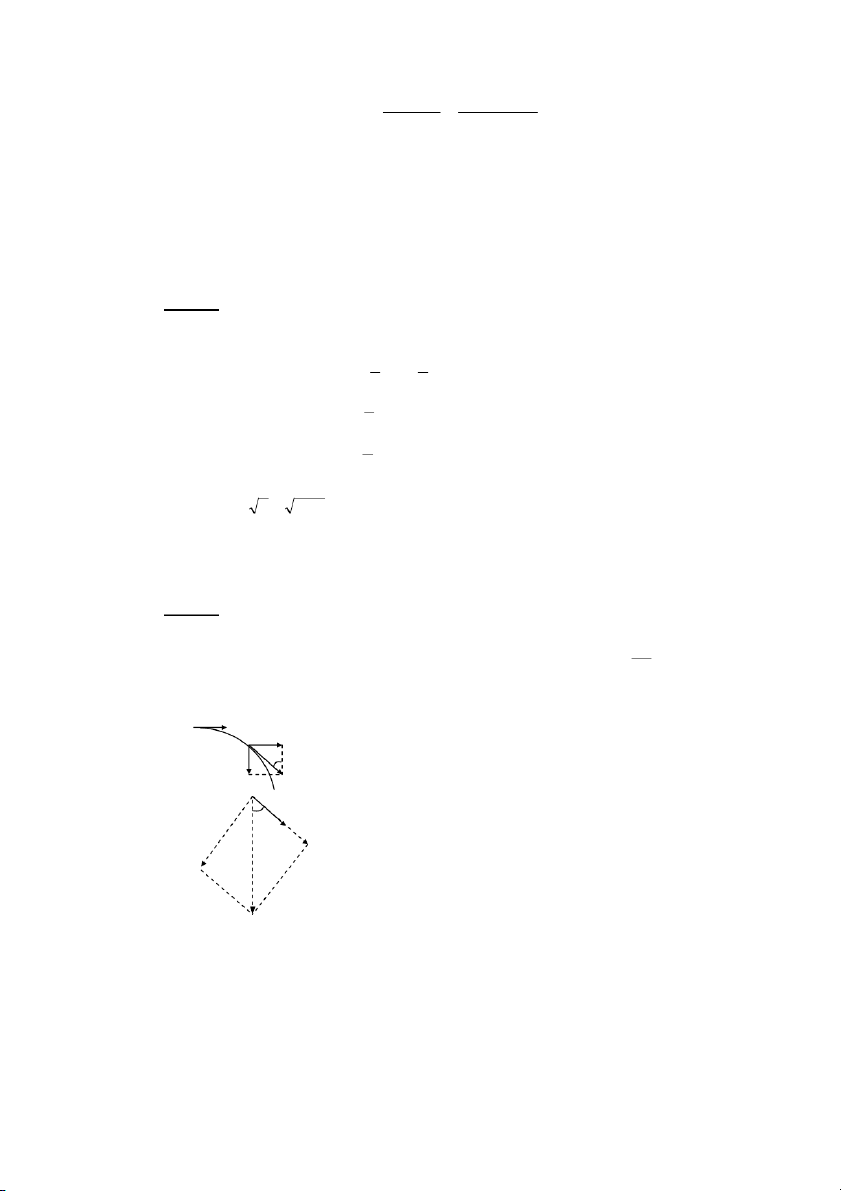
FG6]0Z0o4Add+W+=6AB8HB
>c-J>]R)VAdd"f .S$0AB>c(V
ZR0AB>6c(VoR8fQAB2LRL40<6Q)!` ] Z o R f .S
vC+A2 3 AB> ! %w0 0AB>! % %w! ^
AMB 0 ! ^ %w! ^ ! ^ %
AMB 0AB>6! S AMB 0S AMC 8
UB0+<RAB12 s 2 4R s 2 s 2 1 2 3 t = = = = t = t = 1 2 3 a g a a 1 2 3
HB06ABqLR1N8
= r AB c - J > G T^ AL AB 3 A ^
6;647La
$FLτ V!AL+,-ABM(`
6$h τ V!AL+,-ABM(`
9 ^_!%8
hD(P>O+</62X 2 v + 2gh − v 2h t 0 0 =
A2P>+M( t = g g
AB !L0 -= r AB 3 (L AL AB 3 A = C ^
- 2 2h v + g 2 h − v 0 0 2 − = τ → v + 2gh = gτ − + 0 (v g 2 h 0 ) g g
Z-A<-, ( 2 g 2 2gh − g τ g ) − τ g 2 (v + gh 2 + = → = 0 ) τ( τ ) 2v 2gh 0 v 0 0 2( 2gh − τ g )
$AB!L0-(ALτ !7 10. (
1 2 2. 10.40 −10. ) 1 v = = , / 0 2( 2 1 . 0 4 . 0 −10 1 . ) 12 ( 7 m s)
HBAB,rJ>3(L8
6$AB0-(ALτ. !7 −10. ( 1 2 2 1 . 0 4 . 0 +10 . ) 1 v = = − , / 0 2( 2.10.40 1 + 0. ) 8 ( 7 m ) s 1
HBAB,rJ>1448
RABJt<)C+]ZYV8
HB3AB/)]6;X_!/)Z6; X_!8F(2)C +]Z8 (
Fc'x03AB v ∆ v − v 15 − 5 5 B A a = = = = ( 2 m / s ) 8 ∆t t 6 3
FG77O)C+]ZcP> 1 2 AB = v t + at A 2
F!3,]ZY^8 *
9:;0AB36J6<t7P>
a606; v + v v A B =
04]Z7(2 2 v + v 5 +15 AB = v.t A B = .t = .6 = 60(m ) 2 2
Rc1D@";4+J$ 0X/8
FD+I0c1D(I0D+!
c1DB(I8HB31Lc1D@76; X^/_+8
Z<;'!3334+6;8FO
$s3c1D8
6$F+c1D<)C+@8
HB36c1D12 v = 50 / 2 = 25km / h8
F+c1D< 0X/212 t = s / v = 1 5 , / 25 = 0 0 , h 6 = 3, 6 B = *(JD 8 v 50km / h max (50 /3, )
s3c1D 6 m / s a = = = = 0 1 , 2 ( 2 9 m / s ) 8 (t / 2) 18 , B 18 , 6 . s 0
K+!L !8E!HM!/02 2 v − v 50km / h 0 ( )2
%+6+G v 2 − v 2 = 2.a s . 2 a = = = 0 1 , 29m / s 8 0 2s 15 , km
1PQ'D0E!.5($R<#
Rc1D6eI(I4+J
)La+)!>ALI>8Z<;c
>)La+)!<+τYV8fQ>!b
)La+)!61V`
-(+,-[8
sm112(2y0 12+I)La+
)!8-(-Jt07
o(2> 1 1 2 2 l = at = aτ 1 2 2
o(2". $ 1 2 (n − ) 1 l = at n 1 − 2
o(2I 1 2 nl = at 8 n 2
FG 7 ! + > ) L a + ) ! ∆t = − = τ − − $8 n t n t n 1 ( n n 1 −
HL[07∆[ 0 g!8
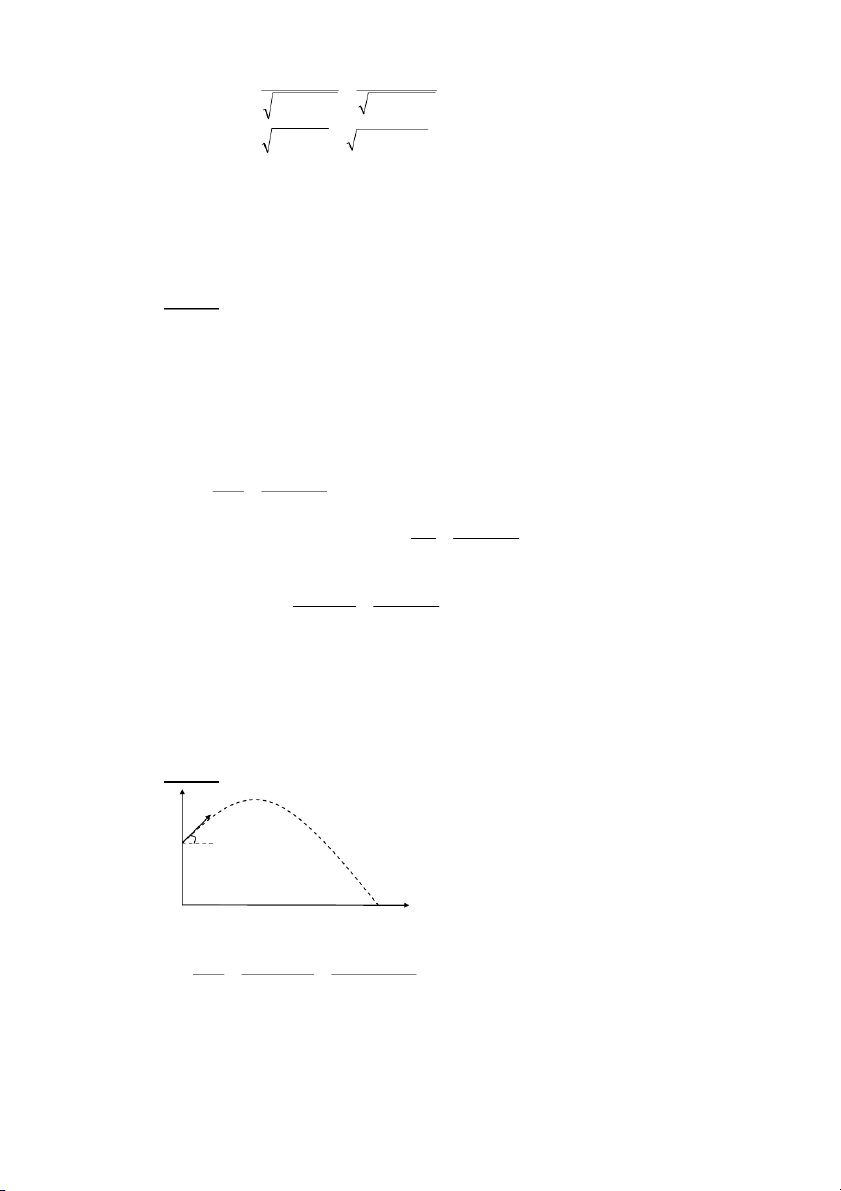
Rd,rc-;ALAB3A^ X_!8FO
3--<A23<-<d!1Nr V8
HB3ABc->!/r !A u0g_!8 s7 v
α@AB3ABA2-J>=C x tgα =
8&c v y Ab648 A ^ A α A A α A 8!α 8!α
FG703--<A23<-<AB1N2O12@2
-I<3
g.v 9 8 , 1 . 5 x a = g sinα = = = 8 2 , m / s n ( 2 ) 2 2 2 2 v + v 15 + 9 8 , x y 2 2 2 2 a = gcos α = g − a =
9,8 − 8,2 = 5, ( 2 4 m/ s ) t n
U+ r )= 67 ALAB 3 A ^_! c - ,- AL a ^
-J;7αT^^8s=!D)=67,rGa8fQ
$1L2)=677,8
6$FI)=678
$F+G1Nr67L1N678
',@1,62a0I1:;07
AB6W/1B-c-
J>A2c-8
oc-J>12J6<tAL
36;0AB36I6;A A 8! ^ ^
α 8oc-12
JALAB3/Pt6;A A 8! ^ α 8
$MA2+AB\14)<AB36Ic
-J>A ^ v 2 0 y v2 2 .sin α y 0 = = = 2, max ( 1 ) m 2g 2g v α
$F+6AB 0 y 2 v . sin t = 2 0 . = = 1, ( 3 s ) g g
6$oP>IABr4 2v si α n v 2 .sin2α L = v t = v 0 0 cos α . = =10m x 0 g g
FG\-f%X+rd14-O4ALAB
3A X_!c-,-ALa-J;7 ^
α S^^8&'
$F+d5
6$n=GV-<yd5
$HB3d1N8 A^ f α z 9
FG\-A4d144, 2 v sinα 0 y ( 2 2 v .sin 0 ) (15 300 ) h = = = = 2 8 , 7m 2g 2g 2 9 . 8 ,
+d v0 2(H + ) h 7 5 , 2 (25 + 2 7 , 8) t y = + = + = 31, ( 5 s) g g 9 8 , 9 8 , FI
L = v cosα t. = 15.cos 30 0.31 , 5 = 4 0 ( 1 m)
HB31N v = g 2 + = . , . + , = , / y (H h) 2 9 8 (25 2 78 ) 23 ( 3 m s) 2 2 2 v = v + v = 23 32 , + .cos = , / y x (15 30 0 ) 26 7 (m s )
C!+?+'%0+8%&HSA3
TNUAV'/9+V&<+Q/W3
X'A !/8U0' x = v t = v cosα t . x 0 1 2 1 2
y = H + v t − g t. = H +v .sin α t. − g t . y 0 2 2
Y<5++!+$+?+'=Z3
Y<"<!<?[/,K+9+Q$!!'</0
%+- !K3
Y</LB<\$97- v = v cosα = const x 0 v = sinα − . y v 0 g t
!#]$(JD^%#_($(<^#*J$2<`D3
FG\-fS^0+rd3ALAB
3A ^_!c-,-ALa-J;7 ^
α S^^8F
$F+dLa/GNr`
6$n=GV-<yd`
$E)*d`
F(q---362 . T8
omzALz;V-8
$ABc2
x = v t = v cosα .t (1) x 0 1 2 1 y = H − v t − g = − α − y .t H v .sin .t g .t 2 0 ( 2 ) 2 2
+0=-^ 0 1
30 −10.sin30 t. − .10 t2 .
= 0 ↔ 30 − 5t − 5t2 = 0 2
om(,+d%!8
6$I{A'OV-640,O8 x =v cosα t. 1 = 0 .co 3 s 00 2 . 1 = 0 m 3 1 ≈ 7 3,m 0
$6<()*A40I-)*
2"-)@A2C/D6<+$
nD+-" $A2"%$6;NG-" $W
A2"%$ x
( 1) → t = v co α s 0 2 1 2 x 1 x
( 2 )→ y = H − v .sinα t . − g t .
= H − v .sinα . − g 0 2 0 v co α s 2 v co α s 0 0 g x2 .
= H − x t.g α − 2v 2 2 cos α 0 x x2 = 30 − −
( /9+ 0 ≤ x ≤10 m 3 ) 3 15
2\;0)*A412-618
fQ-=rABc-,-ALa-J;7α
6;64ALAB36IL0IAB12M8
hD(P>OIAB,r4C1B-,62 . S v2 .sin 2α v2 L 0 0 = ≤ g g v 2
HB!b,IM6; L 0
/!%α 0αTX^8 max = g
n| 1 } K f2 U 12 %0Y[ r8 fQ < t > K & 4c6
/ M"qAB3 6 IA2 7 4$0 /|1 4 !b 126 4`
o6<"f2U$u0[%[_!%5"&4c6$u0g ^_!%8 v2 .sin2α
FG P > I L 0 =
B 0 AL 1M } /P t " A ^ g
/Pt$A27r/Pt"r/7r6;TX^$I9!b\
1'AL3m+8E77',/\1}2
-3&cr6 g 9 7 , 27 L HN = L = 1 . 2 6 , 7 =12 5 , 6(m) XP g HN 9 8 , 10 XP
FAB37
$F))7"F)Ad)
7%T+$8
6$/+A2/-NWW5
$RaF~))F"RaF~))F
Ad%[24$5
($AVF)4)*dAL/6;gg -N8
hD(P>OAB37 2π ω =
A21:/•-=tN3 T
AL12V"!$!b, π
$HB37M)) 2. ω = = 7 2
, 6.10−5(rad / s) 24 3 . 600
6$o/•)/-N12 8n+)<Ad12 %<4AB
37/+A2/-N12 T0X8 ^.X(_!5 0[T8 ^.S(_!
$ol-(P>4AL/•/7AB37
a~)12%0[8 ^.Y(_!5
($oA7/)12gg-N12 0 u8 ^.S(_!
AB3(2)4af2U8
Z<;Axf2U12α% ^8
Fc62 . gAB37M)712
ω[0%Y8 ^.X(_!8Z/O)*f2U"c$12 ω w z α
f62 . u r = Rcosα 8
FG77AB3(2f2U12
Aω8ω8w8! α
F!3A2,ATS^_!8
Y 0<%0+ + 8 "B a 7 - ! ' A !' !
b<H"Gc+L/9+7- !'AO%+6+G/9+
DM-!'ϕ!'.5D$/Lω!'/LH0+/$
+!Lβ !'+!L5!Bde!Kf3
R AP 1~ ! / 6e I ) , -N , AB 3 [^^
Ad_-N8FO37AP1~A2!3Ad2AP1~C),-N
<AP1~12(I8
HB37AP1~ω[^^Ad_-N[^^8%π_Y^"(_!$!+τ -NY^!8 R2 ω 1400π / 60 1400π
ωβ 8τ β = = = = 1 2 , 2( 2 rad / s ) 8 τ 60 3600
s7),!+τ -N12 1 2 1 ϕ = β τ . = 1 . 2 , 2 6 . 02 = 700π (rad) 2 2
EAB0!3Ad), -N12 ϕ 70 π 0 = = = ]R Z /f 8 *π π 2
R 6 c ) B (I0 ! -N AB 3 7 = GS^^
Ad_-N3 g^Ad_-N8F36cA2!3Ad26cC)
,-N8
Fc'xA3771P372 ω − ω 180 2
. π / 60 − 300 2 . π / 60 0 β = = = 0 − 2 , 1 ( 2 rad / s )8 τ 60
s7),(MA23)MAL)A..!
J6<tN 2 2 ω − ω . π / − . π / 0 ( 2 2 180 2 60 ) (300 2 60) ϕ = = = 24 0 1/ f# 8 2β − 2.0 2 , 1
fa(MA2P>AB376 ω + ω 180 + 300 0 ϕ = .τ = .1 = 240 1/ f# 2 2
R6c76/Ow ^1NI>40!7))
7AL376;S0 T(_!%8fQ0!V>
$HB37A2AB3(24A26`
6$ s 3-- <03 <- < A2 3 2-I 4 A26`
$s7@32-IA26/O6c">ALq4 A26`
$hV>0AB37A2AB3(24A2612 ω = β t. = 31 , 4.1 = 31 , 4 (rad / s ) v = ω.R = 31 , 4.0 1 , = 0 3 , 14 (m / ) s
s3<-<7'/PtA23--< α 1N2
f
a = β. R = 3,14. 01 , = 0,314 ( 2 m/ s t ) 2 2 a = ω R . = 3 1 , 4 .01 , = 0 9 , 86 m / s n ( 2 )
od32-I6; 2 2 a = a + a = 1 0
, 3 m / s 8 t n ( 2 )
$s7@32-IA26/O12 α=C a , t 0 314 sin α = = α [^TYj8 a 1 0 , 3
o/)6c6/OX^12^0 V8F
$HB3(2A2AB37A265
6$s3--<@6/O8
HB3(2A2AB374A26 +G H 0+ ! 4 5 f 2 R π 2π 0 . 5 , v = = = = 31 4 , (m / s) 5 ++! ' 4 A < A / f f T 0 1 , v 31 4 , ω = = = 62 8 , (rad / s) R 0 5 ,
6$s3--<{3LV@6/O 2 2 2 a = ω r = ω R . / 2 = 62 8 , 0 . 5
, / 2 = 986 m / s 8 n ( 2 )
R226eIA2+d06/O /0(2Y^^0
ALAB3XT/_+822<)C+7S^V8FAB3(20
3--<03<-<032-IA23722K3
)C+78o2212(I8
ow / ^^^0A XT/_ X_!0!Y^^0S^!8 ^
hD(P>AJA2d6<t!b
O,1,I<8 1 − − . 2 ( 2 s v t) 2(600 15 3 ) 0 1 0 s = v t + a t a = = = ( 2 m / s )8 0 t t 2 2 2 t 30 3
HB3I3+Ad 1
v = v + a t = 15+ .30 = 25 (m / s) = 90 (km / h )8 0 t 3
s3--<{3LVI 2 2 2 v 25 a = ω R = = = 0 6 , 25 m / s n ( 2 ) R 1000
od32-I12 2 2 2 2 1 5 a = a + a = + = 0 7 , 08 m / s t n ( 2 ) 3 8
s372I
a 1/ 3 t −4 β = = ≈ 3,3. 10 ( 2 rad/ s ) R 1000
HB 3 41c4 D P 6; A %0%8 ^g_!8 FO AB
37A23--<41c<c)*712Add6 /O^0X8 ^.g8
€1cA%0%8 ^g_!%0%8 ^Y_!5w^0X8 ^.g^0X8 ^. ^8
HB37A23LV{3--<1I1,
ωA_wT0T8 ^ Y(_!5
ω% wu0Yg8 ^%%_!%
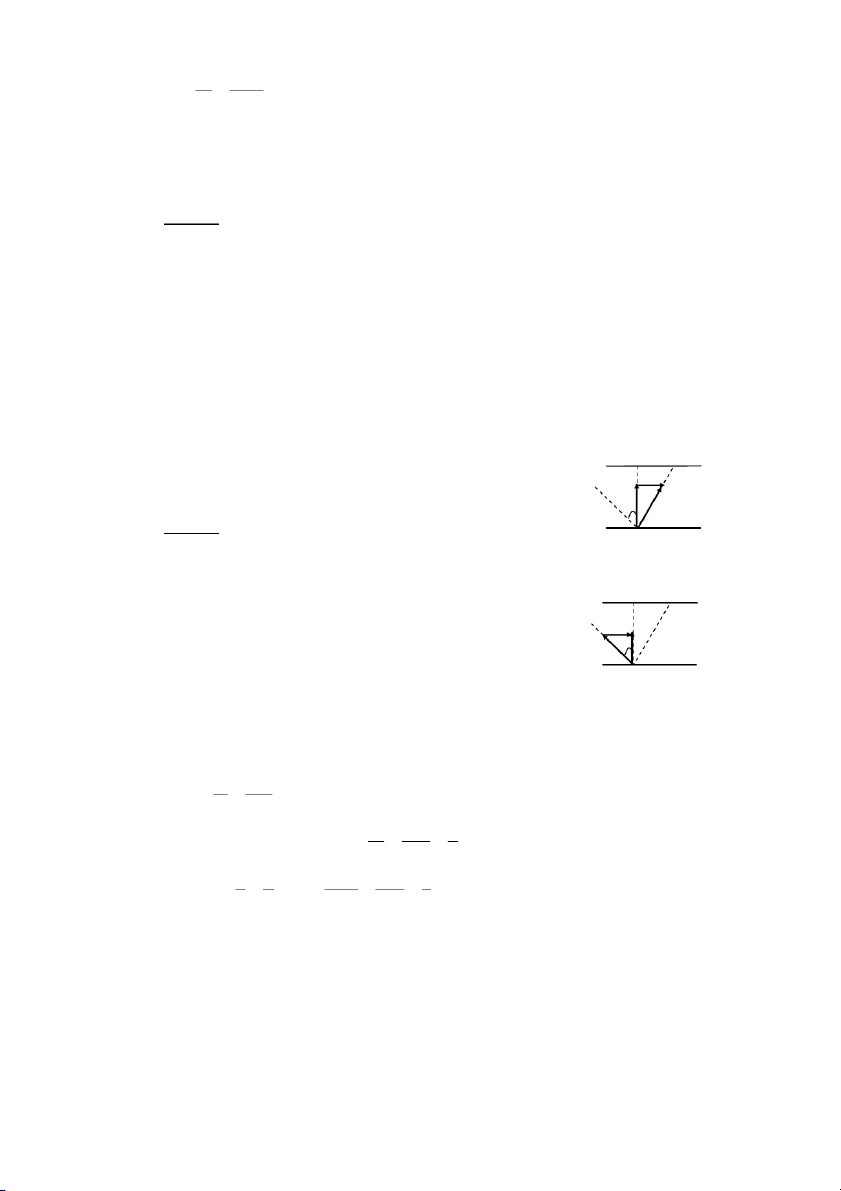
R+3•)!P7(dL=8U<+•
cLGA'O]!A'OZ"]Z⊥AL(d!P0 .T$!+
^-N!bLA'OoZ/=! %^8U<+•
A-O,(d!+ %0X-N!bLNA'OZ8 %
oAB33AL(dL12/Pt8FO
$Z1!P5
6$HB3A3AL(dL5 Z o
$HB3(dL3AL6+!P5 ! ($s7γ8 R A H γ
FG]<o<+ ^-N0]<Z<+ ]
%0X-N0Zo7(2!Zo %^8 f .T %
V 12 62 t ,- AB 38 F W Z o →
+ q AL (d L AL AB 3 u A2 1 →
!AL(dL"( +•$ALAB 3 v 8 H A γ
ot,-O123AL → → →
6+!PALAB3 ] V = v+ u 8
F+,->62>AL .T0+ f .T6
,->>AL .T68
FcAb07-!
!8 51A8 51"A8! 5A8! γ$8 % γ5 s 120 u = = = 0 2 , (m / s)8 t 600 1 t 10 4
l = v.t = v.cosγ .t → cos 1 γ = = = → γ = 360 5 ' 3 1 2 t2 12 ,5 5 3 u u 0 2 , 1 sinγ = = → v = = = = 0 3 , 3 (m / s)8 5 v sinγ 3 / 5 3
o(d!P l= v.t = 0 3
, 3.( 10. 60) = 200 m8 1
U+•)!PcLAP7AL6+!PAL
AB3[0%/_8UL=CA-OP(d/= X^8
F$HB3(dL3AL6+!P5
6$ F+ I ) , !P8 o 6< !P 6; ^0X/8
Z(d!P1^0X/X^^8! X^0H[0%/_%_!8
FGAb Z o u s s 150 ! = → u = v . = 2 . = 0 6 , 0 (m / s)8 v l l 500 A 1
F+<!!P H AC AB l 500 t = = = = = 250 (s )8 ] V v v 2
-!3$^0Y^_!56$%X^!8
f62 .%[
R66GA'O]LA'OZ8]Z;cLFVPA2
/=S^^/8&'+6<
$nP775
6$o77tcLUZe5
$o77tcLFVP8
o6<AB376;A %^_!0AB363AL/P/OA % Y^^/_8
]ZS^^/07A %^_![%/_0A Y^^/_8 %
$F+66M<-G]<Z l 300 t = = = 0 5 , (h )= 3 0 1 B# 8 v 600 2
6$FM62 .%Y063LA'OZ07-=6<A-O
7α!AL-]Z8F7
V = v 2 − v 2 = 6002 − 722 = 596 / 8 2 1 (km h) ] Z
F+66G]<Z12 α A s 300 t = = = 0 5
, 03 (h) = 30, 2 B 8 A% V 596
$s7PGFV!P8F+6
f62 .%g I(q12 s 300 t = = = 0 4
, 46 (h ) = 26 , 8 B 8 v + v 600+ 72 2 1
f .XP=68
$o6<O78
6$x@W'A28
$h!AB368
A % S z f .X A % S z f .Xj
$UA2W'=6212(I 8
6$sW'AL+6<+-
8
$Z012AqL8HB3yABG1N
B/8W'AB32(33AB21L"3
6<!37+J$8FGW'07!!3AB ‚ S ‚ 8 %
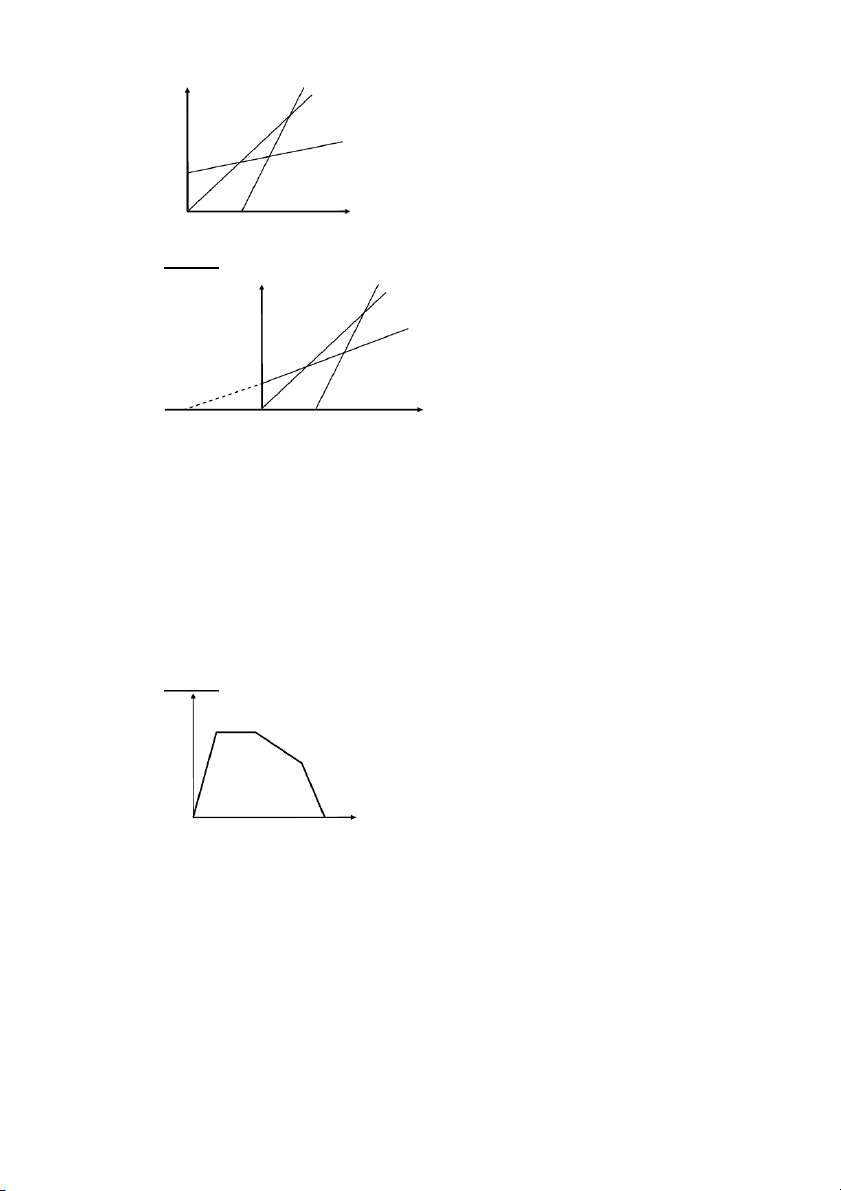
f .YW'AB38fC6<
4yz]0]Z0Zo0oE8 A ] Z o E z f .Y
z]AB-+^W(IAL 3/1L8
W']Z6<AB!8
W'Zo6ABB(I8
W'oEAB<-B(IAL31L
/Zo8HB(G1328
%. 8Rc7/31,%^^^^/0B(I(L(
1M6;Y^^^U0AB36Ic6; X_!8fQ
$s3c5
6$h61Vc(G15
$+cC,/G1NC</c(GJ8
$s3c,Oc'1BiiUcƒ
„_.Y^^^_%^^^^.^0S_!%8
6$F+/G1NC</(G1 ∆ / Z ) (R = ∆t = = =RZ ( ) D 3 ! ) Z$]
$vC+/G1NC</(G1
!A 8#8%_%888S[X8 ^
%.%8 R y a TuU 6' /…- @ a -J J f%.T
> " %.T$8 9M r-J7 4 ya 12 T[U8
fQ 1MQ I Va y` f !3 ! @
yA2ar-/^0%8
9MV ^[0gU51Mu0gU „U „f „ „ ! !%
f%.T f%.T6
n3y3I1M„ L3(L01M! f
4ayL144"f%.T$0d/3Vy14
41M!1L3(L"f%.T6$8
FGAb201M(q"„ $A2V„ y-=7 f U
'Q „ f F + F
− P = 2× k.N − P = 2. 0,2.147 − 49 = 9, m 1 s ms2 ( 8 ) N „UF + F + P = 2 ×k N . + P = 2 0 . 2 , 1 . 47 + 49 =107 8 , m 1 s ms 2 (N)
%.S8fQ-=(1M6;64142>47
(IA2!+S^V7, 8o6<1M!
26;X†m1,28
sm„121M(1428&rc-01MV3
20c'1BU%06;
„.‡ !
F712/31,A2 s 2 a =
123I8 2 t
FG7! 2 s . m . F = f + ma = 5%mg + 8 ms 2 t
F!3! 0S^!0 X0Y XY^^/,„≈g%^^U8
1C"G%0++L+ !!"%&<=(R$J\#3
%.T8R+(<cALAB3/Pt89NI+/r
cA-OL0!7+}cA-O!8F=+,-02c
,-ALa-J;7α8fQ+,-2+-=a14
c1M1L`Z<;m1,c120!3!@6cA2a +12/8
H<-'1BiiUcƒ1M(A2c8F2-I1M
t ,-< c - J > A2 ; 6; ^. /P 7
c-J>0c-./P73
c-4
F+ ,- /r cA-O L"%. j$ 1M rAP 7 c 14a +12
N + F.sin − P = 0 N = P - F. sin
H2 F.cos α − F = 0 F.cosα = F ms ms
R201M!(14c
„ /U/".„! ! α$ kP F co α s = k(P − F sinα) F = cosα + ksinα U Uj „ α „j „! „j ! f%. j f%. j6
F+,-}cA-O!"%. j6$
Z;-VOM0O,1M!a14c+,- 212
„ /Uj/"#„! ! α$
H21M„jIa142c kP ' F =
cosα − k si α n
wk2„j ‚„8UAB+,-}cA-O!+-=(q 1M1L8
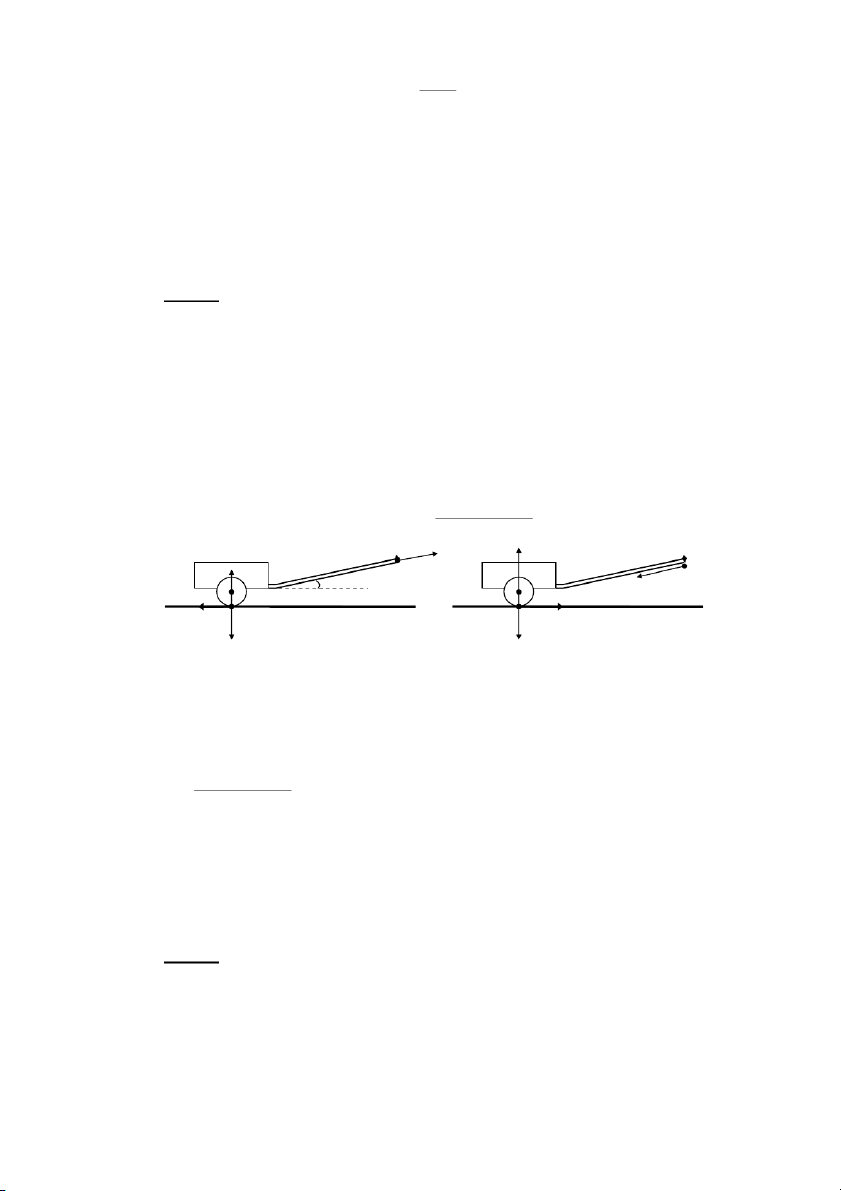
%.X8RAB7/31,X/,a4a-J4,-AL
a-J;7αS^^8f!3!@ABA2a-J46;
/^0%8F3AB4a-J48
F-VO1M(A2ABW S1MJ U
>0 U AP 7 AL a 4 A2 „ ; 4 a ! „ 48 ! z
'1BiiUcƒAB P + N + F α ms = m a .
o< - 2 c - AP 7 AL a
-J4"-z$A2-!!ALa-J
f62%.X
4"-z$, N = Pcos α − Pco α s + N = 0 P si α n − F Psinα − F = ma a = ms ms m
R2„ /8U4 !
P sinα − kP cosα
mg sinα − kmg cosα a = =
= g(sinα − k cosα )8 m m
FαS^^0/^0%0u0gO,S0%T_!%8
[ 7-e!\'$+!L ! /e7UA/0L+ !/3
%.Y8RAB,34a-J4,-ALa-J;
7αTX^8n,,)C+!SY0T0AB,AB3A%_!8&
'!3!@ABA2a-J48
-(P>3AB62%.X7 g si α n − a a
a = g(sinα − k cosα ) k = = t α g − 8 g cosα g cosα
hD(/<>iA3)A..!73AB,2 2 2 2 2 2 12 v − v − 0 v 0 v a = = = 8 2 S . 2S . 2S . 2 v k = tgα − 2.gSc α os
FP!3CαTX^0A%_!0!SY0T^0SYT,/≈^0%8
%.[8R!,(VG,a4a62!-I76Pk
38h,(V6eI,4a62/(2-I6Pk6;
%X†(2(V8&'!3!/@!,(VA2a628 ‡!
f62%.[
sm12m1,=(V0 12m1,-I6Pk8FcI
620(2-I6Pk6;%X†(2(V %X†8
&rc-!,(V0(V'(1M A2‡ 8 !
R3(V6eI,-=7 ‡ ‡ %X†8 ! !
R20‡ /8U/8"[X†$8 !
FG7%X†/8"[X†$ 25 1 k = = ≈ 0 33 , 8 75 3
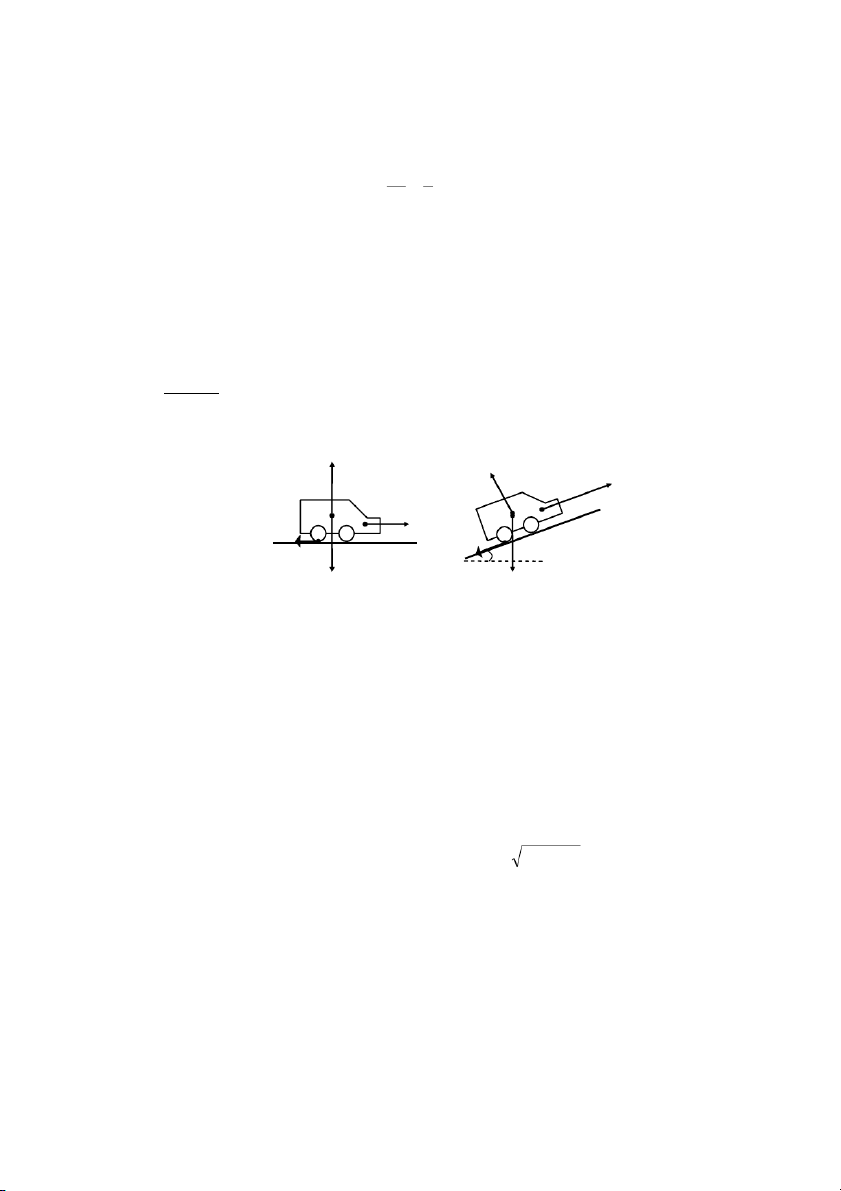
%.g8 $RPP/31,4+6;0!3!
@6PPA2a+12^0 8FO1M/rPP+,-
$ˆP5
6$ˆP(IAL36;%_!%5
%$olVQ4+,-PPA2
$94(37(3T†56$&3(378
f!3!6;^0 !3+8 →
Ft,-1M(14PPW1M/r F PP0m1M P 0-=
1M--< N a+A21M!a+ f 8 ms U Uj „j „ ‡p! ‡ α !
f62%.g → → → → →
'1BiiUcƒPP12 F + P + N + f = m a ms
om(12c8o<-214-
,
$ nc4+; F − f = ma F = ma + f = ma + kmg ms ms
F!3 ^^^/5/^0 5u0g_!%5A2
$n0^ „ug^U8
6$n(IAL3%_!%„%ug^U8
%$ nc4+(3
$ˆP14(3 F− f − P si α n = ma
F = ma + f + Psin α = ma + kmgcosα +mgsinα ms ms
F70!α^0^T12(3(3!α 1 − 0 042 , ≈ 1 0 , F = 1000× 0 + 0 1 , .1000 9 . 8 , .1+ 1000.9 8 , .0 04 , = ( 1372 N )
6$ˆP3(3„"/!α.! α$8 F− f + P si α n = ma
F = ma + f − P sin α = ma + kmgcosα − mg sinα ms ms F!3 F = 1000 ×0 + 0,1.1000. , 9 8.1 −1000.9,8. , 0 04 = 58 ( 8 N)