Bài Tập Thống Kê Nhóm 5 môn Thống kê trong kinh tế và kinh doanh | Trường Đại học Kinh Tế Quốc Dân

BÀI 83/93:
a. Tính trung bình và trung vị:
Sắp xếp dãy số từ bé đến lớn:
4, 4, 5, 5, 5, 5, 6, 6, 6, 6, 7, 8, 8, 9, , 10, 10, 10, 10, 1 9, 9
1, 11, 12, 12, 12, 13, 13, 14, 15, 18
⇒ Trung bình về số lượng sản phẩm = (4+4+5…+15+18) / 30 = 9,5 Hãm số chẵn: 9+9
⇒ Trung vị về số lượng sản phẩm = =9 2
b. Xác định KBT và độ lệch chuẩn
-KBT = x(max)- x(min) = 18-4 = 14
-Độ lệch chuẩn = Căn bậc hai Phương sai ⇒ Tính phương sai:
-Vì hàm số chưa phân tổ và tổng thể là mẫu, cho nên dùng công thức giản đơn sau: Phương sai = 12,879 ⇒
Độ lệch chuẩn = 3.588732367 ⇒
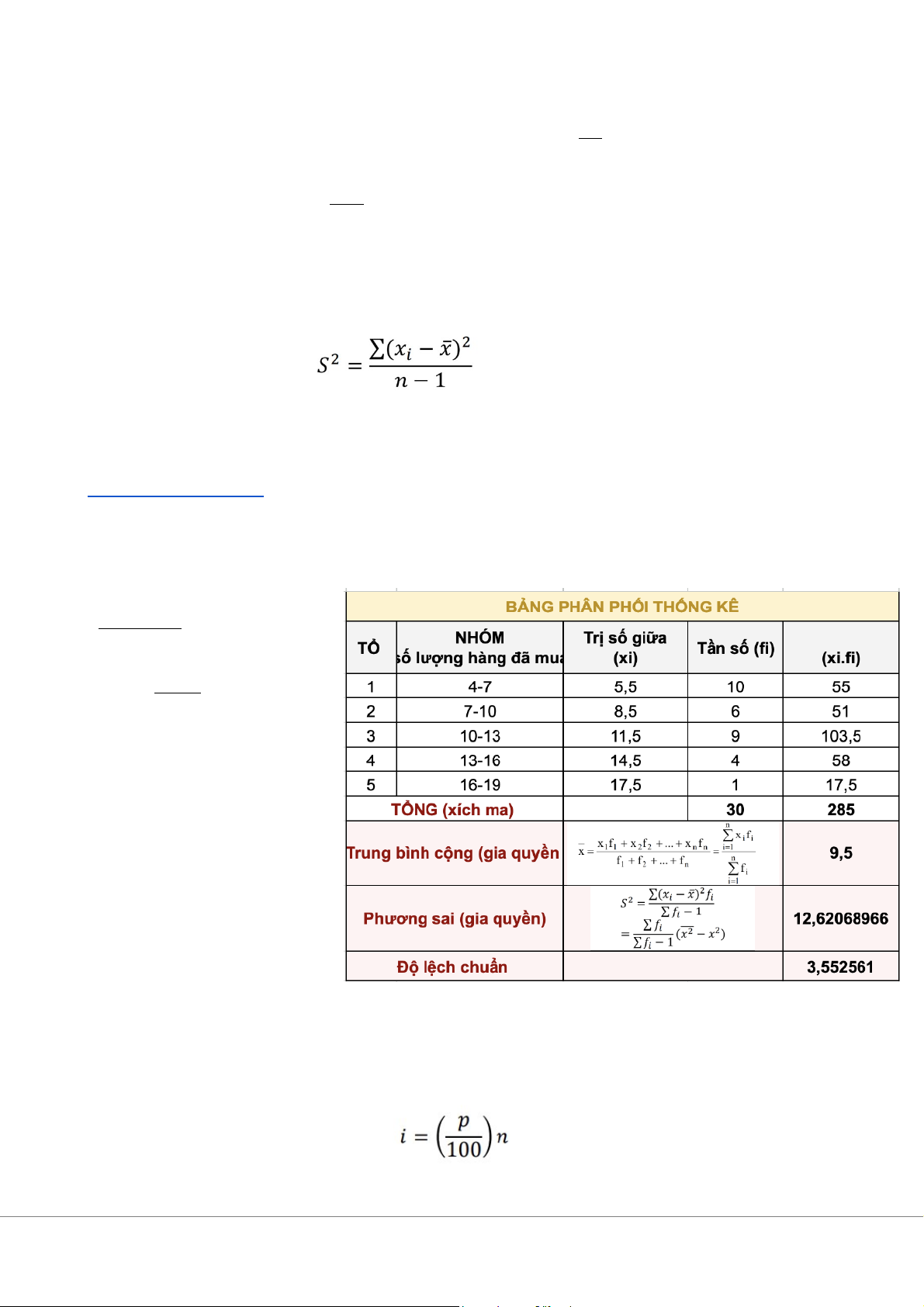
c+d. Bảng tần số phân phối + Tính trung bình và độ lệch chuẩn
Xác định số tổ: áp dụng quy tắc 2 mũ k: quy tắc này cho rằng gía trị nhỏ nhất của số tổ (k) sao cho 2 mũ k lớn hơn số quan sát (n)
Ở đây n=30 => số tổ (k) = 5 (để 25 > n ) Khoảng cách tổ (i) ≥ Max−Min k (i) − ⇒ ≥ 18 4 = 2.8 5 Khoảng cách tổ (i) = 3 ⇒
So sánh trước và sau phân tổ:
-Trung bình cộng bằng nhau
-Phương sai và độ lệch chuẩn
lệch nhau sau khi phân tổ đã
tạo ra sai số, nhưng sai số ở đây khá nhỏ e. Tính phân vị mức 83: + Tính chỉ số i: i = (83 ).30 = 24.9 100
⇒ Vị trí của phân vị mức 83 là số nguyên liền kề lớn hơn 24.9 tức vị trí thứ 25.
⇒ Vậy phân vị mức 83 là 12 mặt hàng
Kết luận: 83% khách mua hàng vào buổi tối mua dưới 12 mặt hàng và 17% mua trên 12 mặt hàng Bài (5 trang 311)
Khoảng tin cậy 95% cho số lượng bản sao trung bình được thực hiện mỗi tuần là S √N−nNt(n−1) S √N−nNt(n−1) x - < < x + (1) √ (anpha (anpha n 2) √n 2) 826+931+1126+918+1011+1101 Mà x = = 985.5 6 ( ) 826−985.5 − ) − ) − ) − ) − )2 S
2+ (931 985.5 2+ (1126 985.5 2+ (918 985.5 2+ (1011 985.5 2+ (1101 985.5 2= 6−1 = 13339.5 => S = 115.496 n=6 N=293 (n−1) t =2,571 anpha/2
thay số vào (1) => 865.52< <1105.47 Bài 45/307:
a). Ước lượng điểm = Σ xi = 87.467 15 Σ (xⅈ−x )2 973.712 b). Phương sai: S = 2 = = 64.91413 15−1 15
Độ lệch chuẩn: S ≈ 8.057
Khoảng tin cậy 95% => 2.145 8.057 8.057
Khoảng tin cậy là: 87.467– x 2.145≤ ≤ 87.467+ x 2.145 √15 √15 83≤ ≤ 92
c). Giả định = 80 không nằm trong (83, 92) => không đủ cơ sở để khẳng định 0 BÀI 15/475 – A, Cỡ mẫu bằng 26 B, SSR = 100 SST = SSR + SSE = 140 SSE = 40 SSR 100 R2 = = = 0,71 SST 140 C, SE = √SSE = √ 40 = 1,41 n− (k+1 ) 26−(5+1) D, Ta có H0:R2=0 H1:R2>0 SSR /k
Tiêu chuẩn kiểm định : F = = 10 SSE /[n−(k+1)]
Với mức ý nghĩa α = 0,05, ta có F0,05(5,20)=2,71
Ta có F > F0,05(5,20) bác bỏ H0
Vậy với mức ý nghĩa 0.05 mô hình phù hợp
E, Với mức ý nghĩa α = 0,05, ta có -2,086 < t0,05(20)< 2,086 Ta có H0:b1=0 H1:b1≠0 TCKĐ t2 = 1,33
Vì -2,086 < t2 < 2,086 nên công nhận H0 Ta có H0:b2=0 H1:b2≠0 TCKĐ t2 = 15
Vì t2 > 2,086 nên bác bỏ H0 Ta có H0:b3=0 H1:b3≠0 TCKĐ t3 = 4
Vì t2 > 2,086 nên bác bỏ H0 Ta có H0:b4=0 H1:b4≠0 TCKĐ t4 = -2,5
Vì t2 < -2,086 nên bác bỏ H0 Ta có H0:b5=0 H1:b5≠0 TCKĐ t2 = 0,75
Vì -2,086 < t2 < 2,086 nên công nhận H0
Có cần loại bỏ biến độc lập đó x1 và x5 Bài 9/312.
Để xác định cỡ mẫu, chúng ta sử dụng công thức sau n= ¿ Trong đó - n là cỡ mẫu cần tìm
- Zα là giá trị Z tương ứng với mức độ tin cậy ( ở đây là 95%, do đó Zα = 1.96 ) 2 2
- σ là độ lệch chuẩn của quần thể. Do không có thông tin về độ lệch chuẩn, ta có thể sử dụng phạm vi dữ liệu để
ước lượng. Trong trường hợp này, phạm vi của dự liệu là 155-5 = 150. Một cách tiếp cận thông thường là chia 150
phạm vi cho 4 để ước lượng độ lệch chuẩn do đó σ = = 37.5 4
- E là sai số chấp nhận được = 4.00 Thay vào công thức: 2 n = (1.96 .37.5 4) n ≈ 388 BÀI 43/344 –
Xét cặp giả thuyết H0:M=1,5 H1:M ≠ 1,5 x−M0 1,3−1,5 Tqs = S = 0,9 = -0,7 √n √10 t9 9
0,005 = 3,25 => | Tqs| < t0,05
Chưa đủ cơ sở bác bỏ H0
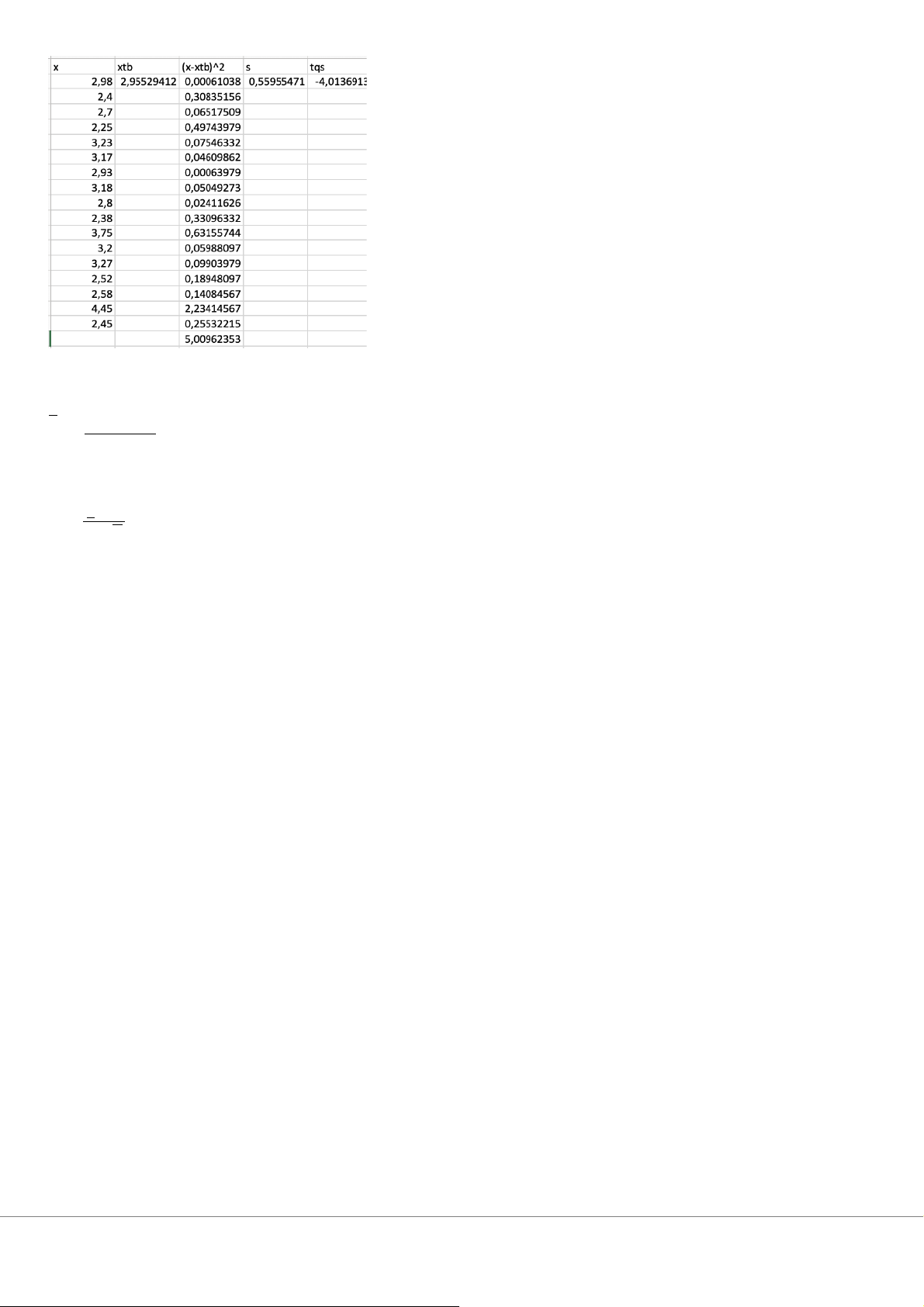
Dữ liệu này không mâu thuẫn với tuyên bố của nxb Bài 38: 38) n = 17, α = 0,05 Ho: μ ≥3,5 H1: μ<3,5 tα(n-1) = t (16) = 1,746 0,05 x = 2,9553 17 s = √ ∑ ❑¿¿¿ i=1 x−μ tqs = = - 4,0137 < -t (16) S/√ 0,05 n => bác bỏ H -> o
Thời gian trung bình của mỗi trận đấu dưới 3,5h BÀI 57/430 -
B1: nhập dữ liệu vaò máy tính cầm tay
B2:nhập AC->OPTN-> tính hồi quy Tính được r=0,834
Và hàm hồi quy mô tả giá phụ thuộc vào tốc độ bộ xử lý Y=703,96X-386,54
C)dựa trên phương trình hồi quy ta thấy
Máy số 10 có mức giá quá cao so với tốc độ xử lý
Máy số 2 và máy số 3 giá lại quá thấp so với tốc độ xử lý
Thay số vào phương trình hồi quy ta thấy được sự chênh lệch đấy