Bài tập thống kê ứng dụng | Trường Đại học Kinh tế – Luật, Đại học Quốc gia Thành phố Hồ Chí Minh

lOMoAR cPSD| 46663874 Ta có
Khoảng tin cậy 95% cho độ lệch chuẩn là
Như vậy máy đóng bịch có độ lệch chuẩn từ 1,99 đến 14, lệch nhiều so với mức
độ cho phép là , vì vậy máy hoạt động không tốt. Bài 3.7
n = 100 > 30, chưa biết độ lệch chuẩn
Trung bình thời gian sử dụng của 100 bóng đèn trên là: (giờ)
a. Ước lượng điểm cho mức phương sai của tuổi thọ bóng đèn là: b. Ta có
Ước lượng tuổi thọ trung bình của loại bóng đèn trên khi độ tin cậy là 95%:
Vậy với độ tin cậy 95% thì tuổi thọ trung bình của loại bóng đèn trên từ
1088,43 giờ đến 1111,57 giờ. c. Ta có Dung sai
Ước lượng chênh lệch tuổi thọ của hai loại bóng đèn với độ tin cậy 0,95 là:
Vậy chênh lệch tuổi thọ của hai loại bóng đèn với độ tin cậy 0,95 là từ 10 giờ lOMoAR cPSD| 46663874 đến 40 giờ. Bài 3.9
Gọi lần lượt là doanh thu trung bình hằng ngày, độ lệch chuẩn mẫu và số ngày theo
dõi của cửa hàng nội thành;
Gọi lần lượt là doanh thu trung bình hằng ngày, độ lệch chuẩn mẫu và số ngày
theo dõi của cửa hàng ngoại thành. Ta có (triệu đồng) a. Dung sai
Ước lượng chênh lệch doanh thu trung bình của hai cửa hàng với độ tin cậy 0,9 là:
Vậy chênh lệch doanh thu trung bình của hai cửa hàng với độ tin cậy 0,9 là từ đến triệu đồng.
b. Ước lượng tỉ số hai phương sai của doanh thu với độ tin cậy 0,95 là: Bài 3.11
Gọi lần lượt là điểm trung bình kiểm tra lần 1, độ lệch chuẩn mẫu và số học viên
trong bài kiểm tra lần 1;
Gọi lần lượt là điểm trung bình kiểm tra lần 2, độ lệch chuẩn mẫu và số học viên
trong bài kiểm tra lần 2.
a. Từ các dữ kiện trong đề bài, ta có
Ước lượng điểm trung bình của điểm kiểm tra lần 1 với độ tin cậy 0,95 là: ; ; [33,85;36,25]
Vậy ước lượng điểm trung bình của điểm kiểm tra lần 1 với độ tin cậy 0,95 là từ 33,85 đến 36,25.
b. Từ các dữ kiện trong đề bài, ta có
Ước lượng phương sai của điểm kiểm tra lần 2 với độ tin cậy 0,95 là: 5,136 18,94
Vậy ước lượng phương sai của điểm kiểm tra lần 2 với độ tin cậy 0,95 là từ 5,136 đến 18,94. c. lOMoAR cPSD| 46663874
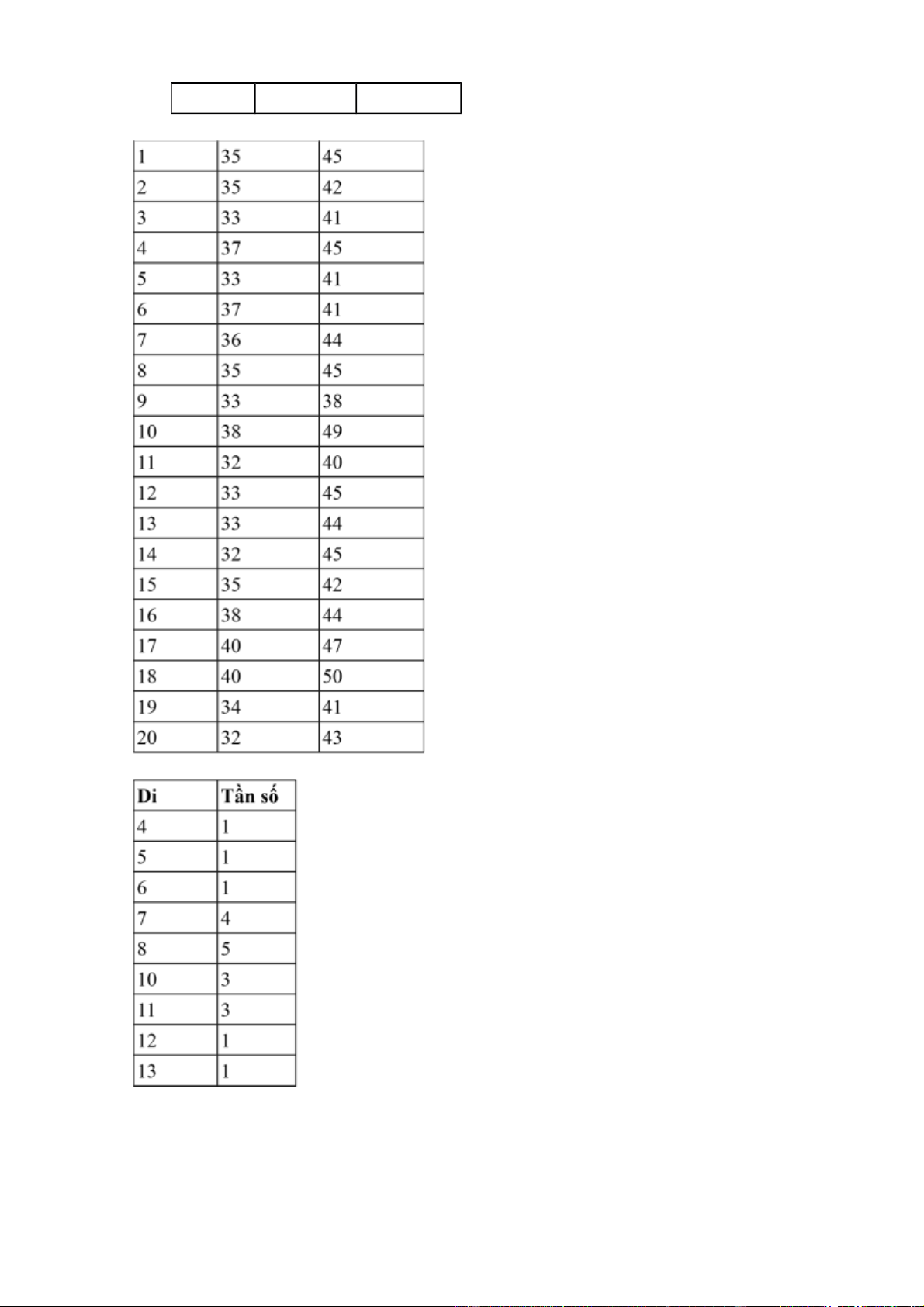
Học viên Điểm lần 1 Điểm lần 2
Sau 1 tháng ta được số điểm chênh lệch giữa lần 1 và lần 2: Di = X2 - X1 = = 8.55 => lOMoAR cPSD| 46663874
Gọi và là số điểm trung bình của điểm kiểm tra lần 1 và lần 2 (sau 1 tháng học với độ tin cậy 0.95) - + 7,44 9,66
Vậy với độ tin cậy 0.95, khoảng ước lượng chênh lệch giữa số điểm kiểm tra lần 1 và
lần 2 trong khoảng (7,44; 9,66). Bài 3.T6
Theo số liệu từ đề bài ta có
Với độ tin cậy 90%, ước lượng sự khác biệt về phương sai thu nhập trung bình giữa
những nhân viên công ty A và B là: Chọn D