BÀI TẬP THỐNG KÊ XÃ HỘI HỌC Khoa Toán tin
Trường Đại học Sư Phạm Hà Nội Hà Nội, tháng 01 năm 2022 MỤC LỤC
1 Bài tập xác suất 3
1.1 Định nghĩa xác suất . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
1.2 Sự độc lập . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
1.3 Biến ngẫu nhiên rời rạc . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
1.4 Phân phối chuẩn . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
2 Bài tập thống kê 7
2.1 Mẫu và các số đặc trưng mẫu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
2.2 Bài toán ước lượng tham số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
2.2.1 Ước lượng khoảng cho giá trị trung bình (trường hợp mẫu lớn) . . . . . . . 8
2.2.2 Ước lượng khoảng cho giá trị trung bình (trường hợp mẫu bé) . . . . . . . . 9
2.2.3 Ước lượng khoảng cho tỉ lệ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
2.2.4 Vấn đề xác định cỡ mẫu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
2.3 Bài toán kiểm định giả thuyết . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
2.3.1 Bài toán kiểm định giả thuyết cho giá trị trung bình một mẫu . . . . . . . 13
2.3.2 Bài toán kiểm định giả thuyết cho tỉ lệ một mẫu . . . . . . . . . . . . . . . . 14
2.3.3 Bài toán kiểm định giả thuyết cho giá trị trung bình hai mẫu . . . . . . . . 15
2.3.4 Bài toán kiểm định giả thuyết cho tỉ lệ hai mẫu . . . . . . . . . . . . . . . . 16
2.4 Bài toán hồi quy và dự báo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17 2 CHƯƠNG 1 BÀI TẬP XÁC SUẤT
1.1 Định nghĩa xác suất
Bài 1. Gieo ngẫu nhiên một con xúc xắc cân đối và đồng chất. Tính xác suất của các biến cố sau:
A: "Mặt chẵn xuất hiện";
B: "Xuất hiện mặt có số chấm chia hết cho 3";
C: "Xuất hiện mặt có số chấm không bé hơn 3".
Bài 2. Gieo ngẫu nhiên một con xúc xắc cân đối và đồng chất hai lần một cách độc lập. Tính
xác suất của các biến cố sau:
A: "Số chấm trong hai lần gieo bằng nhau";
B: "Tổng số chấm trong hai lần gieo bằng 8".
Bài 3. Từ một hộp chứa ba quả cầu trắng và hai quả cầu đen, lấy ngẫu nhiên đồng thời hai
quả. Hãy tính xác suất sao cho hai quả lấy ra cùng màu.
Bài 4. Một khách sạn có 6 phòng đơn. Có 10 khách đến thuê phòng trong đó có 6 nam và 4
nữ. Người quản lí chọn ngẫu nhiên 6 người. Tính xác suất để:
a) Cả 6 người đều là nam. b) Có 4 nam và 2 nữ. c) Có ít nhất 2 nữ.
Bài 5. Lấy ngẫu nhiên ra 6 lá bài từ bộ bài 52 con. Tìm xác suất của các biến cố sau:
a) Lấy được 4 lá bài màu đỏ b) Lấy được 1 lá cơ
c) Lấy được 1 lá Át, 3 lá K và 2 lá chín. 3
Bài tập Thống kê xã hội học 1.2 Sự độc lập
Bài 6. Gieo ngẫu nhiên một con xúc xắc cân đối đồng chất hai lần. Gọi A là biến cố lần thứ
nhất xuất hiện mặt 6 và B là biến cố lần thứ hai xuất hiện mặt 6. Hai biến cố A và B có độc lập với nhau hay không?
Bài 7. Hai sinh viên An và Bình thi môn Thống kê xã hội học. Khả năng đạt của mỗi người
tương ứng là 0,85 và 0,95. Tìm xác suất để xảy ra các tình huống sau: a) Cả hai cùng đạt. b) Không ai đạt.
c) Có đúng 1 người đạt.
d) Có ít nhất một người đạt.
Bài 8. Một bài thi trắc nghiệm gồm 10 câu hỏi, mỗi câu hỏi cho 4 câu trả lời, trong đó chỉ có
1 câu đúng. Giả sử mỗi câu trả lời đúng được 1 điểm, trả lời sai hoặc không trả lời không có
điểm. Một học sinh kém làm bài bằng cách chọn hú họa. Tính xác suất để học sinh này: a) Được 10 điểm. b) Được 0 điểm
c) Được ít nhất 9 điểm.
d) Được không quá 2 điểm.
1.3 Biến ngẫu nhiên rời rạc
Bài 9. Cho biến ngẫu nhiên X có bảng phân phối xác suất: X 4 5 6 7 8 P[X = x] 0,15 0,35 a 0,25 0,15
a) Hãy tìm giá trị của a.
b) Hãy tính các xác suất sau: P[X < 7,5]; P[X > 8]; P[4 ≤ X ≤ 6,5]; P[5 < X < 6].
Bài 10. Cho biến ngẫu nhiên X có bảng phân phối xác suất: X 0 1 2 3 4 P[X = x] 0,1 0,2 0,3 0,25 0,15
a) Tìm kì vọng và phương sai của X.
b) Tìm kì vọng của Y = X2 +3.
Khoa Toán Tin - Trường Đại học Sư Phạm Hà Nội 4
Bài tập Thống kê xã hội học
Bài 11. Xạ thủ 1 có khả năng bắn trúng bia là 0,8; xạ thủ 2 có khả năng bắn trúng bia là 0,7.
Mỗi người bắn vào bia 1 lần. Gọi X là tổng số phát bắn trúng của cả 2 người. Lập bảng phân
phối của X. Tính E[X],Var(X).
Bài 12. Một người đi từ nhà đến cơ quan phải qua 3 ngã tư. Xác suất gặp đèn đỏ tương ứng
tại các ngã tư này là 0,2; 0,25 và 0,3. Giả sử mỗi lần gặp đèn đỏ, người đó phải dừng chờ trên
đường mất 2 phút. Hỏi khi đi từ nhà đến cơ quan, người đó phải dừng chờ trên đường trung bình mất bao nhiêu phút?
Bài 13. Trung bình trong 100 người thì có 7 người mang nhóm máu O âm tính. Chọn ra ngẫu
nhiên 6 người. Tính xác suất:
a) Có đúng 2 người mang nhóm máu O âm tính.
b) Có không ít hơn 2 người mang nhóm máu O âm tính.
Bài 14. Trung bình gieo 1000 hạt giống thì có 650 hạt nảy mầm. Chọn ngẫu nhiên ra 12 hạt
giống để gieo thử nghiệm. Tìm số hạt nảy mầm có xác suất xảy ra cao nhất?
Bài 15. Một nhà máy sản suất sản phẩm với tỉ lệ phế phẩm là 7%. Quan sát ngẫu nhiên n
sản phẩm do máy làm ra. Gọi X là số phế phẩm trong số n sản phẩm này. Xác định phân phối
xác suất của X. Cần chọn n ít nhất là bao nhiêu để biến cố "có ít nhất 1 phế phẩm trong n sản
phẩm quan sát" có xác suất không thấp hơn 0,9?
1.4 Phân phối chuẩn
Bài 16. Chiều cao của nam giới đã trưởng thành là một biến ngẫu nhiên X có phân phối chuẩn N (163;25).
a) Tính tỉ lệ nam giới trưởng thành cao từ 160cm đến 170cm.
b) Chọn ngẫu nhiên 1 nam giới, tìm xác suất để chọn được nam giới cao trên 165cm.
c) Tìm xác suất để khi chọn ngẫu nhiên ra 5 nam giới thì có ít nhất 1 người cao trên 165cm.
Cho biết Φ(0,4) = 0,6554;Φ(0,6) = 0,7257;Φ(1,4) = 0,9192.
Bài 17. Chiều cao của học sinh nam (tính theo đơn vị cm) ở một trường học là biến ngẫu nhiên
có phân phối chuẩn với độ lệch tiêu chuẩn 5,25 cm. Chọn ngẫu nhiên 200 học sinh nam của
trường, đo chiều cao thấy có 57 học sinh có chiều cao trên 170 cm. Xác định chiều cao trung
bình của học sinh nam trường trung học trên.
Bài 18. Thời gian đi từ nhà tới trường của sinh viên An là 1 bnn T (đơn vị là phút) có phân
phối chuẩn. Biết rằng 65% số ngày An đến trường mất hơn 20 phút và 8% số ngày mất hơn 30 phút.
a) Tính thời gian đến trường trung bình của An và độ lệch chuẩn biết Φ(0,3853) = 0,65; Φ(1,405) = 0,92. 5
Khoa Toán Tin - Trường Đại học Sư Phạm Hà Nội
Bài tập Thống kê xã hội học
b) Giả sử An xuất phát từ nhà trước giờ vào học 25 phút. Tính xác suất để An bị muộn học biết Φ(0,51) = 0,695.
Bài 19. Chiều cao của 1 loại cây là 1 biến ngẫu nhiên có phân phối chuẩn. Trong 1 mẫu gồm
640 cây có 25 cây thấp hơn 18m và 110 cây cao hơn 24m.
a) Tính chiều cao trung bình của cây và độ lệch chuẩn biết Φ(0,9463) = 0,8281; Φ(1,762) = 0,961.
b) Ước lượng số cây có chiều cao trong khoảng từ 16m đến 20m trong 640 cây nói trên biết
Φ(0,859) = 0,8051; Φ(2,665) = 0,9964.
Bài 20. Một khách sạn có 200 phòng. Với mỗi khách đã đặt phòng, giả thuyết xác suất hủy
phòng là 0,2. Lễ tân của khách sạn nên chấp nhận nhiều nhất bao nhiêu đề nghị đặt phòng
để khi khách đã đặt phòng đến, xác suất không còn phòng không vượt quá 0,025.
Khoa Toán Tin - Trường Đại học Sư Phạm Hà Nội 6 CHƯƠNG 2 BÀI TẬP THỐNG KÊ
2.1 Mẫu và các số đặc trưng mẫu
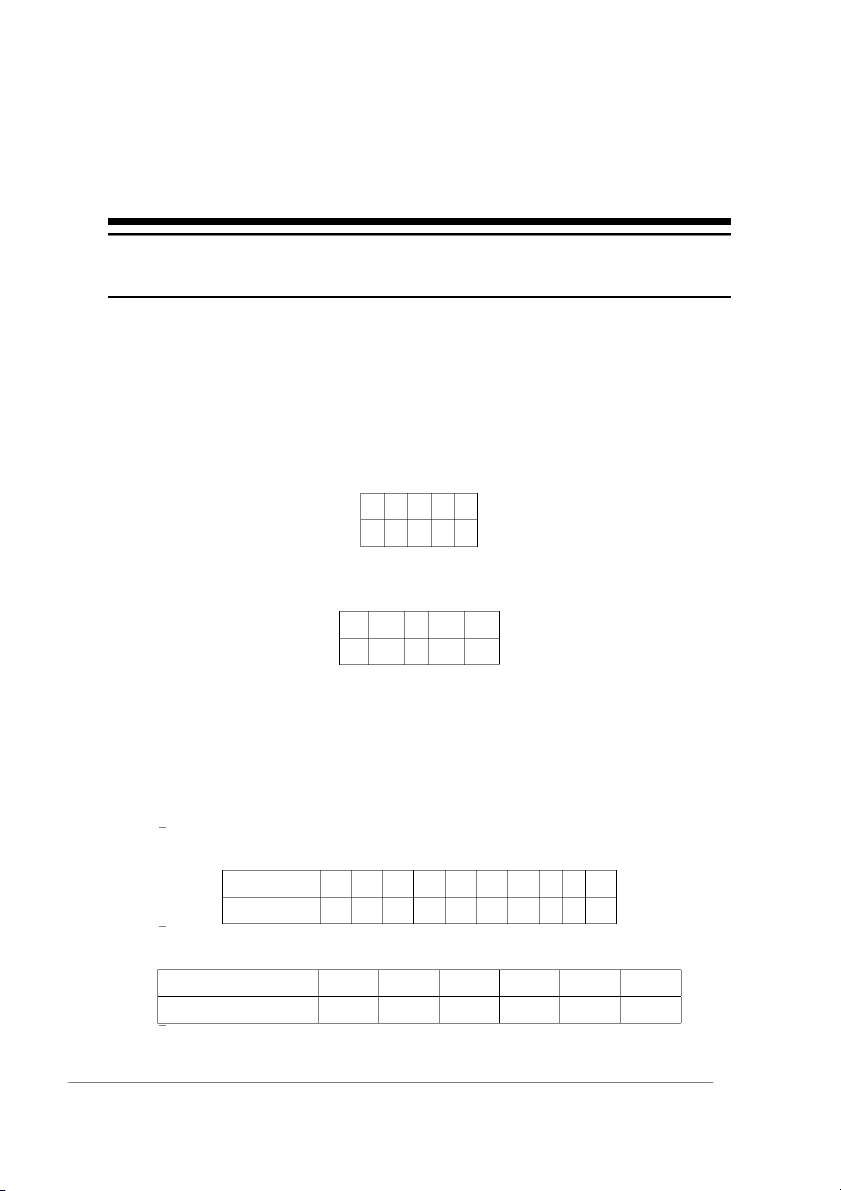
Bài 21. Một mẫu số liệu gồm n = 20 quan sát được cho trong bảng tần số sau: x 1 2 3 4 f 3 a 2 1 Tìm giá trị của a.
Bài 22. Một mẫu số liệu được cho trong bảng tần suất như sau: x 1 2 3 4 fn 0,3 p 0,2 0,1 Tìm giá trị của p. X X X X
Bài 23. Cho mẫu số liệu gồm {1,2,6}. Hãy tính: xi, x2 , i (xi − 3), (xi − 3)2. X X X X
Bài 24. Cho mẫu số liệu gồm {−1,0,1,4}. Hãy tính: xi, x2 , i (xi − 1), (xi − 1)2.
Bài 25. Đo lượng huyết tương của 8 người mạnh khỏe, ta được:
2,86 3,37 2,75 2,62 3,50 3,25 3,12 3,15 Tính n, x, s.
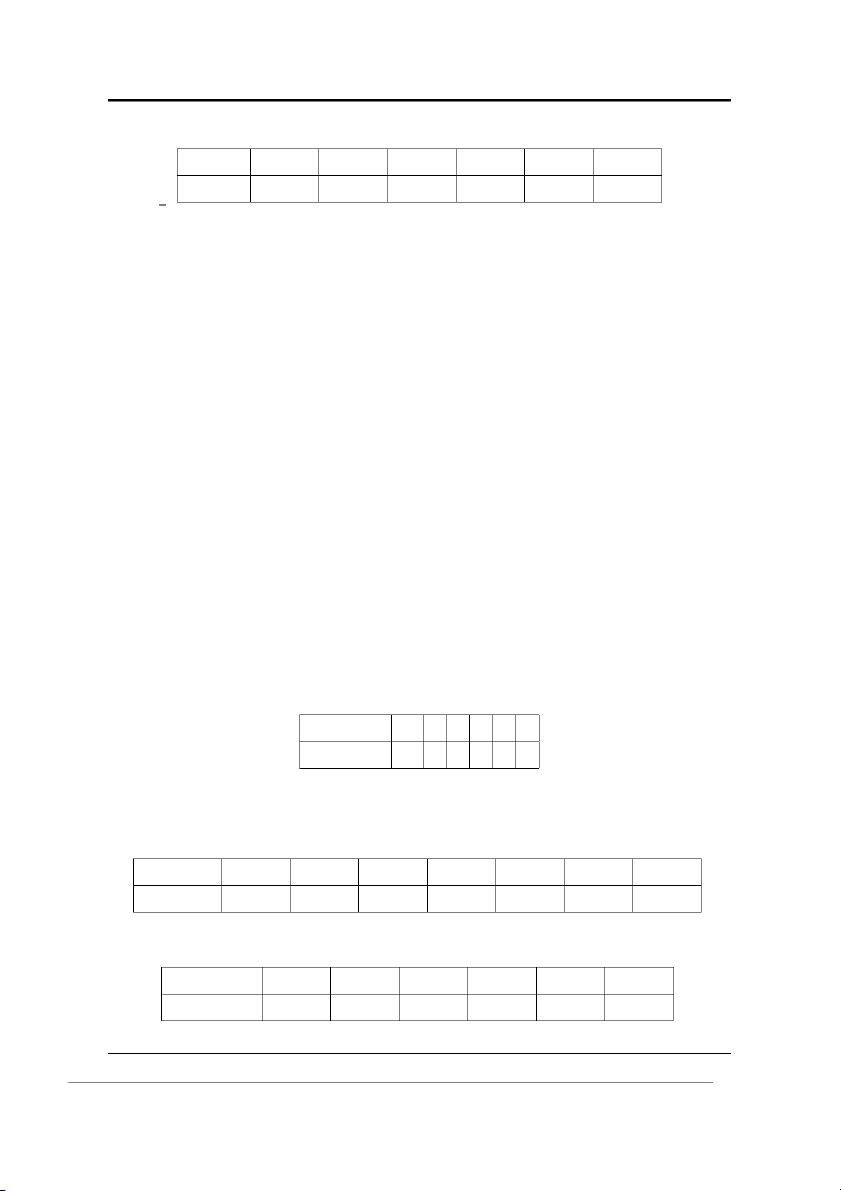
Bài 26. Kết quả thi môn xác suất-thống kê của sinh viên một khoa như sau: X (điểm) 1 2 3 4 5 6 7 8 9 10
Số sinh viên 20 10 25 30 60 20 20 8 5 2 Tính n, x, s.
Bài 27. Đo chiều cao ngẫu nhiên 35 cây bạch đàn trong rừng thu được kết quả:
Khoảng chiều cao (m) 6,5-7,0 7,0-7,5 7,5-8,0 8,0-8,5 8,5-9,0 9,0-9,5 Số cây 2 4 10 11 5 3 Tính n, x, s. 7
Bài tập Thống kê xã hội học
Bài 28. Đo lượng cholesterlemie (đơn vị mg%) của một số người, ta được
X (mg%) 150-160 160-170 170-180 180-190 190-200 200-210 Số người 2 4 5 6 4 3 Tính n, x, s.
2.2 Bài toán ước lượng tham số
2.2.1 Ước lượng khoảng cho giá trị trung bình (trường hợp mẫu lớn)
Bài 29. Hãy xây dựng một khoảng tin cậy 90% cho giá trị trung bình của quần thể dựa trên
thông tin về một mẫu ngẫu nhiên cho trước như sau:
a) n = 36; ¯x = 105,2; s = 11,2.
b) n = 100; ¯x = 105,2; s = 11,2.
Giả sử phương sai quần thể đã biết là 11,3.
Bài 30. Hãy xây dựng một khoảng tin cậy 99% cho giá trị trung bình của quần thể dựa trên
thông tin về một mẫu ngẫu nhiên cho trước như sau:
a) n = 49; ¯x = 17,1; s = 2,1.
b) n = 169; ¯x = 17,1; s = 2,2.
Giả sử phương sai quần thể chưa xác định.
Bài 31. Để nghiên cứu tình trạng nghỉ học của học sinh ở một trường A vào năm học trước,
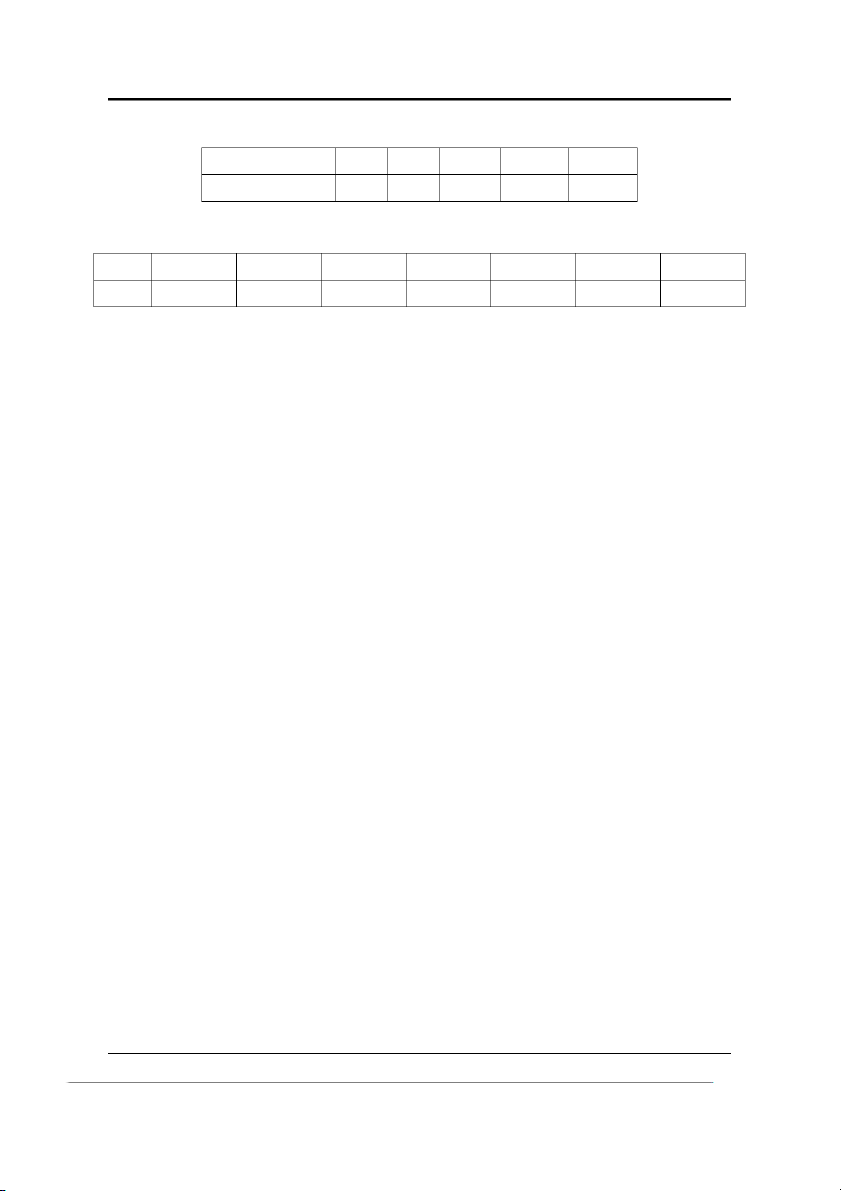
người ta điều tra 40 học sinh và thu được bảng số liệu như sau: X (ngày) 0 1 2 3 4 5 Số học sinh 24 7 5 2 1 1
Hãy xây dựng một khoảng tin cậy 90% về trung bình số ngày nghỉ học của học sinh trường này.
Bài 32. Theo dõi trọng lượng X của một giống Cam ta có bảng số liệu: X (gram)
135-155 155-175 175-195 195-215 215-235 235-255 255-275 Số quả (ni) 5 10 23 35 32 10 5
Với độ tin cậy 99%, xác định khoảng tin cậy cho trọng lượng trung bình của giống cam trên.
Bài 33. Quan sát chiều cao X (cm) của một số người, ta ghi nhận: X (cm)
140-145 145-150 150-155 155-160 160-165 165-170 Số người (ni) 1 3 7 9 5 2
Với độ tin cậy 95%, xác định khoảng tin cậy cho chiều cao trung bình.
Khoa Toán Tin - Trường Đại học Sư Phạm Hà Nội 8
Bài tập Thống kê xã hội học
Bài 34. Số liệu định lượng của mẫu thuốc tiêm vitamin B12 tại một cơ sở thu được như sau:
Hàm lượng (γ/ml) 94-96 96-98 98-100 100-102 102-104 Số ống 4 8 15 12 3
Hãy xác định khoảng tin cậy về hàm lượng trung bình của lô thuốc trên với độ tin cậy 95%.
Bài 35. Khảo sát khối lượng của bộ óc người trên 50 tuổi, người ta thu được các số liệu sau:
KL (g) 1175-1225 1225-1275 1275-1325 1325-1375 1375-1425 1425-1475 1475-1525 SL 6 15 27 25 28 14 8
Tính khoảng tin cậy của trọng lượng trung bình bộ óc của người trên 50 tuổi với độ tin cậy 95%.
2.2.2 Ước lượng khoảng cho giá trị trung bình (trường hợp mẫu bé)
Bài 36. Một mẫu ngẫu nhiên được lấy từ một quần thể có phân phối chuẩn với độ lệch chuẩn
là 5. Hãy xây dựng khoảng tin cậy 95% cho giá trị trung bình của quần txhể dựa trên các
thông tin về mẫu số liệu như sau: a) n = 16; ¯x = 98; s = 5,6. b) n = 9; ¯x = 98; s = 5,6.
Bài 37. Một mẫu ngẫu nhiên được lấy từ một quần thể có phân phối chuẩn với phương sai
chưa biết. Hãy xây dựng khoảng tin cậy 99% cho giá trị trung bình của quần thể dựa trên các
thông tin về mẫu số liệu như sau: a) n = 18; ¯x = 386; s = 24. b) n = 7; ¯x = 386; s = 24.
Bài 38. Đo sức bền chịu lực của một loại ống thí nghiệm, người ta thu được bộ số liệu sau:
4500 6500 5200 4800 4900 5125 6200 5375
Từ kinh nghiệm nghề nghiệp người ta cũng biết rằng sức bền đó có phân phối chuẩn với độ
lệch tiêu chuẩn σ = 300. Hãy xác định khoảng tin cậy 90% cho sức bền trung bình của loại ống trên.
Bài 39. Theo dõi huyết áp của 10 bệnh nhân bị choáng thu được kết quả (tính theo mmHg) như sau: 75 90 85 65 95 75 60 85 85 65
Giả sử huyết áp của người bệnh là biến ngẫu nhiên có phân phối chuẩn. Với độ tin cậy 95%,
hãy xác định khoảng ước lượng cho giá trị trung bình về huyết áp của nhóm bệnh trên.
2.2.3 Ước lượng khoảng cho tỉ lệ
Bài 40. Hãy xây dựng khoảng tin cậy 90% cho tỉ lệ quần thể dựa trên thông tin về mẫu số liệu như sau: a) n = 25; fn = 0,7. 9
Khoa Toán Tin - Trường Đại học Sư Phạm Hà Nội
Bài tập Thống kê xã hội học b) n = 50; fn = 0,7.
Bài 41. Để xác định tỉ lệ này mầm của một loại hạt giống, người ta gieo thử 300 hạt, thấy
có 276 hạt nảy mầm. Với độ tin cậy 95% ta có thể nói tỉ lệ nảy mầm của lô hạt tối đa là bao nhiêu?
Bài 42. Trước bầu cử người ta phỏng vấn ngẫu nhiên 2000 cử tri thì thấy có 1380 người ủng
hộ ứng cử viên K. Với độ tin cậy 95% hỏi ứng cử viên đó thu được tối thiểu bao nhiêu phần trăm phiếu bầu?
Bài 43. Cân thử 100 quả cam ta có bộ số liệu sau:
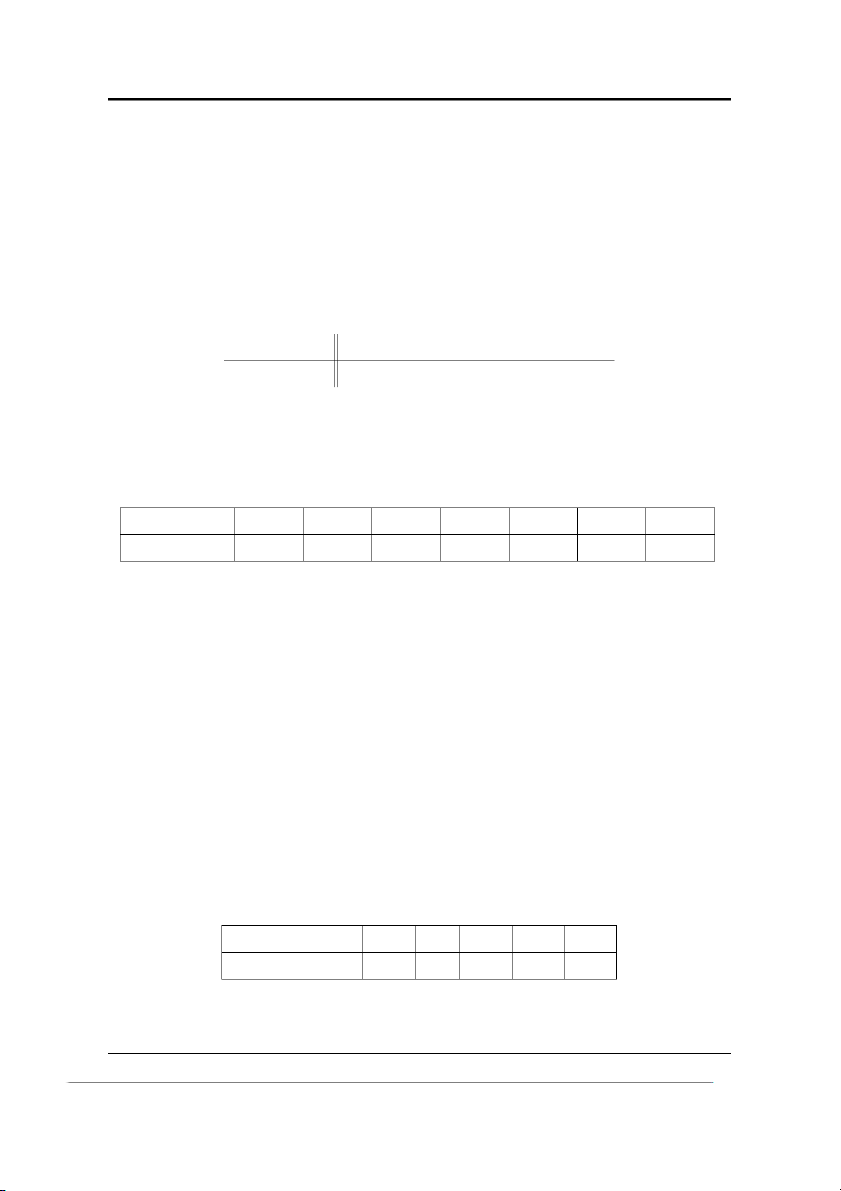
Khối lượng (g) 32 33 34 35 36 37 38 39 40 Số cam 2 3 15 26 28 6 8 8 4
a) Hãy ước lượng khối lượng trung bình các quả cam với độ tin cậy 95%.
b) Cam có khối lượng dưới 34g được coi là cam loại 2. Hãy xác định khoảng ước lượng cho
tỉ lệ số cam loại 2 với độ tin cậy 90%.
Bài 44. Tiến hành đo chiều cao của các học sinh lớp 2 trường Kim Đồng ta có bảng số liệu:
Chiều cao (cm) 112-114 114-116 116-118 118-120 120-122 122-124 124-126 Số học sinh 8 12 20 26 30 14 10
a) Với độ tin cậy 95%, tìm khoảng ước lượng chiều cao trung bình của học sinh lớp 2 trường Kim Đồng.
b) Chọn ngẫu nhiên 250 học sinh lớp 2 trường Kim Đồng. Từ số liệu trên, với độ tin cậy
95%, có thể dự báo nhiều nhất bao nhiêu học sinh trong nhóm được chọn có chiều cao trên 120 cm?
Bài 45. Để xác định số cá trong một cái ao, người ta bắt lên 200 con, đánh dấu chúng rồi thả
lại xuống hồ. Sau một thời gian, người ta lại bắt lên 500 con và thấy có 20 con cá đánh dấu
của lần bắt trước. Dựa vào số liệu đó hãy ước lượng số cá có trong hồ với độ tin cậy 95%.
Bài 46. Để có thể dự đoán được số lượng chim thường nghỉ tại nhà mình, người chủ bắt 89
con, đem đeo khuyên cho chúng rồi thả đi. Sau một thời gian, ông bắt ngẫu nhiên được 120
con và thấy có 7 con có đeo khuyên. Hãy dự đoán số chim giúp ông chủ vườn với độ tin cậy 99%.
2.2.4 Vấn đề xác định cỡ mẫu
Bài 47. Tiến hành điều tra ngẫu nhiên trên 100 con bò, kết quả như sau:
X (sản lượng/ngày) 7-9kg 9-11 11-13 13-15 15-17 Số con bò 10 24 42 16 8
a) Sản lượng sữa trung bình một ngày của một con bò là bao nhiêu?
b) Bao nhiêu % đàn bò cho sản lượng sữa trên 11kg trong ngày?
Khoa Toán Tin - Trường Đại học Sư Phạm Hà Nội 10