Bài Tập Toán 8 Tuần 1 Có Lời Giải Chi Tiết

PHIẾU BÀI TẬP TOÁN 8 TUẦN 01 Bài 1.
Thực hiện các phép tính sau: 1) xy ( 2 3 x − 3y) 2) ( 2 x − )( 2 1 x + 2x) 3) (2x − )
1 (3x + 2)(3− x) 4) ( x + )( 2 3 x + 3x − 5) 5) ( x + )( 2 1 x − x + ) 1 6) ( 3 2x − 3x − ) 1 (5x + 2) 7) ( 2
x − 2x + 3)(x − 4) 8) 3 − x y ( 2 2
2x − 3y + 5yz)
9) ( x − y)( 2 2 2
x y − xy + 2y) 2 2 12) ( − )( 2 2
x y x + xy + y ) 10) xy ( 2
x y − 5x +10y) 11) 2 x y ( 2
3xy − x + y) 5 3 Bài 2.
Rút gọn rồi tính giá trị các biểu thức: 1) x ( 2
x − x + ) − x( 2 5 4 2 1
2 10x − 5x − 2) với x = 15 1 − 1
2) 5x ( x − 4y) − 4y ( y − 5x) với x = ; y = − 5 2 1 3) xy ( 2 xy − y ) 2 − x ( 2 6 8 x − y )
với x = ; y = 2 2  1  2 4) ( 2
y + 2)( y − 4) −( 2 2y + ) 1 y − 2   với y = −  2  3 5) x ( 2 x + ) 2 − x ( x + ) 3 3 2 4 3 + x với x = 5 1 6) xy ( 2 xy − x ) 2 − y ( 2 x − y) 2 − x ( 2 7 3 4 y − xy)
với x = 1; y = 2 Bài 3. Tìm x , biết:
a) 3x(x +1) − (x − 2)(3x +1) = 12 5 b) 2 2
(3x − x +1)(x −1) + x (4 − 3x) = 2
c) (x + 3)(5x −1) = 5(x +1)(x − 2)
d) (2x − 3)(x +1) = 2x(x −1) 1 1 1 e) 2
x − ( x − 4) x = 1 − 4 4 2 2
f) 3(1− 4x)(x −1) + 4(3x − 2)(x + 3) = −27 Bài 4.
Tứ giác ABCD có + = 180o A B
, DB là phân giác góc D . Chứng minh rằng: BC = CD Bài 5.
Cho tam giác ABC vuông cân tại A . Trên nửa mặt phẳng bờ BC không chứa điểm A , vẽ BD
vuông góc BC và BD = BC .
a) Tứ giác ABDC là hình gì? Vì sao?
b) Biết AB = 5 cm. Tính CD . Trang 1 Bài 6.
Hình thang vuông ABCD có 0
A = D = 90 , đường chéo BD vuông góc với cạnh bên BC và BD = BC .
a) Tính các góc của hình thang..
b) Biết AB = 3cm . Tính độ dài các cạnh BC,CD . Bài 7. Cho tứ giác ABCD có 0
B + D = 180 ,CB = CD . Trên tia đối của tia DA lấy điểm E sao cho
DE = AB . Chứng minh
a)Các tam giác ABC và EDC bằng nhau
b) AC là phân giác của góc A Bài 8.
Chứng minh các đẳng thức sau: 4 3 2 2 3 4 5 5
a) (x − y)(x + x y + x y + xy + y ) = x − y 4 3 2 2 3 4 5 5
b) (x + y)(x − x y + x y − xy + y ) = x + y 3 2 2 3 4 4
c) (a + b)(a − a b + ab − b ) = a − b 2 2 3 3
d) (a + b)(a − ab + b ) = a + b Bài 9.
Cho tứ giác ABCD có phân giác trong của góc A và góc B cắt nhau tại E , phân giác ngoài C + D A + B
của góc A và góc B cắt nhau tại F . Chứng minh AEB = và AFB = . 2 2
Bài 10. Cho tứ giác ABCD biết số đo các góc ,
A B,C, D tỉ lệ thuận với 5; 8; 13; và 10.
a) Tính số đo các góc của tứ giác ABCD
b) Kéo dài hai cạnh AB và DC cắt nhau ở E , kéo dài hai cạnh AD và BC cắt nhau tại F .
Hai tia phân giác của góc AED và AFB cắt các cạnh CD và AB tại M và N . Chứng
minh O là trung điểm của đoạn MN .
ĐÁP ÁN BÀI TẬP TĂNG CƯỜNG TOÁN 8 TUẦN 1 Trang 2 Bài 1.
Thực hiện các phép tính sau: 1) xy ( 2 3 x − 3y) 2) ( 2 x − )( 2 1 x + 2x) 3) (2x − )
1 (3x + 2)(3− x) 4) ( x + )( 2 3 x + 3x − 5) 5) ( x + )( 2 1 x − x + ) 1 6) ( 3 2x − 3x − ) 1 (5x + 2) 7) ( 2
x − 2x + 3)(x − 4) 8) 3 − x y ( 2 2
2x − 3y + 5yz)
9) ( x − y)( 2 2 2
x y − xy + 2y) 2 2 12) ( − )( 2 2
x y x + xy + y ) 10) xy ( 2
x y − 5x +10y) 11) 2 x y ( 2
3xy − x + y) 5 3 Lời giải 1) xy ( 2 x − y) 2 3 2 3 3 = 3x . y x − 3x .3
y y = 3x y − 9xy 2) ( 2 x − )( 2 x + x) 2 2 2 2 4 3 2 1 2
= x .x + x .2x − x − 2x = x + 2x − x − 2x 3) (2x − )
1 (3x + 2)(3− x) = (2 .3 x x + 2 .2
x − 3x − 2)(3− x) = ( 2
6x + x − 2)(3− x) 2 2
= 6x .3 − 6x .x + .3 x − .
x x − 2.3 + 2.x 2 3 2
= 18x − 6x + 3x − x − 6 + 2x 3 2
= −6x +17x + 5x − 6 4) ( x + )( 2 x + x − ) 2 2 3 3 5 = . x x + .3 x x − .5
x + 3.x + 3.3x − 3.5 3 2
= x + 6x + 4x −15 5) ( x + )( 2 x − x + ) 2 2 1 1 = . x x − .
x x + x + x − x +1 3 2 2
= x − x + x + x − x +1 3 = x +1 6) ( 3
x − x − )( x + ) 3 3 2 3 1 5
2 = 2x .5x + 2x .2 − 3 .5 x x − 3 .2 x − 5x − 2 4 3 2
= 10x + 4x −15x −11x − 2 7) ( 2
x − x + )(x − ) 2 2 2 3
4 = x .x − x .4 − 2 . x x + 2 .4 x + 3.x − 3.4 3 2 2
= x − 4x − 2x + 8x + 3x −12 3 2
= x − 6x +11x −12 8) 3 − x y ( 2
x − y + yz) 3 2 3 3 2 2 3 5 = 2 − x .2 y x + 2x .3 y y − 2x .5 y yz 5 3 2 3 2 = 4
− x y + 6x y −10x y z Trang 3
9) ( x − y)( 2 2
x y − xy + y) 2 2 2 2 2 2 = . x x y − . x xy + .2 x y − 2 . y x y + 2 . y xy − 2 .2 y y 3 2 2 2 3 2 2
= x y − x y + 2xy − 2x y + 2xy − 4y 3 2 2 3 2 2 2
= x y − 2x y − x y + 2xy + 2xy − 4y 2 2 2 2 10) xy ( 2
x y − 5x +10y) 2 = x . y x y − x .
y 5x + x . y 10y 5 5 5 5 2 3 2 2 2
= x y − 2x y + 4xy 5 2 2 2 2 11) 2 x y ( 2
3xy − x + y) 2 2 2 2 = x .
y 3xy − x . y x + x . y y 3 3 3 3 2 2 3 2 4 2 2
= 2x y − x y + x y 3 3
12) ( x − y)( 2 2
x + xy + y ) 2 2 2 2 = . x x + . x xy + . x y − .
y x − y.xy − y.y 3 2 2 2 2 3
= x + x y + xy − x y − xy − y 3 3 = x − y Bài 2.
Rút gọn rồi tính giá trị các biểu thức: 1) x ( 2
x − x + ) − x( 2 5 4 2 1
2 10x − 5x − 2) với x = 15 1 − 1
2) 5x ( x − 4y) − 4y ( y − 5x) với x = ; y = − 5 2 1 3) xy ( 2 xy − y ) 2 − x ( 2 6 8 x − y )
với x = ; y = 2 2  1  2 4) ( 2
y + 2)( y − 4) −( 2 2y + ) 1 y − 2   với y = −  2  3 5) x ( 2 x + ) 2 − x ( x + ) 3 3 2 4 3 + x với x = 5 1 6) xy ( 2 xy − x ) 2 − y ( 2 x − y) 2 − x ( 2 7 3 4 y − xy)
với x = 1; y = 2 Lời giải 1) x ( 2
x − x + ) − x( 2 x − x − ) 3 2 3 2 5 4 2 1 2 10 5
2 = 20x −10x + 5x − 20x +10x + 4x = 9x
Thay x = 15 vào biểu thức ta được: 9.15 = 135
2) x ( x − y) − y ( y − x) 2 2 2 2 5 4 4 5
= 5x − 20xy − 4y + 20xy = 5x − 4y 1 − 1 2 2  1 −   1  1 1 1 4 − Thay x =
; y = − vào biểu thức ta được: 5. − 4. − = 5. − 4. = −1 =     5 2  5   2  25 4 5 5 Trang 4 3) xy ( 2 xy − y ) 2 − x ( 2 x − y ) 2 2 3 3 2 2 2 2 3 3 6 8
= 6x y − 6xy −8x + 8x y =14x y − 6xy −8x 1
Thay x = ; y = 2 vào biểu thức ta được: 2 2 3  1  1  1  1 1 1 2 3 14. .2 − 6. .2 −8.
=14. .4 − 6. .8 −8. =14 − 24 −1 = 1 − 1      2  2  2  4 2 8  1  1 3 4) ( 2
y + 2)( y − 4) −( 2 2y + ) 3 2 3 2 1
y − 2 = y − 4y + 2y − 8 − y + 4y − y + 2 = y − 6    2  2 2 2 3 2 −
Thay y = − vào biểu thức ta được: . − 6 = 1 − − 6 = 7 − 3 2 3 5) x ( 2 x + ) 2 − x ( x + ) 3 3 3 2 3 2 3 2 4
3 + x = 3x + 2x − 4x − 3x + x = −3x + 2x
Thay x = 5 vào biểu thức ta được: 2 3.
− 5 + 2.5 = −75 +10 = −65 6) xy ( 2 xy − x ) 2 − y ( 2 x − y) 2 − x ( 2 y − xy) 2 2 3 2 2 3 2 2 3 7 3 4
= 7x y − 7x y − 3x y + 3y − 4x y + 4x y 3 3 = −3x y + 3y 1 3 1  1  3 − 3 1 − 2 3 9 −
Thay x = 1; y = vào biểu thức ta được: 3 3 − .1 . + 3. = + = + =   2 2  2  2 8 8 8 8 Bài 3. Tìm x , biết:
a) 3x(x +1) − (x − 2)(3x +1) = 12 5 b) 2 2
(3x − x +1)(x −1) + x (4 − 3x) = 2
c) (x + 3)(5x −1) = 5(x +1)(x − 2)
d) (2x − 3)(x +1) = 2x(x −1) 1 1 1 e) 2
x − ( x − 4) x = 1 − 4 4 2 2
f) 3(1− 4x)(x −1) + 4(3x − 2)(x + 3) = −27 Lời giải
a) 3x(x +1) − (x − 2)(3x +1) = 12  2 2
3x + 3x − 3x − x + 6x + 2 = 12  8x + 2 = 12  8x = 10  5 x = 4 5 b) 2 2
(3x − x +1)(x −1) + x (4 − 3x) = 2 Trang 5  5 3 2 2 2 3 3x 3
− x − x + x + x −1+ 4x − 3x = 2 7  2x = 2 7  x = 4
c) (x + 3)(5x −1) = 5(x +1)(x − 2)  2 2
5x − x +15x − 3 = 5x −10x + 5x −10  14x − 3 = 5 − x −10  19x = 7 −  7 x = − 19
d) (2x − 3)(x +1) = 2x(x −1)  2 2
2x + 2x − 3x − 3 = 2x − 2x
 −x − 3 = −2x  x = 3 1 1 1 e) 2
x − ( x − 4) x = 1 − 4 4 2 2  1 1 2 2
x − x + 2x = 1 − 4 4 4  2x = 14 −  x = −7
f) 3(1− 4x)(x −1) + 4(3x − 2)(x + 3) = −27  2 2
3(x −1− 4x + 4x) + 4(3x + 9x − 2x − 6) = −27  2 2
3(5x −1− 4x ) + 4(3x + 7x − 6) = 2 − 7  2 2
15x − 3 −12x +12x + 28x − 24 = 27 −  43x = 0  x = 0 Bài 4.
Tứ giác ABCD có + = 180o A B
, DB là phân giác góc D .
Chứng minh rằng: BC = CD Lời giải
Tứ giác ABCD có: + = 180o A B (gt) B C 1
Mà hai góc này ở vị trí trong cùng phía  AD//BC (dhnb) 1 2 A D Trang 6
Tứ giác ABCD là hình thang (đn)
 B1 = D2 (slt) (1)
Mà DB là phân giác góc D (gt)  1 D = D2 (2) Từ (1) và (2) ta suy ra 1 B = 1
D  DCB cân tại C (t/c)
 BC = CD (đpcm) Bài 5.
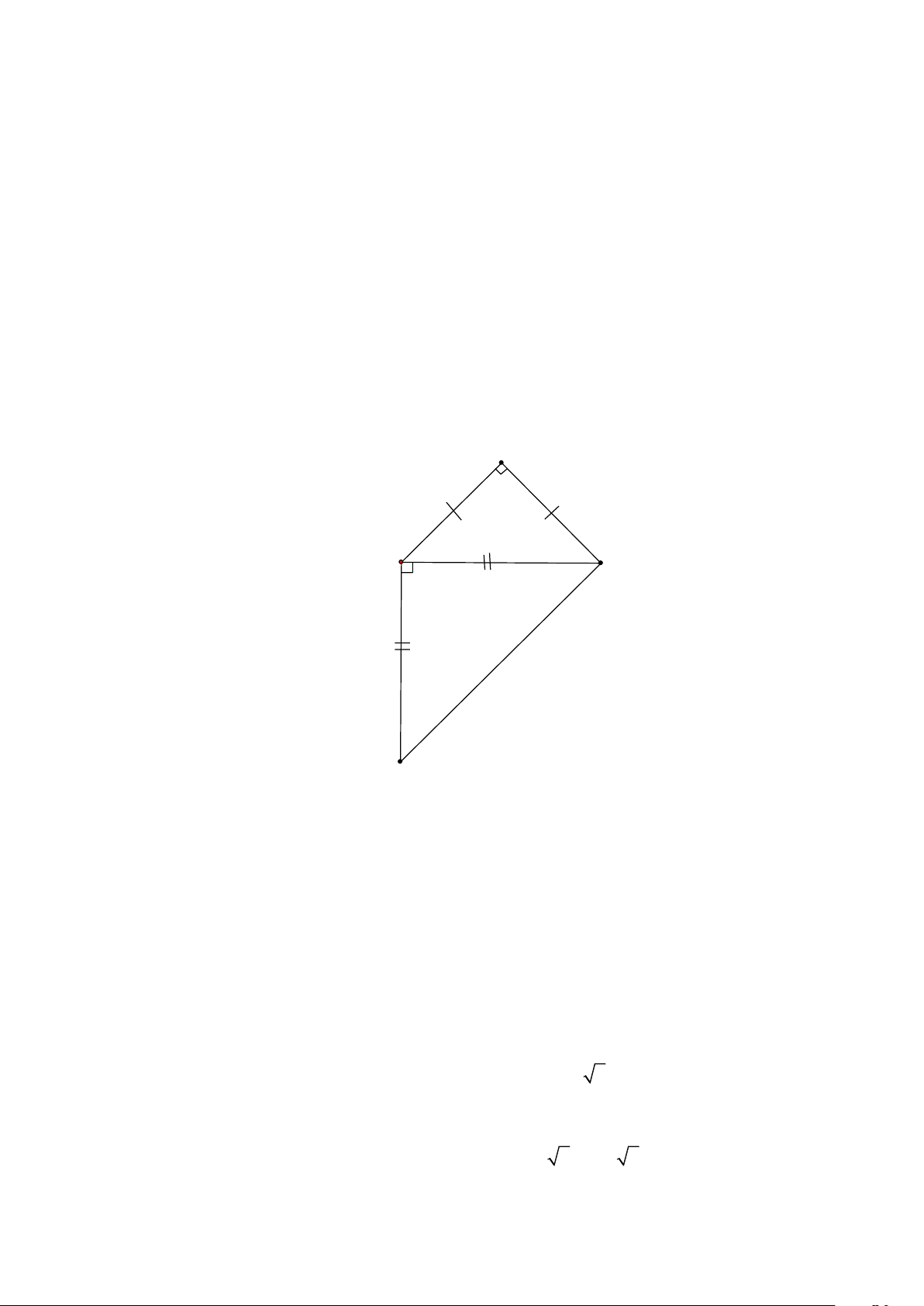
Cho tam giác ABC vuông cân tại A . Trên nửa mặt phẳng bờ BC không chứa điểm A , vẽ BD
vuông góc BC và BD = BC .
a) Tứ giác ABDC là hình gì? Vì sao?
b) Biết AB = 5 cm. Tính CD . Lời giải A B C D
a) Tam giác ABC vuông cân tại A (gt) nên AB ⊥ AC (1) 0 ABC = ACB = 45
Mà BC ⊥ BD và BC = BD (gt) nên tam giác BCD vuông cân tại B Hay 0 BDC = BCD = 45 0 0 0
ACD = ACB + DCB = 45 + 45 = 90 hay AC ⊥ CD (2)
Từ (1) và (2) suy ra AB //CD (3)
Từ (3) và (4) suy ra tứ giác ABDC là hình thang vuông.
b) Dựa vào định lý Pytago cho tam giác ABC vuông cân tại A có AB = AC = 5 cm
Tính được BC = 5 2
Xét tam giác BCD vuông cân tại B có : 2 2 2
CD = BD + BC 2 2 2  CD = (5 2) + (5 2) 2
 CD = 100  CD = 10 Trang 7 Bài 6.
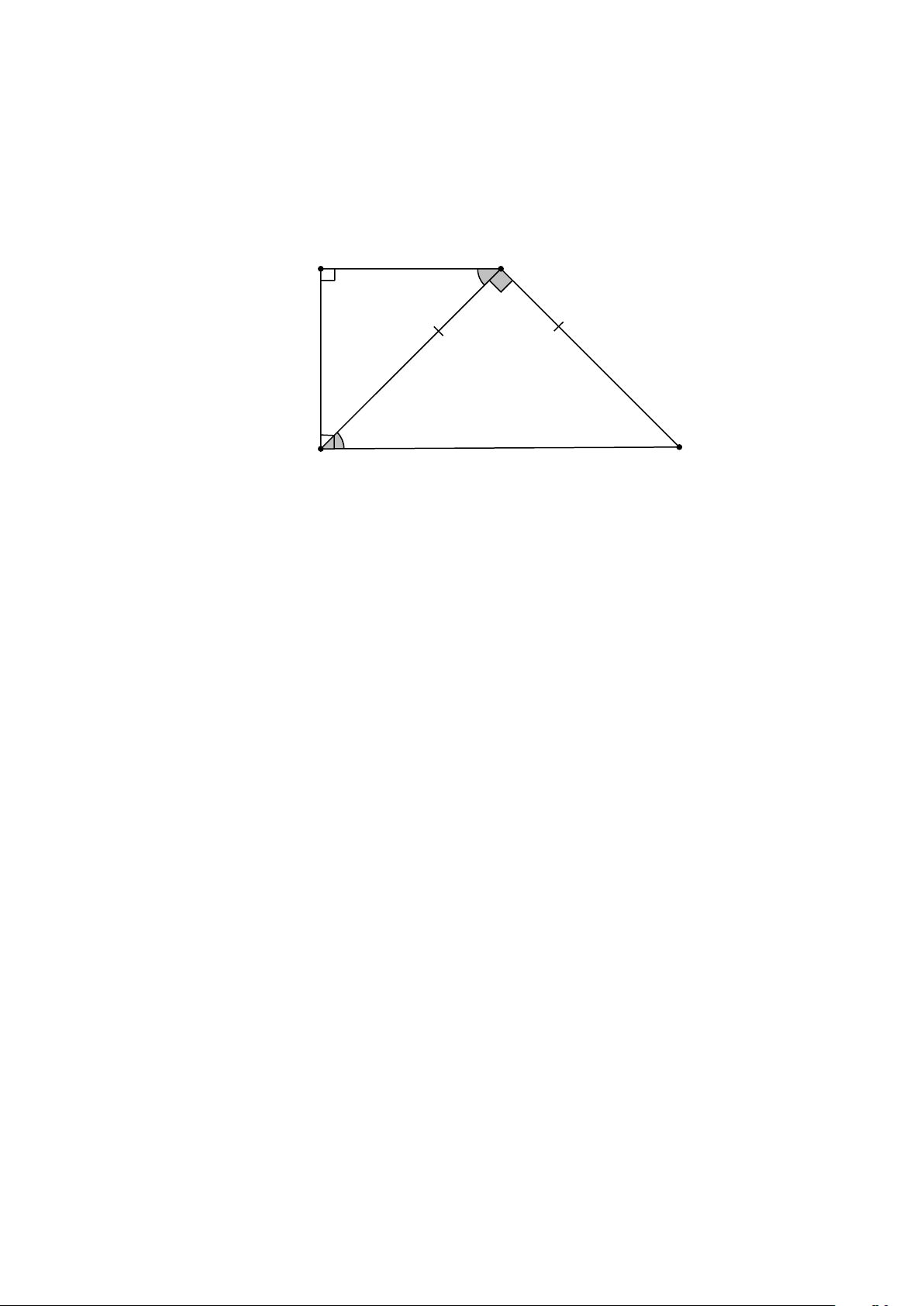
Hình thang vuông ABCD có 0
A = D = 90 , đường chéo BD vuông góc với cạnh bên BC và BD = BC .
a) Tính các góc của hình thang..
b) Biết AB = 3cm . Tính độ dài các cạnh BC,CD . Lời giải A B 1 2 1 1 D C
a) xét DBC có BD = BC (gt)  DBC  cân tại B
 D = C (tính chất tam giác cân) (1) 1 1 Xét DBC có 0
DBC + D + C = 180 mà 0 B = 90 1 1 0
 D + C = 90 (2) 1 1 Từ (1) và (2) suy ra 0 D = C = 45 1 1
Xét tứ giác ABCD có 0
A + ABC + ADC + C = 360 1 Mà 0 0 0
A = 90 , ADC = 90 ,C = 45 1 0 0 0 0 0
 ABC = 360 − 90 − 90 − 45 = 135 0 0 0 0
A = 90 , ABC = 135 ,C = 45 , ADC = 90 1 b) Vì AB// DC (gt)  D = B mà 0 0
D = 45  B = 45 1 1 1 1
Ta có D + D = ADC 1 2 Mà 0 0 0
D = 45 ; ADC = 90  ADC = 45 1 Xét ABD có 0
D = B = 45 (cmt) 2 1 Trang 8
Suy ra ABD là tam giác cân
 AB = AD = 3cm
Xét ABD vuông tại A có 2 2 2
AB + AD = BD 2 2 2  BD = 3 + 3 =18  BD = 18
Xét BDC vuông tại B có 2 2 2
BD + BC = DC  DC = ( )2 +( )2 2 18 18 = 36  DC = 4
Vậy BD = 18 , DC = 4 . Bài 7. Cho tứ giác ABCD có 0
B + D = 180 ,CB = CD . Trên tia đối của tia DA lấy điểm E sao cho
DE = AB . Chứng minh
a) Các tam giác ABC và EDC bằng nhau
b) AC là phân giác của góc A Lời giải B A D C E
a) Các tam giác ABC và EDC bằng nhau Ta có 0
B + ADC = 180 mà 0 EDC + ADC = 180 Trang 9  B = EDC (1)
Xét ABC và EDC có
AB = DE (gt), B = EDC (cmt) , DC = BC (gt)  AB  C = EDC  (c –g-c) b) Vì AB  C = ED  C (cmt)
 AC = EC ( hai cạnh tương ứng)  AC 
E cân tại C
 CAE = AEC (tính chất tam giác cân)
Mà BAC = AEC ( AB  C = ED  C )  CAE = BAC
Hay AC là phân giác của góc A . Bài 8.
Chứng minh các đẳng thức sau: 4 3 2 2 3 4 5 5
a) (x − y)(x + x y + x y + xy + y ) = x − y 4 3 2 2 3 4 5 5
b) (x + y)(x − x y + x y − xy + y ) = x + y 3 2 2 3 4 4
c) (a + b)(a − a b + ab − b ) = a − b 2 2 3 3
d) (a + b)(a − ab + b ) = a + b Lời giải 4 3 2 2 3 4 5 5
a)(x − y)(x + x y + x y + xy + y ) = x − y Xét VT, ta có: 4 3 2 2 3 4 4 3 2 2 3 4 VT = .(
x x + x y + x y + xy + y ) − .(
y x + x y + x y + xy + y ) 5 4 3 2 2 3 4 4 3 2 2 3 4 5
= x + x y + x y + x y + xy − x y − x y − x y − xy − y 5 5
= x − y = VP (đpcm). 4 3 2 2 3 4 5 5
b)(x + y)(x − x y + x y − xy + y ) = x + y Xét VT, ta có: 4 3 2 2 3 4 4 3 2 2 3 4 VT = .(
x x − x y + x y − xy + y ) + .(
y x − x y + x y − xy + y ) 5 4 3 2 2 3 4 4 3 2 2 3 4 5
= (x − x y + x y − x y + xy ) + (x y − x y + x y − xy + y ) 5 5
= x + y = VP (đpcm). Trang 10 3 2 2 3 4 4
c)(a + b)(a − a b + ab − b ) = a − b Xét VT, ta có: 3 2 2 3 3 2 2 3 VT = .(
a a − a b + ab − b ) + .(
b a − a b + ab − b ) 4 3 2 2 3 3 2 2 3 4
= a − a b + a b − ab + a b − a b + ab − b 4 4
= a − b = VP (đpcm). 2 2 3 3
d)(a + b)(a − ab + b ) = a + b Xét VT, ta có: 2 2 2 2 VT = .(
a a − ab + b ) + .(
b a − ab + b ) 3 2 2 2 2 3
= a − a b + ab + a b − ab + b 3 3
= a + b = VP (đpcm). Bài 9.
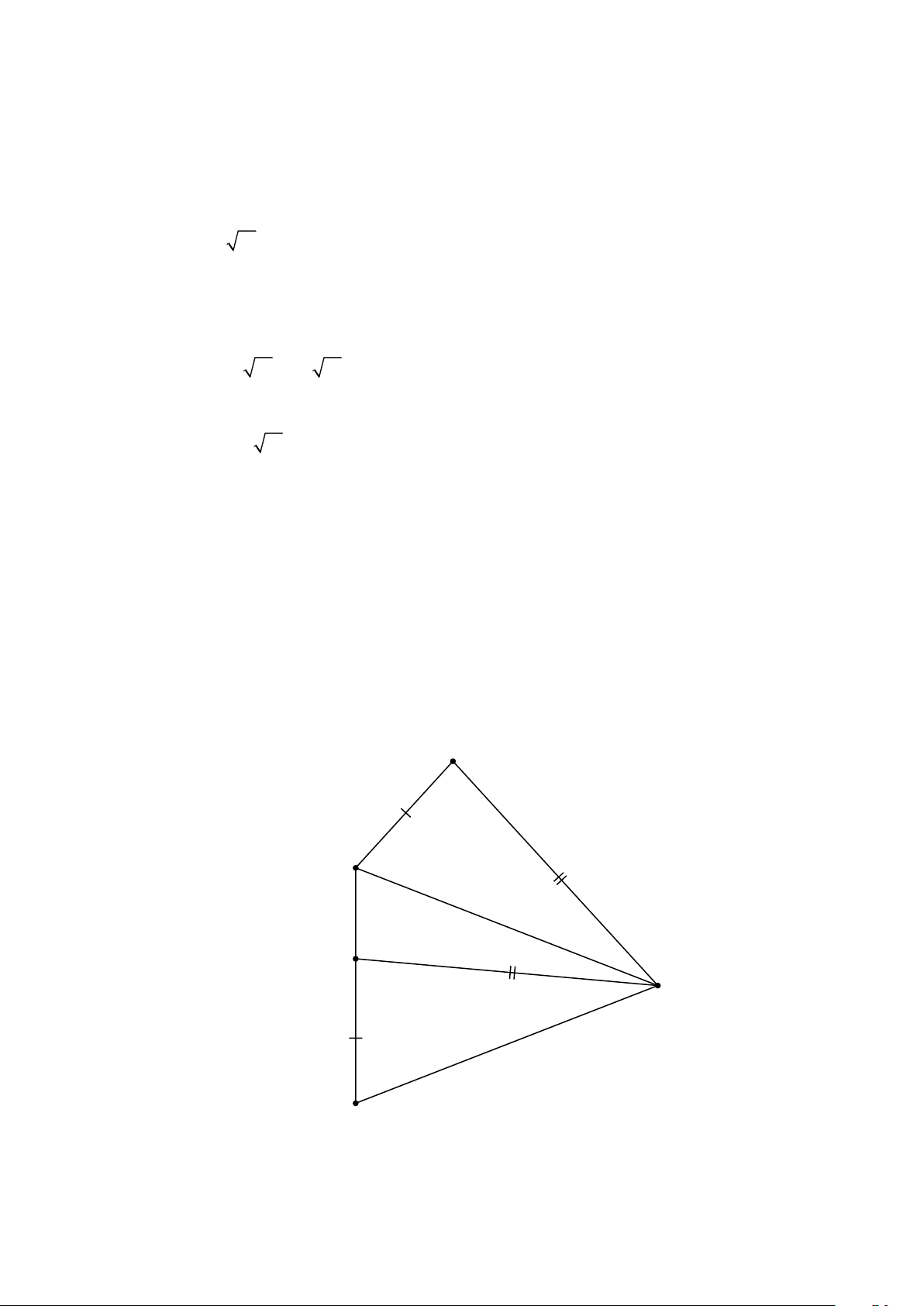
Cho tứ giác ABCD có phân giác trong của góc A và góc B cắt nhau tại E , phân giác ngoài C + D A + B
của góc A và góc B cắt nhau tại F . Chứng minh AEB = và AFB = . 2 2 Lời giải F B A E D C
Xét AEB : AEB = 180 − (EAB + EBA)
 BAD + CBA 
Do EA và EB là phân giác trong của góc A và góc B nên AEB = 180 −    2   
Mà BAD + CBA = 360 − (C + D) ( tổng 4 góc trong tứ giác)
360 − (C + D) C + D  AEB =180 − = . 2 2
EA và FA là phân giác trong và phân giác ngoài của góc A nên EAF = 90 .
Tương tự: FBE = 90 .
Tứ giác AEBF có : EAF + EBF + AEB +AFB = 360 (định lí) Trang 11
 AFB = AEB − EAF − FAE − AEB C + D
 AFB = 360 − 90 − 90 − 2 C + D A + B  AFB =180 − = 2 2
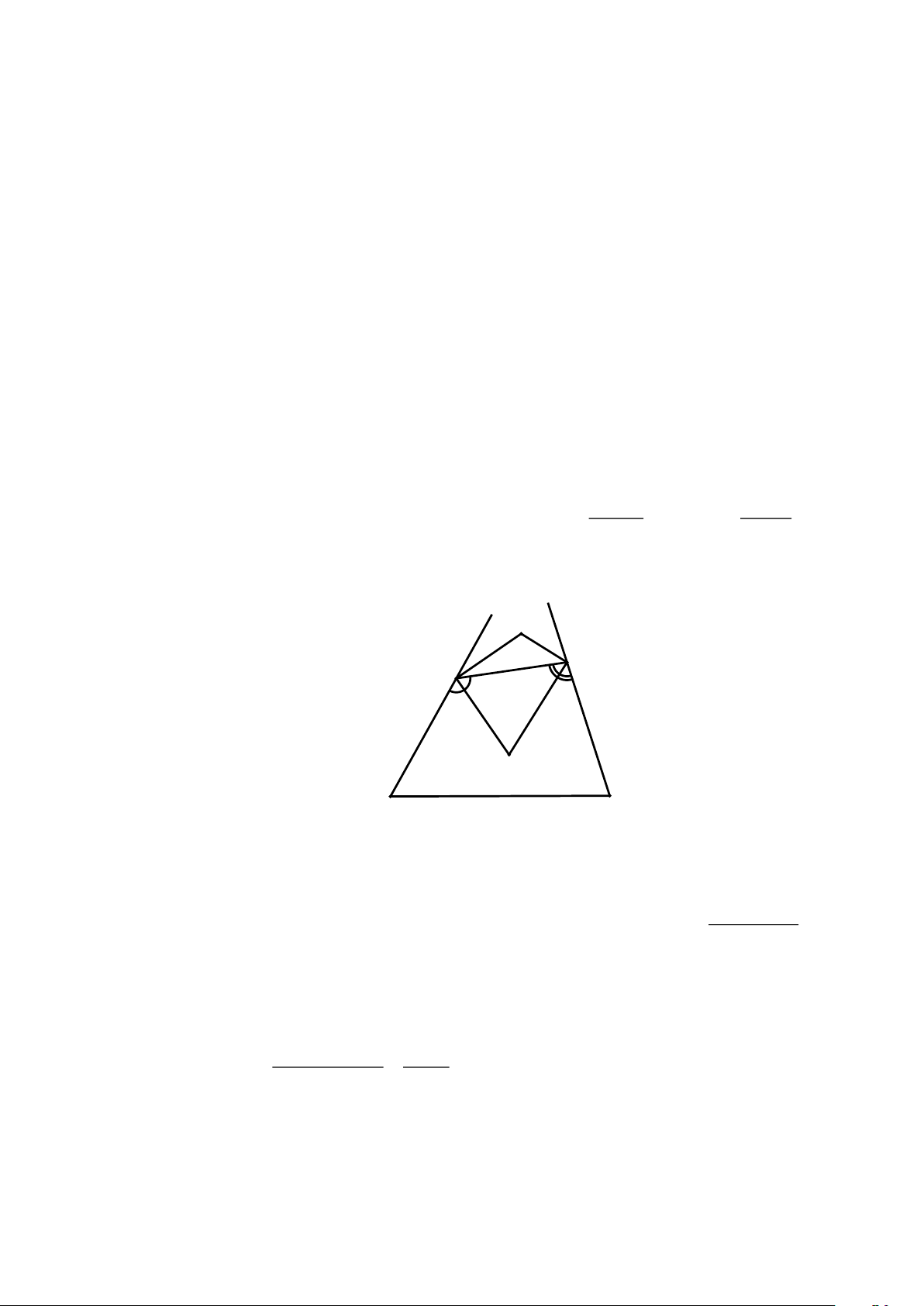
Bài 10. Cho tứ giác ABCD biết số đo các góc ,
A B,C, D tỉ lệ thuận với 5; 8; 13; và 10
a) Tính số đo các góc của tứ giác ABCD
b) Kéo dài hai cạnh AB và DC cắt nhau ở E , kéo dài hai cạnh AD và BC cắt nhau tại F .
Hai tia phân giác của góc AED và AFB cắt các cạnh CD và AB tại M và N . Chứng
minh O là trung điểm của đoạn MN . Lời giải B C A D A B C D a) Theo đề bài: = = = 5 8 13 10 A B C D
A + B + C + D 360
Áp dụng tính chất dãy tỉ số bằng nhau: = = = = = = 10 5 8 13 10 36 36 A = 10.5 = 50 B = 10 .8  = 80 C = 10 .13  =130 D = 10 .10  =100 E B N C O M A D F
b) Xét AED : AED = 180 − (EAD + EDA) =180−(50+100) = 30 Trang 12
ABF : AFB =180 − (FBA+ FAB)=180−(80+50) = 50 AFB 50
FM là tia phân giác của góc AFB nên: BFN = AFN = = = 25. 2 2
BNF là góc ngoài của BNF nên BNF = FAN + AFN = 50 + 25 = 75 .
ENM : EMN =180 − (MEN + ENM ) =180−(30+75) = 75 .
△EMN có: EMN = ENM = 75  ENM cân tại E , mà EO là đường phân giác.
 EO vừa là đường phân giác, vừa là đường trung tuyến.
 O là trung điểm MN .  HẾT  Trang 13