Bài Tập Toán 8 Tuần 10 Có Lời Giải Chi Tiết

PHIẾU BÀI TẬP TOÁN 8 TUẦN 10 Bài 1.
Phân tích các đa thức sau thành nhân tử. a) 2 2
1+ 2xy − x − y b) 2 2 2 2
a + b − c − d − 2ab + 2cd c) 3 3 a b −1 d) 2 2
x ( y − z) + y (z − x) + z(x − y) e) 2 x −15x + 36 f) 12 6 6 12
x − 3x y + 2y Bài 2.
Thực hiện phép tính chia các đa thức sau: ( đặt phép chia vào bài) a) ( 3 2
35x + 41x +13x − 5) : (5x − 2) b) ( 4 3 2 x − x + x − x + ) ( 2 6 16 22
15 : x − 2x + 3) c) ( 4 3 2 2 3
x − x y + x y − xy ) ( 2 2 : x + y ) d) ( 4 3 2 2 4 x − x y − x y + y ) ( 2 2 4 14 24 54
: x − 3xy − 9y ) Bài 3. Tìm x biết: a) 2 x −16x = 0 b) 3 2x − 50x = 0 c) 3 2
x − 4x − 9x + 36 = 0 d) 2 x − ( 2 5 4 x − 2x + ) 1 − 5 = 0 2
e) (x − ) −(x − )2 2 9 3 = 0 f) 3
x − 3x + 2 = 0 Bài 4. Cho hình thoi ABCD có 60o B =
. Kẻ AE ⊥ BC(E  BC), AF ⊥ CD(F CD) a) Chứng minh AE = AF
b) Chứng minh tam giác AEF là tam giác đều
c) Cho BD = 16cm . Tính chu vi của tam giác AEF
Bài 5. Xác định a, b để đa thức f(x)=x4-3x3+x2+ax+b chia hết cho đa thức g(x)=x2-3x+2? Bài 6.
Cho ∆ABC, M là điểm bất kì trên cạnh BC. Qua M kẻ đường thẳng song song với AC cắt AB ở
D, kẻ đường thẳng song song với AB cắt AC ở E. Gọi I là trung điểm của AM.
a) Chứng minh: 3 điểm D, I, E thẳng hàng.
b) Kẻ AK vuông góc với BC, tính góc DKE.
c) Khi M di chuyển trên cạnh BC thì điểm I di chuyển trên đường nào?
Bài 7. Cho tam giác ABC vuông cân tại A, AC = 4cm, M thuộc cạnh BC, D,E theo thứ tự là chân các
đường vuông góc kẻ thừ M đến AB, AC
a) Tứ giác ADME là hình gì? Tính chu vi của tứ giác đó?
b) Điểm M ở vị trí nào trên cạnh BC thì đoạn DE có độ dài nhỏ nhất? Trang 1
ĐÁP ÁN BÀI TẬP TĂNG CƯỜNG TOÁN 8 TUẦN 10
HƯỚNG DẪN GIẢI CHI TIẾT Bài 1.
Phân tích các đa thức sau thành nhân tử. a) 2 2
1+ 2xy − x − y b) 2 2 2 2
a + b − c − d − 2ab + 2cd c) 3 3 a b −1 d) 2 2
x ( y − z) + y (z − x) + z(x − y) e) 2 x −15x + 36 f) 12 6 6 12
x − 3x y + 2y . Lời giải a) 2 2
1+ 2xy − x − y b) 2 2 2 2
a + b − c − d − 2ab + 2cd 2 2
= 1− (x − 2xy + y ) = ( 2 2
a − ab + b ) − ( 2 2 2
c − 2cd + d ) 2 2 = − ( − )2
= (a − b) − (c − d ) 1 x y
= (a − b − c + d).(a − b − c + d)
= (1− x + y).(1+ x − y) c) 3 3 a b −1 d) 2 2
x ( y − z) + y (z − x) + z(x − y) 2 2
= (ab −1).(a b + ab +1) 2 2
= x (y − z) + y (z − x) + z(x − y) 2 2 2 2
= x y − x z + y z − xy + (x − y)
= xy(x − y) − z(x − y)(x + y) + (x − y)
= (x − y)[xy − z(x + y) +1] e) 2 x −15x + 36 f) 12 6 6 12
x − 3x y + 2y . 2
= x − 2x −12x + 36 12 6 6 6 6 12
= x − x y − 2x y + 2y
= (x − 2)(x −12) 6 6 6 6
= (x − y )(x − 2y ) Bài 2.
Thực hiện phép tính chia các đa thức sau: ( đặt phép chia vào bài) a) ( 3 2
35x + 41x +13x − 5) : (5x − 2) b) ( 4 3 2 x − x + x − x + ) ( 2 6 16 22
15 : x − 2x + 3) c) ( 4 3 2 2 3
x − x y + x y − xy ) ( 2 2 : x + y ) d) ( 4 3 2 2 4 x − x y − x y + y ) ( 2 2 4 14 24 54
: x − 3xy − 9y ) Lời giải a) ( 3 2
35x + 41x +13x − 5) : (5x − 2) b) ( 4 3 2 x − x + x − x + ) ( 2 6 16 22
15 : x − 2x + 3) Được thương là 2
7x + 9x dư là 31x − 5 Được thương là 2 x 4
− x + 21 dư là 4x - 48 Trang 2 c) ( 4 3 2 2 3
x − x y + x y − xy ) ( 2 2 : x + y ) d) ( 4 3 2 2 4 x − x y − x y + y ) ( 2 2 4 14 24 54
: x − 3xy − 9y ) 2 2 2 2 2 2 2
= x (x + y ) − xy(x + y ) : (x + y ) 2 2 2 2 2 2  
= (4x − 2xy + 6y ).(x − 3xy − 9y ) : (x − 3xy − 9y ) 2 2 2 2 2 2 2
= (x + y )(x − xy) : (x + y )
= 4x − 2xy + 6y 2 = x − xy Bài 3.
Tìm x biết: a) 2 x −16x = 0 b) 3 2x − 50x = 0 c) 3 2
x − 4x − 9x + 36 = 0 d) 2 x − ( 2 5 4 x − 2x + ) 1 − 5 = 0 2
e) (x − ) −(x − )2 2 9 3 = 0 f) 3
x − 3x + 2 = 0 Lời giải a) 2 x −16x = 0
x ( x −16) = 0 x = 0 x = 0    x 16 0  − = x =16 Vậy x 0  ;16 . b) 3 2x − 50x = 0 x ( 2 2 x − 25) = 0
2x ( x − 5)( x + 5) = 0 x = 0 x = 0 x 5 0   − =  x = 5   x + 5 = 0 x = 5 −   Vậy x  5 − ;0;  5 . c) 3 2
x − 4x − 9x + 36 = 0 2
x ( x − 4) − 9( x − 4) = 0 (x − )( 2 4 x − 9) = 0
(x − 4)(x −3)(x +3) = 0 x − 4 = 0 x = 4 x 3 0   − =  x = 3   x + 3 = 0 x = 3 −   Vậy x  3 − ;3;  4 Trang 3 d) 2 x − ( 2 5 4 x − 2x + ) 1 − 5 = 0 2
x + 8x − 9 = 0 2
x + 9x − x − 9 = 0
(x − )1(x +9) = 0 x −1 = 0 x =1    x 9 0  + = x = 9 − Vậy x  9 −  ;1 . 2
e) (x − ) −(x − )2 2 9 3 = 0
( 2x − − x+ )( 2 9
3 x − 9 + x − 3) = 0
( 2x − x− )( 2
6 x + x −12) = 0
(x + 2)(x −3)(x −3)(x + 4) = 0 x + 2 = 0 x = 2 − x 3 0   − =  x = 3   x + 4 = 0 x = 4 −   Vậy x  4 − ;− 2;  3 . f) 3
x − 3x + 2 = 0 3
x − x − 2x + 2 = 0 x ( 2 x − ) 1 − 2( x − ) 1 = 0 (x − )( 2
1 x + x − 2) = 0
(x − )1(x − )1(x + 2) = 0 x −1 = 0 x =1    x 2 0  + = x = 2 − Vậy x  2 − ;  1 .
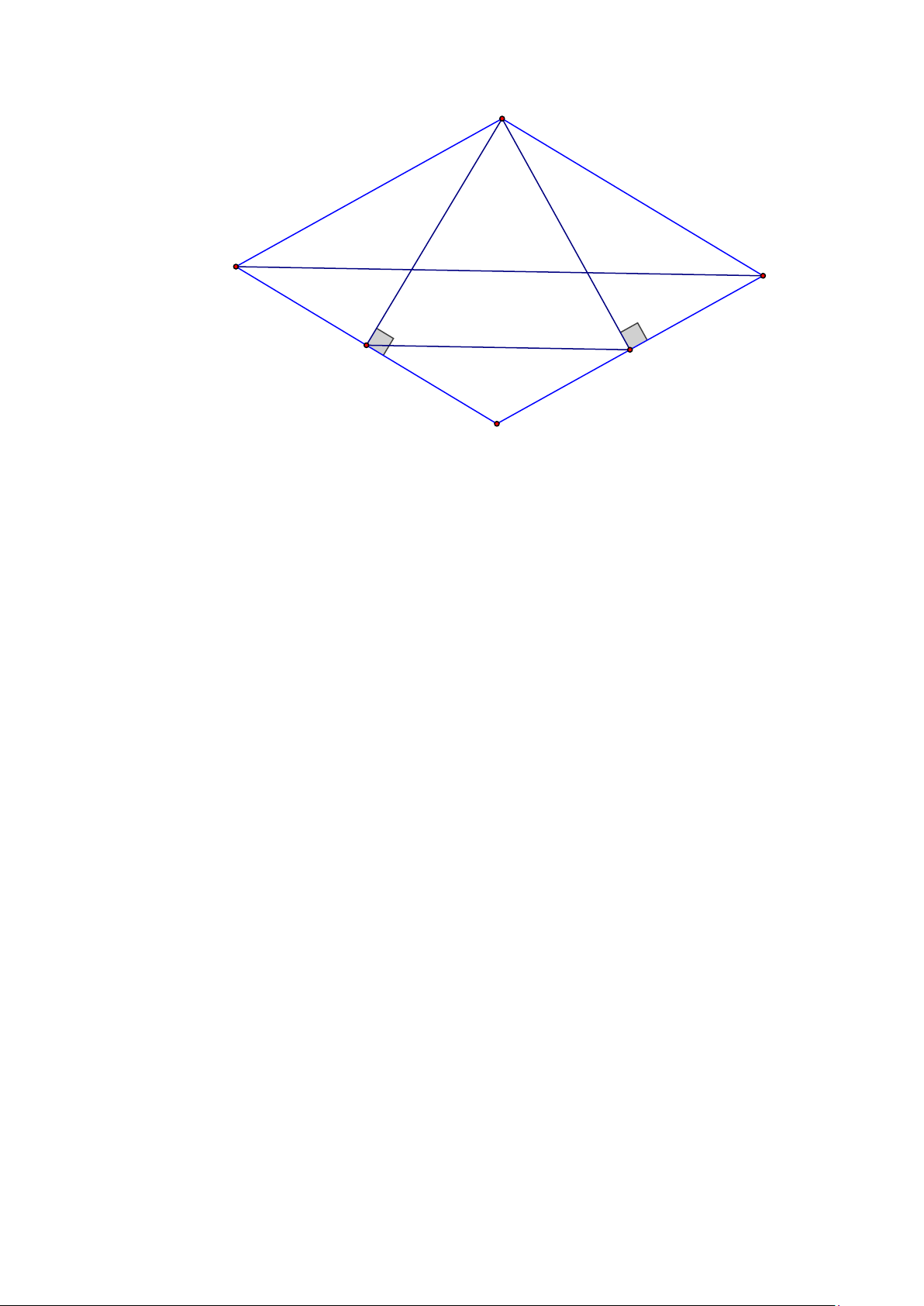
Bài 4. Cho hình thoi ABCD có 60o B =
. Kẻ AE ⊥ BC(E  BC), AF ⊥ CD(F CD) a) Chứng minh AE = AF
b) Chứng minh tam giác AEF là tam giác đều
c) Cho BD = 16cm . Tính chu vi của tam giác AEF Trang 4 Lời giải A B D E F C
a) Xét  AEB và  AFD có: 0
AEB = AFD = 90 (gt)
AB = AD (tứ giác ABCD là hình thoi)
B = D (tứ giác ABCD là hình thoi)
Vậy  AEB =  AFD (ch - gn)  AE = AF . b) Trong  AEB có 0 AEB =90 và 0 B = 60 nên 0 BAE = 30 Tương tự: 0 DAF = 30 Ta có: 0 0
B + DAB = 180  DAB = 120
Mà DAB = DAF + FAE + EAB 0 0 0 0
FAE = 120 − 30 − 30 = 60
Trong  AEF có AE = AF và 0 FAE = 60
Vậy  AEF là tam giác đều.
c) BA = BC   ACB cân tại B Mà 0 B = 60  A  BC đều
 AE vừa là đường cao, vừa là đường trung tuyến
 E là trung điểm của BC . Trang 5
Tương tự ta có F là trung điểm của CD
 EF là đường trung bình của  BCD 1
 EF = BD = 8cm 2
Chu vi  AEF là: 8 + 8 + 8 = 24 cm
Bài 5: Xác định a, b để đa thức f(x)=x4-3x3+x2+ax+b chia hết cho đa thức g(x)=x2-3x+2? Cách 1: Đặt tính chia x4-3x3+x2+ax+b x2-3x+2 x4-3x3+2x2 x2-1 -x2+ax+b -x2+3x-2 (a-3)x+b+2
Để chia hết thì đa thức dư phải bằng 0 với mọi giá trị của x, nên: a − 3 = 0 a = 3    b  + 2 = 0 b  = 2 −
Vậy với a=3; b=-2 thì f(x)=x4-3x3+x2+ax+b chia hết cho đa thức g(x)=x2-3x+2
Cách 2 ( Phương pháp hệ số bất định)
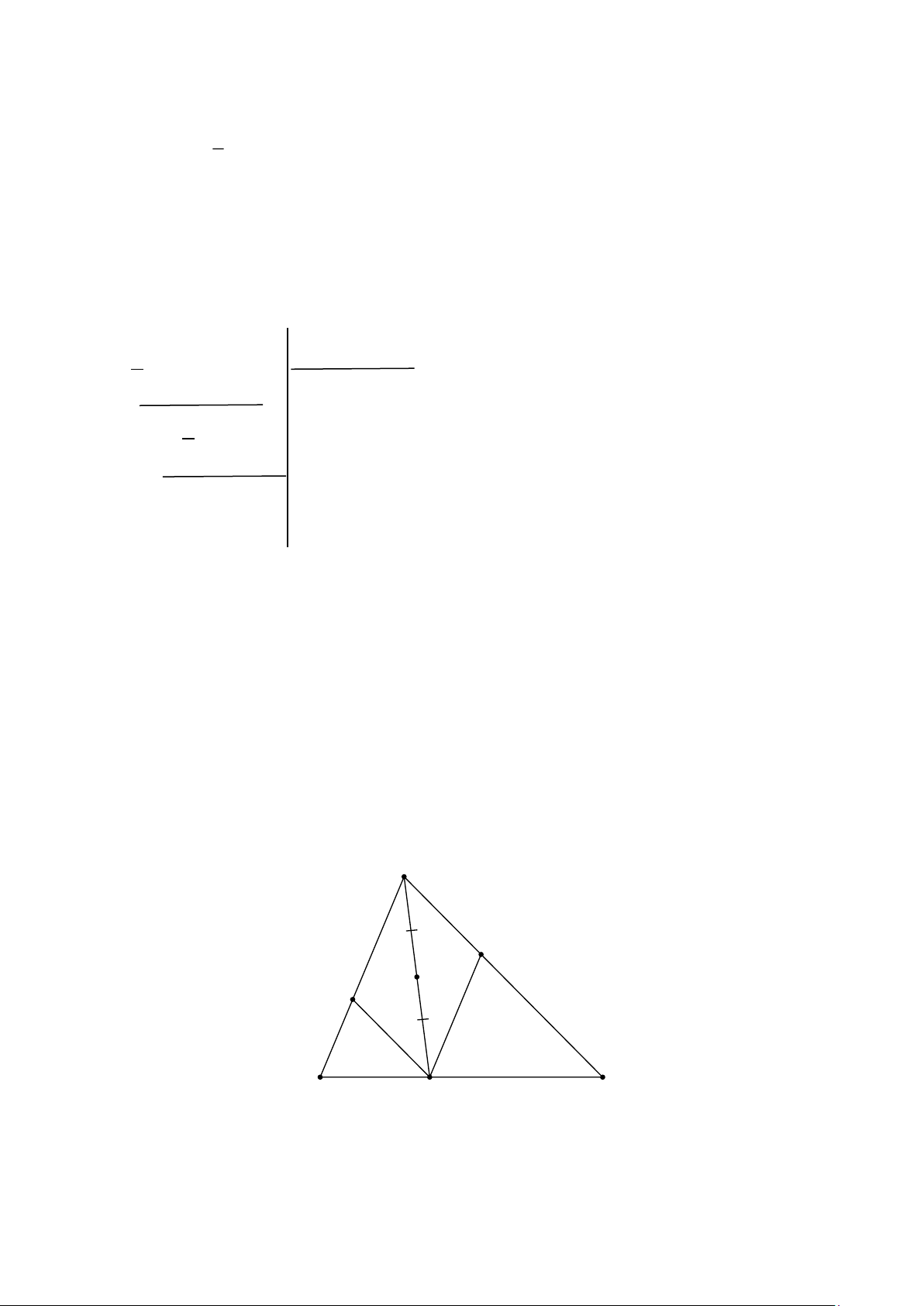
Cách 3( PP xét giá trị riêng) Bài 6. Hình vẽ : a) A E I D B C M Xét tứ giác ADME có:
* MD // AE (vì MD // AC mà E ϵ AC)
* ME // AD (vì ME // AB mà D ϵ AB) Trang 6
=> Tứ giác ADME là hình bình hành (dấu hiệu nhận biết)
Lại có: I là trung điểm của AM (gt); AM là đường chéo của hình bình hành ADME.
=> I đồng thời là trung điểm của DE (tính chất hình bình hành)
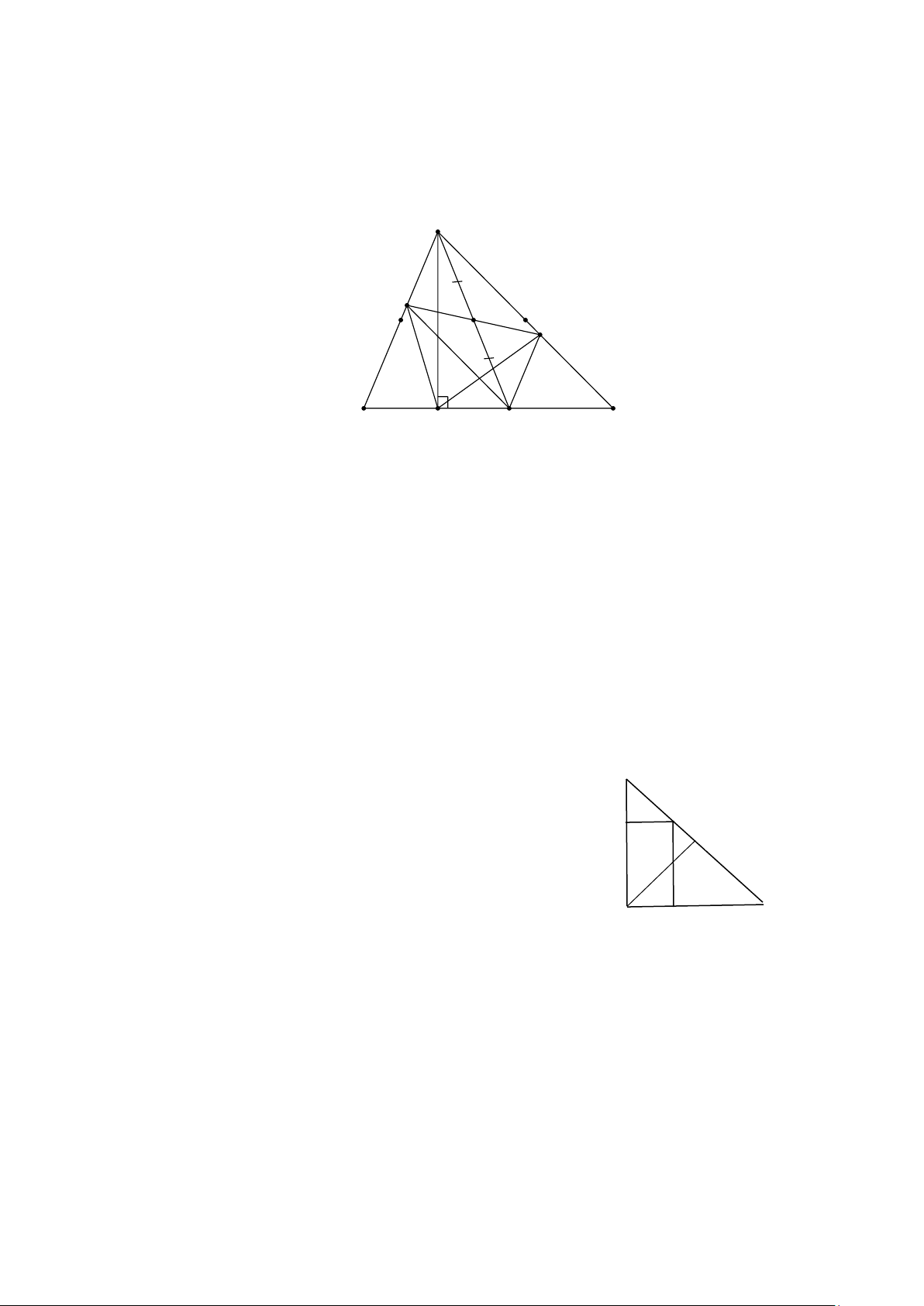
b) Khi M di chuyển trên BC thì số đo góc DKE thay đổi. (Nhờ ad kiểm tra lại đề) c) A D I P N E B C K M
Gọi N và P lần lượt là trung điểm của AB, AC.
Ta sẽ chứng minh N, I, P thẳng hàng.
Thật vậy: N, I lần lượt là trung điểm của AB, AM (cách vẽ, gt)
=> NI là đường trung bình của ∆ABM (định nghĩa đường trung bình)
=> NI // BM ( tính chất đường trung bình)
Hay NI // BC (vì M ϵ BC) (1)
Chứng minh tương tự, có : PI // BC (2)
Từ (1), (2) => IP và IN cùng // BC
=> N, I, P thẳng hàng (theo tiên đề Ơ-clit)
Vậy: do N, P cố định => khi M di chuyển trên BC thì I di chuyển trên NP (đường trung bình của tam giác ABC). Bài 7: B
a) Vì D,E theo thứ tự là chân các đường vuông góc
kẻ thừ M đến AB, AC nên: M 𝑀𝐷𝐴 ̂ = 900; 𝑀𝐸𝐴 ̂ = 900 D H Xét tứ giác ADME có: 𝑀𝐷𝐴 ̂ = 900; 𝑀𝐸𝐴 ̂ = 900 A C 𝐷𝐴𝐸 ̂ = 900 (gt) E
Suy ra tứ giác ADME là hình chữ nhật (DHNB)
∆ ABC vuông cân tại A => 𝐵̂ = 450
Suy ra: ∆ DBM vuông cân tại D ⇒ DM = DB
Chu vi hình chữ nhật ADME bằng :
2(AD + DM) = 2 ( AD + DB) = 2 AB = 2.4 = 8 (cm)
b. Gọi H là trung điểm của BC
Suy ra: AH ⊥ BC (tính chất tam giác cân) Trang 7
AM ≥ AH (dấu “=” xảy ra khi M trùng với H)
Tứ giác ADME là hình chữ nhật
⇒ AM = DE (tính chất hình chữ nhật) Suy ra: DE ≥ AH
Vậy DE = AH có độ dài nhỏ nhất khi điểm M là trung điểm của BC.  HẾT  Trang 8