Bài Tập Toán 8 Tuần 12 Có Lời Giải Chi Tiết

PHIẾU BÀI TẬP TOÁN 8 TUẦN 12
A. PHẦN CƠ BẢN (DÀNH CHO TẤT CẢ CÁC LỚP): Bài 1.
Hãy tìm đa thức A trong mỗi đẳng thức sau: 2 A 9x − 6x +1 2 2x − 3 6x − 7x − 3 4 2 2 x + x x a) = ; b) = ; c) = ; 3x +1 3x −1 A 12x + 4 2 5x + 5 A 3 x + 7 A 2 2 A 6x − 6y 2 3
x + 8 3x + 24x d) = ; e) = ; g) =
3x −1 12x − 4 2 4y − 4x 2x −1 A Bài 2.
Giải thích vì sao các cặp phân thức sau bằng nhau: 2 3 3 4 x y 5x y 2 x (x + 2) x a) = ; b) = ; 5 25xy x(x + 2)2 x + 2 2 3 − x x − 6x + 9 3 2 x − 4x −x − 2x c) = ; d) = ; 2 3 + x 9 − x 10 − 5x 5 Bài 3.
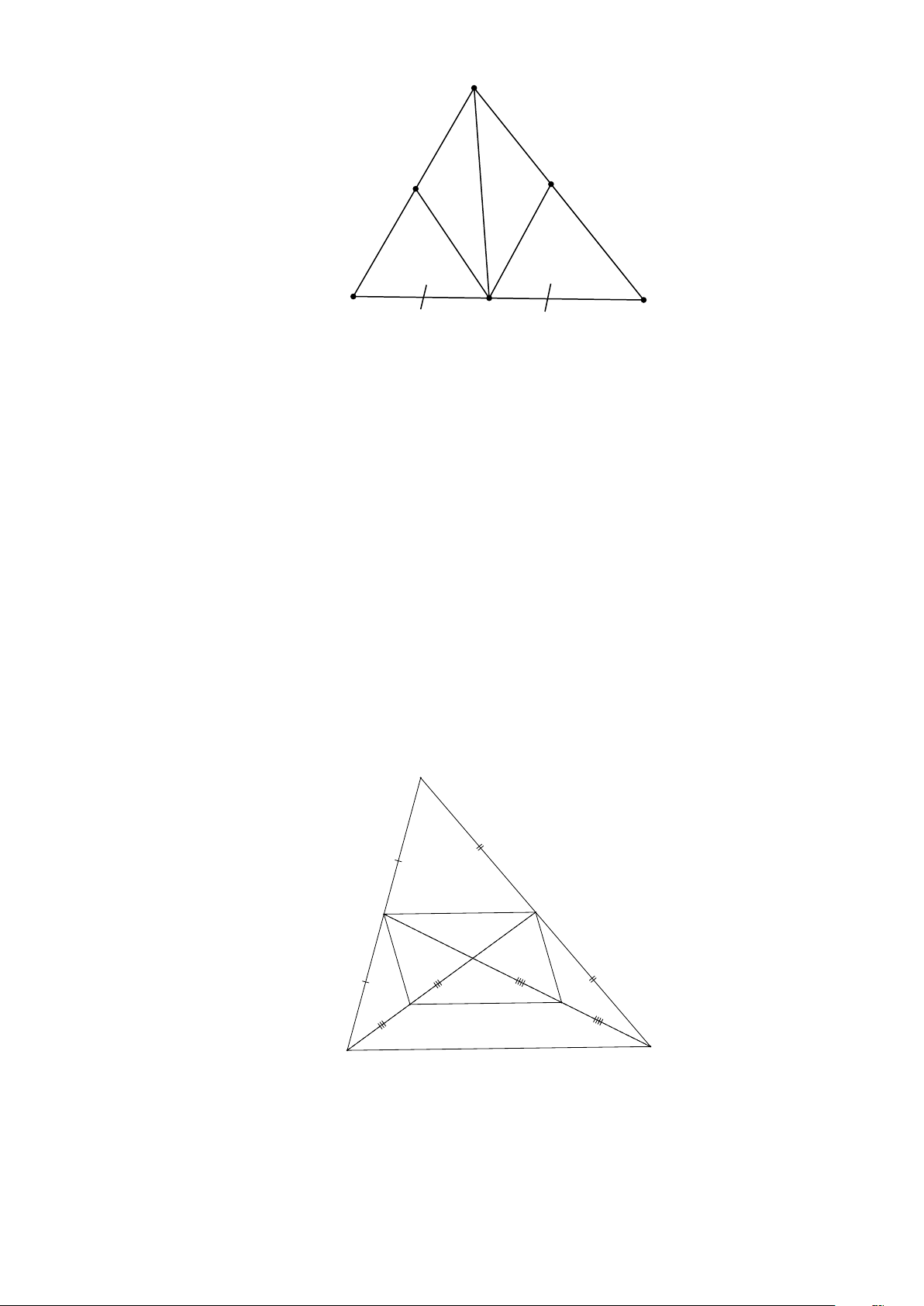
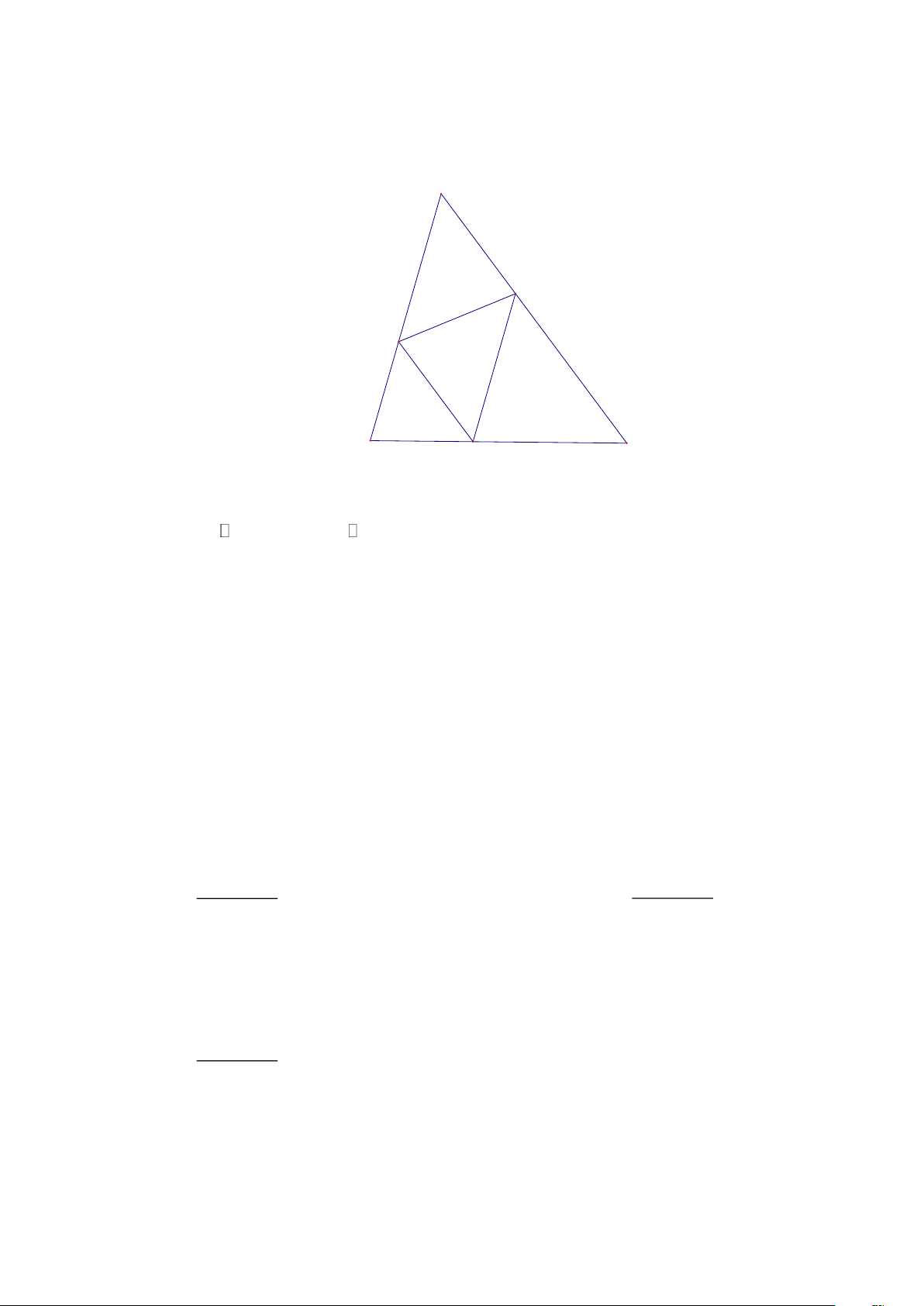
Cho tam giác ABC , trung tuyến AM . Qua kẻ đường thẳng song song với AC cắt AB ở E ,
qua M kẻ đường thẳng song song với AB cắt AC ở F .
a) Tứ giác AEMF là hình gì? Vì sao?
b) Tam giác ABC cần có thêm điều kiện gì thì tứ giác AEMF là hình chữ nhật. Bài 4.
Cho tam giác ABC các đường trung tuyến BD và CE cắt nhau ở G . Gọi H là trung điểm
của GB , K là trung điểm GC
a) Chứng minh tứ giác DEHK là hình bình hành
b) Tam giác ABC cần có thêm điều kiện gì thì tứ giác DEHK là hình chữ nhật ?
c) Nếu các đường trung tuyến BD và CE của tam giác ABC vuông góc với nhau thì tứ giác
DEHK là hình gì? Vì sao? Bài 5.
Cho tam giác ABC , điểm I nằm giữa B và C . Qua I vẽ đường thẳng song song với AB ,
cắt AC ở H . Qua I vẽ đường thẳng song song với AC , cắt AB ở K
a) Tứ giác AHIK là hình gì?
b) Điểm I ở vị trí nào trên cạnh BC thì tứ giác AHIK là hình thoi?
c) Tam giác ABC có điều kiện gì thì tứ giác AHIK là hình chữ nhật?
B. BÀI TẬP NÂNG CAO Bài 6.
Tính giá trị của biến x để. 1 2 x + 4x + 6 a) P =
đạt giá trị lớn nhất. b) Q = đạt giá trị nhỏ 2 x + 2x + 6 3 nhất. Bài 7. Chứng minh rằng. a) 5
n − n chia hết cho 30 với n  N . b) 4 2
n −10n + 9 chia hết cho 384 với mọi n lẻ n  N .
c) 10n +18n − 28 chia hết cho 27 với n  N .
ĐÁP ÁN BÀI TẬP TĂNG CƯỜNG TOÁN 8 Trang 1 TUẦN 12.
HƯỚNG DẪN GIẢI CHI TIẾT Bài 1.
Hãy tìm đa thức A trong mỗi đẳng thức sau: 2 A 9x − 6x +1 2 2x − 3 6x − 7x − 3 4 2 2 x + x x a) = ; b) = ; c) = ; 3x +1 3x −1 A 12x + 4 2 5x + 5 A 3 x + 7 A 2 2 A 6x − 6y 2 3
x + 8 3x + 24x d) = ; e) = ; g) =
3x −1 12x − 4 2 4y − 4x 2x −1 A Lời giải 2 A 9x − 6x +1 a) Ta có: = 3x +1 3x −1 ( x + )( 2 3 1 9x − 6x + ) 1  A = 3x −1 (3x + ) 1 (3x − )2 1  A = = (3x + ) 1 (3x − ) 2 1 = 9x −1 3x −1 Vậy 2 A = 9x −1 2 2x − 3 6x − 7x − 3 b) = A 12x + 4
(2x −3)(12x + 4)  A = 2 6x − 7x − 3
4(2x −3)(3x + ) 1  A = ( = x − )( x + ) 4 2 3 3 1 Vậy A = 4 4 2 2 x + x x c) Ta có = 2 5x + 5 A 2 x ( 2 5x + 5)  A = 4 2 x + x 2 5x ( 2 x + ) 1  A = = 5 2 x ( 2 x + ) 1 Vậy A = 5 3 x + 7 A d) Ta có =
3x −1 12x − 4 Trang 2
( 3x +7)(12x−4) 4( 3x +7)(3x− )1  A = = = 4( 3 x + 7) 3x −1 3x −1 Vậy A = ( 3 4 x + 7) 2 2 2 2 2 2 A 6x − 6y
2(6x − 6y ) 12(x − y ) 12(x + y)(x − y) e) Ta có =  A = = = 2 4y − 4x 4 y − 4x 4 − (x − y) −4(x − y)  A = 3 − (x + y) 2 3 3 2
x + 8 3x + 24x
(3x +24x)(2x− )1 3x(x +8)(2x− )1 g) =  A = = 2x −1 A 2 2 x + 8 x + 8
 A = 3x(2x − ) 1
Bài 2. Giải thích vì sao các cặp phân thức sau bằng nhau: 2 3 3 4 x y 5x y 2 x (x + 2) x a) = ; b) = ; 5 25xy x(x + 2)2 x + 2 2 3 − x x − 6x + 9 3 2 x − 4x −x − 2x c) = ; d) = ; 2 3 + x 9 − x 10 − 5x 5 Lời giải 2 3 3 4 x y 5x y 2 3 2 3 3 4 x y x y .5xy 5x y a) = vì = = 5 25xy 5 5.5xy 25xy 2 x (x + 2) x 2 x ( x + 2) 2
x ( x + 2) : x  ( x + 2) x b) = vì = = ; x(x + 2)2 x + 2 x ( x + 2)2
x ( x + 2)2 : x  ( x + 2) x + 2  2 3 − x x − 6x + 9 3 − x (3− x)(3− x) 2 x − 6x + 9 c) = vì = = ; 2 3 + x 9 − x 3 + x (3+ x)(3− x) 2 9 − x 3 2 x − 4x −x − 2x x − 4x x ( 2 3
x − ) x(x + )(x − ) −  ( x − ) 2 4 2 2 :
2  −x − 2x d) = vì = = = ; 10 − 5x 5 10 − 5x −5( x − 2) −5( x − 2) : −  ( x − 2) 5 
Bài 3. Cho tam giác ABC , trung tuyến AM . Qua kẻ đường thẳng song song với AC cắt AB ở E , qua
M kẻ đường thẳng song song với AB cắt AC ở F .
a) Tứ giác AEMF là hình gì? Vì sao?
b) Tam giác ABC cần có thêm điều kiện gì thì tứ giác AEMF là hình chữ nhật. Lời giải Trang 3 A F E B C M
a) Tứ giác AEMF có AE / /MF (gt) ME / /AF (gt)
tứ giác AEMF là hình bình hành
b) Hình bình hành AEMF là hình chữ nhật nếu 0
EAF = 90 (hình bình hành có một góc vuông).
Vậy tứ giác AEMF là hình chữ nhật khi tam giác ABC vuông tại A . Bài 4.
Cho tam giác ABC các đường trung tuyến BD và CE cắt nhau ở G . Gọi H là trung điểm
của GB , K là trung điểm GC
a) Chứng minh tứ giác DEHK là hình bình hành
b) Tam giác ABC cần có thêm điều kiện gì thì tứ giác DEHK là hình chữ nhật ?
c) Nếu các đường trung tuyến BD và CE của tam giác ABC vuông góc với nhau thì tứ giác
DEHK là hình gì? Vì sao? Lời giải A E D G K H B C
a) BD là đường trung tuyến của ABC nên D là trung điểm của AC (1)
CE là đường trung tuyến của ABC nên E là trung điểm của AB (2)
Từ (1) và (2)  DE là đường trung bình của ABC Trang 4 1
 DE = BC và DE / /BC 2
BGC có H là trung điểm của GB (gt) và K là trung điểm của GC
 HK là đường trung bình của BGC 1
 HK = BC và HK / /BC 2  1 
Tứ giác DEHK có DE / /HK (/ / BC) và DE = HK = BC    2 
 DEHK là hình bình hành
b) Tam giác ABC cần có thêm điều kiện gì thì tứ giác DEHK là hình chữ nhật ?
Vì DEHK là hình bình hành 1  1
HG = GD = HD và EG = GK = EK 2 2
Để tứ giác DEHK là hình chữ nhật thì HD = EK 1 1
 HD == EK  GE = GD và  GH = GK 2 2
GH = GK  2GH = 2GK  GB = GC
Xét GEB và GDC , có: G  E = GD  EGB = DGC G  B = GC   G
 EB = GDC( . c g.c)  BE = CD  2BE = 2CD
 AB = AC  ABC  cân tại A
Kết luận: Để tứ giác DEHK là hình chữ nhật thì ABC cân tại A .
c) Nếu các đường trung tuyến BD và CE của tam giác ABC vuông góc với nhau thì tứ giác
DEHK là hình gì? Vì sao?
BD ⊥ CE  HD ⊥ EK
Hình bình hành DEHK có HD ⊥ EK nên DEHK là hình thoi
Vậy nếu các đường trung tuyến BD và CE vuông góc với nhau thì tứ giác DEHK là hình thoi. Bài 5.
Cho tam giác ABC , điểm I nằm giữa B và C . Qua I vẽ đường thẳng song song với AB ,
cắt AC ở H . Qua I vẽ đường thẳng song song với AC , cắt AB ở K Trang 5
a) Tứ giác AHIK là hình gì?
b) Điểm I ở vị trí nào trên cạnh BC thì tứ giác AHIK là hình thoi?
c) Tam giác ABC có điều kiện gì thì tứ giác AHIK là hình chữ nhật? Lời giải A H K B C I
a) Tứ giác AHIK là hình gì?
Ta có: IK AH (gt) và IH AK (gt)
 AKIH là hình bình hành
b) Điểm I ở vị trí nào trên cạnh BC thì tứ giác AHIK là hình thoi?
Hình bình hành AHIK là hình thoi  AI là đường phân giác của góc A
Vậy nếu I là giao điểm của tia phân giác của góc A với cạnh BC thì AHIK là hình thoi
c) Tam giác ABC có điều kiện gì thì tứ giác AHIK là hình chữ nhật?
Hình bình hành AHIK là hình chữ nhật 0  A = 90 .
Vậy nếu tam giác ABC vuông tại A thì AHIK là hình chữ nhật Bài 6.
Tính giá trị của biến x để. 1 2 x + 4x + 6 a) P =
đạt giá trị lớn nhất. b) Q = đạt giá trị nhỏ 2 x + 2x + 6 3 nhất. Lời giải 1 a) P =
đạt giá trị lớn nhất. 2 x + 2x + 6 Ta có : 2 2
x + 2x + 6 = (x +1) + 5 Vì ( x + )2
1  0 với mọi giá trị của x Trang 6  (x + )2 1 + 5  5 1 1   1  P  2 (x +1) + 5 5 5  1
P có giá trị lớn nhất bằng khi x = −1 5 2 x + 4x + 6 b) Q =
đạt giá trị nhỏ nhất. 3
Ta có: x + x + = ( x + )2 2 4 6 2 + 2
(x + 2)  0 với mọi giá trị của x 2  (x + 2) + 2  0 2 (x + 2) + 2 2 3    P  3 3 2 2
Vậy gía trị nhỏ nhất của P bằng khi x = −2 3 Bài 7. Chứng minh rằng. a) 5
n − n chia hết cho 30 với n  N . b) 4 2
n −10n + 9 chia hết cho 384 với mọi n lẻ n  N .
c) 10n +18n − 28 chia hết cho 27 với n  N . Lời giải a) 5
n − n chia hết cho 30 với n  N . Ta có: 5 4
n − n = n(n −1) 2 2 2
= n(n −1)(n +1) = n(n −1)(n +1)(n − 4 + 5)
= n(n −1)(n +1)(n − 2)(n + 2) + 5n(n −1)(n +1)
Vì n(n −1)(n +1)(n − 2)(n + 2) là tích của 5 số tự nhiên liên tiếp
 n(n −1)(n +1)(n − 2)(n + 2) 2;3;5
 n(n −1)(n +1)(n − 2)(n + 2) 30 (1)
Mà n(n −1)(n +1) là tích của ba số tự nhiên liên tiếp
 n(n −1)(n +1) 2;3  n(n −1)(n +1) 6
5n(n −1)(n +1) 30 (2)
Từ (1) và (2)  n(n −1)(n +1)(n − 2)(n + 2) + 5n(n −1)(n +1) 30 Trang 7 Vậy 5
n − n chia hết cho 30 với n  N b) 4 2
n −10n + 9 chia hết cho 384 với mọi n lẻ n  N 4 2 4 2 2
Ta có: n −10n + 9 = (n − n ) − (9n − 9) = ( 2 n − ) 2
1 (n − 9) = (n −1)(n +1)(n − 3)(n + 3)
Với n lẻ , n = 2k +1(k  N )
 A = (2k − 2)2k(2k + 2)(2k + 4)
 A = (2k − 2)2k(2k + 2)(2k + 4)
= 16(k −1)k(k +1)(k + 2) 16 (I)
Và (k −1)k(k +1)(k + 2) 2;3; 4  A 24 (II)
Từ (I),(II)  A 384
c) 10n +18n − 28 chia hết cho 27 với n  N n n
Ta có : 10 +18n − 28 = (10 − 9n −1) + (27n − 27) Có (27n − 27) 27
10n − 9n = (9...9 + ) 1 − 9n −1   = 99...9 − 9n = 9(11...11− n) 27
 (10n +18n − 28) 27  HẾT  Trang 8