Bài Tập Toán 8 Tuần 13 Có Lời Giải Chi Tiết

PHIẾU BÀI TẬP TOÁN 8 TUẦN 13 Bài 1.
Rút gọn các phân thức sau:. 5x 4xy 2 3 21x y a) ; b) ( y  0); c) (xy  0); 10 2y 6xy 2x + 2y 5x − 5y 15
− x(x − y) d) ; e) (x  y); f) x  y ; 4 3x − 3y 3( y − x) ( ) Bài 2.
Rút gọn các phân thức sau:. 2 x −16 2 x + 4x + 3
15x ( x + y)3 a)
x  0, x  4 ; b) (x  3 − ) ; c) y x + y  0 ; 2 ( ( ) ) 2 ( ) 4x − x 2x + 6
5y ( x + y)
5( x − y) − 3( y − x)
2x + 2y + 5x + 5y 2 x − xy d) x  y ; e)
(x  −y); f)
x  y, y  0 ; 2 ( ) 10( x − y) ( )
2x + 2y − 5x − 5y 3xy − 3y Bài 3.
Rút gọn, rồi tính giá trị các phân thức sau:.
(2x +2x)(x−2)2 2 1 3 2 2
x − x y + xy a) A = ( với x = ; b) B =
với x = −5; y = 10 ; 3
x − 4x)(x + ) 1 2 3 3 x + y
Bài 4. Cho hình bình hành ABCD có 60o A =
, AD = 2AB . Gọi M và N lần lượt là trung điểm của
AD và BC .
a) Chứng minh tứ giác MNCD là hình thoi.
b) Từ C kẻ đường thẳng vuông góc với MN tại E và cắt AB tại F . Chứng minh E là trung điểm của CF .
c) Chứng minh F , N , D thẳng hàng.
d) Chứng minh tam giác CFM là tam giác đều.
Bài 5. Cho tam giác ABC đều. Gọi E , F , D lần lượt là trung điểm của các cạnh AB , AC , BC . Trên tia
đối của tia FE lấy điểm K sao cho FK = FA . Gọi N là trung điểm của EC , M là trung điểm
của ED . Chứng minh rằng:
a) Tứ giác AECK là hình chữ nhật.
b) BF cắt ED tại M . c) MN // EK .
B. BÀI TẬP NÂNG CAO ( DÀNH THÊM CHO LỚP M VÀ KHUYẾN KHÍCH HỌC SINH CÁC LỚP KHÁC)
Bài 6. Chứng minh rằng giá trị của phân thức sau không phụ thuộc vào giá trị của biến x và y:
( 2x +a)(1+a) 2 2 + a x +1 2
3xy − 3x + 2y − 2 9x −1 1  ( − x  ; y  1 2  
x − a)(1− a) 2 2 + a x +1 y −1 3x −1  3  2
ax − a axy + ax − ay − a (x + a)2 2 − − ( x x  1 − ; y  − ) 1 x +1 y +1 2x + a Trang 1 2 2 x − y
2ax − 2x − 3y + 3ay
(x + y)(ax −ay)
4ax + 6x + 9y + 6ay
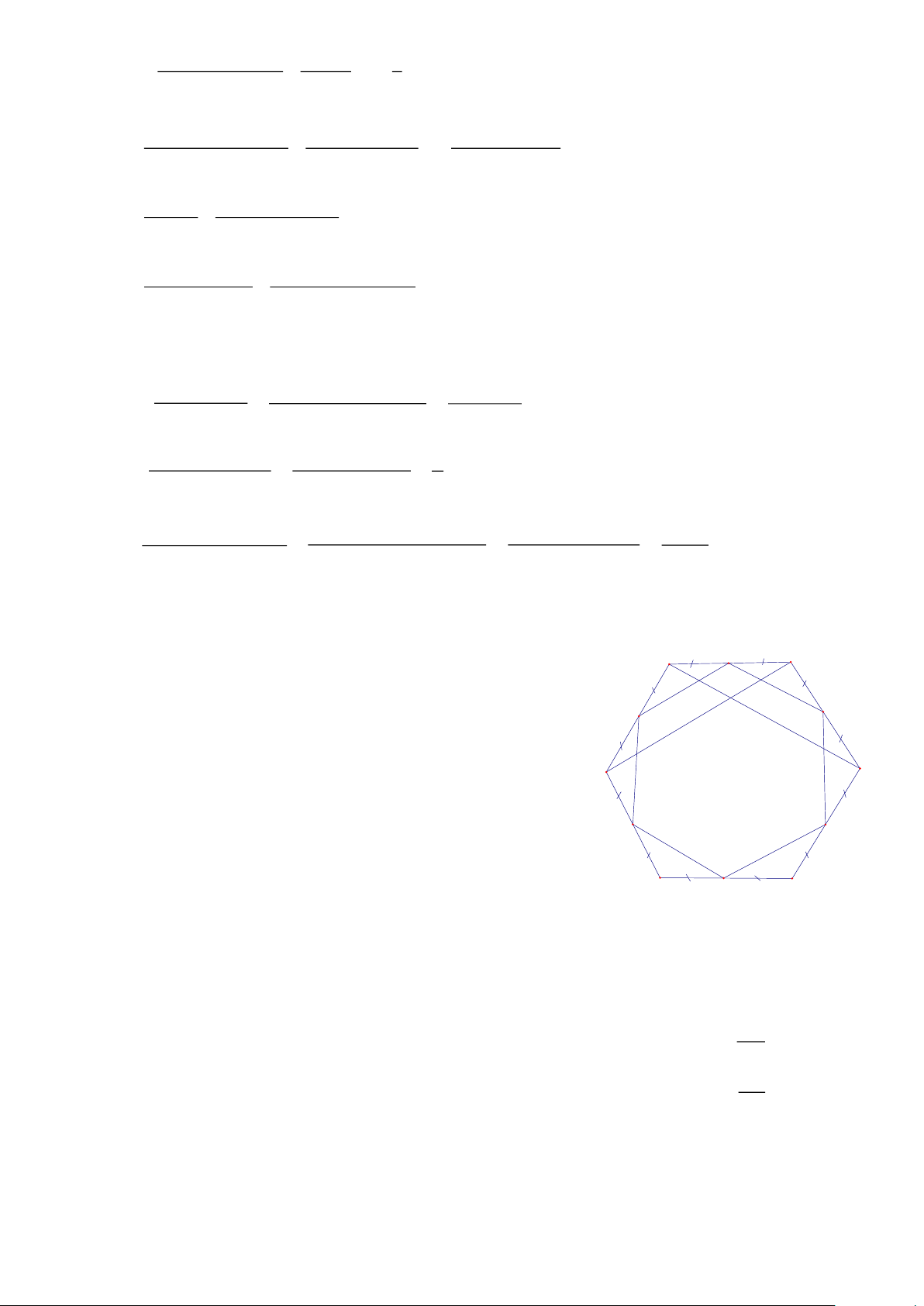
Bài 7. Cho lục giác đều ABCDEF. Gọi A’,B’,C’,D’,E’,F’lần lượt là trung điểm của các cạnh AB, BC, CD,
DE, EF, FA.CMR: A’B’C’D’E’F’ là lục giác đều. Trang 2
ĐÁP ÁN BÀI TẬP TĂNG CƯỜNG TOÁN 8 TUẦN 13
HƯỚNG DẪN GIẢI CHI TIẾT Bài 1.
Rút gọn các phân thức sau:. 5x 4xy 2 3 21x y a) ; b) ( y  0); c) (xy  0); 10 2y 6xy 2x + 2y 5x − 5y 15
− x(x − y) d) ; e) (x  y); f) x  y ; 4 3x − 3y 3( y − x) ( ) Lời giải 5x x 4xy 2 3 2 21x y 7xy a) = ; b) = 2x ; c) = ; 10 2 2y 6xy 2 2x + 2y x + y 5x − 5y 5 1
− 5x(x − y) 1
− 5x(x − y) d) = ; e) = ; f) = = 5x ; 4 2 3x − 3y 3 3( y − x) 3 − (x − y) Bài 2.
Rút gọn các phân thức sau:. 2 x −16 2 x + 4x + 3
15x ( x + y)3 a)
x  0, x  4 ; b) (x  3 − ) ; c) y x + y  0 ; 2 ( ( ) ) 2 ( ) 4x − x 2x + 6
5y ( x + y)
5( x − y) − 3( y − x)
2x + 2y + 5x + 5y 2 x − xy d) x  y ; e) (x  −y); f)
x  y, y  0 ; 2 ( ) 10( x − y) ( )
2x + 2y − 5x − 5y 3xy − 3y Lời giải 2 x −16 (x + 4)(x − 4) x + 4 a) = = − ; 2 4x − x −x(x − 4) x 2
x + 4x + 3 ( x + ) 1 ( x + 3) x +1 b) = = ; 2x + 6 2( x + 3) 2
15x ( x + y)3 3x( x + y) c) = ;
5y ( x + y)2 y
5( x − y) − 3( y − x) 5(x − y) + 3(x − y) 8(x − y) 4 d) = = = ; 10( x − y) 10( x − y) 10( x − y) 5
2x + 2y + 5x + 5y 7x + 7 y 7( x + y) 7 − e) = = = ;
2x + 2y − 5x − 5y 3 − x − 3y 3 − (x + y) 3 Trang 3 2 x − xy
x ( x − y) 1 f) = = ; 2 3xy − 3y
3x ( x − y) 3 Bài 3.
Rút gọn, rồi tính giá trị các phân thức sau:.
(2x +2x)(x−2)2 2 1 3 2 2
x − x y + xy a) A = ( với x = ; b) B =
với x = −5; y = 10 ; 3
x − 4x)(x + ) 1 2 3 3 x + y Lời giải
(2x +2x)(x−2)2 2 1 a) A = ( với x = ; 2
x − 4x)(x + ) 1 2 ( 2
2x + 2x)(x − 2)2 2x(x + ) 1 ( x − 2)2 2x ( x + ) 1 ( x − 2)2 2( x − 2) A = ( = = = ; 3
x − 4x)(x + ) 1 x ( 2 x − 4)(x + ) 1
x ( x − 2)( x + 2)( x + ) 1 x + 2 1
Thay x = vào A ta được: 2  1  2 − 2    2  6 − A = = . 1 5 + 2 2 6 − 1 Vậy A = tại x = . 5 2 3 2 2
x − x y + xy b) B =
với x = −5; y = 10 ; 3 3 x + y
x − x y + xy x ( 2 2 3 2 2
x − xy + y ) x B = = = . 3 3 x + y (x + y)( 2 2
x − xy + y ) x + y
Thay x = −5; y = 10 vào B ta được: 5 − 5 − B = = = 1 − . 5 − +10 5
Vậy B = −1 tại x = −5; y = 10 .
Bài 4. Cho hình bình hành ABCD có 60o A =
, AD = 2AB . Gọi M và N lần lượt là trung điểm của AD và BC .
a) Chứng minh tứ giác MNCD là hình thoi.
b) Từ C kẻ đường thẳng vuông góc với MN tại E và cắt AB tại F . Chứng minh E là trung điểm của CF .
c) Chứng minh F , N , D thẳng hàng.
d) Chứng minh tam giác CFM là tam giác đều. Trang 4 Lời giải
a) Ta có ABCD là hình bình hành
 AB = CD, BC = AD và AB //= CD , BC // AD .
Mà BC = 2AB và M và N lần lượt là trung điểm của AD và BC .  1
AB = CD = AM = MD = BN = NC = BC và MD // NC . 2
Xét tứ giác MNCD có:
MD = NC (chứng minh trên)
MD // NC (chứng minh trên)
 MNCD là hình bình hành
Lại có NC = CD (chứng minh trên)
 MNCD là hình thoi.
b) Chứng minh tương tự câu a ta có ABNM là hình thoi
 AB // MN hay BF // NE Xét BCF có:
N là trung điểm của BC BF // NE
 E là trung điểm của FC c) Gọi '
N là giao điểm của ME và FD  ' N E // CD .
Mặt khác NE // CD (chứng minh trên)  ' N E  NE (1) Xét FCD có:
E là trung điểm của FC Trang 5 ' N E // CD  '
N là trung điểm của FD (2) Từ (1) và (2) suy ra ' N  N
Hay F , N , D thẳng hàng.
d) Ta có ME // CD ( MNCD là hình thoi)
ME ⊥ FC (giả thiết)
 CD ⊥ FC hay 90o FCD = (3)
Xét hình bình hành ABCD có 60o A =  = = 60o NCD A
(tính chất hình bình hành)
Lại có MNCD là hình thoi (câu a)
 CM là phân giác NCD  1 o
BCM = DCM = NCD = 30 (4) 2 Từ (3) và (4) suy ra 60o FCM = . Xét FCM có:
E là trung điểm của FC (câu b)
ME ⊥ FC (giả thiết)
 FCM cân tại M Lại có 60o FCM = (chứng minh trên)
Vậy FCM là tam giác đều.
Bài 5. Cho tam giác ABC đều. Gọi E , F , D lần lượt là trung điểm của các cạnh AB , AC , BC . Trên tia
đối của tia FE lấy điểm K sao cho FK = FA . Gọi N là trung điểm của EC , M là trung điểm
của ED . Chứng minh rằng:
a) Tứ giác AECK là hình chữ nhật.
b) BF cắt ED tại M . c) MN // EK . Trang 6 Lời giải
a) Xét ABC đều, có E , F , D lần lượt là trung điểm của các cạnh AB , AC , BC  1
AE = BE = FA = FC = DB = DC = BC và EF là đường trung bình ABC và 2  1
EF // BC và FE = BC . 2  1
FE = FA = BC 2
 FE = FK (= FA)
Hay F là trung điểm của EK
Xét tứ giác AKCE có
AC cắt EK tại F
F là trung điểm của AC
F là trung điểm của EK
 AKCE là hình bình hành.
Lại có ABC đều
 CE là đường trung tuyến đồng thời là đường cao ứng với AB  EC ⊥ AB Hay 90o AEC =
Vậy AKCE là hình chữ nhật. 1
b) Chứng minh tương tự câu a ta được DE = BE = BC 2 1
Xét tứ giác BDFE có BD = DE = FE = BE = BC 2 Trang 7
 BDFE là hình thoi
hai đường chéo BF, ED cắt nhau tại trung điểm mỗi đường
Mà M là trung điểm của ED
 BF cắt ED tại M c) Xét CDE có
M là trung điểm của ED
N là trung điểm của EC
 MN là đường trung bình CDE  MN // CD
Lại có FE // CD hay EK // CD  MN // EK .
Bài 6. Chứng minh rằng giá trị của phân thức sau không phụ thuộc vào giá trị của biến x và y:
( 2x +a)(1+a) 2 2 + a x +1 a) ( 2
x − a)(1− a) 2 2 + a x +1 2
3xy − 3x + 2y − 2 9x −1 1  b) − x  ; y  1   y −1 3x −1  3  2
ax − a axy + ax − ay − a c) − (x  1 − ; y  − ) 1 x +1 y +1 (x + a)2 2 − x d) 2x + a 2 2 x − y e) (
x + y)(ax − ay)
2ax − 2x − 3y + 3ay f)
4ax + 6x + 9y + 6ay Lời giải ( 2 2 2 2 2
x + a)(1+ a) 2 2 + a x +1 2 2 2 2 2
x + ax + a + a + a x +1
(x + )1+a(x + )1+a (x + )1 a) ( = = 2
x − a)(1− a) 2 2 + a x +1 2 2 2 2 2
x − ax − a + a + a x +1
( 2x + )1−a( 2x + ) 2 1 + a ( 2 x + ) 1
( 2x + )1( 2a +a+ ) 2 1 a + a +1 = ( = 2 x + ) 1 ( 2 a − a + ) 2 1 a − a +1 Trang 8 2
3xy − 3x + 2y − 2 9x −1 1  b) − x  ; y  1   y −1 3x −1  3  3x ( y − ) 1 + 2( y − ) 1 (3x − ) 1 (3x + ) 1
(3x + 2)( y − ) 1 = − = − (3x + )
1 = 3x + 2 − 3x −1 = 1 y −1 3x −1 y −1 2
ax − a axy + ax − ay − a c) − (x  1 − ; y  − ) 1 x +1 y +1 a ( x − ) 1 ( x + ) 1 ax ( y + ) 1 − a ( y + ) 1 = − x +1 y +1
= ax − a − ax + a = 0 (x + a)2 2 − x
(x + a − x)(x + a + x) a(2x + a) d) = = = a 2x + a 2x + a 2x + a 2 2 x − y
(x + y)(x − y) 1 e) ( = =
x + y)(ax − ay) a( x + y)(x − y) a
2ax − 2x − 3y + 3ay 2x(a − ) 1 + 3y (a − ) 1
(a − )1(2x +3y) a −1 f) = = =
4ax + 6x + 9y + 6ay
2x(2a + 3) + 3y (3+ 2a) (2a + 3)(2x + 3y) 2a + 3
Bài 7. Cho lục giác đều ABCDEF.Gọi A’,B’,C’,D’,E’,F’lần lượt là trung điểm của các cạnh AB, BC, CD,
DE,EF, FA.CMR: A’B’C’D’E’F’ là lục giác đều. A' B A j Lời giải F' B'
Ta có ABCDEF là lục giác đều
AB = BC = CD = DE = EF = FA F C   
FAB = ABC = BCD = CDE = DEF = EFA E' C'
Vì A’,B’,C’,D’,E’,F’lần lượt là trung điểm của các cạnh AB, BC, CD, DE, EF, FA E D' D
AA’ = A’B = BB’ = B’C = CC’ = C’D = DD’ =
D’E = EE’ = E’F = FF’ = F’A Ta có: F  AB = A  BC ( .
c g.c)  AC = BF ( ) 1  AC A' B ' =  Xét FAB; A
 BC có A’B’; A’F’ lần lượt là đường trung bình nên : 2  (2) BF A'F ' =  2
Từ (1) và (2) ta có A’B’ = A’F’
CM tương tự ta suy ra: A’B’ = B’C’ = C’D’ = D’E’ = E’F’ = F’A’(3)
Lại có các tam giác A’BB’, A’AF’, F’ FE’ là các tam giác cân bằng nhau từng đôi một nên: Trang 9
BA' B ' = AA' F ' = AF ' A' = FF ' E '
 B ' A' F ' = A' F ' E '
CM tương tự ta suy ra: B ' A' F ' = A' F ' E ' = A' B 'C ' = B 'C ' D ' = C ' D ' E ' = D ' E ' F '(4)
Từ (3) và (4) suy ra A’B’C’D’E’F’ là lục giác đều.  HẾT  Trang 10