Bài Tập Toán 8 Tuần 14 Có Lời Giải Chi Tiết

PHIẾU BÀI TẬP TOÁN 8 TUẦN 14 Bài 1.
Quy đồng mẫu các phân thức. 7x −1 3− 2x 2x −1 x +1 a) và . b) và . 2 2x + 6x 2 x − 9 2 x − x 2 2− 4x + 2x x −1 2x 2 7 4 x − y c) ; và . d) ; và . 3 x +1 2 x − x +1 x +1 5x x − 2y 2 2 8y − 2x 2 6x 3x 2 e) ; và . 3 2
x + 6x +12x + 8 2 x + 4x + 4 2x + 4 Bài 2.
Quy đồng mẫu các phân thức. 7x −1 3− 2x 2x −1 x +1 a) và . b) và . 2 2x + 6x 2 x − 9 2 x − x 2 2− 4x + 2x x −1 2x 2 7 4 x − y c) ; và . d) ; và . 3 x +1 2 x − x +1 x +1 5x x − 2y 2 2 8y − 2x 2 6x 3x 2 e) ; và . 3 2
x + 6x +12x + 8 2 x + 4x + 4 2x + 4 Bài 3.
Diện tích hình vuông tăng thêm bao nhiêu phần trăm nếu mỗi cạnh của nó tăng thêm 20% ? Bài 4.
Cho hình vuông ABCD có cạnh bằng 16 cm, O là giao điểm của AC và BD . Gọi M , N , P
, Q lần lượt là trung điểm của OA , OB , OC , OD .
a) Tứ giác MNPQ là hình gì? Vì sao?
b) Tính diện tích phần hình vuông ABCD nằm ngoài tứ giác MNPQ . Bài 5.
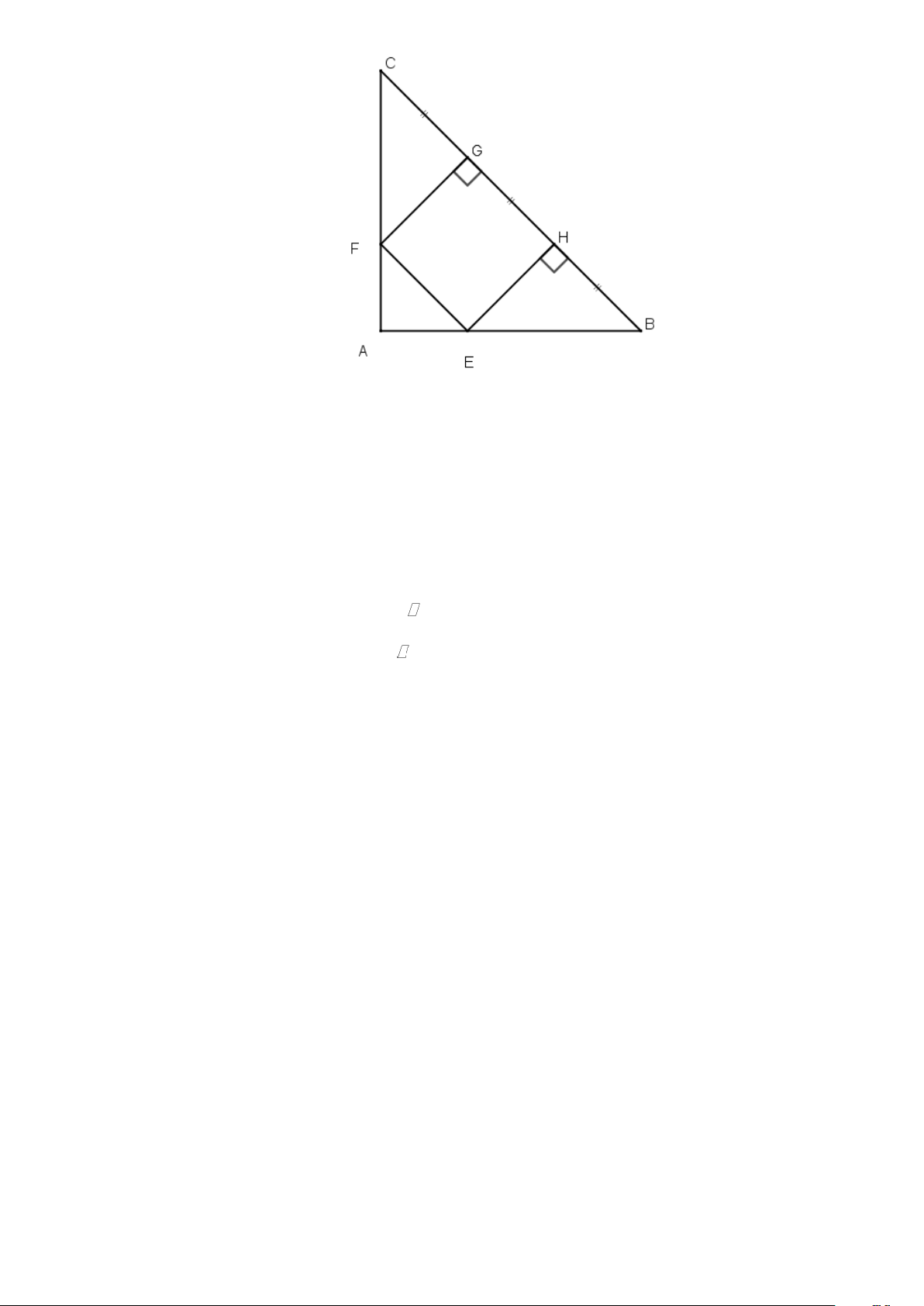
Cho tam giác ABC vuông cân tại A . Trên cạnh BC lấy các điềm H ,G sao cho
BH = HG = GC . Qua H và G kẻ các đường vuông góc với BC , chúng cắt AB và AC theo
thứ tự ở E và F . Tú giác EFGH là hình gì? Vì sao? Bài 6.
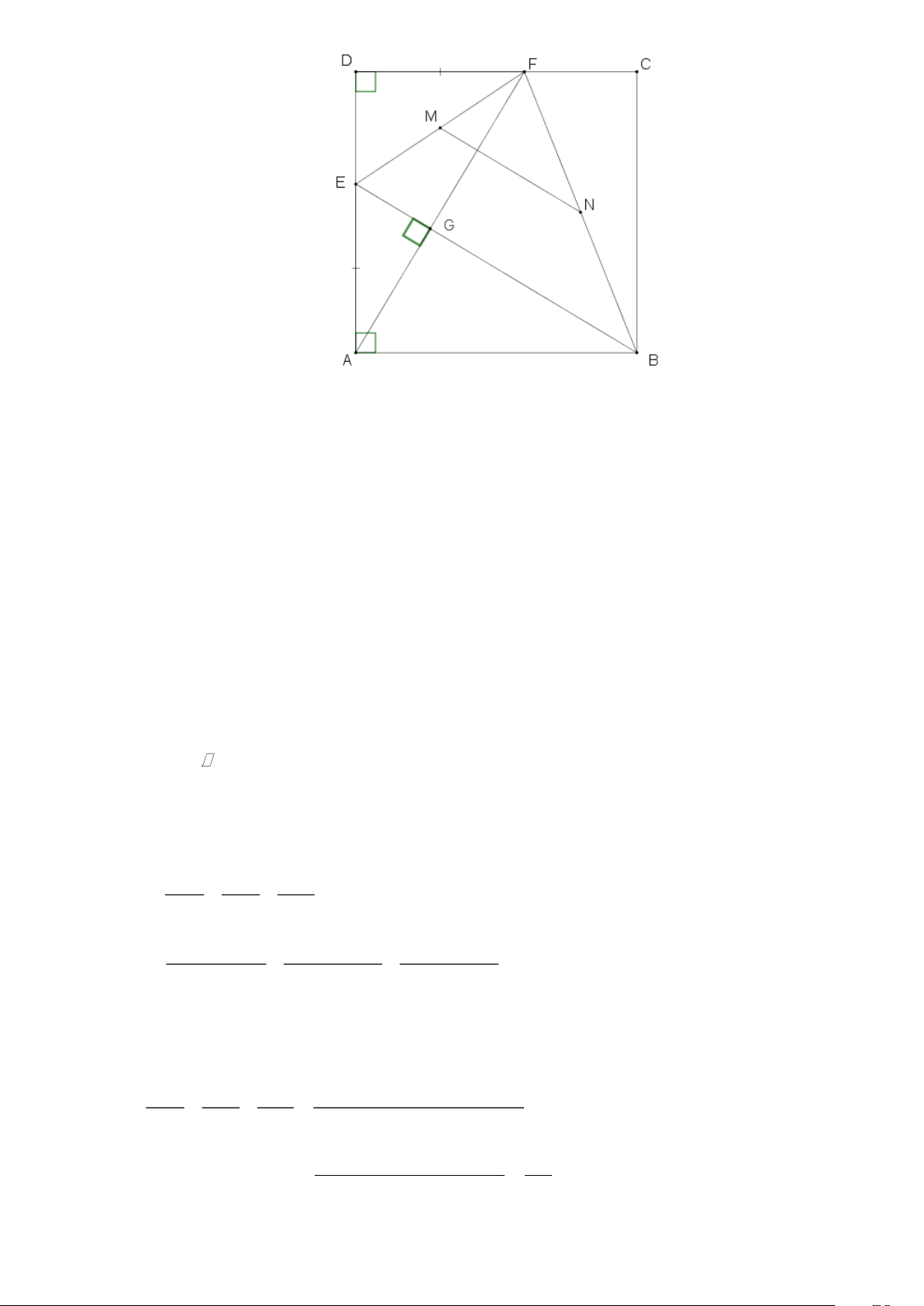
Cho hình vuông ABCD . Trên các cạnh AD , DC lần lượt lấy các điểm E , F sao cho
AE = DF . Goi M , N lần lượt là trung diềm của EF, BF .
a) Chứng minh các tam giác ADF và BAE bằng nhau.
b) Chúng minh MN vuông góc với AF .
B. BÀI TẬP NÂNG CAO ( DÀNH THÊM CHO LỚP M VÀ KHUYẾN KHÍCH HỌC SINH CÁC LỚP KHÁC )
Bài 7. Chứng minh giá trị các biểu thức sau không phụ thuộc vào giá trị của x , y , z x − y y − z z − x 1 1 1 a) + + . b) + + . xy yz zx
(x − y)(y − z) ( y − z)(z − x) (z − x)(x − y) 1 1 2 4 8 16
Bài 8. Tính tổng A = + + + + − . 2 4 8 16
1− x 1+ x 1+ x 1+ x 1+ x 1− x Trang 1
ĐÁP ÁN BÀI TẬP TĂNG CƯỜNG TOÁN 8 TUẦN 14
HƯỚNG DẪN GIẢI CHI TIẾT Bài 1.
Quy đồng mẫu các phân thức. 7x −1 3− 2x a) và . 2 2x + 6x 2 x − 9 2x −1 x +1 b) và . 2 x − x 2 2− 4x + 2x x −1 2x 2 c) ; và . 3 x +1 2 x − x +1 x +1 7 4 x − y d) ; và . 5x x − 2y 2 2 8y − 2x 2 6x 3x 2 e) ; và . 3 2
x + 6x +12x + 8 2 x + 4x + 4 2x + 4 Lời giải 7x −1 3− 2x a) và . 2 2x + 6x 2 x − 9 7x −1 2 7x −1
(7x −1)(x − 3) 7x − 22x + 3 = = = 2 2x + 6x 2 ( x x + 3) 2 (
x x + 3)(x − 3) 2 (
x x + 3)(x − 3) 3− 2x 2 3− 2x (3− 2 ) x 2x 4 − x + 6x = = = . 2 x − 9
(x − 3)(x + 3) 2 (
x x − 3)(x + 3) 2 (
x x + 3)(x − 3) 2x −1 x +1 b) và . 2 x − x 2 2− 4x + 2x 2x −1 2x −1 2(2x − ) 1 (1− x) 2 4 − x + 6x − 2 = = = 2 x − x 2 2 ( x 1− ) x 2 ( x 1− ) x (1− ) x x +1 2 x +1 ( x x +1) x + x = = = 2 2− 4x + 2x 2 2 2 2(1− ) x 2 ( x 1− ) x 2 ( x 1− ) x x −1 2x 2 c) ; và . 3 x +1 2 x − x +1 x +1 x −1 x −1 = 3 x +1 (x + ) 1 ( 2 x − x + ) 1 Trang 2 2x 2x(x + ) 2 1 2x + 2x = = 2
x − x +1 (x + ) 1 ( 2 x − x + ) 1
(x+ )1( 2x − x+ )1 2 2( 2 x − x + ) 2 1 2x − 2x + 2 = = . x +1 (x + ) 1 ( 2 x − x + ) 1
(x+ )1( 2x − x+ )1 7 4 x − y d) ; và . 5x x − 2y 2 2 8y − 2x 7
7.2(2y − x)(2y + x) ( 2 2 y − x ) 2 2 7 8 2 56y −14x = = = 5x 5 .
x 2(2y − x)(2y + x) 10x(2y − x)(2y + x) 10x(2y − x)(2y + x) 4 − x( y + x) 2 4.10 2 8 − 0xy − 40x = = x − 2y
(2y − x)10x(2y + x) 10x(2y − x)(2y + x) x − y 2 x − y 5 ( x x − ) y 5x − 5xy = = = . 2 2 8y − 2x
2(2y− x)(2y+ x) 2.5x(2y − x)(2y + x) 10x(2y − x)(2y + x) 2 6x 3x 2 e) ; và . 3 2
x + 6x +12x + 8 2 x + 4x + 4 2x + 4 2 6x 2 6x = 3 2
x + 6x +12x + 8 (x+2)3 3x 3x 3x(x + 2) 2 3x + 6x = = = 2 x + 4x + 4
(x+2)2 (x+2)3 (x+2)3 2 2 1 (x+2) 2 x + 4x + 4 = = = . 2x + 4 x + 2 (x+2)3 (x+2)3 Bài 2. Thực hiện phép cộng: 4 3 5x + 2 a) + + . 2
x + 2 x − 2 4− x 1− 2x 2x 1 b) + + . 2 2x
2x −1 2x − 4x 1 3xy x − y c) + + . 3 3 2 2
x − y y − x
x + xy + y 3 4 5 d) + + . 2 2 2 2 2 2
x + 2xy + y
2xy − x − y x − y Lời giải Trang 3 4 3 5x + 2 a) + + 2
x + 2 x − 2 4− x 4(x − 2) 3(x + 2) 5x + 2 = + −
(x + 2)(x − 2) (x − 2)(x + 2) (x − 2)(x + 2)
4x − 8+ 3x + 6− 5x − 2 = (x − 2)(x + 2) 2x − 4 = (x − 2)(x + 2) 2(x − 2) = (x − 2)(x + 2) 2 = . x + 2 1− 2x 2x 1 b) + + 2 2x
2x −1 2x − 4x 2 (1− 2 ) x 2 . x 2x 1 = − + 2 ( x 1− 2 ) x 2 ( x 1− 2 ) x 2 ( x 1− 2 ) x 2 2
4x − 4x +1− 4x +1 = 2 ( x 1− 2 ) x 2− 4x = 2 ( x 1− 2 ) x 2(1− 2 ) x 1 = = 2 ( x 1− 2 ) x x 1 3xy x − y c) + + 3 3 2 2
x − y y − x
x + xy + y 2 2 2
x + xy + y 3xy (x − ) y = − + (x − ) y ( 2 2
x + xy + y ) (x − ) y ( 2 2
x + xy + y ) (x − ) y ( 2 2
x + xy + y ) 2 2 2 2
x + xy + y − 3xy + x − 2xy + y = (x − ) y ( 2 2
x + xy + y ) 2 2
2(x − 2xy + y ) = (x − ) y ( 2 2
x + xy + y ) 2 2(x − ) y = (x − ) y ( 2 2
x + xy + y ) Trang 4 2(x − ) y = 2 2
x + xy + y 3 4 5 d) + + 2 2 2 2 2 2
x + 2xy + y
2xy − x − y x − y 3 4 5 = − + (
+ )2 ( − )2 (x + y)(x − y x y x y ) 3(x − y)2 4(x + y)2
5(x + y)(x − y) = − + (
x + y)2 (x − y)2 (x + y)2 (x − y)2 (x + y)2 (x − y)2 2 2 2 2 2 2
3x − 6xy + 3y − 4x − 8xy − 4y + 5x − 5y = (
x + y)2 (x − y)2 2 2
4x −14xy − 6y = ( .
x + y)2 (x − y)2 Bài 3.
Diện tích hình vuông tăng thêm bao nhiêu phần trăm nếu mỗi cạnh của nó tăng thêm 20% ? Lời giải
Gọi cạnh hình vuông ban đầu là x,( x  0) .
Diện tích hình vuông ban đầu là 2 x .
Cạnh hình vuông sau khi tăng 20% là x + 20%.x = x + 0, 2x = 1, 2x .
Diện tích hình vuông sau khi tăng là ( x)2 2 1, 2 =1, 44x .
Khi cạnh hình vuông tăng thì diện tích hình vuông tăng thêm so với ban đầu là 2 2 2
1, 44x − x = 0, 44x .
Vậy khi cạnh hình vuông tăng thì diện tích hình vuông tăng thêm số phần trăm là 2 0, 44x 100% = 44%. 2 x Bài 3.
Cho hình vuông ABCD có cạnh bằng 16 cm , O là giao điểm của AC và BD . Gọi M , N , P
, Q lần lượt là trung điểm của OA , OB , OC , OD .
a) Tứ giác MNPQ là hình gì? Vì sao?
b) Tính diện tích phần hình vuông ABCD nằm ngoài tứ giác MNPQ . Lời giải Trang 5 A B M N O Q P D C
a) Vì ABCD là hình vuông có hai đường chéo cắt nhau tại O (gt)
 OA = OB = OC = OD và AC ⊥ BD (tính chất)
Mà M , N , P , Q lần lượt là trung điểm của OA , OB , OC , OD (gt)
 OM = ON = OP = OQ và MP = QN
Xét tứ giác MNPQ có
OM = OP = ON = OQ (chứng minh trên)
 Tứ giác MNPQ là hình bình hành
Mà MP = QN (chứng minh trên)
 Tứ giác MNPQ là hình chữ nhật
Mà MP ⊥ QN (vì AC ⊥ BD )
 Tứ giác MNPQ là hình vuông (dấu hiệu nhận biết)
b) Xét tam giác AOB có MA = MO (gt) NP = NO (gt)
 MN là đường trung bình của tam giác AOB . 1
 MN = AB (tính chất) 2 1
 MN = 16 = 8 (cm) 2
Diện tích phần hình vuông ABCD nằm ngoài hình vuông MNPQ là: 2 2 16 − 8 = 192 2 (cm ) Bài 5.
Cho tam giác ABC vuông cân tại A . Trên cạnh BC lấy các điềm H ,G sao cho
BH = HG = GC . Qua H và G kẻ các đường vuông góc với BC , chúng cắt AB và AC theo
thứ tự ở E và F . Tú giác EFGH là hình gì? Vì sao? Lời giải Trang 6
ABC vuông cân tại A  ABC = ACB = 45 (tính chất tam giác vuông cân).
Xét CGF và BHE có G = H = 90 ;
 CG = BH; FCG = HBE  CGF = BHE (g – c- g)
 GF = HE (cạnh tương ứng bằng nhau). (1)
CGF có G = 90 ;
 FCG = 45  CF 
G vuông cân tại G  CG = GF (2)
Từ (1) và (2) suy ra CG = GH = HB = GF = HE
Ta có: FG ⊥ BC; EH ⊥ BC  EH FG .
Tứ giác EFGH có HE = GF; HE
FG nên tứ giác EFGH là hình bình hành. Mà G = 90
tứ giác EFGH là hình chữ nhật Mà GF = GH
 tứ giác EFGH là hình vuông. Bài 6.
Cho hình vuông ABCD . Trên các cạnh AD , DC lần lượt lấy các điểm E , F sao cho
AE = DF . Gọi M , N lần lượt là trung điểm của EF, BF .
a) Chứng minh các tam giác ADF và BAE bằng nhau.
b) Chúng minh MN vuông góc với AF . Lời giải Trang 7
a) ABCD là hình vuông  AB = BC = CD = D ;
A ABC = BCD = CDA = DAB (t/c hình vuông).
ADF và BAE có AB = A ; D A = D = 90 ;
 AE = DF  ADF  = BAE (c-g-c)
b) Cho AF cắt BE tại G. A  DF = B
 AE  DAF = ABE (cặp góc tương ứng bằng nhau). (1) A
 BE : A = 90  ABE + AEB = 90 (2)
Từ (1) và (2) suy ra AEB + DAF = 90 .
Tam giác AEG có AEB + DAF = 90  AGE = 90 hay AF ⊥ EB . (3)
Xét BEF có M , N là trung điểm FE, FB suy ra MN là đường trung bình của BEF .  MN EB (4)
Từ (3) và (4) suy ra MN ⊥ AF
Bài 7. Chứng minh giá trị các biểu thức sau không phụ thuộc vào giá trị của x , y , z x − y
y − z z − x a) + + . xy yz zx 1 1 1 b) + + .
(x − y)(y − z) (y − z)(z − x) (z − x)(x − y) Lời giải a) Ta có x − y
y − z z − x
z(x − y) + x(y − z) + y(z − x) + + = xy yz zx xyz
xz − yz + xy − xz + yz − xy 0 = = = 0 xyz xyz
Vậy giá trị của biểu thức trên không phụ thuộc vào giá trị của biến. Trang 8 b) Ta có 1 1 1 + +
(x − y)( y − z) ( y − z)(z − x) (z − x)(x − y)
z − x + x − y + y − z 0 = = = 0
(x − y)( y − z)(z − x) (x − y)(y − z)(z − x)
Vậy giá trị của biểu thức trên không phụ thuộc vào giá trị của biến. 1 1 2 4 8 16
Bài 8. Tính tổng A = + + + + − . 2 4 8 16
1− x 1+ x 1+ x 1+ x 1+ x 1− x Lời giải a) Ta có + + − • 1 1 1 x 1 x 2 + = = . 2 1− x 1+ x
(1− x)(1+ x) 1− x 2 2 2( 2 1+ x ) + 2( 2 1− x ) • 4 + = = . 2 2 1− x 1+ x ( 2 1− x )( 2 1+ x ) 4 1− x Tương tự, ta có • 4 4 8 + = . 4 4 8 1− x 1+ x 1− x • 8 8 16 + = . 8 8 16 1− x 1+ x 1− x 16 6 1 Vậy A = − = 0 . 16 16 1− x 1− x  HẾT  Trang 9