Bài Tập Toán 8 Tuần 15 Có Lời Giải Chi Tiết

PHIẾU BÀI TẬP TOÁN 8 TUẦN 15
A. PHẦN CƠ BẢN (DÀNH CHO TẤT CẢ CÁC LỚP) Bài 1. Thực hiện phép tính. 4x +1 3x + 2 x + 3 x 9 a) − b) − + 2 3 2 x
x − 3 x − 3x x + 3 1 1 4 1 − 0x + 8 c) − d) − − 2 2
x −1 x + x 2 3x − 2 3x + 2 9x − 4 3 2x −1 2 2 4a − 3a + 5 1− 2a 6 e) + − f) − − 2 2 2x + 2x x −1 x 3 2 a −1
a + a +1 a −1 x + 9y 3y 3x + 2 6 3x − 2 g) − h) − − 2 2 2 x − 9y x + 3xy 2 2 2
x − 2x +1 x −1 x + 2x +1 Bài 2.
Rút gọn rồi tính giá trị các biểu thức. 2 2 2
a + b − c + 2ab 2 16x − 40xy x 10 a)
với a = 4; b = 5 − ; c = 6 b) với = 2 2 2
a − b + c + 2ac 2 8x − 24xy y 3 Bài 3.
Cho tam giác ABC vuông tại A , đường trung tuyến AM . Gọi H là điểm đối xứng với M
qua AB , K là điểm đối xứng với M qua AC , E là giao điểm của MH và AB , F là giao
điểm của MK và AC .
a) Các tứ giác AEMF, AM BH , AM
CK là hình gì? Tại sao?
b) Chứng minh rằng điểm H đối xứng với điểm K qua điểm A .
c) Tam giác vuông ABC cần có thêm điều kiện gì để tứ giác AEMF là hình vuông. Khi đó hãy
tính diện tích hình vuông AEMF biết BC = 10cm Bài 4.
Cho hình thoi ABCD , lấy đường chéo AC là cạnh dựng hình bình hành ACEF , cạnh thứ hai
CE có độ dài bằng cạnh của hình thoi, K đối xứng với E qua C .
a) Chứng minh FK , A
C cắt nhau tại trung điểm của mỗi đường.
b) Chứng minh FD//BK .
c) Tính số đo góc KBE .
d) Chứng minh B là trực tâm của tam giác DEF .
B. BÀI TẬP NÂNG CAO Bài 5.
1) Tìm các số a , b , c để: 2 x + 2x −1 a bx + c ( = + x − ) 1 ( 2 x + ) 2 1 x −1 x +1
2) Xác định các số hữu tỉ a , b , c , d sao cho: 2 9x −16x + 4 a b c 3 x a b cx + d a) = + + b) = + + 3 2
x − 3x + 2x x x −1 x − 2 4 2 x −1 x −1 x +1 x +1
ĐÁP ÁN BÀI TẬP TĂNG CƯỜNGTOÁN 8 TUẦN 15
HƯỚNG DẪN GIẢI CHI TIẾT Bài 1. Thực hiện phép tính. 4x +1 3x + 2 x + 3 x 9 a) − b) − + 2 3 2 x
x − 3 x − 3x x + 3 1 1 4 1 − 0x + 8 c) − d) − − 2 2
x −1 x + x 2 3x − 2 3x + 2 9x − 4 3 2x −1 2 2 4a − 3a + 5 1− 2a 6 e) + − f) − − 2 2 2x + 2x x −1 x 3 2 a −1
a + a +1 a −1 x + 9y 3y 3x + 2 6 3x − 2 g) − h) − − 2 2 2 x − 9y x + 3xy 2 2 2
x − 2x +1 x −1 x + 2x +1 Lời giải 4x +1 3x + 2 3(4x + )
1 − 2(3x + 2) 6x −1 a) − = = 2 3 6 6 x + 3 x 9 (x +3)(x −3) 2 x 9 b) − + = − + = 0 2 x
x − 3 x − 3x x (x − 3)
x (x − 3) x(x − 3) x + 3 1 x( x + 3) x −1 (x + )2 1 x +1 c) − = − = = 2 2
x −1 x + x x (x − ) 1 (x + ) 1 x (x + ) 1 (x − ) 1 x (x − ) 1 (x + ) 1 x (x − ) 1 1 4 1 − 0x + 8 d) − − 2 3x − 2 3x + 2 9x − 4 3x + 2 4(3x − 2) 1 − 0x + 8 + = x 2 ( − − =
3x + 2)(3x − 2) (3x + 2)(3x − 2) (3x + 2)(3x − 2) (3x + 2)(3x − 2) 3 2x −1 2 e) + − 2 2 2x + 2x x −1 x 3( x − ) 1 2x (2x − ) 1 2.2( x − ) 1 ( x + ) 1 x +1 1 = + − = = 2x ( x + ) 1 ( x − ) 1 2x ( x − ) 1 (x + ) 1 2x (x − ) 1 (x + ) 1 2x(x + ) 1 (x − ) 1 2x (x − ) 1 2 4a − 3a + 5 1− 2a 6 f) − − 3 2 a −1
a + a +1 a −1 4a − 3a + 5
(1− 2a)(a − ) 1 6( 2 2 a + a + ) 1 = − − 12 − a ( = a − ) 1 ( 2 a + a + ) 1 (a − ) 1 ( 2 a + a + ) 1 (a − ) 1 ( 2 a + a + ) 1 (a − ) 1 ( 2 a + a + ) 1 x + 9y 3y g) − 2 2 2 x − 9y x + 3xy
x ( x + y)
y (x − y) (x + y)2 9 3 3 3 x + 3y = − = =
x( x + 3y)( x − 3y) x(x + 3y)(x − 3y) x(x + 3y)(x − 3y) x(x − 3y) 3x + 2 6 3x − 2 h) − − 2 2 2
x − 2x +1 x −1 x + 2x +1 (3x + 2)(x + )2 1 6( x − ) 1 ( x + ) 1
(3x − 2)(x − )2 2 1 10x +10 = − − = (x − )2 1 ( x + )2 1 (x − )2 1 ( x + )2 1 (x + )2 1 ( x − )2 1 (x − )2 1 ( x + )2 1 Bài 2.
Rút gọn rồi tính giá trị các biểu thức. 2 2 2
a + b − c + 2ab a)
với a = 4; b = 5 − ; c = 6 2 2 2
a − b + c + 2ac 2 16x − 40xy x 10 b) với = 2 8x − 24xy y 3 Lời giải 2 2 2
a + b − c + 2ab (a +b)2 2 − c
(a +b + c)(a +b −c) a +b −c a) = = = 2 2 2
a − b + c + 2ac (a + c)2 2 − b
(a +b + c)(a −b + c) a −b + c
a + b − c 4 − 5 − 6 7 −
Thay a = 4; b = 5
− ; c = 6 vào biểu thức ta được: = =
a − b + c 4 + 5 + 6 15 2 16x − 40xy
8x (2x − 5y) 2x − 5y b) = = 2 8x − 24xy
8x (x − 3y) x − 3y 20 − x 10 10 10 y 5 2 − 5 y x y Ta có =  x = y . Thay x = y ta được: 3 = = 5 y 3 3 3 x − 3y 10 y −3y 3 Bài 3.
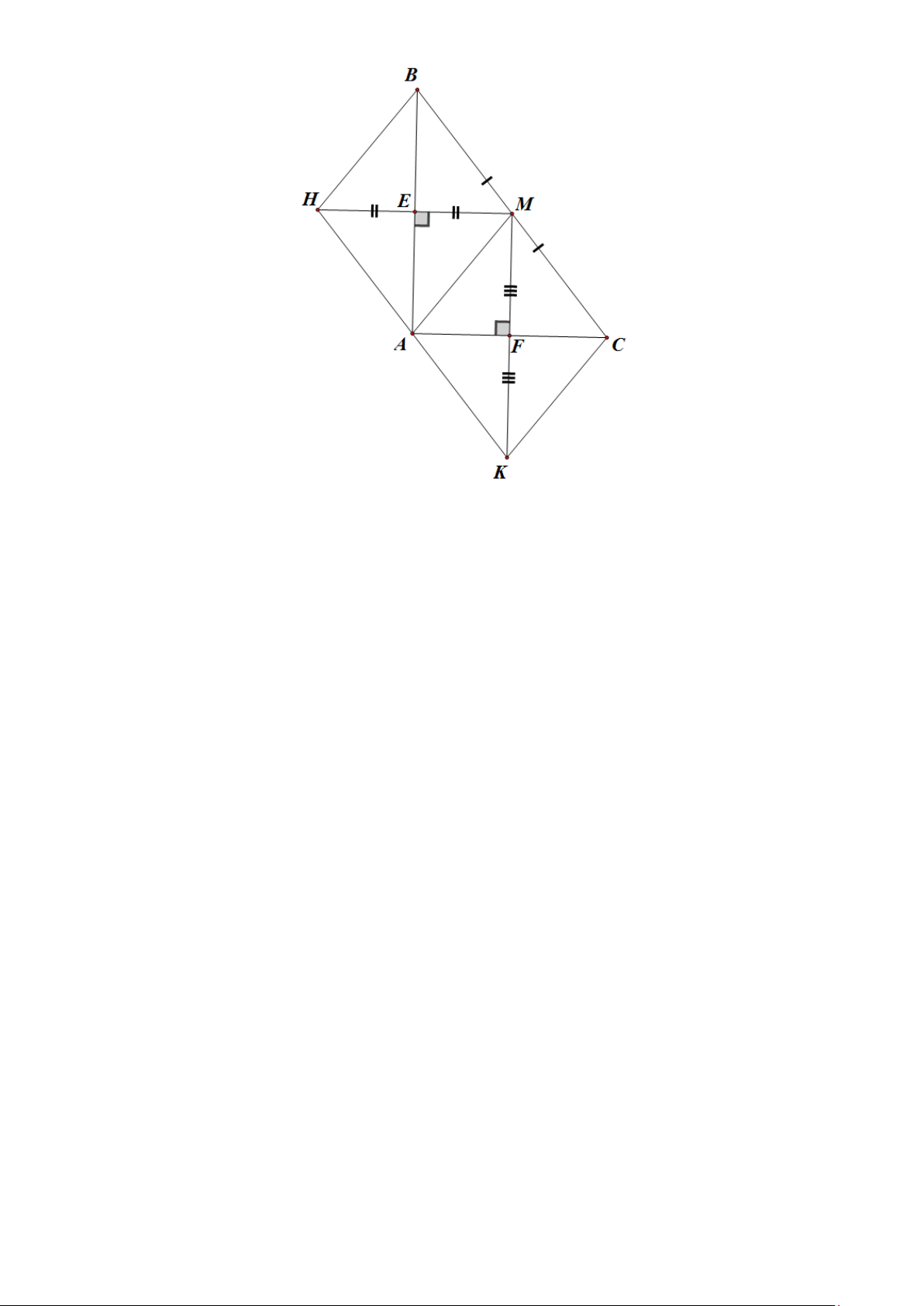
Cho tam giác ABC vuông tại A , đường trung tuyến AM . Gọi H là điểm đối xứng với M
qua AB , K là điểm đối xứng với M qua AC , E là giao điểm của MH và AB , F là giao
điểm của MK và AC .
a) Các tứ giác AEMF, AM BH , AM
CK là hình gì? Tại sao?
b) Chứng minh rằng điểm H đối xứng với điểm K qua điểm A .
c) Tam giác vuông ABC cần có thêm điều kiện gì để tứ giác AEMF là hình vuông. Khi đó hãy
tính diện tích hình vuông AEMF biết BC = 10cm Lời giải
a) Các tứ giác AEMF, AM BH , AM
CK là hình gì? Tại sao?
*Xét tứ giác AEMF ta có A M E
= AFM = 90 vì H là điểm đối xứng với M qua AB , K là điểm đối xứng với M qua AC
EAF = 90 vì tam giác ABC vuông tại A .
Vậy tứ giác AEMF có 3 góc vuông nên AEMF là hình chữ nhật.
*Xét tam giác ABC ta có M là trung điểm của BC (gt)
MF //AB (Vì AEMF là hình chữ nhật)
Nên MF là đường trung bình của tam giác ABC nên F là trung điểm của AC
*Xét tứ giác AMCK có 2 đường chéo MK và AC vuông góc và cắt nhau tại trung điểm của
mỗi đường nên tứ giác AMCK là hình thoi.
*Chứng minh tương tự ta có tứ giác AMBH là hình thoi.
b) Chứng minh rằng điểm H đối xứng với điểm K qua điểm A.
* Vì tứ giác AMCK là hình thoi nên MAF = FAK
* Vì tứ giác AMBH là hình thoi nên HAE = EAM Mà 0
MAF + EAM = 90 vậy 0
MAF + FAK + HAE + EAM = 180 Hay 0 HAK = 180 Vậy 3 điểm H , , A K thẳng hàng (1)
Cũng có tứ giác AMCK là hình thoi nên AM = AK tứ giác AMBH là hình thoi nên
AM = AH Vậy AH = AK (2)
Từ (1) và (2) suy ra điểm H đối xứng với điểm K qua điểm A
c) Tam giác vuông ABC cần có thêm điều kiện gì để tứ giác AEMF là hình vuông. Khi đó hãy
tính diện tích hình vuông AEMF biết BC = 10cm
Vì tứ giác AEMF là hình chữ nhật nên để tứ giác AEMF là hình vuông thì AM là đường phân giác góc BAC
Khi đó AM vừa là đường phân giác vừa là đường trung tuyến của tam giác vuông ABC , vậy
tam giác ABC là tam giác vuông cân tại A.
Vậy tam giác vuông ABC cần có thêm điều kiện là tam giác cân tại để tứ giác AEMF là hình vuông. 1
Xét tam giác vuông ABM vuông tại M có AM = BM = BC = 5cm 2 5 2 nên 2 2 2 2 2
AB = BM + MA = 5 + 5 = 50 Vậy AB = 5 2 suy ra AE = 2 2  5 2  25
Vậy diện tích hình vuông AEMF là 2 2 AE =   = cm  2  2   Bài 4.
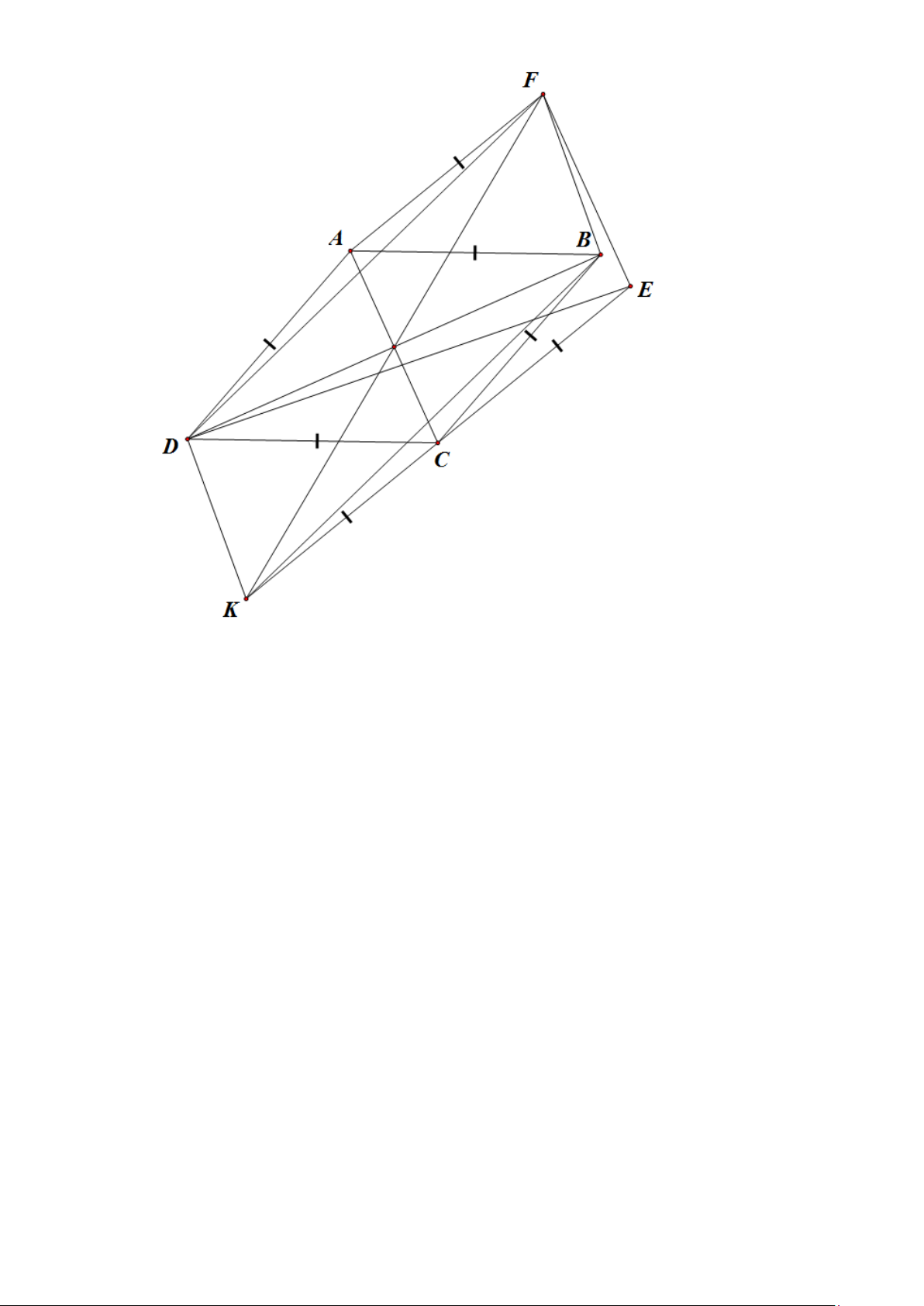
Cho hình thoi ABCD , lấy đường chéo AC là cạnh dựng hình bình hành ACEF , cạnh thứ hai
CE có độ dài bằng cạnh của hình thoi, K đối xứng với E qua C .
a) Chứng minh FK , A
C cắt nhau tại trung điểm của mỗi đường.
b) Chứng minh FD//BK .
c) Tính số đo góc KBE .
d) Chứng minh B là trực tâm của tam giác DEF . Lời giải
a) Chứng minh FK , A
C cắt nhau tại trung điểm của mỗi đường.
Vì ACEF là hình bình hành nên AF //CE, AF = CE (1)
Vì K đối xứng với E qua C nên KC = CE và K,C,E thẳng hàng (2)
Từ (1) và (2) suy ra KC//AF, KC = AF nên tứ giác ACFK là hình bình hành Nên FK , A
C cắt nhau tại trung điểm của mỗi đường.
b) Chứng minh FD//BK .
Vì ABCD là hình bình hành nên BD, A
C cắt nhau tại trung điểm của mỗi đường.
Theo câu a) FK , A
C cắt nhau tại trung điểm của mỗi đường. Vậy FK , B
D cắt nhau tại trung điểm của mỗi đường nên tứ giác DFBK là hình bình hành Do đó FD//BK
c) Tính số đo góc KBE .
Theo giả thiết CE có độ dài bằng cạnh của hình thoi nên CE = BC
Lại có K đối xứng với E qua C nên CE = CK
Xét tam giác KBE có CB = CK = CE nên đường trung tuyến BC bằng một nửa cạnh tương
ứng KE .Vậy tam giác KBE vuông tại B nên KBE = 90
d) Chứng minh B là trực tâm của tam giác DEF .
Ta có AFEC là hình bình hành nên AC//FE
Mà AC ⊥ BD nên BD ⊥ EF (3)
Theo chứng minh c) BK ⊥ BE mà tứ giác tứ giác DFBK là hình bình hành nên BK //DF
Vậy BE ⊥ DF (4)
Từ (3) và (4) suy ra B là trực tâm của tam giác DEF. Bài 5.
1) Tìm các số a , b , c để: 2 x + 2x −1 a bx + c ( = + x − ) 1 ( 2 x + ) 2 1 x −1 x +1
2) Xác định các số hữu tỉ a , b , c , d sao cho: 2 9x −16x + 4 a b c 3 x a b cx + d a) = + + b) = + + 3 2
x − 3x + 2x x x −1 x − 2 4 2 x −1 x −1 x +1 x +1 Lời giải 2 x + 2x −1 a bx + c 1) ( = + x − ) 1 ( 2 x + ) 2 1 x −1 x +1 x + 2x −1 a ( 2 2 x + )
1 + (bx + c)( x − ) 1  ( = x − ) 1 ( 2 x + ) 1 (x − ) 1 ( 2 x + ) 1 2 2 2 x + 2x −1
ax + a + bx − bx + cx − c  ( = x − ) 1 ( 2 x + ) 1 (x − ) 1 ( 2 x + ) 1 2 x + 2x −1 (a + b) 2
x + (c − b) x + (a − c)  ( = x − ) 1 ( 2 x + ) 1 (x − ) 1 ( 2 x + ) 1 a + b = 1 a = 1  
 c − b = 2  b = 0 a c 1  − = − c = 2   2) 2 9x −16x + 4 a b c a) = + + 3 2
x − 3x + 2x x x −1 x − 2 2 9x −16x + 4 a ( x − )
1 (x − 2) + bx (x − 2) + cx (x − ) 1  = x ( 2 x − 3x + 2) x (x − ) 1 ( x − ) 1 2 9x −16x + 4
(ax − a)(x − 2) 2 2
+ bx − 2bx + cx − cx  = x ( 2
x − x − 2x + 2) x ( x − ) 1 ( x − 2) 2 2 2 2 9x −16x + 4
ax − 2ax − ax + 2a + bx − 2bx + cx − cx  = x x  ( x − ) 1 − 2(x − ) 1  x  (x − ) 1 (x − 2) 2 9x −16x + 4
(a + b + c) 2
x − (3a + 2b + c) x + 2a  = x (x − ) 1 (x − 2) x (x − ) 1 (x − 2)
a + b + c = 9 a = 2  
 3a + 2b + c = 16  b = 3 2a 4  = c = 4   3 x a b cx + d b) = + + 4 2 x −1 x −1 x +1 x +1 x a ( x + ) 1 ( 2 x + ) 1 + b ( x − ) 1 ( 2 3 x + )
1 + (cx + d )( x − ) 1 (x + ) 1  ( = 2 x − ) 1 ( 2 x + ) 1 (x + ) 1 ( x − ) 1 ( 2 x + ) 1 x
(ax + a)( 2x + )1 + (bx − b)( 2x + )1 + (cx + d )( 2 3 x − ) 1  ( = x + ) 1 ( x − ) 1 ( 2 x + ) 1 (x + ) 1 ( x − ) 1 ( 2 x + ) 1 3 3 2 3 2 3 2 x
ax + ax + ax + a + bx − bx + bx − b + cx + dx − cx − d  ( = x + )(x − )( 2 x + )
(x + )(x − )( 2 1 1 1 1 1 x + ) 1 3 x
(a + b + c) 3
x + (a − b + d ) 2
x + (a + b − c) x + a − b − d  ( = x + )(x − )( 2 x + )
(x + )(x − )( 2 1 1 1 1 1 x + ) 1  1 a =  4
a + b + c = 1   1
a − b + d = 0 b =     4
a + b − c = 0   1  − − = 0 c a b d = 2  d = 0