Bài Tập Toán 8 Tuần 16 Có Lời Giải Chi Tiết

PHIẾU BÀI TẬP TOÁN 8 TUẦN 16 Bài 1. Thực hiện phép tính: x - 3 3- 2x 3- 3x x + 1 x- 1 x- 2 a) . b) . c) . 2 2 2x - 3x x - 9 (x + )2 2 1 6x - 6 2 x - 3x + 2 x 2 xy 3- 2x 2 15x 2y 5x + 10 4- 2x d) . e) . f) . 2x xy - y 3 2 7 y x 4x - 8 x + 2 2 x - 36 3 2 1- 4x 2- 4x
x + 1 x + 2 x + 3 g) . h) : k) : : 2x + 10 6- x 2 x + 4x 3x
x + 2 x + 3 x + 1 Bài 2.
Rút gọn các biểu thức sau: 2 2 2 2 x −1 x x −1 1− x 2 2
x + y ( x − y) 2 y (x − y) a)  +  b)  −  .
x +10 x + 2 x +10 x + 2 2 2 x + y x x + y x
x + y − z Bài 3.
Tính giá trị biểu thức: 2 2 2
A = (x − y − z + 2yz) :
với x = 8,6; y = 2; z = 1, 4. z + y + z Bài 4. Tìm x , biết: 2 2 2 2
a − 2ab + b a − b 2 2 3 3
a + b − ab a + b a) .x = b) .x = 4 4 2 2 a − b a + b 2 2 2 2 a − b
a + b − 2ab Bài 5.
Cho tam giác ABC, trung tuyến BD và CE cắt nhau ở G. Cho biết BC=10cm, BD=9cm, CE=12cm.
a) Chứng minh: BGC = 90
b) Tính diện tích tam giác ABC. Bài 6.
Cho tam giác ABC , trung tuyến AM . Qua B kẻ đường thẳng song song với AM cắt CA ở
E . Gọi I là giao điểm của EM với AB . Chứng minh: S = s ABC MEC S = s IEA IMB Bài 7.
Tính diện tích lớn nhất của tam giác vuông có cạnh huyền BC = a . Bài 8.
Tìm giá trị nguyên của x để mỗi biểu thức sau là số nguyên: 3 2
2x − 6x + x − 8 2 3x − x + 3 a) M = b) N = x − 3 3x + 2 Trang 1
ĐÁP ÁN BÀI TẬP TĂNG CƯỜNGTOÁN 8 TUẦN 16
HƯỚNG DẪN GIẢI CHI TIẾT Bài 1. Thực hiện phép tính. x - 3 3- 2x 3- 3x x + 1 x- 1 x- 2 a) . b) . c) . 2 2 2x - 3x x - 9 (x + )2 2 1 6x - 6 2 x - 3x + 2 x 2 xy 3- 2x 2 15x 2y 5x + 10 4- 2x d) . e) . f) . 2x xy - y 3 2 7 y x 4x - 8 x + 2 2 x - 36 3 2 1- 4x 2- 4x
x + 1 x + 2 x + 3 g) . h) : k) : : 2x + 10 6- x 2 x + 4x 3x
x + 2 x + 3 x + 1 Lời giải x - 3 3- 2x x - 3 3- 2x 1 1 - 1 a) . = . = . = 2 2 2x - 3x x - 9
- x(3- 2x) (x- ) 3 (x + ) 3 - x (x + ) 3 x(x + ) 3 3- 3x x + 1 3(1- x) x + 1 - 3(x- ) 1 x + 1 - 3 - 1 b) . = . = . = = (x + )2 2 1 6x - 6 (x + )2 1 6( 2 x - ) 1 (x + )2 1 6(x- ) 1 (x + ) 1 6(x + )2 1 2(x + )2 1 x- 1 x- 2 x - 1 x - 2 x- 1 x- 2 1 c) . = . = . = 2 x - 3x + 2 x 2 x - 3x + 2 x (x- ) 1 (x- ) 2 x x 2 xy 3- 2x 2 xy 3- 2x 2 xy (3- 2x) y(3- 2x) d) . = . = = 2x xy - y 2x xy - y 2xy(x- ) 1 2(x- ) 1 2 15x 2y 30 e) . = 3 2 7 y x 7xy 5x + 10 4- 2x
5(x + 2) - 2(x- 2) - 5 f) . = . = 4x - 8 x + 2 4(x- ) 2 x + 2 2 2 x - 36 3 2 2 x - 6 3 3(x + ) 6 (x- 6) - 3(x + 6) g) . = . = = 2x + 10 6- x 2(x + ) 5 6- x - 2(x + ) 5 (x- ) 6 2(x + ) 5 2 2 1- 4x 2- 4x 2 1- 4x 3x 1- (2x) 3x
(1- 2x)(1+ 2x)3x 3(1+ 2x) h) : = . = . = = 2 x + 4x 3x 2
x + 4x 2- 4x x(x + ) 4 2(1- 2x) 2x(x + ) 4 (1- 2x) 2(x + ) 4
x + 1 x + 2 x + 3 (x + ) 1 (x + ) 3 (x + ) 1 (x + )2 1 k) : : = . . =
x + 2 x + 3 x + 1 (x + ) 2 (x + ) 2 (x + ) 3 (x + 2)2 Bài 2.
Rút gọn các biểu thức sau: 2 2 2 2 x −1 x x −1 1− x 2 2
x + y ( x − y) 2 y (x − y) a)  +  b)  −  .
x +10 x + 2 x +10 x + 2 2 2 x + y x x + y x Trang 2 Lời giải 2 2 x −1 x x −1 1− x a)  + 
(x  −2 ; x  −10)
x +10 x + 2 x +10 x + 2 2 2 x −1  x 1− x  x −1 1 (x − ) 1 ( x + ) 1 =  + =  =   x +  x + x +  x + x + (x + )(x + ). 10 2 2 10 2 10 2
x + y ( x − y)2 y (x − y)2 2 2 2 b)  − 
x  0 ; x  − y 2 2 ( ) x + y x x + y x
(x − y)2  x + y y  ( x − y)2 x (x − y)2 2 2 2 2 =  −  =  = . 2 2 x  x + y x + y  x x + y x + y
x + y − z Bài 3.
Tính giá trị biểu thức: 2 2 2
A = (x − y − z + 2yz) :
với x = 8,6; y = 2; z = 1, 4. z + y + z Lời giải + − 2 2 2 x y z
A = (x − y − z + 2 yz) : x + y + z + − 2 2 x y z
= [x − ( y − z) ]: x + y + z
(x − y + z)(x + y − z)(x + y + z) =
x + y − z
= (x − y + z)(x + y + z) 2 2
= (x + z) − y
Thay x = 8,6; y = 2; z = 1, 4 vào biểu thức A ta được: 2 2 A = (8,6+1,4) − 2 2 2 = 10 − 2 = 100 − 4 = 96
Vậy với x = 8,6; y = 2; z = 1, 4 ta có A = 96 Bài 4. Tìm x, biết: 2 2 2 2
a − 2ab + b a − b 2 2 3 3
a + b − ab a + b a) .x = b) .x = 4 4 2 2 a − b a + b 2 2 2 2 a − b
a + b − 2ab Lời giải 2 2 2 2
a − 2ab + b a − b a) .x = a  b 4 4 2 2 ( ) a − b a + b Trang 3 (a −b)2 a − b a − b (a −b)2 2 2 2 2  ( .x =  x = : 2 2 a − b )( 2 2 a + b ) 2 2 2 2 a + b a + b ( 2 2 a − b )( 2 2 a + b )
(a −b)(a +b) (a −b)(a +b)( 2 2 a + b )  x = .
 x = a + b 2 2 2 ( )2 a + b (a −b) 2 2 3 3
a + b − ab a + b b) .x = 2 2 2 2 a − b
a + b − 2ab
a + b − ab (a +b)( 2 2
a + b − ab) (a +b)( 2 2 2 2
a + b − ab ) 2 2
a + b − ab  .x =  x = : 2 2 a − b (a −b)2 (a −b)2 2 2 a − b (a +b)( 2 2
a + b − ab) 2 2 a − b  x = . (a −b)2 2 2
a + b − ab (a +b)( 2 2
a + b − ab) (a + b)(a − b) (a +b)2  x = .  x = (a −b)2 2 2
a + b − ab a − b Bài 5.
Cho tam giác ABC, trung tuyến BD và CE cắt nhau ở G. Cho biết BC = 10c ,
m BD = 9c , m CE = 12c . m
a) Chứng minh: BGC = 90
b) Tính diện tích tam giác ABC. Lời giải A E D G 12 9 B 10 C
Ta có: trung tuyến BD và CE cắt nhau ở G nên G là trọng tâm  2 2 BG = BD = .9 = 6  3 3   2 2 CG  = CE = .12 = 8  3 3 Xét tam giác BCG ta có: Trang 4 2 2 BC = 10 = 100 2 2 2 2
BG + CG = 6 + 8 = 100 2 2 2
 BC = BG + CG
 Tam giác BCG vuông tại G hay 0 BGC = 90 . 1 1 Ta có S = S + S = .B . G CG + 1 1 .G .
D GC = .9.8 + .8.3 = 36 +12 = 48 BDC BGC GDC 2 2 2 2 Lại có: S = 2S = 2.48 = 96 ABC BDC Vậy 2 S = 96cm ABC Bài 6.
Cho tam giác ABC , trung tuyến AM . Qua B kẻ đường thẳng song song với AM cắt CA ở
E . Gọi I là giao điểm của EM với AB . Chứng minh: S = s ABC MEC S = s IEA IMB Lời giải a) Chứng minh S = S ABC MEC
Qua A và E kẻ đường thẳng vuông góc với BC , cắt BC lần lượt tại H và F . CEB có
M là trung điểm BC và AM // EB (gt) nên A là trung điểm của EC . CEF có A là trung
điểm CE và AH // EF ( vì cùng vuông góc với BC nên H là trung điểm của FC . Suy ra AH
là đường trung bình của  1
CEF  AH = EF 2 Ta có: 1 1 1 1 S
= .AH.BC = . EF.BC = .EF.BC ABC 2 2 2 4 1 1 1 1 S
= .EF.MC = .EF. BC = .EF.BC MEC 2 2 2 4 Trang 5 Suy ra S = S ABC MEC b) Chứng minh S = S IEA IMB Ta có: S = S + S MEC IAE IACM S = S + S ABC IMB IACM Mà S = S
( cm câu a) do đó S = S . ABC MEC IEA IMB Bài 7.
Tính diện tích lớn nhất của tam giác vuông có cạnh huyền BC = a . Lời giải
Gọi tam giác vuông đó là: D ABC có cạnh huyền BC = a
- Kẻ đường cao AH ,( H Î BC ) 1
- Diện tích tam giác vuông ABC là: S = AH.BC DABC 2
Vì BC = a không đổi nên diện tích D ABC lớn nhất khi AH lớn nhất.
- Gọi M là trung điểm BC Þ AM là đường trung tuyến ứng với BC
- Xét D AHM vuông tại H có: AH £ AM dấu bằng H º M hay AH vừa là đường cao vừa là
đường trung tuyến của D ABC 1 a Þ AH = BC = max 2 2 1 1 a 1 2 Þ S = AH .BC = . .a = a DABC a M x Max 2 2 2 4 Trang 6 1
Vậy diện tích lớn nhất của tam giác vuông có cạnh huyền BC = a là 2 a . 4 Bài 8.
Tìm giá trị nguyên của x để mỗi biểu thức sau là số nguyên: 3 2
2x − 6x + x − 8 2 3x − x + 3 a) M = b) N = x − 3 3x + 2 Lời giải 3 2 3 2 2
2x − 6x + x − 8
2x − 6x + x − 3 − 5
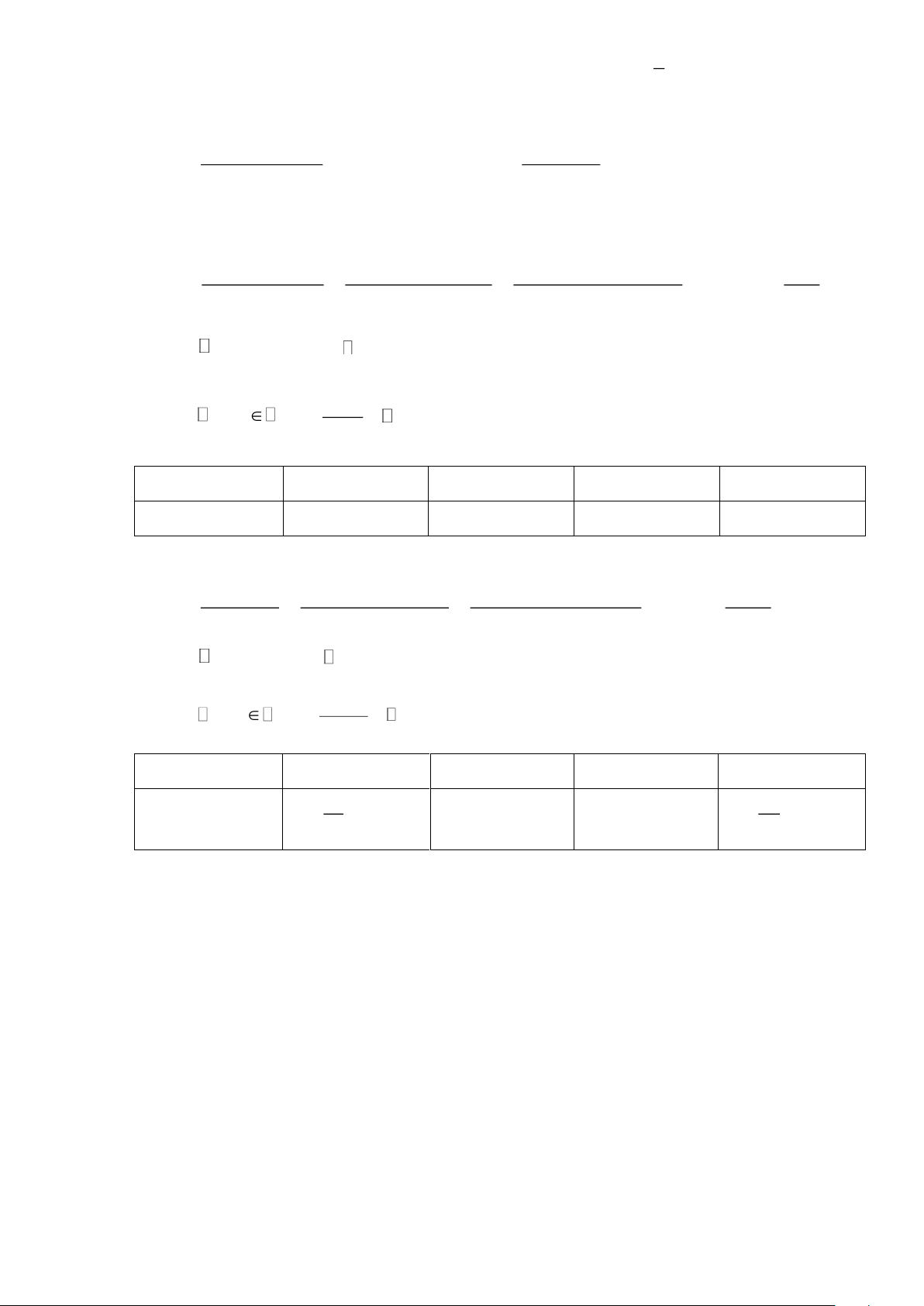
2x ( x − 3) + ( x − 3) − 5 a) M = = = =( 5 2 2x + ) 1 − x − 3 x − 3 x − 3 x − 3 Vì x  nên ( 2 2x + ) 1  5 Vì x  ; M  nên
  x − 3 Ư (5) = 1 ;−1 ; 5 ;−  5 x − 3 x − 3 1 –1 5 –5 x 4 2 8 –2
Vậy x 4 ; 2 ; 8 ; −  2 . 2 2 3x − x + 3
3x + 2x − 3x − 2 + 5
x (3x + 2) − (3x + 2) + 5 = = = = (x − ) 5 b) N 1 + . 3x + 2 3x + 2 3x + 2 3x + 2
Vì x  nên ( x − ) 1  . 5 Vì x  ; N  nên
  3x + 2  Ư (5) = { 1 ; –1; 5 ; – 5 }. 3x + 2 3x + 2 1 –1 5 –5 1 − 7 − x (loại) –1 1 (loại) 3 3
Vậy x 1 ; −  1 . Trang 7