Bài Tập Toán 8 Tuần 2 Có Lời Giải Chi Tiết

PHIẾU BÀI TẬP TOÁN 8 TUẦN 02
A. BÀI TẬP CƠ BẢN (DÀNH CHO TẤT CẢ CÁC LỚP): Bài 1. Tìm x, biết: a) ( 2 x + x + ) 1 ( x − ) 3 1 = 2x d) ( x + )2 1 − 4 = 0 b) ( x + )2 1 − 2x = 0 2
e) x − 2x +1 = 0 2 c) x ( 2 x + x + ) 2 1 − x ( x + ) 1 − x + 5 = 2 f ) (2x + ) 1 − 2( 2 2x + 3) = 0 Bài 2. Chứng minh rằng: a) ( x + )( 2 x − x + ) 3 1 1 = x +1. b) ( 3 2 2 3 + + + )( − ) 4 4 x x y xy y
x y = x − y
c) ( x + y + z)2 2 2 2
= x + y + z + 2xy + 2yz + 2xz Bài 3. Tính: a) ( x + )2 1 ; b) ( + )2 2x y ; c) ( x − y)2 3 2 ; 2  1  d) ( x − )2 2 ; e) 5x − y   ;
f) ( x + 2y)( x − 2y) .  2  Bài 4.
Dùng hằng đẳng thức, hoàn thành vế còn lại: 2  1  a) ( − )2 2x y = b) ( − )2 2 2x y z = c) x + y =    2 
d) ( x − 2y)(2y + x) = e) ( x + y)2 2 5 = f) ( − )2 3x y = Bài 5. Rút gọn biểu thức 2 a) ( 2
x + ) −(x + )(x − )( 2 2 2 2 x + 4) b)
(x y)(x y) (x y)2 (x y)2 2 − + + + + −
c) ( x y)2 ( x y)2 + − −
d) ( x − y + z)2 + ( z − y)2 + 2( x − y + z)( y − z) Bài 6.
Tính giá trị của các biểu thức sau: a) 2 2
x − y tại x = 87 và y = 13 b) 2
x + 6x + 9 tại x = 97 c) 2
x − 4x + 4 tại x = 102 d) 2 2
x − 2xy + y tại x = 2021; y = 2020 Trang 1 Bài 7.
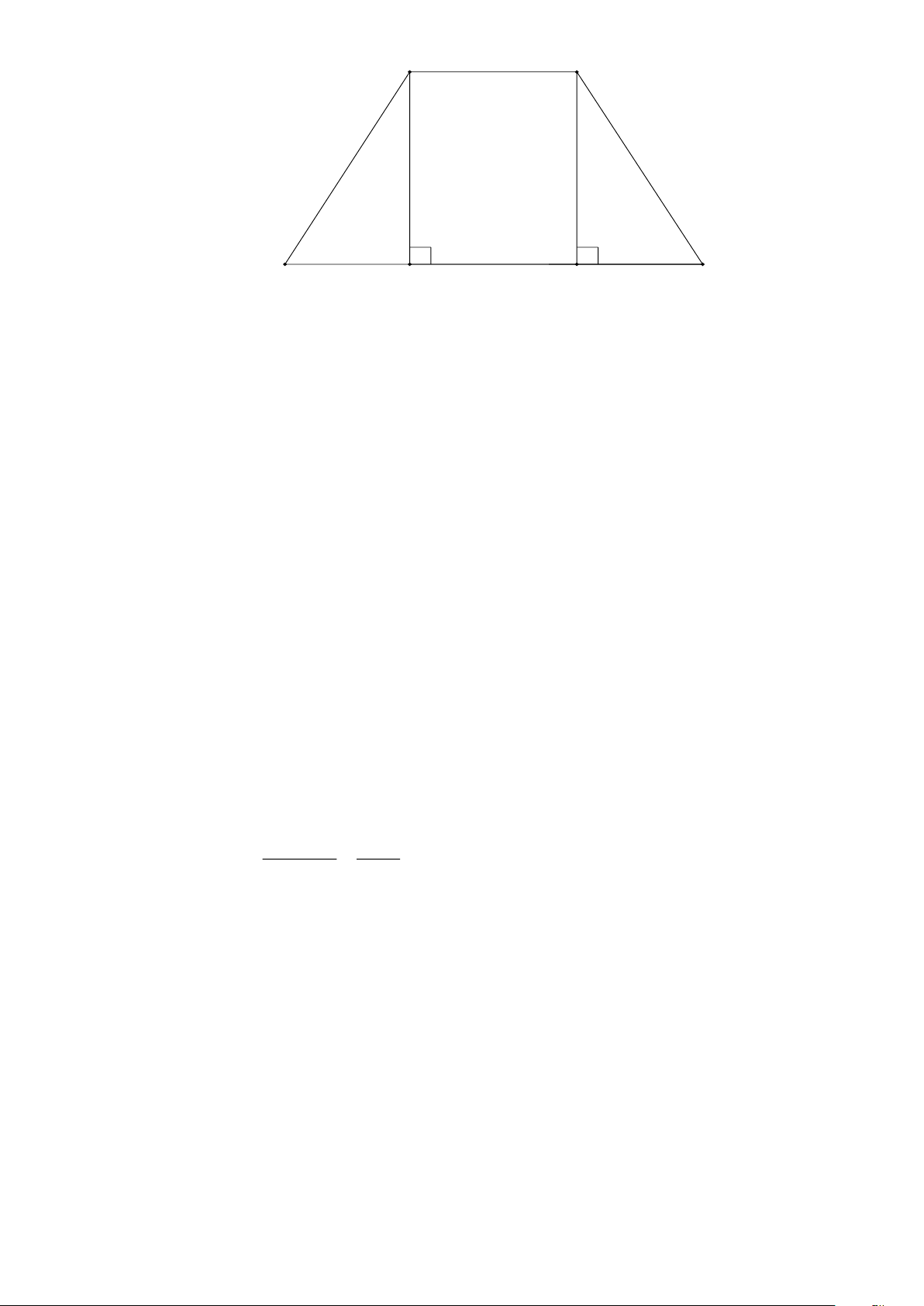
Hình thang cân ABCD có AB//CD , AB  CD . Kẻ hai đường cao AH , BK .
a) Chứng minh rằng HD = KC .
b) Biết AB = 6 cm; CD = 15 cm; C = 60 . Tính độ dài các cạnh BC; BK . Bài 8.
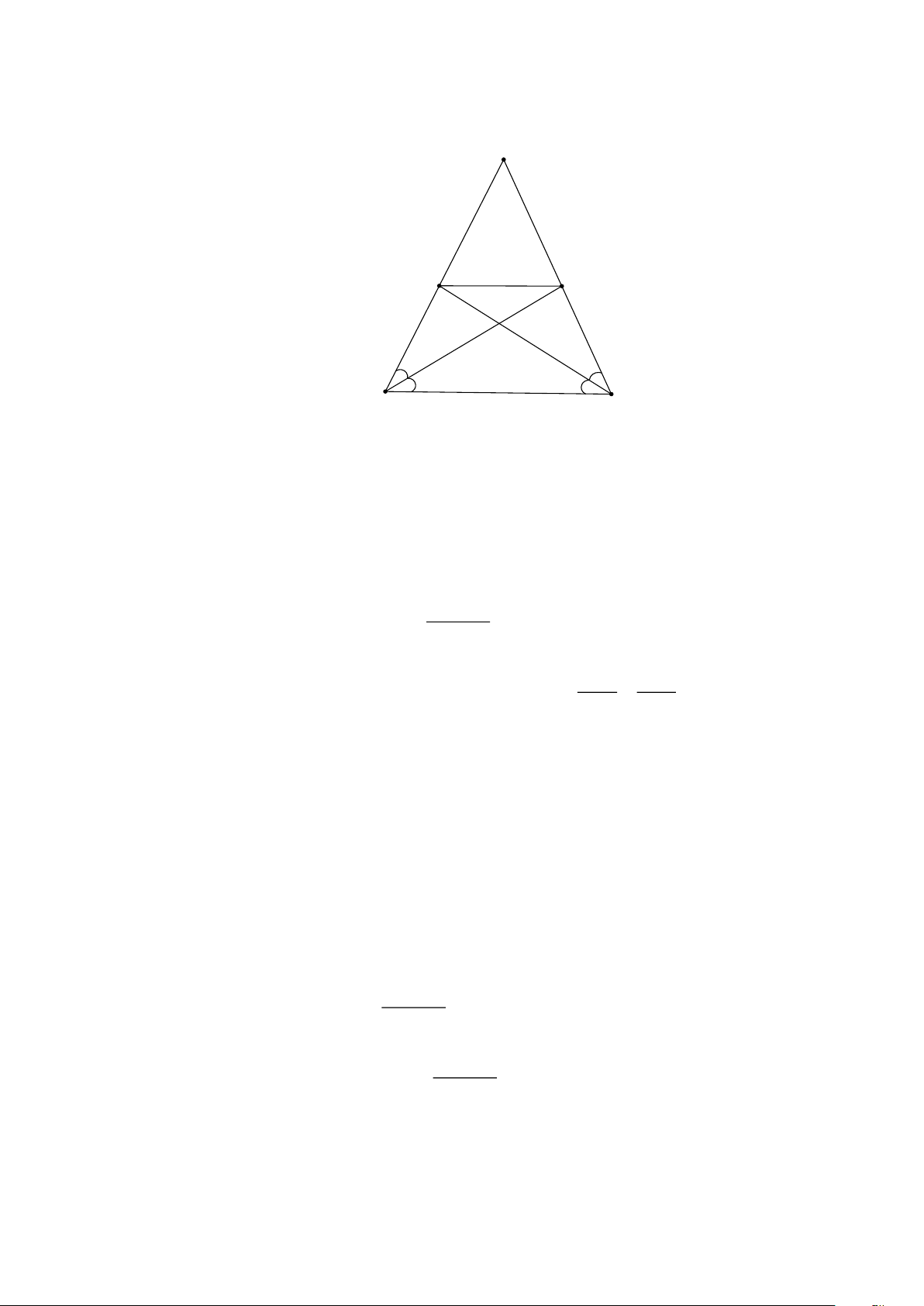
Cho ABC cân tại đỉnh A có BD,CE là phân giác của tam giác.
a) Tứ giác BEDC là hình gì? Vì sao?
b) Chứng minh BE = ED = DC .
c) Biết A = 50 . Tính các góc còn lại của tứ giác BEDC . Bài 9.
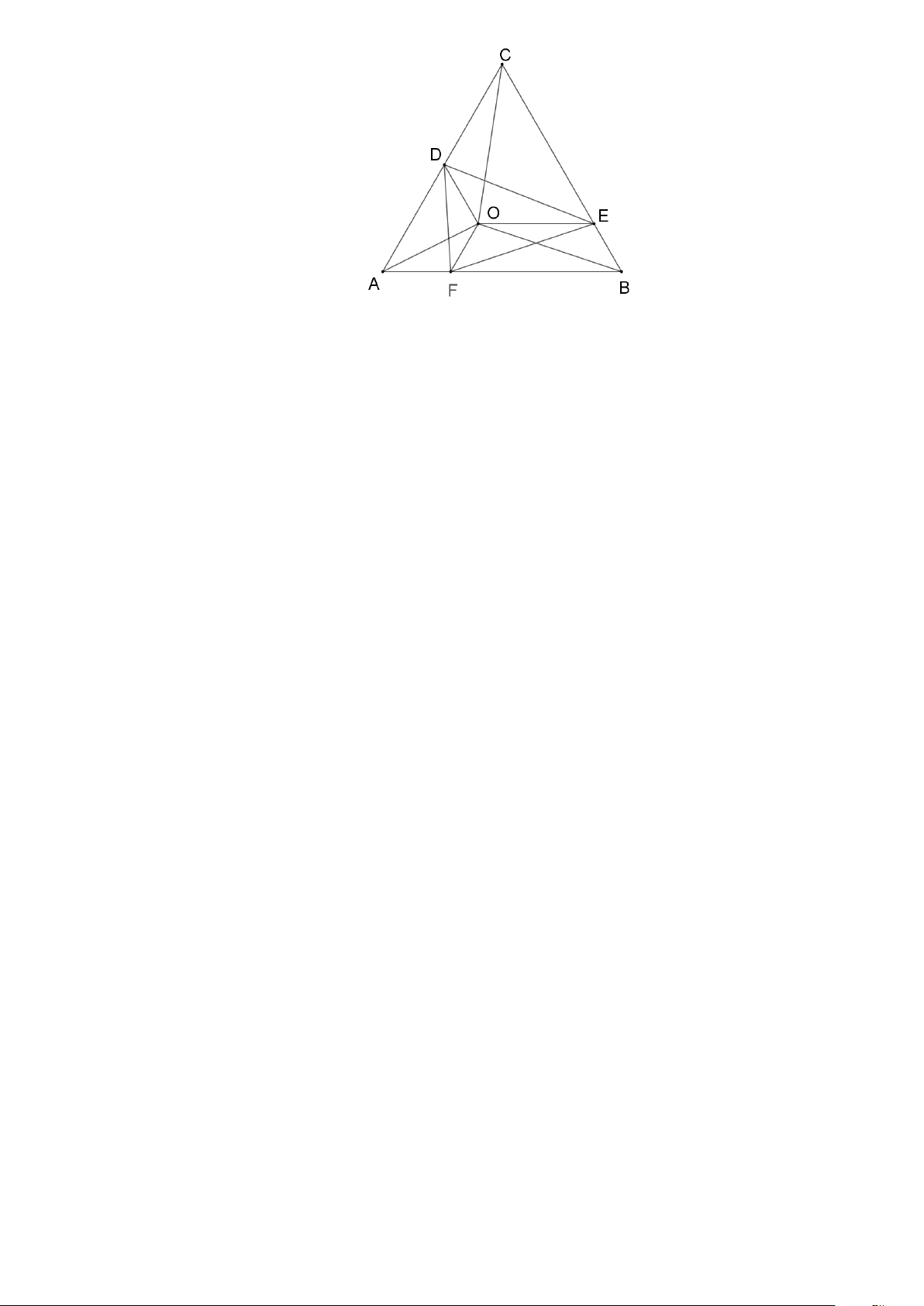
Cho tam giác đều ABC có O là một điểm nằm trong tam giác đó. Qua O kẻ đường thẳng song
song với BC cắt AC ở D , kẻ đường thẳng song song với AB cắt BC ở E , kẻ đường thẳng
song song với AC cắt AB ở F .
a) Tứ giác ADOF là hình gì? Vì sao?
b) So sánh chu vi của tam giác DEF với tổng độ dài các đoạn thẳng OA , OB , OC .
B. BÀI TẬP NÂNG CAO (DÀNH THÊM CHO LỚP M VÀ KHUYẾN KHÍCH HỌC SINH CÁC LỚP KHÁC)
Bài 10. Tìm GTLN hoặc GTNN nếu có của các biểu thức: 2
A = x − 2x −1; 2
B = 4x + 4x + 5; 2
C = 2x − x − 4 ; 2
D = −x − 4x
Bài 11. Giải phương trình: ( x + )2 5
1 − (5x + 3)(5x − 3) = 30 .
Bài 12. Cho x + y + z = 0 ; xy + yz + zx = 0 . Chứng minh rằng: x = y = z . HẾT Trang 2
ĐÁP ÁN BÀI TẬP TĂNG CƯỜNG TOÁN 8 TUẦN2
HƯỚNG DẪN GIẢI CHI TIẾT
A. BÀI TẬP CƠ BẢN (DÀNH CHO TẤT CẢ CÁC LỚP):
Bài 1. Tìm x, biết: a) ( 2 x + x + ) 1 ( x − ) 3 1 = 2x d) ( x + )2 1 − 4 = 0 b) ( x + )2 1 − 2x = 0 2
e) x − 2x +1 = 0 2 c) x ( 2 x + x + ) 2 1 − x ( x + ) 1 − x + 5 = 2 f ) (2x + ) 1 − 2( 2 2x + 3) = 0 a) ( 2 x + x + ) 1 ( x − ) 3 1 = 2x d) ( x + )2 1 − 4 = 0 3 3  x −1 = 2x  (x + )2 1 = 4 = 2 = ( 2 − )2 2 3  x = −1 x +1 = 2 x = 1    x = −1  x 1 2  + = − x = 3 − b) ( x + )2 1 − 2x = 0 2
e) x − 2x +1 = 0 2
 x + 2x +1− 2x = 0 2 2   (x − ) x +1 = 0 1 = 0 2   − = x = 1 − (Vô nghiem) x 1 0  x = 1 c) x ( 2 x + x + ) 2 1 − x ( x + ) 1 − x + 5 = 2 f ) (2x + )2 1 − 2( 2 2x + 3) = 0 3 2 3 2
 x + x + x − x − x − x + 5 = 2 2 2
 4x + 4x +1− 4x − 6 = 0
 5 = 2 (Vô ngh m ie )  4x − 5 = 0  4x = 5 5  x = 4
Bài 2: Chứng minh rằng: a) ( x + )( 2 x − x + ) 3 1 1 = x +1. b) ( 3 2 2 3 + + + )( − ) 4 4 x x y xy y
x y = x − y
c) ( x + y + z)2 2 2 2
= x + y + z + 2xy + 2yz + 2xz Lời giải a) Biến đổi vế trái: Trang 3 VT = ( x + )( 2 1 x − x + ) 1 3 2 2
= x − x + x + x − x +1 3 = x +1 = VP Vậy: ( x + )( 2 x − x + ) 3 1 1 = x +1 b) Biến đổi vế trái: = ( 3 2 2 3 VT
x + x y + xy + y )(x − y) 4 3 3 2 2 2 2 3 3 4
= x − x y + x y − x y + x y − xy + xy − y 4 4
= x − y = VP Vậy: ( 3 2 2 3 + + + )( − ) 4 4 x x y xy y
x y = x − y c) Biến đổi vế phải 2 2 2
VP = x + y + z + 2xy + 2yz + 2xz = 2 x + xy + 2 2
y + 2( x + y)z
= (x + y)2 + (x + y) 2 2 z + z = ( + + )2 x y z = VT
Vậy: ( x + y + z)2 2 2 2
= x + y + z + 2xy + 2yz + 2xz Bài 3. Tính: a) ( x + )2 1 ; b) ( + )2 2x y ; c) ( x − y)2 3 2 ; 2  1  d) ( x − )2 2 ; e) 5x − y   ;
f) ( x + 2y)( x − 2y) .  2  Lời giải a) ( x + )2 2 1 = x + 2x +1 b) ( x + y)2 2 2 2
= 4x + 4xy + y c) ( x − y)2 2 2 3 2
= 9x −12xy + 4y ; d) ( x − )2 2
2 = x − 4x + 4 2  1  1 e) 2 2 5x − y
= 25x − 5xy + y    2  4
f) ( x + y)( x − y) 2 2 2 2 = x − 4y . Trang 4
Bài 4. Dùng hằng đẳng thức, hoàn thành vế còn lại: 2  1  a) ( − )2 2x y = b) ( − )2 2 2x y z = c) x + y =    2 
d) ( x − 2y)(2y + x) = e) ( x + y)2 2 5 = f) ( − )2 3x y = Lời giải
a) ( x − y)2 2 2 2
= 4x − 4xy + y
b) ( x y − z)2 2 4 2 2 2 2
= 4x y − 4x z + z 2  1  1 c) 2 2 x + y
= x + xy + y    2  4
d) ( x − y)( y + x) 2 2 2 2 = x − 4y e) ( x + y)2 2 2 2 5
= 4x + 20xy + 25y f) ( x − y)2 2 2 3
= 9x − 6xy + y Bài 5. Rút gọn biểu thức 2 a) ( 2
x + ) −(x + )(x − )( 2 2 2 2 x + 4) b)
(x y)(x y) (x y)2 (x y)2 2 − + + + + −
c) ( x y)2 ( x y)2 + − −
d) ( x − y + z)2 + ( z − y)2 + 2( x − y + z)( y − z) Lời giải 2 a) ( 2
x + ) −(x + )(x − )( 2 2 2 2 x + 4) 4 2
= x + 4x + 4 − ( 2 x − 4)( 2 x + 4) 4 2
= x + 4x + 4 − ( 4 x −16) 4 2 4
= x + 4x + 4 − x +16 2 = 4x + 20 b)
(x y)(x y) (x y)2 (x y)2 2 − + + + + −
= (x + y) + (x − y) 2   
= (x + y + x − y)2 = (2x)2 2 = 4x
c) ( x y)2 ( x y)2 + − − Trang 5
= (x + y) + (x − y) (x + y) − (x − y)    
= x + y + x − yx + y − x + y = 2 .2 x y = 4xy
d) ( x − y + z)2 + ( z − y)2 + 2( x − y + z)( y − z)
= (x − y + z)2 + 2(x − y + z)( y − z) + ( y − z)2
= (x − y + z) + ( y − z) 2   
= x − y + z + y − z2 2 = x Bài 6.
Tính giá trị của các biểu thức sau: a) 2 2
x − y tại x = 87 và y = 13 b) 2
x + 6x + 9 tại x = 97 c) 2
x − 4x + 4 tại x = 102 d) 2 2
x − 2xy + y tại x = 2021; y = 2020 Lời giải a) Ta có: 2 2
x − y = ( x + y)( x − y)
Thay x = 87 và y = 13 vào biểu thức ta được:
(87 +13)(87 −13) =100.74 = 7400
b) Ta có: x + x + = ( x + )2 2 6 9 3
Thay x = 97 vào biểu thức ta được: ( + )2 2 97 3 = 100 = 10000
c) Ta có: x − x + = ( x − )2 2 4 4 2
Thay x = 102 vào biểu thức ta được: ( − )2 2 102 2 = 100 = 10000
d) Ta có: x − xy + y = ( x − y)2 2 2 2
Thay x = 2021; y = 2020 ta được: ( − )2 2 2021 2020 = 1 = 1 Bài 7.
Hình thang cân ABCD có AB//CD , AB  CD . Kẻ hai đường cao AH , BK .
a) Chứng minh rằng HD = KC .
b) Biết AB = 6 cm; CD = 15 cm; C = 60 . Tính độ dài các cạnh BC; BK . Lời giải Trang 6 A B K H C D
a) Chứng minh rằng HD = KC .
Vì ABCD là hình thang cân nên C = D ( theo định nghĩa )
và AD = BC ( tính chất ).
Xét AHD vuông tại H và BKC vuông tại K có:
C = D ( chứng minh trên );
AD = BC ( chứng minh trên ).
 AHD = BKC ( cạnh huyền – góc nhọn ).
 HD = KC ( hai cạnh tương ứng ).
b) Biết AB = 6 cm; CD = 15 cm; C = 60 . Tính độ dài các cạnh BC; BK .
Xét hình thang ABKH ( AB//KH ) có H = K = 90 nên A = 90 và B = 90
 ABKH là hình chữ nhật.
 KH = AB = 6 cm.
Mà DH + HK + KC = DC vả DH = KC ( chứng minh trên ). DC − HK 15 − 6  DH = KC = = = 4,5 cm. 2 2
Xét BKC vuông tại K có C = 60  BK 
C là nửa tam giác đều cạnh BC
 BC = 2KC = 2.4,5 = 9 cm.
Áp dụng định lí Pytago vào BKC vuông tại K ta có: 2 2 2
BK + KC = BC 2 2 2 2 2
 BK = BC − KC = 9 − 4,5 = 60,75  BK  7,8 cm. Bài 8.
Cho ABC cân tại đỉnh A có BD,CE là phân giác của tam giác.
a) Tứ giác BEDC là hình gì? Vì sao?
b) Chứng minh BE = ED = DC . Trang 7
c) Biết A = 50 . Tính các góc còn lại của tứ giác BEDC . Lời giải A E D B C
a) Tứ giác BEDC là hình gì? Vì sao?
+ Tứ giác BEDC là hình thang cân. + Giải thích:
Xét ABC cân tại A , ta có: B = C . 180 − A
Mà A + B + C = 180 . Do đó B = C = . ( ) 1 2  ABC ACB 
Mà BD,CE là phân giác của ABC nên ABD = ACE  = =   2 2   
Xét ABD và ACE có: DAE chung;
AB = AC ( ABC cân tại A ); ABD = ACE.
 ABD = ACE ( g - c - g ).
 AD = AE ( hai cạnh tương ứng ).  ADE  cân tại A . 180 − A  AED = ADE = . (2) 2  180− A  Từ ( )
1 và (2) suy ra AED = ABC  =   2   
Mà AED đồng vị với ABC nên DE//CB .
Tứ giác BEDC là hình thang.
Mặt khác EBC = DCB ( ABC cân tại A ). Trang 8
Vậy BEDC là hình thang cân.
b) Chứng minh BE = ED = DC .
• BEDC là hình thang cân ( chứng minh a )
 BE = DC . (3)
• DE//CB ( chứng minh trên )
 EDB = DBC ( sole trong )
Mà DBC = DBE ( BD là phân giác của ABC ).
 EDB = DBE (= DBC)
 EBD cân tại E
 ED = EB .(4)
Từ (3) và (4) suy ra BE = ED = DC
c) Biết A = 50 . Tính các góc còn lại của tứ giác BEDC .
180 − A 180 − 50
Xét ABC cân tại A , ta có: B = C = = = 65 . 2 2
Xét hình thang cân BEDC có BED = CDE ;
Mà BED trong cùng phía với EBC và DE//CB
 BED + EBC =180
 BED = 180 − EBC = 180 − 65 = 115.
Vậy BED = CDE = 115. Bài 9.
Cho tam giác đều ABC có O là một điểm nằm trong tam giác đó. Qua O kẻ đường thẳng song
song với BC cắt AC ở D , kẻ đường thẳng song song với AB cắt BC ở E , kẻ đường thẳng
song song với AC cắt AB ở F .
a) Tứ giác ADOF là hình gì? Vì sao?
b) So sánh chu vi của tam giác DEF với tổng độ dài các đoạn thẳng OA , OB , OC . Lời giải Trang 9
a) Ta có OF // AC . Mà D  AC nên OF // AD . Do đó ADOF là hình thang ( ) 1 .
Do OD // EC nên ADO = ACB (hai góc đồng vị). Mặt khác FAD = ACB (do tam giác ABC đều).
Vì vậy: ADO = FAD (2) . Từ ( )
1 và (2) suy ra ADOF là hình thang cân.
b) Theo phần a) ADOF là hình thang cân nên hai đường chéo của ADOF bằng nhau. Do đó: AO = DF
Chứng minh tương tự phần a) ta được:
DOEC là hình thang cân nên OC = DE .
FOEB là hình thang cân nên OB = EF .
Do đó: DE + EF + FD = OC + OB + OA
Vậy chu vi của tam giác DEF bằng tổng độ dài các đoạn thẳng OA , OB , OC .
B. BÀI TẬP NÂNG CAO (DÀNH THÊM CHO LỚP M VÀ KHUYẾN KHÍCH HỌC SINH CÁC LỚP KHÁC)
Bài 10. Tìm GTLN hoặc GTNN nếu có của các biểu thức: 2
A = x − 2x −1; 2
B = 4x + 4x + 5; 2
C = 2x − x − 4 ; 2
D = −x − 4x Lời giải
A = x − x − = x − x + − = ( x − )2 2 2 2 1 2. .1 1 2 1 − 2 . Vì ( x − )2
1  0 với mọi x nên ( x − )2 1 − 2  2 − .
Đẳng thức xảy ra khi ( x − )2 1 = 0  x = 1.
Vậy A đạt giá trị nhỏ nhất là −2 khi x = 1 .
B = x + x + = ( x)2 + x + + = ( x + )2 2 2 4 4 5 2 2.2 .1 1 4 2 1 + 4 Vì ( x + )2 2
1  0 với mọi x nên ( x + )2 2 1 + 4  4 . Trang 10
Đẳng thức xảy ra khi ( x + )2 1 2 1 = 0  x = − . 2 1
Vậy B đạt giá trị nhỏ nhất là 4 khi x = − . 2
C = x − x − = −(x − x + ) − = −(x − )2 2 2 2 4 2 1 3 1 − 3 Vì −( x − )2
1  0 với mọi x nên −( x − )2 1 − 3  3 − .
Đẳng thức xảy ra khi ( x − )2 1 = 0  x = 1.
Vậy C đạt giá trị lớn nhất là 3 − khi x = 1.
D = −x − x = −(x + x + ) + = −(x + )2 2 2 2 4 2. .2 2 4 2 + 4 Vì −( x + )2
2  0 với mọi x nên −( x + )2 2 + 4  4 .
Đẳng thức xảy ra khi ( x + )2 2 = 0  x = 2 − .
Vậy D đạt giá trị lớn nhất là 4 khi x = −2 .
Bài 11. Giải phương trình: ( x + )2 5
1 − (5x + 3)(5x − 3) = 30 . Lời giải Ta có ( x + )2 5
1 − (5x + 3)(5x − 3) = 30  2 x + x + − ( 2 25 10 1 25x − 9) = 30  2 2
25x +10x +1− 25x + 9 = 30  10x = 20  x = 2 Vậy x = 2 .
Bài 12. Cho x + y + z = 0 ; xy + yz + zx = 0 . Chứng minh rằng: x = y = z . Lời giải
Ta có x + y + z = 0
Suy ra ( x + y + z)2 = 0 2 2 2
x + y + z + 2xy + 2 yz + 2xz = 0 2 2 2
x + y + z + 2( xy + yz + xz) = 0
Vì xy + yz + zx = 0 nên 2 2 2
x + y + z = 0 Ta có 2 2 2
x + y + z  0, với mọi x, y, z
Dấu “=” xảy ra khi x = y = z = 0 . Trang 11