Bài Tập Toán 8 Tuần 3 Có Lời Giải Chi Tiết

PHIẾU BÀI TẬP TOÁN 8 TUẦN 03 Bài 1. Tìm x , biết a) ( x − )2 1 −1 = 0 . b) 3 2
x − 3x + 3x −1 = 0 . c) 2 x + 4x = 21. 1 1
d) ( x − )2 + ( x + )2 2 1
3 − 5( x + 7)( x − 7) = 0 . e) 3 2
x + x + x + = 0 . 3 27 Bài 2.
a) Chứng minh rằng, nếu:
(x − y)2 +( y − z)2 +(z − x)2 = ( y + z − x)2 +(z + x − y)2 + (x + y − z)2 2 2 2
thì x = y = z .
b) Chứng minh rằng giá trị của biểu thức sau không phụ thuộc vào x, y : (x + y)( 2 2
x − xy + y ) + (x − y)( 2 2
x + xy + y ) 3 − 2x . Bài 3.
Cho tam giác ABC . Gọi M là trung điểm của BC , I là trung điểm của AM . Tia BI cắt AC
ở D . Qua M kẻ đường thẳng song song với BD cắt AC ở E . Chứng minh rằng :
a) AD = DE = EC . 1 b) ID = BD . 4 Bài 4.
Cho tam giác ABC ( AB  AC ). Trên cạnh AB lấy điểm E sao cho BE = AC . Gọi I , D , F
lần lượt là trung điểm các đoạn thẳng CE , AE và BC . Chứng minh rằng :
a) Tam giác IDF là tam giác cân. b) BAC = 2IDF . Bài 5.
Cho hình thang vuông ABCD có A = D = 90 . Gọi M , N lần lượt là trung điểm của các cạnh
BC , AD . Chứng mính rằng:
a) MAD là tam giác cân. b) MAB = MDC . Bài 6.
Cho tam giác ABC . Gọi M , N , P theo thứ tự là trung điểm của các cạnh AB , AC , BC .
Tính chu vi của tam giác MNP , biết AB = 8 cm, AC = 10 m, BC = 12 m. Bài 7.
Cho hình thang vuông ABCD có A = D = 90. Gọi F là trung điểm của BC . Chứng minh BAF = CDF .
B. BÀI TẬP NÂNG CAO (DÀNH THÊM CHO LỚP M VÀ KHUYẾN KHÍCH HỌC SINH CÁC LỚP KHÁC) Bài 8.
Chứng minh rằng các bất đẳng thức sau luôn đúng với mọi giá trị của x , y a) 2 2
x + xy + y +1  0 b) 2 2
x + 5y + 2x − 4xy −10 y +14  0 c) 2 2
5x +10y − 6xy − 4x − 2 y + 3  0 Bài 9.
Cho hình thang ABCD ( AB // CD).Gọi E, F lần lượt là trung điểm AD và BC . Đường thẳng
EF cắt BD ở I , cắt AC ở K .
a) Chứng minh : AK = KC ; BI = ID .
b) Cho AB = 6 , CD = 10 . Tính EI, KF, IK.
ĐÁP ÁN BÀI TẬP TĂNG CƯỜNG TOÁN 8 TUẦN 3 Bài 1. Tìm x , biết Trang 1 a) ( x − )2 1 −1 = 0 . b) 3 2
x − 3x + 3x −1 = 0 . c) 2 x + 4x = 21. 1 1
d) ( x − )2 + ( x + )2 2 1
3 − 5( x + 7)( x − 7) = 0. e) 3 2
x + x + x + = 0 . 3 27 Lời giải x = 2 a) ( x − )2
1 −1 = 0  ( x − 2).x = 0   . x = 0
b) x − x + x − =  ( x − )3 3 2 3 3 1 0
1 = 0  x −1 = 0  x = 1. x + 2 = 5 x = 3
c) x + 4x = 21  ( x + 2)2 2 = 25    . x 2 5  + = − x = 7 −
d) ( x − )2 + ( x + )2 2 1
3 − 5( x + 7)( x − 7) = 0 . 2 2
 x − x + + x + x + − ( 2 4 4 1 6 9 5 x − 49) = 0 255 −
 2x + 255 = 0  x = . 2 3 1 1  1  1 1 e) 3 2
x + x + x + = 0  x +
= 0  x + = 0  x = −   . 3 27  3  3 3 Bài 2.
a) Chứng minh rằng, nếu:
(x − y)2 +( y − z)2 +(z − x)2 = ( y + z − x)2 +(z + x − y)2 + (x + y − z)2 2 2 2
thì x = y = z .
b) Chứng minh rằng giá trị của biểu thức sau không phụ thuộc vào x, y : (x + y)( 2 2
x − xy + y ) + (x − y)( 2 2
x + xy + y ) 3 − 2x . Lời giải a) Ta có:
= ( − )2 + ( − )2 + ( − )2 VT x y y z z x = ( 2 2 2
2 x + y + z − ( xy + yz + zx))
VP = ( y + z − x)2 + ( z + x − y)2 + ( x + y − z)2 2 2 2 = ( 2 2 2
6 x + y + z − ( xy + yz + zx))
Vì VT = VP  VT −VP =  ( 2 2 2 0
4 x + y + z − (xy + yz + zx)) = 0 x − y = 0 x = y  (  
x − y)2 + ( y − z)2 + (z − x)2 2  = 0  
 y − z = 0  y = z  x = y = z . z x 0  − = z = x   b) ( x + y)( 2 2
x − xy + y ) + (x − y)( 2 2
x + xy + y ) 3 − 2x 3 3 3 3 3
= x + y + x − y − 2x = 0
vậy biểu thức sau không phụ thuộc vào x, y . Bài 3.
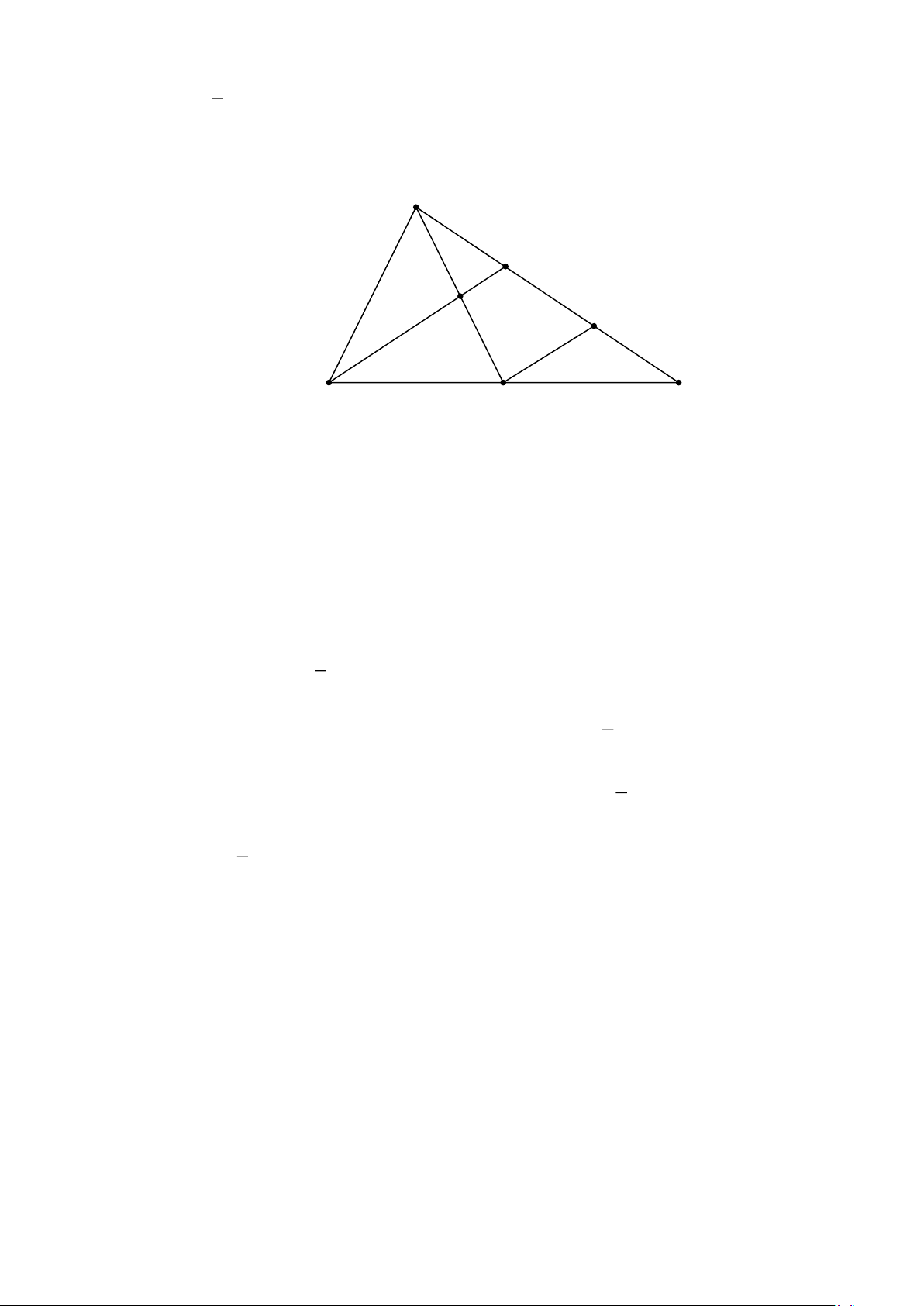
Cho tam giác ABC . Gọi M là trung điểm của BC , I là trung điểm của AM . Tia BI cắt AC
ở D . Qua M kẻ đường thẳng song song với BD cắt AC ở E . Chứng minh rằng : Trang 2
a) AD = DE = EC . 1 b) ID = BD . 4 Lời giải A D I E B M C
a) Chứng minh : AD = DE = EC .
Tam giác IME có I là trung điểm của AM ; ID // ME nên ID là đường trung bình của tam
giác AME . Suy ra AD = DE . (1)
Tam giác CBD có M là trung điểm của BC ; ME // BD nên ME là đường trung bình của tam
giác CBD . Suy ra ED = EC . (2)
Từ (1) và (2) suy ra AD = DE = EC . Đpcm 1
b) Chứng minh: ID = BD . 4 1
Do ID là đường trung bình của tam giác AME . Suy ra ID = ME . (3) 2 1
Do ME là đường trung bình của tam giác CBD . Suy ra ME = BD . (4) 2 1
Suy ra ID = BD . Đpcm 4 Bài 4.
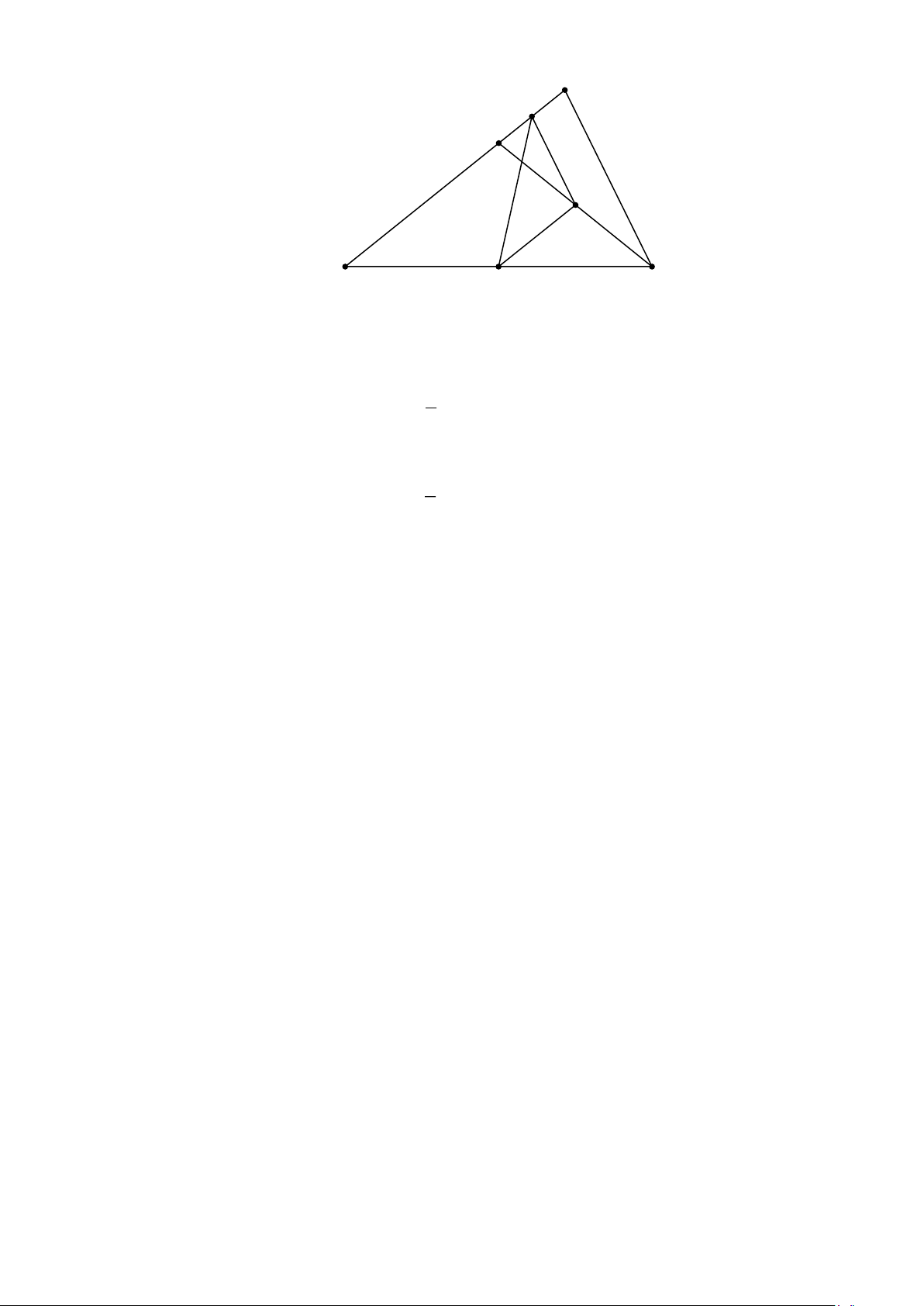
Cho tam giác ABC ( AB  AC ). Trên cạnh AB lấy điểm E sao cho BE = AC . Gọi I , D , F
lần lượt là trung điểm các đoạn thẳng CE , AE và BC . Chứng minh rằng :
a) Tam giác IDF là tam giác cân. b) BAC = 2IDF . Lời giải Trang 3 A D E I B F C
a) Tam giác IDF là tam giác cân.
Tam giác EAC có I là trung điểm của EC , D là trung điểm của EA nên ID là đường trung 1
bình của tam giác EAC . Suy ra ID = AC . 2
Tam giác CBE có I là trung điểm của EC , F là trung điểm của BC nên IF là đường trung 1
bình của tam giác CBE . Suy ra IF = BE . 2
Theo bài ra AC = BE , suy ra ID = IF . Suy ra tam giác IDF cân tại I . Đpcm
b) BAC = 2IDF .
Do IF là đường trung bình của tam giác CBE nên IF // AB . Suy ra IFD = FDE (so le trong)
Mặt khác IFD = IDF (do tam giác IDF cân tại I ). Suy ra IDF = FDE .
Suy ra 2IDF = IDF + FDE = IDE .
Do ID là đường trung bình của tam giác EAC nên ID // AC . Suy ra IDE = BAC (đồng vị)
Suy ra BAC = 2IDF . Đpcm Bài 5.
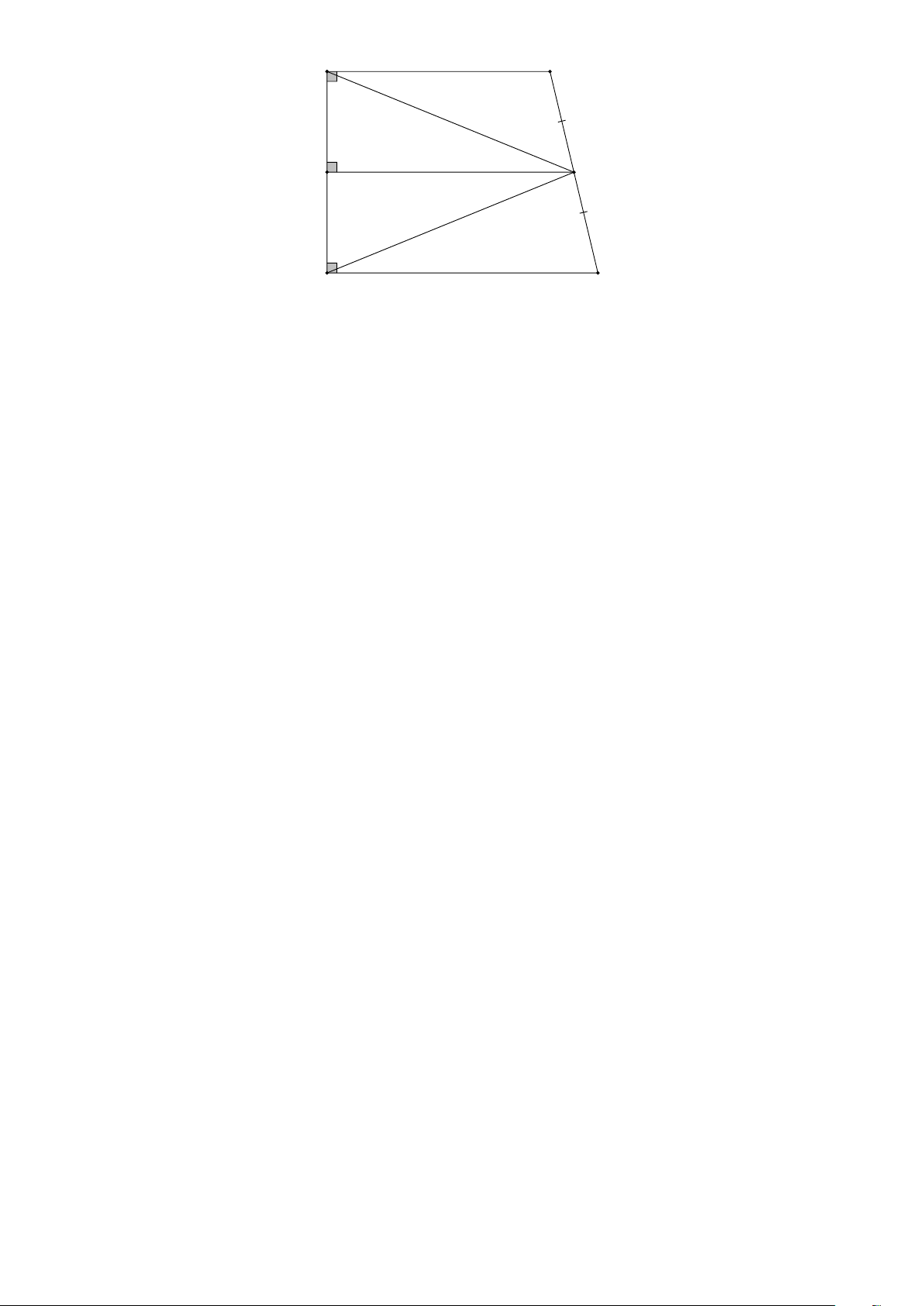
Cho hình thang vuông ABCD có A = D = 90 . Gọi M , N lần lượt là trung điểm của các cạnh
BC , AD . Chứng mính rằng:
a) MAD là tam giác cân. b) MAB = MDC Lời giải Trang 4
a) Theo đề ta ta có M , N lần lượt là trung điểm của BC , AD nên MN là đường trung bình
của hình thang ABCD
 MN //AB//DC  MN ⊥ AD
Xét MAD có MN vừa là đường cao vừa là đường trung tuyến.  MAD  cân tại M
b) Ta có MAD là tam giác cân tại M, suy ra MAN = MDN
Mà MAN + MAB = 90 và MDN + MDC = 90
Suy ra MAB = MDC (đpcm). Bài 6.
Cho tam giác ABC . Gọi M , N , P theo thứ tự là trung điểm của các cạnh AB , AC , BC .
Tính chu vi của tam giác MNP , biết AB = 8 cm, AC = 10 m, BC = 12 m. Lời giải
Ta có M , N , P theo thứ tự là trung điểm của các cạnh AB , AC , BC nên MN , NP , PM là
3 đường trung bình của tam giác ABC .
Áp dụng tính chất đường trung bình của tam giác ta có: BC 12 MN = = = 6 (m) 2 2 AB 8 NP = = = 4 (m) 2 2 AC 10 PM = = = 5 (m) 2 2
Chu vi hình tam giác MNP là: C = 6 + 4 + 5 = 15 (m) Bài 7.
Cho hình thang vuông ABCD có A = D = 90. Gọi F là trung điểm của BC . Chứng minh BAF = CDF .
Lời giải Trang 5 A B H F D C
Kẻ FH ⊥ AD; H  AD .
Ta có: AB ⊥ AD (gt)
DC ⊥ AD (gt)
 FH // AB // DC
Mà F là trung điểm của BC (gt)
 HA = HD (tc đường trung bình)
Xét AHF và DHF có: HA = HD (cmt)
AHF = DHF = 90 HF chung
 AHF = DHF (c.g.c)
 AFH = DFH (góc tương ứng) (1)
Ta có: FH // AB (cmt)  BAF = AFH (so le trong) (2)
Lại có: FH // DC (cmt)  CDF = DFH (so le trong) (3)
Từ (1), (2) và (3)  BAF = CDF (đpcm)
B. BÀI TẬP NÂNG CAO (DÀNH THÊM CHO LỚP M VÀ KHUYẾN KHÍCH HỌC SINH CÁC LỚP KHÁC) Bài 8.
Chứng minh rằng các bất đẳng thức sau luôn đúng với mọi giá trị của x , y a) 2 2
x + xy + y +1  0 b) 2 2
x + 5y + 2x − 4xy −10 y +14  0 c) 2 2
5x +10y − 6xy − 4x − 2 y + 3  0 Lời giải a) Ta có: 2 2
x + xy + y +1 Trang 6 2 2 y y 3y 2 = x + 2x + + +1 2 4 4 2 2  y  3y = x + + +11  0  
với  x , y  2  4 2  y  2 3y Vì x +  0,    0, x  , y  2  4 b) Ta có: 2 2
x + 5y + 2x − 4xy −10 y +14 2 2 2
= (x − 4xy + 4y ) + y + 2x − 4y − 6y +14
= (x − y)2 + x − y + + ( 2 2 2( 2 ) 1
y − 6y + 9) + 4
= (x − y + )2 + ( y − )2 2 1
3 + 4  4  0 với  x , y
Vì ( x − y + )2  ( y − )2 2 1 0, 3  0, x  , y c) Ta có: 2 2
5x +10y − 6xy − 4x − 2y + 3 = ( 2
x − x + ) + ( 2 2
x − xy + y ) + ( 2 4 4 1 6 9 y − 2y + ) 1 +1
= ( x − )2 + (x − y)2 + ( y − )2 2 1 3
1 +1  1  0 với  x , y
Vì ( x − )2  ( x − y)2  ( y − )2 2 1 0, 3 0, 1  0, x  , y Bài 9.
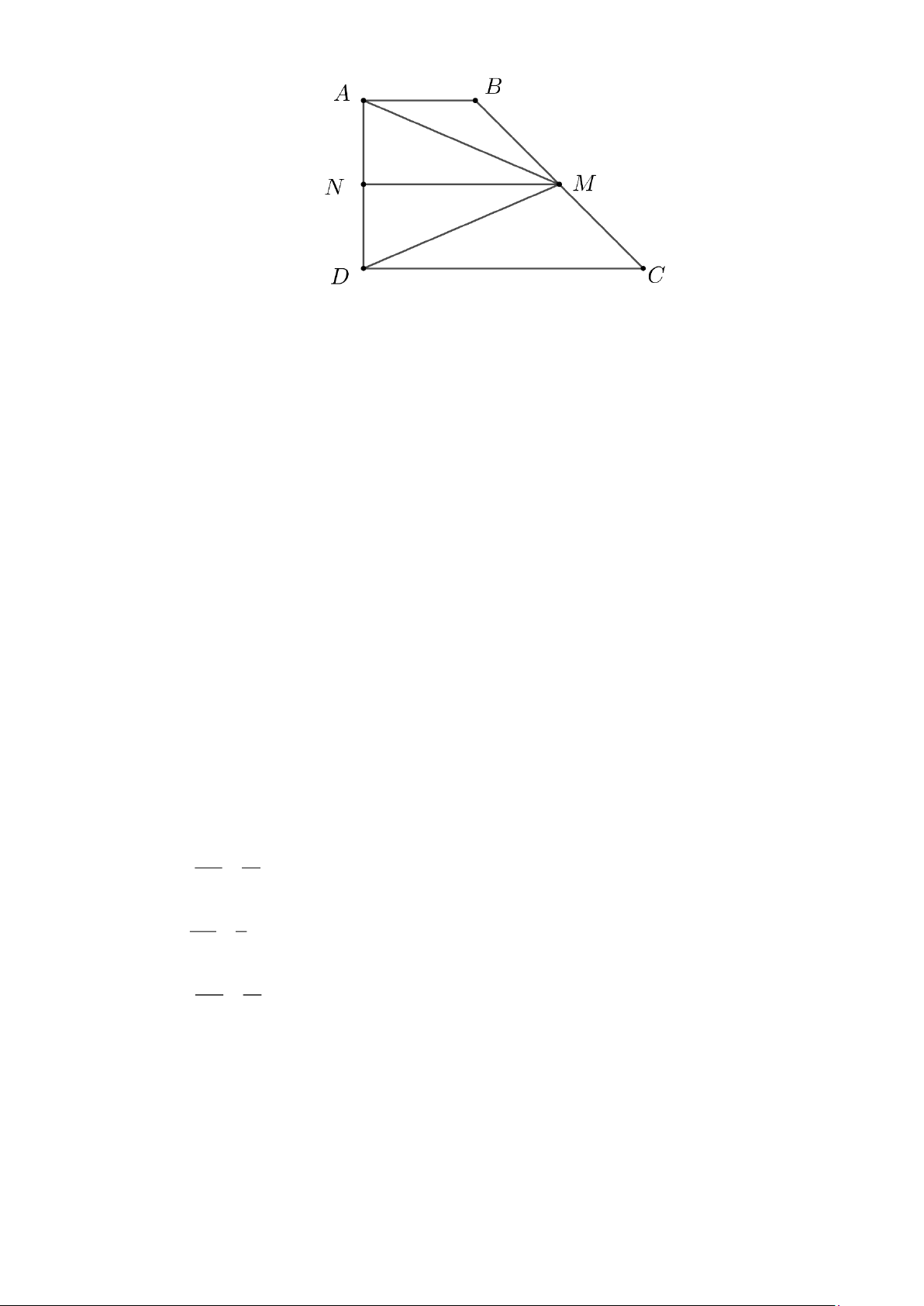
Cho hình thang ABCD ( AB // CD).Gọi E, F lần lượt là trung điểm AD và BC . Đường thẳng
EF cắt BD ở I , cắt AC ở K .
a) Chứng minh : AK = KC ; BI = ID .
b) Cho AB = 6 , CD = 10 . Tính EI, KF, IK. Lời giải
GT Cho hình thang ABCD (AB A 6 B CD).
E là trung điểm AD : EA = ED. E F
F là trung điểm BC : FB = FC. I K EF BD tại I. D C 10 EF AC tại K.
KL a)Chứng minh : AK = KC ; BI = ID.
b)Cho AB = 6, CD = 10. Tính EI, KF, IK. Trang 7
a)Xét hình thang ABCD có:
AE = ED (gt) 
BF = EC (gt)
 EF là đường trung bình của hình thang ABCD (định nghĩa đường trung bình của hình thang) (*)
Mà EF  BD tại I (gt); EF  AC tại K (gt)  EI AB CD 
 KF AB CD
 IK AB CD  Xét tam giác ABD có:
AE = ED ( gt)
  IB = ID ( định lý 1 đường trung bình của tam giác) (đpcm)
EI AB (cmt)  Xét tam giác ABC có:
FB = FC ( gt)
  AK = KC ( định lý 1 đường trung bình của tam giác) (đpcm)
KF AB (cmt)  b)Xét tam giác ABD có:
IB = ID (cma)
  EI là đường trung bình của tam giác ABD (đ/n đường trung
AE = ED (gt)  bình của tam giác) 1 1
 EI = AB = .6 = 3 ( ) 1 2 2 Xét tam giác ABC có:
AK = KC (cma)
  FK là đường trung bình của tam giác ABC (đ/n đường trung
FB = FC (gt)  bình của tam giác) 1 1
 FK = AB = .6 = 3 (2) (định lý 2 đường trung bình của tam giác) 2 2
Có EF là đường trung bình của hình thang ABCD (theo *) 1 1
 EF = .( AB + CD) = .(6 +10) = 8 (3) (định lý 2 đường trung bình của tam giác) 2 2
Có EF = EI + IK + KF
Mà: EF = 8 (theo 3); EI = 3 (theo 1); FK = 3 (theo 2) ⇒ IK = 2. Trang 8 Trang 9