Bài Tập Toán 8 Tuần 4 Có Lời Giải Chi Tiết

PHIẾU BÀI TẬP TOÁN 8 TUẦN 04
Bài 1. Viết các đa thức sau dưới dạng tích: a) 3 3 x + 8 y b) 6 3 a − b c) 3 8y −125 d) 3 8z + 27 Bài 2.
Dùng hằng đẳng thức viết nối vế còn lại 1) 2
(2x − y) = ..................... 2) 2 2
(2x − z) = ..................... 3) 2
4x − 9 = .....................
4) (x − 2 y)(2 y+ x) = ........... 5) 3
(2x − y) = ..................... 6) 3
(3x − y) = ..................... 7) 2
4x + 4x + 4 = ............ 8) 2
x − 6x + 9 = ................ 9) (x − 5)(x + 5) = .......... 10) 3 2
x +12x + 48x + 64 = ...... 11) 3 2
x − 6x +12x − 8 = ...... 12) (x + 2)(x − 2x + 4) = .......... 13) 2
(x − 3)(x + 3x + 9) = ..... 14) 2
x + 2x +1 = ............. 15) 2 x −1 = ...... 16) 2
9x + 6x +1 = ..... 17) 2
36x + 36x + 9 = ............. 18) 3 x + 27 = ...... Bài 3.
Rút gọn rồi tính giá trị của biểu thức. a) 2
(x −10) − x(x + 80) với x = 0,98. b) 2
4x − 28x + 49 với x = 4 . c) 3 2
x − x + 27x − 27 với x = 5 . d) 3 3 3
(x +1) + (x −1) + x − 3x(x−1)(x+1) với x = 100 Bài 4.
Cho tam giác ABC vuông cân tại đỉnh A . Trên cạnh AB lấy điểm D , trên cạnh AC lấy điểm
E sao cho AD = AE . Qua C kẻ đường thẳng vuông góc với BE cắt BA tại I .
a) Chứng minh: BE = CI
b) Qua D và A kẻ đường thẳng vuông góc với BE cắt BC lần lượt ở M và N . Chứng minh: MN = NC .
Bài 5. Cho hình thang ABCD (AB // CD) . Gọi E, F lần lượt là trung điểm AD, BC . Phân giác góc A
và góc B cắt EF theo thứ tự ở I và K .
a) Chứng minh tam giác AIE và tam giác BKF là các tam giác cân.
b) Chứng minh tam giác AID và tam giác BKC là tam giác vuông. 1 1
c) Chứng minh IE = AD và KF = BC . 2 2 d) Cho AB = 5c , m CD = 15c ,
m BC = 2cm . Tính độ dài đoạn thẳng IK . Bài 6.
Tìm giá trị lớn nhất; nhỏ nhất của biểu thức 1) 2
A = x − 6x +11 2) 2
B = x − 5x +12 3) 2
C = −x + 6x −11 4) 2
D = 5x − x 5) 2
D = 2x − 8x + 5 6) 2
E = 12 − 6x − 3x 7) 2 2
F = 4x +12xy +10y −10y + 35 8) 2 2
G = x − 4xy + 5y +10x − 22y + 28 Trang 1
ĐÁP ÁN BÀI TẬP TĂNG CƯỜNG TOÁN 8 TUẦN 4
HƯỚNG DẪN GIẢI CHI TIẾT
Bài 1. Viết các đa thức sau dưới dạng tích: a) 3 3 x + 8 y b) 6 3 a − b c) 3 8y −125 d) 3 8z + 27 Lời giải a) 3 3 2 2
x + 8y = (x + 2y)(x − 2xy + y ) b) 6 3 2 4 2 2
a − b = (a − b)(a + a b + b ) c) 3 2
8y −125 = (2 y − 5)(4 y +10 y + 25) d) 3 2
8z + 27 = (2z + 3)(4z − 3z + 9) Bài 2.
Dùng hằng đẳng thức viết nối vế còn lại 1) 2
(2x − y) = ..................... 2) 2 2
(2x − z) = ..................... 3) 2
4x − 9 = .....................
4) (x − 2 y)(2 y+ x) = ........... 5) 3
(2x − y) = ..................... 6) 3
(3x − y) = ..................... 7) 2
4x + 4x +1 = ............ 8) 2
x − 6x + 9 = ................ 9) (x − 5)(x + 5) = .......... 10) 3 2
x +12x + 48x + 64 = ...... 11) 3 2
x − 6x +12x − 8 = ...... 12) (x + 2)(x − 2x + 4) = .......... 13) 2
(x − 3)(x + 3x + 9) = ..... 14) 2
x + 2x +1 = ............. 15) 2 x −1 = ...... 16) 2
9x + 6x +1 = ..... 17) 2
36x + 36x + 9 = ............. 18) 3 x + 27 = ...... Lời giải
Dùng hằng đẳng thức viết nối vế còn lại 1) 2 2 2
(2x − y) = 4x − 4xy + y 2) 2 2 4 2 2
(2x − z) = 4x − 4x z + z 3) 2
4x − 9 = (2x − 3)(2x + 3) 4) 2 2
(x − 2y)(2 y+ x) = x − 4y 5) 3 3 2 2 3
(2x − y) = 8x −12x y + 6xy − y 6) 3 3 2 2 3
(3x − y) = 27x − 27x y + 9xy − y 7) 2 2
4x + 4x +1 = (2x +1) 8) 2 2
x − 6x + 9 = (x − 3) 9) 2
(x − 5)(x + 5) = x − 25 10) 3 2 3
x +12x + 48x + 64 = (x + 4) 11) 3 2 2
x − 6x +12x − 8 = (x − 2) 12) 3
(x + 2)(x − 2x + 4) = x + 8 13) 2 3
(x − 3)(x + 3x + 9) = x − 27 14) 2 2
x + 2x +1 = (x +1) 15) 2
x −1 = (x −1)(x +1) 16) 2 2
9x + 6x +1 = (3x +1) 17) 2 2
36x + 36x + 9 = (6x + 3) 18) 3 2
x + 27 = (x + 3)(x − 3x + 9) Bài 3.
Rút gọn rồi tính giá trị của biểu thức. a) 2
(x −10) − x(x + 80) với x = 0,98. b) 2
4x − 28x + 49 với x = 4 . Trang 2 c) 3 2
x − x + 27x − 27 với x = 5 . d) 3 3 3
(x +1) + (x −1) + x − 3x(x−1)(x+1) với x = 100 . Lời giải a) 2
(x −10) − x(x + 80) với x = 0,98 Ta có: 2 2 2
(x −10) − x(x + 80) = x − 20x +100 − x − 80x = 100 − x +100
Với x = 0,98 biểu thức có giá trị: 100.0 − ,98 +100 = 98 − +100 = 2 b) 2
4x − 28x + 49 với x = 4 Ta có: 2 2
x − 28x + 49 = (x − 7)
Với x = 4 biểu thức có giá trị: 2 2 (4 − 7) = ( 3 − ) = 9 c) 3 2
x − 9x + 27x − 27 với x = 5 Ta có: 3 2 3
x − 9x + 27x − 27 = (x − 3)
Với x = 5 biểu thức có giá trị: 3 3 (5 − 3) = 3 = 27 d) 3 3 3
(x +1) + (x −1) + x − 3x(x−1)(x+1) với x=100 Ta có: 3 3 3 3 2 3 2 2
(x +1) + (x −1) + x − 3x(x−1)(x+1) = x + 3x + 3x +1+ x − 3x + 3x −1− 3 ( x x −1) 3 2 3 2 3
= x + 3x + 3x +1+ x − 3x + 3x −1− 3x + 3x = 9x
Với x = 100 biểu thức có giá trị: 9.100 = 900 . Bài 4.
Cho tam giác ABC vuông cân tại đỉnh A . Trên cạnh AB lấy điểm D , trên cạnh AC lấy điểm
E sao cho AD = AE . Qua C kẻ đường thẳng vuông góc với BE cắt BA tại I .
a) Chứng minh: BE = CI
b) Qua D và A kẻ đường thẳng vuông góc với BE cắt BC lần lượt ở M và N . Chứng minh: MN = NC . Lời giải B M D N A E C F I Trang 3
a) Chứng minh: BE = CI
Gọi giao điểm của CI và BE là F .
 CF ⊥ BE tại F .
Xét CEF vuông tại F , có:
FCE + CEF = 90 (hai góc phụ nhau).
 ACI = 90 − FCE .
Mà FEC = AEB (tính chất hai góc đối đỉnh).
Do đó: ACI = 90 − AEB . ( ) 1
Xét AEB vuông tại A , ta có:
ABE + AEB = 90 (hai góc phụ nhau).
 ABE = 90 − AEB (2) Từ ( )
1 và (2)  ACI = ABE .
Xét ACI vuông tại A và ABE vuông tại A có:
AC = AB ( ABC vuông cân tại A )
ACI = ABE (chứng minh trên)  AC  I = ABE 
(cạnh góc vuông – góc nhọn kề)
 CI = BE (hai cạnh tương ứng) (điều phải chứng minh)
b) Qua D và A kẻ đường thẳng vuông góc với BE cắt BC lần lượt ở M và N . Chứng minh: MN = NC .
Ta có: ACI = ABE (chứng minh trên).
 AI = AE (hai cạnh tương ứng).
Mà AD = AE (giả thiết)
Nên AI = AD  A là trung điểm của ID .
CI ⊥ BE (giaû thie ) át 
Ta có: MD ⊥ BE (giaû thie )
át   CI // MD // NA (từ vuông góc đến song song). 
NA ⊥ BE (giaû thie ) át 
Xét tứ giác MDIC có MD // IC (chứng minh trên).
 MDIC là hình thang (định nghĩa hình thang).
Lại có: A là trung điểm của ID (chứng minh trên).
AN // MD // CI (chứng minh trên). Trang 4
Do đó: N là trung điểm của CM (đường trung bình của hình thang).
 NM = NC (điều phải chứng minh).
Bài 5. Cho hình thang ABCD (AB // CD) . Gọi E, F lần lượt là trung điểm AD, BC . Phân giác góc A
và góc B cắt EF theo thứ tự ở I và K .
a) Chứng minh tam giác AIE và tam giác BKF là các tam giác cân.
b) Chứng minh tam giác AID và tam giác BKC là tam giác vuông. 1 1
c) Chứng minh IE = AD và KF = BC . 2 2 d) Cho AB = 5c , m CD = 15c ,
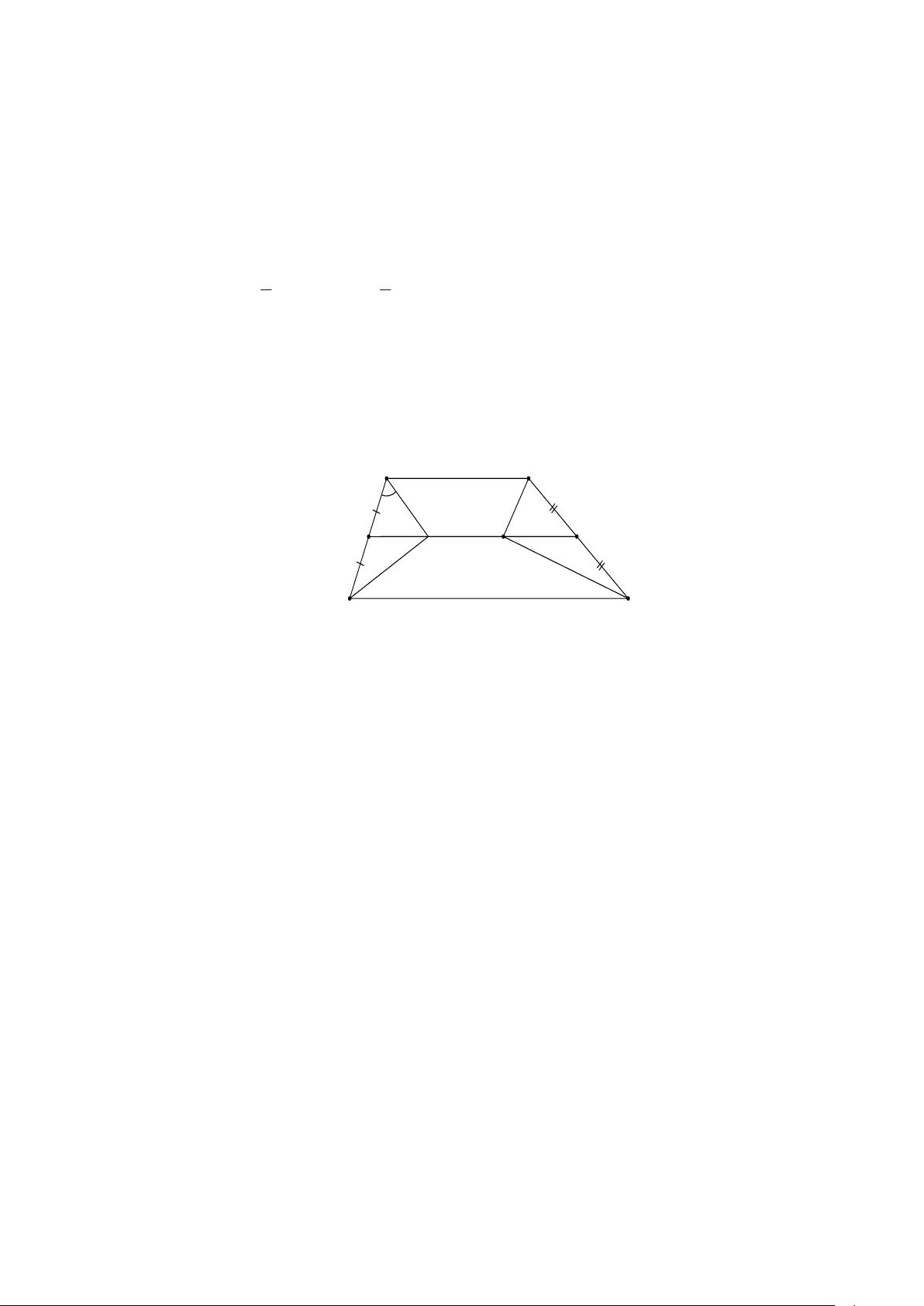
m BC = 2cm . Tính độ dài đoạn thẳng IK . Lời giải a) Xét hình thang ABCD A B 1 2 1 E F 2 K 1 2 D C
Có EA = ED ; FB = FC (giả thiết)
 EF là đường trung bình của hình thang ABCD
 EF // AB // CD
Vì AB // EF => A = I (Hai góc so le trong) 1 1 Mà A = A 1 2
 A = I  E
 AI cân tại E 2 1
Chứng minh tương tự BKF cân tại K b)
Vì IAE cân tại I  EAI cân tại E  EA = EI  A = I 2 1 Mà EA = ED
 EI = ED  IED cân tại I  I = D 2 1 Xét IAD có: Trang 5 A I D 180 + + = (Định lý tổng 3 góc) A I I D 180 + + + = 2 1 2 1 2I 2I 180 + = 1 2 2AID 180  = AID 90 =  AI
 D vuông tại I
Chứng minh tương tự BKC vuông tại K c)
Xét AID vuông tại I có IE là đường trung tuyến ứng với cạnh huyền AD 1  IE = AD 2 1
Chứng minh tương tự KF = BC 2 d)
Xét hình thang ABCD (AB // CD) có EF là đường trung bình hình thang. AB + CD 5 +15  EF = = =10cm 2 2 1 1
Xét AID vuông tại I có IE = AD = .6 = 3cm 2 2 1 1
Xét BKC vuông tại K có KF = BC = .7 = 3,5cm 2 2
Ta có: EF = EI + IK + KF 10 = 3 + IK + 3,5
 IK = 10 − 6,5 = 3,5cm
Vậy IK = 3,5cm Bài 6.
Tìm giá trị lớn nhất; nhỏ nhất của biểu thức 1) 2
A = x − 6x +11 2) 2
B = x − 5x +12 3) 2
C = −x + 6x −11 4) 2
D = 5x − x 5) 2
D = 2x − 8x + 5 6) 2
E = 12 − 6x − 3x 7) 2 2
F = 4x +12xy +10y −10y + 35 8) 2 2
G = x − 4xy + 5y +10x − 22y + 28 Lời giải 1) 2
A = x − 6x +11 Trang 6 Ta có: 2
A = x − 6x +11 = ( 2
x − 6x + 9) + 2 = ( x − )2 3 + 2 . Có: ( x − )2 3  0 x  .  (x − )2 3 + 2  2 x  . Hay A  2 x
 . Dấu “=” xảy ra khi x − 3 = 0  x = 3 .
Vậy min A = 2 khi x = 3 . 2) 2
B = x − 5x +12  5 25  23 2  5  23 Ta có: 2
B = x − 5x +12 2 = x − 2. . x + +   = x − +   .  2 4  4  2  4 2  5  Có: x −  0   x  .  2  2  5  23 23  x − +    x  .  2  4 4 23 5 Hay B  x
 . Dấu “=” xảy ra khi x − = 5 0  x = . 4 2 2 23 5 Vậy min B = khi x = . 4 2 3) 2
C = −x + 6x −11 Ta có: 2
C = −x + 6x −11 = −  = −  − +  ( 2
x − 6x + 9) + 2 (x )2 3 2   = −( x − )2 3 − 2 Có: ( x − )2 3  0 x  .  −( x − )2 3  0 x  .  −(x − )2 3 − 2  2 − x  . Hay C  −2 x
 . Dấu “=” xảy ra khi x − 3 = 0  x = 3 . Vậy max C = 2 − khi x = 3 . 4) 2
D = 5x − x  5 25  25 2  5 25   2  5  25 Ta có: 2
D = 5x − x 2 = − x − 2. . x + −   = −  x − −    = − x − +   .  2 4 4      2  4    2  4 2  5  Có: x −  0   x  .  2  2  5  − x −  0   x  .  2  Trang 7 2  5  25 25  − x − +    x  .  2  4 4 25 5 Hay D  x
 . Dấu “=” xảy ra khi x − = 5 0  x = . 4 2 2 25 5 Vậy max D = khi x = . 4 2 5) 2
D = 2x − 8x + 5  5   3 Ta có: 2
D = 2x − 8x + 5 2 = 2 x − 4x +   = 2 ( 2
x − 4x + 4) −  2  2     = (x − )2 3 2 2 −  = ( x − )2 2 2 − 3. 2   Có ( x − )2 2  0 x  .  (x − )2 2 2  0 x  .  (x − )2 2 2 − 3  3 − x  . Hay D  −3 x
 . Dấu “=” xảy ra khi x − 2 = 0  x = 2. Vậy min D = 3 − khi x = 2 . 6) 2
E = 12 − 6x − 3x Ta có: 2
E = 12 − 6x − 3x = − ( 2
3 x − 2x − 4) = − ( 2 3 x − 2x + ) 1 − 5 = − (x − )2 3 1 − 5   = − ( x − )2 3 1 +15 . Có ( x − )2 1  0 x  .  − (x − )2 3 1  0 x  .  − ( x − )2 3 1 +15  15 x  . Hay E  15 x
 . Dấu “=” xảy ra khi x −1 = 0  x = 1.
Vậy max E = 15 khi x = 1 . 7) 2 2
F = 4x +12xy +10y −10y + 35 Ta có: 2 2
F = 4x +12xy +10y −10y + 35 = ( 2 2 x + xy + y ) + ( 2 4 12 9
y −10 y + 25) +10
= ( x + y)2 + ( y − )2 2 3 5 +10 Có: ( x + y)2 2 3  0 x  , y . Trang 8 ( y − )2 5  0 y  .
 ( x + y)2 + ( y − )2 2 3 5 +10  10 x  , y . y = 5 y − 5 = 0  Hay F  10 x
 , y . Dấu “=” xảy ra khi    15 − 2x + 3y = 0 x =  2 15 −
Vậy min F = 10 khi x = và y = 5 . 2 8) 2 2
G = x − 4xy + 5y +10x − 22y + 28 Ta có: 2 2
G = x − 4xy + 5y +10x − 22y + 28 = ( 2 2
x − xy + y ) + ( x − y) + ( 2 4 4 10 20 y − 2y) + 28
= (x − y)2 + (x − y) + + ( 2 2 10 2 25 y − 2y + ) 1 + 2
= (x − y)2 + (x − y) + + ( y − )2 2 2 2. 2 .5 5 1 + 2
= (x − y + )2 + ( y − )2 2 5 1 + 2 .
Có: ( x − 2y + 5)2  0 x  , y . ( y − )2 1  0 y  .
 (x − y + )2 + ( y − )2 2 5 1 + 2  2 x  , y .
x − 2y + 5 = 0 x = 3 − Hay G  2 x
 , y . Dấu “=” xảy ra khi    y −1 = 0 y =1
Vậy min G = 2 khi x = −3 và y = 1.  HẾT  Trang 9