Bài Tập Toán 8 Tuần 5 Có Lời Giải Chi Tiết

PHIẾU BÀI TẬP TOÁN 8 TUẦN 05
A. PHẦN CƠ BẢN (DÀNH CHO TẤT CẢ CÁC LỚP) Bài 1.
Phân tích các đa thức sau thành nhân tử: a) 7x + 7xy b) 2 2 2x y − 6xy c) x ( x − ) 2 3 1 + 7x ( x − ) 1 d) 2 2
x − 6xy + 9 y e) 3 x − 64
f) 3x ( x − a) + 5a (a − x) Bài 2.
Phân tích đa thức thành nhân tử: a) 2
16x ( x − y) −10y ( y − x) e) 2 x − 9 i) ( + )2 2 x y − x b) 2x ( x + ) 1 + 2 ( x + ) 1 f) 2 4x − 25 k) 2 1 − y + 9 c) 2 ( 2 + ) 2 y x
y − zx − zy g) 2 x − 5 m) 4 2 x − y
d) 4x ( x − 2 y) − 8y ( x − 2 y) h) 6 6 x − y
n) ( x + )2 − ( x + )2 3 1 1 Bài 3.
Tính giá trị của biểu thức sau: 2 2 43 −11 3 3 97 + 83 a) ; b) − 97.80; 2 2 36,5 − 27,5 180
c) A = x(2x − y) − z( y − 2x) với x = 1, 2 ; y = 1,4 ; z = 1,8 d) 2
B = (x −1)x − 4x(x −1) + 4(x −1) với x = 3 . Bài 4.
Tìm x , biết:
a) 3x(x −1) + x −1 = 0 ; c) 3 x − 50x = 0 b) 2
2(x + 3) − x − 3x = 0 d) 2 2
(x − 2)(x + 2x + 7) + 2(x − 4) − 5(x − 2) = 0 Bài 5.
Cho tam giác ABC cân tại A , có đường cao AH ( H  BC ). Lấy E thuộc cạnh AB , F
thuộc cạnh AC sao cho BE = CF .
a) Chứng minh E, F đối xứng nhau qua AH .
b) Gọi O là giao điểm của EF với AH . Các tia BO, CO cắt AC, AB lần lượt tại I và K .
Chứng minh EK = IF . B. BÀI TẬP NÂNG CAO Bài 6.
Cho tam giác ABC có AM là trung tuyến thuộc cạnh BC . Gọi G là trọng tâm của tam
giác ABC . Qua G kẻ đường thẳng d cắt hai cạnh AB , AC . Gọi AA , BB , CC , MM  là các
đường vuông góc kẻ từ A , B , C , M đến đường thẳng d ( A , B, C , M  thuộc d ). Chứng minh: BB + CC a) MM  =
b) AA = BB + CC 2 Bài 7. Chứng minh rằng: 1) 2 a (a + ) 1 + 2a (a + )
1 chia hết cho 6 với a  .
2) a (2a − 3) − 2a (a + )
1 chia hết cho 5 với a  . Trang 1
HƯỚNG DẪN GIẢI CHI TIẾT Bài 1.
Phân tích các đa thức sau thành nhân tử: a) 7x + 7xy b) 2 2 2x y − 6xy c) x ( x − ) 2 3 1 + 7x ( x − ) 1 d) 2 2
x − 6xy + 9 y e) 3 x − 64
f) 3x ( x − a) + 5a (a − x) Lời giải
a) 7x + 7xy = 7x (1+ y) b) 2 2
2x y − 6xy = 2xy ( x − 3y) c) x ( x − ) 2 3 1 + 7x ( x − ) 1 = x ( x − ) 1 (3 + 7x)
d) x − xy + y = ( x − y)2 2 2 6 9 3 e) 3 x − = (x − )( 2 64 4 x + 4x +16)
f) 3x ( x − a) + 5a (a − x) = 3x (x − a) − 5a (x − a) = (x − a)(3x − 5a) Bài 2.
Phân tích đa thức thành nhân tử: a) 2
16x ( x − y) −10y ( y − x) e) 2 x − 9 i) ( + )2 2 x y − x b) 2x ( x + ) 1 + 2 ( x + ) 1 f) 2 4x − 25 k) 2 1 − y + 9 c) 2 ( 2 + ) 2 y x
y − zx − zy g) 2 x − 5 m) 4 2 x − y
d) 4x ( x − 2 y) − 8y ( x − 2 y) h) 6 6 x − y
n) ( x + )2 − ( x + )2 3 1 1 Lời giải a) 2
x ( x − y) − y ( y − x) 2 =
x ( x − y) +
y (x − y) = (x − y)( 2 16 10 16 10 2 8x + 5y )
b) x ( x + ) + ( x + ) = ( x + )( x + ) = ( x + )2 2 1 2 1 2 1 1 2 1 c) 2 ( 2 + ) 2 2 − − =
( 2 + )− ( 2 + ) = ( 2 + )( 2 y x y zx zy y x y z x y x y y − z)
d) x ( x − y) − y ( x − y) = ( x − y)( x − y) = ( x − y)2 4 2 8 2 4 2 2 4 2 e) 2
x − 9 = ( x − ) 3 (x + ) 3 f) 2
4x − 25 = (2x − 5)(2x + 5) g) 2
x − 5 = (x + 5)(x − 5) 3 3 h) 6 6 − = ( 2 ) − ( 2 ) = ( 2 2 − )( 4 2 2 4 + + ) = ( − )( + )( 4 2 2 4 x y x y x y x x y y
x y x y x + x y + y ) i) ( x + y)2 2
− x = (x + y − x)(x + y + x) = y (2x + y) Trang 2 1 1  1  1  k) 2 2
− y + = − y = − y + y    9 9  3  3  m) 4 2 − = ( 2 + )( 2 x y x y x − y)
n) ( x + )2 − ( x + )2 3 1
1 = (3x +1+ x + )
1 (3x +1− x − ) 1 Bài 3.
Tính giá trị của biểu thức sau: 2 2 43 −11 3 3 97 + 83 a) ; b) − 97.80; 2 2 36,5 − 27,5 180
c) A = x(2x − y) − z( y − 2x) với x = 1, 2 ; y = 1,4 ; z = 1,8 d) 2
B = (x −1)x − 4x(x −1) + 4(x −1) với x = 3 . Lời giải 2 2 43 −11 (43−1 ) 1 (43 +1 ) 1 32.54 a) = = = 3 2 2 36,5 − 27,5
(36,5− 27,5)(36,5+ 27,5) 9.64 97 + 83 ( + )( 2 2 3 3 97 83 97 − 97.83 + 83 ) b) − 97.80 = − 97.8 180 180 ( 2 2 180 97 − 97.83 + 83 ) = − 97.80 180 = ( 2 2 97 − 97.83 + 83 ) − 97.80 2 2 = 97 − 2.97.83 + 83 = ( − )2 2 97 83 = 14 = 196
c) A = x(2x − y) − z( y − 2x) = x(2x − y) + z(2x − y) = (2x − y) (x + z)
Thay x = 1,2 ; y = 1,4 ; z = 1,8 ta được:
A = (2.1,2 −1,4)(1,2 +1,8) = 3
d) B = ( x − ) x − x ( x − ) + ( x − ) = (x − )(x − x + ) = (x − )(x − )2 2 2 1 4 1 4 1 1 4 4 1 2
Thay x = 3 vào ta được: B = ( − )( − )2 3 1 3 2 = 2 Bài 4.
Tìm x , biết: a) 3x ( x − ) 1 + x −1 = 0 ; c) 3 x − 50x = 0 b) ( x + ) 2 2
3 − x − 3x = 0 d) ( x − )( 2 x + x + ) + ( 2 2 2 7
2 x − 4) − 5(x − 2) = 0 Lời giải a) 3x ( x − ) 1 + x −1 = 0 Trang 3  ( x − ) 1 (3x + ) 1 = 0  =  x 1 x −1 = 0     1 3x +1 = 0 x = −  3 1
Vậy x = 1 ; x = − . 3 b) (x + ) 2 2
3 − x − 3x = 0  2(x + ) 3 − x ( x + ) 3 = 0
 (x + 3)(2 − x) = 0 x + 3 = 0 x = 3 −    2 x 0  − =  x = 2
Vậy x = −3 ; x = 2 . c) 3 x − 50x = 0  x ( 2 x − 50) = 0  x = 0  x = 0    2  x − 50 = 0 x = 5  2
Vậy x = 0 ; x = 5  2 . d) 2 2
(x − 2)(x + 2x + 7) + 2(x − 4) − 5(x − 2) = 0  (x − )( 2
2 x + 2x + 7) + 2(x − 2)(x + 2) − 5(x − 2) = 0  (x − ) ( 2 2
x + 2x + 7) + 2(x + 2) − 5 = 0   (x − )( 2
2 x + 2x + 7 + 2x + 4 − 5) = 0  (x − )( 2
2 x + 4x + 6) = 0  (x − ) ( 2 2
x + 4x + 4) + 2 = 0 
 (x − ) (x + )2 2 2 + 2 = 0   Ta thấy: ( x + )2 2 + 2  0; x 
Suy ra: x − 2 = 0  x = 2 Vậy x = 2 . Bài 5.
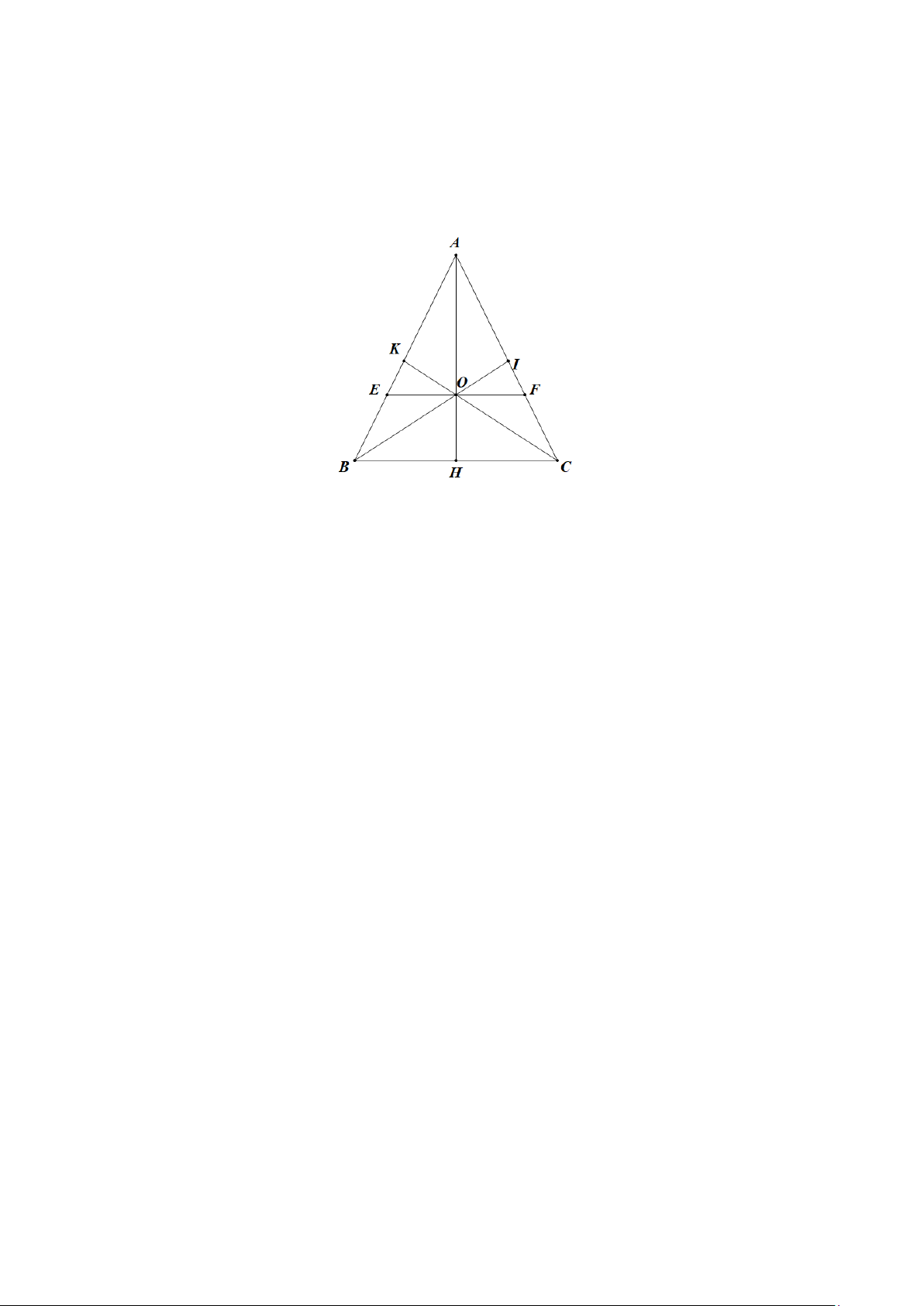
Cho tam giác ABC cân tại A , có đường cao AH ( H  BC ). Lấy E thuộc cạnh AB , F
thuộc cạnh AC sao cho BE = CF . Trang 4
a) Chứng minh E, F đối xứng nhau qua AH .
b) Gọi O là giao điểm của EF với AH . Các tia BO, CO cắt AC, AB lần lượt tại I và K .
Chứng minh EK = IF . Lời giải
a) Chứng minh E, F đối xứng nhau qua AH .
Ta có: AB = AC (tam giác ABC cân tại A ),
BE = CF (giả thiết) nên AE = AF
suy ra: AEF cân tại A ( ) 1
ABC cân tại A , AH là đường cao
nên AH là đường phân giác góc BAC (cũng là góc FAE ) (2) Từ ( )
1 và (2) suy ra AH là đường trung trực của FE .
Vậy E, F đối xứng nhau qua AH .
b) Gọi O là giao điểm của EF với AH . Các tia BO, CO cắt AC, AB lần lượt tại I và K .
Chứng minh EK = IF .
Vì O  AH là trung trực của BC nên OB = OC  OBC  cân tại O  OCB = OBC  KCB = IBC
Xét KCB và IBC có: Trang 5
KCB = IBC , BC chung, KBC = ICB (do ABC cân tại A )  K  CB = I  BC  KB = IC
 KB − EB = IC − FC
 EK = I F (đpcm) Bài 6.
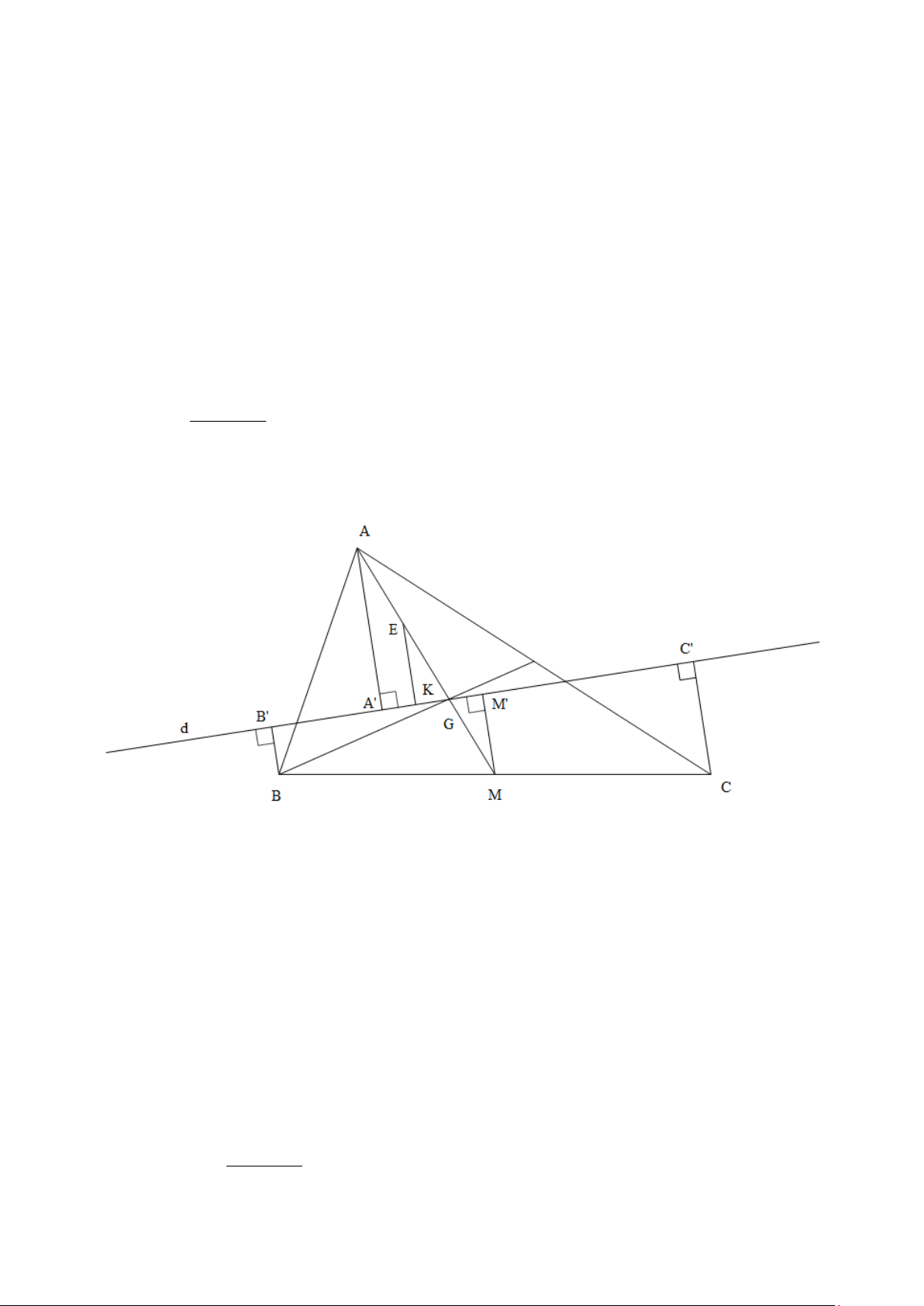
Cho tam giác ABC có AM là trung tuyến thuộc cạnh BC . Gọi G là trọng tâm của tam
giác ABC . Qua G kẻ đường thẳng d cắt hai cạnh AB , AC . Gọi AA , BB , CC , MM  là các
đường vuông góc kẻ từ A , B , C , M đến đường thẳng d ( A , B, C , M  thuộc d ). Chứng minh: BB + CC a) MM  =
b) AA = BB + CC 2 Lời giải
a) Ta có: BB ⊥ d (B d ) ; CC ⊥ d (C d ) ; AA ⊥ d ( A d ) ; MM  ⊥ d (M d )
 BB// CC ' // AA// MM 
Ta có: BB // CC '  tứ giác BB C  C  là hình thang
Mà MB = MC (giả thiết)
 MM // CC// BB  M B   = M C  
Suy ra: MM  là đường trung bình của hình thang BB C  C  BB + CC  MM  = 2 Trang 6 1
b) Gọi E là trung điểm của AG  AE = EG = AG . 2
Kẻ EK ⊥ d (K d ) .
Vì AA ⊥ d ( Ad )
 AA // EK ( từ vuông góc đến song song)
Xét tam giác AAG có: AA // EK
E là trung điểm của AG
 K là trung điểm của AG
 EK là đường trung bình của tam giác AAG 1
 EK = AA (2) 2 GM 1 1
Do G là trọng tâm của tam giác ABC nên =  GM = AG . AG 2 2  1 
 AE = EG = GM = AG    2 
Xét EGK và MGM  có : EKG = M M  G (= 90) EGK = M GM  ( 2 góc đối đỉnh) EG = GM
 EGK = MGM  (cạnh huyền-góc nhọn)
 EK = MM  (3). AA BB + CC Từ ( ) 1 ,(2),(3) ta có: =
 AA = BB + CC 2 2 Bài 7. Chứng minh rằng: 1) 2 a (a + ) 1 + 2a (a + )
1 chia hết cho 6 với a  .
2) a (2a − 3) − 2a (a + )
1 chia hết cho 5 với a  . Lời giải 1) 2 a (a + ) 1 + 2a (a + ) 1 = a (a + ) 1 (a + 2) Ta có a (a + ) 1 2 nên a (a + )
1 (a + 2) 2 và a(a + ) 1 (a + 2) 3
Mặt khác 2 và 3 là hai số nguyên tố cùng nhau nên a (a + ) 1 (a + 2) 6 Vậy 2 a (a + ) 1 + 2a (a + )
1 chia hết cho 6 với a  .
2) Với a  , ta có:
a ( a − ) − a(a + ) 2 2 2 3 2
1 = 2a − 3a − 2a − 2a = 5 − a Mà −5a 5 Trang 7
Vậy a (2a − 3) − 2a(a + )
1 chia hết cho 5 với a  . Trang 8