Bài Tập Toán 8 Tuần 6 Và 7 Có Lời Giải Chi Tiết
Cho hình bình hành ABCD lấy E và F lần lượt là trung điểm của AB và CD, lấy M thuộc tia đối của tia AD sao cho AM = AD. Chứng minh các tứ giác sau là hình bình hành: Tứ giác AEFD. E và F đối xứng nhau qua I. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem!
Chủ đề: Tài liệu chung Toán 8 271 tài liệu
Môn: Toán 8 2.2 K tài liệu
Tác giả:
Preview text:
PHIẾU BÀI TẬP TOÁN 8 TUẦN 06 + 07 A. ĐẠI SỐ Dạng 1. Tính
Bài 1. Thực hiện phép tính: a) 2 x ( 3 3 2x − x + 5) b) ( x + )( 2 4 x − 4x +16) 4 − 1 1 2 c) ( 2
3x y − 6xy + 9x) d) 2 2 x + 2 y
x − xy + 4 y 3xy 3 9 3 e) ( x − )( 2
x − x + ) + x ( 2 2 5 1 x +1 ) 1 f) ( x − y)( 2 2 3
x + 3xy + 9 y ) g) ( + x)( 2 3 x + 3x − 5) h) ( 3 2
12x y +18x y) : 2xy i) ( 3 2 2 3 4 4 2 2
x y − x y + x y − x y ) 2 2 4 6 8 12 : 2x y j) ( 5 2 4 3 3 4 x y − x y + x y ) 3 2 6 9 15 : 3x y
Dạng 2. Phân tích đa thức thành nhân tử
Bài 2. Phân tích các đa thức sau thành nhân tử: a) 3 2
2xy − 6x +10xy b) 3 2 3
x − 3x + 3x −1 − y c) 2 2
x − 25 + y + 2xy d) 6 5 3 2
a − a − 2a + 2a e) 6 125 − x f) 4 2 2 4
4x + 4x y − 8y g) 2 2
a + 2ab + b − ac − bc h) 2 x ( x − ) 1 + 16(1− x) i) 2 x + 8x +15 j) 2 x − x −12 k) 2 x + 4x + 3 l) 2 4x + 4x − 3
Bài 3. Phân tích đa thức sau thành nhân tử: 1) 2
3x − 3xy − 5x + 5y 2) 2 2
x + 4x − y + 4 3) 2 2 2
3x + 6xy + 3y − 3z 4) 2 2 2 2
x − 2xy + y − z + 2zt − t
5) xy − 5y + 2x −10
6) 2xy + z + 2x + yz 7) 3 2 2
5x +10x y + 5xy 8) 2 2
x − 2xy + y − 4 9) 3 3 2
2x y − 2xy − 4xy − 2xy 10) 2 2
x + 2x − y +1
Bài 4. Phân tích các đa thức sau thành nhân tử: 2 a) ( 2 x + x) + ( 2 4 x + x) −12 b) ( 2 x + x + )( 2
1 x + x + 2) −12 2 c) ( 2
x + x + ) + x( 2 x + x + ) 2 4 8 3 4 8 + 2x d) ( x + )
1 ( x + 2)( x + 3)( x + 4) − 24
Dạng 3. Tìm x
Bài 5. Tìm x , biết: a) 2
x − 7x + 6 = 0 b) ( x − )2 2 − 4 = 0 c) 3
x −19x − 30 = 0
Bài 6. Tìm x , biết:
a) 2x ( x − 5) − x(3+ 2x) = 0 Trang 1 b) 5x ( x − ) 1 = x −1 c) (x + ) 2 2
5 − x − 5x = 0
d) ( x − )2 − ( x + )2 2 3 5 = 0 e) 3
3x − 48x = 0 f) 3 2
x + x − 4x = 4 Dạng 4. Chứng minh
Bài 7. Chứng minh các đẳng thức sau:
1) a + b = (a + b)2 2 2 − 2ab .
2) a + b = (a + b )2 4 4 2 2 2 2 − 2a b . 3) a b (a b )(a b )2 6 6 2 2 2 2 2 2 3a b + = + + − . 4) 2 ( − ) 2 + ( − ) 2 a b c
b c a + c (a − b) = (a − c)(b − a)(c −b) . B. HÌNH HỌC Bài 1.
Cho tam giác ABC cân tại A . Trên tia đối của tia AC lấy điểm D , trên tia đối của tia AB lấy
điểm E sao cho AD = AE . Tứ giác DECB là hình gì? Vì sao? Bài 2.
Cho tam giác ABC(AB AC) đường cao AH . Gọi M , N , P lần lượt là trung điểm của BC,C ,
A AB . Chứng minh rằng
a) NP là đường trung trực của AH .
b) MHNP là hình thang cân Bài 3.
Cho hình bình hành ABCD . Từ A kẻ AI vuông góc với BD , từ C kẻ CK vuông góc với
BD (I, K BD) .
a) Tứ giác AICK là hình gì?
b) Tia AI cắt CD tại M , Tia CK cắt AB tại N . Chứng minh rằng trung điểm của đoạn thẳng
MN thuộc đường chéo BD Bài 4.
Cho hình bình hành ABCD . Gọi M , N theo thứ tự là trung điểm của BC, .
AD AM cắt BD tại
P, CN cắt BD tại Q .
a) Chứng minh BP = PQ = QD
b) Gọi I là giao điểm của AM với BN , K là giao điểm của DM với CN . Chứng minh
AC, BD, MN, IK đồng quy. Bài 5.
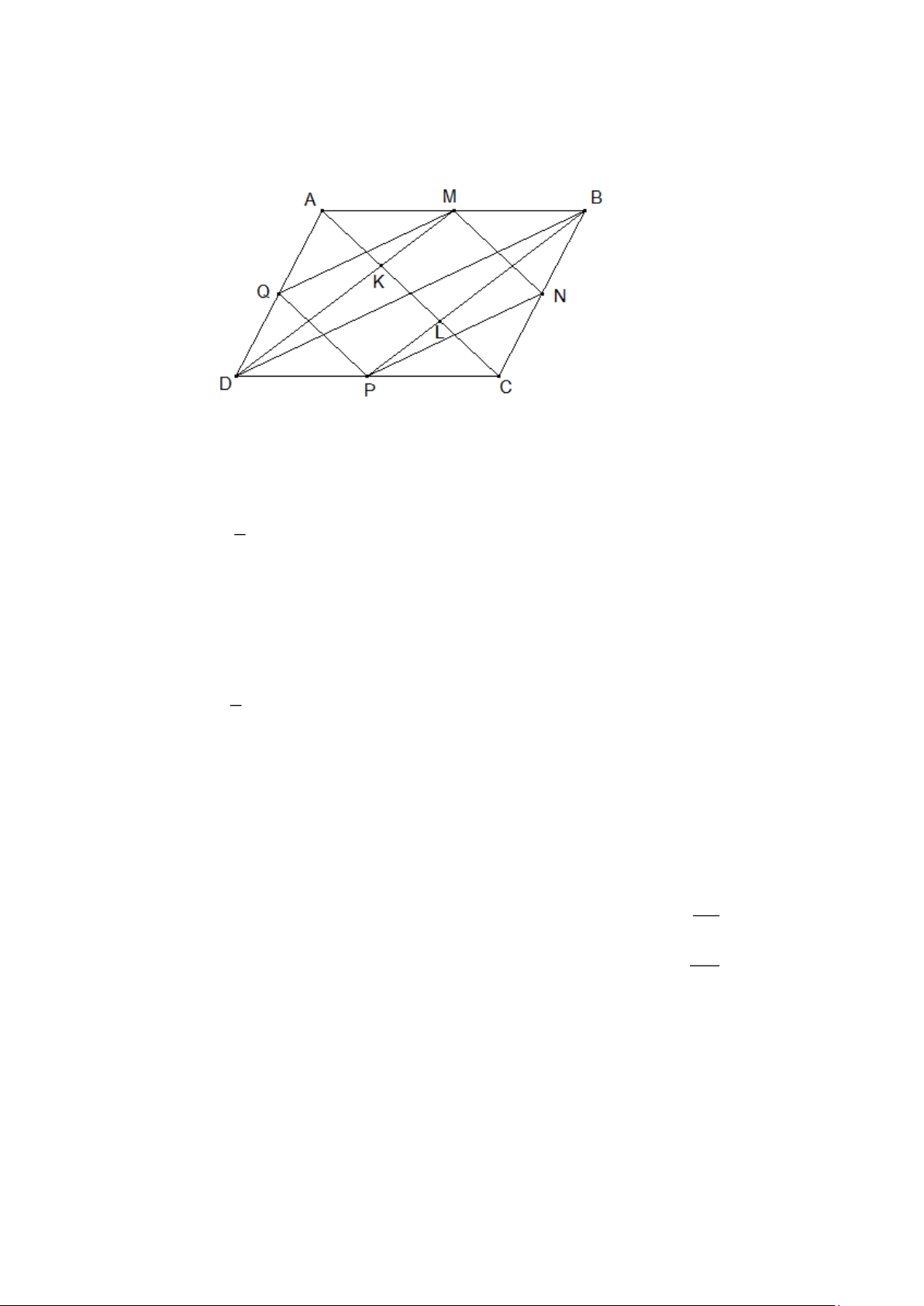
Cho hình bình hành ABCD . Gọi M , N, P, Q lần lượt là trung điểm của AB, BC, CD, D . A
Gọi K là giao điểm của AC và DM , L là giao điểm của BP và CA .
a) MNPQ là hình gì? Vì sao?
b) MDPB là hình gì? Vì sao?
c) Chứng minh: AK = KL = LC. Bài 6.
Cho ABC vuông tại A , có AB = 6 cm, AC = 8cm . M là trung điểm của BC a. Tính BC . Trang 2 b. Kẻ MH
AC (H AB) , MK
AB K AC . Tứ giác AHMK là hình gì? Vì sao? Bài 7.
Cho hình bình hành ABCD . Kẻ AE và CF vuông góc với BD (E, F BD) .
a. Tứ giác AECF là hình gì ? vì sao?
b. Gọi I là giao điểm của AE và CD , K là giáo điểm của CF và AB . Chứng minh: AI = CK .
c. Chứng minh BE = DF . Bài 8.
Cho tam giác ABC , D là một điểm trên cạnh BC . Qua D kẻ đường thẳng song song với AB cắt
AC ở E . Trên AB lấy điểm F sao cho AF = DE . Gọi I là trung điểm của AD . Chứng minh: a) DF = AE
b) E và F đối xứng nhau qua I . Bài 9.
Cho hình bình hành ABCD lấy E và F lần lượt là trung điểm của AB và CD , lấy M thuộc tia
đối của tia AD sao cho AM = AD . Chứng minh các tứ giác sau là hình bình hành: a) Tứ giác AEFD b) Tứ giác AMEF c) Tứ giác AMBC
Bài 10. Cho tứ giác ABCD . Gọi M , N, P,Q thứ tự là trung điểm của AB, BC,CD, DA .
a) Chứng minh rằng tứ giác MNPQ là hình bình hành
b) So sánh chu vi tứ giác MNPQ với tổng hai đường chéo của tứ giác ABCD .
Bài 11. Cho hình bình hành ABCD , AD = 2AB . Từ C vẽ CE vuông góc với AB . Nối E với trung
điểm M của AD . Từ M vẽ MF vuông góc với CE , MF cắt BC tại N .
a) Tứ giác MNCD là hình gì?
b) Tam giác EMC là tam giác gì? C. PHẦN NÂNG CAO Bài 1.
Tìm giá trị nhỏ nhất của các đa thức sau: 2
A = x − 4x + 6; 2 B = 2x + 6 ; x
C = (x −1)(x + 2)(x+ 3)(x+ 6); 2 2
D = (2x −1) + (x + 2) ;
E = x(x +1)(x + 2)(x + 3); 2 2
F = (x −1) + (x − 3) . Bài 2.
Tìm giá trị lớn nhất của các đa thức sau : 2
A = 4 − x + 2 ; x 2
B = 10x − 23 − x ; 2 C = −x + 6 . x a) Rút gọn A .
b) Với giá trị x ; y nguyên dương nào thỏa mãn x + 2y = 14 thì A nhận giá trị nguyên dương. Bài 3.
Cho x là số nguyên. Chứng minh rằng 4 3 2
B = x − 4x − 2x +12x + 9 là bình phương số nguyên. Bài 4.
Cho x, y, z là số nguyên. Chứng minh rằng 2 2
C = 4x(x + y)(x + y + z)(x + z) + y z là một số chính phương.
ĐÁP ÁN BÀI TẬP TĂNG CƯỜNG TOÁN 8 TUẦN 6 + 7 Trang 3
HƯỚNG DẪN GIẢI CHI TIẾT A. ĐẠI SỐ Dạng 1. Tính
Bài 1. Thực hiện phép tính: a) 2 x ( 3 3 2x − x + 5) b) ( x + )( 2 4 x − 4x +16) 4 − 1 1 2 c) ( 2
3x y − 6xy + 9x) d) 2 2 x + 2 y
x − xy + 4 y 3xy 3 9 3 e) ( x − )( 2
x − x + ) + x ( 2 2 5 1 x +1 ) 1 f) ( x − y)( 2 2 3
x + 3xy + 9 y ) g) ( + x)( 2 3 x + 3x − 5) h) ( 3 2
12x y +18x y) : 2xy i) ( 3 2 2 3 4 4 2 2
x y − x y + x y − x y ) 2 2 4 6 8 12 : 2x y j) ( 5 2 4 3 3 4 x y − x y + x y ) 3 2 6 9 15 : 3x y Lời giải a) 2 x ( 3 x − x + ) 5 3 2 3 2
5 = 6x − 3x +15x b) ( x + )( 2 x − x + ) 3 3 3 4 4
16 = x + 4 = x + 64 4 − 12 c) ( 2
3x y − 6xy + 9x). = 4 − x + 8 − 3xy y 3 1 1 2 1 1 d) x + 2 y
x − xy + 4 y = x + (2y)3 2 2 3 3 = x + 8y 3 9 3 3 27 e) ( x − )( 2
x − x + ) + x( 2 x + ) 3 2 2 3 2 5 1
11 = x − 5x + x − 2x +10x − 2 + x +11x 3 2
= 2x − 7x + 22x − 2
f) ( x − y)(x + xy + y ) = x − ( y)3 2 2 3 3 3 3 3 9 3 = x − 27 y g) ( + x)( 2 x + x − ) 3 3 2 3 2 3 3
5 = 3x + 9x −15 + x + 3x − 5x = 4x + 3x + 4x −15 h) ( 3 2 x y + x y) 2 12 18
: 2xy = 6x + 9x i) ( 3 2 2 3 4 4 2 2
x y − x y + x y − x y ) 2 2 2 2 4 6 8 12
: 2x y = 2x − 3y + 4x y − 6 j) ( 5 2 4 3 3 4 x y − x y + x y ) 3 2 2 2 6 9 15
: 3x y = 2x − 3xy + 5y
Dạng 2. Phân tích đa thức thành nhân tử
Bài 2. Phân tích các đa thức sau thành nhân tử: a) 3 2
2xy − 6x +10xy b) 3 2 3
x − 3x + 3x −1 − y c) 2 2
x − 25 + y + 2xy d) 6 5 3 2
a − a − 2a + 2a e) 6 125 − x f) 4 2 2 4
4x + 4x y − 8y g) 2 2
a + 2ab + b − ac − bc h) 2 x ( x − ) 1 + 16(1− x) i) 2 x + 8x +15 j) 2 x − x −12 k) 2 x + 4x + 3 l) 2 4x + 4x − 3 Lời giải a) 3 2 xy − x + xy = x ( 3 2 6 10 2
y − 3x + 5y)
b) x − x + x − − y = ( x − )3 − y = ( x − − y) ( x − )2 3 2 3 3 + (x − ) 2 3 3 1 1 1 1 1 y + y
= (x − y − )( 2 2
1 x − 2x +1+ xy − y + y ) Trang 4 c) x −
+ y + xy = (x + y)2 2 2 2 25 2
− 5 = (x + y − 5)(x + y + 5) d) 6 5 3 2 5
a − a − a + a = a (a − ) 2 − a (a − ) 2 = a (a − )( 3 2 2 1 2 1 1 a − 2) 3 e) 6 3 − x = − ( 2 x ) = ( 2 − x )( 2 4 125 5 5 25 + 5x + x ) f) 4 2 2 4 4 2 2 2 2 4 2
x + x y − y = x + x y − x y − y = x ( 2 2 x + y ) 2 − y ( 2 2 4 4 8 4 8 4 8 4 2 4 x + 2 y ) = ( 2 2 x + y )( 2 2 − y ) = ( 2 2 4 2 x
4 x + 2 y )(x − y)(x + y)
g) a + ab + b − ac − bc = (a + b)2 2 2 2
− c (a + b) = (a + b)(a + b − c) h) 2
x ( x − ) + ( − x) 2
= x (x − ) − (x − ) = (x − )( 2 1 16 1 1 16 1
1 x −16) = (x − )
1 (x − 4)(x + 4) i) 2 2
x + 8x +15 = x + 3x + 5x +15 = x (x + )
3 + 5(x + 3) = (x + 3)(x + 5) j) 2 2
x − x −12 = x − 4x + 3x −12 = x (x − 4) + 3(x − 4) = (x − 4)(x + 3) k) 2 2
x + 4x + 3 = x + 3x + x + 3 = x (x + )
3 + x + 3 = (x + 3)(x + ) 1 l) 2 2
4x + 4x − 3 = 4x + 6x − 2x − 3 = 2x (2x + 3) − (2x + 3) = (2x + 3)(2x − ) 1
Bài 3. Phân tích đa thức sau thành nhân tử: 1) 2
3x − 3xy − 5x + 5y 2) 2 2
x + 4x − y + 4 3) 2 2 2
3x + 6xy + 3y − 3z 4) 2 2 2 2
x − 2xy + y − z + 2zt − t
5) xy − 5y + 2x −10
6) 2xy + z + 2x + yz 7) 3 2 2
5x +10x y + 5xy 8) 2 2
x − 2xy + y − 4 9) 3 3 2
2x y − 2xy − 4xy − 2xy 10) 2 2
x + 2x − y +1 Lời giải 1) 2
3x − 3xy − 5x + 5y = ( 2
3x − 3xy) −(5x −5y) = 3x(x − y) − 5(x − y) = (3x −5)(x − y) 2) 2 2
x + 4x − y + 4 = ( 2 x + x + ) 2 4
4 − y = ( x + )2 2
2 − y = ( x + 2 − y)( x + 2 + y) 3) 2 2 2
3x + 6xy + 3y − 3z = ( 2 2
3 x + 2xy + y − ) 1 = ( x + y)2 2 3 −1
= 3( x + y − t)( x + y + t) 4) 2 2 2 2
x − 2xy + y − z + 2zt − t = ( 2 2
x − xy + y ) −( 2 2 2
z − 2zt + t ) = ( − )2 − ( − )2 x y z t
= (x − y − z + t)(x − y + z −t)
5) xy − 5y + 2x −10 = ( xy − 5y) + (2x −10) = y ( x − 5) + 2( x − 5) = ( y + 2)( x − 5)
6) 2xy + z + 2x + yz = (2xy + 2x) + ( z + yz) = 2x( y + ) 1 + z ( y + )
1 = (2x + z)( y + ) 1 7) 3 2 2
5x +10x y + 5xy = x ( 2 2
5 x + 2xy + y ) = ( + )2 5x x y 8) 2 2
x − 2xy + y − 4 = ( 2 2
x − xy + y ) 2 2
− 2 = (x − y)2 2
− 2 = (x − y − 2)(x − y + 2) 9) 3 3 2
2x y − 2xy − 4xy − 2xy 2
= xy x − ( 2 2 y − 2y + = − −
)1 xy x (y )2 2 2 1
= 2xy (x − y + ) 1 ( x + y − ) 1 Trang 5 10) 2 2
x + 2x − y +1 = ( 2 x + x + ) 2 2
1 − y = ( x + )2 2
1 − y = ( x +1− y)( x +1+ y)
Bài 4. Phân tích các đa thức sau thành nhân tử: 2 a) ( 2 x + x) + ( 2 4 x + x) −12 b) ( 2 x + x + )( 2
1 x + x + 2) −12 2 c) ( 2
x + x + ) + x( 2 x + x + ) 2 4 8 3 4 8 + 2x d) ( x + )
1 ( x + 2)( x + 3)( x + 4) − 24 Lời giải 2 a) ( 2 x + x) + ( 2 4 x + x) −12 Đặt 2
x + x = a . Khi đó đa thức trở thành : 2 a + 4a −12 2
= a + 6a − 2a −12 = ( 2
a + 6a) − (2a +12) = (a − 2)(a + 6) Thay 2
a = x + x ta được 2
a − 2 = x + x − 2 và 2
a + 6 = x + x + 6 (1) Xét : 2 x + x − 2 2
= x + x − x − = ( 2 2 2
x + 2x) − (x + 2) = (x − ) 1 (x + 2) (2) Từ (1) và (2) ta được: (x + x)2 2 + ( 2
x + x) − = (x − )(x + )( 2 4 12 1 2 x + x + 6) b) ( 2 x + x + )( 2
1 x + x + 2) −12 Đặt 2
x + x +1 = a , đa thức trở thành : a (a + ) 2
1 −12 = a + a −12 Xét 2 a + a −12 2
= a + a − a − = ( 2 4 3 12
a + 4a) − (3a +12) = a (a + 4) − 3(a + 4) = (a − 3)(a + 4) Thay 2
x + x +1 = a ta được 2 2
a − 3 = x + x +1− 3 = x + x − 2 và 2
a + 4 = x + x + 5 (1) Xét 2 x + x − 2 2
= x − x + 2x − 2 = x( x − ) 1 + 2( x − )
1 = ( x + 2)( x − ) 1 (2) Từ (1) và (2) ta có: ( 2 x + x + )( 2
x + x + ) − = (x + )(x − )( 2 1 2 12 2 1 x + x + 5) 2 c) ( 2
x + x + ) + x( 2 x + x + ) 2 4 8 3 4 8 + 2x Đặt 2
x + 4x + 8 = a , khi đó đa thức trở thành : 2 2
a + 3ax + 2x . Xét 2 2
a + 3ax + 2x 2 2
= a + 2ax + ax + 2x = ( 2 a + ax) + ( 2 2
ax + 2x ) = a(a + 2x) + x(a + 2x)
= (a + x)(a + 2x) (1) Thay 2
x + 4x + 8 = a ta được 2
a + x = x + 5x + 8 và 2
a + 2x = x + 6x + 8 Xét 2 x + 6x + 8 2
= x + 4x + 2x + 8 = x (x + 4) + 2( x + 4) = (x + 2)(x + 4) (2) 2
Từ (1) và (2) ta được ( 2
x + x + ) + x( 2 x + x + ) 2 + x = ( 2 4 8 3 4 8 2
x + 5x + 8)(x + 2)(x + 4) . Trang 6 d) ( x + )
1 ( x + 2)( x + 3)( x + 4) − 24
Có : ( x + )( x + )( x + )(x + ) − = ( 2 x + x + )( 2 1 2 3 4 24 5
4 x + 5x + 6) − 24 2
x +5x + 4 = a −1 Đặt 2
x + 5x + 5 = a 2
x + 5x + 6 = a +1
Khi đó đa thức trở thành (a − ) 1 (a + ) 1 − 24 Xét (a − ) 1 (a + ) 1 − 24 2
= a − 25 = (a − 5)(a + 5) Thay 2
a = x + 5x + 5 vào ta có: 2 2
a − 5 = x + 5x + 5 − 5 = x + 5x = x ( x + 5) và 2 2
a + 5 = x + 5x + 5 + 5 = x + 5x +10 .
Vậy ( x + )( x + )( x + )( x + ) − = x(x + )( 2 1 2 3 4 24 5 x + 5x +10)
Dạng 3. Tìm x
Bài 5. Tìm x , biết: a) 2
x − 7x + 6 = 0 b) ( x − )2 2 − 4 = 0 c) 3
x −19x − 30 = 0 Lời giải a) 2
x − 7x + 6 = 0 2
x − x − 6x + 6 = 0
( 2x − x)−(6x−6) = 0 x ( x − ) 1 − 6( x − ) 1 = 0
(x − )1(x −6) = 0
x −1 = 0 hay x − 6 = 0 x = 1 hay x = 6 b) ( x − )2 2 − 4 = 0
(x − 2− 2)(x − 2+ 2) = 0
(x − 4) . x = 0
x − 4 = 0 hay x = 0 x = 4 hay x = 0 c) 3
x −19x − 30 = 0 3
x − 9x −10x − 30 = 0
( 3x −9x)−(10x+30) = 0
x (x − 3)( x + 3) −10(x + 3) = 0 (x +3)x
( x − 3) −10 = 0 (x + )( 2
3 x − 3x −10) = 0 (x + )( 2
3 x − 5x + 2x −10) = 0 Trang 7 (x + )( 2 3
x − 5x) + (2x −10) = 0 (x +3)x
( x − 5) + 2( x − 5) = 0
(x +3)(x −5)(x + 2) = 0
x + 3 = 0 hay x − 5 = 0 hay x + 2 = 0
x = −3 hay x = 5 hay x = −2
Bài 6. Tìm x , biết: a)
2x ( x − 5) − x(3+ 2x) = 0 b) 5x ( x − ) 1 = x −1 c) (x + ) 2 2
5 − x − 5x = 0
d) ( x − )2 − ( x + )2 2 3 5 = 0 e) 3
3x − 48x = 0 f) 3 2
x + x − 4x = 4 Lời giải
a) 2x ( x − 5) − x(3+ 2x) = 0 x 2
( x − 5) − (3 + 2x) = 0
x (2x −10 − 3− 2x) = 0 . x ( 13 − ) = 0 x = 0 b) 5x ( x − ) 1 = x −1 5x ( x − ) 1 − ( x − ) 1 = 0
(x − )1(5x − )1 = 0
x −1 = 0 hay 5x −1 = 0
x = 1 hay 5x = 1 1 x = 1 hay x = 5 c) (x + ) 2 2
5 − x − 5x = 0
2( x + 5) − x(x + 5) = 0
(x +5)(2− x) = 0
x + 5 = 0 hay 2 − x = 0
x = −5 hay − x = −2 x = 5 − hay x = 2
d) ( x − )2 − ( x + )2 2 3 5 = 0
(2x −3)−(x +5)
(2x − 3) + ( x + 5) = 0
(2x −3− x −5)(2x −3+ x +5) = 0
(x −8)(3x + 2) = 0
x − 8 = 0 hay 3x + 2 = 0
x = 8 hay 3x = 2 − Trang 8 2 − x = 8 hay x = 3 e) 3 3x − 48x = 0 x ( 2 3 x −16) = 0
3x ( x − 4)( x + 4) = 0
3x = 0 hay x − 4 = 0 hay x + 4 = 0
x = 0 hay x = 4 hay x = −4 f) 3 2
x + x − 4x = 4 ( 3 2
x + x ) − (4x + 4) = 0 2 x ( x + ) 1 − 4( x + ) 1 = 0 (x + )( 2 1 x − 4) = 0
(x + )1(x − 2)(x + 2) = 0
x +1 = 0 hay x − 2 = 0 hay x + 2 = 0
x = −1 hay x = 2 hay x = −2 Dạng 4. Chứng minh
Bài 7. Chứng minh các đẳng thức sau:
1) a + b = (a + b)2 2 2 − 2ab .
2) a + b = (a + b )2 4 4 2 2 2 2 − 2a b . 3) a b (a b )(a b )2 6 6 2 2 2 2 2 2 3a b + = + + − . 4) 2 ( − ) 2 + ( − ) 2 a b c
b c a + c (a − b) = (a − c)(b − a)(c − b) . Lời giải 1) Ta có 2 2 2 2
VP = a + 2ab + b − 2ab = a + b = VT ĐPCM. 2) Ta có 4 2 2 4 2 4 4
VP = a + 2a b + b − 2a b2 = a + b = VT ĐPCM. 3 3 2 3) Ta có VT ( 2 a ) ( 2 b ) ( 2 2 a b )( 4 2 2 4 a a b b ) ( 2 2 a b ) ( 2 2 a b ) 2 2 3a b = + = + − + = + + − = VP ĐPCM. 4) 2 = ( − ) 2 + ( − + − ) 2 VT a b c
b c b b a + c (a − b) 2
= a (b − c) 2
− b (b − c) 2
− b (a − b) 2
+ c (a − b) = ( 2 2
a − b )(b − c) − ( 2 2
b − c )(a − b)
= (a − b)(b − c) (a + b) − (b + c)
= (a − b)(b − c)(a − c) = (a − c)(b − a)(c − b) =VP ĐPCM B. HÌNH HỌC Trang 9 Bài 1.
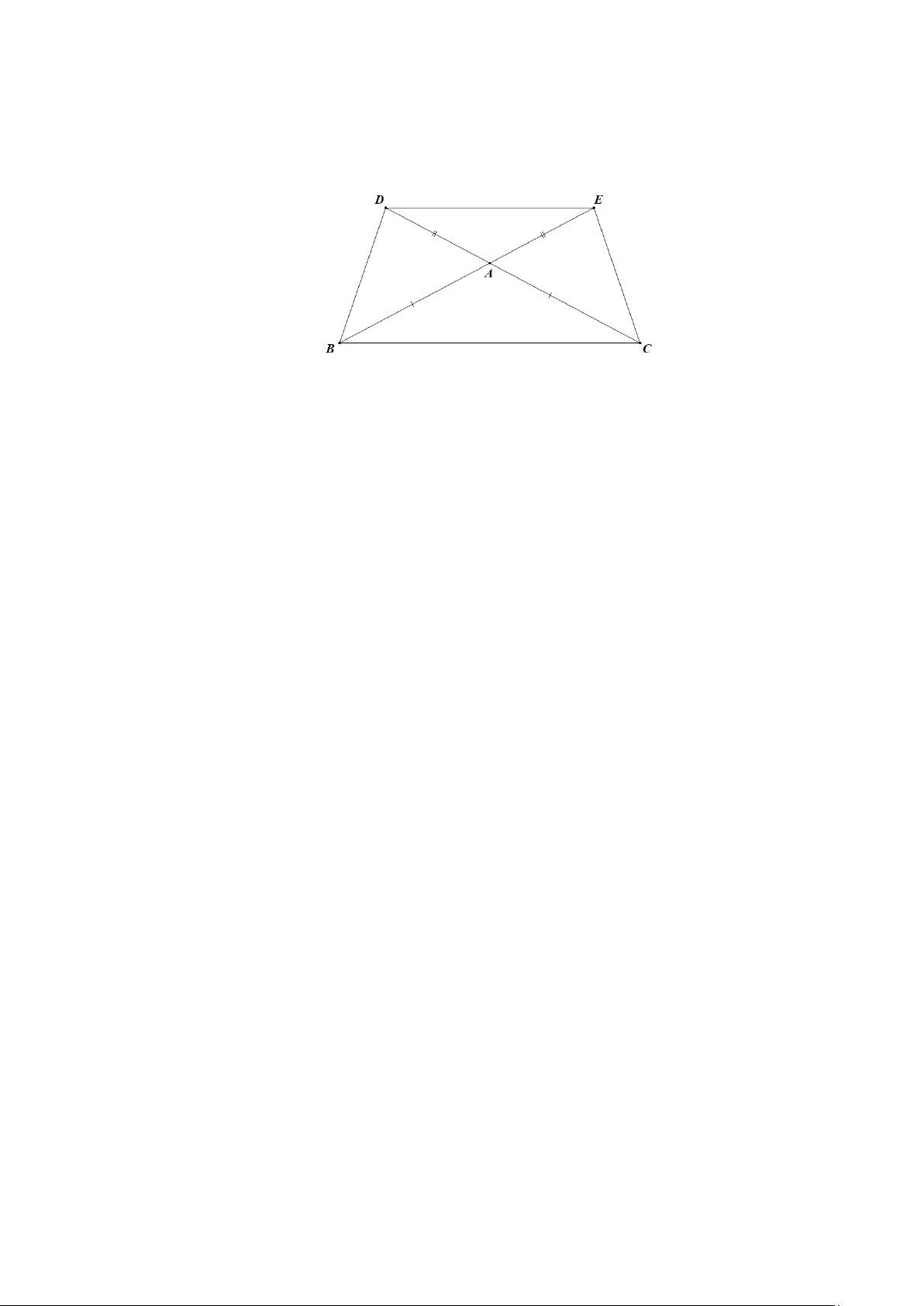
Cho tam giác ABC cân tại A . Trên tia đối của tia AC lấy điểm D , trên tia đối của tia AB lấy
điểm E sao cho AD = AE . Tứ giác DECB là hình gì? Vì sao? Lời giải
Xét hai tam giác ABD và tam giác ACE ta có: AD = AE ( )
1 tam giác ADE cân tại A ADE + AED + DAE = 2ADE + DAE = 180
tam giác ABC cân tại A ABC + ACB + BAC = 2ACB + BAC = 180
mà BAC = DAE (đối đỉnh) ADE = ACB DE//BC (2) .
Lại có AB = AC (3) . Từ ( )
1 , (3) DC = BE (DC = DA + AC ; BE = BA + AE) (4) .
Từ (2) , (4) DECB là hình thang cân. Bài 2.
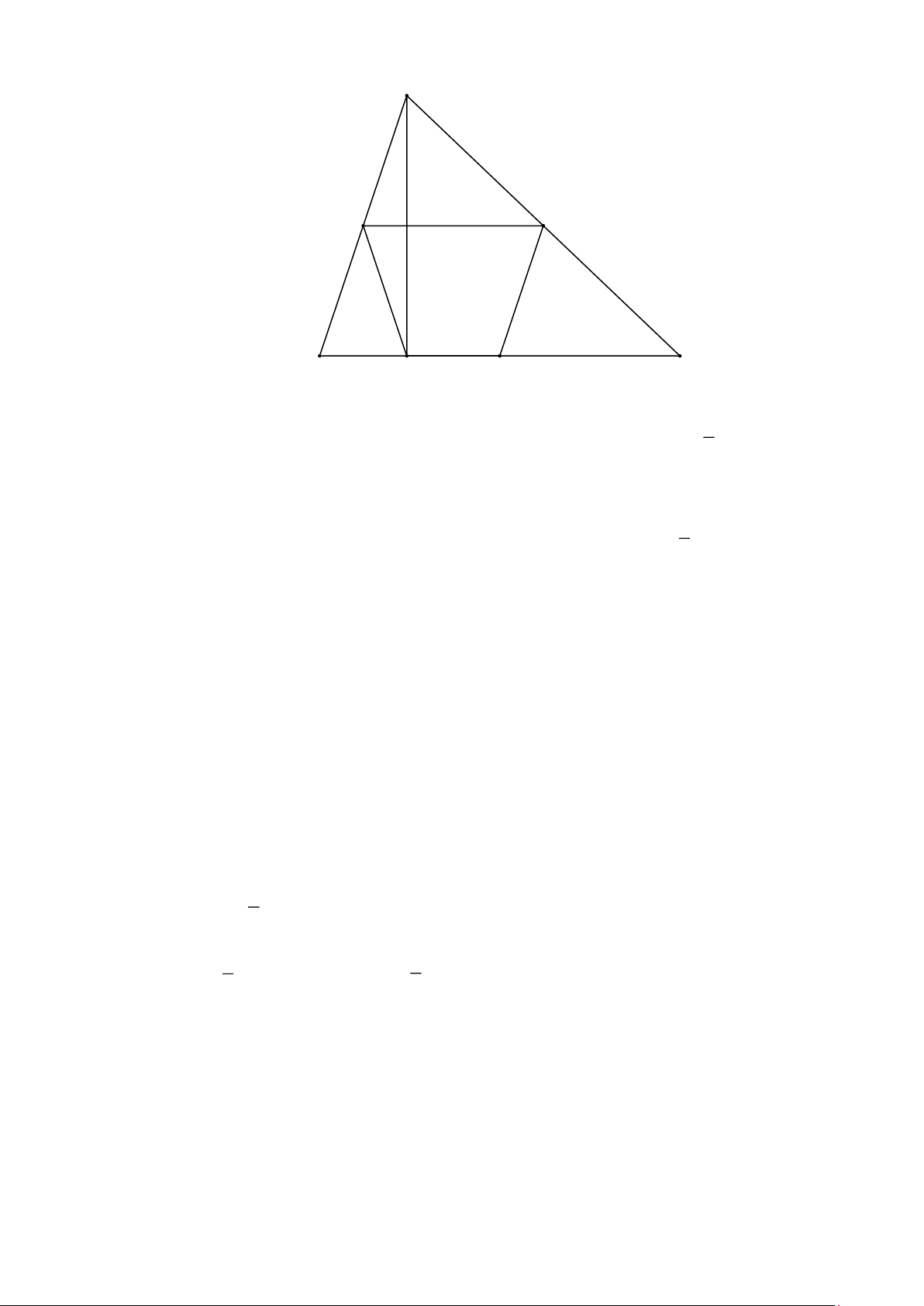
Cho tam giác ABC(AB AC) đường cao AH . Gọi M , N , P lần lượt là trung điểm của BC,C ,
A AB . Chứng minh rằng
a) NP là đường trung trực của AH .
b) MHNP là hình thang cân Lời giải Trang 10 A N P B C H M 1
a) Xét ABH vuông tại H đường trung tuyến HP nên HP = PA = PB = AB . 2
Suy ra P thuộc đường trung trực của AH 1
Xét ACH vuông tại H đường trung tuyến HN nên HN = NA = NC = AC . 2
Suy ra N thuộc đường trung trực của AH
Suy ra NP là đường trung trực của AH . b) Xét ABC có
P là trung điểm của AB ; N là trung điểm của AC nên PN là đường trung bình của ABC
Suy ra PN / /BC hay PN / / HM
Suy ra PHMN là hình thang (1) Xét ABC có
P là trung điểm của AB ; M là trung điểm của BC nên PM là đường trung bình của ABC 1 Suy ra PM = AC 2 1 1
Mà HN = AC nên PM = AN = AC (2) 2 2
Từ (1) và (2) suy ra MHNP là hình thang cân Bài 3.
Cho hình bình hành ABCD . Từ A kẻ AI vuông góc với BD , từ C kẻ CK vuông góc với
BD (I, K BD) .
a) Tứ giác AICK là hình gì?
b) Tia AI cắt CD tại M , Tia CK cắt AB tại N . Chứng minh rằng trung điểm của đoạn thẳng
MN thuộc đường chéo BD Trang 11 Lời giải A N B K P I D M C
a) Có ABCD là hình bình hành nên AD / /CB; AD = BC
Xét ADI và BCK có AD = BC
ADI = KBC (hai góc so le trong AD / /CB ) AID = BKC ( 0 = 90 ) AD I = C
BK(ch − gn)
AI = CK (hai cạnh tương ứng) (1) Có AI ⊥ ;
BD CK ⊥ BD AI / /CK (2)
Từ (1) và (2) ta có AICK là hình bình hành.
b) Gọi P là trung điểm của MN
Xét tứ giác AMCN có AM / /CN; AN/ / MC
Nên AMCN là hình bình hành
Suy ra hai đường chéo MN , AC cắt nhau tại trung điểm mỗi đường.
Mà P là trung điểm của MN nên P là trung điểm của AC
Có ABCD là hình bình hành
Suy ra hai đường chéo BD, AC cắt nhau tại trung điểm mỗi đường.
Mà P là trung điểm của AC nên P là trung điểm của BD
Suy ra trung điểm của đoạn thẳng MN thuộc đường chéo BD Bài 4.
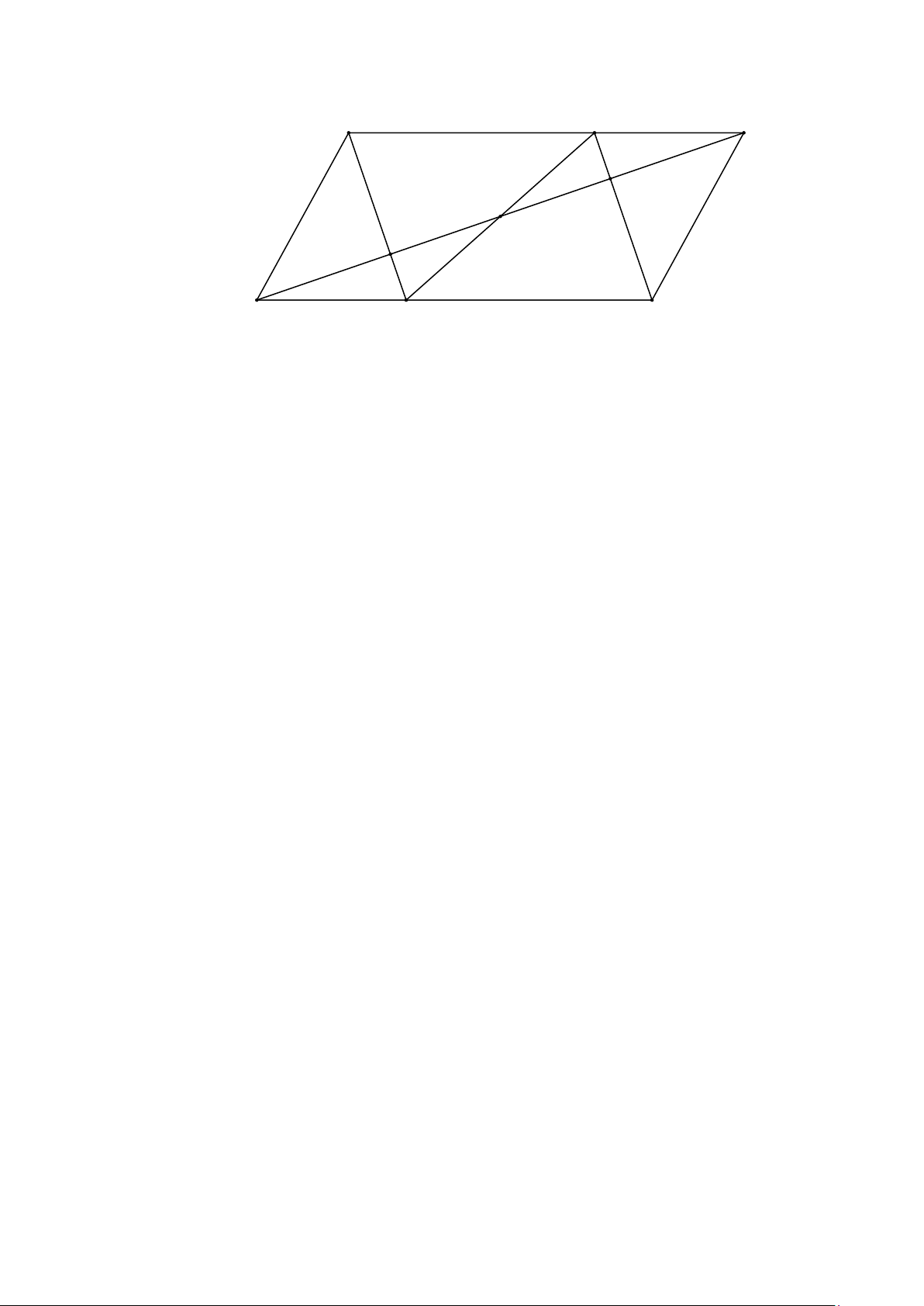
Cho hình bình hành ABCD . Gọi M , N theo thứ tự là trung điểm của BC, .
AD AM cắt BD
tại P, CN cắt BD tại Q .
a) Chứng minh BP = PQ = QD b)
Gọi I là giao điểm của AM với BN , K là giao điểm của DM với CN . Chứng minh
AC, BD, MN, IK đồng quy. Trang 12 Lời giải AB//C ,
D AB = CD
a) Vì ABCD là hình bình hành
AD//BC, AD = BC 1
AN = ND = AD mà 2 AN = CM 1
BM = MC = BC 2
mặt khác, ta có: AN //CM (AD//BC) AMCN là hình bình hành AM //CN BM = MC (gt)
Xét BCQ có PB = PQ ( ) PM CQ ( AM CN ) 1 // // NA = ND (gt)
Xét ADP có DQ = QP (2) NQ//AP ( AM //NC) Từ ( )
1 , (2) BP = PQ = QD(dpcm)
b) Gọi O = IK MN BM = DN
xét tứ giác BMDN có:
BMDN là hình bình hành BM //DN
BN //MD và O là trung điểm của BD và MN ( ) 1
Có BN //MD NI //MQ (2)
Từ câu a MI //NK (3) ( vì AMCN là hình bình hành)
Từ (2)(3) NIMK là hinh bình hành
O là trung điểm của IK và MN (4)
Mặt khác, AMCN là hình bình hành O là trung điểm của AC và MN (5) Từ ( )
1 (4)(5) AC, BD, MN, IK đồng quy tại O .
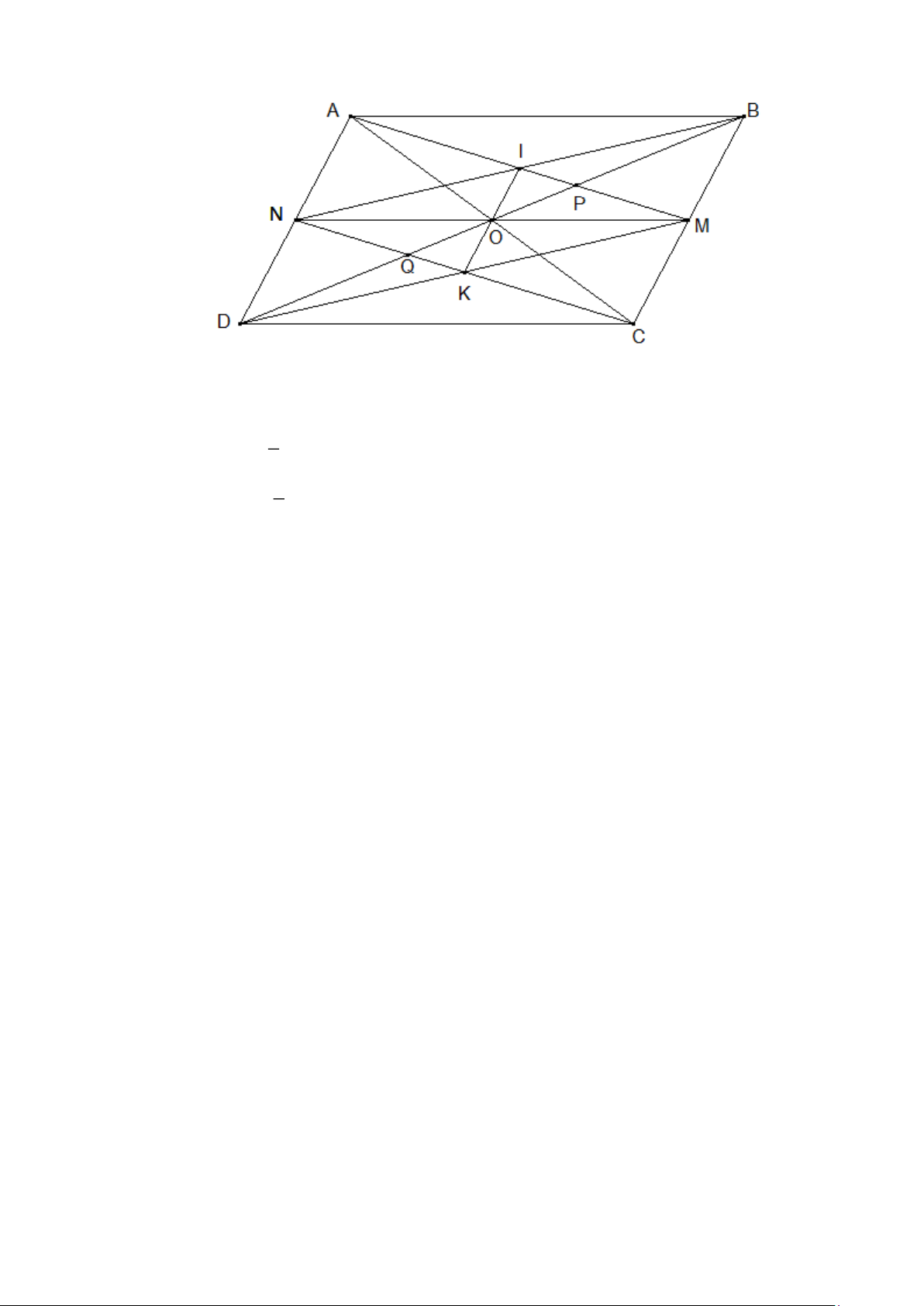
Bài 5. Cho hình bình hành ABCD . Gọi M , N, P, Q lần lượt là trung điểm của AB, BC, CD, D . A
Gọi K là giao điểm của AC và DM , L là giao điểm của BP và CA . Trang 13
a) MNPQ là hình gì? Vì sao?
b) MDPB là hình gì? Vì sao?
c) Chứng minh: AK = KL = LC. Lời giải
MA = MB(gt) a) Xét A BC ó c
MN là đường trung bình của ABC
BN = NC( t g ) MN //AC 1 (1) MN = AC 2 Q
A = QD(gt) Xét A DC ó c
PQ là đường trung bình của ADC
DP = PC( t g ) PQ//AC 1 (2) PQ = AC 2 MN PQ Từ ( )(2) // 1
ANPQ là hình bình hành MN = PQ MB//DP(AB//CD) (1)
b) Ta có ABCD là hình bình hành AB = DC (2) AB MB = MA =
Mặt khác, M và P lần lượt là trung điểm của AB, DC 2 (3) DC DP = PC = 2 Từ ( )(2)(3) MB//DP 1
MBPD là hình bình hành. MB=DP KD//LP
c) Vì MBPD là hình bình hành MD//BP KM//BL M K //LB d) Xét ALB có:
K là trung điểm của AL AK=KL (4)
AM = MB(gt) Trang 14 KD//LP Xét KDC có:
L là trung điểm của KC KL=LC (5)
DP = PC(gt)
Từ (4)(5) AK = KL = LC ( đpcm)
Bài 6. Cho ABC vuông tại A , có AB = 6 cm, AC = 8cm . M là trung điểm của BC a. Tính BC b. Kẻ MH
AC (H AB) , MK
AB K AC . Tứ giác AHMK là hình gì? Vì sao? Lời giải
a. Do ABC vuông tại A , nên áp dụng định lí Pi-ta-go. 2 2 2
BC = AB + AC 2 2 2 BC = 6 + 8 = 100 BC = 10 cm b. 0
HAK = 90 (GT) (1) MH AC Do MH ⊥ AB AC ⊥ AB 0 AMH = 90 (2) MK AB Do MK ⊥ AC AB ⊥ AC 0 AKM = 90 (3)
Bài 7. Cho hình bình hành ABCD . Kẻ AE và CF vuông góc với BD (E, F BD) .
a. Tứ giác AECF là hình gì ? vì sao?
b. Gọi I là giao điểm của AE và CD , K là giáo điểm của CF và AB . Chứng minh: AI = CK
c. Chứng minh BE = DF . Lời giải Trang 15 C F ⊥ BD a. Do
AE ⊥ FC (1) AE ⊥ BD
Xét hai tam giác vuông ABE và FDC
ABD = BDC ( do 2 góc sole trong)
AB = DC vì ABCD là hình bình hành
ABE = FDC
FC = AE (2)
Từ (1) và (2) tứ giác AECF là hình bình hành
AK ⊥ IC(HBH ) b. Do
AKCI là hình bình hành
AE ⊥ BD(CMT ) KC = AI
Do ABE = FDC DF = EB Bài 8.
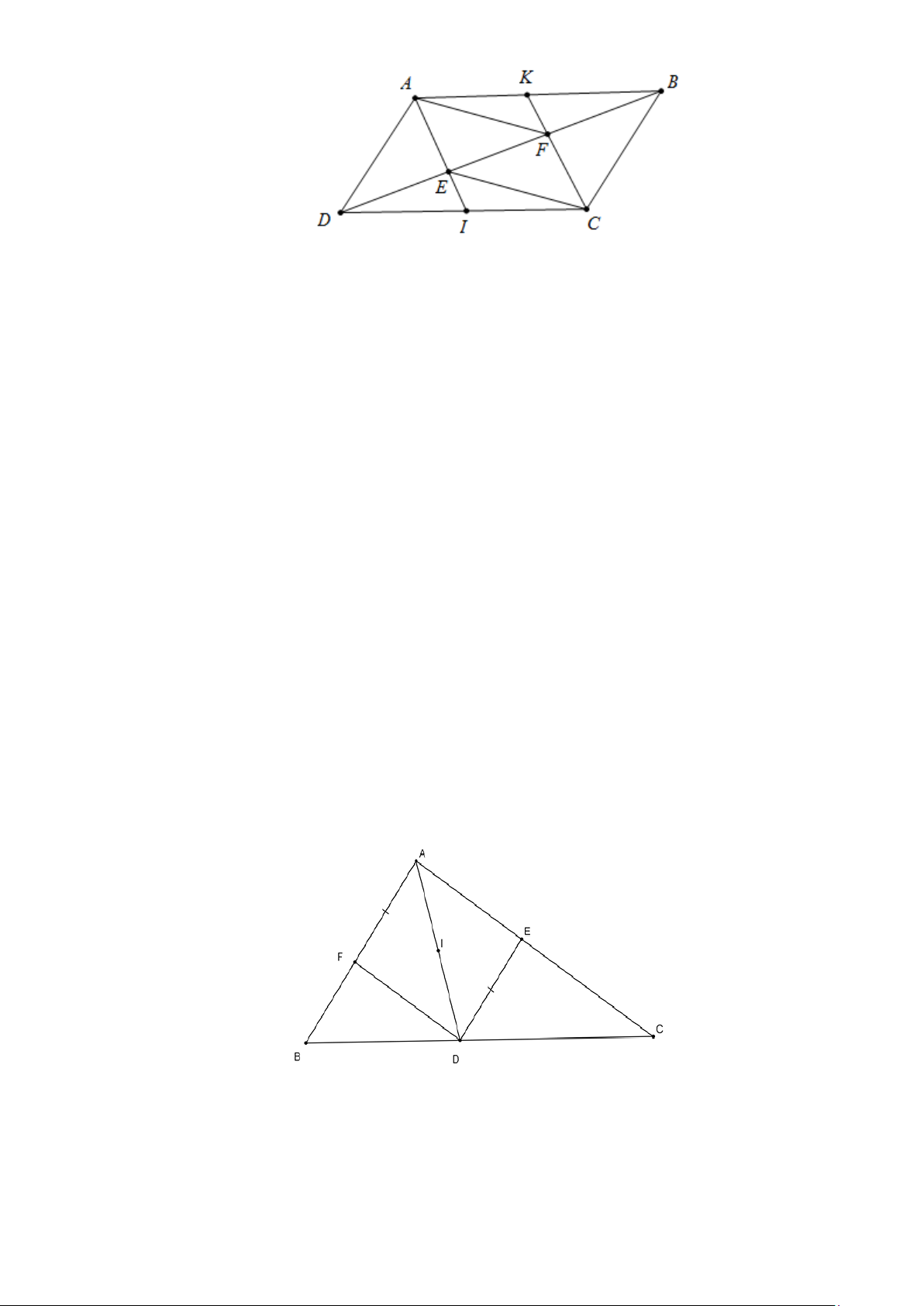
Cho tam giác ABC , D là một điểm trên cạnh BC . Qua D kẻ đường thẳng song song với AB
cắt AC ở E . Trên AB lấy điểm F sao cho AF = DE . Gọi I là trung điểm của AD . Chứng minh: a) DF = AE
b) E và F đối xứng nhau qua I . Lời giải
a) Xét tứ giác AEDF có:
DE / / AF (gỉa thiết)
DE = AF (gỉa thiết)
Suy ra tứ giác AEDF là hình bình hành (Dấu hiệu nhận biết)
DF = AE (tính chất) Trang 16
b) Tứ giác AEDF là hình bình hành, lại có I là trung điểm của AD nên I là trung điểm của EF
hay E và F đối xứng nhau qua I . Bài 9.
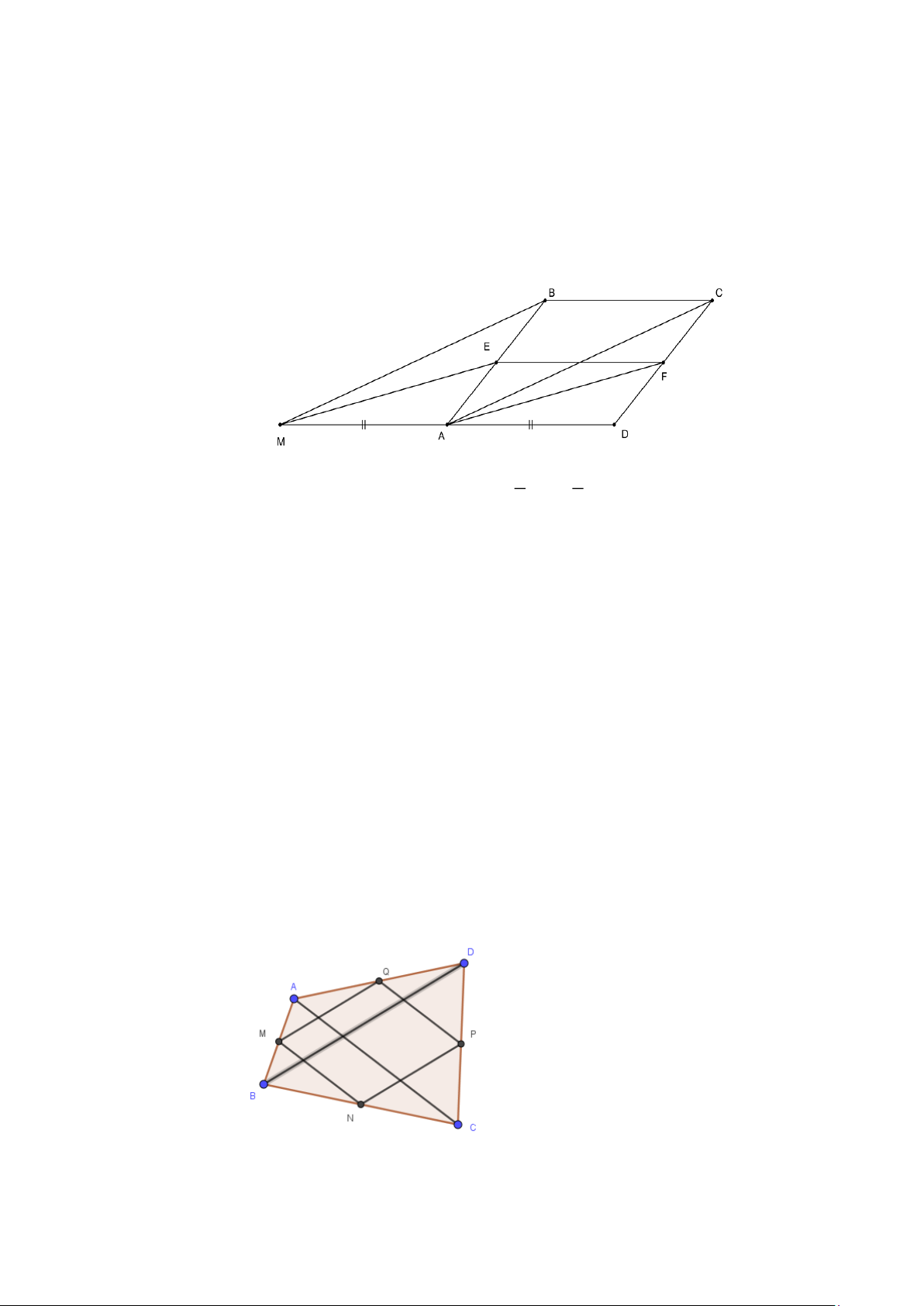
Cho hình bình hành ABCD lấy E và F lần lượt là trung điểm của AB và CD , lấy M thuộc
tia đối của tia AD sao cho AM = AD . Chứng minh các tứ giác sau là hình bình hành: a) Tứ giác AEFD b) Tứ giác AMEF c) Tứ giác AMBC Lời giải 1 1
a) Vì ABCD là hình bình hành nên AB = CD AB = CD 2 2 AE = DF
Xét tứ giác AEFD có AE / /DF, AE = DF (cmt).
Do đó Tứ giác AEFD là hình bình hành (Dấu hiệu nhận biết).
b) Vì AEFD là hình bình hành ( câu a) nên EF / / AD, EF = AD (tính chất)
Xét tứ giác AMEF có EF / /MA , EF=MA (= AD) .
Do đó tứ giác AMEF là hình bình hành (Dấu hiệu nhận biết).
c) Vì ABCD là hình bình hành nên BC / / AD, BC = AD
Xét tứ giác AMBC có BC / /MA , BC=MA (= AD) . Do đó tứ giác AMBC là hình bình hành (Dấu hiệu nhận biết).
Bài 10. Cho tứ giác ABCD . Gọi M , N, P,Q thứ tự là trung điểm của AB, BC,CD, DA .
a) Chứng minh rằng tứ giác MNPQ là hình bình hành
b) So sánh chu vi tứ giác MNPQ với tổng hai đường chéo của tứ giác ABCD . Lời giải
a) Trong tam giác ABD có:
M là trung điểm của AB Trang 17
Q là trung điểm của AD
Suy ra, MQ là đường trung bình của tam giác ABD 1 MQ = D B và MQ / / D B ( ) 1 2
Trong tam giác BCD có:
N là trung điểm của BC
P là trung điểm của CD
Suy ra, NP là đường trung bình của tam giác BCD 1 NP = D B và NP / / D B (2) 2 Từ ( )
1 và (2) suy ra: MQ = NP và MQ / /NP
Vậy tứ giác MNPQ là hình bình hành.
b) Chu vi tứ giác MNPQ là: C = MN + NP + PQ + QM D B AC Mà QM = NP = và MN = PQ = nên: 2 2 D B AC
C = MN + NP + PQ + QM = 2. + 2. = D B + AC 2 2
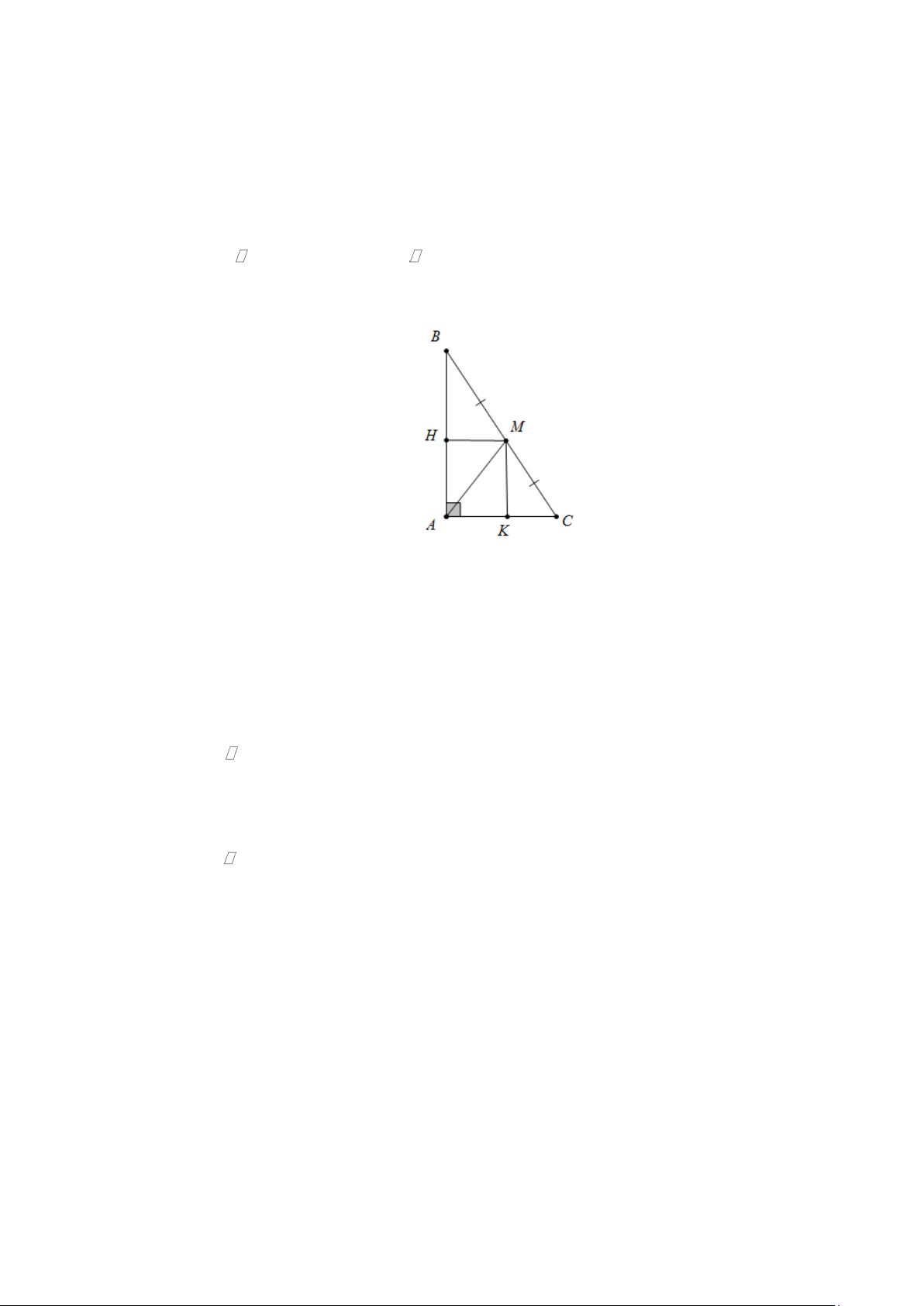
Bài 11. Cho hình bình hành ABCD , AD = 2AB . Từ C vẽ CE vuông góc với AB . Nối E với trung
điểm M của AD . Từ M vẽ MF vuông góc với CE , MF cắt BC tại N .
a) Tứ giác MNCD là hình gì?
b) Tam giác EMC là tam giác gì? Lời giải
a) Ta có MN / / AB (cùng vuông CE)
MN / /CD mà DM / /CN nên tứ giác MNCD là hình bình hành
b) Xét tam giác BEC vuông tại E có: N là trung điểm BC 1
suy ra, NE = NC = BC (t/c trung tuyến tam giác vuông) 2
Xét tam giác ENF và CNF có:
NE = NC , NF chung, EFN = NFC Trang 18 F = C F ENF = FNC
Xét tam giác và C có NE = NC , NM chung, ENF = FNC
= C = C
Vậy tam giác EMC cân tại M . C. PHẦN NÂNG CAO
Bài 1. Tìm giá trị nhỏ nhất của các đa thức sau: 2
A = x − 4x + 6; 2 B = 2x + 6 ; x
C = (x −1)(x + 2)(x+ 3)(x+ 6); 2 2
D = (2x −1) + (x + 2) ;
E = x(x +1)(x + 2)(x + 3); 2 2
F = (x −1) + (x − 3) . Lời giải a) 2
A = x − 4x + 6; Ta có: 2 2
A = x − 4x + 6 = (x− 2) + 2 Vì 2 2
(x − 2) 0 x
(x − 2) + 2 2 x
Vậy MinA = 2 khi x = 2. b) 2 B = 2x + 6 ; x 3 9 9 3 9 Ta có: 2 2 2
A = 2x + 6x = 2(x + 2x + − ) = 2(x+ ) + 2 4 4 2 2 3 3 9 9 Vì 2 2 2(x + ) 0 x (x + ) + x 2 2 2 2 9 3 −
Vậy MinB = khi x = . 2 2
c) C = (x −1)(x + 2)(x+ 3)(x+ 6);
= [(x −1)(x+ 6)][(x + 2)(x+ 3)] 2 2
= (x + 5x − 6)(x + 5x + 6) 2 2
= (x + 5x) − 36 Vì 2 2 2 2
(x + 5 x) 0 x
(x + 5 x) − 36 36 − x
Vậy MinC = −36 khi x = 0 hoặc x = −5. d) 2 2
D = (2x −1) + (x + 2) ; 2 2
= 4x − 4x +1+ x + 4x + 4 2 = 5x + 5 Vì 2 2 5 x 0 x
5x + 5 5 x
Vậy MinD = 5 khi x = 0.
e) E = x(x +1)(x + 2)(x + 3); Trang 19
=[x(x + 3)][(x + 2)(x + 3)] 2 2
= (x + 3x)(x + 3x + 2) 2 2 2
= (x + 3x) + 2(x + 3x) +1−1 2 2
= (x + 3x +1) −1 Vì 2 2
(x + 3x+1) 0 x E 1 − x 3 − + 5 3 − + 5
Vậy MinE = −1 khi x = hoặc x = . 2 2 f) 2 2
F = (x −1) + (x − 3) . 2 2
= x − 2x +1+ x − 6x + 9 2 = 2x − 8x +10 2
= 2(x − 4x + 5) 2 = 2(x − 2) + 2 Vì 2 2 2(x− 2) 0 x
2(x− 2) + 2 2 x
Vậy MinE = 2 khi x = 2.
Bài 2. Tìm giá trị lớn nhất của các đa thức sau : 2
A = 4 − x + 2 ; x 2
B = 10x − 23 − x ; 2 C = −x + 6 . x Lời giải a) 2
A = 4 − x + 2 ; x 2
= 5 − (x − 2x +1) 2 = 5 − (x −1) Vì 2 2 (x−1) 0 x
5 − (x−1) 5 x
Vậy MaxA = 5 khi x = 1. b) 2
B = 10x − 23 − x ; 2
= 2 − (x −10x + 25) 2 = 2 − (x − 5) Vì 2 2 (x− 5) 0 x
2 − (x− 5) 2 x
Vậy MaxA = 2 khi x = 5. c) 2 C = −x + 6 . x 2
= 9 − (x − 2.3.x + 9) 2 = 9 − (x − 3) Vì 2 2 (x− 3) 0 x
9 − (x− 3) 9 x
Vậy MaxA = 9 khi x = 3. Trang 20