Bài Tập Toán 8 Tuần 8 Có Lời Giải Chi Tiết

PHIẾU BÀI TẬP TOÁN 8 TUẦN 08
A. PHẦN CƠ BẢN ( DÀNH CHO TẤT CẢ CÁC LỚP): Bài 1.
Phân tích các đa thức sau thành nhân tử . a) 4 3
x + x + x +1; b) 4 3 2
x − x − x +1 ; c) 2 2
x y + xy − x − y ; d) 2 2
ax − ay − 7x − 7 y ; e) 2 2
ax + ay − bx − by ; f) 2 2
x − y − x + y . Bài 2. Tìm x biết: a) 2
x − x − 3x + 3 = 0 ; b) 2 (x − 3) − 4 = 0 ; c) 3
x − 4x −15x − 30 = 0 ; d) 3
x + 27 + (x + 3)(x − 9) = 0 . Bài 3.
Thực hiện phép chia đơn thức: 1) 12 x ( 10 : −x ) 2) ( 7 − y ) ( 3 : − y )  1  3) ( 5 2 3 − x + x x ) 2 2 3 - 4 : 2x 4) ( 3 2 2
x − 2x y + 3xy ): − x .    2  Bài 4. Làm tính chia : ( 3 2
1) x − 3x + x − 3):(x −3)
(x − y − z)5 (x − y − z)3 2) : ( 4 2 3
x − x + x − − ) ( 2 3) 2 5 3 3x : x − 3) ( 2 2
4) x + 2x +x − 4):(x + 2) ( 3 2 x + x − ) ( 2 5) 2 5 2x+3 : 2x − x + ) 1 ( 3 2
6) 2x 05x +6x−15):(2x- 5). Bài 5. Chứng minh rằng :
a) (a − b)3 + (a + b)3 = a( 2 2 2 a + 3b )
b) ( x + y + z)2 − ( x − y − z)2 = 4x( y + z)
Bài 6. Cho tam giác ADC (AD  AC) . Đường trung trực d của cạnh CD cắt AC ở O . Trên tia đối
của tia OD lấy điểm B sao cho OB = OA .
a) Chứng minh điểm B đối xứng với điểm A qua đường thẳng d ;
b) Tứ giác ABCD là hình gì? Vì sao? Bài 7.
Cho hình bình hành ABCD có CD=2AD . Gọi M là trung điềm của cạnh CD .
a) Chứng minh AM , BM theo thứ tự là tia phân giác của góc A và góc B ;
b) Chứng minh góc AMB là góc vuông. Bài 8. Chứng minh rằng a) 2
x + 2x + 2  0 với x  Z ; b) 2
x − x +1  0 với x  Z ; c) 2
−x + 4x − 5  0 với x  Z Bài 9.
Tìm các cặp số nguyên x, y sao cho a) (
y x − 2) + 3x − 6 = 2.
b) xy + 3x − 2y − 7 = 0 .
c) xy − x + 5y − 7 = 0 .
Bài 10. Cho a + b + c = 0 . Chứng minh các đẳng thức sau a) 3 3 3
a + b + c = 3abc . b) 5 5 5 2 2 2
2(a + b + c ) = 5ab (
c a + b + c ).
ĐÁP ÁN BÀI TẬP TĂNG CƯỜNG TOÁN 8 Trang 1 TUẦN 8
HƯỚNG DẪN GIẢI CHI TIẾT
A. PHẦN CƠ BẢN ( DÀNH CHO TẤT CẢ CÁC LỚP): Bài 1.
Phân tích các đa thức sau thành nhân tử . a) 4 3
x + x + x +1; b) 4 3 2
x − x − x +1 ; c) 2 2
x y + xy − x − y ; d) 2 2
ax − ay − 7x − 7 y ; e) 2 2
ax + ay − bx − by ; f) 2 2
x − y − x + y . Lời giải a) 4 3 3
x + x + x + = x x + + x + = x + ( 3 x + ) 2 = x + ( 2 1 ( 1) ( 1) ( 1) 1 ( 1) x − x + ) 1 . b) 4 3 2 3 2 3
x − x − x + = x x − − x − = x x − − x − x + = x − ( 3 1 ( 1) ( 1) ( 1) ( 1)( 1) ( 1) x − x − ) 1 . c) 2 2
x y + xy − x − y = xy(x + y) − (x + y) = (x + y)(xy −1) . d) 2 2
ax − ay − x − y = a ( 2 2 7 7
x − y ) − 7(x + y) = a(x − y)(x + y) − 7(x + y) = (x + y)(ax −by − 7) . e) 2 2 2
ax + ay − bx − by = a − b x + y a − b = a − b ( 2 ( ) ( ) ( ) x + y) . f) 2 2
x − y − x + y = (x − y)(x + y) − (x − y) = (x − y)(x + y −1) . Bài 2. Tìm x biết: a) 2
x − x − 3x + 3 = 0 ; b) 2 (x − 3) − 4 = 0 ; c) 3
x − 4x −15x − 30 = 0 ; d) 3
x + 27 + (x + 3)(x − 9) = 0 . Lời giải a) 2
x − x − 3x + 3 = 0 x −1 = 0 x =1
 x(x −1) − 3(x −1) = 0  (x −1)(x − 3) = 0    . x 3 0  − = x = 3 Vậy x 1;  3 . x − 3 = 2 x = 5 b) 2 2
(x − 3) − 4 = 0  (x − 3) = 4    . x 3 2  − = − x =1 Vậy x 1;  5 . c) 3
x − 4x −15x − 30 = 0  x(x − 2)(x + 2) −15(x + 2) = 0  x + ( 2 x − x − ) =  x+ ( 2 ( 2) 2 15 0 (
2) x − 5x + 3x −15) = 0  (x + 2)x(x − 5) + 3(x − 5) = 0 Trang 2 x = 2 −
(x 2)(x 3)(x 5) 0   + + − =  x = 3 −  . x = 5  Vậy x  2 − ; 3 − ;  5 . d) 3 x + + x + x − =  x + ( 2 27 ( 3)( 9) 0 (
3) x − 3x + 9) + (x + 3)(x −9) = 0 x = 0 (x 3)( 2 x 2x) 0
x(x 3)(x 2) 0   + − =  + − =  x = 3 −  . x = 2  Vậy x 0; 3 − ;  2 . Bài 3.
Thực hiện phép chia đơn thức: 1) 12 x ( 10 : −x ) 2) ( 7 − y ) ( 3 : − y ) 3) ( 5 2 3 − x + x x ) 2 2 3 - 4 : 2x  1  4) ( 3 2 2
x − 2x y + 3xy ): − x .    2  Lời giải 12 x ( 10 −x ) 12 1 − 0 2 1) : = −x = −x ( 7 −y ) ( 3 −y ) 7−3 4 2) : = y = y ( 5 2 3 − x + x x ) 2 3) 2 3 -4 : 2x 5 2 2 2 3 2
=− 2x : 2x + 3x : 2x − 4x : 2x 3 3
= −x + − 2x 2   4)( 1 3 2 2
x − 2x y + 3xy ): − x    2   1   1   1 3 2 2 
= x : − x − 2x y : − x + 3xy : − x        2   2   2  2 3 2 2 = 2
− x + 4x y − 6x y Bài 4. Làm tính chia : ( 3 2
1) x − 3x + x − 3):(x −3)
(x − y − z)5 (x − y − z)3 2) : Trang 3 ( 4 2 3
x − x + x − − ) ( 2 3) 2 5 3 3x : x − 3) ( 2 2
4) x + 2x +x − 4):(x + 2) ( 3 2 x + x − ) ( 2 5) 2 5 2x+3 : 2x − x + ) 1 ( 3 2
6) 2x 05x +6x−15):(2x- 5). Lời giải ( 3 2
1) x − 3x + x − 3):(x −3) 2
=x (x − 3) + x − 3 :(x − 3)   = (x − ) ( 2 x − ) (x − ) 2 3 . 1 : 3 = x −1
(x − y − z)5 (x − y − z)3 = (x − y − z)2 2) : ( 4 2 3
x − x + x − − ) ( 2 3) 2 5 3 3x : x − 3) 4 2 3 2
= x − x + x − + x −    ( 2 2 6 3x 3 : x − 3) 2
=  x ( 2x − )+ x( 2x − )+( 2x − ) ( 2 2 3 3 3 : x − 3) =( 2 x − )( 2 x + x + ) ( 2 3 2 1 : x − 3) 2 = 2x + x +1 ( 2 2
4) x + 2x +x − 4):(x + 2) = ( 2x + ) ( 2
2x + x − 4) :(x + 2) 
= x(x + 2) +(x + 2)(x − 2) :  ( x + 2)
= (2x − 2)(x + 2):(x + 2) = 2x − 2 ( 3 2 x + x − ) ( 2 5) 2 5 2x+3 : 2x − x + ) 1 = ( 3 2 x + x ) −( 2 x + x) + ( ) ( 2 2 6 3 x+3 : 2x − x +   )1 2 =  x ( )− x(x + )+( ) ( 2 2 x+3 3 x+3 : 2x − x +   )1 = ( )( 2 − x + ) ( 2 x+3 2x 1 : 2x − x + ) 1 = x + 3 ( 3 2
6) 2x 05x +6x−15):(2x- 5) Trang 4 = ( 3 2
2x 05x )+(6x−15) :(2x- 5)  2
= x (2x05) + 3(2x05) :(2x- 5)   = ( x )( 2 2 05 x + 3):(2x- 5) 2 = x + 3 Bài 5. Chứng minh rằng :
a) (a − b)3 + (a + b)3 = a( 2 2 2 a + 3b )
b) ( x + y + z)2 − ( x − y − z)2 = 4x( y + z) Lời giải Xét VT = ( − )3 + ( + )3 a b a b
= ( − + + ) ( − )2 − ( − )( + ) + ( + )2 a b a b a b a b a b a b    2 2
= a a − ab + b −  ( 2 2 a − b ) 2 2 2 2
+ a + 2ab + b  = a ( 2 2 2 2
2 2a + 2b − a + b ) = a ( 2 2 2 a + 3b )
Vậy (a − b)3 + (a + b)3 = a ( 2 2 2 a + 3b ) .
b) ( x + y + z)2 − ( x − y − z)2 = 4x( y + z)
Xét VT = ( + + )2 − ( − − )2 x y z x y z
= ( x + y + z + x − y − z)( x + y + z − x + y + z)
= 2x (2y + 2z)
= 4x ( y + z)
Vậy ( x + y + z)2 − ( x − y − z)2 = 4x ( y + z) .
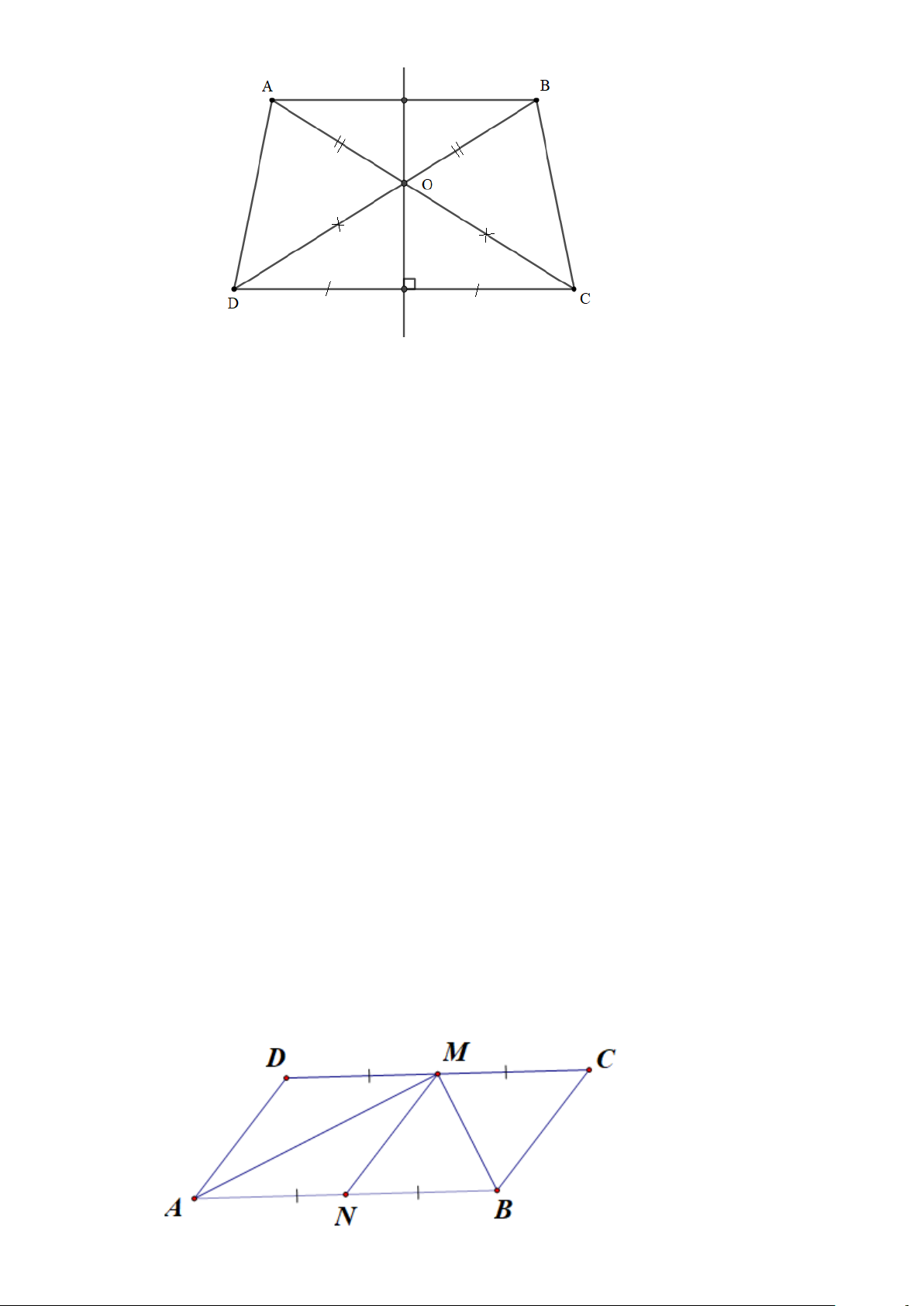
Bài 6. Cho tam giác ADC (AD  AC) . Đường trung trực d của cạnh CD cắt AC ở O . Trên tia đối
của tia OD lấy điểm B sao cho OB = OA .
a) Chứng minh điểm B đối xứng với điểm A qua đường thẳng d ;
b) Tứ giác ABCD là hình gì? Vì sao? Lời giải Trang 5 a) Ta có A  OD = B
 OC ( .cg.c)  AD = BC và OAD = OBC (2 góc tương ứng)
Mà OA = OB (gt)  OAB cân tại O  OAB = OBA
Suy ra: OAD + OAB = OBC + OBA . Hay DAB = CBA
Chứng minh tương tự ta có: ADC = BCD . Tứ giác ABCD có 0
DAB + CBA + ADC + BCD = 360 Hay 0 0
2DAB + 2ADC = 360  DAB + ADC = 180
Suy ra AB / / CD . Mà d ⊥ CD nên d ⊥ AB .
Ta có: d đi qua O và OAB cân tại O nên d là đường trung trực của AB .
Vậy A đối xứng với B qua đường thẳng d .
b) Tứ giác ABCD có AB / / CD nên ABCD là hình thang.
Mà OD = OC ; OA = OB suy ra AC = BD .
Hình thang ABCD có hai đường chéo AC = BD nên tứ giác ABCD là hình thang cân. Bài 7.
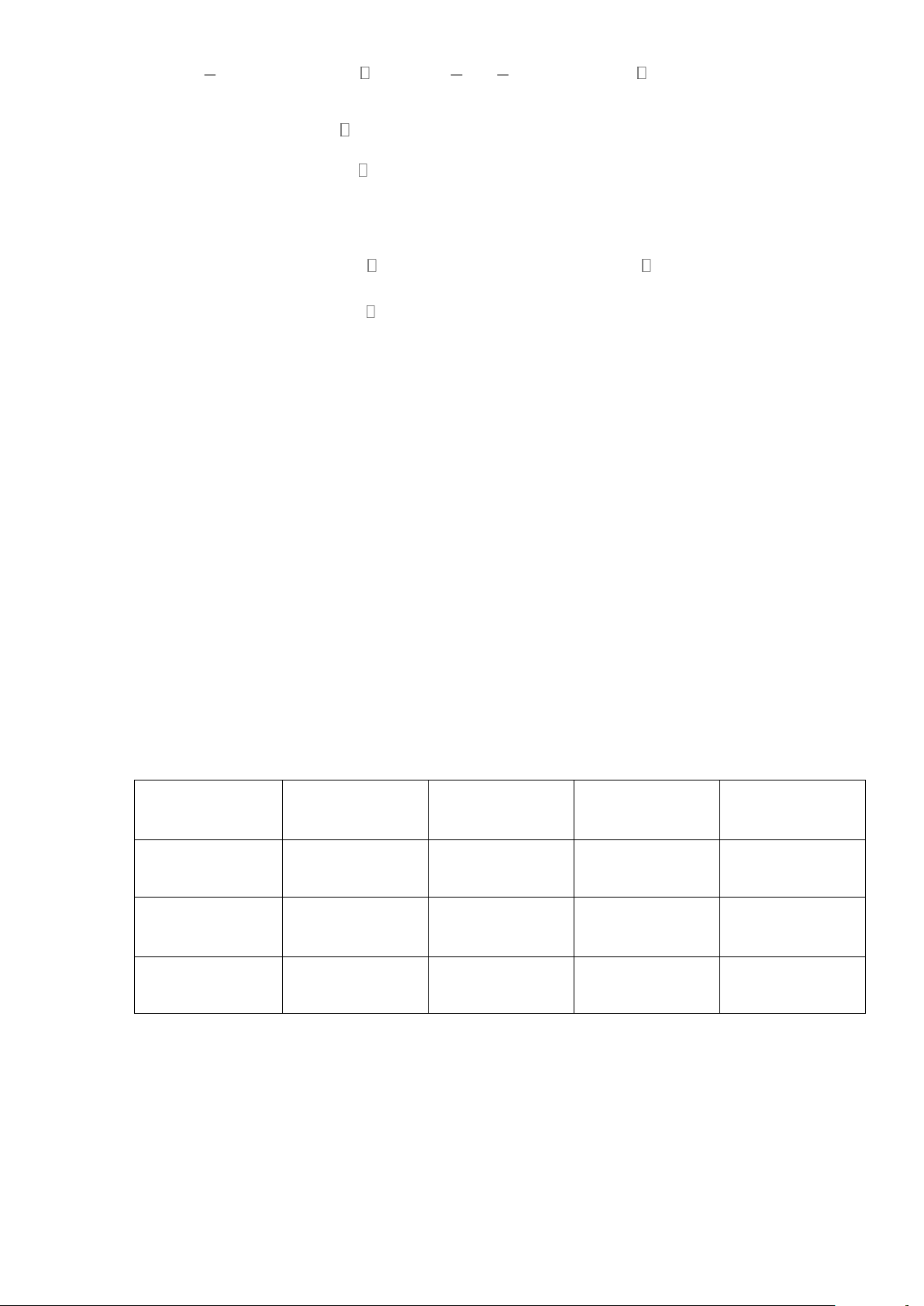
Cho Cho hình bình hành ABCD có CD=2AD . Gọi M là trung điềm của cạnh CD .
a) Chứng minh AM , BM theo thứ tự là tia phân giác của góc A và góc B ;
b) Chứng minh góc AMB là góc vuông. Lời giải
a) Chứng minh AM , BM theo thứ tự là tia phân giác của góc A và góc B ; Trang 6
Gọi N là trung điểm của AB . Ta có: AB AN = NB = 2 CD DM = MC = 2
Mà AB = CD và AB//CD ( ABCD là hình bình hành)
Suy ra: AN = DM , AN//DM và NB = MC , NB//MC .
 ABMN , NMCB là hình bình hành. Ta lại có: CD=2AD Suy ra: AD = DM = CM = BC
 ABMN , NMCB là hình thoi.
 AM , BM theo thứ tự là tia phân giác của góc A và góc B ;
b) Chứng minh góc AMB là góc vuông. Xét ABM , ta có:
AN = BA  MN là trung tuyến của ABM . AB Mà MN = AN = 2 Suy ra ABM vuông tại M.  AMB = 90 Bài 8. Chứng minh rằng a) 2
x + 2x + 2  0 với x  ; b) 2
x − x +1  0 với x  ; c) 2
−x + 4x − 5  0 với x  Lời giải a) 2
x + 2x + 2  0 với x  ;
Ta có: x + x + = (x + x + ) + = (x + )2 2 2 2 2 2 1 1 1 +1. Vì ( x + )2
1  0 với mọi x  nên ( x + )2
1 +1  0 với mọi x  . Vậy 2
x + 2x + 2  0 với x  ; b) 2
x − x +1  0 với x  ; 2  1 1  1  1  3 Ta có: 2 2
x − x + 2 = x − 2. . x + − +1 = x − +     .  2 4  4  2  4 Trang 7 2  1  2  1  3 Vì x −  0  
với mọi x  nên x − +  0   với mọi x  .  2   2  4 Vậy 2
x − x +1  0 với x  ; c) 2
−x + 4x − 5  0 với x  . Ta có: − +
− = −(x − x + )+ − = −(x − )2 2 2 x 4x 5 2. .2 4 4 5 2 −1. Vì −( x − )2
2  0 với mọi x  nên −( x − )2
2 −1  0 với mọi x  . Vậy 2
−x + 4x − 5  0 với x  . Bài 9.
Tìm các cặp số nguyên x, y sao cho :
a) y(x − 2) + 3x − 6 = 2.
b) xy + 3x − 2y − 7 = 0 .
c) xy − x + 5y − 7 = 0 . Lời giải
a) y(x − 2) + 3x − 6 = 2
 y(x − 2) + 3(x − 2) = 2
 (x − 2)(y+ ) 3 = 2
 (x − 2),(y+ ) 3 Ö (2) =  1  ;  2 x − 2 −2 −1 1 2 x 0 1 3 4 y + 3 −1 −2 2 1 y −4 5 − −1 −2 Vậy ( ; x y) (  0; 4 − );(1;− ) 5 ;(3;− ) 1 ;(4; 2 − ).
b) xy + 3x − 2y − 7 = 0 .  x(y+ ) 3 − 2(y+ ) 3 = 1
 (x − 2)(y+ ) 3 = 1 Trang 8 x − 2 −1 1 x 1 3 y + 3 −1 1 y −4 −2
 (x − 2),(y+ ) 3 Ö ( ) 1 =   1 Vậy ( ; x y) (  1; 4 − );(3; 2 − ).
c) xy − x + 5y − 7 = 0 .  x(y− ) 1 + 5(y− ) 1 = 2  (x + ) 5 (y − ) 1 = 2  (x + ) 5 ,(y − ) 1 Ö (2) =  1  ;  2 x + 5 −2 −1 1 2 x −7 6 − −4 3 − y −1 −1 −2 2 1 y 0 −1 3 2 Vậy ( ; x y) (  7 − ;0);( 6 − ;− ) 1 ;( 4 − ; ) 3 ;( 3 − ;2).
Bài 10. Cho a + b + c = 0 . Chứng minh các đẳng thức sau a) 3 3 3
a + b + c = 3abc . b) 5 5 5 2 2 2
2(a + b + c ) = 5ab (
c a + b + c ). Lời giải a) 3 3 3
a + b + c = 3abc . Trang 9 Xét 3 3 3
a + b + c − 3abc 3 2 2 3 3 2 2
= a + 3a b + 3ab + b + c − 3a c
b − 3a b − 3ab = (a + b)3 3
+ c − 3ab(a + b + c)
= (a + b + c)(a + b)2 −(a + b) 2
c + c  − 3ab(a + b + c)   (a b c)( 2 2 2 = + +
a + b + c − ab − ac − bc)
Vì a + b + c = 0  (a + b + c)( 2 2 2
a + b + c − ab − ac − bc) = 0 3 3 3
 a + b + c − 3abc = 0 3 3 3
 a + b + c = 3abc (đpcm) b) 5 5 5 2 2 2
2(a + b + c ) = 5ab (
c a + b + c ). Theo câu a) ta có: 3 3 3
a + b + c = 3abc  ( 3 3 3
a + b + c )( 2 2 2
a + b + c ) = 3abc( 2 2 2
a + b + c ) 5 5 5 3
 a + b + c + a ( 2 2 b + c ) 3 + b ( 2 2 a + c ) 3 + c ( 2 2
a + b ) = 3abc( 2 2 2
a + b + c ) ( ) 1 Mặt khác ta có:
a + b + c = 0  b + c = −a 2 2 2
 b + c + 2bc = a 2 2 2
 b + c = a − 2bc
Chứng minh tương tự ta có: 2 2 2
a + c = b − 2ac và 2 2 2
a + b = c − 2ab Thay vào ( ) 1 ta có: 5 5 5 3
 a + b + c + a ( 2 a − bc) 3 + b ( 2 b − ac) 3 + c ( 2 2 2
c − 2ab) = 3abc( 2 2 2
a + b + c ) 5 5 5 5 3 5 3 5 3
 a + b + c + a − 2a bc + b − 2b ac + c − 2c ab = 3abc ( 2 2 2
a + b + c )  ( 5 5 5
a + b + c ) − abc( 2 2 2
a + b + c ) = abc( 2 2 2 2 2 3
a + b + c ) 5 5 5 2 2 2
 2(a + b + c ) = 5abc(a + b + c ) (đpcm).  HẾT  Trang 10