Bài Tập Toán 8 Tuần 9 Có Lời Giải Chi Tiết

PHIẾU BÀI TẬP TOÁN 8 TUẦN 09
A. PHẦN CƠ BẢN (DÀNH CHO TẤT CẢ CÁC LỚP): Bài 1.
Phân tích các đa thức sau thành nhân tử 1) 2 x − 7x + 6 2) 3 2
x + 4x − 7x −10 3) 3 2 x + x − 2 4) 2 x + 5x + 6 5) 3 2
x − 6x +11x − 6 6) 5 3 2
x + x + x +1 Bài 2. Thực hiện phép chia: 1) ( 3 4 2 4 3
x y − x y + xy ) ( 2 15 10 5 : 5 − xy )
2)  ( x − y)( x + y) −  ( 2 2 7 2 5 2 5
2 14x − 3y ) :( 3 − y) 
Bài 3. Thực hiện phép tính: a) ( 3 2
x − 3x ) :(x − ) 3 b) ( 2
2x + 2x − 4) :(x + 2) c) ( 4
x − x −14) : (x − 2) d) ( 3 2
x − 3x + x − ) 3 : (x − ) 3 e) ( 3 2
x + x −12) :(x − 2) f) ( 3 2
2x − 5x + 6x −1 ) 5 : (2x − ) 5 g) ( 2 2 3
− x + 5x − 9x +1 ) 5 : (5−3x) h) ( 2 3
−x + 6x − 26x + 2 ) 1 : (2x − ) 3
Bài 4. Cho tam giác ABC vuông tại A . Về phía ngoài tam giác ABC , vẽ hai tam giác vuông cân ADB
(DA= DB) và ACE (EA= EC). Gọi Mlà trung điểm của BC, I là giao điểm của DM với AB, K là
giao điểm của EM với AC . Chứng minh:
a) Ba điểm D , A , E thẳng hàng.
b) Tứ giác IAKM là hình chữ nhật.
c) Tam giác DME là tam giác vuông cân.
Bài 5. Tìm số nguyên n sao cho: a) 2 n + 2n − 4 11 b) 3 2
2n + n + 7n +1 2n −1 c) 4 3 2 4
n − 2n + 2n − 2n +1 n −1 d) 3 2 2
n − n + 2n + 7 n +1
Bài 6. Chứng minh rằng. a) 2 9 1945
A = x − x − x chia hết cho 2
B = x − x +1 b) 9 8
C = 8x − 9x +1 chia hết cho D = ( x − )2 1 c) = ( + )2n 2 ( ) 1 n C x x
− x − 2x −1 chia hết cho D(x) = x(x + ) 1 (2x + ) 1
Bài 7. Cho hình chữ nhật ABCD. Kẻ BH vuông góc với AC. Gọi M là trung điểm của AH, K là trung
điểm của CD. Chứng minh BM vuông góc với MK.
Bài 8. Cho hình bình hành ABCD có góc ADC = 750 và O là giao điểm hai đường chéo. Từ D hạ DE và
DF lần lượt vuông góc với AB và BC (E thuộc AB, F thuộc BC). Tính góc EOF. Trang 1
ĐÁP ÁN BÀI TẬP TĂNG CƯỜNG TOÁN 8 TUẦN 9
HƯỚNG DẪN GIẢI CHI TIẾT Bài 1.
Phân tích các đa thức sau thành nhân tử 1) 2 x − 7x + 6 2) 3 2
x + 4x − 7x −10 3) 3 2 x + x − 2 4) 2 x + 5x + 6 5) 3 2
x − 6x +11x − 6 6) 5 3 2
x + x + x +1 Lời giải 1) 2 2
x − 7x + 6 = x − x − 6x + 6 = x( x − ) 1 − 6( x − ) 1 = ( x − ) 1 ( x − 6) 2) 3 2 3 2 2
x + 4x − 7x −10 = x + x + 3x + 3x −10x −10 2 = x (x + ) 1 + 3x ( x + ) 1 −10( x + ) 1 = ( x + )( 2 1 x + 3x −10) = (x + )( 2
1 x − 2x + 5x −10) = (x + )
1 x ( x − 2) + 5( x − 2)   = (x + )
1 ( x − 2)( x + 5) 3) 3 2 3 2 2
x + x − 2 = x − x + 2x − 2 2
= x (x − ) + ( 2 1 2 x − ) 1 2 = x (x − ) 1 + 2( x − ) 1 ( x + ) 1 = (x − )( 2 1 x + 2x + 2) 4) 2 2
x + 5x + 6 = x + 2x + 3x + 6
= x(x + 2) + 3(x + 2)
= (x + 2)(x + 3) 5) 3 2 3 2 2
x − 6x +11x − 6 = x − 3x − 3x + 9x + 2x − 6 2
= x (x − 3) − 3x(x − 3) + 2(x −3) = (x − )( 2 3 x − 3x + 2) Trang 2 = ( x − ) 2
3 x − 2x − x + 2  
= (x −3) x(x − 2) − (x − 2)  
= (x − 3)(x − 2)(x − ) 1 6) 5 3 2 3
x + x + x + = x ( 2 x + ) + ( 2 1 1 x + ) 1 = ( 2 x + )( 3 1 x + ) 1 Bài 2.
Thực hiện phép chia: 1) ( 3 4 2 4 3
x y − x y + xy ) ( 2 15 10 5 : 5 − xy )
2)  ( x − y)( x + y) −  ( 2 2 7 2 5 2 5
2 14x − 3y ) :( 3 − y)  Lời giải 1) 3 4 2 4 3 2
x y − x y + xy = − xy ( 2 2 2 15 10 5 5 3
− x y + 2xy − y) Khi đó: ( 3 4 2 4 3
x y − x y + xy ) ( 2 − xy ) 2 = − xy ( 2 2 2
− x y + xy − y) ( 2 15 10 5 : 5 5 3 2 : 5 − xy ) 2 2 2
= −3x y + 2xy − y .
2) ( x − y)( x + y) − ( 2 2
x − y ) = ( x − y)( x + y) 2 2 7 2 5 2 5 2 14 3 14 35 2 5 − 28x + 6y 2 2 2 2
= 28x + 70xy − 70xy −175y − 28x + 6y 2 = 169 − y 169
Khi đó: 7(2x − 5y)(2x + 5y) − 2  ( 2 2
14x − 3y ) :( 3 − y) 2 = 1 − 69y : ( 3 − y) = y  3
Bài 3. Thực hiện phép tính: a) ( 3 2
x − 3x ) :(x − ) 3 b) ( 2
2x + 2x − 4) :(x + 2) c) ( 4
x − x −14) : (x − 2) d) ( 3 2
x − 3x + x − ) 3 : (x − ) 3 e) ( 3 2
x + x −12) :(x − 2) f) ( 3 2
2x − 5x + 6x −1 ) 5 : (2x − ) 5 g) ( 2 2 3
− x + 5x − 9x +1 ) 5 : (5−3x) h) ( 2 3
−x + 6x − 26x + 2 ) 1 : (2x − ) 3 Trang 3 Lời giải a) ( 3 2
x − 3x ) :(x − ) 3 2
= x (x − ) (x − ) 2 3 : 3 = x b) ( 2
2x + 2x − 4) :(x + 2) = (x + 2)(2x − 2) : (x + 2) = 2x − 2 c) ( 4
x − x −14) : (x − 2) = ( 3 2
x + x + x + )(x − ) (x − ) 3 2 2 4 7 2 :
2 = x + 2x + 4x + 7 d) ( 3 2
x − 3x + x − ) 3 : (x − ) 3 = ( 2
x − )(x − ) (x − ) 2 1 3 : 3 = x −1 e) ( 3 2
x + x −12) :(x − 2) = ( 2
x + x + )(x − ) (x − ) 2 3 6 2 : 2 = x + 3x + 6 f) ( 3 2
2x − 5x + 6x −1 ) 5 : (2x − ) 5 = ( 2
x + )( x − ) ( x − ) 2 3 2 5 : 2 5 = x + 3 g) ( 2 2 3
− x + 5x − 9x +1 )
5 : (5−3x) = (x + ) 3 ( 3 − x + )
5 : (5−3x) = x + 3 h) ( 2 3
−x + 6x − 26x + 2 ) 1 : (2x − ) 3 = ( 2
x + x − )( x − ) ( x − ) 2 3 4 7 2 3 : 2
3 = 3x + 4x − 7
Bài 4. Cho tam giác ABC vuông tại A . Về phía ngoài tam giác ABC , vẽ hai tam giác vuông cân ADB
(DA= DB) và ACE (EA= EC). Gọi Mlà trung điểm của BC, I là giao điểm của DM với AB, K là
giao điểm của EM với AC . Chứng minh:
a) Ba điểm D , A , E thẳng hàng.
b) Tứ giác IAKM là hình chữ nhật.
c) Tam giác DME là tam giác vuông cân. Lời giải A E D K I C M B
a) Chứng minh ba điểm D , A , E thẳng hàng.
Xét tam giác AEM và tam giác CEM BC Ta có AM = MC =
(Tam giác ABC vuông tại A ; đường trung tuyến ứng với cạnh huyền) 2
AE = EC (giả thuyết) EM là cạnh chung Trang 4
Vậy AEM = CEM ( cạnh – cạnh – cạnh)
AEM = EMC (Hai góc tương ứng)
Mà hai góc này ở vị trí so le trong
Suy ra MC / / AE vậy BC / / AE ( ) 1
Chứng minh tương tự suy ra DBM = DAM (cạnh – cạnh – cạnh)
Suy ra DAB = ABM (hai góc tương ứng)
Mà hai góc này ở vị trí so le trong
Suy ra BC / / DA (2) Từ ( )
1 và (2) Theo tiên đề ơ- clit D, , A E thẳng hàng.
b) Chứng minh tứ giác IAKM là hình chữ nhật
Ta có AD = DB (giả thuyết)
AM = MB (đường trung tuyến ứng với cạnh huyền BC )
DM là đường trung trực của AB Suy ra 0 AIM = 90 ( ) 3
Chứng minh tương tự ta được EM là đường trung trực của AC Suy ra 0 AKM = 90 (4) Lại có 0 BAC = 90 ( ) 5 Từ ( ) 3 , (4) , ( )
5 suy ra tứ giac IAKM là hình chữ nhật ( tứ giác có 3 góc vuông)
c) Tam giác DME là tam giác vuông cân 0
IME = 90 suy ra tam giác DME là tam giác vuông tại M
Bài 5. Tìm số nguyên n sao cho: a) 2 n + 2n − 4 11 b) 3 2
2n + n + 7n +1 2n −1 c) 4 3 2 4
n − 2n + 2n − 2n +1 n −1 d) 3 2 2
n − n + 2n + 7 n +1 Lời giải a) 2 n + 2n − 4 11 Có: 2 n + 2n − 4 2
= n + 2n −15 +11 2
= n + 5n − 3n −15 +11
= n(n + 5) − 3(n + 5) +11
= (n − 3)(n + 5) +11 Để 2 n + 2n − 4 11 Trang 5
hay (n − 3)(n + 5) +11 11
 (n − 3)(n + 5) 11
 n − 3 11 hoặc n + 5 11 Do 11 là số nguyên tố
Nên n − 3 11  n = 11k + 3 (k  )
n + 5 11  n = 11k '− 5 (k ' )
Vậy n = 11k + 3 (k  ) hoặc n =11k '− 5 (k ' ) thì 2 n + 2n − 4 11 b) 3 2
2n + n + 7n +1 2n −1 Có: 3 2
2n + n + 7n +1 3 2 2
= 2n − n + 2n − n + 8n − 4 + 5 2 = n (2n − ) 1 + n(2n − ) 1 + 4(2n − ) 1 + 5 = ( n − )( 2 2
1 n + n + 4) + 5 Để 3 2
2n + n + 7n +1 2n −1 hay ( n − )( 2 2
1 n + n + 4) + 5 2n −1  5 2n −1
 2n −1 U (5) =  5 − ; 1 − ;1;  5
Với 2n −1 = −5  n = −2 2n −1 = 1 −  n = 0
2n −1 = 1  n = 1
2n −1 = 5  n = 3 Vậy n =  2 − ;0;1;  3 thì 3 2
2n + n + 7n +1 2n −1 c) 4 3 2 4
n − 2n + 2n − 2n +1 n −1 Có: 4 3 2
n − 2n + 2n − 2n +1 = ( 4 2 n + n + ) 3 2
1 − 2n − 2n 2 = ( 2 n + ) − n( 2 1 2 n + ) 1
= (n + )(n − )2 2 1 1 Và 4 n − = ( 2 n + )( 2 1 1 n − ) 1 Để 4 3 2 4
n − 2n + 2n − 2n +1 n −1 với n  1 (n + )1(n − )2 2 2 1 n −1 2  ( = =1− 2 n + ) 1 ( 2 n − ) 1 n +1 n +1 Trang 6
 n +1 U (2) =  2 − ; 1 − ;1;  2
Với n +1 = −2  n = −3
n +1 = −1  n = −2
n +1 = 1  n = 0
n +1 = 2  n = 1(loại) Vậy n = −3; 2 − ;  0 thì 4 3 2 4
n − 2n + 2n − 2n +1 n −1 d) 3 2 2
n − n + 2n + 7 n +1 Có: 3 2
n − n + 2n + 7 3 2
= n + n − n −1+ n + 8 = n( 2 n + ) −( 2 1 n + ) 1 + n + 8 = ( 2 n + ) 1 (n − ) 1 + n + 8 Để 3 2 2
n − n + 2n + 7 n +1 n + 8 hay ( 2 n + )(n − ) 2 1
1 + n + 8 n +1   2 n +1 2 n − 64 2 n +1− 65 65 Do 2
n + 8 n +1  (n + )(n − ) 2 8 8 n +1  = =1− 2 n +1 2 n +1 2 n +1 n + 8  2  65 n +1 2
 n +1 U(65) = 1;5;13;  65 Vì 2 n +1  1 2 n +1 Với 2
n +1 = 1  n = 0 ; 2
n +1 = 5  n = 2 ; 2
n +1 = 13  n = 12 (loại); 2
n +1 = 65  n = 8
Vậy n = 0;n = 2;n = 8 thì 3 2 2
n − n + 2n + 7 n +1
Bài 6. Chứng minh rằng. a) 2 9 1945
A = x − x − x chia hết cho 2
B = x − x +1 b) 9 8
C = 8x − 9x +1 chia hết cho D = ( x − )2 1 c) = ( + )2n 2 ( ) 1 n C x x
− x − 2x −1 chia hết cho D(x) = x(x + ) 1 (2x + ) 1 Lời giải a) 2 9 1945
A = x − x − x 2 9 1945
= x − x +1−1− x + x − x 3 2 x x ( 3x)  = − + − + − x( 1944 1 1 x − ) 1    = ( 2
x − x + ) − ( 3 x + )( 6 3
x − x + ) − x( 972 x − )( 972 1 1 1 1 x + ) 1 = ( 2
x − x + ) −(x + )( 2 x − x + )( 6 3
x − x + ) − x( 972 x − )( 972 1 1 1 1 1 x + ) 1 Trang 7 324 Do 972 x + = ( 3 x ) 324 + = ( 3 x + )( 323 322 x
− x + − x + ) 3 1 1 1 ... 1 x +1 Mà 3 2
x +1 x − x +1 Nên 972 3 x +1 x +1 Vậy 2 9 1945 2
A = x − x − x x − x +1 9 8
C = 8x − 9x +1 9 8
= 8x – 8 − 9x + 9 = ( 9 x − ) − ( 8 8 1 9 x − ) 1 = ( x − )( 8 7 6
x + x + x + + ) − (x − )( 7 6 5 8 1 ... 1 9
1 x + x + x + ...+ ) 1 = ( x − )( 8 7 6 7 6 5
1 8x + 8x + 8x + ...+ 8 − 9x − 9x − 9x −...− 9) = ( x − )( 8 7 6 5 4 3 2
1 8x − x − x − x − x − x − x − x − ) 1 Do 8 + ( 1 − ) + ( 1 − ) + ( 1 − ) + ( 1
− ) + (−1) + (−1) + (−1) + (−1) = 0 Nên ( 8 7 6 5 4 3 2
8x − x − x − x − x − x − x − x − ) 1 x −1
Suy ra ( x − )( x − x − x − x − x − x − x − x − ) (x − )2 8 7 6 5 4 3 2 1 8 1 1 Vậy C D c) = ( + )2n 2 ( ) 1 n C x x
− x − 2x −1 chia hết cho D(x) = x(x + ) 1 (2x + ) 1 1 −
Ta có đa thức: D(x) = x ( x + ) 1 (2x + )
1 có nghiệm là x = 0; x = 1 − ; x = 2 Với x = 0 ( )2n 2 C(0) 0 1 0 n  = + − − 2.0 −1 2 1 n = −1 = 0
nên x = 0 là nghiệm của C(x) Với x = −1 ( )2n ( )2 C( 1) 1 1 1 n  − = − + − − − 2.(− ) 1 −1 = 0 −1+ 2 −1 = 0
nên x = −1 là nghiệm của C(x) 1 − 2n 2  1  1   1 n −   1  Với x =  C = − +1 − − − 2 .− −1 2          2   2   2   2  2n 2 1 1 n     = − +1−1 = 0      2   2  1 − nên x =
là nghiệm của C(x) 2
Do nghiệm của D(x) là nghiệm của C(x) Suy ra = ( + )2n 2 ( ) 1 n C x x
− x − 2x −1 chia hết cho D(x) = x(x + ) 1 (2x + ) 1 Trang 8
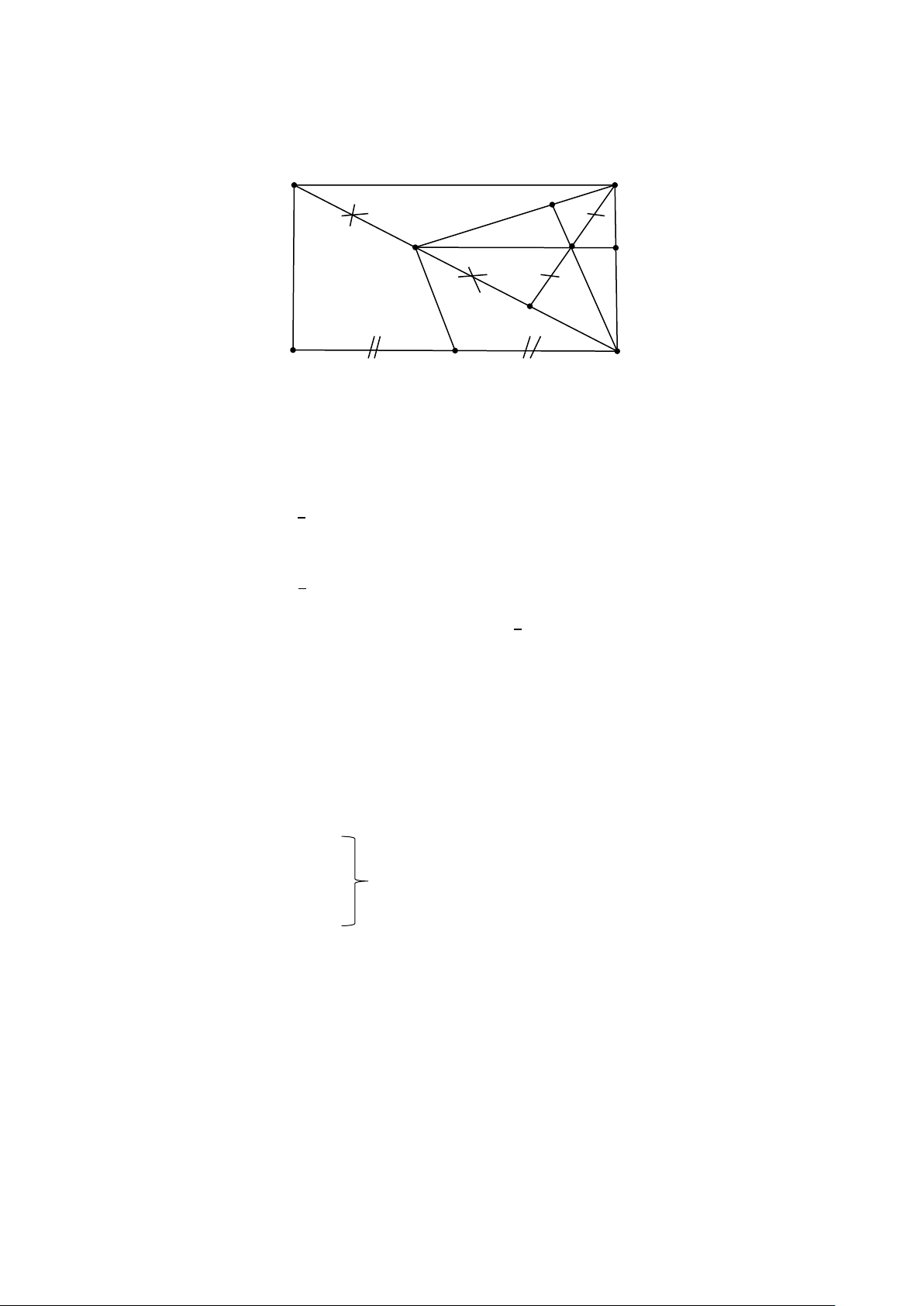
Bài 7. Cho hình chữ nhật ABCD. Kẻ BH vuông góc với AC. Gọi M là trung điểm của AH, K là trung
điểm của CD. Chứng minh BM vuông góc với MK. Lời giải A B M N E D C K
Gọi N là trung điểm của BH. Gọi E là giao điểm của MN và BC.
* Xét ∆ABH có: M là trung điểm của AH, N là trung điểm của BH
=> MN là đường trung bình của ∆ABH (đn)
=> MN // AB và MN = 1 AB (tc) 2 Mà AB = CD và AB // CD => MN // CD và MN = 1 CD 2
* Xét tứ giác MNCK có: MN // CD và MN = CK (= 1 CD) 2
=> tứ giác MNCK là hình bình hành (dhnb) => NC // MK(đn)
Ta có: MN // AB và AB ⊥ BC (vì ABCD là hình chữ nhật)
=> MN ⊥ BC (quan hệ vuông góc và song song) hay ME ⊥ BC * Xét ∆ABC có:
BH là đường cao (BH ⊥ MC)
ME là đường cao (ME ⊥ BC
=> N là trực tâm của ∆ABC BH cắt ME tại N => CN ⊥ BM (2)
Từ (1) và (2) suy ra: MK ⊥ BM.
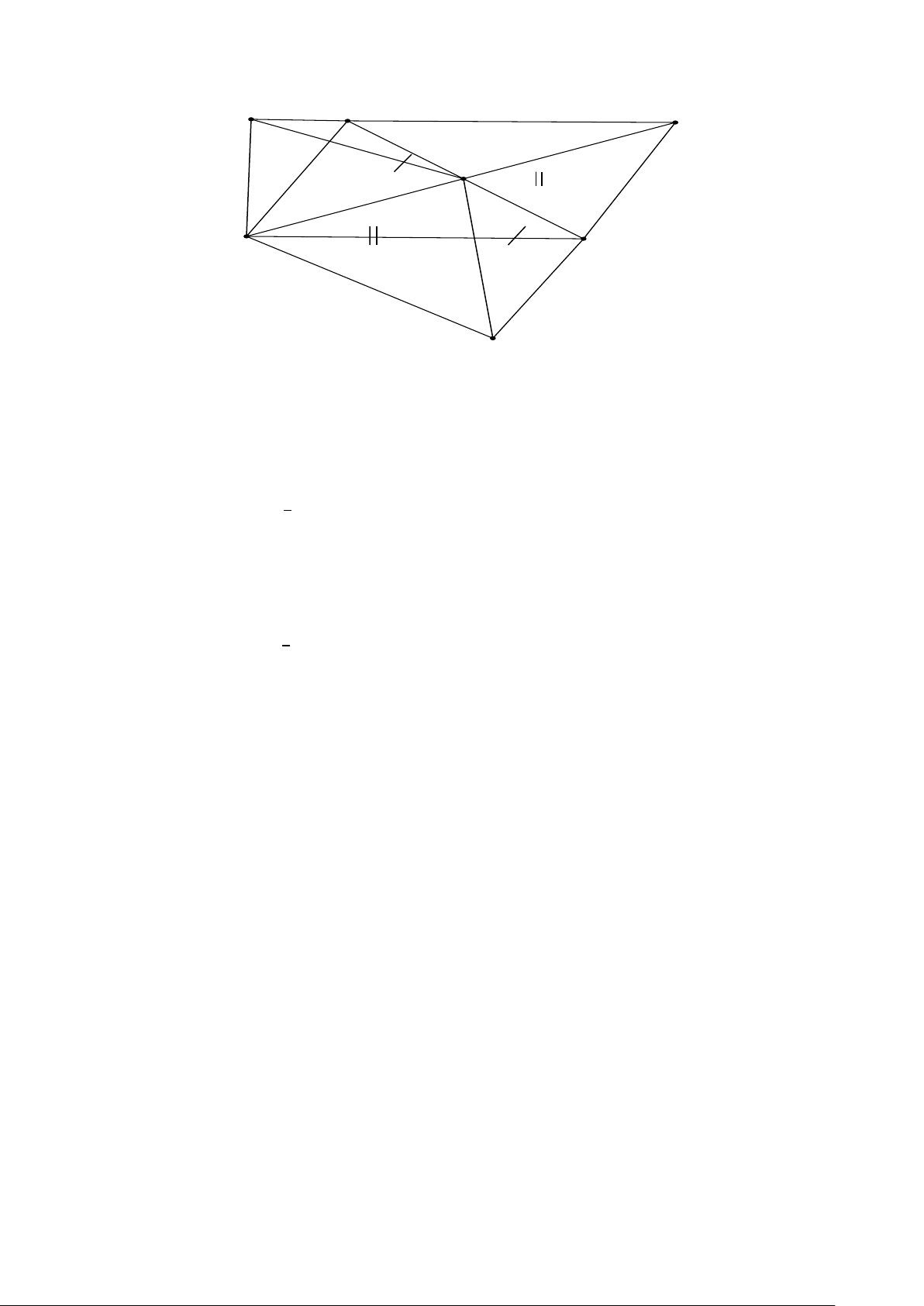
Bài 8. Cho hình bình hành ABCD có góc ADC = 750 và O là giao điểm hai đường chéo. Từ D hạ DE và
DF lần lượt vuông góc với AB và BC (E thuộc AB, F thuộc BC). Tính góc EOF. Trang 9 Lời giải E A B O D C F
* Xét hình bình hành ABCD có O là giao điểm của hai đường chéo (gt)
=> O là trung điểm của AC và O là trung điểm của BD (tính chất) => OA = OC, OB = OD
* Xét ∆EBD vuông tại E (DE ⊥ AB) có EO là đường trung tuyến:
=> OE = OB = OD = 1 BD (định lí) 2 => ∆EBO cân tại O => 𝑂𝐸𝐵 ̂ = 𝑂𝐵𝐸 ̂ (tính chất)
* Xét ∆FBD vuông tại E (DF ⊥ BC) có FO là đường trung tuyến:
=> OF = OB = OD = 1 BD (định lí) 2 => ∆FBO cân tại O => 𝑂𝐹𝐵 ̂ = 𝑂𝐵𝐹 ̂ (tính chất) * Xét ∆EBO có 𝐸𝑂𝐷
̂ là góc ngoài tại đỉnh O => 𝐸𝑂𝐷 ̂ = 𝑂𝐸𝐵 ̂ + 𝑂𝐵𝐸 ̂ = 2𝑂𝐵𝐸
̂ (tính chất góc ngoài) (1) * Xét ∆FBO có 𝐹𝑂𝐷
̂ là góc ngoài tại đỉnh O => 𝐹𝑂𝐷 ̂ = 𝑂𝐹𝐵 ̂ + 𝑂𝐵𝐹 ̂ = 2𝑂𝐵𝐹
̂ (tính chất góc ngoài) (2) Từ (1) và (2) suy ra: 𝐸𝑂𝐷 ̂ + 𝐹𝑂𝐷 ̂ = 2𝑂𝐵𝐸 ̂ + 2𝑂𝐵𝐹 ̂ Hay: 𝐸𝑂𝐹 ̂ = 2𝐸𝐵𝐹
̂ = 2.750 = 1500 (vì 𝐸𝐵𝐹 ̂ = 𝐴𝐷𝐶 ̂ = 750) Vậy 𝐸𝑂𝐹 ̂ = 1500  HẾT  Trang 10