Bài tập toán 9 tuần 11 (có đáp án và lời giải chi tiết)

BÀI TẬP TOÁN 9 TUẦN 11 I. ĐẠI SỐ Bài 1.
Cho hàm số y  2m   1 x  5
a) Với điều kiện nào của m thì hàm số đã cho là hàm số bậc nhất.
b) Với điều kiện nào của m thì hàm số đồng biến, nghịch biến. Bài 2.
Cho hàm số: y   2
k  5k  6 x 5
a) Với giá trị nào của k thì hàm số đồng biến.
b) Với giá trị nào của k thì hàm số nghịch biến. Bài 3.
Tìm điều kiện của m và k để hàm số sau là hàm số bậc nhất:
y  f  x 2  kx   2 2
m  mk  k  2 6
x  9x  5 . Bài 4.
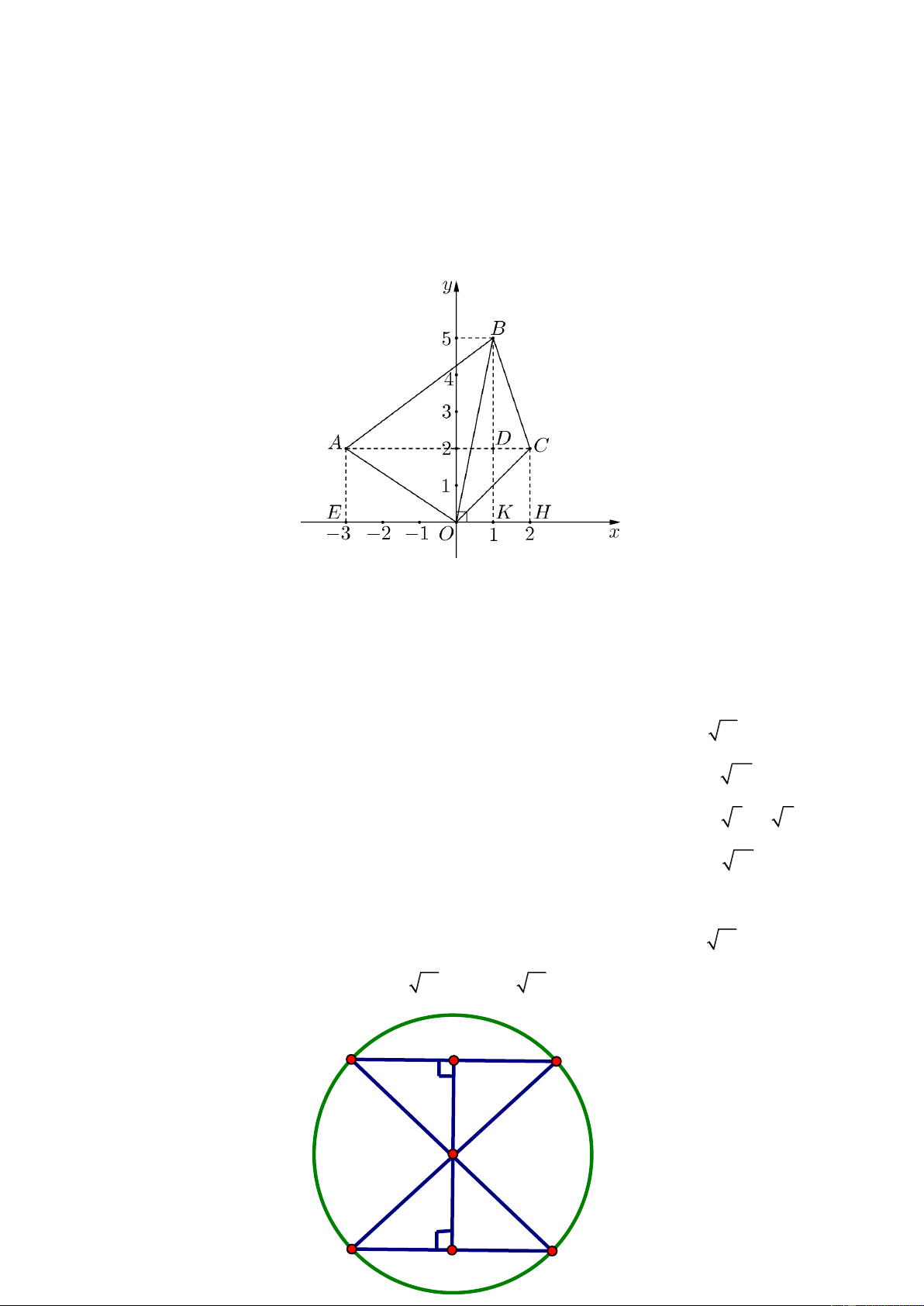
Vẽ tam giác ABC trên mặt phẳng tọa độ Oxy biết ( A 3
 ;2); B(1;5);C(2;2)
a) Tính khoảng cách từ các đỉnh ,
A B, C của tam giác đến gốc tọa độ O .
b) Tam giác ABC là tam giác gì ?
c) Tính chu vi của tam giác ABC . II. HÌNH HỌC Bài 1.
Cho đường tròn tâm O đường kính AB , kẻ hai dây AC , BD song song với nhau. Chứng minh: a) AC  B . D
b) Ba điểm C , O , D thẳng hàng. Bài 2.
Cho nửa đường tròn O, R đường kính AB , đường thẳng d cắt nửa đường tròn tại C và D .
Gọi P, Q lần lượt là hình chiếu của ,
A B trên d . Chứng minh rằng : a) CP  DQ . b) OP  OQ . Bài 3.
Cho đường tròn tâm O đường kính AD  2R , gọi I là trung điểm của OD , qua I kẻ dây BC
vuông góc với AD . a) Chứng minh ABC  đều .
b) Tính độ dài các cạnh của ABC  theo R .
……………………………….HẾT……………………………….. Trang 1
HƯỚNG DẪN GIẢI CHI TIẾT I. Đại số Bài 1.
Cho hàm số y  2m   1 x  5
a) Với điều kiện nào của m thì hàm số đã cho là hàm số bậc nhất.
b) Với điều kiện nào của m thì hàm số đồng biến, nghịch biến. Lời giải
a) Để hàm số đã cho là hàm số bậc nhất thì: 1
2m 1  0  2m  1   m   . 2
b) Để hàm số đã cho đồng biến thì: 1
2m 1  0  2m  1   m   . 2
Điều kiện để hàm số đã cho nghịch biến là: 1
2m 1  0  2m  1   m   2 Bài 2.
Cho hàm số: y   2
k  5k  6 x 5
a) Với giá trị nào của k thì hàm số đồng biến.
b) Với giá trị nào của k thì hàm số nghịch biến. Lời giải
a) Để hàm số đồng biến thì: 2
k  5k  6  0  k  2k  3  0 k  2  0 k  2 - Trường hợp 1:     k  3. k  3  0 k  3 k  2  0 k  2 - Trường hợp 2:     k  2. k  3  0 k  3
Vậy với k  3 hoặc k  2 thì hàm số đồng biến.
b) Để hàm số nghịch biến thì: 2
k  5k  6  0  k  2k  3  0 k  2  0 k  2 - Trường hợp 1:     2  k  3 . k  3  0 k  3 k  2  0 k  2 - Trường hợp 2:    (loại). k  3  0 k  3
Vậy với 2  k  3 thì hàm số nghịch biến. Bài 3.
Tìm điều kiện của m và k để hàm số sau là hàm số bậc nhất:
y  f  x 2  kx   2 2
m  mk  k  2 6
x  9x  5 . Lời giải
Ta có: y  f  x 2  kx   2 2
m  mk  k  2 6 x  9x  5 Trang 2
Hay y  f  x  k   2 x   2 2 9
m  mk  6k  x  5.
Để hàm số là hàm số bậc nhất thì: k  9  0 k  9 k  9  k  9        . 2 2
m  mk  6k  0 2
m  9m  486  0   m  27  m 18  0
m  27 vaø m  18 
Vậy với k  9 , m  27 và m  18
 thì hàm số đã cho là hàm số bậc nhất. Bài 4. a) Ta có: A 3
 ;2 ; B1;5 ; C 2;2  AC  5
Gọi E , K , H theo thứ tự là hình chiếu của A , B , C trên trục Ox; D là giao điểm của AC và BK
OE  3; AE  2 ; OH  2; CH  2 ; OK 1; BK  5; AD  4 ; BD  3; CD 1  O
 AE vuông tại E , ta có: 2 2 2 2 2
OA  OE  AE  3  2  9  4  13  OA  13  O
 BK vuông tại K , ta có: 2 2 2 2 2
OB  OK  BK  1  5  1 25  26  OB  26  O
 CH vuông tại H , ta có: 2 2 2 2 2
OC  OH  CH  2  2  4  4  8  OC  8  2 2  ABD 
vuông tại D , ta có: 2 2 2 2 2
AB  AD  BD  4  3  16  9  25  AB  25  5
b) Ta có: AC  5 và AB  5  AC  AB  ABC  cân tại A c) B
 CD vuông tại D , ta có: 2 2 2 2 2
BC  BD  CD  3 1  9 1  10  BC  10 Chu vi ABC 
là: AB  BC  CA  5  10  5  10  10 II. Hình học H A C Bài 1. O D Trang 3 B K
a) Từ O kẻ OH  AC ( H  AC ); OK  BD ( K  BD ) Vì AC
BD  O ; H ; K thẳng hàng Xét A  OH và B  OK có:
OA  OB (cùng bằng bán kính)
AHO  BKO  90
AOH  BOK ( 2 góc đối đỉnh)  A  OH  B
 OK (cạnh huyền - góc nhọn)
 AH  BK ( 2 cạnh tương ứng) Xét (O) có:
 OH là 1 phần đường kính, AC là dây cung mà OH  AC (cách vẽ)  AC  2.AH
 OK là 1 phần đường kính, BD là dây cung mà OK  BD (cách vẽ)  BD  2.BK
Mà AH  BK  AC  BD b) Xét C  OH và DOK  có:
OH  OK (vì A  OH  B  OK )
HOD  KOD  90
OC  OD (cùng bằng bán kính)  C  OH  D
 OH (cạnh huyền - cạnh góc vuông)
 COH  DOH
Mà COH  COK  180 ( 2 góc kề bù)
 DOH  COK 180
Ba điểm C ; O ; D thẳng hằng Bài 2.
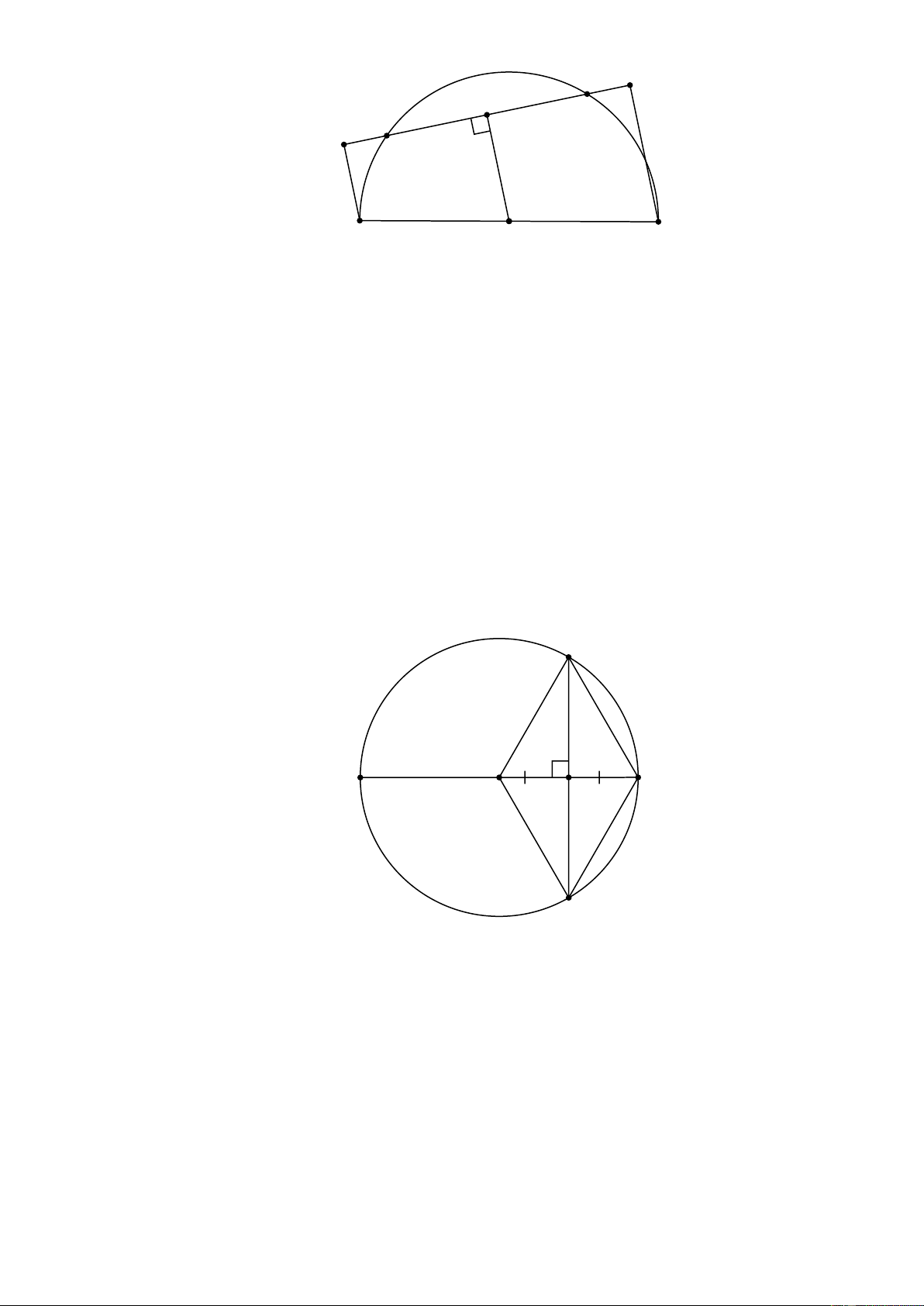
Cho nửa đường tròn O, R đường kính AB , đường thẳng d cắt nửa đường tròn tại C vả D .
Gọi P, Q lần lượt là hình chiếu của ,
A B trên d . Chứng minh rằng : a) CP  DQ . b) OP  OQ . Lời giải Trang 4 Q D I C P A O B
a) Kẻ OI  CD tại I  IC  ID .
Ta có AP//OI //BQ ( cùng vuông góc với PQ )  APQB là hình thang
Vì OA  OB, OI //AP//BQ  IP  IQ . Suy ra : IP  IC  IQ  ID  CP  DQ .
b) Theo câu a): OI  PQ, IP  IQ  OI vừa là đường trung tuyến vừa là đường cao của O  PQ  O
 PQ cân tại O  OP  OQ . Bài 3.
Cho đường tròn tâm O đường kính AD  2R , gọi I là trung điểm của OD , qua I kẻ dây BC
vuông góc với AD . a) Chứng minh ABC  đều .
b) Tính độ dài các cạnh của tam giác ABC theo R . Lời giải B A I D O C
a) Vì OI  BC tại I  IB  IC  Tứ giác OBDC là hình thoi (có hai đường chéo cắt nhau tại
trung điểm của mỗi đường và vuông góc với nhau). Do đó :
BD  OB  R  O
 BD là tam giác đều ( có BD  OB  OD  R ) BDO  60 . Vì ABD 
nội tiếp trong đường tròn có đường kính là cạnh AD  A
 BD vuông tại B
 BAD  90  BDO  30. Lại có ABC 
cân tại A (Vì AI vừa là đường cao vừa là đường trung tuyến ) nên AI cũng là
phân giác của BAC  BAC  2.BAD  60. ABC 
cân và BAC  60  A
 BC là tam giác đều. Trang 5 R b) Xét B
 IO vuông tại I , có OB  R,OI  . Theo Pitago ta có: 2 2  R  3 2 2 2
BI  OB  OI  R   R  
. Do đó : BC  2.BI  3R .  2  2 ABC 
đều nên: AB  BC  CA  3R .  HẾT  Trang 6