Bài Tập Toán Lớp 8 Tuần 1 Có Lời Giải Chi Tiết (Tiếp Theo)

PHIẾU BÀI TẬP TOÁN 8 TUẦN 01 Bài 1.
Cho tứ giác ABCD . Gọi M , N, P,Q thứ tự là trung điểm của AB, BC,CD, DA .
a) Chứng minh rằng tứ giác MNPQ là hình bình hành
b) So sánh chu vi tứ giác MNPQ với tổng hai đường chéo của tứ giác ABCD . Bài 2.
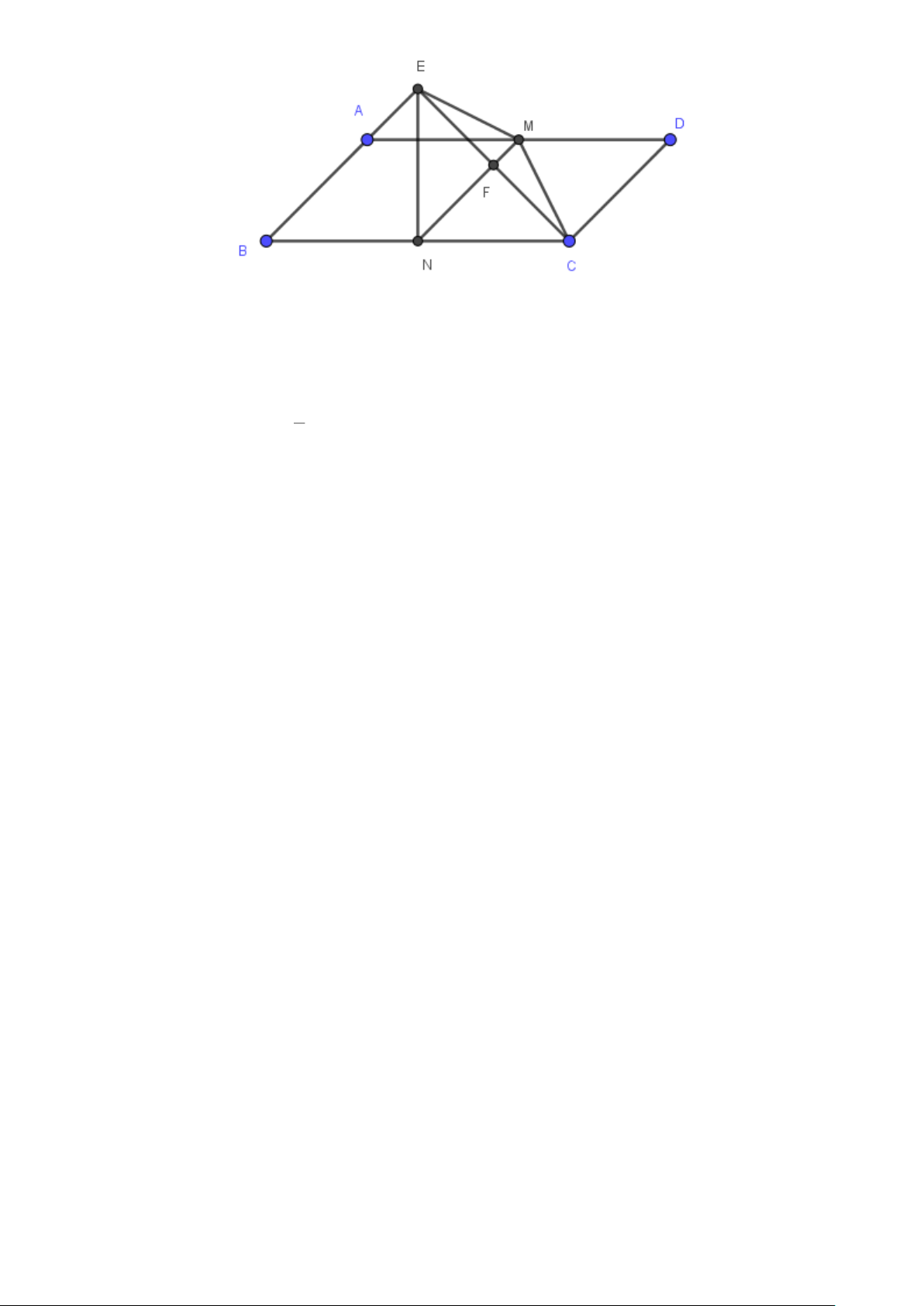
Cho hình bình hành ABCD , AD = 2AB . Từ C vẽ CE vuông góc với AB . Nối E với trung
điểm M của AD . Từ M vẽ MF vuông góc với CE , MF cắt BC tại N .
a) Tứ giác MNCD là hình gì?
b) Tam giác EMC là tam giác gì?
C. PHẦN NÂNG CAO (DÀNH THÊM CHO LỚP M VÀ KHUYẾN KHÍCH HỌC SINH CÁC LỚP KHÁC Bài 1.
Tìm giá trị nhỏ nhất của các đa thức sau: 2
A = x − 4x + 6; 2 B = 2x + 6 ; x
C = (x −1)(x + 2)(x+ 3)(x+ 6); 2 2
D = (2x −1) + (x + 2) ;
E = x(x +1)(x + 2)(x + 3); 2 2
F = (x −1) + (x − 3) . Bài 2.
Tìm giá trị lớn nhất của các đa thức sau : 2
A = 4 − x + 2 ; x 2
B = 10x − 23 − x ; 2 C = −x + 6 . x a) Rút gọn A .
b) Với giá trị x ; y nguyên dương nào thỏa mãn x + 2y = 14 thì A nhận giá trị nguyên dương. Bài 3.
Cho x là số nguyên. Chứng minh rằng 4 3 2
B = x − 4x − 2x +12x + 9 là bình phương số nguyên. Bài 4.
Cho x, y, z là số nguyên. Chứng minh rằng 2 2
C = 4x(x + y)(x + y + z)(x + z) + y z là một số chính phương. HẾT
ĐÁP ÁN BÀI TẬP TĂNG CƯỜNG TOÁN 8 TUẦN …
HƯỚNG DẪN GIẢI CHI TIẾT Bài 1.
Cho tứ giác ABCD . Gọi M , N, P,Q thứ tự là trung điểm của AB, BC,CD, DA .
a) Chứng minh rằng tứ giác MNPQ là hình bình hành
b) So sánh chu vi tứ giác MNPQ với tổng hai đường chéo của tứ giác ABCD . Lời giải Trang 1
a) Trong tam giác ABD có:
M là trung điểm của AB
Q là trung điểm của AD
Suy ra, MQ là đường trung bình của tam giác ABD 1  MQ = D B và MQ / / D B ( ) 1 2
Trong tam giác BCD có:
N là trung điểm của BC
P là trung điểm của CD
Suy ra, NP là đường trung bình của tam giác BCD 1  NP = D B và NP / / D B (2) 2 Từ ( )
1 và (2) suy ra: MQ = NP và MQ / /NP
Vậy tứ giác MNPQ là hình bình hành.
b) Chu vi tứ giác MNPQ là: C = MN + NP + PQ + QM D B AC Mà QM = NP = và MN = PQ = nên: 2 2 D B AC
C = MN + NP + PQ + QM = 2. + 2. = D B + AC 2 2 Bài 2.
Cho hình bình hành ABCD , AD = 2AB . Từ C vẽ CE vuông góc với AB . Nối E với trung
điểm M của AD . Từ M vẽ MF vuông góc với CE , MF cắt BC tại N .
a) Tứ giác MNCD là hình gì?
b) Tam giác EMC là tam giác gì? Lời giải Trang 2
a) Ta có MN / / AB (cùng vuông CE)
 MN / /CD mà DM / /CN nên tứ giác MNCD là hình bình hành
b) Xét tam giác BEC vuông tại E có: N là trung điểm BC 1
suy ra, NE = NC = BC (t/c trung tuyến tam giác vuông) 2
Xét tam giác ENF và CNF có:
NE = NC , NF chung, EFN = NFC   F  = C  F   ENF = FNC
Xét tam giác  và C có NE = NC , NM chung, ENF = FNC
  = C   = C
Vậy tam giác EMC cân tại M .
PHẦN NÂNG CAO (DÀNH THÊM CHO LỚP M VÀ KHUYẾN KHÍCH HỌC SINH CÁC LỚP KHÁC
Bài 1. Tìm giá trị nhỏ nhất của các đa thức sau: 2
A = x − 4x + 6; 2 B = 2x + 6 ; x
C = (x −1)(x + 2)(x+ 3)(x+ 6); 2 2
D = (2x −1) + (x + 2) ;
E = x(x +1)(x + 2)(x + 3); 2 2
F = (x −1) + (x − 3) . Lời giải a) 2
A = x − 4x + 6; Ta có: 2 2
A = x − 4x + 6 = (x− 2) + 2 Vì 2 2
(x − 2)  0 x
  (x − 2) + 2  2 x 
Vậy MinA = 2 khi x = 2. b) 2 B = 2x + 6 ; x Trang 3 3 9 9 3 9 Ta có: 2 2 2
A = 2x + 6x = 2(x + 2x + − ) = 2(x+ ) + 2 4 4 2 2 3 3 9 9 Vì 2 2 2(x + )  0 x   (x + ) +  x  2 2 2 2 9 3 −
Vậy MinB = khi x = . 2 2
c) C = (x −1)(x + 2)(x+ 3)(x+ 6);
= [(x −1)(x+ 6)][(x + 2)(x+ 3)] 2 2
= (x + 5x − 6)(x + 5x + 6) 2 2
= (x + 5x) − 36 Vì 2 2 2 2
(x + 5 x)  0 x
  (x + 5 x) − 36  36 − x 
Vậy MinC = −36 khi x = 0 hoặc x = −5. d) 2 2
D = (2x −1) + (x + 2) ; 2 2
= 4x − 4x +1+ x + 4x + 4 2 = 5x + 5 Vì 2 2 5 x  0 x
  5x + 5  5 x 
Vậy MinD = 5 khi x = 0.
e) E = x(x +1)(x + 2)(x + 3);
=[x(x + 3)][(x + 2)(x + 3)] 2 2
= (x + 3x)(x + 3x + 2) 2 2 2
= (x + 3x) + 2(x + 3x) +1−1 2 2
= (x + 3x +1) −1 Vì 2 2
(x + 3x+1)  0 x   E  1 − x  3 − + 5 3 − + 5
Vậy MinE = −1 khi x = hoặc x = . 2 2 f) 2 2
F = (x −1) + (x − 3) . 2 2
= x − 2x +1+ x − 6x + 9 2 = 2x − 8x +10 2
= 2(x − 4x + 5) 2 = 2(x − 2) + 2 Vì 2 2 2(x− 2)  0 x
  2(x− 2) + 2  2 x 
Vậy MinE = 2 khi x = 2.
Bài 2. Tìm giá trị lớn nhất của các đa thức sau : Trang 4 2
A = 4 − x + 2 ; x 2
B = 10x − 23 − x ; 2 C = −x + 6 . x Lời giải a) 2
A = 4 − x + 2 ; x 2
= 5 − (x − 2x +1) 2 = 5 − (x −1) Vì 2 2 (x−1)  0 x
  5 − (x−1)  5 x 
Vậy MaxA = 5 khi x = 1. b) 2
B = 10x − 23 − x ; 2
= 2 − (x −10x + 25) 2 = 2 − (x − 5) Vì 2 2 (x− 5)  0 x
  2 − (x− 5)  2 x 
Vậy MaxA = 2 khi x = 5. c) 2 C = −x + 6 . x 2
= 9 − (x − 2.3.x + 9) 2 = 9 − (x − 3) Vì 2 2 (x− 3)  0 x
  9 − (x− 3)  9 x 
Vậy MaxA = 9 khi x = 3.
Lời giải bài 3, bài 4 của thầy Nguyễn Duy Tân
Bài 3. Cho x là số nguyên. Chứng minh rằng 4 3 2
B = x − 4x − 2x +12x + 9 là bình phương số nguyên. Lời giải 4 3 2
B = x − 4x − 2x +12x + 9
B = (x )2 − x x + ( x)2 2 2 2 2. .2 2
− 6x +12x + 9
B = (x − x)2 2 2 2
− 6(x − 2x) + 9
B = (x − x)2 2 2 2 2
− 2.(x − 2x).3+ 3 2 2
B = (x − 2x − 3)
Vì x là số nguyên nên 2
x − 2x − 3 là số nguyên
Bài 4. Cho x, y, z là số nguyên. Chứng minh rằng 2 2
C = 4x(x + y)(x + y + z)(x + z) + y z là một số chính phương. Trang 5 Lời giải 2 2
C = 4x(x + y)(x + y + z)(x + z) + y z 2 2 2 2
C = 4(x + xy + xz)(x + xz + xy + yz) + y z yz Đặt 2
t = x + xy + xz + 2  yz  yz  2 2 C = 4 t − t + + y z     2  2  2   yz  2  2 2
C = 4 t −    + y z   2    2 2 2 2 2
C = 4t − y z + y z 2 C = 4t 2  yz 2 
C = 4 x + xy + xz +    2 
C = ( x + xy + yz)2 2 2 2
Vì x, y, z là số nguyên nên 2
2x + 2xy + yz là số nguyên
Suy ra C là một số chính phương
Lời giải bài 3, bài 4 của thầy Bùi Cảm Bài 3.
Cho x là số nguyên. Chứng minh rằng: 4 3 2
B = x − 4x − 2x +12x + 9 là bình phương của một số nguyên. Lời giải 4 3 2 4 2 2 2
B = x − 4x − 2x +12x + 9 = x − 2. x .2x + 4x − 6x +12x + 9
= (x − x)2 − (x − x) + = (x − x − )2 2 2 2 2 6 2 9 2 3 .
Vậy B là bình phương của một số nguyên. Bài 4.
Cho x, y, z là số nguyên. Chứng minh rằng:
C = x ( x + y)( x + y + z)(x + z) 2 2 4
+ y z là một số chính phương. Lời giải
C = x ( x + y)( x + y + z)(x + z) 2 2 4 + y z
= (x + y)(x + z) 
 x ( x + y + z) 2 2 4 .  +  y z
= (x + y)(x + z)   ( 2
x + xy + xz + yz − yz) 2 2 4 . + y z Trang 6
= (x + y)(x + z) 
 ( x + y)( x + z) 2 2 4 . − yz +  y z
= (x + y)2 (x + z)2 − (x + y)(x + z) 2 2 4 4 . yz + y z
=  (x + y)(x + z) 2 2 − yz   .
Vậy C là một số chính phương.  HẾT  Trang 7