Bài tập trắc nghiệm một số phương trình lượng giác thường gặp (có đáp án)

Bài tập trắc nghiệm một số phương trình lượng giác thường gặp có đáp án và lời giải chi tiết gồm 75 câu trắc nghiệm. Bài tập gồm các dạng toán:phương trình bậc nhất đối với một hàm số lượng giác; phương trình bậc nhất đối với sinx và cosx; phương trình bậc hai đối với một hàm số lượng giác; phương trình đẳng cấp bậc hai đối với sinx và cosx; phương trình chứa sinx+cosx và sinxcosx. Bài tập được viết dưới dạng file PDF gồm 30 trang. Các bạn xem và tải về ở dưới.

24 12 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Hàm số lượng giác và phương trình lượng giác (KNTT)

Môn: Toán 11

Thông tin:

36 trang 7 tháng trước

Tác giả:

Profile Thùy Dương (H)
! Trang!1!
BÀI TẬP TRẮC NGHIỆM
MỘT SỐ PHƯƠNG TRÌNH LƯỢNG GIÁC
THƯỜNG GẶP
Vấn đề 1. PHƯƠNG TRÌNH BẬC NHẤT
ĐỐI VỚI MỘT HÀM SỐ LƯỢNG GIÁC
Câu 1. Gọi là tập nghiệm của phương trình . Khẳng định nào sau đây là
đúng?
A. B. C. D.
Câu 2. Hỏi là một nghiệm của phương trình nào sau đây?
A. B.
C. D.
Câu 3. Tìm nghiệm dương nhỏ nhất của phương trình
A. B. C. D.
Câu 4. Số vị trí biểu diễn các nghiệm của phương trình trên đường
tròn lượng giác là?
A. . B. . C. . D. .
Câu 5. Hỏi trên đoạn , phương trình có bao nhiêu nghiệm?
A. B. C. D.
Câu 6. Trong các phương trình sau, phương trình nào tương đương với phương trình
?
A. B. C. D.
Câu 7. Phương trình nào dưới đây có tập nghiệm trùng với tập nghiệm của phương trình
?
A. B. C. D.
Câu 8. Giải phương trình .
A. B.
C. D.
S
2cos 3 0x -=
5
.
6
S
p
Î
11
.
6
S
p
Î
13
.
6
S
p
Ï
13
.
6
S
p
-Ï
7
3
x
p
=
2sin 3 0.x -=
2sin 3 0.x +=
2sin 4 1 0.
3
x
p
æö
--=
ç÷
èø
.
4
x
p
=
7
.
24
x
p
=
.
8
x
p
=
.
12
x
p
=
tan 2 3 0
3
x
p
æö
-+=
ç÷
èø
4
3
2
1
[ ]
0; 2018
p
3cot 3 0x -=
6339.
6340.
2017.
2018.
2
2cos 1x =
2
sin .
2
x =
2sin 2 0.x +=
tan 1.x =
2
tan 1.x =
2
tan 3x =
1
cos .
2
x =-
2
4cos 1.x =
1
cot .
3
x =
1
cot .
3
x =-
2
4sin 3x =
( )
2
3
, .
2
3
xk
k
xk
p
p
p
p
é
=+
ê
Î
ê
ê
=- +
ê
ë
!
( )
2
3
, .
2
2
3
xk
k
xk
p
p
p
p
é
=+
ê
Î
ê
ê
=+
ê
ë
!
( )
, .
33
3
k
x
k
k
pp
ì
=+
ï
Î
í
ï
¹
î
!"
!
( )
, .
3
3
k
x
k
k
p
ì
=
ï
Î
í
ï
¹
î
!"
!
! Trang!2!
Câu 9. Trong các phương trình sau, phương trình nào tương đương với phương trình
?
A. B. C. D.
Câu 10. Với thuộc , hỏi phương trình có bao nhiêu nghiệm?
A. B. C. D.
Câu 11. Có tất cả bao nhiêu giá trị nguyên của tham số để phương trình
có nghiệm?
A. B. C. D. Vô số.
Câu 12. Có bao nhiêu giá trị nguyên của tham số thuộc đoạn để phương
trình có nghiệm?
A. B. C. D.
Câu13. Tìm giá trị thực của tham số để phương trình nhận
làm nghiệm.
A. B. C. D.
Câu 14. Tìm tất cả các giá trị của tham số để phương trình có
nghiệm.
A. B. C. D.
Câu 15. Tìm tất cả các giá trị của tham số để phương trình vô
nghiệm.
A. B.
C. D.
Vấn đề 2. PHƯƠNG TRÌNH BẬC NHẤT ĐỐI VỚI và
Câu 16. Gọi là tập nghiệm của phương trình . Khẳng định nào sau đây là
đúng?
A. B. C. D.
Câu 17. Số nghiệm của phương trình trên khoảng là?
A. B. C. D.
Câu 18. Tính tổng các nghiệm của phương trình trên
khoảng
22
3sin cosxx=
1
sin .
2
x =
3
cos .
2
x =
2
3
sin .
4
x =
2
cot 3.x =
x
( )
0;1
( )
2
3
cos 6
4
x
p
=
8.
10.
11.
12.
m
3cos 1 0xm+-=
1.
2.
3.
m
[ ]
2108; 2018-
cos 1 0mx+=
2018.
2019.
4036.
4038.
m
( )
2sin2 1mxm-=+
12
x
p
=
2.m ¹
( )
231
.
32
m
+
=
-
4.m =-
1.m =-
m
( )
1sin 2 0mxm++-=
1.m £-
1
.
2
m ³
1
1.
2
m-< £
1.m >-
m
( )
2sin2 1mxm-=+
1
;2 .
2
m
éù
Î
êú
ëû
( )
1
;2;.
2
m
æö
Î-¥ È +¥
ç÷
èø
( )
1
;2 2; .
2
m
æö
ÎÈ+¥
ç÷
èø
1
;.
2
m
æö
Î+¥
ç÷
èø
sin x
cos x
S
cos 2 sin 2 1xx-=
.
4
S
p
Î
.
2
S
p
Î
3
.
4
S
p
Î
5
.
4
S
p
Î
sin 2 3 cos 2 3xx+=
0;
2
p
æö
ç÷
èø
1.
2.
3.
4.
T
22
cos sin 2 2 sinxx x-=+
( )
0; 2 .
p
! Trang!3!
A. B. C. D.
Câu 19. Tìm nghiệm dương nhỏ nhất của
A. B. C. D.
Câu 20. Số nghiệm của phương trình trên khoảng là?
A. B. C. D.
Câu 21. Giải phương trình
A. B.
C. D.
Câu 22. Gọi là nghiệm âm lớn nhất của . Mệnh
đề nào sau đây là đúng?
A. B. C. D.
Câu 23. Biến đổi phương trình về dạng
với , thuộc khoảng . Tính .
A. B. C. D.
Câu 24. Giải phương trình
A. B.
C. D.
Câu 25. Hàm số có tất cả bao nhiêu giá trị nguyên?
A. B. C. D.
Câu 26. Gọi là nghiệm dương nhỏ nhất của
Mệnh đề nào sau đây là đúng?
7
.
8
T
p
=
21
.
8
T
p
=
11
.
4
T
p
=
3
.
4
T
p
=
0
x
3
3sin 3 3 cos 9 1 4sin 3 .xx x-=+
0
.
2
x
p
=
0
.
18
x
p
=
0
.
24
x
p
=
0
.
54
x
p
=
sin 5 3 cos 5 2sin 7xxx+=
0;
2
p
æö
ç÷
èø
2.
1.
3.
4.
3 cos sin 2sin 2 .
22
xx x
pp
æöæö
++ -=
ç÷ç÷
èøèø
5
2
6
, .
2
18 3
xk
k
xk
p
p
pp
é
=+
ê
Î
ê
ê
=+
ê
ë
!
7
2
6
, .
2
18 3
xk
k
xk
p
p
pp
é
=+
ê
Î
ê
ê
=- +
ê
ë
!
5
2
6
, .
7
2
6
xk
k
xk
p
p
p
p
é
=+
ê
Î
ê
ê
=+
ê
ë
!
2
18 3
, .
2
18 3
xk
k
xk
pp
pp
é
=+
ê
Î
ê
ê
=- +
ê
ë
!
0
x
sin 9 3 cos 7 sin 7 3 cos 9xxxx+=+
0
;0 .
12
x
p
æö
Î-
ç÷
èø
0
;.
6 12
x
pp
éù
Î- -
êú
ëû
0
;.
36
x
pp
éö
Î- -
÷
ê
ëø
0
;.
23
x
pp
éö
Î- -
÷
ê
ëø
( )
cos 3 sin 3 cos sin 3xx x x-= -
( ) ( )
sin sinax b cx d+= +
b
d
;
22
pp
æö
-
ç÷
èø
bd+
.
12
bd
p
+=
.
4
bd
p
+=
.
3
bd
p
+=-
.
2
bd
p
+=
cos 3 sin
0.
1
sin
2
xx
x
-
=
-
, .
6
xkk
p
p
=+ Î!
2, .
6
xkk
p
p
=+ Î!
7
2, .
6
xkk
p
p
=+ Î!
7
, .
6
xkk
p
p
=+ Î!
2sin 2 cos 2
sin 2 cos 2 3
xx
y
xx
+
=
-+
1.
2.
3.
4.
0
x
cos 2 3 sin 2 3 sin cos 2.xxxx++-=
! Trang!4!
A. B. C. D.
Câu 27. Có bao nhiêu giá trị nguyên của tham số thuộc đoạn để phương trình
vô nghiệm.
A. B. C. D.
Câu 28. Tìm tất cả các giá trị thực của tham số để phương trình
vô nghiệm.
A. B.
C. D.
Câu 29. Có bao nhiêu giá trị nguyên của tham số thuộc đoạn để phương trình
có nghiệm.
A. B. C. D.
Câu 30. Có bao nhiêu giá trị nguyên của tham số thuộc đoạn để phương
trình có nghiệm.
A. B. C. D.
Vấn đề 3. PHƯƠNG TRÌNH BẬC HAI
ĐỐI VỚI MỘT HÀM SỐ LƯỢNG GIÁC
Câu 31. Hỏi trên , phương trình có bao nhiêu nghiệm?
A. B. C. D.
Câu 32. Số vị trí biểu diễn các nghiệm của phương trình trên đường
tròn lượng giác là?
A. B. C. D.
Câu 33. Cho phương trình Đặt , ta được phương trình
nào sau đây?
A. B. C. D.
Câu 34. Số nghiệm của phương trình trên là?
A. 3. B. 4. C. 2. D. 1.
Câu 35. Số nghiệm của phương trình trên đoạn là?
A. B. C. D.
Câu 36. Tính tổng tất cả các nghiệm của phương trình trên đoạn
A. B. C. D.
Câu 37. Số nghiệm của phương trình trên là?
0
0; .
12
x
p
æö
Î
ç÷
èø
0
;.
12 6
x
pp
éù
Î
êú
ëû
0
;.
63
x
pp
æù
Î
ç
ú
èû
0
;.
32
x
pp
æù
Î
ç
ú
èû
m
[ ]
10 ;10-
sin 3 cos 2
33
xxm
pp
æö æö
-- -=
ç÷ ç÷
èø èø
21.
20.
18.
9.
m
( )
2
cos sin 2 1xx m+= +
( ) ( )
;1 1; .mÎ-¥- È +¥
[ ]
1; 1 .mÎ-
( )
;mÎ-¥+¥
( ) ( )
;0 0; .mÎ-¥ È +¥
m
[ ]
10 ;10-
( )
1sin cos 1mxmxm+- =-
21.
20.
18.
11.
m
[ ]
2018; 2018-
( )
2
1sin sin2 cos2 0mxxx+-+=
4037.
4036.
2019.
2020.
0;
2
p
éö
÷
ê
ëø
2
2sin 3sin 1 0xx-+=
1.
2.
3.
4.
2
2cos 5cos 3 0xx++=
1.
2.
3.
4.
2
cot 3 3 cot 3 2 0.xx-+=
cottx=
2
320.tt-+=
2
3920.tt-+=
2
920.tt-+=
2
620.tt-+=
( )
2
4 sin 2 2 1 2 sin 2 2 0xx-+ +=
( )
0;
p
2
sin 2 cos 2 1 0xx-+=
[ ]
;4
pp
-
2.
4.
6.
8.
T
2
2sin 3cos 0
44
xx
-=
[ ]
0;8 .
p
0.T =
8.T
p
=
16 .T
p
=
4.T
p
=
( ) ( )
2
1
31cot 31 0
sin
x
x
-- -+=
( )
0;
p
! Trang!5!
A. B. C. D.
Câu 38. Tính tổng tất cả các nghiệm của phương trình trên
đoạn .
A. B. C. D.
Câu 39. Số vị trí biểu diễn các nghiệm của phương trình trên đường
tròn lượng giác là?
A. B. C. D.
Câu 40. Cho phương trình . Nếu đặt , ta được phương trình nào
sau đây?
A. B. C. D.
Câu 41. Số nghiệm của phương trình thuộc là?
A. B. C. D.
Câu 42. Tìm tất cả các giá trị thực của tham số để phương trình có
nghiệm.
A. B. C. D.
Câu 43. Tìm tất cả các giá trị thực của tham số để phương trình
có nghiệm trên khoảng .
A. . B. . C. . D. .
Câu 44. Biết rằng khi thì phương trình
có đúng nghiệm phân biệt thuộc khoảng . Mệnh đề nào sau đây là đúng?
A. B. . C. D.
Câu 45. Tìm tất cả các giá trị thực của tham số để phương trình
có đúng nghiệm thuộc khoảng
A. B. C. D.
Vấn đề 4. PHƯƠNG TRÌNH ĐẲNG CẤP BẬC HAI ĐỐI VỚI và
Câu 46. Giải phương trình
A. B.
C. D.
1.
2.
3.
4.
T
2cos 2 2cos 2 0xx+-=
[ ]
0; 3
p
17
.
4
T
p
=
2.T
p
=
4.T
p
=
6.T
p
=
cos 2 3sin 4 0xx++=
1.
2.
3.
4.
cos cos 1 0
2
x
x ++=
cos
2
x
t =
2
20.tt+=
2
210.tt-++=
2
210.tt+-=
2
20.tt-+=
5
cos 2 4 cos
362
xx
pp
æö æö
++ -=
ç÷ ç÷
èø èø
[ ]
0; 2
p
1.
2.
3.
4.
m
tan cot 8xm x+=
16.m >
16.m <
16.m ³
16.m £
m
( )
cos 2 2 1 cos 1 0xm xm-+ ++=
3
;
22
pp
æö
ç÷
èø
10m-£ £
10m-£ <
10m-< <
1
1
2
m-£ <
0
mm=
( )
22
2sin 5 1 sin 2 2 0mxmmx -+ + +=
5
;3
2
p
p
æö
-
ç÷
èø
3.m =-
1
2
m =
0
37
;.
5 10
m
æù
Î
ç
ú
èû
0
32
;.
55
m
æö
Î- -
ç÷
èø
m
( )
2
2cos 3 3 2 cos3 2 0xmxm+- +-=
3
;.
63
pp
æö
-
ç÷
èø
1 1.m-£ £
1 2.m<£
1 2.m££
1 2.m£<
sin x
cos x
( )
22
sin 3 1 sin cos 3 cos 0.xxxx-+ + =
( )
2 .
3
xkk
p
p
=+ Î!
( )
.
4
xkk
p
p
=+ Î!
( )
2
3
.
2
4
xk
k
xk
p
p
p
p
é
=+
ê
Î
ê
ê
=+
ê
ë
!
( )
3
.
4
xk
k
xk
p
p
p
p
é
=+
ê
Î
ê
ê
=+
ê
ë
!
! Trang!6!
Câu 47. Gọi là tập nghiệm của phương trình .
Khẳng định nào sau đây là đúng?
A. B. C. D.
Câu 48. Trong các phương trình sau, phương trình nào tương đương với phương trình
.
A. . B. .
C. . D. .
Câu 49. Phương trình nào dưới đây có tập nghiệm trùng với tập nghiệm của phương trình
?
A. . B.
.
C. . D.
.
Câu 50. Cho phương trình . Mệnh đề nào sau đây là sai?
A. không là nghiệm của phương trình.
B. Nếu chia hai vế của phương trình cho thì ta được phương trình
.
C. Nếu chia 2 vế của phương trình cho thì ta được phương trình
.
D. Phương trình đã cho tương đương với .
Câu 51. Số vị trí biểu diễn các nghiệm phương trình trên
đường tròn lượng giác là?
A. . B. . C. . D. .
Câu 52. Số nghiệm của phương trình trên ?
A. . B. . C. . D. .
Câu 53. Nghiệm dương nhỏ nhất của phương trình là:
A. . B. . C. . D. .
Câu 54. Cho phương trình . Trong các
mệnh đề sau, mệnh đề nào sai?
A. là một nghiệm của phương trình.
B. Nếu chia hai vế của phương trình cho thì ta được phương trình
.
S
22
2 sin 3 3 sin cos cos 2xxxx+-=
;.
3
S
p
p
ìü
Ì
íý
îþ
;.
62
S
pp
ìü
Ì
íý
îþ
5
;.
412
S
pp
ìü
Ì
íý
îþ
5
;.
26
S
pp
ìü
Ì
íý
îþ
( )
22
sin 3 1 sin cos 3 cos 3xxxx-+ + =
sin 0x =
sin 1
2
x
p
æö
+=
ç÷
èø
( )
31
cos 1 tan 0
13
xx
æö
+
--=
ç÷
ç÷
-
èø
( )
( )
2
tan 2 3 cos 1 0xx++ - =
2
sin 3 sin cos 1xxx+=
( )
2
cos cot 3 0xx-=
sin . tan 2 3 0
24
xx
pp
éù
æöæö
++--=
ç÷ç÷
êú
èøèø
ëû
( )
2
cos 1 . tan 3 0
2
xx
p
éù
æö
+- - =
ç÷
êú
èø
ëû
( )
( )
sin 1 cot 3 0xx--=
2
cos 3sin cos 1 0xxx-+=
xk
p
=
2
cos x
2
tan 3 tan 2 0xx-+=
2
sin x
2
2cot 3cot 1 0xx++=
cos 2 3sin 2 3 0xx-+=
22
sin 4 sin cos 4 cos 5xxx x-+=
4
3
2
1
22
cos 3sin cos 2 sin 0xxx x-+=
( )
2;2
pp
-
2
4
6
8
22
4 sin 3 3 sin 2 2 cos 4xxx+-=
12
p
6
p
4
p
3
p
( ) ( )
22
2 1 sin sin 2 2 1 cos 2 0xx x-+++ -=
7
8
x
p
=
2
cos x
2
tan 2 tan 1 0xx--=
! Trang!7!
C. Nếu chia hai vế của phương trình cho thì ta được phương trình
.
D. Phương trình đã cho tương đương với .
Câu 55. Giải phương trình
A. . B. . C. . D. .
Câu 56. Có bao nhiêu giá trị nguyên của tham số thuộc đoạn để phương trình
có nghiệm?
A. B. C. D.
Câu 57. Có bao nhiêu giá trị nguyên của tham số thuộc để phương trình
có nghiệm?
A. B. C. D. Vô số.
Câu 58. Tìm điều kiện để phương trình với có
nghiệm.
A. . B. . C. . D. .
Câu 59. Tìm tất cả các giá trị của tham số để phương trình vô
nghiệm.
A. . B. , . C. . D. , .
Câu 60. Có tất cả bao nhiêu giá trị nguyên của tham số thuộc đoạn để phương trình
có nghiệm.
A. . B. . C. . D. .
Vấn đề 5. PHƯƠNG TRÌNH CHỨA và
Câu 61. Giải phương trình .
A. B.
C. D.
Câu 62. Cho phương trình . Đặt , ta
được phương trình nào dưới đây?
A. B.
2
sin x
2
cot 2 cot 1 0xx+-=
cos 2 sin 2 1xx-=
( ) ( )
22
2 sin 1 3 sin cos 1 3 cos 1.xxx x+- +- =
6
p
-
4
p
-
2
3
p
-
12
p
-
m
[ ]
10 ;10-
( )
22
11sin 2 sin 2 3cos 2xm x x+- + =
16.
21.
15.
6.
m
( ) ( )
22
sin 2 1 sin cos 1 cosxm xxm xm-- -- =
2.
1.
0.
22
sin sin c o s cos 0axaxxb x++=
0a ¹
4ab³
4ab£-
4
1
b
a
£
4
1
b
a
£
m
2
2sin sin 2 2xm x m+=
4
0
3
m££
0m <
4
3
m >
4
0
3
m<<
4
3
m <-
0m >
m
[ ]
3; 3-
( )
22
2 cos 2 sin 2 1 0mxmx+- +=
3
7
6
4
sin cosxx±
sin cos .xx
( )
sin cos 2 sin cos 2xx x x++=
, .
2
xk
k
xk
p
p
p
é
=+
ê
Î
ê
=
ë
!
2
, .
2
2
xk
k
xk
p
p
p
é
=+
ê
Î
ê
=
ë
!
2
, .
2
2
xk
k
xk
p
p
p
é
=- +
ê
Î
ê
=
ë
!
, .
2
xk
k
xk
p
p
p
é
=- +
ê
Î
ê
=
ë
!
( )
3 2 sin cos 2sin 2 4 0xx x++ +=
sin costxx=+
2
23220.tt++=
2
43240.tt++=
! Trang!8!
C. D.
Câu 63. Cho phương trình . Trong các phương trình sau,
phương trình nào tương đương với phương trình đã cho?
A. B.
C. D.
Câu 64. Nghiệm âm lớn nhất của phương trình là:
A. B. C. D.
Câu 65. Cho thỏa mãn phương trình . Tính
A. hoặc . B.
hoặc .
C. . D. hoặc
.
Câu 66. Từ phương trình , ta tìm được có
giá trị bằng:
A. B. C. D.
Câu 67. Cho thỏa mãn . Tính
A. B.
C. D.
Câu 68. Từ phương trình , nếu ta đặt
thì giá trị của nhận được là:
A. hoặc . B. hoặc .
C. . D. .
Câu 69. Nếu thì bằng bao nhiêu?
A. . B. hoặc .
C. hoặc . D. hoặc .
2
23220.tt+-=
2
43240.tt+-=
5sin 2 sin cos 6 0xx x++ +=
2
sin .
42
x
p
æö
+=
ç÷
èø
3
cos .
42
x
p
æö
-=
ç÷
èø
tan 1.x =
2
1tan 0.x+=
1
sin cos 1 sin 2
2
xx x+=-
.
2
p
-
.
p
-
3
.
2
p
-
2.
p
-
x
sin 2 sin cos 1xx x+- =
sin .
4
x
p
æö
-
ç÷
èø
sin 0
4
x
p
æö
-=
ç÷
èø
sin 1
4
x
p
æö
-=
ç÷
èø
sin 0
4
x
p
æö
-=
ç÷
èø
2
sin
42
x
p
æö
-=
ç÷
èø
2
sin
42
x
p
æö
-=-
ç÷
èø
sin 0
4
x
p
æö
-=
ç÷
èø
2
sin
42
x
p
æö
-=-
ç÷
èø
( )
5sin 2 16 sin cos 16 0xxx--+=
sin
4
x
p
æö
+
ç÷
èø
2
.
2
2
.
2
-
1.
2
.
2
±
x
( )
6sin cos sin cos 6 0xx xx-+ +=
cos .
4
x
p
æö
+
ç÷
èø
cos 1.
4
x
p
æö
+=-
ç÷
èø
cos 1.
4
x
p
æö
+=
ç÷
èø
1
cos .
4
2
x
p
æö
+=
ç÷
èø
1
cos .
4
2
x
p
æö
+=-
ç÷
èø
( )
( )
1 3 cos sin 2sin cos 3 1 0xx xx++- --=
cos sintxx=+
t
1t =
2t =
1t =
3t =
1t =
3t =
( )
( )
1 5 sin cos sin 2 1 5 0xx x+-+--=
sin x
2
sin
2
x =
2
sin
2
x =
2
sin
2
x =-
sin 1x =-
sin 0x =
sin 0x =
sin 1x =
! Trang!9!
Câu 70. Nếu thì bằng bao nhiêu?
A. B. C. D.
Câu 71. Cho thỏa mãn . Tính
A. B. C. D.
Câu 72. Hỏi trên đoạn , phương trình có bao nhiêu
nghiệm?
A. B. C. D.
Câu 73. Từ phương trình , ta tìm được có giá trị
bằng:
A. B. C. D.
Câu 74. Từ phương trình , ta tìm được có giá trị
bằng:
A. B. C. D.
Câu 75. Có bao nhiêu giá trị nguyên của tham số để phương trình
có nghiệm?
A. B. C. D.
ĐÁP ÁN VÀ LỜI GIẢI
Vấn đề 1. PHƯƠNG TRÌNH BẬC NHẤT
ĐỐI VỚI MỘT HÀM SỐ LƯỢNG GIÁC
Câu 1. Gọi là tập nghiệm của phương trình . Khẳng định nào sau đây là
đúng?
A. B. C. D.
Lời giải. Ta có
Nhận thấy với nghiệm Chọn B
Câu 2. Hỏi là một nghiệm của phương trình nào sau đây?
A. B.
C. D.
( )( )
1sin 1cos 2xx++=
cos
4
x
p
æö
-
ç÷
èø
1.-
1.
2
.
2
2
.
2
-
x
2sin 2 3 6 sin cos 8 0xxx-++=
sin 2 .x
1
sin 2 .
2
x =-
2
sin 2 .
2
x =-
1
sin 2 .
2
x =
2
sin 2 .
2
x =
[ ]
0; 2018
p
in co ss4sin21xxx+=-
4037.
4036.
2018.
2019.
( )
2 sin cos tan cotxx xx+=+
cos x
1.
2
.
2
-
2
.
2
1.-
33
3
1 sin cos sin 2
2
xx x++ =
cos
4
x
p
æö
+
ç÷
èø
1.
2
.
2
-
2
.
2
2
.
2
±
m
sin cos sin cos 0xx x xm-- +=
1.
2.
3.
4.
S
2cos 3 0x -=
5
.
6
S
p
Î
11
.
6
S
p
Î
13
.
6
S
p
Ï
13
.
6
S
p
-Ï
( )
2
6
2cos 3 0 cos cos .
6
2
6
xk
xx k
xk
p
p
p
p
p
é
=+
ê
-=Û = Û Î
ê
ê
=- +
ê
ë
!
1
11
2.
66
k
xk x S
pp
p
=
=- + ¾¾¾® = Î
7
3
x
p
=
2sin 3 0.x -=
2sin 3 0.x +=
! Trang!10!
Lời giải. Với , suy ra . Chọn A
Cách 2. Thử lần lượt vào từng phương trình.
Câu 3. Tìm nghiệm dương nhỏ nhất của phương trình
A. B. C. D.
Lời giải. Ta có
TH1. Với
TH2. Với
So sánh hai nghiệm ta được là nghiệm dương nhỏ nhất. Chọn C
Câu 4. Số vị trí biểu diễn các nghiệm của phương trình trên đường
tròn lượng giác là?
A. . B. . C. . D. .
Lời giải. Ta có
Quá dễ để nhận ra có 4 vị trí biểu diễn nghiệm của phương trình đã cho trên đường tròn lượng giác
là A, B, C, D. Chọn A
Cách trắc nghiệm. Ta có có vị trí biểu diễn.
7
3
x
p
=
73
sin sin
2sin 3 0
32
7 1 2 cos 1 0
cos cos
32
x
x
x
x
p
p
ì
==
ï
ì
-=
ïï
Û
íí
-=
ï
î
ï
==
ï
î
7
3
x
p
=
2sin 4 1 0.
3
x
p
æö
--=
ç÷
èø
.
4
x
p
=
7
.
24
x
p
=
.
8
x
p
=
.
12
x
p
=
1
2sin 4 1 0 sin 4 sin 4 sin
33236
xxx
pppp
æö æö æö
--=Û -=Û -=
ç÷ ç÷ ç÷
èø èø èø
( )
42
42
36
282
.
7
7
42
42
6
36
24 2
k
xk
xk x
k
k
xk
xk
x
pp
ppp
p
p
p
pp
pp
p
pp
é
éé
-=+
=+ =+
ê
êê
ÛÛÛÎ
ê
êê
ê
êê
=+
-=-+
=+
ê
êê
ëë
ë
!
Cho 0
min
1
00.
82 82 4 8
kk
xkkx
pp pp p
>
=+ ¾¾¾¾®+ >Û>-® =Þ=
Cho 0
min
77 7 7
00.
24 2 24 2 12 24
kk
xkkx
pp pp p
>
=+¾¾¾¾®+>Û>-® =Þ=
8
x
p
=
tan 2 3 0
3
x
p
æö
-+=
ç÷
èø
4
3
2
1
tan 2 3 0 tan 2 3 tan 2 tan
3333
xxx
pppp
æö æö æöæö
-+=Û -=-Û -= -
ç÷ ç÷ ç÷ç÷
èø èø èøèø
( )
22 .
33 2
k
xkxkxk
pp p
pp
Û-=-+ Û= Û= Î!
2
24
k
xk
pp
== ¾¾®
4
O
C
D
A
B
! Trang!11!
Câu 5. Hỏi trên đoạn , phương trình có bao nhiêu nghiệm?
A. B. C. D.
Lời giải. Ta có
Theo giả thiết, ta có
. Vậy có tất cả giá trị nguyên của tương ứng với có
nghiệm thỏa mãn yêu cầu bài toán. Chọn D
Câu 6. Trong các phương trình sau, phương trình nào tương đương với phương trình
?
A. B. C. D.
Lời giải. Ta có . Mà
Do đó . Vậy Chọn D
Câu 7. Phương trình nào dưới đây có tập nghiệm trùng với tập nghiệm của phương trình
?
A. B. C. D.
Lời giải. Ta có
Vậy . Chọn B
Câu 8. Giải phương trình .
A. B.
C. D.
Lời giải. Ta có .
= Với
= Với
[ ]
0; 2018
p
3cot 3 0x -=
6339.
6340.
2017.
2018.
( )
cot 3 cot cot .
66
xxxkk
pp
p
=Û = Û=+ Î!
xap xi
1
02018 2017,833
66
kk
p
pp
£+ £ ¾¾¾®-££
{ }
30;1;...;2017
k
k
Î
¾¾¾® Î
!
2018
k
2018
2
2cos 1x =
2
sin .
2
x =
2sin 2 0.x +=
tan 1.x =
2
tan 1.x =
22
1
2cos 1 cos
2
xx=Û =
22 2
1
sin cos 1 sin .
2
xx x+=¾¾®=
2
2
2
sin
tan 1
cos
x
x
x
==
22
2cos 1 tan 1.xx=Û =
2
tan 3x =
1
cos .
2
x =-
2
4cos 1.x =
1
cot .
3
x =
1
cot .
3
x =-
2
222
2
sin
tan 3 3 sin 3cos
cos
x
xxx
x
=Û =Û =
22 2
1cos 3cos 4cos 1.xx xÛ- = Û =
22
tan 3 4 cos 1xx=Û =
2
4sin 3x =
( )
2
3
, .
2
3
xk
k
xk
p
p
p
p
é
=+
ê
Î
ê
ê
=- +
ê
ë
!
( )
2
3
, .
2
2
3
xk
k
xk
p
p
p
p
é
=+
ê
Î
ê
ê
=+
ê
ë
!
( )
, .
33
3
k
x
k
k
pp
ì
=+
ï
Î
í
ï
¹
î
!"
!
( )
, .
3
3
k
x
k
k
p
ì
=
ï
Î
í
ï
¹
î
!"
!
22
33
4sin 3 sin sin
42
xxx=Û = Û =±
( )
2
3
3
sin sin sin .
2
23
2
3
xk
xx k
xk
p
p
p
p
p
é
=+
ê
=Û = Û Î
ê
ê
=+
ê
ë
!
( )
2
3
3
sin sin sin .
4
23
2
3
xk
xx k
xk
p
p
p
p
p
é
=- +
ê
æö
=- Û = - Û Î
ê
ç÷
èø
ê
=+
ê
ë
!
! Trang!12!
Nhận thấy chưa có đáp án nào phù hợp. Ta biểu diễn các nghiệm trên đường tròn lượng giác (hình
vẽ).
Nếu tính luôn hai điểm A, B thì có tất cả 6 điểm cách đều nhau nên ta gộp được 6 điểm này thành
một họ nghiệm, đó là .
Suy ra nghiệm của phương trình Chọn D
Câu 9. Trong các phương trình sau, phương trình nào tương đương với phương trình
?
A. B. C. D.
Lời giải. Ta có . Chi hai vế phương trình cho ta được .
Chọn D
Câu 10. Với thuộc , hỏi phương trình có bao nhiêu nghiệm?
A. B. C. D.
Lời giải. Phương trình
= Với .
có nghiệm.
= Với .
có nghiệm.
Vậy phương trình đã cho có nghiệm. Chọn D
Câu 11. Có tất cả bao nhiêu giá trị nguyên của tham số để phương trình
có nghiệm?
A. B. C. D. Vô số.
3
xk
p
=
( )
3
, .
3
3
3
k
xk
x
k
k
kl
p
p
p
p
ì
=
ì
ï
=
ïï
ÛÎ
íí
ïï
¹
¹
î
ï
î
!"
!
22
3sin cosxx=
1
sin .
2
x =
3
cos .
2
x =
2
3
sin .
4
x =
2
cot 3.x =
22
3sin cosxx=
2
sin ,x
2
cot 3x =
x
( )
0;1
( )
2
3
cos 6
4
x
p
=
8.
10.
11.
12.
( ) ( )
2
33
cos 6 cos 6 .
42
xx
pp
=Û =±
3
cos 6 cos 6 cos 6 2
266
xxxk
pp
pppp
=Û = Û =±+
( )
( )
{ }
{ }
1
135
0;1
0;1; 2
36 3
12 12
1137
0;1 1; 2;3
36 3 12 12
k
k
k
x
kk
k
xkk
Î
Î
é
é
=+Î
-<< ¾¾¾®=
ê
ê
ÛÛ ®
ê
ê
ê
ê
=- + Î < < ¾¾¾® =
ê
ê
ë
ë
!
!
6
355
cos 6 cos 6 cos 6 2
266
xxxk
pp
pppp
=- Û = Û =± +
( )
( )
{ }
{ }
5
531
0;1
0;1; 2
36 3
12 12
5541
0;1 1; 2;3
36 3 12 12
k
k
k
x
kk
k
xkk
Î
Î
é
é
=+Î
- < < ¾¾¾® =
ê
ê
ÛÛ ®
ê
ê
ê
ê
= - + Î < < ¾¾¾® =
ê
ê
ë
ë
!
!
6
12
m
3cos 1 0xm+-=
1.
2.
3.
O
! Trang!13!
Lời giải. Ta có .
Phương trình có nghiệm
Vậy có tất cả 3 giá trị nguyên của tham số . Chọn C
Câu 12. Có bao nhiêu giá trị nguyên của tham số thuộc đoạn để phương
trình có nghiệm?
A. B. C. D.
Lời giải. Ta có
Phương trình có nghiệm
.
Vậy có tất cả giá trị nguyên của tham số . Chọn A
Câu13. Tìm giá trị thực của tham số để phương trình nhận
làm nghiệm.
A. B. C. D.
Lời giải. Vì là một nghiệm của phương trình nên ta có:
.
Vậy là giá trị cần tìm. Chọn C
Câu 14. Tìm tất cả các giá trị của tham số để phương trình có
nghiệm.
A. B. C. D.
Lời giải. Phương trình
Để phương trình có nghiệm
là giá trị cần tìm. Chọn B
Câu 15. Tìm tất cả các giá trị của tham số để phương trình vô
nghiệm.
A. B.
C. D.
1
3cos 1 0 cos
3
m
xm x
-
+-=Û =
{ }
1
111313 0;1;2.
3
m
m
mm
Î
-
Û- £ £ Û - £ £ + ¾¾¾® Î
!
m
m
[ ]
2108; 2018-
cos 1 0mx+=
2018.
2019.
4036.
4038.
1
cos 1 0 cos .mx x
m
+= Û =-
[ ]
{ }
2018;2018
1
111 1;2;3;...;2018
m
m
mm
m
Î
Î-
Û- £- £ Û ³ ¾¾¾¾¾¾¾® Î
!
2018
m
m
( )
2sin2 1mxm-=+
12
x
p
=
2.m ¹
( )
231
.
32
m
+
=
-
4.m =-
1.m =-
12
x
p
=
( )
2sin2 1mxm-=+
( )
22
2 .sin 1 1 2 2 2 4
12 2
m
mm mmmm
p
-
-=+Û=+Û-=+Û=-
4m =-
m
( )
1sin 2 0mxm++-=
1.m £-
1
.
2
m ³
1
1.
2
m-< £
1.m >-
( ) ( )
2
1 sin 2 0 1 sin 2 sin .
1
m
mxm mxm x
m
-
++-=Û+=-Û=
+
2
11
1
m
m
-
Û- £ £
+
1
221
01 0
2
1
11
1
23
2
10 0
11
1
mm
m
mm
m
m
m
mm
m
ì
é
--
ìì
³
£+ ³
ï
ê
ïï
ïïï
++
ê
ÛÛÛÛ³
ííí
<-
-
ë
ïïï
-£ - £
ïï
ï
++
>-
îî
î
m
( )
2sin2 1mxm-=+
1
;2 .
2
m
éù
Î
êú
ëû
( )
1
;2;.
2
m
æö
Î-¥ È +¥
ç÷
èø
( )
1
;2 2; .
2
m
æö
ÎÈ+¥
ç÷
èø
1
;.
2
m
æö
Î+¥
ç÷
èø
! Trang!14!
Lời giải. TH1. Với , phương trình : vô lý.
Suy ra thì phương trình đã cho vô nghiệm.
TH2. Với , phương trình
Để phương trình vô nghiệm
Kết hợp hai trường hợp, ta được là giá trị cần tìm. Chọn D
Vấn đề 2. PHƯƠNG TRÌNH BẬC NHẤT ĐỐI VỚI và
Câu 16. Gọi là tập nghiệm của phương trình . Khẳng định nào sau đây là
đúng?
A. B. C. D.
Lời giải. Phương trình
Xét nghiệm , với ta được Chọn C
Câu 17. Số nghiệm của phương trình trên khoảng là?
A. B. C. D.
Lời giải. Phương trình
= không có giá trị thỏa mãn.
= Chọn A
Câu 18. Tính tổng các nghiệm của phương trình trên
khoảng
A. B. C. D.
Lời giải. Phương trình
2m =
( )
2sin2 1 0 3mxm-=+Û=
2m =
2m ¹
( )
1
2 sin 2 1 sin 2 .
2
m
mxm x
m
+
-=+Û=
-
( )
*
[ ]
1
2
1
1
2
1;1 .
1
1
2
2
1
2
2
m
m
m
m
m
m
m
m
+
é
>
>
é
ê
+
-
ê
ÛÏ-Û Û
ê
ê
+
-
<<
ê
<-
ë
ê
-
ë
1
2
m >
sin x
cos x
S
cos 2 sin 2 1xx-=
.
4
S
p
Î
.
2
S
p
Î
3
.
4
S
p
Î
5
.
4
S
p
Î
1
2cos 2 1 cos 2
44
2
xx
pp
æö æö
Û+=Û+=
ç÷ ç÷
èø èø
22
44
cos 2 cos , .
44
22
4
44
xk
xk
xk
xk
xk
pp
p
p
pp
p
pp
p
p
é
=
+=+
é
ê
æö
ê
Û+=Û Û Î
ê
ç÷
ê
=- +
èø
ê
+=-+
ë
ê
ë
!
4
xk
p
p
=- +
1k =
3
.
4
x
p
=
sin 2 3 cos 2 3xx+=
0;
2
p
æö
ç÷
èø
1.
2.
3.
4.
13 3 3
sin 2 cos 2 sin 2
22 2 32
xx x
p
æö
Û+ =Û+=
ç÷
èø
22
33
sin 2 sin , .
33
22
6
33
xk
xk
xk
xk
xk
pp
p
p
pp
p
pp
p
pp
é
=
+=+
é
ê
æö
ê
Û+=Û Û Î
ê
ç÷
ê
=+
èø
ê
+=-+
ë
ê
ë
!
1
00
22
k
kk
p
p
Î
<<Û<<¾¾¾®
!
k
11
00.
6263 6
k
kkkx
pp p
p
Î
<+ <Û-<<¾¾¾®=®=
!
T
22
cos sin 2 2 sinxx x-=+
( )
0; 2 .
p
7
.
8
T
p
=
21
.
8
T
p
=
11
.
4
T
p
=
3
.
4
T
p
=
22
cos sin sin 2 2 cos 2 sin 2 2xxx xxÛ--=Û-=
! Trang!15!
Do
Chọn C
Câu 19. Tìm nghiệm dương nhỏ nhất của
A. B. C. D.
Lời giải. Phương trình
So sánh hai nghiệm ta được nghiệm dương nhỏ nhất là Chọn B
Cách trắc nghiệm. Thử từng nghiệm của đáp án vào phương trình và so sánh nghiệm nào thỏa
mãn phương trình đồng thời là nhỏ nhất thì ta chọn.
Câu 20. Số nghiệm của phương trình trên khoảng là?
A. B. C. D.
Lời giải. Phương trình
=
( )
cos 2 1 2 2 .
44 8
xxkxkk
pp p
pp
æö
Û+=Û+=Û=-+Î
ç÷
èø
!
7
1
117
8
02 0 2
15
888
2
8
k
kx
xkk
kx
p
p
ppp
p
Î
é
=® =
ê
<< ¾¾®<- + < Û<< ¾¾¾®
ê
ê
=®=
ê
ë
!
71511
.
884
T
pp
p
¾¾® = + =
0
x
3
3sin 3 3 cos 9 1 4 sin 3 .xx x-=+
0
.
2
x
p
=
0
.
18
x
p
=
0
.
24
x
p
=
0
.
54
x
p
=
3
3sin 3 4 sin 3 3 cos 9 1 sin 9 3 cos 9 1xx x x xÛ- - =Û- =
131 1
sin 9 cos 9 sin 9
22 2 32
xx x
p
æö
Û- =Û-=
ç÷
èø
2
92
36 18 9
sin 9 sin
72
36
92
36 549
k
xk x
x
k
xkx
pp p p
p
pp
pp pp
pp
éé
-=+ = +
êê
æö
Û-=Û Û
êê
ç÷
èø
êê
-=-+ = +
êê
ëë
min
Cho 0
min
21
00
18 9 4 18
.
72 7 7
00
54 9 12 54
k
k
k
kkx
k
kkx
pp p
pp p
Î
>
Î
é
+>Û>-¾¾¾®=®=
ê
¾¾¾¾®
ê
ê
+>Û>-¾¾¾®=®=
ê
ë
!
!
.
18
x
p
=
sin 5 3 cos 5 2sin 7xxx+=
0;
2
p
æö
ç÷
èø
2.
1.
3.
4.
13
sin 5 cos 5 sin 7 sin 5 sin 7
22 3
xxxx x
p
æö
Û+ =Û+=
ç÷
èø
( )
75 2
3
6
sin 7 sin 5 .
3
75 2
3
18 6
xx k
xk
xx k
k
xxk
x
p
p
p
p
p
p
pp
pp
é
é
=++
=+
ê
ê
æö
ê
Û= +Û Û Î
ê
ç÷
æö
èø
ê
ê
=- + +
=+
ç÷
ê
ê
ë
èø
ë
!
11
00.
6263 6
k
kkkx
pp p
p
Î
<+ <Û-<<¾¾¾®=®=
!
! Trang!16!
=
Vậy có nghiệm thỏa mãn. Chọn D
Câu 21. Giải phương trình
A. B.
C. D.
Lời giải. Ta có và .
Do đó phương trình
Xét nghiệm .
Vậy phương trình có nghiệm Chọn B
Câu 22. Gọi là nghiệm âm lớn nhất của . Mệnh
đề nào sau đây là đúng?
A. B. C. D.
Lời giải. Phương trình
0
18
18 2
01.
18 6 2 3 3 9
7
2
18
k
kx
kkkx
kx
p
ppp p
p
Î
é
=®=
ê
ê
ê
<+ <Û-<<¾¾¾®=®=
ê
ê
ê
=®=
ê
ë
!
4
3 cos sin 2 sin 2 .
22
xx x
pp
æöæö
++ -=
ç÷ç÷
èøèø
5
2
6
, .
2
18 3
xk
k
xk
p
p
pp
é
=+
ê
Î
ê
ê
=+
ê
ë
!
7
2
6
, .
2
18 3
xk
k
xk
p
p
pp
é
=+
ê
Î
ê
ê
=- +
ê
ë
!
5
2
6
, .
7
2
6
xk
k
xk
p
p
p
p
é
=+
ê
Î
ê
ê
=+
ê
ë
!
2
18 3
, .
2
18 3
xk
k
xk
pp
pp
é
=+
ê
Î
ê
ê
=- +
ê
ë
!
cos sin
2
xx
p
æö
+=-
ç÷
èø
sin cos
2
xx
p
æö
-=-
ç÷
èø
3sin cos 2sin2 3sin cos 2sin2xx x xx xÛ- - = Û + =-
( )
31
sin cos sin 2 sin sin 2 sin sin 2
22 6 6
xx x x x x x
pp
æö æö
Û+=-Û+=-Û+=-
ç÷ ç÷
èø èø
( )
2
22
6183
.
5
22 2
66
xxk xk
k
xxkxk
ppp
p
pp
pp p
éé
+=-+ =-+
êê
ÛÛÎ
êê
êê
+=+ + =- -
êê
ëë
!
1'
, '
57
2'2
66
kk
kk
xk xk
pp
pp
=- -
ÎÎ
=- - ¾¾¾¾¾® = +
!!
( )
27
, '2 , ' .
18 3 6
xkxkkk
pp p
p
=- + = + Î!
0
x
sin 9 3 cos 7 sin 7 3 cos 9xxxx+=+
0
;0 .
12
x
p
æö
Î-
ç÷
èø
0
;.
6 12
x
pp
éù
Î- -
êú
ëû
0
;.
36
x
pp
éö
Î- -
÷
ê
ëø
0
;.
23
x
pp
éö
Î- -
÷
ê
ëø
sin 9 3 cos 9 sin 7 3 cos 7xxxxÛ- =-
97 2
33
sin 9 sin 7
5
33
972
48 8
33
xxk
xk
xx
k
x
xxk
pp
p
p
pp
pp
pp
pp
é
-= -+
=
é
ê
æöæö
ê
ê
Û-=-Û Û
ç÷ç÷
ê
æö
=+
èøèø
ê
-=- - +
ë
ç÷
ê
èø
ë
! Trang!17!
So sánh hai
nghiệm ta được nghiệm âm lớn nhất của phương trình là Chọn A
Câu 23. Biến đổi phương trình về dạng
với , thuộc khoảng . Tính .
A. B. C. D.
Lời giải. Phương trình
Suy ra Chọn D
Câu 24. Giải phương trình
A. B.
C. D.
Lời giải. Điều kiện
Điều kiện bài toán tương đương với bỏ đi vị trí hai điểm trên đường tròn lượng giác (Hình 1).
Phương trình
max
Cho 0
max
00 1
.
55
01
48 8 6 48
k
k
kk k x
k
kkx
pp
pp p
Î
<
Î
é
<Û<¾¾¾® =-®=-
ê
¾¾¾¾®
ê
+<Û<-¾¾¾® =-®=-
ê
ë
!
!
;0 .
48 12
x
pp
æö
=- Î -
ç÷
èø
( )
cos 3 sin 3 cos sin 3xx x x-= -
( ) ( )
sin sinax b cx d+= +
b
d
;
22
pp
æö
-
ç÷
èø
bd+
.
12
bd
p
+=
.
4
bd
p
+=
.
3
bd
p
+=-
.
2
bd
p
+=
3sin3 cos3 sin 3cosxxx xÛ+=+
31 1 3
sin 3 cos 3 sin cos sin 3 sin .
2222 6 3
xxx x x x
pp
æöæö
Û+=+Û+=+
ç÷ç÷
èøèø
.
63 2
bd
pp p
+= + =
cos 3 sin
0.
1
sin
2
xx
x
-
=
-
, .
6
xkk
p
p
=+ Î!
2, .
6
xkk
p
p
=+ Î!
7
2, .
6
xkk
p
p
=+ Î!
7
, .
6
xkk
p
p
=+ Î!
( )
2
11
6
sin 0 sin sin sin .
5
226
2
6
xk
xxx k
xk
p
p
p
p
p
ì
¹+
ï
ï
-¹Û ¹Û ¹ Û Î
í
ï
¹+
ï
î
!
cos 3 sin 0 cos 3 sinxx x xÛ- =Û=
( )
cot 3 cot cot .
66
xxxll
pp
p
Û=Û= Û=+Î!
O
Hình 1
! Trang!18!
Biểu diễn nghiệm trên đường tròn lượng giác ta được 2 vị trí như Hình 2.
Đối chiếu điều kiện, ta loại nghiệm . Do đó phương trình có nghiệm
Chọn C
Câu 25. Hàm số có tất cả bao nhiêu giá trị nguyên?
A. B. C. D.
Lời giải. Ta có
Điều kiện để phương trình có nghiệm
nên có giá trị nguyên. Chọn B
Câu 26. Gọi là nghiệm dương nhỏ nhất của
Mệnh đề nào sau đây là đúng?
A. B. C. D.
Lời giải. Phương trình
.
Đặt
Phương trình trở thành
=
6
xl
p
p
=+
2
6
xk
p
p
=+
( )
7
2 .
6
xll
p
p
=+ Î!
2sin 2 cos 2
sin 2 cos 2 3
xx
y
xx
+
=
-+
1.
2.
3.
4.
( ) ( )
2sin 2 cos 2
2 sin 2 1 cos 2 3 .
sin 2 cos 2 3
xx
yyxyxy
xx
+
=Û--+=-
-+
( ) ( ) ( )
222
2
2137250yy yyyÛ- ++ ³- Û +-£
{ }
5
11;0
7
y
yy
Î
Û- £ £ ¾¾¾® Î -
!
2
0
x
cos 2 3 sin 2 3 sin cos 2.xxxx++-=
0
0; .
12
x
p
æö
Î
ç÷
èø
0
;.
12 6
x
pp
éù
Î
êú
ëû
0
;.
63
x
pp
æù
Î
ç
ú
èû
0
;.
32
x
pp
æù
Î
ç
ú
èû
1331
cos 2 sin 2 sin cos 1
22 22
xxxxÛ+ +-=
sin 2 sin 1
66
xx
pp
æöæö
Û++-=
ç÷ç÷
èøèø
22 2 2 .
66362
tx xt x t x t
ppppp
=- ¾¾®=+ ® = + ® + = +
sin 2 sin 1 cos 2 sin 1
2
tt tt
p
æö
Û++=Û+=
ç÷
èø
( )
2
2sin sin 0 sin 2sin 1 0.tt t tÛ-=Û -=
min
1
sin 0 0 0 .
66 6
k
ttk xk k k x
pp
pp
Î
=Û= ¾¾®= + >Û>-¾¾¾® =®=
!
O
Hình 2
! Trang!19!
=
Suy ra nghiệm dương nhỏ nhất của phương trình là Chọn B
Câu 27. Có bao nhiêu giá trị nguyên của tham số thuộc đoạn để phương trình
vô nghiệm.
A. B. C. D.
Lời giải. Phương trình vô nghiệm
có giá trị. Chọn C
Câu 28. Tìm tất cả các giá trị thực của tham số để phương trình
vô nghiệm.
A. B.
C. D.
Lời giải. Phương trình vô nghiệm
Chọn D
Câu 29. Có bao nhiêu giá trị nguyên của tham số thuộc đoạn để phương trình
có nghiệm.
A. B. C. D.
Lời giải. Phương trình có nghiệm
có giá trị. Chọn C
Câu 30. Có bao nhiêu giá trị nguyên của tham số thuộc đoạn để phương
trình có nghiệm.
A. B. C. D.
Lời giải. Phương trình
Phương trình có nghiệm
có giá trị. Chọn D
min
min
1
220 0.
1
63 6 3
sin
51
2
220 0.
62
k
k
tk xk k k x
t
tk xk k k x
pp p
pp
p
ppp p
Î
Î
é
=+ ¾¾®=+ >Û>-¾¾¾® =®=
ê
=Û
ê
ê
=+ ¾¾®=+ >Û>-¾¾¾® =®=
ê
ë
!
!
;.
6 12 6
x
ppp
éù
=Î
êú
ëû
m
[ ]
10 ;10-
sin 3 cos 2
33
xxm
pp
æö æö
-- -=
ç÷ ç÷
èø èø
21.
20.
18.
9.
( )
( )
2
2
22
1
132 440
1
m
mm
m
<-
é
Û+- < Û ->Û
ê
>
ë
[ ]
{ }
10;10
10 ; 9 ; 8;...; 2;2 ;...;8;9;10
m
m
m
Î
Î-
¾¾¾¾¾® Î - - - - ¾¾®
!
18
m
( )
2
cos sin 2 1xx m+= +
( ) ( )
;1 1; .mÎ-¥- È +¥
[ ]
1; 1 .mÎ-
( )
;mÎ-¥+¥
( ) ( )
;0 0; .mÎ-¥ È +¥
( )
2
22 2
11 2 1m
éù
Û+< +
êú
ëû
( )
42 22 2
20 20 0 0.mm mm m mÛ+ >Û +>Û>Û¹
m
[ ]
10 ;10-
( )
1sin cos 1mxmxm+- =-
21.
20.
18.
11.
( ) ( )
22
22
0
11 40
4
m
mmmmm
m
³
é
Û++ ³- Û + ³Û
ê
£-
ë
[ ]
{ }
10;10
10 ; 9 ; 8;...; 4;0;1; 2 ;...;8;9;10
m
m
m
Î
Î-
¾¾¾¾¾® Î - - - - ¾¾®
!
18
m
[ ]
2018; 2018-
( )
2
1sin sin2 cos2 0mxxx+-+=
4037.
4036.
2019.
2020.
( )
1cos2
1 sin 2 cos 2 0
2
x
mxx
-
Û+ - + =
( )
2sin 2 1 cos 2 1.xmxmÛ- + - =- -
( ) ( ) ( )
22 2
21 1 44 1mm m mÛ- + - ³- - Û £ Û £
[ ]
{ }
2018;2018
2018; 2017;...; 0 ;1
m
m
m
Î
Î-
¾¾¾¾¾¾¾® Î - - ¾¾®
!
2020
! Trang!20!
Vấn đề 3. PHƯƠNG TRÌNH BẬC HAI
ĐỐI VỚI MỘT HÀM SỐ LƯỢNG GIÁC
Câu 31. Hỏi trên , phương trình có bao nhiêu nghiệm?
A. B. C. D.
Lời giải. Phương trình
Theo giả thiết
Vậy phương trình có duy nhất một nghiệm trên . Chọn A
Câu 32. Số vị trí biểu diễn các nghiệm của phương trình trên đường
tròn lượng giác là?
A. B. C. D.
Lời giải. Phương trình
Suy ra có duy nhất 1 vị trí biểu diễn nghiệm của phương trình trên đường tròn lượng giác. Chọn A
Câu 33. Cho phương trình Đặt , ta được phương trình
nào sau đây?
A. B. C. D.
Lời giải. Chọn A
Câu 34. Số nghiệm của phương trình trên là?
A. 3. B. 4. C. 2. D. 1.
Lời giải. Phương trình
0;
2
p
éö
÷
ê
ëø
2
2sin 3sin 1 0xx-+=
1.
2.
3.
4.
2
1
sin
2 sin 3sin 1 0
2
sin 1
x
xx
x
é
=
ê
-+=Û
ê
=
ë
( )
2
6
sin sin
5
2 .
6
6
sin 1
2
2
xk
x
xkk
x
xk
p
p
p
p
p
p
p
é
=+
ê
ê
é
=
ê
ê
ÛÛ=+Î
ê
ê
=
ê
ë
ê
=+
ê
ë
!
11
02 0
6 2 12 6 6
551
002 .
2 6 2 12 12
1
0
02
4
22
k
k
k
kkkx
xk kk
kk
k
pp p
p
ppp
p
pp
p
Î
Î
Î
éé
£+ < - <<¾¾¾®=®=
êê
êê
êê
£< Û £ + < Û- <<- ¾¾¾®ÎÆ
êê
êê
êê
-<<¾¾¾®ÎÆ
£+ <
êê
ëë
!
!
!
0;
2
p
éö
÷
ê
ëø
2
2cos 5cos 3 0xx++=
1.
2.
3.
4.
( )
2
cos 1
2 cos 5 cos 3 0
3
cos
2
x
xx
x
=-
é
ê
Û++=Û
ê
=-
ë
loaÔi
( )
cos 1 2 .xxkk
pp
Û=-Û=+ Î!
2
cot 3 3 cot 3 2 0.xx-+=
cot 3tx=
2
320.tt-+=
2
3920.tt-+=
2
920.tt-+=
2
620.tt-+=
( )
2
4 sin 2 2 1 2 sin 2 2 0xx-+ +=
( )
0;
p
( )
2
2
sin 2
2
4sin 2 2 1 2 sin 2 2 0 .
1
sin 2
2
x
xx
x
é
=
ê
ê
-+ +=Û
ê
=
ê
ë
! Trang!21!
=
=
Vậy có tất cả 4 nghiệm thỏa mãn. Chọn B
Câu 35. Số nghiệm của phương trình trên đoạn là?
A. B. C. D.
Lời giải. Phương trình
Do
Vậy phương trình có 6 nghiệm thỏa mãn. Chọn C
Câu 36. Tính tổng tất cả các nghiệm của phương trình trên đoạn
A. B. C. D.
Lời giải. Phương trình
Chọn B
Câu 37. Số nghiệm của phương trình trên là?
A. B. C. D.
Lời giải. Điều kiện:
Phương trình
( )
( )
0;
0;
22
2
88
4
sin 2 sin .
33 3
24
22
48 8
xk x
xk
x
xk xk x
p
p
pp
p
p
p
p
pp p
pp
é
é
=+ ¾¾¾®=
=+
ê
ê
== Û Û
ê
ê
ê
ê
=+ =+¾¾¾®=
ê
ê
ë
ë
( )
( )
0;
0;
22
1
6
12 12
sin 2 sin .
55 5
26
22
612 12
xk
xk x
x
xkxk x
p
p
p
pp
p
p
p
pp p
pp
é
é
=+
=+¾¾¾®=
ê
ê
== Û Û
ê
ê
ê
ê
=+ =+¾¾¾®=
ê
ê
ë
ë
2
sin 2 cos 2 1 0xx-+=
[ ]
;4
pp
-
2.
4.
6.
8.
22
sin 2 cos 2 1 0 cos 2 cos 2 2 0xx xx-+=Û- -+=
( )
cos 2 1
cos 2 1 2 2 , .
cos 2 2
x
xxkxkk
x
pp
=
é
ÛÛ=Û=Û=Î
ê
=-
ë
!
loaÔi
[ ]
{ }
;4 4 1 4 1;0;1;2;3;4 .
k
xkkk
pp p p p
Î
Î- ¾¾®- £ £ Û- £ £ ¾¾¾® Î-
!
T
2
2sin 3cos 0
44
xx
-=
[ ]
0;8 .
p
0.T =
8.T
p
=
16 .T
p
=
4.T
p
=
22
2sin 3cos 0 2 1 cos 3cos 0
44 4 4
xx x x
æö
-=Û- -=
ç÷
èø
( )
2
1
cos
1
42
2cos 3cos 2 0 cos cos cos
44 4243
cos 2
4
x
xx x x
x
p
é
=
ê
Û- - + = Û Û = Û =
ê
ê
=-
ê
ë
loaÔi
[ ]
[ ]
0; 8
0; 8
44
28
420
43 3 3
8.
420
33
28
43 3 3
x
x
x
kxk x
T
x
kx k x
p
p
pp p
pp
pp
p
pp p
pp
Î
Î
éé
=+ = + ¾¾¾¾®=
êê
ÛÛ ®=+=
êê
êê
=- + =- + ¾¾¾¾® =
êê
ëë
( ) ( )
2
1
31cot 31 0
sin
x
x
-- -+=
( )
0;
p
1.
2.
3.
4.
( )
sin 0 .xxkk
p
¹Û¹ Î!
( )
( ) ( ) ( )
22
1cot 31cot 31 0 cot 31cot 3 0xx xxÛ+ - - - +=Û - - - =
! Trang!22!
Vậy phương trình đã cho có 2 nghiệm thỏa mãn. Chọn B
Câu 38. Tính tổng tất cả các nghiệm của phương trình trên
đoạn .
A. B. C. D.
Lời giải. Phương trình
Chọn
A
Câu 39. Số vị trí biểu diễn các nghiệm của phương trình trên đường
tròn lượng giác là?
A. B. C. D.
Lời giải. Phương trình
Suy ra có duy nhất 1 vị trí đường tròn lượng giác biểu diễn nghiệm. Chọn A
Câu 40. Cho phương trình . Nếu đặt , ta được phương trình nào
sau đây?
A. B. C. D.
Lời giải. Ta có
Do đó phương trình
Đặt , phương trình trở thành Chọn A
Câu 41. Số nghiệm của phương trình thuộc là?
A. B. C. D.
( )
( )
( )
( )
0;
0;
3
cot cot
cot 1
4
44
.
cot 3
cot cot
66
6
x
x
x
xk x
x
x
xk x
x
p
p
p
pp
p
pp
p
p
Î
Î
é
æö
é
=-
=- + ¾¾¾¾® =
ç÷
ê
ê
=-
é
èø
ê
ÛÛ Û
ê
ê
=
ê
ê
ë
=+ ¾¾¾¾®=
=
ê
ê
ë
ë
tho˚a maın
tho˚a maın
T
2cos 2 2cos 2 0xx+-=
[ ]
0; 3
p
17
.
4
T
p
=
2.T
p
=
4.T
p
=
6.T
p
=
( )
2
2cos2 2cos 2 0 2 2cos 1 2cos 2 0xx x x+-=Û -+-=
( )
2
2
cos
2
2
4 cos 2 cos 2 2 0 cos
2
21
cos
2
x
xx x
x
é
=
ê
ê
Û+--=Û Û=
ê
+
=-
ê
ë
loaÔi
[ ]
[ ]
0;3
0;3
9
2;
9717
444
.
7
44 4 4
2
44
x
x
xk xx
T
xk x
p
p
ppp
p
ppp p
pp
p
Î
Î
é
=+ ¾¾¾¾®= =
ê
Û¾¾®=++=
ê
ê
=- + ¾¾¾¾® =
ê
ë
cos 2 3sin 4 0xx++=
1.
2.
3.
4.
( )
22
1 2 sin 3sin 4 0 2sin 3sin 5 0xx xxÛ- + +=Û- + +=
( )
( )
sin 1
sin 1 2 .
5
2
sin
2
x
xxkk
x
p
p
=-
é
ê
ÛÛ=-Û=-+Î
ê
=
ë
!
loaÔi
cos cos 1 0
2
x
x ++=
cos
2
x
t =
2
20.tt+=
2
210.tt-++=
2
210.tt+-=
2
20.tt-+=
2
cos 2 cos 1.
2
x
x =-
22
2cos 1 cos 1 0 2cos cos 0.
22 22
xx xx
æö
Û-++=Û+=
ç÷
èø
cos
2
x
t =
2
20.tt+=
5
cos 2 4 cos
362
xx
pp
æö æö
++ -=
ç÷ ç÷
èø èø
[ ]
0; 2
p
1.
2.
3.
4.
! Trang!23!
Lời giải. Ta có .
Do đó phương trình
.
Ta có ; .
Vậy có hai nghiệm thỏa mãn. Chọn B
Câu 42. Tìm tất cả các giá trị thực của tham số để phương trình có
nghiệm.
A. B. C. D.
Lời giải. Phương trình
.
Để phương trình đã cho có nghiệm khi và chỉ khi .
Chọn D
Câu 43. Tìm tất cả các giá trị thực của tham số để phương trình
có nghiệm trên khoảng .
A. . B. . C. . D. .
Lời giải. Phương trình
Nhận thấy phương trình không có nghiệm trên khoảng (Hình vẽ). Do đó
yêu cầu bài toán có nghiệm thuộc khoảng .
Chọn B
22
cos 2 1 2 sin 1 2 cos
336
xx x
ppp
æö æö æö
+=- +=- -
ç÷ ç÷ ç÷
èø èø èø
2
3
2cos 4cos 0
662
xx
pp
æö æö
Û- - + - - =
ç÷ ç÷
èø èø
( )
1
cos
2
62
1
6
cos 2 ,
626 3
3
2
cos
2
62
x
xk
xxk k
xk
x
p
p
p
ppp
p
p
p
p
é
æö
é
-=
=- +
ç÷
ê
ê
èø
æö
ê
ÛÛ-=Û-=±+ÛÎ
ê
ç÷
ê
èø
æö
ê
=+
-=
ê
ç÷
ê
ë
èø
ë
!
loaÔi
[ ]
0;2
11
2
66
x
xk x
p
pp
p
Î
=- + ¾¾¾¾® =
[ ]
0;2
2
22
x
xk x
p
pp
p
Î
=+ ¾¾¾¾®=
m
tan cot 8xm x+=
16.m >
16.m <
16.m ³
16.m £
2
tan cot 8 tan 8 tan 8 tan 0
tan
m
xm x x x xm
x
+=Û+=Û-+=
( )
2
4016mm
¢
D= - - ³ Û £
m
( )
cos 2 2 1 cos 1 0xm xm-+ ++=
3
;
22
pp
æö
ç÷
èø
10m-£ £
10m-£ <
10m-< <
1
1
2
m-£ <
( )
2
1
cos
2 cos 2 1 cos 0 .
2
cos
x
xm xm
xm
é
=
ê
Û-++=Û
ê
=
ë
1
cos
2
x =
3
;
22
pp
æö
ç÷
èø
cos xmÛ=
3
;10
22
m
pp
æö
Û- £ <
ç÷
èø
O
! Trang!24!
Câu 44. Biết rằng khi thì phương trình
có đúng nghiệm phân biệt thuộc khoảng . Mệnh đề nào sau đây là đúng?
A. B. . C. D.
Lời giải. Đặt .
Phương trình trở thành
Yêu cầu bài toán tương đương với:
= TH1: Phương trình có một nghiệm (có một nghiệm ) và một nghiệm
(có bốn nghiệm ) (Hình 1).
a Do .
a Thay vào phương trình , ta được
= TH2: Phương trình có một nghiệm (có hai nghiệm ) và một nghiệm
(có ba nghiệm ) (Hình 2).
a Do .
a Thay vào phương trình , ta được
Vậy thỏa mãn yêu cầu bài toán. Do Chọn D
Câu 45. Tìm tất cả các giá trị thực của tham số để phương trình
có đúng nghiệm thuộc khoảng
A. B. C. D.
Lời giải. Đặt . Phương trình trở thành
0
mm=
( )
22
2sin 5 1 sin 2 2 0mxmmx -+ + +=
5
;3
2
p
p
æö
-
ç÷
èø
3.m =-
1
2
m =
0
37
;.
5 10
m
æù
Î
ç
ú
èû
0
32
;.
55
m
æö
Î- -
ç÷
èø
( )
sin 1 1tx t=-££
( )
22
2512 20.tm mm-++ +=
( )
*
( )
*
1
1t =-
x
2
01t<<
x
2
12
1
c
ttmm
a
=- ¾¾® =- =- -
1
1t =-
( )
*
( )( )
( )( )
2
2
3 6 0;1
.
11
0;1
24
mt
mt
é
= - ¾¾® = - Ï
ê
ê
= - ¾¾® = Î
ê
ë
loaÔi
tho˚a
( )
*
1
1t =
x
2
10t-< £
x
2
12
1
c
ttmm
a
=¾¾® = = +
1
1t =
( )
*
(
]
( )
(
]
( )
2
2
121;0
.
13
1; 0
24
mt
mt
é
=¾¾® = Ï-
ê
ê
=¾¾®=Ï-
ê
ë
loaÔi
loaÔi
1
2
m =-
132
;.
255
m
æö
=- Î - -
ç÷
èø
m
( )
2
2cos 3 3 2 cos3 2 0xmxm+- +-=
3
;.
63
pp
æö
-
ç÷
èø
1 1.m-£ £
1 2.m<£
1 2.m££
1 2.m£<
( )
cos 1 1tx t=-££
( )
2
232 20.tmtm+- +-=
O
O
Hình 1
Hình 2
! Trang!25!
Ta có . Suy ra phương trình có hai nghiệm
Ta thấy ứng với một nghiệm thì cho ta hai nghiệm thuộc khoảng Do đó
yêu cầu bài toán Chọn B
Cách 2. Yêu cầu bài toán tương đươn với phương trình có hai
nghiệm thỏa mãn
Vấn đề 4. PHƯƠNG TRÌNH BẬC NHẤT ĐỐI VỚI và
Câu 46. Giải phương trình
A. B.
C. D.
Lời giải. Phương trình
Chọn D
Câu 47. Gọi là tập nghiệm của phương trình .
Khẳng định nào sau đây là đúng?
A. B. C. D.
( )
2
25mD= -
1
2
1
.
2
2
t
tm
é
=
ê
ê
=-
ë
1
1
2
t =
x
;.
63
pp
æö
-
ç÷
èø
2
1012012.tm m-< £ Û-< - £ Û < £
( )
2
232 20tmtm+- +-=
12
, tt
( )
( )
21
0
101.10.
.10
P
tt af
af
ì
£
ï
-< £ < < Û >
í
ï
->
î
sin x
cos x
( )
22
sin 3 1 sin cos 3 cos 0.xxxx-+ + =
( )
2 .
3
xkk
p
p
=+ Î!
( )
.
4
xkk
p
p
=+ Î!
( )
2
3
.
2
4
xk
k
xk
p
p
p
p
é
=+
ê
Î
ê
ê
=+
ê
ë
!
( )
3
.
4
xk
k
xk
p
p
p
p
é
=+
ê
Î
ê
ê
=+
ê
ë
!
( )
2
t
tan 3 1 t
an 1
an
tan
3 0
3
x
x
x
xÛ-+ +=
=
=
Û
é
ê
ë
( )
4
.
3
xk
k
xk
p
p
p
p
é
=+
ê
ÛÎ
ê
ê
=+
ê
ë
!
S
22
2 sin 3 3 sin cos cos 2xxxx+-=
;.
3
S
p
p
ìü
Ì
íý
îþ
;.
62
S
pp
ìü
Ì
íý
îþ
5
;.
412
S
pp
ìü
Ì
íý
îþ
5
;.
26
S
pp
ìü
Ì
íý
îþ
O
! Trang!26!
Lời giải. Phương trình
=
=
Vậy tập nghiệm của phương trình chứa các nghiệm và . Chọn B
Câu 48. Trong các phương trình sau, phương trình nào tương đương với phương trình
.
A. . B. .
C. . D. .
Lời giải. Phương trình
=
=
Vậy phương trình đã cho tương đương với . Chọn D
Câu 49. Phương trình nào dưới đây có tập nghiệm trùng với tập nghiệm của phương trình
?
A. . B.
.
C. . D.
.
Lời giải. Phương trình
=
( )
2222
2sin 3 3 sin cos cos 2 sin cosxxxxxxÛ+ -= +
( )
2
3 3 sin cos 3cos 0 3cos 3 sin cos 0.xx x x x xÛ-=Û -=
( )
0
cos 0 .
22
k
xxkk x
pp
p
=
=Û= + Î ¾¾¾®=!
3sin cos 0 3sin cosxx x x-=Û =
( )
0
1
tan tan tan .
66 6
3
k
xxxkk x
pp p
p
=
Û=Û= Û=+ ξ¾¾®=!
6
p
2
p
( )
22
sin 3 1 sin cos 3 cos 3xxxx-+ + =
sin 0x =
sin 1
2
x
p
æö
+=
ç÷
èø
( )
31
cos 1 tan 0
13
xx
æö
+
--=
ç÷
ç÷
-
èø
( )
( )
2
tan 2 3 cos 1 0xx++ - =
( )
( )
2222
sin 3 1 sin cos 3 cos 3 sin cosxxxxxxÛ-+ + = +
( ) ( ) ( ) ( )
2
1 3 sin 3 1 sin cos 0 sin 1 3 sin 3 1 cos 0.xxxxx x
éù
Û- - + =Û - - + =
ëû
22
sin 0 cos 1 cos 1 0.xxx=Û =Û -=
( ) ( ) ( ) ( )
1 3 sin 3 1 cos 0 1 3 sin 3 1 cosxx x x--+=Û-=+
31
tan tan 2 3 tan 2 3 0.
13
xx x
+
Û= Û=--Û++=
-
( )
( )
2
tan 2 3 cos 1 0xx++ - =
2
sin 3 sin cos 1xxx+=
( )
2
cos cot 3 0xx-=
sin . tan 2 3 0
24
xx
pp
éù
æöæö
++--=
ç÷ç÷
êú
èøèø
ëû
( )
2
cos 1 . tan 3 0
2
xx
p
éù
æö
+- - =
ç÷
êú
èø
ëû
( )
( )
sin 1 cot 3 0xx--=
222
sin 3 sin cos sin cosxxxxxÛ+ =+
( )
2
3 sin cos cos 0 cos 3 sin cos 0.xx x x x xÛ-=Û -=
cos 0 sin 0.
2
xx
p
æö
=Û + =
ç÷
èø
! Trang!27!
=
Ta có
Vậy phương trình đã cho tương đương với .Chọn B
Câu 50. Cho phương trình . Mệnh đề nào sau đây là sai?
A. không là nghiệm của phương trình.
B. Nếu chia hai vế của phương trình cho thì ta được phương trình
.
C. Nếu chia 2 vế của phương trình cho thì ta được phương trình
.
D. Phương trình đã cho tương đương với .
Lời giải.
=
Với Thay vào phương trình ta thấy
thỏa mãn. Vậy A đúng.
=
Phương trình
. Vậy B đúng.
=
Phương trình
. Vậy C sai. Chọn C
=
Phương trình Vậy D đúng.
Câu 51. Số vị trí biểu diễn các nghiệm phương trình trên
đường tròn lượng giác là?
A. . B. . C. . D. .
Lời giải. Phương trình
có 2 vị trí biểu diễn nghiệm trên đường tròn lượng gác. Chọn C
Câu 52. Số nghiệm của phương trình trên ?
A. . B. . C. . D. .
Lời giải. Phương trình
1
3 sin cos 0 tan .
3
xx x-=Û=
1
1
tan tan
3
4
tan 2 3 tan 2 3 0.
1
44
1 tan . tan 1 .1
4
3
x
xx
x
p
pp
p
+
+
æö æö
+= = =+Û +--=
ç÷ ç÷
èø èø
--
sin . tan 2 3 0
24
xx
pp
éù
æöæö
++--=
ç÷ç÷
êú
èøèø
ëû
2
cos 3sin cos 1 0xxx-+=
xk
p
=
2
cos x
2
tan 3 tan 2 0xx-+=
2
sin x
2
2cot 3cot 1 0xx++=
cos 2 3sin 2 3 0xx-+=
2
sin 0
sin 0
.
cos 1
cos 1
x
x
xk
x
x
p
=
ì
=
ì
ï
=¾¾® Û
íí
=±
=
îï
î
222
cos 3sin cos sin cos 0xxxx xÛ- ++=
222
sin 3sin cos 2 cos 0 tan 3 tan 2 0xxx x x xÛ- + =Û -+=
222
cos 3sin cos sin cos 0xxxx xÛ- ++=
222
2cos 3sin cos sin 0 2cot 3cot 1 0xxxx xxÛ- +=Û-+=
1 cos 2 sin 2
3 1 0 cos 2 3sin 2 3 0.
22
xx
xx
+
Û-+=Û-+=
22
sin 4 sin cos 4 cos 5xxx x-+=
4
3
2
1
( )
2222
sin 4sin cos 4 cos 5 sin cosxxx x xxÛ- + = +
( )
2
22
4sin 4sin cos cos 0 2sin cos 0 2sin cos 0xxxx xx xxÛ- - - = Û + = Û + =
1
tan
2
xÛ = - ¾¾®
22
cos 3sin cos 2 sin 0xxx x-+=
( )
2;2
pp
-
2
4
6
8
2
tan 1
4
1 3 tan 2 tan 0 .
1
1
tan
arctan
2
2
x
xk
xx
x
xk
p
p
p
é
=
=+
é
ê
ê
Û- + = Û Û
ê
ê
=
ê
=+
ë
ê
ë
! Trang!28!
= Vì
.
= Vì
.
Vậy có tất cả 8 nghiệm. Chọn D
Câu 53. Nghiệm dương nhỏ nhất của phương trình là:
A. . B. . C. . D. .
Lời giải. Phương trình
So sánh hai nghiệm ta được là nghiệm dương nhỏ nhất. Chọn B
Câu 54. Cho phương trình . Trong các
mệnh đề sau, mệnh đề nào sai?
A. là một nghiệm của phương trình.
B. Nếu chia hai vế của phương trình cho thì ta được phương trình
.
C. Nếu chia hai vế của phương trình cho thì ta được phương trình
.
D. Phương trình đã cho tương đương với .
Lời giải. Chọn D
Câu 55. Giải phương trình
A. . B. . C. . D. .
Lời giải. Phương trình
( ) { }
97
2 ;2 2 2 2; 1;0;1
444
k
xkkk
p
pp p p p
Î
Î- ¾¾®- < + < ®- < < ¾¾¾® Î- -
!
( )
1
2 ;2 2 arctan 2
2
xk
pp p p p
Î- ¾¾®- < + <
{ }
CA SIO
xapxi
28 ,565 24,565 28; 27; 26; 25
k
kk
Î
¾¾¾¾®- < < - ¾¾¾® Î - - - -
!
22
4 sin 3 3 sin 2 2 cos 4xxx+-=
12
p
6
p
4
p
3
p
( )
2222
4sin 3 3 sin 2 2cos 4 sin cosxxxxxÛ+ - = +
( )
2
cos 0
3 3 sin 2 6 cos 0 6 cos 3 sin cos 0
1
tan
3
x
xx xxx
x
=
é
ê
Û-=Û -=Û
ê
=
ê
ë
min
Cho 0
min
1
00
22 2 2
.
1
00
66 6 6
k
k
xk k k k x
xk k k k x
pp p
pp
pp p
pp
Î
>
Î
éé
=+ + >Û>-¾¾¾® =®=
êê
Û¾¾¾¾®
êê
êê
=+ + >Û>-¾¾¾® =®=
êê
ëë
!
!
6
x
p
=
( ) ( )
22
2 1 sin sin 2 2 1 cos 2 0xx x-+++ -=
7
8
x
p
=
2
cos x
2
tan 2 tan 1 0xx--=
2
sin x
2
cot 2 cot 1 0xx+-=
cos 2 sin 2 1xx-=
( ) ( )
22
2 sin 1 3 sin cos 1 3 cos 1.xxx x+- +- =
6
p
-
4
p
-
2
3
p
-
12
p
-
( ) ( )
2222
2 sin 1 3 sin cos 1 3 cos sin cosxxx xxxÛ+- +- =+
( )
22
sin 1 3 sin cos 3 cos 0xxxxÛ+- - =
( )
2
an 1
4
an
tan
t
tan 1 3 t 3 0
3
3
xk
x
x
x
xk
x
p
p
p
p
é
=- +
ê
=-
é
Û
ê
ê
=
ê
ë
=+
ê
ë
Û+- -=Û
! Trang!29!
So sánh hai nghiệm ta được là nghiệm âm lớn nhất. Chọn B
Câu 56. Có bao nhiêu giá trị nguyên của tham số thuộc đoạn để phương trình
có nghiệm?
A. B. C. D.
Lời giải. Phương trình
Phương trình có nghiệm
có giá trị nguyên. Chọn A
Câu 57. Có bao nhiêu giá trị nguyên của tham số thuộc để phương trình
có nghiệm?
A. B. C. D. Vô số.
Lời giải. Phương trình
Phương trình có nghiệm
có giá trị nguyên. Chọn A
Câu 58. Tìm điều kiện để phương trình với có
nghiệm.
A. . B. . C. . D. .
Lời giải. Phương trình .
Phương trình có nghiệm
Chọn C
Câu 59. Tìm tất cả các giá trị của tham số để phương trình vô
nghiệm.
A. . B. , . C. . D. , .
Lời giải. Phương trình
max
Cho 0
max
1
00
44 4
.
12
01
33 3
k
k
kk k x
kk k x
pp
p
pp
p
Î
<
Î
é
-+ <Û<¾¾¾® =®=-
ê
¾¾¾¾®
ê
ê
+<Û<-¾¾¾® =-®=-
ê
ë
!
!
4
x
p
=-
m
[ ]
10 ;10-
( )
22
11sin 2 sin 2 3cos 2xm x x+- + =
16.
21.
15.
6.
( )
22
9sin 2 sin 2 cos 0xm x xÛ+- +=
( ) ( )
1cos2 1cos2
9. 2 sin 2 0 2 sin 2 4 cos 2 5.
22
xx
mx mxx
-+
Û+-+=Û--=-
( ) ( )
22
5
21625 2 9
1
m
mm
m
³
é
Û- +³Û- ³Û
ê
£-
ë
[ ]
{ }
10;10
10 ; 9 ;...; 1;5; 6 ;...;10
m
m
m
Î
Î-
¾¾¾¾¾® Î - - - ¾¾®
!
16
m
( ) ( )
22
sin 2 1 sin cos 1 co sxm xxm xm-- -- =
2.
1.
0.
( ) ( ) ( )
22
1sin21sincos21cos 0mxm xxm xÛ- - - - - =
( ) ( ) ( )
1cos2 1cos2
1 . 1 sin 2 2 1 . 0
22
xx
mmxm
-+
Û- - - - - =
( )
21sin2 cos223.mxmxmÛ- + =-
( ) ( )
22
22
41 23 4 400 1mm mmm m-+³- Û - £Û££
{ }
0;1
m
m
Î
¾¾¾® Î ¾¾®
!
2
22
sin sin cos cos 0axaxxb x++=
0a ¹
4ab³
4ab£-
4
1
b
a
£
4
1
b
a
£
2
tan tan 0axaxb++=
( )
2
40 40aab aabÛD= - ³ Û - ³
( )
44
40 0 1.
ba b
aba
aa
-
Û-£Û £Û£
m
2
2sin sin 2 2xm x m+=
4
0
3
m££
0m <
4
3
m >
4
0
3
m<<
4
3
m <-
0m >
1cos2
2. sin 2 2 sin 2 cos 2 2 1.
2
x
mxmmx xm
-
Û+=Û-=-
! Trang!30!
Phương trình vô nghiệm Chọn B
Câu 60. Có tất cả bao nhiêu giá trị nguyên của tham số thuộc đoạn để phương trình
có nghiệm.
A. . B. . C. . D. .
Lời giải. Phương trình
.
Phương trình có nghiệm
có giá trị nguyên. Chọn C
Vấn đề 5. PHƯƠNG TRÌNH CHỨA và
Câu 61. Giải phương trình .
A. B.
C. D.
Lời giải. Đặt . Vì
.
Ta có .
Khi đó, phương trình đã cho trở thành
Với , ta được .
( )
2
22
0
12 1 3 4 0 .
4
3
m
mm mm
m
<
é
ê
Û+< -Û ->Û
ê
>
ë
m
[ ]
3; 3-
( )
22
2 cos 2 sin 2 1 0mxmx+- +=
3
7
6
4
( )
2
1cos2
2 . 2 sin 2 1 0
2
x
mmx
+
Û+ - +=
( )
22
4 sin 2 2 cos 2 4mxm xmÛ-+=+
( ) ( )
22
22 2 2 2
16 2 4 12 12 1 1mm m m m mÛ++³+Û³Û³Û³
[ ]
{ }
3;3
3; 2; 1;1; 2; 3
m
m
m
Î
Î-
¾¾¾¾® Î - - - ¾¾®
!
6
sin cosxx±
sin cos .xx
( )
sin cos 2 sin cos 2xx x x++=
, .
2
xk
k
xk
p
p
p
é
=+
ê
Î
ê
=
ë
!
2
, .
2
2
xk
k
xk
p
p
p
é
=+
ê
Î
ê
=
ë
!
2
, .
2
2
xk
k
xk
p
p
p
é
=- +
ê
Î
ê
=
ë
!
, .
2
xk
k
xk
p
p
p
é
=- +
ê
Î
ê
=
ë
!
sin cos 2 sin
4
txx x
p
æö
=+ = +
ç÷
èø
[ ]
sin 1;1 2; 2
4
xt
p
æö
éù
+Î-ÞÎ-
ç÷
ëû
èø
( )
2
2
222
1
sin cos sin cos 2 sin cos sin cos
2
t
txx xxxxxx
-
=+ = + + Þ =
( )
2
2
1
1
22 450 .
5
2
t
t
ttt
t
=
é
-
+=Û+-=Û
ê
=-
ë
loaÔi
1t =
1
sin cos 1 sin sin sin
444
2
xx x x
ppp
æö æö
+=Û +=Û +=
ç÷ ç÷
èø èø
! Trang!31!
. Chọn B
Câu 62. Cho phương trình . Đặt , ta
được phương trình nào dưới đây?
A. B.
C. D.
Lời giải. Đặt
Phương trình đã cho trở thành Chọn A
Câu 63. Cho phương trình . Trong các phương trình sau,
phương trình nào tương đương với phương trình đã cho?
A. B.
C. D.
Lời giải. Đặt . Điều kiện
Ta có
Khi đó, phương trình đã cho trở thành : vô nghiệm.
Nhận thấy trong các đáp án A, B, C, D thì phương trình ở đáp án D vô nghiệm.
Vậy phương trình đã cho tương đương với phương trình Chọn D
Câu 64. Nghiệm âm lớn nhất của phương trình là:
A. B. C. D.
Lời giải. Đặt . Điều kiện
Ta có
Phương trình đã cho trở thành
Với , ta được
.
TH1. Với
2
44
2
44
xk
xk
pp
p
pp
pp
é
+=+
ê
Û
ê
ê
+=-+
ê
ë
2
,
2
2
xk
k
xk
p
p
p
=
é
ê
ÛÎ
ê
=+
ë
!
( )
3 2 sin cos 2sin 2 4 0xx x++ +=
sin costxx=+
2
23220.tt++=
2
43240.tt++=
2
23220.tt+-=
2
43240.tt+-=
2
sin cos sin 2 1.txx xt=+ ¾¾® =-
( )
22
32 2 1 4 0 2 32 2 0.tt t t+-+=Û+ +=
5sin 2 sin cos 6 0xx x++ +=
2
sin .
42
x
p
æö
+=
ç÷
èø
3
cos .
42
x
p
æö
-=
ç÷
èø
tan 1.x =
2
1tan 0.x+=
sin cos 2 sin
4
txx x
p
æö
=+ = +
ç÷
èø
22.t-££
( )
2
222 2
sin cos sin cos 2.sin .cos sin 2 1.txx xxxxxt=+ = + + Þ =-
( )
22
51 605 10tt tt-++=Û ++=
2
1tan 0.x+=
1
sin cos 1 sin 2
2
xx x+=-
.
2
p
-
.
p
-
3
.
2
p
-
2.
p
-
sin cos 2 sin
4
txx x
p
æö
=+ = +
ç÷
èø
22.t-££
( )
2
222 2
sin cos sin cos 2sin cos sin 2 1.txx xxxxxt=+ = + + Þ =-
( )
2
2
1
1
1230 .
3
2
t
t
ttt
t
=
é
-
=- Û + - = Û
ê
=-
ë
loaÔi
1t =
1
2 sin 1 sin sin sin
44 44
2
xx x
pp pp
æö æö æö
+=Û += Û +=
ç÷ ç÷ ç÷
èø èø èø
2
2
44
,
2
2
2
44
xk
xk
k
xk
xk
pp
p
p
p
pp
p
pp
é
=
+=+
é
ê
ê
ÛÛÎ
ê
ê
=+
ê
+=-+
ë
ê
ë
!
max
20 0 1 2.
k
xk k k x
pp
Î
=<Û<¾¾¾® =-®=-
!
! Trang!32!
TH2. Với
Vậy nghiệm âm lớn nhất của phương trình là . Chọn C
Câu 65. Cho thỏa mãn phương trình . Tính
A. hoặc . B.
hoặc .
C. . D. hoặc
.
Lời giải. Đặt . Điều kiện
Ta có
Phương trình đã cho trở thành .
Với , ta được
Với , ta được
Chọn B
Câu 66. Từ phương trình , ta tìm được có
giá trị bằng:
A. B. C. D.
Lời giải. Đặt . Điều kiện
Ta có
Phương trình đã cho trở thành
Với
max
13
20 1 .
24 2
k
xk k k x
pp
p
Î
=+ <Û<-¾¾¾® =-®=-
!
3
2
x
p
=-
x
sin 2 sin cos 1xx x+- =
sin .
4
x
p
æö
-
ç÷
èø
sin 0
4
x
p
æö
-=
ç÷
èø
sin 1
4
x
p
æö
-=
ç÷
èø
sin 0
4
x
p
æö
-=
ç÷
èø
2
sin
42
x
p
æö
-=
ç÷
èø
2
sin
42
x
p
æö
-=-
ç÷
èø
sin 0
4
x
p
æö
-=
ç÷
èø
2
sin
42
x
p
æö
-=-
ç÷
èø
sin cos 2 sin
4
txx x
p
æö
=- = -
ç÷
èø
22.t-££
( )
2
222 2
sin cos sin cos 2 sin cos sin 2 1 .txx xxxxxt=- = + - Þ =-
22
0
11 0
1
t
tt tt
t
=
é
-+=Û-=Û
ê
=
ë
1t =
1
2 sin 1 sin .
44
2
xx
pp
æö æö
-=Û -=
ç÷ ç÷
èø èø
0t =
2 sin 0 sin 0.
44
xx
pp
æö æö
-=Û -=
ç÷ ç÷
èø èø
( )
5sin 2 16 sin cos 16 0xxx--+=
sin
4
x
p
æö
+
ç÷
èø
2
.
2
2
.
2
-
1.
2
.
2
±
sin cos 2 sin
4
txx x
p
æö
=- = -
ç÷
èø
22.t-££
( )
2
222 2
sin cos sin cos 2.sin cos sin 2 1 .txx xxxxxt=- = + - Þ =-
( )
( )
2
1
5 1 16 16 0 .
21
5
t
tt
t
=
é
ê
--+=Û
ê
=-
ë
loaÔi
1 sin cos 1.txx=Þ - =
( )
*
! Trang!33!
Mặt khác , kết hợp với suy ra
. Chọn D
Câu 67. Cho thỏa mãn . Tính
A. B.
C. D.
Lời giải. Đặt . Điều kiện
Ta có
Phương trình đã cho trở thành
Chọn C
Câu 68. Từ phương trình , nếu ta đặt
thì giá trị của nhận được là:
A. hoặc . B. hoặc .
C. . D. .
Lời giải. Đặt
Phương trình trở thành
Chọn C
Câu 69. Nếu thì bằng bao nhiêu?
A. . B. hoặc .
C. hoặc . D. hoặc .
Lời giải. Đặt
Phương trình trở thành
( ) ( )
22
sin cos sin cos 2xx xx++-=
( )
*
( )
2
2
sin cos 1 2 sin cos 1 sin
42
xx xx x
p
æö
++=Û+=±Û+=±
ç÷
èø
x
( )
6sin cos sin cos 6 0xx xx-+ +=
cos .
4
x
p
æö
+
ç÷
èø
cos 1.
4
x
p
æö
+=-
ç÷
èø
cos 1.
4
x
p
æö
+=
ç÷
èø
1
cos .
4
2
x
p
æö
+=
ç÷
èø
1
cos .
4
2
x
p
æö
+=-
ç÷
èø
sin cos 2 sin
4
txx x
p
æö
=- = -
ç÷
èø
22.t-££
( )
2
2
222
1
sin cos sin cos 2 sin cos sin cos .
2
t
txx xxxxxx
-
=- = + - Þ =
( )
2
1
1
660
13
2
t
t
t
t
=-
é
-
++=Û
ê
=
ë
loaÔi
11
2 sin 1 sin sin
444
22
xx x
ppp
æö æö æö
Þ-=-Û-=-Û-=
ç÷ ç÷ ç÷
èø èø èø
11
cos cos .
24 4
22
xx
pp p
éù
æö æö
Þ--=Û+=
ç÷ ç÷
êú
èø èø
ëû
( )
( )
1 3 cos sin 2sin cos 3 1 0xx xx++- --=
cos sintxx=+
t
1t =
2t =
1t =
3t =
1t =
3t =
( )
2
1
sin cos 2 2 sin cos .
2
t
txx t xx
-
=- -££¾¾® =
( )
( )
2
13 1 310tt+----=
( )
( )
2
1
13 30 1.
3
t
tt t
t
=
é
Û-+ + =Û Û=
ê
=
ê
ë
loa Ôi
( )
( )
1 5 sin cos sin 2 1 5 0xx x+-+--=
sin x
2
sin
2
x =
2
sin
2
x =
2
sin
2
x =-
sin 1x =-
sin 0x =
sin 0x =
sin 1x =
( )
2
1
sin cos 2 2 sin cos .
2
t
txx t xx
-
=- -££¾¾® =
( )
2
15 1 150tt++---=
! Trang!34!
.
Mặt khác Chọn D
Câu 70. Nếu thì bằng bao nhiêu?
A. B. C. D.
Lời giải. Ta có
Đặt
Khi đó trở thành
.
Ta có Chọn C
Câu 71. Cho thỏa mãn . Tính
A. B. C. D.
Lời giải. Đặt . Vì
.
Ta có
Phương trình đã cho trở thành
Chọn C
Câu 72. Hỏi trên đoạn , phương trình có bao nhiêu
nghiệm?
A. B. C. D.
Lời giải. Đặt . Vì
.
( )
( )
2
1
15 50
5
t
tt
t
=
é
Û-+ + =Û
ê
=
ê
ë
loaÔi
sin cos 1 cos sin 1xx xxÞ- =Û =-
( )
2
22 2
sin 0
sin cos 1 sin sin 1 1 .
sin 1
x
xx xx
x
=
é
+=Þ+-=Û
ê
=
ë
( )( )
1sin 1cos 2xx++=
cos
4
x
p
æö
-
ç÷
èø
1.-
1.
2
.
2
2
.
2
-
( )( )
1sin 1cos 2 1sin cos sin.cos 2xx xxxx++=Û+++ =
( )
sin cos sin .c os 1 2 sin cos 2.sin .cos 2.xxxx xx xxÛ++ =Û + + =
( )
*
( )
2
1
sin cos 2 2 sin cos .
2
t
txx t xx
-
=+ -££¾¾® =
( )
*
( )
22
1
212 230
3
t
tt t t
t
=
é
+-=Û+-=Û
ê
=-
ë
loa Ôi
sin cos 1xxÞ+ =
( )
22
cos cos cos sin sin cos sin .
4442 2
xxx xx
ppp
æö
-= + = + =
ç÷
èø
x
2sin 2 3 6 sin cos 8 0xxx-++=
sin 2 .x
1
sin 2 .
2
x =-
2
sin 2 .
2
x =-
1
sin 2 .
2
x =
2
sin 2 .
2
x =
sin cos 2 sin
4
txx x
p
æö
=+ = +
ç÷
èø
[ ]
sin 1;1 0; 2
4
xt
p
æö
éù
+Î-ÞÎ
ç÷
ëû
èø
( )
2
222 2
sin cos sin cos 2sin cos sin 2 1.txx xxxxxt=+ = + + Þ =-
( )
( )
2
6
213680
2
6
t
tt
t
é
=
ê
-- +=Û
ê
ê
=
ë
loaÔi
2
1
sin 2 1 .
2
xt=-=
[ ]
0; 2018
p
in co ss4sin21xxx+=-
4037.
4036.
2018.
2019.
sin cos 2 sin
4
txx x
p
æö
=- = -
ç÷
èø
[ ]
sin 1;1 0; 2
4
xt
p
æö
éù
-Î-ÞÎ
ç÷
ëû
èø
! Trang!35!
Ta có
Phương trình đã cho trở thành
Với , ta được .
Theo giả thiết
có giá trị của nê có nghiệm. Chọn
A
Câu 73. Từ phương trình , ta tìm được có giá trị
bằng:
A. B. C. D.
Lời giải. Điều kiện .
Ta có
Đặt
Phương trình trở thành
Mà
. Chọn C
Câu 74. Từ phương trình , ta tìm được có giá trị
bằng:
A. B. C. D.
Lời giải. Phương trình
Đặt
Phương trình trở thành
( )
2
222 2
sin cos sin cos 2 sin cos sin 2 1 .txx xxxxxt=- = + - Þ =-
( )
( )
2
1
41 1 .
3
4
t
tt
t
=
é
ê
+-=Û
ê
=-
ë
loaÔi
1t =
sin 2 0 2 ,
2
k
xxkxk
p
p
=Û = Û= Î!
[ ]
0; 2018 0 2018 0 4046
2
k
xk
p
pp
ξ¾®££Û££
{ }
0;1 ; 2; 3 ;...; 4036
k
k
Î
¾¾¾® Î ¾¾®
!
4037
k
4037
( )
2 sin cos tan cotxx xx+=+
cos x
1.
2
.
2
-
2
.
2
1.-
sin 0
sin 2 0
cos 0
x
x
x
¹
ì
Û¹
í
¹
î
( ) ( )
sin cos
2 sin cos tan cot 2 sin cos
cos sin
xx
xx xx xx
xx
+=+Û +=+
( ) ( )
22
sin cos
2sin cos 2sin cos.2sin cos 2.
sin cos
xx
xx xx xx
xx
+
Û+= Û +=
( )
2
1
sin cos 2 2 sin cos .
2
t
txx t xx
-
=+ -££¾¾® =
( )
23
212 20 2tt t t tÛ-=Û--=Û=
sin cos 2 sin 2 cos .xx x xÞ+ =Û =-
( )
2
22 2 2
sin cos 1 cos 2 cos 1 2 cos 2 2 cos 1 0xx x x x x+=Þ+- =Û - +=
( )
2
1
2cos 1 0 cos
2
xxÛ-=Û=
33
3
1 sin cos sin 2
2
xx x++ =
cos
4
x
p
æö
+
ç÷
èø
1.
2
.
2
-
2
.
2
2
.
2
±
( )( )
sin cos 1 sin co
3
1 sin 2
2
sxx xx x+=+Û -
( )( )
2sin cos 2sin2 3sin2.xx x xÛ+ + - =
( )
2
1
sin cos 2 2 sin cos .
2
t
txx t xx
-
=+ -££¾¾® =
( ) ( )
22
22 13 1tt t+-+= -
! Trang!36!
Với , ta được .
Mà
Chọn D
Câu 75. Có bao nhiêu giá trị nguyên của tham số để phương trình
có nghiệm?
A. B. C. D.
Lời giải. Đặt
Phương trình trở thành .
Do .
Vậy để phương trình có nghiệm
Chọn C
( )
32
1
3350 .
16
t
ttt
t
=-
é
Û+ --=Û
ê
=- ±
ê
ë
loa Ôi
1t =-
1
sin cos 1 sin
4
2
xx x
p
æö
+=-Û +=-
ç÷
èø
22 2
12
sin cos 1 cos cos .
44 4242
xx x x
pp p p
æö æö æö æö
++ +=¾¾® +=Û +=±
ç÷ ç÷ ç÷ ç÷
èø èø èø èø
m
sin cos sin cos 0xx x xm-- +=
1.
2.
3.
4.
( )
2
1
sin cos 2 2 sin cos .
2
t
txx t xx
-
=+ -££¾¾® =
( )
2
2
2
1
02 21 1 22
2
t
tm mt t t m
-
-+ = Û- = - -Û - =- +
( )
2
22 2112101322tt t-££ ¾¾®--£-£ -¾¾®£- £+
0322
122
22 1
2
mm
+
-+ -Û£ Û £+ ££
{ }
1; 0; 1 .
m
m
Î
¾¾¾® Î -
!
| 1/36
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

BÀI TẬP TRẮC NGHIỆM
MỘT SỐ PHƯƠNG TRÌNH LƯỢNG GIÁC THƯỜNG GẶP
Vấn đề 1. PHƯƠNG TRÌNH BẬC NHẤT
ĐỐI VỚI MỘT HÀM SỐ LƯỢNG GIÁC
Câu 1. Gọi S là tập nghiệm của phương trình 2cos x - 3 = 0. Khẳng định nào sau đây là đúng? 5p p p p A. Î 11 S. B. Î 13 S. C. Ï 13 S. D. - Ï S. 6 6 6 6 7p
Câu 2. Hỏi x =
là một nghiệm của phương trình nào sau đây? 3
A. 2sin x - 3 = 0.
B. 2sin x + 3 = 0.
C. 2cos x - 3 = 0.
D. 2cos x + 3 = 0. æ p ö
Câu 3. Tìm nghiệm dương nhỏ nhất của phương trình 2sin 4x - -1 = 0. ç ÷ è 3 ø p p p p A. x = 7 . B. x = . C. x = . D. x = . 4 24 8 12 æ p ö
Câu 4. Số vị trí biểu diễn các nghiệm của phương trình tan 2x - + 3 = 0 trên đường ç ÷ è 3 ø tròn lượng giác là? A. 4 . B. 3 . C. 2 . D. 1.
Câu 5. Hỏi trên đoạn [0;2018p ], phương trình 3 cot x - 3 = 0 có bao nhiêu nghiệm? A. 6339. B. 6340. C. 2017. D. 2018.
Câu 6. Trong các phương trình sau, phương trình nào tương đương với phương trình 2 2cos x =1? 2 A. sin x =
. B. 2sin x + 2 = 0. C. tan x = 1. D. 2 tan x =1. 2
Câu 7. Phương trình nào dưới đây có tập nghiệm trùng với tập nghiệm của phương trình 2 tan x = 3? 1
A. cos x = - . B. 2 4cos x = 1 1. C. cot x = 1 . D. cot x = - . 2 3 3
Câu 8. Giải phương trình 2 4sin x = 3. é p é p x = + k2p ê x = + k2p 3 ê 3 A. ê , (k Î!) . B. ê , (k Î!). p ê 2p x = - + k2p ê ê x = + k2p ë 3 êë 3 ì p kp ì kp ïx = + ïx = C. í 3 3 (k,! Î"). D. í 3 (k,! Î"). ïîk ¹ 3! ïîk ¹ 3! Trang 1
Câu 9. Trong các phương trình sau, phương trình nào tương đương với phương trình 2 2 3sin x = cos x? 1 A. sin x = 3 . B. cos x = . C. 2 3 sin x = . D. 2 cot x = 3. 2 2 4 3
Câu 10. Với x thuộc (0 ) ;1 , hỏi phương trình 2
cos (6p x) = có bao nhiêu nghiệm? 4 A. 8. B. 10. C. 11. D. 12.
Câu 11. Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình
3 cos x + m -1 = 0 có nghiệm? A. 1. B. 2. C. 3. D. Vô số.
Câu 12. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [ 2108 - ; ] 2018 để phương
trình m cos x +1 = 0 có nghiệm? A. 2018. B. 2019. C. 4036. D. 4038. p
Câu13. Tìm giá trị thực của tham số m để phương trình (m - 2)sin 2x = m +1 nhận x = 12 làm nghiệm. 2( 3 + ) 1
A. m ¹ 2. B. m = . C. m = 4. - D. m = 1. - 3 - 2
Câu 14. Tìm tất cả các giá trị của tham số m để phương trình (m + )
1 sin x + 2 - m = 0 có nghiệm. A. m £ 1. - 1 B. m ³ 1 . C. 1 - < m £ . D. m > 1. - 2 2
Câu 15. Tìm tất cả các giá trị của tham số m để phương trình (m - 2)sin 2x = m + 1 vô nghiệm. é1 ù æ 1 ö A. m Î ;2 . B. m Î - ; ¥ È(2;+¥ ç ÷ ). ê2 ú ë û è 2 ø æ 1 ö æ 1 ö C. m Î ;2 È (2;+¥ ç ÷ ). D. m Î ;+¥ . ç ÷ è 2 ø è 2 ø
Vấn đề 2. PHƯƠNG TRÌNH BẬC NHẤT ĐỐI VỚI sin x và cos x
Câu 16. Gọi S là tập nghiệm của phương trình cos 2x - sin 2x = 1. Khẳng định nào sau đây là đúng? p p p p A. Î S. B. Î 3 S. C. Î 5 S. D. Î S. 4 2 4 4 æ p ö
Câu 17. Số nghiệm của phương trình sin 2x + 3 cos 2x = 3 trên khoảng 0; là? ç ÷ è 2 ø A. 1. B. 2. C. 3. D. 4.
Câu 18. Tính tổng T các nghiệm của phương trình 2 2
cos x - sin 2x = 2 + sin x trên khoảng (0;2p ). Trang 2 7p p p p A. T = 21 . B. T = 11 . C. T = 3 . D. T = . 8 8 4 4
Câu 19. Tìm nghiệm dương nhỏ nhất của x - x = + x 0 x 3 3sin 3 3 cos9 1 4sin 3 . p p p p A. x = B. x = C. x = D. x = 0 . 2 0 . 18 0 . 24 0 . 54 æ p ö
Câu 20. Số nghiệm của phương trình sin 5x + 3 cos5x = 2sin 7x trên khoảng 0; là? ç ÷ è 2 ø A. 2. B. 1. C. 3. D. 4. æ p ö æ p ö
Câu 21. Giải phương trình 3 cos x + + sin x - = 2sin 2 . x ç ÷ ç ÷ è 2 ø è 2 ø é 5p é 7p x = + k2p ê x = + k2p 6 ê 6 A. ê , k Î! . B. ê , k Î . ! p 2p ê p 2p x = + k ê ê x = - + k ë 18 3 êë 18 3 é 5p é p 2p x = + k2p ê x = + k 6 ê 18 3 C. ê , k Î . ! D. ê , k Î . ! 7p ê p 2p x = + k2p ê ê x = - + k ë 6 êë 18 3 Câu 22. Gọi
là nghiệm âm lớn nhất của x + x = x + x. Mệnh 0 x sin 9 3 cos7 sin 7 3 cos9
đề nào sau đây là đúng? æ p ö é p p ù é p p ö é p p ö A. x Î - B. x Î - - C. x Î - - D. x Î - - 0 ;0 . ç ÷ ê ÷ ê ÷ è 12 ø 0 ; . ê 6 12ú ë û 0 ; . ë 3 6 ø 0 ; . ë 2 3 ø
Câu 23. Biến đổi phương trình cos 3x - sin x = 3 (cos x - sin 3x) về dạng æ p p ö
sin(ax +b) = sin(cx + d ) với b , d thuộc khoảng - ;
. Tính b + d . ç ÷ è 2 2 ø p p p p
A. b + d =
. B. b + d = .
C. b + d = - .
D. b + d = . 12 4 3 2 cos x - 3 sin x
Câu 24. Giải phương trình = 0. 1 sin x - 2 p p A. x = + kp , k Î . ! B. x = + k2p , k Î . ! 6 6 7p 7p C. x = + k2p , k Î . ! D. x = + kp , k Î! . 6 6 2sin 2x + cos 2x
Câu 25. Hàm số y =
có tất cả bao nhiêu giá trị nguyên?
sin 2x - cos 2x + 3 A. 1. B. 2. C. 3. D. 4. Câu 26. Gọi
là nghiệm dương nhỏ nhất của x + x + x - x = 0 x cos 2 3 sin 2 3 sin cos 2.
Mệnh đề nào sau đây là đúng? Trang 3 æ p ö é p p ù æ p p ù æ p p ù A. x Î B. x Î C. x Î D. x Î 0 0; . ç ÷ ç ç è 12 ø 0 ; . ê12 6 ú ë û 0 ; . 6 3 ú è û 0 ; . 3 2 ú è û
Câu 27. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [ 10 - ; ] 10 để phương trình æ p ö æ p ö sin x - - 3 cos x - = 2m vô nghiệm. ç ÷ ç ÷ è 3 ø è 3 ø A. 21. B. 20. C. 18. D. 9.
Câu 28. Tìm tất cả các giá trị thực của tham số m để phương trình 2
cos x + sin x = 2 m +1 vô nghiệm. ( ) A. mÎ(- ; ¥ - ) 1 È(1;+¥). B. mÎ[ 1 - ; ] 1 . C. mÎ(- ; ¥ +¥) D. mÎ(- ;0 ¥ )È(0;+¥).
Câu 29. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [ 10 - ; ] 10 để phương trình
(m+ )1sin x-mcos x =1-m có nghiệm. A. 21. B. 20. C. 18. D. 11.
Câu 30. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [ 2018 - ; ] 2018 để phương trình (m + ) 2
1 sin x -sin 2x + cos 2x = 0 có nghiệm. A. 4037. B. 4036. C. 2019. D. 2020.
Vấn đề 3. PHƯƠNG TRÌNH BẬC HAI
ĐỐI VỚI MỘT HÀM SỐ LƯỢNG GIÁC é p ö Câu 31. Hỏi trên 0; , phương trình 2
2sin x - 3sin x +1 = 0 có bao nhiêu nghiệm? ê ÷ ë 2 ø A. 1. B. 2. C. 3. D. 4.
Câu 32. Số vị trí biểu diễn các nghiệm của phương trình 2
2cos x + 5cos x + 3 = 0 trên đường tròn lượng giác là? A. 1. B. 2. C. 3. D. 4.
Câu 33. Cho phương trình 2
cot 3x - 3cot 3x + 2 = 0 . Đặt t = cot x , ta được phương trình nào sau đây? A. 2
t - 3t + 2 = 0. B. 2
3t - 9t + 2 = 0 . C. 2
t - 9t + 2 = 0. D. 2
t - 6t + 2 = 0.
Câu 34. Số nghiệm của phương trình 2
4sin 2x - 2(1+ 2)sin 2x + 2 = 0 trên (0;p ) là? A. 3. B. 4. C. 2. D. 1.
Câu 35. Số nghiệm của phương trình 2
sin 2x - cos 2x +1 = 0 trên đoạn [ p - ;4p ] là? A. 2. B. 4. C. 6. D. 8. x x
Câu 36. Tính tổng T tất cả các nghiệm của phương trình 2 2sin - 3cos = 0 trên đoạn 4 4 [0;8p]. A. T = 0. B. T = 8p . C. T = 16p . D. T = 4p . 1
Câu 37. Số nghiệm của phương trình - 3 -1 cot x - 3 +1 = 0 (0;p ) 2 ( ) ( ) trên là? sin x Trang 4 A. 1. B. 2. C. 3. D. 4.
Câu 38. Tính tổng T tất cả các nghiệm của phương trình 2cos 2x + 2cos x - 2 = 0 trên đoạn [0;3p ]. 17p A. T = . B. T = 2p . C. T = 4p . D. T = 6p . 4
Câu 39. Số vị trí biểu diễn các nghiệm của phương trình cos 2x + 3sin x + 4 = 0 trên đường tròn lượng giác là? A. 1. B. 2. C. 3. D. 4. x x
Câu 40. Cho phương trình cos x + cos +1 = 0 . Nếu đặt t = cos , ta được phương trình nào 2 2 sau đây? A. 2
2t + t = 0. B. 2 2
- t + t +1 = 0. C. 2 2t + t -1 = 0. D. 2 2 - t + t = 0. æ p ö æ p ö 5
Câu 41. Số nghiệm của phương trình cos 2 x + + 4cos
- x = thuộc [0;2p ]là? ç ÷ ç ÷ è 3 ø è 6 ø 2 A. 1. B. 2. C. 3. D. 4.
Câu 42. Tìm tất cả các giá trị thực của tham số m để phương trình tan x + m cot x = 8 có nghiệm.
A. m > 16.
B. m < 16.
C. m ³ 16.
D. m £ 16.
Câu 43. Tìm tất cả các giá trị thực của tham số m để phương trình æ p p ö cos 2x -(2m + ) 1 cos x + m +1 = 3 0 có nghiệm trên khoảng ; . ç ÷ è 2 2 ø A. 1
- £ m £ 0 . B. 1 - £ m < 0 . C. 1 - < m < 1 0 . D. 1 - £ m < . 2
Câu 44. Biết rằng khi m = m thì phương trình 2 x -( m+ ) 2 2sin 5
1 sin x + 2m + 2m = 0 0 æ p ö
có đúng 5 nghiệm phân biệt thuộc khoảng -
;3p . Mệnh đề nào sau đây là đúng? ç ÷ è 2 ø æ 3 7 ù æ 3 2 ö A. m = 3. - 1 B. m = . C. m Î ; . D. m Î - ; - . ç ç ÷ 2 0 5 10 ú è û 0 è 5 5 ø
Câu 45. Tìm tất cả các giá trị thực của tham số m để phương trình 2 æ p p ö
2cos 3x + (3- 2m)cos3x + m- 2 = 0 có đúng 3 nghiệm thuộc khoảng - ; . ç ÷ è 6 3 ø A. 1
- £ m £ 1. B. 1 < m £ 2. C. 1 £ m £ 2.
D. 1 £ m < 2.
Vấn đề 4. PHƯƠNG TRÌNH ĐẲNG CẤP BẬC HAI ĐỐI VỚI sin x và cos x
Câu 46. Giải phương trình 2 x -( + ) 2 sin
3 1 sin x cos x + 3 cos x = 0. p p A. x = + k2p (k Î!). B. x = + kp (k Î!). 3 4 é p é p x = + k2p ê x = + kp 3 ê 3 C. ê (k Î!). D. ê (k Î!). p ê p x = + k2p ê ê x = + kp ë 4 êë 4 Trang 5
Câu 47. Gọi S là tập nghiệm của phương trình 2 2
2sin x + 3 3 sin x cos x - cos x = 2 .
Khẳng định nào sau đây là đúng? ìp ü ìp p ü ìp 5p ü ìp 5p ü
A. í ;p ý Ì S. B. í ; ý Ì S. C. í ; ý Ì S. D. í ; ý Ì S. î 3 þ î 6 2 þ î 4 12 þ î 2 6 þ
Câu 48. Trong các phương trình sau, phương trình nào tương đương với phương trình 2 x -( + ) 2 sin
3 1 sin x cos x + 3 cos x = 3 . æ p ö A. sin x = 0 . B. sin x + =1. ç ÷ è 2 ø æ + ö C. ( x - ) 3 1 cos 1 ç tan x - ÷ = 0. D. 2
tan x + 2 + 3 cos x -1 = 0. ( )( ) ç 1 3 ÷ - è ø
Câu 49. Phương trình nào dưới đây có tập nghiệm trùng với tập nghiệm của phương trình 2
sin x + 3 sin x cos x =1? A. 2
cos x cot x - 3 = 0 . B. ( ) æ p ö é æ p ö ù sin x + . tan x + - 2 - 3 = 0. ç ÷ ê ç ÷ 2 ë 4 ú è ø è ø û é æ p ö ù C. 2 cos x + -1 . ê ç ÷ ú (tan x - 3) = 0. D. ë è 2 ø û
(sin x - )1(cot x- 3) = 0.
Câu 50. Cho phương trình 2
cos x - 3sin x cos x +1 = 0. Mệnh đề nào sau đây là sai?
A. x = kp không là nghiệm của phương trình.
B. Nếu chia hai vế của phương trình cho 2
cos x thì ta được phương trình 2
tan x - 3tan x + 2 = 0.
C. Nếu chia 2 vế của phương trình cho 2
sin x thì ta được phương trình 2
2cot x + 3cot x +1 = 0.
D. Phương trình đã cho tương đương với cos 2x - 3sin 2x + 3 = 0 .
Câu 51. Số vị trí biểu diễn các nghiệm phương trình 2 2
sin x - 4sin xcos x + 4cos x = 5 trên
đường tròn lượng giác là? A. 4 . B. 3 . C. 2 . D. 1.
Câu 52. Số nghiệm của phương trình 2 2
cos x - 3sin x cos x + 2sin x = 0 trên ( 2 - p;2p )? A. 2 . B. 4 . C. 6 . D. 8 .
Câu 53. Nghiệm dương nhỏ nhất của phương trình 2 2
4sin x + 3 3 sin 2x - 2cos x = 4 là: p p p p A. . B. . C. . D. . 12 6 4 3
Câu 54. Cho phương trình ( - ) 2 x + x + ( + ) 2 2 1 sin sin 2
2 1 cos x - 2 = 0 . Trong các
mệnh đề sau, mệnh đề nào sai? 7p A. x =
là một nghiệm của phương trình. 8
B. Nếu chia hai vế của phương trình cho 2
cos x thì ta được phương trình 2
tan x - 2 tan x -1 = 0. Trang 6
C. Nếu chia hai vế của phương trình cho 2
sin x thì ta được phương trình 2
cot x + 2cot x -1 = 0 .
D. Phương trình đã cho tương đương với cos 2x - sin 2x = 1.
Câu 55. Giải phương trình
2 x + ( - ) x x+( - ) 2 2sin 1 3 sin cos 1 3 cos x =1. p p p p A. - . B. - 2 . C. - . D. - . 6 4 3 12
Câu 56. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [ 10 - ; ] 10 để phương trình 2 x +(m- ) 2 11sin
2 sin 2x + 3cos x = 2 có nghiệm? A. 16. B. 21. C. 15. D. 6.
Câu 57. Có bao nhiêu giá trị nguyên của tham số m thuộc để phương trình
2 x - (m- ) x x -(m- ) 2 sin 2 1 sin cos
1 cos x = m có nghiệm? A. 2. B. 1. C. 0. D. Vô số.
Câu 58. Tìm điều kiện để phương trình 2 2
asin x + asin x cos x + bcos x = 0 với a ¹ 0 có nghiệm. b b
A. a ³ 4b . B. a £ 4 - 4 b . C. £ 4 . 1 D. £1. a a
Câu 59. Tìm tất cả các giá trị của tham số m để phương trình 2
2sin x + msin 2x = 2m vô nghiệm. 4 A. 0 £ m £ . B. m < 4 0 , m > 4 . C. 0 < m < 4 .
D. m < - , m > 0 . 3 3 3 3
Câu 60. Có tất cả bao nhiêu giá trị nguyên của tham số m thuộc đoạn [ 3; - ]3 để phương trình 2 2
m + 2 cos x - 2msin 2x +1 = 0 có nghiệm. ( ) A. 3 . B. 7 . C. 6 . D. 4 .
Vấn đề 5. PHƯƠNG TRÌNH CHỨA sin x ± cos x và sin x cos . x
Câu 61. Giải phương trình sin x cos x + 2(sin x + cos x) = 2. é p é p x = + kp x = + k2p A. ê 2 , k Î . ! B. ê 2 , k Î . ! ê ê ëx = kp ëx = k2p é p é p x = - + k2p x = - + kp C. ê 2 , k Î . ! D. ê 2 , k Î . ! ê ê ëx = k2p ëx = kp
Câu 62. Cho phương trình 3 2 (sin x + cos x) + 2sin 2x + 4 = 0. Đặt t = sin x + cos x , ta
được phương trình nào dưới đây? A. 2
2t + 3 2 t + 2 = 0. B. 2
4t + 3 2 t + 4 = 0. Trang 7 C. 2
2t + 3 2 t - 2 = 0. D. 2
4t + 3 2 t - 4 = 0.
Câu 63. Cho phương trình 5sin 2x + sin x + cos x + 6 = 0 . Trong các phương trình sau,
phương trình nào tương đương với phương trình đã cho? æ p ö 2 æ p ö 3 A. sin x + = . B. cos x - = . ç ÷ ç ÷ è 4 ø 2 è 4 ø 2
C. tan x = 1. D. 2 1+ tan x = 0. 1
Câu 64. Nghiệm âm lớn nhất của phương trình sin x + cos x = 1- sin 2x là: 2 p 3p A. - . B. -p . C. - . D. - 2p . 2 2 æ p ö
Câu 65. Cho x thỏa mãn phương trình sin 2x + sin x - cos x = 1. Tính sin x - . ç ÷ è 4 ø æ p ö æ p ö æ p ö A. sin x -
= 0 hoặc sin x - =1. B. sin x - = 0 ç ÷ ç ÷ ç ÷ è 4 ø è 4 ø è 4 ø æ p ö 2 hoặc sin x - = . ç ÷ è 4 ø 2 æ p ö 2 æ p ö C. sin x - = - . D. sin x - = 0 hoặc ç ÷ ç ÷ è 4 ø 2 è 4 ø æ p ö 2 sin x - = - . ç ÷ è 4 ø 2 æ p ö
Câu 66. Từ phương trình 5sin 2x -16(sin x - cos x) +16 = 0, ta tìm được sin x + có ç ÷ è 4 ø giá trị bằng: 2 2 2 A. . B. - . C. 1. D. ± . 2 2 2 æ p ö
Câu 67. Cho x thỏa mãn 6(sin x - cos x) + sin xcos x + 6 = 0. Tính cos x + . ç ÷ è 4 ø æ p ö æ p ö A. cos x + = 1 - . B. cos x + =1. ç ÷ ç ÷ è 4 ø è 4 ø æ p ö 1 æ p ö 1 C. cos x + = . D. cos x + = - . ç ÷ ç ÷ è 4 ø 2 è 4 ø 2
Câu 68. Từ phương trình (1+ 3)(cos x + sin x) - 2sin xcos x - 3 -1= 0, nếu ta đặt
t = cos x + sin x thì giá trị của t nhận được là:
A. t = 1 hoặc t = 2 .
B. t = 1 hoặc t = 3 . C. t = 1. D. t = 3 .
Câu 69. Nếu (1+ 5)(sin x - cos x) + sin 2x -1- 5 = 0 thì sin x bằng bao nhiêu? 2 A. sin x = 2 . B. sin x = 2 hoặc sin x = - . 2 2 2 C. sin x = 1 - hoặc sin x = 0.
D. sin x = 0 hoặc sin x = 1. Trang 8 æ p ö
Câu 70. Nếu (1+ sin x)(1+ cos x) = 2 thì cos x - bằng bao nhiêu? ç ÷ è 4 ø 2 2 A. 1. - B. 1. C. . D. - . 2 2
Câu 71. Cho x thỏa mãn 2sin 2x - 3 6 sin x + cos x + 8 = 0. Tính sin 2 . x 1 A. sin 2x = - 2 . B. sin 2x = - 1 . C. sin 2x = 2 . D. sin 2x = . 2 2 2 2
Câu 72. Hỏi trên đoạn [0;2018p ], phương trình in
s x - cos x + 4sin 2x =1 có bao nhiêu nghiệm? A. 4037. B. 4036. C. 2018. D. 2019.
Câu 73. Từ phương trình
2 (sin x + cos x) = tan x + cot x, ta tìm được cos x có giá trị bằng: 2 A. 1. B. - 2 . C. . D. -1. 2 2 æ p ö
Câu 74. Từ phương trình 3 3 3
1+ sin x + cos x = sin 2x, ta tìm được cos x + có giá trị ç ÷ 2 è 4 ø bằng: 2 2 A. 1. B. - 2 . C. . D. ± . 2 2 2
Câu 75. Có bao nhiêu giá trị nguyên của tham số m để phương trình
sin x cos x - sin x - cos x + m = 0 có nghiệm? A. 1. B. 2. C. 3. D. 4.
ĐÁP ÁN VÀ LỜI GIẢI
Vấn đề 1. PHƯƠNG TRÌNH BẬC NHẤT
ĐỐI VỚI MỘT HÀM SỐ LƯỢNG GIÁC
Câu 1. Gọi S là tập nghiệm của phương trình 2cos x - 3 = 0. Khẳng định nào sau đây là đúng? 5p p p p A. Î 11 S. B. Î 13 S. C. Ï 13 S. D. - Ï S. 6 6 6 6 é p x = + k2p p ê 6
Lời giải. Ta có 2cos x - 3 = 0 Û cos x = cos Û ê (k Î!). 6 p êx = - + k2p êë 6 p k 1 11p
Nhận thấy với nghiệm x k2p = = - + ¾¾¾ ® x = Î S. Chọn B 6 6 7p
Câu 2. Hỏi x =
là một nghiệm của phương trình nào sau đây? 3
A. 2sin x - 3 = 0.
B. 2sin x + 3 = 0.
C. 2cos x - 3 = 0.
D. 2cos x + 3 = 0. Trang 9 ì 7p 3 ï = = 7p sin x sin ï 3 2 ìï2sin x - 3 = 0
Lời giải. Với x = , suy ra í Û í . Chọn A 3 7 ï p 1 ïî2cos x -1 = 0 cos x = cos = ïî 3 2 7p
Cách 2. Thử x =
lần lượt vào từng phương trình. 3 æ p ö
Câu 3. Tìm nghiệm dương nhỏ nhất của phương trình 2sin 4x - -1 = 0. ç ÷ è 3 ø p p p p A. x = 7 . B. x = . C. x = . D. x = . 4 24 8 12 æ p ö æ p ö 1 æ p ö p
Lời giải. Ta có 2sin 4x - -1 = 0 Û sin 4x - = Û sin 4x - = sin ç ÷ ç ÷ ç ÷ è 3 ø è 3 ø 2 è 3 ø 6 é p p é p é p kp 4x - = + k2p 4x = + k2p x = + ê 3 6 ê 2 ê 8 2 Û ê Û ê Û ê (k Î!). p p 7p 7 ê p kp 4x - = p - + k2p ê4x k2p ê = + x = + êë 3 6 êë 6 êë 24 2 p kp Cho>0 p kp 1 p TH1. Với x = + ¾¾¾¾ ® +
> 0 Û k > - ® k = 0 Þ x = . min 8 2 8 2 4 8 7p kp Cho>0 7p kp 7 7p TH2. Với x = + ¾¾¾¾ ® + > 0 Û k > - ® k = 0 Þ x = . min 24 2 24 2 12 24 p
So sánh hai nghiệm ta được x =
là nghiệm dương nhỏ nhất. Chọn C 8 æ p ö
Câu 4. Số vị trí biểu diễn các nghiệm của phương trình tan 2x - + 3 = 0 trên đường ç ÷ è 3 ø tròn lượng giác là? A. 4 . B. 3 . C. 2 . D. 1. Lời giải. Ta có æ p ö æ p ö æ p ö æ p ö tan 2x - + 3 = 0 Û tan 2x - = - 3 Û tan 2x - = tan - ç ÷ ç ÷ ç ÷ ç ÷ è 3 ø è 3 ø è 3 ø è 3 ø p p kp
Û 2x - = - + kp Û 2x = kp Û x = (k Î!). 3 3 2 B C A O D
Quá dễ để nhận ra có 4 vị trí biểu diễn nghiệm của phương trình đã cho trên đường tròn lượng giác
là A, B, C, D. Chọn A kp 2p
Cách trắc nghiệm. Ta có x = = k ¾¾
® có 4 vị trí biểu diễn. 2 4 Trang 10
Câu 5. Hỏi trên đoạn [0;2018p ], phương trình 3 cot x - 3 = 0 có bao nhiêu nghiệm? A. 6339. B. 6340. C. 2017. D. 2018. p p
Lời giải. Ta có cot x = 3 Û cot x = cot
Û x = + kp (k Î!). 6 6 p xap xi 1
Theo giả thiết, ta có 0 £
+ kp £ 2018p ¾¾¾®- £ k £ 2017,833 6 6 3 kÎ ¾¾¾ !®k Î{0;1;...;201 }
7 . Vậy có tất cả 2018 giá trị nguyên của k tương ứng với có
2018 nghiệm thỏa mãn yêu cầu bài toán. Chọn D
Câu 6. Trong các phương trình sau, phương trình nào tương đương với phương trình 2 2cos x =1? 2 A. sin x =
. B. 2sin x + 2 = 0. C. tan x = 1. D. 2 tan x =1. 2 Lời giải. Ta có 2 2 1
2cos x = 1 Û cos x = . Mà 2 2 2 1
sin x + cos x =1¾¾ ®sin x = . 2 2 2 sin x Do đó 2 tan x = = 1. Vậy 2 2
2cos x =1 Û tan x =1. Chọn D 2 cos x
Câu 7. Phương trình nào dưới đây có tập nghiệm trùng với tập nghiệm của phương trình 2 tan x = 3? 1
A. cos x = - . B. 2 4cos x = 1 1. C. cot x = 1 . D. cot x = - . 2 3 3 2 sin x Lời giải. Ta có 2 2 2 tan x = 3 Û
= 3 Û sin x = 3cos x 2 cos x 2 2 2
Û1- cos x = 3cos x Û 4cos x =1. Vậy 2 2
tan x = 3 Û 4cos x =1. Chọn B
Câu 8. Giải phương trình 2 4sin x = 3. é p é p x = + k2p ê x = + k2p 3 ê 3 A. ê , (k Î!) . B. ê , (k Î!). p ê 2p x = - + k2p ê ê x = + k2p ë 3 êë 3 ì p kp ì kp ïx = + ïx = C. í 3 3 (k,! Î"). D. í 3 (k,! Î"). ïîk ¹ 3! ïîk ¹ 3! Lời giải. Ta có 2 2 3 3
4sin x = 3 Û sin x = Û sin x = ± . 4 2 é p x = + k2p 3 p ê 3 = Với sin x = Û sin x = sin Û ê (k Î!). 2 3 2p êx = + k2p êë 3 é p x = - + k2p 3 p ê æ ö 3 = Với sin x = - Û sin x = sin - Û ç ÷ ê (k Î!). 2 è 3 ø 4p êx = + k2p êë 3 Trang 11
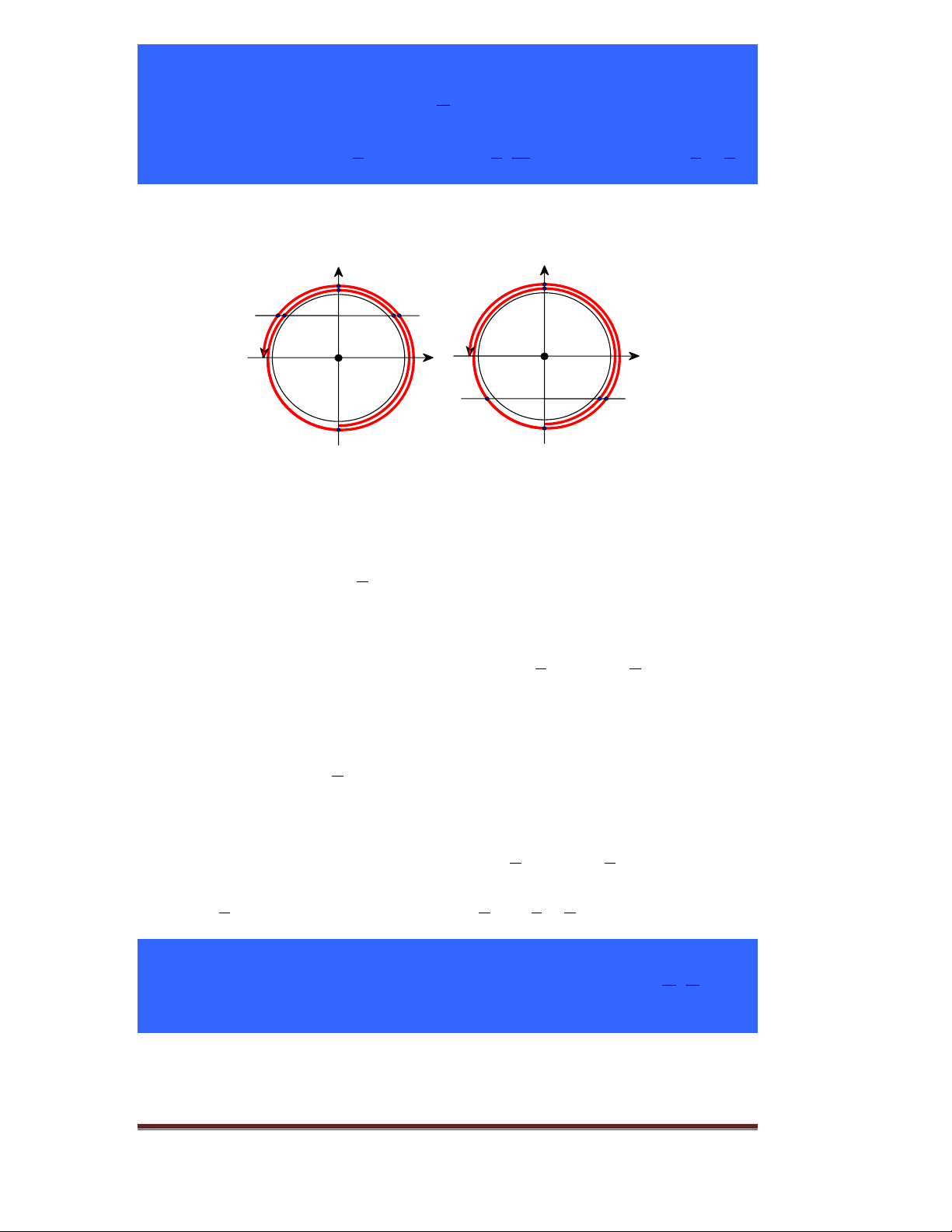
Nhận thấy chưa có đáp án nào phù hợp. Ta biểu diễn các nghiệm trên đường tròn lượng giác (hình vẽ). O
Nếu tính luôn hai điểm A, B thì có tất cả 6 điểm cách đều nhau nên ta gộp được 6 điểm này thành p
một họ nghiệm, đó là x = k . 3 ì p x = k ì kp ïï 3 ïx =
Suy ra nghiệm của phương trình í Û í
3 (k,! Î"). Chọn D p ïk ¹ lp ïîk ¹ 3 ï ! î 3
Câu 9. Trong các phương trình sau, phương trình nào tương đương với phương trình 2 2 3sin x = cos x? 1 A. sin x = 3 . B. cos x = . C. 2 3 sin x = . D. 2 cot x = 3. 2 2 4 Lời giải. Ta có 2 2
3sin x = cos x. Chi hai vế phương trình cho 2 sin x, ta được 2 cot x = 3. Chọn D 3
Câu 10. Với x thuộc (0 ) ;1 , hỏi phương trình 2
cos (6p x) = có bao nhiêu nghiệm? 4 A. 8. B. 10. C. 11. D. 12. 3 3
Lời giải. Phương trình 2
cos (6p x) = Û cos(6p x) = ± . 4 2 3 p p = Với cos 6p x =
Û cos6p x = cos Û 6p x = ± + k2p . 2 6 6 é 1 k é x = + Î( ) 1 35 0;1 k - < k Î < ¾¾¾ !®k = {0;1; } 2 ê 36 3 ê 12 12 Û ê Û ê ® có 6 nghiệm. 1 k êx = - + Î( ) 1 37 0;1 ê k < k Î < ¾¾¾ !®k = {1;2; } 3 êë 36 3 êë12 12 3 5p 5p = Với cos 6p x = - Û cos6p x = cos Û 6p x = ± + k2p . 2 6 6 é 5 k é x = + Î( ) 5 31 0;1 k - < k Î < ¾¾¾ !®k ={0;1; } 2 ê 36 3 ê 12 12 Û ê Û ê ® có 6 nghiệm. 5 k êx = - + Î( ) 5 41 0;1 ê k < k Î < ¾¾¾ !®k = {1;2; } 3 êë 36 3 êë12 12
Vậy phương trình đã cho có 12 nghiệm. Chọn D
Câu 11. Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình
3 cos x + m -1 = 0 có nghiệm? A. 1. B. 2. C. 3. D. Vô số. Trang 12 1- m
Lời giải. Ta có 3 cos x + m -1 = 0 Û cos x = . 3 1- m mÎ
Phương trình có nghiệm Û 1 - £
£1Û1- 3 £ m £1+ 3 ¾¾¾ !®mÎ{0;1; } 2 . 3
Vậy có tất cả 3 giá trị nguyên của tham số m . Chọn C
Câu 12. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [ 2108 - ; ] 2018 để phương
trình m cos x +1 = 0 có nghiệm? A. 2018. B. 2019. C. 4036. D. 4038. 1
Lời giải. Ta có m cos x +1 = 0 Û cos x = - . m Phương trình có nghiệm 1 Û 1 - £ - £1 Û m ³1 mÎ ¾¾¾¾¾ ! ¾¾ ®mÎ 1;2;3;...;2018 . m m [ Î - ] { } 2018;2018
Vậy có tất cả 2018 giá trị nguyên của tham số m . Chọn A p
Câu13. Tìm giá trị thực của tham số m để phương trình (m - 2)sin 2x = m +1 nhận x = 12 làm nghiệm. 2( 3 + ) 1
A. m ¹ 2. B. m = . C. m = 4. - D. m = 1. - 3 - 2 p
Lời giải. Vì x =
là một nghiệm của phương trình (m - 2)sin 2x = m + 1 nên ta có: 12 ( p - m - ) 2 m 2 2 .sin = m +1 Û
= m +1 Û m - 2 = 2m + 2 Û m = -4. 12 2
Vậy m = - 4 là giá trị cần tìm. Chọn C
Câu 14. Tìm tất cả các giá trị của tham số m để phương trình (m + )
1 sin x + 2 - m = 0 có nghiệm. A. m £ 1. - 1 B. m ³ 1 . C. 1 - < m £ . D. m > 1. - 2 2 Lời giải. Phương trình ( - m + )
x + - m = Û (m + ) m 2 1 sin 2 0
1 sin x = m - 2 Û sin x = . m +1 m - 2
Để phương trình có nghiệm Û -1 £ £1 m +1 ì m - 2 ì2m -1 ìé 1 0 £ 1+ ³ 0 m ³ ï ï ïê ï m +1 ï m +1 ï 2 1 Û í Û í Û ê í
Û m ³ là giá trị cần tìm. Chọn B m - 2 3 ëm < -1 2 ï 1 0 ï 0 ï - £ - £ ïî m +1 ïî m +1 ïîm > -1
Câu 15. Tìm tất cả các giá trị của tham số m để phương trình (m - 2)sin 2x = m + 1 vô nghiệm. é1 ù æ 1 ö A. m Î ;2 . B. m Î - ; ¥ È(2;+¥ ç ÷ ). ê2 ú ë û è 2 ø æ 1 ö æ 1 ö C. m Î ;2 È (2;+¥ ç ÷ ). D. m Î ;+¥ . ç ÷ è 2 ø è 2 ø Trang 13
Lời giải. TH1. Với m = 2 , phương trình (m - 2)sin 2x = m +1Û 0 = 3: vô lý.
Suy ra m = 2 thì phương trình đã cho vô nghiệm. m +
TH2. Với m ¹ 2 , phương trình (m - ) 1
2 sin 2x = m +1 Û sin 2x = . m - 2 é m +1 >1 ém > 2 m 1 ê + m - 2
Để phương trình (*) vô nghiệm [ 1 ] ;1 ê Û Ï - Û ê Û 1 . m - 2 m +1 ê ê < m < 2 < -1 ë2 êëm - 2 1
Kết hợp hai trường hợp, ta được m > là giá trị cần tìm. Chọn D 2
Vấn đề 2. PHƯƠNG TRÌNH BẬC NHẤT ĐỐI VỚI sin x và cos x
Câu 16. Gọi S là tập nghiệm của phương trình cos 2x - sin 2x = 1. Khẳng định nào sau đây là đúng? p p p p A. Î S. B. Î 3 S. C. Î 5 S. D. Î S. 4 2 4 4 æ p ö æ p ö 1
Lời giải. Phương trình Û 2 cos 2x + =1 Û cos 2x + = ç ÷ ç ÷ è 4 ø è 4 ø 2 é p p 2x + = + k2p éx = kp p p ê æ ö 4 4 cos 2x cos ê Û + = Û ç ÷ ê Û p , k Î . ! è 4 ø 4 p p ê ê x = - + kp 2x + = - + k2p ë 4 êë 4 4 p p Xét nghiệm x = - + kp , với k = 3 1 ta được x = .Chọn C 4 4 æ p ö
Câu 17. Số nghiệm của phương trình sin 2x + 3 cos 2x = 3 trên khoảng 0; là? ç ÷ è 2 ø A. 1. B. 2. C. 3. D. 4. 1 3 3 æ p ö 3
Lời giải. Phương trình Û sin 2x + cos 2x = Û sin 2x + = ç ÷ 2 2 2 è 3 ø 2 é p p 2x + = + k2p éx = kp p p ê æ ö 3 3 sin 2x sin ê Û + = Û ç ÷ ê Û p , k Î . ! è 3 ø 3 p p ê ê x = + kp 2x + = p - + k2p ë 6 êë 3 3 p 1 kÎ! = 0 < kp < Û 0 < k < ¾¾¾
® không có giá trị k thỏa mãn. 2 2 p p 1 1 kÎ! p = 0 <
+ kp < Û - < k < ¾¾¾
®k = 0 ® x = . Chọn A 6 2 6 3 6
Câu 18. Tính tổng T các nghiệm của phương trình 2 2
cos x - sin 2x = 2 + sin x trên khoảng (0;2p ). 7p p p p A. T = 21 . B. T = 11 . C. T = 3 . D. T = . 8 8 4 4
Lời giải. Phương trình 2 2
Û cos x -sin x -sin 2x = 2 Û cos 2x -sin 2x = 2 Trang 14 æ p ö p p Û cos 2x +
=1 Û 2x + = k2p Û x = - + kp (k Î ç ÷ !). è 4 ø 4 8 é 7p k = 1 ® x p = 1 17 ê kÎ! 8
Do 0 < x < 2p ¾¾
®0 < - + kp < 2p Û < k < ¾¾¾ ® ê 8 8 8 15p êk = 2 ® x = êë 8 7p 15p 11 ¾¾ ®T = + = p. Chọn C 8 8 4
Câu 19. Tìm nghiệm dương nhỏ nhất của x - x = + x 0 x 3 3sin 3 3 cos9 1 4sin 3 . p p p p A. x = B. x = C. x = D. x = 0 . 2 0 . 18 0 . 24 0 . 54
Lời giải. Phương trình 3
Û 3sin 3x - 4sin 3x - 3 cos9x =1 Û sin 9x - 3 cos9x = 1 1 3 1 æ p ö 1 Û sin 9x -
cos9x = Û sin 9x - = ç ÷ 2 2 2 è 3 ø 2 é p p é p k2p 9x - = + k2p x p p = + ê 3 6 ê æ ö 18 9 Û sin 9x - = sin Û ç ÷ ê Û ê è 3 ø 6 p p 7p k2p ê9x p k2p ê - = - + x = + êë 3 6 êë 54 9 é p k2p 1 Î! p + > 0 k Û k > - ¾¾¾
®kmin = 0 ® x = ê Cho>0 18 9 4 18 ¾¾¾¾ ® ê . 7p k2p 7 ê kÎ! 7p + > 0 Û k > - ¾¾¾
®kmin = 0 ® x = êë 54 9 12 54 p
So sánh hai nghiệm ta được nghiệm dương nhỏ nhất là x = . Chọn B 18
Cách trắc nghiệm. Thử từng nghiệm của đáp án vào phương trình và so sánh nghiệm nào thỏa
mãn phương trình đồng thời là nhỏ nhất thì ta chọn. æ p ö
Câu 20. Số nghiệm của phương trình sin 5x + 3 cos5x = 2sin 7x trên khoảng 0; là? ç ÷ è 2 ø A. 2. B. 1. C. 3. D. 4. 1 3 æ p ö
Lời giải. Phương trình Û sin 5x +
cos5x = sin 7x Û sin 5x + = sin 7x ç ÷ 2 2 è 3 ø é p é p 7x = 5x + + k2p x = + kp p ê 3 ê æ ö 6
Û sin 7x = sin 5x + Û ê Û ç ÷ ê (k Î!). è 3 ø ê æ p ö p kp 7x p 5x k2p ê = - + + ê ç ÷ x = + ë è 3 ê ø ë 18 6 p p 1 1 kÎ! p = 0 <
+ kp < Û - < k < ¾¾¾
®k = 0 ® x = . 6 2 6 3 6 Trang 15 é p k = 0 ® x = ê 18 ê p p p 1 8 kÎ! 2p ê = 0 < + k < Û - < k < ¾¾¾ ® k = 1® x = . 18 6 2 3 3 ê 9 ê 7p êk = 2 ® x = êë 18
Vậy có 4 nghiệm thỏa mãn. Chọn D æ p ö æ p ö
Câu 21. Giải phương trình 3 cos x + + sin x - = 2sin 2 . x ç ÷ ç ÷ è 2 ø è 2 ø é 5p é 7p x = + k2p ê x = + k2p 6 ê 6 A. ê , k Î! . B. ê , k Î . ! p 2p ê p 2p x = + k ê ê x = - + k ë 18 3 êë 18 3 é 5p é p 2p x = + k2p ê x = + k 6 ê 18 3 C. ê , k Î . ! D. ê , k Î . ! 7p ê p 2p x = + k2p ê ê x = - + k ë 6 êë 18 3 æ p ö æ p ö
Lời giải. Ta có cos x +
= -sin x và sin x - = -cos x. ç ÷ ç ÷ è 2 ø è 2 ø
Do đó phương trình Û - 3 sin x - cos x = 2sin 2x Û 3 sin x + cos x = 2 - sin 2x 3 1 æ p ö æ p ö Û
sin x + cos x = -sin 2x Û sin x +
= -sin 2x Û sin x + = sin ç ÷ ç ÷ ( 2 - x) 2 2 è 6 ø è 6 ø é p é p 2p x + = 2 - x + k2p x = - + k ê 6 ê 18 3 Û ê Û ê (k Î!). p 5p êx p 2x k2p ê + = + + x = - - k2p êë 6 êë 6 5p k= 1 - -k ' 7p Xét nghiệm x = - - k2p ¾¾¾¾¾ ® x = + k '2p . kÎ!, k ' 6 Î! 6 p 2p 7p
Vậy phương trình có nghiệm x = - + k , x =
+ k '2p (k,k 'Î!). Chọn B 18 3 6 Câu 22. Gọi
là nghiệm âm lớn nhất của x + x = x + x. Mệnh 0 x sin 9 3 cos7 sin 7 3 cos9
đề nào sau đây là đúng? æ p ö é p p ù é p p ö é p p ö A. x Î - B. x Î - - C. x Î - - D. x Î - - 0 ;0 . ç ÷ ê ÷ ê ÷ è 12 ø 0 ; . ê 6 12ú ë û 0 ; . ë 3 6 ø 0 ; . ë 2 3 ø
Lời giải. Phương trình Û sin 9x - 3 cos9x = sin 7x - 3 cos 7x é p p 9x - = 7x - + k2p ê éx = kp æ p ö æ p ö 3 3 Û sin 9x - = sin 7x - Û ê ê Û ç ÷ ç ÷ p p 5 k è 3 ø è 3 ø ê p æ p ö ê = + 9 - = p - 7 - + 2 x x x k p ê ç ÷ ë 48 8 ë 3 è 3 ø Trang 16
ékp < 0 Û k < 0 kÎ ¾¾¾ !®kmax = 1 - ® x = p - Cho<0 ê ¾¾¾¾ ® . So sánh hai ê5p kp 5 Î! p + < 0 k Û k < - ¾¾¾ ®kmax = 1 - ® x = - êë 48 8 6 48 p æ p ö
nghiệm ta được nghiệm âm lớn nhất của phương trình là x = - Î - ;0 .Chọn A ç ÷ 48 è 12 ø
Câu 23. Biến đổi phương trình cos 3x - sin x = 3 (cos x - sin 3x) về dạng æ p p ö
sin(ax +b) = sin(cx + d ) với b , d thuộc khoảng - ;
. Tính b + d . ç ÷ è 2 2 ø p p p p
A. b + d =
. B. b + d = .
C. b + d = - .
D. b + d = . 12 4 3 2
Lời giải. Phương trình Û 3 sin 3x + cos3x = sin x + 3 cos x 3 1 1 3 æ p ö æ p ö Û
sin 3x + cos3x = sin x +
cos x Û sin 3x + = sin x + . ç ÷ ç ÷ 2 2 2 2 è 6 ø è 3 ø p p p Suy ra b + d = + = . Chọn D 6 3 2 cos x - 3 sin x
Câu 24. Giải phương trình = 0. 1 sin x - 2 p p A. x = + kp , k Î . ! B. x = + k2p , k Î . ! 6 6 7p 7p C. x = + k2p , k Î . ! D. x = + kp , k Î! . 6 6 Lời giải. Điều kiện ì p x ¹ + k2p 1 1 p ïï 6
sin x - ¹ 0 Û sin x ¹ Û sin x ¹ sin Û í (k Î!). 2 2 6 5p ïx ¹ + k2p ïî 6 O Hình 1
Điều kiện bài toán tương đương với bỏ đi vị trí hai điểm trên đường tròn lượng giác (Hình 1).
Phương trình Û cos x - 3 sin x = 0 Û cos x = 3 sin x p p
Û cot x = 3 Û cot x = cot Û x = + lp (l Î!). 6 6 Trang 17 O Hình 2 p
Biểu diễn nghiệm x =
+ lp trên đường tròn lượng giác ta được 2 vị trí như Hình 2. 6 p
Đối chiếu điều kiện, ta loại nghiệm x =
+ k2p . Do đó phương trình có nghiệm 6 7p x =
+ 2lp (l Î!). Chọn C 6 2sin 2x + cos 2x
Câu 25. Hàm số y =
có tất cả bao nhiêu giá trị nguyên?
sin 2x - cos 2x + 3 A. 1. B. 2. C. 3. D. 4. 2sin 2x + cos 2x
Lời giải. Ta có y =
Û ( y - 2)sin 2x -( y + ) 1 cos 2x = 3 - . y
sin 2x - cos 2x + 3 Điều kiện để phương trình có nghiệm
Û ( y - )2 +( y + )2 ³ (- y)2 2 2 1 3
Û 7y + 2y -5 £ 0 5 1 y y Î Û - £ £ ¾¾¾ !® yÎ{ 1 - ; }
0 nên có 2 giá trị nguyên. Chọn B 7 Câu 26. Gọi
là nghiệm dương nhỏ nhất của x + x + x - x = 0 x cos 2 3 sin 2 3 sin cos 2.
Mệnh đề nào sau đây là đúng? æ p ö é p p ù æ p p ù æ p p ù A. x Î B. x Î C. x Î D. x Î 0 0; . ç ÷ ç ç è 12 ø 0 ; . ê12 6 ú ë û 0 ; . 6 3 ú è û 0 ; . 3 2 ú è û 1 3 3 1
Lời giải. Phương trình Û cos 2x + sin 2x +
sin x - cos x = 1 2 2 2 2 æ p ö æ p ö Û sin + 2x + sin x - =1. ç ÷ ç ÷ è 6 ø è 6 ø p p p p p Đặt t = x - ¾¾
® x = t + ® 2x = 2t + ® 2x + = 2t + . 6 6 3 6 2 æ p ö
Phương trình trở thành Û sin 2t +
+ sin t =1 Û cos 2t + sin t = 1 ç ÷ è 2 ø 2
Û 2sin t -sint = 0 Û sint (2sint - ) 1 = 0 . p 1 kÎ! p
= sin t = 0 Û t = kp ¾¾
® x = + kp > 0 Û k > - ¾¾¾ ®k = 0 ® x = . min 6 6 6 Trang 18 = é p p 1 Î! p t = + k2p ¾¾
® x = + k2p > 0 k Û k > - ¾¾¾ ®k ê min = 0 ® x = . 1 6 3 6 3 sin t = Û ê 2 5p 1 êt = + k2p ¾¾
® x = p + k2p > 0 k Û k Î > - ¾¾¾
!®kmin = 0 ® x =p. êë 6 2 p é p p ù
Suy ra nghiệm dương nhỏ nhất của phương trình là x = Î ; . Chọn B 6 ê12 6 ú ë û
Câu 27. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [ 10 - ; ] 10 để phương trình æ p ö æ p ö sin x - - 3 cos x - = 2m vô nghiệm. ç ÷ ç ÷ è 3 ø è 3 ø A. 21. B. 20. C. 18. D. 9. 2 2 2 ém < -
Lời giải. Phương trình vô nghiệm Û + (- ) < ( m) 2 1 1 3 2 Û 4m - 4 > 0 Û ê ëm >1 mÎ ¾¾¾¾ ! ¾®mÎ 10 - ; 9 - ; 8 - ;...; 2 - ;2;...;8;9;10 ¾¾
® có 18 giá trị. Chọn C m [ Î - ] { } 10;10
Câu 28. Tìm tất cả các giá trị thực của tham số m để phương trình 2
cos x + sin x = 2 m +1 vô nghiệm. ( ) A. mÎ(- ; ¥ - ) 1 È(1;+¥). B. mÎ[ 1 - ; ] 1 . C. mÎ(- ; ¥ +¥) D. mÎ(- ;0 ¥ )È(0;+¥).
Lời giải. Phương trình vô nghiệm é m ù Û + < + êë ( ) 2 2 2 2 1 1 2 1 úû 4 2 2 2 2
Û m + 2m > 0 Û m m + 2 > 0 Û m > 0 Û m ¹ 0. Chọn D ( )
Câu 29. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [ 10 - ; ] 10 để phương trình
(m+ )1sin x-mcos x =1-m có nghiệm. A. 21. B. 20. C. 18. D. 11. Lời giải. Phương trình có nghiệm Û ( é ³ m + )2 2 + m ³ ( - m)2 2 m 0 1 1
Û m + 4m ³ 0 Û ê ëm £ 4 - mÎ ¾¾¾¾ ! ¾®mÎ 10 - ; 9 - ; 8 - ;...; 4 - ;0;1;2;...;8;9;10 ¾¾
® có 18 giá trị. Chọn C m [ Î - ] { } 10;10
Câu 30. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [ 2018 - ; ] 2018 để phương trình (m + ) 2
1 sin x -sin 2x + cos 2x = 0 có nghiệm. A. 4037. B. 4036. C. 2019. D. 2020. - x
Lời giải. Phương trình Û (m + )1 cos 2 1
- sin 2x + cos 2x = 0 2 Û 2s
- in 2x + (1- m)cos2x = -m-1. 2 2 2
Phương trình có nghiệm Û ( 2
- ) +(1- m) ³ (-m- )
1 Û 4m £ 4 Û m £ 1 mÎ ¾¾¾¾¾ ! ¾¾ ®mÎ 2018 - ; 2017 - ;...;0;1 ¾¾
® có 2020 giá trị. Chọn D m [ Î - ] { } 2018;2018 Trang 19
Vấn đề 3. PHƯƠNG TRÌNH BẬC HAI
ĐỐI VỚI MỘT HÀM SỐ LƯỢNG GIÁC é p ö Câu 31. Hỏi trên 0; , phương trình 2
2sin x - 3sin x +1 = 0 có bao nhiêu nghiệm? ê ÷ ë 2 ø A. 1. B. 2. C. 3. D. 4. é 1 sin x =
Lời giải. Phương trình 2
2sin x 3sin x 1 0 ê - + = Û 2 ê ësin x =1 é p x = + k2p ê 6 é p ê sin x = sin 5p ê Û 6 ê Û x = + k2p (k Î!). ê ê 6 ësin x =1 ê p êx = + k2p êë 2 Theo giả thiết é p p é 1 1 Î! p 0 £ + k2 k p < - < k < ¾¾¾ ® k = 0 ® x = ê 6 2 ê 12 6 6 ê ê p 5p p 5 1 0 £ x ê < Û 0 £ + k2 ê k p < Û - < k Î < - ¾¾¾ !®k ÎÆ . 2 ê 6 2 ê 12 12 ê p p ê 1 ê0 £ + k2p <
ê- < k < 0 kÎ ¾¾¾ !®k ÎÆ êë 2 2 êë 4 é p ö
Vậy phương trình có duy nhất một nghiệm trên 0; . Chọn A ê ÷ ë 2 ø
Câu 32. Số vị trí biểu diễn các nghiệm của phương trình 2
2cos x + 5cos x + 3 = 0 trên đường tròn lượng giác là? A. 1. B. 2. C. 3. D. 4. écos x = 1 -
Lời giải. Phương trình 2
2cos x 5cos x 3 0 ê Û + + = Û 3 êcos x = - (loa )Ôi ë 2 Û cos x = 1
- Û x = p + k2p (k Î!).
Suy ra có duy nhất 1 vị trí biểu diễn nghiệm của phương trình trên đường tròn lượng giác. Chọn A
Câu 33. Cho phương trình 2
cot 3x - 3cot 3x + 2 = 0 .Đặt t = cot 3x , ta được phương trình nào sau đây? A. 2
t - 3t + 2 = 0. B. 2
3t - 9t + 2 = 0 . C. 2
t - 9t + 2 = 0. D. 2
t - 6t + 2 = 0. Lời giải. Chọn A
Câu 34. Số nghiệm của phương trình 2
4sin 2x - 2(1+ 2)sin 2x + 2 = 0 trên (0;p ) là? A. 3. B. 4. C. 2. D. 1. é 2 êsin 2x =
Lời giải. Phương trình 2 x - ( + ) 2 4sin 2 2 1 2 sin 2x + 2 = 0 Û ê . ê 1 sin 2x = êë 2 Trang 20 é p é p (0;p ) p 2x = + k2p x =
+ kp ¾¾¾® x = 2 p ê 4 ê 8 8 = sin 2x = = sin Û ê Û ê . 2 4 3p 3p ê ê (0;p ) 3p 2x = + k2p x =
+ kp ¾¾¾® x = êë 4 êë 8 8 é p é p (0;p ) p 2x = + k2p x =
+ kp ¾¾¾® x = 1 p ê 6 ê 12 12 = sin 2x = = sin Û ê Û ê . 2 6 5p 5p ê ê (0;p ) 5p 2x = + k2p x =
+ kp ¾¾¾® x = êë 6 êë 12 12
Vậy có tất cả 4 nghiệm thỏa mãn. Chọn B
Câu 35. Số nghiệm của phương trình 2
sin 2x - cos 2x +1 = 0 trên đoạn [ p - ;4p ] là? A. 2. B. 4. C. 6. D. 8.
Lời giải. Phương trình 2 2
sin 2x - cos 2x +1 = 0 Û -cos 2x - cos 2x + 2 = 0 écos 2x =1 Û ê
Û cos 2x =1Û 2x = k2p Û x = kp, k Î . ! cos 2x = - 2 ë (loa )Ôi kÎ! Do x Î[ p - ;4p ] ¾¾
®-p £ kp £ 4p Û -1£ k £ 4 ¾¾¾ ®k Î{ 1 - ;0;1;2;3 } ;4 .
Vậy phương trình có 6 nghiệm thỏa mãn. Chọn C x x
Câu 36. Tính tổng T tất cả các nghiệm của phương trình 2 2sin - 3cos = 0 trên đoạn 4 4 [0;8p]. A. T = 0. B. T = 8p . C. T = 16p . D. T = 4p . x x æ x ö x
Lời giải. Phương trình 2 2 2sin - 3cos = 0 Û 2 1- cos - 3cos = 0 ç ÷ 4 4 è 4 ø 4 é x 1 cos = ê 2 x x 4 2 x 1 x p Û 2c - os - 3cos + 2 = 0 Û ê Û cos = Û cos = cos 4 4 x ê = - (loa ) 4 2 4 3 cos 2 ê Ô i ë 4 é x p é 4p x [ Î 0;8p ] 4p = + k2p x =
+ k8p ¾¾¾¾® x = ê4 3 ê 3 3 4p 20p Û ê Û ê ® T = + = 8p. x p 4p x ê ê [ Î 0;8p ] 20p 3 3 = - + k2p x = -
+ k8p ¾¾¾¾® x = êë4 3 êë 3 3 Chọn B 1
Câu 37. Số nghiệm của phương trình
- 3 -1 cot x - 3 +1 = 0 trên (0;p ) là? 2 ( ) ( ) sin x A. 1. B. 2. C. 3. D. 4.
Lời giải. Điều kiện: sin x ¹ 0 Û x ¹ kp (k Î!). Phương trình 2 2
Û 1+ cot x - 3 -1 cot x - 3 +1 = 0 Û cot x - 3 -1 cot x - 3 = 0 ( ) ( ) ( ) ( ) Trang 21 é æ p ö é p x ( Î 0;p ) 3p cot x = cot - é = - ê ç ÷
x = - + kp ¾¾¾¾ ® x = (tho˚a maın) cot x 1 è 4 ê ø 4 4 Û ê Û ê Û ê . ëcot x = 3 ê p p x ê ( Î 0;p ) p cot x = cot x =
+ kp ¾¾¾¾® x = (tho˚a maın) êë 6 êë 6 6
Vậy phương trình đã cho có 2 nghiệm thỏa mãn. Chọn B
Câu 38. Tính tổng T tất cả các nghiệm của phương trình 2cos 2x + 2cos x - 2 = 0 trên đoạn [0;3p ]. 17p A. T = . B. T = 2p . C. T = 4p . D. T = 6p . 4
Lời giải. Phương trình 2
2cos 2x + 2cos x - 2 = 0 Û 2 2cos x -1 + 2cos x - 2 = 0 ( ) é 2 êcos x = 2 2 2
Û 4cos x + 2cos x - 2 - 2 = 0 Û ê Û cos x = ê 2 +1 êcos x = - (loa ) 2 Ô i ë 2 é p x [ Î 0;3p ] p 9p x =
+ k2p ¾¾¾¾® x = ; x = ê 4 4 4 p 9p 7p 17p Û ê ¾¾ ®T = + + = . Chọn p x ê [ Î 0;3p ] 7p 4 4 4 4
x = - + k2p ¾¾¾¾® x = êë 4 4 A
Câu 39. Số vị trí biểu diễn các nghiệm của phương trình cos 2x + 3sin x + 4 = 0 trên đường tròn lượng giác là? A. 1. B. 2. C. 3. D. 4.
Lời giải. Phương trình 2 2
Û 1- 2sin x + 3sin x + 4 = 0 Û 2
- sin x + 3sin x + 5 = 0 ( ) ésin x = 1 - p ê Û 5 Û sin x = 1
- Û x = - + k2p (k Î!). êsin x = (loa )Ôi 2 ë 2
Suy ra có duy nhất 1 vị trí đường tròn lượng giác biểu diễn nghiệm. Chọn A x x
Câu 40. Cho phương trình cos x + cos +1 = 0 . Nếu đặt t = cos , ta được phương trình nào 2 2 sau đây? A. 2
2t + t = 0. B. 2 2
- t + t +1 = 0. C. 2 2t + t -1 = 0. D. 2 2 - t + t = 0. x Lời giải. Ta có 2 cos x = 2cos -1. 2 æ x ö x x x Do đó phương trình 2 2 Û 2cos -1 + cos +1 = 0 Û 2cos + cos = 0. ç ÷ è 2 ø 2 2 2 x
Đặt t = cos , phương trình trở thành 2
2t + t = 0. Chọn A 2 æ p ö æ p ö 5
Câu 41. Số nghiệm của phương trình cos 2 x + + 4cos
- x = thuộc [0;2p ]là? ç ÷ ç ÷ è 3 ø è 6 ø 2 A. 1. B. 2. C. 3. D. 4. Trang 22 æ p ö æ p ö æ p ö Lời giải. Ta có 2 2 cos 2 x + =1- 2sin x + =1- 2cos - x . ç ÷ ç ÷ ç ÷ è 3 ø è 3 ø è 6 ø æ p ö æ p ö Do đó phương trình 2 3 Û - 2cos - x + 4cos - x - = 0 ç ÷ ç ÷ è 6 ø è 6 ø 2 é æ p ö 1 cos - x é p = ê ç ÷ x = - + k2p 6 2 p 1 p p ê è ø æ ö 6 Û ê Û cos
- x = Û - x = ± + k2p Û ç ÷ ê , k Î ! ê æ p ö 3 è ø p cos - x = ê ç ÷ (loa ) 6 2 6 3 ê Ô i x = + k2p ë è 6 ø 2 êë 2 . p x [0;2p ] 11p p x 0;2p p Ta có x k2p Î = - + ¾¾¾¾® x = [ ] ; x k2p Î = + ¾¾¾¾® x = . 6 6 2 2
Vậy có hai nghiệm thỏa mãn. Chọn B
Câu 42. Tìm tất cả các giá trị thực của tham số m để phương trình tan x + m cot x = 8 có nghiệm.
A. m > 16.
B. m < 16.
C. m ³ 16.
D. m £ 16. Lời giải. Phương trình m 2
tan x + mcot x = 8 Û tan x +
= 8 Û tan x -8tan x + m = 0. tan x
Để phương trình đã cho có nghiệm khi và chỉ khi ¢ D = (- )2
4 - m ³ 0 Û m £16. Chọn D
Câu 43. Tìm tất cả các giá trị thực của tham số m để phương trình æ p p ö cos 2x -(2m + ) 1 cos x + m +1 = 3 0 có nghiệm trên khoảng ; . ç ÷ è 2 2 ø A. 1
- £ m £ 0 . B. 1 - £ m < 0 . C. 1 - < m < 1 0 . D. 1 - £ m < . 2 é 1 cos x =
Lời giải. Phương trình 2 2cos x (2m )1cos x m 0 ê Û - + + = Û 2 . ê ëcos x = m O 1 æ p p ö
Nhận thấy phương trình cos x = 3
không có nghiệm trên khoảng ; (Hình vẽ). Do đó ç ÷ 2 è 2 2 ø æ p p ö
yêu cầu bài toán Û cos x = 3
m có nghiệm thuộc khoảng ; Û 1 - £ m < 0. ç ÷ è 2 2 ø Chọn B Trang 23
Câu 44. Biết rằng khi m = m thì phương trình 2 x -( m+ ) 2 2sin 5
1 sin x + 2m + 2m = 0 0 æ p ö
có đúng 5 nghiệm phân biệt thuộc khoảng -
;3p . Mệnh đề nào sau đây là đúng? ç ÷ è 2 ø æ 3 7 ù æ 3 2 ö A. m = 3. - 1 B. m = . C. m Î ; . D. m Î - ; - . ç ç ÷ 2 0 5 10 ú è û 0 è 5 5 ø
Lời giải. Đặt t = sin x ( 1 - £ t £ ) 1 . Phương trình trở thành 2 t -( m+ ) 2 2 5
1 + 2m + 2m = 0 . ( ) * O O Hình 1 Hình 2
Yêu cầu bài toán tương đương với:
= TH1: Phương trình ( )
* có một nghiệm t = - (có một nghiệm x ) và một nghiệm 1 1 0 < t <
1 (có bốn nghiệm x ) (Hình 1). 2 c 2 a Do t = 1 - ¾¾
®t = - = -m - m. 1 2 a ém = 3 - ¾¾ ®t2 = 6 - Ï(0 ) ;1 (loa ) ê Ô i
a Thay t = - vào phương trình ( ) * , ta được . 1 1 ê 1 1 m = - ¾¾ ®t2 = Î ê (0 ) ;1 (tho˚a) ë 2 4
= TH2: Phương trình ( )
* có một nghiệm t = (có hai nghiệm x ) và một nghiệm 1 1 1
- < t £ 0 (có ba nghiệm x ) (Hình 2). 2 c 2 a Do t = 1 ¾¾
®t = = m + m. 1 2 a
ém =1¾¾®t2 = 2Ï( 1 - ;0](loa ) ê Ô i
a Thay t = vào phương trình ( ) * , ta được . 1 1 ê 1 3 m = ¾¾ ®t ê 2 = Ï( 1 - ;0](loa ) Ô i ë 2 4 1 æ ö Vậy m = - 1 3 2
thỏa mãn yêu cầu bài toán. Do m = - Î - ; - . Chọn D ç ÷ 2 2 è 5 5 ø
Câu 45. Tìm tất cả các giá trị thực của tham số m để phương trình 2 æ p p ö
2cos 3x + (3- 2m)cos3x + m- 2 = 0 có đúng 3 nghiệm thuộc khoảng - ; . ç ÷ è 6 3 ø A. 1
- £ m £ 1. B. 1 < m £ 2. C. 1 £ m £ 2.
D. 1 £ m < 2.
Lời giải. Đặt t = cos x ( 1 - £ t £ )
1 . Phương trình trở thành 2
2t + (3- 2m)t + m- 2 = 0. Trang 24 é 1 t = Ta có D = ( m - )2 2
5 . Suy ra phương trình có hai nghiệm ê 1 2 . êtë2 = m-2 O 1 æ p p ö
Ta thấy ứng với một nghiệm t =
thì cho ta hai nghiệm x thuộc khoảng - ; . Do đó 1 ç ÷ 2 è 6 3 ø yêu cầu bài toán 1 - < t £ 0 Û 1
- < m - 2 £ 0 Û1< m £ 2. Chọn B 2
Cách 2. Yêu cầu bài toán tương đươn với phương trình 2
2t + (3- 2m)t + m - 2 = 0 có hai ìP £ 0 ï
nghiệm t , t thỏa mãn 1
- < t2 £ 0 < 1t <1Û í . a f ( ) 1 > 0 . 1 2 ï .af î (- )1 > 0
Vấn đề 4. PHƯƠNG TRÌNH BẬC NHẤT ĐỐI VỚI sin x và cos x
Câu 46. Giải phương trình 2 x -( + ) 2 sin
3 1 sin x cos x + 3 cos x = 0. p p A. x = + k2p (k Î!). B. x = + kp (k Î!). 3 4 é p é p x = + k2p ê x = + kp 3 ê 3 C. ê (k Î!). D. ê (k Î!). p ê p x = + k2p ê ê x = + kp ë 4 êë 4 étan x =1
Lời giải. Phương trình 2
Û tan x - 3 +1 tan x + 3 = 0 Û ( ) ê ëtan x = 3 é p x = + kp ê 4 Û ê
(k Î!). Chọn D p êx = + kp êë 3
Câu 47. Gọi S là tập nghiệm của phương trình 2 2
2sin x + 3 3 sin x cos x - cos x = 2 .
Khẳng định nào sau đây là đúng? ìp ü ìp p ü ìp 5p ü ìp 5p ü
A. í ;p ý Ì S. B. í ; ý Ì S. C. í ; ý Ì S. D. í ; ý Ì S. î 3 þ î 6 2 þ î 4 12 þ î 2 6 þ Trang 25
Lời giải. Phương trình 2 2 2 2
Û 2sin x + 3 3 sin xcos x - cos x = 2 sin x + cos x ( ) 2
Û 3 3 sin x cos x - 3cos x = 0 Û 3cos x( 3sin x -cos x) = 0. p k= p = x = Û x = + kp (k Î!) 0 cos 0 ¾¾¾ ® x = . 2 2
= 3 sin x - cos x = 0 Û 3 sin x = cos x 1 p p = p Û tan x =
Û tan x = tan Û x = + kp (k Î!) k 0 ¾¾¾ ® x = . 3 6 6 6 p p
Vậy tập nghiệm của phương trình chứa các nghiệm và . Chọn B 6 2
Câu 48. Trong các phương trình sau, phương trình nào tương đương với phương trình 2 x -( + ) 2 sin
3 1 sin x cos x + 3 cos x = 3 . æ p ö A. sin x = 0 . B. sin x + =1. ç ÷ è 2 ø æ + ö C. ( x - ) 3 1 cos 1 ç tan x - ÷ = 0. D. ( x + + ) 2 tan 2 3 cos x -1 = 0. ( ) ç 1 3 ÷ - è ø Lời giải. Phương trình 2 Û x - ( + ) 2 2 2 sin
3 1 sin x cos x + 3 cos x = 3 sin x + cos x ( ) Û ( - ) 2 1 3 sin x - ( 3 + )
1 sin x cos x = 0 Û sin x éë(1- 3)sin x-( 3 + )1cos xù = 0. û 2 2
= sin x = 0 Û cos x = 1 Û cos x -1 = 0. = (1- 3)sin x - ( 3 + )
1 cos x = 0 Û (1- 3)sin x = ( 3 + ) 1 cos x 3 +1 Û tan x = Û tan x = 2
- - 3 Û tan x + 2 + 3 = 0. 1- 3
Vậy phương trình đã cho tương đương với ( x + + ) 2 tan 2
3 cos x -1 = 0. Chọn D ( )
Câu 49. Phương trình nào dưới đây có tập nghiệm trùng với tập nghiệm của phương trình 2
sin x + 3 sin x cos x =1? A. 2
cos x cot x - 3 = 0 . B. ( ) æ p ö é æ p ö ù sin x + . tan x + - 2 - 3 = 0. ç ÷ ê ç ÷ 2 ë 4 ú è ø è ø û é æ p ö ù C. 2 cos x + -1 . ê ç ÷ ú (tan x - 3) = 0. D. ë è 2 ø û
(sin x - )1(cot x- 3) = 0.
Lời giải. Phương trình 2 2 2
Û sin x + 3 sin x cos x = sin x + cos x 2
Û 3 sin x cos x - cos x = 0 Û cos x( 3 sin x -cos x) = 0. æ p ö
= cos x = 0 Û sin x + = 0. ç ÷ è 2 ø Trang 26 1
= 3 sin x - cos x = 0 Û tan x = . 3 p 1 tan x + tan +1 æ p ö 4 3 æ p ö Ta có tan x + = = = 2 + 3 Û tan x + - 2 - 3 = 0. ç ÷ ç ÷ è 4 ø p 1 è 4 1 tan . x tan 1 .1 ø - - 4 3 æ p ö é æ p ö ù
Vậy phương trình đã cho tương đương với sin x + . tan x + - 2 - 3 = 0.Chọn B ç ÷ ê ç ÷ 2 ë 4 ú è ø è ø û
Câu 50. Cho phương trình 2
cos x - 3sin x cos x +1 = 0. Mệnh đề nào sau đây là sai?
A. x = kp không là nghiệm của phương trình.
B. Nếu chia hai vế của phương trình cho 2
cos x thì ta được phương trình 2
tan x - 3tan x + 2 = 0.
C. Nếu chia 2 vế của phương trình cho 2
sin x thì ta được phương trình 2
2cot x + 3cot x +1 = 0.
D. Phương trình đã cho tương đương với cos 2x - 3sin 2x + 3 = 0 . si ì n x = 0 si ì n x = 0 ï
Lời giải. = Với x = kp ¾¾ ®í Û í
. Thay vào phương trình ta thấy 2 co î s x = 1 ± co ïî s x =1
thỏa mãn. Vậy A đúng. 2 2 2
= Phương trình Û cos x - 3sin x cos x + sin x + cos x = 0 2 2 2
Û sin x -3sin xcos x + 2cos x = 0 Û tan x -3tan x + 2 = 0. Vậy B đúng. 2 2 2
= Phương trình Û cos x - 3sin x cos x + sin x + cos x = 0 2 2 2
Û 2cos x -3sin xcos x + sin x = 0 Û 2cot x -3cot x +1 = 0. Vậy C sai. Chọn C 1+ cos 2x sin 2x = Phương trình Û - 3
+1 = 0 Û cos 2x - 3sin 2x + 3 = 0 .Vậy D đúng. 2 2
Câu 51. Số vị trí biểu diễn các nghiệm phương trình 2 2
sin x - 4sin xcos x + 4cos x = 5 trên
đường tròn lượng giác là? A. 4 . B. 3 . C. 2 . D. 1.
Lời giải. Phương trình 2 2 2 2
Û sin x - 4sin xcos x + 4cos x = 5 sin x + cos x ( ) 2 2 Û 4s
- in x - 4sin xcos x - cos x = 0 Û (2sin x +cos x)2 = 0 Û 2sin x +cos x = 0 1 Û tan x = - ¾¾
® có 2 vị trí biểu diễn nghiệm trên đường tròn lượng gác. Chọn C 2
Câu 52. Số nghiệm của phương trình 2 2
cos x - 3sin x cos x + 2sin x = 0 trên ( 2 - p;2p )? A. 2 . B. 4 . C. 6 . D. 8 . Lời giải. Phương trình é p étan x =1 x = + kp ê 2 ê 4
Û 1- 3tan x + 2 tan x = 0 Û 1 Û ê . êtan x = 1 ê ë 2 x = arctan + kp êë 2 Trang 27 = Vì ( p p ) p 9 7 2 ;2 2p p 2 k x k p k Î Î - ¾¾ ®- < + < ® - < < ¾¾¾ !®k Î{ 2 - ; 1 - ;0 } ;1 . 4 4 4 = Vì x Î(- p p ) 1 2 ;2 ¾¾ ® 2
- p < arctan + kp < 2p 2 CASIO 28,565 24,565 k k Î ¾¾¾¾ ®- < < - ¾¾¾ !®k Î{ 28 - ; 27 - ; 26 - ;- } 25 . xapxi
Vậy có tất cả 8 nghiệm. Chọn D
Câu 53. Nghiệm dương nhỏ nhất của phương trình 2 2
4sin x + 3 3 sin 2x - 2cos x = 4 là: p p p p A. . B. . C. . D. . 12 6 4 3
Lời giải. Phương trình 2 2 2 2
Û 4sin x + 3 3 sin 2x - 2cos x = 4 sin x + cos x ( ) écos x = 0 2
3 3 sin 2x 6cos x 0
6cos x ( 3sin x cos x) 0 ê Û - = Û - = Û 1 êtan x = êë 3 é p ép 1 Î! p x = + kp + kp > 0 k Û k > - ¾¾¾ ®k ê min = 0 ® x = ê 2 Cho>0 2 2 2 Û ê ¾¾¾¾ ® ê . p p 1 ê ê Î! p x = + kp + kp > 0 k Û k > - ¾¾¾
®kmin = 0 ® x = êë 6 êë 6 6 6 p
So sánh hai nghiệm ta được x =
là nghiệm dương nhỏ nhất. Chọn B 6
Câu 54. Cho phương trình ( - ) 2 x + x + ( + ) 2 2 1 sin sin 2
2 1 cos x - 2 = 0 . Trong các
mệnh đề sau, mệnh đề nào sai? 7p A. x =
là một nghiệm của phương trình. 8
B. Nếu chia hai vế của phương trình cho 2
cos x thì ta được phương trình 2
tan x - 2 tan x -1 = 0.
C. Nếu chia hai vế của phương trình cho 2
sin x thì ta được phương trình 2
cot x + 2cot x -1 = 0 .
D. Phương trình đã cho tương đương với cos 2x - sin 2x = 1.
Lời giải. Chọn D
Câu 55. Giải phương trình
2 x + ( - ) x x+( - ) 2 2sin 1 3 sin cos 1 3 cos x =1. p p p p A. - . B. - 2 . C. - . D. - . 6 4 3 12 Lời giải. Phương trình 2 Û x + ( - ) x x + ( - ) 2 2 2 2sin 1 3 sin cos 1
3 cos x = sin x + cos x 2 Û x + ( - ) 2 sin 1
3 sin x cos x - 3 cos x = 0 é p é an t = 1 x = - + k x p - ê 2 4
Û tan x + 1- 3 tan x - 3 = 0 Û ê Û ê ( ) ëtan x = 3 p êx = + kp êë 3 Trang 28 é p 1 Î! p - + kp < 0 k Û k < ¾¾¾
®kmax = 0 ® x = - ê Cho<0 4 4 4 ¾¾¾¾ ® ê . p 1 ê kÎ! 2p
+ kp < 0 Û k < - ¾¾¾
®kmax = -1® x = - êë 3 3 3 p
So sánh hai nghiệm ta được x = -
là nghiệm âm lớn nhất. Chọn B 4
Câu 56. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [ 10 - ; ] 10 để phương trình 2 x +(m- ) 2 11sin
2 sin 2x + 3cos x = 2 có nghiệm? A. 16. B. 21. C. 15. D. 6.
Lời giải. Phương trình 2 Û x + (m- ) 2 9sin
2 sin 2x + cos x = 0 1- cos 2x ( + Û + m - ) 1 cos 2x 9. 2 sin 2x +
= 0 Û (m - 2)sin 2x - 4cos2x = 5 - . 2 2 2 2 ém ³ 5
Phương trình có nghiệm Û (m - 2) +16 ³ 25 Û (m - 2) ³ 9 Û ê ëm £ 1 - mÎ ¾¾¾¾ ! ¾®mÎ 10 - ; 9 - ;...; 1 - ;5;6;...;10 ¾¾
® có 16 giá trị nguyên. Chọn A m [ Î - ] { } 10;10
Câu 57. Có bao nhiêu giá trị nguyên của tham số m thuộc để phương trình
2 x - (m- ) x x -(m- ) 2 sin 2 1 sin cos
1 cos x = m có nghiệm? A. 2. B. 1. C. 0. D. Vô số.
Lời giải. Phương trình Û ( - m)
2 x - (m- ) x x -( m- ) 2 1 sin 2 1 sin cos 2 1 cos x = 0 ( - +
Û - m) 1 cos2x -(m - )
x - ( m - ) 1 cos 2x 1 . 1 sin 2 2 1 . = 0 2 2 Û 2(m- )
1 sin 2x + mcos 2x = 2 -3 . m 2 2 2
Phương trình có nghiệm (m - ) + m ³ ( - m) 2 4 1 2 3
Û 4m - 4m £ 0 Û 0 £ m £1 mÎ ¾¾¾ !®mÎ{0; } 1 ¾¾
® có 2 giá trị nguyên. Chọn A
Câu 58. Tìm điều kiện để phương trình 2 2
asin x + asin x cos x + bcos x = 0 với a ¹ 0 có nghiệm. b b
A. a ³ 4b . B. a £ 4 - 4 b . C. £ 4 . 1 D. £1. a a
Lời giải. Phương trình 2
a tan x + a tan x + b = 0. Phương trình có nghiệm 2
Û D = a - 4ab ³ 0 Û a(a -4b) ³ 0 ( - Û b - a) 4b a 4b a 4 £ 0 Û £ 0 Û £1 .Chọn C a a
Câu 59. Tìm tất cả các giá trị của tham số m để phương trình 2
2sin x + msin 2x = 2m vô nghiệm. 4
A. 0 £ m £ . B. m < 4 0 , m > 4 . C. 0 < m < 4 .
D. m < - , m > 0 . 3 3 3 3 1- cos 2x
Lời giải. Phương trình Û 2.
+ msin 2x = 2m Û msin 2x - cos 2x = 2m -1. 2 Trang 29 ém < 0 Phương trình vô nghiệm 2 m 1 (2m )2 2 1 3m 4m 0 ê Û + < - Û - > Û 4 . Chọn B êm > ë 3
Câu 60. Có tất cả bao nhiêu giá trị nguyên của tham số m thuộc đoạn [ 3; - ]3 để phương trình 2 2
m + 2 cos x - 2msin 2x +1 = 0 có nghiệm. ( ) A. 3 . B. 7 . C. 6 . D. 4 . + x
Lời giải. Phương trình 2 1 cos 2 Û m + 2 .
- 2msin 2x +1 = 0 ( ) 2 2 2
Û 4msin 2x - m + 2 cos 2x = m + 4. ( ) Phương trình có nghiệm 2 2 2 2 2 2 2
Û16m + m + 2 ³ m + 4 Û12m ³12 Û m ³1Û m ³1 ( ) ( ) mÎ ¾¾¾¾ ! ®mÎ 3; - 2 - ; 1 - ;1;2;3 ¾¾
® có 6 giá trị nguyên. Chọn C m [ Î - ] { } 3;3
Vấn đề 5. PHƯƠNG TRÌNH CHỨA sin x ± cos x và sin x cos . x
Câu 61. Giải phương trình sin x cos x + 2(sin x + cos x) = 2. é p é p x = + kp x = + k2p A. ê 2 , k Î . ! B. ê 2 , k Î . ! ê ê ëx = kp ëx = k2p é p é p x = - + k2p x = - + kp C. ê 2 , k Î . ! D. ê 2 , k Î . ! ê ê ëx = k2p ëx = kp æ p ö Lời giải. Đặt
t = sin x + cos x = 2 sin x + . Vì ç ÷ è 4 ø æ p ö sin x + Î ç ÷ [-1 ]
;1 Þ t Î é- 2; 2 ù. 4 ë û è ø 2 2 2 t - Ta có t = ( x + x) 2 2 1 sin cos
= sin x + cos x + 2sin xcos x Þ sin xcos x = . 2 2 t -1 ét =1
Khi đó, phương trình đã cho trở thành 2
+ 2t = 2 Û t + 4t -5 = 0 Û ê . 2 t = -5 ë (loa )Ôi æ p ö æ p ö p Với t = 1
1, ta được sin x + cos x = 1 Û sin x + = Û sin x + = sin . ç ÷ ç ÷ è 4 ø 2 è 4 ø 4 Trang 30 é p p x + = + k2p ê éx = k2p 4 4 Û ê ê Û p
, k Î !. Chọn B p p ê êx = + k2p x + = p - + k2p ê ë ë 2 4 4
Câu 62. Cho phương trình 3 2 (sin x + cos x) + 2sin 2x + 4 = 0. Đặt t = sin x + cos x , ta
được phương trình nào dưới đây? A. 2
2t + 3 2 t + 2 = 0. B. 2
4t + 3 2 t + 4 = 0. C. 2
2t + 3 2 t - 2 = 0. D. 2
4t + 3 2 t - 4 = 0. Lời giải. Đặt 2
t = sin x + cos x ¾¾
®sin 2x = t -1.
Phương trình đã cho trở thành 2 2
3 2 t + 2 t -1 + 4 = 0 Û 2t + 3 2 t + 2 = 0. Chọn A ( )
Câu 63. Cho phương trình 5sin 2x + sin x + cos x + 6 = 0 . Trong các phương trình sau,
phương trình nào tương đương với phương trình đã cho? æ p ö 2 æ p ö 3 A. sin x + = . B. cos x - = . ç ÷ ç ÷ è 4 ø 2 è 4 ø 2
C. tan x = 1. D. 2 1+ tan x = 0. æ p ö
Lời giải. Đặt t = sin x + cos x = 2 sin x +
. Điều kiện - 2 £ t £ 2 ç ÷ . è 4 ø Ta có 2 t = ( x + x)2 2 2 2 sin cos
= sin x + cos x + 2.sin .
x cos x Þ sin 2x = t -1.
Khi đó, phương trình đã cho trở thành 2 2
5 t -1 + t + 6 = 0 Û 5t + t +1 = 0: vô nghiệm. ( )
Nhận thấy trong các đáp án A, B, C, D thì phương trình ở đáp án D vô nghiệm.
Vậy phương trình đã cho tương đương với phương trình 2
1+ tan x = 0. Chọn D 1
Câu 64. Nghiệm âm lớn nhất của phương trình sin x + cos x = 1- sin 2x là: 2 p 3p A. - . B. -p . C. - . D. - 2p . 2 2 æ p ö
Lời giải. Đặt t = sin x + cos x = 2 sin x +
. Điều kiện - 2 £ t £ 2 ç ÷ . è 4 ø Ta có 2 t = ( x + x)2 2 2 2 sin cos
= sin x + cos x + 2sin xcos x Þ sin 2x = t -1. 2 t -1 t é =1
Phương trình đã cho trở thành 2 t =1-
Û t + 2t - 3 = 0 Û ê 2 t = - ë (loa ). 3 Ô i æ p ö æ p ö æ p ö p Với t = 1
1, ta được 2 sin x + =1 Û sin x + = Û sin x + = sin ç ÷ ç ÷ ç ÷ è 4 ø è 4 ø 2 è 4 ø 4 é p p x + = + k2p éx = k2p ê 4 4 ê Û ê Û p , k Î!. p p ê ê x = + k2p x + = p - + k2p ë 2 êë 4 4 kÎ
TH1. Với x = k2p < 0 Û k < 0 ¾¾¾ !® k = 1 - ® x = -2p. max Trang 31 p 1 kÎ! 3p TH2. Với x =
+ k2p < 0 Û k < - ¾¾¾ ® k = -1® x = - . max 2 4 2 3p
Vậy nghiệm âm lớn nhất của phương trình là x = - . Chọn C 2 æ p ö
Câu 65. Cho x thỏa mãn phương trình sin 2x + sin x - cos x = 1. Tính sin x - . ç ÷ è 4 ø æ p ö æ p ö æ p ö A. sin x -
= 0 hoặc sin x - =1. B. sin x - = 0 ç ÷ ç ÷ ç ÷ è 4 ø è 4 ø è 4 ø æ p ö 2 hoặc sin x - = . ç ÷ è 4 ø 2 æ p ö 2 æ p ö C. sin x - = - . D. sin x - = 0 hoặc ç ÷ ç ÷ è 4 ø 2 è 4 ø æ p ö 2 sin x - = - . ç ÷ è 4 ø 2 æ p ö
Lời giải. Đặt t = sin x - cos x = 2 sin x -
. Điều kiện - 2 £ t £ 2 ç ÷ . è 4 ø Ta có 2 t = ( x - x)2 2 2 2 sin cos
= sin x + cos x - 2sin xcos x Þ sin 2x =1-t . ét =
Phương trình đã cho trở thành 2 2 0
1- t + t = 1 Û t - t = 0 Û . ê ët =1 æ p ö æ p ö Với t = 1
1, ta được 2 sin x - =1 Û sin x - = . ç ÷ ç ÷ è 4 ø è 4 ø 2 æ p ö æ p ö
Với t = 0 , ta được 2 sin x - = 0 Û sin x - = 0. ç ÷ ç ÷ è 4 ø è 4 ø Chọn B æ p ö
Câu 66. Từ phương trình 5sin 2x -16(sin x - cos x) +16 = 0, ta tìm được sin x + có ç ÷ è 4 ø giá trị bằng: 2 2 2 A. . B. - . C. 1. D. ± . 2 2 2 æ p ö
Lời giải. Đặt t = sin x - cos x = 2 sin x -
. Điều kiện - 2 £ t £ 2 ç ÷ . è 4 ø Ta có 2 t = ( x - x)2 2 2 2 sin cos
= sin x + cos x - 2.sin xcos x Þ sin 2x =1-t . ét =1
Phương trình đã cho trở thành 2 5 1 t 16t 16 0 ê - - + = Û ( ) 21 êt = - (loa ). Ô i ë 5
Với t = 1 Þ sin x - cos x = 1. (*) Trang 32 2 2
Mặt khác (sin x + cos x) + (sin x - cos x) = 2 , kết hợp với (*) suy ra ( æ p ö x + x)2 2 sin cos
+1 = 2 Û sin x + cos x = ±1 Û sin x + = ± . Chọn D ç ÷ è 4 ø 2 æ p ö
Câu 67. Cho x thỏa mãn 6(sin x - cos x) + sin xcos x + 6 = 0. Tính cos x + . ç ÷ è 4 ø æ p ö æ p ö A. cos x + = 1 - . B. cos x + =1. ç ÷ ç ÷ è 4 ø è 4 ø æ p ö 1 æ p ö 1 C. cos x + = . D. cos x + = - . ç ÷ ç ÷ è 4 ø 2 è 4 ø 2 æ p ö
Lời giải. Đặt t = sin x - cos x = 2 sin x -
. Điều kiện - 2 £ t £ 2 ç ÷ . è 4 ø 2 2 2 -t Ta có t = ( x - x) 2 2 1 sin cos
= sin x + cos x - 2sin xcos x Þ sin xcos x = . 2 2 1- t ét = -1
Phương trình đã cho trở thành 6t + + 6 = 0 Û ê 2 t =13 ë (loa )Ôi æ p ö æ p ö 1 æ p ö 1 Þ 2 sin x - = 1 - Û sin x - = - Û sin - x = ç ÷ ç ÷ ç ÷ è 4 ø è 4 ø 2 è 4 ø 2 ép æ p öù 1 æ p ö 1 Þ cos - - x = Û cos x + = . Chọn C ê ç ÷ú ç ÷ ë 2 è 4 øû 2 è 4 ø 2
Câu 68. Từ phương trình (1+ 3)(cos x + sin x) - 2sin xcos x - 3 -1= 0, nếu ta đặt
t = cos x + sin x thì giá trị của t nhận được là:
A. t = 1 hoặc t = 2 .
B. t = 1 hoặc t = 3 . C. t = 1. D. t = 3 . -t
Lời giải. Đặt t = x - x - £ t £ ¾¾ ® x x = ( ) 2 1 sin cos 2 2 sin cos . 2
Phương trình trở thành ( + ) 2 1
3 t - t -1 - 3 -1 = 0 ( ) ét =1 2
Û t - 1+ 3 t + 3 = 0 Û ê
Û t =1. Chọn C ( ) êt = 3 ë (loa )Ôi
Câu 69. Nếu (1+ 5)(sin x - cos x) + sin 2x -1- 5 = 0 thì sin x bằng bao nhiêu? 2 A. sin x = 2 . B. sin x = 2 hoặc sin x = - . 2 2 2 C. sin x = 1 - hoặc sin x = 0.
D. sin x = 0 hoặc sin x = 1. -t
Lời giải. Đặt t = x - x - £ t £ ¾¾ ® x x = ( ) 2 1 sin cos 2 2 sin cos . 2
Phương trình trở thành ( + ) 2 1
5 t +1- t -1- 5 = 0 Trang 33 t é =1 2
Û t - 1+ 5 t + 5 = 0 Û ê ( ) t ê = 5 ë (loa )Ôi
Þ sin x - cos x =1 Û cos x = sin x -1. ésin x = 0 Mặt khác 2 2 2
sin x + cos x =1Þ sin x + (sin x - )2 1 =1 Û . Chọn D ê ësin x =1 æ p ö
Câu 70. Nếu (1+ sin x)(1+ cos x) = 2 thì cos x - bằng bao nhiêu? ç ÷ è 4 ø 2 2 A. 1. - B. 1. C. . D. - . 2 2
Lời giải. Ta có (1+ sin x)(1+ cos x) = 2 Û1+ sin x + cos x + sin . x cos x = 2
Û sin x + cos x +sin .
x cos x =1 Û 2(sin x + cos x) + 2.sin . x cos x = 2. (*) t - Đặt t = x + x - £ t £ ¾¾ ® x x = ( ) 2 1 sin cos 2 2 sin cos . 2 ét =1 Khi đó (*) trở thành 2 2
2t + t -1 = 2 Û t + 2t - 3 = 0 Û êt = -3 ë (loa )Ôi
Þ sin x + cos x =1. æ p ö p p 2 2 Ta có cos x -
= cos xcos + sin xsin = ç ÷ (cos x +sin x) = . Chọn C è 4 ø 4 4 2 2
Câu 71. Cho x thỏa mãn 2sin 2x - 3 6 sin x + cos x + 8 = 0. Tính sin 2 . x 1 A. sin 2x = - 2 . B. sin 2x = - 1 . C. sin 2x = 2 . D. sin 2x = . 2 2 2 2 æ p ö Lời giải. Đặt
t = sin x + cos x = 2 sin x + . Vì ç ÷ è 4 ø æ p ö sin x + Î ç ÷ [-1 ] ;1 Þ t Î é0; 2 ù . 4 ë û è ø Ta có 2 t = ( x + x)2 2 2 2 sin cos
= sin x + cos x + 2sin xcos x Þ sin 2x = t -1. é 6 êt =
Phương trình đã cho trở thành 2
2 t -1 - 3 6 t + 8 = 0 Û 2 ( ) ê êt = 6 ë (loa )Ôi 2 1
sin 2x = t -1 = . Chọn C 2
Câu 72. Hỏi trên đoạn [0;2018p ], phương trình in
s x - cos x + 4sin 2x =1 có bao nhiêu nghiệm? A. 4037. B. 4036. C. 2018. D. 2019. æ p ö Lời giải. Đặt
t = sin x - cos x = 2 sin x - . Vì ç ÷ è 4 ø æ p ö sin x - Î ç ÷ [-1 ] ;1 Þ t Î é0; 2 ù . 4 ë û è ø Trang 34 Ta có 2 t = ( x - x)2 2 2 2 sin cos
= sin x + cos x - 2sin xcos x Þ sin 2x =1-t . ét = 1
Phương trình đã cho trở thành 2 t 4 1 t 1 ê + - = Û 3 . ( ) êt = - (loa )Ôi ë 4 kp
Với t = 1, ta được sin 2x = 0 Û 2x = kp Û x = , k Î!. 2 kp
Theo giả thiết x Î[0;2018p ] ¾¾ ®0 £
£ 2018p Û 0 £ k £ 4046 2 kÎ ¾¾¾
!®k Î{0;1;2;3;...;403 } 6 ¾¾
® có 4037 giá trị của k nê có 4037 nghiệm. Chọn A
Câu 73. Từ phương trình
2 (sin x + cos x) = tan x + cot x, ta tìm được cos x có giá trị bằng: 2 A. 1. B. - 2 . C. . D. -1. 2 2 s ì in x ¹ 0
Lời giải. Điều kiện í Û sin 2x ¹ 0. îcos x ¹ 0 x x Ta có ( x + x) = x + x Û ( x + x) sin cos 2 sin cos tan cot 2 sin cos = + cos x sin x 2 2 ( + Û x +
x) sin x cos x 2 sin cos = Û 2sin xcos .
x 2 (sin x + cos x) = 2. sin x cos x t - Đặt t = x + x - £ t £ ¾¾ ® x x = ( ) 2 1 sin cos 2 2 sin cos . 2 Phương trình trở thành 2 3
Û 2 t t -1 = 2 Û t - t - 2 = 0 Û t = 2 ( )
Þsin x +cos x = 2 Û sin x = 2 -cos . x Mà x + x = Þ x + - x = Û x - x + = ( )2 2 2 2 2 sin cos 1 cos 2 cos 1 2cos 2 2 cos 1 0 Û ( x - )2 1 2 cos 1 = 0 Û cos x = . Chọn C 2 æ p ö
Câu 74. Từ phương trình 3 3 3
1+ sin x + cos x = sin 2x, ta tìm được cos x + có giá trị ç ÷ 2 è 4 ø bằng: 2 2 A. 1. B. - 2 . C. . D. ± . 2 2 2 3
Lời giải. Phương trình Û 1+ (sin x + cos x)(1- sin x cos x) = sin 2x 2
Û 2 + (sin x + cos x)(2-sin 2x) = 3sin 2x . t - Đặt t = x + x - £ t £ ¾¾ ® x x = ( ) 2 1 sin cos 2 2 sin cos . 2 Phương trình trở thành 2 2
2 + t 2 - t +1 = 3 t -1 ( ) ( ) Trang 35 ét = -1 3 2
Û t + 3t - 3t - 5 = 0 Û ê êt = - ± ë (loa ). 1 6 Ô i æ p ö Với t = 1 - 1
, ta được sin x + cos x = -1 Û sin x + = - . ç ÷ è 4 ø 2 æ p ö æ p ö æ p ö æ p ö Mà 2 2 2 1 2 sin x + + cos x + =1¾¾ ®cos x + = Û cos x + = ± . ç ÷ ç ÷ ç ÷ ç ÷ è 4 ø è 4 ø è 4 ø 2 è 4 ø 2 Chọn D
Câu 75. Có bao nhiêu giá trị nguyên của tham số m để phương trình
sin x cos x - sin x - cos x + m = 0 có nghiệm? A. 1. B. 2. C. 3. D. 4. t -
Lời giải. Đặt t = x + x - £ t £ ¾¾ ® x x = ( ) 2 1 sin cos 2 2 sin cos . 2 2 t -1 2 2 Phương trình trở thành -t + m = 0 Û 2
- m = t - 2t -1Û (t - ) 1 = 2 - m + 2. 2 Do - £ t £ ¾¾ ®- - £ t - £ - ¾¾ ® £ (t - )2 2 2 2 1 1 2 1 0 1 £ 3+ 2 2. 1+ 2 2
Vậy để phương trình có nghiệm Û 0 £ 2 - m + 2 £ 3+ 2 2 Û - £ m £ 1 2 mÎ ¾¾¾ !®mÎ{ 1 - ;0; } 1 . Chọn C Trang 36