Bài Tập Tuần 4: Tìm Hàm Truyền Hệ Thống (3 Cách) - Kỹ Thuật Điện. Môn Lý thuyết điều khiển tự động (UET) | Trường Đại học Công nghệ, Đại học Quốc gia Hà Nội.

lOMoAR cPSD| 58833082 Bài tập tuần 4
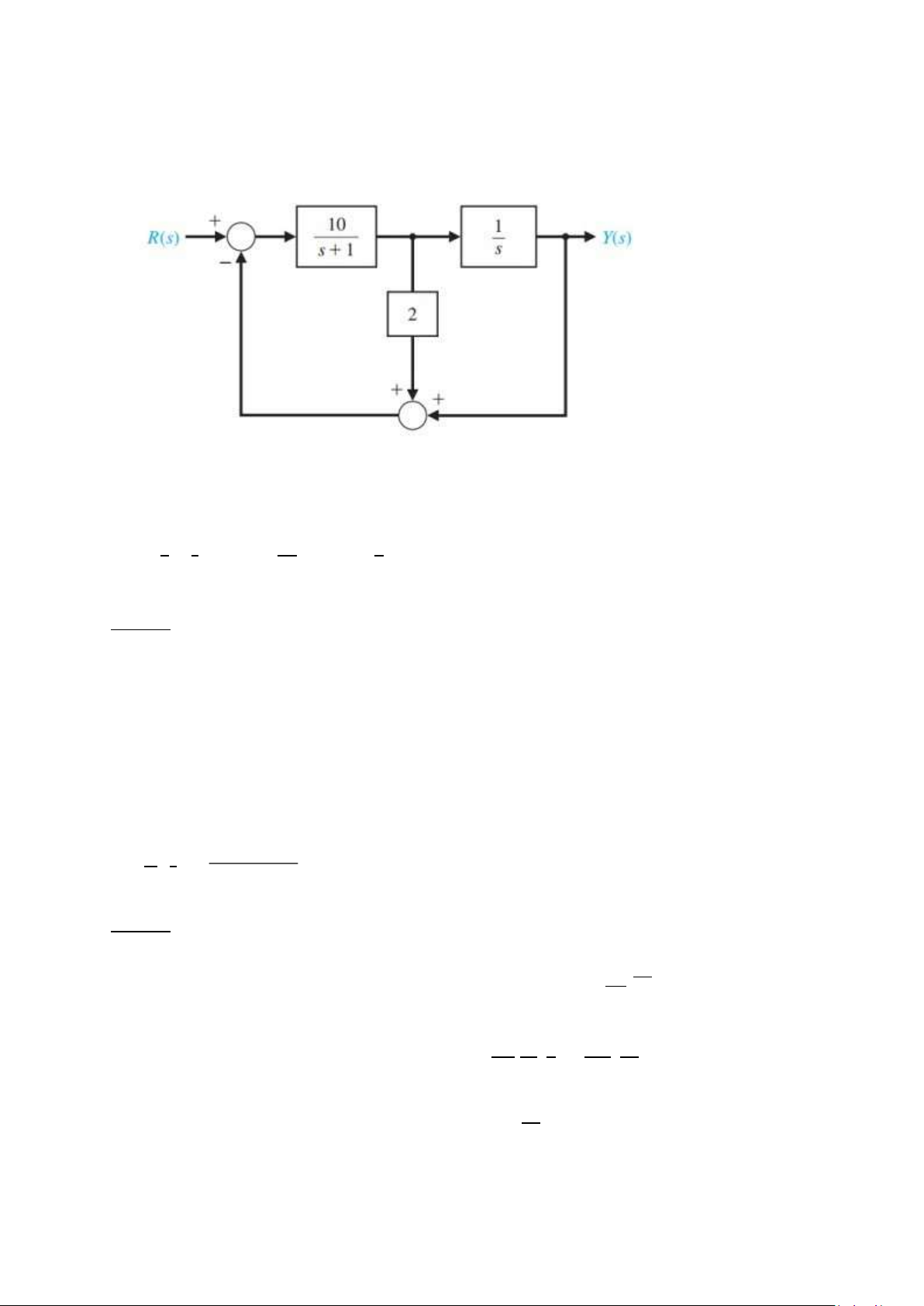
Bài 1: Tìm hàm truyền của hệ thống (bằng 3 cách) Gọi hàm truyền:
G (s)= YH( ss) ;H1( s)=s10+1 ;H2( s)=1s ;H3 (s)=2; ( ) Cách 1:
Gọi tín hiệu vào H1 (s), H2 (s)lần lượt là: e1,e2
Gọi tín hiệu ra H3 (s)là:e3 Ta có: e2=sY (s);e3=2sY
(s );e1=R ( s)−2sY (s )−Y ( s)
→ xéthàmtruyền H1( s):e1. H1 (s)=sY (s)
→10[ R ( s)−(2s+1) Y (s)]=( s+1) sY ( s)
→10R ( s)=[s ( s+1)+20 s+10 ]Y (s) → HY ((ss)) =
s2+2110s+10=G ( s) Cách 2: Xóa lối ra của H +1
2 (s) và bộ tổng sau đó thay H3 (s)=H3 (s)+H2( s)=2 ss
Sau đó chuyển lối ra của H1 (s) ra phía trước và nối thêm H1 (s) vào cụm H3 (s) và H2(s) 10 (2s+1) 20s+10
Khi đó cụm hàm truyền này sẽ có dạng U1 (s)= s(s+1) = s2+s 10
Cụm hàm truyền H1 (s)và H2 (s) sẽ có dạng U2 (s)= 2 s +s lOMoAR cPSD| 58833082
Xét tín hiệu ra và vào hàm truyền này ta có: Gọi
tín hiệu vào hàm truyền H1 (s ) là e1
→R ( s )−e1. 202s+10=e1→e1=
2 s2+s R (s)
s +s s +21s+10 Mặt khác 2
e1U2( s)=Y ( s) →
2 s +sR (s) . 102 =Y (s) s +21s+10 s +s →
s2 2110s+10=HY ((ss)) =G ( s) + Cách 3:
Chuyển điểm rẽ nhánh ở lối vào H3 (s) ra trước H1 (s ) 20
Khi đó ta thay hàm truyền H3 (s)bằngU1( s)=H3( s) H1( s)=s+1
Khi đó ta cũng thay hai hàm truyền nối tiếp H1 (s) và H2( s) thành 10
U2 (s) bằngH1( s) H2( s)= 2 s +s
Gọi tín hiệu đầu vào của U1 là e1 Ta có:
R (s)−e1U1( s)−e1U2 (s)=e1 →e1= R (s) (1)
U1 (s)+U2 (s)+1
Mặt khác: e1U2( s)=Y ( s) (2)
Từ (1) và (2) 10 U
→ U1 (s)+U2( s2)(s)+1=HY )
((ss)) =s20+1+s2s+102s+s+1
=s2+2110s+10=G ( s) lOMoAR cPSD| 58833082
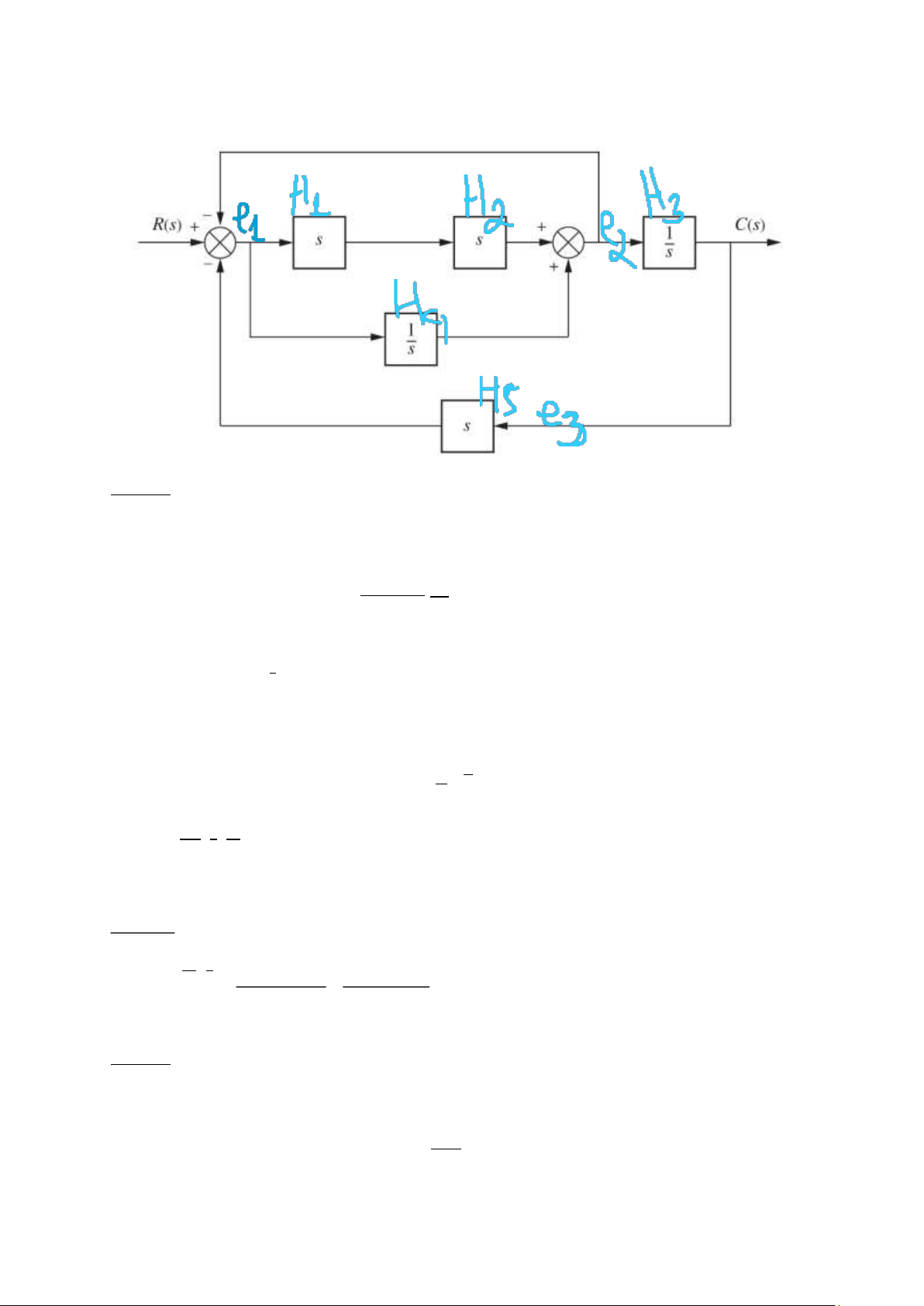
Bài 2: Tìm hàm truyền của hệ thống (bằng 3 cách) Cách 1:
Gọi H1,H2, H3, H4, H5 là các hàm truyền như hình vẽ Gọi tín
hiệu đầu vào H1,H3, H5 là e1,e2,e3 2 e1 s3+1
→e2=e1. H1. H2+e1H4=e1.s + s =e1. s e2
Mà mặt khác: e3= s 3 Mà: e . +1)
1=R (s)−e3.s−e2=R (s)−2e2=R (s)−2e1 (s s 3
→R ( s )=2s +s+2 e1 s Mặt
khác: H3e2=C (s)=
e1(s32+1) s C ( s) s3+1 s3+1
→G( s)=R ( S)
=s (2s3+s+2 )=2s4+s2+2 s Cách 2:
Vì H1 và H2 nối tiếp nên thay H1và H2 bằng U1=H1 H2=s2 3
Thay H4 vàU1 và bộ tổng bằng U2=U1+H4=s +1 s lOMoAR cPSD| 58833082
Chuyển điểm rẽ nhánh ngay trước H3 về trước U2
→ Dây hồi tiếp này sẽ có thêm U2 3 Khi đó U 1
2và H3 đang nối tiếp nên ta thay U2và H3 thành U3=U2H3= s +2 s
Gọi tín hiệu đầu vào của U2,H5làe1,e2
→e2=e1U3=C (s ) Mặt khác
e1=R (s)−e1U2−e2H5=R (s)−e1U2−e1U3 H5
→R ( s )=e1(1+U2+U3 H5) Mà C
( s)=e1U3 s3+1 C (s) U3 s2 s3+1
→G( s)=R ( s) = 1+U2+ = 3 3 = 4 2
U3 1+s +1+s +1 2s +s +2s s s Cách 3:
Vì H1và H2 nối tiếp nên thay H1và H2bằng U1=H1 H2=s2 Thay H4U1
và bộ tổng bằng U2=U1+H4=s3+1 s
Chuyển điểm rẽ nhánh ngay trước H3 về sau H3 1
→Nhánh phản hồi phía trên sẽ có thêm hàm truyền U3= H3=s 3 →U 1
2và H3 nối tiếp, ta thay bằng hàm truyền tương đương U4=U2 H3=s +2 s
Lúc này ta sẽ thấy U3và H5 song song
→ Thay bằng hàm truyền tương đương U5=U3+H5=2s
Giờ đây mạch đã có dạng hồi tiếp âm chỉ còn U4 vàU5 Ta sẽ
thay mạch hồi tiếp âm bằng hàm truyền tương đương s3+1 U4 s2 s3+1
G (s)=1+U4U5=1+ s3+212 s=2s4+s2+2s s
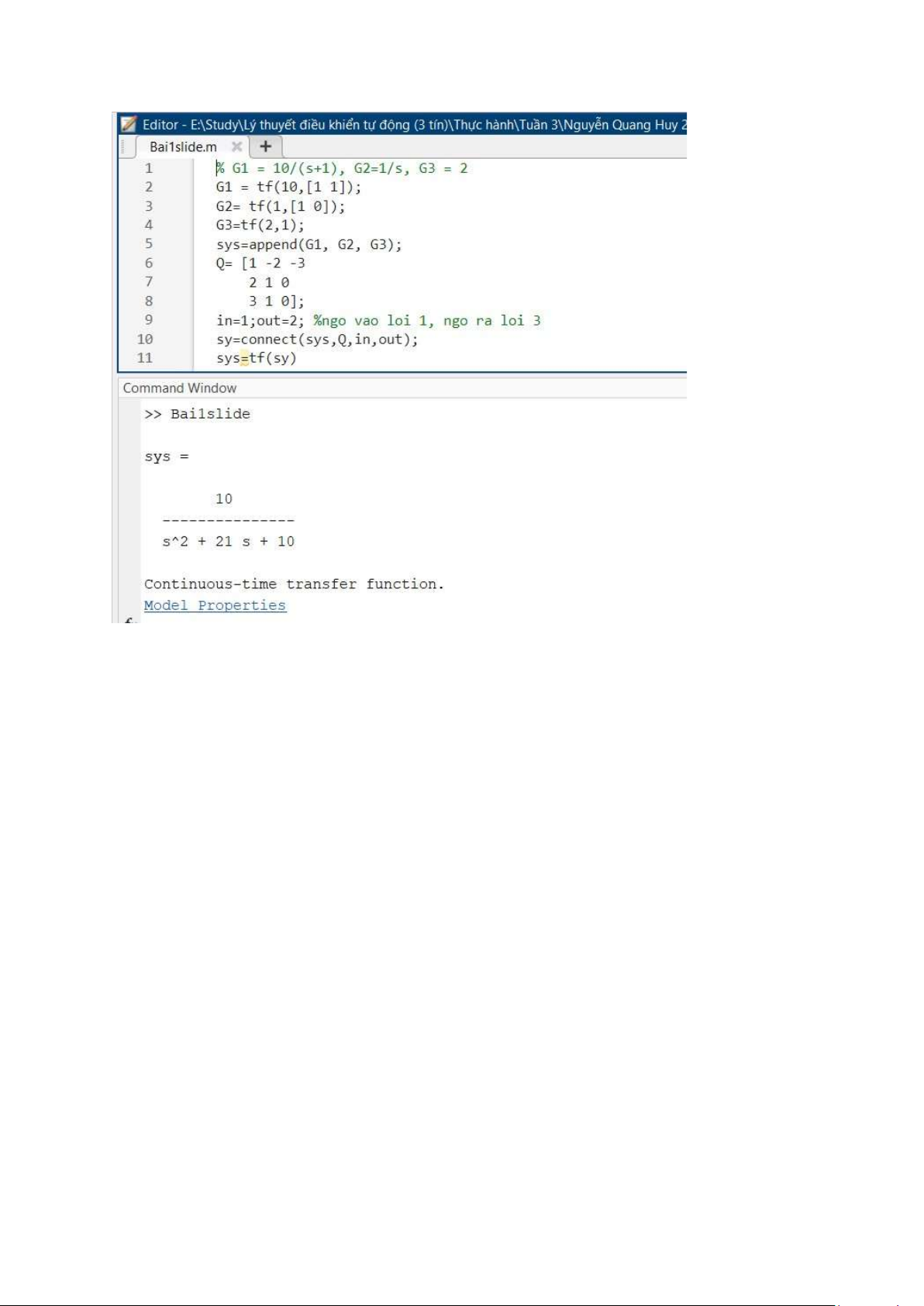
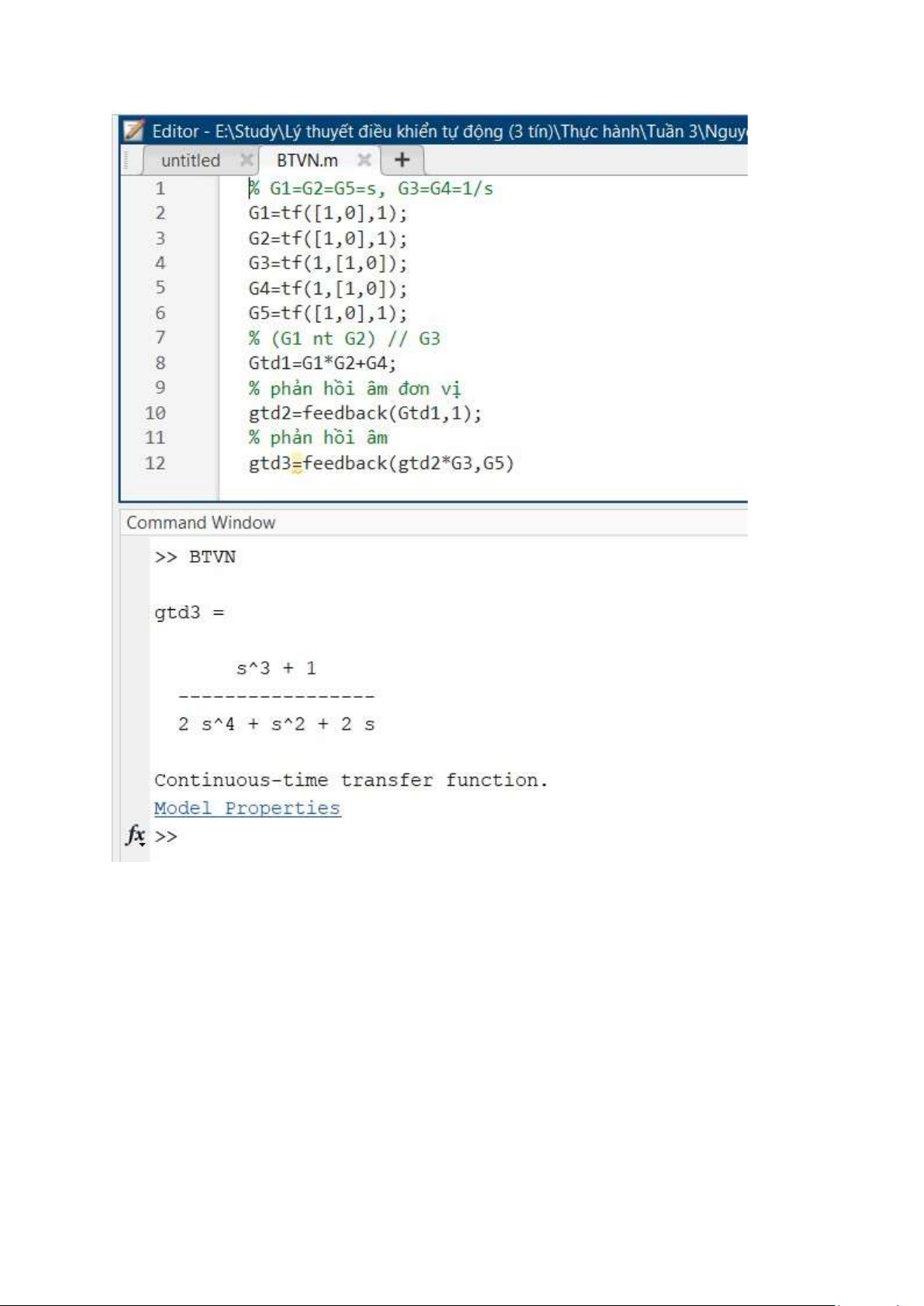
Kiểm tra bằng matlab Bài 1 : lOMoAR cPSD| 58833082 Bài 2 : lOMoAR cPSD| 58833082