Bài tập và tính toán thực hành Chương 9 | Phương trình vi phân đạo hàm riêng | Trường Đại học Khoa học Tự nhiên, Đại học Quốc gia Hà Nội
Giải phương trình vi phân thường trên chương trình Maple bằng lệnh dsolve, đã được trình bày trong giáo trình giải tích một biến. Dưới đây chúng ta nhắc lại và bổ xung thêm một số bài tập mới. Các bước giải phương trình hệ vi phân tương tự như giải phương trình vi phân bậc nhất. Nghiệm tổng quát của hệ 2 phương trình vi phân bậc nhất phụ thuộc vào 2 tham số tự do. Tài liệu được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!
Môn: Phương trình vi phân đạo hàm riêng 10 tài liệu
Trường: Trường Đại học Khoa học tự nhiên, Đại học Quốc gia Hà Nội 0.9 K tài liệu
Tác giả:
Preview text:
Bài tập và tính toán thực hành Chương 9 1. 1 .H ệ p h p ươ ư ng n g t r t ì r n ì h n h v i v ip h p â h n â n t h t ườ ư ng
n ....................................................................................................................................................................32 3 7 2
1.1. Khái niệm......................................................................................................................... 327
1.2. Hệ phương trình vi phân tuyến tính ................................................................................. 328
1.3. Hệ phương trình vi phân tuyến tính không thuần nhất..................................................... 328
1.4. Hệ phương trình vi phân với hệ số không đổi.................................................................. 328 2. 2 .P h P ươ ư ng n g t r t ì r n ì h n h đạ đ o o h à h m à m r i r ê i n ê g n
g ........................................................................................................................................................................... .32 3 8 2 3. 3 .T h T ực c h à h n à h n h t ítn í h n h t o t á o n á n t rê r n ê n m á m y á .
y ........................................................................................................................................................................ .32 3 9 2
3.1. Giải hệ phương trình vi phân thông thường .................................................................... 329
3.2. Tìm nghiệm dưới các dạng khác nhau và bằng các phương pháp tuỳ chọn..................... 330
3.3. Giải phương trình vi phân đạo hàm riêng ........................................................................ 332
3.4. Vẽ đồ thị nghiệm phương trình vi phân ........................................................................... 334
1. Hệ phương trình vi phân thường
1.1. Khái niệm
Bài 1. Hãy tìm các tích phân độc lập của những hệ phương trình sau: dx dy dz dx dy dz 1) = = ; 2) = = ; x y z x y x + y dx dy dz dx dy dz 3) = = ; 4) = = . cos x cos x cos x cos y z(x + z)
−y( y + z) 0
Bài 2. Giải bài toán Cauchy cho các hệ phương trình sau: dx 2 2 = x − y dt x = −1 1)
với điều kiện ban đầu khi t =1. dy y = 0 = 2 xy dt dx − = x e cos y dt x =1 2)
với điều kiện ban đầu khi t = 0 . dy − y =0 = − x e sin y dt 328
Giải tích các hàm nhiều biến
1.2. Hệ phương trình vi phân tuyến tính
Giải các hệ phương trình vi phân tuyến tính thuần nhất sau: dx d x = 2x + y = 2y −3x dt dt 1) 2) dy dy = 3x + 4 y = y −2x dt dt dx d x =
2x − y − z
= x − y + z dt dt dy d y 3)
= 12x − 4 y −12z 4)
= x + y −z dt dt dz = − dz
4x + y + 5z = 2x − y dt dt
1.3. Hệ phương trình vi phân tuyến tính không thuần nhất
Giải các hệ phương trình vi phân tuyến tính không thuần nhất sau: dx 3 dy
= 5x −3 y + 2 t e
= 2y + 4z + cos x dt 1) dx 2) dy = dz x + y + 5 t e−
= −y −2z +sin x dt dx
1.4. Hệ phương trình vi phân với hệ số không đổi
Giải các hệ phương trình vi phân tuyến tính thuần nhất sau bằng phương pháp biến đổi ma trận: dx = dx 3x − y = 5x + 3y dt dt 1) 2) dy dy = 4x − y = −3x − y dt dt dx dx = 4x − y
= 3x − 2y − z dt dt dy dy 3)
= 3x + y −z 4)
= 3x −4 y−3 z dt dt dz = dz x + z = 2x− 4 y dt dt
2. Phương trình đạo hàm riêng
Bài 1. Giải các phương trình tuyến tính cấp một thuần nhất sau:
Bài tập và tính toán thực hành Chương 9 329 ∂ z ∂ z ∂ z ∂ z 1) y + x = 0 ; 2) 2 x +( y + x ) = 0 ; ∂ x ∂ y ∂ x ∂ y u ∂ u ∂ u ∂ ∂ u( , x , y ) z ∂ u( . x . y ) z 3) z x + y + = 0 ; 4) x + yz = 0 ; ∂ x ∂ y 2 ∂ z ∂ x ∂ y ∂ z ∂ z ∂ u ∂ u ∂ u 5) x − z = 0 ; 6) 3 2 3 2 (x + 3xy ) + 2y + 2y z = 0 ∂ x ∂ y ∂ x ∂ y ∂ z
Bài 2. Giải các phương trình tuyến tính cấp một không thuần nhất sau: ∂ z ∂ z ∂ z ∂ z 1) 2 x y − x = yz ; 2) 2 x + 2y = x y + z ; ∂ x ∂ y ∂x ∂ y ∂u ∂u ∂z ∂z 3) + 3 = sin(xy) ; 4) 2 (z − y ) +xz = xy . ∂ x ∂ y ∂x ∂ y
Bài 3. Giải các phương trình đạo hàm riêng cấp hai và cấp cao sau: 2 ∂u ∂ u 2 2 ∂ u ∂ u 1)3 + 7 = xy ; 2) − = 0 ; ∂x ∂x∂ y 2 2 ∂ x ∂ y 5 ∂ u 5 ∂ u 3) = 0 ; 4) = sin(x y) . 2 3 ∂ x ∂ y 2 3 ∂ x ∂ y
3. Thực hành tính toán trên máy
3.1. Giải hệ phương trình vi phân thông thường Giải phư n
ơ g trình vi phân thường trên chương trình Maple bằng lệnh
dsolve, đã được trình bày trong giáo trình giải tích một biến. Dưới đây chúng ta
nhắc lại và bổ xung thêm một số bài tập mới. Các bước giải phương trình hệ vi
phân tương tự như giải phương trình vi phân ậ b c n ấ h t. Nghiệm ổ t ng quát ủ c a ệ h 2
phương trình vi phân bậc nhất phụ thuộc vào 2 tham số tự do.
Thí dụ 1. Giải hệ phương trình vi phân dy = z dx dz = y dx
với điều kiện ban đầu:
y(0) = 0, z(0) = 2 .
Bước 1 Gán tên sys (viết tắt của chữ system - hệ) cho hệ phương trình:
[> sys:={diff(y(x),x)=z(x),diff(z(x),x)=y(x),y(0)=0,z(0)=2}; ∂ ∂
sys := { y(x)= z(x),
z( x) = y(x), y(0) = 0, z(0)= x ∂ x ∂ }2
Bước 2 Gán tên cho nghiệm: 330
Giải tích các hàm nhiều biến
[> fcns:={y(x),z(x)}; fcns :={ ( y )
x , z( x)}
Bước 3 Giải hệ phương trình vi phân:
[> dsolve(sys,fcns); { ( ) x x − = − , ( ) x − x y x e e z x = e + e }
Thí dụ 2. Giải hệ phương trình vi phân thường cấp 2 (không có điều kiện ban đầu) sau: y ' = z z ' = y
Chú ý rằng nếu đưa phương trình này về hệ bậc nhất thì ta có hệ 4 phương trình.
Bước 1 Gán tên sys cho hệ phương trình cần giải:
[> sys:=(D@@2)(y)(x)=z(x),(D@@2)(z)(x)= y(x); 2 2
sys := (D )(y )(x )= z (x ), (D )(z )(x )= y (x )
Bước 2 Giải hệ phương trình vi phân bằng lệnh
[> dsolve({sys},{y(x),z(x)}); 1 (−x ) 1 x 1 1 −x 1 x 1 { ( y ) x = _ 1 C e + _ 1 C e + _ 1 C cos( )
x − _ C2 e + _ C2 e + _ C2sin( ) x 4 4 2 4 4 2 1 −x 1 x 1 1 1 x 1 + _ 3 + _ 3
− _ 3cos( ) − _ 4sin( ) + _ 4 − _ 4 −x C e C e C x C x C e C e , 4 4 2 2 4 4 1 −x 1 x 1 1 1 x 1 ( z ) x = _ 1 C e + _ 1 C e − _ 1 C cos( x) − _ C2sin( )
x + _ C2e − _ C2 −x e + 4 4 2 2 4 4 1 −x 1 x 1 1 −x 1 x 1 + _ C 3e + _C 3e
+ _C 3cos(x) − _C 4e
+ _ C 4e + _ C 4sin(x)} 4 4 2 4 4 2
3.2. Tìm nghiệm dưới các dạng khác nhau và bằng các phương
pháp tuỳ chọn
Trong trường hợp tổng quát, lệnh giải phương trình vi phân có cú pháp là:
[> dsolve(deqns,vars,keyword);
Trong đó deqns là các phương trình vi phân, vars là các biến nghiệm, phần
keyword cho phép ta xác định phư n
ơ g pháp giải và dạng biểu diễn nghiệm. Cách
biểu diễn mặc định là "chính xác " (exact). Nếu chọn cách biểu diễn nghiệm như
vậy ta sẽ không phải cho giá trị ở phần keyword. Nếu cách biểu diễn ấy không
thành (như ta thấy trong ví dụ trên đây), hoặc không phải là ý ta muốn, thì ta có thể
yêu cầu máy cho ta một trong các cách biểu diễn sau đây:
Bài tập và tính toán thực hành Chương 9 331 ♦ Với key e w y o w r o d
r được cho dưới dạng ty t pe p =
e series thì máy sẽ cho ta
nghiệm dưới dạng chuỗi. ♦ Với ke k y e w y o w r o d
r được cho dưới dạng ty t p y e p =
e numeric thì máy sẽ sử dụng
các phương pháp số (có một khối lượng lớn các phương pháp này trong
MAPLE để giải phương trình vi phân). Kết quả máy cho ta ngh ệ i m dưới
dạng một hàm tượng trưng mà có thể đánh giá được giá trị số của nó ạ t i bất kỳ điểm nào. ♦ Với ke k y e w y o w r o d
r được cho dưới dạng ou o p u u p t
u =basic thì máy sẽ cho ta tập
hàm cơ sở mà tập nghiệm được căng trên đó (như một bao tuyến tính). Nếu
phương trình không phải là thuần nhất thì máy sẽ cho ta thêm một nghiệm
riêng, để mọi nghiệm ấ
b t kỳ đều có thể biểu diễn qua tập nghiệm cơ sở và nghiệm riêng này.
Thông thường, nghiệm có t ể
h được cho dưới dạng một hàm ẩn (tức là ộ m t phương
trình hay hệ phương trình tạo bởi các tích phân đầu), hoặc dưới dạng các biến phụ
thuộc tham số. Nếu ta muốn bắt nó phải cho ta nghiệm dư i
ớ dạng hiển (tức là một
hàm số của y theo x ) thì ta cho ke k y e w y o w r o d r là ex e p x l p ilc i i c ti=
t true. (Vì khả năng
này thường khó xảy ra nên giá trị mặc định là ex e p x l p ilc i i c ti= t false ).
Muốn có được nghiệm biểu diễn thông qua các hàm đặc biệt kiểu Di D ira r c( c . ( ) . , ) , He H a e v a i v s i i s d i e d (. ( ) . ,... thì ta phải cho ke k yw y o w r o d r là m e m t e h t o h d o =laplace. . dy
= z − y− x Thí dụ 1. dx Giải hệ
với giá trị ban đầu y(0) = 0, z(0) =1. dz = y dx
1) Theo phương pháp mặc định sẵn trong máy, ta dùng các lệnh:
[> sys:=diff(y(x),x)=z(x)-y(x)-x,diff(z(x),x)=y(x): fcns:={y(x),z(x)}:
[> dsolve({sys,y(0)=0,z(0)=1},fcns); 1 ( 1 − + )x 1 (1 ( 5 1) ( 5 1 − ) x 2 2 ) ( z ) x = 5 e − 5 e + x +1, ( y ) x = 5 5 1 ( 1 − + )x 1 (1 − x) 1 ( 1 − x) 1 ( 1 ( 5 1) ( 5 1) ( 5 1) − ( 5 1 + )x 2 2 2 2 ) 5e 5e 1 e e − + + − − 10 10 2 2
2) Muốn tìm nghiệm dưới dạng chuỗi, ta dùng lệnh
[> dsolve({sys,y(0)=0,z(0)=1},fcns,type=series); 2 1 3 5 4 1 5 6
{ y( x)= x− x + x − x + x + ( O x ), 2 24 15 1 2 1 3 1 4 1 5 6 (
z x ) =1+ x − x + x −
x +O (x )} 2 3 8 24 332
Giải tích các hàm nhiều biến
3) Tìm nghiệm dưới dạng một lưới điểm số ta dùng các lệnh:
[> F:=dsolve({sys,y(0)=0,z(0)=1},fcns,type=numeric);
F := proc(rkf45_x) ... end
và, tiếp theo, để biết giá trị của nghiệm tại một điểm nào đ ó ta dùng lệnh [> F(1);
[x = 1, y(x) = .343731408276753914, z(x) = 1.25897207653682308] [> F(1.5);
[x = 1.5, y(x) = .237649509495644756, z(x) = 1.40935827136441327] [> F(1.7);
[x = 1.7, y(x) = .163416733680997378, z(x) = 1.44974926864546538].
Thí dụ 2. Tìm nghiệm phương trình vi phân cấp hai 3
y" = 2x y (với điều kiện ban
đầu y(0) =1, y '(0) =1 ) dưới dạng lưới điểm số, bằng chương trình mang tên
dverk78, và cho giá trị của nghiệm và đạo hàm của nó tại các điểm x = 1, x =
1.5, x = 1.7 dưới dạng bảng số liệu:
[> deq3:={(D@@2)(y)(x)=2*x^3*y(x),y(0)=1,D(y)(0)=1};
[> s:=dsolve(deq3,{y(x)},type=numeric,method=dverk78,
value=array([1.0,1.5,1.7])); s := ∂ x, y(x), y(x) x ∂ 1.
2.17013243525314170 1.93603788311791480
1.50000000000000000 4.26826796627041372 8.36391691654069902 1
.69999999999999996 6.71039854665199442 17 2
. 757972122874470
Thí dụ 3. Giải phương trình vi phân tuyến tính cấp 2 không thuần nhất
2xy "+ y '+ 3y = x
và cho biết hệ cơ sở (basis) của tập nghiệm cùng với một nghiệm riêng:
[> solve(2*x*diff(y(x),x$2)+diff(y(x),x)+3*y(x)=x,y(x), output=basis); 1 4 1 4 x cos( 6 x ) x sin( 6 x ) 1 1 , , − + x . 9 3 6 x 6 x
3.3. Giải phương trình vi phân đạo hàm riêng
Muốn giải phương trình vi phân đạo hàm riêng ta dùng lệnh pdesolve với cú pháp:
Bài tập và tính toán thực hành Chương 9 333 [> pdesolve(pt,s);
trong đó pt là phương trình đạo hàm riêng cần giải, s là nghiệm (hàm nhiều
biến) cần tìm. Đối với rất nhiều phương trình vi phân đạo hàm riêng, lệnh
pdesolve cho ta nghiệm dưới dạng hiển. Hàm tùy ý thường được kí hiệu là
_F1,_F2,v.v... Dưới đây là một số ví dụ giải phương trình đạo hàm riêng trên Maple.
1. Phương trình đạo hàm riêng cấp một
Thí dụ 1. Giải phương trình ∂z ∂z y + x = 0 . ∂ x ∂ y
[>pdesolve(y*diff(z(x,y),x)+x*diff(z(x,y),y)=0,z(x,y)); 2 2 ( z , x )
y = F −x + y 1( ) ∂z ∂z
Thí dụ 2. Giải phương trình 2 x + (y + x ) = 0. ∂x ∂ y
[>pdesolve(x*diff(z(x,y),x)+(y+x^2)*diff(z(x,y),y)=0,z(x,y)); 2 y x − ( z , x y) = F 1 x
2. Phương trình tuyến tính cấp một không thuần nhất ∂ z
Thí dụ 3. Giải phương trình y = z . ∂ x
[>pdesolve(y*diff(z(x,y),x)=z(x,y),z(x,y)); x ( , ) y z x y = e 1 F ( ) y ∂ z
Thí dụ 4. Giải phương trình = z. ∂ x
[>pdesolve(diff(z(x,y),x)=z(x,y),z(x,y)); ( , ) x
z x y = e F (y ) 1
Chú ý rằng đây là một phương trình đạo hàm riêng (trong lệnh pdesolve hàm z dz
phụ thuộc vào hai biến x, y ) chứ không phải phương trình vi phân thường = z dx
( z là hàm của một biến x ). Vì vậy nghiệm tổng quát phụ thuộc vào một hàm F (y ) 1
, chứ không phải là một hằng số như trong trường hợp phương trình vi phân thường. ∂ u ∂ u
Thí dụ 5. Giải phương trình + 3 = sin(x ) y . ∂ x ∂ y 334
Giải tích các hàm nhiều biến
[>pdesolve(diff(u(x,y),x)+3*diff(u(x,y),y)=sin(x*y),u(x,y));
Nghiệm được viết thông qua các hàm đ c ặ biệt.
3. Phương trình đạo hàm riêng cấp hai 2 ∂ u ∂ u
Thí dụ 6. Giải phương trình 3 + 7 = x y. ∂ x ∂ x∂ y
[>pdesolve(3*diff(g(x,y),x)+7*diff(g(x,y),x,y)=x*y,g(x,y)); 3 1 − 2 7 2 y 7 (
g x, y) = x y − x + 1
F ( y) + e 2 F (x) . 6 18 2 2 ∂ u ∂ u
Thí dụ 7. Giải phương trình − = 0 . 2 2 ∂ x ∂ y
[>pdesolve(diff(u(x,y),x,x)-diff(u(x,y),y,y)=0,u(x,y));
u(x, y) = F ( y + x) + F ( y − x) 1 2
4. Phương trình đạo hàm riêng cấp cao 5 ∂ u
Thí dụ 8. Giải phương trình = 0. 2 3 ∂ x ∂ y
[>pde:=D[1,1,2,2,2](U)(x,y)=0; pde := [
D 1,1, 2, 2, 2](U )( , x y) = 0
[>pdesolve(pde,U(x,y)); 2 U ( ,
x y) = F ( y) + F ( y)x + F (x) + F (x) y + F (x) y 1 2 3 4 5
3.4. Vẽ đồ thị nghiệm phương trình vi phân
1. Vẽ đồ thị nghiệm của hệ phương trình vi phân thường
Để vẽ đồ thị nghiệm của ệ
h phương trình vi phân, ta ầ
c n gọi gói công cụ : [> with(DEtools):
Và tiến hành vẽ đồ thị nghiệm của hệ phương trình vi phân bằng lệnh:
[>DEplot(deqns,vars,trange,inits,eqns); hoặc lệnh
[>DEplot(deqns,vars,trange,inits,xrange,yrange,eqns); Trong đó: deqns
- bảng các phương trình vi phân bậc nhất hoặc một phương trình vi phân cấp cao. vars
- biến phụ thuộc hoặc bảng các biến phụ thuộc.
Bài tập và tính toán thực hành Chương 9 335 trange
- miền thay đổi của biến độc lập. inits
- điều kiện ban đầu xác định đường cong nghiệm cần vẽ. yrange
- miền thay đổi của biến phụ thuộc thứ nhất. xrange
- miền thay đổi của biến phụ thuộc thứ hai. eqns
- các tuỳ chọn (màu, tiêu đề, độ đậm nhạt của đồ thị,...).
x '= x(1− y)
Thí dụ. Vẽ đồ thị của nghiệm ủ
c a hệ phương trình vi phân với y' = 0,3 ( y x 1 − )
biến độc lập t thay đổi trong đoạn [-2,2], biến phụ thuộc x thay đổi trong đoạn [-
1,2], biến phụ thuộc y thay đổi trong đoạn [-1,2], và thêm tiêu đề (tuỳ chọn) là:
‘Lotka-Volterra model’ (Mô hình Lotka-Volterra).
[> DEplot({diff(x(t),t)=x(t)*(1-y(t)),
diff(y(t),t)=.3*y(t)* (x(t)-1)},[x(t),y(t)],t=-
2..2,x=-1..2,y=-1..2, title=`Lotka-Volterra model`); Hình 9.1
2. Vẽ đồ thị nghiệm của phương trình vi phân thường trong không gian ba chiều
Để vẽ đồ thị nghiệm của phương trình vi phân trong không gian ba chiều ta
phải dùng lệnh DEplot3d thay cho DEplot ở trên:
[> DEplot3d(deqns,vars,trange,inits,xrange,yrange,eqns); x ' = y Thí dụ.
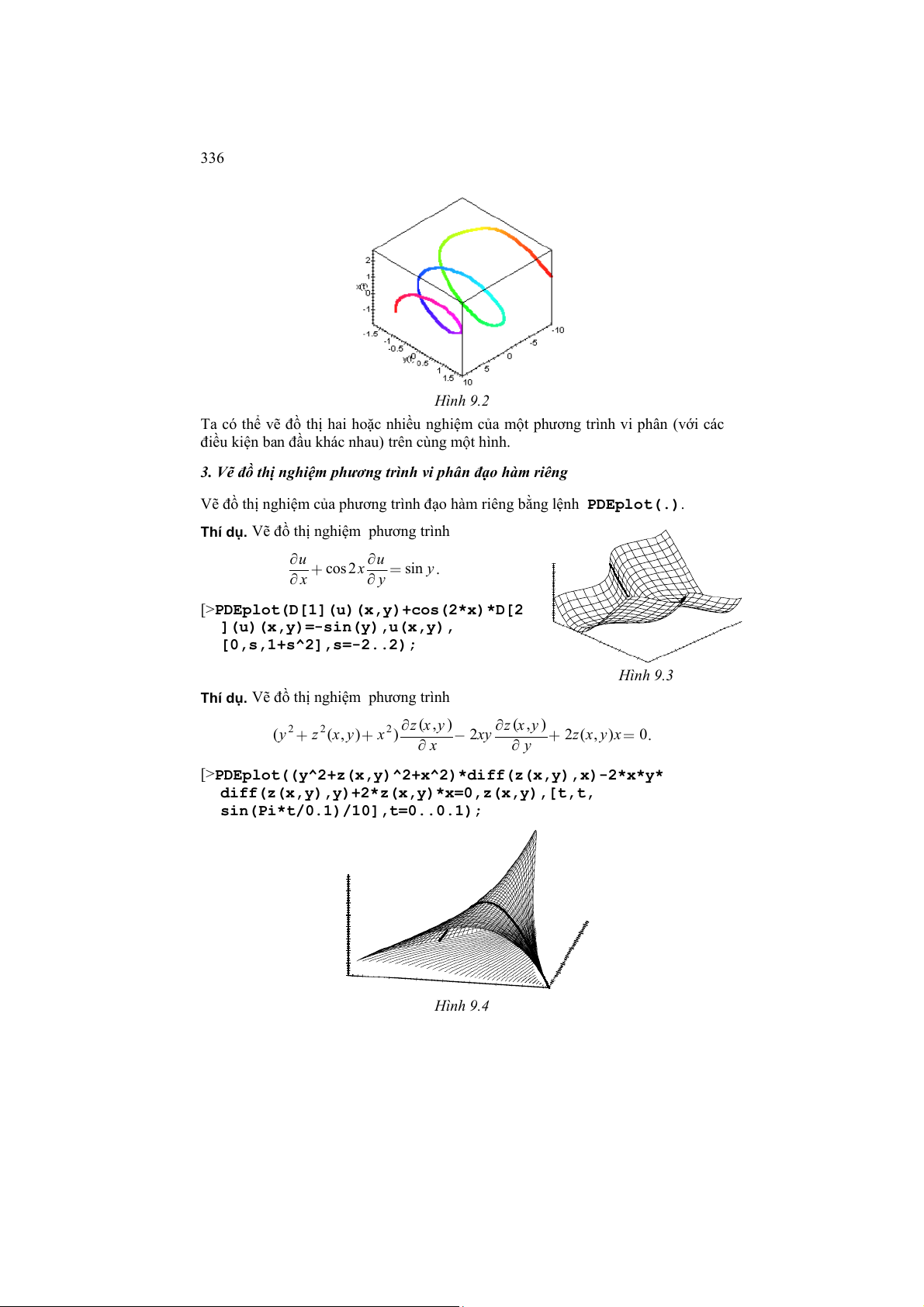
Vẽ đồ thị nghiệm của hệ phương trình vi phân y với điều y ' = −sin x − 10
kiện ban đầu là [x(0)=0, y(0)=1]; t thay đổi trong đoạn [-10,10].
[> DEplot3d({diff(x(t),t)=y(t),diff(y(t),t)=-sin(x(t))-
y(t)/10},{x(t),y(t)},t=-10..10,stepsize=.1,
[[x(0)=1,y(0)=1]],linecolor=t); 336
Giải tích các hàm nhiều biến Hình 9.2
Ta có thể vẽ đồ thị hai hoặc nh ề i u nghiệm của ộ
m t phương trình vi phân (với các
điều kiện ban đầu khác nhau) trên cùng một hình.
3. Vẽ đồ thị nghiệm phương trình vi phân đạo hàm riêng
Vẽ đồ thị nghiệm của phương trình đạo hàm riêng bằng lệnh PDEplot(.).
Thí dụ. Vẽ đồ thị nghiệm phương trình ∂u ∂u + cos 2x = sin y . ∂ x ∂ y
[>PDEplot(D[1](u)(x,y)+cos(2*x)*D[2 ](u)(x,y)=-sin(y),u(x,y), [0,s,1+s^2],s=-2..2); Hình 9.3
Thí dụ. Vẽ đồ thị nghiệm phương trình 2 2
2 ∂ z (x , y )
∂z (x ,y )
(y + z (x, y)+ x ) − 2xy
+ 2z(x, y)x = 0. ∂ x ∂ y
[>PDEplot((y^2+z(x,y)^2+x^2)*diff(z(x,y),x)-2*x*y*
diff(z(x,y),y)+2*z(x,y)*x=0,z(x,y),[t,t,
sin(Pi*t/0.1)/10],t=0..0.1); Hình 9.4