Bài tập Vật lý điện tử | Vật lý điện tử | Trường Đại học Bách Khoa Hà Nội

Bài tập Vật lý điện tử | Vật lý điện tử | Trường Đại học Bách Khoa Hà Nội. Tài liệu gồm 48 trang giúp bạn tham khảo ôn tập đạt kết quả cao trong kỳ thi sắp tới. Mời bạn đọc đón xem.

35 18 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: Vật lý điện tử

Trường: Đại học Bách Khoa Hà Nội

Thông tin:

48 trang 3 tháng trước

Tác giả:

Profile Trịnh Thảo Anh
Bài tập vật lý điện tử
Đỗ Đức Thọ
Bài tập chương I
Bài 1:
Dữ kiện:
0
900V
U
=
1
2cm
l
=
1
2
20cm
2
l
l+ =
1
d
=
1
d
=
?
S
=
Giải:
2
4
1 1
2
3
0
0,2.2.10 m
4,5.10
2 2 900.2.5.10 V
K
l lD
S l
U U d
−
−
−
= = + = =
Bài tập chương I
Bài 2:
Dữ kiện:
0
900V
U
=
1
2 5cm
l R
= =
1
2
35cm
2
l
l+ =
2 200 400;
W
= × =
6
1,26.10 Tm/A
µ
−
=
1
l
2
l
2
R
B
⊗
0
U
K
D
M
Giải:
( )
2
3 2
2 2
;
2
i WR
H
R z
=
+
2 200 400;
W
= × =
?
S
=
0
1,26.10 Tm/A
µ
=
19
1,6.10 C;
e
−
=
31
9.10 kg
m
−
=
0
B H
µ
=
( )
2
0
1
3 2
1 2
2 2
0
2 2
2
R W
l
D e
S l l
i mU
R z
µ
= = +
+
( )
19 4 2 6
2 2
3 2
31
4 4
1,6.10 6,25.10 .4.10 .1.26.10 m
5.10 .35.10 0,618
2.9,1.10 900 A
2 6,25.10 6,25.10
S
− − −
− −
−
− −
= =
+
Bài tập chương I
Bài 3:
Dữ kiện:
Giải
:
giả
sử
chùm
điện
tử
chuyển
động
song
song
với
trục
của
hệ
hai
3cm
R
=
1
300V
U
=
2
500V
U
=
?
f
=
z
R
1
θ
1
θ
2
θ
ϕ
A
C
B
O
Giải
:
giả
sử
chùm
điện
tử
chuyển
động
song
song
với
trục
của
hệ
hai
lưới và cách trục một khoảng z << R. Tia tới và tia khúc xạ hợp thành
với pháp tuyến mặt lưới (bán kính OA) các góc
θ
1
,
θ
2
. Do các góc này
nhỏ nên ta có:
1
2 2
1 1
2
sin
sin
U
k
U
θ θ
θ θ
= =
≃
Bài tập chương I
Từ hình học ta có:
1
1 2
1
R
R
CB
k
θ
θ θ
= =
− −
1 2
;
ϕ θ θ
= −
;
CB AC
ϕ
=
1
AC R
θ
≃
Như vậy CB không phụ thuộc vào góc
θ
1
⇒ có thể xem là tiêu cự
1
3
13,25cm
300
1
500
f CB= = =
−
Bài tập chương I
Bài 5:
Dữ kiện:
1
100V;
D A
U U
= =
1cm
d
=
2
?
D
U
=
Giải
:
Chúng
ta
có
thể
biểu
diễn
hệ
d
d
d
0
K
U
=
Giải
:
Chúng
ta
có
thể
biểu
diễn
hệ
quang học điện tử giống như hệ
quang học tia sáng. Ứng dụng định luật
quang học với hai thấu kính ta có:
2
1 1 1
a b f
+ =
a- khoảng cách vật, b- khoảng cách ảnh đối với thấu kính thứ 2
Bài tập chương I
Điều kiện để cho chùm điện tử hội tụ trên anôt là:
2 1
1 1 1
f d f d
= +
−
Từ công thức tính tiêu cự ta có:
1
1
2 1
4
;
D
U
f
E E
=
−
2
2
3 2
4
;
D
U
f
E E
=
−
(
)
*
Thay vào phương trình (*) ta nhận được:
(
)
1 2
1
1
2
2
1
4
4
2
U U
f
U d
U d
d
U U
−
= =
−
−
2 1
2
d
U U
−
−
Giải phương trình này ta nhận được:
(
)
1
2
432,28V
U
=
(
)
2
2
27,72V
U
=
Bài tập chương IIBài tập chương I
Bài 1:
Dữ kiện:
100W
P
=
0
1A
d
=
2,2eV
K
ϕ
=
5%P
b
P
=
R
75cm
R
=
d
?
t
=
Giải: Cường độ ánh sáng trên bề mặt nguyên tử K là:
2
4
b
P
I
R
π
=
R
75cm
R
=
Công suất hấp thụ bởi nguyên tử:
2
2
2 2
.
4 2 16
b b
a a
P Pd
d
P I S
R R
π
π
= = ⋅ =
Thời gian cần thiết để nguyên tử K hấp thụ năng lượng
ϕ
K
là:
57,6s
K
a
t
P
ϕ
= =
Mẫu sóng ánh sáng cho kết quả rất lớn so với
thực nghiệm:
Bài tập chương IBài tập chương II
Bài 2:
Dữ kiện:
0
2500A ;
λ
=
2,2eV;
K
ϕ
=
max
?
T
=
Giải: từ công thức:
2
W
2 ;
m
I =
?
e
N
=
max
K
hc
T
ϕ
λ
= −
34 8 18
6,626.10 .3.10 .6,24.10
−
Số photon đập vào bề mặt K trong 1s là:
18
2
ph
2,52.10
m .s
ph
I I I
N
hc
E hc
λ
λ
= = = =
34 8 18
max
10
6,626.10 .3.10 .6,24.10
2,2 2,75eV
2500.10
T
−
−
= − =
Nếu mỗi photon đập vào bề mặt K bứt ra một e thì số điện tử phát ra từ
1m
2
bề mặt K trong 1s sẽ là:
18
2
ph
2,52.10
m .s
e
N N= =
Bài tập chương IBài tập chương II
Bài 3:
Dữ kiện:
0,3MeV;
ph
hc
E
λ
= =
v ?
e
=
Giải: áp dụng định luật bảo toàn năng lượng ta có:
0 2
'
e e
hc
E E m c
λ
+ = +
λ
'
λ
e
p
(
)
1
Mặt khác theo định luật bảo toàn động lượng:
'
e
h h
p
λ λ
= − +
(
)
2
Từ (1) và (2)
0 2
'
'
ph e e
e
hc
E E m c
hc hc
p c
λ
λ λ
+ = +
= − +
2
0
2
ph e e
E E m c p c
+ = +
(
)
2
0 0 0 0
2 v v
ph
E E m c m c m c c
γ γ γ
+ = + = +
( )
2
2
0 0
v
1
2
v
1
ph
c
E E E
c
+
+ =
−
Bài tập chương II
v 1
;
1
c
α
α
−
=
+
2 2
2
0
0 0
2 2
2.0,3
1 1 4.73
0,511
ph ph
E E E
E E
α
+
= = + = + =
v 4,73 1
0,65;
4,73 1c
−
= =
+
Bài 4:
Dữ
kiện
:
0
1A ;
λ
=
?
U
=
(
)
(
)
2
12,2 12,2 12,2
150V
1
e
e
U
U
λ
λ
=
⇒
= = =
Giải:
Dữ
kiện
:
0
e e
E E
>>
?
e
λ
Giải:
Bài tập chương II
(
)
2
2 2
0
e e
E p c E
= +
Ta có: . Do E
e
>> E
0
⇒ p
e
c
≈
E
e
Bài 5:
Dữ kiện:
(
)
0
e e
E p c E
= +
e
0
e
e
e
e e e
h hc hc
p p c E
λ
= = =
Đối với photon ta có:
hc hc
E
E
λ
λ
=
⇒
=
Như vậy ta có bước sóng kết hợp của hạt gần đúng bằng bước sóng của
photon có cùng năng lượng. Đây là điều phải chứng minh
v
h h
p m
λ
= =
v ,v ?
f g
Giải
:
Bài tập chương II
Bài 6:
Dữ kiện:
Giải
:
Ta có:
2 2
v ;
v v
f
E mc c
p m
= = =
(
)
(
)
(
)
2
2 2 2
0
2 2 2
E pc m c EdE pc d pc pc dp
= +
⇒
= =
2
2
2 v
v v
2
g
dE pc m c
dp E mc
= = = =
3
6,625.10 Js;
h
−
=
y
∆
Giải:
Bài tập chương II
Bài 8:
Dữ kiện:
v 5m/s;
=
12m;
L
=
0,6m
d
=
Ta có:
3
3
6,625.10 .12
v
0,4m
v 66,25.10 .5.0,6
h
L
L hL
m
y
d d m d
λ
−
−
∆ = = = = =
3
=10 ;
p
p
−
∆
Giải:
Bài tập chương II
Bài 9:
Dữ kiện:
)
5mg;v 2m/s; ?
a m x
= = ∆
)
31 8
9,1.10 kg;v 1,8.10 m/s; ?
e
b m x
−
= = ∆
a)
.
2
x
h
x p
π
∆ ∆ ≥
20 0
10,577.10 A
2 .
x
h
x
p
π
−
∆ ≥ =
∆
b)
.
2
x
h
x p
π
∆ ∆ ≥
2
2
0
3
0
v
1
5,14A
2 . 2 .10 . v
x
h
h
c
x
p m
π π
−
−
∆ ≥ = =
∆
0
=2500A ;
λ
Giải:
Bài tập chương II
Bài 10:
.
2
h
E t
π
∆ ∆ ≥
Dữ kiện:
?
t
2
9
2
8,493.10 s
2 . 2
2 .
h h
t
hc
E c
λ
π π λ
π λ
λ
−
≥ = = =
∆ ∆
∆
0
=1A ;
λ
∆
2
λ
= ;
h
p p
λ
∆ =
Giải:
Bài 11:
.
2
h
x p
π
∆ ∆ ≥
Dữ kiện:
?
x
∆
2 . 2
2 .
h h
x
h
p
λ
π π
π
λ
∆ ≥ = =
∆
Giải:
Bài 12:
.
2
h
p x
π
∆ ∆ ≥ v. . v
2
h
m p x m
π
∆ ∆ ≥
Bài tập chương II
( )
2
2 . v
2
h
p m x
π
∆ ∆ ≥
.
2
h
E t
π
∆ ∆ ≥
Bài 13:
Giải:
.
2
h
p x
π
∆ ∆ ≥ v. . v
2
h
m p x m
π
∆ ∆ ≥
( )
2
2 . v
2
h
p m x
π
∆ ∆ ≥
.
2
h
E t
π
∆ ∆ ≥
Giải:
Bài tập chương II
Bài 15:
2
2 34
2
16
1
2
2
1 6,625.10
8
v 3,3.10 m/s
h
E
h h
mL
−
−
= = = = = =
Dữ kiện:
min
v ?
14
10 kg;
m
−
=
0,1mm;
L
=
16
1
min
2 2 14 4
2
1 6,625.10
8
v 3,3.10 m/s
4 2 2.10 .1.10
E
h h
mL
m m m L mL
−
− −
= = = = = =
2
1
.
n
E E n
=
2
2
2
2 2
1
v
8
8 2. . .v
2
m
mL
E EmL m L
n
E h h h
⋅
= = = =
14 4 5
10
34
2.10 .10 .1.10
3.10
6.625.10
n
− − −
−
= =
Bài tập chương II
Bài 16:
ˆ
d
L i L
dx
Ψ
Ψ = = Ψ
1
d
Ldx iLdx
i
Ψ
= = −
Ψ
.
iLx
C e
−
Ψ =
Giải:
Chúng ta thấy rằng hàm Ψ(x) thỏa mãn phương trình, với mọi giá trị L
hàm Ψ(x) liên tục, đơn trị và hữu hạn. Như vậy bất kì giá trị L thực nào
cũng
là
trị
riêng
của
và
Ψ
(x)
là
hàm
riêng
của
C const
=
ˆ
L
cũng
là
trị
riêng
của
và
Ψ
(x)
là
hàm
riêng
của
ˆ
L
Áp dụng kết quả này cho trường hợp toán tử hình chiếu xung lượng ta
có:
x
d
i p
dx
Ψ
− = Ψ
ℏ
.
x
ip x
C e
−
Ψ =
C const
=
Hàm Ψ(x) là khác không trong khoảng: -∞ < x < ∞, liên tục, đơn trị,
hữu hạn với mọi giá trị p
x
là số thực ⇒ như vậy đại lượng hình chiếu
xung lượng của một hạt tự do không bị lượng tử hóa
Bài tập chương II
Bài 17:
Dữ kiện:
50eV;
E
=
0
70eV;
U
=
)
1nm; ?
a L D
=
)
0,1nm; ?
b L D
=
Giải:
19
2.10
2
L
−
a)
( )
( )
19
31 19
34
0
2.10
2
2.9,1.10 70 50 .1,6.10
2
20
6,625.10
1,3.10
L
m U E
D e e
−
− −
−
− −
− −
−
= =
ℏ
≃
b)
( )
( )
10
31 19
34
0
2.10
2
2.9,1.10 70 50 .1,6.10
2
6,625.10
0,01
L
m U E
D e e
−
− −
−
− −
− −
= =
ℏ
≃
| 1/48
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

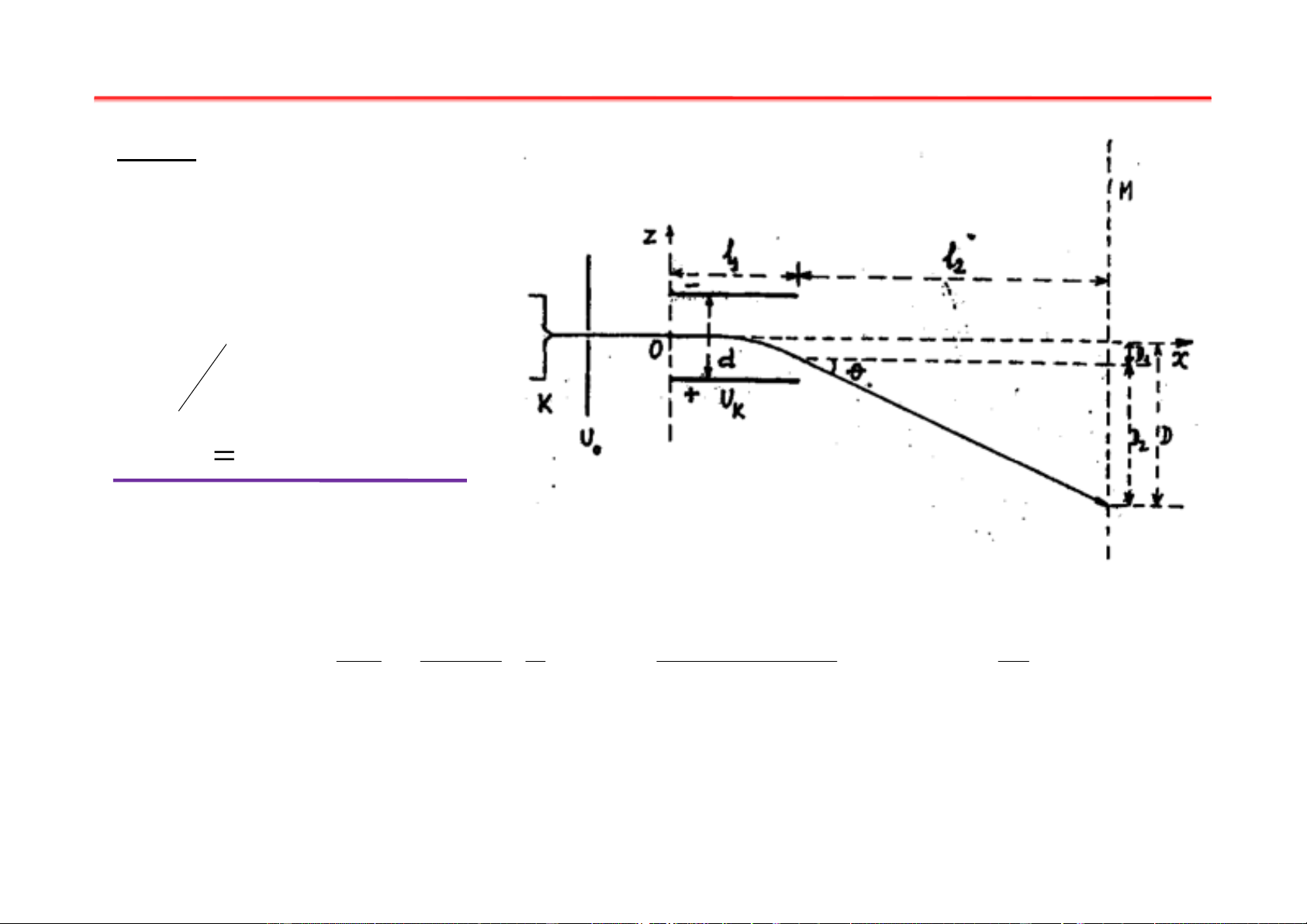
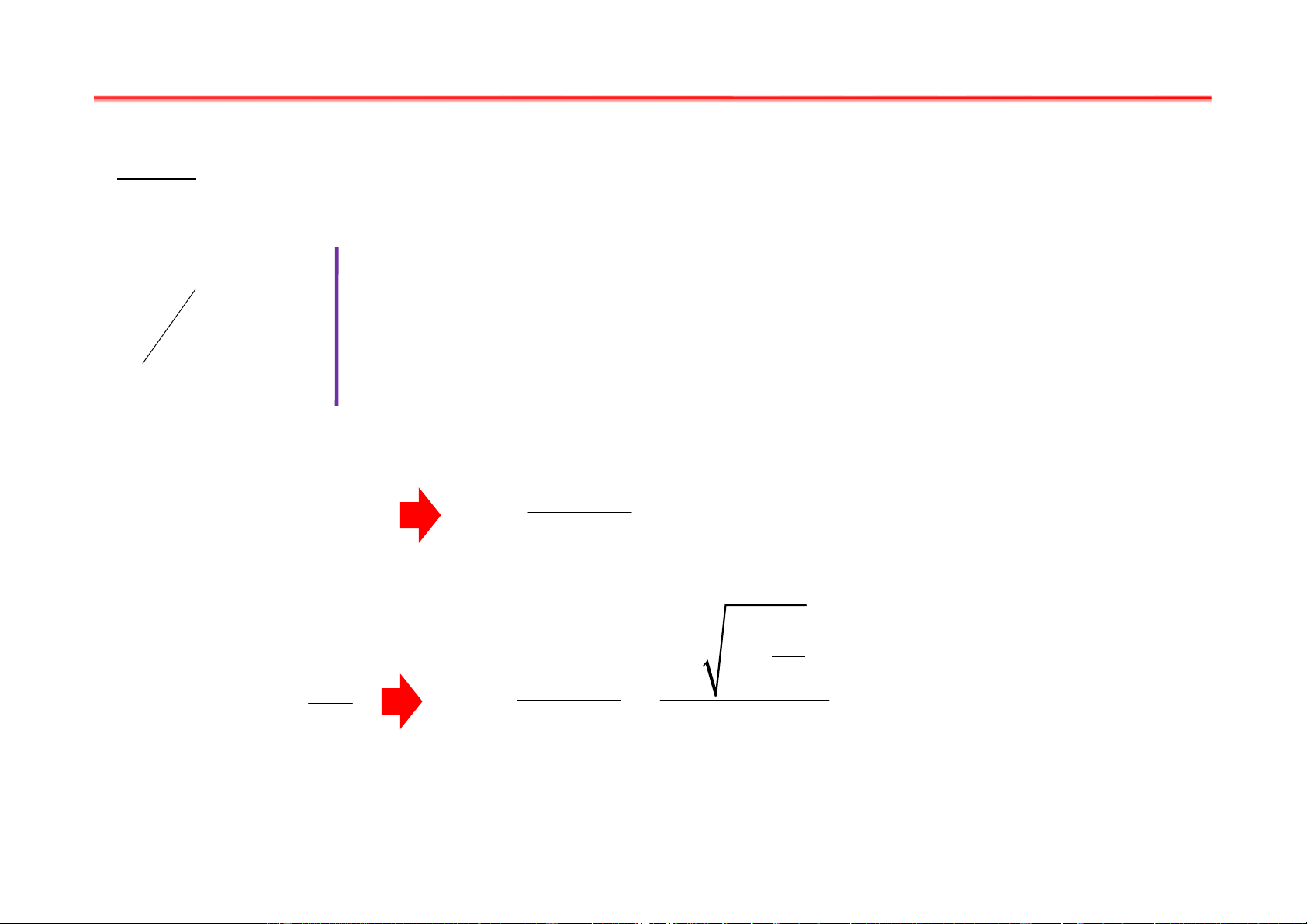
Bài tập vật lý điện tử Đỗ Đức Thọ Bài tập chương I Bài 1: Dữ kiện: U = 900V 0 l = 2cm 1 l1 + l = 20cm 2 2 d = 0,5cm 1 = 0, 5c 1 S = ? Giải: 2 D ll  0, 2.2.10− − m 4 1 1 S = =  + l  = = 4,5.10 2 −3 U U 2d  2  900.2.5.10 V K 0 Bài tập chương I Bài 2: l M 1 Dữ kiện: U l 0 2 U = 900V 0 K 2R l = 2R = 5cm 1 l B⊗ 1 + l = 35cm D 2 2 W = 2× 20 2 0 0 = 40 4 0; 6 0; µ = 1, 1 26 2 . 6 1 . 0− 10 Tm/A 0 = Tm/ −19 −31 2
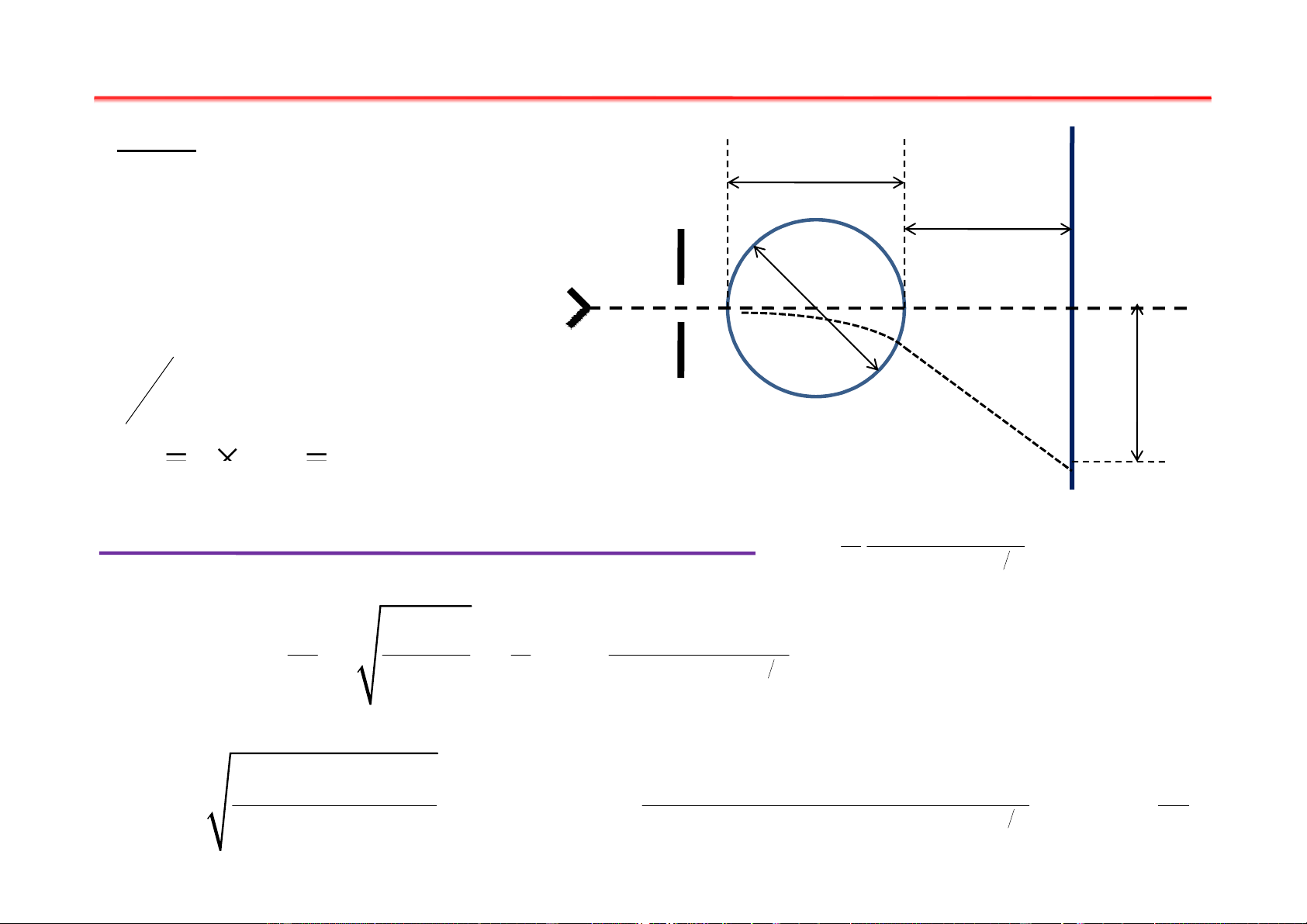
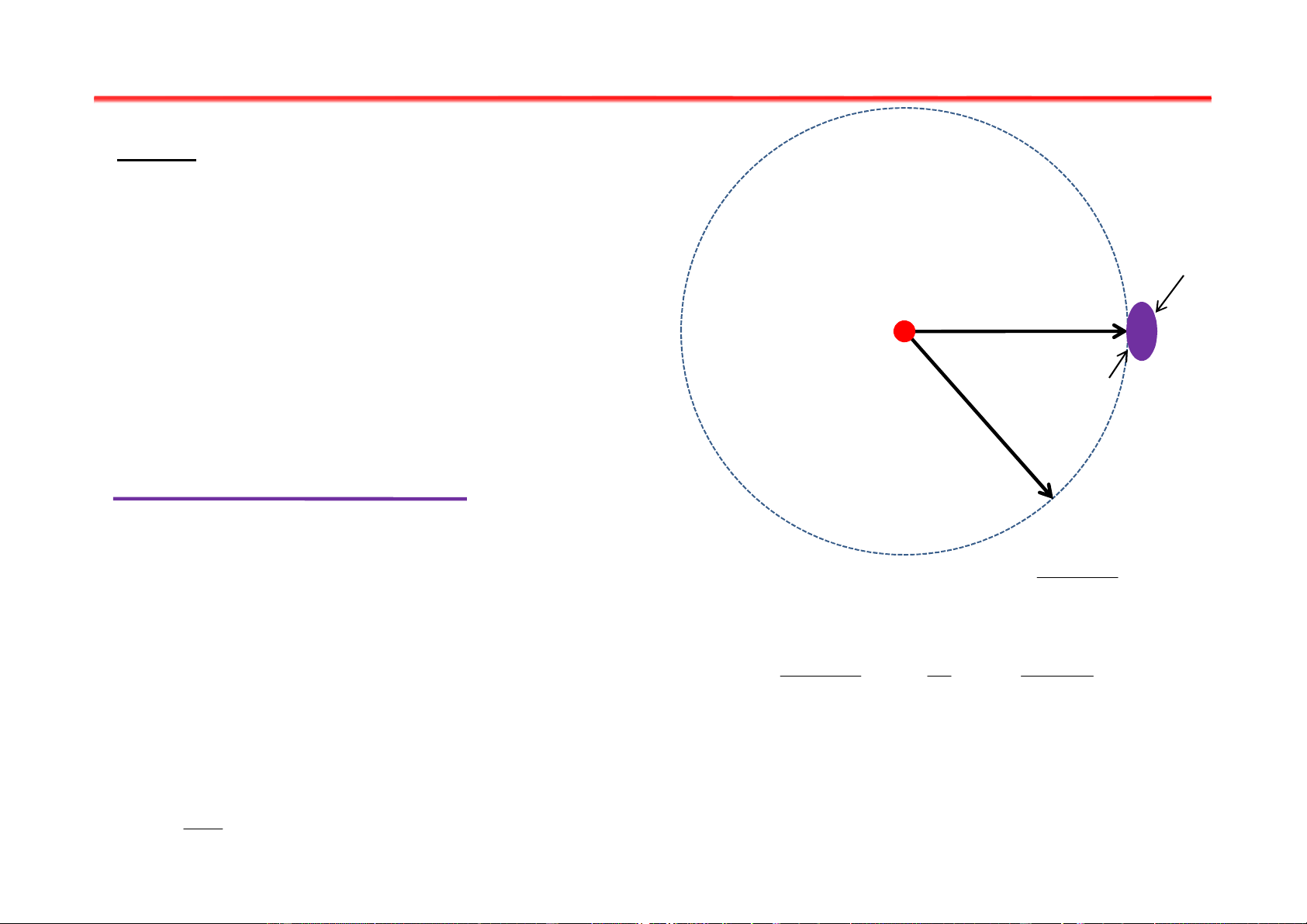
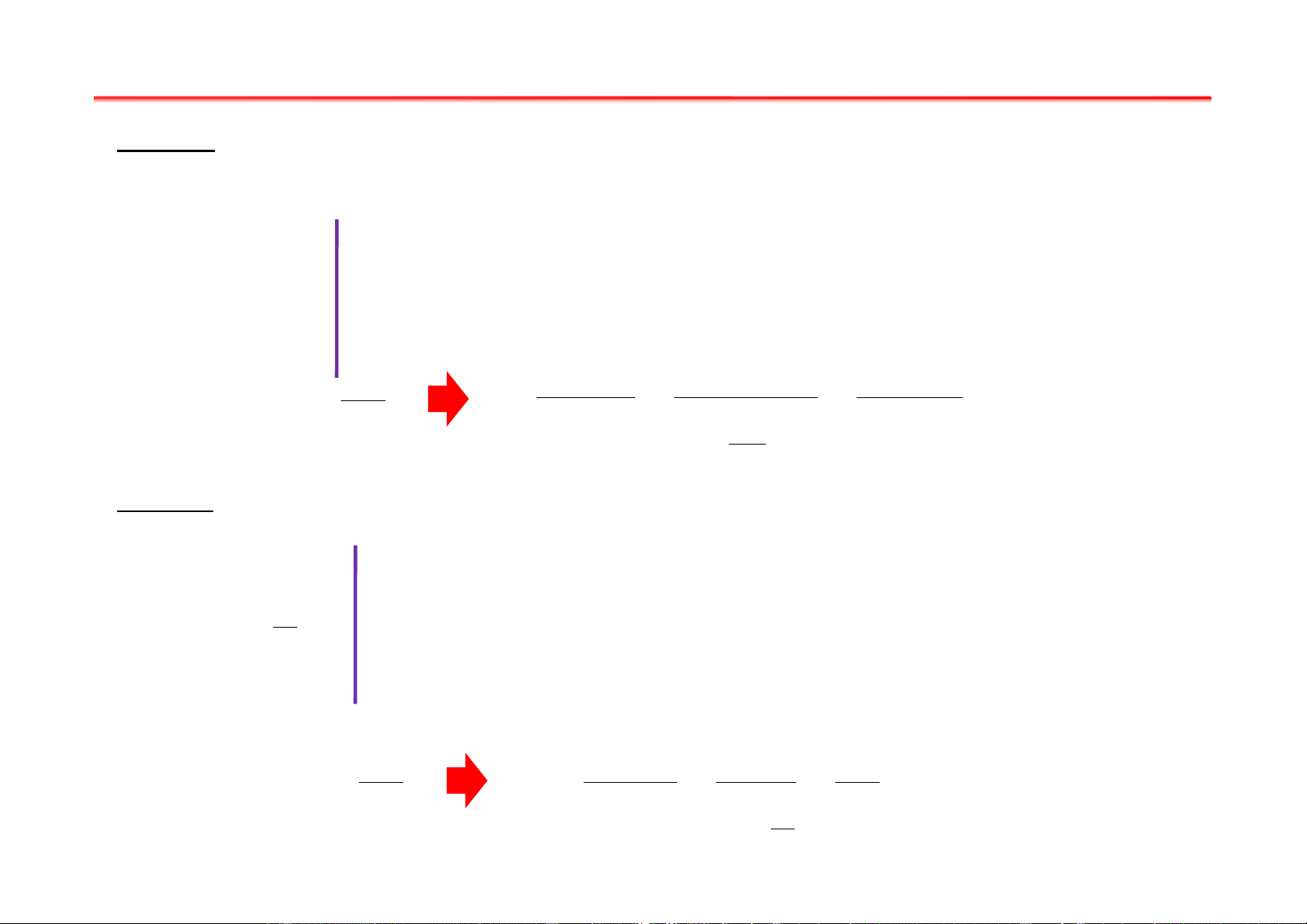
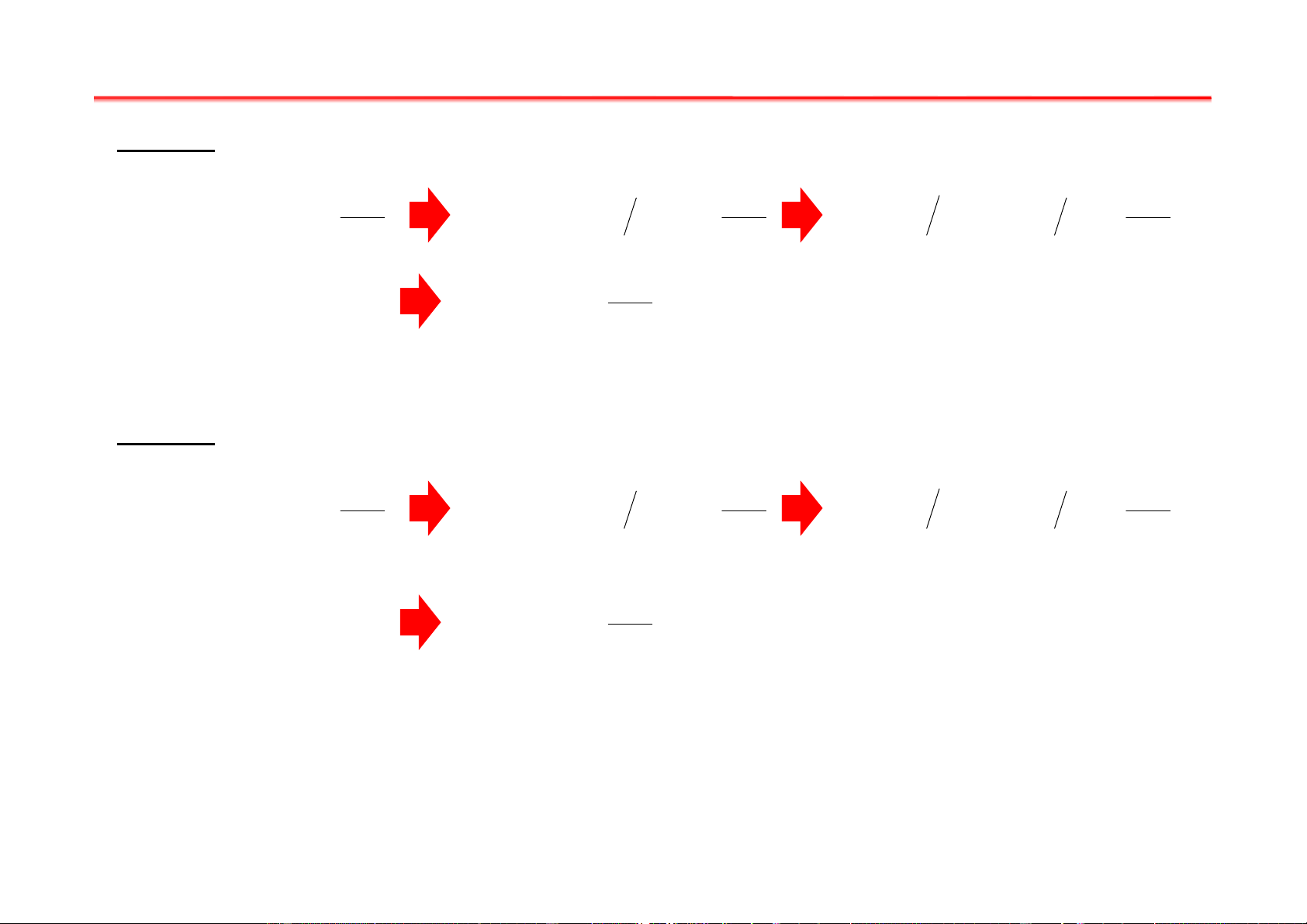
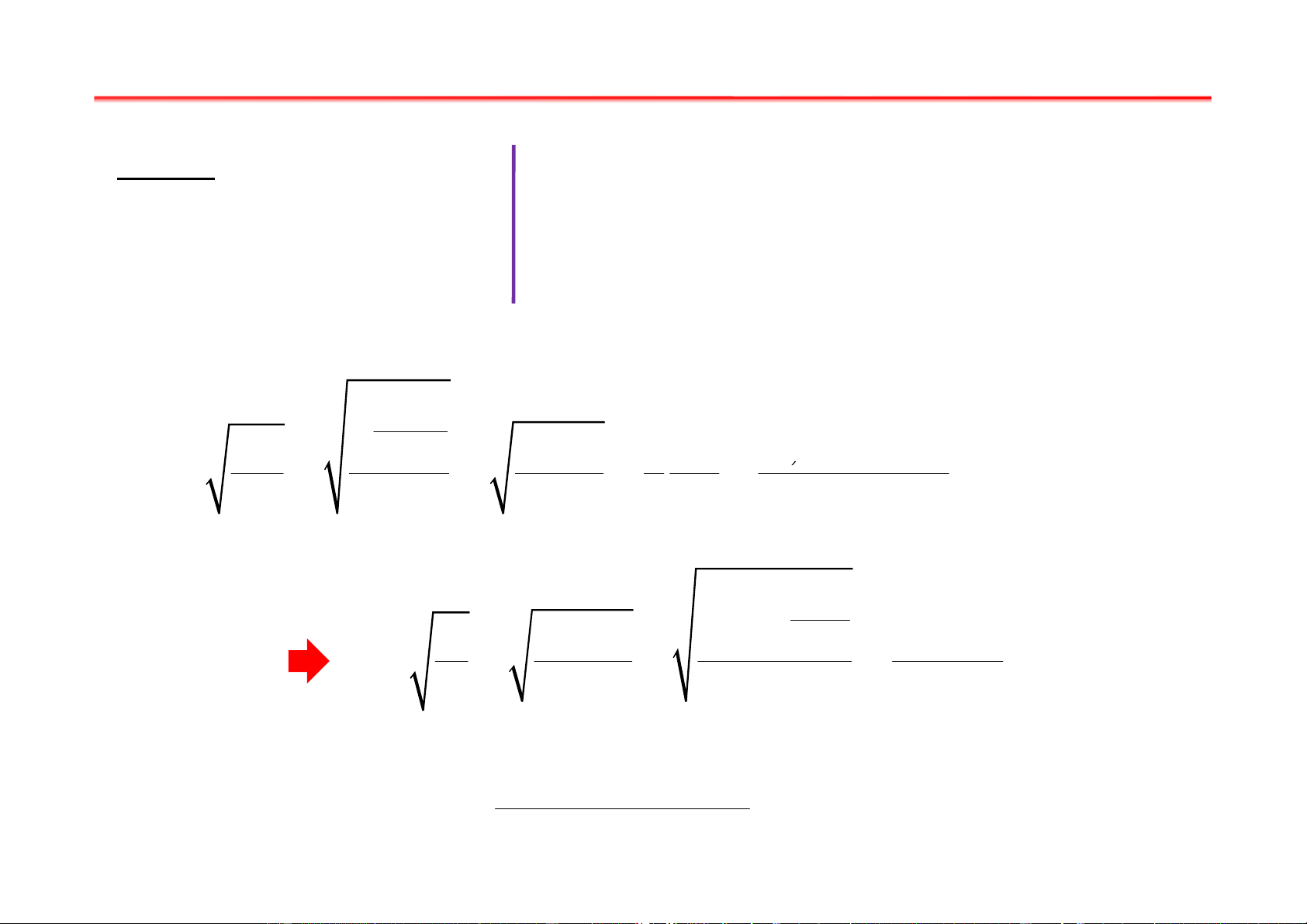
e = 1,6.10 C; m = 9.10 kg i WR H = B = µ H 2 (R + z ) ; 3 2 2 2 0 S = ? 2 D elR W µ Giải: 1 0 S = = l  + l  1 2 i 2mU  2  2( 2 2 R + z 0 )32 −19 −4 2 −6 1, 6.10 − − 6, 25.10 .4.10 .1.26.10 m 2 2 S = 5.10 .35.10 = 0,618 −31 2.9,1.10 900 2( −4 −4 6, 25.10 + 6, 25.10 )3 2 A Bài tập chương I Bài 3: A Dữ kiện: θ1 R = 3cm z θ θ ϕ U = 300V 2 1 1 O U = 500V C R B 2 f = ?
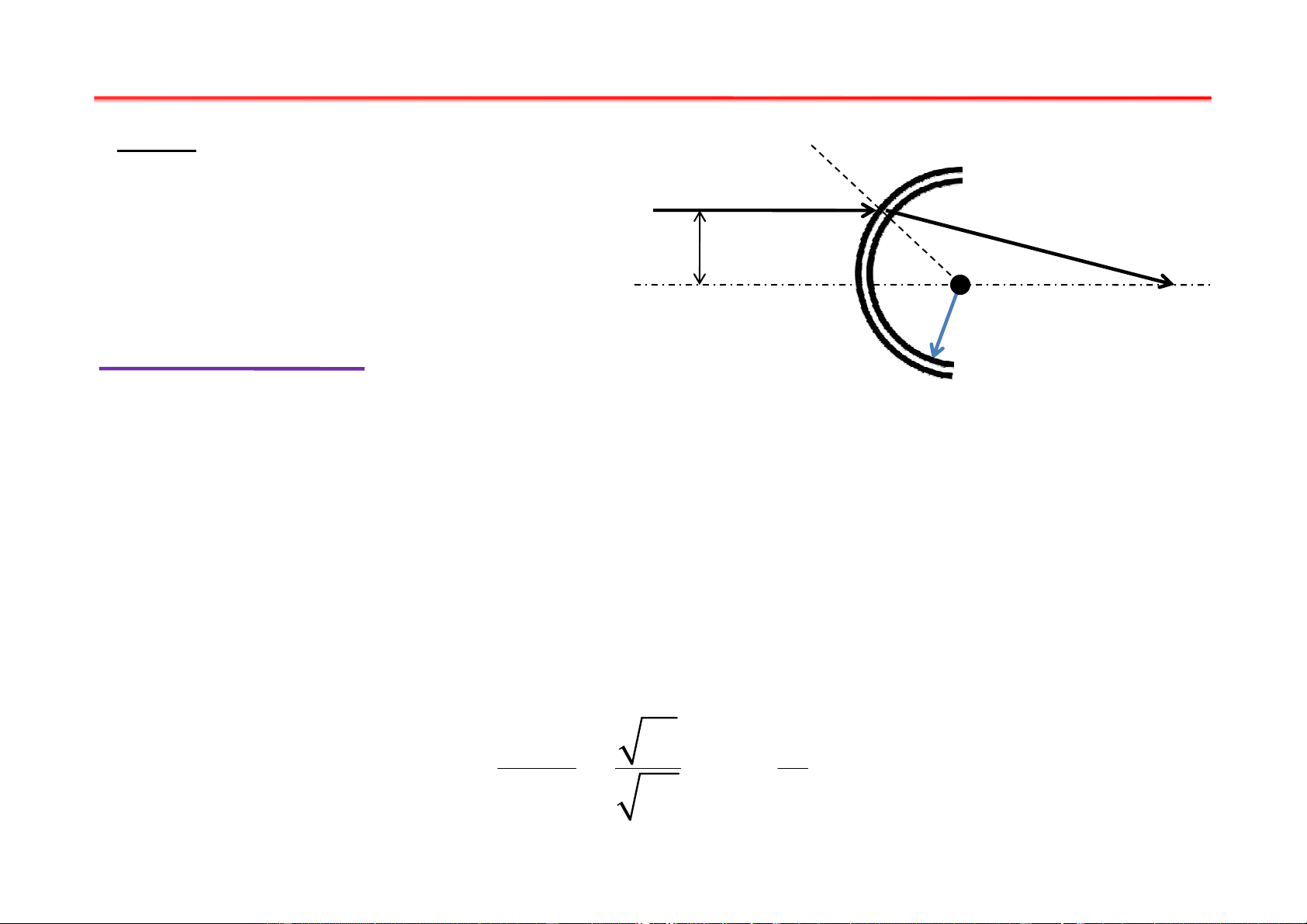
Giải: giả sử chùm điện tử chuyển động song song với trục ụ của hệ ha h i
lưới và cách trục một khoảng z << R. Tia tới và tia khúc xạ hợp thành
với pháp tuyến mặt lưới (bán kính OA) các góc θ , θ . Do các góc này 1 2 nhỏ nên ta có: sinθ U θ 2 1 2 = = k ≃ sinθ U θ 1 2 1 Bài tập chương I Từ hình học ta có:
ϕ = θ −θ ; CB = AC ϕ ; AC ≃ Rθ 1 2 1 Rθ R 1 CB = = θ −θ 1− k 1 2
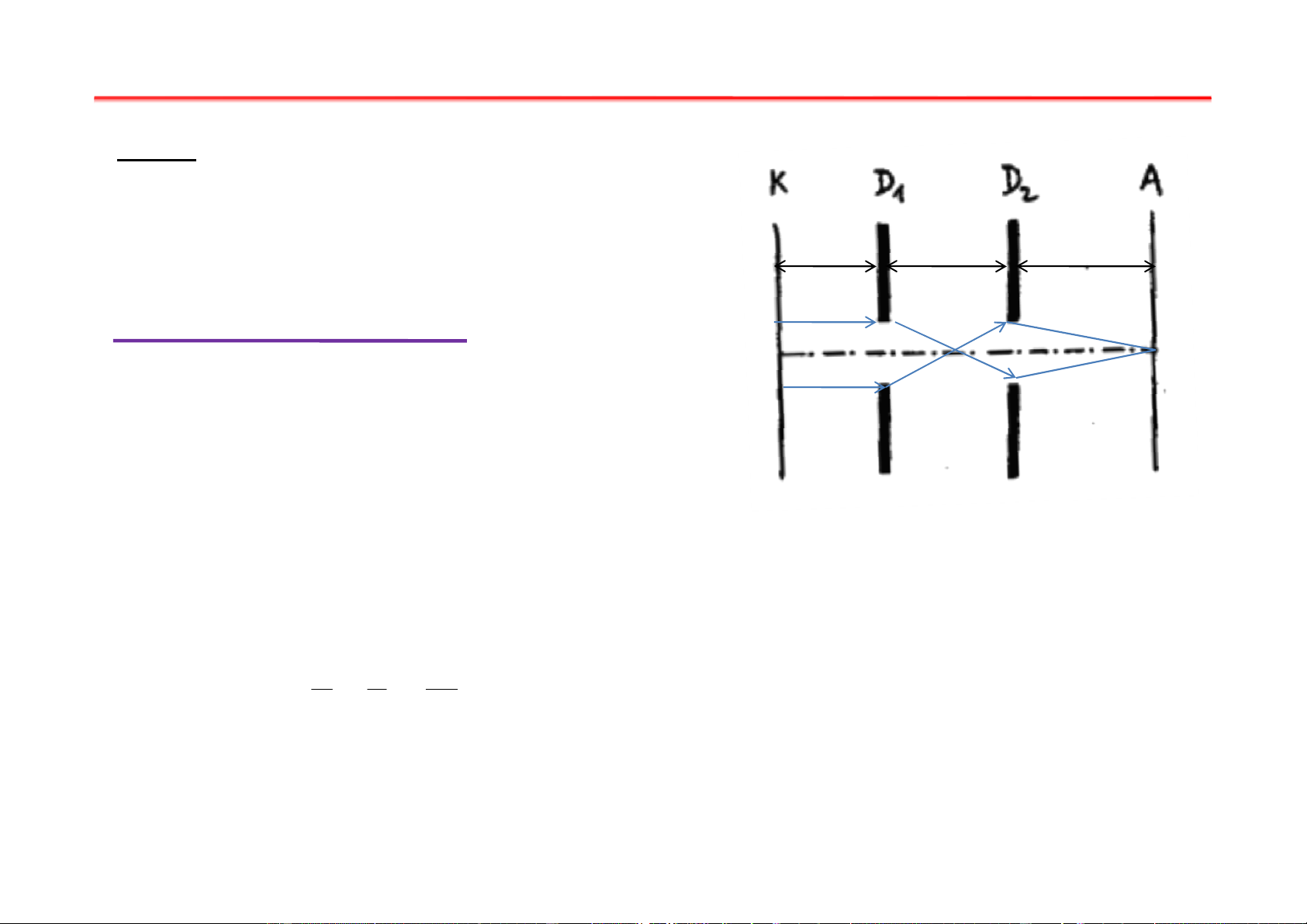
Như vậy CB không phụ thuộc vào góc θ ⇒ có thể xem là tiêu cự 1 3 f = CB = =13,25cm 300 1− 500 Bài tập chương I Bài 5: Dữ kiện: U = U =100V; d d d U = 0 D1 A K d = 1cm U = ? D 2 Gi G ải ả : Chúng C ta có thể h biểu diễn hệ h
quang học điện tử giống như hệ
quang học tia sáng. Ứng dụng định luật
quang học với hai thấu kính ta có: 1 1 1 + = a b f2
a- khoảng cách vật, b- khoảng cách ảnh đối với thấu kính thứ 2 Bài tập chương I Đ 1 1 1
iều kiện để cho chùm điện tử hội tụ trên anôt là: = + ( ) * f d − f d 2 1 4U 4U
Từ công thức tính tiêu cự ta có: D1 f = ; D 2 f = ; 1 E − E 2 E − E 2 1 3 2
Thay vào phương trình (*) ta nhận được: 2(U −U 1 1 2 ) f = = 1 4U d 4U d 1 2
d − U −2U 2 − 2 1
Giải phương trình này ta nhận được: ( )1 U = 432,28V (2) U = 27,72V 2 2 Bài à tậ t p ậ ch c ương II I Bài 1: Dữ kiện: P = 100W d P = 5%P b 0 d = 1A ϕ = 2,2eV K R R = 75cm 75c t = ? P
Giải: Cường độ ánh sáng trên bề mặt nguyên tử K là: b I = 2 4π R 2 2 Pd Pd
Công suất hấp thụ bởi nguyên tử: P = I. b b S = ⋅π   = a a 2 2 4π R  2  16R
Thời gian cần thiết để nguyên tử K hấp thụ năng lượng ϕ là: K ϕK t = =
Mẫu sóng ánh sáng cho kết quả rất lớn so với 57,6s P thực nghiệm: a Bài à tậ t p ậ ch c ương II Bài 2: Dữ kiện: 0 λ = 2500A ; ϕ = 2,2eV; W I = 2 ; K 2 m T = ? N = ? max e hc
Giải: từ công thức: T = −ϕ max K λ 3 − 4 3 8 18 6, 6 62 6 6 2 . 6 1 . 0 1 .3 . . 3 1 . 0 1 .6 . , 6 24 2 . 4 1 . 01 10 T = − 2,2 = 2,75eV max 1 − 0 2500.10
Số photon đập vào bề mặt K trong 1s là: I I I λ ph 18 N = = = = 2,52.10 2 E hc hc m .s ph λ
Nếu mỗi photon đập vào bề mặt K bứt ra một e thì số điện tử phát ra từ ph
1m2 bề mặt K trong 1s sẽ là: 18 N = N = 2,52.10 2 e m .s Bài à tậ t p ậ ch c ương II Bài 3: λ ' λ pe Dữ kiện: hc E = = 0,3MeV; ph λ v = ? e hc
Giải: áp dụng định luật bảo toàn năng lượng ta có: 0 2 E + E = + m c (1) e λ ' e h h
Mặt khác theo định luật bảo toàn động lượng: = − + p (2) λ λ ' ehc 0 2 E + E = + m c ph e  λ ' e 2 Từ (1) và (2) 
2E + E = m c + p c hc hc ph 0 e e  = − + p c  λ λ  v  ' e 1+    2 c
2E + E = m γ c + m γ vc = m cγ c + v
(2E + E = E ph 0 )2 2 ph 0 0 0 0 ( ) 0  v  1−   c  Bài tập chương II 2 2 2 v α −1  2E + E   2E    ph ph 2.0,3 = 0 ; α =   =  +1 =  +1 = 4.73 c α +1  E   E   0,511  0 0 v 4, 73 −1 = = 0,65; c 4, 73 +1 Bài 4: Dữ kiện: 0 λ =1A ; U = ? Giải: λ = ⇒ U = = = e U ( λe)2 12, 2 12, 2 (12,2 ) 150V 1 Bài tập chương II Bài 5: Dữ kiện: 0 E >> E e e λ ? e Giải:
Ta có: E = p c + E e = ( p c e
) + . Do E >> E ⇒ p c e 0 e ≈ E e ( e )2 2 2 0 e 0 e e h hc hc λ = = = e p p c E e e e Đố hc hc
i với photon ta có: E = ⇒ λ = λ E
Như vậy ta có bước sóng kết hợp của hạt gần đúng bằng bước sóng của
photon có cùng năng lượng. Đây là điều phải chứng minh Bài tập chương II Bài 6: Dữ kiện: h h λ = = p v m v , v ? f g Giải: Ta có: 2 2 E mc c v = = = ; f p v m v E = ( pc)2 2 2
+ m c ⇒ 2EdE = 2( pc)d ( pc) 2 = 2 pc dp 0 2 dE 2 pc v m c v = = = = v g 2 dp 2E mc Bài tập chương II Bài 8: Dữ kiện: −3
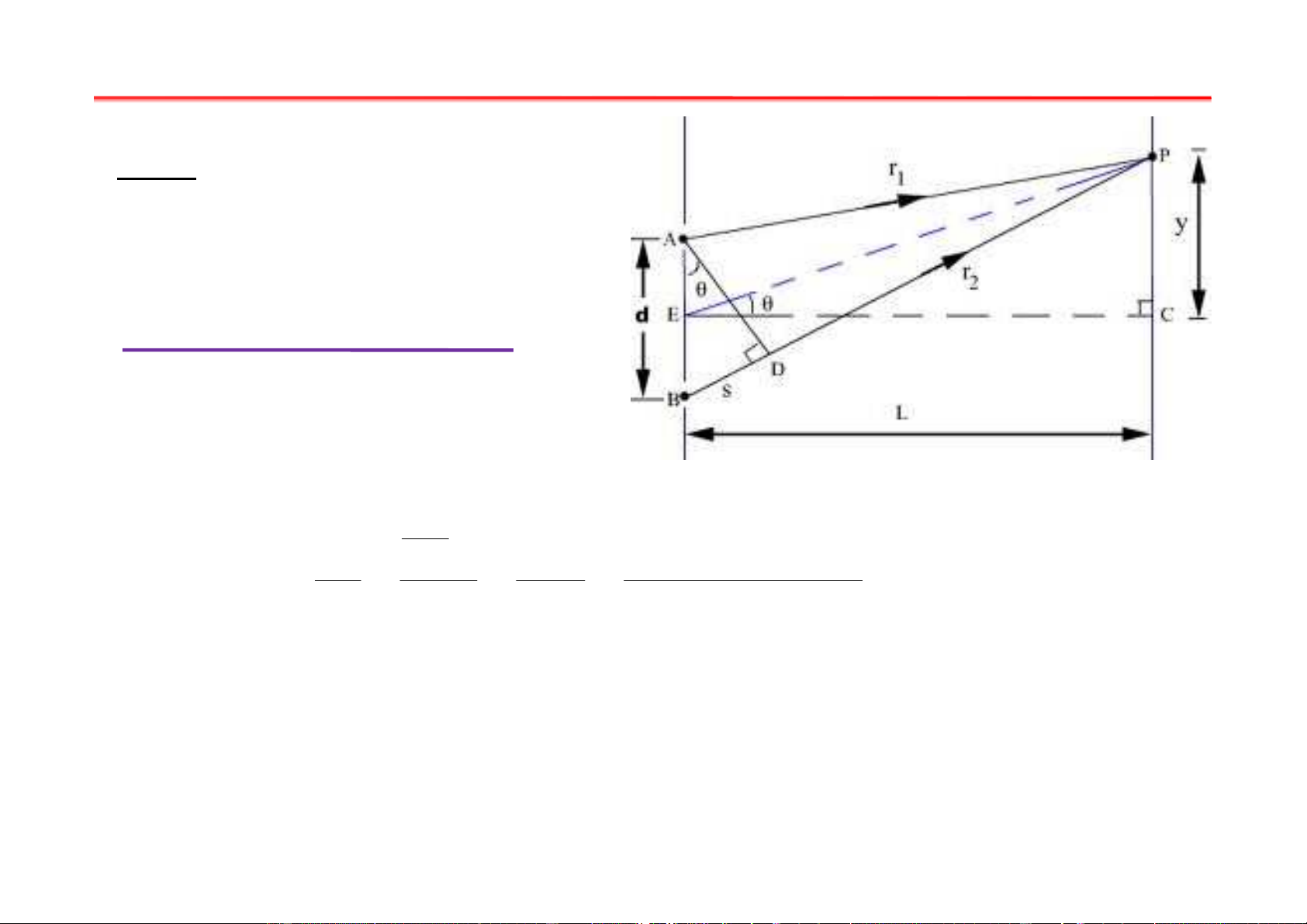
h = 6,625.10 Js; L = 12m; v = 5m/s; d = 0,6m y ∆ Giải: h L −3 λL hL 6, 625.10 .12 Ta có: v m y ∆ = = = = = 0,4m −3 d d v m d 66, 25.10 .5.0, 6 Bài tập chương II Bài 9: Dữ kiện:
a) m = 5mg;v = 2m/s; x ∆ ? p ∆ 3 =10− ; p b) −31 8
m = 9,1.10 kg; v = 1,8.10 m/s; x ∆ ? e Giải: h h − a) ∆ . x p ∆ ≥ 20 0 x ∆ ≥ =10,577.10 A x 2π 2π . p ∆ x 2 v h 1− h 2 h c 0 b) ∆ . x p ∆ ≥ x ∆ ≥ = = 5,14A x − 2π 3 2π . p ∆ 2π .10 .m v x 0 Bài tập chương II Bài 10: Dữ kiện: 0 λ=2500A ; t ? 0 λ ∆ =1A ; h 2 h h λ −9 Giải: E ∆ . t ∆ ≥ t ≥ = = = 8,493.10 s 2π 2π . E ∆ hc 2π c λ ∆ 2π . λ ∆ 2 λ Bài 11: Dữ kiện: h p ∆ = p= ; λ x ∆ ? h h h λ Giải: ∆ . x p ∆ ≥ x ∆ ≥ = = 2π 2π . p ∆ h 2π 2π .λ Bài tập chương II Bài 12: h h h Giải: ∆ . p x ∆ ≥ v m .∆ . p x ∆ v m ≥
∆( 2p 2m). x ∆ v ≥ 2π 2π 2π h E ∆ . t ∆ ≥ 2π Bài 13: h h h Giải: ∆ . p x ∆ ≥ v m .∆ . p x ∆ v m ≥
∆( 2p 2m). x ∆ v ≥ 2π 2π 2π h E ∆ . t ∆ ≥ 2π Bài tập chương II Bài 15: −14 m = 10 kg; Dữ kiện: v ? min L = 0,1mm; Giải: 2 h 2 2 −34 2 2E h 1 h 6, 6 62 6 5 2 . 5 1 . 0 1 8mL −16 1 8 v mL v = = = = = = 3,3.10 m/s min = = = = = = 3,3.10 16 1 m/ 2 2 1 − 4 4 m m 4m L 2 mL 2.10 .1.10− 2 v m 2 ⋅ 2 8mL E 8EmL 2. . m . L v 2 E = E .n 2 n = = = = n 1 2 2 E h h h 1 −14 −4 −5 2.10 .10 .1.10 10 n = = 3.10 3 − 4 6.625.10 Bài tập chương II Bài 16: Ψ Ψ ˆ d d Giải: LΨ = i = LΨ 1 = Ldx = i − Ldx dx Ψ i . iLx C e− Ψ = C = const
Chúng ta thấy rằng hàm Ψ(x) thỏa mãn phương trình, với mọi giá trị L
hàm Ψ(x) liên tục, đơn trị và hữu hạn. Như vậy bất kì giá trị L thực nào
cũng là trị riêng của và Ψ(x) là hàm riêng của ˆ a L
Áp dụng kết quả này cho trường hợp toán tử hình chiếu xung lượng ta có: dΨ i − ℏ = p Ψ ip x = x C. x e− Ψ = C const dx
Hàm Ψ(x) là khác không trong khoảng: -∞ < x < ∞, liên tục, đơn trị,
hữu hạn với mọi giá trị p là số thực ⇒ như vậy đại lượng hình chiếu x
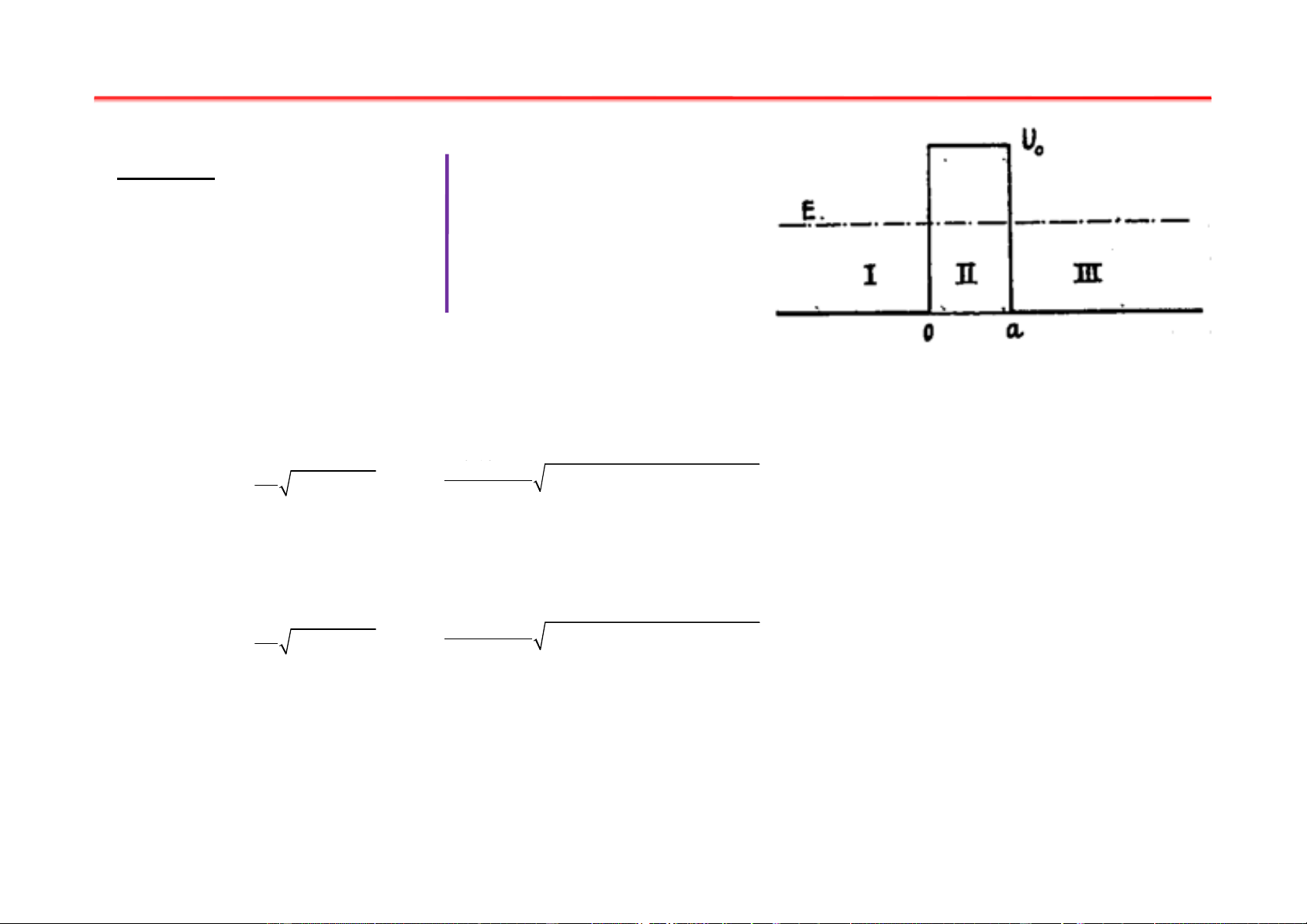
xung lượng của một hạt tự do không bị lượng tử hóa Bài tập chương II Bài 17:
a) L = 1nm; D?
Dữ kiện: E = 50eV; U = 70eV;
b) L = 0,1nm; D? 0 Giải: −19 2. 2 1 . 0 1 2 L − − − m( 10 2 − − 2.9,1.10 70−50 .1,6.10 2 U E 0 ) 31 −34 ( ) 19 a) ℏ 6,625.10 −20 D = e = e ≃ 1,3.10 1 − 0 L − − − m( 2.10 2 − − 2.9,1.10 70−50 .1,6.10 2 U E 0 ) 31 −34 ( ) 19 b) ℏ 6,625.10 D = e = e ≃ 0,01