Bài tập về tiêu chuẩn ổn định đại số trong điều khiển tự động. Môn Lý thuyết điều khiển tự động (UET) | Trường Đại học Công nghệ, Đại học Quốc gia Hà Nội.
Bài tập về tiêu chuẩn ổn định đại số trong điều khiển tự động. Môn Lý thuyết điều khiển tự động (UET) | Trường Đại học Công nghệ, Đại học Quốc gia Hà Nội.
Tài liệu gồm 17 trang giúp bạn tham khảo, củng cố kiến thức và ôn tập đạt kết quả cao trong kỳ thi sắp tới. Mời bạn đọc đón xem!
Môn: Lý thuyết điều khiển tự động (UET) 17 tài liệu
Trường: Trường Đại học Công nghệ, Đại học Quốc gia Hà Nội 755 tài liệu
Tác giả:
Preview text:
lOMoAR cPSD| 59735516 CSTĐ_Nguyễn Đức Hoàng 2010
Bộ môn ĐKTĐ - Khoa ĐĐT - BKHCM
Bài tập về tiêu chuẩn ổn định đại số Routh – Hurwitz
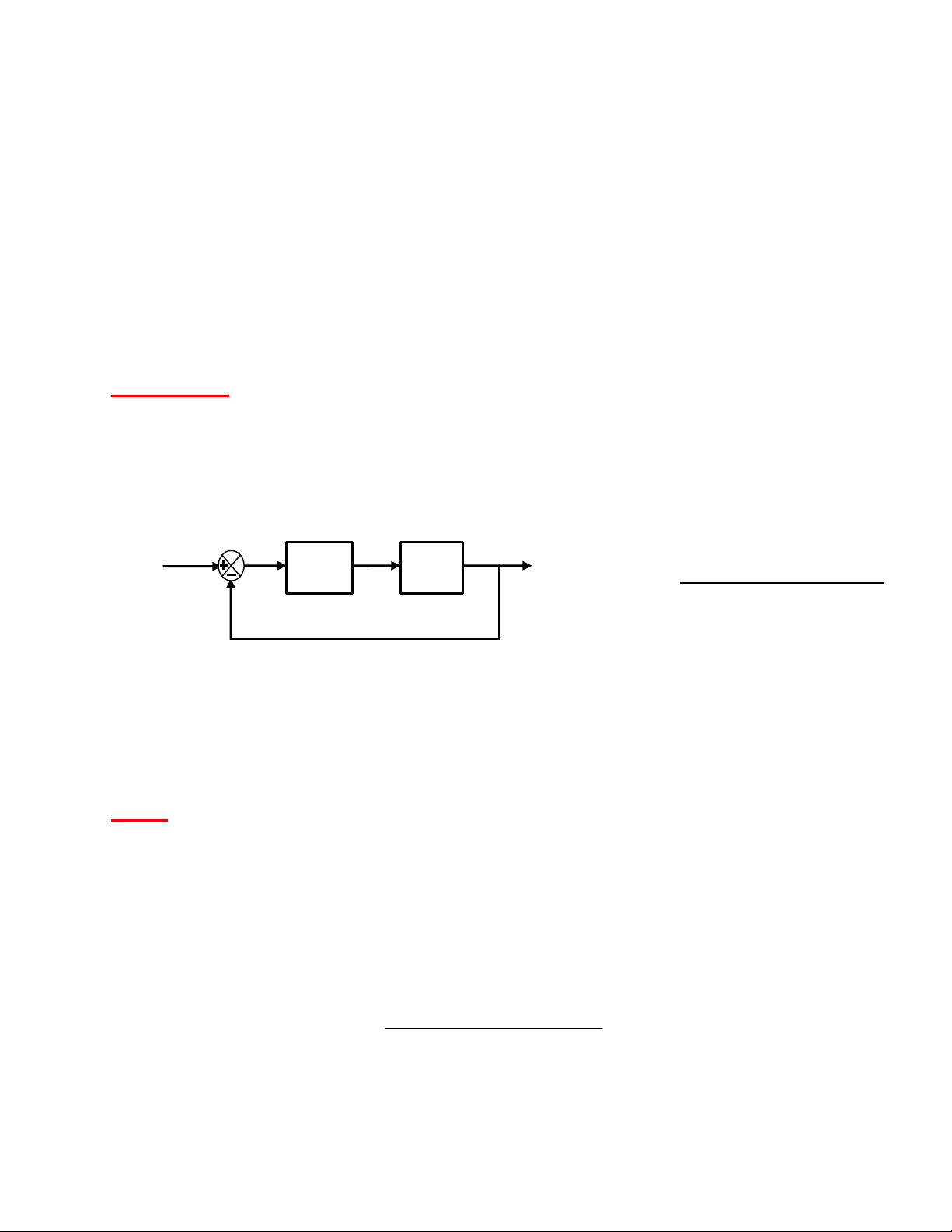
Bài tập 1: Cho hệ thống như Hình 1. Hệ thống vòng kín có ổn định không? 1000 R(s) C(s) G C (s ) G o (s) G sO( )=
(s+ + +2)(s 3)(s 5) G s Hình 1 C( ) 1= Giải: PTĐT: 1+G s G s ( ) ( ) C 0 =0 1000 ⇔ +1 =0
Bài tập lấy từ sách: Control Systems Engineering by Norman S. Nise 1 lOMoAR cPSD| 59735516 CSTĐ_Nguyễn Đức Hoàng 2010
Bộ môn ĐKTĐ - Khoa ĐĐT - BKHCM (
s+2)(s+3)(s+5)
⇔ +s3 10s2 +31 1030 0s+ = Dùng tiêu chuẩn Routh Bảng Routh: S3 1 31 S2 10→1 1030→103 S1 -72 0 S0 1030 0
(Ở hàng s2 ta chia các hệ số cho 10 để dễ tính toán mà
không ảnh hưởng đến kết quả)
Kết luận: Cột 1 bảng Routh đổi dấu 2 lần nên hệ thống
không ổn định, 2 cực bên phải mpp. Dùng tiêu chuẩn Hurwitz 10 1030 0 Ma trận Hurwitz: H=1 31 0 0 10 1030
Bài tập lấy từ sách: Control Systems Engineering by Norman S. Nise 2 lOMoAR cPSD| 59735516 CSTĐ_Nguyễn Đức Hoàng 2010
Bộ môn ĐKTĐ - Khoa ĐĐT - BKHCM ∆ = >1 1 0
Các định thức con: ∆ =210 1030=310 1030− =−720 0< 1 31 ∆ =3 1030*∆ <2 0
Kết luận: Vì tất cả các định thức con không dương nên hệ không ổn định.
Bài tập 2: Xét ổn định của PTĐT sau:
s5 +2s4 +3s3 +6s2 + + =5 3 0s Giải: Bảng Routh: S5 1 3 5 S4 2 6 3 S3 0 → ε 7/2 0 S2 6 7 3 0 0 S1 42 49 6 0 0 0 S0 3 0 0
Bài tập lấy từ sách: Control Systems Engineering by Norman S. Nise 3 lOMoAR cPSD| 59735516 CSTĐ_Nguyễn Đức Hoàng 2010
Bộ môn ĐKTĐ - Khoa ĐĐT - BKHCM
Kết luận: PTĐT không ổn định, có 2 nghiệm bên phải mpp.
Bài tập 3: Xét ổn định của PTĐT sau:
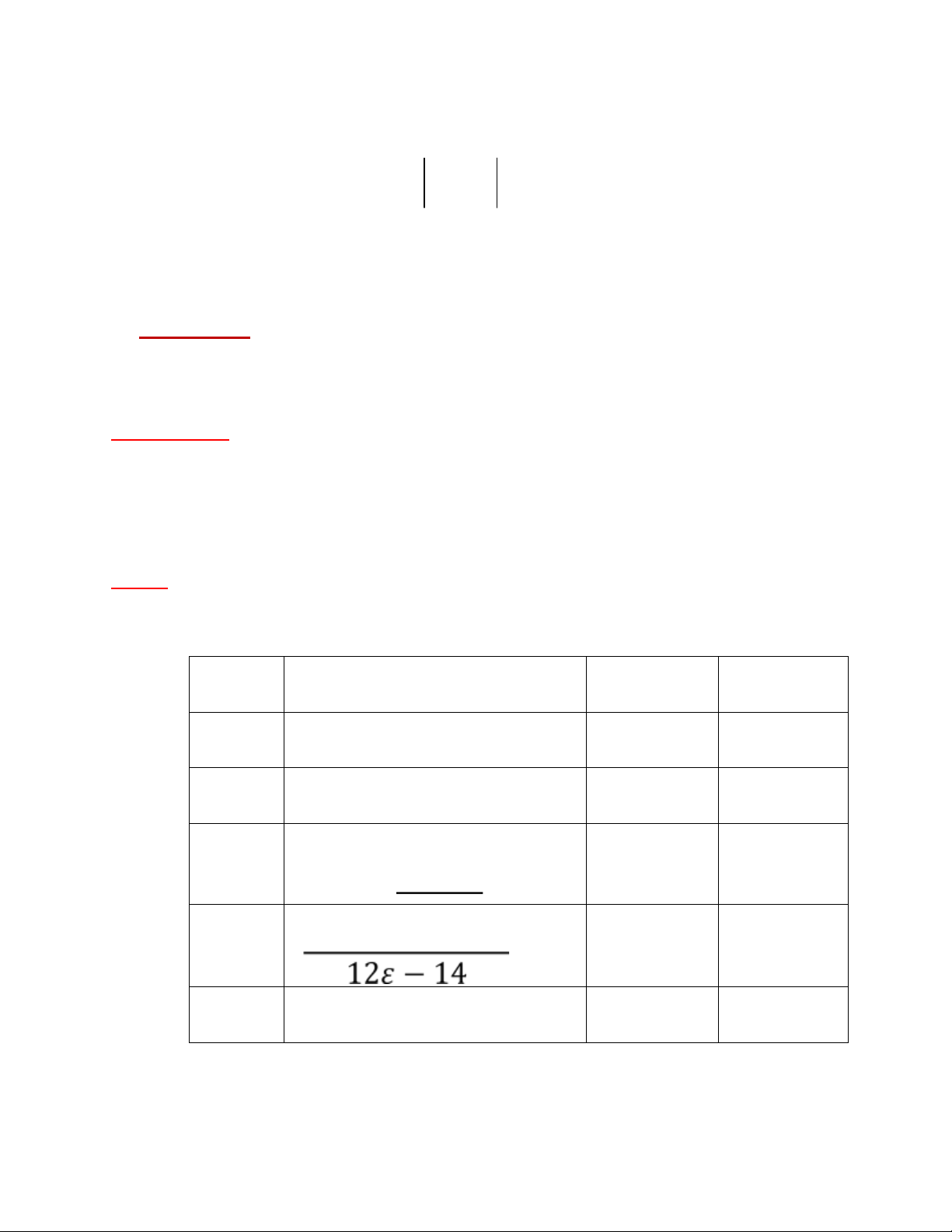
s5 +7s4 +6s3 +42s2 + + =8 56 0s Giải: Bảng Routh: S5 1 6 8 S4 7→1 42→6 56→8 S3 0→4→1 0→12→3 0→0→0 S2 3 8 0 S1 1/3 0 0 S0 8 0 0
Hàng s3 có các hệ số bằng 0 → lập đa thức phụ
A s( )= +s4 6s2 +8
Bài tập lấy từ sách: Control Systems Engineering by Norman S. Nise 4 lOMoAR cPSD| 59735516 CSTĐ_Nguyễn Đức Hoàng 2010
Bộ môn ĐKTĐ - Khoa ĐĐT - BKHCM ⇒ dA s( ) =4s3 +12s ds
Kết luận: PTĐT ổn định vì các hệ số cột 1 bảng Routh dương.
Bài tập 4: Cho hệ thống như Hình 4. Hệ thống vòng kín có ổn định không? 200 R(s) C(s) G C (s ) G o (s) = G s O( ) 3 2 s s( + + +6s 11 6s ) G s Hình 4 C( ) 1=
ĐS: Hệ thống không ổn định, 2 cực bên phải mpp.
Bài tập 5: Cho hệ thống như Hình 5. Hệ thống vòng kín có ổn định không? 1
Bài tập lấy từ sách: Control Systems Engineering by Norman S. Nise 5 lOMoAR cPSD| 59735516 CSTĐ_Nguyễn Đức Hoàng 2010
Bộ môn ĐKTĐ - Khoa ĐĐT - BKHCM R(s) C(s) = G C (s ) G o (s) Gs 0() 4 3 2 s s s s s(2 + + + + 3 2 3 2 ) Gs Hình 5 c() 1=
ĐS: Hệ thống không ổn định, 2 cực bên phải mpp.
Bài tập 6: Cho hệ thống như Hình 6. Tìm K để hệ thống vòng kín ổn định? K R(s) C(s) G C (s ) G o (s) G s0( )= s
s( +7)(s+11) G s Hình 6 c( ) 1= ĐS: 0 < K < 1386.
Bài tập lấy từ sách: Control Systems Engineering by Norman S. Nise 6 lOMoAR cPSD| 59735516 CSTĐ_Nguyễn Đức Hoàng 2010
Bộ môn ĐKTĐ - Khoa ĐĐT - BKHCM
Bài tập 7: Cho hệ thống như Hình 7. Tìm K để hệ thống vòng kín ổn định? K s( +20) R(s) C(s) G C (s ) G o (s) G s0( )= s s( +2)(s+3) G s Hình 7 c( ) 1= ĐS: 0 < K < 2.
Bài tập 8: Xét ổn định của hệ thống được cho bởi hệ PTTT sau: 0 3 1 10
x= −210 − −85 21 x+ 00
Bài tập lấy từ sách: Control Systems Engineering by Norman S. Nise 7 lOMoAR cPSD| 59735516 CSTĐ_Nguyễn Đức Hoàng 2010
Bộ môn ĐKTĐ - Khoa ĐĐT - BKHCM
y=[1 0 0]x
Tính ĐTĐT: det(sI-A)=0 rồi dùng tiêu chuẩn Routh hoặc Hurwitz.
ĐS: Hệ thống không ổn định, 1 cực bên phải mpp.
Bài tập 9: Xét ổn định của hệ thống được cho bởi hệ PTTT sau: 2 1 1 0
x= −1 7 13 4 −5 x+ 10
y=[0 1 0]x
Tính ĐTĐT: det(sI-A)=0 rồi dùng tiêu chuẩn Routh hoặc Hurwitz.
ĐS: Hệ thống không ổn định, 2 cực bên phải mpp.
Bài tập lấy từ sách: Control Systems Engineering by Norman S. Nise 8 lOMoAR cPSD| 59735516 CSTĐ_Nguyễn Đức Hoàng 2010
Bộ môn ĐKTĐ - Khoa ĐĐT - BKHCM
Bài tập 10: Cho hệ thống có hàm truyền G0(s) sau: 0.25K s( + 0.435) G s ( ) 0
= s4 +3.456s3 +3.457s2 + 0.719s+ 0.0416
Tìm điều kiện của K để hệ thống hồi tiếp âm đơn vị ổn định.
ĐS: -0.382 < K < 25.87.
Bài tập 11: Cho hệ thống có hàm truyền vòng kín Gk(s) sau: G s ( )= k s3
+151.32s76.392 +198Ks+ 76.39K
Tìm điều kiện của K để hệ thống ổn định. ĐS: 0 < K < 392.2.
Bài tập lấy từ sách: Control Systems Engineering by Norman S. Nise 9 lOMoAR cPSD| 59735516 CSTĐ_Nguyễn Đức Hoàng 2010
Bộ môn ĐKTĐ - Khoa ĐĐT - BKHCM
Bài tập 12: Cho hệ thống có hàm truyền vòng kín Gk(s) sau:
(0.25s+ 0.10925)K G s ( ) k = 4 3 2
s +3.483s +3.465s + 0.25(K + 2.4288)s+ 0.10925K
Tìm điều kiện của K để hệ thống ổn định. ĐS: 0 < K < 26.42.
Bài tập 13: Cho hệ thống có hàm truyền G0(s) sau: G s ( ) 0 = K
s(s(−+23)()s(s−+45))
Tìm điều kiện của K để hệ thống hồi tiếp âm đơn vị ổn định.
Bài tập lấy từ sách: Control Systems Engineering by Norman S. Nise 10 lOMoAR cPSD| 59735516 CSTĐ_Nguyễn Đức Hoàng 2010
Bộ môn ĐKTĐ - Khoa ĐĐT - BKHCM ĐS: K > 6/8.
Bài tập 14: Cho hệ thống có hàm truyền G0(s) sau:
K s( + 2)(s− 2) ( )= ( ) G s0 2 s +3
Tìm điều kiện của K để hệ thống hồi tiếp âm đơn vị ổn định. ĐS: -1 < K < 3/4.
Bài tập 15: Cho hệ thống có hàm truyền G0(s) sau: K s( +1) G s ( ) ( 0 = s s4 + 2)
Tìm điều kiện của K để hệ thống hồi tiếp âm đơn vị ổn định. ĐS: Không tồn tại K.
Bài tập lấy từ sách: Control Systems Engineering by Norman S. Nise 11 lOMoAR cPSD| 59735516 CSTĐ_Nguyễn Đức Hoàng 2010
Bộ môn ĐKTĐ - Khoa ĐĐT - BKHCM
Bài tập 16: Cho hệ thống có hàm truyền G0(s) sau: G s ( ) 0
= K s( − 2()(2s+ 4))(s+5) s +3
Tìm điều kiện của K để hệ thống hồi tiếp âm đơn vị ổn định. ĐS: 1/54 < K < 3/40.
Bài tập 17: Cho hệ thống có hàm truyền G0(s) sau: K s( + 2)
Bài tập lấy từ sách: Control Systems Engineering by Norman S. Nise 12 lOMoAR cPSD| 59735516 CSTĐ_Nguyễn Đức Hoàng 2010
Bộ môn ĐKTĐ - Khoa ĐĐT - BKHCM ( )= ( ) G s0 2
s +1 (s+ 4)(s−1)
Tìm điều kiện của K để hệ thống hồi tiếp âm đơn vị ổn định. ĐS: Không tồn tại K.
Bài tập 18: Cho hệ thống có hàm truyền G0(s) sau: G s ( ) 0 =
(s+15)(s+K27)(s+38)
Tìm điều kiện của K để hệ thống hồi tiếp âm đơn vị dao động.
ĐS: K = 144690, tần số dao động 44.73 rad/s.
Bài tập lấy từ sách: Control Systems Engineering by Norman S. Nise 13 lOMoAR cPSD| 59735516
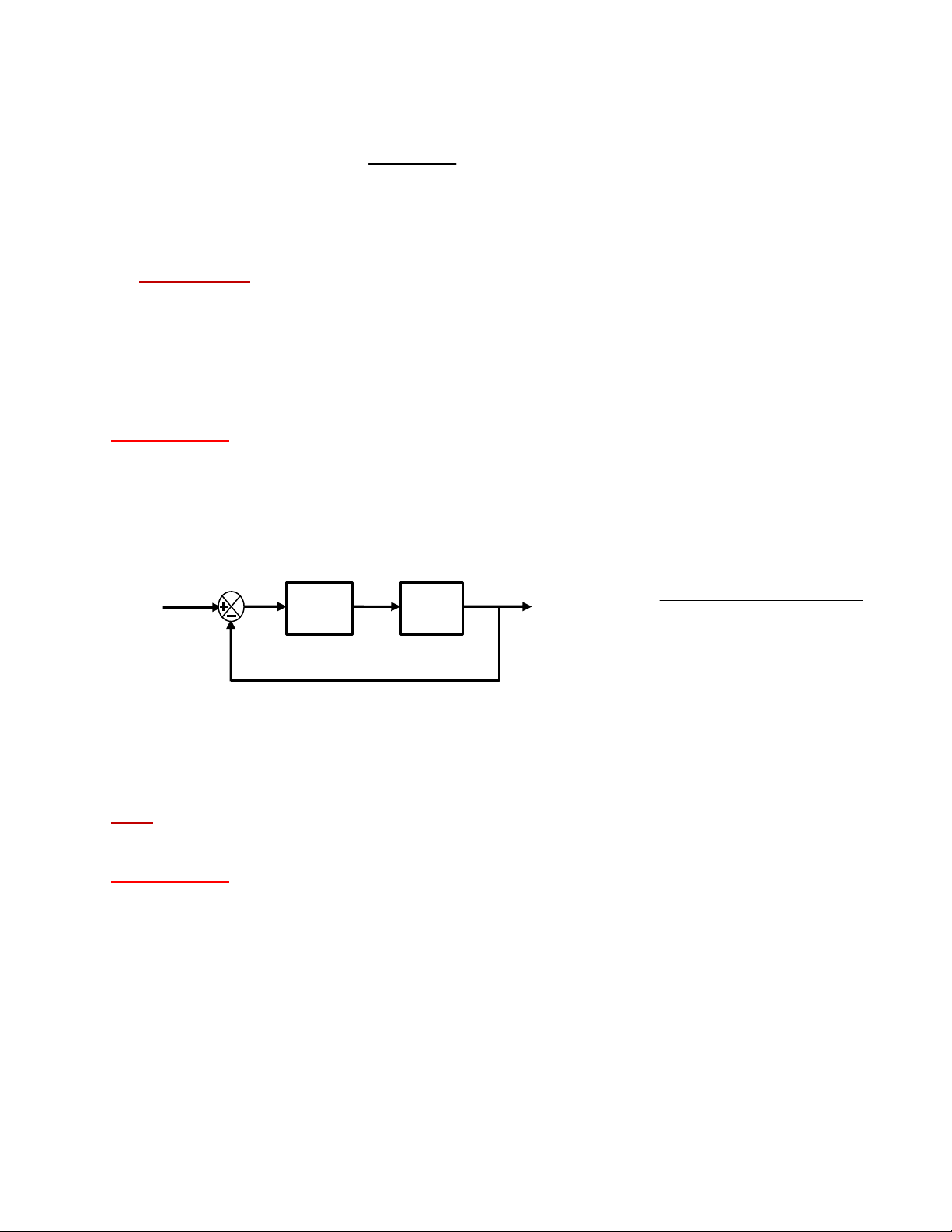
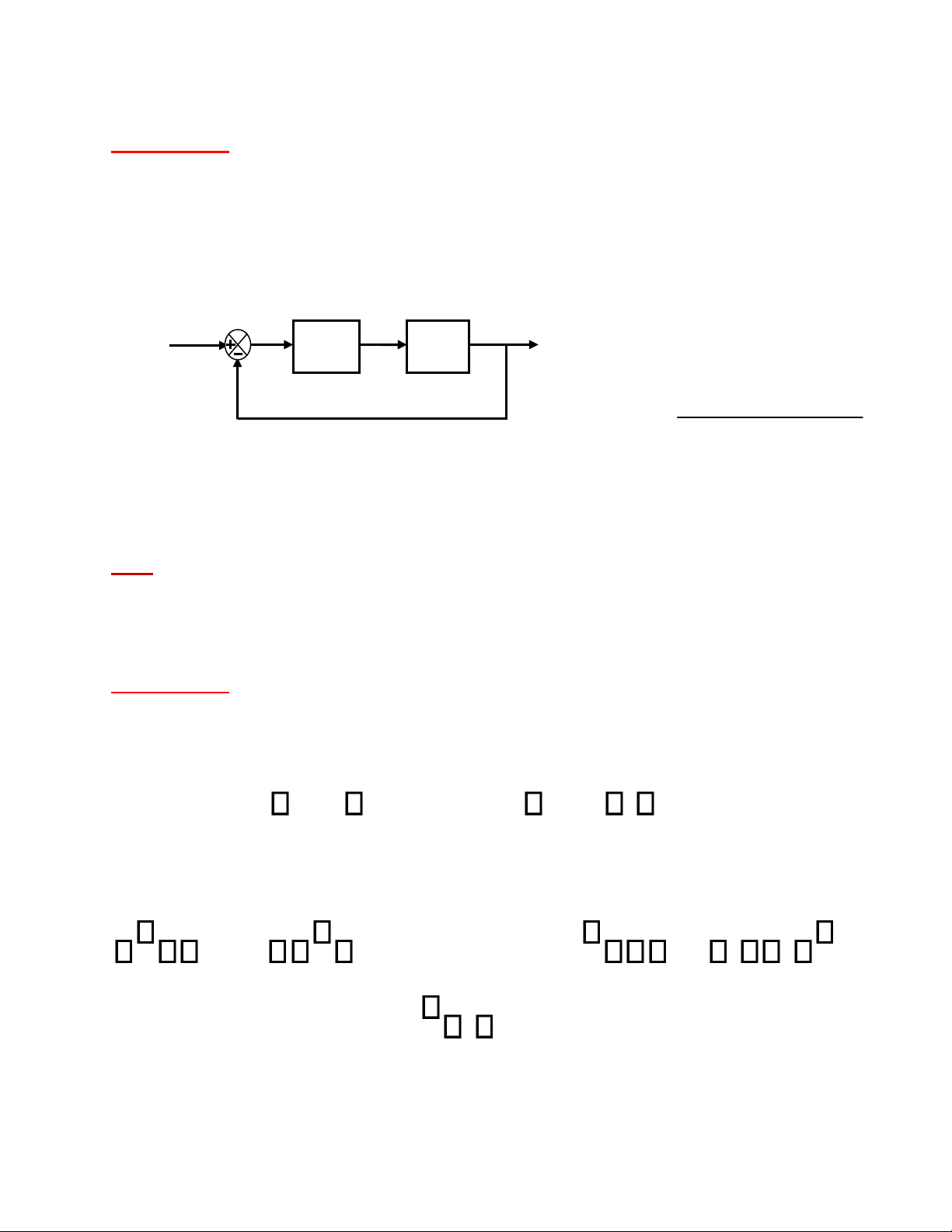
CSTĐ_Nguyễn Đức Hoàng 2010 Bộ môn ĐKTĐ - Khoa ĐĐT - BKHCM Cho hệ thống sau: Bài tập 19: Hình 19
Tìm điều kiện của K để hệ thống kín ổn định. ĐS: -1/2 < K < 1.
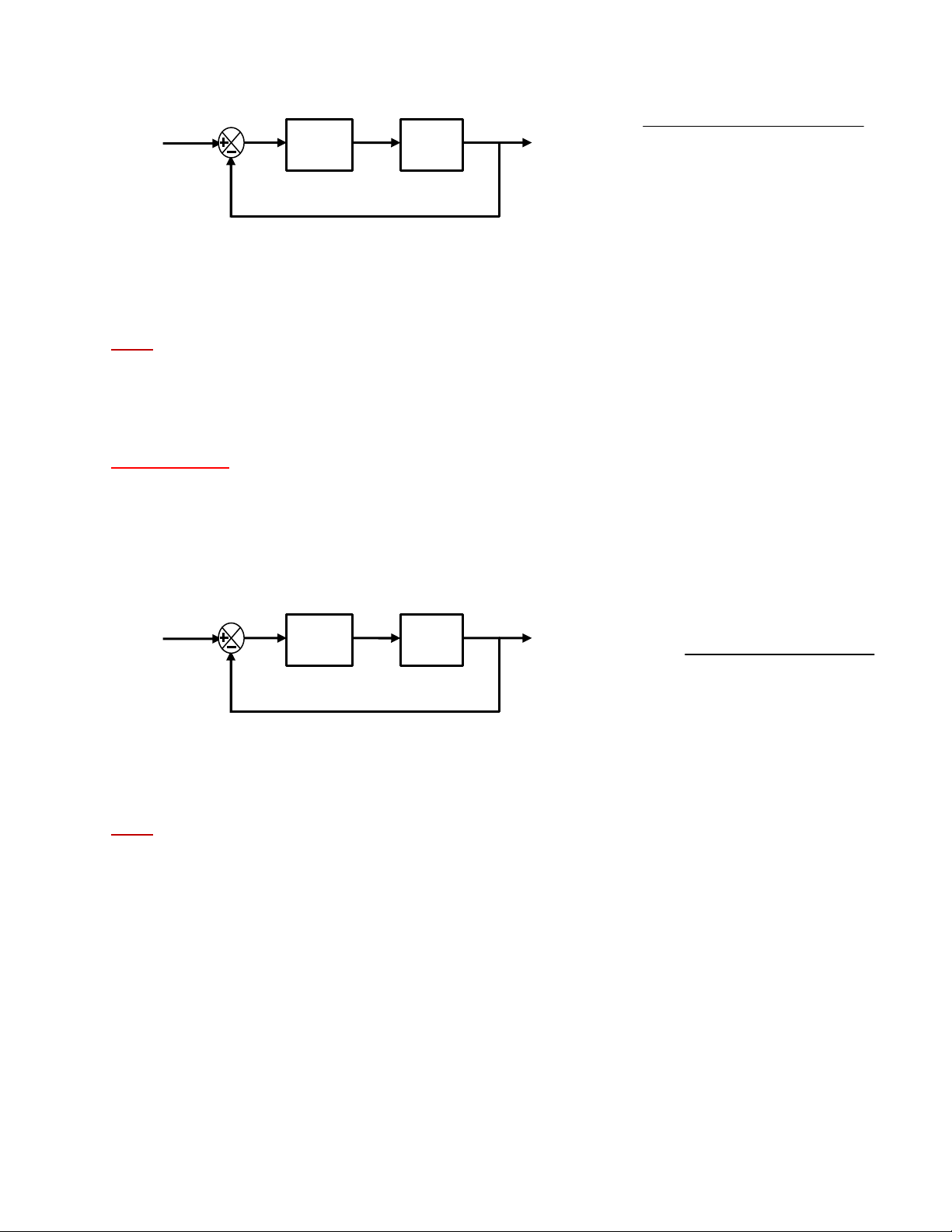
Bài tập 20: Cho hệ thống sau: Hình 20
Tìm điều kiện của K để hệ thống kín ổn định. ĐS: 0 < K.
Bài tập lấy từ sách: Control Systems Engineering by Norman S. Nise 14 lOMoAR cPSD| 59735516
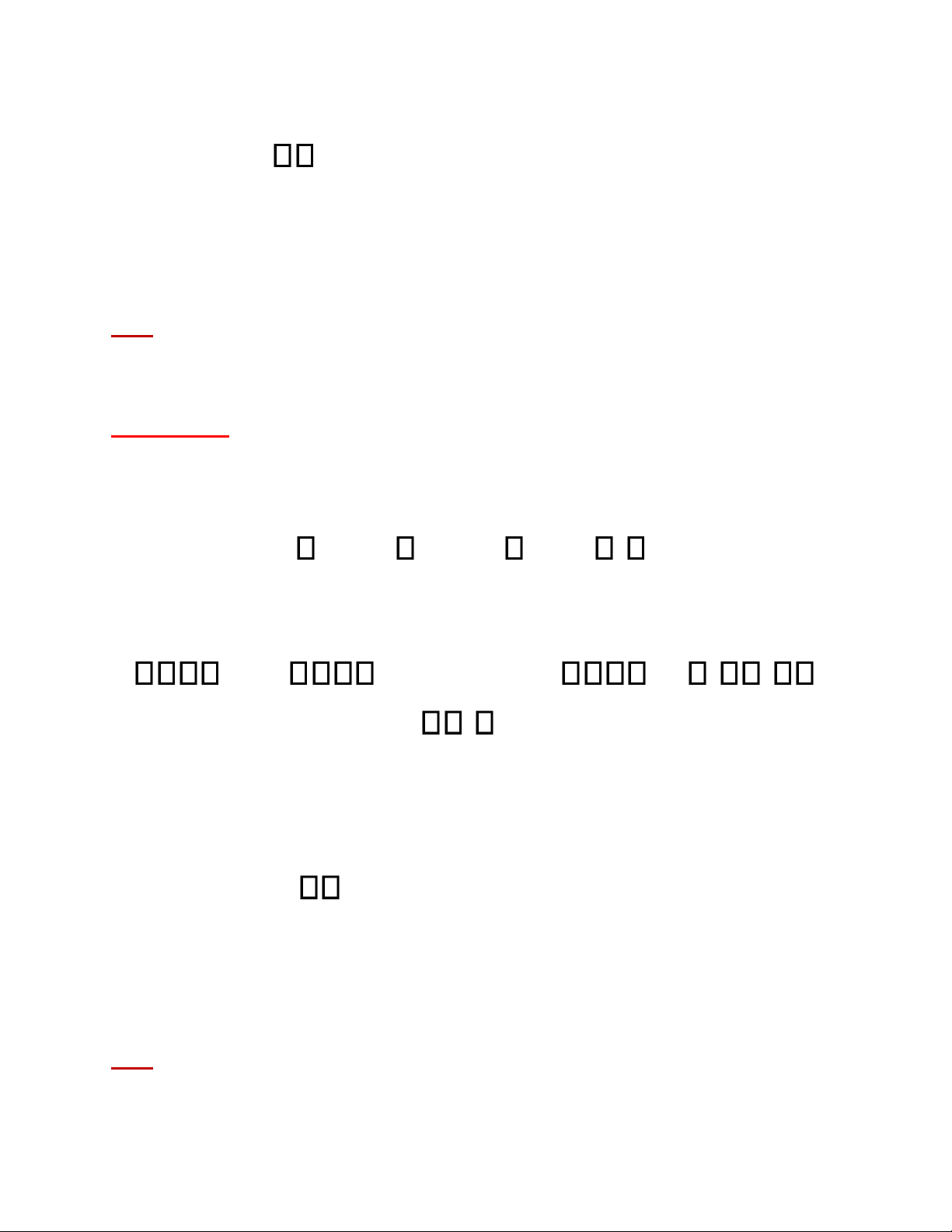
CSTĐ_Nguyễn Đức Hoàng 2010 Bộ môn ĐKTĐ - Khoa ĐĐT - BKHCM Cho hệ thống sau: Bài tập 21: Hình 21
Tìm điều kiện của K để hệ thống kín ổn định. ĐS: -0.36772 < K.
Bài tập 22: Cho hệ thống sau:
Tìm điều kiện của K để hệ thống kín ổn định.
Bài tập lấy từ sách: Control Systems Engineering by Norman S. Nise 15 lOMoAR cPSD| 59735516
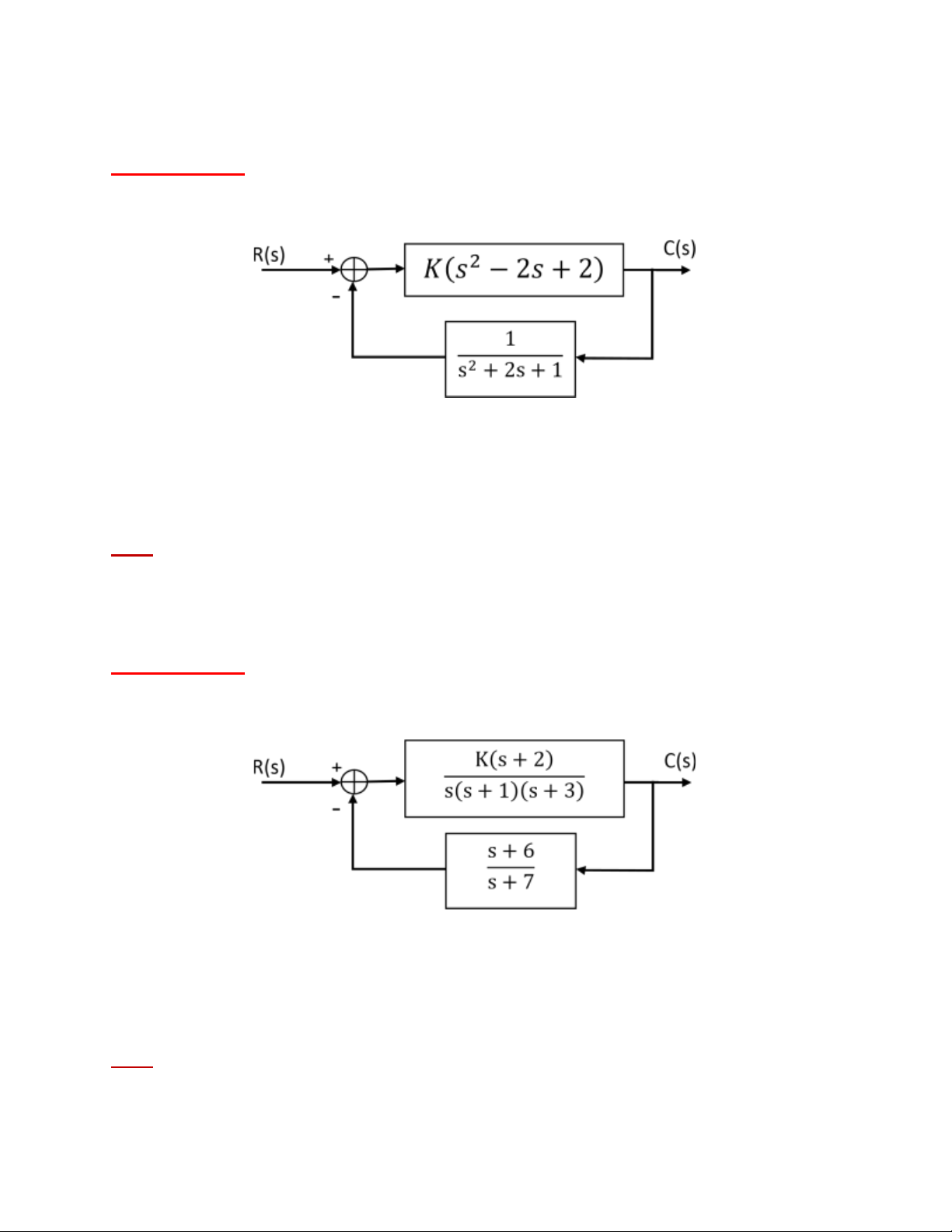
CSTĐ_Nguyễn Đức Hoàng 2010 Bộ môn ĐKTĐ - Khoa ĐĐT - BKHCM Cho hệ thống sau:
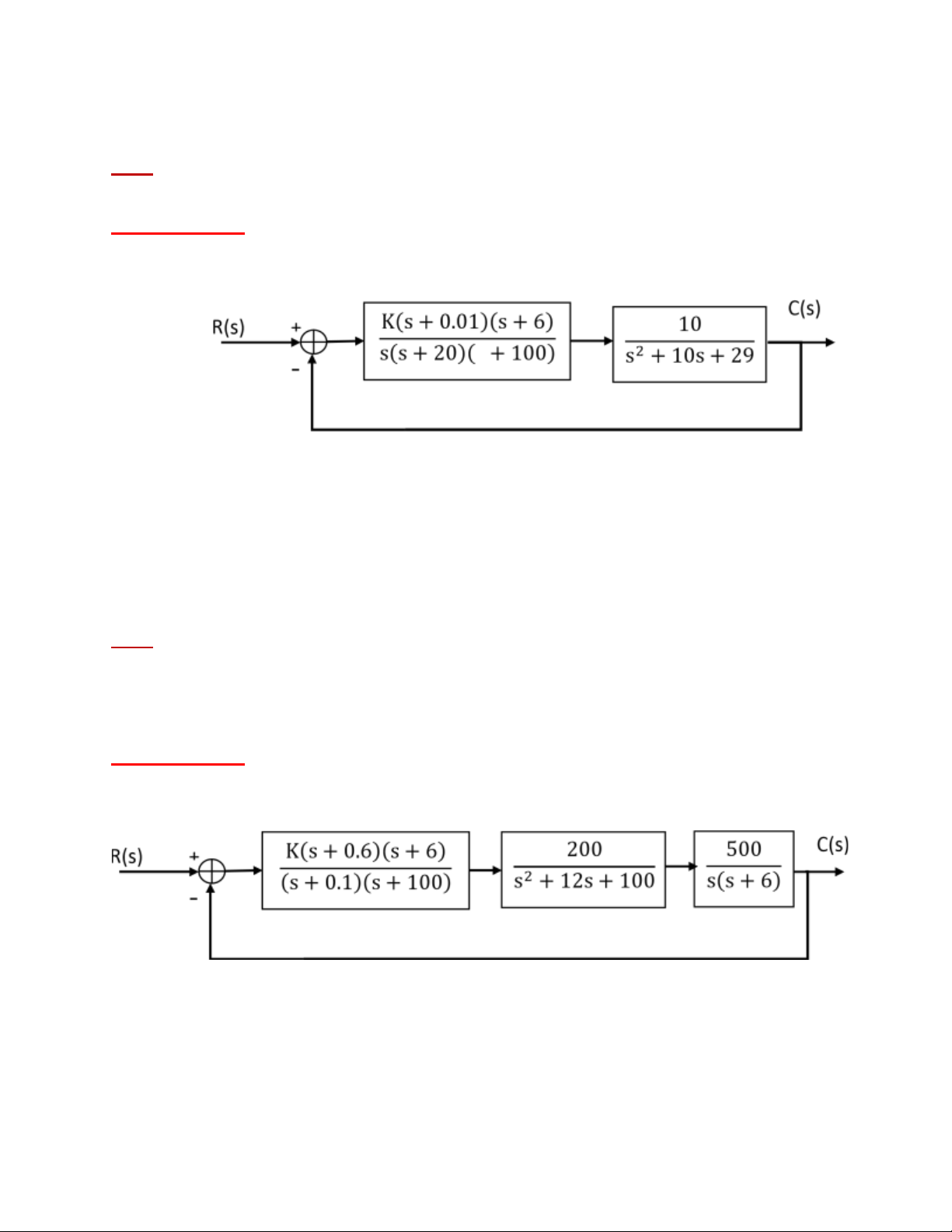
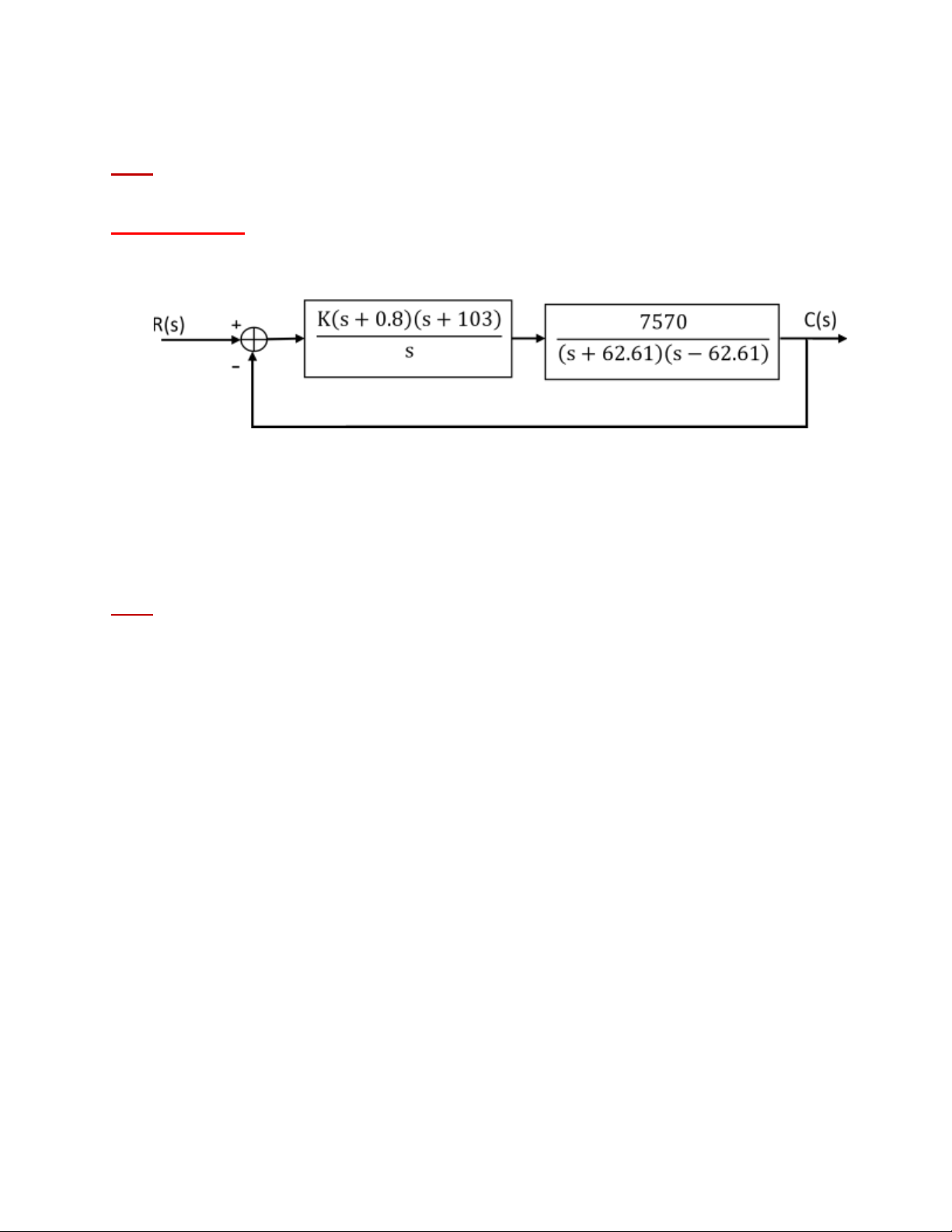
ĐS: -0.1429 < K < 1.1759. Bài tập 23: s Hình 23
Tìm điều kiện của K để hệ thống kín ổn định. ĐS: 0 < K < 29908.07.
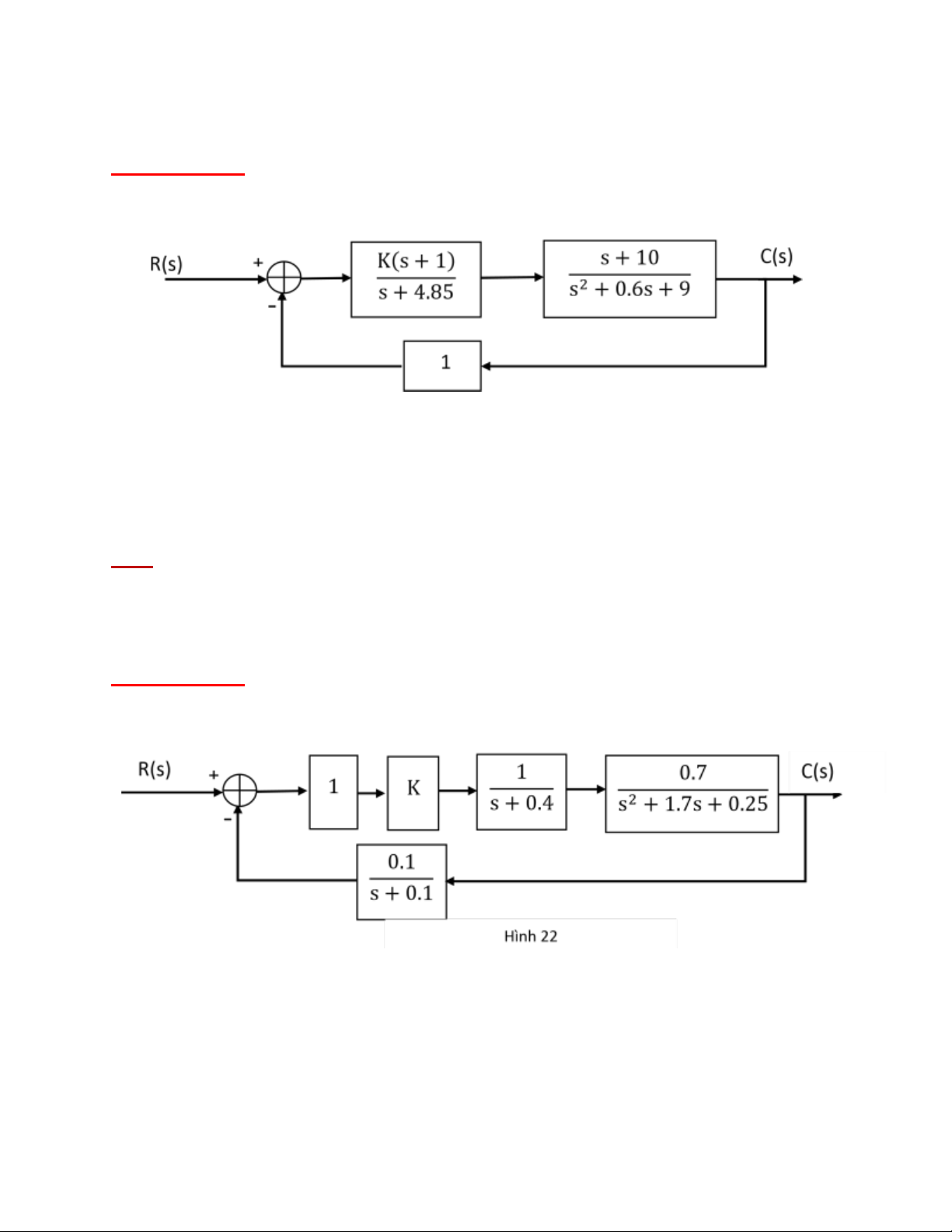
Bài tập 24: Cho hệ thống sau: Hình 2 4
Tìm điều kiện của K để hệ thống kín ổn định.
Bài tập lấy từ sách: Control Systems Engineering by Norman S. Nise 16 lOMoAR cPSD| 59735516
CSTĐ_Nguyễn Đức Hoàng 2010 Bộ môn ĐKTĐ - Khoa ĐĐT - BKHCM Cho hệ thống sau: ĐS: 0 < K < 1.0192. Bài tập 25: Hình 25
Tìm điều kiện của K để hệ thống kín ổn định. ĐS: 0.00509 < K.
Bài tập lấy từ sách: Control Systems Engineering by Norman S. Nise 17