Bài tập Xác suất thống kê

66 33 lượt tải Tải xuống




 !
"#$% &'
"#$%'
'
 (
"#$%))!
!
 *
+$,$%-./
01/
0 (
23.45678
9&$:;-<;7*
=>-.+6?@

$:



 

A11B((.C$-4$%4D4((EF-CG<

4HI?JKDG;-6=43L

 EF4$%-C#?.1B-M

 EF4$%-C#?.1-?!

N6

 NOPLQR-CGF4$%#?.1B-MQ24B

 NOLQR-CGF4$%#?.1-?!Q

24BCJ-6.1G?(5,10,...,100STCJ.1G?

//CT#A 7G$U% %?99.20S

A11J-';6VGW0;6V4IX+$,EFXF8

;6V=43G?4BBL

 R-;6V4I

 Y;6V4I

0 =6VGW

N6ZV[\-+]-. 

 NOPLQ=G?8;6VGFG-B;64IQ

ZG$U%B367G-P ^?4B .

 NOLQ=G?8;6VGFG-B-;64IQ



P (A)=

100

9.8

100.99

≈ 0, 0073

P (B )=

99.20

100

=0 , 2

P (A )=

=0 , 3

ZG$U%B367G- 

^?4B .

0 NOLQ=68;6VGFG-VGWQ24B .

A01]7V738&B!-.0MK73S._$U4)B:1

J73--=43G?8$U4BL

 B+];-.

 BM

0 B0MS`GaBM4b4$%73

N6

"HA

LQBk -.4$%73G?8&Q

 NOPLQB+];-.Q

 NOLQB.1MQ

c43+]B$UM?4$%73P(A

)24B



0 NOLQB0MS`.1M4b4$%73QA 7



A8114)G-G?c4,1-4d[5G7)d

IGISB30% 1[G7)dS20% 1[IGI15% 1[6-

5G")G-.11-4dS4317L

 2][5?

 2]XIGIS`$U74bXG7)d

N6

"HPLQR1-4d[G7)dQeLQR1-

4d[IGIQ

=-BLP(A) = 0,3;P(B) = 0,2;P(AB) = 0,15

+ C

P (B )=

+ C

P (C )=

P (A )= P (A

)+ P (A

+ C

P (B )=1 − P (A

)=1 −

P (C )= P (A

/B )=

P (A

)

P (B )

 c431-4d+]X5?P(A.¯ B¯) = P(A¯) + P(B¯) − P(AB¯ ) =



 cV 

A!"3 4173;-).1.]3-?S$U-fJ.1173

<.0TATJ780% STJ-770% 4b;-TJS

TJ`-745% 4b;-TJ-

 =43.1`+d4$%?4173

 7`5?#S43`5?#gTJ-

N6

"HA

LQ=4$%OgTJQSi {1∈ ,2,3}

=-BLP(A

) = 0,8;P(A

) = 0,7;P(A

) = 0,45

 c434$%?4173 P(A

)=I?]J&-BL

P(A

) = P(A

).P(A

) = 0,8.0,7.0,45 = 0,252

 "H2LQ=4B`5?#Q24BP(K) = P(A¯

) + P(A

A¯

) + P(A

A¯

)

P(A¯

) = 1 − P(A

) = 0,2;

P(A

A¯

) = P(A

).P(A¯

) = P(A

)(1 − P(A

)) = 0,8.0,3 = 0,24; P(A

A¯

) =

P(A

)P(A

)P(A¯

) = 0,8.0,7.0,55 = 0,308

→ P(A

A¯

) = 0,2. + 0,24 + 0,308 = 0,748

A 7434B`5?#gT-S`Ga4b`5?#LP(A¯

/K) =



A*B`-1PSS4KOR1PB(O!OhS1B*O8O

he1B!O!Oh

 i7D._1G-.1OS434$%0OX?#

 i7.11G<D4B7G-0Od4$%OOh=

4314$%O1P

N6

 NOA

LQiO7G-D1JQSi {1∈ ,2,3}

c434$%0OX?#P(A

+A¯

A¯

) = P(A

)P(A

)+P(A¯

)P(A¯

) =

−

100

P (

B/A )=

P (A

B )

P (A )

P (A ) − P (AB )

P (A )

0, 3 − 0, 15

0, 3

P (

.K )

P (K )

P (A

)

P (K )

0, 24

0, 748

=0 , 3209



 NOH

LQi74$%1JQSi {∈ A,B,C}ecLQi74$%OOhQ

24B c431P4$%OP(H

/X)=I?]

J-7IL



=I?]J4V74\S-BL

P(X) = P(H

)P(X/H

) + P(H

)P(X/H

) + P(H

)P(X/H

)

iV$%B 

=-7?]J-BL ^?4BP(H

/X) = 0,2347

A'=+j.OG$,\-.1G$U4#OSk>G$%.]=?34%S

G$%.]l?#M20.5%SG?G$%=?B50% G$%

.]l?#M

 O12 \-G$US)+6jB`-?

G$%6-.]=?l?#Mm=$:J

 96O`-?-??G?4BS,+]`:99%SB

.14_6-.]m

N6

NO=LQZG$%.]=?QelLQZG$%.]l?#MQ

=-BLP(T) = 0,34; P(N) = 0,205; P(N/T) = 0,5

 cG$%6-.]P(T.N) = P(T).P(N/T) = 0,34.0,5 = 0,17O

n-K>[IG?,G$%6-.]p = 0,17Z

)+6jG$%6-.][(n + 1)p] = [13.0,17] = 2

c$:J 

 c4_6-.]P(T.¯ N¯) = 1−P(T ∩N) = 1−P(T)−P(N)+P(T.N) =

0,625

NOn VOc434_6-.]+]4fS-B;

GdIG?B(n,p)

NOoLQY.14_6-.]Q=I?4)`-BL

P(I) = 1 − P

(0) = 1 − (1 − 0,625)

≥ 0,99 0⇔ ,375

≤ 0,01 ⇔ n ≥ 4,69.

A 7VO!

15·

P (H

)= P (H

P (H

/X )=

P (XH

)

P (X )

P (H

)P (X/H

)

P (X )

P (X/H

; P (X/H

P (X )=

5113

16380

≈

0, 312

(2)= C

(0, 17)

(1 − 0, 17)

0=0 , 296

  

=D.11J-@`4h!`GWS7VS._V.1S+]

?#=4374$%L

 `4he

 R-+.e

0 AJ-GW

1]<.((6p.SG?4B*6p.?#oo86p.?#oooST#

6p.?#oOXF06p.=434$%L

 -6p.+?#e

 06p.X?#e

0 "$%4F6p.?#oe

8 "$%6p.?#o

0114)G-?7S43.11-4dB.7 j.

G!(G>0,75=G?14$%4)G-d60% B G!(G>52% B.7

=43.11-4d4$%OL

 B.7B j.G!(G>e

 B.7S$+]B j.G!(G>e

0 B j.G!(G>S`Ga14B+]B.7

81.76`F.7B90% 4#qp+r N6[ 

6p.4#qp+r 95%c43 6p.+]4#qp+r

 8%=436p.4$% 4#qp+r 

!1]B/6p.-_V+3.G-S$U-O06p.S

+3.G-?#G6?]=43-0V+3.G-S/6p.4)4$%+3.G-

*=G?.14173B0 41PSS4,WV$%0,6;0,7 

0,8N6[._$U4.1G 41 -=43L

 "173W.1G e

 "173W-G e

0 A 41P-G?G$U%4173W-G 

'1&+3.? 715% `6J--V.=G?`6

J--V.S60% 4$%I.G5`$U?,D=G?6

`6d20% MG5`$Ul.1?g.1`6`$U

d434B.1-V.`-?m

@1b6\#$,+?680% $UX\#B4O;6??

b6=G?4BB30% .-\#\-b10% +]4O;6?s.-\

#\-b=43.1$UqX4b.-\#\-b.B4O;6?

/B-]6p.i]JBk>6p.?#o90%S]J-Bk>6p.?#

70%O.1]G<D]4B7G-6p.d4$%6p.?#o

=G6#6p.4B?]4bOSG<sD]4B7.16p.=43

6p.7VJ-?#o

(1]J-!6p.SG?4BB*6p.+]4#7Vi7V$%D

6p.+]?#43+3.G-S?4+H06p.+]4#7VdD

 =43>+3.G-D#g6p.J`-mZ6p.Jm

 l>+3.G-D#g6p.JS436p.4$%+3.G-4V

q+]4#7Vm

R1JB8`GW`-S1J-B0`GW0`-S+t$

-73.1`D1J--1JSG<7.1D1J

=43`7G-`GW

R1JB@6p.?#P6p.?#e1J-B!6p.?#P0

6p.?#i7D._16p.

 =434$%06p.?#Pe

 N6[74$%.16p.?#-6p.?#Pl)+6j6V.?#

11?S#-?m

01]?0.7PSS6Sk>6p.\-0.7V$%

30%,20%,50% k>p.$:J1%,2%,3%O6p.D]

=436p.7p.

8R1JB@6p.?#P6p.?#e1J-B!6p.?#P0

6p.?#i7.11SG<786p.G?4B

 =434$%06p.?#Pe

11?S#-?m

!B01S1oB!S1ooB8S1oooB0

i7.11GFG-D14B.1d4$%

=43711oo

*1]<.!(6p.G?4BB6% p.l$U-X$:

O.43+3.G-];7$,GaL23.G-V$%+]?#*6p.lB

6p.p.d?#]=43 ]

'1GT:BW._1/50l.1$U:!(d43

$U4BW.1`-?m

@=G?.1Sk>$UI.`B465%O$U=

43G?4BB4F!$UI.`B4

/NI?.1?FWq*V=43B.1V>.H*

.

NI?.1H-?FW8V=43.1V6-?4)>

.H*.

(=k>6G-p.\-.1.78%26?.1]<.'!6p.?

.74B6

 =43G?]SB(p.e

 =G?]S)+6jB`-?p.m=$:J

l$U-.7.1#D.1]#Bk># 3% 43

JRh67`-?#-??43B.1#+]`

:95%m

$:

"#$% &

 "#$%

 

ANI?-?FW&44<S;-F>g.HG\-

-?FWSOc"illk,G?->

 i `6&\-ce

 =d.P(X ≤ 3)eP(2 ≤ X < 5)

N6X {1∈ ,2,3,4,5,6}.

=-B`6&\-c$-L

P (X =1)= P ({(1, 1)} )=

P (X =2)= P ({ (1, 2) (2; , 1) (2; , 2)} )=

; ...

c   0 8 ! *

9uc

1/3

3/3

5/3

7/3

9/3

11/3

e

0

AB`-1PS4KOR1PB(O!OhS1B*O8

OhS1B!O'Ohi7D._1G-.1O

 =d. &?OG?0O7G-e

 =d.434$%Oe4$%0OX?#

N6NOc`kOG?0O7G-X {0∈ ,1,2,3}

 NOA

LQiO7G-D1JOQ

6&\-cL

c (   0

9uc

7/9

59/18

77/18

 c434$%-OL ec

434$%`-OX?#L 

A0114K!6p.SG?4BB-p.iV$%+3.G-D6p.

u+]?#v?4+H-p.dD#=d. &?6

p.4$%+3.G-=V+3.G-G`d

N6NOc"illk6p.4$%+3.G-X {2∈ ,3,4,5}"HA

LQiV

J+3.G-4$%p.Q

P (X ≤ 3)= P (X =1)+ P (X =2)+ P (X =3)=

P (2

≤

X< 5)= P (2P (3)+ P (4)=



P (X =0)= P (

P (X =1)= P (A

+ A

)

180

P (X =2)= P (A

+ A

180

P (X =3)= P (A



P (X ≥ 2)= P (X =2)+ P (X =3)=

107

180

P (X =0)+ P (X =3)=

P (X =2)= P (A

)= P (A

)P (A

=$:KL 

=-B`6&\-cL

c  0 8 !

9uc

1/1

2/1

3/1

4/1

ZV+3.G-G`dLEX = 4

A8?"illcB.. 41L

=d.aSF(x) P(0 < X < 3)

N6=DR S-BR .

R.&F 4$%45`gL



A!1#\B84#P-V$%`WD?`-wD`W+B.1

GF`-e+]S--w`W?4+4#Ga`WGF`-g._

V`W0,8NOc4#.#\4b`WRb7x. &\-ce+yO

$:-\-c

N6)G5\-X {1,2,3,4}

P(X = 1) = 0,8eP(X = 2) = 0,2.0,8 = 0,16eP(X = 3) = 0,2

.0,8 = 0,032eP(X = 4) = 0,2

= 0,0086&

\-cL

c   0 8

9ucv

0,8 0,16 0,032 0,008

2dO\-cLEX = 1.0,8 + 2.0,16 + 3.0,032 + 4.0,008 = 1,248

9$:-\-cLDX = 1

.0,8 + 2

.0,16 + 3

.0,032 + 4

.0,008 − 1,248

= 0,2985

A*1:g6`-?+z?Z+z?G?._`-?.14#$%cB

&$-L

c @ / (  

9ucv

0,14 0,24 0,32 0,21 0,09

P (X =3)= P (A

+ A

P (X =4)=

; P (X =5)=

f (x)=

(

,x> 1

0 x, ≤ 1

∞

− ∞

f (x)dx =1

∞

− ∞

dx =1

⇔

a =2

F (x)=

− ∞

0dt =0



x ≤ 1

(x)=

dt =1 −



1 x.<

P (0 X << 3)=

f (x)dx = F (3) − F (0)=

 =d.G`d$:-\-+z?G?._`-?e

 6\-._`-?+z?3X + 16=)`._`-?+z?100$2]&`>

+z?G?`-?=d.% G`d41>p\-% ?._`-?+z?e

0 R-`-?+z?4$%O=43.1G?-`-?J-(

+z?

N6

 =G`d$:-\-+z?G?._`-?L

 NO{"illk% ?._`-?+z?S-BY = 100 − (3X + 16) = 84 − 3X

i%     G  `d e

"1>pσ(Y ) = DY = 3 DX = 3,4879

0 "HPL|-?J-(+z?}P(A) = P(X = 20)+P(X = 21)+P(X = 22) = 0,62ec

43.1G?-`-?J-(+z?L0,62+0,62.0,38 = 0,8556

  

11J-(.C4h*.C-O0.C

 NOcC4h=d.&\-ce

 N6[GF4$%C4h4$%!43.GF._.C-4$%@43.NO{43.

f1-+GF0C=d.&\-{

0=G?.11B!`B4~SG?4BB`BS0`BhO

D`B4I.4[u?+]G6#v?4+4$%`BNOcV[V

=d.&\-c=G`dV[`-?Vm

81]<.'6p.SG?4BB0p.O86p.43+3.

G-NOc6p.G?86p.7G-=d.&\-c•c

!R-#\P `W_$U`W-c`WGF\-PV$%0,4

0,5

 NOcGF\-PGD4`WGF\-=d.&\-ce

 =d.&\-Y = |X|

*=G?.14173S`- 41PSS4,WV$%0,6;0,7;0,8

=G?.14%4S._ 41.1G 41 -

EX =

=18

k.P (X = k)=19 , 87

DX = E (X

) − (EX )

=1 , 3531



EY = E (84

−

3X )=84

−

3EX =24 , 39

√ √

=d. &?G W\-41e=

4341-)G eWG e

0 41WG S43P-G 

8 =G WG`d$:-\-G W\-4173

'1$U4)+3`-.7K41?#4141 ,-c`5GGHG?

._-6\-.7oSoooooV$%0,1;0,2 0,3

 i `6&?.7?#41G?.1-6e

 =G`dSG?.1-SB`-?.7?#41m=41>p\-.7?#

41G?.1-6e

0 GaG?-6kB.1.7?#41=43.74B.7

o

@1]<.!OSG?4BB.1O623.G-V$%DO?4

+7O6dD=d.&?-4$%+3.G-

/EF8`G?`1`F:+:S-4B+?-NOc:

G?4$%+?-

 =d.&\-ce

 =G?4BkB.1:

0(=+6?+G.17I`€uZ2•v#.17-?]S

$U-4$%>-L

Z2• ! 0( 0! 8( 8!

c (S! (S (S0 (S

(S

 =+yO41>p\-Z2•e

 N6[?._7I`€((4<S+]1?+4G

IS]76;745`-?43B34$%q)UG`d?._

7I((4<m

0N6[c`$%I]]..14#€`4$%G?.1VB&

$-L

c (   0 8 !

9ucv (S (S (S (S (S

(S

 =434#€4B`4$%)0IG?.1V=+yO$:-

\-I.4#€`4$%G?.1j.e



 N6[??#41\-4#€`aj` -\-I`4$%,!uG>4<v

=d.??#41G`d??#41\-4#€G?.1V

0?-4#$%cS{B&$-L

c (   0 8

9ucv (S (S (S0 (S! (S!

c"illY = X

− 4X

+ 10

 =d.&\-{e

 =•{`a-e

0 =^{

00?.

 Jhf(x) .. 41\-.1`ce

 =d..&F(x) \-ce=d.+dO$:-\-ce

0 = 

08?.

 Jhf(x) .. 41\-.1`ce

 =d..&F(x) \-ce

0 =P(0 < X < 3)

0!?"illcB.. 41

 =d.aae

 =d..&F(x) \-c

0*?"illcB.. 41f(x) = (



≤

0 G#

 =d.a+e

 =P(X > 2)e

0 =.I-\-ce

f (x)=

(

2x,x ∈ [0, 1]

0, x/

∈

[0, 1]

P (0 < <X

)

f (x)=







,x> 1

0, x ≤ 1

f (x)=

(

,x> 1

0, x ≤ 1

8 =d. 

0'2$%\-.1?*f.1"illcu4:5+v,.. 41&

$-L

=d.+$%G`d\-?*f41>qp

0@1]<.@((6p.?#o((6p.?#ooi7G-!6p.B

?#NOc6p.?#o74$%

 c&I?;7 ?mA`3Jf;m

 =+dO$:-\-c

0/ZB-4:..1]7P 4$%G?.17.1"illcB&

9?],-. λ = 1,5=43G?.17L

 ]7+] 4$%B-4:?e

 ]7 4$%B-4:e

0 ]7 4$%)B-4:e

8 ]7 4$%8B-4:

8(1[-B8]]?S+BVG?7.1"illcB

&9?]

 GaEX = 2Sb7]]G`d.[-?G?.17e

 [-VB`-?]]43,+]h:0,98S[-4J

4$%V\-+G?7m

8NI?.14<q)?4+>.H[-dD#c>.H[-

pNOc"illkVI?V

 =d.&\-ce

 =d.&\-c,4)+>G?n VI?4Vqk4FV4<

>.H[-

81]BG)6p.S,k>630%

 i7D]G-(6p.S43B)6p.6

 l$U-7G-D6p..143+3.G-?4+?H6p.6d

D=d. &+yO\-6p. 4b+3.G-

0

P (X<a )=

f (x)=

(

k(x

− 1),

,

2 ≤ x ≤ 3

,T#

801+.-I#.14#€SIBK+r d4$%;7)G6IG?

T07-+.-4$%7#7q).-I_I`5G6#$.

>#?4#€!(dAl"B!(I4$%`G-c43.1I`5G6#0,1

=d.+yO$:-\-I`5G6=43B)I`5G6#e=d.

+yO41>p\-f>#.f4#€65?>G6#I

88#-.K.1+y,dJ6..14)GW>.+;-<.

(&S._&B8U6+-SG?4BkB.1U64Fw4$%.4 

G6U4F*&

 N6[+]O`S.kOU6G?6(&=43

4 e

 Rh6K.7V43B.1V4 +]h:97%m

8!=k>hg]PP

= 0,1Sg]P

= 0,08 g]P

= 0,15Ga._]B

G)-

 i70-g]P=d. &\--hBG?0-=43

B-heB-he

 967`-?-ug]Pv43B.1-h+]h:94%m

0 O]G<7D]4BG-0-=43B-h

8*Z_G.]6.1`&I? &??23.G-

]6S$U-798% B_A 7G`d._.]6B`-?_m

8'1:g6SG`dG?.1VS 4$%84:4HGa4:

4Hc.:g 4$%G?.1V.1llB&9??=43:

g4BL

 l 4$%:!4:4HG?.1Ve

 l 4$%*4:4HG?-Vq

8@=U-436.16p.?#P.1ll&I? &p,

-.µ = 10  σ = 1 u4:5Fv

 =43.16p.?#P?4B4$%6G?+?6U-D/F

4Fe

 =U-V436.16p.?#P`+y

8/?`c&I? &pN(µ,σ)Gac7G5h:*(

,0,1003 7G5,:/(,0,0516Sb7µ σ!("$U+

\-.1?#q?.1.76B&pS+yO20 ..S$:-0,2

..

=7.1qL

 B4$U+G?+?619,9 ..420,3 ..e

 B4$U+-+,+yO+];0,3 ..

 "#$%))

 

A'?c{-"illB&4<U$-L

c{ ‚ 

‚



(



Rb7EX,EY,Cov(X,Y ) ρ(X,Y )

N6

Cov(X,Y ) = E(XY ) − EX.EY e=-B`6&\-XY L

c{ ‚ ( 

9uc{v

5/12 7/24 7/24

A 7 e

A@N6[X ∼ B(2;0,4); Y ∼ B(2;0,7)c{-"ill41 

 =d.&\-X + Y e

 J.GaX + Y +]B&5J

N6

6&\-c{$-L



!

EX = − 1(

)+1(

)= −

EY =

−

1.3.

+1 .(

)=0

E (XY )=

−

⇒

Cov (X,Y )=

ρ(X,Y )=

Cov (X,Y )

= − 0, 15

c (  

9ucv

0,36 0,48 0,16

{ (  

9u{v

0,09 0,42 0,49

 "HZ = X + Y S-BL

P(Z = 0) = P(X = 0).P(Y = 0) = 0,0324e

P(Z = 1) = P(X = 0)P(Y = 1) + P(X = 1)P(Y = 0) = 0,1944e

=$:KLP(Z = 2) = 0,3924; P(Z = 3) = 0,3024; P(Z = 4) = 0,0784=D4?-B

`6&\-Z = X + Y L

ƒ (   0 8

9uƒv

0,032

0,1944 0,3924 0,302

0,0784

 N6[$%#SZ = X + Y B&5JSZ = B(4,p)

24BP(Z = 4) = p

= 0,0784

H+P(Z = 0) = (1 − p)

= 0,0324S7G-6Bp = √

0,0784 p = 1 − √

0,0324S]

A 7X + Y +]B&5J

A/?cS{-"illB.. 414<UL

f(x,y) = ( − x y e ( + ) x > 0,y > 0

0 G#

 =d... 41\- e

 JhGa„A41 Sc{41 

N6

 94f` S,x,y > 0 -B

R.. 414<U\-„ALu > 0,0 < v < 1S…-?`-|J| = u f(u,v) = e−uv−u

uvu =

u.e−u u > 0,0 < v < 1 f(u,v) = 0 G#

R.. 41\-„ u > 0 f(u) = 0 

G#e R R

R.. 41\-A 0 < v < 1 f(v) = 0 

G# R R

 ^†7Gaf(u,v) = f(u)f(v) „A41 1$:KSc{s41 

  

!?"illc{B`6&4<U$-L

U = X + Y,V =

X + Y

u = x + y,v =

x + y

⇔ x = uv,y = u(1 − v)

f (u)=

∞

− ∞

f (u,v )dv =

u.e

−

dv = ue

−

f (v)=

∞

− ∞

f (u,v )du =

∞

u.e

−

du =1

c{   0

 (S



(S

(S(

 (S

(S0

(S(

 J.Gac{41 e

 =d.;7 &\-ƒ‡c{e

0 =•ƒ`a-+3.G-EZ = EX.EY 

!?c{-"illB&$-L

c (   0

9ucv (S8 (S0 (S



(S



{ (   0 8

9u{v (S (S0 (S8 (S! (S(!

 =d.&4<U\-c{e

 =P(X > Y )

!0?c{-"illB&4<U$-L

c{ ‚ ( 

‚

(



0 0

 =EX,EY,cov(X,Y ) ρ(X,Y );

 c{B41 -7+]m

!8?c{-"ill41 

 N6[X ∼ B(1;0,2) Y ∼ B(2;0,2)i `6&\-X,Y X + Y e

 N6[X ∼ B(1;0,5) Y ∼ B(2;0,2)i `6&\-X + Y X + Y B&

5J-7+]m

!!?c{-"illB.. 414<U



0 G#

=d... 41\-c\-{ 

'

f (x,y )=





6π

< 1

!*?-"illc{B.. 414<UL

0 < x < 1,0 < y < 2

( ) = (

0 G#

 =d.ake

 =d..&4<U\-c{

!'?-"illc{B.. 414<UL

 =d.ake

 =d..&4<U\-c{e

0 c{B41 +]m

8 =4343.(X,Y ) G:?dM ,4kA(1,1)SB(√ 3,1),

C(1,0), D(√3 ,0)

!@N6[c{-"ill41 BX&.s,-.λ

 =d..&.. 41\-Z =



 =d..&.. 41\-U = X − Y 

!/N6[c{-"ill41 B&4)G4?#[0,1]

 =d..&.. 41\-Z = X + Y e

 =d..&.. 41\-U = XY 

*(?c{-"illB&p4<U,EX = 35,EY = 20,DX = 36,DY = 16 

ρ(X,Y ) = 0,8=d.+dO$:-\-2X − 3Y 

*?X ∼ N(7;1,2

) Y ∼ N(5;0,9

)N6Gac{41 

 =d.P(X + Y < 9,5)e

 =d.P(X < Y )e

0 =d.P(X > 2Y )

*N6[GaGO$%+4.7`-7B&p,+dO'8u+vGO

$%.-I?B&p,+dO(u+v

f x,y

k(x

)

f (x,y )=

(1+ x

)(1+ y

)

 GaB10% +BGO$%,:@!u+v20% +B

H:8u+v=d.41>qp\-GO$%+GO$%e

 GaB 10% +.fGO$%\-O.-I?,:

(@u+v=d.>$:;-\-GO$%+

$:0

+$,$%-.

0 1

A0N6[+$%\-#X ?.1.764#$%

B&`p,G5G`dE(X) = ae$:-D(X) = σ

$-`"345

+$%G`d\-.1#-7.tn = 50 4$%`6-

2$%u+v S!‚

S0(

S0(‚

S0!

S0!‚

S8(

S8(‚

S8!

#un

v ' ( @ !

Rb7$,$%+]>\-E(X) D(X)=-B

$,$%+]>\-E(X) = a

=

);

$,$%+]>\-D(X) = σ



√

= s

≈ 0,0429kg $,$%\-σ

A0"345ˆ>#p.G?f#\-.1.7$U-+3.G-

$%!(#B*+]4#$%Rb7$,$%ˆ>#p.\-.7

7

J2,4%

/

x =

7.2, 275+20 .2, 325+18 .2, 375+5 .2, 425

=2 , 346kg

−

x )

=0 , 001809(kg

−

≈ 0, 001845(kg

)

∗

250

=0 , 024

0  

*0Aw4-V-

 0 ! *

( 

! (

6-

! ( 

0( 0!

( ! 0

(

0! (

6`

*8^K`34<V.?$,4&7

2?6G5[x

−

] ‚! !‚

@‚



‚

8

=fVG5G:?+?6 * ( 8 !

*!=G`d.S$:-.41>p.4)k\-.?`g`6

-

 8 ! * @ 0 08

( ( 0( ! ( ( !

**l$U-4?@V4#$%X 4$%b7>-Rb7X, s

, s



*'l$U-4?)-?\-((4$%O`+y4$%`6>-

)-?(cm) !8‚

!@

!@‚

*

*‚

**

**‚

'(

'(‚

'8

'8‚

'@

'@‚

@

Z ( 8 * @  @ 

=d.)-?G`d.J41&\-)-??,)-?G`d\-B.

4$%OG

*@=I?‰U-?.16p.\--f]&S$U-4$%>

-

- =fL

` =fL

Rb7U-G`d43?.16p..J41&U-?

.16p.?,U-G`dg-f]&G

*/R-?7>?.14:56p..14#$%,&

p(µ,σ

) , σ = 0,03l$U-6[0*6p.4$%`6>-

J-?7>u-.v Z6p.

=U-uFv 8 88 8! !

*( *8

Z]& 8 ! ( 

(

@ 0

=U-uFv 8* 8@ !

Z]&  8( @

/!‚/' @

/'‚// @

//‚( @

(‚(0 

Rb7x.41q 74J/!Š?.J-?7>G`d?.14:56

p.BG

'(l$U-+3.G-((`B4~X?#7GafOG`d\-]

`B4~7(((uUvA,41q 7(S/!b7$,$%fOG`d\-?#`B4~

G`a+?6q 74JN6GafOG`d4#$%B&

p,41>p σ = 40uUv

'?.1?#]]#7[0(VD45-43.A ,45-43.BS$U- 4$%$%

j-?$-

i$%j-.uv ZV#7

/*‚/@ 0

//‚(( !

((‚( (

(‚(8 @

(8‚(* 8

 A,41q 7//ŠSb7$,$%j-?G`d\-?#]]7+#7DA 4B

`a+?6q 74J

 A,41q 7//ŠSb7$,$%j-?G`d4-\-?#]]7+#7DA

4B

Ga$%j-?4#$%B&p

'"345.JU--]?.16p.S$U-I?‰;Gd-

]!6p.4$%>-

=U--]uFv Z6p.

!‚' 

'‚/ 0

/‚ 8

‚0 

0‚! 0

!‚' 

 A,41q 7(S/!Sb7$,$%U--]G`d?.16p.`a+?6

q 74J

 A,41q 7(S/!Sb7$,$%U--]3?.16p.

N6U--]?.16p.4#$%B&p

'0&[0*`-?`1?7GO$%G`d.1`-?8(+S41>p.4)

k



= 5kg.

Rb7$,$%GO$%G`d\-`-?`1`a+?6q 74J,41q 7/!Š

N6GaGO$%\-`-?`14#$%B&p'8)

?#6p.A ?.1.7K416.14#$%B&p,41

>p σ = 3cml$U-q4?0*6p.A 7)G`d

\-F150cm

 A,41q 7(S/!b7$,$%)G`d\-6p.A `a+?6q 7

4J

 `964?3`-?6p.A 4341q 7(S//$,$%4#41 ε =

0,3

'!23.G-((6p.\-.7A d7B(p.

 Rb7$,$%ˆ>p.\-.7P`a+?6q 74J,41q 7(S/!

 Rb7$,$%ˆ>p.3\-.7A ,41q 7(S/!

'*O!(\-.1G$U4#Od7BMA,41q 7/(Šb7

$,$%ˆ>MgG$U4#O4B`a+?6q 74J

''i.>.-?(((($Ud7B(($UB+;6$:c>.

q4,M$U7dB8($U.W`>-A,41q 7//Šb7$,$%$U

.W`>-G??;`a+?6q 74J

'@NI?[8((#dB(#+]67.V.A,41q 7/!Šb7$,$%ˆ>

#+]67.V.4-`-?m

'/‹.1<$U-4`W(((?S4FG<6<-4B`W#8((

?d7B@(?`54

 Rb7$,$%G?<,41q 7/!Š

 `A,41q 7/!Šb7$,$%G?<B)`-??

@(2$%.16p.B&p&!6p.?#4B$U-

4$%+;64B

2$%u-.v /0 /' 0( 0(! 0('

Z6p. 8 ! @ ! 0

 =d.$,$%+]>?$:-\-+$%6p.

 A,41q 7/!Šb7x.+?6q 7?$:-\-+$%6p.S`

+$%G`d\-?#6p.4B0(-.

0 A,  41  q   7  /!Š  b7  x.  +?6  q   7  ?  $:  -  \-  +  $%  6  p.

G?G$U%$-`+$%G`d\-?#6p.4B

@"3$,$%.W`>A ,41q 7/!Š-+]$%;ŠdV

6+.3`-?$US`Gaˆ>.W`>A K>.?`a(S/

0

$:8

23.4567

@l.7.B?#41`d$UdGO$%\-6p.(X) 4#$%

&I? p,µ = 100gamS σ = 2gamŒ-.1U-6$U-U

GO$%6p.jjJ((6p.dGO$%G`d\-F

100,4gamA,.J€n- α = 0.05 b7+ 4)UG

"LW

= (1,645;+∞);g = 2 e=GO$%G`dj

@0=G?4)+>j]`d$US$%M-G`d\-.1?`T14kg .1

7lU4)+>j]`T+.4.?$%M-6.l$U-4)G-

!?`T4$%$%M-G`d\-.1?G?.1712,5kg 41>

qp.4)ks = 2,5kgA,.J€n- α = 0.05 b7+ )4)UG

Ga$%M-`T4#$%&p

"W

= (−∞;−1,711);g = −3ei$%M-`TB$,6.

@8"5.Js436.16p.(Fl-7?6q+r $U-6

[((6p.4$%+;6-L

=U-436.16p. Z6p.$:J

*‚' *

'‚@ (

@‚/ 8

/‚( 0(

(‚ @

‚ 

A,.J€n- α = 0,05 B3B>6q+n 4b.6.`,U-6.1

6p.-7+]mGaU-6.16p.4#$%&

p"W

= (−∞;−1,645);g = −5,18e=U-6.16p.4b6.

@!=ˆ>p.?.1.7K416!Š23.G-0((6p.7

B86p.p.B€+?Gaˆ>p.?.74B64bjRb7

+ €+G,.J€n- α = 0.05

"W

= (1,645;+∞);g = 2,39e=k>p.j

@*=ˆ>-.h(SZ-.1U-`6?;678((;67*(;6`5h

B€+?Ga>`6?;6-.+]Rb7+ €+G,.J€n- α = 0,01

"W

= (2,575;+∞);g = 3,33eA>`6?;6-.

@'=GO$%\-?.,g4#$%&plU414<

4))GO$%?6.F$U-&[?x.4$%s

= 11,41gam

A,.J€

n- α = 0.05 b7+ )4)UG`Ga`d$U41&\-GO$%

?10gam



"W

= (0;3,82)(21,9;+∞);g = 12,55e=GO$%?+]6.F

@@l.7.B?#41`d$UdGO$%6p.&I?;7 p

kgB3?.7.BT?#41`d$U+]-&[0(6p.

741>qp4)k.kg{V+ ,.J€n- α = 0.01

"W

= (49,6;+∞);g = 35,09e7.B?#41`d$U

@/l$U-6[((6p.4$%+;6-

=U-436.16p. Z6p.$:J

*‚' *

'‚@ (

@‚/ 8

/‚( 0(

(‚ @

‚ 

A,.J€n- α = 0,01 B3I.U-436.16p.4#$%

&I?7 p4$%+]

"x = 19,3;s = 1,34;W

= (11,34,+∞);g = 2,07e=&I? p

/(")G-8(((-4d-B4$%

Z?G- Z-4d$:J

( 8!(

 8*(

 !0(

0 !*(

A,.J€n- α = 0,05 B3?X ?G-G?-4dB`-?&I?;7

 5J4$%+]m

"LW

= (6;+∞),g = 13,68 e+]&I?;7 5J

/Z?\-M\4]$,!f?g`6-

X u?v ZM

( (/(

 *!(

 (

0 0(

8 (

A,.J€n-  α = 0,05 B3I. X &I? 9??4$%+]m"

eW

= (6;+∞),g = 0,32 =&I?;7 9??e

!

/lJ6$gVJj\-`.z(X) 4,,\-?(Y ) -B

+;6-

=VJj

N,

2]BA-. BA-.

?G- 0 8!

? !0 !(

A,.J€n- α = 0,05 -B3I.X Y 41 ,-4$%+]m

/0lJK6$g\-?6-4d4,xG##.1\-GCI.5

;-4)G--B+;6-

?H.z4b .z] T6`.z

2]#.1 ( ! 0

9#.1 / 80 @

A,.J€n- α = 0,05 B3+ Ga?6-4d41&,xG##.1

\-GCI.-7+]m

$:!

9&$:;-<;7

/8?`6&\-4#$%-)GUG#

* 0( 8 !(

S

(S(

(S



(S(

S

(S(

(S0

(

(S



(S



 =d.`6&\-VX Y 

 =d.`6&B4)+>\-Y +X = 26 \-X +Y = 27 /!?

`6&\-4#$%-)GUG#$-

 0 8 @

0 (S

(S(

(S

(S(

* (S0

(

(S

(

(S(

-v =d.+yOB4)+>\-Y ,X = 1

`v =d.+yOE(X),E(Y ) $:-D(X),D(Y )

v =d..?.I$:;->$:;-M-X Y 

"L

-v E(Y/X = 1) = 5

`v E(X) = 2,93;E(Y ) = 4,5;D(Y ) = 2,25

v µ

= −0,555,Γ

= −0,168

/*?`6&\-:(X,Y )

  0

 (S

(S

(S

 (S

(

(S0

(

(S(

-v =d..-G >$:-

`v =d.>$:;-ρ

"L

-v

"−0,25 −0,06#

0,06 0,57

= −0,159

/'?`6&4#$%-)



(



(



(

λ 2

c45

-v =-.λ

`v =d.+yOE(X),E(Y )

v =d..-G >$:-

v =d.>$:;-

-v λ = 1/20

`v E(X) = 22,E(Y ) = 41

'

v

vρ

= 0,56

/@=d.434#$%-)(X,Y )  G5G?dM ,#

`g4$U•x = 1;x = 2;y = 3;y = 5 `.&

"ZLp = 0,0234

(1 e−2x)(1 e−3y) x 0,y 0

//F(x,y) =− − ≥ ≥

0 x < 0,y < 0

"ZLf(x,y) = 6e

2x+3y

=>-.+6?

Ž• "HRX=WSg4Vi€7JSlcN?S///

Ž• "HRX=WS SlcN?S///

Ž0• "?RMR<Sc‚+Slc"#OŒ-Rl1S(('

Ž8• l7†^7=Si€7SlcN?S((*

x x



≥

0,y

≥



x< 0,y< 0

F (x,y )=

(

1 − 2

−

− 2

−

− 2

− −

(

56 57

67 259

Bấm Tải xuống để xem toàn bộ.

Thông tin :

29 trang 10 tháng trước

Môn:

Xác suất thống kê (Xs)

Trường:

Đại Học Nội Vụ Hà Nội

Tác giả:

Thái Huyền

| 1/29

| | Tải xuống

Preview text:

Mục lục

Biến cố ngẫu nhiên và phép tính xác suất 1

1.1 Các ví dụ 1

1.2 Bài tập 5

Đại lượng ngẫu nhiên và luật phân phối xác suất 7

2.1 Đại lượng ngẫu nhiên 7

2.1.1 Các ví dụ 7

2.1.2 Bài tập 10

2.2 Đại lượng ngẫu nhiên nhiều chiều 15

2.2.1 Các ví dụ 15

2.2.2 Bài tập 16

Mẫu thống kê và ước lượng tham số 19

3.1 Một số ví dụ 19

3.2 Bài tập 19

Kiểm định giả thuyết 23

Phân tích tương quan và hồi quy 25

Tài liệu tham khảo 27

Chương 1

Biến cố ngẫu nhiên và phép tính xác suất

1.1 Các ví dụ

Ví dụ 1.1. Một hộp có 100 tấm thẻ như nhau được đánh số từ 1 đến 100. Rút ngẫu nhiên hai thẻ rồi đặt theo thứ tự từ trái qua phải. Tính xác suất để:

Rút được hai thẻ tạo thành một số có hai chữ số.
Rút được hai thẻ tạo thành một số chia hết cho 5.

Giải.

Gọi A:"Hai thẻ rút được tạo thành một số có hai chữ số". Khi đó

(

100

≈

0073

Gọi B:"Hai thẻ rút được tạo thành một số chia hết cho 5 ".

Khi đó thẻ thứ hai là phải là một trong 20 số 5,10,...,100, còn thẻ thứ nhất là một trong

99 thẻ còn lại.Vậy số trường hợp thuận lợi cho B là 99.20,

(

100

Ví dụ 1.2. Một hộp chứa 7 quả cầu trắng và 3 quả cầu đen cùng kích thước. Rút ngẫu nhiên cùng lúc 4 quả cầu. Tính xác suất để trong đó có:

Hai quả cầu đen.
Ít nhất 2 quả cầu đen.
Tất cả là cầu trắng.

Giải. Số phần tử của không gian mẫu là.

Gọi A:"Trong 4 quả cầu rút ra có 2 quả đen".

Số trường hợp có thể xảy ra A là . Do đó .

(

Gọi B:"Trong 4 quả cầu rút ra có ít nhất hai quả đen".

Số trường hợp có thể xảy ra B là.

Do đó .

(

Gọi C:"Tất cả 4 quả cầu rút ra là cầu trắng". Khi đó .

(

Ví dụ 1.3. Một công ty cần tuyển 4 nhân viên. Có 5 nam và 3 nữ dự tuyển, mỗi người đều có cơ hội ứng tuyển ngang nhau. Tính xác suất để trong 4 người đó:

Có không quá 2 nam.
Có ít nhất 1 nữ.
Có 3 nữ, biết rằng có ít nhất 1 nữ đã được tuyển.

Giải.

Đặt A_k: "Có k nam được tuyển trong 4 nhân viên".

Gọi A:" Có không quá 2 nam".

(

Gọi B:"Có ít nhất một nữ".

Xác suất để không có người nữ nào được tuyển là P(A₄). Khi đó

(

)=1

−

(

)=1

−

Gọi C:"Có 3 nữ, biết ít nhất một nữ đã được tuyển".Vậy

(

)

(

)

Ví dụ 1.4. Một cuộc điều tra trong thành phố X đối với các hộ gia đình sử dụng dịch vụ truyền hình cáp và internet, có 30% hộ sử dụng truyền hình cáp, 20% hộ sử dụng internet và 15% hộ sử dụng cả hai dịch vụ trên. Điều tra ngẫu nhiên một hộ gia đình, tính xác suất để hộ này:

Không sử dụng dịch vụ nào.
Không dùng internet, biết người này đã dùng truyền hình cáp.

Giải.

Đặt A:"Hộ gia đình sử dụng truyền hình cáp"; B:"Hộ gia đình sử dụng internet ".

Ta có: P(A) = 0,3;P(B) = 0,2;P(AB) = 0,15.

Xác suất để hộ gia đình không dùng dịch vụ nào là P(A.¯ B¯) = P(A¯) + P(B¯) − P(AB¯ ) =

−

100

Xác suất cần tính là.

(

B/A

(

)

(

)

(

)

−

(

)

(

)

−

Ví dụ 1.5. Để thành lập đội tuyển quốc gia về một môn thể thao, người ta tổ chức một cuộc thi tuyển gồm 3 vòng. Vòng thứ nhất lấy 80% thí sinh, vòng thứ hai lấy 70% thí sinh đã qua vòng thứ nhất, vòng thứ ba lấy 45% thí sinh đã qua vòng thứ hai.

Tính xác suất để một thí sinh bất kì được vào đội tuyển.
Biết thí sinh này bị loại, tính xác suất để thí sinh bị loại ở vòng thứ hai.

Giải.

Đặt A_i: "Thí sinh được chọn ở vòng thứ i ", i ∈ {1,2,3}.

Ta có: P(A₁) = 0,8;P(A₂/A₁) = 0,7;P(A₃/A₁A₂) = 0,45.

Xác suất để thí sinh được vào đội tuyển là P(A₁A₂A₃). Theo công thức nhân xác suất ta có: P(A₁A₂A₃) = P(A₁).P(A₂/A₁).P(A₃/A₁A₂) = 0,8.0,7.0,45 = 0,252.
Đặt K: "Thí sinh đó bị loại". Khi đó P(K) = P(A¯₁) + P(A₁A¯₂) + P(A₁A₂A¯₃).

P(A¯₁) = 1 − P(A₁) = 0,2;

P(A₁A¯₂) = P(A₁).P(A¯₂/A₁) = P(A₁)(1 − P(A₂/A₁)) = 0,8.0,3 = 0,24; P(A₁A₂A¯₃) = P(A₁)P(A₂/A₁)P(A¯₃/A₁A₂) = 0,8.0,7.0,55 = 0,308.

→ P(A₁A₂A¯₃) = 0,2. + 0,24 + 0,308 = 0,748.

Vậy xác suất để thí sinh đó bị loại ở vòng hai, biết rằng thí sinh đã bị loại là: P(A¯₂/K) =

(

)

(

)

(

)

(

)

748

3209

Ví dụ 1.6. Có ba hộp A, B, C đựng các lọ thuốc. Hộp A có 10 lọ tốt và 5 lọ hỏng, hộp B có 6 lọ tốt và 4 lọ hỏng; hộp C có 5 lọ tốt và 5 lọ hỏng.

Lấy ngẫu nhiên từ mỗi hộp ra một lọ thuốc, tính xác suất để được 3 lọ cùng loại.
Lấy ngẫu nhiên một hộp rồi từ đó lấy ra 3 lọ thuốc thì được 1 lọ tốt và 2 lọ hỏng. Tính xácsuất để hộp được chọn là hộp A.

Giải.

Gọi A_i: " Lọ lấy ra từ hộp thứ i là tốt", i ∈ {1,2,3}.

Xác suất để được 3 lọ cùng loại là P(A₁A₂A₃+A¯₁A¯₂A¯₃) = P(A₁)P(A₂)P(A₃)+P(A¯₁)P(A¯₂)P(A¯₃) =

Gọi H_i: "Lấy được hộp thứ i", i ∈ {A,B,C}; X:"Lấy được 1 lọ tốt và 2 lọ hỏng".

Khi đó . Xác suất để hộp A được chọn là P(H_A/X). Theo công thức Bayes:

(

)

(

)

(

)

(

X/H

)

(

)

Theo công thức xác suất đầy đủ, ta có:

P(X) = P(H_A)P(X/H_A) + P(H_B)P(X/H_B) + P(H_C)P(X/H_C).

Lần lượt có.

(

X/H

;

(

X/H

;

(

X/H

Thay vào công thức ta có:. Do đó P(H_A/X) = 0,2347.

(

5113

16380

≈

312

Ví dụ 1.7. Thống kê năm học trước của một trường đại học, tỉ lệ sinh viên thi trượt môn Toán là 34%, thi trượt môn Ngoại ngữ là 20.5%, và trong số các sinh viên thi trượt Toán có 50% sinh viên thi trượt môn Ngoại ngữ.

Chọn ngẫu nhiên 12 sinh viên của trường, nhiều khả năng nhất là có bao nhiêu sinh viên thi trượt cả hai môn Toán và Ngoại ngữ? Tính xác suất tương ứng.
Phải chọn bao nhiêu sinh viên sao cho trong số đó, với xác suất không bé hơn 99%, có ít nhất một sinh viên đỗ cả hai môn?

Giải.

Gọi T:"Sinh viên thi trượt môn Toán"; N:"Sinh viên thi trượt môn Ngoại ngữ".

Ta có: P(T) = 0,34; P(N) = 0,205; P(N/T) = 0,5.

Xác suất sinh viên trượt cả hai môn là P(T.N) = P(T).P(N/T) = 0,34.0,5 = 0,17. Chọn 12 sinh viên nghĩa là thực hiện phép thử Bernoulli với xác suất trượt cả hai môn là p = 0,17. Số sinh viên nhiều khả năng trượt cả hai môn nhất là [(n + 1)p] = [13.0,17] = 2.

Xác suất tương ứng là.

(2)=

17)

−

17)

0=0

296

Xác suất sinh viên đỗ cả hai môn là P(T.¯ N¯) = 1−P(T ∩N) = 1−P(T)−P(N)+P(T.N) =

0,625.

Gọi n là số sinh viên cần chọn. Xác suất để sinh viên đỗ cả hai môn là không đổi, nên ta có quá trình Bernoulli B(n,p).

Gọi I: "Ít nhất một sinh viên đỗ cả hai môn". Theo đề bài ta có:

P(I) = 1 − P_n(0) = 1 − (1 − 0,625)ⁿ≥ 0,99 ⇔ 0,375ⁿ≤ 0,01 ⇔ n ≥ 4,69.

Vậy cần chọn ít nhất 5 sinh viên.

1.2 Bài tập

Bài 1. Từ một hộp chứa 8 viên bi đỏ và 5 viên bi trắng, lấy ngẫu nhiên 2 lần, mỗi lần một viên, không hoàn lại. Tính xác suất để lấy được:

2 viên bi đỏ;
Hai viên khác màu;
Viên thứ hai là trắng.

Bài 2. Một lô hàng gồm 100 sản phẩm, trong đó 6 sản phẩm loại II và 4 sản phẩm loại III, số còn lại là sản phẩm loại I. Chọn ngẫu nhiên cùng lúc 3 sản phẩm. Tính xác suất để được:

Ba sản phẩm khác loại;
3 sản phẩm cùng loại;
Được đúng 1 sản phẩm loại I;
Được ít nhất 1 sản phẩm loại I.

Bài 3. Một cuộc điều tra cho thấy, xác suất để một hộ gia đình có máy vi tính nếu thu nhập hàng năm trên 50 triệu là 0,75. Trong số các hộ được điều tra thì 60% có thu nhập trên 50 triệu và 52% có máy vi tính. Tính xác suất để một hộ gia đình được chọn ngẫu nhiên:

Có máy vi tính và có thu nhập hàng năm trên 50 triệu;
Có máy vi tính, nhưng không có thu nhập hàng năm trên 50 triệu;
Có thu nhập hàng năm trên 50 triệu, biết rằng hộ đó không có máy vi tính.

Bài 4. Một nhà máy sản xuất bút máy có 90% đạt tiêu chuẩn kỹ thuật. Giả sử xác suất chấp nhận 1 sản phẩm đạt tiêu chuẩn kỹ thuật là 95%. Xác suất để chấp nhận 1 sản phẩm không đạt tiêu chuẩn kỹ thuật là 8%. Tính xác suất để sản phẩm được chấp nhận đạt tiêu chuẩn kỹ thuật.

Bài 5. Một lô hàng có 9 sản phẩm giống nhau. Mỗi lần kiểm tra, người ta chọn ngẫu nhiên 3 sản phẩm, kiểm tra xong lại trả vào lô hàng. Tính xác suất để sau 3 lần kiểm tra, 9 sản phẩm đều được kiểm tra.

Bài 6. Trong mội đội tuyển có 3 vận động viên A, B, C thi đấu với xác suất thắng lần lượt là 0,6;0,7 và 0,8. Giả sử mỗi người thi đấu một trận độc lập nhau. Tính xác suất để:

Đội tuyển thắng ít nhất một trận;
Đội tuyển thắng hai trận;
Vận động viên A thua trong trường hợp đội tuyển thắng hai trận.

Bài 7. Một nhân viên kiểm toán nhận thấy 15% các bảng thu chi chứa các sai lầm. Trong các bảng chứa sai lầm, 60% được xem là các giá trị bất thường so với các số xuất phát từ gốc. Trong tất cả các bảng thu chi thì 20% là những giá trị bất thường. Nếu một con số ở một bảng thu chi là bất thường thì xác suất để số đó là một sai lầm là bao nhiêu?

Bài 8. Một hãng sản xuất tủ lạnh ước tính khoảng 80% số người dùng tủ lạnh có đọc quảng cáo do hãng sản xuất. Trong số đó có 30% mua tủ lạnh của hãng. 10% không đọc quảng cáo cũng mua tủ lạnh của hãng. Tính xác suất để một người tiêu dùng đã mua tủ lạnh của hãng mà có đọc quảng cáo.

Bài 9. Có hai lô sản phẩm. Lô thứ nhất có tỉ lệ sản phẩm loại I là90%, lô thứ hai có tỉ lệ sản phẩm loại 1 là 70%. Chọn ngẫu nhiên một lô rồi từ lô đó lấy ngẫu nhiên ra 1 sản phẩm thì được sản phẩm loại I. Trả lại sản phẩm đó vào lô đã chọn, rồi cũng từ lô đó lấy ngẫu nhiên một sản phẩm. Tính xác suất để sản phẩm lấy lần thứ hai là loại I.

Bài 10. Một lô hàng chứa 15 sản phẩm, trong đó có 6 sản phẩm không đạt yêu cầu. Lấy lần lượt từng sản phẩm không hoàn lại để kiểm tra, cho đến khi gặp 3 sản phẩm không đạt yêu cầu thì dừng.

Tính xác suất để việc kiểm tra dừng lại ở sản phẩm thứ ba? Sản phẩm thứ sáu?
Nếu việc kiểm tra dừng lại ở sản phẩm thứ sáu, tính xác suất để sản phẩm được kiểm tra đầu tiên là không đạt yêu cầu?

Bài 11. Hộp thứ nhất có 4 bi trắng và 2 bi xanh, hộp thứ hai có 3 bi trắng và 3 bi xanh, kích cỡ như nhau. Chuyển một viên bi từ hộp thứ hai sang hộp thứ nhất, rồi lấy ngẫu nhiên một viên từ hộp thứ nhất. Tính xác suất để viên bi lấy ra là bi trắng.

Bài 12. Hộp thứ nhất có 8 sản phẩm loại A và 2 sản phẩm loại B; hộp thứ hai có 5 sản phẩm loại A và 3 sản phẩm loại B. Lấy ngẫu nhiên từ mỗi hộp 2 sản phẩm.

Tính xác suất để được 3 sản phẩm loại A;
Giả sử lấy được một sản phẩm loại B và hai sản phẩm loại A. Nhiều khả năng là sản phầmloại B thuộc hộp nào, tại sao?

Bài 13. Một lô hàng do 3 nhà máy A, B, C sản xuất, tỉ lệ sản phẩm của 3 nhà máy lần lượt là

30%,20%,50% và tỉ lệ phế phẩm tương ứng là 1%,2%,3%. Chọn ngẫu nhiên 1 sản phẩm từ lô hàng. Tính xác suất để sản phẩm này là phế phẩm.

Bài 14. Hộp thứ nhất có 8 sản phẩm loại A và 2 sản phẩm loại B; hộp thứ hai có 5 sản phẩm loại A và 3 sản phẩm loại B. Lấy ngẫu nhiên một hộp, rồi lấy ngẫu nhiên 4 sản phẩm trong đó.

Tính xác suất để được 3 sản phẩm loại A;
Giả sử lấy được một sản phẩm loại B và hai sản phẩm loại A. Nhiều khả năng là sản phầmloại B thuộc hộp nào, tại sao?

Bài 15. Có 3 hộp thuốc, hộp I có 5 ống tốt và 2 ống xấu, hộp II có 4 ống tốt và 1 ống xấu, hộp III có 3 ống tốt và 2 ống xấu. Lấy ngẫu nhiên một hộp và rút ra từ hộp đó một ống thuốc thì được ống tốt. Tính xác suất để ống này thuộc hộp II.

Bài 16. Một lô hàng gồm 150 sản phẩm trong đó có 6% là phế phẩm. Người ta dùng phương pháp chọn mẫu để kiểm tra lô hàng và quy ước rằng: Kiểm tra lần lượt không hoàn lại 6 sản phẩm. Nếu có ít nhất 1 sản phẩm là phế phẩm thì loại lô hàng. Tính xác suất để chấp nhận lô hàng.

Bài 17. Một trò chơi có xác suất thắng mỗi ván là 1/50. Nếu một người chơi 50 ván thì xác suất để người đó thắng ít nhất một ván là bao nhiêu?

Bài 18. Trong một thành phố, tỉ lệ người thích xem bóng đá là 65%. Chọn ngẫu nhiên 12 người. Tính xác suất để trong đó có đúng 5 người thích xem bóng đá.

Bài 19. 1. Gieo một con xúc xắc liên tiếp 6 lần. Tính xác suất để ít nhất có một lần xuất hiện mặt 6 chấm.

2. Gieo một cặp hai con xúc xắc 24 lần. Tính xác suất để ít nhất một lần cả hai con đều xuất hiện mặt 6 chấm.

Bài 20. Tỉ lệ sản xuất ra phế phẩm của một nhà máy là 8%. Khảo sát một lô hàng gồm 75 sản phẩm do nhà máy đó sản xuất.

Tính xác suất để trong lô hàng, có 10 phế phẩm;
Trong lô hàng, nhiều khả năng là có bao nhiêu phế phẩm? Tính xác suất tương ứng.

Bài 21. Người ta muốn lấy ngẫu nhiên một số hạt giống từ một lô hạt giống có tỉ lệ hạt lép là 3% để nghiên cứu. Hỏi phải lấy ít nhất bao nhiêu hạt sao cho xác suất để có ít nhất một hạt lép không bé hơn 95%?

Chương 2

Đại lượng ngẫu nhiên và luật phân phối xác suất

2.1 Đại lượng ngẫu nhiên

2.1.1 Các ví dụ

Ví dụ 2.1. Gieo ngẫu nhiên hai con xúc xắc cân đối đồng chất, quan sát số nút xuất hiện ở mặt trên của hai con xúc xắc, gọi X là ĐLNN chỉ số lớn nhất trong hai số xuất hiện.

Lập bảng phân phối xác suất của X;
Tìm P(X ≤ 3); P(2 ≤ X < 5).

Giải. X ∈ {1,2,3,4,5,6}.

;

(

=1)=

(

{

}

(

=2)=

(

{

;

}

;

...

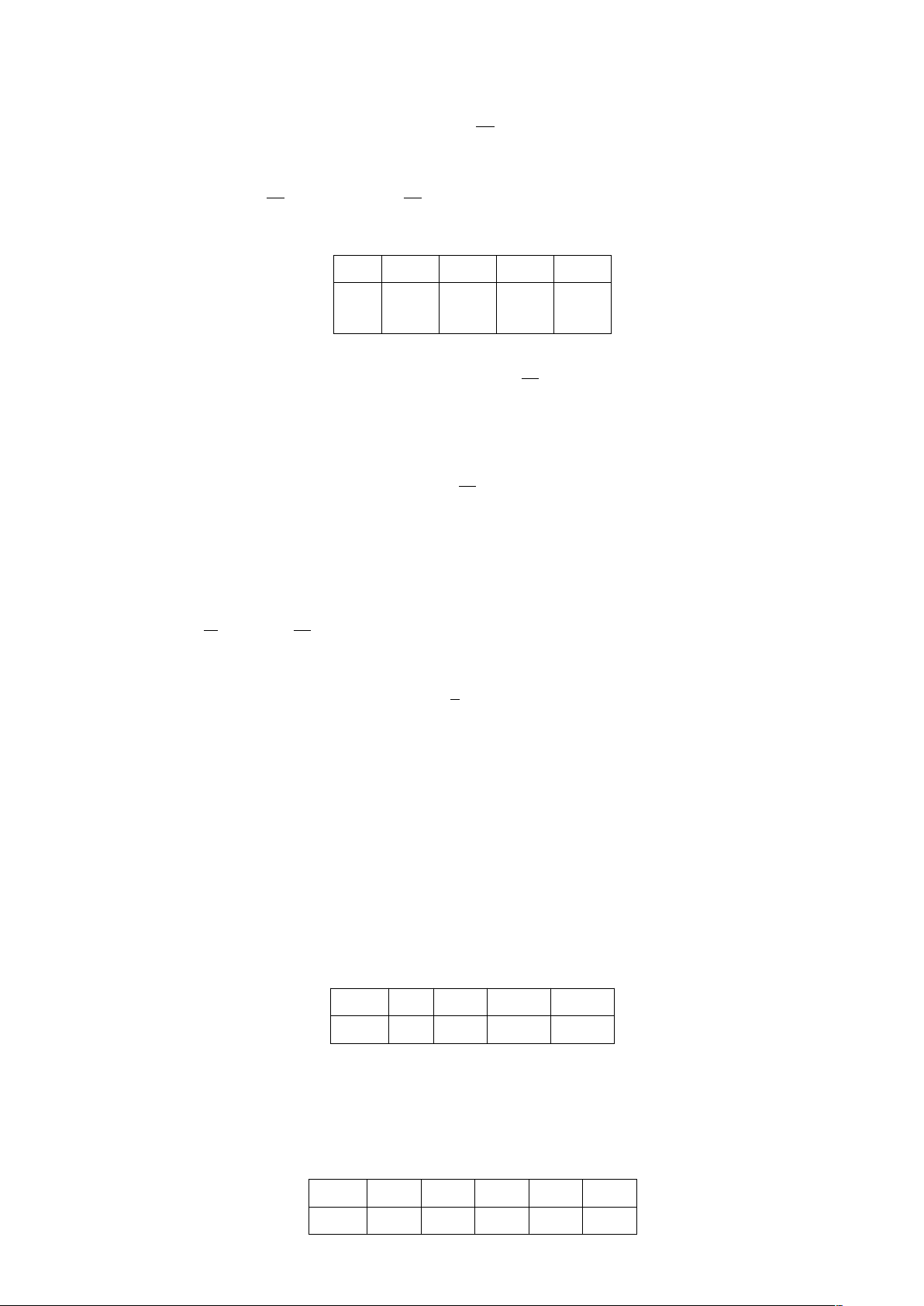
1. Ta có bảng phân phối xác suất của X như sau:

X	1	2	3	4	5	6
P(X)	1/36	3/36	5/36	7/36	9/36	11/36

2.;

(

≤

3)=

(

=1)+

(

=2)+

(

=3)=

≤

5)=

(3)+

(4)=

Ví dụ 2.2. Có ba hộp A, B và C đựng các lọ thuốc. Hộp A có 10 lọ tốt và 5 lọ hỏng, hộp B có 6 lọ tốt và 4 lọ hỏng, hộp C có 5 lọ tốt và 7 lọ hỏng. Lấy ngẫu nhiên từ mỗi hộp ra một lọ thuốc.

Tìm luật phân phối xác suất cho số lọ thuốc tốt trong 3 lọ lấy ra;
Tìm xác suất để được ít nhất 2 lọ tốt; được 3 lọ cùng loại.

Giải. Gọi X là biến ngẫu nhiên chỉ số lọ thuốc tốt trong 3 lọ lấy ra. X ∈ {0,1,2,3}.

Gọi A_i: "Lọ thuốc lấy ra từ hộp thứ i là lọ tốt".

;

(

=0)=

(

;

(

=1)=

(

)

180

;

(

=2)=

(

180

(

=3)=

(

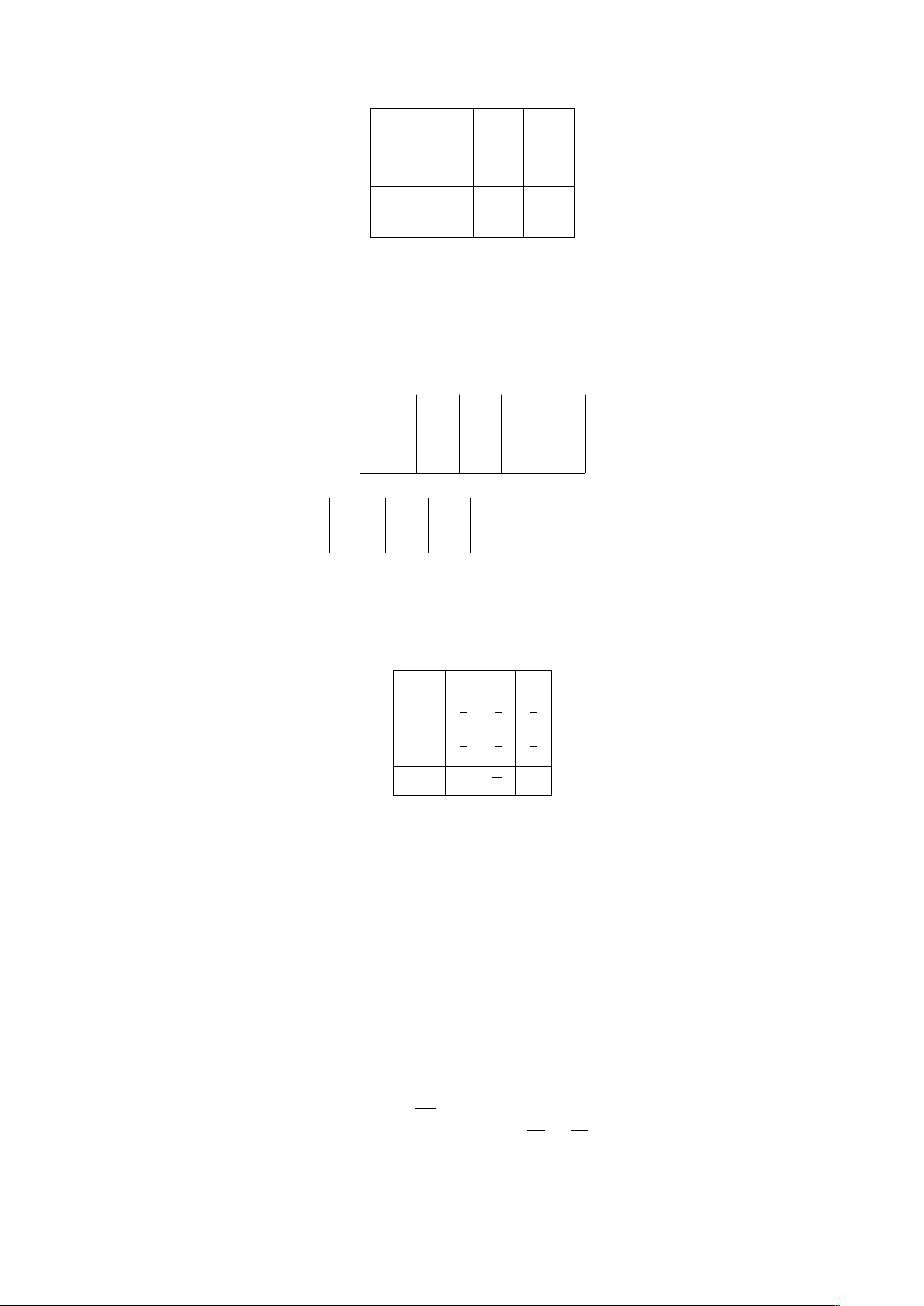
Bảng phân phối xác suất của X:

X	0	1	2	3
P(X)	7/90	59/180	77/180	1/6

Xác suất để được ít nhất hai lọ tốt:; Xác suất để được ba lọ cùng loại: .

(

≥

2)=

(

=2)+

(

=3)=

107

180

(

=0)+

(

=3)=

Ví dụ 2.3. Một hộp đựng 5 sản phẩm, trong đó có hai phế phẩm. Lần lượt kiểm tra từng sản phẩm (không hoàn lại) cho đến khi gặp hai phế phẩm thì dừng lại. Tìm luật phân phối xác suất cho số sản phẩm được kiểm tra. Tính số lần kiểm tra trung bình.

Giải. Gọi X là ĐLNN chỉ số sản phẩm được kiểm tra. X ∈ {2,3,4,5}. Đặt A_i: "Lần thứ i kiểm tra được phế phẩm".

;

(

=2)=

(

)

(

;

(

=3)=

(

Tương tự:.

(

=4)=

;

(

=5)=

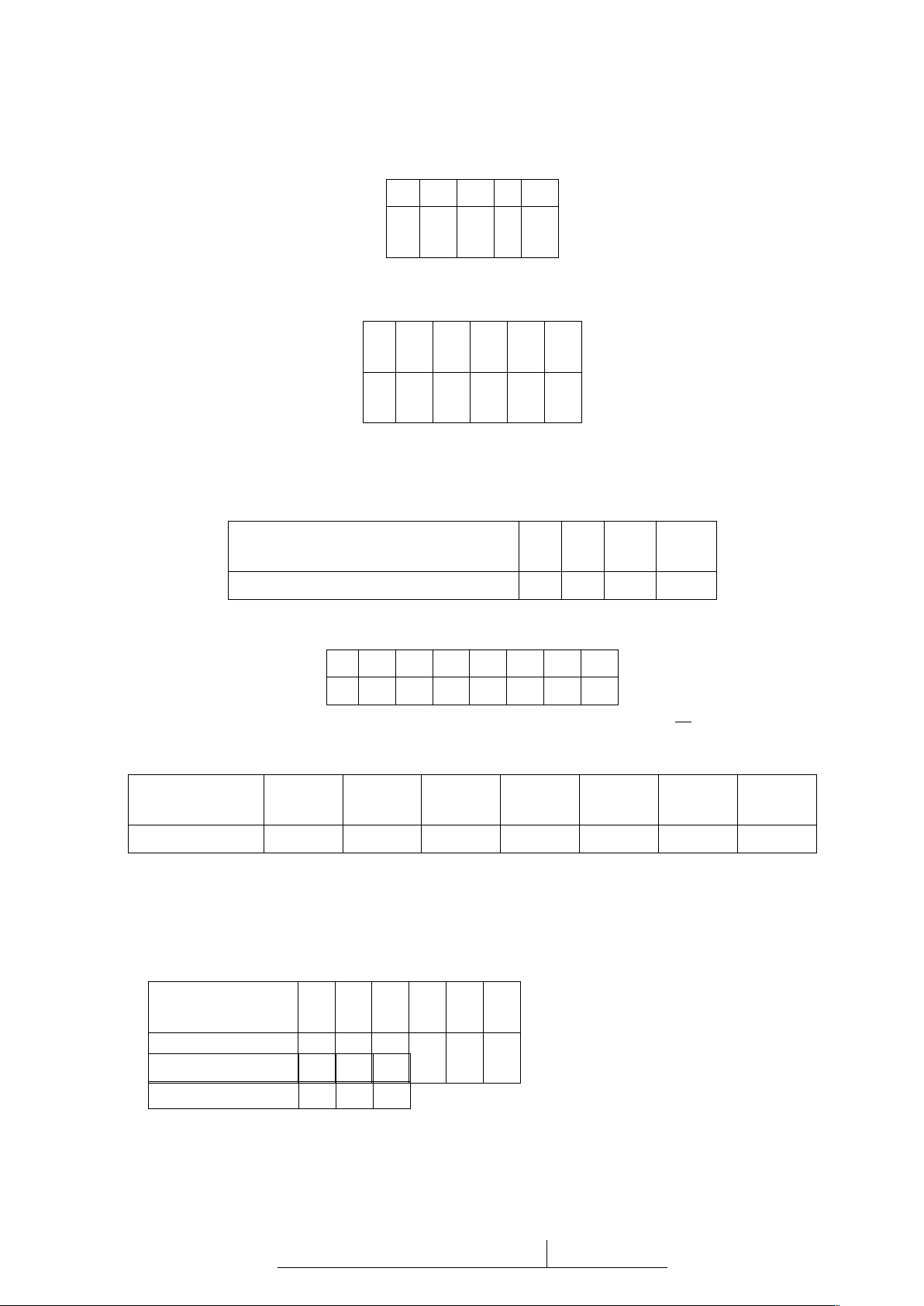
Ta có bảng phân phối xác suất của X:

X	2	3	4	5
P(X)	1/10	2/10	3/10	4/10

Số lần kiểm tra trung bình: EX = 4.

Ví dụ 2.4. Cho ĐLNN liên tục X có hàm mật độ:

(

,x>

≤

Tìm a, F(x) và P(0 < X < 3).

Giải. Từ tính chất R, ta có R.

∞

−

∞

(

)

∞

−

∞

⇔

Hàm phân phối F được xác định bởi:

;

(

−

∞

nếu

≤

(

−

nếu

3)=

(

)

(3)

−

(0)=

Ví dụ 2.5. Một xạ thủ có 4 viên đạn. Anh ta lần lượt bắn từng viên vào bia và sẽ ngừng bắn khi có một viên trúng bia; nếu không, anh ta sẽ bắn cho đến khi hết đạn. Biết rằng xác suất bắn trúng bia ở mỗi lần bắn là 0,8. Gọi X là số đạn mà xạ thủ đã bắn. Hãy tìm luật phân phối xác suất của X; tính kỳ vọng và phương sai của X.

Giải. Miền giá trị của X là {1,2,3,4}.

P(X = 1) = 0,8; P(X = 2) = 0,2.0,8 = 0,16; P(X = 3) = 0,2².0,8 = 0,032; P(X = 4) = 0,2³= 0,008. Bảng phân phối xác suất của X:

X	1	2	3	4
P(X)	0,8	0,16	0,032	0,008

Kì vọng của X: EX = 1.0,8 + 2.0,16 + 3.0,032 + 4.0,008 = 1,248.

Phương sai của X: DX = 1².0,8 + 2².0,16 + 3².0,032 + 4².0,008 − 1,248²= 0,2985.

Ví dụ 2.6. Một cơ sở sản xuất các bao kẹo. Số kẹo trong mỗi bao là một đại lượng ngẫu nhiên X có phân phối xác suất như sau:

X	18	19	20	21	22
P(X)	0,14	0,24	0,32	0,21	0,09

Tìm trung bình và phương sai của số viên kẹo trong mỗi bao;
Chi phí sản xuất của mỗi bao kẹo là 3X + 16. Tiền bán mỗi bao kẹo là 100$. Không phân biệt số kẹo trong bao. Tìm lợi nhuận trung bình và độ lệch chuẩn của lợi nhuận cho mỗi bao kẹo;
Hai bao kẹo được chọn ngẫu nhiên. Tính xác suất để ít nhất một trong hai bao chứa ít nhất20 viên kẹo.

Giải.

Trung bình và phương sai của số viên kẹo trong mỗi bao:

;

=18

k.P

(

)=19

(

)

−

(

)

3531

Gọi Y là ĐLNN chỉ lợi nhuận cho mỗi bao kẹo, ta có Y = 100 − (3X + 16) = 84 − 3X.

Lợi nhuận trung bình;

(84

−

)=84

−

=24

√

Độ lệch chuẩn σ(Y ) = DY = 3 DX = 3,4879.

Đặt A: “Bao chứa ít nhất 20 viên kẹo” . P(A) = P(X = 20)+P(X = 21)+P(X = 22) = 0,62; Xác suất để ít nhất một trong hai bao chứa ít nhất 20 viên kẹo: 0,62+0,62.0,38 = 0,8556.

2.1.2 Bài tập

Bài 22. Một hộp chứa 10 tấm thẻ đỏ và 6 tấm thẻ xanh. Chọn ngẫu nhiên 3 tấm thẻ.

Gọi X là số thẻ đỏ. Tìm phân phối xác suất của X;
Giả sử rút được thẻ đỏ được 5 điểm và rút mỗi tấm thẻ xanh được 8 điểm. Gọi Y là số điểm tổng cộng sau khi rút 3 thẻ. Tìm phân phối xác suất của Y.

Bài 23. Trong một chiếc hộp có 5 bóng đèn, trong đó có 2 bóng tốt, 3 bóng hỏng. Chọn ngẫu nhiên từng bóng đem đi thử (xong không trả lại) cho đến khi thu được 2 bóng tốt. Gọi X là số lần thử cần thiết. Tìm phân phối xác suất của X. Trung bình cần thử bao nhiêu lần?

Bài 24. Một lô hàng gồm 7 sản phẩm, trong đó có 3 phế phẩm. Chọn ngẫu nhiên 4 sản phẩm để kiểm tra. Gọi X là số sản phẩm tốt trong 4 sản phẩm lấy ra. Tìm phân phối xác suất của X và tính EX.

Bài 25. Hai xạ thủ A và B tập bắn. Mỗi người bắn hai phát. Xác suất bắn trúng của A và B lần lượt là 0,4 và 0,5.

Gọi X là số phát trúng của A trừ đi số phát bắn trúng của B. Tìm phân phối xác suất củaX;
Tìm phân phối xác suất của Y = |X|

Bài 26. Trong một đội tuyển, ba vận động viên A, B, C thi đấu với xác suất thắng lần lượt là 0,6;0,7;0,8. Trong một đợt thi đấu, mỗi vận động viên thi một trận độc lập nhau.

1. Tìm luật phân phối xác suất cho số trận thắng của đội; 2. Tính xác suất để đội thua nhiều nhất 1 trận; thắng ít nhất 1 trận;

Biết đội thắng 2 trận, tính xác suất để A thua trận.
Tính số trận thắng trung bình và phương sai của số trận thắng của đội tuyển.

Bài 27. Một người điều khiển ba máy tự động hoạt động độc lập với nhau. Xác suất bị trục trặc trong mỗi ca sản xuất của máy I, II và III lần lượt là 0,1;0,2 và 0,3.

Lập bảng phân phối xác suất cho số máy hoạt động tốt trong một ca sản xuất;
Trung bình, trong một ca, có bao nhiêu máy hoạt động tốt? Tính độ lệch chuẩn của số máy hoạt động tốt trong một ca sản xuất;
Biết rằng trong ca sản xuất chỉ có một máy hoạt động tốt. Tính xác suất để máy đó là máy

Bài 28. Một lô hàng gồm 5 lọ thuốc, trong đó có một lọ thuốc giả. Kiểm tra lần lượt từng lọ cho đến khi thấy lọ thuốc giả thì dừng.Tìm phân phối xác suất cho số chai được kiểm tra.

Bài 29. Rút ngẫu nhiên 4 lá bài trong bộ bài tú lơ khơ, sau đó khoanh ngẫu nhiên 2 lá. Gọi X là số lá cơ trong 2 lá được khoanh.

Tìm phân phối xác suất của X;
Tính xác suất trong 2 lá đó chỉ có một lá cơ.

Bài 30. Tiến hành khảo sát số khách trên một chuyến xe buýt (SK/1C) tại một chuyến giao thông, người ta thu được số liệu sau:

SK/1C	25	30	35	40	45
Xác suất	0,15	0,2	0,3	0,25	0,1

Tính kỳ vọng và độ lệch chuẩn của SK/1C;
Giả sử chi phí cho mỗi chuyến xe buýt là 200 ngàn đồng, không phụ thuộc vào số khách đitrên xe, công ty phải quy định giá vé là bao nhiêu để có thể thu được số tiền lời trung bình cho mỗi chuyến xe là 100 ngàn đồng?

Bài 31. Giả sử X là biến ngẫu nhiên số lượng xe ô tô mà một đại lý bán được trong một tuần có phân phối xác suất như sau:

X	0	1	2	3	4	5
P(X)	0,1	0,1	0,2	0,2	0,3	0,1

Tính xác suất để đại lý đó bán được nhiều nhất 3 xe trong một tuần. Tính kỳ vọng vàphương sai của số xe mà đại lý bán được trong một năm;
Giả sử chi phí cho hoạt động của đại lý bằng căn bậc hai của số xe bán được với 5 (triệuđồng). Tìm chi phí cho hoạt động trung bình cho hoạt động của đại lý trong một tuần.

Bài 32. Cho hai đại lượng ngẫu nhiên X, Y có phân phối xác suất như sau:

X	0	1	2	3	4
P(X)	0,1	0,2	0,3	0,25	0,15

Xét ĐLNN Y = X³− 4X²+ 10.

Tìm phân phối xác suất của Y;
Tính EY bằng hai cách;
Tính DY.

Bài 33. Cho hàm

(

x,x

∈

Chứng tỏ f(x) là hàm mật độ xác suất của một biến ngẫu nhiên liên tục X;
Tìm hàm phân phối xác suất F(x) của X; Tìm kì vọng và phương sai của X;
Tính xác suất .

)

Bài 34. Cho hàm

(







,x>

≤

Chứng tỏ f(x) là hàm mật độ xác suất của một biến ngẫu nhiên liên tục X;
Tìm hàm phân phối xác suất F(x) của X;
Tính xác suất P(0 < X < 3).

Bài 35. Cho ĐLNN X có hàm mật độ

(

,x>

≤

Tìm hằng số a;
Tìm hàm phân phối xác suất F(x) của X.

Bài 36. Cho ĐLNN liên tục X có hàm mật độ f(x) = ( ^kx²^,^{nếu 0}≤ ^x≤ ³

0 nếu trái lại

Tìm hằng số k;
Tính P(X > 2);
Tính median của X;
Tìm .

để

(

X<a

Bài 37. Khối lượng của một con gà 6 tháng tuổi là một ĐLNN X (đơn vị kg) với hàm mật độ phân phối như sau:

(

−

với

≤

với x còn lại

Tìm khối lượng trung bình của con gà 6 tháng tuổi và độ lệch tiêu chuẩn.

Bài 38. Một lô hàng gồm 800 sản phẩm loại I và 200 sản phẩm loại II. Lấy ngẫu nhiên ra 5 sản phẩm có hoàn lại. Gọi X là số sản phẩm loại I lấy được.

X tuân theo quy luật nào? Viết biểu thức xác suất tổng quát?
Tính kì vọng và phương sai của X.

Bài 39. Số hóa đơn mà một công ty A nhận được trong một ngày là một ĐLNN X có phân phối Poátxông với tham số λ = 1,5. Tính xác suất để trong một ngày:

Công ty không nhận được hóa đơn nào;
Công ty nhận được 2 hóa đơn;
Công ty nhận được nhiều nhất 2 hóa đơn;
Công ty nhận được ít nhất 4 hóa đơn.

Bài 40. Một cửa hàng có 4 chiếc ô tô cho thuê, số khách có nhu cầu thuê trong ngày là một ĐLNN X có phân phối Poátxông.

Biết rằng EX = 2, hãy tính số ô tô trung bình mà cửa hàng cho thuê trong một ngày;
Cửa hàng cần có ít nhất bao nhiêu ô tô để với xác suất không nhỏ hơn 0,98, cửa hàng đáp ứng được nhu cầu của khách hàng trong ngày?

Bài 41. Gieo một đồng tiền cho đến khi xuất hiện mặt ngửa thì dừng lại. Xác suất xuất hiện mặt ngửa là p. Gọi X là ĐLNN chỉ số lần gieo cần thiết.

Tìm phân phối xác suất của X;
Tìm phân phối xác suất của X với điều kiện trong n lần gieo đầu tiên chỉ đúng 1 lần đồng xu xuất hiện mặt ngửa.

Bài 42. Một lô hàng có rất nhiều sản phẩm, với tỉ lệ hàng giả là 30%.

Lấy ngẫu nhiên từ lô hàng ra 10 sản phẩm, tính xác suất để có nhiều nhất 2 sản phẩm giả.
Người ta lấy ngẫu nhiên ra từng sản phẩm một để kiểm tra cho đến khi nào gặp sản phẩmgiả thì dừng. Tìm luật phân phối xác suất và tính kỳ vọng của số sản phẩm thật đã kiểm tra.

Bài 43. Một khách hàng mua xe tại một đại lý, nếu xe có sự cố kỹ thuật thì được quyền trả xe trong vòng 3 ngày sau khi mua và được lấy lại nguyên số tiền mua xe. Mỗi chiếc xe bị trả lại như thế làm thiệt hại cho đại lý 250 nghìn VNĐ. Có 50 xe được bán ra. Xác suất để một xe bị trả lại là 0,1.

1. Tìm kỳ vọng và phương sai của số xe bị trả. Tính xác xuất để có nhiều nhất 2 xe bị trả lại; 2. Tìm kỳ vọng và độ lệch chuẩn của tổng thiệt hại mà tổng đại lý phải chịu do việc trả lại xe.

Bài 44. Bạn Minh tham dự một kỳ thi với hình thức phải làm một đề thi trắc nghiệm khách quan gồm 10 câu, mỗi câu có 4 lời giải khác nhau, trong đó chỉ có một lời giải đúng. Minh sẽ được chấm đậu nếu trả lời đúng ít nhất 6 câu.

Giả sử Minh không học bài, mà chỉ chọn ngẫu nhiên lời giải trong cả 10 câu. Tính xác suấtđể Minh thi đậu;
Hỏi Minh phải dự thi ít nhất mấy lần để xác suất có ít nhất một lần thi đậu không nhỏ hơn97%?

Bài 45. Tỉ lệ thuốc hỏng ở lô A là P_A= 0,1, ở lô B là P_B= 0,08 và ở lô C là P_C= 0,15. Biết rằng mỗi lô có rất nhiều chai thuốc.

Lấy 3 chai ở lô A. Tìm luật phân phối xác suất của số chai hỏng có trong 3 chai. Tính xác suất để có 2 chai hỏng; có ít nhất 1 chai hỏng;
Phải lấy bao nhiêu chai (ở lô A) để xác suất có ít nhất một chai hỏng không nhỏ hơn 94%?
Chọn ngẫu nhiên 1 lô thuốc rồi lấy từ lô đó ra 3 chai. Tính xác suất để có ít nhất 1 chaihỏng.

Bài 46. Số lỗi trên 1 mét vuông vải là một biến ngẫu nhiên tuân theo luật phân phối poison. Kiểm tra lô vải, người ta thấy 98% có lỗi. Vậy trung bình mỗi mét vuông vải có bao nhiêu lỗi?

Bài 47. Một cơ sở sản xuất, trung bình trong một tuần, nhận được 4 đơn đặt hàng. Biết rằng số đơn đặt hàng X mà cơ sở nhận được trong một tuần là một BNN có phân phối Poisson. Tính xác suất để cơ sở đó :

Nhận được hơn 5 đơn đặt hàng trong một tuần;
Nhận được 6 đơn đặt hàng trong hai tuần liên tiếp.

Bài 48. Thời gian để sản xuất một sản phẩm loại A là một BNN tuân theo luật phân phối chuẩn với các tham số µ = 10 và σ = 1 (đơn vị là phút).

Tính xác suất để một sản phẩm loại A nào đó được sản xuất trong khoảng thời gian từ 9 phút đến 12 phút;
Tính thời gian cần thiết để sản xuất một sản phẩm loại A bất kỳ.

Bài 49. Cho biến ngẫu nhiên X tuân theo luật phân phối chuẩn N(µ,σ). Biết rằng X lấy giá trị nhỏ hơn 60 với xác suất 0,1003 và lấy giá trị lớn hơn 90 với xác suất 0,0516, hãy tính µ và σ. Bài 50. Đường kính của một loại chi tiết do một máy sản xuất có phân phối chuẩn, kỳ vọng 20 mm, phương sai 0,2²mm. Tính xác suất lấy ngẫu nhiên một chi tiết:

Có đường kính trong khoảng 19,9 mm đến 20,3 mm;
Có đường kính sai khác với kỳ vọng không quá 0,3 mm.

2.2 Đại lượng ngẫu nhiên nhiều chiều

2.2.1 Các ví dụ

Ví dụ 2.7. Cho X và Y là hai ĐLNN có phân phối xác suất đồng thời như sau:

X Y	-1	1
-1	1/6	1/4
0	1/6	1/8
1	1/6	1/8

Hãy tính EX,EY,Cov(X,Y ) và ρ(X,Y ).

Giải.

;

−

)+1(

−

;

−

(

)=0

Cov(X,Y ) = E(XY ) − EX.EY ; Ta có bảng phân phối xác suất của XY :

XY	-1	0	1
P(XY)	5/12	7/24	7/24

Vậy;

(

−

⇒

Cov

(

X,Y

(

X,Y

Cov

(

X,Y

)

−

Ví dụ 2.8. Giả sử X ∼ B(2;0,4); Y ∼ B(2;0,7). X và Y là hai ĐLNN độc lập.

Tìm phân phối xác suất của X + Y ;
Chứng minh rằng X + Y không có phân phối nhị thức.

Giải.

Bảng phân phối xác suất của X và Y như sau:

X	0	1	2
P(X)	0,36	0,48	0,16

Y	0	1	2
P(Y)	0,09	0,42	0,49

và

Đặt Z = X + Y , ta có:

P(Z = 0) = P(X = 0).P(Y = 0) = 0,0324;

P(Z = 1) = P(X = 0)P(Y = 1) + P(X = 1)P(Y = 0) = 0,1944;

Tương tự: P(Z = 2) = 0,3924; P(Z = 3) = 0,3024; P(Z = 4) = 0,0784. Từ đo ta có bảng phân phối xác suất của Z = X + Y :

Z	0	1	2	3	4
P(Z)	0,0324	0,1944	0,3924	0,3024	0,0784

Giả sử ngược lại, Z = X + Y có phân phối nhị thức, Z = B(4,p).

Khi đó P(Z = 4) = p⁴= 0,0784.

Mặt khác P(Z = 0) = (1 − p)⁴= 0,0324, suy ra phải có p = √⁴0,0784 và p = 1 − √⁴0,0324, vô lí.

Vậy X + Y không có phân phối nhị thức.

Ví dụ 2.9. Cho X, Y là hai ĐLNN có hàm mật độ đồng thời là:

f(x,y) = ( − x y e ( + ) nếu x > 0,y > 0

0 nếu trái lại

Tìm hàm mật độ của;

Y,V

Chứng tỏ rằng U và V độc lập, X và Y độc lập.

Giải.

Phép đổi biến , với x,y > 0 ta có

y,v

⇔

uv,y

−

)

Hàm mật độ đồng thời của U và V là:u > 0,0 < v < 1, Jacobian |J| = u. f(u,v) = e−uv−u₊uvu = u.e−u nếu u > 0,0 < v < 1 và f(u,v) = 0 nếu trái lại.

Hàm mật độ của U là nếu u > 0 và f(u) = 0 nếu trái lại; R R

(

∞

−

∞

(

u,v

)

u.e

−

Hàm mật độ của V là nếu 0 < v < 1 và f(v) = 0 nếu trái lại. R R

(

∞

−

∞

(

u,v

)

∞

u.e

−

Dễ thấy rằng f(u,v) = f(u)f(v) nên U và V độc lập. Một cách tương tự, X và Y cũng độc lập.

2.2.2 Bài tập

Bài 51. Cho các ĐLNN X và Y có bảng phân phối xác suất đồng thời như sau:

X Y	1	2	3
1	0,12	0,15	0,03
2	0,28	0,35	0,07

Chứng minh rằng X và Y độc lập;
Tìm quy luật phân phối của Z=XY;
Tính EZ bằng hai cách và kiểm tra EZ = EX.EY .

Bài 52. Cho X và Y là hai ĐLNN có phân phối xác suất như sau:

X	0	1	2	3
P(X)	0,4	0,3	0,2	0,1

và

Y	0	1	2	3	4
P(Y)	0,1	0,3	0,4	0,15	0,05

Tìm phân phối xác suất đồng thời của X và Y;
Tính P(X > Y ).

Bài 53. Cho X và Y là hai ĐLNN có phân phối xác suất đồng thời như sau:

X Y	-1	0	1
-1	4 15	1 15	4 15
0	1 15	2 15	1 15
1	0	2 15	0

Tính EX,EY,cov(X,Y ) và ρ(X,Y );
X và Y có độc lập hay không?

Bài 54. Cho X và Y là hai ĐLNN độc lập.

Giả sử X ∼ B(1;0,2) và Y ∼ B(2;0,2). Lập bảng phân phối xác suất của X,Y và X + Y ;
Giả sử X ∼ B(1;0,5) và Y ∼ B(2;0,2). Lập bảng phân phối xác suất của X + Y . X + Y có phân phối nhị thức hay không?

Bài 55. Cho X và Y là hai ĐLNN có hàm mật độ đồng thời là

nếu

(

x,y





0 nếu trái lại

Tìm hàm mật độ của X và của Y. 

Bài 56. Cho hai ĐLNN X và Y có hàm mật độ đồng thời:

nếu 0 < x < 1,0 < y < 2

( ) = (

x,y

(

)

0 nếu trái lại

Tìm hằng số k;
Tìm hàm phân phối đồng thời của X và Y.

Bài 57. Cho hai ĐLNN X và Y có hàm mật độ đồng thời:

(

x,y

(1+

)(1+

)

Tìm hằng số k;
Tìm hàm phân phối đồng thời của X và Y;
X và Y có độc lập không?
Tính xác suất để điểm ngẫu nhiên (X,Y ) rơi vào hình chữ nhật với các đỉnh là A(1,1), B(√3,1), C(1,0), D(√3,0).

Bài 58. Giả sử X và Y là hai ĐLNN độc lập có cùng phân phối mũ với tham số λ.

Tìm hàm phân phối và hàm mật độ của Z = ^X_Y.
Tìm hàm phân phối và hàm mật độ của U = X − Y .

Bài 59. Giả sử X và Y là hai ĐLNN độc lập có phân phối đều trên đoạn [0,1].

Tìm hàm phân phối và hàm mật độ của Z = X + Y ;
Tìm hàm phân phối và hàm mật độ của U = XY .

Bài 60. Cho X và Y là hai ĐLNN có phân phối chuẩn đồng thời với EX = 35,EY = 20,DX = 36,DY = 16 và ρ(X,Y ) = 0,8. Tìm kì vọng và phương sai của 2X − 3Y .

Bài 61. Cho X ∼ N(7;1,2²) và Y ∼ N(5;0,9²). Giả thiết rằng X và Y độc lập.

Tìm P(X + Y < 9,5);
Tìm P(X < Y );
Tìm P(X > 2Y ).

Bài 62. Giả sử rằng trọng lượng hành khách đi máy bay có phân phối chuẩn với kì vọng 74(kg) và trọng lượng hành lí mang theo có phân phối chuẩn với kì vọng 20(kg).

Biết rằng có 10% hành khách có trọng lượng lớn hơn 85(kg) và 20% hành khách có hành lí nặng hơn 24(kg). Tìm độ lệch tiêu chuẩn của trọng lượng hành khách và trọng lượng hành lí;
Biết rằng có 10% hành khách mà tổng trọng lượng của họ và hành lí mang theo lớn hơn 108(kg). Tìm hệ số tương quan của trọng lượng hành khách và hành lí.

Chương 3

Mẫu thống kê và ước lượng tham số

3.1 Một số ví dụ

Ví dụ 3.1. Giả sử khối lượng của các viên gạch nung X do một nhà máy sản suất là đại lượng ngẫu nhiên có phân bố chuẩn với giá trị trung bình E(X) = a; phương sai D(X) = σ²chưa biết. Để xác định khối lượng trung bình của một viên gạch ta lấy mẫu cỡ n = 50 và được bảng sau

Khối lượng (kg)	2,25-2,30	2,30-2,35	2,35-2,40	2,40-2,45
số viên gạch (n_i)	7	20	18	5

Hãy ước lượng không chệch của E(X) và D(X). Ta có

275+20

325+18

375+5

425

346

là ước lượng không chệch của E(X) = a.

Tính

);

(

−

)

001809(

−

≈

001845(

)

là ước lượng không chệch của D(X) = σ².

√

s⁰= s⁰²≈ 0,0429kg là ước lượng của σ.

Ví dụ 3.2. Để xác định tỷ lệ gạch phế phẩm trong tổng số gạch của một nhà máy người ta kiểm tra chất lượng 250 viên gạch có 6 viên không đạt chất lượng. Hãy ước lượng tỷ lệ gạch phế phẩm của nhà mày này.

∗

250

024

tức là 2,4%.

3.2 Bài tập

Bài 63. Vẽ các đa giác tần số sau.

x_i	2	3	5	6
n_i	10	15	5	20

Bảng a

x_i	15	20	25	30	35
n_i	10	15	30	35	20

Bảng b

Bài 64. Dựng biểu đồ tần xuất các mẫu cho dưới đây.

Khoảng giá trị [x_i−₁,x_i]	2-5	5-8	8-11	11-14
Tổng tần số giá trị rơi vào khoảng	6	10	4	5

Bài 65. Tính trung bình mẫu, phương sai mẫu và độ lệch chuẩn mẫu điều chỉnh của mẫu cho bởi bảng sau.

x_i	21	24	25	26	28	32	34
n_i	10	20	30	15	10	10	5

Bài 66. Người ta đo 8 lần đại lượng X và thu được dãy số liệu sau. Hãy tính X, s², s⁰.

Bài 67. Người ta đo chiều cao của 100 sinh viên được chọn bất kỳ và thu được bảng số liệu sau.

Chiều cao(cm)	154-158	158-162	162-166	166-170	170-174	174-178	178-182
Số sinh viên	10	14	26	28	12	8	2

Tìm chiều cao trung bình và mức độ phân tán của chiều cao so với chiều cao trung bình của nhóm sinh viên được chọn trên.

Bài 68. Theo dõi thời gian hoàn thành một sản phẩm của hai tổ công nhân, người ta thu được số liệu sau.

Thời gian (phút)	42	44	45	58	60	64
Số công nhân	4	5	20	10	8	3

Tổ 1:

Thời gian (phút)	46	48	51
Số công nhân	2	40	8

Tổ 2:

Hãy tính số thời gian trung bình để hoàn thành một sản phẩm và mức độ phân tán thời gian hoàn thành một sản phẩm so với thời gian trung bình ở hai tổ công nhân trên.

Bài 69. Hao phí nguyên liệu cho một đơn vị sản phẩm là một đại lượng ngẫu nhiên với phân phối chuẩn (µ,σ²) với σ = 0,03. Người ta sản xuất thử 36 sản phẩm và được bảng số liệu sau.

Mức hao phí nguyên liệu (gam)	Số sản phẩm
19.5-19.7	8
19.7-19.9	8
19.9-20.1	18
20.1-20.3	2

Hãy tìm độ tin cậy đối xứng 95% cho mức hao phí nguyên liệu trung bình cho một đơn vị sản phẩm nói trên.

Bài 70. Người ta kiểm tra ngẫu nhiên 100 bóng đèn cùng loại và thấy rằng tuổi thọ trung bình của lô bóng đèn này là 1000(giờ). Với độ tin cậy là 0,95 hãy ước lượng tuổi thọ trung bình của loại bóng đèn trên bằng khoảng tin cậy đối xứng. Giả thiết rằng tuổi thọ trung bình là đại lượng ngẫu nhiên có phân phối chuẩn với độ lệch chuẩn σ = 40(giờ).

Bài 71. Cho một loại ô tô chạy thử 30 lần từ địa điểm A tới địa điểm B, người ta ghi nhận được lượng xăng hao phí như sau.

Lượng xăng ham phí (lít)	Số lần chạy
9.6-9.8	3
9.9-10.0	5
10.0-10.2	10
10.2-10.4	8
10.4-10.6	4

Với độ tin cậy 99%, hãy ước lượng xăng hao phí trung bình của loại ô tô này khi chạy từ A đến B bằng khoảng tin cậy đối xứng.
Với độ tin cậy 99%, hãy ước lượng xăng hao phí trung bình tối đa của loại ô tô này khi chạytừ A đến B.

Biết rằng lượng xăng hao phí là đại lượng ngẫu nhiên có phân phối chuẩn.

Bài 72. Để định mức thời gian gia công cho một sản phẩm, người ta theo dõi ngẫu nhiên quá trình gia công 25 sản phẩm và thu được số liệu sau.

Thời gian gia công (phút)	Số sản phẩm
15-17	1
17-19	3
19-21	4
21-23	12
23-25	3
25-27	2

Với độ tin cậy 0,95, hãy ước lượng thời gian gia công trung bình cho một sản phẩm bằngkhoảng tin cậy đối xứng.
Với độ tin cậy 0,95, hãy ước lượng thời gian gia công tối thiểu cho một sản phẩm.

Giả thiết thời gian gia công cho một sản phẩm là đại lượng ngẫu nhiên có phân phối chuẩn.

Bài 73. Cân thử 36 bao bột cho thấy trọng lượng trung bình một bao là 40kg, độ lệch chuẩn mẫu điều chỉnh là

s⁰= 5kg.

Hãy ước lượng trọng lượng trung bình của bao bột bằng khoảng tin cậy đối xứng với độ tin cậy 95%. Giả thiết rằng trọng lượng của bao bột là đại lượng ngẫu nhiên có phân phối chuẩn. Bài 74. Chiều dài loại sản phẩm A do một máy tự động sản xuất là một đại lượng ngẫu nhiên có phân phối chuẩn với độ lệch chuẩn σ = 3cm. Người ta tiến hành đo ngẫu nhiên 36 sản phẩm A và thấy chiều dài trung bình của chúng là 150cm.

Với độ tin cậy là 0,95 hãy ước lượng chiều dài trung bình của sản phẩm A bằng khoảng tin cậy đối xứng.
b. Phải đo tối thiểu bao nhiêu sản phẩm A để độ tin cậy 0,99 ước lượng đạt độ chính xác ε = 0,3.

Bài 75. Kiểm tra ngẫu nhiên 100 sản phẩm của nhà máy A thì thấy có 10 phế phẩm.

Hãy ước lượng tỷ lệ chính phẩm của nhà máy A bằng khoảng tin cậy đối xứng với độ tincậy 0,95.
Hãy ước lượng tỷ lệ chính phẩm tối thiểu của nhà máy A với độ tin cậy 0,95.

Bài 76. Chọn ngẫu nhiên 50 sinh viên của một trường đại học thì thấy có 21 nữ. Với độ tin cậy 90% hãy ước lượng tỷ lệ nữ ở trường đại học đó bằng khoảng tin cậy đối xứng.

Bài 77. Làm xét nghiệm sida cho 10000 người thì thấy có 200 người có kết quả dương tính. Xét nghiệm tiếp đối với những người này thì có 40 người mắc bệnh sida. Với độ tin cậy 99% hãy ước lượng người mắc bệnh sida trong toàn quốc bằng khoảng tin cậy đối xứng.

Bài 78. Gieo thử 400 hạt giống thì có 20 hạt không nảy mầm. Với độ tin cậy 95% hãy ước lượng tỷ lệ hạt giống không nảy mầm tối đa là bao nhiêu?

Bài 79. Ở một hồ người ta đánh bắt 2000 con cá, đánh dấu chúng rồi thả xuống hồ. sau đó bắt lại 400 con thì thấy có 80 con bị đánh dấu.

Hãy ước lượng số cá trong hồ với độ tin cậy 95%.
b. Với độ tin cậy 95% hãy ước lượng trong hồ có nhiều nhất bao nhiêu con cá.

Bài 80. Khối lượng một sản phẩm có phân phối chuẩn. Cân ngẫu nhiên 25 sản phẩm loại đó người ta thu được kết quả đó.

Khối lượng (gam)	29.3	29.7	30	30.5	30.7
Số sản phẩm	4	5	8	5	3

Tìm ước lượng không chệch cho phương sai của khối lượng sản phẩm.
Với độ tin cậy 95% hãy tìm khoảng tin cậy cho phương sai của khối lượng sản phẩm, nếubiết khối lượng trung bình của loại sản phẩm đó là 30gam.
Với độ tin cậy 95% hãy tìm khoảng tin cậy cho phương sai của khối lượng sản phẩm trongtrường hợp chưa biết khối lượng trung bình của loại sản phẩm đó.

Bài 81. Để ước lượng xác xuất mắc bệnh A với độ tin cậy 95% và sai số không vượt quá 1% thì cần phải khám tối thiểu bao nhiêu người, biết rằng tỷ lệ mắc bệnh A thực nghiệm cho bằng 0,9.

Chương 4

Kiểm định giả thuyết

Bài 82. Nếu máy móc hoạt động bình thường thì trọng lượng của sản phẩm (X) là đại lượng ngẫu nhiên tuân theo luật chuẩn với µ = 100gam, σ = 2gam. Qua một thời gian sản xuất người ta nhi ngờ trọng lượng sản phẩm tăng lên. Căn cứ 100 sản phẩm thì trọng lượng trung bình của chúng là 100,4gam. Với mức ý nghĩa α = 0.05 hãy kết luận điều nghi ngờ trên.

Đáp số: W_α= (1,645;+∞);g = 2 ; Trọng lượng trung bình tăng.

Bài 83. Trong điều kiện chăn nuôi bình thường , lượng sữa trung bình của một con bò là 14kg một ngày. Nghi ngờ điều kiện chăn nuôi bò kém đi làm cho lượng sữa giảm xuống. Người ta điều tra ngẫu nhiên 25 con bò và tính được lượng sữa trung bình của một con trong một ngày là 12,5kg và độ lệch tiêu chuẩn mẫu điều chỉnh là s = 2,5kg. Với mức ý nghĩa α = 0.05 hãy kết luận về điều nghi ngờ trên. Biết rằng lượng sữa bò là đại lượng ngẫu nhiên phân phối chuẩn.

Đáp số. W_α= (−∞;−1,711);g = −3; Lượng sữa bò có xu hướng giảm.

Bài 84. Định mức cũ để sản xuất một sản phẩm là 20 phút. Nay do cải tiến kỹ thật người ta sản xuất thử 100 sản phẩm và thu được kết quả sau:

Thời gian để sản xuất một sản phẩm	Số sản phẩm tương ứng
16-17	6
17-18	10
18-19	24
19-20	30
20-21	18
21-22	12

Với mức ý nghĩa α = 0,05 có thể nói việc cải tiến kĩ thuật đã làm giảm bớt thời gian sản xuất một sản phẩm hay không ? Biết rằng thời gian sản xuất một sản phẩm là đại lượng ngẫu nhiên phân phối chuẩn. Đáp số. W_α= (−∞;−1,645);g = −5,18; Thời gian sản xuất một sản phẩm đã giảm

Bài 85. Tỷ lệ phế phẩm do một máy tự động sản xuất là 5%. Kiểm tra ngẫu nhiên 300 sản phẩm thấy có 24 sản phẩm là phế phẩm. Có ý kiến cho rằng tỷ lệ phế phẩm do máy đó sản xuất đã tăng lên. Hãy kết luận ý kiến nêu trên với mức ý nghĩa α = 0.05.

Đáp số. W_α= (1,645;+∞);g = 2,39; Tỉ lệ phế phẩm tăng lên.

Bài 86. Tỷ lệ cam hỏng là 0,1. Sau một thời gian bảo quản lấy ngẫu nhiên 400 quả thấy 60 quả bị hỏng. Có ý kiến cho rằng việc bảo quản cam không tốt. Hãy kết luận ý kiến nêu trên với mức ý nghĩa α = 0,01.

Đáp số. W_α= (2,575;+∞);g = 3,33; Việc bảo quản cam tốt

Bài 87. Trọng lượng của gà con mới nở là đại lượng ngẫu nhiên phân phối chuẩn. Nghi ngờ độ đồng đều về trọng lượng gà con giảm sút người ta cân thử 12 con và tìm được s⁰²= 11,41gam². Với mức ý nghĩa α = 0.05 hãy kết luận về điều nghi ngờ trên biết rằng bình thường độ phân tán của trọng lượng gà con là 10gam².

Đáp số. W_α= (0;3,82)(21,9;+∞);g = 12,55; Trọng lượng gà con không giảm sút.

Bài 88. Nếu máy móc hoạt động bình thường thì trọng lượng sản phẩm tuân theo quy luật chuẩn là 1 kg. Có thể coi là máy móc còn hoạt động bình thường không nếu ta cân thử ngẫu nhiên 30 sản phẩm thấy độ lệch tiêu chuẩn điều chỉnh mẫu là 1.1 kg. Yêu cầu kết luận với mức ý nghĩa α = 0.01.

Đáp số. W_α= (49,6;+∞);g = 35,09; Máy móc hoạt động bình thường.

Bài 89. Người ta sản xuất thử 100 sản phẩm và thu được kết quả sau

Thời gian để sản xuất một sản phẩm	Số sản phẩm tương ứng
16-17	6
17-18	10
18-19	24
19-20	30
20-21	18
21-22	12

Với mức ý nghĩa α = 0,01 có thể xem thời gian để sản xuất một sản phẩm là đại lượng ngẫu nhiên tuân theo uy luật chuẩn được không

Đáp số. x = 19,3;s = 1,34;W_α= (11,34,+∞);g = 2,07; Tuân theo luật chuẩn.

Bài 90. Điều tra 4000 gia đình ta có được

Số con trai	Số gia đình tương ứng
0	450
1	1460
2	1530
3	560

Với mức ý nghĩa α = 0,05 có thể coi X là số con trai trong gia đình có ba con phân phối theo quy luật nhị thức được không?

Đáp số:W_α= (6;+∞),g = 13,68 ; không tuân theo quy luật nhị thức.

Bài 91. Số con của phụ nữ thủ đô dưới 25 tuổi cho ở bảng sau

X (số con)	Số phụ nữ
0	1090
1	650
2	220
3	30
4	10

Với mức ý nghĩa α = 0,05 có thể xem X tuân theo luật Poisson được không? Đáp số;W_α= (6;+∞),g = 0,32 Tuân theo quy luật Poisson ;

Bài 92. Nghiên cứu ảnh hưởng thành phần thức ăn của bố mẹ (X) đối với giới tính của con (Y ) ta có kết quả sau

Thành phần thức ăn Giới tính	Không có Vitamin	Có Vitamin
Con trai	123	145
Con gái	153	150

Với mức ý nghĩa α = 0,05 ta có thể xem X và Y độc lập với nhau được không ?

Bài 93. Nghiên cứu sự ảnh hưởng của hoàn cảnh gia đình đối với tình trạng phạm tội của trẻ em vị thành niên qua điều tra ngẫu nhiên ta có kết quả sau

	Bố hoặc mẹ đã chết	Bố mẹ li hôn	Còn cả bố mẹ
Không phạm tội	20	25	13
Phạm tội	29	43	18

Với mức ý nghĩa α = 0,05 Có thể kết luận rằng hoàn cảnh gia đình độc lâp với tình trạng phạm tội của trẻ em hay không ?

Chương 5

Phân tích tương quan và hồi quy

Bài 94. Cho bảng phân phối xác suất của các đại lượng ngẫu nhiên hai chiều rời rạc

	26	30	41	50
2,5	0,05	0,08	0,12	0,04
2,7	0,09	0,30	0,11	0,21

Tìm bảng phân phối xác suất của các tành phần X và Y .
Tìm bảng phân phối xác xuất có điều kiện của Y khi X = 26 và của X khi Y = 27 Bài 95. Cho bảng phân phối xác suất của đại lượng ngẫu nhiên hai chiều rời rạc như sau

	1	3	4	8
3	0,15	0,06	0,25	0,04
6	0,30	0,10	0,03	0,07

Tìm kỳ vọng có điều kiện của Y với X = 1.
Tìm các kỳ vọng E(X),E(Y ) và các phương sai D(X),D(Y ).
Tìm momen tương quan và hệ số tương quan giữa X và Y .

Đáp số:

E(Y/X = 1) = 5
E(X) = 2,93;E(Y ) = 4,5;D(Y ) = 2,25
µ_XY= −0,555,Γ_XY= −0,168

Bài 96. Cho bảng phân phối xác suất của véc tơ ngẫu nhiên (X,Y )

	1	2	3
1	0,17	0,13	0,25
2	0,10	0,30	0,05

Tìm ma trận hiệp phương sai
Tìm hệ số tương quan ρ_XY

Đáp số:

"−0,25 −0,06#

0,06 0,57

ρ_XY= −0,159

Bài 97. Cho bảng phân phối xác suất đại lượng ngẫu nhiên hai chiều

	20	40	60
10	3λ	λ	0
20	2λ	4λ	2λ
30	λ	2λ	5λ

Xác định

Tham số λ
Tìm các kỳ vọng E(X),E(Y ).
Tìm ma trận hiệp phương sai
Tìm hệ số tương quan
λ = 1/20
E(X) = 22,E(Y ) = 41

259

d) ρ_XY= 0,56

Bài 98. Tìm xác xuất để đại lượng ngẫu nhiên hai chiều (X,Y ) nhận giá trị trong hình chữ nhật giới hạn bởi các đường thẳng x = 1;x = 2;y = 3;y = 5 nếu biết hàm phân phối xác suất

nếu

≥

nếu

,y<

(

x,y

(

−

ĐS: p = 0,0234

(1 e−2x)(1 e−3y) nếu x 0,y 0

(

Bài 99. F(x,y) =− − ≥ ≥

0 nếu x < 0,y < 0

ĐS: f(x,y) = 6e²^x⁺³^y

Tài liệu tham khảo

Đặng Hùng Thắng, Mở đầu Lý thuyết xác suất và ứng dụng, NXB Giáo dục, 1999.
Đặng Hùng Thắng, Bài tập xác suất, NXB Giáo dục, 1999.
Đào Hữu Hồ, Xác suất - thống kê, NXB Đại học Quốc gia Hà Nội, 2007.
Nguyễn Duy Tiến, Lý thuyết xác suất, NXB Giáo dục, 2006.