

Preview text:
lOMoAR cPSD| 45740153
Chương 1: Biến cố ngẫu nhiên và xác suất
Câu 1: Cho hệ đầy đủ ba biến cố {A,B,C} với 2P(A)=P(B)=2P(C). Biết biến cố F thỏa mãn:
P(F/A)=0,01; P(F/B)=0,02 và P(F/C)=0,03. Hãy tính:
1. Xác suất P(F). 2. Xác suất P{(A+ B)| F}
Câu 2: Cho hai biến cố A, B. Biết P(A+B) = 0,7; P(A) = 0,3; P(B) =0,6.
2. Tìm xác suất P(AB). 2. Đặt C A B= + , tính xác suất: P(A|C)
Câu 3: Cho hai biến cố A và B biết: P( B) = 0,4; P(A) = a; P(A/B) = 0,25; P(B/ A) = 0,5
1. Tìm giá trị của a=? 2. Cho biến cố C độc lập với biến cố A.B và P(A.B.C)=0,05. Tính P(C+AB).
Câu 4: Cho 2 biến cố A, B thỏa mãn: P(A)=0,15; P(B)=0,35 và P(B|A)=0,4.
1. Tính xác suất P( AB. ) 2. Tính xác suất để chỉ có một trong hai biến cố A, B xảy ra.
Câu 5: Cho 2 biến cố A, B độc lập nhau. Biết P(A)=0,8 và P(A+B)=0,93.
1. Tính xác suất P(B). 2. Đặt C = A+B. Tính xác suất P( B /C).
Câu 6: Cho hai biến cố A và B. Biết: P(A) = 0,5; P(B)=0,6 và P(A+B)=0,7.
1. Chứng tỏ rằng hai biến cố A và B phụ thuộc nhau. 2. Tính P( BA)
Câu 7: Cho ba biến cố A, B và C độc lập nhau. Biết: P(A)=0,6; P(B)=0,5 và P(A+B+C)=0,94.
1. Tính P(C). 2. Tính P{(A+B)/(A+B+C)}. P{(A+B)/(A+B+C)}=0,851
Câu 8: Cho hai biến cố A, B. Biết P(A+B) = 0,8; P(A) = 0,7; P(B) =0,4.
1. Tìm xác suất P(AB) và chứng tỏ A và B phụ thuộc nhau.
2. Tính xác suất để chỉ có biến cố A xảy ra.
Câu 9: Cho hai biến cố A và B độc lập nhau. Biết: P(A) = 0,25 và P(B)=0,35.
1.Tìm P(A+B) 2. Tính P(A| B) +P(B | A)
Câu 10: Cho 3 biến cố A, B, C có quan hệ độc lập. Đặt T = A + B + C. Biết P(A) = 0,25 , P(AB) = 0,05 , P(T) = 0,46.
1. Tính P(C). 2. Tính P( {A + C}|T).
Câu 11 : Cho hệ đầy đủ ba biến cố {A,B,C} với P(A)=P(B)=2P(C). Biết biến cố F thỏa mãn:
P(F/A)=0,25; P(F/B)=0,35 và P(F/C)=0,15.
1. Tính xác suất P(F)
2. Cho D là biến cố độc lập với A+B thỏa mãn P(D.(A+B)) =0,4. Tính P(D+A+B) Câu 12: Cho
hệ biến cố đầy đủ {A, B, C} và biến cố F. Biết P(A)=0,4; P(B)=2P(C); P(F/A)=0,3;
P(F/B)=0,6 và P(F/C)=0,5.
1. Tính xác suất P(F). 2. Tính P A F( / ).
1 . Tính xác suất P(F). 2. Tính xác suất P(B | F)
Câu 15: Cho hệ đầy đủ ba biến cố {A,B,C} với P(A)=2P(B); P(C)=0,1. Biết biến cố F thỏa mãn:
P(F/A)=0,25; P(F/B)=0,35 và P(F/C)=0,45
2 . Tính xác suất P(F). 2. Tính xác suất: P(A+B+AB+ABC) Câu
16: Cho hệ đầy đủ {A, B, C} có P(F|A) = 0,15, P(F|B) = 0,32, P(F|C) = 0,48, P(C ) = 0,2, P( F ) = 0,335. lOMoAR cPSD| 45740153
Câu 13: Cho hệ đầy đủ ba biến cố {A,B,C} với P(A)=0,2; P(B)=3P(C). Biết biến cố F thỏa mãn:
P(F/A)=m; P(F/B)=0,015 và P(F/C)=0,25. 1. Tìm m biết P(F)=0,179.
2. Tính xác suất để có ít nhất hai trong ba biến cố A; B; C xảy ra.
Câu 14: Cho hệ đầy đủ ba biến cố {A,B,C} với P(A)=P(B)=2P(C). Biết biến cố F thỏa mãn:
P(F|A)=0,25; P(F|B)=0,35 và P(F|C)=0,45. Tính các xác suất sau:
1. Tính P(A), P(B). 2. Tính P( A + B + BC| ).
Câu 17: Cho hệ biến cố đầy đủ { A, B, C}. Biết rằng P(F|A) = 0,35, P(F|B) = 0,24; P(F|C) = 0,45, P(AF) = 0,7, P(B) = 7P(C).
1. Tính P(F)? 2. Tính P( A + B + BC| )?
Câu 18: Cho hệ đầy đủ ba biến cố {A,B,C} với P(A)=2P(B)=2P(C). Biết biến cố F thỏa mãn:
P(F/A)=0,08; P(F/B)=0,09 và P(F/C)=0,05. Hãy tính:
1. Xác suất P(F) 2. Xác suất: P{(A+ B)| F} Chương 2 Câu
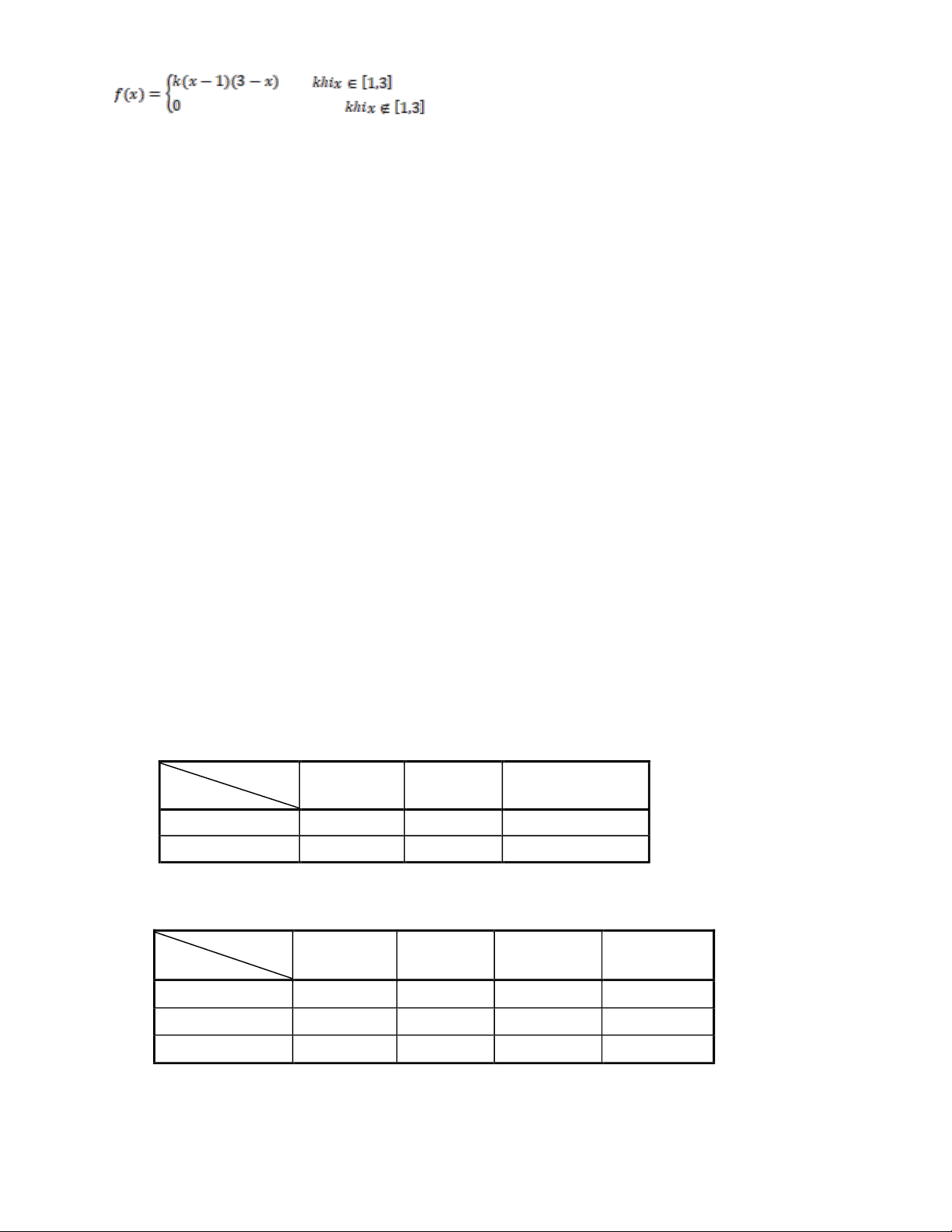
1: Cho hàm mật độ của biến ngẫu nhiên X:
a) Tìm k để f(x) là hàm mật độ. b) Tính xác suất P(X<1 ).
Câu 2: Cho hàm mật độ của biến ngẫu nhiên X:
ìïïk.x(x - 6) khi x Î [0;6] f x( )= íïïî 0 khi x Ï [0;6]
a) Tìm k để f(x) là hàm mật độ. b) Tính P(X < 2) Câu
3 Cho hàm mật độ của biến ngẫu nhiên liên tục X:
a) Tìm k để f(x) là hàm mật độ. b) Tính P(X<1).
Câu 4: Cho hàm mật độ của biến ngẫu nhiên X:
a) Tìm k để f(x) là hàm mật độ. b) Tính xác suất P(X >3) Câu
5: Cho hàm mật độ của biến ngẫu nhiên X:
a) Tìm k để f(x) là hàm mật độ. b) Tính P(X > 1,5) Câu
6: Cho hàm mật độ của biến ngẫu nhiên X:
a) Tìm k để f(x) là hàm mật độ. b) Tính E(100 – 2X). lOMoAR cPSD| 45740153
Câu 7: Cho hàm mật độ của biến ngẫu nhiên X:
a) Tìm k để f(x) là hàm mật độ. b) Tính E(2X-15)
Câu 8: Cho biến ngẫu nhiên X ~ N(5; 4), xét biến ngẫu nhiên Y= X2 -2X, hãy:
a) Tính giá trị kỳ vọng E(Y). b) Tính xác suất P(Y > modX).
Câu 9. X là biến ngẫu nhiên tuân theo quy luật chuẩn chỉ độ dày của một loại sách, biết độ dày
trung bình là 5cm; độ lệch chuẩn 2,1cm.
a). Hãy tính D(Z) biết Z=X.EX- modX b). Tính P(X2 +3X< 0).
Câu 10: Cho 2 biến ngẫu nhiên độc lập: X ~ N(4; 0,64) và Y ~ B(5; 0,3); đặt Z =2X-Y+100
a) Hãy tính D(Z). b) Tính P(MedX-ModY
Câu 11: Cho 2 biến ngẫu nhiên độc lập: X ~ N(8; 1,44) và Y ~ B(10; 0,6); đặt Z =X – 2Y+1000.
a) Hãy tính D(Z). b) Tính P(X<10, Y=E(Y)).
Câu 12: Cho X ~ N(6; 4,41); Y ~ B(10; 0,21) và đặt T = X – Y
a) Hãy tính giá trị của E(T). b) Tính xác suất P(X2 -2X > ModY).
Câu 13: Có 10 loại vắc-xin với xác suất sẽ được đưa vào sử dụng trong tháng đều là 0,8. Gọi X là
số vắc-xin sẽ được đưa vào sử dụng.
a) Tính trung bình có bao nhiêu vắc-xin sẽ được sử dụng? b) Tính P(X>2)
Câu 14: Cho X~ B(50; 0,4)
a). Hãy tính giá trị của E(2X+DX ) b). Tính P(X2 < 4).
Câu 15: Cho 2 biến ngẫu nhiên độc lập: X ~ N(6; 0,49) và Y ~ B(5; 0,4); đặt
Z =X.E(Y) – Y.MedX + 2.
a) Hãy tính E(Z). b) Tính xác suất P(X>5, Y=ModY). Chương 3
Câu 1: Cho biến ngẫu nhiên X và Y có bảng phân phối đồng thời như sau : Y - 1 0 1 X - 1 0 ,5a 0 ,5a a 2 0 ,2 a a
a). Tìm hệ số a từ bảng phân phối. b). Tính xác suất P(X2< 4). Câu
2: Cho biến ngẫu nhiên X và Y có bảng phân phối đồng thời như sau : Y 1 2 3 P(X) X – 1 0 1 , 0 , 1 1 0 , 25 P(Y) 0 25 , 0 45 , 1
a). Điền các giá trị còn thiếu vào bảng. b). Tính xác suất P(Y>2|X=-1) Câu
3: Cho biến ngẫu nhiên X và Y có bảng phân phối đồng thời như sau : lOMoAR cPSD| 45740153 Y - 2 - 1 0 X - 2 ,5a 1 0 ,5a a - 1 0 ,1 a a 0 0 1 , 0 1 , 0 , 2
a). Tìm hệ số a từ bảng phân phối. b). Tính MedY
Câu 4: Cho biến ngẫu nhiên X và Y có bảng phân phối đồng thời như sau : Y - 2021 0 2021 X - 2021 0 ,5a a a 0 0,05 1,5a 1,5a 2021 0,15 1,5a a
a). Tìm hệ số a từ bảng phân phối. b). Tính P(X>-2|Y=0) Câu
5: Cho biến ngẫu nhiên X và Y có bảng phân phối đồng thời như sau : Y - 4 - 3 - 2 X 0 0 15 , a a 1 0 ,05 a a
a). Tìm hệ số a từ bảng phân phối. b). Tính P(Y=-2|X=1) Câu
6: Cho biến ngẫu nhiên X và Y có bảng phân phối đồng thời như sau : Y 0 1 2 X 0 a 0 15 , a 2 a 2 a 3 0 , 15
a). Xác định giá trị của a. b). Tính MedY



