Bài Thực Hành 1
1. Phân biệt các văn phạm theo tiêu chuẩn của Chomsky? -
Văn phạm loại 0: Là tập hợp tất cả các ngôn ngữ hợp lệ. Một văn phạm
thuộc loạinày không bị giới hạn bởi bất kỳ quy tắc nào, và có thể biểu diễn mọi ngôn ngữ hợp lệ. -
Văn phạm loại 1 (Văn phạm phụ thuộc vào ngữ nghĩa): Là tập hợp các ngôn
ngữ có thể được biểu diễn bằng ngữ pháp bậc cao hơn, có sự phụ thuộc vào ngữ
nghĩa, được gọi là Ngữ pháp trưởng thành hoặc Ngữ pháp phụ thuộc vào ngữ nghĩa. -
Văn phạm loại 2 (Văn phạm miễn định): Là tập hợp các ngôn ngữ có thể
được biểu diễn bằng ngữ pháp miễn định hoặc Ngữ pháp context-free. -
Văn phạm loại 3 (Văn phạm hữu hạn): Là tập hợp các ngôn ngữ có thể được
biểu diễn bằng ngữ pháp hữu hạn hoặc Ngữ pháp regular.
Điểm khác biệt giữa các loại văn phạm này chủ yếu liên quan đến mức độ giới hạn
trong cách biểu diễn ngôn ngữ. Văn phạm loại 0 là loại văn phạm mạnh nhất,
không có bất kỳ giới hạn nào trong việc biểu diễn ngôn ngữ, trong khi văn phạm
loại 3 là loại văn phạm yếu nhất, có giới hạn rất nghiêm ngặt trong cách biểu diễn ngôn ngữ.
2. Sự tương đương của văn phạm và Ôtômát?
Về cơ bản, văn phạm và ôtômát đều liên quan đến việc mô tả và đại diện cho ngôn ngữ tự nhiên.
Văn phạm là một bộ quy tắc mô tả cách mà các từ và câu được tạo thành trong một
ngôn ngữ cụ thể. Văn phạm bao gồm các quy tắc ngữ pháp và cú pháp để xây dựng
các câu đúng ngữ pháp. Các văn phạm thường được sử dụng trong các lĩnh vực
như xử lý ngôn ngữ tự nhiên, trí tuệ nhân tạo, và lập trình máy tính.
Ôtômát là một cấu trúc tương tự một máy tính hoặc một tập hợp các luật để đọc và
sản xuất các chuỗi các từ trong một ngôn ngữ. Ôtômát có thể được sử dụng để
phân tích cú pháp hoặc tự động sinh ra các câu trong một ngôn ngữ cụ thể. Các
ôtômát thường được sử dụng trong các lĩnh vực như xử lý ngôn ngữ tự nhiên, máy
học, và trí tuệ nhân tạo.
Tóm lại, văn phạm và ôtômát đều là các công cụ quan trọng trong việc mô tả và đại
diện cho ngôn ngữ tự nhiên. Tuy nhiên, chúng có phạm vi và ứng dụng khác nhau
trong các lĩnh vực khác nhau của khoa học máy tính và xử lý ngôn ngữ tự nhiên.
3. So sánh Ôtômát đơn định (DFA) và Ô tô mát không đơn định (NFA)?
Cả ôtômát đơn định (DFA) và ôtômát không đơn định (NFA) đều là các mô hình
tính toán được sử dụng để mô tả các ngôn ngữ hình thức. Tuy nhiên, chúng có sự
khác biệt về cách thức hoạt động và sức mạnh tính toán.
Độ phức tạp tính toán:
DFA: DFA có tính chất đơn định, tức là với mỗi trạng thái và ký tự đầu vào, chỉ có
một trạng thái kết thúc và một trạng thái tiếp theo. Do đó, DFA có tính chất tổng
quát hơn NFA và có thể giải quyết các vấn đề với độ phức tạp thấp hơn NFA.
NFA: NFA không đơn định, có thể có nhiều trạng thái kết thúc hoặc nhiều trạng
thái tiếp theo cho mỗi ký tự đầu vào. Vì vậy, NFA có thể giải quyết các vấn đề
phức tạp hơn, nhưng cũng có thể dẫn đến mâu thuẫn về trạng thái. Số lượng trạng thái:
DFA: Số lượng trạng thái của DFA ít hơn hoặc bằng với số lượng trạng thái của
NFA. Vì vậy, DFA thường có độ phức tạp tính toán thấp hơn.
NFA: Số lượng trạng thái của NFA có thể lớn hơn số lượng trạng thái của DFA.
Hiệu quả trong việc tối ưu hoá ôtômát:
DFA: DFA là một dạng đặc biệt của NFA, do đó nó có thể được chuyển đổi từ
NFA. Tuy nhiên, quá trình chuyển đổi này có thể dẫn đến tăng số lượng trạng thái
và giảm hiệu quả tính toán.
NFA: NFA không thể được chuyển đổi trực tiếp thành DFA mà phải thông qua quá
trình tối ưu hóa. Tuy nhiên, quá trình này không đảm bảo tối ưu hoá tối đa và có
thể dẫn đến một DFA không tối ưu.
Tóm lại, DFA và NFA đều có ưu điểm và hạn chế của riêng mình. DFA phù hợp
với các bài toán đơn giản, có tính chất tổng quát và ít trạng thái. NFA phù hợp với các bài toán phức tạp. 4.
Cho các Biểu thức chính quy (BTCQ) sau. Hãy xây dựng Các Ô tô mát đơn
định đoán nhận chúng. a. 10 ∪ (0 ∪ 11)0 ∗1 b. 1 ∗00∗ c. 00∗11∗ 5.
Ngôn ngữ nào được tạo ra bởi các ngữ pháp sau đây? Trong mỗi
trường hợp biện minh cho câu trả lời của bạn. a. S -> 0 S 1 | 0 1
b. S -> + S S | - S S | a
c. S -> S (S) S | ε
d. S -> a S b S | b S a S | ε
e. S -> a | S + S | S S | S * | ( S ) a.
Ngữ pháp trên tạo ra ngôn ngữ gồm tất cả các chuỗi nhị phân có dạng
0^n1^n hoặc 01, với n là một số nguyên không âm. Cụ thể, ngữ pháp này cho phép
tạo ra các chuỗi bằng cách đệ quy thêm các ký tự 0 và 1 vào đầu và cuối chuỗi, sao
cho số lượng ký tự 0 và 1 bằng nhau. b.
Ngữ pháp trên tạo ra ngôn ngữ gồm tất cả các biểu thức số học đơn giản, bao
gồm các số và phép ”+”, “-” và số a. Các biểu thức này có thể được tạo ra bằng
cách đệ quy thêm các phép tính và số vào biểu thức, với điều kiện rằng mỗi phép
tính đều được bao quanh bởi hai biểu thức con. c.
Ngữ pháp trên tạo ra ngôn ngữ bao gồm tất cả các chuỗi có thể được tạo ra
bằng cách đặt các cặp dấu ngoặc đơn vào bất kỳ vị trí nào trong chuỗi. Ngoài ra,
chuỗi rỗng cũng là một phần của ngôn ngữ này. d.
Ngữ pháp trên tạo ra ngôn ngữ gồm tất cả các chuỗi có thể được tạo ra bằng
cách lấy hai chuỗi con bắt đầu và kết thúc bằng chữ cái 'a' và 'b', xen kẽ nhau hoặc
không xen kẽ nhau. Cụ thể, các chuỗi có thể được tạo ra bằng cách đệ quy thêm
chuỗi 'aSbS' hoặc 'bSaS' vào chuỗi, với điều kiện rằng chuỗi con 'aSbS' hoặc 'bSaS'
không bao gồm bất kỳ chuỗi con 'aSbS' hoặc 'bSaS' nào. e.
Ngữ pháp trên tạo ra ngôn ngữ gồm tất cả các chuỗi có thể được tạo ra từ
các ký tự 'a', '+', '', '(', ')' và có cấu trúc của một biểu thức toán học đơn giản. Các
chuỗi này có thể được tạo ra bằng cách đệ quy thêm các ký tự vào biểu thức, theo
cấu trúc cho trước. Ví dụ, chuỗi 'a+(aa)' có thể được tạo ra bằng cách sử dụng ngữ
pháp trên như sau: 'S -> a | S + S | S * | ( S )', sau đó sử dụng quy tắc S -> S (S) 6.
Mô tả các ngôn ngữ được biểu thị bằng các biểu thức chính quy sau: a. a(a|b)*a b. ((ε|a)b*)* c. (a|b)*a(a|b)(a|b) d. a*ba*ba*ba*
e. !! (aa|bb)*((ab|ba)(aa|bb)*(ab|ba)(aa|bb)*)*
A, Phần đầu tiên của biểu thức chính quy, $a$, chỉ định rằng mỗi chuỗi trong ngôn
ngữ bắt đầu bằng "a".
Phần tiếp theo, $(a|b)$, chỉ định rằng sau "a", ta có thể có bất kỳ số lượng tùy ý các
ký tự "a" hoặc "b". Dấu " | " biểu thị phép toán lựa chọn, có nghĩa là có thể lựa
chọn giữa "a" hoặc "b". Dấu "" biểu thị lặp lại 0 hoặc nhiều lần.
Phần cuối cùng của biểu thức chính quy, $a$, chỉ định rằng mỗi chuỗi trong ngôn ngữ kết thúc bằng "a".
B, Phần đầu tiên của biểu thức chính quy, (ε|a), chỉ định rằng mỗi chuỗi trong ngôn
ngữ có thể bắt đầu bằng "a" hoặc có thể rỗng (epsilon). • Phần tiếp theo của biểu
thức chính quy, b*, chỉ định rằng mỗi chuỗi trong ngôn ngữ có thể có bất kỳ số
lượng tùy ý các ký tự "b". Dấu "*" biểu thị lặp lại 0 hoặc nhiều lần.
Sau đó, toàn bộ biểu thức chính quy được bao quanh bởi dấu ngoặc đơn và dấu "*"
ở cuối biểu thức cho biết mỗi chuỗi trong ngôn ngữ có thể bao gồm bất kỳ số
lượng tùy ý các chuỗi bắt đầu bằng "a" hoặc rỗng và theo sau là bất kỳ số lượng tùy ý các ký tự "b".
C, Phần đầu tiên của biểu thức chính quy, (a|b), chỉ định rằng mỗi chuỗi trong ngôn
ngữ có thể bắt đầu bằng bất kỳ số lượng tùy ý các ký tự "a" hoặc "b". Dấu " | " biểu
thị phép toán lựa chọn, có nghĩa là có thể lựa chọn giữa "a" hoặc "b". Dấu "" biểu
thị lặp lại 0 hoặc nhiều lần.
Phần tiếp theo của biểu thức chính quy, a, chỉ định rằng mỗi chuỗi trong ngôn ngữ
phải có một ký tự "a".
Phần sau của biểu thức chính quy, (a|b), chỉ định rằng sau "a", ta có thể chọn giữa ký tự "a" hoặc "b".
Phần cuối cùng của biểu thức chính quy, (a|b), cũng chỉ định rằng mỗi chuỗi trong
ngôn ngữ có thể kết thúc bằng "a" hoặc "b".
D, Phần đầu tiên của biểu thức chính quy, a*, chỉ định rằng mỗi chuỗi trong ngôn
ngữ có thể bắt đầu bằng bất kỳ số lượng tùy ý các ký tự "a". Dấu "*" biểu thị lặp lại 0 hoặc nhiều lần.
Phần tiếp theo của biểu thức chính quy, bababa*, chỉ định rằng chuỗi "baba" lặp lại
bất kỳ số lần. Ký tự "b" chỉ xuất hiện một lần trong chuỗi, và giữa các ký tự "b" là
một chuỗi bất kỳ các ký tự "a" (0 hoặc nhiều lần).
E, Biểu thức chính quy (aa|bb)((ab|ba)(aa|bb)(ab|ba)(aa|bb)) biểu diễn ngôn ngữ
gồm các chuỗi có dạng:
Một chuỗi bắt đầu bằng "aa" hoặc "bb" và lặp lại bất kỳ số lần (phần đầu biểu thị bằng (aa|bb)*).
Sau phần đầu, chuỗi chứa một số cặp (ab|ba), mỗi cặp được theo sau bởi một chuỗi
bất kỳ số lần các chuỗi "aa" hoặc "bb". Mỗi cặp (ab|ba) đều được phân tách bởi một chuỗi (aa|bb)*. |ba
7. Các ngôn ngữ nào trong câu 6 là nhập nhằng?
11. Dùng biểu thức chính quy xây dựng các khái niệm: chữ cái, chữ số, tên
quan hệ trong ngôn ngữ Pascal.
Trong ngôn ngữ Pascal, ta có thể định nghĩa các khái niệm như sau bằng cách sử
dụng biểu thức chính quy:
Chữ cái: Chữ cái trong ngôn ngữ Pascal là một ký tự từ 'A' đến 'Z' hoặc từ 'a' đến
'z'. Ta có thể sử dụng biểu thức chính quy để mô tả tập hợp các chữ cái như sau: [A-Za-z]
Chữ số: Chữ số trong ngôn ngữ Pascal là một ký tự từ '0' đến '9'. Ta có thể sử dụng
biểu thức chính quy để mô tả tập hợp các chữ số như sau: [0-9]
Tên quan hệ: Tên quan hệ trong ngôn ngữ Pascal là một chuỗi các chữ cái và chữ
số bắt đầu bằng một chữ cái. Ta có thể sử dụng biểu thức chính quy để mô tả tập
hợp các tên quan hệ như sau: [A-Za-z][A-Za-z0-9]*
Trong đó, [A-Za-z] mô tả một ký tự chữ cái đầu tiên và [A-Za-z0-9]* mô tả các ký
tự tiếp theo có thể là chữ cái hoặc chữ số. Dấu '*' trong biểu thức chính quy này
cho phép xuất hiện 0 hoặc nhiều lần các ký tự có trong tập hợp.
12. Xây dựng bộ phân tích các từ loại: chữ cái, chữ số, tên quan hệ trong ngôn
ngữ Pascal bằng đồ thị chuyển.
Để xây dựng bộ phân tích các từ loại chữ cái, chữ số, tên quan hệ trong ngôn ngữ
Pascal bằng đồ thị chuyển, ta có thể sử dụng phương pháp xây dựng đồ thị chuyển
từ biểu thức chính quy. Cụ thể, ta sẽ xây dựng 3 đồ thị chuyển tương ứng với từng từ loại.
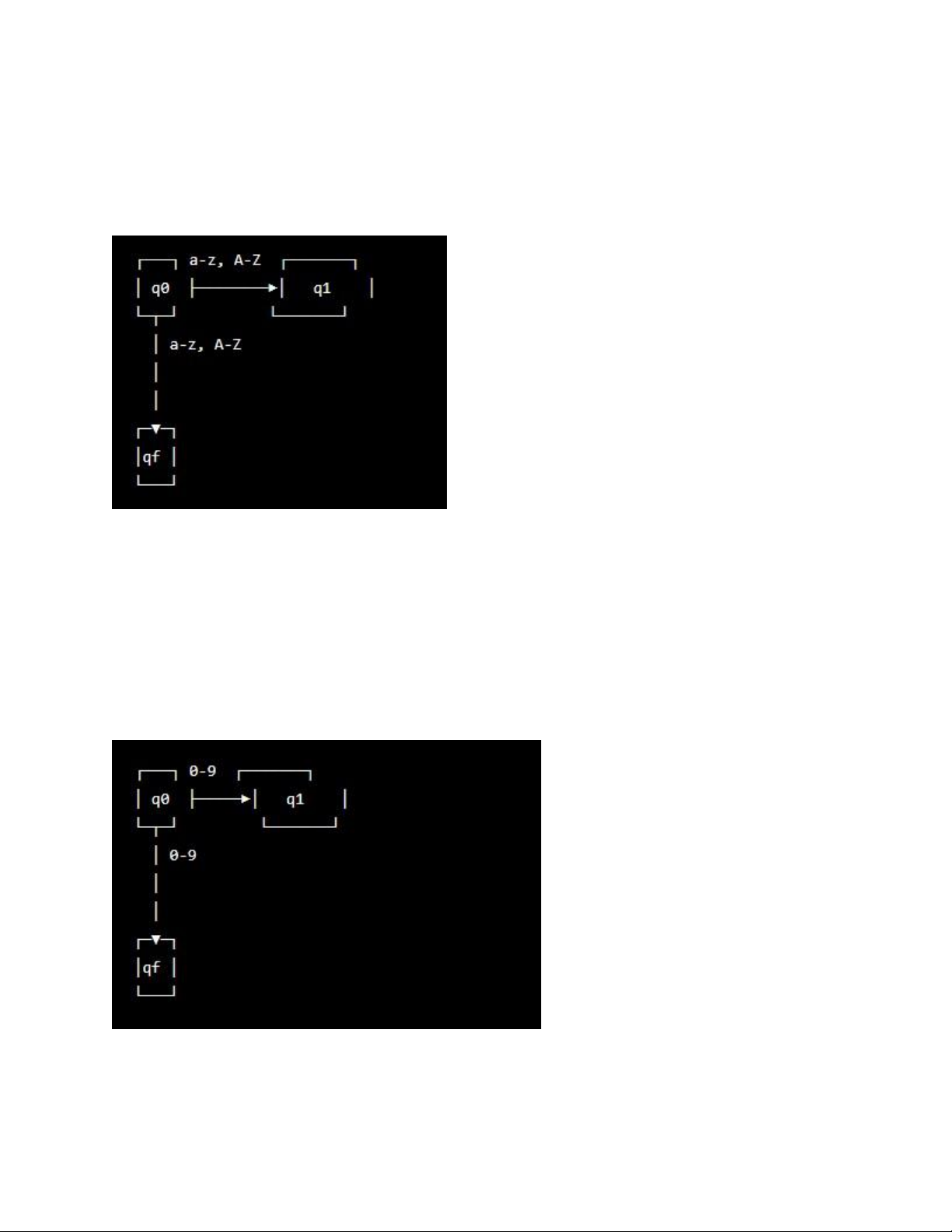
Đồ thị chuyển cho chữ cái:
Để phân tích các chữ cái trong ngôn ngữ Pascal, ta có thể sử dụng đồ thị chuyển sau đây:
Trong đồ thị chuyển này, q0 là trạng thái bắt đầu, qf là trạng thái kết thúc và có một
cạnh đi từ q0 đến q1 được gắn thẻ với bộ chữ cái a-z và A-Z. Cạnh này cho phép
chuyển từ trạng thái q0 sang trạng thái q1 nếu đầu vào là một chữ cái.
Đồ thị chuyển cho chữ số:
Để phân tích các chữ số trong ngôn ngữ Pascal, ta có thể sử dụng đồ thị chuyển sau đây:
Trong đồ thị chuyển này, q0 là trạng thái bắt đầu, qf là trạng thái kết thúc và có một
cạnh đi từ q0 đến q1 được gắn thẻ với bộ chữ số 0-9. Cạnh này cho phép chuyển từ
trạng thái q0 sang trạng thái q1 nếu đầu vào là một chữ số.
Đồ thị chuyển cho tên quan hệ:
Để phân tích các tên quan hệ trong ngôn ngữ Pascal, ta có thể sử dụng đồ thị chuyển sau đây: Câu 13
Để xây dựng bộ phân tích từ loại cho ngôn ngữ Pascal, ta có thể sử dụng đồ thị
chuyển (finite state machine) để mô hình hóa quá trình xác định từ loại của một từ.
Trong đó, ta có thể định nghĩa các trạng thái và các chuyển trạng thái giữa các
trạng thái để mô tả quá trình xác định từ loại. Dưới đây là một bộ phân tích từ loại
đơn giản cho ngôn ngữ Pascal bằng đồ thị chuyển, chỉ xác định được ba loại từ:
chữ cái, chữ số và tên quan hệ. #include #include using
namespace std; enum State { START, LETTER,
DIGIT, RELATION }; bool isLetter(char c) { return
(c >= 'a' && c <= 'z') || (c >= 'A' && c <= 'Z'); } bool isDigit(char c)
{ return c >= '0' && c <= '9';
} bool isRelation(string word) { string relations[] = { "program", "var",
"integer", "real", "begin", "end" }; for (string relation : relations) { if (word == relation) { return true; } } return false; } int main() { string input;
cout << "Enter a string: "; getline(cin, input); State state = START; string word = ""; for (char c : input) { switch (state) { case START: if (isLetter(c)) { state = LETTER; word += c; } else if (isDigit(c)) { state = DIGIT; word += c; } break; case LETTER: if (isLetter(c)) { word += c; } else {
state = isRelation(word) ? RELATION : START;
cout << "Letter: " << word << endl; word = "";
if (isDigit(c)) { state = DIGIT; word += c; } } break; case DIGIT: if (isDigit(c)) { word += c; } else { state =
START; cout << "Digit: " << word << endl; word = ""; if
(isLetter(c)) { state = LETTER; word += c; } } break; case RELATION: if (isLetter(c)) { state = LETTER; word = c; } else { state = START;
cout << "Relation: " << word << endl; word = ""; if (isDigit(c)) { state = DIGIT; word += c; } } break; } } if (!word.empty()) { switch (state) { case LETTER:
cout << "Letter: " << word << endl;
break; case DIGIT: cout <<
"Digit: " << word << endl; break; case RELATION:
cout << "Relation: " << word << endl; break; } } return 0; }