1. Khái niệm
Có một số bài toán cho biết kết quả sau khi thực hiện liên tiếp một số phép
tính đối với số phải tìm. Khi giải các bài toán dạng này, ta thường dùng
phương pháp tính ngược từ cuối (đôi khi còn gọi là phương pháp suy ngược từ cuối) 2. Nhận diện
- Ta bắt đầu với một đại lượng chưa biết
- Bài toán sẽ đưa ra 1 chuỗi các phép toán
- Kết quả cuối cùng đã được cho sẵn
3. Phương pháp giải
Cách giải bài toán bằng phương pháp tính ngược từ cuối như sau:
Bước 1: Xác định thứ tự các số liệu đã cho trong đề bài theo thứ tự từ cuối lên.
Bước 2: Xác định các phép tính ngược với đề bài theo thứ tự từ cuối lên (Ngược
với phép cộng là phép trừ, ngược với phép trừ là phép cộng.)
Bước 3: Đặt lời giải cho bài toán, thực hiện phép tính và ghi đáp số của bài toán.
● Giải bài toán bằng phương pháp tính ngược có 3 dạng:
- Bài toán giải bằng lưu đồ.
- Bài toán giải bằng dùng sơ đồ đoạn thẳng.
- Bài toán giải bằng cách lập bảng.
● Các bước giải các bài toán dùng sơ đồ đoạn thẳng
Bước 1: Tìm hiểu đề bài.
Bước 2: Lập luận để vẽ sơ đồ.
★ Tóm tắt được bài toán bằng sơ đồ đoạn thẳng một cách cẩn thận, chính
xác. Từ đó, suy nghĩ và tìm tòi để phát hiện mối liên hệ giữa cái đã cho và cái cần tìm.
★ Khi vẽ sơ đồ phải chọn độ dài các đoạn thẳng và sắp xếp các đoạn thẳng
đó một cách thích hợp để có thể dễ dàng thấy được mối quan hệ phụ
thuộc giữa các đại lượng, tạo ra một hình ảnh cụ thể giúp ta suy nghĩ tìm
tòi cách giải một bài toán.
★ Để có thể thực hiện những bài toán bằng sơ đồ đoạn thẳng thì nắm được
cách biểu thị các phép tính ( cộng, trừ, nhân, chia), các mối quan hệ (quan
hệ về tổng, hiệu, quan hệ về tỉ số) là hết sức quan trọng. Vì nó làm một
công cụ biểu đạt mối quan hệ 4. Ví dụ minh họa Ví dụ 1: Lớp 1
Bài 1: Cô giáo có một số kẹo. Cô chia cho các bạn nam 20 cái và chia cho các
bạn nữ 15 cái. Cô giáo còn lại 10 cái kẹo. Hỏi lúc đầu cô giáo có bao nhiêu cái kẹo?
- Ở đây, cần chú ý học sinh: Chia cho các bạn tức là số kẹo của cô giáo bị trừ đi.
- Yêu cầu đặt ra đối với học sinh là:
+ Xác định thứ tự các số liệu đã cho từ cuối lên đó là: 10; 15; 20.
+ Xác định thứ tự các phép tính ngược từ cuối lên tạo thành dãy tính: 10 + 15 + 20.
+ Đặt lời giải cho bài toán, thực hiện phép tính và ghi đáp số của bài toán.
Lúc đầu cô giáo có số cái kẹo là: 10 + 15 + 20 = 45 (cái). Đáp số: 45 cái kẹo.
Ví dụ 2: Lớp 1A có 42 học sinh. Nếu chuyển 2 em của tổ 2 sang tổ 1, chuyển 3
em của tổ 2 sang tổ 3 và cuối cùng chuyển 8 em từ tổ 1 sang tổ 3 thì số học sinh
của tổ 3 sẽ gấp 2 lần số học sinh của tổ 2 và số học sinh của tổ 2 gấp 2 lần số
học sinh của tổ 1. Hỏi mỗi tổ lúc đầu có bao nhiêu học sinh? Bài giải
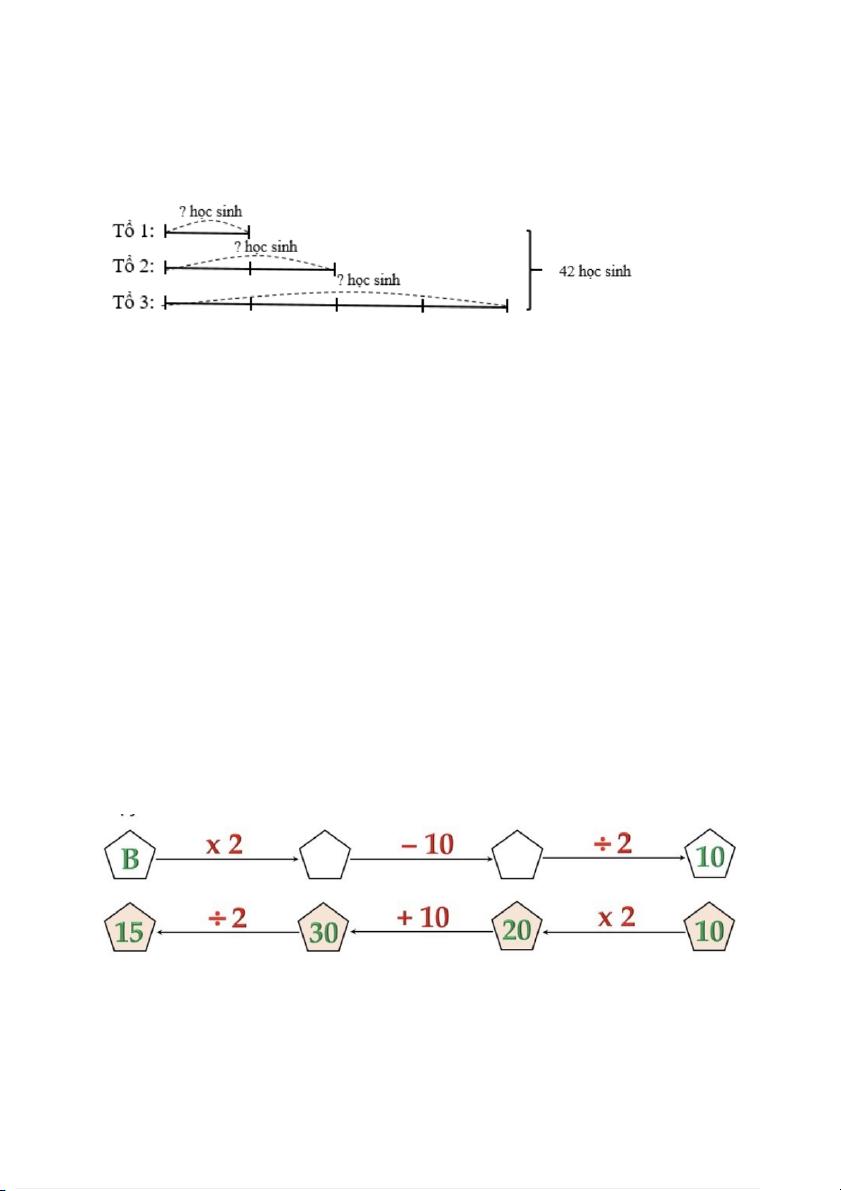
Ta có sơ đồ số học sinh mỗi tổ sau khi chuyển đổi:
Số học sinh của tổ 1 sau khi chuyển đổi là:
42 : (1 + 2 + 4) = 6 (học sinh)
Số học sinh của tổ 2 sau khi chuyển đổi là: 6 x 2 = 12 (học sinh)
Số học sinh của tổ 3 sau khi chuyển đổi là: 12 x 2 = 24 (học sinh)
Số học sinh của tổ 1 trước khi chuyển 8 em sang tổ 3 là: 6 + 8 = 14 (học sinh)
Số học sinh ban đầu của tổ 1 là: 14 - 2 = 12 (học sinh)
Số học sinh của tổ 2 trước khi chuyển 2 em sang tổ 1 và 3 em sang tổ 3 là: 12 + 2 + 3 = 17 (học sinh)
Số học sinh của tổ 3 trước khi nhận 3 em của tổ 2 là: 24 - 3 = 21 (học sinh)
Số học sinh ban đầu của tổ 2 là: 21 - 8 = 13 (học sinh)
Đáp số: Tổ 1: 12 học sinh Tổ 2: 17 học sinh Tổ 3: 13 học sinh Ví dụ 3: Bài 3: Tìm B? Lớp 3
Bài 3: Tìm hai số biết rằng sau khi giảm số thứ nhất đi 7 lần và số thứ 2 đi 4 lần
thì phần còn lại bằng nhau và tổng là 12 Bài giải
Số thứ nhất sau khi giảm 7 lần và số thứ 2 sau khi giảm 4 lần có giá trị là: 12 : 2 = 6 Số thứ nhất là: 6 x 7 = 42 Số thứ hai là: 6 x 4 = 24
Đáp số: Số thứ nhất là 42 Số thứ hai là 24 Ví dụ 4: Lớp 4
Bài 4: Mạnh, Hùng, Dũng, Minh có một số quyển vở. Mạnh lấy 1/3 số vở để
dùng, Hùng lấy 1/3 số vở còn lại để dùng, tiếp theo Dũng cũng lấy 1/3 số vở
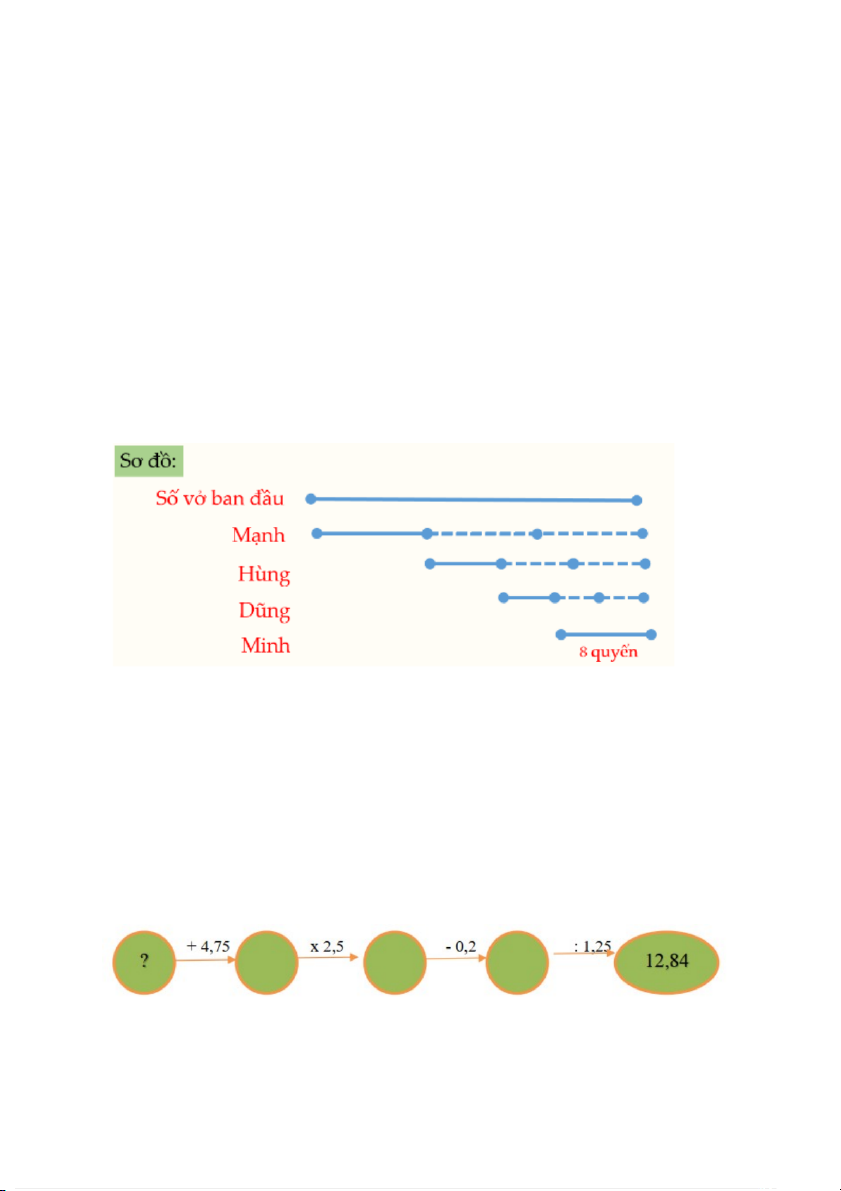
còn lại. Cuối cùng Minh dùng nốt 8 quyển. Hỏi lúc đầu cả 4 bạn có bao nhiêu quyển vở? Bài giải Theo bài ra ta có sơ đồ: Nhìn vào sơ đồ ta có:
Số quyển vở còn lại sau khi Hùng lấy là: ( 8 : 2 ) x 3 = 12 (quyển vở)
Số quyển vở còn lại sau khi Mạnh lấy là: ( 12 : 2 ) x 3 = 18 (quyển vở)
Lúc đầu cả 4 bạn có số quyển vở là: ( 18 : 2 ) x 3 = 27 (quyển vở)
Đáp số: 27 quyển vở Ví dụ 5: Lớp 5:
Bài 5: Tìm một số thập phân, biết nếu lấy số đó cộng với 4,75; sau đó nhân với
2,5; rồi trừ đi 0,2 và cuối cùng chia cho 1,25 thì được kết quả là 12,84 Bài giải Ta có lưu đồ:
Số cần tìm là: (12,84 x 1,25 + 0,2) : 2,5 - 4,75 = 1,75