Báo cáo lớn Mô hình suy hao PathLoss môn Thông tin vô tuyến | Trường Đại học Bách Khoa Hà Nội

TRƯỜNG ĐẠI HỌC BÁCH KHOA HÀ NỘI
VIỆN ĐIỆN TỬ VIỄN THÔNG  BÁO CÁO BÀI TẬP LỚN THÔNG TIN VÔ TUYẾN
Tên đề tài: CÁC
MÔ HÌNH SUY HAO KÊNH
( PATHLOSS )
Giảng viên :
PGS-TS Vũ Văn Yêm
Viện Điện tử Viễn Thông - BKHN
Nhóm sinh viên thực hiện:
Nguyễn Văn Tú. Tăng Thiên Vũ.
Nguyễn Kim Sơn
Hà Nội, 12/2013
Trường Đại học Bách Khoa Hà nội Viện
Điện tử Viễn thông
Báo cáo bài tập lớn môn Thông tin vô tuyến.
Tên đề tài:
Các mô hình suy hao kênh PathLoss
Giảng viên: PGS-TS Vũ Văn Yêm
Viện Điện tử Viễn thông Đại học Bách khoa Hà Nội.
Nhóm sinh viên: 1./ Nguyễn Văn Tú. 2./ Tăng Thiên Vũ. 3./ Nguyễn Kim Sơn.
Lớp KSTN-ĐTVT-K55 – trường Đại học Bách Khoa Hà Nội
Hà Nội, 12/2013. Mục lục:
1./ Giới thiệu đề tài:.......................................................................................................4
2./ Mô hình suy hao truyền sóng trong môi trường tự do:.............................................5
3. Log-distance PathLoss:..............................................................................................8
4. Outdoor Propagation Model:.....................................................................................9
4.1. Okumura Model:.................................................................................................9
4.2. HATA...............................................................................................................12
5. Kết quả mô phỏng trong Matlab:.............................................................................13
5.1. Mô hình lan truyền sóng trong không gian tự do:.............................................13
a. Suy hao truyền sóng L trong môi trường tự do:.............................................13
b. Công suất nhận được ở máy thu:......................................................................14
5.1. Mô hình Log-distance – Không gian thực:........................................................14
5.2. Out door Propagation:.......................................................................................21
a. Okumura Model:............................................................................................21
b. Hata Model:......................................................................................................22
Phụ lục 1: Code mô phỏng trong Matlab.....................................................................23
Phụ lục 2: Tài liệu tham khảo......................................................................................30
1./ Giới thiệu đề tài:
Khác với hệ thống truyền thông có đường dây cố định, tín hiệu vô tuyến mang
tính chất ngẫu nhiên và chịu ảnh hưởng lớn bởi những yếu tố môi trường không gian
truyền. Đường truyền giữa máy phát và máy thu có thể đơn giản là truyền thẳng trong
một toàn nhà (Light-of-Sight) nhưng cũng có thể là bị ảnh hưởng bởi các yếu tố, các
vật cản như các tòa nhà, ngon núi, rừng cây hoặc sự thay đổi môi trường. Những yếu
tố này làm ảnh hưởng đến thông tin được mang theo trong tín hiệu sóng điện từ. Để
đánh giá được mức ảnh hưởng của môi trường đến kênh truyền nay, nhà nghiên cứu
phải mô hình hóa được ảnh hưởng của môi trường thành các mô hình toán học để có
thể tính toán mô phỏng.
“Các mô hình suy hao kênh” mô hình hóa, số liệu hóa được một số ảnh hưởng
đến kênh truyền vô tuyến. Tìm hiểu về các mô hình suy hao kênh trong các môi
trường khác nhau, trong các môi trường cụ thể trên lí thuyết và mô phỏng có thể tìm
cách khắc phục, hạn chế ảnh hưởng của môi trường đến kênh truyền trong thực tế.
Đề tài tìm hiểu về “Các mô hình suy hao kênh - PathLoss” và một số kết quả
mô phỏng trên Matlab. Tìm hiểu về các mô hình trong lí thuyết cũng như một số mô
hình được ứng dụng trong thực tế, qua đó đưa ra nhận xét chung của nhóm.
Nhóm sinh viên lớp KSTN-ĐTVT-K55
Đại học Bách Khoa Hà Nôi.
2./ Mô hình suy hao truyền sóng trong môi trường tự do:
Mô hình truyền sóng trong không gian tự do được sử dụng để dự đoán cường độ
tín hiệu khi giữa máy phát và máy thu không có vật cản giữa chúng, truyền sóng được
thực hiện trong tầm nhìn thẳng (line – of – sight). Hệ thống thông tin vệ tinh và thông
tin vi ba trong tầm nhìn thẳng là điển hình của truyền sóng trong không gian tự do.
Giống như hầu hết các mô hình truyền sóng vô tuyến large-scale, mô hình truyền sóng
trong không gian tự do dự đoán công suất thu được suy giảm phụ thuộc vào khoảng
cách truyền sóng. Công suất thu được khi truyền sóng trong không gian tự do với
khoảng cách giữa anten phát và anten thu là d được cho bởi công thức Friis: • Công thức Friis: 2
𝑃 (𝑑) = 𝑃𝑡𝐺𝑡𝐺rƛ (2.1) 𝑟 (4𝜋)2𝑑2𝐿 Trong đó:
o 𝑃𝑡 là công suất phát (W)
o 𝑃𝑟(𝑑) là công suất nhận được tại điểm thu (W) o 𝐺𝑡 là hệ số tăng
ích của anten phát o 𝐺𝑟 là hệ số tăng ích của anten thu o 𝑑 là
khoảng cách giữa máy phát và máy thu (m) o ƛ là bước sóng (m)
o L là hệ số suy hao của anten ( L ≥ 1)
o Hệ số tăng ích của anten G phụ thuộc vào độ mở hiệu dụng của anten 𝐴𝑒; 𝐺 = 4𝜋𝐴𝑒 . Trong đó:
𝐴𝑒 là độ mở hiệu dụng của anten phụ thuộc vào kích
thước vật lý của anten
ƛ = 𝑐𝑓 với f là tần số sóng mang (Hz), c là tốc độ ánh sáng
Công thức Friis cho ta thấy công suất nhận được tại điểm thu suy giảm tỉ lệ với
bình phương khoảng cách d giữa anten phát và anten thu. ( cũng có nghĩa là
suy giảm 20dB/10 đơn vị khoảng cách) •
Công suất bức xạ đẳng hướng hiệu dụng (EIRP) được định nghĩa là: EIRP
= 𝑃𝑡. 𝐺𝑡 dùng để biểu diễn công suất phát lớn nhất có thể từ máy phát theo
hướng cực đại của hệ số tăng ích của anten. Thông thường EIRP thường
được tính theo đơn vị dB. •
Path Loss biểu diễn sự suy hao tín hiệu trong quá trình truyền sóng, được
tính theo đơn vị dB, được định nghĩa là sự sai khác ( dB ) giữa công suất
phát hiệu dụng và công suất nhận được ở máy thu.
o Path loss trong mô hình không gian tự do khi bao gồm cả hệ số tăng ích của anten: 2 PL(dB) = 10log 𝑃𝑡 = - 10log[ (2.2) 𝑃r
o Nếu không tính đến hệ 𝑃𝑡số = tăng -10log ích[ củaƛ 2anten] = thì
10log[(4𝜋)2.𝑑2.𝑓2] (2.3) PL(dB) = 10log 𝑃r (4𝜋)2.𝑑2 𝑐2 •
Tính công suất thu 𝑃𝑟(𝑑)dựa trên công suất thu tại điểm tham chiếu o Nếu
tính theo đơn vị W hoặc mW (
𝑃𝑟 𝑑) mW = 𝑃𝑟(𝑑0) . (𝑑0)2 (2.4)
o Trong đó: 𝑑0là cự ly tiêumW chuẩn
𝑃𝑟(𝑑0) là công suất thu được tại cự ly tham chiếu
𝑑𝑓 = 2 𝐷2 là cự ly đảm bảo điều kiện trường bức xạ (far – field ƛ0 distance 𝑑𝑓 ≤ 𝑑0 ≤ 𝑑
D là kích thước vật lý của anten
o Nếu tính theo đơn vị dBm 𝑃 (𝑑) = 𝑃 (𝑑 ) – 20log( 𝑑 ) (2.5) 𝑟 dBm 𝑟 0 dBm 𝑑0 • Các ví dụ minh họa: Ví dụ 1:
Tìm cự ly đảm bảo điều kiện trường bức xạ 𝑑𝑓 (far-field distance) với
anten có kích thước lớn nhất là D = 1m và tần số hoạt động là 900MHz. Giải: Theo bài, D = 1m, f = 900MHz ƛ = c = 3.108 m/s (m) f 900.106 Hz Áp dụng công thức d 2 f = 2Dƛ0 ta tính được df = 6m Ví dụ 2:
a) Công suất của máy phát là 50W, biểu diễn công suất phát theo đơn vị dBm và dBW.
b) Cho tần số sóng mang 900MHz, tìm công suất thu được ( tính theo
đơn vị dBm) tại khoảng cách 100m Cũng câu hỏi trên với khoảng
cách 10 km. c) Tính path loss tại khoảng cách 100m
Giả thiết hệ số tăng ích của anten phát và thu đều bằng 1 6 Giải:
a) Công suất𝑃 (𝑑𝐵𝑚 phát) =tính 10 theo𝑙𝑜𝑔 𝑃đơn𝑡 (𝑚𝑊 vị )dBm =
10 là: log[50. 103] = 47.0 𝑑𝐵𝑚 𝑡 1𝑚𝑊
Công suất phát tính theo đơn𝑃 𝑡vị (𝑊 dBW) là:
𝑃 (𝑑𝐵𝑊) = 10𝑙𝑜𝑔
= 10 log[50] = 17.0 𝑑𝐵𝑊 𝑡 1𝑊
b) Công suất nhận được tại khoảng cách 100m là (tính theo dBm) Áp
dụng công thức Friis ta có:
( 𝑑) = (4𝑃𝜋𝑡𝐺)𝑡2𝐺𝑑2𝑟ƛ𝐿2 =50.(4 𝜋(1)2)(. 100(1).) (12. /(1)3)2 = 3.5. 10 −6 𝑊 = 3.5. 10 −3 𝑚𝑊 𝑃𝑟
𝑃𝑟(𝑑𝐵𝑚) = 10𝑙𝑜𝑔𝑃𝑟(𝑚𝑊) = 10 log(3.5. 10−3𝑚𝑊) = −24.5 𝑑𝐵𝑚
Công suất nhận được tại khoảng cách 10km có thể áp dụng công thức (….) với 𝑑0 = 100𝑚 và d = 10 km 100
𝑃 10 𝑘𝑚 = 𝑃 100 + 20 log [
] = −24.5 𝑑𝐵𝑚 − 40𝑑𝐵𝑚 𝑟 ( ) 𝑟 ( ) 10000 = −64.5 𝑑𝐵𝑚 c) Path loss
𝑃𝐿(𝑑𝐵) = 10 log [𝑃𝑡] = 10 log [ 50 ] = 69.3 dB 𝑃r 3.5.10−6
3. Mô hình Log-distance PathLoss:
Cả tính toán lí tuyết và thực nghiệm đều cho thấy cường độ trung bình của tín
hiệu nhận được suy giảm logarit theo khoảng cách, bất kể là môi trường indoor hay
outdoor. Cường độ suy giảm tín hiệu trung bình theo khoảng cách giữa máy phát và
máy thu là một hàm mũ của khoảng cách: 𝑑 ( ) 𝑛 𝑃𝐿 𝑑 ~ ( ) (3.1) 𝑑0 Tính theo dB:
𝑃𝐿(𝑑𝐵) = 𝑃𝐿(𝑑 ) + 10𝑛 log 𝑑 (3.2) 0 𝑑0 Trong đó:
• 𝑃𝐿(𝑑0) : Path loss tại cự li tham chiếu
• 𝑑0: cự li tham chiếu, thỏa mãn 𝑑𝐹 ≤ 𝑑0 ≤ 𝑑,
• 𝑑𝐹∶ đảm bảo điều kiện trường khu xa (các mặt sóng cầu đến có thể coi là phẳng) 𝑑𝐹 = 2𝐷ƛ02 (3.3)
D: kích thước vật lí của anten phát
ƛ0∶ bước sóng làm việc
Việc xác định khoảng cách tham chiếu là rất quang trọng. trong các hệ thống
cell lớn, khoảng cách tham chiếu thường dùng là 1km. trọng các hệ thống cell nhỏ
(micro cells) khoảng cách tham chiếu nhỏ hơn (100m đến 1m). hệ số n được tính từ
thực nghiệm. thông thường, n tuân theo bảng sau: Môi trường Hệ số n Không gian tự do 2 Đô thị 2.7 đến 3.5 Đô thị (bị che phủ) 3 đến 5
Trong các tòa nhà (có LOS) 1.6 đến 1.8
Trong tòa nhà (có vật cản) 4 đến 6
Trong nhà máy (có vật cản) 2 đến 3
4. Outdoor Propagation Model: 4.1. Okumura Model:
Mô hình Okumura là một trong những mô hình được sử dụng rộng rãi nhất trong
khu vực đô thị . Mô hình này được áp dụng cho các tần số từ 150 MHz đến 1920 MHz
(mặc dù nó thường được ngoại suy lên đến 3000 Mhz ) và khoảng cách từ 1 km đến 100
km. Mô hình Okumura có thể được sử dụng cho các trạm cơ sở có chiều cao ăng ten
khác nhau, từ 30 m đến 1000m.
Bằng thực nghiệm, mô hình Okumura đưa ra công thức sau:
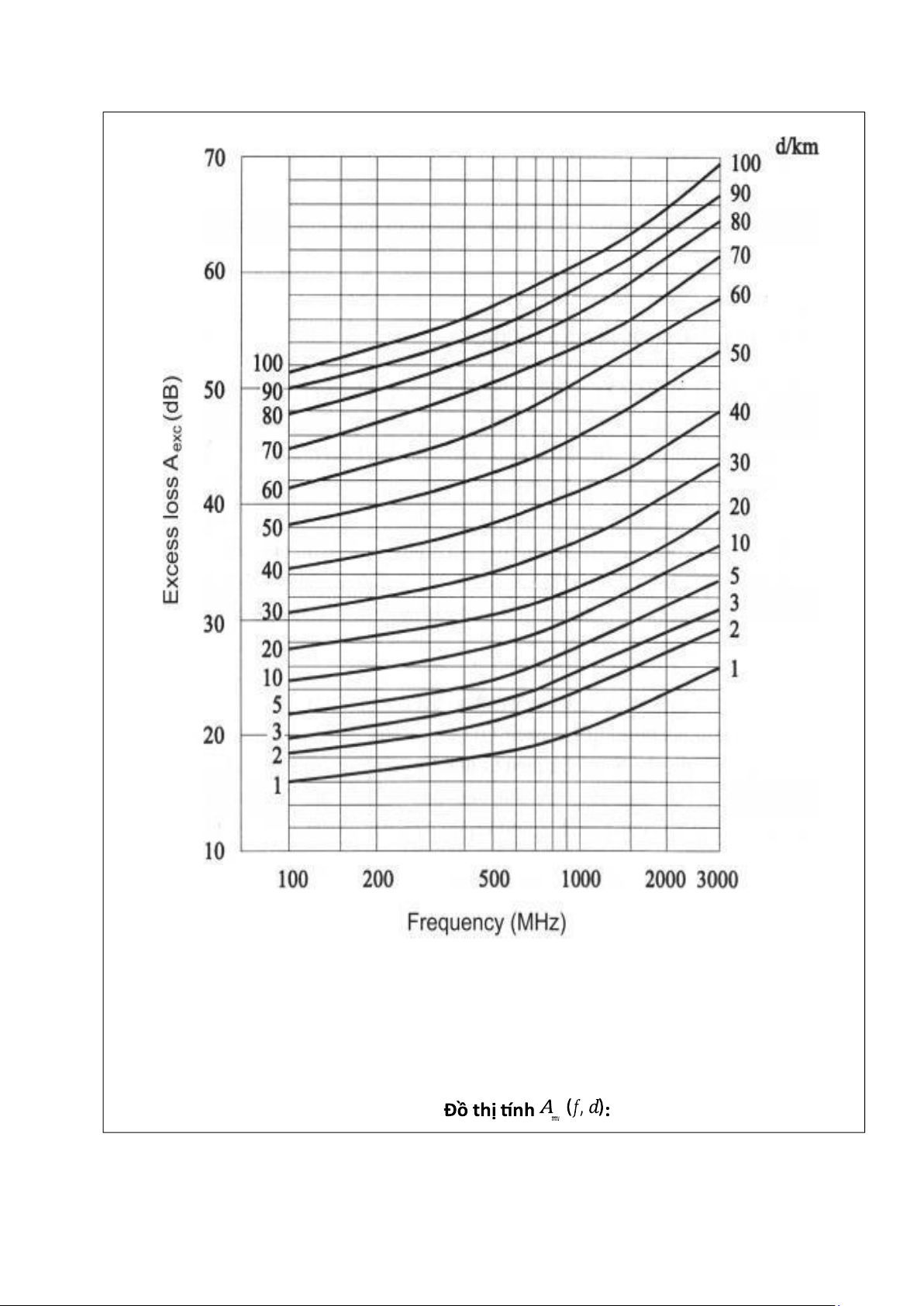
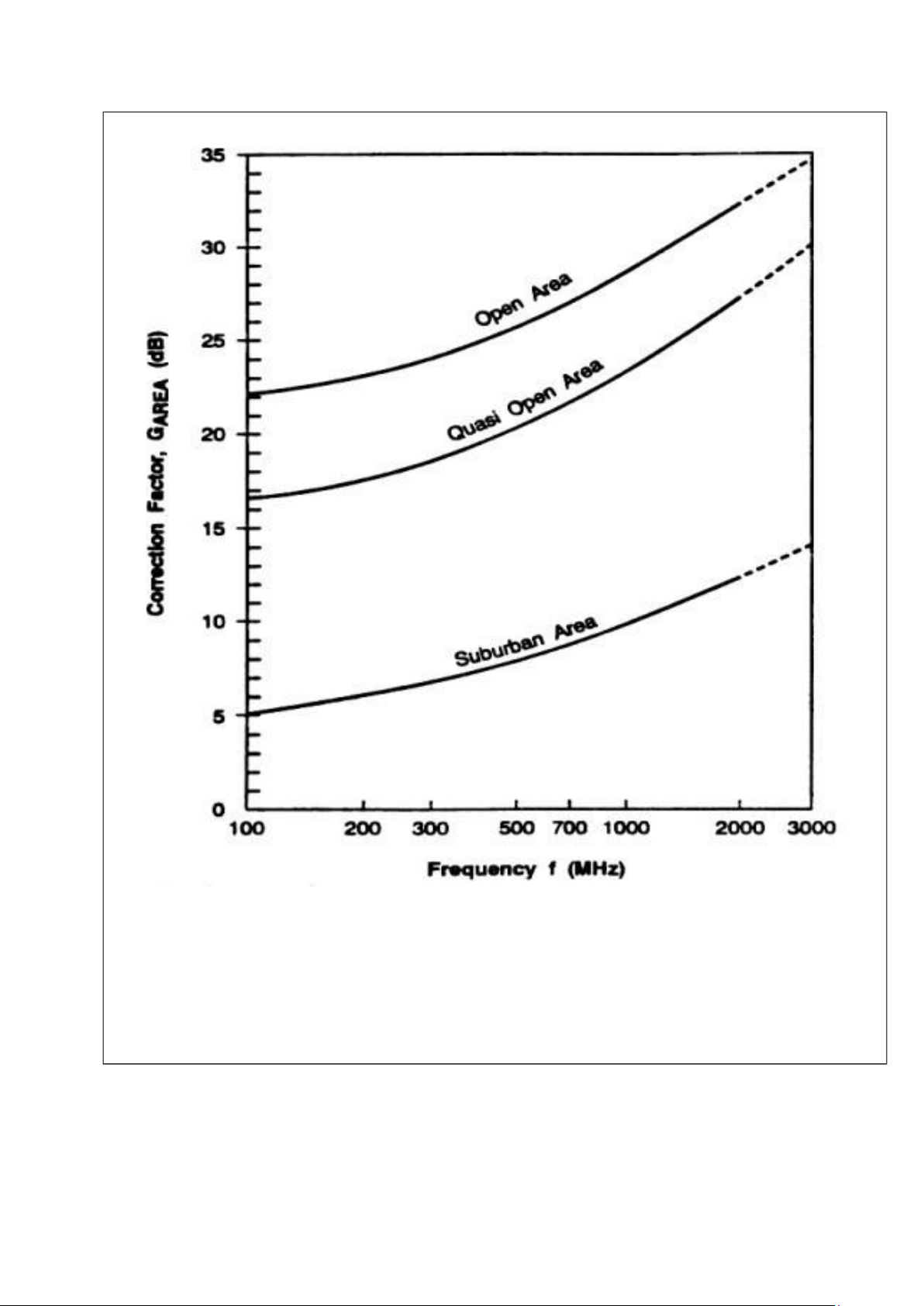
𝐿50(𝑑𝐵) = 𝐿𝐹 + 𝐴𝑚𝑢(𝑓, 𝑑) − 𝐺(ℎ𝑡𝑒) − 𝐺(ℎ𝑟𝑒) − 𝐺𝑎𝑟𝑒𝑎 (4.1) Trong đó:
• 𝐿50(𝑑𝐵) : là 50% giá trị của Pathloss
• 𝐿𝐹 : là pathloss trong không gian tự do
• 𝐴𝑚𝑢(𝑓, 𝑑) : là sự suy giảm tương đối trung bình trong không gian tự do
• 𝐺(ℎ𝑡𝑒) : là chiều cao tăng ích của trạm anten cơ sở (the base station
antenna height gain factor) ; 𝐺(ℎ𝑡𝑒) = 20 log ( ℎ𝑡𝑒 ) với 1000 m > ℎ𝑡𝑒 > 2 30 m
• 𝐺(ℎ𝑟𝑒) : là chiều cao tăng ích của anten di động (the mobile antenna
height gain factor); 𝐺(ℎ𝑟𝑒) = 10 log (ℎ𝑟𝑒) với ℎ𝑟𝑒 ≤ 3 𝐺 m 3
• 𝐺𝑎𝑟𝑒𝑎 là hệ số khuếch đại (tùy thuộc môi trường xét)
Mô hình Okumura hoàn toàn được xây dựng từ thực nghiệm và không có một
luận giải lí thuyết nào cho mô hình này.2 hệ số 𝐴𝑚𝑢(𝑓, 𝑑) và 𝐺𝑎𝑟𝑒𝑎 được lấy từ đồ thi thực
nghiệm. Tuy nhiên mô hình Okumura vẫn rất chính xác khi áp dụng trong thực tế. Nó
đã trở thành mô hình chuẩn được áp dụng trong việc xây dựng các hệ thống vô tuyến ở
Nhật Bản. Khuyết điểm lớn nhất của mô hình này là không áp dụng được cho khu vực
nông thôn. Độ lệch trung bình giữa mô hình và thực tế rơi trong khoảng từ 10 dB đến 14 dB. Hình 4.1.
Hình vẽ 4.2. Đồ thị G area 4.2. Hata Model:
Mô hình Hata là một mô hình thực nghiệm được xây dựng bởi Okumura, được
áp dụng với dải tần từ 150 MHZ đến 1500 MHZ cho môi trường đô thị. Tuy nhiên nó
cũng được đưa vào các tham số chỉnh sửa để áp dụng vào các trường hợp khác. Công
thức chuẩn của mô hình Hata như sau:
𝐿50(𝑢𝑟𝑏𝑎𝑛)(𝑑𝐵) = 69. 55 + 26. 16 𝑙𝑜𝑔 𝑓𝑐 − 13. 82 𝑙𝑜𝑔 ℎ𝑡𝑒 − 𝑎(ℎ𝑟𝑒)
+(44. 9 − 6. 55 𝑙𝑜𝑔 ℎ𝑡𝑒) 𝑙𝑜𝑔 𝑑 (4.2) Trong đó:
• 𝑓𝑐 : tần số hoạt động (150 MHZ đến 1500 MHZ)
• ℎ𝑡𝑒 : chiều dài hiệu dụng của anten trạm phát (30m đến 200m)
• ℎ𝑟𝑒 : chiều dài hiệu dụng của anten thu (1m đến 10m)
• 𝑑 : khoảng cách truyền sóng (km)
• 𝑎(ℎ𝑟𝑒) : là hệ số cân chỉnh, tùy thuộc vào độ rộng vùng được xét Đối với
thành phố cỡ nhỏ hoặc trung bình, 𝑎(ℎ𝑟𝑒) tính như sau:
𝑎(ℎ𝑟𝑒) = (1. 1 log 𝑓𝑐 − 0. 7)ℎ𝑟𝑒 − (1. 56 log 𝑓𝑐 − 0. 8) 𝑑𝐵 (4.3) Đối với thành phố lớn:
𝑎(ℎ𝑟𝑒) = 8. 29(log 1. 54ℎ𝑟𝑒)2 − 1. 1 𝑑𝐵 với fc ≤ 300 MHZ (4.4)
𝑎(ℎ𝑟𝑒) = 3. 2(log 11. 75ℎ𝑟𝑒)2 − 4. 97 𝑑𝐵 với fc ≥ 300 MHZ (4.5) Để áp dụng cho
vùng ngoại ô, mô hình Hata chỉnh sửa công thức như sau : 𝐿 (𝑑𝐵) = 𝐿 ( ) 𝑓𝑐 2 (4.6) 50 50 𝑢𝑟𝑏𝑎𝑛 − 2 [log ] − 5. 4 28
Đối với vùng nông thôn :
𝐿50(𝑑𝐵) = 𝐿50(𝑢𝑟𝑏𝑎𝑛) − 4. 78(log 𝑓𝑐)2 − 18. 33 log 𝑓𝑐 − 40. 98 (4.7)
Mặc dù mô hình Hata không có hệ số chỉnh sửa đường như trong mô hình
okumura, thì các biểu thức trên vẫn có những ứng dụng thực tế. kết quả của mô hình
Hata rất giống với mô hình Okumura , khi d > 1 km. Mô hình Hata phù hợp với các hệ
thống cell lớn, nhưng không phù hợp với các hệ thống PCS (Personal Comunications
Systems) – vì các hệ thống PCS có bán kính cell thường < 1 km. Tuy vậy, hiệp hội
EURO-COST cũng đã nghiên cứ và đưa ra một số mở rộng cho mô hình Hata để có
thể áp dụng được cho mô hình cell có bán kính < 1km.
5. Kết quả mô phỏng trong Matlab:
5.1. Mô hình lan truyền sóng trong không gian tự do:
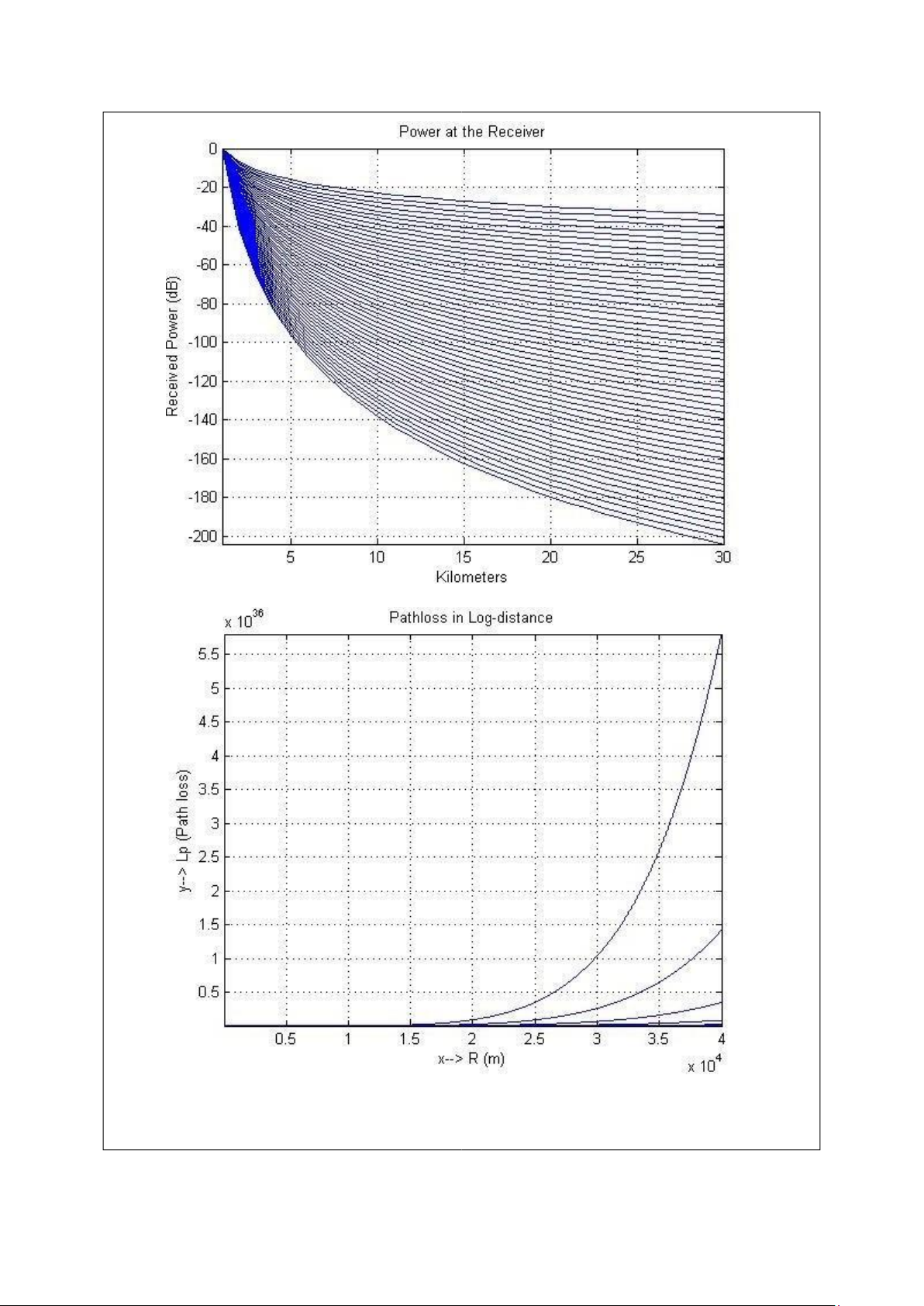
Hình 2 . Đồ thị phụ thuộc công suất nhận trong không gian tự do theo khoảng cách d (km) theo mô hìn
Hình 1 . Đồ thị phụ thuộc Suy hao truyền sóng trong không gian tự do vào khoảng cách (PathLoss – Pa
a. Suy hao truyền sóng L trong môi trường tự do:
Suy hao truyền sóng trong môi trường tự do với hệ số mũ truyền sóng n = 2. Khoảng
cách truyền nhận ảnh hưởng rất lớn đến Suy hao truyền sóng và Công suất nhận của
tại vi trí máy thu. Chênh lệch L giữa R = 3 km và R = 4 km lên đến 18*10^11.
b. Công suất nhận được ở máy thu:
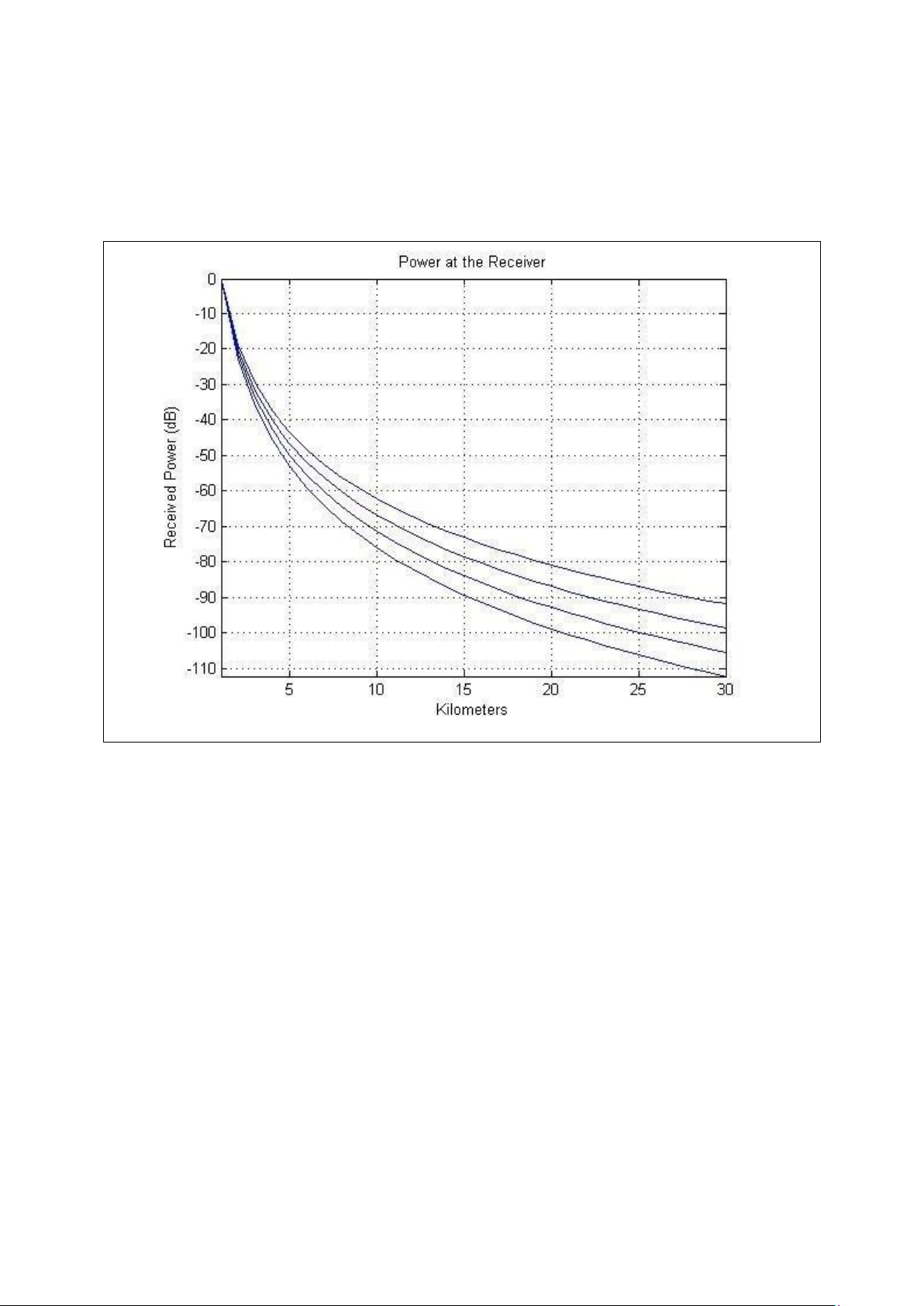
5.1. Mô hình Log-distance – Không gian thực:
Công suất nhận phụ thuộc vào môi trường thực tế (Hệ số mũ truyền sóng). Một số
kết quả mô phỏng với nhưng không gian thực thế khác nhau (có số mũ lan truyền khác nhau).
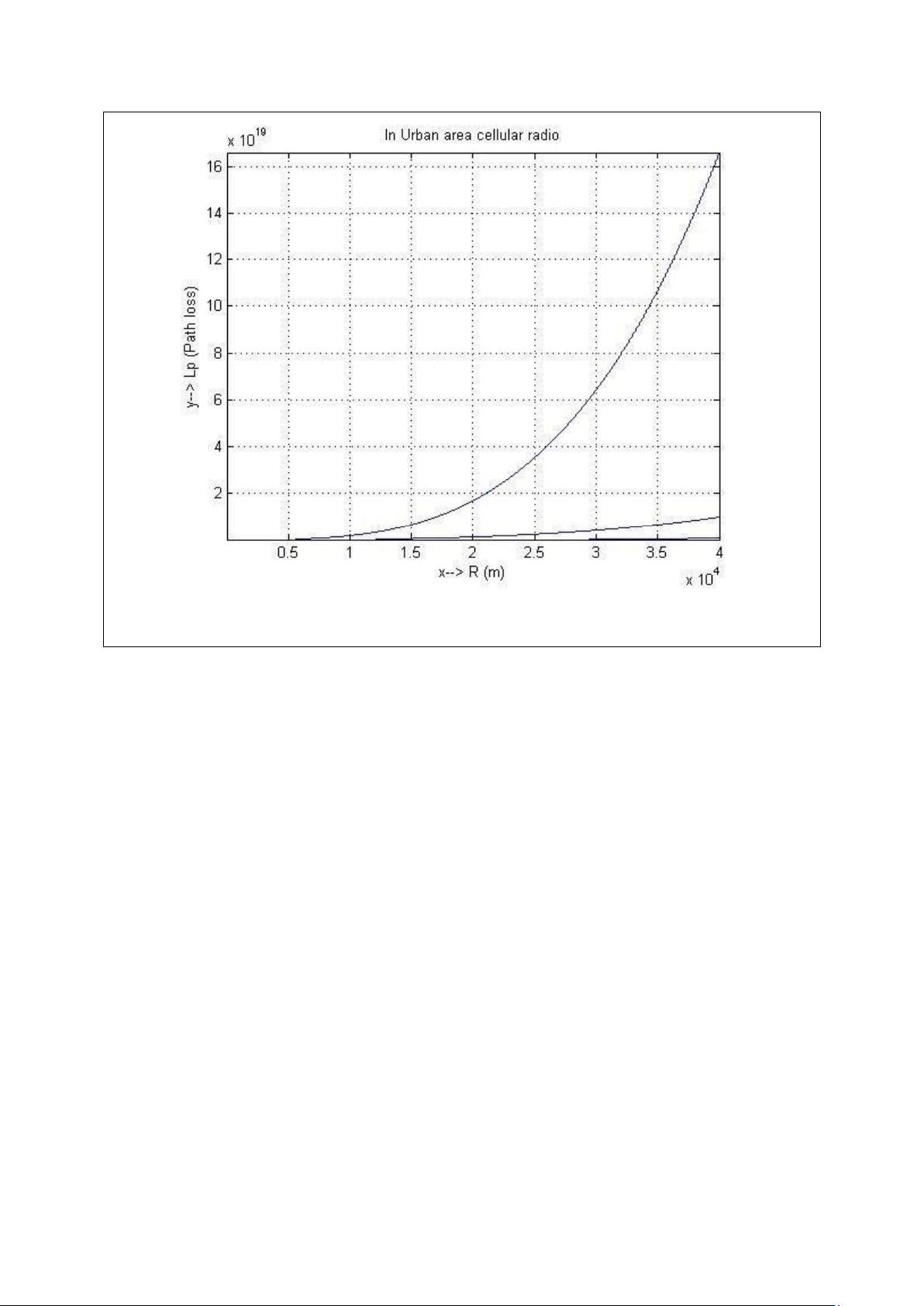
Hình 3. Công suất nhận trong môi trường “Urban area cellular radio” với hệ số mũ
suy hao truyền sóng trong 2.7:3.5.
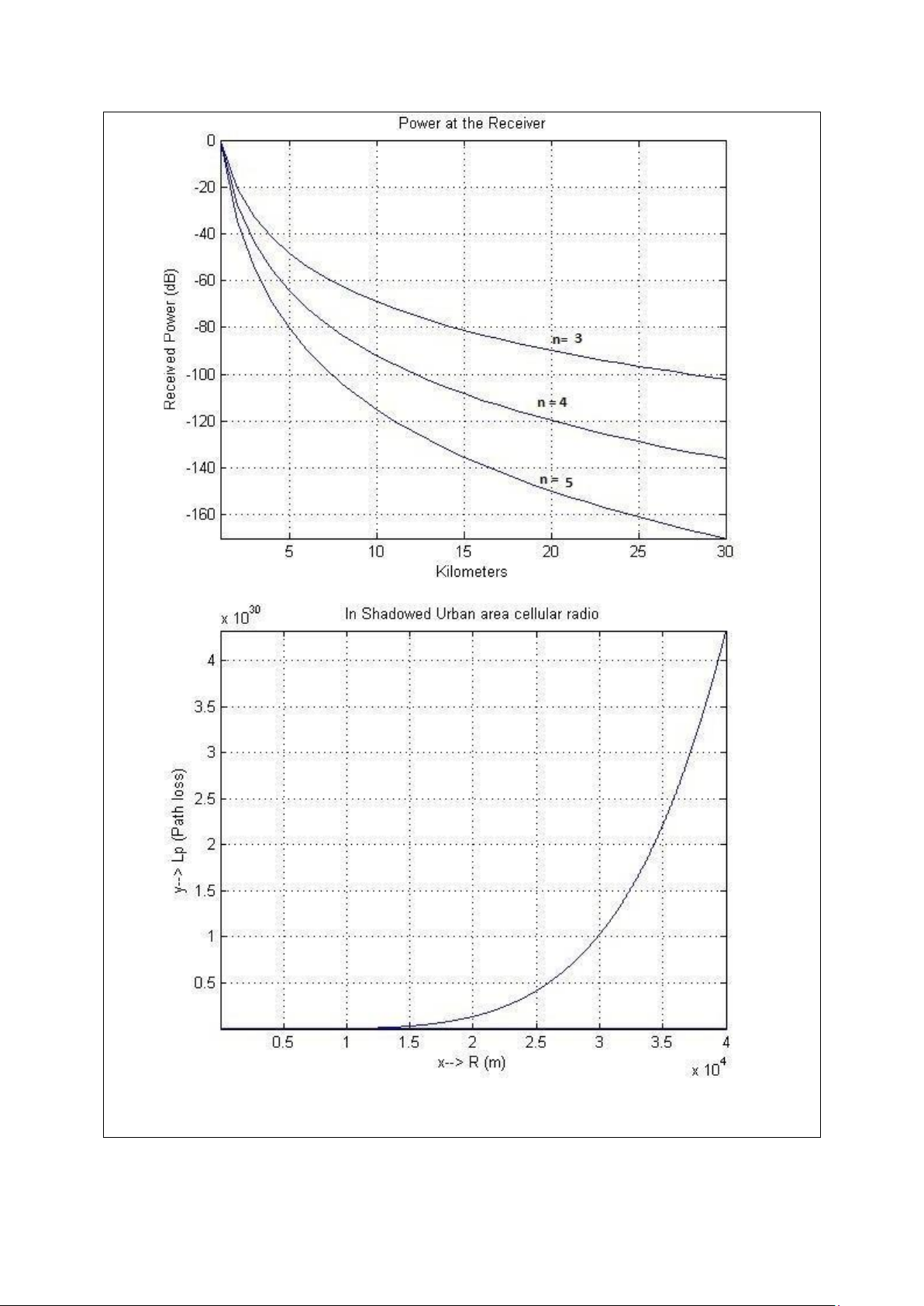
Hình 4. Công suất nhận trong môi trường “Shadowed Urban area cellular radio” với
hệ số mũ suy hao truyền sóng trong 3:5.
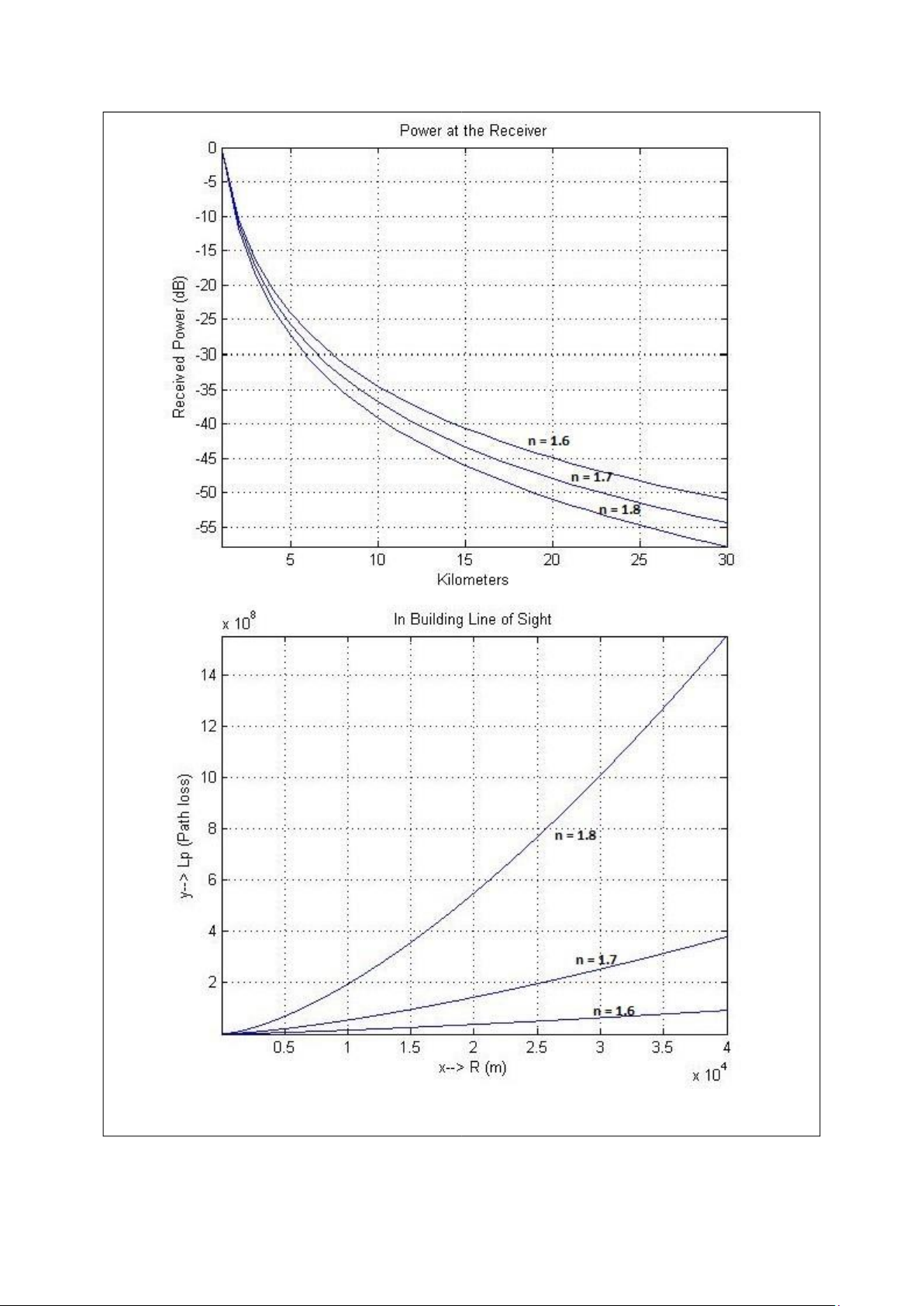
Hình 5. Công suất nhận trong môi trường “In building Light of Sight” với hệ số mũ
suy hao truyền sóng trong 1.6: 1.8.
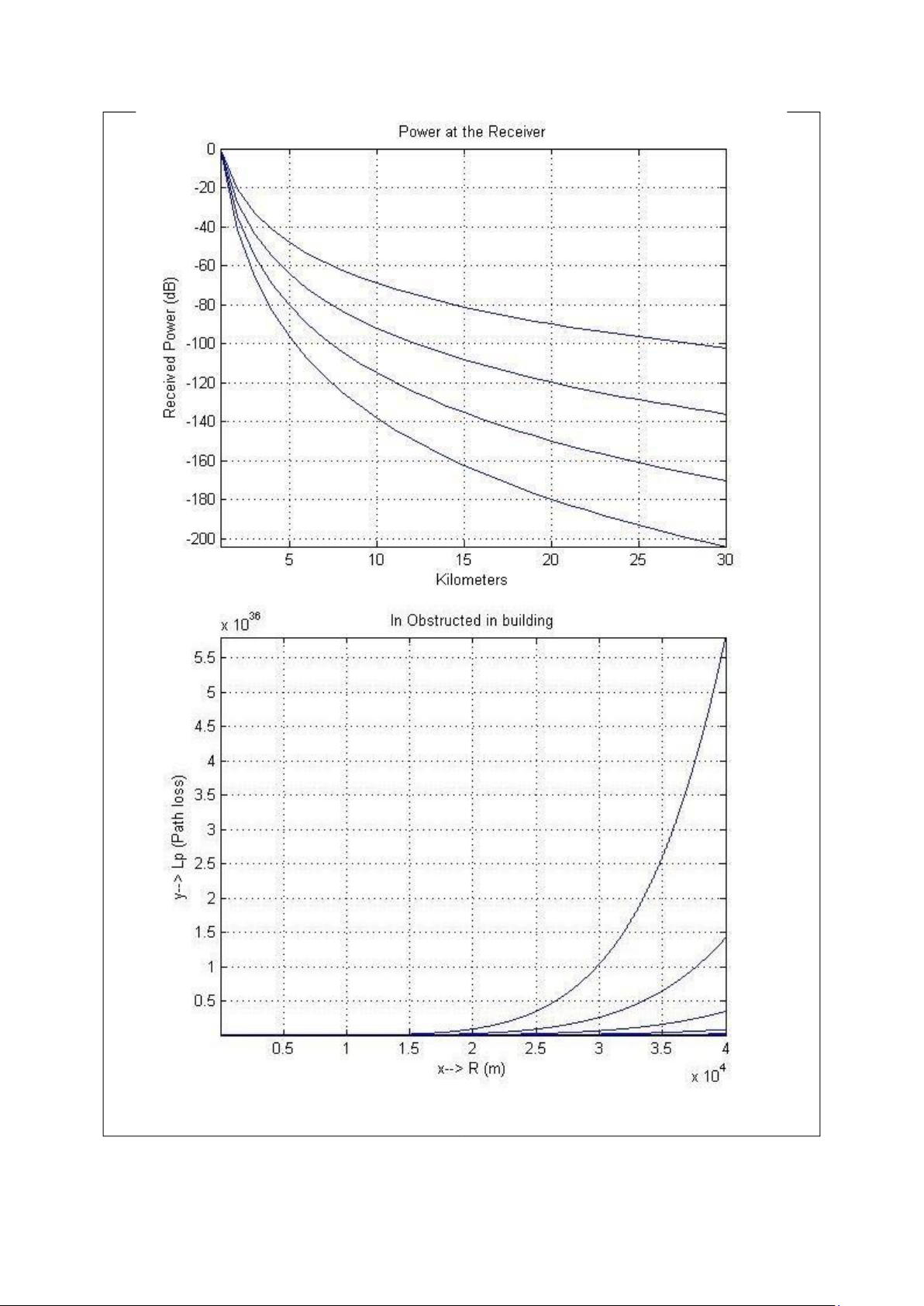
Hình 6. Công suất nhận trong môi trường “Obstructed in building” với hệ số mũ suy hao truyền sóng trong 4:6.
Hình 7 . Công suất nhận trong môi trường thực với hệ số mũ suy hao truyền sóng thay đổi trong trong 1:6.
Chú thích: với hệ số mũ lớn hơn thì đồ thị sẽ nằm phía trên.