Báo cáo Thí Nghiệm : Phép Đo Tiêu Cự Bằng Bessel & Silbermann PFIEV môn Vật lý đại cương 2 | Học viện Công Nghệ Bưu Chính Viễn Thông

BÁO CÁO THÍ NGHIỆM VẬT LÍ Bài 1
CÁC PHÉP ĐO TIÊU CỰ CƠ BẢ N
Họ và tên: Dương Lê Hoàng MSSV: 20212435 Lớp: Tin h c
ọ công nghiệp và tự động hoá Trang 1
I Mục đích thí nghiệm
-Đo tiêu cự của thấu kính hội tụ bằng 2 phương pháp: Bessel và Silbermann
II Cơ sở lý thuyết 1 Công thức Bessel:
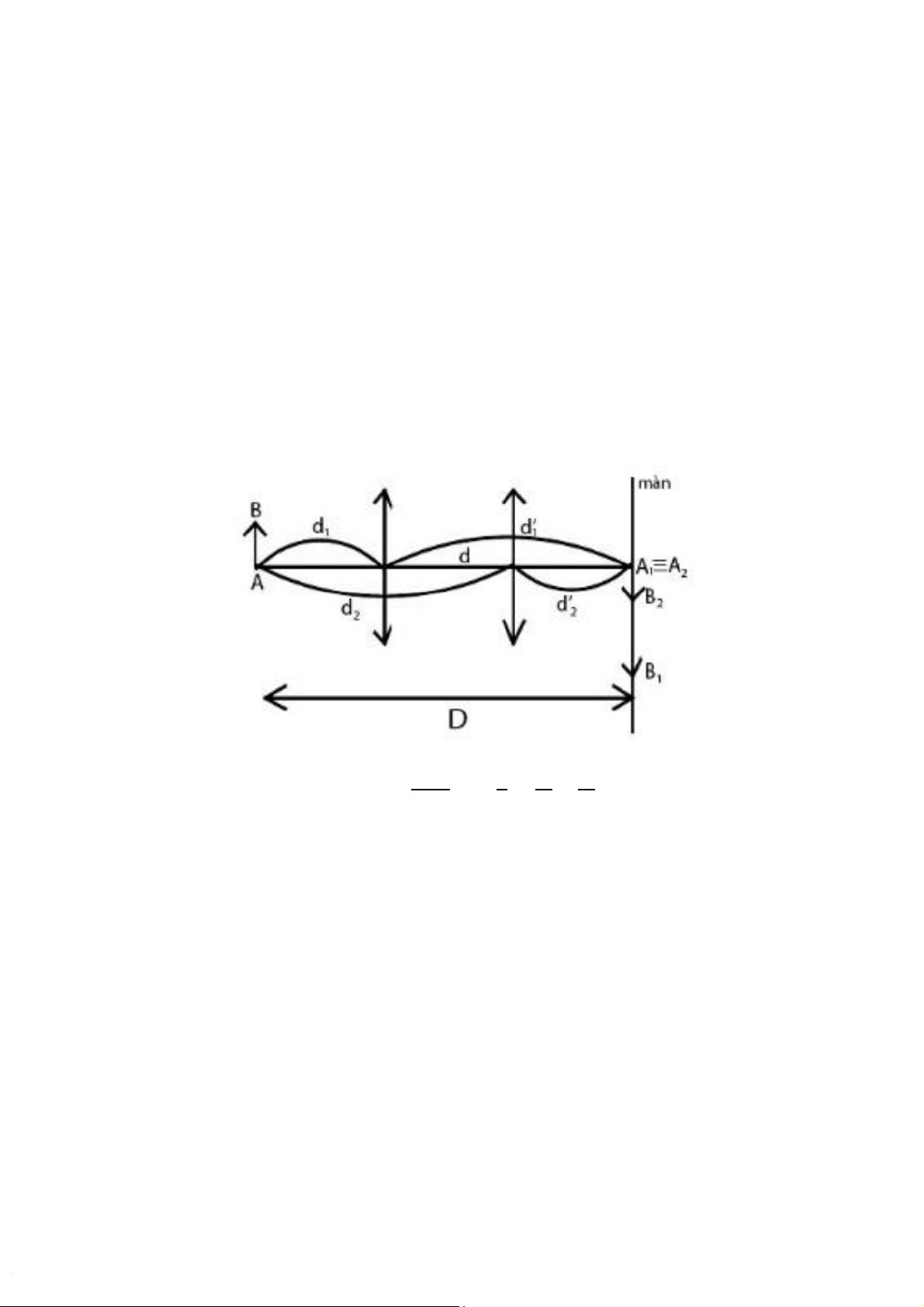
Ta cố định khoảng cách D giữa vật và màn. Tìm 2 vị trí của thấu kính mà
đối với các vị trí đó một ảnh rõ nét được tạo ra trên màn. Nếu điều đó không
thực hiện được, hãy tăng khoảng cách D (để D > 4f’). Gọi d là khoảng cách
giữa 2 vị trí của thấu kính.
Ta có: D = d1+ d′1= d1+d1f′ d1−f′ ( vì 1f′=1 d1+1 ′ ) d1 → d12− Dd1+ Df′= 0 Xét phương trình: x2−Dx + Df′= 0 (*)
Để tồn tại 2 vị trí của thấu kính thì phương trình (*) phải có ∆> 0 ∆= D2−4Df′> 0 → D > 4f′
Nhận xét: để thực hiện được phép đo tiêu cự với phương pháp Bessel, nếu
f’ cố định thì ta phải chọn D sao cho lớn hơn 4f’, hoặc nếu D cố định thì ta phải
chọn thấu kính có f’ nhỏ hơn D/4. Trang 2
Nghiệm của phương trình (*): d1=D − √D2−4Df′ 2 và d2=D+√D2−4Df′ 2 Ta có:
d2− d1= d → D+√D2−4Df′−D+√D2−4Df′ 2= d →√D2−4Df′= d → d2= D2− 4Df′ → f′=D2− d2 4D
Dễ dàng thấy được d1, d2, d1’, d2’ được biểu diễn theo D,d: ′=D + d ′=D − d 2; 𝑑2+ 𝑑12=𝐷 d1= d2 2; d2= d1 2
và hai vị trí của thấu kính đối xứng qua mặt phẳng trung trực vật- màn.
Vậy chỉ cần xác định d, D là xác định được f’: 𝐟′=𝐃𝟐− 𝐝𝟐 𝟒𝐃 2 Phương pháp Silbermann
Phương pháp Silbermann sử dụng điều ghi nhận dưới đây đối với các thấu
kính hội tụ : khoảng cách tối thiểu D giữa một vật thật và ảnh của nó, trong
trường hợp đó là ảnh thật, là bằng 4f’, từ đó : D ≥ 4f′.
III Các bước thí nghiệm
1 Tìm tiêu cự thấu kính dựa trên công thức Bessel:
Đèn và màn ảnh là cố định, thực hiên dịch chuyển thấu kính giữa đèn và
màn ảnh và tìm 2 vị trí sao cho có ảnh rõ trên màn. Xác định bằng ống ngắm
các giá trị D và d. Chứng minh bằng thực nghiệm rằng hai vị trí trên đối xứng
nhau qua trung điểm khoảng cách nguồn – màn ảnh và độ phóng đại khoảng
cách d tỷ lệ nghịch với khoảng cách D. Trang 3
Nếu khoảng cách D là xác định, tiêu cự cực đại của thấu kính là bao nhiêu
để có thể thực hiện được phép đo trên ? Cái đó gợi nhớ một cái gì tương tự ? 2 Phương pháp Silbermann
Ta đặt lần lượt trên bàn quang học nguồn sáng chiếu vật AB, một thấu kính
hội tụ LC làm thực hiện ảnh A’B’ của vật trên màn chiếu được đặt tiếp theo sau.
Chỉ có vật là cố định ở đây.
Tồn tại duy nhất một vị trí các mặt phẳng vật và ảnh tương ứng với độ
khuếch đại –1. Chứng minh rằng khoảng cách vật-ảnh lúc đó có giá trị bằng 4f’.
Dịch chuyển màn để một ảnh rõ nét được tạo ra ở đó. Nếu không thực hiện
được thì phải dịch thấu kính ra xa vật. Từ từ đưa thấu kính lại gần vật đến khi
tìm được một vị trí của màn mà trên đó ảnh là rõ nét. Lúc đó khoảng cách giữa
màn và vật là bằng 4f’. độ phóng đại ảnh khi đó bằng -1.
Thực hiện bằng thực nghiệm luận đề trên để xác định tiêu cự của một thấu kính hội tụ.
Sử dụng thị kính micro chia độ của vật và ảnh như thế nào để xác định độ
khuếch đại tuyến tính giữa chúng
IV Xử lí số liệu
1 Phương pháp Bessel:
1.1 Tìm khoảng cách giữa vật và màn D
-Ta có: sai số dụng cụ ( sai số của thước ): ∆ddc=1(mm) Vị trí đặt vật: d = v 20 (mm) ∆dv= ∆ddc = 1(mm) Vậy vị trí đặt vật:
dv=20 ± 1 (mm), ε = 5%
Vị trí đặt màn dm=980(mm) ∆dm= ∆ddc = 1(mm)
Vậy vị trí đặt màn dm=980 ± 1 (mm) , ε = 0,1% -Ta có: D = dm− dv → D=980 −20 =960(mm)
Mặt khác: ∆D = ∆dm+ ∆dv= 2(mm)
Vậy khoảng cách giữa vật và màn : Trang 4
D = D+ ∆D = 960 ± 2(mm) , ε = 0,2%
1.2 Tìm 2 vị trí cho ảnh rõ nét trên màn -Vị trí thứ nhất d :1 Lần đo d1 ∆d1 Lần 1 479 7,4 Lần 2 481 5,4 Lần 3 475 11,4 Lần 4 502 15,6 Lần 5 495 8,6 Trung bình d1 = 486,4 ∆d  1  = 9,68
-Sai số tuyệt đối của d1: ∆d1= ∆d
1+ ∆ddc = 9,68 + 1 = 10,68 ≈11
Vậy vị trí thứ nhất của thấu kính cho ảnh rõ nét trên màn:
d1= d1± ∆d1=486 ±11(mm), ε = 2,2% -Vị trí thứ hai d :2 Lần đo d2 ∆d2 Lần 1 623 12,6 Lần 2 585 25,4 Lần 3 615 4,6 Lần 4 608 2,4 Lần 5 621 10,6 Trung bình d2 = 610,4 ∆d  2  = 11,12
-Sai số tuyệt đối của d1: ∆d2= ∆d
 2+ ∆ddc =11,12 + 1 = 12,12 ≈12
Vậy vị trí thứ hai của thấu kính cho ảnh rõ nét trên màn:
d2= d2± ∆d2=610 ±12 (mm), ε = 1,9% -Nhận xét:
Vị trí điểm trung trực của mặt phẳng vật- màn: dmid =dv+ dm 2=20 +9602=490 → dmid =490 ± 1(mm) Trang 5
Trung điểm của 2 vị trí của thấu kính: ′=d1+ d2 ′=486,4 + 610,4 dmid 2 → dmid 2=548,4 ≈ 548 → dm′id =548 ±11(mm)
Vậy 2 vị trí của thấu kính cho ảnh rõ nét trên màn đối xứng qua mặt
phẳng trung trực vật-màn, kết quả thực tế đúng so với lý thuyết.
-Khoảng cách giữa 2 vị trí của thấu kính cho ảnh rõ nét trên màn: d = d2− d1
→ d= d2 − d1
 =610,4 − 486,4 = 124 (mm)
Mặt khác: ∆d = ∆d2+ ∆d1=11,12 + 9,68 =20,8 ≈ 21 (mm)
Vậy d = d± ∆d = 124 ±21 (mm), ε = 17% 1.3 Tính f’:
-Dựa vào công thức bessel: f′=D2− d2 4D =D2− d  2 =9602−1242 → f′ 4.960 ≈235,9967(mm) 4D
-Tính sai số tương đối của f’: lnf′=ln D2− d2 4D → d(lnf′) = d(ln D2− d2 4D ) →d(f′)
f= d(ln(D2− d2)) − d(ln 4D) →d(f′f)′=2D. d(D)+ D 2 2 d − . d d2(d − ) d(D) D
→ εf′ =∆f′=2D . ∆D + 2d 2. ∆ + d ∆D  f′ D 2− d D → εf′ =2.960. 9 2 6 + 02 2 − .1 1 2 2 4 42.1 +12 960 ≈ 0,009 Trang 6
-Sai số tuyệt đối của f’:
∆f′= εf′. f′=235,9967.0,012 ≈ 2,2 (mm)
Vậy tiêu cự của thấu kính hội tụ đã dùng:
𝐟′= 𝐟′± ∆𝐟′=𝟐𝟑𝟔, 𝟎 ± 𝟐, 𝟐 (𝐦𝐦), 𝛆 = 𝟎, 𝟗%
2 Phương pháp Silbermann
Khi tồn tại duy nhất 1 vị trí các mặt phẳng vật và ảnh tương ứng với độ
khuếch đại -1, phương trình (*) sẽ có nghiệm duy nhất: → ∆= 0 → D2−4Df′= 0 → D = 4f′ 2.1 Tính D:
Ta có kết quả đo vị trí của màn khi ảnh rõ nét trên màn với độ khuếch đại -1: Lần đo dm ∆dm Lần 1 532 5,8 Lần 2 543 5,2 Lần 3 537 0,8 Lần 4 531 6,8 Lần 5 546 8,2 Trung bình dm  = 537,8 ∆d m= 5,36
-Sai số dụng cụ: ∆ddc = 1(mm)
-Sai số tương đối của dm: ∆dm= ∆d
m+ ∆ddc = 5,36 + 1 = 6,36 ≈ 6,4(mm) -Vậy kết quả đo dm:
dm= dm± ∆dm=537,8 ± 6,4(mm), ε = 1%
-Vị trí của vật d :v dv= dv± ∆dv=20 ± 1 (mm), ε = 5% -Tính D: D = dm− dv → D= dm
 − dv =537,8 − 20 =517,8 (mm) Trang 7 Ta có:
∆D = ∆dm+ ∆dv= 6,36 + 1 = 7,36 ≈ 7,4 (mm)
-Vậy khoảng cách giữa vật và màn D:
D = D± ∆D = 517,8 ± 7,4 (mm), ε = 1,4%
2.2 Tính tiêu cự thấu kính f’: -Theo lí thuyết: f′=D 4 =D4=517,8 → f′ 4=129,45 (mm)
Mặt khác: lnf′=ln D 4 → lnf′= lnD − ln4
→ d(lnf′)= d(lnD − ln4)→ d(f′)f′ =d(D)D
→∆f′=∆D → ∆f′=7,36.129,45 517,8 = 1,84 ≈ 1,8 (mm) f′ D
Vậy tiêu cự của thấu kính đã dùng là:
𝐟′= 𝐟′± ∆𝐟′=𝟏𝟐𝟗, 𝟓 ± 𝟏, 𝟖 (𝐦𝐦), 𝛆 = 𝟏, 𝟒% Trang 8