












































Preview text:
1 2
PHẦN 1. DÃY SỐ, CẤP SỐ CỘNG VÀ CẤP SỐ NHÂN ....................................................................... 5
I. PHƯƠNG PHÁP QUY NẠP TOÁN HỌC ......................................................................................... 5
II. DÃY SỐ................................................................................................................................................ 8
DẠNG 1: THIẾT LẬP CÔNG THỨC TÍNH SỐ HẠNG TỔNG QUÁT u THEO N ................. 8 n
DẠNG 2: TÍNH TĂNG, GIẢM CỦA DÃY SỐ ............................................................................... 10
DẠNG 3: DÃY SỐ BỊ CHẶN ............................................................................................................ 11
III. CẤP SỐ CỘNG ............................................................................................................................... 13
DẠNG 1: CHỨNG MINH MỘT DÃY SỐ u LÀ CẤP SỐ CỘNG ........................................... 13 n
DẠNG 2: TIM SỐ HẠNG ĐẦU TIEN, CÔNG SAI CỦA CẤP SỐ CỘNG, TIM SỐ HẠNG
THỨ K CỦA CẤP SỐ CỘNG, TINH TỔNG K SỐ HẠNG ĐẦU TIÊN ...................................... 14
DẠNG 3: DỰA VÀO TÍNH CHẤT CỦA CẤP SỐ CỘNG, CHỨNG MINH ĐẲNG THỨC ..... 16
IV. CẤP SỐ NHÂN ................................................................................................................................ 17
DẠNG 1: CHỨNG MINH MỘT DÃY un LÀ CẤP SỐ NHÂN ................................................. 17
DẠNG 2: XÁC ĐỊNH SỐ HẠNG ĐẦU CÔNG BỘI, XÁC ĐỊNH SỐ HẠNG THỨ K, TÍNH
TỔNG CỦA N SỐ HẠNG ĐẦU TIÊN ............................................................................................. 19
DẠNG 3: DỰA VÀO TÍNH CHẤT CỦA CẤP SỐ NHÂN, CHỨNG MINH ĐẲNG THỨC ..... 22
PHẦN 2: GIỚI HẠN ................................................................................................................................. 23
I. GIỚI HẠN DÃY SỐ ........................................................................................................................... 23 P n
DẠNG 1: u LÀ MỘT PHÂN THỨC HỮU TỈ DẠNG u
( TRONG ĐÓ P n,Q n n n Q n
LÀ HAI ĐA THỨC CỦA N). ............................................................................................................ 23 P n
DẠNG 2: u LA MỘT PHÂN THỨC HỮU TỈ DẠNG u
( TRONG ĐÓ P n,Q n LÀ n n Q n
CÁC BIỂU THỨC CHỨA CĂN CỦA N). ....................................................................................... 25 P n
DẠNG 3: u LÀ MỘT PHÂN THỨC HỮU TỈ DẠNG u
( TRONG ĐÓ P n,Q n n n Q n
LÀ CÁC BIỂU THỨC CHỨA HÀM MŨ n , n, n
a b c ,…. ) ............................................................... 26
DẠNG 4 : NHÂN LƯỢNG LIÊN HỢP ............................................................................................ 27
DẠNG 5. GIỚI HẠN CỦA MỘT TỔNG DÀI DÀI ........................................................................ 29
II. GIỚI HẠN HÀM SỐ ........................................................................................................................ 31
DẠNG 1. THAY TRỰC TIẾP ĐƯỢC SỐ ....................................................................................... 31 P(x) DẠNG 2. L = lim
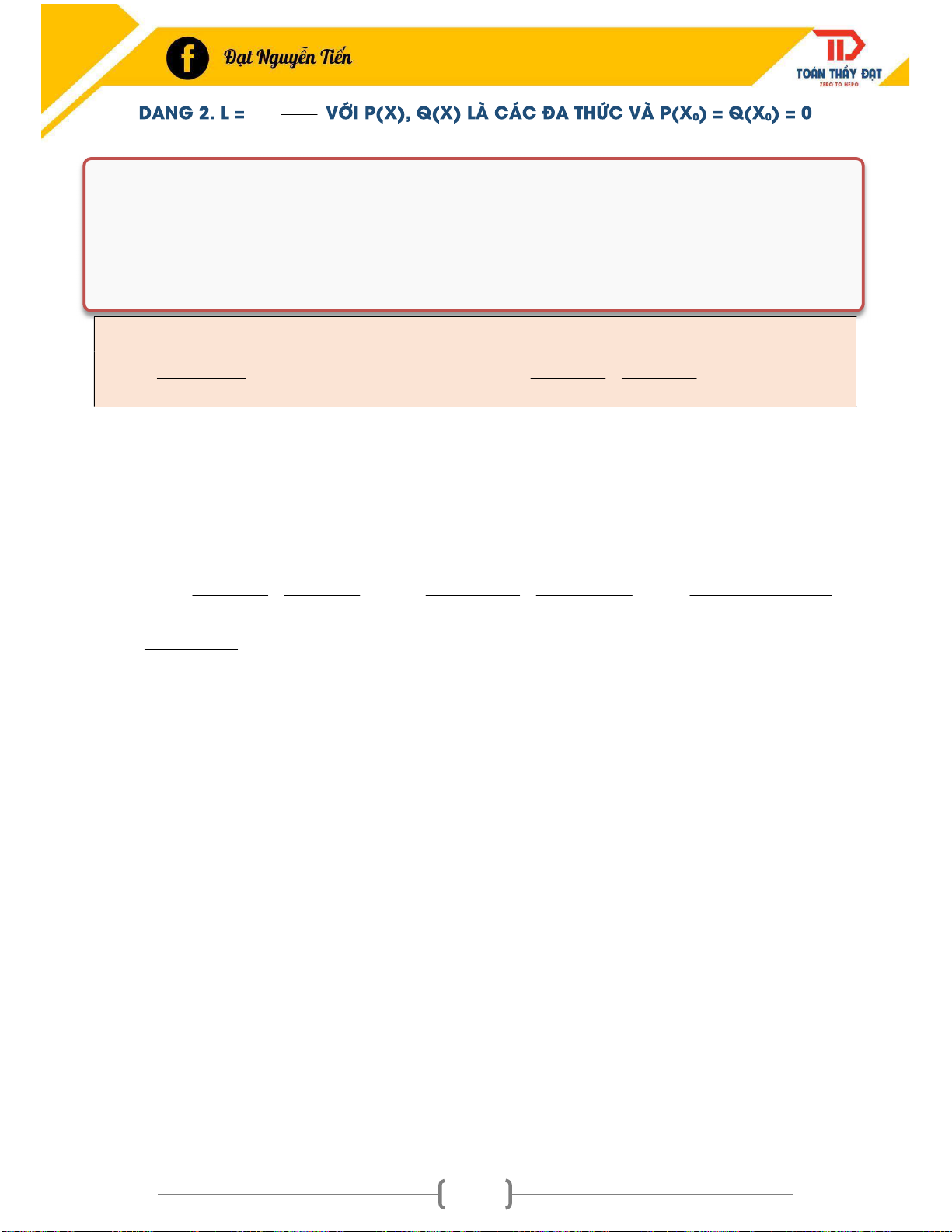
VỚI P(X), Q(X) LÀ CÁC ĐA THỨC VÀ P(X0) = Q(X0) = 0................. 32 x 0 x Q(x) P(x) DẠNG 3. L = lim
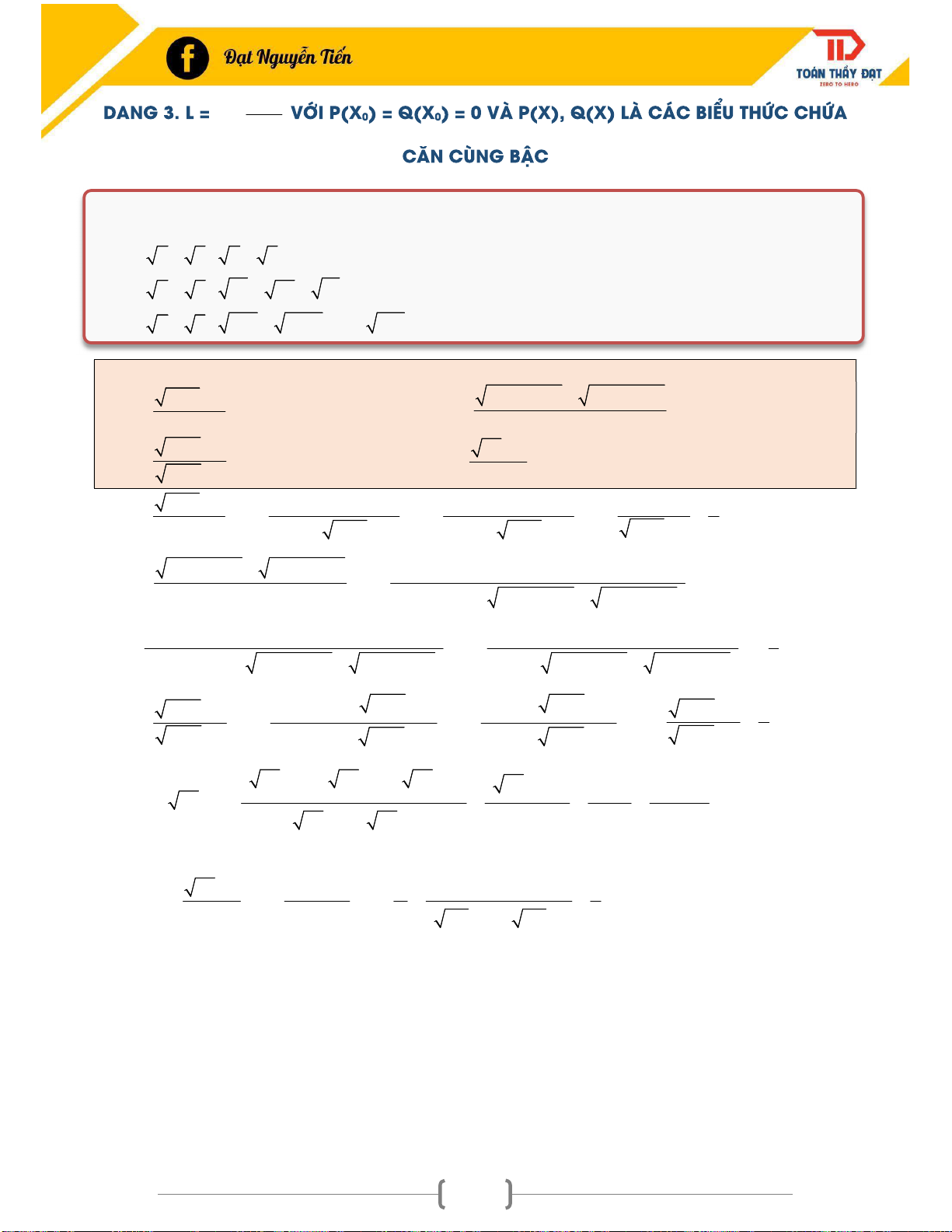
VỚI P(X0) = Q(X0) = 0 VÀ P(X), Q(X) LÀ CÁC BIỂU THỨC CHỨA x 0 x Q(x)
CĂN CÙNG BẬC ............................................................................................................................... 33 3
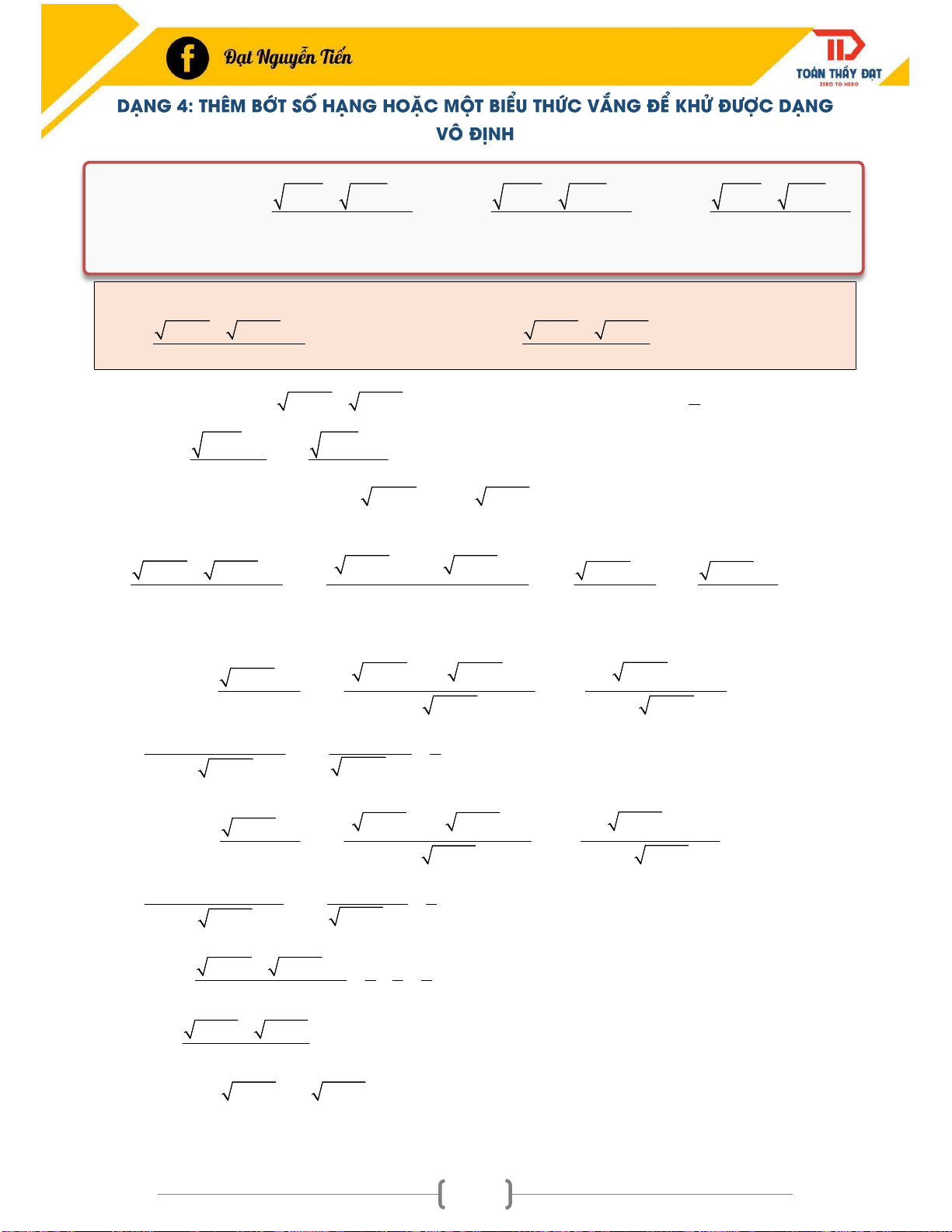
DẠNG 4: THÊM BỚT SỐ HẠNG HOẶC MỘT BIỂU THỨC VẮNG ĐỂ KHỬ ĐƯỢC DẠNG
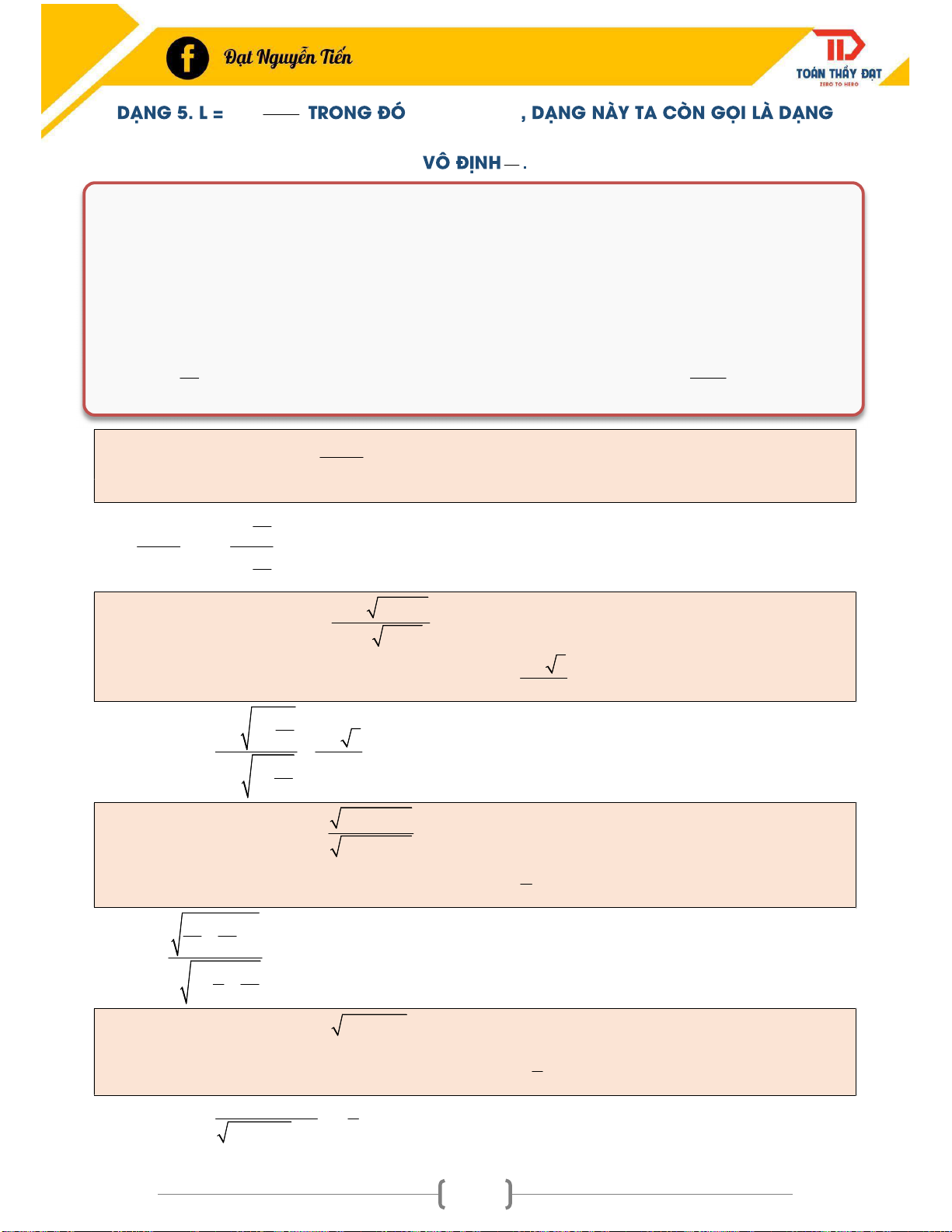
VÔ ĐỊNH ............................................................................................................................................. 34 P(x) DẠNG 5. L = lim
TRONG ĐÓ P(x),Q(x) , DẠNG NÀY TA CÒN GỌI LÀ DẠNG x Q(x) VÔ ĐỊNH
. ....................................................................................................................................... 36
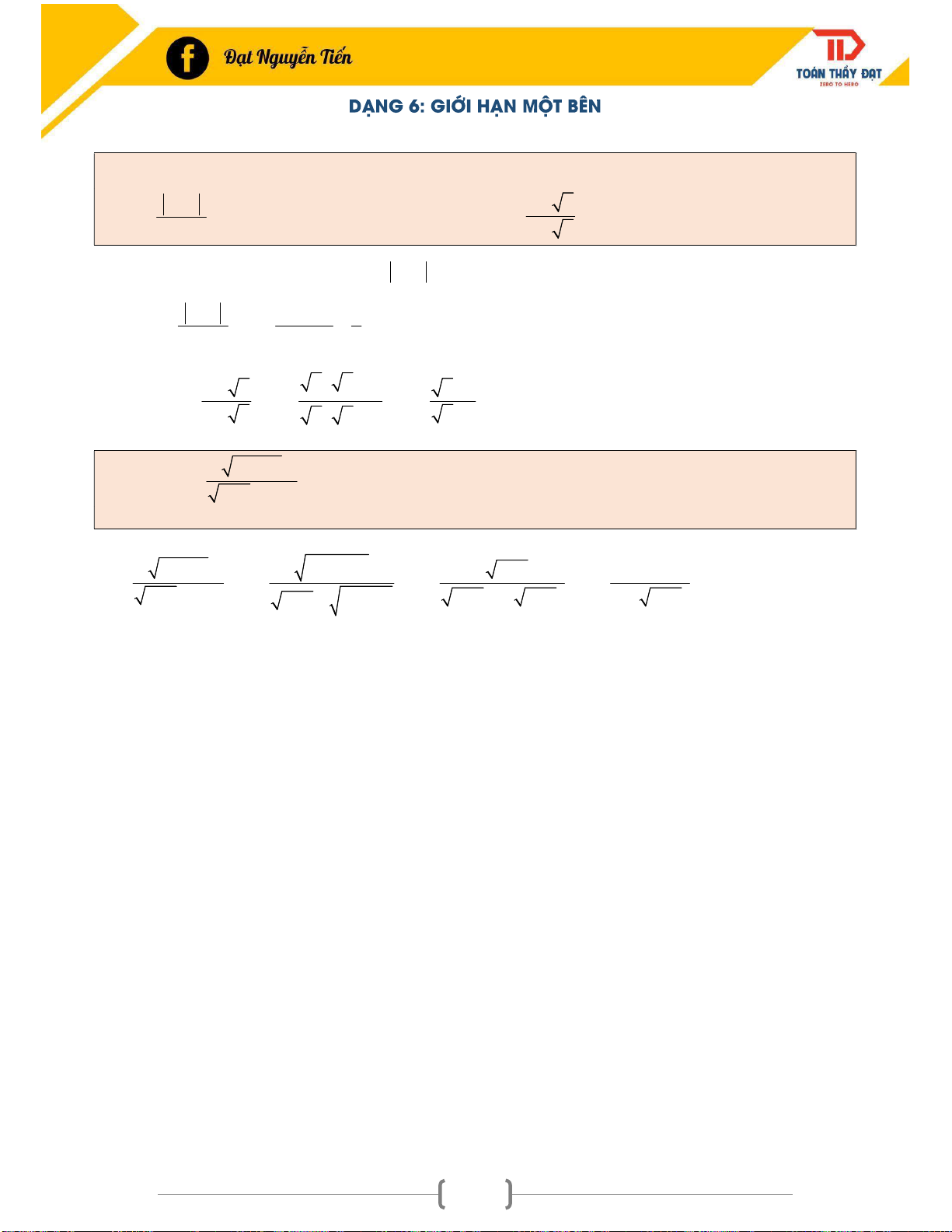
DẠNG 6: GIỚI HẠN MỘT BÊN ...................................................................................................... 37
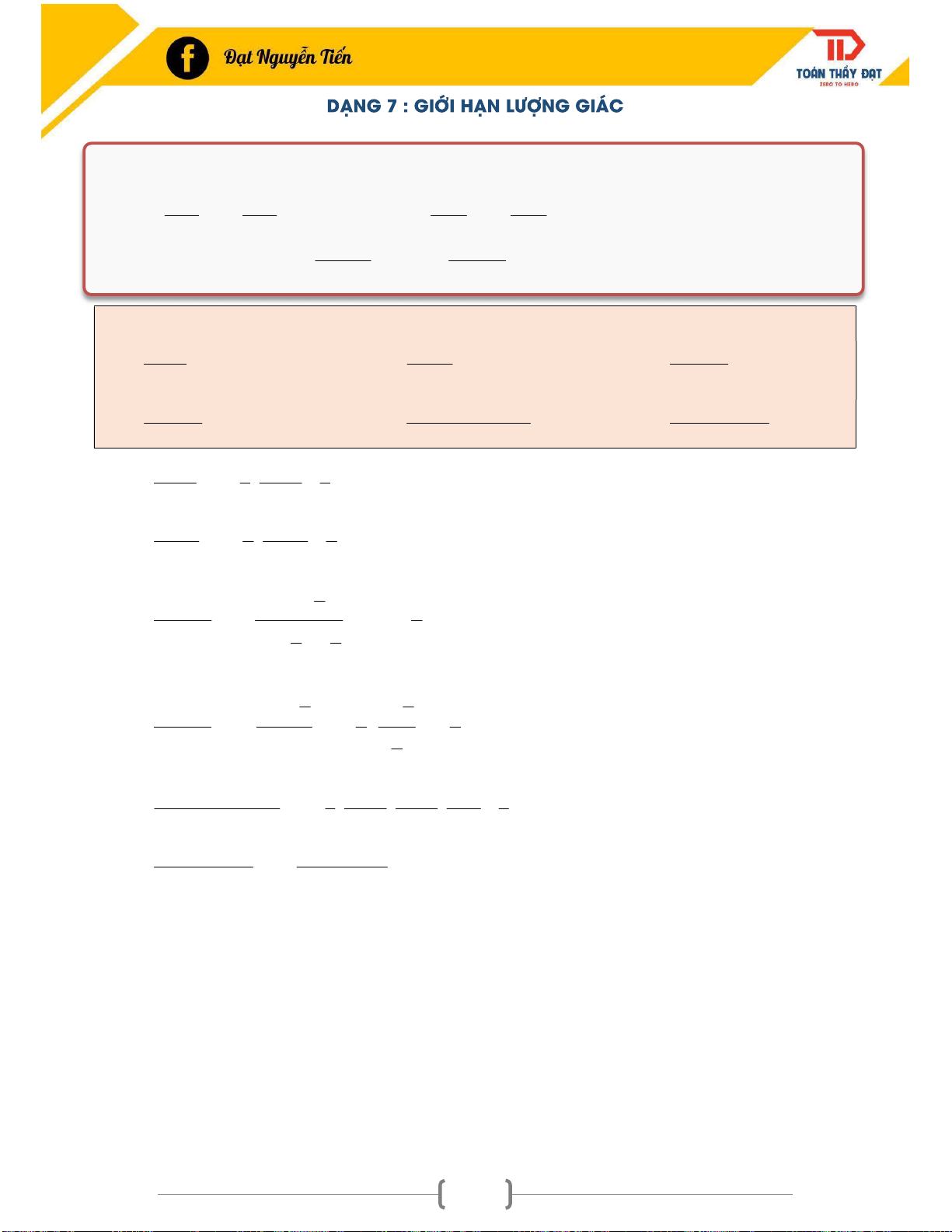
DẠNG 7 : GIỚI HẠN LƯỢNG GIÁC ............................................................................................. 38
DẠNG 8: SỬ DỤNG MÁY TÍNH: TÍNH GIỚI HẠN .................................................................... 39
III. HÀM SỐ LIÊN TỤC ....................................................................................................................... 41
DẠNG 1: XÉT TÍNH LIÊN TỤC CỦA HÀM SỐ TẠI MỘT ĐIỂM ............................................ 41
DẠNG 2: HÀM SỐ LIÊN TỤC TRÊN MỘT TẬP HỢP ............................................................... 43
DẠNG 3: CHỨNG MINH PHƯƠNG TRÌNH CÓ NGHIỆM ....................................................... 45
PHẦN 3: ĐẠO HÀM ................................................................................................................................. 48
I. QUY TẮC TÍNH ĐẠO HÀM ............................................................................................................ 48
II. ĐẠO HÀM CẤP CAO ...................................................................................................................... 53
DẠNG 1: TÍNH ĐẠO HÀM CẤP CAO CỦA HÀM SỐ. ............................................................... 53
DẠNG 2: TÌM ĐẠO HÀM CẤP N CỦA MỘT HÀM SỐ .............................................................. 54
DẠNG 3: CHỨNG MINH ĐẲNG THỨC ........................................................................................ 55
III. PHƯƠNG PHÁP CASIO – VINACAL ......................................................................................... 57
PHẦN 4: PHƯƠNG TRÌNH TIẾP TUYẾN ........................................................................................... 61
KĨ THUẬT LẬP PHƯƠNG TRÌNH TIẾP TUYẾN CỦA ĐỒ THỊ HÀM SỐ BẰNG MÁY
TÍNH CASIO - VINACAL ................................................................................................................ 69
PHẦN 5. QUAN HỆ VUÔNG GÓC TRONG KHÔNG GIAN ............................................................. 72
DẠNG 1: CHỨNG MINH ĐƯỜNG THẲNG VUÔNG GÓC MẶT PHẲNG ................................. 72
DẠNG 2: CHỨNG MINH ĐƯỜNG THẲNG VUÔNG GÓC ĐƯỜNG THẲNG .......................... 74
DẠNG 3: CHỨNG MINH MẶT PHẲNG VUÔNG GÓC VỚI MẶT PHẲNG .............................. 75
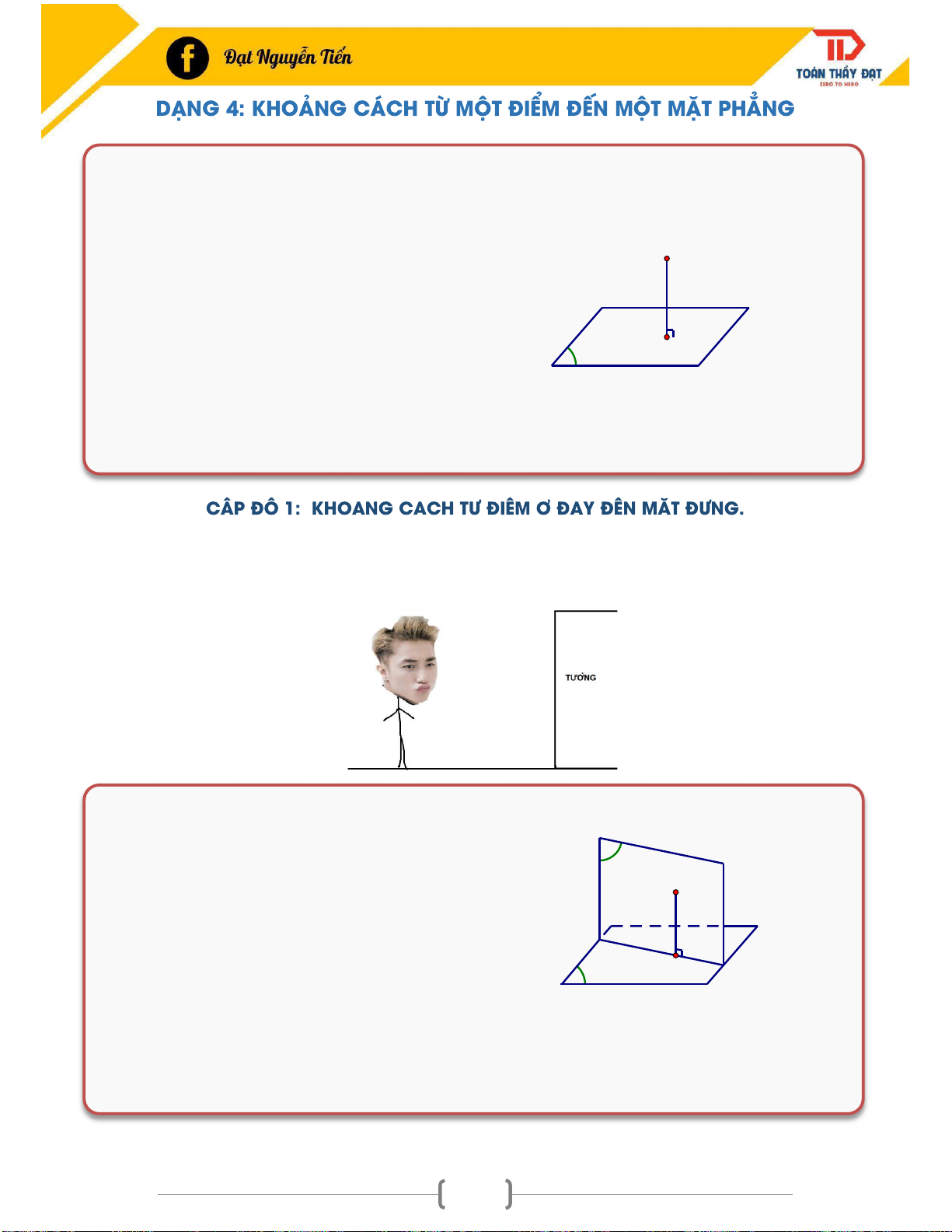
DẠNG 4: KHOẢNG CÁCH TỪ MỘT ĐIỂM ĐẾN MỘT MẶT PHẲNG ...................................... 78
CẤP ĐỘ 1: KHOẢNG CÁCH TỪ ĐIỂM Ở ĐÁY ĐẾN MẶT ĐỨNG. ....................................... 78
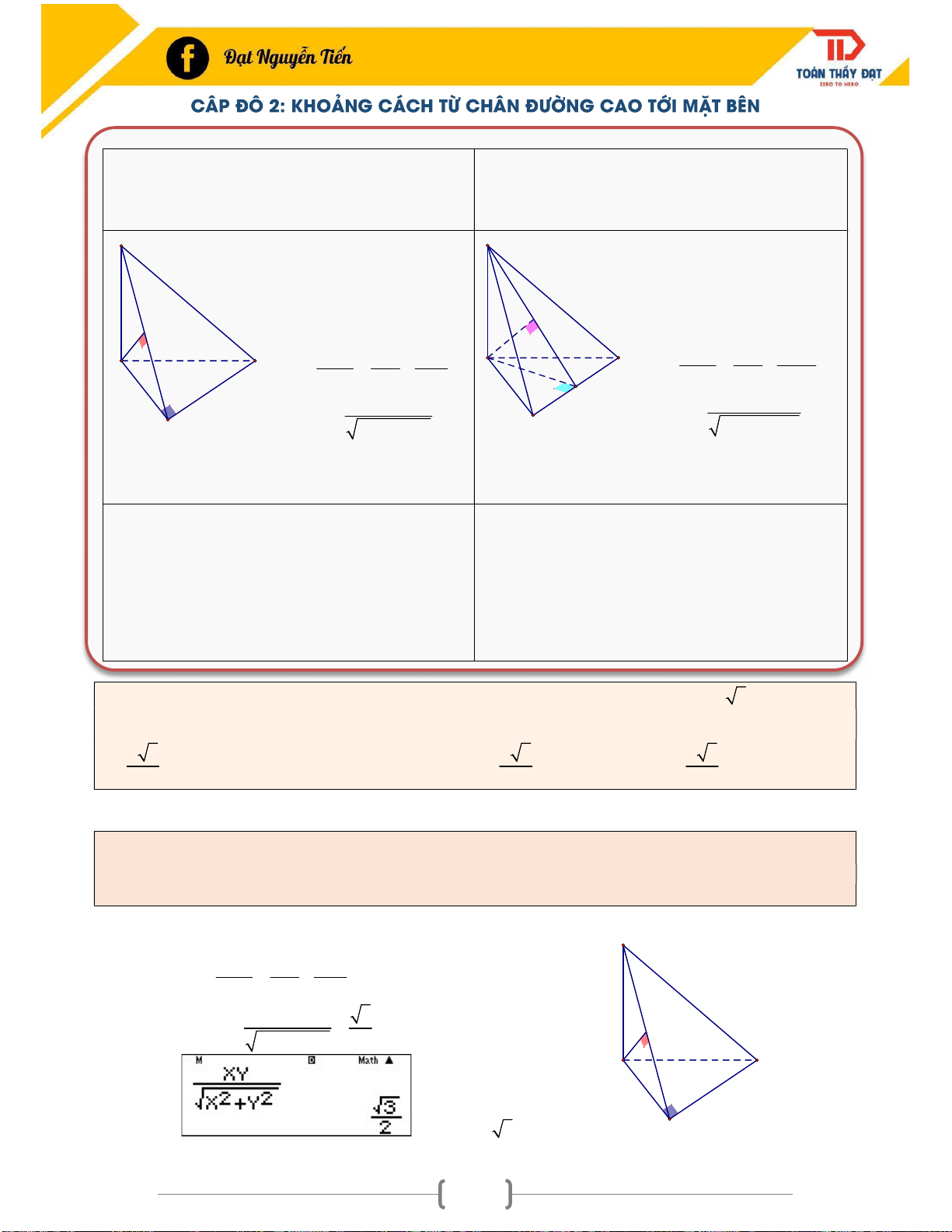
CẤP ĐỘ 2: KHOẢNG CÁCH TỪ CHÂN ĐƯỜNG CAO TỚI MẶT BÊN ................................. 81
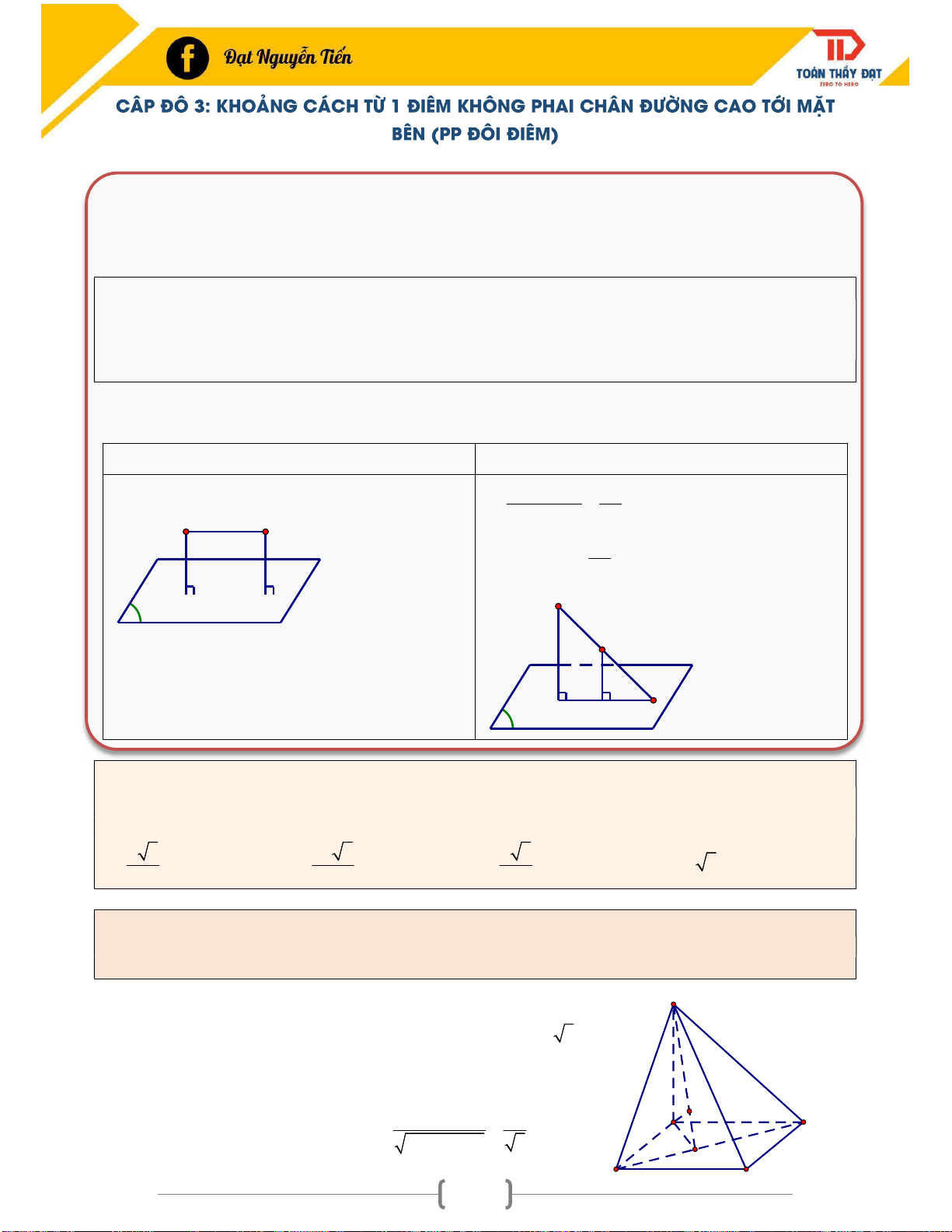
CẤP ĐỘ 3: KHOẢNG CÁCH TỪ 1 ĐIỂM KHÔNG PHẢI CHÂN ĐƯỜNG CAO TỚI MẶT
BÊN (PP ĐỔI ĐIỂM) ......................................................................................................................... 84
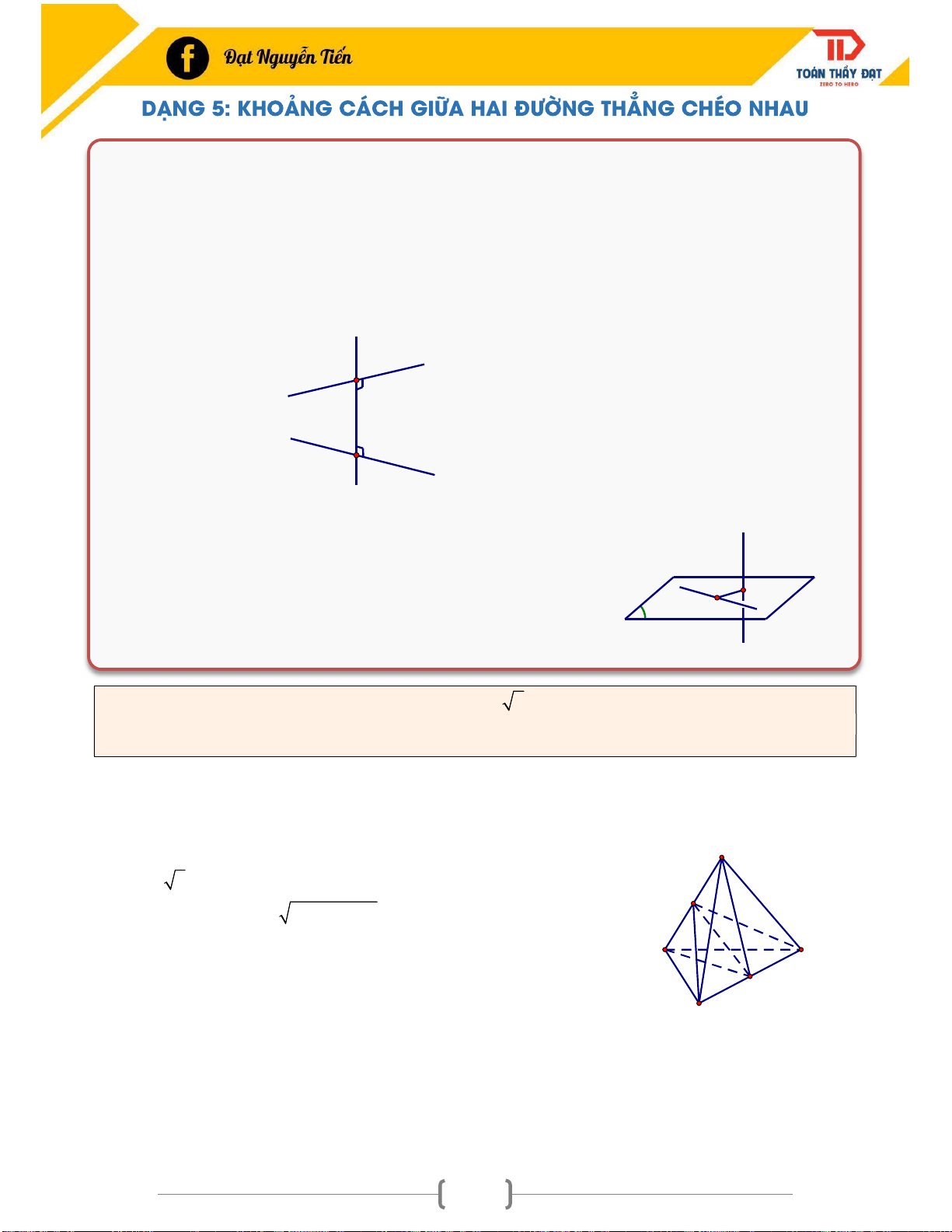
DẠNG 5: KHOẢNG CÁCH GIỮA HAI ĐƯỜNG THẲNG CHÉO NHAU .................................... 87
BÀI TOÁN TỔNG QUÁT 2 BƯỚC TÍNH KHOẢNG CÁCH TỪ A ĐẾN B .............................. 90
DẠNG 6: GÓC TRONG KHÔNG GIAN ............................................................................................ 92
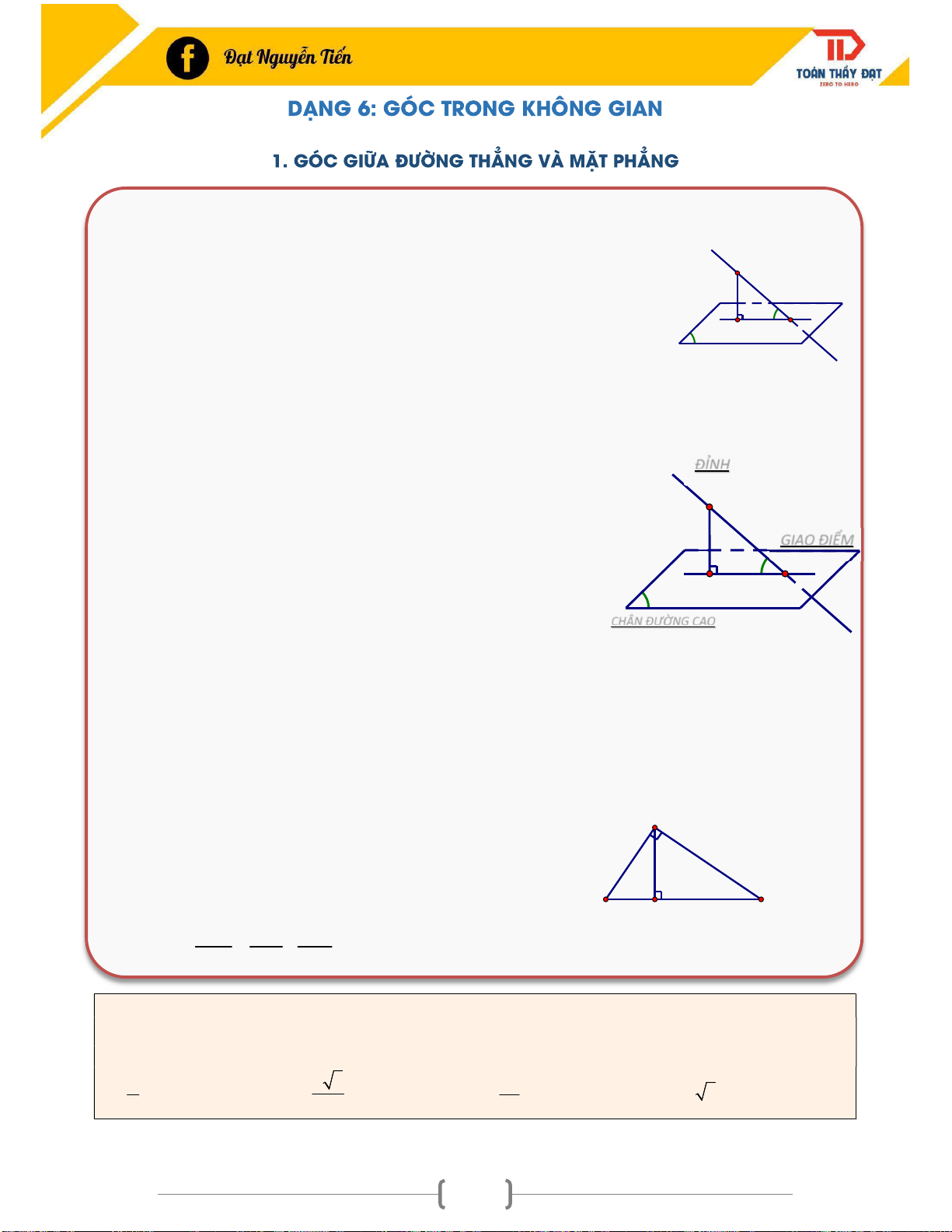
1. GÓC GIỮA ĐƯỜNG THẲNG VÀ MẶT PHẲNG ..................................................................... 92
2. GÓC GIỮA HAI MẶT PHẲNG ................................................................................................... 94 4 TÓM TẮT GIÁO KHOA
Nguyên lý quy nạp toán học:
Giả sử P n là một mệnh đề phụ thuộc vào số tự nhiên n. Nếu cả hai điều kiện i và ii dưới đây được
thỏa mãn thì P n đúng với mọi n m (m là số tự nhiên cho trước). iPm đúng.
ii Với mỗi số tự nhiên k m, nếu Pk 1 đúng.
Phương pháp chứng minh dựa trên nguyên lý quy nạp toán học gọi là phương pháp quy nạp toán học( hay
gọi tắt là phương pháp quy nạp). Phương pháp:
Để chứng minh một mệnh đề P n phụ thuộc vào số tự nhiên n đúng với mọi n m (m là số tự nhiên
cho trước), ta thực hiện theo hai bước sau:
Bước 1: Chứng minh rằng P n đúng khi n m .
Bước 2: Với k là một số tự nhiên tùy ý, k m . Giả sử P n đúng khi n k , ta sẽ chứng minh P n
cũng đúng khi n k 1. Theo nguyên lý quy nạp toán học, ta kết luận rằng P n đúng với mọi số tự nhiên n . m CÁC VÍ DỤ
Ví dụ 1: Chứng minh rằng với mọi số nguyên n, ta có: a).
n n nn 2 1.4 2.7 3 1 1 1 1 1 n n 3 b). 1.2.3 2.3.4 n n 1 n 2 4n 1 n 2 a).
n n nn 2 1.4 2.7 3 1 1 (1)
Với n = 1: Vế trái của (1) 1.4 4 ; Vế phải của (1) 2
1(11) 4 . Suy ra Vế trái của (1) = Vế phải của (1). Vậy (1) đúng với n = 1.
Giả sử (1) đúng với n k . Có nghĩa là ta có:
k k k k 2 1.4 2.7 3 1 1 2
Ta phải chứng minh (1) đúng với n k 1. Có nghĩa ta phải chứng minh:
k k k k k k 2 1.4 2.7 3 1 1 3 4 1 2 5
Thật vậy 1.4 2.7 k 3k 1 k
1 3k 4 k k 2 1 k 1 3k 4
k k 2 1 2 (đpcm). kk 2 1
Vậy (1) đúng khi n k 1. Do đó theo nguyên lí quy nạp, (1) đúng với mọi số nguyên dương n. 1 1 1 n n 3 b). (1) 1.2.3 2.3.4 n n 1 n 2 4n 1 n 2 1 1 1(1 3) 1
Với n = 1: Vế trái của (1)
; Vế phải của (1) . 1.2.3 6 4(11)(1 2) 6
Suy ra Vế trái của (1) = Vế phải của (1). Vậy (1) đúng với n = 1. 1 1 1 k k 3
Giả sử (1) đúng với n k . Có nghĩa là ta có: 1.2.3 2.3.4 k k 1 k 2 4k 1 k 2 2
Ta phải chứng minh (1) đúng với n k 1. Có nghĩa ta phải chứng minh: 1 1 1 1 k 1 k 4 1.2.3 2.3.4 k k 1 k 2 k
1 k 2k 3 4k 2k 3 2 1 1 1 1 Thật vậy 1.2.3 2.3.4 k k 1 k 2 k 1 k 2k 3
k k 3 4k 1k2 k k 3 1 1 4 k k 4k 1 k 2 k
1 k 2k 3 4k 1 k 2 3 k 3 k 6k 9k 4 k 2 3 2 1 k 4 k 1 k 4 (đpcm). 4k
1 k 2k 3 4k
1 k 2k 3 4k 2k 3
Vậy (1) đúng khi n k 1. Do đó theo nguyên lí quy nạp, (1) đúng với mọi số nguyên dương n.
Ví dụ 2: Với mỗi số nguyên dương n, gọi u 9n 1 . Chứng minh rằng với mọi số nguyên dương n thì n u luôn chia hết cho 8. n Ta có 1
u 9 1 8 chia hết cho 8 (đúng). 1
Giả sử u 9k 1chia hết cho 8. k Ta cần chứng minh k 1 u
9 1 chia hết cho 8. k 1 Thật vậy, ta có k 1 u
9 1 9.9k 1 9 9k 1 8 9u 8. Vì 9u và 8 đều chia hết cho 8, nên u k 1 k k k 1 cũng chia hết cho 8.
Vậy với mọi số nguyên dương n thì u chia hết cho 8. n 6
Ví dụ 3: Chứng minh rằng với mọi số tự nhiên n 2 , ta luôn có: n 1 2 2n 3 (*) Với n 2 ta có 2 1
2 2.2 3 8 7 (đúng). Vậy (*) đúng với n 2 .
Giả sử với n k, k 2 thì (*) đúng, có nghĩa ta có: k 1 2 2k 3 (1).
Ta phải chứng minh (*) đúng với n k 1, có nghĩa ta phải chứng minh: k 2 2 2(k 1) 3
Thật vậy, nhân hai vế của (1) với 3 ta được: k 1 k k 2 2.2 2 2 3 2
4k 6 2(k 1) 3 . Vậy k2 2 2(k 1) 3 (đúng).
Do đó theo nguyên lí quy nạp, (*) đúng với mọi số nguyên dương n 3 . 7 un Phương pháp: n Nếu u
u a a . . a . . a a n có dạng n 1 2 k n (kí hiệu u
a ) thì biến đổi k thành hiệu của hai số n k k1
hạng, dựa vào đó thu gọn un .
Nếu dãy số un được cho bởi một hệ thức truy hồi, tính vài số hạng đầu của dãy số ( chẳng hạn tính u ,u ,. . u 1 2
), từ đó dự đoán công thức tính n theo n, rồi chứng minh công thức này bằng phương pháp quy
nạp. Ngoài ra cũng có thể tính hiệu u u u n1
n dựa vào đó để tìm công thức tính n theo n. n
Ví dụ 1: Cho dãy số a . Đặt u a . Tính u ,u ,u ,u và xác định công thức tính u theo n trong n n k 1 2 3 4 n k 1 1 trường hợp a k k k 1 1 1 1 1 2 u a ; u a a 1 1 1.2 2 2 1 2 2 2.(2 1) 3 2 1 3
u a a a u a 3 1 2 3 2 3 3 3(3 1) 4 3 1 4
u a a a a u a 4 1 2 3 4 3 4 4 4.5 5 1 1 1 Ta có a , do đó: k k k 1 k k 1 n 1 1 1 1 1 1 1 1 u a 1 ... 1 . n k k 1 2 2 3 n 1 n n n 1 n 1 u 1
Ví dụ 2: Dãy số u được xác định bằng cộng thức: 1 n 1. n 3 u u n n 1 n
a). Tìm công thức của số hạng tổng quát.
b). Tính số hạng thứ 100 của dãy số. a). Ta có: 3 3 u
u n u u n . n 1 n n 1 n Từ đó suy ra: u 1 1 3 u u 1 2 1 3 u u 2 3 2 3 u u 3 4 3 ..............………… 8 u u n 2 n n 3 1 2 u u n 3 1 n n 1
Cộng từng vế n đẳng thức trên:
u u u u u ... u u u u
11 2 3 ... n n n n n n 23 3 3 3 3 1 1 2 1 3 2 1 2 1 u
n 3 n 3 3 3 3 1 1 2 3 ... 2 1 . n n 1 .n
Bằng phương pháp quy nạp ta chứng minh được: 1 2 3 ... n 2 2 3 3 3 3 1 4 n n 2 2 1 Vậy u 1 n 4 2 2 100 .99 b). u 1 24502501. 100 4 9 Phương pháp:
Cách 1: Xét dấu của biểu thức u u n1 n Nếu n N*,u u 0 un n1 n thì là dãy số tăng; Nếu n N*,u u 0 un n1 n thì là dãy số giảm. u Cách 2: Khi n N*,u 0 n1 n thì có thể so sánh với 1 un u
Nếu n1 1 thì un là dãy số tăng; un u
Nếu n1 1 thì un là dãy số giảm. un
Cách 3: Nếu dãy số un được cho bởi một hệ thức truy hồi thì ta có thể sử dụng phương pháp chứng
minh quy nạp để chứng minh u u u u n1 n (hoặc n1 n ) Chú ý: Nếu k N* : u u un k1 k thì dãy số không giảm. Nếu k N* : u un u k 1 k thì dãy số không tăng.
Ví dụ 3 : Xét tính tăng giảm của dãy số u biết: n 1 n 1 a). u 2 b). u c). u (1)n 2n n 1 n n n n 1 1 1 1 1 1 a). u u 2 2 0 n * n 1 n n 1 n n 1 n n(n 1)
Kết luận dãy số u là dãy số giảm. n n 1 2 b). u 1 n n 1 n 1 2 2 1 1 1 Ta có u u 1 1 0 n * n 1 n n 2
n 1 n 1 n 2 (n 1)(n 2)
Kết luận dãy số u là dãy số tăng. n c). u (1)n 2n n 1 Ta có u 3 ,u 5,u 9
, từ đó suy ra dãy số u là dãy không tăng không giảm. n 1 2 3 10 Phương pháp n 1). Nếu u a thì: n k k1 Thu gọn u u
n , dựa vào biểu thức thu gọn để chặn n . n
Ta cũng có thể chặn tổng a bằng một tổng mà ta có thể biết được chặn trên, chặn dưới của nó. k k1
2). Nếu dãy số ( un ) ho bởi một hệ thức truy hồi thì:
Dự đoán chặn trên, chặn dưới rồi chứng minh bằng phương pháp chứng minh quy nạp.
Ta cũng có thể xét tính đơn điệu ( nếu có) sau đó giải bất phương trình u u u n1 n dựa vào đó chặn ( n ). 2n 1
Ví dụ 4: Xét tính tăng hay giảm và bị chặn của dãy số : u ; n N * n n 3 2 2
2n 1 2n 1 2n 7n 3 2n 7n 4 7 Ta có: u u 0; n N * n 1 n n 4 n 3 n 4n 3 n 4n 3
Vậy: u là dãy số tăng. n 2n 1 2(n 3) 7 7 Ta có u 2 , suy ra: n n 3 n 3 n 3 1 n *
,u 2 nên u bị chặn trên. Vì u là dãy số tăng n *
,u u Nên u bị chặn n n n n 1 4 n
dưới. Vậy u bị chặn. n
Ví dụ 5: Cho dãy số u với u 1 n n 1 .2n n
a). Viết 5 số hạng đầu của dãy số.
b). Tìm công thức truy hồi.
c). Chứng minh dãy số tăng và bị chặn dưới. a).Ta có: u 1 1 1 1 .2 1 1 u 1 2 2 1 .2 5 2 u 1 3 3 1 .2 17 3 u 1 4 4 1 .2 49 4 u 1 5 5 1 .2 129 5 b). Xét hiệu: n 1 u u 1 . n 2 1 n 1 .2n n 1 n 2 .2n 1 .2n 2 1 .2n 1 .2n n n n n n u u n 1 2n. n 1 n 11 u 1 Vậy công thức truy hồi: 1 n 1. u u n 1 .2n n 1 n c). Ta có: u
u n 1 .2n 0 n 1. Từ đó suy ra dãy số u là dãy số tăng. n n 1 n Ta có: u 1 n
n Kết luận u là dãy số bị chặn dưới. n n 1 .2n 1 1. 12 TÓM TẮT GIÁO KHOA
1. Cấp số cộng là một dãy số ( vô hạn hay hữu hạn) mà trong đó, kể từ số hạng thứ hai, mỗi số hạng đều
bằng tổng của số hạng đứng ngay trước nó và một số d không đổi, nghĩa là:
( u ) là cấp số cộng n 2,u u d n n n 1
Số d được gọi là công sai của cấp số cộng.
2.Định lý 1: Nếu ( u ) là một cấp số cộng thì kể từ số hạng thứ hai, mỗi số hạng ( trừ số hạng cuối đối với n u u
cấp số cộng hữu hạn) đều là trung bình cộng của hai số hạng đứng kề nó trong dãy, tức là k 1 k 1 u k 2
Hệ quả: Ba số a, b, c ( theo thứ tự đó) lập thành một cấp số cộng a c 2b .
1). Định lý 2: Nếu một cấp số cộng có số hạng đầu u và công sai d thì số hạng tổng quát u của nó được 1 n
xác định bởi công thức sau: u u n 1 d n 1
2). Định lý 3: Giả sử u là một cấp số cộng có công sai d. n n
Gọi S u u u ... u n k 1 2 n k 1 n u u n 2u n 1 d 1 n 1
( S là tổng của n số hạng đầu tiên của cấp số cộng). Ta có : S . n n 2 2 PHƯƠNG PHÁP GIẢI TOÁN. un Phương pháp:
Để chứng minh dãy số u là một cấp số cộng, ta xét A u u n n 1 n
Nếu A là hằng số thì u là một cấp số cộng với công sai d A. n
Nếu A phụ thuộc vào n thì u không là cấp số cộng. n
Ví dụ 1: Trong các dãy số sau, dãy nào là cấp số cộng. Tìm số hạng đầu và công sai của cấp số cộng đó:
Dãy số u với u 19n 5 n n
Dãy số u với u 19n 5 n n Ta có u
u 19 n 1 5 19n 5 19 . Vậy u là một cấp số cộng với công sai d 19 và số n n 1 n
hạng đầu u 19.1 5 14 . 1 13 Phương pháp:
Ta thiết lập một hệ phương trình gồm hai ẩn u và d. Sau đó giải hệ phương trình này tìm được u và d. 1 1
Muốn tìm số hạng thứ k, trước tiên ta phải tìm u và d. Sau đó áp dụng công thức: u u k 1 d . k 1 1
Muốn tính tổng của k số hạng đầu tiên, ta phải tìm u và d. Sau đó áp dụng công thức: 1 k u u k 2u (k 1)d 1 k 1 S k 2 2
Ví dụ 2: Tìm số hạng đầu tiên, công sai, số hạng thứ 20 và tổng của 20 số hạng đầu tiên của các cấp số cộng sau, biết rằng: u 19 u u u 10 u u 14 u 8 a) 5 b) 2 3 5 c) 3 5 d) 6 u 35 u u 26 s 129 2 2 u u 16 9 4 6 12 2 4 u 19 u 4d 19 u 3 a) 5
1 . Áp dụng công thức u u n 1 d , ta có: 1 1 1 n 1 u 35 u 8d 35 d 4 9 1
Vậy số hạng đầu tiên u 3, công sai d 4 . 1
Số hạng thứ 20: u u 19d 3 19.4 79 . 20 1 202u 19d 1
Tổng của 20 số hạng đầu tiên: S 10 2.3 19.4 820 20 2 u u u 10 b) 2 3 5
1 . Ta cũng áp dụng công thức u u n 1 d : n 1 u u 26 4 6
u d u 2d u 4d 10 u 3d 10 u 1 1 1 1 1 1 1
u 3d u 5d 26 2u 8d 26 d 3. 1 1 1
Vậy số hạng đầu tiên u 1, công sai d 3. 1
Số hạng thứ 20: u u 19d 119.3 58 . 20 1 202u 19d 1
Tổng của 20 số hạng đầu tiên: S 10 2.119.3 590 20 2 u u 14 n2u (n 1)d 1 c) 3 5
1 . Áp dụng công thức u u n 1 d , S Ta có: n 1 s 129 n 2 12 5 2 4 14 u u d u d 1 1 1 2u 6d 14 2 1 6 u u 1 129 12u 66d 129 3 1 12 1 d . 2 14 5 3
Vậy số hạng đầu tiên u , công sai d . 1 2 2 5 3
Số hạng thứ 20: u u 19d 19. 31 . 20 1 2 2 202u 19d 5 3 1
Tổng của 20 số hạng đầu tiên: S 10 2. 19. 335 20 2 2 2 u 8 u 5d 8 u 8 5d d) 6 1 1 2 2 u u 16
u d u 3d 16
8 5d d 8 5d 3d 16 2 4 1 2 1 2 2 2 u 8 5d 1 8 4d
2 8 2d2 16 14 Giải : 2
20d 96d 112 0 d d = 2 . 5 14 Với d u 6 1 5 14 236
Số hạng thứ 20: u u 19d 6 19. . 20 1 5 5 202u 19d 1 14
Tổng của 20 số hạng đầu tiên: S 10 2.(6) 19. 412 20 2 5 Với d 2 u 2 1
Số hạng thứ 20: u u 19d 2 19.2 36 . 20 1 202u 19d 1
Tổng của 20 số hạng đầu tiên: S 10 2.( 2 ) 19.2 340 20 2 15
Ví dụ 3: Cho a, b, c là ba số hạng liên tiếp của một cấp số cộng, chứng minh rằng: a). 2 2 a 2bc c 2ab
b). a bc b c2 2 8 2 c). 2 2 2 2 2 2
a ab b , a ac c ,b bc c là cấp số cộng.
a). Vì a, b, c là ba số hạng liên tiếp của một cấp số cộng: a c 2b a 2b c Ta có: 2 2
a 2ab a a a c ac c b c 2 2 c 2bc Vậy 2 2 2 2
a 2ab c 2bc a 2bc c 2a . b
b). Ta có a bc b c2 2 8 2 8bc 2 2 4b 4bc c 8bc 2 2
4b 4bc c b c2 2 . c). Ta cần chứng minh: 2 2 a ab b 2 2 b bc c 2 2 2 a ac c 2 2 2
2b ab bc a 2ac c
2 2 2b b a c a c b b b2 2 2 2 2 2 2 2 4b 4b (đúng). 16 TÓM TẮT GIÁO KHOA
1). Cấp số nhân là một dãy số ( hữu hạn hay vô hạn) mà trong đó kể từ số hạng thứ hai, mỗi số hạng đều
bằng tích của số hạng đứng ngay trước nó và một số q không đổi, nghĩa là: u n 2,u u .q n là cấp số nhân n n1
Số q được gọi là công bội của cấp số nhân.
2). Định lý 1: Nếu un là một cấp số nhân thì kể từ số hạng thứ hai, bình phương của mỗi số hạng ( trừ
số hạng cuối đối với cấp số nhân hữu hạn) bằng tích của hai số hạng đứng kề nó trong dãy, tức là: 2 u u .u k 2 k k 1 k 1 .
Hệ quả: Nếu a, b, c là ba số khác 0, thì “ba số a, b, c ( theo thứ tự đó) lập thành một cấp số nhân khi và chỉ khi 2 b ac ”.
3). Định lý 2: Nếu một cấp số nhân có số hạng đầu u q 0 u 1 và công bội
thì số hạng tổng quát n của nó
được tính bởi công thức: n 1 u u .q n 1 . n
4). Định lý 3: Giả sử ( u
n ) là một cấp số nhân có công bội q. Gọi S u u u . . u (S là tổng n k 1 2 n n k1
cuản số hạng đầu tiên của cấp số nhân). Ta có: Nếu q=1 thì S nu n 1 . u n 1 q 1 Nếu q 1 thì S n 1 q PHƯƠNG PHÁP GIẢI TOÁN. un Phương pháp: Chứng minh n 1,u u .q n1 n
trong đó q là một số không đổi. u Nếu u 0 n N * n với mọi thì ta lập tỉ số n 1 T un
T là hằng số thì un là cấp số nhân có công bội q T .
T phụ thuộc vào n thì un không là cấp số nhân.
Ví dụ 1: Xét trong các dãy số số sau, dãy số nào là cấp số nhân, (nếu có) tìm công bối của cấp số nhân đó: u 3 u 2 1 a). 2 1 u ( 3) n b). n 3n2 u (1) .5 c). 1 d). 9 n n 2 u u u n 1 n n 1 u n 2n3 u ( 3 ) a). Ta có n 1 2 ( 3
) 9 (không đổi). Kết luận u là cấp số nhân với công bội q 9 . n 2n 1 u ( 3 ) n n 1 3(n 1 )2 u ( 1 ) .5 b). Ta có n 1 3 1 .5 1
25 (không đổi). Kết luận u là cấp số nhân với công bội n n 3n2 u ( 1 ) .5 n q 125. 17 u 4 u 256 u u c). Ta có 2 u u 4 , 2 u u 16 , 2 u u 256 , suy ra 2 2 và 4 16 2 4 . Do 2 1 3 2 4 3 u 2 u 16 u u 1 3 1 3
đó u không là cấp số nhân. n 9 u u u d). n 1 n n 1
u u ,n 2 . Do đó có: n 1 n 1 u 9 u n n un 1 u u u .... u .... (1) 1 3 5 2n 1
Và u u u .... u ... (2) 2 4 6 2n 9
Theo đề bài có u 3 u 3 (3) 1 2 u1
Từ (1), (2) ,(3) suy ra u u u u u .... u u
.... Kết luận u là cấp số nhân với công n 1 2 3 4 5 2n 2n 1 bội q 1. u 2
Ví dụ 2: Cho dãy số u được xác định bởi 1 , n
1. Chứng minh rằng dãy số v xác n n u 4u 9 n 1 n định bởi v u 3, n
1 là một cấp số nhân. Hãy xác định số hạng đầu và công bội của cấp số nhân đó. n n
Vì có v u 3 (1) v u 3 (2) . n n n 1 n 1 Theo đề u
4u 9 u 3 4 u 3 (3). n 1 n n 1 n v
Thay (1) và (2) vào (3) được: n 1 v 4v ,n 1
4 (không đổi). Kết luận v là cấp số nhân với n n 1 n vn
công bội q 4 và số hạng đầu v u 3 5 . 1 1 18 Phương pháp:
Dựa vào giả thuyết, ta lập một hệ phương trình chứa công bội q và số hạng đầu u , giải hệ phương trình 1 này tìm được q và u . 1
Để xác định số hạng thứ k, ta sử dụng công thức: 1 u u . k q . k 1 1 n q
Để tính tổng của n số hạng , ta sử dụng công thức: S u . , q 1. Nếu q 1 thì n 1 1 q
u u u ... u , do đó S nu . 1 2 3 n n 1
Ví dụ 3: Tìm số hạng đầu và công bội của cấp số nhân, biết: u u 51 u u u 135 u 6 a) 1 5 b) 1 2 3 c) 2 u u 102 u u u 40 S 43. 2 6 4 5 6 3 u u 51 u u q 51 u 4 4 1 q 51 1 1 5 1 1 a). 5 u u 102 u q u q 102 u q 4 2 6 1 q 102 1 1 1 u q 4 1 q 1 102 51 51 Lấy q 2 u 3. u 4 1 q 51 1 4 1 q 17 1
Kết luận có công bội q 2 và số hạng đầu tiên u 3. 1
Kết luận: u 3 và q 2 1 2 u u u 135 u u q u q 135 b) 1 2 3 1 1 1 3 4 5 u u u 40 4 5 6 u .q u q u q 40 1 1 1 u 2 1 q q 135 1 3 u q 2 1 q q 40 1 3 u q 2 1 q q 1 40 8 2 Lấy 3 q q u 2 1 q q 135 27 3 1 135 1215 u . 1 2 1 q q 19 2 1215
Kết luận có công bội q và số hạng đầu tiên u . 3 1 19 u 6 u q 6 u q 6 c) 2 1 1 2 S 43 u u u 43 u u q u q 43 3 1 2 3 1 1 1 19 u q 6 1 u q 6 . Lấy 1 u 2 2 1 q q 43 u 1 q q 43 1 1 1 q 2 43 6 1 q q 2
6q 37q 6 0 q 6 q 6 1
Với q 6 u 1. Với q u 36. 1 1 6 1 q 6 q Kết luận hoặc 6 u 1 1 u 36 1 u u 51
Ví dụ 4: Cho CSN u có các số hạng thỏa: 1 5 n u u 102 2 6
a). Tìm số hạng đầu và công bội của CSN.
b). Hỏi tổng bao nhiêu số hạng đầu tiên bằng 3069?
c). Số 12288 là số hạng thứ mấy? 4 4 u u 51 u u q 51 u (1 q ) 51 ( ) a). Ta có 1 5 1 1 1 5 4 u u 102 2 6 u q u q 102 u q(1 q ) 102 ( ) 1 1 1 4 ( ) u q(1 q ) 102 Lấy 1 q 2 u 3 . 4 1 ( ) u (1 q ) 51 1 1 n q 1 2n b). Có S 3069 u . 3069 3.
3069 2n 1024 n 10 . Kết luận tổng của 10 số n 1 1 q 1 2
hạng đầu tiên bằng 3069. c).Có k 1 k 1 k 1 12
u 12288 u .q 12288 3.2 12288 2 4096 2 k 1
k 1 12 k 13. Kết luận số 12288 là số hạng thứ 13.
Ví dụ 5: Tính các tổng sau: a). 2 3
S 2 2 2 2n n 1 1 1 1 b). S n 2 3 2 2 2 2n 2 2 2 1 1 n 1 c). S 3 9 3 n 3 9 3n
d). S 6 66 666 666...6 n n so 6 a). Ta có dãy số 2 3 2, 2 , 2 , , 2n
là một cấp số nhân với n số hạng, có số hạng đầu u 2 và công bội 1 2 2 1 n q 1 2n q 2 . Do đó S u . 2. 2 2n 1 . n 1 2 1 q 1 2 20 1 1 1 1 1 b). Ta có dãy số , , , ,
là một cấp số nhân với n số hạng, có số hạng đầu u và công bội 2 3 2 2 2 2n 1 2 n 1 1 1 2 1 2 1 n q 1 2 1 q . Do đó S u . . 1 . 1 2 n 1 1 q 2 1 2n 1 2 2 2 2 2 1 1 n 1 c). S 3 9 3 n 3 9 3n 1 1 n 1 2 4 2 3 2 3 2 3 2 2 4 2 3 3 3 n n 1 1 1 2 4 2
3 3 3
2 2 2 2 2 4 2 3 3 3 n n 4 3 Có dãy số 2 4 2 3 ,3 , ,3 n
là cấp số nhân với n số hạng, có số hạng đầu 2 u 3 và công bội q 9 . 1 2 3 1 n q 1 9n 9 Do đó S u . 9. 9n 1 . 1 1 1 q 1 9 8 1 1 1 1 1 Có dãy số , , ,
là cấp số nhân với n số hạng, có số hạng đầu u và công bội q . Do 2 4 2 3 3 3 n 1 2 3 9 1 n 1 1 q 1 1 1 9n n 1 đó 9 S u . . 1 . 1 1 1 q 9 1 8 9n 8.9n 1 9 n n 1 9 9n n 1 9 1 9 1 Vậy S n n . n 9 1 2 2 8 8.9n 8.9n 6
d). S 6 66 666 666...6
9 99 999 999...9 n 9 n so 6 n 2
(10 1) (100 1) (1000 1) (10n 1) 3 2 2 10n n n 1 20 n 2 2 3 1
0 10 10 10 n 10. n 10 1 . 3 3 10 1 27 3 21
Ví dụ 6: Cho a, b, c, d là bốn số hạng liên tiếp của một cấp số nhân. Chứng minh:
a ab bc ca3 abc a b c3 ).
b a b b c ab bc2 2 2 2 2 ).
c a b ca b c 2 2 2 ). a b c
d). 2 2 2 2 b c c a d b a d
Vì a, b, c là ba số hạng liên tiếp của một cấp số nhân, nên có 2 ac b . 3 3 3 a). Ta có
3 3 2 abc a b c b a b c ab b bc ab bc ca (đpcm). b). Ta có: 2 2 a b 2 2 b c 2 2 2 2 4 2 2 2 2 4 2 2
a b a c b b c a b 2b b c
a b ab bc b c ab bc2 2 2 2 2 2 . (đpcm).
c). Ta có 2 2 a b c a b c a c b a c b a c b 2 2 2 2 2 2 2 2 2 2
a 2ac c b a 2b c b a b c (đpcm).
d). Vì a, b, c, d lập thành CSN nên có: 2 2 . a d bc, . a c b , . b d c
Khai triển: b c2 c a2 d b2 2 2 2 2
a 2b 2c d 2bc 2ca 2bd
a 2b 2c d 2ad 2b 2c a 2ad d a d 2 2 2 2 2 2 2 2 2 22 GIỚI HẠN HỮU HẠN GIỚI HẠN VÔ CỰC
1. Giới hạn đặc biệt:
1. Giới hạn đặc biệt: 1 1 k lim 0 ; lim 0 (k ) lim n lim n (k ) n n k n n lim n q (q 1) lim n
q 0 ( q 1) ; lim C C 2. Định lí: n n 2. Định lí : 1
a) Nếu lim u thì lim 0 a) Nếu lim u n n = a, lim vn = b thì un lim (un + vn) = a + b u lim (u
b) Nếu lim un = a, lim vn = thì lim n = 0 n – vn) = a – b v lim (u n n.vn) = a.b u c) Nếu lim u a n = a 0, lim vn = 0 lim n (nếu b 0) nÕu . a v 0 v b u n n thì lim n = v nÕu . a v 0 b) Nếu u n n 0, n và lim un= a n thì a 0 và lim u a
d) Nếu lim un = +, lim vn = a n nÕu a 0
c) Nếu u v ,n và lim v thì lim(u n n n = 0 n.vn) = nÕu a 0 thì lim un = 0
d) Nếu lim un = a thì lim u a n
* Khi tính giới hạn có một trong các dạng vô
3. Tổng của cấp số nhân lùi vô hạn 0 u định: ,
, – , 0. thì phải tìm cách khử S = u 0 1 + u1q + u1q2 + … = 1 q 1 1 q dạng vô định. P n u u P n,Q n n n Q n
Phương pháp: Chia cả tử và mẫu cho k n với k
n là lũy thừa có số mũ lớn nhất của P n và Q n
Ví dụ 1: Tìm giới hạn của dãy u biết: n 2 2n 3n 1 3 2 2n 3n 4 a). u b). u n 2 5n 3 n 4 3 n 4n n a). Ta thấy 2
n là lũy thừa cao nhất của tử và mẫu, nên chia cả tử và mẫu của u cho 2 n được: n 2 2n 3n 1 3 1 2 2 2 2 2n 3n 1 n n n 3 1 3 u . Ta có : lim 0, lim 0 và lim 0 nên n 2 2 5n 3 5n 3 3 2 2 5 n n n 2 2 n n 2 0 0 2 lim u . n 5 0 5 b). Dễ dàng thấy 4
n là lũy thừa cao nhất của tử và mẫu, nên chia cả tử và mẫu của u cho 4 n được: n 23 3 2 2n 3n 4 2 3 4 3 2 4 2 4 2n 3n 4 n n n n 2 3 4 4 u . Ta có lim 0, lim 0, lim 0 , lim 0 n 4 3 4 3 n 4n n n 4n n 4 1 2 4 1 n n n n 4 3 n n n 1 0 0 0 và lim 0 . Do đó lim u 0 . 3 n n 1 0 0 24 P n u u P n,Q n n n Q n
Phương pháp : Rút bậc lớn nhất ra ngoài và rút gọn dần.
Ví dụ 2: Tìm giới hạn của dãy u biết: n 2 4n n 1 n 2n 1 n 3 a). u b). u n 2 n 9n 3n 4n 5 2 2 4n n 1 1 1 1 1 n n 2 2 n 4 n 4 1 2 2 4n n 1 n n 1 a). n n n n u . Vì có lim 0, n 2 2 9n 3n 9n 3n 3 3 n 2 n n 9 9 2 n n n 1 3 4 0 0 1 1 lim
0, và lim 0 . Nên limu . 2 n n n 9 0 3 2n 1 n 3 1 3 n n 1 3 n. 2 n. 1 2 1 2n 1 n 3 n n b). n n u n n . n 4n 5 4n 5 5 5 n n. 4 4 n n n 1 3 5
Vì có lim 0, lim 0 và lim 0 . n n n 2 0 1 0 2 1 Từ đó có limu . n 4 0 2 25 P n u u P n,Q n n n Q n n , n, n a b c
Phương pháp : Chia cả tử và mẫu cho n
a với a là cơ số lớn nhất.
Ví dụ 3: Tìm giới hạn của dãy u biết: n 2n 4n n n n2 2 3 4.5 a). u b) u n 4n 3n n n 1 n2 n 1 2 3 5 n 2n 4n 2n 4n 2 1 2n 4n n n 4n 4n 4n 4 2 3 a).Ta có u . Ta có lim 0 và lim 0 . n 4n 3n 4n 3n 4n 3n 3 n 4 4 n n n 1 4 4 4 4 0 1 Nên lim u 1. n 1 0 2n 3n 100.5n n n n2 2 3 4.5 2n 3n 100.5n n b) Ta có 5 u n n 1 n2 n 1 2 3 5 2.2n 9.3n 5.5n 2.2n 9.3n 5.5n 5n n n 2n 3n 5n 2 3 100. 100 n n 5n 5n 5n 5 5 2 3 . Vì lim 0 và lim 0 2n 3n 5n 2 n 3 n 5 5 2. 9. 5. n n n 2. 9. 5 5 5 5 5 5 0 0 100 Nên lim u 20. n 2.0 9.0 5 26
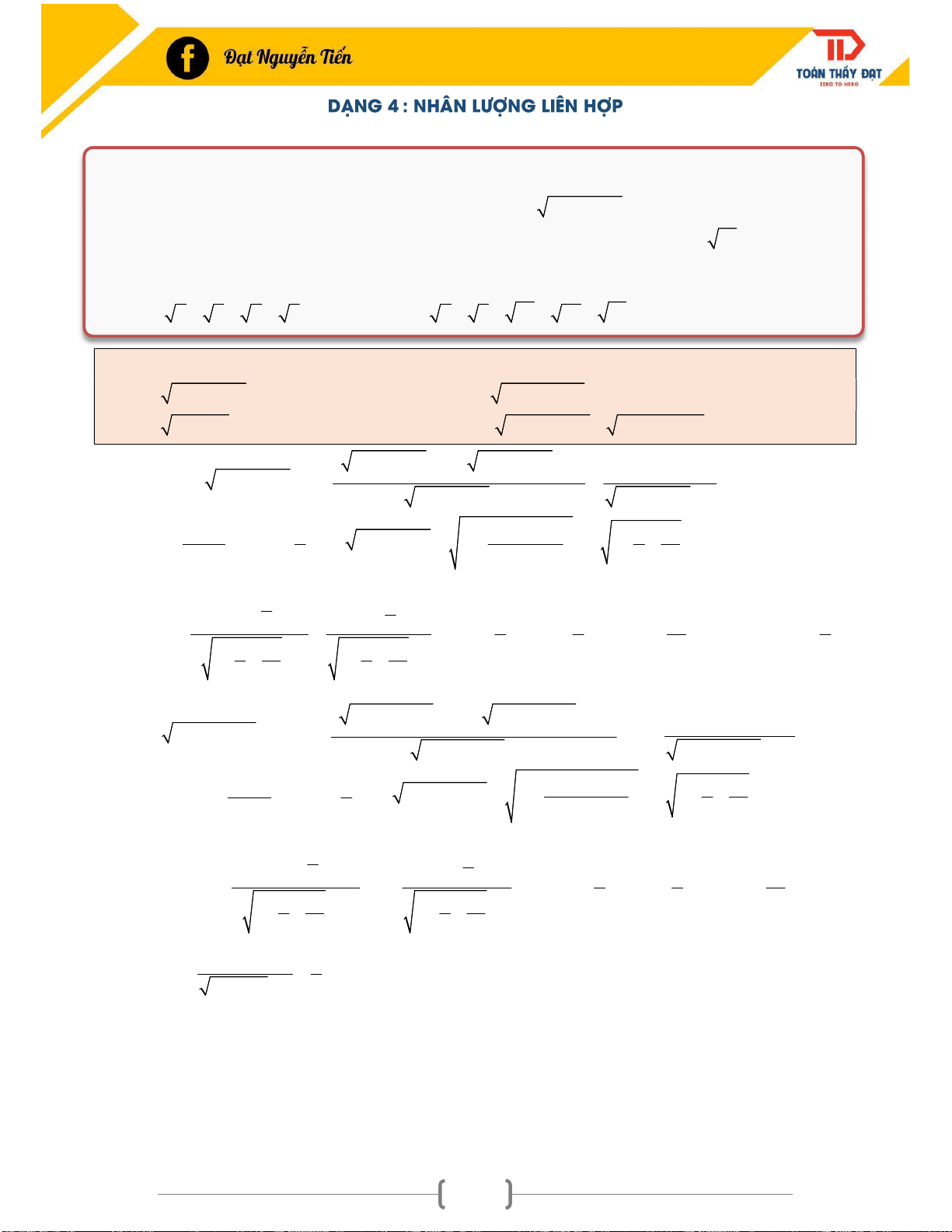
Dấu hiệu nhận biết nhân lượng liên hợp : Để nhận biết một bài tập có nhân lượng liên hợp hay không các
bạn chỉ chú ý tới n có mũ cao nhất sau đó đưa ra ngoài dấu căn thức, nếu chúng trừ nhau bằng 0 thì bài
này ta phải nhân lượng liên hợp. Cụ thể ta làm lại câu a) 2
u n 3n 5 n biểu thức trong căn thức có n 2
n là cao nhất và ta quan tâm đến « nó », những thừa số sau bỏ hết có nghĩa xem 2
u n n n n 0 n
(nên các bạn phải nhân lượng liên hợp).
Dùng các hằng đẳng thức:
a b a b a b; 3 3 a b 3 2 3 3 2
a ab b a b
Ví dụ 4: Tìm giới hạn của dãy u biết: n a). 2
u n 3n 5 n b). 2
u 9n 3n 4 3n 2 n n c). 3 3 2 u n 3n n d). 2 3 3 2
u 4n 3n 7 8n 5n 1 n n
2n 3n5n 2n 3n5n 3n 5 2
a). Ta có u n 3n 5 n . Và có n 2 2 n 3n 5 n n 3n 5 n 3n 5 5 2 n 3n 5 3 5 3n 5 n n 3 và 2 2 n 3n 5 n n 1 . n n 2 2 n n n 5 5 n 3 3 n 5 3 5 3 Do đó n u
, vì lim 0, lim 0 và lim 0 . Nên lim u . n 3 5 3 5 n n 2 n n 2 n 1 n 1 1 2 2 n n n n 2 9n 3n 4 3n 2 9n 3n 4 3n 3n 4 2
b). u 9n 3n 4 3n 2 2 2 . n 2 9n 3n 4 3n 2 9n 3n 4 3n 3n 2 2 2 9n 3n 4 3 4 Ta có 3n 2 n n 3 và 2 2 9n 3n 4 n n 9 . n n 2 2 n n n 2 2 n 3 3 n 2 3 4 Từ đó suy ra 2 n u
2 , vì lim 0, lim 0 và lim 0 . n 3 4 3 4 n n 2 n n 9 3n 9 3 2 2 n n n n 3 0 1 Nên lim u . n 9 0 0 3 2 27
n 3n n n 3n 2 3 3 2 3 3 2 3 3 2 2 . n n 3n n c). 3 3 2 u n 3n n n n 3n 2 3 3 2 3 3 2 2 . n n 3n n 2 3n 3 2 3 3 2 3 n 3n 3 . Ta có n 3n 3 3 n . n 1 . 3 n 3n 2 3 3 2 3 3 2 2 . n n 3n n n n 2 3n 3 3 Do đó u
, ta có lim 0 . Nên lim u 1 n 2 2 n n 2 3 2 3 2 3 3 3 3 3 3
n 1 n . 1 n 1 1 1 n n n n d). 2 3 3 2 u n n n n 2 n n n 3 3 2 4 3 7 8 5 1 4 3 7 2 2n 8n 5n 1 n 7 3 3n 7 3 Tính lim 2 4 3 7 2 lim lim n n n n 2 4n 3n 7 2n 3 7 4 4 2 2 n n Tính 3 3 2 lim 2n 8n 5n 1
2n 8n 5n 1 4n 2 .n 8n 5n 1 8n 5n 12 3 3 2 2 3 3 2 3 3 2 lim 4n 2 .
n 8n 5n 1 8n 5n 12 2 3 3 2 3 3 2 2 5n 1 lim (1) 4n 2 .
n 8n 5n 1 8n 5n 12 2 3 3 2 3 3 2 3 2 8n 5n 1 5 1 Có 3 3 2 3 8n 5n 1 3 3 n . n 8 3 3 n n n 2 1 n 5 2 n Nên 1 lim 2 2 2 5 1 2 5 1 3 3 4n 2n . 8 n . 8 3 3 n n n n 1 5 2 5 3 5 1 lim n
. Từ đó suy ra lim u . 2 12 n 5 1 5 1 4 12 3 3 3 4 2. 8 8 3 3 n n n n 28 ̣ ̣ ̉ ̣ ̉ ̀ ̀
Ví dụ 3 : Tìm giới hạn của dãy u biết: n 1 1 1 1 1 1 1 a). u b). u n 1.2 2.3 n(n 1) n 1.4 4.7 7.10 (3n 2)(3n 1) 1 1 1
1 3 5 (2n 1) c). u 1 1 ... 1 d). u n 2 2 2 2 3 n n 2 3n 4 2 2 2 2
1 2 3 n 1 1 1 e). u f). lim n n(n 1)(n 2) 1.2.3 2.3.4 n(n 1)(n 2) 1 k 1 k k 1 k 1 1 a). Ta có . k n k k 1 k k 1 k k 1 k k , 1, 2,..., 1 k k 1 1 1 1 1 1 1 1 1 1 Từ đó u
1 1 . n 1.2 2.3 n(n 1) 2 2 3 n n 1 n 1 1 1 Nên lim u lim 1 lim1 lim 1 0 1 . n n 1 n 1 1 1 (3k 1) (3k 2) 1 3k 1 3k 2 b). Ta có (3k 2)3k 1 3 (3k 2)3k
1 3 (3k 2)3k 1 (3k 2)3k 1 1 1 1 1 1 1 1 , k
1, 2,3..., n . Từ đó u 3 3k 2 3k 1 n 1.4 4.7 7.10 (3n 2)(3n 1) 1 1 1 1 1 1 1 1 1 1 1 1 1 , có lim 0 . 3 4 4 7 7 10 3n 2 3n 1 3 3n 1 3n 1 1 1 Do đó lim u . n 1 0 3 3 2 1 k 1 (k 1)(k 1) 1 1 1 c). k 2 ta có 1 . Do đó u 1 1 ... 1 2 2 2 k k k n 2 2 2 2 3 n 1.3 2.4 3.5 4.6
(n 3)(n 1) (n 2)n (n 1)(n 1) 1 n 1 . 2 2 2 2 2 2 2 2 3 4 5 (n 2) (n 1) n 2 n 1 1 n 1 1 Nên lim lim lim n u . n 2n 2 2
1 3 5 (2n 1) d). u . n 2 3n 4 29
Ta có dãy số 1 3 5 (2n 1) là một cấp số cộng với u 1 công sai d 31 2 và số hạng tổng 1
quát u 2n 1 u m 1 d 2n 1 1 m 1 .2 2n 1 m n 1, nên tổng của dãy số trên là 1 m 2 1 2 1 m n 1 n n 1 4 S u u n n . Từ đó u có lim 0 và lim 0 m 1 1 2 1 2 1 1 2 2 n 2 3n 4 4 2 3 n n 2 n 1 Từ đó suy ra lim u . n 3 2 2 2 2
1 2 3 n n n 1 2n 1 2 2 2 2 e). u
. Ta có tổng 1 2 3 n
(được chứng minh bằng n n(n 1)(n 2) 6 1 2 2n 1 1 2 2 1
phương pháp quy nạp). Nên n u
vì lim lim 0 do đó lim u . n 6(n 2) 2 n 6 1 n n 6 3 n 1 1 1 1 1 1 f). Ta có
(Chứng minh dựa vào nguyên lý quy 1.2.3 2.3.4 n(n 1)(n 2) 2 2 (n 1)(n 2) 1 1 1 1 1 1 1 nạp). Do đó L lim lim lim 0 . 2 2 (n 1)(n 2) 4 2(n 1)(n 2) 4 4 30 Giới hạn hữu hạn
Giới hạn vô cực, giới hạn ở vô cực
1. Giới hạn đặc biệt:
1. Giới hạn đặc biệt:
lim x x lim c c (c: hằng số) neáu k chaün 0 x 0 x x 0 x lim k x ; lim k x 2. Định lí: x x neáu k leû
a) Nếu lim f (x) L và lim g(x) M c x lim c c ; lim 0 0 x x 0 x x k x x
thì: lim f (x) g(x) L M x 1 1 0 x lim ; lim
lim f (x) g(x) L M x 0 x x 0 x x 0 x 1 1 lim f (x).g(x) . L M lim lim x x0 x0 x x 0 x f (x) L 2. Định lí: lim (nếu M 0) x
Nếu lim f (x) L 0 và lim g(x) thì: 0 x g(x) M x 0 x x 0 x
b) Nếu f(x) 0 và lim f (x) L
neáu L vaø lim g(x) cuøng daáu x 0 x x 0 x thì L 0 và lim f (x)g(x) lim f (x) L x 0 x
neáu L vaø lim g(x) traùi daáu x 0 x x 0 x
c) Nếu lim f (x) L thì lim f (x) L 0 neáu lim g(x) x 0 x x 0 x xx 3. Giới hạn một bên: 0 f (x) lim
neáu lim g(x) 0 vaø . L g(x) 0
lim f (x) L lim f (x) lim f (x) L x 0 x g(x) x 0 x x 0 x x 0 x x 0 x
neáu lim g(x) 0 vaø . L g(x) 0 x 0 x
lim f (x) lim f (x) L 0 x
* Khi tính giới hạn có một trong các dạng vô định: , 0 x x 0 x 0
, – , 0. thì phải tìm cách khử dạng vô định. ̣ ̣ ́ ̣ ́ 3 2 x 2x 1
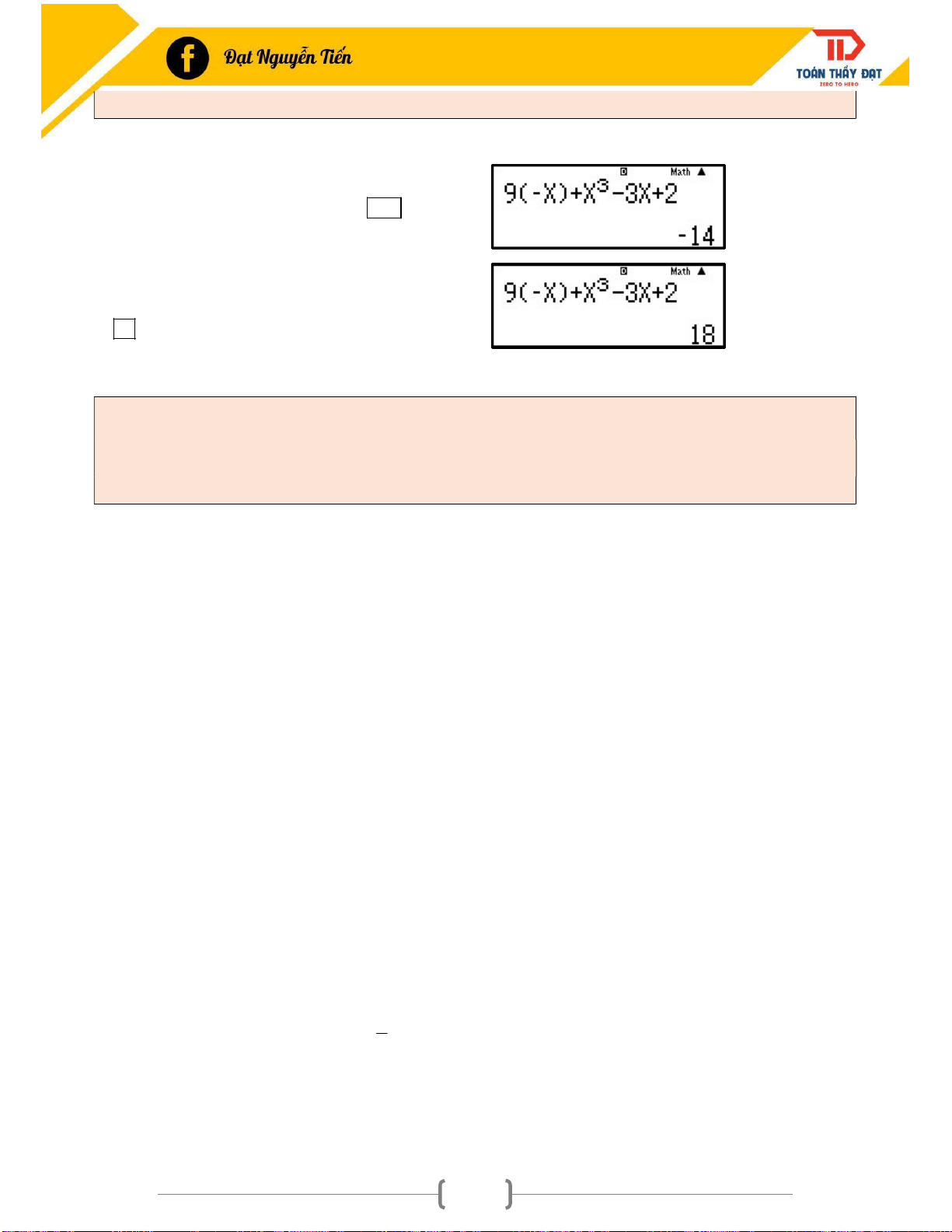
Ví dụ 1: Chọn kết quả đúng trong các kết quả sau của lim là: 5 x 1 2x 1 1 1 A. 2 . B. . C. . D. 2 . 2 2 Chọn A. x 2x 1 3 1 2. 2 3 2 1 1 lim 2 5 x1 2x 1 2 5 1 1 31 P(x) ̣ lim x 0 x Q(x)
Phân tích cả tử và mẫu thành nhân tử và rút gọn. Chú ý: + Nếu tam thức bậc hai 2
ax bx+c có hai nghiệm x , x thì ta luôn có sự phân tích 1 2 2
ax bx c a(x x )(x x ) . 1 2 + n n n 1 n2 n2 n 1 a b (a b)(a a b ... ab b )
Ví dụ 2: Tìm các giới hạn sau: 3 x 8 1 1 a). lim b). lim 2 x2 x 11x 18 2 2 x2 x 3x 2 x 5x 6 a).Ta có 3 3 3 x x x 2 8 2
2 x 2x 4 (áp dụng hằng đẳng thức), và 2
x 11x 18 x 2 x 9 (với x 2 và x 9
là hai nghiệm của phương trình 2 x 11x 18 0 ). 1 2 x x 2 2 3 x 2x 4 8 2 x 2x 4 12 Do đó lim lim lim . 2 x 2 x 2 x 11x 18 x 2x 9 x 2 x 9 7 1 1 1 1 2 x 2 f). L lim lim lim 2 2 x2 x 3x 2 x 5x 6 x2 x
1 x 2 x 2 x 3 x2 x 1 x 2 x 3 2 lim 2 x2 x 1 x 3 32 P(x) ̣ lim x 0 x Q(x)
Sử dụng các hằng đẳng thức để nhân lượng liên hợp ở tử và mẫu. Các lượng liên hợp:
+ ( a b )( a b) a b 3 3 3 2 3 3 2
+ ( a b)( a ab b ) a b + n n n n 1 n n2 n n 1 ( a b)( a a b ... b ) a b
Ví dụ 3: Tìm các giới hạn sau : x 3 2 2 2
x 2x 6 x 2x 6 a). lim b). lim x 1 x 1 2 x3 x 4x 3 x 2 2 3 4x 2 c). lim d) lim x2 x 7 3 x2 x 2 2 x 3 2 x 3 2 x 1 1 1 a). lim lim lim lim . x 1 x 1 x 1 x 1 x 3 2 x 1 x 1 x 3 2 x 1 x 3 2 4 x x x x 2x 2x6 2 2 2 x 2x 6 2 6 2 6 b). lim lim 2 x3 x3 x 4x 3 2x 4x3 2 2
x 2x 6 x 2x 6 4 x 3 4 1 lim lim .
x3 x x 2 2
x x x x x3 x 2 2
x x x x 3 1 3 2 6 2 6 1 2 6 2 6 x 2
x 2 2 x 7 3 x 2 x 7 3 2 2 x 7 3 3 c). lim lim lim lim . x2 x2 x 7 3 2
x 7 3 x 2 2 x2 x 2 x 2 2 x2 x 2 2 2
4x 2 4x2 2. 4x 4 3 4x 2 4x 8 2 x 2 3 3 3 3 3 3 d) Ta có 4x 2 . 4 2 3 3 2. 4 4 A A A x x A 3 4x 2 2 x 2 2 2 1 Do đó lim lim . x x x x lim 2 2 . x A A 2 2 2 2 3 3 6 4.2 2. 4.2 4 33 k f x k g x c k f x m g x c k f x m g x c Các dạng hay gặp lim hoặc lim hoặc lim x n 0 x x x x x x x x 0 x x x0 0 0 0
. Trong đó k, m, n * và n min(k, m) .
Ví dụ 4: Tìm các giới hạn sau : 2x 2 5x 4 5 3 3x 2 5x 6 a). lim b). lim x 1 x 1 x2 x 2 0
a). Ta có khi x 1 thì 2x 2 5x 4 5 0 do đó đây là bài dạng vô định , ta phải tách được 0 f x c g x m về dạng lim lim
sao cho mỗi giới hạn nhân lượng liên hợp đều khử được dạng x 1 x 1 x 1 x 1
vô định . Kỹ thuật ta thay x 1 vào 2x 2 2 và 5x 4 3 nên số 5
tách thành 2 3 và gom lại như sau : x x
2x2 2 5x4 3 2 2 5 4 5 2x 2 2 5x 4 3 lim lim lim lim . x 1 x 1 x 1 x 1 x 1 x 1 x 1 x 1
Sau đó tính từng giới hạn. 2 x
2x2 2 2x2 2 2 2 2 2x2 4 Tính L lim lim lim 1 x 1 x 1 x 1
x 1 2x 2 2 x 1 x 1 2x 2 2 2 x 1 2 1 lim lim . x 1 x 1 2x 2 2 x 1 2x 2 2 2 2 x
5x4 3 5x4 3 5 4 3 5x4 9 Tính L lim lim lim 2 x 1 x 1 x 1
x 1 5x 4 3 x 1 x 1 5x 4 3 5 x 1 5 5 lim lim . x 1 x 1 5x 4 3 x 1 5x 4 3 6 2x 2 5x 4 5 1 5 4 Kết luận lim . x 1 x 1 2 6 3 3 3x 2 5x 6 b). L lim . x2 x 2
Thay x 2 vào 3 3x 2 và 5x 6 đều bằng 2. Suy ra 2 là giá trị ta cần thêm bớt. 34 x x 3 3
3x 2 2 2 5x 6 3 2 5 6
Cụ thể làm như sau: L lim lim x2 x2 x 2 x 2 3 3x 2 2 2 5x 6 lim lim . x2 x2 x 2 x 2 3x 2 2 3x 2 2 3 3 3 2. 3x 2 4 3 3x 2 2 3 x 2 3 1 Tính L lim lim lim lim . 1 x x 2 x x 2 3x 22 2 2 3 3 2. 3x 2 4 x2 x 2 x2 .A A 4
A x
2 5x62 5x6 2 5 6 4 (5x 6) Tính L lim 2 x2 x 2
x 22 5x 6
x 22 5x 6 5 x 2 5 5 1 5
. Do đó L L L 1.
x 22 5x 6 2 5x 6 4 1 2 4 4 35 P(x) lim P(x),Q(x) x Q(x)
Phương pháp: (làm giống giới hạn dãy số)
với P(x), Q(x) là các đa thức hoặc các biểu thức chứa căn.
– Nếu P(x), Q(x) là các đa thức thì chia cả tử và mẫu cho luỹ thừa cao nhất của x.
– Nếu P(x), Q(x) có chứa căn thì có thể chia cả tử và mẫu cho luỹ thừa cao nhất của x hoặc nhân lượng liên hợp.
Tương tự như cách khử dạng vô định ở dãy số. Ta cần tìm cách đưa về các giới hạn: + 2 lim k x ; 2k 1
lim x () . x x ( x) ( x) k k + lim 0 (n 0;k 0) .
+ lim f (x) () lim 0 (k 0) . n x x x 0 x x 0 x f (x) ( x) 4 x 7
Ví dụ 5: Giá trị đúng của lim là: 4 x x 1 A. 1 . B. 1. . C. 7. . D. . 7 4 1 4 x 7 lim lim x 1. 4 x x 1 x 1 1 4 x 2 2x 3x 2
Ví dụ 6: Tìm giới hạn C lim là: x 2 5x x 1 2 3 A. B. C. D. 0 6 2 2 3 2 x 2 3 Ta có: C lim x 1 6 5 1 2 x 3 4 6 1 x x
Ví dụ 7: Tìm giới hạn D lim là: x 3 4 1 x x 4 A. B. C. D. 1 3 1 1 3 1 6 2 lim x x D 1 x 1 1 1 4 x x Ví dụ 8: Tìm giới hạn 2
E lim ( x x 1 x) là: x 1 A. B. C. D. 0 2 x 1 1 Ta có: E lim x 2 x x 1 x 2 36
Ví dụ 9: Tìm các giới hạn sau: x 3 x x a). lim b). lim . x 3 5x 15 x 0 x x a). Vì x 3
x 3 x 3 0 . Vậy x 3 x 3 x 3 x 3 1 Ta có lim lim . x 3 x 3 5x 15 5 x 3 5 x x x x 1 x 1 b). Ta có lim lim lim 1 . x 0 x 0 x x x x x 0 1 x 1 3 2 x x Ví dụ 10: lim bằng: x 1 x 1 1 x A. 1. B. 0 . C. 1. D. . Chọn C. 2 3 2 x x x x 1 x x 1 x lim lim lim lim 1. x 1 x 1 x 1 1 x x 1 x 2 x 1 1 x 11 x 1 x 1 1 x1 37 Phương pháp:
Ta sử dụng các công thức lượng giác biến đổi về các dạng sau: sin x x tan x x lim lim 1, từ đây suy ra lim lim 1. x0 x0 x sin x x0 x0 x tan x sin u(x) tan u(x) Nếu lim u(x) 0 lim 1 và lim 1. x 0 x x 0 x u(x) x 0 x u(x)
Ví dụ 11: Tìm các giới hạn sau sin 5x tan 2x 1 cos x 1. lim 2. lim 3. lim x0 x x0 3x x0 sin x 1 cos x sin 5 . x sin 3 . x sin x sin 7x sin 5x 4. lim 5. lim 6. lim 2 x0 x 3 x0 45x x0 sin x sin 5x 1 sin 5x 1 1). lim lim x0 x0 x 5 5x 5 tan 2x 2 tan 2x 2 2). lim lim x0 x0 3x 3 2x 3 2 x 2sin 1 cos x x 3). 2 lim lim lim tan 0 x0 x0 x x x x0 sin 2 2sin cos 2 2 2 2 x x 1 cos x 2sin sin 1 1 4). lim 2 2 lim lim 2 x0 x 2 x0 x0 x 2 x 2 2 sin 5 . x sin 3 . x sin x 1 sin 5x sin 3x sin x 1 5). lim lim 3 x0 45x x0 3 5x 3x x 3 sin 7x sin 5x 2cos 6x sin x 6). lim lim lim 2cos6x 2 x0 x0 x0 sin x sin x 38 ̣
Gán cho biến X một giá trị gần đúng rồi tính giá trị biểu thức (dùng phím CALC) Giới hạn CACL X = x a a + 0.00000001 x a a – 0,00000001 x 1 1.000000001 hoặc 0,99999999 x 9999999999 x - 999999999
(Nếu máy báo lỗi thì lấy ít chữ số 0 hơn)
Các kết quả hay gặp trong máy Ý nghĩa
Số có số mũ lớn: VD: 2.1020 Dương vô cực
Số có số mũ lớn: VD: -2.1020 Âm vô cực
Số có số mũ nhỏ: VD: 2.10-20 0
Số chưa đẹp: VD: 2,3333.
Cách 1. Ta gõ lại vào máy tính lần nữa: 2,3333333333333
Máy sẽ tự làm tròn giúp. Cách 2. Ta ấn 2.Qs3 3 n 4n 5
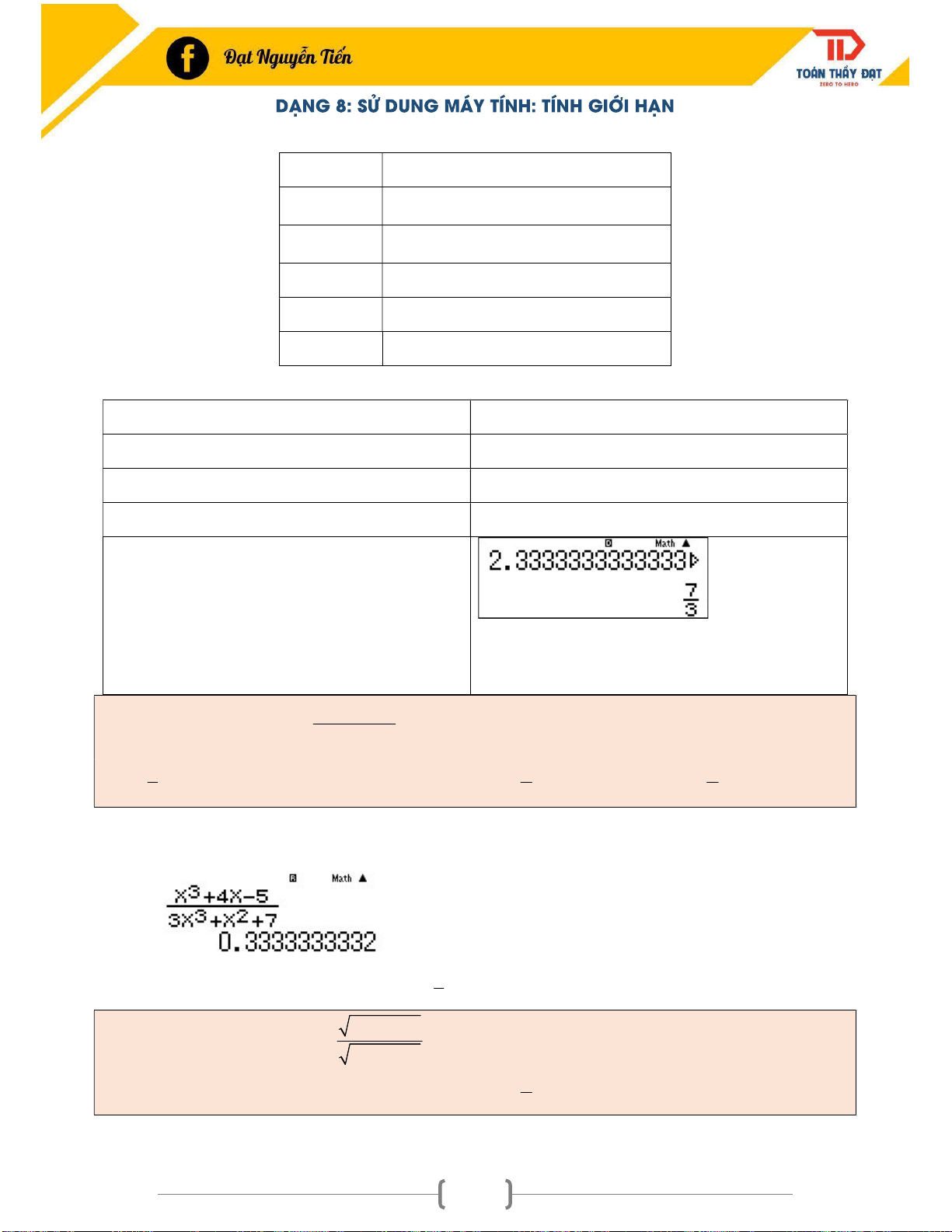
Ví dụ 12: Tính giới hạn : lim 3 2 3n n 7 1 1 1 A. B. 1 C. D. 3 4 2
Đề bài không cho x tiến tới bao nhiêu thì ta hiểu đây là giới hạn dãy số và x
Nhập biểu thức vào máy tính ta ấn CALC x = 999999999 1
Ta nhận được kết quả 0.3333333332 A là đáp án chính xác 3 3 4 6 1 x x
Ví dụ 13: Tìm giới hạn D lim : x 3 4 1 x x 4 A. B. C. D. 1 3
Nhập biểu thức vào máy tính ta ấn CALC x = -999999 39
Ta được kết quả bằng -1 3 4x 1 x 2
Ví dụ 14: Tìm giới hạn E lim : x7 4 2x 2 2 8 A. B. C. D. 1 27
Ta nhập biểu thức vào máy tính và ấn CALC x = 7+0,000000001 hoặc CALC x = 7 – 0,000000001 8
Ta được kết quả bằng 27 3 2 x x Ví dụ 15: lim bằng: x 1 x 1 1 x A. 1. B. 0 . C. 1. D. .
Ta nhập biểu thức vào máy tính và ấn CALC x = 1+0,000000001
Ta được kết quả bằng 1 1 1 1
Ví dụ 16: Tính giới hạn: lim .... 1.2 2.3 n n 1 3 A. 0 B.1. C. . D. Không có giới hạn. 2 1 1 1 n 1 Ta có: .... 1.2 2.3 nn 1 x 1 x x 1
Ta cho n tăng đến n = 50. Nhập vào máy tính qia1RQ)(Q)+1)R1E50=
Ta thấy kết quả xấp xỉ bằng 1. Chọn B 3 3 3 (n 1) 1 2 ... n
Ví dụ 17: Tính giới hạn của dãy số u : n 3 3n n 2 1 A. B. C. D. 1 9 n 3 (n 1) x 3 3 3 (n 1) 1 2 ... n Ta có: x 1 3 3 3n n 2 3n n 2
Ta cho n tăng đến n = 50. Nhập vào máy tính 50 3 (50 1) x x 1
0,1733 . Gấn nhất với đáp án C. 3 3.50 50 2 40
1. Hàm số liên tục tại một điểm: y = f(x) liên tục tại x0 lim f (x) f (x ) 0 x 0 x
Để xét tính liên tục của hàm số y = f(x) tại điểm x0 ta thực hiện các bước: B1: Tính f(x0).
B2: Tính lim f (x) (trong nhiều trường hợp ta cần tính lim f (x) , lim f (x) ) x 0 x x 0 x x 0 x
B3: So sánh lim f (x) với f(x0) và rút ra kết luận. x 0 x
2. Hàm số liên tục trên một khoảng: y = f(x) liên tục tại mọi điểm thuộc khoảng đó.
3. Hàm số liên tục trên một đoạn [a; b]: y = f(x) liên tục trên (a; b) và
lim f (x) f (a), lim f (x) f (b) x a x b
Hàm số đa thức liên tục trên R.
Hàm số phân thức, các hàm số lượng giác liên tục trên từng khoảng xác định của chúng.
Giả sử y = f(x), y = g(x) liên tục tại điểm x0. Khi đó:
Các hàm số y = f(x) + g(x), y = f(x) – g(x), y = f(x).g(x) liên tục tại x0. f (x) Hàm số y =
liên tục tại x0 nếu g(x0) 0. g(x)
4. Nếu y = f(x) liên tục trên [a; b] và f(a). f(b)< 0 thì tồn tại ít nhất một số c (a; b): f(c) = 0.
Nói cách khác: Nếu y = f(x) liên tục trên [a; b] và f(a). f(b)< 0 thì phương trình f(x) = 0 có ít nhất một nghiệm c (a; b).
Mở rộng: Nếu y = f(x) liên tục trên [a; b]. Đặt m = min f (x) , M = max f (x) . Khi đó với mọi a;b a;b
T (m; M) luôn tồn tại ít nhất một số c (a; b): f(c) = T. Phương pháp 1: Bước 1: Tính f x . 0
Bước 2: Tính lim f x . Nếu lim f x f x thì hàm số f(x) liên tục tại x . 0 0 x 0 x x 0 x Phương pháp 2:
Bước 1: Tìm lim f x x 0 x
Bước 2: Tìm lim f x . x 0 x
Nếu lim f x lim f x f x thì hàm số f(x) liên tục tại x . 0 0 x 0 x x 0 x 41 2 3 x 5 x 2 2
Ví dụ 1. Cho hàm số: y f x x 4 1 x 2 6 a). Tính lim f x. x2
b). Xét tính liên tục của hàm số f x tại x 2; x 2. 2 2 3 x 5 9 x 5 1 1
a).Ta có lim f x lim lim lim . 2 x2 x2 x2 x 4 2x 4 2 3 x 5 x2 2 3 x 5 6
b). Từ câu a) suy ra lim f x f 2. Vậy hàm số đã cho liên tục tại x 2. x2
hàm số đã cho không xác định tại x 2
, do đó hàm số không liên tục tại x 2 . 2 x 3x 2 x 2
Ví dụ 2. Cho hàm số f x x 2 a x 2
Với giá trị nào của a thì hàm số đã cho liên tục tại điểm x 2 ? 2 x 3x 2 x 1 x 2 Ta có lim f x lim lim lim x 1 1. x2 x2 x2 x2 x 2 x 2
Hàm liên tục tại x 2 khi và chỉ khi lim f x f 2 a 1. x2
Vậy hàm số đã cho liên tục tại x 2 khi a 1. 2 2x 7x 6 khi x < 2
Ví dụ 3: Cho hàm số y f x x 2
. Xác định a để hàm số f(x) liên tục tại x 2 0 1 x a + khi x 2 2 x . Ta có : 2 2x 7x 6 x 2 2x 3 2 x 2x 3 lim f x lim lim x 2 x 2 x 2 x 2 x 2 x 2 lim 3 2x 1 x 2 1 x 1 lim f x lim a + a f 2 . x 2 x 2 2 x 4 1 3
Hàm số liên tục tại x 2 lim f x lim f x f 2 a 1 a . 0 x 2 x 2 4 4 42
Ví dụ 4: Chứng minh các hàm số sau liên tục trên R. 3 2x x 3 x 1 2 x 4x 3 3 x 1 a). f x x 1 b). f x x 1 7 x 1 5 x x 1 3 3 2x x 3 x 1 3 a) f x x 1
. Tập xác định của f(x) là D 7 x 1 3 3 2x x 3 Nếu x 1 thì f x
là hàm số phân thức hữu tỉ, nên liên tục trên các khoảng ; 1 và 3 x 1 1; (1).
Bây giờ ta xét tính liên tục của f(x) tại x 1 0 7
Ta có: f (x ) f (1) 0 3 x x x 1 2 3 2x 2x 3 2 3 2 2x 2x 3 7 Ta có: lim f x lim lim lim 3 x x x 1 x x 1 2 1 1 1 x x 2 x1 1 x x 1 3
Vì lim f x f
1 Hàm số liên tục tại x 1 (2). x 1 0
Từ (1) và (2) suy ra hàm số f(x) liên tục trên R. 2 x 4x 3 x 1 b) f x x 1
. Tập xác định của f(x) là D 5 x x 1 2 2 x 4x 3 x 4x 3
Với mọi x 1; , ta có 0 0 lim f (x) lim
f (x ) . Suy ra hàm số f(x) liên tục 0 0 x 0 x x 0 x x 1 x 1 0
trên khoảng 1; (1).
Với mọi x ;1 , ta có lim f (x) lim
. Suy ra hàm số f(x) liên tục trên 5 x 5 x f (x ) 0 0 0 x 0 x x 0 x khoảng ;1 (2).
Ta xét tính liên tục của f(x) tại x 1 0 2 x 4x 3 x 1 x 3 Ta có: lim f x lim lim lim(x 3) 2. x 1 x 1 x 1 x 1 x 1 x 1 43
Ta có: lim f x lim 5 x 2. x 1 x 1 Và có f 1 5 1 2
Vì lim f x lim f x f
1 Hàm số liên tục tại 1 (3) x 1 x 1
Từ (1) (2) và (3) suy ra f(x) liên tục trên R. 1 x 3
Ví dụ 5: Cho hàm số f x ax b 3 x 5 7 x 5
Xác định a, b để hàm số liên tục trên R.
Ta có tập xác định của hàm số f(x) là D .
Ta có: hàm số liên tục trên khoảng ;3,3;5,5; (vì là hàm đa thức).
Do đó hàm số liên tục trên R khi và chỉ khi hàm số liên tục tại các điểm x 3 và x 5 . Tại x 3 :
Ta có lim f x lim1 1 và lim f x lim ax b 3a b và f 3 1. x 3 x 3 x 3 x 3
Do đó hàm liên tục tại x 3 khi và chỉ khi
lim f x lim f x f 3 3a b 1 1 x 3 x 3 Tại x 5
Ta có lim f x 5a b và lim f x 7 f 5. x 5 x 5
Do đó hàm số liên tục tại x 5 khi và chỉ khi
lim f x lim f x f 5 5a b 7 2 x 5 x 5 3 a b 1 a 3 Từ
1 và 2 suy ra hàm số liên tục trên R khi và chỉ khi: . 5 a b 7 b 8
Vậy với a 3,b 8 thì hàm số liên tục trên R. 44 Phương pháp:
Bước 1: Biến đổi phương trình về dạng f x 0 .
Bước 2: Tìm hai số a và b sao cho f a. f b 0 .
Bước 3: Chứng minh hàm số f(x) liên tục trên đoạn a;b .
Từ đó suy ra phương trình f x 0 có ít nhất một nghiệm thuộc a;b . Chú ý:
Nếu f a. f b 0 thì phương trình có ít nhất một nghiệm thuộc a;b
Nếu hàm số f(x) liên tục trên a; và có f a. lim f x 0 thì phương trình f x 0 có ít nhất x
một nghiệm thuộc a; .
Nếu hàm số f(x) liên tục trên ;a và có f a. lim f x 0 thì phương trình f x 0 có ít nhất x
một nghiệm thuộc ;a .
Ví dụ 6: Chứng minh rằng phương trình 3 2
4x 8x 1 0 có nghiệm trong khoảng 1; 2 Hàm số f x 3 2
4x 8x 1 liên tục trên R. Ta có f
1 11, f 2 1 nên f 1 . f 2 0
Do đó theo tính chất hàm số liên tục, phương trình đã cho có ít nhất một nghiệm thuộc khoảng 1; 2
Ví dụ 7: Chứng minh phương trình 4 2
4x 2x x 3 0 có ít nhất 2 nghiệm thuộc khoảng 1; 1 . Đặt f x 4 2
4x 2x x 3 thì fx liên tục trên R. f
1 4 2 1 3 4; f 0 3; f 1 2. Vì f
1 . f 0 0 nên phương trình có nghiệm thuộc khoảng 1;0 f
1 . f 0 0 suy ra phương trình có nghiệm thuộc khoảng 0; 1 .
Mà hai khoảng 1;0 ,0;
1 không giao nhau. Từ đó suy ra phương trình đã cho có ít nhất 2 nghiệm thuộc khoảng 1; 1 .
Ví dụ 8: Chứng minh rằng phương trình 2 2n m
m 3 x 2x 4 0 với n * luôn có ít nhất một nghiệm
âm với mọi giá trị của tham số m.
Đặt 2 2n f x m m 3 x 2x 4 . 45
Ta có 2n 2
2 2n f 2 m m 3 2 2 2 4 m m 3 .2 0, m
, f 0 4 0, m . Từ đó có
f 2.f 0 0,m (1). Do hàm số xác định và liên tục trên R nên hàm số liên tục trên đoạn 2 ;0 (2).
Từ (1) và (2) f x 0 có ít nhất một nghiệm thuộc 2;0 , m .
Kết luận phương trình f x 0 luôn có ít nhất một nghiệm âm với mọi giá trị tham số m.
Ví dụ 9: Chứng minh phương trình sau có nghiệm với mọi m a). m x
1 x 2 2x 1 0 (1) b). m 3 4 1 x m 1 x m 0 (1) a). m x
1 x 2 2x 1 0 (1)
Đặt f x m x 1 x 2 2x 1.
Tập xác định của hàm số f(x) là D R . Vì f(x) là hàm đa thức f x liên tục trên R.
Ta có f 2 m2
1 2 2 22 1 3 và có f 1 m 1
1 1 2 2.11 3. Vì f 2. f
1 3.3 9 0 với mọi m.
Do đó f x 0 luôn có ít nhất 1 nghiệm trong khoảng x 2,1 với mọi m. 0
Kết luận phương trình (1) luôn có nghiệm với mọi giá trị m. b). m 3 4 1 x m 1 x m 0 (1)
Đặt f x m 3 4 1 x m
1 x m . Tập xác định của hàm số f(x) là D R . Vì f(x) là hàm đa thức
f x liên tục trên R.
Ta có f 0 m và có f m 3 1 4 1 1 m 1
1 m 2m . Từ đó suy ra f f 2 1 .
0 2m 0 m 0 f x 0 luôn có ít nhất 1 nghiệm x 1;0 0 Xét trường hợp: m 0 3x 3 4.0 1 .
0 1 x 0 0 x x 0 x 1 x 0
Kết luận phương trình (1) luôn có nghiệm với mọi giá trị m.
Ví dụ 10: Chứng minh rằng với mọi a, b, c phương trình 3 2
x ax bx c 0 luôn có nghiệm. Đặt 3 2
f x x ax bx c thì f x liên tục trên R.
Ta có: lim f x x 0 để f x 0. 1 1 x
lim f x x 0 để f x 0. 2 2 x 46
Như vậy có x , x để f x . f x 0 suy ra phương trình có nghiệm x x ; x vậy phương trình đã 1 2 1 2 1 2 cho luôn có nghiệm.
Ví dụ 11: Chứng minh rằng với mọi a, b, c phương trình 4 3 2
x ax bx cx 1 0 có ít nhất hai nghiệm phân biệt. Đặt f x 4 3 2
x ax bx cx 1 thì f x liên tục trên R. Ta có: f 0 1;
lim f x x 0 để f x 0. 1 1 x
lim f x x 0 để f x 0. 2 2 x
Do đó f 0. f x 0 suy ra phương trình có nghiệm trong khoảng x ;0 2 2
f 0. f x 0 suy ra phương trình có nghiệm trong khoảng 0; x mà các khoảng x ;0 và 0; x 1 2 1 1
không giao nhau, do đó phương trình có ít nhất hai nghiệm phân biệt. 47
Giả sử u u(x),v v(x),w w(x) là các hàm số có đạo hàm, khi đó:
1). (u + u - w)' = u' + v' - w'; 2). (uv)' = u'v + v'u; 3) (k.u)' = k.u' ( k R ) / u u'v v'u / 1 v' 4). 5). . 2 v v 2 v v
BẢNG ĐẠO HÀM CỦA CÁC HÀM SỐ SƠ CẤP CƠ BẢN
Đạo hàm của hàm số sơ cấp cơ bản
Đạo hàm của hàm số hợp (u = u(x)) (C)' = 0 / x / 1 x , , x 0 u 1 u u', , u 0 1 ( x)' u' (x > 0) ( u)' (u > 0) 2 x 2 u 1 1 ( )' 1 u' (x 0) ( )' (u 0) 2 x x 2 u u / 1 n / 1 n ,x 0 .u',u 0 n n 1 x x n n 1 u u (sinx)' = cosx (sinu)' = cosu.u' (cosx)' = -sinx (cosu)' = -sinu.u' u ' tan x 1 2 ' 1 tan x tanu' 2 1 tan u u ' 2 2 cos x cos u (x k , k Z) (u k , k Z) 2 2 u ' x 1 cot ' 2 1 cot x cotu' 2 1 cot u u ' 2 2 sin x sin u (x k, k Z). (u k, k Z).
CÔNG THỨC TÍNH ĐẠO HÀM NHANH HAY DÙNG / ax b ad bc 2 cx d (cx d) 48
Ví dụ 1: Đạo hàm các hàm số sau: 1 2 3 1 1: 5 4 3 2 y
x x x x 4x 5 2: 4 3 y 2x x 2 x 5 2 3 2 3 1 2 3 1: 5 4 3 2 y
x x x x 4x 5 2 3 2 / 1 2 3 / / / 1 2 3 5 4 3 2 / y '
x x x x 4x 5 / 5 4 y ' x x 3 x 2 x 4x / 5 2 3 2 2 3 2 5 8 4 3 2
y ' x x 3x 3x 4. 2 3 1 2: 4 3 y 2x x 2 x 5 3 / / / / 4 1 3 1 1 y ' 2x x 2 x 5 y ' 4 2x 3 x 2 x / 5 3 2 y ' 8x x . 3 3 x
Ví dụ 2: Đạo hàm các hàm số sau: 2x 1 a). y 2 x 3x2 x. b) 2 y x x . c) y . 4x 3 2 3 1 2 x 3 x d). 2 7 y x x . f). y . g). y . 2 x x 5 2 1 1 x x 1 x k). y . 1 x / / a). y 2
x 3x2 x. y x x x x x x x x x/ 2 2 2 ' 3 2 3 . 2 3 . 2
x x 2 x x 2 2 3 2 3 1 3 x 2x 6. / / / 1 1 5x x b) 2 y x x y ' 2 x x 2 x . x x 2 2 .x 2 . x x .x 2x x x x . 2 x 2 2 2x 1 / 2x 1 c) y y ' 4x 3 4x 3 2x /
1 4x 3 4x 3/ 2x 1
24x 3 42x 1 2 . 4x 32 4x 32 4x 32 d). 2 7 y x
x . Sử dụng công thức u / 1 .u .u ' (với 7 u x x )
y x x x x/ 7 7 7 x x 6 ' 2 . 2 7x 1 49 1 / 1 f). y
. Đầu tiên sử dụng công thức với u x x 5 2 1 x x 5 2 1 u
2xx 1 /5 5 2xx 41. 2xx /1 52x 1 y ' 2 x x 10 1 x x x x 6 5 2 2 2 1 1 2 2 x 3 3 x / u g). y . Đầu tiên sử dụng 2 1 x x v
2 x 3 x / .
1 x x 1 x x / 2 3 2 2 2 2 x 3 3 x y ' 1 x x 2 2 / / / Tính 2 x 3 x 2 x 3 x 3 x 2 2 3 2 3 3 2 x x 3 x 2 x 2 x 4 2 2 3 3 2 5x 6x 6 . x 4 2 5x 6x 6x 2 1 x x 1 2x 2 2 x 3 3 x Vậy y ' 1 x x 2 2 x/ 1 / / 1 x .1 x 1 x / u
1 x 1 x 1 x 1 x k). y . Sử dụng 2 1 x được: y ' 1 x v 1x2 1 x 21 x 1 x 3 x x x x x . 2 1 . 1 2 1 1
Ví dụ 3: Đạo hàm các hàm số sau: 3 sin x a). y x cos x . b) y . c). 3 y sin 2x 1 . 1 cos x d). y tan 3x cot 3x e). y x cot 2x
a). y x cos x . Ta áp dụng đạo hàm tích. y x x x x/ ' 'cos . cos cos x xsin . x 3 sin x sin x b) y
. Bước đầu tiên ta áp dụng công thức / u với u 1 cos x 1 cos x 2 / sin x sin y ' 3 .
1 cos x 1 cos x 50 / sin x
sin x/ 1 cos x1 cos x/ .sin x cos x1 cos x 2 sin x Tính : 1 cos x 1 cos x2 1cos x2 2 2 cos x cos x sin x 1 . 1 cos x2 1 cos x 2 2 sin x 1 3sin x Vậy y ' 3 . .
1 cos x 1 cos x 1 cos x3 c). 3 y sin 2x
1 . Bước đầu tiên áp dung công thức /
u với u sin 2x 1 / Vậy y x
x x / 3 2 ' sin 2 1 3sin 2 1 . sin 2 1 . Tính x / sin 2 1 : Áp dụng /
sin u , với u 2x 1 Ta được:
x / x x / sin 2 1 cos 2 1 . 2 1 2cos 2x 1 . 2 y x x 2 ' 3.sin 2 1 .2 cos 2 1 6sin 2x 1 cos 2x 1 . d). 2
y sin 2 x . Áp dụng công thức / sin u với 2 u 2 x x x
y ' cos 2 x . 2 x 2 /2 / 2 2 2 2 cos 2 x . .cos 2 x . 2 2 2 2 x 2 x d). y tan 3x cot 3x y x/ x/ x x/ x x/ 2 2 ' tan 3 cot 3 1 tan 3 3 1 cot 3 3 2 x 2 x 2 2 3 1 tan 3 3 1 cot 3 3 2 tan 3x cot 3x. e). y x cot 2x y x x x x/ x x x x/ 2 x x 2 ' '.cot 2 cot 2 cot 2 1 cot 2 . 2 cot 2 2 1 cot 2x. Ví dụ 4: Tính 1 2 3 1 1 1). Cho f x . Tính f ' 1 . 2). Cho f x 2 x . Tính f ' 1 2 3 x x x x x 1 2 3 1). Cho f x . Tính f ' 1 . 2 3 x x x / 1
Bước đầu tiên tính đạo hàm sử dụng công thức 1 x x 51 / f x 1 2 3 1 4 9 ' f '
1 1 4 9 14 2 3 2 3 4 x x x x x x 1 1 2). Cho f x 2 x . Tính f ' 1 x x 1 1 1 x 1 1 2 / / Ta có f ' x x 2x 2x 2 2 x x x x x 2x x Vậy f 1 1 ' 1 1 2 2 2 3 2 x x Ví dụ 5: Cho f x
2x . Với những giá trị nào của x thì: 3 2 a. f ' x 0 b. f ' x 2 c. f ' x 10 3 2 x x Ta có f x 2 '
2x x x 2 3 2 a). f x 2 '
0 x x 2 0 x 1 x 2 b). f x 2 2 '
2 x x 2 2 x x 0 x 0 x 1 c). f x 2 2 '
10 x x 2 10 x x 12 0 x 3 x 4 Ví dụ 5: a). Cho f x 3 x x g x 2 2 2,
3x x 2 . Giải bất phương trình f 'x g 'x . 2 x b).Cho f x 3 2 x x g x 3 2 3, x
3 . Giải bất phương trình f 'x g 'x . 2
a). Ta có f x x x / 3 2 ' 2
2 6x 1, g x x x / 2 ' 3 2 6x 1 f x g x 2 2 ' '
6x 1 6x 1 6x 6x 0 x ;0 1; / 2 / x b). f x 3 2 x x 2 x x g x 3 2 ' 2 3 6 2 , ' x 3 3x x 2 f x g x 2 2 2 ' '
6x 2x 3x x 3x 3x 0 x ;0 1; 52
1. Cho hàm số y f x có đạo hàm f ' x . Hàm số f ' x còn gọi là đạo hàm cấp 1 của hàm số f x
. Nếu hàm số f ' x có đạo hàm thì đạo hàm đó được gọi là đạo hàm cấp 2 của hàm số f x , kí hiệu là
y’’ hay f ' x . Đạo hàm của đạo hàm cấp 2 được gọi là đạo hàm cấp 3 của hàm số f x , kí hiệu là y’’’
hay f’’’ x . Tương tự, ta gọi đạo hàm của đạo hàm cấp n
1 là đạo hàm cấp n của hàm số f x , kí hiệu là n y hay n f
x , tức là ta có: n n y 1 y 'nN,n 1 .
2.Đạo hàm cấp 2 của hàm số f(t) là gia tốc tức thời của chuyển động s f (t) tại thời điểm t. Phương pháp:
Áp dụng trực tiếp định nghĩa: n n y 1 y
' để tính đạo hàm đến cấp mà đề bài yêu cầu.
Ví dụ 1: Tính đạo hàm đến cấp đã chỉ ra của các hàm số sau:
a). y x sin 2x, y '' b). 2 y cos x, y '' c). 4 3 2 ( ) 4 3 1, n y x x x y d). 4 y x x (4) sin 2 , y
a). Có y ' x 'sin 2x .
x (sin 2x) ' sin 2x 2x cos 2x
y ' (sin 2x) ' (2x) 'cos 2x 2x(cos 2x) ' 4 cos 2x 4x sin 2x
y '' 4(cos 2 x) ' (4 x) 'sin 2 x 4 x(sin 2 x) ' 8sin 2 x 4sin 2 x 8cos 2 x 1 2sin 2 x8cos 2 x . 1 b). Ta có 2
y cos x 1 cos 2x y ' sin 2x y ' 2cos 2x y '' 4sin 2x 2 c). 4 3 2 y x 4x 3x 1 3 2 2
y ' 4x 12x 6x y ' 12x 24x 6 y '' 24x 24 (4) (5) (n)
y 24 y 0 ... y 0 . d). 4 y x sin 2x 3 2
y ' 4x 2cos 2x y ' 12x 4sin 2x (4)
y '' 24x 8cos 2x y 24 16sin 2x 53 Phương pháp:
Bước 1: Tính y ', y ', y '' . Dựa vào các đạo hàm vừa tính, dự đoán công thức tính (n) y .
Bước 2: Chứng minh công thức vừa dự đoán là đúng bằng phương pháp quy nạp.
Chú ý: Cần phân tích kĩ các kết quả của đạo hàm y ', y ', y '' tìm ra quy luật để dự đoán công thức (n) y chính xác.
Ví dụ 2: Tìm đạo hàm cấp n của hàm số y x * sin n N
Bước 1: Ta có: y ' cos x sin x 1.
; y ' sin x sin x 2 2 2 Dự đoán: n y x n * sin 1 , n N 2
Bước 2: Chứng minh 1 bằng quy nạp: n 1: 1 hiển nhiên đúng. Giả sử
1 đúng với n k 1 nghĩa là ta có: k y sin x k
ta phải chứng minh 1 cúng đúng với 2
n k 1 nghĩa là ta phải chứng minh k 1 y sin x k 1 2 2 / /
Thật vậy : vế trái k 1 2 k y y sin x k cos x k sin x k 1 =vế phải 2 2 2
2 2 đúng, nghĩa là 1 đúng với n k 1.
Bước 3: theo nguyên lí quy nạp suy ra n * y sin x n , n N . 2 1
Ví dụ 2: Tìm đạo hàm cấp n của hàm số y * n N x 3 1 1! Ta có: y ' / 1 1 ; 2 / x 3 x 32 y 2 1.2 2! ' 1 . 1 . . 3 2 x 3 x33 n n n! Dự đoán: y 1 1 , n N . n 1 * x 3 54 Chứng minh
1 bằng phương pháp quy nạp: n 1: 1 hiển nhiên đúng. k k k ! Giả sử
1 đúng với n k 1 , nghĩa là ta có: y 1
ta phải chứng minh 1 cúng đúng x 3k 1 k k 1 !
với n k 1 , nghĩa là ta phải chứng minh: k y 1 1 1 2 k 2 x 3 Thật vậy: vế trái / / / k k ! k k ! 2 y
y 1 1 . . x 3 k k k k 1 1 2 1 1 x 3 x 3k 1
k 1 k !k 1 k k 1 ! 1 . 1 . vt 2 k 2 1 k 2 x 3 x 3
Vậy 2 đúng nghĩa là 1 đúng với n k 1. n n n!
Theo nguyên lí quy nạp ta suy ra y * 1 . , n N . x 3n 1 Ví dụ 3:
a). Cho hàm số y x sin x . Chứng minh .
x y ' 2 y ' sin x xy 0 b). Cho hàm số : 2 y 2x x chứng minh: 3 y .y ' 1 0
c). Cho hàm số: y x tan x chứng minh: 2 x y 2 2
. ' 2 x y 1 y 0 x 3 d). Cho hàm số: y chứng minh: y 2 2 ' y 1 .y ' x 4
a). Cho hàm số y x sin x . Chứng minh .
x y ' 2 y ' sin x xy 0 Ta có y x x/ y x x x x/ ' sin ' '.sin . sin y ' sin x x cos x y x x x/ x/ x x/ x x x x x/ ' sin cos sin cos cos '.cos . cos 2cos x xsin x x x x x x x x x 2 1 2 cos sin 2 sin cos sin x sin x 0 2 2
2x cos x x sin x 2x cos x x sin x 0 0 0 (đpcm). b). Cho hàm số : 2 y 2x x chứng minh: 3 y .y ' 1 0 55 / 1 / 1 x Ta có: y ' 2 2x x y ' . 2 2x x . 2 2 2 2x x 2x x 1 x
1 x . 2x x 2x x / .1 x 2 / 2 2 2x x .1 x 2 2 ' x x y 2x x 2 2xx 2 2 2
2x x 1 x2 2 1 2x x . 2x x . 2 2xx 3 2 2 2 2x x 3 1 2 .
(đpcm). 2x x 1 0 1 1 0 3 2
c). Cho hàm số: y x tan x chứng minh: 2 x y 2 2
. ' 2 x y 1 y 0 Ta có: y x x/ x x x x/ x x 2 ' tan '.tan . tan tan 1 tan x y x/ x x x x/ 2 x x x 2 ' tan '. 1 tan . 1 tan 2 1 tan . 2 tan . tan 1 2
2 1 tan x1 x tan x 2 x 2 x x x 2 2 2 2 1 tan . 1 tan
2 x x tan x1 x tan x 0 2 x 2 x x x 2 x 2 2 1 tan 1 tan 2
1 tan x1 x tan x 0 0 0 (đpcm). x 3 d). Cho hàm số: y chứng minh: y 2 2 ' y 1 .y ' x 4 / 2 / 7 x 4 x 3 7 14 Ta có: y ' , y ' x 4 x 42 x 44 x 43 2 7 x 3 1 4 98 98 2 1 . (đpcm).
x 42 x 4 x 43 x 44 x 44 e) Cho hàm số 2
y cos 3x chứng minh: 182y 1 y ' 0 Ta có: 2 y cos 3x y x x/ x x x/ ' 2.cos3 cos3 2cos3 . sin 3 3 3
sin 6x y ' 18cos 6x 2 18 2cos 3x
1 18cos 6x 0 18.cos6x 18cos 6x 0 (đpcm). 56 – Phương pháp:
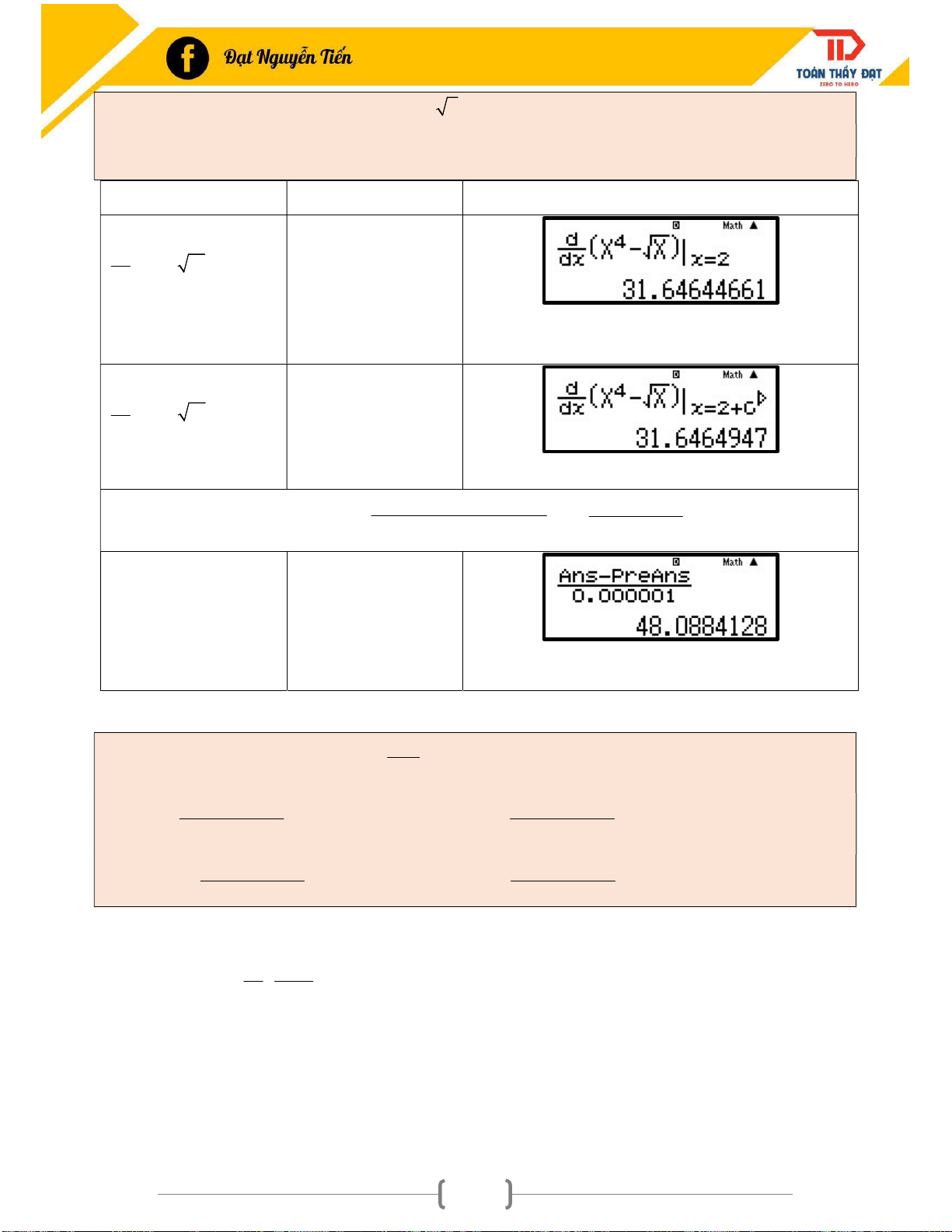
* Tính đạo hàm cấp 1 : qy * Tính đạo hàm cấp 2 : y '
y ' x 0,000001 y ' x 0 0 y ' x lim 0 x0 x 0,000001
* Dự đoán công thức đạo hàm bậc n :
+ Bước 1 : Tính đạo hàm cấp 1, đạo hàm cấp 2, đạo hàm cấp 3
+ Bước 2 : Tìm quy luật về dấu, về hệ số, về số biến, về số mũ rồi rút ra công thức tổng quát.
Quy trình bấm máy tính đạo hàm cấp 1: Bước 1: Ấn qy d
Bước 2: Nhập biểu thức f X và ấn =. X 0 x dx
Quy trình bấm máy tính đạo hàm cấp 2:
Bước 1: Tính đạo hàm cấp 1 tại điểm x x 0
Bước 2: Tính đạo hàm cấp 1 tại điểm x x 0,000001 0 Ans - PreAns
Bước 3: Nhập vào máy tính ấn =. X x 2
Ví dụ 1: Hệ số góc tiếp tuyến của đồ thị hàm số C : y
tại điểm có hoành độ x 1 là 2 0 x 3 1 7 1 A. B. . C. . D. 2 . 4 2 8 d X 2
Hệ số góc tiếp tuyến k y Nhập vào máy tính 1 2 dx X 3 X 1 Phép tính Quy trình bấm máy Màn hình hiển thị d X 2 qyaQ) 2
dx X 3 X 1 +2RsQ)d +3$$$1= d X 2 1 Vậy k y 0,125 Chọn C. 1 2 dx X 3 8 X 1 57
Ví dụ 2: Đạo hàm cấp 2 của hàm số 4
y x x tại điểm có hoành độ x 2 gần số giá trị nào nhất 0 trong các giá trị sau: A. 7. B. 19. C. 25. D. 48. Phép tính Quy trình bấm máy Màn hình hiển thị Tại x 2 0 d 4 X X qyQ)^ X 2 dx 4$psQ )$$2= x 2 0, 000001 0 d 4 X X !!+0.0 X 2 0,000001 dx 00001= y ' 2 0.000001 y ' 2 Ans - PreAns Tính y ' 2 nhờ 0.000001 X aMpQM R0.00 0001=
Vậy y 2 48 Chọn D. x 1
Ví dụ 3: Tính đạo hàm của hàm số y 4x 1 2 x 1 ln 2 1 2x 1 ln 2 A. y ' B. y ' 2 2 x 2 2 x 1 2 x 1 ln 2 1 2x 1 ln 2 C. y ' D. y ' 2 2x 2 2x
Ta chọn tính đạo hàm tại điểm bất kì ví dụ chọn x 0,5 rồi tính đạo hàm của hàm số tại X 0,5 . d X 1 Nhập vào máy tính dx 4X X0,5 58 Phép tính Quy trình bấm máy Màn hình hiển thị d X 1 dx 4X X0,5 qyaQ)+1 R4^Q)$$$ 0.5= Lưu kết quả vừa tìm được qJz vào biến A
Lấy A trừ đi kết quả tính giá trị các biểu thức ở các đáp án nếu ra 0 thì chọn đáp án đó. pa1p2(Q) Đáp án A +1)h2)R2 ^2Q)r 0.5= Số 1 2 8 ,562.10
0 . Nếu chưa ra kết quả là 0 thì thay các đáp án còn
lại bao giờ ra 0 thì chọn Chọn A. Ví dụ 4: Cho hàm số x
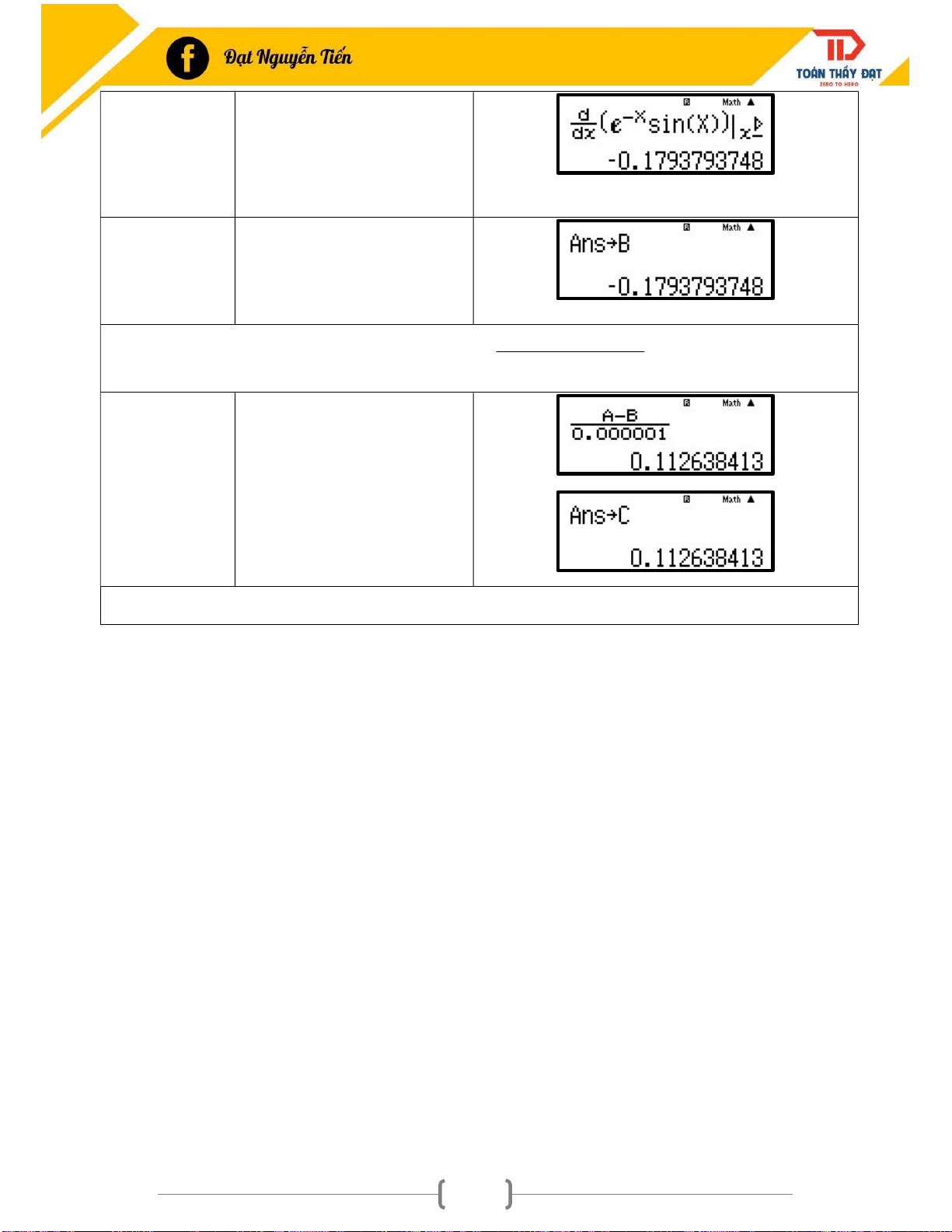
y e sin x , đặt F y ' 2 y ' khẳng định nào sau đây là khẳng định đúng ? A. F 2y B. F y C. F y D. F 2 y Phép tính Quy trình bấm máy Màn hình hiển thị Tính qw4qyQK y '2 0,00 1 ^pQ)$jQ ))$2+0.0 00001 =qJz Lưu kết quả vừa tìm được vào qJz biến A 59 Tính y'0 E!!ooooo oooo=qJx Lưu kết quả vừa tìm được vào qJx biến B f ' x x f ' x
Thay vào công thức f ' x C 0 0 0 x 0 aQzpQxR 0.000001 =qJc
Tính F y ' 2 y ' C 2B 0.2461... 2 y Chọn A. 60
I – Kiến thức cần nhớ
Phương trình tiếp tuyến của C : y f x tại điểm M x ; y có dạng: o o : y k x x y o o
Với k y ' x là hệ số góc tiếp tuyến. o
Để viết phương trình tiếp tuyến , ta
cần tìm ba thành phần x , y , k o o
Điều kiện cần và đủ để hai đường C : y f x và C : y g x tiếp xúc nhau 2 1 f x g x hệ
có nghiệm (nhớ: "hàm hàm, đạo đạo") f ' x g ' x
II – Các dạng toán viết phương trình tiếp tuyến thường gặp
Viết PTTT của C : y f x, biết có hệ số góc k cho trước
Gọi M x ; y là tiếp điểm. Tính y ' y 'x . o o o
Do phương trình tiếp tuyến có hệ số góc k y ' x k i o
Giải i tìm được x y f x
: y k x x y . o o o o o
Lưu ý. Hệ số góc k y '(x ) của tiếp tuyến thường cho gián tiếp như sau: o
Phương trình tiếp tuyến // d : y ax b k a . 1
Phương trình tiếp tuyến d : y ax b k . a
Phương trình tiếp tuyến tạo với trục hoành góc k tan . k a
Phương trình tiếp tuyến tạo với d : y ax b góc tan 1 k.a
Viết PTTT của C : y f x, biết đi qua (kẻ từ) điểm A x ; y A A
Gọi M x ; y là tiếp điểm. Tính y f x và k y 'x theo x . o o o o o o
Phương trình tiếp tuyến tại M x ; y là : y k x x y . o o o o
Do Ax ; y y k x x y i A A A A o o
Giải phương trình i x y và k phương trình . o o
Viết PTTT của C : y f x, biết cắt hai trục tọa độ tại A và B sao cho tam giác OAB
vuông cân hoặc có diện tích S cho trước
Gọi M (x ; y ) là tiếp điểm và tính hệ số góc k y '(x ) theo x . o o o o O
ABvuông cân tạo với Ox một góc 45o và O i Đề cho S S O . A OB 2S ii O AB
Giải i hoặc ii x y ;k
phương trình tiếp tuyến . o o
Tìm những điểm trên đường thẳng d : ax by c 0 mà từ đó vẽ được 1, 2,3,..., n tiếp tuyến với
đồ thị hàm số C : y f x 61
Gọi M x ; y d : ax by c 0 (sao cho có một biến x trong M) M M M
PTTT qua M và có hệ số góc k có dạng : y k x x y . M M f x k x x y i M
Áp dụng điều kiện tiếp xúc: M f ' x k ii
Thế k từ ii vào i, được: f x f 'x.x x y iii M M
Số tiếp tuyến của C vẽ từ M số nghiệm x của iii .
Tìm những điểm M x ; y
mà từ đó vẽ được hai tiếp tuyến với đồ thị hàm số C : y f x M M
và hai tiếp tuyến đó vuông góc nhau
PTTT qua M và có hệ số góc k có dạng : y k x x y . M M f x k x x y i M
Áp dụng điều kiện tiếp xúc: M f ' x k ii
Thế k từ ii vào i, được: f x f 'x.x x y iii M M
Qua M vẽ được hai tiếp tuyến với C iii có hai nghiệm phân biệt x , x . 1 2
Hai tiếp tuyến đó vuông góc nhau k .k 1 y ' x .y ' x 1. 1 2 1 2 Lưu ý.
Qua M vẽ được hai tiếp tuyến với C sao cho hai tiếp điểm nằm về hai phía với trục hoành thì iii :
có hai nghiệm phân biệt x , x . 1 2 f x . f x 0. 1 2
Đối với bài toán tìm điểm M C : y f x sao cho tại đó tiếp tuyến song song hoặc vuông góc với
đường thẳng d cho trước, ta chỉ cần gọi M x ; y và là tiếp tuyến với k f ' x . Rồi áp dụng o o o
k f ' x k nếu cho song song và f ' x k nếu cho vuông góc x y M x ; y . o o o o o . 1 o d d
Ví dụ 1: Cho đường cong C y f x 3 2 :
x 3x . Viết phương trình tiếp tuyến của C trong các trường hợp sau:
a) Tại điểm M 1 ; 2 . 0
b) Tại điểm thuộc C và có hoành độ x 1. 0
c) Tại giao điểm của C với trục hoành .
d) Biết tiếp tuyến đi qua điểm A1 ; 4 . Ta có 2 f '(x) 3x 6x
a). Ta có f '(x ) f '(1) 3 0
Vậy phương trình tiếp tuyến tại điểm M 1 ; 2 : y f '(x )(x x ) y 0 0 0 y 3x 1 3 y 3x
b). Ta có x 1 y 4, f ' x 9 0 0 0
Vậy phương trình tiếp tuyến tại điểm N 1; 4 là y f '(x )(x x ) y 0 0 0 62 y 9 x 1 4 y 9x 5 . x 0
c). Phương trình hoành độ giao điểm của C với trục hoành: 3 2 x 3x 0 x 3
Với x 0 y 0, f '(x ) f '(0) 0 0 0 0
Vậy phương trình tiếp tuyến tại điểm 0;0 là y f '(x )(x x ) y y 0 0 0 0
Với x 3 y 0, f '(x ) f '(3) 9 0 0 0
Vậy phương trình tiếp tuyến tại điểm 3;0 là y f '(x )(x x ) y 0 0 0
y 9 x 3 y 9x 27 .
d). Gọi x ; y là tọa độ tiếp điểm của phương trình tiếp tuyến d đi qua điểm A 0 0
Vì điểm x ; y C 3 2
y x 3x , và f 'x 3x 6x 0 2 0 0 0 0 0 0 0
Phương trình d: y f '(x )(x x ) y y 2 3x 6x x x x 3x 0 0 0 3 2 0 0 0 0 0
Vì A1; 4 d nên: 2 3x 6x 1 x 3 2 x 3x 4 0 0 0 0 0 3
2x 6x 4 0 x 2 x 1 0 0 0 0
Với x 2 y 4, f ' 2 0 , phương trình tiếp tuyến y 4 0 0
Với x 1 y 4, f ' 1 9 , phương trình tiếp tuyến y 9 x 1 4 y 9x 5 0 0 x
Ví dụ 2: Cho đường cong C 3 1 : y . 1 x
a). Viết phương trình tiếp tuyến của C biết tiếp tuyến song song với đường thẳng (d) : x 4 y 21 0 .
b). Viết phương trình tiếp tuyến của C biết tiếp tuyến vuông góc với đường thẳng () : 2x 2y 9 0 .
c). Viết phương trình tiếp tuyến của C biết tiếp tuyến tạo với đường thẳng :
(d ) : x 2y 5 0 một góc 0 30 . 4
Tập xác định D R \{1}. Ta có y ' f ' x 1 x2 a). Có d 1 21 1
: x 4 y 21 0 y x k 4 4 d 4 1
Vì tiếp tuyến song song với d nên k k . tt d 4 4 1
Gọi M x , y là tọa độ tiếp điểm của tiếp tuyến, ta có f 'x k 0 0 0 tt 1 x 2 4 0 x 2
1 16 x 5 x 3 0 0 0 63 Với x 5 y 4
, phương trình tiếp tuyến tại điểm này là: y f '(x )(x x ) y 0 0 0 0 0 1 y x 1 21 5 4 y x (loại, vì trùng với d). 4 4 4 Với x 3 y 2
, phương trình tiếp tuyến tại điểm này là: y f '(x )(x x ) y 0 0 0 0 1 y x 1 5 3 2 y x . 4 4 4 b). 9
: 2x 2 y 9 0 y x k 1 2
Vì tiếp tuyến vuông góc với nên, k .k 1 k 1 tt tt 4
Gọi N x , y là tọa độ tiếp điểm của tiếp tuyến, ta có f ' x k 1 0 0 0 tt 1 x 2 0 x 2 1 4 x 3 x 1 . 0 0 0
Với x 3 y 5 , phương trình tiếp tuyến tại điểm này là: y f '(x )(x x ) y 0 0 0 0
y 1x 3 5 y x 2
Với x 1 y 1, phương trình tiếp tuyến tại điểm này là: y f '(x )(x x ) y 0 0 0 0 y 1x 1 1 y x 2 . 1 5 1
c). (d ) : x 2 y 5 0 y x k 2 2 d 2 k k
Ta có tiếp tuyến hợp với d một góc 300, nên có tt d 0 t an30 1 k k tt d 1 k 2 2 tt 1 1 1 11 2 1 2 3 k 1 k k 4k 0 1 3 tt 2 2 tt 4 tt tt 4 1 k 2 tt 2 x x 2
Ví dụ 3: Cho hàm số y f (x) C x 1
a). Viết phương trình tiếp tuyến của (C) tại điểm M(2; 4).
b). Viết phương trình tiếp tuyến của (C) biết tiếp tuyến có hệ số góc k 1. 2 x 2x 1 Ta có: f '(x) 2 (x 1)
a). Ta có x 2 f '(x ) f '(2) 1 0 0
Phương trình tiếp tuyến của (C) tại điểm M(2; 4) là y f ' x x x y 0 0 0
y 1x 2 4 y x 6 64
b). Gọi x là hoành độ tiếp điểm của tiếp tuyến với đồ thị, ta có f ' x 1 0 0 2 x 2x 1 0 0 1 1 1 (vô lý). 2 (x 1) 0
Kết luận không có tiếp tuyến nào có hệ số góc bằng 1.
Ví dụ 4: Cho hàm số (C): 2
y 1 x x . Tìm phương trình tiếp tuyến với (C): 1
a) Tại điểm có hoành độ x . 0 2
b) Song song với đường thẳng (d): x + 2y = 0. 1 5 1 5 1 2x Tập xác định D ; . Ta có f ' x 2 2 2 2 1 x x 1 1 1 1 1
a). Với x y 1 , f ' x f ' 2 0 0 0 2 2 4 2 2 1 1
Vậy phương trình tiếp tuyến tại điểm ; là y f ' x x x y 0 0 2 2 0 1 1 3 y 2 x y 2x . 2 2 2 1 1
b). Ta có (d ) : x 2 y 0 y x k 2 d 2 1
Vì tiếp tuyến song song với d nên, k k . Gọi x là hoành độ tiếp điểm của tiếp tuyến với đồ thị, tt d 2 0 1 1 2x 1 1 2x 0 ta có f ' x
1 2x 1 x x 0 0 2 0 0 0 0 2 2 2 1 x x 2 x 0 x 1 0 0 0 0
So với điều kiện x 0 (nhận), x 1 (loại) 0 0 1 1
Với x 0 y 1, phương trình tiếp tuyến tại điểm 0;
1 là: y x 0 1 y x 1. 0 0 2 2 Ví dụ 5: Cho hàm số 3 2
y x 3x 9x 5 C . Trong tất cả các tiếp tuyến của đồ thị C , hãy tìm tiếp
tuyến có hệ số góc nhỏ nhất. Ta có y f x 2 ' ' 3x 6x 9
Gọi x là hoành độ tiếp điểm của tiếp tuyến, vậy f ' x 3x 6x 9 0 2 0 0 0
Ta có 3x 6x 9 3x 2x 1 12 3 x 2 2 2 1 12 12, x C 0 0 0 0 0 0
Vậy min f ' x 12 tại x 1 y 16 0 0 0
Suy ra phương trình tiếp tuyến cần tìm: y 12 x
1 16 y 12x 4 65 x 2
Ví dụ 6: Cho hàm số y
1 . Viết phương trình tiếp tuyến của đồ thị hàm số (1), biết tiếp tuyến 2x 3
đó cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A, B và tam giác OAB cân tại gốc tọa độ O. 3 1
Tập xác định D R \ . Ta có y ' f 'x 2 2x 32
Vì tiếp tuyến (d) cắt hai trục Ox, Oy lần lượt tại A, B tạo thành tam giác OAB vuông cân, nên đường
thẳng (d) hợp với trục Ox một góc 450. Vậy có 0
k tan 45 k 1 tt tt
Gọi x là hoành độ tiếp điểm của tiếp tuyến, ta có f ' x 1 0 0 1 Với f ' x 1
1 (phương trình vô nghiệm). 0 2x 32 0 1 Với f ' x 1 1
2x 3 1 x 1 x 2 2 0 2 0 2x 3 0 0 0 Với x 1
y 1, phương trình tiếp tuyến tại điểm này y 1x
1 1 y x . Tiếp tuyến này 0 0
loại vì đường thẳng này đi qua gốc tọa độ nên không tạo thành được tam giác.
Với x 2 y 0 , phương trình tiếp tuyến tại điểm này y 1 x 2 y x 2 0 0 Ví dụ 7: Cho hàm số 3 2
y x 3mx m 1 x 1
1 , m là tham số thực. Tìm các giá trị của m để tiếp
tuyến của đồ thị của hàm số (1) tại điểm có hoành độ x 1
đi qua điểm A1;2. Tập xác định D R 2
y ' f '(x) 3x 6mx m 1 Với x 1
y 2m 1, f '(1) 5 m 4 0 0
Phương trình tiếp tuyến tại điểm M 1; 2m
1 : y 5m 4 x 1 2m 1 (d). Ta có A d m 5 1; 2 ( ) 5
4 .2 2m 1 2 m . 8 3x 1
Ví dụ 8: Cho hàm số y
1 . Tính diện tích của tam giác tạo bởi các trục tọa độ và tiếp tuyến của x 1
đồ thị của hàm số (1) tại điểm M 2;5 . 2
Tập xác định D R \ 1 . Có y ' . x 2 1
Phương trình tiếp tuyến (d) tại điểm M 2;5 : y 2 x 2 5 y 2x 9 9 9
Gọi A là giao điểm của d và trục hoành y 0 x , vậy A ;0 A A 2 2
Gọi B là giao điểm của d và trục tung x 0 y 9 , vậy B 0;9 . B B 1 1 9 81
Ta có tam giác OAB vuông tại O nên S O . A OB 9 O AB 2 2 2 4 66 Ví dụ 9: Cho hàm số 3
y 3x 4 C . Viết phương trình tiếp tuyến của đồ thị C biết tiếp tuyến tạo
với đường thẳng d : x 3y 6 0 góc 0 30 .
Tập xác định D R . Ta có 2 y ' 3 3x d 3 3
: 3y x 6 0 y x 2 3 k 3 d 3 k k
Vì tiếp tuyến tạo với đường thẳng d một góc 0 30 nên thỏa tt d 0 t an30 1 k k tt d 3 2 2 k tt 1 3 3 3 2 3k 1
k k 3k 0 k 0 k 3 3 3 tt 3 3 tt tt tt tt tt 1 k 3 tt
Gọi x là hoành độ tiếp điểm 0 Với 2
k 0 3 3x 0 x 0 y 4 . Phương trình tiếp tuyến tại điểm (0 ; 4): y 4 . tt 0 0 0 1 1 Với 2 2
k 3 3 3x 3 x x tt 0 0 0 3 3 1 13 1 13 10 Với x y
, phương trình tiếp tuyến y 3 x y 3x . 0 0 3 3 3 3 3 1 11 1 11 14 Với x y
, phương trình tiếp tuyến y 3 x y 3x . 0 0 3 3 3 3 3 Ví dụ 10: Cho hàm số 3 2
y x 3x 9x 5 C . Trong tất cả các tiếp tuyến của đồ thị C , hãy tìm
tiếp tuyến có hệ số góc lớn nhất.
Tập xác định D R . Ta có 2 y ' 3 x 6x 9
Gọi x là hoành độ tiếp điểm của tiếp tuyến, ta có f ' x 3x 6x 9 0 2 0 0 0
f 'x 3x 2x 1 12 3 x 2 2 1 12 12 0 0 0 0
Từ đó suy ra max f ' x 12 tại x 1. 0 0 Với x 1 y 1
6 , phương trình tiếp tuyến cần tìm: y 12x 1 16 y 12x 4 0 0 2x 1
Ví dụ 11: Cho hàm số y
C . Gọi I 1 ; 2. Tìm điểm M C sao cho tiếp tuyến của C x 1
tại M vuông góc với đường thẳng IM . 1
Tập xác định D R . Ta có y ' x 2 1 2x 1
Gọi M x , y C 0 y 0 0 0 x 1 0 2x 1 1 1 Ta có 0 IM x 1;
2 IM x 1; k 0 0 x 1 x 1 IM x 1 0 2 0 0 67 1
Hệ số góc của tiếp tuyến tại M k f ' x tt 0 x 2 1 0
Vì tiếp tuyến vuông góc với đường thẳng IM nên có k .k 1 tt IM 1 1 x 1 1 x 0 x 2 x 1 0 4 0 0 0
Vậy có 2 điểm M 0;1 , M 2;3 thỏa yêu cầu bài toán. 1 2 2x
Ví dụ 12: Cho hàm số y
C . Tìm điểm M C , biết tiếp tuyến của C tại M cắt hai trục tọa độ x 1 1
tại A, B và tam giác OAB có diện tích bằng . 4 2
Tập xác định D R \ 1 . Ta có y ' 2 (x 1) 2x
Gọi M x ; y C 0 y 0 0 0 x 1 0
Phương trình tiếp tuyến của (C) tại M: y f ' x x x y 0 0 0 2 2 2x 2 2x y x x y x d 2 0 0 0 2 2 (x 1) x 1 (x 1) (x 1) 0 0 0 0
Gọi A là giao điểm của d và trục Ox, có 2
y 0 x x . Vậy A 2 x ;0 0 A 0 2 2x 2 2x
Gọi B là giao điểm của d và trục Oy, có 0 x 0 y . Vậy 0 B 0; B B 2 (x 1) 2 (x 1) 0 0 1 1 1
Ta có tam giác OAB cân tại O, theo giả thiết ta có: S O . A OB OAB 4 2 4 2 2 2 2x 1 2x x 1 2x x 1 0 2 0 2 2 0 0 0 0 x .
4x (x 1) 0 2 0 0 2 2 (x 1) 2 0 2x x 1 2x x 1 0 0 0 0 0 Với 2
2x x 1 0 phương trình vô nghiệm. 0 0 1 Với 2
2x x 1 0 x 1 x 0 0 0 0 2 1 1
Với x 1 ta có M 1;
1 . Với x ta có M ;2 0 0 2 2 1
Vậy có hai điểm M thỏa mãn yêu cầu bài toán là M 1; 1 , M ; 2 2 68
Phương pháp : Phương trình tiếp có dạng d : y kx . m
+ Đầu tiên tìm hệ số góc tiếp tuyến k y x . 0 d Bấm q y và nhập f X
, sau đó bấm = ta được k. x dx 0 x d
+ Tiếp theo: Bấm phím ! để sửa lại thành f X
x X f X , sau đó bấm phím r với x dx 0 x
X x và bấm phím = ta được . m 0 x
Ví dụ 1: Cho điểm M thuộc đồ thị C 2 1 : y và có hoành độ bằng 1
. Phương trình tiếp tuyến của x 1
đồ thị C tại điểm M là: 3 1 3 1 3 1 3 1 A. y x . B. y x . C. y x . D. y x . 4 4 4 4 4 4 4 4 Phép tính Quy trình bấm máy Màn hình hiển thị d 2X 1 dx X 1 x 1 qya2Q)+ 1RQ)p1$ $p1=
Bấm phím ! để sửa lại thành: d 2X 1 X 2X 1 x dx X 1 X 1 x 1
sau đó bấm phím r với X 1
và bấm phím = ta được kết quả =!(pQ))+a2Q) +1RQ)p1= 3x 1
Vậy phương trình tiếp tuyến tại M là: y Chọn B. 4 4
Ví dụ 2: Phương trình tiếp tuyến của đồ thị C 3
: y x 3x 2 có hệ số góc bằng 9 là:
A. y 9x 18; y 9x 22.
B. y 9x 14; y 9x 18. 69
C. y 9x 18; y 9x 22.
D. y 9x 14; y 9x 18.
Với x 2 ta nhập X 3 9 X 3X 2 r với 0
X 2 rồi bấm = ta được kết quả là 14 d : y 9x 14. 1 Với x 2 ta nhập X 3 9 X 3X 2 r với 0 X 2
rồi bấm = ta được kết quả là 18 d : y 9x 18. 2 Chọn B.
Ví dụ 3: Tiếp tuyến của đồ thị C 3
: y 4x 3x 1 đi qua điểm A1;2 có phương trình là A. y 9
x 7; y x 2. B. y 9
x 11; y x 2. C. y 9 x 11; y 2. D. y 9 x 7; y 2.
Cho f x bằng kết quả các đáp án, từ đó ta thu được các phương trình.
Sử dụng chức năng giải phương trình bậc ba của máy tính bỏ túi bằng cách bấm tổ hợp phím w 5
4 và nhập hệ số phương trình.
Thông thường máy tính cho số nghiệm thực nhỏ hơn số bậc của phương trình là 1 thì ta chọn đáp án đó.
+ Đầu tiên thử với đáp án A, ta cho: 3 3 4 x 3x 1 9
x 7 4x 12x 6 0.
Máy tính cho 3 nghiệm Loại A.
Thử với đáp án B, ta cho: 3 3
4x 3x 1 x 2 4 x 4x 1 0.
Máy tính cho 3 nghiệm Loại B.
Thử với đáp án B, ta cho: 3 3
4x 3x 1 9x 11 4 x 12x 10 0.
Máy tính hiển thị 1 nghiệm thực và 2 nghiệm phức (phương trình có số nghiệm thực là một nhỏ hơn bậc
của phương trình là 2) Loại C. + Thử với đáp án : 3 3
4x 3x 1 9x 7 4 x 12x 8 0
máy tính hiển thị 2 nghiệm x 1; x 2 (nhận). 3 3 4 x 3x 1 2 4 x 3x 1 0 1
máy tính hiển thị 2 nghiệm x 1 ; x (nhận). 2 Chọn D. 70 71 1. Định nghĩa d P d P 0 ( ) ;( ) 90 2. Tính chất
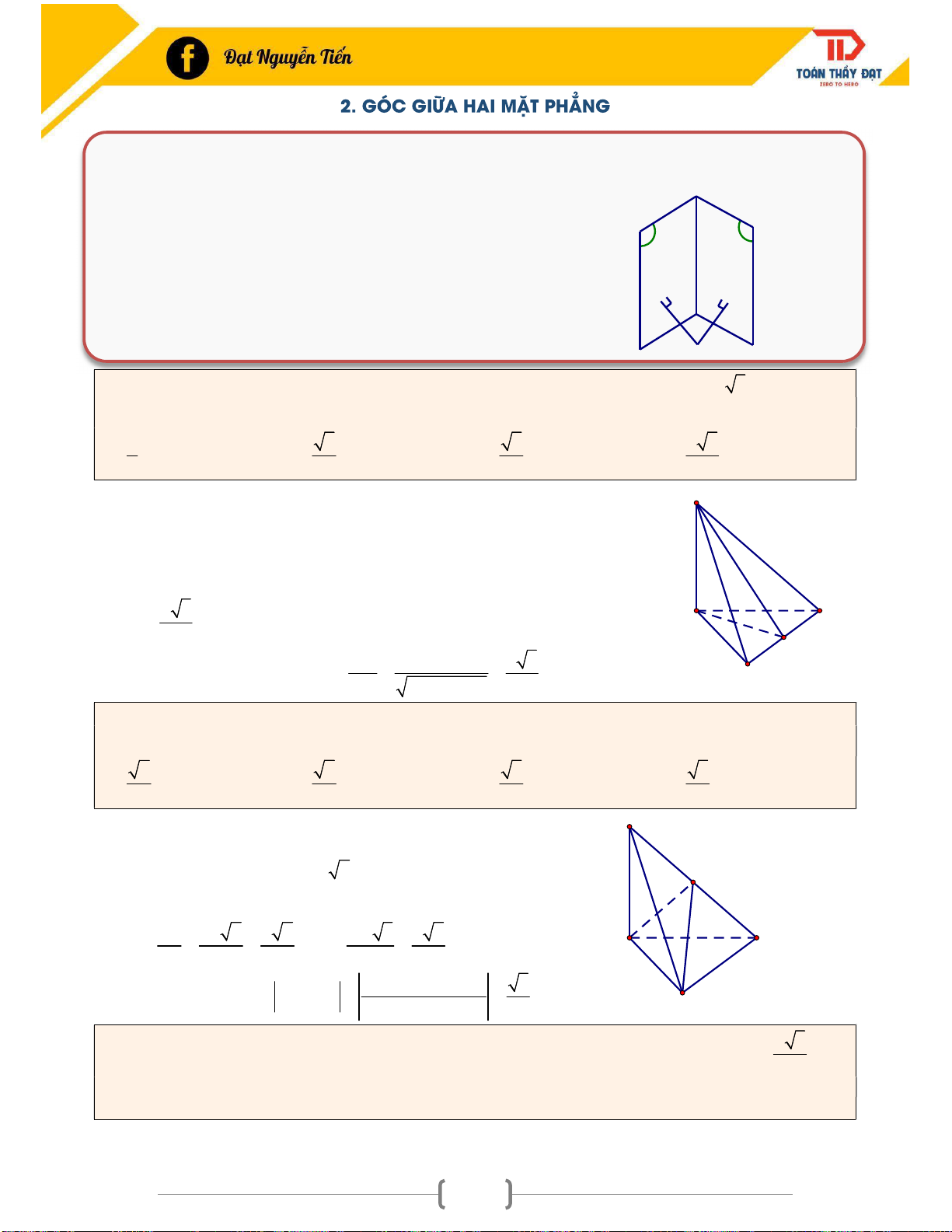
Định lý 1: Nếu một đường thẳng d vuông góc với hai đường thẳng cắt nhau nằm trong (P) thì d vuông góc với (P) . a b M (P) d a d (P) d b
Định lý 2: Nếu đường thẳng d vuông góc với (P) thì d vuông góc với
mọi đường thẳng nằm trong (P) . d (P) d c c ( ) P Chú ý
- Trong không gian, hai đường thẳng vuông góc không nhất thiết phải cắt nhau.
- Trong không gian bảo toàn quan hệ vuông góc.
3. Phương pháp chứng minh d (P) Có sẵn d a (P)
Phải chứng minh d b (P) ?
Chứng minh b vuông góc với một mặt chứa d
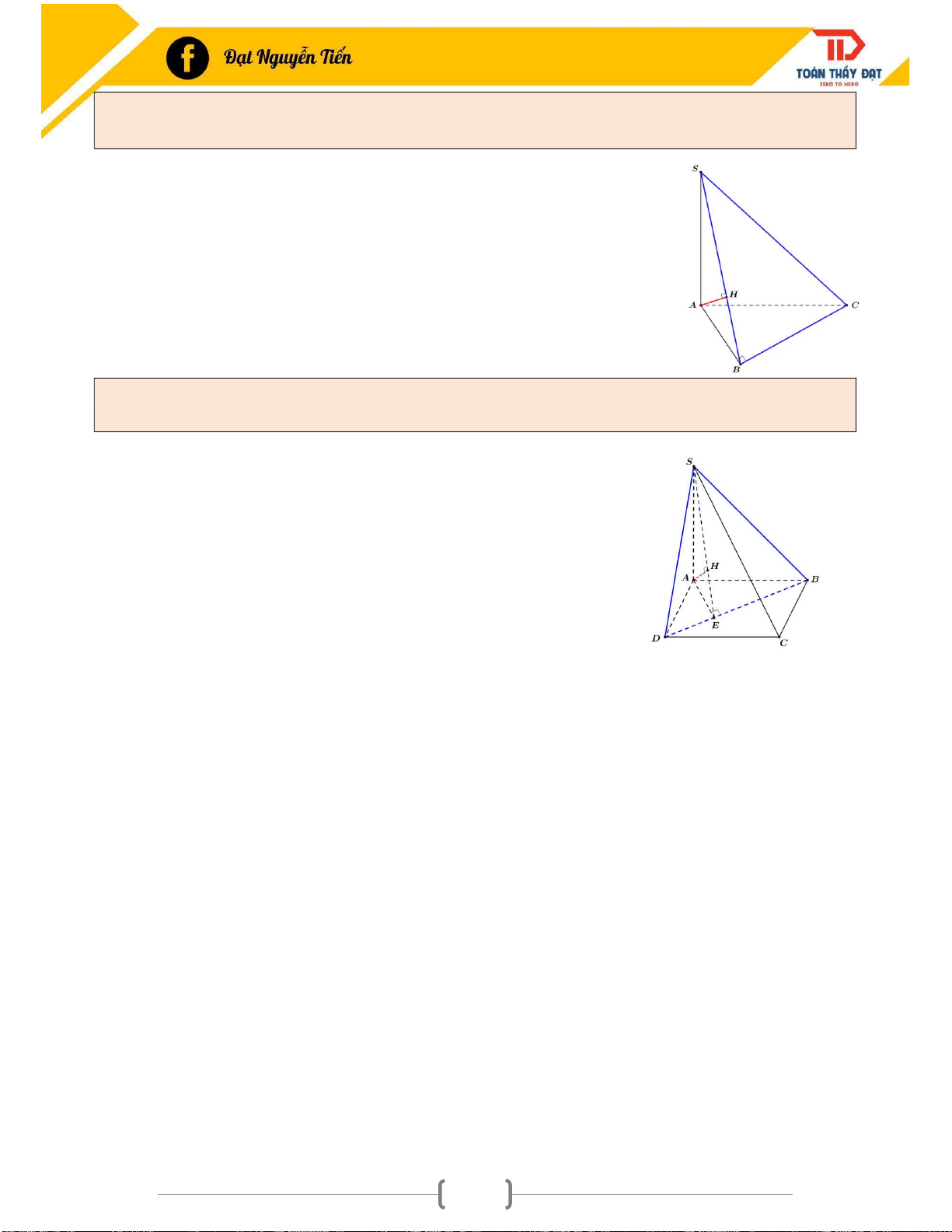
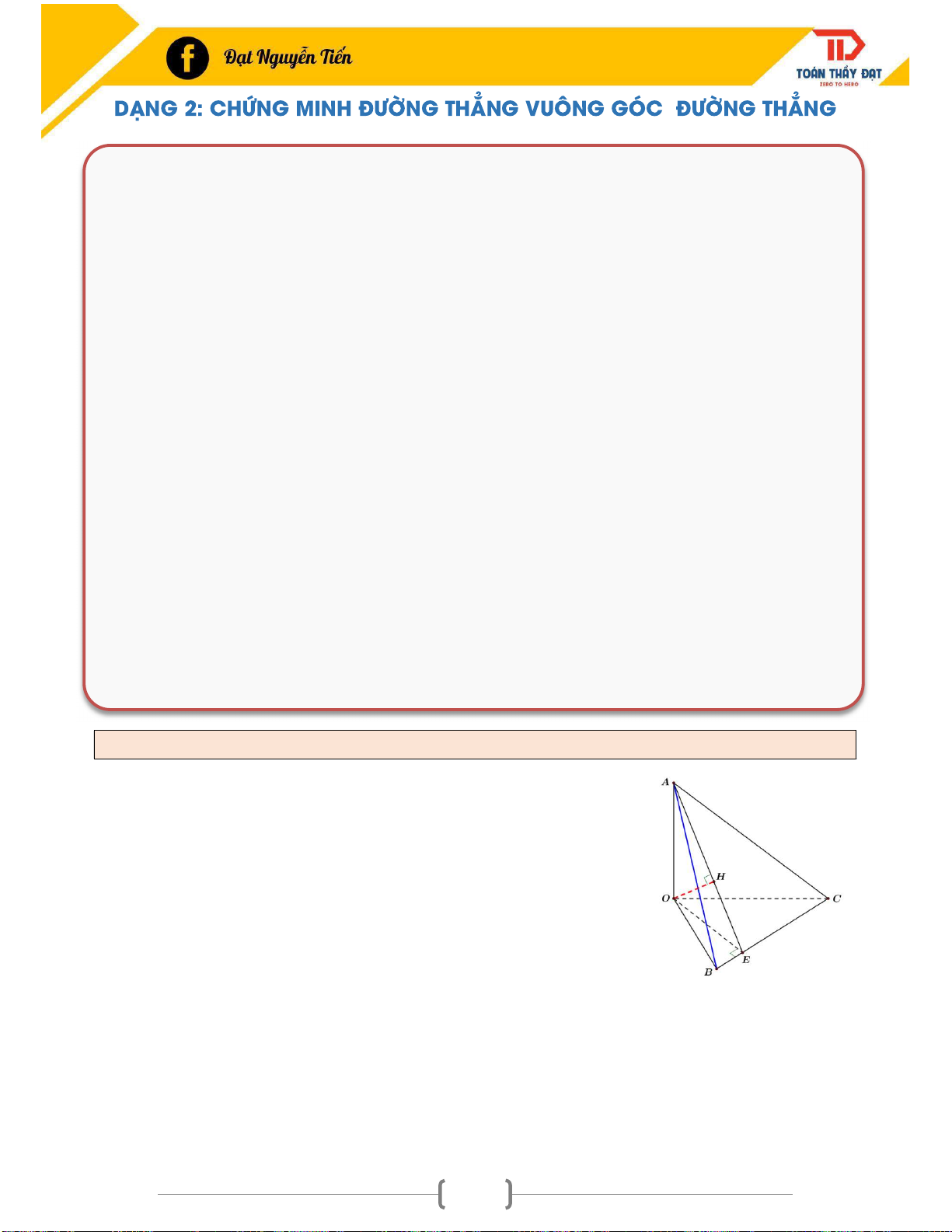
Ví dụ 1: Cho hình chóp S.ABC có SA (ABC),ABC không vuông ở B và C. Vẽ AE BC,
AH SE. Chứng minh AH (SBC) ? Có sẵn AH SE (1) Phải chứng minh AH BC Ta chứng minh BC (SAE) BC AE
BC (SAE) BC AH (2) BC SA
Từ (1) và (2) AH (SBC). 72
Ví dụ 2: Cho hình chóp S.ABC có SA (ABC),ABC vuông ở B. Vẽ AH SB. Chứng minh AH (SBC). Có sẵn AH SB (1) Phải chứng minh AH BC Ta chứng minh BC (SAB) BC AB
BC (SAB) BC AH (2) BC SA
Từ (1) và (2) AH (SBC).
Ví dụ 3: Cho hình chóp S.ABCD có SA ( ABCD), ABCD là hình chữ nhật. Vẽ AE BD, AE SE. Chứng minh AH (SBD)? Có sẵn AH SE (1) Phải chứng minh AH BD BD AE
BD (SAE) BD AH (2) BD SA
Từ (1) và (2) AH (SBD). 73 1. Định nghĩa 0 d a (d; a) 90 2. Tính chất Định lý 1: a b M (P) d a d (P) d b Định lý 2: d (P) d c c ( ) P Chú ý
- Trong không gian, hai đường thẳng vuông góc không nhất thiết phải cắt nhau.
- Trong không gian bảo toàn quan hệ vuông góc.
3. Phương pháp chứng minh d c
Phương pháp không gian: d chéo c
Chứng minh d c d (P) c
Phải chứng minh d b (P) ?
Chứng minh ngược lại b vuông góc với một mặt phẳng chứa d
Ví dụ 4: Cho tứ diện OABC đôi một vuông góc. Vẽ OE BC,OH AE . Chứng minh OH A . B
Chứng minh OH AB Chứng minh OH (ABC). Có sẵn OH AE (1)
Phải chứng minh OH BC BC OE
BC (OAE) BC OH (2) BC OA
Từ (1) và (2) OH (ABC) OH A . B 74 1. Định nghĩa
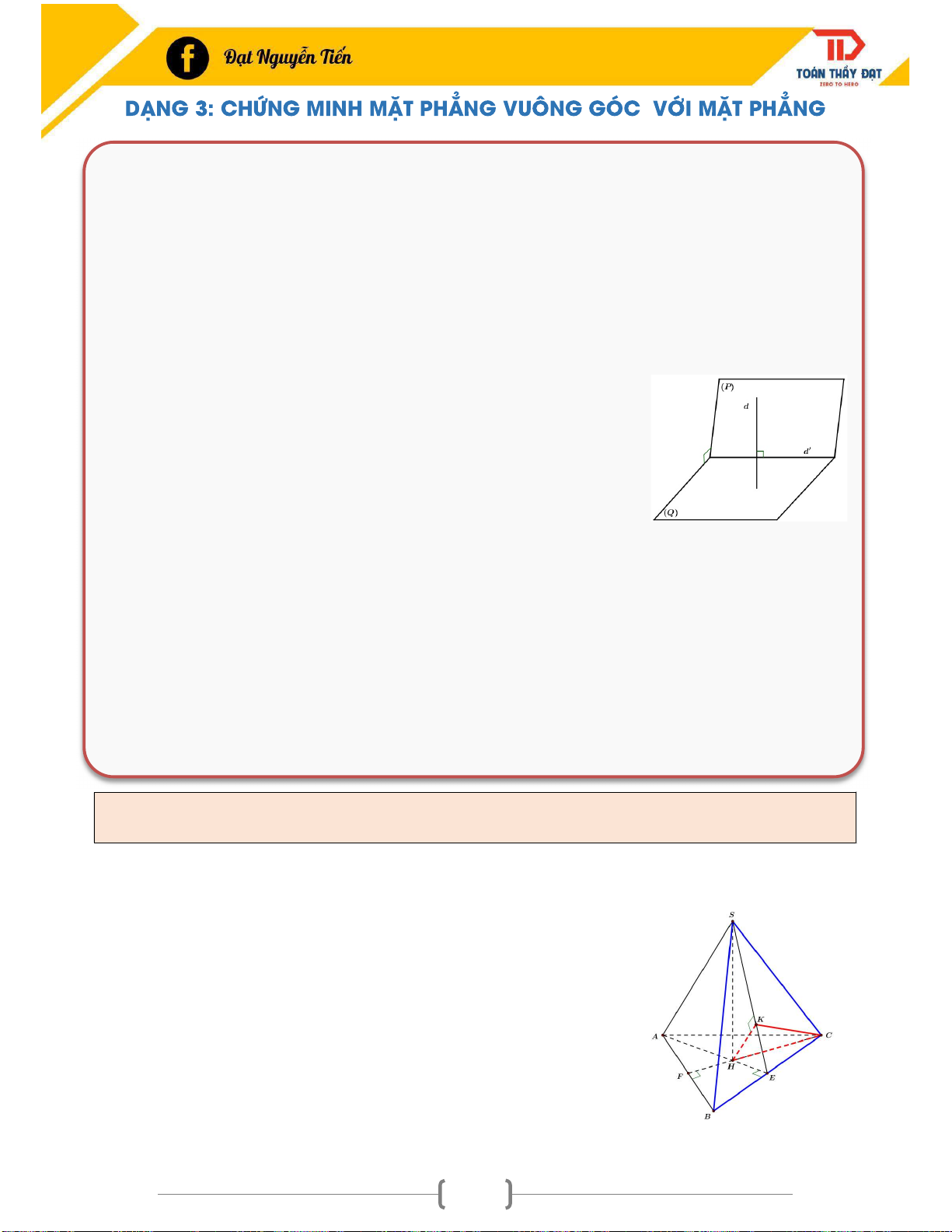
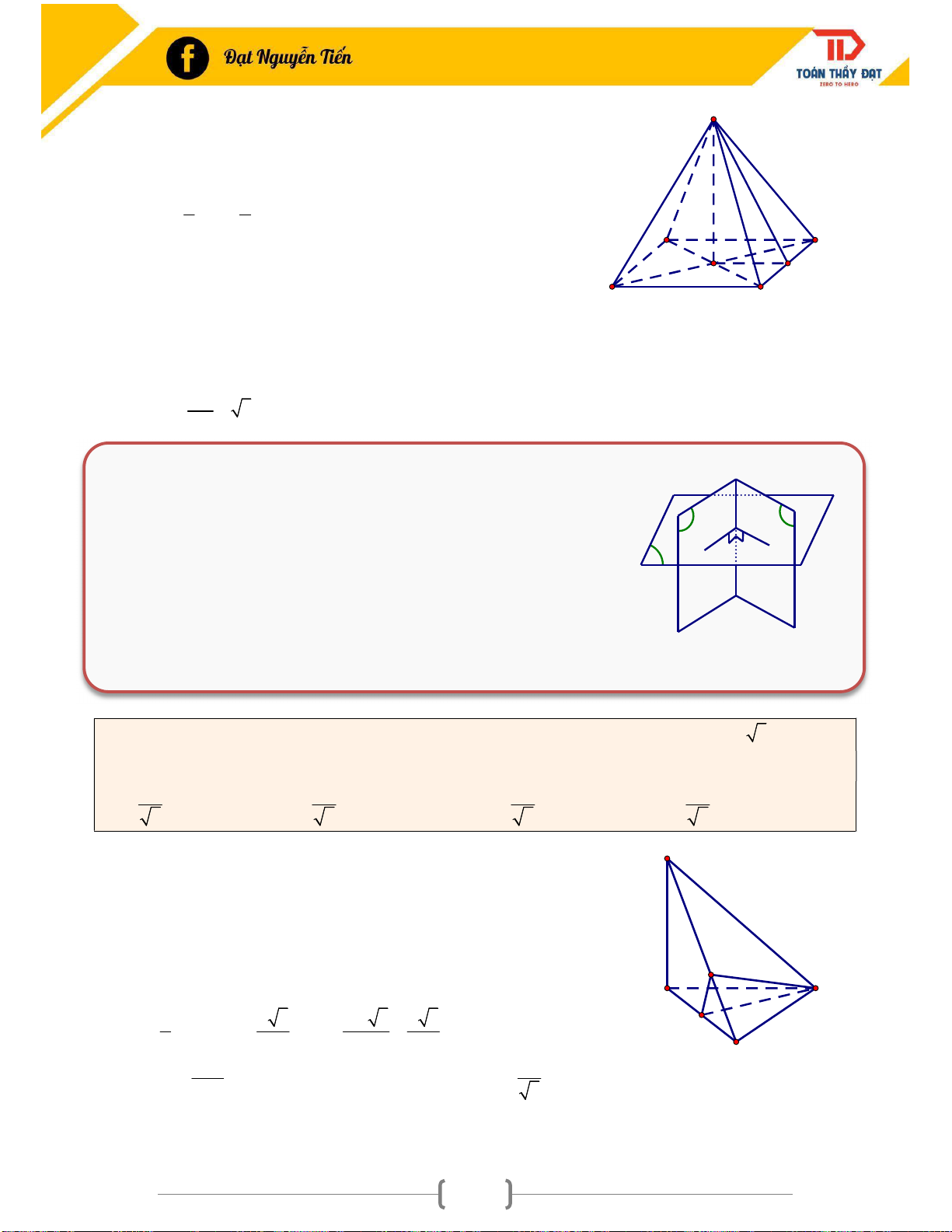
Hai mặt phẳng P Q P Q 0 ( ) ( ) ( );( ) 90 2. Tính chất Định lý 3: d (P) (P) (Q) d (P)
Định lý 4: Hai mặt phẳng vuông góc với nhau, đường thẳng d nằm trong mặt phẳng này và vuông
góc với giao tuyến thì sẽ vuông góc với mặt phẳng còn lại. ( P) (Q) d (Q) d (P),d ' d
Định lý 5: Hai mặt phẳn cùng vuông góc với mặt phẳng thứ ba thì giao tuyến của nó cũng vuông
góc với mặt phẳng thứ ba. (Q) (P),(R) (P) d (P) (Q) (R) d
3. Phương pháp chứng minh (P) (Q)
Chứng minh d (P), d (Q)
Có sẵn d a (P) ?
Phải chứng minh d b (P)
Ví dụ 5: Cho hình chóp đều S.ABC, H là tâm đáy, E là trung điểm BC. Vẽ HK SE . Chứng minh (CHK) (SBC) .
Chứng minh (CHK) (SBC) Chứng minh HK (SBC). Có sẵn HK SE (1)
Phải chứng minh HK BC (Chứng minh BC vuông góc với một mặt chứa HK) BC HE
BC (SHE) BC HK (2) BC SH
Từ (1) và (2) (CHK ) (SBC). 75
Phương pháp sử dụng định lý 4:
Tìm giao tuyến của (P) và (Q)
Vẽ đường thẳng d vuông góc với giao tuyến. Nếu d (P) d (Q)
Suy ra các kết quả tiếp theo.
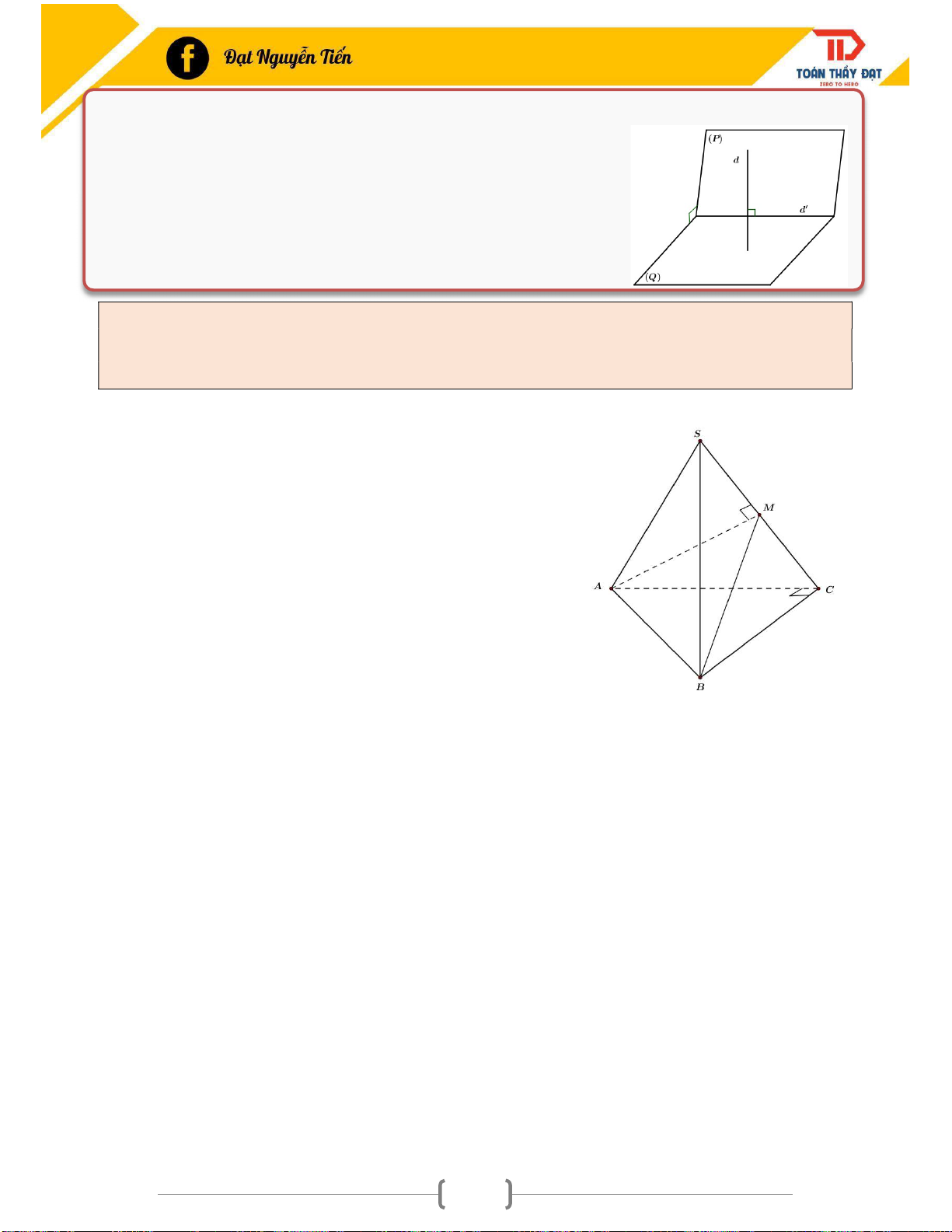
Ví dụ 6: Cho hình chóp S.ABC có (SAC) (ABC). ABC vuông ở C, M là trung điểm của SC. Chứng minh: a) (SAC) (SBC). b) (SBC) (ABM ). a) Ta có (SAC) (ABC) Sử dụng định lý 4: (SAC) (ABC) AC BC AC
BC (SAC) (Kết quả ĐL 4) BC (ABC)
Mặt khác BC (SBC) (SAC) (SBC) (ĐL 3) b) Ta có (SAC) (SBC) Sử dụng định lý 4: (SAC) (SBC) SC AM SC
AM (SBC) (Kết quả ĐL 4) AM (SAC)
Mặt khác AM (ABM ) (ABM ) (SBC) (ĐL 3) 76 1
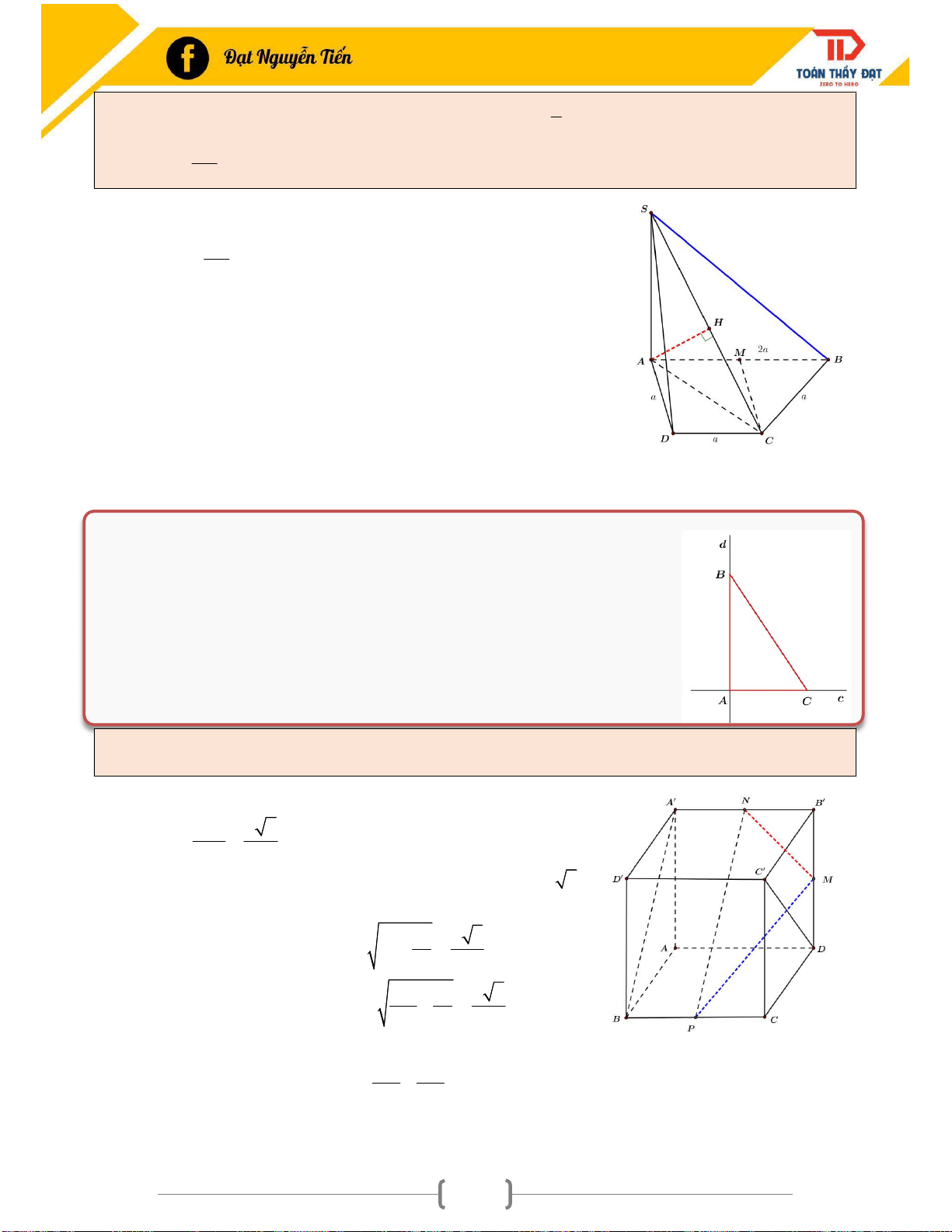
Ví dụ 7: Cho hình chóp S.ABCD có SA (ABCD), ABCD là là hình thang vuông ở A, D, 2 AB AD DC
a . Vẽ AH SC . Chứng minh AH S . B 2
Gọi M là trung điểm của AB Tứ giác ADCM là hình vuông AB CM a ACB vuông ở C. 2
Chứng minh AH SB Chứng minh AH (SBC). Có sẵn AH SC (1)
Phải chứng minh AH BC BC AC
BC (SAC) BC AH (2) BC SA
Từ (1) và (2) AH (SBC) AH S . B Sử dụng PITAGO đảo
Bước 1: Đưa d, c vào tam giác ABC. Tính ba cạnh của tam giác ABC. Bước 2: Thử 2 2 2
AB AC BC ABC vuông tại A. d c
Ví dụ 8: Hình lập phương ABCD.A’B’C’D’ có AB a . M, N, P là trung điểm của BB’, A’B’, CD. Chứng minh MN M . P
Tính MN: A' B 'B có MN là đường trung bình A' B a 2 MN 2 2
Tính PN: Tứ giác A’DPN là hình bình hành PN DA' a 2 Tính MP: 2 a a Trong tam giác vuông BCP: 2 5 BP a 4 2 2 2 5a a a 6
Trong tam giác vuông MBP: PM 4 4 2 2 2 2a 6a Thử tam giác MNP: 2 2 2 2 MN MP 2a PN 4 4
MNP vuông tại M MN MP 77 1. Định nghĩa
Khoảng cách từ điểm M đến mặt phẳng P là MH , với H là hình chiếu vuông góc của M lên mặt phẳng P . MH P M
dM;P MH H P H P
2. Phương pháp tính trực tiếp khoảng cách từ một điểm đến một mặt phẳng
Phương pháp chung: Muốn tìm khoảng cách từ một điểm đến một mặt phẳng, trước hết ta phải tìm hình
chiếu vuông góc của điểm đó trên mặt phẳng. Việc xác định hình chiếu của điểm trên mặt phẳng ta thường
dùng một trong các cách sau: ́ ̣ ̉ ́ ̀ ̉ ̉ ́ ́ ̣ ́
Ví dụ: Làm sao để tìm khoảng cách từ Sơn Tùng đến bức tường?
À, quá dễ, từ Tùng kẻ 1 đường thẳng vuông góc vào tường!
Ta để ý: tường và mặt đất đang vuông góc với nhau thì ta mới có thể kẻ vuông góc vào tường.
Ta có phương pháp như sau:
Bước 1. Tìm một mặt phẳng chứa và vuông góc với P . Q M Q
Bước 2. Xác định giao tuyến: d M P Q . Bước 3. Trong , dựng MH d H d . Q d H P Q P d P Q MH P d M ; P MH Q MH
(Chú ý: Mặt đứng thường chứa đường cao) 78
Ví dụ 1. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. SA vuông góc với đáy. Tìm khoảng cách a) Từ C đến (SAB) b) Từ B đến (SAD) c) Từ B đến (SAC)
d) Từ D đến (SAM), M là trung điểm CD a) Nhận xét: S
(SAB) là mặt đứng (do chứa đường cao SA). Dùng cấp độ 1 Nên theo phương pháp:
Bước 1: Ta xem có mặt phẳng nào chứa C và vuông góc với (SAB)? Đó chính là (ABCD).
Bước 2: Mà giao tuyến chung của (SAB) và (ABCD) là AB D A
Bước 3.Nên từ C ta kẻ 1 đường thẳng vuông góc với AB là xong. Mà
ta có ngay đó chính là BC. B C
Từ đó d C, SAB BC a b) Nhận xét:
(SAD) là mặt đứng (do chứa đường cao SA) -> Dùng cấp độ 1 Nên theo phương pháp:
Bước 1: Ta xem có mặt phẳng nào chứa B và vuông góc với (SAD)? Đó chính là (ABCD).
Bước 2: Mà giao tuyến chung của (SAD) và (ABCD) là AD
Bước 3.Nên từ B ta kẻ 1 đường thẳng vuông góc với AD là xong. Mà ta có ngay đó chính là BA. Từ đó d B,SA D BA a c) Nhận xét: S
(SAC) là mặt đứng (do chứa đường cao SA) -> Dùng cấp độ 1 Nên theo phương pháp:
Bước 1: Ta xem có mặt phẳng nào chứa B và vuông góc với (SAC)? Đó chính là (ABCD). D
Bước 2: Mà giao tuyến chung của (SAC) và (ABCD) là AC A
Bước 3.Nên từ B ta kẻ 1 đường thẳng vuông góc với AC là xong. Mà ta có O
ngay đó chính là BO. (do 2 đường chéo hình vuông sẽ vuông góc với nhau) B C 1 a 2 Từ đó d , B SAC BO BD 2 2 S d) Nhận xét:
(SAM) là mặt đứng (do chứa đường cao SA) -> Dùng cấp độ 1 Nên theo phương pháp: A D D
Bước 1: Ta xem có mặt phẳng nào chứa D và vuông góc với A I
(SAM)? Đó chính là (ABCD). I M M
Bước 2: Mà giao tuyến chung của (SAM) và (ABCD) là AM B C B C
Bước 3.Nên từ D ta kẻ 1 đường thẳng vuông góc với AM là xong.
Ta kẻ DI vuông góc với AM Từ đó d , D SAM DI 79 a . 1 1 1 . a DA DM 5 Ta có 2 DI a 2 2 2 2 2 DI DA DM DA DM a 5 2 2 a ( ) 2 MẸO NHỎ
Ta có thể bấm máy nhanh như sau: ấn CALC X=1; Y = 0,5
Cách này nhanh hơn việc các em nhập từng số vào để bấm 80 ́ ̣ BÀI TOÁN GỐC SỐ 1: BÀI TOÁN GỐC SỐ 2
Cho hình chóp SABC, SA vuông góc (ABC).
Cho hình chóp SABC, SA vuông góc (ABC).
Tam giác ABC vuông tại B (hoặc C).
Tam giác ABC không có góc vuông tại B và C.
Tìm khoảng cách từ A đến (SBC)
Tìm khoảng cách từ A đến (SBC) S Phương pháp: S Phương pháp: (Giả sử tam giác ABC vuông tại B) Kẻ AM vuông góc BC. Kẻ AH vuông góc SB. Kẻ AH vuông góc SM H H d ( ; A (SBC)) AH d ( ; A (SBC)) AH A C 1 1 1 A C 1 1 1 C ´ o C ´ o 2 2 2 AH SA AB 2 2 2 AH SA AM M S . A AB S . A AM AH AH B 2 2 SA B 2 2 AB SA AM
(Mẹo nhớ: Có góc vuông, kẻ 1 đường) (Mẹo nhớ: không có góc vuông, kẻ 2 đường, bản
chất của bài toán gốc số 2 là đưa về bài toán gốc số 1) Chứng minh: Chứng minh: C ´ o BC SA C ´ o BC SA BC (SAB) BC (SAM) BC AB BC AM
Ma` AH (SAB) BC AH
Ma` AH (SAM) BC AH AH (SBC) AH (SBC) C ´ o AH SB C ´ o AH SM d ( ; A (SBC)) AH d ( ; A (SBC)) AH
Ví dụ 2. Cho hình chóp S.ABC có đáy ABC vuông cân tại B , AB= a . Cạnh bên SA a 3 và vuông góc
với mặt đáy ABC . Tính khoảng cách từ A đến mặt phẳng SBC . a 3 a 5 a 3 A. . B. a . C. . D. . 2 5 2
Phân tích: Bài toán hỏi khoảng cách từ A đến mặt phẳng SBC .
1) A là chân đường cao, (SBC) là mặt bên -> CẤP ĐỘ 2
2) Tam giác ABC (đáy) có góc vuông ở B -> BÀI TOÁN GỐC SỐ 1 (kẻ 1 đường) Kẻ AH vuông góc SB. d ( ; A (SBC)) AH S 1 1 1 C ´ o 2 2 2 AH SA AB S . A AB 3 AH H 2 2 SA AB 2 A C (calc x x 3; y 1 ) B 81
Ví dụ 3. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Cạnh bên SA a 3 và vuông góc
với mặt đáy ABC . Tính khoảng cách từ A đến mặt phẳng SBC . a 15 a 5 a 3 A. . B. a . C. . D. . 5 5 2
Phân tích: Bài toán hỏi khoảng cách từ A đến mặt phẳng SBC .
1) A là chân đường cao, (SBC) là mặt bên -> CẤP ĐỘ 2
2) Tam giác ABC (đáy) không có góc vuông ở B hoặc C -> BÀI TOÁN GỐC SỐ 2 (kẻ 2 đường) a 3 S
Kẻ AM BC => M là trung điểm BC (t/c tam giác đều) và AM . 2 Kẻ AK vuông góc SM. suy ra d , A SBC AK . K S . A AM 3a a 15 Trong SAM , có AK . C A 2 2 SA AM 15 5 a 15 M Vậy d , A SBC AK . 5 B
Ví dụ 4. Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh a. Cạnh bên SA a 2 và
vuông góc với đáy ABCD . Tính khoảng cách từ điểm B đến mặt phẳng SCD . a 6 a 3 A. a . B. . C. a 3 . D. . 3 2
Phân tích: Bài toán hỏi khoảng cách từ A đến mặt phẳng SCD .
1) A là chân đường cao, (SCD) là mặt bên -> CẤP ĐỘ 2
2) Tam giác ACD (đáy) có góc vuông ở D -> BÀI TOÁN GỐC SỐ 1 (kẻ 1 đường)
Do AB CD nên d B, SCD d , A SCD . S Kẻ AE SD tại E . Khi đó d , A SCD AE. E
Trong tam giác vuông SAD , ta có: S . A AD a 6 A AE . D 2 2 SA AD 3 O a 6 B Vậy d B, SCD C AE . 3 3a
Ví dụ 5. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a ; SD ; hình chiếu vuông góc 2 d H;SC D
của S trên ABCD trùng với trung điểm H của cạnh AB . Khi đó, tỉ số bằng: a 2 3 2 3 3 3 A. . B. . C. . D. . 2 2 2 2 82
Phân tích: Bài toán hỏi khoảng cách từ H đến mặt phẳng (SC ) D .
1) H là chân đường cao, (SCD) là mặt bên -> CẤP ĐỘ 2
2) Tam giác HCD (đáy) không góc vuông ở C và D -> BÀI TOÁN GỐC SỐ 2 (kẻ 2 đường) Kẻ HI CD I CD S Kẻ HK SI K SI SH.HI K
d H,SCD HK 2 2 SH HI A S a 5 H 2 2 2 2 HD AH AD ; SH SD HD a I 2 B C SH.HI a 2 d H , SCD 2 d H ,SCD 2 2 SH HI 2 a 2
Ví dụ 6. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B với AB BC , a
AD 2a . Cạnh bên SA a và vuông góc với mặt phẳng ABCD . Tính khoảng cách từ điểm A đến mặt phẳng SCD . 2a a 6 A. . B. a 2 . C. . D. 2a . 5 3
Gọi M là trung điểm AD , suy ra ABCM là hình vuông. AD Do đó CM MA
nên tam gác ACD vuông tại C . 2
Phân tích: Bài toán hỏi khoảng cách từ A đến mặt phẳng (SCD) .
1) A là chân đường cao, (SCD) là mặt bên -> CẤP ĐỘ 2
2) Tam giác ACD (đáy) có góc vuông ở C -> BÀI TOÁN GỐC SỐ 1 (kẻ 1 đường) S Kẻ AK SC . Khi đó: S . A AC a 6 d , A SCD AK 2 2 SA AC 3 K M A D B C 83 ́ ̣ ̉ ̉ ̉ ̉
Giả sử ta ta muốn dựng trực tiếp khoảng cách từ điểm A tới mặt phẳng P mà không thực hiện được.
Đồng thời từ điểm B ta lại dựng được trực tiếp khoảng cách tới P khi đó ta sẽ thực hiện tính khoảng cách gián tiếp. PHƯƠNG PHÁP ĐỔI ĐIỂM Bài toán
Giả sử điểm A là chân đường cao
Điểm B không phải là chân đường cao. (P) là mặt bên (nghiêng)
Tìm khoảng cách từ B đến (P)? Phương pháp:
Bước 1. Ta tìm khoảng cách từ điểm A đến (P).
Bước 2. Nối A và B. Đổi điểm dựa vào 1 trong 2 loại sau LOẠI 1. AB P LOẠI 2. AB P I d , A P dB, P d , A P AI A B d B,P BI BI d ( ; B (P)) .d ( ; A (P)) AI A P B I P
Ví dụ 7. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB , a AD 2a . Cạnh bên SA
vuông góc với đáy, góc giữa SD với đáy bằng 0
60 . Tính khoảng cách từ điểm C đến mặt phẳng SBD theo a . a 3 2a 5 a 5 A. . B. . C. . D. a 3 . 2 5 2
Phân tích: Bài toán hỏi khoảng cách từ C đến mặt phẳng (SC ) D .
1) C không là chân đường cao, (SBD) là mặt bên -> CẤP ĐỘ 3 (ĐỔI ĐIỂM VỀ A)
2) Nối AC, ta thấy AC cắt (SBD) => LOẠI 2 S
Bước 1: Tìm khoảng cách từ chân đường cao đến (SBD) 0 60 SD, ABCD SD, AD SD ; A SA A . D tan SDA 2a 3 Ta có d C, SBD d , A SBD .
Kẻ AE BD và kẻ AK SE . Khi đó d , A SBD AK . A . B AD 2a A K
Trong tam giác vuông BAD , ta có AE D . 2 2 AB AD 5 E B C 84 S . A AE a 3
Trong tam giác vuông SAE , ta có AK . 2 2 SA AE 2
Bước 2. Đổi điểm về C
Ta nối A và C thấy AC cắt B tại trung điểm I mỗi đường (Tính chất 2 đường chéo)
Theo công thức đổi điểm LOẠI 2: d ( ; A (P)) AI 1 d (C; (P)) d ( ; A (P)) d(C;(P)) CI a 3 Vậy d C, SBD AK . 2 Ví dụ 8. Cho hình chóp .
S ABCD có đáy là hình vuông cạnh a, mặt bên SAB là tam giác đều và nằm
trong mặt phẳng vuông góc với đáy. Khi đó, khoảng cách từ A đến mặt phẳng SCD bằng a 21 a 21 a 21 a 21 A. . B. . C. . D. . 3 14 7 21
Phân tích: Bài toán hỏi khoảng cách từ A đến mặt phẳng (SCD) .
1) A là không chân đường cao, (SCD) là mặt bên -> CẤP ĐỘ 3 -> Đổi điểm về H
2) Nối AH, ta thấy AH // (SCD) (Do AG//CD) -> CẤP ĐỘ 3: Loại 1 a Gọi H 3
là trung điểm của AB SH . 2 AB // SCD Vì
dA,SCD dH,SCD. H AB
Gọi K là trung điểm của CD HK . a
Kẻ HI SK, I SK . SH.HK a 21
Khi đó: dH,SCD HI 2 2 SH HK 7
Nối AH, ta thấy AH // (SCD) (Do AG//CD) a
Vậy dA SCD dH SCD 21 , , Chọn đáp án C. 7
Ví dụ 9. Cho hình chóp SABCD có đáy ABCD là hình chữ nhật AD=2AB=2a. SA vuông góc với đáy.
Góc giữa (SCD) và (ABCD) là 30o. Gọi M là trung điểm SB. Tìm khoảng cách từ M đến (SCD) a 21 a 21 a a 21 A. . B. . C. D. . 3 14 2 21
Phân tích: Bài toán hỏi khoảng cách từ M đến mặt phẳng (SCD) .
1) M là không chân đường cao, (SCD) là mặt bên -> CẤP ĐỘ 3 -> Đổi điểm
2) Nối MA, nhưng ta không thể biết AM cắt (SCD) hay AM//(SCD) 85
Ố la la. Vậy đối với những bài toán tìm khoảng cách từ những điểm LƠ LỬNG ta sẽ đổi điểm 2 lần.
Lần 1: Ta đổi M về B. (Loại 2: Do BM cắt (SCD) tại S) d(M ;(SCD)) MS 1 1 d (M ;(SCD)) d (B;(SCD)) ??? d( ; B (SCD)) BS 2 2
Lần 2: Ta đổi B về A. (Loại 1: Do AB // (SCD) d (B;(SCD)) d( ; A (SCD)) ???
=> Để tìm d(M ;(SCD)) , ta phải tìm d( ; A (SCD))
Bước 1: Tìm khoảng cách từ chân đường cao A đến (SCD)
Phân tích: Bài toán hỏi khoảng cách từ A đến mặt phẳng (SCD) .
1) A là chân đường cao, (SCD) là mặt bên -> CẤP ĐỘ 2
2) Tam giác ACD (đáy) có góc vuông ở D -> BÀI TOÁN GỐC SỐ 1 (kẻ 1 đường) S . A AD
Kẻ AH vuông góc SD .Khi đó d , A SBD AH ??? . 2 2 SA AD
Tìm SA: Ta có Góc giữa ( SCD ; ABCD ) = SDA =30o S
(Nhắc lại Phương pháp tìm góc: từ chân đường cao A, kẻ 1 đường vuông góc vào H
giao tuyến chung CD, sau đó nối lên đỉnh S) M A D SA o 2 3 tan(SDA).AD tan 30 .2a a 3 S . A AD d , A SCD AH a B C 2 2 SA AD AB / /(SCD) d B, SCD , A SCD a BM (SCD) S d (M ; (SCD)) MS 1 1 a d (M ; (SCD)) d (B;(SCD)) d (B;(SCD)) BS 2 2 2 86 1. Định nghĩa
Đường thẳng d cắt hai đường thẳng chéo nhau a và b và cùng vuông góc với mỗi đường thẳng
ấy được gọi là đường vuông góc chung của a và b .
Nếu đường vuông góc chung d cắt hai đường thẳng chéo nhau a và b lần lượt tại M , N thì độ dài
đoạn thẳng MN là khoảng cách giữa hai đường thẳng chéo nhau a và b .
2. Phương pháp tính khoảng cách giữa hai đường thẳng chéo nhau d M a b N
Cách 1: Dựng đường vuông góc chung (nếu đã biết a và b vuông góc)
Bước 1. Xác định mặt phẳng P chứa b mà P vuông góc a với a .
Bước 2. Tìm giao điểm I P a . I b
Bước 3. Kẻ IA b A b , chứng minh IA a . Khi đó P A d a, b IA .
Ví dụ 1. Cho tứ diện ABCD có độ dài các cạnh bằng 6 2 . Tính khoảng cách giữa hai đường thẳng AB và CD . A. 2 . B. 4 . C. 5 . D. 6 . Gọi ,
M N lần lượt là trung điểm của A , B CD .
Ta có: ACD và BCD là các tam giác đều
CD AN,CD BN CD ABN CD MN A AN 3 6 AB MN M d A , B C 2 2 D MN AN AM 6 B C N D 87
Ví dụ 2. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB a, AD 2a . SA vuông góc
với mặt phẳng ABCD và SA a . Tính khoảng cách giữa hai đường thẳng SB và CD. a A. . B. 2a . C. a . D. a 3 . 3 AB BC S BC SAB SA ABCD SA BC
BC SB dSB,C D BC 2a BC CD A D B C
Ví dụ 3. Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O , cạnh bằng 2 . Đường thẳng SO
vuông góc với mặt phẳng đáy ABCD và SO 3 . Tính khoảng cách giữa hai đường thẳng SA và BD . A. 2 30 . B. . C. 2 2 . D. 2 . 5
Ta có BD SAC . Kẻ OK SA . S S . O OA 30 d S , A BD 2 2 SO OA 5 K A D O B C
Cách 2: Dựng đường vuông góc chung (tổng quát)
Bước 1. Xác định mặt phẳng P chứa b song song với a d a M
Bước 2. Gọi a ' là hình chiếu của a lên P , N a ' b , Q
Q là mặt phẳng chứa a và a ' , d là đường thẳng qua N b
và vuông góc với P , M d a . Khi đó d a,b MN . P a' N
Ví dụ 4. Cho hình chóp S.ABC có mặt bên SBC là tam giác đều cạnh bằng a , cạnh bên SA vuông
góc với mặt phẳng ABC . Lấy điểm M trên cạnh BC sao cho MC 2MB . Biết BAC 120. Tính
khoảng cách giữa hai đường thẳng SM và AC . a 3 a 6 2 2 A. . B. . C. a . D. a . 3 3 7 21 88 Kẻ AH SM H SM S a 2 2 2
SB SC AB AC BC 2AB 2AB .cos120 AB 3 a 6 2 2 SA SB AB H 3 A a a 2 2 AM C AB MB 2A . B M .
B cos120 AM BM 3 3 M BAM ABM 30 MAC 90 AM AC B SA ABC SA AC
AC SAM AC AH S . A AM 2
d AC,SM AH a 2 2 SM AH SA AM 21
Ví dụ 5. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh bằng a và
ABC 60. Hai mặt phẳng
SAC và SBD cùng vuông góc với đáy ABCD , góc giữa hai mặt phẳng SAB và ABCD bằng
30. Tính khoảng cách giữa hai đường thẳng SA và CD. a 3 a 3 a 2 a 2 A. . B. . C. . D. . 4 2 4 2
Gọi O AC BD . Kẻ OI AB . Gọi J OI CD . Kẻ JH SI . CD AB CD SAB S d CD, S
A d CD,SAB d J,SAB JH
SO ABCD SO AB AB SOI OI AB
SAB,ABCD SI,OI SIO 30 H A a 3 a 3 D OI I IJ 2OI 4 2 O a 3 a 3 J B d CD, S A JH IJ.sin 30 C 4 4 89
Bước 1: Dựng (P) chứa b và a Vẽ d thỏa mãn 5 điều: 5 Qua C Thuộc đáy Song song với a
Cắt 1 đườn thẳng dưới đáy tại I Chú ý: Góc vuông (P) ( , b d ) 5
Bước 2: M a;d (a,b) d (M ,(P)) + Mẫu + Đối đỉnh
Ví dụ 6: Cho hình chóp S.ABCD , SA (ABCD) , SA a . ABCD là hình vuông, AB a, AC BD O . Tính d(SO, AB) ?
Bước 1: Qua O vẽ d AB,d AD I
(AMI ) AM và song song với AB
Bước 2: A AB, d (SO, AB) d ( , A (SOI)) AH 1 1 4 5 a Tính AH : AH . 2 2 2 2 AH a a a 5
Ví dụ 7: Cho hình chóp S.ABCD , SA (ABCD), SA 2a , ABCD là hình vuông, AB a . Tính d(SC, BD) ?
Bước 1: Qua C vẽ d BD, d AB I
(AMI ) SC và song song với BD
Bước 2: O BD, d(SC, DB) d (O,(SCI )) CO 1 d O,(SCI) 1 1
d O SCI d A SCI AH CA 2 d , A (SCI ) ,( ) ,( ) 2 2 1 1 1 3 a 3 Tính AH : AH 2 2 2 2 AH 4a 2a 4a 3 a 3 d(SC, BD) 3 90
Ví dụ 8. [Đề THPT Quốc Gia 2018] Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật,
AB a , BC 2a , SA vuông góc với mặt phẳng đáy và SA a . Khoảng cách giữa hai đường thẳng AC và SB bằng 6a 2a a a A. 2 . B. 3 . C. 2 . D. 3 . Chọn B.
Dựng điểm E sao cho ACBE là hình bình hành,
Khi đó: AC//EB AC// SBE.
d AC, SB d AC,SBE d , A SBE. 1
Kẻ AI EB I EB ,
kẻ AH SI H SI d ,
A SEB AH. 2 1 1 1 1 1 5 Tam giác ABE vuông tại 2 2 2 2 2 2 AI AB AE 4a a 4a 1 1 1 1 5 9 2 Xét SAI , ta có: AH a . 2 2 2 2 2 2 3 AH SA AI a 4a 4a 3 a Từ
1 , 2, 3 suy ra h d AC SB 2 , . 3 91 1. Định nghĩa
Cho đường thẳng d và mặt phẳng .
Trường hợp đường thẳng d vuông góc với mặt phẳng thì ta nói rằng góc d A
giữa đường thẳng d và mặt phẳng bằng 90.
Trường hợp đường thẳng d không vuông góc với mặt phẳng góc giữa d d' H O
và hình chiếu d ' của nó trên gọi là góc giữa đường thẳng d và mặt phẳng α . 2. Nhận xét
Góc giữa đường thẳng và mặt phẳng không vượt quá 90.
1. Cách xác định góc giữa đường thẳng và mặt phẳng ĐỈNH
Bước 1: Tìm điểm chung giữa đường thẳng và mặt phẳng.
Bước 2: Tìm hình chiếu của đường thẳng lên mặt phẳng. d A
Bước 3: Tính góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng. GIAO ĐIỂM
Từ đó ta có công thức góc theo thứ tự:
ĐỈNH – GIAO ĐIỂM – CHÂN ĐƯỜNG CAO d' H O α CHÂN ĐƯỜNG CAO
2. Cách tính góc giữa đường thẳng và mặt phẳng
Dựng tam giác chứa góc và sử dụng định lí hàm số côsin: 2 2 2 a b c 2bc cos A 2 2 2 b c a 2ac cos B 2 2 2 c a b 2ab cosC
Sử dụng các hệ thức lượng trong tam giác vuông: 2 2 1 AB BH.BC; AC CH.BC A 2 2 2 2 AB AC BC 3 A . B AC BC.AH 2 4 AH BH.CH B C H 1 1 1 5 2 2 2 AH AB AC
Ví dụ 1. Cho hình chóp S.ABC có SAB là tam giác đều cạnh a , ABC cân tại C . Hình chiếu vuông
góc của S xuống mặt ABC là trung điểm của AB . Góc giữa SC và mặt đáy bằng 30. Tính độ dài đoạn SC . a a 3 3a A. . B. . C. . D. a 3 . 2 2 4 92
Gọi H là trung điểm của AB S
SH ABC SH HC SC, ABC SC,CH SCH 30 a 3 SH SH SC a 3 2 sin SCH A C H B
Ví dụ 2. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a , cạnh bên SA 2a và vuông góc
với đáy. Tính sin của góc giữa đường thẳng SC với mặt phẳng SAB . 85 51 3 15 A. . B. . C. . D. . 10 17 2 10 Gọi M là trung điểm AB S CM AB CM SAB
SA ABC SA CM
SC,SAB SC,SM CSM a 3 1 a 2 2 CM M
; AM AB ; SC SA AC a 5 2 2 2 A N CM 15
sin SC,SAB sin CSM SC 10 C
Ví dụ 3. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , tâm O . Cạnh bên SA 2a và
vuông góc với mặt đáy. Tính tan của góc giữa SO và mặt phẳng ABCD . A. 2 2 . B. 3 . C. 2. D. 1. SA ABC
D SO,ABCD SO,O A SOA S 1 a 2 AC a 2 OA AC 2 2 SA
tan SO,ABCD tan SOA 2 2 A OA D O B C 93
Để xác định góc giữa hai mặt phẳng và
, ta có thể thực hiện theo một trong các cách sau: P Q
1. Cách 1: Theo định nghĩa a P Q P , Q a,b P b Q a b
Ví dụ 4. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a . Cạnh bên SA a 3 và vuông góc
với mặt đáy ABC . Tính sin của góc giữa hai mặt phẳng SBC và ABC . 1 5 3 2 5 A. . B. . C. . D. . 2 5 2 5
Gọi M là trung điểm của BC AM BC S
AM BC BC SAM BC SM BC SA
SBC,ABC SM, AM SMA a 3 AM A C 2 M SA SA 2 5 sin
SBC,ABC sin SMA B 2 2 SM SA AM 5
Ví dụ 5. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A , AB AC a ; cạnh bên SA a
và vuông góc với đáy. Tính côsin của góc giữa hai mặt phẳng SAC và SBC . 6 2 3 3 A. . B. . C. . D. . 3 2 3 2 S
Gọi H là trung điểm SC .
Tam giác SAC có SA AC a AH SC
Tam giác SBC có SB BC a 2 BH SC H
SAC,SBC AH,BH SC SA 2 a 2 BC 3 a 6 AH ; BH A C 2 2 2 2 2 HA HB AB 3 cos
SAC,SBC co 2 2 2 s AHB B 2H . A HB 3 a 3
Ví dụ 6. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a , chiều cao hình chóp bằng . Góc 2
giữa mặt bên và mặt đáy là: A. 30. B. 45 . C. 60 . D. 75 . 94
Gọi O là tâm của hình vuông ABCD và E là trung điểm của S CD .
OE là đường trung bình của ACD O E AD 1 a O E AD 2 2 A D
OE AD OE CDCD SOECD SE CD SO O E B C ABCD SCD CD SE CD,OE CD ABC
D ,SCD SE,OE SEO SO tan SEO 3
ABCD,SCD SEO 60 OE 2. Cách 2:
Khi xác định được P Q c thì ta làm như sau: Q P
Bước 1. Tìm mặt phẳng . R c p q R p R P Bước 2. Tìm . Khi đó P , Q p, q q R Q P p c Đặc biệt: P , Q p, q . Q q c
Ví dụ 7. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA ABC , SA a 3 . Côsin của
góc giữa hai mặt phẳng SBC và SAB bằng: 2 2 1 1 A. . B. . C. . D. . 5 5 5 5
Gọi M là trung điểm của AB . Kẻ MH SB S CM AB CM SAB
SA ABCD SA CM
CM SB SB MHC SB CH SB MH H SAB , SBC MH ,CH CHM A C 1 a 3 AB 3 a 3 MH d , A SB ; MC M 2 4 2 2 B CM 1 ta n BHD 2 cos
SAB,SBC co s CHM MH 5 95




