


























































































































































































Preview text:
LƯỢNG GIÁC
MỘT SỐ CHUYÊN ĐỀ VÀ ỨNG DỤNG
TẬP 1 : BIẾN ĐỔI LƯỢNG GIÁC VÀ HỆ THỨC LƯỢNG
VÕ ANH KHOA – HOÀNG BÁ MINH
VÕ ANH KHOA – HOÀNG BÁ MINH LƯỢNG GIÁC
MỘT SỐ CHUYÊN ĐỀ VÀ ỨNG DỤNG
TẬP 1 : BIẾN ĐỔI LƯỢNG GIÁC VÀ HỆ THỨC LƯỢNG TP. HỒ CHÍ MINH --------------------- TOANMATH.com LỜI NÓI ĐẦU
Cuốn sách “LƯỢNG GIÁC – MỘT SỐ CHUYÊN ĐỀ VÀ ỨNG DỤNG” này được biên
soạn với mục đích cung cấp, bổ sung kiến thức cho học sinh THPT và một số bạn đọc
quan tâm đến mảng kiến thức này trong quá trình học tập và làm việc. Ở cuốn sách này,
ngoài việc đưa ra những khái niệm và dạng bài tập cơ bản, chúng tôi sẽ thêm vào đó lịch
sử và ứng dụng của môn học này để các bạn hiểu rõ hơn “Nó xuất phát từ đâu và tại sao
chúng ta lại phải học nó?”.
Ở các chương chính, chúng tôi chia làm 3 phần : -
Phần I : Nêu lý thuyết cùng ví dụ minh họa ngay sau đó, giúp bạn đọc hiểu và biết
cách trình bày bài. Đồng thời đưa ra các dạng toán cơ bản, thường gặp trong quá trình
làm bài trên lớp của học sinh THPT. Ở phần này, chúng tôi sẽ trình bày một số bài để bạn
đọc có thể nắm vững hơn, tránh sai sót. -
Phần II : Trong quá trình tham khảo và tổng hợp tài liệu, chúng tôi sẽ đưa vào
phần này các dạng toán khó nhằm giúp cho các học sinh bồi dưỡng, rèn luyện kĩ năng
giải LƯỢNG GIÁC thành thạo hơn khi gặp phải những dạng toán này. -
Phần III : Chúng tôi sẽ đưa ra lời giải gợi ý cho một số bài, qua đó bạn đọc kiểm
tra lại đáp số, lời giải hoặc cũng có thể tham khảo thêm.
Trong quá trình biên soạn, mặc dù chúng tôi đã cố gắng bằng việc tham khảo một lượng
rất lớn các tài liệu có sẵn và tiếp thu có chọn lọc ý kiến từ các bạn đồng nghiệp để dần
hoàn thiện cuốn sách này, nhưng khó tránh khỏi những thiếu sót bởi tầm hiểu biết và kinh
nghiệm còn hạn chế, chúng tôi rất mong nhận được ý kiến đóng góp quý báu của bạn đọc gần xa.
Chi tiết liên hệ tại : anhkhoavo1210@gmail.com minh.9a1.dt@gmail.com CÁC TÁC GIẢ
VÕ ANH KHOA – HOÀNG BÁ MINH. --------------------- TOANMATH.com LỜI CẢM ƠN
Trong quá trình biên soạn, chúng tôi xin cám ơn đến những bạn đã cung cấp tài liệu tham
khảo và vui lòng nhận kiểm tra lại từng phần của bản thảo hoặc bản đánh máy, tạo điều
kiện hoàn thành cuốn sách này :
- Tô Nguyễn Nhật Minh (ĐH Quốc Tế Tp.HCM)
- Ngô Minh Nhựt (ĐH Kinh Tế Tp.HCM)
- Mai Ngọc Thắng (ĐH Kinh Tế Tp.HCM)
- Trần Lam Ngọc (THPT Chuyên Trần Đại Nghĩa Tp.HCM)
- Nguyễn Huy Hoàng (THPT Chuyên Lê Hồng Phong Tp.HCM)
- Nguyễn Hoài Anh (THPT Chuyên Phan Bội Châu Tp.Vinh)
- Phan Đức Minh (ĐH Khoa Học Tự Nhiên Hà Nội)
và một số thành viên diễn đàn MathScope. --------------------- TOANMATH.com MỤC LỤC
TẬP 1 : BIẾN ĐỔI LƯỢNG GIÁC VÀ HỆ THỨC LƯỢNG
CHƯƠNG 1 : SƠ LƯỢC VỀ KHÁI NIỆM VÀ LỊCH SỬ ....................................... 1
CHƯƠNG 2 : CÁC BIẾN ĐỔI LƯỢNG GIÁC ........................................................ 4
2.1 CHỨNG MINH MỘT ĐẲNG THỨC LƯỢNG GIÁC ................................... 7
BÀI TẬP TỰ LUYỆN ................................................................................... 15
2.2 TÍNH GIÁ TRỊ CỦA BIỂU THỨC ............................................................... 21
BÀI TẬP TỰ LUYỆN ................................................................................... 33
2.3 CHỨNG MINH ĐẲNG THỨC LƯỢNG GIÁC SUY TỪ ĐẲNG THỨC
LƯỢNG GIÁC KHÁC CHO TRƯỚC .......................................................... 36
BÀI TẬP TỰ LUYỆN ................................................................................... 45
2.4 CHỨNG MINH BIỂU THỨC LƯỢNG GIÁC KHÔNG PHỤ THUỘC VÀO
BIẾN SỐ ....................................................................................................... 46
BÀI TẬP TỰ LUYỆN ................................................................................... 51
CHƯƠNG 3 : HỆ THỨC LƯỢNG TRONG TAM GIÁC ....................................... 52
3.1 CHỨNG MINH ĐẲNG THỨC LƯỢNG GIÁC TRONG TAM GIÁC ......... 55
BÀI TẬP TỰ LUYỆN ................................................................................... 77
3.2 CHỨNG MINH BẤT ĐẲNG THỨC LƯỢNG GIÁC
TRONG TAM GIÁC ..................................................................................... 81
BÀI TẬP TỰ LUYỆN .................................................................................. 133
3.3 NHẬN DẠNG TAM GIÁC VÀ TÍNH CÁC GÓC TRONG TAM GIÁC..... 143
BÀI TẬP TỰ LUYỆN .................................................................................. 191 --------------------- TOANMATH.com ĐỌC THÊM :
TÓM LƯỢC TIỂU SỬ CÁC NHÀ KHOA HỌC
CÓ ẢNH HƯỚNG ĐẾN LƯỢNG GIÁC .................................................. 199
TÀI LIỆU THAM KHẢO ........................................................................................... 205 --------------------- TOANMATH.com
Chương 1 : Sơ lược về khái niệm và lịch sử CHƯƠNG 1
SƠ LƯỢC VỀ KHÁI NIỆM VÀ LỊCH SỬ I. KHÁI NIỆM
Trong toán học nói chung và lượng giác học nói riêng, các hàm lượng giác là các
hàm toán học của góc, được dùng khi nghiên cứu tam giác và các hiện tượng có tính chất
tuần hoàn. Các hàm lượng giác của một góc thường được định nghĩa bởi tỷ lệ chiều dài
hai cạnh của tam giác vuông chứa góc đó, hoặc tỷ lệ chiều dài giữa các đoạn thẳng nối
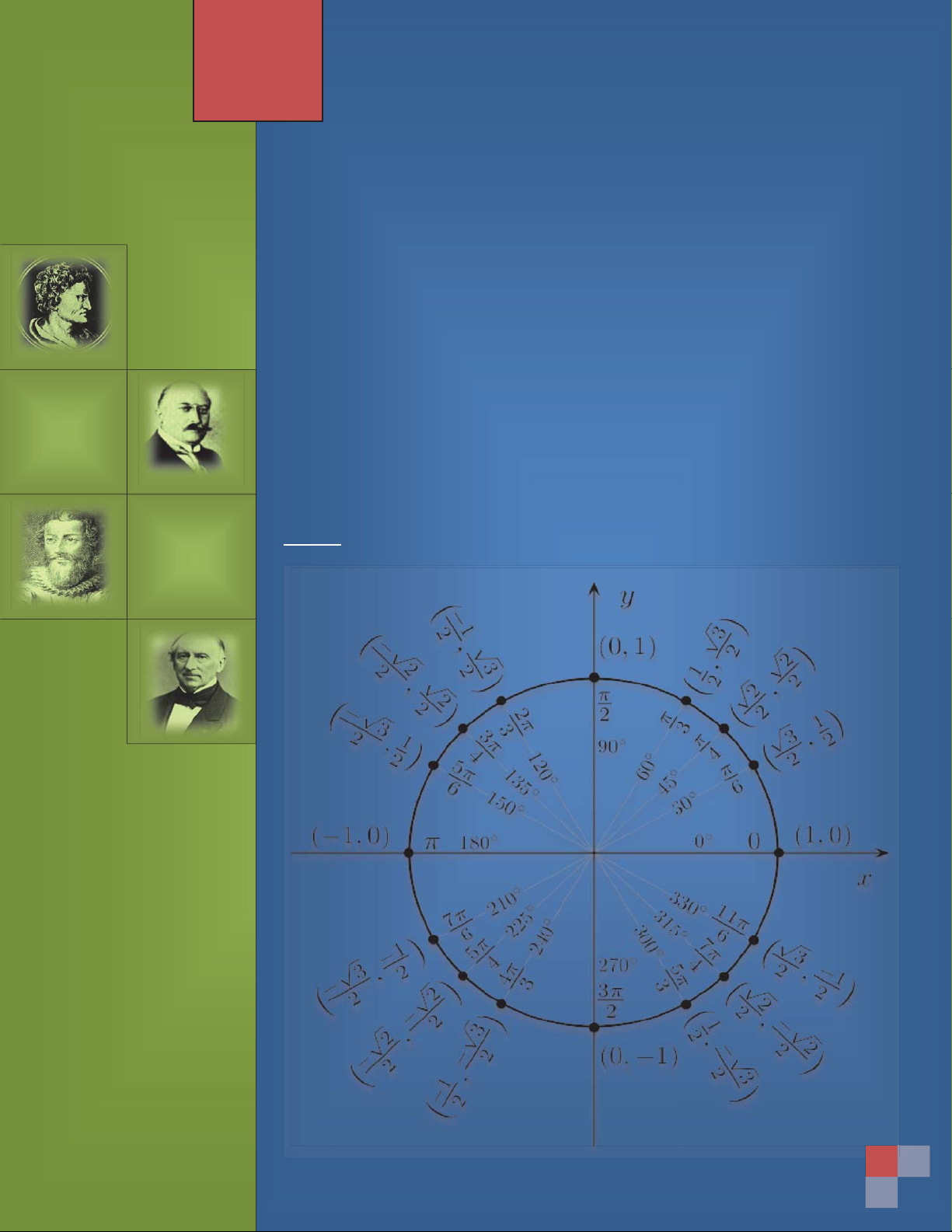
các điểm đặc biệt trên vòng tròn đơn vị. Sâu xa hơn, ở khía cạnh hiện đại hơn, định nghĩa
hàm lượng giác là chuỗi vô hạn hoặc là nghiệm của phương trình vi phân, điều này cho phép phép hàm
hàm llưượợnngg ggiiáácc có có tthhể có
có đđốốii số llàà mộtt số thực hay một số phức bất kỳ.
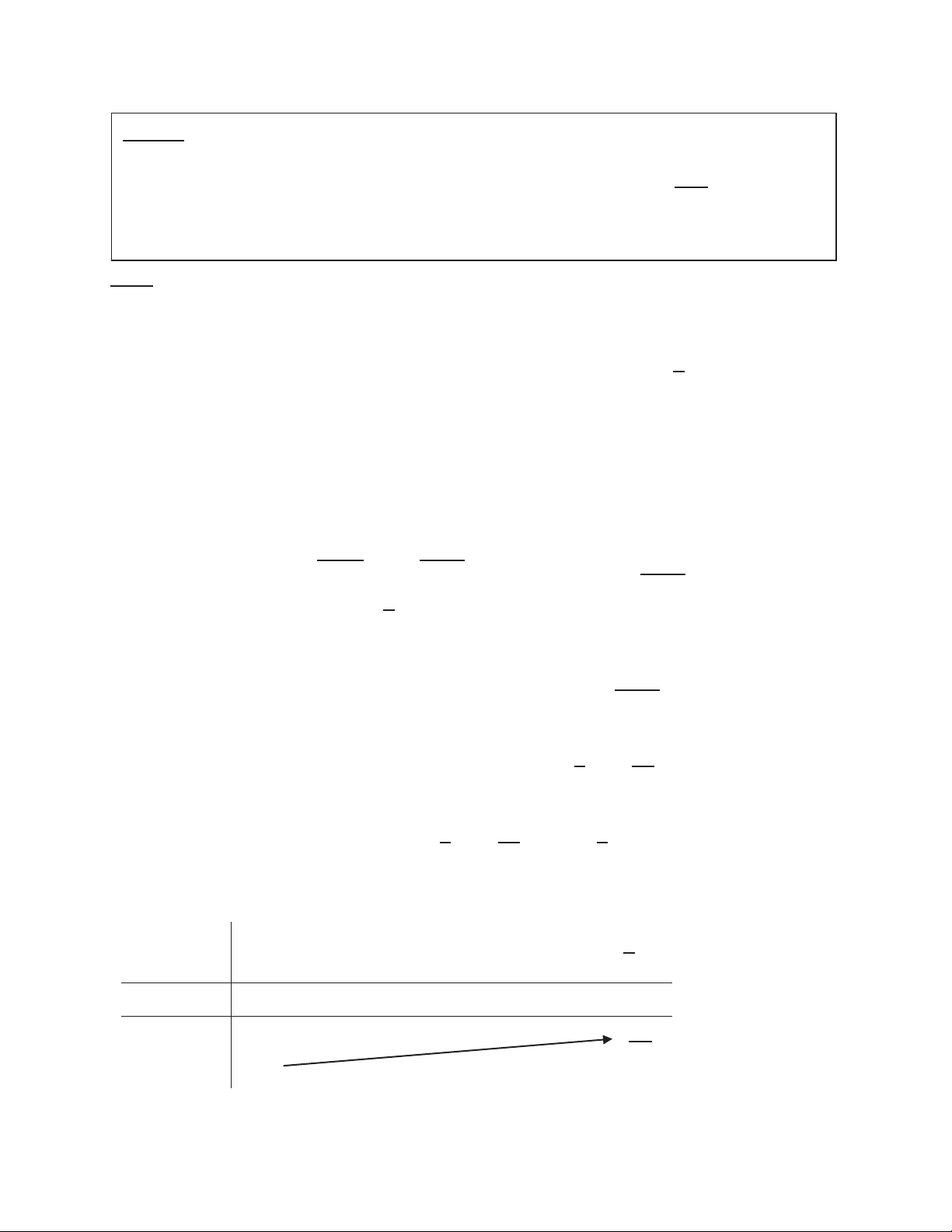
( Dạng đồ thị hàm sin ) II. LỊC CH H SỬ
Những nghiên cứu một cách hệ thống và việc lập bảng tính các hàm lượng giác
được cho là thực hiện đầu tiên bởi Hipparchus(1) (180-125 TCN), người đã lập bảng tính
độ dài các cung tròn và chiều dài của dây cung tương ứng. Sau đó, Ptomely(2) tiếp tục
phát triển công trình, tìm ra công thức cộng và trừ cho ሺ ሻ và ሺ ሻ,
Ptomely cũng đã suy diễn ra được công thức hạ bậc, cho phép ông lập bảng tính với bất
kỳ độ chính xác cần thiết nào. Tuy nhiên, những bảng tính trên đều đã bị thất truyền.
Các phát triển tiếp theo diễn ra ở Ấn Độ, công trình của Surya Siddhanta(3) (thế kỷ
4-5) định nghĩa hàm sin theo nửa góc và nửa dây cung. Đến thế kỷ 10, người Ả Rập đã
dùng cả 6 hàm lượng giác cơ bản với độ chính xác đến 8 chữ số thập phân.
Các công trình đầu tiên này về các hàm lượng giác cơ bản đều được phát triển
nhằm phục vụ trong các công trình thiên văn học, cụ thể là dùng để tính toán các đồng hồ mặt trời. 1 --------------------- TOANMATH.com
Chương 1 : Sơ lược về khái niệm và lịch sử
Ngày nay, chúng được dùng để đo khoảng cách tới các ngôi sao gần, giữa các mốc
giới hạn hay trong các hệ thống hoa tiêu vệ tinh. Rộng hơn nữa, chúng được áp dụng vào
nhiều lĩnh vực khác : quang học, phân tích thị trường tài chính, điện tử học, lý thuyết xác
suất, thống kê, sinh học, dược khoa, hóa học, lý thuyết số, địa chấn học, khí tượng học, hải dương học…
Ta lấy ví dụ từ một bài toán sau trích từ Lucia C. Hamson, Daylight, Twilight, Darkness and Time :
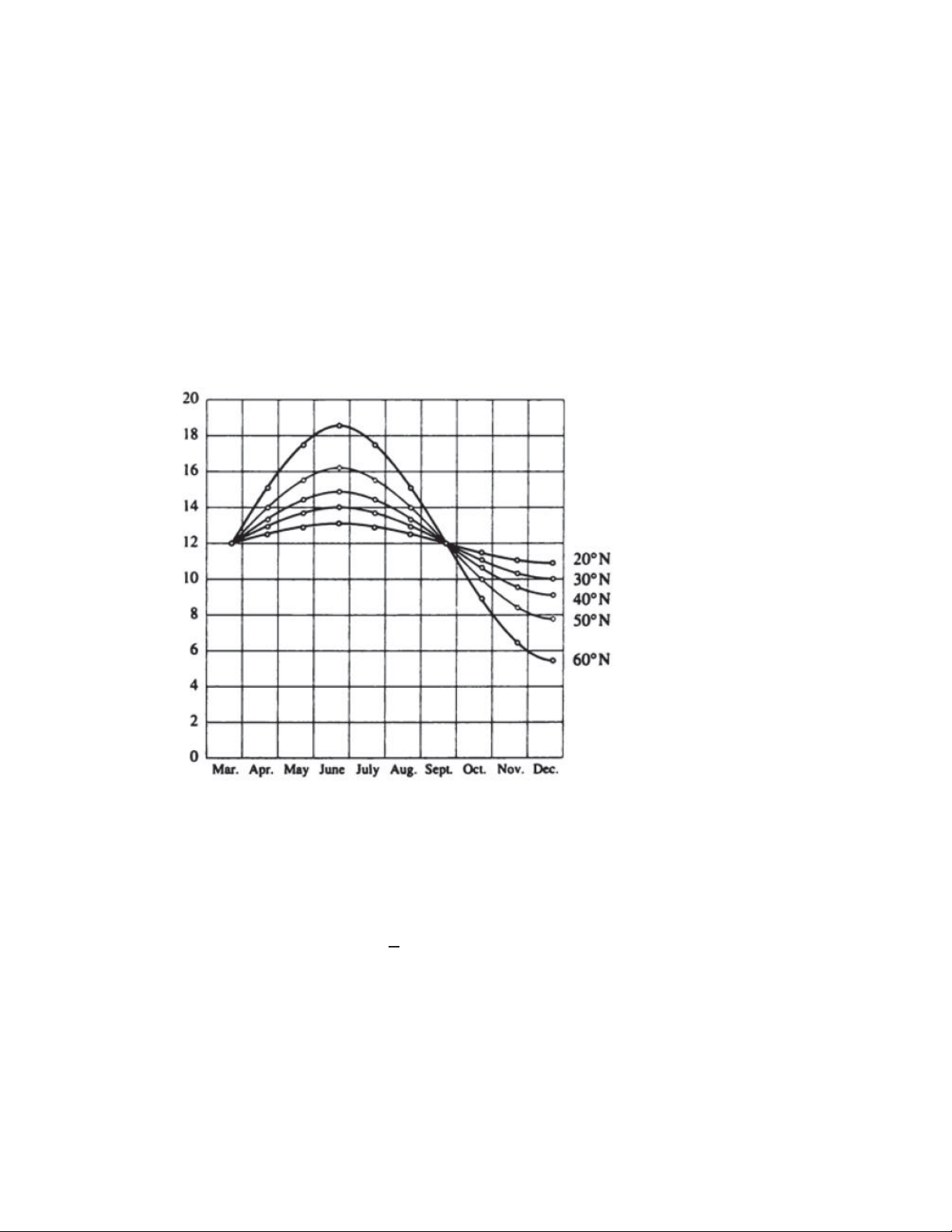
Việc mô hình hóa về số giờ chiếu sáng của mặt trời là hàm thời gian trong năm tại
nhiều vĩ độ khác nhau. Cho biết Philadelphia nằm ở vĩ độ ͶͲ୭ Bắc, tìm hàm biểu thị số
giờ chiếu sáng của mặt trời tại Philadelphia.
Chú ý rằng mỗi đường cong tương tự với một hàm số sin mà bị di chuyển và kéo
căng ra. Tại độ cao của Philadelphia, thời gian chiếu sáng kéo dài 14,8 giờ vào ngày 21
tháng 6 và 9,2 giờ vào ngày 21 tháng 12, vậy nên biên độ của đường cong (hệ số kéo
căng theo chiều dọc) là :
ͳ ሺͳͶǡͺ െ ͻǡʹሻ ൌ ʹǡͺ ʹ
Hệ số nào mà chúng ta cần để kéo căng đồ thị hình sin theo chiều ngang nếu
chúng ta đo thời gian ݐ trong ngày? Bởi có 365 ngày/ năm, chu kỳ của mô hình nên là 365.
Nhưng mà giai đoạn của ݕ ൌ ݐ là ʹߨ, nên hệ số kéo căng theo chiều ngang là : 2 --------------------- TOANMATH.com
Chương 1 : Sơ lược về khái niệm và lịch sử ʹߨ ܿ ൌ ͵ͷ
Chúng ta cũng để ý rằng đường cong bắt đầu một chu trình của nó vào ngày 21
tháng 3, ngày thứ 80 của năm nên chúng ta phải phải dịch chuyển đường cong về bên
phải 80 đơn vị. Ngoài ra, chúng ta phải đưa nó lên trên 12 đơn vị. Do đó chúng ta mô
hình hóa số giờ chiếu sáng của của mặt trời trong năm ở Philadelphia vào ngày thứ ݐ của năm bằng hàm số : ʹߨ
ܮሺݐሻ ൌ ͳʹ ʹǡͺ ሺݐ െ ͺͲሻ൨ ͵ͷ 3 --------------------- TOANMATH.com
Chương 2 : Các biến đổi lượng giác CHƯƠNG 2
CÁC BIẾN ĐỔI LƯỢNG GIÁC I.
BẢNG GIÁ TRỊ LƯỢNG GIÁC CỦA CÁC CUNG CÓ LIÊN QUAN ĐẶC BIỆT
Ta gọi cung có liên quan đặc biệt với cung ߙ là các cung : - Đối với ߙ : െߙ - Bù với ߙ : ߨ െ ߙ - Hiệu ߨ với ߙ : ߨ ߙ - గ గ
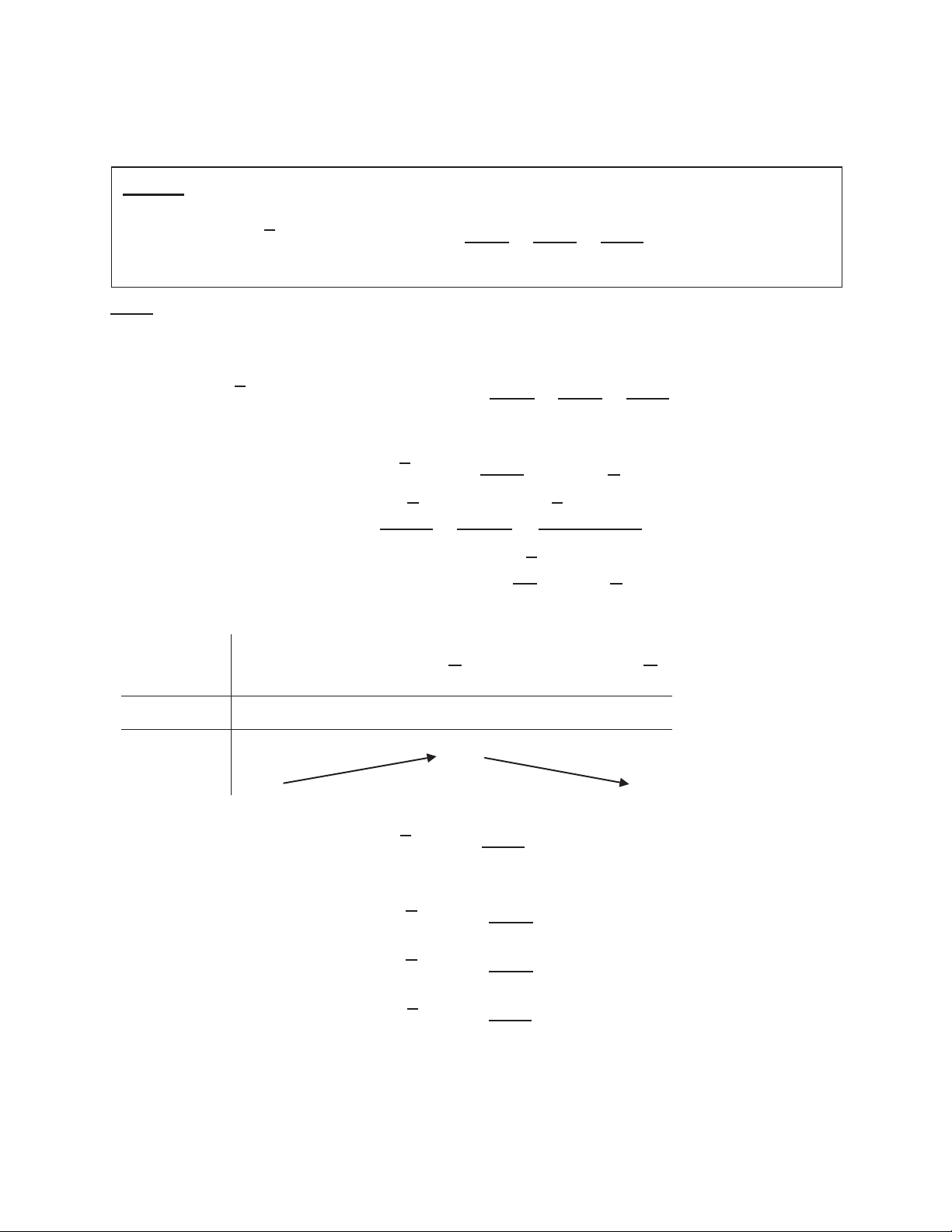
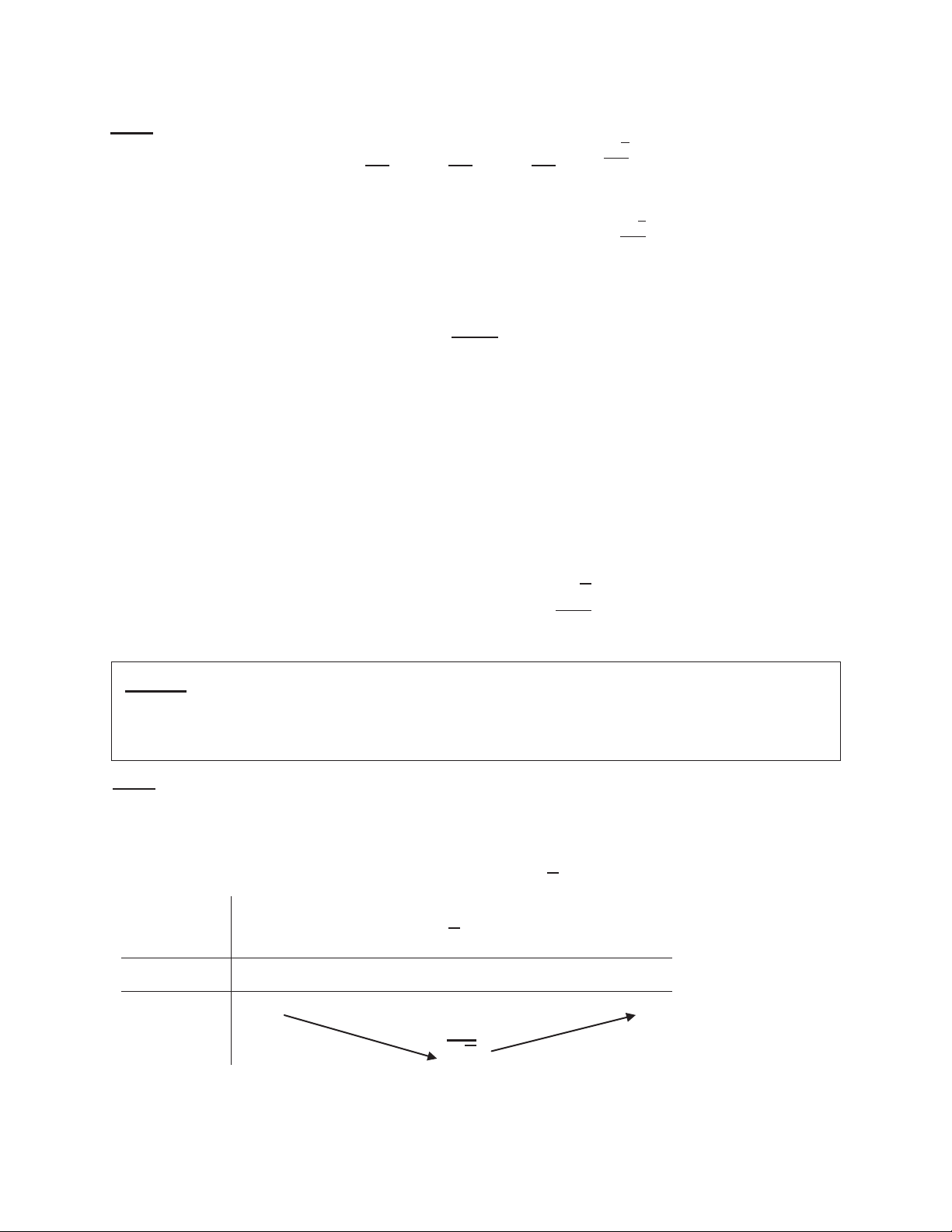
Hơn kém với ߙ : േ ߙ ଶ ߨ ߨ െߙ ߨ െ ߙ ߨ ߙ െ ߙ ߙ ʹ ʹ cos ߙ െ ߙ െ ߙ ߙ െ ߙ sin െ ߙ ߙ െ ߙ ߙ ߙ tan െ ߙ െ ߙ ߙ ߙ െ ߙ cot െ ߙ െ ߙ ߙ ߙ െ ߙ
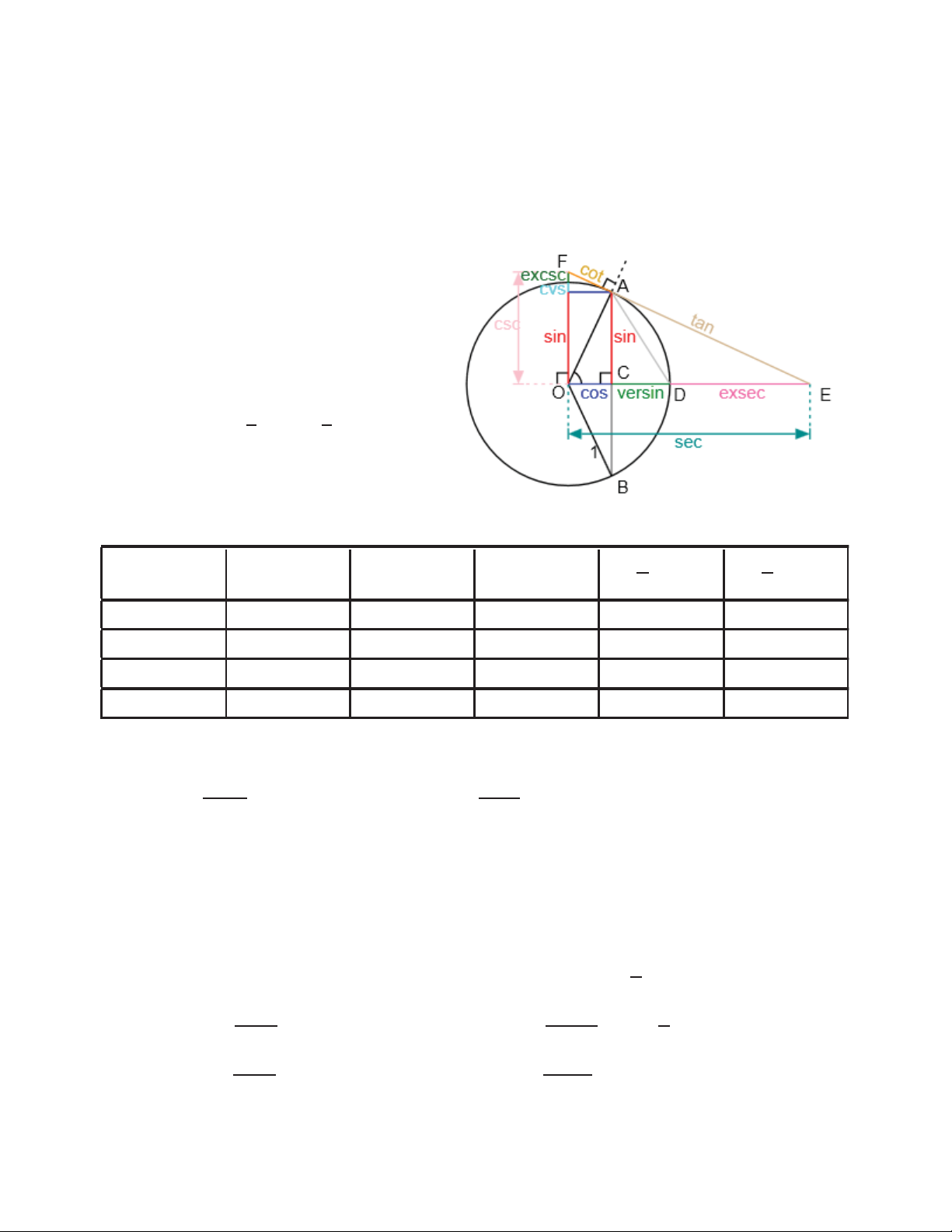
Ngoài ra, có một số hàm lượng giác khác : ͳ ͳ െ ߙ ൌ െ ߙ ൌ ߙ ߙ
െߙ ൌ ͳ െ ߙ െ ߙ ൌ ߙ െ ͳ II.
CÔNG THỨC LƯỢNG GIÁC 1. CÔNG THỨC CƠ BẢN ߨ
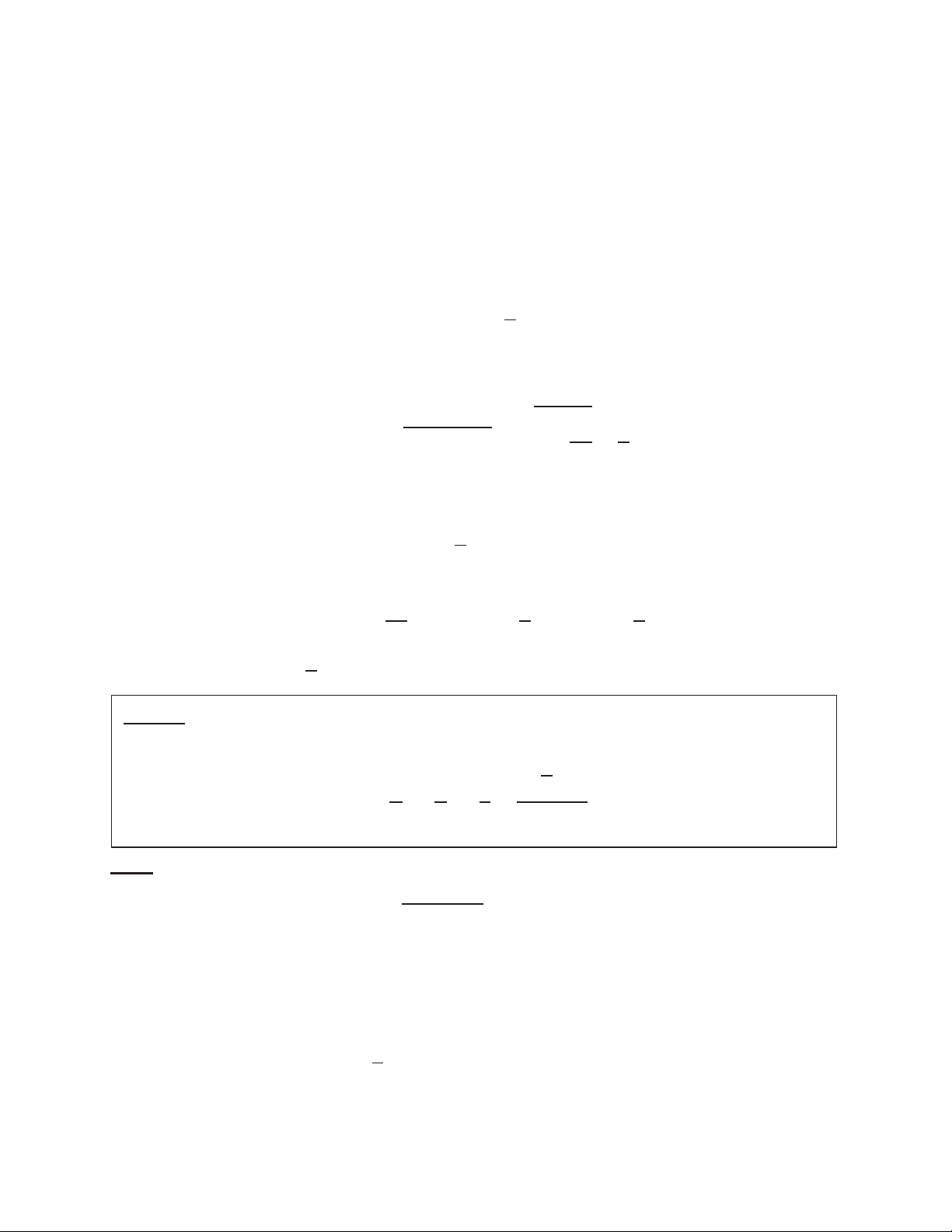
ଶ ݔ ଶ ݔ ൌ ͳ ݔ ݔ ൌ ͳ ቀݔ ് ݇ ǡ ݇ א Ժቁ ʹ ݔ ͳ ߨ ݔ ൌ ͳ ଶ ݔ ൌ
ቀݔ ് ݇ߨǡ ݇ א Ժቁ ݔ ଶ ݔ ʹ ݔ ͳ ݔ ൌ ͳ ଶ ݔ ൌ ሺݔ ് ݇ߨǡ ݇ א Ժሻ ݔ ଶ ݔ 4 --------------------- TOANMATH.com
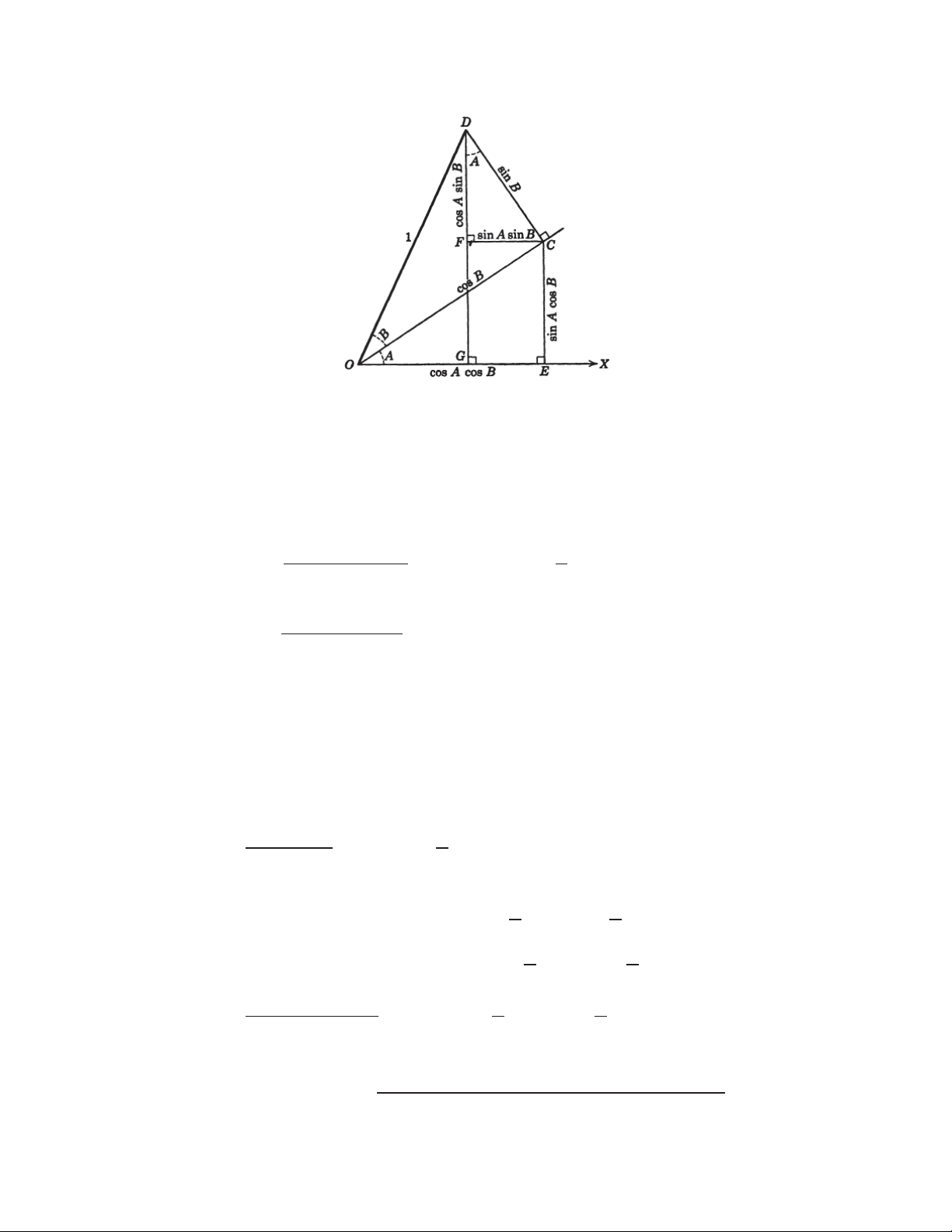
Chương 2 : Các biến đổi lượng giác
Từ hình vẽ thực tiễn trên, ta rút ra được một số công thức cơ bản về hàm lượng giác : 2. CÔNG THỨC CỘNG
ሺܽ േ ܾሻ ൌ ܽ ܾ േ ܾ ܽ
ሺܽ ܾሻ ൌ ܽ ܾ ט ܽ ܾ ܽ േ ܾ ߨ
ሺܽ േ ܾሻ ൌ ͳ ט ܽ ܾቀܽǡܾǡܽ േ ܾ ് ݇ߨǡ݇ א Ժቁ ʹ ܽ ܾ ט ͳ ሺܽ േ ܾሻ ൌ
ሺܽǡ ܾǡ ܽ േ ܾ ് ݇ߨǡ ݇ א Ժሻ ܽ േ ܾ 3. CÔNG THỨC NHÂN a. CÔNG THỨC NHÂN 2 ʹݔ ൌ ʹ ݔ ݔ ଶ ݔ െ ଶ ݔ ʹݔ ൌ ൝ ʹ ଶ ݔ െ ͳ ͳ െ ʹ ଶ ݔ ʹ ݔ ߨ ʹݔ ൌ
ቀݔǡ ʹݔ ് ݇ߨǡ ݇ א Ժቁ ͳ െ ଶ ݔ ʹ b. CÔNG THỨC NHÂN 3 ߨ ߨ
͵ݔ ൌ ͵ ݔ െ Ͷ ଷ ݔ ൌ Ͷ ݔ ቀ െ ݔቁ ቀ ݔቁ ͵ ͵ ߨ ߨ
͵ݔ ൌ Ͷ ଷ ݔ െ ͵ ݔ ൌ Ͷ ݔ ቀ െ ݔቁ ቀ ݔቁ ͵ ͵ ͵ ݔ െ ଷ ݔ ߨ ߨ ͵ݔ ൌ
ൌ ݔ ቀ െ ݔቁ ቀ ݔቁ ͳ െ ͵ ଶ ݔ ͵ ͵
Công thức tổng quát đối với hàm tan : ܽ ܾ ܿ െ ܽ ܾ ܿ
ሺܽ ܾ ܿሻ ൌ ͳ െ ܽ ܾ െ ܾ ܿ െ ܿ ܽ 5 --------------------- TOANMATH.com
Chương 2 : Các biến đổi lượng giác c.
CÔNG THỨC TÍNH THEO ݐ ൌ ݔ ʹݐ ʹݔ ൌ ͳ ݐଶ ͳ െ ݐଶ ߨ ʹݔ ൌ
ቀݔ ് ݇ߨǡ ݇ א Ժቁ ͳ ݐଶ ʹ ʹݐ ʹݔ ൌ ͳ െ ݐଶ d. CÔNG THỨC HẠ BẬC ͳ െ ʹݔ ͳ ʹݔ ͳ െ ʹݔ ଶ ݔ ൌ ଶ ݔ ൌ ଶ ݔ ൌ ʹ ʹ ͳ ʹݔ െ ͵ݔ ͵ ݔ ͵ݔ ͵ ݔ ଷ ݔ ൌ ଷ ݔ ൌ Ͷ Ͷ 4.
CÔNG THỨC BIẾN ĐỔI a. TÍCH THÀNH TỔNG ͳ
ܽ ܾ ൌ ሾሺܽ ܾሻ ሺܽ െ ܾሻሿ ʹͳ
ܽ ܾ ൌ െ ሾሺܽ ܾሻ െ ሺܽ െ ܾሻሿ ʹ ͳ
ܽ ܾ ൌ ሾሺܽ ܾሻ ሺܽ െ ܾሻሿ ʹ ͳ
ܽ ܾ ൌ ሾሺܽ ܾሻ െ ሺܽ െ ܾሻሿ ʹ b. TỔNG THÀNH TÍCH ܽ ܾ ܽ െ ܾ ܽ ܾ ൌ ʹ ʹ ʹ ܽ ܾ ܽ െ ܾ ܽ െ ܾ ൌ െʹ ʹ ʹ ܽ ܾ ܽ െ ܾ ܽ ܾ ൌ ʹ ʹ ʹ ܽ ܾ ܽ െ ܾ ܽ െ ܾ ൌ ʹ ʹ ʹ ሺܽ േ ܾሻ ߨ ܽ േ ܾ ൌ
ቀܽǡ ܾ ് ݇ߨǡ ݇ א Ժቁ ܽ ܾ ʹ ሺܾ േ ܽሻ ܽ േ ܾ ൌ
ሺܽǡ ܾ ് ݇ߨǡ ݇ א Ժሻ ܽ ܾ ሺܽ െ ܾሻ ߨ ܽ ܾ ൌ
ቀܽ ് ݇ߨǡ ܾ ് ݈ߨǡ ݇ǡ ݈ א Ժቁ ܽ ܾ ʹ ሺܽ ܾሻ ߨ ܽ െ ܾ ൌ
ቀܽ ് ݇ߨǡ ܾ ് ݈ߨǡ ݇ǡ ݈ א Ժቁ ܽ ܾ ʹ 6 --------------------- TOANMATH.com
Chương 2 : Các biến đổi lượng giác c. CÔNG THỨC BỔ SUNG ߨ
ܽ േ ܽ ൌ ξʹ ቀܽ േ ቁ Ͷߨ
ܽ േ ܽ ൌ ξʹ ቀܽ ט ቁ Ͷߨ ߨ
ξ͵ ܽ േ ܽ ൌ ʹ ቀܽ േ ቁ ൌ ʹ ቀܽ ט ቁ ͵ ߨ ߨ
ܽ േ ξ͵ ܽ ൌ ʹ ቀܽ േ ቁ ൌ ʹ ቀܽ ט ቁ ͵
݉ ܽ ݊ ܽ ൌ ඥ݉ଶ ݊ଶ ሺܽ ܾሻ Trong đó ݉ଶ ݊ଶ Ͳ ൝ ݉ ݊ ܾ ൌ Ǣ ܾ ൌ ξ݉ଶ ݊ଶ ξ݉ଶ ݊ଶ III.
CÁC LOẠI TOÁN VÀ PHƯƠNG PHÁP GIẢI 1.
CHỨNG MINH MỘT ĐẲNG THỨC LƯỢNG GIÁC
- Ta thường sử dụng các phương pháp : biến đổi vế phức tạp hoặc nhiều số hạng
thành vế đơn giản; biến đổi tương đương; xuất phát từ đẳng thức đúng nào đó, biến
đổi về đẳng thức cần chứng minh.
- Trong khi biến đổi ta sử dụng các công thức thích hợp hướng đến kết quả phải đạt được.
- Lưu ý một số công thức trên phải chứng minh trước khi sử dụng.
Bài 1: Chứng minh các đẳng thức sau : a. ܽ െ ܽ ൌ ʹ ʹܽ b. ʹܽ ሺ ܽ ܽሻ ൌ ʹ Giải: a. Ta có : ܽ ܽ ଶ ܽ െ ଶ ܽ ʹ ʹܽ ൌ െ ൌ ൌ ൌ ܽ ܽ ܽ ܽ ʹܽ b. Ta có : ܽ ܽ ൌ ʹ ܽ ൬
൰ ൌ ʹሺଶ ܽ ଶ ܽሻ ൌ ʹ ܽ ܽ 7 --------------------- TOANMATH.com
Chương 2 : Các biến đổi lượng giác
Bài 2: Chứng minh đẳng thức sau : ݔ ݔ
Ǥ ଷ ݔ ଶ ݔ ݔ ͳ ൌ ଷ ݔ ͳ ݔ ݔ ͳ Ǥ ൌ ͳ െ ݔ ݔ െ ͳ ʹ Ͷݔ Ǥ ൌ ଶ ݔ ଶ ݔ ͳ െ Ͷݔ ݔ െ ݔ ͳ Ǥ ൌ ଷ ݔ ݔ ሺͳ ݔሻ Giải: a. Ta có : ݔ ቀݔ ͳቁ
ൌ ଶ ݔ ሺ ݔ ͳሻ ݔ ͳ ൌ ሺ ݔ ͳሻሺଶ ݔ ͳሻ ൌ ଶ ݔ ݔ ݔ ൌ ൌ ଷ ݔ b.
Ta có điều cần chứng minh tương đương với
ሺͳ ݔሻሺ ݔ െ ͳሻ ൌ ሺ ݔ ͳሻሺͳ െ ݔሻ
ݔ െ ͳ ݔ ݔ െ ݔ ൌ ݔ െ ݔ ݔ ͳ െ ݔ
Điều này hiển nhiên đúng nên ta có điều phải chứng minh. c. Ta có : Ͷ Ͷ ʹ Ͷݔ
ൌ ሺ ݔ ݔሻଶ െ ʹ ൌ െ ʹ ൌ െ ʹ ൌ ൌ ଶ ʹݔ ͳ െ Ͷݔ ͳ െ Ͷݔ ʹ d. Ta có : ͳ ݔ ቀ ͳ െ ݔ ͳ ൌ ݔ െ ͳቁ ൌ ൌ ൌ ଷ ݔ
ݔ ሺͳ െ ݔሻሺͳ ݔሻ ݔ ሺͳ ݔሻ 8 --------------------- TOANMATH.com
Chương 2 : Các biến đổi lượng giác Bài 3: Chứng minh : a.
ͷ ͵ Ͷݔ ൌ ͺሺ ݔ ݔሻ b. ʹݔ ݔ ൌ ͳ െ ʹݔ Suy ra giá trị : ߨ ͵ߨ ͷߨ ൌ ଶ ଶ ଶ ͳʹ ͳʹ ͳʹ Giải: a. Ta có :
ݔ ݔ ൌ ሺଶ ݔ ଶ ݔሻሺସ ݔ െ ଶ ݔ ଶ ݔ ସ ݔሻ ͵ ͵
ൌ ሺଶ ݔ ଶ ݔሻଶ െ ͵ ଶ ݔ ଶ ݔ ൌ ͳ െ ଶ ʹݔ ൌ ͳ െ ሺͳ െ Ͷݔሻ Ͷ ͺ ͷ ͵ ସ ݔ ൌ ͺ
Vậy ta có điều phải chứng minh. b. Ta có : ͳ െ ʹݔ ʹ ଶ ݔ ൌ ൌ ݔ ʹݔ ʹ ݔ ݔ Nên ߨ ߨ ͳ െ ͳ െ ξ͵ ൌ ൌ ʹ ൌ ʹ െ ξ͵ ͳʹ ߨ ͳ ʹ ͵ߨ ͵ߨ ͳ െ ൌ ൌ ͳ ͳʹ ͵ߨ ͷߨ ͷߨ ͳ െ ൌ ൌ ʹ ξ͵ ͳʹ ͷߨ ଶ ଶ
Vậy ൌ ൫ʹ െ ξ͵൯ ͳ ൫ʹ ξ͵൯ ൌ ͳͷ Bài 4: Chứng minh ͵ ͳ ͳ ସ ݔ ൌ െ ʹݔ Ͷݔ ͺ ʹ ͺ Áp dụng tính tổng sau : ߨ ͵ߨ ͷߨ ߨ ൌ ସ ସ ସ ସ ͳ ͳ ͳ ͳ 9 --------------------- TOANMATH.com
Chương 2 : Các biến đổi lượng giác Giải: Ta có : ͳ Ͷݔ ͳ െ ʹݔ ଶ ͳ ଶ ʹݔ െ ʹ ʹݔ ͳ ସ ݔ ൌ ൬ ൰ ൌ ൌ ʹ െ ʹ ʹݔ ʹ Ͷ Ͷ ͵ Ͷݔ ͳ ൌ െ ʹݔ ͺ ͺ ʹ Suy ra ߨ ͵ ͳ ߨ ͳ ߨ ସ ൌ െ ͳ ͺ ʹ ͺ ͺ Ͷ ͵ߨ ͵ ͳ ͵ߨ ͳ ͵ߨ ସ ൌ െ ͳ ͺ ʹ ͺ ͺ Ͷ ͷߨ ͵ ͳ ͷߨ ͳ ͷߨ ସ ൌ െ ͳ ͺ ʹ ͺ ͺ Ͷ ߨ ͵ ͳ ߨ ͳ ߨ ସ ൌ െ ͳ ͺ ʹ ͺ ͺ Ͷ Vì ͵ߨ ͷߨ ߨ ߨ ߨ ͵ߨ ͷߨ ߨ ൌ ൌ ൌ ൌ Ͳ ͺ ͺ ͺ ͺ Ͷ Ͷ Ͷ Ͷ Nên ͵ ൌ ʹ
Bài 5: Cho ݔǡ ݕǡ ݖ với ݔ ݕ ݖ ൌ ݊ߨ ሺ݊ א Գሻ Chứng minh
ଶ ݔ ଶ ݕ ଶ ݖ ൌ ͳ ʹǤ ሺെͳሻ ݔ ݕ ݖ Giải: Ta có : ͳ ʹݔ ͳ ʹݕ ଶ ݔ ଶ ݕ ൌ
ൌ ͳ ሺݔ ݕሻ ሺݔ െ ݕሻ ʹ ʹ
ଶ ݖ ൌ ଶ൫݊ߨ െ ሺݔ ݕሻ൯ ൌ ଶሺݔ ݕሻ 10 --------------------- TOANMATH.com
Chương 2 : Các biến đổi lượng giác Nên
ൌ ͳ ሺݔ ݕሻ ሾሺݔ ݕሻ ሺݔ െ ݕሻሿ ൌ ͳ ʹ ሺݔ ݕሻ ݔ ݕ
ൌ ͳ ʹ ሺ݊ߨ െ ݖሻ ݔ ݕ Khi
- ݊ ൌ ʹ݉ thì ሺ݊ߨ െ ݖሻ ൌ ݖ
- ݊ ൌ ʹ݉ ͳ thì ሺ݊ߨ െ ݖሻ ൌ െ ݖ
Vậy ta có điều phải chứng minh. Bài 6: Chứng minh ߨ ʹߨ ͵ߨ ͳ െ ൌ ʹ (ĐH Đà Nẵng 1998) Giải: Đặt ߨ ʹߨ ͵ߨ ൌ െ Ta có : ߨ ʹߨ ߨ ʹߨ ߨ ͵ߨ ʹ ൌ െ ʹ ʹ ʹߨ ͵ߨ ߨ Ͷߨ ʹߨ ൌ െ ቀെ ቁ൨ ൬െ ൰൨ ʹߨ ͵ߨ ߨ Ͷߨ ʹߨ ߨ Ͷߨ ͵ߨ ൌ െ െ ൌ ൬ ൌ ൰ Do đó ͳ ൌ ʹ Bài 7: Chứng minh ͳ
ݔ ଶ ݔ ଶ ݔ ݔ ൌ ሺͳ െ ସ ʹݔሻ ͺ 11 --------------------- TOANMATH.com
Chương 2 : Các biến đổi lượng giác
Giải: Ta có điều cần chứng minh tương đương với ͳ
ଶ ݔ ଶ ݔ ሺସ ݔ ସ ݔሻ ൌ ሺͳ െ ଶ ʹݔሻሺͳ ଶ ʹݔሻ ͺ
ͺ ଶ ݔ ଶ ݔ െ ͳ ସ ݔ ସ ݔ ൌ ଶ ʹݔ ሺͳ ଶ ʹݔሻ
ʹ ଶ ʹݔ െ ସ ʹݔ ൌ ଶ ʹݔ ଶ ʹݔ ଶ ʹݔ
ଶ ʹݔ ൌ ଶ ʹݔ ሺଶ ʹݔ ଶ ʹݔሻ
Điều này hiển nhiên đúng nên ta có điều phải chứng minh. Bài 8: Chứng minh ܽ ܽ ܽ ܽ ൬ ൰ ൌ ǡ ݊ א Գ ͳ ܽ ܽ ͳ ܽ ܽ Giải: Ta có : ܽ ܽ ܽ ܽ ൌ ቌ ͳ ቍ ൌ ൬ ܽ ൰ ൌ ܽ ͳ ܽ ܽ ܽ ܽ ܽ ܽ ܽ ܽ ൌ ൌ ܽ ͳ ൌ ܽ ܽ ܽ ͳ ܽ ܽ
Do đó, ta có điều phải chứng minh. Bài 9: Chứng minh ଶ ܽ ͳ െ ଶ ܽ
ଶ ܽ െ ʹ ସ ܽ ͵ ଶ ܽ ൌ
ܽ ܽ ʹ ଶ ܽ ଶ ܽ ͳ ܽ ͳ ܽ Giải: Ta có :
ൌ ଶ ܽ ଶ ܽ ʹ ଶ ܽ ሺͳ െ ଶ ܽሻ ͳ ൌ
ሺଶ ܽ ܽ ଶ ܽሻ ܽ ܽ ʹ ଶ ܽ ଶ ܽ ͳ ܽ 12 --------------------- TOANMATH.com
Chương 2 : Các biến đổi lượng giác ܽ ଷ ܽ ଷ ܽ ൌ ቆ
ቇ ܽ ܽ ʹ ଶ ܽ ଶ ܽ ܽ ܽ ܽ
ൌ ͳ െ ܽ ܽ ܽ ܽ ʹ ଶ ܽ ଶ ܽ ൌ ͳ ʹ ଶ ܽ ଶ ܽ
Do đó, ta có điều phải chứng minh. Bài 10: Chứng minh ξͷ െ ͳ
ʹ୭ ͳͺ୭ ʹʹ୭ ͵ͺ୭ Ͷʹ୭ ͷͺ୭ ʹ୭ ͺ୭ ͺʹ୭ ൌ ͳͲʹͶ (ĐHSP Hải Phòng 2001) Giải: Đặt
ൌ ʹ୭ ͳͺ୭ ʹʹ୭ ͵ͺ୭ Ͷʹ୭ ͷͺ୭ ʹ୭ ͺ୭ ͺʹ୭ Ta có :
͵ܽ ൌ Ͷ ܽ ሺͲ୭ ܽሻ ሺͲ୭ െ ܽሻ
Áp dụng công thức trên, ta được :
Ͷ ʹ୭ ሺͲ୭ ʹ୭ሻ ሺͲ୭ െ ʹ୭ሻ ൌ ୭
Ͷ ͳͺ୭ ሺͲ୭ ͳͺ୭ሻ ሺͲ୭ െ ͳͺ୭ሻ ൌ ͷͶ୭
Ͷ ʹʹ୭ ሺͲ୭ ʹʹ୭ሻ ሺͲ୭ െ ʹʹ୭ሻ ൌ ୭ Nhân lại, ta được :
Ͷ ൌ ୭ ͷͶ୭ ୭ ͳ ͳ െͳ ξͷ
Ͷ ൌ ୭ ሺͲ୭ ୭ሻ ሺ୭ െ ୭ሻ ൌ ͳͺ୭ ൌ Ͷ Ͷ ͳ Vậy ξͷ െ ͳ ൌ ͳͲʹͶ 13 --------------------- TOANMATH.com
Chương 2 : Các biến đổi lượng giác
Bài 11: Chứng minh rằng ͳ ܽ ͳ ܽ ͳ ܽ ܽ ǥ ൌ െ ʹ ʹܽ ʹ ʹ ʹ ʹ ʹ ʹ ʹ݊ܽ ߨ
ܽ ͵ܽ ǥ ሺʹ݊ െ ͳሻܽ ൌ
ǡ ܽ א ቀͲǢ ቁ ǡ ݊ א Գ ʹ ܽ ʹ ଶ ݊ܽ ߨ
ܽ ͵ܽ ǥ ሺʹ݊ െ ͳሻܽ ൌ
ǡ ܽ א ቀͲǢ ቁ ǡ ݊ א Գ ܽ ʹ Giải:
x Ta có : ݔ ൌ ݔ െ ʹ ʹݔ
Sử dụng công thức này, ta được : ܽ ൌ ܽ െ ʹ ʹܽ ͳ ܽ ͳ ܽ ൌ െ ʹ ܽ ʹ ʹ ʹ ʹ ͳ ܽ ͳ ܽ ͳ ܽ ൌ െ Ͷ Ͷ ʹଶ Ͷ ʹ ʹ
……………………………………….. ͳ ܽ ͳ ܽ ͳ ܽ ൌ െ ʹ ʹ ʹ ʹ ʹିଵ ʹିଵ
Cộng lại, ta có được điều phải chứng minh.
x Ta sử dụng công thức ʹ ݔ ݕ ൌ ሺݔ ݕሻ ሺݔ െ ݕሻ
Ta có : ʹ ܽ ൌ ʹܽ ሺ Ͷܽ െ ʹܽሻ ሺ ܽ െ Ͷܽሻ ǥ
ሾ ʹ݊ܽ െ ሺʹ݊ െ ʹሻܽሿ ൌ ʹ݊ܽ
Vậy ta có điều phải chứng minh.
x Ta sử dụng công thức ʹ ݔ ݕ ൌ ሺݔ െ ݕሻ െ ሺݔ ݕሻ
Ta có : ʹ ܽ ൌ ሺͳ െ ʹܽሻ ሺ ʹܽ െ Ͷܽሻ ሺ Ͷܽ െ ܽሻ ǥ
ሾሺʹ݊ െ ʹሻܽ െ ʹ݊ܽሿ ൌ ͳ െ ʹ݊ܽ ൌ ʹ ଶ ݊ܽ
Vậy ta có điều phải chứng minh. 14 --------------------- TOANMATH.com
Chương 2 : Các biến đổi lượng giác - BÀI TẬP TỰ LUYỆN
2.1.1. Chứng minh các đẳng thức sau a.
͵ݔ ଷ ݔ ͵ݔ ଷ ݔ ൌ ଷ ʹݔ b.
Ͷ ଷ ݔ ͵ݔ Ͷ ଷ ݔ ͵ݔ ൌ ͵ Ͷݔ c. ݔ ʹ ʹݔ ൌ ݔ 2.1.2. Chứng minh
ሺଶ ݔ ଶ ݔ ͳሻሺଶ ݔ െ ଶ ݔ ͳሻ ൌ ͳ
ሺଶ ݔ ଶ ݔ ͳሻሺଶ ݔ ଶ ݔ െ ͳሻ
2.1.3. Chứng minh ߨ ߨ
ଶ ݔ ଶ ቀ െ ݔቁ ଶ ቀ ݔቁ ൌ ͻ ଶ ͵ݔ ͵ ͵ Áp dụng tính tổng :
ൌ ଶ ͷ୭ ଶ ͳͲ୭ ڮ ଶ ͺͷ୭
2.1.4. Chứng minh ܽ ሻሺ݊ െ ͳሻܽ ܽ ൌ ሺ݊ െ ͳሻܽ െ ݊ܽ
ሻሺ݊ െ ͳሻܽ ݊ܽ ൌ ܽ ሾ ݊ܽ െ ሺ݊ െ ͳሻܽሿ െ ͳ ͳ ʹܽ ሻͳ ൌ ʹܽ ʹିଵܽ ͳ ͳ ͳ ͳ ሻ ൌ െ Ͷ ଶ ܽ Ͷିଵ ʹ ଶ ܽ ʹ െ ͳ Ͷ ଶ ܽ ʹ
2.1.5. Chứng minh ଶ ʹͲ୭,ଶ ͶͲ୭,ଶ ͺͲ୭ là nghiệm của phương trình ݔଷ െ
͵͵ݔଶ ʹݔ െ ͵ ൌ Ͳ
Từ đó suy ra giá trị của
ൌ ଶ ʹͲ୭ ଶ ͶͲ୭ ଶ ͺͲ୭
ൌ ଶ ʹͲ୭ ଶ ͶͲ୭ ଶ ͶͲ୭ ଶ ͺͲ୭ ଶ ͺͲ୭ ଶ ʹͲ୭
ൌ ଶ ʹͲ୭ ଶ ͶͲ୭ ଶ ͺͲ୭ 15 --------------------- TOANMATH.com
Chương 2 : Các biến đổi lượng giác
2.1.6. Cho 3 góc ǡ ǡ thỏa ൌ Ͷͷ୭ Chứng minh
െ ൌ ͳ െ െ െ
2.1.7. Chứng minh ͷ ͵
ݔ ݔ ൌ Ͷݔ ͺ ͺ
2.1.8. Chứng minh ସ ܽ ସ ܽ െ ͳ ʹ ൌ ܽ ܽ െ ͳ ͵ (ĐHQG Hà Nội 1996)
2.1.9. Chứng minh ͳ ܽ ሺͳ െ ܽሻଶ ଶ ܾ െ ଶ ܿ ቈͳ െ
െ ଶ ܾ ଶ ܿ ൌ ܽ െ ͳ ʹ ܽ ଶ ܽ ଶ ܾ ଶ ܿ
2.1.10. Chứng minh ͳ ͳ ͳ ͳ ൌ ݔ െ ͳݔ ʹݔ Ͷݔ ͺݔ ͳݔ ݇ߨ
ừ¯×ǡ ứ ớọ݊ א Գǡ ݔ ് ሺ݇ א Ժǡ ݈ א Գሻ ʹ ͳ ͳ ͳ ǥ ൌ ݔ െ ʹݔ ʹݔ Ͷݔ ʹݔ
2.1.11. Chứng minh ͵ͷ ͳ ଼ ݔ ଼ ݔ ൌ Ͷݔ ͺݔ Ͷ ͳ Ͷ
2.1.12. Chứng minh ξ͵ ͳ
ͳʹ୭ ͳͺ୭ െ Ͷ ͳͷ୭ ʹͳ୭ ʹͶ୭ ൌ െ ʹ (ĐHQG Hà Nội 2001) 16 --------------------- TOANMATH.com
Chương 2 : Các biến đổi lượng giác
2.1.13. Chứng minh Ͷ ͳͺ୭ ͷͶ୭ ൌ ͳ
(ĐH Phòng Cháy Chữa Cháy 2001)
2.1.14. Chứng minh ͺ
͵Ͳ୭ ͶͲ୭ ͷͲ୭ Ͳ୭ ൌ ʹͲ୭ ξ͵ (ĐHQG Hà Nội 1995)
2.1.15. Chứng minh
ሻ ͳ ͳͲ୭ ͵Ͳ୭ ͷͲ୭ Ͳ୭ ൌ ͳ ߨ ߨ ߨ ߨ ሻ ͺ Ͷ ʹ ൌ ͺ ͳ ͵ʹ ͵ʹ
2.1.16. Chứng minh ߨ ʹߨ ͵ߨ Ͷߨ ͷߨ ߨ ߨ ͳ Ǥ ൌ ͳͷ ͳͷ ͳͷ ͳͷ ͳͷ ͳͷ ͳͷ ʹ
Ǥ ͷ୭ ͷͷ୭ ͷ୭ ͷ୭ ൌ ͳ 2.1.17. Chứng minh
ͳͲ୭ ʹͲ୭ ͵Ͳ ǥ Ͳ୭ ͺͲ୭ ൌ ͳ
2.1.18. Chứng minh ሺܽ െ ܾሻ ሺܾ െ ܿሻ ሺܿ െ ܽሻ ൌ Ͳ ܽ ܾ ܾ ܿ ܿ ܽ 2.1.19. Chứng minh ͳ െ ʹ ଶ ܽ ߨ ߨ ൌ ͳ
ʹ ቀͶ ܽቁ ଶ ቀͶ െ ܽቁ
2.1.20. Chứng minh
ͳ ܽ ʹܽ ͵ܽ ൌ ʹܽ ʹ ଶ ܽ ܽ െ ͳ 17 --------------------- TOANMATH.com
Chương 2 : Các biến đổi lượng giác
2.1.21. Chứng minh
ܽ െ ܽ െ ʹ ʹܽ െ Ͷ Ͷܽ െǥെ ʹ ʹܽ ൌ ʹାଵ ʹାଵܽ
2.1.22. Chứng minh
଼ ܽ െ ଼ ܽ െ Ͷ ܽ ସ ܽ െ Ͷ ଶ ܽ ൌ ͳ -
GỢI Ý GIẢI BÀI TẬP TỰ LUYỆN
2.1.1. ǡ – Sử dụng công thức hạ bậc. 2.1.3. Đặt ݐ ൌ ݔ Khi đó ଶ ଶ ξ͵ െ ݐ ξ͵ ݐ ൌ ݐଶ ቆ ቇ ቆ ቇ ͳ ξ͵ݐ ͳ െ ξ͵ݐ
Áp dụng tính tổng, viết lại thành
ൌ ሺଶ ͷ୭ ଶ ͷͷ୭ ଶ ͷ୭ሻ ሺଶ ͳͲ୭ ଶ ͷͲ୭ ଶ Ͳ୭ሻ
ሺଶ ͳͷ୭ ଶ Ͷͷ୭ ଶ ͷ୭ሻ ሺଶ ʹͲ୭ ଶ ͶͲ୭ ଶ ͺͲ୭ሻ
ሺଶ ʹͷ୭ ଶ ͵ͷ୭ ଶ ͺͷ୭ሻ ଶ ͵Ͳ୭ ଶ Ͳ୭
Rồi sử dụng công thức đã chứng minh ở trên. 2.1.4. a) Để ý ܽ ൌ ൌ ሺ݊ܽ െ ݊ܽ ܽሻ ሺ݊ െ ͳሻܽ ݊ܽ b) Để ý ͳ ܽ െ ݊ܽ ሺ݊ െ ͳሻܽ ൌ
ൌ ʹ ሾ ܽ െ ሺʹ݊ െ ͳሻܽሿ ݊ܽ ሺ݊ െ ͳሻܽ ݊ܽ ሺ݊ െ ͳሻܽ c) Ta có : ͳ ʹܽ
ʹ ଶ ʹିଵܽ ʹିଵܽ ʹܽ ʹିଵܽ ൌ ൌ ൌ ൌ ʹܽ ʹܽ ʹିଵܽ ʹܽ ʹିଵܽ d)
Ta có điều cần chứng minh tương đương với : ͳ ͳ ͳ ͳ ൌ Ͷ ଶ ܽ Ͷିଵ ʹ Ͷ ଶ ܽ ʹ ଶ ܽ ʹିଵ 18 --------------------- TOANMATH.com
Chương 2 : Các biến đổi lượng giác
2.1.5. Sử dụng công thức ͵ ܽ െ ଷ ܽ ͵ܽ ൌ ͳ െ ͵ଶ ܽ Cho ܽ ൌ ʹͲ୭, ta có :
͵ ʹͲ୭ െ ଷ ʹͲ୭ ൌ ξ͵ ͳ െ ͵ ଶ ʹͲ୭ Suy ra
ሺ͵ ʹͲ୭ െ ଷ ʹͲ୭ሻଶ ൌ ͵ሺͳ െ ͵ ଶ ʹͲ୭ሻଶ
2.1.6. Áp dụng công thức : ܽ ܾ ܿ െ ܽ ܾ ܿ
ሺܽ ܾ ܿሻ ൌ ͳ െ ܽ ܾ െ ܾ ܿ െ ܿ ܽ
2.1.9. Cần chứng minh ͳ ܽ ሺͳ െ ܽሻଶ ቈͳ െ ൌ ܽ ʹ ܽ ଶ ܽ
ଶ ܾ െ ଶ ܿ െ ଶ ܾଶ ܿ ൌ െͳ ଶ ܾ ଶ ܿ 2.1.10. Để ý ͳ ͳ ݔ െ ʹݔ ൌ Ǣ ʹݔ െ Ͷݔ ൌ ʹݔ Ͷݔ ͳ ͳ Ͷݔ െ ͺݔ ൌ Ǣ ͺݔ െ ͳݔ ൌ ͺݔ ͳݔ 2.1.12. Ta có :
ൌ ʹ ͳͷ୭ ͵୭ െ ʹ ͳͷ୭ ሺ Ͷͷ୭ ͵୭ሻ ൌ ͵Ͳ୭ െ Ͳ୭
2.1.13. Nhân 2 vế cho ͳͺ୭.
2.1.14. Áp dụng công thức ሺܽ ܾሻ ܽ ܾ ൌ ܽ ܾ 19 --------------------- TOANMATH.com
Chương 2 : Các biến đổi lượng giác
Viết lại thành ሺ ͷͲ୭ ͶͲ୭ሻ ሺ ͵Ͳ୭ Ͳ୭ሻ 2.1.15. a) Để ý ͳ
ͳͲ୭ ൌ ͺ ʹͲ୭ ͶͲ୭ ʹͲ୭ ʹ b) Sử dụng công thức ܽ െ ܽ ൌ ʹ ʹܽ
Ta có điều phải chứng minh tương đương với ߨ ߨ ߨ ߨ ቂ െ ቃ െ ʹ െ Ͷ ൌ ͺ ͵ʹ ͵ʹ ͳ ͺ 2.1.16. a. Cần chứng minh ߨ ߨ ͵ߨ ͷߨ ߨ ʹ ൌ ʹଷ ͳͷ ͳͷ ͳͷ ͳͷ ͳͷ Suy ra ͵ߨ ߨ ߨ ͷߨ ʹ ൌ ʹଶ ͳͷ ͳͷ ͳͷ ͳͷ b.
Ta có điều cần chứng minh tương đương với
ሺ ͷ୭ ͷ୭ሻሺ ͷͷ୭ ͷ୭ሻ ൌ ሺ ͷ୭ ͷ୭ሻሺ ͷͷ୭ ͷ୭ሻ 2.1.17.
Để ý rằng ଶ ൌ ሺ ͳͲ୭ ͳͲ୭ሻሺ ʹͲ୭ ʹͲ୭ሻ ǥ ሺ ͺͲ୭ ͺͲ୭ሻ ൌ ͳ
2.1.18. Áp dụng công thức ሺݔ െ ݕሻ ݔ െ ݕ ൌ ݔ ݕ
2.1.19. Ta chỉ cần chứng minh ߨ ߨ ߨ ߨ
ʹ ቀ ܽቁ ଶ ቀ െ ܽቁ ൌ ʹ ቀ െ ܽቁ ቀ െ ܽቁ Ͷ Ͷ Ͷ Ͷ 20 --------------------- TOANMATH.com
Chương 2 : Các biến đổi lượng giác
2.1.21. Sử dụng công thức sau : ܽ െ ܽ ൌ ʹ ʹܽ 2.
TÍNH GIÁ TRỊ CỦA BIỂU THỨC
- Ở loại bài tập này, ngoài các công thức biến đổi cơ bản, ta cần chú ý thêm các công thức sau : ߨ ߨ ߨ
ܽ ൌ ቀ െ ܽቁ Ǣ ܽ ൌ ቀ െ ܽቁ Ǣ ܽ ൌ ቀ െ ܽቁ ʹ ʹ ʹ
- Nhờ cung liên kết ta có thể đưa các cung lớn hơn ͻͲ୭ hay cung âm về cung trong
khoảng ሺͲ୭ǡ ͻͲ୭ሻ.
- Khi cần rút gọn biểu thức ൌ ܽ ʹܽ Ͷܽ ǥ ʹܽ Ta dùng công thức ʹܽ ܽ ൌ ʹܽ
- Khi cần rút gọn biểu thức
ൌ ܽ ʹܽ Ͷܽ ڮ ʹ݊ܽ Ta viết ܽ ʹ ൌ ʹ ܽ ʹ ʹ
Và dùng công thức biến đổi tích thành tổng để rút gọn.
- Ngoài ra, để tính giá trị một biểu thức ta chứng tỏ các số hạng trong biểu thức là
nghiệm của một phương trình, từ đó ta dùng công thức Viète(4) để tính tổng hoặc
tích của lượng phải tìm.
- Cần nhớ lại công thức Viète bậc 3 sau:
Gọi ݔଵǡ ݔଶǡ ݔଷ là 3 nghiệm của phương trình ܽݔଷ ܾݔଶ ܿݔ ݀ ൌ Ͳ thì 21 --------------------- TOANMATH.com
Chương 2 : Các biến đổi lượng giác ܾ
ۓ ݔଵ ݔଶ ݔଷ ൌ െ ۖ ܽ ܿ ݔ
۔ ଵݔଶ ݔଶݔଷ ݔଷݔଵ ൌ ܽ ۖ ݀ ە ݔଵݔଶݔଷ ൌ െ ܽ Từ đó có thể suy ra ܾଶ ʹܿ ݔଶ ଶ ଶ
ଵ ݔଶ ݔଷ ൌ ሺݔଵ ݔଶ ݔଷሻଶ െ ʹሺݔଵݔଶ ݔଶݔଷ ݔଷݔଵሻ ൌ െ ܽଶ ܽ ͳ ͳ ͳ ݔ ܿ
ൌ ଵݔଶ ݔଶݔଷ ݔଷݔଵ ൌ െ ݔଵ ݔଶ ݔଷ ݔଵݔଶݔଷ ݀ Bài 1: Tính
ൌ ଶ ͷͲ୭ ଶ Ͳ୭ െ ͷͲ୭ Ͳ୭ ͳ
ʹ ʹͷͷͲ୭ ሺെͳͺͺ୭ሻ ൌ ͵ͺ୭ ʹ ͵ͺ୭ ͻͺ୭ Giải: Ta có : ͳ ͳ ͳ
ൌ ሺͳ െ ͳͲͲ୭ሻ ሺͳ െ ͳͶͲ୭ሻ െ ሺ ͳʹͲ୭ ʹͲ୭ሻ ʹ ʹ ʹ ͳ ͳ ͳ
ൌ ͳ െ ሺ ͳͲͲ୭ ͳͶͲ୭ሻ െ ൬െ ʹͲ୭൰ ʹ ʹ ʹ ͳ ͳ ͷ
ൌ ͳ െ ሺ ͳʹͲ୭ ʹͲ୭ሻ െ ʹͲ୭ ൌ Ͷ ʹ Ͷ ͳ ʹ ሺെ͵Ͳ୭ሻ ͺ୭ ͺ୭ ൌ ൌ ͺ୭ െ ൌ Ͳ ͺ୭ ʹ ͺ୭ െ ͺ୭ ͺ୭
Bài 2: Rút gọn biểu thức ͳ ݔ ሺͳ െ ݔሻଶ ൌ ቈͳ ݔ ଶ ݔ Tính giá trị của nếu ͳ ߨ
ݔ ൌ െ ǡ ݔ א ቀ ǡ ߨቁ ʹ ʹ 22 --------------------- TOANMATH.com
Chương 2 : Các biến đổi lượng giác Giải: Ta có : ͳ ݔ ʹሺͳ െ ݔሻ ʹሺͳ െ ଶ ݔሻ ʹ ଶ ݔ ʹ ൌ Ǥ ൌ ൌ ൌ ݔ ଶ ݔ ଷ ݔ ଷ ݔ ݔ Mặt khác ͳ ͵ ξ͵ ʹ Ͷ
ଶ ݔ ൌ ͳ െ ଶ ݔ ൌ ͳ െ ൌ ฺ ݔ ൌ ฺ ൌ ൌ Ͷ Ͷ ʹ ݔ ξ͵
Bài 3: Tính giá trị của các biểu thức sau
ൌ ଶ ͵୭ ଶ Ͷ୭ ͵୭ Ͷ୭
ൌ ୭ Ͷʹ୭ ୭ ͺ୭ ߨ Ͷߨ ͷߨ ൌ ʹߨ Ͷߨ ߨ ൌ ͳ ൌ െ Ͷ Ͳ୭ ͳͲ୭ Giải: Ta có :
ൌ ሺ ͵୭ Ͷ୭ሻଶ െ ͵୭ Ͷ୭ ͳ
ൌ ሺʹ Ͳ୭ ͳͺ୭ሻଶ െ ሺ ͳʹͲ୭ ͵୭ሻ ʹ ͳ ͳ ͳ ͵୭ ͳ ͳ ͵
ൌ ଶ ͳͺ୭ െ ൬െ ͵୭൰ ൌ െ ͵୭ ൌ ʹ ʹ ʹ Ͷ ʹ Ͷ
ൌ ୭ Ͷʹ୭ ୭ ͺ୭ ൌ ୭ Ͷͺ୭ ʹͶ୭ ͳʹ୭ ͳʹ୭ ʹͶ୭ Ͷͺ୭ ͻ୭ ͻ୭ ሺͻͲ୭ ୭ሻ ൌ Ǥ Ǥ Ǥ ൌ ൌ
ʹ ୭ ʹ ͳʹ୭ ʹ ʹͶ୭ ʹ Ͷͺ୭ ͳ ୭ ͳ ୭ ͳ ൌ ͳ 23 --------------------- TOANMATH.com
Chương 2 : Các biến đổi lượng giác ʹߨ Ͷߨ ͺߨ ߨ Ͷߨ ͷߨ ߨ Ͷߨ ʹߨ ൌ ൌ െ ൌ െ Ǥ Ǥ ߨ ʹ ʹߨ Ͷߨ ʹ ʹ ͺߨ ߨ ቀߨ ͳ ൌ െ ቁ ߨ ൌ െ ߨ ൌ ͺ ͺ ͺ ߨ ʹߨ Ͷߨ ߨ ʹ ൌ ቀ ቁ ߨ ʹ ߨ ʹߨ ߨ Ͷߨ ߨ ߨ ʹ ൌ
ʹ ʹ ߨ ʹ ͵ߨ ߨ ͷߨ ͵ߨ ͷߨ ቀെ ቁ ቀെ ቁ ߨ ቀെ ൌ ቁ ߨ ʹ ߨ െ ͳ ൌ ߨ ൌ െ ʹ ʹ ͳ െ Ͷ Ͳ୭ ͳͲ୭
ͳ ʹሺ ͺͲ୭ െ Ͳ୭ሻ ൌ ൌ ൌ ʹ ͳͲ୭ ͳͲ୭
Bài 4: Rút gọn biểu thức sau với ܾ ܽ Ͳ ͳ ටܾ െ ܽ ܽ ݔ ൌ ඥܽ ܾ ଶ ݔ ξܾ െ ܽ ට ܾ െ ܽ ͳ ܽ ଶ ݔ Giải: Ta có : ͳ ݔ ܾ ଶ ݔ ݔ ܽ ଶ ݔ ܾ ଶ ݔ ൌ ξܽ ඨܽ ൌ ඨ ଶ ݔ ଶ ݔ ට ܾ െ ܽ ξܾ ଶ ݔ ܽ ଶ ݔ ͳ ܽ ଶ ݔ ߨ ߨ ݔ ݔǡ ݔ א ቀെ ǡ ቁ ൌ ൌ ൞ ʹ ʹ ȁ ݔȁ ߨ ͵ߨ െ ݔ ǡ ݔ א ൬ ǡ ൰ ʹ ʹ 24 --------------------- TOANMATH.com
Chương 2 : Các biến đổi lượng giác
Bài 5: Tính ͳͺ୭. Từ đó chứng minh ͳ୭ là số vô tỷ. Giải: Ta có :
ͻͲ୭ ൌ ͵Ǥͳͺ୭ ʹǤͳͺ୭
Nên ʹǤͳͺ୭ ൌ ͵Ǥͳͺ୭
Suy ra ͳ െ ʹ ଶ ͳͺ୭ ൌ ͵ ͳͺ୭ െ Ͷ ଷ ͳͺ୭
Đặt ൌ ͳͺ୭ Ͳ ; ݐ là nghiệm của phương trình
Ͷݐଷ െ ʹݐଶ െ ͵ݐ ͳ ൌ Ͳ Hay
ሺݐ െ ͳሻሺͶݐଶ ʹݐ െ ͳሻ ൌ Ͳ Vì ͳͺ୭ ് ͳ nên െͳ േ ξͷ ݐ ൌ Ͷ Vì ݐ Ͳ nên െͳ ξͷ ͳͺ୭ ൌ Ͷ
Giả sử ͳ୭ là số hữu tỷ, suy ra ͵୭ ൌ ͵ ͳ୭ െ Ͷ ଷ ͳ୭ cũng là số hữu tỷ.
Như vậy lần lượt ta có ͻ୭ ൌ ͵ ͵୭ െ Ͷ ଷ ͵୭ ; ʹ୭ ൌ ͵ ͻ୭ െ Ͷ ଷ ͻ୭ ;
ͺͳ୭ ൌ ͵ ʹ୭ െ Ͷ ଷ ʹ୭ cũng là những số hữu tỷ.
Do đó, ͳͺ୭ ൌ ʹ ͻ୭ ͻ୭ ൌ ʹ ͻ୭ ͺͳ୭ cũng là số hữu tỷ. Mà െͳ ξͷ ͳͺ୭ ൌ Ͷ
Nên ξͷ là số hữu tỷ. (vô lý)
Vậy ta có điều phải chứng minh. 25 --------------------- TOANMATH.com
Chương 2 : Các biến đổi lượng giác
Bài 6: Cho phương trình ܽݔଶ ܾݔ ܿ ൌ Ͳ có 2 nghiệm ݔଵ ൌ ݑ ǡ ݔଶ ൌ ݒ. Hãy
tính biểu thức sau đây theo ܽǡ ܾǡ ܿ.
ൌ ܽଶሺݑ ݒሻ ܾ ሺݑ ݒሻ ሺݑ ݒሻ ܿ ଶሺݑ ݒሻ
Giải: Ta xét 2 trường hợp sau
* Nếu ሺݑ ݒሻ ൌ Ͳ thì ൌ ܽ.
* Nếu ሺݑ ݒሻ ് Ͳ thì
ൌ ଶሺݑ ݒሻ ሾܽ ଶሺݑ ݒሻ ܾ ሺݑ ݒሻ ܿሿ ͳ ൌ
ሾܽ ଶሺݑ ݒሻ ܾ ሺݑ ݒሻ ܿሿ ͳ ଶሺݑ ݒሻ Mà ܽ ݑ ݒ ݔ െ ܾ ሺݑ ݒሻ ൌ ൌ ଵ ݔଶ ൌ ܾ ൌ ͳ െ ݑ ݒ ͳ െ ݔ ܿ ଵݔଶ ͳ െ ܿ െ ܽ ܽ Vậy ͳ ܾ ଶ ܾଶ ൌ ൰ ܿ ൌ ܿ ܾ ଶ ቈܽ ൬ܿ െ ܽ ܿ െ ܽ ͳ ቀܿ െ ܽቁ
Bài 7: Tìm 1 phương trình bậc 3 có các nghiệm là ߨ ͵ߨ ͷߨ ݔଵ ൌ ǡ ݔ ǡ ݔ ଶ ൌ ଷ ൌ Từ đó, tính tổng ͳ ͳ ͳ ൌ ߨ ͵ߨ ͷߨ Giải: Nếu ta có
ݔଵ ݔଶ ݔଷ ൌ ܽ
൝ݔଵݔଶ ݔଶݔଷ ݔଷݔଵ ൌ ܾ ݔଵݔଶݔଷ ൌ ܿ 26 --------------------- TOANMATH.com
Chương 2 : Các biến đổi lượng giác
Thì ݔଵǡ ݔଶǡ ݔଷ là 3 nghiệm của phương trình bậc 3
ݔଷ െ ܽݔଶ ܾݔ െ ܿ ൌ Ͳ Ta có : ߨ ͵ߨ ͷߨ
ݔଵ ݔଶ ݔଷ ൌ ߨ ߨ ߨ ͵ߨ ߨ ͷߨ ߨ ʹ ͳ ൌ
ʹ ʹ ߨ ൌ ߨ ൌ ʹ ʹ ʹ ߨ ͵ߨ ͵ߨ ͷߨ ͷߨ ߨ
ݔଵݔଶ ݔଶݔଷ ݔଷݔଵ ൌ ʹߨ Ͷߨ ߨ ͳ ൌ ൌ െ ʹ ߨ ͵ߨ ͷߨ ͳ ͺߨ ʹߨ ߨ ݔଵݔଶݔଷ ൌ ൌ ൬ ൰ ʹ ͳ ͻߨ ͵ߨ ߨ ൌ ൬ ߨ ൰ Ͷ ͳ ߨ ͵ߨ ͷߨ ͳ ͳ ͳ ൌ ൬
െ ͳ൰ ൌ ൬ െ ͳ൰ ൌ െ Ͷ Ͷ ʹ ͺ
Vậy phương trình cần tìm là ͳ ͳ ͳ
ݔଷ ݔଶ െ ݔ ൌ Ͳ ʹ ʹ ͺ Suy ra ൌ Ͷ.
Bài 8: Chứng minh rằng య య ʹߨ య Ͷߨ య ͺߨ య ඨ ඨ ඨ ൌ ඨͷ െ ͵ξ ʹ
(Đề nghị Olympic 30-4, 2006) Giải: ʹߨ Ͷߨ ͺߨ 0ểýằ Ǣ Ǣ
ệủươ¿ݔ ൌ ʹߨ ݇ʹߨሺ݇ א Ժሻ 27 --------------------- TOANMATH.com
Chương 2 : Các biến đổi lượng giác Hay ͵ݔ ൌ Ͷݔ ሺכሻ
Từ ሺכሻ ta có ݔ ൌ ͳ ݔ ൌ ݇ʹߨ (loại vì không thỏa 3 nghiệm trên) Như vậy ʹߨ Ͷߨ ͺߨ Ǣ Ǣ
ệủươ¿ݐଷ ݐଶ െ ʹݐ െ ͳ ൌ Ͳሺݐ ൌ ʹ ݔሻ ¯ịnh lý Viète, ta có
ݐଵ ݐଶ ݐଷ ൌ െͳ
൝ݐଵݐଶ ݐଶݐଷ ݐଷݐଵ ൌ െʹ ݐଵݐଶݐଷ ൌ ͳ Đặt ൌ ඥ య ݐ ඥ య ݐ ඥ య ݐ ቊ ଵ ଶ ଷ ൌ ඥ య ݐ య య
ଵݐଶ ඥݐଶݐଷ ඥݐଷݐଵ Khi đó ଷ ൌ ሺݐ య ൌ ͵ െ Ͷ ቊ
ଵ ݐଶ ݐଷሻ ͵ െ ͵ ඥݐଵݐଶݐଷ ଷ ൌ ሺݐ య
ଵݐଶ ݐଶݐଷ ݐଷݐଵሻ ͵ െ ͵ ඥሺݐଵݐଶݐଷሻଶ ൌ ͵ െ ͷ Suy ra
ሺሻଷ ൌ ሺ͵ െ Ͷሻሺ͵ െ ͷሻ ሺ െ ͵ሻଷ ൌ െ Do đó ൌ ͵ െ ξ య Nên ൌ ඥ య ͷ െ ͵ξయ Vậy య య ʹߨ య Ͷߨ య ͺߨ య ඨ ඨ ඨ ൌ ൌ ඨͷ െ ͵ξ ξ య ʹ ʹ 28 --------------------- TOANMATH.com
Chương 2 : Các biến đổi lượng giác Bài 9: Tính tổng
൜ ଵ ൌ ଶ ܽ ଶ ʹܽ ǥ ଶ ݊ܽ
ଶ ൌ ଶ ܽ ଶ ʹܽ ǥ ଶ ݊ܽ
Với ݊ א Գǡ ܽ ് ݇ߨǡ ݇ א Ժ.
Giải: Từ hệ ta có : ൜ ଶ ଵ ൌ ݊
ଶ െ ଵ ൌ ʹܽ Ͷܽ ǥ ʹ݊ܽ Suy ra
ʹ ܽ ሺଶ െ ଵሻ ൌ ʹ ܽ ʹܽ ʹ ܽ Ͷܽ ǥ ʹ ܽ ʹ݊ܽ
ൌ ͵ܽ െ ܽ ͷܽ െ ͵ܽ ǥ ሺʹ݊ ͳሻܽ െ ሺʹ݊ െ ͳሻܽ
ൌ ሺʹ݊ ͳሻܽ െ ܽ ൌ ʹ ሺ݊ ͳሻܽ ݊ܽ Do đó ଶ ଵ ൌ ݊ ൝ ሺ݊ ͳሻܽ ݊ܽ ଶ െ ଵ ൌ ܽ
ሺ݊ ͳሻܽ ݊ܽ ݊ ܽ ଶ ൌ ฺ ൞ ʹ ܽ
݊ ܽ െ ሺ݊ ͳሻܽ ݊ܽ ଵ ൌ ʹ ܽ
Bài 10: Cho ܽ ܾ ൌ ʹ ሺܽ ܾሻ Ǣ ܽ ܾ ് ʹ݇ߨǡ ݇ א Ժ Hãy tìm ܽ ܾ ൌ ʹ ʹ
Giải: Từ giả thuyết, ta có : ܽ ܾ ܽ െ ܾ ܽ ܾ ܽ ܾ ʹ ൌ Ͷ ʹ ʹ ʹ ʹ Vì ܽ ܾ ് ʹ݇ߨ nên 29 --------------------- TOANMATH.com
Chương 2 : Các biến đổi lượng giác ܽ ܾ ܽ ܾ ് ݇ߨ ֜ ് Ͳ ʹ ʹ ܽ െ ܾ ܽ ܾ ǡ ൌ ʹ ʹ ʹ ܽ ܾ ܽ ܾ ܽ ܾ ܽ ܾ ฺ ൌ ʹ ൬ െ ൰ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ܽ ܾ ܽ ܾ ฺ ͵ ൌ ʹ ʹ ʹ ʹ ͳ ฺ ൌ ͵
Bài 11: Rút gọn biểu thức sau
ൌ ඥͳ Ͷ ଶ ܽ ଶ ܽ Ͷ ܽ ܽ
ඥସ ܽ െ ͷ ସ ܽ െ Ͷ ܽ ܽ ଶ ܽ Giải: Ta có :
ൌ ඥͳ Ͷ ଶ ܽ ଶ ܽ Ͷ ܽ ܽ ሺଶ ܽ ଶ ܽሻ
ඥସ ܽ െ ͷሺͳ െ ଶ ܽሻଶ െ Ͷ ܽ ܽ ሺଶ ܽ ଶ ܽሻ ଶ ܽ
ൌ ඥସ ܽ ସ ܽ ଶ ܽ ଶ ܽ Ͷ ଷ ܽ ܽ Ͷ ܽ ଷ ܽ
ඥସ ܽ ସ ܽ ଶ ܽ ଶ ܽ െ Ͷ ଷ ܽ ܽ െ Ͷ ܽ ଷ ܽ
ൌ ඥሺ ܽ ܽሻସ ඥሺ ܽ െ ܽሻସ
ൌ ሺ ܽ ܽሻଶ ሺ ܽ െ ܽሻଶ
ൌ ଶ ܽ ଶ ܽ ʹ ܽ ܽ ଶ ܽ ଶ ܽ െ ʹ ܽ ܽ ൌ ʹ Bài 12: ͵ π ߨ
ߙ ൌ à ൏ ߙ ൏ ߨǤí ቀ െ ߙቁǤ ͷ ʹ Ͷ (ĐH Huế 1996) Giải: Ta có : ߨ ߨ ͳ െ ߙ ቀ െ ߙቁ ൌ Ͷ െ ߙ ൌ Ͷ ߨ ͳ ͳ ߙ Ͷ ߙ 30 --------------------- TOANMATH.com
Chương 2 : Các biến đổi lượng giác Mặt khác : ͳ
ଶ ߙ ൌ ͳ െ ଶ ߙ ൌ ʹͷ Do ߙ ൏ Ͳ nên Ͷ ߙ ൌ െ ͷ Suy ra ͵ ߙ ͵ ߙ ൌ ൌ ͷ ൌ െ ߙ Ͷ െ Ͷ ͷ ͵ ߨ ͳ ฺ ቀ െ ߙቁ ൌ Ͷ ൌ Ͷ ͵ ͳ െ Ͷ
Bài 13: Tính giá trị của biểu thức ߨ ͷߨ ߨ ൌ ͳͺ ͳͺ ͳͺ
Giải: Ta sẽ áp dụng vào bài toán trên bằng hằng đẳng thức
ܽଷ ܾଷ ܿଷ െ ͵ܾܽܿ ൌ ሺܽ ܾ ܿሻଷ െ ͵ሺܽ ܾ ܿሻሺܾܽ ܾܿ ܿܽሻ Dễ thấy ߨ ͷߨ ߨ ͳ ଶ ͵ ቀ ቁ ൌ ଶ ͵ ൬ ൰ ൌ ଶ ͵ ൬ ൰ ൌ ͳͺ ͳͺ ͳͺ ͵ ߨ ͷߨ ߨ ͳ Ǣ Ǣ ệủươ¿ ଶ ͵ݔ ൌ ͳͺ ͳͺ ͳͺ ͵ ͵ ݔ െ ଷ ݔ ଶ ͳ ቆ ቇ ൌ ͳ െ ͵ ଶ ݔ ͵
͵ ݔ െ ʹ ସ ݔ ͵͵ ଶ ݔ െ ͳ ൌ Ͳ ư vậy : ߨ ͷߨ ߨ ଶ Ǣ ଶ Ǣ ଶ
ệủươ¿͵ݕଷ െ ʹݕଶ ͵͵ݕ െ ͳ ൌ Ͳ ͳͺ ͳͺ ͳͺ ¯ịnh lý Viète, ta có :
ݕଵ ݕଶ ݕଷ ൌ ͻ ݕ
൞ ଵݕଶ ݕଶݕଷ ݕଷݕଵ ൌ ͳͳ ͳ ݕଵݕଶݕଷ ൌ ͵ Suy ra ൌ ݕଷ ଷ ଷ
ଵ ݕଶ ݕଷ ൌ ሺݕଵ ݕଶ ݕଷሻଷ െ ͵ሺݕଵ ݕଶ ݕଷሻሺݕଵݕଶ ݕଶݕଷ ݕଷݕଵሻ ͵ݕଵݕଶݕଷ ൌ Ͷ͵͵ 31 --------------------- TOANMATH.com
Chương 2 : Các biến đổi lượng giác
Bài 14: Cho ݔ Ǣ ݕ Ǣ ݖ là 3 nghiệm của phương trình : ߨ
ܽݐଷ ܾݐଶ ܿݐ ݀ ൌ Ͳሺܽ ് ͲሻǢ Ͳ ൏ ݔǡ ݕǡ ݖ ൏ ʹ Chứng minh rằng ܾଷܿଶ
ݔ ݕ ݖ െ ͺͳܽହ
Giải: Ở bài toán này, ta thấy ݔ Ǣ ݕ Ǣ ݖ Ͳ.
Do đó, theo định lý Viète, ta có : ܾ ݔ ݕ ݖ ൌ െ ൞ ܽ ܿ
ݔ ݕ ݕ ݖ ݖ ݔ ൌ ܽ Mặt khác : ͳ ܾ ଷ ܿ ଶ ൌ െ ൬ ൰ ቀ ቁ ͺͳ ܽ ܽ ͳ ൌ
ሺ ݔ ݕ ݖሻଷሺ ݔ ݕ ݕ ݖ ݖ ݔሻଶ ͺͳ
Áp dụng bất đẳng thức :
݉ଶ ݊ଶ ݇ଶ ݉݊ ݊݇ ݇݉
ฺ ሺ݉ ݊ ݇ሻଶ ͵ሺ݉݊ ݊݇ ݇݉ሻ ͳ
ฺ ሺ݉ ݊ ݇ሻସ ሺ݉݊ ݊݇ ݇݉ሻଶ ͻ Ta được :
ͳ ሺݔ ݕ ݖሻଷሺݔ ݕ ݕݖ ݖݔሻଶ ͺͳ ͳ ሺ ݔ ݕ ݖሻ ͺͳǤͻ
Cần chứng minh bất đẳng thức :
ͳ ሺݔ ݕ ݖሻ ͺͳǤͻ
Thật vậy, với ݔ ݕ ݖ Ͳ, ta có : ଶ
ሺ ݔ ݕ ݖሻ ቀξ ݔ Ǥ ඥ ݔ ඥ ݕ Ǥ ඥ ݕ ξ ݖ Ǥ ඥ ݖቁ ͳ ͳ
Ǥ ͻሺସ ݔ ସ ݕ ସ ݖሻଶ
ሺଶ ݔ ଶ ݕ ଶ ݖሻସǤ ͵ସ ͻ ͺͳǤͻ ͳ ሺ ݔ ݕ ݖሻ଼ ͺͳǤͻ 32 --------------------- TOANMATH.com
Chương 2 : Các biến đổi lượng giác Do đó, ܾଷܿଶ
ݔ ݕ ݖ െ ͺͳܽହ
Vậy ta có được điều phải chứng minh. - BÀI TẬP TỰ LUYỆN
2.2.1. Tính giá trị của các biểu thức sau:
Ǥ ͻ୭ െ ʹ୭ െ ͵୭ ͺͳ୭
ሺ ͶͶ୭ ʹʹ୭ሻ ͶͲ୭ Ǥ െ ʹ୭ ͳͺ୭ ͵ͳ୭ ሺെʹͲ୭ሻ Ͳ୭
Ǥ ͳͲ୭ ͵ͶͲ୭ ʹͷͲ୭
2.2.2. Tìm 1 phương trình bậc 3 có các nghiệm là ʹߨ Ͷߨ ͺߨ ݔଵ ൌ Ǣ ݔ Ǣ ݔ ͻ ଶ ൌ ͻ ଷ ൌ ͻ Từ đó, tính tổng ʹߨ Ͷߨ ͺߨ ൌ ଶ ଶ ଶ ͻ ͻ ͻ 2.2.3. Cho ͻͺ
͵ ସ ݔ ʹ ସ ݔ ൌ ͺͳ
Tính ൌ ʹ ସ ݔ ͵ ସ ݔ.
2.2.4. Tính ሺݔ െ Ͷͷ୭ሻ , biết ͻ ͵ߨ ݔ ൌ െ ǡ ݔ א ൬ߨǡ ൰ Ͷͳ ʹ
2.2.5. Rút gọn các biểu thức sau : ͳ ݔ ݔ ൌ ଶ െ ଶ ݔ ͳ െ ݔ ʹ ଶ ʹݔ െ Ͷ ଶ ݔ
ൌ ଶ ʹݔ Ͷଶ ݔ െ Ͷ 33 --------------------- TOANMATH.com
Chương 2 : Các biến đổi lượng giác ሺͲ୭ ݔሻ ൌ ݔ ݔ
Ͷ ቀʹͷ୭ Ͷቁ ቀͷ୭ െ Ͷቁ ͵ߨ ߨ
ൌ ሺߨ ݔሻ ሺݔ െ ߨሻ െ ʹ ସሺʹߨ ݔሻ െ ସ ൬
ݔ൰ ଶ ቀ െ ݔቁ ʹ ʹ ߨ ͵ߨ ߨ ቀݔ െ ൌ
ʹቁ ቀ ʹ ݔቁ െ ଷ ቀ ʹ െ ݔቁ ߨ ͵ߨ
ቀݔ െ ʹቁ ቀ ʹ ݔቁ ݔ ݉ ͵ݔ ͷݔ ൌ ͵ݔ ݉ ͷݔ ݔ ξʹ െ ݔ െ ݔ ൌ ݔ െ ݔ ߨ
ൌ ඪʹ ඩʹ ඨʹ ටǥ ξʹ ʹ ݔቆݔ א ቀͲǡ ቁቇ ʹ
ᇣᇧᇧᇧᇧᇧᇧᇧᇧᇧᇧᇧᇤᇧᇧᇧᇧᇧᇧᇧᇧᇧᇧᇧᇥ ୢấ୳ୡ£୬
ଶሺܽ ܾሻ െ ଶ ܽ െ ଶ ܾ ൌ
ଶሺܽ ܾሻ െ ଶ ܽ െ ଶ ܾ ܽ ܽ ൌ Ͷଶ ʹܽ ଶ ʹܽ
Ͷܽ െ Ͷ ͵ܽ ʹܽ െ Ͷ ܽ ൌ ʹܽ ሺͳ െ ܽሻ
ൌ ʹ Ͷܽ ͷ ܽ ʹ ʹܽ ͺܽ 2.2.6. Tính ܽ ʹܽ ͵ܽ ݊ܽ ൌ ͳ ǥ ܽ ଶ ʹܽ ଷ ܽ ܽ
2.2.7. Tính ൌ ݉ ʹܽ ݊ ʹܽ biết ݉ ܽ ൌ ǡ ݊ ് Ͳ ݊ 34 --------------------- TOANMATH.com
Chương 2 : Các biến đổi lượng giác
2.2.8. Tính ܽ ܾ theo ݉ǡ ݊ biết ሺܽ ܾሻ ݉ ൌ ሺܽ െ ܾሻ ݊
2.2.9. Cho ݔ ൌ Ͷ. Tính giá trị của các biểu thức sau
ହ ݔ െ ͵ ସ ݔ ݔ ʹ ଶ ݔ ଷ ݔ െ ͷ ݔ ସ ݔ െ ͳ͵ ହ ݔ
ൌ ସ ݔ ݔ െ ͳͳଷ ݔ ଶݔ ʹଶ ݔ ଷ ݔ െ ͻݔ ସ ݔ ͷହݔ
͵ ସ ݔ െ ͺ ଷ ݔ ݔ ଶ ݔ ଶ ݔ െ Ͷ ݔ ଷ ݔ െ ʹ ସ ݔ
ൌ ସ ݔ ͷଷ ݔ ݔ െ Ͷଶ ݔ ଶ ݔ ݔ ଷݔ െ ͵ସ ݔ
2.2.10. Cho ݔ ݔ ൌ ݉. Tính
ൌ ଶ ݔ െ ଶ ݔǢ ൌ ଷ ݔ െ ଷ ݔǢ ൌ ହ ݔ െ ହ ݔ
2.2.11. Cho ݔ െ ݔ ൌ ݊. Tính
ൌ ଶ ݔ ଶ ݔǢ ൌ ଷ ݔ െ ଷ ݔǢ ൌ ݔ െ ݔ
2.2.12. Cho ሺܽ ܾሻ ൌ ݉ và ሺܽ െ ܾሻ ൌ ݊. Tính ʹܽ. -
GỢI Ý GIẢI BÀI TẬP TỰ LUYỆN 2.2.3. Đặt
ቄܽ ൌ ଶ ݔሺܽǢ ܾ א ሾͲǡͳሿሻ ܾ ൌ ଶ ݔ Ta có hệ phương trình ͻͺ
൝͵ܽଶ ʹܾଶ ൌ ͺͳ ܽ ܾ ൌ ͳ 2.2.4. Để ý ݔ െ Ͷͷ୭
ሺݔ െ Ͷͷ୭ሻ ൌ ͳ െ ݔ Ͷͷ୭ 2.2.6. Để ý ͳ ݇ܽ ܽ ݇ܽ ሺ݇ ͳሻܽ ݇ܽ ൌ
ൌ ʹ ሾሺ݇ ͳሻܽ െ ሺ݇ െ ͳሻܽሿ ൌ െ ܽ ܽ ܽ ܽ ܽ ܽ ܽ ܽ ିଵ ܽ 2.2.7. Để ý ʹ ܽ ͳ െ ଶ ܽ ʹܽ ൌ Ǣ ʹܽ ൌ ͳ ଶ ܽ ͳ ଶ ܽ 35 --------------------- TOANMATH.com
Chương 2 : Các biến đổi lượng giác
2.2.8. Từ hệ thức ݉ ͳ െ ܽ ܾ ൌ ݊ ͳ ܽ ܾ
Ta biến đổi ܽ ܾ theo ݉ǡ ݊.
2.2.9. Để ý bậc của tử bằng bậc của mẫu, do ݔ có giá trị thực nên ݔ ് Ͳ, từ đó ta
lần lượt chia tử và mẫu cho ହ ݔ đối với và cho ସ ݔ cho . 2.2.10. Để ý ൌ ݉ 2.2.11. Để ý
ൌ ሺସ ݔ ସ ݔሻ െ ݊ 3.
CHỨNG MINH ĐẲNG THỨC LƯỢNG GIÁC SUY TỪ ĐẲNG THỨC
LƯỢNG GIÁC KHÁC CHO TRƯỚC
- Đây là loại bài tập chứng minh đẳng thức lượng giác có điều kiện và từ điều kiện
kết hợp với các công thức lượng giác phù hợp để suy ra điều cần phải chứng minh. ܽ ൌ ݔ
Bài 1: Cho ൝ ܾ ൌ ݔ ݕ. Chứng minh rằng : ܽଶ ܾଶ ܿଶ ൌ ͳ ܿ ൌ ݔ ݕ Giải: Ta có :
ܽଶ ܾଶ ܿଶ ൌ ଶ ݔ ଶ ݔ ሺͳ െ ଶ ݕሻ ଶ ݔ ଶ ݕ
ൌ ଶ ݔ ଶ ݔ െ ଶ ݔ ଶ ݕ ଶ ݔ ଶ ݕ ൌ ͳ
Vậy ta có điều phải chứng minh.
Bài 2: Chứng minh rằng nếu ܽǡ ܾ Ͳ và ସ ݔ ସ ݔ ͳ ൌ ܽ ܾ ܽ ܾ Thì ଶଵଶ ݔ ଶଵଶ ݔ ͳ ൌ ܽଵହ ܾଵହ ሺܽ ܾሻଵହ 36 --------------------- TOANMATH.com
Chương 2 : Các biến đổi lượng giác Giải: Ta có : ସ ݔ ସ ݔ ሺܽ ܾሻ ቆ
ቇ ൌ ሺଶ ݔ ଶ ݔሻଶ ܽ ܾ ܽ ܾ
ସ ݔ ସ ݔ െ ʹ ଶ ݔ ଶ ݔ ൌ Ͳ ܾ ܽ ଶ ݔ ଶ ݔ ͳ ͳ ൌ ൌ ൬ݐ ൌ Ͳ൰ ܽ ܾ ܽ ܾ ܽ ܾ Suy ra ଶଵଶ ݔ ଶଵଶ ݔ ͳ ͳ ܽ ܾ ൌ ሺܽݐሻଵ ሺܾݐሻଵ ൌ ܽଵହ ܾଵହ ܽଵହ ܾଵହ
ሺܽ ܾሻଵ ሺܽ ܾሻଵ ͳ ൌ ሺܽ ܾሻଵହ
Bài 3: Cho ʹ ݔ ݕ െ ͵ ݔ ݕ ൌ Ͳ Chứng minh rằng ͳ ͳ ͷ ൌ ʹ ଶ ݔ ͵ ଶ ݔ ʹ ଶ ݕ ͵ ଶ ݕ
Giải: Ta có : ʹ ݔ ݕ െ ͵ ݔ ݕ ൌ Ͳ ݔ ݕ ͵ ฺ ʹ ൌ ͵ ฺ ʹ ݔ ൌ ͵ ݕ ฺ ݕ ൌ ݔ ݕ ʹ ݔ Khi đó : ͳ ͳ ଶ ݕ ൌ ଶ ݔ ʹ ଶ ݔ ͵ ଶ ݔ ʹ ଶ ݕ ͵ ଶ ݕ ଶ ݔ ଶ ݕ ͳ ଶ ݔ ͳ ଶ ݕ ͳ ଶ ݔ Ͷ ଶ ݔ ͻ ൌ ൌ ʹ ଶ ݔ ͵ ʹ ଶ ݕ ͵ ʹ ଶ ݔ ͵ ሺ͵ ଶ ݔሻ
ሺͳ ଶ ݔሻ Ͷ ଶ ݔ ͻ ͷሺ͵ ʹ ଶ ݔሻ ͷ ൌ ൌ ൌ ሺ͵ ʹ ଶ ݔሻ ሺ͵ ʹ ଶ ݔሻ
Vậy ta có điều phải chứng minh. 37 --------------------- TOANMATH.com
Chương 2 : Các biến đổi lượng giác
Bài 4: Cho ȟ và ݉ǡ ݊ǡ thỏa ݉ ݊ ߨ ൌ Ͳǡ ൏ ܥ ൏ ʹ ʹ
Chứng minh rằng : ݉ݔଶ ݊ݔ ൌ Ͳ có nghiệm ݔ א ሺͲǢ ͳሻ
(Đề nghị Olympic 30-4, 2006) Giải: Ta có : ͳ ͳ
ൌ ሾሺ െ ሻ ሺ ሻሿ ൏ ሺͳ െ ሻ ൌ ଶ ʹ ʹ ʹ ߨ ߨ ߨ Ͳ ൏ ൏ ܥ ൏ ฺ ʹ ൏ ߨ ฺ Ͳ ൏ ൏ െ ൏ ฺ ൏ ʹ ʹ ʹ ʹ ʹ ݒ 0 ൏ ͳ
ặݑ ൌ Ǣ ݒ ൌ Ǣ ݓ ൌ ฺ ൝ Ͳ ൏ ʹ ݑ Ͳ ൏ ݑݓ ൏ ݒଶ
Và ݂ሺݔሻ ൌ ݉ݔଶ ݊ݔ
Ta có 2 trường hợp sau : ݉ ݊ ế ൌ Ͳ¿ ൌ Ͳ ݑ ݒ
- Nếu ݉ ൌ Ͳ ฺ ݂ሺݔሻ ൌ Ͳ có vô số nghiệm thuộc ሺͲǢ ͳሻ - Nếu ݉ ് Ͳ thì ݊ ݑ ݊ െ ൌ
א ሺͲǢ ͳሻ ฺ ݂ሺݔሻ ൌ ݉ݔ ቀݔ ቁ ൌ Ͳ×ệộሺͲǢ ͳሻ ݉ ݒ ݉ ݊ ݑ ݒଶ ݒ ݑݓ െ ݒଶ ế ് Ͳ¿ ൌ Ͳ ቆ݉ ݊ ቇ ൌ ݑ ݒ ݓ ݒଶ ݑଶ ݑ ݒଶݓ ݒ ݑݓ െ ݒଶ ݂ ቀ ቁ ൌ ݂ሺͲሻ ݑ ݑݓ
Ở đây, ta sẽ sử dụng định lý : Nếu hàm số ݂ liên tục trên đoạn ሾܽǢ ܾሿ và ݂ሺܽሻǤ ݂ሺܾሻ ൏ Ͳ
thì tồn tại ít nhất 1 điểm ܿ א ሺܽǢ ܾሻ sao cho ݂ሺܿሻ ൌ Ͳ. Như vậy, ta thấy 38 --------------------- TOANMATH.com
Chương 2 : Các biến đổi lượng giác ݒ
݂²ụ²Թ ฺ ݂²ụ² ቂͲǢ ቃ ݑ ൞ ݒ ݑݓ െ ݒଶ ݂ ቀ ቁ ݂ሺͲሻ ൌ ݂ଶሺͲሻ ൏ Ͳ ݑ ݑݓ
Do đó, ݂ሺݔሻ ൌ Ͳ có nghiệm thuộc ሺͲǢ ͳሻ.
Vậy ta có điều phải chứng minh. ͵ ଶ ݔ ʹ ଶ ݕ ൌ ͳ
Bài 5: Cho ݔǡ ݕ là 2 góc nhọn thỏa hệ ൜͵ ʹݔ െ ʹʹݕ ൌ Ͳ ߨ ứݔ ʹݕ ൌ ʹ
Giải: Ta cần chứng minh ሺݔ ʹݕሻ ൌ Ͳ
Thật vậy, ta có ሺݔ ʹݕሻ ൌ ݔ ʹݕ െ ݔ ʹݕ Mà
͵ ଶ ݔ ʹ ଶ ݕ ൌ ͳ ฺ ͵ ଶ ݔ ൌ ʹݕ ቐ ͵
͵ ʹݔ െ ʹ ʹݕ ൌ Ͳ ฺ ʹݕ ൌ ʹݔ ൌ ͵ ݔ ݔ ʹ Suy ra
ሺݔ ʹݕሻ ൌ ݔ Ǥ ͵ ଶ ݔ െ ݔ Ǥ ͵ ݔ ݔ ൌ Ͳ
Mà ݔǡ ݕ là 2 góc nhọn nên ta có điều phải chứng minh.
Bài 6: Chứng minh rằng nếu ݔ ൌ ʹ ሺݔ ݕሻ ൝ ߨ
ݔ ݕ ് ݇ߨǡ ݇ א Ժ ʹ Thì ݕ ሺݔ ݕሻ ൌ ݕ െ ʹ
(ĐH Thương Mại Hà Nội 1998) 39 --------------------- TOANMATH.com
Chương 2 : Các biến đổi lượng giác Giải: ߨ
ݔ ݕ ് ݇ߨǡ ݇ א Ժ ݕ െ ʹ ് Ͳ²¯ềệ¯ượ¯ịǤ ʹ
×ǣ ݔ ൌ ሾሺݔ ݕሻ െ ݕሿ ൌ ሺݔ ݕሻ ݕ െ ሺݔ ݕሻ ݕ ¯×
ሺݔ ݕሻ ݕ െ ሺݔ ݕሻ ݕ ൌ ʹ ሺݔ ݕሻ
ฺ ሺ ݕ െ ʹሻ ሺݔ ݕሻ ൌ ሺݔ ݕሻ ݕ ݕ ฺ ሺݔ ݕሻ ൌ ݕ െ ʹ Bài 7: Cho ሺݔ െ ߙሻ ܽ ሺݔ െ ߙሻ ൌ Ǣ ൌ ሺݔ െ ߚሻ ܾ ሺݔ െ ߚሻ Chứng minh rằng ܽ ܾ ሺߙ െ ߚሻ ൌ Ǣ ܽ ܾ ് Ͳ ܽ ܾ ải: Ta có : ሺݔ െ ߙሻ ሺݔ െ ߚሻ ܾ ܽ ܾ ܽ ቀ ቁ
ሺݔ െ ߚሻ ሺݔ െ ߙሻ ൌ ܽ ൌ ܽ ܾ ܾ
ሺݔ െ ߚሻ ሺݔ െ ߙሻ ܽ ቀͳ Ǥ ቁ ͳ ܽ
ሺݔ െ ߙሻ Ǥ ሺݔ െ ߚሻ ͳ
ሺʹݔ െ ߙ െ ߚሻ ሺߙ െ ߚሻ ൌ
ʹ ሾ ʹሺݔ െ ߙሻ ʹሺݔ െ ߚሻሿ ൌ
ሺݔ െ ߙሻ ሺݔ െ ߚሻ ሺݔ െ ߚሻ ሺݔ െ ߙሻ ሺʹݔ െ ߙ െ ߚሻ ൌ ሺߙ െ ߚሻ
Vậy ta có điều phải chứng minh. 40 --------------------- TOANMATH.com
Chương 2 : Các biến đổi lượng giác Bài 8: Cho
ܽଷ ݔ ͵ܽ ݔ ଶ ݔ ൌ ݉ሺͳሻ ൜
ܽ ଷ ݔ ͵ܽ ଶ ݔ ݔ ൌ ݊ሺʹሻ Chứng minh rằng : ඥ య ሺ݉ ݊ሻଶ ඥ
య ሺ݉ െ ݊ሻଶ ൌ ʹξ య ܽଶ
Giải: Lấy ሺͳሻ ሺʹሻ suy ra :
݉ ݊ ൌ ܽሺଷ ݔ ଷ ݔሻ ͵ܽ ݔ ݔ ሺ ݔ ݔሻ
ൌ ܽሺ ݔ ݔሻሾሺଶ ݔ ଶ ݔ െ ݔ ݔሻ ͵ ݔ ݔሿ
ൌ ܽሺ ݔ ݔሻሺ ݔ ݔሻଶ ൌ ܽሺ ݔ ݔሻଷ Vậy ඥ
య ሺ݉ ݊ሻଶ ൌ ሺ ݔ ݔሻଶǤ ξ య ܽଶ
Lấy ሺͳሻ െ ሺʹሻ suy ra :
݉ െ ݊ ൌ ܽሺଷ ݔ െ ଷ ݔሻ െ ͵ܽ ݔ ݔ ሺ ݔ െ ݔሻ
ൌ ܽሺ ݔ െ ݔሻሾሺଶ ݔ ଶ ݔ ݔ ݔሻ െ ͵ ݔ ݔሿ ൌ ܽሺ ݔ െ ݔሻଷ
Vậy యඥሺ݉ െ ݊ሻଶ ൌ ሺ ݔ െ ݔሻଶ య Ǥ ξܽଶ Do đó, ta được :
ൌ ሾሺ ݔ ݔሻଶ ሺ ݔ െ ݔሻଶሿǤ యඥܽଶ ൌ ʹయඥܽଶ
Bài 9: Chứng minh rằng nếu ܿ ൌ ܽ ܾ , với ܽǡ ܾǡ ܿ thỏa các điều kiện xác định cần thiết thì ܿ ܽ ܿ െ ܽ ܾ ൌ ଶ ʹ ʹ ʹ
Giải: Ở bài toán này, ta sẽ sử dụng công thức ͳ െ ݔ ݔ ൌ ଶ ͳ ݔ ʹ ܿ ܽ ܿ െ ܽ ܽ െ ܿ ܽ െ ܽ ܾ ͳ െ ܾ ܾ ൌ ൌ ൌ ൌ ଶ ʹ ʹ ܽ ܿ ܽ ܽ ܾ ͳ ܾ ʹ 41 --------------------- TOANMATH.com
Chương 2 : Các biến đổi lượng giác
Bài 10: Cho ܽ ܾ ܿ ൌ Ͳ.
Chứng minh rằng : ͳʹ ܽ ܾ ܿ ൌ ͵ܽ ͵ܾ ͵ܿ Giải: Đặt ݔ ൌ ܽ
ቊݕ ൌ ܾ ฺ ݔ ݕ ݖ ൌ Ͳ ݖ ൌ ܿ
Ta cần chứng minh: ͳʹݔݕݖ ൌ Ͷݔଷ Ͷݕଷ Ͷݖଷ െ ͵ሺݔ ݕ ݖሻ
Hay ͵ݔݕݖ ൌ ݔଷ ݕଷ ݖଷ Thật vậy, ta có :
Ͳ ൌ ሺݔ ݕ ݖሻଷ ൌ ݔଷ ݕଷ ݖଷ ͵ሾݔݕሺݔ ݕሻ ݕݖሺݕ ݖሻ ݖݔሺݖ ݔሻሿ ݔݕݖ
ൌ ݔଷ ݕଷ ݖଷ ͵ሾݔݕሺെݖሻ ݕݖሺെݔሻ ݖݔሺെݕሻሿ ݔݕݖ
ൌ ݔଷ ݕଷ ݖଷ െ ͵ݔݕݖ
Vậy ta có điều phải chứng minh.
Bài 11: Cho 3 số ܽǡ ܾǡ ܿ đôi một khác nhau và 4 góc ݔǡ ݕǡ ݖǡ ݐ được liên hệ với nhau bởi hệ thức : ܽ ܾ ܿ ൌ ൌ ሺݔ ݕሻ ሺݔ ݖሻ ሺݔ ݐሻ Chứng minh rằng ܽ ܾ ܾ ܿ ܿ ܽ ଶሺݕ െ ݖሻ ଶሺݖ െ ݐሻ ଶሺݐ െ ݕሻ ൌ Ͳ ܽ െ ܾ ܾ െ ܿ ܿ െ ܽ
Giải: Áp dụng tính chất của tỷ lệ thức, ta có : ܽ ܾ ܽ െ ܾ ൌ
ሺݔ ݕሻ ሺݔ ݖሻ
ሺݔ ݕሻ െ ሺݔ ݖሻ ܽ ܾ
ሺݔ ݕሻ ሺݔ ݖሻ ሺʹݔ ݕ ݖሻ ฺ ൌ ൌ ܽ െ ܾ
ሺݔ ݕሻ െ ሺݔ ݖሻ ሺݕ െ ݖሻ Do đó, 42 --------------------- TOANMATH.com
Chương 2 : Các biến đổi lượng giác ܽ ܾ ͳ
ଶሺݕ െ ݖሻ ൌ ሺʹݔ ݕ ݖሻ ሺݕ െ ݖሻ ൌ ሾሺʹݔ ʹݖሻ െ ሺʹݔ ʹݕሻሿ ܽ െ ܾ ʹ Tương tự, ta được : ܾ ܿ ͳ
ଶሺݖ െ ݐሻ ൌ ሾሺʹݔ ʹݐሻ െ ሺʹݔ ʹݖሻሿ ܾ െ ܿ ʹ ܿ ܽ ͳ
ଶሺݐ െ ݕሻ ൌ ሾሺʹݔ ʹݕሻ െ ሺʹݔ ʹݐሻሿ ܿ െ ܽ ʹ
Cộng các đẳng thức trên lại, ta có được điều phải chứng minh. Bài 12: Cho ݔ ݕ ݖ ݔ ݕ ݖ ൌ ൌ ܽ ሺݔ ݕ ݖሻ ሺݔ ݕ ݖሻ
Chứng minh rằng : ሺݔ ݕሻ ሺݕ ݖሻ ሺݖ ݔሻ ൌ ܽ
(Đề nghị Olympic 30-4, 2006)
Giải: Để ý rằng :
ሺݔ ݕሻ ൌ ሾሺݔ ݕ ݖሻ െ ݖሿ ൌ ሺݔ ݕ ݖሻ ݖ ሺݔ ݕ ݖሻ ݖ Tương tự vậy, ta có :
ሺݕ ݖሻ ൌ ሺݔ ݕ ݖሻ ݔ ሺݔ ݕ ݖሻ ݔ
ሺݖ ݔሻ ൌ ሺݔ ݕ ݖሻ ݕ ሺݔ ݕ ݖሻ ݕ
Cộng 3 đẳng thức lại, ta được :
ൌ ሺ ݔ ݕ ݖሻ ሺݔ ݕ ݖሻ ሺ ݔ ݕ ݖሻ ሺݔ ݕ ݖሻ
ൌ ܽ ଶሺݔ ݕ ݖሻ ܽ ଶሺݔ ݕ ݖሻ ൌ ܽ 43 --------------------- TOANMATH.com
Chương 2 : Các biến đổi lượng giác Bài 13: Cho ߨ
Ͳ ൏ ݔǡ ݕǡ ݖ ൏ ǡ ݔ ് ݕǡ ݕ ് ݖ ʹ ൞ ݔ െ ݕ ଶ ݕ ݖ ൌ ݔ െ ݖ ଶ ݖ ݕ Chứng minh rằng ݔ ݕ ݖ ൌ ʹ ʹ ʹ
Giải: Từ giả thuyết, ta có :
ݔ ݕ ଶ ݖ െ ݔ ଶ ݕ ݖ ൌ ଶ ݖ ଶ ݕ െ ଶ ݕ ଶ ݖ Hay
ݔ ሺ ݕ ଶ ݖ െ ଶ ݕ ݖሻ ൌ ሺ ݖ ݕ െ ݕ ݖሻሺ ݖ ݕ ݕ ݖሻ
ݔ ሾ ݕ ሺͳ െ ଶ ݖሻ െ ͳሺͳ െ ଶ ݕሻ ݖሿ ൌ ሺݖ െ ݕሻ ሺݖ ݕሻ
ݔ ሺ ݕ െ ݖሻሺͳ ݕ ݖሻ ൌ ଶ ݕ െ ଶ ݖ ݕ ݖ ݔ ൌ ͳ ݕ ݖ ݔ ͳ െ ݔ ͳ ݕ ݖ െ ݕ െ ݖ ሺͳ െ ݕሻሺͳ െ ݖሻ ฺ ଶ ൌ ൌ ൌ ʹ ͳ ݔ ͳ ݕ ݖ ݕ ݖ ሺͳ ݕሻሺͳ ݖሻ ݕ ݖ ൌ ଶ ଶ ʹ ʹ ߨ ݔ ݕ ݖ
Ͳ ൏ ݔǡ ݕǡ ݖ ൏ ǡ ݔ ് ݕǡ ݕ ് ݖ ฺ ǡ ǡ Ͳ ʹ ʹ ʹ ʹ Khi đó, ݔ ݕ ݖ ൌ ʹ ʹ ʹ
Vậy ta có điều phải chứng minh. 44 --------------------- TOANMATH.com
Chương 2 : Các biến đổi lượng giác - BÀI TẬP TỰ LUYỆN
2.3.1. Cho 3 góc ܽǡ ܾǡ ܿ thỏa điều kiện
ଶ ܽ ଶ ܾ ଶ ܾ ଶ ܿ ଶ ܿ ଶ ܽ ʹ ଶ ܽ ଶ ܾ ଶ ܿ ൌ ͳ
Chứng minh : ଶ ܽ ଶ ܾ ൌ ଶ ܿ
2.3.2. Cho ሺܽ ܾሻ ൌ ݇ ሺܽ െ ܾሻ Ǣ ݇ ് െͳ Chứng minh rằng ͳ െ ݇ ܽ ܾ ൌ ͳ ݇
2.3.3. Cho ܽ ܾ ܿ ൌ ͻͲ୭. Chứng minh :
ଶ ܽ ଶ ܾ ଶ ܿ ൌ ͳ െ ʹ ܽ ܾ ܿ
2.3.4. Cho ܽ ܾ ܿ ൌ ܽ ܾ ܿ. Chứng minh ߨ
ܽ ܾ ܿ ൌ ݇ߨǡ ݇ א Ժ ʹ
2.3.5. Chứng minh rằng nếu ܽ ൌ Ǣ ܾ ൌ Ǣሺܽ ܾሻ ൌ Thì ଶ ൌ ଶ ଶ 2.3.6. Cho
ሺ ʹͲ୭ െ ͵͵ ସ ʹͲ୭ ʹ ଶ ʹͲ୭ሻ െ ͳ ڭ ʹଶସǡ ݊ א Գ
Chứng minh rằng : ݊ ʹଶଶ.
(Đề nghị Olympic 30-4, 2004) -
GỢI Ý GIẢI BÀI TẬP TỰ LUYỆN
2.3.1. Đặt ݔ ൌ ଶ ܽǢ ݕ ൌ ଶ ܾǢ ݖ ൌ ଶ ܿ
Ta sẽ chứng minh ݔ ݕ ݖ ൌ ͳ
Biến đổi từ giả thuyết sau : ݔ ݕ ݕ ݖ ݖ ݔ ݔ ݕ ݖ Ǥ Ǥ Ǥ ʹ Ǥ Ǥ ൌ ͳ ͳ െ ݔ ͳ െ ݕ ͳ െ ݕ ͳ െ ݖ ͳ െ ݖ ͳ െ ݔ ͳ െ ݔ ͳ െ ݕ ͳ െ ݖ
2.3.2. Từ giả thuyết, ta rút ra được
ሺͳ െ ݇ሻ ܽ ܾ ൌ ሺͳ ݇ሻ ܽ ܾ
Chỉ cần chứng minh ܽ ܾ ് Ͳ khi ݇ ് െͳ thì ta có được điều phải chứng minh.
2.3.3. Để ý, từ giả thuyết, ta được : ܽ ൌ ሺܾ ܿሻ ൜ܽ ൌ ሺܾ ܿሻ
2.3.4. Điều cần chứng minh tương đương với ሺܽ ܾ ܿሻ ൌ Ͳ hay ܽ ܾ ܿ െ ܿ െ ܽ െ ܾ
Ͳ ൌ ሺܽ ܾ ܿሻ ൌ ܽ ܾ െ ͳ ܿ ሺܽ ܾሻ 45 --------------------- TOANMATH.com
Chương 2 : Các biến đổi lượng giác
2.3.5. Từ giả thuyết, ta biến đổi như sau : ܽ ܾ െ ܽ ܾ ൌ
ฺ ሺͳ െ ଶ ܽሻሺͳ െ ଶ ܾሻ ൌ ሺ ܽ ܾ െ ሻଶ ଶ ଶ ͳ ଶ ฺ ቆͳ െ ቇ ቆͳ െ ቇ ൌ ଶ ଶ ൬ െ ͳ൰ ൌ ଶ ଶ ସ ଶ ଶ ଶ
Chia 2 vế của đẳng thức cho ଶ ଶ , ta được : ͳ ͳ ͳ ͳ ൬ െ ൰ ൬ െ ൰ ൌ ସ ଶ ଶ ଶ ଶ
ฺ ሺଶ െ ଶ ሻሺଶ െ ଶ ሻ ൌ ସ
ฺ ଶ ଶ ൌ ଶ ሺଶ ଶ ሻ ͳ ͳ ͳ ฺ ൌ ଶ ଶ ଶ
Từ đó, ta có điều phải chứng minh.
2.3.6. Để ý ở bài 2.1.5 ta đã chứng minh ଶ ʹͲ୭ là nghiệm của phương trình ݔଷ െ
͵͵ݔଶ ʹݔ െ ͵ ൌ Ͳ, nên ʹͲ୭ െ ͵͵ ସ ʹͲ୭ ʹ ଶ ʹͲ୭ ൌ ͵
Do đó, giả thuyết tương đương với : ͵ െ ͳ ڭ ʹଶସ
Lưu ý mệnh đề : ܽȁܾ ݒሺܽሻ ݒሺܾሻǡ nguyên tố.
Suy ra : ͵ െ ͳ ڭ ʹଶସ ݒଶሺ͵ െ ͳሻ ݒଶሺʹଶସሻ ൌ ʹͲͲͶ.
Mặt khác, ta có bổ đề : ܽଶ െ ܾଶ
ݒଶሺܽ െ ܾሻ ൌ ݒଶ ቆ ቇ ݒଶሺ݊ሻ ʹ
Nên ݒଶሺ͵ െ ͳሻ ൌ ݒଶሺͶሻ ݒଶሺ݊ሻ ʹͲͲͶ
Do đó, ݒଶሺ݊ሻ ʹͲͲʹ ฺ ݊ ʹଶଶ
Trong đó, ݒሺݔሻ ൌ ܽ được hiểu là ܽȁݔ nhưng ܽାଵ ץ ݔ. 4.
CHỨNG MINH BIỂU THỨC LƯỢNG GIÁC KHÔNG PHỤ THUỘC VÀO BIẾN SỐ
- Khi gặp biểu thức ݂ሺݔሻ có chứa ଶ ݔǢ ଶ ݔ, ta thường sử dụng các phương pháp sau :
x Đặt ẩn phụ ܽ ൌ ଶ ݔǢ ܾ ൌ ଶ ݔ với kết quả sau : ܽ ܾ ൌ ͳǢ ܽଶ ܾଶ ൌ ͳ െ
ʹܾܽǢ ܽଷ ܾଷ ൌ ͳ െ ͵ܾܽǢ ܽସ ܾସ ൌ ͳ ʹܽଶܾଶ െ Ͷܾܽ ǥ
x Dùng các công thức hạ bậc
x Đặt ẩn phụ theo ݐ ൌ ଶ ݔ
- Chú ý : Đối với những bạn đọc đã biết về các khái niệm của đạo hàm các hàm số
lượng giác, ta có thể dùng kiến thức
Nếu ݂ᇱሺݔሻ ൌ Ͳ với mọi ݔ א thì ݂ሺݔሻ là hàm hằng với mọi ݔ א . 46 --------------------- TOANMATH.com
Chương 2 : Các biến đổi lượng giác
Bài 1: Chứng minh các biểu thức sau không phụ thuộc vào ݔ
ൌ ସ ݔ ሺ͵ െ ʹ ଶ ݔሻ ସ ݔ ሺ͵ െ ʹ ଶ ݔሻ
ൌ ͵ሺ଼ ݔ െ ଼ ݔሻ Ͷሺ ݔ െ ʹ ݔሻ ସ ݔ
ൌ ଶ ݔ ଶሺܽ ݔሻ െ ʹ ܽ ݔ ሺܽ ݔሻ
ൌ ଶሺܽ ݔሻ ଶሺܽ െ ݔሻ ʹ ሺܽ ݔሻ ሺܽ െ ݔሻ ʹܽ
ൌ ଼ ݔ ଼ ݔ ସ ݔ ସ ݔ Ͷ ଶ ݔ ଶ ݔ ሺସ ݔ ସ ݔሻ Giải:
ൌ ͵ሺସ ݔ ସ ݔሻ െ ʹሺ ݔ ݔሻ
ൌ ͵ሾሺଶ ݔ ଶ ݔሻଶ െ ʹ ଶ ݔ ଶ ݔሿ
െ ʹሺଶ ݔ ଶ ݔሻሺସ ݔ െ ଶ ݔ ଶ ݔ ସ ݔሻ ͳ ͵
ൌ ͵ ൬ͳ െ ଶ ʹݔ൰ െ ʹ ൬ͳ െ ଶ ʹݔ൰ ൌ ͳ ʹ Ͷ
ൌ ͵ሾܽସ െ ሺͳ െ ܽሻସሿ Ͷሾሺͳ െ ܽሻଷ െ ʹܽଷሿ ܽଶǢ ܽ ൌ ଶ ݔ
ൌ ͵ሺͶܽଷ െ ܽଶ Ͷܽ െ ͳሻ Ͷሺെ͵ܽଷ ͵ܽଶ െ ͵ܽ ͳሻ ܽଶ
ൌ ͳʹܽଷ െ ͳͺܽଶ ͳʹܽ െ ͵ െ ͳʹܽଷ ͳʹܽଶ െ ͳʹܽ Ͷ ܽଶ ൌ ͳ
ൌ ଶ ݔ ሺܽ ݔሻ ሾሺܽ ݔሻ െ ʹ ܽ ݔሿ
ൌ ଶ ݔ ሺܽ ݔሻ ሾെ ܽ ݔ െ ܽ ݔሿ ͳ ͳ ͳ
ൌ ଶ ݔ െ ሺܽ ݔሻ ሺܽ െ ݔሻ ൌ ʹݔ െ ሺ ʹܽ ʹݔሻ ʹ ʹ ʹ ൌ ଶ ܽ
ൌ ଶሺܽ െ ݔሻ ሺܽ ݔሻ ሾሺܽ ݔሻ ʹ ሺܽ െ ݔሻ ʹܽሿ
ൌ ଶሺܽ െ ݔሻ ሺܽ ݔሻ ሾሺܽ ݔሻ ሺ͵ܽ െ ݔሻ ሺെܽ െ ݔሻሿ
ൌ ଶሺܽ െ ݔሻ ሺܽ ݔሻ ሺ͵ܽ െ ݔሻ ͳ െ ሺʹܽ െ ʹݔሻ ͳ ͳ ͳ ൌ
ሺെʹܽ ʹݔሻ െ Ͷܽ ൌ ሺͳ െ Ͷܽሻ ʹ ʹ ʹ ʹ ൌ ଶ ʹܽ
ൌ ଼ ݔ ଼ ݔ ସ ݔ ସ ݔ Ͷ ଶ ݔ ଶ ݔ ሺସ ݔ ସ ݔሻ Đặt ݐ ൌ ଶ ݔ 47 --------------------- TOANMATH.com
Chương 2 : Các biến đổi lượng giác ݐ ͳ ฺ ଶ ݔ ൌ Ǣ ଶ ݔ ൌ ݐ ͳ ݐ ͳ ݐସ ͳ ݐଶ ݐ ݐଶ ͳ ฺ ൌ Ͷ ቈ
ሺݐ ͳሻସ ሺݐ ͳሻସ ሺݐ ͳሻସ
ሺݐ ͳሻଶ ሺݐ ͳሻଶ ሺݐ ͳሻଶ
ݐସ Ͷݐଷ ݐଶ Ͷݐ ͳ ൌ ൌ ͳ ሺݐ ͳሻସ
Bài 2: Chứng minh : Nếu ݉ ሺܽ ܾሻ ൌ ሺܽ െ ܾሻ ǡ ܽ െ ܾ ് ݇ߨǡ ݇ א Ժǡ ݉ ് േͳ
thì biểu thức sau không phụ thuộc vào ܽǡ ܾ ͳ ͳ ൌ ͳ െ ݉ ʹܽ ͳ െ ݉ ʹܾ Giải: Ta có : ʹ െ ݉ሺ ʹܽ ʹܾሻ ൌ
ͳ െ ݉ሺ ʹܽ ʹܾሻ ݉ଶ ʹܽ ʹܾ
ʹ െ ʹ݉ ሺܽ ܾሻ ሺܽ െ ܾሻ ൌ ݉ଶ
ͳ െ ʹ݉ ሺܽ ܾሻ ሺܽ െ ܾሻ ʹ ሾʹሺܽ െ ܾሻ െ ʹሺܽ ܾሻሿ
Mà ݉ ሺܽ ܾሻ ൌ ሺܽ െ ܾሻ nên ଶሺܽ െ ܾሻ ൌ ݉ଶ ଶሺܽ ܾሻ Do đó,
ʹሾͳ െ ݉ଶ ଶሺܽ ܾሻሿ ൌ ݉ଶ
ͳ െ ʹ݉ଶ ଶሺܽ ܾሻ
ሾʹ ଶሺܽ െ ܾሻ െ ʹ ʹ ଶሺܽ ܾሻሿ ʹ
ʹሾͳ െ ݉ଶ ଶሺܽ ܾሻሿ
ൌ ͳ െ ʹ݉ଶ ଶሺܽ ܾሻ ݉ସ ଶሺܽ ܾሻ െ ݉ଶ ݉ଶ ଶሺܽ ܾሻ
ʹሾͳ െ ݉ଶ ଶሺܽ ܾሻሿ
ൌ ͳ െ ݉ଶ ଶሺܽ ܾሻ ݉ଶሾ݉ଶ ଶሺܽ ܾሻ െ ͳሿ
ʹሾͳ െ ݉ଶ ଶሺܽ ܾሻሿ ʹ ൌ ൌ
ሾͳ െ ݉ଶ ଶሺܽ ܾሻሿሺͳ െ ݉ଶሻ ͳ െ ݉ଶ
Do ܽ െ ܾ ് ݇ߨ nên ݉ ሺܽ ܾሻ ൌ ሺܽ െ ܾሻ ് േͳ ฺ ݉ଶ ଶሺܽ ܾሻ ് ͳ. 48 --------------------- TOANMATH.com
Chương 2 : Các biến đổi lượng giác Bài 3: Cho ͵
݂ሺݔሻ ൌ ݔ ଶ ʹݔ ݔ Ͷ
a. Chứng minh : ݂ᇱሺݔሻ ൌ Ͳǡ ݔ א Թ b. Tính giá trị của ߨ ݂ ቀ ቁ ͳͻͻͺ (ĐH Hồng Đức 1998)
Giải: Ở bài này, ta có 2 cách chứng minh.
Cách 1: Ta chứng minh ݂ሺݔሻ là hàm hằng ݔ א Թ. Thật vậy, ta có : ͵ ͵
݂ሺݔሻ ൌ ݔ ଶ ʹݔ ݔ ൌ ସ ݔ ସ ݔ െ ଶ ݔ ଶ ݔ ଶ ʹݔ Ͷ Ͷ ͵
ൌ ͳ െ ͵ ଶ ݔ ଶ ݔ ଶ ʹݔ ൌ ͳ Ͷ ߨ ฺ ݂ ቀ ቁ ൌ ͳ ͳͻͻͺ Cách 2: Ta có :
݂ᇱሺݔሻ ൌ ହ ݔ ݔ െ ହ ݔ ݔ ͵ ʹݔ ʹݔ ͵
ൌ ݔ ݔ ሺସ ݔ െ ସ ݔሻ Ͷݔ ʹ ͵ ͵
ൌ ͵ ʹݔ ሺଶ ݔ െ ଶ ݔሻ Ͷݔ ൌ െ͵ ʹݔ ʹݔ Ͷݔ ൌ Ͳ ʹ Ͷ Như vậy, ߨ ߨ ݂ ቀ ቁ ൌ ݂ ቀ ቁ ൌ ͳ ͳͻͻͺ ʹ
Bài 4: Tìm ݉ để giá trị của hàm số sau không phụ thuộc vào biến số
݂ሺݔሻ ൌ ݔ ݔ ݉ሺସ ݔ ସ ݔሻ ʹ ଶ ʹݔ 49 --------------------- TOANMATH.com
Chương 2 : Các biến đổi lượng giác Giải: Ta có : ͵
ݔ ݔ ൌ ସ ݔ ସ ݔ െ ଶ ݔ ଶ ݔ ൌ ͳ െ ଶ ʹݔ Ͷ ͳ
݉ሺସ ݔ ସ ݔሻ ൌ ݉ሺͳ െ ଶ ݔ ଶ ݔሻ ൌ ݉ ൬ͳ െ ଶ ʹݔ൰ Ͷ Vậy ͵ ͳ ͷ ݉
݂ሺݔሻ ൌ ͳ െ ଶ ʹݔ ݉ ൬ͳ െ ଶ ʹݔ൰ ʹ ଶ ʹݔ ൌ ͳ ݉ ൬ െ ൰ ଶ ʹݔ Ͷ Ͷ Ͷ Ͷ
Để ݂ሺݔሻ không phụ thuộc vào biến số thì ݉ ൌ ͷ, khi đó ݂ሺݔሻ ൌ . 50 --------------------- TOANMATH.com
Chương 2 : Các biến đổi lượng giác - BÀI TẬP TỰ LUYỆN
2.4.1. Chứng minh các biểu thức sau không phụ thuộc vào biến số
ൌ ʹሺସ ݔ ସ ݔ ଶ ݔ ଶ ݔሻଶ െ ሺ଼ ݔ ଼ ݔሻ ߨ ߨ
ൌ ଶ ݔ ଶ ቀ ݔቁ ଶ ቀ െ ݔቁ ͵ ͵ ߨ ߨ ͵ߨ
ൌ ସ ݔ ସ ቀݔ ቁ ସ ቀݔ ቁ ସ ൬ݔ ൰ Ͷ ʹ Ͷ ʹ ݔ ͳ ൌ ݔ െ ͳ ݔ െ ͳ ݔ ଶ ݔ ߨ ൌ െ ǡ Ͳ ൏ ݔ ൏ ݔ െ ξଶ ݔ െ ଶ ݔ ʹ ଶ ݔ െ ͳ ʹ
ൌ ඥସ ݔ Ͷ ଶ ݔ ඥସ ݔ Ͷ ଶ ݔ య ͳ ͵ ͳ
ൌ ඨସ ݔ െ ଶ ݔ ൬ െ ʹ ʹݔ Ͷݔ൰ Ͷ ʹ ʹ య ͳ ͳ
ඨସ ݔ ଶ ݔ ଶ ʹݔ െ ଶ ݔ ʹ ʹ
2.4.2. Tìm ݉ để giá trị của hàm số sau không phụ thuộc vào biến số
݂ሺݔሻ ൌ ሺݔ ݉ሻ ሺݔ ʹ݉ሻ ݔ ܽ -
GỢI Ý GIẢI BÀI TẬP TỰ LUYỆN 2.4.2. Để ý
݂ሺݔሻ ൌ ʹ ሺݔ ݉ሻ ݉ ሺݔ ݉ሻ ܽ ൌ ሺͳ ʹ ݉ሻ ሺݔ ݉ሻ ܽ
Do đó, để ݂ሺݔሻ không phụ thuộc vào biến số thì ͳ ݉ ൌ െ ʹ 51 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác CHƯƠNG 3
HÊ THỨC LƯỢNG TRONG TAM GIÁC I.
CÁC KÝ HIỆU CƠ BẢN
െǡ ǡ : các góc đỉnh ǡ ǡ
െܽǡ ܾǡ ܿ : độ dài cạnh đối diện với đỉnh ǡ ǡ
െ݄ǡ ݄ǡ ݄ : độ dài đường cao hạ từ đỉnh ǡ ǡ
െ݉ǡ ݉ǡ ݉ : độ dài đường trung tuyển kẻ từ đỉnh ǡ ǡ
െ݈ǡ ݈ǡ ݈ : độ dài đường phân giác trong kẻ từ đỉnh ǡ ǡ
െܴ : bán kính đường tròn ngoại tiếp tam giác
െݎ : bán kính đường tròn nội tiếp tam giác
െݎǡ ݎǡ ݎ : bán kính đường tròn bàng tiếp tam giác đỉnh ǡ ǡ
െ : nửa chu vi tam giác
െܵ : diện tích tam giác II.
CÁC ĐỊNH LÝ VÀ CÔNG THỨC CƠ BẢN 1.
ĐỊNH LÝ HÀM SỐ SIN
Trong tam giác , ta luôn có : ܽ ܾ ܿ ൌ ൌ ൌ ʹܴ
Từ đó, ta có hệ quả sau :
ܽ ൌ ʹܴ Ǣ ܾ ൌ ʹܴ Ǣ ܿ ൌ ʹܴ 2.
ĐỊNH LÝ HÀM SỐ COS
Trong tam giác , ta luôn có :
ܽଶ ൌ ܾଶ ܿଶ െ ʹܾܿ ൌ ሺܾ െ ܿሻଶ Ͷܾܿ ଶ ʹ
ܾଶ ൌ ܿଶ ܽଶ െ ʹܿܽ ൌ ሺܿ െ ܽሻଶ Ͷܿܽ ଶ ʹ 52 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
ܿଶ ൌ ܽଶ ܾଶ െ ʹܾܽ ൌ ሺܽ െ ܾሻଶ Ͷܾܽ ଶ ʹ
Từ đó, ta có hệ quả sau để tính số đo góc của tam giác : ܾଶ ܿଶ െ ܽଶ ܿଶ ܽଶ െ ܾଶ ܽଶ ܾଶ െ ܿଶ ൌ Ǣ ൌ Ǣ ൌ ʹܾܿ ʹܿܽ ʹܾܽ
Từ hệ quả trên, ta có thêm được kết quả sau : ߨ ߨ ߨ
ܾଶ ܿଶ ൏ ܽଶǢ
ܿଶ ܽଶ ൏ ܾଶǢ ܽଶ ܾଶ ൏ ܿଶ ʹ ʹ ʹ 3.
ĐỊNH LÝ HÀM SỐ TAN
Trong tam giác , ta luôn có : െ െ െ ܽ െ ܾ ܾ െ ܿ ܿ െ ܽ ൌ ʹ Ǣ ൌ ʹ Ǣ ൌ ʹ ܽ ܾ ܿ ܽ ܾ ܿ ʹ ʹ ʹ 4.
ĐỊNH LÝ HÀM SỐ COT
Trong tam giác , ta luôn có : ܽଶ ܾଶ ܿଶ ൌ Ͷܵ 5.
ĐỊNH LÝ CÁC HÌNH CHIẾU
Trong tam giác , ta luôn có :
ܽ ܿ ൌ ܾǢ ܽ ܾ ൌ ܿǢ ܾ ܿ ൌ ܽ 6.
CÔNG THỨC VỀ ĐỘ DÀI TRUNG TUYẾN
Trong tam giác , độ dài 3 đường trung tuyến được xác định bởi công thức : ʹܾଶ ʹܿଶ െ ܽଶ ܽଶ ݉ଶ ଶ ൌ ฺ ʹ݉ ൌ ܾଶ ܿଶ Ͷ ʹ ʹܿଶ ʹܽଶ െ ܾଶ ܾଶ ݉ଶ ଶ ൌ ฺ ʹ݉ ൌ ܿଶ ܽଶ Ͷ ʹ ʹܽଶ ʹܾଶ െ ܿଶ ܿଶ ݉ଶ ଶ ൌ ฺ ʹ݉ ൌ ܽଶ ܾଶ Ͷ ʹ
Từ đó, ta có công thức về tổng bình phương của 3 đường trung tuyến trong tam giác : ͵ ݉ଶ ଶ ଶ ݉ ݉ ൌ
ሺܽଶ ܾଶ ܿଶሻ Ͷ 53 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác 7.
CÔNG THỨC VỀ ĐỘ DÀI PHÂN GIÁC TRONG
Trong tam giác , độ dài 3 đường phân giác trong được xác định bởi công thức : ʹܾܿ ʹܾܿ ሺ െ ܽሻ ݈ ඨ ൌ ൌ ܾ ܿ ʹ ܾ ܿ ܾܿ ʹܿܽ ʹܿܽ ሺ െ ܾሻ ݈ ඨ ൌ ൌ ܿ ܽ ʹ ܿ ܽ ܿܽ ʹܾܽ ʹܾܽ ሺ െ ܿሻ ݈ ඨ ൌ ൌ ܽ ܾ ʹ ܽ ܾ ܾܽ 8.
CÔNG THỨC VỀ ĐỘ DÀI ĐƯỜNG CAO
Trong tam giác , độ dài 3 đường cao được xác định bởi công thức : ʹܵ ʹܵ ʹܵ ݄ ൌ Ǣ݄ Ǣ݄ ܽ ൌ ܾ ൌ ܿ 9.
CÔNG THỨC VỀ ĐỘ DÀI BÁN KÍNH a.
BÁN KÍNH ĐƯỜNG TRÒN NỘI TIẾP ܵ
ݎ ൌ ൌ ሺ െ ܽሻ ൌ ሺ െ ܾሻ ൌ ሺ െ ܿሻ ʹ ʹ ʹ b.
BÁN KÍNH ĐƯỜNG TRÒN NGOẠI TIẾP ܾܽܿ ܽ ܾ ܿ ܴ ൌ ൌ ൌ ൌ Ͷܵ ʹ ʹ ʹ c.
BÁN KÍNH ĐƯỜNG TRÒN BÀNG TIẾP ܵ ݎ ൌ ൌ ʹ െ ܽ ܵ ݎ ൌ ൌ ʹ െ ܾ ܵ ݎ ൌ ൌ ʹ െ ܿ 54 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác 10.
CÔNG THỨC VỀ DIỆN TÍCH TAM GIÁC
Ta có công thức tính diện tích tam giác bằng nhiều công thức khác nhau : ͳ ͳ ͳ ۓ
݄ܽ ൌ ܾ݄ ൌ ݄ܿ ۖ ʹ ʹ ʹ ۖͳ ͳ ͳ ۖ ܾܿ ൌ ܿܽ ൌ ܾܽ ʹ ʹ ʹ
ܵ ൌ ݎሺ െ ܽሻ ൌ ݎሺ െ ܾሻ ൌ ݎሺ െ ܿሻ ۔ ۖ
ඥሺ െ ܽሻሺ െ ܾሻሺ െ ܿሻ ۖ ܾܽܿ ۖ Ͷܴ ە ݎ
Lưu ý: Công thức ܵ ൌ ඥሺ െ ܽሻሺ െ ܾሻሺ െ ܿሻ được nhà toán học và vật lý Heron(5)
phát hiện nên thường được gọi là “Công thức Heron”. III.
CÁC LOẠI TOÁN VÀ PHƯƠNG PHÁP GIẢI 1.
CHỨNG MINH ĐẲNG THỨC LƯỢNG GIÁC TRONG TAM GIÁC
- Để chứng minh loại toán này, chúng ta có nhiều phương pháp giải khác nhau,
chẳng hạn như : biến đổi vế này thành vế kia, xuất phát từ một hệ thức đúng đã
biết để suy ra đẳng thức cần chứng minh, chứng minh tương đương…
- Trong lúc chứng minh, ta chú ý một số kỹ thuật sau :
x Sử dụng biến đổi lượng giác : sử dụng các công thức biến đổi tích thành
tổng hoặc ngược lại, công thức hạ bậc, công thức cung có liên quan đặc biệt như :
ሺ ሻ ൌ Ǣሺ ሻ ൌ െ Ǣ ൬ ൰ ൌ Ǣ ʹ ʹ ൬
൰ ൌ Ǣሺ ሻ ൌ െ Ǣ ሺ ሻ ൌ െ Ǣ ʹ ʹ ൬ ൰ ൌ Ǣ ൬ ൰ ൌ ʹ ʹ ʹ ʹ
x Sử dụng định lý hàm số sin, hàm số cos : Ta thường dùng định lý này để
biến đổi hệ thức phải chứng minh thành một hệ thức chỉ có hàm số lượng
giác và dùng các công thức biến đổi lượng giác để chứng minh.
x Sử dụng công thức tính diện tích : dùng để tìm mối quan hệ giữa các cạnh,
góc, bán kính đường tròn ngoại tiếp, nội tiếp, bàng tiếp. 55 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
Trước hết, ta nên nhớ một số đẳng thức cơ bản trên trong tam giác nhằm giúp cho chúng
ta sử dụng thành thạo các kỹ thuật chứng minh trong dạng toán này, đồng thời làm tăng
“độ nhạy” khi gặp những bài toán phức tạp khác.
Bài 1: Chứng minh các đẳng thức cơ bản trong tam giác : Ǥ ൌ Ͷ ʹ ʹ ʹ Ǥ ൌ ͳ Ͷ ʹ ʹ ʹ Ǥ ʹ ʹ ʹ ൌ Ͷ
Ǥ ʹ ʹ ʹ ൌ െͳ െ Ͷ
Ǥ ଶ ଶ ଶ ൌ ʹ ʹ
Ǥ ଶ ଶ ଶ ൌ ͳ െ ʹ
Ǥ ଶ ଶ ଶ ൌ ͳ െ ʹ ʹ ʹ ʹ ʹ ʹ ʹ
Ǥ ଶ ଶ ଶ ൌ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ
Ǥ ൌ (ĐH Tổng Hợp Tp.HCM 1995) Ǥ ൌ ͳ ʹ ʹ ʹ ʹ ʹ ʹ Giải: a. Ta có : െ െ ൌ ʹ ʹ ൌ ʹ ൬ ൰ ʹ ʹ ʹ ʹ ʹ ʹ ʹ െ ൌ ʹ ൬ ൰ ൌ Ͷ ʹ ʹ ʹ ʹ ʹ ʹ b. Ta có : െ െ ൌ ʹ
ͳ െ ʹ ଶ ൌ ͳ ʹ ൬ െ ൰ ʹ ʹ ʹ ʹ ʹ ʹ െ ൌ ͳ ʹ ൬ െ ൰ ൌ ͳ Ͷ ʹ ʹ ʹ ʹ ʹ ʹ c. Ta có :
ൌ ʹ ሺ ሻ ሺ െ ሻ ʹ ൌ ʹ ሾሺ െ ሻ ሿ
ൌ ʹ ሾሺ െ ሻ െ ሺ ሻሿ ൌ Ͷ 56 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác d. Ta có :
ൌ ʹ ሺ ሻ ሺ െ ሻ െ ͳ ʹ ଶ ൌ െʹ ሾሺ െ ሻ െ ሿ െ ͳ
ൌ െʹ ሾሺ െ ሻ ሺ ሻሿ െ ͳ ൌ െͳ െ Ͷ e. Ta có : ͳ െ ʹ ͳ െ ʹ ͳ ൌ
ͳ െ ଶ ൌ ʹ െ ሺ ʹ ʹሻ െ ଶ ʹ ʹ ʹ
ൌ ʹ െ ሺ ሻ ሺ െ ሻ െ ଶ ൌ ʹ ሾሺ െ ሻ െ ሿ
ൌ ʹ ሾሺ െ ሻ ሺ ሻሿ ൌ ʹ ʹ f. Ta có : ͳ ʹ ͳ ʹ ͳ ൌ ଶ ൌ ͳ ʹ ʹ ʹ ሺ ʹ ʹሻ ଶ
ൌ ͳ ሺ ሻ ሺ െ ሻ ଶ ൌ ͳ െ ሾሺ െ ሻ െ ሿ
ൌ ͳ െ ሾሺ െ ሻ ሺ ሻሿ ൌ ͳ െ ʹ g. Ta có : ͳ െ ͳ െ െ ൌ ଶ ൌ ͳ െ ଶ ʹ ʹ ʹ ʹ ʹ ʹ െ െ ൌ ͳ െ ൬ െ ൰ ൌ ͳ െ ൬ െ ൰ ʹ ʹ ʹ ʹ ʹ ʹ ൌ ͳ െ ʹ ʹ ʹ ʹ h. Ta có : ͳ ͳ െ ൌ ଶ ൌ ͳ ͳ െ ଶ ʹ ʹ ʹ ʹ ʹ ʹ െ ൌ ʹ ൬ െ ൰ ൌ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ i.
Ta có : ൌ ߨ ฺ ൌ ߨ െ
ฺ ሺ ሻ ൌ ሺߨ െ ሻ ൌ െ ฺ ൌ െ ͳ െ ฺ ൌ j. Ta có : ߨ ߨ ͳ
ൌ െ ฺ ൬ ൰ ൌ ൬ െ ൰ ฺ ʹ ʹ ൌ ൌ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ͳ െ ʹ ʹ ʹ ʹ ฺ ൌ ͳ ʹ ʹ ʹ ʹ ʹ ʹ 57 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
Bài 2: Chứng minh trong tam giác , ta luôn có
ଶ ଶ ଶ ൌ ʹሺ ሻ
(ĐH Giao Thông Vận Tải 1995)
Giải: Ta có 2 cách chứng minh bài toán này Cách 1: Ta có : ൌ ሺ ሻ ൌ ሺ ሻ ൌ ଶ Tương tự : ൌ ଶ ൌ ଶ
Cộng 3 đẳng thức trên, ta có điều phải chứng minh.
Cách 2: Theo định lý hàm số cos, ta có :
ܽଶ ൌ ܾଶ ܿଶ െ ʹܾܿ
൝ܾଶ ൌ ܿଶ ܽଶ െ ʹܿܽ ฺ ܽଶ ܾଶ ܿଶ ൌ ʹሺܾܽ ܾܿ ܿܽ ሻ
ܿଶ ൌ ܽଶ ܾଶ െ ʹܾܽ
Theo định lý hàm số sin, ta có : ܽ ൌ ʹܴ ൝ܾ ൌ ʹܴ ܿ ൌ ʹܴ Suy ra :
Ͷܴଶሺଶ ଶ ଶ ሻ ൌ ͺܴଶሺ ሻ
ฺ ଶ ଶ ଶ ൌ ʹሺ ሻ
Vậy ta có điều phải chứng minh.
Bài 3: Trong tam giác , chứng minh đẳng thức
݊ ݊ ݊ ൌ ݊ ݊ ݊ǡ ݊ א Գ (ĐH Y Hải Phòng 1998)
Giải: Ta có : ݊ ݊ ݊ ൌ ݊ߨ ฺ ݊ ݊ ൌ ݊ߨ െ ݊
ฺ ሺ݊ ݊ሻ ൌ ሺ݊ߨ െ ݊ሻ ൌ െ ݊ ݊ ݊ ฺ ൌ െ ݊ ͳ െ ݊ ݊
ฺ ݊ ݊ ݊ ൌ ݊ ݊ ݊ 58 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
Bài 4: Chứng minh rằng trong tam giác ta luôn có ͳ ͳ ͳ ͳ Ǥ ൌ ൬ ൰ ʹ ʹ ʹ ʹ ʹ ʹ ʹ
(ĐH Ngoại Thương Hà Nội 1998) ͵ Ǥ ൌ ʹ ʹ ʹ
(ĐH Ngoại Thương Tp.HCM 2001) ሺ െ ሻ ܽଶ െ ܾଶ Ǥ ൌ ܿଶ
(ĐH Ngoại Ngữ Hà Nội 1998) Ǥ ʹ ʹ ʹ ൌ ʹ ʹ ʹ ʹ ʹ ʹ ʹ (ĐHQG Hà Nội 1998) ܽଶ ܾଶ ܿଶ Ǥ ൌ Ͷܵ (ĐH Dược Hà Nội 1998) Giải: a.
Trong tam giác , ta luôn có : ൌ ʹ ʹ ʹ ʹ ʹ ʹ Mặt khác, ta lại có : ʹ ʹ ʹ ൌ Ǣ ൌ Ǣ ൌ ʹ ʹ ʹ ʹ ʹ ʹ
Cộng 3 đẳng thức trên và thêm hệ thức sẵn có, ta có được điều phải chứng minh. b. Ta có : ൌ
ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ 59 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác Mặt khác : ͳ െ ͳ െ ൌ ൬ ൰ ൌ ൬ ൰ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ͳ െ ͳ ͳ െ ͳ ൌ ൬ଶ ൰ ൌ ሺ ሻ൨ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ͳ ൌ ሺͳ െ ሻ Ͷ Tương tự, ta có : ͳ ൌ ሺͳ െ ሻ ʹ ʹ ʹ Ͷ ͳ ൌ ሺͳ െ ሻ ʹ ʹ ʹ Ͷ Suy ra ͳ
ൌ ሺ͵ ሻ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ Ͷ Ta xét : ͳ െ ͳ െ ൌ ൬ ൰ ൌ ൬ ൰ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ͳ ͳ ͳ ͳ
ൌ ሺ ሻ൨ ൌ ሺ ሻ ʹ ʹ ʹ Ͷ
Vậy ta đã có được điều phải chứng minh. c. Ta có : ܽ ܿଶ ܽଶ െ ܾଶ ܾ ܾଶ ܿଶ െ ܽଶ െ ൌ ൌ ʹܴ Ǥ ʹܽܿ െ ʹܴ Ǥ ʹܾܿ ܿ ʹܴ
ሺܿଶ ܽଶ െ ܾଶሻ െ ሺܾଶ ܿଶ െ ܽଶሻ ܽଶ െ ܾଶ ൌ ൌ ʹܿଶ ܿଶ d. Ta có : ʹ ʹ ʹ ʹ െ ʹ ʹ ൌ ൌ ൌ ͳ െ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ Tương tự, ta có : ʹ ൌ ͳ െ ʹ ʹ ʹ ʹ ʹ ൌ ͳ െ ʹ ʹ ʹ ʹ 60 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
Cộng 3 đẳng thức trên lại, ta có : ൌ ͵ െ ൬ ൰ ʹ ʹ ʹ ʹ ʹ ʹ Mà ൌ ͳ ʹ ʹ ʹ ʹ ʹ ʹ Nên ൌ ʹ. e. Theo định lý cos, ta có :
ܽଶ ൌ ܾଶ ܿଶ െ ʹܾܿ ൌ ܾଶ ܿଶ െ ʹܾܿ ൌ ܾଶ ܿଶ െ Ͷܵ Tương tự, ta có :
ܾଶ ൌ ܿଶ ܽଶ െ Ͷܵ
ܿଶ ൌ ܽଶ ܾଶ െ Ͷܵ
Cộng 3 đẳng thức trên ta được :
ܽଶ ܾଶ ܿଶ ൌ ʹሺܽଶ ܾଶ ܿଶሻ െ Ͷܵሺ ሻ ܽଶ ܾଶ ܿଶ ฺ ൌ Ͷܵ
Vậy ta có được điều phải chứng minh.
Bài 5: Chứng minh rằng trong tam giác ta luôn có Ǥ ൌ െ ʹ ʹ
(Học Viện Quan Hệ Quốc Tế 1998) Ǥ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ൌ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ
(Học Viện Quan Hệ Quốc Tế 2000) െ Ǥ ൌ െ ͳ ʹ ʹ ʹ
(Học Viện Ngân Hàng 2000) Giải: a. Ta có : ൌ Ͷ ʹ ʹ ʹ 61 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác Mặt khác : െ െ ൌ ʹ െ ʹ ʹ ʹ ʹ ʹ െ ൌ ʹ ൬ െ ൰ ൌ െͶ ൬െ ൰ ʹ ʹ ʹ ʹ ʹ ʹ ൌ Ͷ ʹ ʹ ʹ Vậy Ͷ ൌ ʹ ʹ ʹ ൌ Ͷ ʹ ʹ ʹ ʹ ʹ b. Ta có : ൌ ͳ ʹ ʹ ʹ ʹ ʹ ʹ
Do đó, điều cần chứng minh tương đương với : ൌ ͳ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ
൬ െ ൰ ൬ ൰ ൌ ͳ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ൌ ͳ ʹ ʹ ʹ ʹ ൬ ൰ ൌ ͳ ʹ
Điều này hiển nhiên đúng, ta có điều phải chứng minh. c.
Ở câu a, ta đã chứng minh : െ ൌ Ͷ ʹ ʹ ʹ Ta xét : െ െ ͳ ൌ ʹ ʹ ଶ ʹ ʹ ʹ െ ൌ ʹ ൬ ൰ ൌ Ͷ ʹ ʹ ʹ ʹ ʹ ʹ Do đó, Ͷ ൌ ʹ ʹ ʹ ൌ Ͷ ʹ ʹ ʹ ʹ ʹ ʹ 62 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
Bài 6: Cho tam giác . Chứng minh rằng :
Ǥܽଷ ሺ െ ሻ ܾଷ ሺ െ ሻ ܿଷ ሺ െ ሻ ൌ Ͳ ܽ ܾ ܿ Ǥ ൌ ܽ ܾ ܿ
Ǥሺܽ െ ܾሻ ሺܾ െ ܿሻ ሺܿ െ ܽሻ ൌ Ͳ ʹ ʹ ʹ ʹ ʹ ʹ Giải: a. Ta có : ͳ
ଷ ሺ െ ሻ ൌ ଶ ሺ ሻ ሺ െ ሻ ൌ െ ሺͳ െ ʹሻሺ ʹ െ ʹሻ Ͷ ͳ
ൌ ሺ ʹ െ ʹ ʹ ʹ െ ʹ ʹሻ Ͷ Tương tự, ta có : ͳ
ଷ ሺ െ ሻ ൌ ሺ ʹ െ ʹ ʹ ʹ െ ʹ ʹሻ Ͷ ͳ
ଷ ሺ െ ሻ ൌ ሺ ʹ െ ʹ ʹ ʹ െ ʹ ʹሻ Ͷ
Cộng 3 đẳng thức trên, ta được :
ଷ ሺ െ ሻ ଷ ሺ െ ሻ ଷ ሺ െ ሻ ൌ Ͳ
Vậy theo định lý hàm số sin, ta có điều phải chứng minh. b. Ta có : ʹ ʹ ʹ ൌ Ͷ
Do đó, theo định lý hàm số sin, ta có : ʹܴሺଶ ଶ ଶ ሻ ʹሺଶ ଶ ଶ ሻ ൌ ൌ ʹܴሺ ሻ ʹ ʹ ʹ ଶ ଶ ଶ ൌ ൌ ʹ ʹ ʹ ʹ ሺ ሻ ሺ ሻ ሺ ሻ ൌ ʹ ʹ ʹ ͳ ͳ ͳ
ൌ ሺ ሻ ሺ ሻ ሺ ሻ ʹ ʹ ʹ ൌ c. Ta có : ܽ െ ܾ ܾ െ ܿ ܿ െ ܽ ൌ ʹ ʹ ʹ 63 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác Mặt khác, ta có :
ܽ ൌ െ ܾ െ ܿ ൌ ݎ ൬ ൰Ǣ ܾ ൌ ݎ ൬ ൰ ʹ ʹ ʹ ʹ
ฺ ܽ െ ܾ ൌ ݎ ൬ െ ൰ ฺ ሺܽ െ ܾሻ ൌ ݎ ൬ െ ൰ ʹ ʹ ʹ ʹ ʹ ʹ Tương tự :
ሺܾ െ ܿሻ ൌ ݎ ൬ െ ൰ ʹ ʹ ʹ ʹ
ሺܿ െ ܽሻ ൌ ݎ ൬ െ ൰ ʹ ʹ ʹ ʹ
Cộng 3 đẳng thức trên, ta có được điều phải chứng minh.
Bài 7: Với ݊ א Ժ. Ta có một số đẳng thức tổng quát trong tam giác
Ǥ ሺʹ݊ ͳሻ ሺʹ݊ ͳሻ ሺʹ݊ ͳሻ
ൌ ሺെͳሻͶ ሺʹ݊ ͳሻ ሺʹ݊ ͳሻ ሺʹ݊ ͳሻ ʹ ʹ ʹ
Ǥ ʹ݊ ʹ݊ ʹ݊ ൌ ሺെͳሻାଵͶ ݊ ݊ ݊
Ǥ ଶ ݊ ଶ ݊ ଶ ݊ ൌ ʹ ሺെͳሻାଵʹ ݊ ݊ ݊
Ǥ ሺʹ݊ ͳሻ ሺʹ݊ ͳሻ ሺʹ݊ ͳሻ
ൌ ͳ ሺെͳሻͶ ሺʹ݊ ͳሻ ሺʹ݊ ͳሻ ሺʹ݊ ͳሻ ʹ ʹ ʹ
Ǥ ʹ݊ ʹ݊ ʹ݊ ൌ െͳ ሺെͳሻͶ ݊ ݊ ݊
Ǥ ଶ ݊ ଶ ݊ ଶ ݊ ൌ ͳ ሺെͳሻʹ ݊ ݊ ݊ Giải: a. Ta có :
ሺʹ݊ ͳሻ ሺʹ݊ ͳሻ
ሺʹ݊ ͳሻ െ ሺʹ݊ ͳሻ ൌ ʹ ʹ ʹ
ʹ ሺʹ݊ ͳሻ ሺʹ݊ ͳሻ ʹ ʹ െ ൌ ʹ ሺʹ݊ ͳሻ ሺʹ݊ ͳሻ
ʹ ሺʹ݊ ͳሻ ሺʹ݊ ͳሻ ʹ ʹ ʹ ʹ Ta xét : ߨ ߨ ൌ െ ฺ ሺʹ݊ ͳሻ
ൌ ሺʹ݊ ͳሻ ൬ െ ൰ ʹ ʹ ʹ ʹ ʹ ʹ 64 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác ߨ ߨ ฺ ሺʹ݊ ͳሻ
ൌ ሺʹ݊ ͳሻ ൬ െ ൰ ൌ ൬݊ߨ െ ሺʹ݊ ͳሻ ൰ ʹ ʹ ʹ ʹ ʹ
ൌ ሺെͳሻ ሺʹ݊ ͳሻ ʹ Tương tự vậy, ta có : ߨ
ሺʹ݊ ͳሻ ൌ ሺʹ݊ ͳሻ ൬ െ ൰ ʹ ʹ ʹ ߨ
ฺ ሺʹ݊ ͳሻ ൌ ൬݊ߨ െ ሺʹ݊ ͳሻ
൰ ൌ ሺെͳሻ ሺʹ݊ ͳሻ ʹ ʹ ʹ ʹ Suy ra െ
ൌ ʹǤ ሺെͳሻ ሺʹ݊ ͳሻ ሺʹ݊ ͳሻ ൬ ൰ ሺʹ݊ ͳሻ ൬ ൰൨ ʹ ʹ ʹ
ൌ ሺെͳሻͶ ሺʹ݊ ͳሻ ሺʹ݊ ͳሻ ሺʹ݊ ͳሻ ʹ ʹ ʹ b. Ta có :
ൌ ʹ ݊ሺ ሻ ݊ሺ െ ሻ ʹ ݊ ݊ Ta thấy :
ൌ ߨ െ ฺ ݊ሺ ሻ ൌ ݊ߨ െ ݊
ฺ ݊ሺ ሻ ൌ ሺ݊ߨ െ ݊ሻ ൌ ሺെͳሻାଵ ݊ Và
݊ ൌ ݊ߨ െ ݊ሺ ሻ ฺ ݊ ൌ ൫݊ߨ െ ݊ሺ ሻ൯ ൌ ሺെͳሻ ݊ሺ ሻ Suy ra
ൌ ʹሺെͳሻାଵ ݊ ݊ሺ െ ሻ ʹሺെͳሻ ݊ሺ ሻ ݊
ൌ ʹሺെͳሻ ݊ ሾ ݊ሺ ሻ െ ݊ሺ െ ሻሿ
ൌ ሺെͳሻାଵͶ ݊ ݊ ݊ c. Ta có : ͳ െ ʹ݊ ͳ െ ʹ݊ ൌ ͳ െ ଶ ݊ ʹ ʹ ͳ
ൌ ʹ െ ሺ ʹ݊ ʹ݊ሻ െ ଶ ݊ ʹ
ൌ ʹ െ ݊ሺ ሻ ݊ሺ െ ሻ െ ଶ ݊
ൌ ʹ െ ሺെͳሻ ݊ ሾ ݊ሺ െ ሻ ݊ሺ ሻሿ
ൌ ʹ ሺെͳሻାଵʹ ݊ ݊ ݊ d. Ta có : െ ൌ ʹ ሺʹ݊ ͳሻ ሺʹ݊ ͳሻ
ͳ െ ʹ ଶሺʹ݊ ͳሻ ʹ ʹ ʹ Mà ߨ ሺʹ݊ ͳሻ
ൌ ሺʹ݊ ͳሻ ൬ െ ൰ ʹ ʹ ʹ 65 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác ߨ ߨ ฺ ሺʹ݊ ͳሻ
ൌ ሺʹ݊ ͳሻ ൬ െ ൰ ൌ ൬݊ߨ െ ሺʹ݊ ͳሻ ൰ ʹ ʹ ʹ ʹ ʹ
ൌ െͳǤ ሺെͳሻିଵ ሺʹ݊ ͳሻ ൌ ሺെͳሻ ሺʹ݊ ͳሻ ʹ ʹ Và ߨ
ሺʹ݊ ͳሻ ൌ ሺʹ݊ ͳሻ ൬ െ ൰ ʹ ʹ ʹ ߨ ߨ
ฺ ሺʹ݊ ͳሻ ൌ ሺʹ݊ ͳሻ ൬ െ
൰ ൌ ൬݊ߨ െ ሺʹ݊ ͳሻ ൰ ʹ ʹ ʹ ʹ ʹ
ൌ ሺെͳሻ ሺʹ݊ ͳሻ ʹ Suy ra െ
ൌ ͳ ʹሺെͳሻ ሺʹ݊ ͳሻ ሺʹ݊ ͳሻ െ ሺʹ݊ ͳሻ ൨ ʹ ʹ ʹ
ൌ ͳ ሺെͳሻͶ ሺʹ݊ ͳሻ ሺʹ݊ ͳሻ ሺʹ݊ ͳሻ ʹ ʹ ʹ e. Ta có :
ൌ ʹ ݊ሺ ሻ ݊ሺ െ ሻ ʹ ଶ ݊ െ ͳ
ൌ ʹ ሺ݊ߨ െ ݊ሻ ݊ሺ െ ሻ ʹ ଶ ݊ െ ͳ
ൌ െͳ ʹሺെͳሻ ݊ ሾ ݊ሺ െ ሻ ݊ሺ ሻሿ
ൌ െͳ ሺെͳሻͶ ݊ ݊ ݊ f. Ta có : ͳ ʹ݊ ͳ ʹ݊ ͳ ൌ
ଶ ݊ ൌ ͳ ሺ ʹ݊ ʹ݊ሻ ଶ ݊ ʹ ʹ ʹ
ൌ ͳ ݊ሺ ሻ ݊ሺ െ ሻ ଶ ݊
ൌ ͳ ሺ݊ߨ െ ݊ሻ ݊ሺ െ ሻ ଶ ݊
ൌ ͳ ሺെͳሻ ݊ ݊ሺ െ ሻ ሺെͳሻ ݊ ݊ሺ ሻ
ൌ ͳ ሺെͳሻ ݊ ሾ ݊ሺ െ ሻ ݊ሺ ሻሿ
ൌ ͳ ሺെͳሻʹ ݊ ݊ ݊
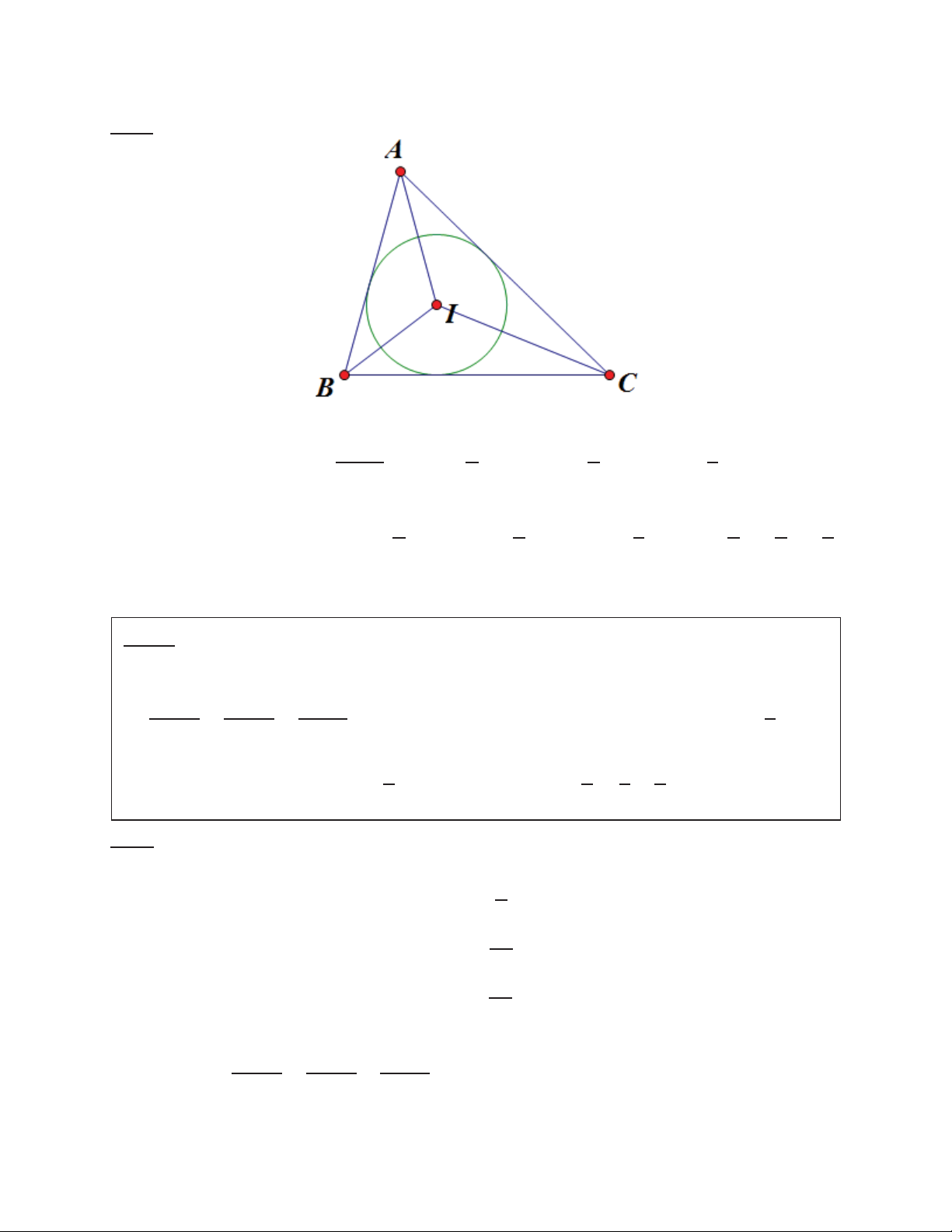
Bài 8: Gọi là tâm đường tròn nội tiếp tam giác . Đặt ݔ ൌ ǡ ݕ ൌ ǡ ݖ ൌ . Chứng minh rằng ൌ Ͷ ݔ ݕ ݖ 66 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác Giải: Ta có : ݔ ൌ ͳͺͲ୭ െ
ൌ ͻͲ୭ ǡ ݕ ൌ ͻͲ୭ ǡ ݖ ൌ ͻͲ୭ ʹ ʹ ʹ ʹ Suy ra
Ͷ ݔ ݕ ݖ ൌ Ͷ ൬ͻͲ୭ ൰ ൬ͻͲ୭ ൰ ൬ͻͲ୭ ൰ ൌ Ͷ ʹ ʹ ʹ ʹ ʹ ʹ ൌ
Bài 9: Cho tam giác có 3 góc ǡ ǡ theo thứ tự tạo thành cấp số nhân công bội ݍ ൌ ʹ. Chứng minh ͳ ͳ ͳ ͳ Ǥ ൌ ͺ Ǥ ൌ െ ଶ ଶ ଶ ͺ ͷ ͳ ͳ ͳ
Ǥ ଶ ଶ ଶ ൌ Ǥ ൌ Ͷ ܽ ܾ ܿ Giải:
Từ giả thuyết, ta suy ra ߨ ۓ ൌ ۖ ʹߨ ൌ ۔ ۖ Ͷߨ ە ൌ a. Ta có : ͳ ͳ ͳ
ൌ ଶ ଶ ʹ ଶ Ͷ ͵ ଶ ଶ ଶ 67 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
ൌ ሺଶ െ ͳሻ ሺଶ ʹ െ ͳሻ ሺଶ Ͷ െ ͳሻ ʹ Ͷ ͺ ൌ ଶ ଶ ʹ ଶ Ͷ ʹ ʹ ʹ Ͷ ʹ ʹ ͺ Ͷ ൌ ʹ ଶ ʹ ଶ ʹ ʹ ʹ ଶ Ͷ Ͷ
ൌ ʹ ʹ ʹ Ͷ ʹ ʹ ͺ Ͷ ൌ ʹሺ ሻ
(vì ͺ ൌ ሺߨ ሻ ൌ )
Mặt khác, trong tam giác ta luôn có : ൌ ͳ Nên ൌ ͺ.
Do đó, ta có điều phải chứng minh. b. Ta có : ʹ Ͷ ͺ ͺ ͳ ൌ ʹ Ͷ ൌ Ǥ Ǥ ൌ ൌ െ ʹ ʹ ʹ ʹ Ͷ ͺ ͺ
(vì ͺ ൌ ሺߨ ሻ ൌ െ )
Vậy ta có điều phải chứng minh. c.
Trong tam giác , ta luôn có : ͳ ͷ
ଶ ଶ ଶ ൌ ͳ െ ʹ ൌ ͳ െ ʹ ൬െ ൰ ൌ ͺ Ͷ
Vậy ta có điều phải chứng minh. d.
Theo định lý hàm số sin, điều cần chứng minh tương đương với ͳ ͳ ͳ ൌ ߨ ʹߨ Ͷߨ Ta có : ʹߨ Ͷߨ ͵ߨ ߨ ߨ ͳ ͳ ʹ ʹ ͳ ʹߨ ൌ Ͷߨ ʹߨ Ͷߨ ൌ ʹߨ ͵ߨ ൌ ߨ ߨ ൌ ߨ ʹ
Vậy ta có điều phải chứng minh. 68 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác Bài 10: Ǥ
Cho tam giác , ൌ ܽǡ ൌ ܾǡ ൌ ܿ. Chứng minh rằng ʹܾ ൌ ܽ ܿ ൌ ͵ ʹ ʹ (ĐH Cần Thơ 1998) b.
Chứng minh rằng : trong tam giác nếu ǡ ǡ theo thứ tự tạo
thành cấp số cộng thì ܽଶǡ ܾଶǡ ܿଶ cũng tạo thành cấp số cộng.
(ĐH Thương Mại Hà Nội 2000) c.
Cho tam giác có ܽଶ ܾଶ െ ܿଶ ൌ Ͷܴଶ. Chứng minh rằng ͳ ൌ ଶ െ ͳ
(Tạp chí “Toán học và Tuổi trẻ”) Giải: a.
Ta có giả thuyết tương đương với ൌ ͵ ʹ ʹ ʹ ʹ ʹ ൬ െ ൰ ൌ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ െ ʹ ൌ ʹ ʹ െ ʹ ൌ ʹ ʹ ʹ ʹ െ Ͷ ൌ ʹ ʹ ʹ ʹ ʹ ʹ ൌ
Theo định lý hàm số sin, ta có điều phải chứng minh. b.
ǡ ǡ lập thành cấp số cộng ൌ ʹ ሺ ሻ ʹ ൌ ଶ ൌ ʹ
ଶ ൌ ሾሺ െ ሻ ሿ
ଶ ൌ െ ሺ ሻ ሺ െ ሻ ଶ 69 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác ͳ
ଶ ൌ ͳ െ ଶ െ ሺ ʹ ʹሻ ʹ ͳ
ʹ ଶ ൌ ͳ െ ሺͳ െ ʹ ଶ ͳ െ ʹ ଶ ሻ ʹ ʹ ଶ ൌ ଶ ଶ
Theo định lý hàm số sin, ta có điều phải chứng minh. c.
Theo định lý hàm số sin, ta suy ra ܽଶ ܾଶ ܿଶ ൌ ൌ ൌ Ͷܴଶ ଶ ଶ ଶ
Áp dụng tính chất tỷ lệ thức, ta có : ܽଶ ܾଶ െ ܿଶ ൌ Ͷܴଶ ଶ ଶ െ ଶ Ͷܴଶ ฺ ൌ Ͷܴଶ ଶ ଶ െ ଶ
ฺ ଶ ଶ ൌ ͳ ଶ ͳ
െ ሺ ʹ ʹሻ ൌ ଶ ʹ ሺ െ ሻ ൌ ଶ
Ở đẳng thức này ta thấy được ǡ ሺ െ ሻ ് Ͳ nên ሺ െ ሻ ൌ ൌ ሺ ሻ
Giả sử ൌ Ͳ thì ሺ ሻ ሺ െ ሻ ൌ Ͳ hay ሺ െ ሻ ൌ . Khi
đó ൌ ͻͲ୭ǡ ൌ ൌ Ͷͷ୭
Mặt khác, do ് Ͳ nên ് .
Đến đây, ta có được mâu thuẫn. Do đó : ͳ ͳ ሺ ሻ ൌ ൌ ͳ െ ͳ െ (vì ് ฺ ് ͳ) ͳ ൌ ሺ ሻ ൌ ଶ ͳ െ
Bài 11: Cho tam giác có là tâm đường tròn nội tiếp. Chứng minh các đẳng thức sau : ݎ Ǥͳ ൌ ܴ Ǥ݉ଶ ଶ ଶ
݉ ݉ ൌ ͵ܴଶሺʹ ʹ ሻ 70 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác ͳ ͳ ͳ ͳ ͳ ͳ Ǥ ൬ ൰ ݈ ൰ ݈ ൰ ݈ ൰ ܽ ܾ ൬ܾ ܿ ൬ܿ ܽ ൌ ʹ ൬ ʹ ʹ ʹ Ǥܽ ൌ ʹ ʹ ʹ ǤǤ Ǥ ൌ Ͷܴݎଶ Giải: a. Ta cần chứng minh : ݎ ൌ Ͷ ܴ ʹ ʹ ʹ Thật vậy, ta có : ͳ ܾܽ
ܵ ൌ ܾܽ ൌ ݎ ฺ ݎ ൌ ʹ ܽ ܾ ܿ
Mà theo định lý hàm số sin, ta được : ܾܽ ʹܴ ʹܴ ݎ ൌ ൌ ܽ ܾ ܿ ʹܴሺ ሻ Suy ra ݎ Ͷ ൌ ܴ Mặt khác, ta lại có : ൌ ʹ ʹ ʹ ൞ ʹ ʹ ʹ ʹ ʹ ʹ ൌ Ͷ ʹ ʹ ʹ Do đó, ݎ ൌ Ͷ ܴ ʹ ʹ ʹ ݎ ฺ ͳ ൌ ͳ Ͷ ൌ ܴ ʹ ʹ ʹ b. Ta có : ʹܾଶ ʹܿଶ െ ܽଶ ʹܽଶ ʹܿଶ െ ܾଶ ʹܽଶ ʹܾଶ െ ܿଶ ͵ ൌ
ൌ ሺܽଶ ܾଶ ܿଶሻ Ͷ Ͷ Ͷ Ͷ
ൌ ͵ܴଶሺଶ ଶ ଶ ሻ ൌ ͵ܴଶሺʹ ʹ ሻ 71 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác c. Ta có : ܽ ܾ ܾ ܿ ܿ ܽ ൌ ݈ ݈ ݈
ܾܽ ܾܿ ܿܽ ܽ ܾ ʹܾܽ ܾ ܿ ʹܾܿ ܿ ܽ ʹܿܽ ൌ Ǥ Ǥ Ǥ ൌ ܾܽ ܽ ܾ ʹ ܾܿ ܾ ܿ ʹ ܿܽ ܿ ܽ ʹ d.
Theo định lý hàm số sin, ta có : ܽ ʹܴ Ͷܴ ͺܴ ൌ ʹǤ ൌ ൌ ʹ ʹ ൌ ʹ ܽ ܾ ܿ ʹܴሺ ሻ ͺܴ ʹ ʹ ʹ ʹ ʹ
Vậy ta có điều phải chứng minh. e.
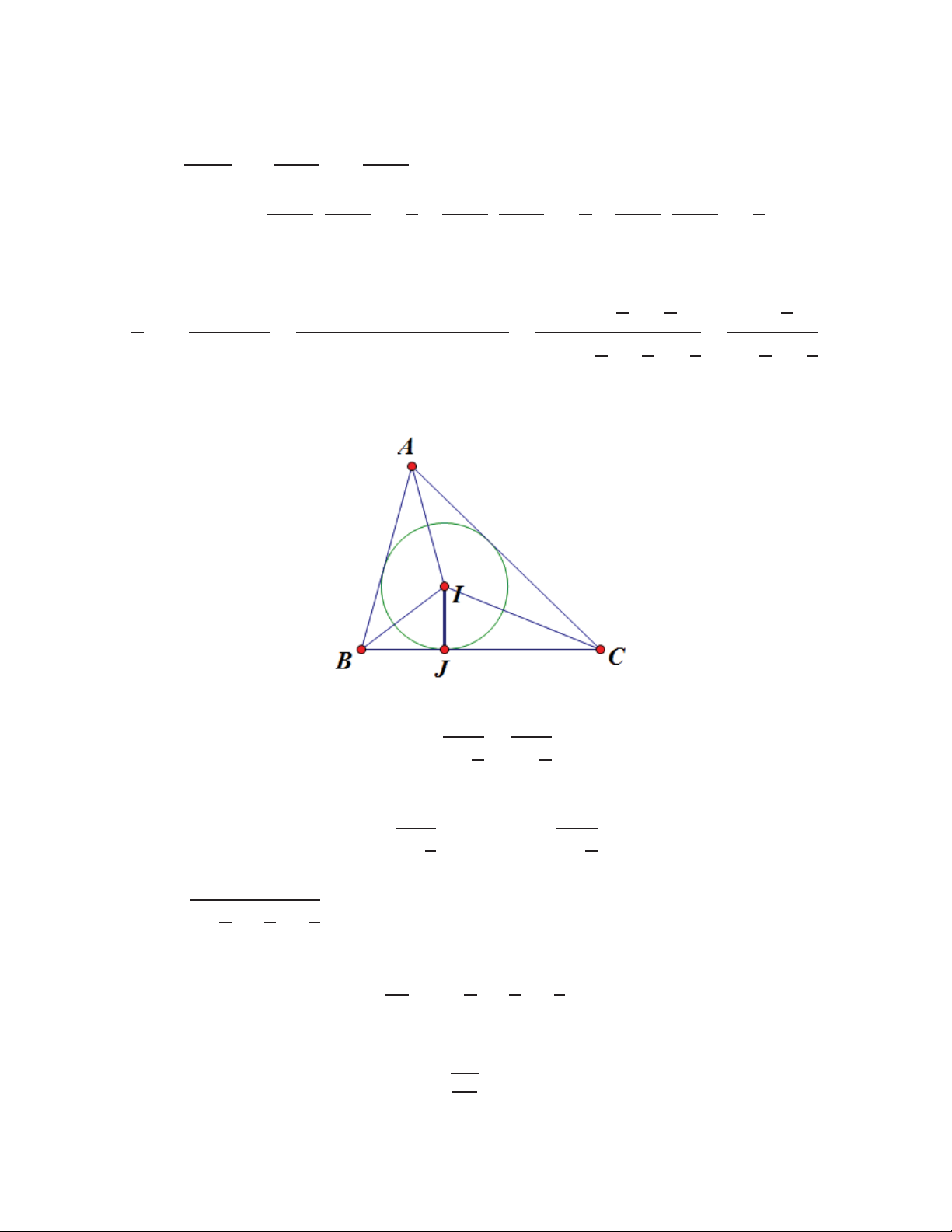
Ta thấy tam giác vuông tại nên ݎ ൌ ൌ ʹ ʹ Tương tự, ta có : ݎ ݎ ൌ Ǣ ൌ ʹ ʹ ݎଷ ฺ ൌ ʹ ʹ ʹ Mặt khác, ta lại có : ݎ ൌ Ͷܴ ʹ ʹ ʹ Nên ݎଷ ൌ ݎ ൌ Ͷܴݎଶ Ͷܴ 72 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
Bài 12: Cho tam giác . Chứng minh rằng ta luôn có :
ଶ ݎଶ ൌ ʹܴሺ݄ ݄ ݄ െ ʹݎሻ
(Đề nghị Olympic 30-4, 2007) Giải:
Trước hết ta sẽ chứng minh : ʹܴሺ݄ ݄ ݄ െ ʹݎሻ ൌ ܾܽ ܾܿ ܿܽ െ Ͷܴݎ Thật vậy ta có : ʹܵ ʹܵ ʹܵ
Ͷܴܵሺܾܽ ܾܿ ܿܽሻ
ʹܴሺ݄ ݄ ݄ሻ ൌ ʹܴ ൬ ൰ ൌ ൌ ܽ ܾ ܿ ܽ ܾ ܿ ܾܽܿ
֜ ʹܴሺ݄ ݄ ݄ െ ʹݎሻ ൌ ܾܽ ܾܿ ܿܽ െ Ͷܴݎ ֜ ଶ ݎଶ Ͷܴݎ ൌ ܾܽ ܾܿ ܿܽ Lại có : ʹݎ ʹ ܽ െ ܽ ൌ ʹ ֜ ൌ ʹܴ ͳ ଶ ݎଶ ʹ ͳ ሺ െ ܽሻଶ
֜ ܽଷ െ ʹܽଶ ሺଶ ݎଶ Ͷܴݎሻܽ െ Ͷܴݎ ൌ Ͳ
Tương tự thì ta cũng có :
ܾଷ െ ʹܾଶ ሺଶ ݎଶ Ͷܴݎሻܾ െ Ͷܴݎ ൌ Ͳ
ܿଷ െ ʹܿଶ ሺଶ ݎଶ Ͷܴݎሻܿ െ Ͷܴݎ ൌ Ͳ
Vậy ܽǡ ܾǡ ܿ là nghiệm của phương trình sau :
ݐଷ െ ʹݐଶ ሺଶ ݎଶ Ͷܴݎሻݐ െ Ͷܴݎ ൌ Ͳ
Theo định lý Viète thì :
ܾܽ ܾܿ ܿܽ ൌ ଶ ݎଶ Ͷܴݎ
Vậy ta có điều phải chứng minh. 73 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
Bài 13: Chứng minh rằng trong tam giác ta luôn có : a.
ݎ ݎ ݎ ൌ Ͷܴ ݎ b.
ݎ ݎ ݎ ൌ Ͷܴ ݎ c. ݎݎݎ ൌ ݎଶ d.
ݎଶሺݎݎ ݎݎ ݎݎሻ ൌ ܵଶ e.
ሺܾ ܿሻସ െ ʹሺܽଶ ʹ݈ଶ ଶ
ሻሺܾ ܿሻଶ ܽଶሺܽଶ Ͷ݄ሻ ൌ Ͳ Giải: a. Ta có : ͳ ͳ ͳ ͳ െ ܽ െ ܾ െ ܿ
ݎ ݎ ݎ െ ݎ ൌ ܵ ൬ െ ൰ ൌ ܵ ൨ െ ܽ െ ܾ െ ܿ ሺ െ ܽሻሺ െ ܾሻ ሺ െ ܿሻ ͳ ͳ
ሺ െ ܿሻ ሺ െ ܽሻሺ െ ܾሻ ൌ ܵܿ ൨ ൌ ܵܿ
ሺ െ ܽሻሺ െ ܾሻ ሺ െ ܿሻ
ሺ െ ܽሻሺ െ ܾሻሺ െ ܿሻ ܿ ܾܽܿ
ൌ ሾʹଶ െ ሺܽ ܾ ܿሻ ܾܽሿ ൌ ൌ Ͷܴ ܵ ܵ b. Ta có : ͳ ͳ ܿ
ݎ ݎ ݎ െ ݎ ൌ ܵܿ െ
൨ ൌ ሾሺܽ ܾ ܿሻ െ ܾܽሿ ሺ െ ܽሻሺ െ ܾሻ ሺ െ ܿሻ ܵ ܿ ͳ
ൌ ሺܽ ܾ ܿሻሺܽ ܾ െ ܿሻ െ ܾܽ൨ ܵ ʹ ʹܴଶܿ ൌ ሾሺ ܾܽܿ
ሻሺ െ ሻ െ ʹ ሿ Ͷܴ ͺܴଷ ൌ ൬Ͷ Ͷ െ ʹ ൰ ܾܽ ʹ ʹ ʹ ʹ ʹ ʹ ͺܴଷ ͺܴଷ ൌ ൬Ͷ ଶ െ ʹ ൰ ൌ ൬Ͷ ଶ െ ʹ൰ ܾܽ ʹ Ͷܴଶ ʹ ൌ Ͷܴ c. Ta có : ܵଷ ܵଶݎ ൌ ൌ ൌ ݎଶ
ሺ െ ܽሻሺ െ ܾሻሺ െ ܿሻ ܵଶ d. Ta có : ͳ ͳ ͳ ൌ ܵଶݎଶ ൨
ሺ െ ܽሻሺ െ ܾሻ ሺ െ ܾሻሺ െ ܿሻ ሺ െ ܿሻሺ െ ܽሻ 74 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
െ ܽ െ ܾ െ ܿ ܵଶݎଶ ൌ ܵଶݎଶ ൌ ൌ ଶݎଶ ൌ ܵଶ
ሺ െ ܽሻሺ െ ܾሻሺ െ ܿሻ ܵଶ e. Ta có :
ൌ ሺܾ ܿሻସ െ ʹܽଶሺܾ ܿሻଶ ܽସ െ Ͷ݈ଶ ଶ
ሺܾ ܿሻଶ Ͷܽଶ݄ Ͷܾଶܿଶ
ൌ ሾሺܾ ܿሻଶ െ ܽଶሿଶ െ Ͷሺܾ ܿሻଶǤ ଶ ͳܵଶ ሺܾ ܿሻଶ ʹ Ͷܾଶܿଶ ͳ
ൌ ሺܾ ܿ െ ܽሻଶሺܾ ܿ ܽሻଶ െ Ͷሺܾ ܿሻଶǤ Ǥ ͳܵଶ ሺܾ ܿሻଶ ʹ ܾଶ ܿଶ െ ܽଶ
ൌ ሺܾ ܿ െ ܽሻଶሺܾ ܿ ܽሻଶ െ ͺܾଶܿଶ ቆͳ ቇ ͳܵଶ ʹܾܿ
ൌ ሺܾ ܿ െ ܽሻଶሺܾ ܿ ܽሻଶ െ Ͷܾܿሾሺܾ ܿሻଶ െ ܽଶሿ ͳܵଶ
ൌ ሺܾ ܿ െ ܽሻଶሺܾ ܿ ܽሻଶ െ Ͷܾܿሺܾ ܿ െ ܽሻሺܾ ܿ ܽሻ ͳܵଶ
ൌ ሺܾ ܿ െ ܽሻሺܾ ܿ ܽሻሺܾ െ ܿ െ ܽሻሺܾ െ ܿ ܽሻ ͳܵଶ
Mặt khác, theo công thức Heron, ta có :
ܽ ܾ ܿ ܾ ܿ െ ܽ ܽ ܿ െ ܾ ܽ ܾ െ ܿ
ܵଶ ൌ ሺ െ ܽሻሺ െ ܾሻሺ െ ܿሻ ൌ Ǥ Ǥ Ǥ ʹ ʹ ʹ ʹ
Suy ra ͳܵଶ ൌ ሺܽ ܾ ܿሻሺܾ ܿ െ ܽሻሺܽ ܿ െ ܾሻሺܽ ܾ െ ܿሻ Vậy ൌ Ͳ.
Bài 14: Chứng minh rằng trong tam giác , ta luôn có ʹݎ ͳ Ǥ ൌ ͳ െ ൌ ʹ ʹ ݄ ʹݎ ݄ ͳ
Ǥ ሺ െ ܽሻଶ ሺ െ ܾሻଶ ሺ െ ܿሻଶ
ൌ ݎሺʹܴ െ ݎሻሺ ሻ Giải: a. Ta có : ʹݎ ʹܵ ܽ ʹܽ Ͷܴ ͳ െ ൌ ͳ െ Ǥ ൌ ͳ െ ൌ ͳ െ ݄ ʹܵ ܽ ܾ ܿ ʹܴሺ ሻ ͺܴ ൌ ͳ െ ʹ ʹ ʹ ൌ ͳ െ ͺܴ ʹ ʹ ʹ ʹ ʹ 75 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác ൌ ͳ െ ʹ ʹ െ ʹ ʹ ൌ ʹ ʹ ʹ ʹ Ta lại có : ʹݎ ʹܵ ܽ ܽ ʹܽ Ͷܴ ൌ Ǥ ൌ ൌ ൌ ൌ ʹ ʹ ݄ െ ܽ ʹܵ െ ܽ ܾ ܿ െ ܽ ʹܴሺ െ ሻ ʹ ʹ ʹ ൌ ʹ ʹ ʹ െ ʹ ʹ ൌ ൌ െ ͳ ʹ ʹ ʹ ʹ ʹ ʹ Suy ra ͳ ͳ ʹݎ ൌ ൌ ʹ ʹ ݄ ͳ ʹ ʹ െ ͳ ͳ b. Ta có :
ൌ ݎሺʹܴ ʹܴ ʹܴ ሻ െ ݎଶሺ ሻ
ൌ ݎሺܽ ܾ ܿሻ െ ݎଶሺ ሻ
ൌ ʹݎ െ ݎଶሺ ሻ ൌ ʹܵ െ ݎଶሺ ሻ
Do đó, điều cần chứng minh tương đương với
ሺ െ ܽሻଶ ሺ െ ܾሻଶ ሺ െ ܿሻଶ ൌ ʹܵ െ ݎଶሺ ሻ
ሾሺ െ ܽሻଶ ݎଶሿ ሾሺ െ ܾሻଶ ݎଶሿ ሾሺ െ ܿሻଶ ݎଶሿ ൌ ʹܵ Mặt khác, ta thấy : ʹ
ሾሺ െ ܽሻଶ ݎଶሿ ൌ ሺ െ ܽሻଶ ൬ͳ ଶ ൰ ൌ ʹ ʹ ሺ െ ܽሻଶ ʹ ଶ ʹ ܵ െ ܽ ܾ ܿ െ ܽ ൌ ʹ ሺ െ ܽሻǤ ʹ ൌ ʹܵǤ ൌ ʹܵǤ ܾ ܿ ܽ ʹ െ Ͷ ൌ ʹܵǤ ൌ ʹܵǤ ʹ ʹ ʹ ൌ ʹܵ Ͷ ʹ ʹ ʹ ʹ ʹ Tương tự vậy, ta có :
ሾሺ െ ܾሻଶ ݎଶሿ ൌ ʹܵ ʹ ʹ
ሾሺ െ ܿሻଶ ݎଶሿ ൌ ʹܵ ʹ ʹ 76 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác Mà ta lại có : ൌ ͳ ʹ ʹ ʹ ʹ ʹ ʹ
Vậy cộng 3 đẳng thức trên, ta có được điều phải chứng minh. - BÀI TẬP TỰ LUYỆN
3.1.1. Cho tam giác . Chứng minh rằng ͳ
Ǥܵ ൌ ሺܽଶ ʹ ܾଶ ʹሻ Ͷ Ǥ Ͷ Ͷ Ͷ Ͷ Ͷ Ͷ Ͷ Ͷ Ͷ ൌ ͳ Ͷ Ͷ Ͷ
Ǥሺܽ ܾሻ ሺܾ ܿሻ ሺܿ ܽሻ ൌ ʹ
Ǥܾܽሺܽ ܾሻ ܾܿሺܾ ܿሻ ܿܽሺܿ ܽሻ ൌ ܽଷ ܾଷ ܿଷ ͵ ͵ ͵
Ǥ ଷ ଷ ଷ ൌ ͳ ͵ െ ʹ ʹ ʹ ʹ ʹ ʹ
3.1.2. Cho tam giác , ൌ ܽǡ ൌ ܾǡ ൌ ܿ và ͷ ൌ ͳ ʹ ʹ
Chứng minh rằng ͵ܿ ൌ ʹሺܽ ܾሻ. (ĐH Cần Thơ 2000)
3.1.3. Cho tam giác có : ܿ ݉ ൌ ് ͳ ܾ ݉
Chứng minh rằng : ʹ ൌ . (ĐH Tổng Hợp 1995)
3.1.4. Cho tam giác có ݈ ൌ ݈. Chứng minh rằng ܽ ൌ ܾ.
(Định lý Steiner(6) – Lehmus(7))
3.1.5. Cho tam giác thỏa hệ thức : ൌ ʹ ʹ ʹ Chứng minh rằng : 77 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác ͳ Ǥ ൌ ʹ ʹ ʹ ͳ Ǥ ൌ ʹ ʹ ʹ ʹ ʹ (ĐH Dược Hà Nội 1998)
3.1.6. Cho tam giác có ܽସ ൌ ܾସ ܿସ. Chứng minh rằng tam giác nhọn và ൌ ʹ ଶ .
3.1.7. Trong tam giác , chứng minh rằng : Ǥݎ ൌ ݎ Ͷܴ ଶ ʹ ݎ Ǥ ൌ ʹ
ඥሺݎ ݎሻሺݎ ݎሻ ʹܴ ݎ െ ݎ Ǥ ൌ ʹܴ Ǥ ൌ ܾ ܿ ܽ ܿ ܾ ܽ ʹܴ
Ǥ ሺܾ െ ܿሻሺ െ ܽሻ ሺܿ െ ܽሻሺ െ ܾሻ ሺܽ െ ܾሻሺ െ ܿሻ ൌ Ͳ -
GỢI Ý GIẢI BÀI TẬP TỰ LUYỆN 3.1.1. a.
Theo định lý hàm số sin, ta có :
ͳ ሺܽଶ ʹ ܾଶ ʹሻ ൌ ܴଶሺଶ ʹ ଶ ʹሻ Ͷ
ൌ ʹܴଶ ሺ ሻ ൌ ʹܴଶ ͳ ൌ ܾܽ ൌ ܵ ʹ b. Cần chứng minh Ͷ Ͷ ͳ െ Ͷ ൌ ͳ െ Ͷ Ͷ ͳ Ͷ c.
Áp dụng định lý các hình chiếu d.
Áp dụng định lý hàm số cos e. Sử dụng công thức ൌ ͳ Ͷ ʹ ʹ ʹ 78 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
3.1.2. Để ý, từ giả thuyết ta có : Ͷ ൌ െ ʹ ʹ ʹ ʹ ʹ ʹ െ ʹ ൬ െ ൰ ൌ ʹ ʹ ʹ െ ͵ ൬ʹ ൰ ൌ Ͷ ʹ ʹ ʹ ʹ ͵ ൌ ʹሺ ሻ 3.1.3. Để ý : ܿଶ ݉ଶ
ʹሺܽଶ ܿଶሻ െ ܾଶ ൌ ൌ
ʹܽଶ ൌ ܾଶ ܿଶ ܾଶ ݉ଶ
ʹሺܽଶ ܾଶሻ െ ܿଶ
3.1.4. Ta sử dụng công thức về độ dài phân giác trong : ʹܿܽ ሺ െ ܾሻ ʹܾܽ ሺ െ ܿሻ ݈ ඨ ൌ ඨ ൌ ݈ ܿ ܽ ܿܽ ܽ ܾ ܾܽ
ܽሺܽ ܾ ܿሻሾሺܽ ܾ ܿሻሺܽଶ ʹܾܿሻ ʹܾܽܿሿሺܾ െ ܿሻ ൌ Ͳ ܾ ൌ ܿ 3.1.5. a. Để ý : ൌ ൌ െ ʹ ʹ ʹ ʹ ʹ ʹ b. Sử dụng đẳng thức : ൌ ͳ ʹ ʹ ʹ ʹ ʹ ʹ
3.1.6. Từ giả thuyết, ta có ܽ ൌ ሼܽǡ ܾǡ ܿሽ. Do đó
ቄܾଶ ൏ ܽଶ ฺ ቄܾସ ൏ ܽଶܾଶ ฺ ܽସ ൌ ܾସ ܿସ ൏ ܽଶሺܾଶ ܿଶሻ ܿଶ ൏ ܽଶ ܿସ ൏ ܽଶܿଶ
ฺ ܽଶ ൏ ܾଶ ܿଶ ฺ Ͳ 79 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác Ͷܽଶܾܿ ൌ ൌ ʹܽଶ Ǥ ൌ ʹ ଶ
ܽସ െ ሺܾଶ െ ܿଶሻଶ ܾ ܿ 3.1.7. a. Ta có :
ݎ െ ݎ ൌ െ ሺ െ ܽሻ ൌ ܽ ൌ Ͷܴ ൌ Ͷܴ ଶ ʹ ʹ ʹ ʹ ʹ ʹ ʹ b. Để ý : ൌ ʹ ൌ ʹ ൌ ʹ ටቀ ʹ ʹቁ ቀ ʹ ʹቁ ඩ ʹ ʹ ଶ ʹ ʹ ʹ c. Để ý : ݎ െ ݎ Ͷܴ ଶ ൌ ͳ ൌ ͳ െ ʹ ൌ ʹܴ ʹܴ d.
Áp dụng định lý các hình chiếu. e. Ta có : ݎ
ሺܾ െ ܿሻሺ െ ܽሻ ൌ ʹܴሺ െ ሻ ʹ െ െ ൌ ʹܴݎǤ ʹ Ǥ ʹ Ǥ ൌ Ͷܴݎ ʹ ʹ ʹ ʹ ʹ ൌ ʹܴݎሺ െ ሻ Tương tự vậy, ta có :
ሺܿ െ ܽሻሺ െ ܾሻ ൌ ʹܴݎሺ െ ሻ
ሺܽ െ ܾሻሺ െ ܿሻ ൌ ʹܴݎሺ െ ሻ 80 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác 2.
CHỨNG MINH BẤT ĐẲNG THỨC LƯỢNG GIÁC TRONG TAM GIÁC
- Ngoài việc nhớ các đẳng thức cơ bản và áp dụng các kỹ thuật biến đổi để chứng
minh đẳng thức lượng giác vào dạng toán này, thì ta cũng nên nắm được một số kỹ
thuật chứng minh bất đẳng thức, chẳng hạn như :
x Dùng các quan hệ giữa cạnh và góc : Trong tam giác , ta có :
ܽ ൏ ܾ ൏ ܿ ൏ ܤ ൏ ܥ ቄͲ ൏ ൏ ൏
Từ tính chất trên, ta có được kết quả sau :
ሺܽ െ ܾሻሺ െ ሻ Ͳ ܽ ܾ ܽ ܾ
ሺܽ െ ܾሻሺ െ ሻ Ͳ ܽ ܾ ܽ ܾ
x Dùng các bất đẳng thức cổ điển : i.
Bất đẳng thức Cauchy(8) :
Cho ݊ số không âm : ܽଵǡ ܽଶǡ ǥ ǡ ܽሺ݊ א Ժǡ ݊ ʹሻ thì :
ܽଵ ܽଶ ǥ ܽ ݊ ඥܽଵܽଶ ǥ ܽ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi ܽଵ ൌ ܽଶ ൌ ǥ ൌ ܽ ii.
Bất đẳng thức Bunyakovsky(9) :
Cho hai dãy số thực : ܽଵǡ ܽଶǡ ǥ ǡ ܽሺ݊ א Ժǡ ݊ ʹሻ và ܾଵǡ ܾଶǡ ǥ ǡ ܾሺ݊ א Ժǡ ݊ ʹሻ thì : ଶ ଶ ଶ ȁܽ ଶ ଶ ଶ
ଵܾଵ ܽଶܾଶ ǥ ܾܽȁ ටሺܽଵ ܽଶ ǥ ܽሻሺܾଵ ܾଶ ǥ ܾሻ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi : ܽଵ ܽ ܽ ൌ ଶ ൌ ǥ ൌ ܾଵ ܾଶ ܾ iii.
Bất đẳng thức Chebyshev(10) :
Cho hai dãy số thực tăng : ܽଵ ܽଶ ǥ ܽ và ܾଵ ܾଶ ǥ ܾ thì :
ܽଵ ܽଶ ǥ ܽ ܾ ܽ
Ǥ ଵ ܾଶ ǥ ܾ ଵܾଵ ܽଶܾଶ ǥ ܾܽ ݊ ݊ ݊ 81 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
Cho dãy số thực tăng : ܽଵ ܽଶ ǥ ܽ và dãy số thực giảm ܾଵ ܾଶ ǥ ܾ thì :
ܽଵ ܽଶ ǥ ܽ ܾ ܽ
Ǥ ଵ ܾଶ ǥ ܾ ଵܾଵ ܽଶܾଶ ǥ ܾܽ ݊ ݊ ݊ ܽ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi ቄ ଵ ൌ ܽଶ ൌ ǥ ൌ ܽ ܾ ଵ ൌ ܾଶ ൌ ǥ ൌ ܾ iv.
Bất đẳng thức Bernoulli(11) :
Với ܽ െͳ thì với mọi א Գ :
ሺͳ ܽሻ ͳ ݊ܽ ܽ ൌ Ͳ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi ݊ ൌ Ͳ ݊ ൌ ͳ v.
Bất đẳng thức Jensen(12) :
Cho hàm số ݂ሺݔሻ có đạo hàm cấp 2 trong khoảng ൌ ሺܽǡ ܾሻ
Nếu với mọi ݔ א ǡ ݂ᇱᇱሺݔሻ Ͳ và ݔଵǡ ݔଶǡ ǥ ǡ ݔ א thì :
݂ሺݔଵሻ ݂ሺݔଶሻ ǥ ݂ሺݔሻ ݔ
݂ ൬ ଵ ݔଶ ǥ ݔ൰ ݊ ݊
Nếu với mọi ݔ א ǡ ݂ᇱᇱሺݔሻ ൏ Ͳ và ݔଵǡ ݔଶǡ ǥ ǡ ݔ א thì :
݂ሺݔଵሻ ݂ሺݔଶሻ ǥ ݂ሺݔሻ ݔ
݂ ൬ ଵ ݔଶ ǥ ݔ൰ ݊ ݊
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi ݔଵ ൌ ݔଶ ൌ ǥ ൌ ݔ
x Dùng đạo hàm để áp dụng tính chất đồng biến, nghịch biến của hàm số.
Tương tự như ở dạng chứng minh đẳng thức lượng giác trong tam giác, ở dạng này trước
hết ta cũng cần nắm rõ một số bất đẳng thức lượng giác cơ bản trong tam giác. 82 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
Bài 1: Cho tam giác , chứng minh rằng : ͵ξ͵ ͵ Ǥ Ǥ ʹ ʹ ͵ξ͵ ͳ Ǥ Ǥ ͺ ͺ ͵ ͵ξ͵ Ǥ Ǥ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ͳ ͵ξ͵ Ǥ Ǥ ʹ ʹ ʹ ͺ ʹ ʹ ʹ ͺ Giải: a. Ta có : െ ൌ ʹ ʹ ʹ ߨ െ ߨ െ Ͳ ߨ െ ฺ ͲͲ ͳ ʹ ʹ ʹ ʹ ʹ ʹ
Vậy ta chứng minh được ʹ ʹ Tương tự, ta có : ߨ ߨ ʹ ቌ ͵ቍ ͵ ʹ Suy ra ߨ ߨ ߨ ʹ ቌ ͵ቍ Ͷ ൬ ൰ ͵ ʹ ʹ Ͷ Ͷ ͳʹ ߨ ߨ ฺ Ͷ ͵ ͵ Do đó, ߨ ͵ξ͵ ͵ ൌ ͵ ʹ b. Ta có : െ ൌ ʹ ʹ ʹ 83 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác െ ൌ ͲͲ ͳ ʹ ʹ ʹ Suy ra ʹ ʹ Tương tự, ta có : ߨ ߨ ʹ ቌ ͵ቍ ͵ ʹ Do đó, ߨ ߨ ʹ ቌ ͵ቍ ͵ ʹ ʹ ߨ Ͷ ൬ ൰ Ͷ Ͷ ͳʹ Suy ra ߨ ߨ Ͷ ͵ ͵ Hay ߨ ͵ ͵ ൌ ͵ ʹ c.
Theo bất đẳng thức Cauchy, ta có : ଷ ଷ ͵ξ͵ ͵ξ͵ ൬ ൰ ቆ ቇ ൌ ͵ ͺ d. Ta thấy :
- Nếu tam giác có một góc tù thì bất đẳng thức hiển nhiên đúng.
- Nếu tam giác nhọn thì theo bất đẳng thức Cauchy, ta có : ଷ ͳ ൬ ൰ ൌ ͵ ͺ e.
Áp dụng bất đẳng thức cơ bản đã chứng minh ở câu a, ta được : ߨ ߨ ߨ ʹ ൬ ൰൨ Ͷ ൬ ൰ ʹ ʹ ʹ Ͷ Ͷ ͳʹ ͺ ͺ ʹͶ Suy ra ߨ ߨ Ͷ ʹ ʹ ʹ 84 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác Vậy ta được : ߨ ͵ ͵ ൌ ʹ ʹ ʹ ʹ f.
Áp dụng bất đẳng thức cơ bản đã chứng minh ở câu b, ta được : ߨ ߨ ʹ ൬ ൰൨ ʹ ʹ ʹ Ͷ Ͷ ͳʹ ߨ ߨ Ͷ ൬ ൰ ൌ Ͷ ͺ ͺ ʹͶ Suy ra ߨ ͵ξ͵ ͵ ൌ ʹ ʹ ʹ ʹ g.
Theo bất đẳng thức Cauchy, ta có : ଷ ͳ ቌ ʹ ʹ ʹቍ ൌ ʹ ʹ ʹ ͵ ͺ h.
Theo bất đẳng thức Cauchy, ta có : ଷ ଷ ξ͵ ͵ξ͵ ቌ
ʹ ʹ ʹቍ ൌ ቆ ቇ ൌ ʹ ʹ ʹ ͵ ʹ ͺ
Bài 2: Cho tam giác , chứng minh rằng : ͻ ͵
Ǥ ଶ ଶ ଶ Ǥ ଶ ଶ ଶ Ͷ Ͷ ͵ ͻ
Ǥ ଶ ଶ ଶ Ǥʹ ൏ ଶ ଶ ଶ ʹ ʹ ʹ Ͷ ʹ ʹ ʹ Ͷ ͻ Ǥ Ͷ ͵ Ǥ Ͷ ͵ Ǥ ʹ ʹ ʹ ʹ ʹ ʹ Ͷ 85 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác Giải: a. Ta có : ͳ െ ʹ ͳ െ ʹ ଶ ଶ ଶ ൌ ͳ െ ଶ ʹ ʹ ͳ
ൌ ʹ െ ሺ ʹ ʹሻ െ ଶ ʹ
ൌ ʹ െ ሺ ሻ ሺ െ ሻ െ ଶ ൌ ʹ ሾሺ െ ሻ െ ሿ
- Nếu góc tù thì ሾሺ െ ሻ െ ሿ ൏ Ͳ. Suy ra ͻ
ଶ ଶ ଶ ൏ ʹ ൏ Ͷ
- Nếu góc không tù thì ሺͳ െ ሻ ଶ ͻ
ଶ ଶ ଶ ʹ ሺͳ െ ሻ ʹ ቈ ൌ ʹ Ͷ b. Ta có : ͳ ʹ ͳ ʹ ଶ ଶ ଶ ൌ ଶ ʹ ʹ
ൌ ͳ ሺ ሻ ሺ െ ሻ ଶ ൌ ͳ െ ሾሺ െ ሻ െ ሿ
- Nếu góc tù thì െ ሾሺ െ ሻ െ ሿ Ͳ. Suy ra ͵
ଶ ଶ ଶ ͳ Ͷ
- Nếu góc không tù thì ͳ െ ଶ ͵
ଶ ଶ ଶ ͳ െ ሺͳ െ ሻ ͳ െ ൬ ൰ ൌ ʹ Ͷ c. Ta có : ͳ െ ͳ െ ͳ െ ଶ ଶ ଶ ൌ ʹ ʹ ʹ ʹ ʹ ʹ ͵ ͳ ͵ ͳ ͵ ͵
ൌ െ ሺ ሻ െ Ǥ ൌ ʹ ʹ ʹ ʹ ʹ Ͷ d. Ta có : ͳ ͳ ͳ ଶ ଶ ଶ ൌ ʹ ʹ ʹ ʹ ʹ ʹ ͵ ͳ ͻ ൌ ሺ ሻ ʹ ʹ Ͷ 86 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác Mặt khác : ͵ ͳ
ଶ ଶ ଶ ൌ ሺ ሻ ʹ ʹ ʹ ʹ ʹ ͵ ͳ
ൌ ൬ͳ Ͷ ൰ ൌ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ Ǣ Ǣ Ͳ ʹ ʹ ʹ e.
Theo bất đẳng thức Bunyakovsky, ta có : ͻ
ଶ ଶ ଶ Ͷ f. Ta có : ሺ ሻଶ
ൌ ଶ ଶ ଶ ʹሺ ሻ ͵ ʹሺ ሻ Ͷ Suy ra ͵ ͻ
ʹሺ ሻ ሺ ሻଶ Ͷ Ͷ Do đó, ͵ Ͷ g. Ta có : ଶ ൬ ൰ ʹ ʹ ʹ
ൌ ଶ ଶ ଶ ʹ ൬ ൰ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ͵ ʹ ൬ ൰ Ͷ ʹ ʹ ʹ ʹ ʹ ʹ Suy ra ͵ ͻ ʹ ൬ ൰ Ͷ ʹ ʹ ʹ ʹ ʹ ʹ Ͷ Do đó, ͵ ʹ ʹ ʹ ʹ ʹ ʹ Ͷ 87 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
Bài 3: Cho tam giác , chứng minh rằng : ͳ ͳ ͳ ͳ ͳ ͳ Ǥ ʹξ͵Ǥ ሺọnሻ ͳ ͳ ͳ ͳ ͳ ͳ Ǥ Ǥ ʹξ͵ ʹ ʹ ʹ ʹ ʹ ʹ ͳ ͳ ͳ ͳ ͳ ͳ Ǥ Ͷ Ǥ ͳʹ ଶ ଶ ଶ ଶ ଶ ଶ ͳ ͳ ͳ ͳ ͳ ͳ Ǥ ͳʹǤ Ͷ ଶ ʹ ଶ ʹ ଶ ʹ ଶ ʹ ଶ ʹ ଶ ʹ Giải: a.
Theo bất đẳng thức Cauchy, ta có : ͳ ͳ ͳ ͵ ͻ ͻ ʹξ͵ యξ ͵ξ͵ ʹ b.
Theo bất đẳng thức Cauchy, ta có : ͳ ͳ ͳ ͵ ͻ ͻ ൌ యξ ͵ ʹ c.
Theo bất đẳng thức Cauchy, ta có : ͳ ͳ ͳ ͵ ͻ య ʹ ට ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ d.
Theo bất đẳng thức Cauchy, ta có : ͳ ͳ ͳ ͵ ͻ ʹξ͵ య ʹ ʹ ʹ ට ʹ ʹ ʹ ʹ ʹ ʹ e.
Theo bất đẳng thức Cauchy, ta có : ͳ ͳ ͳ ͵ ͻ ͻ ൌ Ͷ ଶ ଶ ଶ ξ య ଶ ଶ ଶ ଶ ଶ ଶ ͻ Ͷ f.
Theo bất đẳng thức Cauchy, ta có : ͳ ͳ ͳ ͵ ͵ ൌ ͳʹ ଶ ଶ ଶ ξ య ଶ ଶ ଶ ͳ Ͷ 88 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác g.
Theo bất đẳng thức Cauchy, ta có : ͳ ͳ ͳ ͵ ͻǤͶ ൌ ͳʹ ଶ య ͵ ʹ ଶ ʹ ଶ ʹ ටଶ ʹଶ ʹଶʹ h.
Theo bất đẳng thức Cauchy, ta có : ͳ ͳ ͳ ͵ ͵ǤͶ ൌ Ͷ ଶ య ͵ ʹ ଶ ʹ ଶ ʹ ටଶʹଶʹଶʹ
Chú ý : Từ câu e, f, g, h ta rút ra được kết quả sau :
Ǥ ଶ ଶ ଶ ͳǤ ଶ ଶ ଶ ͻ
Ǥ ଶ ଶ ଶ ͻǤ ଶ ଶ ଶ ͳ ʹ ʹ ʹ ʹ ʹ ʹ
Bài 4: Cho tam giác , chứng minh rằng :
Ǥ ͵ξ͵ሺọሻ Ǥ ξ͵ሺọሻ
Ǥ ξ͵Ǥ ͵ξ͵ ʹ ʹ ʹ ʹ ʹ ʹ Giải: a. Ta có 2 cách chứng minh :
Cách 1: Sử dụng đẳng thức ൌ .
Theo bất đẳng thức Cauchy, ta có :
ሺ ሻଷ ʹ ൌ ʹሺ ሻ Suy ra ͵ξ͵ Cách 2: Ta có ሺ ሻ ൌ Mặt khác :
Ͳ ൏ ʹ ൌ ሺ ሻ ሺ െ ሻ ͳ ሺ ሻ ൌ ʹ ଶ ʹ 89 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác Nên ʹ ʹ ʹ ൌ ʹ ଶ ʹ ʹ Tương tự, ta được : ߨ ߨ ʹ ൬ ൰ ͵ ʹ Do đó, ߨ ߨ ߨ ʹ ൬ ൰൨ Ͷ ͵ ʹ ʹ ͵ Suy ra ߨ ͵ ൌ ͵ξ͵ ͵ b. Ta có : ሺ ሻଶ
ൌ ଶ ଶ ଶ ʹሺ ሻ ͳ ʹ ൌ ͵ Do đó, ξ͵ c. Ta có : ଶ ൬ ൰ ʹ ʹ ʹ
ൌ ଶ ଶ ଶ ʹ ൬ ൰ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ͵ ¯×ǡ ξ͵ ʹ ʹ ʹ d. Ta sử dụng đẳng thức ൌ ʹ ʹ ʹ ʹ ʹ ʹ
Theo bất đẳng thức Cauchy, ta có : ଷ
൬ ൰ ʹ ൌ ʹ ൬ ൰ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ Suy ra ͵ξ͵ ʹ ʹ ʹ 90 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
Bài 5: Chứng minh rằng trong tam giác , ta luôn có : a.
ʹሺܽ ܾ ܿ ሻ ܽ ܾ ܿ b.
ʹሺܽ ܾ ܿ ሻ ሺܽ ܾሻ ሺܾ ܿሻ ሺܿ ܽሻ c.
ͺ݉݉݉ ʹܴଷ (ĐH Ngoại Thương 1996) d. ܴ ʹݎ e. ଶ ܴଶ ͵ݎଶ
(Đề nghị Olympic 30-4, 2007) Giải: a.
Áp dụng định lý các hình chiếu, ta có : ܿ ൌ ܽ ܾ Mà
ሺܽ െ ܾሻሺ െ ሻ Ͳ ܽ ܾ ܽ ܾ
Suy ra ܽ ܾ ܿ. Tương tự, ta có : ܾ ܿ ܽ ܿ ܽ ܾ
Cộng 3 bất đẳng thức trên, ta suy ra được điều phải chứng minh.
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi tam giác đều. b. Ta có :
ሺܽ െ ܾሻሺ െ ሻ Ͳ ܽ ܾ ܽ ܾ Tương tự, ta có : ܾ ܿ ܾ ܿ ܿ ܽ ܿ ܽ
Cộng 3 bất đẳng thức trên, ta suy ra được điều phải chứng minh.
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi tam giác đều. c.
Theo bất đẳng thức Cauchy, ta có : ݉ ଷ ͳ ݉ ݉ ݉
݉ ݉ ൬ ൰ ൌ ሺ݉ ͵ ʹ ݉ ݉ሻଷ
Mặt khác, theo bất đẳng thức Bunyakovsky và định lý hàm số sin : ͻ ሺ݉ ଶ ଶ ଶ
݉ ݉ሻଶ ͵ሺ݉ ݉ ݉ ሻ ൌ
ሺܽଶ ܾଶ ܿଶሻ Ͷ
ൌ ͻܴଶሺଶ ଶ ଶ ሻ
Mà ta có bất đẳng thức cơ bản : ͻ ଶ ଶ ଶ Ͷ 91 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác Do đó, ͺͳ
ሺ݉ ݉ ݉ሻଶ ܴଶ Ͷ Suy ra ͳ ͻܴ ଷ ʹ ݉݉݉ Ǥ ൬ ൰ ൌ ܴଷ ʹ ʹ ͺ
Từ đó ta có được điều phải chứng minh.
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi tam giác đều. d. Ta có : ܾܽܿ ܾܽܿ ͺܴଷ ܵ ൌ ݎ ൌ ฺ ݎ ൌ ൌ Ͷܴ Ͷܴ ܽ ܾ ܿ ͶܴǤ ʹ Ͷܴଶ ฺ ݎ ൌ ൌ ʹܴǤ ʹܴሺ ሻ ൌ Ͷܴ ʹ ʹ ʹ Ͷ ʹ ʹ ʹ ͳ ܴ ͶܴǤ ൌ ͺ ʹ
Từ đó, ta có được điều phải chứng minh.
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi tam giác đều. e. Ta có :
ܵ ൌ ݎ ൌ ඥሺ െ ܽሻሺ െ ܾሻሺ െ ܿሻ
֜ ଶݎଶ ൌ ሺ െ ܽሻሺ െ ܾሻሺ െ ܿሻ ൌ ሾଷ െ ሺܽ ܾ ܿሻଶ ሺܾܽ ܾܿ ܿܽሻ െ ܾܽܿሿ
ൌ ଶሾଶ െ ሺܽ ܾ ܿሻ ሺܾܽ ܾܿ ܿܽሻ െ Ͷܴݎሿ
֜ ݎଶ ൌ ଶ െ ሺܽ ܾ ܿሻ ሺܾܽ ܾܽ ܿܽሻ െ Ͷܴݎ
֜ ଶ ൌ ሺܾܽ ܾܿ ܿܽሻ െ ݎሺͶܴ ݎሻ Do đó,
Ͷଶ ൌ ሺܽ ܾ ܿሻଶ ൌ ʹሺܽଶ ܾଶ ܿଶሻ ͶݎሺͶܴ ݎሻሺכሻ Mặt khác : ͻ
ܽଶ ܾଶ ܿଶ ൌ Ͷܴଶሺଶ ଶ ଶ ሻ ͶܴଶǤ ൌ ͻܴଶሺככሻ Ͷ
Từ (*) và (**) thì ta được :
Ͷଶ ͳͺܴଶ ͳܴݎ Ͷݎଶ ֜ ʹଶ ͳʹܴଶ ݎଶ െ ሺܴ െ ʹݎሻሺ͵ܴ െ ʹݎሻ ͳʹܴଶ ݎଶ 92 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
ሺ¿ܴ ʹݎ ֜ ሺܴ െ ʹݎሻሺ͵ܴ െ ʹݎሻ Ͳሻ Vậy ta có : ଶ ܴଶ ͵ݎଶ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi tam giác đều.
Bài 6: Chứng minh rằng trong tam giác ta có : ͷ ݎ Ǥ ʹ ʹ ʹ ʹ ʹ ʹ ͺ Ͷܴ
(Đề nghị Olympic 30-4, 2006) Ǥݎଶ ଶ ଶ ଶ ଶ ଶ
ݎ ݎ ݉ ݉ ݉
ሺ0ề nghị Olympic 30-4, 2006ሻ
Ǥܽଶ ܾଶ ܿଶ ܴଶ
(Đề nghị Olympic 30-4, 2008) ܽଷ ܾଷ ܿଷ ଷ ܣ ଷ ܤ ଷ ܥ
Ǥݎሺݎ ݎ ݎሻ ͵
(Đề nghị Olympic 30-4, 2010) Giải: a. Ta có : ሺ ሻ ൌ ʹ ሺ ሻ ൌ ʹ ሺ ሻ ൌ ʹ Và ݎ Ͷܴ ൌ ʹ ʹ ʹ ൌ െ ͳ ܴ ܴ
Theo bất đẳng thức Cauchy, ta có : ʹඨ ʹ ʹ ʹ ʹ 93 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác Hay ͳ ൬ ൰ ʹ ʹ Ͷ ʹ ʹ Tương tự, ta được : ͳ ൬ ൰ ʹ ʹ Ͷ ʹ ʹ ͳ ൬ ൰ ʹ ʹ Ͷ ʹ ʹ
Cộng 3 bất đẳng thức trên, ta có : ʹ ʹ ʹ ʹ ʹ ʹ ʹ ͳ ݎ ൌ Ͷ Ͷ Ͷܴ
Ta lại có bất đẳng thức cơ bản : ͵ ʹ
Do đó, ta có được điều phải chứng minh.
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi tam giác đều. b. Ta có : ܵଶ ܵଶ ܵଶ ݎଶ ଶ ଶ ݎ ݎ ൌ
ሺ െ ܽሻଶ ሺ െ ܾሻଶ ሺ െ ܿሻଶ
ሺ െ ܾሻሺ െ ܿሻ ሺ െ ܽሻሺ െ ܿሻ ሺ െ ܾሻሺ െ ܽሻ ൌ ቈ െ ܽ െ ܾ െ ܿ ͵ ݉ଶ ଶ ଶ ݉ ሺ ݉ ൌ ܽଶ ܾଶ ܿଶሻ Ͷ Ta đặt : ݔ ൌ െ ܽ ݔ ݕ ൌ ܿ ݔ ݖ ൌ ܾ ൞ݕ ൌ െ ܾ ฺ ൞ ݖ ൌ െ ܿ ݕ ݖ ൌ ܽ ݔ ݕ ݖ ൌ
Ta đưa điều cần chứng minh tương đương với ݕݖ ݔݖ ݔݕ ͵ ሺݔ ݕ ݖሻ ൬
൰ ሾሺݔ ݕሻଶ ሺݕ ݖሻଶ ሺݖ ݔሻଶሿ ݔ ݕ ݖ Ͷ Thật vậy, ta có : ݕ ݖ ݔ ݖ ݔ ݕ
ݔଶ ൬ ൰ ݕଶ ቀ ቁ ݖଶ ൬ ൰ ʹሺݔଶ ݕଶ ݖଶሻ ݖ ݕ ݖ ݔ ݕ ݔ Suy ra ݕݖ ݔݖ ݔݕ ሺݔ ݕ ݖሻ ൬
൰ ʹሺݔଶ ݕଶ ݖଶሻ ݔݕ ݕݖ ݖݔ ݔ ݕ ݖ 94 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
Theo bất đẳng thức Cauchy, ta có : ͳ ͳ
ሺݔଶ ݕଶ ݖଶሻ ሺݔݕ ݕݖ ݖݔሻ ʹ ʹ Do đó, ݕݖ ݔݖ ݔݕ ͵ ሺݔ ݕ ݖሻ ൬
൰ ሺݔଶ ݕଶ ݖଶ ݔݕ ݕݖ ݖݔሻ ݔ ݕ ݖ ʹ ͵
ൌ ሾሺݔ ݕሻଶ ሺݕ ݖሻଶ ሺݖ ݔሻଶሿ Ͷ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi tam giác đều. c.
Bất đẳng thức tương đương với
Ͷ ଶ Ͷ ଶ Ͷ ଶ ͳ
Ͷሺͳ െ ଶ ሻ ʹሺͳ െ ʹሻ ʹሺͳ െ ʹሻ ͳ
Ͷ ଶ െ ʹሺ ʹ ʹሻ ͳ Ͳ
Ͷ ଶ Ͷ ሺ െ ሻ ͳ Ͳ
ሾʹ ሺ െ ሻሿଶ ଶሺ െ ሻ Ͳ
Điều này hiển nhiên đúng.
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi ሺ െ ሻ ൌ ʹ ሺ െ ሻ ൌ Ͳ hay tam giác
cân tại và có góc là ͳʹͲ୭. d. Ta có : ۓ ۖܿ ൌ ݎ ൬ ൰ ʹ ʹ ݎ ݎ ۔ ܿ ൌ ۖ ە ʹ ʹ ʹ ʹ
ฺ ܿଶ ൌ ݎ ݎ ቌʹ ቍ Ͷݎݎ ʹ ʹ
Tương tự thế thì ta có
ܽଶ Ͷݎݎଶ Ͷݎݎ ܽଶ ܾଶ ܿଶ
ฺ ݎሺݎ ݎ ݎሻ Ͷ Mặt khác: 95 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác ܽଶ ܾଶ ܿଶ ͳ
ൌ ሾሺܽଶ ܾଶ െ ܿଶሻ ሺܾଶ ܿଶ െ ܽଶሻ ሺܿଶ ܽଶ െ ܾଶሻሿ Ͷ Ͷ ͳ
ൌ ሺܾܽ ܾܿ ܿܽ ሻ ʹ
Theo bất đẳng thức Cauchy, ta có : ͳ ͳ
ሺܾܽ ܾܿ ܿܽ ሻ ሾʹሺܽଷ ܾଷ ܿଷሻ ଷ ଷ ଷ ሿ ʹ ܽଶ ܾଶ ܿଶ ܽଷ ܾଷ ܿଷ ଷ ܣ ଷ ܤ ଷ ܥ ฺ Ͷ ͵ ܽଷ ܾଷ ܿଷ ଷ ܣ ଷ ܤ ଷ ܥ
ฺ ݎሺݎ ݎ ݎሻ ͵
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi tam giác đều.
Bài 7: Cho tam giác , chứng minh rằng : ͻ ͳ
Ǥ ଷ ଷ ଷ ሺ ͵ ͵ ͵ሻ ͺ Ͷ (ĐH An Ninh Hà Nội 1997) Ǥ ଶ ʹ (ĐHQG Hà Nội 1997) ξ య య య ξ ξ Ǥ ͳ ට య య య ʹ ට ට ʹ ʹ
(ĐH Bách Khoa Hà Nội 2000) Ǥ Ǥ Ǥ Ǥ ൏ Ͷ ଶ Ͷ ଶ Ͷ ଶ Ͷ ଶ Ͷ ଶ Ͷଶ Ͷ
(Đề nghị Olympic 30-4, 2008) ͳ Ǥ ඨ ʹ ʹ ʹ ͵ξ͵ 96 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác Giải: a.
Điều cần chứng minh tương đương với : ͵ ͵ ͵ ͵ ͵ ͵ Ͷ Ͷ Ͷ ͻ ͳ
ሺ ͵ ͵ ͵ሻ ͺ Ͷ
Khi đó ta đưa bài toán về dạng bất đẳng thức cơ bản : ͵ ʹ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi tam giác đều. b. Ta có : ͳ ͳ
ൌ ሾሺ െ ሻ െ ሺ ሻሿ ሾͳ െ ሺ ሻሿ ൌ ଶ ൌ ଶ ʹ ʹ ʹ ʹ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi ൌ .
Chú ý: Từ bài toán này, ta rút ra được kết quả sau bằng cách chứng minh tương tự : ͳ
൬ଶ ଶ ଶ ൰ ʹ ʹ ʹ ʹ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi tam giác đều. c.
Ta chứng minh bất đẳng thức sau : Với ܽǡ ܾ א Թ và ܽ ܾ Ͳ, ଷ ܽଷ ܾଷ ܽ ܾ ൬ ൰ ʹ ʹ
Thật vậy, bất đẳng thức tương đương với :
Ͷሺܽଷ ܾଷሻ ܽଷ ܾଷ ͵ܾܽଶ ͵ܽଶܾ
ሺܽ ܾሻሺܽଶ ܾଶ െ ʹܾܽሻ Ͳ
ሺܽ ܾሻሺܽ െ ܾሻଶ Ͳ
Điều này hiển nhiên đúng.
Áp dụng bất đẳng thức trên, ta có : య య ଷ ξ ξ െ ቆ ቇ ൌ ʹ ʹ ʹ ʹ ʹ Suy ra ξ య ξ య య ඨ ʹ ʹ Tương tự, ta được : ξ య ξ య య ඨ ʹ ʹ 97 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác ξ య ξ య య ඨ ʹ ʹ
Cộng 3 bất đẳng thức trên, ta có được điều phải chứng minh.
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi tam giác đều. d. Ta chứng minh ൏ ʹ ଶ ʹ Ͷ Thật vậy, xét hàm số ߨ
݂ሺݔሻ ൌ ݔ ݔ െ ʹݔǡ ݔ א ቀͲǢ ቁ ʹ ͳ ͳ ฺ ݂ᇱሺݔሻ ൌ ݔ െ ʹ Ͳ ଶ ݔ ξ ݔ ߨ
¯×ǡ ݂ሺݔሻ¯ồế² ቀͲǢ ቁ ʹ
Với ݔ Ͳ ฺ ݂ሺݔሻ ݂ሺͲሻ ฺ ݔ ݔ െ ʹݔ Ͳ Suy ra െ Ͳ ʹ ʹ Hay ൏ ʹ ʹ ଶ Ͷ
Chứng minh tương tự, ta có : ൏ ʹ ଶ ʹ Ͷ ൏ ʹ ଶ ʹ Ͷ Như vậy, ta được :
൏ Ͷ ൬ ൰ ൌ Ͷ ʹ ʹ ʹ ʹ ʹ ʹ e.
Bất đẳng thức tương đương với ͳ ଶ ଶ ʹ ʹ ʹ ʹ Ta có : 98 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác ͳ െ ଶ ͳ ଶ ଶ ଶ ൌ ൬ െ ൰ ൬ͳ െ ൰ ʹ ʹ ʹ Ͷ ʹ ʹ ʹ Ͷ ʹ ʹ ͳ
ൌ ൬ͳ െ ൰ ൬ͳ െ ൰ ʹǤ ͺ ʹ ʹ ʹ
Theo bất đẳng thức Cauchy, ta có : ଷ ͳ െ ͺ
൬ͳ െ ൰ ൬ͳ െ ൰ ʹǤ ቌ
ʹ ͳ െ ʹ ʹ ʹቍ ൌ ʹ ʹ ʹ ͵ ʹ Do đó, ͳ ଶ ଶ ʹ ʹ ʹ ʹ ͳ
ấ̶ ൌ ̶ảỉạ××ỏ ൌ Ǥ ʹ ͵
Chú ý: Ở bài toán này, ta có kết quả tổng quát sau : ݊ ඨ ʹ ʹ ʹ
ʹሺ݊ ͳሻξ݊ ͳ
Bài 8: Trong tam giác , chứng minh rằng : ξͳ ʹ ଶ ξͳ ʹ ଶ ξͳ ʹ ଶ Ǥ ͵ξʹ ͳ ͳ ͳ Ǥ ʹ ʹ ʹ ͵ξ͵ ͳ ͳ ͳ Ǥ
െ ൬ ൰ ͵ξ͵ Ͷ Ͷ Ͷ ʹ ʹ ʹ
(ĐH Bách Khoa Hà Nội 1999)
Ǥሺͳ െ ሻሺͳ െ ሻሺͳ െ ሻ (ĐHQG Hà Nội 2000) 99 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác Giải: a.
Theo bất đẳng thức Bunyakovsky, ta có : ͳ ͳ ͳ ͳ ͳ ଶ
ͳ ʹ ଶ ൌ ʹ ଶ ൬ ξʹ ൰ ʹ ʹ ͵ ξʹ ξʹ ʹ ͺ
ฺ ͳ ʹ ଶ ሺͳ ሻଶ ൌ ସ ͵ ͵ ʹ Tương tự, ta có : ͺ ͳ ʹ ଶ ସ ͵ ʹ ͺ ͳ ʹ ଶ ସ ͵ ʹ
Theo bất đẳng thức Cauchy, ta có : య
ξͳ ʹ ଶ ξͳ ʹ ଶ ͵ඨξͳ ʹ ଶ Ǥ Ǥ ͳξʹ య ଶ ଶ య ʹ ଶ ʹ ʹ ʹ ͵ ξʹ ͵ඪ ξ͵ ൌ ͵ඨ ͵ξ͵ ʹ ʹ ʹ ͺ ʹ ʹ ʹ ʹ ʹʹ Mặt khác : ൌ ͵ξ͵ ʹ ʹ ʹ ʹ ʹ ʹ Do đó, య ͵ටʹξʹ ൌ ͵ξʹ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi tam giác đều. b. Ta chứng minh ݔଶ ݔ ͳ െ ǡ ݔ Ͳ ʹ Thật vậy, xét hàm số ݔଶ ݂ሺݔሻ ൌ ݔ െ ͳ ʹ
݂ᇱሺݔሻ ൌ െ ݔ ݔ
Đặt ݃ሺݔሻ ൌ ݂ᇱሺݔሻ,
݃ᇱሺݔሻ ൌ െ ݔ ͳ Ͳ
Do đó, ݃ሺݔሻ đồng biến. Suy ra
݃ሺݔሻ ݃ሺͲሻ ൌ Ͳ 100 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
Ta có ݂ሺݔሻ đồng biến. Suy ra
݂ሺݔሻ ݂ሺͲሻ ൌ Ͳ
Vậy bất đẳng thức trên đúng.
Áp dụng vào bài toán, ta được : ଶ ͳ ʹ ͳ െ ฺ ʹ െ ʹ ͺ ʹ ͺ Tương tự, ta có : ͳ ʹ ʹ െ ʹ ͺ ͳ ʹ ʹ െ ʹ ͺ Do đó, ͳ ͳ ͳ ʹ ൬ ൰ െ ͺ
Ta có bất đẳng thức cơ bản : ͳ ͳ ͳ ͳ ͳ ͳ ͻ
ሺ ሻ ൬ ൰ ͻ ฺ ߨ Vậy ͳͺ ߨ െ ͵ξ͵ ߨ ͺ c.
Ta có đẳng thức cơ bản sau :ͳ െ ൌ ʹ Ͷ ʹ Do đó, ͳ െ ൌ ʹ Ͷ ʹ ͳ െ ൌ ʹ Ͷ ʹ Suy ra ൌ ͵ξ͵ ʹ ʹ ʹ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi tam giác đều. 101 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác d. Ta có 2 trường hợp :
- Nếu tam giác vuông hoặc tù thì bất đẳng thức hiển nhiên đúng.
- Nếu tam giác nhọn :
Điều cần chứng minh tương đương với : ͳ െ ଶ ͳ െ ଶ ͳ െ ଶ ቌͳ െ ʹቍ ቌͳ െ ʹቍ ቌͳ െ ʹቍ ͳ ଶ ʹ ͳ ଶ ʹ ͳ ଶ ʹ ͳ െ ଶ ͳ െ ଶ ͳ െ ଶ ʹ Ǥ ʹ Ǥ ʹ ͳ ଶ ʹ ͳ ଶ ʹ ͳ ଶ ʹ Hay
ͺ ଶ ଶ ଶ ൬ͳ െ ଶ ൰ ൬ͳ െ ଶ ൰ ൬ͳ െ ଶ ൰ ʹ ʹ ʹ ʹ ʹ ʹ ߨ Ͳ ൏ ǡ ǡ ൏ ฺ ǡ ǡ Ͳ ʹ ʹ ʹ ʹ ʹ ʹ ʹ Áp dụng công thức ʹ ൌ ʹ ͳ െ ଶ ʹ
Ta đưa bài toán trở thành : ͳ ͳ ͳ Ǥ Ǥ ʹ ʹ ʹ ʹ ʹ ʹ Mặt khác : ሺ ሻ ʹ ʹ ൌ ൌ ൌ ʹ ሺ ሻ ሺ െ ሻ ͳ െ ʹ Tương tự, ta có : ʹ ʹ ʹ ʹ Suy ra 102 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
ʹሺ ሻ ʹ ൬ ൰ ʹ ʹ ʹ ൌ ʹ ʹ ʹ ʹ ʹ ʹ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi tam giác đều.
Bài 9: Cho tam giác nhọn, chứng minh rằng : ξʹ Ǥ ͳ ʹ
(ĐH Kinh Tế Quốc Dân 1997) ͵݊
Ǥ ͵ ǡ ݊ א Գ ʹ
Ǥ͵ ସ ͻ ଼ ͺ Ͷ ʹͶ ଼ ʹ ସ ʹ ʹ ʹ ʹ ʹ ʹ ͺͶ
ǤయඥͶୱ୧୬ାୱ୧୬ାୱ୧୬େ యඥʹ୲ୟ୬ା୲ୟ୬ା୲ୟ୬େ ʹଵାగଶ
(Đề nghị Olympic 30-4, 2008) Giải: a. Ta có : െ െ ʹ ʹ ൌ ʹ ʹ ൌ ʹ ʹ െ െ ʹ ʹ ʹ ʹ ʹ ʹ Ta sẽ chứng minh െ ʹ ʹ ʹ ʹʹ െ ʹ ʹ ʹ ʹ ʹ
Thật vậy, điều trên tương đương với െ ൬ʹ ൰ ൬ʹ ൰ ʹ ʹ ʹ െ ൬ʹ ൰ ൬ʹ ൰ ʹ ʹ ʹ െ െ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ 103 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác െ ൬ െ ͳ൰ ൬ െ ൰ Ͳ ʹ ʹ ʹ െ ͵ ൬ െ ͳ൰ Ͳ ʹ ʹ Giả sử ൌ ሼǡ ǡ ሽ. ߨ ߨ ͵ ߨ ͵ߨ ͵ ฺ א ቂ ǡ ቃ ฺ א ǡ ൨ ฺ Ͳ ͵ ʹ ʹ ʹ Ͷ ʹ
Do đó, bất đẳng thức trên hiển nhiên đúng. Ta xét hàm số : ݔ ʹ ߨ ߨ ݂ሺݔሻ ൌ ʹ ݔ ݔ ǡ ݔ א ቂ ǡ ቃ ʹ ͵ ʹ ʹ ݔ ͵ݔ ߨ ߨ ݂ᇱሺݔሻ ൌ ʹ െ ͳ Ͳǡ ݔ א ቂ ǡ ቃ ݔ ଶ ቀʹ ͵ ʹ ʹ ݔቁ
Suy ra ݂ሺݔሻ nghịch biến. Do đó, ߨ ξʹ
݂ሺݔሻ ݂ ቀ ቁ ൌ ͳ ʹ ʹ Từ đó, ta có : ξʹ ͳ ʹ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi tam giác vuông cân tại . b.
Theo bất đẳng thức Cauchy và bất đẳng thức cơ bản, ta có : య ͳ
͵యඥሺ ሻ ͵ට൫͵ξ͵൯ ͵ ൬ͳ ൰ ʹ
Theo bất đẳng thức Bernoulli, ta có : ͳ ݊
͵ ൬ͳ ൰ ͵ ቀͳ ቁ ʹ ʹ Do đó, ͵݊
͵ ʹ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi ݊ ൌ Ͳ. c.
Theo bất đẳng thức Cauchy, ta có : ͳ ସ ͵ ͵ ସ ͵ ൬ ൰ ଶ ʹ ʹ ʹ ʹ ͳ ͳ ͵
ͺ ͺ ൬ ൰ ͺ ൬ ൰ ଶ ʹ ʹ ʹ ʹ ʹ 104 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác ͳ ଼ ͳ ଼ ͳ ଼ ͵
ʹͶ ଼ ʹͶ ൬ ൰ ʹͶ ൬ ൰ ʹͶ ൬ ൰ ଶ ʹ ʹ ʹ ʹ ʹ ʹ ͳ ଼ ͳ ଼ ͳ ଼ Ͷ ͻ ଼ ͻ ൬ ൰ ͻ ൬ ൰ ͻ ൬ ൰ ଶ ʹ ξ͵ ξ͵ ξ͵ ͵ ʹ ͳ ͳ Ͷ Ͷ Ͷ ൬ ൰ Ͷ ൬ ൰ ଶ ʹ ξ͵ ξ͵ ͵ ʹ ͳ ସ Ͷ ʹ ସ ʹ ൬ ൰ ଶ ʹ ξ͵ ͵ ʹ
Mặt khác, theo bất đẳng thức cơ bản, ta có : ͵ ͻ ൬ଶ ଶ ଶ ൰ ʹ ʹ ʹ ʹ ͺ Ͷ Ͷ ൬ଶ ଶ ଶ ൰ ͵ ʹ ʹ ʹ ͵
Cộng 8 bất đẳng thức trên, ta có được điều phải chứng minh.
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi tam giác đều. d.
Theo bất đẳng thức Cauchy, ta có : ଶ ଵ ଶ ൌ ଷ
ʹ ሺୱ୧୬ାୱ୧୬ାୱ୧୬େሻ ଷ
ʹ ሺ୲ୟ୬ା୲ୟ୬ା୲ୟ୬େሻ ʹටʹଷሺୱ୧୬ାୱ୧୬ାୱ୧୬େሻାଵଷሺ୲ୟ୬ା୲ୟ୬ା୲ୟ୬େሻ Ta cần chứng minh : ଶ ʹට ଷ
ʹ ሺୱ୧୬ାୱ୧୬ାୱ୧୬େሻାଵଷሺ୲ୟ୬ା୲ୟ୬ା୲ୟ୬େሻ ʹଵାగଶ ʹ ͳ
ሺ ሻ ሺ ሻ ߨ ͵ ͵ ʹ ͳ ʹ ͳ ʹ ͳ
൬ െ ൰ ൬ െ ൰ ൬ െ ൰ Ͳ ͵ ͵ ͵ ͵ ͵ ͵ Xét hàm số ʹ ͳ ߨ
݂ሺݔሻ ൌ ݔ ݔ െ ݔǡ ݔ א ቀͲǡ ቁ ͵ ͵ ʹ ʹ ͳ ͳ ͳ ͳ ͳ ݂ᇱሺݔሻ ൌ ݔ Ǥ െ ͳ ൌ ൬ ݔ ݔ
൰ െ ͳ Ǥ ͵ െ ͳ ൌ Ͳ ͵ ͵ ଶ ݔ ͵ ଶ ݔ ͵
Ta thấy rằng dấu ̶ ൌ ̶ trong bất đẳng thức ͳ ݔ ݔ ͵ ଶ ݔ không thể xảy ra.
Do đó, ݂ሺݔሻ đồng biến. Nên ݂ሺݔሻ ݂ሺͲሻ Suy ra ʹ ͳ ݔ ݔ െ ݔ Ͳ ͵ ͵ 105 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
Lần lượt thay ݔ ൌ ሼǡ ǡ ሽ. Ta có điều phải chứng minh.
Bài 10: Cho tam giác và các số thực ݔǡ ݕǡ ݖ Ͳ Hãy chứng minh rằng ݔ ݕ ݖ ݔ ݕ ݖ ʹݕݖ ʹݖݔ ʹݔݕ Giải:
Bất đẳng thức cần chứng minh tương đương với
ʹݕݖ ʹݔݖ ʹݔݕ ݔଶ ݕଶ ݖଶ
ʹݕݖ ʹݔݖ ʹݔݕ
ݔଶሺଶ ଶ ሻ ݕଶሺଶ ଶ ሻ ݖଶ
ʹݕݖ ʹݔݖ െ ʹݔݕሺ െ ሻ
ݔଶሺଶ ଶ ሻ ݕଶሺଶ ଶ ሻ ݖଶ
ሺݔଶ ଶ െ ʹݔݕ ݕଶ ଶ ሻ
ሺݔଶ ଶ ݕଶ ଶ ݖଶ ʹݔݕ െ ʹݔݖ െ ʹݕݖ ሻ Ͳ
ሺݔ െ ݕ ሻଶ ሺݔ ݕ െ ݖሻଶ Ͳ
Điều này hiển nhiên đúng. Do đó, ta có được điều phải chứng minh.
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi ݔ ݔ ൌ ݖ ݔ െ ݕ ൌ Ͳ ݔ ൌ ݖ ൜
ݔ ݕ െ ݖ ൌ Ͳ ൞ ݔ ൜ݔ ൌ ݕ ݕ ൌ
ݔǣ ݕǣ ݖ ൌ ܽǣ ܾǣ ܿ
Bài 12: Cho tam giác nhọn, hãy chứng minh rằng ߨ ܽ ܾ ܿ
Ǥ ܽ ܾ ܿ ൬ ൰ ͵ ܽ ܾ ܿ Ǥ ʹξ͵ ݉ ݉ ݉ ܽ ܾ ܾ ܿ ܿ ܽ Ǥ ൬ െ ܿ൰ ൬ െ ܽ൰ ቀ െ ܾቁ ʹܾܽܿ ͵ Ǥ െ െ െ ቀ Ͷ ʹ ቁ ቀ ʹ ቁ ቀ ʹ ቁ
(Đề nghị Olympic 30-4, 2006) 106 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác Giải: a.
Giả sử ܽ ܾ ܿ ฺ ͻͲ୭. Ta xét hàm số ݔ ߨ ݂ሺݔሻ ൌ ǡ ݔ א ቀͲǢ ቁ ݔ ʹ ݔ െ ݔ ݂ᇱሺݔሻ ൌ ݔଶ ݔ Lại xét hàm số ߨ
݃ሺݔሻ ൌ ݔ െ ݔǡ ݔ א ቀͲǢ ቁ ʹ
݃ᇱሺݔሻ ൌ ଶ ݔ Ͳ
Do đó, ݃ሺݔሻ đồng biến. Suy ra
݃ሺݔሻ ݃ሺͲሻ ݔ ݔ ݂ᇱሺݔሻ ൏ Ͳ
Ta có ݂ሺݔሻ nghịch biến. Suy ra ܽ ܾ ܿ
Theo bất đẳng thức Chebyshev cho 2 dãy ൝ܽ ܾ ܿ ܽ ܾ ܿ ܽ ܾ ܿ Ǥ ܽ ܾ ܿ Ǥ Ǥ Ǥ ൌ ͵ ͵ ͵ ͵
Vậy ta có được điều phải chứng minh.
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi tam giác đều. b. Ta có : ͳ ଶ
݉ ൌ ሺʹܾଶ ʹܿଶ െ ܽଶሻ ൌ ܴଶሺʹ ଶ ʹ ଶ െ ଶ ሻ Ͷ
ൌ ܴଶሾͳ െ ሺ ʹ ʹሻ ଶ ሿ
ൌ ܴଶሾͳ ʹ ሺ െ ሻ ଶ ሿ Suy ra
݉ଶ ܴଶሺͳ ʹ ଶ ሻ ൌ ܴଶሺͳ ሻଶ ൌ Ͷܴଶ ସ ʹ ฺ ݉ଶ ʹܴ ଶ ʹ
Theo định lý hàm số sin, ta có : ܽ ܽ ൌ ൌ ʹ ݉ ʹܴ ଶ ʹ ʹ ଶ ʹ Tương tự, ta được : 107 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác ܾ ۓ ʹ ݉ ʹ ۔ ܿ ʹ ە݉ ʹ
Cộng 3 bất đẳng thức trên, ta có : ʹ ൬ ൰ ʹ ʹ ʹ
Mặt khác, theo bất đẳng thức cơ bản, ta có : ξ͵ ʹ ʹ ʹ
Do đó, ta có điều phải chứng minh.
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi tam giác đều. c.
Theo định lý hàm số sin, điều cần chứng minh tương đương với ʹܴ ʹܴ ʹܴ ʹܴ ʹܴ ൬ െ ʹܴ ൰ ൬ െ ʹܴ ൰ ൬ ʹܴ
െ ʹܴ ൰ ʹǤʹܴ Ǥ ʹܴ Ǥ ʹܴ ൬ െ ൰ ൬ െ ൰ ൬ െ ൰ ʹ ͳ െ ͳ െ ͳ െ Ǥ Ǥ ʹ Ta cần chứng minh ʹ ቀଶ ͳ െ ൌ ʹ ଶ ʹቁ ቀͳ െ ଶ ʹቁ ቀͳ െ ଶ ʹቁ Thật vậy, ʹ ቀଶ ʹ ଶ ʹቁ ʹ ቀଶ ൌ ʹ ଶ ʹቁ ଶ ʹ ଶ ʹ ቀͳ െ ଶ ʹቁ ቀͳ െ ଶ ʹቁ ʹ ቀଶ ൌ ʹ ଶ ʹ ଶ ʹ ଶ ʹቁ
ሺͳ െ ሻሺͳ ሻ ሺͳ െ ሻሺͳ ሻ ͳ െ ൌ ൌ ʹ
Theo bất đẳng thức Cauchy, ta có : 108 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác ͳ െ ʹ ቀଶ ʹ ଶ ʹ ଶ ൌ ʹ ଶ ʹቁ ʹ Ǥ ʹ ൌ ቀͳ െ ଶ ʹቁ ቀͳ െ ଶ ʹቁ ͳ െ ଶ ʹ ͳ െ ଶ ʹ Tương tự, ta có : ͳ െ ͳ െ Như vậy ͳ െ ͳ െ ͳ െ Ǥ Ǥ ଶ ଶ ଶ
Mà theo bất đẳng thức cơ bản, ta có :
͵ξ͵ ฺ ଶ ଶ ଶ ʹ
Vậy ta có điều phải chứng minh.
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi tam giác đều. d.
Theo bất đẳng thức Cauchy, ta có : ʹ െ ൌ Ͷ Ǥ ʹξ ଶ ቀ ʹ ʹ ʹ ʹ ቁ Tương tự, ta có : ʹ െ ଶ ʹ ቀ ʹ ቁ ʹ െ ଶ ʹ ቀ ʹ ቁ
Cộng 3 bất đẳng thức trên, ta được : ଶ ʹ ଶ ଶ ʹ ʹ ʹ ͳ ͳ
ሾ͵ െ ሺ ሻሿ ሺ ሻଶ ʹ ͵
Áp dụng bất đẳng thức cơ bản, ta có : ͵
ሺ ሻଶ ሺ ሻ ʹ Do đó, ͳ ͳ ͵
ʹ ሺ ሻ ሾ͵ െ ሺ ሻሿ ൌ ʹ ʹ ʹ
Vậy ta có điều phải chứng minh.
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi tam giác đều. 109 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
Bài 13: Chứng minh rằng nếu các góc của tam giác nhọn thỏa điều kiện ʹ
͵ ൌ ߨ thì các cạnh của nó thỏa mãn ͷ ܽ ܾ ൏ ܿ Ͷ
(Đề nghị Olympic 30-4, 2008) Giải: Ta có : ߨ ͵ ߨ ʹ ͵ ൌ ߨ ฺ ൌ െ ฺ ൌ ʹ ʹ ʹ ʹ Suy ra ߨ ͵ ͵ ൌ ൬ െ ൰ ൌ ൌ ൬Ͷ ଶ െ ͵൰ ʹ ʹ ʹ ʹ ʹ ߨ ൌ ൬ ൰ ൌ ʹ ʹ ʹ
Theo định lý hàm số sin, ta có : ܽ ܾ ܿ ൌ ൌ ܽ ܾ ܿ ൌ ൌ
ʹ ቀͶ ଶ ʹ െ ͵ቁ ʹ ʹ ʹ ʹ ܽ ܾ ൌ ൌ ܿ Ͷ ଶ ʹ െ ͵ ʹ ʹ
Theo tính chất tỷ lệ thức, ta có : ܽ ܾ ܿ ൌ Ͷ ଶ ʹ െ ͵ ʹ ʹ Suy ra
ܽ ܾ ൌ ܿ ൬െͶ ଶ ʹ ͳ൰ ʹ ʹ Mặt khác ߨ ߨ ͳ ʹ ͵ ൌ ߨ ฺ ൌ െ ฺ Ͳ ൏ ൏ ฺ Ͳ ൏ ൏ ʹ ͵ ʹ ʹ ʹ 0ặݐ ൌ ǡ ±ố ʹ ͳ
݂ሺݐሻ ൌ െͶݐଶ ʹݐ ͳǡ ݐ א ൬ͲǢ ൰ ʹ
݂ᇱሺݐሻ ൌ െͺݐ ʹ 110 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác ͳ
݂ᇱሺݐሻ ൌ Ͳ ݐ ൌ Ͷ ଵ ଵ ݐ Ͳ ସ ଶ ݂Ԣሺݐሻ Ͳ െ ହ ݂ሺݐሻ ସ ͳ ͳ
Dựa vào bảng biến thiên, ta rút ra kết quả ͷ
ܽ ܾ ൌ ܿ ൬െͶ ଶ ʹ ͳ൰ ܿ ʹ ʹ Ͷ
Tuy nhiên, dấu ̶ ൌ ̶ không xảy ra vì ͻͲ୭. Do đó, ta có điều phải chứng minh.
Bài 14: Cho tam giác không vuông. Chứng minh rằng tam giác tù khi và chỉ khi ͳ ͳ ͳ ͳ ͳ ͳ ൏ ʹ ʹ ʹ
(Đề nghị Olympic 30-4, 2009) Giải:
Chiều thuận: Giả sử tam giác có góc tù và ܤ ܥ. Khi đó ߨ Ͳ ൏ ൏ ͳ ͳ ͳ Ͳ ൏ ൏ ฺ ൝ ฺ Ͳ ൏ ൏ ൏ ฺ Ͷ Ͳ ൏ ൏ ʹ ʹ ʹ െ െ ߨ ¿ ൏ Ͳǡ Ͳ Ͳ ൬Ͳ ൏ ൏ ൰ ² ʹ ʹ ʹ െ ͳ ͳ ʹ ͳ ͳ ൌ ʹ ʹ ൏ Ͳ ൏ ʹ ʹ
Do đó, chiều thuận đúng.
Chiều nghịch: Giả sử tam giác nhọn. Ta suy ra ǡ ǡ Ͳ.
Theo bất đẳng thức Cauchy, ta có : 111 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác ͳ ͳ ʹ Ͷ ʹ ʹ ൌ ξ െ ʹ ʹ ʹ Tương tự, ta có ; ͳ ͳ ʹ ʹ ͳ ͳ ʹ ʹ Do đó, ͳ ͳ ͳ ͳ ͳ ͳ ʹ ʹ ʹ
Điều này vô lí. Vậy chiều nghịch đúng.
Vậy ta có điều phải chứng minh.
Bài 15: Cho tam giác chứng minh rằng ܿ ͳ ξ͵ ൌ ฺ ݄ ܽ ܾ ξ͵ ʹ
(Đề nghị Olympic 30-4, 2010) Giải:
Không mất tính tổng quát nên ta sẽ giả sử ܿ ൌ ͳǢ ܾ ൌ ξ͵ Ta có: ݄ ൌ ܿ ൌ .
Bài toán sẽ đưa về chứng minh: ξ͵ ܽ ʹ Áp dụng hàm số sin thì ܽ ܾ ܾ ξ͵ ൌ ֜ ܽ ൌ ൌ Áp dụng hàm số cos thì
ܽଶ ൌ ܾଶ ܿଶ െ ʹܾܿ ൌ Ͷ െ ʹξ͵ 112 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác Ta có : ߨ
ξ͵ ൌ ʹ ቀ ቁ ʹ ֜ ʹ െ ξ͵ ͵ ξ͵ ξ͵ ֜ ʹ ܽଶ ֜ ʹ ܽ ֜ ܽ ʹ
Vậy ta có điều phải chứng minh.
Bài 16: Cho tam giác có chu vi bằng ͳ. Chứng minh rằng : ͳ
ܽଶ ܾଶ ܿଶ Ͷܾܽܿ ൏ ʹ
(Đề nghị Olympic 30-4, 2007) Giải: Ta có ͳ ͳ ͳ ͳ
ܵ ൌ ඥሺ െ ܽሻሺ െ ܾሻሺ െ ܿሻ ൌ ඨ ൬ െ ܽ൰ ൬ െ ܾ൰ ൬ െ ܿ൰ ʹ ʹ ʹ ʹ
֜ ͳܵଶ ൌ ሺͳ െ ʹܽሻሺͳ െ ʹܾሻሺͳ െ ʹܿሻ ൌ ͳ െ ʹሺܽ ܾ ܿሻ Ͷሺܾܽ ܾܿ ܿܽሻ െ ͺܾܽܿ
ൌ െͳ Ͷሺܾܽ ܾܿ ܿܽሻ െ ͺܾܽܿ Mặt khác
ʹሺܾܽ ܾܿ ܿܽሻ ൌ ሺܽ ܾ ܿሻଶ െ ሺܽଶ ܾଶ ܿଶሻ
֜ Ͷሺܾܽ ܾܿ ܿܽሻ ൌ ʹ െ ʹሺܽଶ ܾଶ ܿଶሻ Suy ra
ͳܵଶ ൌ െͳ െ ʹሺܽଶ ܾଶ ܿଶሻ െ ͺܾܽܿ Ͳ Vậy ͳ
ܽଶ ܾଶ ܿଶ Ͷܾܽܿ ൏ ʹ 113 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
Bài 17: Cho tam giác có chu vi bằng ͵. Chứng minh rằng ͳ͵
͵ሺଶ ଶ ଶ ሻ ͺܴ Ͷܴଶ (ĐH Sư Phạm Vinh 2001)
Giải: Theo định lý hàm số sin, ta có điều cần chứng minh tương đương với
͵ܽଶ ͵ܾଶ ͵ܿଶ Ͷܾܽܿ ͳ͵
Giả sử ܽ ܾ ܿ. Ta có : ܽ ܾ ܿ ൌ ͵ nên ͵ ൜ ܽ ܾ ܿ
ቄ͵ െ ܿ ܿ ͳ ܿ ൏
͵ܿ ܽ ܾ ܿ ൌ ͵ ܿ ͳ ʹ Mặt khác
͵ܽଶ ͵ܾଶ ͵ܿଶ Ͷܾܽܿ ൌ ͵ሾሺܽ ܾሻଶ െ ʹܾܽሿ ͵ܿଶ Ͷܾܽܿ
ൌ ͵ሺ͵ െ ܿሻଶ ͵ܿଶ Ͷܾܽܿ െ ܾܽ ൌ ͵ሺ͵ െ ܿሻଶ ͵ܿଶ െ ʹܾܽሺ͵ െ ʹܿሻ Vì ଶ ଶ ۓ ܽ ܾ ͵ െ ܿ ܾܽ ൏ ൬ ൰ ൌ ൬ ൰ ଶ ͵ െ ܿ ʹ ʹ ൰ ฺ ൝െʹܾܽ െʹ ൬ ۔ ͵ ʹ ە ܿ ൏ ͵ െ ʹܿ Ͳ ʹ Nên ͵ െ ܿ ଶ
͵ܽଶ ͵ܾଶ ͵ܿଶ Ͷܾܽܿ ͵ሺ͵ െ ܿሻଶ ͵ܿଶ െ ʹ ൬ ൰ ሺ͵ െ ʹܿሻ ʹ Hay ͵ ʹ
͵ܽଶ ͵ܾଶ ͵ܿଶ Ͷܾܽܿ ܿଷ െ ܿଶ ʹ ʹ Xét hàm số ͵ ʹ ͵
݂ሺܿሻ ൌ ܿଷ െ ܿଶ ǡ ܿ א ͳǢ ൰ ʹ ʹ ʹ
݂ᇱሺܿሻ ൌ ͵ܿଶ െ ͵ܿ
݂ᇱሺܿሻ ൌ Ͳ ܿ ൌ ͳ ଷ ܿ ͳ ଶ ݂Ԣሺܿሻ Ͳ ଶ ݂ሺܿሻ ଶ ͳ͵ 114 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
Từ bảng biến thiên, ta có được
͵ܽଶ ͵ܾଶ ͵ܿଶ Ͷܾܽܿ ͳ͵
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi tam giác đều.
Bài 18: Cho tam giác trong đó ܽ ܾ ܿ. Chứng minh rằng
ሺܽ ܾ ܿሻଶ ͻܾܿ
Hơn nữa, nếu ܽ ൏ ܾ ൏ ܿ. Chứng minh rằng
ܽଷሺܾଶ െ ܿଶሻ ܾଷሺܿଶ െ ܽଶሻ ܿଷሺܽଶ െ ܾଶሻ ൏ Ͳ Giải:
Do ܽ ܾ ܿ nên ܽ ܾ ܿ ʹܾ ܿ. Suy ra
ሺܽ ܾ ܿሻଶ ሺʹܾ ܿሻଶ Mặt khác do ܾ ܿ nên
ቄʹܾ െ ܿ ʹܾ െ ܾ ൌ ܾ ฺ ሺʹܾ െ ܿሻଶ ܾܿ
ʹܾ െ ܿ ʹܿ െ ܿ ൌ ܿ Vậy
ሺܽ ܾ ܿሻଶ ͻܾܿ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi tam giác đều. Ta lại có :
ܽଷሺܾଶ െ ܿଶሻ ܾଷሺܿଶ െ ܽଶሻ ܿଷሺܽଶ െ ܾଶሻ
ൌ ܽଷሺܾଶ െ ܿଶሻ ܾଶܿଶሺܾ െ ܿሻ െ ܽଶሺܾଷ െ ܿଷሻ
ൌ ሺܾ െ ܿሻሾܽଷሺܾ ܿሻ ܾଶܿଶ െ ܽଶሺܾଶ ܿଶ ܾܿሻሿ
ൌ ሺܾ െ ܿሻሺܽଷܾ ܽଷܿ ܾଶܿଶ െ ܽଶܾଶ െ ܽଶܿଶ െ ܽଶܾܿሻ
ൌ ሺܾ െ ܿሻሾܽଶܾሺܽ െ ܾሻ ܽଶܿሺܽ െ ܾሻ ܿଶሺܾଶ െ ܽଶሻሿ
ൌ ሺܾ െ ܿሻሺܽ െ ܾሻሾܽଶܾ ܽଶܿ െ ܿଶሺܽ ܾሻሿ
ൌ ሺܾ െ ܿሻሺܽ െ ܾሻሾܽܿሺܽ െ ܿሻ ܾሺܽଶ െ ܿଶሻሿ
ൌ ሺܾ െ ܿሻሺܽ െ ܾሻሺܽ െ ܿሻሾܽܿ ܾሺܽ ܿሻሿ
Vì ܽ ൏ ܾ ൏ ܿ nên ሺܾ െ ܿሻሺܽ െ ܾሻሺܽ െ ܿሻ ൏ Ͳ
Vậy ta có điều phải chứng minh.
Bài 19: Cho tam giác có chu vi bằng ʹ. Chứng minh rằng
ͷʹ ܽଶ ܾଶ ܿଶ ʹܾܽܿ ൏ ʹ ʹ 115 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác Giải:
Giả sử ܽ ܾ ܿ. Ta suy ra được
ʹܿ ൏ ܽ ܾ ܿ ൌ ʹ ฺ ܿ ൏ ͳ Do đó :
ܽଶ ܾଶ ܿଶ ʹܾܽܿ ൌ ሺܽ ܾ ܿሻଶ െ ʹሺܾܽ ܾܿ ܿܽሻ ʹܾܽܿ
ൌ ʹ ʹሺܽ ܾ ܿ െ ܾܽ െ ܾܿ െ ܿܽ ܾܽܿሻ
ൌ ʹ ʹሺͳ െ ܿሻሺܽ െ ͳሻሺͳ െ ܾሻ ൏ ʹ
Mặt khác, theo bất đẳng thức Cauchy, ta có :
ሺͳ െ ܽሻ ሺͳ െ ܾሻ ሺͳ െ ܿሻ ඥయሺͳ െ ܽሻሺͳ െ ܾሻሺͳ െ ܿሻ ͵ Suy ra ͳ
ሺͳ െ ܽሻሺͳ െ ܾሻሺͳ െ ܿሻ ʹ Hay ͳ
ͳ െ ܽ െ ܾ െ ܿ ܾܽ ܾܿ ܿܽ െ ܾܽܿ ʹ ͳ
ܽ ܾ ܿ ൌ ʹ ฺ ܾܽ ܾܿ ܿܽ ൌ ʹ െ ሺܽଶ ܾଶ ܿଶሻ ʹ Nên ͳ ͳ
ͳ െ ʹ ʹ െ ሺܽଶ ܾଶ ܿଶሻ െ ܾܽܿ ʹ ʹ Do đó ͷʹ
ܽଶ ܾଶ ܿଶ ʹܾܽܿ ʹ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi tam giác đều.
Bài 20: Cho tam giác không vuông thỏa ͷ ଶ ଶ ଶ ൌ ʹ. Chứng minh rằng ͵ ͷ Giải: Ta có : ͷ ଶ ଶ ଶ ൌ ʹ ͳ ʹ ͳ ʹ ͷሺͳ െ ଶ ሻ ൌ ʹ ʹ ʹ ͳ
െͷ ଶ ሺ ʹ ʹሻ ൌ ʹ ʹ
െͷ ଶ Ͷ ሺ ሻ ሺ െ ሻ ൌ Ͳ 116 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
െͷ ଶ Ͷ ൌ ሺ െ ሻ Ta xét 2 trường hợp :
- Nếu góc nhọn thì Ͳ. Do ሺ െ ሻ ͳ, ta suy ra
െͷ ଶ Ͷ ൌ ሺ െ ሻ
Suy ra ͷ ଶ െ Ͷ Ͳ. Do đó Ͷ ͷ
Vì góc nhọn nên ta cũng có Ͳ, suy ra ͳ ͵
ൌ ඥͳ െ ଶ ඨͳ െ ൌ ʹͷ ͷ
- Tương tự, nếu góc tù thì െͷ ଶ Ͷ ൌ ሺ െ ሻ Ͷ
ฺ ͷ ଶ െ Ͷ Ͳ ͷ Do ൏ Ͳ và Ͳ nên ͳ ͻ ͵ ଶ ฺ ଶ ฺ ʹͷ ͷ ͷ ͵ ậØ× Ǥ ͷ
Bài 21: Cho tam giác có các cạnh và nửa chu vi thỏa mãn Ͷሺ െ ܽሻ ܾܿ. Chứng minh rằng ʹξ͵ െ ͵ ʹ ʹ ʹ ͺ Giải: Ta có : ܽ ܾ ܿ
Ͷሺ െ ܽሻ ܾܿ ʹሺܽ ܾ ܿሻ ൬ െ ܽ൰ ܾܿ ʹ
ሺܾ ܿ ܽሻሺܾ ܿ െ ܽሻ ܾܿ
ሺܾ ܿሻଶ െ ܽଶ ܾܿ
ܾଶ ܿଶ െ ܽଶ ʹܾܿ ܾܿ ʹܾܿ െܾܿ ͳ െ ͳʹͲ୭ ൏ ͳͺͲ୭ ʹ 117 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác Mặt khác ͳ െ ͳ ൌ ൬ െ ൰ ൬ͳ െ ൰ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ Vì ͳ ͳ ͳ ͳ ଶ ͳ
൬ͳ െ ൰ ൌ ൬ െ ଶ ൰ ൌ ቈെ ൬ െ ൰ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ Ͷ ଶ ͳ ͳ ͳ ଶ ͳ ͳ ξ͵ ͳ ʹξ͵ െ ͵
ൌ െ ൬ െ ൰ െ ቆ െ ቇ ൌ ͺ ʹ ʹ ʹ ͺ ʹ ʹ ʹ ͺ Do đó, ʹξ͵ െ ͵ ʹ ʹ ʹ ͺ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi ൜ ൌ ͳʹͲ୭ ൌ ൌ ͵Ͳ୭
Bài 22: Cho tam giác vuông tại . Chứng minh rằng ͳ ߨ Giải:
- Nếu Ͷͷ୭ ൏ ͻͲ୭ thì ฺ
- Nếu Ͳ ൏ ൏ Ͷͷ୭ thì ൏ Vậy ta luôn có ߨ
ቀ െ ቁ ሺ െ ሻ Ͳ Ͷ ߨ ߨ
െ െ Ͳ Ͷ Ͷ ߨ ߨ
ቀ െ ቁ ሺ ሻ ʹ Ͷ ߨ ͵ ߨ
൬ͳ െ ଶ ʹ൰ Ͷ Ͷ ͳ ߨ ͳ Mặt khác ଶ ߨଶ ൬ ൰ ൌ ʹ ͳ 118 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác Nên ͳ ߨ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi tam giác vuông cân tại .
Bài 23: Cho tam giác nhọn. Chứng minh rằng ଷξଷ ʹ ଶ
ሺ ሻୱ୧୬ሺ ሻୱ୧୬ሺ ሻୱ୧୬େ ൬ ൰ ͵
(Đề nghị Olympic 30-4, 2006)
Giải: Ta xét hàm số
݂ሺݔሻ ൌ ݔ ݔ ǡ ݔ Ͳ ͳ
ฺ ݂ᇱሺݔሻ ൌ ݔ ͳ ฺ ݂ᇱᇱሺݔሻ ൌ Ͳ ݔ
Theo bất đẳng thức Jensen, ta có :
݂ሺ ሻ ݂ሺ ሻ ݂ሺ ሻ ݂ ൬ ൰ ͵ ͵ Do đó, Ǥ Ǥ Ǥ ͵ ൬ ൰ Ǥ ൬ ൰ ͵ ͵
Mà theo bất đẳng thức cơ bản, ta có : ͵ξ͵ ʹ
Mặt khác do tam giác nhọn, suy ra
ଶ ଶ ଶ ൌ ʹ ʹ ʹ
Và hàm số ݃ሺݔሻ ൌ ݔ ǡ ݔ Ͳ đồng biến nên ta có ͵ξ͵ ʹ ሺ ሻ ൬ ൰ ͵ ʹ ͵ Do đó, ଷξଷ ʹ ଶ
ሺ ሻୱ୧୬ሺ ሻୱ୧୬ሺ ሻୱ୧୬େ ൬ ൰ ͵ 119 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
Bài 24: Cho tam giác nhọn. Chứng minh rằng ଶξଶ ଶξଶ ଶξଶ ൬ ൰ ൬ ൰ ൬ ൰ ͵ଵିξଶ ʹ ʹ ʹ
Giải: Ta xét hàm số ߨ
݂ሺݔሻ ൌ ሺ ݔሻଶξଶǡ ݔ א ቀͲǡ ቁ ʹ
݂ᇱሺݔሻ ൌ ʹξʹሺͳ ଶ ݔሻሺ ݔሻଶξଶିଵ
݂ᇱᇱሺݔሻ ൌ Ͷξʹ ݔ ሺͳ ଶ ݔሻሺ ݔሻଶξଶିଵ
ʹξʹ൫ʹξʹ െ ͳ൯ሺͳ ଶ ݔሻଶሺ ݔሻଶξଶିଶ Ͳ
Do đó, theo bất đẳng thức Jensen, ta có :
݂ ൬ ൰ ݂ ൬ ൰ ݂ ൬ ൰ ͵݂ ൬ ൰ ʹ ʹ ʹ Hay ଶξଶ ଶξଶ ଶξଶ ଶξଶ ൬ ൰ ൬ ൰ ൬ ൰ ൬ ൰ ൌ ͵ଵିξଶ ʹ ʹ ʹ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi tam giác đều.
Bài 25: Cho tam giác nhọn, chứng minh rằng ʹߨ
Giải: Ta xét hàm số ߨ
݂ሺݔሻ ൌ ݔ ݔ െ ʹݔǡ ݔ א ቀͲǡ ቁ ʹ ͳ ଷ ݔ െ ʹ ଶ ݔ ͳ
ሺ ݔ െ ͳሻሺଶ ݔ െ ݔ െ ͳሻ ݂ᇱሺݔሻ ൌ ݔ െ ʹ ൌ ൌ ଶ ݔ ଶ ݔ ଶ ݔ
ሺͳ െ ݔሻሺ ݔ ଶ ݔሻ ൌ Ͳ ଶ ݔ
Vậy hàm số ݂ሺݔሻ đồng biến. Suy ra
݂ሺݔሻ ݂ሺͲሻ ൌ Ͳ ฺ ݔ ݔ ʹݔ
Áp dụng bất đẳng thức trên, ta có : ʹ ൝ ʹ ʹ 120 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác Do đó,
ʹሺ ሻ ൌ ʹߨ
Bài 26: Cho tam giác nhọn. Chứng minh rằng ͳ ͳ ͳ ξ͵ ʹ ൬ ൰ ʹͳ
Giải: Theo đẳng thức cơ bản, ta có : ൌ
Bất đẳng thức trên tương đương với ͳ ͳ ͳ ξ͵ሺ ሻ ʹ ൬ ൰ ʹͳ Ta xét hàm số ʹ ߨ ݂ሺݔሻ ൌ ξ͵ ݔ ǡ ݔ א ቀͲǡ ቁ ݔ ʹ ξ͵ ʹ ݔ ξ͵ െ ʹ ݔ ݂ᇱሺݔሻ ൌ െ ൌ ଶ ݔ ଶ ݔ ଶ ݔ ξ͵ ߨ
݂ᇱሺݔሻ ൌ Ͳ ݔ ൌ ݔ ൌ ʹ ͵ గ గ ݐ Ͳ ସ ଶ ݂Ԣሺݐሻ Ͳ െ ݂ሺݐሻ
Từ bảng biến thiên, ta có : ʹ ξ͵ ݔ ݔ
Áp dụng bất đẳng thức trên, ta suy ra ʹ ۓξ͵ ۖ ʹ ξ͵ ۔ ۖ ʹ ەξ͵
Cộng 3 bất đẳng thức trên, ta có điều phải chứng minh.
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi tam giác đều. 121 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
Bài 27: Cho tam giác không tù và mỗi góc không nhỏ hơn Ͷͷ୭. Chứng minh rằng
͵ Ͷ൫ʹ െ ξʹ൯
Giải: Giả sử . Ta suy ra ߨ ߨ Ͷ ͵ Ta có : ͵
ൌ ͵ ሾͳ െ ሺ ሻሿ
ൌ Ͷ ሺͳ െ ͵ ଶ ሻሺ ሻ Vì ߨ ଶ ͳ
ฺ ͳ െ ͵ ଶ ͳ െ ͵ ൬ ൰ Ͳ ͵ ξ͵ ʹ ൌ ʹ Ͳ ʹ ʹ Suy ra
Ͷ ሺͳ െ ͵ ଶ ሻሺ ሻ Ͷ ሺͳ െ ͵ ଶ ሻʹ ʹ ଶ ଶ ͳ െ ଶ ͳ െ ଶ Ͷ െ ͵ ቀͳ െ ଶ ൌ ͶǤ ʹ ʹ ʹቁ ൦ͳ െ ͵ ቌ ቍ ൪ ʹǤ ൌ ʹ ʹ ʹ ʹ ʹ ʹ ʹ Ta xét hàm số Ͷ െ ͵ሺͳ െ ݔଶሻଶ ͳ ݂ሺݔሻ ൌ ǡ ݔ א ξʹ െ ͳǡ ൨ ʹݔ ξ͵ ሺ͵ݔଶ െ ͳሻଶ ݂ᇱሺݔሻ ൌ െ ʹݔଶ
Suy ra hàm số ݂ሺݔሻ nghịch biến. Do đó,
݂ሺݔሻ ݂൫ξʹ െ ͳ൯ ൌ Ͷ൫ʹ െ ξʹ൯
Vậy ta có điều phải chứng minh.
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi tam giác cân ở và có góc ൌ Ͷͷ୭.
Bài 28: Cho tam giác . Chứng minh rằng ଷξଷ
ሺʹܴ ܽሻሺʹܴ ܾሻሺʹܴ ܿሻ ൏ ͺܴଷ݁ ଶ 122 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
Giải: Ta có điều phải chứng minh tương đương với ܽ ܾ ܿ ଷξଷ ቀͳ ቁ ൬ͳ ൰ ቀͳ ቁ ൏ ݁ ଶ ʹܴ ʹܴ ʹܴ
Theo định lý hàm số sin, ta được ଷξଷ
ሺͳ ሻሺͳ ሻሺͳ ሻ ൏ ݁ ଶ Ta xét hàm số :
݂ሺݔሻ ൌ ሺͳ ݔሻ െ ݔǡ ݔ א ሺͲǡͳሻ ͳ ݂ᇱሺݔሻ ൌ െ ͳ ൏ Ͳ ͳ ݔ
Suy ra hàm số ݂ሺݔሻ nghịch biến. Do đó,
݂ሺݔሻ ൏ ݂ሺͲሻ ൌ Ͳ Vậy ሺͳ ݔሻ ൏ ݔ.
Áp dụng bất đẳng thức trên, ta có :
ሺͳ ሻ ሺͳ ሻ ሺͳ ሻ ൏ Hay
ሺͳ ሻሺͳ ሻሺͳ ሻ ൏ ݁ሺୱ୧୬ାୱ୧୬ାୱ୧୬େሻ
Mặt khác, theo bất đẳng thức cơ bản, ta có : ͵ξ͵ ʹ
Vậy ta có điều phải chứng minh.
Bài 29: Cho tam giác . Chứng minh rằng
ሺ ሻୱ୧୬ ሺ ሻୱ୧୬େ ሺ ሻୱ୧୬ ͳǡͳͻ
Giải: Ta xét hàm số
݂ሺݔሻ ൌ ݔ௫ǡ ݔ א ሺͲǢ ͳሻ
݂ᇱሺݔሻ ൌ ݔ௫ሺͳ ݔሻ ͳ
݂ᇱሺݔሻ ൌ Ͳ ݔ ൌ ݁ ଵ ݔ Ͳ ͳ ݂Ԣሺݔሻ െ Ͳ ͳ ͳ ݂ሺݔሻ ଵ ξ 123 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
Từ bảng biến thiên, ta có : ͳ ݂ሺݔሻ ξ݁
Theo bất đẳng thức Bernoulli, với ǡ ݒ א ሺͲǡͳሻ , ta có : ݑ ݑ ݑ ݑ ݑ௩ ൌ ൌ
ሾͳ െ ሺͳ െ ݑሻሿଵି௩
ͳ െ ሺͳ െ ݒሻሺͳ െ ݑሻ ݑ ݒ െ ݑݒ ݑ ݒ Do đó,
ሺ ሻୱ୧୬େ ሺ ሻୱ୧୬ Giả sử : Suy ra ͳ ۓ
ሺ ሻୱ୧୬ ሺ ሻୱ୧୬ ξ݁ ۔ ەʹሺ ሻ ʹሺ ሻ Khi đó ͳ ͳ ͳ
ሺ ሻୱ୧୬ ሺ ሻୱ୧୬େ ሺ ሻୱ୧୬ ൌ ͳǡͳͻ ξ݁ ʹሺ ሻ ξ ݁ ʹ
Vậy ta có điều phải chứng minh.
Bài 30: Cho tam giác . Chứng minh rằng మ ͵ ξ ξ ξ ͵ ඨͶ
Giải: Theo bất đẳng thức Cauchy, ta có : ିଵ ξ͵ ξ͵ ξ͵ ǥ ݊ ඨቆ ቇ ʹ ᇣᇧᇧᇧᇤᇧᇧ ʹ ᇧᇥ ʹ ሺିଵሻୱố Do đó, ିଵ ξ͵ ξ͵ ݊ ඨቆ ቇ
͵ሺ݊ െ ͳሻ ʹ ʹ
Theo bất đẳng thức cơ bản, ta có : ͵ξ͵ ʹ 124 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác Suy ra ିଵ ξ͵ ͵݊ξ͵ ݊ ඨቆ ቇ ʹ ʹ Hay ିଵ ඨ ξ͵ ͵ξ͵ ቆ ቇ ʹ ʹ Vậy మ ͵ ͵ ඨͶ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi tam giác đều.
Chú ý: Chứng minh tương tự bài toán trên, ta có các bất đẳng thức sau : ͵ ඨ ඨ ඨ ʹ ʹ ʹ ξʹ ͵ ξ ξ ξ ͵ ඨͶ ͵ ඨ ඨ ඨ ʹ ʹ ʹ ʹ ʹ ʹ ξ Ͷ
Bài 31: Cho tam giác . Chứng minh rằng ͳ ͳ ͳ ʹ ͵ ൬ ൰ ξ͵
Giải: Theo bất đẳng thức Cauchy, ta có : ͳ ʹ ʹ ͳ ʹ ሺିଵሻ ʹ ିଵ ͳ ൬ ൰ ǥ ൬ ൰ ݊ ඨ ൬ ൰ ൌ ݊ ൬ ൰ ξ ᇣ ͵
ᇧᇧᇧᇧᇧᇧᇤᇧᇧᇧ ξ ᇧ ͵ ᇧᇧᇥ ξ͵ ξ͵ ሺିଵሻୱố 125 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác Do đó, ʹ ʹ ିଵ ͳ ͳ ͳ ͵ሺ݊ െ ͳሻ ൬ ൰ ݊ ൬ ൰ ൬ ൰ ξ͵ ξ͵
Theo bất đẳng thức cơ bản, ta có : ͳ ͳ ͳ ʹξ͵ Suy ra ʹ ʹ ିଵ ʹ ͵ሺ݊ െ ͳሻ ൬ ൰ ʹξ͵݊ ൬ ൰ ൌ ͵݊ ൬ ൰ ξ͵ ξ͵ ξ͵ Vậy ʹ ͵ ൬ ൰ ξ͵
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi tam giác đều.
Chú ý: Chứng minh tương tự bài toán trên, ta có các bất đẳng thức sau : ͳ ͳ ͳ ͵Ǥʹ ʹ ʹ ʹ ͵ ǡ ݊ ʹ ʹ ʹ ʹ ʹ
Bài 32: Cho tam giác . Chứng minh rằng với ݊ א Գ, ta có : ͳ ͳ ͳ ቌ݊ ቍ ቌ݊ ቍ ቌ݊ ቍ ሺ݊ ʹሻଷ ʹ ʹ ʹ Giải: Ta có : ͳ ͳ ͳ ͳ ͳ ͳ ൌ ݊ଷ ݊ଶ ቌ ቍ ݊ ቌ ቍ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ͳ ʹ ʹ ʹ 126 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
Theo bất đẳng thức cơ bản, ta có : ͳ ʹ ʹ ʹ ͺ
Do đó, theo bất đẳng thức Cauchy ۓ ͳ ͳ ͳ ͳ య ͵ඨ ۖ ۖ ʹ ʹ ʹ ʹ ʹ ʹ ଶ ۔ ͳ ͳ ͳ య ͳ ۖ ۖ ͵ඩቌ ቍ ͳʹ ە ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ Suy ra
݊ଷ ݊ଶ ͳʹ݊ ͺ ൌ ሺ݊ ʹሻଷ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi tam giác đều.
Chú ý: Chứng minh tương tự bài toán trên, ta có bất đẳng thức sau : ۇ ͳ ͳ ͳ ଷ ͳ ۊ ۇͳ ۊ ۇͳ ۊ ൫ͳ ξ ʹ൯ ට ට ට ۉ ʹیۉ ʹیۉ ی ʹ
Bài 33: Cho tam giác . Chứng minh rằng ݊ ඨ ʹ ʹ ʹ ሺ݊ ͳሻ ඥ ʹሺ݊ ͳሻ Giải: Ta có : ͳ െ ͳ ൌ ൬ െ ൰ ൬ͳ െ ൰ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ
Mặt khác, theo bất đẳng thức Cauchy, ta có : ͳ ͳ ͳ ݊ ାଵ ൬ͳ െ ൰ ൌ ቌͳ ᇣᇧ ᇧǥ ᇤ ᇧᇧ ͳ ᇥ െ െ ǥെ ቍ ቀ ቁ ʹ ʹ ʹ ʹ݊ ʹ ᇣᇧʹ
ᇧᇧᇧᇧᇤᇧᇧᇧᇧᇧ ʹ ᇥ ʹ݊ ݊ ͳ ୱố ୱố ݊ ൌ ʹሺ݊ ͳሻାଵ 127 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác Do đó, ݊ ඨ ʹ ʹ ʹ ሺ݊ ͳሻ ඥ ʹሺ݊ ͳሻ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi tam giác cân ở và có góc thỏa mãn : ݊ ൌ ʹ ݊ ͳ
Bài 34: Cho tam giác . Chứng minh rằng ͳ ͳ ͳ ͳ ඨଶ ͵ ඨ ʹ ඨଶ ඨଶ ଶ ʹ ʹ Ͷ ʹ ଶ ʹ ଶ ʹ
Giải: Theo bất đẳng thức Cauchy, ta có : ͳ ͳ ͳ భళ ଶ ଶ ൌ ଶ ǥ ͳ ඩ ʹ ʹ ଶ ʹ ଶ ଶ ʹ ͳଵ ଷଶ ᇣ
ͳᇧᇧᇧᇧʹᇧᇧᇧᇤᇧᇧᇧͳᇧᇧᇧᇧᇥʹ ʹ ଵୱố Suy ra భళ ଶ భళ ଶ భళ ଶ ξ ͳ ൮ ඩ ʹ ඩ ʹ ඩ ʹ ൲ ͳଵ ଷଶ ʹ ͳଵ ଷଶ ʹ ͳଵ ଷଶ ʹ
Theo bất đẳng thức Cauchy, ta được : భళ ଶ భళ ଶ భళ ଶ ඩ ʹ ඩ ʹ ඩ ʹ ͳଵ ଷଶ ʹ ͳଵ ଷଶ ʹ ͳଵ ଷଶ ʹ ఱభ ଶ ଶ ଶ ͵ ඩ ʹ Ǥ ʹ Ǥ ʹ ͳଵ ଷଶ
ʹ ͳଵ ଷଶ ʹ ͳଵ ଷଶ ʹ ͳ
ൌ ͵ఱభඨͳସ଼ଷଶʹଷଶʹଷଶʹ 128 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác Do đó, ͳ ͵ ξ
ͳǤ ఱభඨͳସ଼ଷʹଷʹଷʹ
Mặt khác, theo bất đẳng thức cơ bản, ta có : ͳ ʹ ʹ ʹ ͺ Vậy ͳ ͳ ͳ ͳ ඨଶ ͵ ඨ ʹ ඨଶ ඨଶ ଶ ʹ ʹ Ͷ ʹ ଶ ʹ ଶ ʹ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi tam giác đều.
Bài 35: Cho tam giác . Chứng minh rằng ʹ ʹ ʹ ͵ ʹ ʹ ʹ ʹ ʹ ʹ ʹ
Giải: Theo bất đẳng thức Cauchy, ta có : మ ʹ ʹ ʹ ͳ ͳ ݊ ඩ ʹ ݊ ͳ ǥ ൌ ଶ Ǥ ʹ ʹ ʹ ᇣᇧᇧᇧᇤᇧᇧᇧᇥ ʹ ʹ ʹ ʹିଶ ʹ ʹ
ʹǤ ʹቀଶିଶቁ ቀ ଶିଶቁୱố Do đó, ta được ͳ ͵ ݊ ݊ Ǥ ʹ ൬ ൰ ቀ െ ʹቁ ൬ଶ ଶ ଶ ൰ ʹ ʹ ʹ ʹ ʹ ʹ ʹିଵ ʹ ʹ ʹ
Áp dụng bất đẳng thức cơ bản ͵ ൞ ʹ ʹ ʹ ʹ ͵ ଶ ଶ ଶ ʹ ʹ ʹ Ͷ Ta suy ra ͵ ݊ ͵݊ ͵ ቀ െ ʹቁ െ ʹ ʹ ʹାଵ ʹ Hay 129 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác ʹ ʹ ʹ ͵ ʹ ʹ ʹ ʹ ʹ ʹ ʹ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi tam giác đều.
Chú ý: Từ bài toán trên, ta có kết quả sau : Với tam giác không tù ʹ ξ͵ ʹ ʹ ʹ Với tam giác nhọn ାଵ ͵ ଶ ʹ
Bài 36: Cho tam giác nhọn. Chứng minh rằng với ݊ ݉ ͳǡ ݉ Ͳ thì ାଶ ʹ͵ ଶ ʹ ʹ ʹ
Giải: Theo bất đẳng thức Cauchy, ta có :
ʹାଵ൫ξ͵൯ ǥ ʹାଵ൫ξ͵൯ ᇣᇧᇧᇧᇧᇧᇧᇧᇧ ʹ
ᇧᇧᇧᇧᇤᇧᇧᇧᇧᇧᇧᇧᇧᇧᇧᇧᇧ ʹ ᇥ ʹ ୱố శభ
ሺ݉ ͳሻ ට Ǥ ቂʹାଵ൫ξ͵൯ ቃ Do đó,
݉ʹାଵ൫ξ͵൯ ൬ ൰ ʹ ʹ ʹ
ሺ݉ ͳሻʹ൫ξ͵൯ାଵ൫ ξ
శభ శξభ ξ శభ ൯ Ta xét hàm số ߨ
݂ሺݔሻ ൌ ݔ ǡ ݔ א ቀͲǡ ቁ ǡ ߙ ͳ ʹ
݂ᇱሺݔሻ ൌ ߙ ାଵ ݔ ߙ ିଵ ݔ 130 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
݂ԢԢሺݔሻ ൌ ߙሺߙ ͳሻ ݔ ሺଶ ݔ ͳሻ ߙሺߙ െ ͳሻ ିଶ ݔ ሺଶ ݔ ͳሻ Ͳ
Theo bất đẳng thức Jensen, ta có :
݂ሺሻ ݂ሺሻ ݂ሺሻ ͵݂ ൬ ൰ ͵ Hay ఈ ͵ ൌ ͵Ǥ ൫ξ͵൯ ͵
Áp dụng bất đẳng thức trên, ta được ξ శభ ξ శభ శξ
భ ͵Ǥ ൫ξ͵൯ାଵ
Theo bất đẳng thức cơ bản, ta có ͵ ʹ ʹ ʹ ʹ Do đó, ͵
ሺ݉ ͳሻʹ൫ξ͵൯ାଵǤ ͵Ǥ ൫ξ͵൯ାଵ െ ݉ʹାଵ൫ξ͵൯ Ǥ ʹ ାଶ
ൌ ͵ሺ݉ ͳሻʹ൫ξ͵൯ െ ͵݉ʹ൫ξ͵൯ ൌ ͵Ǥʹ൫ξ͵൯ ൌ ʹ͵ ଶ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi tam giác đều.
Chú ý: Từ bài toán trên, ta có các bất đẳng thức tổng quát sau : ʹඥ͵ଶାି ାଶ ʹ͵ ଶ ʹඥ͵ଶାି ʹ ʹ ʹ
Bài 37: Cho tam giác nhọn. Chứng minh rằng với ݊ ʹǡ ݔǡ ݕǡ ݖ Ͳ thì ͻǤ͵ଶݔݕݖ
ݔǤ ݕǤ ݖǤ ݔݕ ݕݖ ݖݔ 131 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
Giải: Theo bất đẳng thức Bunyakovsky, ta có : ͳ ͳ ͳ ଶ
ሺݔǤ ݕǤ ݖǤ ሻ ൬ ൰ ቀଶ ଶ ଶ ቁ ݔ ݕ ݖ
Áp dụng bất đẳng thức : ఈ
͵Ǥ ൫ξ͵൯ Do đó, ͻǤ͵ଶ ͻǤ͵ଶݔݕݖ
ݔǤ ݕǤ ݖǤ ͳ ͳ ͳ ൌ ݔݕ ݕݖ ݖݔ ݔ ݕ ݖ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi ݔ ൌ ݕ ൌ ݖ
൝ݔǤ ଶ ൌ ݕǤ ଶ ൌ ݖǤ ଶ ቄ ൌ ൌ ൌ Ͳ୭ ଶ ൌ ଶ ൌ ଶ
Bài 38: Cho tam giác . Chứng minh rằng ʹ ඩ ʹ ʹ ʹ ඩ ඩ ͵ ඨ ͵ ʹ ʹ ʹ ʹ ʹ ʹ
Giải: Điều cần chứng minh tương đương với ʹ
ඨͳ െ ඨͳ െ ඨͳ െ ͵ ඨ ʹ ʹ ʹ ʹ ʹ ʹ ͵
Theo bất đẳng thức Cauchy, ta có : ʹ ʹ ʹ ିଵ
ͳ െ ڮ ݊ ඨ൬ͳ െ ൰ ൬ ൰ ʹ ʹ ͵ᇣᇧᇧᇤᇧᇧ ͵ ᇥ ʹ ʹ ͵ ሺିଵሻୱố Do đó, ʹ ʹ ଵିଵ
͵ െ ൬ ൰ ͵Ǥ ሺ݊ െ ͳሻ ݊ ൬ ൰ Ǥ ʹ ʹ ʹ ʹ ʹ ʹ ͵ ͵
Mặt khác, theo đẳng thức cơ bản, ta có : ൌ ͳ ʹ ʹ ʹ ʹ ʹ ʹ 132 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác Suy ra ʹ ͵ ඨ͵
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi tam giác đều.
Chú ý: Từ bài toán trên, ta có bất đẳng thức tổng quát sau െ െ െ Ͷ ඩ ʹ ʹ ʹ ඩ ඩ ͵ ඨ ͵ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ͵Ǥ ൬ ൰ ͵ ʹ ʹ ʹ ʹ ʹ ʹ െ ʹ െ െ Ͷ ʹ ʹ ͵Ǥ ൬ ൰ ͵ ʹ ʹ ʹ ʹ ʹ ʹ - BÀI TẬP TỰ LUYỆN
3.2.1. Chứng minh rằng trong tam giác ta luôn có : ܽ ܾ ܾ ܿ ܿ ܽ Ǥ ܽ ܾ ܿ
Ǥܽଶ൫ͳ െ ξ͵ ൯ ܾଶ൫ͳ െ ξ͵ ൯ ܿଶ൫ͳ െ ξ͵ ൯ Ͳ Ǥ݈݈݈ ܾܽܿ ʹ ʹ ʹ ͵ ͵
Ǥ ଷ ଷ ଷ ൬ ൰ ͵ ͵ ͵ ͺ Ͷ ͵ ͵ ͵ (ĐHQG Hà Nội 1998) െ െ െ Ǥ ʹ ʹ ʹ ͳ ߨ ͳ ߨ ͳ ߨ
ቀ െ ቁ ቀ െ ቁ ቀ െ ቁ ͵ ͵ ͵ ͵ ͵ ͵ (ĐHQG Hà Nội 1995) 133 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác ܵ
Ǥ ൬ͳ ൰ ൬ͳ ൰ ൬ͳ ൰ ʹ ξ͵ ʹ ʹ ʹ ଶ (ĐH Ngoại Thương 1997) ͳ ͳ ͳ ͳ ͳ ͳ Ǥ Ͷܾܽܿ ൬ ൰ ଶ ܽଷ ܾଷ ܿଷ ʹ ଶ ʹ ଶ ʹ
Ǥܴሾʹሺܾ ܿሻ െ ܽሿ ξ͵ ͳ ͳ ͳ ͳ ͳ ͳ ͳ ͳ ͳ Ǥ ൬ ൰
൬ ൰ ൬ ൰ ͵ξ͵ ݈ ܾ ܿ ݈ ܿ ܽ ݈ ܽ ܾ
(ĐH Kỹ Thuật Quân Sự 1997) െ െ െ Ǥ ʹ ʹ ʹ ʹ ʹ ʹ ݔଶ Ǥͳ
ݔ ݔ ǡ ݔ א Թ ʹ ͳ
Ǥݕݖ ଶ ݖݔ ଶ ݔݕ ଶ ሺݔ ݕ ݖሻଶ Ͷ ͳ
Ǥʹ ξ͵ሺ ሻ Ͷ
Ǥξ ξ ξ ඨ ඨ ඨ ʹ ʹ ʹ (ĐH Bách Khoa Tp.HCM 1995)
Ǥξ ξ ξ ඨ ඨ ඨ ǡ ȟọ ʹ ʹ ʹ (ĐH Ngoại Thương 1996) ͵
Ǥʹሺ ሻ ሺ െ ሻ ሺ െ ሻ ሺ െ ሻ െ ʹ ʹ ͳ ͳ Ǥ ͳ ͳ ଶ ͳ ଶ ʹݎ Ǥ ܴ ʹ ʹ ʹ ͳͷ Ǥඨ
ሺ െ ሻ ሺ െ ሻ ሺ െ ሻ Ͷ
(Đề nghị Olympic 30-4, 2007) 134 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác ͷ ͳ
Ǥ ሺ ሻǡ ȟọ ʹ ʹ ʹ Ͷ
(Đề nghị Olympic 30-4, 2010)
3.2.2. Cho tam giác nhọn, chứng minh rằng với ݊ א Գ ݊൫͵ మబబ ξ͵ െ ͳ൯ ͲͲͲ ξ బ ξ మబబబ ξ మబబబ ʹͲͲͲ
3.2.3. Chứng minh rằng ͳ ͵ ܵେ ൌ ฺ ൬
൰ ܽଶ ܾଶ ܿଶ Ͷ ߨ
3.2.4. Cho tam giác có diện tích là ͳ. Gọi ܴ và ݎ là bán kính đường tròn ngoại tiếp
và nội tiếp tam giác , chứng minh rằng ʹ ͵ ర Ͷξʹ ܴ ݎ
3.2.5. Cho tam giác có ܽǡ ܾǡ ܿ thỏa ܽଶ ܾଶ ܿଶ. Chứng minh rằng ʹ ݎ ͳ ൏ ൏ ͷ ݄ ʹ
3.2.6. Cho tam giác có 2 góc ǡ thỏa ൌ ͳ ʹ ʹ Chứng minh rằng ͵ ൏ ͳ Ͷ ʹ
(ĐH Bách Khoa Hà Nội 1998)
3.2.7. Cho tam giác có các góc thỏa mãn : ʹ ʹ ʹ െͳ Chứng minh rằng ͳ ξʹ 135 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
3.2.8. Cho tam giác có Ͳ ൏ ൏ ͻͲ୭. Chứng minh rằng ʹ ͵ െ Ͷ ʹ ͳ ʹ
3.2.9. Cho tam giác có độ dài 3 đường phân giác trong đều nhỏ hơn ͳ. Chứng minh rằng ͳ ܵେ ൏ ξ͵
3.2.10. Cho tam giác nhọn thì ͳ ʹ
Ǥ ሺ ሻ ሺ ሻ ߨ ͵ ͵
Ǥ͵ ൬ ൰ ξ͵ ʹ ʹ ʹ ʹ ʹ ʹ ͳ ͳ ͳ
Ǥ ͵ξ͵ ʹ ൬ ൰ -
GỢI Ý GIẢI BÀI TẬP TỰ LUYỆN 3.2.1. a.
Điều cần chứng minh tương đương với ܽ ܾ ͳ ܾ ܿ ͳ ܿ ܽ ͳ െ ሺܽ ܾሻ൨ െ ሺܾ ܿሻ൨ െ ሺܿ ܽሻ൨ Ͳ ʹ ʹ ʹ ʹሺ െ ሻሺܽ െ ܾሻ ʹሺ െ ሻሺܾ െ ܿሻ ʹሺ െ ሻሺܿ െ ܽሻ Ͳ b.
Theo định lý hàm số sin, ta có :
ଶ ଶ ଶ ξ͵ሺ ሻ ξ͵ ଶ ଶ ଶ ሺ ʹ ʹ ʹሻ ʹ
ଶ ଶ ଶ ʹξ͵ 136 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
Theo bất đẳng thức Cauchy, ta có : ଶ ଶ ଶ ͵ඥ య ሺ ሻଶ
Mà theo bất đẳng thức cơ bản thì ξ͵ ξ య ʹ Suy ra ͵ඥ య ሺ ሻଶ ʹξ͵ c.
Áp dụng công thức độ dài trung tuyến và bất đẳng thức Cauchy ʹܾܿ ݈ ൌ ξܾܿ ܾ ܿ ʹ ʹ d. Cần chứng minh : ͳ ͵
ൌ ሺ ሻ ൬ ൰ Ͷ Ͷ ͵ ͵ ͵ e. Ta có : െ െ െ െ ʹ ߨ ͵ ൌ ʹ ʹ ൬ െ ൰ ʹ ʹ Ͷ Ͷ Ͷ Ͷ Để ý ͳ ߨ ߨ ͵ ߨ
Ͳ ฬ ቀ െ ቁฬ ฬ െ ฬ ൏ Ͷ ͵ Ͷ Ͷ ʹ Do đó, ߨ ͵ ͳ ߨ ൬ െ ൰ ቀ െ ቁ Ͷ Ͷ ͵ ͵ f. Ta đặt : ݔ ൌ ǡݕ ൌ ǡݖ ൌ ʹ ʹ ʹ
ฺ ൌ ͳ ݔ ݕ ݖ ݔݕ ݕݖ ݖݔ ൌ ʹ ݔ ݕ ݖ ݔݕݖ 137 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác Để ý rằng ܵ ܵ ܵ ݔ ൌ ǡ ݕ ൌ ǡ ݖ ൌ ሺ െ ܽሻ ሺ െ ܾሻ ሺ െ ܿሻ ܵ
² ൌ ʹ ݔ ݕ ݖ ଶ
Khi đó chỉ cần chứng minh ݔ ݕ ݖ ξ͵ g.
Áp dụng định lý hàm số cos, ta chứng minh ͳ Ͷܾܿ
ܽଶ ൌ ሺܾ െ ܿሻଶ Ͷܾܿ ଶ ฺ ܽଶ Ͷܾܿ ଶ ฺ ʹ ʹ ܽଶ ଶ ʹ h.
Áp dụng định lý hàm số sin, điều cần chứng minh tương đương với ͳ െ ξ͵ ʹ ͳ ξ͵ ͳ ξ͵ ቆͳ െ െ ቇ ቆͳ െ െ ቇ Ͳ ʹ ʹ ʹ ʹ ߨ ߨ
ቂͳ െ ቀ െ ቁቃ ቂͳ െ ቀ െ ቁቃ Ͳ ͵ ͵ i. Cần chứng minh ͳ ͳ ݈ ൬ ൰ ൌ ʹ ܾ ܿ ʹ j.
Theo bất đẳng thức Cauchy, ta có : െ െ െ య ͵ඩ ʹ ʹ ʹ ʹ ʹ ʹ Để ý െ െ െ ʹ ʹ ʹ
ሺ ሻሺ ሻሺ ሻ ൌ ʹ ʹ ʹ 138 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
Theo bất đẳng thức Cauchy, ta có : ʹξ ቐ ʹξ ʹξ Suy ra
ሺ ሻሺ ሻሺ ሻ ͺ k.
Ta coi điều cần chứng minh là bài toán xét dấu của tam thức bậc hai
ܽݔଶ ܾݔ ܿ Ͳǡ ݔ א Թ ቄȟ Ͳ ܽ Ͳ l. Tương tự như câu k. m.
Ta có đẳng thức cơ bản ଶ ଶ െ ଶ ൌ ʹ
Biến đổi điều phải chứng minh thành ଶ ଶ ଶ ξ͵ ξ͵ ξ͵ ቆ െ ቇ ቆ െ ቇ ቆ െ ቇ Ͳ ʹ ʹ ʹ n. Để ý
ξ ξ ඥʹሺ ሻ ʹඨ ʹ o. Để ý ర ర
ξ ξ ʹξ ʹඨଶ ൌ ʹඨ ʹ ʹ p. Ta đi từ
ሺͳ െ ሻሺ ሻ Ͳ q.
Ta sử dụng phép biến đổi tương đương và để ý rằng ͳ ͳ ͳ ͳ െ െ ͳ ͳ ଶ ͳ ͳ ଶ ሺ െ ሻଶ ͳ െ ൌ ൨
ͳ ሺͳ ଶ ሻሺͳ ଶ ሻ r.
Theo định lý hàm số sin, ta có : ൌ ܴ
Bất đẳng thức tương đương với
ଶ ʹܵ ൬ ൰ ʹ ʹ ʹ 139 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác ଶ
ଷ Ͷሺ െ ܽሻሺ െ ܾሻሺ െ ܿሻ ൬ ൰ ʹ ʹ ʹ Ta có :
ሺ െ ܽ െ ܾ െ ܿሻଷ ଷ
ሺ െ ܽሻሺ െ ܾሻሺ െ ܿሻ ൌ ʹ ʹ ଶ ʹ ൬ ൰ ʹ ʹ ʹ Ͷ s.
Ta có bất đẳng thức đã cho tương đương với ͳͷ ሺ ሻଶ
ሺ െ ሻ ሺ െ ሻ ሺ െ ሻ Ͷ
֞ ଶ ଶ ଶ ሺ െ ሻ ሺ െ ሻ ͵ ሺ െ ሻ Ͳ Ͷ ͵
֞ ଶ ଶ ଶ ሺ ሻ ሺ ሻ ሺ ሻ Ͳ Ͷ ͵
֞ ଶ ଶ ଶ െ ሺ ሻ Ͳ Ͷ ͳ ଶ ͳ ଶ ͳ ଶ
֞ ൬ െ ൰ ൬ െ ൰ ൬ െ ൰ Ͳ ʹ ʹ ʹ t. Ta có : ൌ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ Ͷ ʹ ʹ Để ý ͳ
ൌ ሺ ሻ ሺ ሻ ሺ ሻ൨ ʹ ʹ ʹ ʹ ʹ ൬ ൰ ʹ ʹ ʹ ʹ ʹ ʹ Hay ଶ
ଶ ଶ ଶ ൌ ൬ ൰ ʹ ʹ ʹ ʹ ʹ ʹ 140 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác Mặt khác ͵ ଶ
֜ ʹ ൬ ൰ െ ͵൨ Ͳ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ଶ
ฺ Ͷ ൬ ൰ ͻ ͳʹ ൬ ൰ ʹ ʹ ʹ ʹ ʹ ʹ
ฺ Ͷ ൬ଶ ଶ ଶ ൰ ͻ ͳʹ ൬ ൰ ʹ ʹ ʹ ʹ ʹ ʹ
ฺ ʹሺ͵ ሻ ͻ ͳʹ ൬ ൰ ʹ ʹ ʹ ͷ ͳ
ฺ ሺ ሻ ʹ ʹ ʹ Ͷ
3.2.2. Chứng minh tương tự Bài 9 câu b, để ý rằng ݊
͵Ǥ ൫͵ξ͵൯ ൌ ͵ൣͳ ൫͵ξ͵ െ ͳ൯൧ ͵ ቂͳ ൫͵ξ͵ െ ͳ൯ቃ ͲͲͲ 3.2.3. Ta có :
ሺ െ ሻሺ െ ሻ Ͳ ֜ Để ý
ʹሺ ሻ ሺ ሻ ሺ ሻ ሺ ሻ
ฺ ͵ሺ ሻ ሺ ሻሺ ሻ ܽଶ ܾଶ ܿଶ ฺ ͵ሺ ሻ ߨ Ͷܵ 3.2.4. Để ý ʹ ͵ ͺܵ ͵ ͺ ൌ ൌ ͵ ܴ ݎ ܾܽܿ ܵ ܾܽܿ
Theo bất đẳng thức Cauchy, ta có : ܽ ܾ ܿ ଷ ʹ ଷ ܾܽܿ ൬ ൰ ൌ ൬ ൰ ͵ ͵ Suy ra 141 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác ʹ ʹ ర ʹ ͵ ൌ Ͷඨ ଷ ൌ Ͷξ ర ʹ ଷ ଷ ଷ 3.2.5. Ta có : ݎ ܿ ܿ ܿ ͳ ൌ ൌ ൏ ൌ ݄ ʹ ܽ ܾ ܿ ʹܿ ʹ
Mặt khác theo bất đẳng thức Bunyakovsky, ta có :
Ͷሺܽ ܾሻଶ ͺሺܽଶ ܾଶሻ ͺܿଶ ൏ ͻܿଶ Do đó ݎ ܿ ʹ ൌ ݄ ܽ ܾ ܿ ͷ 3.2.6. Để ý ͳ െ ൌ ʹ ʹ ൌ ͳ െ ൏ ͳ ʹ ʹ ʹ ʹ ʹ Và ͵
ͳ ൌ ʹඨ ฺ ͳ െ ʹ ʹ ʹ ʹ ʹ ʹ Ͷ 3.2.7. Để ý
ʹ ʹ ʹ െͳ Ͳ Do đó, chọn góc sao cho ߨ ߨ ฺ Ͳ ൏ ʹ ʹ Ͷ Khi đó െ ߨ ͳ ʹ ͳ ʹ ൌ ͳ ξʹ ʹ ʹ Ͷ
3.2.8. Từ giả thuyết ta có Ͳ୭. Do đó, bất đẳng thức tương đương với ͳ
ͺ ଷ െ ͺ ଶ െ ͺ ͷ Ͳǡ א ൬ͲǢ ൨ ʹ
Khi đó ta chỉ cần khảo sát hàm số ͳ
݂ሺݔሻ ൌ ͺݔଷ െ ͺݔଶ െ ͺݔ ͷǡ ݔ א ൬ͲǢ ൨ ʹ 3.2.9. Để ý : ݄ ݈ ൏ ͳ
Giả sử ܽ ܾ ܿ. Ta suy ra 142 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác ͳ ͳ ͳ ൝ ܽ ܾ ܿ Mặt khác ʹܾܿ ͳ ͳ ͳ ͳ ݈ ʹ ൌ ฺ ൏ ൬ ൰ ܾ ܿ ʹ ʹ ܾ ܿ ܽ Do ߨ ξ͵ ʹ
ฺ ฺ ฺ ܽ ͵ ʹ ʹ ξ͵ 3.2.10. a. Ta xét hàm số ͳ ʹ ߨ
݂ሺݔሻ ൌ ݔ ݔ െ ݔǡ ݔ א ቀͲǡ ቁ ͵ ͵ ʹ b. Ta xét hàm số ͳ ߨ
݂ሺݔሻ ൌ ͵ݔ ǡ ݔ א ቀͲǡ ቁ ݔ ʹ c. Ta xét hàm số ʹ ߨ ݂ሺݔሻ ൌ ݔ െ ǡ ݔ א ቀͲǡ ቁ ݔ ʹ 3.
NHẬN DẠNG TAM GIÁC VÀ TÍNH CÁC GÓC TRONG TAM GIÁC
- Đây là loại toán cơ bản được tổng kết các loại toán và từ những phương pháp trên.
Khi một tam giác thỏa 1 hay 2 đẳng thức hoặc bất đẳng thức giữa các cạnh và hàm
số lượng giác của các góc, ta phải tìm tính chất của tam giác đó, chẳng hạn như :
tìm số đo của góc, chứng tỏ giá trị hàm lượng giác của góc, hoặc chứng minh là
tam giác cân, vuông, đều…
- Một số kỹ thuật cần chú ý : nếu giả thuyết cho từ 2 hệ thức hoặc bất đẳng thức trở
lên, ta phải biến đổi hệ thức dễ trước, ngoài ra ta phải để ý sử dụng bất đẳng thức ở dạng trên. 143 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
Bài 1: Tính các góc của tam giác , biết rằng ͵ Ǥ ሺ െ ሻ ൌ ʹ (ĐH Mở Hà Nội 2000) ͵ Ǥ ൌ െ ʹ
(ĐH Sư Phạm Kỹ Thuật Tp.HCM 2001) ͷ
Ǥ ʹ ξ͵ሺ ʹ ʹሻ ൌ Ͳ ʹ
(ĐH Sư Phạm Hà Nội 2001) Giải: a.
Giả thuyết tương đương với ͵
ሺ െ ሻ ሺ ሻ ൌ ʹ ͳ ͵
ሺ ʹ െ ʹሻ ൌ ʹ ʹ ͳ ͵
ሺͳ െ ʹ ଶ ͳ െ ʹ ଶ ሻ ൌ ʹ ʹ ͳ ͳ
൬ଶ െ ൰ ൬ଶ െ ൰ ൌ Ͳ Ͷ Ͷ ͳ ଶ ͳ ଶ
൬ െ ൰ ൬ െ ൰ ൌ Ͳ ʹ ʹ ͳ ൌ ୭ ൞
ʹͳ ቄ ൌ ͵Ͳ୭ ฺ ൌ ͻͲ୭ ൌ Ͳ ൌ ʹ b.
Giả thuyết tương đương với െ ͳ ͳ ൌ ʹ െ ʹ ʹ ʹ െ ͳ ʹ ଶ ൌ ʹ െ ʹ ʹ ʹ ʹ െ ͳ ଶ െ ൌ Ͳ ʹ ʹ ʹ Ͷ 144 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác െ ͳ െ ͳ ͳ െ ൬ଶ െ ଶ ൰ െ ଶ ൌ Ͳ ʹ ʹ ʹ Ͷ ʹ Ͷ Ͷ ʹ ͳ െ ଶ ͳ െ ൬ െ ൰ ଶ ൌ Ͳ ʹ ʹ ʹ Ͷ ʹ ͳ െ െ ൌ Ͳ ൞ ʹ ʹ ʹ െ ቄ ൌ ͳʹͲ୭ ൌ ൌ ͵Ͳ୭ ൌ Ͳ ʹ c.
Giả thuyết tương đương với ͷ
ʹ ଶ െ ͳ ʹξ͵ ሺ ሻ ሺ െ ሻ ൌ Ͳ ʹ ͵
ଶ െ ξ͵ ሺ െ ሻ ൌ Ͳ Ͷ
Ta thấy đây là phương trình bậc 2 có nghiệm . Khi đó െ െ ȟ ൌ ͵ ଶ െ ͵ Ͳ ଶ Ͳ ʹ ʹ Suy ra ൌ . Như vậy ͵ ξ͵
ଶ െ ξ͵ ൌ Ͳ ൌ Ͷ ʹ
Do đó : ൌ ͵Ͳ୭ǡ ൌ ൌ ͷ୭
Bài 2: Tính các góc của tam giác biết Ǥ ൌ ൌ ͳ ξ͵ ʹ (ĐH An Ninh 1998)
Ǥ ʹ ʹξʹ ʹξʹ ൌ ͵ሺȟØîሻ (Tuyển sinh Khối A 2004) Giải: a.
Theo định lý hàm số sin, ta có : ܽ ܾ ܿ ൌ ൌ ൌ ൌ ൜ܾ ൌ ܽξ͵ ͳ ξ͵ ʹ ͳ ξ͵ ʹ ܿ ൌ ʹܽ
Theo định lý hàm số cos, ta được : 145 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác ܾଶ ܿଶ െ ܽଶ ͵ܽଶ Ͷܽଶ െ ܽଶ ξ͵ ൌ ൌ ൌ ฺ ൌ ͵Ͳ୭ ʹܾܿ ʹܽξ͵Ǥ ʹܽ ʹ Ͷܽଶ ܽଶ െ ͵ܽଶ ͳ ൌ ൌ ฺ ൌ Ͳ୭ ʹܽǤ ʹܽ ʹ Do đó, ൌ ͻͲ୭. b.
Giả thuyết tương đương với െ ʹ ଶ െ ͳ Ͷξʹ ൌ ͵ ʹ ʹ െ ଶ ʹξʹ ൌ ʹ ʹ ʹ Mặt khác :
Do tam giác không tù nên א ሾͲǢ ͳሻ ฺ ଶ Nên െ െ ʹ ൌ ଶ ʹξʹ ʹξʹ ʹ ʹ ʹ ʹ െ
ʹ ͳ െ ʹ ଶ ʹξʹ ʹ ʹ ʹ െ ͳ ଶ െ ξʹ Ͳ ʹ ʹ ʹ ʹ ξʹ ଶ െ ͳ െ ቆ െ ቇ ଶ Ͳ ʹ ʹ ʹ ʹ ʹ ۓ ξʹ െ െ ൌ Ͳ ʹ ʹ ʹ ቄ ൌ ͻͲ୭ ۔ െ ൌ ൌ Ͷͷ୭ ە ൌ Ͳ ʹ 146 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
Bài 3: Số đo 3 góc của tam giác lập thành cấp số cộng và thỏa mãn đẳng thức ͵ ξ͵ ൌ ʹ a. Tính các góc ǡ ǡ . b.
Biết nửa chu vi tam giác bằng 50. Tính các cạnh của tam giác.
(ĐH Sư Phạm Kỹ Thuật Tp.HCM 1993) Giải: a.
Giả sử . Do đó, ta có : ൌ ʹ
Mặt khác : ൌ ͳͺͲ୭ ฺ ቄ ൌ ͳʹͲ୭ ൌ Ͳ୭ Khi đó : െ െ ൌ ʹ ൌ ʹ Ͳ୭ Ͳ୭ ʹ ʹ ʹ െ ξ͵ ൌ ξ͵ ʹ ʹ Như vậy െ ξ͵ ͵ ξ͵ െ ξ͵ ξ͵ ൌ ฺ ൌ ฺ െ ൌ Ͳ୭ ʹ ʹ ʹ ʹ ʹ
Vậy ൌ ͻͲ୭ǡ ൌ Ͳ୭ǡ ൌ ͵Ͳ୭. b.
Tam giác vuông tại nên ta có : ۓ ξ͵ ൌ Ͳ୭ ൌ ʹ ۔ ە ൌ ͵Ͳ୭ ൌ ʹ Mặt khác ͳ
ൌ ሺ ሻ ൌ ͷͲ ʹ 147 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác Suy ra ʹͲͲ ۓ ൌ ͵ ξ͵ ξ͵ ۖ ۖ ͳͲͲ ൌ ͳͲͲ ൌ ʹ ʹ ۔ ͵ ξ͵ ۖ ۖ ͳͲͲξ͵ ൌ ە ͵ ξ͵
Bài 4: Xác định các góc của tam giác thỏa các điều kiện sau : ൜ ൌ ξʹ ଶ ଶ ଶ ͳ
(ĐH Tổng Hợp Hà Nội 1992)
Giải: Theo đẳng thức cơ bản, ta có :
ͳ െ ʹ ൌ ଶ ଶ ଶ ͳ ฺ Ͳ
Do đó, tam giác tồn tại 1 góc tù hoặc vuông.
Chọn ͻͲ୭. Ta xét : ൌ ξʹ െ ͳ െ ʹ ଶ ʹ ൌ ξʹ ʹ ʹ ʹ െ
ͳ െ ξʹ ൌ ʹ ଶ െ ʹ ʹ ଶ െ ʹ ʹ ʹ ʹ ʹ ʹ ͳ െ ξʹ ଶ െ ʹ ʹ ʹ Ta xét hàm số ξʹ
݂ሺݔሻ ൌ ݔଶ െ ݔǡ ݔ א ቈ Ǣ ͳቇ ʹ
݂ᇱሺݔሻ ൌ ʹݐ െ ͳ Ͳ
Do đó, hàm số ݂ሺݔሻ đồng biến. Suy ra 148 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác ξʹ ͳ െ ξʹ ݂ሺݔሻ ݂ ቆ ቇ ൌ ʹ ʹ Như vậy, ta được : ۓ ξʹ ൌ ʹ ʹ ቄ ൌ ͻͲ୭ ۔ െ ൌ ൌ Ͷͷ୭ ە ൌ ͳ ʹ
Bài 5: Cho các góc của tam giác thỏa mãn hệ thức ଶ ଶ ൌ మశඥ భ ଶ
Biết rằng góc ǡ nhọn. Hãy tính giá trị góc .
Giải: Ta xét 3 trường hợp sau :
- ͻͲ୭ thì ൏ Ͳ. Mà theo định lý hàm số cos, ta có ܽଶ ܾଶ െ ܿଶ ൌ
൏ Ͳ ฺ ܽଶ ܾଶ ൏ ܿଶ ʹܾܽ
Mặt khác, theo định lý hàm số sin, ta suy ra : మశభ ଶ ଶ ൏ ଶ ൏ ඥଶ
Điều này mâu thuẫn với giả thuyết. - మశభ
൏ ͻͲ୭ thì ଶ ൏ ͳ ฺ ξଶ ൏ ͳ Mà ͳ െ ʹ ͳ െ ʹ ଶ ଶ ൌ
ൌ ͳ െ ሺ ሻ ሺ െ ሻ ʹ ʹ ൌ ͳ ሺ െ ሻ
Vì góc nhọn nên Ͳ và ሺ െ ሻ Ͳ. Do đó, మశඥ
భ ଶ ൌ ଶ ଶ ൌ ͳ ሺ െ ሻ ͳ Điều này mâu thuẫn. 149 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
- ൌ ͻͲ୭, dễ thấy giá trị này thỏa đẳng thức đã cho.
Bài 6: Cho tam giác có các góc thỏa mãn điều kiện ͳ ܾ ܿ ʹ ൌ ʹ ʹ ʹ ܽ ʹ Hãy tính góc .
(ĐH Mỏ-Địa Chất Hà Nội 1997)
Giải: Theo công thức biến đổi và định lý hàm số sin, giả thuyết tương đương với െ ͳ ൌ Ǥ ʹ ʹ ʹ ʹ െ െ ͳ ʹ ൌ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ െ ͳ െ ൌ ʹ ʹ ʹ ʹ ͳ ൌ ൌ Ͳ୭ ʹ ʹ
Bài 7: Cho tam giác có các góc thỏa mãn hệ thức ሺ ሻ ൌ ሺ െ ሻ Hãy tính :
Giải: Giả thuyết tương đương với െ Ǥ ʹ ൌ ʹ ሺ െ ሻ ʹ ʹ ʹ ʹ െ ൌ ሺ െ ሻ ʹ ʹ െ െ ൬ͳ െ ʹ ଶ ൰ ൌ ൬ʹ ଶ െ ͳ൰ ʹ ʹ ʹ ʹ െ െ െ ൌ ʹ ൬ ൰ ʹ ʹ ʹ ʹ ʹ ʹ 150 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác Mặt khác, do െ ് Ͳ ʹ ʹ Nên െ ʹ ൌ ͳ ൌ ͳ ʹ ʹ
Bài 8: Chứng minh rằng tam giác cân khi có các góc thỏa mãn hệ thức ܽ Ǥ ൌ ʹ ʹξܾܿ
(ĐH Khoa Học Tự Nhiên Hà Nội 1994) ଶ ଶ ͳ Ǥ ൌ ሺଶ ଶ ሻ ଶ ଶ ʹ
(ĐH Dân Lập Phương Đông 1997) Ǥ ଷ ൌ ଷ ʹ ʹ ʹ ʹ (ĐH Thương Mại 1999) Giải: a.
Giả thuyết tương đương với ܽଶ ଶ ൌ ʹ Ͷܾܿ ͳ ܽଶ ܾଶ ܿଶ െ ܽଶ ܽଶ ሺͳ െ ሻ ൌ ͳ െ ൌ ʹ Ͷܾܿ ʹܾܿ ʹܾܿ
ሺܾ െ ܿሻଶ ൌ Ͳ ܾ ൌ ܿ Vậy tam giác cân tại . b.
Giả thuyết tương đương với
ʹሺଶ ଶ ሻ ൌ ଶ ଶ ଶ ଶ ଶ ଶ
ଶ െ ଶ ଶ ൌ ଶ ଶ െ ଶ
ଶ ሺଶ െ ଶ ሻ ൌ ଶ ሺଶ െ ଶ ሻ
ሺଶ െ ଶ ሻሺଶ െ ଶ ሻ ൌ Ͳ 151 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
ቂଶ ൌ ଶ ቂ ൌ േ ൌ ଶ ൌ ଶ ൌ Vậy tam giác cân tại . c.
Giả thuyết tương đương với ʹ ͳ ʹ ͳ Ǥ ൌ Ǥ ʹ ଶ ʹ ʹ ଶ ʹ
൬ͳ ଶ ൰ ൌ ൬ͳ ଶ ൰ ʹ ʹ ʹ ʹ
ଷ െ ଷ െ ൌ Ͳ ʹ ʹ ʹ ʹ
൬ െ ൰ ቌଶ ଶ ͳቍ ൌ Ͳ ʹ ʹ ᇣᇧ ʹ ᇧᇧᇧᇧᇧᇧᇧ ʹ ᇧᇧᇤᇧᇧᇧʹ ᇧᇧᇧᇧʹ ᇧᇧᇧᇥ வ ൌ ൌ ʹ ʹ Vậy tam giác cân tại .
Bài 9: Chứng minh rằng tam giác cân khi có các góc thỏa mãn hệ thức ൌ ൫ξʹ െ ൯ Ǥ ቊ ൌ ൫ξʹ െ ൯
(ĐH Thủy Lợi Hà Nội 2000) ͳ ʹܽ ܿ Ǥ ൌ ξͶܽଶ െ ܿଶ
(ĐH Giao Thông Vận Tải 2001) ʹሺͳ ሻ Ǥ ൌ
(ĐH Kiến Trúc Tp.HCM 2001) Giải: a.
Ta lấy hệ thức trên trừ cho hệ thức dưới thì : െ ൌ ሺ െ ሻ 152 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác െ െ ʹ ൌ െʹ ʹ ʹ ʹ ʹ െ ቌ ቍ ൌ Ͳ ʹ ᇣᇧᇧ ʹ
ᇧᇧᇧᇧᇧᇤᇧᇧᇧᇧᇧ ʹ ᇧᇧᇥ வ െ ൌ Ͳ ൌ ʹ Vậy tam giác cân tại . b.
Giả thuyết tương đương với ሺͳ ሻଶ ሺʹܽ ܿሻଶ ൌ ଶ Ͷܽଶ െ ܿଶ ͳ ʹܽ ܿ ൌ ͳ െ ʹܽ െ ܿ ͳ ʹܽ ܿ ͳ ൌ ͳ ͳ െ ʹܽ െ ܿ ͳ ʹܽ ൌ ܿ ൌ ʹܽ ͳ െ ʹܽ െ ܿ ܿଶ ܽଶ െ ܾଶ ܿ ൌ ʹܽ ቆ ቇ ܽ ൌ ܾ ʹܽܿ Vậy tam giác cân tại . c.
Giả thuyết tương đương với Ͷ ଶ ʹ ሺ ሻ ൌ ʹ ʹ ʹ ʹ ʹ ൌ ʹ ʹ ൌ ʹ ଶ ʹ
ሺ ሻ ሺ െ ሻ ൌ ͳ െ
ሺ െ ሻ ൌ ͳ ൌ Vậy tam giác cân tại . 153 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
Bài 10: Chứng minh rằng tam giác cân khi có các góc thỏa mãn hệ thức
Ǥܽ ൬ െ ൰ ൌ ܾ ൬ െ ൰ ʹ ʹ ଶ ଶ Ǥ ൌ ʹ ܿଶ Ǥܽଶ ʹ ܾଶ ʹ ൌ ʹ Ǥݎ ൌ Ͷܴ െ ݎ Giải: a.
Giả thuyết tương đương với ܽ ൬ െ ൰ ൌ ܾ ൬ െ ൰ ʹ ʹ ቀ ቀ െ ܽǤ ʹ െ ቁ ʹ ቁ ൌ ܾǤ ʹ ʹ െ െ ܽǤ ʹ ൌ ܾǤ ʹ െ ʹܴ ʹܴ ൬ െ ൰ ൌ Ͳ ʹ െ ൌ Ͳ ʹ ൌ ൌ Vậy tam giác cân tại . b.
Giả thuyết tương đương với ൌ ሺ ሻ ʹ ൬ െ ൰ ൬ െ ൰ ൌ Ͳ ʹ ʹ 154 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác ቀ െ ቀ െ Ǥ ʹ ቁ ʹ ቁ Ǥ ൌ Ͳ ʹ ʹ െ െ Ǥ ʹ Ǥ ʹ ൌ Ͳ െ ሺ െ ሻ ൌ Ͳ ʹ െ ൌ Ͳ ʹ ൌ ൌ Vậy tam giác cân tại . c.
Theo định lý hàm số sin, ta có :
ൌ Ͷܴଶ ଶ Ǥ ʹ Ͷܴଶ ଶ Ǥ ʹ ൌ ͺܴଶ ሺ ሻ
ൌ ሺʹܴ ሻሺʹܴ ሻʹ ൌ ͶܾܽǤ ʹ ʹ Do đó, ܿଶ ͶܾܽǤ ൌ ʹ ʹ ʹ Ͷܾܽ ଶ ൌ ܿଶ ʹ
ʹܾܽሺͳ െ ሻ ൌ ܽଶ ܾଶ െ ʹܾܽ
ʹܾܽ ൌ ܽଶ ܾଶ ܽ ൌ ܾ Vậy tam giác cân tại . d. Ta có : ݎ ൌ ሺ െ ܽሻ ൞ ʹ
ฺ ݎ ݎ ൌ ሺʹ െ ܽሻ ൌ ሺܾ ܿሻ ʹ ʹ ݎ ൌ ʹ
Theo định lý hàm số sin, ta được െ ݎ ݎ ʹ ʹ ൌ ʹܴሺ ሻǤ ൌ ͶܴǤ Ǥ ൌ ʹ ʹ ʹ ʹ െ ൌ Ͷܴ ൌ ʹܴሺ ሻ ʹ ʹ Do đó,
ʹܴሺ ሻ ൌ Ͷܴ ൌ ൌ Vậy tam giác cân tại . 155 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
Bài 11: Chứng minh rằng tam giác cân khi nó thỏa mãn hệ thức ͳ
Ǥܵ ൌ ሺܽଶ ܾଶሻ Ͷ Ǥ݄ ൌ ξܾܿ ʹ Ǥ݉ ൌ ξܾܿ ʹ
Ǥ ସ ʹ ସ ʹ ସ ൌ ʹ ଶ ሺଶ ଶ ሻ Giải: a.
Theo bất đẳng thức Cauchy, ta có : ͳ ͳ ͳ
ሺܽ ܾሻଶ ܾܽ ܾܽ ൌ ܵ Ͷ ʹ ʹ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi ܽ ൌ ܾ. Do đó, tam giác cân tại . b. Ta luôn có : ݄ ݈
Mặt khác, theo bất đẳng thức Cauchy, ta có : ʹܾܿ ξܾܿ ʹܾܿ ൞ܾ ܿ ฺ ξܾܿ ʹ ܾ ܿ ʹ Ͳ ʹ Suy ra ξܾܿ ݈ ʹ ݄
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi ܾ ൌ ܿ. Do đó, tam giác cân tại . c. Ta có : ͳ ͳ ͳ
݉ଶ ൌ ሺʹܾଶ ʹܿଶ െ ܽଶሻ ൌ ሾܾଶ ܿଶ ሺܾଶ ܿଶ െ ܽଶሻሿ ሺܾଶ ܿଶ ʹܾܿ ሻ Ͷ Ͷ Ͷ
Mặt khác, theo bất đẳng thức Cauchy, ta có : ͳ ͳ ͳ
݉ଶ ൌ ሺܾଶ ܿଶ ʹܾܿ ሻ ሺʹܾܿ ʹܾܿ ሻ ൌ ܾܿሺͳ ሻ ൌ ܾܿ ଶ Ͷ Ͷ ʹ ʹ Suy ra
݉ ξܾܿ ൬¿ Ͳ൰ ʹ ʹ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi ܾ ൌ ܿ. Do đó, tam giác cân tại . 156 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác d.
Theo định lý hàm số sin, giả thuyết tương đương với :
ͳܴସሺܿସ ʹܽସ ʹܾସሻ ൌ ͳܴସǤ ʹܿଶሺܽଶ ܾଶሻ
ܿସ െ ʹሺܽଶ ܾଶሻܿଶ ʹܽସ ʹܾସ ൌ Ͳ
ấy đây là phương trình bậc hai theo ݔ ൌ ܿଶ, ta xét :
ȟᇱ ൌ ሺܽଶ ܾଶሻଶ െ ሺʹܽସ ʹܾସሻ ൌ െሺܽସ െ ʹܽଶܾଶ ܾସሻ ൌ െሺܽଶ െ ܾଶሻଶ Ͳ
Do đó, phương trình có nghiệm khi và chỉ khi ቄ ȟᇱ ൌ Ͳ
ݔ ൌ ܽଶ ܾଶ ൜ ܽଶ െ ܾଶ ൌ Ͳ ܿଶ ൌ ܽଶ ܾଶ
Vậy tam giác vuông cân tại .
Bài 12: Chứng tỏ rằng tam giác vuông khi thỏa mãn hệ thức Ǥ ʹ ʹ ൌ Ͷ (ĐH Kinh Tế Tp.HCM 1990) ܾ ܿ Ǥ ൌ ܽ
(ĐH Kiến Trúc Hà Nội 1997) ܾ ܿ ܽ Ǥ ൌ (ĐH Đà Nẵng 1997) ͳ Ǥ െ ൌ ʹ ʹ ʹ ʹ ʹ ʹ ʹ (ĐH Ngoại Thương 2001) Giải: a.
Giả thuyết tương đương với
ʹ ሺ ሻ ሺ െ ሻ ൌ ʹሾሺ െ ሻ െ ሺ ሻሿ
ሺ െ ሻ ൌ ሺ െ ሻ
ሺͳ െ ሻ ሺ െ ሻ ൌ Ͳ
ଶ ሺ െ ሻ ሺͳ ሻ ൌ Ͳ ቈ ᇣᇧ ᇧ ᇧᇧ ሺ ᇧ ᇧ െ ᇧᇧ ᇤ ሻ ᇧ ᇧ ͳ ᇧᇧ ᇧ ᇧ ᇧ ᇧ ᇥ ൌ Ͳ வ ൌ ͻͲ୭
Vậy tam giác vuông tại . 157 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác b.
Theo định lý hàm số sin, giả thuyết tương đương với ൌ െ െ ʹ ʹ ൌ ʹ ʹ ʹ ʹ ʹ ʹ ʹ െ െ ൌ ʹ ʹ ʹ ʹ ʹ ʹ ʹ
ʹ ଶ ൌ ͳ ൌ ͻͲ୭ ʹ
Vậy tam giác vuông tại . c.
Theo định lý các hình chiếu, ta có : ܾ ܿ ܽ ൌ ൌ
Nên từ giả thuyết, ta được : ܽ ܽ ൌ ൌ
ሺ ሻ ൌ Ͳ ൌ ͻͲ୭
Vậy tam giác vuông tại . d.
Giả thuyết tương đương với െ െ ൬ ൰ െ ൬ െ ൰ ൌ ͳ ʹ ʹ ʹ ʹ ʹ ʹ െ ൬ െ ൰ െ ͳ െ ଶ ൌ Ͳ ʹ ʹ ʹ ʹ ʹ ʹ െ ൬ െ ൰ െ ଶ ൌ Ͳ ʹ ʹ ʹ ʹ ʹ ʹ െ ൬ െ ൰ െ ൬ െ ൰ ൌ Ͳ ʹ ʹ ʹ ʹ ʹ ʹ െ ൬ െ ൰ ൬ െ ൰ ൌ Ͳ ʹ ʹ ʹ ʹ ൌ ൌ ͳ ൌ ͻͲ୭ ൦ ʹ ʹ ʹ െ ൦ െ ቈ ൌ ͻͲ୭ ൌ ൌ േ ൌ ͻͲ୭ ʹ ʹ ʹ ʹ Vậy tam giác vuông. 158 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
Bài 13: Chứng minh rằng tam giác vuông nếu nó thỏa mãn hệ thức
Ǥ͵ሺ ʹ ሻ Ͷሺ ʹ ሻ ൌ ͳͷ (ĐH Cần Thơ 1996)
Ǥ ሺ ሻ ሺ െ ሻ ൌ ʹ (ĐH Sư Phạm Vinh 2001) ʹܾܿ Ǥ ʹ ൌ ܾଶ െ ܿଶ Giải: a.
Từ giả thuyết, ta viết lại thành
͵ Ͷ ʹሺ͵ Ͷ ሻ ൌ ͳͷ
Theo bất đẳng thức Bunyakovsky, ta có : ͵ Ͷ ͷ ʹ ൜ ሺ͵ Ͷሻ ͳͲ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi ൌ ൞ ͵ Ͷ ฺ ൌ ฺ ൌ ͻͲ୭ ൌ ͵ Ͷ
Vậy tam giác vuông tại . b.
Giả thuyết tương đương với
ሺ ሻ ሺ െ ሻ ൌ ሺ െ ሻ െ ሺ ሻ
ሺ െ ሻ ൌ ሺ െ ሻ Ta đặt ݐ ൌ Ͳ ʹ Ta được ʹݐ ͳ െ ݐଶ
Ǥ ሺ െ ሻ ൌ ሺ െ ሻ ͳ ݐଶ ͳ ݐଶ
ʹݐǤ ሺ െ ሻ ൌ ሺͳ ݐଶሻ ሺ െ ሻ ͳ െ ݐଶ
ሺݐ െ ͳሻଶ ሺ െ ሻ ͳ െ ݐଶ ൌ Ͳ
ሺͳ െ ݐሻሾሺͳ െ ݐሻ ሺ െ ሻ ͳ ݐሿ ൌ Ͳ ݐ ൌ ͳ ݐሾͳ ᇣᇧെ ᇧᇧ ᇧ ᇧሺ ᇤ ᇧ െ ᇧᇧ ᇧ ሻሿ ᇧᇥ ሾͳ ᇣ ᇧᇧ ᇧ ᇧ ሺ ᇤᇧ െ ᇧ ᇧ ሻሿ ᇧᇥ ൌ Ͳ வ வ 159 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
ݐ ൌ ൌ ͳ ൌ ͻͲ୭ ʹ
Vậy tam giác vuông tại . c.
Theo định lý hàm số sin, ta có ͺܴଶ ʹ ൌ ൌ Ͷܴଶሺଶ െ ଶ ሻ ଶ െ ଶ
Do đó, giả thuyết tương đương với ʹ ʹ ൌ ʹ ଶ െ ଶ
ሺଶ െ ଶ ሻ ൌ ሺଶ െ ଶ ሻ
ሺ െ ሻ ଶ ሺ െ ሻ ൌ Ͳ
ሺ െ ሻሺ ଶ ሻ ൌ Ͳ ൌ ሺͳሻ ଶ ൌ Ͳሺʹሻ Ta xét :
ሺͳሻ ൌ ሺͻͲ୭ െ ሻ ൌ ͻͲ୭
Vậy tam giác vuông tại . ሺʹሻ:
- Nếu tam giác vuông tại thì ൌ ฺ ଶ ଶ ൌ Ͳ. Điều này vô lý.
- Nếu tam giác vuông tại thì ǡ phải nhọn và ۍ ͳ ξͷ ൌ ێ ʹ
ൌ ͳ ฺ ͳ െ ଶ ൌ Ͳ ێێ ͳ െ ξͷ ۏ ൌ ʹ Điều này vô lý.
- Nếu tam giác vuông tại thì ൌ Ͳ ฺ ଶ ൌ Ͳ. Điều này vô lý.
Vậy tam giác vuông tại . 160 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
Bài 14: Cho tam giác thỏa mãn hệ thức : ͳ ൌ ʹ ʹ ʹ
Chứng minh rằng điều kiện cần và đủ để tam giác vuông là ͳ ൌ ʹ ʹ ʹ ͳͲ
(Đề nghị Olympic 30-4, 2006) Giải: Ta có :
ܵ ൌ ሺ െ ܽሻ ൌ ሺ െ ܾሻ ൌ ඥሺ െ ܽሻሺ െ ܾሻሺ െ ܿሻ ʹ ʹ ܵଶ െ ܿ ܽ ܾ െ ܿ ฺ ൌ ൌ ൌ ʹ ʹ
ଶሺ െ ܽሻሺ െ ܾሻ ܽ ܾ ܿ
Do đó, từ giả thuyết ta có : ͳ ܽ ܾ െ ܿ ൌ
ܽ ܾ ൌ ͵ܿ ൌ ʹܿሺͳሻ ʹ ܽ ܾ ܿ Mặt khác : ܾܽܿ ݎ ܵ ൌ ݎ ൌ ฺ Ǥ ܾܽܿǤ
ൌ ܵଶ ൌ ሺ െ ܽሻሺ െ ܾሻሺ െ ܿሻሺʹሻ Ͷܴ Ͷܴ
Thay ሺͳሻ vào ሺʹሻ, ta được : ݎ ݎ ܾܽǤ
ൌ ଶ െ ሺܽ ܾሻ ܾܽ ฺ ቀͳ െ ቁ ܾܽ ൌ ʹܿଶ Ͷܴ Ͷܴ
Chiều thuận: Giả sử ͳ ݎ ͳ ൌ ฺ ൌ ʹ ʹ ʹ ͳͲ Ͷܴ ͳͲ Do đó, ʹͲ ܾܽ ൌ
ܿଶ ฺ ʹͲܽଶ ʹͲܾଶ െ Ͷͳܾܽ ൌ Ͳ ͻ 161 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác ܽ ͷ ൌ ฺ ൦ܾ Ͷ ܽ Ͷ ൌ ܾ ͷ Xét ܽ ܾ, ta có : ܽ ͷ ൌ ൞ܾ Ͷ ܽ
ͷ ฺ ܾଶ ܿଶ ൌ ܽଶ ൌ ܿ ͵
Vậy tam giác vuông tại .
Chiều nghịch: Giả sử tam giác vuông tại , ta có : ܽ ൌ ʹܴ ܽ ൌ ʹܴ ܽ ൌ ʹܴ ሺଵሻ ൞ ܽଶ ൌ ܾଶ ܿଶ ͳ
ሳሰ ൝ሺ͵ܿ െ ܾሻଶ ൌ ܾଶ ܿଶ ฺ ൝ܾ ൌ Ͷݎ ܵ ൌ ܾܿ ൌ ݎ ܾ ൌ Ͷݎ ܿ ൌ ͵ݎ ʹ Từ ሺͳሻ ta được ʹ ͳ
ͷݎ ൌ ʹܴ ฺ Ͷ ൌ ฺ ൌ ʹ ʹ ʹ ͷ ʹ ʹ ʹ ͳͲ
Vậy ta có điều phải chứng minh.
Bài 15: Chứng minh rằng tam giác vuông nếu nó thỏa mãn hệ thức
ܽଶሺܾ ܿ െ ܽሻ ܾଶሺܽ ܿ െ ܾሻ ܿଶሺܽ ܾ െ ܿሻ Ǥξʹ ሺ Ͷͷ୭ሻ ൌ ʹܾܽܿ ݎ ͳ ۓ ൌ Ǥ ݎ ͵ ۔ ݎ ʹ ە ൌ ܴ ͷ െ Ǥݎሺ ሻ ൌ ξʹܿǤ ʹ ʹ 162 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác Giải: a. Ta có :
ܽଶܾ ܽଶܿ െ ܽଷ ܾଶܽ ܾଶܿ െ ܾଷ ܿଶܽ ܿଶܾ െ ܿଷ ൌ ʹܾܽܿ
ܽሺܾଶ ܿଶ െ ܽଶሻ ܾሺܽଶ ܿଶ െ ܾଶሻ ܿሺܽଶ ܾଶ െ ܿଶሻ ൌ ʹܾܽܿ ܾଶ ܿଶ െ ܽଶ ܽଶ ܿଶ െ ܾଶ ܽଶ ܾଶ െ ܿଶ ൌ ൌ ʹܾܿ ʹܽܿ ʹܾܽ
Do đó, hệ thức tương đương với
ξʹ ሺ Ͷͷ୭ሻ ൌ ൌ ൌ െ ʹ ൌ ʹ ʹ ʹ ʹ ʹ െ ൌ ʹ ʹ െ ൌ ൦ʹ ʹ
െ ቂ ൌ ቂ ൌ ͻͲ୭ ൌ ൌ ͻͲ୭ ൌ ʹ ʹ
Vậy tam giác vuông tại hoặc . b. Ta áp dụng công thức : ܵ ۓ ݎ ൌ ͳ ݎ െ ܽ ܵ ฺ ൌ ൌ ۔ ͵ ݎ ݎ ൌ ە െ ܽ ͵ܽ
ൌ ͵ሺ െ ܽሻ ൌ
ܾ ܿ ൌ ʹܽሺͳሻ ʹ Mặt khác, ta lại có : ܾܽܿ ܵ ൌ ൌ ݎ Ͷܵଶ ʹ ൞ Ͷܴ ݎ ʹ ฺ ൌ ܾܽܿǤ ͷ ൌ ܴ ͷ
Theo công thức Heron, ta suy ra
ሺ െ ܽሻሺ െ ܾሻሺ െ ܿሻ ͳ ൌ ܾܽܿǤ ͳͲ ͵ܽ ܽ ܿ െ ܾ ܽ ܾ െ ܿ ͳͲ ൬ െ ܽ൰ ൬ ൰ ൬ ൰ ൌ ܾܽܿ ʹ ʹ ʹ 163 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
ͷܽሾܽ െ ሺܾ െ ܿሻሿሾܽ ሺܾ െ ܿሻሿ ൌ Ͷܾܽܿ Ͷ
ܽଶ െ ሺܾ െ ܿሻଶ ൌ ܾܿ ͷ
ͷܽଶ െ ͷሺܾଶ ܿଶሻ ܾܿ ൌ Ͳ
Từ ሺͳሻ ta suy ra : ܾଶ ܿଶ ʹܾܿ ൌ Ͷܽଶ ܾଶ ܿଶ ൌ Ͷܽଶ െ ʹܾܿ. Do đó,
ͷܽଶ െ ͷሺܾଶ ܿଶሻ ܾܿ ൌ Ͳ ͳͷ
ͷܽଶ െ ͷሺͶܽଶ െ ʹܾܿሻ ܾܿ ൌ Ͳ ܾܿ ൌ ܽଶሺʹሻ ͳ
Từ ሺͳሻǡ ሺʹሻ; theo định lý Viète, ta có ܾǡ ܿ là nghiệm của phương trình ͵ܽ ͳͷ ݔ ൌ ݔଶ െ ʹܽݔ ܽଶ ൌ Ͳ ฺ ൦ Ͷ ͳ ͷܽ ݔ ൌ Ͷ
Giả sử rằng ܾ ܿ, suy ra ͷܽ ܾ ൌ ͻܽଶ ʹͷܽଶ ൞ Ͷ ͵ܽ ฺ ܽଶ ൌ ܽଶ ܿଶ ൌ ܾଶ ͳ ͳ ܿ ൌ Ͷ
Vậy tam giác vuông tại . c.
Ở bài toán này, ta sẽ sử dụng công thức ܿ ൌ ݎ ൬ ൰ ʹ ʹ
Do đó, giả thuyết tương đương với െ െ ʹݎ ൌ ξʹݎ ൬ ൰ ሺכሻ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ൌ ξʹǤ ʹ Ǥ ʹ ʹ ʹ ʹ ʹ ൌ ξʹ ʹ ʹ ʹ ξʹ ൌ ൌ ͻͲ୭ ʹ ʹ
Vậy tam giác vuông tại . 164 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
Bài 16: Chứng minh nếu tam giác không tù và thỏa mãn hệ thức ܴ ൌ ݉ ʹ thì vuông cân tại .
(Đề nghị Olympic 30-4, 2007) Giải: Ta có ͳ
ܾଶ ܿଶ ൌ ʹ݉ଶ ܽଶ ʹ݉ ʹ ܽ Suy ra : ͳ ܽ ܽ ܽଶ ʹ݉ ܾଶ ܿଶ ʹ݉ ܾଶ ܿଶ
Theo định lý hàm số sin, ta có : ʹܴ ܾଶ ܿଶ െ ʹܾܿ ܾଶ ܿଶ ʹ݉
Theo bất đẳng thức Cauchy, ta lại có : ܾଶ ܿଶ െ ʹܾܿ ʹܾܿ ൌ ͳ െ ͳ െ ܾଶ ܿଶ ܾଶ ܿଶ Do đó, ʹܴ ʹܴ ฺ ͳ െ ʹ ʹ ʹ ଶ ʹ݉ ݉ ʹ ߨ
¿ א ቀͲǢ ቁ ² ͲǤ¯ượ ʹ ʹ ʹ ʹ ܴ ݉ ʹ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi tam giác vuông cân tại . 165 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
Bài 17: Chứng minh rằng tam giác đều nếu thỏa mãn hệ thức
Ǥ͵ܵ ൌ ʹܴଶሺଷ ଷ ଷ ሻ ܽ Ǥܾ ܿ ൌ ݄ ʹ ξ͵
Ǥʹሺܽ ܾ ܿ ሻ ൌ ܽ ܾ ܿ Ǥ ൌ Giải: a.
Theo công thức tính diện tích và định lý hàm số sin, giả thuyết tương đương với ͵ܾܽܿ ܽ ଷ ܾ ଷ ܿ ଷ ൌ ʹܴଶ ቈቀ ቁ ൬ ൰ ቀ ቁ Ͷܴ ʹܴ ʹܴ ʹܴ
ܽଷ ܾଷ ܿଷ ൌ ͵ܾܽܿ
Mặt khác, theo bất đẳng thức Cauchy, ta có :
ܽଷ ܾଷ ܿଷ ͵ܾܽܿ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi ܽ ൌ ܾ ൌ ܿ. Vậy tam giác đều. b. Trong tam giác ta luôn có : ݄ ൌ ܿ ൌ ܾ
Nên từ giả thuyết ta có : ܽ
ܾ ܿ ൌ ξ͵ሺܿ ܾ ሻ ʹ
Theo định lý hàm số sin thì từ đẳng thức trên, ta có :
ʹ ʹ ൌ ξ͵ሺ ሻ
Ta viết lại đẳng thức thành
ʹ ʹ ൌ ൫ξ͵ ͳ൯ሺ ሻ
ʹ ሾͳ െ ሺͲ୭ െ ሻሿ ʹ ሾͳ െ ሺͲ୭ െ ሻሿ ൌ Ͳ Mặt khác, ta lại có Ǣ Ͳ
൜ሺͲ୭ െ ሻ ǢሺͲ୭ െ ሻ ͳ Do đó
ʹ ሾͳ െ ሺͲ୭ െ ሻሿ ʹ ሾͳ െ ሺͲ୭ െ ሻሿ Ͳ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi 166 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác ሺͲ୭ െ ሻ ൌ ͳ ൜ ൌ ൌ Ͳ୭ ሺͲ୭ െ ሻ ൌ ͳ Vậy tam giác đều. c.
Theo định lý các hình chiếu, giả thuyết tương đương với ʹሺܽ ܾ ܿ ሻ
ൌ ሺܾ ܿ ሻ ሺܿ ܽ ሻ ሺܽ ܾ ሻ ൌ
Hệ thức trên được viết lại thành
ሺܽ െ ܾሻሺ െ ሻ ሺܾ െ ܿሻሺ െ ሻ ሺܿ െ ܽሻሺ െ ሻ ൌ Ͳ
Mà trong tam giác ta luôn có :
ሺܽ െ ܾሻሺ െ ሻ Ͳ
ቐሺܾ െ ܿሻሺ െ ሻ Ͳ
ሺܿ െ ܽሻሺ െ ሻ Ͳ
ฺ ሺܽ െ ܾሻሺ െ ሻ ሺܾ െ ܿሻሺ െ ሻ ሺܿ െ ܽሻሺ െ ሻ Ͳ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi ቄܽ ൌ ܾ ൌ ܿ ൌ ൌ Vậy tam giác đều. d.
Theo định lý hàm số sin, giả thuyết tương đương với ܽ ܾ ܾ ܿ ܿ ܽ ൌ ܽ ܾ ܿ
Hệ thức trên được viết lại thành ͳ ሺ െ ሻሺܽ െ ܾሻ
ሺ െ ሻሺܾ െ ܿሻ ሺ െ ሻሺܿ െ ܽሻ ቈ ൌ Ͳ ʹ ሺ ሻሺܽ ܾሻ
ሺ ሻሺܾ ܿሻ ሺ ሻሺܿ ܽሻ
Mà trong tam giác ta luôn có :
ሺ െ ሻሺܽ െ ܾሻ Ͳ
ቐሺ െ ሻሺܾ െ ܿሻ Ͳ
ሺ െ ሻሺܿ െ ܽሻ Ͳ
ሺ െ ሻሺܽ െ ܾሻ ሺ െ ሻሺܾ െ ܿሻ ሺ െ ሻሺܿ െ ܽሻ ฺ Ͳ
ሺ ሻሺܽ ܾሻ ሺ ሻሺܾ ܿሻ ሺ ሻሺܿ ܽሻ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi ቄܽ ൌ ܾ ൌ ܿ . ൌ ൌ Vậy tam giác đều. 167 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
Bài 18: Chứng minh rằng tam giác đều nếu thỏa mãn hệ thức Ǥ ቄ ʹ ʹ ͵ ͵ ͵ ൌ Ͳ Ǥ ൝ ൌ ଶ ʹ
(ĐH Kiến Trúc Hà Nội 1997) ͳ ൌ Ǥ ൞ Ͷ ܽଷ െ ܾଷ െ ܿଷ ܽଶ ൌ ܽ െ ܾ െ ܿ
(ĐH Ngoại Ngữ Hà Nội 1997) Ǥ ቄ ൌ ʹ ൌ ʹ (ĐH Sư Phạm Vinh 1999) Giải: a. Ta kí hiệu ʹ ሺͳሻ ൜ ʹሺʹሻ
Từ ሺͳሻ ta nhận xét không là góc lớn nhất vì nếu lớn nhất thì cạnh đối diện ܿ cũng lớn
nhất và theo định lý hàm số sin, ta sẽ có ቄ ฺ ʹ
Điều này mâu thuẫn với giả thuyết.
Vậy phải là góc nhọn. Ta được : Ͳ nên 2 vế của 2 bất đẳng thức ሺͳሻ và ሺʹሻ đều dương. Do đó ሺ ሻଶ Ͷ ଶ ൜ ሺ ሻଶ Ͷ ଶ
ฺ ሺ ሻଶ ሺ ሻଶ Ͷሺଶ ଶ ሻ
ʹ ʹ ሺ െ ሻ Ͷ ሺ െ ሻ ͳ
Vì ሺ െ ሻ ͳ nên ሺ െ ሻ ൌ ͳ. Vậy ൌ .
Từ ሺͳሻ ta có ܽ ܿ
Mặt khác, do hàm số ݂ሺݔሻ ൌ ݔ nghịch biến trong khoảng ሺͲǡ ߨሻ nên từ ሺʹሻ ta có 168 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác ฺ Như vậy, ൌ .
Tóm lại, ta chứng minh được tam giác đều. b. Ta có : ൌ ଶ ʹ ͳ ͳ
ሾሺ ሻ ሺ െ ሻሿ ൌ ሺͳ െ ሻ ʹ ʹ
െ ሺ െ ሻ ൌ ͳ െ
ሺ െ ሻ ൌ ͳ ൌ Khi đó, ͵ ͵ ͵ ൌ Ͳ
ʹ ͵ ሺͷͶͲ୭ െ ሻ ൌ Ͳ ʹ ͵ ൌ Ͳ ͵ ሺͳ ͵ሻ ൌ Ͳ
ቂ ͵ ൌ Ͳ ൌ Ͳ୭ ͵ ൌ െͳ Vậy tam giác đều. c. Ta có : ܽଷ െ ܾଷ െ ܿଷ ܽଶ ൌ
ܽଷ െ ܽଶሺܾ ܿሻ ൌ ܽଷ െ ܾଷ െ ܿଷ ܽ െ ܾ െ ܿ
ܾଷ ܿଷ ൌ ܽଶሺܾ ܿሻ
ܾଶ ܿଶ െ ܾܿ ൌ ܽଶ ܾଶ ܿଶ െ ܽଶ ͳ ൌ ʹܾܿ ʹ ͳ ൌ ൌ Ͳ୭ ʹ Mặt khác, ͳ ͳ
ൌ െ ሺ െ ሻ ൌ Ͷ ʹ
ሺ െ ሻ ൌ ͳ ൌ Vậy tam giác đều. d. Ta có : െ ൌ ʹ ൌ ʹ ʹ ʹ ʹ ʹ െ ൌ ʹ ʹ ʹ 169 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác Mặt khác, ሺ ሻ ൌ ʹ ൌ ʹ ൌ ʹǤ ൌ ʹ ൌ െ ሺ െ ሻ െ
ʹ ൬ͳ െ ʹ ଶ ൰ ൌ ʹ ଶ െ ͳ ʹ ʹ Do ta đã có െ ൌ ʹ ʹ ʹ Nên ͳ
ʹ ൬ͳ െ ʹ ଶ ൰ ൌ ͺ ଶ െ ͳ ଶ ൌ ൌ Ͳ୭ ʹ ʹ ʹ Ͷ Do đó, െ ൌ ͳ ൌ ʹ Vậy tam giác đều.
Bài 19: Chứng minh rằng tam giác đều nếu thỏa mãn hệ thức Ǥ ൌ Ͷ
(Học viện Bưu Chính Viễn Thông 1997) ͳ ʹܽ ܾ ൌ Ǥ ቐ ξͶܽଶ െ ܾଶ
ܽଶሺܾ ܿ െ ܽሻ ൌ ܾଷ ܿଷ െ ܽଷ (ĐH Y Thái Bình 2000) ߨ ǡ ǡ א ቀͲǡ ቁ Ǥ ൝ ʹ
ଶ ൌ ܾܽ ଶ ܾܿ ଶ ܿܽ ଶ Giải: a.
Theo đẳng thức cơ bản, ta có : ൌ Ͷ ʹ ʹ ʹ
Giả thuyết tương đương với 170 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác ൌ ʹ ʹ ʹ ൌ ͺ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ͳ ൌ ʹ ʹ ʹ ͺ
Theo bất đẳng thức cơ bản, ta lại có ͳ ʹ ʹ ʹ ͺ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi ൌ ൌ . Vậy tam giác đều. b.
Từ ܽଶሺܾ ܿ െ ܽሻ ൌ ܾଷ ܿଷ െ ܽଷ, ta suy ra được
ܽଶ ൌ ܾଶ ܿଶ െ ܾܿ
Theo định lý hàm số cos thì ͳ
ܾଶ ܿଶ െ ʹܾܿ ൌ ܾଶ ܿଶ െ ܾܿ ൌ ൌ Ͳ୭ ʹ Mặt khác ͳ ʹܽ ܾ ൌ ξͶܽଶ െ ܾଶ ͳ ଶ ሺʹܽ ܾሻଶ ʹܽ ܾ ൬ ൰ ൌ ൌ Ͷܽଶ െ ܾଶ ʹܽ െ ܾ ଶ ʹ ଶ ʹܽ ܾ ଶ ʹܽ ܾ ቌ ʹ ʹ ቍ ൌ ൌ ʹ ʹܽ െ ܾ ʹܽ െ ܾ ʹ ʹ ଶ ʹ ͳ ʹܽ ܾ ܾ ൌ ൌ ͳ െ ʹܽ െ ܾ ʹܽ ܾଶ ܽଶ െ ܿଶ ܾ ൌ ʹܾܽ ʹܽ ܽ ൌ ܿ Vậy tam giác đều. c.
Giả thuyết tương đương với
ሺܽ ܾ ܿሻଶ ൌ ʹܾܽሺͳ െ ʹሻ ʹܾܿሺͳ െ ʹሻ ʹܿܽሺͳ െ ʹሻ
ܽଶ ʹሺܾ ʹ ܿ ʹሻܽ ܾଶ ܿଶ ʹܾܿ ʹ ൌ Ͳሺͳሻ Ta xét :
ȟᇱ ൌ ሺܾ ʹ ܿ ʹሻଶ െ ܾଶ െ ܿଶ െ ʹܾܿ ʹ
ൌ െܾଶ ଶ ʹ െ ܿଶ ଶ ʹ ʹܾܿሾ ʹ ʹ െ ሺʹሻ ʹሿ
ൌ െܾଶ ଶ ʹ െ ܿଶ ଶ ʹ ʹܾܿ ʹ ʹ
ൌ െሺܾ ʹ െ ܿ ʹሻଶ Ͳ 171 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác Do đó,
ሺͳሻ ቄܽ ൌ െܾ ʹ െ ܿ ʹ ܾ ʹ ൌ ܿ ʹ
ฺ ൜ܽଶ ൌ ܾଶ ଶ ʹ ܿଶ ଶ ʹ ʹܾܿ ʹ ʹ
Ͳ ൌ ܾଶ ଶ ʹ ܿଶ ଶ ʹ െ ʹܾܿ ʹ ʹܥ
ฺ ܽଶ ൌ ܾଶ ܿଶ ʹܾܿ ሺʹ ʹሻ
ʹ ൌ െ ൌ ሺߨ െ ሻ
ʹ ൌ ߨ െ ݇ʹߨሺʹሻ
ฺ ʹ ൌ െ ߨ ݇ʹߨሺ͵ሻሺ݇ א Ժሻ Ta thấy : ሺʹሻ െ ൌ ݇ʹߨ
Do ݇ א Ժ và ȁ െ ȁ ൏ ߨ ȁ݇ʹߨȁ ൏ ߨ ݇ ൌ Ͳ. Suy ra : ൌ
ሺ͵ሻ ʹ െ ൌ ሺʹ݇ െ ͳሻߨ
Do ݇ א Ժ và Ͳ ൏ ǡ ൏ ߨ nên ݇ ൌ ͳ. Suy ra : ʹ ൌ ߨ.
Vậy tù, điều này mâu thuẫn giả thuyết.
Do đó, từ hệ thức ܾ ʹ ൌ ܿ ʹ, ta được : െ Ͷ ൌ ʹ ͳ ʹ ൌ െ ʹ ͳ ൌ ൌ Ͳ୭ ʹ Vậy tam giác đều.
Bài 20: Chứng minh rằng tam giác đều nếu thỏa mãn hệ thức ܽ ܾ ܿ ʹ Ǥ ൌ ܽ ܾ ܿ ͻܴ (ĐH Y Dược Tp.HCM 2001) ͳ െ െ െ
Ǥ ଶ ଶ ଶ െ ʹ ൌ ʹ ʹ ʹ Ͷ ʹ ʹ ʹ ͻͲ୭ Ǥ ൝ െ െ െ
ʹ ʹ ʹ ൌ Ͷ ʹ ʹ ʹ Giải: a.
Theo định lý hàm số sin, ta có :
ܽ ܾ ܿ ൌ ܴሺʹ ʹ ʹ ሻ ൌ ܴሺ ʹ ʹ ʹሻ 172 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
Theo đẳng thức cơ bản, ta có : ʹ ʹ ʹ ൌ Ͷ Do đó, ܽ ܾ ܿ ൌ Ͷܴ
Mặt khác, theo bất đẳng thức Cauchy thì :
ܽ ܾ ܿ ൌ ܴሺʹ ʹ ʹ ሻ ͵ܴ ඥ య ͺ ଶ ଶ ଶ Suy ra ܽ ܾ ܿ Ͷܴ ʹ ൌ ξ య ܽ ܾ ܿ ܴ ξ య ଶ ଶ ଶ ͵ Trong khi đó : ʹ ܽ ܾ ܿ ʹܴሺ ሻ ʹ ൌ ൌ యξ ͻܴ ͻܴ ͻܴ ͵
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi ൌ ൌ . Vậy tam giác đều. b.
Theo đẳng thức cơ bản, ta có : ൌ ʹ ʹ െ ʹ ൌ ʹ ʹ ʹ ʹ ʹ ʹ ʹ
Do đó, giả thuyết tương đương với െ െ െ ͺ ൌ ʹ ʹ ʹ ʹ ʹ ʹ Ͷ ʹ ʹ ʹ ʹ ʹ ʹ െ െ െ ൌ ͺ ʹ ʹ ʹ ʹ ʹ ʹ
ͺ ൌ ሺ ሻሺ ሻሺ ሻ
ͺܾܽܿ ൌ ሺܽ ܾሻሺܾ ܿሻሺܿ ܽሻ
Mặt khác, theo bất đẳng thức Cauchy, ta có : ܽ ܾ ʹξܾܽ
ቐܾ ܿ ʹξܾܿ ฺ ሺܽ ܾሻሺܾ ܿሻሺܿ ܽሻ ͺܾܽܿ ܿ ܽ ʹξܿܽ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi ܽ ൌ ܾ ൌ ܿ. Vậy tam giác đều. c. Ta có : െ െ െ െ െ ʹ െ Ͷ ൌ ʹ ൬ െ ൰ ʹ ʹ ʹ ʹ ʹ ʹ െ െ ʹ െ െ ൌ ʹ െ ʹ ʹ ʹ ʹ ʹ 173 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
ൌ ሺ െ ሻ ሺ െ ሻ ሺ െ ሻ
Do đó, giả thuyết tương đương với ʹ ʹ ʹ
ൌ ሺ ሻ ሺ ሻ ሺ ሻ ሺ െ ሻ ሺ െ ሻ ሺ െ ሻ ൌ
ሺ െ ሻ ሺ െ ሻ ሺ െ ሻ ൌ Ͳ
െ ሾሺ െ ሻ ሺ െ ሻሿ ሺ െ ሻ ሺ െ ሻ ൌ Ͳ ሺ ᇣᇧᇧ ᇧ െ ᇧᇤ ᇧᇧᇧ ᇧ ሻ ᇥ ሺ ᇣᇧ ᇧ െ ᇧᇤ ᇧᇧ ᇧ ሻ ᇥ ሺ ᇣᇧᇧ ᇧ െ ᇧᇤ ᇧᇧᇧ ᇧ ሻ ᇥ ሺ ᇣᇧ ᇧ െ ᇧᇤ ᇧᇧ ᇧ ሻ ᇥ ൌ Ͳ ஹ ஸ ஹ ஸ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi ൌ ൌ . Vậy tam giác đều.
Bài 21: Chứng minh tam giác khi thỏa mãn đẳng thức sau ͻ Ǥ ൌ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ͺ
Ǥܽ ܾ ܿ ൌ ʹට݉ଶ ଶ ଶ ݉ ݉
(Đề nghị Olympic 30-4, 2006) ͵ ͵ െ Ǥ ൌ ʹ ʹ ʹ ʹ (Olympic 30-4, 2007) ͳ ͳ ͳ ͳ ͳ ͳ Ǥ ൌ ʹ ቌ ቍ ଶ ʹ ଶ ଶ ʹ ʹ ʹ ʹ ʹ
(Đề nghị Olympic 30-4, 2008) Giải: a. Ta có : ͳ െ ͳ ͳ െ ൌ ൬ ൰ ൌ ଶ Ǥ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ͳ ͳ
ൌ ሺͳ െ ሻ ሺ ሻ Ͷ Ͷ Tương tự vậy, ta có : 174 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác ͳ ͳ
ൌ ሺͳ െ ሻ ሺ ሻ ʹ ʹ ʹ Ͷ Ͷ ͳ ͳ
ൌ ሺͳ െ ሻ ሺ ሻ ʹ ʹ ʹ Ͷ Ͷ Do đó, ͳ
ൌ ሺ͵ ሻ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ Ͷ ͳ ͵ ͻ ൬͵ ൰ ൌ Ͷ ʹ ͺ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi ൌ ൌ . Vậy tam giác đều. b. Ta có :
ʹሺܾଶ ܿଶሻ െ ܽଶ ͵ ۓ݉ଶ ۓ ଶ ଶ ଶ
ܽ ൌ ටʹሺ݉ ݉ ሻ െ ݉ ൌ ʹ ۖ ۖ Ͷ ۖ ۖ
ʹሺܿଶ ܽଶሻ െ ܾଶ ͵ ݉ଶ ൌ ଶ ଶ ܾ ൌ ටʹሺ݉ ݉ ଶ ۔ Ͷ ۔ʹ ሻ െ ݉ ۖ ۖ
ʹሺܽଶ ܾଶሻ െ ܿଶ ͵ ଶ ۖ ۖ ଶ ଶ ଶ ە݉ ൌ ܿ ൌ ටʹሺ݉ ሻ െ ݉ Ͷ ەʹ ݉ Suy ra ͵ ଶ ଶ ଶ ଶ ଶ ଶ ଶ
ሺܽ ܾ ܿሻ ൌ ටʹሺ݉ ݉ ሻ െ ݉ ݉ ටʹሺ݉ ଶሻ െ ݉ଶ ʹ ටʹሺ݉ ሻ െ ݉ ݉
Khi đó, theo bất đẳng thức Bunyakovsky, ta được : ଶ ଶ ଶ ଶ ଶ ଶ ଶ ටʹሺ݉ ሻ ଶሻ ଶ
݉ െ ݉ ටʹሺ݉ ݉ሻ െ ݉ ටʹሺ݉ ݉ െ ݉ ଶ ξ͵Ǥ ට͵ሺ݉ ଶ ଶ ݉ ሻ ݉ Hay ଶ ܽ ܾ ܿ ʹට݉ ଶ ଶ ݉ ݉
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi ݉ ൌ ݉ ൌ ݉. Vậy tam giác đều. c. Ta có: ͵ ͵ ͵ሺ ሻ ͵ሺ െ ሻ ൌ ʹ ʹ ʹ Ͷ Ͷ Ta dự đoán : ͵ ͵ െ ʹ ʹ ʹ ʹ 175 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
Vậy thì ta cần chứng minh ͵ሺ െ ሻ െ Ͳ ሺכሻ Ͷ ʹ Ta có : െ ͵ሺ ሻ ͵ሺ െ ሻ ͵ሺ െ ሻ Ͳ ֜ ʹ Ͳ ֜ Ͳሺככሻ ʹ Ͷ Ͷ Ͷ ͵ሺ ሻ ቆ Ͳቇ Ͷ Lại có : ȁ െ ȁ ͵ȁ െ ȁ Ͳ ߨ ʹ Ͷ ȁ െ ȁ ͵ȁ െ ȁ ሺ െ ሻ ͵ሺ െ ሻ ฺ ฺ ሺכככሻ ʹ Ͷ ʹ Ͷ
ừ ሺכሻǡ ሺככሻ và ሺכככሻ, ta có : ͵ ͵ െ ʹ ʹ ʹ ʹ
Dấu ̶ ൌ ̶ xảy ra khi tam giác đều. d.
Theo bất đẳng thức Bunyakovsky, ta có : ଶ ͳ ͳ ͳ ͳ ͳ ͳ ͳ ቌ ቍ ଶ ଶ ଶ ͵ ʹ ʹ ʹ ʹ ʹ ʹ
Mặt khác, theo bất đẳng thức Cauchy, ta có : ͳ ͳ ͳ ͵ య ʹ ʹ ʹ ට ʹʹʹ
Theo bất đẳng thức cơ bản, ta được : ͳ ʹ ʹ ʹ ͺ Do đó, ͳ ͳ ͳ ʹ ʹ ʹ 176 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác Suy ra ͳ ͳ ͳ ͳ ͳ ͳ ʹ ቌ ቍ ଶ ʹ ଶ ʹ ଶ ʹ ʹ ʹ ʹ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi ൌ ൌ . Vậy tam giác đều.
Bài 22: Chứng tỏ rằng tam giác đều nếu ͻܴ
Ǥ݉ ݉ ݉ ൌ ʹ ܽ ܾ ܿ Ǥ ൌ ൌ ݉ ݉ ݉ ͳ ͳ ͳ ʹ Ǥ ଶ ଶ ଶ ൌ ܽ ʹ ܾ ʹ ܿ ʹ ͺ ͳ ͳ ͳ ͳͺܴ Ǥ ൌ ݎ ݎ ݎ ܾܽ ܾܿ ܿܽ Giải: a.
Theo bất đẳng thức Bunyakovsky, ta có : ଶ ሺ݉ ଶ ଶ
݉ ݉ሻଶ ͵ሺ݉ ݉ ݉ ሻ Mặt khác, ta có :
ʹሺܾଶ ܿଶሻ െ ܽଶ ۓ ଶ ݉ ൌ ۖ ۖ Ͷ
ʹሺܿଶ ܽଶሻ െ ܾଶ ͵ ݉ଶ ൌ
ฺ ݉ଶ ݉ଶ ݉ଶ ൌ ሺܽଶ ܾଶ ܿଶሻ ۔ Ͷ Ͷ ۖ ۖ
ʹሺܽଶ ܾଶሻ െ ܿଶ ଶ ە݉ ൌ Ͷ Do đó, ͻ
ሺ݉ ݉ ݉ሻଶ ሺܽଶ ܾଶ ܿଶሻ Ͷ
Theo định lý hàm số sin và bất đẳng thức cơ bản, ta có : ͻ
ܽଶ ܾଶ ܿଶ ൌ Ͷܴଶሺଶ ଶ ଶ ሻ ͶܴଶǤ ൌ ͻܴଶ Ͷ Khi đó ͺͳ
ሺ݉ ݉ ݉ሻଶ ܴଶ Ͷ 177 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác Hay ͻܴ
݉ ݉ ݉ ʹ ൌ ൌ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi ൜݉ . ൌ ݉ ൌ ݉ Vậy tam giác đều. b. Ta có : ܽ ܾ ܽଶ ݉ଶ ʹܾଶ ʹܿଶ െ ܽଶ ൌ ൌ ݉ ଶ ൌ ݉ ܾଶ ݉ ʹܽଶ ʹܿଶ െ ܾଶ
ܽଶሺʹܽଶ ʹܿଶ െ ܾଶሻ ൌ ܾଶሺʹܾଶ ʹܿଶ െ ܽଶሻ
ʹܽସ ʹܽଶܿଶ െ ܽଶܾଶ ൌ ʹܾସ ʹܾଶܿଶ െ ܾଶܽଶ
ሺܽଶ െ ܾଶሻሺܽଶ ܾଶ ʹܿଶሻ ൌ Ͳ ܽ ൌ ܾ Tương tự vậy, ta có : ܾ ܿ ൌ ܾ ൌ ܿ ݉ ݉ Vậy tam giác đều. c.
Theo định lý hàm số cos, ta có : ܾଶ ܿଶ െ ܽଶ ൌ ʹܾܿ ܾଶ ܿଶ െ ܽଶ
ܾଶ ܿଶ ʹܾܿ െ ܽଶ ฺ ʹ ଶ െ ͳ ൌ ฺ ଶ ൌ ʹ ʹܾܿ ʹ Ͷܾܿ ሺܾ ܿሻଶ െ ܽଶ
ሺܾ ܿ െ ܽሻሺܾ ܿ ܽሻ ሺ െ ܽሻ ฺ ଶ ൌ ൌ ൌ ʹ Ͷܾܿ Ͷܾܿ ܾܿ Tương tự, ta được : ሺ െ ܾሻ ଶ ൌ ൞ ʹ ܿܽ ሺ െ ܿሻ ଶ ൌ ʹ ܾܽ Do đó, ͳ ͳ ͳ ሺ െ ܽሻ ሺ െ ܾሻ ሺ െ ܿሻ ଶ ଶ ଶ ଶ ൌ ൌ ܽ ʹ ܾ ʹ ܿ ʹ ܾܽܿ ܾܽܿ ܾܽܿ ܾܽܿ
Mặt khác, theo bất đẳng thức Cauchy, ta có : ሺܽ ܾ ܿሻଷ ʹ ଷ ൌ ܾܽܿ ͺ ͺ Hay ͳ ͳ ͳ ଶ ʹ ଶ ଶ ଶ ൌ ܽ ʹ ܾ ʹ ܿ ʹ ܾܽܿ ͺ 178 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi ܽ ൌ ܾ ൌ ܿ. Vậy tam giác đều. d. Ta có : ͳ ͳ ͳ െ ܽ െ ܾ െ ܿ ܽ ܾ ܿ ۓ ൌ ൌ ൌ ۖݎ ݎ ݎ ܵ ܵ ܵ ܵ ʹܵ ͳͺܴ ͳͺܾܽܿ ͻ ͳ ۔ ൌ ൌ Ǥ ۖ ܾܽ ܾܿ ܿܽ
Ͷܵሺܾܽ ܾܿ ܿܽሻ ʹܵ ͳ ͳ ͳ ە ܽ ܾ ܿ
Do đó, giả thuyết tương đương với ͳ ͳ ͳ
ሺܽ ܾ ܿሻ ൬ ൰ ൌ ͻ ܽ ܾ ܿ
Mặt khác, theo bất đẳng thức Cauchy, ta lại có : ܽ ܾ ܿ ͵ξ య ܾܽܿ ͳ ͳ ͳ ቐ ͳ ͳ ͳ ͵
ฺ ሺܽ ܾ ܿሻ ൬ ൰ ͻ ܽ ܾ ܿ ܽ ܾ ܿ ξ య ܾܽܿ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi ܽ ൌ ܾ ൌ ܿ. Vậy tam giác đều.
Bài 23: Xác định đặc điểm của tam giác nếu nó thỏa mãn hệ thức Ǥ ൌ Ͳ Ǥ ൌ ξ͵ ܵ ൌ ͳ
Ǥ ൜ξ͵ሺܽ ܾ ܿሻଶ ൌ ͵ (ĐH Luật Hà Nội 1995) Giải: a. Ta có :
ൌ ʹ ͵ሺ ሻ ͵ሺ െ ሻ ൜
ൌ െʹ ͵ሺ ሻ ͵ሺ ሻ
ฺ ൌ െʹ ͵ሺ ሻ ሾ ͵ሺ െ ሻ െ ͵ሺ ሻሿ
ൌ െʹ ͵ ሺെʹ ͵ ͵ሻ ൌ Ͷ ͵ ͵ ͵
Do đó, giả thuyết tương đương với ͵ ൌ Ͳ
Ͷ ͵ ͵ ͵ ൌ Ͳ ͵ ൌ Ͳ ͵ ൌ Ͳ
Vậy tam giác có ít nhất một góc bằng Ͳ୭ hoặcͳʹͲ୭. 179 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác b.
Giả thuyết tương đương với
൫ െ ξ͵ ൯ ൫ െ ξ͵ ൯ ൫ െ ξ͵ ൯ ൌ Ͳ ߨ ߨ ߨ
ቀ െ ቁ ቀ െ ቁ ቀ െ ቁ ൌ Ͳ ͵ ͵ ͵ ߨ െ ߨ ߨ ʹ ൬ െ ൰ െ ʹ ൬ െ ൰ ൬ െ ൰ ൌ Ͳ ʹ ͵ ʹ ʹ ͵ ʹ ͵ ߨ െ ߨ ʹ ൬ െ ൰ െ ൬ െ ൰൨ ൌ Ͳ ʹ ͵ ʹ ʹ ͵ ߨ ߨ ߨ ൬
െ ൰ ൬ െ ൰ ൬ െ ൰ ൌ Ͳ ʹ ͵ ʹ ʹ ߨ ߨ ߨ
െ ൬ െ ൰ ൬ െ ൰ ൬ െ ൰ ൌ Ͳ ʹ ʹ ʹ ߨ ۍ ൬ െ ൰ ൌ Ͳ ێ ʹ ߨ ێ ൬ െ ൰ ൌ Ͳ ێ ʹ ێ ߨ ۏ ൬ െ ൰ ൌ Ͳ ʹ Ta xét : ߨ
൬ െ ൰ ൌ Ͳ ฺ ൌ Ͳ୭ ʹ
Vậy tam giác có ít nhất một góc bằng Ͳ୭. c.
Theo công thức Heron và bất đẳng thức Cauchy, ta có :
െ ܽ െ ܾ െ ܿ ଷ
ͳ ൌ ܵଶ ൌ ሺ െ ܽሻሺ െ ܾሻሺ െ ܿሻ ൬ ൰ ͵ Do đó, ସ ͳ ʹ Suy ra ଶ ͵ξ͵ Hay
ξ͵ሺܽ ܾ ܿሻଶ ͵
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi ܽ ൌ ܾ ൌ ܿ. Vậy tam giác đều. 180 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
Bài 24: Nhận dạng tam giác nếu biết rằng Ǣ ệủươ¿ݔଶ ܽ Ͷ Ͷ ଵݔ ܾଵ ൌ Ͳ Ǣ ệủươ¿ݔଶ ܽ Ͷ Ͷ ଶݔ ܾଶ ൌ Ͳ Ǣ ệủươ¿ݔଶ ܽ Ͷ Ͷ ଷݔ ܾଷ ൌ Ͳ Và
ሺͳ െ ܽଵ ܾଵሻሺͳ െ ܽଶ ܾଶሻሺͳ െ ܽଷ ܾଷሻ ൌ ͷͳ െ ͵ʹͶͲξ͵
Giải: Từ giả thuyết, ta có :
ۓݔଶ ܽଵݔ ܾଵ ൌ ൬ݔ െ ൰ ൬ݔ െ ൰ ۖ Ͷ Ͷ ݔଶ ܽ ൰ ൬ݔ െ ൰ ۔
ଶݔ ܾଶ ൌ ൬ݔ െ Ͷ Ͷ ۖ
ەݔଶ ܽଷݔ ܾଷ ൌ ൬ݔ െ ൰ ൬ݔ െ ൰ Ͷ Ͷ Lấy ݔ ൌ െͳ, ta có : ଶ ଶ ଶ
ሺͳ െ ܽଵ ܾଵሻሺͳ െ ܽଶ ܾଶሻሺͳ െ ܽଷ ܾଷሻ ൌ ൬ͳ ൰ ൬ͳ ൰ ൬ͳ ൰ Ͷ Ͷ Ͷ ൌ ͳ ൬ ൰ Ͷ Ͷ Ͷ ଶ ൬ ൰ ൨ Ͷ Ͷ Ͷ Ͷ Ͷ Ͷ Ͷ Ͷ Ͷ Mặt khác : ߨ ߨ ൬ ൰ ൌ ൬ െ ൰ ฺ Ͷ Ͷ ൌ Ͷ െ Ͷ Ͷ Ͷ Ͷ ߨ ͳ െ Ͷ Ͷ ͳ Ͷ Ͷ
ฺ ൬ ൰ ൬ͳ ൰ ൌ ൬ͳ െ ൰ ൬ͳ െ ൰ Ͷ Ͷ Ͷ Ͷ Ͷ Ͷ ฺ Ͷ Ͷ Ͷ Ͷ Ͷ Ͷ Ͷ Ͷ Ͷ ൌ ͳ Ͷ Ͷ Ͷ ଶ
ฺ ሺͳ െ ܽଵ ܾଵሻሺͳ െ ܽଶ ܾଶሻሺͳ െ ܽଷ ܾଷሻ ൌ Ͷ ൬ͳ ൰ Ͷ Ͷ Ͷ ߨ
Ǣ Ǣ א ቀͲǢ ቁ ฺ Ǣ Ǣ א ሺͲǢ ͳሻ ฺ א ሺͲǢ ͳሻ Ͷ Ͷ Ͷ Ͷ Ͷ Ͷ Ͷ Ͷ Ͷ Ͷ 181 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
Theo bất đẳng thức Cauchy, ta có : ͳ ݔଷ ൌ ͳ Ͷ Ͷ Ͷ ൌ Ͷ Ͷ Ͷ Ͷ Ͷ Ͷ Ͷ Ͷ Ͷ య ଶ య
͵ඨ ͵ඨ൬ ൰ ൌ ͵ݔ ͵ݔଶ Ͷ Ͷ Ͷ Ͷ Ͷ Ͷ
ݔଷ െ ͵ݔଶ െ ͵ݔ ͳ Ͳ
ሺݔ ͳሻ൫ݔ െ ʹ ξ͵൯൫ݔ െ ʹ െ ξ͵൯ Ͳ Ͳ ൏ ݔ ʹ െ ξ͵ Do đó, ଷ ଶ
ሺͳ െ ܽଵ ܾଵሻሺͳ െ ܽଶ ܾଶሻሺͳ െ ܽଷ ܾଷሻ ൌ Ͷሺͳ ݔଷሻଶ Ͷ ቂͳ ൫ʹ െ ξ͵൯ ቃ ൌ ͷͳ െ ͵ʹͶͲξ͵
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi tam giác đều.
Bài 25: Tìm tất cả các đặc điểm của tam giác đồng thời thỏa điều kiện Ǥ ൜
ܵ ൌ ܽଶ െ ሺܾ െ ܿሻଶ
ଶ ଶ ଶ ൌ
Ǥ ሺͳ ܾ ܿ െ ܾܿሻ ሺͳ ܿ ܽ െ ܿܽሻ ሺͳ ܽ ܾ െ ܾܽሻ ൌ ͵ ͵ୱ୧୬ ۓ Ͷ ൌ ͳ Ͷ Ǥ ͵ୱ୧୬ ۔͵ୱ୧୬ ە Ͷ ൌ ͳ Ͷ ͵ୱ୧୬େ ͵ሺ ሻ Ǥ ൌ Giải: a.
Theo định lý hàm số cot, ta có : ܽଶ ܾଶ ܿଶ ൌ Ͷܵ
Theo định lý hàm số sin, ta được : Ͷܴଶ ൌ ሺଶ ଶ ଶ ሻ Ͷܵ
Do ଶ ଶ ଶ ൌ nên ܵ ൌ ܴଶ. 182 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
Theo định lý hàm số sin, ta lại có :
ܴଶ ൌ ܵ ൌ ܽଶ െ ሺܾ െ ܿሻଶ ൌ Ͷܴଶሾଶ െ ሺ െ ሻଶሿ ͳ
ൌ ሺ െ ሻሺ െ ሻ Ͷ െ െ ൌ ൬ʹ െ ʹ ൰ ൬ʹ െ ʹ ൰ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ െ െ ൌ ʹ ൬ െ ൰ ʹ ൬ െ ൰ ʹ ʹ ʹ ʹ ʹ ʹ ൌ ͳ ʹ ʹ ʹ ʹ ʹ ʹ Do đó, ͳ Ͷ ଶ ൌ ʹ Ͷ
Mặt khác, theo định lý hàm số sin, ta lại có : ܾܽܿ ܵǤ Ͷܴ ͳ ൌ ൌ ൌ ͺܴଷ ͺܴଷ ʹ Nên ͳ ଶ ͳ ͳ ൌ ʹ ൌ ൌ ͳ ʹ Ͷ ʹ ʹ Ͷ Ta biết rằng ͳ ͺ ͳ ൌ ൌ ʹ ൌ ฺ ൌ ͳ ʹ ͳ ͳ ͳ ଶ ʹ
Điều này không thể xảy ra.
Vậy không tồn tại tam giác thỏa mãn hai hệ thức đã cho. b.
Từ giả thuyết, ta viết lại thành
ሺܽ ܾ ሻ ሺܾ ܿ ሻ ሺܽ ܿ ሻ
െ ሺܾܿ ܿܽ ܾܽ ሻ ൌ Ͳ
Theo định lý các hình chiếu và định lý hàm số cos, ta có :
ሺܽ ܾ ሻ ሺܾ ܿ ሻ ሺܽ ܿ ሻ ൌ ܿ ܽ ܾ ൝ ͳ
ܾܿ ܿܽ ܾܽ ൌ ሺܽଶ ܾଶ ܿଶሻ ʹ
Do đó, giả thuyết tương đương với ͳ
ൌ ሺܽଶ ܾଶ ܿଶሻ െ ሺܽ ܾ ܿሻ ͵ ʹ
Mặt khác, theo bất đẳng thức Bunyakovsky, ta có :
͵ሺܽଶ ܾଶ ܿଶሻ ሺܽ ܾ ܿሻଶ 183 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác Nên ͳ ͳ
ሺܽଶ ܾଶ ܿଶሻ െ ሺܽ ܾ ܿሻ ͵ ሺܽ ܾ ܿሻଶ െ ሺܽ ܾ ܿሻ ͵ ʹ ͳ ͵ ͵
ൌ ሺܽ ܾ ܿ െ ͵ሻଶ ʹ ʹ
Theo bất đẳng thức cơ bản, ta có : ͵ ʹ
Do đó, dấu ̶ ൌ ̶ xảy ra khi và chỉ khi ܽ ൌ ܾ ൌ ܿ ൌ ͳ.
Vậy tam giác đều, có độ dài các cạnh bằng ͳ. c.
Hệ đã cho được viết lại thành
൜͵ୱ୧୬ିୱ୧୬ Ͷሺ െ ሻ ൌ ͳሺͳሻ
͵ୱ୧୬ିୱ୧୬େ െ Ͷሺ െ ሻ ൌ ͳሺʹሻ
Xét ሺͳሻ, ta đặt ݑ ൌ െ . Khi đó : ͵௨ Ͷݑ ൌ ͳ Ta xét hàm số
݂ሺݑሻ ൌ ͵௨ Ͷݑǡ ݑ א Թ
݂ᇱሺݑሻ ൌ ͵௨ ͵ Ͷ Ͳ
Do đó, hàm số đồng biến.
Ta thấy ݑ ൌ Ͳ là nghiệm của phương trình và là hàm hằng nên ݑ ൌ Ͳ là nghiệm duy nhất của phương trình. Suy ra : ൌ ൌ
Xét ሺʹሻ, ta đặt ݒ ൌ െ . Khi đó : ͵௩ െ Ͷݒ ൌ ͳ Ta xét hàm số
݂ሺݒሻ ൌ ͵௩ െ Ͷݒǡ ݒ א Թ
݂ᇱሺݒሻ ൌ ͵௩ ͵ െ Ͷ
݂ᇱᇱሺݒሻ ൌ ͵௩ ଶ ͵ Ͳ
Suy ra ݒ ൌ Ͳ và ݒ ൌ ʹ là hai nghiệm duy nhất của phương trình.
Với ݒ ൌ Ͳ thì ൌ ൌ .
Với ݒ ൌ ʹ thì ൌ ʹ ʹ (vô lý). Vậy tam giác đều. d.
Theo các đẳng thức cơ bản, ta có : Ͳ
൞ ൌ ͳ Ͷ ͳ ʹ ʹ ʹ ൌ
Kết hợp với giả thuyết, ta suy ra 184 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác Ͳ
Tương đương tam giác nhọn. Giả sử : ߨ
Ͳ ൏ ൏ ฺ ቄ Ͳ ʹ Ͳ ൏
Theo bất đẳng thức Chebyshev, ta có : Ǥ ͵ ͵ ͵
Ta viết lại bất đẳng thức trên thành ͵ሺ ሻ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi ൌ ൌ . Vậy tam giác đều.
Bài 26: Tìm đặc điểm của tam giác nếu nó thỏa mãn điều kiện
Ǥʹሺܽଶ ܿଶ െ ܾଶሻሺܽଶ ܾଶ െ ܿଶሻ ൌ ʹͷܾܴܿଶ
Ǥݎ݈ ݎ݈ ݎ݈ ൌ ଶ
ଶଵଶ ଶଵଶ ଶଵଶ ߨ ଶଵଶ Ǥ ൌ ቀ ቁ ͵ ͵ Ͷ ܽ ܾ ܿ Ǥ ൌ ܾܽ ܾܿ ܿܽ ͳͺܴଷ Giải: a.
Theo định lý hàm số cos, ta có :
൜ܽଶ ܿଶ െ ܾଶ ൌ ʹܽܿ
ܽଶ ܾଶ െ ܿଶ ൌ ʹܾܽ
Do đó, giả thuyết tương đương với Ͷܴଶ
ʹǤʹܽܿ Ǥ ʹܾܽ ൌ ʹͷܾܴܿଶ ܽଶ ൌ ʹ
Theo định lý hàm số sin, ta viết hệ thức trên thành ͳ ଶ ൌ ʹ
Theo bất đẳng thức Cauchy, ta có : ͳ
ଶ ൌ ሺͳ െ ଶ ሻሾሺ െ ሻ െ ሿ ʹ ͳ ͳ
ሺͳ െ ଶ ሻሺͳ െ ሻ ൌ ሺʹ ʹ ሻሺͳ െ ሻሺͳ െ ሻ ʹ Ͷ 185 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
ͳ ʹ ʹ ͳ െ ͳ െ ଷ ͳ ൬ ൰ ൌ Ͷ ͵ ʹ
Do đó, dấu ̶ ൌ ̶ xảy ra khi và chỉ khi ቄ ሺ െ ሻ ൌ ͳ ʹ ʹ ൌ ͳ െ ൌ ൝ ͳ ൌ െ ͵ͳ ậạỏ ൌ െ ͵ b. Ta có : ۓ ܵ
ሺ െ ܾሻሺ െ ܿሻ ۖݎ ൌ ൌ ඨ െ ܽ െ ܽ ۔ ۖ ʹ ە ݈ ൌ ඥܾܿሺ െ ܽሻ ܾ ܿ
Theo bất đẳng thức Cauchy, ta có : ʹξܾܿ ܾ ܿ െ ܾ െ ܿ ܽ ݎ݈ ൌ
ඥሺ െ ܾሻሺ െ ܿሻ Ǥ ൌ ܾ ܿ ܾ ܿ ʹ ʹ Tương tự, ta được : ܾ ݎ݈ ൞ ʹ ܿ ݎ݈ ʹ Do đó,
ݎ݈ ݎ݈ ݎ݈ ଶ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi ܽ ൌ ܾ ൌ ܿ. Vậy tam giác đều. c. Ta xét hàm số
݂ሺݔሻ ൌ ݔଶଵଶǡ ݔ א ሺͲǢ ߨሻ
݂ᇱሺݔሻ ൌ ʹͲͳʹݔଶଵଵ
݂ᇱᇱሺݔሻ ൌ ʹͲͳʹǤʹͲͳͳǤ ݔଶଵ Ͳ
Theo bất đẳng thức Jensen, ta có :
݂ሺሻ ݂ሺሻ ݂ሺሻ ߨ ଶଵଶ ݂ ൬ ൰ ൌ ቀ ቁ ͵ ͵ ͵
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi ൌ ൌ . Vậy tam giác đều. 186 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác d.
Theo định lý hàm số sin và đẳng thức cơ bản, ta có : ܽ ܾ ܿ Ͷ ൌ ൌ ʹ ʹ ʹ ͳͺܴଷ ͻܴଶ ͻܴଶ
Do đó, giả thuyết tương đương với
ʹܴଶ ൌ ܾܽ ܾܿ ܿܽ ʹ ʹ ʹ
Mặt khác, ta lại có kết quả sau : ۓ ݎ ൌ Ͷܴ ʹ ʹ ʹ ۔ ܾܽܿ ܾܽܿ ܵ ൌ ݎ ൌ ฺ ܴݎ ൌ ە Ͷܴ Ͷ
Nên hệ thức trên được viết lại thành
ͳͺܴݎ ൌ ܾܽ ܾܿ ܿܽ ܾܽܿ ͳͺǤ ൌ ܾܽ ܾܿ ܿܽ Ͷ
ͻܾܽܿ ൌ ሺܾܽ ܾܿ ܿܽሻሺܽ ܾ ܿሻ
Theo bất đẳng thức Cauchy, ta có :
ቊܾܽ ܾܿ ܿܽ ͵యඥܽଶܾଶܿଶ య
ܽ ܾ ܿ ͵ξܾܽܿ
ฺ ሺܾܽ ܾܿ ܿܽሻሺܽ ܾ ܿሻ ͻܾܽܿ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi ܽ ൌ ܾ ൌ ܿ. Vậy tam giác đều.
Bài 27: Tìm đặc điểm của tam giác nếu nó thỏa mãn đẳng thức
Ǥ ൜ଶ ଶ ଶ ൏ ͳ ͷ ͷ ͷ ൌ Ͳ Giải:
a. Ǥ ൜ܽଶ ʹ ܾଶ ʹ ൌ Ͷܾܽ Ta có :
ʹ ʹ ൌ Ͷ ͷ ͷ ͷ െͷ ଶ ͷ ଶ ͷ ൌ ௧ ͷ ൌ ʹ ͷሺ ሻ ʹ ʹ Ǥ ൝ ߨ ǡ א ቀͲǡ ͷ ቁ Ǣ ݐ אͷ ሺͲǢ ʹሻ ͷ െ ͷ ͷ ͷ ൌ ʹ ʹ ൬ ൰ ൌ ʹ ʹ ʹ ʹ ʹ ʹ ʹ Do đó, 187 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác ߨ ͵ߨ ۍ ൌ Ͳ ۍ ൌ ש ൌ ێ ʹ ͷ ͷ ێ ߨ ͵ߨ
ͷ ͷ ͷ ൌ Ͳ ێ ൌ Ͳ ێ ൌ ש ൌ ێ ʹ ێ ͷ ͷ ێ ێ ߨ ͵ߨ ۏ ൌ Ͳ ൌ ש ൌ ʹ ۏ ͷ ͷ
Mặt khác, theo đẳng thức cơ bản ta có :
ͳ െ ʹ ൌ ଶ ଶ ଶ ൏ ͳ Ͳ Suy ra, ta chọn ߨ ۍ ൌ ێ ͷ ߨ ێ ൌ ێ ͷ ێ ߨ ۏ ൌ ͷ
Vậy tam giác có ít nhất một góc ͵୭. b.
Theo định lý hàm số sin, ta có :
ܽଶ ʹ ܾଶ ʹ ൌ Ͷܾܽ
ଶ Ǥ ʹ ଶ Ǥ ʹ ൌ Ͷ െ ൌ Ͳ
ሺ െ ሻ ൌ Ͳ ൌ
Khi đó, thay ൌ vào hệ thức ʹ ʹ ൌ Ͷ . Ta được : ʹ ʹ ൌ Ͷ ଶ ൌ ൌ Ͷͷ୭
Vậy tam giác vuông cân tại . c.
Từ đẳng thức cơ bản :
ଶ ଶ ଶ ൌ ʹ ʹ
Ta suy ra : ௧ ଶ ൌ ʹ ʹ
Mà Ͳ ൏ ͳ ฺ ௧ ଶ ʹ ฺ ʹ ʹ ʹ ฺ Ͳ ฺ Ͳ
Mặt khác cũng từ : Ͳ ൏ ͳ ฺ ௧ ଶ ฺ ଶ ଶ ଶ
ฺ ܽଶ ܾଶ ܿଶ ൌ ܽଶ ܾଶ െ ʹܾܽ ฺ Ͳ
Do đó, ൌ Ͳ ൌ ͻͲ୭.
Vậy tam giác vuông tại . 188 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
Bài 28: Tìm tất cả các tam giác có độ dài 3 cạnh là các số nguyên dương, không
có ước chung và thỏa mãn đẳng thức ଶ
ଶ Ͷ ଶ ͻ ଶ ൌ ൬ ൰ ʹ ʹ ʹ ݎ
(Đề nghị Olympic 30-4, 2006) Giải: Ta có công thức :
ݎ ൌ ሺ െ ܽሻ ൌ ሺ െ ܾሻ ൌ ሺ െ ܿሻ ʹ ʹ ʹ
ฺ ݎଷ ൌ ሺ െ ܽሻሺ െ ܾሻሺ െ ܿሻ ʹ ʹ ʹ
Mà theo công thức Heron, ta lại có : ܵଶ ଶݎଶ
ሺ െ ܽሻሺ െ ܾሻሺ െ ܿሻ ൌ ൌ ൌ ݎଶ Do đó, ൌ ݎ ʹ ʹ ʹ
Theo đẳng thức cơ bản, ta có : ൌ ሺכሻ ʹ ʹ ʹ ʹ ʹ ʹ
Kết hợp với giả thuyết, ta được ଶ
Ͷͻ ൬ଶ Ͷ ଶ ͻ ଶ ൰ ൌ ͵ ൬ ൰ ʹ ʹ ʹ ʹ ʹ ʹ
Theo bất đẳng thức Bunyakovsky, ta có : ଶ
͵ ൬ ൰ Ͷͻ ൬ଶ Ͷ ଶ ͻ ଶ ൰ ʹ ʹ ʹ ʹ ʹ ʹ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi ʹ ʹ ͵ ൌ ʹ ൌ ʹ ͵ ʹ
Kết hợp với ሺכሻ, ta có : ۓ ൌ ۓ ൌ ۖ ʹ ۖ ʹͷ ͷ ൌ ൌ ۔ ʹ Ͷ ۔ ͷ ۖ ۖ ͵ ە ൌ ൌ ʹ ͻ ە ͷ 189 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
Chú ý: Đến đây, cơ bản bài toán đã hoàn thành, nhưng ta có thể có được một kết quả đẹp
hơn nữa bằng việc áp dụng định lý hàm số sin, khi đó : ʹͷܽ ͷܾ ͷܿ ൌ ൌ ͷ ͵
Ta chọn : ܽ ൌ ͳ͵ǡ ܾ ൌ ͶͲǡ ܿ ൌ Ͷͷ.
Vậy tam giác có 3 cạnh thỏa mãn hệ thức :
ܽǣ ܾǣ ܿ ൌ ͳ͵ǣ ͶͲǣ Ͷͷ
Bài 29: Xác định hình dạng của tam giác có 3 góc ǡ ǡ thỏa mãn Ͷ ൬ ൰ ൌ ʹ ʹ ʹ ʹ ʹ ʹ
(Đề nghị Olympic 30-4, 2008) Giải: ߨ Ǣ Ǣ א ቀͲǢ ቁ ² ʹ ʹ ʹ ʹ
ൌ Ͷ ൬ ൰ Ͳ ʹ ʹ ʹ ʹ ʹ ʹ
Do đó, tam giác nhọn. Theo bất đẳng thức cơ bản, ta có : ͵ξ͵ Ta có thể giả sử : ߨ
Ͳ ൏ ൏ ฺ ൬ െ ൰ ൬ െ ൰ Ͳ ʹ ʹ ʹ ʹ ʹ ฺ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ Mà ͳ െ ͳ ൌ ൬ ൰൨ ʹ ʹ ʹ ʹ ʹ ʹ ʹ Suy ra :
Ͷ ൬ ൰ Ͷ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ Ta xét hàm số ݔ ߨ
݂ሺݔሻ ൌ Ͷ ʹ ݔ ǡ ݔ א ቀͲǡ ቁ ʹ ʹ ݔ
݂ᇱሺݔሻ ൌ ʹ ቀ ݔ െ ቁ ʹ 190 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác ߨ
݂ᇱሺݔሻ ൌ Ͳ ݔ ൌ ͵ గ గ ݔ Ͳ ଷ ଶ ݂Ԣሺݔሻ Ͳ െ ͵ξ͵ ݂ሺݔሻ
Từ bảng biến thiên, ta được ݂ሺݔሻ ͵ξ͵ Do đó,
Ͷ ൬ ൰ Ͷ ʹ ͵ξ͵ ʹ ʹ ʹ ʹ ʹ ʹ ʹ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi ൌ ቊ ߨ ൌ ͵ Vậy tam giác đều. - BÀI TẬP TỰ LUYỆN
3.3.1. Tính các góc của tam giác nếu nó thỏa mãn
Ǥ ଶ ଶ ଶ ൌ ଶ ଶ ଶ ʹ ʹ ʹ (ĐH Công Đoàn 2001)
Ǥ ሺͳ ሻሺͳ ሻ ൌ ʹ (ĐH Vinh 2000) Ǥ െ ʹ ൌ ʹ ʹ ʹ ʹ (ĐH An Ninh 2000) ܾଶ ܿଶ ܽଶ Ǥ ൜ ൌ ͳ ξʹ
(ĐH Ngoại Thương Tp.HCM 1998) 191 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác ߨ ൌ ሼǡ ǡ ሽ Ǥ ൝ Ͷ ሺ െ ሻ
3.3.2. Hãy xác định các góc của tam giác , biết rằng ͷ ͷ ͷ ͵ξ͵ ൌ ʹ ʹ ʹ ʹ
(Đề nghị Olympic 30-4, 2006)
3.3.3. Tính các góc của tam giác nhọn biết Ͷ ͵
ሺଷ ଷ ଷ ሻ ʹ ൌ ͵ Ͷ
(Đề nghị Olympic 30-4, 2007)
3.3.4. Tính số đo các góc của tam giác có diện tích ܵ và các cạnh ܽǡ ܾǡ ܿ thỏa mãn hệ thức :
൫ξʹ െ ͳ൯ሺܽଶ ܾଶሻ ܿଶ ൌ Ͷܵ
(Đề nghị Olympic 30-4, 2008)
3.3.5. Tính diện tích tam giác , biết rằng ܾ ሺܾ ܿ ሻ ൌ ʹͲ
3.3.6. Cho tam giác có các góc thỏa mãn െ ሺ െ ሻ ൌ Ͳ ʹ ʹ Tính .
3.3.7. Chứng minh tam giác cân khi các góc thỏa mãn hệ thức Ǥ ൌ ʹ ଶ Ǥ ൌ ଶ ͳ Ǥ ൌ ሺ ሻ ʹ 192 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác Ǥ ʹ ൌ ଶ ʹ Ǥ ൌ ʹ
Ǥܽ ሺ െ ሻ ܾ ሺ െ ሻ ൌ Ͳ Ǥܽ ൌ ܽ ʹ ʹܾ ʹ
Ǥሺܽଶ ܾଶሻ ሺ െ ሻ ൌ ሺܽଶ െ ܾଶሻ
Ǥ ൜ܽଶ ʹ ܾଶ ʹ ൌ Ͷܾܽ ʹ ʹ ൌ Ͷ
3.3.8. Chứng minh tam giác vuông khi nó thỏa mãn hệ thức ܽ ܿ Ǥ ൌ ʹ ܾ Ǥ ൌ ͳ Ǥ ൌ ͳ െ ͳ
Ǥܵ ൌ ሺܽ ܾ െ ܿሻሺܽ ܾ ܿሻ Ͷ ͳ ܿ ܾ Ǥ ൌ ܽ Ǥ ଶ ଶ ൌ ͳ ଶ െ ܿ െ ܾ Ǥ ൌ ʹ ܿ ܾ ܾ െ ܿ ଶ Ͷ ଶ െ Ǥ ൬ ൰ ൌ ʹ ܾ ͳ െ ʹ Ǥ݄ ൌ ʹξʹǤ ʹ ʹ
3.3.9. Chứng minh rằng tam giác đều nếu nó thỏa mãn hệ thức Ǥ ൌ ʹ ʹ ʹ 193 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác Ǥ ൌ ʹ ʹ ʹ
Ǥξ ξ ξ ൌ ඨ ඨ ඨ ʹ ʹ ʹ
Ǥξ ξ ξ ൌ ඨ ඨ ඨ ʹ ʹ ʹ Ǥ ൌ ʹ ʹ ʹ ͳ ͳ ͳ ͳ ͳ ͳ Ǥ ൌ ʹ ʹ ʹ
Ǥʹξ͵ െ ʹሺ ሻ ൌ Ͳ
Ǥ ʹ ʹ ʹ ൌ Ͳ
Ǥ͵ሺଶ ଶ ଶ ሻ ൌ ଶ ଶ ଶ
Ǥ ൌ ൫ െ Ͷξ͵൯൫ʹ െ ξ͵൯ Ͷ Ͷ Ͷ
Ǥܽሺͳ െ ʹ ሻ ܾሺͳ െ ʹ ሻ ܿሺͳ െ ʹ ሻ ൌ Ͳ ܽ ൌ ʹܾ Ǥ ൝ ܾଷ ܿଷ െ ܽଷ ܽଶ ൌ ܾ ܿ െ ܽ ܽ ܾ ܿଶ െ ൌ ͳ Ǥ ൞ܾ ܽ ܾܽ ͳ ൌ Ͷ
3.3.10. Cho tam giác nhọn thỏa điều kiện
ͳ െ ሺ ሻ ൌ ʹ 194 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
Chứng minh rằng tam giác là tam giác đều.
(Đề nghị Olympic 30-4, 2006)
3.3.11. Nhận dạng đặc điểm của tam giác nếu biết Ǥ ଶ ଶ ଶ ൌ ͳ Ǥܿ ൌ ܿ ʹ ܾ ʹ
Ǥܽଶ ܾଶ ܿଶ ͺ ܽ ܾ ܿ Ǥ ൌ ܾ ܿ ܿ ܽ ܽ ܾ
Ǥܽଶ ʹ ܾଶ ʹ ൌ ܿଶ ʹ
Ǥ ሺ ሻ ሺ െ ሻ ൌ ʹ ʹ Ǥ ൌ ʹ మబభమ మబభమ మబభమ Ǥ ξ మబభమ ξ మబభమ ξ మబభమ ൌ ඨ ඨ ඨ ʹ ʹ ʹ ʹ ʹ ʹ ͵ʹξ͵ Ǥ ൌ ଶ ͻ ʹ ଶ ʹ ଶ ʹ ͳʹ Ǥ ൌ ʹ ʹ ʹ Ǥ݈ଶ ଶ ଶ
݈ ݈ ൌ ଶ -
GỢI Ý GIẢI BÀI TẬP TỰ LUYỆN 3.3.1. a.
Theo đẳng thức cơ bản, giả thuyết tương đương với 195 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác ൌ ʹ ʹ ʹ (Tam giác đều) b.
Biến đổi tương đương, chú ý xét trường hợp െ ͳ ൌ Ͳ và െ ͳ ് Ͳ
(Tam giác có góc ൌ Ͷͷ୭) c.
Theo đẳng thức cơ bản, ta có ൌ Ͷ ʹ ʹ ʹ
(Tam giác có góc ൌ ͳʹͲ୭) d.
Theo bất đẳng thức Bunyakovsky, ta có :
ܾ ܿ ඥʹሺܾଶ ܿଶሻ ܽξʹ
Theo định lý hàm số sin, ta lại có : ξʹ Suy ra
൫ͳ ξʹ൯ ͳ ξʹ (Tam giác vuông cân ở ) e.
Từ giả thuyết ta suy ra tam giac không tù. Do đó ʹ ʹ ൌ ቄ ʹ ʹ ฺ ൞ ʹ ʹ ൌ ʹ ʹ
(Tam giác vuông cân ở hoặc ở hoặc đều) 3.3.2. ߨ ͵ߨ ͷ ͷ ͷ ͵ξ͵ ếǡ ǡ א Ǣ ൨ ¿ ൏ ʹ ൏ ሺẫሻ ͷ ͷ ʹ ʹ ʹ ʹ Do đó, ߨ ͵ߨ ǡ ǡ א ቀͲǡ ቁ ൬ ǡ ߨ൰ ͷ ͷ
Giả sử , chỉ có thể xảy ra khả năng ߨ ͵ߨ ǡ א ቀͲǡ ቁ Ǣ א ൬ ǡ ߨ൰ ͷ ͷ ͷ ͷ ߨ ߨ ߨ Ǣ
א ቀͲǡ ቁ ؿ ቀെ Ǣ ቁ ฺ ൞ ʹ ʹ ʹ ʹ ʹ ͷ െ Ͷߨ ߨ ߨ ͷ െ Ͷߨ ͷ א ቀെ Ǣ ቁ Ǣ ൬ ൰ ൌ ʹ ʹ ʹ ʹ ʹ
Theo bất đẳng thức Jensen, ta có : 196 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác ͷ ͷ ͷ ͷ ͷ ͷ െ ߨ ͵ξ͵ ͵ ൬ ൰ ൌ ʹ ʹ ʹ ʹ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi ߨ ൌ ൌ
ቄͷ ൌ ͷ ൌ ͷ െ Ͷߨ ൞ ͳͷ ൌ ߨ ͳ͵ߨ ൌ ͳͷ
3.3.3. Áp dụng đẳng thức cơ bản :
ʹ ʹ ʹ ൌ െͳ െ Ͷ
Khi đó giả thuyết tương đương với Ͷ ͳ ͷ
ሺଷ ଷ ଷ ሻ െ ሺ ʹ ʹ ʹሻ ൌ ͵ ʹ Ͷ Ta sẽ xét hàm số Ͷ ͳ ߨ
݂ሺݔሻ ൌ ଷ ݔ െ ʹݔ Ǣ ݔ א ቀͲǢ ቁ ͵ ʹ ʹ
݂ᇱሺݔሻ ൌ െͶ ଶ ݔ ݔ ʹݔ ൌ ሺͳ െ ʹݔሻ ʹݔ ߨ
݂ᇱሺݔሻ ൌ Ͳ ֞ ݔ ൌ ͵ ߨ ߨ ͷ
ậảế²݂ሺݔሻ² ቀͲǢ ቁ ¿×݂ሺݔሻ ݂ ቀ ቁ ൌ ʹ ͵ ͳʹ ͷ
ฺ ܵ ൌ ݂ሺሻ ݂ሺሻ ݂ሺሻ Ͷ
3.3.4. Theo bất đẳng thức Cauchy, với ݇ Ͳ ta có :
ሺܽ ܾ݇ሻଶ Ͷܾ݇ܽ Ͷܾ݇ܽ ሺ Ͷͷ୭ሻ
(Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi ܽ ൌ ܾ݇ và ൌ Ͷͷ୭)
ሺܽ ܾ݇ሻଶ ʹܾ݇ܽξʹ ʹܾ݇ܽξʹ
Do ሺܽ ܾ݇ሻଶ ʹሺܽଶ ݇ଶܾଶሻ
ฺ ʹሺܽଶ ݇ଶܾଶሻ Ͷ݇ξʹܵ ݇ξʹሺܽଶ ܾଶ െ ܿଶሻ
൫ʹ െ ݇ξʹ൯ܽଶ ൫ʹ݇ଶ െ ݇ξʹ൯ܾଶ ݇ξʹܿଶ Ͷ݇ξʹܵ
Khi đó, chọn ݇ ൌ ͳ, ta có :
൫ξʹ െ ͳ൯ሺܽଶ ܾଶሻ ܿଶ Ͷܵ 197 --------------------- TOANMATH.com
Chương 3 : Hệ thức lượng trong tam giác
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi tam giác cân tại và góc ൌ Ͷͷ୭.
3.3.10. Đề đã cho được viết lại
ሺͳ െ ሻሺͳ െ ሻሺͳ െ ሻ ൌ Ta sẽ chứng minh : ͳ െ ͳ െ ͳ െ ൬ ൰ ൬ ൰ ൬ ൰ ͳ Ta đặt : ͳ െ ݔଶ ۓݔ ൌ ۓ ൌ ۖ ʹ ͳ ݔଶ ۖ ۖ ͳ െ ݕଶ
ݕ ൌ ሺݔǡ ݕǡ ݖ Ͳሻ ฺ ൌ ۔ ʹ ۔ ͳ ݕଶ ۖ ۖ ۖ ͳ െ ݖଶ ەݖ ൌ ʹ ە ൌ ͳ ݖଶ
Do đó, điều cần chứng minh tương đương với ʹݔ ʹݕ ʹݖ ͳ ൬ ൰ ൬ ൰ ൬ ൰ ͳ െ ݔଶ ͳ െ ݕଶ ͳ െ ݖଶ ݔݕݖ ʹ ʹ ʹ ʹ ʹ ʹ 198 --------------------- TOANMATH.com
Đọc thêm : Tóm lược tiểu sử các nhà khoa học có ảnh hưởng đến lượng giác Đọc Thêm
TÓM LƯỢC TIỂU SỬ CÁC NHÀ KHOA HỌC
CÓ ẢNH HƯỞNG ĐẾN LƯỢNG GIÁC (1)HIPPARCHUS (190–120 TCN)
Hipparchus là một nhà thiên văn học, địa lý học, nhà toán học Hy Lạp. Ông được xem là
người sáng lập ra môn lượng giác học bởi những tính toán hàm số lượng giác đầu tiên
được gọi là bảng lượng giác. Qua đó, ông tính toán các giá trị đặc biệt của lượng giác
bằng các mô hình hình học. Nhờ đó, ông có thể giải được các bài toán lượng giác phẳng,
cũng như lượng giác cầu.
Hipparchus đã phát minh và sử dụng các dụng cụ thiên văn có vòng chia độ. Ông đã xác
định được khoảng cách đến Mặt Trời và Mặt Trăng, là người đầu tiên đưa ra một mô hình
về lượng mô tả chính xác sự chuyển động của Mặt Trời và Mặt Trăng. Với lý thuyết về
nhật nguyệt và lượng giác của mình, ông trở thành người đầu tiên xây dựng và phát triển
phương pháp tiên đoán nhật thực. Một thành tựu khác của ông cũng được biết đến đó là
việc thiết lập danh mục tọa độ khoảng 850 ngôi sao có chỉ rõ độ chói theo thang độ quy ước.
(2)PTOMELY (khoảng 85-165 TCN)
Ptomely là nhà bác học cổ Hy Lạp có sức ảnh hưởng lớn đến các vấn đề về thiên văn học,
địa lý học, quang học và lượng giác học. 199 --------------------- TOANMATH.com
Đọc thêm : Tóm lược tiểu sử các nhà khoa học có ảnh hưởng đến lượng giác
Là một người có nhu cầu nghiên cứu thiên văn học và địa lý học nên ông đã góp phần mở
rộng thêm các ứng dụng của hình học và lượng giác học. Ông được cho là người đầu tiên
tìm ra công thức cộng và trừ cho ሺ ሻ và ሺ ሻ, từ đó suy ra được công thức
hạ bậc, cho phép ông lập bảng tính với bất kỳ độ chính xác cần thiết nào. Tuy nhiên,
những bảng tính trên đều đã bị thất truyền. Ngoài ra, ông còn nghiên cứu phép chiếu
trong không gian mà ông cho là có ích cho việc nghiên cứu bầu trời.
(3)SURYA SIDDHANTA (khoảng thế kỷ 4-5)
Surya Siddhanta là một nhà thiên văn học người Ấn Độ, nhưng những công trình nghiên
cứu của ông đã góp phần phát triển các vấn đề về hàm lượng giác, đó là việc định nghĩa
hàm sin theo nửa góc và nửa dây cung, được cho là mở rộng các kết quả lượng giác của Ptomely.
Xoay quanh các công trình nghiên cứu của ông, ngoài những phép tính lượng giác phục
vụ cho thiên văn học, ông được biết đến bởi những ước tính gần đúng về đường kính của
các hành tinh. Chẳng hạn như đường kính của sao Thủy là 3.008 dặm, sao Thổ là 73.882
dặm, sao Hỏa là 3.772 dặm…
(4)FRANNCOIS VIÈTE (1540-1603)
Francois Viète là một luật gia, một nghị sĩ và là nhà toán học vĩ đại người Pháp, ông tổ
của môn đại số học. Ông viết nhiều công trình về lượng giác, đại số và hình học, và là
người đề ra cách giải thống nhất các phương trình bậc 2, bậc 3 và bậc 4 bằng việc khám
phá ra mối liên hệ giữa các nghiệm của một đa thức với các hệ số của đa thức đó, ngày
nay được gọi là định lý Viète. 200 --------------------- TOANMATH.com
Đọc thêm : Tóm lược tiểu sử các nhà khoa học có ảnh hưởng đến lượng giác
Cũng chính định lý Viète của ông đã góp phần phát triển những kỹ thuật tính toán quan
trọng trong các bài toán về biến đổi lượng giác, cũng như xác định được chính xác giá trị
của các hàm lượng giác ứng với mỗi góc qua việc giải phương trình. Ngoài ra, ông là
người đầu tiên phát triển hệ thống những phương pháp giải các tam giác phẳng và tam
giác cầu bằng cách dùng cả sáu hàm lượng giác. Đặc biệt chú ý là ông đã tìm ra được các
biểu thức cho ݊ݔ theo ݔ một cách tổng quát và có gợi ý cách giải lượng giác cho
trường hợp bất khả quy của các phương trình bậc 3.
Trong công trình nổi tiếng của Viète, ông đã phát triển nhiều ký hiệu đại số và trình bày
một quá trình có hệ thống để tìm xấp xỉ liên tiếp nghiệm của phương trình. (5)HERON (10-75)
Heron là nhà toán học và vật lý người Hy Lạp, vào thời đó ông được biết đến như một tác
gia bách khoa trong hai lĩnh vực này bởi những công trình của ông quá phong phú về nội
dung cũng như nhiều về số lượng. Mọi luận văn của ông thường hướng tới tính hữu dụng
thực tiễn hơn là tính hoàn chỉnh về lý thuyết.Công trình của Heron có thể chia thành hai
loại : Cơ học và Hình học.
Nói về cơ học thì ông có các công trình nổi bật như mô tả và xây dựng thiết bị mà các
phản ứng bên trong tương tự như động cơ tên lửa và động cơ hơi nước, công trình về máy bán hàng tự động…
Còn về hình học, đây là công trình quan trọng nhất của ông, tiêu biểu là tuyển tập
“Metrica” gồm 3 bộ. Trong tác phẩm này, Heron đã rút ra được công thức nổi tiếng để
tính diện tích tam giác theo ba cạnh và nửa chu vi, nay được gọi là công thức Heron.
Ngoài ra, ông còn đưa ra cách tính xấp xỉ về căn bậc hai của một số nguyên không chính
phương, cách tính thể tích các hình nón, hình trụ, hình hộp, hình lăng trụ, hình chóp, hình nón cụt, hình cầu… 201 --------------------- TOANMATH.com
Đọc thêm : Tóm lược tiểu sử các nhà khoa học có ảnh hưởng đến lượng giác (6)JAKOB STEINER (1796-1863)
Jakob Steiner là nhà toán học người Thụy Sỹ, được biết đến với các công trình nổi tiếng
về hình học, và hầu hết ông chỉ nghiên cứu về môn học này. Do đó, đã ảnh hưởng không
nhỏ đến các vấn đề về lượng giác, cụ thể là hệ thức lượng trong tam giác, vốn dĩ được xây
dựng trên nền tảng của hình học và thiên văn học.
Từ một đề xuất của nhà toán học người Đức – (7)Daniel Christian Ludolph Lehmus (1780-
1863), ông đã chứng minh được định lý rằng điều kiện cần và đủ để tam giác cân là hai
đường phân giác trong bằng nhau, ngày nay định lý này mang tên Steiner – Lahmus. Các
nghiên cứu quan trọng nhất của ông là hình học xạ ảnh và nguyên lý đối ngẫu.
(8)AUGUSTIN LOUIS CAUCHY (1789-1857)
Augustin Louis Cauchy là nhà toán học người Pháp, được xem là người đi đầu trong lĩnh
vực giải tích toán học. Những công trình của ông hầu hết đặt nền móng cơ sở cho toán
học hiện đại như lý thuyết hàm, vật lý và giải tích toán học. Đặc biệt các định nghĩa của
chúng ta hiện nay về giới hạn, tính liên tục, khả vi chủ yếu là do ông đề nghị, ông đã đặt
ra tiêu chuẩn Cauchy nổi tiếng để nghiên cứu về sự hội tụ của dãy trong các không gian riêng biệt.
Ngoài ra, ông còn phát triển lý thuyết chuỗi, lý thuyết định thức, phép tính tích phân, lý
thuyết hàm biến phức và có hàng loạt công trình cho các lĩnh vực hình học, đại số và lý
thuyết số… Một hệ quả nhỏ trong các công trình nghiên cứu của ông là bất đẳng thức
Cauchy, có ảnh hưởng to lớn đến toán học, trong đó có bất đẳng thức lượng giác. 202 --------------------- TOANMATH.com
Đọc thêm : Tóm lược tiểu sử các nhà khoa học có ảnh hưởng đến lượng giác
(9)VIKTOR YAKOVLEVICH BUNYAKOVSKY (1804-1889)
Viktor Yakovlevich Bunyakovsky là nhà toán học người Nga, được biết đến với khoảng
150 công trình về toán học và cơ học. Và ông còn được biết nhiều hơn về bất đẳng thức
Bunyakovsky, ngày nay chúng ta vẫn thường gọi là bất đẳng thức Bunyakovsky-Cauchy- Schwarz.
Ông còn nghiên cứu trong các lĩnh vực lý thuyết số, lý thuyết xác suất và ứng dụng, hình
học-đặc biệt là lý thuyết các đường song song, cơ học ứng dụng và thủy tĩnh học… và
quan tâm đến cả tính toán trong thực tiễn, bằng chứng là một loạt công trình về thống kê
và xác suất đã góp phần đáng kể vào việc phát triển lý thuyết thống kê của nước Nga.
(10)PAFNUTY LVOVICH CHEBYSHEV (1821-1894)
Pafnuty Lvovich Chebyshev là một nhà toán học người Nga, được coi là cha đẻ của nền
toán học Nga. Ông được biết tới bởi các công trình về lý thuyết xác suất, lý thuyết thống
kê và lý thuyết số, đặc biệt trong việc nghiên cứu sự phân bố các số nguyên tố trong dãy số tự nhiên.
Ông còn nghiên cứu về giải tích toán học, chẳng hạn như phương trình vi phân. Ông đã
thiết lập một ngành hoàn toàn mới nổi tiếng là “Lý thuyết xấp xỉ tốt nhất các hàm số bằng
đa thức”. Ngoài ra, trong nền toán học sơ cấp, ông cũng đóng góp không nhỏ, đó chính là
bất đẳng thức Chebyshev nổi tiếng. 203 --------------------- TOANMATH.com
Đọc thêm : Tóm lược tiểu sử các nhà khoa học có ảnh hưởng đến lượng giác
(11)JAKOB BERNOULLI (1654-1705)
Jakob Bernoulli là nhà toán học người Thụy Sĩ. Công trình của ông chủ yếu là hình học
giải tích, lý thuyết xác suất và phép tính biến phân. Ông được biết đến khi đã cùng với hai
nhà bác học Isaac Newton (1643-1689) người Anh và Gottfried Wilhelm Leibniz (1646-
1716) người Đức, phát triển phép tính vi phân và tích phân.
Ông là người nghiên cứu sớm về xác suất toán học. Có nhiều loại trong toán học mang
tên ông : sự phân phối Bernoulli, định lý Bernoulli trong xác suất và thống kê, phương
trình Bernoulli trong phương trình vi phân, bất đẳng thức Bernoulli…
(12)JOHAN LUDWIG WILLIAM VALDERMAR JENSEN (1859-1925)
Johan Ludwig William Valdermar Jensen là nhà toán học và kỹ sư người Đan Mạch. Tuy
công việc chính của ông là một kỹ sư xuất sắc cho một công ty ở Copenhagen và hầu hết
các nghiên cứu toán học của ông chỉ được thực hiện trong thời gian rảnh rỗi nhưng ông
đã đạt đến mức độ rất cao về toán học. Ông nghiên cứu về chuỗi dài vô tận, hàm gamma,
hàm lồi. Qua đó, ông đã đóng góp vào nền toán học sơ cấp : bất đẳng thức Jensen. 204 --------------------- TOANMATH.com TÀI LIỆU THAM KHẢO
[1] Trần Phương, Tuyển tập các chuyên đề luyện thi Đại học môn Toán – Hệ thức
lượng giác, NXB Đại học Quốc Gia Hà Nội, 2010.
[2] Huỳnh Công Thái, Đậu Thế Cấp, Các chuyên đề - Tìm cực trị và Chứng minh bất
đẳng thức chứa hàm lượng giác, NXB Đại học Quốc Gia Tp.HCM, 2007.
[3] Nguyễn Văn Nho, Nguyễn Văn Thổ, Chuyên đề Lượng giác, NXB Tổng hợp Tp.HCM, 2007.
[4] Võ Giang Giai, Tuyển tập 400 bài toán lượng giác, NXB Đại học Sư Phạm, 2007.
[5] Phạm Tấn Phước, Các chuyên đề Lượng giác, NXB Tp.HCM, 1999.
[6] Huỳnh Công Thái, Chuyên đề lượng giác – Đẳng thức, Bất đẳng thức trong tam giác,
Nhận dạng tam giác, NXB Đại học Quốc Gia Tp.HCM, 2002.
[7] James Stewart, Calculus – Concepts and Contexts, Richard Stratton, 2005.
[8] Tuyển tập đề thi Olympic 30 tháng 4, Lần XII – 2006, Toán học, NXBGD, 2006.
Tuyển tập đề thi Olympic 30 tháng 4, Lần XIII – 2007, Toán học, NXBGD, 2007.
Tuyển tập đề thi Olympic 30 tháng 4, Lần XIV – 2008, Toán học, NXBGD, 2008.
Tuyển tập đề thi Olympic 30 tháng 4, Lần XV – 2009, Toán học, NXBGD, 2009.
Tuyển tập đề thi Olympic 30 tháng 4, Lần XVI – 2006, Toán học, NXBGD, 2010. [9]
Nguyễn Phúc Lộc, Lịch sử Toán học, NXBGD, 2008. 205 --------------------- TOANMATH.com
Document Outline
- Untitled
- Untitled
- Untitled
- Untitled
- Untitled
- Untitled




