











Preview text:
SỞ GD & ĐT BẮC NINH
ĐỀ KIỂM TRA GIỮA HỌC KÌ I NĂM HỌC 2025 - 2026
TRƯỜNG THPT YÊN DŨNG SỐ 1 Môn: TOÁN, Lớp
Thời gian làm bài: 90 phút, không kể thời gian phát đề
(Đề gồm có 3 trang) Mã đề
Họ và tên: ……………………………………………….... Số báo danh: …………...... 0102
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Học sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi học
sinh chỉ chọn một phương án.
Câu 1. Lập mệnh đề phủ định của mệnh đề 2 " x
: x + x + 2025 0". A. 2 x
: x + x + 2025 0 . B. 2 x
: x + x + 2025 0 . C. 2 x
: x + x + 2025 0. D. 2 x
: x + x + 2025 0 .
Câu 2. Phát biểu nào sau đây là một mệnh đề?
A. 151 là số chẵn phải không?
B. 2x −1là số chẵn. C. 3 x +1 = 0 .
D. Số 27 là số lẻ.
Câu 3. Cho hai tập hợp A = (1;
5 ; B = (2;7. Tập hợp A\ B là A. (2;5) B. ( 1 − ;2) C. (1;2 D. ( 1 − ;7
Câu 4. Miền nghiệm của bất phương trình x − 2 + 2( y − )
1 2x + 4 chứa điểm nào sau đây?
A. D(0 ; 4).
B. B(1 ; 5). C. A(1 ; ) 1 . D. C (4 ; 3).
Câu 5. Hãy liệt kê các phần tử của tập hợp X = 2
x | 2x − 3x +1 = 0 . 3 1 A. X = 1 B. X = 1; C. X = 0 D. X = 1; 2 2
Câu 6. Trong các bất phương trình sau, bất phương trình nào là bất phương trình bậc nhất hai ẩn?
A. 2x + 5y 3 . B. 2
2x + 3y 5 . C. 2
4x + 2y − 4 0 .
D. 4x − 5y + 3xy 0 .
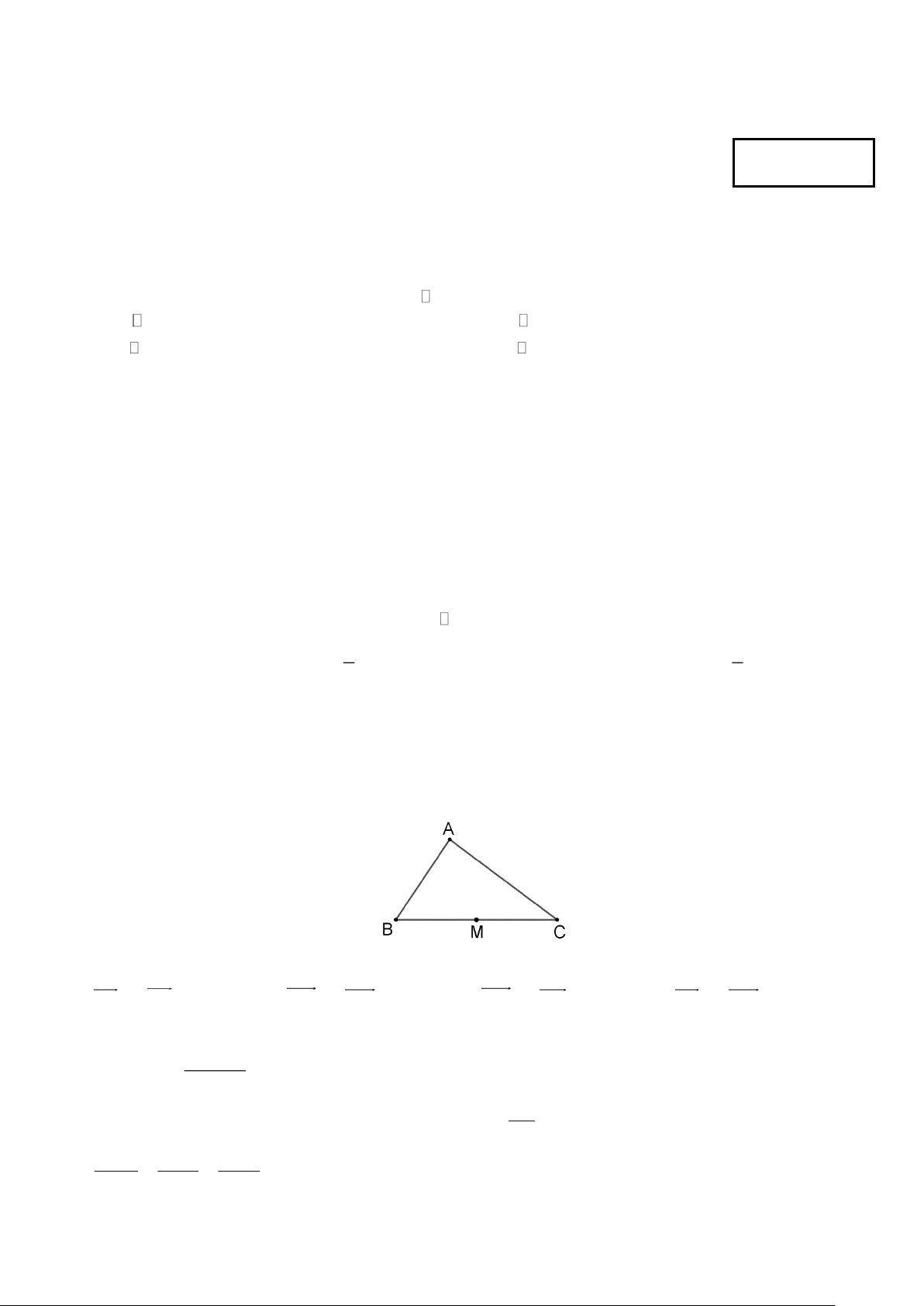
Câu 7. Cho tam giác ABC có M là trung điểm cạnh BC .
Hỏi cặp vectơ nào sau đây ngược hướng?
A. AB và AC .
B. MC và BM .
C. MC và MB .
D. AB và BM .
Câu 8. Cho tam giác ABC , có độ dài ba cạnh là BC = a, AC = b, AB = c . Gọi R là bán kính đường tròn ngoại a + b + c tiếp tam giác, p =
là nửa chu vi và S là diện tích tam giác đó. Mệnh đề nào sau đây sai? 2 abc
A. S = pr . B. S = . 4R a b c C. = = = 2R. D. 2 2 2
a = b +c + 2bccos A .
sin A sin B sinC Trang 1
Câu 9. Cho tam giác ABC có AB = 2, AC =1 và µ 0
A = 60 . Tính độ dài cạnh . BC
A. BC = 2.
B. BC = 2.
C. BC = 3.
D. BC =1.
Câu 10. Trong các đẳng thức sau đây, đẳng thức nào đúng?
A. cot (180 −a ) = −cota
B. cos(180 −a ) = cosa
C. sin(180 −a ) = −sina .
D. tan(180 −a ) = tana .
Câu 11. Cho góc thoả mãn 0 . Khẳng định nào sau đây là đúng?
A. tan 0 .
B. cot .
C. cos .
D. sin 0 .
Câu 12. Cho hình bình hành ABCD. Vectơ nào sau đây bằng vectơ AD ? A. BC B. AC C. CB D. DA
PHẦN II. Câu trắc nghiệm đúng sai. Học sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu,
học sinh chọn đúng hoặc sai.
x + y − 2 0
Câu 1. Cho hệ bất phương trình: x − y + 2 0 ( )
1 . Xét tính đúng sai của các mệnh đề sau
x − 2y + 2 0
a) Hệ bất phương trình ( )
1 là hệ bất phương trình bậc nhất hai ẩn.
b) Cặp số (0;0) là một nghiệm của hệ bất phương trình.
c) Miền nghiệm của hệ trên là miền tam giác (bao gồm cả các cạnh của tam giác).
d) Cho biểu thức F = 3x + 4y với x, y thoả mãn hệ ( )
1 . Giá trị nhỏ nhất của biểu thức F đạt được khi x = 0; y = 2 . 2 Câu 2. Cho sina (0 a 90 = ). Khi đó: 3 5 5 a) 2 cos a = b) cosa = − 9 3 2 5 sina + 5 cosa 7 c) tan x = d) = 5 2sina + cosa 4 + 5
PHẦN III. Câu trắc nghiệm trả lời ngắn. Học sinh trả lời từ câu 1 đến câu 4. Câu 1. Cho A BC có AB = 6; A = 40;
B = 60 . Tính được góc o
C = a , khi đó a có giá trị bằng bao nhiêu?
Câu 2. Bạn Minh mua một số quyển vở và bút chuẩn bị cho năm học mới. Biết rằng giá một quyển vở là
12.000 đồng và giá của một cây bút là 8.000 đồng. Gọi x, y lần lượt là số quyển vở và số bút được mua. Điều
kiện của x và y để tổng số tiền bạn Minh phải trả không quá 200.000 đồng là 3x + ay b . Khi đó P = a + b có giá trị bằng bao nhiêu?
Câu 3. Khối 10 của một trường THPT có 540 học sinh trong đó có 295 học sinh thích môn Văn, 340 học sinh
thích học môn Toán. Hỏi số học sinh chỉ thích học một môn trong hai môn Toán và Văn là bao nhiêu? Biết
rằng mỗi học sinh trong trường đều thích học môn Toán hoặc thích học môn Văn. Trang 2 2
Câu 4. Cho sin x =
. Tính giá trị biểu thức 2 2
P = 3sin x + 8cos x ? (kết quả làm tròn đến hàng phần trăm) 3
PHẦN IV: Tự luận (3,0 điểm) Bài 1. (1,0 điểm)
a) Cho tập hợp A = 0;1;2;5; 6 ; B = 0;3;4;
5 . Tìm A B .
b) Cho các tập hợp M = 2 − ; 5 ; N = (3; 9 .
Tìm các tập hợp M N; M N .
Bài 2. (1,0 điểm) Cho tam giác ABC có AB = 5 , AC = 6 và 0 A =120 .
a) Tính độ dài cạnh BC .
b) Tính diện tích tam giác ABC .
Bài 3. (1,0 điểm) Tại một trường THPT, câu lạc bộ Hóa học tổ chức cuộc thi “Pha chế hương vị tuổi học trò”.
Mỗi đội được sử dụng tối đa 8 gam hương liệu, 14 lít nước và 180 gam đường để pha hai loại nước giải khát:
Loại Kỷ niệm (K) và Loại Tự hào (T). Để pha 1 lít nước loại K cần 30 gam đường, 1 lít nước và 1 gam hương
liệu. Để pha 1 lít nước loại T cần 10 gam đường, 2 lít nước và 1 gam hương liệu. Mỗi lít nước loại K được 60
điểm thưởng, mỗi lít loại T được 70 điểm thưởng. Hỏi cần pha chế bao nhiêu lít nước mỗi loại để đội chơi có
tổng điểm thưởng cao nhất?
-------------- HẾT -------------- ĐÁP ÁN
PHẦN I: Trắc nghiệm nhiều lựa chọn
- Mỗi câu đúng được 0,25 điểm. Mã đề 1 2 3 4 5 6 7 8 9 10 11 12 0102 D D C B A A C D C A C A
PHẦN II: Trắc nghiệm đúng sai
- Điểm tối đa mỗi câu là 1 điểm.
- Đúng 1 ý được 0,1 điểm; đúng 2 ý được 0,25 điểm; đúng 3 ý được 0,5 điểm; đúng 4 ý được 1 điểm. Mã đề Câu 1 Câu 2 0102
a)Đ - b)S - c)Đ - d)S
a)Đ - b)S - c)Đ - d)Đ
PHẦN III: Trắc nghiệm trả lời ngắn - tự luận
- Mỗi câu đúng được 0,5 điểm. Mã đề Câu 1 Câu 2 Câu 3 Câu 4 0102 80 52 445 5,78 PHẦN IV: Tự luận Bài Nội dung Điểm 1.a(0,5
A B = 0;1;2;3;4;5; 6 0.5 điểm) Trang 3 1.b(0, 5
+ Tìm và biểu diễn đúng M N = (3; 5 0,25 điểm) 0,25
+ Tìm và biểu diễn đúng M N = 2 − ; 9 2.a(0,5 đ)
+ Áp dụng định lí cosin cho tam giác ABC ta có 2 2 2
BC = AB + AC − 2.A . B AC.cos A 0,25 2 25 36 2.5.6.cos120o BC = + − = 91 0,25 Suy ra BC = 91 2.b(0,5 đ) 1 0,25
+ Diện tích tam giác ABC là S = .A . B AC.sin A 2 1 o 15 3 S = .5.6.sin120 = 0,25 2 2 3(1 điểm)
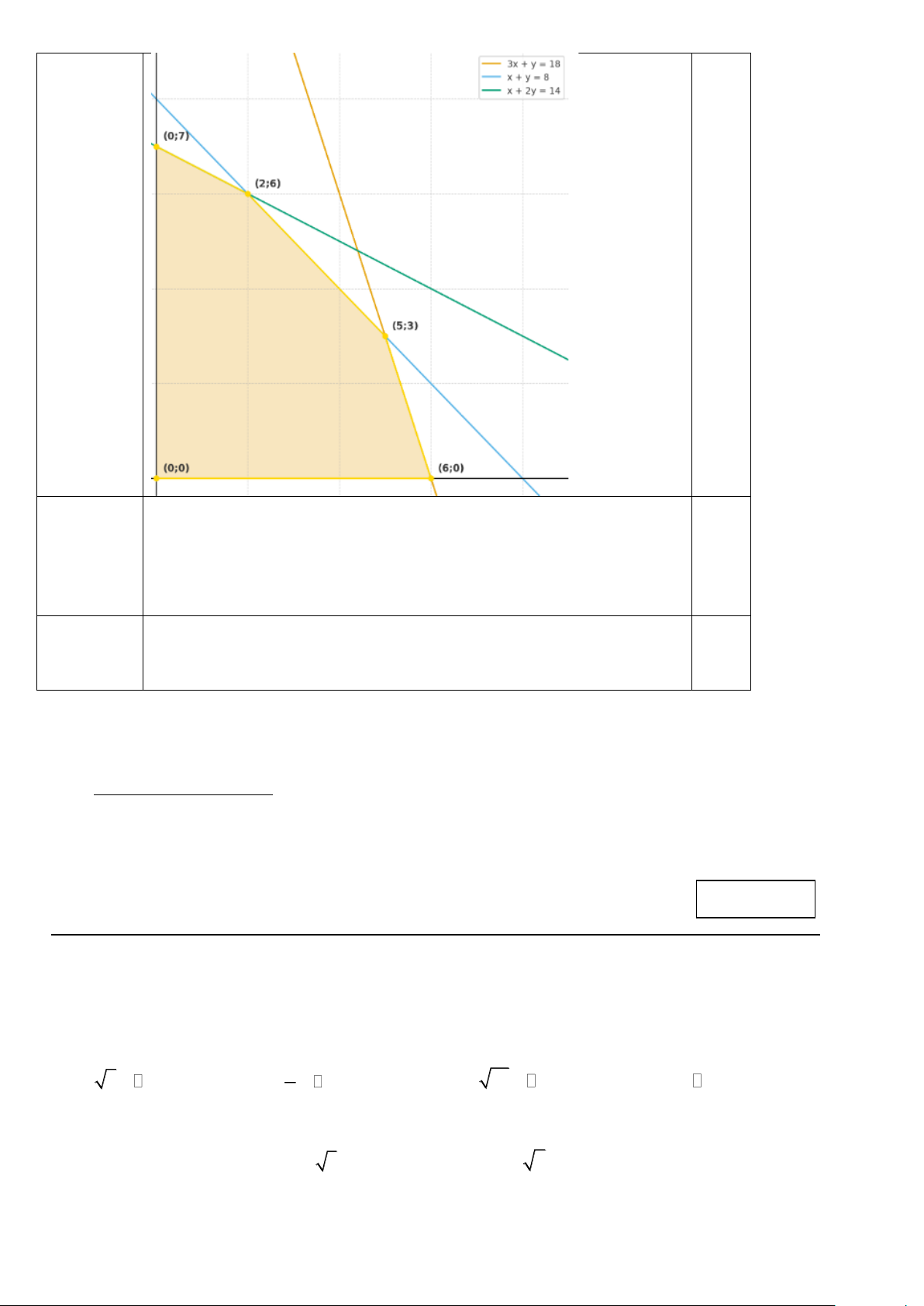
Gọi x và y lần lượt là số lít nước loại K và T cần pha chế .
Theo đề bài, ta có hệ bất phương trình bậc nhất hai ẩn x , y sau: x 0 x 0 y 0 y 0 0,25 3
0x +10y 180 hay 3x + y 18 (*) x + y 8 x + y 8 x + 2y 14 x + 2y 14
Biểu diễn miền nghiệm của hệ (*) trên mặt phẳng tọa độ (Oxy), ta
được miền ngũ giác OABCD (lấy cả các điểm trên các cạnh của ngũ 0,25
giác) với tọa độ các đỉnh là O(0;0) , A(0;7) , B(2;6) , C (5;3) , D(6;0) . Trang 4
Số điểm thưởng đội chơi nhận được là F( ;
x y) = 60x + 70 y (điểm).
Tìm x, y để F ( ;
x y) đạt giá trị lớn nhất. 0,25
F (0;0) = 0, F (0;7) = 490 , F (2;6) = 540, F (5; ) 3 = 510, F (6;0) = 360
Giá trị lớn nhất của F ( ;
x y) bằng 540 khi x = 2, y = 6
Kết luận: Vậy cần pha chế 2 lít nước loại K và 6 lít nước loại T thì số 0,25 điểm thưởng cao nhất.
SỞ GD&ĐT HẢI PHÒNG
ĐỀ KIỂM TRA GIỮA HỌC KÌ I
TRƯỜNG THPT NHỊ CHIỂU NĂM HỌC 2025 - 2026 MÔN: Toán 10
Thời gian làm bài : 90 phút
(Đề thi có 03 trang)
(không kể thời gian phát đề)
Họ và tên học sinh :..................................................... Số báo danh : ................... Mã đề 102
PHẦN I( 3 điểm): Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu hỏi thí sinh chỉ chọn một
phương án, mỗi câu trả lời đúng được 0,25 điểm.
Câu 1. Chọn khẳng định đúng trong các khẳng định dưới đây? A. 5 . B. 1 − . C. 10 . D. 7 . 2
Câu 2. Cho tam giác ABC có AB = 2, AC =1 và
A = 60 . Độ dài cạnh BC bằng:
A. BC = 2.
B. BC = 3 .
C. BC = 2 . D. BC =1.
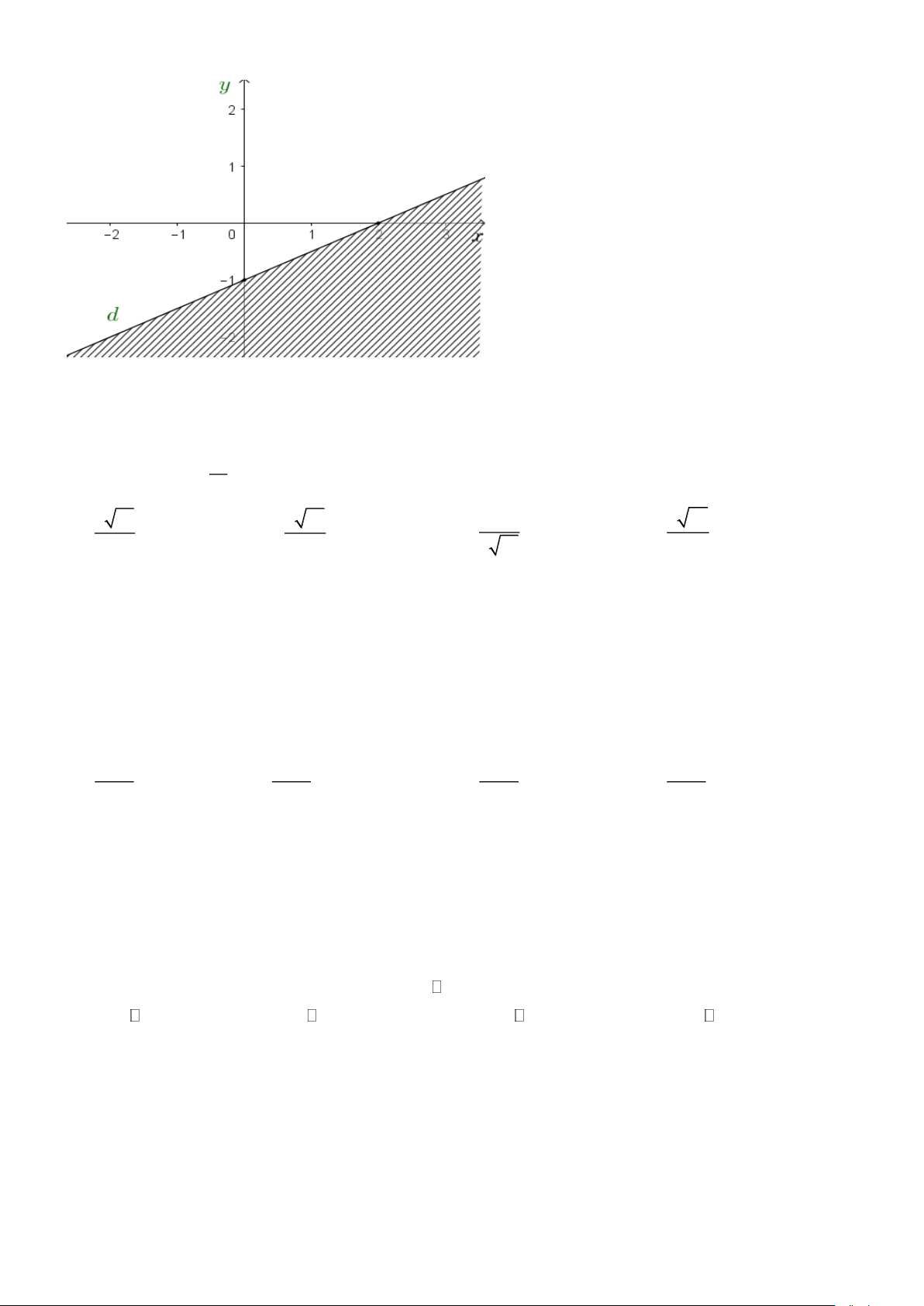
Câu 3. Phần gạch chéo trong hình vẽ dưới đây (không bao gồm đường thẳng d ) là miền nghiệm của Trang 5
bất phương trình bậc nhất hai ẩn nào dưới đây?
A. x − 2y 2.
B. x − 2y 1.
C. x − 2y 3 .
D. 2x − y 0 .
Câu 4. Cho 90 a 180. Trong các khẳng định sau, khẳng định nào đúng?
A. sin a 0
B. tana 0
C. cot a 0 D. cosa 0 4
Câu 5. Cho cosa =
và 0 < a < 90°. Khi đó sin a bằng: 13 4 3 17 A. 3 17 . B. 3 17 − . C. . D. . 14 13 3 17 13
Câu 6. Trong các mệnh đề sau, mệnh đề nào là mệnh đề đúng?
A. Tổng của hai số tự nhiên là số lẻ khi và chỉ khi cả hai số đó đều là số lẻ.
B. Tích của hai số tự nhiên là số chẵn khi và chỉ khi cả hai số đó đều là số chẵn.
C. Tích của hai số tự nhiên là số lẻ khi và chỉ khi cả hai số đó đều là số lẻ.
D. Tổng của hai số tự nhiên là số chẵn khi và chỉ khi cả hai số đó đều là số chẵn.
Câu 7. Xét tam giác ABC tùy ý, đường tròn ngoại tiếp tam giác có bán kính R, BC = . a Mệnh đề nào dưới đây đúng? A. a = a a a 2R . B. = R . C. = 3R . D. = 4R . sin A sin A sin A sin A
Câu 8. Điểm A( 1
− ;3) thuộc miền nghiệm của bất phương trình nào dưới đây?
A. 2x + y − 4 0 .
B. x + 3y 0 .
C. x − 3y 0 . D. 3
− x + 2y − 4 0 .
Câu 9. Điểm O(0;0) không thuộc miền nghiệm của hệ bất phương trình nào dưới đây?
x + 3y − 6 0 x + 3y 0
x + 3y − 6 0 x + 3y 0 A. . B. . C. . D. .
2x + y + 4 0
2x + y − 4 0
2x + y + 4 0
2x + y + 4 0
Câu 10. Mệnh đề phủ định của mệnh đề: “ 2 x
: x x −1” là: A. 2 x
: x x −1. B. 2 x
: x x −1. C. 2 x
: x x −1. D. 2 x
: x x −1.
x − y + 2 0
Câu 11. Miền nghiệm của hệ bất phương trình
là phần mặt phẳng chứa điểm nào dưới 2x + y 3 đây ? A. (1; ) 1 . B. (1;2) . C. (2; ) 1 − . D. ( 1 − ;2) .
Câu 12. Cho hai tập hợp A = 3
− ;5) và B = (0;7. Xác định tập hợp A B ? A. 5;7. B. (0;5). C. 3 − ;7. D. 3 − ;0 . Trang 6
PHẦN II( 2 điểm): Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a),
b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1( 1 điểm): Cho tam giác ABC biết cạnh a = BC = 5 c ;
m b = AC = 6 c ;
m c = AB = 7 cm . R là bán
kính đường tròn ngoại tiếp tam giác ABC, S là diện tích tam giác ABC. Khi đó: a) 12 6 Sin B = 35
b) Cos(A+B) = - CosC
c) Sin(A + B) = −Sin C d) = abc S 2R
Câu 2( 1 điểm): Cho các tập hợp A = 1 − ;
5 ; B ={0;1;2};C = m+1;m+ 6 . Khi đó ta có:
a) Phát biểu: “ Tập A là tập con của tập B” là mệnh đề sai
b) Tập các giá trị của m để AC là 7 − m 4
c) A\ B = 1 − ;2).
d) Phát biểu: “Nếu x thuộc tập B thì x thuộc tập A” là mệnh đề sai
PHẦN III ( 2 điểm): Câu trắc nghiệm trả lời ngắn. Mỗi câu hỏi thí sinh chỉ ghi đáp số và tô vào
phiếu trả lời trắc nghiệm.
Câu 1(0,5 điểm): Cho tan = 3 ( 0 0 0
0 180 , 90 ) . 2 2
2sin − 3cos sin − 3 o c s
Tính giá trị của biểu thức A = 2 2
5sin + 2cos sin − o c s
(Kết quả làm tròn đến hàng phần trăm)
Câu 2(0,5 điểm): Có tất cả bao nhiêu giá trị nguyên của tham số m thuộc đoạn 0;2 0 để cặp số x=3 và
y=2 là nghiệm của bất phương trình 2x + (m −1) y 24 ?
Câu 3(0,5 điểm): Để chuẩn bị đồ dùng học tập cho năm học mới, mẹ cho Hoa 100000 đồng để đi mua
dụng cụ học tập. Sau khi lên danh sách đồ dùng còn thiếu, Hoa quyết định đi mua bút bi và quyển vở
để ghi chép. Biết giá tiền của một chiếc bút bi là 5000 đồng và giá tiền một quyển vở là 7000 đồng.
Hỏi Hoa có thể mua tối đa bao nhiêu chiếc bút bi để không quá số tiền mà mẹ cho, biết rằng Hoa đã mua 10 quyển vở?
Câu 4(0,5 điểm): Cho 3 sin = ( 0 0
90 180 ) . Tính cos ? (Kết quả làm tròn đến hàng phần 7 chục)
PHẦN IV: Tự luận (3 điểm): Đề chẵn Trang 7
Câu 1( 1 điểm): Một lớp học có 25 học sinh chơi bóng đá, 23 học sinh chơi bóng bàn, 14 học sinh
chơi cả bóng đá và bóng bàn, 6 học sinh không chơi môn nào. Tìm số học sinh chỉ chơi một môn thể thao?
Câu 2( 1 điểm): Một gia đình cần ít nhất 1200 đơn vị protein và 800 đơn vị lipit trong thức ăn mỗi
ngày. Mỗi kilôgam thịt bò chứa 800 đơn vị protein và 400 đơn vị lipit. Mỗi kilôgam thịt lợn chứa 600
đơn vị protein và 800 đơn vị lipit. Biết rằng gia đình này chỉ mua nhiều nhất 1,8 kg thịt bò và 1, 2 kg
thịt lợn. Giá tiền một kilôgam thịt bò là 200 nghìn đồng, một kilôgam thịt lợn là 150 nghìn đồng. Gọi
x , y lần lượt là số kilôgam thịt bò và thịt lợn mà gia đình đó cần mua. Tìm x , y để tổng số tiền họ
phải trả là ít nhất mà vẫn đảm bảo lượng protein và lipit trong thức ăn mỗi ngày? + +
Câu 3( 1 điểm): Cho tam giác 1 cos B 2a c ABC thoả mãn =
.Chứng minh tam giác ABC cân. 2 2 sin B 4a − c
……………………………………………………Hết…………………………………………
Học sinh không được sử dụng tài liệu. Giáo viên coi thi không giải thích gì thêm! ĐÁP ÁN
Phần I: Trắc nghiệm nhiều lựa chọn( 3 điểm, 12 câu, mỗi câu 0,25 điểm) 102 1 C 2 B 3 A 4 A 5 D 6 C 7 A 8 D 9 D 10 B 11 B 12 C
Phần II: Trắc nghiệm chọn đúng hoặc sai( 2 điểm, 2 câu, mỗi câu 1 điểm).
- Thí sinh chỉ lựa chọn chính xác 01 ý trong 1 câu hỏi được 0,1 điểm
- Thí sinh chỉ lựa chọn chính xác 02 ý trong 1 câu hỏi được 0,25 điểm
- Thí sinh chỉ lựa chọn chính xác 03 ý trong 1 câu hỏi được 0,5 điểm
- Thí sinh lựa chọn chính xác cả 04 ý trong 1 câu hỏi được 1 điểm Câu\Mã đề 102 Câu 1 DDSS Câu 2 DDSS Trang 8
Phần III:Trả lời ngắn( 2 điểm, 4 câu, mỗi câu 0,5 điểm) Câu\Mã đề 102 Câu 1 0,12 Câu 2 11 Câu 3 6 Câu 4 -0,9
PHẦN IV: TỰ LUẬN (3 điểm, 3 câu, mỗi câu 1 điểm) A.Đề chẵn:
Câu 1. Một lớp học có 25 học sinh chơi bóng đá, 23 học sinh chơi bóng bàn, 14 học sinh chơi cả bóng
đá và bóng bàn, 6 học sinh không chơi môn nào. Tìm số học sinh chỉ chơi một môn thể thao?
Giải : Gọi A là tập gồm các học sinh chơi bóng đá
B là tập gồm các học sinh chơi bóng bàn
A B là tập các học sinh chơi cả bóng đá và bóng bàn
n(A)=25; n(B)=23; n( A B )=14 0,25đ
Số học sinh chỉ chơi bóng bàn là 23-14=9 0,25đ
Số học sinh chỉ chơi bóng đá là 25-14=11 0,25đ
Vậy số học sinh chỉ chơi một môn là 9+11=20 0,25đ
Câu 2: Theo bài ra ta có số tiền gia đình cần trả là T(x, y)= 200.x +150.y (nghìn đồng) với x , y thỏa 0 x 1,8 mãn: . 0 y 1,2
Số đơn vị protein gia đình đó sử dụng là 800.x + 600.y
Số đơn vị lipit gia đình đó sử dụng là 400.x + 800.y . 0,25đ 0 x 1,8 0 x 1,8 0 y 1,2 0 y 1,2
Theo đề, ta được hệ bất phương trình 0,25đ
800x + 600y 1200 4x + 3y 6
400x +800y 800
x + 2y 2 Trang 9 0 x 1,8 0 y 1, 2
Bài toán trở thành: Tìm x, y thỏa mãn hệ bất phương trình
sao cho T = 200.x +150.y nhỏ 4x + 3y 6
x + 2y 2 nhất.
Vẽ mặt phẳng tọa độ Oxy ta tìm
được miền nghiệm của hệ bất
phương trình là miền tứ giác
ABCD với tọa độ các điểm
A(0,6;1 ,2); B(1,8;1 ,2) ; C (1,8; 0, ) 1 ; D(1,2; 0,4) 0,25đ
Nhận xét: T ( A) = 300 nghìn.;
T (B) = 540 nghìn, T (C) = 375 nghìn, T (D) = 300 nghìn
Vậy tổng số tiền họ phải trả là ít nhất mà vẫn đảm bảo lượng protein và lipit trong thức ăn khi x = 0,6
và y =1, 2 hoặc x=1,2 và y=0,4. 0,25đ Câu 3: Ta có 2 2 1+ cos B 2a + c (1+ cos B) (2a + c) = = , 0 25đ 2 2 2 2 2 sin B 4a − c sin B 4a − c 1+ cos B 2a + c 1+ cos B 2a + = − c 1 = −1 , 0 25đ 1− cos B 2a − c 1− cos B 2a − c 2 2 2 2 2 2 2 2
2accos B = c a + c −b = c a = b = b a = b , 0 25đ
Vậy tam giác ABC cân tại C . (0,25)
SỞ GD&ĐT PHÚ THỌ
KIỂM TRA GIỮA KỲ I - NĂM HỌC 2025 - 2026
TRƯỜNG THPT NGUYỄN VĂN CHẤT Môn: TOÁN, Lớp 10 ĐỀ CHÍNH THỨC
Thời gian: 90 phút (Không kể thời gian phát đề)
(Đề thi có 04 trang) Mã đề thi
Họ và tên thí sinh:.............................................................................. SBD:..................... 102 Trang 10
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 18. Mỗi câu hỏi thí
sinh chỉ chọn một phương án. 2x − y 1
Câu 1. Điểm nào dưới đây thuộc miền nghiệm của hệ bất phương trình ?
x + y + 4 0
A. (0 ; − 4).
B. (0 ; − 2).
C. (0 ; − 5). D. (0 ; 0).
Câu 2. Tập hợp I = x x
1 khi được viết bằng ký hiệu khoảng, nửa khoảng, đoạn là A. ( ;1 − .
B. I = (1;+) .
C. I = 1;+) . D. ( ) ;1 − .
Câu 3. Bất phương trình nào dưới đây là bất phương trình bậc nhất hai ẩn?
A. (2x − y)(−x + 3y) 1. B. 2 2x − y 1. C. 2 2
x + y 1.
D. 2025x − 2026y 1.
Câu 4. Chọn công thức đúng trong các đáp án sau 1 1 1 1
A. S = bc sin C .
B. S = bc sin A.
C. S = bc sin B.
D. S = ac sin A. 2 2 2 2 Câu 5. Cho ,
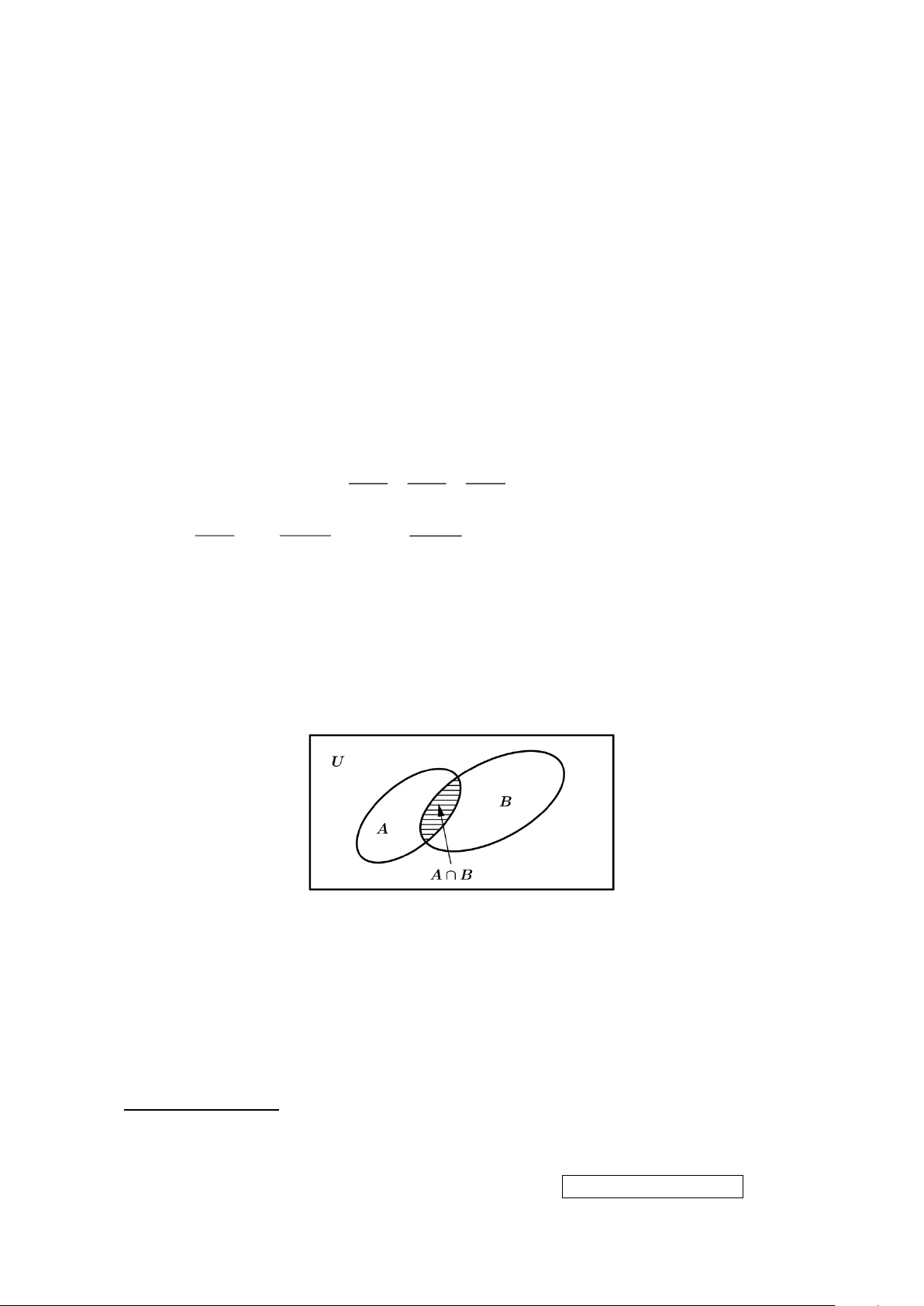
A B là hai tập hợp được minh họa như hình vẽ. Phần gạch sọc trong hình vẽ là tập hợp nào sau đây?
A. B \ A.
B. A B .
C. A B .
D. A \ B .
Câu 6. Hệ bất phương trình nào dưới đây là hệ bất phương trình bậc nhất hai ẩn? 2
−x + y 3 −x + y = 3 x + 2y 1
x − 2y 3 A. . B. . C. . D. . 2
2x − 3y 1 2x − 3y =1 2 2 x + y 4
2x − y 1 −
Câu 7. Cho bất phương trình −x − y 2 . Điểm nào dưới đây thuộc miền nghiệm của bất phương trình đã cho? A. (0; 5 − ) . B. (0;3) . C. (0;1) . D. (5;0) .
Câu 8. Phát biểu nào dưới đây là một mệnh đề ?
A. Hãy học tập thật chăm chỉ vào.
B. Trường THPT Nguyễn Văn Chất tỉnh Phú Thọ là một trường công lập được thành lập năm 2025.
C. Bạn có bao giờ đến Hoà Bình chưa?
D. Học ở THPT Nguyễn Văn Chất thật là tuyệt vời!
Câu 9. Hình nào sau đây minh họa tập hợp A là con của tập hợp B ? A. . B. . C. . D. .
Câu 10. Cho tập A = 2;3;5;
7 . Tập nào sau đây là tập con của A A. 1; 5 . B. 2;3;5;7; 9 . C. 2; 7 . D. 2; 4 . Câu 11. Cho góc 0 0
90 180 . Khẳng định nào sau đây là đúng?
A. cot 0 .
B. cos 0.
C. tan 0 . D. sin 0 . Trang 11 Câu 12. Biểu thức 0
A = sin 30 có giá trị bằng 1 3 1 3 A. . B. − . C. − . D. . 2 2 2 2
Câu 13. Cách viết nào sau đây để viết câu: ‘‘Mọi số tự nhiên đều không âm’’ A. ‘‘ n
N, n 1’’. B. ‘‘ n
N,n 0 ’’. C. ‘‘ n
N, n 0 ’’. D. ‘‘ n
N, n 1’’. Câu 14. Cho ABC
có BC = a ,
BAC =120 . Bán kính đường tròn ngoại tiếp ABC là a 3 a a 3 A. R = . B. R = .
C. R = a . D. R = . 3 2 2
Câu 15. Trong các đẳng thức sau, đẳng thức nào đúng? A. ( o
sin 180 − ) = −sin . B. ( o sin 180 − ) = cos . C. ( o
sin 180 − ) = sin . D. ( o
sin 180 − ) = −cos .
Câu 16. Tập hợp A = ; a
b . Tập A có bao nhiêu tập con? A. 4 . B. 5 . C. 1. D. 2 .
Câu 17. Hình vẽ nào sau đây (phần không bị gạch) minh họa cho tập hợp (1;4? A. . B. . C. . D. .
Câu 18. Mệnh đề phủ định của mệnh đề 2 Q : x
, x − 2025 0 là A. 2 Q : x
, x − 2025 0 . B. 2 Q : x
, x − 2025 0 . C. 2 Q : x
, x − 2025 0 . D. 2 Q : x
, x − 2025 = 0 .
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu,
thí sinh chọn đúng hoặc sai.
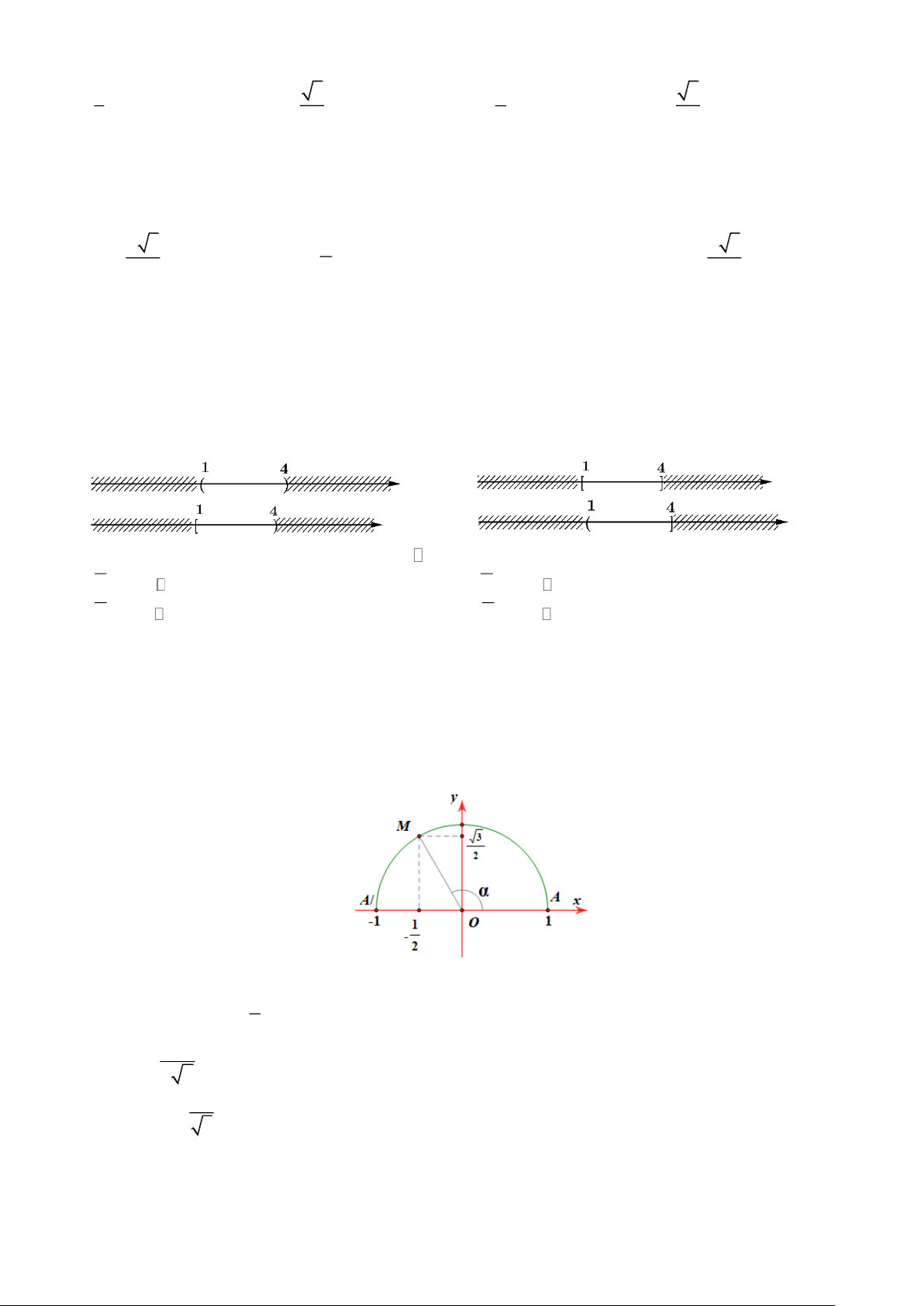
Câu 1. Trên nửa đường tròn đơn vị cho điểm M sao cho
xOM = (hình vẽ). Trong các mệnh đề sau mệnh đề
nào đúng, mệnh đề nào sai:
a) M (x ; y là điểm biểu diễn góc tù. 0 0 ) 1
b) Giá trị của cos = − . 2 1 c) cot = − . 2 2 1
d) tan xOM = − . 3
Câu 2. Một cửa hàng dành tối đa 10 triệu để nhập x tạ gạo và y tạ mì. Biết mỗi tạ gạo mua hết 1,5 triệu, mỗi
tạ mì mua hết 1,2 triệu. Khi đó các khẳng định sau đúng hay sai:
a) Cửa hàng sẽ không đủ vốn để nhập được 4 tạ gạo và 5 tạ mì. Trang 12
b) Nếu mua 2 tạ gạo và mua 3 tạ mì thì mất số tiền là 6,6 triệu, cửa hàng vẫn còn dư tiền để nhập tiếp.
c) Bất phương trình bậc nhất hai ẩn biểu thị mối liên hệ giữa x và y là: 1,5x +1, 2y 10 .
d) Miền nghiệm của bất phương trình 1,5x +1, 2y 10 là nửa mặt phẳng bờ là đường thẳng
d :1,5x +1, 2 y = 10 chứa gốc toạ độ O.
Câu 3. Cho tam giác ABC có độ dài các cạnh AB = 5, AC = 8, BC = 7 . 1
a) Giá trị của cos B = . 12 abc
b) Một công thức tính diện tích tam giác nữa được học trong chương 3 toán 10 KNTT đó là S = . Dựa 4R 7 3
vào công thức vừa cho ta tính được bán kính đường tròn ngoại tiếp tam giác ABC bằng . 3
c) Heron xứ Alexandria, là một nhà phát minh người Hy Lạp sinh vào năm 10 SCN tại Alexandria, hiện thuộc
Ai Cập. Đây là thành phố lớn thứ hai của nước này, sau Cairo. Không có nhiều điều được biết đến về cuộc đời
của Heron, tuy nhiên chúng ta biết rằng cha mẹ ông là người Hy Lạp di cư đến Alexandria sau cuộc xâm lăng
của Alexander Đại đế. Heron là một nhà toán học và kỹ sư được xem là một trong những nhà phát minh vĩ đại
nhất thời cổ đại. Một trong số đó có công thức tính diện tích tam giác mà ông tìm ra. Công thức đó là
S = p( p − a)( p − )
b ( p − c)
Diện tích tam giác ABC tính theo công thức Heron bằng 10 3.
d) Tam giác ABC là tam giác nhọn.
Câu 4. Cho tập hợp A và B có biểu diễn trên trục số như sau:
a) Tập hợp B chứa đúng 7 số nguyên.
b) Biểu diễn dưới dạng các khoảng, đoạn, nửa khoảng trong ℝ của tập hợp A là [−3;3].
c) A B = [−2; 4].
d) A B = [−2;3] .
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ Câu 1 đến Câu 3.
Câu 1. Anh An là nhân viên bán hàng tại một cửa hàng. Anh An sẽ được thưởng hoa hồng 100 nghìn đồng cho
mỗi cái điện thoại bán được và 250 nghìn đồng cho mỗi cái laptop bán được. Nếu tháng này anh An bán được 7
laptop thì để nhận được từ 3 triệu đồng trở lên tiền hoa hồng, anh An cần bán tối thiểu bao nhiêu cái điện thoại?
Câu 2. Một mảnh đất hình tam giác có các cạnh có độ dài lần lượt là 23m, 27m, 32m người ta muốn trồng cỏ
trang trí lên đó. Biết giá một mét vuông cỏ là 65.000đ. Hỏi để mua cỏ phủ kín lên mảnh đất thì phải mất bao
nhiêu triệu đồng? (làm tròn đến hàng đơn vị) Trang 13
Câu 3. Đoàn trường THPT Nguyễn Văn Chất theo nhu cầu và nguyện vọng của học sinh có thành lập câu lạc
bộ thể thao, để học sinh được tham gia phát triển toàn diện trí và lực. Câu lạc bộ đã thành lập và bước đầu đi
vào hoạt động nhận được sự hưởng ứng rất nhiệt tình của các em học sinh. Câu lạc bộ thể thao của nhà trường
hiện đang có hai môn thể thao là bóng chuyền và cầu lông. Theo thống kê có tổng 90 em đăng kí vào câu lạc
bộ. Trong đó, có 60 em đăng kí môn bóng chuyền và có 45 em đăng kí vào môn cầu lông. Hỏi có bao nhiêu bạn
đang đồng thời đăng kí cả hai môn thể thao? -------- HẾT-------- ĐÁP ÁN
PHẦN I: Trắc nghiệm nhiều lựa chọn
- Mỗi câu đúng được 0,25 điểm. Mã đề 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 102 D D D B B D A B B C A A B A C A D A
PHẦN II: Trắc nghiệm đúng sai
- Điểm tối đa mỗi câu là 1 điểm.
- Đúng 1 câu được 0,1 điểm; đúng 2 câu được 0,25 điểm; đúng 3 câu được 0,5 điểm; đúng 4 câu được 1 điểm. Mã đề Câu 1 Câu 2 Câu 3 Câu 4 102
a)Đ - b)Đ - c)S - d)S
a)Đ - b)Đ - c)Đ - d)Đ
a)S - b)Đ - c)Đ - d)Đ
a)Đ - b)Đ - c)S - d)Đ
PHẦN III: Trắc nghiệm trả lời ngắn - tự luận
- Mỗi câu đúng được 0,5 điểm. Mã đề Câu 1 Câu 2 Câu 3 102 13 20 15
SỞ GD & ĐT HÀ TĨNH
ĐỀ KIỂM TRA, ĐÁNH GIÁ GIỮA HỌC KỲ I
TRƯỜNG THPT NGUYỄN VĂN TRỖI NĂM HỌC 2025 - 2026
Môn: TOÁN - Lớp 10 - Sách KNTT ĐỀ CHÍNH THỨC
Thời gian: 90 phút (Không kể thời gian phát đề)
(Đề có 3 trang) Mã đề thi
Họ và tên thí sinh:.............................................................................. SBD:..................... 102
PHẦN I. (3,0 điểm) Câu trắc nghiệm nhiều phương án lựa chọn. Học sinh trả lời từ câu 1 đến
câu 12. Mỗi câu hỏi học sinh chỉ chọn một phương án.
Câu 1. Sơ đồ Ven nào sau đây biểu thị tập A là con của tập B ? A. B. C. D.
Câu 2. Cho tập hợp X = d; ;
e f . Số phần tử của tập hợp X là: A. 1. B. 3 . C. 8 . D. 0 . Trang 14
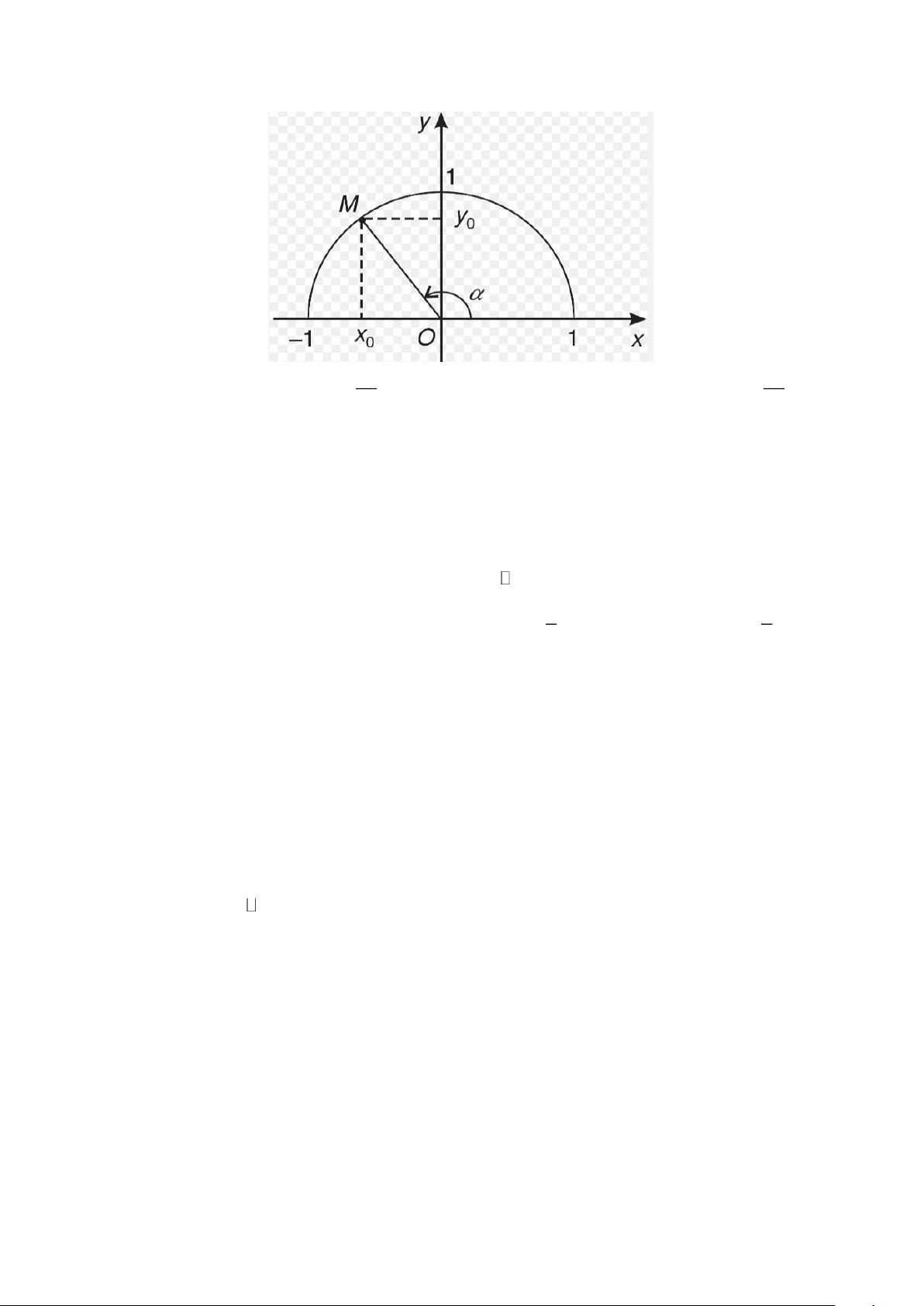
Câu 3. Trên nửa đường tròn đơn vị, cho điểm M(x ; y sao cho
xOM = . Khẳng định nào dưới đây 0 0 ) đúng? y x
A. sin = y .. B. 0 sin = ..
C. sin = x . . D. 0 sin = .. 0 x 0 y 0 0
Câu 4. Nếu + =180 thì khẳng định nào sau đây đúng
A. cot = cot .
B. tan = tan .
C. cos = − cos .
D. sin = −sin .
Câu 5. Cho các tập hợp A = 1;3; 4 , B = 1;3;
5 . Chọn phát biểu sai?
A. A B = 1 .
B. A B = 1;3;4; 5 .
C. B \ A = 5 .
D. A\ B = 4 .
Câu 6. Liệt kê các phần tử của phần tử tập hợp X = 2
x | 3x − 5x + 2 = 0 . A. X = 0 . B. X = 1 . C. 2 X = . D. 2 X = 1; . 3 3
Câu 7. Trong các câu sau đây, câu nào là mệnh đề?
A. Học lớp10 thật vui.
B. Cơn bão để lại hậu quả nặng nề quá!.
C. 2026 là một số lẻ.
D. Bài toán này dễ quá phải không?
Câu 8. Cho mệnh đề: “Nếu một tam giác có hai cạnh bằng nhau thì tam giác đó là tam giác cân”.
Mệnh đề đảo của mệnh đề trên là:
A. Nếu một tam giác là tam giác cân thì tam giác đó có hai cạnh bằng nhau.
B. Để một tam giác là tam giác cân thì điều kiện cần và đủ là nó có hai cạnh bằng nhau.
C. Tam giác là tam giác cân nếu và chỉ nếu tam giác đó có hai cạnh bằng nhau.
D. Nếu tam giác có hai cạnh bằng nhau thì tam giác đó không là tam giác cân.
Câu 9. Tập hợp A = x | 5 − x
3 là tập hợp nào trong các tập hợp dưới đây ? A. 5 − ; ) 3 . B. 5 − ; 3 . C. ( 5 − ;3) . D. ( 5 − ; 3 .
Câu 10. Trong các bất phương trình sau, bất phương trình nào là bất phương trình bậc nhất hai ẩn?
A. 2x − 5y 0 . B. 2
x + y − 4 0 .
C. 2x + y z . D. 2 2x + y 1.
Câu 11. Hệ bất phương trình nào sau đây là hệ bất phương trình bậc nhất hai ẩn ? 2
x − 3y 0 2 x − y 7 . x y +1 0 x + y 2
A. y − 3 0 . B. y − x 0 . C. y − 3x 2 − . D. y 0 . x 0 2 y 5 3x + y 5 3 x + y 1 −
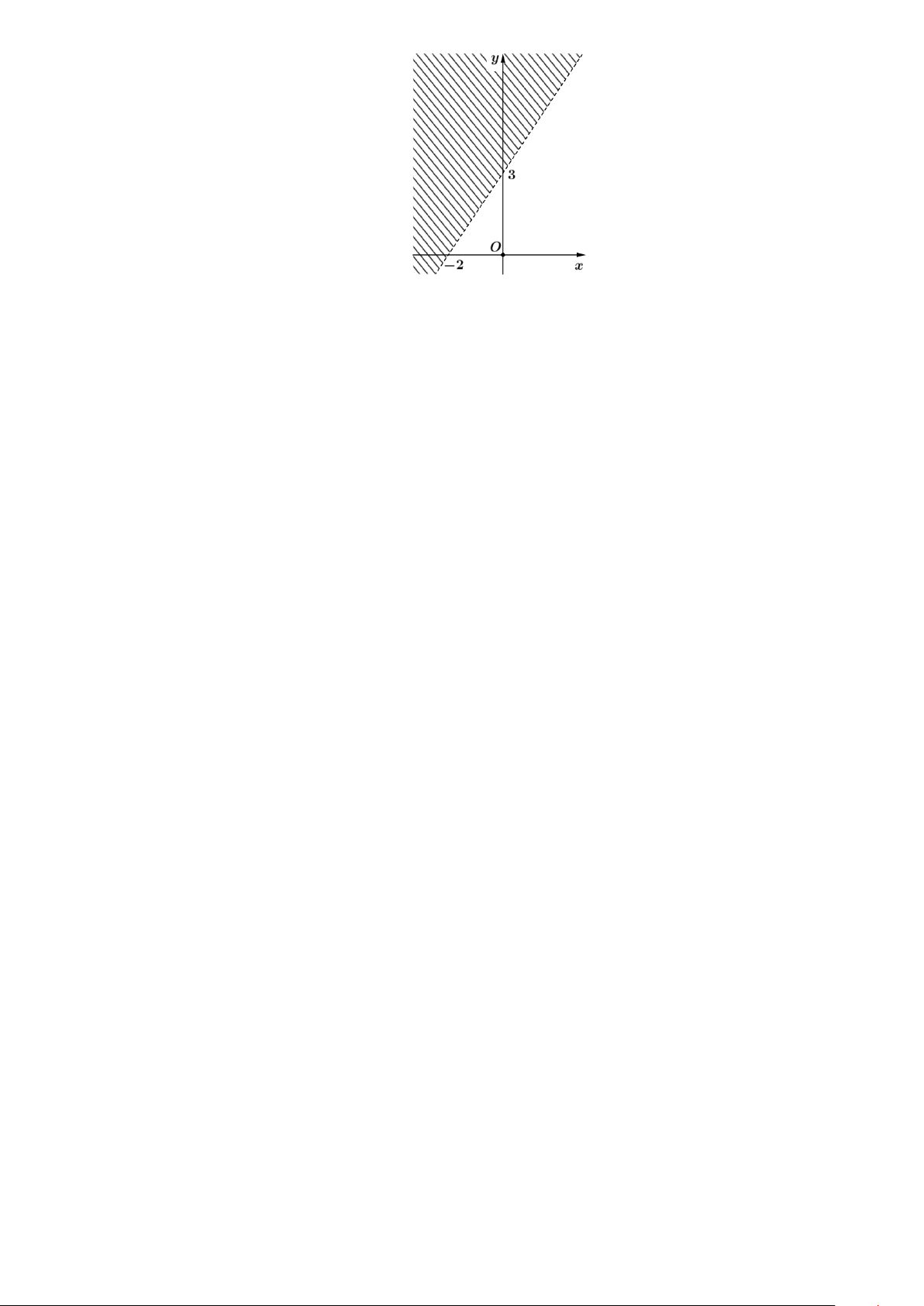
Câu 12. Phần không bị gạch chéo trong hình vẽ bên dưới là miền nghiệm của bất phương trình nào? Trang 15
A. 3x − 2y 6 − .
B. 3x − 2y 6 − .
C. 3x − 2y 0 .
D. 3x − 2y 0 .
PHẦN II. (2,0 điểm) Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý
a), b), c), d) ở mỗi câu, thí sinh chọn đúng (Đ) hoặc sai (S).
Câu 1. Gọi A là tập hợp các học sinh lớp 10 học giỏi môn Toán và B là tập hợp các học sinh lớp 10
học giỏi môn Ngữ Văn. Vậy:
a) A B là tập hợp các học sinh lớp 10 học giỏi môn Toán và học giỏi môn Ngữ Văn.
b) A\ B là tập hợp những học sinh lớp 10 không học giỏi môn Toán nhưng học giỏi môn Ngữ Văn.
c) A B là tập hợp các học sinh lớp 10 học giỏi môn Toán hoặc học giỏi môn Ngữ Văn.
d) B \ A là tập hợp các học sinh lớp 10 học giỏi môn Toán nhưng không học giỏi môn Ngữ Văn.
Câu 2. Hạnh thích ăn hai loại trái cây là cam và xoài, mỗi tuần mẹ cho Hạnh 200000 đồng để mua trái
cây. Biết rằng giá cam là 15000 đồng/ 1 kg, giá xoài là 30000 đồng/1 kg. Gọi , x y( ,
x y 0) lần lượt là
số kilôgam cam và xoài mà Hạnh có thể mua về sử dụng trong một tuần. Các mệnh đề sau đúng hay sai?
a) Trong tuần, số tiền Hạnh có thể mua cam là 15000x , số tiền Hạnh có thể mua xoài là 30000y .
b) Bất phương trình biểu thị số tiền Hạnh có thể mua cam và xoài là 15000x + 30000y 200000( ) 1
c) Cặp số (5;4) là nghiệm của bất phương trình ( ) 1
d) Hạnh có thể mua 4 kg cam, 5 kg xoài trong tuần.
PHẦN III. (2,0 điểm) Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 4.
Câu 1 : Trong các mệnh đề sau, có bao nhiêu câu là mệnh đề đúng?
A: 2 là một số nguyên âm.
B: Lào là một nước thuộc Đông Nam Á. C: Phương trình 2
x + 3x - 4 = 0 có nghiệm kép.
D: Số 2026 chia hết cho 2. x 0 y 0
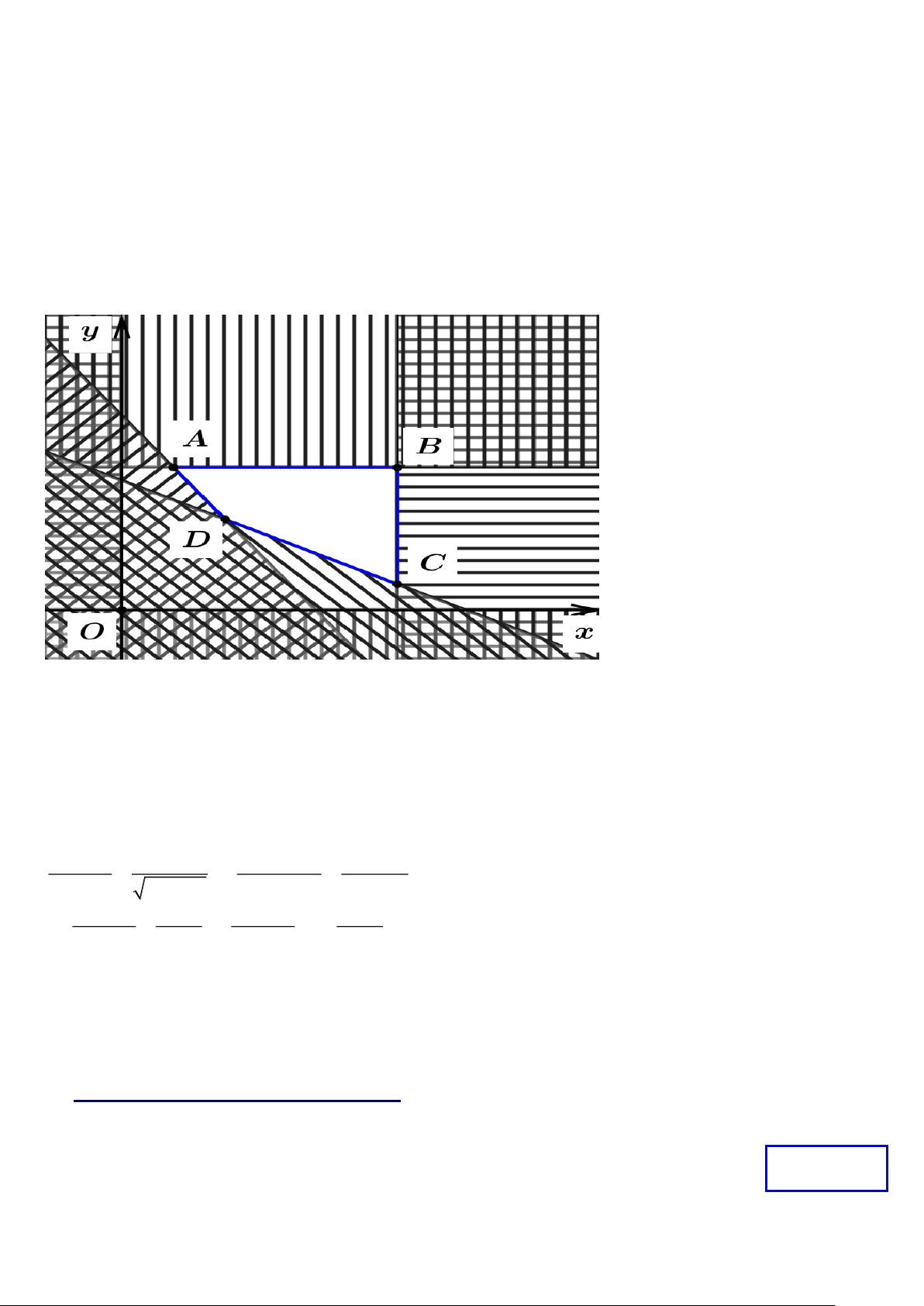
Câu 2. Miền nghiệm của hệ bất phương trình x + y 9 (I ) là miền ngũ giác OABCD ( miền không 3x + y 21 x + 4y 24
bị gạch trong hình vẽ dưới đây) với O(0;0) , A(7;0) , B(6;3) , C (4;5) , D(0;6) . Biết F = 6x + 8y, với
( ;x y)là nghiệm của hệ (I) đạt giá trị lớn nhất tại x = a; y = b. Tính a+2b Trang 16
Câu 3. Tính giá trị 0 cos 60
Câu 4. Lớp 10A có 19 học sinh chỉ thích chơi nhảy dây, 17 học sinh chỉ thích chơi đá cầu và 6 học
sinh vừa thích chơi nhảy dây vừa thích chơi đá cầu. Tìm số học sinh thích chơi ít nhất một trong hai môn thể thao nói trên.
PHẦN IV. (3,0 điểm) Tự luận
Câu 1. Cho góc ( 0 0
0 180 ) thỏa mãn 1
cot = . Tính giá trị biểu thức P = tan + 2026. 2
Câu 2. Cho hai tập hợp A = 2 − ;7) ; B = (1;
9 . Tìm các tập hợp A B , A B . Câu 3
a) Một nhóm học sinh dự định làm dự án vẽ tay 2 loại sản phẩm là bao lỳ xì và tờ lịch năm 2026 để
bán trong một hội chợ Tết năm 2026 do Đoàn trường tổ chức. Biết rằng cả nhóm cần 1 giờ để làm 4
một bao lỳ xì có giá 5 nghìn đồng và 1 giờ để vẽ một tờ lịch có giá 30 nghìn đồng. Nhóm học sinh này
dự định có nhiều nhất 30 giờ để thực hiện dự án và dự kiến sẽ làm được ít nhất được 48 sản phẩm
(gồm cả 2 loại). Hỏi nhóm học sinh đó có thể thu được số tiền nhiều nhất là bao nhiêu nghìn đồng?
b) Cho 2 tập hợp A = (30;4 )
1 , B = (39;50) , biết số học sinh lớp 10A thuộc A B , trong đó có 22 em
học giỏi môn Toán, 20 em học giỏi môn Lý, 23 em học giỏi môn Hóa, 11 em học giỏi cả môn Toán và
môn Lý, 8 em học giỏi cả môn Lý và môn Hóa, 9 em học giỏi cả môn Toán và môn Hóa. Hỏi lớp 10A
có bao nhiêu bạn học giỏi cả ba môn Toán, Lý, Hóa, biết rằng mỗi học sinh trong lớp học giỏi ít nhất
một trong 3 môn Toán, Lý, Hóa? SỞ GD&ĐT CÀ MAU
KIỂM TRA GIỮA KỲ I
TRƯỜNG THPT HỒ THỊ KỶ NĂM HỌC 2025 - 2026
MÔN TOÁN – Khối lớp 10
Thời gian làm bài : 90 phút
(Đề thi có 03 trang)
(không kể thời gian phát đề)
Họ và tên học sinh :..................................................... Số báo danh : ................... Mã đề 1102
I. PHẦN TRẮC NGHIỆM (7,0 điểm)
PHẦN 1. Câu trắc nghiệm nhiều phương án lựa chọn. Học sinh trả lời từ câu 1 đến câu 16. Mỗi câu hỏi học sinh chỉ chọn một
phương án. (4,0 điểm)
Câu 1. Hệ bất phương trình nào dưới đây là hệ bất phương trình bậc nhất hai ẩn? Trang 17 x − y 2 x 0 A. x − y x − y . B. . C. 2 3 . D. 0 . 2 x + y 1 2 2 x + y 1 x + y 1 − 2xy 1
Câu 2. Cho hai tập hợp X = 1;3;5; 8 , Y = 3;5;7;
9 . Tập hợp X Y bằng tập hợp nào sau đây A. 3; 5 . B. 1;3;5;7;8; 9 . C. 1;7; 9 . D. 1;3; 5 .
Câu 3. Cho p là một số tự nhiên. Xét mệnh đề Q : “ Nếu p là số nguyên tố thì p là số vô tỷ”. Mệnh đề nào dưới đây là mệnh
đề đảo của mệnh đề Q ?
A. Nếu p là số vô tỷ thì p là số nguyên tố.
B. Nếu p là số vô tỷ thì p không là số nguyên tố.
C. Nếu p không là số vô tỷ thì p không là số nguyên tố.
D. Nếu p không là số nguyên tố thì p không là số vô tỷ.
Câu 4. Giá trị lượng giác sin (135o ) bằng 3 2 2 1 A. . B. . C. − . D. . 2 2 2 2
Câu 5. Cho tam giác ABC có 0
b = 4,c = 6, A =120 . Độ dài cạnh a bằng A. 2 19 . B. 19 . C. 3 19 . D. 2 7 .
Câu 6. Cho 0º 90º . Mệnh đề nào sau đây là mệnh đề đúng? A. sin (90º − ) = −cos . B. cos(90º − ) = sin . C. cot (90º − ) = −tan . D. tan (90º − ) = −cot .
Câu 7. Bất phương trình nào sau đây là bất phương trình bậc nhất đối với hai ẩn x và y ?
A. 2x − y + 7 0 . B. x − y + z − 5t 0 . C. 2
x − 4x + 2 0 .
D. x − y + z + 5 0 .
Câu 8. Công thức nào sau đây đúng? A. 2 2 2
a = b + c + 2bc cosA . B. 2 2 2
a = b + c − 2b c sinA . C. 2 2 2
a = b + c − 2ac cosA. D. 2 2 2
a = b + c − 2b c cosA .
Câu 9. Trong các câu dưới đây, câu nào là mệnh đề toán học? A. Phương trình 2
x − 2x + 2 = 0 vô nghiệm.
B. Bạn có thích học toán không?
C. Trời hôm nay lạnh quá!
D. Bạn bao nhiêu tuổi?
Câu 10. Tập hợp nào sau đây có đúng hai tập hợp con? A. x; . B. x; y . C. x .
D. x; y; .
Câu 11. Cho tam giác ABC có
AB = 8, AC = 6, BAC = 30 . Khi đó diện tích tam giác ABC bằng A. 24 3 . B. 12. C. 12 3 . D. 24.
Câu 12. Cho bất phương trình x − 2 y + 5 0 có tập nghiệm là S .Mệnh đề nào sau đây là đúng? A. ( 2 − ;4)S . B. ( 2 − ;2)S .
C. (2;2)S . D. (1;3)S . 1 2sin − cos
Câu 13. Cho tan = − . Khi đó giá trị của biểu thức T = 3 4cos . Trang 18 12 7 5 5 A. − B. − C. − . D. 5 4 12 12
Câu 14. Mệnh đề nào sau là mệnh đề sai? A. 2 n
: n = n . B. n
: n 2n . C. 2 x
: x x . D. 2 x : x 0 .
Câu 15. Điểm O (0 ;0) thuộc miền nghiệm của hệ bất phương trình nào sau đây?
x + 3y − 6 0
x + 3y − 6 0
x + 3y − 6 0
x + 3y − 6 0 A. . B. . C. . D. .
2x + y + 4 0
2x + y + 4 0
2x + y + 4 0
2x + y + 4 0 Câu 16. Cho ABC có µ µ B = 45 , C = 30 ,
AC = 2. Độ dài cạnh AB là 1 A. . B. 1+ 3 . C. 2 2 . D. 2 . 2 2
PHẦN 2. Câu trắc nghiệm đúng sai. Học sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, học sinh chọn đúng
hoặc sai. (2,0 điểm)
Câu 1. Cho hai tập hợp A và B, trong đó tập hợp A gồm các số nguyên tố có một chữ số và tập hợp B = 2
x | x − 2x − 3 = 0
a) Các số tự nhiên lẻ có một chữ số đều thuộc tập hợp A .
b) Tập hợp A có 4 phần tử. c) B = 1 − ; 3 .
d) Số phần tử của tập A gấp 4 lần số phần tử của tập hợp B .
Câu 2. Xét tính đúng, sai của các mệnh đề sau: 2x + y 0 a) (2; 3
− )không là một nghiệm của hệ bất phương trình x + y 0 x + 2y 2 x + 3y 0
b) (1;0) không là nghiệm của hệ phương trình y − 2x 0 3
x +3y −1 0 x + 3y 0 c) ( 1
− ;2) là nghiệm của hệ bất phương trình y − 2x 0 3
x +3y −1 0
2x − y 1 d) (2; 3
− )là một nghiệm của hệ bất phương trình x 0 … y„ 0
PHẦN 3. Câu trắc nghiệm trả lời ngắn. Học sinh trả lời từ câu 1 đến câu 2. (1,0 điểm)
Câu 1. Để đo khoảng cách từ A đến B người ta không thể đo trực tiếp được vì phải qua một đầm nuôi cá. Nên người ta xác định được
một điểm C mà từ đó có thể nhìn được A và B dưới một góc 0
60 . Biết CA = 200m , CB =180m. Khoảng cách AB làm
tròn đến hàng đơn vị là bao nhiêu mét?
Câu 2. Để chuẩn bị đồ dùng học tập cho năm học mới, mẹ cho Hoa 100.000 đồng để đi mua dụng cụ học tập. Sau khi lên danh sách
đồ dùng còn thiếu, Hoa quyết định đi mua ít nhất 2 chiếc bút bi và một số vở để ghi chép. Biết giá tiền của một chiếc bút bi là 5.000
đồng và giá tiền một quyển vở là 7.000 đồng. Hỏi bạn Hoa có thể mua tối đa bao nhiêu quyển vở mà vẫn đảm bảo đủ đồ dùng học tập.
II. PHẦN TỰ LUẬN (3,0 điểm)
Câu 1. (1,0 điểm) Cho hai tập hợp A = [ 2
− ;3] và B = (1;+). Hãy xác định và biểu diễn trên trục số các tập hợp sau: A B , B \ ; A A B .
Câu 2. (1,0 điểm) Cho tam giác ABC có ˆ A 45 = , c = 12 và ˆ B 70 =
. Tính số đo góc C, độ dài cạnh a . Trang 19
Câu 3. (1,0 điểm) Trong một cuộc khảo sát người tiêu dùng, trong 100 người uống cà phê được khảo sát, có 55 người thêm đường, 65
người thêm sữa và 30 người thêm cả đường và sữa. Trong số 100 người đó có bao nhiêu người thêm ít nhất đường hoặc sữa?
------ HẾT ------
- Học sinh không được sử dụng tài liệu;
- Giáo viên coi kiểm tra không giải thích gì thêm. ĐÁP ÁN
Câu 1 (1,0 điểm) Cho hai tập hợp A = [ 2
− ;3] và B = (1;+). Hãy xác định và biểu diễn trên trục số các tập
hợp sau: A B , B \ ; A A B . Gợi ý làm bài:
1. Xác định hợp của hai tập hợp: A B = [ 2 − ;3](1;+) = [ 2 − ;+) .
Xác định đúng 0,25. Biểu diễn đúng 0,25
2. Xác định hiệu của hai tập hợp: B ‚ A = (1; +) ‚ [ 2 − ;3] = (3;+ ) .
Xác định đúng 0,25. Biểu diễn đúng 0,25
Câu 2 (1,0 điểm) Cho tam giác ABC có ˆA 45 =
, c =12 và ˆB 70 =
. Tính số đo góc C, độ dài cạnh a . Gợi ý làm bài: 1. Tính góc ˆ C : Trong tam giác ABC, ta có tổng ba góc bằng 180 . ˆ ˆ ˆ C 180
(A B) 180 (45 70) 180 115 65 = − + = − + = − = .(0,25 điểm) a b c
2. Tính độ dài cạnh a (Áp dụng Định lí sin): = = sin A sin B sin C sin A sin 45 0.7071
Tính cạnh a : a = c =12 => a 12
9.36 9 (0,25 điểm) sin C sin 65 0.9063
Câu 3 (1,0 điểm) Trong một cuộc khảo sát người tiêu dùng, trong 100 người uống cà phê được khảo sát, có 55
người thêm đường, 65 người thêm sữa và 30 người thêm cả đường và sữa. Trong số 100 người đó có bao nhiêu
người thêm ít nhất đường hoặc sữa? Gợi ý làm bài:
Kí hiệu U là tập hợp 100 người được khảo sát, A là tập hợp người thêm đường, B là tập hợp người thêm sữa (trong số 100 người đó).
Khi đó tập A B là tập hợp người thêm cả đường và sữa và A B là tập hợp người thêm ít nhất đường hoặc sữa. Sơ đồ Ven:
Theo giả thiết ta có n( A) = 55; n(B) = 65 ; n( A B) = 30 .
Số người thêm ít nhất đường hoặc sữa là
n(A B) = n( )
A + n(B) − n(A B) = 55+ 65− 30 = 90. SỞ GD&ĐT HẢI PHÒNG
ĐỀ KIỂM TRA GIỮA HỌC KỲ I
TRƯỜNG THPT THÁI PHIÊN NĂM HỌC 2025 - 2026 MÔN THI: TOÁN 10
(Đề thi có 04 trang)
Thời gian làm bài: 90 phút, không kể thời gian phát đề Mã đề: 2356
Họ tên thí sinh: ................................................................. Trang 20