Bộ 10 Đề Kiểm Tra Giữa Kỳ 2 Toán 9 Cấu Trúc Mới 2025-2026 Có Đáp Án Ma Trận Đặc Tả
Chu vi một mảnh vườn hình chữ nhật là 30m. Biết chiều dài hơn chiều rộng 5 m. Tính diện tích hình chữ nhật. Số học sinh của một trường sau 2 năm tăng từ 500 lên 720 học sinh. Vậy, trung bình hàng năm, số học sinh trường đó tăng lên bao nhiêu phần trăm? Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem!
Chủ đề: Đề giữa HK2 Toán 9 187 tài liệu
Môn: Toán 9 2.6 K tài liệu
Tác giả:
Preview text:
ĐỀ 1
ĐỀ KIỂM TRA GIỮA HỌC KỲ II MÔN:TOÁN - LỚP 9
NĂM HỌC: 2025 – 2026
Thời gian làm bài: 90 phút
A. Trắc nghiệm (7 điểm)
I. Trắc nghiệm nhiều lựa chọn (5 điểm) 2
Câu 1_ NB_ Điểm nào sau đây thuộc đồ thị hàm số y = −2x ? A. (−1; 2) . B. (1;2) .
C. (−1; −2) . D. (2; −1) .
Câu 2_ NB_ Đồ thị của hình bên dưới là đồ thị của hàm số nào trong các hàm số sau? 1 1 2 2 2 y = x y = x 2
A. y = 4x . B. 2 . C. 4
. D. y = 2x . 2
Câu 3_TH_ Toạ độ giao điểm của đường thẳng y = x - 2 và parabol y = - x là
A. (1;- 1) và (2;- 4) .
B. (1;1) và (- 2; 4) .
C. (- 1;- 1) và (2;- 4) .
D. (1;- 1) và (- 2;- 4) .
Câu 4_NB_Phương trình nào dưới đây là phương trình bậc hai một ẩn? 1 A. 2
3x − 2 x +1 = 0 . B. 2 2x − 2022 = 0 .
C. 3x + − 5 = 0 .
D. 4x −1 = 0 . x
Câu 5. _NB_Khẳng định nào sau đây sai? A. 2
x − 4x − 3 = 0 trong đó: a = 1;b = −4;c = −3. B. 2
4x − 2x +1 = 0 trong đó: a = 4;b = − 2;c =1. C. 2
x − 4x + 5 = 0 trong đó: a = 1;b = −4;c = −3. D. 2 2
5x − m = 1 5x − m −1 = 0 trong đó: a = 5;b = 0;c = −m −1.
Câu 6._VD_Một tam giác vuông có một cạnh góc vuông bằng 2cm , chu vi bằng 10cm . Cạnh góc vuông còn lại bằng A. 2, 4 cm . B. 3, 75cm . C. 1cm . D. 3cm .
Câu 7_NB_ Cho phương trình 2
ax + bx + c = 0 (a 0) có hai nghiệm x , x . Chọn phát biểu đúng 1 2 b b b b x + x = − x + x = x + x = x + x = 1 2 1 2 1 2 1 2 A. a a a a B. . C. . D. . c c c c x .x = x .x = − x .x = x .x = − 1 2 a 1 2 a 1 2 a 1 2 a
Câu 8 _TH_ Gọi x , x là nghiệm của phương trình 2
x − 5x + 2 = 0 . Không giải phương trình, tính 1 2 giá trị của biểu thức 2 2
A = x + x . 1 2 A. 20 . B. 21 . C. 22 . D. 23 .
Câu 9 _VD_ Biết rằng phương trình 2
x − (2a −1)x − 4a − 3 = 0 luôn có hai nghiệm x , x với mọi 1 2
a . Tìm hệ thức liên hệ giữa hai nghiệm không phụ thuộc a .
A. 2( x + x − x x = 5 .
B. 2( x + x + x x = −5. 1 2 ) 1 2 ) 1 2 1 2
C. 2( x + x + x x = 5.
D. 2( x + x − x x = 5 − . 1 2 ) 1 2 ) 1 2 1 2
Câu 10_TH_ Chu vi một mảnh vườn hình chữ nhật là 30 m . Biết chiều dài hơn chiều rộng 5 m .
Tính diện tích hình chữ nhật. A.100 2 m . B. 70 2 m . C. 50 2 m . D. 55 2 m . Trang 1
Câu 11_VD_ Số học sinh của một trường sau 2 năm tăng từ 500 lên 720 học sinh. Vậy, trung bình
hàng năm, số học sinh trường đó tăng lên bao nhiêu phần trăm? A. 10% . B. 15% . C. 20% . D. 25% .
Câu 12_NB_Góc nội tiếp là
A. góc có đỉnh nằm trên đường tròn.
B. góc có đỉnh trùng với tâm của đường tròn.
C. góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó.
D. góc có hai cạnh chứa hai dây cung của đường tròn đó.
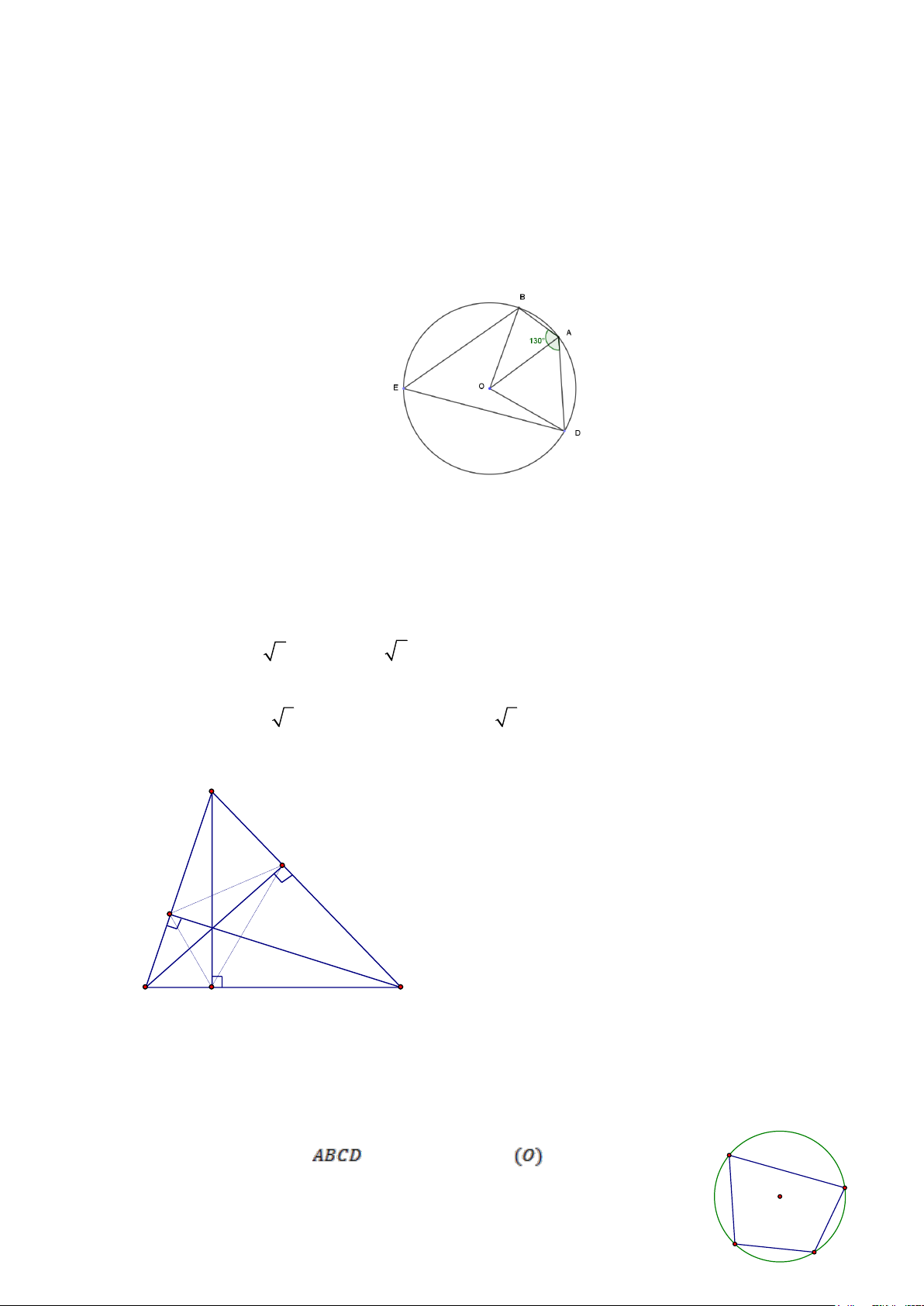
Câu 13_TH_ Cho đường tròn ( )
O và góc nội tiếp 0
BAD = 130 như hình vẽ. E là một điểm thuộc
cung lớn CD . Số đo của BED bằng A. 0 130 . B. 0 100 . C. 0 260 . D. 0 50 .
Câu 14_NB_Đường tròn ngoại tiếp đa giác là đường tròn
A. Tiếp xúc với tất cả các cạnh của đa giác đó.
B. Đi qua tất cả các đỉnh của đa giác đó.
C. Cắt tất cả các cạnh của đa giác đó.
D. Đi qua tâm của đa giác đó.
Câu 15 TH_ Đường tròn ngoại tiếp hình vuông cạnh bằng 2 có bán kính là
A. 1. B. 2 . C. 2 . D. 2 2 . (O;2cm)
Câu 16 VD_ Tính diện tích tam giác đều nội tiếp đường tròn 2 2 2 2 A. 6 cm .
B. 6 3 cm . C. 3cm . D. 3 3 cm .
Câu 17_NB_Cho hình vẽ sau: B P N Q C A M
Số tứ giác nội tiếp được trong đường tròn là:
A. Có 3 hình tứ giác nội tiếp.
B. Có 4 hình tứ giác nội tiếp.
C. Có 5 hình tứ giác nội tiếp.
D. Có 6 hình tứ giác nội tiếp. A
Câu 18_VD_Cho tứ giác nội tiếp đường tròn . Biết 0 0
ADO = 50 ;OCD = 40 B
. Khi đó số đo ABC là: 0 0 0 0 O
A. 40 . B. 50 . C. 90 . D. 10 . D Trang 2 C 0
Câu 19_VDC_Cho ABC cân tại ;
A B = 40 điểm D thuộc cạnh AB . Đường vuông góc với AB tại
D cắt BC tại E và cắt đường thẳng vuông góc với AC tại C ở K . Gọi I là trung điểm của BE .
Khi đó số đo IAK là: 0 0 0 0 A. 40 . B. 50 . C. 90 . D. 60 .
Câu 20 NB Đa giác đều là một đa giác lồi có
A. Các cạnh bằng nhau.
B. Các góc bằng nhau.
C. Các cạnh bằng nhau và các góc khác nhau.
D. Các cạnh bằng nhau và các góc bằng nhau.
II. Trắc nghiệm đúng sai (2 điểm)
Câu 21: Cho phương trình 2 x + (m + ) 2 2
1 x + m = 0 ( m là tham số).
A. Với m = −1 phương trình vô nghiệm
B. Khi phương trình có hai nghiệm x ; x thì x + x = 2 m + 1 1 2 ( ) 1 2 1 −
C. để phương trình có nghiệm thì m . 2
D. Có 2 giá trị của m để phương trình có hai nghiệm x ; x thỏa mãn 2 3
x + x = 4 1 2 1 2 (O)
Câu 22. Cho tam giác ABC cân tại A , nội tiếp đường tròn
. Đường cao AH cắt đường tròn ở
D . Cho BC = 24cm, AC = 20cm (O)
A. AD là đường kính của đường tròn . .
B. Góc ACD là góc nhọn. C. AH = 16 cm (O)
D. Bán kính đường tròn bằng 25cm A O H B C D B. Tự luận
Câu 23 (1 điểm). Cho parabol (P): 2
y = x và đường thẳng (d): y = 2x − 3m +1.
A. Cho hai điểm A và B thuộc (P) có hoành độ lần lượt là 3
− và 9 . Tìm toạ độ hai điểm A và B.
B. Tìm các giá trị của m để (P) và (d ) cắt nhau tại hai điểm có hoành độ x , x thỏa mãn điều kiện 1 2 2 2
x + x = 10 1 2
Câu 24 (2 điểm). Cho đường tròn tâm (O) đường kính AB, điểm C cố định trên đoạn thẳng OB
( C khác O và B ). Điểm M chuyển động trên đường tròn. Đường vuông góc với AB tại C cắt M ,
A MB theo thứ tự ở E và F.
A. Chứng minh tứ giác BCME nội tiếp.
B. Tia AF cắt EB tại N. Chứng minh BF.BM = BE.NE không đổi.
C. Chứng minh đường tròn ngoại tiếp tam giác AEF luôn đi qua một điểm cố định khác điểm . A
ĐÁP ÁN VÀ LỜI GIẢI Trang 3 A. TRẮC NGHIỆM
I. Trắc nghiệm nhiều lựa chọn
(5 điểm) (mỗi câu đúng 0,25 điểm) Câu 1 2 3 4 5 6 7 8 9 10 Đáp C D D B C B A B B C án Câu 11 12 13 14 15 16 17 18 19 20 Đáp C C D B C D D C B D án Thang Câu Đáp án điểm
II. Trắc nghiệm Đúng / Sai (2 điểm)
Cho phương trình x 2 + (m + )x + m 2 2 1
= 0 (m là tham số).
A. Với m = −1 phương trình vô nghiệm
B. Khi phương trình có hai nghiệm x ; x thì x + x = 2 m + 1 1 2 ( ) 1 2 Câu 21 1 −
C. để phương trình có nghiệm thì m . 2
D. Có 2 giá trị của m để phương trình có hai nghiệm x ; x thỏa mãn 1 2 2 3
x + x = 4 1 2 A
Với m = −1 thì ta có PT: 2 x + 1 = 0 . phương trình 2
x + 1 = 0 vô nghiệm nên A đúng
Khi phương trình có hai nghiệm x ; x , Theo định lý Viet thì B 1 2 x + x = 2
− m + 1 nên B sai 1 2 ( ) 2
Phương trình có nghiệm khi ' = (m + ) − m 2 1 0 Chính xác C −1 01 ý: 0,1 m 2 + 1 0 m
. Nên C đúng. 2 điểm, chính xác 02 ý: −
Phương trình có hai nghiệm x , x khi m 1 .Theo Vi-ét ta có 1 2 0,25 điểm, 2 chính xác x + x = − ( 2 m + ) 1 1 2 03 ý: 0,5 x x = m2 1 2 điểm, chính Khi đó xác cả 04 ý: 2 2 1,0 điểm) x + x = 4 nên D 1 2 2
(x + x − 2x x = 4 1 2 ) 1 2 2 4 (m + 1) 2 − 2m = 4 2 2m + 8m = 0
Suy ra m = 0 ( C) hoặc m = −4 ( KTM)
Vậy chỉ có 1 giá trị của m để phương trình có hai nghiệm x ; x thỏa mãn 1 2 2 3
x + x = 4 nên D sai 1 2 Câu 22
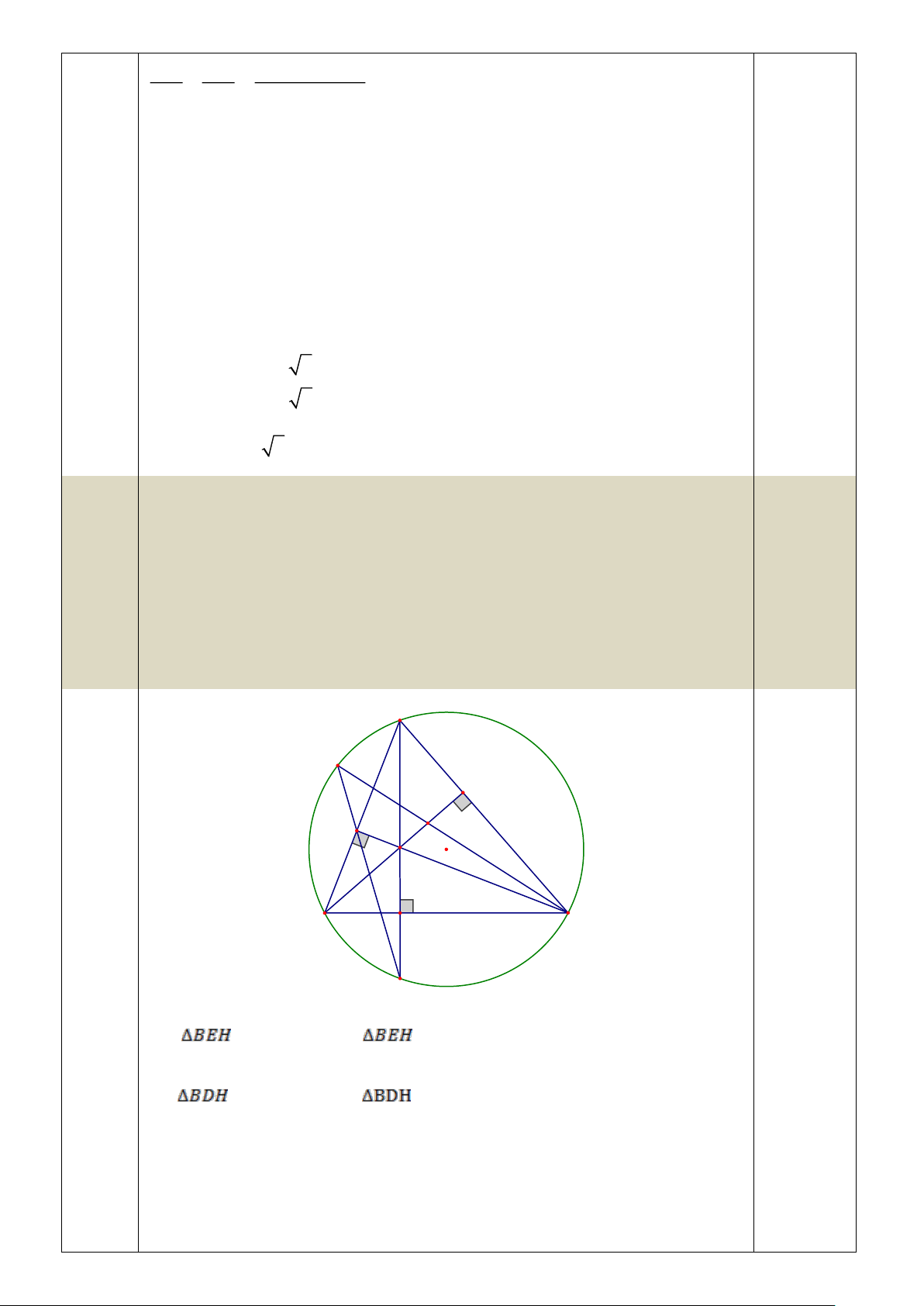
Câu 22. Cho tam giác ABC cân tại A , nội tiếp đường tròn(O) . Đường cao Trang 4
AH cắt đường tròn ở D
A. AD là đường kính của đường tròn (O) . Cho BC = 24cm, AC = 20cm .
B. Góc ACD là góc nhọn. C. AH = 16 cm
D. Bán kính đường tròn (O) bằng 25cm A O H B C D
ABC cân tại A nên AH là đường cao, cũng là đường trung trực của BC
Mà tam giác ABC cân tại A , nội tiếp đường tròn (O) nên O AH A
Mặt khác đường cao AH cắt đường tròn ở D
suy ra AD là đường kính của đường tròn nên A Đúng Chính xác 01 ý: 0,1 B điểm, chính
Vì AD là đường kính của đường tròn (O) nên ACD = 90 nên B sai. xác 02 ý:
Xét ABC cân tại A có AH ⊥ BC 0,25 điểm, 1 = = chính xác HC BC 12(cm) C 2 03 ý: 0,5 AC = 20cm điểm, chính Nên 2 2 2 2
AH = AC − HC = 20 −12 = 400 −144 = 256 = 16cm nên C xác cả 04 ý: 1,0 điểm) đúng. AH AC 2 2 AC 20
Vì AHC ∽ACD nên = hay AD = = = 25 D AC AD AH 16 25
Suy ra bán kính của đường tròn (O) là = 12,5 nên D sai 2
B. TỰ LUẬN ( 3 điểm) Câu 23 Vì ,
A B (P) và có hoành độ lần lượt bằng −3;9 nên 0,5 A
A(−3;9) ; B(9;81) .
Phương trình hoành độ giao điểm của (P) và (d) là: 0,25 2
x = 2x − 3m +1 2
x − 2x + 3m −1 = 0 B Ta có: = (− )2 1 − (3m − )
1 = 1− 3m +1 = 2 − 3m .
Để phương trinh có nghiệm x ; x thì 1 2 Trang 5 0 2 − 3m 0 2 m 3 x + x = 2 Theo hệ thức viet ta có: 1 2 (3)
x .x = 3m −1 1 2 Theo bài ra ta có: 2 2 x + x = 10 1 2
(x + x )2 − 2x x =10(4) 0,25 1 2 1 2
Thay (3) vào (4) ta được: 2 2 − 2(3m − ) 1 = 10 4 − 6m + 2 = 10 6m = 4 − 2 − m = (tm). 3 Câu 24 0,75 A
Chứng minh tứ giác BCME nội tiếp. - Ta có BMA = 0
90 ( Góc nội tiếp chắn nửa đường tròn) suy ra BME = 0 90 ( kề bù)
Ta có EC ⊥ A B suy raBCE = 0 90
Xét tứ giác BCME ta có BME = BCE = 0
90 suy ra tứ giác BCME nội tiếp
( Đỉnh M ,C cùng nhìn BE góc bằng nhau)
Chứng minh: BF.BM = BE.NE 0,75
- Xét ABE ta có F là trực tâm suy raEB ⊥ A N B B NF B
ME (g.g) BF BE = BN BM
BF.BM = BN.BE (1). Trang 6 B CF B
MA(g.g) BF BC = BA BM
BF.BM = BC.BA (2).
Mà BC, BA cố định suy ra BC.BA không đổi (3)
- Từ (1),(2),(3) suy ra (đpcm)
Chứng minh đường tròn ngoại tiếp tam giác AEF luôn đi qua qua một điểm 0,5 cố định khác điểm .
A Gọi K là giao điểm của đường tròn ngoại tiếp AEF với cạnh .
AB Ta có BFC = BA M (cùng phụ với B ) (4). - Ta có 4 điểm ,
A K, E, F cùng thuộc đường tròn ngoại tiếp AEF suy ra
KFC = BA M (cùng bù với EFK góc ngoài đỉnh đối tứ giác nội tiếp) (5). C
Từ (4), (5) suy ra KFC = BFC
- Xét BFK ta có KFC = BFC suy ra FC là phân giác , mà FC ⊥ A B
nên BFK cân tại F suy ra FC là trung trực của KC.
- Vì FC là trung trực BC = CK. Do B,C cố định, nên K là điểm cố định.
Vậy đường tròn ngoại tiếp tam giác AEF luôn đi qua điểm K cố định khác . A
KHUNG MA TRẬN ĐỀ KIỂM TRA GIỮA KỲ II MÔN TOÁN 9 CẤP THCS
Mức độ đánh giá
Trắc nghiệm khách quan Chủ Nội dung/Đơn vị Tự luận TT
Nhiều lựa chọn Đúng/Sai đề/Chương kiến thức Vận Vận Biết Hiểu Biết Hiểu Biết Hiểu dụng dụng TN 1 TN3 TL 23A Hàm số TN 2 2 Chủ đề 1
y = ax (a 0) Hàm số 2 y = ax Phương trình TN 4 TN TN TN 1
(a 0). bậc hai một ẩn TN 5 TN 6 21A 21B 21C Phương
trình bậc hai Hệ thức Viète TN 7 TN 8 TN 9 TN một ẩn 21D Giải bải toán TN 10 TN 11 bằng cách lập phương trình Góc ở tâm, góc TN 12 TN TN Chủ đề 2 nội tiếp 13 22B Đường tròn Đường tròn nội TN 14 TN 15 TN 16 TN TN 2 ngoại tiêp
tiếp, đường tròn 22A 22C và đường ngoại tiếp TN tròn nội tiếp 22D Trang 7
Tứ giác nội tiếp TN 17 TN 18 TL 24A TN 19 Đa giác đều TN 20 Tổng số câu 9 5 6 2 2 4 2 Tổng số điểm 5 2 3 Tỷ lệ % 50% 20% 30%
KHUNG BẢN ĐẶC TẢ ĐỀ KIỂM TRA GIỮA KÌ II MÔN TOÁN 9 CẤP THCS
Số câu hỏi/ý hỏi ở các mức độ đánh giá
Trắc nghiệm khách quan Chủ Nội dung/Đơn TT
Yêu cầu cần đạt
đề/Chương vị kiến thức Nhiều lựa chọn Đúng/Sai Vận Biết Hiểu Biết Hiểu dụng Hàm số
- Biết: Nhận biết hàm 2 y = ax số 2
y = ax (a 0) . (a 0) TN1
- Hiểu: Thiết lập được TN3 bảng giá trị của hàm TN2
số . Tìm tọa độ điểm - Vận dụng: Phương trình
- Biết: Phương trình
bậc hai một ẩn bậc hai TN4 - Hiểu: TN5 TN6 TN21A - Vận dụng: Tìm Chủ đề 1. nghiệm của phương Hàm số trình bậc hai 2 y = ax Hệ thức Viète
- Biết: Hệ thức Viète 1 (a 0). - Hiểu: Cách tính Phương tổng, hiệu hai nghiệm trình bậc của pt bậc hai hai một ẩn - Vận dụng: Giải
được phương trình bậc hai một ẩn. TN7 TN 8 TN 9 TN21B
– Ứng dụng được định lí Viète vào tính nhẩm nghiệm của phương trình bậc hai, tìm hai số biết tổng và tích của chúng, ... Giải bải toán - Biết: TN 10 TN 11 bằng cách lập Trang 8 phương trình
- Hiểu: lập được phương trình.
- Vận dụng: Bài toán thực tế Góc nội tiếp
Biết : nhận biết góc với đường tròn TN 12 TN 13 TN22B
Hiểu : Tính số đo góc
Đường tròn nội Biết : Đường tròn nội tiếp, đường
tiếp, đường tròn ngoại
tròn ngoại tiếp tiếp đa giác
Hiểu Tính bán kính Chủ đề 2. của đường tròn TN 14 TN 15 TN 16 TN22A Đường tròn
Vận dụng Tính diện 2 ngoại tiêp tích đa giác nội tiếp, và đường
ngoại tiếp đường tròn. tròn nội Điểm cố định, tính tiếp không đổi. Tứ giác nội
- Biết: nhận biết tứ tiếp giác nội tiếp
- Hiểu: chứng minh tứ TN 18 giác nội tiếp TN 17 TN 19
- Vận dụng: Tính số đo góc. Chứng minh hệ thức hình học Đa giác đều
Biết nhận biết đa giác TN 20 đều Tổng số câu 9 5 6 2 2 Tổng số điểm 5 2 Tỷ lệ % 50% 20% ĐỀ 2
ĐỀ KIỂM TRA GIỮA HỌC KỲ II MÔN:TOÁN - LỚP 9
NĂM HỌC: 2024 – 2025
Thời gian làm bài: 90 phút
Phần 1. Câu hỏi trắc nghiệm nhiều lựa chọn (5 điểm)
Em hãy khoanh tròn vào phương án đúng nhất.
Câu 1 (NB): Đồ thị hàm số là đồ thị: A. nhận trục làm trục đối xứng B. nhận trục làm trục đối xứng
C. không có trục đối xứng D. nhận hai trục và làm trục đối xứng
Câu 2 (NB): Điểm đối xứng với điểm qua trục là: A. B. C. D. Trang 9
Câu 3 (TH): Điểm nào sau đây thuộc hàm số A. B. C. D.
Câu 4 (NB): Trong các phương trình sau, phương trình nào là phương trình bậc hai một ẩn A. B. C. D.
Câu 5 (NB): Phương trình bậc hai một ẩn có 2 nghiệm phân biệt khi: A. B. C. D.
Câu 6 (TH): Nghiệm của phương trình là A. B. C. D.
Câu 7 (VD): Tìm để phương trình
có nghiệm kép và tính nghiệm kép với vừa tìm được. A. và B. và C. và D. và
Câu 8 (NB): Tổng hai nghiệm của phương trình là: A. B. C. D.
Câu 9 (TH): Lập phương trình bậc hai có hai nghiệm là 3 và A. B. C. D.
Câu 10 (VD): Tìm để phương trình có hai nghiệm thỏa mãn A. B. C. D.
Câu 11 (TH): Một mảnh đất hình chữ nhật có độ dài đường chéo là 13 m, chiều dài hơn chiều rộng là 7m.
Nếu gọi chiều rộng của mạnh đất là (m) với x > 0. Khi đó, chiều dài của mảnh đất hình chữ nhật tính theo là: A. (m) B. (m) C. (m) D. (m)
Câu 12 (NB): Góc nội tiếp chắn nửa đường tròn bằng bao nhiêu độ? A. 45 B. 90 C. 60 D. 120 C
Câu 13 (TH): Cho hình vẽ bên biết COA = 64 . Số đo CBA bằng A. 64 B. 32 A B O C. 128 D. 116
Câu 14 (TH): Tam giác đều ABC nội tiếp đường tròn (O), khi đó số đo cung BC lớn là A. 60 B. 120 C. 240 D. 270
Câu 15 (VD): Cho tam giác vuông tại , có và . Tính bán kính đường
tròn ngoại tiếp tam giác A. B. C. D. Trang 10
Câu 16 (NB): Trong các tứ giác sau, tứ giá c nào nội tiếp được đường tròn? A. Hình bình hành. B. Hình chữ nhật. C. Hình thang. D. Hình thang vuông.
Câu 17 (NB): Trong một tứ giác nội tiếp, tổng số đo 2 góc đối nhau bằng A. B. C. D.
Câu 18 (VD): Người ta muốn dựng một khung cồng hình chữ nhật cao 2m, rộng 3m, bên ngoài khung
cổng được bao bởi một khung thép dạng nửa đường tròn (như hình vẽ). Chiều dài của đoạn thép làm kung
nửa đường tròn đó là A. B. C. D.
Câu 19 (NB): Đa giác đều là một đa giác
A. Có 3 cạnh và 3 góc bằng nhau
B. Có 7 cạnh và 7 góc bằng nhau
C. Có các cạnh và các góc bằng nhau
D. Có 8 cạnh và 8 góc bằng nhau
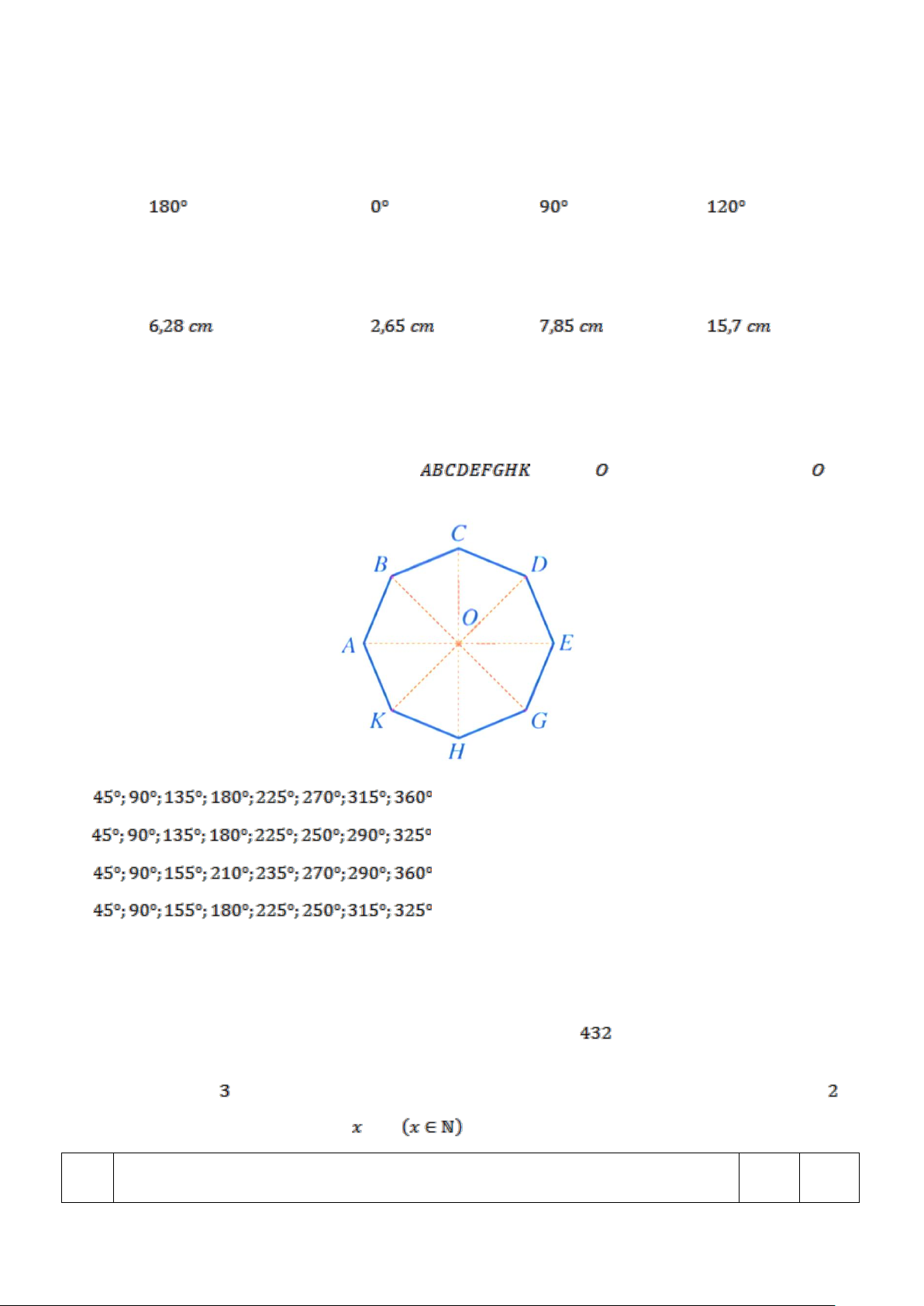
Câu 20 (TH): Cho hình đa giác đều có 8 cạnh
với tâm . Chỉ ra các phép quay tâm giữ
nguyên hình đa giác đều đã cho A. B. C. D.
Phần 2. Câu hỏi trắc nghiệm Đúng – Sai (2 điểm)
Em hãy đánh dấu vào ô trống ứng với mỗi khẳng dịnh sau.
Câu 21: Trong dịp kỉ niệm 75 năm chiến thắng Điện Biên Phủ có
học sinh được điều về thăm quan
diễu hành, người ta tính nếu dùng loại xe lớn chuyên chở một lượt hết số học sinh thì phải điều động ít hơn
dùng loại xe nhỏ là chiếc. Biết rằng mỗi ghế ngồi một học sinh và mỗi xe lớn nhiều hơn xe nhỏ là chỗ
ngồi. Gọi số xe lớn được huy động là (xe)
. Xét tính đúng-sai của các khẳng định sau. STT Khẳng định Đúng Sai Trang 11 1
Số xe nhỏ được huy động là (xe) . 2
Mỗi xe nhỏ có số ghế ngồi là ghế .
Mỗi xe lớn nhiều hơn xe nhỏ là chỗ ngồi nên ta biến đổi được về phương trình 3 . 4 Cần huy động xe lớn .
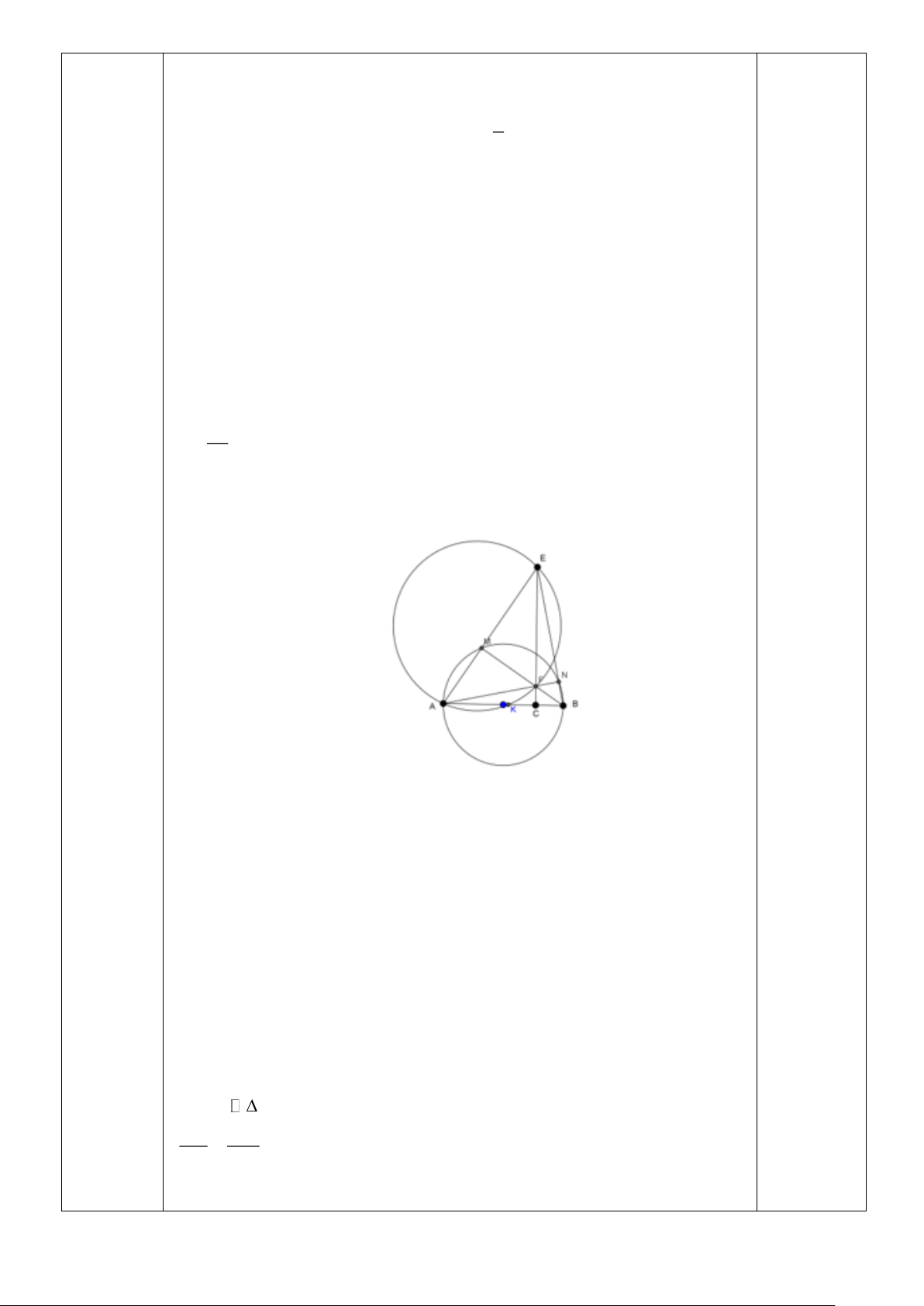
Câu 22: Cho tam giác nhọn ABC. Đường tròn (O) đường kính BC cắt AB
và AC theo thứ tự tại D và E. Gọi H là giao điểm của BE và CD, tia AH A
cắt BC tại F (Như hình vẽ). Xét tính đúng-sai của các khẳng định sau: E STT Khẳng định Đúng Sai D H 1
Tứ giác BDEC không nội tiếp đường tròn.
4 điểm A, D, H, E cùng thuộc 1 đường B C 2 F O tròn. 3
Có 4 tứ giác nội tiếp trong hình. 4 .
Phần 3. Tự luận (3 điểm) Câu 23. (1,5 điểm)
a) Giải phương trình: 2
2x − 3x − 5 = 0 b) Cho phương trình 2 2
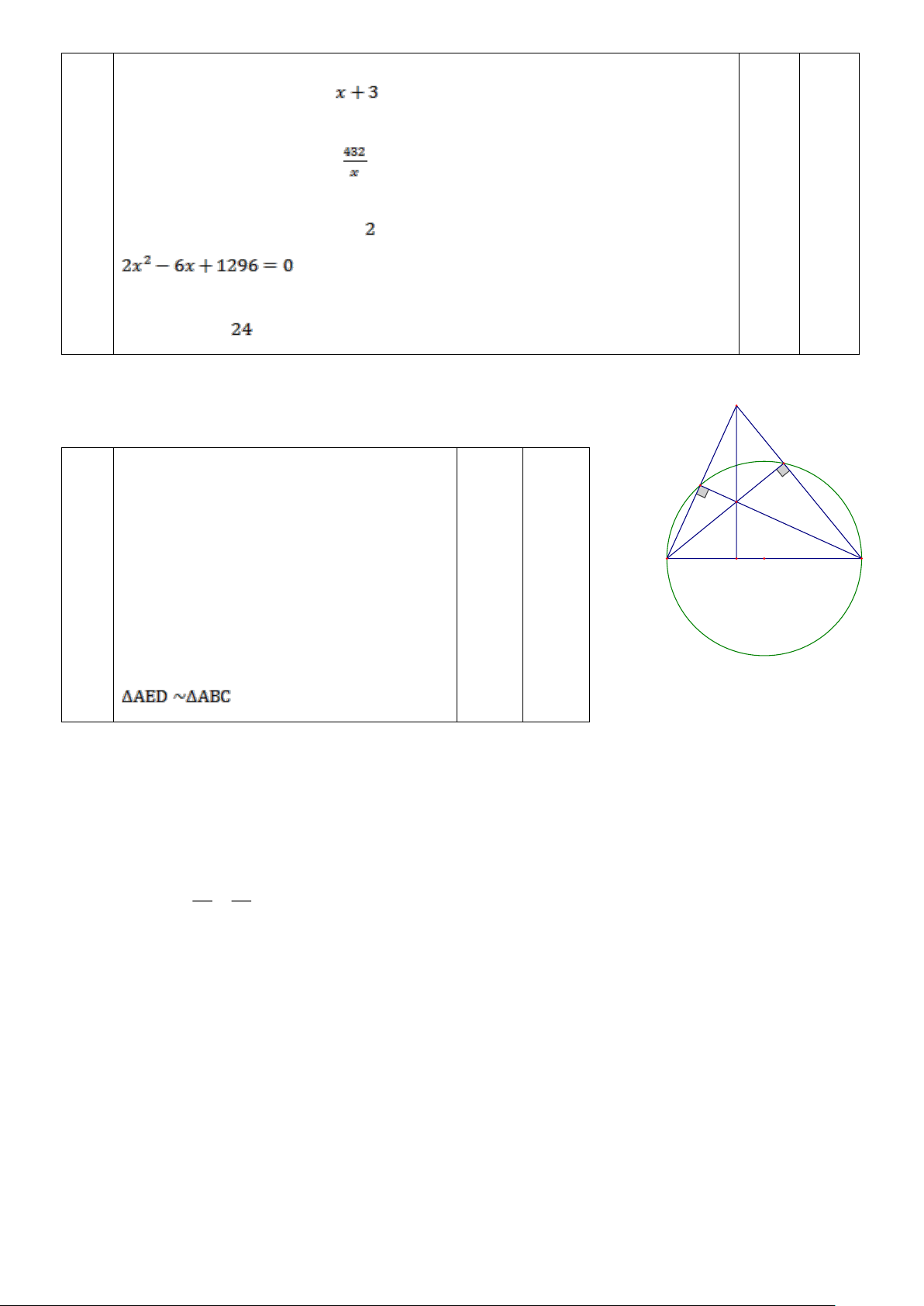
x − 2(m −1)x + m = 0 (*). Tìm m để phương trình có hai nghiệm phân biệt 2 2 x x
x ; x thỏa mãn: 1 2 + = 5(x + x . 2 1 ) 1 2 x x 2 1
Câu 24. (1,5 điểm) Cho ABC có ba góc nhọn nội tiếp đường tròn (O; R) . Các đường cao AD , BF ,
CE của ABC cắt nhau tại H .
a. Chứng minh tứ giác BEHD nội tiếp một đường tròn.
b. Kéo dài AD cắt đường tròn (O) tại điểm thứ hai K . Kéo dài KE cắt đường tròn (O) tại điểm
thứ hai I . Gọi N là giao điểm của CI và EF . Chứng minh 2
CE = CN.CI . Trang 12
ĐÁP ÁN VÀ HƯỚNG DẪN CHẤM
Phần 1. Câu hỏi trắc nghiệm nhiều lựa chọn (5 điểm) 1. B 2. A 3. D 4. B 5.C 6. C 7. D 8. A 9. B 10. A 11. A 12. B 13. B 14. C 15. D 16. B 17. A 18. C 19. C 20. A
Phần 2. Câu hỏi trắc nghiệm Đúng – Sai (2 điểm)
Câu 21. 1 – Đúng; 2 – Sai; 3 – Sai; 4 – Đúng.
Trong dịp kỉ niệm 75 năm chiến thắng Điện Biên Phủ có
học sinh được điều về thăm quan diễu hành,
người ta tính nếu dùng loại xe lớn chuyên chở một lượt hết số học sinh thì phải điều động ít hơn dùng loại
xe nhỏ là chiếc. Biết rằng mỗi ghế ngồi một học sinh và mỗi xe lớn nhiều hơn xe nhỏ là chỗ ngồi. Gọi
số xe lớn được huy động là (xe) .
a) Khẳng định đã cho là khẳng định đúng.
Số xe nhỏ được huy động là (xe)
b) Khẳng định đã cho là khẳng định sai.
Mỗi xe lớn có số ghế ngồi là ghế
Mỗi xe nhỏ có số ghế ngồi là ghế
c) Khẳng định đã cho là khẳng định sai. ta có phương trình
d) Khẳng định đã cho là khẳng định đúng.
Giải phương trình ta tìm được hoặc (Loại) Vậy cần huy động xe lớn.
Câu 22: 1 – Sai; 2 – Đúng; 3 – Sai; 4 – Đúng
Cho tam giác nhọn ABC. Đường tròn (O) đường kính BC cắt AB và AC
theo thứ tự tại D và E. Gọi H là giao điểm của BE và CD, tia AH cắt BC A tại F (Như hình vẽ)
1. Khẳng định đã cho là khẳng định Sai. Vì 4 điểm B, C, D, E đều nằm E
trên đường tròn (O) nên tứ giác BCED nội tiếp D
2. Khẳng định đã cho là khẳng định đúng. H Vì
vuông tại D nên nội tiếp đường tròn đường tròn đường B C F O kính AH. Trang 13 Vì
vuông tại E nên nội tiếp đường tròn đường tròn đường kính AH.
Do đó 4 điểm A, D, H, E cùng thuộc 1 đường tròn.
3. Khẳng định đã cho là khẳng định Sai.
Có 6 tứ giác nội tiếp: ADHE, BDHF, CEHF, BDEC, AEFB, ADFC.
4. Khẳng định đã cho là khẳng định đúng.
Vì tứ giác BDEC nội tiếp (O) nên: Mà (Hai góc kề bù) Nên . Từ đó suy ra (g.g)
Phần 3. Tự luận (3 điểm) Thang Câu
Đáp án – Hướng dẫn điểm a) Giải phương trình: 2
2x − 3x − 5 = 0 b) Cho phương trình 2 2
x − 2(m −1)x + m = 0 (*). Tìm m để phương trình có 23 1,5 2 2 x x
hai nghiệm phân biệt x ; x thỏa mãn: 1 2 + = 5(x + x . 2 1 ) 1 2 x x 2 1 Ta có: 2
2x − 3x − 5 = 0 2
2x + 2x − 5x − 5 = 0 0,25 2x ( x + ) 1 − 5( x + ) 1 = 0 (x + ) 1 (2x − 5) = 0 a
x + 1 = 0 Hoặc 2x − 5 = 0 5
x = −1 Hoặc x = 2 0,25 5
Vậy x = −1 và x = là các nghiệm của phương trình. 2 Ta có: = − (m − ) 2 2 ' 1 − m 2 2
= m − 2m +1− m =1− 2m 0,25 1
Phương trình có hai nghiệm phân biệt x , x ' 0 1− 2m 0 m 1 2 2
x + x = 2 m −1 1 2 ( ) b Theo vi-ét ta có: 2 x x = m 1 2 0,25 2 2 x x x 0 Theo đề bài ta có: 1 2 +
= 5(x + x ( ĐK 1
x x 0 m 0) 2 1 ) 0,25 x x 1 2 x 0 2 1 2 Trang 14 3 3 x x 5 x + x x x 1 2 ( 2 1) 1 2 + = x x x x x x 1 2 1 2 1 2 3 3
x + x − 5 x + x x x = 0 (x + x )( 2 2
x + x x + x − 5 x + x x x = 0 1 2 1 1 2 2 ) ( 1 2 ) 1 2 ( 2 1) 1 2 1 2 (x + x )( 2 2
x + x − 6x x = 0 1 2 1 2 1 2 )
(x + x )(x + x )2 −8x x = 0 1 2 1 2 1 2 Suy ra : m − ( 2 2( 1) 3
− m − 8m + 4) = 0 m =1(L) Suy ra: m = 2 − − 6(TM ) 0,25 m = 2 − + 6(TM ) Vậy: m = 2 − 6
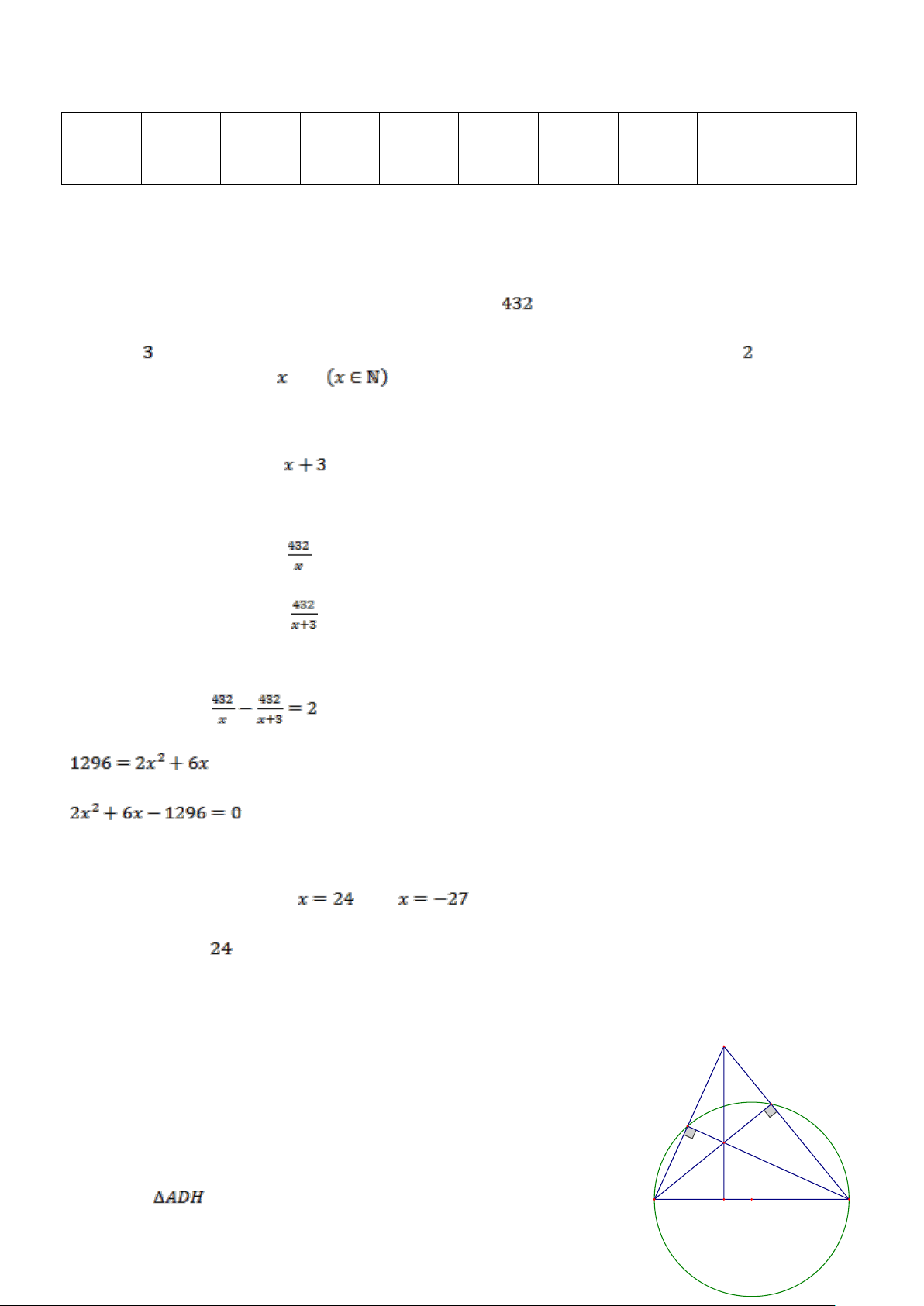
Cho ABC có ba góc nhọn nội tiếp đường tròn (O; R) . Các đường cao AD ,
BF , CE của ABC cắt nhau tại H .
a. Chứng minh tứ giác BEHD nội tiếp một đường tròn. 24 1,5
b. Kéo dài AD cắt đường tròn (O) tại điểm thứ hai K . Kéo dài KE cắt
đường tròn (O) tại điểm thứ hai I . Gọi N là giao điểm của CI và EF . Chứng minh 2
CE = CN.CI . A I F N E H O B D C K Vì vuông tại E nên
nội tiếp đường tròn đường tròn đường kính 0,25 BH. Vì vuông tại D nên
nội tiếp đường tròn đường tròn đường kính a 0,25 BH.
Suy ra 4 điểm B, E, H, D cùng thuộc đường tròn đường kính BH. 0,25
Hay Tứ giác BEHD nội tiếp. b
Chứng minh được tứ giác AEHF nội tiếp 0,25 Trang 15
Xét đường tròn ngoại tiếp tứ giác AEHF có
FEH = FAH (hai góc nội tiếp cùng chắn FH ) hay CEN = KAC ( ) 1
Xét (O) có KAC = KIC (hai góc nội tiếp cùng chắn KC ) hay KAC = EIC (2) 0,25 Từ ( )
1 và (2) suy ra CEN = EIC
Xét CEN và CIE có: ECI : chung; CEN = EIC (cmt) CE CN 0,25 Nên CEN ∽ CI
E ( g − g )Suy ra 2 =
CE = CN.CI (đpcm) CI CE
Nếu học sinh giải theo cách khác mà vẫn đúng thì vẫn cho điểm tối đa.
KHUNG MA TRẬN ĐỀ KIỂM TRA GIỮA KÌ II MÔN TOÁN CẤP THCS Mức độ đánh giá Trắc nghiệm khách quan Chủ Nội dung/Đơn vị Tự luận TT Nhiều lựa chọn Đúng/Sai đề/Chương kiến thức Vận Vận Vận Biết Hiểu Biết Hiểu Biết Hiểu dụng dụng dụng Hàm số 2 2 1
y = ax (a 0) Chủ đề 1: Phương trình bậc 2 1 1 1 Hàm số hai một ẩn 1 2 y = ax Định lí Viete và 1 1 1 1 ứng dụng (a 0) Giải bài toán bằng cách lập phương 1 2 1 1 trình Góc nội tiếp 1 1 1 Chủ đề 2: Đường tròn ngoại Đường tròn tiếp và đường 2 ngoại tiếp 1 1 tròn nội tiếp của và đường một tam giác tròn nội tiếp Tứ giác nội tiếp 2 2 1 1 1 1 Đa giác đều 1 1 Tổng số câu 10 6 4 4 2 2 Tổng số điểm 5 2 3 Tỷ lệ % 50% 20% 30%
KHUNG BẢN ĐẶC TẢ ĐỀ KIỂM TRA GIỮA HỌC KÌ II MÔN TOÁN CẤP THCS
Số câu hỏi/ý hỏi ở các mức độ đánh giá Chủ Nội dung/Đơn TT Yêu cầu cần đạt Trắc nghiệm khách quan đề/Chương vị kiến thức Nhiều lựa chọn Đúng/Sai Trang 16 Vận Biết Hiểu Biết Hiểu dụng Hàm số Nhận biết: 2
y = ax (a 0) - Nhận biết được tính đối xứng (trục) và
trục đối xứng của đồ
thị hàm số y = ax2 (a ≠ 0). Câu 1, 2 Câu 3 Thông hiểu: Thiết lập được bảng
giá trị của hàm số y = ax2 (a ≠ 0). Phương trình Nhận biết: bậc hai một ẩn
- Nhận biết được khái niệm phương trình bậc hai một ẩn.
- Nhận biết được khái niệm nghiệm của hệ hai phương trình bậc nhất hai ẩn. Chủ đề 1: Thông hiểu: Hàm số Câu 4, 5 Câu 6 Câu 7 - Tính được nghiệm 1 2 y = ax phương trình bậc hai (a 0) một ẩn bằng máy tính cầm tay. Vận dụng: – Giải được phương trình bậc hai một ẩn.
Định lí Viete và Nhận biết: ứng dụng - Tính được tổng và tích hai nghiệm của phương trình bậc hai theo định lí Viet. Thông hiểu: Câu 8 Câu 9 Câu 10
- Giải thích được định lí Viète. Vận dụng:
- Ứng dụng được định lí Viète vào tính nhẩm nghiệm của phương Trang 17
trình bậc hai, tìm hai số biết tổng và tích của chúng, ... Giải bài toán Thông hiểu bằng cách lập - Vận dụng được phương trình phương trình bậc hai Câu Câu
vào giải quyết bài toán Câu 11 21.1, 21.3
thực tiễn (đơn giản, 21.2 quen thuộc). Vận dụng Nhận biết
– Nhận biết được góc nội tiếp. Thông hiểu
– Giải thích được mối Góc nội tiếp
liên hệ giữa số đo của Câu 12 Câu 13
cung với số đo góc nội tiếp.
– Giải thích được mối
liên hệ giữa số đo góc
nội tiếp và số đo góc ở tâm cùng chắn một cung.
– Xác định được tâm và bán kính đường tròn Chủ đề 2: Đường tròn ngoại tiếp tam giác, 2 ngoại tiếp trong đó có tâm và bán và đường Đường tròn kính đường tròn ngoại tròn nội tiếp ngoại tiếp và tiếp tam giác vuông, tam đường tròn nội Câu 14 Câu 15 tiếp của một giác đều. tam giác
– Xác định được tâm và
bán kính đường tròn nội tiếp tam giác, trong đó có tâm và bán kính
đường tròn nội tiếp tam giác đều. Nhận biết
– Nhận biết được tứ giác nội tiếp đường Câu Câu 16, Câu
Tứ giác nội tiếp tròn. Câu 18 22.1, 17 22.3 22.2 Thông hiểu
– Giải thích được định
lí về tổng hai góc đối Trang 18 của tứ giác nội tiếp bằng 180o.
– Xác định được tâm và bán kính đường tròn ngoại tiếp hình
chữ nhật, hình vuông. Vận dụng
– Giải quyết được một
số vấn đề thực tiễn (đơn giản, quen
thuộc) gắn với đường
tròn (ví dụ: một số bài toán liên quan đến chuyển động tròn
trong Vật lí; tính được diện tích một số hình phẳng có thể đưa về những hình phẳng gắn với hình tròn, chẳng hạn hình viên phân,...). Nhận biết - Nhận dạng được đa giác đều. Đa giác đều Thông hiểu Câu 19 Câu 20
- Mô tả được các phép quay giữ nguyên hình đa giác đều. Tổng số câu 9 7 4 4 2 Tổng số điểm 5 2 Tỷ lệ % 50% 20% ĐỀ 3
ĐỀ KIỂM TRA GIỮA HỌC KỲ II MÔN:TOÁN - LỚP 9
NĂM HỌC: 2024 – 2025
Thời gian làm bài: 90 phút
PHẦN I. Câu hỏi trắc nghiệm nhiều phương án lựa chọn (5 điểm). Thí sinh trả lời câu hỏi từ 1 đến 20.
Mỗi câu hỏi có 4 phương án trả lời A, B,C,D trong đó chỉ có 1 phương án đúng.
Câu 1. [B] Điểm nào sau đây thuộc đồ thị hàm số 2 y = 2x ? A. (2; ) 1 . B. (1;2) . C. (1;4) . D. (4; ) 1 . Trang 19
Câu 2. [H] Cho hàm số y = f (x )= (- m + ) 2 2
1 x .Tìm giá trị m để đồ thị đi qua điểm A (- 2; ) 4 A. m = 0 . B. m = 1. C. m = 2 . D. m = - 2 .
Câu 3. [B] Phương trình nào sau đây là phương trình bậc hai một ẩn ? A. 2
- 5x + 2x + 1 = 0 . B. 3
2x + x + 5 = 0 . C. 2
4x + xy + 5 = 0 . D. 2
0x - 3x + 1 = 0 .
Câu 4. [B] Phương trình nào dưới đây có hai nghiệm là - 2 và - 3 ? A. 2
x + 5x + 6 = 0 . B. 2
x - 5x + 6 = 0 . C. 2
x - 5x - 6 = 0 . D. 2
x + 5x - 6 = 0 .
Câu 5. [VD] Phương trình 2
x - 2(m - 2)x - 5m = 0 có một nghiệm x = 5 . Khi đó nghiệm còn lại là. A. 3 . B. - 3 . C. - 5. D. 2 .
Câu 6. [H] Tính nhẩm nghiệm của phương trình: 2
- 4x + 5x - 1 = 0 1 1 1
A. x = 1;x = .
B. x = - 1;x = -
C. x = - 1;x = .
D. x = - 1;x = - 4 4 4 4
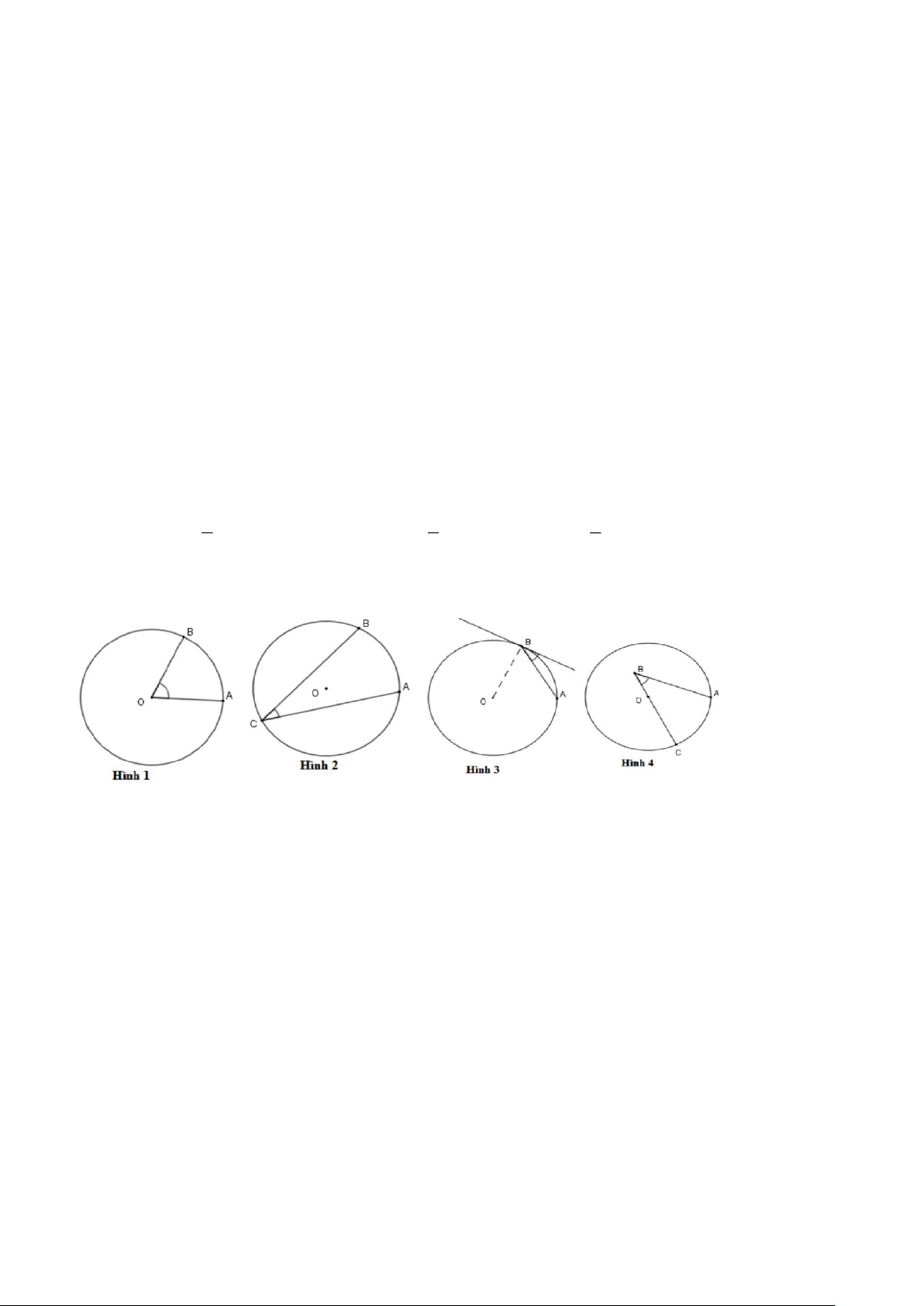
Câu 7. [B] Hình nào dưới đây biểu diễn góc nội tiếp? A. Hình 1. B.Hình 2. C.Hình 3. D. Hình 4.
Câu 8. [B] Góc nội tiếp có số đo
A. Bằng hai lần số đo góc ở tâm cùng chắn một cung.
B. Bằng số đo góc ở tâm cùng chắn một cung.
C. Bằng số đo cung bị chắn.
D. Bằng nửa số đo cung bị chắn.
Câu 9. [B] Trong các khẳng định dưới đây, khẳng định đúng là A. Phương trình 2
2x - 5x + 35 = 0 có hai nghiệm trái dấu. B. Phương trình 2
2x - 3x - 5 = 0 có hai nghiệm. C. Phương trình 2
- 3x + 4x - 1 = 0 có hai nghiệm âm. D. Phương trình 2
- 2x + 6x - 4 = 0 có một nghiệm duy nhất. Trang 20