






Preview text:
ĐỀ 1
ĐỀ ÔN TẬP CUỐI HỌC KỲ I NĂM HỌC 2025-2026 MÔN: TOÁN 9
PHẦN I. (3 điểm) Câu trắc nghiệm nhiều phương án lựa chọn.
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi chỉ chọn một phương án.
Câu 1. Cặp số nào sau đây là nghiệm của phương trình 2x − y = 3 ? A. (2; ) 1 B. (1; ) 1 C. (0; ) 3 D. (3;0)
Câu 2. Giá trị nào sau đây không phải là nghiệm của bất phương trình x −3 0 A. 2 B. 3 C. 5 − D. 5
Câu 3. Cho bất đẳng thức a b . Khẳng định nào sau đây là đúng?
A. a + 2 b + 2
B. a −3 b −3 C. 2 − a 2 − b
D. 5a 5b
Câu 4. Các căn bậc hai của 9 là? A. 3. B. 3. − C. 3 và 3 − D. 9 và 9 − .
Câu 5. x −1 xác định khi? A. x 1. B. x 1.
C. x 1. D. x 1.
Câu 6. Biểu thức nào sau đây là căn thức bậc ba? 8x 3 x A. 3 x +1. B. 3 5x + 2. C. . D. . 3 9 7 + x
Câu 7. Cho hình vẽ bên, hệ thức nào trong các hệ thức sau là đúng A. c c sin B = B. cosC = A a b b b b c C. tan B = D. cot C = c a a B C
Câu 8. Giá trị của sin30 bằng bao nhiêu? A. 1 B. 3 C. 1 D. 2 2 2 2
Câu 9. Trong các phát biểu sau đây, phát biểu nào sai?
A. Đường tròn có vô số trục đối xứng.
B. Trục đối xứng của đường tròn là đường kính của đường tròn đó.
C. Mỗi đường thẳng đi qua tâm đường tròn là một trục đối xứng của đường tròn đó.
D. Đường tròn có duy nhất một trục đối xứng.
Câu 10. Đường thẳng a được gọi là tiếp tuyến của đường tròn ( ; O R) nếu:
A. Đường thẳng a và đường tròn ( ;
O R) không có điểm chung.
B. Đường thẳng a và đường tròn ( ;
O R) có hai điểm chung phân biệt.
C. Đường thẳng a và đường tròn ( ;
O R) có một điểm chung duy nhất.
D. Đường thẳng a đi qua tâm O của đường tròn ( ; O R) .
Câu 11. Hình nào dưới đây biểu diễn góc nội tiếp đường tròn (O) ? Trang 1 A. Hình 1.
B. Hình 2. C. Hình 3. D. Hình 4.
Câu 12. Cho hình vẽ bên, góc nào sau đây là góc ở tâm? A A. ABC B. BAO C. AOC D. ABC và AOC O B
PHẦN II. (2 điểm) Câu trắc nghiệm đúng/sai
Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí siCnh chọn đúng hoặc sai
Câu 1. Xét các biến đổi căn thức sau đây: a) 32 = 4 2. b) Với 2
y 0, ta có 4y = 2 . y 3 c) Với a
a 0 , biểu thức
có thể biến đổi thành 6 . 2a 4a x −1 2 − − d) Với x 3 x 2
x 0 , biểu thức − được rút gọn thành . x +1 x x ( x + ) 1
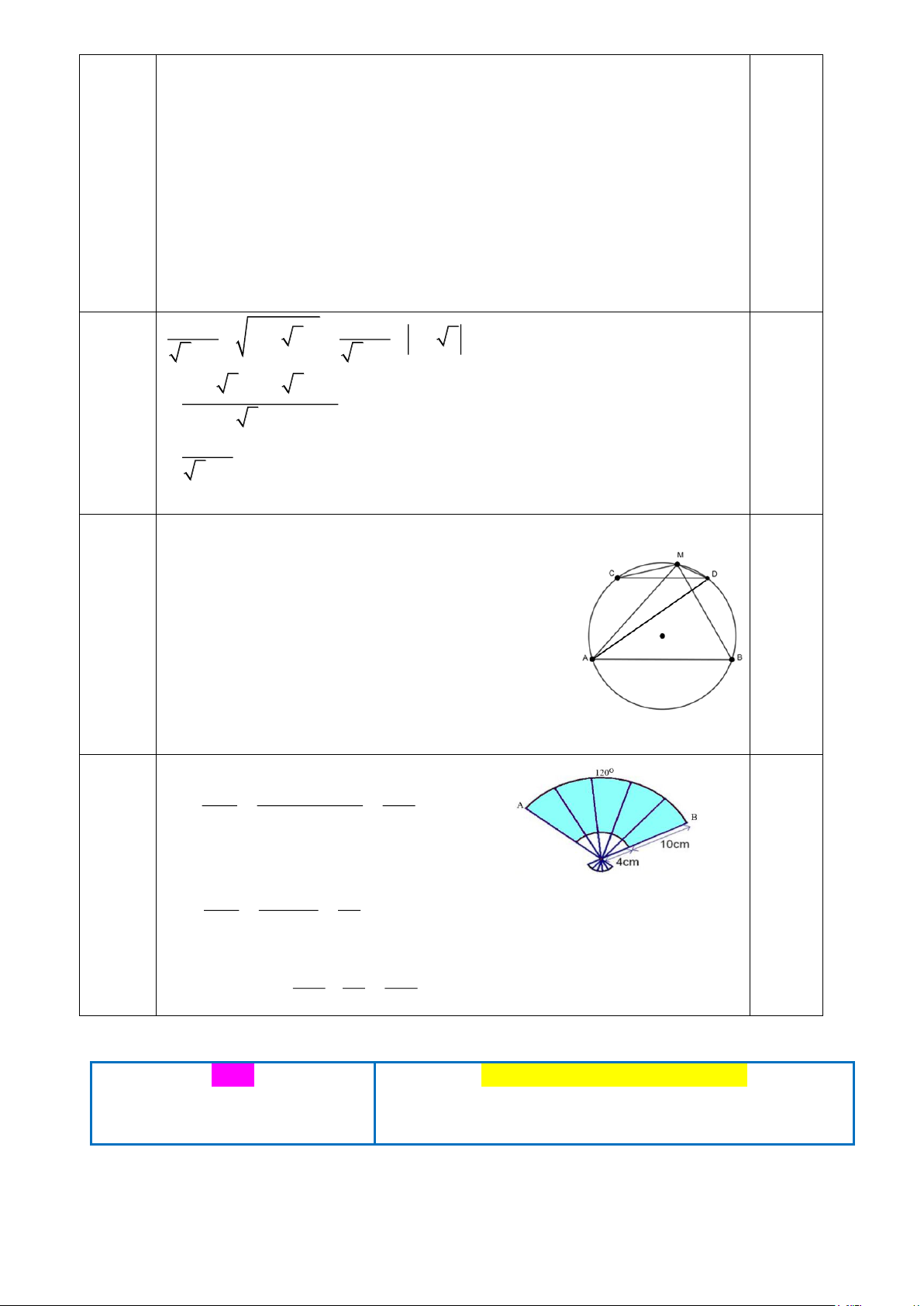
Câu 2. Cho tam giác ABC có ba đỉnh A, B, C nằm trên đường tròn (O) sao cho 0 AOC = 80 ,
nối OA, OC như hình vẽ bên. Xét tính đúng sai của các khẳng định sau. a)
ABC là góc nội tiếp. 1 b) ABC = AOC 3 c) 0 ABC = 40
d) Số đo cung nhỏ AD bằng 1000
PHẦN III. (2 điểm) Câu trắc nghiệm trẳ lời ngắn.
Thí sinh trả lời từ Câu 1 đến Câu 4. Đối với mỗi câu, thí sinh chỉ
viết kết quả dưới dạng số thập phân, không trình bày suy luận.
Câu 1. Tìm nghiệm lớn nhất của bất phương trình 4x − 7 0
Câu 2. Tìm điều kiện xác định của biểu thức 5x + 8
Câu 3. Giá trị x thỏa mãn 3 3 − 2x = 2
Câu 4. Một người quan sát đứng cách gốc một cây 20 m . Góc nâng từ mắt người quan sát đến
ngọn cây là 30. Biết rằng khoảng cách từ mắt người quan sát đến mặt đất là 1,6 m . Tính chiều
cao của cây (làm tròn kết quả đến chữ số thập phân thứ nhất).
PHẦN IV (3 điểm). TỰ LUẬN
Thí sinh trả lời từ Câu 1 đến Câu 5. Đối với mỗi câu, thí sinh trình bày quá trình suy luận và kết quả. Trang 2 3x + 2y = 1
Câu 1. Giải hệ phương trình: 2x − 3y = 5
Câu 2. Một người mua hai loại hàng và phải trả tổng cộng là 21,7 triệu đồng, kể cả thuế giá trị
gia tăng (VAT) với mức 10% đối với loại hàng thứ nhất và 8% đối với loại hàng thứ hai. Nếu
thuế VAT đối với cả hai loại hàng là 9% thì người đó phải trr tổng cộng 21,8 triệu đồng. Hỏi
nếu không kể thuế VAT thì người đó phải trả bao nhiêu tiền cho mỗi loại hàng.
Câu 3. Tính giá trị biểu thức: − ( − )2 4 2 6 6 + 2
Câu 4. Cho đường tròn tâm O và hai dây cung song song AB, CD. Trên cung AB lấy điểm M. Chứng minh rằng
AMC = BMD .
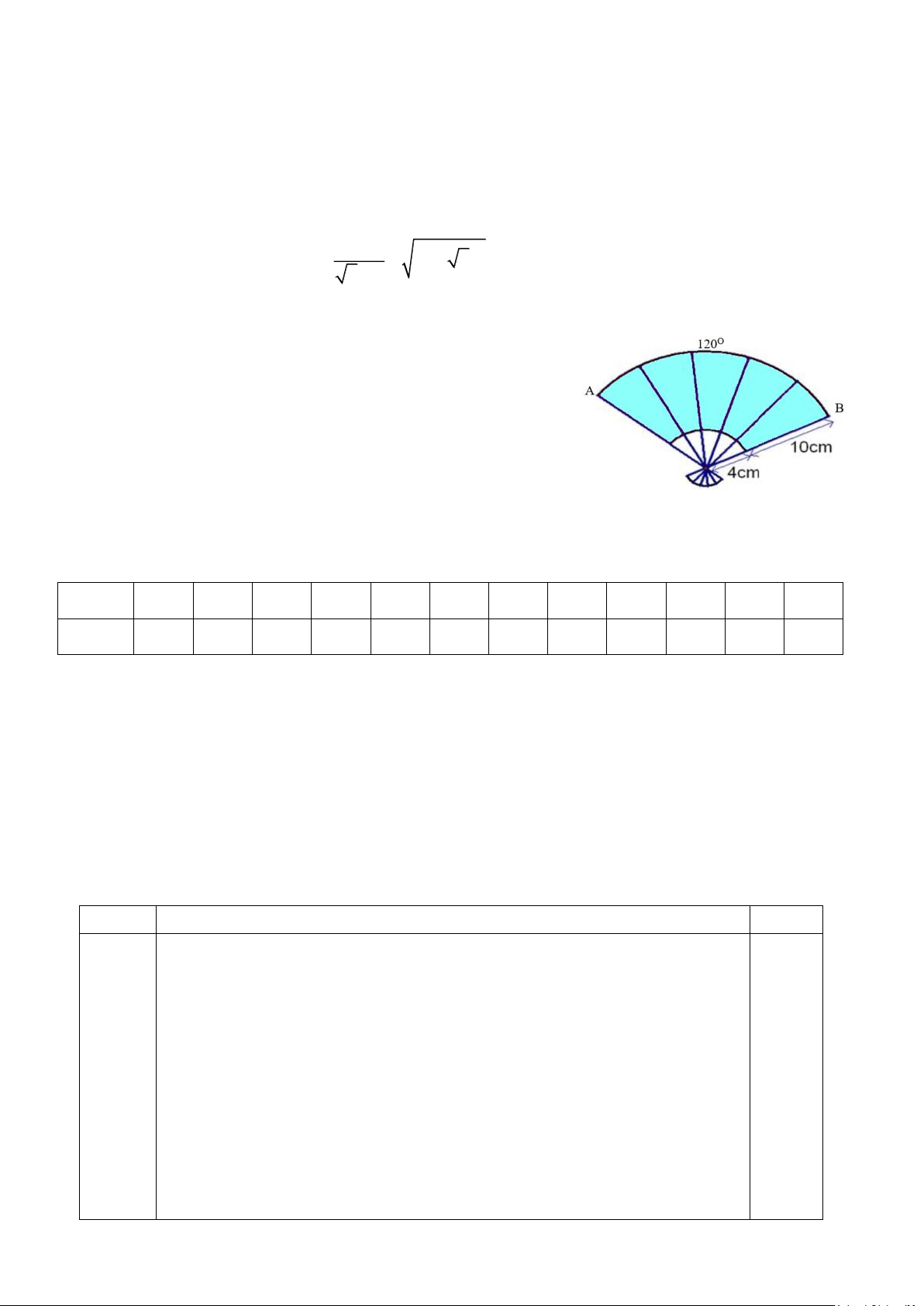
Câu 5. Cho hình vẽ bên. Tính diện tích của phần giấy để
làm chiếc quạt (Biết quạt dán cả hai mặt và phần mép gấp
không đáng kể)? (làm tròn đến hàng đơn vị của cm2)
ĐÁP ÁN VÀ HƯỚNG DẪN CHẤM
PHẦN I. (Mỗi câu đúng được 0,25 điểm) Câu 1 2 3 4 5 6 7 8 9 10 11 12 Đáp án A D B C A A C A D C B C
PHẦN II. (Mỗi ý đúng được 0,25 điểm)
Câu 1. a) đúng ; b) sai ; c) đúng ; d) sai
Câu 2. a) đúng ; b) sai ; c) đúng ; d) đúng.
PHẦN III. (Mỗi câu đúng được 0,5 điểm) Câu 1. 1,75 Câu 2. -1,6 Câu 3. -2,5 Câu 4. 13,1 PHẦN IV. Câu Hướng dẫn giải Điểm 3 x + 2y = 1 2x − 3y = 5 Câu 1 6x + 4y = 2 0,25
6x − 9y = 15 13 y = 13 − 3 x + 2y = 1 0,25 y = −1 x = 1 0,25
Vậy hệ phương trình có nghiệm duy nhất ( ; x y) = (1; 1 − ) Trang 3
Gọi x, y (triệu đồng) lần lượt là giá của loại hàng thứ nhất và loại hàng thứ 2 (Đk:
0 x 21,7;0 y 21,7) Câu 2 1
,1x +1,08y = 21,7
Lập luận để lập được hệ phương trình 0,25 x + y = 2 x = 5
Giải hệ phương trình ta được y = 15 0,25 Trả lời bài toán. Câu 3. 0,25 − ( − )2 4 4 2 6 = − 2 − 6 6 + 2 6 + 2 4 − ( 6 − 2)( 6 + 2) = 0,25 6 + 2 2 = 6 + 2 0,25 -Vẽ hình. Ta có:
AMC là góc nội tiếp chắn cung AC, BMD
Câu 4 là góc nội tiếp chắn cung BD (1) Vì AB//CD nên
ADC = DAB (hai góc song song) 0,25
AC = BD (2) Từ (1) và (2), suy ra
AMC = BMD 0,25
Ta có diện tích hình quạt lớn là.
Rn .(10 + 4).120 28 S = = = Câu 5 1 180 180 3 0,25
Diện tích hình quạt nhỏ là Rn .4.120 8 S = = = 2 180 180 3
Vì quạt dán cả hai mặt nên diện tích giấy để làm quạt là 0,25 28 8 20 2
S = 2.(S − S ) = − = 21(cm ) 1 2 3 3 3
(Ghi chú: Nếu học sinh làm cách khác đúng, giáo viên chia điểm theo các bước tương ứng) ĐỀ 2
ĐỀ ÔN TẬP CUỐI HỌC KỲ I NĂM HỌC 2025-2026 MÔN: TOÁN 9
Bài 1 (2,5 điểm).
1) (NB) Thực hiện phép tính Trang 4 1 1 a) 3 3 (1− 2) b) B = + 2 − 3 2 + 3
2) (TH) Giải phương trình, bất phương trình và hệ phương trình 2 1 3 a) + = b) 2 − x − 5 1 x + 1 x - 2 (x + 1)(x - 2) x − 5 2x + 2 x x
Bài 2 (2,0 điểm). Cho hai biểu thức A = và B = − x x −1 x −1 với x>0, x≠1
a) (NB) Tính giá trị biểu thức A khi x=36.
b) (TH) Rút gọn biểu thức B.
c) (VD) Biểu thức P=A.B+1.Tìm tất cả các giá trị của x để P=0.
Bài 3 (1,5 điểm). (VD) Theo kế hoạch hai tổ sản xuất 600 sản phẩm trong một thời gian nhất
định. Do áp dụng kỹ thuật mới nên tổ I đã vượt mức 18% và tổ II vượt mức 21%. Vì vậy trong
thời gian quy định họ đã hoàn thành được 720 sản phẩm. Hỏi số sản phẩm được giao của mỗi tổ theo kế hoạch?
Bài 4 (3, 5 điểm).
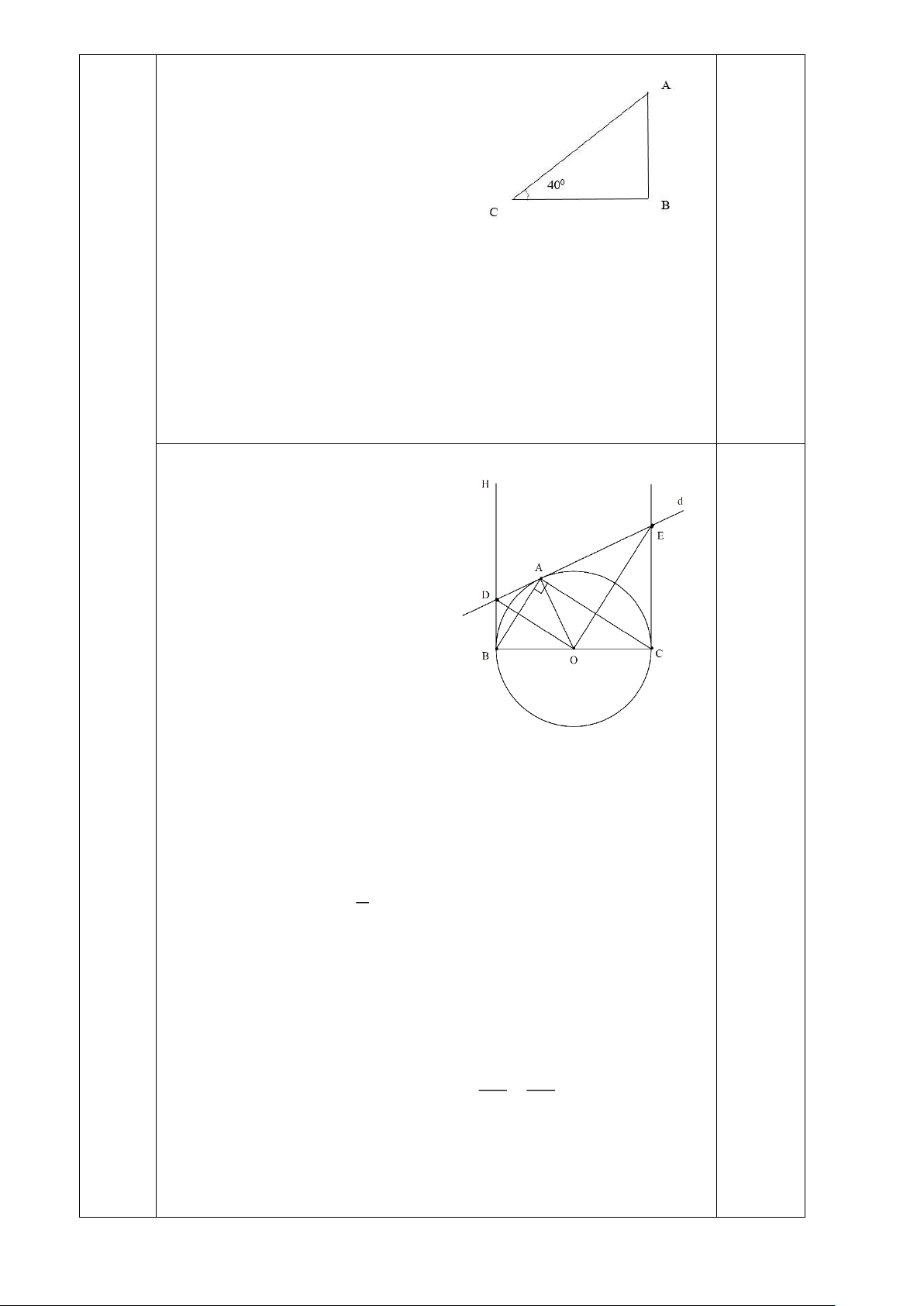
1) (VD) Bóng trên mặt đất của một cái cây dài
25 m. Tính chiều cao của cây (làm tròn đến dm),
biết rằng tia nắng mặt trời tạo với mặt đất góc 40.
2) Cho tam giác ABCvuông tại A. Gọi O là tâm đường tròn ngoại tiếp tam giác ABC ; d là
tiếp tuyến của đường tròn tại A . Các tiếp tuyến của đường tròn tại B và C cắt d theo thứ tự ở D và E.
a) (VD)Tính góc DOE .
b) (VD)Chứng minh : DE = BD+CE . c) (VDC)Chứng minh : 2
BD.CE = R (R là bán kính đường tròn tâm O)
Bài 5 (0,5 điểm). (VDC) Cho ,
a b 0 thỏa mãn a + b =1. 1 1
Chứng minh rằng (1+ ).(1+ ) 9 . a b ---HẾT----
ĐÁP ÁN, BIỂU ĐIỂM ĐỀ KIỂM TRA CUỐI KÌ I Trang 5 BÀI ĐÁP ÁN ĐIỂM 1 1a) ta có: 0,5đ 3 3 (1− 2) =1− 2 1b) Ta có 0,5đ 1 1 B= + 2 − 3 2 + 3 2 + 3 + 2 − 3 B = ( 2 − 3)(2 + 3) 4 B = = 4 1 Vậy B = 4 2 1 3 2 a) + = x + 1 x - 2 (x + 1)(x - 2) ĐKXĐ: 0,25đ
x −1; x 2
Quy đồng mẫu thức ta được: 2(x - 2) 1(x + 1) 3 + = x + 1 x - 2 (x + 1)(x - 2) 2x - 4 + x + 1 3 = (x + 1)(x - 2) (x + 1)(x - 2) Khử mấu ta được: 3x - 3 = 3 0,25đ 3x = 6 x = 2 0,25đ
Giá trị x=2 không thoả mãn điều kiện xác định.
Vậy phương trình đã cho vô nghiệm. 2b) Ta có: 0,25đ 2 − x − 5 1 2 − x > 6 x < − 3 0,25đ
Vậy Bất phương trình có nghiệm là x < -3 0,25đ Trang 6 2
a) Khi x = 36 (thoả mãn điều kiện) thay vào biểu thức A − 0,25đ Ta có : 36 5 31 A = = 36 6 0,25đ Vậy 31 A = khi x = 36. 6 2x + 2 x x b) Ta có B = − x −1 x −1 0,25đ 2 x( x +1) x B = − ( x −1)( x +1) x −1 0,25đ 2 x x B = − 0,25đ x −1 x −1 x B= x −1 x Vậy B= x −1 0,25đ c) ta có P = A.B+1 x − 5 x P = . +1 x x −1 x − 5 P = +1 x −1 x − 5 + x −1 P = x −1 x + x − 6
( x + 3)( x − 2) P = = x −1 x −1
Để P=0 thì ( x + 3)( x − 2) = 0 suy ra x − 2 = 0 x = 4 Vậy khi x=4 thì P=0. 3
Gọi x (sản phẩm) số sản phẩm được giao theo kế hoạch của tổ I
y (sản phẩm) số sản phẩm được giao theo kế hoạch của tổ II 0,25đ (x, y ∈ N*; x, y <600)
Theo kế hoạch 2 tổ sản xuất 600 sản phẩm: Ta có pt: x + y = 600 (1) 0,25đ Trang 7
Do cải tiến kỹ thuật nên 2 tổ sản xuất được 720 sản phẩm
Ta có pt: x + 18%.x + y + 21%. y= 720 1,18x + 1,21y = 720 (2) 0,25đ
Từ (1) và (2) ta có hệ pt: x + y = 600 1 ,18x +1,21y = 720 0,25đ
Giải hệ ta được x=200; y=400 (thoả mãn điều kiện) 0,25đ
Vậy theo kế hoạch tổ I sản xuất 200 sản phẩm, tổ II sản xuất 400 sản phẩm. 0,25đ Trang 8 4 1) Vẽ hình Chiều cao của cây BA, 0,25đ
Bóng cây trên mặt đất CB
Góc tạo bởi tia nắng với mặt đất là góc ACB 0,25đ
DABC vuông tại B, Áp dụng hệ thức hai cạnh góc vuông
AB = BC.tan C 0 AB = 25.tan 40 0,25đ AB= 18,1635…(m)≈182(dm) Vậy cây cao gần 182dm. 0,25đ 2) Vẽ hình đúng 0,25đ
a) Sử dụng tính chất 2 tiếp tuyến ta được : 1,0đ
OD là phân giác của góc AOB OE là phân giác của AOC 0,75đ 1 DOE=DOA+EOA= (BOA+COA) 0 =90 2
b) Sử dụng tính chất 2 tiếp tuyến ta chứng minh: 0,5đ
DA=DB; EA=EC mà DE=DA+AE nên suy ra DE = BD+CE c) Chứng minh D A AO D A O ∽ A E O suy ra 2 = D A . E A = AO OA E A 2 BD.CE = R . Trang 9 5 Ta có 1 1 1+ . 1+ 9 (1) a b a +1 b +1 . 9 a b
ab + a + b +1 9ab (vi ab 0) a + b +1 8ab 2 8ab 0,25đ 1 4ab (vi a + b =1) (a + b)2 4ab 2 (a − b) 0
Bất đẳng thức trên luôn đúng suy ra BĐT (1) luôn đúng. 0,25đ
Dấu “=” xảy ra khi a = b, a + b = 1 suy ra 1 a = b = 2
(Học sinh có cách giải khác đúng vẫn cho điểm tối đa). ĐỀ 3
ĐỀ ÔN TẬP CUỐI HỌC KỲ I NĂM HỌC 2025-2026 MÔN: TOÁN 9
Bài 1 (NB) (1điểm). Tính giá trị của các biểu thức sau: 2 1 a) 81 - 16; 3 2 b) 3 0, 5 0, 04 + 5 8
Bài 2 (TH) (1điểm). Giải phương trình sau: 3x (x - 7)+ 5(x - 7)= 0 2 + 3 2 − 3
Câu 3 (TH) (1) điểm Cho A = + . Rút gọn A 2 − 3 2 + 3
Câu 4 (VD) (1,5 điểm) Một nhóm khách vào cửa hàng bán trà sữa. Nhóm khách đó đã mua 6
cốc trà sữa gồm trà sữa trân châu và trà sữa phô mai. Giá mỗi cốc trà sữa trân châu là 33000
đồng, trà sữa phô mai là 28000 đồng. Tổng số tiền nhóm khách thanh toán cho cửa hàng là
188000 đồng. Hỏi nhóm khách hàng đó mua bao nhiêu cốc trà sữa mỗi loại? Câu 5 (2điểm)
a) (TH) (1 điểm) Cho a > b chứng minh rằng - 3a + 4 < - 3b + 4 Trang 10
b) (TH) (1,0 điểm) : Bạn An có 90 nghìn đồng. Bạn muốn mua một bộ thước giá 15 nghìn
đồng và một số quyển vở, mỗi quyển vở giá 8 nghìn đồng. Hỏi bạn An mua được nhiều nhất bao nhiêu quyển vở.
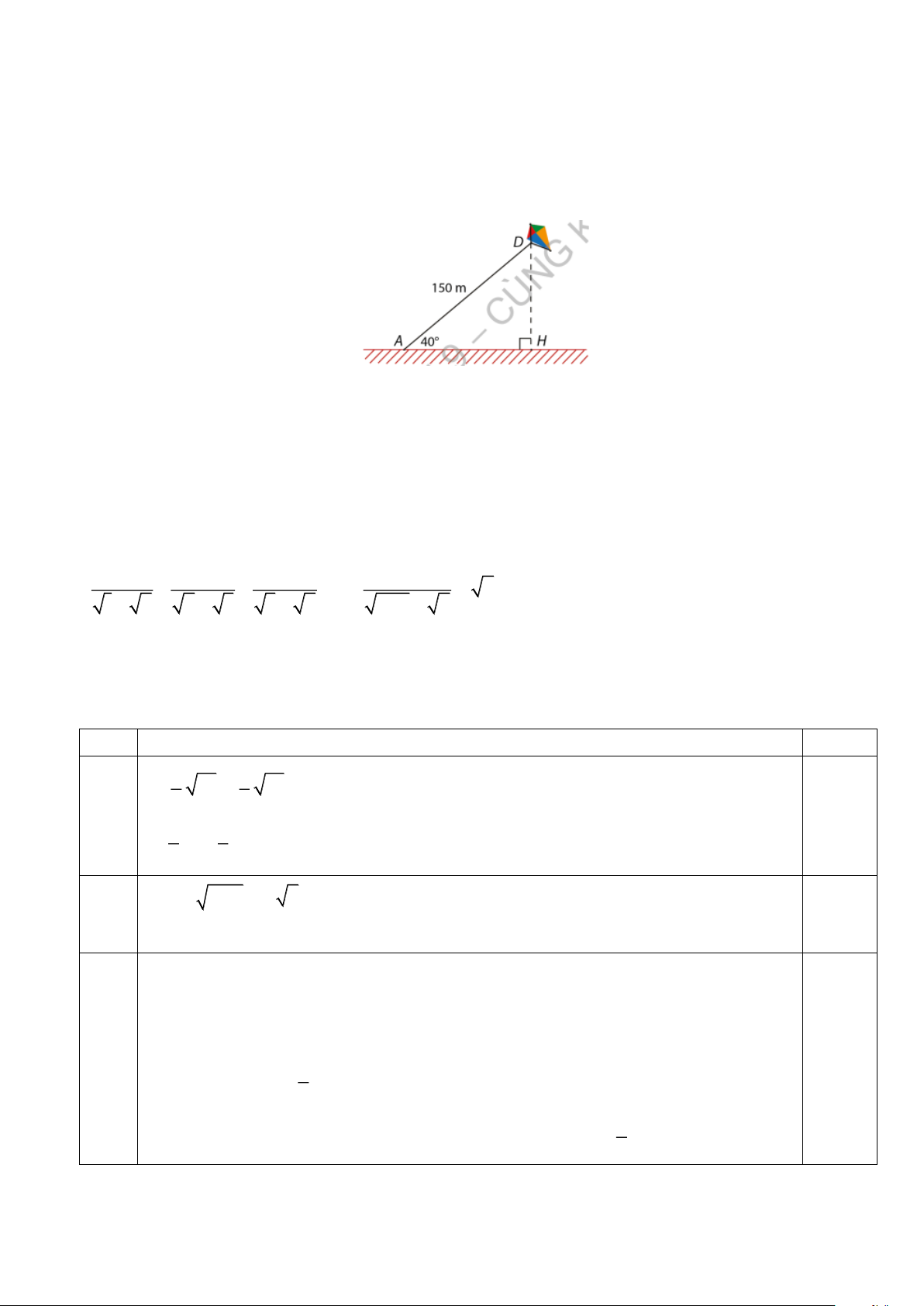
Câu 6 (TH) (1 điểm) Trong hình vẽ dưới đây, một cánh diều được thả trên bầu trời với chiều
dài dây là A D = 150 m, góc tạo bởi dây diều và phương nằm ngang là · 40o DA H = . Tính độ
cao DH của cánh diều so với mặt đất.
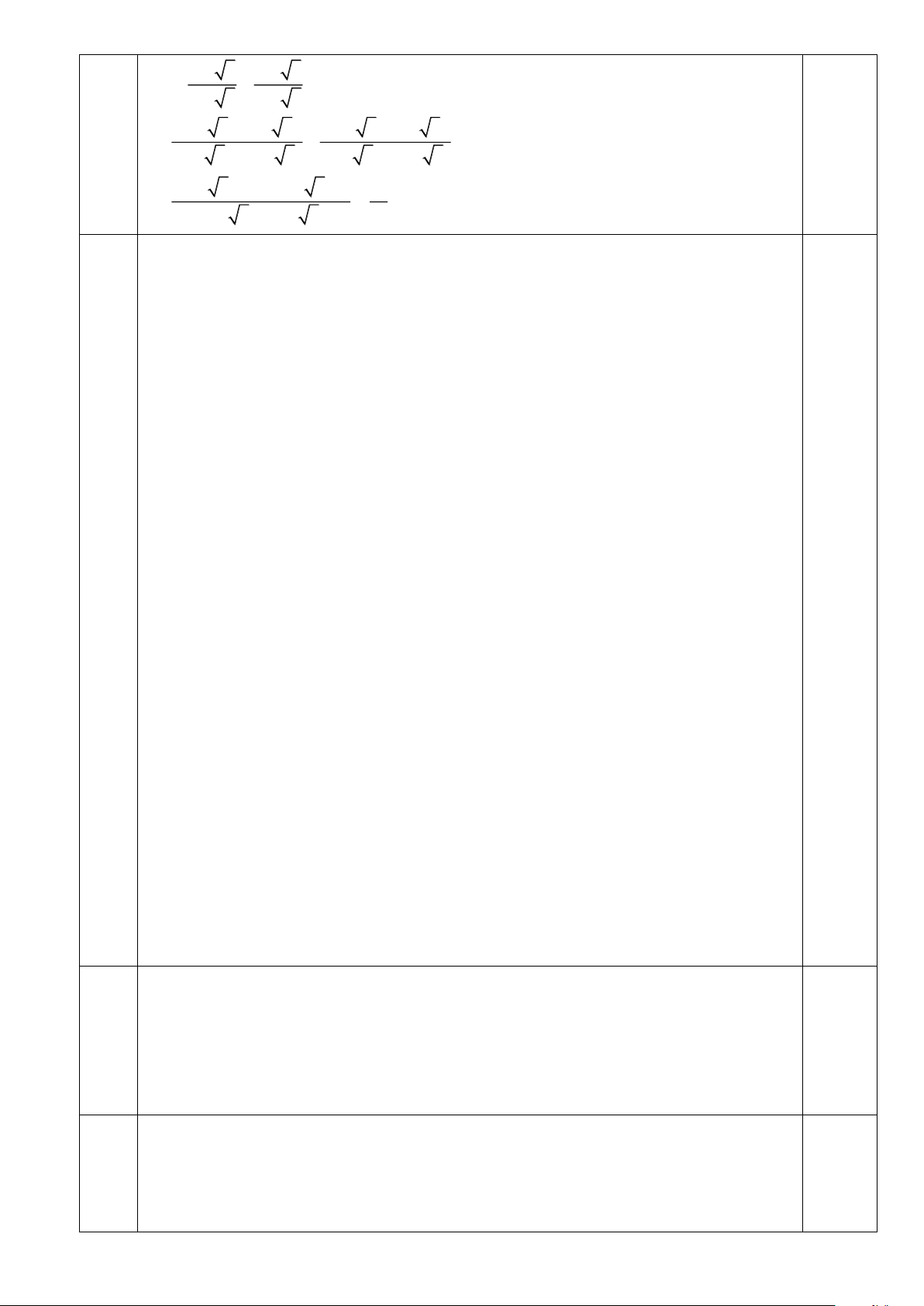
Câu 7 (VD) (2 điểm) Qua điểm M nằm ở ngoài đường tròn (O) kẻ hai tiếp tuyến MA, MB (A,
B là các tiếp điểm) và cát tuyến MPQ (MP < MQ). Gọi I là trung điểm của dây PQ, E là giao
điểm thứ hai của đường thẳng BI và đường tròn (O).
a) (1 điểm) Chứng minh các điểm O, I, A, M, B cùng thuộc một đường tròn..
b) (1 điểm) Chứng minh BOM = BE . A Câu 8 (VDC)
(0,5điểm) Chứng minh rằng: 1 1 1 1 + + +...+ = n −1 1 + 2 2 + 3 3 + 4 n −1 + n HẾT.
ĐÁP ÁN VÀ THANG ĐIỂM
(Đáp án này gồm 04 trang) Câu Nội dung Điểm 1a 2 1 0,5 a) 81 - 16 3 2 2 1 = .9 - .4 = 4 3 2 1b b) 3 0,5 0, 5 0, 04 + 5 8 = = 0, 5.0, 2 + 5.2 = 10,1 2
3x (x - 7)+ 5(x - 7) = 0 1đ
(x - 7)(3x + 5)= 0
x - 7 = 0 hoặc 3x + 5 = 0 5
x = 7 hoặc x = - . 3 5
Vậy phương trình đã cho có hai nghiệm là: x = 7 , x = - 3 Trang 11 3 2 + 3 2 − 3 = + (1đ) A 2− 3 2+ 3 (2 + 3).(2 + 3) (2 − 3).(2 − 3) 0,5đ = +
(2 − 3).((2 + 3) (2 − 3).((2 + 3) 0,25đ 0,25đ 4 + 4 3 + 3 + 4 − 4 3 + 3 14 = = =14 (2 − 3).((2 + 3) 1 4
Một nhóm khách vào của hàng bán trà sữa. Nhóm khách đó đã mua 6 cốc trà
(1,5 sữa gồm trà sữa trân châu và trà sữa phô mai.Giá mỗi cốc trà sữa trân châu, trà đ)
sữa phô mai lần lượt là 33 000 đồng và 28 000 đồng. Tổng số tiền nhóm khách
thanh toán cho cửa hàng là
188 000 đồng. Hỏi nhóm khách hàng đó mua bao
nhiêu cốc trà sữa mỗi loại? Lời giải: 0,25
Gọi x,y (cốc) lần lượt là số cốc trà sữa trân châu và trà sữa phô mai mà nhóm
khách đã mua ( x,y Î ¥ ,x < 6;y < 6) 0,25
Vì nhóm khách đã mua 6 cốc trà sữa nên ta có phương trình: x + y = 6
Mà nhóm khách thanh toán cho cửa hàng là 188 000 đồng nên ta có phương 0,25 trình
33 000x + 28 000y = 188 000 hay 33x + 28y = 188 0,25 ìï x + y = 6 (1)
Do đó, ta có hệ phương trình ïí
ï 33x + 28y = 188 (2) ïî 0,25
Từ phương trình (1) ta có: x = 6 - y
Thế (3) và (2) ta được:
33.(6 - y) + 28y = 188 0,25
198 - 33y + 28y = 188 10 = 5y y = 2
Thay giá trị y = 2 vào phương trình (3) ta có: x = 6 - 2 = 4
Do đó hệ phương trình có nghiệm duy nhất (x;y) = (4;2)
Vậy nhóm khách hàng đó đã mua 4 cốc trà sữa trân châu và 2 cốc trà sữa phô mai
a) a > b 0,5 5a
- 3a < - 3b (Nhân cả hai vế với – 3 < 0) (1,0 0,5
- 3a + 4 < - 3b + 4 (Cộng cả hai vế với 4)a đ) KL: …. 5b
Bạn An có 90 nghìn đồng. Bạn muốn mua một bộ thước giá 15 nghìn đồng và
(1đ) một số quyển vở, mỗi quyển vở giá 8 nghìn đồng. Hỏi bạn An mua được nhiều
nhất bao nhiêu quyển vở? Lời giải: Trang 12
Gọi x (quyển vở) là số vở bạn An có thể mua. 0,25 (ĐK: x Î ¥ ) 0,25
Theo đề bài, ta có bất phương trình: 8x + 15 £ 90 0,25 8x £ 90 - 15 8x £ 75 0,25 x £ 9, 375
Vì số vở là số tự nhiên nên An có thể mua được nhiều nhất 9 quyển vở.: ….
Trong hình vẽ dưới đây, một cánh diều được thả trên bầu trời với chiều dài dây 6
là A D = 150 m, góc tạo bởi dây diều và phương nằm ngang là · 40o DA H = .
(1đ) Tính độ cao DH của cánh diều so với mặt đất. 0,5đ 0,5đ
Giải: Xét DA DH vuông tại H ta có µ = . sin = 150. sin 40o DH A D A » , 96 42 (m) KL:… 7 (2,0 đ)
a) Chứng minh OI vuông góc MQ 0,5đ
Gọi T là trung điểm OM. Tam giác OIM, OAM, OBM vuông tại O có T là 0,25đ 1 0,25đ
trung điểm cạnh huyền OM nên TO = TI = TA = TM = TB = OM nên các 2
điểm O, I, A, M, B cùng thuộc đường tròn tâm T 1 1 0,5đ b) Chứng minh
BOM = BOA BOM = d s A .
B (Góc ở tâm có số đo bằng số 2 2 đo của cung bị chắn). 1 0,5đ Trong (O) ta có BEA = d s A .
B (góc nội tiếp có số đo bằng nửa số đo cung bị 2 chắn). Trang 13 Do đó BEA = BOM.
Câu (0,5điểm) Chứng minh rằng: 8 1 1 1 1 + + + ...+ = n −1 1 + 2 2 + 3 3 + 4 n −1 + n Giải 1 1( 2 − 1) 1( 2 − 1) 0,25 Ta có = = = ( 2 − 1) 1 + 2 ( 1 + 2)( 2 − 1) 2 −1 Tương tự 1 = 3 − 2 2 + 3 1 = 4 − 3 3 + 4 1 = 5 − 4 4 + 5 . . 0,25 . . 1 = n − n −1 n −1 + n Cộng lại ta có 1 1 1 1 + + +...+ = n −1 (đpcm) 1 + 2 2 + 3 3 + 4 n −1 + n ĐỀ 4
ĐỀ ÔN TẬP CUỐI HỌC KỲ I NĂM HỌC 2025-2026 MÔN: TOÁN 9
Bài I. (1,5 điểm) Giải các phương trình, bất phương trình sau: x + 3 3x − 2 a) x − 3 = 2 b) 2
25x + 50 + 3 x + 2 − 9x +18 = 12 c) − −1 3 4 6 x x − x + 2 2 1
Bài II. (2,0 điểm) Cho biểu thức A = và B = + + với 𝑥≥0;𝑥≠4 3 x +1 x − 4 x + 2 x − 2
1) Tính giá trị của biểu thức A khi x = 25 . x 2) Chứng minh B = . x − 2
3) Cho P = B : A. Tìm x là số nguyên lớn nhất để P < 2.
Bài III. (2,5 điểm)
Giải các bài toán sau bằng cách lập phương trình, hệ phương trình, bất phương trình.
1) Bà Minh dùng số tiền 5 tỉ để mua hai mảnh đất. Hai năm sau bà quyết định bán hai mảnh
đất đó và được tổng số tiền lãi là 1tỉ 100 triệu. Mảnh đất thứ nhất bà lãi 20% so với lúc mua, Trang 14
mảnh đất thứ hai bà lãi 25% so với lúc mua. Tính số tiền bà Minh bỏ ra mua mỗi mảnh đất trên?
2) Bạn Mai làm một bài thi Toán gồm 30 câu hỏi trắc nghiệm, mỗi câu đúng được cộng 4
điểm, mỗi câu sai bị trừ 1 điểm, câu nào không làm thì không bị trừ cũng không được
cộng điểm. Bạn Mai đã làm 25 câu và đạt hơn 82 điểm. Hãy cho biết bạn Mai cần trả lời
ít nhất bao nhiêu câu hỏi đúng để đạt số điểm như trên?
Bài IV. (3,5 điểm)
1) Một bồn hoa trong công viên có dạng hình vành khăn (tô đậm như hình vẽ)
người ta muốn trồng hoa bên trong phần tô đậm. Tính diện tích phần trồng hoa,
biết rằng bán kính đường tròn lớn là 12m và bán kính đường tròn nhỏ là 10m.
2) Cho đường tròn (O;R ) và điểm M (OM > R). Vẽ hai tiếp tuyến MA, MB với đường tròn
(O) (A, B là các tiếp điểm). Nối OM cắt đoạn thẳng A B tại điểm H .
a) Chứng minh bốn điểm M, , A ,
O B cùng thuộc một đường tròn.
b) Chứng minh OM ⊥ AB và 2
OH.OM = R .
c) Vẽ đường kính AC của đường tròn (O), đường thẳng vuông góc với AC tại O lần
lượt cắt các đường thẳng BC và MB theo thứ tại các điểm K và N . Hai đường thẳng MK
và OB cắt nhau tại điểm Q. Chứng minh QN ^ MO.
Bài V. (0,5 điểm) Một công ty sản xuất dụng cụ thể thao nhận được một đơn đặt hàng sản
xuất 8000 quả bóng tennis. Công ty này sở hữu một số máy móc, mỗi máy móc có thể sản xuất
30 quả bóng trong một giờ. Chi phí thiết lập các máy này là 200 nghìn đồng cho mỗi máy.
Khi được thiết lập, hoạt động sản xuất sẽ hoàn toàn diễn ra tự động dưới sự giám sát. Số tiền
phải trả cho người giám sát là 192 nghìn đồng một giờ (người này sẽ giám sát tất cả các máy
hoạt động). Số máy móc công ty nên sử dụng là bao nhiêu để chi phí sản xuất là thấp nhất?
--------------HẾT--------------
(Cán bộ coi kiểm tra không giải thích gì thêm) ĐÁP ÁN BÀI Ý Nội dung Điể m 1 a a) x −3 = 2 (x 0) 0,5 1,5đ
x = 25 (tm) vậy x = 25 thì TMĐB b 2
b) 25x + 50 + 3 x + 2 − 9x +18 = 12 (x 2) − 3 0,5 (x + ) 2 25 2 + 3 x + 2 − 9( x + 2) =12 3 2
5 x + 2 + 3 x + 2 − .3. x + 2 = 12 3 6 x + 2 = 12 x + 2 = 2 x + 2 = 4 x = 2(tm) Trang 15 Vậy x = 2 thì TMĐB c x + 3 3x − 2 − 1 − 4 6
3(x + 3) 2(3x − 2) 12 − − 12 12 12 0,5
3x + 9 − 6x + 4 +12 0 3 − x −25 25 x 3 Vậy 25 x thì TMĐB 3
1 1) Tính giá trị của biểu thức A khi x = 25 . Với (TM) ( ) ta thay vào A x 25 5 = = = x = 25 x 0; x 9 3 x +1 3 25 +1 16 0,25 0,25 Vậy x = 25 thì A= 5 16
Rút gọn biểu thức B, Với x 0; x 9 , ta có: 0,25 x − x + 2 + 2 x − x +
( x −2)+1( x +2 2 2 1 ) II B = + + = = 0,25 2đ x − 4 x + 2 x − 2 ( x −2)( x +2) 2 0,25 x 0,25 x − x + + x − + x + x + x ( x +2 2 2 4 2 2 ) x = ( = = = x − 2)( x + 2)
( x −2)( x +2) ( x −2)( x +2) x −2
Với x 0; x 9 , ta có: x x 3 x +1 0,25
P = B : A = : = để P < 2 Hay x − 2 3 x +1 x − 2 0,25 3 3 x +1 3 x +1 x + 5 2 hay − 2 0 hay
0 mà x + 5 0 nên x − 2 x − 2 x − 2
x − 2 0 hay x 4 mà x nguyên lớn nhất nên x = 3 Vậy x = 3 thì P < 2 III 3,5đ 1,75
1 Gọi số tiền Bà Minh đầu tư mua mảnh đất thứ nhất là x ( 0 < x < 5, tỉ đồng) 0,25 đ
Số tiền Bà Minh đầu tư mua mảnh đất thứ hai là: y ( tỉ đồng) 0,25
Vì tổng tiền là 5 tỉ ta có pt : x + y = 5
Số tiền lãi Bà Minh thu được sau khi bán mảnh đất thứ nhất là 0,2x ( tỉ) 0,25
Số tiền lãi Bà Minh thu được sau khi bán mảnh đất thứ hai là 0,25y ( tỉ) 0,25
Vì tổng tiền lãi là 1,1 tỉ ta có pt : 0,2x + 0,25y = 1,1 0,25 Trang 16 x + y = 5 x = 3 0,25 Ta có hpt giải hệ pt có (tm)
0,2x + 0,25y =1,1 y = 2 0,25
Vậy Bà Minh mua mảnh đất thứ nhất là 3 tỉ đồng
Bà Minh mua mảnh đất thứ hai là 2 tỉ đồng. 0,75
Gọi số câu trả lời đúng là x (Câu , x N ) đ
Số câu trả lời sai là 25 – x câu 0,25
Số điểm đạt được là 4x điểm
2 Số điểm bị trừ là 1(25 – x ) điểm
Vì điểm ít nhất là 82 nên ta có bất phương trình 0,25 4x – 1(25 – x ) 82 x 107 = 21,4 5 0,25
Vậy số câu đúng tối thiểu mà Mai cần phải làm đúng là 22 câu
1 Diện tích trồng hoa là 2 2
S = R − r ( 2 2 ( ) 3,14 12 −10 ) =138,16m2 IV
2 Vẽ đúng hình đến câu a A 0,25 3,5đ H I O M N C K B Q
a Vì MA,MB là hai tiếp tuyến (O) ta có MA ⊥ OA;MB ⊥ OB 0,25
Gọi I là trung điểm OM. Xét tam giác vuông MAO có trung tuyến AI ứng 0,25
với cạnh huyền OM =>IM=IO=IA=OM/2 0,25
Tương tự với tam giác vuông MBO ta có IM=IO=IB=MO/2 0,25 =>IM=IO=IA=IB 0,25
=> 4 điểm A,M,B,O cùng thuộc một đường tròn
b * (O) có tiếp tuyến MA,MB cắt nhau tại M nên
MA=MB. Có OA=OB =R => M,O thuộc đường trung trực của AB 0,25
=> MO là đường trung trực AB => MO ⊥ AB
* Xét tam giác OHA và tam giác OAM có 0,25 0
OHA = OAM = 90 OH OA => O HA O AM = = 0,25 AOM chung OA OM 2 2 = 0,25
OH.OM = OA = R => đpcm
c Ta chứng minh QN ⊥ MO
*Chứng minh OH là đường trung bình của tam giác ABC =>OH//BC 0,25
*Chứng minh tam giác MAO=tam giác KOC (gcg)=>OM=CK=>OMKC là hbh
* Chứng minh MAOK là hcn => OKM=900 =>N là trực tâm tam giác 0,25 QOM Trang 17
=>N là trực tâm => QN ⊥ MO V
Gọi số máy móc công ty nên sử dụng là x (máy, x 0) 0,25 0,5đ
Trong một giờ, số quả bóng tennis sản xuất được là 30x (quả bóng)
Như vậy, số giờ để sản xuất 8000 quả bóng là 8000 (giờ) 30x
Mỗi giờ phải trả 192 nghìn đồng cho người giám sát và chi phí thiết lập
cho mỗi máy là 200 nghìn đồng nên chi phí sản xuất là 8000 51200000 B = 200000x + .192000 = 200000x + (đồng). 30x x
Với hai số không âm a và b ta có ( a − b )2 0 suy ra a + b 2 ab 0,25 51200000
Áp dụng bất đẳng thức trên với hai số dương 200000x và , ta x được : 51200000 51200000 200000x + 2 200000 . x = 6400000 . x x 51200000 Dấu "=" xảy ra khi 2 200000x =
x = 256 x = 16 (nhận) hay x x = 16 − (loại).
Vậy số máy móc công ty nên sử dụng là 16 máy để chi phí sản xuất là thấp nhất.
Lưu ý: Học sinh làm theo cách khác đúng vẫn cho điểm tối đa ĐỀ 5
ĐỀ ÔN TẬP CUỐI HỌC KỲ I NĂM HỌC 2025-2026 MÔN: TOÁN 9
Bài 1. (1,0 đ) (NB) Thực hiện phép tính: 20
a, 2. 27 + 48 + 30 . 12,1 ; b, 3 64 − + 3 27 + 16
Bài 2. (1,5 điểm). (VD )
Một mảnh đất hình chữ nhật có chu vi 48m. Nếu tăng chiều rộng thêm 2m và tăng chiều dài
thêm 3m thì diện tích hình chữ nhật tăng thêm 2 64 m
. Tính độ dài các cạnh của mảnh đất hình chữ nhật ban đầu.
Bài 3. (1,5 điểm). (TH). Giải phương trình và bất phương trình sau: x x −1 5 a) − = 2 x −1 x +1 x −1
b) 5(x − 3) + 7 2(x + 3) −11.
Bài 4. (2.0 điểm). (TH-VD) Trang 18 x +12 3 1 1 Cho hai biểu thức A = và B = + : với x 0, x 1 x −1 x −1 x +1 x +1
a) Tính giá trị của biểu thức A khi x = 9.
b) Rút gọn biểu thức B. c) Đặt A M =
. Tìm x để biểu thức M < 0 B
Bài 5.(1 điểm) (TH)
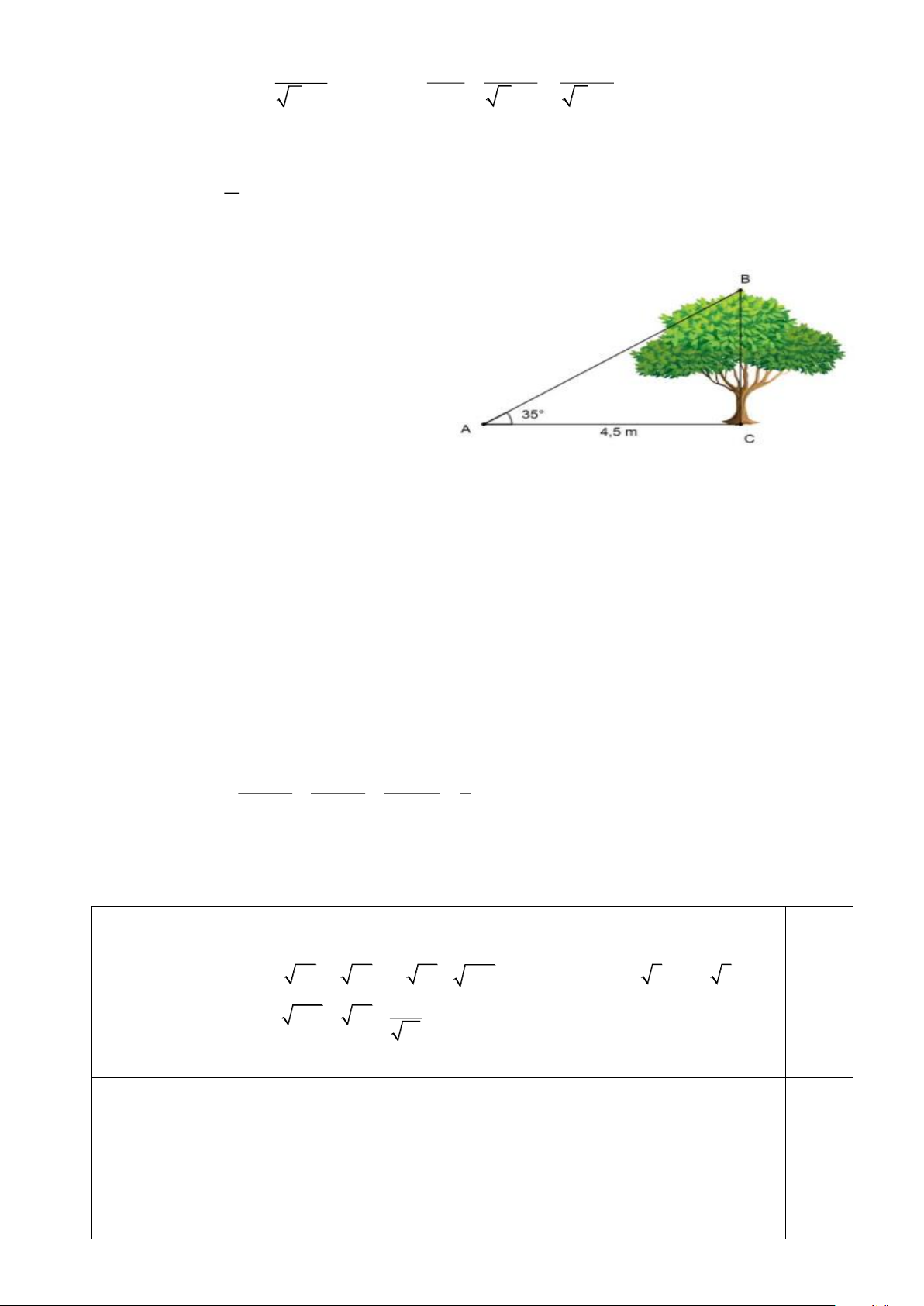
Trên sân trường một cây xanh có bóng dài
4,5m. Biết tại thời điểm đó tia nắng mặt
trời tạo với mặt đất một góc bằng 35 .
Tính chiều cao của cây đó theo đơn vị mét
(kết quả làm tròn đến chữ số thập phân thứ nhất).
Bài 6:(2,5đ) Cho đường tròn tâm O bán kính R, điểm A nằm ngoài đường tròn. Kẻ tiếp tuyến
AB với đường tròn (B là tiếp điểm). Kẻ BH vuông góc với AO(HAO), tia BH cắt đường tròn (O) tại điềm C.
a) Chứng minh: Ba điểm A; O; B thuộc một đường tròn.
b) Chứng minh AC là tiếp tuyến của (O).
c) Điểm E thuộc cung nhỏ BC, điểm F thuộc cung lớn BC. Tiếp tuyến tại E cắt tia AB, AC lần
lượt tại P và Q. Tiếp tuyến tại F cắt tia AB, AC lần lượt tại M và N. Chứng minh rằng C
= AM + AN - MN (trong đó C là chu vi tam giác APQ ) V APQ V APQ
Bài 7 (0,5đ) VDC: Cho các số thực dương a, b, c thỏa mãn 2 2 2
a + b + c = 1. 2 2 2 a b c 3 Chứng minh rằng + +
1+ 2bc 1+ 2ca 1+ 2ab 5
-------- Hết--------- HƯỚNG DẪN CHẤM Câu Nội dung đáp án Biểu điểm Bài 1
Câu a: 2. 27 + 48 + 30 . 12,1 = (2.3+ 4 + 11). 3 = 21. 3 0,5 (1,0đ) 20 0,5 Câu b: 3 64 − + 3 27 + = - 4 + 3 +5 = 4 16 Bài 2
Gọi chiều dài, chiều rộng của hình chữ nhật lần lượt là x ( m), y ( m) 0,25 (1,5 đ)
. ĐK: x, y 0, x y . 0,25
Vì mảnh vườn có chu vi là 48m nên 2( x + y) = 48 x + y = 24 0,25 ( ) 1 0,25 Trang 19
Diện tích của hình chữ nhật ban đầu là ( 2 xy m ) 0,25
Nếu tăng chiều rộng thêm 2m thì chiều rộng là y + 2 ( m) và tăng 0,25
chiều dài thêm 3m thì chiều dài là x + 3( m) . Khi đó diện tích hình chữ nhật tăng thêm 2 64 m nên (x + )
3 ( y + 2) = xy + 64 2x + 3y = 58 (2) x + y = 24 x =14 Từ ( ) 1 , (
2) ta có hệ phương trình (thỏa mãn) 2x + 3y = 58 y =10
Vậy chiều dài, chiều rộng của hình chữ nhật ban đầu là 14m và 10m. Bài 3 x x −1 5 − = (1,5đ) a, 2 x −1 x +1
x −1 ĐKXĐ: x 1 và x -1
suy ra: x(x+1) – (x – 1).(x -1) = 5 0,25 x2 + x - x2 + 2x – 1= 5 3.x = 6 0,25 x = 2 (tmđkxđ)
Vậy phương trình đã cho có nghiệm là: x = 2. 0,25
b) 5(x − 3) + 7 2(x + 3) −11 0,25
5x −15 + 7 2x + 6 −11
5x − 2x 6 −11+15 − 7 0,25 3x 6 −11+15− 7 0,25 3x 3 x 1
Vậy nghiệm của bất phương trình là x 1 Bài 4 9 +12 21 21 0,25
a) Thay x = 9 (TMĐK) vào A ta có: A = = = (2,0 điểm) 9 −1 3 −1 2 21 0,25 Vậy x = 9 thì A = 2
b) Điều kiện: x 0, x 1 0,5 3 + x −1 1 x + 2 x +1 x + 2 B = : = = 0,5 ( x −1)( x +1) x +1 ( x −1)( x +1) 1 x −1 x + 2 0,25 Vậy B = với x 0, x 1. x −1 0,25 A x +12 x −1 x +12 c) Ta có: M = = = B x −1 x + 2 x + 2
Vì x + 2 >0 nên M < 0 khi x + 12 < 0 suy ra x < - 12 (ktmđk)
Vậy không có giá trị nào của x thỏa mãn đề bài. Bài 5
Xét DABC vuông tại C ta có: 0,75 (1điểm) = . tan = 4, 5. tan 35o BC A C A » 3, 2 (m) 0,25
Vậy chiều cao của cây xanh khoảng 3,2m Trang 20




