






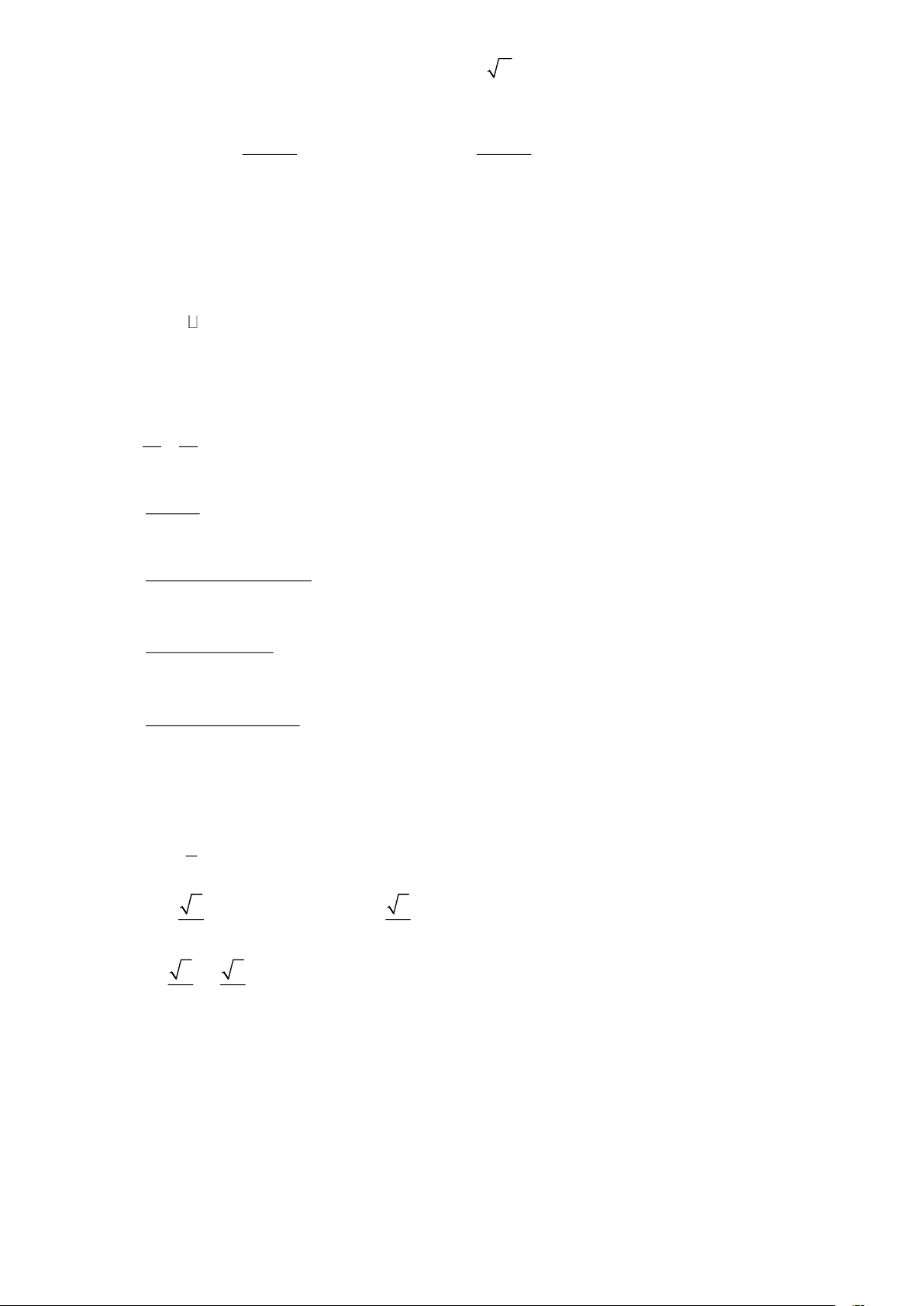






Preview text:
PHÒNG GIÁO DỤC & ĐÀO TẠO …
ĐỀ KIỂM TRA GIỮA HỌC KÌ 2 TRƯỜNG …
MÔN: TOÁN – LỚP 9 ĐỀ SỐ 01 NĂM HỌC: 2025-2026 Thời gian: 90 phút
(không kể thời gian giao đề)
A. TRẮC NGHIỆM (7,0 điểm)
Phần 1. Câu trắc nghiệm nhiều phương án lựa chọn (3,0 điểm)
Trong mỗi câu hỏi từ câu 1 đến câu 12, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm. Câu 1. Hàm số 2
y = ax (a 0) xác định với
A. mọi giá trị x .
B. mọi giá trị x .
C. mọi giá trị x . D. mọi giá trị * x . Câu 2. Cho hàm số 2 y = 3
− x . Giá trị của y ứng với giá trị của x = −2 là A. −6. B. 6. C. −12. D. 12.
Câu 3. Điểm đối xứng với điểm có tọa độ (−a; b) qua trục Oy là A. ( ; b − a). B. (− ; b a). C. (a; b). D. (a; − b).
Câu 4. Phương trình nào sau đây không phải là phương trình bậc hai một ẩn? 3 A. 2 5x − 4 = 0. B. 2 x − x = 0. 5 C. 2
2x + (1− 3) x − 3 = 0. D. 2
0x + 7x + 5 = 0.
Câu 5. Phương trình 2
2x + 2 = 0 là phương trình bậc hai một ẩn có các hệ số a, b, c lần lượt là A. 2, 2, 0. B. 2, 0, 2. C. 0, 2, 2. D. 2, 0, 0.
Câu 6. Phương trình 2
ax + bx + c = 0 (a 0) có biệt thức 2 = b − 4 .
ac Phương trình này có hai nghiệm phân biệt khi A. 0. B. = 0. C. 0. D. 0.
Câu 7. Phương trình 2
x + 3x −1 = 0 có các nghiệm là 3 + 13 3 − + 13 3 + 13 3 − + 13 A. x = ; x = . B. x = − ; x = − . 1 2 2 2 1 2 2 2 3 + 13 3 − + 13 3 + 13 C. x = − ; x = . D. x = x = . 1 2 2 2 1 2 2
Câu 8. Nhận định nào sau đây là sai?
A. Trong một đường tròn, góc nội tiếp chắn nửa đường tròn là góc vuông.
B. Trong một đường tròn, hai góc nội tiếp chắn hai cung bằng nhau thì bằng nhau.
C. Trong một đường tròn, hai góc nội tiếp cùng chắn một cung thì bằng nhau.
D. Trong một đường tròn, hai góc nội tiếp bằng nhau thì cùng chắn một cung. Trang 1
Câu 9. Tâm đường tròn nội tiếp của một tam giác là giao điểm của A. ba đường trung trực. B. ba đường phân giác.
C. ba đường trung tuyến. D. ba đường cao.
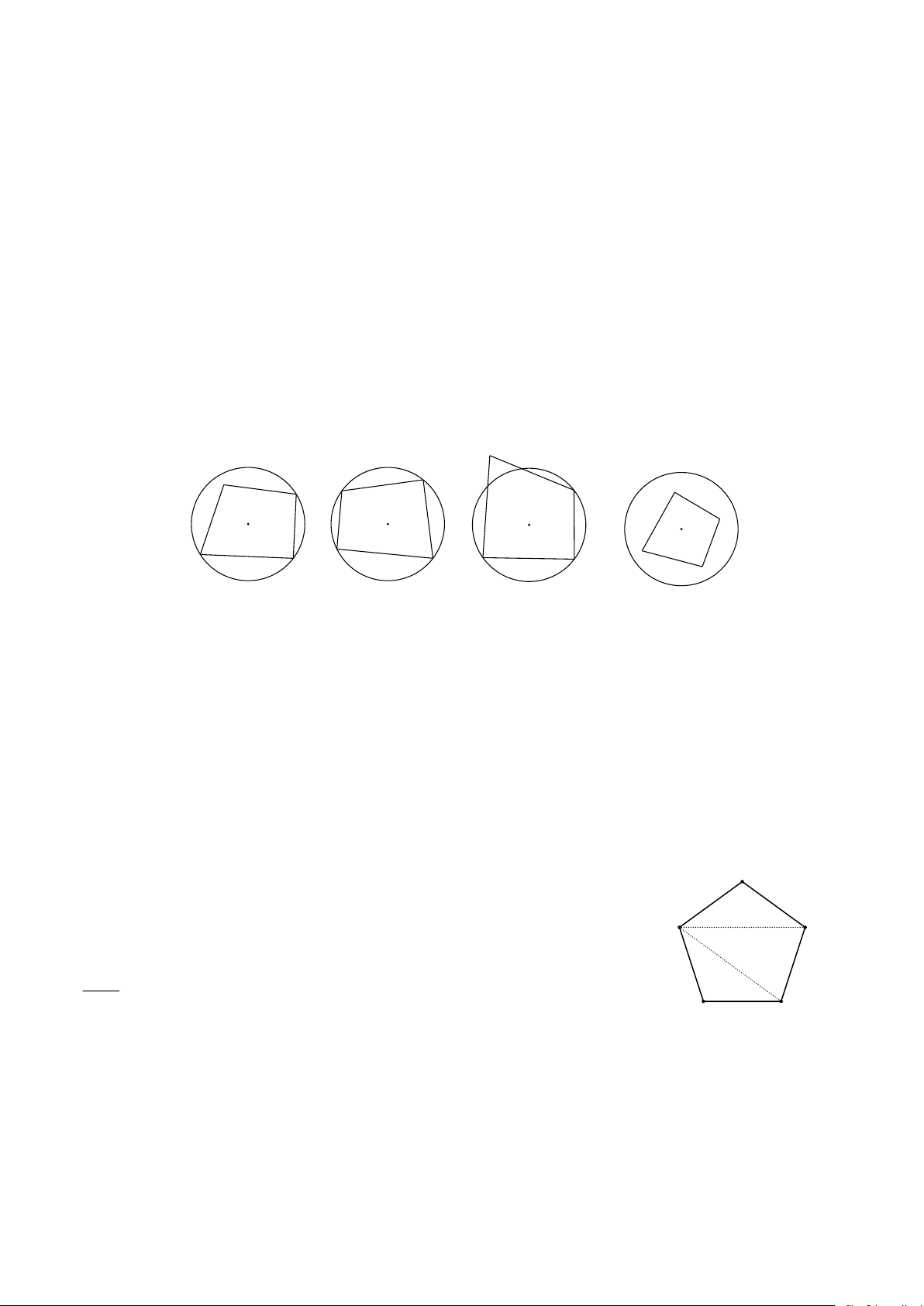
Câu 10. Tứ giác nào dưới đây là tứ giác nội tiếp? E N A M F R B S Q V D C P H G T A. ABC . D B. MNP . Q C. EFGH. D. RSTV .
Câu 11. Mỗi góc của ngũ giác đều có số đo là A. 36 . B. 72 . C. 108 . D. 144 .
Câu 12. Cho hình vuông ABCD có tâm O. Có bao nhiêu phép quay thuận chiều tâm O biến hình vuông thành chính nó? A. 1. B. 2. C. 3. D. 4.
Phần 2. Câu trắc nghiệm đúng sai (2,0 điểm)
Trong câu 13 và câu 14, hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d). Câu 13. Cho hàm số 2 y = 0 − ,5x .
a) Đồ thị hàm số có trục đối xứng là . Ox
b) Đồ thị hàm số nằm phía trên trục hoành.
c) Đồ thị hàm số đi qua điểm ( 3 − ; − 4,5).
d) Giá trị lớn nhất của hàm số là 0.
Câu 14. Cho tứ giác ABCD có ABC = ADC = 90 nội tiếp đường tròn tâm O. a) ACB = . ADB
b) Tâm O là giao điểm ba đường phân giác của tam giác ABC.
c) BAD + BCD = 200 . 1
d) Bán kính đường tròn ngoại tiếp tam giác BCD bằng AC. 2
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn (2,0 điểm)
Trong mỗi câu hỏi từ câu 15 đến câu 18, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày
lời giải chi tiết.
Câu 15. Tìm giá trị nguyên lớn nhất của m để phương trình 2
x − 2x + m = 0 có nghiệm.
Câu 16. Phương trình bậc hai 2 mx + (2m + )
1 x + 3 = 0 có một nghiệm là x = −1. Tìm giá trị 1
nghiệm còn lại (viết dưới dạng số thập phân) của phương trình.
Câu 17. Cho tứ giác ABCD nội tiếp đường tròn (O), biết ABC = 106 .
Số đo cung ADC là bao Trang 2 nhiêu độ?
Câu 18. Cho tam giác đều ABC. Góc quay của phép quay thuận chiều kim đồng hồ với tâm A biến
điểm B thành điểm C là bao nhiêu độ?
B. TỰ LUẬN (3,0 điểm)
Bài 1. (1,5 điểm)
1. Giải bài toán sau bằng cách lập phương trình:
Người ta trộn 8 g chất lỏng I với 6 g chất lỏng II có khối lượng riêng nhỏ hơn 0, 2 g/cm3 để
được một hỗn hợp có khối lượng riêng là 0,7 g/cm3 (quá trình trộn lẫn không xảy ra phản ứng hóa
học). Tìm khối lượng riêng của mỗi chất lỏng.
2. Cho phương trình 2 2
x − 2mx − 2m −1 = 0 (m là tham số). Tìm m để phương trình đã cho có x x
hai nghiệm x , x thỏa mãn 1 2 + = 3. − 1 2 x x 2 1
Bài 2. (1,5 điểm) Cho tam giác ABC nhọn. Ba đường cao AI, BK, CL cắt nhau tại H. Chứng minh:
1. Tứ giác BIHL là các tứ giác nội tiếp.
2. AKL = IKC.
3. H là tâm đường tròn nội tiếp tam giác IK . L -----HẾT----- Trang 3
ĐÁP ÁN & HƯỚNG DẪN ĐỀ KIỂM TRA GIỮA HỌC KÌ 2 – TOÁN 9 – KẾT NỐI TRI THỨC
PHÒNG GIÁO DỤC & ĐÀO TẠO …
ĐÁP ÁN & HƯỚNG DẪN GIẢI TRƯỜNG …
KIỂM TRA GIỮA HỌC KÌ 2 ĐỀ SỐ 01
MÔN: TOÁN – LỚP 9 NĂM HỌC: 2024-2025
A. TRẮC NGHIỆM (7,0 điểm)
Bảng đáp án trắc nghiệm: Câu 1 2 3 4 5 6 7 8 9 10 11 12 Đáp án A C C D B C C D B B C D Câu
13a 13b 13c 13d 14a 14b 14c 14d 15 16 17 18 Đáp án S S Đ Đ Đ S S Đ 1 –1,5 148 300
Hướng dẫn giải chi tiết
Phần 1. Câu trắc nghiệm nhiều phương án lựa chọn (3,0 điểm) Câu 1. Hàm số 2
y = ax (a 0) xác định với
A. mọi giá trị x .
B. mọi giá trị x .
C. mọi giá trị x . D. mọi giá trị * x . Hướng dẫn giải
Đáp án đúng là: A Hàm số 2
y = ax (a 0) xác định với mọi giá trị x . Câu 2. Cho hàm số 2 y = 3
− x . Giá trị của y ứng với giá trị của x = −2 là A. −6. B. 6. C. −12. D. 12. Hướng dẫn giải
Đáp án đúng là: C
Thay x = −2 vào hàm số 2
y = −3x ta được: y = − (− )2 3 2 = 3 − 4 = 1 − 2.
Câu 3. Điểm đối xứng với điểm có tọa độ (−a; b) qua trục Oy là A. ( ; b − a). B. (− ; b a). C. (a; b). D. (a; − b). Hướng dẫn giải
Đáp án đúng là: C
Hai điểm (a; b) và (−a; b) đối xứng với nhau qua trục tung . Oy
Câu 4. Phương trình nào sau đây không phải là phương trình bậc hai một ẩn? 3 A. 2 5x − 4 = 0. B. 2 x − x = 0. 5 C. 2
2x + (1− 3) x − 3 = 0. D. 2
0x + 7x + 5 = 0. Trang 4 Hướng dẫn giải
Đáp án đúng là: D
Phương trình bậc hai một ẩn là phương trình có dạng 2
ax + bx + c = 0 (a 0). Như vậy phương trình 2
0x + 7x + 5 = 0 không là phương trình bậc hai một ẩn.
Câu 5. Phương trình 2
2x + 2 = 0 là phương trình bậc hai một ẩn có các hệ số a, b, c lần lượt là A. 2, 2, 0. B. 2, 0, 2. C. 0, 2, 2. D. 2, 0, 0. Hướng dẫn giải
Đáp án đúng là: B Phương trình 2
2x + 2 = 0 viết lại thành 2
2x + 0x + 2 = 0 là phương trình bậc hai một ẩn có các hệ số
a, b, c lần lượt là: a = 2, b = 0, c = 2.
Câu 6. Phương trình 2
ax + bx + c = 0 (a 0) có biệt thức 2 = b − 4 .
ac Phương trình này có hai nghiệm phân biệt khi A. 0. B. = 0. C. 0. D. 0. Hướng dẫn giải
Đáp án đúng là: C Phương trình 2
ax + bx + c = 0 (a 0) có hai nghiệm phân biệt khi 0.
Câu 7. Phương trình 2
x + 3x −1 = 0 có các nghiệm là 3 + 13 3 − + 13 3 + 13 3 − + 13 A. x = ; x = . B. x = − ; x = − . 1 2 2 2 1 2 2 2 3 + 13 3 − + 13 3 + 13 C. x = − ; x = . D. x = x = . 1 2 2 2 1 2 2 Hướng dẫn giải
Đáp án đúng là: C
Sử dụng máy tính cầm tay, ta lần lượt bấm các phím: MODE 5 3 1 = 3 = − 1 = = 3 − + 13
Trên màn hình hiện lên kết quả: x =
, ấn thêm phím = , màn hình hiện kết quả 1 2 3 − − 13 x = . 2 2 3 − − 13 3 + 13 Ta thấy x = = −
và vai trò của x , x là như nhau nên ta chọn phương án C. 2 2 2 1 2
Câu 8. Nhận định nào sau đây là sai?
A. Trong một đường tròn, góc nội tiếp chắn nửa đường tròn là góc vuông.
B. Trong một đường tròn, hai góc nội tiếp chắn hai cung bằng nhau thì bằng nhau.
C. Trong một đường tròn, hai góc nội tiếp cùng chắn một cung thì bằng nhau. Trang 5
D. Trong một đường tròn, hai góc nội tiếp bằng nhau thì cùng chắn một cung. Hướng dẫn giải
Đáp án đúng là: D
Trong một đường tròn, hai góc nội tiếp bằng nhau thì cùng chắn một cung hoặc hai cung bằng nhau.
Do đó nhận định ở phương án D là sai.
Câu 9. Tâm đường tròn nội tiếp của một tam giác là giao điểm của A. ba đường trung trực. B. ba đường phân giác.
C. ba đường trung tuyến. D. ba đường cao. Hướng dẫn giải
Đáp án đúng là: B
Tâm đường tròn nội tiếp của một tam giác là giao điểm của ba đường phân giác.
Câu 10. Tứ giác nào dưới đây là tứ giác nội tiếp? E N A M F R B S Q V D C P H G T A. ABC . D B. MNP . Q C. EFGH. D. RSTV . Hướng dẫn giải
Đáp án đúng là: B
Tứ giác MNPQ có tất cả các đỉnh đều nằm trên một đường tròn nên là tứ giác nội tiếp.
Câu 11. Mỗi góc của ngũ giác đều có số đo là A. 36 . B. 72 . C. 108 . D. 144 . Hướng dẫn giải
Đáp án đúng là: C
Ngũ giác đều được chia làm 3 tam giác nên có tổng số đo các góc là: 3180 = 540 .
Ngũ giác đều có 5 góc bằng nhau nên mỗi góc của ngũ giác đều có số đo là: 540 =108 . 5
Câu 12. Cho hình vuông ABCD có tâm O. Có bao nhiêu phép quay thuận chiều tâm O biến hình vuông thành chính nó? A. 1. B. 2. C. 3. D. 4. Hướng dẫn giải
Đáp án đúng là: D
Có bốn phép quay thuận chiều tâm O giữ nguyên hình vuông ABCD với lần lượt nhận các giá trị 90 ; 180 ; 270 ; 360 . Trang 6
Phần 2. Câu trắc nghiệm đúng sai (2,0 điểm) Câu 13. Cho hàm số 2 y = 0 − ,5x .
a) Đồ thị hàm số có trục đối xứng là . Ox
b) Đồ thị hàm số nằm phía trên trục hoành.
c) Đồ thị hàm số đi qua điểm ( 3 − ; − 4,5).
d) Giá trị lớn nhất của hàm số là 0. Hướng dẫn giải Đáp án: a) Sai. b) Sai. c) Đúng. d) Đúng. Xét hàm số 2 y = 0 − ,5x .
⦁ Đồ thị hàm số có trục đối xứng là .
Oy Do đó ý a) là sai.
⦁ Hàm số có hệ số a = −0,5 0 nên đồ thị hàm số nằm phía dưới trục hoành. Do đó ý b) là sai.
⦁ Thay x = −3 vào hàm số, ta được: y = − (− )2 0,5 3 = 4 − ,5.
Như vậy, đồ thị hàm số 2 y = 0
− ,5x đi qua điểm ( 3
− ; − 4,5). Do đó ý c) là đúng.
⦁ Đồ thị có đỉnh là gốc tọa độ O (0; 0) mà a = −0,5 0 nên điểm O (0; 0) là điểm cao nhất của đồ
thị hàm số. Như vậy giá trị lớn nhất của hàm số là 0. Do đó ý d) là đúng.
Câu 14. Cho tứ giác ABCD có ABC = ADC = 90 nội tiếp đường tròn tâm O. a) ACB = . ADB
b) Tâm O là giao điểm ba đường phân giác của tam giác ABC.
c) BAD + BCD = 200 . 1
d) Bán kính đường tròn ngoại tiếp tam giác BCD bằng AC. 2 Hướng dẫn giải
Đáp án: a) Đúng. b) Sai. c) Sai. d) Đúng.
⦁ Tứ giác ABCD nội tiếp đường tròn (O) nên ACB = ADB (hai B
góc nội tiếp cùng chắn cung AB). Do đó ý a) là đúng.
⦁ Vì tam giác ABC nội tiếp đường tròn (O) nên tâm O là giao A O C
điểm ba đường trung trực của tam giác ABC. Do đó ý b) là sai. ⦁ Tứ giác
ABCD nội tiếp đường tròn (O) nên D
BAD + BCD = 180 . Do đó ý c) là sai.
⦁ Tam giác ABC vuông tại B và tam giác ADC vuông tại D nên các điểm ,
A B, C, D nằm trên
đường tròn đường kính AC. Như vậy tam giác BCD nội tiếp đường tròn đường kính AC, khi đó 1
bán kính đường tròn này là AC. Do đó ý d) là đúng. 2 Trang 7
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn (2,0 điểm)
Câu 15. Tìm giá trị nguyên lớn nhất của m để phương trình 2
x − 2x + m = 0 có nghiệm. Hướng dẫn giải Đáp số: 1. Phương trình 2
x − 2x + m = 0 có = (− )2 1 −1 m = 1− . m Phương trình 2
x − 2x + m = 0 có nghiệm khi 0 hay 1− m 0, suy ra m 1.
Như vậy, giá trị nguyên lớn nhất của m thỏa mãn yêu cầu đề bài là m = 1.
Câu 16. Phương trình bậc hai 2 mx + (2m + )
1 x + 3 = 0 có một nghiệm là x = −1. Tìm giá trị 1
nghiệm còn lại (viết dưới dạng số thập phân) của phương trình. Hướng dẫn giải
Đáp số: −1,5. Để phương trình 2 mx + (2m + )
1 x + 3 = 0 nhận x = −1 là nghiệm thì x = −1 thỏa mãn phương 1 1
trình đó, tức là: m (− )2 1 + (2m + ) 1 (− ) 1 + 3 = 0
m − 2m −1+ 3 = 0 −m = −2 m = 2.
Thay m = 2 vào phương trình đã cho, ta được phương trình 2
2x + 5x + 3 = 0.
Sử dụng máy tính cầm tay, ta lần lượt bấm các phím: MODE 5 3 2 = 5 = 3 = = 3
Trên màn hình hiện lên kết quả: x = −1, ấn thêm phím = , màn hình hiện kết quả x = − . 1 2 2
Vậy nghiệm còn lại cần tìm là −1,5.
Câu 17. Cho tứ giác ABCD nội tiếp đường tròn (O), biết ABC =106 .
Số đo cung ADC là bao nhiêu độ? Hướng dẫn giải A Đáp số: 148. D O
Vì tứ giác ABCD nội tiếp nên ABC + ADC = 180 (tổng hai góc đối của 106° B tứ giác nội tiếp) C
Suy ra ADC = 180 − ABC = 180 −106 = 74 .
Khi đó, sđ ADC = 2ADC = 274 = 148 (số đo cung gấp hai lần số đo góc nội tiếp chắn cung đó).
Câu 18. Cho tam giác đều ABC. Góc quay của phép quay thuận chiều kim đồng hồ với tâm A biến
điểm B thành điểm C là bao nhiêu độ? Hướng dẫn giải Đáp số: 300. Trang 8
Xét ABC đều có AB = AC và BAC = 60 .
Phép quay thuận chiều kim đồng hồ với tâm A biến điểm B thành A
điểm C tạo nên cung lớn BC có số đo là:
360 − sđBC = 360 − BAC = 360 − 60 = 300 . B C
Vậy góc quay của phép quay đó là 300 .
B. TỰ LUẬN (3,0 điểm)
Bài 1. (1,5 điểm)
1. Giải bài toán sau bằng cách lập phương trình:
Người ta trộn 8 g chất lỏng I với 6 g chất lỏng II có khối lượng riêng nhỏ hơn 0, 2 g/cm3 để
được một hỗn hợp có khối lượng riêng là 0,7 g/cm3 (quá trình trộn lẫn không xảy ra phản ứng hóa
học). Tìm khối lượng riêng của mỗi chất lỏng.
2. Cho phương trình 2 2
x − 2mx − 2m −1 = 0 (m là tham số). Tìm m để phương trình đã cho có x x
hai nghiệm x , x thỏa mãn 1 2 + = 3. − 1 2 x x 2 1 Hướng dẫn giải
1. Gọi x (g/cm3) là khối lượng riêng của chất lỏng I (x 0,2).
Khi đó, khối lượng riêng của chất lỏng II là x − 0, 2 (g/cm3). 8
Thể tích của chất lỏng I là: (cm3). x 6
Thể tích của chất lỏng II là: (cm3). x − 0, 2
Khối lượng hỗn hợp sau khi trộn là: 8 + 6 = 14 (g). 14
Thể tích của hỗn hợp sau khi trộn là: = 20 (cm3). 0,7 8 6 Ta có phương trình: + = 20 . x x − 0, 2 Giải phương trình: 8 6 + = 20 x x − 0, 2 8(x − 0,2) 6x 20x (x − 0,2) + =
x (x − 0,2) x(x − 0,2) x (x − 0,2)
8( x − 0, 2) + 6x = 20x( x − 0, 2) 2
8x −1,6 + 6x = 20x − 4x 2
20x −18x +1,6 = 0 2
50x − 45x + 4 = 0 Trang 9
Phương trình có = (− )2
45 − 450 4 = 1 225 0 và = 35.
Phương trình có hai nghiệm phân biệt là: 45 + 35 45 − 35 x =
= 0,8 (thỏa mãn); x = = 0,1 (không thỏa mãn). 1 250 2 250
Vậy khối lượng riêng của chất lỏng I là 0,8 g/cm3; khối lượng riêng của chất lỏng I là 0,8 − 0, 2 = 0,6 (g/cm3).
2. Xét phương trình 2 2
x − 2mx − 2m −1 = 0 có = (−m)2 − ( 2 − m − ) 2 2 2 1 2
1 = m + 2m +1 = 3m +1.
Với mọi m ta thấy 2
3m +1 0 nên 0.
Do đó, phương trình đã cho có hai nghiệm phân biệt x , x với mọi giá trị của . m 1 2
Theo định lí Viète, ta có: 2 x + x = 2 ; m x x = 2 − m −1. 1 2 1 x x x Ta có: 1 2 + = 3 − x x 2 1 2 2 x + x 1 2 = 3 − x x 1 2 2 2
x + 2x x + x − 2x x 1 1 2 2 1 2 = 3 − x x 1 2
(x + x )2 −2x x 1 2 1 2 = 3 − x x 1 2 (2m)2 −2( 2 2 − m − ) 1 = 3 − 2 2 − m −1 2 2 2
4m + 4m + 2 = 6m + 3 2 2m = 1 2 1 m = 2 2 2 m =
(thỏa mãn) hoặc m = − (thỏa mãn). 2 2 2 2 Vậy m ; − . 2 2
Bài 2. (1,5 điểm) Cho tam giác ABC nhọn. Ba đường cao AI, BK, CL cắt nhau tại H. Chứng minh:
1. Tứ giác BIHL là các tứ giác nội tiếp.
2. AKL = IKC.
3. H là tâm đường tròn nội tiếp tam giác IK . L Hướng dẫn giải Trang 10
1. Vì AI , CL là đường cao của tam giác ABC nên AI ⊥ BC và A CL ⊥ .
AB Do đó AIB = BLC = 90 hay HIB = BLH = 90 .
Suy ra hai điểm I, L cùng nằm trên đường tròn đường kính K BH. H L O
Vậy bốn điểm B, I, L, H cùng nằm trên đường tròn đường kính
BH hay tứ giác BIHL nội tiếp đường tròn đường kính BH. B I C
2. Chứng minh tương tự câu 1, ta có tứ giác CIHK nội tiếp
đường tròn đường kính CH.
Suy ra IKC = IHC (hai góc nội tiếp cùng chắn cung IC)
Chứng minh tương tự, ta có tứ giác AKHL nội tiếp đường tròn đường kính AH nên AKL = AHL
(hai góc nội tiếp cùng chắn cung AL).
Lại có IHC = AHL (đối đỉnh)
Do đó AKL = IKC.
3. Ta có AKL + LKB = 90 và IKC + IKB = 90
Mà AKL = IKC (câu 2) nên LKB = IKB hay KB tức KH là tia phân giác của IK . L
Chứng minh tương tự, ta có IH là tia phân giác của LIK.
Xét tam giác IKL có KH , IH là hai đường phân giác của tam giác cắt nhau tại H nên H là tâm
đường tròn nội tiếp tam giác IK . L -----HẾT-----
PHÒNG GIÁO DỤC & ĐÀO TẠO …
ĐỀ KIỂM TRA GIỮA HỌC KÌ 2 TRƯỜNG …
MÔN: TOÁN – LỚP 9 ĐỀ SỐ 02 NĂM HỌC: 2024-2025 Thời gian: 90 phút
(không kể thời gian giao đề)
A. TRẮC NGHIỆM (7,0 điểm)
Phần 1. Câu trắc nghiệm nhiều phương án lựa chọn (3,0 điểm)
Trong mỗi câu hỏi từ câu 1 đến câu 12, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm.
Câu 1. Trong các hàm số sau đây, hàm số nào có dạng 2
y = ax (a 0) ? − 2 2 A. 2 1 y = x . B. = x y . C. y = . D. 2 y = 2 x . 2 0 2 x
Câu 2. Đồ thị của hàm số 2
y = ax (a 0) luôn đi qua điểm nào sau đây? A. (0; ) 1 . B. (1; 0). C. (0; 0). D. (1; ) 1 . Trang 11
Câu 3. Kết luận nào sau đây là sai khi nói về đồ thị của hàm số 2
y = ax (a 0)?
A. Đồ thị hàm số nhận trục tung làm trục đối xứng.
B. Với a 0 đồ thị nằm phía trên trục hoành và O là điểm cao nhất của đồ thị.
C. Với a 0 đồ thị nằm phía dưới trục hoành và O là điểm cao nhất của đồ thị. D. Nếu điểm ( ;
x y) thuộc đồ thị hàm số thì điểm (− ;
x y) cũng thuộc đồ thị hàm số.
Câu 4. Cho phương trình bậc hai 2 x − 2(2m + )
1 x + 2m = 0, hệ số b của phương trình là A. 2(2m + ) 1 . B. 2m +1. C. 2m . D. 2 − (2m + ) 1 .
Câu 5. Giá trị của m để phương trình 2 mx − 2(m − )
1 x + m +1 = 0 là phương trình bậc hai một ẩn x là A. m 0 . B. m 1. C. m −1.
D. m 0, m 1 và m −1.
Câu 6. Cho phương trình bậc hai ẩn x có 0. Khẳng định nào sau đây là đúng khi nói về số
nghiệm của phương trình?
A. Phương trình vô nghiệm.
B. Phương trình có nghiệm kép.
C. Phương trình có nghiệm.
D. Phương trình có hai nghiệm phân biệt.
Câu 7. Phương trình 2
2x −17x +1 = 0 có tổng và tích hai nghiệm lần lượt là 17 − 1 17 1 A. và . B. 17 và 2. C. và . D. −17 và 2. 2 2 2 2
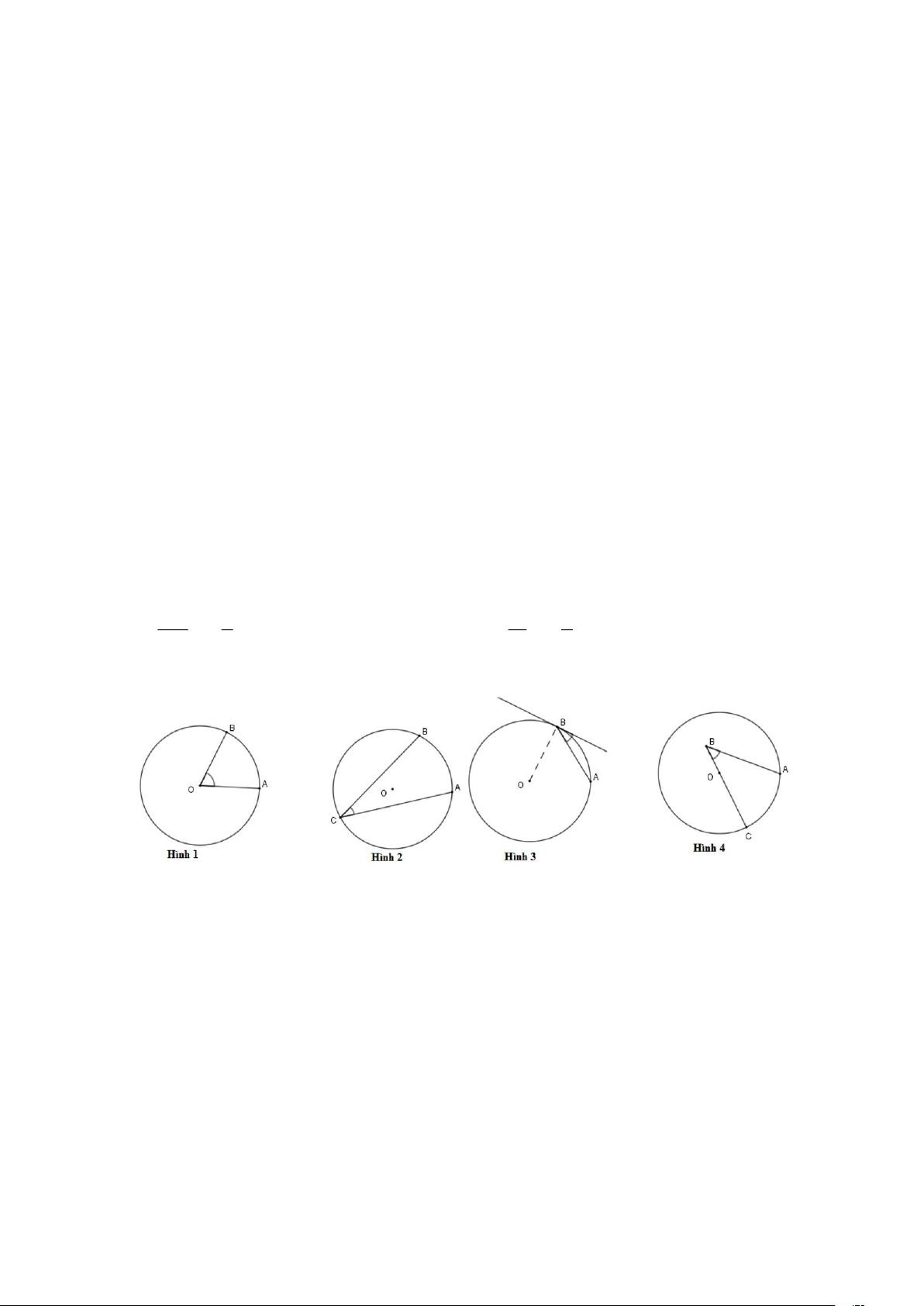
Câu 8. Hình nào dưới đây biểu diễn góc nội tiếp? A. Hình 1. B. Hình 2. C. Hình 3. D. Hình 4.
Câu 9. Tâm đường tròn ngoại tiếp của một tam giác là giao điểm của A. ba đường trung trực. B. ba đường phân giác.
C. ba đường trung tuyến. D. ba đường cao.
Câu 10. Khẳng định nào sau đây là đúng?
A. Tứ giác có 4 đỉnh nằm trên một đường thẳng là tứ giác nội tiếp.
B. Tứ giác có 3 đỉnh nằm trên một đường tròn là tứ giác nội tiếp.
C. Tứ giác có 4 đỉnh nằm trong một đường tròn là tứ giác nội tiếp.
D. Tứ giác có 4 đỉnh nằm trên một đường tròn là tứ giác nội tiếp.
Câu 11. Khẳng định nào sau đây là không đúng về ngũ giác đều? A. Có 6 cạnh bằng nhau.
B. Các góc ở đỉnh bằng nhau. C. Các cạnh bằng nhau.
D. Mỗi góc ở đỉnh bằng 108 . Trang 12
Câu 12. Cho hình vuông ABCD có tâm O. Phép quay ngược chiều 180 tâm O biến điểm A thành điểm A. A . B. B. C. C. D. . D
Phần 2. Câu trắc nghiệm đúng sai (2,0 điểm)
Trong câu 13 và câu 14, hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d).
Câu 13. Diện tích của đường tròn bán kính R (cm) được cho bởi công thức 2 2
S = R (cm ).
a) Khi bán kính đường tròn R = 1 cm thì diện tích của đường tròn bằng 2 (cm ).
b) Nếu diện tích của đường tròn bằng 2 S =
(cm ) thì bán kính của đường tròn là 2 R = 0,5 (cm). c) Công thức 2
S = R là một hàm số có biến R và đồ thị hàm số đi qua điểm (0;0).
d) Diện tích của đường tròn không có giá trị lớn nhất.
Câu 14. Cho ngũ giác đều ABCDE nội tiếp đường tròn tâm O.
a) ABC = ADC = AEC.
b) Tâm O là giao điểm ba đường trung trực của tam giác ABC.
c) Có 4 tứ giác nội tiếp đường tròn (O;OA).
d) Đường kính đường tròn ngoại tiếp tam giác ABD lớn hơn . AD
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn (2,0 điểm)
Trong mỗi câu hỏi từ câu 15 đến câu 18, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày
lời giải chi tiết.
Câu 15. Có bao nhiêu giá trị nguyên dương của m để phương trình 2
x − 4x + 3m −11 = 0 có hai nghiệm trái dấu?
Câu 16. Với giá trị nào của m để parabol (P) 2
: y = x và đường thẳng
(d ): y = 5x − m cắt nhau tại hai điểm phân biệt có hoành độ x , x là 1 2 A số nguyên tố? D
Câu 17. Cho hình vẽ bên. Số đo góc ADC bằng bao nhiêu độ? O
Câu 18. Trên mặt phẳng toạ độ Oxy cho A( 2 − ; − 2). Phép quay thuận chiều 60°
90 tâm O biến điểm A thành điểm I. Khi đó, hãy tính 40° B C
tổng bình phương hoành độ và tung độ của điểm I.
B. TỰ LUẬN (3,0 điểm)
Bài 1. (1,5 điểm) Trang 13
1. Giải bài toán sau bằng cách lập phương trình: E
Một mảnh vườn hình chữ nhật ABCD có chu vi A B Khu tiểu c K ảnh hu
và diện tích lần lượt là 70 m và 2 250 m . Người ta trồng hoa
chia mảnh vườn đó thành ba khu vực: khu tiểu cảnh Khu thư giãn
ADE, khu trồng hoa BEDF , khu thư giãn BCF với D C F
BE = DF = 6 m như mô tả ở hình bên.
Người chủ vườn đã thuê người trồng hoa ở khu trồng hoa với chi phí là 50 000 đồng/m2. Tính số
tiền chủ vườn phải trả cho người trồng hoa để trồng hết khu vườn hoa đó.
2. Cho phương trình 2
x − 2x − m = 0. Tìm m để phương trình có hai nghiệm phân biệt x , x 1 2 thỏa mãn 2
4x − 8x + 4 − x x = 2m − 7. 1 1 1 2
Bài 2. (1,5 điểm) Cho hai đường tròn (O) và (O) cắt nhau tại hai điểm phân biệt , A . B Đường
thẳng AO cắt hai đường tròn (O) và (O) lần lượt tại hai điểm C, E (khác điểm ). A Đường thẳng
AO cắt hai đường tròn (O) và (O) lần lượt tại hai điểm D, F (khác điểm ). A Chứng minh:
1. C, B, F thẳng hàng.
2. Tứ giác CDEF nội tiếp đường tròn.
3. A là tâm đường tròn nội tiếp tam giác BDE. -----HẾT----- Trang 14
ĐÁP ÁN & HƯỚNG DẪN ĐỀ KIỂM TRA GIỮA HỌC KÌ 2 – TOÁN 9 – KẾT NỐI TRI THỨC
PHÒNG GIÁO DỤC & ĐÀO TẠO …
ĐÁP ÁN & HƯỚNG DẪN GIẢI TRƯỜNG …
KIỂM TRA GIỮA HỌC KÌ 2 ĐỀ SỐ 02
MÔN: TOÁN – LỚP 9 NĂM HỌC: 2024-2025
A. TRẮC NGHIỆM (7,0 điểm)
Bảng đáp án trắc nghiệm: Câu 1 2 3 4 5 6 7 8 9 10 11 12 Đáp án A C B D A C V B A D A C Câu
13a 13b 13c 13d 14a 14b 14c 14d 15 16 17 18 Đáp án Đ S Đ Đ S Đ Đ Đ 3 6 80 8
Hướng dẫn giải chi tiết
Phần 1. Câu trắc nghiệm nhiều phương án lựa chọn (3,0 điểm)
Câu 1. Trong các hàm số sau đây, hàm số nào có dạng 2
y = ax (a 0) ? − 2 2 A. 2 1 y = x . B. = x y . C. y = . D. 2 y = 2 x . 2 0 2 x Hướng dẫn giải
Đáp án đúng là: A − 1 − 1 − Hàm số 2 1 y = x hay 2 y = x có dạng 2
y = ax với a = 0. 2 2 2
Câu 2. Đồ thị của hàm số 2
y = ax (a 0) luôn đi qua điểm nào sau đây? A. (0; ) 1 . B. (1; 0). C. (0; 0). D. (1; ) 1 . Hướng dẫn giải
Đáp án đúng là: C Đồ thị hàm số 2
y = ax (a 0) luôn đi qua gốc tọa độ là điểm O có tọa độ (0; 0).
Câu 3. Kết luận nào sau đây là sai khi nói về đồ thị của hàm số 2
y = ax (a 0)?
A. Đồ thị hàm số nhận trục tung làm trục đối xứng.
B. Với a 0 đồ thị nằm phía trên trục hoành và O là điểm cao nhất của đồ thị.
C. Với a 0 đồ thị nằm phía dưới trục hoành và O là điểm cao nhất của đồ thị. D. Nếu điểm ( ;
x y) thuộc đồ thị hàm số thì điểm (− ;
x y) cũng thuộc đồ thị hàm số. Hướng dẫn giải
Đáp án đúng là: B
Với a 0 đồ thị nằm phía trên trục hoành và O là điểm thấp nhất của đồ thị.
Câu 4. Cho phương trình bậc hai 2 x − 2(2m + )
1 x + 2m = 0, hệ số b của phương trình là Trang 15 A. 2(2m + )
1 . B. 2m +1. C. 2m . D. 2 − (2m + ) 1 . Hướng dẫn giải
Đáp án đúng là: D
Phương trình bậc hai một ẩn có dạng 2
ax + bx + c = 0 (a 0) .
Do đó, phương trình bậc hai 2 x − 2(2m + )
1 x + 2m = 0, hệ số b của phương trình là 2 − (2m + ) 1 .
Câu 5. Giá trị của m để phương trình 2 mx − 2(m − )
1 x + m +1 = 0 là phương trình bậc hai một ẩn x là A. m 0 . B. m 1. C. m −1.
D. m 0, m 1 và m −1. Hướng dẫn giải
Đáp án đúng là: A
Phương trình bậc hai một ẩn có dạng 2
ax + bx + c = 0 (a 0) . Phương trình 2 mx − 2(m − )
1 x + m +1 = 0 là phương trình bậc hai một ẩn x khi m 0.
Câu 6. Cho phương trình bậc hai ẩn x có 0. Khẳng định nào sau đây là đúng khi nói về số
nghiệm của phương trình?
A. Phương trình vô nghiệm.
B. Phương trình có nghiệm kép.
C. Phương trình có nghiệm.
D. Phương trình có hai nghiệm phân biệt. Hướng dẫn giải
Đáp án đúng là: C
Phương trình bậc hai ẩn x có 0 hay 0 hoặc = 0 nên phương trình có hai nghiệm phân
biệt hoặc có nghiệm kép, tức là phương trình có nghiệm.
Câu 7. Phương trình 2
2x −17x +1 = 0 có tổng và tích hai nghiệm lần lượt là 17 − 1 17 1 A. và . B. 17 và 2. C. và . D. −17 và 2. 2 2 2 2 Hướng dẫn giải
Đáp án đúng là: C Phương trình 2
2x −17x +1 = 0 có = (− )2
17 − 4 21 = 281 0 nên có hai nghiệm phân biệt x , x . 1 2 17 1
Theo định lí Viète, ta có: x + x = ; x x = . 1 2 1 2 2 2
Câu 8. Hình nào dưới đây biểu diễn góc nội tiếp? Trang 16 A. Hình 1. B. Hình 2. C. Hình 3. D. Hình 4. Hướng dẫn giải
Đáp án đúng là: B
Góc nội tiếp là góc có đỉnh nằm trên đường tròn và có hai cạnh chứa hai dây cung của đường tròn đó.
Như vậy, chỉ có hình 2 thỏa mãn.
Câu 9. Tâm đường tròn ngoại tiếp của một tam giác là giao điểm của A. ba đường trung trực. B. ba đường phân giác.
C. ba đường trung tuyến. D. ba đường cao. Hướng dẫn giải
Đáp án đúng là: A
Tâm đường tròn ngoại tiếp của một tam giác là giao điểm của ba đường trung trực.
Câu 10. Khẳng định nào sau đây là đúng?
A. Tứ giác có 4 đỉnh nằm trên một đường thẳng là tứ giác nội tiếp.
B. Tứ giác có 3 đỉnh nằm trên một đường tròn là tứ giác nội tiếp.
C. Tứ giác có 4 đỉnh nằm trong một đường tròn là tứ giác nội tiếp.
D. Tứ giác có 4 đỉnh nằm trên một đường tròn là tứ giác nội tiếp. Hướng dẫn giải
Đáp án đúng là: D
Tứ giác có 4 đỉnh nằm trên một đường tròn là tứ giác nội tiếp.
Câu 11. Khẳng định nào sau đây là không đúng về ngũ giác đều? A. Có 6 cạnh bằng nhau.
B. Các góc ở đỉnh bằng nhau. C. Các cạnh bằng nhau.
D. Mỗi góc ở đỉnh bằng 108 . Hướng dẫn giải
Đáp án đúng là: A
Ngũ giác đều có 5 cạnh bằng nhau, các góc ở đỉnh bằng nhau và mỗi góc bằng 108 .
Câu 12. Cho hình vuông ABCD có tâm O. Phép quay ngược chiều 180 tâm O biến điểm A thành điểm A. A . B. B. C. C. D. . D Hướng dẫn giải A B
Đáp án đúng là: C
Ta có O là tâm hình vuông ABCD nên O là trung điểm của AC, do đó O
OA = OC và AOC = 180 . D C
Như vậy, phép quay ngược chiều 180 tâm O biến điểm A thành điểm C.
Phần 2. Câu trắc nghiệm đúng sai (2,0 điểm)
Câu 13. Diện tích của đường tròn bán kính R (cm) được cho bởi công thức 2 2
S = R (cm ). Trang 17
a) Khi bán kính đường tròn R = 1 cm thì diện tích của đường tròn bằng 2 (cm ).
b) Nếu diện tích của đường tròn bằng 2 S =
(cm ) thì bán kính của đường tròn là 2 R = 0,5 (cm). c) Công thức 2
S = R là một hàm số có biến R và đồ thị hàm số đi qua điểm (0;0).
d) Diện tích của đường tròn không có giá trị lớn nhất. Hướng dẫn giải
Đáp án: a) Đúng. b) Sai. c) Đúng. d) Đúng.
⦁ Khi R = 1 cm, thay vào công thức 2
S = R , ta được 2 2
S = 1 = (cm ). Do đó ý a) là đúng. 2 ⦁ Nếu 2 S =
(cm ), thay vào công thức 2
S = R , ta được 2
= R , suy ra R = (cm) (do 2 2 2 R 0). Do đó ý b) là sai. ⦁ Công thức 2
S = R là một hàm số có biến R và đồ thị hàm số đi qua điểm (0;0). Do đó ý c) là đúng. ⦁ Do hàm số 2
S = R có hệ số a = 0 nên đồ thị của hàm số có điểm thấp nhất là (0; 0) và
không có điểm cao nhất, như vậy diện tích của đường tròn không có giá trị lớn nhất. Do đó ý d) là đúng.
Câu 14. Cho ngũ giác đều ABCDE nội tiếp đường tròn tâm O.
a) ABC = ADC = AEC.
b) Tâm O là giao điểm ba đường trung trực của tam giác ABC.
c) Có 4 tứ giác nội tiếp đường tròn (O;OA).
d) Đường kính đường tròn ngoại tiếp tam giác ABD lớn hơn . AD Hướng dẫn giải Đáp án: a) Sai.
b) Đúng. c) Đúng. d) Đúng.
⦁ Ta có ABC là góc nội tiếp chắn cung nhỏ AC, ADC là hai góc nội A
tiếp chắn cung lớn AC. Nên số đo ABC khác ADC. Do đó ý a) là E B sai. O
⦁ Ngũ giác đều ABCDE nội tiếp đường tròn tâm O nên O là tâm
đường tròn ngoại tiếp tam giác ABC, hay D C
O là giao điểm ba đường
trung trực của tam giác ABC. Do đó ý b) là đúng.
⦁ Có 4 tứ giác nội tiếp đường tròn (O;OA) là: ABCD, ABCE, ACDE, BCDE. Do đó ý c) là đúng.
⦁ Đường tròn (O; OA) đi qua ba điểm ,
A B, D nên ngoại tiếp tam giác .
ABD Như vậy đường kính
của đường tròn ngoại tiếp tam giác ABD bằng 2OA = OA + . OD Trang 18
Xét OAD có OA + OD AD (bất đẳng thức trong tam giác)
Như vậy, đường kính đường tròn ngoại tiếp tam giác ABD lớn hơn .
AD Do đó ý d) là đúng.
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn (2,0 điểm)
Câu 15. Có bao nhiêu giá trị nguyên dương của m để phương trình 2
x − 4x + 3m −11 = 0 có hai nghiệm trái dấu? Hướng dẫn giải Đáp số: 3. Phương trình 2
x − 4x + 3m −11 = 0 có a = 1 0 và c = 3m −11. c
Phương trình có hai nghiệm trái dấu khi tích hai nghiệm là số âm, hay 0 a 3m −11 11 Tức là 0, suy ra m . 1 3
Các giá trị nguyên dương của m thỏa mãn là m 1; 2; 3 .
Vậy có 3 giá trị nguyên dương của m cần tìm.
Câu 16. Với giá trị nào của m để parabol (P) 2
: y = x và đường thẳng (d ) : y = 5x − m cắt nhau tại
hai điểm phân biệt có hoành độ x , x là số nguyên tố? 1 2 Hướng dẫn giải Đáp số: 6.
Phương trình hoành độ giao điểm của (P) và (d ) có dạng 2
x − 5x + m = 0 (1) Ta có: = (− )2
5 − 4 m = 25 − 4 . m
Để parabol (P) cắt đường thẳng (d ) tại hai điểm phân biệt thì phương trình hoành độ giao điểm 25
luôn có hai nghiệm phân biệt, tức là 0 hay 25 − 4m 0 nên m . 4 x + x = 5
Theo định lí Viète ta có 1 2 x x = m 1 2
Vì x , x có giá trị là số nguyên tố nên x , = 2; x = 3, suy ra m = 6. 1 2 1 2
Vậy m = 6 là giá trị cần tìm.
Câu 17. Cho hình vẽ bên. Số đo góc ADC bằng bao nhiêu độ? Hướng dẫn giải A Đáp số: 80. D O
Xét đường tròn (O), ta có ABD = ACD = 60 (hai góc nội tiếp cùng chắn cung AD) 60° 40° B C
Tứ giác ABCD nội tiếp đường tròn nên ADC + ABC = 180
Suy ra ADC = 180 − ABC = 180 − ( ABD + DBC) =180−(60+ 40) = 80 . Trang 19
Câu 18. Trên mặt phẳng toạ độ Oxy cho A( 2
− ; − 2). Phép quay thuận chiều 90 tâm O biến điểm
A thành điểm I. Khi đó, hãy tính tổng bình phương hoành độ và tung độ của điểm I. Hướng dẫn giải Đáp số: 8.
Gọi H là hình chiếu của A trên . Ox Ta có A( 2 − ; − 2) nên y 2 I
OH = AH = –2 = 2. 1
Do đó AOH vuông cân tại H , nên AOH = 45 . H 2 O 1 1 x
Xét AOH vuông tại H , theo định lí Pythagore ta có: 1 2 2 2
OA = OH + AH A 2 Suy ra 2 2 2 2
OA = OH + AH = 2 + 2 = 8 = 2 2.
Gọi I là điểm đối xứng với A qua Ox, do đó I (–2; 2).
Ta cũng chứng minh được HOI = 45 và OI = 2 2.
Như vậy, phép quay thuận chiều 90 tâm O biến điểm A( 2
− ; − 2) thành điểm I (–2; 2).
Tổng bình phương hoành độ và tung độ của điểm I là (− )2 2 2 + 2 = 8.
B. TỰ LUẬN (3,0 điểm)
Bài 1. (1,5 điểm)
1. Giải bài toán sau bằng cách lập phương trình: E
Một mảnh vườn hình chữ nhật ABCD có chu vi A B Khu tiểu c K ảnh hu
và diện tích lần lượt là 70 m và 2 250 m . Người ta trồng hoa
chia mảnh vườn đó thành ba khu vực: khu tiểu cảnh Khu thư giãn
ADE, khu trồng hoa BEDF , khu thư giãn BCF với D C F
BE = DF = 6 m như mô tả ở hình bên.
Người chủ vườn đã thuê người trồng hoa ở khu trồng hoa với chi phí là 50 000 đồng/m2. Tính số
tiền chủ vườn phải trả cho người trồng hoa để trồng hết khu vườn hoa đó.
2. Cho phương trình 2
x − 2x − m = 0. Tìm m để phương trình có hai nghiệm phân biệt x , x 1 2 thỏa mãn 2
4x − 8x + 4 − x x = 2m − 7. 1 1 1 2 Hướng dẫn giải
1. Gọi chiều dài và chiều rộng mảnh vườn lần lượt là x (m) và y (m) ( x 0, y 0).
Vì mảnh vườn có chu vi là 70 m nên ta có phương trình 2( x + y) = 70 hay x + y = 35 .
Vì mảnh vườn có diện tích là 2
250 m nên ta có phương trình xy = 250 .
Ta có: x + y = 35 và xy = 250 và 2
35 − 4 250 = 225 0 nên x, y là nghiệm của phương trình: 2
t − 35t + 250 = 0. Trang 20




