Bộ 5 Đề Luyện Thi Cấp Tốc Tốt Nghiệp THPT 2021 Môn Toán Có Lời Giải Chi Tiết Và Đáp Án-Bộ 1

Bộ 5 đề luyện thi cấp tốc tốt nghiệp THPT 2021 môn toán được biên soạn dưới dạng file PDF gồm 118 trang. Mỗi đề thi là kiến thức từ cơ bản đến nâng cao khác nhau và kèm sẵn đáp án để các em học sinh dễ dàng so sánh kết quả sao cho chuẩn xác nhất. Mời các em tham khảo thêm nhé!

35 18 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

Trang1

Đề 1

ĐỀ LUYỆN THI CẤP TỐC TỐT NGHIỆP THPT NĂM 2021

BÀI THI: TOÁN

Thời gian: 90 phút

Câu1. S cách sp xp 6 bn hc sinh vào 6 gh kê thành hang ngang là

. B.

120

. C.

. D.

720

Câu 2. Din tích ca mt cu có bán kính

3r 

là



. B.



. C.



. D.



Câu 3. m M trong hình v bên biu din s ph

2 4 .zi

4 2 .zi

4 2 .zi

2 4 .zi

Câu 4. cho hàm s

 

y f x

có bng bin thiên sau:

S nghim c

 

20fx

là

Câu5. Trong các hàm s sau, hàm s nào có mt nguyên hàm là hàm s

 

cosF x x

 

cosf x x

. B.

 

sinf x x

. C.

 

cosf x x

. D.

 

sinf x x

Câu6. Cho cp s cng

 

có

3; 7uu

. Công sai ca cp s cng

. B.

. C.

4

. D.

2

Câu 7.  th ca hàm s  có dng cong trong hình bên

Trang2

31y x x   

31y x x  

31y x x   

31y x x  

Câu 8.  th

 

 th 

Hàm s ch bin trong kho

 

;0

 

0;1

 

0;

 

1;0

Câu 9. Phn thc và phn o ca s phc

13zi

lt là:

và

. B.

và

. C.

và

. D.

và

Câu 10. Tp nghim ca b

log 3x 

là

 

;8

. B.





;8

. C.





8;

. D.

 

8;

Câu 11. Th tích ca khi hp ch nhc

,2 ,3a a a

bng

. B.

36a

. C.

. D.

Câu12. 

5r 

 ng sinh

6.l 

Din tích xung quanh ca



12 5S





. B.

20S





. C.

10 5S





. D.

65S





Câu 13. Cho hai s phc

2 3 , 4 6z i z i   

. Tính

z z z

29zi=+

. B.

29zi=-

. C.

29zi= - +

. D.

29zi= - -

Câu 14. Tim cn ngang và tim cng c th hàm s

là

1; 2yx= - =

. B.

1; 2yx==

. C.

1, 2yx= = -

. D.

1; 2yx= - = -

Câu15. Cho hàm s

 

liên t n

 

0;8

, tha mãn

 

d9f x x 



và

 

d6f x x 



. Tính

 

dI f x x



4I 

. B.

3I 

. C.

15I 

. D.

3I 

Câu16. Trong không gian

Oxyz

ng thng

1 2 1

2 3 4

x y z

  





t

 a

 

2; 3; 4u    



. B.

 

1;2;1u 



. C.

 

2; 3;4u   



. D.

 

2;3;4u 



Câu17. Tnh ca hàm s

 

log 2yx

là.





;2

. B.





2;

. C.

 

;2

. D.

 

2;

Trang3

Câu18. Trong không gian

Oxyz

, cho mt phng

 



2 4 1 0x y z   

c

 



 

3;0; 1M 

. B.

 

0;3;1Q

. C.

 

3;0;1P

. D.

 

3;1;0N

Câu19. Trong không gian

Oxyz

, cho mt cu

       

2 2 2

: 1 2 5 16S x y z     

. T tâm và bán

kính ca

 

lt là

 

1;2; 5 , 4IR

. B.

 

1; 2; 5 , 4IR  

. C.

 

1; 2;5 , 4IR

. D.

 

1; 2;5 , 16IR

Câu20. Cho hình chóp

.S ABCD



ABCD

là hình vuông cnh

. Cnh

vuông góc vi mt

ph dài bng

. Th tích khi t din

.S BCD

bng

. B.

. C.

. D.

Câu21. Nghi

2 16

x



là

2x 

. B.

4x 

. C.

1x 

. D.

3x 

Câu22. Cho

0a 

1a 

, giá tr ca

log

bng

. B.



. C.

3

. D.

Câu 23. Trong không gian

Oxyz



 

1; 2;1u 



và

 

2;1;1v 



, góc gi

bng



Câu 24. Th tích ca khi cu có bán kính

là

2.a



4.a



Câu 25. Cho hàm s

 

y f x

có b

Giá tr ci ca hàm s ng

2

. B.

1

. C.

. D.

Câu 26. Gi

là din tích hình phng gii hn bng

, 0, 2, 5.   

y e y x x

M nào









S e dx

. B.







S e dx

. C.





S e dx

. D.





S e dx

Trang4

Câu 27. Cho không gian

Oxyz

  m

 

0;1;2A

  ng thng

: 1 2

d y t







  









2 1 1

x y z







. Vit phng

 





và song song vng

thng

,dd

 

: 3 5 13 0x y z



   

. B.

 

: 2 13 0x y z



   

 

:3 13 0x y z



   

. D.

 

: 3 5 13 0x y z



   

Câu 28. Cho s phc

tha mãn

 

1 3 5z i i  

a

16z 

. B.

4z 

. C.

17z 

. D.

17z 

Câu 29.  u có tt c các cnh bng a. Tính cosin ca góc gia hai

ng thng và

A. B. C. D.

Câu 30. Tp nghim ca b là

A. B. C.

éù

êú

ëû

Câu31. Tích phân

2 1dI x x x



bt

1tx

. M 

I t t



. B.

dI t t



. C.

2dI t t



. D.

2dI t t



Câu 32. Cho

,,a b x

là các s tha mãn

log 2log 3logx a b

. M 



. B.

43x a b

. C.



. D.

x a b

Câu33. Cho hàm s

()y f x

có bng xét du

'( )fx



S m cc tr ca hàm s 

. B.

. C.

. D. 1.

Câu34. Giá tr ln nht ca hàm s

32y x x  

n

 

2;0

bng

. B.

. C.

. D. 2.

Câu 35. Trong không gian

Oxyz

m

(1;2;3), (3; 4;5)AB

không

phng thng

. ' ' 'ABC A B C

'AB

'BC

2 2 1

3 16

x x x+ - -

æ ö æ ö

÷÷

çç

÷÷

çç

÷÷

çç

è ø è ø

æö

èø

( ]

;0 ;

éö

- ¥ È + ¥

( )

;0 ;

æö

- ¥ È + ¥

èø

Trang5

















. B.







  









. C.







  









. D.







  









Câu36. Mt hình tr có chiu cao gp

lt th tích khi tr ng





th tích. Din tích thit din qua trc ca hình tr bng

. B.

. C.

. D.

Câu37. Gi

và

là hai nghim phc c  

2 5 0  zz

. Giá tr ca biu thc

zz

bng

6

. B.

. C.

. D.

Câu38. S m c th hàm s

2 2 1   y x x x

ng thng

1yx

là

. B.

. C.

. D.

Câu39. Bit

a b c

  





vi

là các s hu t. Tính

P a b c  

5P 

. B.

P 

. C.

P 

. D.

P 

Câu40. 

. ' ' ' 'ABCD A B C D



ABCD

là hình vuông cnh bng 2a.

AA' 3a

hình chiu ca

lên mt phng

ABCD

trùng vm

ca

. Gi

m

ca

. Tính khong cách t

n

( ' )A KD

. B.

3 38

. C.

. D.

Câu41. Có bao nhiêu giá tr nguyên ca tham s

thu n

 

10;10

 hàm s

3 3 2020y x x mx   

nghch bin trên khong

 

1;2

. B.

. C.

. D.

Câu42. Ông Bn d nh gi vào ngân hàng mt s tin vi lãi sut

69,%

mt rng, c sau

m tin lãi s c nhp vào vu. Tính s tin ti thiu

(tring,

x 

)

ông Bn g   mua mt chic xe máy có giá tr 32 triu

ng.

A. 224 tring. B. 252 tring. C. 242 tring. D. 225 tring.

Câu 43. Ba bn Tun, An, Bình mi bn vit ngu nhiên lên bng mt s t nhiên thun

 

1;17



1079

4913

. B.

1637

4913

. C.

. D.

1728

4913

Câu 44. Mt cái cc hình tr u cao 20 cm. Trong cng

c, khong cách gic và mc là 12 cm. Ta lt th vào cc nhng viên bi

hình c c dâng lên cao thêm ít nht 2 cm thì cn th vào cc ít nht

bao nhiêu viên bi?

A. 20 viên bi. B. 19 viên bi. C. 18 viên bi. D. 17 viên bi.

Trang6

Câu45. Cho các s th 

và

tha mãn

 

2 2 2

2 2 2 2

5 9.3 5 9 .7 .

x y x y y x   

  

Tìm giá tr nh

nht ca biu thc

2 11xy





6P 

. B.

9P 

. C.

7P 

. D.

8P 

Câu46. Cho t din

.S ABC

và

m thuc các cnh

và

sao cho

3MA SM

2SN NB

()



là mt phng qua

và song song vi

. Kí hiu

()H

và

()H

là các khi

c khi chia khi t din

.S ABC

bi mt phng

()





()H

chm

()H

chm

;

và

lt là th tích ca

()H

và

()H

Tính t s

VV

119

. B.

. C.

. D.

Câu47. Cho hàm s

 





2 2019 2 2020

1 ln 1 sin 3f x a x x bx x     

, vi

,ab

là các s thc và

 

log3

29f 

. Tính

 

log2

3f 

 

log2

33f 

. B.

 

log2

33f   

. C.

 

log2

32f 

. D.

 

log2

32f   

Câu48. Cho hàm s

 

y f x

o hàm liên tc trên



 th hàm s

 

y f x





 bên

Hi hàm s

     

21g x f x x  

ng bin trên khong nào trong các khong sau?

 

3;1

. B.

 

1;3

. C.

 

;3

. D.

 

3; 

Câu 49. Gi

là tp hp tt c các s nguyên

 hàm s

1 19

y x x x m   

có giá tr ln

nhn

 

0;2

t quá

. Tng các phn t ca

là

195

. B.

195

. C.

210

. D.

210

Câu50. Cho hàm s

 

y f x

, hàm s

 

y f x





liên tc trên



 th .

Trang7

B

 

38f x m x x x   

(

là tham s thc) nghii mi

 

0;3x

khi và ch khi

 

0mf

. B.

 

3 24mf

. C.

 

0mf

. D.

 

3 24mf

--------------HT---------------

Trang8

ĐÁP ÁN ĐỀ THI

1.D

2.A

3.C

4.B

5.B

6.A

7.D

8.B

9.C

10.C

11.A

12.D

13.D

14.B

15.D

16.D

17.C

18.C

19.C

20.A

21.A

22.A

23.A

24.B

25.D

26.D

27.A

28.C

29.C

30.C

31.B

32.C

33.A

34.B

35.B

36.D

37.D

38.A

39.D

40.B

41.A

42.D

43.B

44.C

45.D

46.A

47.B

48.B

49.A

50.D

HƯỚNG DẪN GIẢI CHI TIẾT

Câu1. S cách sp xp 6 bn hc sinh vào 6 gh kê thành hang ngang là

. B.

120

. C.

. D.

720

Lời giải

Mi cách xp 6 bn hc sinh vào 6 gh kê thành hang ngang là mt hoán v ca 6.

Vy có

6! 720

cách xp.

Câu 2. Din tích ca mt cu có bán kính

3r 

là



. B.



. C.



. D.



Lời giải

Din tích mt cu

4 4 .9 36 .Sr

  

  

Câu 3. m M trong hình v bên biu din s phc 

2 4 .zi

4 2 .zi

4 2 .zi

2 4 .zi

Lời giải

T hình v c t

 

4,2M

Suy ra

4 2 .zi

Câu 4. cho hàm s

 

y f x

có bng bin thiên sau:

S nghim c

 

20fx

là

Lời giải

Ta có

 

20fx

 

2fx

Trang9

T bng bin thiên suy ra

 

2fx

có 3 nghim.

Câu5. Trong các hàm s sau, hàm s nào có mt nguyên hàm là hàm s

 

cosF x x

 

cosf x x

. B.

 

sinf x x

. C.

 

cosf x x

. D.

 

sinf x x

Lời giải

Ta có :

sin dx cosx x C  



Vy hàm s

 

sinf x x

có mt nguyên hàm là hàm s

 

cosF x x

Câu6. Cho cp s cng

 

có

3; 7uu

. Công sai ca cp s cng

. B.

. C.

4

. D.

2

Lời giải

Ta có:

 

u u n d  

vi

là công sai ca cp s cng

2 7 3 2 2u u d d d      

Câu 7.  th ca hàm s ng cong trong hình bên

31y x x   

31y x x  

31y x x   

31y x x  

Lời giải

Da vào hình dng  th ta nhn thy  th hàm s bc ba

 

( 0)f x ax bx cx d a    

Xét m

 

0;1

là m ca  th hàm s vi trc tung

0x 

c

.0 .0 .0 1a b c d   

1d

Vy t n D.

Câu 8.  th

 

 th 

Trang10

Hàm s ch bin trong kho

 

;0

 

0;1

 

0;

 

1;0

Lời giải

D th ta thc 2 khong nghch bin là

 

;1 

và

 

0;1

Chn  B.

Câu 9. Phn thc và phn o ca s phc

13zi

lt là:

và

. B.

và

. C.

và

. D.

và

Lời giải

Phn thc , phn o ca s phc

z a bi

lt là

,ab

. Chn C.

Câu 10. Tp nghim ca b

log 3x 

là

 

;8

. B.





;8

. C.





8;

. D.

 

8;

Lời giải

log 3 8





   







. Vy tp nghim ca b





8;S   

Câu 11. Th tích ca khi hp ch nhc

,2 ,3a a a

bng

. B.

36a

. C.

. D.

Lời giải

Th tích ca khi hp ch nht là

.2 .3 6 .V a a a a

Câu12. 

5r 

 ng sinh

6.l 

Din tích xung quanh ca



12 5S





. B.

20S





. C.

10 5S





. D.

65S





Lời giải

Din tích xung quanh ca ca hình nón là

. 5.6 6 5 .S rl

  

  

Câu 13. Cho hai s phc

2 3 , 4 6z i z i   

. Tính

z z z

29zi=+

. B.

29zi=-

. C.

29zi= - +

. D.

29zi= - -

Trang11

Lời giải

Ta có

(2 3 ) (4 6 ) 2 9z z z i i i        

Câu 14. Tim cn ngang và tim cng c th hàm s

là

1; 2yx= - =

. B.

1; 2yx==

. C.

1, 2yx= = -

. D.

1; 2yx= - = -

Lời giải

Lý thuyt: Hàm s

,( 0, )

ax b

y c ad bc

cx d



  





1. Tim cn ngang



2. Tim cng



Áp dng tim cn ngang, tim cng cn

t là

1, 2yx

Câu15. Cho hàm s

 

liên t n

 

0;8

, tha mãn

 

d9f x x 



và

 

d6f x x 



. Tính

 

dI f x x



4I 

. B.

3I 

. C.

15I 

. D.

3I 

Lời giải

Ta có:

     

8 5 8

0 0 5

d d df x x f x x f x x

  

Suy ra:

     

8 8 5

5 0 0

d d d 9 6 3f x x f x x f x x    

  

Câu16. Trong không gian

Oxyz

ng thng

1 2 1

2 3 4

x y z

  





t

 a

 

2; 3; 4u    



. B.

 

1;2;1u 



. C.

 

2; 3;4u   



. D.

 

2;3;4u 



Lời giải

T ng thng suy ra

 

2;3;4u 



là vtcp ca d

Câu17. Tnh ca hàm s

 

log 2yx

là.





;2

. B.





2;

. C.

 

;2

. D.

 

2;

Lời giải

u kin

2 0 2xx   

Tnh

 

;2D  

Trang12

Câu18. Trong không gian

Oxyz

, cho mt phng

 



2 4 1 0x y z   

c

 



 

3;0; 1M 

. B.

 

0;3;1Q

. C.

 

3;0;1P

. D.

 

3;1;0N

Lời giải

+ Thay t m

 

3;0; 1M 

t phng

 



c

 

3 2.0 4. 1 1 8VT VP      

. Vy

 





+ Thay t m

 

0;3;1Q

t phng

 



c

0 2.3 4.1 1 3VT VP     

. Vy

 





+ Thay t m

 

3;0;1P

t phng

 



c

3 2.0 4.1 1 0VT VP     

. Vy

 





Câu19. Trong không gian

Oxyz

, cho mt cu

       

2 2 2

: 1 2 5 16S x y z     

. T tâm và bán

kính ca

 

lt là

 

1;2; 5 , 4IR

. B.

 

1; 2; 5 , 4IR  

. C.

 

1; 2;5 , 4IR

. D.

 

1; 2;5 , 16IR

Lời giải

Mt cu

 

có tâm

 

1; 2;5I 

, bán kính

4R 

Câu20. Cho hình chóp

.S ABCD



ABCD

là hình vuông cnh

. Cnh

vuông góc vi mt

ph dài bng

. Th tích khi t din

.S BCD

bng

. B.

. C.

. D.

Lời giải

BCD ABCD

SS

.S BCD

BCD

S SA

. .2

a



Câu21. Nghi

2 16

x



là

2x 

. B.

4x 

. C.

1x 

. D.

3x 

Trang13

Lời giải

Ta có:

2 2 4

2 16 2 2 2 4 2.



       

Câu22. Cho

0a 

1a 

, giá tr ca

log

bng

. B.



. C.

3

. D.

Lời giải

Ta có:

log log .

aa

Câu 23. Trong không gian

Oxyz



 

1; 2;1u 



và

 

2;1;1v 



, góc gi

bng



Lời giải

 

   

2 2 2 2

1. 2 2 .1 1.1

cos ;

1 2 1 . 2 1 1

   

   

     





 

; 120uv 



Vy góc ging



Câu 24. Th tích ca khi cu có bán kính

là

2.a



4.a



Lời giải

Th tích ca khi cu có bán kính

là





Câu 25. Cho hàm s

 

y f x

có b

Giá tr ci ca hàm s ng

2

. B.

1

. C.

. D.

Lời giải

Giá tr ci ca hàm s ng 2.

Trang14

Câu 26. Gi

là din tích hình phng gii hn bng

, 0, 2, 5.   

y e y x x

M nào









S e dx

. B.







S e dx

. C.





S e dx

. D.





S e dx

Lời giải

Din tích hình phng cn tìm là:





S e dx e dx

Câu 27. Cho không gian

Oxyz

  m

 

0;1;2A

  ng thng

: 1 2

d y t







  









2 1 1

x y z







. Vit phng

 





và song song vng

thng

,dd

 

: 3 5 13 0x y z



   

. B.

 

: 2 13 0x y z



   

 

:3 13 0x y z



   

. D.

 

: 3 5 13 0x y z



   

Lời giải

 ng thng

,dd

lt là

   

1; 2;1 ; 2;1; 1aa   

 

Vì mt phng

 



song song vng thng

,dd

nên :

 

; 1;3;5n a a









  

Vt phng

 



cn tìm là:

     

1 0 3 1 5 2 0.

3 5z 13 0.

x y z

     

    

Câu 28. Cho s phc

tha mãn

 

1 3 5z i i  

a

16z 

. B.

4z 

. C.

17z 

. D.

17z 

Lời giải

Ta có:

 

1 3 5 1 4

z i i z i



       



Va

là:

   

1 4 17z     

Câu 29.  u có tt c các cnh bng a. Tính cosin ca góc gia hai

ng thng và

A. B. C. D.

Lời giải

. ' ' 'ABC A B C

'AB

'BC

Trang15

Ta có

Mà

Vy

Câu 30. Tp nghim ca b là

A. B. C.

éù

êú

ëû

Lời giải

Ta có b

Vy tp nghim

Câu31. Tích phân

2 1dI x x x



bt

1tx

. M 

I t t



. B.

dI t t



. C.

2dI t t



. D.

2dI t t



Lời giải

( )

'. '

sin ', ' sin ', '

' . '

AB BC

co AB BC co AB BC

AB BC

uuur uuur

' '; ' 'AB AB BB BC BC CC= + = +

uuur uuur uuur uuur uuur uuur

'. ' . '. '

AB BC AB BC AA CC aÞ = + = - + =

uuur uuur uuur uuur uuur uuur

( )

'. '

sin ', '

2. 2

' . '

AB BC

co AB BC

AB BC

= = =

uuur uuur

2 2 1

3 16

x x x+ - -

æ ö æ ö

÷÷

çç

÷÷

çç

÷÷

çç

è ø è ø

æö

èø

( ]

;0 ;

éö

- ¥ È + ¥

( )

;0 ;

æö

- ¥ È + ¥

èø

2 2 4 2

4 4 3

2 2 4 2 2 3 0 0

3 3 2

x x x

x x x x x x

- - - -

æ ö æ ö

÷÷

çç

³ Û - - ³ - - Û - £ Û £ £

÷÷

çç

÷÷

çç

è ø è ø

éù

êú

ëû







Trang16

Xét tích phân

2 1dI x x x



t

1 d 2 dt x t x x   

Khi

1x 

thì

2t 

, khi

2x 

thì

5t 

Suy ra :

dI t t



Câu 32. Cho

,,a b x

là các s tha mãn

log 2log 3logx a b

. M 



. B.

43x a b

. C.



. D.

x a b

Lời giải

Vi

,,a b x

là các s th

5 1 5 5 5 5 5 5

log 2log 3log log 4log 3log log log log

log log

x a b x a b x a b

       

   

Câu33. Cho hàm s

()y f x

có bng xét du

()fx





S m cc tr ca hàm s 

. B.

. C.

. D. 1.

Lời giải

T bng bin thiên ta thy

()fx



có ba nghi

()fx



i d 

m cc tr.

Câu34. Giá tr ln nht ca hàm s

32y x x  

n

 

2;0

bng

. B.

. C.

. D. 2.

Lời giải

Ta có

33yx





 

1 2;0

0 3 3 0

1 2;0



  



    



   





( 2) 0f 

( 1) 4f 

(0) 2f 

Vy

 

 

2;0

max ( ) 1 4f x f



  

Trang17

Câu 35. Trong không gian

Oxyz

m

(1;2;3), (3; 4;5)AB

không

phng thng

















. B.







  









. C.







  









. D.







  









Lời giải

Ta có

(2; 6;2)AB 



là m 

i



Chng th

hoc

Câu36. Mt hình tr có chiu cao gp

lt th tích khi tr ng





th tích. Din tích thit din qua trc ca hình tr bng

. B.

. C.

. D.

Lời giải

Gi

u cao

3hr

Ta có :

2 2 3

. . . .3 3 1 1V r h r r r r

  

      

và

3h 

Thit din qua trc là hình ch nht có din tích là:

2 . 2.3 6S r h  

Câu37. Gi

và

là hai nghim phc c  

2 5 0  zz

. Giá tr ca biu thc

zz

bng

6

. B.

. C.

. D.

Lời giải

Ta có:

2 5 0

  



   



  





2 2 2 2

1 2 1 2 10       z z i i

Câu38. S m c th hàm s

2 2 1   y x x x

ng thng

1yx

là

. B.

. C.

. D.

Lời giải

 m là:

3 2 3 2

2 2 1 1 2 3 0 0          x x x x x x x x

 th hàm s

2 2 1   y x x x

ng thng

1yx

ct nhau tm

 

0;1

Vy s m là

Câu39. Bit

a b c

  





vi

là các s hu t. Tính

P a b c  

5P 

. B.

P 

. C.

P 

. D.

P 

Trang18

Lời giải

Ta có

 

1 1 1

x x dx x x x x



      









16 4 2

2 3 2

3 3 3

   

   

   

   

4 14

2 3 2

  

Vy

2a 

;

b 

;

c 

. Suy ra

4 14 16

3 3 3

P    

Câu40. 

. ' ' ' 'ABCD A B C D



ABCD

là hình vuông cnh bng 2a.

AA' 3a

hình chiu ca

lên mt phng

ABCD

trùng vm

ca

. Gi

m

ca

. Tính khong cách t

n

( ' )A KD

. B.

3 38

. C.

. D.

Lời giải

ABCD

là hình vuông nên có

IC DK

ti

K

' (1)IH A N

ti H.



DK IC

DK A I











(2)DK IH

T (1) và (2) ta có

( ' )IH A DK

Vy

( ,( ' ))d I A DK IH

Xét tam giác

'A IA

có

' ' 2A I A A AI a  

Xét tam giác

DKC

có

2 2 2

1 1 1

CN CK DC



CN

Xét tam giác

IBC

có

5IC a

IN

Xét tam giác

'A IN

có

2 2 2

1 1 1

'IH IN A I



3 2 3 38

IH  

Câu41. Có bao nhiêu giá tr nguyên ca tham s

thu n

 

10;10

 hàm s

3 3 2020y x x mx   

nghch bin trên khong

 

1;2

. B.

. C.

. D.

Lời giải

3 6 3y x x m



  

Hàm s ch bin trên khong

 

1;2

 

0, 1;2



   yx

Trang19

 

3 6 3 0, 1;2     x x m x

 

2 , 1;2     m x x x

Xét hàm s:

 

( ) 2 , 1;2g x x x x   

( ) 2 2g x x



  

( ) 0 1g x x



  

Bng bin thiên:

1 2

()gx





()gx

Da vào bng bin thiên ta có:

 

2 , 1;2 0m x x x m      

Mà

 

10;10m

nên có

giá tr nguyên ca tham s

th.

Câu42. Ông Bn d nh gi vào ngân hàng mt s tin vi lãi sut

69,%

mt rng, c sau

m tin lãi s c nhp vào vu. Tính s tin ti thiu

(tring,

x 

)

ông Bn g   mua mt chic xe máy có giá tr 32 triu

ng.

A. 224 tring. B. 252 tring. C. 242 tring. D.225 tring.

Lời giải

Gi

là s tin ti thiu mà ông Bn phi g  mua mt chit

69,%r

m

Tng s tin vn nhc là

   

11T a r

. Vy s tin lãi là

Ta

 ta có:

32 32    T a T a

Thay vào

 

c

   

32 1 32 1 069 224 15,,       a a r a a a

Vy s tin ti thiu mà ông Bn cn gi là 225 tring.

Câu 43. Ba bn Tun, An, Bình mi bn vit ngu nhiên lên bng mt s t nhiên thun

 

1;17



1079

4913

. B.

1637

4913

. C.

. D.

1728

4913

Lời giải

Ta có:

Trang20

 

17.17.17 4913n   

Gi A là bin c c vit ra có tng chia h

n

 

1;17

có 5 s chia ht cho 3; có 6 s  

TH1: Ba s vit ra cùng chia ht cho 3, có

5.5.5 125

cách.

TH2: Ba s vi

6.6.6 216

cách.

TH3: Ba s vi

6.6.6 216

cách.

TH4: Ba s vit ra có 1 sô chia ht cho 3, 1 s  

 

5.6.6 .3! 1080

cách.

 

125 2.216 1080 1637nA   

Vy xác sut  ba s c vit ra có tng chia ht cho 3 bng

 

1637

4913





c, khong cách gic và mc là 12 cm. Ta lt th vào cc nhng viên bi

hình c c dâng lên cao thêm ít nht 2 cm thì cn th vào cc ít nht

bao nhiêu viên bi?

A. 20 viên bi. B. 19 viên bi. C. 18 viên bi. D. 17 viên bi.

Lời giải

Gi

là s viên bi cn th vào cc, (

là s 

Theo yêu cu bài toán thì

phi tha mãn

 

4 6000

. 0,7 .2 .2 17,493

3 343



   

Suy ra s viên bi ít nht cn th vào cc là 18 viên.

Câu45. Cho các s th 

và

tha mãn

 

2 2 2

2 2 2 2

5 9.3 5 9 .7 .

x y x y y x   

  

Tìm giá tr nh

nht ca biu thc

2 11xy





6P 

. B.

9P 

. C.

7P 

. D.

8P 

Lời giải

Ta có

 

   

  

2 2 2

2 2 2 2

2 2 2

2 2 2 2

2 2 2 2 2 2 2 2

2 2 2 2 2 2

2 2 2 2

5 9.3 5 9 .7

5 3 5.7 3 .7

3 7 1 5 7 1 0

7 1 3 5 0

x y x y y x

x y y x x y y x

x y y x y x

y x x y

   

       

     

   

  

   

    

   

2 2 2 2

2 2 2

7 1 0 3 5 0

7 1 2 2 0

y x x y

   



    

     

  

Trang21

Vì

0 2 0 2y x x     

Suy ra

2 11 9 9

x x x x

x x x

    

    

Xét hàm s

 

1f x x

  

trên khong

 

2,

   

1 , 0 3

f x f x x





     

Ta có bng bin thiên hàm

 

Da vào BBT ta có

min 7 3, 5P khi x y  

Câu46. Cho t din

.S ABC

và

m thuc các cnh

và

sao cho

3MA SM

2SN NB

()



là mt phng qua

và song song vi

. Kí hiu

()H

và

()H

là các khi

c khi chia khi t din

.S ABC

bi mt phng

()





()H

chm

()H

chm

;

và

lt là th tích ca

()H

và

()H

Tính t s

VV

119

. B.

. C.

. D.

Lời giải

Kí hiu

là th tích khi t din

SABC

. Gi

lm ca

()



vi các

ng thng

. Ta có

// //NP MQ SC

. Khi chia khi

()H

bi mt phng

()QNC

, ta

c hai khi chóp

.N SMQC

và

.N QPC

Với khối chóp N.SMQC:

Trang22

Vì





N SMQC B SMQC

VV

Li có:

3 9 7

4 16 16

AMQ SAC SMQC SAC

S S S S

    

Vy

N SMQC S ABC

VV

Với khối chóp N.QPC:

Vì

2 1 1

3 4 6

CPQ

CBA

CP CQ

S CB CA

  



6 18

N PQC N ABC SABC

V V V

Suy ra:

1 2 1

7 1 25 25 47 25

24 18 72 72 72 47

SABC SABC

V V V

        

Vy:

1 2 1

1 1 1 47

2 25

2 119

V V V

   



Câu47. Cho hàm s

 





2 2019 2 2020

1 ln 1 sin 3f x a x x bx x     

, vi

,ab

là các s thc và

 

log3

29f 

. Tính

 

log2

3f 

 

log2

33f 

. B.

 

log2

33f   

. C.

 

log2

32f 

. D.

 

log2

32f   

Lời giải

Ta có:

 





   

2 2019 2 2020

1 ln 1 sin 3f x a x x b x x         

 





2 2019 2 2020

1 ln 1 sin 3a x x bx x



     

 





2 2019 2 2020

1 ln 1 sin 3a x x bx x      

 





2 2019 2 2020

1 ln 1 sin 3a x x bx x



      





 

33fx   





 

6fx  

Áp dng tính cht này, ta có:

     

log2 log3 log3

3 2 2 6 9 6 3f f f          

Câu48. Cho hàm s

 

y f x

o hàm liên tc trên



 th hàm s

 

y f x





 bên

Trang23

Hi hàm s

     

21g x f x x  

ng bin trên khong nào trong các khong sau?

 

3;1

. B.

 

1;3

. C.

 

;3

. D.

 

3; 

Lời giải

Ta có

     

2 2 1g x f x x



  

Hàm s

 

ng bin khi

       

0 2 2 1 0 1g x f x x f x x

  

        

D th ca hàm s

 

y f x





và

1yx  

c

 

;3x  

hoc

 

1;3x

thì

hàm s

 

ng bin.

Câu 49. Gi

là tp hp tt c các s nguyên

 hàm s

1 19

y x x x m   

có giá tr ln

nhn

 

0;2

t quá

. Tng các phn t ca

là

195

. B.

195

. C.

210

. D.

210

Lời giải

- 2

- 1

- 3

- 4

- 6

- 2

- 1

- 3

- 4

- 6

Trang24

Xét hàm s

 

1 19

f x x x x m   

n

 

0;2

 

19 30f x x x



  

 

 

5 0;2

3 0;2

f x x



  





   







   

0 ; 2 26f m f m  

 

 

 

 

0;2

max 26; minf x m f x m   

Suy ra

 

 

0;2

max max , 26y m m

YCBT

 

0;2

26 20

20 26 20

max 20 20 6

20 20

  

   





        



  









m

nên

 

20, 19,..., 7, 6mS     

Vy tng các phn t ca

bng

 

15. 20 6

195





Câu50. Cho hàm s

 

y f x

, hàm s

 

y f x





liên tc trên



 th .

B

 

38f x m x x x   

(

là tham s thc) nghii mi

 

0;3x

khi và ch khi

 

0mf

. B.

 

3 24mf

. C.

 

0mf

. D.

 

3 24mf

Lời giải

 

38f x m x x x    

 

38f x x x x m   

t

   

38h x f x x x x   

     

 

3 6 8 3 6 8 .h x f x x x f x x x

  

        

t

 

3 6 8g x x x  

và v  th ca

 

lên h trc Oxy.

T hình v, ta thy

     

, 0;3 .f x g x x



  



   

0, 0;3 .h x x



  

Vì vy ta có bng bin thiên

Trang25

T bng bin thiên, yêu cu bài toán

   

3 3 24.m h m f    

--------------HT---------------

Đề 2

ĐỀ LUYỆN THI CẤP TỐC TỐT NGHIỆP THPT NĂM 2021

Thuvienhoclieu.Com

BÀI THI: TOÁN

Thời gian: 90 phút

Câu1. Mt nguyên hàm ca

 







là

3 6ln 1

xx  

. B.

3 6ln 1

xx  

3 6ln 1

xx  

. D.

3 6ln 1

xx  

Câu2. Tìm s phc liên hp ca s phc

 

32z i i

32zi  

. B.

32zi

. C.

32zi  

. D.

32zi  

Câu3. Cho

 ng th   m

 

1;2;3A

và vuông góc vi mt phng

 

:4 3 7 1 0x y z   



c ca

là

1 2 3

4 3 7

x y z  



  

. B.

1 2 3

4 3 7

x y z  





4 3 7

1 2 3

x y z  



. D.

1 2 3

4 3 7

x y z  





Câu4. 

, chiu cao là

. Din tích toàn phn ca hình nón bng

36 a



. B.

32 a



. C.

38 a



. D.

30 a



Câu5. Vu kin nào ca

 hàm s

 

ya

ng bin trên



0a 

. B.

 

;1 1;



  





1a 

. D.

;



 





Câu6. m biu din ca s phc

 

34z m i  

là

 

3;2M

khi

bng

2m 

. B.

4m 

. C.

6m 

. D.

2m 

Câu7. Tìm s m

c th

32y x x  

và

2yx

4n 

. B.

2n 

. C.

0n 

. D.

1n 

Trang26

Câu 8. Cho hàm s

 

có bng bi

S ngim thc c

 

2 3 0fx

là

. B.

. C.

. D.

Câu 9. Cho hình tr ng

 

3 cm

ng cao

 

6 cm

. Din tích xung quanh ca hình

tr này là

 

36 cm



. B.

 

20 cm



. C.

 

24 cm



. D.

 

18 cm



Câu 10. Trong không gian

Oxyz

m

 

2;4;6K

, gi



là hình chiu ca

trên



m



có t là

 

1;0;0

. B.

 

1;2;3

. C.

 

0;0;3

. D.

 

0;2;0

Câu11. 









.S ABC



ABC



BC a

. 



lên

 

ABC



. 

SB a

. 



 

ABC

75

. B.

30

. C.

60

. D.

45

Câu 12. 



11A1 25 20 . 

?

A. 500. B. 20. C. 25. D. 45.

Câu 13. Trong không gian vi h t

Oxyz

, mt phi mt phng

 

Oyz

20x

. B.

2 1 0z  

. C.

20z 

. D.

2 1 0x  

Câu 14. Tìm s tim cng c th hàm s

42x







. B.

. C.

. D.

Câu15. ng cong trong hình v  th ca hàm s 

1y x x  

. B.

1y x x   

. C.

21y x x   

. D.

21y x x  

Câu16. Nu

 

7 7 7

log 8log 2log , 0x ab a b a b  

thì

bng:

8 14

. B.

6 12

. C.

. D.

2 14

Trang27

Câu17. Cho hàm s

 

y f x

có bng xét d

M 

A.Hàm s ng bin trên khong

 

;0

B.Hàm s ng bin trên khong

 

2;0

C.Hàm s nghch bin trên khong

 

0;2

D.Hàm s nghch bin trên khong

 

;2 

Câu18. Tính th tích mt khi chóp bit khng cao bng

12a

, ding

12a

. B.

. C.

12a

. D.

Câu19. Cho hàm s

log

6 x

có tnh là

 

;6

. B.

 

0;

. C.

 

6;

. D.



Câu20. Mt mt cu có din tích

 

36 m



. Th tích ca khi cu này bng

 

108 m



. B.

 

72 m



. C.

 



. D.

 

36 m



Câu21. a s phc

tha mãn

 

2 13 1z i i  

34z 

. B.

34z 

. C.

5 34

z 

. D.

z 

Câu22. 

.ABCD A B C D

   

u có m

A.Hình thoi. B. Hình bình hành. C. Hình ch nht. D. Hình vuông.

Câu23. Cho hàm s

 

o hàm

   

2f x x x





x

. S m cc tr ca hàm s 

là

. B.

. C.

. D.

Câu24. Giá tr ln nht ca hàm s

 

49y f x x x   

n

 

2;3

bng

201

. B.

. C.

. D.

Câu 25. Nghim c

125











là



. B.



. D.

Câu26. Trong các khnh sau, khnh nào sai?

 

5 cosF x x

là mt nguyên hàm ca hàm s

 

sinf x x

Trang28

 

d log

x u x C







C.Nu

 

là mt nguyên hàm ca hàm s

 

thì mi nguyên hàm ca

 

u có

dng

 

F x C

(

là hng s) .

 

1 tanF x x

là mt nguyên hàm ca hàm s

 

1 tanf x x

Câu27. Cho cp s nhân

 

, bit

81, 9





. La chđúng.

q 

. B.

9q 

. C.

q 

. D.

9q 

Câu28. Cho

0,2 0,2

log logxy

. Chn kh

0xy

. B.

0xy

. C.

0yx

. D.

0yx

Câu29. Trong không gian vi h t

Oxyz

, 









 

tâm

 

1; 2;2I 





23R 



     

2 2 2

1 2 2 12x y z     

. B.

     

2 2 2

1 2 2 6x y z     

     

2 2 2

1 2 2 12x y z     

. D.

     

2 2 2

1 2 2 6x y z     

Câu30. Cho hàm s

y ax bx cx d   

 th  bên. M 

0, 0, 0, 0a b c d   

. B.

0, 0, 0, 0a b c d   

0, 0, 0, 0a b c d   

. D.

0, 0, 0, 0a b c d   

Câu31. Trong không gian vi h t

Oxyz

ng thng

: 6 2

d y t

















và mt phng

 

: 2 2 0x y z



   

. Chn kh

 

//d



. B.

 





. C.

 





. D.

ct

 



Câu32. Gi s

d ln5 ln3; ,

x a b a b



  







. Tính

.P ab

5P 

. B.

4P 

. C.

8P 

. D.

6P 

Câu33. nh

ng tròn là

. Mt mt phng qua

to vi m

mt góc

60

ct hình nón theo thit diu

IBC

cnh

. Tính th tích khi nón.



. B.



. C.



. D.



Trang29

Câu34. Cho hình chóp

.S ABCD

i

và

vuông góc mt

ph

, 3 , 2 ,SA a AD a AB a BC a= = = =

. Tính khong cách ging thng

và

. B.

. C.

. D.

Câu35. Áp sut không khí

suy gi cao

theo công thc

PP



760P mmHg

là áp sut  mc bin

 

0x 

là h s suy gim. Bit rng   cao

1000m

thì áp sut ca không khí là

672,71mmHg

. Áp sut không khí   cao 3343

xp x

bng

A.495,34

mmHg

. B.530,23

mmHg

. C.485,36

mmHg

. D.505,45

mmHg

Câu 36. Cho hàm s

()fx

có

()

( 1) 1

x x x x





  

0x

và

(1) 2 2f 



( )df x x



bng



. B.



. C.

4 2 10



. D.



Câu37. Tính th tích khi tròn xoay sinh ra khi quay quanh trc

hình phng gii hn b th

46y x x  

và

26y x x   





. B.



. C.



. D.



Câu38.  bng

4cm

, chiu cao bng

6cm

 ng chéo ca thit din qua

trc bng

5cm

. B.

6cm

. C.

8cm

. D.

10cm

Câu39.   

   

7 6 0z z z z    

có bn nghim phc

. Tính

1 2 3 4

S z z z z   

2

. B.

5

. C.

3

. D.

1

Câu 40. Cho hàm s

1 2020y x mx   

(

là tham s thc). Có bao nhiêu giá tr nguyên ca

thun

 

10;10

 ng bin trên khong

 

; 

. B.

. C.

. D.

Câu41. Tìm s phc

bit

5z 

và

là s thun o.

5i

. B.

. C.

5i

. D.

5i

Câu42. Chn mt s t nhiên có

ch s c lp t tp

 

0;1;2;3;4;5

. Xác sut

 s c chn chia ht cho

bng

. B.

. C.

. D.

Câu43. m

 

3;2;3A

và

 

3;4;1B

. Vit phng

 

là mt phng trung

trc ca

 

: 1 0  P y z

. B.

 

: 1 0  P y z

. C.

 

: 1 0  P y z

. D.

 

: 1 0  P y z

Trang30

Câu44. B

2 10













có bao nhiêu nghi

. B.

. C.

. D.

Câu45. 

   

5 5 5

log 5 6log 11 log 3 0

x m x m



     





(

là tham s thc). Tp

hp tt c các giá tr ca tham s

     m phân bit thu n

 

1;625

là

 

1;2

. B.

 

1;2

. C.

 

2;

. D.





1;2

Câu46. Cho hàm s

 

có bng bi

S nghim thun

7 13

;











c

 

sin cos 1 0  f x x

là

. B.

. C.

. D.

Câu47. Cho hàm s

( ) 8f x x ax b  



,ab

là tham s thc. Bit rng giá tr ln nht ca

hàm s

()fx

n

 

1;1

bng

. Tính

ba

A.10. B.8. C.7. D.9.

Câu48. 









.S ABC



ABC





90SCA SBA  

. 















. 













.S ABC



. B.

. C.

. D.

Câu49. Cho hàm s bc bn

 

y f x

 th  

S m cc tr ca hàm s

 

23g x f x x

là

. B.

. C.

. D.

0,75

-2

-1

Trang31

Câu50. Trong h t

Oxy

m

( ; )M x y

vi

; ; 6 6; 0x y x y    Z

và th

trình

36 2

3 36

3 2 log





  





. Hm

tha yêu cu nêu trên?

A. Bm. B.Mm. C. m. D. m.

--------------HT---------------

ĐÁP ÁN ĐỀ THI

10C

11C

12D

13D

14B

15D

16D

17C

18B

19A

20D

21B

22D

23D

24B

25C

26B

27A

28D

29C

30A

31D

32D

33D

34A

35D

36A

37D

38D

39A

40D

41D

42D

43C

44B

45D

46C

47D

48A

49B

50D

HƯỚNG DẪN GIẢI CHI TIẾT

Câu1. Mt nguyên hàm ca

 







là

3 6ln 1

xx  

. B.

3 6ln 1

xx  

3 6ln 1

xx  

. D.

3 6ln 1

xx  

Lời giải

Ta có:

 

2 2

2 3 6

3 3 6ln 1d d d

112

f Cxx x x

xxx





    







  





  

Vy mt nguyên hàm ca hàm s

 







là

3 6ln 1

xx  

Câu2. Tìm s phc liên hp ca s phc

 

32z i i

32zi  

. B.

32zi

. C.

32zi  

. D.

32zi  

Lời giải

Ta có

 

3 2 3 2 3 2 3 2z i i i i i z i          

Câu3. Cho

 ng th   m

 

1;2;3A

và vuông góc vi mt phng

 

:4 3 7 1 0x y z   



c ca

là

1 2 3

4 3 7

x y z  



  

. B.

1 2 3

4 3 7

x y z  





4 3 7

1 2 3

x y z  



. D.

1 2 3

4 3 7

x y z  





Lời giải

Ta có

 

:4 3 7 1 0x y z



   

 

4;3; 7n



  



là VTPT ca mt phng

 



Trang32

ng thng

 





 

4;3; 7n



  



là VTCP cng thng

Ta li có

 

1;2;3Ad

c cng thng

là:

1 2 3

4 3 7

x y z  





Câu4. 

, chiu cao là

. Din tích toàn phn ca hình nón bng

36 a



. B.

32 a



. C.

38 a



. D.

30 a



Lời giải



4ra

, chiu cao là

3ha

ng sinh

   

4 3 5l r h a a a    

Mà din tích toàn phn bng:

    

4 5 4 36rl r aS a a a    

    

Câu5. Vu kin nào ca

 hàm s

 

ya

ng bin trên



0a 

. B.

 

;1 1;



  





1a 

. D.

;



 





Lời giải

 hàm s ng bin trên



thì

2 1 1a

1a

Câu6. m biu din ca s phc

 

34z m i  

là

 

3;2M

khi

bng

2m 

. B.

4m 

. C.

6m 

. D.

2m 

Lời giải

 s phm biu din là

 

3;2M

khi:

42m

2m  

Câu7. Tìm s m

c th

32y x x  

và

2yx

4n 

. B.

2n 

. C.

0n 

. D.

1n 

Lời giải

 m c th

32y x x  

và

2yx

là:

4 2 2

3 2 2x x x   

4 4 0xx   















Vy có

m c th

32y x x  

và

2yx

Câu 8. Cho hàm s

 

có bng bi

Trang33

S ngim thc c

 

2 3 0fx

là

. B.

. C.

. D.

Lời giải

Ta có

 

2 3 0fx

 

fx

S ngim thc c

 

2 3 0fx

chính bng s m c th hàm s

 

y f x

ng thng

y 

Da bng bin thiên ca hàm s

 

y f x

ta th

 

2 3 0fx

có

nghim

thc.

Câu 9. Cho hình tr ng

 

3 cm

ng cao

 

6 cm

. Din tích xung quanh ca hình

tr này là

 

36 cm



. B.

 

20 cm



. C.

 

24 cm



. D.

 

18 cm



Lời giải

Ta có

 

2 36 cm

S rh





Câu 10. Trong không gian bi h t

Oxyz

m

 

2;4;6K

, gi



là hình chiu ca

trên

m



có t là

 

1;0;0

. B.

 

1;2;3

. C.

 

0;0;3

. D.

 

0;2;0

Lời giải

Ta có

 

0;0;6K



m ca



có t là

 

0;0;3

Câu11. 









.S ABC



ABC



BC a

. 



lên

 

ABC



. 

SB a

. 



 

ABC

75

. B.

30

. C.

60

. D.

45

Lời giải

Trang34















 

SH ABC





 

ABC





SAH







2 2 2

SH SB BH a    



AH BC







 

tan 3 60

SAH SAH

     





 



 

ABC



60

Câu 12. 



?

A. 500. B. 20. C. 25. D.45.

Lời giải

25  



.

20 .











25 20 45

.

Câu 13. Trong không gian vi h t

Oxyz

, mt phi mt phng

 

Oyz

20x

. B.

2 1 0z  

. C.

20z 

. D.

2 1 0x  

Lời giải

Mt phng song song vi mt phng

 

Oyz



0Ax D

 

0D 

Dn mt ph

2 1 0x  

Câu 14. Tìm s tim cng c th hàm s

42x







. B.

. C.

. D.

Lời giải

u kinh:











0, 1









  



Trang35

Ta có:

 

0 0 0

4 2 4 4 1 1

lim lim lim

4 2 4 2 1

x x x

x x x x x

  

  



   

  





     



Ta có:

 

0 0 0

4 2 4 4 1 1

lim lim lim

4 2 4 2 1

x x x

x x x x x

  

  



   

  





     



Suy ra

0x 

không là tim cng c th hàm s.

Ta có:

 

lim









 







Suy ra

1x 

là tim cng c th hàm s.

V th hàm s ng tim cng

1x 

Câu15. ng cong trong hình v  th ca hàm s 

1y x x  

. B.

1y x x   

. C.

21y x x   

. D.

21y x x  

Lời giải

D th, ta th th hàm s c bc bi h s ca



lim



 

Câu16. Nu

 

7 7 7

log 8log 2log , 0x ab a b a b  

thì

bng:

8 14

. B.

6 12

. C.

. D.

2 14

Lời giải

Ta có

7 7 7

8 16 6 2

7 7 7

8 16

2 14

log 8log 2log

log log log

log log

x ab a b

x a b a b

x a b



  



Câu17. Cho hàm s

 

y f x

có bng xét d

M i 

A. Hàm s ng bin trên khong

 

;0

Trang36

B. Hàm s ng bin trên khong

 

2;0

C. Hàm s nghch bin trên khong

 

0;2

D. Hàm s nghch bin trên khong

 

;2 

Lời giải

Nhìn vào bng xét du co hàm ta thy:

Hàm s ng bin trên mi khong

 

;2 

và

 

2;

Hàm s nghch bin trên mi khong

 

2;0

và

 

0;2

T Hàm s nghch bin trên khong

 

0;2

Câu18. Tính th tích mt khi chóp bit khng cao bng

12a

, ding

12a

. B.

. C.

12a

. D.

Lời giải

Th tích ca khi chóp là:

. .12 4

V a a a

Câu19. Cho hàm s

log

6 x

có tnh là

 

;6

. B.

 

0;

. C.

 

6;

. D.



Lời giải

 u kin:

0 6 0 6

     



 Tnh

 

;6D  

Câu20. Mt mt cu có din tích

 

36 m



. Th tích ca khi cu này bng

 

108 m



. B.

 

72 m



. C.

 



. D.

 

36 m



Lời giải

 Din tích mt cu

4 36 9 3S R R R



     

 Th tích khi cu

.3 36

  

  

Câu21. a s phc

tha mãn

 

2 13 1z i i  

34z 

. B.

34z 

. C.

5 34

z 

. D.

z 

Lời giải

Ta có:

 

1 13

2 13 1 3 5

z i i z i



      



. Vy

34z 

Câu22. 

.ABCD A B C D

   

u có m

A. Hình thoi. B. Hình bình hành. C. Hình ch nht. D.Hình vuông.

Trang37

Lời giải

 t u có m

Câu23. Cho hàm s

 

o hàm

   

2f x x x





x

. S m cc tr ca hàm s 

là

. B.

. C.

. D.

Lời giải

Ta có:

   

0 2 0

f x x x







    







Bng bin thiên

Vy hàm s m cc tr.

Câu24. Giá tr ln nht ca hàm s

 

49y f x x x   

n

 

2;3

bng

201

. B.

. C.

. D.

Lời giải

Ta có:

48y x x





 

2 2;3

0 4 8 0 2 2;3

0 2;3

y x x x



  







        



  





 

     

2 5; 0 9; 2 9; 3 54f f f f     

Vy giá tr ln nht ca hàm s

 

49y f x x x   

n

 

2;3

bng

Câu 25. Nghim c

125











là



. B.



. D.

Lời giải

Ta có:

 

2 2 3

125 5 5







  





2 2 6





   

  

Trang38

Câu26. Trong các khnh sau, khnh nào sai?

 

5 cosF x x

là mt nguyên hàm ca hàm s

 

sinf x x

 

d log

x u x C







C. Nu

 

là mt nguyên hàm ca hàm s

 

thì mi nguyên hàm ca

 

u có

dng

 

F x C

(

là hng s) .

 

1 tanF x x

là mt nguyên hàm ca hàm s

 

1 tanf x x

Lời giải

Ta có:

 

   

 

d d ln

x u x u x C

u x u x



  



nên đáp án B sai.

Câu27. Cho cp s nhân

 

, bit

81, 9





. La chđúng.

q 

. B.

9q 

. C.

q 

. D.

9q 

Lời giải

Ta có





Câu28. Cho

0,2 0,2

log logxy

. Chn kh

0xy

. B.

0xy

. C.

0yx

. D.

0yx

Lời giải

Ta có

0,2 0,2

log log 0x y y x   

Câu29. 

















Oxyz

, 









 

tâm

 

1; 2;2I 



23R 

:

     

2 2 2

1 2 2 12x y z     

     

2 2 2

1 2 2 6x y z     

     

2 2 2

1 2 2 12x y z     

     

2 2 2

1 2 2 6x y z     

Lời giải

Ta có

 

1; 2;2













     

2 2 2

1 2 2 12x y z      

Câu30. Cho hàm s

y ax bx cx d   

 th  bên. M 

Trang39

0, 0, 0, 0a b c d   

. B.

0, 0, 0, 0a b c d   

0, 0, 0, 0a b c d   

. D.

0, 0, 0, 0a b c d   

Lời giải

T  th nhn thy:

- Khi

x 

 th ng

0a

-  th ct trc

t âm

0d

- m cc tr c th nm v hai phía







có hai nghim trái

du

00ac c   

- Gi

,xx

m cc tr ca hàm s thì t  th có

0xx

. Mà

,xx

là hai nghim

c

3 2 0 0 0

ax bx c b

       

Vy

0, 0, 0, 0a b c d   

Câu31. Trong không gian vi h t

Oxyz

ng thng

: 6 2

d y t

















và mt phng

 

: 2 2 0x y z



   

. Chn kh

 

//d



. B.

 





. C.

 





. D.

ct

 



Lời giải

ng thng

: 6 2

d y t

















 

 

1; 2; 5u 



Mt phng

 

: 2 2 0x y z



   

n là

 

1; 2 ; 1n 



Ta có:

. 1 4 5 10 0un    



suy ra



và



không vuông góc

d

ct

 



Ta có:

1 2 5

1 2 1







suy ra



và





d

không vuông góc vi

 



Câu32. Gi s

d ln5 ln3; ,

x a b a b



  







. Tính

.P ab

5P 

. B.

4P 

.C.

8P 

. D.

6P 

Lời giải

Ta có

4 3 ( 3)( 1) 3 1

x x A B

x x x x x x



  

     

( ) 3

( 3)( 1)

A B x A B

  





ng nht thc ta có

3 1 2

A B B

A B A

   







   



Trang40

Suy ra

1 2 1

4 3 3 1

x x x x





   

Suy ra

1 2 1

4 3 3 1

x x x x









   





2 2ln 3 ln 1

     





2ln5 2ln3 ln3 2ln5 3ln3    

Suy ra

2; 3ab  

. Vy

.6P ab  

Câu33. nh

ng tròn là

. Mt mt phng qua

to vi m

mt góc

60

ct hình nón theo thit diu

IBC

cnh

. Tính th tích khi nón.



. B.



. C.



. D.



Lời giải

Ta có

()IBC

giao vi mn

HJ BC

nên



60IJH 

Mt khác

IJ 

Xét

IHJ





3 3 3

sin .sin60 .

2 2 4

HI a a

HJI HI IJ

     



3 1 3

cos .cos60 .

2 2 4

HJ a a

HJI HJ IJ

     

Xét

BHJ



4 16 4

a a a

HB R   

1 1 7 3 7

3 3 16 4 64

non

a a a

V R h





  

Câu34. Cho hình chóp

.S ABCD

i

và

vuông góc mt ph

, 3 , 2 ,SA a AD a AB a BC a   

. Tính khong cách ging thng

và

Trang41

. B.

. C.

. D.

Lời giải

Gi

thuc cnh

sao cho

2AN DN



//( ) ( , ) ( ,( )) ( ,( ))CD SBN d CD SB d CD SBN d D SBN  

Ta có

( ,( )) 1 1

( ,( )) ( ,( ))

( ,( )) 2 2

d D SBN DN

d D SBN d A SBN

d A SBN AN

   

Gi

m ca

và

là hình chiu vuông góc ca

trên

Ta có

BN AK

và

BN SA

suy ra

()BN SAK

AH SK

và

AH BN

suy ra

()AH SBN



( ,( ))d A SBN AH

Xét

ABN

vuông cân ti

ta có

1 2 2

AK BN a  

Xét

SAK

vuông cân ti

ta có

2 2 2 2 2 2

1 1 1 1 1 3 6

2 2 3

AH AK AS a a a

      

Vy

( , )

d CD SB 

Câu35. Áp sut không khí

suy gi cao

theo công thc

PP



760P mmHg

là áp sut  mc bin

 

0x 

là h s suy gim. Bit rng   cao

1000m

thì áp sut ca không khí là

672,71mmHg

. Áp sut không khí   cao 3343

xp x

bng

A. 495,34

mmHg

. B. 530,23

mmHg

. C. 485,36

mmHg

. D.505,45

mmHg

Lời giải

Áp dng công thc

PP

vi

760P mmHg

1000x 

thì

672,71P 

c h s

suy gim

672,71

760

0,000122004

1000





   

   

Trang42

Vy vi

3343x 

thì

PP

 

3343. 0,000122004

760.e 505,45





Câu 36. Cho hàm s

()fx

có

()

( 1) 1

x x x x





  

0x

và

(1) 2 2f 



( )df x x



bng



. B.



. C.

4 2 10



. D.



Lời giải

Ta có

 

( ) ( )d d d

( 1) 1

f x f x x x x

x x x x



  

  

  

  

1 1 1

( ) d d 2 1 2

( 1) 1

f x x x x x C

x x x x





      









Vì

(1) 2 2f 

nên

2C 

và

( ) 2 1 2 2f x x x   



 

4 4 10

( )d 2 1 2 2 d ( 1) 1 2 4 3

3 3 3

f x x x x x x x x x x



          







Câu37. Tính th tích khi tròn xoay sinh ra khi quay quanh trc

hình phng gii hn b th

46y x x  

và

26y x x   





. B.



. C.



. D.



Lời giải

 m c th hàm s

46y x x  

và

26y x x   

2 2 2

4 6 2 6 2 2 0

x x x x x x





         







 tích khi tròn xoay sinh ra khi quay quanh trc

hình phng gii hn b

th

46y x x  

và

26y x x   



   

4 6 2 6 d 3V x x x x x



       



Câu38.  bng

4cm

, chiu cao bng

6cm

 ng chéo ca thit din qua

trc bng

5cm

. B.

6cm

. C.

8cm

. D.

10cm

Lời giải

Thit din qua trc hình tr là hình ch nht có chiu dài

8cm

, chiu rng

6cm

 ng chéo bng

6 8 10cm

Câu39.   

   

7 6 0z z z z    

có bn nghim phc

. Tính

1 2 3 4

S z z z z   

2

. B.

5

. C.

3

. D.

1

Trang43

Lời giải

Ta có

   

 

6 1

7 6 0

1 2

z z z z



  

     



  





Gi s

là hai nghim c

 

là hai nghim c

 

áp dnh lí Vi-ét ta có :

1 2 3 4

1; 1

z z z z



       



1 2 3 4

2S z z z z     

Cách 2 :

   

2 2 4 3 2

7 6 0 2 8 7 6 0z z z z z z z z          

Theo Vi-ét ta có

1 2 3 4

S z z z z



      

Câu 40. Cho hàm s

1 2020y x mx   

(

là tham s thc). Có bao nhiêu giá tr nguyên ca

thun

 

10;10

 ng bin trên khong

 

; 

. B.

. C.

. D.

Lời giải

Có







Hàm s   ng bin trên khong

 

; 



  



 

;x   

, du

"=" xy ra ti hu hm.

T ta có:

()

g x m





 

;x   

Hàm s

()gx

 nh và liên tc trên khong

 

; 

và

 

( ) 0

1. 1







 

;x   

nên

()gx

ng bin trên khong

 

; 

Ta có:

lim ( ) lim 1; lim ( ) lim 1

x x x x

g x g x

   

    



và hàm s ng bin vi mi

 

;x  

nên t suy ra

1m

, kt hp gi thit

 

10;10m

và

nguyên nên ta có 10

giá tr ca

(

nhn các giá tr :

10; 9; 8; 7; 6; 5; 4; 3; 2; 1         

Câu41. Tìm s phc

bit

5z 

và

là s thun o.

5i

. B.

. C.

5i

. D.

5i

Lời giải

Ta có

là s thun o nên

 

z bi b



5 5 . 5 5 5.z bi b i b b         

Vy

5.zi

Trang44

Câu42. Chn mt s t nhiên có

ch s c lp t tp

 

0;1;2;3;4;5

. Xác sut

 s c chn chia ht cho

bng

. B.

. C.

. D.

Lời giải

Có

5 5 4 3 2 600    

s có

ch s t khác nhau.

Gi s có

ch s t khác nhau và chia ht cho

có dng

abcde

 Nu

04de 

ta có

4 3 2 24  

s tha mãn.

 Nu

12de 

ta có

3 3 2 18  

s tha mãn.

 Nu

20de 

ta có

4 3 2 24  

s tha mãn.

 Nu

24de 

ta có

3 3 2 18  

s tha mãn.

 Nu

32de 

ta có

3 3 2 18  

s tha mãn.

 Nu

40de 

ta có

4 3 2 24  

s tha mãn.

 Nu

52de 

ta có

3 3 2 18  

s tha mãn.

Theo quy tc cng ta có

24 3 18 4 144   

s tha mãn yêu c bài.

Xác sut cn tìm là

144 6

600 25



Câu43. m

 

3;2;3A

và

 

3;4;1B

. Vit phng

 

là mt phng trung

trc ca

 

: 1 0  P y z

. B.

 

: 1 0  P y z

. C.

 

: 1 0  P y z

. D.

 

: 1 0  P y z

Lời giải

Mt phng trung trc

 

cn thng

m

 

3;3;2I

ca

và nhn

 

0;2; 2



n.

t phng

 

là

   

2 3 2 2 0 1 0       y z y z

Câu44. B

2 10













có bao nhiêu nghi

. B.

. C.

. D.

Lời giải

Ta có:

2 10

3 4 3 4 10 2 2

2 2 2 3 4 10 2



    



       





x x x x x

x x x

6 0 2 3x x x       

Suy ra tp các nghi

 

 1;2;3S

. Vy s nghi

Trang45

Câu45. 

   

5 5 5

log 5 6log 11 log 3 0

x m x m



     





(

là tham s thc). Tp

hp tt c các giá tr ca tham s

     m phân bit thu n

 

1;625

là

 

1;2

. B.

 

1;2

. C.

 

2;

. D.





1;2

Lời giải

u kin:

0x 

   

5 5 5

log 5 6log 11 log 3 0

x m x m



     





     

5 5 5

1 log 6 log 1 11 log 3 0x x m x m        

t

logtx

c

 

3 4 2 0t t m t m     

Vi

 

1;625x

thì

 

0;4t 

. Vy ta cn tìm tt c các giá tr ca tham s

 

nghim phân bit thun

 

0;4

Ta có

   

 

* 1 2 2 0

2 2 0 (**)

t t t m

t t m





      



   



Vy ta cn tìm

 có hai nghim phân bit khác 1 thun

 

0;4

Ta có

2 2 0 2 2t t m m t t       

Xét hàm s

 

22f t t t  

có bng bin

 

0;4



u kin ca

là





1;2m

. Ch

Câu46. Cho hàm s

 

có bng bi

S nghim thun

7 13

;











c

 

sin cos 1 0  f x x

là

. B.

. C.

. D.

Trang46

Lời giải

Xét hàm s

 

sin cos 2sin

t t x x x x





    





n

7 13

;











ta có

5 3 7 11

2cos 0 ; ; ; ;

4 4 4 4 4 4

     

   



      





   

t x x

Suy ra bng bin thiên

t

sin cost x x



 

sin cos 1 0  f x x

 

tr thành

   

1 0 1    f t f t

 

, vi

2; 2







Da vào bng bin thiên ca hàm s

 

ta nhn th

 

có hai nghim

và

tha

20  t

và

02t

a vào bng bin thiên ca hàm s

 

t t x

ta có:



sin cosx x t

 

20t  

: có 4 nghim

phân bit.



sin cosx x t

 

02t

: có 6 nghim

phân bit.

V

 

sin cos 1 0  f x x

có 10 nghim.

Câu47. Cho hàm s

( ) 8f x x ax b  



,ab

là tham s thc. Bit rng giá tr ln nht ca

hàm s

()fx

n

 

1;1

bng

. Tính

ba

A. 10. B. 8. C. 7. D.9.

Lời giải

Theo gii thit:

 

1;1

max ( ) 1fx





nên

 

8 1, 1;1x ax b x     

Suy ra

(1) 1

(0) 1





























8. . 1









   





  





1 1 1 1

1 8 1 9 7 (*)

2 2 4 2 6 2 2

a b a b

     





           





         



T

  







  



, mt khác

1b 

nên

1b 

Th

1b 

vào ta có:

9 1 7 10 8

6 2 2 8 4

        



   



        



Trang47

Khi

8, 1ab  

8 8 1.y x x   

t

cosx





, vi

 





cos4y





Vy

( ) 1fx

khi

1x 



9ba

Câu48. 









.S ABC



ABC





90SCA SBA  

. 















. 













.S ABC



. B.

. C.

. D.

Lời giải





, 





AH BC

. 





,HI SA I SA







SBC SCA  

nên

SB SC

SBC







SH BC











 

BC SAH



 

HI SAH

nên

BC HI







 

SA BC

HI d a















 

ABC

 

SD ABC SD AB   

mà

 

SB AB AB SBD AB BD ABD      





















ACD













ABD ACD DB DC D     





























AHB

:

2 2 2 2

43AH AH BH a a a    



ABD

:

2 2 2 2 2 2 2 2 2

1 1 1 1 1 1 1 1 3 2

BH BD BA BD BH BA a a a

         

2 2 2

AD BD BA a    

Trang48







, / /DK SA K SA DK HI  





4 2 3

3 3 3

AH HI AD HI a

AD DK AH

    



SDA

, 



2 2 2 2 2 2 2 2 2

1 1 1 1 1 1 27 3 15 8

64 16 64

DK SD AD SD DK AD a a a

         















.S ABC



1 1 1 1 8 8

. . . . . . . .2 . 3

3 3 2 6

15 3 5

S ABC ABC

V SD S SD AH BC a a   

Câu49. Cho hàm s bc bn

 

y f x

 th  

S m cc tr ca hàm s

 

23g x f x x

là

. B.

. C.

. D.

Lời giải

 

   

2 3 2

6 6 . 2 3g x x x f x x



  

;

 

   

 

2 3 2

0 6 6 . 2 3 0 1

2 3 0

g x x x f x x x

f x x









       











 

   

 

3 2 3 2

2 3 1 2 1

2 3 0 2 3 2 1 0

2 3 3 0

x x a a

f x x x x b b

x x c c





     





       







   









t

 

23P x x x

 

66P x x x





Bng bin thiên:

0,75

-2

-1

Trang49

Da vào BBT ta có:

PT có nghi

khác 0 và

1

PT có nghi

khác 0,

1

và

PT có 3 nghit khác 0,

1

và



 

0gx





có 7 nghit .

Vy hàm s

 

23g x f x x

m cc tr.

Câu50. Trong h t

Oxy

m

( ; )M x y

vi

; ; 6 6; 0x y x y    Z

và th

trình

36 2

3 36

3 2 log





  





. Hm

tha yêu cu nêu trên?

A.  B. Mm C.  D.

Lời giải

Ta có:

36 2

3 36

3 2 log





  





9 36

3 3 log 2







   





9 36

3 3 log







  





 

9 36 2 2

3 3 log 36 log 9



    

 

9 2 2 36

3 log 9 log 36 3



    

(1)

Xét hàm s

( ) 3 log

f x x

vi

0x 

Có

( ) 3 .ln3 0, 0

.ln3

f x x



    



Hàm s

()y f x

ng bin trên khong

(0; )



(1)

(9 ) (36 )f y f x  

9 36yx  

9 36xy  

Vì

; ; 6 6; 0x y x y    Z

nên nhc











(0;2); (0; 2)MM

--------------HT---------------

Đề 3

ĐỀ LUYỆN THI CẤP TỐC TỐT NGHIỆP THPT NĂM 2021

Thuvienhoclieu.Com

BÀI THI: TOÁN

Thời gian: 90 phút

Câu 1: Din tích toàn phn ca hình lnh

là

. B.

72a

. C.

54a

. D.

36a

Câu 2: Tìm tnh ca hàm s

 

log 1yx

 

;1D   

. B.

 

1;D   

. C.

[ 1; )D   

. D.

 

\1

Trang50

Câu 3: H nguyên hàm ca hàm s

 

4f x x



là:

 

F x x C

  

. B.

 

12F x x C

  

 

F x x C

  

. D.

 

lnF x x x C  

Câu 4: Có bao nhiêu cách chn

hc sinh t

hc sinh?

1860480

cách. B.

120

cách. C.

15504

cách. D.

100

cách.

Câu 5: Cho cp s cng

 

có s hu

3u 

và công sai

2d 

. Giá tr ca

bng:

. B.

. C.

. D.

Câu 6: Tìm tp nghim c

xx



 

1;3S 

. B.

 

0; 2S 

. C.

 

1; 3S 

. D.

 

0;2S 

Câu 7: Cho hàm s

 

y f x

nh và liên tc trên



, có bng bi

M đúng?

A. ch bin trên khong

 

;1

B. Hàm s ng bin trên khong

 

;2 

C. ch bin trên khong

 

1; 

D. Hàm s ng bin trên khong

 

1; 

Câu 8: Bii biu thc



.A a a

v da vi s u t c



. B.



. C.

Aa

. D.



Câu 9: Cho hình tr ng

và chiu cao bng

. Din tích xung quanh ca hình tr 

cho bng:

175



. B.

175

. C.

70

. D.

35

Câu 10:Cho khi chóp

.S ABC

có

vuông góc

 

ABC

và

2SA 

, tam giác

ABC

vuông cân ti

và

1AB 

. Th tích khi chóp

.S ABC

bng

. B.

. C.

. D.

Câu 11: Mt kh ng sinh

 

13l cm



 

5r cm



tích khi nón bng

Trang51

 

100V cm





. B.

 

300V cm





. C.

 

325

V cm





. D.

 

20V cm





Câu 12: Khi cu có bán kính

6R 

có th tích bng bao nhiêu?

144



. B.

288



. C.



. D.



Câu 13: B

 

log 3 1 3x 

có nghim là:

 3x

. B.

 3x

. C.



. D.



Câu 14:  th ca hàm s

 

y f x

 bên.

S nghim c

 

4 3 0fx

là

. B.

. C.

. D.

Câu 15:Nu

 

5f x dx 



và

 

2f x dx 



thì

 

f x dx



bng

. B.

. C.

. D.

3

Câu 16:Cho hàm s

 

y f x

có bng bi

Hàm s t ci t

2x 

. B.

3x 

. C.

2x 

. D.

4x 

Câu 17: ng cong trong hình v  th ca hàm s nào?

Trang52

3  y x x

. B.

3y x x

. C.

1   y x x

. D.

1  y x x

Câu 18: ng thng

1x 

là tim cng c th hàm s 







. B.







. C.







. D.

2 3 2







Câu 19: Trong không gian

Oxyz

, hình chiu vuông góc cm

 

2;3;4A

lên trc

m nào



 

2;0;0M

. B.

 

0;3;0M

. C.

 

0;0;4M

. D.

 

0;2;3M

Câu 20:Mt cu

 

2 2 2

: 8 10 8 0S x y z x y     

có tâm

và bán kính

lt là:

 

4; 5;4 , 8IR

. B.

 

4; 5;0 , 33IR

 

4;5;0 , 7IR

. D.

 

4; 5;0 , 7IR

Câu 21: Trong không gian vi h t

Oxyz

, cho mt phng

 

:3 2 0P x z  



là mn ca

 

1;0; 1n   



. B.

 

3; 1;2n 



. C.

 

3; 1;0n 



. D.

 

3;0; 1n 



Câu 22: Phn thc và phn o ca s phc

12zi

lt là

và

. B.

và

. C.

và

. D.

và

Câu 23: Cho 2 s phc

1zi=+

và

2 3 .zi=-

Tính modun ca s phc

zz+

bng

zz+=

13.

zz+=

Câu 24: Cho s phc

6 17zi=+

m biu din ca s phc

trên mt phng t

Oxy

là:

 

6; 17M

. B.

 

17; 6M

. C.

 

17;6M

. D.

 

6;17M

Câu 25: Tìm tp nghim ca b

6 13.6 6 0

xx

  

 

1;1

. B.

   

; 1 1;   

. C.

log ;log







. D.

 

;log 2

Câu 26: Tính th tích khu

ABC

cnh bng 1 quanh



. B.



. C.



. D.



Trang53

Câu 27: Nt

sinx a t

thì tích phân

 

dx a







tr 





. B.





. C.





. D.





Câu 28: Din tích phn hình phng gch chéo trong hình v c tính theo công th

 

2 2 4x x dx







. B.

 

22x dx







 

22x dx





. D.

 

2 2 4x x dx



  



Câu 29: Cho hai s phc

1 2 , 2z i z i    



là

. B.

. C.

. D.

Câu 30: Gi

và

lt là nghim c

2 5 0zz  

. Tính

F z z

. B.

. C.

. D.

Câu 31: ng thng

   

: 2 2

y t t R







   









m

ng thng

 



 

1; 2;3M 

. B.

(2;0;4)M

. C.

 

1;2; 3M 

. D.

 

2;1;3M

Câu 32: Cho t diu

ABCD

cnh

m ca

. Tính cosin ca góc ging

thng

và

. B.

. C.

. D.

Câu 33: Cho hàm s

 

o hàm

    

' 1 2f x x x x  

. S m cc tr ca hàm s 

. B.

. C.

. D.

Câu 34: Giá tr nh nht ca hàm s

3y x x

n

 

4; 1

là

4

. B.

16

. C.

. D.

Trang54

Câu 35: Cho

,,a b c

là các s th

và tha mãn

log

log 2

c=-

. Giá tr ca

log

æö

èø

bng

. B.

. C.

. D.

Câu 36:S m c th hàm s

2y x x  

ng thng

21yx  

là

. B.

. C.

. D.

Câu 37: S ng ca mt loi vi khun

trong phòng thí nghic tính theo công thc

   

0 .2

x t x



 

là s ng vi khun

u,

 

là s ng vi khun

. Bit sau 2 phút thì s ng vi khun

là 625 nghìn con. Hi sau bao lâu, k t lúc bt

u, s ng vi khun

là 10 triu.

A. 7 phút. B. 5 phút. C. 8 phút. D. 6 phút.

Câu 38:  th hàm s

 

23y f x x x   

:

T  th c s nghim c

23x x m  

vi

 

3;4m

là:

A. 3. B. 2. C. 4. D.

Câu 39: Mt hình tr ng a, mt phng qua trc ct hình tr theo mt thit din có din

tích bng

. Tính din tích xung quanh ca hình tr.

4 a



. B.

8 a



. C.

16 a



. D.

2 a



Câu 40: Cho hàm s

 

tha mãn

   

f x x e





và

 

01f 

. Tính

 

2 4e 1.f 

 

2 2e 1.f 

 

2 3e 1.f 

 

2 e 1.f 

Câu 41:Trong không gian

Oxyz

  m

( 3;2;0)M 

 ng thng

()d

  

1 1 2

x y z





. Via mt phm

và vuông góc vng

thng

()d

2 5 0x y z   

20xy  

2 5 0x y z   

50x y z   

Câu 42:Trong không gian

Oxyz

ng thm

 

1;2;3A

và

 

5;4; 1B 

là

Trang55

5 4 1

2 1 2

x y z  



. B.

1 2 3

4 2 4

x y z  





1 2 3

4 2 4

x y z  



. D.

3 3 1

2 1 2

x y z  





Câu 43:Xp

nam và

n vào mt bàn dài gm

ch ngi. Tính xác su

n không ngi cnh

nhau?

. B.

. C.

. D.

Câu 44: Cho hàm s

(4 9) 5y x mx m x     

. Có bao nhiêu giá tr nguyên ca

 hàm s

nghch bin trên khong

( ; )  

A. 7. B. 6. C. 5. D. 8.

Câu 45: Cho hình chóp

.S ABC



ABC

u cnh

, ( )a SA ABC

, góc ging

thng SB và bng

. Tính khong cách ging thng

và

. B.

. C.

. D.

Câu 46:Cho hàm s

 

y f x

o hàm trên



 th  i.

t

   

g x f f x





. Tìm s nghim c

 

0gx





. B.

. C.

. D.

Câu 47: Tp nghim ca b

 

log log 2 1 0x 

là:









. B.









. C.

 

0;1S 

. D.









Câu 48: Cho hàm s

y = f x

( )

o hàm cp hai trên



. Bit

 

03f





 

2 2018f





và bng xét

du ca

f '' x

( )



Hàm s

y = f x +2017

( )

+ 2018x

t giá tr nh nht ti

thuc kho

0;2

( )

. B.

-¥;-2017

( )

. C.

-2017;0

( )

. D.

2017;+¥

( )

Trang56

Câu 49: Xét các s th

,xy

tha mãn

 

1 1 1

2 2 2

log log logx y x y  

. Tìm giá tr nh nht

min

ca biu thc

3P x y

min

P 

. B.

min

8P 

. C.

min

9P 

. D.

min

25 2

P 

Câu 50: Có tt c bao nhiêu giá tr nguyên ca tham s

thuc khong

 

0,2019



9 3 1

lim

5 9 2187

n n a







2018

. B.

2011

. C.

2012

. D.

2019

--------------HT---------------

ĐÁP ÁN ĐỀ THI

1.C

2.B

3.A

4.C

5.D

6.B

7.B

8.A

9.C

10.B

11.A

12.B

13.A

14.A

15.C

16.C

17.A

18.A

19.A

20.D

21.D

22.A

23.A

24.D

25.C

26.B

27.A

28.D

29.A

30.A

31.B

32.B

33.A

34.B

35.D

36.D

37.D

38.D

39.B

40.B

41.C

42.D

43.C

44.A

45.A

46.A

47.A

48.B

49.C

50.C

HƯỚNG DẪN GIẢI CHI TIẾT

Câu 1: Din tích toàn phn ca hình lnh

là:

. B.

72a

. C.

54a

. D.

36a

Lời giải

Hình lt, nên din tích toàn phn ca hình lng 6 ln din tích

mi mt:

 

3 .6 54

S a a

Câu 2: Tìm tnh ca hàm s

 

log 1yx

 

;1D   

. B.

 

1;D   

. C.

[ 1; )D   

. D.

 

\1

Lời giải

Hàm s

 

log 1yx

nh khi

1 0 1xx    

Vy tnh

 

1;D   

Câu 3: H nguyên hàm ca hàm s

 

4f x x



là:

 

F x x C

  

. B.

 

12F x x C

  

 

F x x C

  

. D.

 

lnF x x x C  

Trang57

Lời giải

Câu 4: Có bao nhiêu cách chn

hc sinh t

hc sinh?

1860480

cách. B.

120

cách. C.

15504

cách. D.

100

cách.

Lời giải

S cách chn

hc sinh t

hc sinh là:

15504C 

cách.

Câu 5: Cho cp s cng

 

có s hu

3u 

và công sai

2d 

. Giá tr ca

bng:

. B.

. C.

. D.

Lời giải

Ta có:

   

3 2 1 3 2 10 1 21

u n u       

Câu 6: Tìm tp nghim c

xx



 

1;3S 

. B.

 

0; 2S 

. C.

 

1; 3S 

. D.

 

0;2S 

Lời giải

Ta có:

3 1 2 0







    







Vy tp nghim c

 

0; 2S 

Câu 7: Cho hàm s

 

y f x

nh và liên tc trên



, có bng bi

M đúng?

A. ch bin trên khong

 

;1

B. Hàm s ng bin trên khong

 

;2 

C. ch bin trên khong

 

1; 

D. Hàm s ng bin trên khong

 

1; 

Lời giải

T bng bin thiên ca hàm s

 

y f x

, ta có hàm s

 

y f x

ng bin trên khong

 

;1 

Suy ra, hàm s

 

y f x

ng bin trên khong

 

;2 

Câu 8: Bii biu thc



.A a a

v da vi s u t c

Trang58



. B.



. C.

Aa

. D.



Lời giải

Vi

là s th

ta có:



   

1 2 1 2 7

2 3 2 3 6

..A a a a a a a

Câu 9: Cho hình tr ng

và chiu cao bng

. Din tích xung quanh ca hình tr 

cho bng:

175



. B.

175

. C.

70

. D.

35

Lời giải

Din tích xung quanh ca hình tr:

2 2.5.7 70

S rh

  

  

Câu 10:Cho khi chóp

.S ABC

có

vuông góc

 

ABC

và

2SA 

, tam giác

ABC

vuông cân ti

và

1AB 

. Th tích khi chóp

.S ABC

bng

. B.

. C.

. D.

Lời giải

Do tam giác

ABC

vuông cân ti

và

1AB 

nên

ABC

S AB AC

Vy th tích khi chóp

.S ABC

là:

1 1 1 1

. . .2.

3 3 2 3

S ABC ABC

V SA S  

Câu 11: Mt kh ng sinh

 

13l cm



 

5r cm



tích khi nón bng

 

100V cm





. B.

 

300V cm





. C.

 

325

V cm





. D.

 

20V cm





Lời giải

Trang59

Chiu cao ca khi nón là

 

2 2 2 2

13 5 12h l r cm    

Th tích ca khi nón là:

 

2 2 3

.5 .12 100

V r h cm  



Câu 12: Khi cu có bán kính

6R 

có th tích bng bao nhiêu?

144



. B.

288



. C.



. D.



Lời giải

Ta có th tích khi cu là:

. .6 288

VR  

  

Câu 13: B

 

log 3 1 3x 

có nghim là:

 3x

. B.

 3x

. C.



. D.



Lời giải

Ta có:

 

3 1 0

log 3 1 3

3 1 2





  













  









Vy bm

3x 

Câu 14:  th ca hàm s

 

y f x

 bên.

S nghim c

 

4 3 0fx

là

. B.

. C.

. D.

Lời giải

Trang60



   

4 3 0

f x f x   

S nghim c  

 

4 3 0fx

là s  m c  th hàm s

 

y f x

và

ng thng

y 

T  th m.

Câu 15:Nu

 

5f x dx 



và

 

2f x dx 



thì

 

f x dx



bng

. B.

. C.

. D.

3

Lời giải

Ta có

   

22f x dx f x dx   



Suy ra:

     

2 1 2

0 0 1

5 2 3f x dx f x dx f x dx    

  

Vy

 

3f x dx 



Câu 16:Cho hàm s

 

y f x

có bng bi

Hàm s t ci t

2x 

. B.

3x 

. C.

2x 

. D.

4x 

Lời giải

Da vào bng bim ci ca hàm s là

 2x

Câu 17: ng cong trong hình v  th ca hàm s nào?

Trang61

3  y x x

. B.

3y x x

. C.

1   y x x

. D.

1  y x x

Lời giải

Ta th th 

(0;0)O

nên lo

 th ta th th ca hàm bc ba có h s

0a

nên lo

V th a hàm s

3  y x x

Câu 18: ng thng

1x 

là tim cng c th hàm s 







. B.







. C.







. D.

2 3 2







Lời giải

Xét hàm s









 

\1D  

lim







 



;

lim







 



1x

là tim cng c th hàm s







Câu 19: Trong không gian

Oxyz

, hình chiu vuông góc cm

 

2;3;4A

lên trc

m nào



 

2;0;0M

. B.

 

0;3;0M

. C.

 

0;0;4M

. D.

 

0;2;3M

Lời giải

m

thuc trc

nên t có dng

 

;0;0Mx

là hình chiu vuông góc cm

 

2;3;4A

lên trc

AM i

uuur r

20x  

2x

Vy

 

2;0;0 .M

Câu 20:Mt cu

 

2 2 2

: 8 10 8 0S x y z x y     

có tâm

và bán kính

lt là:

 

4; 5;4 , 8IR

. B.

 

4; 5;0 , 33IR

 

4;5;0 , 7IR

. D.

 

4; 5;0 , 7IR

Lời giải

Trang62

Gi

 

;;I a b c

là tâm ca mt cu

 

Ta có:

 

5 4; 5;0













    













 

có bán kính

   

2 2 2 2

4 5 8 7R a b c d         

Vy mt c

 

4; 5;0I 

và bán kính

7R 

Câu 21: Trong không gian vi h t

Oxyz

, cho mt phng

 

:3 2 0P x z  



là mn ca

 

1;0; 1n   



. B.

 

3; 1;2n 



. C.

 

3; 1;0n 



. D.

 

3;0; 1n 



Lời giải

Mt phng quát dng:

2 2 2

0 ( 0)ax by cz d a b c      

có mn là

( ; ; )n a b c



Vy mt phng

( ) :3 2 0P x z  

có mn là

 

3;0; 1n 



Câu 22: Phn thc và phn o ca s phc

12zi

lt là

và

. B.

và

. C.

và

. D.

và

Lời giải

Phn thc và phn o ca s phc

12zi

lt là

và

Câu 23: Cho 2 s phc

1zi=+

và

2 3 .zi=-

Tính modun ca s phc

zz+

bng

zz+=

13.

zz+=

Lời giải

Ta có

(1 ) (2 3 ) 3 2z z i i i+ = + + - = -

Suy ra

3 ( 2) 13zz+ = + - =

Câu 24: Cho s phc

6 17zi=+

m biu din ca s phc

trên mt phng t

Oxy

là:

 

6; 17M

. B.

 

17; 6M

. C.

 

17;6M

. D.

 

6;17M

Lời giải

m biu din ca s phc

m

 

6;17M

Câu 25: Tìm tp nghim ca b

6 13.6 6 0

xx

  

Trang63

 

1;1

. B.

   

; 1 1;   

. C.

log ;log







. D.

 

;log 2

Lời giải

Ta có

6 13.6 6 0

xx

  

6.6 13.6 6 0

   

  

log log

x  

Vy tp nghim ca b

log ;log







Câu 26: Tính th tích khu

ABC

cnh bng 1 quanh



. B.



. C.



. D.



Lời giải

Vì tam giác

ABC

u cnh bng 1 nên

CD 

Gi

m ca

Quay tam giác

ABC

quanh

c

+) Khi nón

 

ng cao

h AD



R CD

Suy ra th tích ca khi nón

 

là:

  

  

1 1 3 1 1

. . . .

3 3 4 2 8

V R h

+) Khi nón

 

ng cao

h BD



R CD

Suy ra th tích ca khi nón

 

là:

  

  

1 1 3 1 1

. . . .

3 3 4 2 8

V R h

Vy th tích ca khi tròn xoay là:

1 1 1

8 8 4

V V V

  

    

Trang64

Câu 27: Nt

sinx a t

thì tích phân

 

dx a







tr 





. B.





. C.





. D.





Lời giải

t

sin cos .x a t dx a t dt  

Ta có

 

2 2 2 2 2 2

1 sin os cosa x a t a c t a t    

i cn:

x a t



  







  





Suy ra

 

2 2 2

0 0 0 0

1 1 1

. cos . . cos .

cos

1 sin

dx a t dt a t dt dt

  

  



   

Câu 28: Din tích phn hình phng gch chéo trong hình v c tính theo công th

 

2 2 4x x dx







. B.

 

22x dx







 

22x dx





. D.

 

2 2 4x x dx



  



Lời giải

Hình phng

c gii hn bng

3yx  

21y x x  

1x 

và

2x 

Din tích hình phng

cn tìm là:

     

2 2 2

3 2 1 2 2 4S x x x dx x x dx





         





Câu 29: Cho hai s phc

1 2 , 2z i z i    



là

. B.

. C.

. D.

Lời giải

Ta có

  

1 2 2 5 .z z i i i     

Trang65



5 5.z z i  

Câu 30: Gi

và

lt là nghim c

2 5 0zz  

. Tính

F z z

. B.

. C.

. D.

Lời giải

Ta có:

2 5 0 1 2z z z i     

Suy ra

1 2 1 2

5 2 5z z F z z     

Câu 31: ng thng

   

: 2 2

y t t R







   









m

ng thng

 



 

1; 2;3M 

. B.

(2;0;4)M

. C.

 

1;2; 3M 

. D.

 

2;1;3M

Lời giải

m

 

2;0;4M

Thay

  2, 0, 4x y z

ng thng

 



c:

0 2 2 1







   









Vm

 

2;0;4M

thung thng

 



Câu 32: Cho t diu

ABCD

cnh

m ca

. Tính cosin ca góc ging

thng

và

. B.

. C.

. D.

Lời giải

Gi

m ca

ng thng

ng thng

bng

góc ging thng

ng thng

Ta có

ND MD MN  

Trang66

Áp dnh lí Cô sin trong tam giác

MND

ta có:



2 2 2

2 . .cosND MN MD MN MD NMD  

Suy ra



3 3 3

2. . .cos

2 2 2 2 2

a a a a a

NMD

     

   

  

     

   

     

   

     



cos

NMD

Vy

 



 



cos , cos ,

AB DM MN DM

Câu 33: Cho hàm s

 

o hàm

    

' 1 2f x x x x  

. S m cc tr ca hàm s 

. B.

. C.

. D.

Lời giải

Ta có:

    

' 0 1 2 0 1

f x x x x x







      







Bng bin thiên:

Da vào bng bin thiên ta thy hàm s

 

m cc tr.

Câu 34: Giá tr nh nht ca hàm s

3y x x

n

 

4; 1

là

4

. B.

16

. C.

. D.

Lời giải

Ta có

' 0 3 6 0

y x x





    







. Do ch n

 

4; 1

nên ta ch ly

2x 

Bng bin thiên:

Da vào bng bin thiên , suy ra giá tr nh nht ca hàm s

3y x x

n

 

4; 1

là

 

   

4; 1

min 4 16f x f



   

Trang67

Câu 35: Cho

,,a b c

là các s th

và tha mãn

log

log 2

c=-

. Giá tr ca

log

æö

èø

bng

. B.

. C.

. D.

Lời giải

Ta có:

æö

= + -

èø

log log log log

a a a a

a b c

=+-

4log log 3log

a a a

a b c

= + -

4 3log

3log

= + - - =

4 3.( 2) 11

Câu 36:S m c th hàm s

2y x x  

ng thng

21yx  

là

. B.

. C.

. D.

Lời giải

 m c th hàm s

2y x x  

ng thng

21yx  

là nghim

c

2 2 1 3 1 0x x x x x        

Xét hàm s

 

31f x x x  

trên



Ta có

 

3 3 0f x x x



    

Suy ra

 

ng bin trên





 

0fx

có nhiu nht 1 nghim

 

D thy do

 

c nên

 

liên tc trên



, li có

   

1 . 0 3.1 3 0ff     



 

0fx

có ít nht 1 nghim trong khong

 

1;0

 

T

 

và

 



 

0fx

m.

 th hàm s

2y x x  

cng thng

21yx  

ti duy nht 1

m.

Câu 37: S ng ca mt loi vi khun

trong phòng thí nghic tính theo công thc

   

0 .2

x t x



 

là s ng vi khun

u,

 

là s ng vi khun

. Bit sau 2 phút thì s ng vi khun

là 625 nghìn con. Hi sau bao lâu, k t lúc bt

u, s ng vi khun

là 10 triu.

A. 7 phút. B. 5 phút. C. 8 phút. D. 6 phút.

Lời giải

Trang68

Sau 2 phút thì s ng vi khun



   

0 .2 625000 0 156250xx  

Th s ng vi khun X là 10 triu:

 

0 0 2

156250.2 10.10 2 64 log 64 6

x t t      

Câu 38:  th hàm s

 

23y f x x x   

:

T  th c s nghim c

23x x m  

vi

 

3;4m

là

A. 3. B. 2. C. 4. D. 6.

Lời giải

T  th hàm s

 

23y f x x x   

 th hàm s

 

y f x

 sau:

T  th ta thy s nghim c

23x x m  

vi

 

3;4m

là 6.

Câu 39: Mt hình tr ng a, mt phng qua trc ct hình tr theo mt thit din có din

tích bng

. Tính din tích xung quanh ca hình tr.

4 a



. B.

8 a



. C.

16 a



. D.

2 a



Lời giải

Trang69

Vì mt phc ca hình tr nên nó ct hình tr theo thit din là mt hình ch nht

ABCD   c là

2,AB a BC h

   n tích ca thit din bng

2 . 8 4 .a h a h a  

Vy din tích xung quanh ca hình tr là

2 8 .Rh a





Câu 40: Cho hàm s

 

tha mãn

   

f x x e





và

 

01f 

. Tính

 

2 4e 1.f 

 

2 2e 1.f 

 

2 3e 1.f 

 

2 e 1.f 

Lời giải

Hàm s

   

f x x e





liên tc trên



nên liên tn

 

0;2



       

d 2 0 .f x x f x f f



  



 bài cho ta có

   

d 1 d

f x x x e x







t

1 d d

u x u x

v e x v e

  













     

 

2 2 2

2 0 2 0 2

0 0 0

' d 1 d 1 3 2 .

x x x x

f x x x e e x x e e e e e e e          



Suy ra

     

2 0 2 2 1 2f f e f e    

 

2 2 1.fe  

Vy

 

2 2 1.fe

Câu 41:Trong không gian

Oxyz

  m

( 3;2;0)M 

 ng thng

()d

  

1 1 2

x y z





. Via mt phm

và vuông góc vng

thng

()d

2 5 0x y z   

. B.

20xy  

. C.

2 5 0x y z   

. D.

50x y z   

Lời giải

Trang70

Gi

()P

là mt phng cn tìm.

ng thng

()d

ca m 

 

()

1; 1; 2

u   



Vì

()P

vuông góc vng thng

()d

nên

()P

có mn:

 

()

1; 1; 2

n   



t phng

()P

m

 

3;2;0M 

và vuông góc vng thng

()d

là:

     

1. 3 1. 2 2. 0 0x y z     

2 5 0x y z    

Vy mt phng cn tìm là:

2 5 0x y z   

Câu 42:Trong không gian

Oxyz

ng thm

 

1;2;3A

và

 

5;4; 1B 

là

5 4 1

2 1 2

x y z  



. B.

1 2 3

4 2 4

x y z  





1 2 3

4 2 4

x y z  



. D.

3 3 1

2 1 2

x y z  





Lời giải

Ta có

 

4;2; 4AB 



ng thm

,AB

có m 

 

  2; 1;2



. Suy ra lo

án A và C.

Thay t m

 

1;2;3A



3 3 1

2 1 2

x y z  

  



c:

1 3 2 3 3 1

111

2 1 2

  

       



. Suy ra

A

Thay t m

 

5;4; 1B 



3 3 1

2 1 2

x y z  

  



c:

5 3 4 3 1 1

111

2 1 2

   

       



. Suy ra

B

Vng thm

,AB

là:

3 3 1

2 1 2

x y z  





Câu 43:Xp

nam và

n vào mt bàn dài gm

ch ngi. Tính xác su

n không ngi cnh

nhau?

. B.

. C.

. D.

Lời giải

S phn t ca không gian mu

 

7! 5040n   

Gi

là bin c 

n không ngi c

là bin c 

n ngi c

Ta có

 

2.6! 1440nA

Trang71

Xác xut ca bin c

là

 

1440 2

5040 7

  



Vy xác xut ca bin c

là

 

P A P A    

Câu 44: Cho hàm s

(4 9) 5y x mx m x     

. Có bao nhiêu giá tr nguyên ca

 hàm s

nghch bin trên khong

( ; )  

A. 7. B. 6. C. 5. D. 8.

Lời giải



D  

3 2 4 9y x mx m



    

Hàm s nghch bin trên khong

( ; )  

khi





vi mi

( ; )x   

3 2 4 9 0x mx m     

vi mi

( ; )x   

12 27 0



  

   

    

Có 7 giá tr nguyên ca

tha yêu cu bài toán.

Câu 45: Cho hình chóp

.S ABC



ABC

u cnh

, ( )a SA ABC

, góc ging

thng SB và bng

. Tính khong cách ging thng

và

. B.

. C.

. D.

Lời giải

Vì

 

SA ABC

nên

 



,, ABC SB AB SBASB 



60SBA  

Trong

SAB

có



.tan .tan60 3SA AB SBA a a   

Dng hình bình hành

ACBD

, ta có

 

//AC SBD

nên:

   

 

, , ,d AC SB d AC SBD d A SBD

Gi

m

, có

ABD

cân ti A , suy ra

BD AM

T

 

SA ABC

ta có

BD SA



 

BD SAM

 

()SAM SBD

Trang72

Trên

 

SAM

k

AH SM

(

H SM

) thì

 

AH SBD

nên

 

,d A SBD AH

u

ABD

cnh

nên

AM 

Trong tam giác

SAM

vuông ti

, ta có

 

2 2 2 2

1 1 1 1 1 5 3 15

AH AM SA a

       







Vy

   

 

d AC SB d A SBD AH  

Câu 46:Cho hàm s

 

y f x

o hàm trên



 th  i.

t

   

g x f f x





. Tìm s nghim c

 

0gx





. B.

. C.

. D.

Lời giải

Ta có:

     

.g x f x f f x

  







;

 

   

f f x

























D th ta thy:



 















 

2;3x 



 

f f x

f x x





















 

2;3x 



   

03fx

Nhn xét s nghi

 

là s m c th hàm s

 

y f x

và trc

hoành. D th ta th th hàm s

 

y f x

ct trc hoành tm phân bit khi



 

; 1;0

; 3;4

x x x

f x x

x x x

  





  









   

4f x x

Nhn xét s nghim c

 

là s m c th hàm s

 

y f x

và

ng thng

yx

Trang73

D th ta th th hàm s

 

y f x

cng thng

yx

tm phân bit



 

2 2 1

6 4 4

8 8 7

; ;0

; 0;1

;;

x x x x

f x x x x x

x x x x







   



  



V

 

'0gx

có

nghim phân bit

1 2 4 6 7 8

; ;0; ;1; ; ;x x x x x x



1 2 4 6 7 8

1 0 1 2 3x x x x x x          

Câu 47: Tp nghim ca b

 

log log 2 1 0x 

là









. B.









. C.

 

0;1S 

. D.









Lời giải

B

 

log log 2 1 0x 

 

2 1 0

log 2 1 0 2 1 1

2 1 2

log 2 1 1















      

  



  









Vy tp nghim ca b









Câu 48: Cho hàm s

y = f x

( )

o hàm cp hai trên



. Bit

 

03f





 

2 2018f





và bng xét

du ca

f '' x

( )



Trang74

Hàm s

y = f x +2017

( )

+ 2018x

t giá tr nh nht ti

thuc kho

0;2

( )

. B.

-¥;-2017

( )

. C.

-2017;0

( )

. D.

2017;+¥

( )

Lời giải

t

g x

( )

= f x + 2017

( )

+ 2018 x

Ta có

   

2017 2018g x f x



  

Cho

   

0 2017 2018.g x f x



    

Da vào bng bin thiên

Ta có

x +2017 = 2

hay

x + 2017 = x

Suy ra

x = -2015

hay

x = x

- 2017.

t

= x

-2017

thì

< -2017.

Ta có

   

0 2017 2018 0.gf



  

T ng bin thiên ca hàm

 



Da vào bng bin thiên, ta thy hàm

 

t giá tr nh nht ti

, vi

Î -¥;-2017

( )

Câu 49: Xét các s th

,xy

tha mãn

 

1 1 1

2 2 2

log log logx y x y  

. Tìm giá tr nh nht

min

ca biu thc

3P x y

Trang75

min

P 

. B.

min

8P 

. C.

min

9P 

. D.

min

25 2

P 

Lời giải

u kinh ca

 

1 1 1

2 2 2

log log logx y x y  

là

0x 

và

0y 

Suy ra

 

.1x y x y x y y    

, vì

0x 

nên

10y 

   

 

1x y y

suy ra





   

3 3 4 1 5 2 4 1 . 5 9

1 1 1

P x y y y y

y y y

           

  

min

9P 

khi

   

(N)

4 1 4 1 1

(L)







     













Vi

y 

c

x 

Câu 50: Có tt c bao nhiêu giá tr nguyên ca tham s

thuc khong

 

0,2019



9 3 1

lim

5 9 2187

n n a







2018

. B.

2011

. C.

2012

. D.

2019

Lời giải

Ta có

9 3 9 3.3 1 1

lim lim lim

5 9 5 9 9 3

n n n n

n n a n n a a a









   











Vì

9 3 1 1 1

lim 3 2187 7

5 9 2187 3 2187

n n a a



      



Kt hp vi gi thit

thuc khong

 

0;2019

nên có 2012 giá tr nguyên ca

--------------HT---------------

Đề 4

ĐỀ LUYỆN THI CẤP TỐC TỐT NGHIỆP THPT NĂM 2021

Thuvienhoclieu.Com

BÀI THI: TOÁN

Thời gian: 90 phút

Trang76

Câu 1: Trong không gian

Oxyz

, cho mt phng

 

: 5 0P x y  

. Mn ca mp

 

là:

 

1;1;0

. B.

 

1;0; 1

. C.

 

1; 1;5

. D.

 

1;1;0

Câu 2: Cho hàm s







. Kh

A. Hàm s ch bin trên



B. Hàm s 









   

;2 2;  

C. Hàm s 



n trên tng khonh.

D. Hàm s n trên tng khonh.

Câu 3: Trong không gian

Oxyz

ng thng

m

 

1; 1;0A 

và song song vng thng

2 1 5

x y z

  





2 1 5

x y z





. B.

3 2 5

2 1 5

x y z  





2 1 5

x y z



. D.

3 2 5

2 1 5

x y z  





Câu 4: Cho





1. Hàm s

log

yx

có tnh là

 

0;D  

2. Hàm s

log

yx

u trên khong

 

0;

 th hàm s

log

yx

 th hàm s

ya

i xng thng

yx

 th hàm s

log

yx

nh





là mt tim cn.

. B.

. C.

. D.

Câu 5: Tp xác nh ca hàm s

 

27yx





là

 

3;D  

. B.

 

\3D  

. C.





3;D  

. D.

D  

Câu 6: Bit

 

là mt nguyên hàm ca hàm

 

 n

 

;ab

và

   

d 1; 2.

f x x F b



Tính

 

. B.

. C.

. D.

1

Câu 7: Trong không gian

,Oxyz



2u j k

  

có t là

 

0;2; 1

. B.

 

2; 1;0

. C.

 

0;2;1

. D.

 

0; 1;2

Câu 8: Gi



là góc gi

 

2;1; 2u 



 

3;4;0v 



. Tính

cos



. B.

. C.



. D.

Câu 9: Quay tam giác

ABC

vuông ti

vi

2, 1AB BC

quanh trc

. Tính th tích khi tròn

c.



. B.



. C.



. D.



Câu 10: Cho hình chóp

.S ABCD

 nht vi

2,AB a BC a

u

SAB

nm

trên mt phng vuông góc vng cách gia

và

là

. B.

. C.

. D.

Trang77

Câu 11: Tip tuyn c th hàm s

31y x x  

có h s góc nh nhng thng

yx

. B.

0y 

. C.

32yx  

. D.

32yx  

Câu 12: Trong không gian

Oxyz

, mp

 

ct ba trc t tm phân bit to thành mt tam

giác có trng tâm

 

3;2; 1G 

. Vi









 

9 6 3

x y z

  

. B.

9 6 3

x y z

  

. C.

9 6 3

x y z

  

. D.

9 6 3

x y z

  

Câu 13: 

























2020 3.2020 1 0

  



. B.

. C.

. D. 



.

Câu 14: Trong không gian

Oxyz



 

1;2;4M



 

: 2 2 5 0P x y z   







 

là:

. B.

. C.

. D.

Câu 15: Trong không gian

,Oxyz



 

1;0;2A



1 1 2

x y z















1 3 1

x y z

  



1 1 1

x y z

  

2 2 1

x y z

  

. D.

1 1 1

x y z

  



Câu 16:   

 

    

 

3;3

   

DABC

  

 





f x x



. B.

. C.



. D.

Câu 17: 

 









. B.



. C.



. D.



Câu 18: 



 

21x



2 C

. B.

2 C

. C.

2 A

. D.

2 A

Câu 19: Tp nghim

ca b

xx









là:

   

;1 3;S     

. B.

 

1;S   

 

;3S  

. D.

 

1;3S 

Trang78

Câu 20: Trong mt phng tm

 m biu din s phc

. Tính

 

1 z

2

 

18zi  

. B.

 

1 2 2zi   

. C.

 

11zi   

. D.

 

12zi  

Câu 21: Cho t din

OABC

có

,,OA OB OC

t vuông góc và

1; 2; 12OA OB OC  

. Tính th

tích t din

OABC

. B.

. C.

. D.

Câu 22: Cho hàm s

 

y f x



     

' 1 3f x x x x  

. 















 hàm s

 

y f x

:

. B.

. C.

. D.

Câu 23: S 



























:

. B.

. C.

. D.

Câu 24: Cho 

ABC.A'B'C'



, 

. 











 

AB'C'



 

A'B'C'

. B.

. C.

. D.

Câu 25: Cho s phc

z a bi

vi

,ab

tha mãn

   

1 2 13 2i z i z i    

. Tính tng

ab

1ab

. B.

2ab

. C.

0ab

. D.

2ab  

Câu 26: 

 

log 5 4x 

có nghim là.

11x 

. B.

3x 

. C.

13x 

. D.

21x 

Câu 27: Trong không gian

Oxyz

, cho mt cu

     

: 1 4 9S x y z    

. T m

 

4;0;1A

nm

ngoài mt cu, k mt tip tuyn bt k n

 

vi tim

. Tp hm

ng

tròn có bán kính bng

. B.

. C.

. D.

Câu 28: Gi s

( )

2 x

F x ax bx c e= + +

là mt nguyên hàm ca hàm s

( )

2 x

f x x e=

. Tính tích

P abc=

4P =-

. B.

1P =

. C.

5P =-

. D.

3P=

Câu 29: Mt nhóm có

bn nam và

bn n. Chn ngu nhiên

b

trong cách cht

bn n.

. B.

. C.

. D.

Câu 30: Trong không gian

Oxyz

m

( )

1;2;4A -

m

( )

3;0; 6B -

m cn

có t là:

( )

4; 2; 10--

. B.

( )

4;2;10-

. C.

( )

1;1; 1-

. D.

( )

2;2; 2-

Câu 31: 

2log 2

log 20

log 5













,,abc

. 

T a b c  

Trang79

1T 

. B.

3T 

. C.

3T 

. D.

1T 

Câu 32: Cho hàm s

 

y f x









có bng bin thiên sau:

Kh

A. Hàm s t ci ti

2x 

. B. Hàm s t ci ti

2x 

C. Hàm s t ci ti

4x 

. D. Hàm s t ci ti

3x 

Câu 33: Giá tr nh nht ca hàm s

34y x x  

n

 

0;2

là

 

0;2

min 4y 

. B.

 

0;2

min 1y 

. C.

 

0;2

min 2y 

. D.

 

0;2

min 6y 

Câu 34:  th ca mt hàm s c lit kê  bA, B, C, D 



31y x x   

. B.

31y x x   

. C.

31y x x  

. D.

31y x x  

Câu 35: Tính

Ix



ln 2

C

. B.

2 ln 2

C

. C.

C

. D.



Câu 36: Hàm s a hàm s

 



trên khong

 

0; .

ln x

. B.

 

ln 1x 

. C.

ln2x

. D.

Câu 37: 















có t là

 

1;0

. B.

 

1;1

. C.

 

1; 1

. D.

 

0;1

Câu 38: Bit

 

x1f x d 



và

 

2 1 x 3.f x d



Tính

 

x.f x d



4.

Câu 39: 

















2020y x x  

:

Câu 40: Cho s phc

tho mãn

30zi  

a

bng

. B.

. C.

. D.

Câu 41: Cho hàm s

 

y f x

c bc b th

 





Trang80



 

0fx

có 4 nghim phân bit khi và ch khi

 

00f 

   

00f f m

. C.

   

0f m f n

. D.

   

00f f n

Câu 42: Cho hàm s

 

    ng bin trên

 

1;4

, tho mãn

   

 

2 . , 1;4x x f x f x x



   





. Bit rng

 

f 

. Tính tích phân

 

I f x dx



. B.

1187

. C.

1188

1186

Câu 43: Cho hàm s

 

3 2 2

3 3 1 2020y x mx m x    

. Có tt c bao nhiêu giá tr nguyên ca

sao

cho hàm s có giá tr nh nht trên khong

 

0;

. B.

. C. vô s. D.

Câu 44: Có tt c bao nhiêu s t nhiên gm

ch s 

ch s

chn

60000

. B.

72000

. C.

36000

. D.

64800

Câu 45: 

 

y f x











 

y f x









 

2 2 20201g x f xx x

?

 

2;0

. B.

 

3;1

. C.

 

1;3

. D.

 

0;1

Câu 46: 







x x mx

  





 

1;2

1m

. B.

8m 

. C.

8m

. D.

1m

Câu 47:  ng

.ABC A BC

  

có chiu cao bng



ABC

là tam giác cân ti

vi



2; 120AB AC BAC  

. Din tích mt cu ngoi ti trên



. B.



. C.

64 2



. D.

32 2



Câu 48: Cho b

   

log 2 2 1 log 6 5x x x x m      

. Có tt c bao nhiêu giá tr

nguyên ca tham só

 bp nghim cha khong

 

1;3

. B.

. C.

. D. Vô s.

Trang81

Câu 49: 

.ABCD A B CD

   

có

2AA







ABCD

 

ABC

là tam





,,M N P



,,B C C D DD

    

và



sao cho

3.QC QB



.MNPQ

. B.

. C.

. D. n

Câu 50: 





 

y f x











 

1;4































 

10;10



 

2f x m m

























 

1;4

. B.

. C.

. D.

ĐÁP ÁN

1-D

2-C

3-B

4-D

5-A

6-B

7-A

8-C

9-B

10-C

11-C

12-C

13-B

14-B

15-D

16-D

17-B

18-A

19-A

20-D

21-D

22-D

23-C

24-A

25-A

26-D

27-C

28-A

29-B

30-C

31-D

32-B

33-C

34-D

35-A

36-B

37-B

38-A

39-D

40-A

41-B

42-D

43-C

44-D

45-D

46-A

47-B

48-C

49-C

50-C

LỜI GIẢI CHI TIẾT

Câu 51: Chọn D

Ta có mn ca mp

 

là

 

1; 1;0n 



hay

 

1;1;0n 



Câu 52: Chọn C

Ta có

 

0, 2





   



Câu 53: Chọn B

Vì

m

 

1; 1;0A 

và song song vng thng

2 1 5

x y z

  



nên

có

VTCP

 

2; 1;5u 





d y t







  









Vi

1t 

d

m

 

3; 2;5M 

a

là

3 2 5

2 1 5

x y z  





Trang82

Câu 54: Chọn D.

Hàm s

log

yx



 

0;D  





log

yx



 

0;



1a 

, nghch bin trên

 

0;



01a

 

 th hàm s

log

yx

và

ya



yx

, nên m 3





log

yx











Câu 55: Chọn A.

Hàm s nh khi

27 0 3.xx   

Vy tnh ca hàm s là

 

3;D  

Câu 56: Chọn B.

Ta có

     

f x x F b F a  



, suy ra

   

1 2 1 1.F a F b    

Câu 57: Chọn A

Ta có:

 

2 0;2; 1u j k u    

   

Câu 58: Chọn C

Ta có:

. 6 4 0 2

cos

4 1 4. 9 16 0

  

    

   



Câu 59: Chọn B

Khi quay tam giác

ABC

vuông ti

quanh trc

 c kh     

1r BC

và có chiu cao

2h AB

 tích khi nón to ra là:

1 1 2

.1 .2

3 3 3

V r h



    

Câu 60: Chọn C

Trang83





thì

 

SH ABCD

Vì

 

BC SAD¤¤

nên

   

 

, , ,d BC SD d BC SAD d B SAD





thì

BI SA

thì

 

BI SAD

(do

 

AD SAB BI

Suy ra

 

d B SAD BI a  

Câu 61: Chọn C



 

3 6 3 1 3 3y x x x



      



3k 



11xy   



 

3 1 1 3 2y x y x       

Câu 62: Chọn C



     

;0;0 , 0; ;0 , 0;0;cA a B b C



 



,,Ox Oy Oz

Vì



ABC

nên suy ra

9, 6, 3a b c   



9 6 3

x y z

  

Câu 63: Chọn B

2020

log

2020

2020 3.2020 1 0

2020

log



























    

























1 2 2020 2020 2020 2020

3 5 3 5 3 5 3 5

log log log . log 1 0

2 2 2 2

     

   

     

     

     

Câu 64: Chọn B

Ta có

 

1.1 2.2 2.4 5

1 2 2

d M P

  



  

Câu 65: Chọn D

Gi

 

1 ; ; 1 2B d B t t t      

 

; ;2 3AB t t t  



Ta có

 

. 0 4 6 0 1 2;1;1

d AB a t t t t B           

 

Trang84



AB

ng thng



qua

 

 

1;1; 1AB 



là:

1 1 1

x y z

  



Câu 66: Chọn D



:3AB y x

:1BC y

  CD y x

Suy ra

 

3 khi 3 2

1 khi 2 1

khi1 3





    



   





   



f x x



   

3 2 1 3

3 3 2 1

d 3 d d d



  



     





   

f x x x x x x x



Câu 67: Chọn B





3SO

2OA

1CD

Ta có

1 1 2 4

3 3 3 3

       

AC CD

CD SO AC AO OC

AO SO



2 . .





S OC CD

Câu 68: Chọn A

S hng th

1k

trong khai trin

 

21x

là

 

1 10

. 2 .1







T C x

10 10

.2 .





k k k

Xét

4 10 6   kk

Vy h s ca s hng cha

là

6 10 6 6 4 4 4

10 10 10

.2 .2 .2



C C C

Câu 69: Chọn A

Ta có:

4 3 2

8 2 2 4 3







      





4 3 0





    







Câu 70: Chọn D

Ta có:

 

2;1 2M z i    

Vy

   

1 1 1 2 2z i i i i        

Câu 71: Chọn D

Trang85

Ta có:

. . 24

OABC

OAOB OC

V   

Câu 72: Chọn D

Ta có: Bng bi

Da vào bng bin thiên ta thy hàm s có 2 cc tr.

Ch D.

Câu 73: Chọn C

Ta có: Tnh

 

2;2D 

 

3 2;2xD    

 th hàm s m cng.

 th hàm s không có tim cn ngang do

không th tin ti



Ch C.

Câu 74: Chọn A

Gi

m

B'C'

nên

   



;AB'C' A'B'C' AIA









T 

AI a

Trong tam giác vuông

'AIA

có:



tan '

AA a

AIA

  

Vy

   

 



' ' ; ' ' ' ' 30AB C A B C AIA

Ch A.

Câu 75: Chọn A

z a bi z a bi    

Theo gi thit

   

1 2 13 2i z i z i    

     

1 2 13 2i a bi i a bi i       

3 2 13 2 1

a b bi i a b





        







Câu 76: Chọn D

u kin

5x 

Trang86



 

log 5 4 5 2 21x x x      

Câu 77: Chọn C

Hình v minh ha mt c

 

4;0;1A

và tâm

mt cu.

Gi

là tâm và

ng tròn là tp hp các tim ca các tip tuyn vi mt

cu

 

Mt cu

 

có tâm

 

1;0;4I

và bán kính

3R 

Ta có

     

2 2 2

1 4 0 0 4 1 3 2AI       

18 9 3AM AI R     

Vng tròn tp hm

là

. 3.3 3 2

AM IM

  

Câu 78: Chọn A

( )

là nguyên hàm ca

( )

( ) ( )

( )

22xx

F x f x ax bx c e x e

éù

Û = Û + + =

êú

ëû

( ) ( )

2 2 0 2

ax a b x b c e x e a b b

b c c

íí

ïï

éù

Û + + + + = Û + = Û = -

ìì

êú

ëû

ïï

+ = =

ïï

îî

Suy ra:

4P =-

Câu 79: Chọn B

S cách chn

bn bt k là:

10C =

TH1 Chn

bn n,

bn nam: Có

.2 6C =

cách.

TH2 Chn

bn n: Có

cách.

Suy ra s cách chn

bt

n là

cách.

Xác sut cn tìm là:

Câu 80: Chọn C

Áp dng công thc tính t m ta có t m

là:

( )

1 3 2 0

; ; 1;1; 1

2 2 2

æö

- + +

èø

Câu 81: Chọn D

 

3 3 3

log 2 .5

log 20 2log 2 log 5

log 20

log 15 log 5.3 log 5 1



  



3 3 3

2log 2 1 1 log 5 2log 2 1

log 5 1 log 5 1

   

  





1a 

;

1b 

;

11c T a b c     

Câu 82: Chọn B

Hàm s t ci ti

2x 

Câu 83: Chọn C

Trang87

33yx





;

 

1 0;2











  



Ta có:

 

04y 

;

 

12y 

;

 

26y 

Vy

 

 

0;2

min 1 2yy

Câu 84: Chọn D



lim ; lim 0

y y a

 

     



1; 1xx  

nên

   

1 0; 1 0yy



  



31y x x  

Câu 85: Chọn A

ln2

I x C  



Câu 86: Chọn B

 

ln 1





  







 

ln 1yx



 



Câu 87: Chọn B

i xng c th m cng tim cn

ng tim cng:

1x 

ng tim cn ngang:

1.y 

Vi xng c th có t là

 

1;1

Ch B.

Câu 88: Chọn A

t :

21tx

2.dt dx

   

2 1 d 3

f x x f t dt  



 

6f x dx



Mà

     

3 1 3

0 0 1

1 6 5.f x dx f x dx f x dx     

  

Câu 89: Chọn D



2020 0xx  

t

0.tx

m trái dm

,.xx

Vy ch D.

Câu 90: Chọn A

Ta có:

 

3 0 3 3 1 10z i z i z z           

Câu 91: Chọn B

Ta có

 

f x x









  







ng bin thiên

Trang88

Ta có

               

f x dx f x dx f m f f n f f m f n



      



Da vào bng bi 

 

0fx

có 4 nghim thì

   

00f f m

Câu 92: Chọn D

Vì

 

ng bin trên

 

1;4

suy ra

 

 

0, 1;4f x x



  



       

 

2 . 1 2 1 2

x x f x f x x f x f x x f x





        

     

     



 

f x x C   

Mà

   

3 2 4

1 1 3

2 3 3 2

f C C f x









        

 

1186

2 45

I f x dx dx









   



Câu 93: Chọn C

Ta có:

 

3 6 3 1y x mx m



   

   

2 2 2 2

0 3 6 3 1 0 2 1 0 1y x mx m x mx m x m



             

Bng bin thiên

Da vào bng bi hàm s có giá tr nh nht thuc khong

 

0;

 

   

 

1 0;

1 3 1 3 1 2020 2020

m m m m

f m f





  









      







2 2 0









  



1m  

Vy có vô s giá tri nguyên

Câu 94: Chọn D

Trường hợp 1: (Ba số chẵn không có mặt số

)

+ Chn

s chn:

(cách)

+ Chn

s l:

(cách)

+ Sp xp

s n:

(cách)

Suy ra có:

. .6! 28800CC 

(cách)

Trường hợp 2: (Ba số chẵn có mặt số

)

+ Sp xp s

(khác v u):

(cách).

f(m+1)

m+1

m-1



f(m-1)

Trang89

+ Chn

s chn:

(cách).

+ Chn

s l:

(cách).

+ Sp xp

s n:

(cách).

Suy ra có:

5. . .5! 36000CC 

(cách).

Vy có

28800 36000 64800

(cách).

Câu 95: Chọn D.

Ta có:

 

2 2 2020 112 2021 1g x f x g x xx f xx     



     

1 2 1 1 2021k x f x x     



1tx



   

2 2021h t f t t  

   

22h t f t t



  



yx





     

00h t f t t f t t

  

     















 

1 1 0

1 1 3 2 4

   





   



    





     

1 2 1 1 2021k x f x x     



 

2 1 20211g x f xx 





1x 



Câu 96: Chọn A.

Tnh:

D  

x x mx

  



 

2 .ln2. 3 2

x x mx

y x x m

  



   



x x mx

  





 

1;2



 

0, 1;2yx



  

 

2 .ln2. 3 2 0, 1;2

x x mx

x x m x

  

     

 

3 2 0, 1;2x x m x     

 

3 2 , 1;2m x x x     

Trang90

 

 

1;2

max 3 2 1m x x     

Câu 97: Chọn B

Gi

ng tròn ngoi tip ca tam giác

ABC

và

m cn

Dng thng

vuông góc vi mt phng

( )

ABC

ti

ng thng trung trc

cn

nm trong mt phng

( )

;dd

m

ca

và

là tâm mt cu ngoi

ti ng

.ABC A BC

  

và

R AI=

là bán kính ca mt cu này.

Ta có

2 2 o

2 . cos120 2 3BC AB AC AB AC   

Áp dnh lý sin cho tam giác

ABC

ta có



sin

AH AH

BAC

= Þ =

Xét hình ch nht

AKIH

ta có

22R AI IH AH= = + =

Vy din tích mt cu bng

4 32SR



Câu 98: Chọn C

Ta có:

   

log 2 2 1 log 6 5x x x x m      

 

   

log 7 14 14 log 6 5x x x x m      

7 14 14 6 5 0x x x x m       

6 8 9 6 5x x m x x       

 

Bp nghim cha khong

 

1;3

khi và ch khi

 

i mi

 

1;3x 

Ta có bng bin thiên ca hai hàm s

6 8 9y x x  

65y x x   

trên khan

 

1;3



Suy ra

12 23m  

, mà

*mN

nên

 

11,...2,3,4,5,22m

. Vy tng các giá tr

tha

mãn bài là

Trang91

Câu 99: Chọn C

Ly

: 3 // //K CD KC KD KQ BD MN  

 

,,d Q PMN d K PMN

. . .Q PMN K PMN M PKN

V V V  

Ta có:

PKN DCC D DKP PND KCC N

S S S S S

   

  

   

 

1 1 1 3

4.2 .1.1 .1.2 . 2 3 .2

2 2 2 2

     

Vì

   

A B C D DCC D C D

       



và

 

M A B C D

   



 

     

, , , do //d M DCC D d M C D d M A B A B C D

         

  

Li có

   

1 1 1

, . . . .sin . , .

2 2 2

ABM

S d M A B A B A B B M B d M A B A B





           

  

 

, .sin 2.sin 60 3d M A B B M B

   

    

Vy th tích ca khi t din

MNPQ

là:

 

1 1 3 3

. , . . 3.

3 3 2 2

MNPQ M PKN PKN

V V d M A B S





   

Câu 100: Chọn C



là:

0m 



     

2 2 2 3f x m m m f x m m m f x m          



3 2 3







     











m

và

 

 

10;10 4,5,6,7,8,9,10mm    

có





Đề 5

ĐỀ LUYỆN THI CẤP TỐC TỐT NGHIỆP THPT NĂM 2021

Thuvienhoclieu.Com

BÀI THI: TOÁN

Thời gian: 90 phút

Câu 1. Khi tr tròn xoay có th tích bng

144



ng sinh ca khi tr

bng

. B.

. C.

. D.

Câu 2. Trong các hàm s  nào nghch bin trên tp







. B.









. C.

y 

. D.

y 

Trang92

Câu 3. Giá tr ca tích phân



bng

. B.

. C.

. D.

Câu 4. ng cong  hình  th ca hàm s 

21   y x x

. B.







. C.







. D.

1  y x x

Câu 5. Trong không gian

Oxyz

, cho mt phng

 

: 2 3 2020 0P x y z   

    

không phi là mn ca mt phng

 

2;4; 6n   



. B.

 

1;2; 3n   



. C.

 

1; 2;3n 



. D.

 

2;3;2020n 



Câu 6. Cho s phc

53zi

. S phc liên hp ca

là

53i

. B.

53i

. C.

53i

. D.

53i 

Câu 7. Trong mt phng

 

Oxy

m

biu din s phc

13zi  

có t là

 

1; 3M 

. B.

 

1; 3M 

. C.

 

1;3M 

. D.

 

1;3M

Câu 8. Cho các s th

,ab

và

1a 

. Biu thc

log

bng

 

2 1 log

b

. B.

2log

. C.

2 log

b

. D.

1 log

b

Câu 9. Th tích kh tam giác có chiu cao bng

, ct bng

là:

. B.

12.

. C.

. D.

28.

Câu 10. Trong các khi hình sau, khi không phi khi tròn xoay là:

A. Khi cu. B. Khi tr. C. Kh. D. Khi nón.

Câu 11. H tt c các nguyên hàm ca hàm s

 

sinf x x



là

cos 2lnx x C

. B.

cosxC



cos 2lnx x C  

. D.

cos 2lnx x C  

Câu 12. Trong không gian vi h t

Oxyz

, cho

2 3 5a i j k   

   

. T ca



là

 

2;3;5

. B.

 

2;3;5

. C.

 

2;3; 5

. D.

 

2; 3; 5

Câu 13. Cho

s th

tha mãn

1x 

và

log 3

y 

. Tính

log

Ty

Trang93

T 

. B.

T 

. C.

T 

. D.

5T 

Câu 14. Trong không gian

Oxyz

m

 

2; 1;3M 

và mt phng

 

:2 5 1 0x y z



   



trình mt phm

và song song vi

 



2 5 12 0x y z   

. B.

2 5 12 0x y z   

2 5 12 0x y z   

. D.

2 5 12 0x y z   

Câu 15. Cho hàm s

 

y f x

 th  bên.

Hàm s ch bin trên khong

 

0 ; 2

. B.

 

3 ; 1

. C.

 

1 ; 0

. D.

 

1 ; 3

Câu 16.  th hàm s







ng tim cng th

1x 

. B.

2y 

y 

. D.





Câu 17. Gi

là tp nghim c

9 10.3 9 0

  

. Tng các phn t ca

bng

. B.

. C.

. D.

Câu 18. Mu vi vn tc

16 /ms

i lái xe nhìn thy mng

ngi vp phanh tng chm du vi vn tc

 

2 16v t t  



là thi gian (tính bng giây) k t c

trong

giây cui cùng bng

60m

. B.

64m

. C.

160m

. D.

96m

Câu 19. Cho hàm s

 

y f x

o hàm

 

1,fx





.x

M 

   

12ff

. B.

   

12ff

. C.

   

12ff

. D.

   

12ff

Câu 20. Cho hình vuông

ABCD

tâm

 dài cnh là

4.cm

ng cong

BOC

là mt phn parabol

nh

chia hình vuông thành hai hình phng có din tích lt là

và

(tham kho hình

v).

Trang94

T s

bng

. B.

. C.

. D.

Câu 21. Mt cp s nhân có s hng th 3 và s hng th 6 lt là

và

243

 hng th

ca cp s nhân bng:

2187

. B.

2187

. C.

729

. D.

243

Câu 22. Tìm hàm s

 

không là nguyên hàm ca hàm s

 

sin2f x x

 

cosF x x

. B.

 

sinF x x

. C.

 

cos2

F x x

. D.

 

cos2F x x

Câu 23. Cho hàm s

 

nh, liên tc trên



và có bng bi



1













1



 th hàm s

 

y f x

cng thng

2y 

tm?

. B.

. C.

. D.

Câu 24. Trong không gian

Ox ,yz

m

   

2;1; 0 , 2; 5; 4 .AB

t cng

kính

là

   

2 1 12x y z    

. B.

   

3 2 48x y z    

     

2 2 2

4 4 4 48x y z     

. D.

   

3 2 12x y z    

Câu 25. Tp nghim ca b

   

log 3 1 log 25 25xx  

là









. B.

;









. C.

;









. D.







Câu 26. Cho hàm s

 

y f x

liên tc trên

 

3;3

và có bng xét du c

Trang95

M sai?

A. Hàm s t cc tiu ti

1x 

. B. Hàm s t ci ti

2x 

C. Hàm s t ci ti

1x 

. D. Hàm s t cc tiu ti

0x 

Câu 27. Cho hình hp

.ABCD A B C D

   

. B ng phng là:

, , ' 'AC BD A D

  

. B.

, ', 'AC AC BB

  

, ', ' 'AB BD C D

  

. D.

' , ' , 'A C B D BD

  

Câu 28. Cho hai s phc

,zz

tha mãn

1 1 2

4, 3z z z

. Giá tr biu thc

P z z

bng

A. 13. B. 25. C. 7. D. 19.

Câu 29. Trong không gian vi h t

Oxyz

, cho

 

2; 1;3M

 

3;2; 4N

 

1; 1;2P

nh ta

 m



MNPQ

là hình bình hành?

 

2;2; 5Q

. B.

 

2; 3; 5Q

. C.

 

0; 4;9Q

. D.

 

1;3; 2Q

Câu 30. Giá tr nh nht ca hàm s







n

 

0;3

là

 

0;3

min 3





. B.

 

0;3

min 2





. C.

 

0;3

min





. D.

 

0;3

min





Câu 31. 

 

y f x



 

0;1



 

d3f x x 



và

 

14f 

Tích phân

 

dxf x x









. B.

. C.

. D.

1

Câu 32. Trong không gian vi h trc t

Oxyz

m

 

1;0;3A

;

 

5;2; 1B 



ng chính tc cng thm

và

5 2 1

x y z





. B.

2 1 2

x y z





3 1 1

2 1 2

x y z  





. D.

5 2 1

2 1 2

x y z  



Câu 33. Có 3 qu c cha trong mt hp hình tr (hình v bên) vi chiu cao

và

bán kính

3,5

Th tích bên trong hình tr không b chim ly bi các qu bóng tennis (b  dày ca v

hp) bng bao nhiêu?

82,75



. B.

87,25



. C.

85,75



. D.

87,75



Câu 34. Có bao nhiêu s t nhiên có hai ch s khác nhau?

A. 72. B. 81. C. 90. D. 18.

Trang96

Câu 35. Cho hàm s

 

o hàm

 

   

2 4 , .f x x x x x x



     

S m cc tr ca

hàm s

 

là

. B.

. C.

. D.

Câu 36. Cho hàm s

 

y f x

 th hàm s

 

y f x

 bên

Hàm s

 

12y f x x x   

ng bin trên khong?

 

2; 1

. B.

 

3; 2

. C.

 

3;0

. D.

 

0;1

Câu 37. Trong không gian vi h t 

Oxyz

  m

 

1( 2;1;I

và mt phng

 

:2 2 1 0P x y z   

. Mt cu

 

có tâm

, ct

 

theo m ng tròn có bán kính

4r 

. Mt cu

 

 là:

     

2 2 2

2 1 1 20x y z     

. B.

     

2 2 2

2 1 1 18x y z     

     

2 2 2

2 1 1 20x y z     

. D.

     

2 2 2

2 1 1 2 5x y z     

Câu 38. u tháng m i gi ngân hàng

400.000.000

ng (

400

tri ng) vi lãi sut gi là

0,6%

mi tháng theo hình thc lãi sut kép. Cui mn gi vào ngân

hàng s tin là

10.000.000

(

tring). Hi sau ít nht bao nhiêu tháng ( k t i

này ra ngân hàng gi tin) thì s tic l

700.000.000

(b

tring)?

tháng. B.

tháng. C.

tháng. D.

tháng.

Câu 39.  th hàm s

y ax bx cx d   









:

Trang97

 th ca hàm s

 

   

f x f x



















?

. B.

. C.

. D.

Câu 40. Cho hàm s

 

có bng xét du c

Hàm s

 

1y f x

nghch bin trên khong

 

1;4

. B.

 

0;2

. C.

 

0;1

. D.

 

2; 1

Câu 41. Trong không gian vi h t 

Oxyz

, cho hình hp

.ABCD A B C D

   

bit

 

1;2;3A

 

2;0; 1B





 

3;0; 3C 

và

 

2;4; 3D





. T nh

ca hình hp

.ABCD A B C D

   

là

 

4; 1;1B 

. B.

 

2; 1;2B 

. C.

 

4;1; 1B 

. D.

 

0;1; 3B 

Câu 42. Cho hình chóp

.S ABCD

nh

2AB a

SAB

là tam giác cân ti

và

nm trong mt phng vuông góc vi mt phng

 

ABCD

. Gi

,MN

lm ca

,AB BC

và

là trng tâm

SCD

. Bit khong cách t m

n mt phng

 

SND

bng

. Th tích ca khi chóp

.G AMND

bng

. B.

. C.

. D.

Câu 43. Cho hình thang

ABCD

 

//AB CD

bit

5AB 

3BC 

10CD 

4AD 

. Th tích khi tròn

xoay to thành khi quay hình thang

ABCD

 

//AB CD

quanh trc

bng

128



. B.



. C.

112



. D.



Câu 44. 

.ABC AB C

  

u cnh

, hình chiu vuông góc cnh



lên

 

ABC

  m

ca cnh

. Góc gi ng thng



và m  ng

60

Khong cách gia



và



là

. B.

3 13

. C.

2 13

. D.

Câu 45. Tnh ca hàm s

 

1 4 1 16 1

2 4 16

log log log log logf x x











là mt kho dài

vi

và

là s  

mn

bng:

240

. B.

271

. C.

241

. D.

241

Câu 46. S m ci c th hàm s

     

1 2 3 ... 100y x x x x    

bng

. B.

. C.

. D.

100

Câu 47. Cho các s th 

tha mãn

log log log log 100x y x y   

và

log x

log y

log x

log y

là các s t qu

bng

200

. B.

100

. C.

164

. D.

144

Câu 48. Cho hàm s

y ax bx cx d   

 th  bên

Trang98

Giá tr nguyên ln nht ca tham s

 hàm s

 

y f x m

ng bin trên khong

 

10;

là

10

. B.

. C.

. D.

Câu 49. Cho hàm s

 

liên tc trên



và tho mãn

   

xf x f x e x    



 

df x x





bng:

. B.

 

31e 

. C.

 

31 e

. D.

Câu 50. Mt hng

th  t

n

. Rút ngu nhiên hai th t hp nêu  trên, tính

xác su tích ca hai s trên hai th này là s chn.

. B.

. C.

. D.

…..HẾT…..

BẢNG ĐÁP ÁN

1.A

2.B

3.D

4.C

5.D

6.C

7.B

8.C

9.B

10.C

11.C

12.B

13.D

14.A

15.C

16.C

17.B

18.D

19.A

20.A

21.B

22.D

23.B

24.D

25.C

26.D

27.D

28.A

29.C

30.B

31.C

32.C

33.C

34.B

35.B

36.D

37.C

38.B

39.A

40.D

41.A

42.D

43.B

44.B

45.D

46.C

47.C

48.C

49.B

50.B

LỜI GIẢI CHI TIẾT

Câu 1. Khi tr tròn xoay có th tích bng

144



ng sinh ca khi tr

bng

. B.

. C.

. D.

Lời giải

Chọn A

Gi

,,h l r

lt là chia khi tr.

Ta có:

V r h





144 .6 . 4hh



   

Vy khi tr  ng sinh là:

4lh

Câu 2. Trong các hàm s  nào nghch bin trên tp







. B.









. C.

y 

. D.

y 

Lời giải

Chọn B

Trang99

Hàm s 

ya

nghch bin trên tp



khi và ch khi

01a

Câu 3. Giá tr ca tích phân



bng

. B.

. C.

. D.

Lời giải

Chọn D

Ta có:

2 2 2

2 d 2 0 4   



x x x

Câu 4. ng cong   th ca hàm s 

21   y x x

. B.







. C.







. D.

1  y x x

Lời giải

Chọn C

Da vào hình v  th hàm s ng tim cn là

1x

và

1y

Vng cong   th hàm s







Câu 5. [Mức độ 1] Trong không gian

Oxyz

, cho mt phng

 

: 2 3 2020 0P x y z   



i là mn ca mt phng

 

2;4; 6n   



. B.

 

1;2; 3n   



. C.

 

1; 2;3n 



. D.

 

2;3;2020n 



Lời giải

Chọn D

+) Mt phng

 

: 2 3 2020 0P x y z   

có mn là

 

1; 2;3

n 



 A;B;Ci



n ca

 



 

2;3;2020n 



 D i



nên không ph

pháp tuyn ca

 

Trang100

Câu 6. Cho s phc

53zi

. S phc liên hp ca

là

53i

. B.

53i

. C.

53i

. D.

53i 

Lời giải

Chọn C

S phc

 

,;z a bi a b  

có s phc liên hp là

z a bi

Vy s phc

53zi

có s phc liên hp là

53zi

Câu 7. Trong mt phng

 

Oxy

m

biu din s phc

13zi  

có t là

 

1; 3M 

. B.

 

1; 3M 

. C.

 

1;3M 

. D.

 

1;3M

Lời giải

Chọn B

m

biu din s phc

13zi  

là

 

1; 3M 

Câu 8. Cho các s th

,ab

và

1a 

. Biu thc

log

bng

 

2 1 log

b

. B.

2log

. C.

2 log

b

. D.

1 log

b

Lời giải

Chọn C

Ta có:

log log log 2log log 2 log

a a a a a a

a b a b a b b     

Câu 9. Th tích kh tam giác có chiu cao bng

, ct bng

là:

. B.

12.

. C.

. D.

28.

Lời giải

Chọn B

Kh tam giác có ct là

Vnh góc vuông lt là

Th tích kh:

. .3.4.2 12

V B h  

Câu 10. Trong các khi hình sau, khi không phi khi tròn xoay là:

A. Khi cu. B. Khi tr.

C. Kh. D. Khi nón.

Lời giải

Chọn. C.

Kh không phi khi tròn xoay.

Câu 11. H tt c các nguyên hàm ca hàm s

 

sinf x x



là

cos 2lnx x C

. B.

cosxC



cos 2lnx x C  

. D.

cos 2lnx x C  

Lời giải

Chọn C

Trang101

sin d cos 2lnx x x x C



    







Câu 12. Trong không gian vi h t

Oxyz

, cho

2 3 5a i j k   

   

. T ca



là

 

2;3;5

. B.

 

2;3;5

. C.

 

2;3; 5

. D.

 

2; 3; 5

Lời giải

Chọn B

T ca



là

 

2;3;5

Câu 13. Cho

s th

tha mãn

1x 

và

log 3

y 

. Tính

log

Ty

T 

. B.

T 

. C.

T 

. D.

5T 

Lời giải

Chọn D

Ta có

log 3

y y x  

Suy ra

 

3 15

log log .15.log 5

T x x x   

Vy

5T 

Câu 14. Trong không gian

Oxyz

m

 

2; 1;3M 

và mt phng

 

:2 5 1 0x y z



   



trình mt phm

và song song vi

 



2 5 12 0x y z   

. B.

2 5 12 0x y z   

2 5 12 0x y z   

. D.

2 5 12 0x y z   

Lời giải

Chọn A

Gi

 

là mt phm

và song song vi

 



Ta có

   

//P



nên

 

có mt véc-n là

 

2; 5;1

n 



Mt phng

 

m

và song song vi

 





   

2 2 5 1 3 0 2 5 12 0x y z x y z          

Câu 15. Cho hàm s

 

y f x

 th  bên.

Trang102

Hàm s ch bin trên khong

 

0 ; 2

. B.

 

3 ; 1

. C.

 

1 ; 0

. D.

 

1 ; 3

Lời giải

Chọn C

D th ta thy: Hàm s nghch bin trên các khong là

 

1 ; 1

và

 

2 ; 3

Nên hàm s ch bin

 

1 ; 0

Câu 16.  th hàm s







ng tim cng thng 

1x 

. B.

2y 

y 

. D.





Lời giải

Chọn C

Ta có:

lim

2 1 2









;

lim

2 1 2









m cn ngang c th hàm s ng thng

y 

Câu 17. Gi

là tp nghim c

9 10.3 9 0

  

. Tng các phn t ca

bng

. B.

. C.

. D.

Lời giải

Chọn B

3 1 0

9 10.3 9 0







    









 

0 , 2S 

Trang103

Vy tng các phn t ca

bng

Câu 18. Mu vi vn tc

16 /ms

i lái xe nhìn thy mng

ngi vp phanh tng chm du vi vn tc

 

2 16v t t  



là thi gian (tính bng giây) k t c

trong

giây cui cùng bng

60m

. B.

64m

. C.

160m

. D.

96m

Lời giải

Chọn D

Ly mc thi gian lúc ô tô bp phanh.

Khi ô tô dng hn thì

 

0 2 16 0 8v t t t      

c trong

giây cui:

 

2 16 16 64 .

t dt t t m     



 bài: ô tô c 10 giây cuc:

16.2 32m

Vc trong 10 giây cui:

64 32 96m

Câu 19. Cho hàm s

 

y f x

o hàm

 

1,fx





.x

M 

   

12ff

. B.

   

12ff

. C.

   

12ff

. D.

   

12ff

Lời giải

Chọn A

Vì

 

10fx





x

nên

 

là hàm s ng bin trên

.

   

1 2 1 2 .ff    

Câu 20. Cho hình vuông

ABCD

tâm

 dài cnh là

4.cm

ng cong

BOC

là mt phn parabol

nh

chia hình vuông thành hai hình phng có din tích lt là

và

(tham kho hình

v).

T s

bng

. B.

. C.

. D.

Lời giải

Chọn A

Chn h trc t

,Oxy

vi

là gc t, trc



m ca

và

.CD

Trang104

Parabol có dng

 

:.P y ax

m

   

2 ; 2CP

nên

2 4 .

aa  

Vy

 

P y x

1 16

2 d .

S x x





  







16 32

16 .

ABCD

S S S    

Vy



Câu 21. Mt cp s nhân có s hng th 3 và s hng th 6 lt là

và

243

 hng th

ca cp s nhân bng:

2187

. B.

2187

. C.

729

. D.

243

Lời giải

Chọn B

Gi

là s hu,

là công bi ca cp s nhân.

Ta có:

u u q















243

27 3



       



243.9 2187u u q    

Câu 22. Tìm hàm s

 

không là nguyên hàm ca hàm s

 

sin2f x x

 

cosF x x

. B.

 

sinF x x

. C.

 

cos2

F x x

. D.

 

cos2F x x

Lời giải

Chọn D

Vì

 

cos2 2sin2xx





nên

 

cos2F x x

không phi là mt nguyên hàm ca hàm s

 

sin2f x x

Câu 23. Cho hàm s

 

nh, liên tc trên



và có bng bi



1













1



 th hàm s

 

y f x

cng thng

2y 

tm?

. B.

. C.

. D.

Lời giải

Trang105

Chọn B

Vì

21  

ng thng

2y 

nng thng

1.y 



1











1

2y 



T bng bi th hàm s

 

y f x

cng thng

2y 

tm phân

bit.

Câu 24. Trong không gian

Ox ,yz

m

   

2;1; 0 , 2; 5; 4 .AB

t cng

kính

là

   

2 1 12x y z    

. B.

   

3 2 48x y z    

     

2 2 2

4 4 4 48x y z     

. D.

   

3 2 12x y z    

Lời giải

Chọn D

Gi

m cn

suy ra

 

0; 3; 2 .I 

Ta có:

 

4; 4; 4 ,AB 



 

4 4 4 2 12.AB     

Mt cng kính

có tâm

 

0; 3; 2I 

và bán kính

R AB



   

3 2 12.x y z    

Câu 25. Tp nghim ca b

   

log 3 1 log 25 25xx  

là









. B.

;









. C.

;









. D.







Lời giải

Chọn C

u kin:

3 1 0

25 25 0











    













Ta có:

   

log 3 1 log 25 25xx  

3 1 25 25xx   

28 24 .

xx   

Kt hp vu kin ta có tp nghim ca b









Câu 26. Cho hàm s

 

y f x

liên tc trên

 

3;3

và có bng xét du c

Trang106

M 

A. Hàm s t cc tiu ti

1x 

. B. Hàm s t ci ti

2x 

C. Hàm s t ci ti

1x 

. D. Hàm s t cc tiu ti

0x 

Lời giải

Chọn D

Ta có bng bin thiên:

Vy hàm s t cc tiu ti

1;x 

hàm s t ci ti

1x 

và

2.x 

Câu 27. [Mức độ 1] Cho hình hp

.ABCD A B C D

   

. B ng phng là:

, , ' 'AC BD A D

  

. B.

, ', 'AC AC BB

  

, ', ' 'AB BD C D

  

. D.

' , ' , 'A C B D BD

  

Lời giải

Chọn D

ng phng nu các giá ca chúng cùng song song vi mt mt phng.

, , ' 'AC BD A D

  

có giá cùng song song vi mt phng

 

ABCD

, ', 'AC AC BB

  

có giá cùng song song vi mt phng





ACC A



, ', ' 'AB BD C D

  

có giá cùng nm trên mt phng





ABC D



Câu 28. [Mức độ 2]Cho hai s phc

,zz

tha mãn

1 1 2

4, 3z z z

. Giá tr biu thc

P z z

bng

A. 13. B. 25. C. 7. D. 19.

Trang107

Lời giải

Chọn A

Có

1 1 1

4z z z

;

39zz  



4 9 13.P z z    

Câu 29. [Mức độ 2] Trong không gian vi h t

Oxyz

, cho

 

2; 1;3M

 

3;2; 4N

 

1; 1;2P

nh t m



MNPQ

là hình bình hành?

 

2;2; 5Q

. B.

 

2; 3; 5Q

. C.

 

0; 4;9Q

. D.

 

1;3; 2Q

Lời giải

Chọn C

MNPQ

là hình bình hành khi và ch khi



 

PQ NM



 

1 2 3

1 1 2

2 3 4



  



   





   











  









Vy

 

0; 4;9Q

Câu 30. [Mức độ 2] Giá tr nh nht ca hàm s







n

 

0;3

là

 

0;3

min 3





. B.

 

0;3

min 2





. C.

 

0;3

min





. D.

 

0;3

min





Lời giải

Chọn B

Hàm s







liên tn

 

0;3

Ta có

 

 

0 0;3



   



Vy

 

 

0;3

min 0 2



  

Câu 31. 

 

y f x



 

0;1



 

d3f x x 



và

 

14f 

Tích phân

 

dxf x x





 là



. B.

. C.

. D.

1

Lời giải

Chọn C

Ta có

 

dxf x x





 

dx f x



   

dxf x f x x



   

1df f x x



43

1

Trang108

Câu 32. [Mư



c đô



1] Trong không gian vi h trc t

Oxyz

m

 

1;0;3A

;

 

5;2; 1B 

ng chính tc cng thm

và

5 2 1

x y z





. B.

2 1 2

x y z





3 1 1

2 1 2

x y z  





. D.

5 2 1

2 1 2

x y z  



Lời giải

Chọn C

M ng thng

là:

 

4;2; 4AB 



Suy ra m a

là

 

2;1; 2u 



Lm

 

1;0;3A

thung thng  

1 3 0 1 3 1

2 1 2

  

   



Vy chn C

Câu 33. Có 3 qu c cha trong mt hp hình tr (hình v bên) vi chiu cao

và

bán kính

3,5

Th tích bên trong hình tr không b chim ly bi các qu bóng tennis (b  dày ca v

hp) bng bao nhiêu?

82,75



. B.

87,25



. C.

85,75



. D.

87,75



Lời giải

Chọn C

Th tích khi tr là:

 

. 3,5 .21 257,25V





Mi qu ng

3,5cm

nên 3 qu bóng có th tích là:

 

3. . . 3,5 171,5





Vy th tích cn tìm là

257,25 171,5 85,75V V V

  

    

Câu 34. Có bao nhiêu s t nhiên có hai ch s khác nhau?

A. 72. B. 81. C. 90. D. 18.

Lời giải

Chọn B

Gi

là s t nhiên có hai ch s khác nhau

 

 

, 0;1;2;...;9 ; 0a b a

Ta có:

có 9 cách chn (do

0a 

Trang109

ng vi mi cách chn

ta có 9 cách chn

(do

ab

Theo quy tc

9.9 81

s t nhiên có hai ch s khác nhau.

Câu 35. [Mư



c đô



2] Cho hàm s

 

o hàm

 

   

2 4 , .f x x x x x x



      

S m

cc tr ca hàm s

 

là

. B.

. C.

. D.

Lời giải

Chọn B



 

   

2 4 0f x x x x x



    

ta có:

nghi

0; 1.xx  

+ 1 nghim bi l là

4.x 

+ 1 nghim bi chn là

2.x 

Vy hàm s

 

t cc tr tm

0; 1; 4.x x x   

Câu 36. Cho hàm s

 

y f x

 th hàm s

 

y f x

 bên

Hàm s

 

12y f x x x   

ng bin trên khong?

 

2; 1

. B.

 

3; 2

. C.

 

3;0

. D.

 

0;1

Lời giải

Chọn D

Trang110

t

   

12g x f x x x   

   

1 2 2g x f x x



    

 

2f t t





( vi

1tx

)

 th nhn thy

02t

thì

 

2f t t





hay

 

0gx







0 1 2x  

11x   

Câu 37. Trong không gian vi h t 

Oxyz

  m

 

1( 2;1;I

và mt phng

 

:2 2 1 0P x y z   

. Mt cu

 

có tâm

, ct

 

theo m ng tròn có bán kính

4r 

. Mt cu

 

 là:

     

2 2 2

2 1 1 20x y z     

. B.

     

2 2 2

2 1 1 18x y z     

     

2 2 2

2 1 1 20x y z     

. D.

     

2 2 2

2 1 1 2 5x y z     

Lời giải

Chọn C

Ta có

 

2 2 2

2.2 1 2.1 1

;

I Pd

  







Vì mt cu

 

có tâm

, ct

 

theo mng tròn có bán kính

4r 

nên mt cu

 

có

bán kính

 

2 2 2 2

42 25; PR r d I    

Vt cu

 

là

     

2 2 2

2 1 1 20x y z     

Câu 38. u tháng m i gi ngân hàng

400.000.000

ng (

400

tri ng) vi lãi sut gi là

0,6%

mi tháng theo hình thc lãi sut kép. Cui mn gi vào ngân

hàng s tin là

10.000.000

(

tring). Hi sau ít nht bao nhiêu tháng ( k t i

này ra ngân hàng gi tin) thì s tic l

700.000.000

(b

tring)?

tháng. B.

tháng. C.

tháng. D.

tháng.

Lời giải

Chọn B

Tng quát bài toán:

Gi

là s tiu.

Trang111

là lãi sut mi tháng.

là s tii vào thêm mi tháng.

là s tic sau

tháng.

u tháng 1, s tii vào là

ST

Cui tháng 1,

 

1 0 0 0

. % . 1 %S T T r a T r a     

Cui tháng 2,

   

2 1 1 1 0

. % . 1 % .(1 %) . 1 %S S S r a S r a T r a r a          

Cui tháng 3,

.(1 %) .(1 %) .(1 %)S T r a r a r a      



Cui tháng n,

       

 

1 2 1

. 1 % 1 % 1 % ... 1 % 1

1 % 1

. 1 % .

n n n

S T r a r r r

T r a





         





  

Theo yêu cu bài toán:

 

1 0,6%

1 % 1

. 1 % . 700.000.000

1 0,6% 1

40. 1 0,6% 70

0,6%

1 0,6% 1,14515129

log 1,14515129 22,65

T r a





  



   

  

  

Vy phi sau ít nhc l

700.000.000

(b

tring).

Câu 39.  th hàm s

y ax bx cx d   









:

 th ca hàm s

 

   

f x f x



















?

. B.

. C.

. D.

Lời giải

Chọn A

Trang112



   

 

3 6 0

f x f x





  

















 th, 





 

0fx













(





2x 







1x 







    

21f x a x x   

 

0a 



 

2fx

 

x m m

x n n







     







(

0, ,x x m x n  



    

2f x ax x m x n    

 

0a 

Suy ra

 

  

   

  

     

1 3 2 1 3 2

3 2 1

x x x x

f x f x

a x x x x m x n

   







   



 

0a 





 th hàm s

 

có

















.

Câu 40. Cho hàm s

 

có bng xét du c

Hàm s

 

1y f x

nghch bin trên khong

 

1;4

. B.

 

0;2

. C.

 

0;1

. D.

 

2; 1

Lời giải

Chọn D

Xét hàm s

 

1y f x

có

 

1y f x



  

T bng xét du ca

 



ta có:

 

3 1 2 3 1 2 3 4

0 1 0

1 1 3 1 1 3 2 0

x x x

y f x

x x x

         

  



      

  

          

  

Suy ra hàm s

 

1y f x

nghch bin trên các khong

 

3;4

và

 

2;0

Mà

   

2; 1 2;0   

nên hàm s nghch bin trên khong

 

2; 1

Câu 41. [Mức độ 2]Trong không gian vi h t 

Oxyz

, cho hình hp

.ABCD A B C D

   

bit

 

1;2;3A

 

2;0; 1B





 

3;0; 3C 

và

 

2;4; 3D





. T  nh

ca hình hp

.ABCD A B C D

   

là

 

4; 1;1B 

. B.

 

2; 1;2B 

. C.

 

4;1; 1B 

. D.

 

0;1; 3B 

Lời giải

Chọn A

Trang113

Gi

,II



lm ca

và



Ta có

 

2;1;0I

 

0;2; 2I





và

 

2;1; 2II



  



Gi s

 

;;B a b c

 

2 ; ; 1BB a b c



     



Theo tính cht ca hình hp ta có

BB II





 

  





  





   









  









Vy

 

4; 1;1B 

Câu 42. Cho hình chóp

.S ABCD

nh

2AB a

SAB

là tam giác cân ti

và

nm trong mt phng vuông góc vi mt phng

 

ABCD

. Gi

,MN

lm ca

,AB BC

và

là trng tâm

SCD

. Bit khong cách t m

n mt phng

 

SND

bng

. Th tích ca khi chóp

.G AMND

bng

. B.

. C.

. D.

Lời giải

Chọn A

SAB

là tam giác cân ti

và

là trung

m ca

c

SM AB

. Thêm



   

SAB ABCD

nên chúng ta có th suy

c

 

SM ABCD

Ta k

MH DN

tm

và

MK SH

ti

m



 

MH DN

DN SHM DN MK

SM DN





   







. Mà



MK SH

c

   

 

MK SDN MK d M SDN   

Trang114

Mt khác:

 

2 2 2

ABCD MBN NCD MAD

MND

a a a

S S S S

NC DC

  





  



  



   



Xét trong

SMH

, ta có:

2 2 2

1 1 1

3SM a

SM MK MH

   

D thy:

 

d G ABCD SM

. Vy:

 

1 1 3 3 5 5 3

. , . . . .

3 3 3 9 2 18

G AMND AMND ABCD MBN NDC

a a a a

V d G ABCD S S S S



     

Câu 43. Cho hình thang

ABCD

 

//AB CD

bit

5AB 

3BC 

10CD 

4AD 

. Th tích khi tròn

xoay to thành khi quay hình thang

ABCD

 

//AB CD

quanh trc

bng

128



. B.



. C.

112



. D.



Lời giải

Chọn B

Gi

m ca

D thy t giác

ABCE

là hình bình hành

3AE BC  

DAE

vuông ti

Gi

m ca

và

DHC

vuông ti

Ta có

4AH BE

8DH

và

3HB 

Khi quay

DHC

quanh trc

c hình nón tròn xoay có chiu cao

8h 



6r 

nên có th tích

1 1 1

.36.8 96

V r h

  

  

Khi quay

AHB

quanh trc

c hình nón tròn xoay có chiu cao

4h 



3r 

nên có th tích

2 2 2

.9.4 12

V r h

  

  

Vy th tích khi tròn xoay to thành khi quay hình thang

ABCD

 

//AB CD

quanh trc

bng

96 12 84VV

  

   

Trang115

Câu 44. 

.ABC AB C

  

u cnh

, hình chiu vuông góc cnh



lên

 

ABC

  m

ca cnh

. Góc gi ng thng



và m  ng

60

Khong cách gia



và



là

. B.

3 13

. C.

2 13

. D.

Lời giải

Chọn B

Ta có

 

A H ABC





 

; ; 60A C ABC A C HC A HC

  

     

.tan60 . 3

A H HC



   

Gi

m ca

, t

k

HN AC HN BM   

T

k

HI A N





 

HI A AC





   

 

'; ' ; ; 2 ; 2d BB A C d BB A AC d B A AC d H A AC HI

   

   

Xét tam giác vuông

A HI



vuông ti

2 2 2

. 3 13

HN HA a

HN HA



   













 

3 13

; 2 .

d BB A C HI



  

Câu 45. Tnh ca hàm s

 

1 4 1 16 1

2 4 16

log log log log logf x x











là mt kho dài

vi

và

là s  

mn

bng:

Trang116

240

. B.

271

. C.

241

. D.

241

Lời giải

Chọn D

Hàm s

 

1 4 1 16 1

2 4 16

log log log log logf x x











nh khi và ch khi

4 1 16 1

4 16

log log log log 0x









1 16 1

4 16

log log log 1x









16 1

0 log log



  





log 1

log 16











































256 16

x  

Suy ra tnh ca hàm s là

;

256 16







 dài ca khong

;

256 16







là

1 1 15

15, 256

16 256 256

mn    

Vy

241mn  

Câu 46. [Mức độ 3] S m ci c th hàm s

     

1 2 3 ... 100y x x x x    

bng

. B.

. C.

. D.

100

Lời giải

Chọn C

*Ta thy hàm s c bc 100, liên tc trên

m phân

bit (

1; 2;...; 100x x x  

), nên hàm s m cc tr (

1 2 99

; ;...;x x x

), mm

cc tr nm gia 2 nghim c

0y 

. Mt khác



 lim

nên s m cc tiu

nhi m ci là m th hàm s m ci là

2 4 98

; ;...;x x x

Vy hàm s m ci.

Câu 47. Cho các s th 

tha mãn

log log log log 100x y x y   

và

log x

log y

log x

log y

là các s t qu

bng

200

. B.

100

. C.

164

. D.

144

Lời giải

Chọn C

Trang117

Ta có:

   

log log log log 100 log 1 log 1 202x y x y x y        

Vì

log x

log y

là các s 

 

log 1x 

và

 

log 1y 

là các s

n phân tích 202 thành tng 2 s 

 chn nên 2 s i cùng chn hoc cùng l.

+) Nu 2 s

 

log 1x 

và

 

log 1y 

cùng chn thì

   

log 1 log 1 4xy   

còn

202 không chia ht cho 4 nên không tn ti

ng hp này.

+) Nu 2 s

 

log 1x 

và

 

log 1y 

cùng l, suy ra ch s tn cùng ca 2 s t

trong các ch s 1, 5, hoc 9. Vì tng 2 ch s tn cùng là 2 nên 2 s

 

log 1x 

 

log 1y 

u có tn cùng bng 1.



 thit và kt lun nên ta ch ng hp:

 

log 1 81

log 1 121















. T 

164

100

















Câu 48. Cho hàm s

y ax bx cx d   

 th  bên

Giá tr nguyên ln nht ca tham s

 hàm s

 

y f x m

ng bin trên khong

 

10;

là

10

. B.

. C.

. D.

Lời giải

Chọn C

Hàm s

 

y f x m

ng bin trên khong

 

10;

   

' ' 0, 10 ' 0, 10

y f x m x f x m x

          

, 10

  

  



  





, 10

  

  









10 1 9mm    

Trang118

Vy s nguyên ln nht ca tham s

là

Câu 49. Cho hàm s

 

liên tc trên



và tho mãn

   

xf x f x e x    



 

df x x





bng:

. B.

 

31e 

. C.

 

31 e

. D.

Lời giải

Chọn B

Nhân hai v ca

   

xf x f x e x    

vi

 c:

   

2 3 2

x f x xf x xe x     

Ly tích phân t

1

n

hai v c:

   

0 0 0

2 3 2

1 1 1

1 (1)

x f x dx xf x dx xe dx

  

  

  

Kí hiu

   

0 0 0

2 3 2

1 1 1

; 1 ;

I x f x dx K xf x dx H xe dx

  

   

  

t

ux

c

 

   

0 0 0

1 1 1

I x f x dx f u du f x dx

  

  

  

t

1ux

c

 

   

0 0 0

1 1 1

K xf x dx f v dv f x dx

  

     

  

Và

 

2 2 2

1 1 1

2 2 2

x x x

H xe dx e d x e e





    



Nên

         

0 0 0

1 1 1

(1) 1 3 1

3 2 2

f x dx f x dx e f x dx e

  

      

  

Câu 50. Mt hng

th  t

n

. Rút ngu nhiên hai th t hp nêu  trên, tính

xác su tích ca hai s trên hai th này là s chn.

. B.

. C.

. D.

Lời giải

Chọn B

 

nC

Gi

là bin c tích ca hai s trên hai th là s l, ta có xác xut cn tính là

 

Nhn thy bin c

xy ra khi và ch c c hai th mang s l. Trong 9 th 

5 th mang s l, vì th nên

 

n A C

Ta có

 





và

 

1P A P A



 

PA

…..HẾT…..

Bấm Tải xuống để xem toàn bộ.

| 1/118

| | Tải xuống

Preview text:

Đề 1
ĐỀ LUYỆN THI CẤP TỐC TỐT NGHIỆP THPT NĂM 2021 BÀI THI: TOÁN
Thời gian: 90 phút Câu1.
Số cách sắp xếp 6 bạn học sinh vào 6 ghế kê thành hang ngang là A. 60 . B. 120 . C. 12 . D. 720 . Câu 2.
Diện tích của mặt cầu có bán kính r  3là A. 36 . B. 18 . C. 9 . D. 6 . Câu 3.
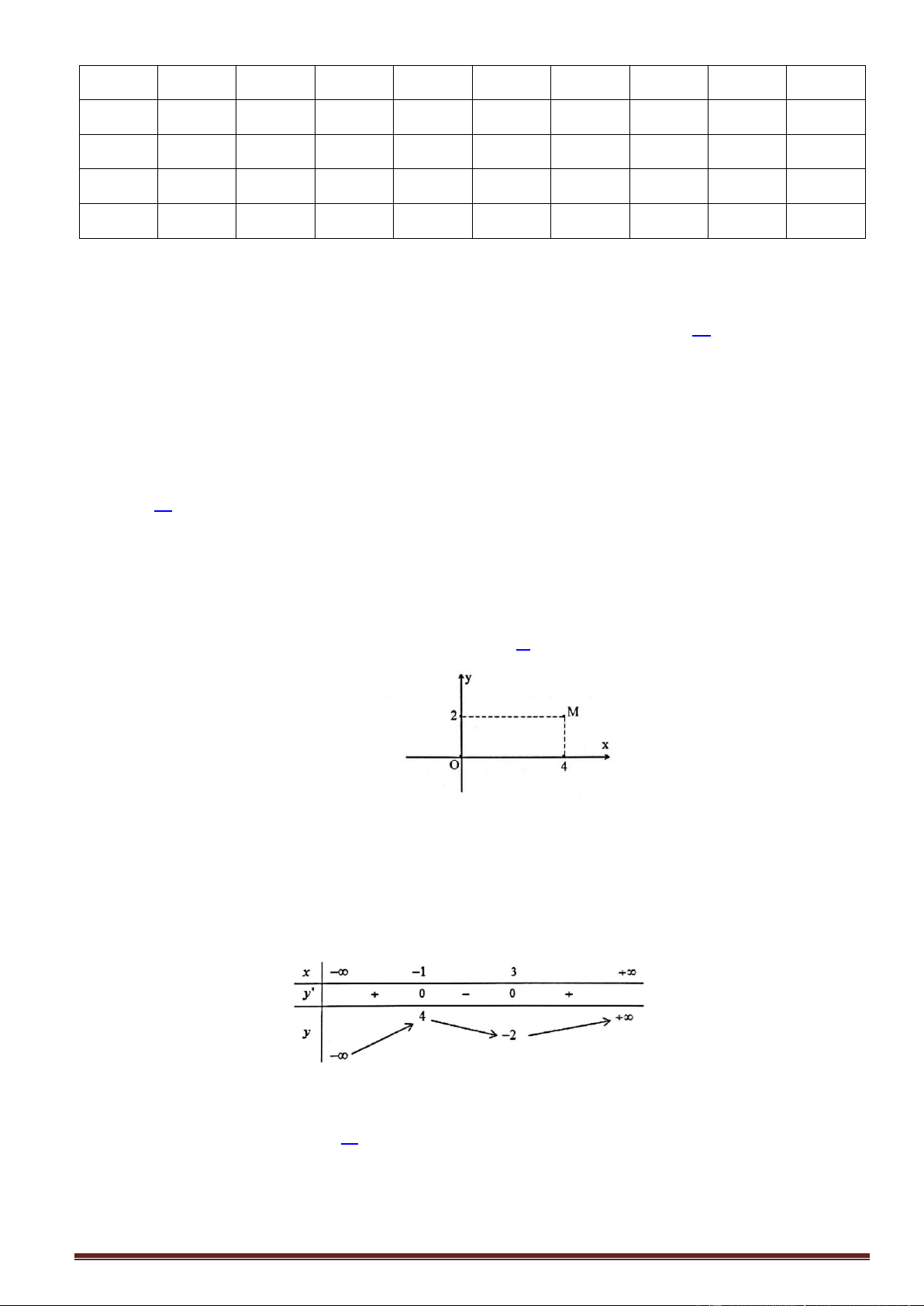
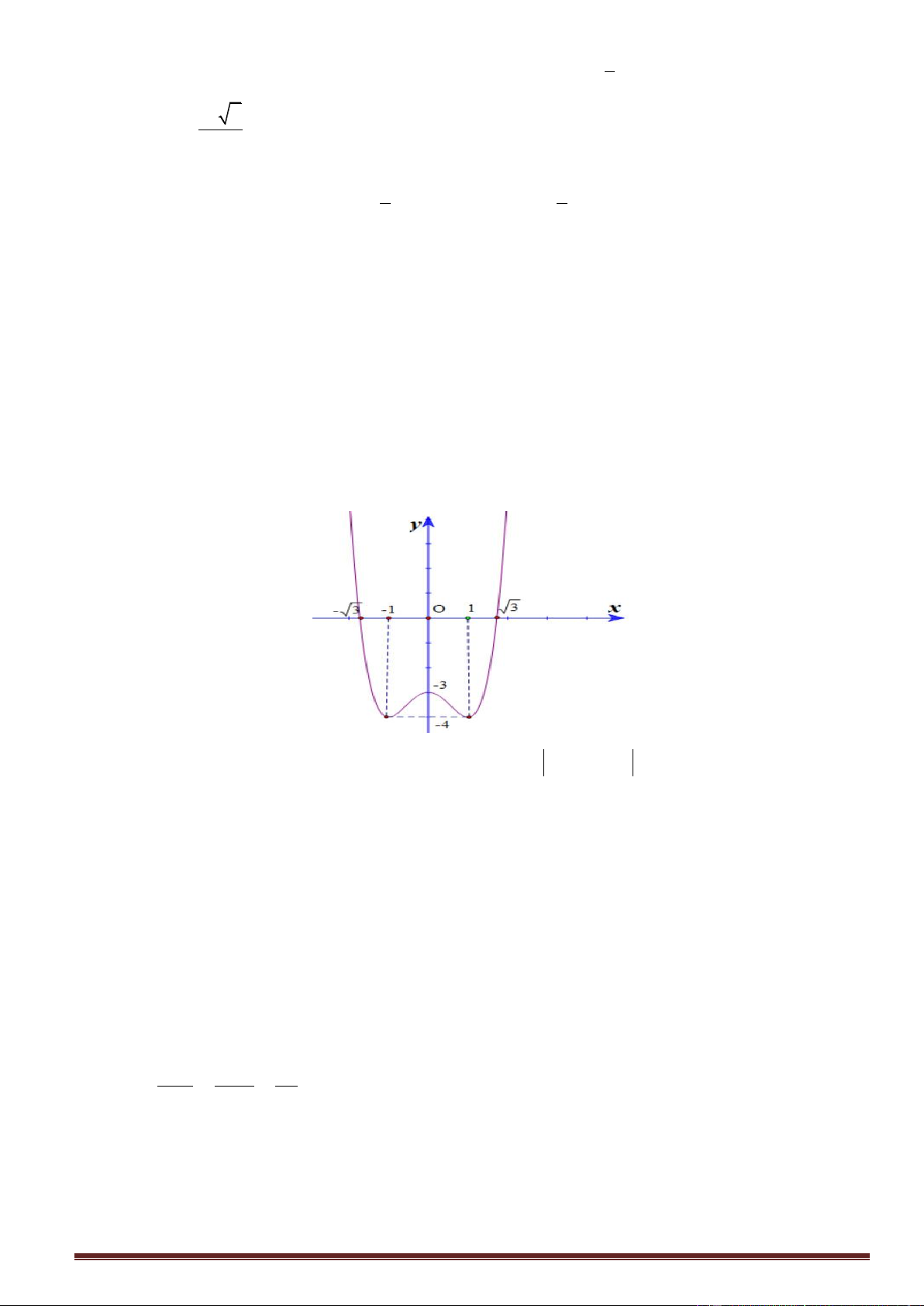
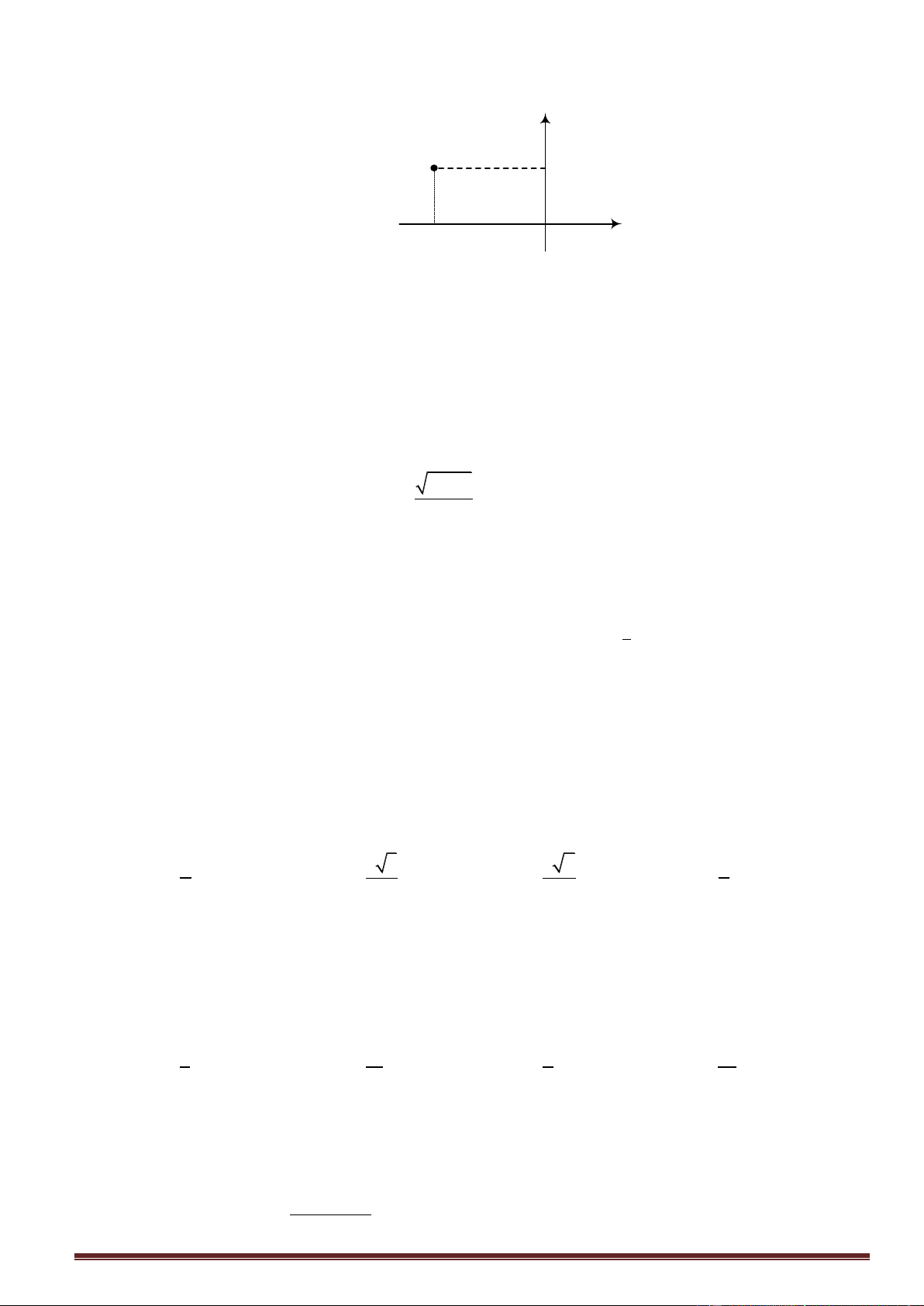
Điểm M trong hình vẽ bên biểu diễn số phức nào dưới đây?
A. z  2  4 . i
B. z  4  2 . i
C. z  4  2 . i
D. z  2  4 . i Câu 4.
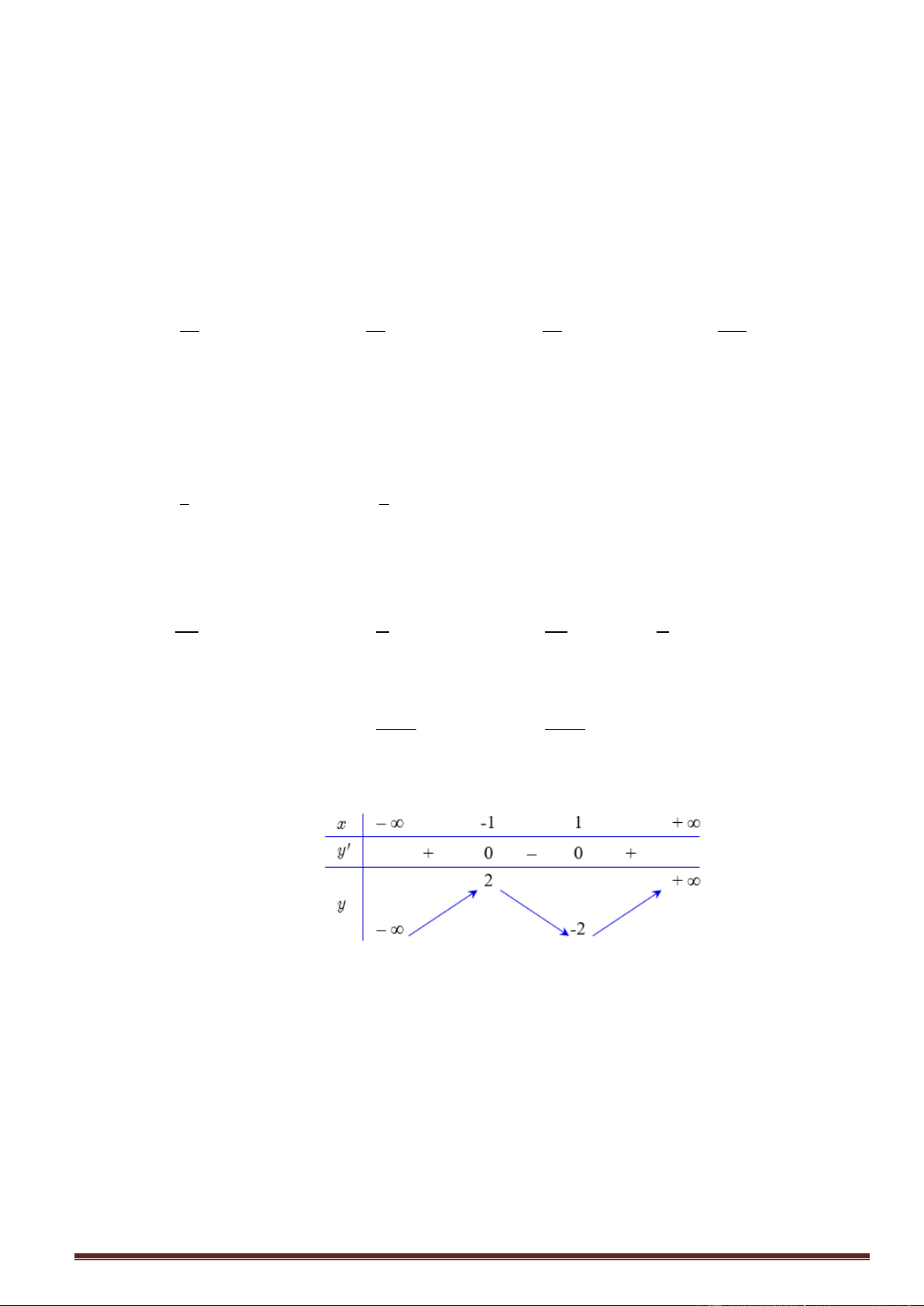
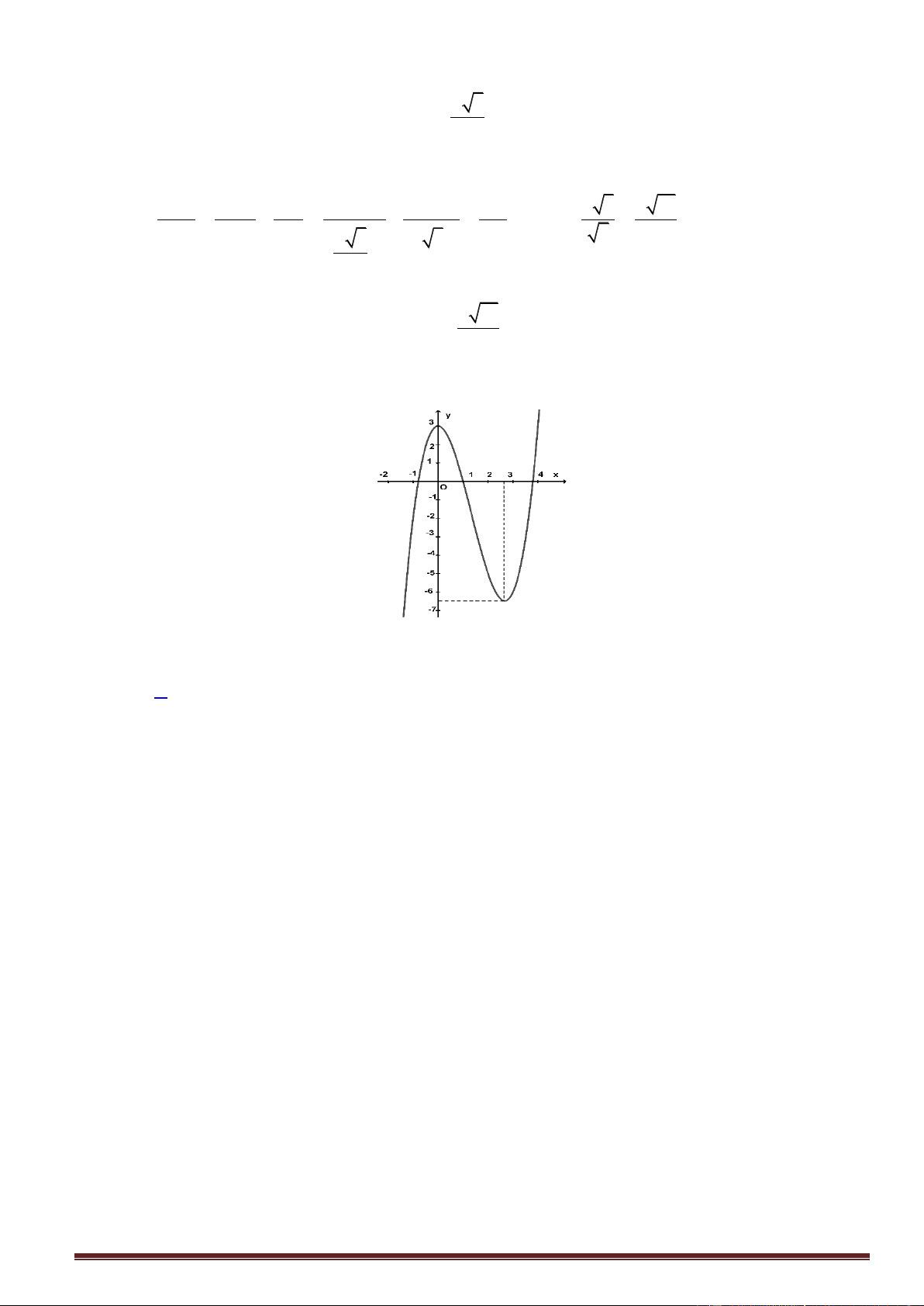
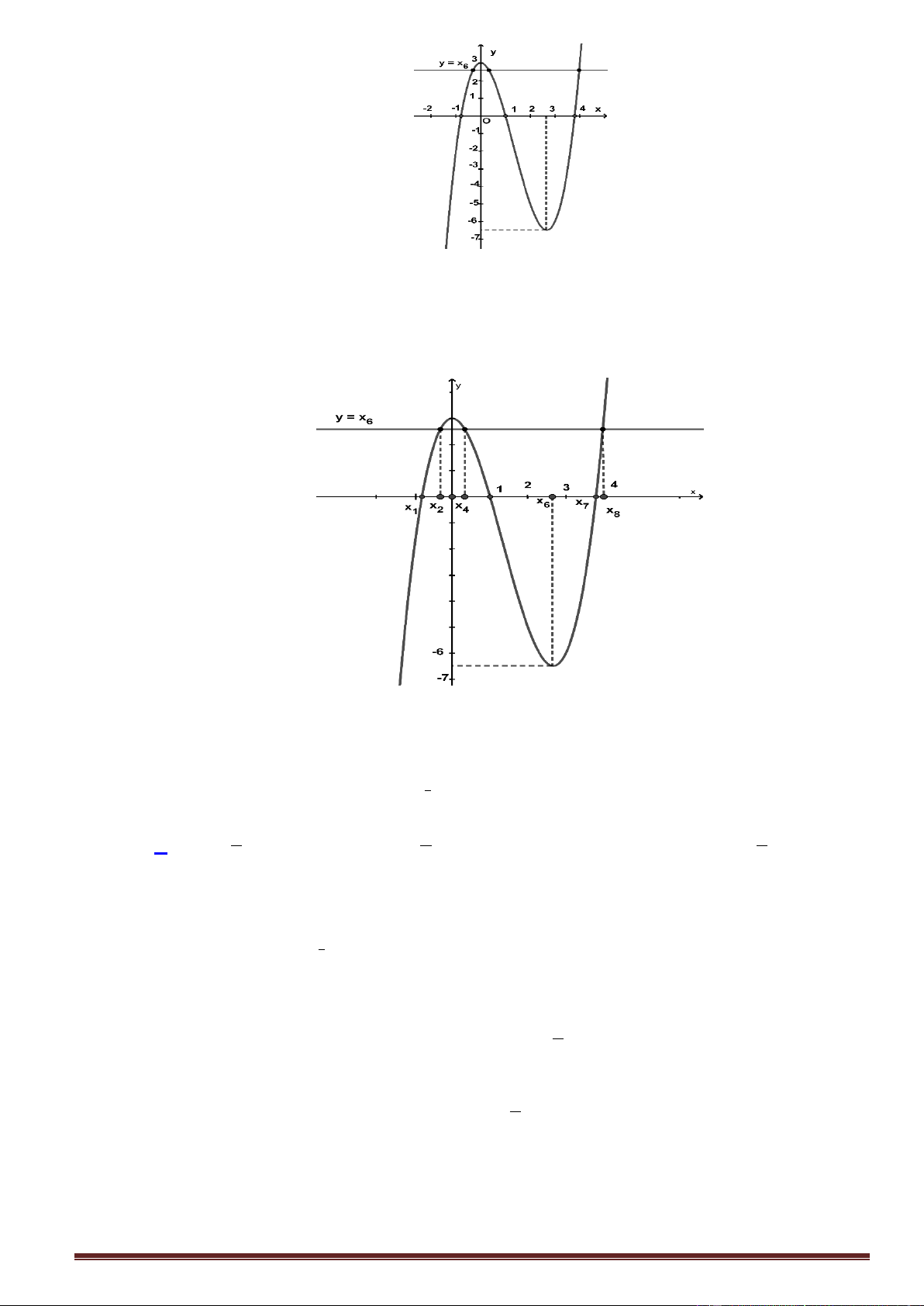
cho hàm số y  f  x có bảng biến thiên sau:
Số nghiệm của phương trình f  x  2  0 là A. 2. B. 3. C. 1. D. 0. Câu5.
Trong các hàm số sau, hàm số nào có một nguyên hàm là hàm số F  x  cos x ?
A. f  x   cos x .
B. f  x  sin x .
C. f  x  cos x .
D. f  x  sin x . Câu6.
Cho cấp số cộng u có u  3;u  7 . Công sai của cấp số cộng đã cho bằng n  1 3 A. 2 . B. 4 . C. 4  . D. 2  . Câu 7.
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên Trang1 A. 3
y  x  3x 1 B. 3
y  x  3x 1 C. 3
y  x  3x 1 D. 3
y  x  3x 1 Câu 8.
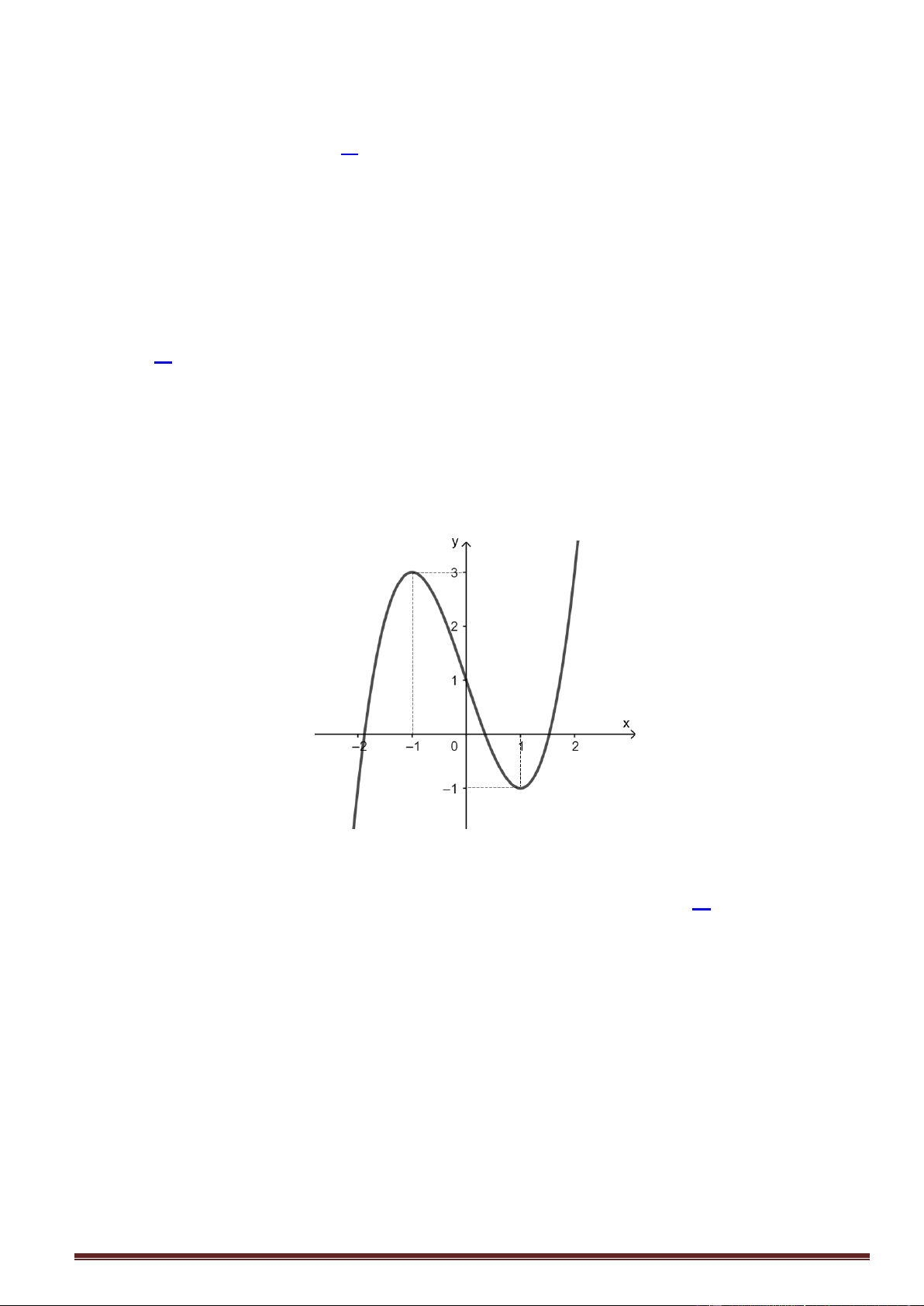
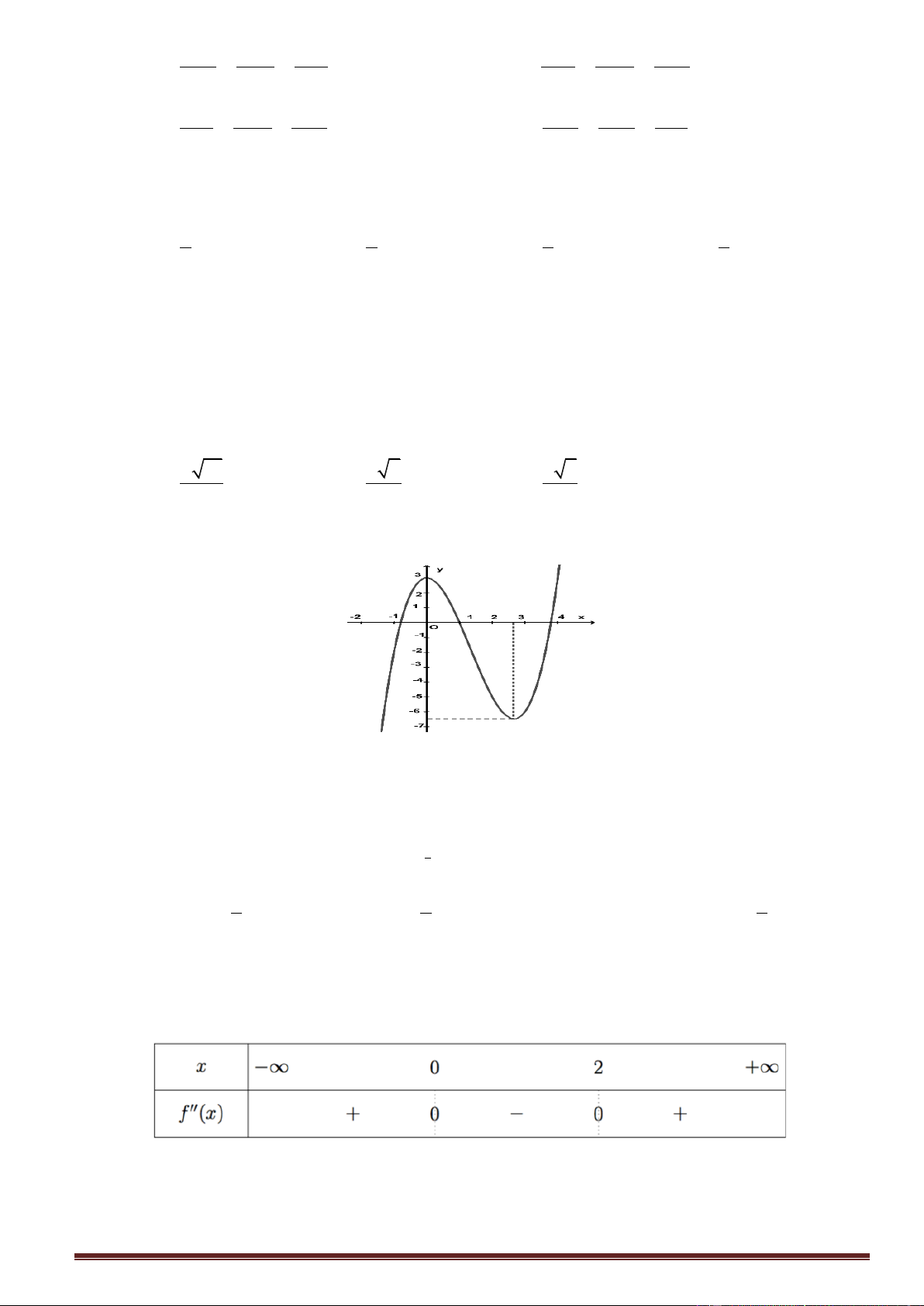
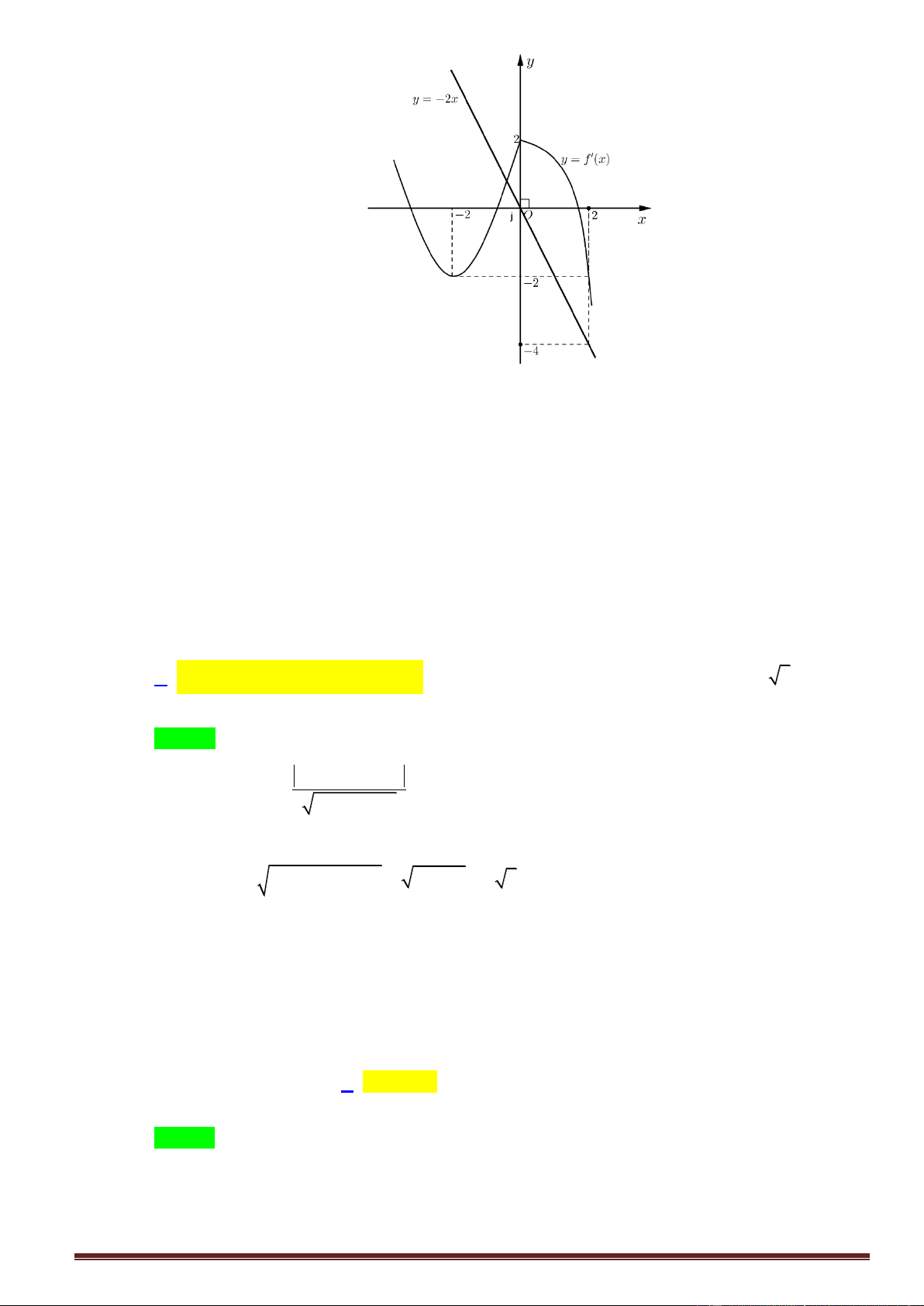
Cho đồ thị f  x có đồ thị như hình vẽ
Hàm số đã cho nghịch biến trong khoảng nào dưới đây? A.  ;  0 B. 0;  1 C. 0;  D.  1  ;0 Câu 9.
Phần thực và phần ảo của số phức z  1 3i lần lượt là: A. 1và i . B. 3 và 1. C. 1và 3 . D.1và 3i .
Câu 10. Tập nghiệm của bất phương trình log x  3 là 2 A. ;8 . B.   ;8 . C. 8;  . D. 8;   .
Câu 11. Thể tích của khối hộp chữ nhật có ba kích thước a, 2a,3a bằng A. 3 6a . B. 3 36a . C. 3 5a . D. 3 2a .
Câu12. Cho hình nón có bán kính đáy là r  5 và độ dài đường sinh l  6. Diện tích xung quanh của hình nón đã cho là
A. S  12 5 .
B. S  20 .
C. S  10 5 .
D. S  6 5 .
Câu 13. Cho hai số phức z  2  3i, z  4  6i . Tính z  z  z . 1 2 1 2
A. z = 2 + 9i .
B. z = 2 - 9i .
C. z = - 2 + 9i .
D. z = - 2 - 9i . x + 1
Câu 14. Tiệm cận ngang và tiệm cận đứng của đồ thị hàm số y = là x - 2
A. y = - 1;x = 2 .
B. y = 1;x = 2 .
C. y = 1, x = - 2 .
D. y = - 1;x = - 2 . 8 5
Câu15. Cho hàm số f  x liên tục trên đoạn 0;  8 , thỏa mãn f
 xdx  9 và f
 xdx  6. Tính 0 0 8 I  f  xdx . 5 A. I  4 . B. I  3  . C. I 15 . D. I  3 . x 1 y  2 z 1
Câu16. Trong không gian Oxyz , cho đường thẳng d :  
. Vectơ nào dưới đây là mộ  t 2 3 4
vectơ chỉ phương của d ?     A. u     2
 2; 3; 4 . B. u   1  1;2;  1 . C. u    3
 2; 3;4. D. u   4  2;3;4 .
Câu17. Tập xác định của hàm số y  log 2  x là. 3   A. ;2 . B. 2;  . C. ;2 . D. 2;  . Trang2
Câu18. Trong không gian Oxyz , cho mặt phẳng   : x  2y  4z 1  0 . Điểm nào dưới đây thuộc   ?
A. M 3;0;  1 . B. Q 0;3;  1 . C. P 3;0;  1 .
D. N 3;1;0 . 2 2 2
Câu19. Trong không gian Oxyz , cho mặt cầu S  :  x  
1   y  2   z  5  16 . Tọa độ tâm và bán
kính của S  lần lượt là A. I 1;2; 5  , R  4 . B. I 1; 2  ; 5
 , R  4. C. I 1; 2
 ;5, R  4. D. I 1; 2  ;5, R 16 .
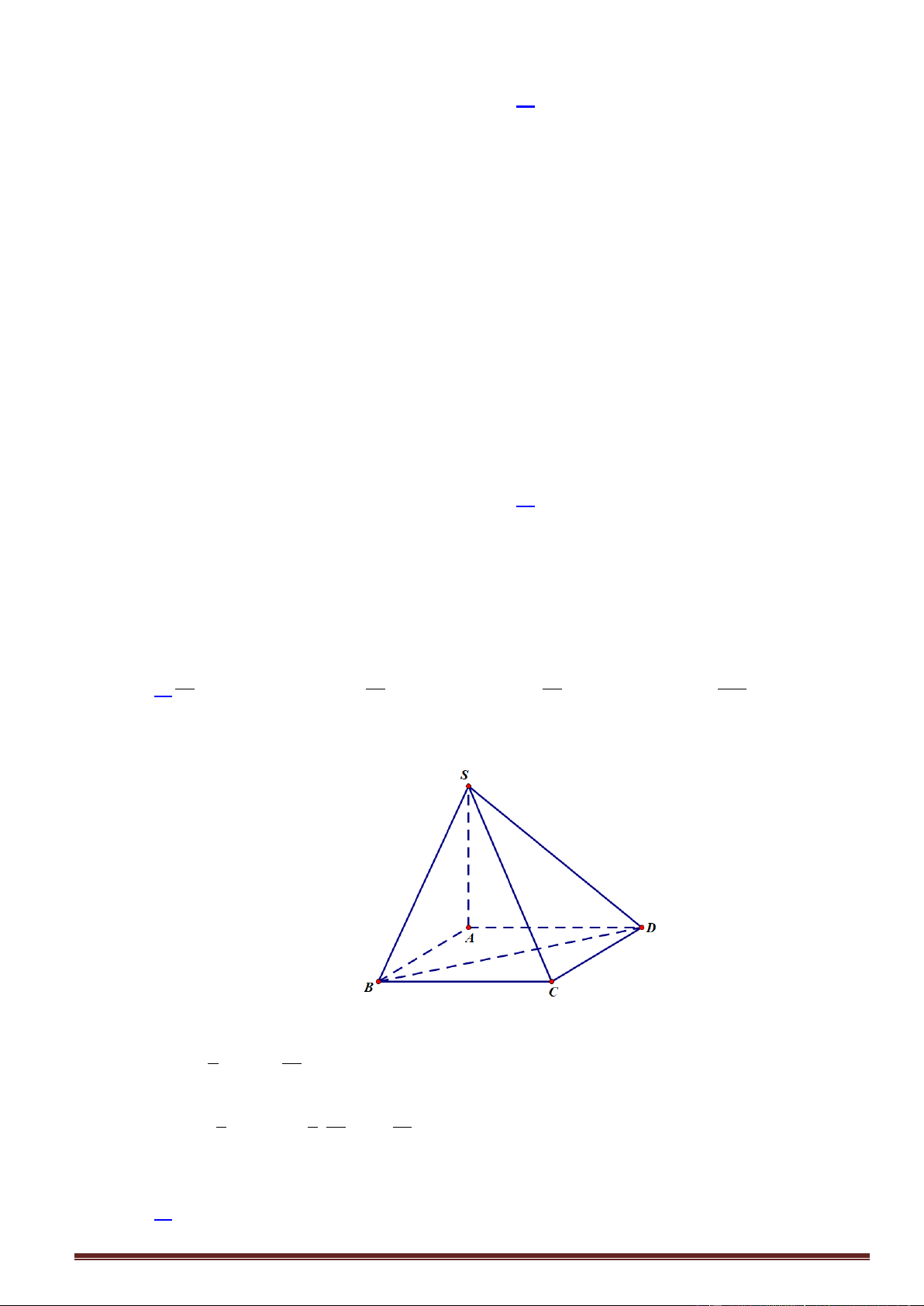
Câu20. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Cạnh SA vuông góc với mặt
phẳng đáy và có độ dài bằng 2a . Thể tích khối tứ diện S.BCD bằng 3 a 3 a 3 a 3 2a A. . B. . C. . D. . 3 4 8 3
Câu21. Nghiệm phương trình x2 2  16 là A. x  2 . B. x  4 . C. x 1. D. x  3.
Câu22. Cho a  0 , a 1, giá trị của log a bằng 3 a 1 1 A. . B.  . C. 3  . D. 3 . 3 3  
Câu 23. Trong không gian Oxyz cho hai véctơ u  1; 2  ;  1 và v   2  ;1; 
1 , góc giữa hai véctơ đã cho bằng 2  5  A. . B. . C. . D. . 3 3 6 6
Câu 24. Thể tích của khối cầu có bán kính a là 3 4 a 2 4 a A. 2 2 a . B. . C. . D. 2 4 a . 3 3
Câu 25. Cho hàm số y  f  x có bảng biên thiên như sau:
Giá trị cực đại của hàm số đã cho bằng A. 2  . B. 1  . C. 1 . D. 2 .
Câu 26. Gọi S là diện tích hình phẳng giới hạn bởi các đường  x y
e , y  0, x  2, x  5. Mệnh đề nào dưới đây đúng? 5 5 5 5 A.    x S e dx . B. 2    x S e dx . C. 2   x S e dx . D.   x S e dx . 2 2 2 2 Trang3 x 1 t 
Câu 27. Cho không gian Oxyz , cho điểm A0;1;2 và hai đường thẳng d :  y  1   2t , 1 z  2t  x y 1 z 1 d :    2
đi qua A và song song với hai đường 2 1 1
 . Viết phương trình mặt phẳng   thẳng d , d 1 2 .
A.   : x  3y  5z 13  0 .
B.   : x  2y  z 13  0 .
C.   : 3x  y  z 13  0.
D.   : x  3y  5z 13  0 .
Câu 28. Cho số phức z thỏa mãn z 1 i  3  5i . Tính môđun của z . A. z  16 . B. z  4 . C. z  17 . D. z  17 .
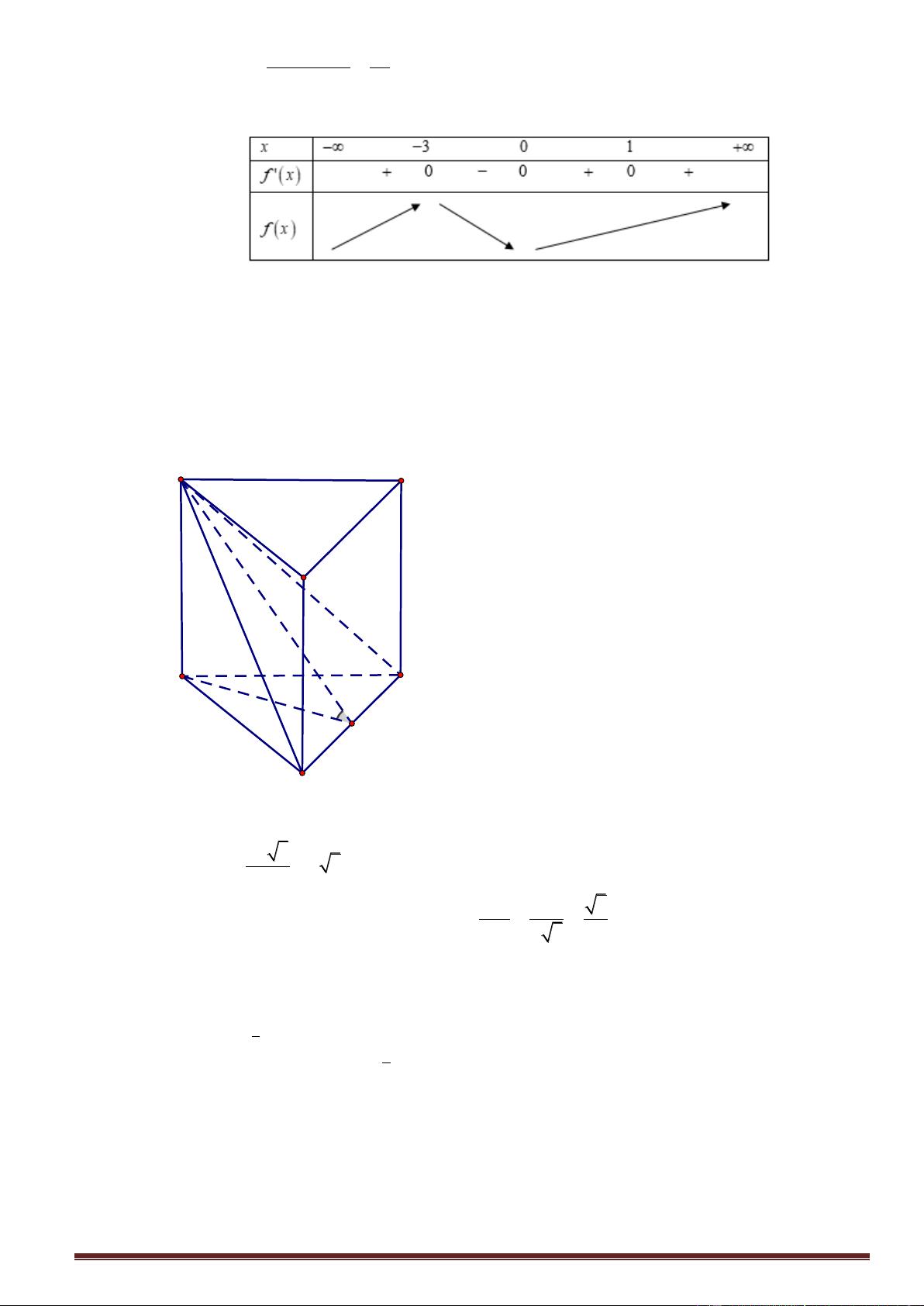
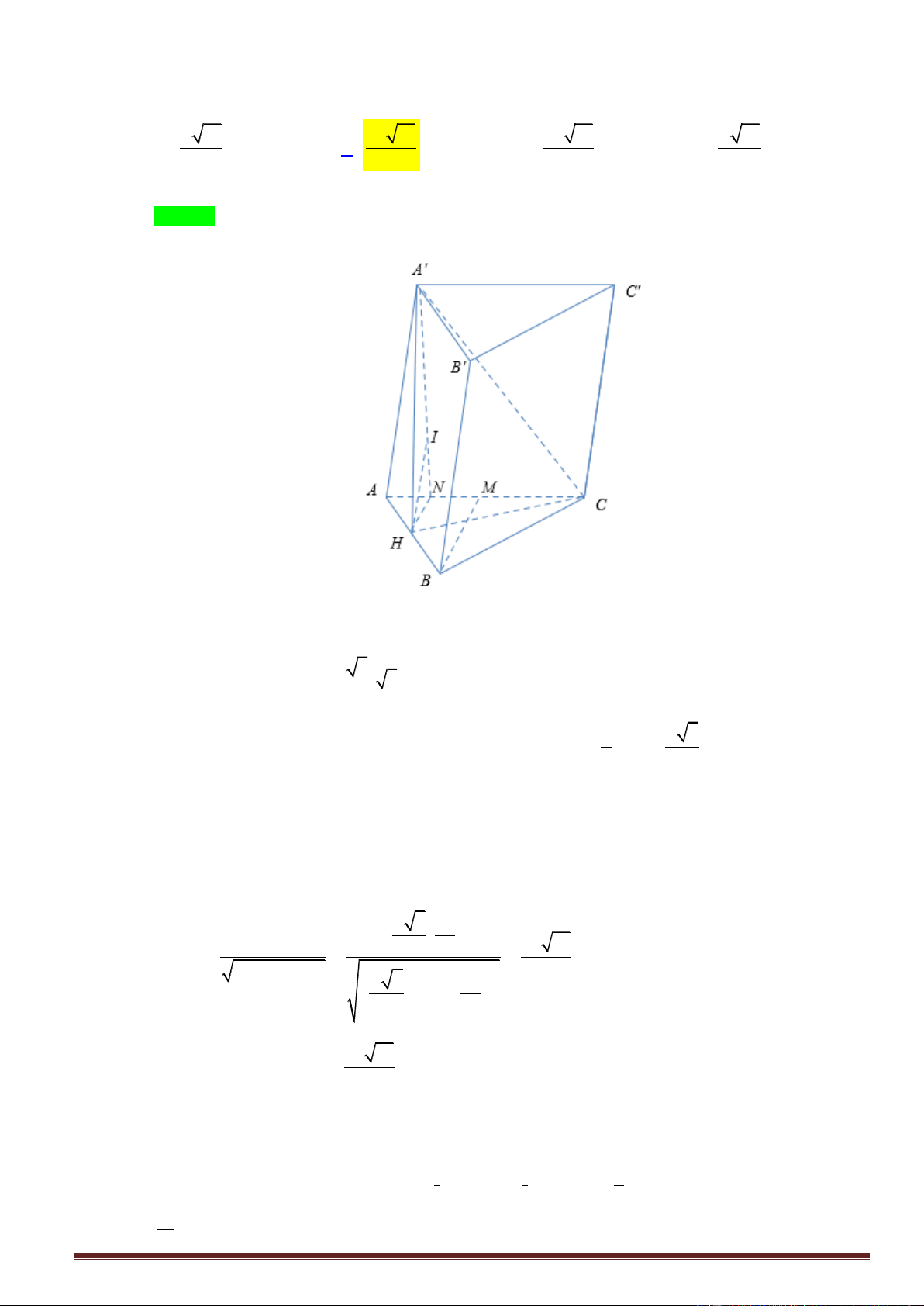
Câu 29. Cho lăng trụ tam giác đều AB .
C A' B 'C ' có tất cả các cạnh bằng a. Tính cosin của góc giữa hai
đường thẳng AB ' và BC ' 1 3 1 1 A. - B. C. D. 4 4 4 3 2 x+ 2 x - 2 x- 1 3 æ ö 1 æ 6ö
Câu 30. Tập nghiệm của bất phương trình ç ÷ ç ÷ ³ ç ÷ ç ÷ là çè4÷ø çè 9 ÷ø æ 3ö 3 é ö é 3ù 3 æ ö A. 0; çç ÷ ÷ B. (- ¥ ;0]È ;+ ¥ ÷ ê ÷ C. - ¥ Èç ÷ 0; ê ú D. ( ; ) 0 ;+ ¥ ç ç ÷ è 2÷ø 2 ÷ ê ø ê ë ç ÷ 2ú ë û è2 ø 2 Câu31. Tích phân 2
I  2x x 1dx  bằng cách đặt 2
t  x 1. Mệnh đề nào dưới đây đúng ? 1 5 1 5 5 8 A. I  tdt  . B. I  tdt  . C. I  2 tdt  . D. I  2 tdt  . 2 2 2 2 2
Câu 32. Cho a, ,
b x là các số thực dương thỏa mãn log x  2 log
a  3log b . Mệnh đề nào là đúng ? 5 1 5 5 4 a 4 a A. x  .
B. x  4a 3b . C. x  . D. 4 3
x  a  b . b 3 b
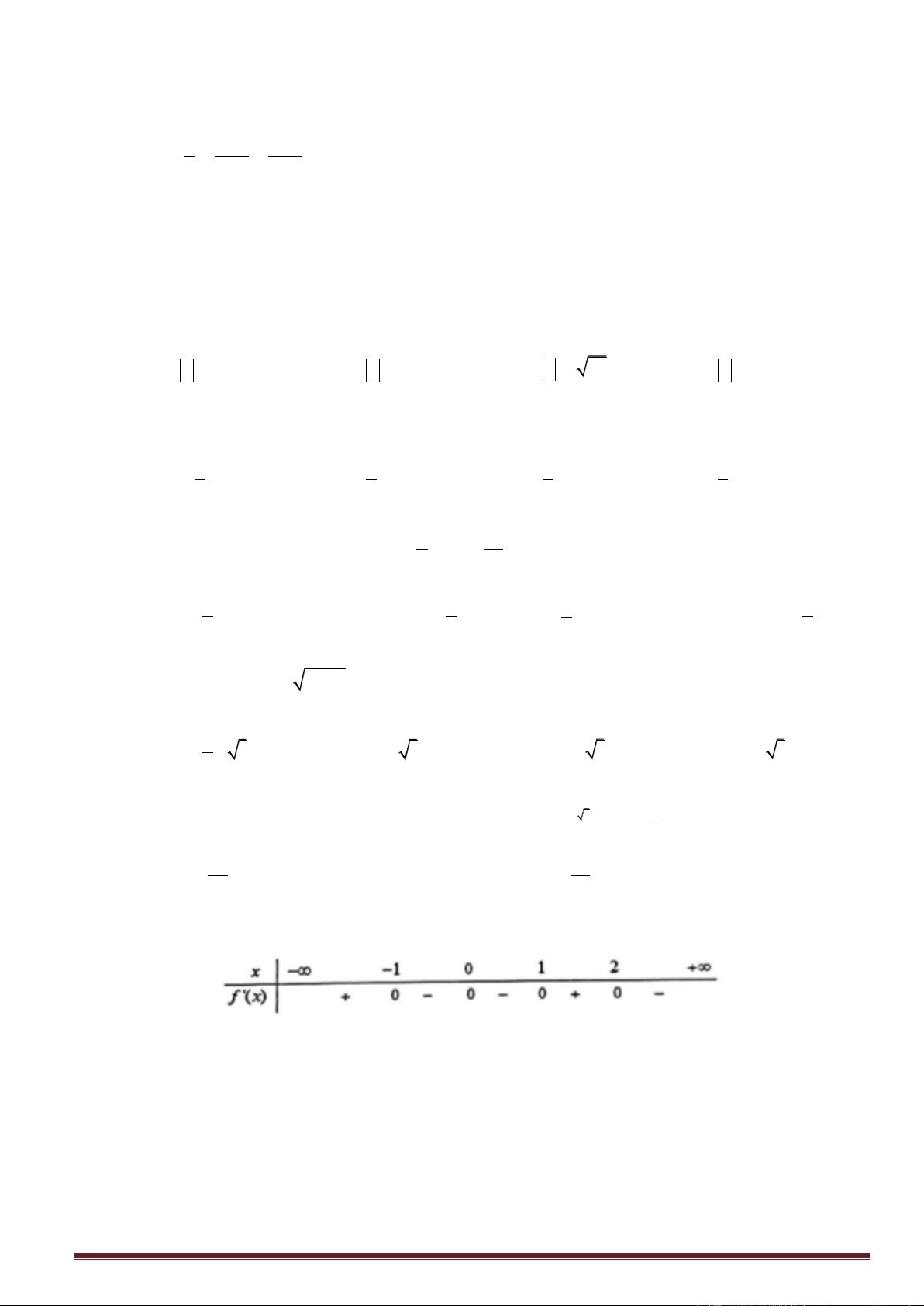
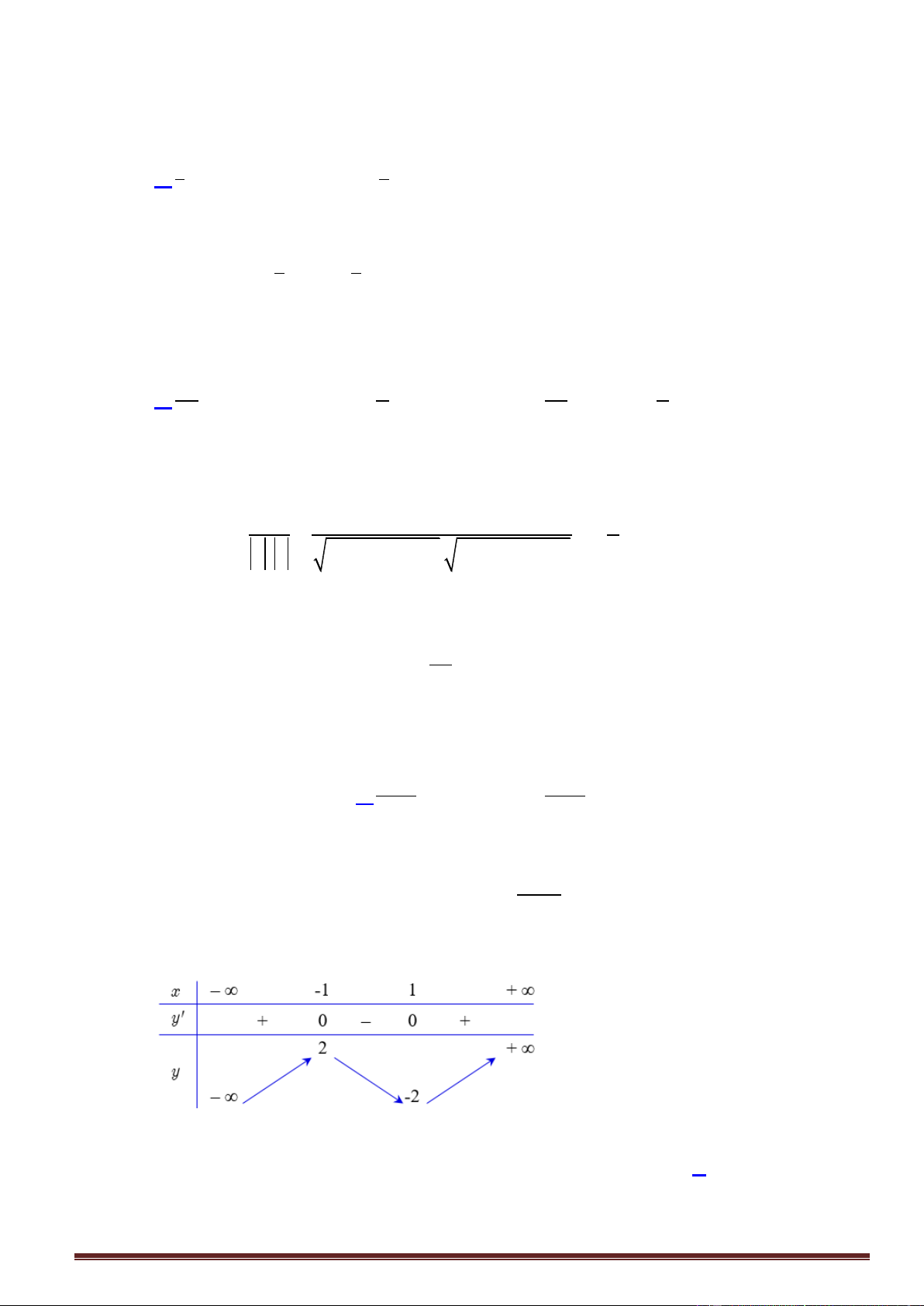
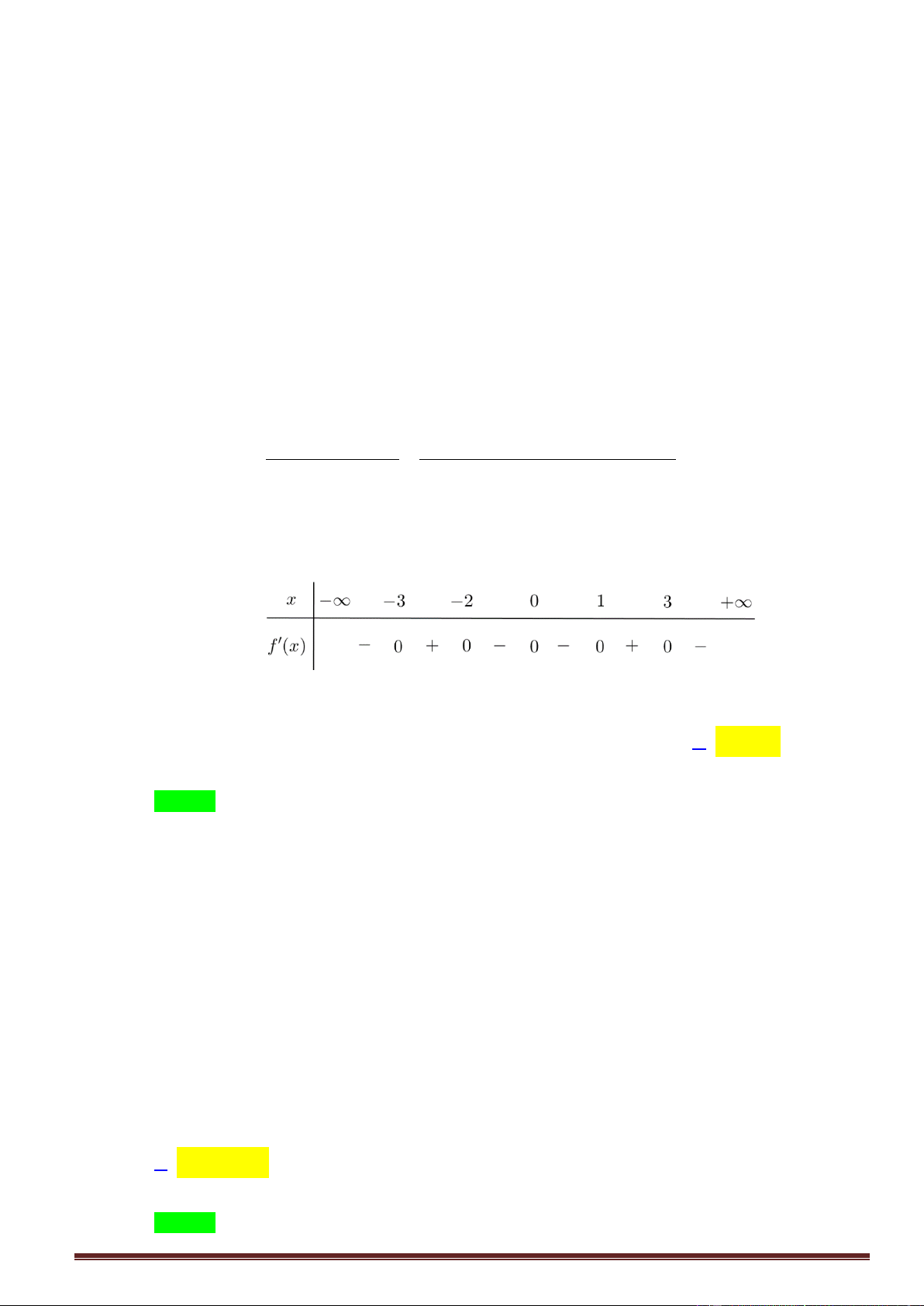
Câu33. Cho hàm số y  f (x) có bảng xét dấu f '(x) như sau:
Số điểm cực trị của hàm số đã cho là A. 3 . B. 2 . C. 4 . D. 1.
Câu34. Giá trị lớn nhất của hàm số 3
y  x  3x  2 trên đoạn  2  ;0 bằng A. 0 . B. 4 . C. 8 . D. 2.
Câu 35. Trong không gian Oxyz , cho hai điểm (
A 1; 2;3), B(3; 4;5) . Phương trình nào sau đây không
phải là phương trình của đường thẳng AB ? Trang4 x 1 2t x 1 2t x  3 t x  3 t    
A.  y  2  6t . B.  y  4   6t . C.  y  4   3t . D.  y  4   3t .     z  3  2t  z  1 2t  z  5  t  z  5  t 
Câu36. Một hình trụ có chiều cao gấp 3 lần bán kính đáy, biết thể tích khối trụ đã cho bằng 3 đơn vị
thể tích. Diện tích thiết diện qua trục của hình trụ bằng A. 3 . B. 3 6 9 . C. 3 3 9 . D. 6 .
Câu37. Gọi z và z là hai nghiệm phức của phương trình 2
z  2z  5  0 . Giá trị của biểu thức 1 2 2 2 z  z bằng 1 2 A. 6  . B. 10 . C. 4 . D. 10 .
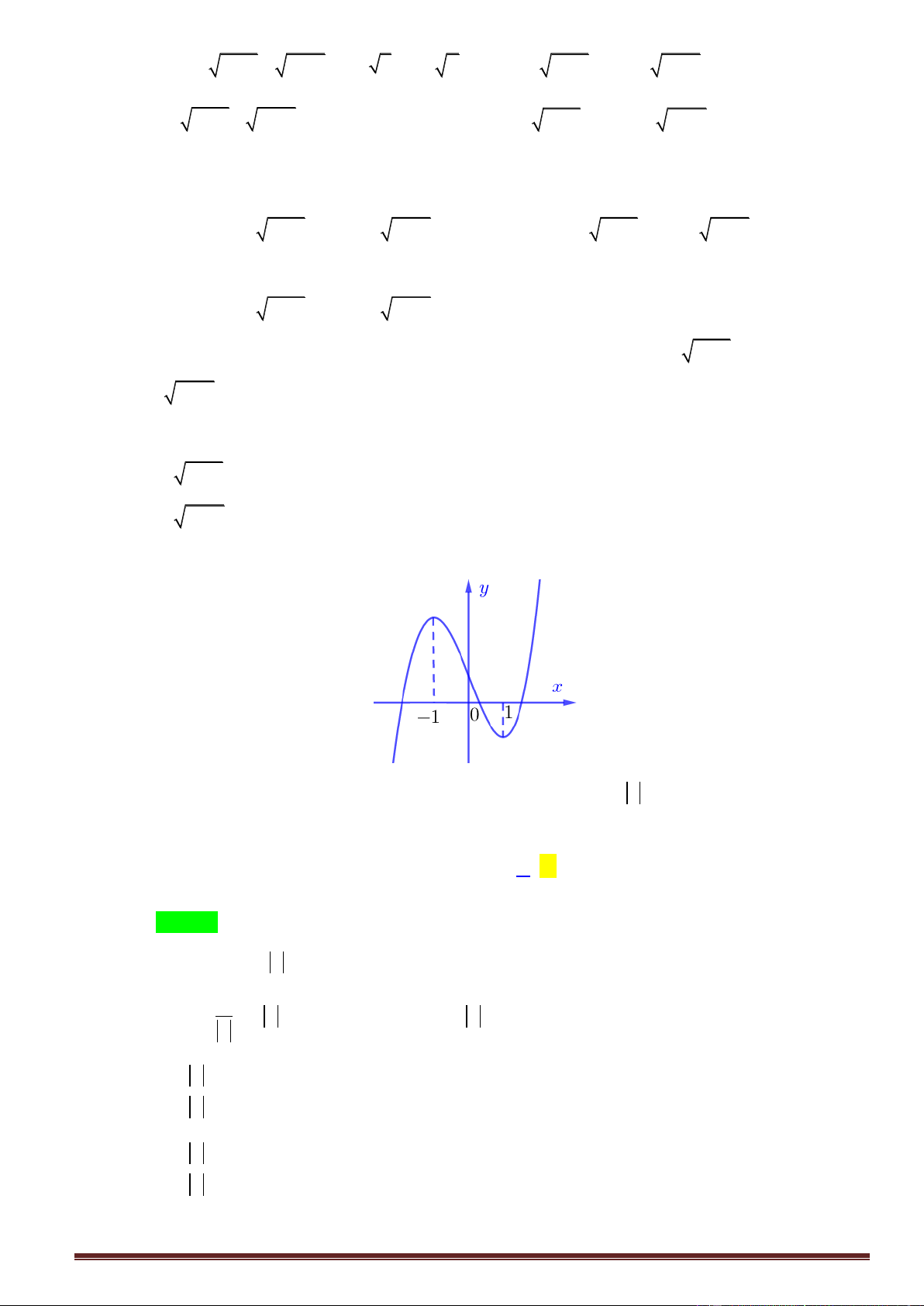
Câu38. Số giao điểm của đồ thị hàm số 3 2
y  x  2x  2x 1 và đường thẳng y  1 x là A. 1. B. 2 . C. 3 . D. 0 . 3 dx Câu39. Biết
 a 3  b 2  c 
với a , b , c là các số hữu tỷ. Tính P  a  b  c . x 1  x 1 2 13 16 A. P  5. B. P  . C. P  . D. P  . 3 2 3
Câu40. Cho hình lăng trụ ABC .
D A' B'C ' D' có đáy ABCD là hình vuông cạnh bằng 2a. AA '  a 3 ,
hình chiếu của A ' lên mặt phẳng ABCD trùng với trung điểm I của AB . Gọi K là trung điểm
của BC . Tính khoảng cách từ I đến ( A ' KD) . 3a 2 3 38a 4a 2 3a 2 A. . B. . C. . D. . 19 19 3 8
Câu41. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn  1  0;1  0 để hàm số 3 2
y  x  3x  3mx  2020 nghịch biến trên khoảng 1; 2 ? A. 11. B. 20 . C. 21 . D. 10 .
Câu42. Ông Bốn dự định gửi vào ngân hàng một số tiền với lãi suất 6,9% một năm. Biết rằng, cứ sau
mỗi năm số tiền lãi sẽ được nhập vào vốn ban đầu. Tính số tiền tối thiểu x (triệu đồng, x  )
ông Bốn gửi vào ngân hàng để sau 2 năm số tiên lãi đủ mua một chiếc xe máy có giá trị 32 triệu đồng.
A. 224 triệu đồng.
B. 252 triệu đồng.
C. 242 triệu đồng.
D. 225 triệu đồng.
Câu 43. Ba bạn Tuấn, An, Bình mỗi bạn viết ngẫu nhiên lên bảng một số tự nhiên thuộc đoạn A.
1;17. Xác suất để ba số được viết ra có tổng chia hết cho 3 bằng 1079 1637 23 1728 A. . B. . C. . D. . 4913 4913 68 4913
Câu 44. Một cái cốc hình trụ có bán kính đáy là 2 cm, chiều cao 20 cm. Trong cốc đang có một lượng
nước, khoảng cách giữa đáy cốc và mặt nước là 12 cm. Ta lần lượt thả vào cốc những viên bi
hình cầu có bán kính 0,7 cm. Để nước dâng lên cao thêm ít nhất 2 cm thì cần thả vào cốc ít nhất bao nhiêu viên bi? A. 20 viên bi. B. 19 viên bi. C. 18 viên bi. D. 17 viên bi. Trang5 2 2 2
Câu45. Cho các số thực dương    
x và y thỏa mãn x 2 y    x 2 y   2y x 2 5 9.3 5 9 .7 . Tìm giá trị nhỏ x  2 y 11
nhất của biểu thức P  ? x A. P  6 . B. P  9. C. P  7 . D. P  8 .
Câu46. Cho tứ diện S.ABC , M và N là các điểm thuộc các cạnh SA và SB sao cho MA  3SM ,
SN  2NB , ( ) là mặt phẳng qua MN và song song với SC . Kí hiệu (H ) và (H ) là các khối 1 2
đa diện có được khi chia khối tứ diện S.ABC bởi mặt phẳng ( ) , trong đó, (H ) chứa điểm S , 1
(H ) chứa điểm A ; V và V lần lượt là thể tích của (H ) và (H ) . 2 1 2 1 2 V Tính tỉ số 2 ? V  2V 1 2 47 35 4 35 A. . B. . C. . D. . 119 90 5 45
Câu47. Cho hàm số f  x   2 a   2019  2 x   x  2020 1 ln 1  bxsin
x  3 , với a, b là các số thực và f  log3 2
 9. Tính f  log2 3  . A. f  log2 3   3. B. f  log2 3    3  . C. f  log2 3    2. D. f  log2 3    2  .
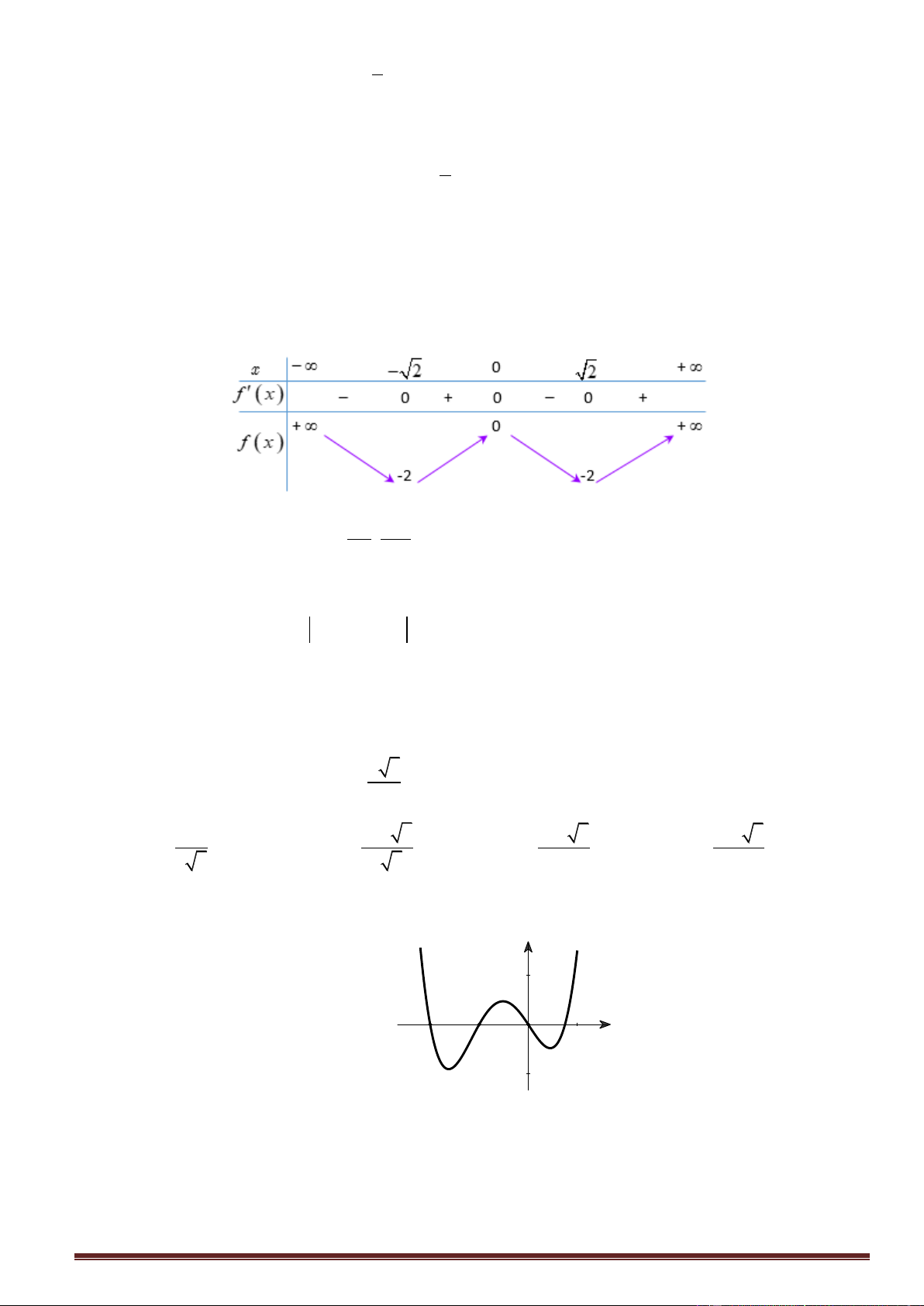
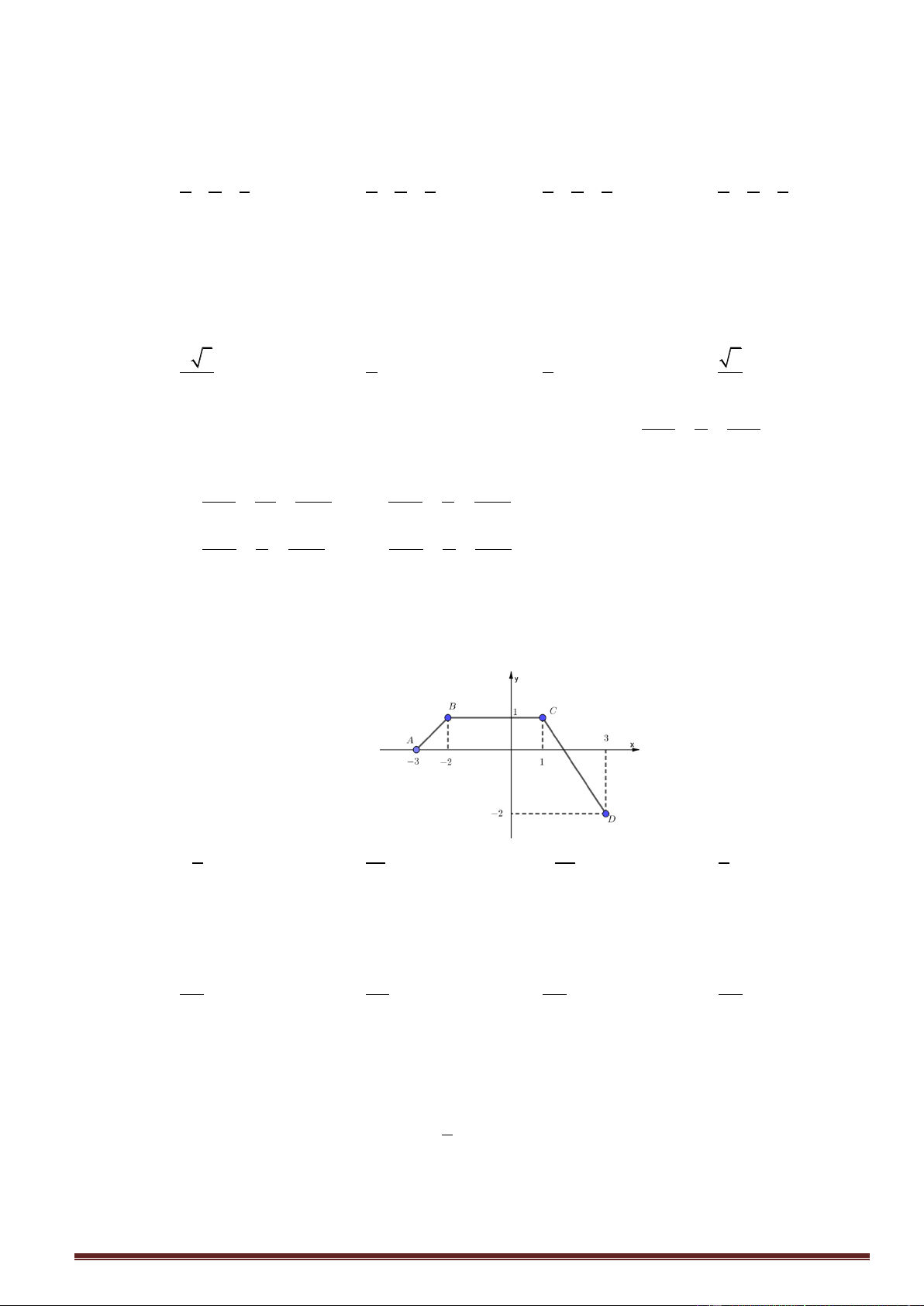
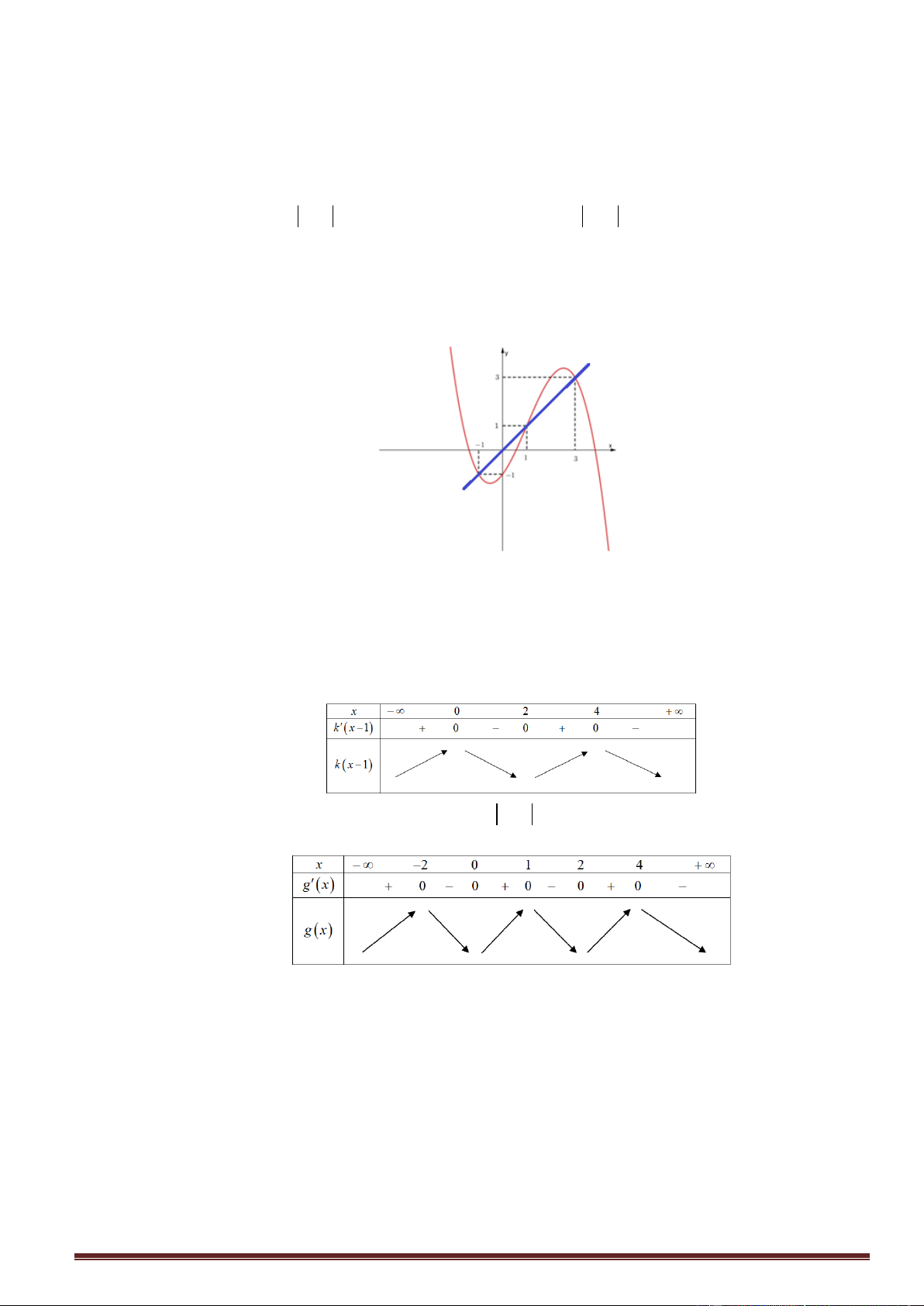
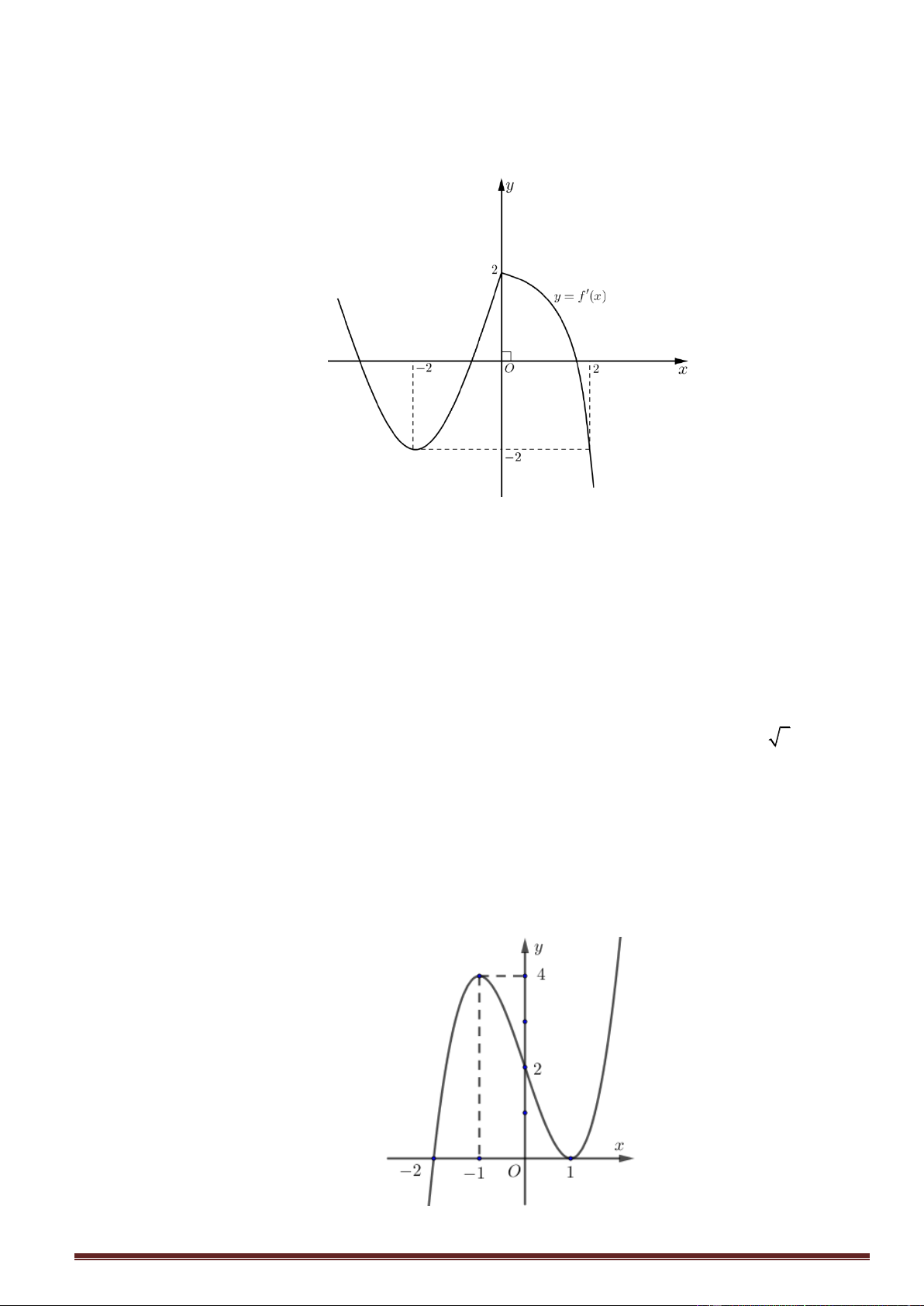
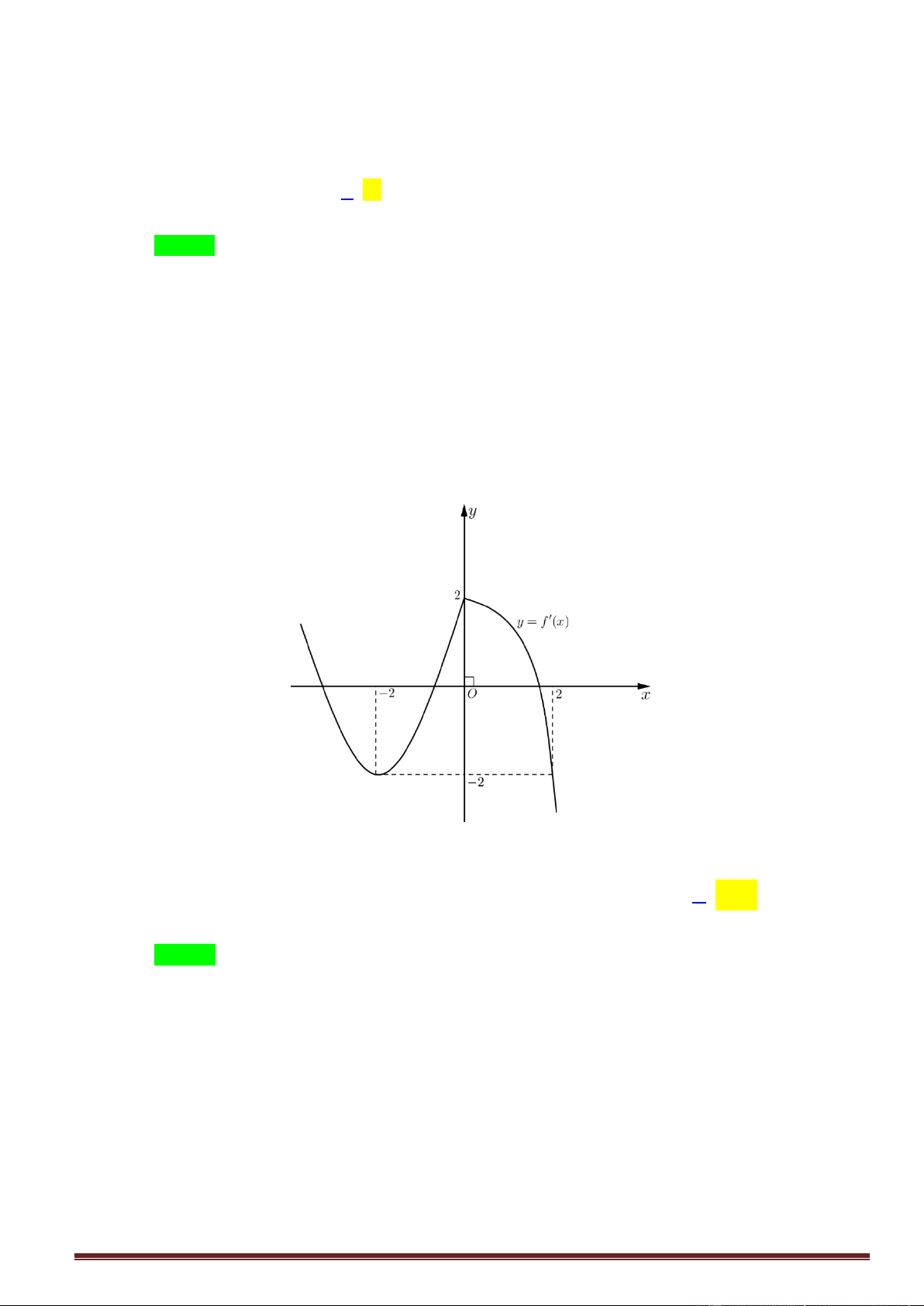
Câu48. Cho hàm số y  f  x có đạo hàm liên tục trên  . Đồ thị hàm số y  f  x như hình vẽ bên
Hỏi hàm số g  x  f  x   x  2 2
1 đồng biến trên khoảng nào trong các khoảng sau? A.  3   ;1 . B. 1;3 . C.  ;3   . D. 3;  . 1 19
Câu 49. Gọi S là tập hợp tất cả các số nguyên m để hàm số 4 2 y  x 
x  30x  m có giá trị lớn 4 2
nhất trên đoạn 0;2 không vượt quá 20 . Tổng các phần tử của S là A. 195  . B.195 . C. 210 . D. 210  .
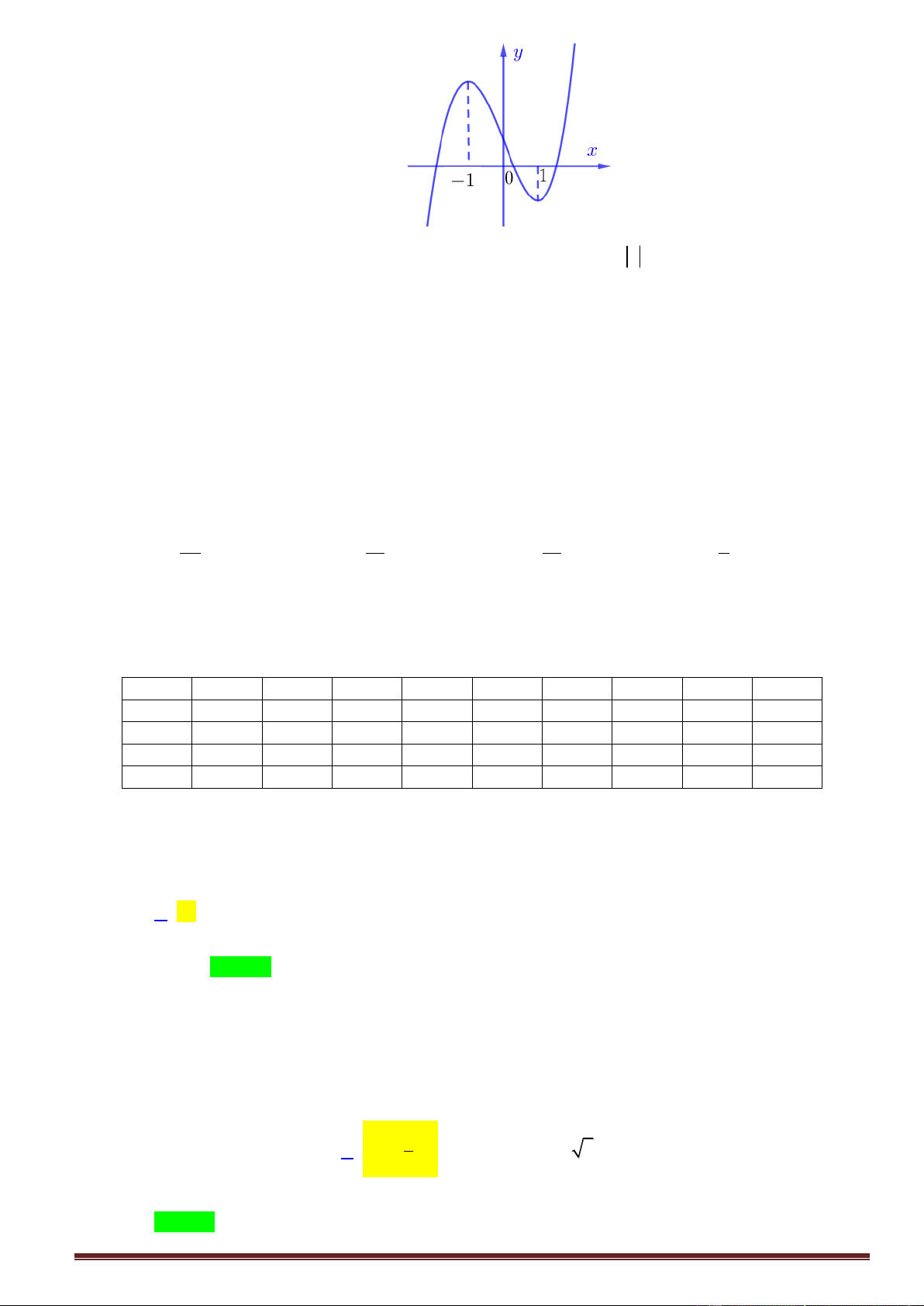
Câu50. Cho hàm số y  f  x , hàm số y  f  x liên tục trên  và có đồ thị như hình vẽ. Trang6
Bất phương trình f  x 3 2
 m  x  3x  8x ( m là tham số thực) nghiệm đúng với mọi x0;3 khi và chỉ khi
A. m  f 0 .
B. m  f 3  24 .
C. m  f 0 .
D. m  f 3  24 .
--------------HẾT--------------- Trang7 ĐÁP ÁN ĐỀ THI 1.D 2.A 3.C 4.B 5.B 6.A 7.D 8.B 9.C 10.C 11.A 12.D 13.D 14.B 15.D 16.D 17.C 18.C 19.C 20.A 21.A 22.A 23.A 24.B 25.D 26.D 27.A 28.C 29.C 30.C 31.B 32.C 33.A 34.B 35.B 36.D 37.D 38.A 39.D 40.B 41.A 42.D 43.B 44.C 45.D 46.A 47.B 48.B 49.A 50.D
HƯỚNG DẪN GIẢI CHI TIẾT Câu1.
Số cách sắp xếp 6 bạn học sinh vào 6 ghế kê thành hang ngang là A. 60 . B. 120 . C. 12 . D. 720 . Lời giải
Mỗi cách xếp 6 bạn học sinh vào 6 ghế kê thành hang ngang là một hoán vị của 6.
Vậy có 6! 720 cách xếp. Câu 2.
Diện tích của mặt cầu có bán kính r  3là A. 36 . B. 18 . C. 9 . D. 6 . Lời giải Diện tích mặt cầu 2
S  4 r  4 .9  36 . Câu 3.
Điểm M trong hình vẽ bên biểu diễn số phức nào dưới đây?
A. z  2  4 . i
B. z  4  2 . i
C. z  4  2 . i
D. z  2  4 . i Lời giải
Từ hình vẽ ta xác định được tọa độ M 4,2 . Suy ra z  4  2 . i Câu 4.
cho hàm số y  f  x có bảng biến thiên sau:
Số nghiệm của phương trình f  x  2  0 là A. 2. B. 3. C. 1. D. 0. Lời giải
Ta có f  x  2  0  f  x  2 Trang8
Từ bảng biến thiên suy ra f  x  2 có 3 nghiệm. Câu5.
Trong các hàm số sau, hàm số nào có một nguyên hàm là hàm số F  x  cos x ?
A. f  x   cos x .
B. f  x  sin x .
C. f  x  cos x .
D. f  x  sin x . Lời giải Ta có : sin d
x x  cos x  C 
Vậy hàm số f  x  sin x có một nguyên hàm là hàm số F  x  cos x Câu6.
Cho cấp số cộng u có u  3;u  7 . Công sai của cấp số cộng đã cho bằng n  1 3 A. 2 . B. 4 . C. 4  . D. 2  . Lời giải
Ta có: u  u  n 1 d với d là công sai của cấp số cộng n 1  
u  u  2d  7  3  2d  d  2 3 1 Câu 7.
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên A. 3
y  x  3x 1 B. 3
y  x  3x 1 C. 3
y  x  3x 1 D. 3
y  x  3x 1 Lời giải
Dựa vào hình dạng đồ thị ta nhận thấy đây là đồ thị hàm số bậc ba f  x 3 2
 ax  bx  cx  d (a  0) Xét điểm 0; 
1 là giao điểm của đồ thị hàm số với trục tung Oy : x  0 ta được . a 0  . b 0  .
c 0  d 1  d 1
Vậy từ 4 đáp án trên chọn đáp án D. Câu 8.
Cho đồ thị f  x có đồ thị như hình vẽ Trang9
Hàm số đã cho nghịch biến trong khoảng nào dưới đây? A.  ;  0 B. 0;  1 C. 0;  D.  1  ;0 Lời giải
Dựa vào đồ thị ta thấy được 2 khoảng nghịch biến là  ;    1 và 0;  1 Chọn đáp án B. Câu 9.
Phần thực và phần ảo của số phức z  1 3i lần lượt là: A. 1và i . B. 3 và 1. C.1và 3 . D.1và 3i . Lời giải
Phần thực , phần ảo của số phức z  a  bi lần lượt là a , b . Chọn C.
Câu 10. Tập nghiệm của bất phương trình log x  3 là 2 A. ;8 . B.   ;8 . C.8;  . D. 8;   . Lời giải x  0 log x  3  
 x  8 . Vậy tập nghiệm của bất phương trình: S  8;  2 3 x  2
Câu 11. Thể tích của khối hộp chữ nhật có ba kích thước a, 2a,3a bằng A. 3 6a . B. 3 36a . C. 3 5a . D. 3 2a . Lời giải
Thể tích của khối hộp chữ nhật là 3 V  .2 a .3 a a  6a .
Câu12. Cho hình nón có bán kính đáy là r  5 và độ dài đường sinh l  6. Diện tích xung quanh của hình nón đã cho là
A. S  12 5 .
B. S  20 .
C. S  10 5 .
D. S  6 5 . Lời giải
Diện tích xung quanh của của hình nón là S   rl   . 5.6  6 5 .
z  2  3i, z  4  6i
z  z  z
Câu 13. Cho hai số phức 1 2 . Tính 1 2 .
A. z = 2 + 9i .
B. z = 2 - 9i .
C. z = - 2 + 9i .
D. z = - 2 - 9i . Trang10 Lời giải
Ta có z  z  z  (2  3i)  (4  6i)  2   9i . 1 2 x + 1
Câu 14. Tiệm cận ngang và tiệm cận đứng của đồ thị hàm số y = là x - 2
A. y = - 1;x = 2 .
B. y = 1;x = 2 .
C. y = 1, x = - 2 .
D. y = - 1;x = - 2 . Lời giải ax  b
Lý thuyết: Hàm số y 
, (c  0, ad  bc) . ĐTHS có: cx  d a
1. Tiệm cận ngang y  c d
2. Tiệm cận đứng x   c
Áp dụng ta được đường tiệm cận ngang, tiệm cận đứng của ĐTHS trên có phương trình lần
lượt là y  1, x  2 . 8 5
Câu15. Cho hàm số f  x liên tục trên đoạn 0;  8 , thỏa mãn f
 xdx  9 và f
 xdx  6. Tính 0 0 8 I  f  xdx . 5 A. I  4 . B. I  3  . C. I 15 . D. I  3 . Lời giải 8 5 8 Ta có: f
 xdx  f
 xdx f  xdx 0 0 5 8 8 5 Suy ra: f
 xdx  f
 xdx f
 xdx  96  3. 5 0 0 x 1 y  2 z 1
Câu16. Trong không gian Oxyz , cho đường thẳng d :  
. Vectơ nào dưới đây là mộ  t 2 3 4
vectơ chỉ phương của d ?     A. u     2
 2; 3; 4 . B. u   1  1;2;  1 . C. u    3
 2; 3;4. D.u   4  2;3;4 . Lời giải 
Từ pt đường thẳng suy ra u   4  2;3;4 là vtcp của d
Câu17. Tập xác định của hàm số y  log 2  x là. 3   A. ;2 . B. 2;  . C. ;2 . D. 2;  . Lời giải
Điều kiện 2  x  0  x  2.
Tập xác định D  ;2 . Trang11
Câu18. Trong không gian Oxyz , cho mặt phẳng   : x  2y  4z 1  0 . Điểm nào dưới đây thuộc   ?
A. M 3;0;  1 . B. Q 0;3;  1 . C. P 3;0;  1 .
D. N 3;1;0 . Lời giải
+ Thay tọa độ điểm M 3;0; 
1 vào phương trình mặt phẳng   ta được
VT  3  2.0  4. 
1 1  8  VP . Vậy M   .
+ Thay tọa độ điểm Q 0;3; 
1 vào phương trình mặt phẳng   ta được
VT  0  2.3  4.1 1  3  VP . Vậy Q   .
+ Thay tọa độ điểm P 3;0; 
1 vào phương trình mặt phẳng   ta được
VT  3  2.0  4.1 1  0  VP . Vậy P    . 2 2 2
Câu19. Trong không gian Oxyz , cho mặt cầu S  :  x  
1   y  2   z  5  16 . Tọa độ tâm và bán
kính của S  lần lượt là A. I 1;2; 5  , R  4 . B. I 1; 2  ; 5
 , R  4. C. I 1; 2
 ;5, R  4. D. I 1; 2  ;5, R 16 . Lời giải
Mặt cầu S  có tâm I 1; 2
 ;5 , bán kính R  4 .
Câu20. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Cạnh SA vuông góc với mặt
phẳng đáy và có độ dài bằng 2a . Thể tích khối tứ diện S.BCD bằng 3 a 3 a 3 a 3 2a A. . B. . C. . D. . 3 4 8 3 Lời giải 2 1 a S  S  BCD 2 ABCD 2 1 2 1 a 3 a V  S .SA  . .2a  . S .BCD 3 BCD 3 2 3
Câu21. Nghiệm phương trình x2 2  16 là A. x  2 . B. x  4 . C. x 1. D. x  3. Trang12 Lời giải Ta có: x2 x2 4 2  16  2
 2  x  2  4  x  2.
Câu22. Cho a  0 , a 1, giá trị của log a bằng 3 a 1 1 A. . B.  . C. 3  . D. 3 . 3 3 Lời giải 1 1 Ta có: log a  log a  . 3 3 a a 3  
Câu 23. Trong không gian Oxyz cho hai véctơ u  1; 2  ;  1 và v   2  ;1; 
1 , góc giữa hai véctơ đã cho bằng 2  5  A. . B. . C. . D. . 3 3 6 6 Lời giải     . u v 1. 2   2  .11.1 1 cosu;v           . u . v 1   2  2 1 .  2  2 2 2 2 2 2 1 1    u v 0 ;  120 . 2
Vậy góc giữa hai véctơ đã cho bằng . 3
Câu 24. Thể tích của khối cầu có bán kính a là 3 4 a 2 4 a A. 2 2 a . B. . C. . D. 2 4 a . 3 3 Lời giải 3 4 a
Thể tích của khối cầu có bán kính a làV  . 3
Câu 25. Cho hàm số y  f  x có bảng biên thiên như sau:
Giá trị cực đại của hàm số đã cho bằng A. 2  . B. 1  . C. 1 . D. 2 . Lời giải
Giá trị cực đại của hàm số đã cho bằng 2. Trang13
Câu 26. Gọi S là diện tích hình phẳng giới hạn bởi các đường  x y
e , y  0, x  2, x  5. Mệnh đề nào dưới đây đúng? 5 5 5 5 A.    x S e dx . B. 2    x S e dx . C. 2   x S e dx . D.   x S e dx . 2 2 2 2 Lời giải
Diện tích hình phẳng cần tìm là: 5 5  x    x S e dx e dx 2 2 x 1 t 
Câu 27. Cho không gian Oxyz , cho điểm A0;1;2 và hai đường thẳng d :  y  1   2t , 1 z  2t  x y 1 z 1 d :    2
đi qua A và song song với hai đường 2 1 1
 . Viết phương trình mặt phẳng   thẳng d , d 1 2 .
A.   : x  3y  5z 13  0 .
B.   : x  2y  z 13  0 .
C.   : 3x  y  z 13  0.
D.   : x  3y  5z 13  0 . Lời giải  
Ta có: Vectơ chỉ phương của hai đường thẳng d , d a  1; 2  ;1 ; a  2;1; 1  1 2 lần lượt là 1   2  .
Vì mặt phẳng   song song với hai đường thẳng d , d 1 2 nên :   
n  a ;a   1;3;5  . 1 2    
Vậy phương trình mặt phẳng   cần tìm là: 
1 x  0  3 y  
1  5 z  2  0.
 x  3y  5z 13  0.
Câu 28. Cho số phức z thỏa mãn z 1 i  3  5i . Tính môđun của z . A. z  16 . B. z  4 . C. z  17 . D. z  17 . Lời giải  i
Ta có: z   i 3 5 1
 3  5i  z   1 4i 1 . i 2 2
Vậy môđun của z là: z    1   4    17 .
Câu 29. Cho lăng trụ tam giác đều AB .
C A' B 'C ' có tất cả các cạnh bằng a. Tính cosin của góc giữa hai
đường thẳng AB ' và BC ' 1 3 1 1 A. - B. C. D. 4 4 4 3 Lời giải Trang14 A’ C’ B’ A C B uuur uuur uuur uuur AB '.BC '
Ta có co sin (AB ', BC )
' = co sin(AB ', BC )' = uuur uuur AB ' . BC ' uuur uuur uuur uuur uuur uuur 2 2 uuur uuur uuur uuur uuur uuur a a
Mà AB ' = AB + BB '; BC ' = BC + CC ' 2
Þ AB '.BC ' = A .
B BC + AA'.CC ' = - + a = 2 2 2 uuur uuur a AB '.BC ' 1 2
Vậy co sin(AB ', BC ) ' = uuur uuur = = AB ' . BC ' a 2.a 2 4 2 x+ 2 x - 2 x- 1 3 æ ö 1 æ 6ö
Câu 30. Tập nghiệm của bất phương trình ç ÷ ç ÷ ³ ç ÷ ç ÷ là çè4÷ø çè 9 ÷ø æ 3ö 3 é ö é 3ù 3 æ ö A. 0; çç ÷ ÷ B. (- ¥ ;0]È ;+ ¥ ÷ ê ÷ C. - ¥ Èç ÷ 0; ê ú D. ( ; ) 0 ;+ ¥ ç ç ÷ è 2÷ø 2 ÷ ê ø ë ê ç ÷ 2ú ë û è2 ø Lời giải Ta có bất phương trình: 2 - x- 2 2 x - 4 x- 2 4 æ ö 4 æ ö 3 2 2 ç ÷ ç ÷ ³ ç ÷ ç ÷
Û - x - 2 ³ 2x - 4x- 2 Û 2x - 3x £ 0 Û 0 £ x £ çè3÷ø çè3÷ø 2 é 3ù
Vậy tập nghiệm S = 0; ê ú ê 2ú ë û 2 Câu31. Tích phân 2
I  2x x 1dx  bằng cách đặt 2
t  x 1. Mệnh đề nào dưới đây đúng ? 1 5 1 5 5 8 A. I  tdt  . B. I  tdt  . C. I  2 tdt  . D. I  2 tdt  . 2 2 2 2 2 Lời giải Trang15 2 Xét tích phân 2
I  2x x 1dx  . 1 Đặt 2
t  x 1  dt  2 d x x .
Khi x 1 thì t  2, khi x  2 thì t  5 . 5 Suy ra : I  tdt  . 2
Câu 32. Cho a, ,
b x là các số thực dương thỏa mãn log x  2 log
a  3log b . Mệnh đề nào là đúng ? 5 1 5 5 4 a 4 a A. x  .
B. x  4a 3b . C. x  . D. 4 3
x  a  b . b 3 b Lời giải Với a, ,
b x là các số thực dương. Ta có : 4 3 log x  2 log
a  3log b  log x  4 log a  3log b  log x  log a  log b 5 1 5 5 5 5 5 5 5 5 4 4 a a  log x  log  x  5 5 3 3 b b
Câu33. Cho hàm số y  f (x) có bảng xét dấu f (  x) như sau:
Số điểm cực trị của hàm số đã cho là A. 3 . B. 2 . C. 4 . D. 1. Lời giải
Từ bảng biến thiên ta thấy f (
 x) có ba nghiệm mà qua đó f (x) đổi dấu, do đó hàm số đã cho có ba điểm cực trị.
Câu34. Giá trị lớn nhất của hàm số 3
y  x  3x  2 trên đoạn  2  ;0 bằng A. 0 . B. 4 . C. 8 . D. 2. Lời giải Ta có 2
y  3x  3 x 1 2  ;0 2
y  0  3x  3  0   x  1     2  ;0 f ( 2)   0 f (1)  4 f (0)  2 Vậy max f ( ) x  f  1   4 .  2  ;0 Trang16
Câu 35. Trong không gian Oxyz , cho hai điểm (
A 1; 2;3), B(3; 4;5) . Phương trình nào sau đây không
phải là phương trình của đường thẳng AB ? x 1 2t x 1 2t x  3 t x  3 t    
A.  y  2  6t . B.  y  4   6t . C.  y  4   3t . D.  y  4   3t .     z  3  2t  z  1 2t  z  5  t  z  5  t  Lời giải  Ta có AB  (2; 6
 ;2) là một vec tơ chỉ phương thỏa mãn các phương án vì các vec tơ này cùng  phương với AB .
Chọn B, vì các phương án còn lại đường thẳng đi qua A hoặc B .
Câu36. Một hình trụ có chiều cao gấp 3 lần bán kính đáy, biết thể tích khối trụ đã cho bằng 3 đơn vị
thể tích. Diện tích thiết diện qua trục của hình trụ bằng A. 3 . B. 3 6 9 . C. 3 3 9 . D. 6 . Lời giải
Gọi r là bán đường tròn đáy thì chiều cao h  3r . Ta có : 2 2 3
V   .r .h   .r .3r  3  r  1  r  1 và h  3.
Thiết diện qua trục là hình chữ nhật có diện tích là: S  2 . r h  2.3  6.
Câu37. Gọi z và z là hai nghiệm phức của phương trình 2
z  2z  5  0 . Giá trị của biểu thức 1 2 2 2 z  z bằng 1 2 A. 6  . B. 10 . C. 4 . D.10 . Lời giải z  1   2i Ta có: 2 1
z  2z  5  0   z  1   2  i 2 Khi đó 2 2 2 2 z  z  1   2i  1   2i 10 . 1 2
Câu38. Số giao điểm của đồ thị hàm số 3 2
y  x  2x  2x 1 và đường thẳng y  1 x là A.1. B. 2 . C. 3 . D. 0 . Lời giải
Phương trình hoành độ giao điểm là: 3 2 3 2
x  2x  2x 1  1 x  x  2x  3x  0  x  0 .
Ta suy ra đồ thị hàm số 3 2
y  x  2x  2x 1 và đường thẳng y  1 x cắt nhau tại điểm 0;  1 .
Vậy số giao điểm là 1. 3 dx Câu39. Biết
 a 3  b 2  c 
với a , b , c là các số hữu tỷ. Tính P  a  b  c . x 1  x 1 2 13 16 A. P  5. B. P  . C. P  . D. P  . 3 2 3 Trang17 Lời giải 3 3 3 dx 2 2  Ta có  
 x1 xdx  x 1 x1 x x   x 1  x 3 3  1 1 1 16   4 2    4 14 2 3  2       2 3  2  .  3   3 3  3 3 4 14 4 14 16
Vậy a  2 ; b   ; c  . Suy ra P  2    . 3 3 3 3 3
Câu40. Cho hình lăng trụ ABC .
D A' B'C ' D' có đáy ABCD là hình vuông cạnh bằng 2a. AA '  a 3 ,
hình chiếu của A ' lên mặt phẳng ABCD trùng với trung điểm I của AB . Gọi K là trung điểm
của BC . Tính khoảng cách từ I đến ( A ' KD) . 3a 2 3 38a 4a 2 3a 2 A. . B. . C. . D. . 19 19 3 8 Lời giải
Do ABCD là hình vuông nên có IC  DK tại N .
Kẻ IH  A ' N (1) tại H. DK  IC Khi đó có 
 DK  IH (2) .
DK  A' I
Từ (1) và (2) ta có IH  ( A ' DK ) .
Vậy d (I ,( A' DK ))  IH .
Xét tam giác A' IA có 2 2 A' I 
A' A  AI  a 2 . 1 1 1
Xét tam giác DKC có   2 2 2 CN CK DC 2a CN  . 5 a
Xét tam giác IBC có IC  3 5 a 5  IN  . 5 1 1 1 a a
Xét tam giác A' IN có   3 2 3 38  IH   . 2 2 2 IH IN A ' I 19 19
Câu41. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn  1  0;1  0 để hàm số 3 2
y  x  3x  3mx  2020 nghịch biến trên khoảng 1; 2 ? A. 11. B. 20 . C. 21 . D. 10 . Lời giải 2
y  3x  6x  3m
Hàm số đã cho nghịch biến trên khoảng 1; 2
 y  0,x 1;2 Trang18 2
 3x  6x  3m  0,x1;2 2
 m  x  2 ,
x x 1;2 Xét hàm số: 2
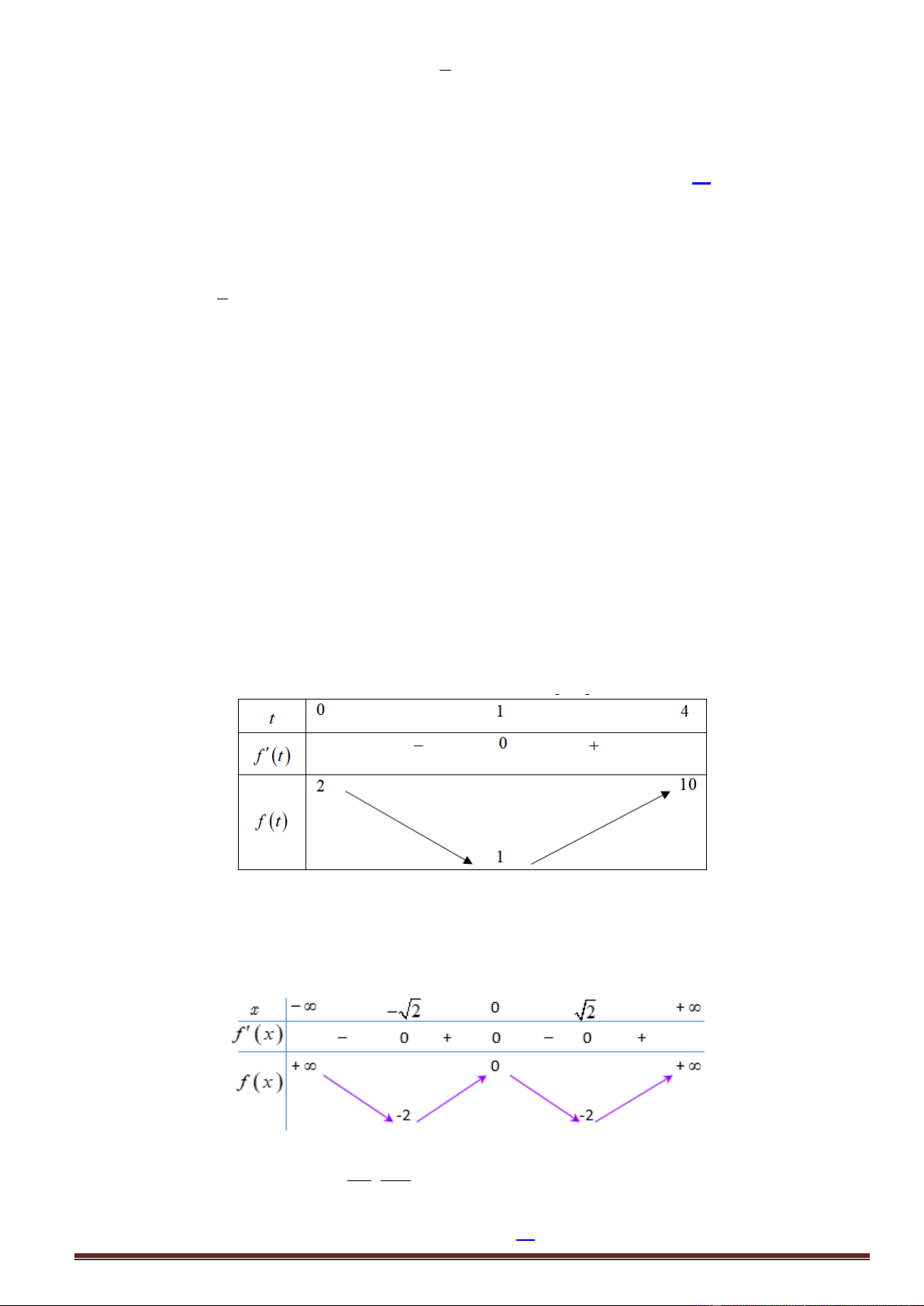
g(x)  x  2x, x 1; 2 g (  x)  2  x  2 g (
 x)  0  x 1 Bảng biến thiên: x 1 2 g (  x)  g(x) 1 0
Dựa vào bảng biến thiên ta có: 2
m  x  2 , x x
 1;2  m  0 Mà m  1
 0;10 nên có 11 giá trị nguyên của tham số m thỏa đề.
Câu42. Ông Bốn dự định gửi vào ngân hàng một số tiền với lãi suất 6,9% một năm. Biết rằng, cứ sau
mỗi năm số tiền lãi sẽ được nhập vào vốn ban đầu. Tính số tiền tối thiểu x (triệu đồng, x  )
ông Bốn gửi vào ngân hàng để sau 2 năm số tiên lãi đủ mua một chiếc xe máy có giá trị 32 triệu đồng.
A. 224 triệu đồng.
B. 252 triệu đồng.
C. 242 triệu đồng. D.225 triệu đồng. Lời giải
Gọi a là số tiền tối thiểu mà ông Bốn phải gửi để đủ mua một chiếc xe máy sau 2 năm, lãi suất r  6,9%mỗi năm. 2
Tổng số tiền vốn và lãi sau 2 năm ông Bốn nhận được là T  a 1 r  
1 . Vậy số tiền lãi là T  a .
Theo đề ta có: T  a  32 T  32 a . 2 2 Thay vào  
1 ta thu được 32  a  a 1 r  32  a  a 1,069  a  224 1 , 5 .
Vậy số tiền tối thiểu mà ông Bốn cần gửi là 225 triệu đồng.
Câu 43. Ba bạn Tuấn, An, Bình mỗi bạn viết ngẫu nhiên lên bảng một số tự nhiên thuộc đoạn B.
1;17. Xác suất để ba số được viết ra có tổng chia hết cho 3 bằng 1079 1637 23 1728 A. . B. . C. . D. . 4913 4913 68 4913 Lời giải Ta có: Trang19 C.
n   17.17.17  4913
Gọi A là biến cố: “ba số được viết ra có tổng chia hết cho 3”.
Trong đoạn 1;17 có 5 số chia hết cho 3; có 6 số chia cho 3 dư 1và có 6 số chia cho 3 dư 2.
TH1: Ba số viết ra cùng chia hết cho 3, có 5.5.5 125 cách.
TH2: Ba số viết ra cùng chia cho 3 dư 1, có 6.6.6  216 cách.
TH3: Ba số viết ra cùng chia cho 3 dư 2, có 6.6.6  216 cách.
TH4: Ba số viết ra có 1 sô chia hết cho 3, 1 số chia cho 3 dư 1, 1 số chia cho 3 dư 2 có 5.6.6.3!1080 cách.
n  A  125  2.216 1080 1637 . n A 1637
Vậy xác suất để ba số được viết ra có tổng chia hết cho 3 bằng P  A     . n  4913
Câu 44. Một cái cốc hình trụ có bán kính đáy là 2 cm, chiều cao 20 cm. Trong cốc đang có một lượng
nước, khoảng cách giữa đáy cốc và mặt nước là 12 cm. Ta lần lượt thả vào cốc những viên bi
hình cầu có bán kính 0,7 cm. Để nước dâng lên cao thêm ít nhất 2 cm thì cần thả vào cốc ít nhất bao nhiêu viên bi? A. 20 viên bi. B. 19 viên bi. C. 18 viên bi. D. 17 viên bi. Lời giải
Gọi n là số viên bi cần thả vào cốc, ( n là số nguyên dương). 4 6000
Theo yêu cầu bài toán thì n phải thỏa mãn . n  0,73 2  .2 .2  n  17, 493 . 3 343
Suy ra số viên bi ít nhất cần thả vào cốc là 18 viên. 2 2 2    
Câu45. Cho các số thực dương x và y thỏa mãn x 2 y    x 2 y   2y x 2 5 9.3 5 9 .7 . Tìm giá trị nhỏ x  2 y 11
nhất của biểu thức P  ? x A. P  6 . B. P  9. C. P  7 . D. P  8 . Lời giải Ta có 2 x 2 5  9.3 y   2 x 2 5  9 y  2 2 y x 2 .7 2 2 2 2 x 2 y2 2 y x 2 x 2 y2 2 y x 2  5  3  5.7  3 .7 2 x 2 y2  3  2 2 y x 2 7   1  5 2 2 y x 2 7   1  0   2 2 y x 2 7  
1  2x2y2 3  5  0 2 2 2 yx 2 x 2 y2  7 1  0 do 3  5  0 2 2 y x 2 2  7
1 2y  x  2  0 2
 2y  x  2 Trang20 Vì 2
y  0  x  2  0  x  2 2 2
x  x  2 11 x  x  9 9 Suy ra P    x  1 x x x
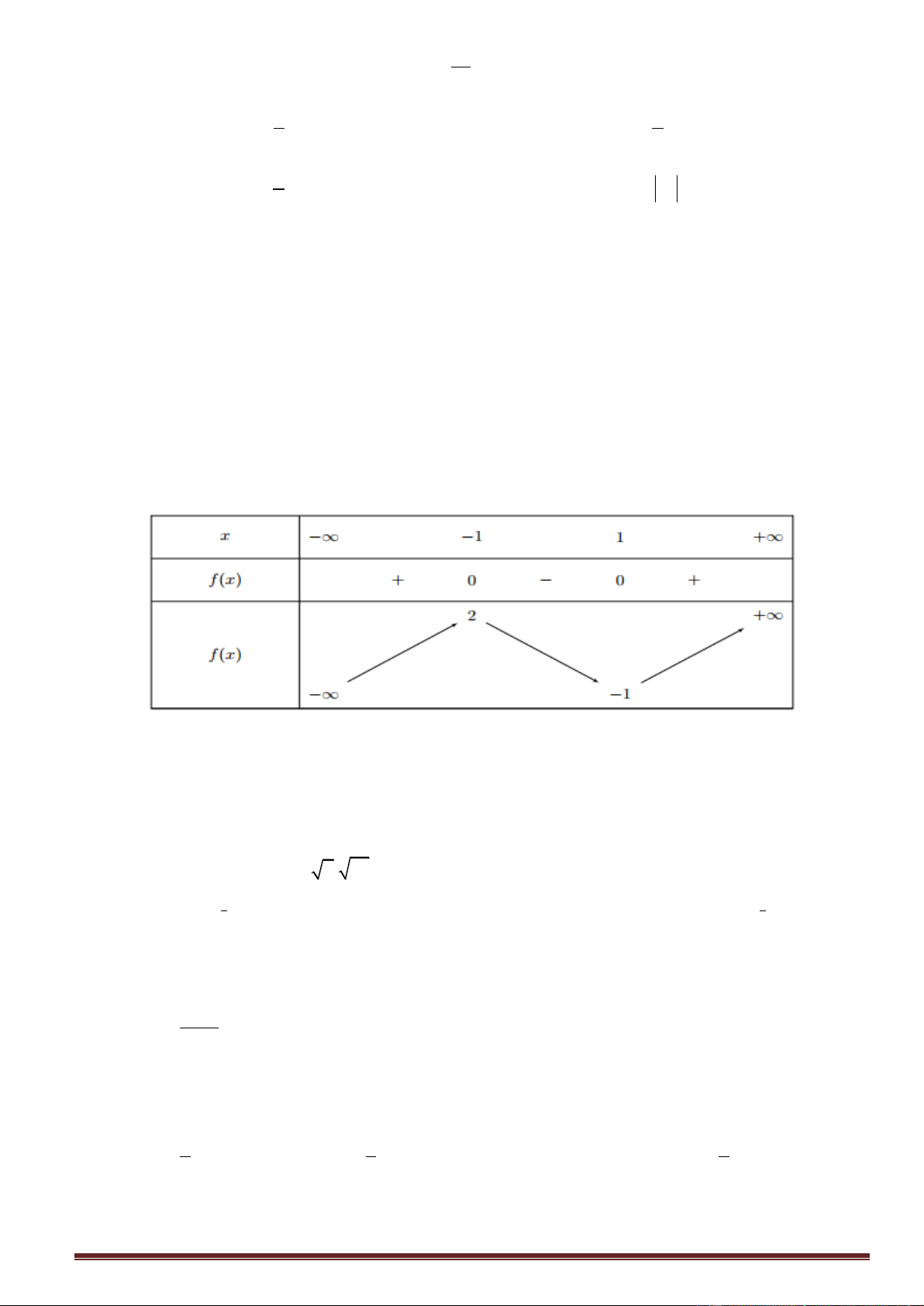
Xét hàm số f  x 9
 x  1 trên khoảng  2, x  f  x 2 9 x 9 1 
, f  x  0  x  3 2 2   x x
Ta có bảng biến thiên hàm f  x
Dựa vào BBT ta có min P  7 khi x  3, y  5
Câu46. Cho tứ diện S.ABC , M và N là các điểm thuộc các cạnh SA và SB sao cho MA  3SM ,
SN  2NB , ( ) là mặt phẳng qua MN và song song với SC . Kí hiệu (H ) và (H ) là các khối 1 2
đa diện có được khi chia khối tứ diện S.ABC bởi mặt phẳng ( ) , trong đó, (H ) chứa điểm S , 1
(H ) chứa điểm A ; V và V lần lượt là thể tích của (H ) và (H ) . 2 1 2 1 2 V Tính tỉ số 2 ? V  2V 1 2 47 35 4 35 A. . B. . C. . D. . 119 90 5 45 Lời giải
Kí hiệu V là thể tích khối tứ diện SABC . Gọi P , Q lần lượt là giao điểm của ( ) với các
đường thẳng BC , AC . Ta có NP//MQ//SC . Khi chia khối (H ) bởi mặt phẳng (QNC) , ta 1
được hai khối chóp N.SMQC và N.QPC .
Với khối chóp N.SMQC: Trang21 NS 2 2 Vì  do đó V  V . BS 3 N .SMQC B. 3 SMQC AM 3 9 7 Lại có:   S  S  S  S . AS 4 AMQ 16 SAC SMQC 16 SAC 7 Vậy V  V . N .SMQC S . 24 ABC
Với khối chóp N.QPC: SCPQ CP CQ 2 1 1 Vì    S CB CA 3 4 6 CBA Do đó 1 1 V  V  V . N .PQC N . 6 ABC 18 SABC V 7 1 25 V 25 47 V 25 Suy ra: 1 2 1     1    . V 24 18 72 V 72 72 V 47 SABC SABC 2 V 1 1 1 47 Vậy: 2     . V  2V V  2V V 25 1 2 1 119 1 2  2  2 V V 47 2 2
Câu47. Cho hàm số f  x   2 a   2019  2 x   x  2020 1 ln 1  bxsin
x  3 , với a, b là các số thực và f  log3 2
 9. Tính f  log2 3  . A. f  log2 3   3. B. f  log2 3    3  . C. f  log2 3    2. D. f  log2 3    2  . Lời giải
Ta có: f x   2 a   2019  2 x 
 x bx 2020 1 ln 1 sin x3    a  
x x  1 2 2019 2 2020 1 ln 1  bxsin x  3   2 a   2019  2 x   x  2020 1 ln 1  bxsin x  3  2    a   2019   2 x   x  2020 1 ln 1  bxsin x  3     f
 x 3  3 
  f x  6 .
Áp dụng tính chất này, ta có: f  log2    f  log3    f  log3 3 2 2 6 9   6  3  .
Câu48. Cho hàm số y  f  x có đạo hàm liên tục trên  . Đồ thị hàm số y  f  x như hình vẽ bên Trang22 y 2 x - 1 1 3 - 3 O - 2 - 4 - 6
Hỏi hàm số g  x  f  x   x  2 2
1 đồng biến trên khoảng nào trong các khoảng sau? A.  3   ;1 . B. 1;3 . C.  ;3   . D. 3;  . Lời giải
Ta có g x  2 f  x  2 x   1 .
Hàm số g  x đồng biến khi g x  0  2 f  x  2 x  
1  0  f  x  x 1. y 2 x 1 3 - 3 - 1 O - 2 - 4 - 6
Dựa vào đồ thị của hàm số y  f  x và y  x 1 ta được x  ;  3
  hoặc x1;3 thì
hàm số g  x đồng biến. 1 19
Câu 49. Gọi S là tập hợp tất cả các số nguyên m để hàm số 4 2 y  x 
x  30x  m có giá trị lớn 4 2
nhất trên đoạn 0;2 không vượt quá 20 . Tổng các phần tử của S là A. 195  . B.195 . C. 210 . D. 210  . Lời giải Trang23 1 19
Xét hàm số f  x 4 2  x 
x  30x  m trên đoạn 0;2 . 4 2 x  5  0;2  f  x 3
 x 19x  30,  f x  0  x  2  . x  3  0;2 f 0  ;
m f 2  m  26  max f  x  m  26; min f  x  m . 0;2 0;2
Suy ra max y  max  m , m  26  0;2  m  26  20   2
 0  m  26  20
YCBT  max y  20      2  0  m  6  . 0;2  m  20   2  0  m  20
Do m nên m  2  0, 1  9,..., 7  ,  6  S . 15. 2  0  6
Vậy tổng các phần tử của S bằng  195  . 2
Câu50. Cho hàm số y  f  x , hàm số y  f  x liên tục trên  và có đồ thị như hình vẽ.
Bất phương trình f  x 3 2
 m  x  3x  8x ( m là tham số thực) nghiệm đúng với mọi x0;3 khi và chỉ khi
A. m  f 0 .
B. m  f 3  24 .
C. m  f 0 .
D. m  f 3  24 . Lời giải f  x 3 2
 m  x 3x  8x  f x 3 2
 x  3x 8x  m .
Đặt hx  f x 3 2
 x  3x 8x  hx  f x 2
 x  x   f x  2 3 6 8
3x  6x  8.
Đặt g  x 2
 3x  6x 8 và vẽ đồ thị của g x lên hệ trục Oxy.
Từ hình vẽ, ta thấy f  x  g x , x  0;3.
Do đó hx  0, x
 0;3. Vì vậy ta có bảng biến thiên Trang24
Từ bảng biến thiên, yêu cầu bài toán  m  h 3  m  f 3  24.
--------------HẾT--------------- Đề 2
ĐỀ LUYỆN THI CẤP TỐC TỐT NGHIỆP THPT NĂM 2021 Thuvienhoclieu.Com BÀI THI: TOÁN
Thời gian: 90 phút x  x  Câu1.
Một nguyên hàm của f  x 2 2 3  x  là 1 2 x 2 x A.
 3x  6ln x 1 . B.
 3x  6ln x 1 . 2 2 2 x 2 x C.
 3x  6ln x 1 . D.
 3x  6ln x 1 . 2 2 Câu2.
Tìm số phức liên hợp của số phức z  i 3i  2 . A. z  3   2i .
B. z  3 2i . C. z  3   2i . D. z  3   2i . Câu3.
Cho d là đường thẳng đi qua điểm A1; 2;3 và vuông góc với mặt phẳng
:4x 3y 7z 1 0 . Phương trình chính tắc của d là x 1 y  2 z  3 x 1 y  2 z  3 A.   . B.   . 4 3 7 4 3 7 x  4 y  3 z  7 x 1 y  2 z  3 C.   . D.   . 1 2 3 4 3 7  Câu4.
Cho hình nón có bán kính đáy là 4a , chiều cao là 3a . Diện tích toàn phần của hình nón bằng A. 2 36 a . B. 2 32 a . C. 2 38 a . D. 2 30 a . x Câu5.
Với điều kiện nào của a để hàm số y  2a   1 đồng biến trên  ?  1  A. a  0 . B. a  ;1  1;   .  2   1  C. a 1. D. a  ;    .  2  Câu6.
Điểm biểu diễn của số phức z  3  4  mi là M 3;2 khi m bằng A. m  2  . B. m  4 . C. m  6  . D. m  2 . Câu7.
Tìm số giao điểm n của hai đồ thị 4 2
y  x  3x  2 và 2 y  x  2 . A. n  4 . B. n  2 . C. n  0 . D. n 1. Trang25 Câu 8.
Cho hàm số f  x có bảng biến thiên như sau:
Số ngiệm thực của phương trình 2 f  x  3  0 là A. 0 . B. 3 . C. 2 . D.1. Câu 9.
Cho hình trụ có bán kính đáy bằng 3cm , đường cao 6cm . Diện tích xung quanh của hình trụ này là A.   2 36 cm  . B.   2 20 cm  . C.   2 24 cm  . D.   2 18 cm  .
Câu 10. Trong không gian Oxyz , cho điểm K 2; 4;6 , gọi K là hình chiếu của K trên Oz . Khi đó
trung điểm OK có tọa độ là A. 1;0;0 . B. 1; 2;3 . C. 0;0;3 . D. 0; 2;0 .
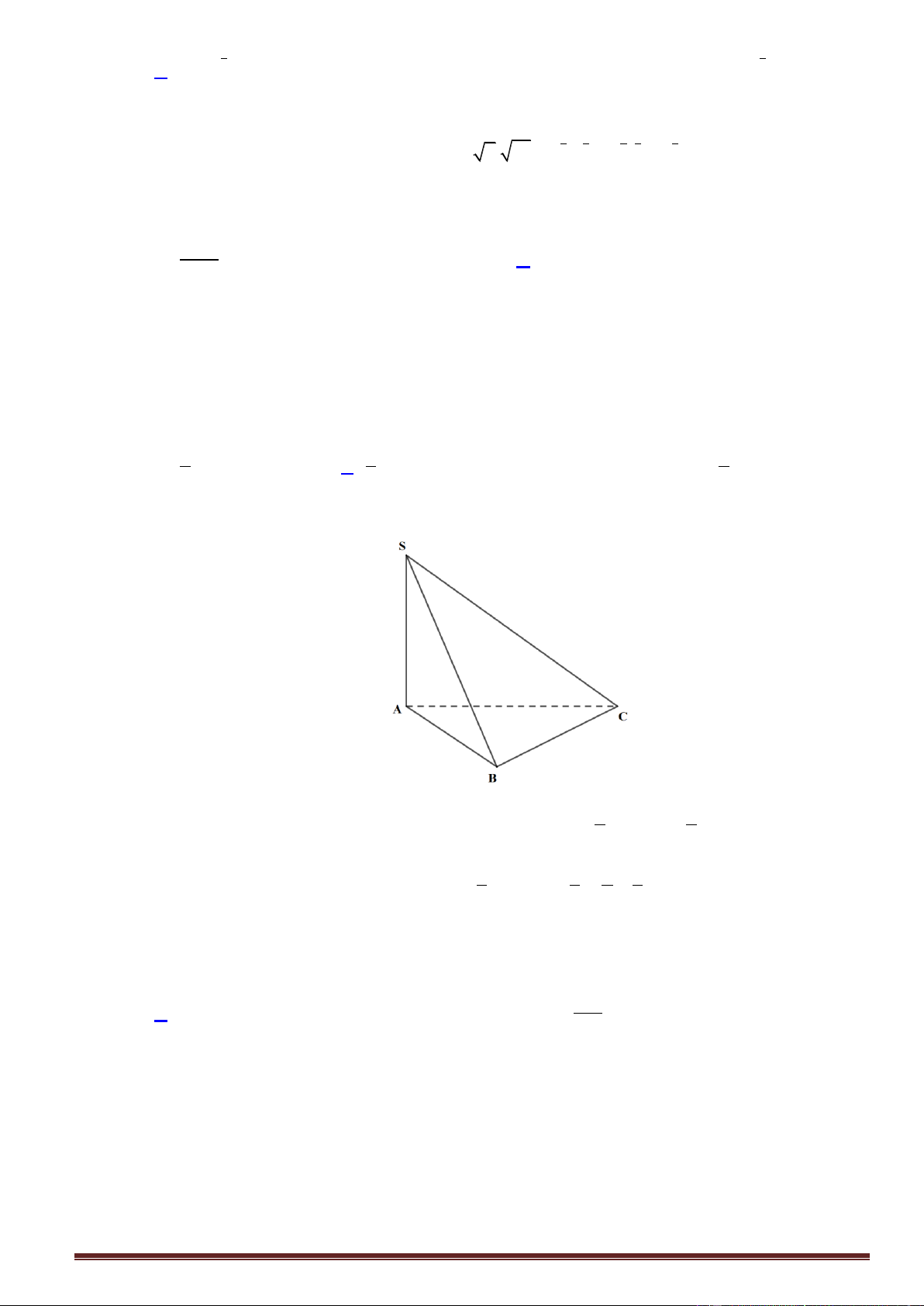
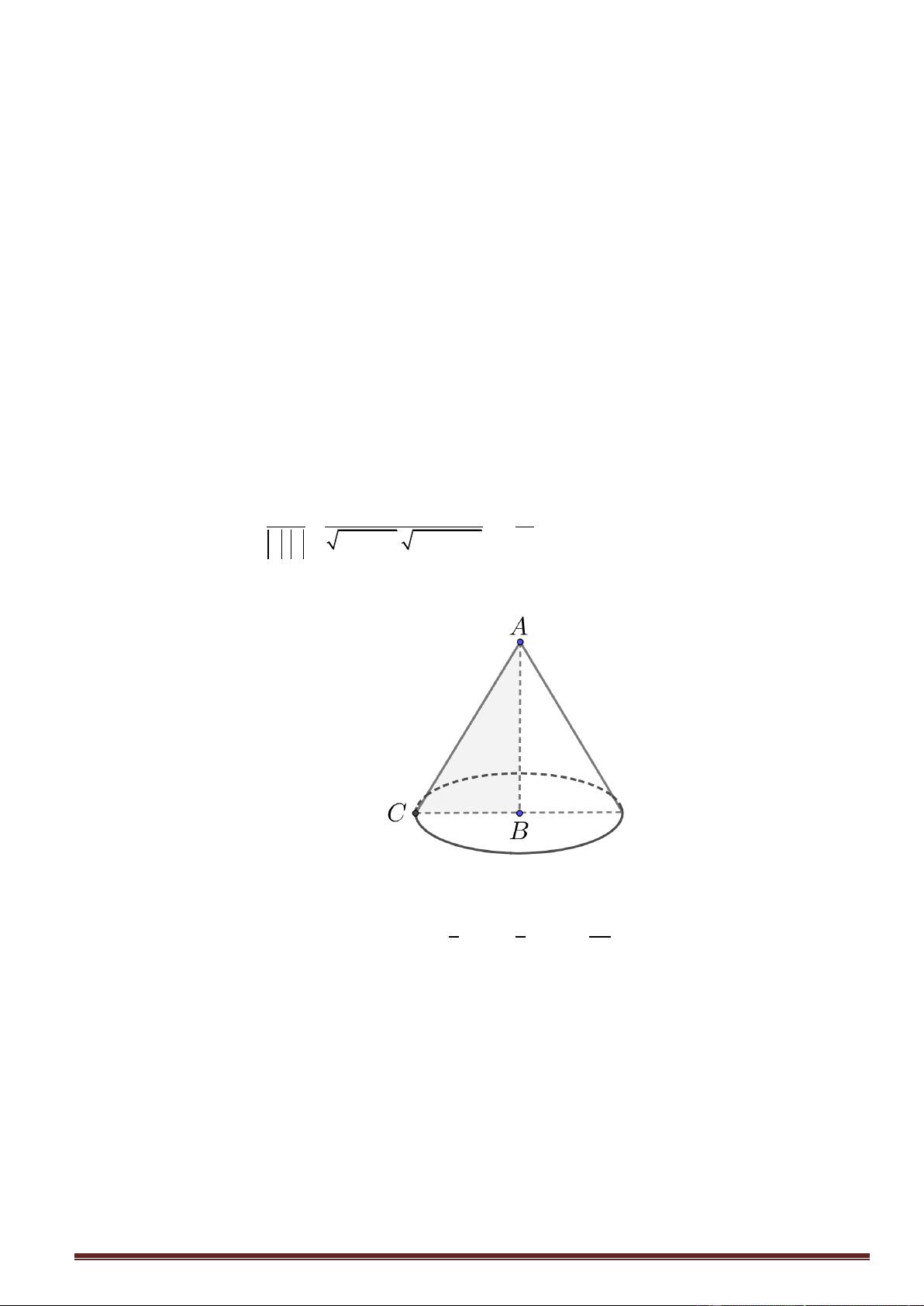
Câu11. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cạnh huyền BC  a . Hình chiếu vuông
góc của S lên  ABC trùng với trung điểm của BC . Biết SB  a . Tính số đo của góc giữa SA và  ABC. A. 75 . B. 30 . C. 60 . D. 45 .
Câu 12. Lớp 11A1 có 25 học sinh nam và 20 học sinh nữ. Hỏi có bao nhiêu cách chọn ngẫu nhiên một
bạn trong lớp làm lớp trưởng? A. 500. B. 20. C. 25. D. 45.
Câu 13. Trong không gian với hệ tọa độ Oxyz , mặt phẳng nào sau đây song song với mặt phẳng Oyz ? A. 2  x  0. B. 2  z 1 0. C. 2z  0 . D. 2  x 1 0 . x  4  2
Câu 14. Tìm số tiệm cận đứng của đồ thị hàm số y  2 x  . x A. 2 . B.1. C. 3 . D. 0 .
Câu15. Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây? y O x A. 3 2
y  x  x 1 . B. 3 2
y  x  x 1 . C. 4 2
y  x  2x 1. D. 4 2
y  x  2x 1. Câu16. Nếu 2 3
log x  8log ab  2 log a b ,
a b  0 thì x bằng: 7 7 7   A. 8 14 a b . B. 6 12 a b . C. 6 6 a b . D. 2 14 a b . Trang26
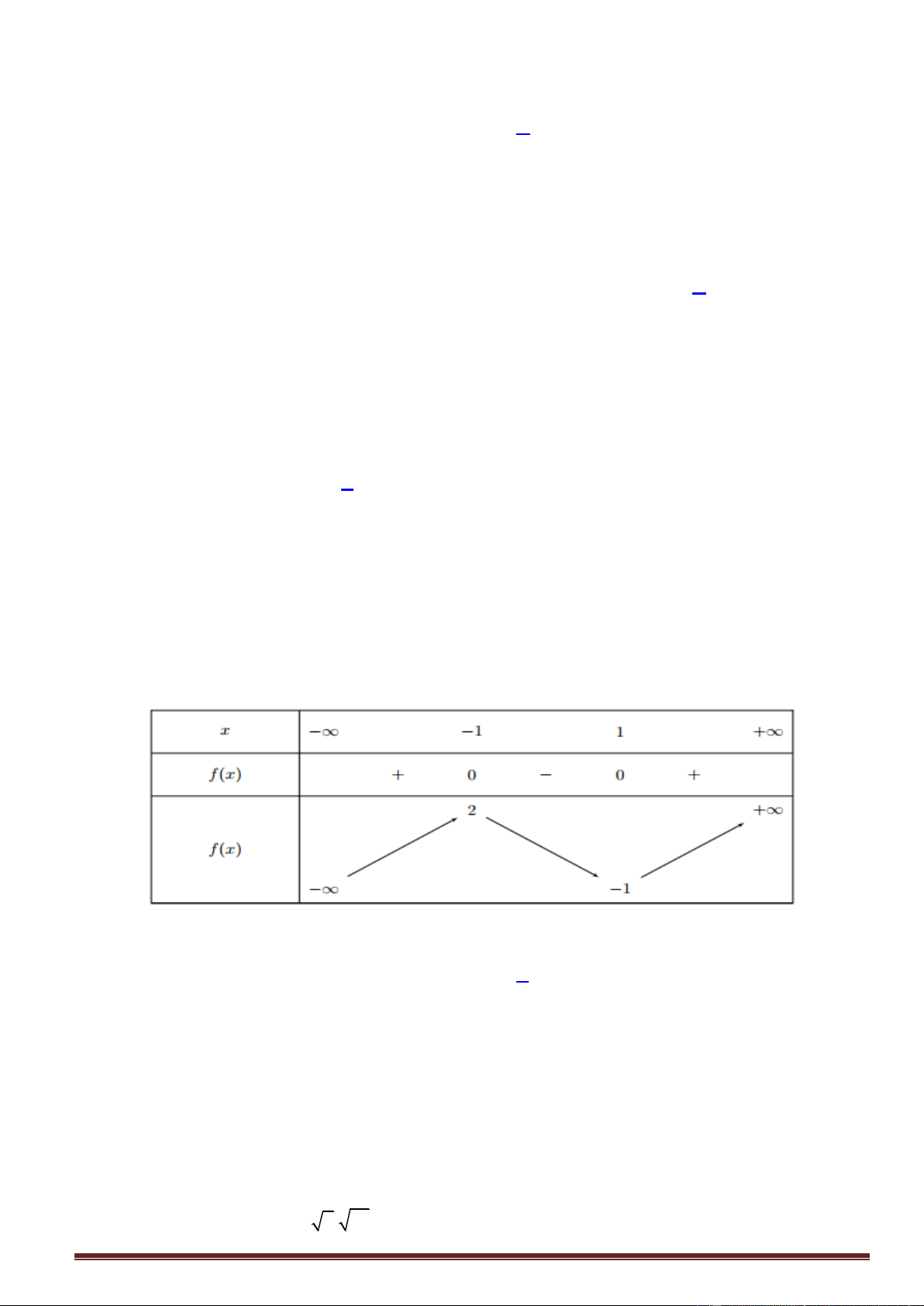
Câu17. Cho hàm số y  f  x có bảng xét dấu đạo hàm như sau.
Mệnh đề nào dưới đây đúng?
A.Hàm số đồng biến trên khoảng  ;0  .
B.Hàm số đồng biến trên khoảng  2  ;0 .
C.Hàm số nghịch biến trên khoảng 0; 2 .
D.Hàm số nghịch biến trên khoảng ;  2 .
Câu18. Tính thể tích một khối chóp biết khối chóp đó có đường cao bằng 12a , diện tích đáy bằng 2 a . A. 3 12a . B. 3 4a . C. 2 12a . D. 2 4a . 1
Câu19. Cho hàm số log3 6 có tập xác định là x A. ;6 . B. 0;  . C. 6;   . D.  .
Câu20. Một mặt cầu có diện tích   2 36
m  . Thể tích của khối cầu này bằng 4 A.   3 108 m  . B.   3 72 m  . C.   3 m  . D.   3 36 m  . 3
Câu21. Tính môđun của số phức z thỏa mãn z 2  i 13i  1. 5 34 34 A. z  34 . B. z  34 . C. z  . D. z  . 3 3
Câu22. Lăng trụ ABC . D A B  C  D
  đều có mặt đáy là A.Hình thoi. B. Hình bình hành. C. Hình chữ nhật. D. Hình vuông.
Câu23. Cho hàm số f  x có đạo hàm f  x  x  x  2 2 , x
  . Số điểm cực trị của hàm số đã cho là A. 0 . B. 3 . C. 2 . D.1.
Câu24. Giá trị lớn nhất của hàm số y  f  x 4 2
 x  4x  9 trên đoạn  2  ;  3 bằng A. 201. B. 54 . C. 9 . D. 2 . x 1   1 
Câu 25. Nghiệm của phương trình 2 125 x   là  25  1 1 A.  . B.1 C.  . D. 4 . 8 4
Câu26. Trong các khẳng định sau, khẳng định nào sai?
A. F  x  5  cos x là một nguyên hàm của hàm số f  x  sin x . Trang27 u x
B.   dx  log ux C . u x
C.Nếu F  x là một nguyên hàm của hàm số f  x thì mọi nguyên hàm của f  x đều có
dạng F  x  C ( C là hằng số) .
D. F  x  1 tan x là một nguyên hàm của hàm số f  x 2 1 tan x .
Câu27. Cho cấp số nhân u , biết u  81,u
 9 . Lựa chọn đáp án đúng. n  n n 1  1 1 A. q  . B. q  9 . C. q   . D. q  9 . 9 9 Câu28. Cho log x  log
y . Chọn khẳng định đúng? 0,2 0,2
A. x  y  0 .
B. x  y  0 .
C. y  x  0 .
D. y  x  0 .
Câu29. Trong không gian với hệ tọa độ Oxyz , phương trình mă ̣t cầu S  tâm I 1; 2  ;2 và có bán
kính R  2 3 là 2 2 2 2 2 2 A.  x  
1   y  2   z  2  12 . B.  x  
1   y  2   z  2  6 . 2 2 2 2 2 2 C.  x  
1   y  2   z  2  12 . D.  x  
1   y  2   z  2  6 . Câu30. Cho hàm số 3 2
y  ax  bx  cx  d có đồ thị như hình vẽ bên. Mệnh đề nào sau đây đúng? y O x
A. a  0, b  0, c  0, d  0 .
B. a  0, b  0, c  0, d  0 .
C. a  0, b  0, c  0, d  0 .
D. a  0, b  0, c  0, d  0 . x 1 t 
Câu31. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :  y  6  2t và mặt phẳng z 15t 
: x  2y  z  2  0. Chọn khẳng định đúng:
A. d / /   .
B. d    .
C. d    .
D. d cắt   . 2 x 1 Câu32. Giả sử
dx  a ln 5  b ln 3; a,b    . Tính P  . a b . 2 x  4x  3 0 A. P  5  . B. P  4  . C. P  8 . D. P  6  .
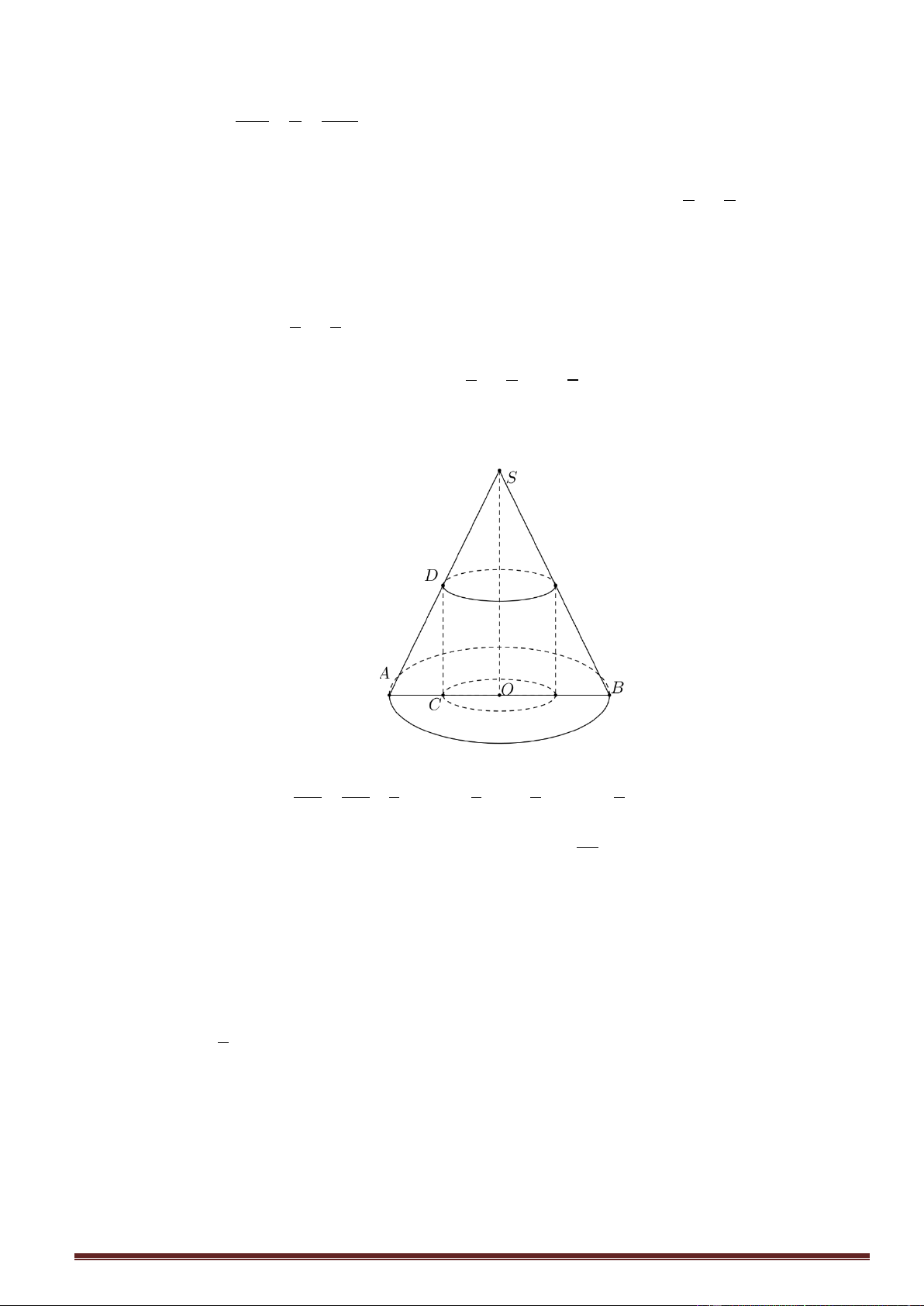
Câu33. Cho hình nón đỉnh I tâm đường tròn là H . Một mặt phẳng qua I tạo với mặt đáy hình nón một góc 
60 cắt hình nón theo thiết diện là tam giác đều IBC cạnh a . Tính thể tích khối nón. 3 11 a 3 5 a 3 9 a 3 7 a A. . B. . C. . D. . 64 64 64 64 Trang28 Câu34.
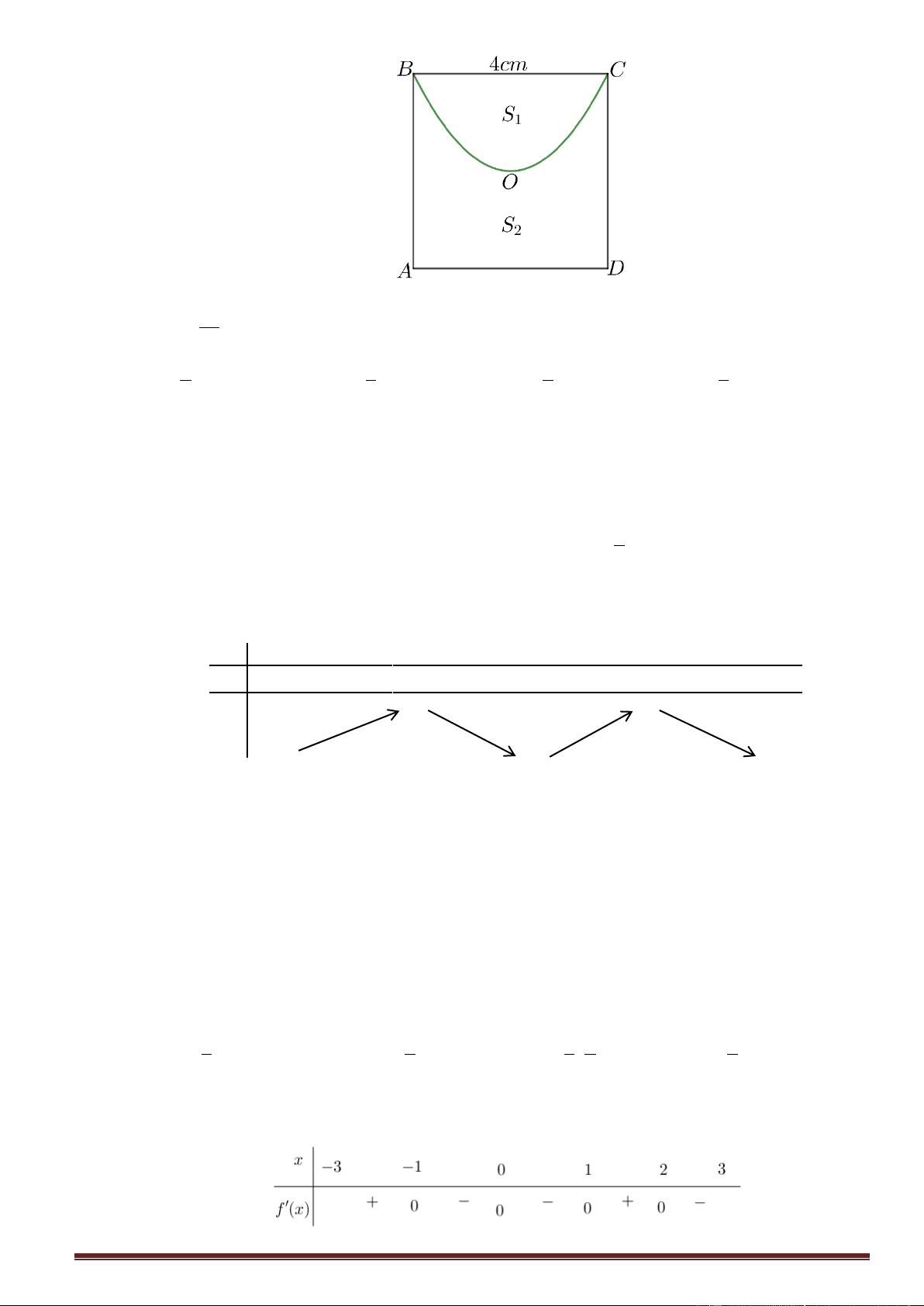
Cho hình chóp S.ABCD đáy là hình thang vuông tại A và B , SA vuông góc mặt
phẳng đáy, SA = a, AD = 3a, AB = 2a, BC = a . Tính khoảng cách giữa hai đường thẳng SB và CD . a 6 a 6 a 6 a 6 A. . B. . C. . D. . 6 3 12 2
Câu35. Áp suất không khí P suy giảm mũ so với độ cao x theo công thức .  .ex i P P , trong đó 0
P  760mmHg là áp suất ở mực nước biển  x  0 , i là hệ số suy giảm. Biết rằng ở độ cao 0
1000m thì áp suất của không khí là 672, 71mmHg . Áp suất không khí ở độ cao 3343 m xấp xỉ bằng A.495,34 mmHg . B.530,23 mmHg . C.485,36 mmHg . D.505,45 mmHg . 1 2
Câu 36. Cho hàm số f (x) có f (  x)  , x
  0 và f (1)  2 2 . Khi đó f (x)dx 
(x 1) x  x x 1 1 bằng 10 10 4 2 10 14 A. 4 3  . B. 4 3  . C. 4 3   . D. 4 3  . 3 3 3 3 3
Câu37. Tính thể tích khối tròn xoay sinh ra khi quay quanh trục Ox hình phẳng giới hạn bởi hai đồ thị 2
y  x  4x  6 và 2
y  x  2x  6 . A.  1 . B. 2 . C. . D. 3 .
Câu38. Bán kính đáy hình trụ bằng 4 cm , chiều cao bằng 6 cm . Độ dài đường chéo của thiết diện qua trục bằng A. 5 cm . B. 6 cm . C. 8 cm . D.10 cm . 2
Câu39. Cho phương trình  2
z  z   2
7 z  z  6  0có bốn nghiệm phức z , z , z , z . Tính 1 2 3 4
S  z  z  z  z 1 2 3 4 A. 2  . B. 5  . C. 3  . D. 1. Câu 40. Cho hàm số 2 y 
x 1  mx  2020 ( m là tham số thực). Có bao nhiêu giá trị nguyên của m thuộc đoạn  1
 0;10 để hàm đã cho đồng biến trên khoảng  ;   ? A. 20 . B. 8 . C.12 . D.10 .
Câu41. Tìm số phức z biết z  5 và z là số thuần ảo. A. 5  i . B. 5i . C.  5i . D. 5  i .
Câu42. Chọn một số tự nhiên có 5 chữ số đôi một khác nhau được lập từ tập 0;1; 2;3; 4;  5 . Xác suất
để số được chọn chia hết cho 4 bằng 4 13 7 6 A. . B. . C. . D. . 25 25 25 25
Câu43. Cho hai điểm A3; 2;3 và B 3; 4 
;1 . Viết phương trình mặt phẳng  P là mặt phẳng trung trực của AB .
A.  P : y  z 1  0 .
B.  P : y  z 1  0 . C.  P : y  z 1  0 . D.  P : y  z 1  0 . Trang29 2 x 1  0 x  x  1 
Câu44. Bất phương trình 2 3 4 2   
có bao nhiêu nghiệm nguyên dương?  2  A. 2 . B. 3 . C. 6 . D. 4 .  x 
Câu45. Cho phương trình 3 log 5x 2  6log
 11 m log x  3 m  0 ( m là tham số thực). Tập 5 5     5  5 
hợp tất cả các giá trị của tham số m để phương trình có ba nghiệm phân biệt thuộc đoạn 1;62 5 là A. 1; 2 . B.1; 2 . C. 2;  . D. 1;2 .
Câu46. Cho hàm số f  x có bảng biến thiên như sau:  7 13 
Số nghiệm thuộc đoạn  ; 
 của phương trình f sin x  cos x 1  0 là  4 4  A. 6 . B. 8 . C.10 . D. 7 . Câu47. Cho hàm số 4 2
f (x)  8x  ax  b , trong đó a, b là tham số thực. Biết rằng giá trị lớn nhất của
hàm số f (x) trên đoạn  1  ; 
1 bằng 1. Tính b  a . A.10. B.8. C.7. D.9.
Câu48. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 2a ,  
SCA  SBA  90 . Khoảng cách
giữa hai ca ̣nh SA và BC là 2 3 a . Thể tích khối chóp S.ABC là 3 3 8a 3 4a 3 3 4a 3 3 8a 3 A. . B. . C. . D. . 3 5 3 5 3 5
Câu49. Cho hàm số bậc bốn y  f  x có đồ thị như hình vẽ dưới đây y x -2 -1 O 0,75
Số điểm cực trị của hàm số g  x  f  3 2
2x  3x  là A.11. B. 7 . C. 3 . D. 5 . Trang30
Câu50. Trong hệ tọa độ Oxy , cho điểm M (x; y) với ; x y  ; Z 6
  x  6; y  0 và thỏa mãn phương 36 2    2 x y 3 36 trình 9 3   2  log 
 . Hỏi có bao nhiêu điểm M thỏa yêu cầu nêu trên? 2 3 2 3x  y  A. Bốn điểm. B.Một điểm. C. Ba điểm. D. Hai điểm.
--------------HẾT--------------- ĐÁP ÁN ĐỀ THI 1B 2C 3B 4A 5C 6A 7B 8B 9A 10C 11C 12D 13D 14B 15D 16D 17C 18B 19A 20D 21B 22D 23D 24B 25C 26B 27A 28D 29C 30A
31D 32D 33D 34A 35D 36A 37D 38D 39A 40D 41D 42D 43C 44B 45D 46C 47D 48A 49B 50D
HƯỚNG DẪN GIẢI CHI TIẾT x  x  Câu1.
Một nguyên hàm của f  x 2 2 3  x  là 1 2 x 2 x A.
 3x  6ln x 1 . B.
 3x  6ln x 1 . 2 2 2 x 2 x C.
 3x  6ln x 1 . D.
 3x  6ln x 1 . 2 2 Lời giải x  x    x Ta có: f  x 2 2 2 3 6 dx  dx  x  3  dx 
 3x  6ln x 1  C    . x 1  x 1  2 x  x  2 x
Vậy một nguyên hàm của hàm số f  x 2 2 3 
 3x  6ln x 1 . x  là 1 2 Câu2.
Tìm số phức liên hợp của số phức z  i 3i  2 . A. z  3   2i .
B. z  3 2i . C. z  3   2i . D. z  3   2i . Lời giải
Ta có z  i  i   2 3
2  3i  2i  3
  2i  z  3   2i . Câu3.
Cho d là đường thẳng đi qua điểm A1; 2;3 và vuông góc với mặt phẳng
:4x 3y 7z 1 0 . Phương trình chính tắc của d là x 1 y  2 z  3 x 1 y  2 z  3 A.   . B.   . 4 3 7 4 3 7 x  4 y  3 z  7 x 1 y  2 z  3 C.   . D.   . 1 2 3 4 3 7 Lời giải 
Ta có   : 4x  3y  7z 1  0  n  4;3; 7
  là VTPT của mặt phẳng   . Trang31 
Mà đường thẳng d     n  4;3; 7
  là VTCP của đường thẳngd .
Ta lại có A1; 2;3  d .   
Suy ra phương trình chính tắ x 1 y 2 z 3
c của đường thẳng d là:   . 4 3 7 Câu4.
Cho hình nón có bán kính đáy là 4a , chiều cao là 3a . Diện tích toàn phần của hình nón bằng A. 2 36 a . B. 2 32 a . C. 2 38 a . D. 2 30 a . Lời giải
Ta có bán kính đáy r  4a , chiều cao là h  3a . Suy ra đườ 2 2 ng sinh 2 2 l 
r  h  4a  3a  5a .
Mà diện tích toàn phần bằng: S   rl   r   . tp
 a a  a2 2 2 4 5 4  36a x Câu5.
Với điều kiện nào của a để hàm số y  2a   1 đồng biến trên  ?  1  A. a  0 . B. a  ;1  1;    .  2   1  C. a 1. D. a  ;    .  2  Lời giải
Để hàm số mũ đã cho đồng biến trên  thì 2a 11  a 1. Câu6.
Điểm biểu diễn của số phức z  3  4  mi là M 3;2 khi m bằng A. m  2  . B. m  4 . C. m  6  . D. m  2 . Lời giải
Để số phức đã cho có điểm biểu diễn là M 3;2 khi: 4 m  2  m  2  . Câu7.
Tìm số giao điểm n của hai đồ thị 4 2
y  x  3x  2 và 2 y  x  2 . A. n  4 . B. n  2 . C. n  0 . D. n 1. Lời giải
Phương trình hoành độ giao điểm của hai đồ thị 4 2
y  x  3x  2 và 2
y  x  2 là: x  4 2 2
x  3x  2  x  2 4 2
 x  4x  4  2 0   . x   2
Vậy có 2 giao điểm của hai đồ thị 4 2
y  x  3x  2 và 2 y  x  2 . Câu 8.
Cho hàm số f  x có bảng biến thiên như sau: Trang32
Số ngiệm thực của phương trình 2 f  x  3  0 là A. 0 . B. 3 . C. 2 . D. 1. Lời giải
Ta có 2 f  x  3  0  f  x 3  . 2
Số ngiệm thực của phương trình 2 f  x  3  0 chính bằng số giao điểm của đồ thị hàm số 3
y  f  x và đường thẳng y  . 2
Dựa bảng biến thiên của hàm số y  f  x ta thấy phương trình 2 f  x  3  0 có 3 nghiệm thực. Câu 9.
Cho hình trụ có bán kính đáy bằng 3cm , đường cao 6cm . Diện tích xung quanh của hình trụ này là A.   2 36 cm  . B.   2 20 cm  . C.   2 24 cm  . D.   2 18 cm  . Lời giải Ta có S  rh    2 2 36 cm . xq 
Câu 10. Trong không gian bởi hệ tọa độ Oxyz , cho điểm K 2; 4;6 , gọi K là hình chiếu của K trên
Oz . Khi đó trung điểm OK có tọa độ là A. 1;0;0 . B. 1; 2;3 . C. 0;0;3 . D. 0; 2;0 . Lời giải
Ta có K0;0;6 .
Trung điểm của OK có tọa độ là 0;0;3 .
Câu11. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cạnh huyền BC  a . Hình chiếu vuông
góc của S lên  ABC trùng với trung điểm của BC . Biết SB  a . Tính số đo của góc giữa SA và  ABC. A. 75 . B. 30 . C. 60 . D. 45 . Lời giải Trang33 S A C H B
Gọi H là trung điểm của BC .
Theo giả thiết ta có SH   ABC và góc giữa SA và  ABC là góc  SAH . 2 Ta co a a 3 a ́ 2 2 2
SH  SB  BH  a   và 1 AH  BC  . 4 2 2 2 a 3 Ta co SH ́  2  tan SAH  
 3  SAH  60 . AH a 2
Vâ ̣y góc giữa SA và  ABC bằng 60.
Câu 12. Lớp 11A1 có 25 học sinh nam và 20 học sinh nữ. Hỏi có bao nhiêu cách chọn ngẫu nhiên một
bạn trong lớp làm lớp trưởng? A. 500. B. 20. C. 25. D.45. Lời giải
Có 25 cách chọn một học sinh nam làm lớp trưởng.
Có 20 cách chọn một học sinh nữ làm lớp trưởng.
Vâ ̣y có 25 20  45 cách chọn ngẫu nhiên một bạn trong lớp làm lớp trưởng.
Câu 13. Trong không gian với hệ tọa độ Oxyz , mặt phẳng nào sau đây song song với mặt phẳng Oyz ? A. 2  x  0. B. 2  z 1 0. C. 2z  0 . D. 2  x 1 0 . Lời giải
Mặt phẳng song song với mặt phẳng Oyz có phương trình: Ax  D  0  D  0 .
Dựa vào đáp án ta chọn mặt phẳng có phương trình: 2  x 1 0 . x  4  2
Câu 14. Tìm số tiệm cận đứng của đồ thị hàm số y  2 x  . x A. 2 . B.1. C. 3 . D. 0 . Lời giải x  4  0 x  4 
Điều kiện xác định:    . 2 x  x  0
x  0, x  1  Trang34  x  4  2  x  4  4 1 1 Ta có: lim    lim  lim  .   2    x  x x x     x4 2 2 0 0
x  x x0  x  4  2x   1 4  x  4  2  x  4  4 1 1 Ta có: lim    lim  lim  .   2    x  x x x     x4 2 2 0 0
x  x x0  x  4  2x   1 4
Suy ra x  0 không là tiệm cận đứng của đồ thị hàm số.  x  4  2  Ta có: lim     .    x  2 1 x  x   Suy ra x  1
 là tiệm cận đứng của đồ thị hàm số.
Vậy đồ thị hàm số có 1 đường tiệm cận đứng x  1  .
Câu15. Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây? y O x A. 3 2
y  x  x 1 . B. 3 2
y  x  x 1 . C. 4 2
y  x  2x 1. D. 4 2
y  x  2x 1. Lời giải
Dựa vào đồ thị, ta thấy đây là dạng đồ thị hàm số đa thức bậc bốn trùng phương với hệ số của 4
x dương do lim y   . x Câu16. Nếu 2 3
log x  8log ab  2 log a b ,
a b  0 thì x bằng: 7 7 7   A. 8 14 a b . B. 6 12 a b . C. 6 6 a b . D. 2 14 a b . Lời giải Ta có 2 3
log x  8 log ab  2 log a b 7 7 7 8 16 6 2
 log x  log a b  log a b 7 7 7 8 16 a b  log x  log 7 7 6 2 a b 2 14
 log x  log a b 7 7 2 14  x  a b
Câu17. Cho hàm số y  f  x có bảng xét dấu đạo hàm như sau
Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng  ;0  . Trang35
B. Hàm số đồng biến trên khoảng  2  ;0 .
C. Hàm số nghịch biến trên khoảng 0; 2 .
D. Hàm số nghịch biến trên khoảng ;  2 . Lời giải
Nhìn vào bảng xét dấu của đạo hàm ta thấy:
Hàm số đồng biến trên mỗi khoảng ;  2 và 2;   .
Hàm số nghịch biến trên mỗi khoảng  2  ;0 và 0;2.
Từ đây suy ra đáp án đúng là: Hàm số nghịch biến trên khoảng 0; 2 .
Câu18. Tính thể tích một khối chóp biết khối chóp đó có đường cao bằng 12a , diện tích đáy bằng 2 a . A. 3 12a . B. 3 4a . C. 2 12a . D. 2 4a . Lời giải 1
Thể tích của khối chóp là: 2 3 V 
.a .12a  4a . 3 1
Câu19. Cho hàm số log3 6 có tập xác định là x A. ;6 . B. 0;  . C. 6;   . D.  . Lời giải  1 Điều kiện:
 0  6  x  0  x  6 6  . x
 Tập xác định D  ;6 .
Câu20. Một mặt cầu có diện tích   2 36
m  . Thể tích của khối cầu này bằng 4 A.   3 108 m  . B.   3 72 m  . C.   3 m  . D.   3 36 m  . 3 Lời giải  Diện tích mặt cầu 2 2
S  4 R  36  R  9  R  3.  4 4 Thể tích khối cầu 3 3 V 
 R  .3  36 . 3 3
Câu21. Tính môđun của số phức z thỏa mãn z 2  i 13i  1. 5 34 34 A. z  34 . B. z  34 . C. z  . D. z  . 3 3 Lời giải  i
Ta có: z   i 1 13 2
13i  1  z 
 3  5i . Vậy z  34 . 2  i
Câu22. Lăng trụ ABC . D A B  C  D
  đều có mặt đáy là A. Hình thoi. B. Hình bình hành. C. Hình chữ nhật. D.Hình vuông. Trang36 Lời giải
Lăng trụ tứ giác đều có mặt đáy là hình vuông.
Câu23. Cho hàm số f  x có đạo hàm f  x  x  x  2 2 , x
  . Số điểm cực trị của hàm số đã cho là A. 0 . B. 3 . C. 2 . D.1. Lời giải x 
Ta có: f  x   x x  2 0 0 2  0   . x  2 Bảng biến thiên
Vậy hàm số đã cho có một điểm cực trị.
Câu24. Giá trị lớn nhất của hàm số y  f  x 4 2
 x  4x  9 trên đoạn  2  ;  3 bằng A. 201. B. 54 . C. 9 . D. 2 . Lời giải Ta có: 3
y  4x  8x x  2  2  ;  3  3
y  0  4x  8x  0  x   2 2;  3  x  0 2  ;  3 
f  2  5; f 0  9; f  2
   9; f 3  54 .
Vậy giá trị lớn nhất của hàm số y  f  x 4 2
 x  4x  9 trên đoạn  2  ;  3 bằng 54 . x 1   1 
Câu 25. Nghiệm của phương trình 2 125 x   là  25  1 1 A.  . B. 1 C.  . D. 4 . 8 4 Lời giải x 1  x 1  2  1 x  Ta có: 2 125 x   2 5       35 .  25  2x2 6  5  5 x
 2x  2  6x 1  x   4 Trang37
Câu26. Trong các khẳng định sau, khẳng định nào sai?
A. F  x  5  cos x là một nguyên hàm của hàm số f  x  sin x . u x
B.   dx  log ux C . u x
C. Nếu F  x là một nguyên hàm của hàm số f  x thì mọi nguyên hàm của f  x đều có
dạng F  x  C ( C là hằng số) .
D. F  x  1 tan x là một nguyên hàm của hàm số f  x 2 1 tan x . Lời giải u x 1 Ta có: dx  d   u x     
   ln ux C nên đáp án B sai. u x u x
Câu27. Cho cấp số nhân u , biết u  81,u
 9 . Lựa chọn đáp án đúng. n  n n 1  1 1 A. q  . B. q  9 . C. q   . D. q  9 . 9 9 Lời giải u 1 Ta có n 1 q    . u 9 n Câu28. Cho log x  log
y . Chọn khẳng định đúng? 0,2 0,2
A. x  y  0 .
B. x  y  0 .
C. y  x  0 .
D. y  x  0 . Lời giải Ta có log x  log
y  y  x  0 . 0,2 0,2
Câu29. Trong không gian với hê ̣ to ̣a đô ̣ Oxyz , phương trình mă ̣t cầu S  tâm I 1; 2  ;2 và có bán kính R  2 3 là: 2 2 2 2 2 2 A.  x  
1   y  2   z  2  12 B.  x  
1   y  2   z  2  6 2 2 2 2 2 2 C.  x  
1   y  2   z  2  12 D.  x  
1   y  2   z  2  6 Lời giải I 1; 2  ;2 2 2 2 Ta có S  :   x  
1   y  2   z  2  12  R  2 3 Câu30. Cho hàm số 3 2
y  ax  bx  cx  d có đồ thị như hình vẽ bên. Mệnh đề nào sau đây đúng? y O x Trang38
A. a  0, b  0, c  0, d  0 .
B. a  0, b  0, c  0, d  0 .
C. a  0, b  0, c  0, d  0 .
D. a  0, b  0, c  0, d  0 . Lời giải
Từ đồ thị nhận thấy:
- Khi x   đồ thị đi xuống  a  0 .
- Đồ thị cắt trục Oy tại điểm có tung độ âm  d  0 .
- Vì 2 điểm cực trị của đồ thị nằm về hai phía Oy nên phương trình y  0 có hai nghiệm trái
dấu  ac  0  c  0
- Gọi x , x là hai điểm cực trị của hàm số thì từ đồ thị có x  x  0 . Mà x , x là hai nghiệm 1 2 1 2 1 2 2b của phương trình 2
3ax  2bx  c  0    0  b  0 3a
Vậy a  0, b  0, c  0, d  0 . x 1 t 
Câu31. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :  y  6  2t và mặt phẳng z 15t 
: x  2y  z  2  0. Chọn khẳng định đúng:
A. d / /   .
B. d    .
C. d    .
D. d cắt   . Lời giải x 1 t  
Đường thẳng d : y  6  2t có vectơ chỉ phương là u  1; 2 ;  5 . z 15t  
Mặt phẳng   : x  2y  z  2  0 có vectơ pháp tuyến là n  1; 2 ;   1 .     Ta có: .
u n 1 4  5 10  0suy ra u và n không vuông góc  d cắt   . 1 2 5    Ta có:  
và n không cùng phương  d không vuông góc với   . 1 2 1  suy ra u 2 x 1 Câu32. Giả sử
dx  a ln 5  b ln 3; a,b    . Tính P  . a b . 2 x  4x  3 0 A. P  5  . B. P  4
 .C. P  8. D. P  6  . Lời giải x 1 x 1 A B
( A  B)x  A  3B Ta có     2 x  4x  3
(x  3)(x 1) x  3 x 1 (x  3)(x  . 1) A B 1 B  1 
Đồng nhất thức ta có    . A 3B  1  A  2 Trang39 x 1 2 1 Suy ra   . 2 x  4x  3 x  3 x 1 2 2 x 1  2 1  Suy ra dx   dx    2 x  4x  3
 x  3 x 1 0 0 2 2 dx dx 2 2  2 
 2ln x  3  ln x 1   0 0 x  3 x 1 0 0
 2ln52ln3ln3  2ln53ln3.
Suy ra a  2; b  3 . Vậy P  . a b  6  .
Câu33. Cho hình nón đỉnh I tâm đường tròn là H . Một mặt phẳng qua I tạo với mặt đáy hình nón
một góc 60 cắt hình nón theo thiết diện là tam giác đều IBC cạnh a . Tính thể tích khối nón. 3 11 a 3 5 a 3 9 a 3 7 a A. . B. . C. . D. . 64 64 64 64 Lời giải I C J H B
Ta có (IBC) giao với mặt đáy theo giao tuyến BC , HJ  BC nên  IJH  60 a 3 Mặt khác IJ  2 Xét I  HJ HI a a  3 3 3 sin HJI 
 HI  IJ.sin 60  .  IJ 2 2 4 HJ a a  3 1 3 cos HJI 
 HJ  IJ.cos60  .  IJ 2 2 4 Xét BHJ 2 2 a 3a a 7 HB  R    4 16 4 2 3 1 1 7a 3a 7 a 2 V   R h    non 3 3 16 4 64
Câu34. Cho hình chóp S.ABCD đáy là hình thang vuông tại A và B , SA vuông góc mặt phẳng đáy,
SA  a, AD  3a, AB  2a, BC  a . Tính khoảng cách giữa hai đường thẳng SB và CD . Trang40 a 6 a 6 a 6 a 6 A. . B. . C. . D. . 6 3 12 2 Lời giải
Gọi N thuộc cạnh AD sao cho AN  2DN .
Khi đó CD // (SBN)  d(CD, SB)  d(CD,(SBN))  d(D,(SBN))
d (D, (SBN )) DN 1 1 Ta có 
  d(D,(SBN))  d( , A (SBN )) d ( , A (SBN )) AN 2 2
Gọi K là trung điểm của BN và H là hình chiếu vuông góc của A trên SK .
Ta có BN  AK và BN  SA suy ra BN  (SAK ) .
AH  SK và AH  BN suy ra AH  (SBN ) . Do đó d( ,
A (SBN ))  AH . 1 2a 2 Xét ABN 
vuông cân tại A ta có AK  BN   a 2 . 2 2 1 1 1 1 1 3 a 6 Xét S
 AK vuông cân tại A ta có       AH  . 2 2 2 2 2 2 AH AK AS a 2a 2a 3 a 6
Vậy d (CD, SB)  . 6
Câu35. Áp suất không khí P suy giảm mũ so với độ cao x theo công thức .  .ex i P P , trong đó 0
P  760mmHg là áp suất ở mực nước biển  x  0 , i là hệ số suy giảm. Biết rằng ở độ cao 0
1000m thì áp suất của không khí là 672, 71mmHg . Áp suất không khí ở độ cao 3343 m xấp xỉ bằng
A. 495,34 mmHg .
B. 530,23 mmHg .
C. 485,36 mmHg . D.505,45 mmHg . Lời giải Áp dụng công thức .  .ex i P P
với P  760mmHg , x  1000 thì P  672, 71 ta tìm được hệ số 0 0  P   672,71 ln   ln   P    760  suy giảm 0 i    0  ,000122004 x 1000 Trang41 3343  . 0  ,000122004
Vậy với x  3343 thì .  .ex i P P = 760.e  505,45 0 1 2
Câu 36. Cho hàm số f (x) có f (  x)  , x
  0 và f (1)  2 2 . Khi đó f (x)dx 
(x 1) x  x x 1 1 bằng 10 10 4 2 10 14 A. 4 3  . B. 4 3  . C. 4 3   . D. 4 3  . 3 3 3 3 3 Lời giải 1 1 Ta có f (x)  f (  x)dx  dx     x  x  x x  x x 
 x  xdx ( 1) 1 ( 1) 1 x 1  x  1 1  f (x)  dx  
dx  2 x 1  2 x  C    x(x 1)  x 1 x 
Vì f (1)  2 2 nên C  2  và f ( )
x  2 x 1  2 x  2 .   Khi đó f x x  
 x  x   2 2 2 4 4 10 ( )d 2 1 2 2 dx 
(x 1) x 1  x x  2x  4 3    . 3 3  3 1 1 1
Câu37. Tính thể tích khối tròn xoay sinh ra khi quay quanh trục Ox hình phẳng giới hạn bởi hai đồ thị 2
y  x  4x  6 và 2
y  x  2x  6 . A.  1 . B. 2 . C.  . D. 3 . Lời giải
Phương trình hoành độ giao điểm của hai đồ thị hàm số 2
y  x  4x  6 và 2
y  x  2x  6 x  0 2 2 2
x  4x  6  x  2x  6  2x  2x  0   . x 1
Khi đó thể tích khối tròn xoay sinh ra khi quay quanh trục Ox hình phẳng giới hạn bởi hai đồ thị 2
y  x  4x  6 và 2
y  x  2x  6 được tính như sau: 1
V    x  4x  62 x  2x  62 2 2 dx  3 . 0
Câu38. Bán kính đáy hình trụ bằng 4 cm , chiều cao bằng 6 cm . Độ dài đường chéo của thiết diện qua trục bằng A. 5 cm . B. 6 cm . C. 8 cm . D.10 cm . Lời giải
Thiết diện qua trục hình trụ là hình chữ nhật có chiều dài 8cm , chiều rộng 6cm .
Do đó độ dài đường chéo bằng 2 2 6  8  10cm . 2
Câu39. Cho phương trình  2
z  z   2
7 z  z  6  0 có bốn nghiệm phức z , z , z , z . Tính 1 2 3 4
S  z  z  z  z . 1 2 3 4 A. 2  . B. 5  . C. 3  . D. 1. Trang42 Lời giải 2     2 z z 6 1 Ta có  2
z  z   7 2 z  z     6  0   . 2 z  z  1   2
Giả sử z , z là hai nghiệm của phương trình  
1 , z , z là hai nghiệm của phương trình 2 , 1 2 3 4
áp dụng định lí Vi-ét ta có : b b z  z 
 1; z  z 
 1. Do đó S  z  z  z  z  2  . 1 2 3 4 a a 1 2 3 4 Cách 2 : z  z2 2   2 z  z 4 3 2 7
 6  0  z  2z 8z  7z  6  0 . 2 
Theo Vi-ét ta có S  z  z  z  z   2 . 1 2 3 4 1 Câu 40. Cho hàm số 2 y 
x 1  mx  2020 ( m là tham số thực). Có bao nhiêu giá trị nguyên của m thuộc đoạn  1
 0;10 để hàm đã cho đồng biến trên khoảng  ;   ? A. 20 . B. 8 . C.12 . D.10 . Lời giải x Có y   m . 2 x 1 x
Hàm số đã cho đồng biến trên khoảng  ;
   y '   m  0 x   ;   , dấu 2 x 1
"=" xảy ra tại hữu hạn điểm. x
Từ ta có: g(x)   m x   ;   . 2 x 1 1
Hàm số g(x) xác định và liên tục trên khoảng  ;
  và g (x)   0 2 x 1. 2 x   1 x   ;
  nên g(x) luôn đồng biến trên khoảng  ;   . x x
Ta có: lim g(x)  lim  1
 ; lim g(x)  lim
1 và hàm số đồng biến với mọi x x 2 x x 2 x 1 x 1 x  ;
  nên từ suy ra m  1
 , kết hợp giả thiết m 1
 0;10 và m nguyên nên ta có 10
giá trị của m ( m nhận các giá trị : 10
 ; 9; 8; 7; 6; 5; 4; 3; 2;1).
Câu41. Tìm số phức z biết z  5 và z là số thuần ảo. A. 5  i . B. 5i . C.  5i . D. 5  i . Lời giải
Ta có z là số thuần ảo nên z  bi b    .
Do đó: z  5  bi  5  b . i  5  b  5  b  5  . Vậy z  5  .i Trang43
Câu42. Chọn một số tự nhiên có 5 chữ số đôi một khác nhau được lập từ tập 0;1; 2;3; 4;  5 . Xác suất
để số được chọn chia hết cho 4 bằng 4 13 7 6 A. . B. . C. . D. . 25 25 25 25 Lời giải
Có 55 43 2  600 số có 5 chữ số đôi một khác nhau.
Gọi số có 5 chữ số đôi một khác nhau và chia hết cho 4 có dạng abcde .
 Nếu de 04 ta có 432  24 số thỏa mãn.  Nếu de  12
 ta có 332 18 số thỏa mãn.
 Nếu de 20 ta có 432  24 số thỏa mãn.
 Nếu de 24 ta có 332 18 số thỏa mãn.
 Nếu de 32 ta có 332 18 số thỏa mãn.
 Nếu de 40 ta có 432  24 số thỏa mãn.
 Nếu de 52 ta có 332 18 số thỏa mãn.
Theo quy tắc cộng ta có 24318 4 144 số thỏa mãn yêu cầu đề bài. 144 6 Xác suất cần tìm là  . 600 25
Câu43. Cho hai điểm A3; 2;3 và B 3; 4 
;1 . Viết phương trình mặt phẳng  P là mặt phẳng trung trực của AB .
A.  P : y  z 1  0 .
B.  P : y  z 1  0 . C.  P : y  z 1  0 .
D.  P : y  z 1  0 . Lời giải
Mặt phẳng trung trực  P của đoạn thẳng AB đi qua trung điểm I 3;3; 2 của AB và nhận  AB  0; 2; 2
  làm vectơ pháp tuyến.
Do đó phương trình mặt phẳng P là 2 y 3  2z  2  0  y  z 1  0 . 2 x 1  0 x  x  1 
Câu44. Bất phương trình 2 3 4 2   
có bao nhiêu nghiệm nguyên dương?  2  A. 2 . B. 3 . C. 6 . D. 4 . Lời giải Ta có: 2 x 1  0 2 2 x  x  1  3 4 x 3x4 102 x 2 2   2  2
 x  3x  4 10  2   x  2  2
 x  x  6  0  2  x  3
Suy ra tập các nghiệm nguyên dương là S  1;2; 
3 . Vậy số nghiệm nguyên dương là 3 . Trang44  x 
Câu45. Cho phương trình 3 log 5x 2  6log
 11 m log x  3 m  0 ( m là tham số thực). Tập 5 5     5  5 
hợp tất cả các giá trị của tham số m để phương trình có ba nghiệm phân biệt thuộc đoạn 1;62 5 là A. 1; 2 . B. 1; 2 . C. 2;  . D. 1;2 . Lời giải
Điều kiện: x  0 .  x  3 log 5x 2  6log
 11 m log x  3 m  0 5 5     5  5 
 1 log x3 6log x  2
1  11 m log x  3  m  0 . 5 5   5
Đặt t  log x ta được 3 2
t  3t  4  mt  m  2  0 . 5 Với x 1;62 
5 thì t 0;4 . Vậy ta cần tìm tất cả các giá trị của tham số m để phương trình có ba
nghiệm phân biệt thuộc đoạn 0;4 . t 1
Ta có *  t   1  2
t  2t  2  m  0   . 2
t  2t  2  m  0 (**)
Vậy ta cần tìm m để có hai nghiệm phân biệt khác 1 thuộc đoạn 0;4 . Ta có 2 2
t  2t  2  m  0  m  t  2t  2 .
Xét hàm số f t  2
 t  2t  2 có bảng biến thiên trên đoạn 0;4 như sau.
Suy ra điều kiện của m là m1;2. Chọn đáp án D.
Câu46. Cho hàm số f  x có bảng biến thiên như sau:  7 13 
Số nghiệm thuộc đoạn  ; 
 của phương trình f sin x  cos x 1  0 là  4 4  A. 6 . B. 8 . C.10 . D. 7 . Trang45 Lời giải     7 13 
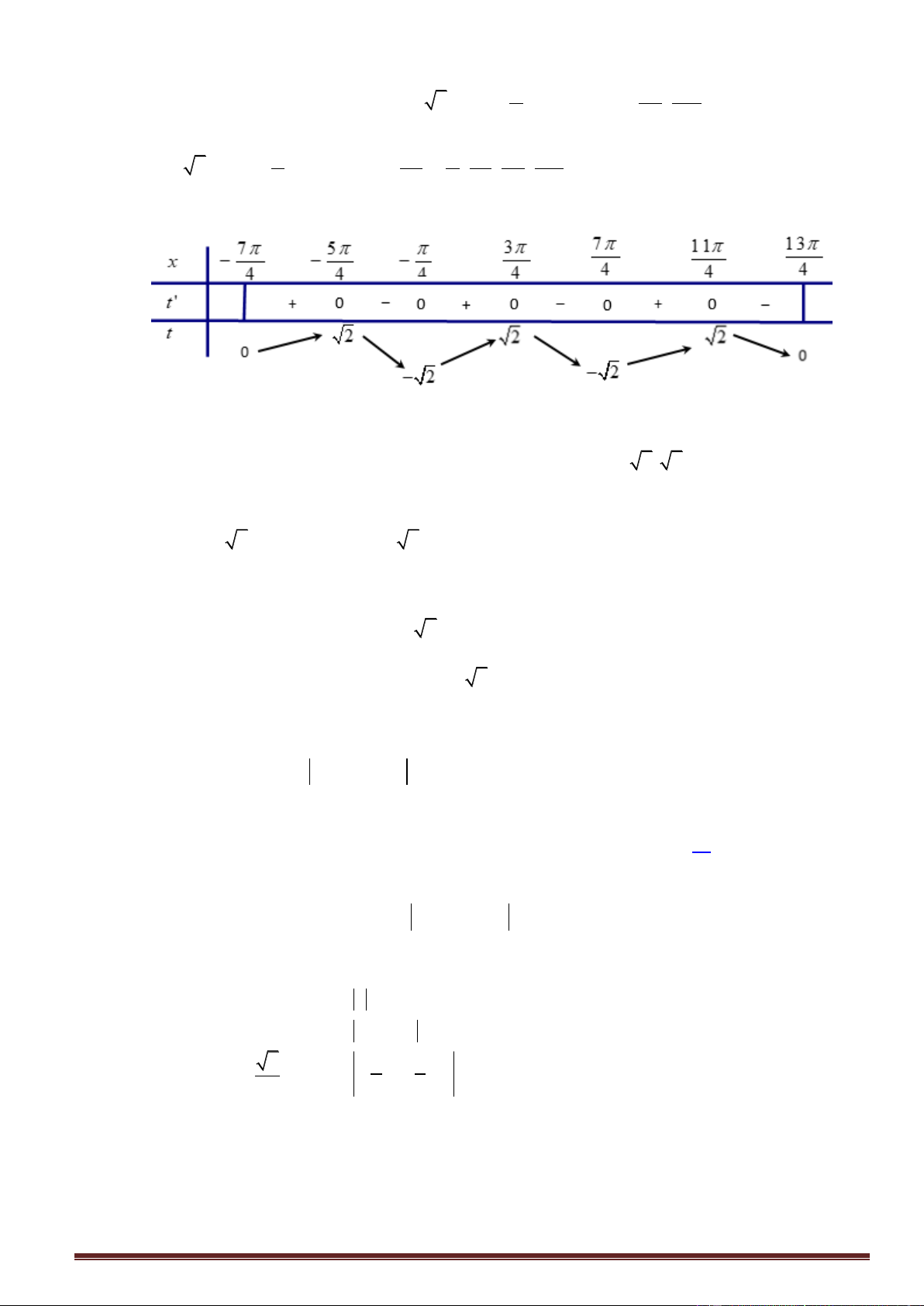
Xét hàm số t  t  x  sin x  cos x  2 sin x    trên đoạn  ; ta có    4   4 4      5  3 7 11 
t  2 cos x   0  x    ;  ; ; ;   4   4 4 4 4 4  Suy ra bảng biến thiên
Đặt t  sin x cos x thì phương trình f sin x  cos x 1 0   1 trở thành
f t  1  0  f t   1
 2 , với t  2; 2  
Dựa vào bảng biến thiên của hàm số f  x ta nhận thấy phương trình 2 có hai nghiệm t và 1
t thỏa  2  t  0 và 0  t  2 . 2 1 2
Khi đó dựa vào bảng biến thiên của hàm số t  t  x ta có:
+ Phương trình sin x  cos x  t ,  2  t  0 : có 4 nghiệm x phân biệt. 1  1
+ Phương trình sin x  cos x  t , 0  t  2 : có 6 nghiệm x phân biệt. 2  2
Vậy phương trình f sin x  cos x 1  0 có 10 nghiệm. Câu47. Cho hàm số 4 2
f (x)  8x  ax  b , trong đó a, b là tham số thực. Biết rằng giá trị lớn nhất của
hàm số f (x) trên đoạn  1  ; 
1 bằng 1. Tính b  a . A. 10. B. 8. C. 7. D.9. Lời giải
Theo giải thiết: max f (x)  1 nên 4 2
8x  ax  b  1, x   1  ;  1  1  ;  1      f (1)  1 b  1  1   b 1  1   b 1     Suy ra  f (0)  1
  8  a  b 1   1
  a  b  8 1   9
  a  b  7  (*)      2   1 1  2
  a  2b  4  2 6
  a  2b  2    f     1       8. . a b 1 2     4 2 a  b  7  Từ 
 b 1, mặt khác b 1 nên b 1
a  2b  6   9   a 1 7   1  0  a  8 
Thế b 1 vào ta có:     a  8  .  6   a  2  2   8   a  4  Trang46 Khi a  8  , b  1 4 2
 y  8x 8x 1. Đặt x  cos , với 0;   y  cos 4 .
Vậy f (x)  1 khi x  1.
Do đó b  a  9.
Câu48. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 2a ,  
SCA  SBA  90 . Khoảng cách
giữa hai ca ̣nh SA và BC là 2 3 a . Thể tích khối chóp S.ABC là 3 3 8a 3 4a 3 3 4a 3 3 8a 3 A. . B. . C. . D. . 3 5 3 5 3 5 Lời giải
Gọi H là trung điểm của BC , ta có AH  BC . Dựng HI  , SA I  SA . Ta có S  BC  S
 CA nên SB  SC  S
 BC cân ta ̣i S  SH  BC .
Từ và  BC  SAH  mà HI  SAH  nên BC  HI . Vâ ̣y 2 3 HI  d  a . S , A BC  3
Gọi D là hình chiếu vuông góc của S lên mă ̣t phẳng  ABC  SD   ABC  SD  AB mà
SB  AB  AB  SBD  AB  BD  A
 BD vuông ta ̣i B .
Tương tự ta cũng có A
 CD vuông ta ̣i C . Ta có A  BD  A
 CD  DB  DC  D thuô ̣c đường trung trực của đoa ̣n thẳng BC .
Xét tam giác vuông AHB có: 2 2 2 2 AH  AH  BH
 4a  a  a 3 .
Xét tam giác vuông ABD có: 1 1 1 1 1 1 1 1 3 2a          BD  . 2 2 2 2 2 2 2 2 2 BH BD BA BD BH BA a 4a 4a 3 2 2 2 4a 2 4a AD  BD  BA   4a  . 3 3 Trang47 Dựng DK  ,
SA K  SA  DK / / HI . 4a 2 3 . a Ta co AH HI A . D HI 3 3 8a ́:   DK    . AD DK AH a 3 3 3
Xét tam giác vuông SDA , ta có : 1 1 1 1 1 1 27 3 15 8a          SD  . 2 2 2 2 2 2 2 2 2 DK SD AD SD DK AD 64a 16a 64a 15
Thể tích khối chóp S.ABC là 3 1 1 1 1 8a 8a     S V . .S . D S .S . D .AH.BC . .2 . a a 3 ABC ABC . 3 3 2 6 15 3 5
Câu49. Cho hàm số bậc bốn y  f  x có đồ thị như hình vẽ dưới đây y x -2 -1 O 0,75
Số điểm cực trị của hàm số g  x  f  3 2
2x  3x  là A.11. B. 7 . C. 3 . D. 5 . Lời giải
g x   2
x  x f  3 2 6 6 . 2x  3x  ; x  0 
g x  0   2
6x  6x. f  3 2
2x  3x   0  x  1  .  f    3 2
2x  3x   0  3 2
2x  3x  a  1  2   a    1  f  3 2 2x  3x  3 2
 0  2x  3x  b 2  1   b  0 .    3  3 2
2x  3x  c 3 0  c       4 
Đặt P  x 3 2
 2x  3x , Px 2  6x  6x . Bảng biến thiên: Trang48 Dựa vào BBT ta có:
PT có nghiệm đơn x khác 0 và 1. 1
PT có nghiệm đơn x khác 0, 1 và x . 2 1
PT có 3 nghiệm đơn phân biệt khác 0, 1, x và x . 1 2
Suy ra phương trình g x  0 có 7 nghiệm đơn phân biệt .
Vậy hàm số g  x  f  3 2
2x  3x  có 7 điểm cực trị.
Câu50. Trong hệ tọa độ Oxy , cho điểm M (x; y) với ; x y  ; Z 6
  x  6; y  0 và thỏa mãn phương 36 2    2 x y 3 36 trình 9 3   2  log 
 . Hỏi có bao nhiêu điểm M thỏa yêu cầu nêu trên? 2 3 2 3x  y  A. Bốn điểm B. Một điểm C. Ba điểm D.Hai điểm Lời giải 36 2    2    2 x  x y x 36 y 3 36 2 2 Ta có: 9 3   2  log   9 36  3  3  log    2 2 3 2 3 2 3x  y   y  2    2 2  x y x 36 9 36  2 2 3  3  log   9 y 36
 3  3 x  log 36  x  log 9y 3  2  2 3 2  9y  3 2 3 y log 9 log 36  2 9 2 2 36 3 x y x       (1) . 3 3
Xét hàm số ( )  3x f x
 log x với x  0 . 3 x 1 Có f (  x)  3 .ln 3   0, x
  0  Hàm số y  f (x) đồng biến trên khoảng (0;) . x ln 3 Khi đó (1) 2 2
 f (9y )  f (36  x ) 2 2
 9y  36  x 2 2
 x  9y  36 x  0 Vì ; x y  ; Z 6
  x  6; y  0 nên nhận được  y  2 
 M (0;2); M (0; 2  ) . 1 2
--------------HẾT--------------- Đề 3
ĐỀ LUYỆN THI CẤP TỐC TỐT NGHIỆP THPT NĂM 2021 Thuvienhoclieu.Com BÀI THI: TOÁN
Thời gian: 90 phút
Câu 1: Diện tích toàn phần của hình lập phương có cạnh 3a là A. 2 9a . B. 2 72a . C. 2 54a . D. 2 36a .
Câu 2: Tìm tập xác định của hàm số y  log  x   1
A. D   ;    1 . B. D   1  ; .
C. D  [ 1; ) . D.  \   1  . Trang49 1
Câu 3: Họ nguyên hàm của hàm số f  x 3  4x  là: 2 x 1 1
A. F  x 4
 x   C .
B. F  x 2
 12x   C . x x 1
C. F  x 4
 x   C .
D. F  x 4 2
 x  ln x  C . x
Câu 4: Có bao nhiêu cách chọn 5 học sinh từ 20 học sinh? A. 1860480 cách. B. 120cách. C. 15504cách. D. 100 cách.
Câu 5: Cho cấp số cộng u có số hạng đầu u  3 và công sai d  2 . Giá trị của u bằng: n  1 10 A. 24 . B. 23. C. 22 . D. 21 . 
Câu 6: Tìm tập nghiệm của phương trình 2 x 2 3 x  1. A. S   1  ;  3 .
B. S  0;   2 .
C. S  1;  3 .
D. S  0;  2 .
Câu 7: Cho hàm số y  f  x xá định và liên tục trên  , có bảng biến thiên như sau:
Mệnh đề nào sau đây đúng?
A. Hàm số nghịch biến trên khoảng   ;1 
B. Hàm số đồng biến trên khoảng  ;  2   .
C. Hàm số nghịch biến trên khoảng 1; 
D. Hàm số đồng biến trên khoảng  1  ;.
Câu 8: Biến đổi biểu thức A  3 2
a. a về dạng lũy thừa với số mũ hữu tỷ ta được 7 7 A.  6 A a . B.  2 A a .
C. A  a . D.  2 A a .
Câu 9: Cho hình trụ có bán kính đáy bằng 5 và chiều cao bằng 7 . Diện tích xung quanh của hình trụ đã cho bằng: 175 A. . B. 175 . C. 70 . D. 35 . 3
Câu 10:Cho khối chóp S.ABC có SA vuông góc  ABC  và SA  2 , tam giác ABC vuông cân tại A và
AB  1. Thể tích khối chóp S.ABC bằng 1 1 2 A. . B. . C. 1. D. . 6 3 3
Câu 11: Một khối nón tròn xoay có độ dài đường sinh l  13cm và bán kính đáy r  5cm . Khi đó thể tích khối nón bằng Trang50 325 A. V    3 100 cm  . B. V    3 300 cm  . C. V    3
cm  . D. V    3 20 cm  . 3
Câu 12: Khối cầu có bán kính R  6 có thể tích bằng bao nhiêu? A. 144 . B. 288 . C. 48 . D. 72 .
Câu 13: Bất phương trình sau log
3x 1  3 có nghiệm là: 2   1 A. x  3. B. x  3. C.  x  3. D. x  10 . 3 3
Câu 14: Đồ thị của hàm số y  f  x như hình vẽ bên.
Số nghiệm của phương trình 4 f  x  3  0 là A. 4 . B. 3 . C. 2 . D. 0 . 1 1 2 Câu 15:Nếu f
 xdx  5 và f
 xdx  2 thì f xdx  bằng 0 2 0 A. 8 . B. 2 . C. 3 . D. 3  .
Câu 16:Cho hàm số y  f  x có bảng biến thiên như sau:
Hàm số đạt cực đại tại điểm nào trong các điểm sao đây? A. x  2  .
B. x  3. C. x  2 . D. x  4
Câu 17: Đường cong trong hình vẽ là đồ thị của hàm số nào? Trang51 A. 3
y  x  3x . B. 3
y  x  3x . C. 2
y  x  x 1. D. 4 2
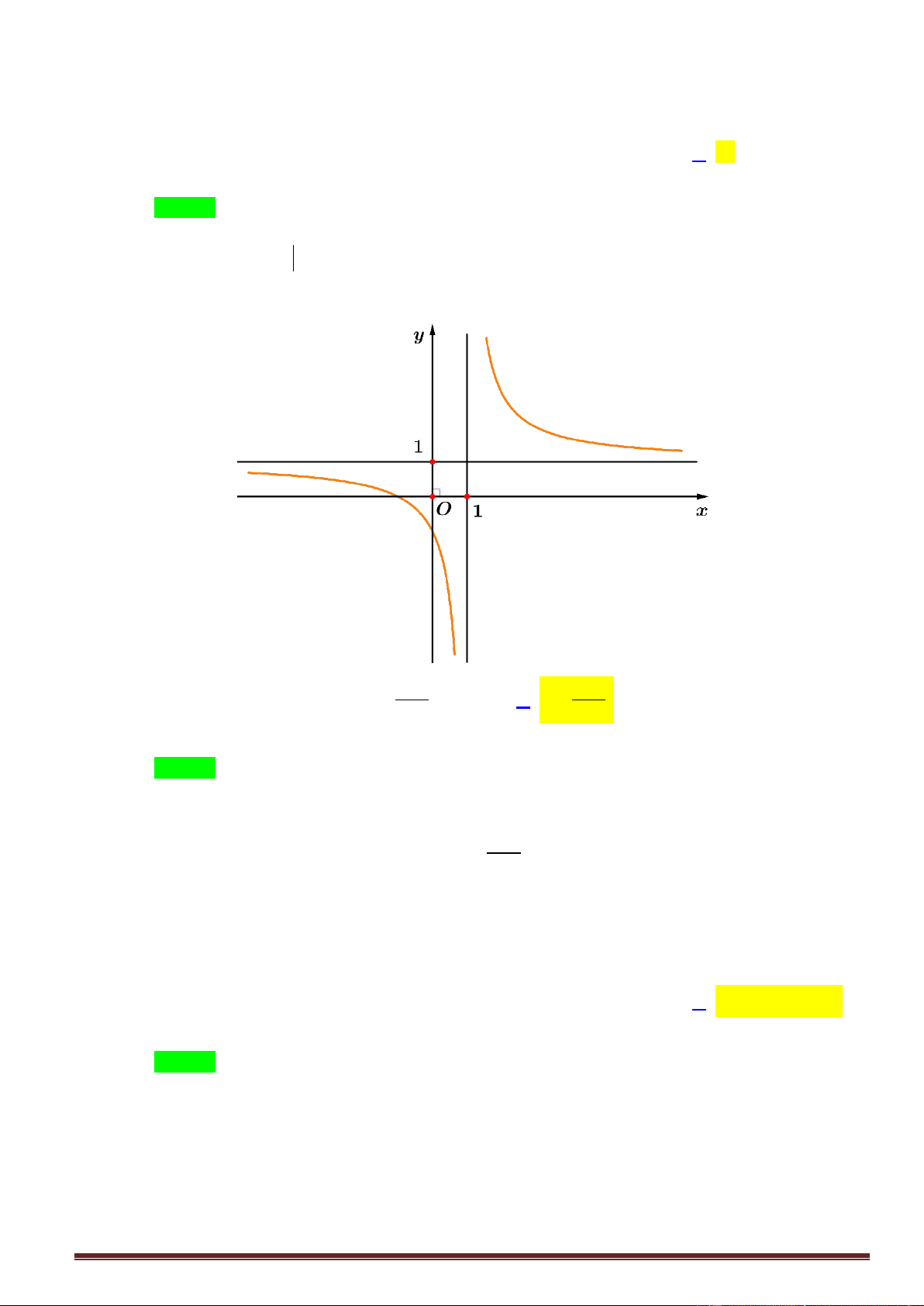
y  x  x 1.
Câu 18: Đường thẳng x 1 là tiệm cận đứng của đồ thị hàm số nào sau đây? 1 x 2x  2 2 1 x 2 2x  3x  2 A. y  . B. y  . C. y  y  1 x x  2 1 . D. x 2  . x
Câu 19: Trong không gian Oxyz , hình chiếu vuông góc của điểm A2;3; 4 lên trục Ox là điểm nào dưới đây?
A. M 2;0;0 .
B. M 0;3;0 .
C. M 0;0; 4 .
D. M 0; 2;3 .
Câu 20:Mặt cầu S  2 2 2
: x  y  z  8x 10 y  8  0 có tâm I và bán kính R lần lượt là: A. I 4; 5  ;4, R  8.
B. I 4; 5;0, R  33 .
C. I 4;5;0, R  7 . D. I 4; 5  ;0, R  7 .
Câu 21: Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng  P : 3x  z  2  0 . Vectơ nào dưới đây
là một vectơ pháp tuyến của  P ?     A.   1 n   1;0;  1 . B. n   2 3; 1;2 . C. n   3 3; 1;0. D. n   4 3;0;  1 .
Câu 22: Phần thực và phần ảo của số phức z 1 2i lần lượt là A. 1 và 2 . B. 1 và i . C. 1 và 2i . D. 2 và 1.
Câu 23: Cho 2 số phức z = 1 + i và z = 2 - 3i. Tính modun của số phức z + z bằng 1 2 1 2
A. z + z = 13.
B. z + z = 5.
C. z + z = 1.
D. z + z = 5. 1 2 1 2 1 2 1 2
Câu 24: Cho số phức z = 6 + 17i . Điểm biểu diễn của số phức z trên mặt phẳng tọa độ Oxy là:
A. M 6;17 .
B. M 17;6 .
C. M 17;6 . D. M 6;17
Câu 25: Tìm tập nghiệm của bất phương trình 2x 1
6  13.6x  6  0 .  2 3  A.  1  ;  1 . B.  ;   
1  1; . C. log ;log  . D.  ;  log 2 . 6  6 6   3 2 
Câu 26: Tính thể tích khối tròn xoay sinh ra khi quay tam giác đều ABC cạnh bằng 1 quanh AB . 3    3 A . B. . C. . D. . 4 4 8 2 Trang52 a 1
Câu 27: Nếu đặt x  asin t thì tích phân dx, 
a  0 trở thành tích phân nào dưới đây? 2 2  0 a x     2 2 1 2 a 4 A. dt  . B. dt  . C. dt  . D. dt  . a t 0 0 0 0
Câu 28: Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây? 2 2 A.   2
2x  2x  4dx . B.   2
 x  2dx . 1  1  2 2
C.  2x  2dx . D.   2 2
 x  2x  4dx . 1  1 
Câu 29: Cho hai số phức z  1 2i, z  2
  i . Khi đó giá trị z z là 1 2 1 2 A. 5 . B. 2 5 . C. 25 . D. 0 .
Câu 30: Gọi z và z lần lượt là nghiệm của phương trình 2
z  2z  5  0 . Tính F  z  z 1 2 1 2 A. 2 5 . B. 10 . C. 3 . D. 6 . x 1 t 
Câu 31: Cho đường thẳng  :  y  2  2t t  R . Điểm M nào sau đây thuộc đường thẳng  . z  3t  A. M 1; 2  ;3 .
B. M (2; 0; 4) . C. M 1; 2; 3  .
D. M 2;1;3 .
Câu 32: Cho tứ diện đều ABCD cạnh a , M là trung điểm của BC . Tính cosin của góc giữa hai đường
thẳng AB và DM . 3 3 3 1 A. . B. . C. . D. . 2 6 3 2
Câu 33: Cho hàm số f  x có đạo hàm f  x  x  x   x  3 ' 1
2 . Số điểm cực trị của hàm số đã cho là A. 3 . B. 2 . C. 5 . D. 1.
Câu 34: Giá trị nhỏ nhất của hàm số 3 2
y  x  3x trên đoạn  4  ;  1 là A. 4  . B. 16  . C. 0 . D. 4 . Trang53 1 Câu 35: Cho , a ,
b c là các số thực dương khác 1và thỏa mãn log a =
, log c = - 2. Giá trị của b 3 a æ 4 3 ö ça b÷ log ç ÷ ç ÷ bằng a 3 ç c ÷÷ è ø 2 5 A. - 2 . B. - . C. - . D. 11. 3 6
Câu 36:Số giao điểm của đồ thị hàm số 3
y  x  x  2 và đường thẳng y  2  x 1 là A. 3 . B. 0 . C. 2 . D. 1.
Câu 37: Số lượng của một loại vi khuẩn X trong phòng thí nghiệm được tính theo công thức    0.2t x t x
, trong đó x0 là số lượng vi khuẩn X ban đầu, xt là số lượng vi khuẩn X
sau t . Biết sau 2 phút thì số lượng vi khuẩn X là 625 nghìn con. Hỏi sau bao lâu, kể từ lúc bắt
đầu, số lượng vi khuẩn X là 10 triệu. A. 7 phút. B. 5 phút. C. 8 phút. D. 6 phút.
Câu 38: Cho đồ thị hàm số y  f  x 4 2
 x  2x  3 như hình vẽ:
Từ đồ thị suy ra được số nghiệm của phương trình 4 2
x  2x  3  m với m 3; 4 là: A. 3. B. 2. C. 4. D. 6 .
Câu 39: Một hình trụ có bán kính đáy bằng a, mặt phẳng qua trục cắt hình trụ theo một thiết diện có diện 2
tích bằng 8a . Tính diện tích xung quanh của hình trụ. 2 2 2 2
A. 4 a .
B. 8 a .
C. 16 a . D. 2 a .
Câu 40: Cho hàm số f  x thỏa mãn       1 x f x x
e và f 0  1. Tính f 2 . A. f   2 2  4e 1. B. f   2 2  2e 1. C. f   2 2  3e 1. D. f   2 2  e 1.
Câu 41:Trong không gian Oxyz , cho điểm M ( 3
 ;2;0) và đường thẳng (d) có phương trình x 1 y  3 z   1 1  2
 . Viết phương trình của mặt phẳng đi qua điểm M và vuông góc với đường thẳng (d) .
A. x  y  2z  5  0
B. x  y  2  0
C. x  y  2z  5  0 D. x  y  z  5  0
Câu 42:Trong không gian Oxyz ,phương trình đường thẳng đi qua hai điểm A1; 2;  3 và B 5;4;   1 là Trang54 x  5 y  4 z 1 x 1 y  2 z  3 A.   . B.   . 2 1 2 4 2 4 x 1 y  2 z  3 x  3 y  3 z 1 C.   . D.   . 4 2 4 2 1  2
Câu 43:Xếp 5 nam và 2 nữ vào một bàn dài gồm 7 chỗ ngồi. Tính xác suất để 2 nữ không ngồi cạnh nhau? 6 4 5 2 A. . B. . C. . D. . 7 7 7 7
Câu 44: Cho hàm số 3 2
y  x  mx  (4m  9)x  5 . Có bao nhiêu giá trị nguyên của m để hàm số
nghịch biến trên khoảng (;  ) ? A. 7. B. 6. C. 5. D. 8.
Câu 45: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA  ( ABC) , góc giữa đường thẳng SB và bằng 0
60 . Tính khoảng cách giữa hai đường thẳng AC và SB a 15 a 2 a 7 A. . B. . C. . D. 2a . 5 2 7
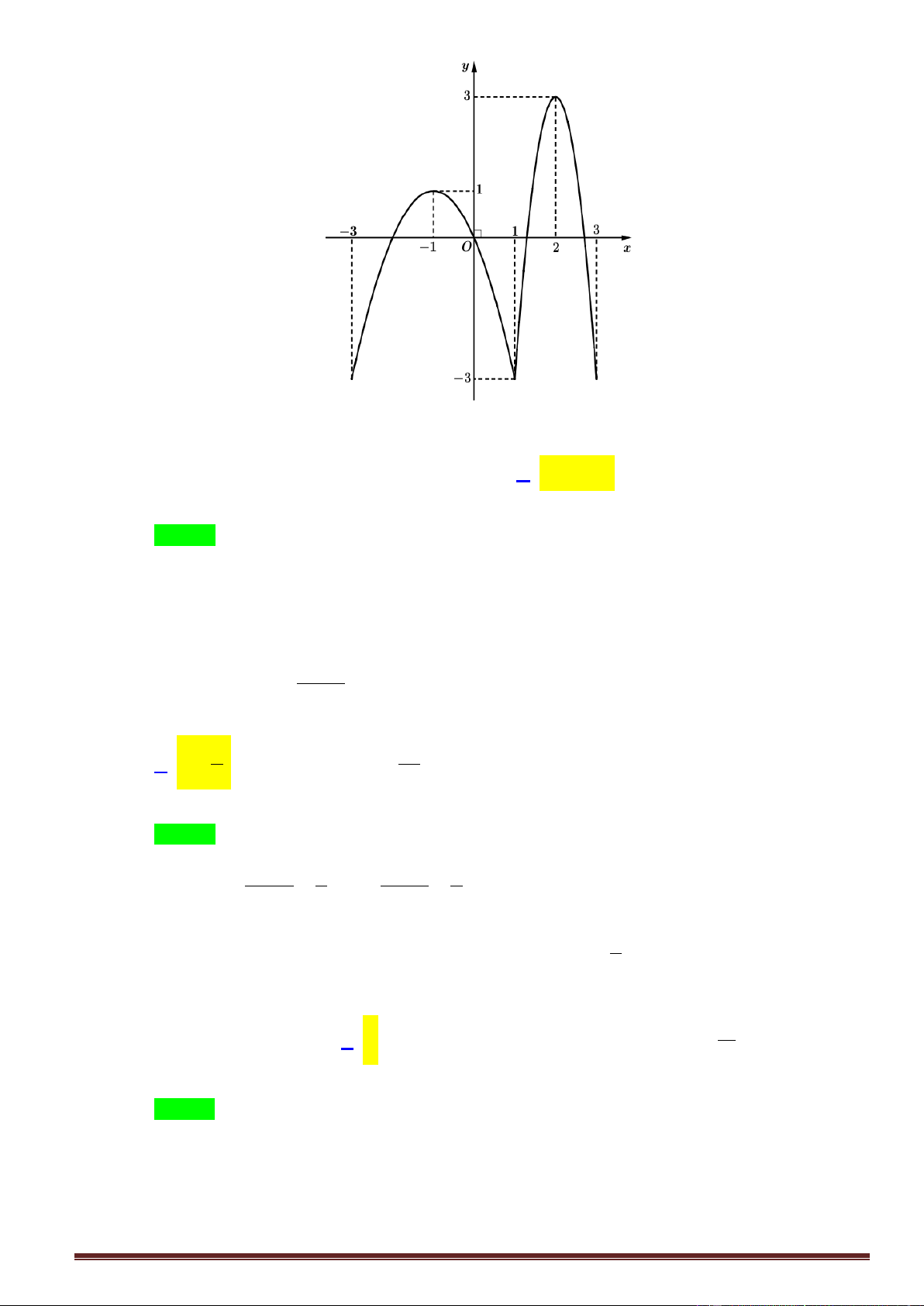
Câu 46:Cho hàm số y  f  x có đạo hàm trên  và có đồ thị là đường cong như hình vẽ dưới.
Đặt g x  f  f x 
 . Tìm số nghiệm của phương trình g x  0 . A. 8 . B. 4 . C. 6 . D. 2 .
Câu 47: Tập nghiệm của bất phương trình log log 2x 1  0 là: 1  2   2  3   3   3  A. S  1;   . B. S  0;   .
C. S  0;  1 . D. S  ; 2  .  2   2   2 
Câu 48: Cho hàm số y = f (x) có đạo hàm cấp hai trên  . Biết f 0  3 , f 2  2  018 và bảng xét
dấu của f ' (x) như sau
Hàm số y = f (x + 2017)+ 2018x đạt giá trị nhỏ nhất tại x thuộc khoảng nào sau đây? A. (0;2). B. (-¥;-2017). C. (-2017;0). D. (2017;+¥). Trang55
Câu 49: Xét các số thực dương x, y thỏa mãn log x  log y  log  2 x  y
. Tìm giá trị nhỏ nhất P 1 1 1  min 2 2 2
của biểu thức P  x  3y . 17 25 2 A. P  . B. P  8. C. P  9 . D. P  . min min min 2 min 4
Câu 50: Có tất cả bao nhiêu giá trị nguyên của tham số a thuộc khoảng 0, 2019 để n n 1 9  3  1 lim 
5n  9na 2187 A. 2018 . B. 2011. C. 2012 . D. 2019 .
--------------HẾT--------------- ĐÁP ÁN ĐỀ THI 1.C 2.B 3.A 4.C 5.D 6.B 7.B 8.A 9.C 10.B 11.A 12.B 13.A 14.A 15.C 16.C 17.A 18.A 19.A 20.D 21.D 22.A 23.A 24.D 25.C 26.B 27.A 28.D 29.A 30.A 31.B 32.B 33.A 34.B 35.D 36.D 37.D 38.D 39.B 40.B 41.C 42.D 43.C 44.A 45.A 46.A 47.A 48.B 49.C 50.C
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Diện tích toàn phần của hình lập phương có cạnh 3a là: A. 2 9a . B. 2 72a . C. 2 54a . D. 2 36a . Lời giải
Hình lập phương có 6 mặt, nên diện tích toàn phần của hình lập phương bằng 6 lần diện tích
mỗi mặt: S   a2 2 3 .6  54a tp
Câu 2: Tìm tập xác định của hàm số y  log  x   1
A. D   ;    1 . B. D   1  ; .
C. D  [ 1; ) . D.  \   1  . Lời giải
Hàm số y  log  x  
1 xác định khi x 1  0  x  1  .
Vậy tập xác định D   1  ; . 1
Câu 3: Họ nguyên hàm của hàm số f  x 3  4x  là: 2 x 1 1
A. F  x 4
 x   C .
B. F  x 2
 12x   C . x x 1
C. F  x 4
 x   C .
D. F  x 4 2
 x  ln x  C . x Trang56 Lời giải
Câu 4: Có bao nhiêu cách chọn 5 học sinh từ 20 học sinh? A. 1860480 cách. B. 120cách. C. 15504cách. D. 100 cách. Lời giải
Số cách chọn 5 học sinh từ 20 học sinh là: 5 C 15504 cách. 20
Câu 5: Cho cấp số cộng u có số hạng đầu u  3 và công sai d  2 . Giá trị của u bằng: n  1 10 A. 24 . B. 23. C. 22 . D. 21 . Lời giải
Ta có: u  3  2n  
1  u  3  2 10 1  21. n 10   
Câu 6: Tìm tập nghiệm của phương trình 2 x 2 3 x  1. A. S   1  ;  3 .
B. S  0;   2 .
C. S  1;  3 .
D. S  0;  2 . Lời giải   2 x 0 Ta có: x 2x 2 3
1 x  2x  0   . x  2 
Vậy tập nghiệm của phương trình đã cho là: S  0;   2 .
Câu 7: Cho hàm số y  f  x xá định và liên tục trên  , có bảng biến thiên như sau:
Mệnh đề nào sau đây đúng?
A. Hàm số nghịch biến trên khoảng   ;1 
B. Hàm số đồng biến trên khoảng  ;  2   .
C. Hàm số nghịch biến trên khoảng 1; 
D. Hàm số đồng biến trên khoảng  1  ;. Lời giải
Từ bảng biến thiên của hàm số y  f  x , ta có hàm số y  f  x đồng biến trên khoảng  ;    1
Suy ra, hàm số y  f  x đồng biến trên khoảng  ;  2   .
Câu 8: Biến đổi biểu thức A  3 2
a. a về dạng lũy thừa với số mũ hữu tỷ ta được Trang57 7 7 A.  6 A a . B.  2 A a .
C. A  a . D.  2 A a . Lời giải 1 2 1 2 7
Với a là số thực dương khác 1 ta có: A  3 2 a a  2 3 a a  2 3 a  6 . . a .
Câu 9: Cho hình trụ có bán kính đáy bằng 5 và chiều cao bằng 7 . Diện tích xung quanh của hình trụ đã cho bằng: 175 A. . B. 175 . C. 70 . D. 35 . 3 Lời giải
Diện tích xung quanh của hình trụ: S
 2rh  2.5.7  70 . xq
Câu 10:Cho khối chóp S.ABC có SA vuông góc  ABC  và SA  2 , tam giác ABC vuông cân tại A và
AB  1. Thể tích khối chóp S.ABC bằng 1 1 2 A. . B. . C. 1. D. . 6 3 3 Lời giải 1 1
Do tam giác ABC vuông cân tại A và AB  1 nên S  .A . B AC  . ABC 2 2 1 1 1 1
Vậy thể tích khối chóp S.ABC là: V  . . SA S  .2.  . S . ABC 3 ABC 3 2 3
Câu 11: Một khối nón tròn xoay có độ dài đường sinh l  13cm và bán kính đáy r  5cm . Khi đó thể tích khối nón bằng 325 A. V    3 100 cm  . B. V    3 300 cm  . C. V    3
cm  . D. V    3 20 cm  . 3 Lời giải Trang58
Chiều cao của khối nón là 2 2 2 2
h  l  r  13  5  12 cm . 1 1
Thể tích của khối nón là: 2 2 V 
 r h  .5 .12  100  3 cm  . 3 3
Câu 12: Khối cầu có bán kính R  6 có thể tích bằng bao nhiêu? A. 144 . B. 288 . C. 48 . D. 72 . Lời giải 4 4
Ta có thể tích khối cầu là: 3 3 V 
 R  ..6  288 . 3 3
Câu 13: Bất phương trình sau log
3x 1  3 có nghiệm là: 2   1 A. x  3. B. x  3. C.  x  3. D. x  10 . 3 3 Lời giải  1 3  x 1  0 x  Ta có: log 3x 1  3     3  x  3. 2   3 3  x 1  2 x  3
Vậy bất phương trình có nghiệm x  3.
Câu 14: Đồ thị của hàm số y  f  x như hình vẽ bên.
Số nghiệm của phương trình 4 f  x  3  0 là A. 4 . B. 3 . C. 2 . D. 0 . Lời giải Trang59
Phương trình f  x    f  x 3 4 3 0  . 4
Số nghiệm của phương trình 4 f  x  3  0 là số giao điểm của đồ thị hàm số y  f  x và đườ 3 ng thẳng y  . 4
Từ đồ thị trên suy ra phương trình đã cho có 4 nghiệm. 1 1 2 Câu 15:Nếu f
 xdx  5 và f
 xdx  2 thì f xdx  bằng 0 2 0 A. 8 . B. 2 . C. 3 . D. 3  . Lời giải 1 2 Ta có
f  x dx  2  f  x dx  2    2 1 2 1 2 Suy ra: f
 xdx  f
 xdx f
 xdx  52  3. 0 0 1 2 Vậy f
 xdx  3. 0
Câu 16:Cho hàm số y  f  x có bảng biến thiên như sau:
Hàm số đạt cực đại tại điểm nào trong các điểm sao đây? A. x  2  .
B. x  3. C. x  2 . D. x  4 Lời giải
Dựa vào bảng biến thiên, điểm cực đại của hàm số là x  2 .
Câu 17: Đường cong trong hình vẽ là đồ thị của hàm số nào? Trang60 A. 3
y  x  3x . B. 3
y  x  3x . C. 2
y  x  x 1. D. 4 2
y  x  x 1. Lời giải
Ta thấy đồ thị đi qua O(0; 0) nên loại đáp án C, D.
Nhìn đồ thị ta thấy đây là đồ thị của hàm bậc ba có hệ số a  0 nên loại phương án D.
Vậy đồ thị đã cho là của hàm số 3
y  x  3x .
Câu 18: Đường thẳng x 1 là tiệm cận đứng của đồ thị hàm số nào sau đây? 1 x 2x  2 2 1 x 2 2x  3x  2 A. y  . B. y  . C. y  y  1 x x  2 1 . D. x 2  . x Lời giải  x Xét hàm số 1 y  1 x
+) TXĐ: D   \  1 1 x 1 x 1 x +) lim   ; lim
   x 1 là tiệm cận đứng của đồ thị hàm số y  .   x 1  1 x x 1  1 x 1 x
Câu 19: Trong không gian Oxyz , hình chiếu vuông góc của điểm A2;3; 4 lên trục Ox là điểm nào dưới đây?
A. M 2;0;0 .
B. M 0;3;0 .
C. M 0;0; 4 .
D. M 0; 2;3 . Lời giải
Do điểm M thuộc trục Ox nên tọa độ có dạng M  ; x 0; 0 uuur r
M là hình chiếu vuông góc của điểm A2;3; 4 lên trục Ox : AM  i  x  2  0  x  2
Vậy M 2;0;0 .
Câu 20:Mặt cầu S  2 2 2
: x  y  z  8x 10 y  8  0 có tâm I và bán kính R lần lượt là: A. I 4; 5  ;4, R  8.
B. I 4; 5;0, R  33 .
C. I 4;5;0, R  7 . D. I 4; 5  ;0, R  7 . Lời giải Trang61 Gọi I  ; a ;
b c là tâm của mặt cầu S  .  8  a   4  2    10 Ta có: b    5   I 4; 5  ;0 . 2   c  0   2 S  có bán kính 2 2 2 2
R  a  b  c  d  4   5
   8  7 .
Vậy mặt cầu đã cho có tâm I 4; 5
 ;0 và bán kính R  7 .
Câu 21: Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng  P : 3x  z  2  0 . Vectơ nào dưới đây
là một vectơ pháp tuyến của  P ?     A.   1 n   1;0;  1 . B. n   2 3; 1;2 . C. n   3 3; 1;0. D. n   4 3;0;  1 . Lời giải
Mặt phẳng có phương trình tổng quát dạng: 2 2 2
ax  by  cz  d  0 (a  b  c  0) 
có một vectơ pháp tuyến là n  ( ; a ; b ) c . 
Vậy mặt phẳng (P) : 3x  z  2  0 có một vectơ pháp tuyến là n   4 3;0;  1 .
Câu 22: Phần thực và phần ảo của số phức z 1 2i lần lượt là A. 1 và 2 . B. 1 và i . C. 1 và 2i . D. 2 và 1. Lời giải
Phần thực và phần ảo của số phức z 1 2i lần lượt là 1 và 2 .
Câu 23: Cho 2 số phức z = 1 + i và z = 2 - 3i. Tính modun của số phức z + z bằng 1 2 1 2
A. z + z = 13.
B. z + z = 5.
C. z + z = 1.
D. z + z = 5. 1 2 1 2 1 2 1 2 Lời giải
Ta có z + z = (1 + i) + (2 - 3i) = 3 - 2i 1 2 Suy ra 2 2 z + z = 3 + (- 2) = 13 . 1 2
Câu 24: Cho số phức z = 6 + 17i . Điểm biểu diễn của số phức z trên mặt phẳng tọa độ Oxy là:
A. M 6;17 .
B. M 17;6 .
C. M 17;6 . D. M 6;17 Lời giải
Điểm biểu diễn của số phức z là điểm M 6;17 .
Câu 25: Tìm tập nghiệm của bất phương trình 2x 1
6  13.6x  6  0 . Trang62  2 3  A.  1  ;  1 . B.  ;   
1  1; . C. log ;log  . D.  ;  log 2 . 6  6 6   3 2  Lời giải Ta có 2x 1
6  13.6x  6  0 2 6.6 x 13.6x    6  0 2 x 3   6  3 2 2 3  log  x  log 6 6 3 2  2 3 
Vậy tập nghiệm của bất phương trình là log ;log  . 6 6   3 2 
Câu 26: Tính thể tích khối tròn xoay sinh ra khi quay tam giác đều ABC cạnh bằng 1 quanh AB . 3    3 A . B. . C. . D. . 4 4 8 2 Lời giải 3
Vì tam giác ABC đều cạnh bằng 1 nên CD  2
Gọi D là trung điểm của AB .
Quay tam giác ABC quanh AB ta thu được 1
+) Khối nón N có đường cao h  AD  , bán kính đáy 3 R  CD  1  1 2 2 1 1 3 1 1
Suy ra thể tích của khối nón N là: V   2
.R .h   . .   . 1  1 1 3 3 4 2 8 1
+) Khối nón N có đường cao h  BD  , bán kính đáy 3 R  CD  2  2 2 2 1 1 3 1 1
Suy ra thể tích của khối nón N là: V   2
.R .h   . .   . 2  2 2 3 3 4 2 8 1 1 1
Vậy thể tích của khối tròn xoay là: V  V  V       . 1 2 8 8 4 Trang63 a 1
Câu 27: Nếu đặt x  asin t thì tích phân dx, 
a  0 trở thành tích phân nào dưới đây? 2 2  0 a x     2 2 1 2 a 4 A. dt  . B. dt  . C. dt  . D. dt  . a t 0 0 0 0 Lời giải
Đặt x  asint  dx  acost.dt Ta có 2 2 2
a  x  a  2  t  2 2 1 sin  a os c
t  a cos t
x  0  t  0  Đổi cận:  
x  a  t    2    a 2 2 2 1 1 1 Suy ra dx 
.a cos t.dt 
.a cos t.dt  dt     . 2 2 2 a  x a  2 a cos t  0 0 1 sin t  0 0
Câu 28: Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây? 2 2 A.   2
2x  2x  4dx . B.   2
 x  2dx . 1  1  2 2
C.  2x  2dx . D.   2 2
 x  2x  4dx . 1  1  Lời giải
Hình phẳng D được giới hạn bởi các đường 2
y  x  3 , 2
y  x  2x 1 , x  1  và x  2 2 2
Diện tích hình phẳng D cần tìm là: S    2  x 3 
 2x 2x 1dx    2 2
 x  2x  4dx . 1  1 
Câu 29: Cho hai số phức z  1 2i, z  2
  i . Khi đó giá trị z z là 1 2 1 2 A. 5 . B. 2 5 . C. 25 . D. 0 . Lời giải
Ta có z z  1 2i 2   i  5  .i 1 2    Trang64 Do đó z z  5  i  5. 1 2
Câu 30: Gọi z và z lần lượt là nghiệm của phương trình 2
z  2z  5  0 . Tính F  z  z 1 2 1 2 A. 2 5 . B. 10 . C. 3 . D. 6 . Lời giải Ta có: 2
z  2z  5  0  z  1 2i .
Suy ra z  z  5  F  z  z  2 5 . 1 2 1 2 x 1 t 
Câu 31: Cho đường thẳng  : y  2  2t t  R . Điểm M nào sau đây thuộc đường thẳng  . z  3t  A. M 1; 2  ;3 .
B. M (2; 0; 4) . C. M 1; 2; 3  .
D. M 2;1;3 . Lời giải
Xét điểm M 2;0;4 .
Thay x  2, y  0, z  4 vào phương trình đường thẳng  . 2 1 t 
Ta được: 0  2  2t  t 1. 4  3t 
Vậy điểm M 2;0; 4 thuộc đường thẳng 
Câu 32: Cho tứ diện đều ABCD cạnh a , M là trung điểm của BC . Tính cosin của góc giữa hai đường
thẳng AB và DM . 3 3 3 1 A. . B. . C. . D. . 2 6 3 2 Lời giải
Gọi N là trung điểm của AC , khi đó góc giữa đường thẳng AB và đường thẳng DM bằng
góc giữa đường thẳng MN và đường thẳng DM . A N B D M C a 3 a
Ta có ND  MD  , MN  2 2 Trang65 2 2 2 
Áp dụng định lí Cô sin trong tam giác MND ta có: ND  MN  MD  2MN.M . D cos NMD . 2 2 2  a 3   a   a 3 
 a   a 3  Suy ra       3        2. .      .cos NMD    cos NMD  . 2    2  2    2  2   6   3
Vậy cos  AB, DM   cos MN , DM   6
Câu 33: Cho hàm số f  x có đạo hàm f  x  x x   x  3 ' 1
2 . Số điểm cực trị của hàm số đã cho là A. 3 . B. 2 . C. 5 . D. 1. Lời giải  x  0 
Ta có: f ' x  0  x  x  
1  x  23  0  x  1  x  2   Bảng biến thiên:
Dựa vào bảng biến thiên ta thấy hàm số f  x có 3 điểm cực trị.
Câu 34: Giá trị nhỏ nhất của hàm số 3 2
y  x  3x trên đoạn  4  ;  1 là A. 4  . B. 16  . C. 0 . D. 4 . Lời giải x  2  Ta có 2
y '  0  3x  6x  0  
. Do chỉ xét trên đoạn  4  ; 
1 nên ta chỉ lấy x  2  x  0 Bảng biến thiên:
Dựa vào bảng biến thiên , suy ra giá trị nhỏ nhất của hàm số 3 2
y  x  3x trên đoạn  4  ;  1 là
min f  x  f  4    1  6 .  4  ;  1 Trang66 1 Câu 35: Cho , a ,
b c là các số thực dương khác 1và thỏa mãn log a =
, log c = - 2. Giá trị của b 3 a æ 4 3 ö ça b÷ log ç ÷ ç ÷ bằng a 3 ç c ÷÷ è ø 2 5 A. - 2 . B. - . C. - . D. 11. 3 6 Lời giải æ 4 3 ö ça b÷ 1 Ta có: log ç ÷= 4 3 3 ç ÷ log a + log
b - log c = 4log a+ log b- 3log c a ç 3 ÷ ç c ÷ a a a è ø a a a 3 l = 4+ - 3log c 3log a a b 1 = 4+ - 3. - ( 2) = 11. 1 3. 3
Câu 36:Số giao điểm của đồ thị hàm số 3
y  x  x  2 và đường thẳng y  2  x 1 là A. 3 . B. 0 . C. 2 . D. 1. Lời giải
Hoành độ giao điểm của đồ thị hàm số 3
y  x  x  2 và đường thẳng y  2
 x 1 là nghiệm của phương trình 3 3
x  x  2  2
 x 1  x  3x 1  0 .
Xét hàm số f  x 3
 x  3x 1 trên 
Ta có f  x 2
 3x  3  0 x  
Suy ra f  x đồng biến trên 
Suy ra phương trình f  x  0 có nhiều nhất 1 nghiệm   1 .
Dễ thấy do f  x là hàm đa thức nên f  x liên tục trên  , lại có f   1 . f 0  3  .1  3   0
nên phương trình f  x  0 có ít nhất 1 nghiệm trong khoảng  1  ;0 2 . Từ  
1 và 2 suy ra phương trình f  x  0 có đúng 1 nghiệm.
Điều đó có nghĩa là đồ thị hàm số 3
y  x  x  2 cắt đường thẳng y  2
 x 1 tại duy nhất 1 điểm.
Câu 37: Số lượng của một loại vi khuẩn X trong phòng thí nghiệm được tính theo công thức    0.2t x t x
, trong đó x0 là số lượng vi khuẩn X ban đầu, xt là số lượng vi khuẩn X
sau t . Biết sau 2 phút thì số lượng vi khuẩn X là 625 nghìn con. Hỏi sau bao lâu, kể từ lúc bắt
đầu, số lượng vi khuẩn X là 10 triệu. A. 7 phút. B. 5 phút. C. 8 phút. D. 6 phút. Lời giải Trang67
Sau 2 phút thì số lượng vi khuẩn X là 625 nghìn con nghĩa là: x   2
0 .2  625000  x 0 156250
Thời gian để số lượng vi khuẩn X là 10 triệu:
 156250.2t 10.10  2t x t
 64  t  log 64  6 . 0  0 6 0 0 2
Câu 38: Cho đồ thị hàm số y  f  x 4 2
 x  2x  3 như hình vẽ:
Từ đồ thị suy ra được số nghiệm của phương trình 4 2
x  2x  3  m với m 3; 4 là A. 3. B. 2. C. 4. D. 6. Lời giải
Từ đồ thị hàm số y  f  x 4 2
 x  2x  3 ta có đồ thị hàm số y  f x như hình vẽ sau:
Từ đồ thị ta thấy số nghiệm của phương trình 4 2
x  2x  3  m với m 3; 4 là 6.
Câu 39: Một hình trụ có bán kính đáy bằng a, mặt phẳng qua trục cắt hình trụ theo một thiết diện có diện 2
tích bằng 8a . Tính diện tích xung quanh của hình trụ. 2 2 2 2
A. 4 a .
B. 8 a .
C. 16 a . D. 2 a . Lời giải Trang68
Vì mặt phẳng đi qua trục của hình trụ nên nó cắt hình trụ theo thiết diện là một hình chữ nhật
ABCD có kích thước là AB  2a, BC  h , do đó diện tích của thiết diện bằng 2 2 .
a h  8a  h  4 . a 2
Vậy diện tích xung quanh của hình trụ là 2 Rh  8 a .
Câu 40: Cho hàm số f  x thỏa mãn       1 x f x x
e và f 0  1. Tính f 2 . A. f   2 2  4e 1. B. f   2 2  2e 1. C. f   2 2  3e 1. D. f   2 2  e 1. Lời giải
Hàm số       1 x f x x
e liên tục trên  nên liên tục trên đoạn 0;2 . Do đó ta có 2 f 
 xdx  f x 2  f 2 f 0. 0 0 2 2 Theo đề bài cho ta có  d       1 x f x x x e dx . 0 0 u   x 1 du  dx Đặt    . d x v  e d x x v  e 2 2 Khi đó f '
 xdx  x  2 1 x x e  e dx   x   2 2 x x 2 0 1 e  e
 3e  e   2 0 e  e  2  2e . 0 0 0 0 0
Suy ra f    f   2
 e  f   2 2 0 2 2 1  2e  f   2 2  2e 1. Vậy f   2 2  2e 1.
Câu 41:Trong không gian Oxyz , cho điểm M ( 3
 ;2;0) và đường thẳng (d) có phương trình x 1 y  3 z   1 1  2
 . Viết phương trình của mặt phẳng đi qua điểm M và vuông góc với đường thẳng (d) .
A. x  y  2z  5  0 . B. x  y  2  0 .
C. x  y  2z  5  0 . D. x  y  z  5  0 . Lời giải Trang69 Gọi ( )
P là mặt phẳng cần tìm. 
Đường thẳng (d) cỏa một véc tơ chỉ phương là: u    (d ) 1; 1; 2  Vì ( )
P vuông góc với đường thẳng (d) nên ( )
P có một véc tơ pháp tuyến: n    ( P) 1; 1; 2
Phương trình mặt phẳng ( )
P đi qua điểm M  3
 ;2;0 và vuông góc với đường thẳng (d) là:
1. x  3 1. y  2  2. z  0  0 .
 x  y  2z  5  0.
Vậy mặt phẳng cần tìm là: x  y  2z  5  0 .
Câu 42:Trong không gian Oxyz ,phương trình đường thẳng đi qua hai điểm A1;2;  3 và B 5;4;   1 là x  5 y  4 z 1 x 1 y  2 z  3 A.   . B.   . 2 1 2 4 2 4 x 1 y  2 z  3 x  3 y  3 z 1 C.   . D.   . 4 2 4 2 1  2 Lời giải 
Ta có AB  4; 2;  4 . 
Đường thẳng đi qua 2 điểm ,
A B có một véc tơ chỉ phương là: u  2;1;2 . Suy ra loại đáp án A và C. x  y  z 
Thay tọa độ điểm A1; 2;  3 vào phương trình 3 3 1  :   ta được: 2  1  2 1 3 2  3 3 1  
 1  1  1. Suy ra A . 2 1  2 x  y  z 
Thay tọa độ điểm B 5; 4;  1 vào phương trình 3 3 1  :   ta được: 2  1  2 5  3 4  3 1  1  
 1  1  1. Suy ra B  . 2 1  2 x  3 y  3 z 1
Vậy phương trình đường thẳng đi qua 2 điểm , A B là:   . 2 1  2
Câu 43:Xếp 5 nam và 2 nữ vào một bàn dài gồm 7 chỗ ngồi. Tính xác suất để 2 nữ không ngồi cạnh nhau? 6 4 5 2 A. . B. . C. . D. . 7 7 7 7 Lời giải
Số phần tử của không gian mẫu n   7!  5040
Gọi A là biến cố “ 2 nữ không ngồi cạnh nhau”, A là biến cố “ 2 nữ ngồi cạnh nhau”
Ta có n A  2.6!1440 Trang70 n A 1440 2
Xác xuất của biến cố A là P  A      n  5040 7
Vậy xác xuất của biến cố A là P  A   P  A 2 5 1  1  . 7 7
Câu 44: Cho hàm số 3 2
y  x  mx  (4m  9)x  5 . Có bao nhiêu giá trị nguyên của m để hàm số
nghịch biến trên khoảng (;  ) ? A. 7. B. 6. C. 5. D. 8. Lời giải TXĐ: D   2 y  3
 x  2mx  4m  9 .
Hàm số nghịch biến trên khoảng (;  ) khi y  0 với mọi x  ( ;   ) 2  3
 x  2mx  4m  9  0 với mọi x ( ;   )    0 2
 m 12m  27  0  9   m  3 
Có 7 giá trị nguyên của m thỏa yêu cầu bài toán.
Câu 45: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA  ( ABC) , góc giữa đường thẳng SB và bằng 0
60 . Tính khoảng cách giữa hai đường thẳng AC và SB a 15 a 2 a 7 A. . B. . C. . D. 2a . 5 2 7 Lời giải S H A C D M B
Vì SA   ABC  nên  ,
SB  ABC  SB AB  ,  
SBA  SBA  60 . Trong S  AB có  SA  A . B tan SBA  .
a tan 60  a 3 .
Dựng hình bình hành ACBD , ta có AC// SBD nên:
d  AC, SB  d  AC,SBD  d  ,
A SBD .
Gọi M là trung điểm BD , có ABD 
cân tại A , suy ra BD  AM .
Từ SA   ABC  ta có BD  SA, do đó BD  SAM  .  SAM   (SBD) Trang71
Trên SAM  kẻ AH  SM ( H SM ) thì AH  SBD nên d  ,
A SBD  AH . Tam giác đề a 3
u ABD cạnh a nên AM  . 2
Trong tam giác SAM vuông tại A , ta có 1 1 1 1 1 5 a 3 a 15       AH   . 2 2 2 2 AH AM SA  a 3  a 32 2 3a 5 5   2   a
Vậy d  AC SB  d  A SBD 15 , ,  AH  . 5
Câu 46:Cho hàm số y  f  x có đạo hàm trên  và có đồ thị là đường cong như hình vẽ dưới.
Đặt g x  f  f x 
 . Tìm số nghiệm của phương trình g x  0 . A. 8 . B. 4 . C. 6 . D. 2 . Lời giải
 f x  0   1
Ta có: g x  f  x. f   f  x 
 ; g x  0   .  f  f
   x  0  2
Dựa vào đồ thị ta thấy: x  0
TH1: Phương trình f ' x  0  
, trong đó x  2;3 . 6   x  x  6
 f x  0
TH2: Phương trình f '  f
  x  0   
, trong đó x  2;3 . 6    f
  x  x6
+) Xét phương trình f  x  0 3 .
Nhận xét số nghiệm phương trình 3 là số giao điểm của đồ thị hàm số y  f  x và trục
hoành. Dựa vào đồ thị ta thấy đồ thị hàm số y  f  x cắt trục hoành tại 3 điểm phân biệt khi
x  x ; x  1;0 1 1   
đó phương trình f  x  0  x  1 
x  x ;x  3;4  7 7  
+) Xét phương trình f x  x 4 . 6  
Nhận xét số nghiệm của phương trình 4 là số giao điểm của đồ thị hàm số y  f  x và
đường thẳng y  x . 6 Trang72
Dựa vào đồ thị ta thấy đồ thị hàm số y  f  x cắt đường thẳng y  x tại 3 điểm phân biệt 6
x  x ; x  x ;0 2 2  1  
nên phương trình f  x  x  x  x ; x  0;1 . 6 4 4  
x  x ;x  x ;  8 8  7 
Vậy phương trình g ' x  0 có 8 nghiệm phân biệt x ; x ;0; x ;1; x ; x ; x 1 2 4 6 7 8 trong đó: 1
  x  x  0  x 1 2  x  3  x  x . 1 2 4 6 7 8
Câu 47: Tập nghiệm của bất phương trình log log 2x 1  0 là 1  2   2  3   3   3  A. S  1;   . B. S  0;   .
C. S  0;  1 . D. S  ; 2  .  2   2   2  Lời giải Bất phương trình: log log 2x 1  0 1  2   2 2x 1  0 2x 1  0 x 1   
 log 2x 1  0  2x 11   2   3 x       2x 1  2 log 2x 1 1   2  2    
Vậy tập nghiệm của bất phương trình là 3 S  1;   .  2 
Câu 48: Cho hàm số y = f (x) có đạo hàm cấp hai trên  . Biết f 0  3 , f 2  2  018 và bảng xét
dấu của f ' (x) như sau Trang73
Hàm số y = f (x + 2017)+ 2018x đạt giá trị nhỏ nhất tại x thuộc khoảng nào sau đây? A. (0;2). B. (-¥;-2017). C. (-2017;0). D. (2017;+¥). Lời giải
Đặt g(x) = f (x + 2017)+ 2018x.
Ta có g x  f  x  2017  2018 .
Cho g x  0  f  x  2017  2  018.
Dựa vào bảng biến thiên
Ta có x + 2017 = 2 hay x + 2017 = x . 0
Suy ra x = -2015 hay x = x - 2017. Đặt x = x - 2017 thì x < -2017. 0 1 0 1
Ta có g0  f 2017  2018  0.
Từ đó, ta có bảng biến thiên của hàm g  x như sau
Dựa vào bảng biến thiên, ta thấy hàm g  x đạt giá trị nhỏ nhất tại x , với x Î(-¥;-2017). 1 1
Câu 49: Xét các số thực dương 2
x, y thỏa mãn log x  log y  log x  y
. Tìm giá trị nhỏ nhất P 1 1 1   min 2 2 2
của biểu thức P  x  3y . Trang74 17 25 2 A. P  . B. P  8. C. P  9 . D. P  . min min min 2 min 4 Lời giải
Điều kiện xác định của log x  log y  log  2 x  y
là x  0 và y  0 . 1 1 1  2 2 2 Suy ra 2
x y  x  y  x  y   2 .
1  y , vì x  0 nên y 1  0 . Do đó từ x  y   2 1  y suy ra 2 y x  . y 1 2 y
P  x  y 
 y   y   1     y   1 3 3 4 1 5 2 4 1 .  5  9 . y 1 y 1 y 1  3 y  (N) 1  P  9 2 khi 4 y   1   4 y  2 1 1   . min y 1 1  y  (L)  2 3 9 Với y  ta tìm được x  . 2 2
Câu 50: Có tất cả bao nhiêu giá trị nguyên của tham số a thuộc khoảng 0, 2019 để n n 1 9  3  1 lim  ?
5n  9na 2187 A. 2018 . B. 2011. C. 2012 . D. 2019 . Lời giải 3  n n 1  n n 1 9  3 9  3.3 n 1 1 Ta có 3 lim  lim  lim   .
5n  9na
5n  9na n a a  5  9 3  9a    9  n n 1 9  3  1 1 1 Vì lim   
 3a  2187  a  7 .
5n  9na 2187 3a 2187
Kết hợp với giả thiết a thuộc khoảng 0; 2019 nên có 2012 giá trị nguyên của a .
--------------HẾT--------------- Đề 4
ĐỀ LUYỆN THI CẤP TỐC TỐT NGHIỆP THPT NĂM 2021 Thuvienhoclieu.Com BÀI THI: TOÁN
Thời gian: 90 phút Trang75 Câu 1:
Trong không gian Oxyz , cho mặt phẳng  P : x  y  5  0 . Một vectơ pháp tuyến của mp  P là: A. 1;1;0 . B. 1;0;  1  . C. 1; 1  ;5. D.  1  ;1;0 . x 1 Câu 2: Cho hàm số y 
. Khẳng định nào sau đây đúng? x  2
A. Hàm số đã cho nghịch biến trên  .
B. Hàm số đã cho nghi ̣ch biến trên tâ ̣p  ;  22; .
C. Hàm số đã cho nghi ̣ch biến trên từng khoảng xác định.
D. Hàm số đã cho đồng biến trên từng khoảng xác định. Câu 3:
Trong không gian Oxyz , đường thẳng d đi qua điểm A1; 1
 ;0và song song với đường thẳng x 1 y z  3  :   2  có phương trình là 1 5 x 1 y 1 z x  3 y  2 z  5 A.   . B.   . 2  1 5 2 1  5 x 1 y 1 z x  3 y  2 z  5 C.   . D.   . 2 1 5 2 1  5 Câu 4:
Cho a là một số thực dương khác 1. Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?
1. Hàm số y  log x có tập xác định là D  0;  . a
2. Hàm số y  log x đơn điệu trên khoảng 0;  . a
3. Đồ thị hàm số y  log x và đồ thị hàm số x
y  a đối xứng nhau qua đường thẳng y  x . a
4. Đồ thị hàm số y  log x nhận tru ̣c Ox là một tiệm cận. a A. 4 . B. 2 . C. 1. D. 3 .  Câu 5:
Tập xác định của hàm số y   3 x  2 27 là
A. D  3;  .
B. D   \   3 .
C. D  3; . D. D   . b Câu 6:
Biết F  x là một nguyên hàm của hàm f  x trên đoạn  ; a b và f
 xd x 1; F b  2. a
Tính F a . A. 2 . B. 1. C. 3 . D. 1.    Câu 7:
Trong không gian Oxyz, vectơ u  2 j  k có tọa độ là A. 0; 2;  1  . B. 2; 1  ;0 . C. 0; 2  ;1 . D. 0; 1  ;2 .   Câu 8:
Gọi  là góc giữa hai vectơ u  2;1; 2 , v   3  ;4;0 . Tính cos  . 2 2 2 2 A.  . B. . C.  . D. . 15 15 15 15 Câu 9:
Quay tam giác ABC vuông tại B với AB  2, BC  1 quanh trục AB . Tính thể tích khối tròn xoay thu được. 4 5 2 4 5 4 A. . B. . C. . D. . 5 3 15 3
Câu 10: Cho hình chóp S.ABCD có đáy là hình chữ nhật với AB  2a, BC  a , tam giác đều SAB nằm
trên mặt phẳng vuông góc với đáy. Khoảng cách giữa BC và SD là 2 5 3 5 A. a . B. a . C. 3a . D. a . 5 2 5 Trang76
Câu 11: Tiếp tuyến của đồ thị hàm số 3 2
y  x  3x 1 có hệ số góc nhỏ nhất là đường thẳng
A. y  x . B. y  0 . C. y  3  x  2 . D. y  3  x  2 .
Câu 12: Trong không gian Oxyz , mp  P cắt ba trục tọa độ tại ba điểm phân biệt tạo thành một tam
giác có trọng tâm G 3; 2;  
1 . Viết phương trình mă ̣t phẳng P : x y z x y z x y z x y z A.    1. B.    0. C.    0 . D.    1. 9 6 3 9 6 3 9 6 3 9 6 3
Câu 13: Tổng tất cả các nghiê ̣m của phương trình 2 2020 x 3.2020x  1  0 là A. 3 . B. 1. C. 0 .
D. Không tồn ta ̣i.
Câu 14: Trong không gian Oxyz , cho điểm M 1;2;4 và mặt phẳng  P : x  2y  2z  5  0. Khoảng
cách từ điểm M đến mp P là: 2 3 2 2 2 A. . B. . C. . D. . 3 3 9 9 x  y z 
Câu 15: Trong không gian Oxyz, cho điểm A1;0; 2 và đường thẳng 1 1 d :   . Viết phương 1 1 2
trình đường thẳng  đi qua ,
A vuông góc và cắt d . x 1 y z  2 x 1 y z  2 A.  :   B.  :   . 1 3  1 1 1 1 x 1 y z  2 x 1 y z  2 C.  :   . D.  :   . 2 2 1 1 1 1 
Câu 16: Cho hàm số f  x có đồ thị trên đoạn  3  ;  3 là đường gấp khúc D
ABC như hình vẽ.Tính 3
 f xdx 3  5 35 35 5 A.  . B. . C.  . D. 2 6 6 2
Câu 17: Cho hình nón có đường cao bằng 3, bán kính đường tròn đáy bằng 2. Hình trụ T  nội tiếp hình
nón (một đáy của hình trụ nằm trên đáy của hình nón). Biết hình trụ có chiều cao bằng 1, tính
diện tích xung quanh của hình trụ đó. 2 8 4 2 A. . B. . C. . D. 3 3 9 9
Câu 18: Hệ số của 4
x trong khai triển  x  10 2 1
thành đa thức là: A. 4 4 2 C . B. 6 4 2 C . C. 6 4 2 A . D. 4 4 2 A . 10 10 10 10 2 x 4 x  1 
Câu 19: Tập nghiệm S của bất phương trình  8   là:  2 
A. S  ;  1  3;  .
B. S  1;   .
C. S  ;3 .
D. S  1;3 . Trang77
Câu 20: Trong mặt phẳng tọa độ, cho điểm M như hình vẽ bên là điểm biểu diễn số phức z . Tính   2 1 z . y M 1 x 2  O A.   z2 1  8  i . B.   z2 1  2
  2i . C.   z2 1  1   i . D.   z2 1  2  i .
Câu 21: Cho tứ diện OABC có ,
OA OB, OC đôi một vuông góc và OA  1; OB  2; OC  12 . Tính thể
tích tứ diện OABC . A. 12 . B. 6 . C. 8 . D. 4 . 2
Câu 22: Cho hàm số y  f  x có đạo hàm f ' x  x x  
1  x  3. Số điểm cực tri ̣ của hàm số
y  f  x là: A. 3 . B. 0 . C. 1. D. 2 . 2 4  x
Câu 23: Số tiê ̣m câ ̣n của đồ thi ̣ hàm số y  x  là: 3 A. 1. B. 2 . C. 0 . D. 3 .
Câu 24: Cho hình lăng trụ đều ABC.A'B'C' có cạnh đáy bằng 2a , cạnh bên bằng a . Tính góc giữa hai
mă ̣t phẳng  AB'C'  và  A'B'C'  . A. 0 30 . B. 0 60 . C. 0 45 . D. 0 75 .
Câu 25: Cho số phức z  a  bi với a, b   thỏa mãn 1 i z  2  i z  13  2i . Tính tổng a  b .
A. a  b 1.
B. a  b  2 .
C. a  b  0.
D. a  b  2  .
Câu 26: Phương trình log
x  5  4 có nghiệm là. 2   A. x  11. B. x  3. C. x  13. D. x  21. 2 2
Câu 27: Trong không gian Oxyz , cho mặt cầu S   x   2 :
1  y   z  4  9 . Từ điểm A4;0  ;1 nằm
ngoài mặt cầu, kẻ một tiếp tuyến bất kỳ đến S  với tiếp điểm M . Tập hợp điểm M là đường tròn có bán kính bằng 3 3 3 3 2 5 A. . B. . C. . D. . 2 2 2 2 Câu 28: Giả sử ( )= ( 2 + + ) x F x ax bx
c e là một nguyên hàm của hàm số ( ) 2 x
f x = x e . Tính tích P = abc . A. P = - 4 . B. P = 1. C. P = - 5 . D. P = 3 .
Câu 29: Một nhóm có 2 bạn nam và 3 bạn nữ. Chọn ngẫu nhiên 3 bạn trong nhóm đó, tính xác suất để
trong cách chọn đó có ít nhất 2 bạn nữ. 3 7 2 3 A. . B. . C. . D. . 5 10 5 10
Câu 30: Trong không gian Oxyz , cho điểm A(- 1; 2; ) 4 và điểm B(3;0;- )
6 . Trung điểm của đoạn AB có tọa độ là: A. (4;- 2;- 1 ) 0 . B. (- 4; 2;1 ) 0 . C. (1;1;- ) 1 . D. (2; 2;- 2). 2 log 2  b Câu 31: Biết 3 log 20  a 
với a, b, c  . Tính T  a b  c. 15 log 5  c 3 Trang78 A. T  1  . B. T  3  . C. T  3. D. T  1.
Câu 32: Cho hàm số y  f  x liên tu ̣c trên  có bảng biến thiên sau:
Khẳng định nào sau đây là đúng?
A. Hàm số đạt cực đại tại x  2  .
B. Hàm số đạt cực đại tại x  2 .
C. Hàm số đạt cực đại tại x  4 .
D. Hàm số đạt cực đại tại x  3.
Câu 33: Giá trị nhỏ nhất của hàm số 3
y  x  3x  4 trên đoạn 0; 2 là
A. min y  4 . B. min y  1  .
C. min y  2 .
D. min y  6 . 0;2 0;2 0;2 0;2
Câu 34: Hình bên là đồ thị của một hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hàm số đó là A. 3
y  x  3x 1. B. 3
y  x  3x 1. C. 3
y  x  3x 1. D. 3
y  x  3x 1.
Câu 35: Tính  2x I dx  2x x 1 2  A.  C .
B. 2x ln 2  C .
C. 2x  C . D.  C ln 2 x  . 1
Câu 36: Hàm số nào dưới đây không là nguyên hàm của hàm số   1 f x 
trên khoảng 0; . x 1 A. ln x .
B. ln  x   1 . C. ln 2x . D. 2 ln x . 2 x 1
Câu 37: Tâm đối xứng của đồ thi ̣ hàm số y  có tọa độ là x 1 A.  1  ;0 . B.  1   ;1 . C. 1; 1  . D. 0;  1 . 1 2 3 Câu 38: Biết f  x x d  1   và f  2x 1 x d  3. Tính f  x x. d  0 1 0 A. 5. B. 2. C. 7. D. 4. 
Câu 39: Số giao điểm của đồ thi ̣ hàm số 4 2
y  x  x  2020 và trục hoành là: A. 3. B. 4. C. 1. D. 2.
Câu 40: Cho số phức z thoả mãn z  3  i  0 . Môđun của z bằng A. 10 . B. 10 . C. 3 . D. 4 .
Câu 41: Cho hàm số y  f  x là hàm đa thức bậc bốn, có đồ thị f  x như hình vẽ Trang79
Phương trình f  x  0 có 4 nghiệm phân biệt khi và chỉ khi
A. f 0  0
B. f 0  0  f m . C. f m  0  f n . D. f 0  0  f n . Câu 42: Cho hàm số
f  x có đạo hàm và đồng biến trên 1; 4, thoả mãn 4
x  x f  x   f   x 2 2 .  , x   
1;4. Biết rằng f   3 1 
. Tính tích phân I  f  xdx ? 2 1 9 1187 1188 1186 A. . B. . C. D. . 2 45 45 45 Câu 43: Cho hàm số 3 2
y  x  mx   2 3 3 m  
1 x  2020 . Có tất cả bao nhiêu giá trị nguyên của m sao
cho hàm số có giá trị nhỏ nhất trên khoảng 0;  A. 3 . B. 1. C. vô số. D. 2 .
Câu 44: Có tất cả bao nhiêu số tự nhiên gồm 6 chữ số đôi một khác nhau trong đó có đúng 3 chữ số chẵn A. 60000 . B. 72000 . C. 36000 . D. 64800
Câu 45: Cho hàm số y  f  x liên tu ̣c trên  có đồ thị hàm số y  f  x cho như hình vẽ.
Hàm số g x  f  x 1 2 2
 x  2x  2020 đồng biến trên khoảng nào? A.  2  ;0 . B.  3   ;1 . C. 1;3 . D. 0;  1 .
Câu 46: Tìm tất cả các giá trị thực của m để hàm số 3 2 1 2x x mx y    
đồng biến trên 1;2 . A. m  1  . B. m  8  . C. m  8  . D. m  1  .
Câu 47: Cho lăng trụ đứng AB . C A B  C
  có chiều cao bằng 4 , đáy ABC là tam giác cân tại A với  O
AB  AC  2;BAC  120 . Diện tích mặt cầu ngoại tiếp lăng trụ trên 64 2 32 2 A. 16 . B. 32 . C.  . D. . 3 3
Câu 48: Cho bất phương trình log  2
x  2x  2 1  log  2
x  6x  5  m . Có tất cả bao nhiêu giá trị 7 7 
nguyên của tham só m để bất phương trình trên có tập nghiệm chứa khoảng 1;3 ? A. 35 . B. 36 . C. 34 . D. Vô số. Trang80
Câu 49: Cho hình hộp đứng ABC . D A B  C  D
  có AA  2 , đáy ABCDlà hình thoi với ABC là tam
giác đều cạnh 4. Gọi M , N, P lần lượt là trung điểm của B C  ,C D
 , DD và Q thuộc cạnh BC
sao cho QC  3Q .
B Tính thể tích tứ diện MNP . Q 3 3 3 3 A. . B. . C. . D. n 3 3 . 4 2 2
Câu 50: Cho hàm số y  f  x liên tu ̣c trên đoa ̣n  1
 ;4 và có đồ thị như hình vẽ
Có tất cả bao nhiêu giá tri ̣ nguyên của m thuô ̣c đoa ̣n 1
 0;10 để bất phương trình
f  x  m  2m đúng với mo ̣i x thuô ̣c đoa ̣n  1  ;4? A. 5 . B. 6 . C. 7 . D. 8 . ĐÁP ÁN 1-D 2-C 3-B 4-D 5-A 6-B 7-A 8-C 9-B 10-C 11-C 12-C 13-B 14-B 15-D 16-D 17-B 18-A 19-A 20-D 21-D 22-D 23-C 24-A 25-A 26-D 27-C 28-A 29-B 30-C 31-D 32-B 33-C 34-D 35-A 36-B 37-B 38-A 39-D 40-A 41-B 42-D 43-C 44-D 45-D 46-A 47-B 48-C 49-C 50-C
LỜI GIẢI CHI TIẾT Câu 51: Chọn D  
Ta có một vectơ pháp tuyến của mp  P là n  1; 1
 ;0 hay n   1  ;1;0 . Câu 52: Chọn C 3  Ta có y      x . x  2 0, 2 2 Câu 53: Chọn B x 1 y z  3
Vì d đi qua điểm A1; 1
 ;0và song song với đường thẳng  :   2  nên d có 1 5  VTCP u  2; 1  ;5 x 1 2t 
Do đó PTĐT d : y  1   t z  5t 
Với t 1  d đi qua điểm M 3; 2  ;5    Do đó PT củ x 3 y 2 z 5 a d là   . 2 1  5 Trang81 Câu 54: Chọn D.
Hàm số y  log x xác định trên D  0;  , nên mệnh đề 1 đúng. a
Hàm số y  log x đồng biến trên 0; nếu a 1, nghịch biến trên 0; nếu 0  a 1, a
do đó mệnh đề 2 đúng.
Đồ thị hàm số y  log x và x
y  a đối xứng nhau qua đường thẳng y  x , nên mệnh đề 3 a đúng.
Đồ thị hàm số y  log x nhận tru ̣c Oy làm tiện cận đứng nên mệnh đề 4 sai. a
Do đó có 3 mệnh đề đúng. Câu 55: Chọn A. Hàm số xác định khi 3
x  27  0  x  3.
Vậy tập xác định của hàm số là D  3;  . Câu 56: Chọn B. b Ta có f
 xd x  F b F a 1, suy ra Fa  F b1 211. a Câu 57: Chọn A    
Ta có: u  2 j  k  u  0; 2;   1 . Câu 58: Chọn C   . u v 6   4  0 2
Ta có: cos        . u . v 4 1 4. 9 16  0 15 Câu 59: Chọn B
Khi quay tam giác ABC vuông tại B quanh trục AB ta được khối nón có bán kính đáy
r  BC 1 và có chiều cao h  AB  2 .  Khi đó, thể 1 1 2
tích khối nón tạo ra là: 2 2 V  r  h  .1  .2  . 3 3 3 Câu 60: Chọn C Trang82
Gọi H là trung điểm AB thì SH   ABCD . Vì BC ¤ 
¤ SAD nên d BC, SD  d BC,SAD  d B,SAD.
Gọi I là trung điểm của SA thì BI  SA thì BI  SAD (do AD  SAB  BI . a
Suy ra d B SAD 2 3 ,  BI   a 3 . 2 Câu 61: Chọn C
Ta có đạo hàm y  x  x  x  2 2 3 6 3 1  3  3  .
Do đó tiếp tuyến có hệ số góc nhỏ nhất k  3
 tại điểm có hoành độ x 1 y  1  . 0 0
Phương trình tiếp tuyến cần tìm là y  3  x   1 1  y  3  x  2 . Câu 62: Chọn C Gọi A ;
a 0;0, B 0; ;
b 0,C 0;0;c là tọa độ các giao điểm của P và các trục Ox,Oy,Oz .
Vì G là trọng tâm ABC nên suy ra a  9, b  6, c  3 .
Vậy phương trình mặt phẳng cần tìm là x y z    0 . 9 6 3 Câu 63: Chọn B   3 5    x 3 5 x  log   2020 2020    2    2 x x 2 2020  3.2020 1  0     .       x 3 5 3 5 2020  x  log   2020  2    2              Khi đó 3 5 3 5 3 5 3 5 x  x  log    log    log  .   log 1  0 . 1 2 2020 2020 2020 2020       2 2 2 2       Câu 64: Chọn B 1.1 2.2  2.4  5 2
Ta có d M ,P   .    2 2 2 3 1 2 2 Câu 65: Chọn D 
Gọi B    d  B 1 t;t;1 2t   AB  t;t; 2t  3 .   Ta có   d  .
AB a  0  t  t  4t  6  0  t  1  B 2;1  ;1 . d Trang83 Khi đó   AB . 
Phương trình đường thẳng  qua A và có véctơ chỉ phương AB  1;1;  1 là: x 1 y z  2  :   . 1 1 1  Câu 66: Chọn D 3 5
Dựa vào đồ thị, ta xác định được AB : y  x  3 , BC : y  1, CD : y   x  2 2  x  3 khi  3  x  2  
Suy ra f  x  1  khi  2  x  1  3 5  x  khi1  x  3  2 2 3 2  1 3   5
Vậy  f x x   x   3 5 d 3 dx  dx   x  d    x  .  2 2  2 3  3  2  1 Câu 67: Chọn B
Từ giải thiết, ta có hình vẽ như sau
Với SO  3, OA  2, CD 1. AC CD 1 1 2 4
Ta có CD// SO  
  AC  AO   OC  . AO SO 3 3 3 3 8
Vậy diện tích xung quanh hình trụ là S  2 .OC.CD  xq 3 Câu 68: Chọn A  k 
Số hạng thứ k 1 trong khai triển  x  10 2 1 là T  k k C . k x 10 10  k .2 . k C x k  2 10 .1 1 10 10
Xét 4 10  k  k  6 . 
Vậy hệ số của số hạng chứa 4 x là 6 10 6 6 4 4 4 C .2
 C .2  C .2 . 10 10 10 Câu 69: Chọn A 2 x 4 x 2  1    Ta có: x 4 x 3 2  8  2
 2  x  4x  3    2   x 1 2
 x  4x  3  0   . x  3 Câu 70: Chọn D Ta có: M  2  ;  1  z  2   i . 2 2
Vậy   z    i 2 1 1
1 2i  i  2  i . Câu 71: Chọn D Trang84 . OA . OB OC 24 Ta có: V    4. OABC 6 6 Câu 72: Chọn D
Ta có: Bảng biến thiên như sau:
Dựa vào bảng biến thiên ta thấy hàm số có 2 cực trị. Chọn đáp án D. Câu 73: Chọn C
Ta có: Tập xác định D   2  ;2 . x  3   D   2
 ;2 nên đồ thị hàm số đã cho không có tiệm cận đứng.
Đồ thị hàm số không có tiệm cận ngang do x không thể tiến tới  Chọn đáp án C. Câu 74: Chọn A A C a B C' A' 2a I B'
Gọi I là trung điểm B'C' nên  AB'C'   A'B'C'   ;   AIA  a Từ đó 2 3 AI   a 3 . 2 AA a
Trong tam giác vuông AIA' có:  ' 3 tan AIA'    . A' I a 3 3
Vậy  AB C  A B C   0 ' ' ; ' ' '  AIA' 30 . Chọn đáp án A. Câu 75: Chọn A
z  a  bi  z  a  bi .
Theo giả thiết 1 i z  2  i z  13  2i
 1 ia bi  2 ia bi 13 2i a  3
 3a  2b bi 13 2i  
 a  b 1. b   2  Câu 76: Chọn D
Điều kiện x  5. Trang85
Phương trình log x 5 4
 4  x 5  2  x  21. 2 Câu 77: Chọn C M R r A I O
Hình vẽ minh họa mặt cắt đi qua A4;0 
;1 và tâm I mặt cầu.
Gọi O là tâm và r là bán kính đường tròn là tập hợp các tiếp điểm của các tiếp tuyến với mặt cầu S  .
Mặt cầu S  có tâm I 1;0; 4 và bán kính R  3. 2 2 2
Ta có AI  1 4  0  0  4   1  3 2 2 2
 AM  AI  R  18 9  3 . AM.IM 3.3 3 2
Vậy bán kính đường tròn tập hợp các điểm M là r    . AI 3 2 2 Câu 78: Chọn A ¢
F (x) là nguyên hàm của f (x) Û ( ¢ )= ( )Û ( 2 é + + ê ) x 2 x F x f x ax bx c e ù = x e ë úû íï a = 1 íï a = 1 ï ï ï Û é + + + + ù ï 2 ax ê
(2a b)x (b c) x 2 x e = x e Û ë ú
ì 2a + b = 0 Û ì b = - 2 û ï ï ï ï ï b + c = 0 ï c = 2 ïî ïî Suy ra: P = - 4 . Câu 79: Chọn B
Số cách chọn 3 bạn bất kỳ là: 3 C = 10 5
TH1 Chọn 2 bạn nữ, 1 bạn nam: Có 2 C .2 = 6 cách. 3
TH2 Chọn 3 bạn nữ: Có 1 cách.
Suy ra số cách chọn 3 bạn sao cho trong đó có ít nhất 2 nữ là 7 cách. 7 Xác suất cần tìm là: 10 Câu 80: Chọn C
Áp dụng công thức tính tọa độ trung điểm ta có tọa độ trung điểm AB là: æ- 1+ 3 2+ 0 4+ (- 6)ö ç ÷ ç ; ; ÷= ç ÷ (1;1;- ) 1 . çè 2 2 2 ÷ø Câu 81: Chọn D log  2 2 .5 log 20      3
 2log 2 log 5 2log 2 1 1 log 5 2 log 2 1 3 3 3 log 20    3 3 3  1 . 15 log 15 log 5.3 log 5 1 log 5 1 log 5 1 3 3   3 3 3
Do đó a 1; b  1
 ; c 1T  a bc 1. Câu 82: Chọn B
Hàm số đạt cực đại tại x  2 . Câu 83: Chọn C Trang86 x 1 2
y  3x  3 ; y  0   . x  1    0;2
Ta có: y 0  4 ; y  
1  2 ; y 2  6 .
Vậy min y  y 1  2 . 0;2 Câu 84: Chọn D
Dễ thấy lim y   ;
 lim y    a  0. x x
Mặt khác hàm số đạt cực trị tại x  1; x  1 nên y  1  0; y  1  0 .
Vậy đây là đồ thị của hàm số 3
y  x  3x 1. Câu 85: Chọn A x 2x I  2 dx   C  . ln 2 Câu 86: Chọn B    x   1 1 ln 1      . x 1 x
Nên hàm số y  ln x  
1 không là nguyên hàm của hàm số   1 f x  . x Câu 87: Chọn B
Ta có: Tâm đối xứng của đồ thị là giao điểm của hai đường tiệm cận
Đường tiệm cận đứng: x  1 
Đường tiệm cận ngang: y  1.
Vậy tâm đối xứng của đồ thị có tọa độ là  1   ;1 . Chọn đáp án B. Câu 88: Chọn A
Ta đặt : t  2x 1  dt  2d . x 2 3 3 f   x  1 2 1 dx  f
 tdt 3  f
 xdx  6 2 1 1 1 3 1 3 Mà f
 xdx  f
 xdx f
 xdx  1   6  5. 0 0 1 Câu 89: Chọn D Xét PT HĐGĐ: 4 2
x  x  2020  0 Đặt 2 t  x  0.
Phương trình có hai nghiệm trái dấu, do đó có hai nghiệm x , x . 1 2
Vậy chọn đáp án D. Câu 90: Chọn A
Ta có: z   i 
 z  i  z  z    2 2 3 0 3 3 1  10 . Câu 91: Chọn B x  m 
Ta có f  x  0  x  0 
. Khi đó ta có bảng biến thiên x  n  Trang87 0 n Ta có f 
 xdx  f 
 xdx  f m f 0  f n f 0  f m  f n. m 0
Dựa vào bảng biến thiên để phương trình f  x  0 có 4 nghiệm thì f 0  0  f m . Câu 92: Chọn D
Vì f  x có đạo hàm và đồng biến trên 1; 4 suy ra f  x  0, x  1;4 . Khi đó f  x  x  2 .
x f  x   f    x 2   x 1   2 f  
x   f     x 2     x   
 12f x
1 2 f  x
 1 2 f x 2 3  x  C . 3 2  2 4  3 x  1   3 2 4  3 3  Mà f   1 
 1 3   C  C   f x  2 3 3 2 2  2 4  3 x  1 4 4    
 I  f x 3 3 1186 dx  dx    . 2 45 1 1 Câu 93: Chọn C Ta có: 2
y  x  mx   2 3 6 3 m   1 . 2 y 
 x  mx   2 m   2
  x  mx   2 0 3 6 3 1 0 2 m  
1  0  x  m 1. Bảng biến thiên x ∞ m-1 m+1 + ∞ y' + 0 0 + f(m-1) y f(m+1)
Dựa vào bảng biến thiên để hàm số có giá trị nhỏ nhất thuộc khoảng 0;  m 1  0; m 1  0  m  1         f  m   1  f 0 m  3
1  3mm  2 1  3 2   2 m   1  2020  2020  2  m  2  0  m  1  .
Vậy có vô số giá tri nguyên m . Câu 94: Chọn D
Trường hợp 1: (Ba số chẵn không có mặt số 0 ) + Chọn 3 số chẵn: 3 C (cách) 4 + Chọn 3 số lẻ: 3 C (cách) 5
+ Sắp xếp 6 số đã chọn: 6!(cách) Suy ra có: 3 3
C .C .6!  28800 (cách) 4 5
Trường hợp 2: (Ba số chẵn có mặt số 0 )
+ Sắp xếp số 0 (khác vị trí đầu): 5 (cách). Trang88 + Chọn 2 số chẵn: 2 C (cách). 4 + Chọn 3 số lẻ: 3 C (cách). 5
+ Sắp xếp 5 số đã chọn: 5!(cách). Suy ra có: 2 3
5.C .C .5!  36000 (cách). 4 5
Vậy có 28800  36000  64800 (cách). Câu 95: Chọn D.
Ta có: g  x  f  x 1   x  x 
 g x  2 f  x 1 x  2 2 2 2 2020 1  20 1 2
Xét hàm số k x    f x   x  2 1 2 1 1  2021 .
Đặt t  x 1
Xét hàm số: ht  f t 2 2
 t  2021  ht  2 f t  2t .
Kẻ đường y  x như hình vẽ. t  1 
Khi đó: ht  0  f t t  0  f t  t   . 1   t  3 x    x 
Do đó: kx   1 1 0 1  0     . 1   x 1 3 2  x  4
Ta có bảng biến thiên của hàm số k x    f x   x  2 1 2 1 1  2021 .
Khi đó, ta có bảng biến thiên của g  x  f  x 1  x  2 2
1  2021 bằng cách lấy đối xứng
qua đường thẳng x 1 như sau: Câu 96: Chọn A.
Tập xác định: D   3 2 1 2x x mx y     3 2
x  x mx 1  y     2 2
.ln 2. 3x  2x  m Hàm số 3 2 1 2x x mx y    
đồng biến trên 1;2 khi và chỉ khi y  0, x  1;2 3 2
x  x mx 1    2 2
.ln 2. 3x  2x  m  0, x  1;2 2
 3x  2x  m  0, x  1;2 2  m  3  x  2 , x x  1;2 Trang89  m  max  2
3x  2x  1. 1;2 Câu 97: Chọn B
Gọi H là tâm đường tròn ngoại tiếp của tam giác ABC và K là trung điểm của đoạn AA¢.
Dựng đường thẳng d vuông góc với mặt phẳng (ABC) tại H và đường thẳng trung trực d ¢
của đoạn AA¢ nằm trong mặt phẳng (d; d )
¢ . Giao điểm I của d và d ¢ là tâm mặt cầu ngoại
tiếp lăng trụ đứng AB . C A B  C
  và R = AI là bán kính của mặt cầu này. Ta có 2 2 o BC 
AB  AC  2A . B AC cos120  2 3
Áp dụng định lý sin cho tam giác ABC ta có BC = Þ =  2 AH AH 2 sin BAC
Xét hình chữ nhật AKIH ta có 2 2 R = AI = IH + AH = 2 2 .
Vậy diện tích mặt cầu bằng 2
S = 4 R = 32 . Câu 98: Chọn C Ta có: log  2
x  2x  2 1  log  2
x  6x  5  m   1 7 7   log  2
7x 14x 14  log  2
x  6x  5  m 4 2
 7x 14x 14  x  6x  5  m  0 7 7  2 2
 6x  8x  9  m  x  6x  5 * .
Bất phương trình trên có tập nghiệm chứa khoảng 1;3 khi và chỉ khi * đúng với mọi x  1;3 .
Ta có bảng biến thiên của hai hàm số 2
y  6x  8x  9 , 2
y  x  6x  5 trên khan 1;3 như sau: Suy ra 1
 2  m  23, mà mN * nên m 1  1,...2,3,4,5,2 
2 . Vậy tổng các giá trị m thỏa mãn bài là 34 . Trang90 Câu 99: Chọn C
Lấy K CD : KC  3KD  KQ //BD //MN  d  ,
Q  PMN   d K,PMN  . V V V . . Q PMN K.PMN M .PKN Ta có: S  S       S S    S PKN DCC D DKP PND KCC N  1 1 1        3 4.2 .1.1 .1.2 . 2 3 .2  . 2 2 2 2 Vì  A B  C  D    DCC D    C D
  và M  A B  C  D  
 d M,DCC D
   d M,C D
   d M, A B   do A B  //C D  . 1 1 1 Lại có S                   d M A B A B A B B M B d M A B A B . A B M  , . . . .sin .  , . 2 2 2
 d M , AB  B M
 .sin B  2.sin 60  3 .
Vậy thể tích của khối tứ diện MNPQ là: 1 1 3 3 V V  .d M, A B   .S  . 3.  . MNPQ M .PKN    3 PKN 3 2 2 Câu 100: Chọn C
Ta có điều kiện của m là: m  0.
Khi đó: f x  m  2m  2
 m  f x m  2m  3
 m  f x  m . m  3 
Yêu cầu bài toán   3  m  2   m  3. m  0 
Lại có m và m 1
 0;10  m4,5,6,7,8,9,1 
0  có 7 giá trị m thỏa mãn. Đề 5
ĐỀ LUYỆN THI CẤP TỐC TỐT NGHIỆP THPT NĂM 2021 Thuvienhoclieu.Com BÀI THI: TOÁN
Thời gian: 90 phút Câu 1.
Khối trụ tròn xoay có thể tích bằng 144 và có bán kính đáy bằng 6. Đường sinh của khối trụ bằng A. 4 . B. 6 . C. 12 . D. 10 . Câu 2.
Trong các hàm số sau đây, hàm số nào nghịch biến trên tập  ? x  1  x A. x y   .
B. y    .
C. y  3 . D. 3x y  .  3  Trang91 2 Câu 3.
Giá trị của tích phân 2 d  x x bằng 0 A. 8 . B. 6 . C. 2 . D. 4 . Câu 4.
Đường cong ở hình bên là đồ thị của hàm số nào dưới đây? x 1 x 1 A. 3
y  x  2x 1 . B. y  . C. y  . D. 3 2
y  x  x 1 . x 1 x 1 Câu 5.
Trong không gian Oxyz , cho mặt phẳng  P : x  2y  3z  2020  0 . Vectơ nào dưới đây
không phải là một vectơ pháp tuyến của mặt phẳng  P ?     A. n   2  ;4;6 .
B. n  1; 2; 3   . C. n  1; 2  ;3 . D. n   2  ;3;2020 . Câu 6.
Cho số phức z  5  3i . Số phức liên hợp của z là A. 5  3i . B. 5  3i . C. 5  3i . D. 5i  3. Câu 7.
Trong mặt phẳng Oxy , điểm M biểu diễn số phức z  1
 3i có tọa độ là A. M 1; 3   . B. M  1  ; 3   . C. M  1  ;3 .
D. M 1;3 . Câu 8.
Cho các số thực dương a, b và a  1. Biểu thức 2 log a b bằng a
A. 21 log b b  b  b a . B. 2 loga . C. 2 loga . D. 1 loga . Câu 9.
Thể tích khối lăng trụ tam giác có chiều cao bằng 2 , cạnh đáy lần lượt bằng 3 , 4 , 5 là: A. 8. . B. 12. . C. 4.. D. 28. .
Câu 10. Trong các khối hình sau, khối không phải khối tròn xoay là: A. Khối cầu. B. Khối trụ. C. Khối lăng trụ. D. Khối nón.
Câu 11. Họ tất cả các nguyên hàm của hàm số f  x 2
 sin x  là x 2
A. cosx  2ln x  C . B. cosx   C . 2 x
C.  cosx  2ln x  C .
D.  cosx  2ln x  C .     
Câu 12. Trong không gian với hệ tọa độ Oxyz , cho a  2
 i  3 j  5k . Tọa độ của a là A. 2;3;5 . B.  2  ;3;5. C. 2;3;  5.
D. 2; 3; 5 .
Câu 13. Cho 2 số thực dương x , y thỏa mãn x 1 và log y  3 . Tính 5  . x T log 3 y x Trang92 5 9 3 A. T  . B. T  . C. T  . D. T  5. 3 5 5
Câu 14. Trong không gian Oxyz , cho điểm M 2;1;3 và mặt phẳng  :2x  5y  z 1  0 . Phương
trình mặt phẳng nào dưới đây đi qua điểm M và song song với   .
A. 2x  5 y  z 12  0 .
B. 2x  5 y  z 12  0 .
C. 2x  5 y  z 12  0 .
D. 2x  5 y  z 12  0 .
Câu 15. Cho hàm số y  f  x có đồ thị như hình vẽ bên.
Hàm số đã cho nghịch biến trên khoảng A. 0 ; 2. B.  3  ;   1 . C.  1  ; 0 . D. 1 ; 3 . x  2
Câu 16. Đồ thị hàm số y 
có đường tiệm cận ngang là đường thẳng nào sau đây? 2x 1 A. x  1  . B. y  2 . 1 1  C. y  . D. x  . 2 2
Câu 17. Gọi S là tập nghiệm của phương trình 9x 10.3x 
 9  0 . Tổng các phần tử của S bằng 10 A. 1. B. 2 . C. 10 . D. . 3
Câu 18. Một xe ô tô đang chuyển động đều với vận tốc 16 m / s thì người lái xe nhìn thấy một chướng
ngại vật nên đạp phanh tại điểm đó, ô tô chuyển động chậm dần đều với vận tốc v t   2  t 16
trong đó t là thời gian (tính bằng giây) kể từ lúc đạp phanh. Quãng đường mà ô tô đi được
trong 10 giây cuối cùng bằng A. 60m . B. 64m . C. 160m. D. 96m .
Câu 19. Cho hàm số y  f  x có đạo hàm f  x  1, x
  . Mệnh đề nào sau đây đúng? A. f   1  f 2 . B. f   1  f 2 . C. f   1  f 2 . D. f   1  f 2 .
Câu 20. Cho hình vuông ABCD tâm O, độ dài cạnh là 4 .
cm Đường cong BOC là một phần parabol
đỉnh O chia hình vuông thành hai hình phẳng có diện tích lần lượt là S và S (tham khảo hình 1 2 vẽ). Trang93 S Tỉ số 1 bằng S2 1 3 2 1 A. . B. . C. . D. . 2 5 5 3
Câu 21. Một cấp số nhân có số hạng thứ 3 và số hạng thứ 6 lần lượt là 9 và 243  . Khi đó số hạng thứ
8 của cấp số nhân bằng: A. 2187 . B. 2187  . C. 729 . D. 243.
Câu 22. Tìm hàm số F  x không là nguyên hàm của hàm số f  x  sin 2x .
A. F  x 2  cos x .
B. F  x 2  sin x .
C. F  x 1
  cos 2x . D. F x  cos2x . 2
Câu 23. Cho hàm số f  x xác định, liên tục trên  và có bảng biến thiên như hình bên x  1 0 1  y '  0  0  0  y 3 3  1 
Đồ thị hàm số y  f x cắt đường thẳng y  2 tại bao nhiêu điểm? A. 0 . B. 2 . C. 1. D. 4 .
Câu 24. Trong không gian Oxyz, cho hai điểm A 2
 ; 1; 0, B2; 5;  4. Phương trình mặt cầu đường kính AB là 2 2 2 2
A.  x     y   2 2 1  z  12 . B. 2
x   y  3   z  2  48 . 2 2 2 2 2
C.  x  4   y  4   z  4  48. D. 2
x   y   3
 z  2 12 .
Câu 25. Tập nghiệm của bất phương trình log 3x 1  log 25  25x là 5   5    1   6   1 6   6  A.  ;1   . B. ;    . C.  ;  . D. ;1   .  3   7   3 7   7 
Câu 26. Cho hàm số y  f  x liên tục trên  3  ; 
3 và có bảng xét dấu của đạo hàm như hình bên. Trang94
Mệnh đề nào sau đây sai?
A. Hàm số đạt cực tiểu tại x 1.
B. Hàm số đạt cực đại tại x  2 .
C. Hàm số đạt cực đại tại x  1  .
D. Hàm số đạt cực tiểu tại x  0 .
Câu 27. Cho hình hộp ABC . D AB C
 D. Bộ 3 vectơ không đồng phẳng là:
  
  
A. AC, B , D A' D' .
B. AC, AC ', BB ' .
  
   C. A ,
B BD ',C ' D ' .
D. A'C, B ' , D BD ' . 2 2
Câu 28. Cho hai số phức z , z thỏa mãn z z  4, z  3 . Giá trị biểu thức P  z  z bằng 1 2 1 1 2 1 2 A. 13. B. 25. C. 7. D. 19.
Câu 29. Trong không gian với hệ tọa độ Oxyz , cho M 2; 1;3 , N 3; 2;  4 , P 1; 1;2 . Xác định tọa
độ điểm Q để MNPQ là hình bình hành?
A. Q 2; 2;  5 .
B. Q 2; 3; 5 .
C. Q 0;  4;9 .
D. Q 1;3;  2 . x  2
Câu 30. Giá trị nhỏ nhất của hàm số y  trên đoạn 0;  3 là x 1 1 1 A. min y  3  . B. min y  2  . C. min y  . D. min y   . x   0;  3 x   0;  3 x   0;  3 4 x   0;  3 2 1
Câu 31. Cho hàm số y  f  x có đạo hàm liên tục trên 0  ;1 , thỏa mãn f
 xdx  3 và f  1  4 . 0 1 Tích phân xf 
 xdx có giá trị là 0 1 1 A.  . B. . C. 1. D. 1. 2 2
Câu 32. Trong không gian với hệ trục tọa độ Oxyz , cho hai điểm A1;0;3 ; B5;2;  1 . Phương trình
nào sau đây là phương trình dạng chính tắc của đường thẳng đi qua hai điểm A và B ? x  1 y z  3 x  1 y z  3 A.   . B.   . 5 2 1 2 1 2 x  3 y  1 z  1 x  5 y  2 z  1 C.   . D.   . 2 1 2 2 1 2
Câu 33. Có 3 quả bóng tennis được chứa trong một hộp hình trụ (hình vẽ bên) với chiều cao 21 cm và bán kính 3,5 cm .
Thể tích bên trong hình trụ không bị chiếm lấy bởi các quả bóng tennis (bỏ qua độ dày của vỏ
hộp) bằng bao nhiêu? A. 82, 75 3 cm . B. 87, 25 3 cm . C. 85, 75 3 cm . D. 87, 75 3 cm .
Câu 34. Có bao nhiêu số tự nhiên có hai chữ số khác nhau? A. 72. B. 81. C. 90. D. 18. Trang95 2 3
Câu 35. Cho hàm số f  x có đạo hàm f  x   2
x  x x  2  x  4 , x
   . Số điểm cực trị của
hàm số f  x là A. 2 . B. 3 . C. 1. . D. 4 .
Câu 36. Cho hàm số y  f  x có đồ thị hàm số y  f  x như hình vẽ bên
Hàm số y  f  x   2
1  x  2x đồng biến trên khoảng? A.  2  ;  1 . B.  3  ; 2   . C.  3  ;0 . D. 0;  1 .
Câu 37. Trong không gian với hệ tọa độ Oxyz , cho điểm I  ( 2;1;  1 và mặt phẳng
P:2x  y  2z 1 0 . Mặt cầu S có tâm I , cắt P theo một đường tròn có bán kính
r  4 . Mặt cầu S  có phương trình là: 2 2 2 2 2 2
A.  x  2   y   1   z   1  20.
B.  x  2   y   1   z   1 18. 2 2 2 2 2 2
C.  x  2   y   1   z   1  20 .
D.  x  2   y   1   z   1  2 5 .
Câu 38. Đầu tháng một người gửi ngân hàng 400.000.000 đồng ( 400 triệu đồng) với lãi suất gửi là
0, 6% mỗi tháng theo hình thức lãi suất kép. Cuối mỗi tháng người đó đều đặn gửi vào ngân
hàng số tiền là 10.000.000 (10 triệu đồng). Hỏi sau ít nhất bao nhiêu tháng ( kể từ lúc người
này ra ngân hàng gửi tiền) thì số tiền người đó tích lũy được lớn hơn 700.000.000 (bảy trăm triệu đồng)? A. 22 tháng. B. 23 tháng. C. 25 tháng. D. 24 tháng.
Câu 39. Cho đồ thị hàm số 3 2
y  ax  bx  cx  d như hình vẽ dưới đây: Trang96 2   Đồ 3x x 2
thị của hàm số g  x 
có bao nhiêu đường tiê ̣m câ ̣n đứng? 2
3 f  x  6 f  x A. 5 . B. 4 . C. 3 . D. 2 .
Câu 40. Cho hàm số f  x có bảng xét dấu của đạo hàm như hình bên.
Hàm số y  f 1 x nghịch biến trên khoảng A. 1; 4 . B. 0; 2 . C. 0;  1 . D.  2  ;  1 .
Câu 41. Trong không gian với hệ tọa độ Oxyz , cho hình hộp ABC . D A B  C  D
  biết A1;2;3 , B2;0; 1
  , C 3;0;3 và D 2
 ;4; 3 . Tọa độ đỉnh B của hình hộp ABC . D A B  C  D   là
A. B 4; 1;  1 .
B. B 2; 1; 2 .
C. B 4;1;   1 .
D. B 0;1;  3 .
Câu 42. Cho hình chóp S.ABCD có đáy là hình vuông cạnh AB  2a , S
 AB là tam giác cân tại S và
nằm trong mặt phẳng vuông góc với mặt phẳng  ABCD . Gọi M , N lần lượt là trung điểm của
AB, BC và G là trọng tâm S
 CD. Biết khoảng cách từ điểm M đến mặt phẳng SND bằng
3a 2 . Thể tích của khối chóp . G AMND bằng 4 3 5 3a 3 5 3a 3 5 3a 3 5 3a A. . B. . C. . D. . 2 6 3 18
Câu 43. Cho hình thang ABCD  AB // CD biết AB  5, BC  3, CD 10 , AD  4 . Thể tích khối tròn
xoay tạo thành khi quay hình thang ABCD  AB // CD quanh trục AD bằng A. 128 . B. 84 . C. 112 . D. 90 .
Câu 44. Cho lăng trụ AB . C A B  C
 có đáy là tam giác đều cạnh a , hình chiếu vuông góc của đỉnh A lên
ABC là trung điểm H của cạnh AB . Góc giữa đường thẳng A C
 và mặt đáy bằng 60.
Khoảng cách giữa BB và A C  là a 13 3a 13 2a 13 a 13 A. . B. . C. . D. . 39 13 13 13     
Câu 45. Tập xác định của hàm số f  x  log  log  log  log  log x  là một khoảng có độ dài 1 4 1 16 1     2 4     16 
m với m và n là số nguyên dương và nguyên tố cùng nhau. Khi đó m  n bằng: n A. 240  . B. 271. C. 241 . D. 241.
Câu 46. Số điểm cực đại của đồ thị hàm số y   x  
1  x  2 x  3... x 100 bằng A. 50 . B. 99 . C. 49 . D. 100 .
Câu 47. Cho các số thực dương x , y thỏa mãn
log x  log y  log x  log y  100 và log x ,
log y , log x , log y là các số nguyên dương. Khi đó kết quả xy bằng A. 200 10 . B. 100 10 . C. 164 10 . D. 144 10 . Câu 48. Cho hàm số 3 2
y  ax  bx  cx  d có đồ thị như hình vẽ bên Trang97
Giá trị nguyên lớn nhất của tham số m để hàm số y  f  x  m đồng biến trên khoảng 10; là A. 10  . B. 10 . C. 9 . D. 11.
Câu 49. Cho hàm số f  x liên tục trên  và thoả mãn      2 3 2 1 x xf x f x  e , x    . 0 Khi đó f
 xdx bằng: 1  A. 0 . B. 3e   1 .
C. 31 e . D. 3e .
Câu 50. Một hộp đựng 9 thẻ được đánh số từ1 đến 9 . Rút ngẫu nhiên hai thẻ từ hộp nêu ở trên, tính
xác suất để tích của hai số trên hai thẻ này là số chẵn. 25 13 5 1 A. . B. . C. . D. . 81 18 18 2 …..HẾT….. BẢNG ĐÁP ÁN 1.A 2.B 3.D 4.C 5.D 6.C 7.B 8.C 9.B 10.C 11.C 12.B 13.D 14.A 15.C 16.C 17.B 18.D 19.A 20.A 21.B 22.D 23.B 24.D 25.C 26.D 27.D 28.A 29.C 30.B 31.C 32.C 33.C 34.B 35.B 36.D 37.C 38.B 39.A 40.D 41.A 42.D 43.B 44.B 45.D 46.C 47.C 48.C 49.B 50.B
LỜI GIẢI CHI TIẾT Câu 1.
Khối trụ tròn xoay có thể tích bằng 144 và có bán kính đáy bằng 6. Đường sinh của khối trụ bằng A. 4 . B. 6 . C. 12 . D. 10 . Lời giải Chọn A
Gọi h, l, r lần lượt là chiều cao, đường sinh và bán kính đáy của khối trụ. Ta có: 2 V   r h 2
 144  .6 .h  h  4 .
Vậy khối trụ có độ dài đường sinh là: l  h  4 . Câu 2.
Trong các hàm số sau đây, hàm số nào nghịch biến trên tập  ? x  1  x A. x y   .
B. y    .
C. y  3 . D. 3x y  .  3  Lời giải Chọn B Trang98 Hàm số mũ x
y  a nghịch biến trên tập  khi và chỉ khi 0  a 1. 2 Câu 3.
Giá trị của tích phân 2 d  x x bằng 0 A. 8 . B. 6 . C. 2 . D. 4 . Lời giải Chọn D 2 2 Ta có: 2 2 2 2 d   2  0  4  x x x . 0 0 Câu 4.
Đường cong ở hình bên là đồ thị của hàm số nào dưới đây? x 1 x 1 A. 3
y  x  2x 1 . B. y  . C. y  . D. 3 2
y  x  x 1 . x 1 x 1 Lời giải Chọn C
Dựa vào hình vẽ suy ra đồ thị hàm số có 2 đường tiệm cận là x 1 và y  1. x 1
Vậy đường cong ở trên là đồ thị hàm số y  . x 1 . Câu 5.
[Mức độ 1] Trong không gian Oxyz , cho mặt phẳng  P : x  2y  3z  2020  0 . Vectơ nào
dưới đây không phải là một vectơ pháp tuyến của mặt phẳng P ?     A. n   2  ;4;6 .
B. n  1; 2; 3   . C. n  1; 2  ;3 . D. n   2  ;3;2020 . Lời giải Chọn D 
+) Mặt phẳng  P : x  2y  3z  2020  0 có một vectơ pháp tuyến là n  1; 2;3 . P  
+) Các vectơ ở phương án A;B;Ccùng phương với n nên cũng là vectơ pháp tuyến của P . P   +) Vectơ n   2
 ;3;2020 ở phương án D không cùng phương với n nên không phải là vectơ P
pháp tuyến của  P . Trang99 Câu 6.
Cho số phức z  5  3i . Số phức liên hợp của z là A. 5  3i . B. 5  3i . C. 5  3i . D. 5i  3. Lời giải Chọn C
Số phức z  a  bi , ;
a b    có số phức liên hợp là z  a  bi .
Vậy số phức z  5  3i có số phức liên hợp là z  5  3i . Câu 7.
Trong mặt phẳng Oxy , điểm M biểu diễn số phức z  1
 3i có tọa độ là A. M 1; 3   . B. M  1  ; 3   . C. M  1  ;3 .
D. M 1;3 . Lời giải Chọn B
Điểm M biểu diễn số phức z  1
 3i là M  1  ; 3   . Câu 8.
Cho các số thực dương a, b và a  1. Biểu thức 2 log a b bằng a
A. 21 log b b  b  b a . B. 2 loga . C. 2 loga . D. 1 loga . Lời giải Chọn C Ta có: 2 2
log a b  log a  log b  2log a  log b  2  log b . a a a a a a Câu 9.
Thể tích khối lăng trụ tam giác có chiều cao bằng 2 , cạnh đáy lần lượt bằng 3 , 4 , 5 là: A. 8. . B. 12. . C. 4.. D. 28. Lời giải Chọn B A' C'
Khối lăng trụ tam giác có cạnh đáy lần lượt là 3 , 4 , 5 . B'
Vậy đáy là tam giác vuông có hai cạnh góc vuông lần lượt là 3 , 4 . 1
Thể tích khối lăng trụ: V  . B h  .3.4.2  12 . A 2 C . B
Câu 10. Trong các khối hình sau, khối không phải khối tròn xoay là: A. Khối cầu. B. Khối trụ. C. Khối lăng trụ. D. Khối nón. Lời giải Chọn. C.
Khối lăng trụ không phải khối tròn xoay.
Câu 11. Họ tất cả các nguyên hàm của hàm số f  x 2
 sin x  là x 2
A. cosx  2ln x  C . B. cosx   C . 2 x
C.  cosx  2ln x  C . D.  cosx  2ln x  C . Lời giải Chọn C Trang100  2  sinx 
dx   cosx  2ln x  C   .  x      
Câu 12. Trong không gian với hệ tọa độ Oxyz , cho a  2
 i  3 j  5k . Tọa độ của a là A. 2;3;5 . B.  2  ;3;5. C. 2;3;  5.
D. 2; 3; 5 . Lời giải Chọn B 
Tọa độ của a là  2  ;3;5 .
Câu 13. Cho 2 số thực dương x , y thỏa mãn x 1 và log y  3 . Tính 5  . x T log 3 y x 5 9 3 A. T  . B. T  . C. T  . D. T  5. 3 5 5 Lời giải Chọn D Ta có 3
log y  3  y  x . x 5 Suy ra 3 15 1 T  log x
 log x  .15.log x  5 . 3   3 3 x x x Vậy T  5.
Câu 14. Trong không gian Oxyz , cho điểm M 2;1;3 và mặt phẳng  :2x  5y  z 1  0 . Phương
trình mặt phẳng nào dưới đây đi qua điểm M và song song với   .
A. 2x  5 y  z 12  0 . B. 2x  5 y  z 12  0 .
C. 2x  5 y  z 12  0 . D. 2x  5 y  z 12  0 . Lời giải Chọn A
Gọi  P là mặt phẳng đi qua điểm M và song song với   . 
Ta có  P //   nên  P có một véc-tơ pháp tuyến là n  2; 5;  1 . P
Mặt phẳng  P đi qua điểm M và song song với   có phương trình là
2 x  2  5 y  
1  z  3  0  2x  5y  z 12  0 .
Câu 15. Cho hàm số y  f  x có đồ thị như hình vẽ bên. Trang101
Hàm số đã cho nghịch biến trên khoảng A. 0 ; 2 . B.  3  ;   1 . C.  1  ; 0 . D. 1 ;  3 . Lời giải Chọn C
Dựa vào đồ thị ta thấy: Hàm số nghịch biến trên các khoảng là 1 ;  1 và 2 ;  3 .
Nên hàm số cũng nghịch biến  1  ; 0 . x  2
Câu 16. Đồ thị hàm số y 
có đường tiệm cận ngang là đường thẳng nào sau đây? 2x  1 A. x  1  . B. y  2 . 1 1 C. y  . D. x  . 2 2 Lời giải Chọn C x  2 1 x  2 1 Ta có: lim  lim 
x 2x  ; 1
2 x 2x  . 1 2 1
Do đó tiệm cận ngang của đồ thị hàm số là đường thẳng y  . 2
Câu 17. Gọi S là tập nghiệm của phương trình 9x 10.3x 
 9  0 . Tổng các phần tử của S bằng 10 A. 1. B. 2 . C. 10 . D. . 3 Lời giải Chọn B 3x 1 x  0
9x 10.3x  9  0     . 3x  9 x  2  S  0 ,  2 Trang102
Vậy tổng các phần tử của S bằng 2 .
Câu 18. Một xe ô tô đang chuyển động đều với vận tốc 16 m / s thì người lái xe nhìn thấy một chướng
ngại vật nên đạp phanh tại điểm đó, ô tô chuyển động chậm dần đều với vận tốc v t   2  t 16
trong đó t là thời gian (tính bằng giây) kể từ lúc đạp phanh. Quãng đường mà ô tô đi được
trong 10 giây cuối cùng bằng A. 60m . B. 64m . C. 160m. D. 96m. Lời giải Chọn D
Lấy mốc thời gian lúc ô tô bắt đầu đạp phanh.
Khi ô tô dừng hẳn thì v t   0  2
 t 16  0  t  8. 8 8
Quãng đường mà ô tô đi được trong 8 giây cuối:  2
 t 16 dt   2t
 16t  64 m. 0 0
Theo đề bài: ô tô đi được 10 giây cuối cùng nên 2 giây đầu ô tô đi được:16.2  32m .
Vậy quãng đường ô tô đi được trong 10 giây cuối: 64  32  96m.
Câu 19. Cho hàm số y  f  x có đạo hàm f  x  1, x
  . Mệnh đề nào sau đây đúng? A. f   1  f 2 . B. f   1  f 2 . C. f   1  f 2 . D. f   1  f 2 . Lời giải Chọn A
Vì f  x  1  0 x
  nên f  x là hàm số đồng biến trên  . 1
  2  f   1  f 2. .
Câu 20. Cho hình vuông ABCD tâm O, độ dài cạnh là 4 .
cm Đường cong BOC là một phần parabol
đỉnh O chia hình vuông thành hai hình phẳng có diện tích lần lượt là S và S (tham khảo hình 1 2 vẽ). S Tỉ số 1 bằng S2 1 3 2 1 A. . B. . C. . D. . 2 5 5 3 Lời giải Chọn A
Chọn hệ trục tọa độ Oxy, với O là gốc tọa độ, trục Ox đi
qua trung điểm của AB và . CD Trang103
Parabol có dạng  P 2 : y  ax . 1
Vì điểm C 2 ; 2P nên 2  4a  a  . 2 1 Vậy  P 2 : y  x . 2 2  1  16 2 S  2  x dx  .  1    2  3 2  16 32 S  S  S  16   . 2 ABCD 1 3 3 S 1 Vậy 1  . . S 2 2
Câu 21. Một cấp số nhân có số hạng thứ 3 và số hạng thứ 6 lần lượt là 9 và 243  . Khi đó số hạng thứ
8 của cấp số nhân bằng: A. 2187 . B. 2187  . C. 729 . D. 243. Lời giải Chọn B
Gọi u là số hạng đầu, q là công bội của cấp số nhân. 1 2 u   u q u 243  Ta có: 3 1  3 6  q    2  7  q  3  . 5 u   u q  u 9 6 1 3 Khi đó 2 u  u q  2  43.9  2  187. 8 6
Câu 22. Tìm hàm số F  x không là nguyên hàm của hàm số f  x  sin 2x .
A. F  x 2  cos x .
B. F  x 2  sin x .
C. F  x 1
  cos 2x . D. F x  cos2x . 2 Lời giải Chọn D 
Vì  cos 2x  2sin 2x nên F  x   cos 2x không phải là một nguyên hàm của hàm số
f  x  sin 2x .
Câu 23. Cho hàm số f  x xác định, liên tục trên  và có bảng biến thiên như hình bên x  1 0 1  y '  0  0  0  y 3 3  1 
Đồ thị hàm số y  f x cắt đường thẳng y  2 tại bao nhiêu điểm? A. 0 . B. 2 . C. 1. D. 4 . Lời giải Trang104 Chọn B Vì 2   1
 nên đường thẳng y  2 nằm dưới đường thẳng y  1. x  1 0 1  y '  0  0  0  y 3 3 1 y  2  
Từ bảng biến thiên suy ra đồ thị hàm số y  f  x cắt đường thẳng y  2 tại 2 điểm phân biệt.
Câu 24. Trong không gian Oxyz, cho hai điểm A 2
 ; 1; 0, B2; 5;  4. Phương trình mặt cầu đường kính AB là 2 2 2 2
A.  x     y   2 2 1  z  12 . B. 2
x   y  3   z  2  48 . 2 2 2 2 2
C.  x  4   y  4   z  4  48. D. 2
x   y   3
 z  2 12 . Lời giải Chọn D
Gọi I là trung điểm của đoạn AB suy ra I 0; 3;  2. 
Ta có: AB  4; 4;  4, AB     2 2 2 4 4 4  2 12. 1
Mặt cầu đường kính AB có tâm I 0; 3;  2 và bán kính R 
AB  12 có phương trình là 2
x   y  2   z  2 2 3 2 12..
Câu 25. Tập nghiệm của bất phương trình log 3x 1  log 25  25x là 5   5    1   6   1 6   6  A.  ;1   . B. ;    . C.  ;  . D. ;1    3   7   3 7   7  Lời giải Chọn C  1 3  x 1  0 x   Điề 1 u kiện:    3    x 1. 25  25x  0 3 x 1
Ta có: log 3x 1  log
25  25x  3x 1 25  6
25x  28x  24  x  . 5   5   7  
Kết hợp với điều kiện ta có tập nghiệm của bất phương trình đã cho là: 1 6 S   ; .   .  3 7 
Câu 26. Cho hàm số y  f  x liên tục trên  3  ; 
3 và có bảng xét dấu của đạo hàm như hình bên. Trang105
Mệnh đề nào sau đây sai?
A. Hàm số đạt cực tiểu tại x 1.
B. Hàm số đạt cực đại tại x  2 .
C. Hàm số đạt cực đại tại x  1  .
D. Hàm số đạt cực tiểu tại x  0 . Lời giải Chọn D Ta có bảng biến thiên:
Vậy hàm số đạt cực tiểu tại x  1; hàm số đạt cực đại tại x  1  và x  2..
Câu 27. [Mức độ 1] Cho hình hộp ABC . D AB C
 D. Bộ 3 vectơ không đồng phẳng là:
  
  
A. AC, B , D A' D' .
B. AC, AC ', BB ' .
  
   C. A ,
B BD ',C ' D ' .
D. A'C, B ' , D BD ' . Lời giải Chọn D
3 vectơ đồng phẳng nếu các giá của chúng cùng song song với một mặt phẳng.
  
A. AC, B ,
D A' D' có giá cùng song song với mặt phẳng  ABCD .
  
B. AC, AC ', BB ' có giá cùng song song với mặt phẳng  ACCA.
   C. A ,
B BD ',C ' D ' có giá cùng nằm trên mặt phẳng  ABCD . 2 2
Câu 28. [Mức độ 2]Cho hai số phức z , z thỏa mãn z z  4, z  3 . Giá trị biểu thức P  z  z 1 2 1 1 2 1 2 bằng A. 13. B. 25. C. 7. D. 19. Trang106 Lời giải Chọn A 2 2 Có z z  z
 4 ; z  3 z  9 . 1 1 1 2 2 Khi đó, 2 2 P  z
 z  4  9 13. . 1 2
Câu 29. [Mức độ 2] Trong không gian với hệ tọa độ Oxyz , cho M 2; 1;3 , N 3; 2;  4 , P 1; 1;2 .
Xác định tọa độ điểm Q để MNPQ là hình bình hành?
A. Q 2; 2;  5 .
B. Q 2; 3; 5 .
C. Q 0;  4;9 .
D. Q 1;3;  2 . Lời giải Chọn C x 1 2 3 x  0    Q  Q
MNPQ là hình bình hành khi và chỉ khi PQ  NM   y 1  1
  2  y  4  . Q Q   z  2  3  z  9 Q  4    Q
Vậy Q 0;  4;9  . x  2
Câu 30. [Mức độ 2] Giá trị nhỏ nhất của hàm số y  trên đoạn 0;  3 là x 1 1 1 A. min y  3  . B. min y  2  . C. min y  . D. min y   . x   0;  3 x   0;  3 x   0;  3 4 x   0;  3 2 Lời giải Chọn B x  2 Hàm số y 
liên tục trên đoạn 0;  3 . x 1 3 Ta có y   0 x  0;3 . 2   x   1
Vậy min y  y 0   2  . x   0;3 1
Câu 31. Cho hàm số y  f  x có đạo hàm liên tục trên 0  ;1 , thỏa mãn f
 xdx  3 và f  1  4 . 0 1 Tích phân xf 
 xdx có giá trị là 0 1 1 A.  . B. . C. 1. D. 1. 2 2 Lời giải Chọn C Ta có 1 1 1 1 xf 
 xdx  d x f
 x  xf x  f  xdx 0 0 0 0 1  f   1  f
 xdx  43 1. 0 Trang107
Câu 32. [Mức đô ̣ 1] Trong không gian với hệ trục tọa độ Oxyz , cho hai điểm A1;0;3 ; B5;2;  1 .
Phương trình nào sau đây là phương trình dạng chính tắc của đường thẳng đi qua hai điểm A và B ? x  1 y z  3 x  1 y z  3 A.   . B.   . 5 2 1 2 1 2 x  3 y  1 z  1 x  5 y  2 z  1 C.   . D.   . 2 1 2 2 1 2 Lời giải Chọn C 
Một vectơ chỉ phương của đường thẳng AB là: AB  4;2; 4 . 
Suy ra một vectơ chỉ phương khác của AB là u  2;1; 2 .   
Lại có điểm A1;0;3 thuộc đường thẳng ở phương án C vì: 1 3 0 1 3 1    1. 2 1 2 Vậy chọn C
Câu 33. Có 3 quả bóng tennis được chứa trong một hộp hình trụ (hình vẽ bên) với chiều cao 21 cm và bán kính 3,5 cm .
Thể tích bên trong hình trụ không bị chiếm lấy bởi các quả bóng tennis (bỏ qua độ dày của vỏ
hộp) bằng bao nhiêu? A. 82,75 3 cm . B. 87,25 3 cm . C. 85,75 3 cm . D. 87,75 3 cm . Lời giải Chọn C
Thể tích khối trụ là: V   .3, 2 5 .21 257,25 3 cm . 1
Mỗi quả bóng tennis cũng có bán kính bằng 3,5cm nên 3 quả bóng có thể tích là: 4
V  3. . .3, 3 5  171,5 3 cm . 2 3
Vậy thể tích cần tìm là V  V V  257,25 171,5  85,75 3 cm . 1 2
Câu 34. Có bao nhiêu số tự nhiên có hai chữ số khác nhau? A. 72. B. 81. C. 90. D. 18. Lời giải Chọn B
Gọi ab là số tự nhiên có hai chữ số khác nhau  a,b0;1;2;...;  9 ; a  0  . Ta có:
a có 9 cách chọn (do a  0 ). Trang108
Ứng với mỗi cách chọn a ta có 9 cách chọn b (do a  b ).
Theo quy tắc nhân ta được 9.9  81 số tự nhiên có hai chữ số khác nhau. 2 3
Câu 35. [Mức đô ̣ 2] Cho hàm số f  x có đạo hàm f  x   2
x  x x  2  x  4 , x    . Số điểm
cực trị của hàm số f  x là A. 2 . B. 3 . C. 1. . D. 4 . Lời giải Chọn B
Xét phương trình f  x  x  xx  2 x  3 2 2 4  0 ta có:
+ 2 nghiệm đơn là x  0; x  1.
+ 1 nghiệm bội lẻ là x  4.
+ 1 nghiệm bội chẵn là x  2.
Vậy hàm số f  x đạt cực trị tại các điểm x  0; x  1  ; x  4.
Câu 36. Cho hàm số y  f  x có đồ thị hàm số y  f  x như hình vẽ bên
Hàm số y  f  x   2
1  x  2x đồng biến trên khoảng? A.  2  ;  1 . B.  3  ; 2   . C.  3  ;0 . D. 0;  1 . Lời giải Chọn D Trang109
Đặt g x  f x   2
1  x  2x  g x  f  x  
1  2x  2  f t   2t ( với t  x 1)
Nhìn vào đồ thị nhận thấy 0  t  2 thì f t  2
 t hay gx  0
Khi đó 0  x 1 2  1   x 1. .
Câu 37. Trong không gian với hệ tọa độ Oxyz , cho điểm I  ( 2;1;  1 và mặt phẳng
P:2x  y  2z 1 0 . Mặt cầu S có tâm I , cắt P theo một đường tròn có bán kính
r  4 . Mặt cầu S  có phương trình là: 2 2 2 2 2 2
A.  x  2   y   1   z   1  20.
B.  x  2   y   1   z   1 18. 2 2 2 2 2 2
C.  x  2   y   1   z   1  20 .
D.  x  2   y   1   z   1  2 5 . Lời giải Chọn C 2.2 1 2.11
Ta có d I;P   2 . 2 2 2 2 1  2
Vì mặt cầu  S  có tâm I , cắt  P theo một đường tròn có bán kính r  4 nên mặt cầu  S  có bán kính 2 2
R  r  d I;P 2 2  4  2  2 5 . 2 2 2
Vậy phương trình mặt cầu  S  là  x  2   y   1   z   1  20 .
Câu 38. Đầu tháng một người gửi ngân hàng 400.000.000 đồng ( 400 triệu đồng) với lãi suất gửi là
0, 6% mỗi tháng theo hình thức lãi suất kép. Cuối mỗi tháng người đó đều đặn gửi vào ngân
hàng số tiền là 10.000.000 (10 triệu đồng). Hỏi sau ít nhất bao nhiêu tháng ( kể từ lúc người
này ra ngân hàng gửi tiền) thì số tiền người đó tích lũy được lớn hơn 700.000.000 (bảy trăm triệu đồng)? A. 22 tháng. B. 23 tháng. C. 25 tháng. D. 24 tháng. Lời giải Chọn B Tổng quát bài toán:
Gọi T là số tiền người đó gửi ban đầu. 0 Trang110
r% là lãi suất mỗi tháng.
a là số tiền người đó gửi vào thêm mỗi tháng.
S là số tiền người đó nhận được sau n tháng. n
Đầu tháng 1, số tiền người đó gửi vào là S  T . 0 0
Cuối tháng 1, S  T  T .r%  a  T . 1 r%  a . 1 0 0 0  
Cuối tháng 2, S  S  S .r%  a  S .1 r% 2
 a  T .(1 r%)  .
a 1 r%  a . 2 1 1 1 0   Cuối tháng 3, 3 2
S  T .(1 r%)  .
a (1 r%)  .
a (1 r%)  a . 3 0 … Cuối tháng n, n n n S  T .  r  a   r   r    r   n 1 %
1 % 1 1 % 2 ... 1 %1 1 0   n   n 1 r% 1
 T . 1 r%  . a 0     r% Theo yêu cầu bài toán: n   n 1 r% 1 T . 1 r%  . a  700.000.000 0     r% n       n 1 0,6% 1 40. 1 0, 6%   70 0, 6%   n 1 0, 6%  1,14515129  n  log 1,14515129  22, 65 10,6%
Vậy phải sau ít nhất 23 tháng thì người đó mới tích lũy được lớn hơn 700.000.000 (bảy trăm triệu đồng).
Câu 39. Cho đồ thị hàm số 3 2
y  ax  bx  cx  d như hình vẽ dưới đây: 2   Đồ 3x x 2
thị của hàm số g  x 
có bao nhiêu đường tiê ̣m câ ̣n đứng? 2
3 f  x  6 f  x A. 5 . B. 4 . C. 3 . D. 2 . Lời giải Chọn A Trang111
 f x  0 Xét phương trình 2
3 f  x  6 f  x  0    f   x  2
Dựa vào đồ thị, ta có x  2 
+) Phương trình f  x  0   (trong đó x  2
 là nghiệm đơn và x 1 là nghiệm bội x 1 2)
 f x  ax  x  2 2 1 , a  0 . x  0 
+) Phương trình f  x  2  x  m  2   m   
1 ( x  0, x  ,
m x  n đều là các nghiệm đơn)
x n n    1
 f x  2  axx  mx  n , a  0. x 1 3x  2 x   1 3x  2
Suy ra g  x      , a  0 .
3 f  x  f
 x  2 3a x  2x  2 2
1 x  x  m x  n
Vâ ̣y đồ thị hàm số g x có 5 đường tiê ̣m câ ̣n đứng.
Câu 40. Cho hàm số f  x có bảng xét dấu của đạo hàm như hình bên.
Hàm số y  f 1 x nghịch biến trên khoảng A. 1; 4 . B. 0; 2 . C. 0;  1 . D.  2  ;  1 . Lời giải Chọn D
Xét hàm số y  f 1 x có y   f 1 x.
Từ bảng xét dấu của f  x ta có:            
y   f   x 3 1 x 2 3 x 1 2 3 x 4 0 1  0       . 1  1 x  3  1   x 1 3   2   x  0
Suy ra hàm số y  f 1 x nghịch biến trên các khoảng 3; 4 và  2  ;0 . Mà  2  ;  1   2
 ;0 nên hàm số nghịch biến trên khoảng  2  ;  1 .
Câu 41. [Mức độ 2]Trong không gian với hệ tọa độ Oxyz , cho hình hộp ABC . D A B  C  D   biết
A1;2;3 , B2;0;  
1 , C 3;0;  3 và D 2
 ;4; 3 . Tọa độ đỉnh B của hình hộp ABC . D A B  C  D   là
A. B 4; 1;  1 .
B. B 2; 1; 2 .
C. B 4;1;   1 .
D. B 0;1;  3 . Lời giải Chọn A Trang112
Gọi I , I  lần lượt là trung điểm của AC và B D   . 
Ta có I 2;1;0 , I0;2;  2 và II   2;1;  2 . 
Giả sử B a;b;c  BB  2  a ;  b; 1 c . 2  a  2  a  4    
Theo tính chất của hình hộp ta có BB  II    b  1  b   1  .   1   c  2   c  1 
Vậy B 4; 1;1 .
Câu 42. Cho hình chóp S.ABCD có đáy là hình vuông cạnh AB  2a , S
 AB là tam giác cân tại S và
nằm trong mặt phẳng vuông góc với mặt phẳng  ABCD . Gọi M , N lần lượt là trung điểm của
AB, BC và G là trọng tâm S
 CD. Biết khoảng cách từ điểm M đến mặt phẳng SND bằng
3a 2 . Thể tích của khối chóp . G AMND bằng 4 3 5 3a 3 5 3a 3 5 3a 3 5 3a A. . B. . C. . D. . 2 6 3 18 Lời giải S Chọn A Do S
 AB là tam giác cân tại S và M là trung
điểm của AB nên ta có được SM  AB . Thêm
vào đó SAB   ABCD nên chúng ta có thể suy
ra được SM   ABCD . G K A
Ta kẽ MH  DN tại điểm H và MK  SH tại D điểm K . M Khi đó: H  B MH  DN 
 DN  SHM   DN  MK . Mà N C SM  DN a
trước đó MK  SH , nên ta có được MK  SDN   MK  d M SDN  3 2 ,  . 4 Trang113 2  a  2 2 2 a   a  a   2S S  S  S  S       a MND  ABCD MBN NCD MAD  2 4 2 2 3 5 Mặt khác: MH     . 2 2 ND NC  DC a 5 5 1 1 1 Xét trong S  MH , ta có:    SM  3a . 2 2 2 SM MK MH a
Dễ thấy: d G  ABCD 1 3 ,  SM  . Vậy: 3 3 1 a a a a V  d G ABCD S  S  S  S   . G AMND    1 3 AMND  ABCD M  BN NDC  2 2 3 5 5 3 . , . . . . . 3 3 3 9 2 18
Câu 43. Cho hình thang ABCD  AB // CD biết AB  5, BC  3, CD 10 , AD  4 . Thể tích khối tròn
xoay tạo thành khi quay hình thang ABCD  AB // CD quanh trục AD bằng A. 128 . B. 84 . C. 112 . D. 90 . Lời giải Chọn B
Gọi E là trung điểm của CD .
Dễ thấy tứ giác ABCE là hình bình hành  AE  BC  3  D
 AE vuông tại A .
Gọi H là giao điểm của AD và BC  DHC  vuông tại H .
Ta có AH  BE  4  DH  8 và HB  3 . Khi quay DHC 
quanh trục DH ta được hình nón tròn xoay có chiều cao h  8 , bán kính đáy 1 1 1
r  6 nên có thể tích 2 V 
 r h  .36.8  96 . 1 1 1 1 3 3 Khi quay A
 HB quanh trục AH ta được hình nón tròn xoay có chiều cao h  4 , bán kính đáy 2 1 1
r  3 nên có thể tích 2 V 
 r h  .9.4  12 . 2 2 2 2 3 3
Vậy thể tích khối tròn xoay tạo thành khi quay hình thang ABCD  AB // CD quanh trục AD
bằngV V  96 12  84 . 1 2 Trang114
Câu 44. Cho lăng trụ AB . C A B  C
 có đáy là tam giác đều cạnh a , hình chiếu vuông góc của đỉnh A lên
ABC là trung điểm H của cạnh AB . Góc giữa đường thẳng A C
 và mặt đáy bằng 60.
Khoảng cách giữa BB và A C  là a 13 3a 13 2a 13 a 13 A. . B. . C. . D. . 39 13 13 13 Lời giải Chọn B Ta có A H
   ABC  A C
 ; ABC  A C  ;HC  A  H  C  60 . a 3 3a 0  A H   HC.tan 60  . 3  . 2 2 1 a 3
Gọi M là trung điểm của AC , từ H kẻ HN  AC  HN  BM  . 2 4
Từ H kẻ HI  A N
  HI   A A  C .
d BB '; A'C  d BB; A A
 C  d B;A A
 C  2d H ;A A
 C  2HI .
Xét tam giác vuông AHI vuông tại H a 3 3a . HN.HA 3a 13 4 2  HI    . 2 2 2 2   26 HN HA  a 3   3a       4    2 
 d BB A C   3a 13 ;  2HI  . 13 .     
Câu 45. Tập xác định của hàm số f  x  log  log  log  log  log x  là một khoảng có độ dài 1 4 1 16 1     2 4     16 
m với m và n là số nguyên dương và nguyên tố cùng nhau. Khi đó m  n bằng: n Trang115 A. 240  . B. 271. C. 241 . D. 241. Lời giải Chọn D     
Hàm số f  x  log  log  log  log  log x  xác định khi và chỉ khi 1 4 1 16 1     2 4     16           1
log  log  log  log x   0  log  log  log x   1  0  log  log x   4 1 16 1    1 16 1   16 1 4   4    16  4   16  16  log x 1  1 1  0  x   16    16 1 1      1  x . 2 4 log x 16   1  256 16 1   x     16  16   1 1 
Suy ra tập xác định của hàm số là ;   .  256 16    Suy ra độ 1 1 1 1 15 dài của khoảng ;   là  
 m  15, n  256 .  256 16  16 256 256
Vậy m  n  241.
Câu 46. [Mức độ 3] Số điểm cực đại của đồ thị hàm số y   x  
1  x  2 x  3... x 100 bằng A. 50 . B. 99 . C. 49 . D. 100 . Lời giải Chọn C
*Ta thấy hàm số đã cho là hàm đa thức bậc 100, liên tục trên ¡ và có đúng 100 nghiệm phân
biệt ( x  1; x  2;...; x  100 ), nên hàm số đã cho có 99 điểm cực trị ( x ; x ;...; x ), mỗi điểm 1 2 99
cực trị nằm giữa 2 nghiệm của phương trình y  0 . Mặt khác lim   nên số điểm cực tiểu x
nhiều hơn số điểm cực đại là một nên đồ thị hàm số đã cho có 49 điểm cực đại là x ; x ;...; x . 2 4 98
Vậy hàm số đã cho có 49 điểm cực đại.
Câu 47. Cho các số thực dương x , y thỏa mãn
log x  log y  log x  log y  100 và log x ,
log y , log x , log y là các số nguyên dương. Khi đó kết quả xy bằng A. 200 10 . B. 100 10 . C. 164 10 . D. 144 10 . Lời giải Chọn C Trang116 2 2
Ta có: log x  log y  log x  log
y  100   log x   1   log y   1  202
Vì log x , log y là các số nguyên dương nên:  x  2 log 1 và  y  2 log 1 là các số
nguyên dương. Do đó cần phân tích 202 thành tổng 2 số chính phương.
Cũng do 202 là số chẵn nên 2 số chính phương đó phải cùng chẵn hoặc cùng lẻ. 2 2 +) Nếu 2 số  x  2 log 1 và  y  2 log
1 cùng chẵn thì  log x   1   log y   1 4 còn
202 không chia hết cho 4 nên không tồn tại x , y trong trường hợp này. +) Nếu 2 số  x  2 log 1 và  y  2 log
1 cùng lẻ, suy ra chữ số tận cùng của 2 số đó là một
trong các chữ số 1, 5, hoặc 9. Vì tổng 2 chữ số tận cùng là 2 nên 2 số  x  2 log 1 ,  y  2 log
1 đều có tận cùng bằng 1.
Cũng do vai trò x , y như nhau trong giả thiết và kết luận nên ta chỉ xét trường hợp:  logx   2 1  81 64 x 10 164     . Từ đó suy ra xy 10 .  100   log y  y 10  2 1  121 Câu 48. Cho hàm số 3 2
y  ax  bx  cx  d có đồ thị như hình vẽ bên
Giá trị nguyên lớn nhất của tham số m để hàm số y  f  x  m đồng biến trên khoảng 10; là A. 10  . B. 10 . C. 9 . D. 11. Lời giải Chọn C
Hàm số y  f  x  m đồng biến trên khoảng 10; x  y ' 
f ' x  m  0, x
 10  f ' x  m  0, x  10 x  x  m 1   , x  10
 x  m  1    x 1 m   , x  10  x  m 1 
10 1 m  m  9. Trang117
Vậy số nguyên lớn nhất của tham số m là 9 .
Câu 49. Cho hàm số f  x liên tục trên  và thoả mãn      2 3 2 1 x xf x f x  e , x    . 0 Khi đó f
 xdx bằng: 1  A. 0 . B. 3e   1 .
C. 31 e . D. 3e . Lời giải Chọn B Nhân hai vế của      2 3 2 1 x xf x f x  e , x    với x ta được:      2 2 3 2 1 x x f x xf x  xe , x    . 0 0 0
Lấy tích phân từ 1 đến 0 hai vế ta được: 2   3    2   2 1 x x f x dx xf x dx  xe dx (1)  1  1  1  0 0 0 Kí hiệu 2  
 3 ;    2   2 1 ; x I x f x dx K xf x dx H  xe dx  1  1  1  0 0 0 Đặ 1 1 t 3
u  x ta tính được 2 I  x f 
 3xdx  f
 udu  f  xdx 3 3 1  1  1  0 0 0 Đặ 1 1 t 2
u  x 1 ta tính được K  xf
  2x  1dx   f
 vdv   f  xdx 2 2 1  1  1  0 0 0 2 2 2 x 1 x 1 x 1 Và H  xe dx  e d  
 2x  e  1e 2 2 2 1  1  1  0 0 0 1 1 1 Nên (1) 
f  x dx 
f  xdx  1 e 
f  xdx  3e      1 . 3 2 2 1  1  1 
Câu 50. Một hộp đựng 9 thẻ được đánh số từ1 đến 9 . Rút ngẫu nhiên hai thẻ từ hộp nêu ở trên, tính
xác suất để tích của hai số trên hai thẻ này là số chẵn. 25 13 5 1 A. . B. . C. . D. . 81 18 18 2 Lời giải Chọn B n  2  C . 9
Gọi A là biến cố tích của hai số trên hai thẻ là số lẻ, ta có xác xuất cần tính là P  A.
Nhận thấy biến cố A xảy ra khi và chỉ khi rút được cả hai thẻ mang số lẻ. Trong 9 thẻ đã cho có
5 thẻ mang số lẻ, vì thế nên n  A 2  C . 5 n A
Ta có P  A   
và P  A  P A 1, do đó P  A 13  . n  18 …..HẾT….. Trang118

Bộ 5 Đề Luyện Thi Cấp Tốc Tốt Nghiệp THPT 2021 Môn Toán Có Lời Giải Chi Tiết Và Đáp Án-Bộ 1

Thông tin :

Tài liệu liên quan:

Đề chính thức kỳ thi tốt nghiệp THPT năm 2024 môn Toán

Đề kiểm tra Toán 12 năm 2024 – 2025 trường THCS&THPT Nguyễn Khuyến – TP HCM (13/09/2024)

Đề kiểm tra Toán 12 năm 2024 – 2025 trường Nguyễn Khuyến & Lê Thánh Tông – TP HCM (22/09/2024)

Đề kiểm tra Toán 12 năm 2024 – 2025 trường Nguyễn Khuyến & Lê Thánh Tông – TP HCM (06/10/2024)

Đề thi thử TN THPT môn Toán đợt tháng 6 năm 2024 cụm trường THPT – Bắc Ninh