Bộ 5 Đề Ôn Thi Cấp Tốc TN THPT 2021 Môn Toán Có Lời Giải Chi Tiết Và Đáp Án-Bộ 2

Bộ 5 đề ôn thi cấp tốc TN THPT được biên soạn dưới dạng file PDF gồm 129 trang. Mỗi đề thi là kiến thức từ cơ bản đến nâng cao khác nhau và kèm sẵn đáp án để các em học sinh dễ dàng so sánh kết quả sao cho chuẩn xác nhất. Mời các em tham khảo thêm nhé!

38 19 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

Trang1

Đề 6

ĐỀ LUYỆN THI CẤP TỐC TỐT NGHIỆP THPT NĂM 2021

Thuvienhoclieu.Com

BÀI THI: TOÁN

Thời gian: 90 phút

Câu 1: Có bao nhiêu s t nhiên có ba ch s t khác nhau?

. B.

. C.

. D.

9.A

Câu 2: Cho cp s cng

 

, bit

6u 

và

2u 

. Giá tr ca

bng

8

. B.

. C.

. D.

22

Câu 3: Cho hàms

 

y f x

nh và liên tc trên khong

 

;, 

có bng bi



1



 

'fx



 



1

Hàm s ch bin trên kho

 

1;0 .

. B.

 

0;1

 

1;4

. D.

 

1; 

Câu 4: Cho hàm s

 

y f x

có bng bi



0 3



 

'fx

+ 0 - 0 +

 





5

Hàms

 

t ci tm

2x 

. B.

5x 

. C.

3x 

. D.

0x 

Câu 5: Cho hàms

 

y f x

liên tc trên



và có bng xét di 



3



 

'fx







S m cc tr ca hàm s là

. B.

. C.

. D.

Câu 6: S ng tim cn c th hàm s







là

Trang2

. B.

. C.

. D.

Câu 7:  th ca hàm s ng cong trong hình bên:

32y x x= - + +

. B.

2y x x= - +

. C.

2y x x= - + -

. D.

32y x x= - +

Câu 8:  th ca hàm s







ct trc hoành t bng

2

. B.

. C.

. D.

3

Câu 9: Vi

là s th

125

log







bng

3 log a

. B.

3log a

. C.

 

log a

. D.

3 log a

Câu 10: Vi

0x 

o hàm ca hàm s

logy x

là

ln 2

. B.

.ln 2x

. C.

.ln2x

. D.

2 .ln 2

Câu 11: Vi

là s th

bng

. B.

. C.

. D.

Câu 12: Nghi

77 1680

x 



là

2x 

. B.

2; 2xx  

. C.

2x 

. D.

4x 

Câu 13: Nghim c

 

log 33x  

là:

11x 

. B.

12x 

. C.

33x 

. D.

32x 

Câu 14: Nguyên hàm ca hàm s

( ) 5 2f x x

là:

 

df x x x x C  



. B.

 

df x x x x C  



 

d2f x x x x C  



. D.

 

d 2f x x x Cx 



Câu 15: Cho hàm s

 

sin2f x x

. Trong các khnh sau, khnh nào đúng?

 

d cos2

f x x x C



. B.

 

d cos2

f x x x C  



 

d 2cos2f x x x C



. D.

 

d 2cos2f x x x C  



Câu 16: Nu

 

d3f x x 



và

 

d1f x x 



thì

 

df x x



bng

. B.

4

. C.

2

. D.

3

Trang3

Câu 17: Tích phân

 

d2 xxx



bng

. B.

. C.

. D.

Câu 18: S phc liên hp ca s phc

23zi

là:

32zi

. B.

23zi

. C.

32zi

. D.

23zi  

Câu 19: Cho hai s phc

23zi

và

5wi

. S phc

z iw

bng

38i

18i

8 i

74i

Câu 20: Trên mt phng tm biu din s phc liên hp ca s phc

95i

có t là

 

5; 9

. B.

 

5;9

. C.

 

9; 5

. D.

 

9;5

Câu 21: Mt khi chóp có th tích bng 90 và ding 5. Chiu cao ca khng

. B.

. C.

. D.

450

Câu 22: Th tích ca khi hp ch nhc 5; 7; 8 bng

. B.

280

. C.

. D.

Câu 23: Mt khi nón tròn xoay có chiu cao

6 cmh 



5 cmr 

 tích khi

nón là:

300V cm





. B.

20V cm





. C.

325

V cm





. D.

50V cm





Câu 24: Cho mt khi tr  ng sinh là

6 cml 



5 cmr 

Din tích toàn phn ca khi tr là

110 cm



85 cm



. C.

55 cm



30 cm



Câu 25: Trong không gian

Oxyz





2OA i j

  



,ij









là

 

2;1;0A

. B.

 

0;2;1A

. C.

 

0;1;1A

. D.

 

1;1;1A

Câu 26:       

Oxyz

   

 

  

2 2 2

2 4 4 7 0x y z x y z      



và bán kính



 

1;2; 2I 

;

4R 

. B.

 

1;2; 2I 

;

2R 

 

1; 2;2I 

;

4R 

. D.

 

1; 2;2I 

;

3R 

Câu 27: 

Oxyz



 

: 3 3 0P x y z   



 





 

1;1;0 .

 

0;1; 2 .

 

2; 1;3 .

 

1;1;1 .

Câu 28: Trong không gian

Oxyz



 

: 2 3 2 0P x y z   



vuông góc



 



 

1; 2;2u 



. B.

 

1;2;3u 



. C.

 

0; 2;3u 



. D.

 

1; 2;3u 



Câu 29: 









 

; 

. B.

 

6;0

. C.

 

1;4

. D.

 

5;1

Câu 30: Trong mt lp hc gm 15 hc sinh nam và 10 hc sinh n. Giáo viên gi ngu nhiên 4 hc

sinh lên gii bài tp. Tính xác su 4 hc g nam và n?

Trang4

219

323

. B.

219

323

. C.

442

506

. D.

443

506

Câu 31: Tìm giá tr ln nht

ca hàm s

2 3 12 2y x x x   

n

 

1;2 .

10M 

. B.

6M 

. C.

11M 

. D.

15M 

Câu 32: Tp nghim ca b

 

7 4 3 7 4 3

a

  

là

 

;0

. B.





;1

. C.

 

0;

. D.

 

1; 

Câu 33: Cho

 

10f x dx 



và

 

5g x dx 



. Tính

   

3 5 2I f x g x x dx  







17.I 

15.I 

5.I 

10.I 

Câu 34: Cho s phc

2 3 .zi

a s phc

 

1 iz

bng

26.

25.

26.

Câu 35: Cho hình hp ch nht

. ' ' ' 'ABCD A B C D

có

22AB AD

và

' 4 3AA 

(tham kho hình

bên). Góc ging thng

'CA

và mt phng

 

ABCD

bng

. B.

. C.

. D.

Câu 36: Cho hình chóp t u

.S ABCD

 dài cng

 dài cnh bên bng

(tham kho hình bên). Khong cách t

n mt phng

 

ABCD

bng

. B.

. C.

. D.

Câu 37: Trong không gian

,Oxyz

mt c   m

(2; 3;1)I 

   m

 

0; 1;2M 

có



     

2 2 2

2 3 1 3.x y z     

   

1 2 3.x y z    

   

1 2 9.x y z    

     

2 2 2

2 3 1 9.x y z     

Câu 38: Trong không gian

,Oxyz

ng thm

 

4;1; 3A 

và

 

0; 1;1B 



tham s là:

Trang5

  





  





  



1 2 .







  















  









1 2 .

  





  





  



Câu 39: Cho hàm s

 

 th hàm s

 

y f x





ng cong trong hình bên. Giá tr nh nht ca

hàm s

 

g x f









n

 

5;3

bng

 

2f 

. B.

 

. C.

 

4f 

. D.

 

Câu 40: Có bao nhiêu s t nhiên

sao cho ng vi mi

có không quá 148 s nguyên

tha mãn









A. 4 B. 5 C. 6 D. 7

Câu 41: Cho hàm s

 

4 1 , 5

2 6 , 5

x x x



  









. Tích phân

 

ln2

3 1 . d

f e e x



bng

. B.

. C.

. D.

Câu 42: Có bao nhiêu s phc

tha mãn

1  z z z

. B.

. C.

. D.

Câu 43: Cho hình chóp

.S ABCD



ABCD



6AB 

3AD 

, tam giác

SAC



 

SAB

 

SAC









tan







3SC 



.S ABCD



. B.

. C.

. D.

Câu 44: S dng mnh inox hình ch nht

ABCD

có din tích bng

và cnh

 

mBC x

 làm

m nht

ABCD

thành

hình ch nht

ADNM

và

BCNM

n hình ch nht

ADNM

c gò

thành phn xung quanh hình tr có chiu cao bng

; phn hình ch nht

BCNM

c ct

ra m a hình tr trên (phn inox thc b 

 c trên có th tích ln nh).

-2

Trang6

0,97m

. B.

1,37m

. C.

1,12m

. D.

1,02m

Câu 45: Trong không gian vi h t

,Oxyz

m

 

3;3;1 ,A

 

0;2;1B

và mt phng

 

: 7 0.P x y z   

ng thng

nm trong

 

sao cho mm ca

u hai

m

, AB

n sau, m 

7 3 .

















7 3 .

















7 3 .

















7 3 .

















Câu 46: Cho hàm s

 

y f x

là hàm s bc bn tha mãn

 

0 0.f 

Hàm s

 

'y f x

có bng bin



Hàm s

 

g x f x x

m cc tr?

. B.

. C.

. D.

Câu 47:       

vi

1m 

sao cho tn ti s thc

tha mãn:

 

log

3 3 1

mx  

. B.

. C.

. D.

Câu 48: Cho hàm s bc ba

 

f x ax bx cx d   

ng thng

 

:d g x mx n

 th 

hình v. Gi

1 2 3

,,S S S

lt là din tích ca các phn gii hu

4S 

thì

t s

bng.

Trang7

. B.

. C.

. D.

Câu 49: Xét hai s phc

,zz

tha mãn

 

2, 1 6z i z  

và

5zz

. Giá tr ln nht

2 2021zz

bng

2044

. B.

23 2021

. C.

23 2021

. D.

2 23 2021

Câu 50: Trong không gian

Oxyz

m

 

1;2;11 , ( 1;2; 1)CH  

, hình nón

 

ng cao

CH h



32R 

. Gi

n

,CH

 

là thit din ca mt

phng

 

vuông góc vi trc

ti

ca hình nón

 

Gi

 



là khnh



 

. Khi th tích khi nón

 



ln nht thì mt cu ngoi tip nón

 



có t tâm

 

; , ,I a b c

bán kính là

. Giá tr

a b c d  

bng

. B.

. C.

. D.

6

BẢNG ĐÁP ÁN

1.D

2.D

3.B

4.D

5.C

6.C

7.D

8.C

9.D

10.B

11.C

12.A

13.A

14.C

15.B

16.A

17.B

18.B

19.B

20.D

21.A

22.B

23.D

24.A

25.A

26.A

27.D

28.D

29.C

30.D

31.D

32.A

33.A

34.D

35.A

36.B

37.D

38.C

39.A

40.C

41.B

42.C

43.B

44.D

45.C

46.C

47.B

48.B

49.C

50.C

HƯỚNG DẪN GIẢI CHI TIẾT

Câu 1: Có bao nhiêu s t nhiên có ba ch s t khác nhau?

. B.

. C.

. D.

9.A

Lờigiải

Chọn D

Gi s s t nhiên cn tìm có dng

abc

0a 

nên có

cách chn ch s

. Hai ch s

và

có

cách chn.

Vy có

9.A

s t nhiên có ba ch s t khác nhau.

Câu 2: Cho cpscng

 

, bit

6u 

và

2u 

. Giátrca

bng

Trang8

8

. B.

. C.

. D.

22

Lờigiải

Chọn D

Tgithit

6u 

và

2u 

suy ra ta có:





2 6 4d u u      

Vy

7 22u u d   

Câu 3: Cho hàms

 

y f x

nhvàliêntctrênkhong

 

;, 

cóbngbi



1



 

'fx



 



1

Hàm s ch bin trên khoi 

 

1;0 .

. B.

 

0;1

 

1;4

. D.

 

1; 

Lờigiải

ChọnB

Tbngbinthiên ta thyhàms nghch bintrênkhong

 

0;1

Câu 4: Cho hàms

 

y f x

có bng bi



0 3



 

'fx

+ 0 - 0 +

 





5

Hàms

 

tcitm

2x 

. B.

5x 

. C.

3x 

. D.

0x 

Lờigiải

Chọn D

vào bng bin thiên ta có

 

0fx





 

0;3x

và

 

0fx





 

3;x  

suy ra hàmstcctiuti

3x 

 

0fx





 

;0x  

và

 

0fx





 

0;3x

suy ra hàmstciti

0x 

Câu 5: Cho hàms

 

y f x

liêntctrên



vàcóbngxétdi



3



 

'fx







Smcctrcahàmslà

. B.

. C.

. D.

Lờigiải

Trang9

ChọnC

Hàmsmcctr.

Câu 6: S ng tim cn c th hàm s







là

. B.

. C.

. D.

Lờigiải

ChọnC

Ta có :

Vì

5 3 5

lim lim

2 1 2

 







ngthng

y 

làtimcnngangcthhàms

Vì

lim







 



lim







 



ngthng

x 

làtingcthhàms.

V th hàm s t c

ng tim cn.

Câu 7:  th ca hàm s ng cong trong hình bên:

32y x x= - + +

. B.

2y x x= - +

. C.

2y x x= - + -

. D.

32y x x= - +

Lời giải

Chọn D

 th ng c th hàm s bc ba

y ax bx cx d   

nên lo

B và C.

D th, ta có

lim 0



   

nên loA.

Câu 8:  th ca hàm s







ct trc hoành t bng

2

. B.

. C.

. D.

3

Lời giải

Chọn C

Trang10

 tìm t cm vi trc hoành, ta cho

0 0 3 0 3

y x x



       



Câu 9: Vi

là s th

125

log







bng

3 log a

. B.

3log a

. C.

 

log a

. D.

3 log a

Lời giải

Chọn D

Ta có:

5 5 5 5

125

log log 125 log 3 logaa



   





Câu 10: Vi

0x 

o hàm ca hàm s

logy x

là

ln 2

. B.

.ln 2x

. C.

.ln2x

. D.

2 .ln 2

Lời giải

Chọn B

Ta có:

 

log

.ln 2





Câu 11: Vi

là s th

bng

. B.

. C.

. D.

Lời giải

Chọn C

Ta có

aa

vi mi

0a 

và

,.mn





Câu 12: Nghi

77 1680

x 



là

2x 

. B.

2; 2xx  

. C.

2x 

. D.

4x 

Lời giải

Chọn A

Ta có

51 21

168 407 77 0







    









Câu 13: Nghim c

 

log 33x  

là:

11x 

. B.

12x 

. C.

33x 

. D.

32x 

Lời giải

Chọn A

Ta có:

 

log 33x  



 

lo32og l gx  



32x 



11x 

Câu 14: Nguyên hàm ca hàm s

( ) 5 2f x x

là:

 

df x x x x C  



. B.

 

df x x x x C  



 

d2f x x x x C  



. D.

 

d 2f x x x Cx 



Lời giải

Chọn C

Ta có:

 

d2d25f x x x x x Cx   



Câu 15: Cho hàm s

 

sin2f x x

. Trong các khnh sau, khnh nào đúng?

Trang11

 

d cos2

f x x x C



. B.

 

d cos2

f x x x C  



 

d 2cos2f x x x C



. D.

 

d 2cos2f x x x C  



Lời giải

Chọn C

Áp dng công thc:

   

sin d cosax b x ax b C

    



Ta có:

 

s did co 2n2 s

f x x x Cx x   



Câu 16: Nu

 

d3f x x 



và

 

d1f x x 



thì

 

df x x



bng

. B.

4

. C.

2

. D.

3

Lời giải

Chọn A

Ta có:

     

1 1 2

d d df x x f x x f x x

  



     

2 1 1

d d df x x f x x f x x

  



   

d 1 3 4f x x    



Câu 17: Tích phân

 

d2 xxx



bng

. B.

. C.

. D.

Lời giải

Chọn B

Ta có:

 

d2 xxx





 

xxx



  









Câu 18: S phc liên hp ca s phc

23zi

là:

32zi

. B.

23zi

. C.

32zi

. D.

23zi  

Lời giải

Chọn B

 phc

 

,z a bi a b  

. S phc liên hp ca s phc

là

z a bi

Ta có: S phc liên hp

ca s phc

23zi

là

23zi

Câu 19: Cho hai s phc

23zi

và

5wi

. S phc

z iw

bng

38i

18i

8 i

74i

Lời giải

Chọn B

Ta có

   

2 3 5 1 8z iw i i i i      

Câu 20: Trên mt phng tm biu din s phc liên hp ca s phc

95i

có t là

 

5; 9

. B.

 

5;9

. C.

 

9; 5

. D.

 

9;5

Lời giải

Trang12

Chọn D

Trên mt phng tm biu din s phc liên hp ca s phc

95i

có t là

 

9;5

Câu 21: Mt khi chóp có th tích bng 90 và ding 5. Chiu cao ca kh

bng

. B.

. C.

. D.

450

Lời giải

Chọn A.

Chia khi chóp có th tích bng 90 và ding 5 là



Câu 22: Th tích ca khi hp ch nhc 5; 7; 8 bng

. B.

280

. C.

. D.

Lời giải

Chọn B

Th tích ca khi hp ch nhc 5; 7; 8 bng

0.. 28V abc

Câu 23: Mt khi nón tròn xoay có chiu cao

6 cmh 



5 cmr 

 tích

khi nón là:

300V cm





. B.

20V cm





. C.

325

V cm





. D.

50V cm





Lời giải

Chọn D

Th tích khi nón:

.5 .6 50

V cm





Câu 24: Cho mt khi tr  ng sinh là

6 cml 



5 cmr 

Din tích toàn phn ca khi tr là

110 cm



85 cm



. C.

55 cm



30 cm



Lời giải

Chọn A

 

22 + S 2 2 110 cm

qp áyt ĐX

S S r rl r r l

   

  

 

+ S 2 2 0 m2 c2 3

tp Đáy Xq

S S r rl r r l

   

  

Câu 25: Trong không gian

Oxyz





2OA i j

  



,ij









là

 

2;1;0A

. B.

 

0;2;1A

. C.

 

0;1;1A

. D.

 

1;1;1A

Lời giải

Chọn A

Vì

   

=2i+ = 2;1;0 2;1;0OA j OA A

   

Câu 26:       

Oxyz

   

 

  

2 2 2

2 4 4 7 0x y z x y z      



và bán kính



 

1;2; 2I 

;

4R 

. B.

 

1;2; 2I 

;

2R 

 

1; 2;2I 

;

4R 

. D.

 

1; 2;2I 

;

3R 

Lời giải

Chọn A

Trang13

 

2 2 2

: 2 4 4 7 0S x y z x y z      

1a

;

2b 

;

2c 

;

7d 





 

có bán kính

2 2 2

R a b c d   

4

và có tâm

 

1;2; 2I 

Câu 27: 

Oxyz



 

: 3 3 0P x y z   



 





 

1;1;0 .

 

0;1; 2 .

 

2; 1;3 .

 

1;1;1 .

Lời giải

Chọn D



 

1;1;1



Câu 28: Trong không gian

Oxyz



 

: 2 3 2 0P x y z   



vuông góc



 



 

1; 2;2u 



. B.

 

1;2;3u 



. C.

 

0; 2;3u 



. D.

 

1; 2;3u 



Lời giải

Chọn D

Vì

 

dP

nên

u





 



hay

 

1; 2;3

n 



là m a

Câu 29: 









 

; 

. B.

 

6;0

. C.

 

1;4

. D.

 

5;1

Lời giải

Chọn C



 

\4D 

Ta có

 







xD



 

;4 

và

 

4; 





 

1;4

Câu 30: Trong mt lp hc gm 15 hc sinh nam và 10 hc sinh n. Giáo viên gi ngu nhiên 4 hc

sinh lên gii bài tp. Tính xác su 4 hc g nam và n?

219

323

. B.

219

323

. C.

442

506

. D.

443

506

Lời giải

Chọn D

Gi

là bin c 4 hc gi có c nam và n

là bin c c

gi toàn là nam hoc toàn là n

S phn t ca không gian mu là

 

12650nC  

Ta có

   

 

15 10

1575

506

n A C C P A

     



Vy xác sut ca bin c

là

 

63 443

506 506

P A P A    

Câu 31: Tìm giá tr ln nht

ca hàm s

2 3 12 2y x x x   

n

 

1;2 .

10M 

. B.

6M 

. C.

11M 

. D.

15M 

Lời giải

Trang14

Chọn D

Ta có

 

6 6 12 6 2y x x x x



     

 

1 1;2

2 1;2



  







   



Ngoài ra

     

1 15; 1 5; 2 6y y y    

nên

15.M 

Câu 32: Tp nghim ca b

 

7 4 3 7 4 3

a

  

là

 

;0

. B.





;1

. C.

 

0;

. D.

 

1; 

Lời giải

Chọn A

Ta có:

  

7 4 3 7 4 3 1  

nên

     

1 1 1

7 4 3 7 4 3 7 4 3 7 4 3

aa  

      

1 1 0aa     

(do

7 4 3 1

Câu 33: Cho

 

10f x dx 



và

 

5g x dx 



. Tính

   

3 5 2I f x g x x dx  







17.I 

15.I 

5.I 

10.I 

Lời giải

Chọn A

   

4 4 4

2 2 2

3 5 2 3.10 5.5 12 17I f x dx g x dx xdx      

  

Câu 34: Cho s phc

2 3 .zi

a s phc

 

1 iz

bng

26.

25.

26.

Lời giải

Chọn D

Ta có

    

1 1 2 3 1 5i z i i i      



   

1 1 5 26.iz    

Câu 35: Cho hình hp ch nht

. ' ' ' 'ABCD A B C D

có

22AB AD

và

' 4 3AA 

(tham kho hình

bên). Góc ging thng

'CA

và mt phng

 

ABCD

bng

. B.

. C.

. D.

Lời giải

Chọn A

Vì

. ' ' ' 'ABCD A B C D

là hình hp ch nht nên

' ( )AA ABCD

ng thng

'CA

và mt phng

 

ABCD

là



'ACA

Trang15

Vì

22AB AD

nên

ABCD

ng chéo

2 2 2. 2 4AC AB  

Tam giác

'ACA

vuông ti

và có

' 4 3AA 

4AC 

nên



' 4 3

tan ' 3

ACA

  

Suy ra



' 60ACA 

. Vy góc ging thng

'CA

và mt phng

 

ABCD

bng

Câu 36: Cho hình chóp t u

.S ABCD

 dài cng

 dài cnh bên bng

(tham kho hình bên). Khong cách t

n mt phng

 

ABCD

bng

. B.

. C.

. D.

Lời giải

Chọn B

Gi

I AC BD

Vì

.S ABCD

là hình chóp t  dài cng



ABCD

là hình vuông

cnh

4AB 

và hình chiu vuông góc ca

trên

 

ABCD

là tâm

ca hình vuông

ABCD

ng cách t

n mt phng

 

ABCD

bng

Ta có

2 4 2 2 2

AC AB IA AC    

Cnh bên

6SA 

và tam giác

SAI

vuông ti

nên

2 2 2 2

6 (2 2) 36 8 28 2 7SI SA AI       

Vy khong cách t

n mt phng

 

ABCD

bng

Câu 37: Trong không gian

,Oxyz

mt c   m

(2; 3;1)I 

   m

 

0; 1;2M 

có



     

2 2 2

2 3 1 3.x y z     

   

1 2 3.x y z    

Trang16

   

1 2 9.x y z    

     

2 2 2

2 3 1 9.x y z     

Lời giải

Chọn D

Mt cm

(2; 3;1)I 

m

 

0; 1;2M 

có bán kính là

Ta có

 

2 2 2

2;2;1 ( 2) 2 1 9 3IM r IM         



t cu là:

     

2 2 2

2 3 1 9.x y z     

Câu 38: Trong không gian

,Oxyz

ng thm

 

4;1; 3A 

và

 

0; 1;1B 



tham s là:

  





  





  



1 2 .







  















  









1 2 .

  





  





  



Lời giải

Chọn C

ng thm

 

4;1; 3A 

và

 

0; 1;1B 

 

   

4; 2;4 2 2; 1;2AB    



 cng thng

()AB

m

 

0; 1;1B 

 

   

4; 2;4 2; 1;2

u AB    

 

là







  









Câu 39: Cho hàm s

 

 th hàm s

 

y f x





ng cong trong hình bên. Giá tr nh nht ca

hàm s

 

g x f









n

 

5;3

bng

 

2f 

. B.

 

. C.

 

4f 

. D.

 

Lời giải

Chọn A

 

g x f















    





















 

0 0 2 4

g x f x





        





Bng bin thiên

-2

Trang17

Giá tr nh nht ca hàm s

 

trên

 

5;3

bng

   

42gf  

Câu 40: Có bao nhiêu s t nhiên

sao cho ng vi mi

có không quá 148 s nguyên

tha mãn









A. 4 B. 5 C.6D. 7

Lời giải

Chọn C

u kin:

















ng hp 1:

ln 0

x e e











  



  











ng hp 2:

ln 0



























Kt hu kin

0; 1

x e e  

. Ta có

xe

 có không quá 148 s nguyên x thì

1 149 0 ln149 5,004

ey     

 

0;1;2;3;4;5y

. Có 6 s nguyên y.

Câu 41: Cho hàm s

 

4 1 , 5

2 6 , 5

x x x



  









. Tích phân

 

ln2

3 1 . d

f e e x



bng

. B.

. C.

. D.

Lời giải

Chọn B

Ta có

     

lim lim 5 4

f x f x f





  

nên hàm s liên tc ti

5x 

Vy hàm s

 

liên tc trên



t

3 1 d d

t e e x t   

i cn :

0x 



4t 

;

ln2x 



7t 



     

 

7 7 5 7

4 4 4 5

1 1 1 77

d d 2 6 d 4 1 d

3 3 3 9

I f t t f x x x x x x x



       





   

Câu 42: Có bao nhiêu s phc

tha mãn

1  z z z

Trang18

. B.

. C.

. D.

Lời giải

Chọn C

Ta có Gi s

z x yi

 

, xy

2     z x yi z z x

Bài ra ta có











  



  













Vi

1 1 3

2 4 2

       x y y

 phc tha mãn là

zi

zi

  zi

  zi

Câu 43: Cho hình chóp

.S ABCD



ABCD



6AB 

3AD 

, tam giác

SAC



 

SAB

 

SAC









tan







3SC 



.S ABCD



. B.

. C.

. D.

Lời giải

Chọn B

. . .

S ABCD S ABC B SAC

V V V

. K

vuông góc vi

ti

Ta có:

3AC 

2BH 

1HC 



tan tan

BKH





KH



sin

SAC





cos

SAC



2 2 2

2 . .cosSC SA AC AS AC SAC  

2SA



. .sin

SAC

S SA AC SAC

1 2 2

.2.3. 2 2



Vy

2. .2 2. 2

S ABCD

V 

Câu 44: S dng mnh inox hình ch nht

ABCD

có din tích bng

và cnh

 

mBC x

 làm

ABCD

thành

hình ch nht

ADNM

và

BCNM

n hình ch nht

ADNM

c gò

thành phn xung quanh hình tr có chiu cao bng

; phn hình ch nht

BCNM

c ct

Trang19

ra m a hình tr trên (phn inox thc b r

 c trên có th tích ln nh).

0,97m

. B.

1,37m

. C.

1,12m

. D.

1,02m

Lời giải

Chọn D

Ta có

 

. 1 m   AB BC AB

BC x

Gi

 

 ng

 

m.BC x



 

  



r x r

y

 

2m      



BM r AM AB BM

Th tích khi tr c là

 

   

    

   

   

  

V r h x x

Xét hàm s

 





f x x x

vi

0x

 







f x x

;

 



  



f x x

;

 

0 0;





  







f x x

và

 





   







f x x

Bi vy

 

ng bin trên khong









và nghch bin trên khong

;











Suy ra

 

max











  

f x f

 

max

V f x

 

1,02 m

  



Câu 45: Trong không gian vi h t

,Oxyz

m

 

3;3;1 ,A

 

0;2;1B

và mt phng

 

: 7 0.P x y z   

ng thng

nm trong

 

sao cho mm ca

u hai

m

, AB

m sau, m 

7 3 .

















7 3 .

















7 3 .

















7 3 .

















Lời giải

ChọnC

Trang20

t phng trung trc cn

là

 

:3 7 0.xy



  

ng thng cn tìm

m

, AB

nên

thuc mt phng

 



Li có

 

,dP

suy ra

   





hay

3 7 0

x y z

   





  



Chn

,xt

 c











Câu 46: Cho hàm s

 

y f x

là hàm s bc bn tha mãn

 

0 0.f 

Hàm s

 

'y f x

có bng bin



Hàm s

 

g x f x x

m cc tr?

. B.

. C.

. D.

Lời giải

Chọn C

t

 

0 0.h x f x x h   

Ta có

 

' 2 ' 2 0 .

h x xf x x





   









Da vào bng bin thiên ca hàm s

 

't f x



 

'1fx

có duy nht mt

nghim và nghii

là nghim c

 

'1fx

Suy ra

 

' 1 .f x x x x x     

Ta có

   

4 3 2 3 2

' 4 3 2y f x ax bx cx dx e f x ax bx cx d          

 

lim ' 0.

f x a



   



 

h x f x x

là hàm bc 8 và

   

lim lim

h x h x

 

  

Lp bng bin thiên ca

 

ta có

Da vào bng bin thiên ta có hàm s

   

g x h x

m cc tr.

Câu 47:       

vi

1m 

sao cho tn ti s thc

tha mãn:

 

log

3 3 1

mx  

. B.

. C.

. D.

Trang21

Lời giải

ChọnB

u kin:

0x 

t

log

mu



 

c:

log log

u x x u    

Vì

log logmu

um

. T  

log













 

f t m

trên



1m 

. Suy ra hàm s

 

ng bin trên





   

log logf x f u x u  

Vì th 

5 5 5

log log log

3 3 3

x m m

x m x x x x       

 

log

5 5 5 5 5 5

log 3

log 3 log log 3 log .log log

log

x x x x m m



       

0x 

nên

3xx

nên

 

log 3

log 1 5

log



   

Suy ra

 

2,3,4















Vy, có

giá tr tham s

tha mãn.

Câu 48: Cho hàm s bc ba

 

f x ax bx cx d   

ng thng

 

:d g x mx n

 th 

hình v. Gi

1 2 3

,,S S S

lt là din tích ca các phn gii hu

4S 

thì

t s

bng.

. B.

. C.

. D.

Lời giải:

Chọn B

D th , ta có:

      

. 2 2f x g x k x x x   

 

3g x x

Trang22

  

2 2 4S S kx x x dx k



    



   

 

0 2 .2

3 5 .2



   

Vì

44SS  

8 4 4S   

. Vy



Câu 49: Xét hai s phc

,zz

tha mãn

 

2, 1 6z i z  

và

5zz

. Giá tr ln nht

2 2021zz

bng

2044

. B.

23 2021

. C.

23 2021

. D.

2 23 2021

Lời giải

Chọn C

t

,z a bi z c di   

vi

, , , .a b c d 

Theo gi thit thì

1z 

4ab

 

1 6 3

i z z

    



3cd  

5zz  

   

5a c b d   



2 2 2 2

2 2 5 1a ac c b bd d ac bd        

Ta có

   

2 2 2z z a c b d i    

nên

   

 

2 2 2 2

2 2 2 4 4 23z z a c b d a b c d ac bd           

Áp dng bng thc

z z z z



  

, ta có

1 2 1 2

2 2021 2 2021 23 2021.z z z z       

Câu 50: Trong không gian

Oxyz

m

 

1;2;11 , ( 1;2; 1)CH  

, hình nón

 

ng cao

CH h



32R 

. Gi

n

,CH

 

là thit din ca mt

phng

 

vuông góc vi trc

ti

ca hình nón

 

Gi

 



là khnh



 

. Khi th tích khi nón

 



ln nht thì mt cu ngoi tip nón

 



có t tâm

 

; , ,I a b c

bán kính là

. Giá tr

a b c d  

bng

. B.

. C.

. D.

6

Lời giải

Chọn C

Trang23

t

HM x

0 xh

. Gi

,,I R r

la nón

()N

ng tròn

 



12CH h

là chiu cao ca

( ), 3 2NR



,,C I H

thng hàng (

nm gia

,CH

Do tam giác

CEM CQH∽

nên

EM CM

QH CH



.QH CM



 

R h x

r EM FM



   

Th tích ca khi nón nh



 

là

V EM HM





 

R h x













 

h x x





Ta có Xét hàm s

   

f x h x x





 

0 xh

    

f x h x h x





  

;

    

f x h x h x x





     

Lp bng bin thiên ta có

T bng bin ta có th tích khnh



 

ln nht khi

x 

Chú ý: Có th a vào

 

1 1 2

( )( ) ( )( )2 ( )

2 2 3

h x h x x

h x x h x h x x h x h x x

   

       

vi

0 xh

.Du "="

xy ra khi ba s

( ) ( ) 2

h x h x x x     



HM x  

. .( )

R CM R h x

r MF



   

Trang24

Gm ca HM vi mt cu ngoi tip nón

 



Ta có

HFP

vuông ti F

.HF HM HP

 

. 16 2 2 4. 6HM MF HM HP HP HP       

3 ( 1;2;2)

d HI HC HI HC I       

 

Vy

6a b c d   

Đề 7

ĐỀ LUYỆN THI CẤP TỐC TỐT NGHIỆP THPT NĂM 2021

Thuvienhoclieu.Com

BÀI THI: TOÁN

Thời gian: 90 phút

Câu 1: Trong mt hp bút gm có 8 cây bút bi, 6 cây bút chì và 10 cây bút màu. Hi có bao nhiêu cách

chn ra mt cây bút t h

480.

24.

48.

60.

Câu 2: Cho cp s cng

 

có s hng tng quát là

un

. Tìm công sai

ca cp s cng.

3d 

. B.

2d 

. C.

2d 

. D.

3d 

Câu 3: Cho hàm s

 

y f x

có bng bi bên. Hàm s

 

y f x

nghch bin trên

khong nào trong các kho

 

1; 0

. B.

 

1; 1

. C.

 

;1 

. D.

 

0; 

Câu 4: Cho hàm s

 

y f x

có bng bii:

Giá tr ci ca hàm s 

1.

. D.

2.

Câu 5: Cho hàm s

3.  y x x

Kh



























Trang25

A. Hàm s m cc tr.

B. Hàm s ch c tr.

C. Hàm s không có cc tr

D. Hàm s ch m cc tr.

Câu 6: Cho hàm s

 

y f x

có bng bi 

Tng s ng tim cn ngang và tim cng c th hàm s 

Câu 7:  th ca mt hàm s trong bn hàm s c lit kê  bn

i hàm s  nào?

-1

2 4 1y x x   

. B.

21y x x  

41y x x   

. D.

21y x x   

Câu 8: S m c th hàm s

2 12y x x x   

và trc

là

. B.

. C.

. D.

Câu 9: Cho

,ab

là các s tht k. M sai?

log(10 ) 2 log( )ab ab

. B.

log(10 ) 2(1 log log )ab a b  

log(10 ) 2 2log( )ab ab

. D.

log(10 ) (1 log log )ab a b  

Câu 10: 

 





 

2.e







. B.

 

2.e







. C.

 

2.e







. D.

 







Câu 11: Rút gn

. , 0.P a a













Câu 12: Tng các nghim c bng

3 81

xx



Trang26

. B.

. C.

. D.

Câu 13: Tp nghim c

log log ( 2) 2xx+ + =

là

 

13S   

. B.

 

1 10; 1 10S     

 

1 10S   

. D.

 

0;2S 

Câu 14: Cho hàm s

( )

21x

. Trong các khnh sau, khnh nào đúng?

( ) ln 2f x dx x x C  



. B.

( ) lnf x dx x x C  



( ) lnf x dx x C



. D.

( ) ln 2f x dx x x C  



Câu 15: Cho hàm s

( )

sin cosf x x x=

. Trong các khnh sau, khnh nào đúng?

( ) sinf x dx x C



. B.

sin

()

f x dx C



cos

()

f x dx C



. D.

( ) cosf x dx x C  



Câu 16: Nu

( )

3f x dx =

và

f dx

æö

èø

thì

( )

f x dx

bng

. B.

. C.

. D.

Câu 17: Tích phân

xdx

bng

. B.

1e

. C.

1e

. D.

Câu 18: Tng phn thc và phn o ca s phc liên hp ca

23zi=-

là

1

. B.

. C.

5

. D.

Câu 19: Cho hai s phc

2zi

và

73zi

. Tìm s phc

z z z

52  zi

. B.

9z

. C.

4zi

. D.

94zi

Câu 20: Trên mt phng t, cho s phc

 

13  i z i

m biu din s phc

là

 

3;2

. B.

 

1; 2

. C.

 

2; 1

. D.

 

1;2

Câu 21: Cho hình chóp

.S ABCD



ABCD

là hình vuông cnh

, cnh

vuông góc v

2SA a

. Th tích khi chóp

.S ABCD

bng

. B.

. C.

. D.

Câu 22: Th tích ca mt khi hp ch nht có các cnh

2 ,4 ,7cm cm cm

là

56cm

. B.

36cm

. C.

48cm

. D.

24cm

Trang27

Câu 23: Cho khng

ng cao

. Th tích ca khng



. B.



. C.



. D.



Câu 24: Cho hình tr  ng sinh bng

, din tích xung quanh bng



. Bán kính hình tròn

a hình tr ng

. B.

. C.

. D.

Câu 25. Trong không gian vi h t

Oxyz

, cho

 

2;0;0A

 

0;3;4B

 n thng

là:

33AB 

. B.

27AB 

. C.

19AB 

. D.

29AB 

Câu 26.Trong không gian

Oxyz

m

   

2;1;1 , 0; 1;1AB

t cng kính

là:

   

1 1 2x y z    

. B.

   

1 1 4x y z    

   

1 1 8x y z    

. D.

   

1 1 2x y z    

Câu 27. Cho bit phng

 

: 13 0P ax by cz   

m

 

1; 1;2A 

 

2;1;0B

 

0;1;3C

. 

abc

bng

. B.

11

. C.

10

. D.

Câu 28.Trong không gian

Oxyz

m

   

1; 2;0 , (2; 1;3), 0; 1;1A B C  

ng trung tuyn

ca tam giác

ABC









  









. B.

















. C.

















. D.







  









Câu 29.Trên giá sách có 4 quyn sách Toán, 3 quyn sách Lí và 2 quyn sách Hóa, ly ngu nhiên 3

quyn sách. Tính xác sut sao cho ba quyn ly ra có ít nht mt quyn sách Toán.

. B.

. C.

. D.

Câu 30. Hàm s nào trong các hàm s ch bin trên

?

0,9

logyx

. B.

y 

. C.

logyx

. D.

 

0,9

y 

Câu 31: Hàm s

y x x x= - + +

t giá tr ln nht và giá tr nh nhn

[ ]

1;3

lt

tm

và



xx+

bng

. B.

. C.

. D.

Câu 32: Tìm tp nghim

ca b

xx









 

1;2S 

. B.

 

;1S  

. C.

 

1;2S 

. D.

 

2;S  

Câu 33: Cho

 

d2f x x







và

 

d1g x x







. Tính

   

2 3 dI x f x g x x





  



Trang28

I 

. B.

I 

. C.

I 

. D.

I 

Câu 34: Cho s phc

12zi

. Tìm tng phn thc và phn o ca s phc

2w z z

. B.

. C.

. D.

Câu 35: Cho hình chóp

.S ABCD

 

ABCD

là hình ch nht,

2, 5AB AD

. Cnh bên

3SA 

và vuông góc vi mt pho hình bên). Góc ging thng

và

mt phng

 

ABCD

bng

30 .



45 .



60 .



90 .



Câu 36:    

. ' ' 'ABC A B C

     u cnh bng

. Bit

' ' ' 2A A A B A C  

. Khong cách t

n mt phng

 

ABC

bng

. B.

Câu 37: Trong không gian

,Oxyz

mt cu có tâm

 

1;0;2I

và tip xúc vi mt phng

 

Oyz



trình là:

   

1 2 1.x y z    

   

1 2 1.x y z    

   

1 2 2.x y z    

   

1 2 4.x y z    

Câu 38: Trong không gian

,Oxyz

ng thm

 

1;3; 2M 

và song song vng thng

2 1 3

x y z







 là:













  















  



1 3 .







  





  



  





  









Trang29

Câu 39: Cho hàm s

 

 th hàm s

 

y f x





ng cong trong hình bên. Giá tr ln nht ca

hàm s

   

2 1 2g x f x x   

n

 

0;2

bng

 

12f

. B.

 

1f

. C.

 

23f

. D.

 

34f

Câu 40.Có bao nhiêu s 

sao cho ng vi mi

có không quá 25 s nguyên

tha

mãn









A. 30 B. 31C. 32 D. 33

Câu 39: Cho hàm s

 

liên tc trên



tha mãn

 

x m x













(m là hng s). Bit

 

f x x a









,ab

là các s hu t. Tính

ab

. B.

. C.

. D.

Câu 42: Có bao nhiêu s phc

tha mãn

z z i

z i z i







. B.

. C.

. D.

Câu 43: Cho hình chóp

.S ABCD



ABCD

là hình thoi tâm

cnh

, góc



30BCA 

 

SO ABCD

và

SO 

 tích ca khi chóp là

. B.

. C.

. D.

Câu 44. T mt tm thép phng hình ch nhi ta mun làm mt ching du hình tr

bng cách ct ra hai hình tròn bng nhau và mt hình ch nht (phi,

  nht làm thành mt xung

quanh cng du (v). Bit ri tip mt tam giác có kích

c là

50 ,70 ,80cm cm cm

(các mi ghép ni khi gò hàn chim di. Ly

3,14





). Din tích ca tm thép hình ch nhu gn nht vi s li

Trang30

6,8

 

. B.

24,6

 

. C.

6,15

 

. D.

3,08

 

Câu 45. Trong không gian

Oxyz

,ng thng

1 1 1

1 2 1

  



x y z

1 3 1

2 1 2

  





x y z

và

mt phng

 

:2 3 0   P x y z

. Bit rng thng



song song vi mt phng

 

, ct

ng thng



lt ti

sao cho

11MN

m

).

ng thng



là

1 1 3







x y z

1 2 4







x y z

1 1 3







x y z

1 2 4







x y z

Câu 46: Cho

 

là hàm s bc bn tha mãn

 

ln2

f 

. Hàm s

 



có bng bi

Hàm s

 

ln2

g x f x x   

m cc tr?

. B.

. C.

. D.

Câu 47: Cho các s thc

,,x y z

tha mãn

   

   

2 2 3 3

log 2 log 2 logx y x y z

. Có bao giá

tr nguyên ca

 p

 

,xy

thng thc trên.

. B.

211

. C.

. D.

Câu 48: Cho hàm s

3y x x m  

 th

 

, vi

là tham s thc. Gi s

 

ct trc

ti bm phân bi

Trang31



              



1 3 2

S S S

là

. B.



. C.

. D.



Câu 49: Xét hai s phc

;zz

tha mãn

1; 4zz

và

5zz

. Giá tr ln nht ca

z 2 7zi

bng

7 89

. B.

7 89

. C.

7 2 89

. D.

7 2 89

Câu 50: Trong không gian

Oxyz

   m

(1;3;0), ( 3;1;4)AB

 ng thng

2 1 2

1 1 3

x y z  

  



. Xét khi nón

()N

nh có t nguyên thung thng



và

ngoi tip mt cng kính

. Khi

()N

có th tích nh nht thì mt phng chng

a

()N

ng

10ax by cz   

. Giá tr

abc

bng

. B.

. C.

. D.

6.

BẢNG ĐÁP ÁN

1.B

2.A

3.A

4.B

5.D

6.D

7.A

8.B

9.D

10.A

11.B

12.D

13.C

14.D

15.B

16.C

17.D

18.B

19.A

20.B

21.D

22.A

23.A

24.C

25.D

26.A

27.A

28.A.

29.A

30.D

31.D

32.C

33.A

34.B

35.A

36.A

37.B

38.A

39.C

40.B

39.A

42.D

43.B

44.C

45.C

46.D

47.B

48.A

49.B

50.A

HƯỚNG DẪN GIẢI CHI TIẾT

Câu 1: Trong mt hp bút gm có 8 cây bút bi, 6 cây bút chì và 10 cây bút màu. Hi có bao nhiêu cách

chn ra mt cây bút t h

480.

24.

48.

60.

Lời giải

Chọn B

Áp dng quy tc cng:

S cách chn ra mt cây bút t h

8 6 10 24.  

Câu 2: Cho cp s cng

 

có s hng tng quát là

un

. Tìm công sai

ca cp s cng.

3d 

. B.

2d 

. C.

2d 

. D.

3d 

Trang32

Lời giải

Chọn A

Ta có

 

3 1 2 3 2 3

u u n n



      

Suy ra

3d 

là công sai ca cp s cng.

Câu 3: Cho hàm s

 

y f x

có bng bi bên. Hàm s

 

y f x

nghch bin trên

khong nào trong các kho

 

1; 0

. B.

 

1; 1

. C.

 

;1 

. D.

 

0; 

Lời giải

Chọn A

Trong khong

 

1; 0

o hàm





nên hàm s nghch bin trên khong

 

1; 0

Câu 4: Cho hàm s

 

y f x

có bng bii:

Giá tr ci ca hàm s 

1.

. D.

2.

Lời giải

Chọn B

Câu 5: Cho hàm s

3.  y x x

Kh

A. Hàm s m cc tr.

B. Hàm s ch c tr.

C. Hàm s không có cc tr

D. Hàm s ch m cc tr.

Lời giải

Chọn D



























Trang33

0 (boi 2)

4 3 0









   







y x x

Vy hàm s c tr.

Câu 6: Cho hàm s

 

y f x

có bng bi 

Tng s ng tim cn ngang và tim cng c th hàm s 

Lời giải

Chọn D

Tim cn ngang:

3.y

Tim cng:

1; 1.  xx

Câu 7:  th ca mt hàm s trong bn hàm s c lit kê  bn

i hàm s  nào?

-1

2 4 1y x x   

. B.

21y x x  

41y x x   

. D.

21y x x   

Lời giải

Chọn A

 th hàm s m

 

0; 1A 

;

 

1;1B

và

 

1;1C 

Trang34

Xét

2 4 1y x x   

Th t m

 

0; 1A 

tha mãn; th t m

 

1;1B

1 2.1 4.1 1   

Th t m

 

1;1C 

tha mãn.

Câu 8: S m c th hàm s

2 12y x x x   

và trc

là

. B.

. C.

. D.

Lời giải

Chọn B

 m:

2 12 0x x x   

3x

Vy có mm duy nht.

Câu 9: Cho

,ab

là các s tht k. M sai?

log(10 ) 2 log( )ab ab

. B.

log(10 ) 2(1 log log )ab a b  

log(10 ) 2 2log( )ab ab

. D.

log(10 ) (1 log log )ab a b  

Lời giải

Chọn D

Ta có

 

log(10 ) 2log(10 ) 2 log10 log 2 2log( )ab ab ab ab    

2(1 log log ) 2 log( )a b ab    

Câu 10: 

 





 

2.e







. B.

 

2.e







. C.

 

2.e







. D.

 







Lời giải

Chọn A

Ta có

   

2 3 2 3

2 3 .e 2.e

f x x





  

Câu 11: Rút gn

. , 0.P a a













Lời giải

Chọn B

Cách 1:

 

2 2 1 2 1 2

.P a a a a a a







   





Cách 2: MTCT

Trang35

B1: Nhp biu thc P và tr 

B2: Bm phím CALC máy hin

? nhp s ng hn là nhp 2) bm du = nu

kt qu là s 0 thì nhn nu khác 0 ta nh s

lp l

Câu 12: Tng các nghim c bng

. B.

. C.

. D.

Lời giải

Chọn D

Ta có

4 2 4 2

3 3 4 4 2

3 81 3 3 3 4

x x x x



     













42xx    

Vy tng các nghim c

3 81

xx



bng

Câu 13: Tp nghim c

log log ( 2) 2xx+ + =

là

 

13S   

. B.

 

1 10; 1 10S     

 

1 10S   

. D.

 

0;2S 

Lời giải

Chọn C

u kin

0x >

Ta có

3 3 3 3

1 10

log log ( 2) 2 log ( ( 2)) log 9 2 9 0

1 10

x x x x x x

= - -

+ + = Þ + = Þ + - = Û

= - +

Vì

0x >

m duy nht là

1 10x = - +

Câu 14: Cho hàm s

( )

21x

. Trong các khnh sau, khnh nào đúng?

( ) ln 2f x dx x x C  



. B.

( ) lnf x dx x x C  



( ) lnf x dx x C



. D.

( ) ln 2f x dx x x C  



Lời giải

Chọn D

Ta có

2 1 1

2 2 ln

dx dx dx x x C

= + = + +

ò ò ò

Câu 15: Cho hàm s

( )

sin cosf x x x=

. Trong các khnh sau, khnh nào đúng?

3 81

xx



Trang36

( ) sinf x dx x C



. B.

sin

()

f x dx C



cos

()

f x dx C



. D.

( ) cosf x dx x C  



Lời giải

Chọn B

Ta có

sin

sin cos sin (sin )

x xdx xd x C= = +

òò

Câu 16: Nu

 

3f x dx 



và

f dx











thì

 

f x dx



bng

. B.

. C.

. D.

Lời giải

Chọn C

Ta có

12 12 4 4

6 6 2 2

3 3 ( ) 3 ( )

3 3 3

x x x

f dx f d f t dt f x dx

æ ö æ ö æ ö

÷ ÷ ÷

ç ç ç

÷ ÷ ÷

= = =

ç ç ç

÷ ÷ ÷

ç ç ç

÷ ÷ ÷

ç ç ç

è ø è ø è ø

ò ò ò ò

Suy ra:

 

f x dx 



T 

4 2 4

1 1 2

2 11

( ) ( ) ( ) 3

f x dx f x dx f x dx= + = + =

ò ò ò

Câu 17: Tích phân

xdx

bng

. B.

1e

. C.

1e

. D.

Lời giải

Chọn D

ln ln ( 1) 1

xdx x x dx e e= - = - - =

òò

Câu 18: Tng phn thc và phn o ca s phc liên hp ca

23zi=-

là

1

. B.

. C.

5

. D.

Lời giải

Chọn B

S phc liên hp là

23zi=+

ng cn tìm bng

Câu 19: Cho hai s phc

2zi

và

73zi

. Tìm s phc

z z z

Trang37

52  zi

. B.

9z

. C.

4zi

. D.

94zi

Lời giải

Chọn A.

Ta có

   

2 7 3 2 7 3 5 2            z z z i i i i i

Câu 20: Trên mt phng t, cho s phc

 

13  i z i

m biu din s phc

là

 

3;2

. B.

 

1; 2

. C.

 

2; 1

. D.

 

1;2

Lời giải

Chọn B.

Ta có:

 

13  i z i







  







12  zi

Vm biu din s phc

là

 

1; 2M

Câu 21: Cho hình chóp

.S ABCD



ABCD

là hình vuông cnh

, cnh

vuông góc v

2SA a

. Th tích khi chóp

.S ABCD

bng

. B.

. C.

. D.

Lời giải

Chọn D.

Ta có th tích khi chóp

.S ABCD

là

1 1 2

. . . .2

3 3 3

  

S ABCD ABCD

V S SA a a

Câu 22: Th tích ca mt khi hp ch nht có các cnh

2 ,4 ,7cm cm cm

là

56cm

. B.

36cm

. C.

48cm

. D.

24cm

Lời giải

Chọn A.

Ta có th tích ca khi hp ch nht có các cnh

2 ,4 ,7cm cm cm

là

 

2.4.7 56V cm

Câu 23: Cho khng

ng cao

. Th tích ca khng



. B.



. C.



. D.



Lời giải

Chọn A.

Trang38

Th tích khi nón là

1 1 2

3 3 3

  

V r h a a





Câu 24: Cho hình tr  ng sinh bng

, din tích xung quanh bng



. Bán kính hình tròn

a hình tr ng

. B.

. C.

. D.

Lời giải

Chọn C.

Ta có

2 48 6.2 4    

S Rl R R

  

Câu 25. Trong không gian vi h t

Oxyz

, cho

 

2;0;0A

 

0;3;4B

 n thng

là:

33AB 

. B.

27AB 

. C.

19AB 

. D.

29AB 

Lời giải

Chọn D

Ta có:

 

0 2 3 4AB    

29

Câu 26.Trong không gian

Oxyz

m

   

2;1;1 , 0; 1;1AB

t cng kính

là:

   

1 1 2x y z    

. B.

   

1 1 4x y z    

   

1 1 8x y z    

. D.

   

1 1 2x y z    

Lời giải

Chọn A

Mt cng kính AB nhm I ca AB là tâm và bán kính

R 

Ta có

 

1;0;1I 

và

R 

Vt cu là

   

1 1 2x y z    

Câu 27. Cho bit phng

 

: 13 0P ax by cz   

m

 

1; 1;2A 

 

2;1;0B

 

0;1;3C

. 

abc

bng

. B.

11

. C.

10

. D.

Lời giải

Chọn A

Trang39

 

: 13 0P ax by cz   

m

     

1; 1;2 , 2;1;0 , 0;1;3A B C

nên ta có h

2 13 6

2 13 1 11

3 13 4

a b c a

a b b a b c

b c c

   





       





  



Câu 28.Trong không gian

Oxyz

m

   

1; 2;0 , (2; 1;3), 0; 1;1A B C  

ng trung tuyn

ca tam giác

ABC









  









. B.

















. C.

















. D.







  









Lời giải

Chọn A

     

1; 2;0 , 1; 1;2 ; 0;1;2A M AM  



ng trung tuyn

ca tam giác

ABC









  









Câu 29.Trên giá sách có 4 quyn sách Toán, 3 quyn sách Lí và 2 quyn sách Hóa, ly ngu nhiên 3

quyn sách. Tính xác sut sao cho ba quyn ly ra có ít nht mt quyn sách Toán.

. B.

. C.

. D.

Lời giải

Chọn A

S phn t không gian mu

 

84nC  

Gi bin c n ly ra có ít nht 1 quy

Ta có

 

1 2 2 1 3

4 5 4 5 4

. . 74n A C C C C C   

Xác sut ca bin c A là

 

74 37

84 42

  



Nhận xét: Có th dùng bin c i

 

10 37

10 1 1

84 42

n A C P A P A       

Câu 30. Hàm s nào trong các hàm s ch bin trên

?

0,9

logyx

. B.

y 

. C.

logyx

. D.

 

0,9

y 

Lời giải

Chọn D

Hàm s:

0,9

logyx

nghch bin trên

 

0;

Hàm s:

y 

ng bin trên



Hàm s:

logyx

ng bin trên

 

0;

Hàm s:

 

0,9

y 

nghch bin trên



V

Trang40

Câu 31: Hàm s

y x x x= - + +

t giá tr ln nht và giá tr nh nhn

[ ]

1;3

lt

tm

và



xx+

bng

. B.

. C.

. D.

Lời giải

Chọn D

Tnh:

D =

56y x x

= - +

;

[ ]

2 1;3

0 5 6 0

3 1;3

y x x

=Î

= Û - + = Û

=Î

Ta có:

( )

y =

( )

y =

( )

y =













  







  





1;3

max 2

min 1

Vy hàm s t giá tr ln nht và giá tr nh nhn

[ ]

1;3

lt tm

2x =

và

1x =

3xxÞ + =

Câu 32: Tìm tp nghim

ca b

xx









 

1;2S 

. B.

 

;1S  

. C.

 

1;2S 

. D.

 

2;S  

Lời giải

Chọn C

Ta có :

3 3 2

1 1 1 1

3 2 3 2 0 1 2

2 4 2 2

x x x x

x x x x x

   

     

             

     

     

Vy tp nghim ca b

 

1;2S 

Câu 33: Cho

 

d2f x x







và

 

d1g x x







. Tính

   

2 3 dI x f x g x x





  



I 

. B.

I 

. C.

I 

. D.

I 

Lời giải

Chọn A

Ta có:

   

2 3 dI x f x g x x



  









   

2 d 3 d

f x x g x x











 

2.2 3 1

  



Câu 34: Cho s phc

12zi

. Tìm tng phn thc và phn o ca s phc

2w z z

. B.

. C.

. D.

Lời giải

Chọn B

Ta có

1 2 1 2z i z i    

Trang41

2 2(1 2 ) 1 2 3 2w z z i i i       

Vy tng phn thc và phn o ca s phc

là

Câu 35: Cho hình chóp

.S ABCD

 

ABCD

là hình ch nht,

2, 5AB AD

. Cnh bên

3SA 

và vuông góc vi mt pho hình bên). Góc ging thng

và

mt phng

 

ABCD

bng

30 .



45 .



60 .



90 .



Lời giải

Chọn A.

là hình chiu vuông góc ca

trên mt phng

 

ABCD

 



,SC ABCD SCA

Xét

SCA

vuông ti

có

 

3, 3 tan 30

SA AC SCA SCA

      

Câu 36:    

. ' ' 'ABC A B C

     u cnh bng

. Bit

' ' ' 2A A A B A C  

. Khong cách t

n mt phng

 

ABC

bng

. B.

Lời giải

Chọn A

Gi

ng tròn ngoi tip

ABC

'''A A A B A C

nên

   

 

' ', 'A H ABC d A ABC A H  

Xét

'A AH

vuông ti

có

2 2 3 2 3 2 6

' 2, . ' '

3 2 3 3

A A AH A H A A AH      

Câu 37: Trong không gian

,Oxyz

mt cu có tâm

 

1;0;2I

và tip xúc vi mt phng

 

Oyz



trình là:

Trang42

   

1 2 1.x y z    

   

1 2 1.x y z    

   

1 2 2.x y z    

   

1 2 4.x y z    

Lời giải

Chọn B

Gi

là hình chiu vuông góc ca

trên mt phng

   

0;0;2Oyz H

Có

1R IH

t cu cn tìm là

   

1 2 1.x y z    

Câu 38: Trong không gian

,Oxyz

ng thm

 

1;3; 2M 

và song song vng thng

2 1 3

x y z







 là:













  















  



1 3 .







  





  



  





  









Lời giải

Chọn A.

ng thng

có VTCP

 

2; 1; 3

u   



ng thng cn lp song song vi

nên có VTCP

 

2; 1; 3

uu   

 

Vng thng cn l là













  



Câu 39: Cho hàm s

 

 th hàm s

 

y f x





ng cong trong hình bên. Giá tr ln nht ca

hàm s

   

2 1 2g x f x x   

n

 

0;2

bng

 

12f

. B.

 

1f

. C.

 

23f

. D.

 

34f

Lời giải

Chọn C

Trang43

     

0 2 2 1 2 0 2 1 1g x f x f x

  

        

2 1 1 0

2 1 1 1

2 1 2 3





   





    













   

2 1 1

0 2 1 1

2 1 2

g x f x





  







     









Bng bin thiên

Giá tr ln nht ca hàm s

 

trên

 

0;2

bng

 



  





Câu 40.Có bao nhiêu s 

sao cho ng vi mi

có không quá 25 s nguyên

tha

mãn









A. 30 B.31C. 32 D. 33

Chọn B

u kin:

















ng hp 1:

 

log 0













  













ng hp 2:

 

log



























Kt hu kin:

0; log log 1 0xy  

. Ta có :

 

0 logxy

Trang44

 có không quá 25 s nguyên x thì

 

1 log 25 1 log 5 2 32y y y       

 

2;3;...;32y

. Có 31 s nguyên y.

Câu 39: Cho hàm s

 

liên tc trên



tha mãn

 

x m x













(m là hng s). Bit

 

f x x a









,ab

là các s hu t. Tính

ab

. B.

. C.

. D.

Lời giải

Chọn A

Do hàm s liên tc trên



nên hàm s liên tc ti

     

0 lim lim 0 1

x f x f x f m





     



       

2 0 2 0 2

1 1 0 1 0

d d d d 1 d

f x x f x x f x x e x x x

  

    

    

2 2 2

1 9 1

2 2 2 2 2 2

e x e





       







;

ab  

Vy

4ab

Câu 42: Có bao nhiêu s phc

tha mãn

z z i

z i z i







. B.

. C.

. D.

Lời giải

Chọn D

Ta có: Gi

z a bi

 

,ab

Ta có:

z z i

z i z i

   





  





   

a b a b



    







    





2 1 2 1

6 9 2 1

    







   















Vy có mt s phc tha mãn là

1zi

Câu 43: Cho hình chóp

.S ABCD



ABCD

là hình thoi tâm

cnh

, góc



30BCA 

 

SO ABCD

và

SO 

 tích ca khi chóp là

. B.

. C.

. D.

Lời giải

Chọn B

Trang45

30

Theo gi thit

ABCD

là hình thoi tâm

cnh

, góc



30BCA 

nên



60BCD 

;

BCD

u suy ra

BD a

CO 

23AC CO a

Ta có

ABCD

S AC BD

. . 3

aa

;

S ABCD ABCD

V SO S

vi

SO 

suy ra

1 3 3 3

3 4 2 8

S ABCD

a a a

V    

Câu 44. T mt tm thép phng hình ch nhi ta mun làm mt ching du hình tr

bng cách ct ra hai hình tròn bng nhau và mt hình ch nht (phi,

quanh cng du (v). Bit ri tip mt tam giác có kích

c là

50 ,70 ,80cm cm cm

(các mi ghép ni khi gò hàn chim di. Ly

3,14





). Din tích ca tm thép hình ch nhu gn nht vi s li

6,8

 

. B.

24,6

 

. C.

6,15

 

. D.

3,08

 

Lờigiải

ChọnC

i:

50 0,5 ;70 0,7 ;80 0,8cm m cm m cm m  

Xét tam giác ni tic lt là

0,5 ;0,7 ;0,8m m m

nên bán kính

ng du là

   

4 1 1 0,5 1

0,5.0,

0,8 7 3









Ta có

2hR

Din tích hình ch nhu gp

ln din tích xung quanh ca hình tr.

Trang46

Vy

7693

3.2

6.3,14.2.R 6.3,14.2 6,1544

1250

S Rh





    





 

Câu 45. Trong không gian

Oxyz

,ng thng

1 1 1

1 2 1

  



x y z

1 3 1

2 1 2

  





x y z

và

mt phng

 

:2 3 0   P x y z

. Bit rng thng



song song vi mt phng

 

, ct

ng thng



lt ti

sao cho

11MN

m

).

ng thng



là

1 1 3







x y z

1 2 4







x y z

1 1 3







x y z

1 2 4







x y z

Lời giải

Chọn C

Gi

 

1 ; 1 2 ;1     M a a a d

(

a¢

) ,

 

1 2 ;3 ;1 2



    N b b b d

 

2 ; 2 4; 2      MN b a b a b a



. Mn ca ca

 

là

 

2;1;1n



Ta có

   

// . 0 5 4 0 5 4 9 8; 7 8; 11 8                 P MN n a b b a MN a a a

  

11 251 432 192 11 251 432 181 0

181

()

251







         







MN a a a a

Suy ra



có mt   ca

 

1;1; 3  u MN





và





 

0;1;2M

Vng thng



là

1 1 3







x y z

Câu 46: Cho

 

là hàm s bc bn tha mãn

 

ln2

f 

. Hàm s

 



có bng bi

Hàm s

 

ln2

g x f x x   

m cc tr?

. B.

. C.

. D.

Lời giải

Trang47

Chọn D

T bng bic

 

3 9 5

4 4 2

f x x x



   

t

 

ln2

h x f x x   

. Ta có

   

0 0 0

ln2

hf  

 

   

2 2 2 2 2 1 2

h x x f x x x x f x



  

           



 

2 1 (*)













  





t

,0t x t  

 thành:

   

f t u t





, vi

 





T  th ta th

   

f t u t t t



  

, vi

1t 

T 

x t x t      

Bng bin thiên

T bng bin thiên suy ra hàm s

   

g x h x

m cc tr.

Câu 47: Cho các s thc

,,x y z

tha mãn

   

   

2 2 3 3

log 2 log 2 logx y x y z

. Có bao giá

tr nguyên ca

 p

 

,xy

thng thc trên.

. B.

211

. C.

. D.

Lời giải

Chọn B

Ta có

   

 

2 2 3 3 3 3

2 3 1

log 2 log 2 log 2 7 2

10 3

x y x y z t x y







       











Trang48

+ Nu

0y 

 

x

thay vào

 

c

2.7 3 log 2

t  





log 2

10z

+ Nu

0y 

T

   

1 & 2

suy ra

 



















   





   



   

   





















2 27

49 49

27 27

2 49

t

  

. Xét

 



  





      











2 6 2 4

2 1 2 1

u u u u

f u f u u

Ta có bng bin thiên

Nhn xét vi mi giá tr

ng vi duy nht 1 cp

 

,xy

th

Yêu c

49 49

27 27

log log 4

log

1 49

10 10

8 27

49 4

0 10

27 33























































Vì

là s nguyên nên có

211

giá tr tha mãn.

Câu 48: Cho hàm s

3y x x m  

 th

 

, vi

là tham s thc. Gi s

 

ct trc

ti bm phân bi

Trang49





1 3 2

S S S

là

. B.



. C.

. D.



Lời giải

Chọn A





30x x m  

, ta có

3m x x  

 

Vì

1 3 2

S S S

và

SS

nên

2SS

hay

 

f x x 



Mà

 

f x x



 

x x m x  



x mx



  





x mx  

x x m



  







x x m



  







xm  

 



 

và

 



2 4 2

1 1 1

x x x   



4 10 0xx  



x 



3m x x  



Câu 49: Xét hai s phc

;zz

tha mãn

1; 4zz

và

5zz

. Giá tr ln nht ca

z 2 7zi

bng

7 89

. B.

7 89

. C.

7 2 89

. D.

7 2 89

Lời giải

Chọn B

t

,z a bi z c di= + = +

vi

, , , .a b c d Î ¡

Theo gi thit thì

2 2 2 2 2 2

1, 16, ( ) ( ) 5.a b c d a c b d+ = + = - + - =



2 2 2 2

2 2 5 6.a ac c b bd d ac bd- + + - + = Þ + =

Ta có

2 ( 2 ) ( 2 )z z a c b d i+ = + + +

nên

2 2 2 2 2 2

2 ( 2 ) ( 2 ) 4( ) 4( ) 89.z z a c b d a b c d ac bd+ = + + + = + + + + + =

Áp dng bng thc

z z z z

¢¢

+ £ +

, ta có ngay

1 2 1 2

2 7 2 7 7 89z z i z z i+ - £ + + - = +

Câu 50: Trong không gian

Oxyz

   m

(1;3;0), ( 3;1;4)AB

 ng thng

2 1 2

1 1 3

x y z  

  



. Xét khi nón

()N

nh có t nguyên thung thng



và

ngoi tip mt cng kính

. Khi

()N

có th tích nh nht thì mt phng chng

a

()N

ng

10ax by cz   

. Giá tr

abc

bng

. B.

. C.

. D.

6.

Lời giải

Trang50

Chọn A

Mt cng kính

có tâm

( 1;2;2)I 

, bán kính

Gi

,Hr

la

()N

nh ca

()N



,,C I H

thng hàng (

nm gia

,CH

3IH IK

t

CI x

CIK

ng dng

CMH

nên

. 3( 3)

IK CK IK CH x

r HM

MH CH CK



    



   

()

3 3 3

. .( 3) 3

3 3 3

V r CH x





      







()N

nh nht

 

()





  



nh nht

( 3)x 

6 27

'( )







'( ) 0













()N

nh nht

9x



9IC 

nên

2 2 2

( ):( 1) ( 2) ( 2) 81C S x y z      

Mt khác

C

nên

 

1;2;11C 

hoc

43 32 41

;;

11 11 11









Vì

có t nguyên nên

 

1;2;11C 

IH IC

 

nên

( 1;2; 1)H 

Trang51

Mt phng cha

()N



và nhn

(0;0;3)IH 





tuyt phng là

10z 



0, 0, 1abc  

nên

1abc  

Đề 8

ĐỀ LUYỆN THI CẤP TỐC TỐT NGHIỆP THPT NĂM 2021

Thuvienhoclieu.Com

BÀI THI: TOÁN

Thời gian: 90 phút

Câu 1: Có bao nhiêu cách sp xp

hng thành mt hàng dc?

. B.

. C.

. D.

Câu 2: Cho cp s nhân

 

có

2u 

và công bi

3q 

. Giá tr ca

là:

6

. B.

18

. C.

. D.

4

Câu 3: Cho hàm s

 

y f x

có bng bi

Hàm s ch bin trên khong nào trong các kho

 

2;0

. B.

 

2; 1

. C.

 

3; 

. D.

 

1; 

Câu 4: Cho hàm s bc ba

 

0y ax bx cx d a    

 th 

Giá tr ci ca hàm s là:

2x 

. B.

4y 

. C.

0x 

. D.

0y 

Trang52

Câu 5: Cho hàm s

 

y f x

nh trên



o hàm

    

 

' 2 1 4f x x x x x   

. Hàm s

m cc tr

A. 3. B.

. C.

. D.

Câu 6: Tim cn ngang c th hàm s





ng thng:

1x 

. B.

1y 

. C.

1y 

. D.

0y 

Câu 7: ng cong   th ca mt trong bn hàm s  

s nào ?

y x x  

y x x  

y x x  

1.y x x x    

Câu 8:  th hàm s

yx   

ct trc hoành ti mm?

Câu 9: Vi

là s th

 

log 125a

bng

3 log a

. B.

3 log a

. C.

 

log a

. D.

2 log a

Câu 10: o hàm ca hàm s

12x





là:





. B.





. C.





. D.





Câu 11: Vi

là s thc tu ý,

bng

. B.

. C.

. D.

Câu 12: Tng các nghim c

3 81

xx



bng

A. B. C. D.

Câu 13: Nghim c

 

log 2 2x 

là:

x 

. B.

3x 

. C.

x 

. D.

1x 

Trang53

Câu 14: Cho hàm s

 

4 2021f x x

. Trong các khnh sau, kh

 

d 4 2021f x x x x C  



. B.

 

d 2021f x x x x C  



 

d 2021f x x x



. D.

 

df x x x C



Câu 15: Cho hàm s

 

sin3f x x

. Trong các khnh sau, kh

 

d cos3

f x x x C



. B.

 

d cos3

f x x x C  



 

d 3cos3f x x x C



. D.

 

d 3cos3f x x x C  



Câu 16: Nu

 

d2f x x 



và

 

d7f x x 



thì

 

df x x



bng

5

. B.

. C.

9

. D.

14

Câu 17: Tích phân

ln3



bng

. B.

. C.

. D.

1e

Câu 18: S phc liên hp ca s phc

34zi

là:

34zi

. B.

43zi

. C.

43zi

. D.

34zi

Câu 19: Cho hai s phc

35zi

và

68zi  

. S phc liên hp ca s phc

zz

là

9 13i

. B.

33i

. C.

33i

. D.

9 13i

Câu 20: Trên mt phng tm biu din s phc liên hp ca s phc

23 5i

có t là

 

23; 5

. B.

 

23;5

. C.

 

23; 5

. D.

 

23;5

Câu 21: Th tích khi  u có cng 2 và chiu cao bng mt na c

Câu 22: Cho khi hnh bng 5 và chiu cao khi hp bng mt na chu vi

 tích ca khi hng

250cm

. B.

125cm

. C.

200cm

. D.

500cm

Câu 23: Công thc tính th tích

ca hình nón có di

4SR





và chiu cao

là:

V R h





. B.

V R h





. C.

V R h





. D.

V Rh





Câu 24: Mt hình tr có bán kính

6R 

 ng sinh

4l 

cm. Tính din tích toàn phn ca

hình tr 

120

S cm

. B.

S cm

. C.

S cm

. D.

S cm

Trang54

Câu 25: Trong không gian

,Oxyz

cho tam giác

ABC

bit

     

1;1;3 , 1;4;0 , 3; 2; 3A B C   

. Trng

tâm

ca tam giác

ABC

có t là

 

3;3;0

. B.

; ;0









. C.

 

1;1;0

. D.

 

1; 1;1

Câu 26: Trong không gian

,Oxyz

mt cu

       

2 2 2

: 1 1 3 9S x y z     

. Tâm

ca mt cu

( )

có t là

 

1; 1; 3

. B.

 

1;1;3

. C.

 

2; 2; 6

. D.

 

2;2;6

Câu 27: Trong không gian

,Oxyz

cho mt phng

 



2 3 0x y z   

m nào sau

c mt phng

 

1; 1; 3M 

. B.

 

1;1;0N 

. C.

 

2; 2;6H 

. D.

 

2;2;3K 

Câu 28: Trong không gian

,Oxyz

không phải  ng thng

2 1 2

x y z







 

2; 1;2u   



. B.

 

2;1; 2u 



. C.

 

4; 2;4u   



. D.

 

1; 1;0u 



Câu 29: Có

chic th  th t t n 30. Chn ngu nhiên mt chic th. Tính xác sut

 chic th c chn mang s chia ht cho 3.

. B.

. C.

. D.

Câu 30: Hàm s ch bin trên

?

41y x x   

. B.

1y x x   

. C.







. D.

23yx  

Câu 31: Cho hàm s

34y x x  

. Gi

,Mm

lt là giá tr ln nht và giá tr nh nht ca hàm

s n

 

0;2

. Khđúng?

8Mm

. B.

22Mm  

. C.

2 10Mm

. D.

8Mm  

Câu 32: B

xx



có tp nghim là

3 17 3 17

;











. B.

3 17 3 17

;;

   



   







   

 

1;2T 

. D.



 



;1 2;T    

Câu 33: Bit

 

d3f x x 



 

d4f x x 



. Tính

 

2df x x x



Trang55

. B.

. C.

. D.

Câu 34: Cho s phc

tha mãn

 

1 2 1 4z i i  

. Phn thc ca s phc

thuc khoi



 

0;2

. B.

 

2; 1

. C.

 

4; 3

. D.









Câu 35: Cho hình chóp

.S ABCD

nh

ng thng

vuông góc vi mt

phng

 

ABCD

SA a

. Góc gia hai mt phng

 

SCD

và

 

ABCD

là





tan



nhn giá tr nào trong các giá tr sau ?

tan 2





. B.

tan





. C.

tan 3





. D.

tan 1





Câu 36: Cho hình chóp t u

.S ABCD



và

,SA a AB a

ng

cách t m

n mt phng

 

SAD

bng bao nhiêu ?

. B.

. C.

. D.

Câu 37: Trong không gian vi h t

Oxyz

m

 

1;1;0A

và

 

1; 1; 4B 

. Vi

trình mt cu

 

nhn

ng kính .

     

: 1 2 5S x y z    

. B.

     

: 1 2 20S x y z    

     

: 1 2 20S x y z    

. D.

     

: 1 2 5S x y z    

Câu 38: Trong không gian vi h t

Oxyz

m

 

2;3;4M 

. Ving thng

 

m

và vuông góc vi mt phng

 

Oxy

 

















. B.

 

  















. C.

 

















. D.

 

  















Câu 39: Cho hàm s

 

,fx

 th ca hàm s

 

y f x

. Giá tr nh nht

ca hàm s

   

2 1 6g x f x x  

n







bng

Trang56







. B.

 

03f 

. C.

 

16f 

. D.

 

3 12f 

Câu 40: Có bao nhiêu s 

sao cho ng vi mi

có không quá

2186

s nguyên

tha mãn

 

log 3 9 0

xy  

. B.

. C.

2186

. D.

Câu 41: Cho hàm s

 

1y f x

 

y g x x

. Giá tr

   

 

min ; dI f x g x x







. B.

. C.

. D.

Câu 42: Có tt c bao nhiêu s phc

mà phn thc và phn o ca nó trái d ng thi tha mãn

4   z z z z

và

2 2 3 2.zi  

. B.

. C.

. D.

Câu 43: Cho hình chóp

.S ABC



ABC

là tam giác vuông ti

và có

,3AB a BC a

. Mt

bên

SAB

u và nm trong mt phng vuông góc vi mt phng

 

ABC

. Tính th

tích

ca khi khóp

.S ABC

V 

. B.

V 

. C.

V 

. D.

V 

Câu 44: Ông An cn làm m . Phi là mt phn ca khi cu bán kính

20 cm

làm bng g c, bán kính cng tròn phn chm cu bng

10 cm

. Phn phía trên

làm bng lp v kính trong sut. Bit giá tin ca

ng, giá

trin ca

g ng. Hi s tin hàng nghìn) mà ông An mua

vt li  trang trí là bao nhiêu.

1.000.000

1.100.000

1.010.000

1.005.000

Câu 45: Trong không gian

Oxyz

   ng thng

1 1 2

x y z







2 1 1

x y z

  

1 2 1

x y z

  

ng thng



vuông góc vi

ng thi ct

,

ng ti

,HK

sao cho

27HK 

ng thng



là

10cm

20cm

Trang57

1 1 1

x y z



. B.

1 1 1

x y z





. C.

2 1 1

x y z



. D.

3 3 1

x y z





Câu 46: 

 

y f x

o hàm

 

' 4 2f x x x

và

 

0 1.f 

S m cc tiu ca hàm s

 

23g x f x x  

là

. B.

. C.

. D.

Câu 47: Tng các nghim c

 

7 6log 6 5 1



  

bng

. B.

. C.

. D.

Câu 48: Cho parabol

 

:4P y x  





















:d y a

 

04a

. 

 





ya

. 

































 





 



. 

SS

(











).



8 48T a a a  

99T 

. B.

64T 

. C.

32T 

. D.

72T 

Câu 49: Cho hai s phc

,uv

tha mãn

10uv==

và

3 4 50uv-=

. Tìm Giá tr ln nht ca biu

thc

4 3 10u v i+-

. B.

. C.

. D.

Câu 50:Trong h trc

Oxyz

, cho hai mt cu

       

2 2 2

: 1 3 2 49S x y z     

và

       

2 2 2

: 10 9 2 400S x y z     

và mt phng

 

:4 3 22 0P x y mz   

. Có bao

nhiêu s   mp (P) ct hai mt cu

   

,SS

theo giao tuy  ng tròn

không có tip tuyn chung?

. B.

. C. Vô s. D.

Trang58

BẢNG ĐÁP ÁN

1.A

2.C

3.B

4.D

5.C

6.C

7.A

8.C

9.B

10.B

11.C

12.A

13.C

14.B

15.B

16.C

17.A

18.D

19.D

20.A

21.B

22.A

23.C

24.A

25.C

26.B

27.B

28.D

29.A

30.B

31.C

32.C

33.A

34.B

35.D

36.C

37.D

38.C

39.C

40.A

41.C

42.C

43.C

44.D

45.A

46.B

47.B

48.B

49.C

50.D

HƯỚNG DẪN GIẢI CHI TIẾT

Câu 1: Có bao nhiêu cách sp xp

hng thành mt hàng dc?

. B.

. C.

. D.

Lời giải

Chọn A.

Câu 2: Cho cp s nhân

 

có

2u 

và công bi

3q 

. Giá tr ca

là:

6

. B.

18

. C.

. D.

4

Lời giải

Chọn C.

Ta có:

18.u u q

Câu 3: Cho hàm s

 

y f x

có bng bi

Hàm s ch bin trên khong nào trong các kho

 

2;0

. B.

 

2; 1

. C.

 

3; 

. D.

 

1; 

Lời giải

Chọn B.

Câu 4: Cho hàm s bc ba

 

0y ax bx cx d a    

 th 

Trang59

Giá tr ci ca hàm s là:

2x 

. B.

4y 

. C.

0x 

. D.

0y 

Lời giải

Chọn D

Câu 5: Cho hàm s

 

y f x

nh trên



o hàm

    

 

' 2 1 4f x x x x x   

. Hàm s

m cc tr

A.3. B.

. C.

. D.

Lời giải

Chọn C.

    

 

' 2 1 4 0

f x x x x x











     











Bng xét du

 

'fx

Vy hàm s m cc tr.

Câu 6: Tim cn ngang c th hàm s





ng thng:

1x 

. B.

1y 

. C.

1y 

. D.

0y 

Lời giải

Chọn C.

Câu 7: ng cong   th ca mt trong bn hàm s i  

s nào ?

Trang60

y x x  

y x x  

y x x  

1.y x x x    

Lời giải

Chọn A

+  C.

+ T  th ta thy

lim

® + ¥

= + ¥

nên h s ca

D.

B ta có:

y x x

  



' 0 1yx   

Suy ra hàm s m cc tr nên loi B.

A.

Câu 8:  th hàm s

yx   

ct trc hoành ti mm?

Lời giải

Chọn C

 m c th hàm s c hoành:

x   

2 3 0xx   













3x  

V

nghi th ct trc hoành ti

m.

Câu 9: Vi

là s th

 

log 125a

bng

3 log a

. B.

3 log a

. C.

 

log a

. D.

2 log a

Lời giải

Chọn B

Ta có

 

5 5 5 5

log 125 log 125 log 3 log .a a a   

Câu 10: o hàm ca hàm s

12x





là:





. B.





. C.





. D.





Lời giải

Chọn B

Trang61

Ta có

 

1 2 1 2

' . 1 2 ' 2 .

y e x e



   

Câu 11: Vi

là s thc tu ý,

bng

. B.

. C.

. D.

Lời giải

Chọn C

Vi s thc

ta có

aa

Câu 12: Tng các nghim c

3 81

xx



bng

A. B. C. D.

Lời giải

Chọn A

Ta có

3 4 2

3 81 3 4



    

3 4 0





   







42xx    

Vy tng các nghim c

3 81

xx



bng

Câu 13: Nghim c

 

log 2 2x 

là:

x 

. B.

3x 

. C.

x 

. D.

1x 

Lời giải

Chọn C



 

log 2 2x 

xx   

Câu 14: Cho hàm s

 

4 2021f x x

. Trong các khnh sau, kh

 

d 4 2021f x x x x C  



. B.

 

d 2021f x x x x C  



 

d 2021f x x x



. D.

 

df x x x C



Lời giải

Chọn B

Áp dng công thn:

 

d 4 2021 d 2021f x x x x x x C    



Câu 15: Cho hàm s

 

sin3f x x

. Trong các khnh sau, kh

 

d cos3

f x x x C



. B.

 

d cos3

f x x x C  



 

d 3cos3f x x x C



. D.

 

d 3cos3f x x x C  



Lời giải

Chọn B

Áp dng công thn:

 

d cos3

f x x x C  



Câu 16: Nu

 

d2f x x 



và

 

d7f x x 



thì

 

df x x



bng

Trang62

5

. B.

. C.

9

. D.

14

Lời giải

Chọn C

Áp dng tính cht tích phân ta có:

     

3 3 2

2 1 1

d d d 7 2 9f x x f x x f x x      

  

Câu 17: Tích phân

ln3



bng

. B.

. C.

. D.

1e

Lời giải

Chọn A

Ta có:

ln3

e x e



ln3 0

2ee  

Câu 18: S phc liên hp ca s phc

34zi

là:

34zi

. B.

43zi

. C.

43zi

. D.

34zi

Lời giải

Chọn D

S phc liên hp ca s phc

 

a bi

là

 

a bi

. Nên

34zi

là s phc liên hp ca s

phc

34zi

Câu 19: Cho hai s phc

35zi

và

68zi  

. S phc liên hp ca s phc

zz

là

9 13i

. B.

33i

. C.

33i

. D.

9 13i

Lời giải

Chọn D

S phc

   

6 8 3 5 9 13z z i i i        

Vy s phc liên hp ca s phc

zz

là

9 13i

Câu 20: Trên mt phng tm biu din s phc liên hp ca s phc

23 5i

có t là

 

23; 5

. B.

 

23;5

. C.

 

23; 5

. D.

 

23;5

Lời giải

Chọn A

S phc liên hp ca s phc

23 5i

là s phc

23 5i

Vm biu din s phc

23 5i

m

 

23; 5M 

Câu 21: Th tích kh u có cng 2 và chiu cao bng mt na c

Lời giải

Chọn B

u nên

S 

Ta có chiu cao bng mt na c :

1h 

Trang63

Vy th tích kh

.3V S h

Câu 22: Cho khi hnh bng 5 và chiu cao khi hp bng mt na chu vi

 tích ca khi hbng

250cm

. B.

125cm

. C.

200cm

. D.

500cm

Lời giải

Chọn A

Ta có ding

25cm



5.4 20 10

P cm h cm    

Vy ta có th tích khi hp là

25.10 250V cm

Câu 23: Công thc tính th tích

ca hình nón có di

4SR





và chiu cao

là:

V R h





. B.

V R h





. C.

V R h





. D.

V Rh





Lời giải

Chọn C

Ding tròn là

4 R





Bán kính hình nón là

 

Nón

V R h R h





Câu 24: Mt hình tr có bán kính

6R 

 ng sinh

4l 

cm. Tính din tích toàn phn ca

hình tr 

120

S cm

. B.

S cm

. C.

S cm

. D.

S cm

Lời giải

Chọn A

   

 

2 . 2 6. 6 4 120

S R R l cm

  

    

Câu 25: Trong không gian

,Oxyz

cho tam giác

ABC

bit

     

1;1;3 , 1;4;0 , 3; 2; 3A B C   

. Trng

tâm

ca tam giác

ABC

có t là

 

3;3;0

. B.

; ;0









. C.

 

1;1;0

. D.

 

1; 1;1

Lời giải

Chọn C

Trng tâm

ca tam giác

ABC

có t là

1; 1; 0.

3 3 3

A B C A B C A B C

G G G

x x x y y y z z z

x y z

     

      

Câu 26: Trong không gian

,Oxyz

mt cu

       

2 2 2

: 1 1 3 9S x y z     

. Tâm

ca mt cu

( )

có t là

Trang64

 

1; 1; 3

. B.

 

1;1;3

. C.

 

2; 2; 6

. D.

 

2;2;6

Lời giải

Chọn B

t cu là:

     

2 2 2

x a y b z c R      

t tâm

 

1;1;3I 

Câu 27: Trong không gian

,Oxyz

cho mt phng

 



2 3 0x y z   

m nào sau

c mt phng

 

1; 1; 3M 

. B.

 

1;1;0N 

. C.

 

2; 2;6H 

. D.

 

2;2;3K 

Lời giải

Chọn B

Câu 28: Trong không gian

,Oxyz

không phải  ng thng

2 1 2

x y z







 

2; 1;2u   



. B.

 

2;1; 2u 



. C.

 

4; 2;4u   



. D.

 

1; 1;0u 



Lời giải

Chọn D

 

2;1; 2u 



 ng thng

d 

 

2; 1;2u   



và

 

4; 2;4u   



 ng thng

d 



Câu 29: Có

chic th  th t t n 30. Chn ngu nhiên mt chic th. Tính xác sut

 chic th c chn mang s chia ht cho 3.

. B.

. C.

. D.

Lời giải

Chọn A

T n 30 có 10 s chia ht cho 3 nên xác su chc 1 chic th mang s chia ht cho

3 là

10 1

30 3



Câu 30: Hàm s ch bin trên

?

41y x x   

. B.

1y x x   

. C.







. D.

23yx  

Lời giải

Trang65

Chọn B

Ta có:

1 3 1 0,y x x y x x



           

nên hàm s ng bin trên

.

Câu 31: Cho hàm s

34y x x  

. Gi

,Mm

lt là giá tr ln nht và giá tr nh nht ca hàm

s n

 

0;2

. Khđúng?

8Mm

. B.

22Mm  

. C.

2 10Mm

. D.

8Mm  

Lời giải

Chọn C

D  

33yx





 

1 0;2

0 3 3 0

1 0;2







     



  







Ta có

     

0 4, 2 2; 1 6y y y     

Vy

2, 6Mm   

Câu 32: B

xx



có tp nghim là

3 17 3 17

;











. B.

3 17 3 17

;;

   



   







   

 

1;2T 

. D.



 



;1 2;T    

Lời giải

Chọn C

3 2 2

5 3 log 3 2 0

25 25

x x x x



       

12x  

Vy tp nghim ca b

 

1;2T 

Câu 33: Bit

 

d3f x x 



 

d4f x x 



. Tính

 

2df x x x



. B.

. C.

. D.

Lời giải

Chọn A

Ta có

         

5 2 5 5 2

1 1 2 1 1

d 4, d 3 d d d 1f x x f x x f x x f x x f x x     

    

 

5 5 5

2 2 2

2 d 2 d d 2.1

f x x x f x x x x     

  

Trang66

Câu 34: Cho s phc

tha mãn

 

1 2 1 4z i i  

. Phn thc ca s phc

thuc khoi



 

0;2

. B.

 

2; 1

. C.

 

4; 3

. D.









Lời giải

Chọn B

Ta có

 

1 2 1 4

z i i z



    



  

1 4 1 2

5 5 5



    

Vy phn thc ca s phc

 

2; 1

z     

Câu 35: Cho hình chóp

.S ABCD

nh

ng thng

vuông góc vi mt

phng

 

ABCD

SA a

. Góc gia hai mt phng

 

SCD

và

 

ABCD

là





tan



nhn giá tr nào trong các giá tr sau ?

tan 2





. B.

tan





. C.

tan 3





. D.

tan 1





Lời giải

Chọn D



Ta có:

 

CD AD

CD SAD CD SD

CD SA





   







   

 

   



 



CD SCD ABCD

SD SCD SD CD

ABCD SCD SD AD SDA

AD ABCD AD CD



  





   













Xét tam giác

SAD



tan tan 1

SA a

SDA

AD a



   

Câu 36: Cho hình chóp t u

.S ABCD



và

,SA a AB a

ng

cách t m

n mt phng

 

SAD

bng bao nhiêu ?

. B.

. C.

. D.

Trang67

Lời giải

Chọn C

Ta có :

 

S ABCD

V AB

4 24

S AOD S ABCD

VV  

Din tích tam giác

SAD

là

SAD

S 

Vy

 

SAOD

SAD

d O SAD

  





Câu 37: Trong không gian vi h t

Oxyz

m

 

1;1;0A

và

 

1; 1; 4B 

. Vi

trình mt cu

 

nhn

ng kính .

     

: 1 2 5S x y z    

. B.

     

: 1 2 20S x y z    

     

: 1 2 20S x y z    

. D.

     

: 1 2 5S x y z    

Lời giải

Chọn D

Gi

là tâm ca mt cu

 

I

m ca

 

1;0; 2I

 

0; 2; 4 2 5AB AB    



Vy mt cu

 

có tâm

 

1;0; 2I 

và bán kính

R 

     

: 1 2 5S x y z     

Câu 38: Trong không gian vi h t

Oxyz

m

 

2;3;4M 

. Ving thng

 

m

và vuông góc vi mt phng

 

Oxy

Trang68

 

















. B.

 

  















. C.

 

















. D.

 

  















Lời giải

Chọn C

   

d Oxy



 a

 

là

 

0;0;1k 



V

   





















Câu 39: Cho hàm s

 

,fx

 th ca hàm s

 

y f x

. Giá tr nh nht

ca hàm s

   

2 1 6g x f x x  

n







bng







. B.

 

03f 

. C.

 

16f 

. D.

 

3 12f 

Lời giải

Chọn C

t

 

2 1 0;3t x t   

, xét hàm s

   

33h t f t t  

trên

 

0;3

Ta có

   

3h x f x

 

h t t







  







     

0 3 1;3h x f x x     

     

0 3 0;1h x f x x     

Ta có bng bin thiên sau

Trang69

Ta có

 

     

0;3

min 1 1 6h t h f  

Câu 40: Có bao nhiêu s 

sao cho ng vi mi

có không quá

2186

s nguyên

tha mãn

 

log 3 9 0

xy  

. B.

. C.

2186

. D.

Lời giải

Chọn A

Ta có

 

log 3 9 0

log











    















Nu



thì bm ( không tha mãn).

Nu

3 2 log 2 0,631

y   

thì bp nghim

 

2T 

( không tha mãn vì



Nu

3 2 log 2 0,631

y   

p nghim

2;3







 mi giá tr

, b     

2021

nghim nguyên

thì

3 2187 log 2187 7

y   

Kt hu kin



0,631 7y

suy ra có

s

tha mãn bài toán.

Câu 41: Cho hàm s

 

1y f x

 

y g x x

. Giá tr

   

 

min ; dI f x g x x







. B.

. C.

. D.

Lời giải

Chọn C

Trang70

Xét b

1x 













Vy

 

min 1; 1x 

khi

1 x

hoc

1x 

 

min 1; xx

khi

11x  

Xét

   

 

min ; dI f x g x x







 

min 1; dxx







 

min 1; dxx







 

min 1; dxx



ddI x x x







0 1 2

1 0 1

d d dx x x x x



   

  



  

=2.

Câu 42: Có tt c bao nhiêu s phc

mà phn thc và phn o ca nó trái d ng thi tha mãn

4   z z z z

và

2 2 3 2.zi  

. B.

. C.

. D.

Lời giải

Chọn C

Gi m

 

;M x y

m trên mp t

Oxy

biu din s phc

( , )z x yi x y z x yi     

4 2 2 2 2z z z z x yi x y         

p hm

 

;M x y

biu din s

phc

là hai cnh i

,AD BC

ca hình vuông

ABCD

 dài cnh bng

và tâm là gc ta



   

2 2 3 2 2 2 18z i x y       

. Tp hm

 

;M x y

biu din s phc

là

ng tròn tâm

 

2;2 , 3 2IR

Vm biu din

,MP

tha yêu cu bài toán.

Câu 43: Cho hình chóp

.S ABC



ABC

là tam giác vuông ti

và có

,3AB a BC a

. Mt

Trang71

bên

SAB

u và nm trong mt phng vuông góc vi mt phng

 

ABC

. Tính th

tích

ca khi khóp

.S ABC

V 

. B.

V 

. C.

V 

. D.

V 

Lời giải

Chọn C

Gi

m cn

. Vì

SAB

u nên

SK AB

   

SAB ABC

theo giao tuyn

 

S ABC ABC

SK ABC V SK S



  

ABC

vuông ti

có

, 3 2AB a BC a AC BC AB a     

1 1 2

. . 2

2 2 2

ABC

S AB AC a a



  

SAB

u

SK

1 1 3 2 6

. . .

3 3 2 2 12

S ABC ABC

a a a

V SK S



  

Câu 44: Ông An cn làm m . Phi là mt phn ca khi cu bán kính

20 cm

làm bng g c, bán kính cng tròn phn chm cu bng

10 cm

. Phn phía trên

làm bng lp v kính trong sut. Bit giá tin ca

ng, giá

trin ca

g ng. Hi s tin hàng nghìn) mà ông An mua

vt li  trang trí là bao nhiêu.

Trang72

1.000.000

1.100.000

1.010.000

1.005.000

Lời giải

Chọn D

Bán kính mt cu là

20R cm

ng tròn phn chm cu là

10r cm

Theo hình v ta có

10 1

sin 30

20 2



   

Din tích phn làm kính là:

 

360 2.30 4000

.4 .20

360 3

S cm







nh là tâm mt cng

10 ; 20 20 10 10 3r cm l R cm h cm      

Th tích phn chm cu bng

hom

2.30 4 1

360 3 3

c cau

V R r h





 

16000 1000 3





Vy s tin ông An cn mua vt liu là:

4000 16000 1000 3

.150 .100 1.005.000

3 9 3

  



  





Câu 45: Trong không gian

Oxyz

   ng thng

1 1 2

x y z







2 1 1

x y z

  

1 2 1

x y z

  

ng thng



vuông góc vi

ng thi ct

,

ng ti

,HK

sao cho

27HK 

ng thng



là

1 1 1

x y z



. B.

1 1 1

x y z





. C.

2 1 1

x y z



. D.

3 3 1

x y z





Lời giải

ChọnA

 

3 2 ; ;1H H t t t   

 

1 ;2 2 ;K K m m m   

Ta có

 

2 2;2 2; 1HK m t m t m t      



ng thng

có mt VTCP là

 

1;1; 2

u 



d  

u HK 

 

 

2 0 2 4; 2; 3 .m t m t HK t t            



Ta có

       

2 2 2 2

4 2 3 2 1 27 27,HK t t t t            

10cm

20cm

Trang73

27 1, 3.HK t m     



 

3; 3; 3 3(1;1;1)HK      



(1; 1;0)H 

ng thng



là

1 1 1

x y z



Câu 46: 

 

y f x

o hàm

 

' 4 2f x x x

và

 

0 1.f 

S m cc tiu ca hàm s

 

23g x f x x  

là

. B.

. C.

. D.

Lời giải

Chọn B

Ta có:

 

3 4 2

42f x x x dx x x C    



và

 

0 1 1.fC  



 

1 0, .f x x x x    

Ta có:

 

2 2 2

' 3(2 2). ( 2 3). '( 2 3)g x x f x x f x x     

 

   

2 2 0

4 2 3 2 2 3 0

x x x x









     











  







Bng bin thiên:

T bng bin thiên suy ra hàm s

 

y g x

có hai cc tiu.

Câu 47: Tng các nghim c

 

7 6log 6 5 1



  

bng

. B.

. C.

. D.

Lờigiải

Chọn B

u kin:

x 

t

 

1 log 6 5yx  

thì ta có h 

 

7 6 1 1

7 6 5

7 6 7 6

1 log 6 5

7 6 5









  







    



  







(2)

Xét hàm s

 

f t t





vi

t 

thì

   

' 7 ln7 6 0,

f t t f t



     

ng bin nên

     

2 f x f y x y   



7 6 5 0.



  

(3)



1



'( )gx









()gx



Trang74

Xét hàm s

 

7 6 5

g x x



  

vi

x 

thì

     

' 7 ln7 6 " 7 ln7 0

g x g x



    

x



 

0gx

có không quá hai nghim.

Mt khác

   

1 2 0gg

nên

1x 

và

2x 

là 2 nghim c

Vm là

1x 

và

2x 

Suy ra tng các nghim c

1 2 3

Câu 48: Cho parabol

 

:4P y x  





















:d y a

 

04a

. 

 





ya

. 

































 





 



. 

SS

(











).



8 48T a a a  

99T 

. B.

64T 

. C.

32T 

. D.

72T 

Lời giải

Chọn B

- 



 



 

2;0A

 

2;0B

4AB

- 



 



 

4;M a a  

 

4;N a a

24MN a  

- 



:

 



y x a  

- :

2 4 .d

S y y



 



  





 

aa  

2 .d

S x a x



  









  







Trang75

- 



:

SS

 

aa   

 

44aa  

8 48 64a a a   

Câu 49: Cho hai s phc

,uv

tha mãn

10uv==

và

3 4 50uv-=

. Tìm Giá tr ln nht ca biu

thc

4 3 10u v i+-

. B.

. C.

. D.

Lời giải

Chọn C

Ta có

.z z z=

t

34T u v=-

43M u v=+



( )

3 4 3 4T u v u v= - -

( )

9 16 12u v uv vu= + - +

 ta có

( )

4 3 4 3M u v u v= + +

( )

16 9 12u v uv vu= + + +



( )

25 5000M T u v+ = + =

Suy ra

5000MT=-

5000 50 2500= - =

hay

50M =

Áp dng

z z z z

¢¢

+ £ +

ta có

4 3 10 4 3 10 50 10 60u v i u v i+ - £ + + - = + =

Suy ra

max 4 3 10 60u v i+ - =

Câu50:Trong h trc

Oxyz

, cho hai mt cu

       

2 2 2

: 1 3 2 49S x y z     

và

       

2 2 2

: 10 9 2 400S x y z     

và mt phng

 

:4 3 22 0P x y mz   

. Có bao

nhiêu s   mp (P) ct hai mt cu

   

,SS

theo giao tuy  ng tròn

không có tip tuyn chung?

. B.

. C.Vô s. D.

Lời giải

Chọn D

Mt cu

 

có tâm

 

1; 3;2I 

, bán kính

7R 

; mt cu

 

có tâm

 

10;9;2J

, bán kính

20R 

. Ta có

 

9;12;0IJ



15IJ 

Mt phng

 

:4 3 22 0P x y mz   

n

 

4; 3;

nm



IJ n 

 

nên

song song hoc cha trong (P).

  ng tròn giao tuyn ca hai mt cu

   

,SS

là

   

2 7 20 15

15 5

p p p p

  



vi

20 7 15





Trang76

t phng chng tròn giao tuyn hai mt cu là (Q):

3 4 30 0xy  

Ta có

 

;( )

d I Q 

 

;( )

d J Q 

nên

   

;( ) ;( )d I Q IJ d J Q

Ta có mp(P) ct hai mt cu

   

,SS

theo giao tuyng tròn

nh  ng tròn ln khi

 

2 35

28 28

;( ) 7 7

d I P



    



45 140 0

684

140 441 0











  





Và có m nguyên, nên

 

2; 1;4;5;6;7m  

Đề 9

ĐỀ LUYỆN THI CẤP TỐC TỐT NGHIỆP THPT NĂM 2021

Thuvienhoclieu.Com

BÀI THI: TOÁN

Thời gian: 90 phút

Câu 1: Cho tp hp

 

1;3;5;7;9S 

. Có bao nhiêu s t nhiên gm ba ch s c lp

t các phn t ca tp

. B.

. C.

. D.

Câu 2: Cho mt dãy cp s nhân

 

có

u 

và

2u 

. Giá tr ca

bng

. B.

. C.

. D.

Câu 3: Cho hàm s

 

y f x

có bng bin thiên sau:

Trang77

Khsai?

A. Hàm s

 

y f x

ng bin trên khong

 

;2 

B. Hàm s nghch bin trên khong

 

2;2

C. Hàm s nghch bin trên khong

 

2;0

D. Hàm s ng biu trên

 

0;2

Câu 4: Hàm s

 

y f x

có bng bi

Tìm kh

A. Hàm s m cc tr. B. Hàm s có giá tr ci là

1x 

C. Hàm s t ci ti

0x 

. D. Hàm s m cc tiu là

1x 

Câu 5: Cho hàm 

 

y f x







 





Hàm s

 

m cc tr?

A. 2. B. 3.

C. 0. D. 1.

Câu 6: C







. T

A. ng thng

1.x 

B. ng thng

2.x 

C. ng thng

2.y 

D. ng thng

1.y 

Câu 7: Cho hàm s  th :



2



 









Trang78

Hàm s  th là hình v trên?

42y x x  

. B.

32y x x  

. C.

42y x x   

. D.

32y x x   

Câu 8:  th ca hàm s

  

22y x x  

ct trc tung tm có t là

 

0;4

. B.

 

0; 4

. C.

 

4;0

. D.

 

4;0

Câu 9: Vi

là s th

 

ln ea



bng

1 lna





. B.

1 lna





. C.

1 lna





. D.

1 ln lna





Câu 10: o hàm ca hàm s





là





. B.



. C.



. D.



Câu 11: Vi

là s th

bng

. B.

. C.

. D.

Câu 12: Nghim c

 

log 2 2 1x 

là

2x 

. B.

1x 

. C.

2x 

. D.

3x 

Câu 13: Nghim c

 

1 log 1 3x  

là

3x 

. B.

1x 

. C.

7x 

. D.

4x 

Câu 14: Cho hàm s

 





. Trong các khnh sau, khnh nào đúng?

 

f x dx C

  



. B.

 

f x dx x C

  



 

f x dx C

  



. D.

 

f x dx C

  



Câu 15: Cho hàm s

( ) sin3 1f x x

. Trong các khnh sau, khnh nào đúng?

( )d cos3

f x x x x C  



( )d cos3

f x x x x C   



( )d 3cos3f x x x x C  



( )d 3cos3f x x x x C   



Câu 16: Nu

 

d3f x x







và

 

d2f x x







thì

 

df x x



bng

. B.

. C.

5

. D.

1

Trang79

Câu 17: Tích phân

ln2



bng

. B.

. C.

. D.

1e 

Câu 18: Tìm s phc

z z z

bit

13zi

22zi  

1zi  

. B.

1zi  

. C.

1zi

. D.

1zi

Câu 19: Tìm s phc liên hp ca s phc

 

31z i i

3zi

. B.

3  zi

. C.

3zi

. D.

3  zi

Câu 20: Cho s phc

2zi  

u din ca s phc

w iz

trên mt phng to

?

 

1; 2 .M 

 

2;1 .P 

 

2;1 .N

 

1;2 .Q

Câu 21: Cho hình chóp

.S ABC



ABC

là tam giác vuông cân ti

SA AB a==

vuông

góc vi mt phng

( )

ABC

. Th tích ca khi chóp

.S ABC

bng

. B.

. C.

. D.

Câu 22: Cho kh nh

và chiu cao bng

. Th tích ca kh

ng

Câu 23: Tính th tích

ca khng

và chiu cao bng

108V





. B.

54V





. C.

36V





. D.

18V





Câu 24: Tính din tích xung quanh

ca hình tr có bán kính bng

và chiu cao bng

36S





. B.

24S





. C.

12S





42S





Câu 25: Trong không gian

Oxyz

, cho tam giác

ABC

vi

     

1;2;1 ; 3;1; 2 ; 2;0;4A B C

. Trng tâm ca

tam giác

ABC

có t là

 

6;3;3

. B.

 

2; 1;1

. C.

 

2;1; 1

. D.

 

2;1;1

Câu 26: Trong không gian

Oxyz

, mt cu

     

: 1 2 16S x y z    

ng kính bng

. B.

. C.

. D.

Câu 27: Trong không gian

Oxyz

, mt phm

 

2;1;1M 

0x y z  

. B.

2 3 0x y z   

10x y z   

. D.

30x y z   

Câu 28: Trong không gian

Oxyz

 ng th

m

 

1;2; 1A 

và

 

1;0;0B 

 

2;2;1u



. B.

 

2;2;1u 



. C.

 

2; 2; 1u 



. D.

 

2;2; 1u 



Câu 29: Chn ngu nhiên mt s trong s 21 s u tiên. Xác su chc s l

bng

. B.

. C.

. D.

Câu 30: Hàm s i ng bin trên

tanyx

. B.

1y x x x   

Trang80

1yx

. D.







Câu 31: Gi

lt là giá tr ln nht, giá tr nh nht ca hàm s

2 3 12 1y x x x   

trên

n

[ 1;5]

. Tng

Mm

bng.

270

. B.

. C.

280

. D.

260

Câu 32: Tp nghim ca b

xx

   



   

   

x 

. B.

x 

. C.

x 

x 

Câu 33: Nu

 

2 ( ) 1 5f x dx



thì

()f x dx



bng ?

. B.

2

. C.

3

Câu 34: Cho s phc

34zi

a s phc

 

1 iz

bng ?

. B.

. C.

Câu 35: Cho hình chóp

.S ABC

 

ABC

là tam giác vuông cân ti

và

2AB a

. Bit

 

SA ABC

và

SA a

. Góc gia hai mt phng

 

SBC

và

 

ABC

bng

30

. B.

45

. C.

60

. D.

90

Câu 36: u có cng , góc gia mt mt bên và mng .

 ng cao

A. B. C. D.

Câu 37: Trong không gian vi h t 

,Oxyz

 

3; 4; 2A 

 

5; 6; 2B 

 

10; 17; 7C 

. Vit

t cu tâm

, bán kính

     

2 2 2

10 17 7 8x y z     

. B.

     

2 2 2

10 17 7 8x y z     

     

2 2 2

10 17 7 8x y z     

. D.

     

2 2 2

10 17 7 8x y z     

Câu 38: Trong không gian vi h trc t

Oxyz

, cho

 

  M

 

0;1; 3N

ng

thm

là

1 2 1

1 3 2

x y z  





. B.

1 3 2

1 2 1

x y z  





1 3 2

x y z





. D.

1 2 1

x y z





Câu 39. Cho hàm s

 

,fx

 th ca hàm s

 

y f x

. Giá tr nh

nht ca hàm s

   

2 1 4 3g x f x x   

n









bng

.S ABC

60

.SH

SH 

Trang81

 

. B.

 

11f 

. C.

 

25f 

. D.

 

13f 

Câu 40.Có bao nhiêu s 

sao cho ng vi mi



2021

s nguyên

tho

mãn

( ) ( )

log 3 1 . log 0x x y

éù

+ - - <

ëû

. B.

. C.

. D.

Câu 41. Cho hàm s

 

2cos 3 0

x m x

y f x

















liên tc trên



. Giá tr

2cos 1sin dI f x x x









. B.

. C.

. D.



Câu 42: Có bao nhiêu s phc

tha

23z i z i   

và

2 3 2zi  

A. Vô s B.

. C.

. D.

Câu 43: Cho hình chóp

.S ABCD

nh

, hình chiu vuông góc ca

lên mt

phng

 

ABCD

trùng vm cnh

, cnh bên

hp vt góc

60

. Tính

theo

th tích

ca khi chóp

.S ABCD

V 

. B.

V 

. C.

V 

. D.

V 

Câu 44: Ông Bo làm mái vòm  c ngôi nhà ca mình bng vt lit

phn ca mt xung quanh ca mt hình tr i. Bit giá tin ca 1

tôn là

300.000

ng. Hi s tin hàng nghìn) mà ông Bo mua tôn là bao nhiêu ?

18.850.000

ng. B.

5.441.000

ng. C.

9.425.000

ng. D.

10.883.000

ng.

5 m

6 m

120

Trang82

Câu 45: Trong không gian vi h t     ng thng

2 1 1

x y z







và

1 2 2

1 3 2

x y z

  





. Gi



 ng thng song song vi

 

: 7 0P x y z   

và ct

,dd

lt ti A, B sao cho AB ngn nhng thng



là:

























. B.













  



























. D.

























Câu 46: Cho hàm s

()y f x

 th

()fx



 sau

Bit

 

00f 

. Hi hàm s

 

g x f x x

m cc tr

. B.

. C.

. D.

Câu 47: Có bao nhiêu s t nhiên

sao cho tn ti s thc

tho

 

3log 1

2021 2020 2020





  

A. 9. B. 8. C. 5. D. 12

Câu 48. 

 

y f x



 



 

y f x



   

1 2 3

,,x x x

 

2xx

     

1 3 2

f x f x f x  

và

 



 

:d x x

    

1 2 3 4

, , ,S S S S

      







Trang83

0,60

. B.

0,55

. C.

0,65

. D.

0,70.

Câu 49: Cho hai s phc

,uv

tha mãn

10uv==

và

3 4 50uv-=

. Tìm Giá tr ln nht ca biu

thc

4 3 10u v i+-

. B.

. C.

. D.

Câu 50. Trong không gian

Oxyz

m

(2;3;3)A

và mt cu

       

2 2 2

: 1 2 3 12S x x x     

. Xét khi tr

 

ni tip mt cu

 

và có tr

m

. Khi khi tr

 

có th tích ln nha

 

nm trên hai mt

phng

0x ay bz c   

và

0x ay bz d   

. Giá tr

a b c d  

bng

4 4 2

. B.

5

. C.

4

. D.

5 4 2

BẢNG ĐÁP ÁN

1.D

2.A

3.B

4.A

5.A

6.A

7.D

8.B

9.C

10.D

11.D

12.A

13.A

14.D

15.B

16.C

17.B

18.A

19.B

20.A

21.B

22.C

23.D

24.B

25.D

26.A

27.B

28.D

29.A

30.B

31.D

32.A

33.A

34.A

35.B

36.C

37.B

38.C

39.D

40.C

41.A

42.A

43.B

44.D

45.A

46.B

47.A

48.A

49.C

50.B

HƯỚNG DẪN GIẢI CHI TIẾT

Câu 1: Cho tp hp

 

1;3;5;7;9S 

. Có bao nhiêu s t nhiên gm ba ch s c lp t

các phn t ca tp

. B.

. C.

. D.

Lời giải

Chọn D

T yêu cu ca bài toán, ta chn 3 ch s t 5 phn t ca tp

ri sp xp li th t là mt

chnh hp chp 3 ca 5 phn t.

Trang84

Câu 2: Cho mt dãy cp s nhân

 

có

u 

và

2u 

. Giá tr ca

bng

. B.

. C.

. D.

Lời giải

Chọn A

Dãy cp s i



Suy ra s hng Tim cng

. .64 32.

u u q  

Câu 3: Cho hàm s

 

y f x

có bng bin thiên sau:

Khsai?

A. Hàm s

 

y f x

ng bin trên khong

 

;2 

B.Hàm s nghch bin trên khong

 

2;2

C. Hàm s nghch bin trên khong

 

2;0

D. Hàm s ng biu trên

 

0;2

Lời giải

Chọn B

Lý thuyt

Câu 4: Hàm s

 

y f x

có bng bi

Tìm kh

A.Hàm s m cc tr. B. Hàm s có giá tr ci là

1x 

C. Hàm s t ci ti

0x 

. D. Hàm s m cc tiu là

1x 

Lời giải

Chọn A

Lý thuyt

Câu 5: Cho hàm 

 

y f x







 





Trang85

Hàm s

 

m cc tr?

A.2. B. 3.

C. 0. D. 1.

Lời giải

Chọn A

Lý thuyt

Câu 6: C







. T

A.ng thng

1.x 

B. ng thng

2.x 

C. ng thng

2.y 

D. ng thng

1.y 

Lời giải

Chọn A

Lý thuyt

Câu 7: Cho hàm s  th :

Hàm s  th là hình v trên?

42y x x  

. B.

32y x x  

. C.

42y x x   

. D.

32y x x   

Lời giải

Chọn D

T  th ta có hàm s i là hàm s bc 3, v

b loi.

Mt khác

 

lim



 

, suy ra h s bc ba âm. Vy ch

Câu 8:  th ca hàm s

  

22y x x  

ct trc tung tm có t là

 

0;4

. B.

 

0; 4

. C.

 

4;0

. D.

 

4;0

Lời giải

Chọn B

Vi

0x 

, suy ra

  

0 2 0 2 4y     

. Vy t m là

 

0; 4

Câu 9: Vi

là s th

 

ln ea



bng

1 lna





. B.

1 lna





. C.

1 lna





. D.

1 ln lna







2



 









Trang86

Lời giải

Chọn C

Ta có:

 

ln ln ln 1 lnea e a a





   

Câu 10: o hàm ca hàm s





là





. B.



. C.



. D.



Lời giải

Chọn D

Ta có:







Câu 11: Vi

là s th

bng

. B.

. C.

. D.

Lời giải

Chọn D

Ta có:

aa

Câu 12: Nghim c

 

log 2 2 1x 

là

2x 

. B.

1x 

. C.

2x 

. D.

3x 

Lời giải

Chọn A

Ta có:

 

log 2 2 1 2 2 2 2 4 2x x x x        

Câu 13: Nghim c

 

1 log 1 3x  

là

3x 

. B.

1x 

. C.

7x 

. D.

4x 

Lời giải

Chọn A

Ta có:

 

1 log 1 3x  

 

log 1 2x  

14x  

3x

Câu 14: Cho hàm s

 





. Trong các khnh sau, khnh nào đúng?

 

f x dx C

  



. B.

 

f x dx x C

  



 

f x dx C

  



. D.

 

f x dx C

  



Lời giải

Chọn D

Ta có

 







suy ra

 

f x dx x dx C



    







Câu 15: Cho hàm s

( ) sin3 1f x x

. Trong các khnh sau, khnh nào đúng?

( )d cos3

f x x x x C  



( )d cos3

f x x x x C   



( )d 3cos3f x x x x C  



( )d 3cos3f x x x x C   



Trang87

Lời giải

Chọn B

Ta có

 

( )d sin3 1f x x x dx



cos3

x x C   

Câu 16: Nu

 

d3f x x







và

 

d2f x x







thì

 

df x x



bng

. B.

. C.

5

. D.

1

Lời giải

Chọn C

Ta có:

     

3 1 3

2 2 1

d d df x x f x x f x x





  

 

3 2 5     

Câu 17: Tích phân

ln2



bng

. B.

. C.

. D.

1e 

Lời giải

Chọn B

Ta có

ln2



ln2

e

2 1 1  

Câu 18: Tìm s phc

z z z

bit

13zi

22zi  

1zi  

. B.

1zi  

. C.

1zi

. D.

1zi

Lời giải

Chọn A

z z z

   

1 3 2 2ii    

1 i  

Câu 19: Tìm s phc liên hp ca s phc

 

31z i i

3zi

. B.

3  zi

. C.

3zi

. D.

3  zi

Lờigiải

ChọnB

 

3 1 3z i i i    

nên suy ra

3zi  

Câu 20: Cho s phc

2zi  

u din ca s phc

w iz

trên mt phng to

?

 

1; 2 .M 

 

2;1 .P 

 

2;1 .N

 

1;2 .Q

Lờigiải

ChọnA

Ta có:

 

2 1 2w iz i i i      

Vm biu din s phc

w iz

m

 

1; 2 .M 

Câu 21: Cho hình chóp

.S ABC



ABC

là tam giác vuông cân ti

SA AB a==

vuông

góc vi mt phng

( )

ABC

. Th tích ca khi chóp

.S ABC

bng

Trang88

. B.

. C.

. D.

Lời gia



Chọn B

Th tích ca khi chóp

.S ABC

S ABC ABC

V SA S==

Câu 22: Cho kh nh

và chiu cao bng

. Th tích ca kh

ng

Lời giải

Chọn C

Ta có:

.V S h

.2aa

2a

Câu 23: Tính th tích

ca khng

và chiu cao bng

108V





. B.

54V





. C.

36V





. D.

18V





Lời gia



Chọn D

Ta có

V R h





.3 .6









Câu 24: Tính din tích xung quanh

ca hình tr có bán kính bng

và chiu cao bng

36S





. B.

24S





. C.

12S





42S





Lời giải

Chọn B

Ta có:

2 2 .3.4 24

S rh

  

  

Câu 25: Trong không gian

Oxyz

, cho tam giác

ABC

vi

     

1;2;1 ; 3;1; 2 ; 2;0;4A B C

. Trng tâm ca

tam giác

ABC

có t là

 

6;3;3

. B.

 

2; 1;1

. C.

 

2;1; 1

. D.

 

2;1;1

Lời giải

Chọn D

là trng tâm tam giác

ABC

thì

2; 1

A B C A B C

x x x y y y

   

   

Câu 26: Trong không gian

Oxyz

, mt cu

     

: 1 2 16S x y z    

ng kính bng

. B.

. C.

. D.

Trang89

Lời giải

Chọn A

Bán kính

16 4r 

ng kính là 8.

Câu 27: Trong không gian

Oxyz

, mt phm

 

2;1;1M 

0x y z  

. B.

2 3 0x y z   

10x y z   

. D.

30x y z   

Lời giải

Chọn B

Câu 28: Trong không gian

Oxyz

 ng th

m

 

1;2; 1A 

và

 

1;0;0B 

 

2;2;1u



. B.

 

2;2;1u 



. C.

 

2; 2; 1u 



. D.

 

2;2; 1u 



Lời giải

Chọn D

ng thm

,AB

nên có m 

 

2;2; 1BA 



Câu 29: Chn ngu nhiên mt s trong s 21 s u tiên. Xác su chc s l

bng

. B.

. C.

. D.

Lời giải

Chọn A

Tp hp 21 s u tiên là

 

0;1;2;3;....;19;20

Không gian mu có 21 phn t. Trong 21 s u tiên có 10 s l 

ng có 10 kt qu thun li. Vy xác sut là

Câu 30: Hàm s ng bin trên

tanyx

. B.

1y x x x   

1yx

. D.







Lời giải

Chọn B

Hàm s

1y x x x   

có

' 3 2 1 0,y x x x     R

ng bin trên

Câu 31: Gi

lt là giá tr ln nht, giá tr nh nht ca hàm s

2 3 12 1y x x x   

trên

n

[ 1;5]

. Tng

Mm

bng.

270

. B.

. C.

280

. D.

260

Lời giải

Chọn D

+) Hàm s

2 3 12 1y x x x   

nh và liên tn

 

1;5

+) Ta có

 

1 1;5

6 6 12 0

2 1;5

y x x

  





    



   





Trang90

 

1 14f 

;

 

16f 

;

 

5 266f 

Vy

 

   

1;5

16m min f x f



   

 

   

1;5

max 5 266M f x f



  

260Mm  

Câu 32: Tp nghim ca b

xx

   



   

   

x 

. B.

x 

. C.

x 

x 

Lời giải

Chọn A

2 2 2

4 2 .

3 3 3

x x x



   

      

   

   

Vy tp nghim ca b

x 

Câu 33: Nu

 

2 ( ) 1 5f x dx



thì

()f x dx



bng ?

. B.

2

. C.

3

Lời giải

Chọn A

Ta có

 

2 2 2 2 2

1 1 1 1 1

2 ( ) 1 2 ( ) 2 ( ) 1 5 ( ) 2f x dx f x dx dx f x dx f x dx       

    

Câu 34: Cho s phc

34zi

a s phc

 

1 iz

bng ?

. B.

. C.

Lời giải

Chọn A

Ta có

 

1 1 2.5i z i z   

Câu 35: Cho hình chóp

.S ABC

 

ABC

là tam giác vuông cân ti

và

2AB a

. Bit

 

SA ABC

và

SA a

. Góc gia hai mt phng

 

SBC

và

 

ABC

bng

30

. B.

45

. C.

60

. D.

90

Lời giải

Chọn B

Trang91

Gi

m

Do tam giác

ABC

vuông cân ti

nên

AM BC

 

SA BC

SAM BC

AM BC













Ta có

   

 

   









 

SBC ABC BC

SAM BC

SBC ABC SM AM

SAM SBC SM

SAM ABC AM























Suy ra góc gia

 

SBC

và

 

ABC

bng góc



SMA

Xét tam giác

ABC

vuông cân ti

và

2AB a

2;BC a AM a  

Xét tam giác

SMA

vuông ti

Ta có

 

tan 1 45

SA a

SMA SMA

AM a

     

Câu 36: u có cng , góc gia mt mt bên và mng .

 ng cao

A. B. C. D.

Lời giải

Chọn C

  .

ABC



AM BC

.S ABC

60

.SH

SH 

Trang92

Vì



60SMA

  . Vì  .

ABC



3 1 3

2 3 6

AM HM AM   

Trong tam giác vuông có

Câu 37: Trong không gian vi h t 

,Oxyz

 

3; 4; 2A 

 

5; 6; 2B 

 

10; 17; 7C 

. Vit

t cu tâm

, bán kính

     

2 2 2

10 17 7 8x y z     

. B.

     

2 2 2

10 17 7 8x y z     

     

2 2 2

10 17 7 8x y z     

. D.

     

2 2 2

10 17 7 8x y z     

Lờigiải

ChọnB

Ta có

 

2;2;0AB 



2 2 2 2AB   

t cu tâm

bán kính

     

2 2 2

10 17 7 8x y z     

Câu 38: Trong không gian vi h trc t

Oxyz

, cho

 

  M

 

0;1; 3N

ng

thm

là

1 2 1

1 3 2

x y z  





. B.

1 3 2

1 2 1

x y z  





1 3 2

x y z





. D.

1 2 1

x y z





Lờigiải

ChọnC

ng thng



 

0;1; 3N

 

 

1; 3; 2MN 





trình là

1 3 2

x y z





Câu 39. Cho hàm s

 

,fx

 th ca hàm s

 

y f x

. Giá tr nh

nht ca hàm s

   

2 1 4 3g x f x x   

n









bng

 

. B.

 

11f 

. C.

 

25f 

. D.

 

13f 

Lời giải

Chọn D

   

 

SBC ABC BC

SM SBC SM BC

AM ABC AM BC

















ABC

.S ABC

 

SH ABC

SHM

.tan60 . 3 .

SH HM   

Trang93

t

 

2 1 2;3t x t    

, xét hàm s

   

21h t f t t  

trên

 

2;3

Ta có

   

2h x f x

 

h t t







  







     

0 2 1;3h x f x x    

     

0 2 2;1h x f x x     

Ta có bng bin thiên sau

Ta có

 

     

min 1 1 3h t h f



  

Câu 40.Có bao nhiêu s 

sao cho ng vi mi



2021

s nguyên

tho

mãn

( ) ( )

log 3 1 . log 0x x y

éù

+ - - <

ëû

. B.

. C.

. D.

Lời giải

Chọn C

u kin:

0x>

Vu kin trên:

( ) ( )

log 3 1 . log 0x x y

éù

+ - - <

ëû

( )

log 3 1 0

log 0

log 3 1 0

log 0

+ - <

+ - >

( )

log 3 1

log

log 3 1

log

êï

( )

2 1

x sai

< < -

Û Û Û - < <

êï

- < <

u kic:

x<<

ng vi mi



2021

s nguyên

2 2021 log 2021

yÛ £ Û £

Vì

là s 

{ }

1;2;3;4;5;6;7;8;9;10y Î

Trang94

Câu 41. Cho hàm s

 

2cos 3 0

x m x

y f x

















liên tc trên



. Giá tr

2cos 1sin dI f x x x









. B.

. C.

. D.



Lời giải

Chọn A

Hàm

 

liên tc trên



suy ra

   

lim lim

f x f x







 

lim lim 2cos 3

x m x





   

1m

Xét b

2cos 1 0x

vi





2cos 1x

cos

x



  

Vy

2cos 1 0x 

khi





2cos 1 0x 

khi





2cos 1sin dI f x x x







2cos 1 sin d 2cos 1sin df x x x f x x x



   



   

2cos 1 sin d 1 2cos sin dI f x x x f x x x



   



Xét

 

2cos 1 sin dI f x x x







Xét

2cos 1tx

d 2sin dt x x  

sin d







Trang95

Suy ra

 

2cos 1 sin dI f x x x







 

-d

ft



 

f t t



 

f x x



 

-1 d

2 6 2 3

I x x



   



Xét

 

1 2cos sin dI f x x x







Xét

1 2costx

d 2sin dt x x

sin d

xx



Suy ra

 

2cos 1 sin dI f x x x







 

ft



 

f t t



 

f x x



 

-1 d

2 6 2 3

I x x



   



Suy ra

I I I



  

Câu 42: Có bao nhiêu s phc

tha

23z i z i   

và

2 3 2zi  

A.Vô s B.

. C.

. D.

Lời giải

Chọn A

Gi m

 

;M x y

m trên mp t

Oxy

biu din s phc

( , )z x yi x y  

23z i z i   

: Tp hp

 

;M x y

là trung trc cn thng

vi

   

2;1 , 0;3AB

2 3 2zi  

: Tp hp

 

;M x y

là hình tròn (k c biên) có bán kính

2r 

và tâm

 

2;3I

 só phc tha yêu cu bài toán.

Câu 43: Cho hình chóp

.S ABCD

nh

, hình chiu vuông góc ca

lên mt

phng

 

ABCD

trùng vm cnh

, cnh bên

hp vt góc

60

. Tính

theo

th tích

ca khi chóp

.S ABCD

V 

. B.

V 

. C.

V 

. D.

V 

Trang96

Lời giải

Chọn B

Gi

m ca

 

SH ABCD



là hình chiu vuông góc ca

trên

 

ABCD



 



, 60SBH SB ABCD   

ABH

vuông ti

2 2 2

BH AB AH a     

SBH

vuông ti

.tan60 .

SH HB   

1 15

S ABCD ABCD

V SH S

Câu 44: Ông Bo làm mái vòm  c ngôi nhà ca mình bng vt lit

phn ca mt xung quanh ca mt hình tr i. Bit giá tin ca 1

tôn là

300.000

ng. Hi s tin hàng nghìn) mà ông Bo mua tôn là bao nhiêu ?

18.850.000

ng. B.

5.441.000

ng. C.

9.425.000

ng. D.

10.883.000

ng.

5 m

6 m

120

Trang97

Lời giải

Chọn D

Gi

a hình tr

2 2 3.

sin120

rr  

S dng h thng trong tam giác, ta có góc  tâm ca cung này bng

120

 dài cung này bng



Suy ra din tích ca mái vòm bng

(vi

là din tích xung quanh ca hình tr).

n ca mái vòm là

 

1 1 1

.300.000 . 2 .300.000 . 2 .2 3.5 .300.000 10882796,19.

3 3 3

S rl



 

Câu 45: Trong không gian vi h t     ng thng

2 1 1

x y z







và

1 2 2

1 3 2

x y z

  





. Gi



 ng thng song song vi

 

: 7 0P x y z   

và ct

,dd

lt ti A, B sao cho AB ngn nhng thng



là:

























. B.













  



























. D.

























Lời giải

Chọn A

   

1 2 ; ; 2 ,B 1 ; 2 3b;2 2A d A a a a d B b b          

 

2 ;3 2; 2 4AB b a b a b a     



(P) có vtpt

 

1;1;1n



   

/ / . 0 2 1;2 5; 6

5 49 49

6 30 62 6

2 2 2

P AB n b a AB a a a

AB a a a

           



       





  

120

6 m

Trang98

min

khi

 

5 5 9 7 5

6; ; , 1;0;1 :

2 2 2 2 2

a A AB y















      





















Câu 46: Cho hàm s

()y f x

 th

()fx



 sau

Bit

 

00f 

. Hi hàm s

 

g x f x x

m cc tr

. B.

. C.

. D.

Lời giải

Chọn B

t

 

3 2 3

h x f x x h x x f x



    

Ta có

 

   

0 , 0 , 1h x f x x



   

t

t x x t  

T

 

ta có:

   

,2ft





Xét

   

2 4 1

m t m t



   

Lúc này ta có hình v  th 

Trang99

Suy ra pt

 

có 1 nghim

0tt  

 

có nghim

0x t x  

Bng bin thiên ca

     

,h x g x h x



Vy hàm s

 

y g x

có

m cc tr.

Câu 47: Có bao nhiêu s t nhiên

sao cho tn ti s thc

tho

 

3log 1

2021 2020 2020





  

A. 9. B. 8. C. 5. D. 12

Lời giải

Chọn A



 

3log 1

2020

2021

2020











u kin:

1x 

   

 

   

 

3log 1 3log 1

2021 2021

3log 1 3log 1

2021 20

log 2020 log 2020

x a a x

x x a a



     

      

Trang100

Xét hàm s

 

( ) log 2020f t t t  

, trên

 

0;

 

'( ) 3 0, 0

2020 ln2021

f t t t

    



nên hàm s

()ft

ng bin trên

 

0;



 



tr thành:

 

log 1x





 

log

1 log log .log( 1)

x x x a x     

 

log

log 1, 1

log 1

     



nên

 

10 1,2,3,4,5,6,7,8,9aa

Câu 48. 

 

y f x



 



 

y f x



   

1 2 3

,,x x x

 

2xx

     

1 3 2

f x f x f x  

và

 



 

:d x x

    

1 2 3 4

, , ,S S S S

      







0,60

. B.

0,55

. C.

0,65

. D.

0,70.

Lời giải

Chọn A



 





:d x x



 



 

y g x

có ba



1 2 3

1, 0, 1x x x   

. Suy ra

 

20y g x k x x c k    



     

1 3 2

2 2 3

0 2 2 0

3 3 4

f x f x f x k c c c k         

Suy ra :

 

y g x k x x k   



3 28 2 17

4 60

S S k x x dx k



    





   

01g g k

1 2 3 4

.1S S S S k k     

Trang101

Suy ra

28 2 17 77 28 2 28 2 17

0,604

60 60

77 28 2

S S k k k



  

      





Câu 49: Cho hai s phc

,uv

tha mãn

10uv==

và

3 4 50uv-=

. Tìm Giá tr ln nht ca biu

thc

4 3 10u v i+-

. B.

. C.

. D.

Lời giải

Chọn C

Ta có

.z z z=

t

34T u v=-

43M u v=+



( )

3 4 3 4T u v u v= - -

( )

9 16 12u v uv vu= + - +

 ta có

( )

4 3 4 3M u v u v= + +

( )

16 9 12u v uv vu= + + +



( )

25 5000M T u v+ = + =

Suy ra

5000MT=-

5000 50 2500= - =

hay

50M =

Áp dng

z z z z

¢¢

+ £ +

ta có

4 3 10 4 3 10 50 10 60u v i u v i+ - £ + + - = + =

Suy ra

max 4 3 10 60u v i+ - =

Câu 50. Trong không gian

Oxyz

m

(2;3;3)A

và mt cu

       

2 2 2

: 1 2 3 12S x x x     

. Xét khi tr

 

ni tip mt cu

 

và có tr

m

. Khi khi tr

 

có th tích ln nha

 

nm trên hai mt

phng

0x ay bz c   

và

0x ay bz d   

. Giá tr

a b c d  

bng

4 4 2

. B.

5

. C.

4

. D.

5 4 2

Lời giải

Chọn B

Gi

,rh

lu cao ca mt tr

 

và

là bán kính mt

cu

 

, ta có :

23R 

2h R r

Trang102

Th tích khi tr

 

là

 

2 2 2 2 2 2 2 2

. 2 2. . 2 2V r h r R r r r R r

  

    

Mà theo Cô-si ta có:

 

2 2 2 2

2 2 2 2 2

2 2 2

. 2 2

r r R r

r r R r R

  

  

Suy ra :

 

2 2 2 2 6 3

8 4 3

. 2 2

27 9

r r R r R V R



   

. Dy ra khi

r 

Vy khi khi tr

 

t th tích ln nht thì chiu cao

6 2 3



   





( Có

th dùng ).

Mt khác tâm ca khi tr

 

chính là tâm

 

1;2;3I

ca mt cu

 

nên trc ca khi tr

 

nng thng

IA y t

















. Va khi tr nm trên 2 mt phng vuông

góc vng thng

và cách tâm

mt khong bng

. Gi

 

1 ;2 ;3M t t IA  

là tâm

cng tròn , ta có

2 2 2

2 2 2 4IM t t t     

 

2 1 2;2 2;3



   







    





Vy 2 mt phng cha mt tr 

   

1 2 2 2 0 3 2 2 0x y x y          

Và

   

1 2 2 2 0 3 2 2 0x y x y          

Vy:

5a b c d    

Đề 10

ĐỀ LUYỆN THI CẤP TỐC TỐT NGHIỆP THPT NĂM 2021

Thuvienhoclieu.Com

BÀI THI: TOÁN

Thời gian: 90 phút

Câu 1: n nghe mt bui hòa nhc. S cách xi này vào mt hàng có 5 gh là:

130

. B.

125

. C.

120

. D.

100

Câu 2: Cho cp s nhân

 

vi

; 32

uu   

. Tìm

2q

. B.

4q

. C.

1q

. D.

q

Câu 3: Cho hàm s

 

y f x

có bng bi

Trang103

Hàm s

 

y f x

nghch bin trên kho

 

;0

. B.

 

;2 

. C.

 

1;0

. D.

 

0;

Câu 4: Cho hàm s

 

y f x

có bng bi

Kh

A. Hàm s t ci ti

3x 

. B. Hàm s t ci ti

4x 

C. Hàm s t ci ti

2x 

. D. Hàm s t ci ti

2x 

Câu 5: Cho hàm s

()y f x

liên tc trên



và có bng xét du

 





Kt lu

A. Hàm s có

m cc tr. B. Hàm s có

m ci.

C. Hàm s có

m cc tr. D. Hàm s có

m cc tiu.

Câu 6: ng thm cn ngang c th hàm s







2y 

. B.

4y 

. C.

y 

. D.

2y 



f '(x)



Trang104

Câu 7: 



2   y x x

. B.

32   y x x

. C.

23  y x x

. D.

1   y x x

Câu 8:  th ca hàm s

31   y x x

ct trc tung t bng

3

. B.

. C.

. D.

1

Câu 9: Cho

0a 

1a 

. Tính

 

log

. B.

2

. C.

. D.

Câu 10: o hàm ca hàm s

3

là

ln3



yx

. B.







. C.

ln3





. D.

3 ln3





Câu 11: Cho

là s th



bng

. B.

. C.

. D.

Câu 12: 

 

log 1 4x

có nghim là

4x

. B.

15x

. C.

3x

. D.

16x

Câu 13: Nghim c

   

log 2 7 log 1 2xx   

là

2x 

. B.

3x 

. C.

x 

. D.

x 

Câu 14: Cho hàm s

 

21f x x x   

. Trong các khnh sau, kh

 

f x dx x x x C    



. B.

 

f x dx x x x C    



 

f x dx x x x C    



. D.

 

f x dx x x x C    



Câu 15: Cho hàm s

 

sin2 3f x x

. Trong các khnh sau, kh

Trang105

 

cos2f x dx x C  



. B.

 

cos2 3

f x dx x x C   



 

cos2 3f x dx x x C   



. D.

 

cos2

f x dx x C  



Câu 16: 

( ) 7f x dx







và

(t) 9f dt







thì

()f x dx





2

. B.

. C.

. D. c.

Câu 17: Tích phân

xdx







. B.

. C.

. D.

Câu 18: S phc liên hp ca s phc

7zi

m biu din trên mt phng t là:

 

0; 7 .M 

 

7;0 .M 

 

7;0 .M

 

0;7 .M

Câu 19: Cho hai s phc

2 ;w 3 2z i i   

. S phc

wz 

bng

13i

. B.

62i

. C.

5 i

. D.

13i

Câu 20: Cho s phc

23zi  

m biu din ca

trên mt phng t là

 

2;3M

. B.

 

2; 3N 

. C.

 

2; 3P 

. D.

 

2;3Q 

Câu 21: Mt khi chóp có ding

và chiu cao bng

. Th tích ca kh

. B.

. C.

. D.

Câu 22: Th tích ca khi hp ch nhc là

2;3;5

là

. B.

. C.

. D.

120

Câu 23: Công thc

ca khi tr có bán kính

và chiu cao

là

V r h





. B.

V r h





. C.

V rh





. D.

V rh





Câu 24: Mt hình tr 

2r cm

 ng sinh

5l cm

. Din tích xung quanh ca

hình tr 

10 cm



. B.

20 cm



. C.

50 cm



. D.

5 cm



Câu 25: Trong không gian vi h trc t

Oxyz

, cho

 

1;2;0a 



 

2;1;0b 



 

3;1;1c 



. Tìm

t c

32u a b c  



  

 

10; 2;13

. B.

 

2;2; 7

. C.

 

2; 2;7

. D.

 

11;3; 2

Câu 26: Trong không gian

Oxyz

, cho mt cu

 

2 2 2

: 2 4 2 0S x y z y z     

. Bán kính ca mt cu

ng

Trang106

. B.

. C.

. D.

Câu 27: Trong không gian

Oxyz

m

   

1;0;1 , 2;1;0AB

. Vit phng

 



và vuông góc vi

 

:3 4 0P x y z   

. B.

 

:3 4 0P x y z   

 

:3 0P x y z  

. D.

 

:2 1 0P x y z   

Câu 28: Trong không gian

Oxyz

ng thng

2 1 7

1 3 5

x y z

  







phi là m a

 

1;3;5u 



. B.

 

1;3; 5u 



. C.

 

1; 3;5u   



. D.

 

2;6; 10u 



Câu 29: Mt hng. Ly ngu nhiên 3 bóng. Tính xác su

trong 3 bóng có 1 bóng hng.

. B.

112

. C.

. D.

Câu 30: Tìm tt c các giá tr ca tham s

 hàm s

 

3 3 2 1 1y x mx m    

ng bin trên



A. Không có giá tr

tha mãn. B.

1m 

1m 

. D.

m

Câu 31: Gi

,Mm

lt là giá tr ln nhât, giá tr nh nht ca hàm s

 

   

7 11 2f x x x x

n

 

0;2 .

Giá tr ca biu thc

25A M m

bng?

 3.A

4.A

 16.A



1037

Câu 32: Tp nghim ca b

xx



là





;3 

. B.

 

3;1

. C.

 

3;1

. D.





3;1

Câu 33: Cho

 

3 2 6f x x dx









 

f x dx





. B.

3

. C.

. D.

1

Câu 34: Cho s phc

1zi

. 

 

. 4 3zi



52z 

2z 

25 2z 

72z 

Câu 35: Cho hình chóp

.S ABCD

 

ABCD

   

 

   

, 3, 2 2AB a AD a SA a  

(tham khảo hình bên). Góc

ging thng

và mt phng

 

SAB

bng



. B.



Trang107



. D.



Câu 36: 

. ' ' 'ABC A B C



ABC

là tam giác vuông



và

2AB 

(tham khảo hình bên). Khong cách t

n mt phng

 

'A BC

bng

. B.

. C.

. D.

6 13

Câu 37: Trong không gian

,Oxyz



   

2;4;1 , 2;2; 3MN



kính

là

   

3 1 9.x y z    

   

3 1 9.x y z    

   

3 1 9.x y z    

   

3 1 3.x y z    

Câu 38: Trong không gian vi h t

,Oxyz

ng

th

 

1;0;2A

và vuông góc vi mt phng

( )

: 3 7 0?P x y z- + - =

































































Câu 39: Cho hàm s

 

 th ca hàm s

 

'y f x

ng cong trong hình bên. Giá tr ln nht

ca hàm s

     

  

21g x f x x

n

 

3;3

bng

 

0 1.f 

 

3 4.f 

 

2 1 4.f 

 

3 16.f 

Câu 40: Có bao nhiêu s nguyên

 n

 

2021;2021

sao cho b  

 

log

10 10





i mi

thuc

 

1;100

: .

2021

. B.

4026

. C.

2013

. D.

4036

Câu 41: Cho hàm s

 

2 2 0

+4 2 0

x khi x

x x khi x













. Tích phân

 

sin2 . cos dI x f x x







bng

Trang108

I 

. B.

I 

. C.

I 

. D.

I 

Câu 42: Có bao nhiêu s phc

tha mãn

13z 

và

 

24z i z i

là s thun o?

. B.

. C.

. D.

Câu 43: Cho hình chóp

.S ABCD

 nht vi

AB a

3BC a

. Cnh bên SA

vuông góc vng thng

to vi mt phng

()SAB

mt góc



. Th tích khi

chóp

.S ABCD

bng

. B.

. C.

. D.

Câu 44: Ông Bo làm mái vòm  c ngôi nhà ca mình bng vt lit

phn ca mt xung quanh ca mt hình tr i. Bit giá tin ca 1

tôn là

300.000

ng. Hi s tin hàng nghìn) mà ông Bo mua tôn là bao nhiêu ?

18.850.000

ng. B.

5.441.000

ng. C.

9.425.000

ng. D.

10.883.000

ng.

Câu 45: Trong không gian

,Oxyz

m

 

2;1;3E

, mt phng

 

:2 2 3 0P x y z   

và mt cu

       

2 2 2

: 3 2 5 36.S x y z     

Gi



ng th

nm trong mt phng

 

và ct

 

tm có khong cách nh nha



là

















. B.

















. C.

















. D.

1 3 .

















5 m

6 m

120

Trang109

Câu 46: Cho hàm s

 

y f x

là mc có bng xét du

 





S m cc tr ca hàm s

 

g x f x x

. B.

. C.

. D.

Câu 47: Có bao nhiêu s nguyên

 

20;20m

 

 

7 6log 6

m x m  

có nghim thc

. B.

. C.

. D.

Câu 48: Cho hàm s bc b

 

y f x

 th ng cong trong hình bên. Bit hàm

s

 

t cc tr tm

1 2 3 1 2 3

, , ( )x x x x x x

tha mãn

4xx

. Gi

và

là

din tích ca hai hình phc gch trong hình. T s

bng

Câu 49: Cho các s phc

1 2 3

,,z z z

tha mãn

1 4 2, 4 6 1z i z i     

và

12z z i   

. Tìm

giá tr nh nht ca biu thc

3 1 3 2

P z z z z   



. B.

29 3

. C.



. D.

85 3

Câu 50: Trong không gian

Oxyz

m

   

1;0;0 , 3;4; 4AB

. Xét khi tr

 

có trng

thng

m trên mt cng kính

. Khi

 

có th tích ln

nh   a

 

nm trên hai mt phng song song l     

0x by cz d   

và

0x by cz d   

 ca biu thc

b c d d  

thuc

kho

 

0;21

. B.

 

11;0

. C.

 

29; 18

. D.

 

20; 11

BẢNG ĐÁP ÁN

1.C

2.A

3.B

4.C

5.D

6.D

7.C

8.C

9.C

10.D

11.D

12.B

13.C

14.B

15.B

16.C

17.A

18.D

19.C

20.B

Trang110

21.C

22.A

23.A

24.B

25.D

26.B

27.A

28.A

29.C

30.B

31.C

32.B

33.C

34.A

35.A

36.D

37.B

38.C

39.C

40.A

41.A

42.B

43.D

44.D

45.C

46.A

47.D

48.B

49.D

50.C

HƯỚNG DẪN GIẢI CHI TIẾT

Câu 1: n nghe mt bui hòa nhc. S cách xi này vào mt hàng có 5 gh là:

130

. B.

125

. C.

120

. D.

100

Lời giải

Chọn C

S cách sp xp là s hoán v ca tp có 5 phn t:

5! 120P 

Câu 2: Cho cp s nhân

 

vi

; 32

uu   

. Tìm

2q

. B.

4q

. C.

1q

. D.

q

Lời giải

Chọn A

Áp dng công thc s hng tng quát cp s nhân ta có

1 6 6

1 7 1

. 64

u u q u u q q







     







Câu 3: Cho hàm s

 

y f x

có bng bi

Hàm s

 

y f x

nghch bin trên kho

 

;0

. B.

 

;2 

. C.

 

1;0

. D.

 

0;

Lời giải

Chọn B

Câu 4: Cho hàm s

 

y f x

có bng bi

Kh

Trang111

A. Hàm s t ci ti

3x 

. B. Hàm s t ci ti

4x 

C.Hàm s t ci ti

2x 

. D. Hàm s t ci ti

2x 

Lời giải

Chọn C

Giá tr ci ca hàm s là

3y 

ti

2x 

Câu 5: Cho hàm s

()y f x

liên tc trên



và có bng xét du

 





Kt lu

A. Hàm s có

m cc tr. B. Hàm s có

m ci.

C. Hàm s có

m cc tr. D.Hàm s có

m cc tiu.

Lời giải

Chọn D

Da vào bng xét du, ta có:

 



i du

lm

1,3,4.

Suy ra loA.

 



i du t m

1,4

i du t m

. Suy ra hàm s có

m cc tiu.

Câu 6: ng thm cn ngang c th hàm s







2y 

. B.

4y 

. C.

y 

. D.

2y 

Lời giải

Chọn D

Ta có

lim 2









. Vng tim cn ngang c th hàm s là

2y 



f '(x)



Trang112

Câu 7:  



2   y x x

. B.

32   y x x

. C.

23  y x x

. D.

1   y x x

Lời giải

Chọn C

 th 

 

0; 3M

, suy ra lo

Câu 8:  th ca hàm s

31   y x x

ct trc tung t bng

3

. B.

. C.

. D.

1

Lời giải

Chọn C

Tr

0x

. Thay

0x

vào

31   y x x

c:

1y

Câu 9: Cho

0a 

1a 

. Tính

 

log

. B.

2

. C.

. D.

Lời giải

Chọn C

 

log 2

Câu 10: o hàm ca hàm s

3

là

ln3



yx

. B.







. C.

ln3





. D.

3 ln3





Lời giải

Chọn D

Theo công tho hàm ta có

3 ln3





Câu 11: Cho

là s th



bng

Trang113

. B.

. C.

. D.

Lời giải

Chọn D

Ta có:

2 2 2 1 1

3 3 3 4 6



   





a a a a a

Câu 12: 

 

log 1 4x

có nghim là

4x

. B.

15x

. C.

3x

. D.

16x

Lời giải

Chọn B



1 0 1    xx

Ta có

 

log 1 4 1 2 1 16 15         x x x x

. Vm

là

15x

Câu 13: Nghim c

   

log 2 7 log 1 2xx   

là

2x 

. B.

3x 

. C.

x 

. D.

x 

Lời giải

Chọn C

u kin

2 7 0











  













Ta có

       

3 3 3 3

log 2 7 log 1 2 log 2 7 log 1 2x x x x        



   

log 2 7 log 9 1xx  





2 7 9 9

x x x     

(thu kin).

Câu 14: Cho hàm s

 

21f x x x   

. Trong các khnh sau, kh

 

f x dx x x x C    



. B.

 

f x dx x x x C    



 

f x dx x x x C    



. D.

 

f x dx x x x C    



Lời giải

Chọn B

Trang114

Câu 15: Cho hàm s

 

sin2 3f x x

. Trong các khnh sau, kh

 

cos2f x dx x C  



. B.

 

cos2 3

f x dx x x C   



 

cos2 3f x dx x x C   



. D.

 

cos2

f x dx x C  



Lời giải

Chọn B

     

sin 2 3 sin 2 2 3 cos2 3 .

f x dx x dx xd x dx x x C       

   

Câu 16: 

( ) 7f x dx







và

(t) 9f dt







thì

()f x dx





2

. B.

. C.

. D. nh c.

Lời giải

Chọn C

Ta có :

(t) ( ) 9f dt f x dx







+) Áp dng công thc :

 

( ) ( ) ( ) .

c b b

a c a

f x dx f x dx f x dx a c b   

  

2 1 2 2 2 1

1 1 1 1 1 1

( ) ( ) ( ) ( ) ( ) ( ) 9 7 2.f x dx f x dx f x dx f x dx f x dx f x dx

   

       

     

Câu 17: Tích phân

xdx







. B.

. C.

. D.

Lời giải

Chọn A

Cách 1 :

1 1 1 1

4 2 4

xdx

    



Cách 2 :S dng máy tính CASIO .

Câu 18: S phc liên hp ca s phc

7zi

m biu din trên mt phng t là:

 

0; 7 .M 

 

7;0 .M 

 

7;0 .M

 

0;7 .M

Lời giải

Chọn D

Trang115

S phc liên hp ca s phc

7zi

là s phc

7zi

m biu din trên mt phng t

m

 

0;7 .M

Câu 19: Cho hai s phc

2 ;w 3 2z i i   

. S phc

wz 

bng

13i

. B.

62i

. C.

5 i

. D.

13i

Lời giải

Chọn C

   

w 2 3 1 2 5z i i       

Câu 20: Cho s phc

23zi  

m biu din ca

trên mt phng t là

 

2;3M

. B.

 

2; 3N 

. C.

 

2; 3P 

. D.

 

2;3Q 

Lời giải

Chọn B

Ta có

23zi  

m biu din ca

là

 

2; 3

Câu 21: Mt khi chóp có ding

và chiu cao bng

. Th tích ca kh

. B.

. C.

. D.

Lời giải

Chọn C

Th tích khi chóp là

.4.6 8

V 

Câu 22: Th tích ca khi hp ch nhc là

2;3;5

là

. B.

. C.

. D.

120

Lời giải

Chọn A

Th tích khi hp ch nht là

2.3.5 30V 

Câu 23: Công thc

ca khi tr có bán kính

và chiu cao

là

V r h





. B.

V r h





. C.

V rh





. D.

V rh





Lời giải

Chọn A

Công thc

ca khi tr có bán kính

và chiu cao

là

V r h





Câu 24: Mt hình tr 

2r cm

 ng sinh

5l cm

. Din tích xung quanh ca

hình tr 

10 cm



. B.

20 cm



. C.

50 cm



. D.

5 cm



Lời giải

Chọn B

Din tích xung quanh ca hình tr 

2 2 .2.5 20S rl

  

  

Trang116

Câu 25: Trong không gian vi h trc t

Oxyz

, cho

 

1;2;0a 



 

2;1;0b 



 

3;1;1c 



. Tìm

t c

32u a b c  



  

 

10; 2;13

. B.

 

2;2; 7

. C.

 

2; 2;7

. D.

 

11;3; 2

Lời giải

Chọn D

Ta có

 

3 6;3;0b 



 

2 6;2;2c 



Suy ra

   

3 2 1 6 ( 6);2 3 2;0 0 2 11;3; 2u a b c             



  

Câu 26: Trong không gian

Oxyz

, cho mt cu

 

2 2 2

: 2 4 2 0S x y z y z     

. Bán kính ca mt cu

ng

. B.

. C.

. D.

Lời giải

Chọn B

Ta có

0; 1; 2; 2a b c d     

Suy ra

   

1 2 2 7R      

Câu 27: Trong không gian

Oxyz

m

   

1;0;1 , 2;1;0AB

. Vit phng

 



và vuông góc vi

 

:3 4 0P x y z   

. B.

 

:3 4 0P x y z   

 

:3 0P x y z  

. D.

 

:2 1 0P x y z   

Lời giải

Chọn A

Ta có:

 

3;1; 1AB 



Mt phng

 

m

 

1;0;1A 

và vuông góc vng thng



tuyn

 

3;1; 1AB 





       

:3 1 1 0 1 1 0 3 4 0P x y z x y z          

Câu 28: Trong không gian

Oxyz

ng thng

2 1 7

1 3 5

x y z

  







phi là m a

 

1;3;5u 



. B.

 

1;3; 5u 



. C.

 

1; 3;5u   



. D.

 

2;6; 10u 



Lời giải

Chọn A

ng thng

2 1 7

1 3 5

x y z

  





có m 

 

1;3; 5u 





v

   

1; 3;5 , 2;6; 10uu    

 

Câu 29: Mt hng. Ly ngu nhiên 3 bóng. Tính xác su

trong 3 bóng có 1 bóng hng.

Trang117

. B.

112

. C.

. D.

Lời giải

Chọn C

Trong 3 bóng có 1 bóng hng.

Ta có

 

220nC  

Gi bin c A y ra có 1 bóng h

c

 

. 112n A C C

Vy

112 28

()

220 55

PA

Câu 30: Tìm tt c các giá tr ca tham s

 hàm s

 

3 3 2 1 1y x mx m    

ng bin trên



A. Không có giá tr

tha mãn. B.

1m 

1m 

. D.

m

Lời giải

Chọn B

nh :

D = ¡

 

3 6 3 2 1y x mx m



   

Ta có:

   

3 3.3. 2 1mm



    

 hàm s ng bin trên



thì





9 18 9 0mm   

 

9 2 1 0 9 1 0m m m      

1m

Câu 31: Gi

,Mm

l t là giá tr ln nhât, giá tr nh nht ca hàm s

 

   

7 11 2f x x x x

n

 

0;2 .

Giá tr ca biu thc

25A M m

bng?

 3.A

4.A

 16.A



1037

Lờigiải

Chọn C

Xét hàm s n

[0 ; 2]

. Hàm s liên tc trên

[0 ; 2]

. Ta có

 

  

' 3 14 11f x x x

 



   









  







1 0; 2

0; 2

Tính

     

   0 2; 1 3, 2 0f f f

. Suy ra

     3, 2 2 5 16M m M m

Câu 32: Tp nghim ca b

xx



là





;3 

. B.

 

3;1

. C.

 

3;1

. D.





3;1

Lờigiải

Chọn B.

Ta có :

2 2 3 2

2 8 2 2 2 3 0 3 1

x x x x

x x x



          

Trang118

Câu 33: Cho

 

3 2 6f x x dx









 

f x dx





. B.

3

. C.

. D.

1

Lờigiải

Chọn C.

     

   

2 2 2 2

1 1 1 1

3 2 6 3 2 6 3 2. 6

3 9 3.

f x x dx f x dx xdx f x dx

f x dx f x dx

       





   

   



Câu 34: Cho s phc

1zi

. 

 

. 4 3zi



52z 

2z 

25 2z 

72z 

Lờigiải

Chọn A.

    

. 4 3 1 4 3z i i i   

7 i

   

1 7 1 5 2.zi     

Câu 35: Cho hình chóp

.S ABCD

 

ABCD

   

 

   

, 3, 2 2AB a AD a SA a  

(tham khảo hình bên). Góc

ging thng

và mt phng

 

SAB

bng



. B.



. D.



Lời giải

Chọn A

Ta có

CB AB

và

CB SA

(vì

 

SA ABCD

) , suy ra

 

CB SAB

ti

Ta có

 

CB SAB

B SAB

S SAB



















ng thng

là hình chiu vuông góc cng thng

trên mt

phng

 

SAB

Suy ra góc ging thng

và mt phng

 

SAB

là



CSB

Trang119

Xét

CSB

vuông ti

, ta có



 



2 2 2

tan 30

BC AD a

CSB CSB

SA AB

      



Câu 36: 

. ' ' 'ABC A B C





ABC

  

và

2AB 

(tham khảo hình

bên). Khong cách t

n mt phng

 

'A BC

bng

. B.

. D.

6 13

Lời giải

Chọn D

* K

   

 

' ' , 'AH A B AH A BC d A A BC AH    

* Chng minh

 

'AH A BC

, tht vy

Ta có

'AH A B

và

AH BC

(vì

 

''BC ABB A

) , suy ra

 

'AH A BC

* Tính

Xét

'A AB

vuông ti

, ta có

2 2 2

1 1 1 1 1 13 36 6 13

' 9 4 36 13 13

AH AA AB

       

Câu 37: Trong không gian

,Oxyz



   

2;4;1 , 2;2; 3MN



kính

là

   

3 1 9.x y z    

   

3 1 9.x y z    

   

3 1 9.x y z    

   

3 1 3.x y z    

Lời giải

Trang120

Chọn B

Mt cng kính

m cn thng

. Suy ra t tâm mt

cu là

 

0;3; 1 .I 

Bán kính mt cu:

1 1 6

16 4 16 3.

2 2 2

R MN     















 

0;3; 1I 

, 

3R 

   

3 1 9.x y z    

Câu 38: Trong không gian vi h t

,Oxyz

ng

th

 

1;0;2A

và vuông góc vi mt phng

( )

: 3 7 0?P x y z- + - =

































































Lời giải

Chọn C

ng thng cn tìm nhn n ca mt phng

( )

là

 

1; 1;3n 



làm m

ch 





 c







 cn tìm 





 

1;0;2A

, 





 

1; 1;3n 



vec

 

















Câu 39: Cho hàm s

 

 th ca hàm s

 

'y f x

ng cong trong hình bên. Giá tr ln nht

ca hàm s

     

  

21g x f x x

n

 

3;3

bng

 

0 1.f 

 

3 4.f 

 

2 1 4.f 

 

3 16.f 

Lờigiải

Chọn C

Ta có

     



  2 2 1g x f x x

Trang121

   





    







g x f x x

Da vào hình v ta có bng bin thiên

Suy ra giá tr ln nht ca hàm s

     

  

21g x f x x

n

 

3;3

là

   

1 2 1 4gf

Câu 40: Có bao nhiêu s nguyên

 n

 

2021;2021

sao cho b  

 

log

10 10





i mi

thuc

 

1;100

: .

2021

. B.

4026

. C.

2013

. D.

4036

Lời giải

Chọn A

   

log

log 11

10 10 log 10 log

10 10

x y x x





   





   

log 11

1 log log 1

10 10

y x x



   





t

log xt

. Ta có

   

1;100 log 0;2xx  

 

0;2t 

. B thành

     

11 10

1 2 1

10 10 10

t t t

y t t y t





     





 

10 1







Xét hàm s

 

10 1







trên khong

 

0;2

, ta có

 

2 10

10 1

  







   

0, 0;2f t t



   

       

0 2 , 0;2f f t f t    

   

0 , 0;2

f t t    

Trang122

Yêu cu bài toán

 

2

i mi

 

0;2t 

   

, 0;2

f t y t y     

Kt hp vu kin

 

2021;2021 ;2021



   





. Vy có tt c

2021

giá tr nguyên

ca

tha mãn yêu cu bài toán.

Câu 41: Cho hàm s

 

2 2 0

+4 2 0

x khi x

x x khi x













. Tích phân

 

sin2 . cos dI x f x x







bng

I 

. B.

I 

. C.

I 

. D.

I 

Lời giải

Chọn A

     

lim lim 0 2

f x f x f





   

nên hàm s

 

liên tc tm

0x 

t

costx

d sin dt x x  

i cn:

01xt  

;

1xt



   

Ta có:

       

0 0 1 1

sin2 . cos d 2sin .cos . cos d 2 . d 2 . dx f x x x x f x x t f t t t f t t





   

   

   

 

0 1 1 0

1 0 0 1

2 . d 2 . d 2 4 2 d 2 . 2 2 dx f x x x f x x x x x x x x x



      

   

4 3 3 2

4 7 10 9

2 4.

4 3 3 2 6 3 2

x x x x



   

       

   

   

Câu 42: Có bao nhiêu s phc

tha mãn

13z 

và

 

24z i z i

là s thun o?

. B.

. C.

. D.

Lời giải

Chọn B

Gi

z x yi

vi

,xy

Ta có

13 13 (1)z x y   

Mà

 

  

 

2 4 2 4 2 8 ( 6 ).z i z i x yi i x yi i x y y x i            

là s thun o khi

2 8 0 13 2 8 0

x y y y y          

T

y 

c













Vy có 2 s phc tho yêu cu bài toán.

Câu 43: Cho hình chóp

.S ABCD

 nht vi

AB a

3BC a

. Cnh bên SA

Trang123

vuông góc vng thng

to vi mt phng

()SAB

mt góc



. Th tích khi

chóp

.S ABCD

bng

. B.

. C.

. D.

Lời giải

Chọn D

Vì

()SA ABCD

nên

SA BC

, do

BC AB

nên

()BC SAB

. Ta có

là hình chiu

vuông góc ca

lên mt phng (

SAB

ng thng

và mt phng

()SAB

là góc



30CSB





. Trong tam giác

SBC

, ta có

.cot30 3. 3 3SB BC a a



  

Trong tam giác

SAB

, ta có

22SA SB AB a  

Vy

1 1 2 6

. . 2 2. . 3

3 3 3

S ABCD

V SA AB BC a a a  

Câu 44: Ông Bo làm mái vòm  c ngôi nhà ca mình bng vt lit

phn ca mt xung quanh ca mt hình tr i. Bit giá tin ca 1

tôn là

300.000

ng. Hi s tin hàng nghìn) mà ông Bo mua tôn là bao nhiêu ?

18.850.000

ng. B.

5.441.000

ng. C.

9.425.000

ng. D.

10.883.000

ng.

Lời giải

5 m

6 m

120

Trang124

Chọn D

Gi

a hình tr

2 2 3.

sin120

rr  

S dng h thng trong tam giác, ta có góc  tâm ca cung này bng

120

 dài cung này bng



Suy ra din tích ca mái vòm bng

(vi

là din tích xung quanh ca hình tr).

n ca mái vòm là

 

1 1 1

.300.000 . 2 .300.000 . 2 .2 3.5 .300.000 10882796,19.

3 3 3

S rl



 

Câu 45: Trong không gian

,Oxyz

m

 

2;1;3E

, mt phng

 

:2 2 3 0P x y z   

và mt cu

       

2 2 2

: 3 2 5 36.S x y z     

Gi



ng th

nm trong mt phng

 

và ct

 

tm có khong cách nh nha



là

















. B.

















. C.

















. D.

1 3 .

















Lời giải

Chọn C

Mt cu

       

2 2 2

: 3 2 5 36,S x y z     

có tâm

 

3;2;5I

và bán kính

6.R 

Ta có:

 

2 2 2

1;1;2 1 1 2 6 6 .EI EI EI R        

 

m

nm trong mt cu

 

Ta li có:

 

EP

và

 















m ca

 



và

 

nng tròn giao tuyn

 

tâm

ca mt phng

 

và mt cu

 



là hình chiu vuông góc ca

lên mt phng

 

Gi s

   

;S A B  

 dài

nh nht khi và ch khi

 

,dK

ln nht.

120

6 m

Trang125

Gi

là hình chiu ca

trên

 





 

;d K KF KE  

Du

""

xy ra khi và ch khi

.FE

Ta có

 

IK P











   









Ta có:

 

, 5; 5;0

n EI











i

 

1; 1;0u 



Vì

 















nên



có m 

 

1; 1;0u 



ng thng







  









Câu 46: Cho hàm s

 

y f x

là mc có bng xét du

 





S m cc tr ca hàm s

 

g x f x x

. B.

. C.

. D.

Lời giải

Chọn A

Ta có

 

g x f x x f x x   

. S m cc tr ca hàm s

 

bng hai ln s

m cc tr a hàm s

 

cng thêm 1.

Xét hàm s

 

   

 

2 2 2

2 1 0 1

h x f x x h x x f x x x x

















           



















Bng xét du hàm s

 

h x f x x

Hàm s

 

h x f x x

  m cc tr  y hàm s

 

g x f x x f x x   

m cc tr.

Câu 47: Có bao nhiêu s nguyên

 

20;20m

 

 

7 6log 6

m x m  

có nghim thc

Trang126

. B.

. C.

. D.

Lời gia



Chọn D

t:

 

log 6 6 7 6 7

t x m x m x m       

 thành

 

7 6 7 6 7 6 7 6

x t x t

x t x t x t        



xm

. Xét hàm s

 

6 7 ;

f x x x  

Có

   

' 6 7 ln7 ' 0 log

ln7

f x f x x x      

. Ta có BBT

T BBT ta thy PT có nghim

 

log

ln7

6log 7 0,389

ln7

m y x   

;

Mà

   

20;20 ; 19; 18;...;0m m m      

Câu 48: Cho hàm s bc b

 

y f x

 th ng cong trong hình bên. Bit hàm

s

 

t cc tr tm

1 2 3 1 2 3

, , ( )x x x x x x

tha mãn

4xx

. Gi

và

là

din tích ca hai hình phc gch trong hình. T s

bng

Lời giải

Chọn B

Rõ ràng kt qu i khi ta tnh ti th sang trái sao cho

0x 

Trang127

Gi

()g x ax bx c  

, ta có hàm s

()gx

là chm cc tr ng là

2;0; 2

là các nghim c

4 2 0ax bx

D th

()gx

, ta có

(0) 0g 

. T 

( ) ( 8 )g x a x x

vi

0a 

i xng cn tích hình ch nht bng

2 (2) .4 64S S g a  

Ta có

là din tích hình phng gii hn b th hàm s

()gx

, trng thng

2, 0xx  

224

( ) d 8 d

S g x x a x x x



   



. Suy ra

224 512

64 2.

15 15

Sa  

Vy

224 7

512 16



Câu 49: Cho các s phc

1 2 3

,,z z z

tha mãn

1 4 2, 4 6 1z i z i     

và

12z z i   

. Tìm

giá tr nh nht ca biu thc

3 1 3 2

P z z z z   



. B.

29 3

. C.



. D.

85 3

Lời giải

Chọn D



1 1 1

z x y i

 

,xy

   

1 1 1

1 4 2 1 4 4z i x y       

Vy tp hm

biu din s phc

ng tròn

     

: 1 4 4C x y   

có tâm

 

1;4I 

, bán kính

2R 



2 2 2

z x y i

 

,xy

   

2 2 2

4 6 1 4 6 1z i x y       

Vy tp hm

biu din s phc

ng tròn

     

: 4 6 1C x y   

có tâm

 

4;6I

, bán kính

1R 



3 3 3

z x y i

 

,xy

Trang128

3 3 3 3

1 2 2 0z z i x y       

Vy tp hm

biu din s phc

ng thng

: 2 0d x y  



3 1 3 2

P z z z z AM AN     

Mt khác,

   

1 1 2 2

, ; , 2 2

d I d R d I d R   

và

,II

ni vi

Gi

 



i xng vi vi

 

qua

, suy ra

     

: 8 2 1C x y



   

và

gi



i xng vi

qua

 



có tâm

 

8;2I



, bán kính





Ta có:

1 1 1 1 1

2AM MI AI AM AI MI AI      

2 2 2 2 2 2

1AN NI AN N I AI AN AI N I AI

        

        

Suy ra

1 2 1 2

3 3 85 3P AM AN AM AN AI AI I I

  

          

ng thc xy ra khi và

ch m

,,I A I



thng hàng.

Vy

min 85 3P 

Câu 50: Trong không gian

Oxyz

m

   

1;0;0 , 3;4; 4AB

. Xét khi tr

 

có trng

thng

m trên mt cng kính

. Khi

 

có th tích ln

nh   a

 

nm trên hai mt phng song song l     

0x by cz d   

và

0x by cz d   

 ca biu thc

b c d d  

thuc

kho

 

0;21

. B.

 

11;0

. C.

 

29; 18

. D.

 

20; 11

Lời giải

Chọn C

Trang129

Mt cng kính

có tâm

 

2;2; 2I 

và bán kính bng 3.

Gi

 

, 0 3xx

a

 



 

có chiu cao bng

29hx



th tích ca

 

bng

 

2 2 2

2 9 4 . . . 9 4 12 3

2 2 3

V x x x

   



  



     





 

có th tích ln nht bng

max

12 3V





khi

6x 

i

 

là mt phng cha

 

ng quát

dng

2 2 0x y z d   

. Khong cách t tâm

 

2;2; 2I 

n

 

bng

nên

 

2 2.2 2. 2

3 3 10



   







  





Vy

2 2 3 3 10 3 3 10 20b c d d          

Bấm Tải xuống để xem toàn bộ.

| 1/129

| | Tải xuống

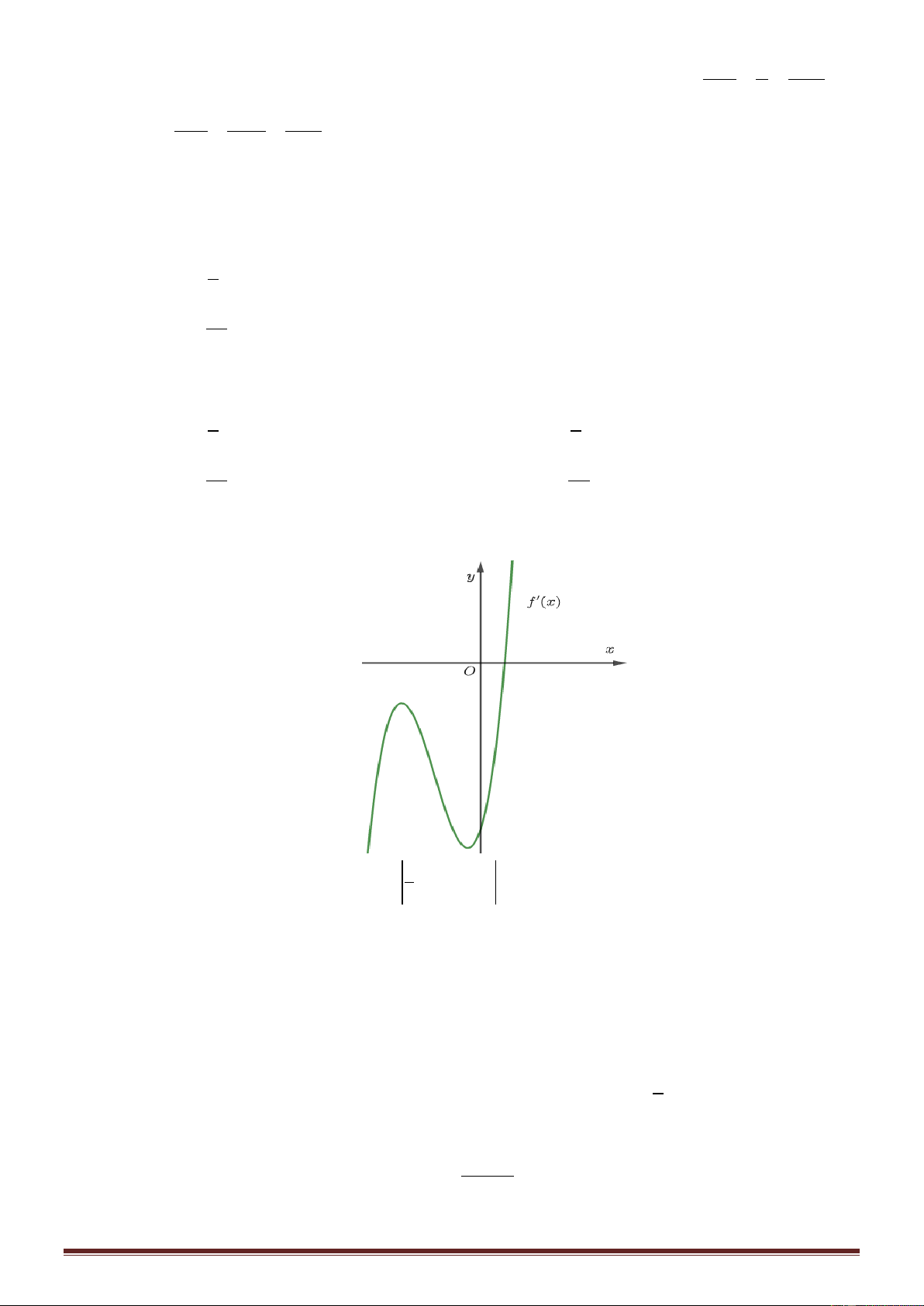
Preview text:

Đề 6
ĐỀ LUYỆN THI CẤP TỐC TỐT NGHIỆP THPT NĂM 2021 Thuvienhoclieu.Com BÀI THI: TOÁN
Thời gian: 90 phút Câu 1:
Có bao nhiêu số tự nhiên có ba chữ số đôi một khác nhau? A. 3 C . B. 10 3 . C. 3 A . D. 2 9.A . 10 10 9 Câu 2:
Cho cấp số cộng u , biết u  6 và u  2
 . Giá trị củau bằng n  1 3 8 A. 8  . B. 22 . C. 34 . D. 22 . Câu 3:
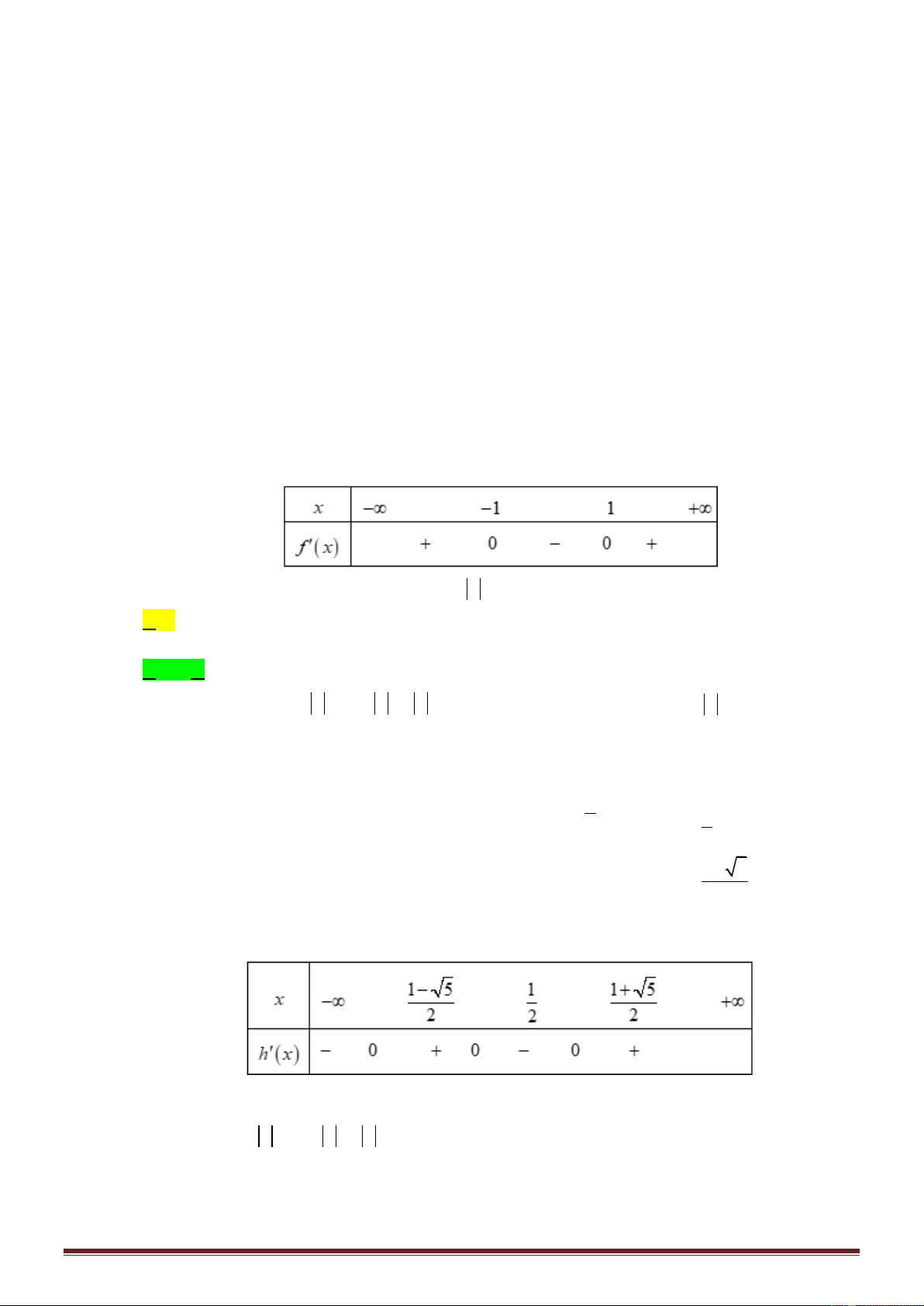
Cho hàmsố y  f  x xác định và liên tục trên khoảng  ;
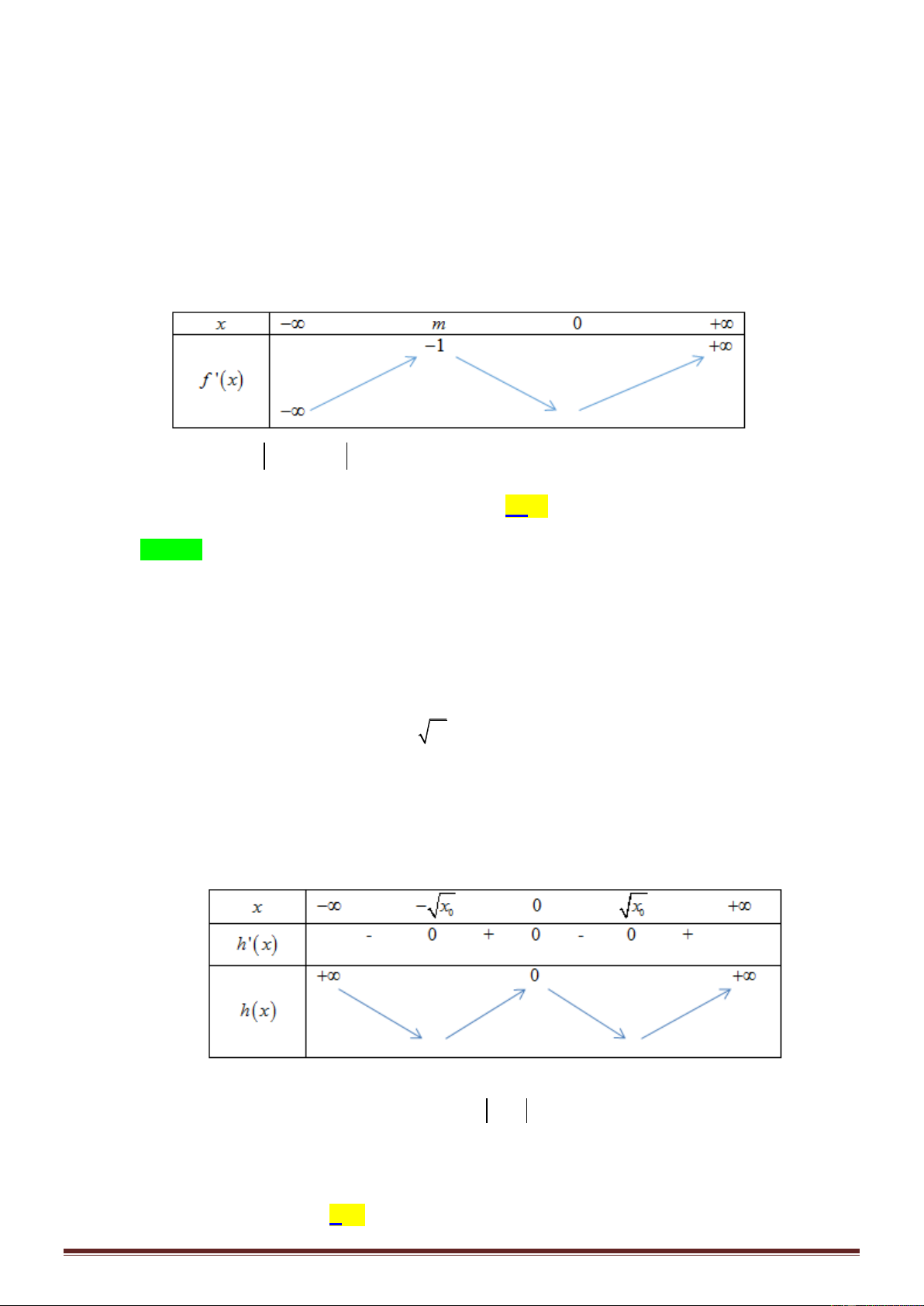
 ,có bảng biến thiên như hình sau: x  1 0 1 
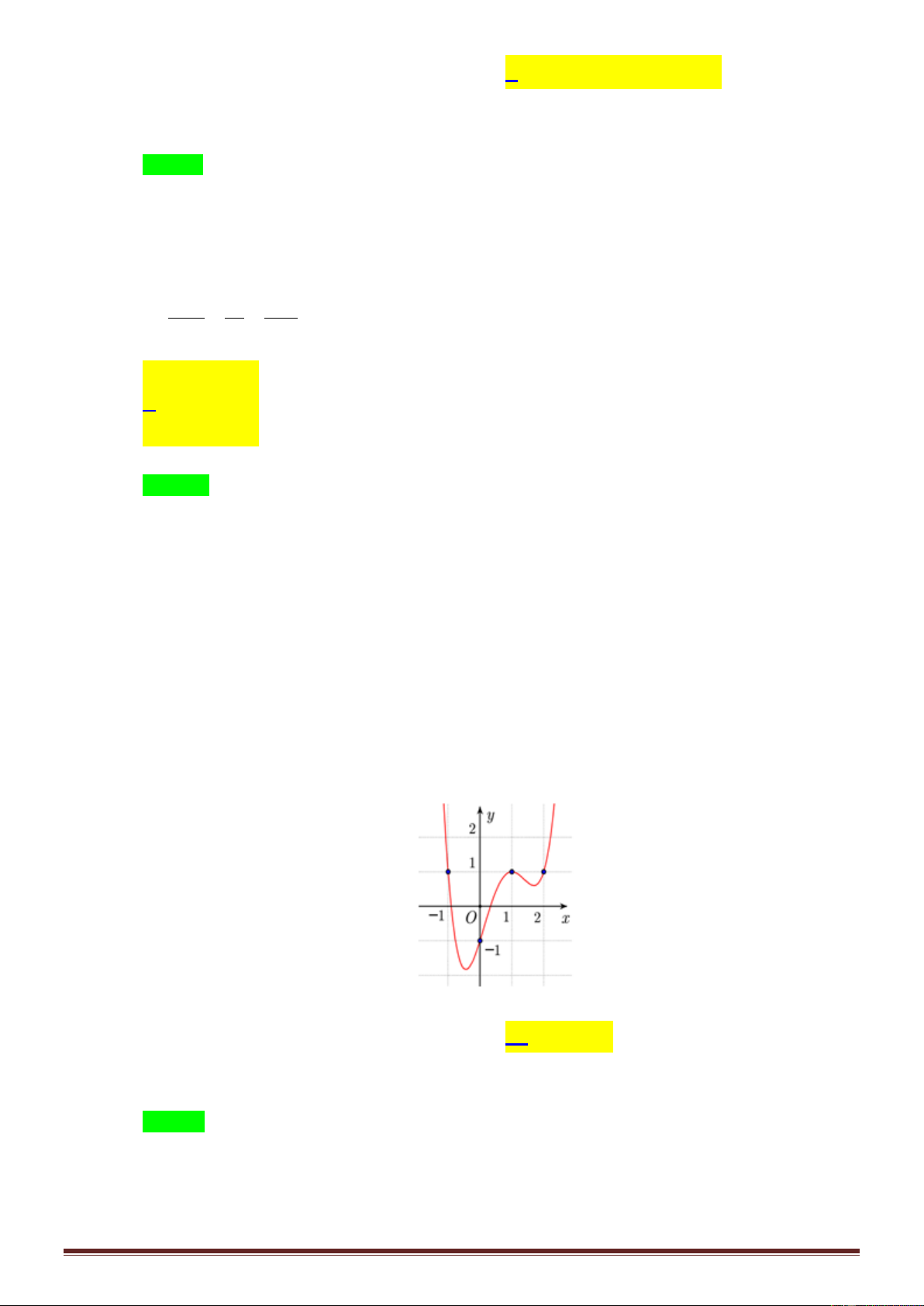
f ' x  0 + 0  0 + f  x  4  1 1
Hàm số đã cho nghịch biến trên khoảng nào dưới đây? A.  1  ;0. . B. 0;  1 . C.  1  ;4 . D. 1;  . Câu 4:
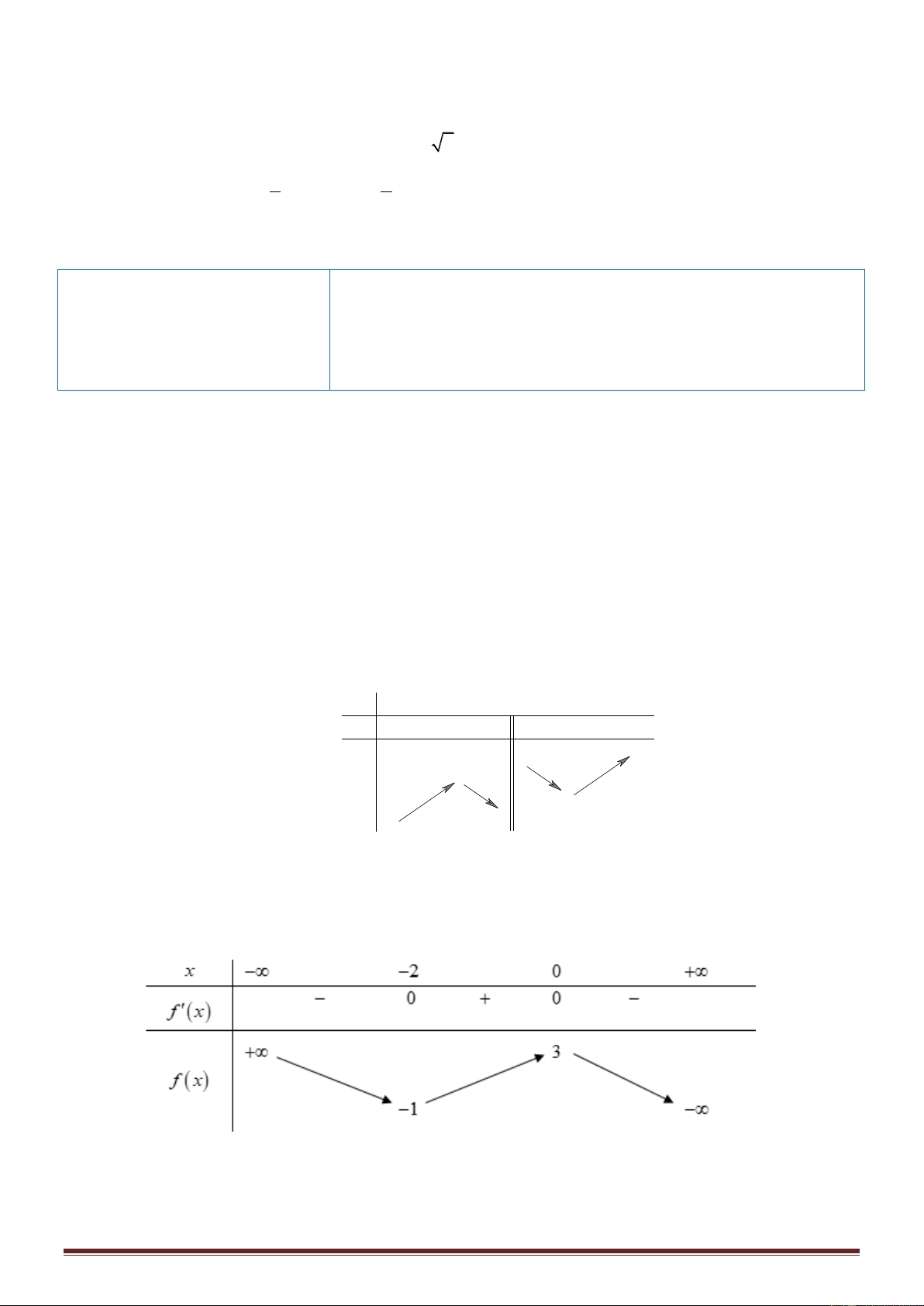
Cho hàm số y  f  x có bảng biến thiên như sau x  0 3 
f ' x + 0 - 0 +
f  x 2   5 
Hàmsố f  x đạt cực đại tại điểm A. x  2 . B. x  5  . C. x  3. D. x  0 . Câu 5:
Cho hàmsố y  f  x liên tục trên  và có bảng xét dấu đạo hàm dưới đây x  3  1 4 
f ' x  0  0  0  .
Số điểm cực trị của hàm số là A. 1 . B. 0 . C. 2 . D. 3 . 5x  3 Câu 6:
Số đường tiệm cận của đồ thị hàm số y  2x  là 1 Trang1 A. 3 . B. 0 . C. 2 . D. 1. Câu 7:
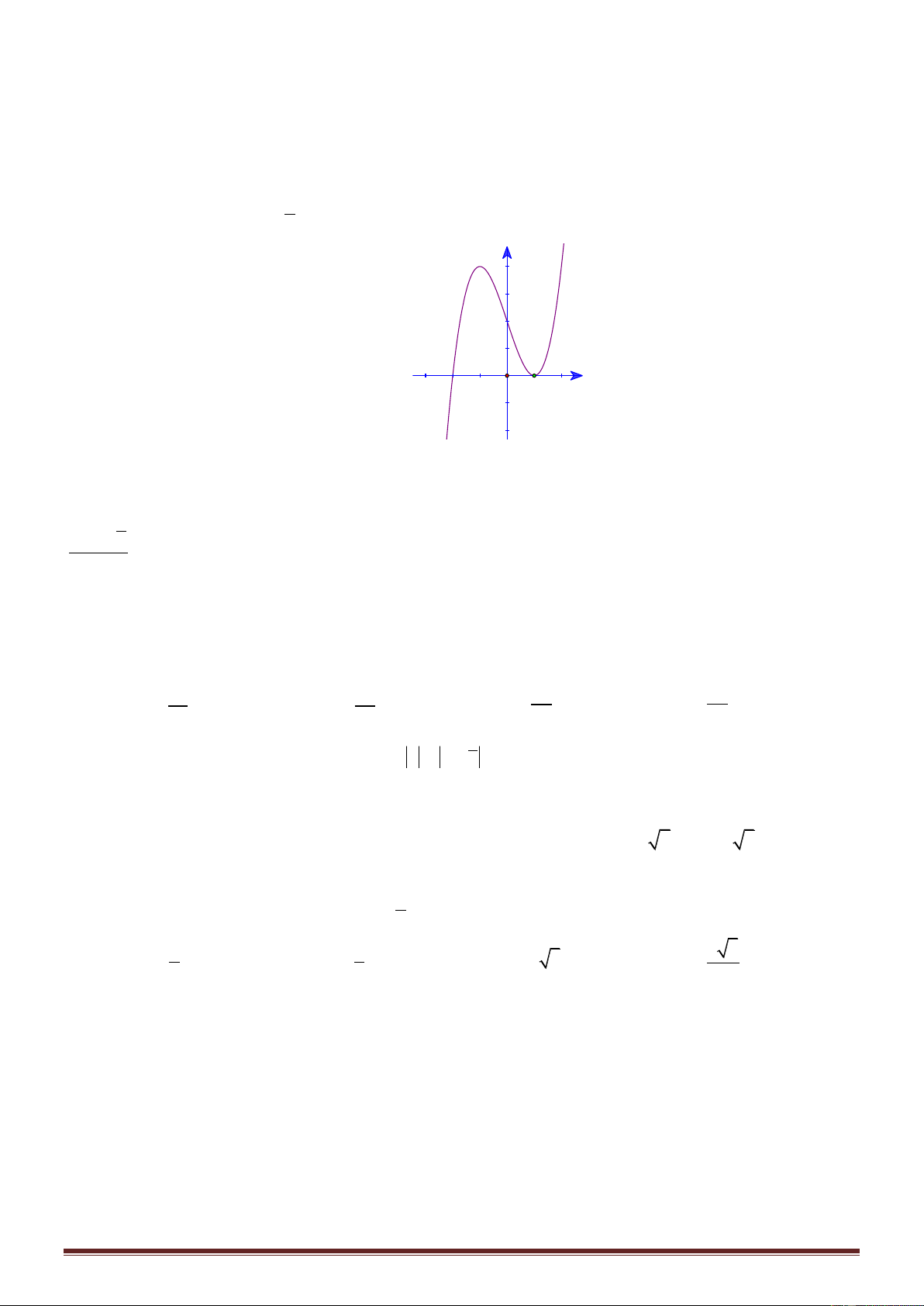
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên: A. 3
y = - x + 3x + 2 . B. 4 2
y = x - x + 2 . C. 2
y = - x + x - 2 . D. 3
y = x - 3x + 2 . x  3 Câu 8:
Đồ thị của hàm số y 
cắt trục hoành tại điểm có hoành độ bằng 2x 1 1 A. 2  . B. . C. 3 . D. 3  . 2 125  Câu 9:
Với a là số thực dương tùy ý, log bằng 5    a 
A. 3  log a .
B. 3log a .
C. log a .
D. 3  log a . 5 3 5 5 5
Câu 10: Với x  0 , đạo hàm của hàm số y  log x là 2 x 1 A. . B. . C. . x ln 2 . D. 2x.ln 2 . ln 2 . x ln 2
Câu 11: Với a là số thực dương tùy ý , 4 7 a bằng 4 7 1 A. 28 a . B. 7 a . C. 4 a . D. 28 a . 
Câu 12: Nghiệm dương của phương trình 2 x 1 7  7 1680 là
A. x  2 .
B. x  2; x  2 . C. x  2  . D. x  4 .
Câu 13: Nghiệm của phương trình log
x  3  3 là: 2  
A. x 11.
B. x 12 .
C. x  3  3 . D. 3 x  3  2 .
Câu 14: Nguyên hàm của hàm số 4
f (x)  5x  2 là: A. f  x 3
dx  x  x  C . B. f  x 5
dx  x  x  C . C. f  x 5
dx  x  2x  C . D. f  x 5
dx  x  2x  C .
Câu 15: Cho hàm số f  x  sin 2x . Trong các khằng định sau, khẳng định nào đúng? A. f  x 1 dx 
cos 2x  C . B. f  x 1 dx  
cos 2x  C . 2 2 C. f
 xdx  2cos2xC. D. f
 xdx  2
 cos 2x  C . 2 3 3 Câu 16: Nếu f
 xdx  3 và f
 xdx 1 thì f xdx  bằng 1 1 2 A. 4 . B. 4  . C. 2  . D. 3  . Trang2 2 Câu 17: Tích phân x
 x 2 dx bằng 1 15 16 7 15 A. . B. . C. . D. . 3 3 4 4
Câu 18: Số phức liên hợp của số phức z  2  3i là:
A. z  3 2i .
B. z  2  3i .
C. z  3 2i . D. z  2  3i . 
Câu 19: Cho hai số phức z  2  3i và w  5  i . Số phức z iw bằng
A. 3 8i
B. 1 8i
C. 8  i D. 7  4i
Câu 20: Trên mặt phẳng tọa độ, điểm biểu diễn số phức liên hợp của số phức 9  5i có tọa độ là A. 5; 9  . B. 5;9 . C. 9; 5   . D. 9;5 .
Câu 21: Một khối chóp có thể tích bằng 90 và diện tích đáy bằng 5. Chiều cao của khối chóp đó bằng A. 54 . B. 18 . C. 15 . D. 450 .
Câu 22: Thể tích của khối hộp chữ nhật có ba kích thước 5; 7; 8 bằng A. 35 . B. 280 . C. 40 . D. 56 .
Câu 23: Một khối nón tròn xoay có chiều cao h  6 cm và bán kính đáy r  5 cm . Khi đó thể tích khối nón là: 325 A. 3
V  300 cm . B. 3
V  20 cm . C. 3 V  cm . D. 3
V  50 cm . 3
Câu 24: Cho một khối trụ có độ dài đường sinh là l  6 cm và bán kính đường tròn đáy là r  5 cm .
Diện tích toàn phần của khối trụ là A. 2 110 cm B. 2 85 cm . C. 2 55 cm D. 2 30 cm     
Câu 25: Trong không gian Oxyz cho điểm A thỏa mãn OA  2i  j với i, j là hai vectơ đơn vị trên hai
trục Ox , Oy . Tọa độ điểm A là
A. A2;1;0 . B. A0; 2  ;1 . C. A0;1  ;1 . D. A1;1  ;1 .
Câu 26: Trong không gian với hệ tọa độ Oxyz , cho mặt cầu S  có phương trình: 2 2 2
x  y  z  2x  4 y  4z  7  0 . Xác định tọa độ tâm I và bán kính R của mặt cầu S  . A. I 1;2; 2
  ; R  4 . B. I 1;2; 2
  ; R  2 . C. I  1  ; 2
 ;2; R  4 . D. I  1  ; 2
 ;2; R  3.
Câu 27: Trong không gian với hệ toạ độ Oxyz , cho mặt phẳng P  : x  3y  z  3  0 . Mặt phẳng  P  đi
qua điểm nào dưới đây?
A. 1;1;0. B. 0;1; 2  . C. 2; 1  ;3. D. 1;1;1.
Câu 28: Trong không gian Oxyz , cho mặt phẳng  P : x  2y  3z  2  0 và đường thẳng d vuông góc
với mặt phẳng P . Vectơ nào dưới đây là một vectơ chỉ phương của d ?     A. u  1; 2  ;2 .
B. u  1; 2;3 .
C. u  0; 2;3 . D. u  1; 2  ;3 . 2   3   4   2   x  Câu 29: Hàm số 7
y  x  đồng biến trên khoảng 4 A.  ;   . B.  6  ;0 . C. 1; 4 . D.  5   ;1 .
Câu 30: Trong một lớp học gồm 15 học sinh nam và 10 học sinh nữ. Giáo viên gọi ngẫu nhiên 4 học
sinh lên giải bài tập. Tính xác suất để 4 học sinh được gọi đó có cả nam và nữ? Trang3 219 219 442 443 A. . B. . C. . D. . 323 323 506 506
Câu 31: Tìm giá trị lớn nhất M của hàm số 3 2
y  2x  3x 12x  2 trên đoạn  1  ;2. A. M 10 . B. M  6 . C. M  11 . D. M 15. a
Câu 32: Tập nghiệm của bất phương trình    1 7 4 3  7  4 3 là A.  ;0  . B.   ;1  .
C. 0;  . D. 1;  . 4 4 f
 xdx 10 g
 xdx  5 4 Câu 33: Cho 2 và 2 . Tính I  3  f
 x5gx2xdx  2 A. I 17. B. I 15. C. I  5.  D. I 10.
Câu 34: Cho số phức z  2  3 .
i Môđun của số phức 1 i z bằng A. 26. B. 25. C. 5. D. 26.
Câu 35: Cho hình hộp chữ nhật ABC .
D A' B'C ' D' có AB  AD  2 2 và AA'  4 3 (tham khảo hình
bên). Góc giữa đường thẳng CA' và mặt phẳng  ABCD bằng A. 0 60 . B. 0 90 . C. 0 30 . D. 0 45 .
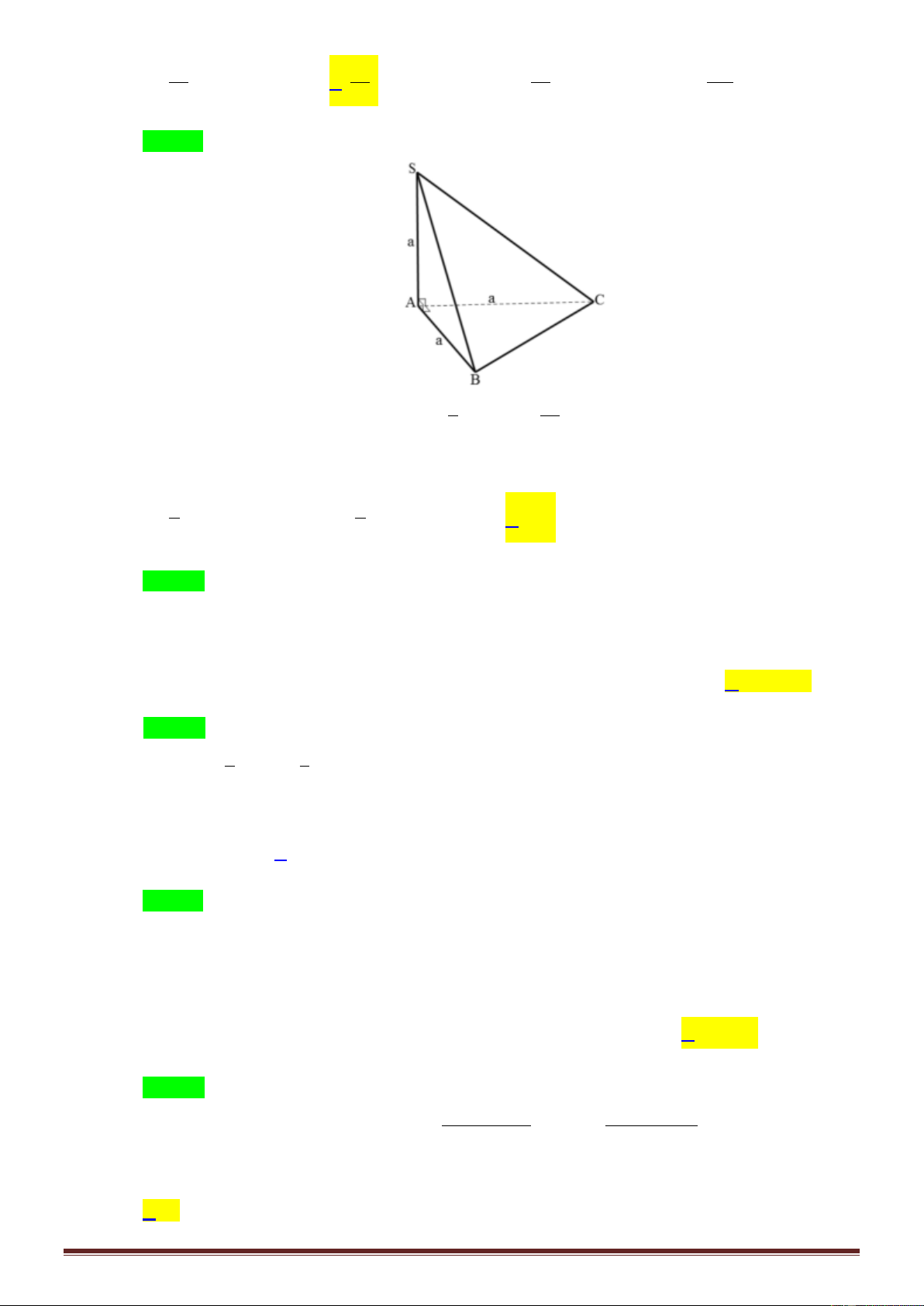
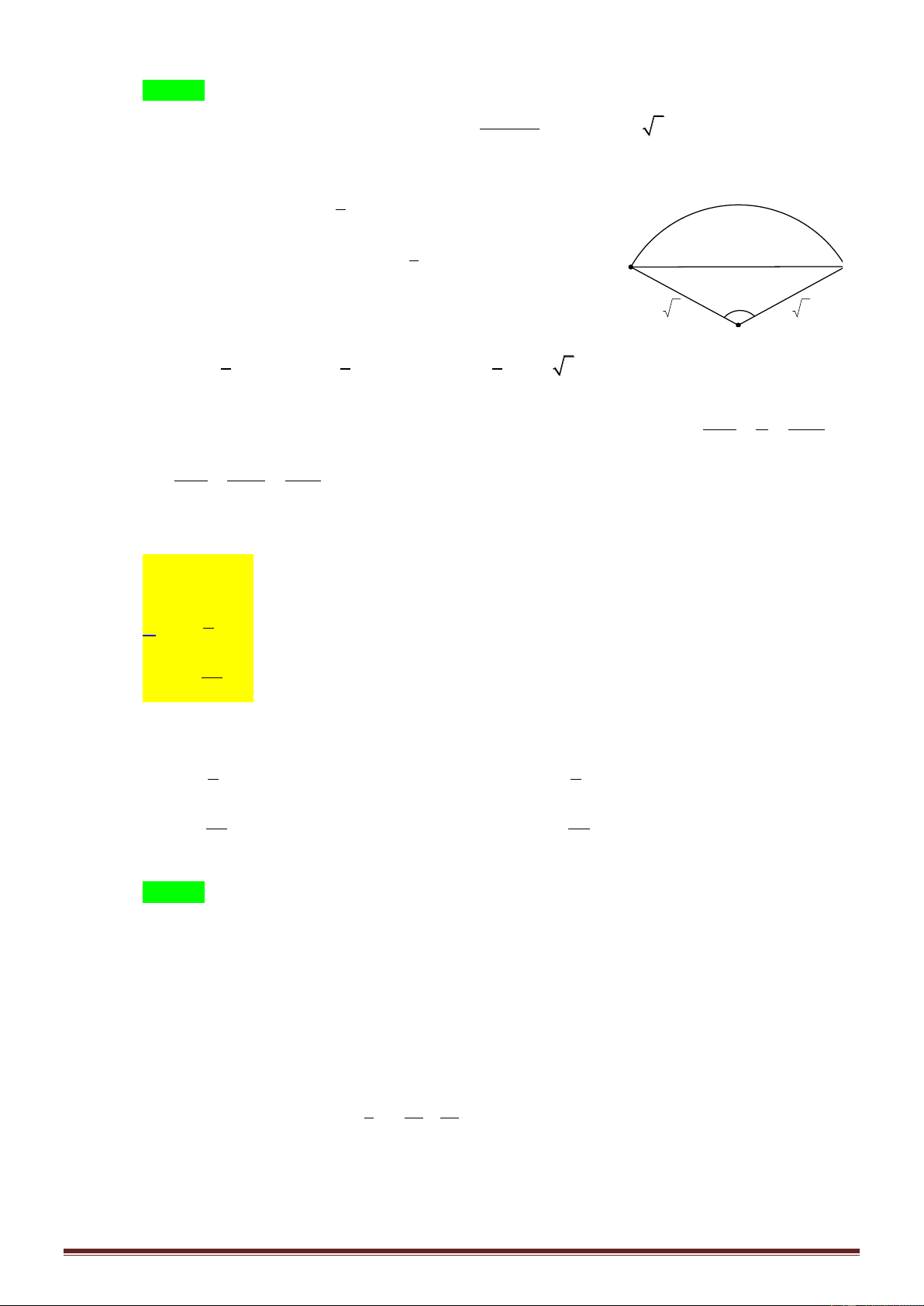
Câu 36: Cho hình chóp tứ giác đều S.ABCD có độ dài cạnh đáy bằng 4 và độ dài cạnh bên bằng 6
(tham khảo hình bên). Khoảng cách từ S đến mặt phẳng  ABCD bằng A. 2 5 . B. 2 7 . C. 2 . D. 7
Câu 37: Trong không gian Oxyz, mặt cầu tâm là điểm I (2; 3;1) và đi qua điểm M 0; 1  ;2 có phương trình là: 2 2 2 2 2
A.  x  2   y  3   z   1  3. B. 2
x   y  
1   z  2  3. 2 2 2 2 2 C. 2
x   y  
1   z  2  9.
D.  x  2   y  3   z   1  9.
Câu 38: Trong không gian Oxyz, đường thẳng đi qua điểm A 4  ;1; 3   và B0; 1   ;1 có phương trình tham số là: Trang4 x  4   2t x  4t x  2t x  4   4t     A.  y  1   t . B.  y  1   2t . C.  y  1   t. D.  y  1   2t .     z  3   2t  z  1 4t  z  1 2t  z  3   4t 
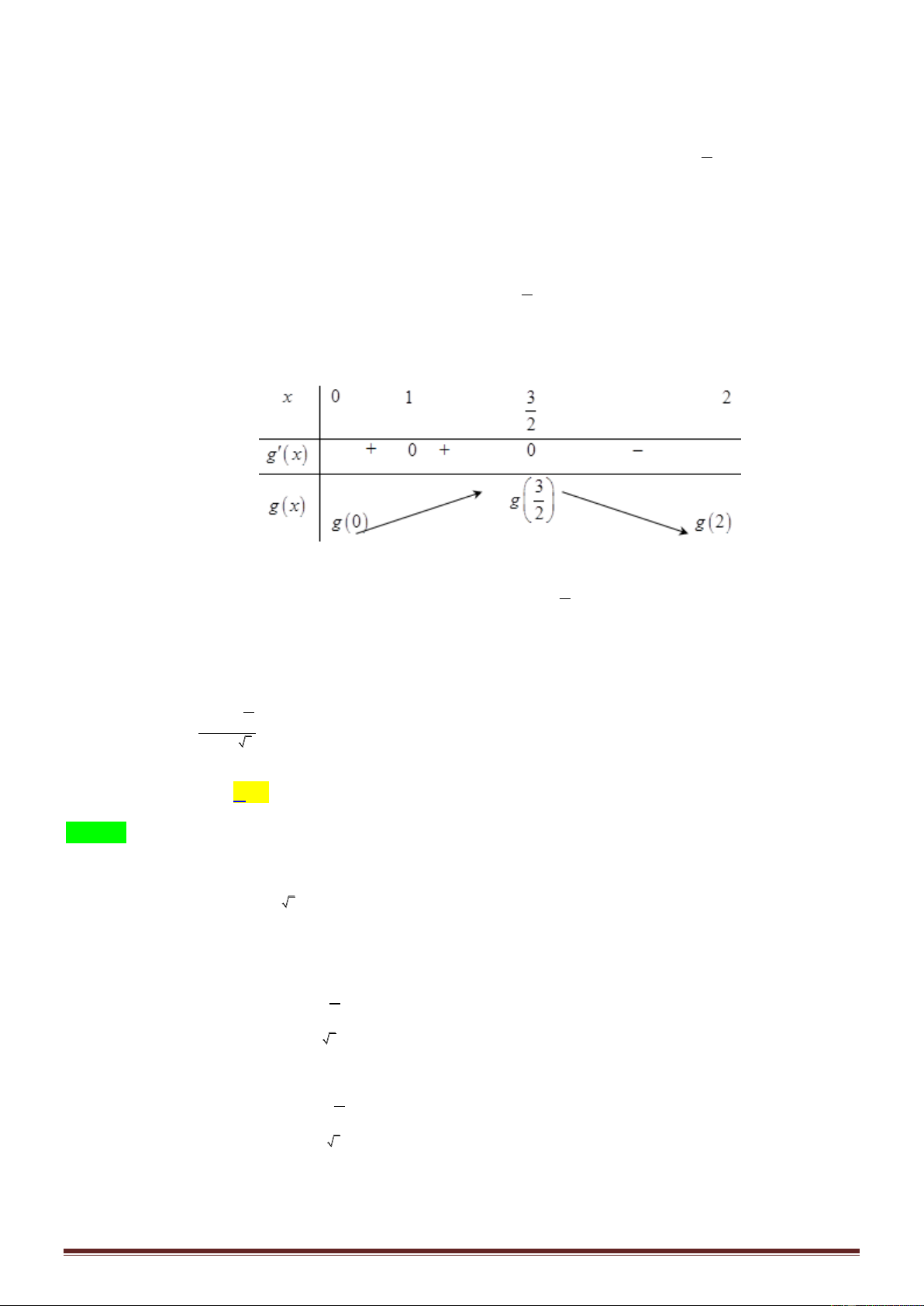
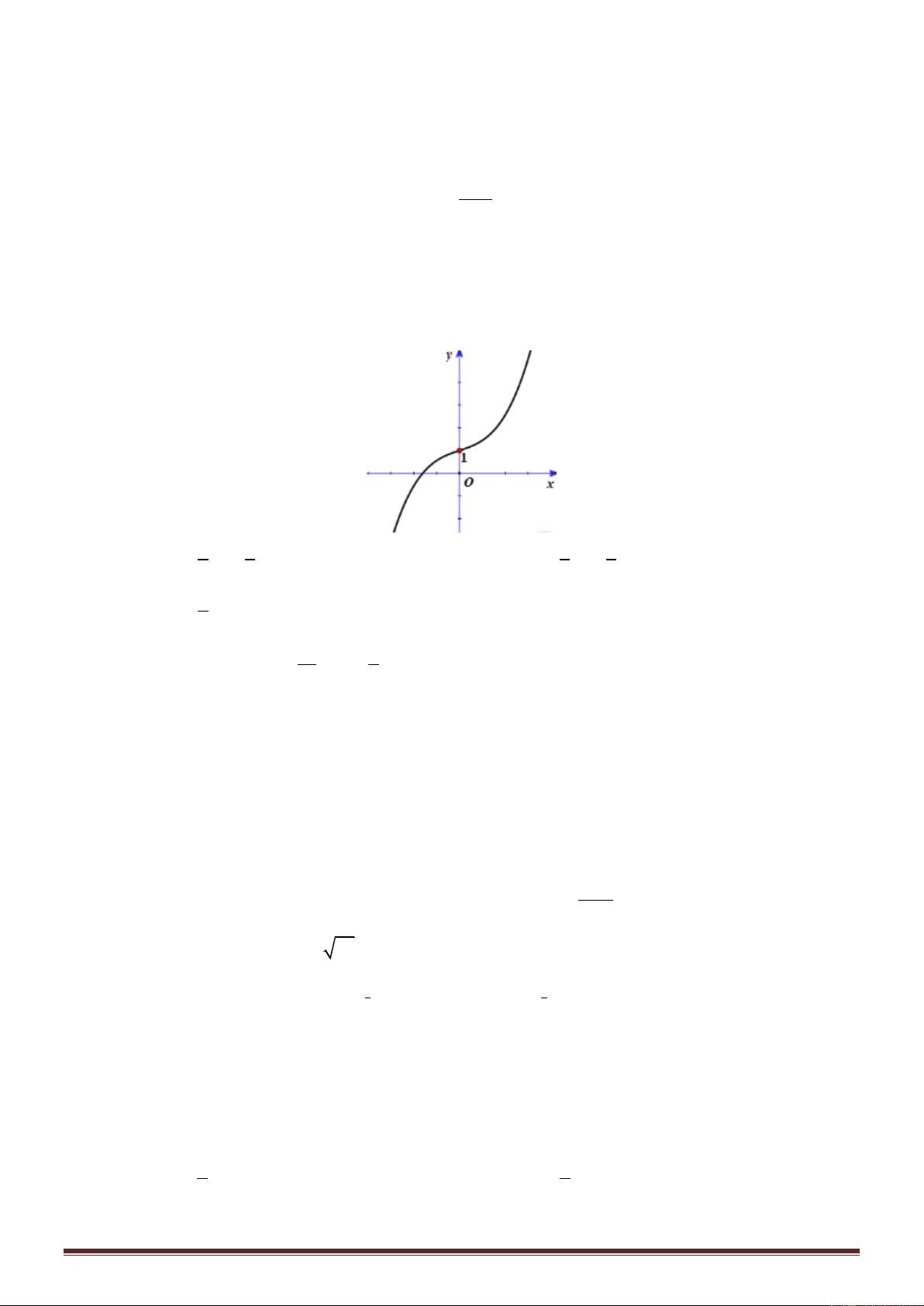
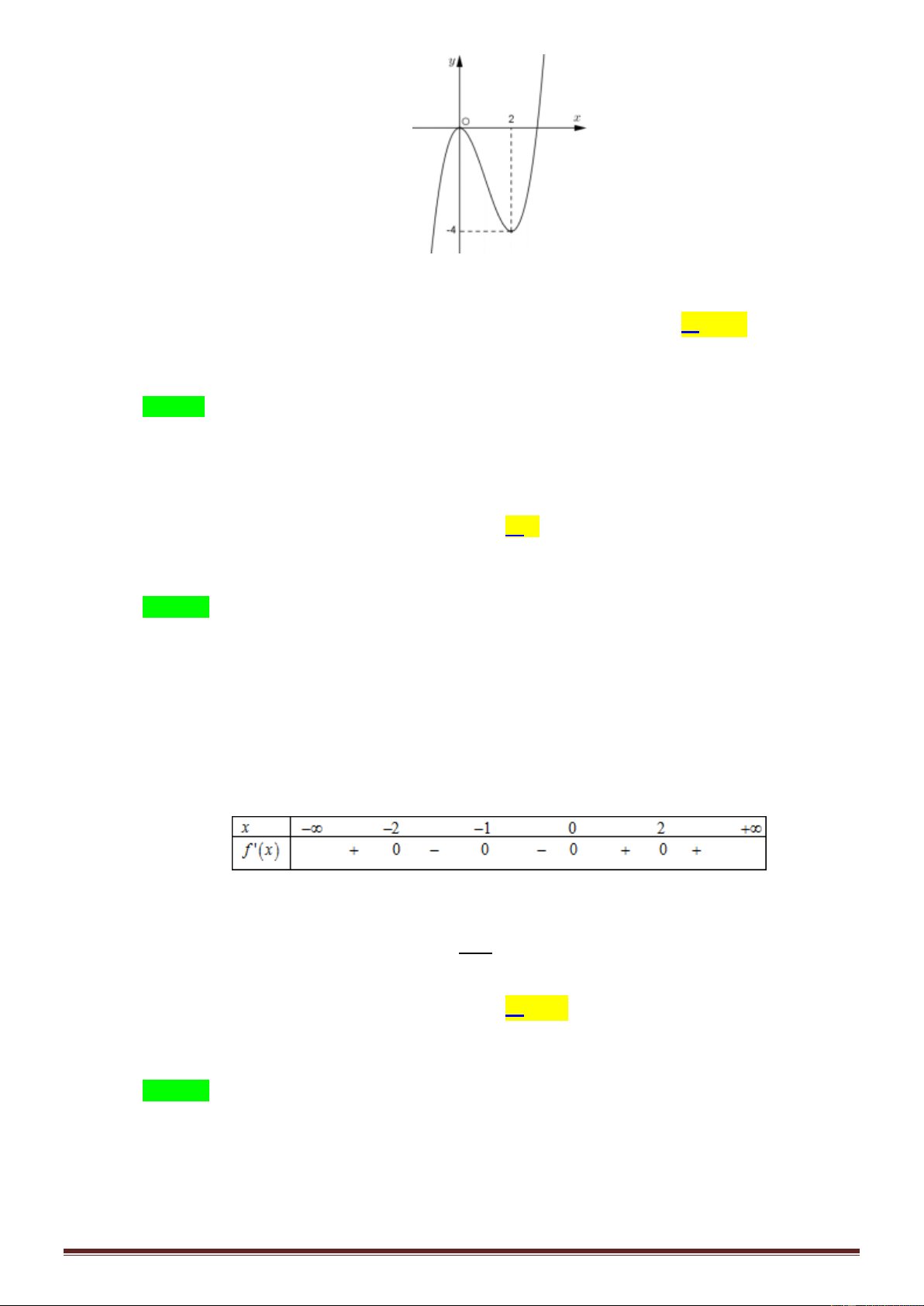
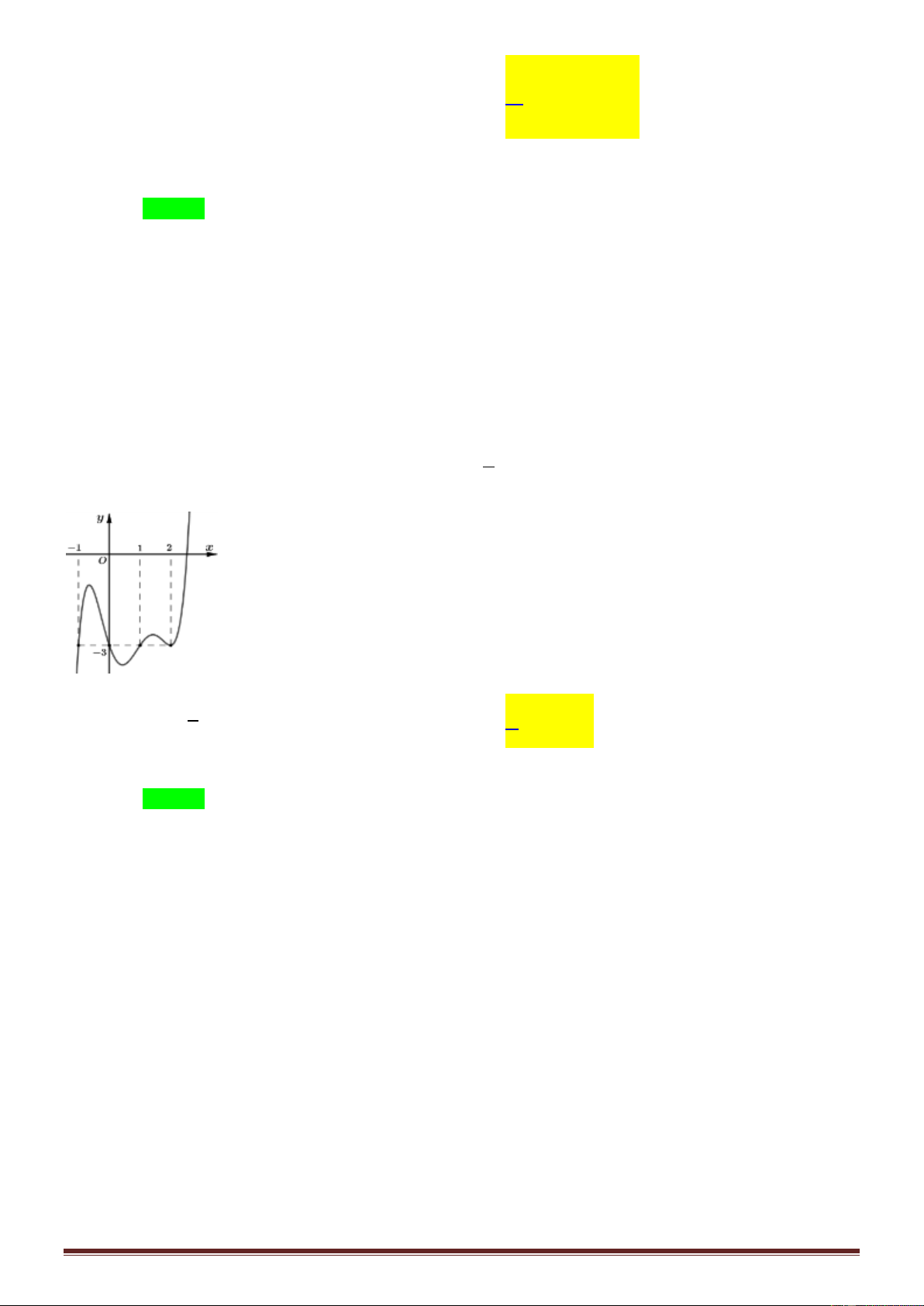
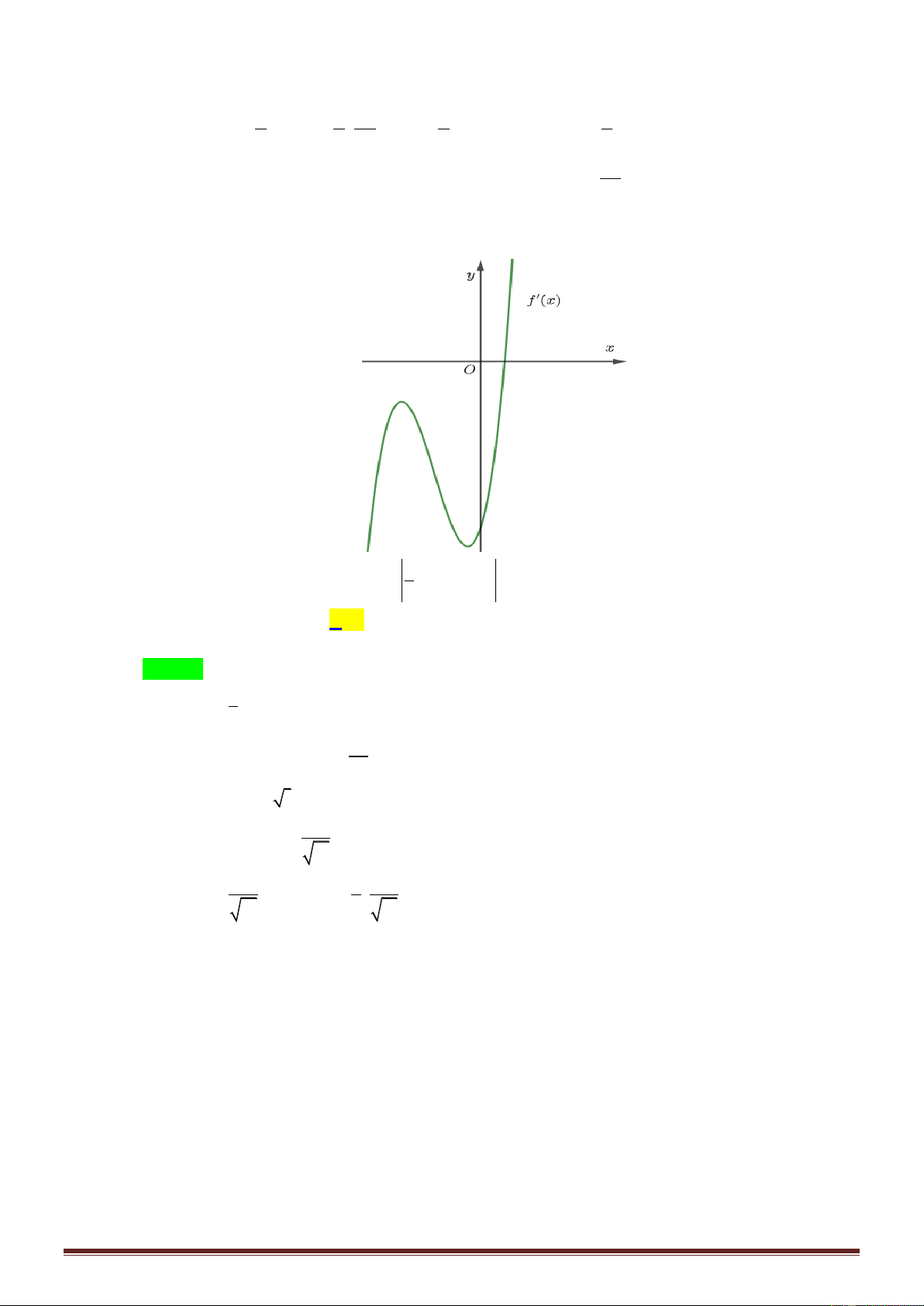
Câu 39: Cho hàm số f  x , đồ thị hàm số y  f  x là đường cong trong hình bên. Giá trị nhỏ nhất của  x 
hàm số g  x  f   trên đoạn 5  ;  3 bằng  2  y 2 1 x -2 O A. f  2  . B. f   1 . C. f  4  . D. f 2 .
Câu 40: Có bao nhiêu số tự nhiên y sao cho ứng với mỗi y có không quá 148 số nguyên x thỏa mãn x 1 2 3  3 0 y  ? ln x
A. 4 B. 5 C. 6 D. 7 x  x  x  ln 2
Câu 41: Cho hàm số f  x 2 4 1 , 5   . Tích phân 3 x   1. x f e e dx bằng 2x  6 , x  5 0 77 77 68 77 A. . B. . C. . D. . 3 9 3 6
Câu 42: Có bao nhiêu số phức z thỏa mãn z  z  z  1? A. 0 . B. 1. C. 4 . D. 3 .
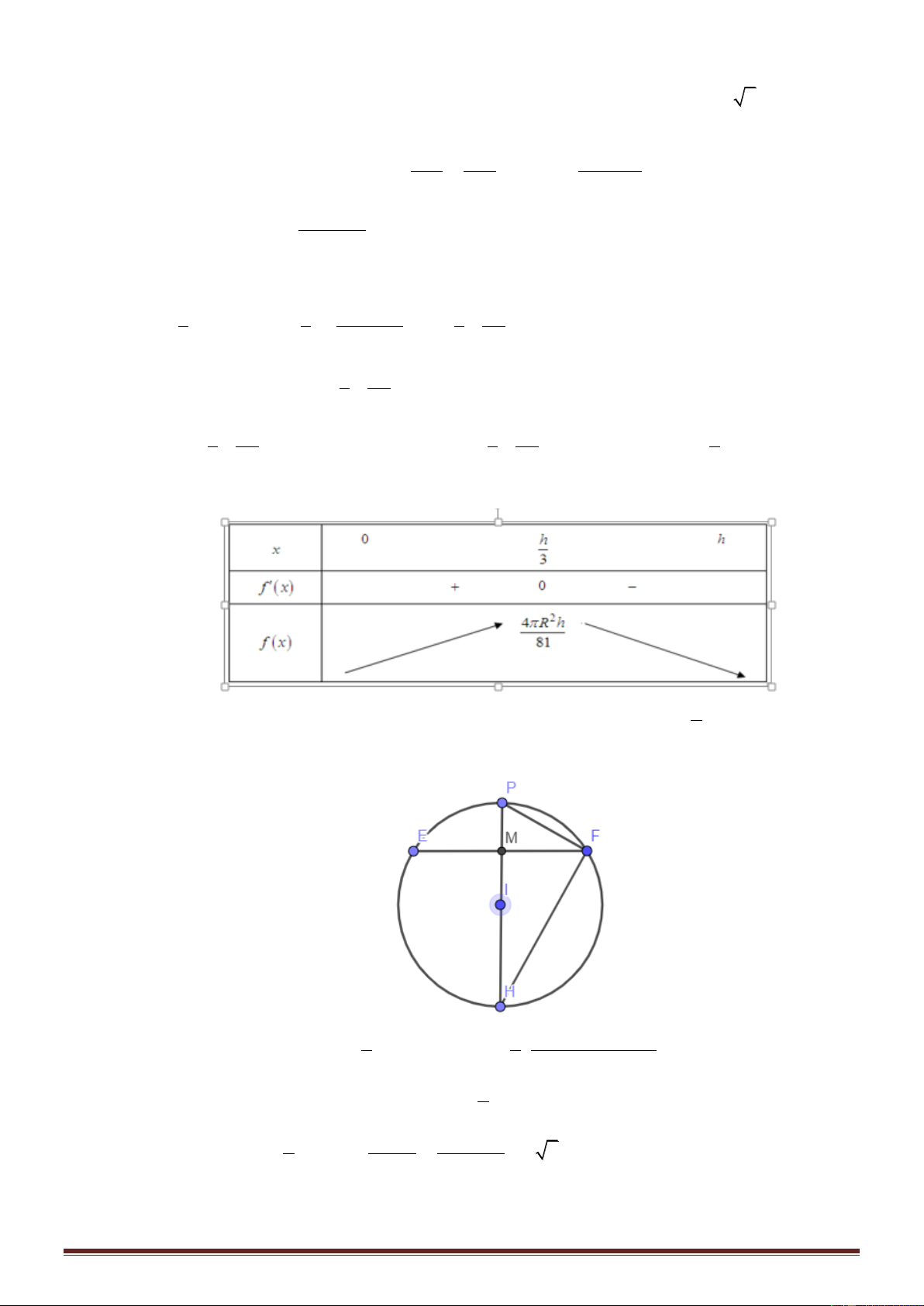
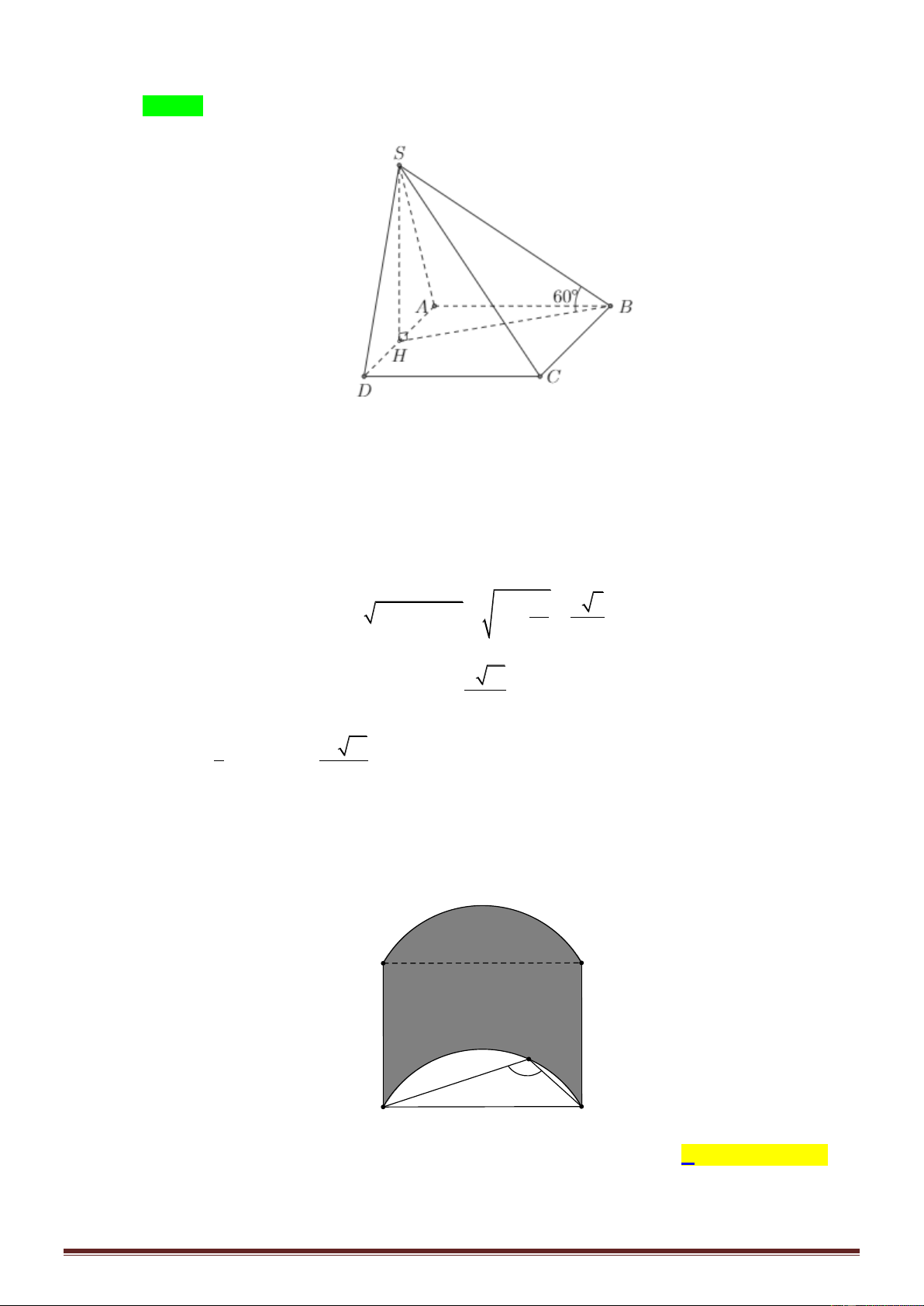
Câu 43: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB  6 , AD  3 , tam giác
SAC nhọn và nằm trong mặt phẳng vuông góc với đáy. Biết hai mặt phẳng SAB , SAC  tạo
với nhau góc  thỏa mãn 3 tan  
và cạnh SC  3 . Thể tích khối S.ABCD bằng: 4 4 8 5 3 A. . B. . C. 3 3 . D. . 3 3 3
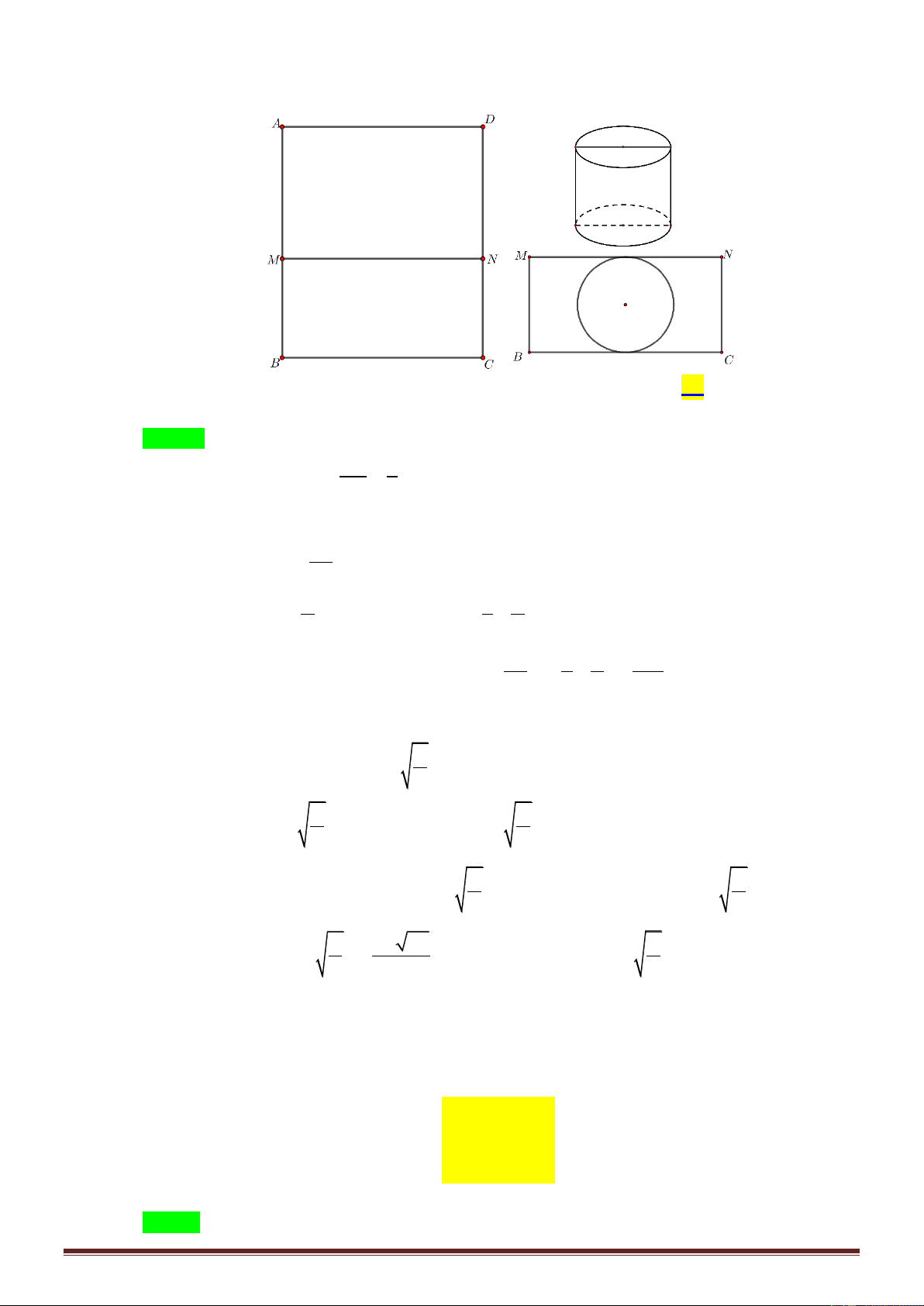
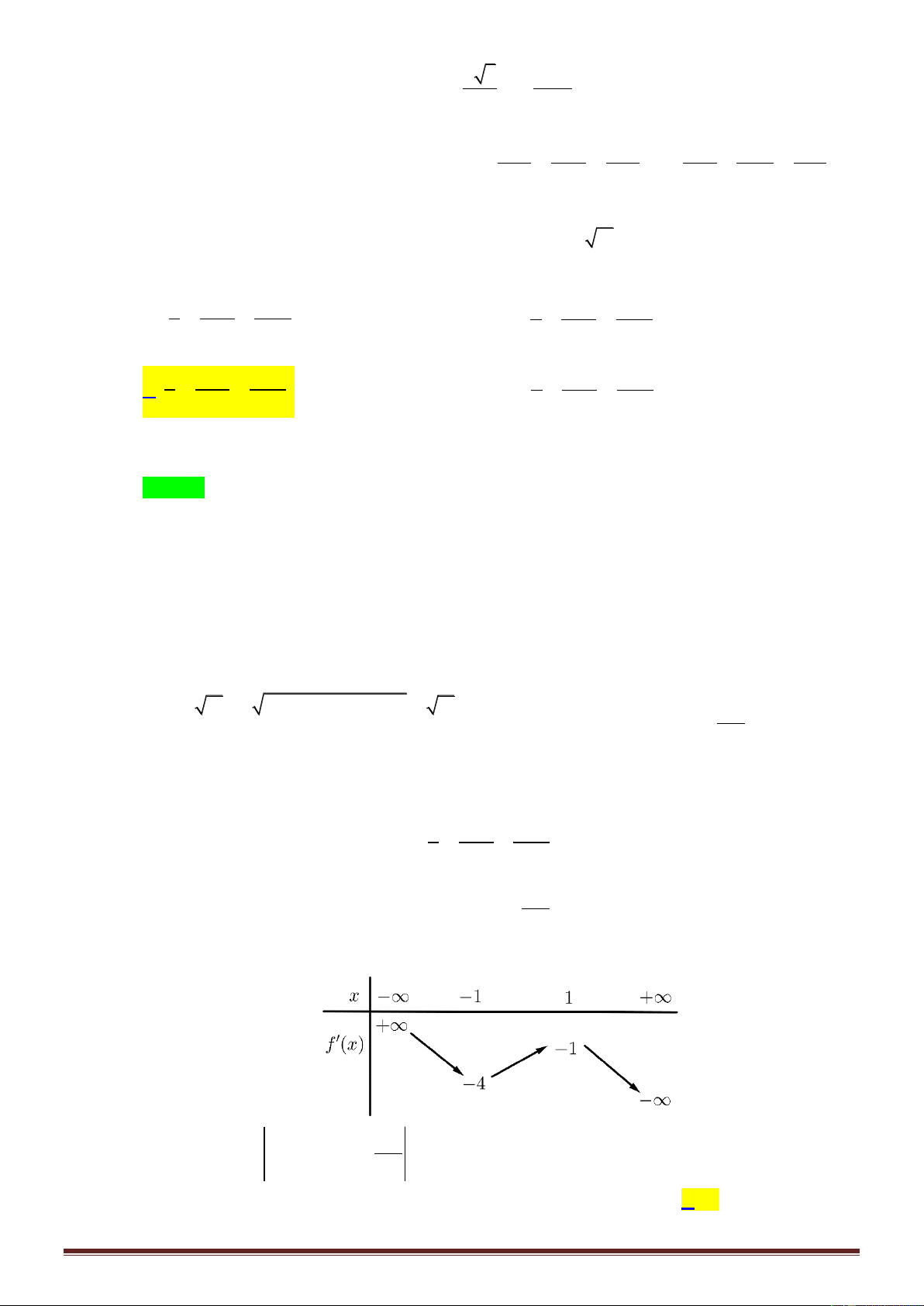
Câu 44: Sử dụng mảnh inox hình chữ nhật ABCD có diện tích bằng 2
1m và cạnh BC  x m để làm
một thùng đựng nước có đáy, không có nắp theo quy trình như sau: Chia hình chữ nhật ABCD
thành 2 hình chữ nhật ADNM và BCNM , trong đó phần hình chữ nhật ADNM được gò
thành phần xung quanh hình trụ có chiều cao bằng AM ; phần hình chữ nhật BCNM được cắt
ra một hình tròn để làm đáy của hình trụ trên (phần inox thừa được bỏ đi) Tính gần đúng giá trị
x để thùng nước trên có thể tích lớn nhất (coi như các mép nối không đáng kể). Trang5
A. 0, 97m .
B. 1, 37m .
C. 1,12m .
D. 1, 02m .
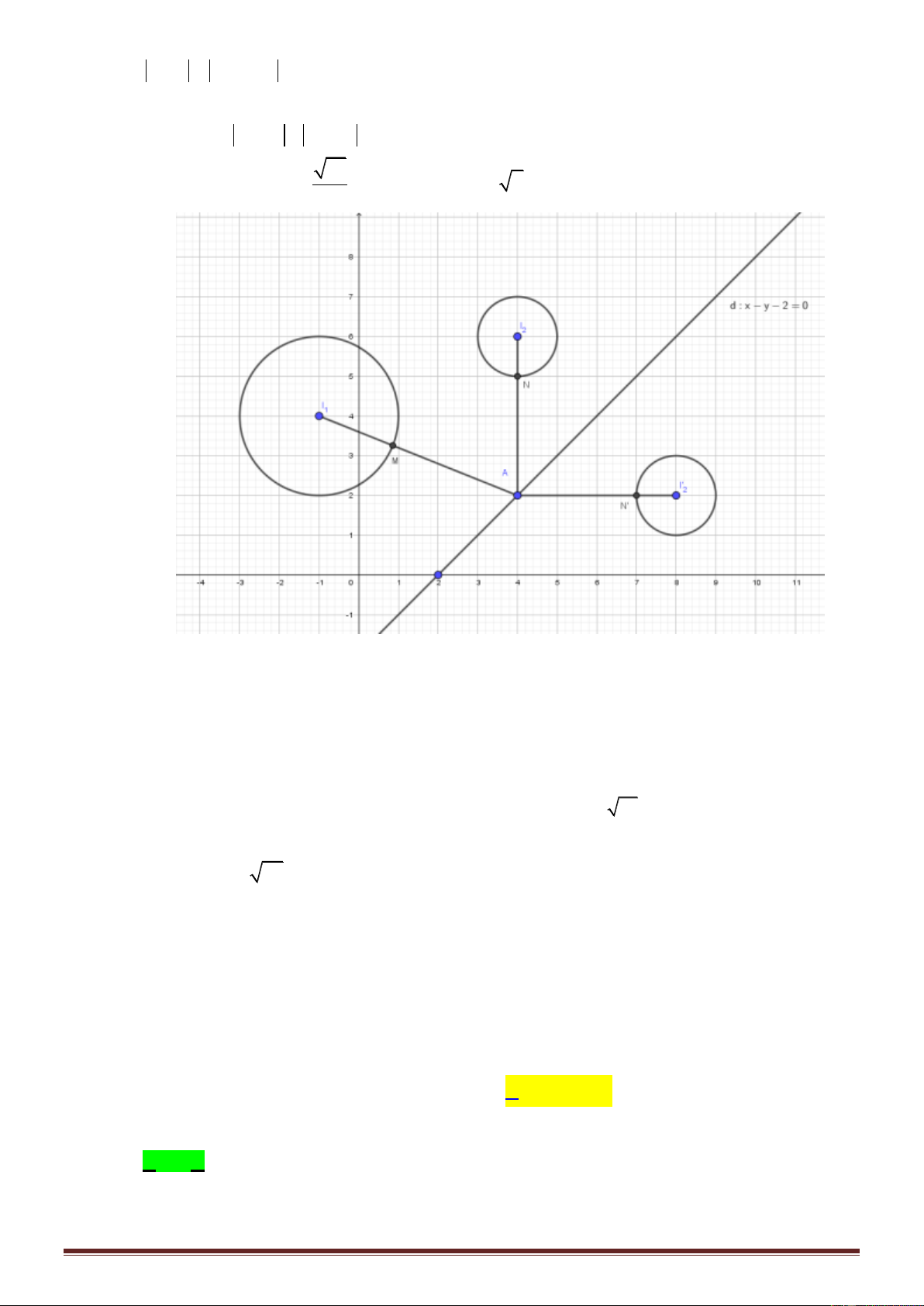
Câu 45: Trong không gian với hệ tọa độ Oxyz, cho hai điểm A3;3  ;1 , B 0; 2  ;1 và mặt phẳng
P: x  y  z 7  0. Đường thẳng d nằm trong P sao cho mọi điểm của d cách đều hai điểm ,
A B có phương trình làcác mệnh đề sau, mệnh đề nào đúng? x  t x  2t x  t x  t     
A.  y  7  3t .
B.  y  7  3t . C.  y  7  3t .
D.  y  7  3t .     z  2t  z  t  z  2t  z  2t 
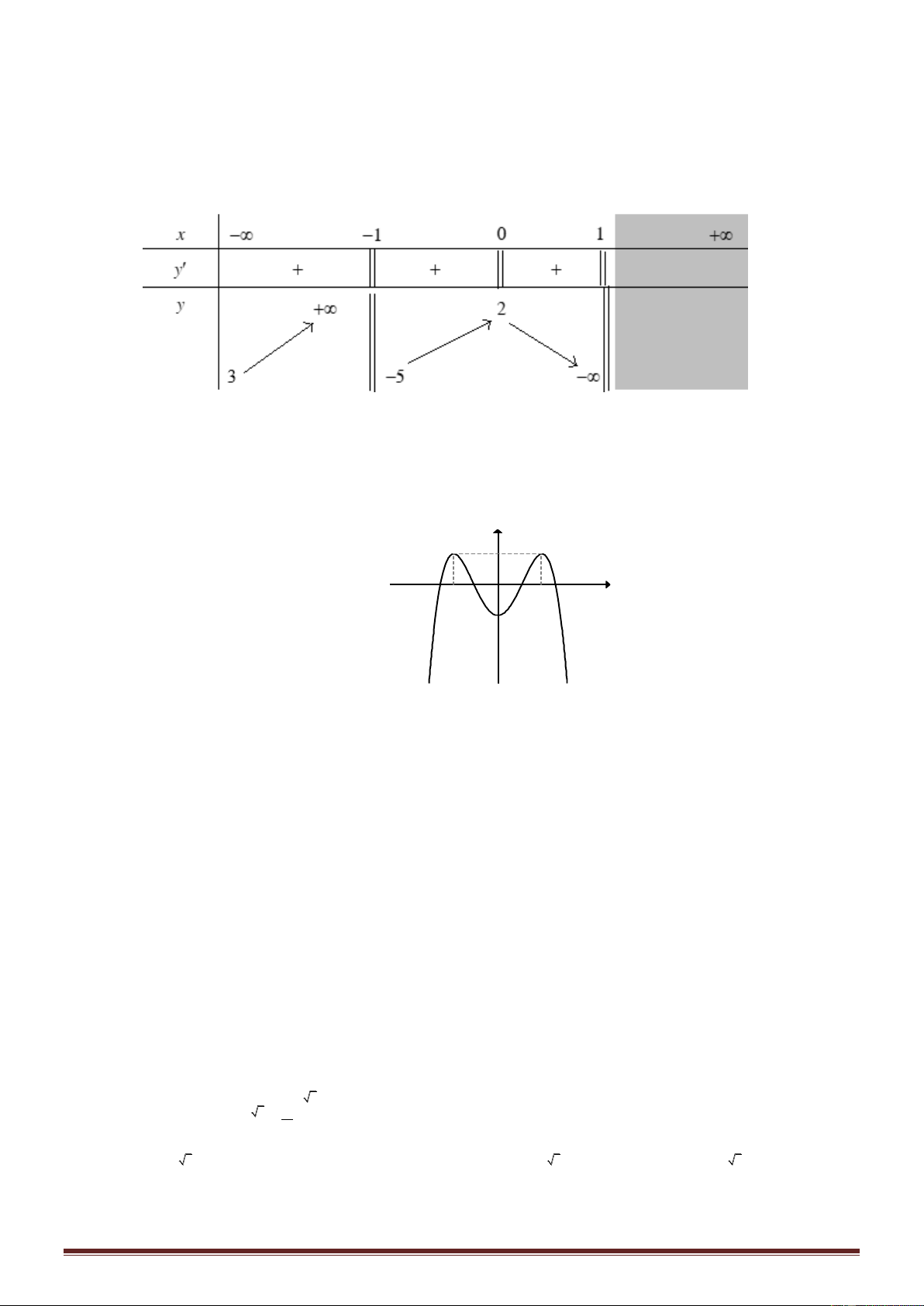
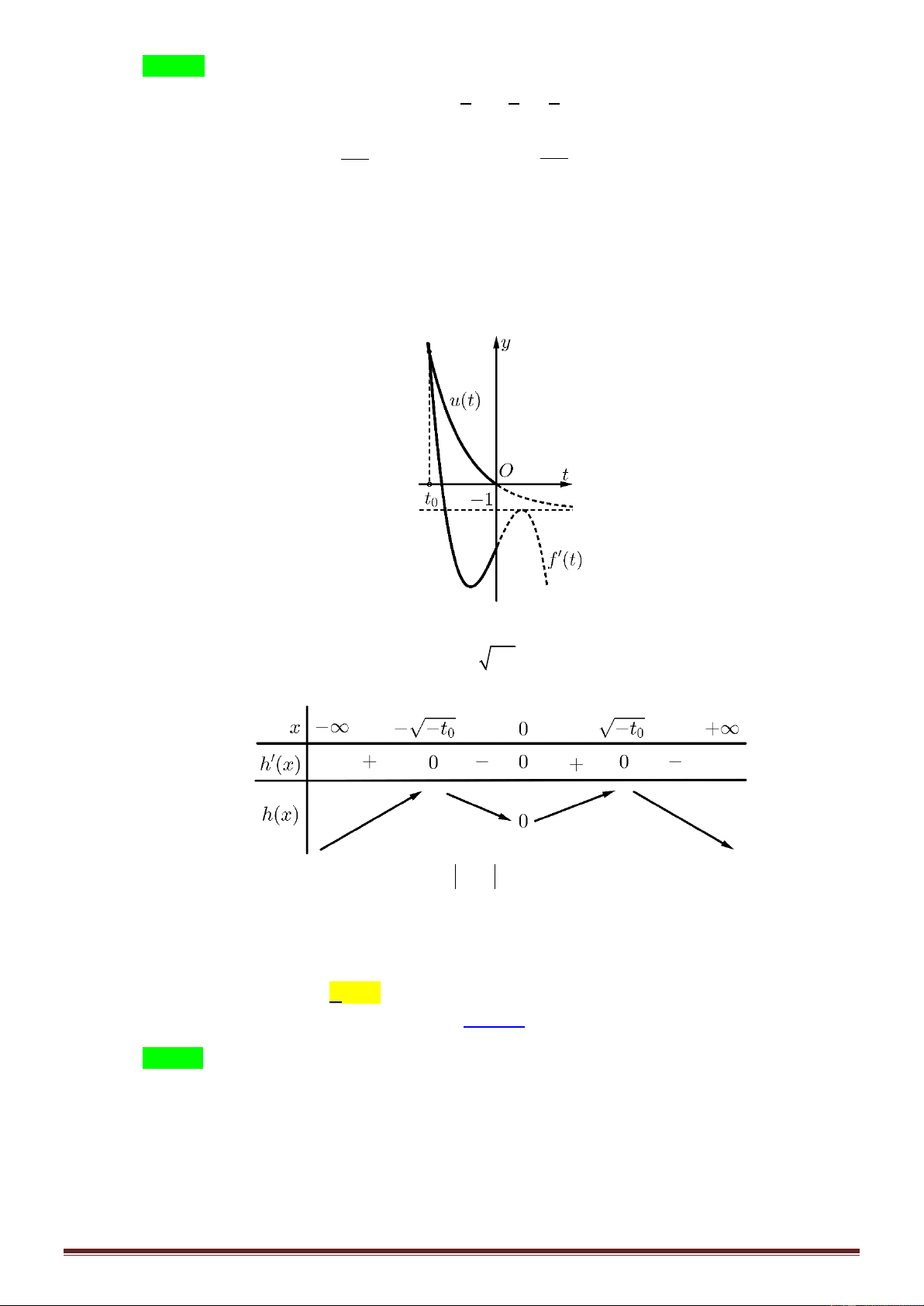
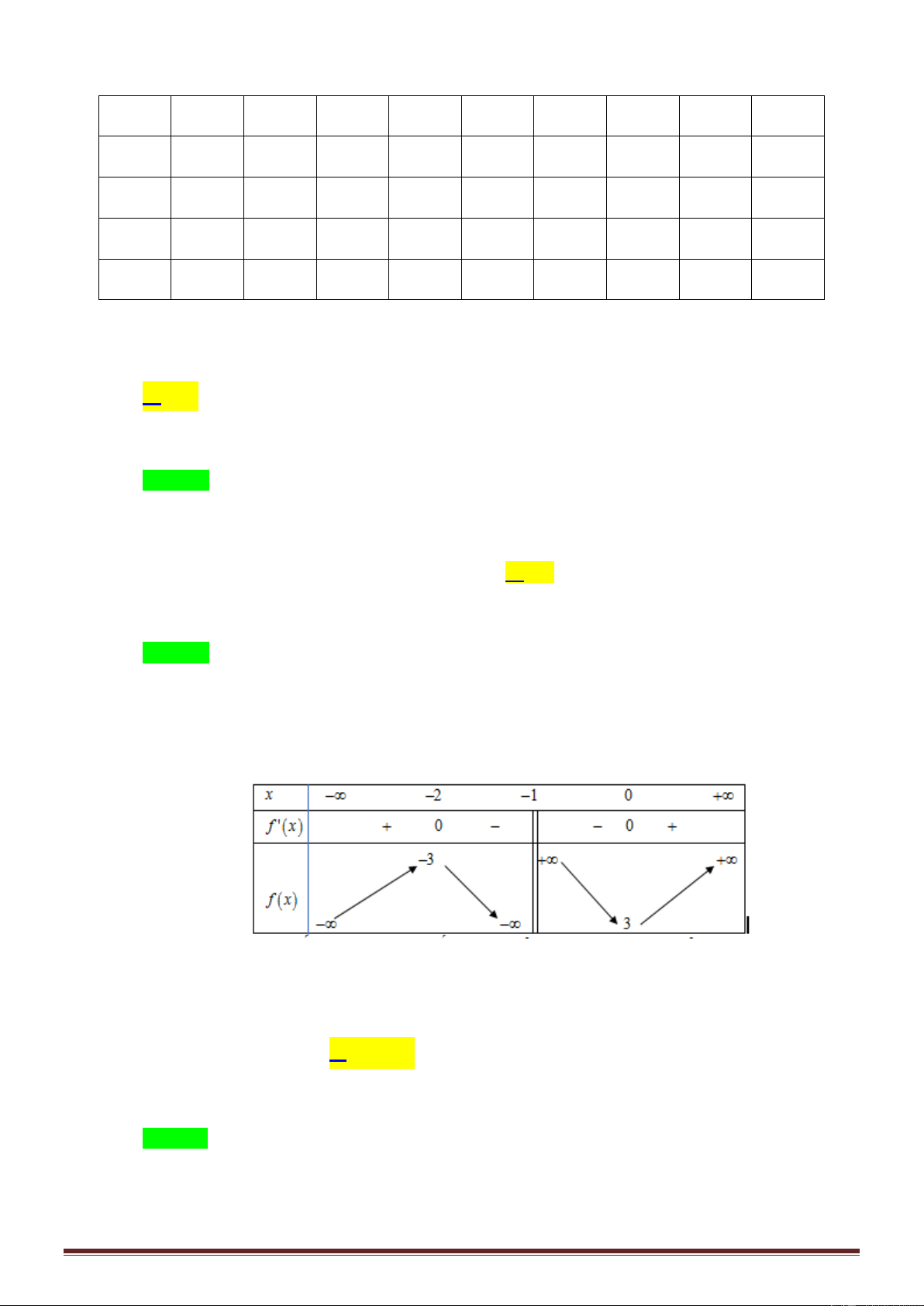
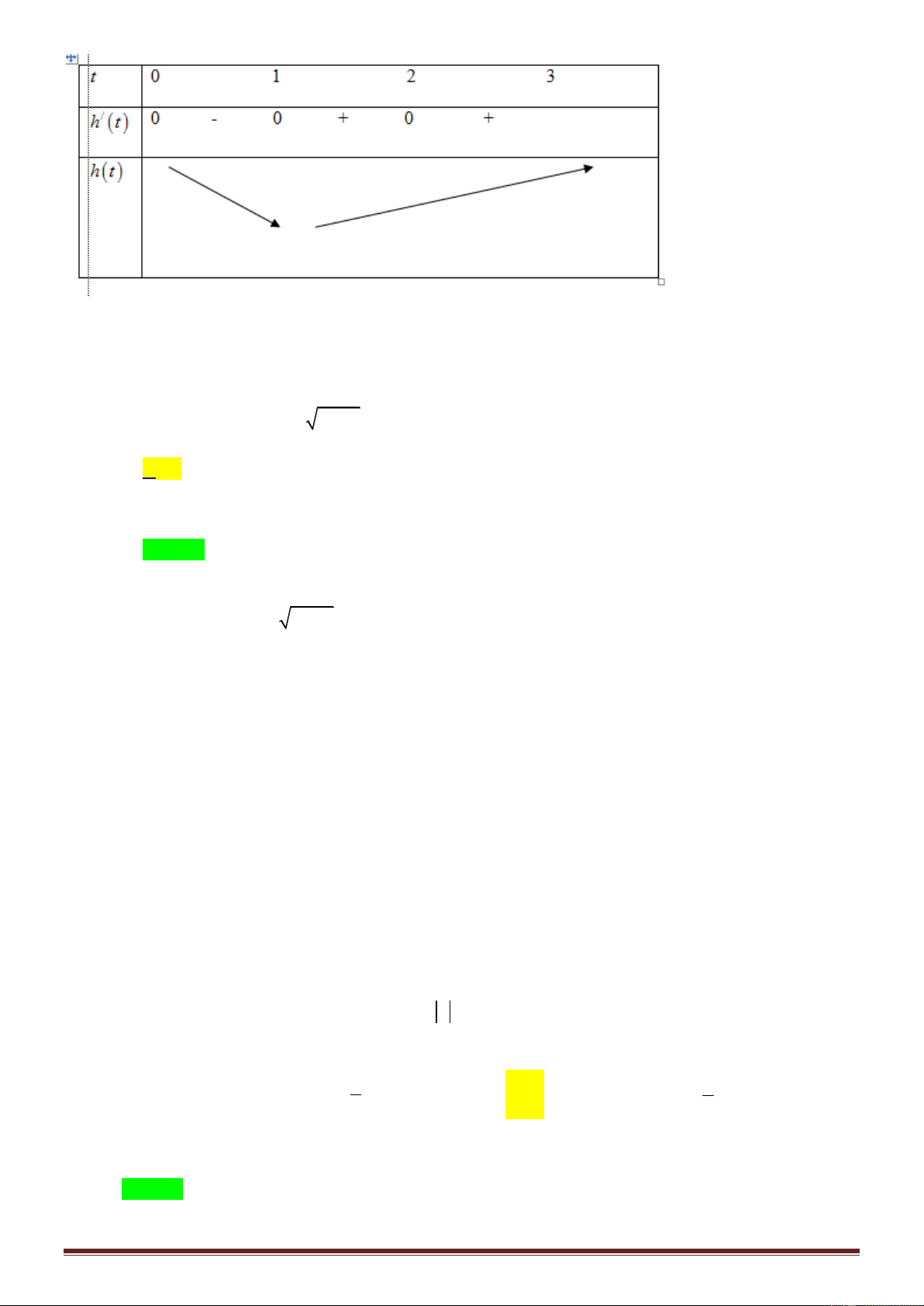
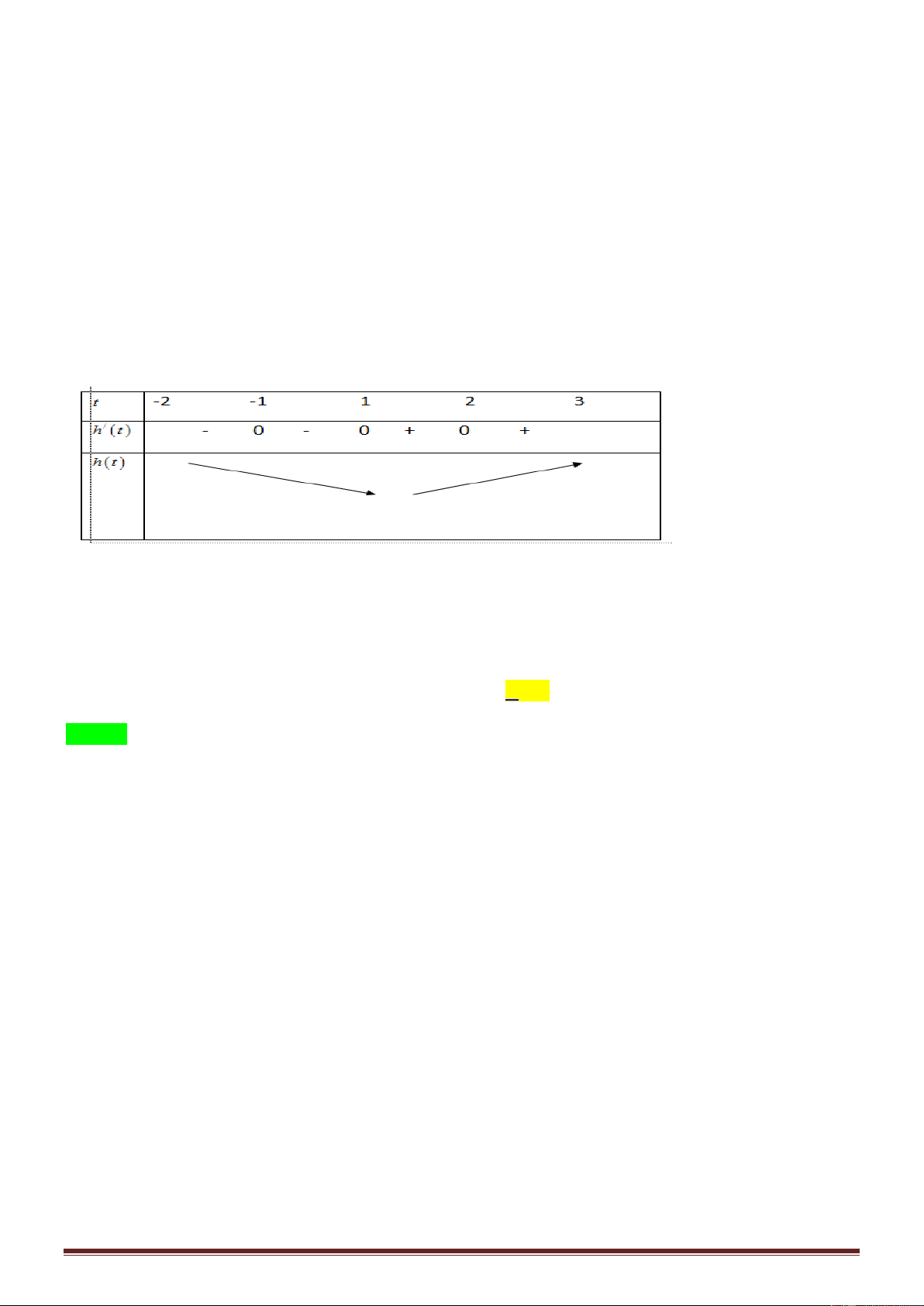
Câu 46: Cho hàm số y  f  x là hàm số bậc bốn thỏa mãn f 0  0. Hàm số y  f ' x có bảng biến thiên như sau: Hàm số     2 2 g x f x
 x có bao nhiêu điểm cực trị? A. 1. B. 3 . C. 5 . D. 7
Câu 47: Có bao nhiêu giá trị nguyên của m với m 1 sao cho tồn tại số thực x thỏa mãn:  m log x m  3log5 5  x 3   1 . A. 4 . B. 3 . C. 5 . D. 8 .
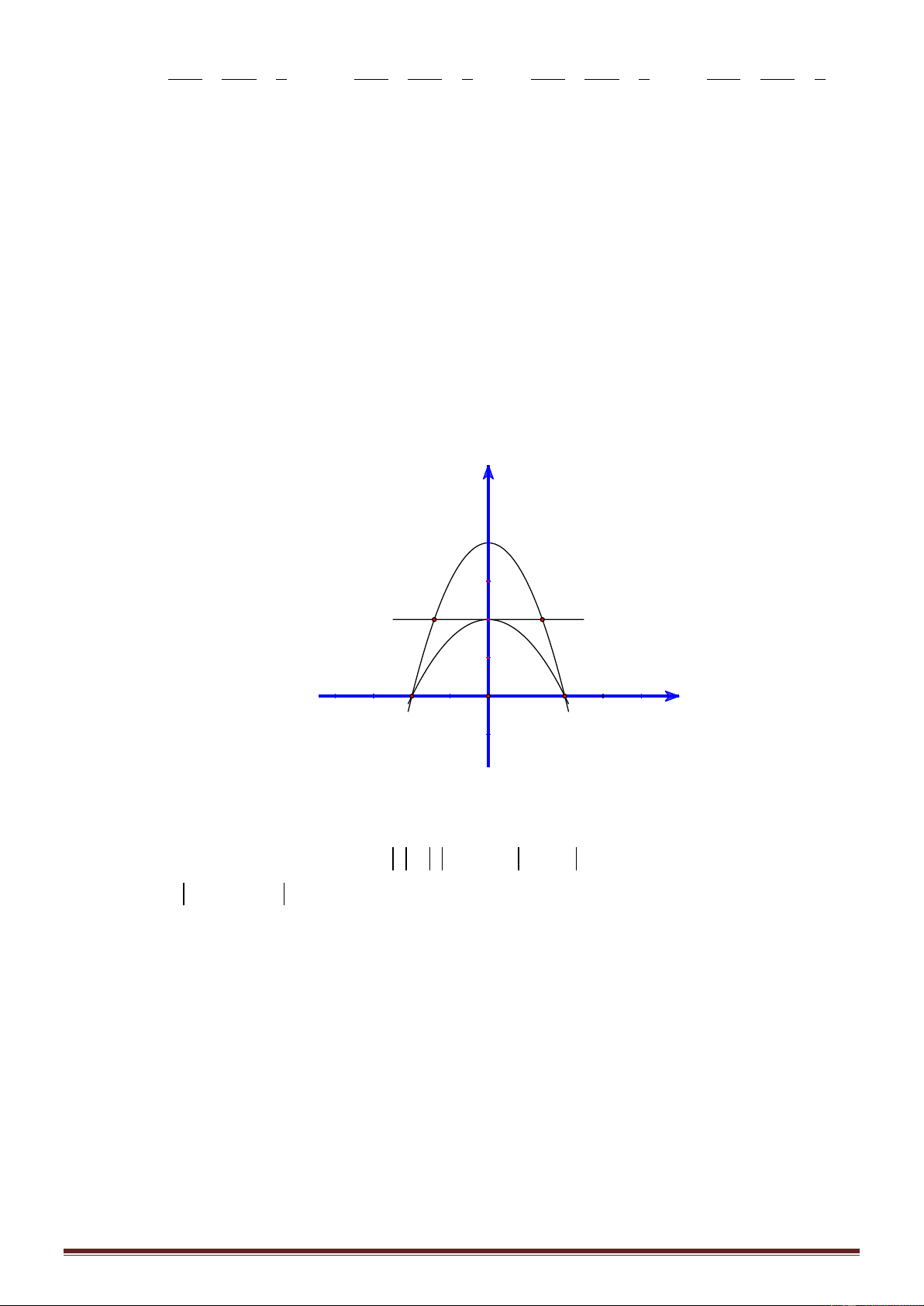
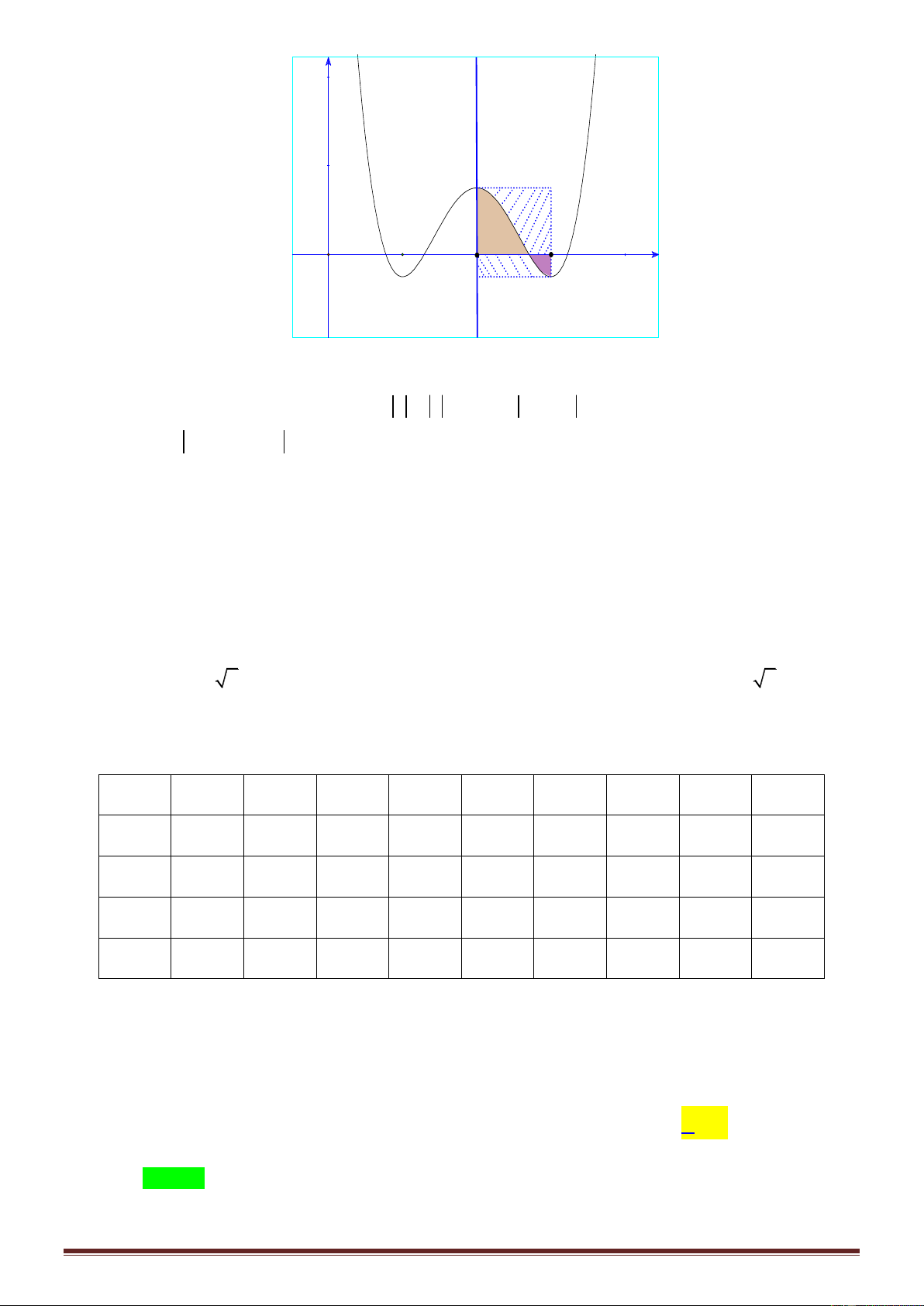
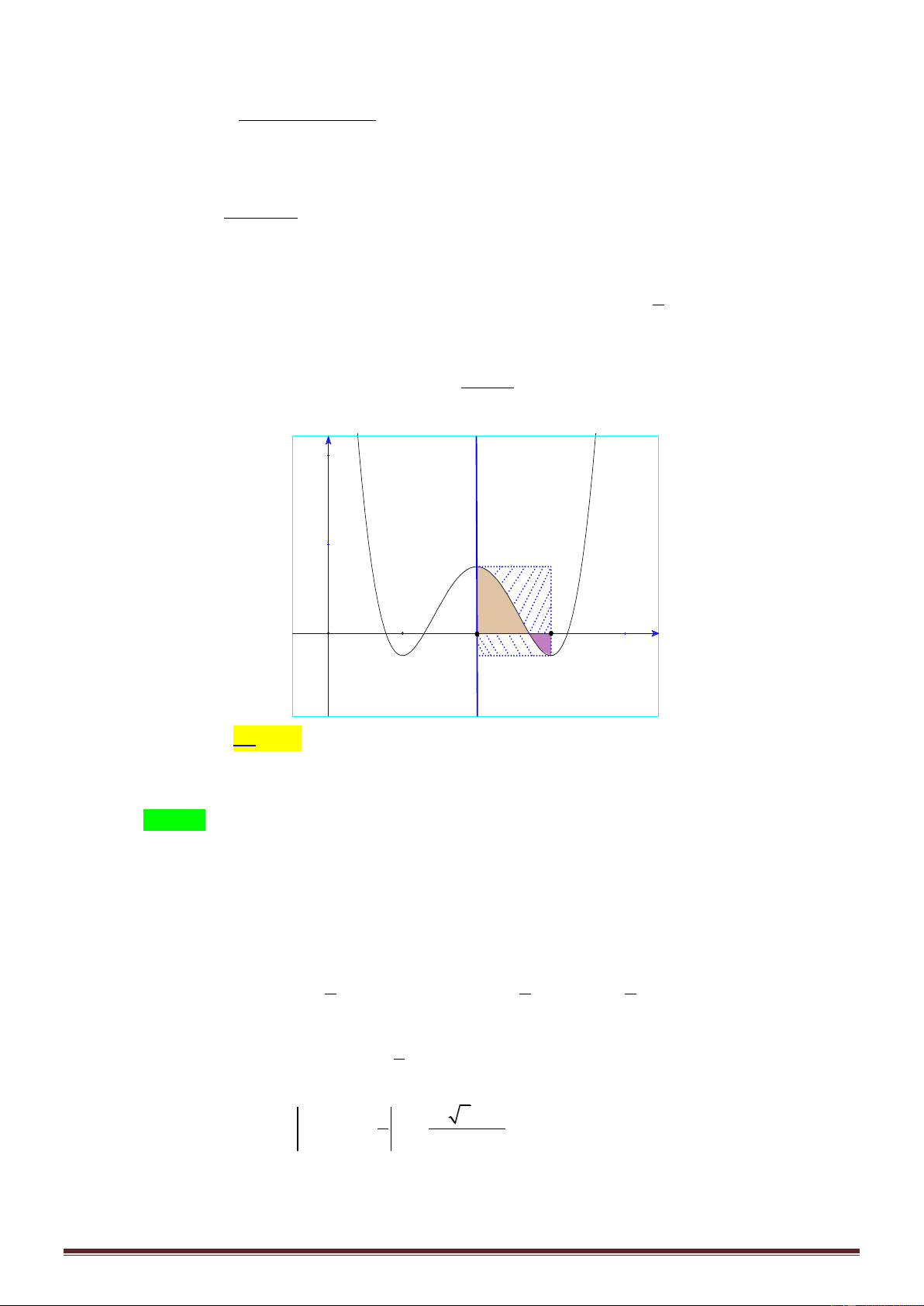
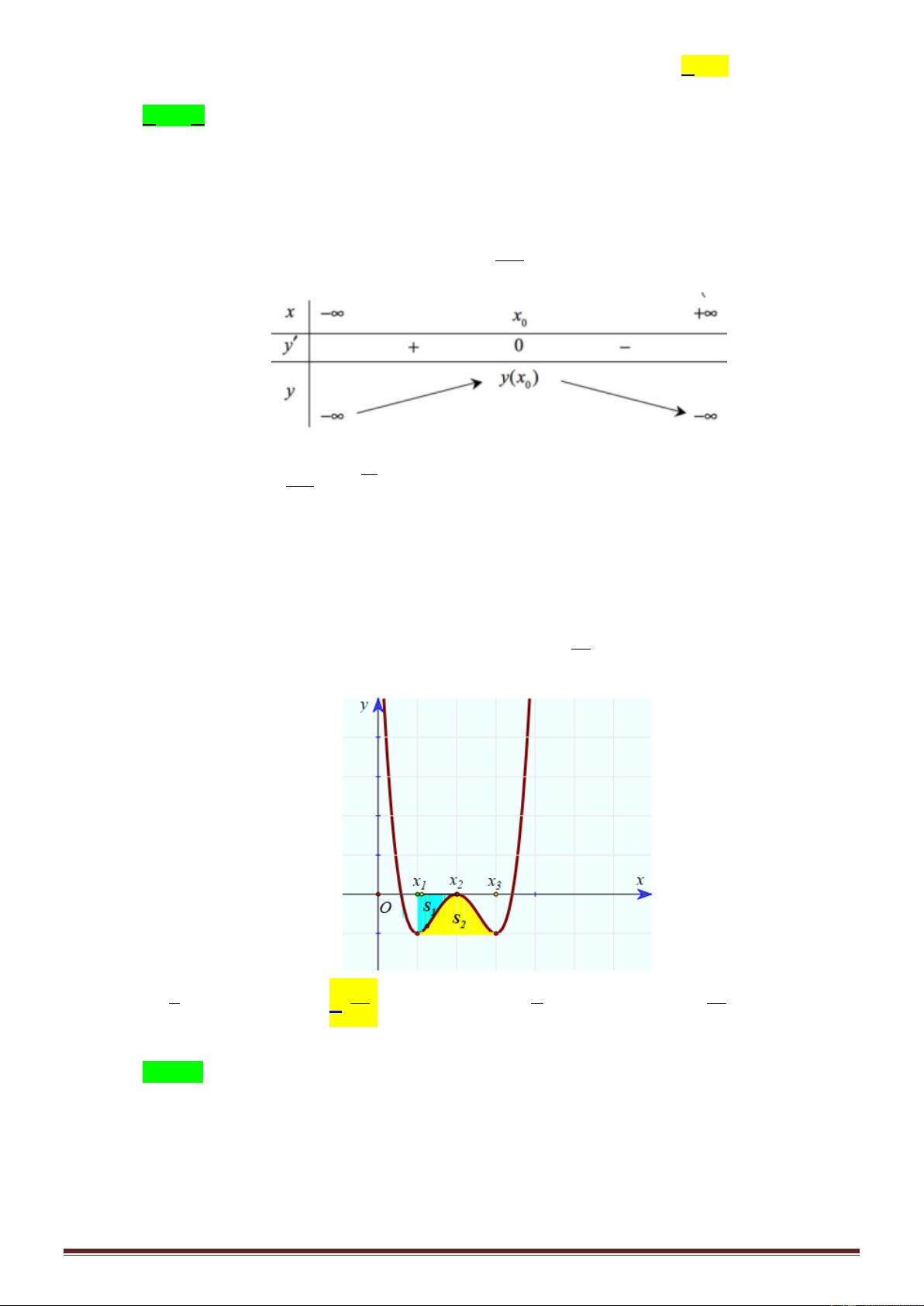
Câu 48: Cho hàm số bậc ba   3 2
f x  ax  bx  cx  d và đường thẳng d : g  x  mx  n có đồ thị như
hình vẽ. Gọi S , S , S lần lượt là diện tích của các phần giới hạn như hình bên. Nếu S  4 thì 1 2 3 1 S tỷ số 2 bằng. S3 Trang6 3 1 A. . B. 1 . C. 2 . D. . 2 2
Câu 49: Xét hai số phức z , z thỏa mãn z  2, 1 i z  6 và z  z  5 . Giá trị lớn nhất 1   1 2 2 1 2
2z  z  2021 bằng 1 2 A. 2044 .
B.  23  2021. C. 23  2021.
D. 2 23  2021.
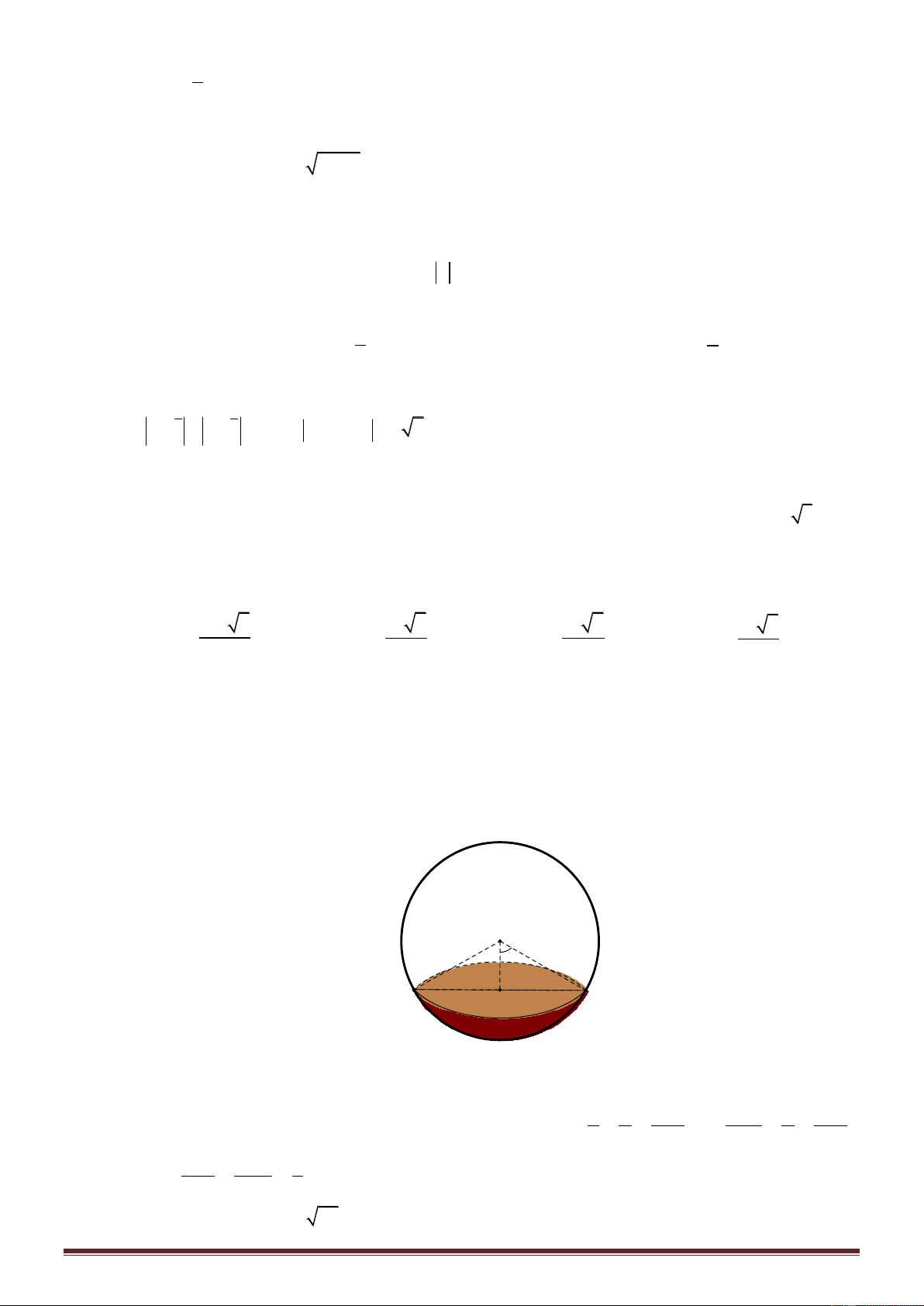
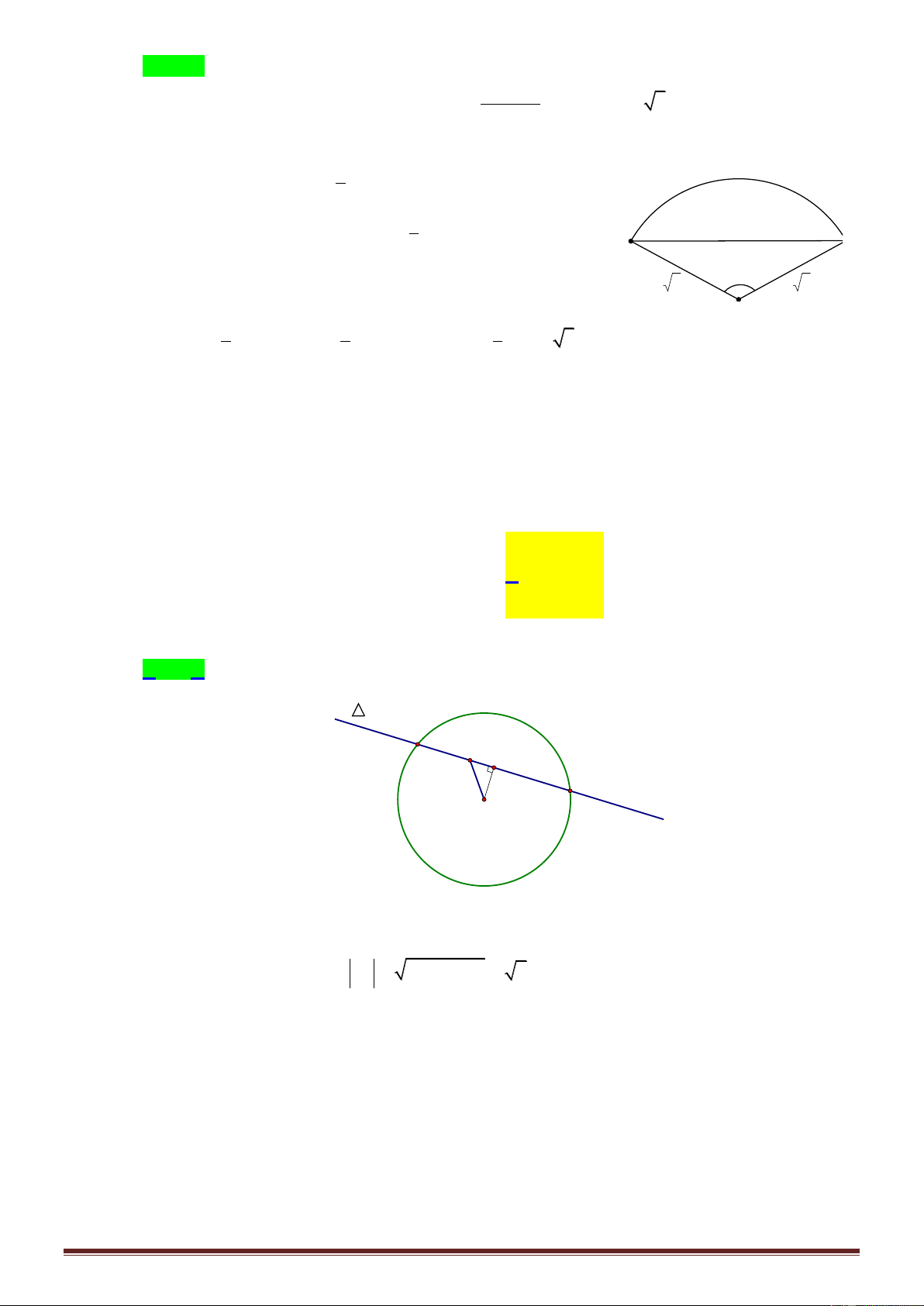
Câu 50: Trong không gian Oxyz , cho hai điểm C  1  ;2;1  1 , H ( 1
 ;2;1) , hình nón N  có đường cao
CH  h và bán kính đáy là R  3 2 . Gọi M là điểm trên đoạn CH , C là thiết diện của mặt
phẳng  P vuông góc với trục CH tại M của hình nón  N . Gọi  N  là khối nón có đỉnh H
đáy là C . Khi thể tích khối nón  N lớn nhất thì mặt cầu ngoại tiếp nón  N có tọa độ tâm I  ; a ,
b c, bán kính là d . Giá trị a  b  c  d bằng A. 1. B. 3 . C. 6 . D. 6  . BẢNG ĐÁP ÁN 1.D 2.D 3.B 4.D 5.C 6.C 7.D 8.C 9.D 10.B 11.C 12.A 13.A 14.C 15.B 16.A 17.B 18.B 19.B 20.D 21.A 22.B 23.D 24.A 25.A 26.A 27.D 28.D 29.C 30.D 31.D 32.A 33.A 34.D 35.A 36.B 37.D 38.C 39.A 40.C 41.B 42.C 43.B 44.D 45.C 46.C 47.B 48.B 49.C 50.C
HƯỚNG DẪN GIẢI CHI TIẾT Câu 1:
Có bao nhiêu số tự nhiên có ba chữ số đôi một khác nhau? A. 3 C . B. 10 3 . C. 3 A . D. 2 9.A . 10 10 9 Lờigiải Chọn D
Giả sử số tự nhiên cần tìm có dạng abc .
Do a  0 nên có 9 cách chọn chữ số a . Hai chữ số b và c có 2 A cách chọn. 9 Vậy có 2
9.A số tự nhiên có ba chữ số đôi một khác nhau. 9 Câu 2:
Cho cấpsốcộng u , biết u  6 và u  2
 . Giátrịcủau bằng n  1 3 8 Trang7 A. 8  . B. 22 . C. 34 . D. 22 . Lờigiải Chọn D u  u
Từgiảthiết u  6 và u  2  suy ra ta có: 1 3 u 
 2  d  u  u  2  6  4  . 1 3 2 2 2 1
Vậy u  u  7d  2  2 . 8 1 Câu 3:
Cho hàmsố y  f  x xácđịnhvàliêntụctrênkhoảng  ;
 ,cóbảngbiếnthiênnhưhìnhsau: x  1 0 1 
f ' x  0 + 0  0 +
f  x  4  1 1
Hàm số đã cho nghịch biến trên khoảng nào dưới đây? A.  1  ;0. . B. 0;  1 . C.  1  ;4 . D. 1;  . Lờigiải ChọnB
Từbảngbiếnthiên ta thấyhàmsố nghịch biếntrênkhoảng 0;  1 . Câu 4:
Cho hàmsố y  f  x có bảng biến thiên như sau x  0 3 
f ' x + 0 - 0 +
f  x 2   5 
Hàmsố f  x đạtcựcđạitạiđiểm A. x  2 . B. x  5  . C. x  3. D. x  0 . Lờigiải Chọn D
Căncứvào bảng biến thiên ta có
f  x  0 , x
 0;3 và f x  0, x
 3;suy ra hàmsốđạtcựctiểutại x  3.
f  x  0, x
 ;0 và f x  0, x
 0;3 suy ra hàmsốđạtcựcđạitại x  0 . Câu 5:
Cho hàmsố y  f  x liêntụctrên  vàcóbảngxétdấuđạohàmdướiđây x  3  1 4 
f ' x  0  0  0 
Sốđiểmcựctrịcủahàmsốlà A. 1 . B. 0 . C. 2 . D. 3 . Lờigiải Trang8 ChọnC
Hàmsốcó hai điểmcựctrị. 5x  3 Câu 6:
Số đường tiệm cận của đồ thị hàm số y  2x  là 1 A. 3 . B. 0 . C. 2 . D. 1. Lờigiải ChọnC Ta có : 3 5  5x  3 5 5 Vì lim  lim
x  nênđườngthẳng y  làtiệmcậnngangcủađồthịhàmsố
x 2x 1 x 1 2 2 2  x 5x  3 5x  3 1 Vì lim   lim
  nênđườngthẳng x  làtiệmcânđứngcủađồthịhàmsố.   1 2x  , 1 1 2x 1 2 x x 2 2
Vậy độ thị hàm số đã cho có tất cả 2 đường tiệm cận. Câu 7:
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên: A. 3
y = - x + 3x + 2 . B. 4 2
y = x - x + 2 . C. 2
y = - x + x - 2 . D. 3
y = x - 3x + 2 . Lời giải Chọn D
Đồ thị đã cho có hình dạng của đồ thị hàm số bậc ba 3 2
y  ax  bx  cx  d nên loại phương án B và C.
Dựa vào đồ thị, ta có lim y    a  0 nên loại phương án A. x x  3 Câu 8:
Đồ thị của hàm số y 
cắt trục hoành tại điểm có hoành độ bằng 2x 1 1 A. 2  . B. . C. 3 . D. 3  . 2 Lời giải Chọn C Trang9  Để x 3
tìm tọa độ của giao điểm với trục hoành, ta cho y  0 
 0  x  3  0  x  3 2x  . 1 125  Câu 9:
Với a là số thực dương tùy ý, log bằng 5    a 
A. 3  log a .
B. 3log a .
C. log a .
D. 3  log a . 5 3 5 5 5 Lời giải Chọn D 125  Ta có: log
 log 125  log a  3 log a . 5   5 5 5  a 
Câu 10: Với x  0 , đạo hàm của hàm số y  log x là 2 x 1 A. . B. . C. . x ln 2 . D. 2x.ln 2 . ln 2 . x ln 2 Lời giải Chọn B 1 
Ta có: y  log x  . 2  . x ln 2
Câu 11: Với a là số thực dương tùy ý , 4 7 a bằng 4 7 1 A. 28 a . B. 7 a . C. 4 a . D. 28 a . Lời giải Chọn C n Ta có m n m
a  a với mọi a  0 và , m n   . 
Câu 12: Nghiệm dương của phương trình 2 x 1 7  7 1680 là
A. x  2 .
B. x  2; x  2 . C. x  2  . D. x  4 . Lời giải Chọn A   2 2 x 2 Ta có x 1  x 1  5 2 7 16807  7
 7  x  4  0   . x  2 
Câu 13: Nghiệm của phương trình log
x  3  3 là: 2  
A. x 11.
B. x 12 .
C. x  3  3 . D. 3 x  3  2 . Lời giải Chọn A Ta có: log x  3  3  log x  3  o l g 2  3
x  3  2  x  11. 2   3 2   2
Câu 14: Nguyên hàm của hàm số 4
f (x)  5x  2 là: A. f  x 3
dx  x  x  C . B. f  x 5
dx  x  x  C . C. f  x 5
dx  x  2x  C . D. f  x 5
dx  x  2x  C . Lời giải Chọn C Ta có: f
 xdx   4 5x  2 5
dx  x  2x  C .
Câu 15: Cho hàm số f  x  sin 2x . Trong các khằng định sau, khẳng định nào đúng? Trang10 A. f  x 1 dx 
cos 2x  C . B. f  x 1 dx  
cos 2x  C . 2 2 C. f
 xdx  2cos2xC. D. f
 xdx  2
 cos 2x  C . Lời giải Chọn C 1 Áp dụng công thức: sin
 ax bdx   cosax bC . a Ta có: f  x 1
dx  sin 2x dx   cos 2x  C  . 2 2 3 3 Câu 16: Nếu f
 xdx  3 và f
 xdx 1 thì f xdx  bằng 1 1 2 A. 4 . B. 4  . C. 2  . D. 3  . Lời giải Chọn A Ta có: 3 f  x 2 x  f  x 3 d dx  f  xdx 1 1 2  3 f  x 3 dx  f  x 2 dx  f  xdx 2 1 1  3 f
 xdx 13  4. 2 2 Câu 17: Tích phân x
 x 2 dx bằng 1 15 16 7 15 A. . B. . C. . D. . 3 3 4 4 Lời giải Chọn B 2  x  2 16 Ta có: x
 x 2 dx    2x 2x 3 2 2 dx    x   . 1 1 3 1 3  
Câu 18: Số phức liên hợp của số phức z  2  3i là:
A. z  3 2i .
B. z  2  3i .
C. z  3 2i . D. z  2  3i . Lời giải Chọn B
Phương pháp: Cho số phức z  a  bi a,b   . Số phức liên hợp của số phức z là z  a bi .
Ta có: Số phức liên hợp z của số phức z  2  3i là z  2  3i . 
Câu 19: Cho hai số phức z  2  3i và w  5  i . Số phức z iw bằng
A. 3 8i
B.1 8i
C. 8  i D. 7  4i Lời giải Chọn B
Ta có z  iw  2  3i  i 5  i  1 8i .
Câu 20: Trên mặt phẳng tọa độ, điểm biểu diễn số phức liên hợp của số phức 9  5i có tọa độ là A. 5; 9  . B. 5;9 . C. 9; 5   . D. 9;5 . Lời giải Trang11 Chọn D
Trên mặt phẳng tọa độ, điểm biểu diễn số phức liên hợp của số phức 9  5i có tọa độ là 9;5 . Câu 21:
Một khối chóp có thể tích bằng 90 và diện tích đáy bằng 5. Chiều cao của khối chóp đó bằng A. 54 . B. 18 . C. 15 . D. 450 . Lời giải Chọn A. 3V
Chiều cao đáy của khối chóp có thể tích bằng 90 và diện tích đáy bằng 5 là h   54 . B Câu 22:
Thể tích của khối hộp chữ nhật có ba kích thước 5; 7; 8 bằng A. 35 . B. 280 . C. 40 . D. 56 . Lời giải Chọn B
Thể tích của khối hộp chữ nhật có ba kích thước 5; 7; 8 bằng V  . a . b c  0 28 . Câu 23:
Một khối nón tròn xoay có chiều cao h  6 cm và bán kính đáy r  5 cm . Khi đó thể tích khối nón là: 325 A. 3
V  300 cm . B. 3
V  20 cm . C. 3 V  cm . D. 3
V  50 cm . 3 Lời giải Chọn D 1 Thể tích khối nón: 2 3
V   .5 .6  50 cm . 3
Câu 24: Cho một khối trụ có độ dài đường sinh là l  6 cm và bán kính đường tròn đáy là r  5 cm .
Diện tích toàn phần của khối trụ là A. 2 110 cm B. 2 85 cm . C. 2 55 cm D. 2 30 cm Lời giải Chọn A 2 S  S + S
 2r  2rl  r r  l   p t áy Đ X   2 2 2 110 cm q 2 S  2S
 r  rl  2r r  l   tp Đáy Xq   2 + S 2 2 0 3 m c     
Câu 25: Trong không gian Oxyz cho điểm A thỏa mãn OA  2i  j với i, j là hai vectơ đơn vị trên hai
trục Ox , Oy . Tọa độ điểm A là
A. A2;1;0 . B. A0; 2  ;1 . C. A0;1  ;1 . D. A1;1  ;1 . Lời giải Chọn A     Vì O =2 A i+ j  O =
A 2;1;0  A2;1;0 .
Câu 26: Trong không gian với hệ tọa độ Oxyz , cho mặt cầu S  có phương trình: 2 2 2
x  y  z  2x  4 y  4z  7  0 . Xác định tọa độ tâm I và bán kính R của mặt cầu S  . A. I 1;2; 2
  ; R  4 . B. I 1;2; 2
  ; R  2 . C. I  1  ; 2
 ;2; R  4 . D. I  1  ; 2
 ;2; R  3. Lời giải Chọn A Trang12 S 2 2 2
: x  y  z  2x  4 y  4z  7  0  a 1; b  2 ; c  2  ; d  7  .
Mặt cầu S  có bán kính 2 2 2
R  a  b  c  d  4 và có tâm I 1;2; 2   .
Câu 27: Trong không gian với hệ toạ độ Oxyz , cho mặt phẳng P  : x  3y  z  3  0 . Mặt phẳng  P  đi
qua điểm nào dưới đây?
A. 1;1;0. B. 0;1; 2  . C. 2; 1  ;3. D. 1;1;1. Lời giải Chọn D
Thay tọa độ từng điểm vào phương trìnhmặt phẳng (P) ta thấy chỉ 1;1;  1 thỏa mãn
Câu 28: Trong không gian Oxyz , cho mặt phẳng  P : x  2y  3z  2  0 và đường thẳng d vuông góc
với mặt phẳng P . Vectơ nào dưới đây là một vectơ chỉ phương của d ?     A. u  1; 2  ;2 .
B. u  1; 2;3 .
C. u  0; 2;3 . D. u  1; 2  ;3 . 2   3   4   2   Lời giải Chọn D   
Vì d   P nên  u cùng phương n hay n  1; 2
 ;3 là một vectơ chỉ phương của d P  d P   x  Câu 29: Hàm số 7
y  x  đồng biến trên khoảng 4 A.  ;   . B.  6  ;0 . C. 1; 4 . D.  5   ;1 . Lời giải Chọn C
Tập xác định D   \  4 . 11 Ta có y      , x D . x  4 0 2
Vậy hàm số đồng biến trên các khoảng  ;  4   và  4;  .
 Hàm số đồng biến trên 1;4 .
Câu 30: Trong một lớp học gồm 15 học sinh nam và 10 học sinh nữ. Giáo viên gọi ngẫu nhiên 4 học
sinh lên giải bài tập. Tính xác suất để 4 học sinh được gọi đó có cả nam và nữ? 219 219 442 443 A. . B. . C. . D. . 323 323 506 506 Lời giải Chọn D
Gọi A là biến cố “4 học sinh được gọi có cả nam và nữ”, suy ra A là biến cố “4 học sinh được
gọi toàn là nam hoặc toàn là nữ”
Số phần tử của không gian mẫu là n 4  C 12650 . 25 n A 63 Ta có n A 4 4
 C  C 1575  P A   . 15 10     n 506
Vậy xác suất của biến cố A là P  A   P  A 63 443 1  1  . 506 506
Câu 31: Tìm giá trị lớn nhất M của hàm số 3 2
y  2x  3x 12x  2 trên đoạn  1  ;2. A. M 10 . B. M  6 . C. M  11 . D. M 15. Lời giải Trang13 Chọn D Ta có 2
y  x  x    2 6 6 12
6 x  x  2  x 1 1  ;2 y  0   x  2     1  ;2 Ngoài ra y   1  15; y   1  5
 ; y2  6 nên M 15. a
Câu 32: Tập nghiệm của bất phương trình    1 7 4 3  7  4 3 là A.  ;0  . B.   ;1  .
C. 0;  . D. 1;  . Lời giải Chọn A a 1  a 1  1 
Ta có: 7  4 37  4 3 1 nên 7  4 3  7  4 3  7  4 3  7  4 3  a 1 1
  a  0 (do 7  4 3 1). 4 4 f
 xdx 10 g
 xdx  5 4 Câu 33: Cho 2 và 2 . Tính I  3  f
 x5gx2xdx  2 A. I 17. B. I 15. C. I  5.  D. I 10. Lời giải Chọn A 4 4 4 I  3 f
 xdx5 g
 xdx 2xdx  3.105.512 17  . 2 2 2
Câu 34: Cho số phức z  2  3 .
i Môđun của số phức 1 i z bằng A. 26. B. 25. C. 5. D. 26. Lời giải Chọn D
Ta có 1 i z  1 i2  3i  1   5i
Do đó   i z   2 2 1 1  5  26.
Câu 35: Cho hình hộp chữ nhật ABC .
D A' B'C ' D' có AB  AD  2 2 và AA'  4 3 (tham khảo hình
bên). Góc giữa đường thẳng CA' và mặt phẳng  ABCD bằng A. 0 60 . B. 0 90 . C. 0 30 . D. 0 45 . Lời giải Chọn A Vì ABC .
D A' B'C ' D' là hình hộp chữ nhật nên AA'  ( ABCD) . Do đó góc giữa đường thẳng
CA' và mặt phẳng  ABCD là  ACA ' . Trang14
Vì AB  AD  2 2 nên ABCD là hình vuông có đường chéo AC  AB 2  2 2. 2  4 . AA
Tam giác ACA' vuông tại A và có AA'  4 3 , AC  4 nên  ' 4 3 tan ACA'    3 . AC 4 Suy ra  0
ACA'  60 . Vậy góc giữa đường thẳng CA' và mặt phẳng  ABCD bằng 0 60 .
Câu 36: Cho hình chóp tứ giác đều S.ABCD có độ dài cạnh đáy bằng 4 và độ dài cạnh bên bằng 6
(tham khảo hình bên). Khoảng cách từ S đến mặt phẳng  ABCD bằng A. 2 5 . B. 2 7 . C. 2 . D. 7 Lời giải Chọn B
Gọi I  AC  BD .
Vì S.ABCD là hình chóp tứ giác đều có độ dài cạnh đáy bằng 4 nên đáy ABCD là hình vuông
cạnh AB  4 và hình chiếu vuông góc của S trên  ABCD là tâm I của hình vuông ABCD .
Do đó, khoảng cách từ S đến mặt phẳng  ABCD bằng SI 1
Ta có AC  AB 2  4 2  IA  AC  2 2 2
Cạnh bên SA  6 và tam giác SAI vuông tại I nên 2 2 2 2 SI  SA  AI  6  (2 2)  36  8  28  2 7
Vậy khoảng cách từ S đến mặt phẳng  ABCD bằng 2 7 .
Câu 37: Trong không gian Oxyz, mặt cầu tâm là điểm I (2; 3;1) và đi qua điểm M 0; 1  ;2 có phương trình là: 2 2 2 2 2
A.  x  2   y  3   z   1  3. B. 2
x   y  
1   z  2  3. Trang15 2 2 2 2 2 C. 2
x   y  
1   z  2  9.
D.  x  2   y  3   z   1  9. Lời giải Chọn D
Mặt cầu tâm là điểm I (2; 3;1) và đi qua điểm M 0; 1
 ;2 có bán kính là IM .  Ta có IM    2 2 2
2; 2;1  r  IM  ( 2  )  2 1  9  3 Phương trình mặ 2 2 2
t cầu là:  x  2   y  3   z   1  9.
Câu 38: Trong không gian Oxyz, đường thẳng đi qua điểm A 4  ;1; 3   và B0; 1   ;1 có phương trình tham số là: x  4   2t x  4t x  2t x  4   4t     A.  y  1   t . B.  y  1   2t . C.  y  1
  t. D. y  1   2t .     z  3   2t  z  1 4t  z  1 2t  z  3   4t  Lời giải Chọn C
Đường thẳng đi qua điểm A 4  ;1; 3   và B0; 1  
;1 có vectơ chỉ phương là  AB  4; 2  ;4  22; 1  ;2
Phương trình tham số của đường thẳng (AB) đi qua điểm B 0; 1  
;1 và có vectơ chỉ phương x  2t  1  1  u  AB  4;2;4  2; 1
 ;2 là y  1   t. 2 2 z 1 2t 
Câu 39: Cho hàm số f  x , đồ thị hàm số y  f  x là đường cong trong hình bên. Giá trị nhỏ nhất của  x 
hàm số g  x  f   trên đoạn 5  ;  3 bằng  2  y 2 1 x -2 O A. f  2  . B. f   1 . C. f  4  . D. f 2 . Lời giải Chọn A  x  2        g x 1 x x 4 2  0  f   0       . 2  2  x  x  2 1 2    x  x
g x  0  f   0   2   x  4    .  2  2 Bảng biến thiên Trang16
Giá trị nhỏ nhất của hàm số g  x trên  5  ;  3 bằng g  4    f  2   .
Câu 40: Có bao nhiêu số tự nhiên y sao cho ứng với mỗi y có không quá 148 số nguyên x thỏa mãn x 1 2 3  3 0 y  ? ln x
A. 4 B. 5 C.6D. 7 Lời giải Chọn C x  0  Điều kiện: y x  e y  0   x 1 1 3    0 x  3  + Trường hợp 1:  3    x y 0 
x  e  e 1
y  ln x  0  x 1 1 3    0 x  3  + Trường hợp 2:  3   y  x  e
y  ln x  0 Kết hợp điều kiện y 0
x  0; e  e  1. Ta có 0 y  x  e
Để có không quá 148 số nguyên x thì 1 y
 e 149  0  y  ln149  5,004
 y0;1;2;3;4;  5 . Có 6 số nguyên y. x  x  x  ln 2
Câu 41: Cho hàm số f  x 2 4 1 , 5   . Tích phân 3 x   1. x f e e dx bằng 2x  6 , x  5 0 77 77 68 77 A. . B. . C. . D. . 3 9 3 6 Lời giải Chọn B
Ta có lim f  x  lim f  x  f 5  4 nên hàm số liên tục tại x  5.   x 5  x 5 
Vậy hàm số f  x liên tục trên  . Đặ x x 1
t t  3e 1  e dx  dt 3
Đổi cận : x  0  t  4 ; x  ln 2  t  7 7 7 5 7 1 1 1   77 Khi đó I  f
 tdt  f
 xdx  2x6dx  2x 4x 1dx  . 3 3 3 9 4 4  4 5 
Câu 42: Có bao nhiêu số phức z thỏa mãn z  z  z  1? Trang17 A. 0 . B. 1. C. 4 . D. 3 . Lời giải Chọn C
Ta có Giả sử z  x  yi  ,
x y     z  x  yi  z  z  2x . 2 2 x  y  2 2 1  z 1    x  y 1  Bài ra ta có      1  z  z 1   2x 1 x     2 1 1 3 Với 2 x  
  y 1  y   . 2 4 2 Do đó có 4 số 1 3 1 3 1 3 1 3
phức thỏa mãn là z   i , z   i , z    i , z    i . 1 2 2 2 2 2 3 2 2 4 2 2
Câu 43: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB  6 , AD  3 , tam giác
SAC nhọn và nằm trong mặt phẳng vuông góc với đáy. Biết hai mặt phẳng SAB , SAC  tạo
với nhau góc  thỏa mãn 3 tan  
và cạnh SC  3 . Thể tích khối S.ABCD bằng: 4 4 8 5 3 A. . B. . C. 3 3 . D. . 3 3 3 Lời giải Chọn B V  2V  2V
. Kẻ BH vuông góc với AC tại H . S .ABCD S .ABC B.SAC
Ta có: AC  3 , BH  2 , HC 1.  BH tan   tan BKH  4 2  KH  . KH 3  KH 2 2 sin SAC    1  cos SAC  . HA 3 3 2 2 2 
SC  SA  AC  2AS.AC.cos SAC  SA  2. 1  S  1 2 2 .
SA AC.sin SAC  .2.3.  2 2 . SAC 2 2 3 1 8 Vậy V  2. .2 2. 2  . S . ABCD 3 3
Câu 44: Sử dụng mảnh inox hình chữ nhật ABCD có diện tích bằng 2
1m và cạnh BC  x m để làm
một thùng đựng nước có đáy, không có nắp theo quy trình như sau: Chia hình chữ nhật ABCD
thành 2 hình chữ nhật ADNM và BCNM , trong đó phần hình chữ nhật ADNM được gò
thành phần xung quanh hình trụ có chiều cao bằng AM ; phần hình chữ nhật BCNM được cắt Trang18
ra một hình tròn để làm đáy của hình trụ trên (phần inox thừa được bỏ đi) Tính gần đúng giá trị
x để thùng nước trên có thể tích lớn nhất (coi như các mép nối không đáng kể).
A. 0, 97m .
B. 1, 37m .
C. 1,12m .
D. 1, 02m . Lời giải Chọn D 1 1 Ta có .
AB BC  1  AB   m. BC x
Gọi r m là bán kính đáy hình trụ inox gò được, ta có chu vi hình tròn đáy bằng BC  x m. Do đó x
2 r  x  r  m . 2 Như vậ x 1 x y BM  2r 
 AM  AB  BM   m  . x  2
 x   1 x  1
Thể tích khối trụ inox gò được là 2
V   r h   . .   x  2       x . 2 
 2   x   4
Xét hàm số f  x x  2
   x  với x  0 .  f  x 2
   3x ; f x  0  x  ; 3    f  x      0  x 0;  
 và f  x  0  x  ;     . 3   3        
Bởi vậy f  x đồng biến trên khoảng  0;  
 và nghịch biến trên khoảng  ;     . 3   3      2 3 
Suy ra max f  x  f    V  f x  x  1,02m . max      0; 3 9   max 3
Câu 45: Trong không gian với hệ tọa độ Oxyz, cho hai điểm A3;3  ;1 , B 0; 2  ;1 và mặt phẳng
P: x  y  z 7  0. Đường thẳng d nằm trong P sao cho mọi điểm của d cách đều hai điểm ,
A B có phương trình làcác mệnh đề sau, mệnh đề nào đúng? x  t x  2t x  t x  t     
A.  y  7  3t .
B.  y  7  3t . C.  y  7  3t .
D.  y  7  3t .     z  2t  z  t  z  2t  z  2t  Lời giải ChọnC Trang19
Phương trình mặt phẳng trung trực của đoạn AB là   :3x  y  7  0.
Đường thẳng cần tìm d cách đều hai điểm ,
A B nên d thuộc mặt phẳng  .
x  y  z  7  0
Lại có d   P, suy ra d   P   hay d : 
. Chọn x  t, ta được 3
 x  y  7  0 z  2t  . y  7 3t
Câu 46: Cho hàm số y  f  x là hàm số bậc bốn thỏa mãn f 0  0. Hàm số y  f ' x có bảng biến thiên như sau: Hàm số     2 2 g x f x
 x có bao nhiêu điểm cực trị? A. 1. B. 3 . C. 5 . D. 7 Lời giải Chọn C
Đặt hx  f  2 x  2
 x  h0  0. x  0
Ta có h ' x  2xf ' 2
x   2x  0    f '   . 2 x   1
Dựa vào bảng biến thiên của hàm số t  f ' x ta có phương trình f ' x  1 có duy nhất một
nghiệm và nghiệm đó dương. Gọi x là nghiệm của phương trình f ' x  1. 0 Suy ra f ' 2 x  2
1  x  x  x   x . 0 0
Ta có y  f  x 4 3 2
 ax  bx  cx  dx  e  f x 3 2 '
 4ax  3bx  2cx  d
lim f ' x    a  0. x Khi đó     2  2 h x f x
 x là hàm bậc 8 và lim hx  lim hx   x x
Lập bảng biến thiên của h  x ta có
Dựa vào bảng biến thiên ta có hàm số g  x  h x có 5 điểm cực trị.
Câu 47: Có bao nhiêu giá trị nguyên của m với m 1 sao cho tồn tại số thực x thỏa mãn:  m log x m  3log5 5  x 3   1 . A. 4 . B. 3 . C. 5 . D. 8 . Trang20 Lời giải ChọnB
Điều kiện: x  0 Đặt log5 x m
 3  u thay vào phương trình   1 ta được: log5 m log5   3 m u x  x  u  3. log5 x u   m  3 Vì log5 m log5 u u  m
. Từ đó ta có hệ Phương trình  . log5 m x  u  3
Xét hàm đặc trưng   t
f t  m  3 trên  .
Do m 1. Suy ra hàm số f t  đồng biến trên  .
Do đó, f log x  f log u  x  u . 5   5 
Vì thế, ta đưa về xét phương trình: log5 x log5 m log5   3    3   3 m x m x x x  x log x  3  log x 3  log m x
 log x 3  log .
x log m  log m  5   5  log  5   5   5 5 5 5 log x 5 log x  3 5  
Do x  0 nên x  3  x nên log m  1 m  5 . 5 log x 5  m Suy ra   m2,3,  4 . 1   m  5
Vậy, có 3 giá trị tham số m thỏa mãn.
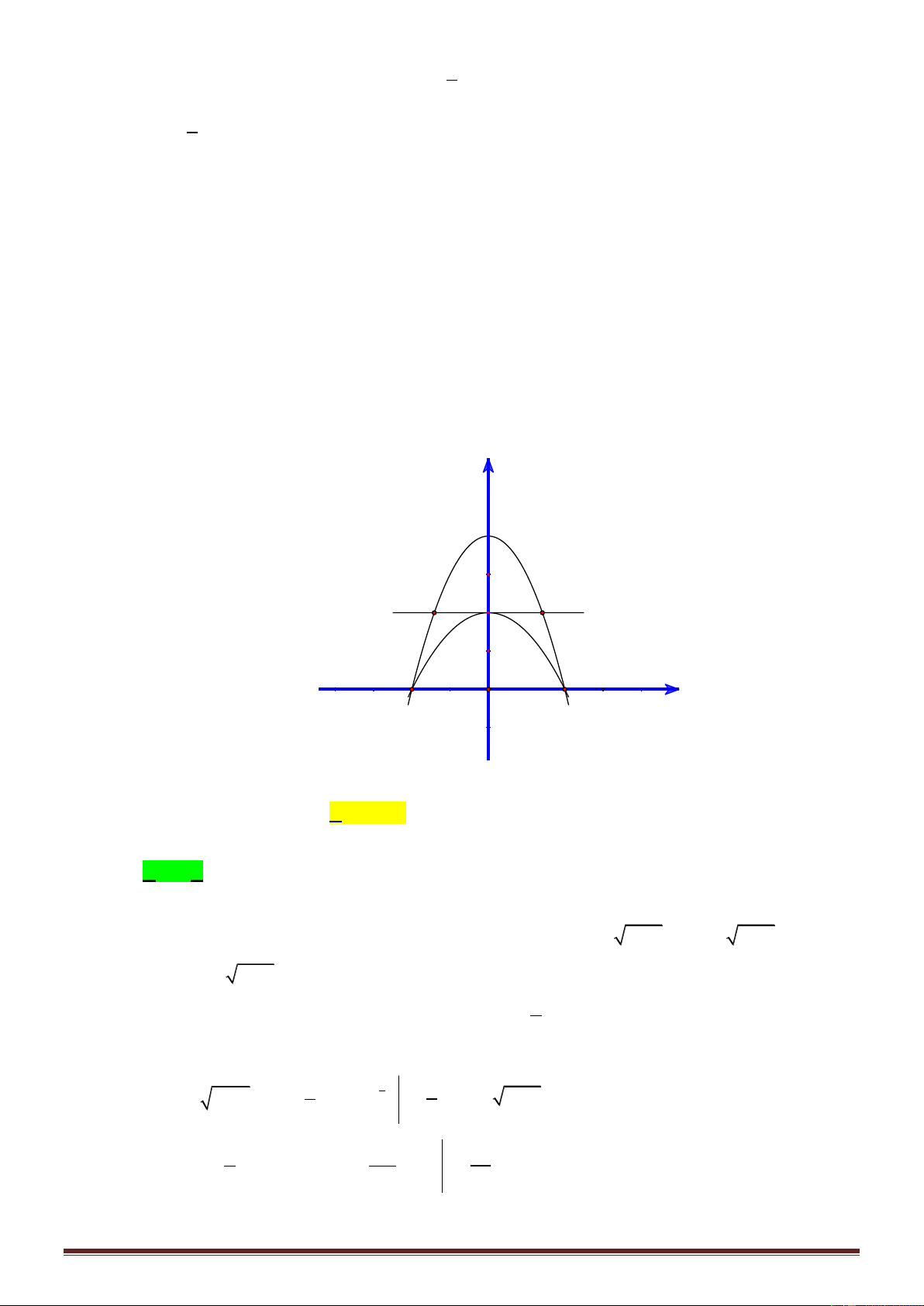
Câu 48: Cho hàm số bậc ba   3 2
f x  ax  bx  cx  d và đường thẳng d : g  x  mx  n có đồ thị như
hình vẽ. Gọi S , S , S lần lượt là diện tích của các phần giới hạn như hình bên. Nếu S  4 thì 1 2 3 1 S tỷ số 2 bằng. S3 3 1 A. . B.1 . C. 2 . D. . 2 2 Lời giải: Chọn B
Dựa vào đồ thị như hình vẽ, ta có: f x  g x  k.xx  2x  2.
g  x  x  3 Trang21 0 S  S  kx x  2
x  2 dx  4k  1 2    2
 g0  g2.2 35.2 S  S    8 2 3 2 2 S
Vì S  4  S  4  S  8  4  4 . Vậy 2  1 . 1 2 3 S3
Câu 49: Xét hai số phức z , z thỏa mãn z  2, 1 i z  6 và z  z  5 . Giá trị lớn nhất 1   1 2 2 1 2
2z  z  2021 bằng 1 2 A. 2044 .
B.  23  2021. C. 23  2021.
D. 2 23  2021. Lời giải Chọn C
Đặt z  a  bi, z  c  di với a,b, c, d   . Theo giả thiết thì 1 2 z  1  2 2 a  b  4 1  i 6 1
z  6  z   3 2 2
 c  d  3 2 2 1 i 2 2
z  z  5  a  c  b  d   5 1 2 Do đó 2 2 2 2
a  2ac  c  b  2bd  d  5  ac  bd  1
Ta có 2z  z  2a  c  2b  d i nên 1 2     2 2z  z
 2a  c2  2b  d 2  4 2 2
a  b    2 2 c  d
 4 ac  bd  23 1 2   
Áp dụng bất đẳng thức z  z  z  z , ta có
2z  z  2021  2z  z  20  21  23  2021. 1 2 1 2
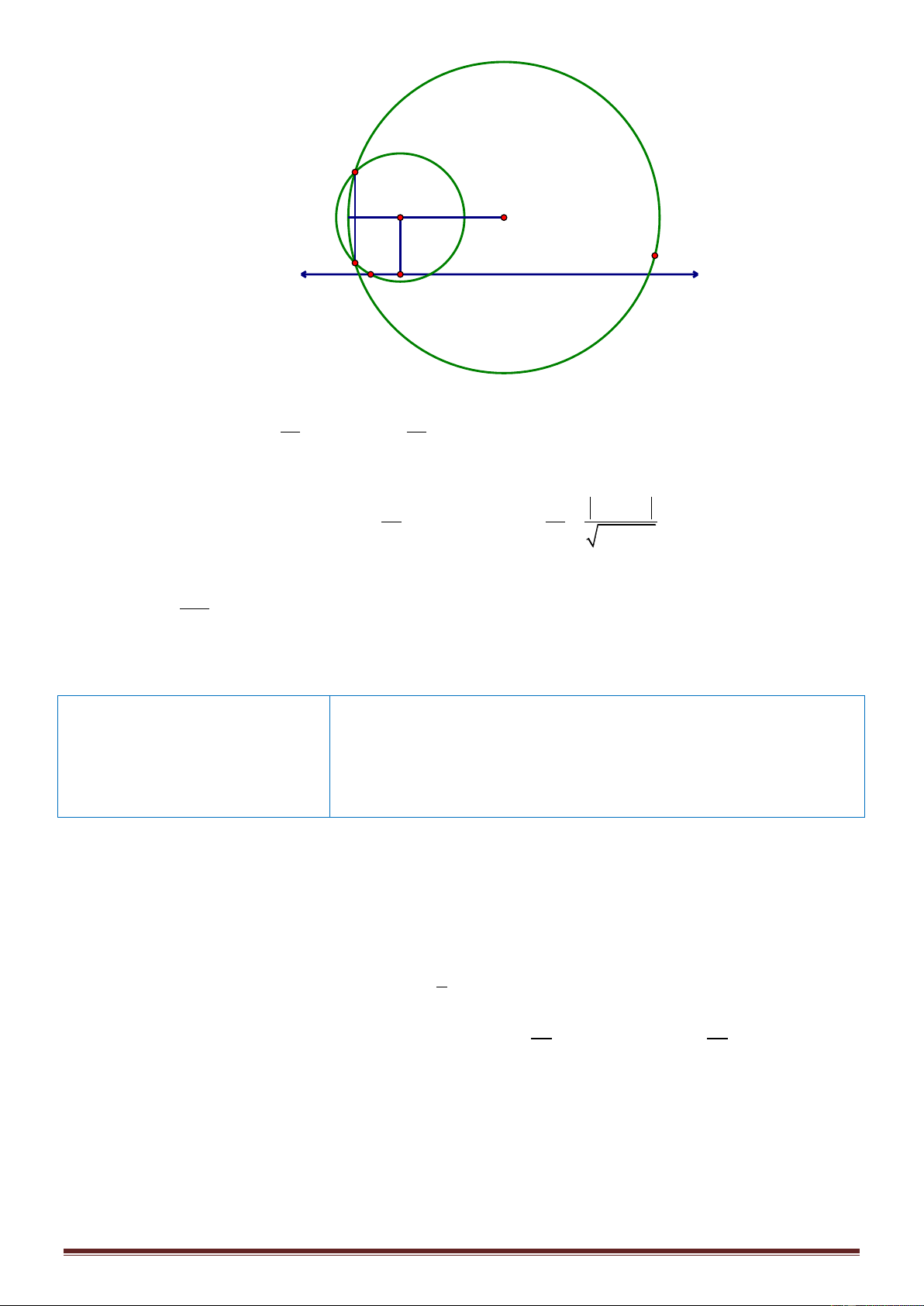
Câu 50: Trong không gian Oxyz , cho hai điểm C  1  ;2;1  1 , H ( 1
 ;2;1) , hình nón N  có đường cao
CH  h và bán kính đáy là R  3 2 . Gọi M là điểm trên đoạn CH , C là thiết diện của mặt
phẳng  P vuông góc với trục CH tại M của hình nón  N . Gọi  N  là khối nón có đỉnh H
đáy là C . Khi thể tích khối nón  N lớn nhất thì mặt cầu ngoại tiếp nón  N có tọa độ tâm I  ; a ,
b c, bán kính là d . Giá trị a  b  c  d bằng A. 1. B. 3 . C. 6 . D. 6  . Lời giải Chọn C Trang22
Đặt HM  x , 0  x  h . Gọi I , R, r lần lượt là tâm và bán kính đường tròn đáy của nón (N ) ,
bán kính đường tròn C. Khi đó ta có CH  h 12 là chiều cao của (N), R  3 2 .
Khi đó C, I , H thẳng hàng ( I nằm giữa C, H ). EM CM QH CM Do tam giác CEM  ∽ CQ  H nên  .  EM  QH CH CH
R h  x
 r  EM  FM  . h
Thể tích của khối nón đỉnh O đáy là C là 1 1
 Rh  x 2  2 2 1 R 2 V 
 EM .HM     x  
h  x x. 3 3 h   2 3 h 2 1 R 2
Ta có Xét hàm số f  x  
h  x x , 0  x  h 2 3 h 2 2   1 R 1 R h f x  
h  xh 3x ; f x  0  
h  xh 3x  x  . 2 3 h 2 3 h 3
Lập bảng biến thiên ta có h
Từ bảng biến ta có thể tích khối nón đỉnh O đáy là C lớn nhất khi x  3
Chú ý: Có thể đánh giá dựa vào      h  x2 1 1 h x h x 2x 3
x  (h  x)(h  x)x 
(h  x)(h  x)2x  (
) với 0  x  h .Dấu "=" 2 2 3 h
xảy ra khi ba số (h  x)  (h  x)  2x  x  . 3  Khi đó h . R CM .( R h x) HM  x   4 , r    2 2  MF 3 h h Trang23
Gọi P là giao điểm của HM với mặt cầu ngoại tiếp nón  N . Ta có H  FP vuông tại F 2
 HF  HM.HP
 HM  MF  HM HP    2 2 2 . 16 2 2
 4.HP  HP  6 1  1 
 d  HI  3  HC  HI  HC  I (1;2;2) . 4 4
Vậy a  b  c  d  6 . Đề 7
ĐỀ LUYỆN THI CẤP TỐC TỐT NGHIỆP THPT NĂM 2021 Thuvienhoclieu.Com BÀI THI: TOÁN
Thời gian: 90 phút Câu 1:
Trong một hộp bút gồm có 8 cây bút bi, 6 cây bút chì và 10 cây bút màu. Hỏi có bao nhiêu cách
chọn ra một cây bút từ hộp bút đó? A. 480. B. 24. C. 48. D. 60. Câu 2:
Cho cấp số cộng u có số hạng tổng quát là u  3n  2 . Tìm công sai d của cấp số cộng. n  n A. d  3. B. d  2 . C. d  2  . D. d  3  . Câu 3:
Cho hàm số y  f  x có bảng biến thiên như hình vẽ bên. Hàm số y  f  x nghịch biến trên
khoảng nào trong các khoảng sau đây? x 0  1 1  y' 0    0    y   A.  1  ; 0 . B.  1  ;  1 . C.  ;    1 . D. 0;   . Câu 4:
Cho hàm số y  f  x có bảng biến thiên như hình dưới:
Giá trị cực đại của hàm số đã cho là: A. 1.  B. 3. C. 0 . D. 2.  Câu 5: Cho hàm số 4 3
y  x  x  3. Khẳng định nào sau đây là đúng? Trang24
A. Hàm số có 3 điểm cực trị.
B. Hàm số chỉ có đúng 2 cực trị.
C. Hàm số không có cực trị
D. Hàm số chỉ có đúng 1 điểm cực trị. Câu 6:
Cho hàm số y  f  x có bảng biến thiên như hình vẽ dưới đây: y
Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là: A. 1. B. 4. C. 0. D. 3. Câu 7:
Đường cong trong hình dưới là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn
phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào? y 1 x -1 O 1 -1 A. 4 2 y  2
 x  4x 1. B. 4 2
y  x  2x 1. C. 4 2
y  x  4x 1. D. 4 2
y  x  2x 1. Câu 8:
Số giao điểm của đồ thị hàm số 3 2
y  x  2x  x 12 và trục Ox là A. 2 . B. 1. C. 3 . D. 0 . Câu 9:
Cho a, b là các số thực dương bất kỳ. Mệnh đề nào sau đây sai? A. 2 2
log(10ab)  2  log(ab) . B. 2
log(10ab)  2(1 log a  log b) . C. 2
log(10ab)  2  2 log(a ) b . D. 2 2
log(10ab)  (1 log a  log b) .
Câu 10: Tính đạo hàm của hàm số   2 3 e x f x   . A.   2 3 2.e x f x    . B.   2 3 2.e x f x     . C.   3 2.ex f x    . D.   2 3 e x f x    . 2 1   1  Câu 11: Rút gọn 2 P  a . , a  0.    a  A. 2 a . B. a. C. 2 2 a . D. 1 2 a  . 4 2 
Câu 12: Tổng các nghiệm của phương trình x 3 3 x  81 bằng Trang25 A. 4 . B. 1. C. 3 . D. 0 .
Câu 13: Tập nghiệm của phương trình log x + log (x + 2) = 2 là 3 3 A. S   1   3. B. S   1   10; 1   10. C. S   1   10.
D. S  0;  2 . x +
Câu 14: Cho hàm số f (x ) 2 1 =
. Trong các khẳng định sau, khẳng định nào đúng? x A.
f (x)dx  ln x  2x  C  . B.
f (x)dx  x  ln x  C  . C.
f (x)dx  ln x  C  . D.
f (x)dx  ln x  2x  C  .
Câu 15: Cho hàm số f (x ) = sin x cos x . Trong các khẳng định sau, khẳng định nào đúng? 2 sin x A. 2
f (x)dx  sin x  C  . B.
f (x)dx   C  . 2 2 cos x C.
f (x)dx   C  . D. 2
f (x)dx   cos x  C  . 2 2 12 4 x æ ö ç ÷ f ò (x)dx = 3 f ç dx ÷ = 2 ò ç ÷ f ò (x)dx çè3÷ø Câu 16: Nếu 1 và 6 thì 1 bằng 7 11 A. 5 . B. . C. . D. 1. 3 3 e Câu 17: Tích phân ln xdx ò bằng 1 A. e . B. e 1. C. e 1. D. 1.
Câu 18: Tổng phần thực và phần ảo của số phức liên hợp của z = 2 - 3i là A. 1. B. 5 . C. 5  . D. 1.
Câu 19: Cho hai số phức z  2  i và z  7  3i . Tìm số phức z  z  z . 1 2 1 2 A. z  5   2i .
B. z  9 . C. z  4  i .
D. z  9  4i .
Câu 20: Trên mặt phẳng tọa độ, cho số phức 1 i z  3  i , điểm biểu diễn số phức z là A. 3; 2 . B. 1; 2   . C. 2;  1  . D.  1  ;2 .
Câu 21: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , cạnh SA vuông góc với đáy và
SA  2a . Thể tích khối chóp S.ABCD bằng 3 4a 3 a 3 2a A. . B. 3 2a . C. . D. . 3 3 3
Câu 22: Thể tích của một khối hộp chữ nhật có các cạnh 2c , m 4c ,
m 7cm là A. 3 56cm . B. 3 36cm . C. 3 48cm . D. 3 24cm . Trang26
Câu 23: Cho khối nón có bán kính đáy bằng a và đường cao 2a . Thể tích của khối nón đã cho bằng 3 2 a 3 3 a 3  a A. . B. . C. 3  a . D. . 3 2 2
Câu 24: Cho hình trụ có độ dài đường sinh bằng 6 , diện tích xung quanh bằng 48 . Bán kính hình tròn
đáy của hình trụ đó bằng A. 1. B. 8 . C. 4 . D. 2 .
Câu 25. Trong không gian với hệ tọa độ Oxyz , cho A2;0;0 , B0;3;4 . Độ dài đoạn thẳng AB là:
A. AB  3 3 .
B. AB  2 7 .
C. AB  19 . D. AB  29 .
Câu 26.Trong không gian Oxyz , cho hai điểm A 2  ;1;  1 , B 0; 1  ; 
1 . Phương trình mặt cầu đường kính AB là: 2 2 2 2 A.  x   2
1  y   z   1  2. B.  x   2
1  y   z   1  4. 2 2 2 2 C.  x   2
1  y   z   1  8 . D.  x   2
1  y   z   1  2 .
Câu 27. Cho biết phương trình mặt phẳng  P:ax  by  cz 13 0 đi qua 3 điểm A1; 1
 ;2, B2;1;0 ,
C 0;1;3 . Khi đó a  b  c bằng A. 11. B. 11  . C. 10  . D. 10 .
Câu 28.Trong không gian Oxyz cho ba điểm A1; 2  ;0, B(2; 1  ;3),C 0; 1  ; 
1 . Đường trung tuyến AM
của tam giác ABC có phương trình là x 1 x 1 2t x 1 t x 1 2t     A. y  2   t . B.  y  2  . C. y  2  . D. y  2   t .     z  2t  z  2  t  z  2  t  z  2t 
Câu 29.Trên giá sách có 4 quyển sách Toán, 3 quyển sách Lí và 2 quyển sách Hóa, lấy ngẫu nhiên 3
quyển sách. Tính xác suất sao cho ba quyển lấy ra có ít nhất một quyển sách Toán. 37 5 10 42 A. . B. . C. . D. . 42 42 21 37
Câu 30. Hàm số nào trong các hàm số sau đây nghịch biến trên  ? x A. y  log x . B. 9x y  .
C. y  log x .
D. y  0,9 . 0,9 9 1 5 Câu 31: Hàm số 3 2 y = x -
x + 6x + 1 đạt giá trị lớn nhất và giá trị nhỏ nhất trên đoạn [1;3] lần lượt 3 2
tại hai điểm x và x . Khi đó x + x bằng 1 2 1 2 A. 2 . B. 4 . C. 5 . D. 3 . 2  x 3x  1  1
Câu 32: Tìm tập nghiệm S của bất phương trình    .  2  4
A. S  1;2 .
B. S    ;1 .
C. S  1; 2 .
D. S  2;   . 2 2 2 f
 xdx  2
g  xdx  1   I  x  2 f  
x3g xdx  Câu 33: Cho 1  và 1  . Tính 1  . Trang27 17 5 7 11 A. I  . B. I  . C. I  . D. I  . 2 2 2 2
Câu 34: Cho số phức z 1 2i . Tìm tổng phần thực và phần ảo của số phức w  2z  z . A. 3 . B. 5 . C. 1. D. 2 .
Câu 35: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB  2, AD  5 . Cạnh bên
SA  3 và vuông góc với mặt phẳng đáy (tham khảo hình bên). Góc giữa đường thẳng SC và
mặt phẳng  ABCD bằng A. 30 .  B. 45 .  C. 60 .  D. 90 . 
Câu 36: Cho hình lăng trụ AB .
C A' B 'C ' có đáy là tam giác đều cạnh bằng 2 . Biết
A' A  A' B  A'C  2 . Khoảng cách từ A ' đến mặt phẳng  ABC  bằng A' B' A C H B 2 6 2 3 2 3 2 2 A. . B. . 3 3 . C. 6 . D. 3
Câu 37: Trong không gian Oxyz, mặt cầu có tâm I 1;0; 2 và tiếp xúc với mặt phẳng Oyz có phương trình là: 2 2 2 2 A.  x   2
1  y   z  2  1. B.  x   2
1  y   z  2 1. 2 2 2 2 C.  x   2
1  y   z  2  2. D.  x   2
1  y   z  2  4.
Câu 38: Trong không gian Oxyz, đường thẳng đi qua điểm M 1;3; 2
  và song song với đường thẳng x  2 y z 1 d :   2 1
 có phương trình tham số là: 3 x 1 2t x 1 2t x  2  t x  1   2t    
A.  y  3  t . B.  y  3 . C.  y  1   3t . D.  y  3   t .     z  2   3t  z  2   t  z  3   2t  z  2  3t  Trang28
Câu 39: Cho hàm số f  x , đồ thị hàm số y  f  x là đường cong trong hình bên. Giá trị lớn nhất của
hàm số g  x   f 2x  
1  2x trên đoạn 0;2 bằng A.  f   1  2 .
B.  f   1 .
C.  f 2  3 .
D.  f 3  4 .
Câu 40.Có bao nhiêu số nguyên dương y sao cho ứng với mỗi y có không quá 25 số nguyên x thỏa x 1 1 2  mãn 4  0 ?  2 x y A. 30
B. 31C. 32 D. 33
x  m , x  0
Câu 39: Cho hàm số f  x liên tục trên  thỏa mãn f  x  
(m là hằng số). Biết 2 x e , x  0 2   b
f x dx  a  
trong đó a, b là các số hữu tỉ. Tính a  b . 2 e 1  A. 4 . B. 3 . C. 0 . D. 1. z 1 z  3i
Câu 42: Có bao nhiêu số phức z thỏa mãn  1? z  i z  i A. 3 . B. 0 . C. 2 . D. 1. 
Câu 43: Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O cạnh a , góc BCA  30 , 3a
SO   ABCD và SO 
. Khi đó thể tích của khối chóp là 4 3 a 2 3 a 3 3 a 2 3 a 3 A. . B. . C. . D. . 4 8 8 4
Câu 44. Từ một tấm thép phẳng hình chữ nhật, người ta muốn làm một chiếc thùng đựng dầu hình trụ
bằng cách cắt ra hai hình tròn bằng nhau và một hình chữ nhật (phần tô đậm) sau đó hàn kín lại,
như trong hình vẽ dưới đây. Hai hình tròn làm hai mặt đáy, hình chữ nhật làm thành mặt xung
quanh của thùng đựng dầu (vừa đủ). Biết rằng đường tròn đáy ngoại tiếp một tam giác có kích
thước là 50cm, 70cm,80cm (các mối ghép nối khi gò hàn chiếm diện tích không đáng kể. Lấy
  3,14 ). Diện tích của tấm thép hình chữ nhật ban đầu gần nhất với số liệu nào sau đây? Trang29 A. 6, 8  2 m  . B. 24, 6  2 m  . C. 6,15  2 m  . D. 3, 08  2 m  . x 1 y 1 z 1 x 1 y  3 z 1
Câu 45. Trong không gian Oxyz ,cho 2 đường thẳng d :   , d ' :   và 1 2 1 2 1 2 
mặt phẳng  P : 2x  y  z  3  0 . Biết rằng đường thẳng  song song với mặt phẳng  P , cắt
các đường thẳng d , d lần lượt tại M , N sao cho MN  11 ( điểm M có tọa độ ngyên).
Phương trình của đường thẳng  là x y 1 z  2 x y 1 z  2 A.   . B.   . 1 1 3 1 2  4 x y 1 z  2 x y 1 z  2 C.   . D.   . 1 1 3  1 2 4
Câu 46: Cho f  x là hàm số bậc bốn thỏa mãn f   1 0  
. Hàm số f  x có bảng biến thiên như ln 2 sau: 2x
Hàm số g  x  f x  2 2 2  x 
có bao nhiêu điểm cực trị? ln 2 A. 3 . B. 2 . C. 4 . D. 5 .
Câu 47: Cho các số thực x, y, z thỏa mãn log  2 2x  2 y   log  3 x  3 2y log z . Có bao giá 3 7  
trị nguyên của z để có đúng hai cặp  x, y thỏa mãn đẳng thức trên. A. 2 . B. 211 . C. 99 . D. 4. Câu 48: Cho hàm số 4 2
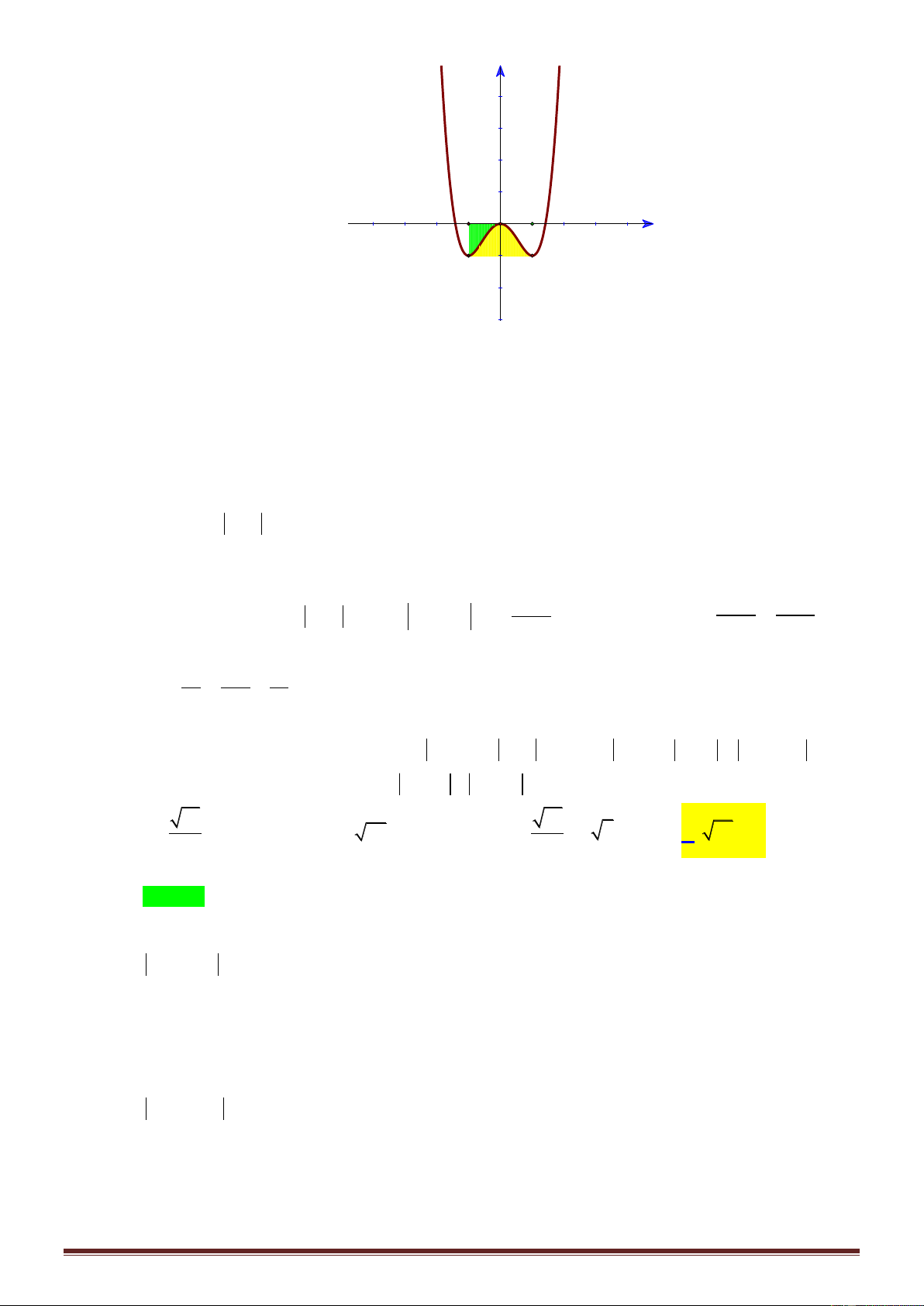
y  x  3x  m có đồ thị C
, với m là tham số thực. Giả sử C cắt trục Ox m  m 
tại bốn điểm phân biệt như hình vẽ Trang30
Gọi S , S , S là diện tích các miền gạch chéo được cho trên hình vẽ. Giá trị của m để 1 2 3
S  S  S là 1 3 2 5 5 5 5 A. . B.  . C. . D.  . 4 4 2 2
Câu 49: Xét hai số phức
z  1; z  4 và z  z 
. Giá trị lớn nhất của 1
z ; z thỏa mãn 2 1 2 1 2 5   1 z 2z2 7i bằng A. 7  89 . B. 7  89 . C. 7  2 89 . D. 7  2 89 .
Câu 50: Trong không gian Oxyz , cho hai điểm (
A 1;3; 0), B(3;1; 4) và đường thẳng x  2 y 1 z  2  :  
. Xét khối nón (N ) có đỉnh có tọa độ nguyên thuộc đường thẳng  và 1 1 3
ngoại tiếp mặt cầu đường kính AB . Khi (N ) có thể tích nhỏ nhất thì mặt phẳng chứa đường
tròn đáy của (N ) có phương trình dạng ax  by  cz 1  0 . Giá trị a b  c bằng A. 1. B. 3 . C. 5 . D. 6.  BẢNG ĐÁP ÁN 1.B 2.A 3.A 4.B 5.D 6.D 7.A 8.B 9.D 10.A 11.B 12.D 13.C 14.D 15.B 16.C 17.D 18.B 19.A 20.B 21.D 22.A 23.A 24.C 25.D 26.A 27.A 28.A. 29.A 30.D 31.D 32.C 33.A 34.B 35.A 36.A 37.B 38.A 39.C 40.B 39.A 42.D 43.B 44.C 45.C 46.D 47.B 48.A 49.B 50.A
HƯỚNG DẪN GIẢI CHI TIẾT Câu 1:
Trong một hộp bút gồm có 8 cây bút bi, 6 cây bút chì và 10 cây bút màu. Hỏi có bao nhiêu cách
chọn ra một cây bút từ hộp bút đó? A. 480. B. 24. C. 48. D. 60. Lời giải Chọn B
Áp dụng quy tắc cộng:
Số cách chọn ra một cây bút từ hộp bút đó là 8  6 10  24. Câu 2:
Cho cấp số cộng u có số hạng tổng quát là u  3n  2 . Tìm công sai d của cấp số cộng. n  n A. d  3. B. d  2 . C. d  2  . D. d  3  . Trang31 Lời giải Chọn A Ta có u
 u  3 n 1  2  3n  2  3 n 1  n  
Suy ra d  3 là công sai của cấp số cộng. Câu 3:
Cho hàm số y  f  x có bảng biến thiên như hình vẽ bên. Hàm số y  f  x nghịch biến trên
khoảng nào trong các khoảng sau đây? x 0  1 1  y' 0    0    y   A.  1  ; 0 . B.  1  ;  1 . C.  ;    1 . D. 0;   . Lời giải Chọn A Trong khoảng  1
 ; 0 đạo hàm y  0 nên hàm số nghịch biến trên khoảng  1  ; 0 . Câu 4:
Cho hàm số y  f  x có bảng biến thiên như hình dưới:
Giá trị cực đại của hàm số đã cho là: A. 1.  B. 3. C. 0 . D. 2.  Lời giải Chọn B Câu 5: Cho hàm số 4 3
y  x  x  3. Khẳng định nào sau đây là đúng?
A. Hàm số có 3 điểm cực trị.
B. Hàm số chỉ có đúng 2 cực trị.
C. Hàm số không có cực trị
D. Hàm số chỉ có đúng 1 điểm cực trị. Lời giải Chọn D Trang32 x  0 (boi 2) 3 2
y  4x  3x  0   3 x   4
Vậy hàm số đã cho có đúng 1 cực trị. Câu 6:
Cho hàm số y  f  x có bảng biến thiên như hình vẽ dưới đây:
Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là: A. 1. B. 4. C. 0. D. 3. Lời giải y Chọn D
Tiệm cận ngang: y  3.
Tiệm cận đứng: x  1; x  1. Câu 7:
Đường cong trong hình dưới là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn
phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào? y 1 x -1 O 1 -1 A. 4 2 y  2
 x  4x 1. B. 4 2
y  x  2x 1. C. 4 2
y  x  4x 1. D. 4 2
y  x  2x 1. Lời giải Chọn A
Ta có đồ thị hàm số đi qua điểm A0;  1 ; B 1;  1 và C  1  ;  1 Trang33 Xét 4 2 y  2
 x  4x 1
Thế tọa độ điểm A0;  
1 thỏa mãn; thế tọa độ điểm B 1;  1 : 1  2  .1 4.11
Thế tọa độ điểm C  1  ;  1 thỏa mãn. Câu 8:
Số giao điểm của đồ thị hàm số 3 2
y  x  2x  x 12 và trục Ox là A. 2 . B.1. C. 3 . D. 0 . Lời giải Chọn B
Phương trình hoành độ giao điểm: 3 2
x  2x  x 12  0  x  3 .
Vậy có một giao điểm duy nhất. Câu 9:
Cho a, b là các số thực dương bất kỳ. Mệnh đề nào sau đây sai? A. 2 2
log(10ab)  2  log(ab) . B. 2
log(10ab)  2(1 log a  log b) . C. 2
log(10ab)  2  2 log(a ) b . D. 2 2
log(10ab)  (1 log a  log b) . Lời giải Chọn D Ta có 2
log(10ab)  2 log(10a )
b  2log10  log ab  2  2log(a ) b 2
 2(1 log a  logb)  2  log(ab) .
Câu 10: Tính đạo hàm của hàm số   2 3 e x f x   . A.   2 3 2.e x f x    . B.   2 3 2.e x f x     . C.   3 2.ex f x    . D.   2 3 e x f x    . Lời giải Chọn A 
Ta có f  x   x   2x3 2 x3 2 3 .e  2.e . 2 1   1  Câu 11: Rút gọn 2 P  a . , a  0.    a  A. 2 a . B. a. C. 2 2 a . D. 1 2 a  . Lời giải Chọn B 2 1  2 1  1     Cách 1: 2 2 P  a .  a    1 a  2 1 2  a a  a .  a  Cách 2: MTCT Trang34
B1: Nhập biểu thức P và trừ đi 1 đáp án tùy ý
B2: Bấm phím CALC máy hiện a ? nhập số dương tùy ý ( chẳng hạn là nhập 2) bấm dấu = nếu
kết quả là số 0 thì nhận nếu khác 0 ta nhấn phím mũi tên sang trái để sửa cho đáp án khác và
lặp lại quy trình trên cho đến khi có đáp án đúng. 4 2
Câu 12: Tổng các nghiệm của phương trình x 3 3 x  81 bằng A. 4 . B. 1. C. 3 . D. 0 . Lời giải Chọn D 2    4 2 4 2 x 1 Ta có x 3x x 3x 4 4 2 3  81  3
 3  x  3x  4   2
 x  4  x  2  . 2  x  4
Vậy tổng các nghiệm của phương trình 4 2 x 3 3 x  81 bằng 0 .
Câu 13: Tập nghiệm của phương trình log x + log (x + 2) = 2 là 3 3 A. S   1   3. B. S   1   10; 1   10. C. S   1   10.
D. S  0;  2 . Lời giải Chọn C
Điều kiện x > 0 . Ta có éx = - 1- 10 ê 2
log x + log (x + 2) = 2 Þ log (x(x + 2)) = log 9 Þ x + 2x - 9 = 0 Û ê 3 3 3 3 x ê = - 1 + 10 ë
Vì x > 0 nên phương trình có nghiệm duy nhất là x = - 1 + 10 . x +
Câu 14: Cho hàm số f (x ) 2 1 =
. Trong các khẳng định sau, khẳng định nào đúng? x A.
f (x)dx  ln x  2x  C  . B.
f (x)dx  x  ln x  C  . C.
f (x)dx  ln x  C  . D.
f (x)dx  ln x  2x  C  . Lời giải Chọn D 2x + 1 1 Ta có dx = 2dx +
dx = 2x + ln x + C ò ò ò . x x
Câu 15: Cho hàm số f (x ) = sin x cos x . Trong các khẳng định sau, khẳng định nào đúng? Trang35 2 sin x A. 2
f (x)dx  sin x  C  . B.
f (x)dx   C  . 2 2 cos x C.
f (x)dx   C  . D. 2
f (x)dx   cos x  C  . 2 Lời giải Chọn B 2 sin x Ta có sin x cos xdx = sin xd(sin x) = + C ò ò . 2 2 12  x  4 Câu 16: Nếu f
 xdx 3 và f dx  2    thì
f  xdx  bằng  3  1 6 1 7 11 A. 5 . B. . C. . D. 1. 3 3 Lời giải Chọn C 12 12 4 4 x æ ö x æ ö x æ ö ç ÷ ç ÷ ç ÷ Ta có f ç dx ÷ = 3 f ç d
÷ ç ÷= 3 f (t)dt = 3 f (x)dx ò ç ÷ ç ÷ ò ç ÷ ò ò . è ø ç ÷ ç ÷ 3 è3ø çè3÷ ø 6 6 2 2 4 2 Suy ra:
f  x dx   . 3 2 4 2 4 2 11 Từ đó suy ra f (x)dx = f (x)dx +
f (x)dx = 3 + = ò ò ò . 3 3 1 1 2 e Câu 17: Tích phân ln xdx ò bằng 1 A. e . B. e 1. C. e 1. D. 1. Lời giải Chọn D e e ln = ln e xdx x x -
dx = e - (e - 1) = 1 ò ò . 1 1 1
Câu 18: Tổng phần thực và phần ảo của số phức liên hợp của z = 2 - 3i là A. 1. B. 5 . C. 5  . D. 1. Lời giải Chọn B
Số phức liên hợp là z = 2 + 3i . Do đó tổng cần tìm bằng 5 .
Câu 19: Cho hai số phức z  2  i và z  7  3i . Tìm số phức z  z  z . 1 2 1 2 Trang36 A. z  5   2i .
B. z  9 . C. z  4  i .
D. z  9  4i . Lời giải Chọn A.
Ta có z  z  z  2  i  7  3i  2  i  7  3i  5   2i . 1 2    
Câu 20: Trên mặt phẳng tọa độ, cho số phức 1 i z  3  i , điểm biểu diễn số phức z là A. 3; 2 . B. 1; 2   . C. 2;  1  . D.  1  ;2 . Lời giải Chọn B. 3  i
3i1i
Ta có: 1 i z  3  i  z   z 
 z 12i . 1 i
1i1i
Vậy điểm biểu diễn số phức z là M 1; 2  .
Câu 21: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , cạnh SA vuông góc với đáy và
SA  2a . Thể tích khối chóp S.ABCD bằng 3 4a 3 a 3 2a A. . B. 3 2a . C. . D. . 3 3 3 Lời giải Chọn D. 3 1 1 2a
Ta có thể tích khối chóp S.ABCD là 2 V  .S
.SA  .a .2a  . S . ABCD 3 ABCD 3 3
Câu 22: Thể tích của một khối hộp chữ nhật có các cạnh 2c , m 4c ,
m 7cm là A. 3 56cm . B. 3 36cm . C. 3 48cm . D. 3 24cm . Lời giải Chọn A.
Ta có thể tích của khối hộp chữ nhật có các cạnh 2c , m 4c ,
m 7cm là V    3 2.4.7 56 cm  .
Câu 23: Cho khối nón có bán kính đáy bằng a và đường cao 2a . Thể tích của khối nón đã cho bằng 3 2 a 3 3 a 3  a A. . B. . C. 3  a . D. . 3 2 2 Lời giải Chọn A. Trang37 h r 3 1 1 2 Thể tích khối nón là 2 2     .2  a V r h a a . 3 3 3
Câu 24: Cho hình trụ có độ dài đường sinh bằng 6 , diện tích xung quanh bằng 48 . Bán kính hình tròn
đáy của hình trụ đó bằng A. 1. B. 8 . C. 4 . D. 2 . Lời giải Chọn C. Ta có S
 2 Rl  48  6.2 R  R  4 . xq
Câu 25. Trong không gian với hệ tọa độ Oxyz , cho A2;0;0 , B0;3;4 . Độ dài đoạn thẳng AB là:
A. AB  3 3 .
B. AB  2 7 .
C. AB  19 . D. AB  29 . Lời giải Chọn D Ta có: AB    2 2 2 0 2  3  4  29 .
Câu 26.Trong không gian Oxyz , cho hai điểm A 2  ;1;  1 , B 0; 1  ; 
1 . Phương trình mặt cầu đường kính AB là: 2 2 2 2 A.  x   2
1  y   z   1  2. B.  x   2
1  y   z   1  4. 2 2 2 2 C.  x   2
1  y   z   1  8 . D.  x   2
1  y   z   1  2 . Lời giải Chọn A AB
Mặt cầu đường kính AB nhận trung điểm I của AB là tâm và bán kính R  . 2 AB Ta có I  1  ;0;  1 và R   2 . 2 2 2
Vậy phương trình mặt cầu là  x   2
1  y   z   1  2.
Câu 27. Cho biết phương trình mặt phẳng  P:ax  by  cz 13 0 đi qua 3 điểm A1; 1
 ;2, B2;1;0 ,
C 0;1;3 . Khi đó a  b  c bằng A.11. B. 11  . C. 10  . D. 10 . Lời giải Chọn A Trang38
Do  P:ax  by  cz 13 0 đi qua 3 điểm A1; 1
 ;2, B2;1;0,C 0;1;  3 nên ta có hệ
a b  2c 13 a 6  
2a  b 13  b
 1 a b  c 11.   b  3c 13 c  4  
Câu 28.Trong không gian Oxyz cho ba điểm A1; 2  ;0, B(2; 1  ;3),C 0; 1  ; 
1 . Đường trung tuyến AM
của tam giác ABC có phương trình là x 1 x 1 2t x 1 t x 1 2t     A. y  2   t . B.  y  2  . C. y  2  . D. y  2   t .     z  2t  z  2  t  z  2  t  z  2t  Lời giải Chọn A  A1; 2  ;0, M 1; 1
 ;2; AM  0;1;2 x 1 
Đường trung tuyến AM của tam giác ABC có phương trình là y  2   t z  2t 
Câu 29.Trên giá sách có 4 quyển sách Toán, 3 quyển sách Lí và 2 quyển sách Hóa, lấy ngẫu nhiên 3
quyển sách. Tính xác suất sao cho ba quyển lấy ra có ít nhất một quyển sách Toán. 37 5 10 42 A. . B. . C. . D. . 42 42 21 37 Lời giải Chọn A
Số phần tử không gian mẫu n  3  C  84 . 9
Gọi biến cố A: “Ba quyển lấy ra có ít nhất 1 quyển Toán”.
Ta có n  A 1 2 2 1 3
 C .C  C .C  C  74 . 4 5 4 5 4 n A 74 37
Xác suất của biến cố A là P  A      . n  84 42 10 37
Nhận xét: Có thể dùng biến cố đối n  A 3
 C  10  P A  1 P A  1  . 5     84 42
Câu 30. Hàm số nào trong các hàm số sau đây nghịch biến trên  ? x A. y  log x . B. 9x y  .
C. y  log x .
D. y  0,9 . 0,9 9 Lời giải Chọn D Hàm số: y  log
x nghịch biến trên 0;  . 0,9 Hàm số: 9x y  đồng biến trên  .
Hàm số: y  log x đồng biến trên 0;  . 9 x
Hàm số: y  0,9 nghịch biến trên  . Vậy đáp án D đúng. Trang39 1 5 Câu 31: Hàm số 3 2 y = x -
x + 6x + 1 đạt giá trị lớn nhất và giá trị nhỏ nhất trên đoạn [1;3] lần lượt 3 2
tại hai điểm x và x . Khi đó x + x bằng 1 2 1 2 A. 2 . B. 4 . C. 5 . D. 3 . Lời giải Chọn D
Tập xác định: D =  . x é = 2 Î [1; ] 3 2
y¢= x - 5x + 6 ; 2
y¢= 0 Û x - 5x + 6 = 0 ê Û ê . x = 3 Î ê [1; ] 3 ë 29 17 11 Ta có: y ( ) 1 = , y(2)= , y( ) 3 = . 6 3 2  y  17 max  x   2 1  Do đó,   ;3  3 .  y  29 min  x   1 1     ;3 6
Vậy hàm số đạt giá trị lớn nhất và giá trị nhỏ nhất trên đoạn [1;3] lần lượt tại hai điểm x = 2 1
và x = 1 Þ x + x = 3. 2 1 2 2  x 3x  1  1
Câu 32: Tìm tập nghiệm S của bất phương trình    .  2  4
A. S  1;2 .
B. S    ;1 .
C. S  1; 2 .
D. S  2;   . Lời giải Chọn C 2 2 x 3x x 3x 2  1  1  1   1  Ta có : 2 2   
 x  3x  2  x  3x  2  0  1 x  2       .  2  4  2   2 
Vậy tập nghiệm của bất phương trình đã cho là S  1; 2 . 2 2 2 f
 xdx  2
g  xdx  1   I  x  2 f  
x3g xdx  Câu 33: Cho 1  và 1  . Tính 1  . 17 5 7 11 A. I  . B. I  . C. I  . D. I  . 2 2 2 2 Lời giải Chọn A 2 2 2 2 2 x 3 Ta có: I  x  2 f  
x3gxdx    2 f
 xdx3 g
 xdx   2.23 1  17 . 2 2 2 1  1  1  1 
Câu 34: Cho số phức z 1 2i . Tìm tổng phần thực và phần ảo của số phức w  2z  z . A. 3 . B. 5 . C. 1. D. 2 . Lời giải Chọn B
Ta có z 1 2i  z 1 2i Trang40
w  2z  z  2(1 2i) 1 2i  3 2i
Vậy tổng phần thực và phần ảo của số phức w là 5 .
Câu 35: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB  2, AD  5 . Cạnh bên
SA  3 và vuông góc với mặt phẳng đáy (tham khảo hình bên). Góc giữa đường thẳng SC và
mặt phẳng  ABCD bằng A. 30 .  B. 45 .  C. 60 .  D. 90 .  Lời giải Chọn A.
AC là hình chiếu vuông góc của SC trên mặt phẳng  ABCD
 SC  ABCD  ,  SCA SA 3 Xét S
 CA vuông tại A có   0
SA  3, AC  3  tan SCA    SCA  30 . CA 3
Câu 36: Cho hình lăng trụ AB .
C A' B 'C ' có đáy là tam giác đều cạnh bằng 2 . Biết
A' A  A' B  A'C  2 . Khoảng cách từ A ' đến mặt phẳng  ABC  bằng A' B' A C H B 2 6 2 3 2 3 2 2 A. . B. . 3 3 . C. 6 . D. 3 Lời giải Chọn A
Gọi H là tâm đường tròn ngoại tiếp ABC  .
Do A' A  A' B  A'C nên A' H   ABC  d  A', ABC  A' H . 2 2 3 2 3 2 6 Xét A
 ' AH vuông tại H có 2 2
A' A  2, AH  . 
 A' H  A' A  AH  . 3 2 3 3
Câu 37: Trong không gian Oxyz, mặt cầu có tâm I 1;0; 2 và tiếp xúc với mặt phẳng Oyz có phương trình là: Trang41 2 2 2 2 A.  x   2
1  y   z  2  1. B.  x   2
1  y   z  2 1. 2 2 2 2 C.  x   2
1  y   z  2  2. D.  x   2
1  y   z  2  4. Lời giải Chọn B
Gọi H là hình chiếu vuông góc của I trên mặt phẳng Oyz  H 0;0;2 2 2
Có R  IH  1, suy ra phương trình mặt cầu cần tìm là  x   2
1  y   z  2 1.
Câu 38: Trong không gian Oxyz, đường thẳng đi qua điểm M 1;3; 2
  và song song với đường thẳng x  2 y z 1 d :   2 1
 có phương trình tham số là: 3 x 1 2t x 1 2t x  2  t x  1   2t    
A.  y  3  t . B.  y  3 . C.  y  1   3t . D.  y  3   t .     z  2   3t  z  2   t  z  3   2t  z  2  3t  Lời giải Chọn A. 
Đường thẳng d có VTCP u  2; 1  ; 3  d   
Vì đường thẳng cần lập song song với d nên có VTCP u  u  2; 1  ; 3  d  x 1 2t 
Vậy đường thẳng cần lập có phương trình tham số là  y  3  t . z  2   3t 
Câu 39: Cho hàm số f  x , đồ thị hàm số y  f  x là đường cong trong hình bên. Giá trị lớn nhất của
hàm số g  x   f 2x  
1  2x trên đoạn 0;2 bằng A.  f   1  2 .
B.  f   1 .
C.  f 2  3 .
D.  f 3  4 . Lời giải Chọn C Trang42  2x 1  1 x  0  
g x  0  2
 f 2x  
1  2  0  f 2x  
1  1  2x 1  1  x  1   . 2x 1  2  3  x   2 x  0    
g x   f  x   2x 1 1 0 2 1  1     3 . 2x 1  2 x   2 Bảng biến thiên  3 
Giá trị lớn nhất của hàm số g  x trên 0;2 bằng g   f   23 .  2 
Câu 40.Có bao nhiêu số nguyên dương y sao cho ứng với mỗi y có không quá 25 số nguyên x thỏa x 1 1 2  mãn 4  0 ?  2 x y A. 30
B.31C. 32 D. 33 Chọn B x  0 
Điều kiện:  y  2 x  0 y 1   x 1 1 2   0 x  3   + Trường hợp 1:  4    x   x  y  x  log 2 0 2 y  2  0  x 1 1 2   0 x  3   + Trường hợp 2:  4    x  y x  log 2 2 y  2  0
Kết hợp điều kiện: x  0; log y  log 1  0 . Ta có : 0  x  log y 2 2 2 2 Trang43
Để có không quá 25 số nguyên x thì 1  log y2  25 1  log y  5  2  y  32 2 2
 y 2;3;...;3  2 . Có 31 số nguyên y.
x  m , x  0
Câu 39: Cho hàm số f  x liên tục trên  thỏa mãn f  x  
(m là hằng số). Biết 2 x e , x  0 2   b
f x dx  a  
trong đó a, b là các số hữu tỉ. Tính a  b . 2 e 1  A. 4 . B. 3 . C. 0 . D. 1. Lời giải Chọn A Do hàm số liên tục trên  nên hàm số liên tục tại
x  0  lim f  x  lim f  x  f 0  m  1   x0 x0 2 0 2 0 2 Khi đó ta có  d   d    2 d x f x x f x x
f x x  e dx   x        1 dx 1  1  0 1  0 0 2 2 x 2 2 e  x  1 e 9 1 
   x    4   . 2 2  2  2 2 2 2e 1  0 Do đó 9 1 a  ; b   . 2 2
Vậy a  b  4 . z 1 z  3i
Câu 42: Có bao nhiêu số phức z thỏa mãn  1? z  i z  i A. 3 . B. 0 . C. 2 . D. 1. Lời giải Chọn D
Ta có: Gọi z  a  bi a,b    . Ta có:
 z 1  z  i    a  2
1  b  a  b   2 2 2 1  2  a 1  2  b 1 a 1        .
 z  3i  z  i         a  
b 32  a b  2 2 2 1 6b 9 2b 1 b 1
Vậy có một số phức thỏa mãn là z  1 i . 
Câu 43: Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O cạnh a , góc BCA  30 , 3a
SO   ABCD và SO 
. Khi đó thể tích của khối chóp là 4 3 a 2 3 a 3 3 a 2 3 a 3 A. . B. . C. . D. . 4 8 8 4 Lời giải Chọn B Trang44 s 3a 4 B A 30 O C a D
Theo giả thiết ABCD là hình thoi tâm O cạnh a , góc  BCA  30 nên 
BCD  60 ; B  CD đề a 3
u suy ra BD  a , CO 
, AC  2CO  a 3 . 2 1 2 1 a 3 1 3a Ta có S
 AC.BD  . . a a 3  ; V  S . O S với SO  suy ra ABCD 2 S . ABCD ABCD 2 2 3 4 2 3 1 3a a 3 a 3 V     . S.ABCD 3 4 2 8
Câu 44. Từ một tấm thép phẳng hình chữ nhật, người ta muốn làm một chiếc thùng đựng dầu hình trụ
bằng cách cắt ra hai hình tròn bằng nhau và một hình chữ nhật (phần tô đậm) sau đó hàn kín lại,
như trong hình vẽ dưới đây. Hai hình tròn làm hai mặt đáy, hình chữ nhật làm thành mặt xung
quanh của thùng đựng dầu (vừa đủ). Biết rằng đường tròn đáy ngoại tiếp một tam giác có kích
thước là 50cm, 70cm,80cm (các mối ghép nối khi gò hàn chiếm diện tích không đáng kể. Lấy
  3,14 ). Diện tích của tấm thép hình chữ nhật ban đầu gần nhất với số liệu nào sau đây? A. 6, 8  2 m  . B. 24, 6  2 m  . C. 6,15  2 m  . D. 3, 08  2 m  . Lờigiải ChọnC Đổi: 50cm  0,5 ;
m 70cm  0, 7 ;
m 80cm  0,8m .
Xét tam giác nội tiếp đường tròn đáy có kích thước lần lượt là 0, 5 ; m 0, 7 ;
m 0,8m nên bán kính
đường tròn đáy của thùng đựng dầu là 0,5.0, 7.0,8 7 3 R   .
4 11 0,51 0,71 0,8 0 3
Ta có h  2R
Diện tích hình chữ nhật ban đầu gấp 3 lần diện tích xung quanh của hình trụ. Trang45 2  7 3  7693 Vậy 2
S  3.2 Rh  6.3,14.2.R  6.3,14.2    6,1544 2   m  . 30 1250   x 1 y 1 z 1 x 1 y  3 z 1
Câu 45. Trong không gian Oxyz ,cho 2 đường thẳng d :   , d ' :   và 1 2 1 2 1 2 
mặt phẳng  P : 2x  y  z  3  0 . Biết rằng đường thẳng  song song với mặt phẳng  P , cắt
các đường thẳng d , d lần lượt tại M , N sao cho MN  11 ( điểm M có tọa độ ngyên).
Phương trình của đường thẳng  là x y 1 z  2 x y 1 z  2 A.   . B.   . 1 1 3 1 2  4 x y 1 z  2 x y 1 z  2 C.   . D.   . 1 1 3  1 2 4 Lời giải Chọn C Gọi M  1   ; a 1   2 ;
a 1 a  d ( a¢ ) , N  1   2 ; b 3  ;
b 1 2b d .  
MN  2b  ;
a b  2a  4; 2
 b  a . Một vectơ pháp tuyến của của P là n  2;1;  1 .   
Ta có //  P  MN.n  0  5
 a  b  4  0  b  5a  4  MN  9a 8;7a  8;11a  8 a 1 2 2  MN  11 
251a  432a 192  11  251a  432a 181  0  181  . a  (l)  251  
Suy ra  có một vectơ chỉ phương của u  MN  1;1; 3
  và  đi qua M 0;1;2 . x y 1 z  2
Vậy phương trình đường thẳng  là   . 1 1 3 
Câu 46: Cho f  x là hàm số bậc bốn thỏa mãn f   1 0  
. Hàm số f  x có bảng biến thiên như ln 2 sau: 2x
Hàm số g  x  f x  2 2 2  x 
có bao nhiêu điểm cực trị? ln 2 A. 3 . B. 2 . C. 4 . D. 5 . Lời giải Trang46 Chọn D 3 9 5
Từ bảng biến thiên, ta tìm được f  x 3
  x  x  . 4 4 2 x Đặ 2
t h  x  f x  2 2 2  x 
. Ta có h    f   1 0 0   0 . ln 2 ln 2
       2 x         2 2 2 2 2 2 2 2 1 2x h x x f x x x x f x    ,   h x x 0  0   .  f   x  2 2  2x 1 (*) Đặt 2
t  x , t  0 . Phương trình (*) trở thành: f t   u t  , với   2 t u t   1
Từ đồ thị ta thấy phương trình f t   u t   t  t , với t  1  . 0 0
Từ đó, phương trình (*) 2
 x  t  x   t . 0 0 Bảng biến thiên
Từ bảng biến thiên suy ra hàm số g  x  h x có 5 điểm cực trị.
Câu 47: Cho các số thực x, y, z thỏa mãn log  2 2x  2 y   log  3 x  3 2y log z . Có bao giá 3 7  
trị nguyên của z để có đúng hai cặp  x, y thỏa mãn đẳng thức trên. A. 2 . B. 211 . C. 99 . D. 4. Lời giải Chọn B 2 2
2x  y  3t 1  Ta có log  2 2
2x  y   log  3 3 x  2y  3 3
 log z  t  x  2y  7t 2 . 3 7   z   10t  3 Trang47 log 2 t 2t 3 3 + Nếu t y  0   3
2  x  7 thay vào   1 ta được 3 2.7  3  t  log 2 do đó z  49 10 . 3 3 49 + Nếu y  0  3 2  x   2 2 2x  3 2  2 y   27t  3x  3 2y      t  y   t 49       49  Từ   1 & 2 suy ra      , * . 2 3   3      3x  3 2y   49t  2 2x  2 y   27   2   27   x    2   2 1   y       u 0 u  22 3 6u 3
u  2u  4   x  Đặ 3 t 3
 u,u   2 . Xét f u   f  u 0 u 2 . 3      4    y  2 2u  1  2 2u  1 u   4 Ta có bảng biến thiên
Nhận xét với mỗi giá trị u tương ứng với duy nhất 1 cặp  x, y thỏa mãn bài toán do đó t  1  49   1   log   log 4    49 49   4  8   27 27 8  27  10  z  10
Yêu cầu bài toán tương đương    . t  4  log    49  49 4    33    27 0     0  z  10   27  33
Vì z là số nguyên nên có 211 giá trị thỏa mãn. Câu 48: Cho hàm số 4 2
y  x  3x  m có đồ thị C
, với m là tham số thực. Giả sử C cắt trục Ox m  m 
tại bốn điểm phân biệt như hình vẽ Trang48
Gọi S , S , S là diện tích các miền gạch chéo được cho trên hình vẽ. Giá trị của m để 1 2 3
S  S  S là 1 3 2 5 5 5 5 A. . B.  . C. . D.  . 4 4 2 2 Lời giải Chọn A
Gọi x là nghiệm dương lớn nhất của phương trình 4 2
x  3x  m  0 , ta có 4 2
m  x  3x   1 . 1 1 1 1 x
Vì S  S  S và S  S nên S  2S hay f
 xdx  0. 1 3 2 1 3 2 3 0 x 1 x 1 x 1 5  x  5 x 4  x  Mà
f  x dx    4 2
x  3x  mdx 3
   x  mx 1 3   x  mx 1 2
 x   x  m .  1 1 5  1 1 5  5  0 0 0 4  x  4 Do đó, x 1 2 x 
 x  m  0  1 2
 x  m  0 2 . 1 1  5  1 5 4 Từ   x 5
1 và 2 , ta có phương trình 1 2 4 2
 x  x  3x  0  4 2 4
 x 10x  0  2 x  . 1 1 1 5 1 1 1 2 Vậy 4 2 m  x  5 3x  . 1 1 4
Câu 49: Xét hai số phức
z  1; z  4 và z  z 
. Giá trị lớn nhất của 1
z ; z thỏa mãn 2 1 2 1 2 5   1 z 2z2 7i bằng A. 7  89 . B. 7  89 . C. 7  2 89 . D. 7  2 89 . Lời giải Chọn B
Đặt z = a + bi, z = c + di với a, , b ,
c d Î ¡ . Theo giả thiết thì 1 2 2 2 2 2 2 2
a + b = 1, c + d = 16, (a - c) + (b - d ) = 5. Do đó 2 2 2 2
a - 2ac + c + b - 2bd + d = 5 Þ ac + bd = 6.
Ta có z + 2z = (a + 2c) + (b + 2d )i nên 1 2 2 2 2 2 2 2 z + 2z =
(a + 2c) + (b + 2d ) =
a + b + 4(c + d ) + 4(ac + bd ) = 89. 1 2
Áp dụng bất đẳng thức z + z¢£ z + z¢ , ta có ngay
z + 2z - 7i £ z + 2z + - 7i = 7 + 89 1 2 1 2
Câu 50: Trong không gian Oxyz , cho hai điểm (
A 1;3; 0), B(3;1; 4) và đường thẳng x  2 y 1 z  2  :  
. Xét khối nón (N ) có đỉnh có tọa độ nguyên thuộc đường thẳng  và 1 1 3
ngoại tiếp mặt cầu đường kính AB . Khi (N ) có thể tích nhỏ nhất thì mặt phẳng chứa đường
tròn đáy của (N ) có phương trình dạng ax  by  cz 1  0 . Giá trị a b  c bằng A. 1. B. 3 . C. 5 . D. 6.  Lời giải Trang49 Chọn A
Mặt cầu đường kính AB có tâm I (1; 2; 2) , bán kính 3 .
Gọi H , r lần lượt là tâm và bán kính đường tròn đáy của (N ) , C là đỉnh của (N ) .
Khi đó C, I , H thẳng hàng ( I nằm giữa C, H ), IH  IK  3
Đặt CI  x IK CK IK.CH 3(x  3) C
 IK đồng dạng C  MH nên   r  HM   2 MH CH CK x  9 1 1  3 x  3 2  x 32 2 V
 r .CH    .(x  3)  3 ( N ) 2 3 3   x  3 x 9  x  2 2 3 x  6x  9 V
nhỏ nhất  f (x)  
nhỏ nhất (x  3) ( N ) x  3 x  3 2 x  6x  27 f '(x)  x  3 x  3 
f '(x)  0   x  9 V
nhỏ nhất  x  9 , khi đó IC  9 nên 2 2 2
C  (S) : (x 1)  ( y  2)  (z  2)  81 ( N )  43 32 41 
Mặt khác C  nên C  1  ;2;1  1 hoặc C ;  ;     11 11 11 
Vì C có tọa độ nguyên nên C  1  ;2;1  1  1  IH   IC nên H ( 1  ;2; 1  ) 3 Trang50 
Mặt phẳng chứa đường tròn đáy của (N ) đi qua H và nhận IH  (0;0;3) làm vectơ pháp
tuyến nên phương trình mặt phẳng là z 1  0
Do đó a  0,b  0, c  1 nên a b  c 1 Đề 8
ĐỀ LUYỆN THI CẤP TỐC TỐT NGHIỆP THPT NĂM 2021 Thuvienhoclieu.Com BÀI THI: TOÁN
Thời gian: 90 phút Câu 1:
Có bao nhiêu cách sắp xếp 5 học sinh đứng thành một hàng dọc? A. 5! . B. 3 5 . C. 5 C . D. 1 A . 5 5 Câu 2:
Cho cấp số nhân u có u  2 và công bội q  3. Giá trị của u là: n  1 3 A. 6  . B. 18  . C. 18 . D. 4  . Câu 3:
Cho hàm số y  f  x có bảng biến thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào trong các khoảng dưới đây? A.  2  ;0 . B.  2  ;  1 . C. 3;  . D.  1  ;. Câu 4: Cho hàm số bậc ba 3 2
y  ax  bx  cx  d a  0 có đồ thị như sau
Giá trị cực đại của hàm số là: A. x  2 . B. y  4 . C. x  0 . D. y  0 . Trang51 2 Câu 5:
Cho hàm số y  f  x xác định trên  có đạo hàm f  x  x  x   x    2 ' 2 1 x  4 . Hàm số
đã cho có bao nhiêu điểm cực trị A. 3. B. 4 . C. 2 . D. 1. 1 Câu 6:
Tiệm cận ngang của đồ thị hàm số y  1 x  là đường thẳng: 1 A. x 1 . B. y  1. C. y  1. D. y  0 . Câu 7:
Đường cong ở hình dưới đây là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào ? 1 1 1 1 A. 3 y  x  x 1. B. 3 y  x  x 1. 9 3 9 3 1 C. 4 2 y 
x  x 1. D. 3 2
y  x  x  x 1. 4 4 x 3 Câu 8: Đồ thị hàm số 2 y  
 x  cắt trục hoành tại mấy điểm? 2 2 A. 4 B. 3 C. 2 D. 0 Câu 9:
Với a là số thực dương tùy ý, log 125a bằng 5  
A. 3  log a .
B. 3  log a .
C. log a .
D. 2  log a . 5 3 5 5 5
Câu 10: Đạo hàm của hàm số 1 2 x y e   là: 12 x e A. 1 2 ' 2 x y e   . B. 1 2 ' 2 x y e    . C. y '   . D. 1 2 ' x y e   2
Câu 11: Với a là số thực tuỳ ý, 3 5 a bằng 3 5 A. 3 a . B. 5 a . C. 3 a . D. 2 a .
Câu 12: Tổng các nghiệm của phương trình 4 2 x 3 3 x  81 bằng A. 0. B. 1. C. 3. D. 4.
Câu 13: Nghiệm của phương trình log 2x  2 là: 3   3 9 A. x  .
B. x  3. C. x  . D. x 1 . 2 2 Trang52
Câu 14: Cho hàm số f  x 3
 4x  2021. Trong các khẳng định sau, khẳng định nào đúng? A. f  x 4
dx  4x  2021x  C . B. f  x 4
dx  x  2021x  C . C. f  x 4
dx  x  2021. D. f  x 4
dx  x  C .
Câu 15: Cho hàm số f  x  sin 3x . Trong các khẳng định sau, khẳng định nào đúng? A. f  x 1 dx 
cos 3x  C . B. f  x 1
dx   cos 3x  C . 3 3 C. f
 xdx 3cos3xC . D. f
 xdx  3
 cos3x  C . 2 3 3 Câu 16: Nếu f
 xdx  2 và f xdx  7   thì
f  xdx  bằng 1 1 2 A. 5  . B. 9 . C. 9  . D. 14 . ln 3 Câu 17: Tích phân x e dx  bằng 0 A. 2 . B. 3 . C. e . D. e 1.
Câu 18: Số phức liên hợp của số phức z  3 4i là:
A. z  3  4i .
B. z  4  3i .
C. z  4  3i .
D. z  3  4i .
Câu 19: Cho hai số phức z  3  5i và z  6
 8i . Số phức liên hợp của số phức z  z là 1 2 2 1 A. 9  13i . B. 3  3i . C. 3  3i . D. 9  13i .
Câu 20: Trên mặt phẳng tọa độ, điểm biểu diễn số phức liên hợp của số phức 23  5i có tọa độ là A. 23; 5   . B. 23;5 . C.  2  3; 5   . D.  2  3;5 .
Câu 21: Thể tích khối lăng trụ tam giác đều có cạnh đáy bằng 2 và chiều cao bằng một nửa cạnh đáy là A. 2 3 B. 3 C. 3 D. 6
Câu 22: Cho khối hộp có đáy là hình vuông cạnh bằng 5 và chiều cao khối hộp bằng một nửa chu vi
đáy. Thể tích của khối hộp đã cho bằng A. 3 250cm . B. 3 125cm . C. 3 200cm . D. 3 500 cm .
Câu 23: Công thức tính thể tích V của hình nón có diện tích đáy 2
S  4 R và chiều cao h là: 1 4 2 A. 2 V   R h . B. 2 V   R h . C. 2 V   R h . D. V   Rh . 3 3 3
Câu 24: Một hình trụ có bán kính R  6 cm và độ dài đường sinh l  4cm. Tính diện tích toàn phần của hình trụ đó. A. 2 S  120cm . B. 2 S  84cm . C. 2 S  96cm . D. 2 S  24cm . tp tp tp tp Trang53
Câu 25: Trong không gian Oxyz, cho tam giác ABC biết A1;1;3, B  1  ;4;0,C 3  ;2;  3 . Trọng
tâm G của tam giác ABC có tọa độ là  3  3  A.  3  ;3;0 . B. ; ; 0  . C.  1  ;1;0 . D. 1; 1  ;  1 .  2 2  2 2 2
Câu 26: Trong không gian Oxyz, mặt cầu S  :  x   1   y   1
 z 3  9 . Tâm I của mặt cầu (S) có tọa độ là A. 1; 1  ; 3  . B.  1  ;1;3. C. 2; 2  ; 6   . D.  2  ;2;6 .
Câu 27: Trong không gian Oxyz, cho mặt phẳng  P có phương trình 2x  y  z  3  0 . Điểm nào sau
đây thuộc mặt phẳng P ? A. M 1; 1  ; 3   . B. N  1  ;1;0. C. H 2; 2  ;6 . D. K  2  ;2;3 .
Câu 28: Trong không gian Oxyz, vectơnào dưới đây không phải là vectơ chỉ phương của đường thẳng x 1 y 1 z d :   2 1  ? 2    
A. u  2; 1; 2 . B. u  2;1; 2  .
C. u  4; 2; 4 . D. u  1; 1  ;0 4   3   2   1  
Câu 29: Có 30 chiếc thẻ được đánh số thứ tự từ 1 đến 30. Chọn ngẫu nhiên một chiếc thẻ. Tính xác suất
để chiếc thẻ được chọn mang số chia hết cho 3. 1 1 3 2 A. . B. . C. . D. . 3 2 10 3
Câu 30: Hàm số nào sau đây nghịch biến trên  ? 3x  2 A. 4 2
y  x  4x 1. B. 3
y  x  x 1 . C. y 
y   x  . x  . D. 2 2 3 1 Câu 31: Cho hàm số 3
y  x  3x  4 . Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm
số trên đoạn 0; 2 . Khẳng định nào sau đây đúng?
A. M  m  8 .
B. 2M  m  2  .
C. M  2m 10 .
D. M  m  8  . x  x 1
Câu 32: Bất phương trình mũ 2 3 5  có tập nghiệm là 25 3 17 3 17   3  17  3 17  A. T   ;  .
B. T    ;     ;    . 2 2   2 2    
C. T  1; 2 .
D. T   ;   1 2; . 2 5 5 Câu 33: Biết f
 xdx 3, f
 xdx  4. Tính 2f x xdx 1 1 2 Trang54 25 17 A. . B. 23. C. . D. 19 . 2 2
Câu 34: Cho số phức z thỏa mãn z 1 2i  1 4i . Phần thực của số phức z thuộc khoảng nào dưới đây?  3  A. 0; 2 . B.  2  ;  1 . C.  4  ; 3   . D.  ; 1    .  2 
Câu 35: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a . Đường thẳng SA vuông góc với mặt
phẳng  ABCD , SA  a . Góc giữa hai mặt phẳng SCD và  ABCD là  . Khi đó, tan
nhận giá trị nào trong các giá trị sau ? 2
A. tan  2 . B. tan  .
C. tan   3 . D. tan 1. 2
Câu 36: Cho hình chóp tứ giác đều S.ABCD , đáy có tâm là O và SA  a, AB  a . Khi đó, khoảng
cách từ điểm O đến mặt phẳng SAD bằng bao nhiêu ? a a a A. . B. . C. . D. a . 2 2 6
Câu 37: Trong không gian với hệ tọa độ Oxyz , cho hai điểm A1;1;0 và B 1; 1;  4 . Viết phương
trình mặt cầu S  nhận AB làm đường kính . 2 2 2 2 A. S  2
: x   y  
1   z  2  5 .
B. S   x   2 :
1  y   z  2  20 . 2 2 2 2
C. S   x   2 :
1  y   z  2  20 .
D. S   x   2 :
1  y   z  2  5 .
Câu 38: Trong không gian với hệ tọa độ Oxyz , cho điểm M  2
 ;3;4 . Viết phương trình đường thẳng
d  qua điểm M và vuông góc với mặt phẳng Oxy. x  2  x  2   t x  2  x  2   t    
A. d  :  y  3  t .
B. d  :  y  3
. C. d  :  y  3 .
D. d  :  y  3  t .     z  4 z  4 z  4  t z  4  t
Câu 39: Cho hàm số f  x, đồ thị của hàm số /
y  f  x là đường cong như hình vẽ. Giá trị nhỏ nhất 1 
của hàm số g  x  f 2x  
1  6x trên đoạn ; 2   bằng  2  Trang55  1  A. f   .
B. f 0  3 . C. f   1  6 .
D. f 3 12.  2 
Câu 40: Có bao nhiêu số nguyên dương y sao cho ứng với mỗi y có không quá 2186 số nguyên x thỏa mãn log  3x x y  9  0 ? 3  A. 7 . B. 8 . C. 2186 . D. 6 . 2
Câu 41: Cho hàm số y  f  x  1, y  g  x  x . Giá trị I  min
 f x;gxdx 1  3 5 A. 1. B. . C. 2 . D. . 2 2
Câu 42: Có tất cả bao nhiêu số phức z mà phần thực và phần ảo của nó trái dấu đồng thời thỏa mãn
z  z  z  z  4 và z  2  2i  3 2. A. 1. B. 3 . C. 2 . D. 0 .
Câu 43: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A và có AB  ,
a BC  a 3 . Mặt
bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng  ABC  . Tính thể
tích V của khối khóp S.ABC . 3 2a 6 3 a 6 3 a 6 3 a 6 A. V  . B. V  . C. V  . D. V  . 12 6 12 4
Câu 44: Ông An cần làm một đồ trang trí như hình vẽ. Phần dưới là một phần của khối cầu bán kính
20 cm làm bằng gỗ đặc, bán kính của đường tròn phần chỏm cầu bằng 10 cm . Phần phía trên
làm bằng lớp vỏ kính trong suốt. Biết giá tiền của 2
1 m kính như trên là 1.500.000 đồng, giá triền của 3
1 m gỗ là 100.000.000 đồng. Hỏi số tiền (làm tròn đến hàng nghìn) mà ông An mua
vật liệu để làm đồ trang trí là bao nhiêu. a 20cm 10cm A. 1.000.000 B. 1.100.000 C. 1.010.000 D. 1.005.000 . . . x y z 1 x  3 y z 1
Câu 45: Trong không gian Oxyz , cho ba đường thẳng d :   ,  :   , 1 1 2 1 2 1 1 x 1 y  2 z  : 
 . Đường thẳng  vuông góc với d đồng thời cắt  , tương ứng tại 2 1 2 1 1 2
H , K sao cho HK 
27 . Phương trình của đường thẳng  là Trang56 x 1 y 1 z x 1 y 1 z x 1 y 1 z x 1 y 1 z A.   . B.     . D.   1 1 1 1 1  . C. 1 2 1 1 3  3  . 1
Câu 46: Cho hàm số y  f  x có đạo hàm f  x 3 '
 4x  2x và f 0 1. Số điểm cực tiểu của hàm số g  x 3  f  2
x  2x  3 là A. 0 . B. 2 . C. 1. D. 3 . 
Câu 47: Tổng các nghiệm của phương trình sau x 1 7
 6log 6x 5 1 bằng 7   A. 2 . B. 3 . C. 1. D. 10 .
Câu 48: Cho parabol  P  2
: y  x  4 cắt tru ̣c hoành ta ̣i hai điểm
A , B và đường thẳng d : y  a 1
0  a  4 . Xét parabol P đi qua A , B và có đỉnh thuộc đường thẳng y  a . Gọi S là 2  1
diê ̣n tích hình phẳng giới ha ̣n bởi P và d . S là diện tích hình phẳng giới hạn bởi P và 2  1  2
trục hoành. Biết S  S (tham khảo hình vẽ bên). 1 2 y M N
y = a A B O x Tính 3 2
T  a  8a  48a . A. T  99 . B. T  64 . C. T  32 . D. T  72 .
Câu 49: Cho hai số phức u, v thỏa mãn u = v = 10 và 3u - 4v = 50 . Tìm Giá trị lớn nhất của biểu
thức 4u + 3v - 10i . A. 30 . B. 40 . C. 60 . D. 50 . 2 2 2
Câu 50:Trong hệ trục Oxyz , cho hai mặt cầu
S : x 1  y 3  z 2  49 và 1       
S :x 102  y 92 z 22  400 và mặt phẳng P:4x 3y  mz  22  0. Có bao 2
nhiêu số nguyên m để mp (P) cắt hai mặt cầu S , S theo giao tuyến là hai đường tròn 1   2 
không có tiếp tuyến chung? A. 5 . B. 11. C. Vô số. D. 6 . Trang57 BẢNG ĐÁP ÁN 1.A 2.C 3.B 4.D 5.C 6.C 7.A 8.C 9.B 10.B 11.C 12.A 13.C 14.B 15.B 16.C 17.A 18.D 19.D 20.A 21.B 22.A 23.C 24.A 25.C 26.B 27.B 28.D 29.A 30.B 31.C 32.C 33.A 34.B 35.D 36.C 37.D 38.C 39.C 40.A 41.C 42.C 43.C 44.D 45.A 46.B 47.B 48.B 49.C 50.D
HƯỚNG DẪN GIẢI CHI TIẾT Câu 1:
Có bao nhiêu cách sắp xếp 5 học sinh đứng thành một hàng dọc? A. 5! . B. 3 5 . C. 5 C . D. 1 A . 5 5 Lời giải Chọn A. Câu 2:
Cho cấp số nhân u có u  2 và công bội q  3. Giá trị của u là: n  1 3 A. 6  . B. 18  . C.18 . D. 4  . Lời giải Chọn C. Ta có: 2
u  u q 18. 3 1 Câu 3:
Cho hàm số y  f  x có bảng biến thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào trong các khoảng dưới đây? A.  2  ;0 . B.  2  ;  1 . C. 3;  . D.  1  ;. Lời giải Chọn B. Câu 4: Cho hàm số bậc ba 3 2
y  ax  bx  cx  d a  0 có đồ thị như sau Trang58
Giá trị cực đại của hàm số là: A. x  2 . B. y  4 . C. x  0 . D. y  0 . Lời giải Chọn D 2 Câu 5:
Cho hàm số y  f  x xác định trên  có đạo hàm f  x  x  x   x    2 ' 2 1 x  4 . Hàm số
đã cho có bao nhiêu điểm cực trị A.3. B. 4 . C. 2 . D.1. Lời giải Chọn C. x  0 x 
f ' x  x  x  2 x  2 1  2 2
x  4  0   x  1   x  2 
Bảng xét dấu f ' x
Vậy hàm số đã cho có hai điểm cực trị. 1 Câu 6:
Tiệm cận ngang của đồ thị hàm số y  1 x  là đường thẳng: 1 A. x 1 . B. y  1. C. y  1. D. y  0 . Lời giải Chọn C. Câu 7:
Đường cong ở hình dưới đây là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào ? Trang59 1 1 1 1 A. 3 y  x  x 1. B. 3 y  x  x 1. 9 3 9 3 1 C. 4 2 y 
x  x 1. D. 3 2
y  x  x  x 1. 4 Lời giải Chọn A
+ Do đây là đồ thị của hàm số bậc ba nên loại đáp án C.
+ Từ đồ thị ta thấy lim y = + ¥ nên hệ số của 3
x dương nên loại đáp ánD. x® + ¥
+ Ở đáp án B ta có: 1 1 3 y  x  x 1 9 3 1 1 2 y '  x  3 3
y '  0  x  1
Suy ra hàm số có hai điểm cực trị nên loại B.
+ Vậy chọn đáp án A. 4 x 3 Câu 8: Đồ thị hàm số 2 y  
 x  cắt trục hoành tại mấy điểm? 2 2 A. 4 B. 3 C. 2 D. 0 Lời giải Chọn C
Phương trình hoành độ giao điểm của đồ thị hàm số đã cho và trục hoành: 4 2 x 3 x  1  2   x   0 4 2
 x  2x  3  0    x   3 . 2 2 2 x  3
Vậy phương trình có 2 nghiệm nên đồ thị cắt trục hoành tại 2 điểm. Câu 9:
Với a là số thực dương tùy ý, log 125a bằng 5  
A. 3  log a .
B. 3  log a .
C. log a .
D. 2  log a . 5 3 5 5 5 Lời giải Chọn B
Ta có log 125a  log 125  log a  3  log . a 5   5 5 5
Câu 10: Đạo hàm của hàm số 1 2 x y e   là: 12 x e A. 1 2 ' 2 x y e   . B. 1 2 ' 2 x y e    . C. y '   . D. 1 2 ' x y e   2 Lời giải Chọn B Trang60   Ta có 1 2 x     1 2 ' . 1 2 '  2 x y e x  e .
Câu 11: Với a là số thực tuỳ ý, 3 5 a bằng 3 5 A. 3 a . B. 5 a . C. 3 a . D. 2 a . Lời giải Chọn C 5
Với số thực a ta có 3 5 3 a  a .
Câu 12: Tổng các nghiệm của phương trình 4 2 x 3 3 x  81 bằng A. 0. B.1. C. 3. D. 4. Lời giải Chọn A 2    4 2 x 1 Ta có x 3x 4 2 3
 81  x  3x  4  4 2
x  3x  4  0   2
 x  4  x  2  . 2  x  4
Vậy tổng các nghiệm của phương trình 4 2 x 3 3 x  81 bằng 0 .
Câu 13: Nghiệm của phương trình log 2x  2 là: 3   3 9 A. x  .
B. x  3. C. x  . D. x 1 . 2 2 Lời giải Chọn C 9
Phương trình: log 2x  2 2
 2x  3  x  . 3   2
Câu 14: Cho hàm số f  x 3
 4x  2021. Trong các khẳng định sau, khẳng định nào đúng? A. f  x 4
dx  4x  2021x  C . B. f  x 4
dx  x  2021x  C . C. f  x 4
dx  x  2021 . D. f  x 4
dx  x  C . Lời giải Chọn B
Áp dụng công thức nguyên hàm cơ bản: f
 x x   3x   4 d 4
2021 dx  x  2021x  C .
Câu 15: Cho hàm số f  x  sin 3x . Trong các khẳng định sau, khẳng định nào đúng? A. f  x 1 dx 
cos 3x  C . B. f  x 1
dx   cos 3x  C . 3 3 C. f
 xdx 3cos3xC . D. f
 xdx  3
 cos3x  C . Lời giải Chọn B
Áp dụng công thức nguyên hàm cơ bản: f  x 1
dx   cos 3x  C . 3 2 3 3 Câu 16: Nếu f
 xdx  2 và f xdx  7   thì
f  xdx  bằng 1 1 2 Trang61 A. 5  . B. 9 . C. 9  . D. 14 . Lời giải Chọn C 3 3 2
Áp dụng tính chất tích phân ta có:
f  xdx  f  xdx  f  xdx  7   2  9     2 1 1 ln 3 Câu 17: Tích phân x e dx  bằng 0 A. 2 . B. 3 . C. e . D. e 1. Lời giải Chọn A ln 3 ln 3 Ta có: x d x e x  e  ln 3 0
 e  e  2 . 0 0
Câu 18: Số phức liên hợp của số phức z  3 4i là:
A. z  3  4i .
B. z  4  3i .
C. z  4  3i .
D. z  3  4i . Lời giải Chọn D
Số phức liên hợp của số phức a  bi là a  bi . Nên z  3  4i là số phức liên hợp của số
phức z  3 4i .
Câu 19: Cho hai số phức z  3  5i và z  6
 8i . Số phức liên hợp của số phức z  z là 1 2 2 1 A. 9  13i . B. 3  3i . C. 3  3i . D. 9  13i . Lời giải Chọn D
Số phức z  z  6
 8i  3 5i  9  13i . 2 1    
Vậy số phức liên hợp của số phức z  z là 9  13i . 2 1
Câu 20: Trên mặt phẳng tọa độ, điểm biểu diễn số phức liên hợp của số phức 23  5i có tọa độ là A. 23; 5   . B. 23;5 . C.  2  3; 5   . D.  2  3;5 . Lời giải Chọn A
Số phức liên hợp của số phức 23  5i là số phức 23 5i .
Vậy điểm biểu diễn số phức 23 5i là điểm M 23; 5   .
Câu 21: Thể tích khối lăng trụ tam giác đều có cạnh đáy bằng 2 và chiều cao bằng một nửa cạnh đáy là A. 2 3 B. 3 C. 3 D. 6 Lời giải Chọn B 2
Ta có đáy là tam giác đề 2 3 u nên S   3 . 4
Ta có chiều cao bằng một nửa cạnh đáy nên : h 1 Trang62
Vậy thể tích khối lăng trụ V  S.h  3 .
Câu 22: Cho khối hộp có đáy là hình vuông cạnh bằng 5 và chiều cao khối hộp bằng một nửa chu vi
đáy. Thể tích của khối hộp đã cho bằng A. 3 250cm . B. 3 125cm . C. 3 200cm . D. 3 500 cm . Lời giải Chọn A
Ta có diện tích đáy bằng 2 25cm Chu vi đáy : P
P  5.4  20 cm  h   10cm 2
Vậy ta có thể tích khối hộp là 3
V  25.10  250cm
Câu 23: Công thức tính thể tích V của hình nón có diện tích đáy 2
S  4 R và chiều cao h là: 1 4 2 A. 2 V   R h . B. 2 V   R h . C. 2 V   R h . D.V   Rh . 3 3 3 Lời giải Chọn C
Diện tích đáy đường tròn là 2
4 R  Bán kính hình nón là 2R . 1 4 V
  R h   R h Nón 2 2 2 . 3 3
Câu 24: Một hình trụ có bán kính R  6 cm và độ dài đường sinh l  4cm. Tính diện tích toàn phần của hình trụ đó. A. 2 S  120cm . B. 2 S  84cm . C. 2 S  96cm . D. 2 S  24cm . tp tp tp tp Lời giải Chọn A
S   R R  l          2 2 . 2 6. 6 4 120 cm . tp 
Câu 25: Trong không gian Oxyz, cho tam giác ABC biết A1;1;3, B  1  ;4;0,C 3  ;2;  3 . Trọng
tâm G của tam giác ABC có tọa độ là  3  3  A.  3  ;3;0 . B. ; ; 0  . C.  1  ;1;0 . D. 1; 1  ;  1 .  2 2  Lời giải Chọn C
Trọng tâm G của tam giác ABC có tọa độ là x       A xB C x y y y z z z x   1; A B C y   1; A B C z   0. G G G 3 3 3 2 2 2
Câu 26: Trong không gian Oxyz, mặt cầu S  :  x   1   y   1
 z 3  9 . Tâm I của mặt cầu (S) có tọa độ là Trang63 A. 1; 1  ; 3  . B.  1  ;1;3. C. 2; 2  ; 6   . D.  2  ;2;6 . Lời giải Chọn B Phương trình mặ 2 2 2
t cầu là:            2 x a y b z c
 R  tọa độ tâm I  1  ;1;3.
Câu 27: Trong không gian Oxyz, cho mặt phẳng  P có phương trình 2x  y  z  3  0 . Điểm nào sau
đây thuộc mặt phẳng P ? A. M 1; 1  ; 3   . B. N  1  ;1;0. C. H 2; 2  ;6 . D. K  2  ;2;3 . Lời giải Chọn B
Câu 28: Trong không gian Oxyz, vectơnào dưới đây không phải là vectơ chỉ phương của đường thẳng x 1 y 1 z d :   2 1  ? 2    
A. u  2; 1; 2 .
B. u  2;1; 2 .
C. u  4; 2; 4 . D. u  1; 1  ;0 4   3   2   1   Lời giải Chọn D    u  2;1; 2
 là 1 vectơ chỉ phương của đường thẳng d  u  2;1;2 và u  4;2;4 3   1   2  
cũng là vectơ chỉ phương của đường thẳng d  đáp án D sai.
Câu 29: Có 30 chiếc thẻ được đánh số thứ tự từ 1 đến 30. Chọn ngẫu nhiên một chiếc thẻ. Tính xác suất
để chiếc thẻ được chọn mang số chia hết cho 3. 1 1 3 2 A. . B. . C. . D. . 3 2 10 3 Lời giải Chọn A
Từ 1 đến 30 có 10 số chia hết cho 3 nên xác suất để chọn được 1 chiếc thẻ mang số chia hết cho 10 1 3 là  . 30 3
Câu 30: Hàm số nào sau đây nghịch biến trên  ? 3x  2 A. 4 2
y  x  4x 1. B. 3
y  x  x 1 . C. y 
y   x  . x  . D. 2 2 3 1 Lời giải Trang64 Chọn B Ta có: 3 2
y  x  x 1  y  3
 x 1 0, x
   nên hàm số đồng biến trên  . Câu 31: Cho hàm số 3
y  x  3x  4 . Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm
số trên đoạn 0; 2 . Khẳng định nào sau đây đúng?
A. M  m  8 .
B. 2M  m  2  .
C. M  2m 10 .
D. M  m  8  . Lời giải Chọn C D   . x 10;2 2
y  3x  3 2
 y  0  3x  3  0   . x  1     0;2 Ta có y 0  4  , y 2  2  ; y   1  6  . Vậy M  2  , m  6  . x  x 1
Câu 32: Bất phương trình mũ 2 3 5  có tập nghiệm là 25 3 17 3 17   3  17  3 17  A. T   ;  .
B.T    ;     ;    . 2 2   2 2    
C. T  1; 2 . D.T   ;   1 2; . Lời giải Chọn C 2 x  x 1 1 3 2 2 5 
 x  3x  log
 x  3x  2  0 1 x  2. 5 25 25
Vậy tập nghiệm của bất phương trình là: T  1; 2 . 2 5 5 Câu 33: Biết f
 xdx 3, f
 xdx  4. Tính 2f x xdx 1 1 2 25 17 A. . B. 23. C. . D.19 . 2 2 Lời giải Chọn A 5 2 5 5 2 Ta có f
 xdx  4, f
 xdx 3 f
 xdx  f
 xdx f
 xdx 1. 1 1 2 1 1 5 5 5 5 2 x 25
2 f x xdx  2 f xdx xdx  2.1     . 2 2 2 2 2 2 Trang65
Câu 34: Cho số phức z thỏa mãn z 1 2i  1 4i . Phần thực của số phức z thuộc khoảng nào dưới đây?  3  A. 0; 2 . B.  2  ;  1 . C.  4  ; 3   . D.  ; 1    .  2  Lời giải Chọn B  i
1 4i1 2i 7 6
Ta có z   i 1 4 1 2
 1 4i  z   z     i 1 2i 5 5 5 7
Vậy phần thực của số phức z   2;  1 . 5
Câu 35: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a . Đường thẳng SA vuông góc với mặt
phẳng  ABCD , SA  a . Góc giữa hai mặt phẳng SCD và  ABCD là  . Khi đó, tan
nhận giá trị nào trong các giá trị sau ? 2
A. tan  2 . B. tan  .
C. tan   3 . D. tan 1. 2 Lời giải Chọn D S A  D B C C  D  AD Ta có: 
 CD  SAD  CD  SD . C  D  SA
 CD  SCD  ABCD   
Do SD  SCD SD  CD
  ABCD SCD   SD AD  , , ,  SDA   . AD  
 ABCD, AD  CD SA a Xét tam giác SAD :  tan SDA  tan     1 . AD a
Câu 36: Cho hình chóp tứ giác đều S.ABCD , đáy có tâm là O và SA  a, AB  a . Khi đó, khoảng
cách từ điểm O đến mặt phẳng SAD bằng bao nhiêu ? a a a A. . B. . C. . D. a . 2 2 6 Trang66 Lời giải Chọn C S a B A O a C D 2 a 2 3 1 a 2 Ta có : V  AB  V  V  . S ABCD   3 3 . 6 6 S.AOD S . 4 ABCD 24 2 a 3
Diện tích tam giác SAD là S  SAD 4 . 3 a 3 3. 3.V a 6 Vậy d O  SAD SAOD 24 ,      . 2 S a SAD 3 6 4
Câu 37: Trong không gian với hệ tọa độ Oxyz , cho hai điểm A1;1;0 và B 1; 1;  4 . Viết phương
trình mặt cầu S  nhận AB làm đường kính . 2 2 2 2 A. S  2
: x   y  
1   z  2  5 .
B. S   x   2 :
1  y   z  2  20 . 2 2 2 2
C. S   x   2 :
1  y   z  2  20 .
D. S   x   2 :
1  y   z  2  5 . Lời giải Chọn D
Gọi I là tâm của mặt cầu  S   I là trung điểm của AB  I 1;0;  2 . 
AB  0;  2;  4  AB  2 5 . AB
Vậy mặt cầu S  có tâm I 1;0;  2 và bán kính R   5 . 2
 S x  2  y z  2 2 : 1 2  5 .
Câu 38: Trong không gian với hệ tọa độ Oxyz , cho điểm M  2
 ;3;4 . Viết phương trình đường thẳng
d  qua điểm M và vuông góc với mặt phẳng Oxy. Trang67 x  2  x  2   t x  2  x  2   t    
A. d  :  y  3  t .
B. d  :  y  3 .
C. d  :  y  3 .
D. d  :  y  3  t .     z  4 z  4 z  4  t z  4  t Lời giải Chọn C 
Do d   Oxy  Vectơ chỉ phương của d  là k  0;0;  1 . x  2  
Vậy phương trình d  :  y  3 t  .  z  4  t
Câu 39: Cho hàm số f  x, đồ thị của hàm số /
y  f  x là đường cong như hình vẽ. Giá trị nhỏ nhất 1 
của hàm số g  x  f 2x  
1  6x trên đoạn ; 2   bằng  2   1  A. f   .
B. f 0  3 . C. f   1  6 .
D. f 3 12.  2  Lời giải Chọn C
Đặt t  2x 1  t 0; 
3 , xét hàm số h t   f t   3t  3 trên 0;  3 . t  0  Ta có / h  x /
 f x  3 , /
h t   0  t  1  . t  2  / h  x /
 0  f x  3   x1;3 / h  x /
 0  f x  3   x 0;  1
Ta có bẳng biến thiên sau Trang68
Ta có min h t   h   1  f   1  6 . 0; 3
Câu 40: Có bao nhiêu số nguyên dương y sao cho ứng với mỗi y có không quá 2186 số nguyên x thỏa mãn log  3x x y  9  0 ? 3  A. 7 . B. 8 . C. 2186 . D. 6 . Lời giải Chọn A  x  0   x  2
Ta có log x  y
3x  9  0  3x  9   3   x  3y log x  y  3
Nếu 3y  2 thì bất phương trình vô nghiệm ( không thỏa mãn).
Nếu 3y  2  y  log 2  0,631 thì bất phương trình có tập nghiệm T    2 3
( không thỏa mãn vì y nguyên dương).
Nếu 3y  2  y  log 2  0,631, khi đó bất phương trình có tập nghiệm  2;3y T   3  
Để mỗi giá trị y , bất phương trình có không quá 2021 nghiệm nguyên x thì
3y  2187  y  log 2187  7 . 3
Kết hợp điều kiện y nguyên dương, 0, 631  y  7 suy ra có 7 số y thỏa mãn bài toán. 2
y  f  x  1 y  g  x  x Câu 41: Cho hàm số , . Giá trị I  min
 f x;gxdx 1  3 5 A.1. B. . C. 2 . D. . 2 2 Lời giải Chọn C Trang69 x 
Xét bất phương trình x  1 1   . x  1 
Vậy min 1; x  1 khi 1 x hoặc x  1 
min1; x   x khi 1   x 1 2 2 1 2 Xét I  min
 f x;gxdx  min
 1; xdx  min
 1; xdx  min
 1; xdx 1  1  1  1 1 2 0 1 2 0 1 2 2 x x 2 I 
xdx  dx 
   dxx dxx dx       x =2. 1 2 2 1  1 1  0 1 1  0
Câu 42: Có tất cả bao nhiêu số phức z mà phần thực và phần ảo của nó trái dấu đồng thời thỏa mãn
z  z  z  z  4 và z  2  2i  3 2. A.1. B. 3 . C. 2 . D. 0 . Lời giải Chọn C Gọi điểm M  ;
x y là điểm trên mp tọa độ Oxy biểu diễn số phức
z  x  yi ( ,
x y  )  z  x  yi
z  z  z  z  4  2x  2yi  2  x  y  2 . Khi đó tập hợp điểm M  ;
x y biểu diễn số
phức z là hai cạnh đối AD, BC của hình vuông ABCD độ dài cạnh bằng 2 2 và tâm là gốc tọa độ O z   i 
 x  2   y  2 2 2 3 2 2 2
18 . Tập hợp điểm M  ;
x y biểu diễn số phức z là
đường tròn tâm I 2;2, R  3 2 . 8 6 4 A 2 I M 15 10 5 5 10 15 D B N P 2 C 4
Vậy có 2 điểm biểu diễn M , P thỏa yêu cầu bài toán. 6
Câu 43: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A và có AB  ,
a BC  a 3 . Mặt Trang70
bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng  ABC  . Tính thể
tích V của khối khóp S.ABC . 3 2a 6 3 a 6 3 a 6 3 a 6 A.V  . B.V  . C.V  . D.V  . 12 6 12 4 Lời giải Chọn C
Gọi K là trung điểm của đoạn AB . Vì S
 AB là tam giác đều nên SK  AB .
SAB  ABC theo giao tuyến AB .
SK   ABC  1  V  SK.S . S . ABC  3 ABC ABC  vuông tại A có 2 2
AB  a, BC  a 3  AC 
BC  AB  a 2 2 1 1 a 2 S  A . B AC  . a a 2  . ABC  2 2 2 a 3 S
 AB là tam giác đều  SK  . 2 2 3 1 1 a 3 a 2 a 6 V  SK.S  . .  . S.ABC  3 ABC 3 2 2 12
Câu 44: Ông An cần làm một đồ trang trí như hình vẽ. Phần dưới là một phần của khối cầu bán kính
20 cm làm bằng gỗ đặc, bán kính của đường tròn phần chỏm cầu bằng 10 cm . Phần phía trên
làm bằng lớp vỏ kính trong suốt. Biết giá tiền của 2
1 m kính như trên là 1.500.000 đồng, giá triền của 3
1 m gỗ là 100.000.000 đồng. Hỏi số tiền (làm tròn đến hàng nghìn) mà ông An mua
vật liệu để làm đồ trang trí là bao nhiêu. Trang71 a 20cm 10cm A.1.000.000 B.1.100.000 C.1.010.000 D.1.005.000 . . . Lời giải Chọn D
Bán kính mặt cầu là R  20 cm ; bán kính đường tròn phần chỏm cầu là r 10cm . 10 1 Theo hình vẽ ta có 0 sin       30 . 20 2 360  2.30 4000
Diện tích phần làm kính là: 2 S  .4 .20   2 cm  . 360 3
Xét hình nón đỉnh là tâm mặt cầu, hình tròn đáy có bán kính bằng 2 2
r  10 cm ; l  R  20 cm  h  20 10  10 3cm
Thể tích phần chỏm cầu bằng 2.30 4 1   3 2 16000 1000 3 V 
.  R   r .h =   3 cm  c hom cau 360 3 3 9 3 4000 16000 1000 3 
Vậy số tiền ông An cần mua vật liệu là: .150    .100 1.005.000   3 9 3   x y z 1 x  3 y z 1
Câu 45: Trong không gian Oxyz , cho ba đường thẳng d :   ,  :   , 1 1 2 1 2 1 1 x 1 y  2 z  : 
 . Đường thẳng  vuông góc với d đồng thời cắt  , tương ứng tại 2 1 2 1 1 2
H , K sao cho HK 
27 . Phương trình của đường thẳng  là x 1 y 1 z x 1 y 1 z x 1 y 1 z x 1 y 1 z A.   . B.     . D.   1 1 1 1 1  . C. 1 2 1 1 3  3  . 1 Lời giải ChọnA
H    H 3  2t;t;1 t , K    K 1 ; m 2  2 ; m m . 2   1    
Ta có HK  m  2t  2; 2m  t  2; m  t  
1 . Đường thẳng d có một VTCP là u  1;1; 2  . d    
  d  u .HK  0  m  t  2  0  m  t  2  HK   t
  4;t  2;3. d 2 2 2 2 Ta có 2 HK   t
  4  t  2   3
   2t   1  27  27, t    . Trang72 
HK  27  t  1  , m  3
 .Khi đó HK  3;3;3  3(1;1;1) , H (1;1;0) .   Phương trình đườ x 1 y 1 z ng thẳng  là   . 1 1 1
Câu 46: Cho hàm số y  f  x có đạo hàm f  x 3 '
 4x  2x và f 0 1. Số điểm cực tiểu của hàm số g  x 3  f  2
x  2x  3 là A. 0 . B. 2 . C.1. D. 3 . Lời giải Chọn B
Ta có: f  x   3 x  x 4 2 4 2
dx  x  x  C và f 0  1 C  1.
Do đó ta có: f  x 4 2
 x  x 1  0,  . x
Ta có: g  x 2 2 2 '
 3(2x  2). f (x  2x 3). f '(x  2x 3) .  x 1 2x  2  0 
g ' x  0    x  1.   4
  x  2x  33 2  2 2
x  2x  3  0 x  3  Bảng biến thiên: x   1 1 3    g '( x)   0 0 0   g(x)
Từ bảng biến thiên suy ra hàm số y  g  x có hai cực tiểu. 
Câu 47: Tổng các nghiệm của phương trình sau x 1 7
 6log 6x 5 1 bằng 7   A. 2 . B. 3 . C.1. D.10 . Lờigiải Chọn B 5
Điều kiện: x  . 6
Đặt y 1  log 6x  5 thì ta có hệ phương trình 7   x 1
7   6 y   x 1 1 1 7   6y 5 x 1  y 1      x    y (2) y 1  log  6x 5 7 6 7 6 y 1 7   6x 5 7  5 t  5
Xét hàm số f t  t 1
 7  6t với t  thì f 't 1
 7 ln 7  6  0, t
   f t đồng biến nên 6 6
2  f x  f  y  x  y 
khi đó ta có phương trình x 1 7
 6x  5  0. (3) Trang73  5
Xét hàm số g  x x 1
 7  6x  5 với x  thì   x   x g x g x       2 1 1 ' 7 ln 7 6 " 7 ln 7  0 6 5 x  6
nên suy ra phương trình g  x  0 có không quá hai nghiệm. Mặt khác g  
1  g 2  0 nên x 1 và x  2 là 2 nghiệm của phương trình (3).
Vậy phương trình đã cho có 2 nghiệm là x 1 và x  2 .
Suy ra tổng các nghiệm của phương trình là 1 2  3.
Câu 48: Cho parabol  P  2
: y  x  4 cắt tru ̣c hoành ta ̣i hai điểm
A , B và đường thẳng d : y  a 1
0  a  4 . Xét parabol P đi qua A , B và có đỉnh thuộc đường thẳng y  a . Gọi S là 2  1
diê ̣n tích hình phẳng giới ha ̣n bởi P và d . S là diện tích hình phẳng giới hạn bởi P và 2  1  2
trục hoành. Biết S  S (tham khảo hình vẽ bên). 1 2 y M N
y = a A B O x Tính 3 2
T  a  8a  48a . A. T  99 . B. T  64 . C.T  32 . D.T  72 . Lời giải Chọn B
- Gọi A , B là các giao điểm của  P và trục Ox  A 2
 ;0, B2;0  AB  4. 1 
- Gọi M , N là giao điểm của  P và đường thẳng d  M  4  a;a, N  4  a;a 1 
 MN  2 4  a . a
- Nhâ ̣n thấy:  P là parabol có phương trình 2 y   x  a . 2  4
- Áp dụng công thức tính diện tích hình phẳng ta được: 4 4 3 4   4 S  2 4  y.dy 
  4  y2  4  a 4  a . 1  3   3 a a 2 2  a  3  ax  8a 2 S  2
 x  a .dx   2  ax  . 2    4   12  3 0 0 Trang74 4 8a
- Theo giả thiết: S  S  4  a 4  a     a3 2 4  4a 3 2
 a  8a  48a  64 . 1 2 3 3
Câu 49: Cho hai số phức u, v thỏa mãn u = v = 10 và 3u - 4v = 50 . Tìm Giá trị lớn nhất của biểu
thức 4u + 3v - 10i . A. 30 . B. 40 . C. 60 . D. 50 . Lời giải Chọn C 2 Ta có z = .
z z . Đặt T = 3u - 4v , M = 4u + 3v . Khi đó 2 2 2
T = (3u - 4v)(3u - 4 )
v = 9 u + 16 v - 12(uv + vu). Tương tự 2 2 ta có 2
M = (4u + 3v)(4u + 3v)= 16 u + 9 v + 12(uv + vu). Do đó M + T = ( 2 2 2 2
25 u + v )= 5000 . Suy ra 2 2 M = 5000 - T 2
= 5000 - 50 = 2500 hay M = 50 .
Áp dụng z + z¢£ z + z¢ta có
4u + 3v - 10i £ 4u + 3v + - 10i = 50 + 10 = 60 .
Suy ra max 4u + 3v - 10i = 60 . 2 2 2 Câu50:Trong hệ trục Oxyz , cho hai mặt cầu
S : x 1  y 3  z 2  49 và 1       
S :x 102  y 92 z 22  400 và mặt phẳng P:4x 3y  mz  22  0. Có bao 2
nhiêu số nguyên m để mp (P) cắt hai mặt cầu S , S theo giao tuyến là hai đường tròn 1   2 
không có tiếp tuyến chung? A. 5 . B.11. C.Vô số. D. 6 . Lời giải Chọn D
Mặt cầu S có tâm I 1; 3
 ;2 , bán kính R  7 ; mặt cầu S có tâm J 10;9;2 , bán kính 2  1  1 
R  20 . Ta có IJ 9;12;0 , IJ 15. 2 
Mặt phẳng  P : 4x  3y  mz  22  0 có vec tơ pháp tuyến n 4; 3; m P   
Do IJ.n  0 nên IJ song song hoặc chứa trong (P). P Bán kính đường tròn giao tuyến của hai mặt cầu S , S là 1   2 
2 p  p  7 p  20 p 15 28 20  7 15 r   với p   21 15 5 2 Trang75 I J r
Phương trình mặt phẳng chứa đường tròn giao tuyến hai mặt cầu là (Q): 3x  4 y  30  0
Ta có d  I Q  21 ; ( )  , d  J Q  96 ; ( ) 
nên d  I;(Q)  IJ  d  J;(Q) 5 5
Ta có mp(P) cắt hai mặt cầu S , S theo giao tuyến là hai đường tròn, trong đó đường tròn 1   2  28 28 2m  35
nhỏ ở trong đường tròn lớn khi
 d I;(P)  7    7 2 5 5 m  25 2
45m 140m  0   684 2
m 140m  441  0  25
Và có m nguyên, nên m  2  ; 1  ;4;5;6;  7 . Đề 9
ĐỀ LUYỆN THI CẤP TỐC TỐT NGHIỆP THPT NĂM 2021 Thuvienhoclieu.Com BÀI THI: TOÁN
Thời gian: 90 phút Câu 1:
Cho tập hợp S  1;3;5;7; 
9 . Có bao nhiêu số tự nhiên gồm ba chữ số khác nhau được lập
từ các phần tử của tập S ? 3 A. 3!. B. 5 3 . C. 5 C . D. 35 A . 1
Câu 2: Cho một dãy cấp số nhân u có u 
và u  2 . Giá trị của u bằng n  1 2 2 4 1 25 A. 32 . B. 6 . C. . D. . 32 2
Câu 3: Cho hàm số y  f  x có bảng biến thiên sau: Trang76
Khẳng định nào sau đây sai?
A. Hàm số y  f  x đồng biến trên khoảng  ;  2   .
B. Hàm số nghịch biến trên khoảng  2  ;2 .
C. Hàm số nghịch biến trên khoảng  2  ;0 .
D. Hàm số đồng biến điệu trên 0; 2 .
Câu 4: Hàm số y  f  x có bảng biến thiên như sau: Tìm khẳng định đúng?
A. Hàm số có ba điểm cực trị.
B. Hàm số có giá trị cực đại là x  1  .
C. Hàm số đạt cực đại tại x  0 .
D. Hàm số có điểm cực tiểu là x 1 .
Câu 5: Cho hàm số y  f  x liên tục trên  và có bảng xét dấu của f  x như sau: x  2  1 5 
f  x  0  0  0 
Hàm số f  x có bao nhiêu điểm cực trị? A. 2. B. 3. C. 0. D. 1. x  Câu 6: Cho hàm số 2 1
y  x  . Tiệm cận đứng của đồ thị hàm số là 1
A. Đường thẳng x  1. B. Đường thẳng x  2.
C. Đường thẳng y  2. D. Đường thẳng y  1.
Câu 7: Cho hàm số có đồ thị như hình vẽ: Trang77
Hàm số nào dưới đây có đồ thị là hình vẽ trên? A. 4 2
y  x  4x  2 . B. 3
y  x  3x  2 . C. 4 2
y  x  4x  2 . D. 3
y  x  3x  2 .
Câu 8: Đồ thị của hàm số y   2 x   2 2
x  2 cắt trục tung tại điểm có tọa độ là A. 0; 4 . B. 0; 4   . C. 4;0 . D.  4  ;0 .
Câu 9: Với a là số thực dương tùy ý,  ln ea  bằng
A. 1 a ln .
B. 1 ln a .
C. 1 ln a .
D. 1 ln  ln a .
Câu 10: Đạo hàm của hàm số x y   là x  A. x 1 x  . B. x   . ln  . C. x  . D. ln
Câu 11: Với a là số thực dương tùy ý, 3 2 a bằng 1 3 2 A. 6 a . B. 6 a . C. 2 a . D. 3 a .
Câu 12: Nghiệm của phương trình log 2x  2  1 là 2  
A. x  2 .
B. x 1. C. x  2  . D. x  3.
Câu 13: Nghiệm của phương trình 1 log x 1  3 là 2  
A. x  3.
B. x 1.
C. x  7 . D. x  4 . x  4
Câu 14: Cho hàm số f  x 5 
. Trong các khẳng định sau, khẳng định nào đúng? 2 x 4 x 4 A. f
 xdx   C . B.    3 4 f x dx  x   C . 4 x x 4 x 1 4 x 4 C. f
 xdx   C. D. f
 xdx   C. 4 x 4 x
Câu 15: Cho hàm số f (x)  sin 3x 1 . Trong các khẳng định sau, khẳng định nào đúng? 1 1 A.
f (x)dx 
cos 3x  x  C  B.
f (x)dx   cos 3x  x  C  3 3 C.
f (x)dx  3cos 3x  x  C  D.
f (x)dx  3
 cos3x  x  C  2 3 3 Câu 16: Nếu f
 xdx  3 và f xdx  2   thì
f  xdx  bằng 1  1  2 A. 1. B. 5 . C. 5  . D. 1. Trang78 ln 2 Câu 17: Tích phân x e dx  bằng 0 A. 2 e . B. 1. C. 2 . D. 2 e 1.
Câu 18: Tìm số phức z  z  z biết z  1 3i , z  2   2i 1 2 1 2 . A. z  1  i . B. z  1  i .
C. z  1 i .
D. z  1 i .
Câu 19: Tìm số phức liên hợp của số phức z  i 3i   1 .
A. z  3 i . B. z  3  i .
C. z  3 i . D. z  3  i .
Câu 20: Cho số phức z  2
 i . Điểm nào dưới đây là biểu diễn của số phức w  iz trên mặt phẳng toạ độ? A. M  1  ; 2  . B. P  2  ;  1 . C. N 2  ;1 .
D. Q 1; 2.
Câu 21: Cho hình chóp S. ABC , có đáy ABC là tam giác vuông cân tại A , SA = AB = a , SA vuông
góc với mặt phẳng (ABC). Thể tích của khối chóp S. ABC bằng 3 a 3 a 3 a 3 3a A. . B. . C. . D. . 3 6 2 2
Câu 22: Cho khối lăng trụ có đáy là hình vuông cạnh a và chiều cao bằng 2a . Thể tích của khối lăng trụ đã cho bằng 2 4 A. 3 a B. 3 a C. 3 2a D. 3 4a 3 3
Câu 23: Tính thể tích V của khối nón có bán kính đáy bằng 3 và chiều cao bằng 6 .
A. V 108 .
B. V  54 .
C. V  36 .
D. V 18 .
Câu 24: Tính diện tích xung quanh S của hình trụ có bán kính bằng 3 và chiều cao bằng 4 .
A. S  36 .
B. S  24 .
C. S 12 D. S  42 .
Câu 25: Trong không gian Oxyz , cho tam giác ABC với A1;2;  1 ; B3;1; 2
 ;C2;0;4 . Trọng tâm của
tam giác ABC có tọa độ là A. 6;3;3. B. 2; 1  ;  1 . C.  2  ;1;  1 . D. 2;1;  1 . 2 2
Câu 26: Trong không gian Oxyz , mặt cầu S   x   2 :
1  y   z  2  16 có đường kính bằng A. 8 . B. 4 . C. 16 . D. 2 .
Câu 27: Trong không gian Oxyz , mặt phẳng nào dưới đây đi qua điểm M  2  ;1;  1 ?
A. x  y  z  0 .
B. x  2 y  z  3  0 .
C. x  y  z 1  0 .
D. x  y  z  3  0 .
Câu 28: Trong không gian Oxyz , vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng đi qua
hai điểm A1;2;  1 và B  1  ;0;0 ?     A. u 2; 2; 1 u 2; 2; 1  1 u 2;2;  1 . B. u  2  2; 2;  1 . C. 3  . D. 4  .
Câu 29: Chọn ngẫu nhiên một số trong số 21 số nguyên không âm đầu tiên. Xác suất để chọn được số lẻ bằng 10 11 9 4 A. . B. . C. . D. . 21 21 21 7
Câu 30: Hàm số nào dưới đây đồng biến trên R ?
A. y  tan x . B. 3 2
y  x  x  x 1. Trang79 2x 1 C. 4 y  x 1.
D. y  x  . 1
Câu 31: Gọi M , m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số 3 2
y  2x  3x 12x 1 trên
đoạn [1;5] . Tổng M  m bằng. A. 270 . B. 8 . C. 280 . D. 260 . 4 x x2  2   2 
Câu 32: Tập nghiệm của bất phương trình      ?  3   3  2 2 2 2 A. x   . B. x  . C. x  D. x  3 3 5 5 2 2
Câu 33: Nếu 2 f (x)  
1 dx  5 thì f (x)dx  bằng ? 1 1 A. 2 . B. 2  . C. 3 D. 3 
Câu 34: Cho số phức z  3 4i . Khi đó mô đun của số phức 1 i z bằng ? A. 5 2 . B. 10 . C. 20 D. 2 5
Câu 35: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A và AB  a 2 . Biết
SA   ABC và SA  a . Góc giữa hai mặt phẳng SBC  và  ABC  bằng A. 30 . B. 45 . C. 60 . D. 90 .
Câu 36: Cho hình chóp đều S.ABC có cạnh đáy bằng a , góc giữa một mặt bên và mặt đáy bằng 60 .
Tính độ dài đường cao SH. a 2 a a a A. SH  3 . B. SH  . C. SH  3 . D. SH  . 3 2 2 3
Câu 37: Trong không gian với hệ tọa độ Oxyz, A 3  ; 4; 2 , B 5  ; 6; 2 , C 1  0; 17; 7   . Viết
phương trình mặt cầu tâm C , bán kính AB . A.  2 2 2 x 
2  y  2 z  2 10 17 7  8 .
B.  x 10   y 17   z  7  8 . C.  2 2 2 x 
2  y  2 z  2 10 17 7  8 .
D.  x 10   y 17   z  7  8 .
Câu 38: Trong không gian với hệ trục tọa độ Oxyz , cho M 1; – 2; 
1 , N 0;1; 3 . Phương trình đường
thẳng qua hai điểm M , N là x 1 y  2 z 1 x 1 y  3 z  2 A.      . B. 1 3 2 1  . 2 1 x y 1 z  3 x y 1 z  3 C.      . D. 1 3 2 1  . 2 1
Câu 39. Cho hàm số f  x, đồ thị của hàm số /
y  f  x là đường cong như hình vẽ. Giá trị nhỏ  3 
nhất của hàm số g  x  f 2x  
1  4x  3 trên đoạn  ;1   bằng  2  Trang80 A. f 0 . B. f   1 1.
C. f 2  5 . D. f   1  3.
Câu 40.Có bao nhiêu số nguyên dương y sao cho ứng với mỗi y luôn có ít hơn 2021 số nguyên x thoả mãn l
éog x+ 3 - 1 .ù log x- y < 0 2 ( ) ( 2 ) ë û A. 20 . B. 9 . C. 10 . D. 11.  2 x  m x  0 2
Câu 41. Cho hàm số y  f  x  
liên tục trên  . Giá trị I 
f 2 cos x 1 sin d x x  2cos x  3  x  0 0 2 1 1 A. . B. 0 . C. . D. . 3 3 3
Câu 42: Có bao nhiêu số phức z thỏa z  2  i  z  3i và z  2  3i  2 ? A. Vô số B. 0 . C. 2 . D. 1.
Câu 43: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , hình chiếu vuông góc của S lên mặt
phẳng  ABCD trùng với trung điểm cạnh AD , cạnh bên SB hợp với đáy một góc 60 . Tính
theo a thể tích V của khối chóp S.ABCD . 3 a 15 3 a 15 3 a 15 3 a 5 A. V  . B. V  . C. V  . D. V  . 2 6 4 6
Câu 44: Ông Bảo làm mái vòm ở phía trước ngôi nhà của mình bằng vật liệu tôn. Mái vòm đó là một
phần của mặt xung quanh của một hình trụ như hình bên dưới. Biết giá tiền của 1 2 m tôn là
300.000 đồng. Hỏi số tiền (làm tròn đến hàng nghìn) mà ông Bảo mua tôn là bao nhiêu ? 5 m 1200 6 m
A. 18.850.000 đồng.
B. 5.441.000 đồng.
C. 9.425.000 đồng.
D. 10.883.000 đồng. Trang81 x 1 y z  2
Câu 45: Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d :   1 2 1 1  và x 1 y  2 z  2 d :   P
x  y  z   và cắt 2 1 3 2
 . Gọi  là đường thẳng song song với   : 7 0
d , d lần lượt tại A, B sao cho AB ngắn nhất. Phương trình đường thẳng  là: 1 2  x  6  t  x 12  t  5  A.  y  . B.  y  5 . 2       z 9 t  9  z   t  2   x  6
x  6  2t    5  5
C.  y   t .
D.  y   t . 2  2   9   9  z   t  z   t   2  2
Câu 46: Cho hàm số y  f (x) có đồ thị f (
 x) như hình vẽ sau 1
Biết f 0  0 . Hỏi hàm số g  x  f  3
x   2x có bao nhiêu điểm cực trị 3 A. 1. B. 3 . C. 4 . D. 5 . Câu 47: Có bao nhiêu số tự nhiên a sao cho tồn tại số thực x thoả 3 3lo  g x  1 x a  3  x   3lo gx 1 2021 2020  a  2020 A. 9. B. 8. C. 5. D. 12
Câu 48. Cho hàm số bậc bốn y  f  x có đồ thị C như hình vẽ bên. Biết hàm số y  f  x đạt cực trị tại các điểm 2
x , x , x thỏa mãn x  x  2 , f  x  f x  f x
 0 và C nhận 1   3  2  1 2 3 3 1 3
đường thẳng d : x  x làm trục đối xứng. Gọi S , S , S , S là diện tích của các miền hình 2 1 2 3 4 
phẳng được đánh dấu như hình bên. Tỉ số S S 1
2 gần kết quả nào nhất S  S 3 4 Trang82 y d S3 S1 x1 x3 O x2 S2 x S4 A. 0, 60 . B. 0, 55 . C. 0, 65 . D. 0, 70.
Câu 49: Cho hai số phức u, v thỏa mãn u = v = 10 và 3u - 4v = 50 . Tìm Giá trị lớn nhất của biểu
thức 4u + 3v - 10i . A. 30 . B. 40 . C. 60 . D. 50 .
Câu 50. Trong không gian Oxyz , cho hai điểm (
A 2;3;3) và mặt cầu
S x  2 x  2 x 2 : 1 2 3
12 . Xét khối trụ T  nội tiếp mặt cầu S  và có trục đi qua
điểm A . Khi khối trụ T có thể tích lớn nhất thì hai đường tròn đáy của T  nằm trên hai mặt
phẳng có phương trình dạng x  ay  bz  c  0 và x  ay  bz  d  0 . Giá trị a  b  c  d bằng A. 4   4 2 . B. 5  . C. 4  . D. 5   4 2 . BẢNG ĐÁP ÁN 1.D 2.A 3.B 4.A 5.A 6.A 7.D 8.B 9.C 10.D 11.D 12.A 13.A 14.D 15.B 16.C 17.B 18.A 19.B 20.A 21.B 22.C 23.D 24.B 25.D 26.A 27.B 28.D 29.A 30.B 31.D 32.A 33.A 34.A 35.B 36.C 37.B 38.C 39.D 40.C 41.A 42.A 43.B 44.D 45.A 46.B 47.A 48.A 49.C 50.B
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Cho tập hợp S  1;3;5;7; 
9 . Có bao nhiêu số tự nhiên gồm ba chữ số khác nhau được lập từ
các phần tử của tập S ? 3 A. 3!. B. 5 3 . C. 5 C . D. 35 A . Lời giải Chọn D
Từ yêu cầu của bài toán, ta chọn 3 chữ số từ 5 phần tử của tập S rồi sắp xếp lại thứ tự là một
chỉnh hợp chập 3 của 5 phần tử. Trang83 1
Câu 2: Cho một dãy cấp số nhân u có u 
và u  2 . Giá trị của u bằng n  1 2 2 4 1 25 A. 32 . B. 6 . C. . D. . 32 2 Lời giải Chọn A u
Dãy cấp số nhân đã cho có công bội 2 q   4 1 u 1
Suy ra số hạng Tiệm cận đứng 3 u    4 1 u .q .64 32. 2
Câu 3: Cho hàm số y  f  x có bảng biến thiên sau:
Khẳng định nào sau đây sai?
A. Hàm số y  f  x đồng biến trên khoảng  ;  2   .
B.Hàm số nghịch biến trên khoảng  2  ;2 .
C. Hàm số nghịch biến trên khoảng  2  ;0 .
D. Hàm số đồng biến điệu trên 0; 2 . Lời giải Chọn B Lý thuyết
Câu 4: Hàm số y  f  x có bảng biến thiên như sau: Tìm khẳng định đúng?
A.Hàm số có ba điểm cực trị.
B. Hàm số có giá trị cực đại là x  1  .
C. Hàm số đạt cực đại tại x  0 .
D. Hàm số có điểm cực tiểu là x 1 . Lời giải Chọn A Lý thuyết
Câu 5: Cho hàm số y  f  x liên tục trên  và có bảng xét dấu của f  x như sau: Trang84 x  2  1 5 
f  x  0  0  0 
Hàm số f  x có bao nhiêu điểm cực trị? A.2. B. 3. C. 0. D. 1. Lời giải Chọn A Lý thuyết x  Câu 6: Cho hàm số 2 1
y  x  . Tiệm cận đứng của đồ thị hàm số là 1
A.Đường thẳng x  1. B. Đường thẳng x  2.
C. Đường thẳng y  2. D. Đường thẳng y  1. Lời giải Chọn A Lý thuyết
Câu 7: Cho hàm số có đồ thị như hình vẽ:
Hàm số nào dưới đây có đồ thị là hình vẽ trên? A. 4 2
y  x  4x  2 . B. 3
y  x  3x  2 . C. 4 2
y  x  4x  2 . D. 3
y  x  3x  2 . Lời giải Chọn D
Từ đồ thị ta có hàm số đã cho phải là hàm số bậc 3, vậy hai phương án A , C bị loại.
Mặt khác lim f  x   , suy ra hệ số bậc ba âm. Vậy chọn phương án D. x
Câu 8: Đồ thị của hàm số y   2 x   2 2
x  2 cắt trục tung tại điểm có tọa độ là A. 0; 4 . B. 0; 4   . C. 4;0 . D.  4  ;0 . Lời giải Chọn B
Với x  0 , suy ra y   2   2 0 2 0  2  4
 . Vậy tọa độ giao điểm là 0; 4   .
Câu 9: Với a là số thực dương tùy ý,  ln ea  bằng
A. 1 a ln .
B. 1 ln a .
C.1 ln a .
D. 1 ln  ln a . Trang85 Lời giải Chọn C Ta có:  
ln ea   ln e  ln a 1 ln a .
Câu 10: Đạo hàm của hàm số x y   là x  A. x 1 x  . B. x   . ln  . C. x  . D. ln Lời giải Chọn D Ta có: x y   ln  .
Câu 11: Với a là số thực dương tùy ý, 3 2 a bằng 1 3 2 A. 6 a . B. 6 a . C. 2 a . D. 3 a . Lời giải Chọn D 2 Ta có: 3 2 3 a  a .
Câu 12: Nghiệm của phương trình log 2x  2  1 là 2  
A. x  2 .
B. x 1. C. x  2  . D. x  3. Lời giải Chọn A Ta có: log
2x  2  1  2x  2  2  2x  4  x  2 . 2  
Câu 13: Nghiệm của phương trình 1 log x 1  3 là 2  
A. x  3.
B. x 1.
C. x  7 . D. x  4 . Lời giải Chọn A Ta có: 1 log x 1  3  log
x 1  2  x 1  4  x  3 . 2   2   x  4
Câu 14: Cho hàm số f  x 5 
. Trong các khẳng định sau, khẳng định nào đúng? 2 x 4 x 4 A. f
 xdx   C . B.    3 4 f x dx  x   C . 4 x x 4 x 1 4 x 4 C. f
 xdx   C. D. f
 xdx   C. 4 x 4 x Lời giải Chọn D x  4 4 4  4  x 4
Ta có f  x 5  3  x  suy ra f  x 3 dx  x  dx    C   . 2 x 2 x 2  x  4 x
Câu 15: Cho hàm số f (x)  sin 3x 1 . Trong các khẳng định sau, khẳng định nào đúng? 1 1 A.
f (x)dx 
cos 3x  x  C  B.
f (x)dx   cos 3x  x  C  3 3 C.
f (x)dx  3cos 3x  x  C  D.
f (x)dx  3
 cos3x  x  C  Trang86 Lời giải Chọn B 1 Ta có
f (x)dx  sin 3x    
1 dx   cos 3x  x  C . 3 2 3 3 Câu 16: Nếu f
 xdx  3 và f xdx  2   thì
f  xdx  bằng 1  1  2 A. 1. B. 5 . C. 5  . D. 1. Lời giải Chọn C Ta có: 3 1  3 f
 xdx  f
 xdx f
 xdx  3    2    5  2 2 1  ln 2 Câu 17: Tích phân x e dx  bằng 0 A. 2 e . B.1. C. 2 . D. 2 e 1. Lời giải Chọn B Ta có ln 2 x e dx  ln 2 x  e  2 1  1. 0 0
Câu 18: Tìm số phức z  z  z biết z  1 3i , z  2   2i 1 2 1 2 . A. z  1  i . B. z  1  i .
C. z  1 i .
D. z  1 i . Lời giải Chọn A
z  z  z  1 3i   2   2i  1   i . 1 2
Câu 19: Tìm số phức liên hợp của số phức z  i 3i   1 .
A. z  3 i . B. z  3  i .
C. z  3 i . D. z  3  i . Lờigiải ChọnB
z  i 3i   1  3
  i nên suy ra z  3  i .
Câu 20: Cho số phức z  2
 i . Điểm nào dưới đây là biểu diễn của số phức w  iz trên mặt phẳng toạ độ? A. M  1  ; 2  . B. P  2  ;  1 . C. N 2  ;1 .
D. Q 1; 2. Lờigiải ChọnA
Ta có: w  iz  i  2   i  1   2i .
Vậy điểm biểu diễn số phức w  iz là điểm M  1  ; 2  .
Câu 21: Cho hình chóp S. ABC , có đáy ABC là tam giác vuông cân tại A , SA = AB = a , SA vuông
góc với mặt phẳng (ABC). Thể tích của khối chóp S. ABC bằng Trang87 3 a 3 a 3 a 3 3a A. . B. . C. . D. . 3 6 2 2 Lời giải Chọn B 3 1 a
Thể tích của khối chóp S. ABC : V = S . A S = . S . ABC 3 ABC 6
Câu 22: Cho khối lăng trụ có đáy là hình vuông cạnh a và chiều cao bằng 2a . Thể tích của khối lăng trụ đã cho bằng 2 4 A. 3 a B. 3 a C. 3 2a D. 3 4a 3 3 Lời giải Chọn C
Ta có: V  S.h 2  a .2a 3  2a .
Câu 23: Tính thể tích V của khối nón có bán kính đáy bằng 3 và chiều cao bằng 6 .
A. V 108 .
B. V  54 .
C. V  36 .
D.V 18 . Lời giải Chọn D 1 1 Ta có 2 V   R h 2
 .3 .6 18 . 3 3
Câu 24: Tính diện tích xung quanh S của hình trụ có bán kính bằng 3 và chiều cao bằng 4 .
A. S  36 .
B. S  24 .
C. S 12 D. S  42 . Lời giải Chọn B Ta có: S
 2rh  2.3.4  24 . xq
Câu 25: Trong không gian Oxyz , cho tam giác ABC với A1;2;  1 ; B3;1; 2
 ;C2;0;4 . Trọng tâm của
tam giác ABC có tọa độ là A. 6;3;3. B. 2; 1  ;  1 . C.  2  ;1;  1 . D. 2;1;  1 . Lời giải Chọn D
x  x  x
y  y  y
G là trọng tâm tam giác ABC thì A B C x   2; A B C y   1. G 3 G 3 2 2
Câu 26: Trong không gian Oxyz , mặt cầu S   x   2 :
1  y   z  2  16 có đường kính bằng A. 8 . B. 4 . C. 16 . D. 2 . Trang88 Lời giải Chọn A
Bán kính r  16  4 nên đường kính là 8.
Câu 27: Trong không gian Oxyz , mặt phẳng nào dưới đây đi qua điểm M  2  ;1;  1 ?
A. x  y  z  0 .
B. x  2 y  z  3  0 .
C. x  y  z 1  0 .
D. x  y  z  3  0 . Lời giải Chọn B
Câu 28: Trong không gian Oxyz , vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng đi qua
hai điểm A1;2;  1 và B  1  ;0;0 ?     A. u 2; 2; 1 u 2; 2; 1  1 u 2;2;  1 . B. u  2  2; 2;  1 . C. 3  . D. 4  . Lời giải Chọn D 
Đường thẳng đi qua hai điểm ,
A B nên có một vectơ chỉ phương là BA2;2;  1
Câu 29: Chọn ngẫu nhiên một số trong số 21 số nguyên không âm đầu tiên. Xác suất để chọn được số lẻ bằng 10 11 9 4 A. . B. . C. . D. . 21 21 21 7 Lời giải Chọn A
Tập hợp 21 số nguyên không âm đầu tiên là 0;1;2;3;....;19;2  0 .
Không gian mẫu có 21 phần tử. Trong 21 số nguyên không âm đầu tiên có 10 số lẻ nên tương ứ 10
ng có 10 kết quả thuận lợi. Vậy xác suất là . 21
Câu 30: Hàm số nào dưới đây đồng biến trên R ?
A. y  tan x . B. 3 2
y  x  x  x 1. 2x 1 C. 4 y  x 1.
D. y  x  . 1 Lời giải Chọn B Hàm số 3 2
y  x  x  x 1 có 2
y '  3x  2x 1  0, x
  R nên đồng biến trên R .
Câu 31: Gọi M , m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số 3 2
y  2x  3x 12x 1 trên
đoạn [1;5] . Tổng M  m bằng. A. 270 . B. 8 . C. 280 . D. 260 . Lời giải Chọn D +) Hàm số 3 2
y  2x  3x 12x 1 xác định và liên tục trên đoạn  1  ;  5 . x 1 1  ;5 +) Ta có 2
y  6x  6x 12  0   . x  2     1  ;5 Trang89 +) f   1  14 ; f   1  6
 ; f 5  266.
Vậy m  min f  x  f   1  6
 , M  max f x  f 5  266  1  ;5  1  ;  5
 M  m  260 4 x x2  2   2 
Câu 32: Tập nghiệm của bất phương trình      ?  3   3  2 2 2 2 A. x   . B. x  . C. x  D. x  3 3 5 5 Lời giải Chọn A 4 x x2  2   2  2 
 4x  x  2  x   .     .  3   3  3
Vậy tập nghiệm của bất phương trình đã cho là 2 x   3 2 2
Câu 33: Nếu 2 f (x)  
1 dx  5 thì f (x)dx  bằng ? 1 1 A. 2 . B. 2  . C. 3 D. 3  Lời giải Chọn A 2 2 2 2 2
Ta có 2 f (x)  
1 dx  2 f (x)dx  dx  2 f (x)dx 1  5 
f (x)dx  2     1 1 1 1 1
Câu 34: Cho số phức z  3 4i . Khi đó mô đun của số phức 1 i z bằng ? A. 5 2 . B. 10 . C. 20 D. 2 5 Lời giải Chọn A
Ta có 1 i z  1 i z  2.5
Câu 35: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A và AB  a 2 . Biết
SA   ABC và SA  a . Góc giữa hai mặt phẳng SBC  và  ABC  bằng A. 30 . B. 45 . C. 60 . D. 90 . Lời giải Chọn B Trang90 S C A M B
Gọi M là trung điểm BC .
Do tam giác ABC vuông cân tại A nên AM  BC . SA  BC  Do
  SAM   BC . AM  BC  
 SBC  ABC  BC  
 SAM   BC  Ta có 
 SBC,ABC 
 SM, AM   . SAM 
SBC  SM   SAM 
 ABC  AM
Suy ra góc giữa SBC  và  ABC  bằng góc  SMA .
Xét tam giác ABC vuông cân tại A và AB  a 2  BC  2a; AM  a SA a
Xét tam giác SMA vuông tại A Ta có   tan SMA 
  1 SMA  45 . AM a
Câu 36: Cho hình chóp đều S.ABC có cạnh đáy bằng a , góc giữa một mặt bên và mặt đáy bằng 60 .
Tính độ dài đường cao SH. a 2 a a a A. SH  3 . B. SH  . C. SH  3 . D. SH  . 3 2 2 3 Lời giải Chọn C
Gọi M là trung điểm của BC .
Do ABC là tam giác đều nên AM  BC . Trang91 
 SBC  ABC  BC  Vì  0
SM  SBC : SM  BC  SMA  60 . AM  
ABC: AM  BC
Gọi H là trọng tâm tam giác ABC . Vì S.ABC là hình chóp đều nên SH   ABC. a 3 1 a 3
Do ABC là tam giác đều AM 
 HM  AM  2 3 6 a 3 a
Trong tam giác vuông SHM có SH  HM .tan 60  . 3  . 6 2
Câu 37: Trong không gian với hệ tọa độ Oxyz, A 3  ; 4; 2 , B 5  ; 6; 2 , C 1  0; 17; 7   . Viết
phương trình mặt cầu tâm C , bán kính AB . A.  2 2 2 x 
2  y  2 z  2 10 17 7  8 .
B.  x 10   y 17   z  7  8 . C.  2 2 2 x 
2  y  2 z  2 10 17 7  8 .
D.  x 10   y 17   z  7  8 . Lờigiải ChọnB  Ta có AB   2  ;2;0 2 2
 AB  2  2  2 2 .
Phương trình mặt cầu tâm C bán kính 2 2 2
AB :  x 10   y 17   z  7  8.
Câu 38: Trong không gian với hệ trục tọa độ Oxyz , cho M 1; – 2; 
1 , N 0;1; 3 . Phương trình đường
thẳng qua hai điểm M , N là x 1 y  2 z 1 x 1 y  3 z  2 A.      . B. 1 3 2 1  . 2 1 x y 1 z  3 x y 1 z  3 C.      . D. 1 3 2 1  . 2 1 Lờigiải ChọnC 
Đường thẳng MN đi qua N 0;1; 3 và có vectơ chỉ phương là MN   1  ; 3; 2 có phương x y 1 z  3 trình là    . 1 3 2
Câu 39. Cho hàm số f  x, đồ thị của hàm số /
y  f  x là đường cong như hình vẽ. Giá trị nhỏ  3 
nhất của hàm số g  x  f 2x  
1  4x  3 trên đoạn  ;1   bằng  2  A. f 0 . B. f   1 1.
C. f 2  5 . D. f   1  3. Lời giải Chọn D Trang92
Đặt t  2x 1  t  2  ; 
3 , xét hàm số h t   f t   2t 1 trên  2  ;  3 . t  1   Ta có / h  x /
 f x  2 , /
h t   0  t  1  . t  2  / h  x /
 0  f x  2  x1;3 / h  x /
 0  f x  2  x 2  ;  1
Ta có bẳng biến thiên sau
Ta có min h t   h  1  f   1  3 .   ;3
Câu 40.Có bao nhiêu số nguyên dương y sao cho ứng với mỗi y luôn có ít hơn 2021 số nguyên x thoả mãn l
éog x+ 3 - 1 .ù log x- y < 0 2 ( ) ( 2 ) ë û A. 20 . B. 9 . C.10 . D. 11. Lời giải Chọn C
Điều kiện: x > 0
éíï log x + 3 - 1< 0 ï 2 ( )
êìêïlog x- y> 0 ïêî 2 Với điều kiện trên: l
éog x+ 3 - 1 .ù log x- y < 0 Û ê 2 ( ) ( 2 ) ë û
íêï log x + 3 - 1> 0 ï 2 ( )
êìêï log x- y< 0 ïî 2 ë éíï log x + 3 < 1 ï éíï x + 3< 2 éíï x < - 1 2 ( ) êì ïê ïê êï ìê ìê log x > y ïêî ï x > 2y ï x > 2y 2y é < x < - 1 ïîê (sai) 2 Û ïîê ê Û ê Û ê Û
Û - 1< x < 2y í ê êï ê log x + 3 > 1 í y í ï êï x + 3> 2 êï x > - 1 - ï ê 1< x < 2 2 ( ) êì ïê ë ê ê ì ì ï log x < y y y ï ïê x < 2 ïî ïê x < 2 ïî î 2 ë ë ë
So điều kiện ta được: 0 < < 2y x
Ứng với mỗi y luôn có ít hơn 2021 số nguyên x Û 2y £ 2021 Û y £ log 2021 2
Vì y là số nguyên dương nên y Î {1; 2;3; 4;5;6;7;8;9;1 } 0 Trang93  2 x  m x  0 2
Câu 41. Cho hàm số y  f  x  
liên tục trên  . Giá trị I 
f 2 cos x 1 sin d x x  2cos x  3  x  0 0 2 1 1 A. . B. 0 . C. . D. . 3 3 3 Lời giải Chọn A
Hàm f  x liên tục trên  suy ra
lim f  x  lim f  x  lim     m 1   2 x
m lim 2cos x 3    x0 x0 x 0  x 0  
Xét bất phương trình 2cos x 1  0 với 0  x  . 2   2cos x  1 1  cos x   0  x  2 3  Vậy 2cos x 1
 0 khi 0  x  , 3   2 cos x 1  0 khi  x  . 3 2    2 3 2 I 
f 2 cos x 1 sin d x x 
 f 2cos x 1 sin d x x 
f 2 cos x 1 sin d x x   0 0  3   3 I  f  2cosx  2 1 sin d x x  f
 12cosxsin dxx 0  3  3 Xét I 
f 2 cos x 1 sin d x x  1   0  t
Xét t  2cos x 1  dt  2  d sin d x x   sin d x x 2 x 0  3 t 1 0 Trang94  3 0 -dt 1 1 1 1 Suy ra I 
f 2 cos x 1 sin d x x   f
 t  f
 tdt  f  xdx 1   2 2 2 0 1 0 0 1 1 3 1 x x 1  I 
 2x-1 dx     1  2 6 2 3 0 0  2 Xét I 
f 1 2 cos x sin d x x  2    3 t
Xét t 1 2cos x  dt  d 2sin d x x   sin d x x 2 x   3 2 t 0 1  2 1 dt 1 1 1 1 Suy ra I 
f 2 cos x 1 sin d x x   f
 t  f
 tdt  f  xdx 2    2 2 2 0 0 0 3 1 1 3 1 x x 1  I 
 2x-1 dx     2  2 6 2 3 0 0 2
Suy ra I  I  I  . 1 2 3
Câu 42: Có bao nhiêu số phức z thỏa z  2  i  z  3i và z  2  3i  2 ? A.Vô số B. 0 . C. 2 . D. 1. Lời giải Chọn A Gọi điểm M  ;
x y là điểm trên mp tọa độ Oxy biểu diễn số phức z  x  yi (x, y   )
z  2  i  z  3i : Tập hợp M  ;
x y  là trung trực của đoạn thẳng AB với A2  ;1 , B 0;3
z  2  3i  2 : Tập hợp M  ;
x y  là hình tròn (kể cả biên) có bán kính r  2 và tâm I 2;3
Do đó có vô số só phức thỏa yêu cầu bài toán.
Câu 43: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , hình chiếu vuông góc của S lên mặt
phẳng  ABCD trùng với trung điểm cạnh AD , cạnh bên SB hợp với đáy một góc 60 . Tính
theo a thể tích V của khối chóp S.ABCD . 3 a 15 3 a 15 3 a 15 3 a 5 A. V  . B.V  . C. V  . D. V  . 2 6 4 6 Trang95 Lời giải Chọn B
Gọi H là trung điểm của AD  SH   ABCD  BH là hình chiếu vuông góc của SB trên  ABCD . 
 SBH  SB  
, ABCD  60 . 2 a a 5 ABH  vuông tại A 2 2 2
 BH  AB  AH  a   . 4 2 a 15 S
 BH vuông tại H  SH  H . B tan 60  . 2 3 1 a 15 V  .SH.S  . S.ABCD 3 ABCD 6
Câu 44: Ông Bảo làm mái vòm ở phía trước ngôi nhà của mình bằng vật liệu tôn. Mái vòm đó là một
phần của mặt xung quanh của một hình trụ như hình bên dưới. Biết giá tiền của 1 2 m tôn là
300.000 đồng. Hỏi số tiền (làm tròn đến hàng nghìn) mà ông Bảo mua tôn là bao nhiêu ? 5 m 1200 6 m
A. 18.850.000 đồng.
B. 5.441.000 đồng.
C. 9.425.000 đồng.
D.10.883.000 đồng. Trang96 Lời giải Chọn D 6
Gọi r là bán kính đáy của hình trụ. Khi đó:
 2r  r  2 3. 0 sin120
Sử dụng hệ thức lượng trong tam giác, ta có góc ở tâm của cung này bằng 0 120 . Và độ 1 dài cung này bằng
chu vi đường tròn đáy. 3 1
Suy ra diện tích của mái vòm bằng S , 6 m 3 xq
(với S là diện tích xung quanh của hình trụ). 1200 xq 2 3 m 2 3 m
Do đó, giá tiền của mái vòm là 1 1 S   rl    xq   1 .300.000 . 2 .300.000
.2 .2 3.5.300.000 10882796,19. 3 3 3 x 1 y z  2
Câu 45: Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d :   1 2 1 1  và x 1 y  2 z  2 d :   P
x  y  z   và cắt 2 1 3 2
 . Gọi  là đường thẳng song song với   : 7 0
d , d lần lượt tại A, B sao cho AB ngắn nhất. Phương trình đường thẳng  là: 1 2  x  6  t  x 12  t  5  A.  y  . B.  y  5 . 2       z 9 t  9  z   t  2   x  6
x  6  2t    5  5
C.  y   t .
D.  y   t . 2  2   9   9  z   t  z   t   2  2 Lời giải Chọn A
A d  A 1 2 ; a ; a 2
  a ,Bd  B 1 ; b 2   3b;2  2b . 1   2    AB b  2 ;
a 3b  a  2; 2
 b  a  4 . 
(P) có vtpt n 1;1;  1 .   
 / / P  A .
B n  0  b  a  2  AB a 1;2a  5; a  6 2  5  49 49 2 2
 AB  6a  30a  62  6 a       2  2 2 Trang97  x  6  t  5  5 9    7  5 AB khi a   A 6; ; , AB     1  ;0  ;1   :  y  min 2  2 2  2 2   9  z   t.  2
Câu 46: Cho hàm số y  f (x) có đồ thị f (
 x) như hình vẽ sau 1
Biết f 0  0 . Hỏi hàm số g  x  f  3
x   2x có bao nhiêu điểm cực trị 3 A. 1. B. 3 . C. 4 . D. 5 . Lời giải Chọn B Đặ 1 t h  x  f  3
x   2x  hx 2  x f  3 x   2 3 2
Ta có h x  0  f  3 x   , x  0,  1 2 x Đặt 3 3
t  x  x  t 2 Từ  
1 ta có: f t  ,2 3 2 t 2 4 1
Xét mt 
 mt   . 3 2 3 3 5 t t
Lúc này ta có hình vẽ 2 đồ thị như sau Trang98
Suy ra pt 2 có 1 nghiệm t  t   pt      0 0 1 có nghiệm 3 x t0 0 x 0
Bảng biến thiên của h x, g x  hx như sau
Vậy hàm số y  g  x có 3 điểm cực trị. Câu 47: Có bao nhiêu số tự nhiên a sao cho tồn tại số thực x thoả 3 3lo  g x  1 x a  3  x   3lo gx 1 2021 2020  a  2020 A. 9. B. 8. C. 5. D. 12 Lời giải Chọn A 3log x  1  3 3lo  g x  Xét phương trình: 1  a x a 2020 2021 
, điều kiện: x  1  , 3 x  2020 3 3log x  1 3log x  3  x  a  log a  2020  log x  2020 2021  1  2021  3 3    x  log x  2020 x  a  log x a  2020  2021   3log 1 3log  20 1 2  1    Trang99 Xét hàm số 3
f (t)  t  log
t  2020 , trên 0; 21  3 20  2 3t 2
f '(t)  3t    0, t
  0 nên hàm số f (t) đồng biến trên 0; 3 t  2020ln 2021 Do đó  lo  g x  a trở thành: 1 x  a
 x  x  log 1  log x  log . a log(x 1) log x  log a  
    nên a 10  a 1,2,3,4,5,6,7,8,  9 x   1, x 1 log 1
Câu 48. Cho hàm số bậc bốn y  f  x có đồ thị C như hình vẽ bên. Biết hàm số y  f  x đạt cực trị tại các điểm 2
x , x , x thỏa mãn x  x  2 , f  x  f x  f x
 0 và C nhận 1   3  2  1 2 3 3 1 3
đường thẳng d : x  x làm trục đối xứng. Gọi S , S , S , S là diện tích của các miền hình 2 1 2 3 4 
phẳng được đánh dấu như hình bên. Tỉ số S S 1
2 gần kết quả nào nhất S  S 3 4 y d S3 S1 x1 x3 O x2 S2 x S4 A. 0, 60 . B. 0, 55 . C. 0, 65 . D. 0, 70. Lời giải Chọn A
Nhận thấy kết quả bài toán không đổi khi ta tịnh tiến đồ thị C sang bên trái sao cho đường
thẳng d : x  x trùng với trục tung khi đó C là đồ thị của hàm trùng phương y  g  x có ba 2
điểm cực trị x  1
 , x  0, x 1. Suy ra y  g x  k  4 2
x  2x   c k  0 1 2 3 2 2 3
Lại có f  x  f x  f x
 0  2k  2c  c  0  c  k 1   3  2  3 3 4 3
Suy ra : y  g  x  k  4 2
x  2x   k 4 1  Khi đó: 3 28 2 17 4 2
S  S  k x  2x  dx  k  . 1 2 4 60 0
Ta lại có : g 0  g  
1  k  S  S  S  S  k.1  k . 1 2 3 4 Trang100 28 2 17 77  28 2 S  S 28 2 17 Suy ra 1 2
S  S  k  k  k    0,604 3 4 60 60 S  S 77  28 2 3 4
Câu 49: Cho hai số phức u, v thỏa mãn u = v = 10 và 3u - 4v = 50 . Tìm Giá trị lớn nhất của biểu
thức 4u + 3v - 10i . A. 30 . B. 40 . C. 60 . D. 50 . Lời giải Chọn C 2 Ta có z = .
z z . Đặt T = 3u - 4v , M = 4u + 3v . Khi đó 2 2 2
T = (3u - 4v)(3u - 4 )
v = 9 u + 16 v - 12(uv + vu). Tương tự 2 2 ta có 2
M = (4u + 3v)(4u + 3v)= 16 u + 9 v + 12(uv + vu). Do đó M + T = ( 2 2 2 2
25 u + v )= 5000 . Suy ra 2 2 M = 5000 - T 2
= 5000 - 50 = 2500 hay M = 50 .
Áp dụng z + z¢£ z + z¢ta có
4u + 3v - 10i £ 4u + 3v + - 10i = 50 + 10 = 60 .
Suy ra max 4u + 3v - 10i = 60 .
Câu 50. Trong không gian Oxyz , cho hai điểm (
A 2;3;3) và mặt cầu
S x  2 x  2 x 2 : 1 2 3
12 . Xét khối trụ T  nội tiếp mặt cầu S  và có trục đi qua
điểm A . Khi khối trụ T có thể tích lớn nhất thì hai đường tròn đáy của T  nằm trên hai mặt
phẳng có phương trình dạng x  ay  bz  c  0 và x  ay  bz  d  0 . Giá trị a  b  c  d bằng A. 4   4 2 . B. 5  . C. 4  . D. 5   4 2 . Lời giải Chọn B
Gọi r, h lần lượt là bán kính đường tròn đáy và chiều cao của mặt trụ T  và R là bán kính mặt
cầu S  , ta có : R  2 3 , 2 2
h  2 R  r . Trang101
Thể tích khối trụ T  là 2 2 2 2 2 2
V   r h   r R  r   r r  2 2 . 2 2. . 2R  2r 
r  r  2R  2r 2
Mà theo Cô-si ta có: r .r 2R  2r  2 2 2 2 2 2 2 2 2 3   R 3 3 8 4 3 R 6 Suy ra : 2 2 r .r  2 2 2R  2r  6 3  R  V 
R . Dấu “=” xẩy ra khi r  27 9 3 2  R 6  2 3R
Vậy khi khối trụ T  đạt thể tích lớn nhất thì chiều cao 2
h  2 R      4  ( Có 3  3  
thể dùng phương pháp hàm số).
Mặt khác tâm của khối trụ T  chính là tâm I 1; 2;3 của mặt cầu S  nên trục của khối trụ x 1 t  
T  nằm trên đường thẳng IA : y  2  t . Vậy hai đáy của khối trụ nằm trên 2 mặt phẳng vuông z  3 
góc với đường thẳng AI và cách tâm I một khoảng bằng 2 . Gọi M 1 t; 2  t;3 IA là tâm
của đường tròn đáy hình trụ, ta có 2 2 2
IM  2  t  t  2  2t  4
t  2  M 1 2;2 2;3   
t   2  M  1 2;2 2;3
Vậy 2 mặt phẳng chứa 2 đường tròn đáy của mặt trụ có phương trình là:
x1 2y2 20 x y32 2 0
Và x 1 2  y  2  2  0  x  y 3 2 2  0
Vậy: a  b  c  d  5  Đề 10
ĐỀ LUYỆN THI CẤP TỐC TỐT NGHIỆP THPT NĂM 2021 Thuvienhoclieu.Com BÀI THI: TOÁN
Thời gian: 90 phút Câu 1:
Có 5 người đến nghe một buổi hòa nhạc. Số cách xếp 5 người này vào một hàng có 5 ghế là: A. 130 . B. 125 . C. 120 . D. 100 . 1 Câu 2:
Cho cấp số nhân u với u   ; u  32 . Tìm q ? n  1 7 2 1
A. q  2 .
B. q  4 .
C. q  1. D. q   . 2 Câu 3:
Cho hàm số y  f  x có bảng biến thiên như sau: Trang102
Hàm số y  f  x nghịch biến trên khoảng nào dưới đây? A.  ;0  . B.  ;  2  . C.  1  ;0 . D. 0; . Câu 4:
Cho hàm số y  f  x có bảng biến thiên như hình bên:
Khẳng định nào sau đây là đúng?
A. Hàm số đạt cực đại tại x  3.
B. Hàm số đạt cực đại tại x  4 .
C. Hàm số đạt cực đại tại x  2 .
D. Hàm số đạt cực đại tại x  2  . Câu 5:
Cho hàm số y  f (x) liên tục trên  và có bảng xét dấu f  x như sau: x -∞ 1 2 3 4 +∞ f '(x) 0 + + 0 +
Kết luận nào sau đây đúng
A. Hàm số có 4 điểm cực trị.
B. Hàm số có 2 điểm cực đại.
C. Hàm số có 2 điểm cực trị.
D. Hàm số có 2 điểm cực tiểu. 1  4x Câu 6:
Đường thẳng nào dưới đây là tiệm cận ngang của đồ thị hàm số y  2x  . 1 1 A. y  2 . B. y  4 . C. y  . D. y  2 . 2 Trang103 Câu 7:
Đường cong trong hình vẽ bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn
phương án A, B, C, D dưới đây. Hỏi đó là hàm số nào? A. 3 2
y  x  x  2 . B. 4 2
y  x  3x  2 . C. 4 2
y  x  2x  3 . D. 2
y  x  x 1. Câu 8: Đồ thị của hàm số 4 2
y  x  3x 1 cắt trục tung tại điểm có tung độ bằng A. 3  . B. 0 . C. 1. D. 1. Câu 9:
Cho a  0 , a 1. Tính  2 log a . a  A. 2a . B. 2  . C. 2 . D. a .
Câu 10: Đạo hàm của hàm số  3x y là 3x
A. y  x ln 3. B. 1 .3x y x    . C. y  . D.   3x y ln 3 . ln 3 2 4
Câu 11: Cho a là số thực dương khác 1. Khi đó 3 a bằng 8 3 A. 3 2 a . B. 3 a . C. 8 a . D. 6 a .
Câu 12: Phương trình log
x 1  4 có nghiệm là 2   A. x  4 . B. x  15. C. x  3. D. x 16 .
Câu 13: Nghiệm của phương trình log 2x  7  log x 1  2 là 3   3   16 13 A. x  2 . B. x  3. C. x  . D. x  . 7 3
Câu 14: Cho hàm số f  x 3  2
 x  x 1. Trong các khẳng định sau, khẳng định nào đúng? 1 1 A.    3 2
f x dx  x  x  x  C . B. f  x 4 2 dx   x 
x  x  C . 2 2 1 1 1 C. f  x 4 2 dx  
x  x  x  C . D. f  x 4 2 dx   x 
x  x  C . 4 4 2
Câu 15: Cho hàm số f  x  sin 2x  3 . Trong các khẳng định sau, khẳng định nào đúng? Trang104 A. f
 xdx  cos2xC . B. f  x 1 dx  
cos 2x  3x  C . 2 C. f
 xdx  cos2x3xC . D. f  x 1 dx   cos 2x  C . 2 1 2 2 Câu 16: Nếu
f (x)dx  7  và f (t)dt  9  thì f (x)dx  bằng 1  1  1 A. 2  . B. 16 . C. 2 .
D. Không xác định được. 4 Câu 17: Tích phân xdx  bằng 1 1 1 A.  . B. . C. 4 . D. 2 . 4 4
Câu 18: Số phức liên hợp của số phức z  7
 i có điểm biểu diễn trên mặt phẳng tọa độ là:
A. M 0;  7. B. M  7  ;0. C. M 7;0. D. M 0;7.
Câu 19: Cho hai số phức z  2  i; w  3  2i . Số phức z  w bằng A. 1  3i . B. 6  2i . C. 5  i . D. 1 3i .
Câu 20: Cho số phức z  2
 3i . Điểm biểu diễn của z trên mặt phẳng tọa độ là
A. M 2;3 . B. N  2  ; 3  . C. P 2; 3   . D. Q  2  ;3 .
Câu 21: Một khối chóp có diện tích đáy bằng 4 và chiều cao bằng 6 . Thể tích của khối chóp đó là A. 24 . B. 12 . C. 8 . D. 6 .
Câu 22: Thể tích của khối hộp chữ nhật có ba kích thước là 2; 3; 5 là A. 30 . B. 10 . C. 15 . D. 120 .
Câu 23: Công thức V của khối trụ có bán kính r và chiều cao h là 1 1 A. 2 V   r h . B. 2 V   r h . C. 2 V   rh . D. 2 V   rh . 3 3
Câu 24: Một hình trụ có bán kính đáy r  2cm và độ dài đường sinh l  5cm . Diện tích xung quanh của hình trụ đó là A. 2 10 cm . B. 2 20 cm . C. 2 50 cm . D. 2 5 cm .   
Câu 25: Trong không gian với hệ trục tọa độ Oxyz , cho a   1
 ;2;0 , b  2;1;0 , c  3;1;  1 . Tìm    
tọa độ của vectơ u  a  3b  2c . A. 10; 2  ;13 . B.  2  ;2; 7   . C.  2  ; 2  ;7 . D. 11;3; 2  .
Câu 26: Trong không gian Oxyz , cho mặt cầu S  2 2 2
: x  y  z  2y  4z  2  0 . Bán kính của mặt cầu đã cho bằng Trang105 A. 1. B. 7 . C. 2 2 . D. 7 .
Câu 27: Trong không gian Oxyz , cho 2 điểm A 1  ;0; 
1 , B 2;1;0 . Viết phương trình mặt phẳng P
đi qua A và vuông góc với AB .
A.  P : 3x  y  z  4  0 .
B.  P : 3x  y  z  4  0 .
C.  P : 3x  y  z  0 .
D.  P : 2x  y  z 1  0 . x  2 y 1 z  7
Câu 28: Trong không gian Oxyz , cho đường thẳng d :  
. Vectơ nào dưới đây không 1 3 5 
phải là một vectơ chỉ phương của d ?    
A. u  1;3;5 .
B. u  1;3;  5 .
C. u  1; 3;5 .
D. u  2; 6; 10  . 2   1   3   4  
Câu 29: Một hộp đèn có 12 bóng, trong đó có 4 bóng hỏng. Lấy ngẫu nhiên 3 bóng. Tính xác suất để
trong 3 bóng có 1 bóng hỏng. 11 13 28 5 A. . B. . C. . D. . 50 112 55 6
Câu 30: Tìm tất cả các giá trị của tham số m để hàm số 3 2
y  x  3mx  32m  
1 1 đồng biến trên  .
A. Không có giá trị m thỏa mãn.
B. m 1.
C. m  1.
D. m .
Câu 31: Gọi M , m lần lượt là giá trị lớn nhât, giá trị nhỏ nhất của hàm số f x  3 x  2
7x  11x  2
trên đoạn 0;2. Giá trị của biểu thức A  2M 5m bằng?
A. A  3.
B. A  4.
C. A  16. D. A  1037 . 27
Câu 32: Tập nghiệm của bất phương trình 2 x 2 2 x  8 là A.  ;    3 . B.  3   ;1 . C.  3   ;1 . D.  3   ;1 . 2 2 Câu 33: Cho 3  f
 x2xdx  6 
. Khi đó f xdx  bằng 1 1 A. 1. B. 3  . C. 3 . D. 1.
Câu 34: Cho số phức z  1 i . môđun của số phức .
z 4  3i bằng A. z  5 2 B. z  2 C. z  25 2 D. z  7 2
Câu 35: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Cạnh bên SA vuông góc với đáy, AB  ,
a AD  a 3, SA  2a 2 (tham khảo hình bên). Góc
giữa đường thẳng SC và mặt phằng SAB bằng A. 30 . B. 45 . Trang106 C. 60 . D. 90 .
Câu 36: Cho hình lăng trụ đứng AB .
C A' B'C ' có độ dài cạnh bên bằng 3, đáy ABC là tam giác vuông
tại B và AB  2 (tham khảo hình bên). Khoảng cách từ A đến mặt phẳng  A' BC bằng 13 13 6 6 13 A. . B. . C. . D. . 13 36 13 13
Câu 37: Trong không gian Oxyz, cho hai điểm M 2;4;  1 , N  2  ;2; 3
  . Phương trình mặt cầu đường kính MN là 2 2 2 2 A. 2
x   y   3  z   1  9. B. 2
x   y  3   z   1  9. 2 2 2 2 C. 2
x   y  3   z   1  9. D. 2
x   y  3   z   1  3.
Câu 38: Trong không gian với hệ tọa độ Oxyz, phương trình nào dưới đây là phương trình của đường
thẳng đi qua A1;0; 2 và vuông góc với mặt phẳng (P): x - y + 3z - 7 = 0? x  t x 1 t x 1 t x 1 t    
A.  y  t  . B.  y  1  .
C.  y  t  .
D.  y  t .     z  3t  z  3  2t  z  2  3t  z  2  3t 
Câu 39: Cho hàm số f  x , đồ thị của hàm số y  f ' x là đường cong trong hình bên. Giá trị lớn nhất 2
của hàm số g x  2 f x x   1 trên đoạn  3  ;  3 bằng
A. f 0 1. B. f  3    4. C. 2 f   1  4.
D. f 3 16.
Câu 40: Có bao nhiêu số nguyên y trong đoạn  2  021;202 
1 sao cho bất phương trình 11   x logx log x y 10 10 10 10
đúng với mọi x thuộc 1;100 : . A. 2021. B. 4026 . C. 2013. D. 4036 .     f  x 2x 2 khi x 0   I  sin 2 . x f  cosxdx 2
x +4x  2 khi x  0 Câu 41: Cho hàm số . Tích phân 0 bằng Trang107 9 9 7 7 A. I  . B. I   . C. I   . D. I  . 2 2 6 6
Câu 42: Có bao nhiêu số phức z thỏa mãn z  13 và  z  2iz  4i là số thuần ảo? A. 1. B. 2 . C. 0 . D. 4 .
Câu 43: Cho hình chóp S.ABCD có đáy là hình chữ nhật với AB  a , BC  a 3 . Cạnh bên SA
vuông góc với đáy và đường thẳng SC tạo với mặt phẳng (SAB) một góc 30 . Thể tích khối
chóp S.ABCD bằng 3 2a 3 3a 3 2 6a A. 3 3a . B. . C. . D. . 3 3 3
Câu 44: Ông Bảo làm mái vòm ở phía trước ngôi nhà của mình bằng vật liệu tôn. Mái vòm đó là một
phần của mặt xung quanh của một hình trụ như hình bên dưới. Biết giá tiền của 1 2 m tôn là
300.000 đồng. Hỏi số tiền (làm tròn đến hàng nghìn) mà ông Bảo mua tôn là bao nhiêu ? 5 m 1200 6 m
A. 18.850.000 đồng.
B. 5.441.000 đồng.
C. 9.425.000 đồng.
D. 10.883.000 đồng.
Câu 45: Trong không gian Oxyz, cho điểm E 2;1; 
3 , mặt phẳng  P : 2x  2y  z  3  0 và mặt cầu
S x  2  y  2 z  2 : 3 2 5
 36. Gọi  là đường thẳng đi qua E, nằm trong mặt phẳng
P và cắt S tại hai điểm có khoảng cách nhỏ nhất. Phương trình của  là
x  2  9t
x  2  5t x  2  t
x  2  4t    
A.  y  1 9t .
B.  y  1 3t .
C.  y  1 t .
D.  y  1 3t.     z  3  8t  z  3  z  3  z  3  3t  Trang108
Câu 46: Cho hàm số y  f  x là một hàm đa thức có bảng xét dấu f  x như sau
Số điểm cực trị của hàm số     2 g x
f x  x  A. 5 . B. 3 . C. 1. D. 7 .
Câu 47: Có bao nhiêu số nguyên m  2
 0;20 để phương trình 7x  m  6log 6x  m có nghiệm thực 7   A. 19 . B. 21 . C. 18 . D. 20 .
Câu 48: Cho hàm số bậc bốn trùng phương y  f  x có đồ thị là đường cong trong hình bên. Biết hàm
số f  x đạt cực trị tại ba điểm x , x , x (x  x  x ) thỏa mãn x  x  4 . Gọi S và S là 1 2 3 1 2 3 1 3 1 2 S
diện tích của hai hình phẳng được gạch trong hình. Tỉ số 1 bằng S2 2 7 1 7 A. . B. . C. . D. . 5 16 2 15
Câu 49: Cho các số phức
z 1 4i  2, z  4  6i  1 và z 1  z  2  i . Tìm 1 z , z2, 3 z thỏa mãn 1 2 3 3
giá trị nhỏ nhất của biểu thức P     3 z 1 z 3 z z2 . 14 14 A.  2 . B. 29  3 . C.  2 2 . D. 85  3 . 2 2
Câu 50: Trong không gian Oxyz cho hai điểm A1;0;0, B 3; 4; 4
  . Xét khối trụ T  có trục là đường
thẳng AB và có hai đường tròn đáy nằm trên mặt cầu đường kính AB . Khi T  có thể tích lớn
nhất, hai đáy của T  nằm trên hai mặt phẳng song song lần lượt có phương trình là
x  by  cz  d  0 và x  by  cz  d  0 . Khi đó giá trị của biểu thức b  c  d  d thuộc 1 2 1 2
khoảng nào sau đây? A. 0;  21 . B.  1  1;0 . C.  2  9; 1  8. D.  2  0; 1   1 . BẢNG ĐÁP ÁN 1.C 2.A 3.B 4.C 5.D 6.D 7.C 8.C 9.C 10.D 11.D 12.B 13.C 14.B 15.B 16.C 17.A 18.D 19.C 20.B Trang109 21.C 22.A 23.A 24.B 25.D 26.B 27.A 28.A 29.C 30.B 31.C 32.B 33.C 34.A 35.A 36.D 37.B 38.C 39.C 40.A 41.A 42.B 43.D 44.D 45.C 46.A 47.D 48.B 49.D 50.C
HƯỚNG DẪN GIẢI CHI TIẾT Câu 1:
Có 5 người đến nghe một buổi hòa nhạc. Số cách xếp 5 người này vào một hàng có 5 ghế là: A. 130 . B. 125 . C.120 . D. 100 . Lời giải Chọn C
Số cách sắp xếp là số hoán vị của tập có 5 phần tử: P  5!  120 . 5 1 Câu 2:
Cho cấp số nhân u với u   ; u  32 . Tìm q ? n  1 7 2 1
A. q  2 .
B. q  4 .
C. q  1. D. q   . 2 Lời giải Chọn A
Áp dụng công thức số hạng tổng quát cấp số nhân ta có q  2 n 1  6 6 u  u q
 u  u .q  q  64  . n 1 7 1  q  2  Câu 3:
Cho hàm số y  f  x có bảng biến thiên như sau:
Hàm số y  f  x nghịch biến trên khoảng nào dưới đây? A.  ;0  . B.  ;  2  . C.  1  ;0 . D. 0;  . Lời giải Chọn B Câu 4:
Cho hàm số y  f  x có bảng biến thiên như hình bên:
Khẳng định nào sau đây là đúng? Trang110
A. Hàm số đạt cực đại tại x  3.
B. Hàm số đạt cực đại tại x  4 .
C.Hàm số đạt cực đại tại x  2 .
D. Hàm số đạt cực đại tại x  2  . Lời giải Chọn C
Giá trị cực đại của hàm số là y  3 tại x  2 . Câu 5:
Cho hàm số y  f (x) liên tục trên  và có bảng xét dấu f  x như sau: x -∞ 1 2 3 4 +∞ f '(x) 0 + + 0 +
Kết luận nào sau đây đúng
A. Hàm số có 4 điểm cực trị.
B. Hàm số có 2 điểm cực đại.
C. Hàm số có 2 điểm cực trị.
D.Hàm số có 2 điểm cực tiểu. Lời giải Chọn D
Dựa vào bảng xét dấu, ta có:
f  x đổi dấu 3 lần khi qua các điểm 1,3, 4. Suy ra loại phương án A.
f  x đổi dấu từ âm sang dương khi qua điểm 1, 4 và đổi dấu từ dương sang âm khi qua điểm
3 . Suy ra hàm số có 2 điểm cực tiểu. 1  4x Câu 6:
Đường thẳng nào dưới đây là tiệm cận ngang của đồ thị hàm số y  2x  . 1 1 A. y  2 . B. y  4 . C. y  . D. y  2 . 2 Lời giải Chọn D 4x 1 Ta có lim  2  y   .
x 2x 
. Vậy đường tiệm cận ngang của đồ thị hàm số là 2 1 Trang111 Câu 7:
Đường cong trong hình vẽ bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn
phương án A, B, C, D dưới đây. Hỏi đó là hàm số nào? A. 3 2
y  x  x  2 . B. 4 2
y  x  3x  2 . C. 4 2
y  x  2x  3 . D. 2
y  x  x 1. Lời giải Chọn C
Đồ thị đi qua M 0;3 , suy ra loại các phương án A, B, D. Câu 8: Đồ thị của hàm số 4 2
y  x  3x 1 cắt trục tung tại điểm có tung độ bằng A. 3  . B. 0 . C. 1. D. 1. Lời giải Chọn C
Trục tung có phương trình: x  0 . Thay x  0 vào 4 2
y  x  3x 1 được: y  1. Câu 9:
Cho a  0 , a 1. Tính  2 log a . a  A. 2a . B. 2  . C. 2 . D. a . Lời giải Chọn C a . a  2 log   2
Câu 10: Đạo hàm của hàm số  3x y là 3x
A. y  x ln 3. B. 1 .3x y x    . C. y  . D.   3x y ln 3 . ln 3 Lời giải Chọn D
Theo công thức đạo hàm ta có   3x y ln 3 . 2 4
Câu 11: Cho a là số thực dương khác 1. Khi đó 3 a bằng Trang112 8 3 A. 3 2 a . B. 3 a . C. 8 a . D. 6 a . Lời giải Chọn D 1 2 2 2 1 1 4   4 . Ta có: 3 3 3 4 6 6
a   a   a  a  a .  
Câu 12: Phương trình log
x 1  4 có nghiệm là 2   A. x  4 . B. x 15. C. x  3. D. x 16 . Lời giải Chọn B
Đk: x 1 0  x  1  .
Ta có log  x   4
1  4  x 1  2  x 1  16  x  15 . Vậy phương trình đã cho có nghiệm 2 là x 15.
Câu 13: Nghiệm của phương trình log 2x  7  log x 1  2 là 3   3   16 13 A. x  2 . B. x  3. C. x  . D. x  . 7 3 Lời giải Chọn C  7 2x  7  0 x   Điều kiện    2  x  1. x 1  0 x 1 Ta có log 2x  7  log x 1  2  log 2x  7  log x 1  2 3   3   3   3  
 log 2x  7  log 9  x 1  3   3    16
 2x  7  9x  9  x  (thỏa mãn điều kiện). 7
Câu 14: Cho hàm số f  x 3  2
 x  x 1. Trong các khẳng định sau, khẳng định nào đúng? 1 1 A.    3 2
f x dx  x  x  x  C . B. f  x 4 2 dx   x 
x  x  C . 2 2 1 1 1 C. f  x 4 2 dx  
x  x  x  C . D. f  x 4 2 dx   x 
x  x  C . 4 4 2 Lời giải Chọn B Trang113
Câu 15: Cho hàm số f  x  sin 2x  3 . Trong các khẳng định sau, khẳng định nào đúng? A. f
 xdx  cos2xC . B. f  x 1 dx  
cos 2x  3x  C . 2 C. f
 xdx  cos2x3xC . D. f  x 1 dx   cos 2x  C . 2 Lời giải Chọn B 1 1 f
 xdx  sin2x 3dx  sin2xd 
2x 3 dx   cos2x 3x C.  2 2 1 2 2 Câu 16: Nếu
f (x)dx  7  và f (t)dt  9  thì f (x)dx  bằng 1  1  1 A. 2  .
B. 16 . C. 2 . D. Không xác định được. Lời giải Chọn C Ta có : 2 2 +)
f (t)dt  f (x)dx 9    . 1  1  c b b +) Áp dụng công thức :
f (x)dx 
f (x)dx  f (x)dx   
a  c  b. a c a 2 1 2 2 2 1
f (x)dx 
f (x)dx 
f (x)dx 
f (x)dx 
f (x)dx 
f (x)dx  9  7  2.       1  1  1 1 1  1  4 Câu 17: Tích phân xdx  bằng 1 1 1 A.  . B. . C. 4 . D. 2 . 4 4 Lời giải Chọn A 4 1 4 1 1 1 Cách 1 : xdx      .  2 x 1 4 2 4 1
Cách 2 :Sử dụng máy tính CASIO .
Câu 18: Số phức liên hợp của số phức z  7
 i có điểm biểu diễn trên mặt phẳng tọa độ là:
A. M 0;  7. B. M  7  ;0. C. M 7;0. D. M 0;7. Lời giải Chọn D Trang114
Số phức liên hợp của số phức z  7
 i là số phức z  7i có điểm biểu diễn trên mặt phẳng tọa độ
là điểm M 0;7.
Câu 19: Cho hai số phức z  2  i; w  3  2i . Số phức z  w bằng A. 1  3i . B. 6  2i . C. 5  i . D. 1 3i . Lời giải Chọn C
z  w  2  3   1
  2i  5 i .
Câu 20: Cho số phức z  2
 3i . Điểm biểu diễn của z trên mặt phẳng tọa độ là
A. M 2;3 . B. N  2  ; 3  . C. P 2; 3   . D. Q  2  ;3 . Lời giải Chọn B Ta có z  2
 3i nênđiểm biểu diễn của z là  2  ; 3   .
Câu 21: Một khối chóp có diện tích đáy bằng 4 và chiều cao bằng 6 . Thể tích của khối chóp đó là A. 24 . B. 12 . C. 8 . D. 6 . Lời giải Chọn C 1
Thể tích khối chóp là V  .4.6  8 . 3
Câu 22: Thể tích của khối hộp chữ nhật có ba kích thước là 2; 3; 5 là A. 30 . B. 10 . C. 15 . D. 120 . Lời giải Chọn A
Thể tích khối hộp chữ nhật là V  2.3.5  30 .
Câu 23: Công thức V của khối trụ có bán kính r và chiều cao h là 1 1 A. 2 V   r h . B. 2 V   r h . C. 2 V   rh . D. 2 V   rh . 3 3 Lời giải Chọn A
Công thức V của khối trụ có bán kính r và chiều cao h là 2 V   r h .
Câu 24: Một hình trụ có bán kính đáy r  2cm và độ dài đường sinh l  5cm . Diện tích xung quanh của hình trụ đó là A. 2 10 cm . B. 2 20 cm . C. 2 50 cm . D. 2 5 cm . Lời giải Chọn B
Diện tích xung quanh của hình trụ đó là S  2rl  2.2.5  20 . Trang115   
Câu 25: Trong không gian với hệ trục tọa độ Oxyz , cho a   1
 ;2;0 , b  2;1;0 , c  3;1;  1 . Tìm    
tọa độ của vectơ u  a  3b  2c . A. 10; 2  ;13 . B.  2  ;2; 7   . C.  2  ; 2  ;7 . D. 11;3; 2  . Lời giải Chọn D  
Ta có 3b  6;3;0 , 2c   6  ;2;2 .    
Suy ra u  a  3b  2c   1   6  ( 6)
 ;2  3  2;0  0  2  11;3; 2   .
Câu 26: Trong không gian Oxyz , cho mặt cầu S  2 2 2
: x  y  z  2y  4z  2  0 . Bán kính của mặt cầu đã cho bằng A. 1. B. 7 . C. 2 2 . D. 7 . Lời giải Chọn B
Ta có a  0;b  1; c  2; d  2 . 2 Suy ra 2
R  1  2  2  7 .
Câu 27: Trong không gian Oxyz , cho 2 điểm A 1  ;0; 
1 , B 2;1;0 . Viết phương trình mặt phẳng P
đi qua A và vuông góc với AB .
A.  P : 3x  y  z  4  0 .
B.  P : 3x  y  z  4  0 .
C.  P : 3x  y  z  0 .
D.  P : 2x  y  z 1  0 . Lời giải Chọn A 
Ta có: AB  3;1;   1 .
Mặt phẳng  P qua điểm A 1  ;0 
;1 và vuông góc với đường thẳng AB nên có 1 véc tơ pháp 
tuyến AB  3;1;  
1   P : 3 x  
1 1 y  0 1 z  
1  0  3x  y  z  4  0 . x  2 y 1 z  7
Câu 28: Trong không gian Oxyz , cho đường thẳng d :   . 1 3 5 
Vectơ nào dưới đây không
phải là một vectơ chỉ phương của d ?    
A. u  1;3;5 .
B. u  1;3;  5 .
C. u  1; 3;5 .
D. u  2; 6; 10  . 2   1   3   4   Lời giải Chọn A     Đườ x 2 y 1 z 7 ng thẳng d :  
u  1;3;  5 cùng phương 1 3
 có một vectơ chỉ phương là 3   5  
với các véc tơ u  1  ; 3  ;5 , u  2;6; 10  . 1   2  
Câu 29: Một hộp đèn có 12 bóng, trong đó có 4 bóng hỏng. Lấy ngẫu nhiên 3 bóng. Tính xác suất để
trong 3 bóng có 1 bóng hỏng. Trang116 11 13 28 5 A. . B. . C. . D. . 50 112 55 6 Lời giải Chọn C
Trong 3 bóng có 1 bóng hỏng. Ta có n  3  C  220 . 12
Gọi biến cố A : “Trong 3 bóng lấy ra có 1 bóng hỏng”.
Tính được n A 1 2
 C .C 112. 4 8 112 28 Vậy P( ) A   . 220 55
Câu 30: Tìm tất cả các giá trị của tham số m để hàm số 3 2
y  x  3mx  32m  
1 1 đồng biến trên  .
A. Không có giá trị m thỏa mãn.
B. m 1.
C. m  1.
D. m . Lời giải Chọn B
Tâp xác định : D = ¡ . 2
y  3x  6mx  32m   1 2 Ta có:     3
 m 3.3.2m   1 .
Để hàm số luôn đồng biến trên  thì    0 2
 9m 18m  9  0
 m  m     m  2 2 9 2 1 0 9 1  0  m 1. Câu 31:
Gọi M , m lần lượt là giá trị lớn nhât, giá trị nhỏ nhất của hàm số f x  3 x  2
7x  11x  2 trên đoạn 0;2. Giá trị của biểu thức A  2M 5m bằng?
A. A  3.
B. A  4.
C. A  16. D. A  1037 . 27 Lờigiải Chọn C
Xét hàm số trên đoạn [0 ; 2]. Hàm số liên tục trên [0 ; 2]. Ta có f x  2 '
3x  14x  11 x  10;2 f 'x     0   x  11  0; 2     3
Tính f 0  2; f  
1  3, f 2  0 . Suy ra M  3, m  2  2M  5m  16 .
Câu 32: Tập nghiệm của bất phương trình 2 x 2 2 x  8 là A.  ;    3 . B.  3   ;1 . C.  3   ;1 . D.  3   ;1 . Lờigiải Chọn B. 2 2 Ta có : x 2x x 2 x 3 2 2  8  2
 2  x  2x  3  0  3   x 1. Trang117 2 2 Câu 33: Cho 3  f
 x2xdx  6 
. Khi đó f xdx  bằng 1 1 A. 1. B. 3  . C. 3 . D. 1. Lờigiải Chọn C. 2 2 2 2 2 x 3 f
 x2xdx  6  3 f 
 xdx2 xdx  6  3 f   x 2 dx  2.  6 2 1 1 1 1 1 2 2  3 f
 xdx  9  f
 xdx  3. 1 1
Câu 34: Cho số phức z  1 i . môđun của số phức .
z 4  3i bằng A. z  5 2 B. z  2 C. z  25 2 D. z  7 2 Lờigiải Chọn A. .
z 4  3i  1 i4  3i  7  i  z   i    2 2 1 7 1  5 2.
Câu 35: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Cạnh bên SA vuông góc với đáy, AB  ,
a AD  a 3, SA  2a 2 (tham khảo hình bên). Góc
giữa đường thẳng SC và mặt phằng SAB bằng A. 30 . B. 45 . C. 60 . D. 90 . Lời giải Chọn A
Ta có CB  AB và CB  SA (vì SA   ABCD ) , suy ra CB  SAB tại B .
CB  SAB 
Ta có B  SAB  đường thẳng SB là hình chiếu vuông góc của đường thẳng SC trên mặt  S   SAB phẳng SAB .
Suy ra góc giữa đường thẳng SC và mặt phẳng SAB là  CSB . Trang118 Xét C
 SB vuông tại B , ta có  BC AD a 3 1  tan CSB      CSB  30 2 2 SB SA  AB a   a 2 2 3 2 2 .
Câu 36: Cho hình lăng trụ đứng AB .
C A' B'C ' có độ dài cạnh bên bằng 3,
đáy ABC là tam giác vuông tại B và AB  2 (tham khảo hình
bên). Khoảng cách từ A đến mặt phẳng  A' BC  bằng 13 13 A. . B. . 13 36 6 6 13 C. . D. . 13 13 Lời giải Chọn D
* Kẻ AH  A' B  AH   A' BC  d  ,
A  A' BC   AH .
* Chứng minh AH   A' BC  , thật vậy
Ta có AH  A' B và AH  BC (vì BC   ABB ' A' ) , suy ra AH   A' BC  . * Tính AH Xét A
 ' AB vuông tại A , ta có 1 1 1 1 1 13 36 6 13       AH   . 2 2 2 AH AA' AB 9 4 36 13 13
Câu 37: Trong không gian Oxyz, cho hai điểm M 2;4;  1 , N  2  ;2; 3
 . Phương trình mặt cầu đường kính MN là 2 2 2 2 A. 2
x   y   3  z   1  9. B. 2
x   y  3   z   1  9. 2 2 2 2 C. 2
x   y  3   z   1  9. D. 2
x   y  3   z   1  3. Lời giải Trang119 Chọn B
Mặt cầu đường kính MN có tâm là trung điểm của đoạn thẳng MN . Suy ra tọa độ tâm mặt
cầu là I 0;3;   1 . 1 1 6
Bán kính mặt cầu: R  MN  16  4 16   3. 2 2 2 Phương tri 2 2
̀nh mă ̣t cầu có tâm I 0;3;  
1 , bán kính R  3: 2
x   y  3   z   1  9.
Câu 38: Trong không gian với hệ tọa độ Oxyz, phương trình nào dưới đây là phương trình của đường
thẳng đi qua A1;0; 2 và vuông góc với mặt phẳng (P): x - y + 3z - 7 = 0? x  t x 1 t x 1 t x 1 t    
A.  y  t  . B.  y  1  .
C.  y  t  .
D.  y  t .     z  3t  z  3  2t  z  2  3t  z  2  3t  Lời giải Chọn C 
Đường thẳng cần tìm nhận vectơ pháp tuyến của mặt phẳng (P) là n  1; 1  ;3 làm một vectơ chỉ phương. 
Phương trình tham số của đường thẳng cần tìm đi qua điểm A1;0;2 , nhâ ̣n n  1; 1  ;3 là vec x 1 t 
tơ chỉ phương là y  t  . z  23t 
Câu 39: Cho hàm số f  x , đồ thị của hàm số y  f ' x là đường cong trong hình bên. Giá trị lớn nhất 2
của hàm số g x  2 f x x   1 trên đoạn  3  ;  3 bằng
A. f 0 1. B. f  3    4. C. 2 f   1  4.
D. f 3 16. Lờigiải Chọn C Ta có 
g x  2 f x  2x   1 Trang120
g x   f x x     x   1 0 1  . x    3
Dựa vào hình vẽ ta có bảng biến thiên 2
Suy ra giá trị lớn nhất của hàm số g x  2 f x x   1 trên đoạn  3  ;  3 là g   1  2 f   1  4 .
Câu 40: Có bao nhiêu số nguyên y trong đoạn  2  021;202 
1 sao cho bất phương trình 11   x logx log x y 10 10 10 10
đúng với mọi x thuộc 1;100 : . A. 2021. B. 4026 . C. 2013. D. 4036 . Lời giải Chọn A 11  x x y  x   log x  11 10x log log log 11 10 10 10  y  log  
10x  log x  y   1 log x  log x   1 .  10  10  10  10
Đặt log x  t . Ta có x 1;100  log x0;2 t 0;2. Bất phương trình trở thành  t  2        t  10t
t    y t   2 11 t 10t y t 1 2 1      y 2 .  10  10 10 10t     1 2 t  10t 2 t   2t 10
Xét hàm số f t  
trên khoảng 0; 2 , ta có f t   10t   1 10t  2 1  8
f t   0, t
 0;2  f 0  f t  f 2, t
 0;2  0  f t  , t  0;2 . 15 Trang121
Yêu cầu bài toán  2 đúng với mọi t 0; 2  f t   y t    8 , 0; 2  y  . 15  
Kết hợp với điều kiện y   8 2021; 2021  y  ; 2021 
 . Vậy có tất cả 2021 giá trị nguyên 15 
của y thỏa mãn yêu cầu bài toán.     f  x 2x 2 khi x 0   I  sin 2 . x f  cosxdx 2
x +4x  2 khi x  0 Câu 41: Cho hàm số . Tích phân 0 bằng 9 9 7 7 A. I  . B. I   . C. I   . D. I  . 2 2 6 6 Lời giải Chọn A
Do lim f  x  lim f  x  f 0  2
 nên hàm số f x liên tục tại điểm x  0 .   x0 x0
Đặt t  cos x  dt  sin d x x .
Đổi cận: x  0  t 1; x    t  1  . Ta có:   1  1 sin 2 . x f 
cosxdx  2sin .xcos .xf 
cosxdx   2t.f 
tdt  2 t.f  tdt 0 0 1 1  0 1 1 0  2 . x f
 xdx2 .xf
 xdx  2 x
  2x 4x2dx2 .x
 2x2dx 1  0 0 1  0 4 3 3 2  x 4x  1  x x  7 10 9 2  2 
 x   4.      .  4 3 0   3 2  6 3 2 1 
Câu 42: Có bao nhiêu số phức z thỏa mãn z  13 và  z  2iz  4i là số thuần ảo? A. 1. B. 2 . C. 0 . D. 4 . Lời giải Chọn B
Gọi z  x  yi với x, y   . Ta có 2 2
z  13  x  y  13 (1) .
Mà  z  iz  i  x  yi  ix  yi  i   2 2 2 4 2 4
x  y  2y  8  ( 6
 x).i là số thuần ảo khi 5 2 2
x  y  2 y  8  0  13  2 y  8  0  y   . 2  3 3 x  5 2 Từ y   thay vào (1) ta được  . 2  3 3 x    2
Vậy có 2 số phức thoả yêu cầu bài toán.
Câu 43: Cho hình chóp S.ABCD có đáy là hình chữ nhật với AB  a , BC  a 3 . Cạnh bên SA Trang122
vuông góc với đáy và đường thẳng SC tạo với mặt phẳng (SAB) một góc 30 . Thể tích khối
chóp S.ABCD bằng 3 2a 3 3a 3 2 6a A. 3 3a . B. . C. . D. . 3 3 3 Lời giải Chọn D
Vì SA  ( ABCD) nên SA  BC , do BC  AB nên BC  (SAB) . Ta có SB là hình chiếu
vuông góc của SC lên mặt phẳng ( SAB ), do đó góc giữa đường thẳng SC và mặt phẳng (SAB) là góc  CSB 30 
. Trong tam giác SBC , ta có SB BC.cot 30 
 a 3. 3  3a .
Trong tam giác SAB , ta có 2 2
SA  SB  AB  2a 2 . 3 1 1 2a 6 Vậy V  S . A AB.BC 
2a 2.a.a 3  . S.ABCD 3 3 3
Câu 44: Ông Bảo làm mái vòm ở phía trước ngôi nhà của mình bằng vật liệu tôn. Mái vòm đó là một
phần của mặt xung quanh của một hình trụ như hình bên dưới. Biết giá tiền của 1 2 m tôn là
300.000 đồng. Hỏi số tiền (làm tròn đến hàng nghìn) mà ông Bảo mua tôn là bao nhiêu ? 5 m 1200 6 m
A. 18.850.000 đồng.
B. 5.441.000 đồng.
C. 9.425.000 đồng.
D.10.883.000 đồng. Lời giải Trang123 Chọn D 6
Gọi r là bán kính đáy của hình trụ. Khi đó:
 2r  r  2 3. 0 sin120
Sử dụng hệ thức lượng trong tam giác, ta có góc ở tâm của cung này bằng 0 120 . Và độ 1 dài cung này bằng
chu vi đường tròn đáy. 3 1
Suy ra diện tích của mái vòm bằng S , 6 m 3 xq
(với S là diện tích xung quanh của hình trụ). xq 1200 2 3 m 2 3 m
Do đó, giá tiền của mái vòm là 1 1 S   rl    xq   1 .300.000 . 2 .300.000
.2 .2 3.5.300.000 10882796,19. 3 3 3
Câu 45: Trong không gian Oxyz, cho điểm E 2;1; 
3 , mặt phẳng  P : 2x  2y  z  3  0 và mặt cầu
S x  2  y  2 z  2 : 3 2 5
 36. Gọi  là đường thẳng đi qua E, nằm trong mặt phẳng
P và cắt S tại hai điểm có khoảng cách nhỏ nhất. Phương trình của  là
x  2  9t
x  2  5t x  2  t
x  2  4t    
A.  y  1 9t .
B.  y  1 3t .
C.  y  1 t .
D.  y  1 3t.     z  3  8t  z  3  z  3  z  3  3t  Lời giải Chọn C A E F B K
Mặt cầu S   x  2   y  2   z  2 : 3 2 5
 36, có tâm I 3;2;5 và bán kính R  6.   Ta có: EI    2 2 2
1;1; 2  EI  EI  1 1  2  6  6  .
R Do đó điểm E nằm trong mặt cầu S. E   
Ta lại có: E  P và 
nên giao điểm của  và S  nằm trên đường tròn giao tuyến    P
C tâm K của mặt phẳng P và mặt cầu S, trong đó K là hình chiếu vuông góc của I
lên mặt phẳng  P.
Giả sử   S    ; A 
B . Độ dài AB nhỏ nhất khi và chỉ khi d  K ,  lớn nhất. Trang124
Gọi F là hình chiếu của K trên  khi đó d  K;   KF  KE .
Dấu "  " xảy ra khi và chỉ khi F  . E
IK  P IK   Ta có     IE   . KE   KE      Ta có: n
, EI   5; 5;0 , cùng phương với u  1;1;  0 . P        P  Vì 
nên  có một vectơ chỉ phương là u  1; 1;0 .   IE x  2  t 
Suy ra phương trình đường thẳng  : y 1 t . z  3 
Câu 46: Cho hàm số y  f  x là một hàm đa thức có bảng xét dấu f  x như sau
Số điểm cực trị của hàm số     2 g x
f x  x  A. 5 . B. 3 . C. 1. D. 7 . Lời giải Chọn A 2 Ta có     2 g x
f x  x   f  x  x  . Số điểm cực trị của hàm số f  x  bằng hai lần số
điểm cực trị dương của hàm số f  x cộng thêm 1. Xét hàm số  1 x    1 2 x   
h  x  f  2
x  x  h x   x   f  2 x  x 2 2 2 1
 0  x  x  1  .   1 5 2 x  x  1 x    2 
Bảng xét dấu hàm số     2 h x f x  x Hàm số     2 h x f x  x có 2 điểm cực trị dương, vậy hàm số
        2 2 g x f x x f
x  x  có 5 điểm cực trị.
Câu 47: Có bao nhiêu số nguyên m  2
 0;20 để phương trình 7x  m  6log 6x  m có nghiệm thực 7   Trang125 A. 19 . B. 21 . C. 18 . D. 20 . Lời giải Chọn D Đặt:  log 6 
 6   7t  6  7t t x m x m x
 m . Khi đó phương trình trở thành 7  
7x  6  7t   6  7x  6  7t x t x
 6t  x  t .
Khi đó ta có PT: 6  7x x
 m . Xét hàm số    6  7x f x x ; x   x 6
Có f ' x  6  7 ln 7  f ' x  0  x  log  x . Ta có BBT 7 0 ln 7
Từ BBT ta thấy PT có nghiệm 6
m  y  x  log 6 7 ln 7  6log  7  0,389 ; 0 7 ln 7 Mà m  2
 0;20;m  m 1  9; 1  8;...;  0
Câu 48: Cho hàm số bậc bốn trùng phương y  f  x có đồ thị là đường cong trong hình bên. Biết hàm
số f  x đạt cực trị tại ba điểm x , x , x (x  x  x ) thỏa mãn x  x  4 . Gọi S và S là 1 2 3 1 2 3 1 3 1 2 S
diện tích của hai hình phẳng được gạch trong hình. Tỉ số 1 bằng S2 2 7 1 7 A. . B. . C. . D. . 5 16 2 15 Lời giải Chọn B
Rõ ràng kết quả bài toán không đổi khi ta tịnh tiến đồ thị sang trái sao cho x  0 . 2 Trang126 y x1 x O x3 S1 S2 Gọi 4 2
g(x)  ax  bx  c , ta có hàm số g(x) là chẵn và có 3 điểm cực trị tương ứng là 2; 0; 2
là các nghiệm của phương trình 3
4ax  2bx  0 .
Dựa vào đồ thị g(x) , ta có g(0)  0 . Từ đó suy ra 4 2
g(x)  a(x  8x ) với a  0 .
Do tính đối xứng của hàm trùng phương nên diện tích hình chữ nhật bằng
2S  S  g(2) .4  64a 1 2
Ta có S là diện tích hình phẳng giới hạn bởi đồ thị hàm số g(x) , trục hoành, đường thẳng 1 0 0 224a 224a 512a
x  2, x  0 . 4 2 S 
g(x) dx  a
x  8x dx   
. Suy ra S  64a  2.  . 1 2 15 15 15 2  2  S 224 7 Vậy 1   . S 512 16 2
Câu 49: Cho các số phức
z 1 4i  2, z  4  6i  1 và z 1  z  2  i . Tìm 1 z , z2, 3 z thỏa mãn 1 2 3 3
giá trị nhỏ nhất của biểu thức P     3 z 1 z 3 z z2 . 14 14 A.  2 . B. 29  3 . C.  2 2 . D. 85  3 . 2 2 Lời giải Chọn D Đặt  
 1x, 1y  . 1 z 1 x 1 y i
z 1 4i  2   x  2 1   y  42  1 1 1 4 . 2 2
Vậy tập hợp điểm M biểu diễn số phức C : x 1
 y  4  4 có tâm 1
z là đường tròn  1      R  2 1
I  1; 4 , bán kính . 1 Đặt z    2 x , 2 y    . 2 2 x y2i
z  4  6i  1   x  42   y  62  2 2 2 1. 2 2
Vậy tập hợp điểm N biểu diễn số phức z là đường tròn      2
C  :  x 4  y 6 1 có tâm 2 I R  1 2  4; 6 , bán kính . 2 Đặt  
 3x, 3y  . 3 z 3 x 3 y i Trang127         3 z 1 3 z 2 i 3 x 3 y 2 0 .
Vậy tập hợp điểm A biểu diễn số phức
d x  y   . 3
z là đường thẳng : 2 0 Khi đó: P       3 z 1 z 3 z z2 AM AN 14
Mặt khác, d  I ,d 
 R ; d I ,d  2 2  R và I , I nằm cùng phía đối với d . 1  1  2  2 2 1 2 2 2
Gọi C là đường tròn đối xứng với với C qua d , suy ra       2
C  :  x 8  y 2 1 và 2  2 
gọi N là điểm đối xứng với N qua d . C có tâm I R  1 2 8; 2 , bán kính . 2  2 Ta có: AM  M       . 1 I A 1 I AM A 1 I M 1 I A 1 I 2 AN  NI                  . 2 AN N I2 AI2 AN AI2 N I2 AI2 1
Suy ra P  AM  AN  AM  AN  A         . Đẳ 1 I AI2 3 1 I I2 3 85 3 ng thức xảy ra khi và
chỉ khi 3 điểm I , , A I  thẳng hàng. 1 2
Vậy min P  85 3 .
Câu 50: Trong không gian Oxyz cho hai điểm A1;0;0, B 3; 4; 4
  . Xét khối trụ T  có trục là đường
thẳng AB và có hai đường tròn đáy nằm trên mặt cầu đường kính AB . Khi T  có thể tích lớn
nhất, hai đáy của T  nằm trên hai mặt phẳng song song lần lượt có phương trình là
x  by  cz  d  0 và x  by  cz  d  0 . Khi đó giá trị của biểu thức b  c  d  d thuộc 1 2 1 2
khoảng nào sau đây? A. 0;  21 . B.  1  1;0 . C.  2  9; 1  8. D.  2  0; 1   1 . Lời giải Chọn C Trang128
Mặt cầu đường kính AB có tâm I 2; 2; 2
  và bán kính bằng 3. Gọi ,
x 0  x  3 là bán kính đáy của T  , khi đó T  có chiều cao bằng 2
h  2 9  x , do đó
thể tích của T  bằng 3 2 2  x x      2  2 2 9 x   x x 2 2 V   x  x    2  x  2 2 2 9 4 . . . 9  4    12 3 . 2 2  3     
T  có thể tích lớn nhất bằng V 12 3 khi x  6 . max
Khi đó gọi P là mặt phẳng chứa đường tròn đáy của T  , P có phương trình tổng quát
dạng x  2 y  2z  d  0 . Khoảng cách từ tâm I 2; 2; 2
  đến P bằng 3 nên 2  2.2  2. 2    d d  3 3 10  3   . 3 d  3  3 10
Vậy b  c  d  d  2  2  3 3 10  3 3 10  2  0 . 1 2 Trang129

Bộ 5 Đề Ôn Thi Cấp Tốc TN THPT 2021 Môn Toán Có Lời Giải Chi Tiết Và Đáp Án-Bộ 2

Thông tin :

Tài liệu liên quan:

Đề chính thức kỳ thi tốt nghiệp THPT năm 2024 môn Toán

Đề kiểm tra Toán 12 năm 2024 – 2025 trường THCS&THPT Nguyễn Khuyến – TP HCM (13/09/2024)

Đề kiểm tra Toán 12 năm 2024 – 2025 trường Nguyễn Khuyến & Lê Thánh Tông – TP HCM (22/09/2024)

Đề kiểm tra Toán 12 năm 2024 – 2025 trường Nguyễn Khuyến & Lê Thánh Tông – TP HCM (06/10/2024)

Đề thi thử TN THPT môn Toán đợt tháng 6 năm 2024 cụm trường THPT – Bắc Ninh