Bộ 5 Đề Ôn Thi Tốt Nghiệp THPT Môn Toán Năm 2021 Có Đáp Án Và Lời Giải-Bộ 1

Bộ 5 đề ôn thi tốt nghiệp THPT Môn Toán năm 2021 được biên soạn dưới dạng file PDF gồm 53 trang. Mỗi đề thi là kiến thức từ cơ bản đến nâng cao khác nhau và kèm sẵn đáp án để các em học sinh dễ dàng so sánh kết quả sao cho chuẩn xác nhất. Mời các em tham khảo thêm nhé!

38 19 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 12

Môn: Toán 12

Thông tin:

53 trang 8 tháng trước

Tác giả:

Profile ha phan
Trang 1
ĐỀ SỐ 01
ĐỀ RÈN LUYỆN MÔN TOÁN 12
HƯỚNG ĐẾN KÌ THI THPT QUỐC GIA
Trắc nghiệm: 50 câu
Thời gian: 90 phút
Nội dung:
FULL KIẾN THỨC TOÁN 12
Câu 1. Cho hàm s
fx
có bng bi
S ng tim cn ngang c th hàm s 
A.
0
. B.
3
. C.
2
. D.
1
.
Câu 2. Trong không gian vi h t
Oxyz
, hình chiu cm
lên trc
Oy
m
A.
1;0;0M
. B.
1;0;3M
. C.
0;2;0M
. D.
0;0;3M
.
Câu 3. Cho
a
là s th
1
, giá tr ca
1
4
log
a
a



bng
A.
1
. B.
1
4
. C.
1
2
. D.
2
.
Câu 4. S phc liên hp ca s phc
23zi
A.
32zi
. B.
23zi
. C.
32zi
. D.
23zi
.
Câu 5. Tính din tích hình phng gii hn bng
2
2, , 0, 2y x y x x x
.
A.
8
3
. B.
8
. C.
26
3
. D.
14
3
.
Câu 6. Trong không gian
Oxyz
ng thng
d
c
O
 
1; 2;3u

có
 là
A.
3
2
xt
yt
zt

. B.
2
3
xt
yt
zt

. C.
1
2
3
x
y
z

. D.
1
2
3
xt
yt
zt

.
Câu 7. Giá tr ca
2021
3
1
dx
x
bng
C.
2021
3
. B.
2021.ln3
. C.
2021.ln3 1
. D.
2021
.
Câu 8. Tìm tnh ca hàm s
3
2
2
32y x x
.
A.
;1 2;
. B.
;1 2;
. C.
1;2
. D.
1;2
.
Câu 9. Vit công thc tính th tích khi tròn xoay to thành khi quay quanh trc hoành hình phng
H
gii
hn bng
xa
,
xb
,
0y
,
y f x

y f x
là hàm s liên tn
;ab
.
Trang 2
A.
22
d
b
a
f x x
. B.
2
d
b
a
V f x x
. C.
2
d
b
a
f x x



. D.
2
d
b
a
f x x



.
Câu 10. Trong không gian vi h trc t
Oxyz
, cho mt phng
:2 3 1 0P x y z
i
c mt phng
P
?
A.
1;2; 8B
. B.
1; 2; 7C
. C.
0;0;1A
. D.
1;5;18D
.
Câu 11. Hàm s
Fx
gi là mt nguyên hàm ca hàm s
fx
trên khong
;ab
nu có
A.
,;f x F x x a b
. B.
,;F x f x C x a b
.
C.
,;f x F x C x a b
. D.
,;F x f x x a b
.
Câu 12. 
R
ng cao
h
. Din tích xung quanh ca hình nón này là
A.
Rh
. B.
2 Rh
. C.
22
R R h
. D.
22
2 R R h
.
Câu 13. Hàm s ng bii
A.
3
3y x x
. B.
3 2
31y x x
. C.
3
3y x x
. D.
3 2
31y x x
.
Câu 14. S nghim c
0,1
log 1 log 4xx
là
A. Vô s. B.
1
. C.
0
. D.
2
.
Câu 15. Cho
a
,
b
là các s 
222
1
log 2log log
3
x a b
. Biu th
x
a ca
a
và
b
.
A.
1
3
x ab
. B.
1
2
3
x a b
. C.
2
2xa
. D.
1
3
2
x a b
.
Câu 16. Tìm s hng không cha
x
trong khai trin nh thc
20
3
2
3 , 0xx
x




.
A.
15 5 15
20
.3 .2C
. B.
15 15
20
.2C
. C.
5 15
3 .2
. D.
15
20
C
.
Câu 17. Trong không gian vi h t 
Oxyz
, mt phng
()P
   m
;
( 1; 2;3)B 
;
(0;0;3)C

20x by cz d
,,b c d
thì
b c d
bng
A.
2
. B.
3
. C.
1
. D.
3
.
Câu 18. Cho hàm s
()y f x
có
9 8 2022
( ) ( 1) ( 2)f x x x x
. S m cc tr ca hàm s
()y f x
là
A.
3
. B.
2
. C.
1
. D.
0
.
Câu 19. Cho hình chóp
.S ABC
có
3SA a
,
SA
vuông góc vi mt phng
()ABC
, tam giác
ABC
vuông
ti
,B AB a
, tam giác
SBC
cân. Th tích khi chóp
.S ABC
bng
A.
3
23
3
a
. B.
3
3a
. C.
3
3
3
a
. D.
3
3
6
a
.
Câu 20. Tìm h nguyên hàm ca hàm s
3
21
e
x
f x x
.
A.
3
3
1
de
3
x
x
f x x C

. B.
3
1
1
de
3
x
f x x C

.
Trang 3
C.
3
1
d 3e
x
f x x C

. D.
3
1
de
x
f x x C

.
Câu 21. o hàm ca hàm s
2
1
2
x
y
.
A.
2
2
1 .2
x
yx

. B.
2
2
.2 .ln2
x
yx
. C.
2
1
2 .ln2
x
y
. D.
2
2
x
y
.
Câu 22. Cho
3
log 5 a
. Tính
729
1
log
125
theo
a
.
A.
1
2
a
. B.
1
2
a
. C.
1
2a
. D.
1
2a
.
Câu 23. Vip tuyn c th hàm s
3
23y x x
ti
2;7M
.
A.
10 27yx
. B.
10 13yx
. C.
77yx
. D.
5yx
.
Câu 24. Cho hai s phc
1
12zi
,
2
26zi
. Tính
12
.zz
.
A.
10 2i
. B.
2 12i
. C.
14 10i
. D.
14 2i
.
Câu 25. Trong không gian
,Oxyz
m
1;1;5A
và
1;2; 1 .B
Mt ph
t phm
,A
B
và vuông góc vi mt phng
?Oxy
A.
3 2 0.xz
B.
2 3 0.xy
C.
6 6 7 0.x y z
D.
6 11 0.yz
Câu 26. Hàm s a hàm s
1
32
fx
x
?
A.
2y 
. B.
1
2 3 2yx
. C.
1
ln 3 2
2
yx
. D.
ln 3 2yx
.
Câu 27. Cho hình l
.ABCD A B C D
, góc gi

AB
và
AC

bng
A.
30
. B.
45
. C.
90
. D.
60
.
Câu 28. Cho s phc
z a bi
,abR
tha mãn
1 3 2 1 4i z i i
. Giá tr ca
ab
bng
A.
2
. B.
0
.
C. 1. D.
2
.
Câu 29. Cho hàm s
y f x
 th  bên.
S nghim c
2 1 0fx
là
A.
0
.
B.
2
.
C.
1
.
D.
3
.
Câu 30.  u
.ABC A B C
có cng
a
,
3AC a
. Th tích kh này
là
A.
3
6
12
a
. B.
3
2
2
a
. C.
3
3
6
a
. D.
3
6
4
a
.
Câu 31. Cho 2 s
,xy
tha mãn
53
x
và
56
y
. Giá tr ca
2
5
xy
bng
A.
3
2
. B.
54
. C.
36
. D.
1
.
Câu 32. Trong không gian vi h trc t 
Oxyz
, cho mt phng
: 2 2 5 0P x y z
 m
0;2;4M
. Tính
,d M P
.
A.
1
3
. B.
1
9
. C.
4
9
. D.
4
3
.
Trang 4
Câu 33. Tp nghim ca b
1
1
34
3
x
x

là
A.
;0
. B.
1; 
. C.
0;1
. D.
0;1
.
Câu 34. Gi
12
;zz
là hai nghim c
2
2 3 0zz
. Tính giá tr ca biu thc
1 2 1 2
.A z z z z
.
A.
5.A 
B.
1.A
C.
5.A
D.
1.A 
Câu 35. Có bao nhiêu giá tr nguyên ca tham s
m
,
10 10m
 
2
1 2 0x x mx
có 3 nghim phân bit.
A.
13
. B.
14
. C.
16
. D.
15
.
Câu 36. H tt c các nguyên hàm ca hàm s
2
41
2
x
fx
x
trên khong
2;
là
A.
4
4ln 2
2
xC
x
. B.
9
4ln 2
2
xC
x
.
C.
4
4ln 2
2
xC
x
. D.
9
4ln 2
2
xC
x
.
Câu 37. Nu
2
1
d1f x x
,
3
1
d1f x x 
thì
3
2
df x x
bng
A.
0
. B.
2
. C.
3
. D.
2
.
Câu 38. Cho hình chóp
.S ABC
có tam giác
ABC
vuông ti
A
,
2 , 3AB a AC a
,
SA
vuông góc vi
ABC
,
5SA a
. Tính bán kính
R
ca mt cu ngoi tip hình chóp
.S ABC
.
A.
38
4
a
R
. B.
38Ra
. C.
38R
. D.
38
2
a
R
.
Câu 39. Trong không gian vi h trc t 
Oxyz
  nh t   m
M
c ng thng
115
:
2 3 4
x y z
vi mt phng
:2 11 0P x y z
.
A.
1;1; 5M 
. B.
4;0; 3M 
. C.
1;4; 9M
. D.
0;0; 11M
.
Câu 40. Ba chic bình có hình tr cùng cha m cao mc trong bình II gp

1 2 3
,,r r r
ca ba bình (theo th t) I,
II, III lp thành mt cp s nhân vi công bi bng
A.
2
. B.
2
. C.
1
2
. D.
1
2
.
Câu 41. Trong không gian vi h to 
Oxyz
, gi
ng thm
1;2;3A
và vuông góc vi
mt phng
:2 2 7 0P x y z
. Khong cách t m
0;3;12B
ng thng
bng
A.
110
. B.
15
. C.
74
. D.
21
.
Câu 42. Cho hình chóp
.S ABC
có
SA
vuông góc vi mt phng
ABC
. Tam giác
ABC
u cnh bng
3a
, tam giác
SAC
cân. Tính khong cách
h
t
A
n
SBC
.
A.
3
7
a
h
. B.
3
4
a
h
. C.
7
a
. D.
3
7
a
h
.
Câu 43. Cho hàm s
fx
liên tc trên
và tha mãn
1
4
d 10f x x
. Giá tr ca
2
1
6 5 df x x
bng
A. 2. B. 1. C. 5. D. 4.
Trang 5
Câu 44. Trong không gian
Oxyz
  ng thng
12
1 1 2 2
12
2 1 2
: 1 5 , : 1
1
x t x t
d y t d y t
z t z t



và mt phng
:0P x y z
ng thng thuc mt phng
P
và ct c ng thng
1
d
và
2
d
là
A.
2
1
1
xt
y
zt


. B.
3
1
1
xt
y
zt


. C.
12
1
3
xt
y
zt

. D.
22
1
13
xt
y
zt


.
Câu 45. Có hai giá tr ca tham s
m
  th hàm s
2
23
21
mx x x
y
x
có mt tim cn ngang là
1y
. Tng hai giá tr này bng
A.
2
. B.
4
. C.
3
. D.
1
.
Câu 46. Cho hàm s
()y f x
liên tc trên
 th  .
Bit
1
H
có din tích bng 7,
2
H
có din tích bng 3. Tính
1
2
2
(2 6) ( 6 7)dI x f x x x
A.
11
.
B.
4
.
C.
1
.
D.
10
.
Câu 47. Cho
fx
là hàm s bc
5.
Hàm s
y f x
có bng bi sau
S m cc tr ca hàm s
32
2 6 9g x f x x x x
là
A.
4.
B.
2.
C.
3.
D.
1.
Câu 48. Cho hàm s
y f x
liên t  n
2;2
và
2
1
23
4
f x f x
x
,
2;2x
. Tính
2
2
dI f x x
.
A.
10
I
. B.
10
I

. C.
20
I

. D.
20
I
.
Câu 49. Cho
, , 0;x y z
, , 1abc
và
3
x y z
a b c abc
. Giá tr ln nht ca biu thc
2
11
P z z
xy
thuc kho
A.
0;2
. B.
3; 
. C.
1;3
. D.
2;4
.
Trang 6
Câu 50. Cho hàm s
3 2 2
( ) 3 2 .f x x x m m
Gi
S
tp hp tt c các giá tr nguyên ca tham s
m
tha
mãn
3;1
3;1
3 2m 2ma in 11x f x f x

. S phn t ca
S
bng
A.
11.
B.
12.
C.
9.
D.
10.
________________HẾT________________
ÑAÙP AÙN ÑEÀ SOÁ 01
1
2
3
4
5
6
7
8
9
10
D
C
C
B
D
B
B
A
B
A
11
12
13
14
15
16
17
18
19
20
D
C
C
B
B
A
D
C
C
B
21
22
23
24
25
26
27
28
29
30
B
A
B
D
B
C
D
D
D
D
31
32
33
34
35
36
37
38
39
40
A
A
C
D
A
D
D
D
C
D
41
42
43
44
45
46
47
48
49
50
C
A
A
A
B
B
B
D
C
A
Lôøi giaûi caâu hoûi vaän duïng cao ñeà soá 01
Câu 45. Có hai giá tr ca tham s
m
  th hàm s
2
23
21
mx x x
y
x
có mt tim cn ngang là
1y
. Tng hai giá tr này bng
A.
2
. B.
4
. C.
3
. D.
1
.
Hướng dẫn giải:
Ta có:
2
2
2
23
23
1
1
2 3 1
lim lim lim lim
11
2 1 2
22
x x x x
xm
mx x
xx
mx x x m
xx
y
x
xx
xx
   




;
2
2
2
23
23
1
1
2 3 1
lim lim lim lim
11
2 1 2
22
x x x x
xm
mx x
xx
mx x x m
xx
y
x
xx
xx
   




.
Theo gi thi th hàm s có mt tim cn ngang
1y
1
1
1
2
13
1
2
m
m
mm


.
Tng hai giá tr m c là
1 3 4
.
Choïn
B
Câu 46. Cho hàm s
()y f x
liên tc trên
 th  . Bit
1
H
có din tích bng 7,
2
H
có
din tích bng 3. Tính
1
2
2
(2 6) ( 6 7)dI x f x x x
Trang 7
A.
11
. B.
4
. C.
1
. D.
10
.
Hướng dẫn giải:
D th ta thy
1
2
1
1
2
1
( )d 7
( ) d 3
H
H
S f x x
S f x x

hay
1
1
2
1
( )d 7
( )d 3
f x x
f x x

.
Xét
1
2
2
(2 6) ( 6 7)dI x f x x x
t
2
6 7 dt (2 6)dt x x x x
i cn:
21
12
xt
xt
.
:
2 2 1 2
1 1 1 1
( )dt ( )d ( )d ( )d 7 ( 3) 4I f t f x x f x x f x x
.Vy
4I
.
Choïn
B
Câu 47. Cho
fx
là hàm s bc
5.
Hàm s
y f x
có bng bi sau
S m cc tr ca hàm s
32
2 6 9g x f x x x x
là
A.
4.
B.
2.
C.
3.
D.
1.
Hướng dẫn giải:
Ta bit
fx
có dng bc bt
4 2 3
42f x ax bx c f x ax bx
.
T bng bin thiên suy ra:
10
03
03
36
10
4 2 0 3
00
f
a b c a
f
cb
f
a b c
f







.
Do vy
22
4 2 2 2
3 6 3 3 1 2 3 4 3f x x x x f x x x

.
Xét hàm s
gx
, ta có
2
2 2 2
2 3 4 3 3 4 3 3 4 3g x f x x x x x x x

;
2
2
1
4 3 0
03
4 3 1
2
x
xx
g x x
xx
x
.Bng bin thiên :
Trang 8
T bng bin thiên suy ra hàm s
gx
có
2
m cc tr.
Choïn
B
Câu 48. Cho hàm s
y f x
liên t  n
2;2
và
2
1
23
4
f x f x
x
,
2;2x
. Tính
2
2
dI f x x
.
A.
10
I
. B.
10
I

. C.
20
I

. D.
20
I
.
Hướng dẫn giải:
Ta có:
2
1
23
4
f x f x
x
,
2;2x
, suy ra
2 2 2
2
2 2 2
1
2 d 3 d d
4
f x x f x x x
x
(1).
Xét
2
2
3df x x
t
t x dt dx
. Ta có:
2 2 2
2 2 2
3 d 3 d 3f x x f t t f x dx

(2).
c:
2 2 2 2
22
2 2 2 2
1 1 1
5 d d d d
4 5 4
f x x x I f x x x
xx

.
t
2
2tan d 2 1 tan dx t x t t
i cn:
2
4
2
4
xt
xt
.
:
44
2
2
44
1 1 1
. 2 1 tan d d
5 4tan 4 10 20
I t t t
t




.
Choïn
D
Câu 49. Cho
, , 0;x y z
, , 1abc
và
3
x y z
a b c abc
. Giá tr ln nht ca biu thc
2
11
P z z
xy
thuc kho
A.
0;2
. B.
3; 
. C.
1;3
. D.
2;4
.
Hướng dẫn giải:
Ta có :
3
x y z
a b c abc
; suy ra
3 3 3
log , log , log
a b c
x abc y abc z abc
vi
, , , 0x y z
.
 :
3 3 3
3 3 3
1 1 1 1 1 1
log log log
log log log
abc abc abc
a b c
abc
x y z
abc abc abc
3
log ( ) 3
abc
abc
. Suy ra :
1 1 1
3
x y z
.
Thay vào biu thc Pc :
32
2
2
1 2 1
3 0 ; 0 1
zz
P f z z z z f z z
zz
.
Trang 9
Bng bin thiên:
Da vào bng bin thiên, ta có
0;
max ( ) (1) 2f z f


.
Vy
max 2P
.
Choïn
C
Câu 50. Cho hàm s
3 2 2
( ) 3 2 .f x x x m m
Gi
S
tp hp tt c các giá tr nguyên ca tham s
m
tha
mãn
3;1
3;1
3 2m 2ma in 11x f x f x

. S phn t ca
S
bng
A.
11.
B.
12.
C.
9.
D.
10.
Hướng dẫn giải:
Xét hàm s
32
2
32f x x x m m
(1). t
tx
;
3;1x
0;3t
.
Hàm s
(1)
tr thành
3 2 2
32f t t t m m
,
0;3t
;
2
3 6 0 2f t t t t
.
Ta có:
2
02f m m
;
2
2 2 4f m m
;
2
32f m m
.
Suy ra:
2
3;1 0;3
2
3;1 0;3
min min 2 4
max max 2
f x f t m m
f x f t m m
.
Ta có:
3;1
3;1
3max 2min 112f x f x

22
3 2 2 2 4 112m m m m
2
5 10 120 0mm
46m
. Vì
m
nên
4; 3;...;6m
.
Vy có
11
giá tr ca
m
tha mãn yêu cu bài toán.
Choïn
A
ĐỀ SỐ 02
ĐỀ RÈN LUYỆN MÔN TOÁN 12
HƯỚNG ĐẾN KÌ THI THPT QUỐC GIA
Trắc nghiệm: 50 câu
Thời gian: 90 phút
Nội dung:
FULL KIẾN THỨC TOÁN 12+
Câu 51. i hai mu có s nh, s cnh và s mt lt là
A.
20, 30, 12
.
B.
30, 20, 12
.
C.
30, 12, 20
.
D.
12, 20, 30
.
Câu 52. Trong không gian vi h trc t
Oxyz
c ca
ng thng
d
m
2; 1;3M
 
1; 2; 4u
là
Trang 10
A.
2 1 3
1 2 4
x y z

. B.
2 1 3
1 2 4
x y z


.
C.
124
2 1 3
x y z

. D.
1 2 4
2 1 3
x y z

.
Câu 53. Cho hàm s
y f x
có bng bin thiên
Hi hàm s có bao nhiêu cc tr?
A.
3
. B.
1
. C.
2
. D.
4
.
Câu 54. Mt hình nón có din tích xung quanh bng
2
2 cm

1
cm
2
r
 ng
sinh ca hình nón.
A.
1cm
. B.
4cm
. C.
2cm
. D.
3cm
.
Câu 55. Htt c các nguyên hàm ca hàm s
2 2022f x x
là
A.
2
2xC
. B.
2
2022x x C
. C.
2
xC
. D.
2
2 2022x x C
.
Câu 56. Tp nghim ca b
2
2
3 27
xx
là
A.
; 3 1; 
. B.
; 1 3;
. C.
1;3
. D.
3;1
.
Câu 57. Trong không gian vi h to 
Oxyz
, khong cách t m
1; 2;3A
n mt phng
: 3 4 9 0P x y z
là
A.
17
26
. B.
8
. C.
26
13
. D.
4 26
13
.
Câu 58. Din tích toàn phn ca hình lnh
3a
là
A.
2
72a
. B.
2
54a
.
C.
2
36a
. D.
2
9a
.
Câu 59. Cho hàm s
y f x
 th . Hãy ch ra
mt khong bin ca hàm s 
A.
0;3
.
B.
3;4
.
C.
3; 2
.
D.
2; 1
.
Câu 60. Cho hàm s
y f x
có
,
2
lim 0
x
y
. Kh
A.  th hàm s có tim cn ngang
2x
và tim cng
2y
.
B. th hàm s không có tim cn ngang và tim cng
2x
.
C. th hàm s có tim cn ngang
2y
và và không có tim cn
ng.
D. th hàm s có tim cn ngang
2y
và tim cng
2x
.
Câu 61. Hàm s  th  ?
A.
42
31y x x
.
Trang 11
B.
21
1
x
y
x
.
C.
1
2
x
y
x
.
D.
2yx
.
Câu 62. Trong không gian vi h to 
Oxyz
, cho mt cu
2 2 2
: 2 2 7 0S x y z x z
. Bán kính ca
mt cng
A.
7
. B. 3. C. 9. D.
15
.
Câu 63. Cho hai s phc
1
12zi
và
2
23zi
. Phn o ca s phc
12
32w z z
là
A.
1
. B.
11
. C.
12
. D.
12i
.
Câu 64. Cho hàm s
ln
2
x
f x x
. Kh
A.Hàm s ng bin trên khong
0;1
.
B.Hàm s ng bin trên khong
0;
.
C.Hàm s ng bin trên khong
2;
.
D.Hàm s ng bin trên các khong
;0
và
2;
.
Câu 65. Cho các s 
, , ,a b c d
. Biu thc
log log log log
a b c d
M
b c d a
bng
A.
1
. B.
log
a b c d
b c d a



. C.
0
. D.
log abcd
.
Câu 66. Tp nghim c
6
log 5 1xx


A.
1;6
. B.
2;3
. C.
1; 6
. D.
4;6
.
Câu 67. Cho hình l
.ABCD A B C D
có
,IJ

,BC BB
. Góc gia hai
ng thng
,AC IJ
bng
A.
0
30
. B.
0
120
. C.
0
60
. D.
0
45
.
Câu 68. Tnh ca hàm s
2
ln 2yx
là:
A.
2;2
. B.
. C.
\ 2; 2


. D.
\ 2; 2
.
Câu 69. Gi
1
z
,
2
z
là nghim c
2
2 4 0zz
. Tính giá tr ca biu thc
22
12
21
zz
P
zz

.
A.
4
. B.
4
. C.
8
. D.
11
4
.
Câu 70. Trong không gian vi h t
Oxyz
t phm
0;1;1A
,
1;0;2B
và vuông góc vi mt phng
P
:
10x y z
là
A.
20yz
. B.
20yz
. C.
20yz
. D.
20yz
.
Câu 71. Cho hàm s
1
1 ln
y
xx

vi
0x

2
y
y
bng
A.
1
1 ln
x
xx

. B.
1 ln
x
xx
. C.
1
1
x
. D.
1
x
x
.
Câu 72. 


.S ABCD

SA






ABCD
 i
A
và
B
,
Trang 12
, 3 ,AB a AD a
.BC a

3,SA a

.S BCD
theo
.a
A.
3
3
6
a
. B.
3
3
4
a
.
C.
3
23
3
a
. D.
3
23a
.
Câu 73. Gi
,,A B C
lm biu din ca các s phc
1
2z
,
2
4zi
,
3
24zi
trong mt
phng t
.Oxy
Tính din tích tam giác
.ABC
A.
8
. B.
2
. C.
6
. D.
4
.
Câu 74. Cho hàm s
42
26y x x
 th
C
. S m c th
C
ng thng
4y
là:
A.
4
. B.
2
. C.
0
. D.
1
.
Câu 75. Trong không gian vi h t
Oxyz
m
1;0;2A
và
3; 1; 3B 
ng thng
AB

A.
12
2 1 5
x y z

. B.
3 1 2
2 1 5
x y z


.
C.
12
2 1 5
x y z


. D.
117
2 1 5
x y z


.
Câu 76. Cho
12
,zz
là 2 nghim phc c
2
2 5 0zz

1
z
là s phc có phn o âm.

12
3zz
bng:
A.
44i
. B.
44i
. C.
44i
. D.
44i
.
Câu 77. Cho hình chóp t u
.S ABCD
có cng
2a
, cnh bên bng
3a
. Tính th tích
V
ca
kh
A.
3
4
.
3
a
V
B.
3
4 7 .Va
C.
3
47
.
9
a
V
D.
3
47
.
3
a
V
Câu 78. Gi
S
là din tích min hình phc gch chéo trong hình v i. Công thc tính
S
là
A.
2
1
( )dS f x x
.
B.
12
11
( )d ( )dS f x x f x x


.
C.
12
11
( )d ( )dS f x x f x x

.
D.
2
1
( )dS f x x
.
Câu 79. Tìm tp hm biu din s phc
z
tho
1 2 3zi
.
A.ng tròn tâm
1;2I
, bán kính
9r
. B.ng tròn tâm
1;2I
, bán kính
9r
.
C.ng tròn tâm
1; 2I
, bán kính
3r
. D.ng tròn tâm
1;2I
, bán kính
3r
.
Câu 80. Cho cp s nhân
()
n
u
có
1
1
1,
10
uq
. S
103
1
10
là s hng th my ca dãy
A.S hng th
101
. B.S hng th
104
.
C.S hng th
102
. D.S hng th
103
.
Câu 81. Gi
0
z
là nghim phc có phn o âm c
2
2 1 0z
a s phc
0
zi
bng
Trang 13
A.
5
. B.
2
.
C.
5
. D.
2
.
Câu 82. Cho hàm s
32
y ax bx cx d
 th  bên. Mnh
 
A.
0, 0, 0, 0a b c d
.
B.
0, 0, 0, 0a b c d
.
C.
0, 0, 0, 0a b c d
.
D.
0, 0, 0, 0a b c d
.
Câu 83. Có bao nhiêu s phc
z
tha mãn
1 i z z
là s thun o và
21zi
A.
2
. B.
1
. C.
0
. D.Vô s.
Câu 84.  ng
.ABC A B C
i
B
,
2AC a
, bit góc gia
A BC
ng
60
. Tính th tích
V
ca kh.
A.
3
3
2
a
V
. B.
3
3
3
a
V
. C.
3
3
6
a
V
.
D.
3
6
6
a
V
.
Câu 85. Bit
e
1
1 ln 2
e1
d .e ln
1 ln e
xx
x a b
xx






a
,
b
là các s  s
a
b
là
A.
1
2
. B.
1
. C.
3
. D.
2
.
Câu 86. Cho hình chóp
.S ABC
có
60ASB BSC CSA
,
SA a
,
2SB a
,
4SC a
. Tính th tích khi
chóp
.S ABC
theo
a
.
A.
3
82
3
a
. B.
3
42
3
a
. C.
3
22
3
a
. D.
3
2
3
a
.
Câu 87. B
2
2
11
28
xx



có tp nghim là khong
;ab
 ca
ab
là
A.
2
. B.
2
. C.
4
. D.
4
.
Câu 88.  th hàm s ng tim cng?
A.
2
2
log 1yx
. B.
2
2
1
32
x
y
xx

. C.
2
1
x
y
x
. D.
yx
.
Câu 89. Trong không gian
Oxyz
m
2;0; 3A
ng thng
: 1 3
5
xt
yt
zt


. Mt ph
A
và vuông góc vng thng

A.
30x y z
. B.
3 1 0x y z
. C.
3 3 0yz
. D.
3 5 0x y z
.
Câu 90. Tp nghim ca b
2
ln ln 4 4xx
là
A.
1;
. B.
2;
. C.
1; \ 2
. D.
\2
.
Câu 91. S ca nhim Covid-19 trong cng mt tnh vào ngày th
x
trong mc tính
theo công thc
.e
rx
f x A

A
là s ca nhim u cn,
r
là t l 
s ca nhim hàng ngày ct n thì
r
n th
nht tính t ngày t
9
ca bu tiên và không dùng bin pháp phòng chng lây nhim nào
n ngày th 6 s ca bnh ca tn th hai (k t ngày th 7 tr 
dng các bin pháp phòng chng lây nhim nên t l  ca nhim hàng ngày gin
so vn ngày th 6 cn th hai thì s ca bnh ca tn nht vi
s 
Trang 14
A. 242. B. 90. C. 16. D. 422.
Câu 92. Cho hàm s
42
y ax bx c
, vi
,,abc
là các s thc,
0a
. Bit
lim
x
y

, hàm s m
cc tr 
0y
vô nghim. Hi trong 3 s
,,abc
có bao nhiêu s 
A.
0
. B.
3
. C.
2
. D.
1
.
Câu 93. Cho
,,abc

0

4 25 10
a b c

. Tính
.
A.
1
2
T
. B.
2T
. C.
10T
. D.
1
10
T
.
Câu 94. Tính th tích cng c có hình d
A.
3
0,238
4
m
.
B.
3
0,238
3
m
.
C.
3
0,238
3
m
.
D.
3
0,238
2
m
.
Câu 95. Có 8 chic gh c kê thành mt hàng ngang. Xp ngu nhiên 8 hc sinh,
gm 3 hc sinh lp A, 3 hc sinh lp B và 2 hc sinh lp C, ngi vào gh
i gh t hc sinh. Xác su c sinh
lp A ngi cnh nhau bng
a
b
vi
, , ; 1a b a b

ab
là
A.
43
. B.
93
. C.
101
. D.
21
.
Câu 96. Cho hàm s
y f x
liên tc trên
 th
y f x

   t
2
21g x f x x
. M    

A.
1 3 3g g g
.
B.
1 3 3g g g
.
C.
3 1 3g g g
.
D.
1 3 3g g g
.
Câu 97. Cho hình chóp
.S ABCD

SAB
u và nm trong mt phng vuông góc
vi mt phng
ABCD
. Bit
2 , 4AC a BD a
. Tính theo
a
khong cách ging thng
AD
và
SC
.
A.
15
2
a
. B.
25
5
a
. C.
2 15
3
a
. D.
4 1365
91
a
.
Câu 98. Xét các s th
vi
ab
tha
4 log log 25log
a b ab
c c c
. Giá tr nh nht ca
biu thc
log log log
b a c
P a c b
bng
A.
5
. B.
3
. C.
8
. D.
17
2
.
Câu 99. Gi s
1
z
,
2
z
là hai trong s các s phc
z
tha mãn
21iz i
và
12
2zz
. Giá tr ln nht
ca
12
zz
bng
Trang 15
A.
4
. B.
23
. C.
32
. D.
3
.
Câu 100. Cho hàm s
y f x
liên tn
1;3
và có bng bi
Gi
S
là tp tt c các giá tr nguyên ca tham s
m
 
2
1
6 12
m
fx
xx


có hai
nghim phân bin
2;4
. Tng các phn t ca
S
là
A.
297
. B.
294
. C.
75
. D.
72
.
________________HẾT________________
ÑAÙP AÙN ÑEÀ SOÁ 02
1
2
3
4
5
6
7
8
9
10
A
B
C
B
B
A
D
B
D
C
11
12
13
14
15
16
17
18
19
20
B
B
C
A
C
B
C
D
B
C
21
22
23
24
25
26
27
28
29
30
C
A
D
B
D
A
D
B
D
B
31
32
33
34
35
36
37
38
39
40
C
C
A
A
B
C
D
A
B
C
41
42
43
44
45
46
47
48
49
50
A
C
B
C
A
B
D
A
A
C
Lôøi giaûi caâu hoûi vaän duïng cao ñeà soá 02
Câu 44. Tính th tích cc có hình dng và 
Trang 16
A.
3
0,238
4
m
. B.
3
0,238
3
m
.
C.
3
0,238
3
m
. D.
3
0,238
2
m
.
Hướng dẫngiải:
Th tích cc là:
12
V V V
vi
1
V
là th tích khi tr ng
1
2 0,6Rm
và chiu cao
1
0,6hm
;
2
V
là th tích khi nón cn
1
2 0,6Rm

2
2 0,4Rm
và chiu cao
2
1 0,6 0,4hm
.
:
2
23
1 1 1
27
. . 0,3 .0,6
500
V R h m

;
22
2 2 1 2 1 2
1
3
V h R R R R
3
1 19
.0,4. 0,09 0,04 0,06
3 750
m
.
Vy
3
12
27 19 199
500 750 1500
V V V m

3
0,238
3
m
.
Choïn
C
Câu 45. Có 8 chic gh c kê thành mt hàng ngang. Xp ngu nhiên 8 hc sinh, gm 3 hc sinh lp A, 3
hc sinh lp B và 2 hc sinh lp C, ngi vào gh i gh t hc sinh. Xác sut
 c sinh lp A ngi cnh nhau bng
a
b
vi
, , ; 1a b a b

ab
là
A.
43
. B.
93
. C.
101
. D.
21
.
Hướng dẫngiải:
Gi
là không gian mu. S phn t ca không gian mu là
.
Gi
X
là bin cXc hàng c sinh lp A ngi c
Vic xp hàng tha mãn bin c X c thc hi
Chia các hc sinh lp A thành hai nhóm (có th t), ta có
2
3
.1A
(cách xp).
Xp 5 hc sinh không phi lp A thành mt hàng ngang, ta có
5!
(cách xp).
Ta có th xp các nhóm ca lp A vào mt trong các v trí: gia hai bn liên tic
hoc hai v c, ta có
2
6
A
(cách xp).
X là:
22
36
5!. . 21 600n X A A
.
Xác sut cn tìm là:
21 600 15
15, 28 43
8! 28
nX
P X a b a b
n
.
Choïn
A
Câu 46. Cho hàm s
y f x
liên tc trên
  th
y f x
     t
2
21g x f x x
. M 
Trang 17
A.
1 3 3g g g
. B.
1 3 3g g g
.
C.
3 1 3g g g
. D.
1 3 3g g g
.
Hướng dẫngiải:
Xét
2
21g x f x x
;
2 2 2 2 1 0 1g x f x x f x x f x x


.
V ng thng
1yx
trên cùng h trc t vi  th
y f x
(Xem hình).
Ta có:
3
0 1 1
3
x
g x f x x x
x


.
Nhận xét:
Ta thy khi
3;1x
 th hàm
y f x
n th hàm
1yx
,
do vy
1
3
1 0 2 1 0 d 0f x x g x f x x g x x


. Lý lun
, ta có:
3
1
0g x dx
.
Xét
3 1 3
12
3 3 1
d d d 0g x x g x x g x x S S

vi
12
,SS
là các phn din tích
ng trong hình v. T i gii.
Xét
11
33
d 2 1 d 0g x x f x x x





1 3 0 1 3g g g g
(1).
Xét
33
11
d 2 1 d 0g x x f x x x




3 1 0 3 1g g g g
(2).
Xét
3
3
d0g x x
3 3 0 3 3g g g g
.
Vy ta có
1 3 3g g g
.
Choïn
B
Câu 47. Cho hình chóp
.S ABCD

SAB
u và nm trong mt phng vuông góc
vi mt phng
ABCD
. Bit
2 , 4AC a BD a
. Tính theo
a
khong cách ging thng
AD
và
SC
.
Trang 18
A.
15
2
a
. B.
25
5
a
. C.
2 15
3
a
. D.
4 1365
91
a
.
Hướng dẫngiải:
Trong (ABCD), gi
O AC BD
. Ta có:
OA a
,
2OB a
.
Xét tam giác
OAB
vuông ti
O
. Ta có
2
2 2 2
25AB OA OB a a a
.
Gi
H
m
AB
, vì
SAB
u và nm trong mt phng vuông góc v
SH ABCD
và
5. 3 15
22
aa
SH 
.
Ta có:
// ,AD SBC SC SBC
, , ,d AD SC d AD SBC d A SBC
.
Ta li có:
,
1
, 2 ,
2
,
d H SBC
HB
d A SBC d H SBC
AB
d A SBC
.
Trong (ABCD), k
HM
vuông góc vi
BC
ti M. K ng cao
HN
ca tam giác
SHM
. Ta chng
c:
HN SBC
hay
,d H SBC HN
.
Ta có:
22
1
.4 .2 4 2
2
ABCD ABC
S a a a S a
.
Suy ra
2
1
2
HBC ABC
S S a


(do H m AB).
Mt khác:
2
11
. . 5
22
HBC
S HM BC a HM a
2
25
5
5
aa
HM
a
.
Xét tam giác
SHM
vuông ti
H
ta có:
2 2 2 2
15 2 5
.
. 2 1365
25
91
15 20
4 25
aa
SH HM a
HN
SH HM a a
.
Vy
4 1365
,2
91
a
d AD SC HN
.
Choïn
D
Câu 48. Xét các s th
vi
ab
tha
4 log log 25log
a b ab
c c c
. Giá tr nh nht ca
biu thc
log log log
b a c
P a c b
bng
A.
5
. B.
3
. C.
8
. D.
17
2
.
Hướng dẫngiải:
Ta có:
4 log log 25log
a b ab
c c c
1 1 1
4 25
log log log log
c c c c
a b a b

2
4 log log 25 log . log
c c c c
a b a b
22
4 log 17. log . log 4 log 0
c c c c
a a b b
log 4log
1
log log
4
cc
cc
ab
ab
4
4
ab
ba
. Vì
1ab
nên
4
ba
không tha mãn.
Trang 19
Vi
4
ab
, ta có:
4
4
log log log
bc
b
P b c b
1
4 log log
4
bc
cb
.
Vì
,1bc
nên
log , log 0
bc
cb
. Do vy
11
4 log log 4 2 log . log 5
44
b c b c
AM GM
P c b c b
.
Du bng xy ra
1
log log
4
bc
cb
2
log 4
b
c
log 2
b
c
2
cb
.
Vy
min 5P
, khi 
42
a b c
.
Choïn
A
Câu 49. Gi s
1
z
,
2
z
là hai trong s các s phc
z
tha mãn
21iz i
và
12
2zz
. Giá tr ln nht
ca
12
zz
bng
A.
4
. B.
23
. C.
32
. D.
3
.
Hướng dẫngiải:
Ta có
2 1 1 2 1 1 2 1 1 2 1 (1)iz i i z i i z i z i


.
Gi
0
12zi
là s phm biu din là
1; 2I
;
A
,
B
m biu din ca
1
z
,
2
z
.
T (1) suy ra
1IA IB
mà
12
2zz
tc là
2AB
nên
I
m ca
AB
.
Ta có :
2
2 2 2 2 2
12
1. 1. 2 2 2 4 16 4
2
Bianhiakopxki
AB
z z OA OB OA OB OI OI AB



.
Du bng xy ra
12
22OA OB z z
. Vy giá tr ln nht ca
12
zz
bng
4
.
A
Choïn
Câu 50. Cho hàm s
y f x
liên tn
1;3
và có bng bi
Gi
S
là tp tt c các giá tr nguyên ca tham s
m
 
2
1
6 12
m
fx
xx


có hai
nghim phân bin
2;4
. Tng các phn t ca
S
là
A.
297
. B.
294
. C.
75
. D.
72
.
Hướng dẫngiải:
Xét hàm s
1y f x
trên
2;4
. Ta có:
1 1 2; 1 2 3; 1 3 4x x x x x x
.
Ta có bng bin thiên cho hàm
1y f x

Trang 20
t
2
2
6 12
33
mm
gx
xx
x



.
Hàm s
y g x
n
2;4
o hàm
2
2
26
6 12
mx
gx
xx


.
S nghim c
2
1
6 12
m
fx
xx


1
là s m c th hàm s
1y f x
và
2
6 12
m
y g x
xx


.
ng hp 1:
0m
.

2
0 , 2;4
33
m
g x x
x

mà
1 1, 2;4f x x
nên (1) vô nghim.
ng hp 2:
0m
. Ta có:
03g x x
. Bng bin thiên ca
y g x
n
2;4
:
Da vào hai bng bin thiên ca
1y f x
và
y g x
, ta khnh:
1
có hai nghim phân bit
6
4
26
3 1 1 12 3
3
43
3
4
m
g
m
gm
g
m






.
Ta li có m nguyên suy ra
12; 11;...; 4; 3S
, s phn t ca S là 10.
Suy ra tng các phn t ca
S
là:
12 3 .10
75
2


.
Choïn
C
Trang 21
ĐỀ SỐ 03
ĐỀ RÈN LUYỆN MÔN TOÁN 12
HƯỚNG ĐẾN KÌ THI THPT QUỐC GIA
Trắc nghiệm: 50 câu
Thời gian: 90 phút
Nội dung:
FULL KIẾN THỨC TOÁN 12+
Câu 1. H nguyên hàm ca hàm s
2xx
y e e

là
A.
2
1
2
xx
e e C

. B.
2
2
xx
e e C

. C.
2
2
xx
e e C

. D.
2
1
2
xx
e e C

.
Câu 2. Tp nghim c
2
5
log 2x
là :
A.
5.
B.
5.
C.
5.
D.
.
Câu 3. Trên mt phng tm
5;1M
biu din s phc
z
. Phn o ca s phc
z
là
A.
5
. B.
i
. C.
1
. D.
5i
.
Câu 4. Cho
n
u
là mt cp s cng có
1
3u
và công sai
2d
. Tìm
20
u
.
A.
39
. B.
43
. C.
41
. D.
45
.
Câu 5. Trong không gian vi h t
Oxyz
t phng
Oyz
?
A.
0yz
. B.
0x
. C.
0y
. D.
0z
.
Câu 6. Cho khi nón có ding
2
a
ng sinh
5.la
Tính th tích kh
A.
3
2
.
3
Va
B.
3
8
.
3
Va
C.
3
2.Va
D.
3
4
.
3
Va
Câu 7. Cho hàm s
Fx
là mt nguyên hàm ca
fx
. Bit
1 3, 2 12FF
. Tính
1
2
dI f x x
?
A.
15I
. B.
36I 
. C.
15I 
. D.
9I
.
Câu 8. Tnh ca hàm s
5
yx
là
A.
;0
. B.
\0
.
C.
;0
. D.
0;
.
Câu 9. Cho hàm s
42
y ax bx c
  th     i. S
nghim thc c
0f x f
là
A.
3
.
B.
0
.
C.
4
.
D.
2
.
Câu 10. Trong không gian vi h t
Oxyz
, hình chiu cm
lên trc
Oy
m
A.
1;0;0R
. B.
1;0;3P
. C.
0;2;0Q
. D.
0;0;3S
.
Câu 11. Trong không gian
Oxyz
, cho mt cu
2 2 2
: 2 3 1 49S x y z
. Tìm t tâm
I
và
tính bán kính
R
ca
.S
A.
2; 3;1 , 49IR
. B.
2; 3;1 , 7IR
. C.
2;3; 1 , 7IR
. D.
2; 3;1 , 7IR
.
Câu 12. Cho hàm s
32
2 9 2021 2022
3
m
f x x mx m x
. Có bao nhiêu giá tr nguyên ca tham s
m
 hàm s ch bin trên
?
A.
4
. B.
3
. C.
2
. D. Vô s.
Trang 22
Câu 13. Cho t diu
ABCD
. Gi
M
m ca
BC
, cosin góc gia
AB
và
DM
bng
A.
2
2
. B.
3
3
. C.
3
6
. D.
3
.
Câu 14. Trong không gian
Oxyz
m
1;2;3A
ng thng
3 1 7
:
2 1 2
x y z
d

ng thng

A
và song song vi
d

A.
13
2
37
xt
yt
zt



. B.
3
12
73
xt
yt
zt


. C.
12
2
32
xt
yt
zt



. D.
2
12
23
xt
yt
zt


.
Câu 15. Cho
5
log 2 a
và
5
log 3 b
. Biu din
5
log 360
i dng
5
log 360 ma nb p
, vi
,,m n p
là
các s nguyên. Tính
2A m n p
.
A.
9A
. B.
7A
. C.
8A
. D.
10A
.
Câu 16. Trong không gian, cho tam giác
ABC
vuông ti
A
,
2AB a
và
AC a
. Khi quay tam giác
ABC
xung quanh cnh góc vuông
AB
ng gp khúc
ACB
to thành mt hình nón. Din tích xung
quanh cng
A.
2
5 a
. B.
2
5 a
. C.
2
20 a
. D.
2
25a
.
Câu 17. Tp nghim ca b
4 6.2 8 0
xx
là
A.
2;4
. B.
0;2
. C.
;1 2; 
. D.
1;2
.
Câu 18. Tng s tim cng và ngang c th hàm s
42
1
2
y
xx

bng:
A.
5
. B.
3
. C.
4
. D.
1
.
Câu 19. Trong không gian
Oxyz
, cho mt cu
()S
:
2 2 2
( 1) ( 1) 4x y z
và mt phng
()P
:
2 2 1 0x y z
. Khong cách t tâm
I
ca
()S
n
()P
bng
A.
2
3
. B. 2. C. 1. D.
4
3
.
Câu 20. Th tích ca vt th tròn xoay sinh bi hình phng gii hn b th hàm s
2
6y x x
và trc
hoành quay quanh trc tính theo công thc
A.
1
2
0
6dx x x
. B.
3
4 3 2
2
2 11 12 36 dx x x x x
.
C.
3
2
2
6dx x x

. D.
1
4 3 2
0
2 11 12 36 dx x x x x
.
Câu 21. Giá tr ln nht và giá tr nh nht ca hàm s
3
2
2 3 4
3
x
y x x
n
4;0
lt là
và Mm
. Giá tr ca tng
Mm
bng bao nhiêu?
A.
4
3
Mm
. B.
4
3
Mm
. C.
28
3
Mm
. D.
4Mm
.
Câu 22. Cho hình chóp
.S ABC
u cnh
a
. Bit
SA
vuông góc vi mt ph
30SBA
. Th tích khi chóp
.S ABC
bng:
A.
3
2
a
. B.
3
4
a
. C.
3
6
a
. D.
3
12
a
.
Câu 23. Xét
1
ln
d
2
e
x
x
x
, nt
lnux
thì
1
ln
d
2
e
x
x
x
bng
A.
1
0
2duu
. B.
1
0
1
d
2
uu
. C.
1
d
e
uu
. D.
1
1
d
2
e
uu
.
Trang 23
Câu 24. Tp nghim ca b
12
2
log 2 3 log 3 1 0xx
là
A.
1
2
3
x
. B.
2
2
3
x
. C.
2x
. D.
2x
.
Câu 25. Cho 
.ABC AB C
có
2AB a
,
M

BC
và
3AM a


A.
3
18 2a
. B.
3
32a
. C.
3
2a
. D.
3
92a
.
Câu 26. Xét
2
0
cos dI f x x x
. Nt
u f x
và
d cos dv x x
thì
A.
2
2
0
0
sin sin dI f x x f x x x

. B.
2
2
0
0
sin sin dI f x x f x x x

.
C.
2
2
0
0
sin sin dI f x x f x x x
. D.
2
2
0
0
sin sin dI f x x f x x x
.
Câu 27. Trong không gian
Oxyz
  ng thng
12
:
2 1 1
x y z
và mt phng
: 2 1 5 1 1 5 0P m x m y m z
. Tìm
m

song song vi
P
.
A.
1m 
. B.
3m 
. C.
1m
. D. Không tn ti
m
.
Câu 28. Gi
S
là tp hp tt c các giá tr ca tham s
m
 hàm s
42
21y x mx m
có giá tr cc tiu
bng
1
. Tng các phn t thuc
S
là
A.
2
. B.
0
. C.
1
. D.
1
.
Câu 29. Trong không gian
Oxyz
   m
2;0;0 , 0; 3;0 , 0;0;6A B C
. T  m  
tuyn ca mt phng
ABC
là
A.
2; 3;6n

. B.
1; 2;3n

. C.
3; 2;1n

. D.
3;2;1n
.
Câu 30. Ký hiu
0
z
là nghim phc có phn o âm c
2
4 13 0.zz
Trên mt phng to ,
m biu din ca s phc
0
?iz
A.
1
(3;2).M
B.
2
(2;3).M
C.
3
(2; 3).M
D.
4
( 3;2).M
Câu 31.     ng
.ABC A B C
 
ABC
là tam giác vuông cân ti
B
có
,2AB a AA a

. Góc ging thng
AC
vi mt phng
AA B B

bng:
A.
60
. B.
30
. C.
45
. D.
90
.
Câu 32. Cho hàm s
fx
o hàm liên tc trên
. Bit
1
0
. 10x f x dx
và
13f
, tính
1
0
f x dx
.
A.
30
. B.
7
. C.
13
. D.
7
.
Câu 33. S phi s thun o?
A.
3zi
. B.
1z i i
. C.
0z
. D.
12zi
.
Câu 34. Trong không gian
Oxyz
cm
1;2;3A
và
3;3;4B
và mt phng
: 2 0.P x y z
Gi
,AB

lt là hình chiu vuông góc ca
A
và
B
lên mt phng
P
. Tính  n thng
AB

.
A.
6
2
. B.
3
. C.
6
. D.
3
2
.
Trang 24
Câu 35. Din tích hình phng gch chéo trong hình v  c tính
theo công th
A.
1
32
1
( 3 3) .x x x dx
B.
1
32
1
( 3 3) .x x x dx
C.
1
32
1
( 3 3) .x x x dx
D.
3
32
1
( 3 3) .x x x dx
Câu 36.  trt
M
(Richterc cho bi công thc
0
log logM A A
, vi
A

rung chn t 
0
A
là m  chun (hng su th k 20, mt trt San

8,3
 Richtert trt khác Nam M
ng 
9,3
 Richter. Hi trt Nam M  rung chn tp my ln
 trt San Francisco?
A.
20
. B.
10
. C.
2
. D.
100
.
Câu 37. Có tt c bao nhiêu giá tr thc ca tham s
m
 ng thng
1y mx m
c th hàm s
32
32y x x x
tm
,AB
và
1;1C
phân bit sao cho
2
4
AB
yy
.
A.
1
. B.
3
. C.
2
. D.
0
.
Câu 38. Cho hình chóp
.S ABCD

ABCD
là hình ch nht cnh
22AB AD a
. Tam giác
SAB
u
nm trong mt phng vuông góc vi mng cách t
A
n mt phng
SBD
bng
A.
a
. B.
3
4
a
. C.
2
a
. D.
3
2
a
.
Câu 39. Trong không gian
Oxyz
ng thng
12
13
: , :
2 1 1 1 1 2
x y z x y z
dd


. Gi
,,M a b c
m ca
1
d
và
2
d
. Tính
23a b c
.
A.
2
. B.
5
. C.
6
. D.
3
.
Câu 40. Cho
1
*
0
82
,
33
21
dx
a b a a b
xx
. Tính
2ab
.
A.
21ab
. B.
28ab
. C.
27ab
. D.
25ab
.
Câu 41. Trong không gian
Oxyz
   ng
12
:
1 1 1
x y z
và mt phng
: 2 2 6 0.P x y z
  ng thng
d
nm trong
P
sao cho
d
c ng thi
vuông góc vi
là
A.
24
33
1
xt
yt
zt



. B.
24
33
1
xt
yt
zt



. C.
24
33
1
xt
yt
zt


. D.
24
33
1
xt
yt
zt


.
Câu 42. Cho hình tr ng
32a
. Bit rng khi ct hình tr i mt mt phng song
song vi trc và cách trc mt khong bng
3a
, thit dic là mt hình vuông. Th tích ca
khi tr c gii hn bi hình tr ng
A.
3
108
3
a
. B.
3
54 a
. C.
3
216 a
. D.
3
108 a
.
Câu 43. Cho hàm s
()fx
có bng bi
Trang 25
 th hàm s
4
2
1
4
x
gx
f x f x
có tt c ng tim cng
A.
2
. B.
5
. C.
4
. D.
3
.
Câu 44. Cho hình chóp
.S ABC

ABC
u cnh
a
, mt bên
SAB
là tam giác cân ti
S
và
nm trong mt phng vuông góc vt rng góc gia
SBC
và
ABC
bng
60
. Tính th
tích khi chóp
.S ABC
.
A.
3
3
4
a
. B.
3
3
16
a
. C.
3
3
8
a
. D.
3
33
16
a
.
Câu 45. Cho s phc
z
tha mãn
10
1 2 2i z i
z
. Khnh nào sau 
A.
1
2
z
. B.
3
2
2
z
. C.
2z
. D.
13
;
22
z



.
Câu 46. Cho hàm s
y f x
 th  bên. S nghim
thc ca b  
3 2 2 3 2
1 3 1 2 3 1 2f x x f x x
là
A.
3
.
B.
5
.
C.
4
.
D.
2
.
Câu 47. 
S

S


0,abc
. Tính
2 2 2
abc
.
A.
15
. B.
10
. C.
17
. D.
16
.
Câu 48. Cho các s th
;;abc
khác
1
và thu kin
22
3
log log 2log log
a b b a
cc
bc
b a b
. Gi
,Mm
lt là giá tr ln nht, giá tr nh nht ca biu thc
log log
ab
P ab bc
. Tìm giá tr ca
biu thc
22
29S m M
.
A.
28S
. B.
25S
. C.
26S
. D.
27S
.
Câu 49. Cho mt cu
2 2 2
( ): 2 2 2 0S x y z x y z
 m
2;2;0A
. Vi   t phng
OAB
bim
B
là mm thuc mt cu
S
 
OAB
u.
A.
20x y z
. B.
20x y z
. C.
0x y z
. D.
20yz
.
Câu 50. Cho hàm s
3
3f x x x m
. Có tt c bao nhiêu s nguyên
m
thuc khong
20;20
 vi
mi b ba s thc
,,abc
2;1
thì
,,f a f b f c
 dài ba cnh ca tam giác ?
Trang 26
A.
24
. B.
26
. C.
28
. D.
30
.
________________HẾT________________
ÑAÙP AÙN ÑEÀ SOÁ 03
1
2
3
4
5
6
7
8
9
10
D
B
C
C
B
A
C
B
A
C
11
12
13
14
15
16
17
18
19
20
D
A
C
C
B
B
D
B
D
B
21
22
23
24
25
26
27
28
29
30
C
D
B
D
B
B
C
B
C
A
31
32
33
34
35
36
37
38
39
40
B
D
B
D
B
B
B
D
C
B
41
42
43
44
45
46
47
48
49
50
D
D
C
B
D
C
C
D
C
B
Lôøi giaûi caâu hoûi vaän duïng cao ñeà soá 03
Câu 43. Cho hàm s
()fx
có bng bi
 th hàm s
4
2
1
4
x
gx
f x f x
có tt c ng tim cng
A.
2
. B.
5
. C.
4
. D.
3
.
Hướng dẫn giải:
Xét
2
0
40
4
fx
f x f x
fx
.
1
1
0
x
fx
xx


1x
là nghim kép,
1
xx
là là nghit tính
tng quát, ta biu din
2
11
1f x a x x x
,
1
0a
.
2
1
4
x
fx
xx



1x 
là nghim kép,
2
xx
là là nghit tính
tng quát, ta biu din
2
22
41f x a x x x
,
2
0a
.
Ta vit li hàm s u:
22
11
4
xx
gx
f x f x



Trang 27
2
2
22
1 2 1 2
1 1 2 2
1 1 1
1
11
11
x x x
x
a a x x x x x x
a x x x a x x x

.
Ta th th hàm s
y g x
có bng tim cng:
12
1, ,x x x x x
.
Choïn
C
Câu 44. Cho hình chóp
.S ABC

ABC
u cnh
a
, mt bên
SAB
là tam giác cân ti
S
và
nm trong mt phng vuông góc vt rng góc gia
SBC
và
ABC
bng
60
. Tính th
tích khi chóp
.S ABC
.
A.
3
3
4
a
. B.
3
3
16
a
. C.
3
3
8
a
. D.
3
33
16
a
.
Hướng dẫn giải:
Gi
H
m ca
AB SH AB
. Ta có
SAB ABC
suy ra
SH ABC
.
Gi
M
m ca
BC
và
I
m ca
BM
.

AM BC
mà
//HI AM
(tính chng trung
bình), suy ra
HI BC
.
Vì
BC HI
BC SHI BC SI
BC SH
.
Ta có:
,
SBC ABC BC
HI BC SI BC


, , 60SBC ABC HI SI SIH
.
Xét
ABC
u cnh
3 1 3
2 2 4
aa
a AM HI AM
.
Xét
SHI
vuông ti
3
tan
4
a
H SH HI SIH
.
Th tích khi chóp:
23
.
1 1 3 3 3
3 3 4 4 16
S ABC ABC
a a a
V SH S
.
Choïn
B
Câu 45. Cho s phc
z
tha mãn
10
1 2 2i z i
z
. Kh
A.
1
2
z
. B.
3
2
2
z
. C.
2z
. D.
13
;
22
z



.
Hướng dẫn giải:
Ta có
10 10
1 2 2 1 2 2 2 2 1 . 10 (*)
a
b
i z i i z i z z i z
zz




.
L c:
22
22
2
2 2 1 . 10 5 5. 10
ab
z z z z z
2
42
2
1 ( )
5 5 10 0
2 ( )
zn
zz
zl

1z
.Vy
13
;
22
z



.
Choïn
D
Câu 46. Cho hàm s
y f x
  th    bên. S nghim thc ca b  
3 2 2 3 2
1 3 1 2 3 1 2f x x f x x
là
Trang 28
A.
3
. B.
5
. C.
4
. D.
2
.
Hướng dẫn giải:
t
32
31t f x x
. B thành:
2
1 2 2tt
2
2
2
1
1
1
2 1 0
1 2 2
t
t
t
tt
tt



.
Ta có:
32
32
32
3 1 2; 1
3 1 1
3 1 1;2
x x a
f x x
x x b
.
Xét hàm s
3 2 2
0
3 1, 3 6 , 0
2
x
g x x x g x x x g x
x

. Bng bin thiên
gx
:
Ta 
32
3 1 2; 1x x a
có ba nghim phân bit
1 2 3
,,x x x
.

32
3 1 1;2x x b
có mt nghim
4
x
khác
1 2 3
,,x x x
.
Vy bbn nghim thc.
Choïn
C
Câu 47. 
S

S


0,abc
. Tính
2 2 2
abc
.
A.
15
. B.
10
. C.
17
. D.
16
.
Hướng dẫn giải:
Cách giải 1:

6
9.10n 
.

A


1 2 3 4 5 6
3a a a a a a
.
Ta có:
1 2 3 4 5 6 1 2 3 4 5 6 1 2 3 4 5 6 1 2 3 4 5 6
3 10. 3 3. 7. 3 7a a a a a a a a a a a a a a a a a a a a a a a a
Trang 29
1 2 3 4 5 6
3. 3 7a a a a a a 
.

1 2 3 4 5 6 1 2 3 4 5 6
3. 3 7 2 1
3
k
a a a a a a k k a a a a a a k

3k m m
.
 :
1 2 3 4 5 6
71a a a a a a m

14 285,8 142 857,1
100 001 1 000 000
100 000 7 1 999 999
77
mm

.
Do
14 286;14 287;...;142 857mm
. Vì vy có
142 857 14 286 1 128 572
giá tr ca
m
tha mãn. Suy ra
128 572nA
.

A
là:
6
128572
0,014
9.10
nA
PA
n
. Suy ra:
0, 1, 4a b c
.
Vây
2 2 2
17abc
.
Choïn
C
Cách giải 2:

6
9.10n 
.

A

Gi s t nhiên tha mãn bin c A là X, ta có:
1 000 013 9 999 983X
.
Ta thy s nh nht mà X có th nhc là
1 000 013
, s ln nht mà X có th nhn là
9 999 983
.
Chênh lch gia hai s liên tip th . Vì vy ta có th thy tp hp các s t
nhiên X s lp nên mt cp s cng có s hu là
1
1 000 013u
, công sai
70d
, s hng cui
là
9 999 983
.
Do vy s các s t nhiên mà X có th nhn là:
9 999 983 1 000 013
1 128 572
70

(s).
Suy ra
128 572nA

A
là:
6
128572
0,014
9.10
nA
PA
n
.
Suy ra:
0, 1, 4a b c
. Vây
2 2 2
17abc
.
Choïn
C
Câu 48. Cho các s th
;;abc
khác
1
và thu kin
22
3
log log 2log log
a b b a
cc
bc
b a b
. Gi
,Mm
lt là giá tr ln nht, giá tr nh nht ca biu thc
log log
ab
P ab bc
. Tìm giá tr ca
biu thc
22
29S m M
.
A.
28S
. B.
25S
. C.
26S
. D.
27S
.
Hướng dẫn giải:
Ta có:
log log log log
a b a b
P ab bc b c
t
log
log
log log .log
b
a
a a b
c x P
bx
c b c x x P


.
Ta có:
22
3
log log 2log log
a b b a
cc
bc
b a b
2
log log 2log .log 2log 2 log 3 log
a b a b b a a
x x P x P x
x x P
P
b c b c c c b




2
2 2 2 3P x x P x P x x P x
2 2 2
2 2 2 2 2 3P x Px x P x Px x
22
3 2 1 0x P x P P
(*).

*
luôn có nghim
x
nên
2
2
3 4 2 1 0P P P
2
3 2 5 0PP
Trang 30
55
1 1,
33
P m M
.
Thay vào ta có
22
2 9 27S m M
.
Choïn
D
Câu 49. Cho mt cu
2 2 2
( ): 2 2 2 0S x y z x y z
 m
2;2;0A
. Vi   t phng
OAB
bim
B
là mm thuc mt cu
S
 
OAB
u.
A.
20x y z
. B.
20x y z
. C.
0x y z
. D.
20yz
.
Hướng dẫn giải:
Gi
vi
0x
và
H
m
1;1;0OA H
.
Gi
P
là mt phng trung trn
OA

P
m
1;1;0H
cn
OA
và
nhn
2;2;0OA
làm n. Suy ra
P
:
2. 1 2. 1 0xy
20xy
.
Theo gi thit:
22
BP
OB AB
OB OA OB OA
B S B S



2 2 2
2 2 2
20
8
2 2 2 0
xy
x y z
x y z x y z
2 2 2 2 2
22
84
2 2 2 8 2
x y x y
x y z x y
x y z z





2
2
2
2 4 0
2
2
xy
xy
x y xy xy
z
z




Suy ra:
2
0 (2;0;2)
2
x
yB
z

, (do
0x
).
Ta có :
2;2;0 , 2;0;2 , 4; 4; 4 4 1; 1; 1OA OB OA OB


.
Mt phng
OAB

O
, nhn
1; 1; 1n
là mn.
V
OAB
là:
0x y z
.
Choïn
C
Câu 50. Cho hàm s
3
3f x x x m
. Có tt c bao nhiêu s nguyên
m
thuc khong
20;20
 vi
mi b ba s thc
,,abc
2;1
thì
,,f a f b f c
 dài ba cnh ca tam giác ?
A.
24
. B.
26
. C.
28
. D.
30
.
Hướng dẫn giải:
Xét
3
3g x x x m
,
2
3 3 0 1g x x x
.
Ta có:
22gm
;
12gm
;
12gm
. Suy ra:
22m f x m
,
2;1x
.
Ta có:
2;1
2;1
Min , , Maxf x f a f b f c f x

.
Không mt tính tng quát, gi s
f a f b f c
.
u kin c 
,,f a f b f c
 dài ba cnh ca tam giác là:
0f a f b f c f a f b f c
.
Yêu cu bài toán cho u kin:
2;1
2;1
2Min Max 0f a f b f c f x f x
(1).
Trang 31
Trường hợp 1:
2 2 0 2m m m

2;1
Max Max 2 ; 2 2 2f x m m m m
;
2;1
Min Min 2 ; 2 2 2f x m m m m
.
Thay vào (1):
2 2 2 0 6 0 6m m m m
. Vì m nguyên thuc khong
20;20
nên
7;8;...;19m
c 13 giá tr m tha mãn.
Trường hợp 2:
2 2 0 2m m m

2;1
Max Max 2 ; 2 2 2f x m m m m
;
2;1
Min Min 2 ; 2 2 2f x m m m m
.
Thay vào (1):
2 2 2 0 6m m m
. Vì m nguyên thuc khong
20;20
nên
19; 18;... 7m
c 13 giá tr m tha mãn.
Trường hợp 3:
2 0 2 2 2m m m
.

2;1
2 2 2 2
Max Max 2 ; 2 2
2
m m m m
f x m m m
;
2;1
Min 0fx
. Do vy (1) tr thành:
2.0 2 0 2 0mm
(vô lí).
Vy s giá tr m th bài là:
13 13 26
.
Choïn
B
ĐỀ SỐ 04
ĐỀ RÈN LUYỆN MÔN TOÁN 12
HƯỚNG ĐẾN KÌ THI THPT QUỐC GIA
Trắc nghiệm: 50 câu
Thời gian: 90 phút
Nội dung:
FULL KIẾN THỨC TOÁN 12+
Câu 1. Cho hai s phc
và
2
1zi
a s phc
12
23zz
bng
A.
58
. B.
113
. C.
82
. D.
137
.
Câu 2. Giá tr nh nht ca hàm s
4
1yx
x
n
3; 1
bng
Trang 32
A.
5
. B.
4
. C.
6
. D.
5
.
Câu 3. Cho
a
là s th
1
. Giá tr ca biu thc
3
log
a
Ta
bng
A.
3 a
. B.
3
2
. C.
6
. D.
3
.
Câu 4. Trong không gian
Oxyz
ng thng
3 2 1
:
1 3 2
x y z
d


c
d
?
A.
3; 2;1Q 
. B.
4; 1;1M
. C.
2;5; 3N
. D.
3;2; 1P
.
Câu 5. S phc liên hp ca s phc
34z i i
là
A.
43zi
. B.
43zi
. C.
43zi
. D.
43zi
.
Câu 6. Cho hàm s
y f x
liên tc trên
, có bng bi
Hàm s t cc tiu ti
A.
4x
. B.
2x
. C.
3x
. D.
2x 
.
Câu 7. Cho hình hng
.ABCD A B C D
có cnh bên
AA h
và din tích tam giác
ABC
bng
S
. Th
tích ca khi hp
.ABCD ABC D
bng:
A.
1
3
V Sh
. B.
2
3
V Sh
. C.
V Sh
. D.
2V Sh
.
Câu 8. Tìm tnh ca hàm s
1
2
log 2 1yx
.
A.
1;D 
. B.
1
;1
2
D


. C.
1;D 
. D.
1
;1
2
D



.
Câu 9. Trong mt phng
Oxy
m
,AB
 m cn thng
AB
m
biu din ca s ph
A.
1
2
2
i
.
B.
12i
.
C.
2 i
.
D.
1
2
2
i
.
Câu 10. Trong không gian
Oxyz
, cho hình hp
.ABCD A B C D
có
1;0;1A
,
2;1;2B
,
1; 1;1D
,
4;5; 5C
. Tính t nh
A
ca hình hp.
A.
4;6; 5A
. B.
2;0;2A
. C.
3;5; 6A
. D.
3;4; 6A
.
Câu 11.  th ca hàm s ng ng cong trong hình bên ?
A.
3
3y x x
.
B.
42
y x x
.
Trang 33
C.
32
3y x x
.
D.
42
y x x
.
Câu 12. 




4a
. 



A.
3
32 a
. B.
3
32
3
a
. C.
3
16 a
. D.
3
8
3
a
.
Câu 13. Trong không gian
Oxyz
m
2;0;0M
,
0;1;0N
và
0;0;2P
. Mt phng
MNP
có

A.
1
2 1 2
x y z
B.
1
1 2 2
x y z
. C.
1
2 1 2
x y z
. D.
1
2 2 1
x y z
.
Câu 14. Cho hàm s
y f x
 th  bên. M  hàm s 
A.ng bin trên khong
0;2
.
B.Nghch bin trên khong
3;0
.
C.ng bin trên khong
1;0
.
D.Nghch bin trên khong
0;3
.
Câu 15. Kí hiu
1
z
,
2
z
,
3
z
,
4
z
là bn nghim c
42
60zz
.
Tính
1 2 3 4
S z z z z
.
A.
23S
. B.
2 2 3S 
. C.
22S
. D.
2 2 3S 
.
Câu 16. Cho
3
12
0
d
e .e .e
1
x
x
a b c
x
. Vi
a
,
b
,
c
là các s nguyên. Tính
S a b c
.
A.
1S
. B.
2S
. C.
0S
. D.
4S
.
Câu 17. Tìm tp nghim
S
c
2
33
log 2 3 log 1 1x x x
.
A.
0;5S
. B.
5S
. C.
0S
. D.
1;5S
.
Câu 18. Cho hình chóp
.S ABCD
. Gi
M
,
N
,
P
,
Q
theo th t m ca
SA
,
SB
,
SC
,
SD
. Tính
t s th tích ca hai khi chóp
.S MNPQ
và
.S ABCD
bng
A.
1
8
. B.
1
2
. C.
1
4
. D.
1
16
.
Câu 19. Tìm stim cn c th hàm s
2
2
76
1
xx
y
x

.
A.
1
. B.
2
. C.
3
. D.
0
.
Câu 20. Tích phân
1
0
d
31
x
x
bng
A.
4
3
. B.
3
2
. C.
1
3
. D.
2
3
.
Câu 21. B
42
log 7 log 1xx
có tp nghim là.
A.
5;
. B.
1;2
. C.
2;4
. D.
3;2
.
Câu 22. Trong không gian
Oxyz
, cho mt phng
:3 2 6 0x y z
. Hình chiu vuông góc cm
2; 1;0A
lên mt phng
có t là
Trang 34
A.
1;0;3
. B.
2; 2;3
. C.
1;1; 1
. D.
1;1; 1
.
Câu 23. Cho hàm s bc bn
()y f x
  th    i, s
nghim c
2 1 0fx
là
A. 2.
B. 4.
C. 3.
D. 1.
Câu 24. Cho hàm s
y f x
tha mãn
2
0
sin . d 0x f x x f
1
. Tính
2
0
cos . dI x f x x
.
A.
1I
. B.
0I
. C.
2I
. D.
1I 
.
Câu 25. Tìm tt c các giá tr ca
m
 hàm s
1
2
mx
xm
y
nghch bin trên
1
;
2




.
A.
1;1m
. B.
1
;1
2
m



. C.
1
;1
2
m



. D.
1
;1
2
m



.
Câu 26. Cho hai s thc
,ab
tho mãn
20ab
và
3 3 3
2log 2 log log .a b a b
Giá tr ca biu thc
b
T
a
bng
A.
1.
B.
4.
C.
3.
D.
2.
Câu 27. Cho hình chóp t u
.S ABCD
có tt c các cu bng
a
,
M
m cnh
SD
. Giá
tr tang ca góc ging thng
BM
và mt phng
ABCD
bng
A.
1
3
. B.
2
2
. C.
3
3
. D.
2
3
.
Câu 28. Th tích khi l
.ABCD A B C D
ng chéo
26AC
bng
A.
24 3
. B.
48 6
. C.
66
. D.
16 2
.
Câu 29. Cho hàm s
fx
, bit
fx
 th  m
cc tr ca hàm s
fx
là
A.
2
.
B.
1
.
C.
3
.
D.
0
.
Câu 30. Trong không gian
Oxyz
m
1;0; 1M
. Mt phng

qua
M
và cha trc
Ox

A.
0y
. B.
0xz
. C.
10yz
. D.
0x y z
.
Câu 31. Giá tr ca biu thc
2 3 4 63
log 3.log 4.log 5...log 64A
bng
A.
7.
B.
6.
C.
8.
D.
10.
Câu 32. Cho s phc
z
tha mãn:
1 2 . 15z i z i i
. Tìm mô-a s phc
z
?
Trang 35
A.
5z
. B.
4z
. C.
25z
. D.
23z
.
Câu 33. Khi quay mu cnh bng
a
(bao gm c m trong tam giác) quanh mt cnh ca nó ta
c mt khi tròn xoay. Tính th tích
V
ca kh
a
.
A.
3
4
a
. B.
3
3
8
a
. C.
3
3
4
a
. D.
3
3
24
a
.
Câu 34. Din tích
S
ca phn hình phc gch chéo trong hình bên bng
A.
3
22
0
1
7 12 d
2
S x x x x
.
B.
23
22
02
1
7 12 d
2
S x dx x x x

.
C.
23
22
02
1
7 12 d
2
S x dx x x x

.
D.
3
22
0
1
7 12 d
2
S x x x x
.
Câu 35. Cho kh
.ABC A B C

ABC
u cnh bng
3a
, cnh bên
AA a
, góc
gia
AA
và mt phng
30
. Tính th tích kh 
a
.
A.
3
33
8
a
. B.
3
3
3
a
. C.
3
3
4
a
. D.
3
3
2
a
.
Câu 36. Tp nghim ca b
2
ln 2ln 3 0xx
là
A.
3
;ee
. B.
;e 
. C.
3
1
;;e
e

 


. D.
3
1
;e
e



.
Câu 37.
Cho
Fx
là mt nguyên hàm ca hàm s
1
2e 3
x
fx
tha mãn
0 10F
. Tìm
Fx
.
A.
1 ln5
ln 2e 3 10
33
x
F x x
. B.
1
10 ln 2e 3
3
x
F x x
.
C.
13
ln e 10 ln5 ln2
32
x
F x x






. D.
1 3 ln5 ln2
ln e 10
3 2 3
x
F x x





.
Câu 38. Tìmgiá tr thc ca tham s
m
 ng thng
: 3 1 3d y m x m
vuông góc vng thng
m cc tr c th hàm s
32
31y x x
.
A.
1
6
m
. B.
1
3
. C.
1
3
. D.
1
6
.
Câu 39. Có bao nhiêu giá tr nguyên ca tham s
m
thuc khong
10;10
 hàm s
10
2
mx
y
xm
nghch
bin trên khong
0;2
.
A.
5
. B.
8
. C.
6
. D.
7
.
Câu 40. Cho s phc
z
tha mãn
2zz
. Bit rng phn thc ca
z
bng
a
. Tính
z
theo
a
A.
1
1
z
a
. B.
2
1
2
aa
z

. C.
2
1
2
aa
z

. D.
2
4
2
aa
z

.
Câu 41. Cho bit
7
3
3
2
0
d
1
xm
x
n
x
vi
m
n
là mt phân s ti gin. Tính
7mn
.
A.
0
. B.
1
. C.
2
. D.
91
.
Trang 36
Câu 42. Cho hình chóp
.S ABCD

ABCD
là hình vuông cnh
a
. Hình chiu ca
S
lên mt ph
trùng vi trng tâm ca tam giác
ABD
. Cnh
SD
to vt góc
60
. Tính th tích ca khi
chóp
.S ABCD
.
A.
3
15
3
a
. B.
3
15
27
a
. C.
3
15
9
a
. D.
3
3
a
.
Câu 43. Mt nhóm các chuyên gia y t u và th nghi chính xác ca mt b xét nghim
19.COVID
Gi s c sau
n
ln th nghiu chnh b xét nghim thì t l chính xác ca b
xét nghic
0,01
1
1 2020.10
n
Sn
. Hi phi tin hành ít nht bao nhiêu ln
th nghiu chnh b xét nghi m bo t l chính xác ca b xét nghit trên
90%?
A.
426
. B.
425
. C.
428
. D.
427
.
Câu 44. Cho hình tr
T
có
O
,
O
l
ABC
ni ting
tròn tâm
O
,
2AB a
,
1
sin
3
ACB
và
OO
to vi mt phng
O AB
mt góc
o
30
(tham kho
i). Th tích khi tr
T
bng
A.
3
2π6a
.
B.
3
3π6a
.
C.
3
π3a
.
D.
3
π6a
.
Câu 45. S
100000
7
có bao nhiêu ch s?
A.
84510
. B.
194591
. C.
194592
. D.
84509
.
Câu 46. Cho hình chóp
.S ABCD

2,AB a AD DC CB a
và
SA
vuông góc vi
mt ph i
M
m ca cnh
AB
. Khong cách
ging thng
CM
và
SD
bng
A.
3
2
a
.
B.
3
4
a
.
C.
3
2
a
.
D.
3a
.
Câu 47. Cho hàm s
33
22
log logf x x x m
(
m
là tham s thc). Gi
S
là tp hp tt c các giá tr ca
m
sao cho
1;4
1;4
max min 6f x f x
. Tt c các phn t ca
S
bng
A.
13
. B.
18
. C.
5
. D.
8
.
Câu 48. Trong không gian
Oxyz
   m
10;6; 2A
,
5;10; 9B
và mt phng
:2 2 12 0x y z
m
M
ng trên
sao cho
MA
,
MB
luôn to vi
các góc
bng nhau. Bit rng
M
luôn thuc mng tròn
C
c  cng tròn
C
bng
Trang 37
A.
4
. B.
9
2
. C.
2
. D.
10
.
Câu 49. Gi s
1
z
,
2
z
là hai trong s các s phc
z
tha mãn
21iz i
và
12
2zz
. Giá tr ln nht
ca
12
zz
bng
A.
4
. B.
23
. C.
32
. D.
3
.
Câu 50. Cho hàm s
2024 4 2024 2024 2 2 2024
1 2 2 3 2024f x m x m m x m
, vi
m
là tham s. S
cc tr ca hàm s
2023y f x
.
A.
3
. B.
5
. C.
6
. D.
7
.
________________HẾT________________
ÑAÙP AÙN ÑEÀ SOÁ 04
1
2
3
4
5
6
7
8
9
10
C
B
C
A
C
A
D
B
A
C
11
12
13
14
15
16
17
18
19
20
C
B
C
C
D
C
A
A
B
D
21
22
23
24
25
26
27
28
29
30
B
D
B
B
D
A
A
D
A
A
31
32
33
34
35
36
37
38
39
40
B
A
A
C
A
D
A
D
C
D
41
42
43
44
45
46
47
48
49
50
B
C
A
B
A
A
B
C
A
D
Lôøi giaûi caâu hoûi vaän duïng cao ñeà soá 04
Câu 44. Cho hình tr
T
có
O
,
O
l
ABC
ni ting
tròn tâm
O
,
2AB a
,
1
sin
3
ACB
và
OO
to vi mt phng
O AB
mt góc
o
30
(tham kho
i). Th tích khi tr
T
bng
A.
3
2π6a
. B.
3
3π6a
. C.
3
π3a
. D.
3
π6a
.
Hướng dẫn giải:
Trang 38
Gi
r
a hình tr. Tam giác
ABC
ni tip trong
ng tròn tâm
O
nên
2
3
1
2sin
2.
3
AB a
ra
ACB
. Gi
I
là
 m c n thng
AB
, ta có:
OI AB
AB O OI
OO AB

. K ng cao OH ca tam giác
O OI
, ta có:
do
OH O I
OH AB AB O OI

, suy ra
OH O AB

OH
là hình chiu vuông góc ca
OO
lên mt phng
O AB
o
30OO H OO I

.
Xét tam giác OAI vuông ti I có:
2 2 2 2
32OI r IA a a a
.
Xét tam giác
OO I
vuông ti O có:
0
6
tan30
OI
OO a h
vi
h
là chiu cao ca khi tr
T
.
Th tích khi tr
T
bng
23
36V r h a


.
Choïn
B
Câu 45. S
100000
7
có bao nhiêu ch s?
A.
84510
. B.
194591
. C.
194592
. D.
84509
.
Hướng dẫngiải:
Ta có:
100 000
log7 100 000.log7 84 509,804 84 509;84 510
.
:
84 509 100 000 84 510
log10 log7 log10
, suy ra s
100 000
7
có 
84 510
10
mt ch s mà
84 510
10
có
84 511 ch s nên
100 000
7
có
84510
ch s.
Choïn
A
Câu 46. Cho hình chóp
.S ABCD

2,AB a AD DC CB a
và
SA
vuông góc vi
mt ph i
M
m ca cnh
AB
. Khong cách
ging thng
CM
và
SD
bng
A.
3
2
a
. B.
3
4
a
. C.
3
2
a
. D.
3a
.
Hướng dẫngiải:
Trang 39
Ta có
M
m ca
//
AM a CD
AD AMCD
AM CD


là
hình bình hành
// //CM AD CM SAD
, mà
SD SAD
, , ,d CM SD d CM SAD d M SAD
1
.
D thy MBCD 
DM BC a
.
Ta thy:
AD AM DM a
nên tam giác
ADM
u cnh
a
.
Gi
H
m ca
(1)AD MH AD
và
3
2
a
MH
.
Ta li có:
(2)MH SA
(do
SA ABCD
). T (1) và (2) suy ra
MH SAD
.

3
,
2
a
d M SAD MH
. Vy
3
,
2
a
d CM SD
.
Choïn
A
Câu 47. Cho hàm s
33
22
log logf x x x m
(
m
là tham s thc). Gi
S
là tp hp tt c các giá tr ca
m
sao cho
1;4
1;4
max min 6f x f x
. Tt c các phn t ca
S
bng
A.
13
. B.
18
. C.
5
. D.
8
.
Hướng dẫngiải:
t
1;4
1;4
max , minM f x N f x
.
t
2
logtx
; vì
1;4 0;2xt
.Hàm s  thành:
3
3g t t t m
.
Ta có
2
3 3 0 1g t t t
.Bng bin thiên ca
gt
:
Suy ra:
0;2
0;2
max 2, min 2g t m g t m
.
ng hp 1:
0 2 2 2m m m
. Ta có
2 2, 2 2M m m N m m
.

6 2 2 6 3M N m m m
(nhn).
ng hp 2:
2 2 0 2m m m
. Ta có:
2 2 , 2 2M m m N m m
.

6 2 2 6 3M m m m m
(nhn).
ng hp 3:
2 0 2 2 2m m m
. Ta có:
22
0
M m M m
N
.
Trang 40
Xét
22
22
0
4 4 4 4
4
4
26
2 0 6
8
26
M
N
M
mm
m
m m m m
m
m
m
m
m
m



(loi).
Xét
22
22
0
4 4 4 4
4
8
26
2 0 6
4
26
M
N
M
mm
m
m m m m
m
m
m
m
m
m



(loi).
Vy
3;3S 
. Suy ra tt c các phn t ca
S
bng 18.
Choïn
B
Câu 48. Trong không gian
Oxyz
   m
10;6; 2A
,
5;10; 9B
và mt phng
:2 2 12 0x y z
m
M
ng trên
sao cho
MA
,
MB
luôn to vi
các góc
bng nhau. Bit rng
M
luôn thuc mng tròn
C
c  cng tròn
C
bng
A.
4
. B.
9
2
. C.
2
. D.
10
.
Hướng dẫngiải:
Gi
,HK
l t là hình chiu vuông góc ca
,AB
trên mt phng
  
2 2 2
2.10 2.6 2 12
;6
2 2 1
AH d A

;
2 2 2
2.5 2.10 9 12
;3
2 2 1
BK d B

.
Vì
MA
,
MB
to vi
các góc bng nhau nên
AMH BMK
mà
2AH BK
suy ra
2MA MB
.
Gi
;;M x y z
, ta có:
2MA MB
22
4MA MB
2 2 2 2 2 2
10 6 2 4 5 10 9x y z x y z


2 2 2
3 3 3 20 68 68 684 0x y z x y z
2 2 2
20 68 68
228 0
3 3 3
x y z x y z
.
m
M
nm trên mt cu
S
có tâm
10 34 34
;;
3 3 3
I



và bán kính
2 10R
.
Mt khác ta có M ng trên
, vì vy tp hm
M
chính
ng tròn giao tuyn
C
c to bi mt cu
S
và mt
phng
. Gi H là tâm cng tròn
C
H là hình
chiu vuông góc ca
I
trên mt phng
.
Trang 41
ng thng
d

I
và vuông góc vi mt phng
là:
10
2
3
34
:2
3
34
3
xt
d y t
zt


. Thay
 ca d vào
:
10 34 34 2
2 2 2 2 12 0
3 3 3 3
t t t t
, t 
suy ra
2;10; 12H
.
Choïn
C
Câu 49. Gi s
1
z
,
2
z
là hai trong s các s phc
z
tha mãn
21iz i
và
12
2zz
. Giá tr ln nht
ca
12
zz
bng
A.
4
. B.
23
. C.
32
. D.
3
.
Hướng dẫngiải:
Ta có :
2
2 1 1 1 2 1 (*)
i
iz i i z z i
i




.
Gi
A
,
B
lm biu din ca
1
z
,
2
z

,AB
tha (*) nên
,AB
ng trên
ng tròn
C
có tâm
1; 2I
, bán kính
1R
.
Ta có :
12
2 2 2z z AB R
, suy ra
AB
ng kính ca
C
hay
I
m ca
AB
.
 :
2
2 2 2 2 2
12
w
2 2 2 4 16 4
2
Cauchy Sch arz
AB
z z OA OB OA OB OI OI AB



.
Du bng khi
OA OB
.
Choïn
A
Câu 50. Cho hàm s
2024 4 2024 2024 2 2 2024
1 2 2 3 2024f x m x m m x m
, vi
m
là tham s. S
cc tr ca hàm s
2023y f x
.
A.
3
. B.
5
. C.
6
. D.
7
.
Hướng dẫngiải:
t
2023g x f x
.Ta có:
2024 3 2024 2024 2
4 1 2 2 2 3g x f x m x m m x

;
2024 2024 2
2
2024
0
2 2 3
0
21
x
mm
fx
x
m


Trang 42
Ta thy
2024 2024 2
2024
2 2 3
0,
21
mm
m

m
nên hàm s
2023g x f x
luôn có
3
cc tr gm
2024 2024 2
1 2,3
2024
2 2 3
0,
21
mm
xx
m

. Ta li có:
2024
10
g
am
 th hàm
gx
có nhánh phi
ng lên trên.
Mt khác:
2024 2024 2024 2 2024 2024 2
1 1 2 2 3 1 2 1 0,g m m m m m m
.
Ta có bng bin thiên hàm
2023g x f x

T bng bin thiên, ta th th hàm s
gx
luôn có ba m cc tr, m cc tiu
ni trc
Ox
. Vì vy s cc tr ca hàm s
2023y f x
là
3 4 7mn

3m
là s cc tr ca hàm
gx
,
4n
là s  m c   th hàm s
.
0
y g x
y Ox
Choïn
D
ĐỀ SỐ 05
ĐỀ RÈN LUYỆN MÔN TOÁN 12
HƯỚNG ĐẾN KÌ THI THPT QUỐC GIA
Trắc nghiệm: 50 câu
Thời gian: 90 phút
Nội dung:
FULL KIẾN THỨC TOÁN 12+
Câu 1. Trong không gian vi h t 
Oxyz
, cho mt cu
2
22
: 1 2S x y z
. Trong các
m nào nm ngoài mt cu
S
?
A.
1;1;1M
. B.
0;1;0N
. C.
1;0;1P
. D.
1;1;0Q
.
Trang 43
Câu 2. Cho hàm s
fx
nh trên
và có bng xét di hàm s có bao nhiêu
m cc tr 
A.2. B.3. C.1. D.4.
Câu 3. t
5
log 3a
. Tính theo
a
giá tr ca biu thc
9
log 1125
.
A.
9
3
log 1125 1
2a

. B.
9
3
log 1125 2
a

. C.
9
2
log 1125 2
3a

. D.
9
3
log 1125 1
a

.
Câu 4. Th tích khi t diu cnh
a
bng
A.
3
3
4
a
. B.
3
3
2
a
. C.
3
2
12
a
. D.
3
2
6
a
.
Câu 5. Gii hn
2
22
lim
2
x
x
x

bng
A.
1
2
. B.
1
4
. C.
0
. D.
1
.
Câu 6. Tp nghim ca b
2
log 1 3x 
là:
A.
;10
. B.
1;9
. C.
1;10
. D.
;9
.
Câu 7.  th hàm bc b th hình v
bên
A.
42
( ) 2f x x x
.
B.
42
( ) 2f x x x
.
C.
42
( ) 2f x x x
.
D.
42
( ) 2 1f x x x
.
Câu 8. Trong không gian
Oxyz
ng thng
1
: 2 2
1
xt
d y t
zt



 a
d
?
A.
1; 2;1n

. B.
1;2;1n
. C.
1; 2;1n
. D.
1;2;1n

.
Câu 9.  th hàm s nào trong các hàm s không có tim cn ngang?
A.
2
2
1
x
y
x
. B.
2
1
x
y
x
. C.
2
1
2
x
y
x
. D.
1
2
y
x
.
Câu 10. Nguyên hàm ca hàm s
2
1
( ) 5cosf x x
x

là hàm s 
A.
1
( ) 5sinF x x C
x
. B.
1
( ) 5sinF x x C
x
.
C.
( ) 5sin lnF x x x C
. D.
1
( ) 5sinF x x C
x
.
Câu 11. Th tích ca khi nón có chiu cao bng
4
ng sinh bng
5
bng
A.
16
. B.
48
. C.
12
. D.
36
.
Câu 12.  th hàm s
3
31y x x
cho    
3
30x x m
(
m
là tham s) có ba nghim phân bit khi
Trang 44
A.
13m
.
B.
22m
.
C.
23m
.
D.
22m
.
Câu 13. Cho khi chóp
.S ABCD
có
SA
vuông góc vi mt ph
3SA a
,
ABCD
là hình ch nht và
2AB a
,
AD a
. Th tích ca khi chóp
.S ABCD
bng
A.
3
3
2
a
. B.
3
3a
.
C.
3
2a
. D.
3
9a
.
Câu 14. Vi
a
và
b
là các s thu thc
2
log
a
ab
bng
A.
2 log
a
b
. B.
2 log
a
b
. C.
1 2log
a
b
. D.
2log
a
b
.
Câu 15. Tính din tích hình phng gii hn b th
2
4y x x
và trc hoành.
A.
41
3
S
. B.
32
3
S
. C.
7
4
S
. D.
9
4
S
.
Câu 16. Trong không gian vi h t
,Oxyz
t
phng
Oyz
?
A.
0y
. B.
0z
. C.
0yz
. D.
0x
.
Câu 17. Cho s phc
2020
1zi
. S phc liên hp ca
z
là
A.
2z
. B.
22zi
. C.
0z
. D.
2z 
.
Câu 18. Cho kh có ding
2
a
và khong cách ging
3a
. Tính th tích
V
ca kh 
A.
3
3
2
Va
. B.
3
3Va
. C.
3
Va
. D.
3
9Va
.
Câu 19. Cho
x
,
y
là các s thc tùy ý. M 
A.
e e e
x y x y

. B.
e e e
x y x y

. C.
e e e
xy x y
. D.
e
e
e
x
xy
y
.
Câu 20. Tích phân
bng.
A.
2ln5
. B.
1
ln5
2
. C.
ln5
. D.
4ln5
.
Câu 21. Hàm s ch bin trên khong
1;5
?
A.
1
32
x
y
x
. B.
3
4
x
x
. C.
31
1
x
y
x
. D.
21
2
x
x
.
Câu 22. Nghim c
21
2 27
38
x



là
A.
2x
. B.
3x
.
C.
1x 
. D.
4x
.
Câu 23. Th tích
V
ca kh u có cng
2a
và cnh bên bng
a
là
A.
3
3
2
a
V
. B.
3
3Va
. C.
3
3
4
a
V
. D.
3
3
3
a
V
.
Câu 24. Cho s phc
z
tha mãn:
2
3 2 2 4i z i i
. Hiu phn thc và phn o ca s phc
z
là
A.
3
. B.
2
. C.
1
. D.
0
.
Câu 25. Trong các hàm s  nào có tnh là
D
?
Trang 45
A.
2
ln 1yx
. B.
2
ln 1yx
. C.
2
ln 1yx
. D.
2
ln 1yx
.
Câu 26. Cho kh
.ABCD A B C D
có th tích bng
12

ABCD
là hình vuông tâm
O
. Th tích
ca khi chóp
.A BCO
bng
A.
1
. B.
4
. C.
3
. D.
2
.
Câu 27. c các s
a
,
b
,
c
  th hàm s
32
y x ax bx c
m
1;0
và có
m cc tr
2;0
. Tính giá tr biu thc
2 2 2
T a b c
.
A.
25
. B.
1
. C.
7
. D.
14
.
Câu 28. Hu
.S ABCD
tt c các cnh bng
a
. Din tích mt cu ngoi tip hình chóp là:
A.
2
4 a
. B.
2
a
. C.
2
2 a
. D.
2
2 a
.
Câu 29. Cho
1,2,3,4A
. T
A
lc bao nhiêu s t nhiên có
4
ch s t khác nhau?
A.
32
. B.
24
. C.
256
. D.
1
.
Câu 30. Tìm tt c các giá tr ca
m
 hàm s
16mx
y
xm
ng bin trên
0;10
.
A.
; 10 4;m 
. B.
; 4 4;m 
.
C.
; 10 4;m 
. D.
; 4 4;m
Câu 31. Trong không gian
Oxyz
  m
2; 2;3M
  ng thng
4 3 2
:
3 1 2
x y z
,
12
:
2 3 1
x y z
 cng th
M
và vuông góc vng thng
và
?
A.
27
2
3 11
xt
yt
zt


. B.
27
23
3 11
xt
yt
zt

. C.
27
2
38
xt
yt
zt


. D.
27
2
38
xt
yt
zt


.
Câu 32. Cho
3
0
d ln2 ln3
3
4 2 1
xa
x b c
x


a
,
b
,
c

abc

A.
1
. B.
2
. C.
7
. D.
9
.
Câu 33. 


.S ABCD

ABCD

a
. 
SA



.



A

SCD

3
2
a
. 
.S ABCD
theo
a
.
A.
3
3
3
a
B.
3
33
4
a
. C.
3
3a
. D.
3
3
4
a
.
Câu 34. Cho hàm s
32
y ax bx cx d
. Hi hàm s ng bin trên
khi nào?
A.
2
0, 0
0 ; 3 0
a b c
a b ac
. B.
2
0, 0
0 ; 3 0
a b c
a b ac
.
C.
2
0, 0
0 ; 3 0
a b c
a b ac
. D.
2
0
0 ; 3 0
abc
a b ac
.
Câu 35. Trong không gian
Oxyz
ng thng
31
:
2 3 1
x y z
m
2; 1;5M

mt phng
P
qua
M
và vuông góc vi
là
A.
2 3 12 0x y z
. B.
2 3 12 0x y z
.
C.
2 5 12 0x y z
. D.
2 5 12 0x y z
.
Trang 46
Câu 36. Cho s phc
z
, bit rm biu din hình hc ca các s phc
z
;
iz
và
z i z
to thành mt
tam giác có din tích bng
18
a s phc
z
bng
A.
23
. B.
32
. C.
6
. D.
9
.
Câu 37. S nghim c
2
5
2
log 3 log 3
x
xx
xx

là:
A.
3
. B.
1
. C.
2
. D.
0
.
Câu 38. Trong không gian
Oxyz
, cho hai mt phng
: 2 2 6 0P x y z
và
: 2 2 3 0Q x y z
.
Khong cách gia hai mt phng
P
và
Q
bng
A.
1
. B.
3
. C.
9
. D.
6
.
Câu 39. Tính th tích
V
ca vt th nm gia hai mt phng
0x
và
x
, bit rng thit din ca vt th b
ct bi mt phng vuông góc vi trc
Ox
t
x
0 x

là mu
cnh
2 sin x
.
A.
3V
. B.
3V
. C.
23V
. D.
23V
.
Câu 40. Cho s phc
z a bi
,
tha mãn
1
1
z
zi
và
. Tính
P a b
.
A.
7P
. B.
1P 
. C.
1P
. D.
2P
.
Câu 41. Cho tam giác
ABC
vuông ti
A
có
1cm, 2cm, AC AB M
m ca
.AB
Quay tam giác
BMC
quanh trc
AB
, gi
V
là th tích kh
V
bng:
A.
3
3
.
4
cm
B.
3
.
3
cm
C.
3
.cm
D.
3
.
2
cm
Câu 42. Tp hp tt c m biu din các s phc
z
tha mãn:
24zi
ng tròn có tâm
I
và
bán kính
R
lt là:
A.
2; 1I 
;
4R
. B.
2; 1I 
;
2R
. C.
2; 1I
;
4R
. D.
2; 1I
;
2; 1I
.
Câu 43. Mt bng cao
2m
nm song song vi tòa nhà và cách
tòa nhà
2m
i ta mun ch to mt chic thang bc t
mt bên ngoài bng, gác qua bng và chm vào
tòa nhà (xem hình v). Hi chiu dài ti thiu ca thang bng
bao nhiêu mét ?
A.
5 13
m
3
.
B.
4 2m
.
C.
6m
.
D.
3 5m
.
Câu 44. Tp các giá tr ca
m
 
4. 5 2 5 2 3 0
xx
m
m âm
phân bit là:
A.
; 1 7; 
. B.
7; 8
. C.
;3
. D.
7; 9
.
Câu 45. Tìm tt c các giá tr ca tham s
m
  th hàm s
2
1
2 2 1
x
y
x x m x
ng
tim cn.
A.
5;4 \ 4m
. B.
5;4m
. C.
5;4 \ 4m
. D.
5;4 \ 4m
.
Câu 46. Cho tp hp
1;2;3;...;10A
. Chn ngu nhiên ba s t
A
. Tìm xác su trong ba s chn ra
không có hai s nào là hai s nguyên liên tip.
Trang 47
A.
7
90
P
. B.
7
24
P
. C.
7
10
P
. D.
7
15
P
.
Câu 47. Cho t din ABCD có
2, 3, 4, 2 5, 5.AB AC AD BC BD CD
Khong cách gia hai
ng thng AC và BD bng.
A.
3 15
4
. B. 2. C.
240
79
. D. 3.
Câu 48. Cho hai hàm s
3 2 3 2
3 1, 2 2 2y x x x y x x mx
 th lt là
12
,CC
và m là
tham s thc. Bit rng tn ti m 
1
C
ct
2
C
tm phân bi là
1 2 3
,,y y y
tha mãn
1 2 3
1 1 1 2
4 4 4 3y y y
:
A.
4;7m
. B.
9;12m
. C.
6;9m
. D.
8;11m
.
Câu 49. Cho
x
,
0y
tha mãn
log 2 log logx y x y
     nh nht ca biu thc
22
4
1 2 1
xy
P
yx


là:
A.
6
. B.
32
5
. C.
31
5
. D.
29
5
.
Câu 50. Cho s phc
z
tha mãn
5 1 3 3 1z i z i z i
. Tìm giá tr ln nht
T
ca
23zi
?
A.
10
3
T
. B.
1 13T 
. C.
45T
. D.
9T
.
________________HẾT________________
ÑAÙP AÙN ÑEÀ SOÁ 05
1
2
3
4
5
6
7
8
9
10
C
B
A
C
B
B
B
D
C
D
11
12
13
14
15
16
17
18
19
20
C
B
C
B
B
D
A
B
D
C
21
22
23
24
25
26
27
28
29
30
A
C
B
D
D
A
A
D
B
A
31
32
33
34
35
36
37
38
39
40
A
A
A
A
A
C
A
B
D
D
41
42
43
44
45
46
47
48
49
50
B
A
B
B
D
D
C
D
B
C
Lôøi giaûi caâu hoûi vaän duïng cao ñeà soá 05
Câu 43. Mt bng cao
2m
nm song song vi tòa nhà và cách tòa nhà
2m
i ta mun ch to mt
chic thang bc t mt bên ngoài bng, gác qua bng và chm vào tòa nhà (xem hình
v). Hi chiu dài ti thiu ca thang bng bao nhiêu mét ?
Trang 48
A.
5 13
m
3
. B.
4 2m
. C.
6m
. D.
3 5m
.
Hướng dẫn giải:
Xét h m
, , , ,A B C D E
.
Gi
0BC x x
. Ta cn tìm
x
  dài
CD
t giá tr
nh nht.
D thy hai tam giác
,CAB CDE
ng dng, suy ra:
2
22
. 4.
2
BC x AC x x
CD AC x
CE x CD x x

.
t
2
2
4.
x
f x x
x

vi
0x
.
Cách giải 1:
22
2
2 2 2
2 2 2
2 2 2 2 4 2 2 4
. 4. 0
4 4 4
x x x x x x
f x x
x x x x
x x x
2 2 3
2 2 4 8 2x x x x x
. Bng bin thiên ca
fx
:
Vy chiu dài ti thiu ca thang bng
42
.
Choïn
B
Cách giải 2:
Ta có:
2
42
4 .2 2
42
AM GM AM GM
xx
xx
fx
xx





. Dng thc xy tra
2
4
2.
2
x
x
x
Câu 44. Tp các giá tr ca
m
 
4. 5 2 5 2 3 0
xx
m
m âm
phân bit là:
A.
; 1 7; 
. B.
7; 8
. C.
;3
. D.
7; 9
.
Trang 49
Hướng dẫn giải:
t
5 2 0
x
t
52
logxt

. Ph  tr thành:
1
4 3 *tm
t
.
Nhận xét:Vi mi
0; 1t
thì ta c t nghim
0x
.
Bài toán tr thành:Tìm
m
 
*
m phân bit
1,2
0; 1t
.
Xét hàm s
1
43f t t
t
vi
0; 1t
;
2
22
1 4 1
4
t
ft
tt
1
0; 1
2
0
1
0; 1
2
t
t


.
Bng bin thiên:
Da vào bng bin thiên ta có:
78m
.
Choïn
B
Câu 45. Tìm tt c các giá tr ca tham s
m
  th hàm s
2
1
2 2 1
x
y
x x m x
ng
tim cn.
A.
5;4 \ 4m
. B.
5;4m
. C.
5;4 \ 4m
. D.
5;4 \ 4m
.
Hướng dẫn giải:
Ta có:
2
1
1
1
lim lim 1 2
21
21
21
xx
x
x
y
m
x
x x x
 






;
2
1
1
1
lim lim 1 2
21
21
21
xx
x
x
y
m
x
x x x
 







  th hàm s có hai đường tiệm
cận ngang là
12y 
và
12y 
. Vì vy ta cn tìm m   th hàm s hai đường
tiệm cận đứng.
Khi tìm tim cng, ta xét:
2
2 2 1 0x x m x
2
2 2 1x x m x
2
22
1
1
4 1 (*)
2 2 2 1
gx
x
x
x x m
x x m x x




.
Yêu cu bài toán
*
có hai nghim phân bit
1,2
1x 
và khác 1 (không trùng nghim ca t s).
Xét hàm s
2
41g x x x
vi
1x 
và
1x
. Ta có:
2 4 0 2g x x x
.
Bng bin thiên:
Trang 50
Da vào bng bin thiên, ta có
5;4 \ 4m
.
D
Choïn
Câu 46. Cho tp hp
1;2;3;...;10A
. Chn ngu nhiên ba s t
A
. Tìm xác su trong ba s chn ra
không có hai s nào là hai s nguyên liên tip.
A.
7
90
P
. B.
7
24
P
. C.
7
10
P
. D.
7
15
P
.
Hướng dẫn giải:
S phn t không gian mu là
3
10
nC
120
.
Gi
B
là bin c  chn ra không có hai s nào là hai s nguyên liên ti
B
là bin c  c chn có ít nht hai s là các s t nhiên liên ti
Tìm các kết quả thuận lợi cho
B
:
Xét b ba s có dng
1
1;2;a
, vi
1
\ 1;2aA
: có
8
b tha mãn.
Xét b ba s có dng
2
2;3;a
, vi
2
\ 1;2;3aA
: có
7
b tha mãn.
Xét b ba s có dng
3
3,4,a
vi
3
\ 2;3;4aA
: có 7 b tha mãn.
Thc hin  mi b ba s dng:
4
4,5,a
,
5
5,6,a
,
6
6,7,a
,
7
7,8,a
,
8
8,9,a
,
9
9,10,a
: u có
7
b tha mãn.
Suy ra:
8 8.7nB
64
. Do vy:
1P B P B
64
1
120

7
15
.
D
Choïn
Câu 47. Cho t din ABCD có
2, 3, 4, 2 5, 5.AB AC AD BC BD CD
Khong cách gia hai
ng thng AC và BD bng.
A.
3 15
4
. B. 2. C.
240
79
. D. 3.
Hướng dẫn giải:
Ta có:
2 2 2
AD AC CD
nên tam giác
ACD
vuông

A
hay
AD AC

2 2 2
AD AB BD
nên tam giác
ABD

A
hay
.
Ta có:
AD AC
AD AB
()AD ABC
.

ACBE

//( )AC BDE
.

, ,( ) ,( ) (1)d AC BD d AC BDE d A BDE
.
ABCD
AF BE

F
, trong
tam giác
,ADF

.AG

( ).AG BDE

()
BE AF
BE ADF
BE AD

mà
( ) .AG ADF AG BE
5
2
5
4
4
3
2
A
B
C
D
E
F
G
Trang 51
Vì
( ) (2).
AG BE
AG BDE
AG DF


(1)&(2)
,d AC BD AG
.

9 3 15
( )( )( )
2 2 4
ABE
AB BE AE
p S p p AB p BE p AE

.

3
1 15
.
22
ABE
S AF BE AF
.
Xét tam giác
ADF

A

22
. 240
79
AD AF
AG
AD AF

.
Choïn
C
Câu 48. Cho hai hàm s
3 2 3 2
3 1, 2 2 2y x x x y x x mx
 th lt là
12
,CC
và m là
tham s thc. Bit rng tn ti m 
1
C
ct
2
C
tm phân bi là
1 2 3
,,y y y
tha mãn
1 2 3
1 1 1 2
4 4 4 3y y y
:
A.
4;7m
. B.
9;12m
. C.
6;9m
. D.
8;11m
.
Hướng dẫn giải:
Cần nhớ:Định lí Vi-ét dành cho phương trình bậc ba.

32
0ax bx cx d

1 2 3
,,x x x
thì
1 2 3
1 2 2 3 1 3
1 2 3
b
x x x
a
c
x x x x x x
a
d
x x x
a

.

12
,CC
:
32
3 3 0x x m x
(*).

,,A B C

,,A B C

3 2 3 2
3 2 3 2
3 1 2 2 2 6 2
2 2 2 2 2 2
y x x x y x x x
y x x mx y x x mx





. Suy ra
64y m x
.

1 1 2 2 3 3
4 6 ; 4 6 ; 4 6y m x y m x y m x

1 2 3
,,x x x

(*).
Theo định lí Vi-ét bậc ba, ta có
1 2 2 3 3 1
1 2 3
3
3
x x x x x x m
x x x

.
T
1 2 2 3 3 1
1 2 3 1 2 3
2 1 1 1 1 3
.
3 4 4 4 6 3 6
x x x x x x
m
y y y m x x x m

. Suy ra
9m
.
 :
9m
thì 
32
6 3 0x x x
. 

9m

Choïn
D
Câu 49. Cho
x
,
0y
tha mãn
log 2 log logx y x y
     nh nht ca biu thc
22
4
1 2 1
xy
P
yx


là:
A.
6
. B.
32
5
. C.
31
5
. D.
29
5
.
Trang 52
Hướng dẫn giải:
Cần nhớ:
Bng thc Cauchy-Schwarz dạng Engel (còn gi là bng thc công mu):
2
22
xy
xy
a b a b

. Dng thc xy ra khi và ch khi
xy
ab
.
u kin:
0, 0xy
.
Ta có:
log 2 log log log 2 log . 2 (*)x y x y x y x y x y xy
.
Áp dng bng thc Cauchy-Schwarz dạng Engel , ta có:
22
2
22
1 2 1 2 2
y x y
x
P
y x x y
.
Theo AM-GM, ta có:
(1)
2
2 2 .2 2 2 2 2 8 2x y x y x y x y x y
2 0 (loaïi)
2 8 (nhaän)
xy
xy
é
+£
ê
Û
ê
+³
ë
u kin
0, 0xy
). Suy ra
28xy+³
.
t
28t x y
, ta có:
2
4
2
22
t
Pt
tt

24
.8
25
1 4 24 52 4 24 52 32
2 2 .8
25 2 25 25 25 25 25 5
AM GM
P t t
t
. Do vy
min
32
5
P
.
Dng thc xy ra
2
8 2 2
1 2 1
4
1 2 1 8 2
.
14
2
2 8; 2
82
25 2
t
xy
yy
yx
x
yy
y
x y t
xy
t




B
Choïn
Câu 50. Cho s phc
z
tha mãn
5 1 3 3 1z i z i z i
. Tìm giá tr ln nht
T
ca
23zi
?
A.
10
3
T
. B.
1 13T 
. C.
45T
. D.
9T
.
Hướng dẫn giải:
Gi M m biu din ca z; gi
0;1A
,
1;3 , 1; 1BC
. Ta thy
A
m ca
BC
.
Ta có :
2
2 2 2 2
2 2 10
2
BC
MB MC MA MA
.
Theo gi thit :
5 1 3 3 1z i z i z i
2
22
2 10
5 3 10.
Cauchy Schwarz
MA
MA MB MC MB MC

22
25 10 2 10MA MA
2
5 100 2 5MA MA
(1).
Xét
2 3 2 4z i z i i
24z i i
2 5 4 5MA
(do (1)).
Du
""
xy ra khi và ch khi:
25
1
0
24
zi
ab



, vi
z a bi
;
, ab
. Suy ra
2 3 (loaïi)
25
zi
zi
é
=-
ê
ê
= - +
ë
.
Vy giá tr ln nht ca
23zi
là
45T
.
Choïn
C
Trang 53
| 1/53
| | Tải xuống

Có thể bạn quan tâm:

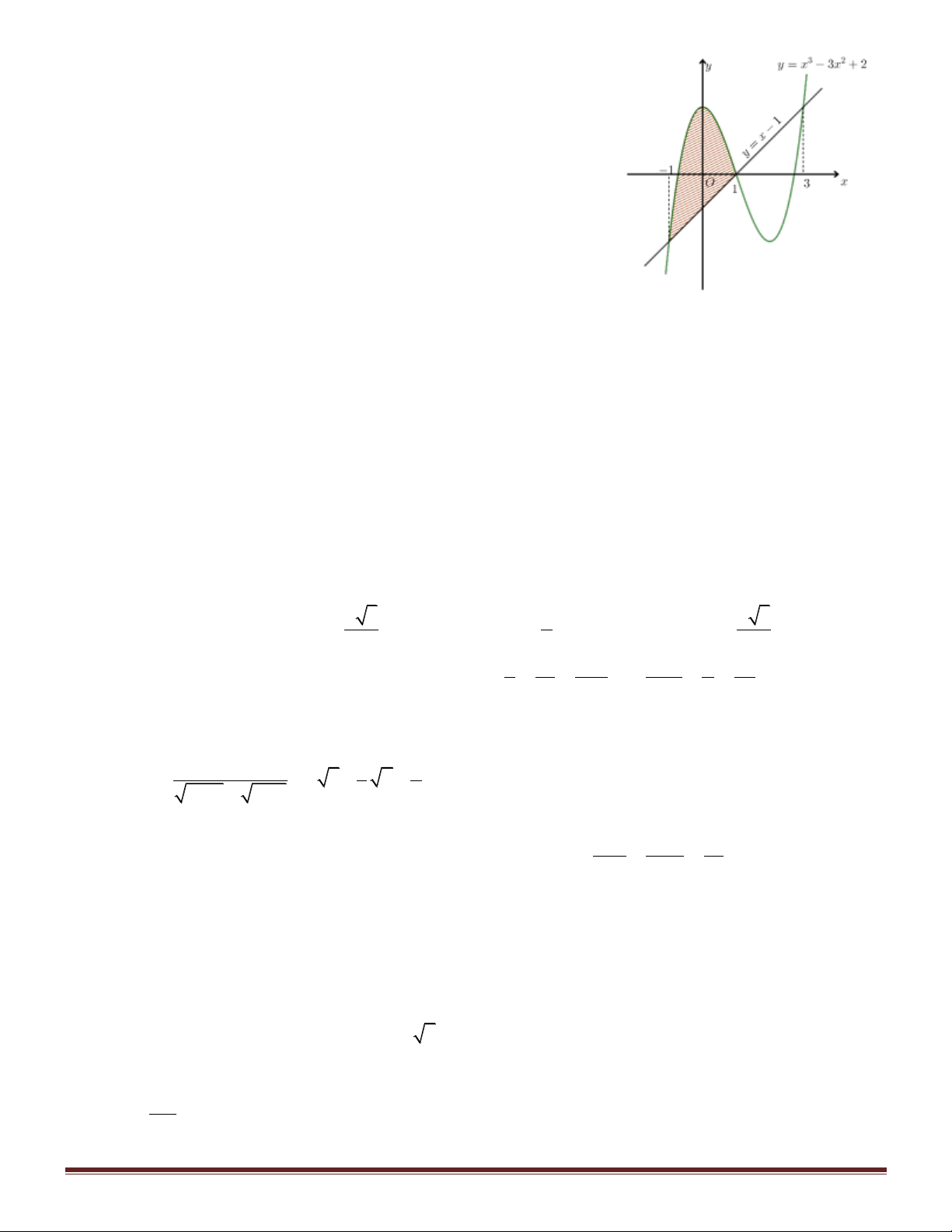
Preview text:

ĐỀ SỐ 01
ĐỀ RÈN LUYỆN MÔN TOÁN 12
HƯỚNG ĐẾN KÌ THI THPT QUỐC GIA
Trắc nghiệm: 50 câu Nội dung:
Thời gian: 90 phút
FULL KIẾN THỨC TOÁN 12
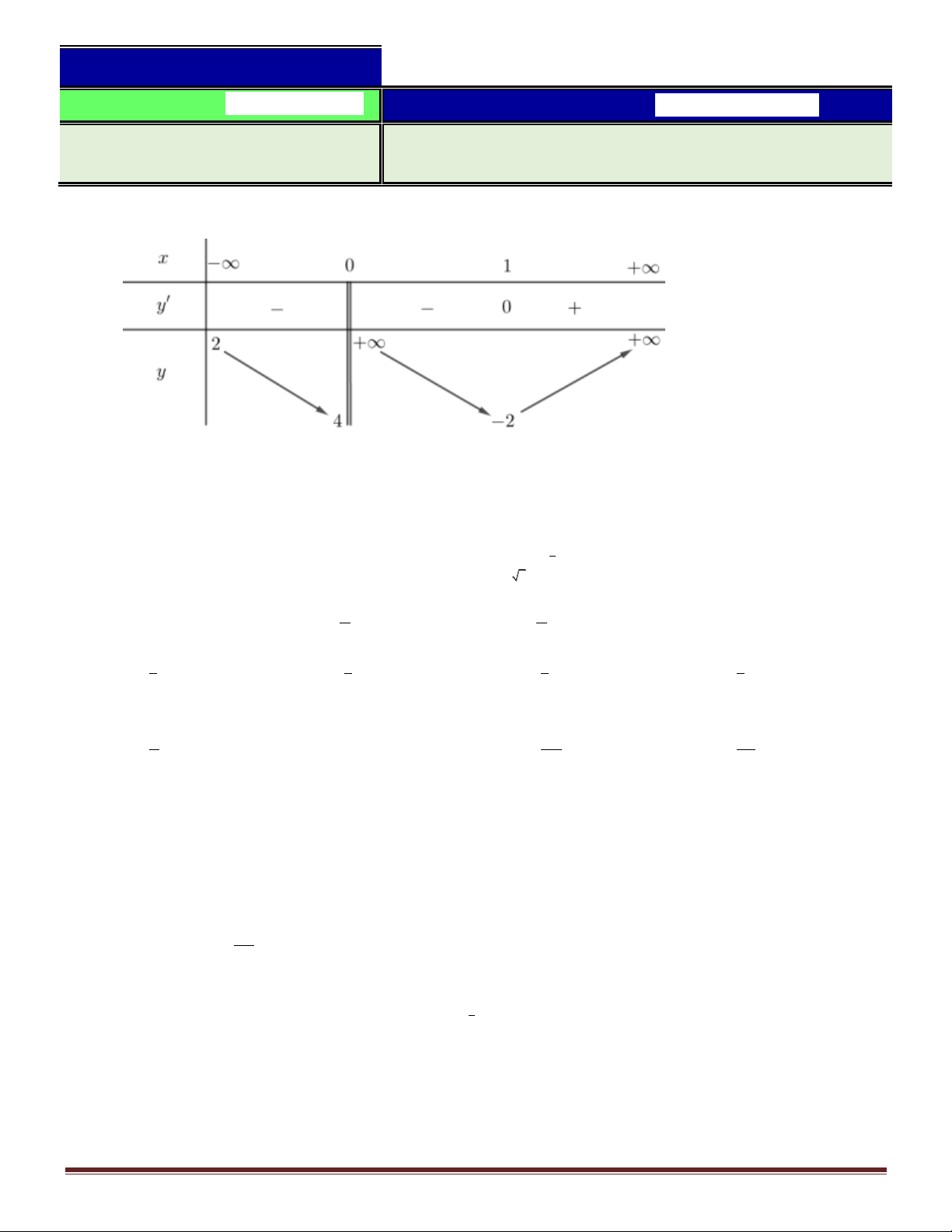
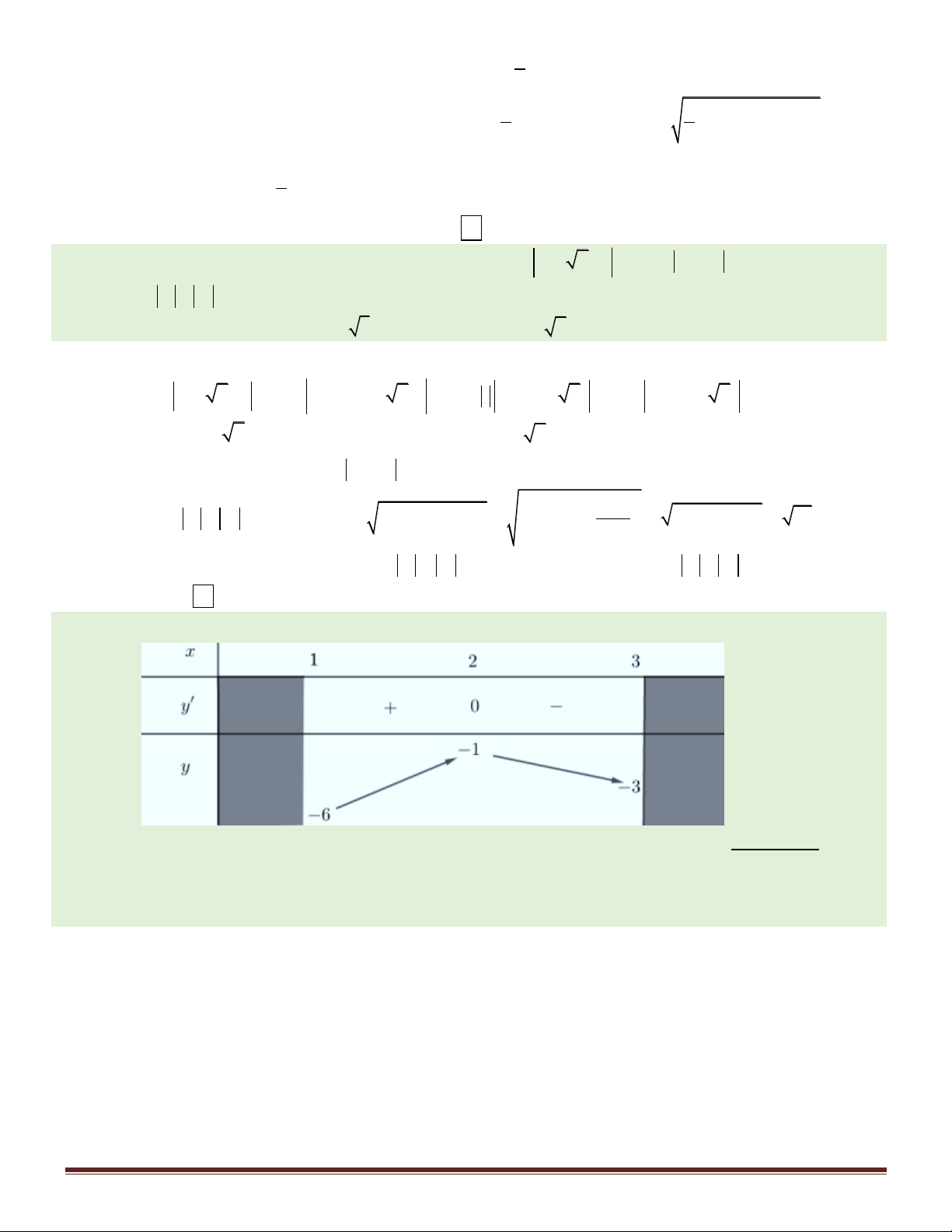
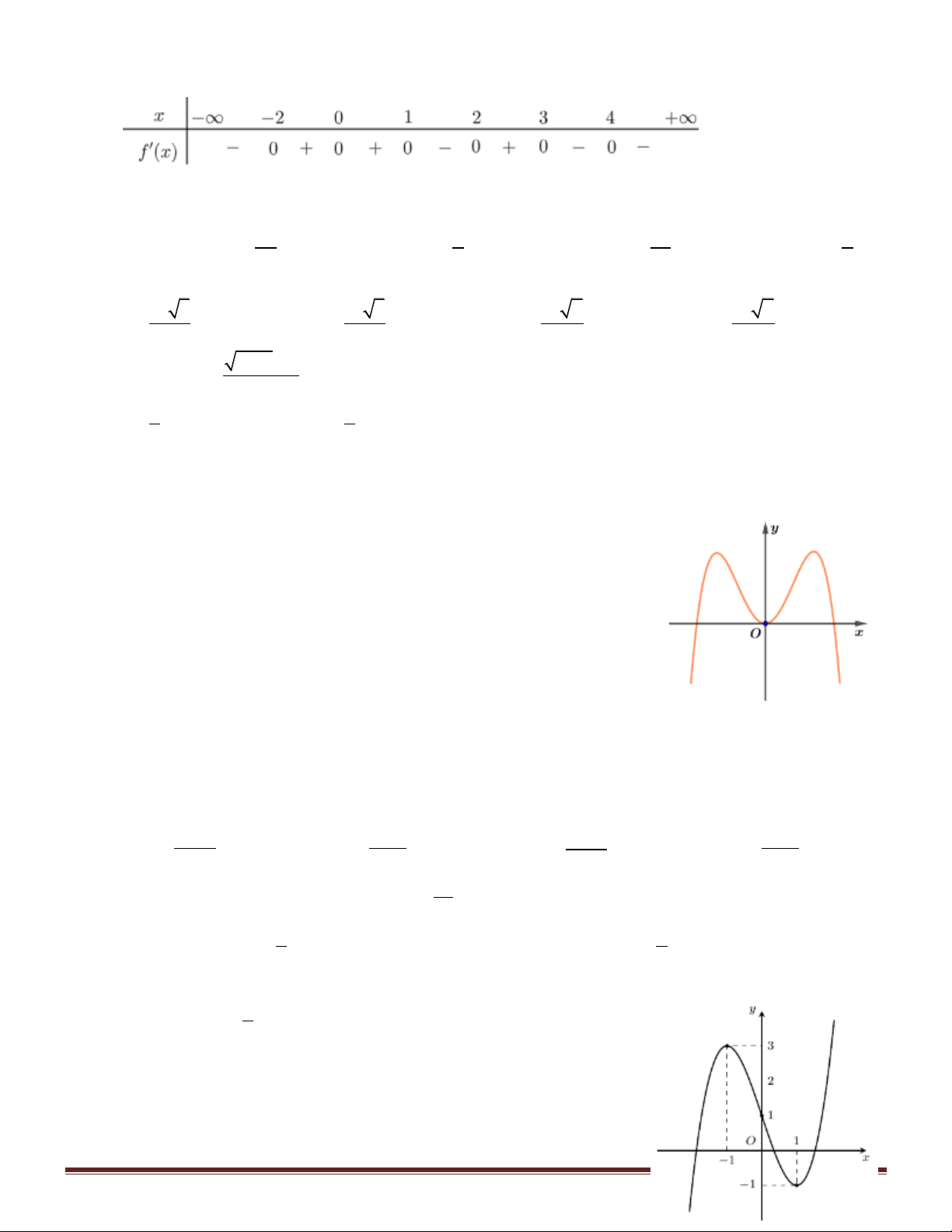
Câu 1. Cho hàm số f x có bảng biến thiên như sau:
Số đường tiệm cận ngang của đồ thị hàm số đã cho là A. 0 . B. 3 . C. 2 . D.1.
Câu 2. Trong không gian với hệ tọa độ Oxyz , hình chiếu của điểm M 1; 2;3 lên trục Oy là điểm
A. M 1;0;0 .
B. M 1;0;3 .
C. M 0; 2;0 .
D. M 0;0;3 . 1  
Câu 3. Cho a là số thực dương tùy ý khác 1, giá trị của 4 log  a  bằng a   1 1 A.1. B. . C. . D. 2 . 4 2
Câu 4. Số phức liên hợp của số phức z  2  3i
A. z  3  2i .
B. z  2  3i . C. z  3   2i . D. z  2   3i .
Câu 5. Tính diện tích hình phẳng giới hạn bởi các đường 2
y x  2, y x , x  0, x  2 . 8 26 14 A. . B. 8 . C. . D. . 3 3 3 
Câu 6. Trong không gian Oxyz , đường thẳng d đi qua gốc O và có vectơ chỉ phương u  1;  2;3 có phương trình tham số là x tx tx 1 x 1 t    
A. y  3t . B. y  2  t . C. y  2  . D. y  2   t .     z  2  tz  3tz  3  z  3t  2021 3 dx
Câu 7. Giá trị của  bằng x 1 C. 2021 3 . B. 2021.ln 3 .
C. 2021.ln 31. D. 2021.
Câu 8. Tìm tập xác định của hàm số y   x x  3 2 2 3 2 . A.  ;   1  2;  . B.  ;  
1 2;  . C. 1; 2 . D.1; 2.
Câu 9. Viết công thức tính thể tích khối tròn xoay tạo thành khi quay quanh trục hoành hình phẳng H giới
hạn bởi các đường x a , x b , y  0 , y f x trong đó y f x là hàm số liên tục trên đoạn  ;ab. Trang 1 2 2 b b b   b   A. 2 2  f  xdx. B. 2 V   f  xdx. C.  f
 xdx . D. f
 xdx . a aa   a
Câu 10. Trong không gian với hệ trục tọa độ Oxyz , cho mặt phẳng  P : 2x  3y z 1  0 . Điểm nào dưới
đây không thuộc mặt phẳng P ? A. B 1; 2; 8   . B. C  1  ; 2  ; 7  . C. A0;0;  1 .
D. D 1;5;18 .
Câu 11. Hàm số F x gọi là một nguyên hàm của hàm số f x trên khoảng a;b nếu có
A. f  x  F x, x   ; a b .
B. F x  f x  C, x   ; a b .
C. f  x  F x  C, x   ; a b .
D. F x  f x, x   ; a b .
Câu 12. Cho hình nón có bán kính đáy R , đường cao h . Diện tích xung quanh của hình nón này là
A. Rh .
B. 2 Rh . C. 2 2
R R h . D. 2 2
2 R R h .
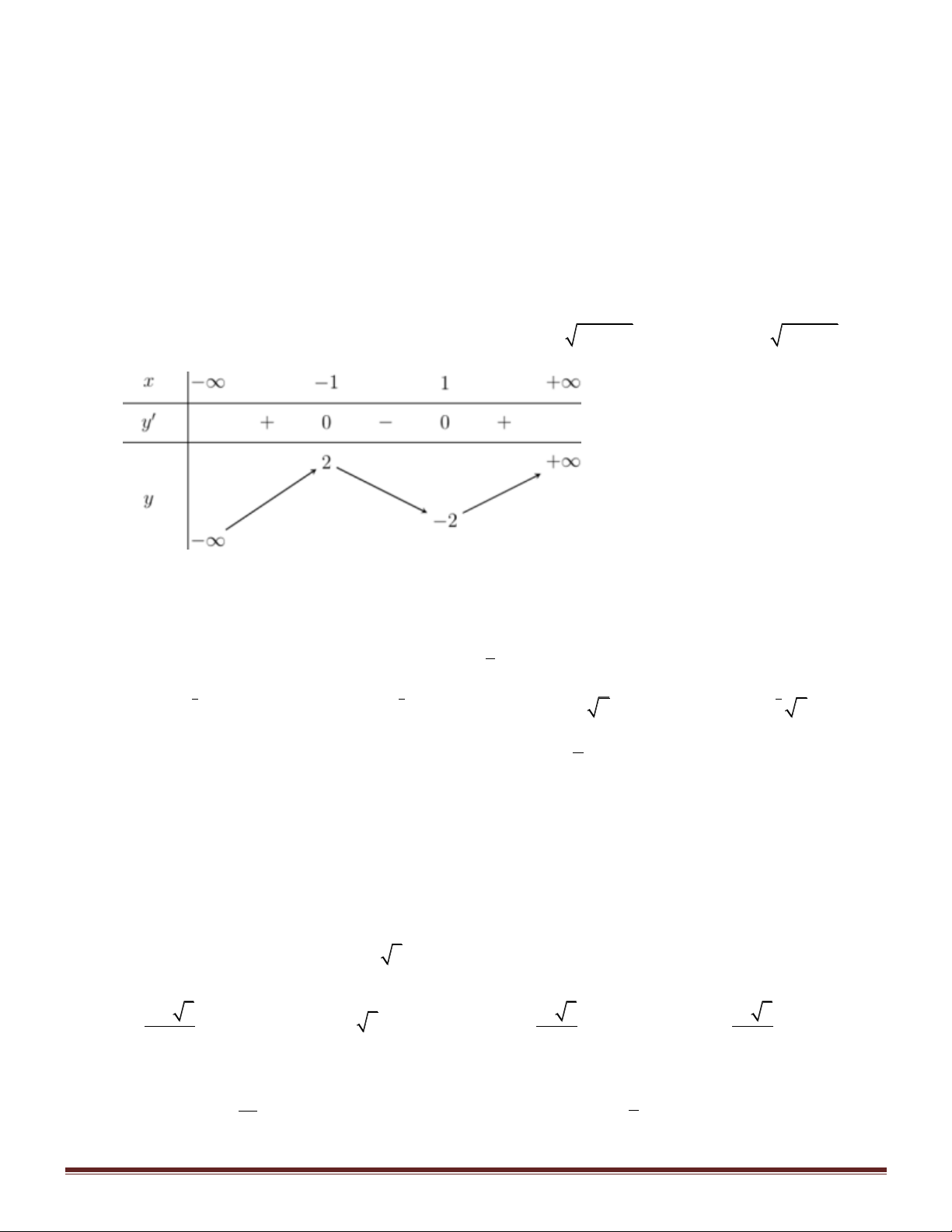
Câu 13. Hàm số nào sau đây có bảng biến thiên như hình dưới A. 3
y  x  3x . B. 3 2
y x  3x 1. C. 3
y x  3x . D. 3 2
y  x  3x 1.
Câu 14. Số nghiệm của phương trình log  x   1  log x  4 là 0,1 A. Vô số. B. 1. C. 0 . D. 2 . 1
Câu 15. Cho a , b là các số dương và log x  2 log a  log b . Biểu thị x theo lũy thừa của a và b . 2 2 2 3 1 1 1 A. 3 x ab . B. 2 3 x a b . C. 2 x a 2 . D. 2 3 x a b . 20  2 
Câu 16. Tìm số hạng không chứa x trong khai triển nhị thức 3 3x  , x  0   .  x A. 15 5 15 C .3 .2 . B. 15 15 C .2 . C. 5 15 3 .2 . D. 15 C . 20 20 20
Câu 17. Trong không gian với hệ tọa độ Oxyz , mặt phẳng (P) đi qua ba điểm (
A 1; 1; 0) ; B(1; 2;3) ;
C(0;0;3) có phương trình là 2x by cz d  0  ,
b c, d    thì b c d bằng A. 2 . B. 3 . C.1. D. 3  .
Câu 18. Cho hàm số y f (x) có 9 8 2022 f (
x)  x (x 1) (x  2)
. Số điểm cực trị của hàm số y f (x) là A. 3 . B. 2 . C.1. D. 0 .
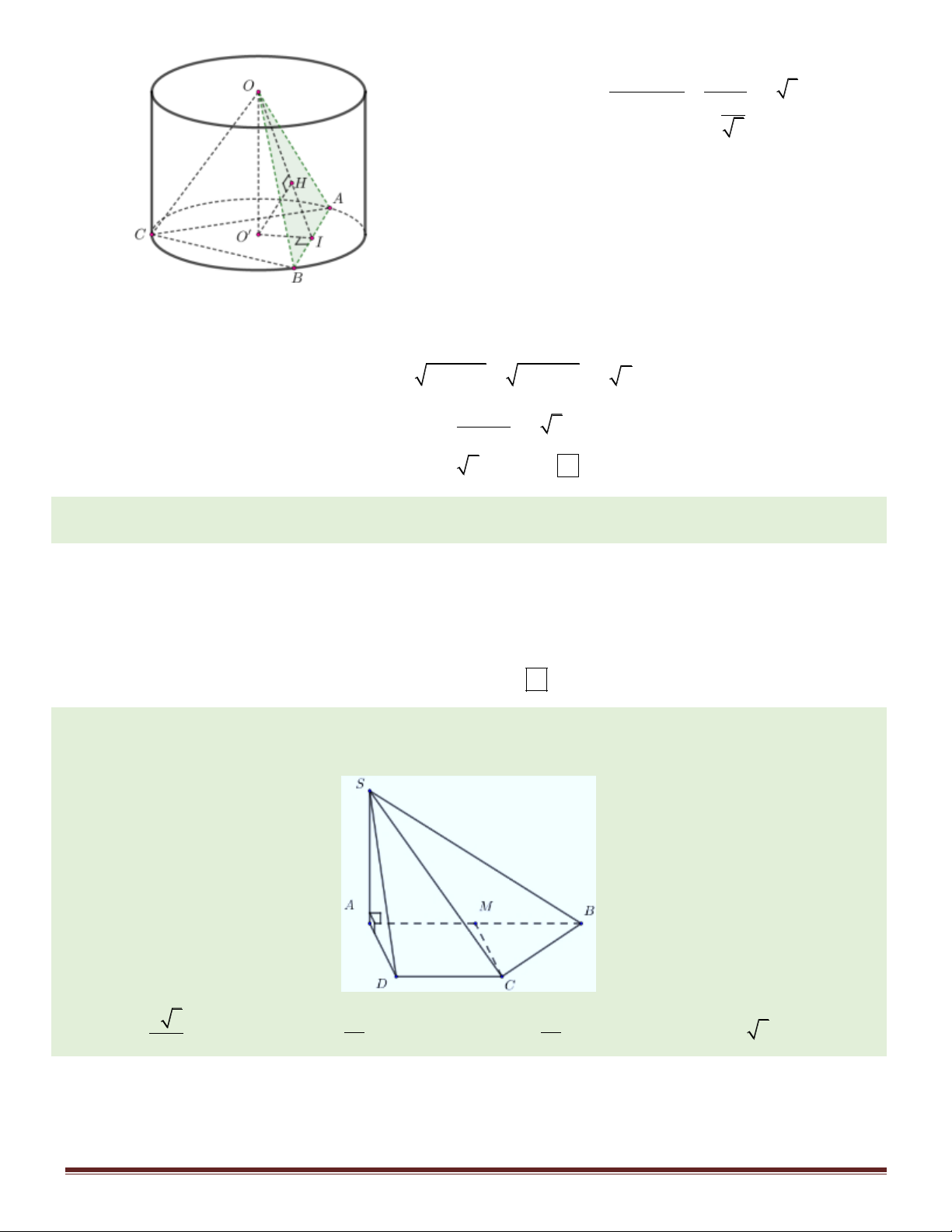
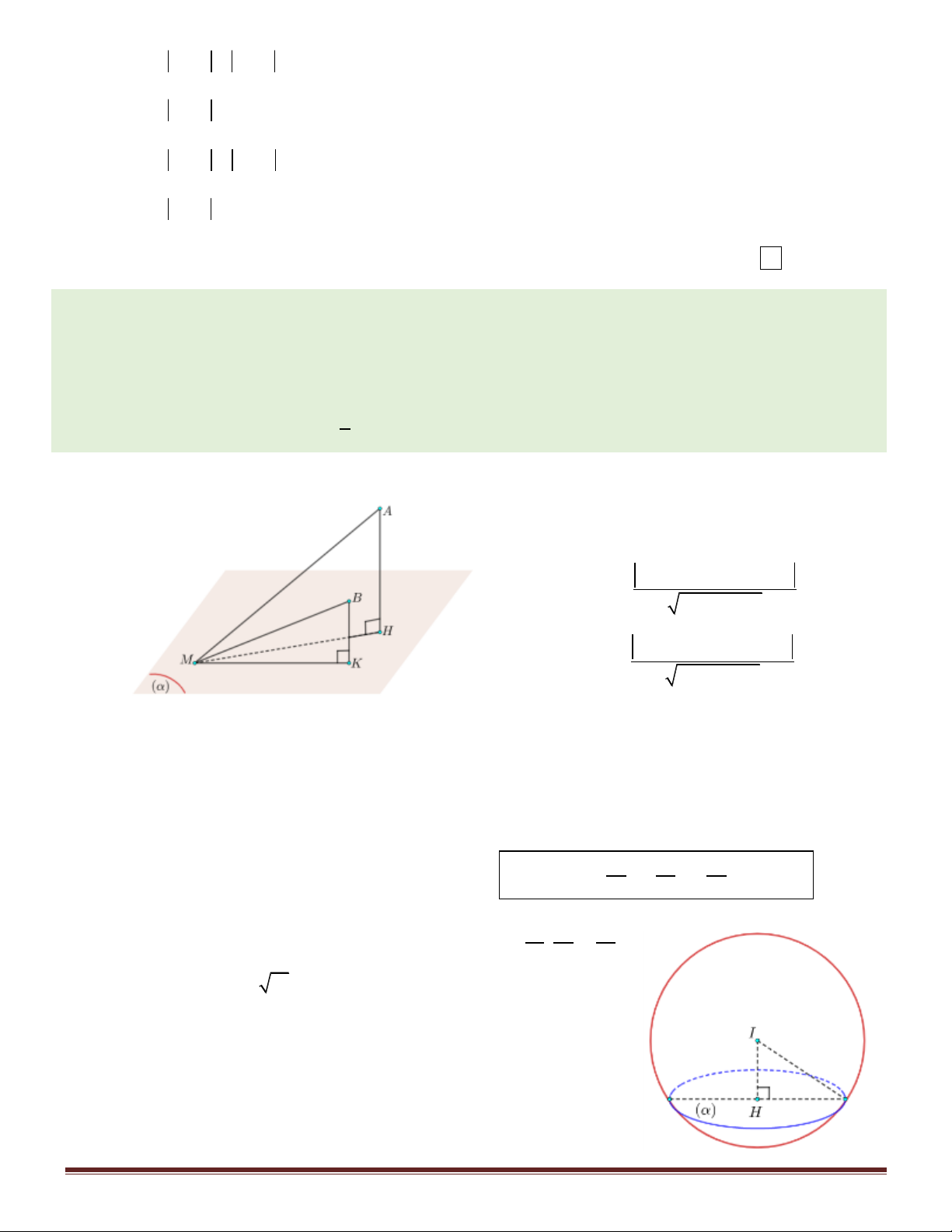
Câu 19. Cho hình chóp S.ABC có SA a 3 , SA vuông góc với mặt phẳng ( ABC) , tam giác ABC vuông
tại B, AB a , tam giác SBC cân. Thể tích khối chóp S.ABC bằng 3 2a 3 3 a 3 3 a 3 A. . B. 3 a 3 . C. . D. . 3 3 6
Câu 20. Tìm họ nguyên hàm của hàm số   3 2 1 ex f x x   . 3 x  1  A. f  x 3 x 1 dx  e  C . B. f  x 3 x 1 dx  e  C . 3 3 Trang 2   C.    3 1 d  3ex f x xC . D.    3 1 d  ex f x xC . 2
Câu 21. Tính đạo hàm của hàm số 1 2x y   . 2  2  2 A.      2 2 1 .2x y x . B. x 2 y  . x 2 .ln 2 . C. x 1 y  2 .ln 2 . D. 2x y  . 1
Câu 22. Cho log 5  a . Tính log theo a . 3 729 125 1 1 1 1 A. a . B. a . C. . D.  . 2 2 2a 2a
Câu 23. Viết phương trình tiếp tuyến của đồ thị hàm số 3
y x  2x  3 tại M 2;7 .
A. y  10x  27 .
B. y  10x 13 .
C. y  7x  7 .
D. y x  5 .
Câu 24. Cho hai số phức z  1 2i , z  2  6i . Tính z .z . 1 2 1 2 A. 1  0 2i .
B. 2 12i . C. 14 10i . D.14  2i .
Câu 25. Trong không gian Oxyz, cho hai điểm A 1
 ;1;5 và B1;2; 
1 . Mặt phẳng có phương trình nào sau
đây là mặt phẳng đi qua hai điểm ,
A B và vuông góc với mặt phẳng Oxy?
A. 3x z  2  0.
B. x  2 y  3  0.
C. 6x  6 y z  7  0.
D. 6 y z 11  0.
Câu 26. Hàm số nào sau đây là nguyên hàm của hàm số f x 1  3 ? 2x  1 A. y  2 .
B. y     x 1 2 3 2 . C. y   ln 3  2x .
D. y  ln 3  2x . 2
Câu 27. Cho hình lập phương ABC . D A BCD
  , góc giữa hai đường thẳng AB và A C   bằng A. 30 . B. 45 . C. 90 . D. 60 .
Câu 28. Cho số phức z a bi a,b  R  thỏa mãn 1 iz  3  2i  1 4i . Giá trị của a b bằng A. 2 . B. 0 . C. 1. D. 2  .
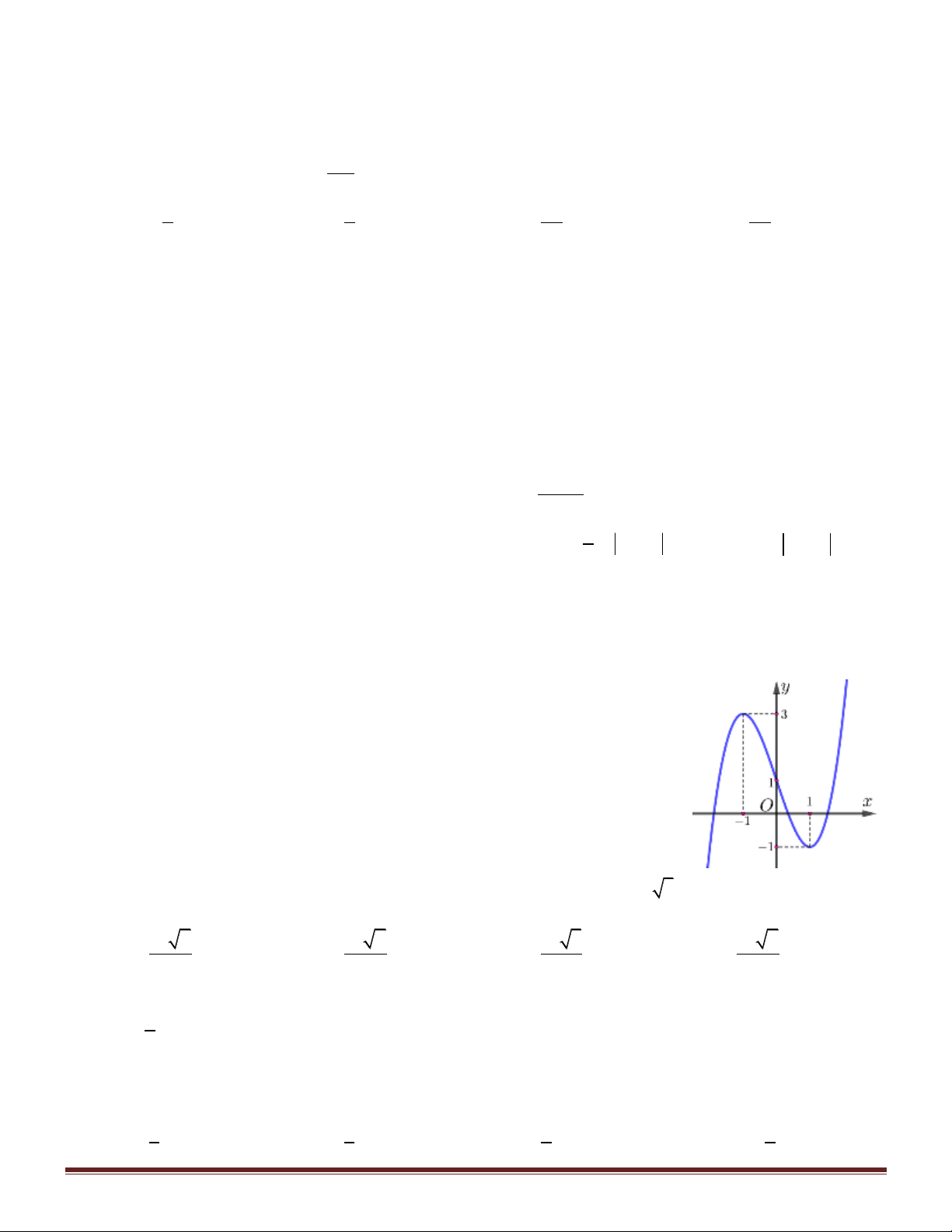
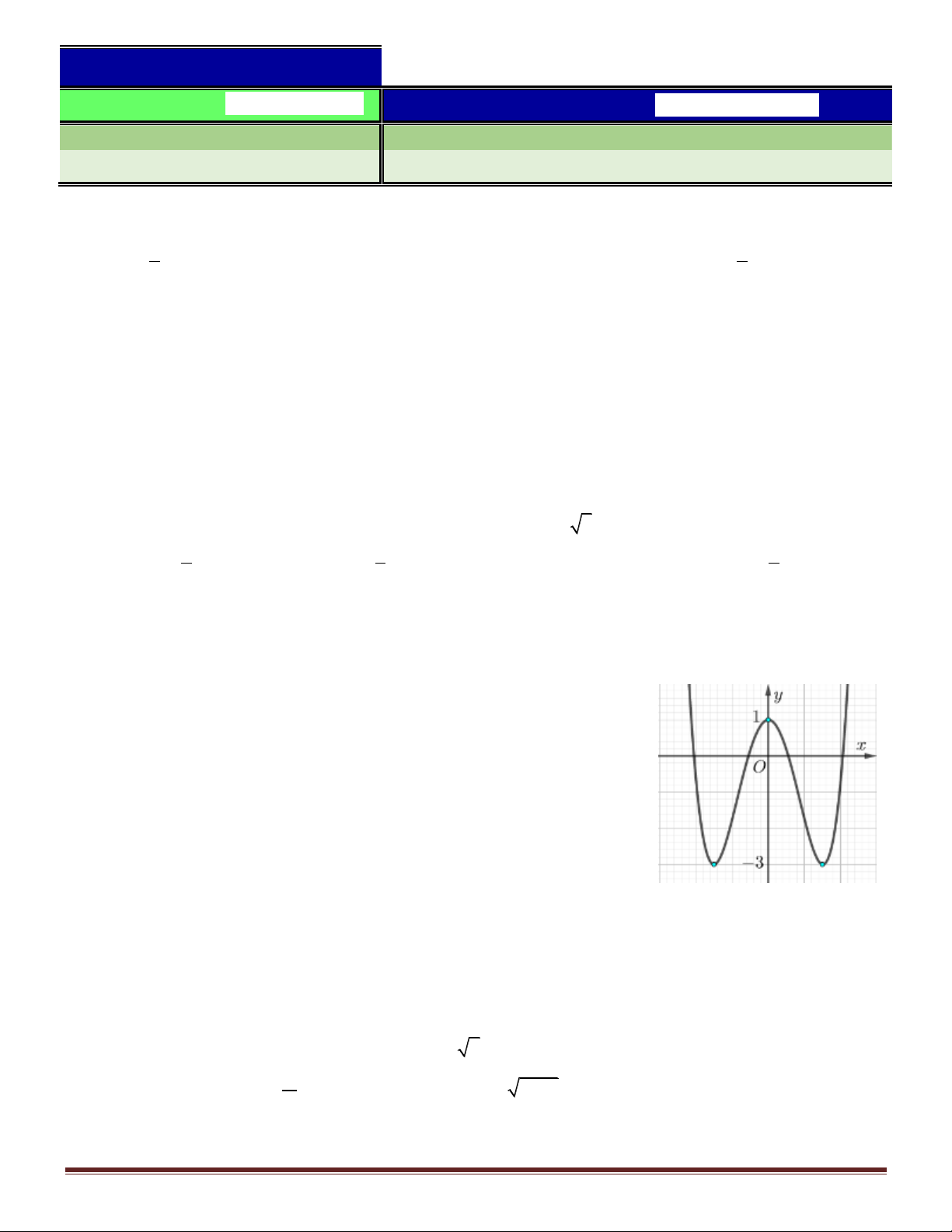
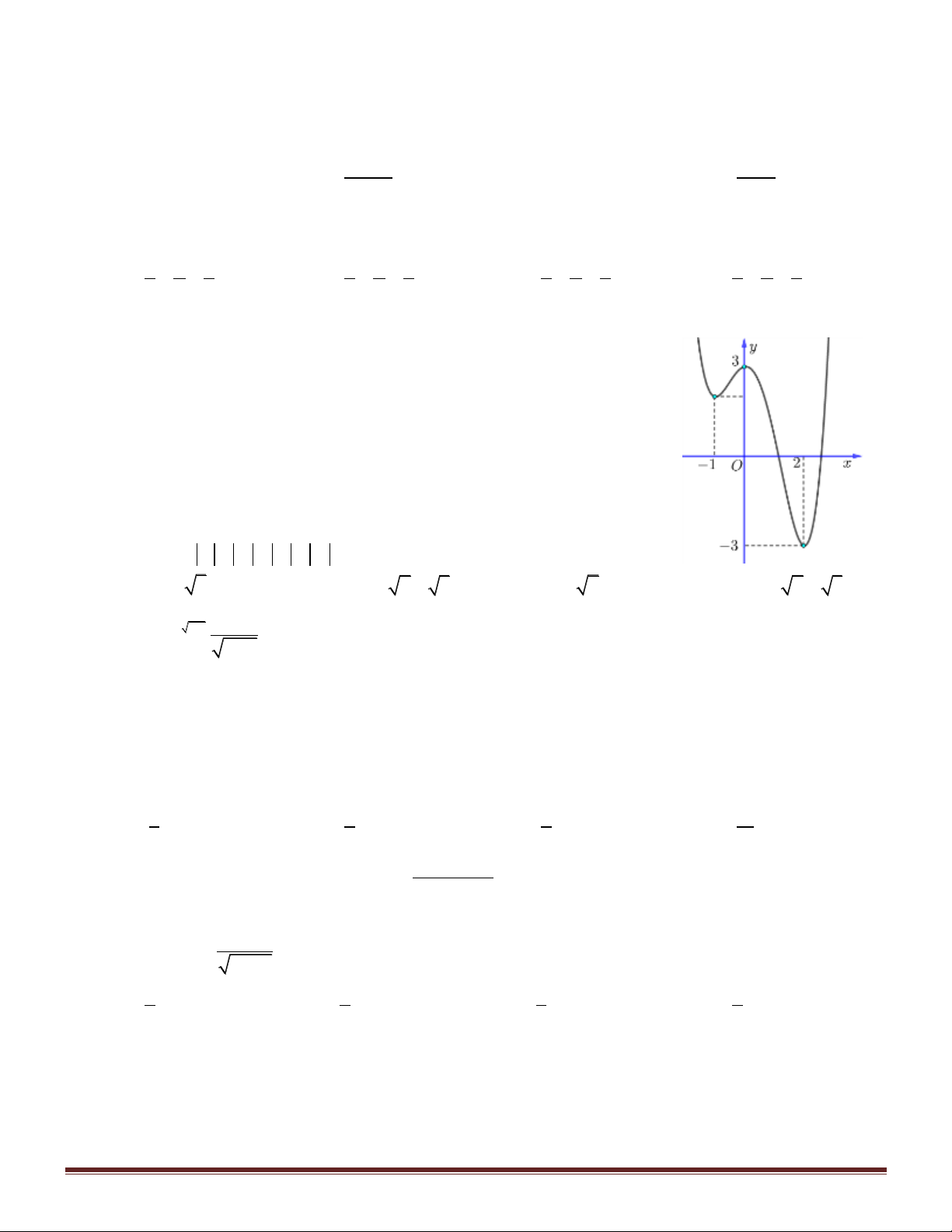
Câu 29. Cho hàm số y f x có đồ thị như hình vẽ bên.
Số nghiệm của phương trình 2 f x 1  0 là A. 0 . B. 2 . C. 1. D. 3 .
Câu 30. Cho lăng trụ tam giác đều AB . C A BC
  có cạnh đáy bằng a , AC  a 3 . Thể tích khối lăng trụ này là 3 a 6 3 a 2 3 a 3 3 a 6 A. . B. . C. . D. . 12 2 6 4 
Câu 31. Cho 2 số x, y thỏa mãn 5x  3 và 5y  6 . Giá trị của 2 5 x y bằng 3 A. . B. 54 . C. 36 . D. 1. 2
Câu 32. Trong không gian với hệ trục tọa độ Oxyz , cho mặt phẳng  P : x  2y  2z  5  0 và điểm
M 0;2;4 . Tính d M ,P . 1 1 4 4 A. . B. . C. . D. . 3 9 9 3 Trang 3 x 1
Câu 33. Tập nghiệm của bất phương trình 3  4  là x 1 3  A.  ;0   . B. 1; . C. 0  ;1 . D. 0;  1 .
Câu 34. Gọi z ; z là hai nghiệm của phương trình 2
z  2z  3  0 . Tính giá trị của biểu thức A z z z .z . 1 2 1 2 1 2 A. A  5.  B. A 1. C. A  5. D. A  1. 
Câu 35. Có bao nhiêu giá trị nguyên của tham số m , 1
 0  m 10 để phương trình x   2
1 x mx  2  0 có 3 nghiệm phân biệt. A. 13 . B. 14 . C. 16 . D. 15 . 4x 1
Câu 36. Họ tất cả các nguyên hàm của hàm số f x   trên khoảng  2;    là x  22 A. x   4 4 ln 2   C x    C x  . B.   9 4 ln 2 2 x  . 2 C. x   4 4 ln 2   C x    C x  . D.   9 4 ln 2 2 x  . 2 2 3 3 Câu 37. Nếu f
 xdx 1, f xdx  1   thì
f x dx  bằng 1 1 2 A. 0 . B. 2 . C. 3 . D. 2  .
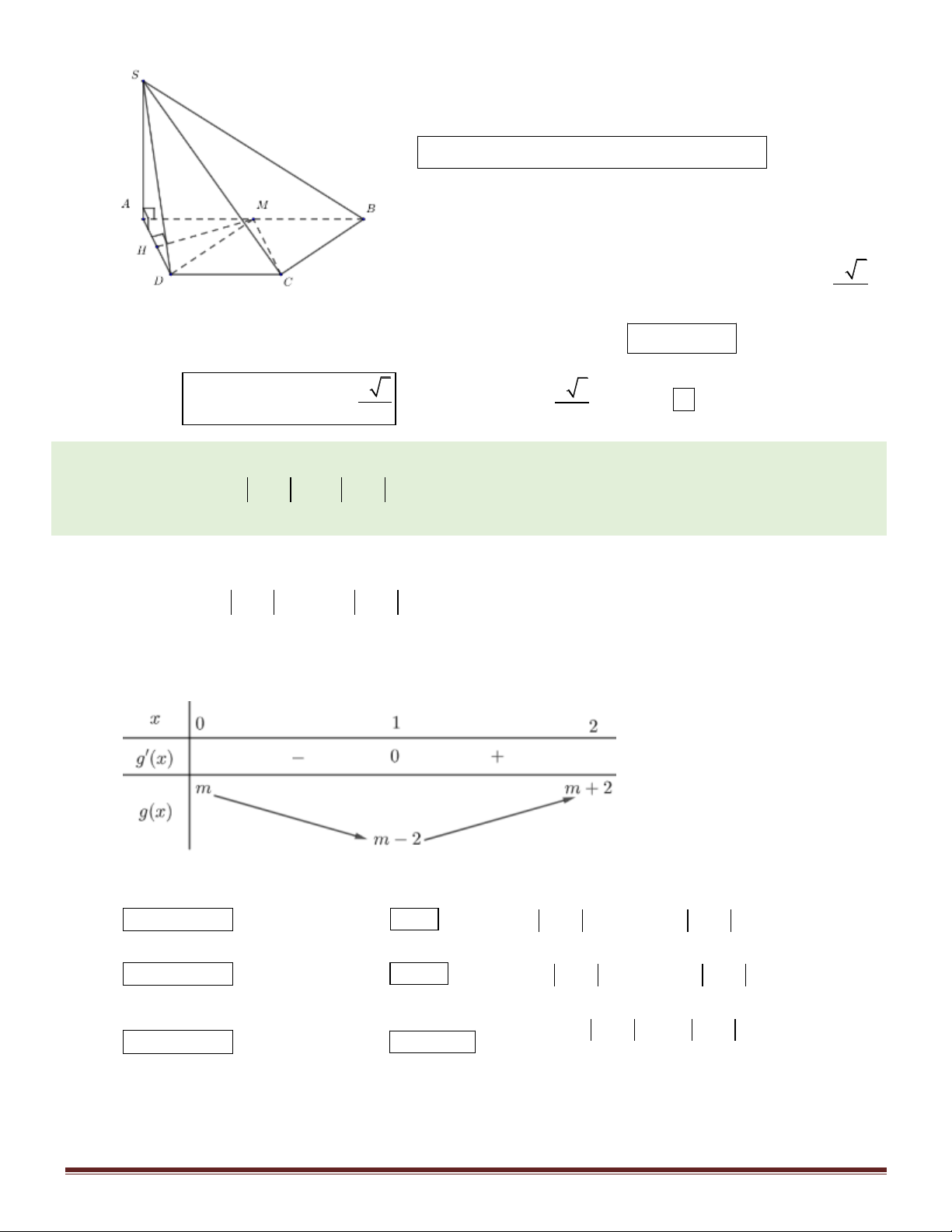
Câu 38. Cho hình chóp S.ABC có tam giác ABC vuông tại A , AB  2a, AC  3a , SA vuông góc với
ABC, SA5a. Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABC. a 38 a 38 A. R  .
B. R a 38 . C. R  38 . D. R  . 4 2
Câu 39. Trong không gian với hệ trục tọa độ Oxyz , xác định tọa độ giao điểm M của đường thẳng x 1 y 1 z  5  :   P
x y z   . 2 3
 với mặt phẳng   :2 11 0 4 A. M  1  ;1; 5. B. M  4  ;0;3 .
C. M 1; 4;  9 .
D. M 0;0; 1  1 .
Câu 40. Ba chiếc bình có hình trụ cùng chứa một lượng nước như nhau, độ cao mức nước trong bình II gấp
đôi bình I và trong bình III gấp đôi bình II. Lúc đó bán kính đáy r , r , r của ba bình (theo thứ tự) I, 1 2 3
II, III lập thành một cấp số nhân với công bội bằng 1 1 A. 2 . B. 2 . C. . D. . 2 2
Câu 41. Trong không gian với hệ toạ độ Oxyz , gọi  là đường thẳng đi qua điểm A1; 2;  3 và vuông góc với
mặt phẳng  P : 2x  2y z  7  0 . Khoảng cách từ điểm B 0;3;12 đến đường thẳng  bằng A. 110 . B. 15 . C. 74 . D. 21 .
Câu 42. Cho hình chóp S.ABC có SA vuông góc với mặt phẳng  ABC  . Tam giác ABC đều cạnh bằng
a 3 , tam giác SAC cân. Tính khoảng cách h từ A đến SBC  . 3a a 3 a a 3 A. h  . B. h  . C. . D. h  . 7 4 7 7 1 2
Câu 43. Cho hàm số f x liên tục trên  và thỏa mãn f
 xdx 10. Giá trị của f
 65xdx bằng 4  1 A. 2. B. 1. C. 5. D. 4. Trang 4
x  2  t
x  1 2t 1 2  
Câu 44. Trong không gian Oxyz cho hai đường thẳng d :  y  1 5t , d :  y  1 t và mặt phẳng 1 1 2 2   z  1 t z t  1  2
P: x y z  0 . Phương trình đường thẳng thuộc mặt phẳng P và cắt cả hai đường thẳng d và 1 d là 2
x  2  tx  3 tx 1 2t
x  2  2t     A. y 1 . B. y  1 . C. y  1 . D. y  1 .     z  1 tz  1 tz  3tz  1 3t  2
mx x  2x  3
Câu 45. Có hai giá trị của tham số m để đồ thị hàm số y y  2x
có một tiệm cận ngang là 1 1
. Tổng hai giá trị này bằng A. 2 . B. 4 . C. 3 . D. 1.
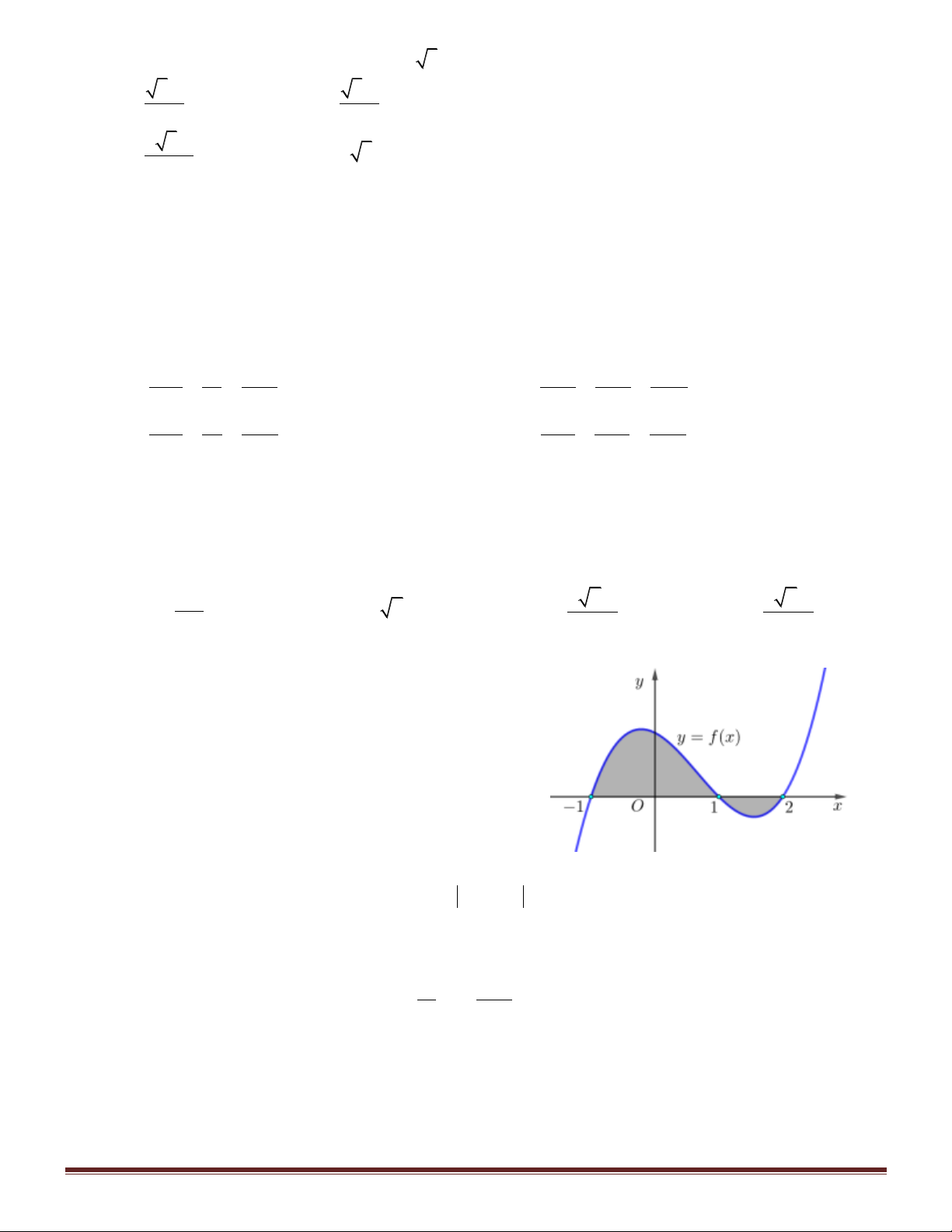
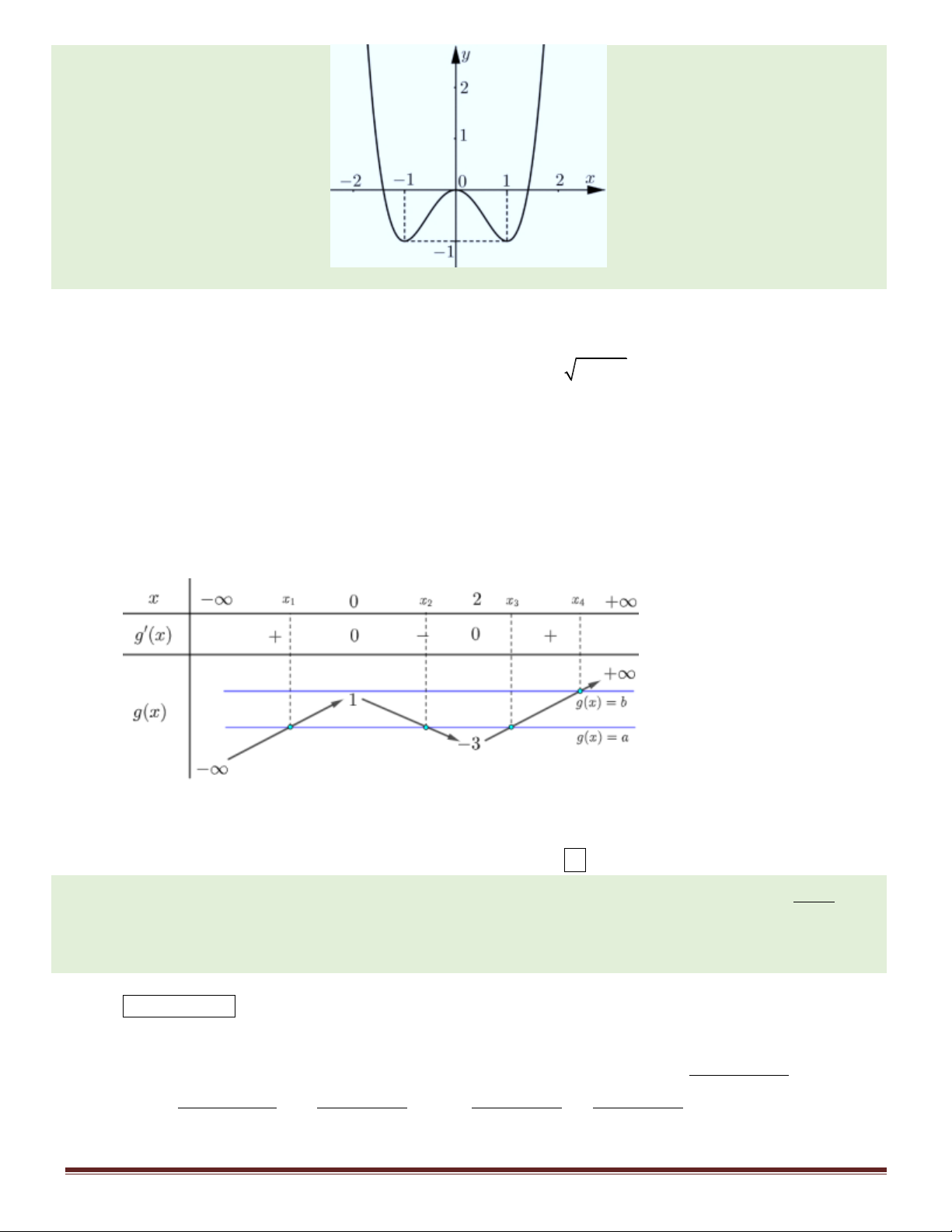
Câu 46. Cho hàm số y f (x) liên tục trên  có đồ thị như hình vẽ .
Biết H có diện tích bằng 7, H có diện tích bằng 3. Tính 1 2 1  2 I
(2x  6) f (x  6x  7)dx  2  A. 11. B. 4 . C. 1. D.10 .
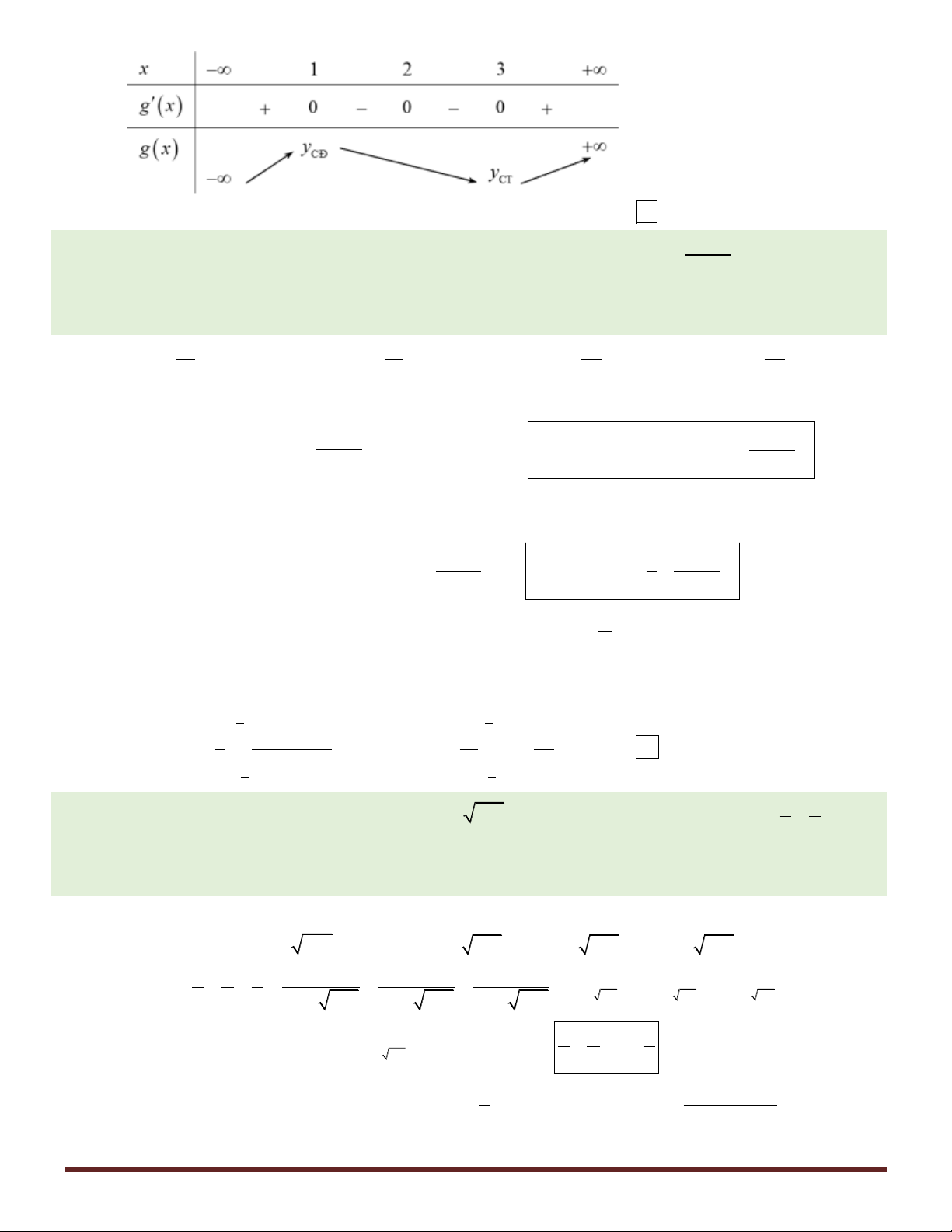
Câu 47. Cho f x là hàm số bậc 5. Hàm số y f  x có bảng biến thiên như hình vẽ sau
Số điểm cực trị của hàm số g x  f x   3 2
2  x  6x  9x là A. 4. B. 2. C. 3. D.1. 1
Câu 48. Cho hàm số y f x liên tục trên đoạn  2
 ;2 và 2 f x  3 f x  x   2  ;2 . Tính 2 x  ,   4 2 I f
 xdx . 2      A. I  . B. I   . C. I   . D. I . 10 10 20 20 1 1
Câu 49. Cho x, y, z  0; a, b, c  1 và x y z 3
a b c abc . Giá trị lớn nhất của biểu thức 2 P
  z z x y
thuộc khoảng nào dưới đây? A. 0; 2 . B. 3;  . C. 1;3 . D. 2; 4 . Trang 5 Câu 50. Cho hàm số 3 2 2
f (x)  x  3x m  2 .
m Gọi S tập hợp tất cả các giá trị nguyên của tham số m thỏa
mãn 3 max f x   2 min f x   112 . Số phần tử của S bằng  3;   1 3; 1 A. 11. B. 12. C. 9. D. 10.
________________HẾT________________
ÑAÙP AÙN ÑEÀ SOÁ 01 1 2 3 4 5 6 7 8 9 10 D C C B D B B A B A 11 12 13 14 15 16 17 18 19 20 D C C B B A D C C B 21 22 23 24 25 26 27 28 29 30 B A B D B C D D D D 31 32 33 34 35 36 37 38 39 40 A A C D A D D D C D 41 42 43 44 45 46 47 48 49 50 C A A A B B B D C A
Lôøi giaûi caâu hoûi vaän duïng cao ñeà soá 01 2
mx x  2x  3
Câu 45. Có hai giá trị của tham số m để đồ thị hàm số y y  2x
có một tiệm cận ngang là 1 1
. Tổng hai giá trị này bằng A. 2 . B. 4 . C. 3 . D. 1. Hướng dẫn giải:  2 3  2 3 x     m  1  mx x 1  2 2 2
mx x  2x  3 x x x x   m 1 Ta có: lim y  lim  lim  lim  ; x x 2x 1 x  1 x   1  2 x 2  x 2       x   x   2 3  2 3 x     m  1  mx x 1  2 2 2
mx x  2x  3 x x x x   m 1 lim y  lim  lim  lim  . x x 2x 1 x  1 x   1  2 x 2  x 2       x   x  m 1 1  m 1 2
Theo giả thiết thì đồ thị hàm số có một tiệm cận ngang y  1     . m 1  m  3 1  2 Choïn
Tổng hai giá trị m tìm được là 1 3  4 .   B
Câu 46. Cho hàm số y f (x) liên tục trên  có đồ thị như hình vẽ . Biết H có diện tích bằng 7, H có 1 2 1  diện tích bằng 3. Tính 2 I
(2x  6) f (x  6x  7)dx  2  Trang 6 A. 11. B. 4 . C. 1. D.10 . Hướng dẫn giải: 1  1 
S f (x)dx  7 
f (x)dx  7  1 H   
Dựa vào đồ thị ta thấy 1  hay 1  . 2  2  S   f x x  
f (x)dx  3   H  ( )d 3   2  1 1 1  x  2   t  1  Xét 2 I
(2x  6) f (x  6x  7)dx  .Đặt 2
t x  6x  7  dt  (2x  6)dx .Đổi cận:  . x  1   t  2 2  2 2 1 2
Khi đó: I f (t)dt  f (x)dx f (x)dx f (x)dx  7  ( 3  )  4     .Vậy I  4 . Choïn   B 1  1  1  1
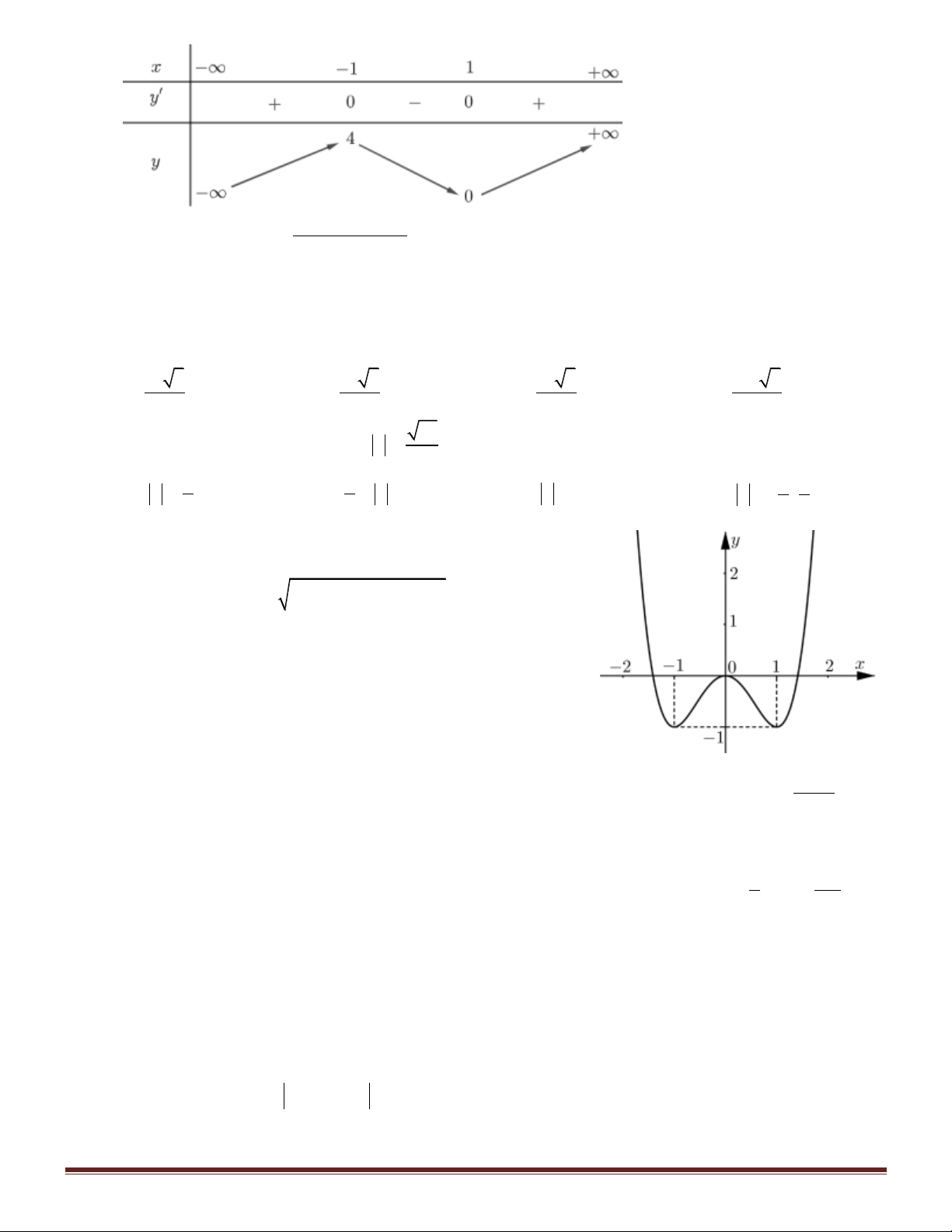
Câu 47. Cho f x là hàm số bậc 5. Hàm số y f  x có bảng biến thiên như hình vẽ sau
Số điểm cực trị của hàm số g x  f x   3 2
2  x  6x  9x là A. 4. B. 2. C. 3. D.1. Hướng dẫn giải:
Ta biết f  x có dạng bậc bốn trùng phương nên đặt f  x 4 2
ax bx c f  x 3
 4ax  2bx .  f   1  0         f   a b c 0 a 3 0  3  
Từ bảng biến thiên suy ra:         . f     c 3 b 6 1  0   4a  2b  0 c  3    f   0  0 2 2
Do vậy f  x 4 2
x x    2
x    f x     2 3 6 3 3 1 2
3 x  4x  3 . 2
Xét hàm số g x , ta có g x  f  x     2
x x     2
x x     2 2 3 4 3 3 4 3
3 x  4x  3 ; x 1 2      g xx 4x 3 0  0  
x  3 .Bảng biến thiên : 2 
x  4x  3  1  x  2  Trang 7
Từ bảng biến thiên suy ra hàm số g x có 2 điểm cực trị. Choïn   B 1
Câu 48. Cho hàm số y f x liên tục trên đoạn  2
 ;2 và 2 f x  3 f x  x   2  ;2 . Tính 2 x  ,   4 2 I f
 xdx . 2      A. I  . B. I   . C. I   . D. I . 10 10 20 20 Hướng dẫn giải: 1 2 2 2 1
Ta có: 2 f x  3 f x  x   2  ;2 , suy ra 2 f
 xdx3 f
 xdx  dx  (1). 2 x  ,   4 2 x  4 2  2  2  2 2 2  2 Xét 3 f
 xdx . Đặt t  xdt d
x . Ta có: 3 f
 xdx 3 f  t d  t  3 f
 xdx (2). 2  2  2 2  2 2 2 2 Thay (2) vào (1), ta đượ 1 1 1 c: 5 f
 xdx  dx I f x dx  dx    . 2   2 x  4 5 x  4 2  2  2  2    x  2   t    Đặ 4 t x t x   2 2 tan d
2 1 tan t dt .Đổi cận:   .
x  2  t   4   4 4 1 1 1  Khi đó: I  . 2   2
1 tan t dt  dt   . Choïn   D 2  5   4 tan t 4 10  20   4 4 1 1
Câu 49. Cho x, y, z  0; a, b, c  1 và x y z 3
a b c abc . Giá trị lớn nhất của biểu thức 2 P
  z z x y
thuộc khoảng nào dưới đây? A. 0; 2 . B. 3;  . C. 1;3 . D. 2; 4 . Hướng dẫn giải: Ta có : x y z 3
a b c abc ; suy ra 3 3 3 x  log abc , y  log abc , z  log
abc với x, , y, z  0 . a b c Khi đó 1 1 1 1 1 1 :       log a  log b  log c 3 3 3 3 3 3 x y z log abc log abc log abc abc abc abc a b c  1 1 1 log (abc)  3 . Suy ra :   3 . 3 abc x y z 1 2  z z 1
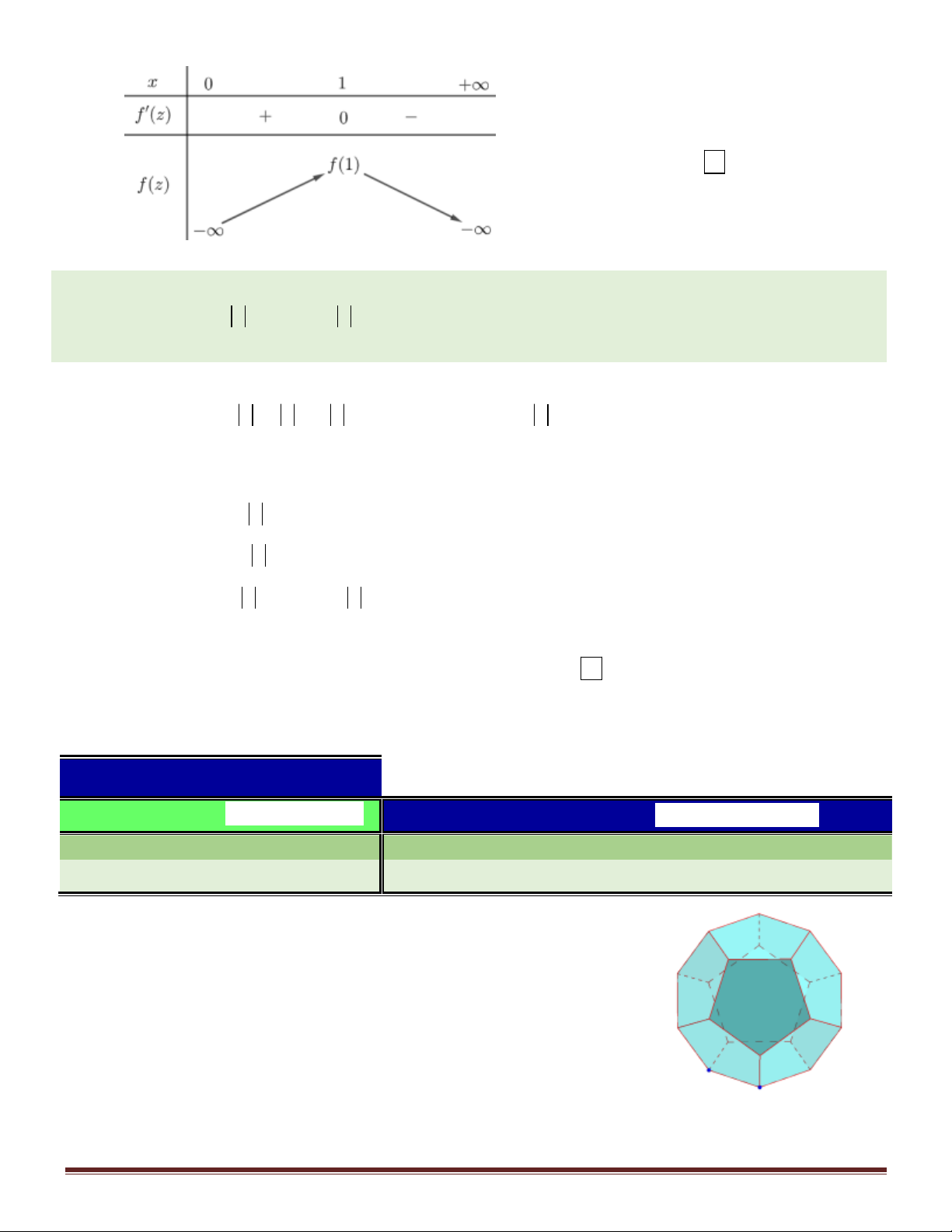
Thay vào biểu thức P, ta được : P f z  3   z z z  0; f  z 3 2 2   0  z  1. 2 z z Trang 8 Bảng biến thiên:
Dựa vào bảng biến thiên, ta có
max f (z)  f (1)  2 . 0; Vậy max P  2 . Choïn   C Câu 50. Cho hàm số 3 2 2
f (x)  x  3x m  2 .
m Gọi S tập hợp tất cả các giá trị nguyên của tham số m thỏa
mãn 3 max f x   2 min f x   112 . Số phần tử của S bằng  3;   1 3; 1 A. 11. B. 12. C. 9. D. 10. Hướng dẫn giải:
Xét hàm số f x  3 2 2
x  3 x m  2m (1). Đặt t x ; x  3   ;1  t 0;  3 .
Hàm số (1) trở thành f t  3 2 2
t  3t m  2m , t 0; 
3 ; f t  2
 3t  6t  0  t  2 . Ta có: f   2
0  m  2m ; f   2
2  m  2m  4 ; f   2
3  m  2m .
min f x   min f t 2
m  2m  4  3; 1 0; 3 Suy ra:  .
max f x   max f t 2  m  2m   3; 1 0; 3
Ta có: 3 max f x   2 min f x   112   2
m m   2 3 2
2 m  2m  4 112  3;   1 3; 1 2
 5m 10m 120  0  4
  m  6. Vì m nên m 4  ; 3  ;...;  6 .
Vậy có 11 giá trị của m thỏa mãn yêu cầu bài toán. Choïn   A ĐỀ SỐ 02
ĐỀ RÈN LUYỆN MÔN TOÁN 12
HƯỚNG ĐẾN KÌ THI THPT QUỐC GIA
Trắc nghiệm: 50 câu Nội dung:
Thời gian: 90 phút
FULL KIẾN THỨC TOÁN 12+
Câu 51. Hình mười hai mặt đều có số đỉnh, số cạnh và số mặt lần lượt là A. 20, 30, 12 . B. 30, 20, 12 . C. 30, 12, 20 . D.12, 20, 30 .
Câu 52. Trong không gian với hệ trục tọa độ Oxyz , phương trình chính tắc của 
đường thẳng d đi qua điểm M 2; 1
 ;3 và có véctơ chỉ phương u  1; 2; 4 là Trang 9 x  2 y 1 z  3 x  2 y 1 z  3 A.     1 2  . B. 4 1 2  . 4 x 1 y  2 z  4 x 1 y  2 z  4 C.     2  . D. 1 3 2 1  . 3
Câu 53. Cho hàm số y f x có bảng biến thiên
Hỏi hàm số có bao nhiêu cực trị? A. 3 . B. 1. C. 2 . D. 4 .
Câu 54. Một hình nón có diện tích xung quanh bằng 2
2 cm và bán kính đáy 1 r
cm . Tính độ dài đường 2 sinh của hình nón. A. 1cm . B. 4 cm . C. 2 cm . D. 3cm .
Câu 55. Họtất cả các nguyên hàm của hàm số f x  2x  2022 là A. 2 2x C . B. 2
x  2022x C . C. 2 x C . D. 2
2x  2022x C . 
Câu 56. Tập nghiệm của bất phương trình 2 x 2 3 x  27 là A.  ;  3
 1; . B.  ;    1  3; . C. 1;3 . D.  3   ;1 .
Câu 57. Trong không gian với hệ toạ độ Oxyz , khoảng cách từ điểm A1;  2;3 đến mặt phẳng
P:x 3y 4z 9  0 là 17 26 4 26 A. . B. 8 . C. . D. . 26 13 13
Câu 58. Diện tích toàn phần của hình lập phương cạnh 3a là A. 2 72a . B. 2 54a . C. 2 36a . D. 2 9a .
Câu 59. Cho hàm số y f x có đồ thị như hình vẽ. Hãy chỉ ra
một khoảng đồng biến của hàm số đã cho. A. 0;3 . B. 3; 4 . C.  3  ; 2   . D.  2  ;  1 .
Câu 60. Cho hàm số y f x có lim y  2 , lim y  0 . Khẳng định nào sau đây đúng? x  x2
A. Đồ thị hàm số có tiệm cận ngang x  2 và tiệm cận đứng y  2 .
B.Đồ thị hàm số không có tiệm cận ngang và tiệm cận đứng x  2 .
C.Đồ thị hàm số có tiệm cận ngang y  2 và và không có tiệm cận đứng.
D.Đồ thị hàm số có tiệm cận ngang y  2 và tiệm cận đứng x  2 .
Câu 61. Hàm số nào dưới đây có đồ thị như hình vẽ ? A. 4 2
y x  3x 1 . Trang 10 2x 1 B. y  . x 1 x 1 C. y  . x  2
D. y  x  2 .
Câu 62. Trong không gian với hệ toạ độ Oxyz , cho mặt cầu S  2 2 2
: x y z  2x  2z  7  0 . Bán kính của mặt cầu đã cho bằng A. 7 . B. 3. C. 9. D. 15 .
Câu 63. Cho hai số phức z  1 2i và z  2  3i . Phần ảo của số phức w  3z  2z là 1 2 1 2 A. 1 . B. 11 . C.12 . D. 12i . x
Câu 64. Cho hàm số f x  ln x  . Khẳng định nào dưới đây đúng? 2
A.Hàm số đồng biến trên khoảng 0;  1 .
B.Hàm số đồng biến trên khoảng 0;  .
C.Hàm số đồng biến trên khoảng 2;  .
D.Hàm số đồng biến trên các khoảng  ;0
  và 2; . a b c d
Câu 65. Cho các số dương a, b, c, d . Biểu thức M  log
 log  log  log bằng b c d aa b c d A. 1 . B. log      . C. 0 .
D. log abcd  .  b c d a
Câu 66. Tập nghiệm của phương trình log x 5  x   1 6    A. 1  ;  6 . B.2;  3 . C.1;  6  . D.4;  6 .
Câu 67. Cho hình lập phương ABC . D A BCD
  có I, J tương ứng là trung điểm của BC, BB . Góc giữa hai
đường thẳng AC, IJ bằng A. 0 30 . B. 0 120 . C. 0 60 . D. 0 45 .
Câu 68. Tập xác định của hàm số 2
y  ln 2  x là: A.  2  ;2 . B.  .
C.  \  2; 2    .
D.  \  2; 2. 2 2 z z
Câu 69. Gọi z , z là nghiệm của phương trình 2
z  2z  4  0 . Tính giá trị của biểu thức 1 2 P   . 1 2 z z 2 1 11 A. 4 . B. 4  . C. 8 . D.  . 4
Câu 70. Trong không gian với hệ tọa độ Oxyz , phương trình mặt phẳng đi qua hai điểm A0;1  ;1 , B  1  ;0;2
và vuông góc với mặt phẳng  P : x y z 1  0 là
A. y z  2  0 .
B. y z  2  0 .
C. y z  2  0 .
D. y z  2  0 . 1 y
Câu 71. Cho hàm số y
với x  0 . Khi đó  bằng x 1 ln x 2 y x 1 x 1 x A. . B. . C.1 . D. . 1  x  ln x 1  x  ln x x x 1
Câu 72. Cho hình chóp S.ABCD có SA vuông góc với mă ̣t phẳng
ABCD, đáy ABCDlà hình thang vuông t ại A và B , Trang 11
AB a, AD  3a, BC  .
a Biết SA a 3, tính thể tích khối chóp S.BCD theo a. 3 3a 3 3a A. . B. . 6 4 3 2 3a C. . D. 3 2 3a . 3 Câu 73. Gọi ,
A B, C lần lượt là các điểm biểu diễn của các số phức z  2 , z  4i , z  2  4i trong mặt 1 2 3
phẳng tọa độ Oxy. Tính diện tích tam giác . ABC A. 8 . B. 2 . C. 6 . D. 4 . Câu 74. Cho hàm số 4 2
y  2x  6x có đồ thị C . Số giao điểm của đồ thị C và đường thẳng y  4 là: A. 4 . B. 2 . C. 0 . D.1.
Câu 75. Trong không gian với hệ tọa độ Oxyz , cho hai điểm A1;0; 2 và B 3; 1;  3 . Đường thẳng AB có phương trình là x 1 y z  2 x  3 y 1 z  2 A.   . B.   . 2 1  5 2 1 5 x 1 y z  2 x 1 y 1 z  7 C.   . D.   . 2 1  5  2 1 5
Câu 76. Cho z , z là 2 nghiệm phức của phương trình 2
z  2z  5  0 , trong đó z là số phức có phần ảo âm. 1 2 1
Khi đó z  3z bằng: 1 2 A. 4   4i . B. 4  4i . C. 4  4i . D. 4  4i .
Câu 77. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a , cạnh bên bằng 3a . Tính thể tích V của khối chóp đã cho 3 4a 3 4 7a 3 4 7a A.V  . B. 3 V  4 7a . C.V  . D.V  . 3 9 3
Câu 78. Gọi S là diện tích miền hình phẳng được gạch chéo trong hình vẽ bên dưới. Công thức tính S là 2 A. S f (x)dx  . 1  1 2 B. S
f (x)dx f (x)dx   . 1  1 1 2
C. S   f (x)dx f (x)dx   . 1  1 2 D. S f (x)dx  . 1 
Câu 79. Tìm tập hợp điểm biểu diễn số phức z thoả z 1 2i  3 .
A.Đường tròn tâm I  1
 ;2, bán kính r  9.
B.Đường tròn tâm I 1; 2 , bán kính r  9 .
C.Đường tròn tâm I 1;  2 , bán kính r  3.
D.Đường tròn tâm I  1
 ;2, bán kính r  3. 1 1
Câu 80. Cho cấp số nhân (u ) có u  1, q   . Số
là số hạng thứ mấy của dãy n 1 10 103 10
A.Số hạng thứ 101.
B.Số hạng thứ 104 .
C.Số hạng thứ 102.
D.Số hạng thứ 103 .
Câu 81. Gọi z là nghiệm phức có phần ảo âm của phương trình  z  2 2
1 0 . Môđun của số phức z i 0 0 bằng Trang 12 A. 5 . B. 2 . C. 5 . D. 2 . Câu 82. Cho hàm số 3 2
y ax bx cx d có đồ thị như hình vẽ bên. Mệnh
đề nào dưới đây đúng?
A. a  0, b  0, c  0, d  0 .
B. a  0, b  0, c  0, d  0 .
C. a  0, b  0, c  0, d  0 .
D. a  0, b  0, c  0, d  0 .
Câu 83. Có bao nhiêu số phức z thỏa mãn 1 iz z là số thuần ảo và z  2i  1 A. 2 . B.1. C. 0 . D.Vô số.
Câu 84. Cho lăng trụ đứng AB . C A BC
  đáy là tam giác vuông cân tại B , AC a 2 , biết góc giữa  A BC
và đáy bằng 60 . Tính thể tích V của khối lăng trụ. 3 a 3 3 a 3 3 a 3 3 a 6 A.V  . B. V  . C.V  . D. V  . 2 3 6 6 e  x   1 ln x  2  e 1 a Câu 85. Biết dx  . a e  b ln  
 trong đó a , b là các số nguyên. Khi đó tỉ số là 1 x ln x  e  b 1 1 A. . B.1. C. 3 . D. 2 . 2
Câu 86. Cho hình chóp S.ABC có   
ASB BSC CSA  60 , SA a , SB  2a , SC  4a . Tính thể tích khối
chóp S.ABC theo a . 3 8a 2 3 4a 2 3 2a 2 3 a 2 A. . B. . C. . D. . 3 3 3 3 2 x 2 x  1  1
Câu 87. Bất phương trình   
có tập nghiệm là khoảng a;b . Khi đó giá trị của a b là  2  8 A. 2  . B. 2 . C. 4 . D. 4  .
Câu 88. Đồ thị hàm số nào sau đây có 2 đường tiệm cận đứng? 2 x 1 x  2
A. y  log  2 x 1 . B. y y  . D. y x . 2  2 x  3x  . C. 2 x 1 x t  
Câu 89. Trong không gian Oxyz , cho điểm A2;0; 3
  và đường thẳng  : y 1 3t . Mặt phẳng đi qua Az  5t
và vuông góc với đường thẳng  có phương trình là:
A. x  3y z  0 .
B. x  3y z 1  0 .
C. 3y z  3  0 .
D. x  3y z  5  0 .
Câu 90. Tập nghiệm của bất phương trình 2
ln x  ln 4x  4 là A. 1;  . B. 2;  .
C. 1; \   2 . D.  \   2 .
Câu 91. Số ca nhiễm Covid-19 trong cộng đồng ở một tỉnh vào ngày thứ x trong một giai đoạn được ước tính theo công thức    .erx f x A
, trong đó A là số ca nhiễm ở ngày đầu của giai đoạn, r là tỷ lệ gia tăng
số ca nhiễm hàng ngày của giai đoạn đó và trong cùng một giai đoạn thì r không đổi. Giai đoạn thứ
nhất tính từ ngày tỉnh đó có 9 ca bệnh đầu tiên và không dùng biện pháp phòng chống lây nhiễm nào
thì đến ngày thứ 6 số ca bệnh của tỉnh là 180 ca. Giai đoạn thứ hai (kể từ ngày thứ 7 trở đi) tỉnh đó áp
dụng các biện pháp phòng chống lây nhiễm nên tỷ lệ gia tăng số ca nhiễm hàng ngày giảm đi 10 lần
so với giai đoạn trước. Đến ngày thứ 6 của giai đoạn thứ hai thì số ca bệnh của tỉnh đó gần nhất với số nào sau đây? Trang 13 A. 242. B. 90. C. 16. D. 422. Câu 92. Cho hàm số 4 2
y ax bx c , với a, b, c là các số thực, a  0 . Biết lim y   , hàm số có ba điểm x
cực trị và phương trình y  0 vô nghiệm. Hỏi trong 3 số a, b, c có bao nhiêu số dương? A. 0 . B. 3 . C. 2 . D.1. c c
Câu 93. Cho a, b, c là các số thực khác 0 thỏa mãn 4a 25b 10c   . Tính T   . a b 1 1 A. T  . B. T  2 . C. T  10 . D.T  . 2 10
Câu 94. Tính thể tích của thùng đựng nước có hình dạng và kích thước như hình vẽ 0, 238 A.  3 m  . 4 0, 238 B.  3 m  3 . 0, 238 C.  3 m  . 3 0, 238 D.  3 m . 2
Câu 95. Có 8 chiếc ghế được kê thành một hàng ngang. Xếp ngẫu nhiên 8 học sinh,
gồm 3 học sinh lớp A, 3 học sinh lớp B và 2 học sinh lớp C, ngồi vào ghế
đó, sao cho mỗi ghế có đúng một học sinh. Xác suất để có đúng 2 học sinh a
lớp A ngồi cạnh nhau bằng với , a b   ,  ;
a b 1. Khi đó giá trị a b là b A. 43. B. 93 . C.101. D. 21 .
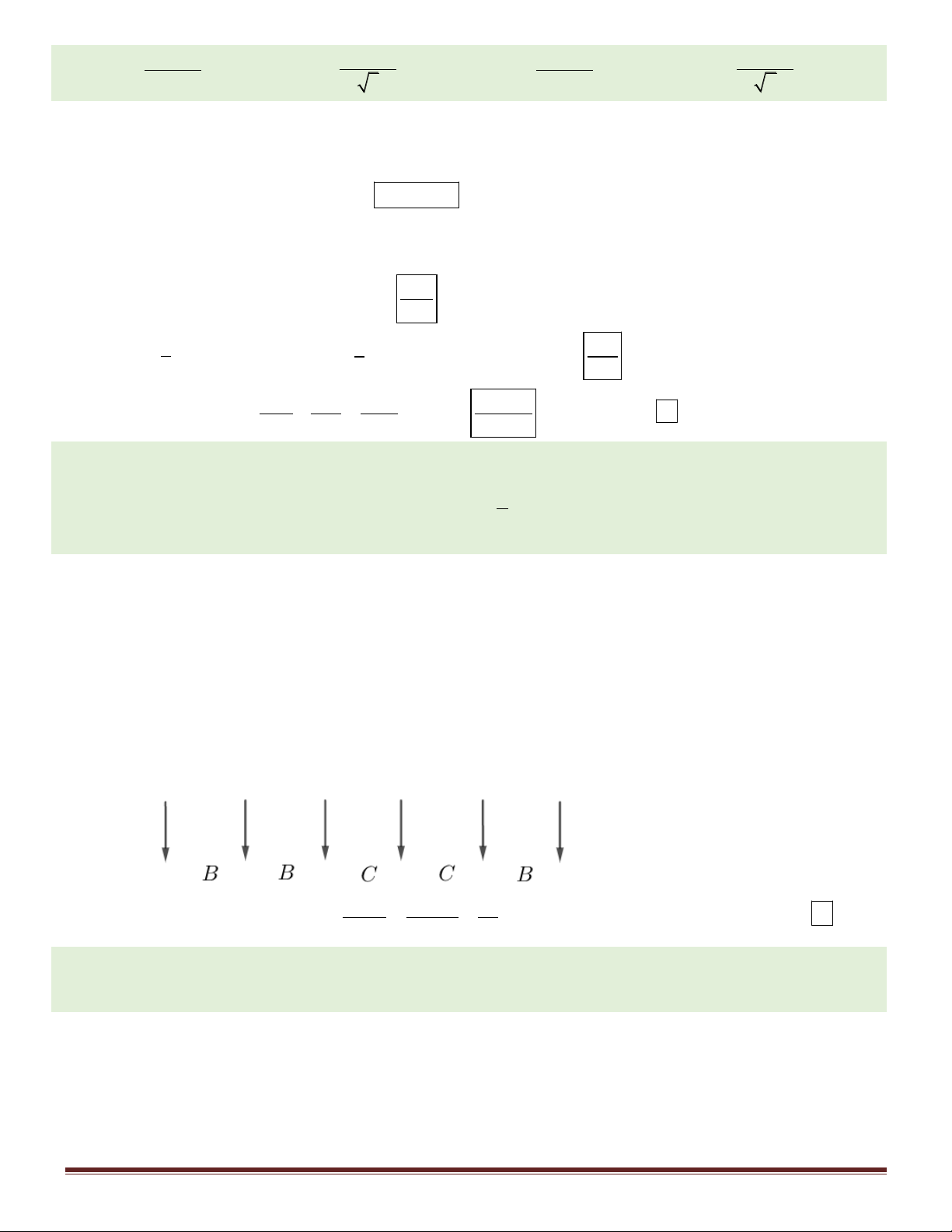
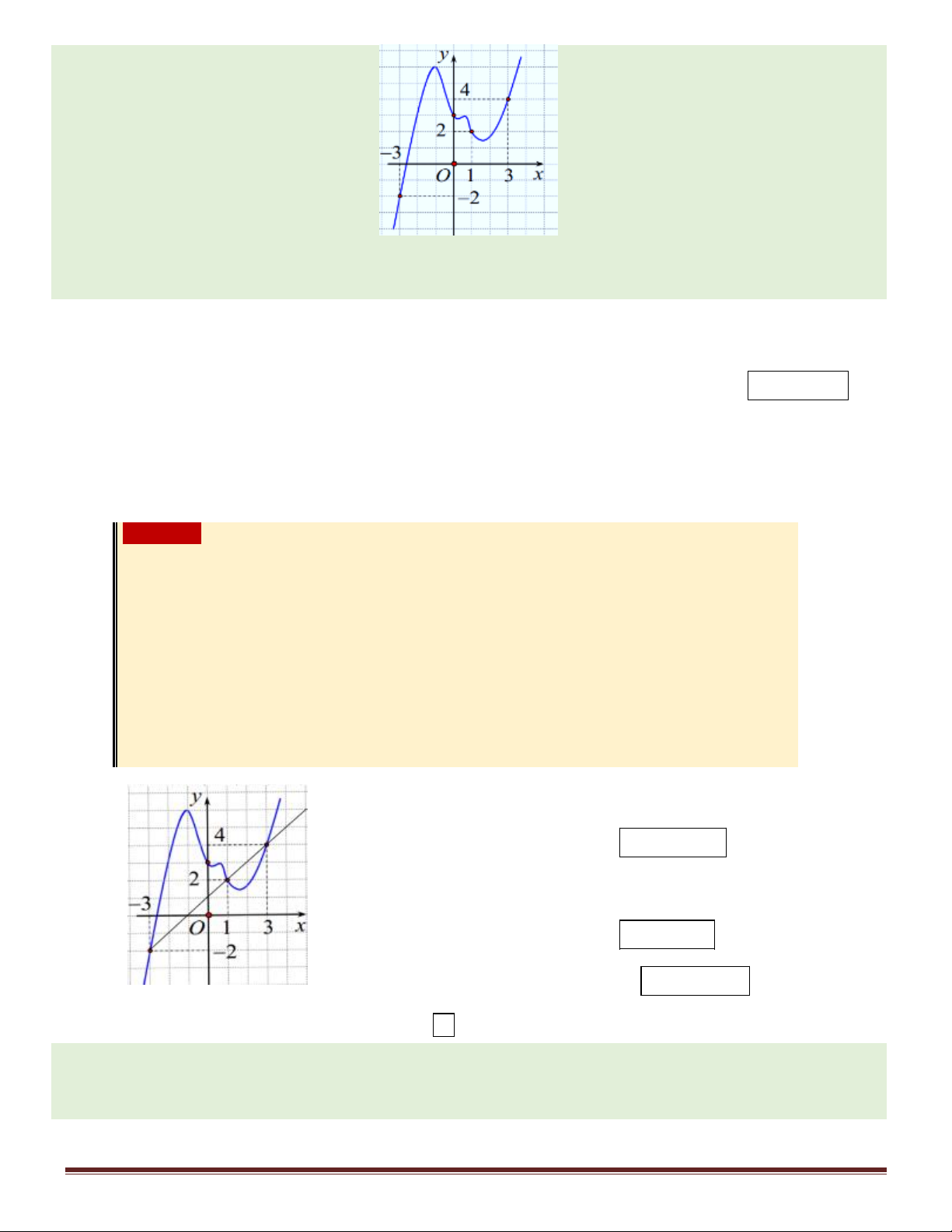
Câu 96. Cho hàm số y f x liên tục trên  có đồ thị y f  x cho như
hình dưới đây. Đặt g x  f x x  2 2
1 . Mệnh đề nào dưới đây đúng. A. g  
1  g 3  g  3   . B. g  
1  g 3  g  3  . C. g  3    g   1  g 3 . D. g   1  g  3    g 3.
Câu 97. Cho hình chóp S.ABCD có đáy là hình thoi, tam giác SAB đều và nằm trong mặt phẳng vuông góc
với mặt phẳng  ABCD . Biết AC  2a, BD  4a . Tính theo a khoảng cách giữa hai đường thẳng AD và SC . a 15 2a 5 2a 15 4a 1365 A. . B. . C. . D. . 2 5 3 91
Câu 98. Xét các số thực dương a, b, c  1 với a b thỏa 4log c  log c  25log c . Giá trị nhỏ nhất của a b ab
biểu thức P  log a  log c  log b bằng b a c 17 A. 5 . B. 3 . C. 8 . D. . 2
Câu 99. Giả sử z , z là hai trong số các số phức z thỏa mãn iz  2  i  1 và z z  2 . Giá trị lớn nhất 1 2 1 2
của z z bằng 1 2 Trang 14 A. 4 . B. 2 3 . C. 3 2 . D. 3 . Câu 100.
Cho hàm số y f x liên tục trên đoạn 1; 
3 và có bảng biến thiên như sau: m
Gọi S là tập tất cả các giá trị nguyên của tham số m để phương trình f x   1  có hai 2 x  6x 12
nghiệm phân biệt trên đoạn 2; 4 . Tổng các phần tử của S là A. 297  . B. 294  . C. 75  . D. 72  .
________________HẾT________________
ÑAÙP AÙN ÑEÀ SOÁ 02 1 2 3 4 5 6 7 8 9 10 A B C B B A D B D C 11 12 13 14 15 16 17 18 19 20 B B C A C B C D B C 21 22 23 24 25 26 27 28 29 30 C A D B D A D B D B 31 32 33 34 35 36 37 38 39 40 C C A A B C D A B C 41 42 43 44 45 46 47 48 49 50 A C B C A B D A A C
Lôøi giaûi caâu hoûi vaän duïng cao ñeà soá 02
Câu 44. Tính thể tích của thùng đựng nước có hình dạng và kích thước như hình vẽ Trang 15 0, 238 0, 238 0, 238 0, 238 A.  3 m  . B.  3 m C.  3 m  . D.  3 m . 4 3 . 3 2 Hướng dẫngiải:
Thể tích của thùng đựng nước là: V V V với V là thể tích khối trụ có đường kính đáy bằng 1 2 1
2R  0, 6 m và chiều cao h  0, 6 m ; V là thể tích khối nón cụt có đường kính đáy lớn 2R  0, 6 m 1 1 2 1
và đường kính đáy nhỏ 2R  0, 4 m và chiều cao h  1 0,6  0, 4 m . 2 2  Khi đó 2 27 : 2
V   R .h   .0,3 .0,6   3 m ; 1 1 1  500 1 1 19 V   h  2 2
R R R R
 .0,4.0,09  0,04  0,06   3 m  . 2 2 1 2 1 2  3 3 750 27 19 199 0, 238
Vậy V V V      3 m   3
m  . Choïn   C 1 2  500 750 1500 3
Câu 45. Có 8 chiếc ghế được kê thành một hàng ngang. Xếp ngẫu nhiên 8 học sinh, gồm 3 học sinh lớp A, 3
học sinh lớp B và 2 học sinh lớp C, ngồi vào ghế đó, sao cho mỗi ghế có đúng một học sinh. Xác suất để a
có đúng 2 học sinh lớp A ngồi cạnh nhau bằng với , a b   , ;
a b 1. Khi đó giá trị a b là b A. 43. B. 93 . C.101. D. 21 . Hướng dẫngiải:
Gọi  là không gian mẫu. Số phần tử của không gian mẫu là n   8!.
Gọi X là biến cố: “Xếp được hàng có đúng 2 học sinh lớp A ngồi cạnh nhau”.
Việc xếp hàng thỏa mãn biến cố X được thực hiện như sau:
Chia các học sinh lớp A thành hai nhóm (có thứ tự), ta có 2 A .1 (cách xếp). 3
Xếp 5 học sinh không phải lớp A thành một hàng ngang, ta có 5! (cách xếp).
Ta có thể xếp các nhóm của lớp A vào một trong các vị trí: ở giữa hai bạn liên tiếp đã xếp trước
hoặc ở hai vị trí đầu hàng đã xếp trước, ta có 2 A (cách xếp). 6
Khi đó, số biến cố thuận lợi của X là: nX  2 2
 5!.A .A  21 600 . 3 6 n X 21 600 15 Choïn
Xác suất cần tìm là: P X             .   A n  a 15, b 28 a b 43 8! 28
Câu 46. Cho hàm số y f x liên tục trên  có đồ thị y f  x cho như hình dưới đây. Đặt
g x  f x   x  2 2
1 . Mệnh đề nào dưới đây đúng. Trang 16 A. g  
1  g 3  g  3   . B. g  
1  g 3  g  3  . C. g  3    g   1  g 3 . D. g   1  g  3    g 3. Hướng dẫngiải:
Xét g x  f x   x  2 2
1 ; g x  2 f  x  2x  2  2  f
  x  x   1   0  f  
x  x 1 .
Vẽ đường thẳng y x 1 trên cùng hệ trục tọa độ với đồ thị y f  x (Xem hình). x  3  
Ta có: g x  0  f  x  x 1  x  1  . x  3  Nhận xét:
Ta thấy khi x  3  
;1 thì đồ thị hàm y f  x nằm phía trên đồ thị hàm y x 1, 1
do vậy f  x   x  
1  0  g x  2  f
 x  x   1   0  g 
 xdx  0 . Lý luận 3  3
tương tự, ta có: g
 xdx  0. 1 3 1 3 Xét g
 xdx g
 xdxg
 xdx S S  0 với S , S là các phần diện tích 1 2 1 2 3  3  1
tương ứng trong hình vẽ. Từ đó, ta có lời giải bên dưới. 1 1 Xét g
 xdx  2  f
  xx 1 dx  0  3  3   g   1  g   3  0  g   1  g  3   (1). 3 3 Xét g
 xdx  2  f
 xx 1 dx  0  1 1  g   3  g   1  0  g   3  g   1 (2). 3 Xét g
 xdx  0  g 3 g 3
   0  g 3  g  3   . 3  Choïn Vậy ta có g  
1  g 3  g  3  .   B
Câu 47. Cho hình chóp S.ABCD có đáy là hình thoi, tam giác SAB đều và nằm trong mặt phẳng vuông góc
với mặt phẳng  ABCD . Biết AC  2a, BD  4a . Tính theo a khoảng cách giữa hai đường thẳng AD và SC . Trang 17 a 15 2a 5 2a 15 4a 1365 A. . B. . C. . D. . 2 5 3 91 Hướng dẫngiải:
Trong (ABCD), gọi O AC BD . Ta có: OA a , OB  2a .
Xét tam giác OAB vuông tại O . Ta có AB OA OB a   a2 2 2 2 2  a 5 .
Gọi H là trung điểm AB , vì S
AB đều và nằm trong mặt phẳng vuông góc với đáy nên a 5. 3 a 15
SH   ABCD và SH   . 2 2
Ta có: AD// SBC , SC  SBC   d AD, SC   d AD,SBC   d  ,
A SBC  .
d H ,SBC  HB 1 Ta lại có:     . d d  ,
A SBC  2d H , SBC  , A SBC      AB 2
Trong (ABCD), kẻ HM vuông góc với BC tại M. Kẻ đường cao HN của tam giác SHM . Ta chứng
minh được: HN  SBC hay d H ,SBC  HN . 1 Ta có: 2 2 S  .4 .2
a a  4a S  2a . ABCD  2 ABC 1 Suy ra 2 SSa
(do H là trung điểm AB). HBC  2 ABC 1 1 Mặt khác: 2 S
HM .BC a HM .a 5 HBC  2 2 2 a 2a 5  HM   . a 5 5
Xét tam giác SHM vuông tại H ta có: a 15 2a 5 . SH.HM 2a 1365 2 5 HN    . 2 2 2 2  91 SH HM 15a 20a  4 25 a Choïn
Vậy d AD SC 4 1365 ,  2HN  .   D 91
Câu 48. Xét các số thực dương a, b, c  1 với a b thỏa 4log c  log c  25log c . Giá trị nhỏ nhất của a b ab
biểu thức P  log a  log c  log b bằng b a c 17 A. 5 . B. 3 . C. 8 . D. . 2 Hướng dẫngiải:    
Ta có: 4log c  log c  25log c  1 1 1 4    25  a b ab log a log b log a  log bc c   c c    2 2 a b2 4 log log
 25log a.log b  4log a a b bc
 17.logc .logc  4logc  0 c c c c
log a  4log b c c 4  a b  1       . Vì a b 1 nên 4 b a không thỏa mãn. log a  log b 4 b a c  4 c Trang 18 Với 4
a b , ta có: 4
P  log b  log c  log b  1 4 
log c  log b . 4 b c b 4 b c 1 1
Vì b, c  1 nên log c, log b  0 . Do vậy P  4 
log c  log b  4  2 c b  . b c
logb .logc  5 b c 4 4  AM GM
Dấu bằng xảy ra  1 log c  log b   c   log c  2  2 c b . b 2 log 4 4 b c b Choïn
Vậy min P  5 , khi đó 4 2
a b c .   A
Câu 49. Giả sử z , z là hai trong số các số phức z thỏa mãn iz  2  i  1 và z z  2 . Giá trị lớn nhất 1 2 1 2
của z z bằng 1 2 A. 4 . B. 2 3 . C. 3 2 . D. 3 . Hướng dẫngiải:
Ta có iz  2  i  1  i z  
1i 2 1 i z 
1i 2 1 z1i 2 1 (1).
Gọi z  1 i 2 là số phức có điểm biểu diễn là I 1; 2 ; A , B là các điểm biểu diễn của z , z . 0 1 2
Từ (1) suy ra IA IB  1 mà z z  2 tức là AB  2 nên I là trung điểm của AB . 1 2  AB
Ta có : z z  1.OA 1.OB  2  OA OB  2 2 2 2 2 2  22OI
  4OI AB  16  4 . 1 2  2  Bianhiakopxki
Dấu bằng xảy ra  OA OB  2  z z  2 . Vậy giá trị lớn nhất của z z bằng 4 . 1 2 1 2  Choï n A
Câu 50. Cho hàm số y f x liên tục trên đoạn 1; 
3 và có bảng biến thiên như sau: m
Gọi S là tập tất cả các giá trị nguyên của tham số m để phương trình f x   1  có hai 2 x  6x 12
nghiệm phân biệt trên đoạn 2; 4 . Tổng các phần tử của S là A. 297  . B. 294  . C. 75  . D. 72  . Hướng dẫngiải:
Xét hàm số y f x  
1 trên 2; 4 . Ta có: x 1  1 x  2; x 1  2  x  3; x 1  3  x  4 .
Ta có bảng biến thiên cho hàm y f x   1 như sau: Trang 19 Đặ m m t g x   . 2 x  6x 12 x 32 3 m 2  x  6
Hàm số y g x xác định trên đoạn 2; 4 và có đạo hàm g x     .
x  6x 122 2 m
Số nghiệm của phương trình f x   1   
1 là số giao điểm của hai đồ thị hàm số 2 x  6x 12 m
y f x  
1 và y g x  . 2 x  6x 12
Trường hợp 1: m  0. Khi đó   m g x   0 , x
  2;4 mà f x   1  1  , x
 2;4 nên (1) vô nghiệm. 2   x 3 3
Trường hợp 2: m  0. Ta có: gx  0  x  3. Bảng biến thiên của y g x trên đoạn 2;4:
Dựa vào hai bảng biến thiên của y f x  
1 và y g x , ta khẳng định: m    g   6   4 2 6     m
1 có hai nghiệm phân biệt  g 3  1     1   1  2  m  3  .   g   3 4  3   m  3   4
Ta lại có m nguyên suy ra S   1  2;11;...; 4; 
3 , số phần tử của S là 10.  12   3.10 Choïn
Suy ra tổng các phần tử của S là:  75  .   C 2 Trang 20 ĐỀ SỐ 03
ĐỀ RÈN LUYỆN MÔN TOÁN 12
HƯỚNG ĐẾN KÌ THI THPT QUỐC GIA
Trắc nghiệm: 50 câu Nội dung:
Thời gian: 90 phút
FULL KIẾN THỨC TOÁN 12+ Câu 1.
Họ nguyên hàm của hàm số 2 x x y e e   là 1   1 A. 2 xx ee C . B. 2 2 x x ee C . C. 2 2 x x ee C . D. 2 xx ee C . 2 2
Câu 2. Tập nghiệm của phương trình : 2 log x  2 là : 5 A.   5 . B.  5 . C.  5 . D. . 
Câu 3. Trên mặt phẳng tọa độ, cho điểm M 5 
;1 biểu diễn số phức z . Phần ảo của số phức z là A. 5 . B. i . C. 1. D. 5i .
Câu 4. Cho u là một cấp số cộng có u  3 và công sai d  2 . Tìm u . n  1 20 A. 39 . B. 43. C. 41 . D. 45 .
Câu 5. Trong không gian với hệ tọa độ Oxyz , phương trình nào dưới đây là phương trình mặt phẳng Oyz ?
A. y z  0 .
B. x  0 .
C. y  0 . D. z  0 .
Câu 6. Cho khối nón có diện tích đáy bằng 2
a và đường sinh l  5 .
a Tính thể tích khối nón đó. 2 8 4 A. 3 V   a . B. 3 V   a . C. 3 V  2 a . D. 3 V   a . 3 3 3 1
Câu 7. Cho hàm số F x là một nguyên hàm của f x . Biết F   1  3  , F  2
  12 . Tính I f  xdx ? 2  A. I  15 . B. I  36  . C. I  15  . D. I  9 .
Câu 8. Tập xác định của hàm số 5 y x  là A.  ;0  . B.  \   0 . C.  ;0   . D.0;   . Câu 9. Cho hàm số 4 2
y ax bx c có đồ thị như hình vẽ bên dưới. Số
nghiệm thực của phương trình f x  f 0 là A. 3 . B. 0 . C. 4 . D. 2 .
Câu 10. Trong không gian với hệ tọa độ Oxyz , hình chiếu của điểm M 1; 2;3 lên trục Oy là điểm
A. R 1;0;0 .
B. P 1;0;3 .
C. Q 0; 2;0 .
D. S 0;0;3 . 2 2 2
Câu 11. Trong không gian Oxyz , cho mặt cầu S  :  x  2   y   3  z   1
 49. Tìm tọa độ tâm I và
tính bán kính R của S . A. I 2; 3  ;  1 , R  49 .
B. I 2; 3;  1 , R  7 . C. I  2  ;3;  1 , R  7 . D. I 2; 3   ;1 , R  7 . m
Câu 12. Cho hàm số f x 3 2 
x  2mx  m  9 x  2021 2022 . Có bao nhiêu giá trị nguyên của tham số 3
m để hàm số đã cho nghịch biến trên  ? A. 4 . B. 3 . C. 2 . D. Vô số. Trang 21
Câu 13. Cho tứ diện đều ABCD . Gọi M là trung điểm của BC , cosin góc giữa AB và DM bằng 2 3 3 A. . B. . C. . D. 3 . 2 3 6 x  3 y 1 z  7
Câu 14. Trong không gian Oxyz , cho điểm A1; 2; 
3 và đường thẳng d :   . Đường thẳng 2 1 2 
 đi qua A và song song với d có phương trình là x 1 3tx  3 tx 1 2t
x  2  t    
A. y  2  t .
B. y  1 2t .
C. y  2  t .
D. y  1 2t .     z  3  7tz  7   3tz  3  2tz  2   3t
Câu 15. Cho log 2  a và log 3  b . Biểu diễn log 360 dưới dạng log 360  ma nb p , với , m , n p là 5 5 5 5
các số nguyên. Tính A m n  2 p . A. A  9. B. A  7 . C. A  8 . D. A  10.
Câu 16. Trong không gian, cho tam giác ABC vuông tại A , AB  2a và AC a . Khi quay tam giác ABC
xung quanh cạnh góc vuông AB thì đường gấp khúc ACB tạo thành một hình nón. Diện tích xung
quanh của hình nón đó bằng A. 2 5 a . B. 2 5 a . C. 2 20 a . D. 2 2 5 a .
Câu 17. Tập nghiệm của bất phương trình 4x 6.2x   8  0 là A. 2; 4 . B. 0; 2 . C.   ;1  2; . D. 1; 2 . 1
Câu 18. Tổng số tiệm cận đứng và ngang của đồ thị hàm số y  bằng: 4 2 x x  2 A. 5 . B. 3 . C. 4 . D. 1.
Câu 19. Trong không gian Oxyz , cho mặt cầu (S ) : 2 2 2
x  ( y 1)  (z 1)  4 và mặt phẳng (P) :
2x y  2z 1  0 . Khoảng cách từ tâm I của (S ) đến (P) bằng 2 4 A. . B. 2. C. 1. D. . 3 3
Câu 20. Thể tích của vật thể tròn xoay sinh bởi hình phẳng giới hạn bởi đồ thị hàm số 2
y x x  6 và trục
hoành quay quanh trục hoành được tính theo công thức 1 3 A.   2
x x  6dx . B.    4 3 2
x  2x 11x 12x  36dx . 0 2 3 1 C.    2
x x  6dx . D.    4 3 2
x  2x 11x 12x  36dx . 2 0 3 x
Câu 21. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số 2 y
 2x  3x  4 trên đoạn  4  ;0 lần lượt là 3
M và m . Giá trị của tổng M m bằng bao nhiêu? 4 4 28
A. M m   .
B. M m  .
C. M m   .
D. M m  4  . 3 3 3
Câu 22. Cho hình chóp S.ABC có đáy là tam giác đều cạnh a . Biết SA vuông góc với mặt phẳng đáy và  SBA 30 
. Thể tích khối chóp S.ABC bằng: 3 a 3 a 3 a 3 a A. . B. . C. . D. . 2 4 6 12 e ln x e ln x Câu 23. Xét dx
, nếu đặt u  ln x thì dx  bằng 2x 2x 1 1 1 1 1 e 1 e A. 2 d u u  . B. d u u  . C. udu  . D. d u u  . 2 2 0 0 1 1 Trang 22
Câu 24. Tập nghiệm của bất phương trình log 2x  3  log 3x 1  0 là 1   2   2 1 2 A.   x  2 . B.   x  2 . C. x  2 . D. x  2 . 3 3
Câu 25. Cho khối lăng trụ đều AB . C A BC
  có AB  2a, M là trung điểm BC và A M
  3a. Thể tích của
khối lăng trụ đã cho bằng A. 3 18a 2 . B. 3 3a 2 . C. 3 a 2 . D. 3 9a 2 .  2
Câu 26. Xét I f  xcos d
x x . Nếu đặt u f x và dv  cos d x x thì 0    2  2
A. I   f xsin x 2  f   xsin d x x .
B. I   f xsin x 2  f   xsin d x x . 0 0 0 0    2  2
C. I    f xsin x 2  f   xsin d x x .
D. I    f xsin x 2  f   xsin d x x . 0 0 0 0 x 1 y  2 z Câu 27. Trong không gian Oxyz , cho đường thẳng  :   và mặt phẳng 2 1 1
P:2m 
1 x  5m  
1 y  m  
1 z  5  0 . Tìm m để  song song với  P . A. m  1  . B. m  3  . C. m 1.
D. Không tồn tại m .
Câu 28. Gọi S là tập hợp tất cả các giá trị của tham số m để hàm số 4 2
y x  2mx m 1 có giá trị cực tiểu
bằng 1. Tổng các phần tử thuộc S là A. 2  . B. 0 . C.1. D. 1.
Câu 29. Trong không gian Oxyz , cho ba điểm A2;0;0, B 0; 3
 ;0, C 0;0;6 . Tọa độ một vectơ pháp
tuyến của mặt phẳng  ABC  là    
A. n  2; 3;6 . B. n  1; 2  ;3 . C. n  3; 2   ;1 .
D. n  3; 2;  1 .
Câu 30. Ký hiệu z là nghiệm phức có phần ảo âm của phương trình 2
z  4z 13  0. Trên mặt phẳng toạ độ, 0
điểm nào dưới đây là điểm biểu diễn của số phức iz ? 0 A. M (3; 2). B. M (2;3). C. M (2; 3  ). D. M ( 3  ;2). 1 2 3 4
Câu 31. Cho hình lăng trụ đứng AB . C A BC
  có đáy ABC là tam giác vuông cân tại B có AB  ,
a AA  a 2 . Góc giữa đường thẳng A C
 với mặt phẳng  AA BB   bằng: A. 60 . B. 30 . C. 45 . D. 90 . 1 1
Câu 32. Cho hàm số f x có đạo hàm liên tục trên  . Biết . x f  
xdx 10 và f   1  3 , tính
f xdx  . 0 0 A. 30 . B. 7 . C. 13 . D. 7  .
Câu 33. Số phức nào sau đây không phải số thuần ảo?
A. z i 3 .
B. z  i   1 i .
C. z  0.
D. z  1 2i .
Câu 34. Trong không gian Oxyz cho hai điểm A1; 2; 
3 và B 3;3;4 và mặt phẳng  P : x  2y z  0. Gọi A ,
B lần lượt là hình chiếu vuông góc của A và B lên mặt phẳng P . Tính độ dài đoạn thẳng AB . 6 3 A. . B. 3 . C. 6 . D. . 2 2 Trang 23
Câu 35. Diện tích hình phẳng gạch chéo trong hình vẽ bên được tính
theo công thức nào dưới đây? 1 A. 3 2
(x  3x x  3)d . x  1  1 B. 3 2
(x  3x x  3)d . x  1  1 C. 3 2
(x  3x x  3)d . x  1  3 D. 3 2
(x  3x x  3)d . x  1 
Câu 36. Cường độ trận động đất M (Richter) được cho bởi công thức M  log A  log A , với A là biên độ 0
rung chấn tối đa và A là một biên độ chuẩn (hằng số). Đầu thế kỷ 20, một trận động đất ở San 0
Francisco có cường độ 8,3 độ Richter. Cũng trong cùng năm đó, một trận động đất khác ở Nam Mỹ
có cường độ 9,3 độ Richter. Hỏi trận động đất ở Nam Mỹ có biên độ rung chấn tối đa gấp mấy lần
biên độ trận động đất ở San Francisco? A. 20 . B. 10 . C. 2 . D. 100 .
Câu 37. Có tất cả bao nhiêu giá trị thực của tham số m để đường thẳng y mx m 1 cắt đồ thị hàm số 3 2
y x  3x x  2 tại ba điểm A, B và C 1; 
1 phân biệt sao cho  y y 2  4 . A B A. 1. B. 3 . C. 2 . D. 0 .
Câu 38. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật cạnh AB  2AD  2a . Tam giác SAB đều
nằm trong mặt phẳng vuông góc với mặt đáy. Khoảng cách từ A đến mặt phẳng SBD bằng a 3 a a 3 A. a . B. . C. . D. . 4 2 2 x y z 1 x  3 y z
Câu 39. Trong không gian Oxyz , cho hai đường thẳng d :   , d :  
. Gọi M a, , b c 1 2 2 1  1 1 1 2 
là giao điểm của d và d . Tính a  2b  3c. 1 2 A. 2 . B. 5 . C. 6 . D. 3 . 1 dx 8 2 Câu 40. Cho  a b a    *
a,b    . Tính a  2b . x  2  x 1 3 3 0
A. a  2b  1  .
B. a  2b  8 .
C. a  2b  7 .
D. a  2b  5. x 1 y  2 z Câu 41. Trong không gian
Oxyz , cho đương thẳng  :   và mặt phẳng 1 1 1 
P: x  2y  2z 6  0. Phương trình đường thẳng d nằm trong P sao cho d cắt, đồng thời vuông góc với  là
x  2  4t
x  2  4t
x  2  4t
x  2  4t    
A. y  3  3t .
B. y  3  3t .
C. y  3  3t .
D. y  3  3t .     z  1 tz  1 tz  1   tz  1   t
Câu 42. Cho hình trụ có bán kính đáy bằng 3a 2 . Biết rằng khi cắt hình trụ đã cho bởi một mặt phẳng song
song với trục và cách trục một khoảng bằng 3a , thiết diện thu được là một hình vuông. Thể tích của
khối trụ được giới hạn bởi hình trụ đã cho bằng 108 A. 3  a . B. 3 54 a . C. 3 216 a . D. 3 108 a . 3
Câu 43. Cho hàm số f (x) có bảng biến thiên như sau. Trang 24 4  Đồ x 1
thị hàm số g x 
có tất cả bao nhiêu đường tiệm cận đứng 2
f x  4 f xA. 2 . B. 5 . C. 4 . D. 3 .
Câu 44. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a , mặt bên SAB là tam giác cân tại S và
nằm trong mặt phẳng vuông góc với đáy. Biết rằng góc giữa SBC  và  ABC  bằng 60 . Tính thể
tích khối chóp S.ABC . 3 a 3 3 a 3 3 a 3 3 3a 3 A. . B. . C. . D. . 4 16 8 16
Câu 45. Cho số phức z thỏa mãn   i 10 1 2 z
 2  i . Khẳng định nào sau đây là đúng? z 1 3 1 3 A. z  . B. z  2 . C. z  2 . D. z  ;   . 2 2 2 2
Câu 46. Cho hàm số y f x có đồ thị như hình vẽ bên. Số nghiệm thực của bất phương trình  f  3 2 x x   2  f  3 2 1 3 1 2 x  3x   1  2 là A. 3 . B. 5 . C. 4 . D. 2 .
Câu 47. Gọi S là tập hợp tất cả các số tự nhiên có 7 chữ số. Lấy ngẫu nhiên một số từ tập S . Xác suất để số
lấy được có tận cùng là 3 và chia hết cho 7 (làm tròn đến chữ số phần nghìn) có dạng 0,abc . Tính 2 2 2
a b c . A. 15 . B. 10 . C. 17 . D. 16 . c c
Câu 48. Cho các số thực dương a; ;
b c khác 1và thỏa mãn điều kiện 2 2
log b  log c  2 log  log . Gọi a b b a 3 b a b
M , m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức P  log ab  log bc . Tìm giá trị của a b biểu thức 2 2
S  2m  9M . A. S  28 . B. S  25 . C. S  26 . D. S  27 .
Câu 49. Cho mặt cầu 2 2 2
(S) : x y z  2x  2 y  2z  0 . Điểm A2; 2;0 . Viết phương trình mặt phẳng
OAB biết điểm B là một điểm thuộc mặt cầu S, có hoành độ dương và tam giác OAB đều.
A. x y  2z  0 .
B. x y  2z  0 .
C. x y z  0 .
D. 2  y z  0 .
Câu 50. Cho hàm số f x 3
x 3x m . Có tất cả bao nhiêu số nguyên m thuộc khoảng  2  0;20 để với
mọi bộ ba số thực a, b, c  2  ; 
1 thì f a, f b, f clà độ dài ba cạnh của tam giác ? Trang 25 A. 24 . B. 26 . C. 28 . D. 30 .
________________HẾT________________
ÑAÙP AÙN ÑEÀ SOÁ 03 1 2 3 4 5 6 7 8 9 10 D B C C B A C B A C 11 12 13 14 15 16 17 18 19 20 D A C C B B D B D B 21 22 23 24 25 26 27 28 29 30 C D B D B B C B C A 31 32 33 34 35 36 37 38 39 40 B D B D B B B D C B 41 42 43 44 45 46 47 48 49 50 D D C B D C C D C B
Lôøi giaûi caâu hoûi vaän duïng cao ñeà soá 03
Câu 43. Cho hàm số f (x) có bảng biến thiên như sau. 4 x 1
Đồ thị hàm số g x 
có tất cả bao nhiêu đường tiệm cận đứng 2
f x  4 f x A. 2 . B. 5 . C. 4 . D. 3 . Hướng dẫn giải:
f x  0 Xét 2
f x  4 f x  0   .  f   x  4   f xx 1  0  
(trong đó x 1 là nghiệm kép, x x là là nghiệm đơn). Không làm mất tính x x  1 1 2
tổng quát, ta biểu diễn f x  a x 1
x x , a  0 . 1    1  1    f xx 1  4   (trong đó x  1
 là nghiệm kép, x x là là nghiệm đơn). Không làm mất tính x x  2 2 2
tổng quát, ta biểu diễn f x  4  a x 1 x x , a  0 . 2    2  2  2x   2 1 x   1
Ta viết lại hàm số ban đầu: g x 
f x  f x  4   Trang 26x   1  x   1  2 x   2 1 x 1   . a x 1 x x a x 1 x x a a
x 1 x 1 x x x x 1  2  1  2  2  2  1 2    1   2 
Ta thấy đồ thị hàm số y g x có bốn đường tiệm cận đứng: x  1
 , x x , x x . Choïn   C 1 2
Câu 44. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a , mặt bên SAB là tam giác cân tại S và
nằm trong mặt phẳng vuông góc với đáy. Biết rằng góc giữa SBC  và  ABC  bằng 60 . Tính thể
tích khối chóp S.ABC . 3 a 3 3 a 3 3 a 3 3 3a 3 A. . B. . C. . D. . 4 16 8 16 Hướng dẫn giải:
Gọi H là trung điểm của AB SH AB . Ta có
SAB  ABC suy ra SH  ABC.
Gọi M là trung điểm của BC và I là trung điểm của BM .
Khi đó: AM BC mà HI //AM (tính chất đường trung
bình), suy ra HI BC . BC HI Vì 
BC  SHI   BC SI . BC SH
 SBC  ABC  BC
Ta có: HI BC, SI BC  
SBC ABC   HI SI   , ,  SIH  60 . a 3 1 a 3 Xét ABC
đều cạnh a AM
HI AM  . 2 2 4 a Xét SHI vuông tại  3
H SH HI  tan SIH  . 4 2 3 1 1 3a a 3 a 3 Choïn
Thể tích khối chóp:VSH S     .   B S. ABC  3 ABC 3 4 4 16
Câu 45. Cho số phức z thỏa mãn   i 10 1 2 z
 2  i . Khẳng định nào sau đây là đúng? z 1 3 1 3 A. z  . B. z  2 . C. z  2 . D. z  ;   . 2 2 2 2 Hướng dẫn giải:   10 10
Ta có 1 2iz
 2  i  1 2iz  2  i
  z  2  2 z  
1 i .z  10 (*) .  z z     ab  2 2 2
Lấy mô đun 2 vế ta được:  z  2  2 z  
1 . z  10  5 z  5. z  10  2 2 a b 2  z 1 ( ) n 4 2  1 3 Choïn
5 z  5 z 10  0  
z 1.Vậy z  ;   .   D 2  z  2  (l)  2 2
Câu 46. Cho hàm số y f x có đồ thị như hình vẽ bên. Số nghiệm thực của bất phương trình  f  3 2 x x   2  f  3 2 1 3 1 2 x  3x   1  2 là Trang 27 A. 3 . B. 5 . C. 4 . D. 2 . Hướng dẫn giải:
Đặt t f  3 2 x  3x  
1 . Bất phương trình trở thành: 2
1 t  2t  2 t   1   t   1       t  .  1 t   1 2 2 2  2t  2  t   2t 1 0 3 2
x  3x 1  a  2  ; 1  Ta có: f  3 2 x  3x     1  1   . 3 2
x  3x 1  b  1;2 x  0
Xét hàm số g x 3 2
x 3x 1, gx 2  3x  6 ,
x g x  0  
. Bảng biến thiên g x : x  2 Ta có:Phương trình 3 2
x  3x 1  a  2  ; 
1 có ba nghiệm phân biệt x , x , x . 1 2 3 Phương trình 3 2
x  3x 1  b 1;2 có một nghiệm x khác x , x , x . 4 1 2 3 Choïn
Vậy bất phương trình đã cho có bốn nghiệm thực.   C
Câu 47. Gọi S là tập hợp tất cả các số tự nhiên có 7 chữ số. Lấy ngẫu nhiên một số từ tập S . Xác suất để số
lấy được có tận cùng là 3 và chia hết cho 7 (làm tròn đến chữ số phần nghìn) có dạng 0,abc . Tính 2 2 2
a b c . A. 15 . B. 10 . C. 17 . D. 16 . Hướng dẫn giải: Cách giải 1:
Số phần tử của không gian mẫu là: n 6  9.10 .
Gọi A là biến cố: “Số lấy được có tận cùng là 3 và chia hết cho 7”.
Gọi số tự nhiên có 7 chữ số chia hết cho 7 và có chữ số tận cùng bằng 3 là: a a a a a a 3 . 1 2 3 4 5 6
Ta có: a a a a a a 3  10.a a a a a a  3  3.a a a a a a  7.a a a a a a  3 7 1 2 3 4 5 6 1 2 3 4 5 6
 1 2 3 4 5 6 1 2 3 4 5 6  Trang 28
 3.a a a a a a 3 7 . 1 2 3 4 5 6  Đặt: k
3.a a a a a a  3  7k
k    a a a a a a  2k 1
là số nguyên nên k  3m m   . 1 2 3 4 5 6   1 2 3 4 5 6 3 Khi đó 100 001 1 000 000
: a a a a a a  7m 1. Do đó: 100 000  7m 1  999 999   m  . 1 2 3 4 5 6 7 7     1  4 285,8 1  42 857,1
Do m    m 14 286;14 287;...;142 85 
7 . Vì vậy có 142 857 14 286 1  128 572 giá trị của
m thỏa mãn. Suy ra n A  128 572 . n A Xác suất của biến cố 128572
A là: P A     
. Suy ra: a  0, b  1, c  4 . n  0, 014 6 9.10 Vây 2 2 2
a b c  17 . Choïn   C Cách giải 2:
Số phần tử của không gian mẫu là: n 6  9.10 .
Gọi A là biến cố: “Số tự nhiên lấy được có tận cùng là 3 và chia hết cho 7”.
Gọi số tự nhiên thỏa mãn biến cố A là X, ta có: 1 000 013  X  9 999 983 .
Ta thấy số nhỏ nhất mà X có thể nhận được là 1 000 013 , số lớn nhất mà X có thể nhận là 9 999 983 .
Chênh lệch giữa hai số liên tiếp thỏa mãn đề bài là 70 đơn vị. Vì vậy ta có thể thấy tập hợp các số tự
nhiên X sẽ lập nên một cấp số cộng có số hạng đầu là u  1 000 013 , công sai d  70 , số hạng cuối 1 là 9 999 983 . 9 999 983 1 000 013
Do vậy số các số tự nhiên mà X có thể nhận là: 1  128 572 (số). 70 n A 128572
Suy ra n A  128 572 .Xác suất của biến cố A là: P A      . n  0, 014 6 9.10 Choïn
Suy ra: a  0, b  1, c  4 . Vây 2 2 2
a b c  17 .   C c c
Câu 48. Cho các số thực dương a; ;
b c khác 1và thỏa mãn điều kiện 2 2
log b  log c  2 log  log . Gọi a b b a 3 b a b
M , m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức P  log ab  log bc . Tìm giá trị của a b biểu thức 2 2
S  2m  9M . A. S  28 . B. S  25 . C. S  26 . D. S  27 . Hướng dẫn giải:
log c x Pb
Ta có: P  log ab  log bc  log b  log c .Đặt log b x   . a b a b a log c  log .
b log c x x Pa a b   c c Ta có: 2 2
log b  log c  2 log  log a b b a 3 b a b 2  
 log b  log c  2           log b.  log c 2  log c 2  log c 3  log b a b a b b a a  P  x xP xP
xxPx 2
P  2xx P  2x P  2  xx P 3 x 2 2 2
P  2x  2Px  2x  2P  2  x Px  3  x 2
x    P 2 3
x P  2P 1  0 (*). Do phương trình  2
* luôn có nghiệm x nên     P   2 3
4 P  2P   1  0 2
 3P  2P  5  0 Trang 29 5 5
 1  P   m  1, M  . 3 3 Thay vào ta có 2 2
S  2m  9M  27 . Choïn   D
Câu 49. Cho mặt cầu 2 2 2
(S) : x y z  2x  2 y  2z  0 . Điểm A2; 2;0 . Viết phương trình mặt phẳng
OAB biết điểm B là một điểm thuộc mặt cầu S, có hoành độ dương và tam giác OAB đều.
A. x y  2z  0 .
B. x y  2z  0 .
C. x y z  0 .
D. 2  y z  0 . Hướng dẫn giải: Gọi B  ;
x y; z với x  0 và H trung điểm OA H 1;1;0 .
Gọi P là mặt phẳng trung trực đoạn OA, do đó P đi qua trung điểm H 1;1;0 của đoạn OA và 
nhận OA  2; 2;0 làm vectơ pháp tuyến. Suy ra P : 2. x   1  2. y  
1  0  x y  2  0 .   B P OB AB
x y  2  0    Theo giả thiết: 2 2 O
B OA OB OA 2 2 2
 x y z  8    B  S B   S 2 2 2 
x y z  2x  2 y  2z  0  x y  2 x y  2 x y  2 x y  2     2 2 2 2 2
 x y z  8  x y  4  
x y2  2xy  4  xy  0    
2x  2 y  2z  8 z  2   z  2 z  2   x  2 
Suy ra:  y  0  B(2;0;2) , (do x  0 ). z  2    
Ta có : OA  2;2;0, OB  2;0;2  O , A OB  4; 4  ; 4    41;1;  1   . 
Mặt phẳng OAB đi qua O , nhận n  1; 1;  
1 là một vectơ pháp tuyến. Choïn
Vậy phương trình OAB là: x y z  0 .   C
Câu 50. Cho hàm số f x 3
x 3x m . Có tất cả bao nhiêu số nguyên m thuộc khoảng  2  0;20 để với
mọi bộ ba số thực a, b, c  2  ; 
1 thì f a, f b, f clà độ dài ba cạnh của tam giác ? A. 24 . B. 26 . C. 28 . D. 30 . Hướng dẫn giải: Xét g x 3
x 3x m , gx 2
 3x 3  0  x  1  . Ta có: g  2
   m  2 ; g  
1  m  2 ; g  
1  m  2 . Suy ra: m  2  f x  m  2 , x   2   ;1 .
Ta có: Min f x  f a, f b, f c  Max f x .  2  ;  1  2  ;  1
Không mất tính tổng quát, giả sử f a  f b  f c .
Điều kiện cần và đủ để f a, f b, f clà độ dài ba cạnh của tam giác là:
f a  f b  f c  f a  f b  f c  0 .
Yêu cầu bài toán cho ta điều kiện: f a  f b  f c  2 Min f x  Max f x  0 (1).  2  ;  1  2  ;  1 Trang 30
Trường hợp 1: m  2  m  2  0  m  2 . Khi đó
Max f x  Max m  2 ; m  2  m  2  m  2 ; Min f x  Min m  2 ; m  2  m  2  m  2 .      2;1  2  ;   1 
Thay vào (1): 2 m  2  m  2  0  m  6  0  m  6 . Vì m nguyên thuộc khoảng  2  0;20
nên m 7;8;...;1 
9 , ta tìm được 13 giá trị m thỏa mãn.
Trường hợp 2: m  2  m  2  0  m  2  . Khi đó:
Max f x  Max m  2 ; m  2  m  2  m  2 ;    2;1 
Min f x  Min m  2 ; m  2  m  2  m  2 .    2;1 
Thay vào (1): 2 m  2  m  2  0  m  6
 . Vì m nguyên thuộc khoảng  2  0;20 nên m  1  9; 1  8;... 
7 , ta tìm được 13 giá trị m thỏa mãn.
Trường hợp 3: m  2  0  m  2  2   m  2 .
m  2  m  2  m  2  m  2
Khi đó: Max f x  Max m  2 ; m  2           m  2 ;  2  ;  1 2
Min f x  0 . Do vậy (1) trở thành: 2.0   m  2  0   m  2  0 (vô lí).  2  ;  1 Choïn
Vậy số giá trị m thỏa mãn đề bài là: 1313  26 .   B ĐỀ SỐ 04
ĐỀ RÈN LUYỆN MÔN TOÁN 12
HƯỚNG ĐẾN KÌ THI THPT QUỐC GIA
Trắc nghiệm: 50 câu Nội dung:
Thời gian: 90 phút
FULL KIẾN THỨC TOÁN 12+ Câu 1.
Cho hai số phức z  2  3i và z  1 i . Môđun của số phức 2z  3z bằng 1 2 1 2 A. 58 . B. 113 . C. 82 . D. 137 . 4
Câu 2. Giá trị nhỏ nhất của hàm số y  1 x  trên đoạn  3  ;  1 bằng x Trang 31 A. 5 . B. 4  . C. 6  . D. 5  .
Câu 3. Cho a là số thực dương và khác 1. Giá trị của biểu thức T   3 log a bằng a  3 A. 3 a . B. . C. 6 . D. 3 . 2 x  3 y  2 z 1
Câu 4. Trong không gian Oxyz , cho đường thẳng d :  
. Điểm nào sau đây không thuộ  c d 1 3 2  ? A. Q  3  ; 2   ;1 . B. M 4; 1   ;1 . C. N 2;5; 3   .
D. P 3; 2;   1 .
Câu 5. Số phức liên hợp của số phức z i 3  4i là
A. z  4  3i . B. z  4  3i .
C. z  4  3i . D. z  4   3i .
Câu 6. Cho hàm số y f x liên tục trên  , có bảng biến thiên như sau:
Hàm số đã cho đạt cực tiểu tại A. x  4 . B. x  2 . C. x  3. D. x  2  .
Câu 7. Cho hình hộp đứng ABC . D A BCD
  có cạnh bên AA  h và diện tích tam giác ABC bằng S . Thể
tích của khối hộp ABC . D A BCD   bằng: 1 2 A.V Sh . B.V Sh .
C.V Sh .
D.V  2Sh . 3 3
Câu 8. Tìm tập xác định của hàm số y  log 2x 1 . 1   2  1   1 
A. D  1;  . B. D  ;1   .
C. D  1;  . D. D  ;1   .  2   2 
Câu 9. Trong mặt phẳng Oxy , cho các điểm ,
A B như hình vẽ bên. Trung điểm của đoạn thẳng AB là điểm
biểu diễn của số phức nào sau đây? 1 A.   2i . 2 B. 1   2i . C. 2  i . 1 D. 2  i . 2
Câu 10. Trong không gian Oxyz , cho hình hộp ABC . D A BCD   có A1;0  ;1 ,
B 2;1; 2 , D 1; 1 
;1 , C4;5;  5 . Tính tọa độ đỉnh A của hình hộp.
A. A4;6;  5 .
B. A2;0; 2 .
C. A3;5;  6 .
D. A3; 4;  6 .
Câu 11. Đồ thị của hàm số nào dưới đây có dạng là đường cong trong hình bên ? A. 3
y  x  3x . B. 4 2
y  x x . Trang 32 C. 3 2
y  x  3x . D. 4 2
y x x .
Câu 12. Cho mă ̣t cầu có đường kính bằng 4a . Thể tích khối cầu tương ứng bằng 3 32 a 3 8 a A. 3 32 a . B. . C. 3 16 a . D. . 3 3
Câu 13. Trong không gian Oxyz , cho ba điểm M 2;0;0 , N 0;1;0 và P 0;0; 2 . Mặt phẳng MNP có phương trình là x y z x y z x y z x y z A.    1 B.    1 . C.    1 . D.    1. 2 1 2 1 2 2 2 1 2 2 2 1
Câu 14. Cho hàm số y f x có đồ thị như hình vẽ bên. Mệnh đề nào sau đây đúng về hàm số đó?
A.Đồng biến trên khoảng 0; 2 .
B.Nghịch biến trên khoảng  3  ;0.
C.Đồng biến trên khoảng  1  ;0 .
D.Nghịch biến trên khoảng 0;3 .
Câu 15. Kí hiệu z , z , z , z là bốn nghiệm của phương trình 4 2
z z  6  0 . 1 2 3 4
Tính S z z z z . 1 2 3 4 A. S  2 3 .
B. S  2 2  3 . C. S  2 2 .
D. S  2 2  3 . 3  x x d Câu 16. Cho 1 2 e  . a e  . b e  c
. Với a , b , c là các số nguyên. Tính S a b c . x 1 0 A. S  1. B. S  2 . C. S  0 . D. S  4 .
Câu 17. Tìm tập nghiệm S của phương trình log  2
x  2x  3  log x 1  1. 3  3  
A. S  0;  5 . B. S    5 . C. S    0 .
D. S  1;  5 .
Câu 18. Cho hình chóp S.ABCD . Gọi M , N , P , Q theo thứ tự là trung điểm của SA , SB , SC , SD . Tính
tỉ số thể tích của hai khối chóp S.MNPQ và S.ABCD bằng 1 1 1 1 A. . B. . C. . D. . 8 2 4 16 2 x  7x  6
Câu 19. Tìm sốtiệm cận của đồ thị hàm số y  2 x  . 1 A. 1. B. 2 . C. 3 . D. 0 . 1 dx
Câu 20. Tích phân  bằng 3x 1 0 4 3 1 2 A. . B. . C. . D. . 3 2 3 3
Câu 21. Bất phương trình log x  7  log
x 1 có tập nghiệm là. 4   2   A. 5;   . B.  1  ;2 . C. 2; 4 . D.  3  ;2.
Câu 22. Trong không gian Oxyz , cho mặt phẳng   : 3x  2y z  6  0 . Hình chiếu vuông góc của điểm A2;1; 
0 lên mặt phẳng   có tọa độ là Trang 33 A. 1;0;3 . B. 2; 2  ;3. C. 1;1;  1  . D.  1  ;1;  1 .
Câu 23. Cho hàm số bậc bốn y f (x) có đồ thị như hình bên dưới, số
nghiệm của phương trình 2 f x 1  0 là A. 2. B. 4. C. 3. D. 1.  2
Câu 24. Cho hàm số y f x thỏa mãn sin . x f
xdx f 0 1. Tính 0  2 I  cos . x f   xdx . 0 A. I  1. B. I  0. C. I  2 . D. I  1  . mx 1   1 
Câu 25. Tìm tất cả các giá trị của m để hàm số  2 xm y nghịch biến trên ;   .  2   1  1   1  A. m  1  ;  1 . B. m  ;1   . C. m  ;1 . D. m   ;1   .    2  2   2 
Câu 26. Cho hai số thực a, b thoả mãn 2a b  0 và 2log 2a b  log a  log .
b Giá trị của biểu thức 3   3 3 b T  bằng a A. 1. B. 4. C. 3. D. 2.
Câu 27. Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a , M là trung điểm cạnh SD . Giá
trị tang của góc giữa đường thẳng BM và mặt phẳng  ABCD bằng 1 2 3 2 A. . B. . C. . D. . 3 2 3 3
Câu 28. Thể tích khối lập phương ABC . D A BCD
  có đường chéo AC  2 6 bằng A. 24 3 . B. 48 6 . C. 6 6 . D. 16 2 .
Câu 29. Cho hàm số f x , biết f  x có đồ thị như hình bên. Số điểm
cực trị của hàm số f x là A. 2 . B. 1. C. 3 . D. 0 .
Câu 30. Trong không gian Oxyz , cho điểm M 1;0; 
1 . Mặt phẳng   đi
qua M và chứa trục Ox có phương trình là A. y  0 .
B. x z  0.
C. y z 1  0 .
D. x y z  0 .
Câu 31. Giá trị của biểu thức A  log 3.log 4.log 5...log 64 bằng 2 3 4 63 A. 7. B. 6. C. 8. D. 10.
Câu 32. Cho số phức z thỏa mãn: z 1 2i  z.i  15  i . Tìm mô-đun của số phức z ? Trang 34 A. z  5 . B. z  4 . C. z  2 5 . D. z  2 3 .
Câu 33. Khi quay một tam giác đều cạnh bằng a (bao gồm cả điểm trong tam giác) quanh một cạnh của nó ta
được một khối tròn xoay. Tính thể tích V của khối tròn xoay đó theo a . 3  a 3  3a 3 3 a 3  3a A. . B. . C. . D. . 4 8 4 24
Câu 34. Diện tích S của phần hình phẳng được gạch chéo trong hình bên bằng 3 1 A. 2 S x  
 2x 7x12 dx . 2 0 2 3 1 B. 2 S x dx  
 2x 7x12dx . 2 0 2 2 3 1 C. 2 S x dx  
 2x 7x12dx. 2 0 2 3 1 D. 2 S x  
 2x 7x12 dx . 2 0
Câu 35. Cho khối lăng trụ AB . C A BC
  có đáy ABC là tam giác đều cạnh bằng a 3 , cạnh bên AA  a , góc
giữa AA và mặt phẳng đáy bằng 30 . Tính thể tích khối lăng trụ đã cho theo a . 3 3a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 8 3 4 2
Câu 36. Tập nghiệm của bất phương trình 2
ln x  2 ln x  3  0 là  1   1  A.  3 ; e e  . B.  ; e  . C.  ;   ; e    . D. ; e   . 3    e  3  e
Câu 37. Cho F x là một nguyên hàm của hàm số f x 1 
thỏa mãn F 0  10 . Tìm F x . 2ex  3 1 1 x ln 5
A. F x   x  ln 2e  3 10  . B.
    10ln2ex F x x  3 . 3 3 3       
C. F x 1 x 3  x  ln e  10  ln5  ln 2    .
D. F x 1 x 3 ln 5 ln 2  x  ln e  10     . 3   2  3   2  3
Câu 38. Tìmgiá trị thực của tham số m để đường thẳng d : y  3m  
1 x  3  m vuông góc với đường thẳng
đi qua hai điểm cực trị của đồ thị hàm số 3 2
y x  3x 1. 1 1 1 1 A. m  . B.  . C. . D.  . 6 3 3 6 mx 10
Câu 39. Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng  1
 0;10 để hàm số y  nghịch 2x m
biến trên khoảng 0; 2 . A. 5 . B. 8 . C. 6 . D. 7 .
Câu 40. Cho số phức z thỏa mãn z z  2 . Biết rằng phần thực của z bằng a . Tính z theo a 1 2 a a 1 2 a a 1 2 a a  4 A. z  . B. z  . C. z  . D. z  . 1 a 2 2 2 7 3 x m m Câu 41. Cho biết dx   với
là một phân số tối giản. Tính m  7n . 3 2  n n 0 1 x A. 0 . B.1. C. 2 . D. 91. Trang 35
Câu 42. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Hình chiếu của S lên mặt phẳng đáy
trùng với trọng tâm của tam giác ABD . Cạnh SD tạo với đáy một góc 60 . Tính thể tích của khối chóp S.ABCD . 3 a 15 3 a 15 3 a 15 3 a A. . B. . C. . D. . 3 27 9 3
Câu 43. Một nhóm các chuyên gia y tế đang nghiên cứu và thử nghiệm độ chính xác của một bộ xét nghiệm
COVID 19. Giả sử cứ sau n lần thử nghiệm và điều chỉnh bộ xét nghiệm thì tỷ lệ chính xác của bộ 1
xét nghiệm đó tuân theo công thức S n  
. Hỏi phải tiến hành ít nhất bao nhiêu lần 0,01 1 2020.10 n
thử nghiệm và điều chỉnh bộ xét nghiệm để đảm bảo tỉ lệ chính xác của bộ xét nghiệm đó đạt trên 90%? A. 426 . B. 425 . C. 428 . D. 427 .
Câu 44. Cho hình trụ T  có O , O lần lượt là tâm hai đường tròn đáy. Tam giác ABC nội tiếp trong đường
tròn tâm O , AB  2a ,  1 sin ACB
và OO tạo với mặt phẳng O AB   một góc o 30 (tham khảo 3
hình bên dưới). Thể tích khối trụ T  bằng A. 3 2πa 6 . B. 3 3πa 6 . C. 3 πa 3 . D. 3 πa 6 . Câu 45. Số 100000 7 có bao nhiêu chữ số? A. 84510 . B.194591. C.194592 . D. 84509 .
Câu 46. Cho hình chóp S.ABCD có đáy là hình thang AB  2a, AD DC CB a và SA vuông góc với
mặt phẳng đáy (minh họa như hình vẽ dưới đây). Gọi M là trung điểm của cạnh AB . Khoảng cách
giữa hai đường thẳng CM và SD bằng a 3 A. . 2 3a B. . 4 3a C. . 2 D. a 3 .
Câu 47. Cho hàm số f x 3 3
 log x  log x m ( m là tham số thực). Gọi S là tập hợp tất cả các giá trị của 2 2
m sao cho max f x  min f x  6 . Tổng bình phương tất cả các phần tử của S bằng 1;4 1;4 A. 13 . B. 18 . C. 5 . D. 8 .
Câu 48. Trong không gian Oxyz , cho hai điểm A10;6; 2   , B5;10; 9   và mặt phẳng
:2x  2y z 12  0 . Điểm M di động trên  sao cho MA, MB luôn tạo với  các góc
bằng nhau. Biết rằng M luôn thuộc một đường tròn C cố định. Hoành độ của tâm đường tròn C bằng Trang 36 9 A. 4  . B. . C. 2 . D.10 . 2
Câu 49. Giả sử z , z là hai trong số các số phức z thỏa mãn iz  2  i  1 và z z  2 . Giá trị lớn nhất 1 2 1 2
của z z bằng 1 2 A. 4 . B. 2 3 . C. 3 2 . D. 3 .
Câu 50. Cho hàm số f x   2024 m   4 x   2024 2024 2  mm   2 2024 1 2 2 3 x m
 2024 , với m là tham số. Số
cực trị của hàm số y f x  2023 . A. 3 . B. 5 . C. 6 . D. 7 .
________________HẾT________________
ÑAÙP AÙN ÑEÀ SOÁ 04 1 2 3 4 5 6 7 8 9 10 C B C A C A D B A C 11 12 13 14 15 16 17 18 19 20 C B C C D C A A B D 21 22 23 24 25 26 27 28 29 30 B D B B D A A D A A 31 32 33 34 35 36 37 38 39 40 B A A C A D A D C D 41 42 43 44 45 46 47 48 49 50 B C A B A A B C A D
Lôøi giaûi caâu hoûi vaän duïng cao ñeà soá 04
Câu 44. Cho hình trụ T  có O , O lần lượt là tâm hai đường tròn đáy. Tam giác ABC nội tiếp trong đường
tròn tâm O , AB  2a ,  1 sin ACB
và OO tạo với mặt phẳng O AB   một góc o 30 (tham khảo 3
hình bên dưới). Thể tích khối trụ T  bằng A. 3 2πa 6 . B. 3 3πa 6 . C. 3 πa 3 . D. 3 πa 6 . Hướng dẫn giải: Trang 37
Gọi r là bán kính đáy của hình trụ. Tam giác ABC nội tiếp trong đườ AB 2a
ng tròn tâm O nên r    
a 3 . Gọi I là 1 2 sin ACB 2. 3 trung điểm của đoạn thẳng AB , ta có: OI AB
AB  O O
I . Kẻ đường cao OH của tam giác OO  AB OH O I  O OI , ta có:  , suy ra OH AB  do AB   O OI  OH  O A
B . Do đó: O H
 là hình chiếu vuông góc của OO
lên mặt phẳng O AB     o  OO H
  OO I  30 .
Xét tam giác OAI vuông tại I có: 2 2 2 2
OI r IA  3a a a 2 . OI Xét tam giác OO I
 vuông tại O có: OO 
a 6  h với h là chiều cao của khối trụ T . 0 tan 30 Choïn
Thể tích khối trụ T  bằng 2 3
V   r h  3 a 6 .   B Câu 45. Số 100000 7 có bao nhiêu chữ số? A. 84510 . B.194591. C.194592 . D. 84509 . Hướng dẫngiải: Ta có: 100 000 log 7
100 000.log7  84 509,80484 509;84 510 . Do đó: 84 509 100 000 84 510 log10  log 7  log10 , suy ra số 100 000 7 có ít hơn 84 510 10 một chữ số mà 84 510 10 có 84 511 chữ số nên 100 000 7 có 84510 chữ số. Choïn   A
Câu 46. Cho hình chóp S.ABCD có đáy là hình thang AB  2a, AD DC CB a và SA vuông góc với
mặt phẳng đáy (minh họa như hình vẽ dưới đây). Gọi M là trung điểm của cạnh AB . Khoảng cách
giữa hai đường thẳng CM và SD bằng a 3 3a 3a A. . B. . C. . D. a 3 . 2 4 2 Hướng dẫngiải: Trang 38
AM a CD
Ta có M là trung điểm của AD    AMCD là AM // CD
hình bình hành  CM // AD CM // SAD , mà SD  SAD
d CM , SD  d CM ,SAD  d M ,SAD   1 .
Dễ thấy MBCD cũng là hình bình hành suy ra DM BC a .
Ta thấy: AD AM DM a nên tam giác ADM đều cạnh a . a 3
Gọi H là trung điểm của AD MH AD (1) và MH  . 2
Ta lại có: MH SA (2) (do SA   ABCD ). Từ (1) và (2) suy ra MH  SAD . Do đó: a
d M SAD a 3 ,  MH Choïn
. Vậy d CM SD  3 ,  .   A 2 2
Câu 47. Cho hàm số f x 3 3
 log x  log x m ( m là tham số thực). Gọi S là tập hợp tất cả các giá trị của 2 2
m sao cho max f x  min f x  6 . Tổng bình phương tất cả các phần tử của S bằng 1;4 1;4 A. 13 . B. 18 . C. 5 . D. 8 . Hướng dẫngiải:
Đặt M  max f x , N  min f x . 1;4 1;4
Đặt t  log x ; vì x 1;4  t 0;2.Hàm số đã cho trở thành: g t 3
t 3t m . 2
Ta có gt  2
 3t  3  0  t  1
 .Bảng biến thiên của g t :
Suy ra: max g t   m  2, min g t   m  2 . 0;2 0;2
Trường hợp 1: 0  m  2  m  2  m  2 . Ta có M m  2  m  2, N m  2  m  2 .
Khi đó: M N  6  m 2  m 2  6  m  3 (nhận).
Trường hợp 2: m  2  m  2  0  m  2
 . Ta có: M m  2  2  ,
m N m  2  m  2 .
Khi đó: M m  6  2 mm 2  6  m  3  (nhận).
M m  2  M m  2
Trường hợp 3: m  2  0  m  2  2
  m  2 . Ta có:  . N  0 Trang 39 2 2
m  2  m  2 
m  4m  4  m  4m  4 m  0    Xét M   m  2  6
 m  4  m  4 (loại). m  2  0  6      m  2  6  m  8  N M 2 2
m  2  m  2 
m  4m  4  m  4m  4 m  0    Xét M   m  2  6
 m  8  m  4  (loại). m  2  0  6      m  2  6  m  4  N M Vậy S   3  ; 
3 . Suy ra tổng bình phương tất cả các phần tử của S bằng 18. Choïn   B
Câu 48. Trong không gian Oxyz , cho hai điểm A10;6; 2   , B5;10; 9   và mặt phẳng
:2x  2y z 12  0 . Điểm M di động trên  sao cho MA, MB luôn tạo với  các góc
bằng nhau. Biết rằng M luôn thuộc một đường tròn C cố định. Hoành độ của tâm đường tròn C bằng 9 A. 4  . B. . C. 2 . D.10 . 2 Hướng dẫngiải:
Gọi H , K lần lượt là hình chiếu vuông góc của , A B trên mặt phẳng  , khi đó:    
AH d A   2.10 2.6  2 12 ;   6 ; 2 2 2 2  2 1    
BK d B   2.5 2.10  9 12 ;   3. 2 2 2 2  2 1
Vì MA , MB tạo với   các góc bằng nhau nên  
AMH BMK mà AH  2BK suy ra MA  2MB . Gọi M  ;
x y; z  , ta có: MA  2MB 2 2  MA  4MB
 x  2   y  2  z  2  x  2   y  2  z  2 10 6 2 4 5 10 9    2 2 2  20 68 68
3x  3y  3z  20x  68y  68z  684  0 2 2 2
x y z x y z  228  0 . 3 3 3   Như vậy, điể 10 34 34
m M nằm trên mặt cầu  S  có tâm I ; ;     3 3 3 
và bán kính R  2 10 .
Mặt khác ta có M di động trên   , vì vậy tập hợp điểm M chính
là đường tròn giao tuyến C được tạo bởi mặt cầu S  và mặt
phẳng   . Gọi H là tâm của đường tròn C , khi đó H là hình
chiếu vuông góc của I trên mặt phẳng   . Trang 40  10 x   2t  3   Phương trình đườ 34
ng thẳng d đi qua I và vuông góc với mặt phẳng   là: d :  y   2t . Thay 3   34 z    t  3       phương trình tham số 10 34 34 2
của d vào   : 2  2t  2  2t  
t 12  0  t         , từ đó  3   3   3  3 suy ra H 2;10; 1  2. Choïn   C
Câu 49. Giả sử z , z là hai trong số các số phức z thỏa mãn iz  2  i  1 và z z  2 . Giá trị lớn nhất 1 2 1 2
của z z bằng 1 2 A. 4 . B. 2 3 . C. 3 2 . D. 3 . Hướng dẫngiải:  2  i
Ta có : iz  2  i  1  i z    1 z   
1i 2 1 (*). i  
Gọi A , B lần lượt là các điểm biểu diễn của z , z . Khi đó , A B thỏa (*) nên , A B di động trên 1 2
đường tròn C có tâm I 1; 2, bán kính R 1.
Ta có : z z  2  AB  2  2R , suy ra AB là đường kính của C hay I là trung điểm của AB . 1 2   Khi đó AB
: z z OA OB
2OA OB  2 2 2 2 2 2  22OI
  4OI AB  16  4. 1 2     2  CauchySc w h arz
Dấu bằng khi OA OB . Choïn   A
Câu 50. Cho hàm số f x   2024 m   4 x   2024 2024 2  mm   2 2024 1 2 2 3 x m
 2024 , với m là tham số. Số
cực trị của hàm số y f x  2023 . A. 3 . B. 5 . C. 6 . D. 7 . Hướng dẫngiải:
Đặt g x  f x  2023 .Ta có: gx  f x   2024 m   3 x   2024 2024 2 4 1 2 2  m  2 m  3 x ; x  0  f  x 2024 2024 2  0  2m  2 m  3 2  x   2  2024 m   1 Trang 41 2024 2024 2 2m  2 m  3 Ta thấy  m
  nên hàm số g x  f x  2023 luôn có 3 cực trị gồm 2 0, 2024 m   1 2024 2024 2 2m  2 m  3 x  0, x   . Ta lại có: 2024 a m
1 0  Đồ thị hàm g x có nhánh phải 1 2,3 g 2 2024 m   1 hướng lên trên.
Mặt khác: g     2024 m   2024 2024 2  mm   2024 2024 2 1 1 2 2 3  m 1 2  m 1  0, m   .
Ta có bảng biến thiên hàm g x  f x  2023 như sau:
Từ bảng biến thiên, ta thấyđồ thị hàm số g x luôn có ba điểm cực trị, trong đó có hai điểm cực tiểu
nằm bên dưới trục Ox . Vì vậy số cực trị của hàm số y f x  2023 là mn  3 4  7 ; trong đó y g  x
m  3 là số cực trị của hàm g x , n  4 là số giao điểm của hai đồ thị hàm số y   Ox. 0 Choïn   D ĐỀ SỐ 05
ĐỀ RÈN LUYỆN MÔN TOÁN 12
HƯỚNG ĐẾN KÌ THI THPT QUỐC GIA
Trắc nghiệm: 50 câu Nội dung:
Thời gian: 90 phút
FULL KIẾN THỨC TOÁN 12+ Câu 1.
Trong không gian với hệ tọa độ Oxyz , cho mặt cầu S x   y  2 2 2 :
1  z  2 . Trong các
điểm cho dưới đây, điểm nào nằm ngoài mặt cầu S  ? A. M 1;1;  1 .
B. N 0;1;0 . C. P 1;0  ;1 .
D. Q 1;1;0 . Trang 42
Câu 2. Cho hàm số f x xác định trên  và có bảng xét dấu đạo hàm như sau. Hỏi hàm số có bao nhiêu
điểm cực trị dương? A.2. B.3. C.1. D.4.
Câu 3. Đặt a  log 3 . Tính theo a giá trị của biểu thức log 1125 . 5 9 3 3 2 3 A. log 1125  1  . B. log 1125  2  . C. log 1125  2  . D. log 1125  1  . 9 2a 9 a 9 3a 9 a
Câu 4. Thể tích khối tứ diện đều cạnh a bằng 3 a 3 3 a 3 3 a 2 3 a 2 A. . B. . C. . D. . 4 2 12 6 x  2  2
Câu 5. Giới hạn lim bằng x2 x  2 1 1 A. . B. . C. 0 . D. 1. 2 4
Câu 6. Tập nghiệm của bất phương trình log x 1  3 là: 2   A. ;10 . B. 1;9 . C. 1;10 . D. ;9 .
Câu 7. Đồ thị hàm bậc bốn trùng phương nào dưới đây có dạng đồ thị hình vẽ bên A. 4 2
f (x)  x  2x . B. 4 2
f (x)  x  2x . C. 4 2
f (x)  x  2x . D. 4 2
f (x)  x  2x 1. x 1 t
Câu 8. Trong không gian Oxyz , cho đường thẳng d : y  2
  2t . Vectơ nào z 1t
dưới đây là vectơ chỉ phương của d ?    
A. n  1;  2  ;1 .
B. n  1; 2  ;1 . C. n   1  ; 2;  1 . D. n   1  ;2  ;1 .
Câu 9. Đồ thị hàm số nào trong các hàm số được cho dưới đây không có tiệm cận ngang? x  2 x  2 2 x 1 1 A. y y y  . D. y  2 x  . B. 1 x  . C. 1 x  2 x  . 2 1
Câu 10. Nguyên hàm của hàm số f (x)  5 cos x
là hàm số nào sau đây: 2 x 1 1
A. F (x)  5
 sin x   C .
B. F (x)  5sin x   C . x x
C. F (x)  5sin x  ln x C . D. 1
F (x)  5sin x   C . x
Câu 11. Thể tích của khối nón có chiều cao bằng 4 và đường sinh bằng 5 bằng A. 16 . B. 48 . C. 12 . D. 36 .
Câu 12. Đồ thị hàm số 3
y x  3x 1 cho ở hình bên. Phương trình 3
x  3x m  0 ( m là tham số) có ba nghiệm phân biệt khi Trang 43 A. 1   m  3. B. 2   m  2 . C. 2   m  3. D. 2   m  2 .
Câu 13. Cho khối chóp S.ABCD có SA vuông góc với mặt phẳng đáy, SA  3a , ABCD là hình chữ nhật và
AB  2a , AD a . Thể tích của khối chóp S.ABCD bằng 3 A. 3 a . B. 3 3a . 2 C. 3 2a . D. 3 9a .
Câu 14. Với a và b là các số thực dương. Biểu thức  2 log a b bằng a
A. 2  log b .
B. 2  log b .
C. 1 2 log b . D. 2 log b . a a a a
Câu 15. Tính diện tích hình phẳng giới hạn bởi đồ thị 2
y x  4x và trục hoành. 41 32 7 9 A. S  . B. S  . C. S  . D. S  . 3 3 4 4
Câu 16. Trong không gian với hệ tọa độ Oxyz, phương trình nào được cho dưới đây là phương trình mặt phẳng Oyz ? A. y  0 . B. z  0.
C. y z  0 . D. x  0 .
Câu 17. Cho số phức 2020 z  1 i
. Số phức liên hợp của z là A. z  2 . B. z  2   2i . C. z  0 . D. z  2 .
Câu 18. Cho khối lăng trụ có diện tích đáy bằng 2
a và khoảng cách giữa hai đáy bằng 3a . Tính thể tích V
của khối lăng trụ đã cho. 3 A. 3 V a . B. 3 V  3a . C. 3 V a . D. 3 V  9a . 2
Câu 19. Cho x , y là các số thực tùy ý. Mệnh đề nào sau đây là đúng? x   e
A. ex y  ex  ey .
B. ex y  ex  ey . C. exy exey  . D.  exy . ey 2 2 Câu 20. Tích phân dx  bằng. 2x 1 0 1 A. 2ln 5 . B. ln 5 . C. ln 5 . D. 4ln 5 . 2
Câu 21. Hàm số nào dưới đây nghịch biến trên khoảng 1;5 ? x 1 x  3 3x 1 2x  1 A. y y  3x  . B. 2 x  . C. 4 x  . D. 1 x  . 2 2 x 1   2  27
Câu 22. Nghiệm của phương trình    là  3  8 A. x  2 . B. x  3. C. x  1  . D. x  4 .
Câu 23. Thể tích V của khối lăng trụ tam giác đều có cạnh đáy bằng 2a và cạnh bên bằng a là 3 a 3 3 a 3 3 a 3 A.V  . B. 3 V a 3 . C.V  . D.V  . 2 4 3
Câu 24. Cho số phức z thỏa mãn:   iz    i2 3 2 2
 4  i . Hiệu phần thực và phần ảo của số phức z là A. 3 . B. 2 . C.1. D. 0 .
Câu 25. Trong các hàm số được cho dưới đây, hàm số nào có tập xác định là D   ? Trang 44 A. y   2 ln x   1 . B. y   2 ln 1 x  . C. y  x  2 ln 1 . D. y   2 ln x   1 .
Câu 26. Cho khối lăng trụ ABC . D A BCD
  có thể tích bằng 12 , đáy ABCD là hình vuông tâm O . Thể tích
của khối chóp A .BCO bằng A. 1. B. 4 . C. 3 . D. 2 .
Câu 27. Ta xác định được các số a , b , c để đồ thị hàm số 3 2
y x ax bx c đi qua điểm 1;0 và có điểm cực trị  2
 ;0 . Tính giá trị biểu thức 2 2 2
T a b c . A. 25 . B. 1. C. 7 . D.14 .
Câu 28. Hình chóp đều S.ABCD tất cả các cạnh bằng a . Diện tích mặt cầu ngoại tiếp hình chóp là: A. 2 4 a . B. 2  a . C. 2 2 a . D. 2 2 a .
Câu 29. Cho A  1, 2,3, 
4 . Từ A lập được bao nhiêu số tự nhiên có 4 chữ số đôi một khác nhau? A. 32 . B. 24 . C. 256 . D.1. mx 16
Câu 30. Tìm tất cả các giá trị của m để hàm số y  0; 10 . x  đồng biến trên   m A. m  ;
 104;   . B. m  ;
  4 4;  . C. m  ;
 104;   . D. m  ;
  44;   x  4 y  3 z  2
Câu 31. Trong không gian Oxyz , cho điểm M 2; 2; 
3 và hai đường thẳng  :   3 1  , 2 x 1 y  2 z  : 
 . Phương trình nào dưới đây là phương trình tham số của đường thẳng đi qua M 2 3 1
và vuông góc với hai đường thẳng  và  ?
x  2  7tx  2   7t
x  2  7tx  2   7t     A. y  2   t .
B. y  2  3t . C. y  2   t .
D. y  2  t .     z  3 11tz  3  11tz  3  8tz  3  8t  3 x a Câu 32. Cho dx
bln 2  c ln 3 
với a , b , c là các số nguyên. Giá trị của a b c bằng 4  2 x 1 3 0 A. 1. B. 2 . C. 7 . D. 9 .
Câu 33. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Cạnh bên SA vuông góc với đáy . Biết khoa a
̉ng cách từ A đến SCD bằng
3 . Tính thể tích khối chóp S.ABCD theo a . 2 3 a 3 3 3a 3 3 a 3 A. B. . C. 3 a 3 . D. . 3 4 4 Câu 34. Cho hàm số 3 2
y ax bx cx d . Hỏi hàm số luôn đồng biến trên  khi nào?
a b  0,c  0
a b  0,c  0 A.  . B.  . 2
a  0 ; b 3ac 0 2
a  0 ; b  3ac  0
a b  0,c  0
a b c  0 C.  . D.  . 2
a  0 ; b  3ac  0 2
a  0 ; b  3ac  0 x  3 y z 1
Câu 35. Trong không gian Oxyz , cho đường thẳng  :   M 2; 1  ;5 . Phương trình 2  và điểm   3 1
mặt phẳng  P qua M và vuông góc với  là
A. 2x  3y z 12  0 .
B. 2x  3y z 12  0 .
C. 2x y  5z 12  0 .
D. 2x y  5z 12  0 . Trang 45
Câu 36. Cho số phức z , biết rằng các điểm biểu diễn hình học của các số phức z ; iz và z i z tạo thành một
tam giác có diện tích bằng 18 . Mô đun của số phức z bằng A. 2 3 . B. 3 2 . C. 6 . D. 9 .
Câu 37. Số nghiệm của phương trình log x  3  log x  3 là: 2     x5   x x 2 A. 3 . B.1. C. 2 . D. 0 .
Câu 38. Trong không gian Oxyz , cho hai mặt phẳng  P : x  2y  2z  6  0 và Q : x  2y  2z  3  0 .
Khoảng cách giữa hai mặt phẳng  P và Q bằng A. 1. B. 3 . C. 9 . D. 6 .
Câu 39. Tính thể tích V của vật thể nằm giữa hai mặt phẳng x  0 và x   , biết rằng thiết diện của vật thể bị
cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x 0  x    là một tam giác đều cạnh 2 sin x .
A.V  3.
B.V  3 .
C.V  2 3 .
D.V  2 3 . z 1 z  3i
Câu 40. Cho số phức z a bi , a,b    thỏa mãn 1 và
1. Tính P a b . z i z i A. P  7 . B. P  1  . C. P  1 . D. P  2 .
Câu 41. Cho tam giác ABC vuông tại A có AC  1cm, AB  2cm, M là trung điểm của . AB Quay tam giác
BMC quanh trục AB , gọi V là thể tích khối tròn xoay thu được, khi đó V bằng: 3   A. 3 cm . B. 3 cm . C. 3  cm . D. 3 cm . 4 3 2
Câu 42. Tập hợp tất cả các điểm biểu diễn các số phức z thỏa mãn: z  2  i  4 là đường tròn có tâm I và
bán kính R lần lượt là: A. I  2  ;  1 ; R  4 . B. I  2  ;  1 ; R  2 .
C. I 2;   1 ; R  4 .
D. I 2;   1 ; I 2;   1 .
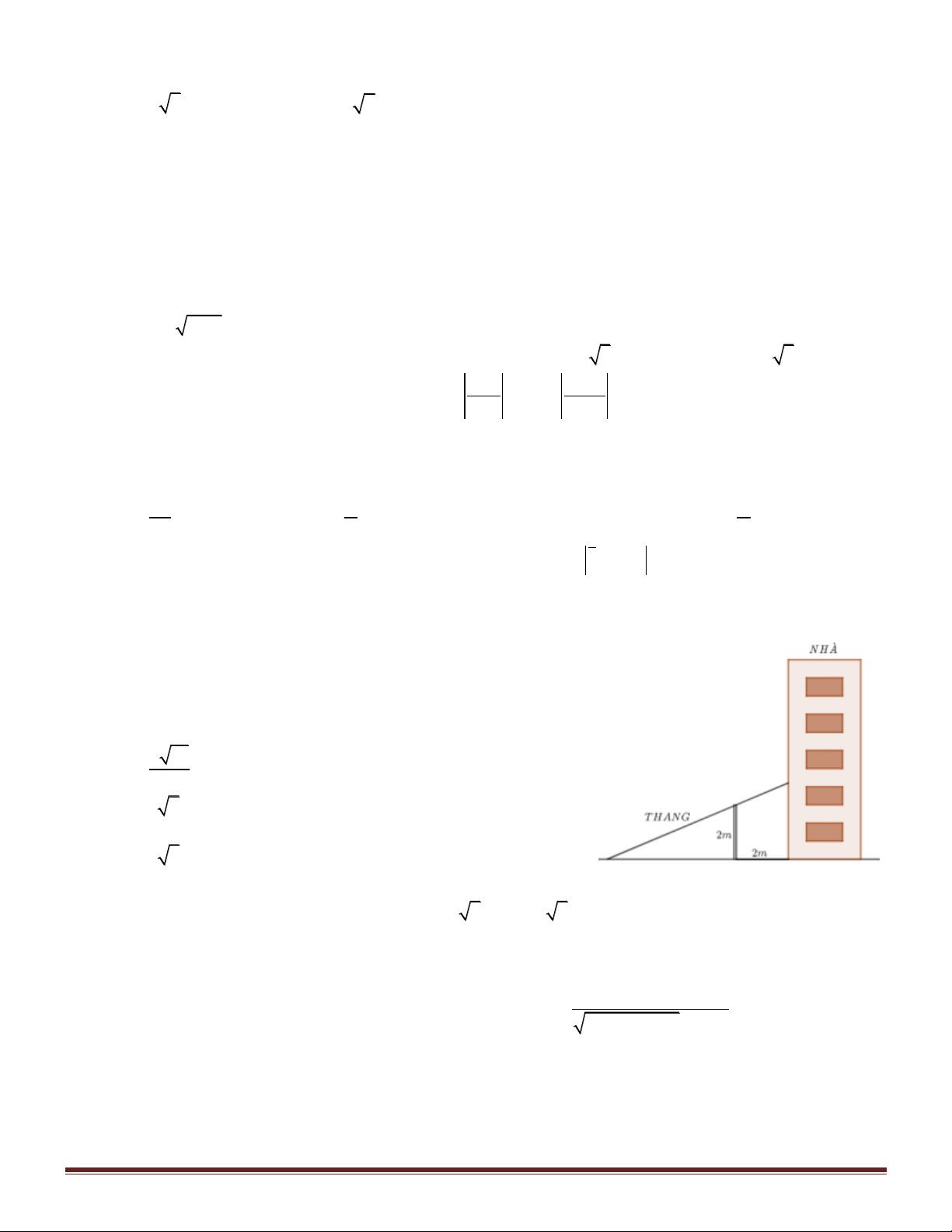
Câu 43. Một bức tường cao 2m nằm song song với tòa nhà và cách
tòa nhà 2m . Người ta muốn chế tạo một chiếc thang bắc từ
mặt đất bên ngoài bức tường, gác qua bức tường và chạm vào
tòa nhà (xem hình vẽ). Hỏi chiều dài tối thiểu của thang bằng bao nhiêu mét ? 5 13 A. m . 3 B. 4 2m . C. 6m . D. 3 5m . x x
Câu 44. Tập các giá trị của m để phương trình 4. 5  2   5  2  m  3  0 có đúng hai nghiệm âm phân biệt là: A.  ;    1  7; . B. 7; 8 . C.  ;  3 . D. 7; 9 . x 1
Câu 45. Tìm tất cả các giá trị của tham số m để đồ thị hàm số y  có đúng bốn đường 2
2x  2x m x 1 tiệm cận. A. m  5  ;4\  4 . B. m  5  ;4. C. m  5  ;4 \  4 . D. m  5  ;4\  4 .
Câu 46. Cho tập hợp A  1;2;3;...;10 . Chọn ngẫu nhiên ba số từ A . Tìm xác suất để trong ba số chọn ra
không có hai số nào là hai số nguyên liên tiếp. Trang 46 7 7 7 7 A. P  . B. P  . C. P  . D. P  . 90 24 10 15
Câu 47. Cho tứ diện ABCD có AB  2, AC  3, AD BC  4, BD  2 5, CD  5. Khoảng cách giữa hai
đường thẳng AC và BD bằng. 3 15 240 A. . B. 2. C. . D. 3. 4 79
Câu 48. Cho hai hàm số 3 2 3 2
y x x  3x 1, y  2x  2x mx  2 có đồ thị lần lượt là C , C và m là 1   2
tham số thực. Biết rằng tồn tại m để C cắt C tại ba điểm phân biệt có tung độ là y , y , y 2  1  1 2 3 1 1 1 2 thỏa mãn    , khi đó: y  4 y  4 y  4 3 1 2 3
A. m  4;7.
B. m  9;12 .
C. m  6;9 .
D. m 8;1  1 .
Câu 49. Cho x , y  0 thỏa mãn log  x  2y  log  x  log  y . Khi đó, giá trị nhỏ nhất của biểu thức 2 2 x 4 y P   1 2 y 1 là: x 32 31 29 A. 6 . B. . C. . D. . 5 5 5
Câu 50. Cho số phức z thỏa mãn 5 z i z 1 3i  3 z 1 i . Tìm giá trị lớn nhất T của z  2  3i ? 10 A. T  .
B. T  1 13 . C.T  4 5 . D.T  9 . 3
________________HẾT________________
ÑAÙP AÙN ÑEÀ SOÁ 05 1 2 3 4 5 6 7 8 9 10 C B A C B B B D C D 11 12 13 14 15 16 17 18 19 20 C B C B B D A B D C 21 22 23 24 25 26 27 28 29 30 A C B D D A A D B A 31 32 33 34 35 36 37 38 39 40 A A A A A C A B D D 41 42 43 44 45 46 47 48 49 50 B A B B D D C D B C
Lôøi giaûi caâu hoûi vaän duïng cao ñeà soá 05
Câu 43. Một bức tường cao 2m nằm song song với tòa nhà và cách tòa nhà 2m . Người ta muốn chế tạo một
chiếc thang bắc từ mặt đất bên ngoài bức tường, gác qua bức tường và chạm vào tòa nhà (xem hình
vẽ). Hỏi chiều dài tối thiểu của thang bằng bao nhiêu mét ? Trang 47 5 13 A. m . B. 4 2m . C. 6m . D. 3 5m . 3 Hướng dẫn giải: Xét hệ điểm ,
A B, C, D, E như hình vẽ.
Gọi BC x x  0 . Ta cần tìm x để độ dài CD đạt giá trị nhỏ nhất.
Dễ thấy hai tam giác CAB, CDE đồng dạng, suy ra: BC x AC x  2 x  2 2    CD AC.  x  4. CE x  . 2 CD x x x  2
Đặt f x 2  x  4. với x  0 . xCách giải 1:       f  x 2 2 x x 2 2 x 2 2 x 4 x 2 2 x 4 2  .  x  4.    0   2 2 2 2 2 2  4 x x  4 x  4 x x x x 2
x x     2 x   3 2 2
4  x  8  x  2 . Bảng biến thiên của f x :
Vậy chiều dài tối thiểu của thang bằng 4 2 . Choïn   B Cách giải 2:   2  x  4   x  2  2       x x x 4 AM GM AM GM 4 .2 2
Ta có: f x  
 4 2 . Dấu đẳng thức xảy tra    x  2. x xx  2 x x
Câu 44. Tập các giá trị của m để phương trình 4. 5  2   5  2  m  3  0 có đúng hai nghiệm âm phân biệt là: A.  ;    1  7; . B. 7; 8 . C.  ;  3 . D. 7; 9 . Trang 48 Hướng dẫn giải: x 1
Đặt t   5  2  0  x  log
t . Phương trình đã cho trở thành: 4t   3  m * . 5 2 t
Nhận xét:Với mỗi t  0; 
1 thì ta tìm được đúng một nghiệm x  0 .
Bài toán trở thành:Tìm m để phương trình * có đúng hai nghiệm phân biệt t  0; 1 . 1,2    1 t  0;  1 1 4t 1  2
Xét hàm số f t  1
 4t   3 với t 0; 
1 ; f t  2  4    0   . t 2 2 t t 1
t   0; 1  2 Bảng biến thiên:
Dựa vào bảng biến thiên ta có: 7  m  8. Choïn   B x 1
Câu 45. Tìm tất cả các giá trị của tham số m để đồ thị hàm số y  có đúng bốn đường 2
2x  2x m x 1 tiệm cận. A. m  5  ;4\  4 . B. m  5  ;4. C. m  5  ;4 \  4 . D. m  5  ;4\  4 . Hướng dẫn giải:  1  x 1    x  1 Ta có: lim y  lim  1 2 ; x x  2 m 1  2 1 x  2   1  2 x x x    1  x 1    x  1 lim y  lim 
 1 2 . Do đó đồ thị hàm số có hai đường tiệm x x  2 m 1   2 1 x   2   1  2 x x x  
cận ngang là y  1 2 và y  1 2 . Vì vậy ta cần tìm m để đồ thị hàm số đã cho có hai đường tiệm cận đứng.
Khi tìm tiệm cận đứng, ta xét: 2
2x  2x m x 1  0 2
 2x  2x m x 1 x  1  x  1      2     . 2 2 x 4x 1 m (*)
2x  2x m x  2x 1   g  x
Yêu cầu bài toán   
* có hai nghiệm phân biệt x  1
 và khác 1 (không trùng nghiệm của tử số). 1,2
Xét hàm số g x 2
x  4x 1 với x  1
 và x 1. Ta có: gx  2x  4  0  x  2 . Bảng biến thiên: Trang 49
Dựa vào bảng biến thiên, ta có m  5  ;4\  4 .  Choï n D
Câu 46. Cho tập hợp A  1;2;3;...;10 . Chọn ngẫu nhiên ba số từ A . Tìm xác suất để trong ba số chọn ra
không có hai số nào là hai số nguyên liên tiếp. 7 7 7 7 A. P  . B. P  . C. P  . D. P  . 90 24 10 15 Hướng dẫn giải:
Số phần tử không gian mẫu là n  3  C 120 . 10
Gọi B là biến cố “Ba số chọn ra không có hai số nào là hai số nguyên liên tiếp”.
B là biến cố “Ba số được chọn có ít nhất hai số là các số tự nhiên liên tiếp”.
Tìm các kết quả thuận lợi cho B :
Xét bộ ba số có dạng 1; 2; a , với a A \ 1; 2 : có 8 bộ thỏa mãn. 1   1 
Xét bộ ba số có dạng 2;3; a , với a A \ 1; 2;3 : có 7 bộ thỏa mãn. 2   2 
Xét bộ ba số có dạng 3, 4, a với a A \ 2;3;4 : có 7 bộ thỏa mãn. 3   3 
Thực hiện tương tự mỗi bộ ba số dạng: 4,5, a , 5,6, a , 6, 7, a , 7,8, a , 8,9, a , 8  7  6  5  4 
9,10,a : đều có 7 bộ thỏa mãn. 9 
Suy ra: nB  88.7  64 . Do vậy: PB 1 64
P B  1 7  .  Choï n D 120 15
Câu 47. Cho tứ diện ABCD có AB  2, AC  3, AD BC  4, BD  2 5, CD  5. Khoảng cách giữa hai
đường thẳng AC và BD bằng. 3 15 240 A. . B. 2. C. . D. 3. 4 79 Hướng dẫn giải: Ta có: 2 2 2
AD AC CD nên tam giác ACD vuông D
tại A hay AD AC . Mặt khác: 2 2 2
AD AB BD
nên tam giác ABD vuông tại A hay AD AB . 5AD AC 2 5 Ta có: 4
AD  (ABC) . AD AB G A 3 C
Dựng hình bình hành ACBE .Khi đó AC//(BDE) . 4
Suy ra khoảng cách cần tìm: 2 d E
AC,BD  d AC,(BDE)  d  ,
A (BDE) (1) . B F
Trong mặt phẳng (ABCD), kẻ AF BE tại F , trong
tam giác ADF , dựng đường cao AG. Ta sẽ chứng minh AG  (BDE). BE AF Thật vậy: 
BE  (ADF) mà AG  (ADF)  AG BE. BE AD Trang 50AG BE Vì 
AG  (BDE) (2). Từ (1) & (2)  d AC, BD  AG . AG DF   Đặt: AB BE AE 9 3 15 p    S
p( p AB)( p BE)( p AE)   . 2 2 ABE 4 Ta lại có: 1 15 S
AF.BE AF  . ABE   2 3 2 A . D AF 240
Xét tam giác ADF vuông tại A có đường cao AG   . Choïn   C 2 2  79 AD AF
Câu 48. Cho hai hàm số 3 2 3 2
y x x  3x 1, y  2x  2x mx  2 có đồ thị lần lượt là C , C và m là 1   2
tham số thực. Biết rằng tồn tại m để C cắt C tại ba điểm phân biệt có tung độ là y , y , y 2  1  1 2 3 1 1 1 2 thỏa mãn    , khi đó: y  4 y  4 y  4 3 1 2 3
A. m  4;7.
B. m  9;12 .
C. m  6;9 .
D. m 8;1  1 . Hướng dẫn giải:
Cần nhớ:Định lí Vi-ét dành cho phương trình bậc ba.  b
x x x    1 2 3 a   Nếu phương trình 3 2 c
ax bx cx d  0 có ba nghiệm x , x , x thì x x x x x x  . 1 2 3 1 2 2 3 1 3 a   d x x x    1 2 3  a
Phương trình hoành độ giao điểm của C , C : 3 2
x x  3  mx  3  0 (*). 1   2
Giả sử A, B, C là giao điểm của hai đồ thị hàm số đã cho thì tọa độ A, B, C thỏa hệ 3 2 3 2
y x x 3x 1
2y  2x  2x  6x  2   
. Suy ra y  m  6 x  4 . 3 2 3 2
y  2x  2x mx  2
y  2x  2x mx  2
Khi đó, ta có: y  4  m  6 x ; y  4  m  6 x ; y  4  m  6 x với x , x , x là nghiệm của 1   1 2   2 3   3 1 2 3 phương trình (*).
x x x x x x  3  m
Theo định lí Vi-ét bậc ba, ta có 1 2 2 3 3 1  . x x x  3   1 2 3 2 1 1 1 1
x x x x x x m  3 Theo giả thiết: 1 2 2 3 3 1     .  m  . 3 y  4 y  4 y  4 m  6 x x x 3 m  . Suy ra 9 6 1 2 3 1 2 3  
Thử lại:với m  9 thì (*) trở thành 3 2
x x  6x  3  0 . Phương trình này có 3 nghiệm phân biệt.
Vậy m  9 là giá trị cần tìm. Choïn   D
Câu 49. Cho x , y  0 thỏa mãn log  x  2y  log  x  log  y . Khi đó, giá trị nhỏ nhất của biểu thức 2 2 x 4 y P   1 2 y 1 là: x 32 31 29 A. 6 . B. . C. . D. . 5 5 5 Trang 51 Hướng dẫn giải: Cần nhớ:
Bất đẳng thức Cauchy-Schwarz dạng Engel (còn gọi là bất đẳng thức công mẫu): x y   2 2 2 x y   x y
. Dấu đẳng thức xảy ra khi và chỉ khi  . a b a b a b
Điều kiện: x  0, y  0 .
Ta có: log  x  2y  log  x  log  y  log  x  2y  log  .
x y  x  2y xy (*) . x
y2 x y2 2 2 2
Áp dụng bất đẳng thức Cauchy-Schwarz dạng Engel , ta có: P    1 2 y 1 x 2  x  . 2 y (1) 2
Theo AM-GM, ta có: x  2 y  2 .
x 2 y  2 2 x  2y   x  2y  8 x  2yx é + 2y £ 0 (loaïi) Û ê
(do điều kiện x  0, y  0 ). Suy ra x + 2y ³ 8 . x ê + 2y ³ 8 (nhaän) ë 2 Đặ t 4
t t x  2 y  8 , ta có: P   t  2  t  2 t  2 1  32 P  t   4 24 52 4 24 52 32 2   t   2  .8   . Do vậy P  . min 25 t  2   25 25 25 25 25 5 5 AM GM 24  .8 25  x 2 y   8  2y 2 y 1 2 y 1 x    x  4
Dấu đẳng thức xảy ra  
 1 2y 18 2y   . 1         x yt  4 y 2 2 8; 2
x  8  2y   25 t  2  t  Choï n B
Câu 50. Cho số phức z thỏa mãn 5 z i z 1 3i  3 z 1 i . Tìm giá trị lớn nhất T của z  2  3i ? 10 A. T  .
B. T  1 13 . C.T  4 5 . D.T  9 . 3 Hướng dẫn giải:
Gọi M là điểm biểu diễn của z; gọi A0;  1 , B  1
 ;3,C 1; 
1 . Ta thấy A là trung điểm của BC . 2 BC Ta có : 2 2 2 2
MB MC  2MA   2MA 10 . 2 CauchySchwarz
Theo giả thiết : 5 z i z 1 3i  3 z 1 i 2 2
 5MA MB  3MC  10. MB MC  2 2MA 1  0 2  MA   2 25 10 2MA 10 2
 5MA 100  MA  2 5 (1).
Xét z  2  3i   z i   2
  4i  z i  2  4i MA 2 5  4 5 (do (1)).
z i  2 5  z é = 2 - 3i (loaïi)
Dấu "  " xảy ra khi và chỉ khi:   ê a b 1
, với z a bi ; a, b  . Suy ra .    ê 0 z = - 2 + 5i ë 2  4 Choïn
Vậy giá trị lớn nhất của z  2  3i là T  4 5 .   C Trang 52 Trang 53