Bộ đề kiểm tra chương 2 Giải tích 12 có đáp án và lời giải chi tiết

Tài liệu gồm 106 trang được biên soạn bởi tập thể quý thầy, cô giáo nhóm Toán học Bắc Trung Nam, tuyển chọn 11 đề kiểm tra chương 2 Giải tích 12 có đáp án và lời giải chi tiết. Bộ đề được sử dụng trong các kỳ kiểm tra định kỳ, kiểm tra tập trung, kiểm tra 1 tiết, kiểm tra 45 phút

26 13 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 12

Môn: Toán 12

Thông tin:

106 trang 8 tháng trước

Tác giả:

Profile Nguyễn Vân
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 1/11 - Mã đề LD-001
TOÁN H
ỌC
B
ẮC
–
TRUNG
–
NAM
Nhóm: THBTN – ĐỀ KIỂM TRA
(25 câu trắc nghiệm)
KIỂM TRA CHƯƠNG 2 GIẢI TÍCH 12
MÃ ĐỀ 001
Thời gian làm bài: 45 phút, không kể thời gian phát đề.
Câu 1. [2D2-1] Giả sử
a
,
là các số thực dương. Biểu thức
5
3
b a
a b
được viết dưới dạng
a
b
. Tìm
giá trị
.
A.
4
15
. B.
2
5
. C.
2
15
. D.
2
15
.
Câu 2. [2D2-1] Cho
a
,
là các số thực dương khác
1
. Trong các khẳng định sau, chọn khẳng định
đúng.
A.
, .
m m
a b a b m
B.
1 1
, 0
m m
a b m
a b
.
C.
1 1
, 0
m m
a b m
a b
. D.
1 1
, 0
m m
a b m
a b
.
Câu 3. [2D2-1] Tìm tập xác định của hàm số
2
2
y x .
A.
\ 2
. B.
2;

. C.
0;

. D.
.
Câu 4. [2D2-2] Cho
3
2 2
.
f x x x
. Tính giá trị của
1
f
.
A.
2
. B.
8
. C.
4
. D.
8
.
Câu 5. [2D2-2]Cho đồ thị ba hàm số
x
y a
,
x
y b
,
x
y c
như hình vẽ. Kết luận nào sau đây đúng.
A.
0 1
a b c
.
B.
0 1
c a b
.
C.
0 1
c b a
.
D.
0 1
a c b
Câu 6. [2D2-1] Tính
3 7
1
log 0, 1
a
a a a
.
A.
7
3
. B.
7
3
. C.
3
7
. D.
3
7
.
Câu 7. [2D2-2] Cho
a
là hai số thực dương khác. Đặt
3
log
a m
. Tính theo
m
giá trị của biểu thức
1
3
3
log log log 9
a
D a a .
A.
2
2 3
m
D
m
. B.
2
3 2
m
D
m
. C.
2
4 3
2
m
D
m
. D.
3
D m
.
Câu 8. [2D2-2]Cho
2
log 5
,
3
log 5
. Hãy biểu diễn
6
log 5
theo
a
và
.
A.
6
1
log 5
a b
. B.
6
log 5
ab
a b
.
C.
6
log 5
a b
. D.
2 2
6
log 5
a b
.
O
x
y
1
x
y a
x
y b
x
y c
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 2/11 - Mã đề LD-001
Câu 9. [2D2-3] Biết
2 2
a b ab
,
0
a
,
0
b
. Chọn đẳng thức đúng.
A.
2ln ln2 ln ln
a b a b
. B.
2 2
ln ln ln
a b a b
.
C.
2 2
lg lg lg
a b a b
. D.
2lg lg3 lg lg
a b a b
.
Câu 10. [2D2-3] Cho hàm số
2
5
2
x
x
f x . Khẳng định nào sau đây là khẳng định sai?
A.
2
5
1 0
log 2
x
f x
x
. B.
2
2
1 log 5 0
f x x x
.
C.
2
5
5
1 log 0
2
x
x
f x
. D.
2
5
1 log 2 0
f x x x
.
Câu 11. [2D2-1] Tìm tập xác định
D
của hàm số
2
2
2 1
log 3
x
f x
x x
.
A.
0;3
D . B.
3 5
0;3 \
2
D
C.
\ 0;3
D
. D.
D
.
Câu 12. [2D2-2] Tìm đạo hàm của hàm số
2
2 3 e 3
x
y x x
trong điều kiện xác định.
A.
2
4 4 e 3
x
y x
. B.
2
4 4 e 3
x
y x x
.
C.
2
4.e 3
x
y
. D.
2
2 1 e 3
x
y x
.
Câu 13. [2D2-2] Mệnh đề nào sau đây là sai?
A. Cho hàm số
2
x
y
thì
1 ln 4
y
.
B. Cho hàm số
log 2 1
y x
thì
2
1
3ln10
y
.
C. Cho hàm số
e
x
y
thì
1 e
x
y
.
D. Cho hàm số
ln
y x
thì
1 1
y
.
Câu 14. [2D2-3] Gọi
M
và
m
là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
x
y xe
trên
1;2
.
Tính
.
M n
.
A.
3
2e
. B.
2
2e
. C.
e
. D.
0
.
Câu 15. [2D2-4] Ông A vay ngân hàng T (triệu đồng) với lãi suất
12
% năm. Ông A thỏa thuận với ngân
hàng cách thức trả nợ như sau: sau đúng một tháng kể từ ngày vay, ông bắt đầu hoàn nợ; hai
lần hoàn nợ liên tiếp cách nhau đúng một tháng. Nhưng cuối tháng thứ ba kể từ lúc vay ông A
mới hoàn nợ lần thứ nhất, cuối tháng thứ tư ông A hoàn nợ lần thứ hai, cuối tháng thứ năm ông
A hoàn nợ lần thứ ba (hoàn hết nợ). Biết rằng số tiền hoàn nợ lần thứ hai gấp đôi số tiền hoàn
nợ lần thứ nhất và số tiền hoàn nợ lần thứ ba bằng tổng số tiền hoàn nợ của hai lần trước. Tính
số tiền ông A đã hoàn nợ ngân hàng lần thứ nhất.
A.
5
2
1 0,01
2,01 2
T
. B.
5
2
1 0,01
1,01 5
T
. C.
5
1 0,01
6
T
. D.
5
1
100
6
T
.
Câu 16. [2D2-1] Tìm nghiệm của phương trình
1
3 27
x
.
A.
9
x
. B.
3
x
.C.
4
x
. D.
10
x
.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 3/11 - Mã đề LD-001
Câu 17. [2D2-2] Gọi
S
là tập nghiệm của phương trình
2
2 3
1
1
7 .
7
x x
x
Tính tổng tất cả các phần tử
của
S
.
A.
5.
B.
0.
C.
1.
D.
2.
Câu 18. [2D2-2] Gọi
S
là tập nghiệm của phương trình
4 8 2 5
2
3 4.3 28 2log 2
x x
. Tính tích tất cả
các phần tử của
S
.
A.
4.
B.
3
.
2
C.
3
.
2
D.
1.
Câu 19. [2D2-1] Cho phương trình
2 2 2 2
2 2 2 2
log 1 .log 2 4 6 log 1 1 4log 2 4 0 1
x x x x x x
Gọi
1
x
,
2
x
là hai nghiệm thực dương của phương trình đã cho
1 2
x x
. Tính
2
1 2
2
T x x
.
A.
3 2 5
T . B.
1 3 5
T . C.
7
T
. D.
6
T
.
Câu 20. [2D2-4] Tìm nghiệm của phương trình
2
0,5
log sin 5sin .cos 2
4
x x x
.
A.
2
1
arctan
5
x k
k
x k
. B.
2
1
arctan
3
x k
k
x k
C.
1
arctan
3
x k
k
x k
. D.
1
arctan
5
x k
k
x k
.
Câu 21. [2D2-1] Tìm tập nghiệm của bất phương trình
2
2 4
2 3 1
1
4
2
x
x x
.
A.
5
0;
4
. B.
1
.
C.
;0 1;
 
. D.
5
;1 ;
4
 
.
Câu 22. [2D2-1] Tìm tập nghiệm của bất phương trình
1
2
log 1 2
x
.
A.
1;S

. B.
3
0;
4
S
. C.
3
1;
4
S
. D.
3
;
4
S

.
Câu 23. [2D2-3] Tìm tập nghiệm của bất phương trình
2
1
5 2 5 2
x
x
x
.
A.
; 1 0;1
 . B.
1;0
. C.
; 1 0;
 
.
D.
1;0 1;

.
Câu 24. [2D2-2] Phương trình
2 4
log 1 2log 3 2 2 0
x x
có mấy nghiệm?
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 25. [2D2-4] Có bao nhiêu giá trị nguyên bé hơn
10
của tham số
m
sao cho bất phương trình
2 2
2 2
log 1 2 log 1 0
x x m
thỏa mãn với mọi
3
1;2
?
A.
3
. B.
4
. C.
5
. D.
6
.
----------HẾT----------
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 4/11 - Mã đề LD-001
ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
C
C
B
B
C
A
A
B
D
A
B
A
C
A
A
C
C
C
D
A
A
C
D
A
B
BÀI GIẢI
Câu 1: [2D2-1] Giả sử
a
,
là các số thực dương. Biểu thức
5
3
b a
a b
được viết dưới dạng
a
b
. Tìm
giá trị
.
A.
4
15
. B.
2
5
. C.
2
15
. D.
2
15
.
Lời giải
Chọn C.
Ta có
1 1 1 1 1 1 2
5 15 5 15 5 15 15
5
3
. .
b a b a a a a a
a b a b b b b b
.
Phân tích phương án nhiễu.
A – sai do biến đổi.
B – sai do tính toán.
D – sai do biến đổi.
Câu 2: [2D2-1] Cho
a
,
là các số thực dương khác
1
. Trong các khẳng định sau, chọn khẳng định
đúng.
A.
, .
m m
a b a b m
B.
1 1
, 0
m m
a b m
a b
.
C.
1 1
, 0
m m
a b m
a b
. D.
1 1
, 0
m m
a b m
a b
.
Lời giải
Chọn C.
Phân tích phương án nhiễu
A – sai vì Ta có:
2 3
mà
2 2
1 1
2 3
4 9
.
B – sai vì Ta Ta có:
2 3
mà
2 2
1 1 1 1
2 4 3 9
.
C – sai vì Ta Ta có:
2 3
mà
2 2
1 1
4 9
2 3
.
Câu 3: [2D2-1] Tìm tập xác định của hàm số
2
2
y x .
A.
\ 2
. B.
2;

. C.
0;

. D.
.
Lời giải
Chọn B.
Ta có:
2 0 2
x x
. Vậy TXĐ của hàm số là:
2;D

.
Câu 4: [2D2-2] Cho
3
2 2
.
f x x x
. Tính giá trị của
1
f
.
A.
2
. B.
8
. C.
4
. D.
8
.
Lời giải
Chọn B.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 5/11 - Mã đề LD-001
Với
0
x
thì
2 8 5
2
3 3 3
8
3
f x x x f x x
nên
8
1
3
f
.
Câu 5: [2D2-2]Cho đồ thị ba hàm số
x
y a
,
x
y b
,
x
y c
như hình vẽ. Kết luận nào sau đây đúng.
A.
0 1
a b c
. B.
0 1
c a b
. C.
0 1
c b a
. D.
0 1
a c b
Lời giải
Chọn C.
Do đồ thị của hàm
x
y a
,
x
y b
là đường đi lên, đồ thị hàm
x
y c
là đường đi xuống, suy ra
hàm
x
y a
,
x
y b
là các hàm đồng biến suy ra
1
a
,
1
b
,
1
c
Xét tại điểm
0
x m
ta có
m m
a b
mà
1
a
,
1
b
suy ra
a b
.
Vậy mệnh đề đúng là:
0 1
c b a
.
Phân tích phương án nhiễu.
A, D – sai do học sinh ko nắm được dáng điệu đồ thị hàm số mũ.
B – sai do xác định nhầm cơ số.
Câu 6: [2D2-1] Tính
3 7
1
log 0, 1
a
a a a
.
A.
7
3
. B.
7
3
. C.
3
7
. D.
3
7
.
Lời giải
Chọn A.
Ta có
1
7
3 7
3
1
7
log log
a
a
a a
.
Phân tích phương án nhiễu.
B – sai do học sinh nhầm dấu.
C – sai do áp dụng sai công thức
3
3 7
7
a a
.
D – sai do áp dụng sai công thức
3
3 7
7
a a
và nhầm dấu khi làm.
Câu 7: [2D2-2] Cho
a
là hai số thực dương khác. Đặt
3
log
a m
. Tính theo
m
giá trị của biểu thức
1
3
3
log log log 9
a
D a a .
A.
2
2 3
m
D
m
. B.
2
3 2
m
D
m
. C.
2
4 3
2
m
D
m
. D.
3
D m
.
Lời giải
Chọn A.
Ta có:
1 3 3
3
3
log log log 9 log 2log 2log 3
a a
D a a a a
2
3
3
2 2 3 2
3log 3
log
m
a m
a m m
Phân tích phương án nhiễu.
B – sai do quên đổi dấu biểu thức.
O
x
y
1
x
y a
x
y b
x
y c
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 6/11 - Mã đề LD-001
B – sai do tính toán.
D – sai do khai triển sai
3
3
1
log log
2
a a
.
Câu 8: [2D2-2]Cho
2
log 5
,
3
log 5
. Hãy biểu diễn
6
log 5
theo
a
và
.
A.
6
1
log 5
a b
. B.
6
log 5
ab
a b
. C.
6
log 5
a b
. D.
2 2
6
log 5
a b
.
Lời giải
Chọn B.
Ta có:
6
5 5 5 5
1 1 1 1
log 5
1 1
log 6 log 2.3 log 2 log 3
ab
a b
a b
.
Phân tích phương án nhiễu.
A – sai do quên nghịch đảo hạng tử.
B – sai do nhầm công thức
5 5 5
log 6 log 2 log 3
.
D – sai do tính toán.
Câu 9: [2D2-3] Biết
2 2
a b ab
,
0
a
,
0
b
. Chọn đẳng thức đúng.
A.
2ln ln2 ln ln
a b a b
. B.
2 2
ln ln ln
a b a b
.
C.
2 2
lg lg lg
a b a b
. D.
2lg lg3 lg lg
a b a b
.
Lời giải
Chọn D.
Ta biến đổi:
2 2
2 2
3 log log 3 2log log3 log log
a b ab a b ab a b ab a b a b
Phân tích phương án nhiễu.
A – sai do tính toán.
B – sai do công thức hàm số logarit.
C – sai do công thức hàm số logarit.
Câu 10: [2D2-3] Cho hàm số
2
5
2
x
x
f x . Khẳng định nào sau đây là khẳng định sai?
A.
2
5
1 0
log 2
x
f x
x
. B.
2
2
1 log 5 0
f x x x
.
C.
2
5
5
1 log 0
2
x
x
f x
. D.
2
5
1 log 2 0
f x x x
.
Lời giải
Chọn A.
2
2 2
2 2
5 5 5 2
5
1 1 5 2 log 5 log 2 log 2 0 log 5 0
2
x
x x x x
x
f x x x x x
.
Đáp án C đúng.
Đáp án D đúng.
Đáp án B đúng và đáp án A sai.
Câu 11: [2D2-1] Tìm tập xác định
D
của hàm số
2
2
2 1
log 3
x
f x
x x
.
A.
0;3
D . B.
3 5
0;3 \
2
D
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 7/11 - Mã đề LD-001
C.
\ 0;3
D
. D.
D
.
Lời giải
Chọn B.
Điều kiện
2
2
2
2
0 3
3 0
0 3
3 5
log 3 0 3 1
2
x
x x
x
x x x x
x
.
Câu 12: [2D2-2] Tìm đạo hàm của hàm số
2
2 3 3
x
y x e x
trong điều kiện xác định.
A.
2
4 4 3
x
y x e
. B.
2
4 4 3
x
y x e x
.
C.
2
4. 3
x
y e
. D.
2
2 1 3
x
y x e
.
Lời giải
Chọn A.
2 2 2
2. 2 2 3 3 4 4 3
x x x
y e e x e x
.
Câu 13: [2D2-2] Mệnh đề nào sau đây là sai?
A. Cho hàm số
2
x
y
thì
1 ln 4
y
. B. Cho hàm số
log 2 1
y x
thì
2
1
3ln10
y
.
C. Cho hàm số
x
y e
thì
1
x
y e
. D. Cho hàm số
ln
y x
thì
1 1
y
.
Lời giải
Chọn C.
Cho hàm số
x
y e
, vậy
1
x
y e y e
.
Câu 14: [2D2-3] Gọi
M
và
m
là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
x
y xe
trên
1;2
.
Tính
.
M n
.
A.
3
2
e
. B.
2
2
e
. C.
e
. D.
0
.
Lời giải
Chọn A.
1
x x x x
y xe y e xe x e
.
0 1
y x l
.
Vậy
1
y e m
và
2
2 2
y e M
. Khi đó
3
. 2
M n e
.
Câu 15: [2D2-4] Ông A vay ngân hàng T (triệu đồng) với lãi suất
12
% năm. Ông A thỏa thuận với ngân
hàng cách thức trả nợ như sau: sau đúng một tháng kể từ ngày vay, ông bắt đầu hoàn nợ; hai
lần hoàn nợ liên tiếp cách nhau đúng một tháng. Nhưng cuối tháng thứ ba kể từ lúc vay ông A
mới hoàn nợ lần thứ nhất, cuối tháng thứ tư ông A hoàn nợ lần thứ hai, cuối tháng thứ năm ông
A hoàn nợ lần thứ ba (hoàn hết nợ). Biết rằng số tiền hoàn nợ lần thứ hai gấp đôi số tiền hoàn
nợ lần thứ nhất và số tiền hoàn nợ lần thứ ba bằng tổng số tiền hoàn nợ của hai lần trước. Tính
số tiền ông A đã hoàn nợ ngân hàng lần thứ nhất.
A.
5
2
1 0,01
2,01 2
T
. B.
5
2
1 0,01
1,01 5
T
. C.
5
1 0,01
6
T
. D.
5
1
100
6
T
.
Lời giải
Chọn A.
Số tiền nợ của ông A sau hai tháng vay là:
2 2
2
1 1% 1,01
A T T .
Số tiền nợ của ông A sau 3 tháng vay là:
3 2
1,01
A A m
.
Số tiền nợ của ông A sau 4 tháng vay là:
4 3
1,01 2
A A m
.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 8/11 - Mã đề LD-001
Số tiền nợ của ông A sau 5 tháng vay là:
5 5
1,01 3
A A m
.
Theo giả thiết bài toán ta có:
5 2
0 .1,01 .1,01 2 .1,01 3 0
A A m m m
.
3 5
3 2
2
2
2
2
.1,01
.1,01
.1,01 1.01 2.1,01 3 0
1,01 2.1,01 1 2
2,01 2
A T
A m m m
.
Câu 16: [2D2-1] Tìm nghiệm của phương trình
1
3 27
x
.
A.
9
x
. B.
3
x
. C.
4
x
. D.
10
x
.
Lời giải
Chọn C.
Ta có
1 1 3
3 27 3 3 1 3 4
x x
x x
.
Câu 17: [2D2-2] Gọi
S
là tập nghiệm của phương trình
2
2 3
1
1
7 .
7
x x
x
Tính tổng tất cả các phần tử
của
S
.
A.
5.
B.
0.
C.
1.
D.
2.
Lời giải
Chọn C.
2
2
2 3
1 2 3 1 2 2
1
1
7 7 7 2 3 1 2 0
2.
7
x x
x x x x
x
x x x x x
x
Vậy
1.
S
Câu 18: [2D2-2] Gọi
S
là tập nghiệm của phương trình
4 8 2 5
2
3 4.3 28 2log 2
x x
. Tính tích tất cả
các phần tử của
S
.
A.
4.
B.
3
.
2
C.
3
.
2
D.
1.
Lời giải
Chọn C.
2
4 8 2 5 2 4 2 4
2
3 4.3 28 2log 2 3 12.3 27 0 1 .
x x x x
Đặt
2 4
3 , 0
x
t t
. Phương trình trở thành:
2
12. 27 0 2 .
t t
Khi đó:
9
2
3.
t
t
Với
2 4
3
3 3 3 2 4 1 .
2
x
t x x
Với
2 4 2
9 3 3 2 4 2 1.
x
t x x
Vậy tích các nghiệm là:
3
.
2
Câu 19: [2D2-1] Cho phương trình
2 2 2 2
2 2 2 2
log 1 .log 2 4 6 log 1 1 4log 2 4 0 1
x x x x x x
Gọi
1
x
,
2
x
là hai nghiệm thực dương của phương trình đã cho
1 2
x x
. Tính
2
1 2
2
T x x
.
A.
3 2 5
T . B.
1 3 5
T . C.
7
T
. D.
6
T
.
Lời giải
Chọn D.
Điều kiện xác định:
1
x
hoặc
1
x
.
2 2 2 2
2 2 2
1 log 1 .log 2 4 3lg 1 2log 2 4 6 0
x
x x x x x x
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 9/11 - Mã đề LD-001
2 2
2 2
log 1 2 log 2 4 3 0
x x x
2
2
2
2
log 1 2 0
log 2 4 3 0
x
x x
2
2
2
2
log 1 2
log 2 4 3
x
x x
2
2
5
2 4 0
x
x x
5
1 5
x
x
So với điều kiện ta được hai nghiệm
1
1 5
x và
2
5
x .
Khi đó:
2
2
1 2
2 5 1 2 5 6
T x x
.
Phân tích phương án nhiễu.
A – Sai do xác định
1
5
x ,
2
1 5
x .
B – Sai do yêu cầu tính
T
(Tính
1 2
2
x x
).
C – Sai do tạo phương trình tích sai và không loại nghiệm:
1
1
x
và
2
3
x
.
Câu 20: [2D2-4] Tìm nghiệm của phương trình
2
0,5
log sin 5sin .cos 2
4
x x x
.
A.
2
1
arctan
5
x k
k
x k
. B.
2
1
arctan
3
x k
k
x k
C.
1
arctan
3
x k
k
x k
. D.
1
arctan
5
x k
k
x k
.
Lời giải
Chọn A.
Điều kiện:
2
sin 5sin cos 2 0
x x x
Lấy logarit cơ số 4 hai vế của phương trình ta được:
2 2
0,5 4
log sin 5sin cos 2 log 3
x x x
2
2 2
log sin 5sin cos 2 log 3
x x x
2
sin 5sin cos 2 3
x x x
(thỏa mãn điều kiện)
cos 5sin cos 0
x x x
*
cos 0
2
x x k k
*
1
5sin cos 0 tan 5 arctan
5
x x x x k k
.
Phân tích phương án nhiễu.
B – sai do tính toán.
C – sai do không đối chiếu điều kiện.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 10/11 - Mã đề LD-001
D – sai do tính toán.
Câu 21: [2D2-1] Tìm tập nghiệm của bất phương trình
2
2 4
2 3 1
1
4
2
x
x x
.
A.
5
0;
4
. B.
1
.
C.
;0 1;
 
. D.
5
;1 ;
4
 
.
Lời giải
Chọn A.
2
2
2 4
1
2 4
2 2 3 1
2 3 1
2
1
4 2 2
2
x
x
x x
x x
2 2
5
4 6 2 2 4 5 0 0;
4
x x x x x x
.
Câu 22: [2D2-1] Tìm tập nghiệm của bất phương trình
1
2
log 1 2
x
.
A.
1;S

. B.
3
0;
4
S
. C.
3
1;
4
S
. D.
3
;
4
S

.
Lời giải
Chọn C.
1
2
1 1
3
log 1 2 1;
1 3
4
1
4 4
x x
x x
x x
.
Câu 23: [2D2-3] Tìm tập nghiệm của bất phương trình
2
1
5 2 5 2
x
x
x
.
A.
; 1 0;1
 . B.
1;0
. C.
; 1 0;
 
.
D.
1;0 1;

.
Lời giải
Chọn D.
Ta có
2 2
1 1
2
5 2 5 2 5 2 5 2
1
x x
x x
x x
x
x
x
2
2
0 0 1 0
1 1
x x x
x x
x x
hoặc
1
x
.
Câu 24: [2D2-2] Phương trình
2 4
log 1 2log 3 2 2 0
x x
có mấy nghiệm?
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
Chọn A.
Điều kiện:
1
1 0
1
3
3 2 0
2
x
x
x
x
x
(*)
Ta có
2 4 2 2
log 1 2log 3 2 2 0 log 4 4 log 3 2
x x x x
4 4 3 2 2
x x x
(thỏa (*))
Vậy phương trình có
1
nghiệm.
Phân tích phương án nhiễu.
B – sai do tính toán.
C – sai do tính toán.
D – sai do tính toán.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 11/11 - Mã đề LD-001
Câu 25: [2D2-4] Có bao nhiêu giá trị nguyên bé hơn
10
của tham số
m
sao cho bất phương trình
2 2
2 2
log 1 2 log 1 0
x x m
thỏa mãn với mọi
3
1;2
?
A.
3
. B.
4
. C.
5
. D.
6
.
Lời giải
Chọn B.
Điều kiện:
0
x
.
2 2 2 2
2 2 2 2
log 1 2 log 1 0 log 1 2 log 1 2 0 1
x x m x x
Đặt:
2
2
log 1
x t
với
3
1;2 1;2
x t
Khi đó,
2
1 2 2
t t m
.
Xét hàm số:
2
2 2
f t t t
trên
1;2
;
2 2 0 1
f t t t
Bảng biến thiên:
Bất phương tình thoả mãn với mọi
x
thuộc
3
1;2
khi
6
m
.
x
1
2
f t
f t
1
6
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 1/10 - Mã đề 002
TOÁN H
Ọ
C
B
Ắ
C
–
TRUNG
-
NAM
Nhóm: THBTN – ĐỀ KIỂM TRA
(25 câu trắc nghiệm)
KIỂM TRA CHƯƠNG 2 GIẢI TÍCH 12
MÃ ĐỀ 002
Thời gian làm bài: 45 phút, không kể thời gian phát đề.
Câu 1. [2D2-1] Rút gọn biểu thức
1
3
0
M a a a
.
A.
5
6
M a
. B.
1
6
M a
. C.
6
5
M a
. D.
3
2
M a
.
Câu 2. [2D2-2] Cho
a
là số thực dương. Đơn giản biểu thức
4 1 2
3 3 3
1 3 1
4 4 4
a a a
P
a a a
.
A.
P a
. B.
1
P a a
. C.
1
P a
. D.
1
P a
.
Câu 3. [2D2-3] Với
, 0
a b
bất kì. Cho biểu thức
2 1
3 3
6 6
a b b a
P
a b
. Tìm mệnh đề đúng.
A.
3
P ab
. B.
P ab
. C.
6
P ab
. D.
P ab
.
Câu 4. [2D2-1] Cho
a
là số thực dương
1
a
và
3
3
log
a
P a
. Mệnh đề nào dưới đây đúng?
A.
3
P
. B.
1
P
. C.
9
P
. D.
P
.
Câu 5. [2D2-1] Giá trị của
2 3 4 63
log 3.log 4.log 5...log 64
A bằng
A.
5
. B.
4
. C.
6
. D.
3
.
Câu 6. [2D2-2] Với các số thực dương
a
,
bất kì. Khẳng định nào sau đây là khẳng định đúng?
A.
log log
ab a b
. B.
log log
b
a
a
b
.
C.
log log log
ab a b
. D.
log log
a
a b
b
.
Câu 7. [2D2-2] Cho log
b
a x
và log
b
c y
. Hãy biểu diễn
2
3
5 4
log
a
b c
theo
x
và
y
:
A.
5 4
6
y
x
. B.
20
3
y
x
. C.
4
2
5 3
3
y
x
. D.
20
20
3
y
x .
Câu 8. [2D2-3] Cho
14 14
log 7 ,log 5
a b
. Tính
35
log 28
theo
,
a b
A.
35
2
log 28
a
a b
. B.
35
2
log 28
a b
.
C.
35
2
log 28
a
a b
. D.
35
log 28
a
a b
.
Câu 9. [2D2-1] Tìm tập xác định
D
của hàm số
1
x
y
.
A.
D
. B.
1;D
. C.
1;D
. D.
;1
D

.
Câu 10. [2D2-1] Tìm tập xác định
D
của hàm số
3
log 2 1
y x
.
A.
1
;
2
D

. B.
1
;
2
D
. C.
0;D
. D.
1
;
2
D
.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 2/10 - Mã đề 002
Câu 11. [2D2-2] Tìm đạo hàm của hàm số
2
log2
.
x
y
x
A.
3
1 4ln 2
.
2 ln10
x
y
x
B.
2
1
.
2 ln10
y
x
C.
3
1 2ln 2
.
ln10
x
y
x
D.
3
1 2log 2
.
x
y
x
Câu 12. [2D2-1] Đạo hàm của hàm số
3
e
x
y
là
A.
3
e
x
y
. B.
3 1
3 e
x
y x
. C.
3
3 e
x
y x
. D.
3
3e
x
y
.
Câu 13. [2D2-1] Tìm giá trị nhỏ nhất của hàm số
ln
y x
trên
1;e
A. Không xác định được giá trị nhỏ nhất. B.
min 1
y
khi
1
x
.
C.
min e
y
, khi
e
x
. D.
min 0
y
, khi
1
x
.
Câu 14. [2D2-1] Tìm giá trị nhỏ nhất của hàm số
1
2
x
y
trên
1;0
A.
min 1
y
, khi
0
x
. B.
1
min
y
khi
1
x
.
C.
min 2
y
, khi
1
x
. D.
1
min
2
y
, khi
1
x
.
Câu 15. [2D2-1] Hình vẽ sau đây là đồ thị của hàm số nào?
A.
ln
y x x
.
B.
ln
y x
.
C.
e
x
y
.
D.
e
x
y x
.
Câu 16. [2D2-2] Cho hàm số
2
ln
y x x
, khẳng định nào sau đây là đúng
A.
3 0
y x y
. B.
2 0
y x y

. C.
2 0
y x y
. D.
3 0
y x y

.
Câu 17. [2D2-2] Nghiệm của phương trình
2 1
1
3
27
x
là
A.
2
x
. B.
2
x
. C.
1
x
. D.
1
x
.
Câu 18. [2D2-2] Nghiệm của phương trình
2
2 2
log 1 log 3 2
x x x
A.
1; 3
x x
. B.
3
x
. C.
1; 3
x x
. D.
3
x
.
Câu 19. [2D2-2] Tập nghiệm của bất phương trình
2
3 1
1
2
2
x x
.
A.
;1 2;T

. B.
;1 2;T
 
.
C.
1;2
T . D.
1;2
T .
Câu 20. [2D2-2] Tập nghiệm của bất phương trình
2
3
log 2 4 5 2
x x
.
A.
T
. B.
\ 1
T
. C.
\ 1
T
. D.
T
.
Câu 21. [2D2-3] Bác Hiếu đầu tư
99
triệu đồng vào một công ty theo thể thức lãi kép với lãi suất
8,25%
một năm. Hỏi sau
5
năm mới rút tiền lãi thì bác Hiếu thu được bao nhiêu tiền lãi? (Giả
sử rằng lãi suất hàng năm không đổi).
A.
48,155
triệu. B.
147,155
triệu. C.
58,004
triệu. D.
8,7
triệu.
O
x
y
1
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 3/10 - Mã đề 002
Câu 22. [2D2-3] Giá trị
m
để phương trình
2
2
5 .5 3 0
x
x
m m
có
2
nghiệm phân biệt sao cho
1 2
2
x x
là
A.
2
. B.
2
. C.
3
. D.
4
.
Câu 23. [2D2-3] Có bao nhiêu số nguyên thỏa mãnbất phương trình
1
2
2.3 9 9 ?
x
x x x
A.
3.
B.
4.
C.
5.
D.
6.
Câu 24. [2D2-2] Số nghiệm nguyên của bất phương trình
3 1
1 3
10 3 10 3
x x
x x
trong khoảng
2018;2018
là
A.
4033
. B.
4032
. C.
4031
. D.
4030
.
Câu 25. [2D2-4] Biết
15
2
x
là một nghiệm của bất phương trình
2
2log 23 23 log 2 15 *
a
a
x x x . Tập nghiệm
T
của bất phương trình
*
là
A.
19
;
2
T
. B.
17
1;
2
T
. C.
2;8
T . D.
2;9
T .
-----------HẾT---------
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 4/10 - Mã đề 002
ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
A
A
B
C
C
C
A
A
D
D
C
D
D
A
A
C
B
D
D
D
A
B
A
D
D
ĐÁP ÁN CHI TIẾT
Câu 1: [2D2-1] Rút gọn biểu thức
1
3
0
M a a a
.
A.
5
6
M a
. B.
1
6
M a
. C.
6
5
M a
. D.
3
2
M a
.
Lời giải
Chọn A.
Ta có
1 1 5
1
3 3 6
2
.
M a a a a a
Câu 2: [2D2-2] Cho
a
là số thực dương. Đơn giản biểu thức
4 1 2
3 3 3
1 3 1
4 4 4
a a a
P
a a a
.
A.
P a
. B.
1
P a a
. C.
1
P a
. D.
1
P a
.
Lời giải
Chọn A.
Ta có
4 1 2
3 3 3
4 1 4 2
2
3 3 3 3
1 3 1 1
1 3 1
4 4 4 4
4 4 4
1
. .
.
1 1
. .
a a a
a a
a a a a a a
P a
a a
a a a a
a a a
Câu 3: [2D2-3] Với
, 0
a b
bất kì. Cho biểu thức
2 1
3 3
6 6
a b b a
P
a b
. Tìm mệnh đề đúng.
A.
3
P ab
. B.
P ab
. C.
6
P ab
. D.
P ab
.
Lời giải
Chọn B.
Phương pháp: Đặt ẩn phụ để biểu thức trở lên gọn gàng hơn
Cách giải: ta đặt
1 2
1
6 3
4 3
2
;
a x a x a x
1 2
1
4 3
6 3 2
;
b y b y b y
;
3 3
4 3 3 4
x x y
x
P ab
x
y
y x y
y x y
.
Câu 4: [2D2-1] Cho
a
là số thực dương
1
a
và
3
3
log
a
P a
. Mệnh đề nào dưới đây đúng?
A.
3
P
. B.
1
P
. C.
9
P
. D.
P
.
Lời giải
Chọn C.
1
3
3
3 3
log log 9log 9
a
a
a
P a a a
.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 5/10 - Mã đề 002
Câu 5: [2D2-1] Giá trị của
2 3 4 63
log 3.log 4.log 5...log 64
A bằng
A.
5
. B.
4
. C.
6
. D.
3
.
Lời giải
Chọn C.
Áp dụng công thức đổi cơ số, ta có
6
2 3 4 63 2 4 63 2 2
log 3.log 4.log 5...log 64 log 4.log 5...log 64 l
og 64 log 2 6
A
.
Câu 6: [2D2-2] Với các số thực dương
a
,
bất kì. Khẳng định nào sau đây là khẳng định đúng?
A.
log log
ab a b
. B.
log log
b
a
a
b
.
C.
log log log
ab a b
. D.
log log
a
a b
b
.
Lời giải
Chọn C.
Theo định nghĩa ta có công thức
log log log
ab a b
và
log log log
a
a b
b
.
Câu 7: [2D2-2] Cho log
b
a x
và log
b
c y
. Hãy biểu diễn
2
3
5 4
log
a
b c
theo
x
và
y
:
A.
5 4
6
y
x
. B.
20
3
y
x
. C.
4
2
5 3
3
y
x
. D.
20
20
3
y
x .
Lời giải
Chọn A.
- Phương pháp: Áp dụng công thức logarit sau:
ln
log ln .ln , 0
ln
b
a
a k a k b a b
b
ln . ln .ln
m n
a b m a n b
Biểu thức cần tính sau khi đưa về cùng loga cơ số e thì việc tối giản biểu thức sẽ đơn giản hơn.
- Cách giải:
ln
log ln .ln , 0
ln
b
a
a x a x b a b
b
lnc
log lnc .ln , 0
ln
b
c y y b b c
b
2
5 4
3 3
3 5 4
3 5 4
5 4 5 4
ln .c
ln ln ln .ln
ln
5 4
3 3 3 3
log
ln 2 2.ln 2.ln 2. .ln 6
a
b
b c b y b
b c
y
b c
ah a a x b x
Cách 2:
2
5 4
3 5 4
3 5 4
2
1
log
log
5 4
3
log
2.log 6
log
b
b
a
b
b
b c
b c
y
b c
a x
a
Trắc nghiệm:
Cho
2
a b c
ta có
1
x y
;
2 2
3 35 4 5 4
2
3
log log 2 .2
2
a
b c
Mà:
1
x y
5 4 3
6 2
y
x
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 6/10 - Mã đề 002
Câu 8: [2D2-3] Cho
14 14
log 7 ,log 5
a b
. Tính
35
log 28
theo
,
a b
A.
35
2
log 28
a
a b
. B.
35
2
log 28
a b
. C.
35
2
log 28
a
a b
. D.
35
log 28
a
a b
.
Lời giải
Chọn A.
Vì logarit cần tính không cùng cơ số với hai logarit đã cho nên ta sẽ đổi logarit cần tính về cơ
số 14
Ta có
14
35
14
log 28
log 28
log 35
Lại thấy
14 14 14 4
log 35 log 7.5 log 7 log 5
a b
Tiếp theo ta biểu diễn
14
log 28
theo các logarit
17
log 7
và
14
log 5
. Muốn vậy ta chỉ biểu diễn số
28 thành tích hoặc thương của các lũy thừa của
14
,
7
và
5
là xong.
Ta có
2
14 14
28 14.2 14.
7 7
Suy ra
2
2
14 14 14 14
14
log 28 log log 14 log 7 2
7
a
Vậy
35
2
log 28
a
a b
Câu 9: [2D2-1] Tìm tập xác định
D
của hàm số
1
x
y
.
A.
D
. B.
1;D
. C.
1;D
. D.
;1
D

.
Lời giải
Chọn D.
Điều kiện
1 0 1
x x
Vậy tập xác định
;1 .
D 
Câu 10: [2D2-1] Tìm tập xác định
D
của hàm số
3
log 2 1
y x
.
A.
1
;
2
D

. B.
1
;
2
D
. C.
0;D
. D.
1
;
2
D
.
Lời giải
Chọn D.
Hàm số
3
log 2 1
y x
xác định khi
1
2 1 0
2
x x
Vậy TXĐ là
1
;
2
D

.
Câu 11: [2D2-2] Tìm đạo hàm của hàm số
2
log2
.
x
y
x
A.
3
1 4ln 2
.
2 ln10
x
y
x
B.
2
1
.
2 ln10
y
x
C.
3
1 2ln 2
.
ln10
x
y
x
D.
3
1 2log 2
.
x
y
x
Lời giải
Chọn C.
ADCT:
a
ln
log
ln
x
a
;
a
1
log
.ln
x
x a
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 7/10 - Mã đề 002
2
'
'
2 2
4 4 4 3
1
1 2 ln 2
. 2 .log2
log2 . .log2
1 2ln 2
.ln10
ln10 ln10
.
ln10
x x
x x x
x x x x
x
x
y
x x x x
Câu 12: [2D2-1] Đạo hàm của hàm số
3
x
y e
là
A.
3
x
y e
. B.
3 1
3
x
y xe
. C.
3
3
x
y xe
. D.
3
3
x
y e
.
Lời giải
Chọn D.
.
u u
e u e
3 3
3 3
x x
y x e e
Câu 13: [2D2-1] Tìm giá trị nhỏ nhất của hàm số
ln
y x
trên
1;
e
A. Không xác định được giá trị nhỏ nhất. B.
min 1
y
khi
1
x
.
C. min
y e
, khi
x e
. D.
min 0
y
, khi
1
x
.
Lời giải
Chọn D.
Vì hàm số đồng biến trên khoảng xác định nên
Vậy hàm số có giá trị nhỏ nhất
min 1 0
y y
khi
1
x
e
.
Câu 14: [2D2-1] Tìm giá trị nhỏ nhất của hàm số
1
2
x
y
trên
1;0
A.
min 1
y
, khi
0
x
. B.
1
min
y
khi
1
x
.
C.
min 2
y
, khi
1
x
. D.
1
min
2
y
, khi
1
x
.
Lời giải
Chọn A.
Vì hàm số nghịch biến trên khoảng xác định nên
Vậy hàm số có giá trị nhỏ nhất
min 0 1
y y
khi
0
x
.
Câu 15: [2D2-1] Hình vẽ sau đây là đồ thị của hàm số nào?
A.
ln
y x x
. B.
ln
y x
. C.
x
y e
. D.
x
y xe
.
Lời giải
Chọn A.
Ta có ĐTHS đi qua điểm
1;0
nên loại đáp án C và D.
Khi
0
lim 0
x
y
nên loại B và Chọn A.
Câu 16: [2D2-2] Cho hàm số
2
ln
y x x
, khẳng định nào sau đây là đúng
O
x
y
1
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 8/10 - Mã đề 002
A.
3 0
y x y
. B.
2 0
y x y

. C.
2 0
y x y
. D.
3 0
y x y

.
Lời giải
Chọn C.
Ta có
2 ln ; 2ln 3 2
y x x x y x y x y
 
.
Câu 17: [2D2-2] Nghiệm của phương trình
2 1
1
3
27
x
là
A.
2
x
. B.
2
x
. C.
1
x
. D.
1
x
.
Lời giải
Chọn B.
Ta có
2 1 2 1 3
1
3 3 3 2 1 3 2
27
x x
x x
.
Câu 18: [2D2-2] Nghiệm của phương trình
2
2 2
log 1 log 3 2
x x x
A.
1; 3
x x
. B.
3
x
. C.
1; 3
x x
. D.
3
x
.
Lời giải
Chọn D.
Ta có PT
2
1 0
3
1 3 2
x
x
x x x
.
Câu 19: [2D2-2] Tập nghiệm của bất phương trình
2
3 1
1
2
2
x x
.
A.
;1 2;T

. B.
;1 2;T
 
.
C.
1;2
T . D.
1;2
T .
Lời giải
Chọn D.
Ta có BPT
2
3 1 1
2 2
1 1
3 1 1 3 2 0 1;2
2 2
x x
x x x x x
.
Câu 20: [2D2-2] Tập nghiệm của bất phương trình
2
3
log 2 4 5 2
x x
.
A.
T
. B.
\ 1
T
. C.
\ 1
T
. D.
T
.
Lời giải
Chọn D.
Ta có BPT
2 2
2 4 5 3 2 4 2 0x x x x x
.
Câu 21: [2D2-3] Bác Hiếu đầu tư
99
triệu đồng vào một công ty theo thể thức lãi kép với lãi suất
8,25%
một năm. Hỏi sau
5
năm mới rút tiền lãi thì bác Hiếu thu được bao nhiêu tiền lãi? (Giả
sử rằng lãi suất hàng năm không đổi).
A.
48,155
triệu. B.
147,155
triệu. C.
58,004
triệu. D.
8,7
triệu.
Lời giải.
Chọn A.
Áp dụng công thức lãi kép, số tiền thu được cả vốn lẫn lãi là
1
N
T A r
, với tiền gửi:
99
A
triệu đồng, lãi suất
0,0825
r
,
5
N
kì. Ta được:
147,155
T
triệu đồng
số tiền lãi là
48,155
T A
triệu đồng.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 9/10 - Mã đề 002
Câu 22: [2D2-3] Giá trị
m
để phương trình
2
2
5 .5 3 0
x
x
m m
có
2
nghiệm phân biệt sao cho
1 2
2
x x
là
A.
2
. B.
2
. C.
3
. D.
4
.
Lời giải
Chọn B
Đặt
2
5 0.
x
t
Ta có:
2
5 3 0
t mt m
Điều kiện cần: pt có hai nghiệm
1 2
2
x x
hay
1 2
2
1 2
. 5 5 3 2.
x x
t t m m
Thử lại.
Câu 23: [2D2-3] Có bao nhiêu số nguyên thỏa mãnbất phương trình
1
2
2.3 9 9 ?
x
x x x
A.
3.
B.
4.
C.
5.
D.
6.
Lời giải
Chọn A.
Đk:
0.
x
2
1
2 2
2
2
3 3
2.3 9 9 2.3 .3 3. 3 3 2. 3. 1 2.3 3. 3 1
3 3
x x
x
x x x x x x x x x x x
x x
Đặt
3 0
x x
t
ta có:
2
3t 2 1 0
t
t

1
1

2
3t 2 1
t
0
0
Suy ra:
2
1
1
3 3 1 1 0
3
x x
t x x x x
Đặt
0
u x
ta có:
2
1 0
u u

1 5
2
1 5
2

2
1
u u
0
0
Khi đó:
1 5 1 5 3 5
0 0 0
2 2 2
u x x
.
Tập nghiệm nguyên
0;1;2
T .
Câu 24: [2D2-2] Số nghiệm nguyên của bất phương trình
3 1
1 3
10 3 10 3
x x
x x
trong khoảng
2018;2018
là
A.
4033
. B.
4032
. C.
4031
. D.
4030
.
Lời giải
Chọn D.
Đk:
3
x
và
1.
x
3 1
1 3
3 1 8
10 3 10 3 0 1 3 0
1 3 1 3
x x
x x
x x
BPT x x
x x x x
x

3
1

Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 10/10 - Mã đề 002
1 3
x x
0
0
Vậy có số nghiệm nguyên trong khoảng
2018;2018
là
4030
Câu 25: [2D2-4] Biết
15
2
x
là một nghiệm của bất phương trình
2
2log 23 23 log 2 15 *
a
a
x x x . Tập nghiệm
T
của bất phương trình
*
là
A.
19
;
2
T
. B.
17
1;
2
T
. C.
2;8
T . D.
2;9
T .
Lời giải
Chọn D.
2 2
2log 23 23 log 2 15 log 23 23 log 2 15
a a a
a
x x x x x x
.
Nếu
1
a
ta có
2
2
2
23 23 2 15
log 23 23 log 2 15 2 19
2 15 0
a a
x x x
x x x x
x x
.
Nếu
0 1
a
ta có
2
2
1 2
23 23 2 15
log 23 23 log 2 15
19
23 23 0
a a
x
x x x
x x x
x
x
.
Mà
15
2
x
là một nghiệm của bất phương trình.
Phân tích phương án nhiễu.
- A sai do quên nghiệm
15
2
x
thuộc tập nghiệm.
- B sai chỉ đúng cho nghiệm
15
2
x
còn sai trong các nghiệm khác.
- C sai do giải sai.
---------HẾT-----------
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 1/11 - Mã đề 003
TOÁN H
Ọ
C
B
Ắ
C
–
TRUNG
–
NAM
Nhóm: THBTN – ĐỀ KIỂM TRA
(25 câu trắc nghiệm)
KIỂM TRA CHƯƠNG 2 GIẢI TÍCH 12
MÃ ĐỀ 003
Thời gian làm bài: 45 phút, không kể thời gian phát đề.
Câu 1. [2D2-1] Cho góc
, giá trị của biểu thức
2 2
sin cos
5 .5
bằng
A.
1
. B.
5
. C.
25
. D.
2 2
sin .cos
5
.
Câu 2. [2D2-2] Cho
a
,
là các số thực dương khác
1
. Hình
vẽ bên là đồ thị của
2
hàm số
1
:
x
C y a
,
2
:
x
C y b
. Mệnh đề nào sau đây là đúng?
A.
1
b a
. B.
1
a b
.
C.
1
a b
. D.
1
b a
.
Câu 3. [2D2-1] Tìm tập xác định
D
của hàm số
2
2
2
y x x
.
A.
D
. B.
\ 1;2
D
.
C.
; 1 2;D

. D.
0;D
.
Câu 4. [2D2-2] Tính đạo hàm của hàm số
13
x
y
x
.
A.
1
13
x
y
. B.
2
13 ln13 1
x
x
y
x
.
C.
13 1
x
y
x
. D.
13 ln13 1
.ln13
x
y
x
.
Câu 5. [2D2-2] Cho hàm số
2
ln 1
2
x
y x
. Khẳng định nào sau đây là đúng.
A. Hàm số đồng biến trên khoảng
0;
. B. Hàm số đạt cực tiểu tại
1
x
.
C. Hàm số nghịch biến trên khoảng
0;1
. D. Hàm số đạt cực đại tại
1
x
.
Câu 6. [2D2-1] Cho
0
a
,
1
a
và
x
,
y
là hai số dương. Mệnh đề nào sau đây là đúng?
A.
log log log
a a a
x y x y
. B.
log log .log
a a a
x y x y
.
C.
log . log log
a a a
x y x y
. D.
log . log .log
a a a
x y x y
.
Câu 7. [2D2-2] Đặt
ln3
a
,
ln5
b
. Tính
3 4 5 123 124
ln ln ln ... ln ln
4 5 6 124 125
S theo
a
và
.
A.
2
I a b
. B.
3
I a b
. C.
2
I a b
. D.
3
I a b
.
Câu 8. [2D2-2] Biết
sin 0
x
,
cos 0
x
và
3 3
log sin log cos 1
x x
. Giá trị của
3
log sin cos
x x
bằng
A.
1
. B.
1
. C.
3
1
log 5 1
2
. D.
3
log 5 1
.
Câu 9. [2D2-3] Cho
0
a
,
0
b
,
0
c
là các số thực khác
0
thỏa
5 15 45
a b c
. Tính
b b
T
a c
.
A.
15
log 5
T . B.
3
T
. C.
2
T
. D.
5
log 45
T .
O
x
y
1
1
C
2
C
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 2/11 - Mã đề 003
Câu 10. [2D2-3] Cho hàm số
2
1 2
log
2 1
x
f x
x
.
Tính tổng:
1 2 3 2015 2016
...
2017 2017 2017 2017 2017
S f f f f f
.
A.
2017
. B.
2016
. C.
4032
. D.
1008
.
Câu 11. [2D2-1] Tìm tập xác định
D
của hàm số
3
0,5
log 3 2
y x x
.
A.
2;
. B.
0;1
. C.
1;
. D.
2; \ 1
.
Câu 12. [2D2-2] Cho bốn hàm số
1
1
2
x
y
,
3 2
x
y ,
1
3
2
x
y
,
4 4
x
y và bốn đường cong
1
C
,
2
C
,
3
C
,
4
C
như hình vẽ bên. Đồ thị hàm số
1
,
2
,
3
,
4
lần lượt là
A.
1 2 3 4
, , ,
C C C C
. B.
3 2 4 1
, , ,
C C C C
.
C.
2 4 1 3
, , ,
C C C C
. D.
4 1 3 2
, , ,
C C C C
.
Câu 13. [2D2-2] Tìm tất cả giá trị thực của tham số
m
để hàm số
2
ln 2
y x mx m
có tập xác định
là
.
A.
0
m
hoặc
1
m
. B.
0 1
m
.
C.
0
m
hoặc
1
m
. D.
0 1
m
.
Câu 14. [2D2-3] Trong mặt phẳng tọa độ
Oxy
cho hình vuông
ABCD
có diện tích bằng
36
, đường
thẳng
AB
song song với trục
Ox
, các đỉnh
A
,
B
và
C
lần lượt nằm trên đồ thị của các hàm
số
log
a
y x
, log
a
y x
,
3
log
a
y x
và
a
là một số thực lớn hơn
1
. Tìm
a
.
A.
3
a . B.
3
6
a .
C.
6
a . D.
6
3
a .
Câu 15. [2D2-4] Cho
a
,
là hai số thực dương thỏa mãn
2 4 8
2 2 4 8
a
a b
b
a b
. Tính giá trị của biểu
thức
2017
2017
a
b
P .
A.
1
. B.
2
2017
. C.
2017
a
. D.
2017
b
.
Câu 16. [2D2-1] Tập nghiệm
S
của phương trình
1 2
2 3
3 2
x x
là
A.
1
S . B.
1
3
S
.
C.
1
S
. D.
2
S .
Câu 17. [2D2-2] Tìm tọa độ giao điểm của đồ thị hàm số
3 2
x
y
và đường thẳng
5
y
.
A.
1;5
. B.
1;5
. C.
2;5
. D.
2;5
.
O
x
y
1
2
C
1
C
4
C
3
C
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 3/11 - Mã đề 003
Câu 18. [2D2-2] Biết rằng phương trình
8
log 9
2018
3 2 0
x
có nghiệm duy nhất
0
x x
. Khẳng định nào
sau đây là đúng?
A.
0
x
là số nguyên tố. B.
0
x
là số chính phương.
C.
0
x
chia hết cho
3
. D.
0
x
là một số chẵn.
Câu 19. [2D2-3] Tính tổng
T
tất cả các nghiệm của phương trình
2 2
3.25 3 10 .5 3 0
x x
x x
.
A.
5
2
4 log
7
T
. B.
5
3 log 2
T . C.
5
4 log 3
T . D.
5
2 log 6
T .
Câu 20. [2D2-4] Tính tổng
T
tất cả các giá trị của tham số
m
để phương trình
2
1
2
2 2
2 log 2 3 4 log 2 2
x mx
x x x m
có đúng ba nghiệm phân biệt.
A.
1
T
. B.
2
T
. C.
3
T
. D.
4
T
.
Câu 21. [2D2-1] Tập nghiệm của bất phương trình
1
1
3
9
x
là
A.
3;
. B.
1;
. C.
; 1

. D.
1;3
.
Câu 22. [2D2-2] Tập nghiệm của bất phương trình
0,5
log 1 2
x
là
A.
5
;
4

. B.
5
;
4
. C.
5
1;
4
. D.
1;3
.
Câu 23. [2D2-2] Gọi
S
là tập nghiệm của bất phương trình
2
2 3
1
0,25
4
x
x
. Khi đó
S
có dạng
;
a b
với
a b
. Tính
P a b
.
A.
2
. B.
2
. C.
1
. D.
0
.
Câu 24. [2D2-2] Có bao nhiêu số nguyên
x
thỏa mãn bất phương trình
log 40 log 60 2
x x
.
A.
20
. B.
18
. C.
21
. D.
19
.
Câu 25. [2D2-4] Có bao nhiêu giá trị nguyên của tham số
m
thuộc khoảng
2018;2018
để bất
phương trình
2 2
1 4 1 4
9 20 .3 2 5 0
x x
m m
có tập nghiệm
2;2
.
A.
2057
. B.
2060
. C.
2058
. D.
2056
.
----------HẾT----------
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 4/11 - Mã đề 003
ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
B C
B B D
C
D
C
C
D
D
B D
D
B B A
C
C
C
A
C
A
B D
HƯỚNG DẪN GIẢI
Câu 1. [2D2-1] Cho góc
, giá trị của biểu thức
2 2
sin cos
5 .5
bằng
A.
1
. B.
5
. C.
25
. D.
2 2
sin .cos
5
.
Lời giải
Chọn B.
Ta có:
2 2 2 2
sin cos sin cos 1
5 .5 5 5 5
x x x x
.
Câu 2. [2D2-2] Cho
a
,
là các số thực dương khác
1
. Hình vẽ bên là đồ thị của
2
hàm số
1
:
x
C y a
,
2
:
x
C y b
. Mệnh đề nào sau đây là đúng?
A.
1
b a
. B.
1
a b
. C.
1
a b
. D.
1
b a
.
Lời giải
Chọn C.
Đồ thị hàm số
x
y a
và
x
y b
đi từ trái sang phải theo chiều hướng xuống nên là những hàm
số nghịch biến
, 1
a b

. Loại A,B.
Từ đồ thị hàm số ta thấy tại cùng một giá trị
0
0
x
thì đồ thị hàm số
x
y a
nằm trên đồ thị
hàm số
x
y b
hay
0
0
x x
x
a b
b a
. Ví dụ:
0
1 1
1
1 1
x
a b
b a
b a
.
Vậy
1
a b
.
Câu 3. [2D2-1] Tìm tập xác định
D
của hàm số
2
2
2
y x x
.
A.
D
. B.
\ 1;2
D
.
C.
; 1 2;D

. D.
0;D
.
Lời giải
Chọn B.
Hàm số xác định khi và chỉ khi
2
1
2 0 \ 1;2
2
x
x x D
x

.
Câu 4. [2D2-2] Tính đạo hàm của hàm số
13
x
y
x
.
A.
1
13
x
y
. B.
2
13 ln13 1
x
x
y
x
.
C.
13 1
x
y
x
. D.
13 ln13 1
.ln13
x
y
x
.
O
x
y
1
1
C
2
C
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 5/11 - Mã đề 003
Lời giải
Chọn B.
Ta có:
2
13 ln13 1
13
x
x
x
y y
x x
.
Câu 5. [2D2-2] Cho hàm số
2
ln 1
2
x
y x
. Khẳng định nào sau đây là đúng.
A. Hàm số đồng biến trên khoảng
0;
. B. Hàm số đạt cực tiểu tại
1
x
.
C. Hàm số nghịch biến trên khoảng
0;1
. D. Hàm số đạt cực đại tại
1
x
.
Lời giải
Chọn D.
Tập xác định
0;D
Đạo hàm:
1
1
0
1
x
y x y
x
x
.
Bảng biến thiên:
Dựa vào bảng biến thiên, hàm số đạt cực đại tại
1
x
.
Câu 6. [2D2-1] Cho
0
a
,
1
a
và
,
x y
là hai số dương. Mệnh đề nào sau đây là đúng?
A.
log log log
a a a
x y x y
. B.
log log .log
a a a
x y x y
.
C.
log . log log
a a a
x y x y
. D.
log . log .log
a a a
x y x y
.
Lời giải
Chọn C.
Câu 7. [2D2-2] Đặt
ln3
a
,
ln5
b
. Tính
3 4 5 123 124
ln ln ln ... ln ln
4 5 6 124 125
S theo
a
và
.
A.
2
I a b
. B.
3
I a b
. C.
2
I a b
. D.
3
I a b
.
Lời giải
Chọn D.
Ta có:
3 4 123 124 3 4 123 124 3
ln ln ... ln ln ln . .... . ln
4 5 124 125 4 5 124 125 125
S
ln3 ln125 ln3 3ln5 3
a b
.
Câu 8. [2D2-2] Biết
sin 0
x
,
cos 0
x
và
3 3
log sin log cos 1
x x
. Giá trị của
3
log sin cos
x x
bằng.
A.
1
. B.
1
. C.
3
1
log 5 1
2
. D.
3
log 5 1
.
Lời giải
Chọn C.
Ta có:
1
3 3 3 3
1
log sin log cos 1 log sin .cos log 3 sin .cos
x x x x x x
.
x

1

y
0
y

1
2

Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 6/11 - Mã đề 003
2
5
sin cos
3
x x

. Mà
15
sin 0,cos 0 sin cos
3
x x x x  .
Do đó:
3 3 3
15 1
log sin cos log log 5 1
3 2
x x
.
Câu 9. [2D2-3] Cho
0
a
,
0
b
,
0
c
là các số thực khác
0
thỏa
5 15 45
a b c
. Tính
b b
T
a c
.
A.
15
log 5
T . B.
3
T
. C.
2
T
. D.
5
log 45
T .
Lời giải
Chọn C.
Giả sử
5
15
45
log
5 15 45 log
log
a b c
a t
t b t
c t
.
Ta có:
15 15
15 15 15
5 45
log log
log 5 log 45 log 225 2
log log
t t
b b
T
a c t t
.
Câu 10. [2D2-3] Cho hàm số
2
1 2
log
2 1
x
f x
x
. Tính tổng:
1 2 3 2015 2016
...
2017 2017 2017 2017 2017
S f f f f f
.
A.
2017
. B.
2016
. C.
4032
. D.
1008
.
Lời giải
Chọn D.
Xét
2 2 2
2 1
1 2 1 1
1 log log log 4 1
2 1 2 2
x
x
f x f x
x x
Do đó:
1 2016
1
2017 2017
f f
,
2 2015
1
2017 2017
f f
Suy ra:
1 2 2015 2016
... 1 1 .. 1 1 1008
2017 2017 2017 2017
S f f f f
.
Câu 11. [2D2-1] Tìm tập xác định
D
của hàm số
3
0,5
log 3 2
y x x
.
A.
2;
. B.
0;1
. C.
1;
. D.
2; \ 1
.
Lời giải
Chọn D.
Hàm số xác định khi và chỉ khi
3
2
3 2 0
1
m
x x
m
.
Câu 12. [2D2-2] Cho bốn hàm số
1
1
2
x
y
,
3 2
x
y ,
1
3
2
x
y
,
4 4
x
y và bốn đường
cong
1
C
,
2
C
,
3
C
,
4
C
như hình vẽ bên. Đồ thị hàm số
1
,
2
,
3
,
4
lần lượt là
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 7/11 - Mã đề 003
A.
1 2 3 4
, , ,
C C C C
. B.
3 2 4 1
, , ,
C C C C
.
C.
2 4 1 3
, , ,
C C C C
. D.
4 1 3 2
, , ,
C C C C
.
Lời giải
Chọn B.
Đồ thị hàm số
3
C
,
4
C
đi từ trái sang phải theo chiều hướng xuống nên là những hàm số
nghịch biến

3
C
,
4
C
tương ứng với
1
hoặc
3
.
Từ đồ thị hàm số ta thấy tại cùng một giá trị
0
0
x
thì đồ thị hàm số
4
C
nằm trên đồ thị hàm
số
3
C
. Chọn
1
1
0
1 1
1
2
2
x

. Do đó
4
3
C ,
3
1
C .
Tương tự:
1
4
C ,
2
2
C .
Câu 13. [2D2-2] Tìm tất cả giá trị thực của tham số
m
để hàm số
2
ln 2
y x mx m
có tập xác định
là
.
A.
0
m
hoặc
1
m
. B.
0 1
m
.
C.
0
m
hoặc
1
m
. D.
0 1
m
.
Lời giải
Chọn D.
YCBT
2 2
2 0, 0 0 0 1
x mx m x m m m
.
Câu 14. [2D2-3] Trong mặt phẳng tọa độ
Oxy
cho hình vuông
ABCD
có diện tích bằng
36
, đường
thẳng
AB
song song với trục
Ox
, các đỉnh
,
A B
và
C
lần lượt nằm trên đồ thị của các hàm số
log
a
y x
, log
a
y x
,
3
log
a
y x
và
a
là một số thực lớn hơn
1
. Tìm
a
.
O
x
y
1
2
C
1
C
4
C
3
C
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 8/11 - Mã đề 003
A.
3
a . B.
3
6
a . C.
6
a . D.
6
3
a .
Lời giải
Chọn D.
Do
,
A B
thuộc đường thẳng song song trục
Ox
, giả sử , : log
a
A B d y m
,
0
m
.
;log , ;log
a a
A m m B m m

, Mà
36 6 6 9
ABCD
S AB m m m

.
Suy ra:
3
3;2log 3 3;3log
a
B C a
 . Ta lại có:
6
3
6
3
6 log 6
1
3
a
BC a
a
.
Đối chiếu với điều kiện
6
1 3
a a .
Câu 15. [2D2-4] Cho
,
a b
là hai số thực dương thỏa mãn
2 4 8
2 2 4 8
a
a b
b
a b
. Tính giá trị của biểu thức
2017
2017
a
b
P .
A.
1
. B.
2
2017
. C.
2017
a
. D.
2017
b
.
Lời giải
Chọn B.
Ta có:
2
2 4 8
2 . 2 4 8 2 . 2 . 2
2 2 4 8
a
a b a b
a b
b
a b a b
a b
.
Xét hàm số
2 . , 0 2 2 . .ln2 0, 0
t t t
f t t t f t t t

Suy ra hàm số đồng biến trên khoảng
0;
.
Do đó:
2 2
f a f b a b
.
Vậy
2
2
2017 2017
2017
2017 2017
a b
b b
P
.
Câu 16. [2D2-1] Tập nghiệm
S
của phương trình
1 2
2 3
3 2
x x
là
A.
1
S . B.
1
3
S
. C.
1
S
. D.
2
S .
Lời giải
Chọn B.
Ta có:
1 2 1 2
2 3 3 3 1
1 2
3 2 2 2 3
x x x x
x x x
.
Câu 17. [2D2-2] Tìm tọa độ giao điểm của đồ thị hàm số
3 2
x
y
và đường thẳng
5
y
.
A.
1;5
. B.
1;5
. C.
2;5
. D.
2;5
.
Lời giải
Chọn A.
Phương trình hoành độ giao điểm:
3 2 5 3 3 1
x x
x
.
Vậy tọa độ giao điểm là
1;5
.
Câu 18. [2D2-2] Biết rằng phương trình
8
log 9
2018
3 2 0
x
có nghiệm duy nhất
0
x x
. Khẳng định nào
sau đây là đúng.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 9/11 - Mã đề 003
A.
0
x
là số nguyên tố. B.
0
x
là số chính phương.
C.
0
x
chia hết cho
3
. D.
0
x
là một số chẵn.
Lời giải
Chọn C.
Ta có:
2
8
2 2
.log 3
.log 9
2018 2018 2018
3 3
3 2 0 2 3 3 3 3027
x
x
x
x
.
Câu 19. [2D2-3] Tính tổng
T
tất cả các nghiệm của phương trình
2 2
3.25 3 10 .5 3 0
x x
x x
.
A.
5
2
4 log
7
T
. B.
5
3 log 2
T . C.
5
4 log 3
T . D.
5
2 log 6
T .
Lời giải
Chọn C.
Đặt
2
5
x
t
,
0
t
. Phương trình trở thành:
2
3 3 10 . 3 0
t x t x
1
.
2 2
2
3 10 12 3 9 48 64 3 8
x x x x x

Phương trình
1
có hai phân biệt
1
3
t
hay
3
t x
.
Với
2
5
1 1
5 2 log 3
3 3
x
t x
.
Với
2
3 5 3
x
t x x
.
2 2
5 5 ln5 0
x x
VT f x f x

Hàm số
đồng biến,
3 1 0VP g x x g x
 
Hàm số nghịch biến.
Do đó:
có nghiệm duy nhất:
2
x
. Tổng hai nghiệm là
5
4 log 3
.
Câu 20. [2D2-4] Tính tổng
T
tất cả các giá trị của tham số
m
để phương trình
2
1
2
2 2
2 log 2 3 4 log 2 2
x mx
x x x m
có đúng ba nghiệm phân biệt.
A.
1
T
. B.
2
T
. C.
3
T
. D.
4
T
.
Lời giải
Chọn C.
Phương trình trở thành:
2
2
2
1
2 2
2 .log 1 2 2 .log 2 2
x m
x
x x m
1
.
Xét hàm số
2 2
2
2 .log 2 , 0 2 .log 2 ln 2 0, 0
2 ln 2
t
t t
f t t t f t t t
t

.

Hàm số đồng biến trên
0;
.
Do đó:
2
2 2
2
1
2
2 2
1 1 2 1 2
1
2
x
m x
f x f x m x x m
x
m
.
Số nghiệm pt
là số giao điểm của đường thẳng
y m
và đồ thị hàm số
2
2
1
2
2 2
1
2
x
x
y
x
.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 10/11 - Mã đề 003
Dựa vào đồ thị hàm số:
có
3
nghiệm phân biệt
1 3
; 1;
2 2
m m m

.
Câu 21. [2D2-1] Tập nghiệm của bất phương trình
1
1
3
9
x
là
A.
3;
. B.
1;
. C.
; 1

. D.
1;3
.
Lời giải
Chọn A.
Bất phương trình trở thành:
1 2
3 3 1 2 3
x
x x
.
Câu 22. [2D2-2] Tập nghiệm của bất phương trình
0,5
log 1 2
x
là
A.
5
;
4

. B.
5
;
4
. C.
5
1;
4
. D.
1;3
.
Lời giải
Chọn C.
Điều kiện:
1 0 1
x x
Bất phương trình trở thành:
2
0,5 0,5
1 5
log 1 log 0,5 1
4 4
x x x
.
Vậy:
5
1;
4
x
.
Câu 23. [2D2-2] Gọi
S
là tập nghiệm của bất phương trình
2
2 3
1
0,25
4
x
x
. Khi đó
S
có dạng
;
a b
với
a b
. Tính
P a b
.
A.
2
. B.
2
. C.
1
. D.
0
.
Lời giải
Chọn A.
Bất phương trình trở thành:
2
2 3
2 2
1 1
2 3 2 3 0 1 3
4 4
x x
x x x x x
.
Vậy
1;3 2
S a b

.
Câu 24. [2D2-2] Có bao nhiêu số nguyên
x
thỏa mãn bất phương trình
log 40 log 60 2
x x
.
A.
20
. B.
18
. C.
21
. D.
19
.
Lời giải
Chọn B.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 11/11 - Mã đề 003
Điều kiện:
40 60
x
.
Bất phương trình trở thành:
2
log 40 60 log100 100 2500 0 50
x x x x x
.
Vậy
40;60 \ 50S
có
18
giá trị nguyên.
Câu 25. [2D2-4] Có bao nhiêu giá trị nguyên của tham số
m
thuộc khoảng
2018;2018
để bất
phương trình
2 2
1 4 1 4
9 20 .3 2 5 0
x x
m m
có tập nghiệm
2;2
.
A.
2057
. B.
2060
. C.
2058
. D.
2056
.
Lời giải
Chọn D.
Điều kiện:
2 2
x
.
Xét hàm số
2
2
1 4 , 2;2 0 0
4
x
f x x x f x f x x
x
.
Ta có:
2 1, 2 1, 0 3 1 3
f f f f x
.
Đặt
2
1 4
3 3;27
x
t t
Bất pt trở thành:
2
20 2 5 0, 3;27
t m t m t
2
20 5
, 3;27
2
t t
m t
t
.
Xét hàm số
2 2
2
9
20 5 4 45
, 3;27 0
5
2
2
t
t t t t
f t t f t f t
t
t
t
.
Bảng biến thiên:
t
f'
t( )
f
t( )
∞
273 9
0
+
_
1274
25
74
38
Dựa vào bảng biến thiên:
, 3;27 38
m f t t m

m
có
2056
giá trị nguyên.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 1/9 - Mã đề 004
TOÁN HỌC BẮC–TRUNG–NAM
Nhóm: THBTN – ĐỀ KIỂM TRA
(25 câu trắc nghiệm)
KIỂM TRA CHƯƠNG 2 GIẢI TÍCH 12
MÃ ĐỀ 004
Thời gian làm bài: 45 phút, không kể thời gian phát đề.
Câu 1. [2D2-1] Cho
. Kết luận nào sau đây là đúng?
A.
0
. B.
. 1
. C.
. D.
.
Câu 2. [2D2-2] Cho biểu thức
3
5
2 3
P x x x
. Mệnh đề nào dưới đây đúng.
A.
14
15
P x
. B.
17
36
P x
. C.
13
15
P x
. D.
16
15
P x
.
Câu 3. [2D2-1] Tìm tập xác định
D
của hàm số
2
2
3 1
y x
A.
1
\
3
D
. B.
1
3
D
.
C.
1 1
; ;
3 3
 
. D.
1 1
;
3 3
D
.
Câu 4. [2D2-2] Đường cong ở hình bên là đồ thị của một hàm số trong
bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây.
Hỏi hàm số đó là hàm số nào?
A.
2
2 1
y x x
. B.
0,5
log
y x
.
C.
1
2
x
y . D.
2
x
y
.
Câu 5. [2D2-1] Hàm số
1
3
1
y x
có đạo hàm là
A.
2
3
1
3 1
y
x
. B.
3
1
3 1
y
x
. C.
3
1
3
x
y
. D.
3
1
3
x
y
.
Câu 6. [2D2-2] Cho
30
log 3
a và
30
log 5
b . Tính
30
log 1350
theo
a
và
.
A.
1 2
a b
B.
1 2 .
a b
C.
1 2
a b
D.
1 2
a b
Câu 7. [2D2-2] Nếu
2 2 2
log 5log 4log ,( , 0)
x a b a b
thì
x
bằng
A.
5 4
a b
. B.
4 5
a b
. C.
5 4 .
a b
D.
4 5 .
a b
Câu 8. [2D2-2] Cho
3 5
2 2 4
3
. . .
log
a
a a a a
A
a
với
0; 1
a a
. Giá trị
A
bằng
A.
16
5
B.
67
5
C.
22
5
D.
62
15
Câu 9. [2D2-3] Cho
x
,
y
là các số thực dương thỏa mãn
9 6 4
log log log
6
x y
x y
. Tính tỉ số
x
y
.
A.
3
x
y
. B.
5
x
y
. C.
2
x
y
. D.
4
x
y
.
O
x
y
1
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 2/9 - Mã đề 004
Câu 10. [2D2-3] Cho các số thực dương khác
1
là
a
,
,
c
. Rút gọn
2
2
2
log .log .log
a
b
c
b c a
ta được
, ,
2
m
m n N
n
, với
m
n
là phân số tối giản. Chọn khẳng định đúng.
A.
2
m n
B.
2 0
m n
C.
2 0
m n
D.
2
4 0
n m
Câu 11. [2D2-1] Đồ thị sau là của hàm số nào sau đây?
A.
3
log
y x
. B.
2
log 2
y x
.
C.
3
2log
y x
. D.
5
log
y x
.
Câu 12. [2D2-2] Hàm số
2
ln 2 4
y x mx
có tập xác định
D
khi:
A.
2
m
. B.
2
2
m
m
. C.
2
m
. D.
2 2
m
.
Câu 13. [2D2-3] Biết rằng giá trị lớn nhất của hàm số
2
ln
x
y
x
trên đoạn
3
1;e
là
e
n
m
M
trong đó
M
,
n
là các số tự nhiên. Tính
2 3
2 .
S m n
A.
22.
S
B.
24.
S
C.
32.
S
D.
135.
S
Câu 14. [2D2-1] Cho
ln
f x x x
. Đạo hàm cấp hai
e
f
bằng:
A.
2.
B.
1
.
e
C.
3.
D.
e
.
Câu 15. [2D2-2] Đồ thị hàm số
ln
x
y
x
có tọa độ điểm cực đại là
;
a b
. Khi đó
ab
bằng
A.
e
. B.
2e
. C.
1
D.
1
Câu 16. [2D2-1] Tìm các nghiệm của phương trình
1
3 27.
x
A.
9.
x
B.
3.
x
C.
4.
x
D.
10.
x
Câu 17. [2D2-1] Phương trình
2
3
log 4 12 2
x x
. Chọn phương án đúng?
A. Có hai nghiệm cùng dương. B. Có hai nghiệm trái dấu.
C. Có hai nghiệm cùng âm. D. Vô nghiệm.
Câu 18. [2D2-2] Cho phương trình
25
log 4.5 2 1
x
x
có hai nghiệm là
1
x
,
2
x
. Tổng
1 2
x x
bằng
A.
50.
B.
5
log 100
C.
30.
D.
5
log 50.
Câu 19. [2D2-2] Bất phương trình
2
2 3 2 3
x x
có tập nghiệm là
A.
1; .

B.
; 1 .

C.
(2; ).

D.
( ; 2).

Câu 20. [2D2-2] Tập nghiệm của bất phương trình
1
3
log 3 1 0
x
có dạng
;
a b
. Khi đó giá trị
3
a b
bằng
A.
15
. B.
13
.
C.
37
3
. D.
30
.
Câu 21. [2D2-2] Tìm số nghiệm nguyên của bất phương trình:
3
log 1 3
x
.
A.
7
.
B.
26
.
C.
15
.
D.
27
.
O
x
y
1
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 3/9 - Mã đề 004
Câu 22. [2D2-2] Anh Nam vay tiền ngân hàng
1
tỷ đồng theo phương thức trả góp (chịu lãi số tiền chưa
trả) với lãi suất
0,5%
/tháng. Nếu cuối mỗi tháng bắt đầu từ tháng thứ nhất anh Nam trả
30
triệu đồng. Hỏi sau bao nhiêu tháng anh Nam trả hết nợ?
A.
35
tháng. B.
36
tháng. C.
37
tháng. D.
38
tháng.
Câu 23. [2D2-3] Tìm tất cả các giá trị của tham số
m
để phương trình
2
3 3
log 2 log 3 1 0
x m x m
có 2 nghiệm
1
x
,
2
x
sao cho
1 2
27
x x
.
A.
4
3
m
. B.
25
m
. C.
28
3
m . D.
1
m
.
Câu 24. [2D2-4] Tìm tập hợp các giá trị của tham số thực
m
để phương trình
6 3 2 0
x x
m m
có
nghiệm thuộc khoảng
0;1
.
A.
3;4
. B.
2;4
. C.
2;4
. D.
3;4
.
Câu 25. [2D2-4] Tìm giá trị nhỏ nhất của biểu thức
2
2
2
log 6 log
a
b
a
b
P b
a
với
a
,
là các số
thực thay đổi thỏa mãn
1.
b a
A.
30.
B.
40.
C.
50.
D.
60.
----------HẾT----------
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 4/9 - Mã đề 004
ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
D
A
A
C
A
B A
D
C
A
A
D
C
B D
C
C
D
B B B C
D
C
D
HƯỚNG DẪN GIẢI
Câu 1. [2D2-1] Cho
. Kết luận nào sau đây là đúng?
A.
0
. B.
. 1
. C.
. D.
.
Lời giải
Chọn D.
Vì
1
nên
.
Câu 2. [2D2-2] Cho biểu thức
3
5
2 3
P x x x
. Mệnh đề nào dưới đây đúng.
A.
14
15
P x
. B.
17
36
P x
. C.
13
15
P x
. D.
16
15
P x
.
Lời giải
Chọn A.
Ta có
1
1
1
3
1
1
3
2 3 2 1 1 14
1
2
3
3
2
5 5 52 3 2 3 2 3
3 5 3 6 10 15
2
. . . .
P x x x x x x x x x x x x x x x x
.
Câu 3. [2D2-1] Tìm tập xác định
D
của hàm số
2
2
3 1
y x
A.
1
\
3
D
. B.
1
3
D
.
C.
1 1
; ;
3 3
 
. D.
1 1
;
3 3
D
.
Lời giải
Chọn A.
Vì
2 0
nên
2
2
3 1
y x
xác định khi
2
1
3 1 0
3
x x
.
Câu 4. [2D2-2] Đường cong ở hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn
phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
A.
2
2 1
y x x
. B.
0,5
log
y x
.
C.
1
2
x
y . D.
2
x
y
.
Lời giải
Chọn C.
Nhìn vào đồ thị ta thấy:.
+ Hàm số nghịch biến trên
. Nên loại đáp án A, D.
O
x
y
1
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 5/9 - Mã đề 004
+ Hàm số xác định trên
nên loại đáp án B ( hàm số
0,5
log
y x
xác định khi
0
x
)
Câu 5. [2D2-1] Hàm số
1
3
1
y x
có đạo hàm là
A.
2
3
1
3 1
y
x
. B.
3
1
3 1
y
x
. C.
3
1
3
x
y
. D.
3
1
3
x
y
.
Lời giải
Chọn A.
1 1 2
1
3 3 3
2
3
1 1 1
1 1 . 1 1
3 3
3 1
y x y x x x
x
.
Câu 6. [2D2-2] Cho
30
log 3
a và
30
log 5
b . Tính
30
log 1350
theo
a
và
.
A.
1 2
a b
B.
1 2 .
a b
C.
1 2
a b
D.
1 2
a b
Lời giải
Chọn B.
Ta có:
2
30 30 30 30
log 1350 log 30.3 .5 1 2log 3 log 5 1 2
a b
.
Câu 7. [2D2-2] Nếu
2 2 2
log 5log 4log ,( , 0)
x a b a b
thì
x
bằng
A.
5 4
a b
. B.
4 5
a b
. C.
5 4 .
a b
D.
4 5 .
a b
Lời giải
Chọn A.
5 4 5 4 5 4
2 2 2 2 2 2 2 2
log 5log 4log log log log log log . .
x a b x a b x a b x a b
.
Câu 8. [2D2-2] Cho
3 5
2 2 4
3
. . .
log
a
a a a a
A
a
với
0; 1
a a
. Giá trị
A
bằng
A.
16
5
B.
67
5
C.
22
5
D.
62
15
Lời giải
Chọn D.
Với
0 1
a
. Ta có:
62
3 52 2 4
15
3
. . . 62
log log
15
a a
a a a a
A a
a
Câu 9. [2D2-3] Cho
x
,
y
là các số thực dương thỏa mãn
9 6 4
log log log
6
x y
x y
. Tính tỉ số
x
y
.
A.
3
x
y
. B.
5
x
y
. C.
2
x
y
. D.
4
x
y
.
Lời giải
Chọn C.
Đặt
9 6 4
9
log log log 6
6
4
6
t
t
t
x
x y
t x y y
x y
2
3 3 3
9 6 6.4 6 2
2 2 2
t t t
t t t
x
y
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 6/9 - Mã đề 004
Câu 10. [2D2-3] Cho các số thực dương khác
1
là
a
,
,
c
. Rút gọn
2
2
2
log .log .log
a
b
c
b c a
ta được
, ,
2
m
m n N
n
, với
m
n
là phân số tối giản. Chọn khẳng định đúng.
A.
2
m n
B.
2 0
m n
C.
2 0
m n
D.
2
4 0
n m
Lời giải
Chọn A.
Ta có
2
2
2
1 2
log .log .log log . log . log
2 2
2
a a b c
b
c
b c a b c a
1 2
. . log . log . log 1, 2.
2 2
2 2 2
a b c
b c a m n
Câu 11. [2D2-1] Đồ thị sau là của hàm số nào sau đây?
A.
3
log
y x
.
B.
2
log 2
y x
.
C.
3
2log
y x
.
D.
5
log
y x
.
Lời giải
Chọn A.
Ta thấy đồ thị hàm số đi qua điểm
3;1
. Do đó ta loại các đáp án B, C, D.
Câu 12. [2D2-2] Hàm số
2
ln 2 4
y x mx
có tập xác định
D
khi:
A.
2
m
. B.
2
2
m
m
. C.
2
m
. D.
2 2
m
.
Lời giải
Chọn D.
Hàm số có tập xác định
2
2
4 0
2 4 0, 2 2
1 0
m
D x mx m m
a
Câu 13. [2D2-3] Biết rằng giá trị lớn nhất của hàm số
2
ln
x
y
x
trên đoạn
3
1;
e
là
n
m
M
e
trong đó
M
,
n
là các số tự nhiên. Tính
2 3
2 .
S m n
A.
22.
S
B.
24.
S
C.
32.
S
D.
135.
S
Lời giải
Chọn C.
2 2
2
2
1
ln 0
ln 2ln ln
0
ln 2
x
x
x x x
y f x f x f x
xx x
x e
.
Ta có:
2 3 2 3
2 3 2
4
4 9 4
1 0, , 2 32.
2
n
m
m
f f e f e S m n
n
e e e e
O
x
y
1
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 7/9 - Mã đề 004
Câu 14. [2D2-1] Cho
ln
f x x x
. Đạo hàm cấp hai
f e
bằng:
A.
2.
B.
1
.
e
C.
3.
D.
.
e
Lời giải
Chọn B.
Ta có:
1 1
ln 1f x x f x f e
x e

.
Câu 15. [2D2-2] Đồ thị hàm số
ln
x
y
x
có tọa độ điểm cực đại là
;
a b
. Khi đó
ab
bằng
A.
.
e
B.
2 .
e
C.
1
D.
1
Lời giải
Chọn D.
Ta có
2
ln 1 ln
0 1 ln 0
x x
y y x x e
x x
Mặt khác
2 4 3
2ln 3
1 ln 1
0
x x
x
y y e
x x e
Suy ra, hàm số đạt cực đại tại
x e
, suy ra tọa độ điểm cực đại là
1
; 1
1
a e
e ab
e
b
e
Câu 16. [2D2-1] Tìm các nghiệm của phương trình
1
3 27.
x
A.
9.
x
B.
3.
x
C.
4.
x
D.
10.
x
Lời giải
Chọn C.
Ta có
1 3
3 3 4
x
x
.
Câu 17. [2D2-1] Phương trình
2
3
log 4 12 2
x x
. Chọn phương án đúng?
A. Có hai nghiệm cùng dương. B. Có hai nghiệm trái dấu.
C. Có hai nghiệm cùng âm. D. Vô nghiệm.
Lời giải
Chọn C.
Phương trình
2
4 12 9 1
x x x
hoặc
3
x
.
Vậy phương trình có hai nghiệm cùng âm.
Câu 18. [2D2-2] Cho phương trình
25
log 4.5 2 1
x
x
có hai nghiệm là
1
x
,
2
x
. Tổng
1 2
x x
bằng
A.
50.
B.
5
log 100
C.
30.
D.
5
log 50.
Lời giải
Chọn D.
1 2
2
25
log 4.5 2 1 5 100.5 50 0 5 50
x xx x x
x
.
Câu 19. [2D2-2] Bất phương trình
2
2 3 2 3
x x
có tập nghiệm là
A.
1; .

B.
; 1 .

C.
(2; ).

D.
( ; 2).

Lời giải
Chọn B.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 8/9 - Mã đề 004
Bất phương trình
2
2 3 2 3 2 1
x x
x x x
.
Câu 20. [2D2-2] Tập nghiệm của bất phương trình
1
3
log 3 1 0
x
có dạng
;
a b
. Khi đó giá trị
3
a b
bằng
A.
15
. B.
13
.
C.
37
3
. D.
30
.
Lời giải
Chọn B.
1 1
3 3
1 10
log 3 1 0 log 3 1 0 3 3
3 3
x x x x . Do đó
3 13
a b
Câu 21. [2D2-2] Tìm số nghiệm nguyên của bất phương trình:
3
log 1 3
x
.
A.
7
.
B.
26
.
C.
15
.
D.
27
.
Lời giải
Chọn B.
Ta có
3
log 1 3 0 3 27 1 28
x x x
.
Nghiệm nguyên của phương trình là
2
;
3
;
4
…,
26
;
27
. Vậy có
26
nghiệm nguyên.
Câu 22. [2D2-2] Anh Nam vay tiền ngân hàng
1
tỷ đồng theo phương thức trả góp (chịu lãi số tiền chưa
trả) với lãi suất
0,5%
/tháng. Nếu cuối mỗi tháng bắt đầu từ tháng thứ nhất anh Nam trả
30
triệu đồng. Hỏi sau bao nhiêu tháng anh Nam trả hết nợ?
A.
35
tháng. B.
36
tháng. C.
37
tháng. D.
38
tháng.
Lời giải
Chọn C.
Gọi
a
là số tiền vay,
r
là lãi,
m
là số tiền hàng tháng trả.
Số tiền nợ sau tháng thứ nhất là
1
1
N a r m
Số tiền nợ sau tháng thứ hai là
2
2
1 1 1 1 1
N a r m a r m r m a r m r
….
Số tiền nợ sau
n
tháng là
1 1
1
n
n
n
r
N a r m
r
Sau
n
tháng anh Nam trả hết nợ:
1 1
1 0 37
n
n
n
r
N a r m n
r
Vậy
37
tháng thì anh Nam trả hết nợ.
Câu 23. [2D2-3] Tìm tất cả các giá trị của tham số
m
để phương trình
2
3 3
log 2 log 3 1 0
x m x m
có 2 nghiệm
1
x
,
2
x
sao cho
1 2
27
x x
.
A.
4
3
m
. B.
25
m
. C.
28
3
m . D.
1
m
.
Lời giải
Chọn D.
Nếu đặt
3
log
t x
, khi đó ta tìm
1 2 3 1 3 2 3 1 2 3
log log log log 27 3 2 3 1
t t x x x x m m
.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 9/9 - Mã đề 004
Câu 24. [2D2-4] Tìm tập hợp các giá trị của tham số thực
m
để phương trình
6 3 2 0
x x
m m
có
nghiệm thuộc khoảng
0;1
.
A.
3;4
. B.
2;4
. C.
2;4
. D.
3;4
.
Lời giải
Chọn C.
Ta có
6 3.2
6 3 2 0
2 1
x x
x x
x
m m m
.
Đặt
6 3.2
2 1
x x
x
f x
với
0;1
x .
Ta có
6 ln6 3.2 ln2 2 1 6 3.2 2 ln 2
2 1
x x x x x x
x
f x
2
6 2 ln6 ln2 6 ln6 3.2 ln2
0 0;1
2 1
x x x x
x
x
Suy ra
f x
đồng biến trên
0;1
ta suy ra
yêu cầu bài toán tương đương với
2 4
m
.
Câu 25. [2D2-4] Tìm giá trị nhỏ nhất của biểu thức
2
2
2
log 6 log
a
b
a
b
P b
a
với
a
,
là các số
thực thay đổi thỏa mãn
1.
b a
A.
30.
B.
40.
C.
50.
D.
60.
Lời giải
Chọn D.
Ta có
2
2
2
2log 6 log
a b
a
b
P b
a
. Đặt
2
2
1
b
x b a x
a
.
Khi đó
2
2
2
2
2 2
1
2log 6 log 4(2 log ) 6 1
log
a x a
a
a x
P a x x
a x
Đặt
2
2
1
log log 1 0 4 2 6
a a
t x P t t
t
Xét hàm số
2
2
1
4 2 6f t t t
t
với
0;t
.Ta có
3
12 1
8 2 0 1
t
f t t t
t
Suy ra
1 60
f t f
. Vậy
3
min
60 log 1
a
P x x a b a
.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 1/10 - Mã đề 005
TOÁN H
ỌC
B
ẮC
–
TRUNG
–
NAM
Nhóm: THBTN – ĐỀ KIỂM TRA
(25 câu trắc nghiệm)
KIỂM TRA CHƯƠNG 2 GIẢI TÍCH 12
MÃ ĐỀ 005
Thời gian làm bài: 45 phút, không kể thời gian phát đề.
Câu 1. [2D2-1] Tính:
3 2 1 2 4 2
4 .2 : 2K
, ta được
A.
5
. B.
6
. C.
7
. D.
8
.
Câu 2. [2D1-2] Với biểu thức
3 5
4 6
2 1 2 1
a a
. Khi đó cơ số
a
phải thỏa điều kiện
A.
1
a
. B.
0 1
a
. C.
1
1
2
a
. D.
1
a
.
Câu 3. [2D2-1] Hàm số y =
4
2
4 1
x
có tập xác định là
A.
. B.
0;

. C.
1 1
\ ;
2 2
. D.
1 1
;
2 2
.
Câu 4. [2D2-2] Tìm đạo hàm của hàm số
e
2
2
1
y x trên
.
A.
e
1
2
2
2 1
y x x
. B.
e 2
2
e 1y x x
.
C.
e
1
2
2
e
1
2
y x
. D.
e
2 2
2
1 ln 1
y x x
.
Câu 5. [2D2-2] Tìm điểm cực trị của hàm số
e
2
2
1
y x trên
.
A.
1
x
. B.
0
x
. C.
1
x
. D.
2
x
.
Lời giải
Câu 6. [2D2-1] Giá trị của biểu thức
2
log 3
4
A
bằng
A.
6
. B.
2
. C.
12
. D.
9
.
Câu 7. [2D2-2] Biết
5
log 3
a
, khi đó giá trị của
3
27
log
25
được tính theo
a
là
A.
3 2
a
a
. B.
3
2
a
. C.
3
2
a
. D.
3 2
a
a
.
Câu 8. [2D2-2] Nếu
30
log 3
a và
30
log 5
b thì
A.
30
log 1350 2 2.
a b
B.
30
log 1350 2 1.
a b
C.
30
log 1350 2 1.
a b
D.
30
log 1350 2 2.
a b
Câu 9. [2D2-3] Giả sử ta có hệ thức
2 2
7 , 0 .
a b ab a b Hệ thức nào sau đây là đúng?
A.
2 2 2
4log log log
6
a b
a b
. B.
2 2 2
log 2 log log
3
a b
a b
.
C.
2 2 2
2log log log
a b a b
. D.
2 2 2
2log log log
3
a b
a b
.
Câu 10. [2D2-3] Tìm tất cả các giá trị thực của tham số
m
để bất phương trình sau có nghiệm
3 4
log 3 12
x
m x x x
.
A.
2 3
m . B.
0
m
. C.
3
2 3 12log 5
m . D.
3
12log 5
m .
Câu 11. [2D2-1] Tìm tập xác định
D
của hàm số
2
log 6 5
y x x
.
A.
;1 5;D
 
. B.
1;5
D .
C.
;1 5;D

. D.
1;5
D .
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 2/10 - Mã đề 005
Câu 12. [2D2-2] Hàm số y =
2
2 2 e
x
x x có đạo hàm là
A.
2
e
x
y x
. B.
2
4 4 e
x
y x x
. C.
2
e
x
y x
. D.
2
e
2
x
y x
.
Câu 13. [2D2-3.2-2] Tính đạo hàm của hàm số
9
x
x
y
tại điểm
2
x
.
A.
2
3
y
. B.
1
2
5
y
. C.
1
2
9
y
. D.
2
1
2
9
y
.
Câu 14. [2D2-3] Hàm số
2
3
1
e
x x
x
y
có giá trị lớn nhất trên đoạn
0;3
là:
A.
2
e
. B.
1
. C.
e
. D.
3
e
.
Câu 15. [2D2-4] Bạn Hùng trúng tuyển vào trường đại học A nhưng vì do không đủ nộp học phí nên
Hùng quyết định vay ngân hàng trong 4 năm mỗi năm vay
3.000.000
đồng để nộp học phí với
lãi suất
3%
/năm. Sau khi tốt nghiệp đại học bạn Hùng phải trả góp hàng tháng số tiền
T
(không đổi) cùng với lãi suất
0,25%
/tháng trong vòng 5 năm. Số tiền
T
hàng tháng mà bạn
Hùng phải trả cho ngân hàng (làm tròn đến kết quả hàng đơn vị) là:
A.
309604
đồng. B.
232518
đồng. C.
232289
đồng. D.
215456
đồng.
Câu 16. [2D2-1] Nghiệm của phương trình
2 1
1
2 0
8
x
là.
A.
2
x
. B.
2
x
. C.
1
x
. D.
1
x
.
Câu 17. [2D2-2] Tìm tập nghiệm
S
của phương trình
2
0,5 2
log 10 23 log 5 0
x x x
.
A.
7
S . B.
2;9
S . C.
9
S . D.
4;7
S .
Câu 18. [2D2-2] Tìm tích các nghiệm của phương trình
2 1 2 1 2 2 0
x x
.
A.
0
. B.
2
. C.
1
. D.
1
.
Câu 19. [2D2-3] Phương trình
3 3
3 log log 3 1 0
x x
có tổng các nghiệm bằng
A.
81
. B.
3
. C.
78
. D.
84
.
Câu 20. [2D2-4] Tổng các nghiệm của phương trình
2
2 1 2
1 .2 2 1 4 2
x x
x x x x
bằng
A.
3
. B.
5
. C.
4
. D.
2
.
Câu 21. [2D2-1] Tập nghiệm của bất phương trình
2 1 2
4 4
5 5
x x
là
A.
. B.
;1

. C.
3;

. D.
1;

.
Câu 22. [2D2-1] Tìm tập nghiệm của bất phương trình
2
1
2
log 3 2 1.
x x
A.
0;2
. B.
;1

. C.
0;1 2;3
. D.
0;2 3;7
.
Câu 23. [2D2-2] Tìm số nghiệm nguyên của bất phương trình
2
3 10 2
1 1
3 3
x x x
.
A.
0
. B.
1
. C.
9
. D.
11
.
Câu 24. [2D2-2] Bất phương trình
2 3
log log 1
x x
có nghiệm là
A.
2
log 6
3x . B.
3
log 6
2x . C.
6
x
. D.
6
log 2
3x .
Câu 25. [2D2-4] Tìm tập hợp tất cả các giá trị của tham số
m
để bất phương trình
2 2 2
sin cos cos
4 5 .7
x x x
m
có nghiệm.
A.
7
m
. B.
7
m
. C.
6
m
. D.
6
m
.
----------HẾT----------
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 3/10 - Mã đề 005
ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
D
C C B B
D
A
C D
B C A
D
B
C
D
A
D
D
B D C C D A
HƯỚNG DẪN GIẢI
Câu 1. [2D2-1] Tính:
3 2 1 2 4 2
4 .2 : 2K
, ta được
A.
5
. B.
6
. C.
7
. D.
8
.
Lời giải
Chọn D.
2 3 2 2 3 2 1 2 4 2
3 2 1 2 4 2 1 2 4 2
4 .2 : 2 2 .2 :2 2 8
K
.
Câu 2. [2D1-2] Với biểu thức
3 5
4 6
2 1 2 1
a a
. Khi đó cơ số
a
phải thỏa điều kiện
A.
1
a
. B.
0 1
a
. C.
1
1
2
a
. D.
1
a
.
Lời giải
Chọn C.
Vì
3 5
4 6
nên
0 2 1 1
a
1
1
2
a
.
Câu 3. [2D2-1] Hàm số y =
4
2
4 1
x
có tập xác định là
A.
. B.
0;

. C.
1 1
\ ;
2 2
. D.
1 1
;
2 2
.
Lời giải
Chọn C.
Vì hàm số xác định khi
2
4 1 0
x
1
2
x
Vậy TXĐ:
1 1
\ ;
2 2
D
.
Câu 4. [2D2-2] Tìm đạo hàm của hàm số
2
2
1
e
y x trên
.
A.
1
2
2
2 1
e
y x x
. B.
2
2
1
e
y ex x
.
C.
1
2
2
1
2
e
e
y x
. D.
2 2
2
1 ln 1
e
y x x
.
Lời giải
Chọn B.
Ta có:
1 1 2
2 2 2 2
2 2 2
1 .2 1 1 1
2
e e e
e
e
y x x x ex x ex x
.
Câu 5. [2D2-2] Tìm điểm cực trị của hàm số
2
2
1
e
y x trên
.
A.
1
x
. B.
0
x
. C.
1
x
. D.
2
x
.
Lời giải
Chọn B.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 4/10 - Mã đề 005
Ta có:
1 1 2
2 2 2 2
2 2 2
1 .2 1 1 1
2
e e e
e
e
y x x x ex x ex x
.
0 0
y x
Lập bảng xét dấu suy ra
0
x
là điểm cực tiểu của hàm số.
Câu 6. [2D2-1] Giá trị của biểu thức
2
log 3
4
A
bằng
A.
6
. B.
2
. C.
12
. D.
9
.
Lời giải
2 2 2
log 3 2log 3 log 9
4 2 2 9
.
Câu 7. [2D2-2] Biết
5
log 3
a
, khi đó giá trị của
3
27
log
25
được tính theo
a
là
A.
3 2
a
a
. B.
3
2
a
. C.
3
2
a
. D.
3 2
a
a
.
Lời giải
Chọn A.
Ta có
3 3 3 3
27 2 3a 2
log log 27 log 25 3 2log 5 3
25
a a
. Ta chọn đáp án A.
Câu 8. [2D2-2] Nếu
30
log 3
a và
30
log 5
b thì
A.
30
log 1350 2 2.
a b
B.
30
log 1350 2 1.
a b
C.
30
log 1350 2 1.
a b
D.
30
log 1350 2 2.
a b
Lời giải
Chọn C.
2
30 30 30 30
log 1350 log 30.3 .5 1 2log 3 log 5 1 2 .
a b
Sử dụng Casio:
30 30
*log 3 ;log 5 .
A B
30
*log 1350 1 2
a b
.
Kết quả bằng
0.
Chọn đáp án C.
Câu 9. [2D2-3] Giả sử ta có hệ thức
2 2
7 , 0 .
a b ab a b Hệ thức nào sau đây là đúng?
A.
2 2 2
4log log log
6
a b
a b
. B.
2 2 2
log 2 log log
3
a b
a b
.
C.
2 2 2
2log log log
a b a b
. D.
2 2 2
2log log log
3
a b
a b
.
Lời giải
Chọn D.
Ta có:
2 2
7 . b
a b a
.
2 2
2 2
2
2 2 2 2 2
9 log log (9 )
log log ( ) 2log log log
3 3
a b ab a b ab
a b a b
ab a b
.
Câu 10. [2D2-3] Tìm tất cả các giá trị thực của tham số
m
để bất phương trình sau có nghiệm
3 4
log 3 12
x
m x x x
.
A.
2 3
m . B.
0
m
.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 5/10 - Mã đề 005
C.
3
2 3 12log 5
m . D.
3
12log 5
m .
Lời giải
Chọn B.
Điều kiện:
3 4 0
3 4 1
0 0 4
12 0
4 0
x
x
x x
x
x
.
Nhận xét:
3 4 3 4 0 1
x
3 4 3 4
log 3 log 1 0
x x
.
3
3 4
3 4
12
log 3 12 12 .log 3 4
log 3
x
x
x x x
m x x x m m x x x x
Đặt
3
12 .log 3 4
f x x x x x
.
3
3 2 1
log 3 4 12 .
2
2 12
3 4 ln3.2 4
f x x x x x x
x
x x
Vì
0
f x
,
0;4
x
f x
tăng trên
0;4
tập giá trị của
f x
là
0;12
.
Bất phương trình có nghiệm
0
m
.
Câu 11. [2D2-1] Tìm tập xác định
D
của hàm số
2
log 6 5
y x x
.
A.
;1 5;D
 
. B.
1;5
D .
C.
;1 5;D

. D.
1;5
D .
Lời giải
Chọn C.
Biểu thức
2
log 6 5
x x
xác định
2
1
6x 5 0
5
x
x
x
.
Câu 12. [2D2-2] Hàm số y =
2
2 2
x
x x e
có đạo hàm là
A.
2
x
y x e
. B.
2
4 4
x
y x x e
.
C.
2
x
y xe
. D.
2 2
x
y x e
.
Lời giải
Chọn A.
2 2 2 2 2
2 2 2 2 2 2 2 2
x x x x x
y x x e e x x x x e e x x x e
.
Câu 13. [2D2-3.2-2] Tính đạo hàm của hàm số
9
x
x
y
tại điểm
2
x
.
A.
2
3
y
. B.
1
2
5
y
. C.
1
2
9
y
. D.
2
1
2
9
y
.
Lời giải
Chọn D.
2
9 9 .ln9 2 1 2 ln9
2
9 9 9
x x
x x x
x x
x
y y
2 2
1 2 2 ln9
1
2
9 9
y
.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 6/10 - Mã đề 005
Câu 14. [2D2-3] Hàm số
2
3
1
x x
x
y e
có giá trị lớn nhất trên đoạn
0;3
là:
A.
2
e
. B.
1
.
C.
e
.
D.
3
e
.
Lời giải
Chọn B.
Tập xác định
\ 1
D
.
Ta có
2 2
3 3
2 2
1 1
2
3 2 3
. .
1
1
x x x x
x x
x x x x
y e e
x
x
.
2
3
2
2
1
2
1
2 3
0 . 0 2 3 0
3
1
0;3
0;3
x x
x
x
x x
y e x x
x
x
.
Mà
1
1 ; 0 3 1
y y y
e
.
Vậy hàm số
2
3
1
x x
x
y e
có giá trị lớn nhất trên đoạn
0;3
là
1.
Câu 15. [2D2-4] Bạn Hùng trúng tuyển vào trường đại học A nhưng vì do không đủ nộp học phí nên
Hùng quyết định vay ngân hàng trong 4 năm mỗi năm vay
3.000.000
đồng để nộp học phí với
lãi suất
3%
/năm. Sau khi tốt nghiệp đại học bạn Hùng phải trả góp hàng tháng số tiền
T
(không đổi) cùng với lãi suất
0,25%
/tháng trong vòng 5 năm. Số tiền
T
hàng tháng mà bạn
Hùng phải trả cho ngân hàng (làm tròn đến kết quả hàng đơn vị) là:
A.
309604
đồng. B.
232518
đồng. C.
232289
đồng. D.
215456
đồng.
Lời giải
Chọn C.
Bạn Hùng nợ sau năm thứ nhất là:
3000000. 1 0,03 3000000.1,03
Bạn Hùng nợ sau năm thứ hai là:
2
3000000 3000000.1,03 . 1 0,03 3000000.1,03 300
0000.1,03
Bạn Hùng nợ sau năm thứ ba là:
2 3
3000000.1,03 3000000.1,03 3000000.1,03
Bạn Hùng nợ sau năm thứ tư là:
2 3 4
3000000.1,03 3000000.1,03 3000000.1,03 3000
000.1,03
Vậy sau
4
năm bạn Hùng nợ ngân hàng số tiền là:
4 3 2
3000000 1,03 12927407,43
N
  
.
Lúc này ta coi như bạn Hùng nợ ngân hàng khoản tiền ban đầu là
12.927.407,43
đồng.
số tiền này bắt đầu được tính lãi và được trả góp trong
5
năm với lãi suất 0,25% /
tháng
.
Tháng thứ nhất Hùng còn nợ ngân hàng là:
. 1 0,0025 .1,0025
N T N T
Tháng thứ hai Hùng còn nợ ngân hàng là:
2
.1,0025 . 1 0,0025 .1.0025 .1,0025
N T T N T T
Tháng thứ ba Hùng còn nợ ngân hàng là:
2 3 2
.1.0025 .1,0025 . 1 0,0025 .1.0025 .1,0025 .1,0025
N T T T N T T T
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 7/10 - Mã đề 005
Tháng thứ tư Hùng còn nợ ngân hàng là:
4 3 2
.1.0025 .1,0025 .1,0025 .1,0025
N T T T T
………………………………
Tháng thứ sáu mươi Hùng còn nợ ngân hàng là:
60 59 2
.1.0025 .1,0025 .......... .1,0025 .1,0025
N T T T T
Vì Hùng trả dần trong
5
năm nên
60
tháng Hùng trả hết nợ do đó ta có:
60 59 2
60 59 2
60
60
60
60
.1.0025 .1,0025 .......... .1,0025 .1,0025 0
.1.0025 .1,0025 .......... .1,0025 .1,0025
1.0025 1
.1.0025
1,0025 1
.1.0025 . 1,0025 1
1.0025 1
N T T T T
N T T T T
N T
N
T
232289
T
.
Câu 16. [2D2-1] Nghiệm của phương trình
2 1
1
2 0
8
x
là.
A.
2
x
. B.
2
x
. C.
1
x
. D.
1
x
.
Lời giải
Chọn D.
Ta có
2 1 2 1 3
1
2 0 2 2 1
8
x x
x
.
Câu 17. [2D2-2] Tìm tập nghiệm
S
của phương trình
2
0,5 2
log 10 23 log 5 0
x x x
.
A.
7
S . B.
2;9
S . C.
9
S . D.
4;7
S .
Lời giải
Chọn A.
Điều kiện:
2
10 23 0
5
5 0
x x
x
x
.
Phương trình tương đương.
2
2 2
2
2 2
2
2
log 10 23 log 5 0
log 5 log 10 23
5 10 23
11 28 0
4 ( )
7 ( )
x x x
x x x
x x x
x x
x l
x n
Vậy
7
S .
Câu 18. [2D2-2] Tìm tích các nghiệm của phương trình
2 1 2 1 2 2 0
x x
.
A.
0
. B.
2
. C.
1
. D.
1
.
Lời giải
Chọn D.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 8/10 - Mã đề 005
Vì
2 1 . 2 1 1
x x
. Đặt t =
2 1
x
(
0
t
) suy ra:
1
2 1
x
t
.
Khi đó, phương trình trở thành:
1
2 2 0
t
t
.
1 2 1 2
1 2 1
1
1 2
1 2 1 2
x
x
t x
x
t
.
Câu 19. [2D2-3] Phương trình
3 3
3 log log 3 1 0
x x
có tổng các nghiệm bằng
A.
81
. B.
3
. C.
78
. D.
84
.
Lời giải
Chọn D.
Điều kiện:
3
0
0
1
log 0
1
x
x
x
x
x
.
3 3 3 3
3 log log 3 1 0 3 log 1 log 1 0
x x x x
.
3 3
log 3 log 2 0
x x
.
Đặt
3
log 0
t x t
.
Ta có
3
2
3
log 1
1 3
3 2 0
2 81
log 2
x
t x
t t
t x
x
.
Vậy tổng các nghiệm bằng
84
.
Câu 20. [2D2-4] Tổng các nghiệm của phương trình
2
2 1 2
1 .2 2 1 4 2
x x
x x x x
bằng
A.
3
. B.
5
. C.
4
. D.
2
.
Lời giải
Chọn B.
2
2 1 2
1 .2 2 1 4 2
x x
x x x x
2
2 2
1 .2 2 1 2.2 4
x x
x x x x
.
2 2
2 2 1 2.2 2 1 2
x x
x x x x x
2 2
2 2 1 2 2 1
x
x x x x x
.
2
2 1 0 1
2 2 2
x
x x
x
.
PT
1
1 2
1 2
x
x
.
PT
2 :2 2 2 2 0
x x
x f x x
.
Xét hàm số
2 2
x
f x x
.
2 ln 2 2
x
f x
.
2
2
0 2 ln 2 2 0 log
ln2
x
f x x
có 1 nghiệm.
0
f x
có không quá
2
nghiệm. Mà nhẩm thấy
1, 2
x x
là
2
nghiệm của PT
0
f x
.
Vậy tổng các nghiệm của phương trình đã cho là:
1 2 1 2 1 2 5
.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 9/10 - Mã đề 005
Câu 21. [2D2-1] Tập nghiệm của bất phương trình
2 1 2
4 4
5 5
x x
là
A.
. B.
;1

. C.
3;

. D.
1;

.
Lời giải
Chọn D.
2 1 2
4 4
2 1 2 1
5 5
x x
x x x
.
Câu 22. [2D2-1] Tìm tập nghiệm của bất phương trình
2
1
2
log 3 2 1.
x x
A.
0;2
. B.
;1

. C.
0;1 2;3
. D.
0;2 3;7
.
Lời giải
Chọn C.
2 2
2
1
2 2
2
0 3
3 2 2 3 0 0 1
log 3 2 1
1
2 3
3 2 0 3 2 0
2
x
x x x x x
x x
x
x
x x x x
x
Vậy tập nghiệm của bất phương trình là:
0;1 2;3
.
Câu 23. [2D2-2] Tìm số nghiệm nguyên của bất phương trình
2
3 10 2
1 1
3 3
x x x
.
A.
0
. B.
1
. C.
9
. D.
11
.
Lời giải
Chọn C.
2
2
3 10 2
2
2
2
3 10 0
1 1
3 10 2 2 0
3 3
3 10 2
2 5
2 5 14
14
x x x
x x
x x x x
x x x
x x
x x
x
.
Vì
x
nguyên nên
5;6;7;8;9;10;11;12;13
x , do đó số nghiệm nguyên là 9.
Câu 24. [2D2-2] Bất phương trình
2 3
log log 1
x x
có nghiệm là
A.
2
log 6
3x . B.
3
log 6
2x . C.
6
x
. D.
6
log 2
3x .
Lời giải
Chọn D.
Ta có
2 3
log log 1
x x
2 3 2
log log 2.log 1
x x
.
3 2
1 log 2 .log 1
x
.
3 2
log 6.log 1
x
.
2 6
3
1
log log 3
log 6
x .
6
log 3
2x
6
log 2
3x .
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 10/10 - Mã đề 005
Câu 25. [2D2-4] Tìm tập hợp tất cả các giá trị của tham số
m
để bất phương trình
2 2 2
sin cos cos
4 5 .7
x x x
m
có nghiệm.
A.
7
m
. B.
7
m
. C.
6
m
. D.
6
m
.
Lời giải
Chọn A.
Ta có
2 2
2 2 2
cos cos
sin cos cos
1 5
4 5 .7 4
28 7
x x
x x x
m m
.
Đặt
2
cos , 0;1
t x t thì BPT trở thành:
1 5
4
28 7
t t
m
.
Xét
1 5
4.
28 7
t t
f t
là hàm số nghịch biến trên
0;1
.
Suy ra:
6
1 0 5
7
f f t f f t
.
Từ đó BPT có nghiệm
6
7
m
.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 1/9 - Mã đề 006
TOÁN H
Ọ
C
B
Ắ
C
–
TRUNG
–
NAM
Nhóm: THBTN – ĐỀ KIỂM TRA
(25 câu trắc nghiệm)
KIỂM TRA CHƯƠNG 2 GIẢI TÍCH 12
MÃ ĐỀ 006
Thời gian làm bài: 45 phút, không kể thời gian phát đề.
Câu 1. [2D2-1] Viết biểu thức
a a
0
a
về dạng lũy thừa của
a
là
A.
5
4
a
. B.
1
4
a
. C.
3
4
a
. D.
1
2
a
.
Câu 2. [2D2-2] Trong các khẳng định sau đây, khẳng định nào sai?
A.
2 2
0,01 10
. B.
2 2
0,01 10
.
C.
2 2
0,1 10
. D.
0
1, 0
a a
.
Câu 3. [2D2-1] Tập xác định của hàm số
2017
(2 1)
y x là
A.
D
.
B.
1
;
2
D

. C.
1
;
2
D

. D.
1
\
2
D
Câu 4. [2D2-2] Hàm số
1
3
1
y x
có đạo hàm là
A.
2
3
1
3 1
y
x
. B.
3
1
3 1
y
x
. C.
3
1
3
x
y
. D.
3
1
3
x
y
Câu 5. [2D2-2] Đồ thị hàm số
ln
x
y
x
có tọa độ điểm cực đại là
;
a b
. Khi đó
ab
bằng
A.
e
. B.
2e
. C.
1
. D.
1
.
Câu 6. [2D2-1] Cho
0
a
,
1
a
, giá trị của biểu thức
log 4
a
a
bằng bao nhiêu?
A.
16
. B.
4
. C.
8
. D.
2
.
Câu 7. [2D2-2] Cho
2
log 6
a
. Khi đó giá trị của
3
log 18
được tính theo
a
là
A.
a
. B.
1
a
a
. C.
2 3
a
. D.
2 1
1
a
a
.
Câu 8. [2D2-2] Cho
2
log 5
,
3
log 5
. Khi đó
6
log 5
tính theo
a
và
là
A.
1
a b
. B.
ab
a b
. C.
a b
. D.
2 2
a b
.
Câu 9. [2D2-3] Cho
, 0
a b
và
2 2
7
a b ab
. Khẳng định nào sau đây là khẳng định đúng?
A.
2log log log
a b a b
. B.
4log log log
6
a b
a b
.
C.
1
log log log
3 2
a b
a b
. D.
log 3 log log
3
a b
a b
.
Câu 10. [2D2-3] Cho hàm số
2
2 sin
2 .3
x x
f x . Khẳng định nào sau đây là khẳng định đúng?
A.
2
1 ln4 sin x ln3 0
f x x
. B.
2
1 2 2sin log 3 0
f x x x
.
C.
2
3
1 log 2 sin 0
f x x x
. D.
2
2
1 2 log 3 0
f x x
.
Câu 11. [2D2-1] Với giá trị nào của
x
thì biểu thức:
2
6
log 2
f x x x
xác định?
A.
0 2
x
. B.
2
x
. C.
1 1
x
. D.
3
x
.
Câu 12. [2D2-2] Đạo hàm của hàm số
2
4
x
y là
A.
2
2.4 ln 4
x
y
. B.
2
4 .ln 2
x
y
. C.
2
4 ln 4
x
y
. D.
2
2.4 ln 2
x
y
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 2/9 - Mã đề 006
Câu 13. [2D2-2] Cho hàm số
2
3
log 2 .
f x x x
Tập nghiệm
S
của phương trình
0
f x
là
A.
1
S . B.
1 2
S
. C.
0;2
S . D.
1
S
.
Câu 14. [2D2-3] Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
2 2
x
y xe x x
trên đoạn
1
;2
2
là
A.
1
;2
2
1
;2
2
max 4e 8
min 0
y
y
. B.
1
;2
2
1
;2
2
max 0
1 5
min
e
y
y
.C.
2
1
;2
2
1
;2
2
max 4e 8
min 0
y
y
. D.
2
1
;2
2
1
;2
2
max 4e 8
min 0
y
y
.
Câu 15. [2D2-4] Bạn Duy Anh trúng tuyển vào đại học nhung vì không đủ nộp tiền học phí Duy Anh
quyết định vay ngân hàng trong
4
năm mỗi năm
3.000.000
đồng để nộp học với lãi suất
3%
/năm. Sau khi tốt nghiệp đại học Duy Anh phải trả góp hàng tháng số tiền
T
(không đổi)
cùng với lãi suất
0,25%
/tháng trong vòng
5
năm. Số tiền
T
mà Duy Anh phải trả cho ngân
hàng (làm tròn đến hàng đơn vị) là
A.
232518
đồng. B.
309604
đồng. C.
215456
đồng. D.
232289
đồng.
Câu 16. [2D2-1] Số nghiệm của phương trình
2
2 7 5
2 1
x x
là
A.
2
. B.
0
. C.
3
. D.
1
.
Câu 17. [2D2-2] Phương trình
2
2 4
log 2 3 2log 1
x x x
có nghiệm là
A.
4
x
. B.
1
x
. C.
4; 1
x x
. D.
2
x
.
Câu 18. [2D2-2] Phương trình
9 3.3 2 0
x x
có hai nghiệm
1
x
,
2
x
với
1 2
x x
. Giá trị
1 2
2 3
A x x
là
A.
2
2log 3
. B.
1
. C.
3
3log 2
. D.
3
4log 2
.
Câu 19. [2D2-3] Phương trình
2 2
4 4
log 7log 4 10 0
x x
có hai nghiệm
1
x
,
2
x
với
1 2
x x
. Giá trị
4
1
2
x
A
x
là
A.
1
4
. B.
16
. C.
64
. D.
1
16
.
Câu 20. [2D2-1] Biết rằng phương trình
2
log 4 2 3
2 4. 2
x
x x
có hai nghiệm
1
x
,
2 1 2
x x x
.
Tính
1 2
2
x x
.
A.
1
. B.
3
. C.
5
. D.
1
.
Câu 21. [2D2-1] Tìm tập nghiệm
S
của bất phương trình
1
1
5 0
5
x
.
A.
1;S
. B.
1;S
. C.
2;S
. D.
; 2
S

.
Câu 22. [2D2-1] Tập nghiệm của bất phương trình:
1
3
log 3 1
x
có dạng
;
a b
. Khi đó giá trị
3
a b
bằng
A.
15
. B.
13
. C.
37
3
. D.
30
.
Câu 23. [2D2-2] Bất phương trình
2
2 10
3 4
1
2
2
x
x x
có bao nhiêu nghiệm nguyên dương?
A.
2
. B.
4
. C.
6
. D.
3
.
Câu 24. [2D2-2] Tập nghiệm của bất phương trình
3 1
3
2log 4 3 log 2 3 2
x x
là
A.
3
;3
8
S
. B.
3
;3
8
S
. C.
; 3
S  . D.
3
;3
4
S
.
Câu 25. [2D2-3] Tìm
m
để bất phương trình
2 2
5 5
1 log 1 log 4
x mx x m
thỏa mãn với mọi
x
.
A.
1 0
m
. B.
1 0
m
. C.
2 3
m
. D.
2 3
m
.
----------HẾT----------
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 3/9 - Mã đề 006
ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
C B A
A
C
A
D
B C A
A
A
A
D
D
A
A
C C D
C B
D
D
C
HƯỚNG DẪN GIẢI
Câu 1. [2D2-1] Viết biểu thức
a a
0
a
về dạng lũy thừa của
a
là
A.
5
4
a
. B.
1
4
a
. C.
3
4
a
. D.
1
2
a
.
Lời giải
Chọn C.
1 3 1 3
.
2 2 2 4
.
a a a a a a
.
Câu 2. [2D2-2] Trong các khẳng định sau đây, khẳng định nào sai?
A.
2 2
0,01 10
. B.
2 2
0,01 10
.
C.
2 2
0,1 10
. D.
0
1, 0
a a
.
Lời giải
Chọn B.
A đúng vì
2 2
2 2
0,01 10 10
C đúng vì
2
2 2
1
0,1 10
10
D đúng vì
0
1, 0
a a
.
Câu 3. [2D2-1] Tập xác định của hàm số
2017
(2 1)
y x là
A.
D
.
B.
1
;
2
D

. C.
1
;
2
D

. D.
1
\
2
D
Lời giải
Chọn A.
Vì 2007
nên hàm số xác định với mọi
x
.
Câu 4. [2D2-2] Hàm số
1
3
1
y x
có đạo hàm là
A.
2
3
1
3 1
y
x
. B.
3
1
3 1
y
x
. C.
3
1
3
x
y
. D.
3
1
3
x
y
Lời giải
Chọn A.
1 1 2
1
3 3 3
2
3
1 1 1
1 1 . 1 1
3 3
3 1
y x y x x x
x
.
Câu 5. [2D2-2] Đồ thị hàm số
ln
x
y
x
có tọa độ điểm cực đại là
;
a b
. Khi đó
ab
bằng
A.
e
. B.
2
e
. C.
1
. D.
1
.
Lời giải
Chọn C.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 4/9 - Mã đề 006
2
1 ln
x
y
x
0
y x e
1
y
e
1
. . 1
a b e
e
.
Câu 6. [2D2-1] Cho
0, 1
a a
, giá trị của biểu thức
log 4
a
a
bằng bao nhiêu?
A.
16
. B.
4
. C.
8
. D.
2
.
Lời giải
Chọn A.
1
2
2
log 4
log 4
2log 4 log 4
2
4 16.
a
a a a
a a a a
.
Câu 7. [2D2-2] Cho
2
log 6
a
. Khi đó giá trị của
3
log 18
được tính theo
a
là
A.
a
. B.
1
a
a
. C.
2 3
a
. D.
2 1
1
a
a
.
Lời giải
Chọn D.
Ta có:
2 2 2 3
1
log 6 log (2.3) 1 log 3 log 2
1
a
a
Suy ra
2
3 3 3
1 2 1
log 18 log (2.3 ) log 2 2 2
1 1
a
a a
.
Câu 8. [2D2-2] Cho
2
log 5
,
3
log 5
. Khi đó
6
log 5
tính theo
a
và
là
A.
1
a b
. B.
ab
a b
. C.
a b
. D.
2 2
a b
.
Lời giải
Chọn B.
6
5
1
log 5
log 6
5 5 5
1 1
log (2.3) log 2 log 3
2 3
2 3
log 5.log 5
log 5 log 5
ab
a b
.
Câu 9. [2D2-3] Cho
, 0
a b
và
2 2
7
a b ab
. Khẳng định nào sau đây là khẳng định đúng?
A.
2log log log
a b a b
. B.
4log log log
6
a b
a b
.
C.
1
log log log
3 2
a b
a b
. D.
log 3 log log
3
a b
a b
.
Lời giải
Chọn C.
2 2
2 2
7 9 log log9
a b ab a b ab a b ab
.
2
log log9 log log
a b a b
2
log log9 log log
a b a b
2
log log log
3
a b
a b
2log log log
3
a b
a b
1
log log log
3 2
a b
a b
.
Câu 10. [2D2-3] Cho hàm số
2
2 sin
2 .3
x x
f x . Khẳng định nào sau đây là khẳng định đúng?
A.
2
1 ln4 sin x ln3 0
f x x
. B.
2
1 2 2sin log 3 0
f x x x
.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 5/9 - Mã đề 006
C.
2
3
1 log 2 sin 0
f x x x
. D.
2
2
1 2 log 3 0
f x x
.
Lời giải
Chọn A.
2
2 sin 2
1 ln 2 .3 ln1 ln4 sin ln3 0
x x
f x x x
.
Câu 11. [2D2-1] Với giá trị nào của
x
thì biểu thức:
2
6
log 2
f x x x
xác định?
A.
0 2
x
. B.
2
x
. C.
1 1
x
. D.
3
x
.
Lời giải
Chọn A.
2
6
log 2
f x x x
xác định khi
2
2 0 0 2
x x x
.
Câu 12. [2D2-2] Đạo hàm của hàm số
2
4
x
y là
A.
2
2.4 ln 4
x
y
. B.
2
4 .ln 2
x
y
. C.
2
4 ln 4
x
y
. D.
2
2.4 ln 2
x
y
Lời giải
Chọn A.
2 2
4 2.4 ln4
x x
y
.
Câu 13. [2D2-2] Cho hàm số
2
3
log 2 .
f x x x
Tập nghiệm
S
của phương trình
0
f x
là
A.
1
S . B.
1 2
S
. C.
0;2
S . D.
1
S
.
Lời giải
Chọn A.
2
2 2
2 ln3
x
y
x x
.
0
y
2 2 0
x
1
x
.
Câu 14. [2D2-3] Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
2 2
x
y xe x x
trên đoạn
1
;2
2
là
A.
1
;2
2
1
;2
2
max 4 8
min 0
y e
y
. B.
1
;2
2
1
;2
2
max 0
1 5
min
y
y
e
.C.
2
1
;2
2
1
;2
2
max 4 8
min 0
y e
y
. D.
2
1
;2
2
1
;2
2
max 4 8
min 0
y e
y
.
Lời giải
Chọn D.
Cách 1: Tự luận
2 2 2 2 2 2 2 2
x x x
y e xe x e x x
2 2 1
x
y x e
1
0 2 2 1 0
0
x
x
y x e
x
0 0
y
1
1 3
2
2 4
y e
2
2 4 8
y e
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 6/9 - Mã đề 006
Cách 2: Sử dụng chức năng MODE 7 của máy tính Casio với thiết lập Start
1
2
End
2
Step
1
2
2
19
Quan sát bảng giá trị
F X
ta thấy giá trị lớn nhất
F X
có thể đạt được là
2
2 21.556 4 8.
f e
Ta thấy giá trị nhỏ nhất
F X
có thể đạt được là
3
1.05 9.95.10 0.
f
.
Câu 15. [2D2-4] Bạn Duy Anh trúng tuyển vào đại học nhung vì không đủ nộp tiền học phí Duy Anh
quyết định vay ngân hàng trong
4
năm mỗi năm
3.000.000
đồng để nộp học với lãi suất
3%
/năm. Sau khi tốt nghiệp đại học Duy Anh phải trả góp hàng tháng số tiền
T
(không đổi)
cùng với lãi suất
0,25%
/tháng trong vòng
5
năm. Số tiền
T
mà Duy Anh phải trả cho ngân
hàng (làm tròn đến hàng đơn vị) là
A.
232518
đồng. B.
309604
đồng. C.
215456
đồng. D.
232289
đồng.
Lời giải
Chọn D.
+ Tính tổng số tiền mà Duy Anh nợ sau 4 năm học:.
Sau
1
năm số tiền Duy Anh nợ là
3 3 3 1
r r
Sau
2
năm số tiền Duy Anh nợ là
2
3 1 3 1
r r
.
Tương tự: Sau
4
năm số tiền Duy Anh nợ là
4 3 2
3 1 3 1 3 1 3 1 12927407,43
r r r r A
.
+ Tính số tiền
T
mà Duy Anh phải trả trong
1
tháng:.
Sau
1
tháng số tiền còn nợ là
1
A Ar T A r T
.
Sau
2
tháng số tiền còn nợ là
2
1 1 1 1
A r T A r T r T A r T r T
.
Tương tự sau
60
tháng số tiền còn nợ là
60 59 58
1 1 1 1T T
A r r r T
T r
Duy Anh trả hết nợ khi và chỉ khi.
60 59 58
1 1 1 1 0
A r r rT T T r T
60 59 58
1 1 1 1 1 0
A r r r rT
60
60
1 1
1 1
1 0
r
A r T
r
60 60
60
60
1 1 1
232.2
1 0
1
9
1
8
r Ar
T
r
r
A r T T
r
.
Câu 16. [2D2-1] Số nghiệm của phương trình
2
2 7 5
2 1
x x
là
A.
2
. B.
0
. C.
3
. D.
1
.
Lời giải
Chọn A.
2
2 7 5 2
1
2 1 2 7 5 0
5
2
x x
x
x x
x
.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 7/9 - Mã đề 006
Câu 17. [2D2-2] Phương trình
2
2 4
log 2 3 2log 1
x x x
có nghiệm là
A.
4
x
. B.
1
x
. C.
4; 1
x x
. D.
2
x
.
Lời giải
Chọn A.
Điều kiện
2
2 3 0
3
1 0
x x
x
x
2 2
2 4 2 2
log 2 3 2log 1 log 2 3 log 1
x x x x x x
2 2
2 3 1 3 4 0
x x x x x
1 ( )
4 ( )
x L
x N
4
S .
Câu 18. [2D2-2] Phương trình
9 3.3 2 0
x x
có hai nghiệm
1
x
,
2
x
với
1 2
x x
. Giá trị
1 2
2 3
A x x
là
A.
2
2log 3
. B.
1
. C.
3
3log 2
. D.
3
4log 2
.
Lời giải
Chọn C.
2 3
1
log 2
9 3.3 2 0
0
x x
x
x
1 2 3
2 3 3log 2
A x x .
Câu 19. [2D2-3] Phương trình
2 2
4 4
log 7log 4 10 0
x x
có hai nghiệm
1
x
,
2
x
với
1 2
x x
. Giá trị
4
1
2
x
A
x
là
A.
1
4
. B.
16
. C.
64
. D.
1
16
.
Lời giải
Chọn C.
2 2
4 4
log 7log 4 10 0
x x
2
4 4
4log 7log 3 0
x x
4
4
log 1
3
log
4
x
x
3
4
4
4
x
x
3
4
1 2
4 , 4
x x
.
Câu 20. [2D2-1] Biết rằng phương trình
2
log 4 2 3
2 4. 2
x
x x
có hai nghiệm
1
x
,
2 1 2
x x x
.
Tính
1 2
2
x x
.
A.
1
. B.
3
. C.
5
. D.
1
.
Lời giải
Chọn D.
Điều kiện
2
x
.
Phương trình thành
2 2
log 4 log 2 3
2 4. 2
x
x x
2
2 log 2 3
2 . 2 4. 2
x
x x x
hay
2
log 2
2 4. 2
x
x x
.
Lấy lôgarit cơ số 2 hai vế ta được
2 2 2
log 2 .log 2 log 4 2
x x x
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 8/9 - Mã đề 006
2
2
2 2
2
log 2 1
log 2 2 log 2
log 2 2
6
x
x
x x
x
x
.
Suy ra
1
5
2
x
và
2
6.
x
Vậy
1 2
5
2 2. 6 1
2
x x
.
Câu 21. [2D2-1] Tìm tập nghiệm
S
của bất phương trình
1
1
5 0
5
x
.
A.
1;S
. B.
1;S
. C.
2;S
. D.
; 2
S

.
Lời giải
Chọn C.
1 1 1
1
5 0 5 5 1 1 2
5
x x
x x
.
Câu 22. [2D2-1] Tập nghiệm của bất phương trình:
1
3
log 3 1
x
có dạng
;
a b
. Khi đó giá trị
3
a b
bằng
A.
15
. B.
13
. C.
37
3
. D.
30
.
Lời giải
Chọn B.
1
3
log 3 1
x
3 0
1
3
3
x
x
3
10
3
x
x
10
3;
3
x
3
10
3
a
b
3 13
a b
.
Câu 23. [2D2-2] Bất phương trình
2
2 10
3 4
1
2
2
x
x x
có bao nhiêu nghiệm nguyên dương?
A.
2
. B.
4
. C.
6
. D.
3
.
Lời giải
Chọn D.
2
2 10
3 4 2 2
1
2 3 4 10 2 6 0 2 3
2
x
x x
x x x x x x
.
Do
1; 2; 3
x x
.
Câu 24. [2D2-2] Tập nghiệm của bất phương trình
3 1
3
2log 4 3 log 2 3 2
x x
là
A.
3
;3
8
S
. B.
3
;3
8
S
. C.
; 3
S  . D.
3
;3
4
S
.
Lời giải
Chọn D.
Điều kiện:
4 3 0
2 3 0
x
x
3
4
3
2
x
x
3
4
x
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 9/9 - Mã đề 006
2
3 3
log 4 3 log 2 3 2
x x
2
3
4 3
log 2
2 3
x
x
2
16 24 9
9
2 3
x x
x
2
16 24 9 18 27
x x x
2
16 42 18 0
x x
8
;3
3
x
Kết luận:
3
;3
4
S
.
Câu 25. [2D2-3] Tìm
m
để bất phương trình
2 2
5 5
1 log 1 log 4
x mx x m
thỏa mãn với mọi
x
.
A.
1 0
m
. B.
1 0
m
. C.
2 3
m
. D.
2 3
m
.
Lời giải
Chọn C.
BPT thỏa mãn với mọi
x
2
2 2
4 0
5 1 4
mx x m
x
x mx x m
2
2
4 0
5 4 5 0
mx x m
x
m x x m
2
2
0
16 4 0
5 0
16 4 5 0
m
m
m
m
0
2
2
5
3
7
m
m
m
m
m
m
2 3
m
.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 1/10 - Mã đề 007
TOÁN HỌC BẮC–TRUNG–NAM
Nhóm: THBTN – ĐỀ KIỂM TRA
(25 câu trắc nghiệm)
KIỂM TRA CHƯƠNG 2 GIẢI TÍCH 12
MÃ ĐỀ 007
Thời gian làm bài: 45 phút, không kể thời gian phát đề.
Câu 1. [2D2-1] Cho
a
là số thực dương. Rút gọn biểu thức
2 1
2 2
2 1
1
.
P a
a
A.
3
P a
. B.
2
P a
. C.
2 2
P a
. D.
2
P a
.
Câu 2. [2D2-2] Mệnh đề nào sau đây là đúng?
A.
1
1
1 1
. B.
0,5 0,5
e
. C.
1 1
e
. D.
3
0
2 0
.
Câu 3. [2D2-1] Tập xác định của hàm số
1
3
1 2
y x
là
A.
. B.
1
;
2

. C.
0;
. D.
1
;
2

.
Câu 4. [2D2-2] Hàm số
4
2
3
3y x
có đạo hàm trên khoảng
3; 3
là
A.
7
2
3
4
3
3
y x
. B.
7
2
3
8
3
3
y x x
.
C.
7
2
3
8
3
3
y x x
. D.
7
2 2
3
4
3
3
y x x
Câu 5. [2D2-2] Hàm số nào sau đây có cực trị?
A.
3
y x
. B.
4
y x
. C.
1
y x
. D.
1
3
y x
.
Câu 6. [2D2-1] Với các số thực dương
a
,
bất kì, đặt
0,3
10
3 5
a
M
b
. Mệnh đề nào dưới đây đúng?
A.
1
log 3log log
2
M a b
. B.
1
log 3log log
2
M a b
.
C.
log 3log 2log
M a b
. D.
log 3log 2log
M a b
.
Câu 7. [2D2-2] Cho
3
log 5
a
,
3
log 6
b
,
3
log 22
c
. Mệnh đề nào dưới đây đúng?
A.
3
270
log
121
3 2
a b c
. B.
3
270
log
121
3 2
a b c
.
C.
3
270
log
121
3 2
a b c
. D.
3
270
log
121
3 2
a b c
.
Câu 8. [2D2-2] Với các số thực dương
a
,
bất kì. Mệnh đề nào dưới đây đúng?
A.
7 3
3
2
ln
3ln
log log
3
a
b
b
a
. B.
3
27 3
ln
3ln3
log log
a
a
b b
.
C.
7 3
3
2
ln
3ln
log log
3
a
b
b
a
. D.
3
27 3
ln
3ln3
log log
a
a
b b
.
Câu 9. [2D2-3] Cho
a
,
,
x
là các số thực dương và khác 1 và các mệnh đề:
Mệnh đề (I) :
log log
b
b
a
a
x x
. Mệnh đề (II) :
log 1 log
log
log
b b
a
b
a x
ab
x a
.
Khẳng định nào dưới đây là đúng ?
A. (II) đúng, (I) sai. B. (I) đúng, (II) sai. C. (I), (II) đều sai. D. (I), (II) đều đúng.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 2/10 - Mã đề 007
Câu 10. [2D2-3] Cho hàm số
2
3 .4
x x
f x . Khẳng định nào sau đây sai?
A.
2
3
9 2 log 2 2
f x x x
. B.
2
9 ln3 ln 4 2ln3
f x x x .
C.
2
2 2
9 log 3 2 2log 3
f x x x . D.
9 2 log3 log4 log9
f x x x .
Câu 11. [2D2-1] Tìm tập xác định
D
của hàm số
2
2
log 2
y x x
.
A.
0;D

. B.
;0 2;D
 
.
C.
;0 2;D

. D.
;0 2;D
 
.
Câu 12. [2D2-2] Đạo hàm của hàm số
2
log e 1
x
y
là
A.
e
e 1 ln2
x
x
y
. B.
2 ln 2
2 1
x
x
y
. C.
2
2 1 ln 2
x
x
y
. D.
e ln2
e 1
x
x
y
.
Câu 13. [2D2-2] Cho hàm số
2 .5
x x
f x . Tính giá trị của
0
f
.
A.
0 10
f
. B.
0 1
f
. C.
1
0
ln10
f
. D.
0 ln10
f
.
Câu 14. [2D2-3] Cho ba số thực
a
,
,
1
;1
4
c
.
Tìm giá trị nhỏ nhất
min
P
của biểu thức
1 1 1
log log log
4 4 4
a b c
P b c a
.
A.
min
3
P
. B.
min
6
P
. C.
min
3 3
P . D.
min
1
P
.
Câu 15. [2D2-4] Bác Hiếu đầu tư
99
triệu đồng vào một công ty theo thể thức lãi kép với lãi suất
8,25%
một năm. Hỏi sau
5
năm mới rút tiền lãi thì bác Hiếu thu được bao nhiêu tiền lãi? (Giả
sử rằng lãi suất hàng năm không đổi).
A.
48,155
triệu. B.
147,155
triệu. C.
58,004
triệu. D.
8,7
triệu.
Câu 16. [2D2-1] Tìm nghiệm của phương trình
1 ln81
9 e
x
.
A.
5
x
. B.
4
x
. C.
6
x
. D.
17
x
.
Câu 17. [2D2-2] Phương trình
2
3 3
log log 9 0
x x
có 2 nghiệm là
1
x
,
2
x
,
1 2
x x
. Khi đó
1 2
3
x x
bằng
A.
28
9
. B.
3
. C.
. D.
10
.
Câu 18. [2D2-2] Phương trình
3 3
3 log log 3 1 0
x x
có tổng các nghiệm bằng
A.
3
. B.
84
. C.
81
. D.
78
.
Câu 19. [2D2-3] Phương trình
4
log 3.2 1 1
x
x
có hai nghiệm
1
x
,
2
x
thì tổng
1 2
x
x
là
A.
4
. B.
2
. C.
2
log 6 4 2
. D.
6 4 2
.
Câu 20. [2D2-4] Tìm tập hợp tất cả các giá trị của tham số thực
m
đề phương trình
2 2
log 5 1 .log 2.5 2
z z
m
có nghiệm thuộc khoảng
0; .

A.
1
;
4

. B.
1
;
4

. C.
;0 2;

. D.
0;2
.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 3/10 - Mã đề 007
Câu 21. [2D2-1] Tìm tập nghiệm
S
của bất phương trình
1
3 1 4 2 3
x
A.
1;S

. B.
1;S

. C.
;1
S

. D.
;1
S

.
Câu 22. [2D2-1] Tìm tập hợp nghiệm
S
của bất phương trình
2
4 4
log 1 log 2 4
x x
.
A.
2; 1
S
. B.
2;S

.
C.
3; 2; 1
S

. D.
3;S

.
Câu 23. [2D2-2] Nghiệm của bất phương trình
1
1
1
5 2 5 2
x
x
x
là
A.
2 1
x
hoặc
1
x
. B.
1
x
.
C.
2 1
x
. D.
3 1
x
.
Câu 24. [2D2-2] Nghiệm của bất phương trình
2
2 1 2
2
log log 2 log 2 3
x x x
là
A.
3
2
x
. B.
3
2
x
.
C.
1 0
x
hoặc
0
x
. D.
3
1
2
x
.
Câu 25. [2D2-4] Tìm tập hợp
X
gồm tất cả các giá trị của tham số thực
m
để bất phương trình
2 2
5 5
1 log 1 log 4
x mx x m
có tập nghiệm là
.
A.
2;3
X . B.
3;5
X . C.
2;3
X . D.
3;5
X .
----------HẾT----------
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 4/10 - Mã đề 007
ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
A
B B B B
A
A
A
D
D
B A
D
B
A
A
D
B B D
D
C
B C
C
HƯỚNG DẪN GIẢI
Câu 1. [2D2-1] Cho
a
là số thực dương. Rút gọn biểu thức
2 1
2 2
2 1
1
.
P a
a
A.
3
P a
. B.
2
P a
. C.
2 2
P a
. D.
2
P a
.
Lời giải
Chọn A.
2
2 1
2 1
2 1
2 2 2 2 2 1 2 2 2 2 3 2 2 3
2 1
1
. . .
P a a a a a a a a
a
.
Câu 2. [2D2-2] Mệnh đề nào sau đây là đúng?
A.
1
1
1 1
. B.
0,5 0,5
e
. C.
1 1
e
. D.
3
0
2 0
.
Lời giải
Chọn B.
Hai đáp án A, D sai do không đúng định nghĩa lũy thừa.
Câu 3. [2D2-1] Tập xác định của hàm số
1
3
1 2
y x
là
A.
. B.
1
;
2

. C.
0;
. D.
1
;
2

.
Lời giải
Chọn B.
Hàm số xác định khi:
1
1 2 0
x x
. Vậy tập xác định là
1
;
2
D
.
Câu 4. [2D2-2] Hàm số
4
2
3
3y x
có đạo hàm trên khoảng
3; 3
là
A.
7
2
3
4
3
3
y x
. B.
7
2
3
8
3
3
y x x
.
C.
7
2
3
8
3
3
y x x
. D.
7
2 2
3
4
3
3
y x x
Lời giải
Chọn B.
Ta có:
4
1
2 2
3
4
3 . 3
3
y x x
4
1
2
3
4
3 . 2
3
x x
7
2
3
8
3
3
x
x
.
Câu 5. [2D2-2] Hàm số nào sau đây có cực trị?
A.
3
y x
. B.
4
y x
. C.
1
y x
. D.
1
3
y x
.
Lời giải
Chọn B.
3
y x
2
3 0
y x
nên hàm số không có cực trị.
4
y x
3
4
y x
có nghiệm
0
x
và đạo hàm đổi dấu khi đi qua
0
x
nên hàm số có cực trị
tại điểm
0
x
.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 5/10 - Mã đề 007
1
y x
2
1
0
y
x
nên hàm số không có cực trị.
1
3
y x
2
3
2
3
1 1
0, 0
3
3
y x x
x
nên hàm số không có cực trị.
Câu 6. [2D2-1] Với các số thực dương
a
,
bất kì, đặt
0,3
10
3 5
a
M
b
. Mệnh đề nào dưới đây đúng?
A.
1
log 3log log
2
M a b
. B.
1
log 3log log
2
M a b
.
C.
log 3log 2log
M a b
. D.
log 3log 2log
M a b
.
Lời giải
Chọn A.
0,3
10
3 5
a
M
b
0,3
10
5
3
a
b
3
0,5
a
b
3
3 0,5
0,5
1
log log log log 3log log
2
a
M a b a b
b
.
Câu 7. [2D2-2] Cho
3
log 5
a
,
3
log 6
b
,
3
log 22
c
. Mệnh đề nào dưới đây đúng?
A.
3
270
log
121
3 2
a b c
. B.
3
270
log
121
3 2
a b c
.
C.
3
270
log
121
3 2
a b c
. D.
3
270
log
121
3 2
a b c
.
Lời giải
Chọn A.
3 3 3 3
log 6 log 3.2 1 log 2 log 2 1
b b b b
3 3
log 22 log 11.2
c c
3 3
log 11 log 2
c
3 3
log 11 log 2 1
c c b
3
270
log
121
3
3
2
2.3 .5
log
11
3
3 3
log 2.3 .5 2log 11
3 3 3
log 2 3 log 5 2log 11
1 3 2 1
b a c b
3 2
a b c
.
Câu 8. [2D2-2] Với các số thực dương
a
,
bất kì. Mệnh đề nào dưới đây đúng?
A.
7 3
3
2
ln
3ln
log log
3
a
b
b
a
. B.
3
27 3
ln
3ln3
log log
a
a
b b
.
C.
7 3
3
2
ln
3ln
log log
3
a
b
b
a
. D.
3
27 3
ln
3ln3
log log
a
a
b b
.
Lời giải
Chọn A.
3 3
3
27 3 3
3 3
3
3
ln ln
ln3 3l
log log log log l
n3
og
a
a b a a
b
b
b
.
Câu 9. [2D2-3] Cho
a
,
,
x
là các số thực dương và khác 1 và các mệnh đề:
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 6/10 - Mã đề 007
Mệnh đề (I) :
log log
b
b
a
a
x x
. Mệnh đề (II) :
log 1 log
log
log
b b
a
b
a x
ab
x a
.
Khẳng định nào dưới đây là đúng ?
A. (II) đúng, (I) sai. B. (I) đúng, (II) sai. C. (I), (II) đều sai. D. (I), (II) đều đúng.
Lời giải
Chọn D.
1
log .log log
b
b
a a
a
x b x x
b
(I) đúng.
log
log log log log 1 log
log
log log log
b
b b b b b
a
b b b
ab
a b x a x
ab
x
x a a a
(II) đúng.
Câu 10. [2D2-3] Cho hàm số
2
3 .4
x x
f x . Khẳng định nào sau đây sai?
A.
2
3
9 2 log 2 2
f x x x
. B.
2
9 ln3 ln 4 2ln3
f x x x .
C.
2
2 2
9 log 3 2 2log 3
f x x x . D.
9 2 log3 log4 log9
f x x x .
Lời giải
Chọn D.
2
9 3 .4 9
x x
f x
2
2
4 3
x x
2
2
log 4 log 3
x x
2
log4 2 log3
x x
2
log3 log4 log9
x x .
Câu 11. [2D2-1] Tìm tập xác định
D
của hàm số
2
2
log 2
y x x
.
A.
0;D

. B.
;0 2;D
 
.
C.
;0 2;D

. D.
;0 2;D
 
.
Lời giải.
Chọn B.
Hàm số xác định khi
2
2 0 0 2
x x x x
.
Vậy tập xác định của hàm số là
;0 2;D
 
.
Câu 12. [2D2-2] Đạo hàm của hàm số
2
log 1
x
y e
là
A.
1 ln 2
x
x
e
y
e
. B.
2 ln 2
2 1
x
x
y
. C.
2
2 1 ln 2
x
x
y
. D.
ln2
1
x
x
e
y
e
.
Lời giải
Chọn A.
Ta có:
1 ln 2
x
x
e
y
e
.
Câu 13. [2D2-2] Cho hàm số
2 .5
x x
f x . Tính giá trị của
0
f
.
A.
0 10
f
. B.
0 1
f
. C.
1
0
ln10
f
. D.
0 ln10
f
.
Lời giải
Chọn D.
2 .5 10
x x x
f x
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 7/10 - Mã đề 007
10 .ln10
x
f x
Vậy
0
0 10 .ln10 ln10
f
.
Câu 14. [2D2-3] Cho ba số thực
a
,
,
1
;1
4
c
. Tìm giá trị nhỏ nhất
min
P
của biểu thức
1 1 1
log log log
4 4 4
a b c
P b c a
.
A.
min
3
P
. B.
min
6
P
. C.
min
3 3
P . D.
min
1
P
.
Lời giải
Chọn B.
Với mọi
1
; 1
4
x
ta có
2
2 2
1 1 1
0
4 2 4
x x x x x
Lấy logarit 2 vế, ta được
2
1
log log
4
t t
x x
(với
0;1
t (*)
Áp dụng BĐT (*) ta được:
2
1
log log 2log
4
a a a
b b b
2
1
log log 2log
4
b b b
c c c
2
1
log log 2log
4
c c c
a a a
Suy ra
3
min
2 log log log 2.3 log .log .log 6
a b c a b c
P b c a b c a P
.
Câu 15. [2D2-4] Bác Hiếu đầu tư
99
triệu đồng vào một công ty theo thể thức lãi kép với lãi suất
8,25%
một năm. Hỏi sau
5
năm mới rút tiền lãi thì bác Hiếu thu được bao nhiêu tiền lãi? (Giả
sử rằng lãi suất hàng năm không đổi).
A.
48,155
triệu. B.
147,155
triệu. C.
58,004
triệu. D.
8,7
triệu.
Lời giải.
Chọn A.
Áp dụng công thức lãi kép, số tiền thu được cả vốn lẫn lãi là
1
N
T A r
, với tiền gửi :
99
A
triệu đồng, lãi suất
0,0825
r
,
5
N
kì. Ta được :
147,155
T
triệu đồng
số tiền lãi là
48,155
T A
triệu đồng.
Câu 16. [2D2-1] Tìm nghiệm của phương trình
1 ln81
9
x
e
.
A.
5
x
. B.
4
x
. C.
6
x
. D.
17
x
.
Lời giải
Chọn A.
Điều kiện :
1
x
.
Ta có :
1 ln81 1
9 9 81 1 2 5 (t/m)
x x
e x x
.
Câu 17. [2D2-2] Phương trình
2
3 3
log log 9 0
x x
có 2 nghiệm là
1
x
,
2
x
,
1 2
x x
. Khi đó
1 2
3
x x
bằng
A.
28
9
. B.
3
. C.
. D.
10
.
Lời giải
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 8/10 - Mã đề 007
Chọn D.
2
3 3
log log 9 0
x x
2
3 3
0
log log 2 0
x
x x
3
3
0
log 1
log 2
x
x
x
1
2
3
9
x
x
.
Khi đó
1
3. 9 10
3
.
Câu 18. [2D2-2] Phương trình
3 3
3 log log 3 1 0
x x
có tổng các nghiệm bằng
A.
3
. B.
84
. C.
81
. D.
78
.
Lời giải
Chọn B.
Điều kiện:
3
0
0
1
log 0
1
x
x
x
x
x
3 3 3 3
3 log log 3 1 0 3 log 1 log 1 0
x x x x
3 3
log 3 log 2 0
x x
Đặt
3
log 0
t x t
Ta có
3
2
3
log 1
1 3
3 2 0
2 81
log 2
x
t x
t t
t x
x
Vậy tổng các nghiệm bằng
84
.
Câu 19. [2D2-3] Phương trình
4
log 3.2 1 1
x
x
có hai nghiệm
1
x
,
2
x
thì tổng
1 2
x
x
là
A.
4
. B.
2
. C.
2
log 6 4 2
. D.
6 4 2
.
Lời giải
Chọn B.
2
1
4
1
log 3.2 1 1 3.2
4
1 4 2 3.
2
2 1 0 2 6
4
x x x x x x
x
.
Vậy
2
4log
2
6x
. Ta có
1 2 2 2
log 6 4 2 log 6 4 2 2
x x
.
Câu 20. [2D2-4] Tìm tập hợp tất cả các giá trị của tham số thực
m
đề phương trình
2 2
log 5 1 .log 2.5 2
z z
m
có nghiệm thuộc khoảng
0; .

A.
1
;
4

. B.
1
;
4

. C.
;0 2;

. D.
0;2
.
Lời giải
Chọn D.
Phương trình đã cho
2 2
log 5 1 .log 2 5 1
z z
m
2 2
log 5 1 1 log 5 1 .
z z
m
Đặt
2
log 5 1
z
t
với
5 1
5 ln5
0
5 1 ln2 5 1 ln 2
z
z
z z
t z
nên hàm
t z
nghịch biến.
1
m t t f t
.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 9/10 - Mã đề 007
Với
0;z

thì
2
0
2
log 1 0
0;1 .
log 5 1 1
t
t
t
Khi đó YCBT
0 1
f m f
hay
0 2.
m
Câu 21. [2D2-1] Tìm tập nghiệm
S
của bất phương trình
1
3 1 4 2 3
x
A.
1;S

. B.
1;S

. C.
;1
S

. D.
;1
S

.
Lời giải
Chọn D.
Ta có
1 1 2
3 1 4 2 3 3 1 3 1 1 2 1.
x x
x x
Vậy tập nghiệm của bất phương trình là
;1 .
S  .
Câu 22. [2D2-1] Tìm tập hợp nghiệm
S
của bất phương trình
2
4 4
log 1 log 2 4
x x
.
A.
2; 1
S
. B.
2;S

.
C.
3; 2; 1
S

. D.
3;S

.
Lời giải.
Chọn C.
Điều kiện:
2 4 0 2
x x
.
Bpt
2
1 2 4
x x
(do
1
4
nên đổi chiều bất phương trình).
2
2 3 0
x x
; 1 3;x
 
, kết hợp với điều kiện:
3; 2; 1
S

.
Câu 23. [2D2-2] Nghiệm của bất phương trình
1
1
1
5 2 5 2
x
x
x
là
A.
2 1
x
hoặc
1
x
. B.
1
x
.
C.
2 1
x
. D.
3 1
x
.
Lời giải
Chọn B.
Điều kiện:
1
x
Ta có
1
5 2
5 2
.
1
2
1
1
1 2
5 2 5 2 1 0 2; 1 1;
1 1
x
x
x
x x x
x x
x x

.
Câu 24. [2D2-2] Nghiệm của bất phương trình
2
2 1 2
2
log log 2 log 2 3
x x x
là
A.
3
2
x
. B.
3
2
x
.
C.
1 0
x
hoặc
0
x
. D.
3
1
2
x
.
Lời giải
Chọn C.
TXĐ:
3
; \ 0
2
D

.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 10/10 - Mã đề 007
Khi đó,
2 2
2 1 2 2 2
2
2
log log 2 log 2 3 log log 2 log 2 3
x x x x x x
2 2
2 2 2 2 2
log log 2 3 log 2 log log 2 3 . 2
x x x x x x
2 2 2
2 7 6 7 6 0 ; 7 1;x x x x x x x
 
.
So với điều kiện
1;0 0;x
.
Câu 25. [2D2-4] Tìm tập hợp
X
gồm tất cả các giá trị của tham số thực
m
để bất phương trình
2 2
5 5
1 log 1 log 4
x mx x m
có tập nghiệm là
.
A.
2;3
X . B.
3;5
X . C.
2;3
X . D.
3;5
X .
Lời giải
Chọn C.
2 2
5 5
1 log 1 log 4
x mx x m
2 2
5 5
log 5 1 log 4
x mx x m
2
2 2
4 0
5 5 4
mx x m
x mx x m
2
2
4 0
5 4 5 0
mx x m
m x x m
Để bất phương trình trên có tập nghiệm là
khi và chỉ khi:
2
2
4 0
5 4 5 0
mx x m x
m x x m x
I
+ Trường hợp
0
m
hoặc
5
m
không thỏa
I
.
+ Với
0
m
và
5
m
I
2
2
0
4 0
5 0
4 5 0
m
m
m
m
0 5
2 2
3 7
m
m m
m m
2 3
m
là giá trị cần tìm.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 1/9 - Mã đề 008
TOÁN HỌC BẮC–TRUNG–NAM
Nhóm: THBTN – ĐỀ KIỂM TRA
(25 câu trắc nghiệm)
KIỂM TRA CHƯƠNG 2 GIẢI TÍCH 12
MÃ ĐỀ 008
Thời gian làm bài: 45 phút, không kể thời gian phát đề.
Câu 1. [2D2-1] Rút gọn biểu thức
5
3
3
:
Q a a
với
0.
a
A.
4
3
.
Q a
B.
4
3
.
Q a
C.
5
9
.
Q a
D.
2
.
Q a
Câu 2. [2D2-1] Nếu
2 3 2 3
x y
thì kết luận nào sau đây đúng?
A.
x y
. B.
x y
. C.
x y
. D.
x y
.
Câu 3. [2D2-1] Tìm tập xác định
D
của hàm số
e
.
y x
A.
;0 .
D  B.
.
D
C.
0; .
D

D.
\ 0 .
D
Câu 4. [2D2-2] Tính đạo hàm của hàm số
1
2
x
y
.
A.
1 2 ln2
x
y x
. B.
1
2 log2
x
y
. C.
1
2
ln2
x
y
. D.
1
2 ln2
x
y
.
Câu 5. [2D2-2] Hình bên là đồ thị của ba hàm số
x
y a
,
x
y b
,
x
y c
0 , , 1
a b c
được vẽ trên cùng một hệ trục tọa độ.
Khẳng định nào sau đây là khẳng định đúng?
A.
b a c
. B.
a b c
.
C.
a c b
. D.
c b a
Câu 6. [2D2-2] Cho
a
là số thực dương khác
2
. Tính
2
2
log
4
a
a
I
.
A.
2
I
. B.
2
I
. C.
1
2
I
. D.
2
I
.
Câu 7. [2D2-2] Cho
6
log 9 .
a
Tính
3
log 2
theo
a
.
A.
.
2
a
a
B.
2
.
a
a
C.
2
.
a
a
D.
2
.
a
a
Câu 8. [2D2-2] Cho
3
log 2
a
và
2
log
2
b
. Tính
2
3 3 1
4
2log log 3 log
I a b
.
A.
4
I
. B.
4
I
. C.
0
I
. D.
3
2
I
.
Câu 9. [2D2-3] Đường cong trong hình bên là đồ thị của một hàm số
trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới
đây. Hỏi hàm số đó là hàm số nào?
A.
2
log
y x
. B.
1
2
log
y x
.
C.
2
log
y x
. D.
2
log 2
y x
Câu 10. [2D2-3] Cho
a
và
là hai số thực dương và
1
a
. Mệnh đề nào sau đây là đúng?
A.
log
x
b
a b x a
. B.
log
x
a
a b x b
.
C.
log
x
a
a b x b
. D.
0 log
x
a
a b x b
O
x
y
x
y c
x
y b
x
y a
1
O
x
y
1
1
2
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 2/9 - Mã đề 008
Câu 11. [2D2-1] Tìm tập xác định
D
của hàm số
2
3
log 4 3
y x x
.
A.
2 2;1 3;2 2
D
. B.
1;3
D .
C.
;1 3;D
 
. D.
;2 2 2 2;D
 
.
Câu 12. [2D2-2] Tính đạo hàm của hàm số
1
2
4
1 xy
.
A.
5
2
4
1
1
4
xy
. B.
5
2
4
5
1
2
x xy
.
C.
5
2
4
5
1
2
xy x
. D.
5
2
4
1
1
2
xy x
.
Câu 13. [2D2-2] Cho hàm số
2
ln 2
f x x x
. Chọn khẳng định đúng trong các khẳng định sau:
A.
4
3
3
f
. B.
1
3
12
f
. C.
1
3
f
. D.
3 ln3
f
Câu 14. [2D2-2] Cho hàm số
x
y ex e
. Nghiệm của phương trình
0
y
?
A.
1
x
. B.
1
x
. C.
0
x
. D.
ln 2
x
Câu 15. [2D2-4] Xét các số thực dương
a
,
thỏa mãn
2
1
log 2 3
ab
ab a b
a b
. Tìm giá trị nhỏ
nhất
min
P
của
2
P a b
.
A.
min
2 10 3
2
P
. B.
min
2 10 5
2
P
. C.
min
3 10 7
2
P
. D.
min
2 10 1
2
P
.
Câu 16. [2D2-2] Gọi
1
x
,
2
x
là hai nghiệm của phương trình:
2
6 10
1
5
5
x x
x
; khi đó
1 2
x x
bằng:
A.
7
2
. B.
7
2
. C.
7
. D.
7
.
Câu 17. [2D2-2] Tìm nghiệm của phương trình
2
log 5 4
x
.
A.
21
x
. B.
3
x
. C.
11
x
. D.
13
x
.
Câu 18. [2D2-3] Số nghiệm của phương trình
1
3 4 0
9
x x
:
A.
1
n
. B.
2
n
. C.
3
n
. D.
4
n
.
Câu 19. [2D2-2] Nghiệm nguyên nhỏ nhất của bất phương trình
3
log 3 log 3 0
x x
là:
A.
3
x
. B.
1
x
. C.
2
x
. D.
4
x
.
Câu 20. [2D2-3] Giá trị của
m
để phương trình
1
4 .2 2 0
x x
m m
có hai nghiệm
1
x
,
2
x
thỏa mãn
1 2
3
x x
là
A.
3
m
. B.
4
. C.
2
m
. D.
3
2
m
.
Câu 21. [2D2-1] Nghiệm của bất phương trình
2
1
3
9
x
là
A.
4
x
. B.
0
x
. C.
0
x
. D.
4
x
.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 3/9 - Mã đề 008
Câu 22. [2D2-1] Tập nghiệm của bất phương trình
2
1
2
log 1
x
là
A.
2;

. B.
2;0 0; 2
.
C.
2; 2
. D.
0; 2
.
Câu 23. [2D2-2] Tập nghiệm của bất phương trình
1 1
2 2 3 3
x x x x
A.
2;x

. B.
2;x

. C.
;2
x  . D.
2;

.
Câu 24. [2D2-2] Bất phương trình
4 2
log 7 log 1
x x
có tập nghiệm là
A.
1;4
. B.
5;

. C.
1;2
. D.
;1

.
Câu 25. [2D2-4] Tìm tất cả các giá trị thực của tham số
m
để hàm số
3
1
log
2 1
y x m
m x
xác định trên
2;3
.
A.
1 2
m
. B.
1 2
m
. C.
1 2
m
. D.
1 2
m
----------HẾT----------
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 4/9 - Mã đề 008
ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
B A
C D
A
B
D
D
A
B C D
A
A
A
D
A
A
D
B A
B
A
C
A
LỜI GIẢI
Câu 1. [2D2-1] Rút gọn biểu thức
5
3
3
:
Q a a
với
0.
a
A.
4
3
.
Q a
B.
4
3
.
Q a
C.
5
9
.
Q a
D.
2
.
Q a
Lời giải
Chọn B.
Ta có:
5 5 1 5 1 4
3
3 3 3 3 3 3
: : .
Q a a a a a a
Câu 2. [2D2-1] Nếu
2 3 2 3
x y
thì kết luận nào sau đây đúng?
A.
x y
. B.
x y
. C.
x y
. D.
x y
.
Lời giải
Chọn A.
Vì
0 2 3 1
nên ta chọn đáp án A.
Câu 3. [2D2-1] Tìm tập xác định
D
của hàm số
.
e
y x
A.
;0 .
D  B.
.
D
C.
0; .
D

D.
\ 0 .
D
Lời giải
Chọn C.
Ta có hàm số xác định khi
0.
x
Câu 4. [2D2-2] Tính đạo hàm của hàm số
1
2
x
y
.
A.
1 2 ln2
x
y x
. B.
1
2 log2
x
y
. C.
1
2
ln2
x
y
. D.
1
2 ln2
x
y
.
Lời giải
Chọn D.
Câu 5. [2D2-2] Hình bên là đồ thị của ba hàm số
x
y a
,
x
y b
,
x
y c
0 , , 1
a b c
được vẽ trên
cùng một hệ trục tọa độ. Khẳng định nào sau đây là khẳng định đúng?
A.
b a c
. B.
a b c
. C.
a c b
. D.
c b a
Lời giải
Chọn A.
Do
x
y a
và
x
y b
là hai hàm đồng biến nên
, 1
a b
.
Do
x
y c
nghịch biến nên
1
c
. Vậy
x
bé nhất.
O
x
y
x
y c
x
y b
x
y a
1
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 5/9 - Mã đề 008
Mặt khác: Lấy
x m
, khi đó tồn tại
1 2
, y 0
y
để
1
2
m
m
a y
b y
Dễ thấy
1 2
m m
y y a b a b
( Có thể so sánh
,
a b
bằng cách kiểm tra tại
1
x
đối với
hai hàm số ,
x x
y a y b
)
Vậy
b a c
.
Câu 6. [2D2-2] Cho
a
là số thực dương khác
2
. Tính
2
2
log
4
a
a
I
.
A.
2
I
. B.
2
I
. C.
1
2
I
. D.
2
I
.
Lời giải
Chọn B.
2
2
2 2 2
log log 2log 2
4 2 2
a a a
a a a
I
.
Câu 7. [2D2-2] Cho
6
log 9 .
a
Tính
3
log 2
theo
a
.
A.
.
2
a
a
B.
2
.
a
a
C.
2
.
a
a
D.
2
.
a
a
Lời giải
Chọn D.
Ta có:
6 2.3
log 9 2log 3
3
2
log 2.3
a
3
2
log 2 1
a
3
2
log 2 .
a
a
.
Câu 8. [2D2-2] Cho
3
log 2
a
và
2
log
2
b
. Tính
2
3 3 1
4
2log log 3 log
I a b
.
A.
4
I
. B.
4
I
. C.
0
I
. D.
3
2
I
.
Lời giải
Chọn D.
Ta có
2
3
log 2 3 9
a a
và
1
2
2
1
log 2 2
2
b b .
2
3 3 1
4
1 3
2log log 3.9 log 2 2
2 2
I
.
Câu 9. [2D2-3] Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở
bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
A.
2
log
y x
. B.
1
2
log
y x
. C.
2
log
y x
. D.
2
log 2
y x
Lời giải
Chọn A.
O
x
y
1
1
2
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 6/9 - Mã đề 008
Nhận thấy đây là đồ thị hàm số
log
a
y x
. Điểm
1
; 1
2
thuộc đồ thị hàm số nên
1
1 1 1 1
1 log 2
2 2 2
a
a a
a
. Hàm số là
2
log
y x
.
Câu 10. [2D2-3] Cho
a
và
là hai số thực dương và
1
a
. Mệnh đề nào sau đây là đúng?
A.
log
x
b
a b x a
.
B.
log
x
a
a b x b
.
C.
log
x
a
a b x b
.
D.
0 log
x
a
a b x b
Lời giải
Chọn B.
Câu 11. [2D2-1] Tìm tập xác định
D
của hàm số
2
3
log 4 3
y x x
.
A.
2 2;1 3;2 2
D
. B.
1;3
D .
C.
;1 3;D
 
. D.
;2 2 2 2;D
 
.
Lời giải
Chọn C.
Điều kiện
2
1
4 3 0
3
x
x x
x
.
Câu 12. [2D2-2] Tính đạo hàm của hàm số
1
2
4
1 xy
.
A.
5
2
4
1
1
4
xy
. B.
5
2
4
5
1
2
x xy
.
C.
5
2
4
5
1
2
xy x
. D.
5
2
4
1
1
2
xy x
.
Lời giải
Chọn D.
Các hàm số đã cho có dạng
y u x
(với
2
1
u x x
và
1/ 4
)
1 5 5
2 2 2 2
4 4 4
1 1
1 1 1 1
4 2
xy x x x x
.
Câu 13. [2D2-2] Cho hàm số
2
ln 2
f x x x
. Chọn khẳng định đúng trong các khẳng định sau:
A.
4
3
3
f
. B.
1
3
12
f
. C.
1
3
f
. D.
3 ln3
f
Lời giải
Chọn A.
2
2 2
2
2 2
2 2
x x
x
f x
x x x x
4
3
3
f
.
Câu 14. [2D2-2] Cho hàm số
x
y ex e
. Nghiệm của phương trình
0
y
?
A.
1
x
. B.
1
x
. C.
0
x
. D.
ln 2
x
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 7/9 - Mã đề 008
Lời giải
Chọn A.
x x
y ex e y e e
. Suy ra
0 0 1
x
y e e x
.
Câu 15. [2D2-4] Xét các số thực dương
a
,
thỏa mãn
2
1
log 2 3
ab
ab a b
a b
. Tìm giá trị nhỏ
nhất
min
P
của
2
P a b
.
A.
min
2 10 3
2
P
. B.
min
2 10 5
2
P
. C.
min
3 10 7
2
P
. D.
min
2 10 1
2
P
.
Lời giải
Chọn A.
Điều kiện:
1
ab
.
Ta có
2 2 2
1
log 2 3 log 2 1 2 1 log *
ab
ab a b ab ab a b a b
a b
.
Xét hàm số
2
log
y f t t t
trên khoảng
0;

.
Ta có
1
1 0, 0
.ln2
f t t
t
.Suy ra hàm số
f t
đồng biến trên khoảng
0;

.
Do đó,
2
* 2 1 2 1 2 1 2
2 1
b
f ab f a b ab a b a b b a
b
.
2
2 2
2 1
b
P a b b g b
b
.
2
2
5 5 10 10 2
2 0 2 1 2 1
2 2 4
2 1
g b b b b
b
(vì
0
b
).
Lập bảng biến thiên ta được
min
10 2 2 10 3
4 2
P g
.
Câu 16. [2D2-2] Gọi
1
x
,
2
x
là hai nghiệm của phương trình:
2
6 10
1
5
5
x x
x
; khi đó
1 2
x x
bằng:
A.
7
2
. B.
7
2
. C.
7
. D.
7
.
Lời giải
Chọn D.
2
6 10
1
5
5
x x
x
2
6 10
5 5
x x x
2
7 10 0
x x
1 2
b
a
x x
7
Câu 17. [2D2-2] Tìm nghiệm của phương trình
2
log 5 4
x
.
A.
21
x
. B.
3
x
. C.
11
x
. D.
13
x
.
Lời giải
Chọn A.
Điều kiện:
5
x
.
Phương trình
2 2
log 5 log 16 5 16 21
x x x
.
Câu 18. [2D2-3] Số nghiệm của phương trình
1
3 4 0
9
x x
:
A.
1
n
. B.
2
n
. C.
3
n
. D.
4
n
.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 8/9 - Mã đề 008
Lời giải
Chọn A.
1
3 4 0
9
x x
2
3 3.3 4 0
x x
3 1
3 4
x
x
3 4
x
.
Câu 19. [2D2-2] Nghiệm nguyên nhỏ nhất của bất phương trình
3
log 3 log 3 0
x x
là:
A.
3
x
. B.
1
x
. C.
2
x
. D.
4
x
.
Lời giải
Chọn D.
Cách 1: Điều kiện:
0; 1; 3
x x x
3
33 3
3
log 0
0 1
1
log 3 log 3 0 0
log 1 3
log . log 1
x x
x
x
x xx x
Cách 2:
Loại B, A vì
1; 3
x x
Loại C vì
2 2
3
2 log 3 log 3 0
x
Vậy chọn đáp án. D.
Câu 20. [2D2-3] Giá trị của
m
để phương trình
1
4 .2 2 0
x x
m m
có hai nghiệm
1
x
,
2
x
thỏa mãn
1 2
3
x x
là
A.
3
m
. B.
4
. C.
2
m
. D.
3
2
m
.
Lời giải
Chọn B.
Đặt
2
x
t
, điều kiện
0
t
. Phương trình đã cho trở thành
2
2 2 0
t mt m
(1).
Ta có
1 2
2 8
x x
1 2
2 .2 8
x x
.
Vậy phương trình (1) phải có hai nghiệm dương
1 2
,
t t
sao cho
1 2
. 8
t t
.
Điều kiện
2
1 2
1 2
0 2 0
0 2 0 4
2 8
. 8
m m
t t m m
m
t t
.
Câu 21. [2D2-1] Nghiệm của bất phương trình
2
1
3
9
x
là
A.
4
x
. B.
0
x
. C.
0
x
. D.
4
x
.
Lời giải
Chọn A.
2 2 2
1
3 3 3 2 2 4
9
x x
x x
.
Câu 22. [2D2-1] Tập nghiệm của bất phương trình
2
1
2
log 1
x
là
A.
2;

. B.
2;0 0; 2
. C.
2; 2
. D.
0; 2
.
Lời giải
Chọn B .
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 9/9 - Mã đề 008
Ta có
2
2
1
1
2
2
2
0
0
0
log 1 2;0 0; 2 .
1
2
2 2
2
x
x
x
x x
x
x
x
.
Câu 23. [2D2-2] Tập nghiệm của bất phương trình
1 1
2 2 3 3
x x x x
A.
2;x

. B.
2;x

. C.
;2
x  . D.
2;

.
Lời giải
Chọn A.
1 1
2 2 3 3
x x x x
4
3.2 .3
3
x x
3 9
2 4
x
2
x
Câu 24. [2D2-2] Bất phương trình
4 2
log 7 log 1
x x
có tập nghiệm là
A.
1;4
. B.
5;

. C.
1;2
. D.
;1

.
Lời giải
Chọn C.
Điều kiện
1
x
Ta có
2
4 2 2
2
log 7 log 1 log 7 log 1
x x x x
2 2
log 7 2log 1
x x
2 2
2 2
log 7 log 1 7 1
x x x x
(do cơ số
2
a
lớn hơn 1, hàm số
log
a
y x
đồng biến)
2
6 0 3 2
x x x
Kết hợp với điều kiện suy ra
1 2
x
.
Câu 25. [2D2-4] Tìm tất cả các giá trị thực của tham số m để hàm số
3
1
log
2 1
y x m
m x
xác
định trên
2;3
.
A.
1 2
m
. B.
1 2
m
. C.
1 2
m
. D.
1 2
m
Lời giải
Chọn A.
Hàm số xác định
2 1 0 2 1
0
m x x m
x m x m
Suy ra, tập xác định của hàm số là
;2 1
D m m
, với
1
m
.
Hàm số xác định trên
2;3
suy ra
2 2
2;3
2 1 3 1
m m
D
m m
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 1/8 - Mã đề 009
TOÁN HỌC BẮC–TRUNG–NAM
Nhóm: THBTN – ĐỀ KIỂM TRA
(25 câu trắc nghiệm)
KIỂM TRA CHƯƠNG 2 GIẢI TÍCH 12
MÃ ĐỀ 008
Thời gian làm bài: 45 phút, không kể thời gian phát đề.
Câu 1. [2D2-1] Cho các số thực dương
a
,
. Khi đó biểu thức
1 4 4 1
3 3 3 3
3 3
a b a b
a b
bằng
A.
.
a b
B.
1 1
3 3
.
a b
C.
.
ab
D.
2 2
3 3
.
a b
Câu 2. [2D2-2] Cho
m
,
n
thoả mãn
5 2 5 2
m n
. Khi đó ta có
A.
.
m n
B.
.
m n
C.
.
m n
D.
.
m n
Câu 3. [2D2-1] Tập xác định của hàm số
1
2
3
4
y x
là
A.
0; .

B.
.
C.
2;2 .
D.
;2 .

Câu 4. [2D2-2] Đạo hàm của hàm số
4
2
3
2 3
y x x là
A.
1
2
3
2 3 .
x x B.
1
2
3
4
2 3 .
3
x x
C.
1
2
3
4
2 3 .
3
x x
D.
1
2
3
8
1 2 3 .
3
x x x
Câu 5. [2D2-2] Số cực trị của hàm số
1
3
y x x
là
A.
0.
B.
1.
C.
2.
D.
3.
Câu 6. [2D2-1] Cho
0 1
a
,
b
. Rút gọn biểu thức
2
2 4
log log
a
a
b b
ta được
A.
4log .
a
b
B.
6log .
a
b
C.
4log .
a
b
D.
6log .
a
b
Câu 7. [2D2-2] Biết
5
log 3,
a khi đó
15
log 27
bằng
A.
3
.
1
a
a
B.
2
.
1
a
a
C.
4 1
.
1
a
a
D.
4 1
.
2 1
a
a
Câu 8. [2D2-2] Đặt
2 2
log 3,b log 5.
a Khi đó
2
log 675
bằng
A.
3 2 .
a b
B.
2 3 .
a b
C.
3 .
a b
D.
3 .
a b
Câu 9. [2D2-3] Cho các số thực dương
a
,
thỏa mãn
a b
và
2 2
3 0.
a ab b
Trong các đẳng
thức sau, đẳng thức nào đúng
A.
ln ln
ln .
2
a b
a b
B.
ln ln
ln .
3
a b
a b
C.
ln ln
ln 2 2 .
2
a b
a b
D.
ln ln
ln .
2
a b
a b
Câu 10. [2D2-3] Cho hai số thực
,
m n
thỏa mãn
2 2
m n
. Khẳng định nào sau đấy đúng
A.
3 3
1 1
2 2
log 3 log 3 .
m m n n
B.
3 3
1 1
2 2
log 3 log 3 .
m m n n
C.
3 3
1 1
2 2
log 3 log 3 .
m m n n
D.
3 3
1 1
2 2
log 3 log 3 .
m m n n
Câu 11. [2D2-1] Tập xác định của hàm số
2
5
log 2
y x x
là
A.
0; .

B.
.
C.
0;2 .
D.
0;2 .
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 2/8 - Mã đề 009
Câu 12. [2D2-2] Đạo hàm của hàm số
2 .e
x x
y x
A.
1 1
2 e .e .
x x x
x
B.
2 ln2 1 e .
x x
x C.
2 1 e .
x x
x D.
2
1 e .
ln2
x
x
x
Câu 13. [2D2-2] Tìm tất cả các khoảng đồng biến của hàm số
2
2
log 2 3
y x x
A.
1; .

B.
;1 .
 C.
0; .

D.
;2 .

Câu 14. [2D2-3] Gọi
M
,
m
lần lượt là giá trị lớn nhất, nhỏ nhất của hàm số
3
e 3e 4
x x
y
trên
1;1 .
Khi đó
M m
bằng
A.
3
e 3e 4.
B.
3
e 3e 6.
C.
3
e 3e 2.
D.
3
1 3
6.
e e
Câu 15. [2D2-4] Một người gửi ngân hàng
100
triệu đồng theo thể thức lãi kép định kì liên tục, với lãi
suất không đổi mỗi năm. Sau
5
năm thì thu được cả vốn lẫn lãi là
200
triệu đồng. Hỏi người
đó muốn thu được
300
triệu đồng khi gửi
100
triều đồng thì cần bao nhiêu năm
A.
7.
B.
8.
C.
9.
D.
10
Câu 16. [2D2-1] Số nghiệm của phương trình
2
2
1
9
3
x x
x
là
A.
0.
B.
1.
C.
2.
D.
3.
Câu 17. [2D2-2] Số nghiệm của phương trình
3
2
2 8
log 1 log 1
x x
là
A.
0.
B.
1.
C.
2.
D.
3.
Câu 18. [2D2-2] Tổng các nghiệm của phương trình
16 10.4 16 0
x x
là
A.
10.
B.
16.
C.
2.
D.
6.
Câu 19. [2D2-3] Tích các nghiệm của phương trình
2 3 3 2
log .log 4 log 4log
x x x x
là
A.
83.
B.
54.
C.
4.
D.
60.
Câu 20. [2D2-4] Số nghiệm của phương trình
3 1 .2 3 1
x
x x
là
A.
0.
B.
1.
C.
2.
D.
3.
Câu 21. [2D2-1] Tập nghiệm của bất phương trình
2
3 1
1
2
2
x x
là
A.
1;2 .
B.
1;3 .
C.
;1 2; .

D.
2; .

Câu 22. [2D2-1] Tập nghiệm của bất phương trình
1
2
log 2 2 1
x
là
A.
1;0 .
B.
0;1 .
C.
;0 .
 D.
1; .

Câu 23. [2D2-2] Tập nghiệm của bất phương trình
2
2 2
3 9
x x x
là
A.
2;3 .
B.
2;3 .
C.
3;2 .
D.
1;3 .
Câu 24. [2D2-2] Khoảng
;
a b
là tập nghiệm của bất phương trình
5
5
log 1 log 3
x x
. Khi đó
2 2
a b
bằng
A.
29.
B.
27.
C.
34.
D.
30.
Câu 25. [2D2-3] Tìm tất cả các giá trị của tham số
m
để bất phương trình
2
log 6 < log 2 m
x x x x
có tập nghiệm chứa
3;4
A.
3
m
B.
4
m
C.
5
m
D.
6
m
----------HẾT----------
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 3/8 - Mã đề 009
ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
A
B C D
B
C
A
A
A
B D
B A
B
B
C B C B C C A
A
C
B
LỜI GIẢI
Câu 1. [2D2-1] Cho các số thực dương
a
,
. Khi đó biểu thức
1 4 4 1
3 3 3 3
3 3
a b a b
a b
bằng
A.
.
a b
B.
1 1
3 3
.
a b
C.
.
ab
D.
2 2
3 3
.
a b
Lời giải
Chọn A.
1 4 4 1
1 13 3 3 3
3 3
1 1
3 3
3 3
a b a b
a b a b
a b
a b
a b
Câu 2. [2D2-2] Cho
m
,
n
thoả mãn
5 2 5 2
m n
. Khi đó ta có
A.
.
m n
B.
.
m n
C.
.
m n
D.
.
m n
Lời giải
Chọn B.
Ta có
0 5 2 1
nên
5 2 5 2
m n
m n
Câu 3. [2D2-1] Tập xác định của hàm số
1
2
3
4
y x
là
A.
0; .

B.
.
C.
2;2 .
D.
;2 .

Lời giải
Chọn C.
Hàm số trên xác định khi
2
4 0 2 2
x x
Câu 4. [2D2-2] Đạo hàm của hàm số
4
2
3
2 3
y x x là
A.
1
2
3
2 3 .
x x B.
1
2
3
4
2 3 .
3
x x
C.
1
2
3
4
2 3 .
3
x x
D.
1
2
3
8
1 2 3 .
3
x x x
Lời giải
Chọn D.
1 1
2 2 2
3 3
4 8
2 3 . 2 3 1 2 3
3 3
y x x x x x x x
Câu 5. [2D2-2] Số cực trị của hàm số
1
3
y x x
là
A.
0.
B.
1.
C.
2.
D.
3.
Lời giải
Chọn B.
TXĐ:
0;

Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 4/8 - Mã đề 009
2
3
3
2
1 1
1 1
3
3
y x
x
1
0
3 3
y x
Lập bảng xét dấu
y
x
0
1
3 3
y
0
Suy ra hàm số có một điểm cực trị
Câu 6. [2D2-1] Cho
0 1
a
,
b
. Rút gọn biểu thức
2
2 4
log log
a
a
b b
ta được
A.
4log .
a
b
B.
6log .
a
b
C.
4log .
a
b
D.
6log .
a
b
Lời giải
Chọn C.
2
2 4
4
log log 2log log 4log
2
a a a a
a
b b b b b
Câu 7. [2D2-2] Biết
5
log 3,
a khi đó
15
log 27
bằng
A.
3
.
1
a
a
B.
2
.
1
a
a
C.
4 1
.
1
a
a
D.
4 1
.
2 1
a
a
Lời giải
Chọn A.
5 5
15
5 5
log 27 3log 3
3
log 27
log 15 1 log 3 1
a
a
Câu 8. [2D2-2] Đặt
2 2
log 3,b log 5.
a Khi đó
2
log 675
bằng
A.
3 2 .
a b
B.
2 3 .
a b
C.
3 .
a b
D.
3 .
a b
Lời giải
Chọn A.
3 2
2 2 2 2
log 675 log 3 .5 3log 3 2log 5 3 2
a b
Câu 9. [2D2-3] Cho các số thực dương
a
,
thỏa mãn
a b
và
2 2
3 0.
a ab b
Trong các đẳng
thức sau, đẳng thức nào đúng
A.
ln ln
ln .
2
a b
a b
B.
ln ln
ln .
3
a b
a b
C.
ln ln
ln 2 2 .
2
a b
a b
D.
ln ln
ln .
2
a b
a b
Lời giải
Chọn A.
2 2
2 2
3 0 ln ln
a ab b a b ab a b ab
ln ln
2ln ln ln ln
2
a b
a b a b a b
Câu 10. [2D2-3] Cho hai số thực
,
m n
thỏa mãn
2 2
m n
. Khẳng định nào sau đấy đúng
A.
3 3
1 1
2 2
log 3 log 3 .
m m n n
B.
3 3
1 1
2 2
log 3 log 3 .
m m n n
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 5/8 - Mã đề 009
C.
3 3
1 1
2 2
log 3 log 3 .
m m n n
D.
3 3
1 1
2 2
log 3 log 3 .
m m n n
Lời giải
Chọn B.
2 2
m n
m n
Xét hàm số
3
3
f t t t
2
3 3 0
f t t
với
t
Suy ra hàm số
f t
là hàm số đồng biến trên
;
 
Mà
3 3
3 3
m n f m f n m m n n
3 3
1 1
2 2
log 3 log 3
m m n n
Câu 11. [2D2-1] Tập xác định của hàm số
2
5
log 2
y x x
là
A.
0; .

B.
.
C.
0;2 .
D.
0;2 .
Lời giải
Chọn D.
Hàm số xác định khi
2
2 0 0 2
x x x
Câu 12. [2D2-2] Đạo hàm của hàm số
2 .
x x
y x e
A.
1 1
2 . .
x x x
e x e
B.
2 ln2 1 .
x x
x e
C.
2 1 .
x x
x e
D.
2
1 .
ln2
x
x
x e
Lời giải
Chọn B.
2 ln 2 . 2 ln . 2 ln 2 1 .
x x x x x x x
y x e x e x e x e
Câu 13. [2D2-2] Tìm tất cả các khoảng đồng biến của hàm số
2
2
log 2 3
y x x
A.
1; .

B.
;1 .
 C.
0; .

D.
;2 .

Lời giải
Chọn A.
TXĐ:
2
2 2
2 3 ln 2
x
y
x x
Hàm số đồng biến khi
' 0 1
y x
Câu 14. [2D2-3] Gọi
,
M m
lần lượt là giá trị lớn nhất, nhỏ nhất của hàm số
3
3 4
x x
y e e
trên
1;1 .
Khi đó
M m
bằng
A.
3
3 4.
e e
B.
3
3 6.
e e
C.
3
3 2.
e e
D.
3
1 3
6.
e e
Lời giải
Chọn B.
Đặt
x
t e
1
1;1 ;
x t e
e
Hàm số trở thành
3
3 4
y f t t t
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 6/8 - Mã đề 009
2
3 3
f t t
;
1
1 ;
' 0
1
1 ;
t e
e
f t
t e
e
3
3
1 1 3
4
3 4
1 2
f
e e e
f e e e
f
Suy ra
3
3 4, 2
M e e m
Câu 15. [2D2-4] Một người gửi ngân hàng
100
triệu đồng theo thể thức lãi kép định kì liên tục, với lãi
suất không đổi mỗi năm. Sau
5
năm thì thu được cả vốn lẫn lãi là
200
triệu đồng. Hỏi người
đó muốn thu được
300
triệu đồng khi gửi
100
triều đồng thì cần bao nhiêu năm
A.
7.
B.
8.
C.
9.
D.
10
Lời giải
Chọn B.
Gọi
r
là lãi suất một năm
Số tiền người đó thu được khi gửi
100
triệu sau
5
năm là
5
100 1
r
Ta có
5
5
200 100. 1 2 1
r r
Số tiền người đó thu được sau
n
năm gửi
100
triệu vào ngân hàng là
5
100. 1 100. 2
n
n
r
Theo giả thiết
5
100. 2 300 8
n
n
Câu 16. [2D2-1] Số nghiệm của phương trình
2
2
1
9
3
x x
x
là
A.
0.
B.
1.
C.
2.
D.
3.
Lời giải
Chọn C.
2 2
2 2 4 2 2
0
1
9 3 3 2 4 2 3 0
3
3
2
x x x x x
x
x
x x x x x
x
Câu 17. [2D2-2] Số nghiệm của phương trình
3
2
2 8
log 1 log 1
x x
là
A.
0.
B.
1.
C.
2.
D.
3.
Lời giải
Chọn B.
ĐK :
2
3
1 0
1
1 0
x
x
x
3
2 2
2 8 2 2
log 1 log 1 log 1 log 1
x x x x
2 2
1
1 1 2 0
2
x
x x x x
x
Suy ra PT có một nghiệm
2
x
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 7/8 - Mã đề 009
Câu 18. [2D2-2] Tổng các nghiệm của phương trình
16 10.4 16 0
x x
là
A.
10.
B.
16.
C.
2.
D.
6.
Lời giải
Chọn C.
2
4 2
2
16 10.4 16 0 4 10.4 16 0
3
4 8
2
x
x x x x
x
x
x
Câu 19. [2D2-3] Tích các nghiệm của phương trình
2 3 3 2
log .log 4 log 4log
x x x x
là
A.
83.
B.
54.
C.
4.
D.
60.
Lời giải
Chọn B.
ĐK:
0
x
2 3 3 2 2 3
log .log 4 log 4log log 1 log 4 0
x x x x x x
2
3
log 1
2
log 3
27
x
x
x
x
Câu 20. [2D2-4] Số nghiệm của phương trình
3 1 .2 3 1
x
x x
là
A.
0.
B.
1.
C.
2.
D.
3.
Lời giải
Chọn C.
Kiểm tra
1
3
x
không phải là nghiệm của PT
Với
1
3
x
3 1
3 1 .2 3 1 2
3 1
x x
x
x x
x
Hàm số
2
x
y
là hàm số đồng biến trên mỗi khoảng
1
;
3

và
1
;
3

Hàm số
3 1
3 1
x
y
x
là hàm số nghịch biến trên mỗi khoảng
1
;
3

và
1
;
3

Suy ra trên mỗi khoảng
1
;
3

và
1
;
3

PT có tối đa 1 nghiệm
Ta thấy
1
x
là nghiệm của PT
Vậy phương trình có 2 nghiệm
1
x
Câu 21. [2D2-1] Tập nghiệm của bất phương trình
2
3 1
1
2
2
x x
là
A.
1;2 .
B.
1;3 .
C.
;1 2; .

D.
2; .

Lời giải
Chọn C.
2 2
3 1 3 1 1 2 2
1
1
2 2 2 3 1 1 3 2 0
2
2
x x x x
x
x x x x
x
Câu 22. [2D2-1] Tập nghiệm của bất phương trình
1
2
log 2 2 1
x
là
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 8/8 - Mã đề 009
A.
1;0 .
B.
0;1 .
C.
;0 .
 D.
1; .

Lời giải
Chọn A.
1
2
log 2 2 1 0 2 2 2 1 0
x x x
Câu 23. [2D2-2] Tập nghiệm của bất phương trình
2
2 2
3 9
x x x
là
A.
2;3 .
B.
2;3 .
C.
3;2 .
D.
1;3 .
Lời giải
Chọn B.
2 2
2 2 2 2 4 2 2
3 9 3 3 2 2 4 6 0 2 3
x x x x x x
x x x x x x
Câu 24. [2D2-2] Khoảng
;
a b
là tập nghiệm của bất phương trình
5
5
log 1 log 3
x x
. Khi đó
2 2
a b
bằng
A.
29.
B.
27.
C.
34.
D.
30.
Lời giải
Chọn C.
ĐK:
3
x
2
5 5 5 5 5
5
log 1 log 3 log 1 2log 3 log 1 log 3
x x x x x x
2
2
1 3 7 10 0 2 5
x x x x x
Kết hợp điều kiện, suy ra
3 5
x
Suy ra
2 2
3, 5 34
a b a b
Câu 25. [2D2-3] Tìm tất cả các giá trị của tham số
m
để bất phương trình
2
log 6 < log 2 m
x x x x
có tập nghiệm chứa
3;4
A.
3
m
B.
4
m
C.
5
m
D.
6
m
Lời giải
Chọn B.
ĐK:
2
6 0
3
2 0
x x
x
x
Với ĐK trên
2 2
log 6 < log 2 m log 6 log 2
x x x x m x x x x
2
6
log log 3
2
x x
m x m x x
x
Đặt
log 3
f x x x
BPT có tập nghiệm chứa
3;4
log 3
m x x
đúng với
3;4
x
Xét hàm số
log 3
f x x x
trên khoảng
3;4
1
' 1 0
3 ln10
f x
x
với
3;4
x
Suy ra hàm số
log 3
f x x x
đồng biến trên
3;4
m f x
đúng với
3;4
x
4 4
m f
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 1/9 - Mã đề 010
TOÁN HỌC BẮC–TRUNG–NAM
Nhóm: THBTN – ĐỀ KIỂM TRA
(25 câu trắc nghiệm)
KIỂM TRA CHƯƠNG 2 GIẢI TÍCH 12
MÃ ĐỀ 010
Thời gian làm bài: 45 phút, không kể thời gian phát đề.
Câu 1. [2D2-1] Cho
m
là số nguyên dương, biểu thức nào sau đây sai?
A.
2
16 4
m m
. B.
3
16 2 . 2
m m m
. C.
16 4 . 2
m m m
. D.
4
16 2
m m
.
Câu 2. [2D2-2] Với
0, 0
a b
. Giá trị của biểu thức
3 1 3 5
2 3
2
. .
. : .
a a b b
A
a b a b b
là:
A.
b a
A
a
. B.
1
A a
. C.
1
a
A
b
. D.
a b
A
b
.
Câu 3. [2D2-1] Tập xác định của hàm số
3
3 1
y x
là tập:
A.
3;

. B.
1
;
3

. C.
1
;
3

. D.
1
\
3
.
Câu 4. [2D2-2] Đạo hàm của hàm số
y x x
A.
4
3
4
y
x
. B.
4
4
3
y
x
. C.
3
4
y
x
. D.
4
3
4
y
x
.
Câu 5. [2D2-2] Hàm số
2
1
x
y x e
có bao nhiêu cực trị?
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 6. [2D2-1] Cho
0
a
và
1.
a
Tìm mệnh đề đúng trong các mệnh đề sau:
A.
log
a
x
có nghĩa với
x
. B. log 1
a
a
và log
0.
a
a
C.
log
.
log
log
a
a
a
x
x y
y
D.
log . log log
a a a
x y x y
0
)
0, .
(x y
Câu 7. [2D2-2] Với
0
m
, cho
3
log
a m
với. Tính
log 27
m
P m
theo
a
A.
6 2
.
a
P
a
B.
6 . .
P a a
C.
6
.
a
P
a
D.
6 2 . .
A a a
Câu 8. [2D2-2] Đặt
2
log 3,
a
5
log 3.
b Hãy biểu diễn
6
log 45
theo
a
và
.
b
A.
6
2
log 45 .
a ab
ab
B.
2
6
2 2
log 45 .
a ab
ab
C.
6
2
log 45 .
a ab
ab b
D.
2
6
2 2
log 45 .
a ab
ab b
Câu 9. [2D2-3] Khẳng định nào sau đây đúng:
A.
2
3 3
log 2log
a a
. B.
3
2 2 2
3
log 4log
a a
. C.
3
2 2 2
3
log 4log
a a
. D.
2
3 3
1
log log
2
a a
.
Câu 10. [2D2-3] Nếu
2
2
3
a a
và
3 4
log log
4 5
b b
thì khẳng định nào sau đây đúng?
A.
0 1
a
và
0 1.
b
B.
0 1
a
và
1.
b
C.
1
a
và
0 1.
b
D.
1
a
và
1.
b
Câu 11. [2D2-2] Tìm tập xác định
D
của hàm số
2
3
log 2 1
y x x
.
A.
;1
D

. B.
1;D
.
C.
;D

. D.
;1 1;D

.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 2/9 - Mã đề 010
Câu 12. [2D2-1] Đạo hàm
f x
của hàm số
2
e
x
f x
là
A.
2e
x
f x
. B.
2e
x
f x
. C.
2e
f x
x
. D.
2
2e
x
f x
.
Câu 13. [2D2-2] Cho hàm số
ln
y x x
, khi đó đạo hàm cấp hai tại
e
x
là
e
y
có giá trị bằng bao
nhiêu?
A.
e
. B.
2
. C.
1
e
. D.
1
.
Câu 14. [2D2-3] Bác Anh đem gửi tiết kiệm ở ngân hàng với lãi suất là
12%
một năm. Biết rằng cứ sau
mỗi một quý (
3
tháng) thì lãi được cộng dồn vào gốc. Hỏi sau tối thiểu bao nhiêu năm thì Bác
Anh nhận lại được số tiền (cả vốn lẫn lãi) gấp ba số tiền ban đầu.
A.
8
năm. B.
9
năm. C.
10
năm. D.
11
năm.
Câu 15. [2D2-4] Tìm giá trị lớn nhất của
2 2
sin cos
2 2
x x
y
A.
3
. B.
2
. C.
4
. D.
5
.
Câu 16. [2D2-1] Cho phương trình
2
4 5
3 9
x x
tổng lập phương các nghiệm thực của phương trình là
A.
28.
B.
27.
C.
26.
D.
25.
Câu 17. [2D2-2] Gọi
1 2
,
x x
là nghiệm của phương trình
16
log 2 log 0
x
x
. Khi đó giá trị
1 2
.
2
x x
bằng
A.
1
. B.
1
. C.
2
. D.
2
.
Câu 18. [2D2-2] Tổng các nghiệm của phương trình:
3 1
1 1
2 5 2
x x
x x
là
A.
0
. B.
2
. C.
2
. D. 4.
Câu 19. [2D2-3] Số nghiệm của phương trình
4 2 2 4
log log log log 2
x x
là
A.
0
. B.
2
. C.
3
. D.
1.
Câu 20. [2D2-4] Biết phương trình
1
5 .8 500
x
x
x
hai nghiệm
1
x
,
2
x
. Tính
1 2
.
5
x x
P .
A.
8
P
. B.
P
. C.
3
P
. D.
P
.
Câu 21. [2D2-1] Bất phương trình
2
1 3 1
3 3
2 2
x x
có tập nghiệm là
A.
(2;5)
. B.
1;2
. C.
1;3
. D.
; 1

.
Câu 22. [2D2-1] Tìm tập nghiệm
S
của bất phương trình
1
2
log 4 3 4
x
.
A.
; 4 .
S

B.
4
;2 .
3
S
C.
4
; .
3
S

D.
.
S
Câu 23. [2D2-2] Nghiệm của bất phương trình
2 4 2 2
3 45.6 9.2 0
x x x
A.
2
x
. B.
2
x
. C.
2
x
. D.
2
x
.
Câu 24. [2D2-2] Có bao nhiêu giá trị nguyên dương của
x
thỏa mãn bất phương trình
log 40 log 60 2
x x
.
A.
10
. B.
19
. C.
18
. D.
20
.
Câu 25. [2D2-4] Tìm tất cả các giá trị thực của tham số
m
để bất phương trình
2 2
log 5 1 .log 2.5 2
x x
m
nghiệm đúng với mọi
1
x
.
A.
6
m
. B.
6
m
. C.
6
m
. D.
6
m
.
----------HẾT----------
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 3/9 - Mã đề 010
ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
C C B D
5 D
A
C B B D
D
C
C
A
A
C C D
B B A
D
C
C
HƯỚNG DẪN GIẢI
Câu 1. [2D2-1] Cho
m
là số nguyên dương, biểu thức nào sau đây sai?
A.
2
16 4
m m
. B.
3
16 2 . 2
m m m
. C.
16 4 . 2
m m m
. D.
4
16 2
m m
.
Lời giải
Chọn C.
Ta có:
. 4 4 3 3 2
16 2 2 2 2 .2 4
n m
m m n m m m m m m m
a a
2 3
4 .2 2 .2 2
m m m m m
. Vậy C sai.
Câu 2. [2D2-2] Với
0, 0
a b
. Giá trị của biểu thức
3 1 3 5
2 3
2
. .
. : .
a a b b
A
a b a b b
là:
A.
b a
A
a
. B.
1
A a
. C.
1
a
A
b
. D.
a b
A
b
.
Lời giải
Chọn C.
Với
0, 0
a b
. Xét
3 1 3 5 2 2
2 3
2
2
. .
1
. : .
a b a b
a a b b a b a b a
A
ab b b a b b b
a b a b b
.
Câu 3. [2D2-1] Tập xác định của hàm số
3
3 1
y x
là tập:
A.
3;

. B.
1
;
3

. C.
1
;
3

. D.
1
\
3
.
Lời giải
Chọn B.
Ta có:
3
không nguyên nên đkxđ của hàm số là
1
3 1 0
3
x x
Suy ra tập xác định:
1
;
3
D

.
Câu 4. [2D2-2] Đạo hàm của hàm số
y x x
A.
4
3
4
y
x
. B.
4
4
3
y
x
. C.
3
4
y
x
. D.
4
3
4
y
x
.
Lời giải
Chọn D.
Áp dụng công thức:
1
. .
n n
u n u u
Suy ra:
3 1
4 4
4
3 3
.
4
4
y x x x y x
x
.
Câu 5. [2D2-2] Hàm số
2
1
x
y x e
có bao nhiêu cực trị?
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 4/9 - Mã đề 010
Chọn A.
Ta có:
2 2 2
1 2 . 1 . 2 1 . 1 . 0
x x x x x
y x e y x e x e x x e x e
với
x
Nên hàm số không có cực trị.
Câu 6. [2D2-1] Cho
0
a
và
1.
a
Tìm mệnh đề đúng trong các mệnh đề sau:
A.
log
a
x
có nghĩa với
x
. B. log 1
a
a
và log
0.
a
a
C.
log
.
log
log
a
a
a
x
x y
y
D.
log . log log
a a a
x y x y
0
)
0, .
(x y
Lời giải
Chọn D.
Ta có:
log
a
x
xác định khi
0
x
nên A sai
log
0
1
a
và log
1
a
a
nên B sai
C không tồn tại
log . log log
a a a
x y x y
0
)
0, .
(x y
Đúng.
Câu 7. [2D2-2] Với
0
m
, cho
3
log
a m
với. Tính
log 27
m
P m
theo
a
A.
6 2
.
a
P
a
B.
6 . .
P a a
C.
6
.
a
P
a
D.
6 2 . .
A a a
Lời giải
Chọn A.
Ta có
3 3
3 2
2.log 27 2. 3 log
6 2
log 27 .
log log
m
m m
a
P m
m m a
Câu 8. [2D2-2] Đặt
2
log 3,
a
5
log 3.
b Hãy biểu diễn
6
log 45
theo
a
và
.
b
A.
6
2
log 45 .
a ab
ab
B.
2
6
2 2
log 45 .
a ab
ab
C.
6
2
log 45 .
a ab
ab b
D.
2
6
2 2
log 45 .
a ab
ab b
Lời giải
Chọn C.
Cách 1: Ta có
2
5 2
2 2
log 3
log 3 log 5
log 5 log 5
a a
b
b
2
2
2 2 2
6
2 2 2
2
log 3 .5
log 45 2log 3 log 5 2
log 45 .
log 6 log 2.3 1 log 3 1
a
a
a ab
b
a ab b
Cách 2: Dùng Casio: Nếu
0.
A B A B
Gán
2
log 3
A
;
5
log 3
B
. Sau đó ta thử các các phương án.
6
2
log 45 0.
A AB
AB
suy ra A loại.
2
6
2 2
log 45 0.
A AB
AB
suy ra B loại.
6
2
log 45 0.
A AB
AB B
suy ra chọn. C.
Câu 9. [2D2-3] Khẳng định nào sau đây đúng:
A.
2
3 3
log 2log
a a
. B.
3
2 2 2
3
log 4log
a a
. C.
3
2 2 2
3
log 4log
a a
. D.
2
3 3
1
log log
2
a a
.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 5/9 - Mã đề 010
Lời giải
Chọn B.
Ta có:
2
3 3
log 2log
a a
nên A sai
2
2
2 2 2 2
3 3 3 3
log log 2log 4log
a a a a
. Vậy B đúng.
Câu 10. [2D2-3] Nếu
2
2
3
a a
và
3 4
log log
4 5
b b
thì khẳng định nào sau đây đúng?
A.
0 1
a
và
0 1.
b
B.
0 1
a
và
1.
b
C.
1
a
và
0 1.
b
D.
1
a
và
1.
b
Lời giải
Chọn B.
Ta có
2 2
3
2
2 2
3 2
0 1
a
a a
và
3 4
4 5
1
3 4
log log
4 5
b b
b
.
Câu 11. [2D2-2] Tìm tập xác định
D
của hàm số
2
3
log 2 1
y x x
.
A.
;1
D

. B.
1;D
.
C.
;D

. D.
;1 1;D

.
Lời giải
Chọn D.
Hàm số
2
3
log 2 1
y x x
xác định khi
2
2 1 0 1
x x x
Vậy TXĐ là
;1 1;D

.
Câu 12. [2D2-1] Đạo hàm
f x
của hàm số
2
x
f x e
là
A.
2
x
f x e
. B.
2
x
f x e
. C.
2
e
f x
x
. D.
2
2
x
f x e
.
Lời giải
Chọn D.
Ta có:
2 2
2 . 2
x x
f x x e e
.
Câu 13. [2D2-2] Cho hàm số
ln
y x x
, khi đó đạo hàm cấp hai tại
x e
là
y e
có giá trị bằng bao
nhiêu?
A.
e
. B.
2
. C.
1
e
. D.
1
.
Lời giải
Chọn C.
Ta có:
1 1
.ln . ln ln 1y x x x x x y y e
x e
.
Câu 14. [2D2-3] Bác Anh đem gửi tiết kiệm ở ngân hàng với lãi suất là
12%
một năm. Biết rằng cứ sau
mỗi một quý (
3
tháng) thì lãi được cộng dồn vào gốc. Hỏi sau tối thiểu bao nhiêu năm thì Bác
Anh nhận lại được số tiền (cả vốn lẫn lãi) gấp ba số tiền ban đầu.
A.
8
năm. B.
9
năm. C.
10
năm. D.
11
năm.
Lời giải
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 6/9 - Mã đề 010
Chọn C.
Gọi số tiền Bác Anh gửi là
A
, lãi suất mỗi quý là
0,03
.
Sau
n
quý, tiền mà người đó nhận được là :
1 0,03
n
A .
Yêu cầu bài toán
1,03
1 0,03 3 log 3 37,16
n
A A n .
Suy ra số năm tổi thiểu xấp xỉ
9,29
năm. Vậy sau
10
năm thì Bác Anh nhận lại được số tiền
thỏa ycbt.
Câu 15. [2D2-4] Tìm giá trị lớn nhất của
2 2
sin cos
2 2
x x
y
A.
3
. B.
2
. C.
4
. D.
5
.
Lời giải
Chọn A.
Xét
2 2
sin cos
2 2
x x
y f x
Đặt
2
sin , 0;1
t x t .
Tìm GTLN của
1
2 2
t t
y f t
trên
0;1
.
1
2 ln 2 2 ln 2 0
t t
y
1
2 2
2
t t
t
.
1
(0) 3; (1) 3; 2 2
2
f f f
.
Vậy
0;1
max 3
y
.
Câu 16. [2D2-1] Cho phương trình
2
4 5
3 9
x x
tổng lập phương các nghiệm thực của phương trình là
A.
28.
B.
27.
C.
26.
D.
25.
Lời giải
Chọn A.
Ta có:
2 2
4 5 4 5 2 2 2
3 9 3 3 4 5 2 4 3 0
3
x x x x
x
x x x x
x
.
Suy ra
3 3
1 3 28
.
Câu 17. [2D2-2] Gọi
1 2
,
x x
là nghiệm của phương trình
16
log 2 log 0
x
x
. Khi đó giá trị
1 2
.
2
x x
bằng
A.
1
. B.
1
. C.
2
. D.
2
.
Lời giải
Chọn C.
Điều kiện:
0 1
x
PT
4
16
2
log 2 log 0 log 2 log 0
x x
x x
2
1
log 2 log 0
4
x
x
1
2
2
1
4
log 2
1
2
log 2
1
1
4
log 2
2
x
x
x
x
x
Vậy
1 2
.
1 2
. 1 2 2
x x
x x
.
Câu 18. [2D2-2] Tổng các nghiệm của phương trình:
3 1
1 1
2 5 2
x x
x x
là:
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 7/9 - Mã đề 010
A.
0
. B.
2
. C.
2
. D. 4.
Lời giải
Chọn C.
Điều kiện:
1
x
Phương trình
2 2 2
1 1
1 1 1
2
1
2
2 5 2 2.2 5
2
x x x
x
Đặt
2
1
2 0
x
t
phương trình trở thành:
2
2
2
2. 5 2 5 2 0
1
2
t
t t t
t
t
Với
2
1
1
2
2 2 2 1 1 2 1
1
x
t x x
x
Với
2
1
1
2
1 2
2 2 1 1 2 3
2 1
x
t x x
x
Nên
1 2
1 3 2
x x
.
Câu 19. [2D2-3] Số nghiệm của phương trình
4 2 2 4
log log log log 2
x x
là
A.
0
. B.
2
. C.
3
. D.
1.
Lời giải
Chọn D.
PT
2 2
2
4
2 2 2 2
2 2
2 2
0
1
log 0
1 1
log 0
log log log log 2
2 2
log log log log 2
x
x
x
x
x x
x x
.
2 2 2 2 2 2 2
1 1
1 1 3
log log log log log 2 log log 1 2
2 2 2
x x
x x x
.
2 2 2
1
1 1
16
log log 2 log 4 16
x
x x
x
x x x
.
Câu 20. [2D2-4] Biết phương trình
1
5 .8 500
x
x
x
hai nghiệm
1 2
,
x x
. Tính
1 2
.
5
x x
P .
A.
8
P
. B.
P
. C.
3
P
. D.
P
.
Lời giải
Chọn B.
Điều kiện:
0.
x
1 3 3 3 3
3 2 3 2
5 5
5 .8 500 5 .2 5 .2 log 5 .2 log 5 .2
x x x
x x x
x x x
1
2
5 5 5 5
2 5
3
3 3
.log 2 3 2log 2 log 2 3 3log 2 0
log 2
x
x
x x x
xx
Vậy
5 51 2
3
3.log 2 log 2.
3
1
5 5 5 2
8
x x
P
.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 8/9 - Mã đề 010
Câu 21. [2D2-1] Bất phương trình
2
1 3 1
3 3
2 2
x x
có tập nghiệm là
A.
(2;5)
. B.
1;2
. C.
1;3
. D.
; 1

.
Lời giải
Chọn B.
Ta có
2
1 3 1
2 2
3 3
1 3 1 3 2 0 1 2
2 2
x x
x x x x x
.
Câu 22. [2D2-1] Tìm tập nghiệm
S
của bất phương trình
1
2
log 4 3 4
x
.
A.
; 4 .
S

B.
4
;2 .
3
S
C.
4
; .
3
S

D.
.
S
Lời giải
Chọn A.
Đk:
4
4 3 0
3
x x
Ta có:
1
2
log 4 3 4
x
4
1
4 3
2
x
4 3 16
x
4
x
.
Kết hợp điều kiện ta có :
4
4
3
x
.
Câu 23. [2D2-2] Nghiệm của bất phương trình
2 4 2 2
3 45.6 9.2 0
x x x
A.
2
x
. B.
2
x
. C.
2
x
. D.
2
x
.
Lời giải
Chọn D.
Ta có:
2
2 4 2 2 2
3 3
3 45.6 9.2 0 81.3 45.6 36.4 0 81. 45. 36 0
2 2
x x
x x x x x x
Đặt
3
, 0
2
x
t t
. Khi đó bất phương trình trở thành
2
4 4 3 4
81 45 36 0 1 0 2
9 9 2 9
x
t t t t x
.
Câu 24. [2D2-2] Có bao nhiêu giá trị nguyên dương của
x
thỏa mãn bất phương trình
log 40 log 60 2
x x
.
A.
10
. B.
19
. C.
18
. D.
20
.
Lời giải
Chọn C.
ĐK:
40 60.
x
Ta có:
log 40 log 60 2
x x
log 40 60 2
x x
40 60 100
xv x
2
100 2500 0
x x
2
50 0
x
50.
x
Số giá trị nguyên dương thỏa bpt là
59 41 1 1 18.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 9/9 - Mã đề 010
Câu 25. [2D2-4] Tìm tất cả các giá trị thực của tham số
m
để bất phương trình
2 2
log 5 1 .log 2.5 2
x x
m
nghiệm đúng với mọi
1
x
.
A.
6
m
. B.
6
m
. C.
6
m
. D.
6
m
.
Lời giải
Chọn C.
BPT
2 2 2 2
log 5 1 .log 2 5 1 log 5 1 . 1 log 5 1
x x x x
m m
Đặt
2
log 5 1
x
t
do
1
x
2;t

Ta được
2
1
t t m t t m f t m
Xét hàm số
2
f t t t
,
2;t

2 1 0
f t t
với
2;t

nên hàm đồng biến trên
2;t

min 2 6
f t f
Do đó để để bất phương trình
2 2
log 5 1 .log 2.5 2
x x
m
nghiệm đúng với mọi
1
x
thì
min 6
m f t m
.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 1/10 - Mã đề 011
TOÁN HỌC BẮC–TRUNG–NAM
Nhóm: THBTN – ĐỀ KIỂM TRA
(25 câu trắc nghiệm)
KIỂM TRA CHƯƠNG 2 GIẢI TÍCH 12
MÃ ĐỀ 011
Thời gian làm bài: 45 phút, không kể thời gian phát đề.
Câu 1. [2D2-1] Biểu thức
4
3
1
27
3
a
( với
0
a
) viết dưới dạng lũy thừa với số mũ hữu tỉ là
A.
1 1
4 12
3 .
a
. B.
1 1
4 2
3 .
a
. C.
1
12
9.
a
. D.
1
1
3
4
3 .
a
Câu 2. [2D2-1] Cho
a
,
là các số thực dương thỏa mãn
4
3
5
4
a a
và
1 2
log log
2 3
b b
. Mệnh đề nào
sau đây đúng?
A.
1, 1
a b
. B. 1,0
a b a
. C.
0 1,0 1
a b
. D.
0 1, 1
a b
.
Câu 3. [2D2-1] Tìm
x
để biểu thức
1
2
3
1
x
có nghĩa:
A.
;1 1;x
 
. B.
; 1 1;x

.
C.
1;1
x . D.
\ 1
x
.
Câu 4. [2D2-2] Đạo hàm của hàm số
1
2
3
5 2
y x x là
A.
3 2
10 1
3 5 2
x
y
x x
. B.
3 2
10 1
5 2
x
y
x x
.
C.
2
2
3
10 1
3 5 2
x
y
x x
. D.
3 2
1
3 5 2
y
x x
.
Câu 5. [2D2-2] Hàm số
2
3 10 2
x
y a a đồng biến trên
;
 
khi:
A.
1
;
3
a

. B.
3;a

. C.
1
;
3
a

. D.
1
;3
3
a
.
Câu 6. [2D2-1] Nếu
1
1
6
2
a a
và
2 3
b b
thì
A.
1;0 1
a b
.
B.
1; 1
a b
.
C.
0 1; 1
a b
.
D.
1;0 1
a b
.
Câu 7. [2D2-2] Cho
0
a
,
0
b
. Nếu viết
0,2
10
5 5 5
6 5
log log log
a
x a y b
b
thì
xy
bằng bao nhiêu?
A.
3
. B.
1
. C.
3
. D.
3
.
Câu 8. [2D2-2] Cho
, 0
x y
và
2 2
4 12
x y xy
. Khẳng định nào sau đây là khẳng định đúng?
A.
2 2 2
2
log log log
4
x y
x y
. B.
2 2 2
1
log 2 2 log log
2
x y x y
.
C.
2 2 2
log 2 log log 1
x y x y
. D.
2 2 2
4log 2 log log
x y x y
.
Câu 9. [2D2-2] Cho
2
log 3
a
,
2
log 7
. Tính
2
log 2016
theo
a
và
.
A.
5 2
a b
. B.
5 3 2
a b
.
C.
2 2 3
a b
. D.
2 3 2
a b
.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 2/10 - Mã đề 011
Câu 10. [2D2-3] Hình bên là đồ thị của ba hàm số
x
y a
,
x
y b
,
x
y c
0 , , 1
a b c
được vẽ trên cùng một hệ
trục tọa độ. Khẳng định nào sau đây là khẳng định đúng?
A.
b a c
.
B.
a b c
.
C.
a c b
.
D.
c b a
.
Câu 11. [2D2-2] ] Cho
a
là số thực dương khác
1
. Xét hai số thực
1
x
,
2
x
. Phát biểu nào sau đây là
đúng?
A. Nếu
1 2
x x
a a
thì
1 2
x x
. B. Nếu
1 2
x x
a a
thì
1 2
1 0
a x x
.
C. Nếu
1 2
x x
a a
thì
1 2
1 0
a x x
. D. Nếu
1 2
x x
a a
thì
1 2
x x
.
Câu 12. [2D2-1] Hàm số
1
log
x
y x
xác định khi và chỉ khi:
A.
1
2
x
x
. B.
1
x
. C.
0
x
. D.
2
x
Câu 13. [2D2-1] Cho hàm số
e
x
f x x
. Gọi
f x
là đạo hàm cấp hai của
f x
. Ta có
1
f
bằng
A.
3e
. B.
2
3e
. C.
3
e
. D.
2
5e
Câu 14. [2D2-1] Cho hàm số
e e
x
y x
.
Nghiệm của phương trình
0
y
?
A.
1
x
. B.
1
x
. C.
0
x
. D.
ln 2
x
Câu 15. [2D2-2] Tính giá trị của biểu thức
ln tan1° ln tan 2 ln tan3 ... ln tan89
P
.
A.
1.
P
B.
1
.
2
P
C.
0.
P
D.
2.
P
Câu 16. [2D2-3] Một người mỗi tháng đều đặn gửi vào ngân hàng một khoản tiền
T
theo hình thức lãi
kép với lãi suất
0,6
% mỗi tháng. Biết sau
15
tháng người đó có số tiền là
10
triệu đồng.Hỏi số
tiền
T
gần với số tiền nào nhất trong các số sau?
A.
535000
. B.
635000
. C.
613000
. D.
643000
.
Câu 17. [2D2-1] Nghiệm của phương trình
1 1
2 2 3 3
x x x x
là
A.
3
2
3
log
4
x . B.
1
x
. C.
0
x
. D.
4
3
2
log
3
x .
Câu 18. [2D2-1] Số nghiệm của phương trình
2
2 2
log 3 log 6 10 1 0
x x
là
A. Vô nghiệm. B.
1
. C.
2
. D.
3
.
Câu 19. [2D2-1] Phương trình
9 5.3 6 0
x x
có tổng các nghiệm là
A.
3
log 6
. B.
3
log
. C.
3
log
. D.
3
log 6
.
Câu 20. [2D2-2] Tìm số nghiệm thực của phương trình
3 2
1
log 2 2 3 1
x
x x x
.
A.
0
. B.
1
.
C.
2
.
D.
3
.
Câu 21. [2D2-3] Hỏi phương trình
3.2 4.3 5.4 6.5
x x x x
có tất cả bao nhiêu nghiệm thực?
A.
2
. B.
4
. C.
1
. D.
3
.
O
x
y
x
y c
x
y b
x
y a
1
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 3/10 - Mã đề 011
Câu 22. [2D2-3] Phương trình
3 2
23 3 2
2 .2 1024 23 10
x x x
x x x
có tổng các nghiệm gần nhất với số
nào dưới đây
A.
0,35.
B.
0,40.
C.
0,50.
D.
0,45.
Câu 23. [2D2-3] Tìm
m
để phương trình
2
2 2
log log 0
x x m
có nghiệm
0;1
x ?
A.
1
m
. B.
1
m
. C.
1
m
. D.
1
m
.
Câu 24. [2D2-2] Cho hàm số
2
2 sin
2 .3
x x
f x . Khẳng định nào sau đây là khẳng định đúng?
A.
2
1 ln4 sin x ln3 0
f x x
. B.
2
1 2 2sin log 3 0
f x x x
.
C.
2
3
1 log 2 sin 0
f x x x
. D.
2
2
1 2 log 3 0
f x x
.
Câu 25. [2D2-4] Cho hàm số
3
e 1 e 1
4
2017
x x
m
y
. Tìm
m
để hàm số đồng biến trên khoảng
1;2
.
A.
3 4
3e 1 3e 1
m
. B.
4
3e 1
m
.
C.
2 3
3e 1 3e 1
m
. D.
2
3e 1
m
.
----------HẾT----------
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 4/10 - Mã đề 011
ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
A
D
B C D
A
C B A
A
B A
A
A
C
B A
B A
B C D
C A
B
LỜI GIẢI
Câu 1. [2D2-1] Biểu thức
4
3
1
27
3
a
( với
0
a
) viết dưới dạng lũy thừa với số mũ hữu tỉ là
A.
1 1
4 12
3 .
a
. B.
1 1
4 2
3 .
a
. C.
1
12
9.
a
. D.
1
1
3
4
3 .
a
Lời giải
Chọn A.
1
1 1
1 1 3 1 1 1
4
1
4
4
3
3 3
4 12 4 12 4 12
1 1 1 1
27 27. 27 27 3 3 .
3 3 3 3
a a a a a a
.
Câu 2. [2D2-1] Cho
a
,
là các số thực dương thỏa mãn
4
3
5
4
a a
và
1 2
log log
2 3
b b
. Mệnh đề nào
sau đây đúng?
A.
1, 1
a b
. B. 1,0
a b a
. C.
0 1,0 1
a b
. D.
0 1, 1
a b
.
Lời giải
Chọn D.
Ta có
3
4
4
5
4
3
5
4
a a
nên hàm số
x
y a
giảm. Suy ra
0 1
a
.
Và
1 2 1 2
log log
2 3 2 3
b b
nên hàm số
log
b
y x
tăng. Suy ra
1
b
.
Câu 3. [2D2-1] Tìm
x
để biểu thức
1
2
3
1
x
có nghĩa:
A.
;1 1;x
 
. B.
; 1 1;x

.
C.
1;1
x . D.
\ 1
x
.
Lời giải
Chọn B.
Biểu thức
1
2
3
1
x
có nghĩa
2
1
1 0
1
x
x
x
.
Câu 4. [2D2-2] Đạo hàm của hàm số
1
2
3
5 2
y x x là
A.
3 2
10 1
3 5 2
x
y
x x
. B.
3 2
10 1
5 2
x
y
x x
.
C.
2
2
3
10 1
3 5 2
x
y
x x
. D.
3 2
1
3 5 2
y
x x
.
Lời giải
Chọn C.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 5/10 - Mã đề 011
Ta có:
1 2
2 2
3 3
2
3
1 10 1
5 2 5 2 10 1
3
3 5 2
x
y x x x x x
x x
Câu 5. [2D2-2] Hàm số
2
3 10 2
x
y a a đồng biến trên
;
 
khi:
A.
1
;
3
a

. B.
3;a

. C.
1
;
3
a

. D.
1
;3
3
a
.
Lời giải
Chọn D.
Hàm số
2
3 10 2
x
y a a đồng biến trên
;
 
khi
2
1
3 10 2 1 3
3
a a a
.
Câu 6. [2D2-1] Nếu
1
1
6
2
a a
và
2 3
b b
thì
A.
1;0 1
a b
.
B.
1; 1
a b
.
C.
0 1; 1
a b
.
D.
1;0 1
a b
Lời giải
Chọn A.
Do
1 1
2 6
nên
1
1
62
1
a a a
.
Vì
2 3
nên
2 3
0 1
b b b
.
Câu 7. [2D2-2] Cho
0
a
,
0
b
. Nếu viết
0,2
10
5 5 5
6 5
log log log
a
x a y b
b
thì
xy
bằng bao nhiêu?
A.
3
. B.
1
. C.
3
. D.
3
.
Lời giải
Chọn C.
Ta có:
0,2
1
10
2
6
5 5 5 5
6 5
1 1
log log . 2log log .
6 3
a
a b a b x y
b
.
Câu 8. [2D2-2] Cho
, 0
x y
và
2 2
4 12
x y xy
. Khẳng định nào sau đây là khẳng định đúng?
A.
2 2 2
2
log log log
4
x y
x y
. B.
2 2 2
1
log 2 2 log log
2
x y x y
.
C.
2 2 2
log 2 log log 1
x y x y
. D.
2 2 2
4log 2 log log
x y x y
.
Lời giải
Chọn B.
Ta có:
2 2
2 2
2 2
4 12 2 16 log 2 log 16
x y xy x y xy x y xy
2 2 2 2 2 2
1
2log 2 4 log log log 2 2 log log
2
x y x y x y x y
.
Câu 9. [2D2-2] Cho
2
log 3
a
,
2
log 7
. Tính
2
log 2016
theo
a
và
.
A.
5 2
a b
. B.
5 3 2
a b
. C.
2 2 3
a b
. D.
2 3 2
a b
.
Lời giải
Chọn A.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 6/10 - Mã đề 011
Ta có:
5 2
2 2
log 2016 log 2 3 7
5 2
2 2 2
log 2 log 3 log 7
5 2
a b
.
Câu 10. [2D2-3] Hình bên là đồ thị của ba hàm số
x
y a
,
x
y b
,
x
y c
0 , , 1
a b c
được vẽ trên
cùng một hệ trục tọa độ. Khẳng định nào sau đây là khẳng định đúng?
A.
b a c
. B.
a b c
. C.
a c b
. D.
c b a
.
Lời giải
Chọn A.
Do
x
y a
và
x
y b
là hai hàm đồng biến nên
, 1
a b
.
Do
x
y c
nghịch biến nên
1
c
. Vậy
x
bé nhất.
Mặt khác: Lấy
x m
, khi đó tồn tại
1 2
, y 0
y
để
1
2
m
m
a y
b y
Dễ thấy
1 2
m m
y y a b a b
Vậy
b a c
.
Câu 11. [2D2-2] ] Cho
a
là số thực dương khác
1
. Xét hai số thực
1
x
,
2
x
. Phát biểu nào sau đây là
đúng?
A. Nếu
1 2
x x
a a
thì
1 2
x x
. B. Nếu
1 2
x x
a a
thì
1 2
1 0
a x x
.
C. Nếu
1 2
x x
a a
thì
1 2
1 0
a x x
. D. Nếu
1 2
x x
a a
thì
1 2
x x
.
Lời giải
Chọn B.
Xét 2 trường hợp:
+) TH1:
1.
a
Khi đó,
1 2
1 2 1 2
0.
x x
a a x x x x
Mà
1 2
1 1 0 1 0.
a a a x x
+) TH1:
0 1.
a
Khi đó,
1 2
1 2 1 2
0.
x x
a a x x x x
Mà
1 2
1 1 0 1 0.
a a a x x
.
Câu 12. [2D2-1] Hàm số
1
log
x
y x
xác định khi và chỉ khi:
A.
1
2
x
x
. B.
1
x
. C.
0
x
. D.
2
x
Lời giải
Chọn A.
Hàm số
1
log
x
y x
xác định khi
0 0
1
1 0 1
2
1 1 2
x x
x
x x
x
x x
.
Câu 13. [2D2-1] Cho hàm số
x
f x xe
. Gọi
f x
là đạo hàm cấp hai của
f x
. Ta có
1
f
bằng
O
x
y
x
y c
x
y b
x
y a
1
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 7/10 - Mã đề 011
A.
3
e
. B.
2
3
e
. C.
3
e
. D.
2
5
e
Lời giải
Chọn A.
. . . 1 3e
x x x x x x
f x x e f x e x e f x e e x e f

.
Câu 14. [2D2-1] Cho hàm số
x
y ex e
.
Nghiệm của phương trình
0
y
?
A.
1
x
. B.
1
x
. C.
0
x
. D.
ln 2
x
Lời giải
Chọn A.
x x
y ex e y e e
. Suy ra
0 0 1
x
y e e x
.
Câu 15. [2D2-2] Tính giá trị của biểu thức
ln tan1° ln tan 2 ln tan3 ... ln tan89
P
.
A.
1.
P
B.
1
.
2
P
C.
0.
P
D.
2.
P
Lời giải
Chọn C.
ln tan1° ln tan 2 ln tan3 ... ln tan89
ln tan1 .tan2 .tan3 ...tan89
ln tan1 .tan2 .tan3 ...tan 45 .cot44 .cot 43 ...c
ot1
P
ln tan 45 ln1 0.
(vì
tan .cot 1
).
Câu 16. [2D2-3] Một người mỗi tháng đều đặn gửi vào ngân hàng một khoản tiền
T
theo hình thức lãi
kép với lãi suất
0,6
% mỗi tháng. Biết sau
15
tháng người đó có số tiền là
10
triệu đồng.Hỏi số
tiền
T
gần với số tiền nào nhất trong các số sau?
A.
535000
. B.
635000
. C.
613000
. D.
643000
.
Lời giải
Chọn B.
Đầu mỗi tháng khách hàng gửi vào ngân hàng số tiền A đồng với lãi kép r% một tháng thì số
tiền khách hàng nhận được cả vốn lẫn lãi sau n tháng
*
n
là
1 1 1
n
n
A
S r r
r
Ta có:
15
10.000.000 1 0,6% 1 . 1 0,6% 635.000
0,6%
T
T
.
Câu 17. [2D2-1] Nghiệm của phương trình
1 1
2 2 3 3
x x x x
là
A.
3
2
3
log
4
x . B.
1
x
. C.
0
x
. D.
4
3
2
log
3
x .
Lời giải
Chọn A.
1 1
3
2
3 3 3
2 2 3 3 3.2 4.3 log
2 4 4
x
x x x x x x
x
.
Câu 18. [2D2-1] Số nghiệm của phương trình
2
2 2
log 3 log 6 10 1 0
x x
là
A. Vô nghiệm. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn B.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 8/10 - Mã đề 011
Điều kiện:
3
x .
Phương trình
2 2
2
2
2
3 3 1
log 1 3 2 0
1
6 10 6 10 2
x
x x
x x
x
x x
So điều kiện nhận nghiệm
2
x
nên phương trình có 1 nghiệm.
Câu 19. [2D2-1] Phương trình
9 5.3 6 0
x x
có tổng các nghiệm là
A.
3
log 6
. B.
3
log
. C.
3
log
. D.
3
log 6
.
Lời giải
Chọn A.
9 5.3 6 0
x x
1
2
2
1 3 5.3 6 0 3 5.3 6 0 1'
x
x x x
Đặt
3 0
x
t
. Khi đó:
2
2
1' 5 6 0
3
t N
t t
t N
Với
3
2 3 2 log 2
x
t x .
Với
3
3 3 3 log 3 1
x
t x
.
Suy ra
3 3 3 3
1 log 2 log 3 log 2 log 6
.
Câu 20. [2D2-2] Tìm số nghiệm thực của phương trình
3 2
1
log 2 2 3 1
x
x x x
.
A.
0
. B.
1
.
C.
2
.
D.
3
.
Lời giải
Chọn B.
Điều kiện:
1
0
x
x
. Ta có phương trình tương đương
3 2 3 2 3 2
2 2 3 1 3 3 1 6 0 0 3 2.
x x x x x x x x x x x x
Kết hợp với điều kiện ta có nghiệm
3
x
.
Câu 21. [2D2-3] Hỏi phương trình
3.2 4.3 5.4 6.5
x x x x
có tất cả bao nhiêu nghiệm thực?
A.
2
. B.
4
. C.
1
. D.
3
.
Lời giải
Chọn C.
2 3 4
3. 4. 5. 6 0
5 5 5
x x x
pt
Xét hàm số
2 3 4
3. 4. 5. 6
5 5 5
x x x
f x
liên tục trên
.
Ta có:
2 2 3 3 4 4
3 ln 4 ln 5 ln 0,
5 5 5 5 5 5
x x x
f x x
Do đó hàm số luôn nghịch biến trên
mà
0 6 0
f
,
2 22 0
f
nên phương trình
0
f x
có nghiệm duy nhất.
Câu 22. [2D2-3] Phương trình
3 2
23 3 2
2 .2 1024 23 10
x x x
x x x
có tổng các nghiệm gần nhất với số
nào dưới đây
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 9/10 - Mã đề 011
A.
0,35.
B.
0,40.
C.
0,50.
D.
0,45.
Lời giải
Chọn D.
Ta có
3 2 3 2
23 3 2 23 3 10 2
2 .2 1024 23 10 2 23 2 10
x x x x x x
x x x x x x
Hàm số
2
t
f t t
đồng biến trên
nên
3 2
23 3 10 2 3 2
2 23 2 10 23 10 0
x x x
x x x x x x x
hoặc
5 2
23
x
Tổng các nghiệm bằng
10
0,4347
23
.
Câu 23. [2D2-3] Tìm
m
để phương trình
2
2 2
log log 0
x x m
có nghiệm
0;1
x ?
A.
1
m
. B.
1
m
. C.
1
m
. D.
1
m
.
Lời giải
Chọn C.
Đặt
2
2
log : 0,
t x PT t t m
do
2
0 1 log 0 0
x x t
Để phương trình đã cho có nghiệm
0;1
x thì phương trình
2
0
t t m
có nghiệm âm
0 1 4 0
0 1 0
m
m
S
Câu 24. [2D2-2] Cho hàm số
2
2 sin
2 .3
x x
f x . Khẳng định nào sau đây là khẳng định đúng?
A.
2
1 ln4 sin x ln3 0
f x x
. B.
2
1 2 2sin log 3 0
f x x x
.
C.
2
3
1 log 2 sin 0
f x x x
. D.
2
2
1 2 log 3 0
f x x
.
Lời giải
Chọn A.
2
2 sin 2
1 ln 2 .3 ln1 ln4 sin ln3 0
x x
f x x x
Câu 25. [2D2-4] Cho hàm số
3
1 1
4
2017
x x
e m e
y
. Tìm
m
để hàm số đồng biến trên khoảng
1;2
.
A.
3 4
3 1 3 1
e m e
. B.
4
3 1
m e
.
C.
2 3
3 1 3 1
e m e
. D.
2
3 1
m e
.
Hướng dẫn giải
Chọn B.
3
1 1
3
4 4
.ln . 1 1
2017 2017
x x
e m e
x x
y e m e
=
3
1 1
3
4 4
.ln . 3 1
2017 2017
x x
e m e
x x
y e m e
Hàm số đồng biến trên khoảng
1;2
3
1 1
3
4 4
.ln . 3 1 0, 1;2
2017 2017
x x
e m e
x x
y e m e x
(*),
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 10/10 - Mã đề 011
mà
3
1 1
4
0,
2017
4
ln 0
2017
x x
e m e
x
.
Nên (*)
3
3 1 0, 1;2
x x
e m e x
2
3 1 , 1;2
x
e m x
Đặt
2
3 1, 1;2
x
g x e x ,
2
3 .2 0, 1;2
x
g x e x
1 2x
g x
g x
| |
| |
. Vậy (*) xảy ra khi
2
m g
4
3 1
m e
.
| 1/106
| | Tải xuống

Có thể bạn quan tâm:

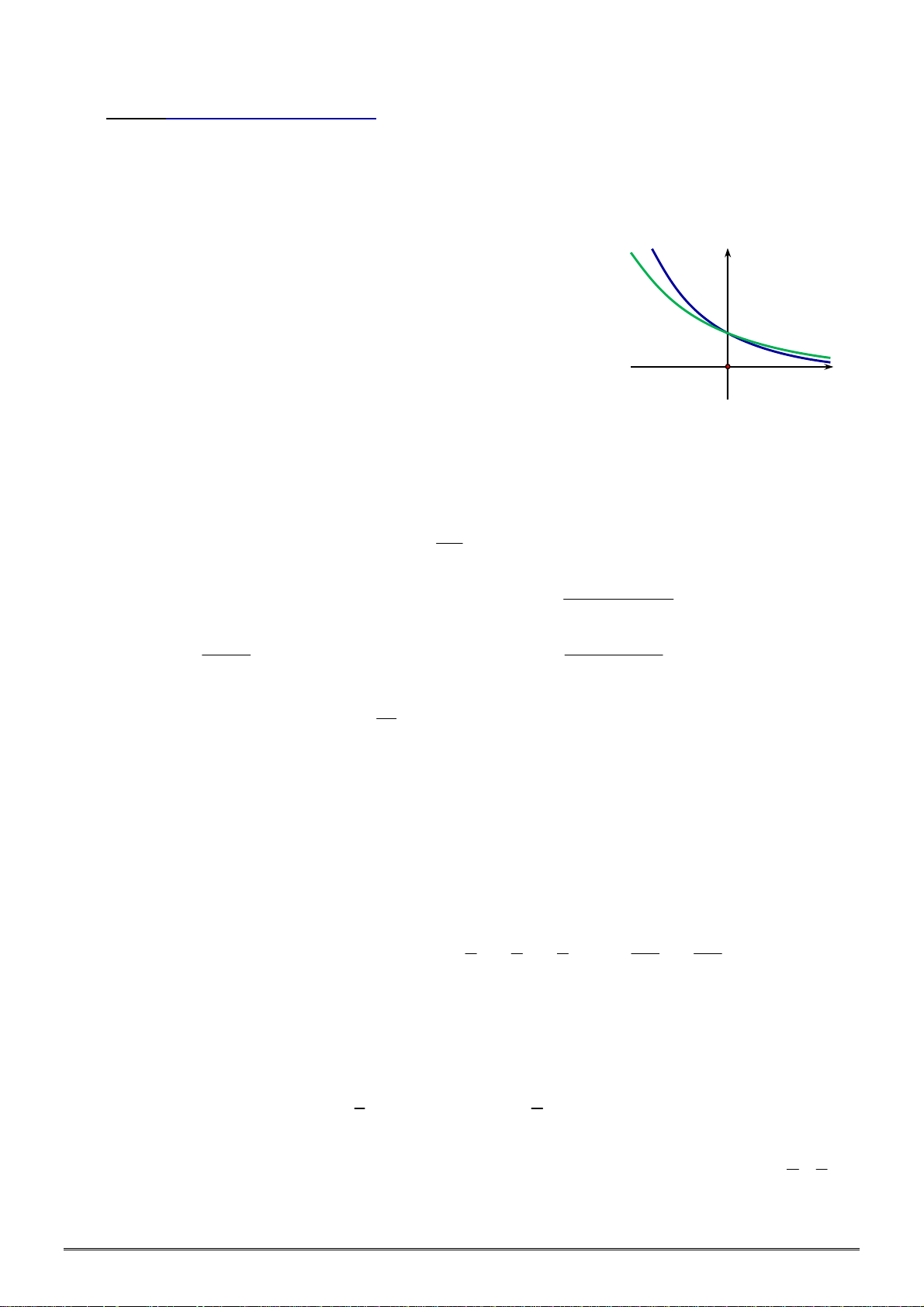
Preview text:

TOÁN HỌC BẮC–TRUNG–NAM
KIỂM TRA CHƯƠNG 2 GIẢI TÍCH 12
Nhóm: THBTN – ĐỀ KIỂM TRA MÃ ĐỀ 001
(25 câu trắc nghiệm)
Thời gian làm bài: 45 phút, không kể thời gian phát đề. b aa Câu 1.
[2D2-1] Giả sử a , b là các số thực dương. Biểu thức 5 3
được viết dưới dạng   . Tìm a bb  giá trị . 4 2 2 2 A. . B. . C.  . D. . 15 5 15 15 Câu 2.
[2D2-1] Cho a , b là các số thực dương khác 1. Trong các khẳng định sau, chọn khẳng định đúng. m m  1   1  A. m m
a b a b , . m
B. a b   , m   0     .  a   b m m m m  1   1   1   1 
C. a b   ,m  0     .
D. a b   , m   0     .  a   b   a   b  2 Câu 3.
[2D2-1] Tìm tập xác định của hàm số y   x   3 2 . A.  \   2 . B.  2  ;  . C. 0;  . D.  . Câu 4.
[2D2-2] Cho f x 2 3 2
x . x . Tính giá trị của f   1 . 8 3 A. 2 . B. . C. 4 . D. . 3 8 Câu 5.
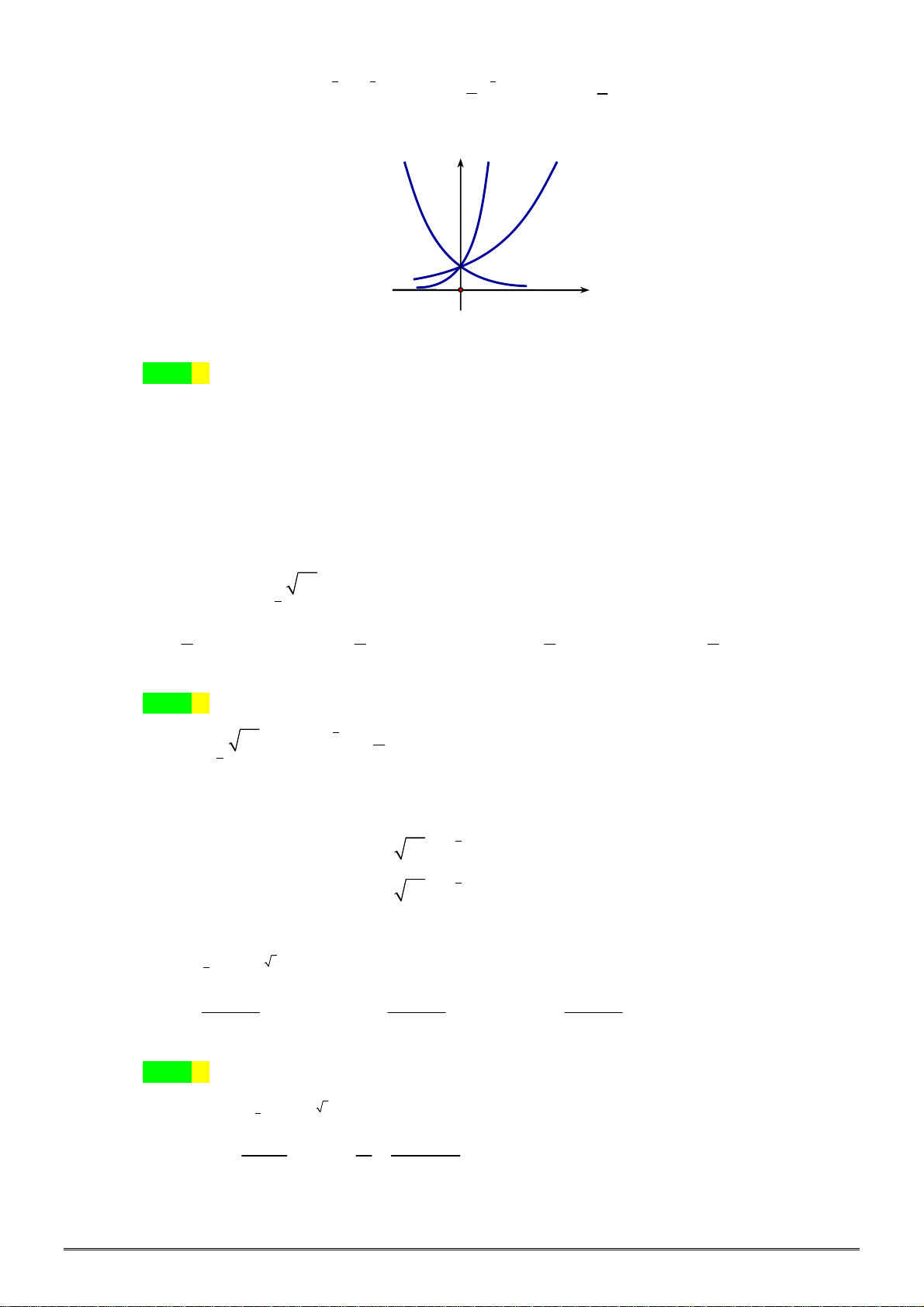
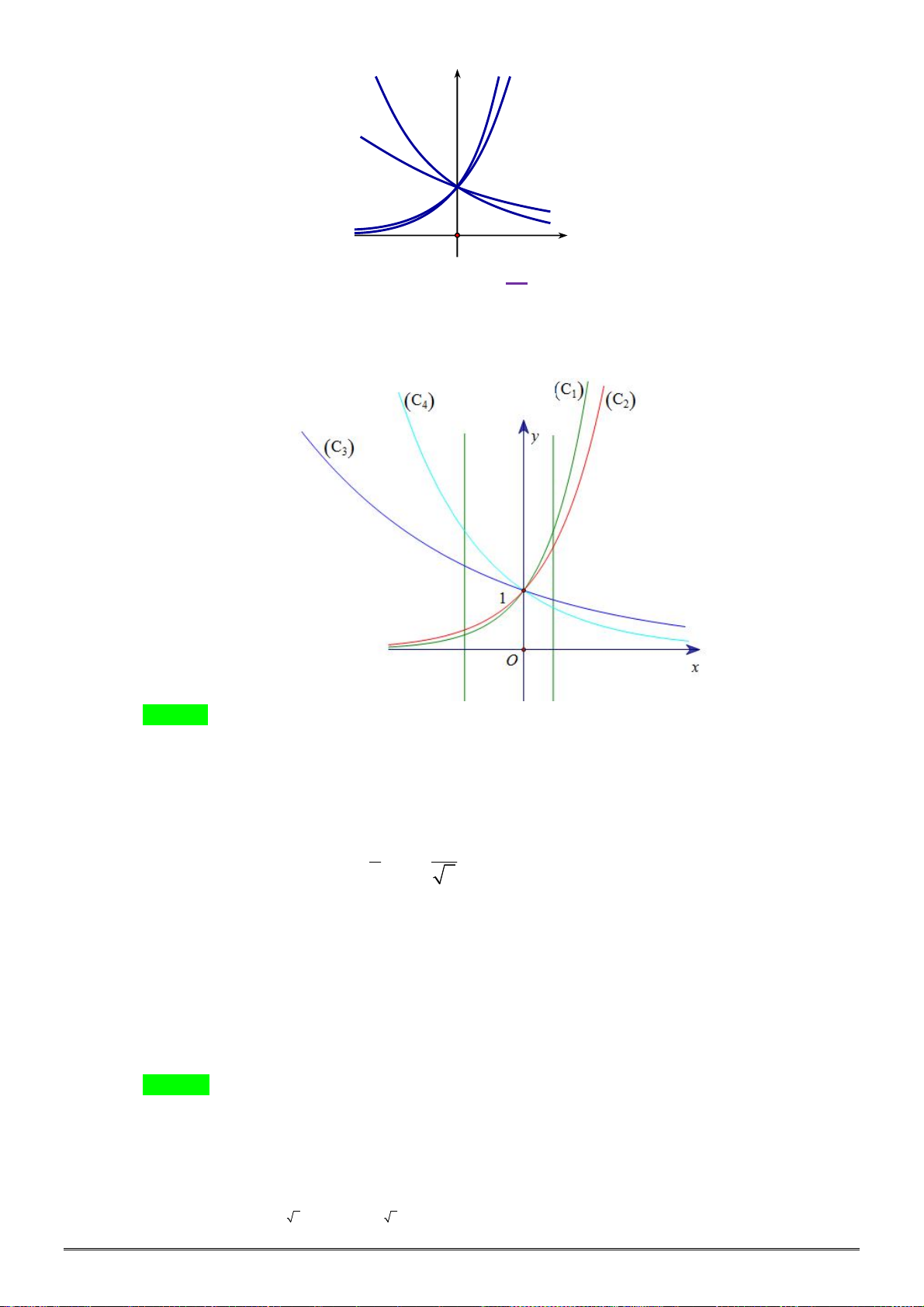
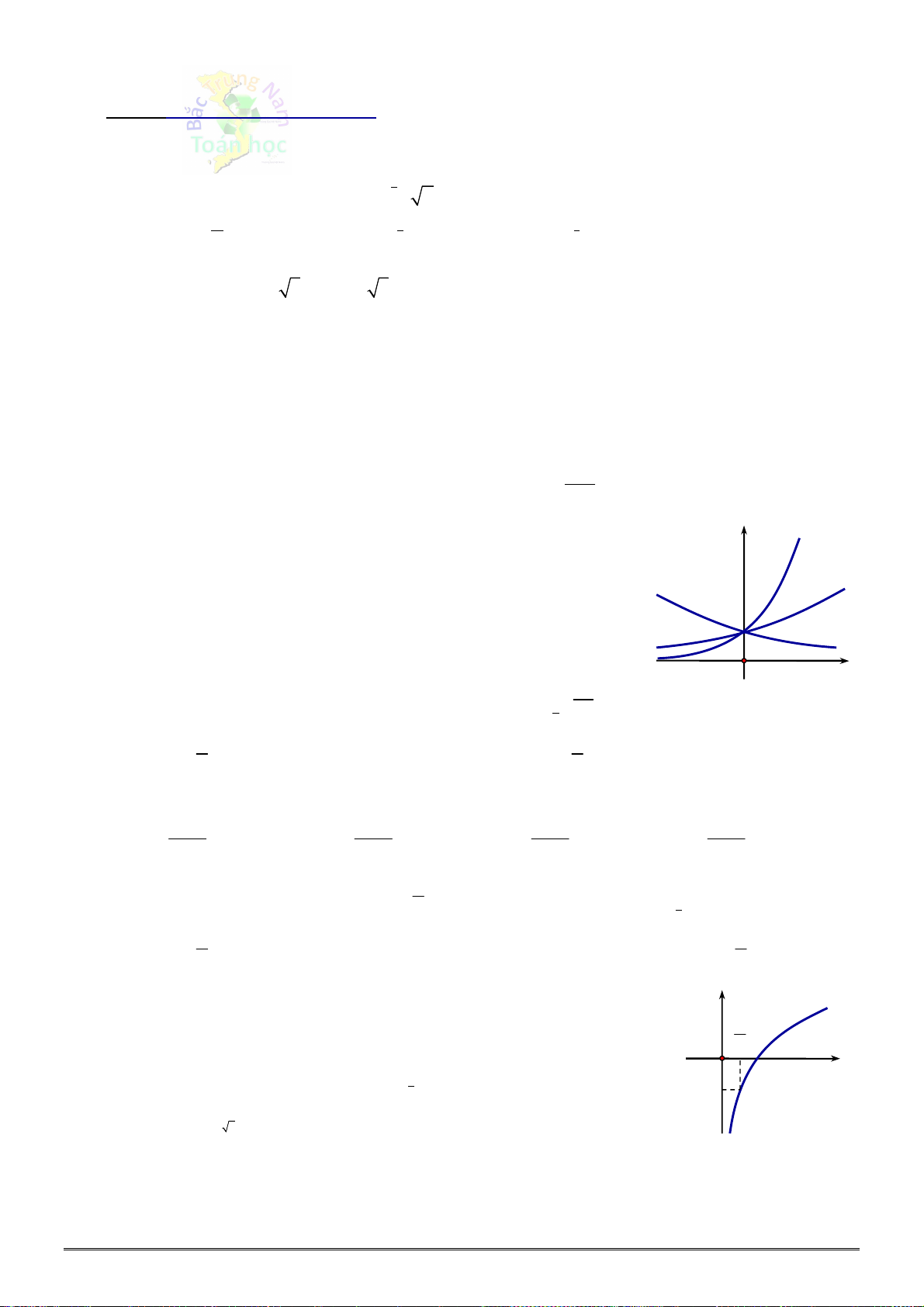
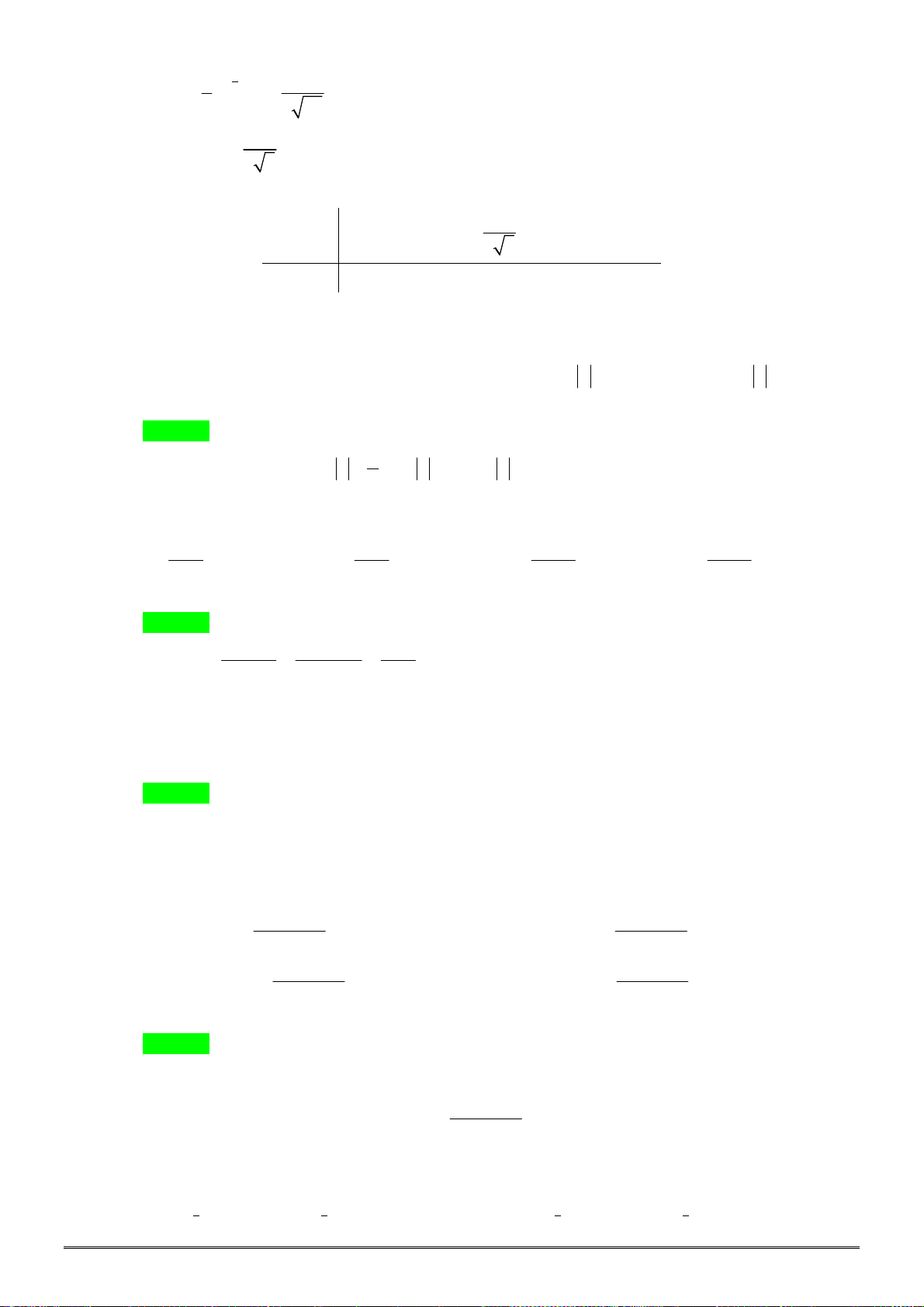
[2D2-2]Cho đồ thị ba hàm số x y a , x y b , x y c x x x
như hình vẽ. Kết luận nào sau đây đúng. y c y y a y b
A. 0  a  1  b c .
B. 0  c  1  a b .
C. 0  c  1  b a .
D. 0  a  1  c b 1 O x Câu 6. [2D2-1] Tính 3 7 log a
a  0, a  1 . 1   a 7 7 3 3 A.  . B. . C.  . D. . 3 3 7 7 Câu 7.
[2D2-2] Cho a là hai số thực dương khác. Đặt log a m . Tính theo m giá trị của biểu thức 3
D  log a  log a  log 9 . 1 3 a 3 2 2  3m 2 3m  2 2 4  3m A. D  . B. D  . C. D  . D. D  3  m . m m 2m Câu 8.
[2D2-2]Cho log 5  a , log 5  b . Hãy biểu diễn log 5 theo a và b . 2 3 6 1 ab A. log 5  . B. log 5  . 6 a b 6 a b
C. log 5  a b . D. 2 2
log 5  a b . 6 6
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 1/11 - Mã đề LD-001 Câu 9. [2D2-3] Biết 2 2
a b ab , a  0 , b  0 . Chọn đẳng thức đúng.
A. 2 ln a b  ln 2  ln a  ln b . B.  2 2
ln a b   ln a  ln b . C.  2 2
lg a b   lg a  lg b .
D. 2 lg a b  lg 3  lg a  lg b . 2 5x
Câu 10. [2D2-3] Cho hàm số f x 
. Khẳng định nào sau đây là khẳng định sai? 2x 2 x
A. f x  1   0 .
B. f x 2
 1  x log 5  x  0 . x log 2 2 5 2  5x
C. f x  1  log    0 .
D. f x 2
 1  x x log 2  0 . 5  2x  5   2x 1
Câu 11. [2D2-1] Tìm tập xác định D của hàm số f x  . log  2  x  3x 2    3   5  
A. D  0;3 .
B. D  0;3 \    2   
C. D   \ 0;  3 .
D. D   .
Câu 12. [2D2-2] Tìm đạo hàm của hàm số     2 2 3 e x y x
 3x trong điều kiện xác định. A.      2 4 4 e x y x  3 . B.      2 4 4 e x y x  3x . C. 2 4.e x y   3 . D.      2 2 1 e x y x  3 .
Câu 13. [2D2-2] Mệnh đề nào sau đây là sai? A. Cho hàm số 2x y  thì y  1  ln 4 . 2
B. Cho hàm số y  log 2x   1 thì y  1  . 3ln10 C. Cho hàm số ex y  thì   1 ex y  .
D. Cho hàm số y  ln x thì y  1  1.
Câu 14. [2D2-3] Gọi M và m là giá trị lớn nhất và giá trị nhỏ nhất của hàm số x
y xe trên 1;2. Tính M .n . A. 3 2e . B. 2 2e . C. e . D. 0 .
Câu 15. [2D2-4] Ông A vay ngân hàng T (triệu đồng) với lãi suất 12 % năm. Ông A thỏa thuận với ngân
hàng cách thức trả nợ như sau: sau đúng một tháng kể từ ngày vay, ông bắt đầu hoàn nợ; hai
lần hoàn nợ liên tiếp cách nhau đúng một tháng. Nhưng cuối tháng thứ ba kể từ lúc vay ông A
mới hoàn nợ lần thứ nhất, cuối tháng thứ tư ông A hoàn nợ lần thứ hai, cuối tháng thứ năm ông
A hoàn nợ lần thứ ba (hoàn hết nợ). Biết rằng số tiền hoàn nợ lần thứ hai gấp đôi số tiền hoàn
nợ lần thứ nhất và số tiền hoàn nợ lần thứ ba bằng tổng số tiền hoàn nợ của hai lần trước. Tính
số tiền ông A đã hoàn nợ ngân hàng lần thứ nhất.  5  5 T 1 T 1 0, 5 01 T 1 0,  01 T   5 1 0, 01    100  A. . B. . C. . D. .  2 2, 2 01  2 1,  01  5 6 6
Câu 16. [2D2-1] Tìm nghiệm của phương trình x 1 3   27 . A. x  9 .
B. x  3 .C. x  4 . D. x  10 .
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 2/11 - Mã đề LD-001 2 x 2x3  1 
Câu 17. [2D2-2] Gọi S là tập nghiệm của phương trình x 1  7  .  
Tính tổng tất cả các phần tử  7  của S . A. 5. B. 0. C. 1. D. 2.
Câu 18. [2D2-2] Gọi S là tập nghiệm của phương trình 4x8 2 x5 3  4.3  28  2 log 2 . Tính tích tất cả 2
các phần tử của S . 3 3 A. 4. B.  . C. . D. 1  . 2 2
Câu 19. [2D2-1] Cho phương trình log  2 x  1 .log  2 x 2x 4 2 2 6 log x 1 1        4 log
x  2x  4  0 1 2 2 2 2    
Gọi x , x là hai nghiệm thực dương của phương trình đã cho  x x . Tính 2
T x  2x . 1 2  1 2 1 2
A. T  3  2 5 . B. T  1   3 5 . C. T  7 .
D. T  6 . log  2 xx x 1 0,5 sin 5sin .cos 2
Câu 20. [2D2-4] Tìm nghiệm của phương trình 4  . 9  x   kx   k 2  2 A.
k  . B.  k  1  1 x  arctan  k
x  arctan  k  5  3  x kx k C.   1
k  . D. 1
k  .
x  arctan  k
x  arctan  k  3  5 2x4 2 x x  1 
Câu 21. [2D2-1] Tìm tập nghiệm của bất phương trình 2 3 1 4    .  2   5  A. 0;  . B.   1 . 4     5  C.  ;
 0 1;  . D.  ;   1  ;    .  4 
Câu 22. [2D2-1] Tìm tập nghiệm của bất phương trình log x 1  2 . 1   2  3   3   3 
A. S  1;  . B. S  0;    .
C. S  1;    .
D. S   ;    .  4   4   4  2 x x
Câu 23. [2D2-3] Tìm tập nghiệm của bất phương trình  x 1 5 2     5  2 . A.  ;    1  0;  1 . B.  1  ; 0 . C.  ;   
1  0;  . D.  1
 ; 0  1;  .
Câu 24. [2D2-2] Phương trình log x 1  2 log
3x  2  2  0 có mấy nghiệm? 2   4   A. 1. B. 2 . C. 3 . D. 4 .
Câu 25. [2D2-4] Có bao nhiêu giá trị nguyên bé hơn 10 của tham số m sao cho bất phương trình 2 2
log x 1 2 log x 1  m  0 thỏa mãn với mọi 3 1  ;2  ? 2 2   A. 3 . B. 4 . C. 5 . D. 6 .
----------HẾT----------
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 3/11 - Mã đề LD-001 ĐÁP ÁN 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
C C B B C A A B D A B A C A A C C C D A A C D A B BÀI GIẢI b aa Câu 1:
[2D2-1] Giả sử a , b là các số thực dương. Biểu thức 5 3
được viết dưới dạng   . Tìm a bb  giá trị . 4 2 2 2 A. . B. . C.  . D. . 15 5 15 15 Lời giải Chọn C. 1 1 1 1 1 1 2     5 15 5 15 5 15 15 b a
b   a   a   a   a   a  Ta có 5 3  .  .               . a b
a   b   b   b   b   b
Phân tích phương án nhiễu.
A – sai do biến đổi.
B – sai do tính toán.
D – sai do biến đổi. Câu 2:
[2D2-1] Cho a , b là các số thực dương khác 1. Trong các khẳng định sau, chọn khẳng định đúng. m m  1   1  A. m m
a b a b , . m
B. a b   , m   0     .  a   b m m m m  1   1   1   1 
C. a b   ,m  0     .
D. a b   , m   0     .  a   b   a   b Lời giải Chọn C.
Phân tích phương án nhiễu  1  1
A – sai vì Ta có: 2  3 mà 2 2 2   3  . 4 9 2 2  1  1  1  1
B – sai vì Ta Ta có: 2  3 mà        .  2  4  3  9 2  2  1   1 
C – sai vì Ta Ta có: 2  3 mà  4   9     .  2   3  2 Câu 3:
[2D2-1] Tìm tập xác định của hàm số y   x   3 2 . A.  \   2 . B.  2  ;  . C. 0;  . D.  . Lời giải Chọn B.
Ta có: x  2  0  x  2
 . Vậy TXĐ của hàm số là: D   2  ;   . Câu 4:
[2D2-2] Cho f x 2 3 2
x . x . Tính giá trị của f   1 . 8 3 A. 2 . B. . C. 4 . D. . 3 8 Lời giải Chọn B.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 4/11 - Mã đề LD-001 2 8 5 2 8 8
Với x  0 thì f x 3 3  x
x f  x 3 
x nên f   1  . 3 3 Câu 5:
[2D2-2]Cho đồ thị ba hàm số x y a , x y b , x
y c như hình vẽ. Kết luận nào sau đây đúng. x y c y x y a x y b 1 O x
A. 0  a  1  b c .
B. 0  c  1  a b .
C. 0  c  1  b a .
D. 0  a  1  c b Lời giải Chọn C. Do đồ thị của hàm x y a , x
y b là đường đi lên, đồ thị hàm x
y c là đường đi xuống, suy ra hàm x y a , x
y b là các hàm đồng biến suy ra a  1 , b  1, c  1
Xét tại điểm x m  0 ta có m m
a b mà a  1 , b  1 suy ra a b .
Vậy mệnh đề đúng là: 0  c  1  b a .
Phân tích phương án nhiễu.
A, D – sai do học sinh ko nắm được dáng điệu đồ thị hàm số mũ.
B – sai do xác định nhầm cơ số. Câu 6: [2D2-1] Tính 3 7 log a
a  0, a  1 . 1   a 7 7 3 3 A.  . B. . C.  . D. . 3 3 7 7 Lời giải Chọn A. 7 7 Ta có 3 7 3 log a  log   . a 1 1 a 3 a
Phân tích phương án nhiễu.
B – sai do học sinh nhầm dấu. 3
C – sai do áp dụng sai công thức 3 7 7 a a . 3
D – sai do áp dụng sai công thức 3 7 7
a a và nhầm dấu khi làm. Câu 7:
[2D2-2] Cho a là hai số thực dương khác. Đặt log a m . Tính theo m giá trị của biểu thức 3
D  log a  log a  log 9 . 1 3 a 3 2 2  3m 2 3m  2 2 4  3m A. D . B. D . C. D . D. D  3  m . m m 2m Lời giải Chọn A.
Ta có: D  log a  log
a  log 9   log a  2 log a  2 log 3 1 a 3 3 3 a 3 2 2 2 3m  2  3  log a   3  m   3 log a m m 3
Phân tích phương án nhiễu.
B – sai do quên đổi dấu biểu thức.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 5/11 - Mã đề LD-001
B – sai do tính toán. 1
D – sai do khai triển sai log a  log a . 3 3 2 Câu 8:
[2D2-2]Cho log 5  a , log 5  b . Hãy biểu diễn log 5 theo a và b . 2 3 6 1 ab A. log 5  . B. log 5  .
C. log 5  a b . D. 2 2
log 5  a b . 6 a b 6 a b 6 6 Lời giải Chọn B. 1 1 1 1 ab Ta có: log 5      . 6 log 6 log 2.3 log 2  log 3 1 1 a b 5 5 5 5  a b
Phân tích phương án nhiễu.
A – sai do quên nghịch đảo hạng tử.
B – sai do nhầm công thức log 6  log 2  log 3 . 5 5 5
D – sai do tính toán. Câu 9: [2D2-3] Biết 2 2
a b ab , a  0 , b  0 . Chọn đẳng thức đúng.
A. 2 ln a b  ln 2  ln a  ln b . B.  2 2
ln a b   ln a  ln b . C.  2 2
lg a b   lg a  lg b .
D. 2 lg a b  lg 3  lg a  lg b . Lời giải Chọn D. Ta biến đổi:
a b ab  a b2  ab  a b2 2 2 3 log
 log 3ab  2log a b  log 3  log a  log b
Phân tích phương án nhiễu. A – sai do tính toán.
B – sai do công thức hàm số logarit.
C – sai do công thức hàm số logarit. 2 5x
Câu 10: [2D2-3] Cho hàm số f x 
. Khẳng định nào sau đây là khẳng định sai? 2x 2 x
A. f x  1   0 .
B. f x 2
 1  x log 5  x  0 . x log 2 2 5 2  5x
C. f x  1  log    0 .
D. f x 2
 1  x x log 2  0 . 5  2x  5   Lời giải Chọn A. 2 5x f x 2 2 x x x x 2 2  1   1  5  2  log 5
 log 2  x x log 2  0  x log 5  x  0 . x 5 5 5 2 2 Đáp án C đúng. Đáp án D đúng.
Đáp án B đúng và đáp án A sai. 2x 1
Câu 11: [2D2-1] Tìm tập xác định D của hàm số f x  . log  2  x  3x 2    3   5  
A. D  0;3 .
B. D  0;3 \    2   
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 6/11 - Mã đề LD-001
C. D   \ 0;  3 .
D. D   . Lời giải Chọn B. 2 0  x  3
x  3x  0  0  x  3  Điều kiện     .    2   x x 2 3 5 log 3  0
x  3x  1   2 x    2
Câu 12: [2D2-2] Tìm đạo hàm của hàm số     2 2 3 x y x e
 3x trong điều kiện xác định. A.      2 4 4 x y x e  3 . B.      2 4 4 x y x e  3x . C. 2   4. x y e  3 . D.      2 2 1 x y x e  3 . Lời giải Chọn A. 2 x 2 x       2 2. 2 2 3  3 x y e e x
e 4x  4  3 .
Câu 13: [2D2-2] Mệnh đề nào sau đây là sai? 2 A. Cho hàm số 2x y  thì y  1  ln 4 .
B. Cho hàm số y  log 2x   1 thì y  1  . 3ln10 C. Cho hàm số x
y e thì   1 x ye .
D. Cho hàm số y  ln x thì y  1  1. Lời giải Chọn C. Cho hàm số x y e , vậy x
y  e y   1  e .
Câu 14: [2D2-3] Gọi M và m là giá trị lớn nhất và giá trị nhỏ nhất của hàm số x
y xe trên 1;2. Tính M .n . A. 3 2e . B. 2 2e . C. e . D. 0 . Lời giải Chọn A. x x x          1 x y xe y e xe x e .
y 0  x  1  l  . Vậy y  
1  e m và y   2
2  2e M . Khi đó 3
M .n  2e .
Câu 15: [2D2-4] Ông A vay ngân hàng T (triệu đồng) với lãi suất 12 % năm. Ông A thỏa thuận với ngân
hàng cách thức trả nợ như sau: sau đúng một tháng kể từ ngày vay, ông bắt đầu hoàn nợ; hai
lần hoàn nợ liên tiếp cách nhau đúng một tháng. Nhưng cuối tháng thứ ba kể từ lúc vay ông A
mới hoàn nợ lần thứ nhất, cuối tháng thứ tư ông A hoàn nợ lần thứ hai, cuối tháng thứ năm ông
A hoàn nợ lần thứ ba (hoàn hết nợ). Biết rằng số tiền hoàn nợ lần thứ hai gấp đôi số tiền hoàn
nợ lần thứ nhất và số tiền hoàn nợ lần thứ ba bằng tổng số tiền hoàn nợ của hai lần trước. Tính
số tiền ông A đã hoàn nợ ngân hàng lần thứ nhất.  5  5 T 1 T 1 0, 5 01 T 1 0,  01 T   5 1 0, 01    100  A. . B. . C. . D. .  2 2, 2 01  2 1,  01  5 6 6 Lời giải Chọn A. 2 2
Số tiền nợ của ông A sau hai tháng vay là: A T 11%  T 1, 01 . 2    
Số tiền nợ của ông A sau 3 tháng vay là: A A 1, 01  m . 3 2  
Số tiền nợ của ông A sau 4 tháng vay là: A A 1, 01  2m . 4 3  
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 7/11 - Mã đề LD-001
Số tiền nợ của ông A sau 5 tháng vay là: A A 1, 01  3m . 5 5  
Theo giả thiết bài toán ta có: A  0   A .1, 01 m .1, 01 2m .1, 01 3m  0 5   2   . 3 5 A .1, 01 T.1, 01 3
A .1, 01  m  2 1.01  2.1, 01 3 2  0  m   m  . 2  2 1, 01  2.1, 01  1  2 2,0 2 1  2
Câu 16: [2D2-1] Tìm nghiệm của phương trình x 1 3   27 . A. x  9 . B. x  3 . C. x  4 . D. x  10 . Lời giải Chọn C. Ta có x 1  x 1  3 3  27  3
 3  x 1  3  x  4 . 2 x 2x3  1 
Câu 17: [2D2-2] Gọi S là tập nghiệm của phương trình x 1  7  .  
Tính tổng tất cả các phần tử  7  của S . A. 5. B. 0. C. 1. D. 2. Lời giải Chọn C. 2 x 2x3 2  1   x  1  x 1   x 2x3 x 1  2 2  7  7  7
 x  2x  3  x 1   x x  2  0      7  x  2.  Vậy S  1.
Câu 18: [2D2-2] Gọi S là tập nghiệm của phương trình 4x8 2 x5 3  4.3  28  2 log 2 . Tính tích tất cả 2
các phần tử của S . 3 3 A. 4. B.  . C. . D. 1  . 2 2 Lời giải Chọn C.
3 x  4.3 x  28  2 log 2  3 x 2 4 8 2 5 2 4 2 x4 12.3  27  0 1 . 2   Đặt 2 x4 t  3
,t  0 . Phương trình trở thành: 2
t 12.t  27  0 2. t  9 2  Khi đó: t  3.  x 3 Với 2 4 t  3  3
 3  2x  4  1  x   . 2 Với 2 x4 2 t  9  3
 3  2x  4  2  x  1. 3
Vậy tích các nghiệm là:  . 2
Câu 19: [2D2-1] Cho phương trình log  2 x  1 .log  2 x 2x 4 2 2 6 log x 1 1        4 log
x  2x  4  0 1 2 2 2 2    
Gọi x , x là hai nghiệm thực dương của phương trình đã cho  x x . Tính 2
T x  2x . 1 2  1 2 1 2
A. T  3  2 5 . B. T  1   3 5 . C. T  7 .
D. T  6 . Lời giải Chọn D.
Điều kiện xác định: x  1 hoặc x  1  .   1  log  2 x   1 .log  2
x  2x  4  3lg x   x x    x  2  1 2 log  2 2 4 6 0 2 2 2 
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 8/11 - Mã đề LD-001  log  2 x   1  2 log  2
x  2x  4  3  0 2 2      log  2 x 1  2  0 2 
 log  2x 2x4 3 0 2   log  2 x 1  2 2 
 log  2x 2x4  3 2   2  x  5   2
x  2x  4  0   x  5   x  1   5 
So với điều kiện ta được hai nghiệm x  1 5 và x  5 . 1 2
Khi đó: T x  2x   5  2 2 1  2 5  6 . 1 2
Phân tích phương án nhiễu.
A – Sai do xác định x  5 , x  1   5 . 1 2
B – Sai do yêu cầu tính T (Tính x  2x ). 1 2
C – Sai do tạo phương trình tích sai và không loại nghiệm: x  1 và x  3 . 1 2 log  2 xx x 1 0,5 sin 5sin .cos 2
Câu 20: [2D2-4] Tìm nghiệm của phương trình 4  . 9  x   kx   k 2  2 A.
k  . B.  k  1  1 x  arctan  k
x  arctan  k  5  3  x kx k C.   1
k  . D. 1
k  .
x  arctan  k
x  arctan  k  3  5 Lời giải Chọn A. Điều kiện: 2
sin x  5sin x cos x  2  0
Lấy logarit cơ số 4 hai vế của phương trình ta được: log  2
sin x  5sin x cos x  2 2  log 3 0,5 4   log  2
sin x  5sin x cos x  2   log 3 2  2 2
 sin x  5sin x cos x  2  3 (thỏa mãn điều kiện)
 cos x 5sin x  cos x  0
* cos x  0  x
k k   2 1
* 5sin x  cos x  0  tan x  5  x  arctan
k k   . 5
Phân tích phương án nhiễu. B – sai do tính toán.
C – sai do không đối chiếu điều kiện.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 9/11 - Mã đề LD-001
D – sai do tính toán. 2x4 2 x x  1 
Câu 21: [2D2-1] Tìm tập nghiệm của bất phương trình 2 3 1 4    .  2   5  A. 0;  . B.   1 . 4     5  C.  ;
 0 1;  . D.  ;   1  ;    .  4  Lời giải Chọn A. 2x4      x x  1 2 x x x 2 3 1  1 2 2 2 3 1 2 4 2 4   2  2    2   5 2 2 
 4x  6x  2  x  2  4x  5x  0  x  0;  . 4   
Câu 22: [2D2-1] Tìm tập nghiệm của bất phương trình log x 1  2 . 1   2  3   3   3 
A. S  1;  . B. S  0;    .
C. S  1;    .
D. S   ;    .  4   4   4  Lời giải Chọn C. x  1 x  1     3  log x 1  2   1   3  x  1  ;  . 1     x 1  x    4  2    4  4 2 x x
Câu 23: [2D2-3] Tìm tập nghiệm của bất phương trình  x 1 5 2     5  2 . A.  ;    1  0;  1 . B.  1  ; 0 . C.  ;   
1  0;  . D.  1
 ; 0  1;  . Lời giải Chọn D. 2 x 2 x x x 2x
Ta có  5  2x 1   5  2   5  2 x 1   5  2   x x 1 2 2x x x   x  0   0  1
  x  0 hoặc x  1 . x 1 x 1
Câu 24: [2D2-2] Phương trình log x 1  2 log
3x  2  2  0 có mấy nghiệm? 2   4   A. 1. B. 2 . C. 3 . D. 4 . Lời giải Chọn A. x  1 x 1  0  Điều kiện:    3  x  1 (*) 3x  2  0  x    2 Ta có log x 1  2 log
3x  2  2  0  log 4x  4  log 3x  2 2   4   2   2  
4x  4  3x  2  x  2 (thỏa (*))
Vậy phương trình có 1 nghiệm.
Phân tích phương án nhiễu. B – sai do tính toán.
C – sai do tính toán.
D – sai do tính toán.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 10/11 - Mã đề LD-001
Câu 25: [2D2-4] Có bao nhiêu giá trị nguyên bé hơn 10 của tham số m sao cho bất phương trình 2 2
log x 1 2 log x 1  m  0 thỏa mãn với mọi 3 1  ;2  ? 2 2   A. 3 . B. 4 . C. 5 . D. 6 . Lời giải Chọn B.
Điều kiện: x  0 . 2 2 2 2
log x 1 2 log x 1  m  0  log x 1 2 log x 1  2  0 1 2 2 2 2   Đặt: 2
log x 1  t với 3 x 1
 ;2   t 1;2 2   Khi đó,   2
1  t  2t  2  m .
Xét hàm số: f t 2
t  2t  2 trên 1;2; f t  2t  2  0  t  1 Bảng biến thiên: x 1 2
f t  6
f t 1
Bất phương tình thoả mãn với mọi x thuộc 3 1
 ;2  khi m  6 .  
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 11/11 - Mã đề LD-001
TOÁN HỌC BẮC – TRUNG - NAM
KIỂM TRA CHƯƠNG 2 GIẢI TÍCH 12
Nhóm: THBTN – ĐỀ KIỂM TRA MÃ ĐỀ 002
(25 câu trắc nghiệm)
Thời gian làm bài: 45 phút, không kể thời gian phát đề. 1 Câu 1.
[2D2-1] Rút gọn biểu thức 3 M a
a a  0 . 5 1 6 3 A. 6 M a . B. 6 M a . C. 5 M a . D. 2 M a . 4 1 2   3 3 3 a aa   Câu 2.
[2D2-2] Cho a là số thực dương. Đơn giản biểu thức   P  . 1 3 1    4 4 4 a a a    
A. P a .
B. P a a   1 .
C. P a 1 .
D. P a 1. 2 1 3 3 a b b a Câu 3. [2D2-3] Với ,
a b  0 bất kì. Cho biểu thức P  . Tìm mệnh đề đúng. 6 6 a b A. 3 P ab . B. P ab . C. 6 P ab .
D. P ab . Câu 4.
[2D2-1] Cho a là số thực dương a  1 và 3 P  log
a . Mệnh đề nào dưới đây đúng? 3 a 1 A. P  3 . B. P  1 . C. P  9 . D. P  . 3 Câu 5.
[2D2-1] Giá trị của A  log 3.log 4.log 5...log 64 bằng 2 3 4 63 A. 5 . B. 4 . C. 6 . D. 3 . Câu 6.
[2D2-2] Với các số thực dương a , b bất kì. Khẳng định nào sau đây là khẳng định đúng?  a
A. log ab  log a b . B. log  log a   . b    b   a
C. log ab  log a  log b . D. log  log   a b .  b Câu 7.
[2D2-2] Cho log a x và log c y . Hãy biểu diễn 3 5 4 log b c
theo x và y : 2 a   b b 5  4 y 20 y 4 5  3y 20 y A. . B. . C. . D. 20x  . 6x 3x 2 3x 3 Câu 8.
[2D2-3] Cho log 7  a, log 5  b . Tính log 28 theo , a b 14 14 35 2  a 2 A. log 28  . B. log 28  . 35 a b 35 a b 2  a a C. log 28  . D. log 28  . 35 a b 35 a b Câu 9.
[2D2-1] Tìm tập xác định D của hàm số 1 x y   . A. D   .
B. D  1;  .
C. D  1;  .
D. D  ;  1 .
Câu 10. [2D2-1] Tìm tập xác định D của hàm số y  log 2x  1 . 3    1   1   1 
A. D  ;    . B. D  ;     .
C. D  0;   .
D. D   ;     .  2   2   2 
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 1/10 - Mã đề 002 log 2x
Câu 11. [2D2-2] Tìm đạo hàm của hàm số y  . 2 x 1 4 ln 2x 1 1 2 ln 2x 1 2 log 2x A. y  . B. y  . C. y  . D. y  . 3 2x ln10 2 2x ln10 3 x ln10 3 x
Câu 12. [2D2-1] Đạo hàm của hàm số 3 e x y  là A. 3 e x y  . B. 3 1 3 e x y x    . C. 3   3 e x y x . D. 3 3e x y  .
Câu 13. [2D2-1] Tìm giá trị nhỏ nhất của hàm số y  ln x trên 1;e
A. Không xác định được giá trị nhỏ nhất.
B. min y  1 khi x  1 .
C. min y  e , khi x  e .
D. min y  0 , khi x  1 . x  1 
Câu 14. [2D2-1] Tìm giá trị nhỏ nhất của hàm số y    trên  1  ; 0  2  1
A. min y  1, khi x  0 . B. min y  khi x  1  . 2 1 
C. min y  2 , khi x  1  . D. min y  , khi x  1  . 2
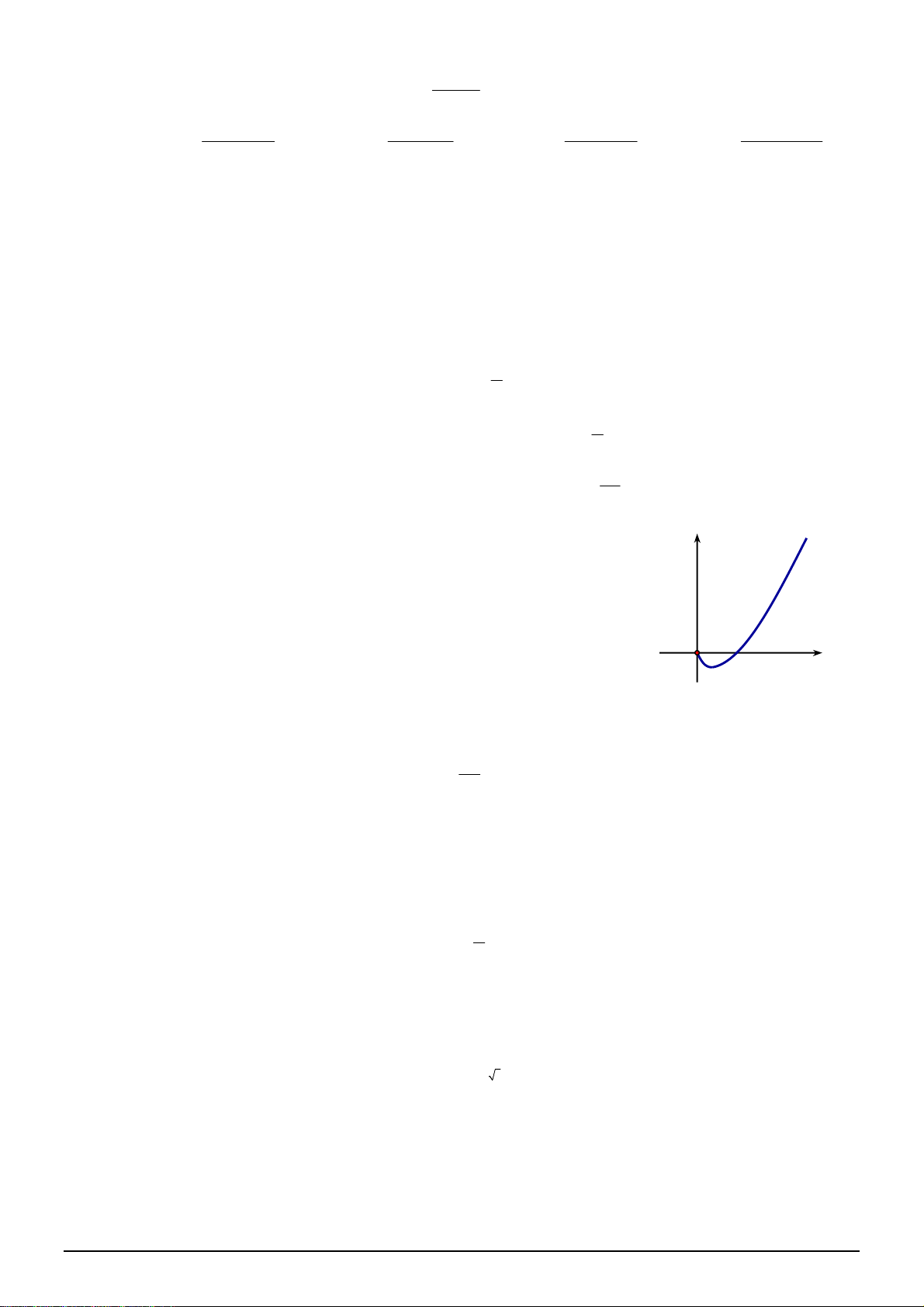
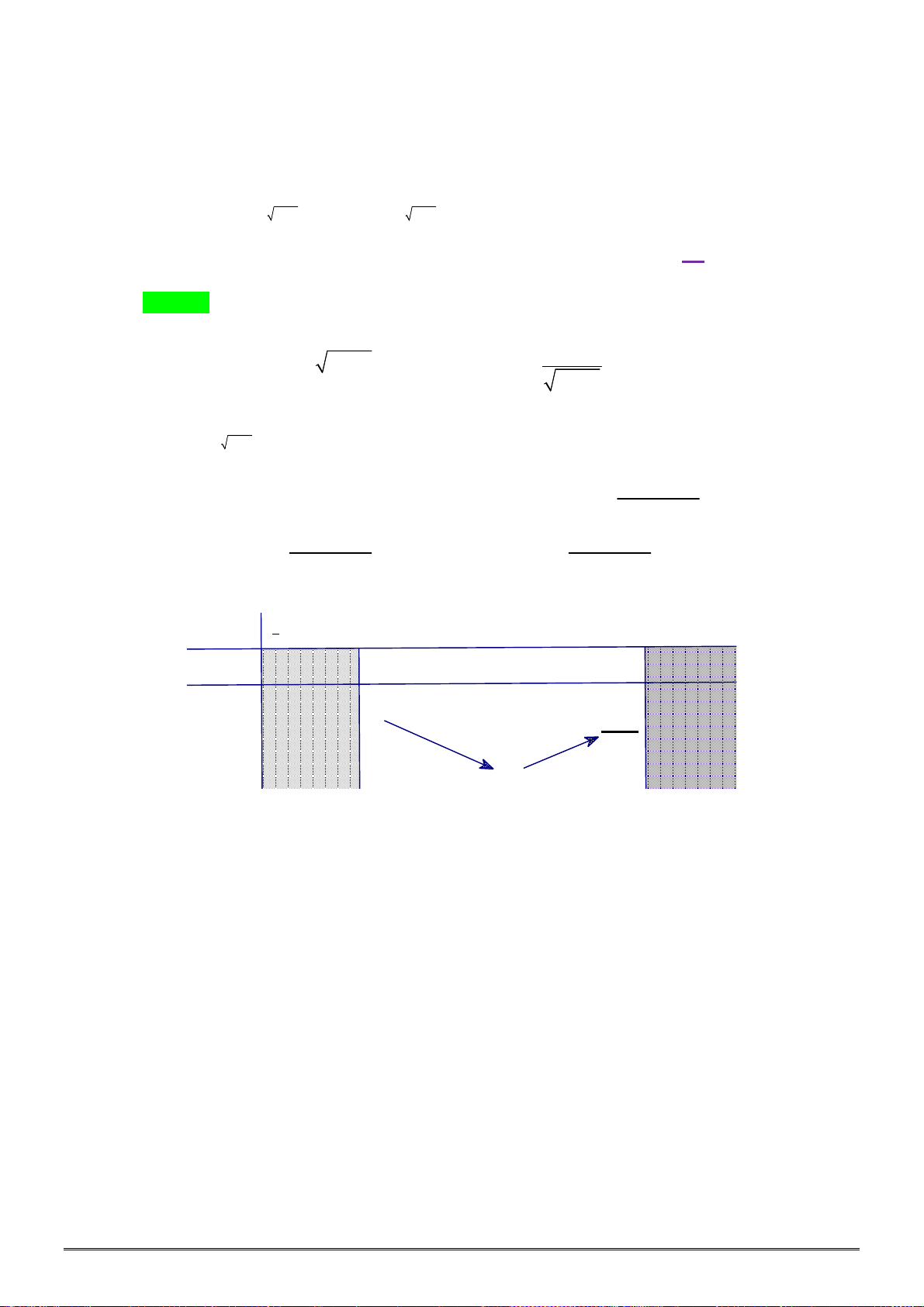
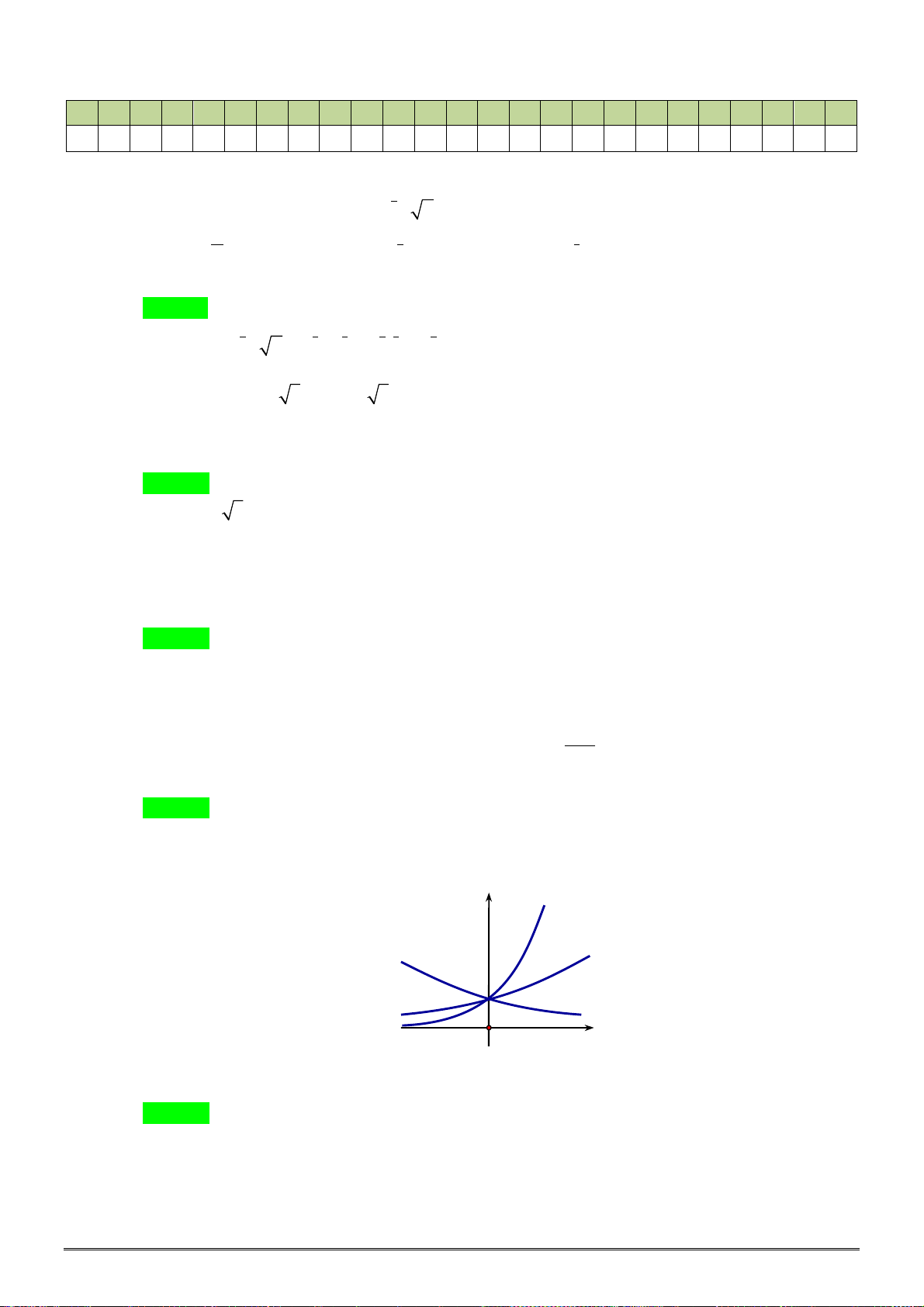
Câu 15. [2D2-1] Hình vẽ sau đây là đồ thị của hàm số nào? y
A. y x ln x .
B. y  ln x . C. ex y  . D.  ex y x . O 1 x
Câu 16. [2D2-2] Cho hàm số 2
y x ln x , khẳng định nào sau đây là đúng
A. y  x 3  y  0 .
B. y  x 2  y  0 . C. y  x 2  y  0 . D. y  x 3  y  0 . x 1
Câu 17. [2D2-2] Nghiệm của phương trình 2 1 3  là 27 A. x  2 . B. x  2  . C. x  1 . D. x  1  .
Câu 18. [2D2-2] Nghiệm của phương trình log  x   1  log  2 x  3x  2 2 2 
A. x  1; x  3 . B. x  3  .
C. x  1; x  3 . D. x  3 . 2 x 3x 1   1 
Câu 19. [2D2-2] Tập nghiệm của bất phương trình  2   .  2 
A. T   ;   1  2;  .
B. T   ;   1  2;  .
C. T  1; 2 .
D. T  1; 2 .
Câu 20. [2D2-2] Tập nghiệm của bất phương trình log  2
2x  4x  5  2 . 3  A. T   .
B. T   \   1 .
C. T   \   1 . D. T   .
Câu 21. [2D2-3] Bác Hiếu đầu tư 99 triệu đồng vào một công ty theo thể thức lãi kép với lãi suất
8, 25% một năm. Hỏi sau 5 năm mới rút tiền lãi thì bác Hiếu thu được bao nhiêu tiền lãi? (Giả
sử rằng lãi suất hàng năm không đổi). A. 48,155 triệu. B. 147,155 triệu. C. 58, 004 triệu. D. 8, 7 triệu.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 2/10 - Mã đề 002 x2
Câu 22. [2D2-3] Giá trị m để phương trình x 2 5  . m 5
 3  m  0 có 2 nghiệm phân biệt sao cho
x x  2 là 1 2 A. 2  . B. 2 . C. 3 . D. 4 . 1 x
Câu 23. [2D2-3] Có bao nhiêu số nguyên thỏa mãnbất phương trình xx 2 2.3  9  9x ? A. 3. B. 4. C. 5. D. 6. 3 x x 1 
Câu 24. [2D2-2] Số nghiệm nguyên của bất phương trình    x 1    x3 10 3 10 3 trong khoảng  2  018; 2018 là A. 4033 . B. 4032 . C. 4031 . D. 4030 . 15 Câu 25. [2D2-4] Biết x  là một nghiệm của bất phương trình 2  x    x x
. Tập nghiệm T của bất phương trình * là a  2 2 log 23 23 log 2 15 * a   19   17  A. T   ;    . B. T  1;   .
C. T  2;8 .
D. T  2;9 .  2   2 
-----------HẾT---------
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 3/10 - Mã đề 002 ĐÁP ÁN 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
A A B C C C A A D D C D D A A C B D D D A B A D D ĐÁP ÁN CHI TIẾT 1 Câu 1:
[2D2-1] Rút gọn biểu thức 3 M a
a a  0 . 5 1 6 3 A. 6 M a . B. 6 M a . C. 5 M a . D. 2 M a . Lời giải Chọn A. 1 1 1 5 Ta có 3 3 2 6 M a
a a .a a 4 1 2   3 3 3 a aa   Câu 2:
[2D2-2] Cho a là số thực dương. Đơn giản biểu thức   P  . 1 3 1    4 4 4 a a a    
A. P a .
B. P a a   1 .
C. P a 1 .
D. P a 1. Lời giải Chọn A. 4 1 2    3 3 3 4 1 4 2 a aa    2 3 3 3 3   a .aa .a a a a a   1 Ta có P      . a 1 3 1 1 3 1 1     a 1 a  1 4 4 4 4 4 4 4 a a a
a .a a .a     2 1 3 3 a b b a Câu 3: [2D2-3] Với ,
a b  0 bất kì. Cho biểu thức P  . Tìm mệnh đề đúng. 6 6 a b A. 3 P ab . B. P ab . C. 6 P ab .
D. P ab . Lời giải Chọn B.
Phương pháp: Đặt ẩn phụ để biểu thức trở lên gọn gàng hơn 1 2 1 Cách giải: ta đặt 6 3 4 3 2
a x a x ; a x 1 2 1 4 3 3 4 3 3 x y x y
x y x y 4 3 6 3 2
b y b y ;b y ; P    ab . x y x y Câu 4:
[2D2-1] Cho a là số thực dương a  1 và 3 P  log
a . Mệnh đề nào dưới đây đúng? 3 a 1 A. P  3 . B. P  1 . C. P  9 . D. P  . 3 Lời giải Chọn C. 3 3 P  log a  log
a  9 log a  9 . 3 1 a a 3 a
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 4/10 - Mã đề 002 Câu 5:
[2D2-1] Giá trị của A  log 3.log 4.log 5...log 64 bằng 2 3 4 63 A. 5 . B. 4 . C. 6 . D. 3 . Lời giải Chọn C.
Áp dụng công thức đổi cơ số, ta có 6
A  log 3.log 4.log 5...log 64  log 4.log 5...log 64  log 64  log 2  6 . 2 3 4 63 2 4 63 2 2 Câu 6:
[2D2-2] Với các số thực dương a , b bất kì. Khẳng định nào sau đây là khẳng định đúng?  a
A. log ab  log a b . B. log  log a   . b    b   a
C. log ab  log a  log b . D. log  log   a b .  b  Lời giải Chọn C. a
Theo định nghĩa ta có công thức log ab  log a  log b và log
 log a  log b   .  b Câu 7:
[2D2-2] Cho log a x và log c y . Hãy biểu diễn 3 5 4 log b c
theo x và y : 2 a   b b 5  4 y 20 y 4 5  3y 20 y A. . B. . C. . D. 20x  . 6x 3x 2 3x 3 Lời giải Chọn A.
- Phương pháp: Áp dụng công thức logarit sau: ln a log a
k  ln a k.ln b a b b  , 0 ln b ln  m. n
a b   m ln a  . n ln b
Biểu thức cần tính sau khi đưa về cùng loga cơ số e thì việc tối giản biểu thức sẽ đơn giản hơn. - Cách giải: ln a log a
x  ln a  . x ln b a b b  , 0 ln b lnc log c   y  lnc  . y ln b b c b  , 0 ln b 5 4   ln  b c  3 3 5 4 5 4 3 5 4 ln b .c   ln b  ln c ln b  . y ln b   5  4 y 3 5 4 3 3 3 3 log b c      2 a   lnah2 2.ln a 2.ln a 2. . x ln b 6x log b c b c b  1 3 5 4 logb 5  4 y 3 5 4   5 4  Cách 2: 3 log b c    2 a   log a a x b  2  2.log 6 b Trắc nghiệm: 3
Cho a b c  2 ta có x y  1 ; 3 5 4 3 5 4 log b c  log 2 .2  2 a   2 2   2 5  4 y 3
Mà: x y  1   6x 2
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 5/10 - Mã đề 002 Câu 8:
[2D2-3] Cho log 7  a, log 5  b . Tính log 28 theo , a b 14 14 35 2  a 2 2  a a A. log 28  . B. log 28  . C. log 28  . D. log 28  . 35 a b 35 a b 35 a b 35 a b Lời giải Chọn A.
Vì logarit cần tính không cùng cơ số với hai logarit đã cho nên ta sẽ đổi logarit cần tính về cơ số 14 log 28 Ta có 14 log 28  35 log 35 14 Lại thấy log 35  log
7.5  log 7  log 5  a b 14 14   14 4
Tiếp theo ta biểu diễn log 28 theo các logarit log 7 và log 5 . Muốn vậy ta chỉ biểu diễn số 14 17 14
28 thành tích hoặc thương của các lũy thừa của 14 , 7 và 5 là xong. 2 14 14 Ta có 28  14.2  14.  7 7 2 14 Suy ra 2 log 28  log
 log 14  log 7  2  a 14 14 14 14 7 2  a Vậy log 28  35 a b Câu 9:
[2D2-1] Tìm tập xác định D của hàm số 1 x y   . A. D   .
B. D  1;  .
C. D  1;  .
D. D  ;  1 . Lời giải Chọn D.
Điều kiện 1 x  0  x  1
Vậy tập xác định D   ;   1 .
Câu 10: [2D2-1] Tìm tập xác định D của hàm số y  log 2x  1 . 3    1   1   1 
A. D  ;    . B. D  ;     .
C. D  0;   .
D. D   ;     .  2   2   2  Lời giải Chọn D. 1 Hàm số y  log
2x  1 xác định khi 2x 1  0  x   3   2  1 
Vậy TXĐ là D   ;    .  2  log 2x
Câu 11: [2D2-2] Tìm đạo hàm của hàm số y  . 2 x 1 4 ln 2x 1 1 2 ln 2x 1 2 log 2x A. y  . B. y  . C. y  . D. y  . 3 2x ln10 2 2x ln10 3 x ln10 3 x Lời giải Chọn C. ln x 1 ADCT: log x
; log x   a  a ln a . x ln a
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 6/10 - Mã đề 002  1  2 1 2x ln 2x '   x' 2 x   2 x  .x 2 . x log 2x log 2 . .log 2x     . x ln10  1 2 ln 2 ln10 ln10 x y     . 4 4 4 3 x x x x ln10
Câu 12: [2D2-1] Đạo hàm của hàm số 3x y e là A. 3x y  e . B. 3 1 3 x y xe    . C. 3   3 x y xe . D. 3   3 x y e . Lời giải Chọn D.
u   . u e ue     3x 3 3  3 x y x e e
Câu 13: [2D2-1] Tìm giá trị nhỏ nhất của hàm số y  ln x trên 1;e
A. Không xác định được giá trị nhỏ nhất.
B. min y  1 khi x  1 .
C. min y e , khi x e .
D. min y  0 , khi x  1 . Lời giải Chọn D.
Vì hàm số đồng biến trên khoảng xác định nên 1
Vậy hàm số có giá trị nhỏ nhất min y y   1  0 khi x  . e x  1 
Câu 14: [2D2-1] Tìm giá trị nhỏ nhất của hàm số y    trên  1  ; 0  2  1
A. min y  1, khi x  0 . B. min y  khi x  1  . 2 1 
C. min y  2 , khi x  1  . D. min y  , khi x  1  . 2 Lời giải Chọn A.
Vì hàm số nghịch biến trên khoảng xác định nên
Vậy hàm số có giá trị nhỏ nhất min y y 0  1 khi x  0 .
Câu 15: [2D2-1] Hình vẽ sau đây là đồ thị của hàm số nào? y O x 1
A. y x ln x .
B. y  ln x . C. x y e . D. x y xe . Lời giải Chọn A.
Ta có ĐTHS đi qua điểm 1;0 nên loại đáp án C và D.
Khi lim y  0 nên loại B và Chọn A. x 0 
Câu 16: [2D2-2] Cho hàm số 2
y x ln x , khẳng định nào sau đây là đúng
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 7/10 - Mã đề 002
A. y  x 3  y  0 .
B. y  x 2  y  0 . C. y  x 2  y  0 . D. y  x 3  y  0 . Lời giải Chọn C.
Ta có y  2x ln x  ;
x y  2 ln x  3  y  x y  2 . x 1
Câu 17: [2D2-2] Nghiệm của phương trình 2 1 3  là 27 A. x  2 . B. x  2  . C. x  1 . D. x  1  . Lời giải Chọn B. x 1 Ta có 2 1 2 x 1  3 3 3 3     2x 1  3   x  2 . 27
Câu 18: [2D2-2] Nghiệm của phương trình log  x   1  log  2 x  3x  2 2 2 
A. x  1; x  3 . B. x  3  .
C. x  1; x  3 . D. x  3 . Lời giải Chọn D. x 1  0 Ta có PT    x  3 . 2
x 1  x  3x  2  2 x 3x 1   1 
Câu 19: [2D2-2] Tập nghiệm của bất phương trình  2   .  2 
A. T   ;   1  2;  .
B. T   ;   1  2;  .
C. T  1; 2 .
D. T  1; 2 . Lời giải Chọn D. 2 x 3x 1  1  1   1  Ta có BPT 2 2  
x  3x 1  1  x  3x  2  0  x      1;2 .  2   2 
Câu 20: [2D2-2] Tập nghiệm của bất phương trình log  2
2x  4x  5  2 . 3  A. T   .
B. T   \   1 .
C. T   \   1 . D. T   . Lời giải Chọn D. Ta có BPT 2 2
2x  4x  5  3  2x  4x  2  0  x   .
Câu 21: [2D2-3] Bác Hiếu đầu tư 99 triệu đồng vào một công ty theo thể thức lãi kép với lãi suất
8, 25% một năm. Hỏi sau 5 năm mới rút tiền lãi thì bác Hiếu thu được bao nhiêu tiền lãi? (Giả
sử rằng lãi suất hàng năm không đổi). A. 48,155 triệu. B. 147,155 triệu. C. 58, 004 triệu. D. 8, 7 triệu. Lời giải. Chọn A.
Áp dụng công thức lãi kép, số tiền thu được cả vốn lẫn lãi là   N T
A 1 r  , với tiền gửi: A  99 triệu đồng, lãi suất r  0, 0825 , N  5 kì. Ta được:
T  147,155 triệu đồng  số tiền lãi là T A  48,155 triệu đồng.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 8/10 - Mã đề 002 x2
Câu 22: [2D2-3] Giá trị m để phương trình x 2 5  . m 5
 3  m  0 có 2 nghiệm phân biệt sao cho
x x  2 là 1 2 A. 2  . B. 2 . C. 3 . D. 4 . Lời giải Chọn B x Đặt 2
t  5  0. Ta có: 2
t  5mt  3  m  0 x x 1 2
Điều kiện cần: pt có hai nghiệm x x  2 hay 2 t .t  5
 5  3  m m  2. 1 2 1 2 Thử lại. 1 x
Câu 23: [2D2-3] Có bao nhiêu số nguyên thỏa mãnbất phương trình xx 2 2.3  9  9x ? A. 3. B. 4. C. 5. D. 6. Lời giải Chọn A. Đk: x  0. 2 1 x x x    2.3xx  9
 9x  2.3x.3 x  3.3 x 2 2  3x 2 3 3 2  2.  3.
  1  2.3 xx  3.   3 xx x x  1 3 3   Đặt 3 x x t    0 ta có: 2 3 t  2t 1  0 1 t  1   3 2 3 t  2t 1  0  0  1 Suy ra: 3 xx t 3     x x  1     x 2 1  x 1  0 3 Đặt u x  0 ta có: 2 u   u 1  0 1 5 1 5 u   2 2 2 u   u 1  0  0  1 5 1 5 3  5 Khi đó: 0  u   0  x   0  x  . 2 2 2
Tập nghiệm nguyên T  0;1;  2 . 3 x x 1 
Câu 24: [2D2-2] Số nghiệm nguyên của bất phương trình    x 1    x3 10 3 10 3 trong khoảng  2  018; 2018 là A. 4033 . B. 4032 . C. 4031 . D. 4030 . Lời giải Chọn D.
Đk: x  3 và x  1. x3 x 1    x x   BPT 10  3 3 1 8 x 1 
  10  3x3     0   x   1  x  3  0 x 1 x  3  x   1  x  3 x  3  1 
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 9/10 - Mã đề 002  x   1  x  3  0  0 
Vậy có số nghiệm nguyên trong khoảng  2  018; 2018 là 4030 15 Câu 25: [2D2-4] Biết x  là một nghiệm của bất phương trình 2  x    x x
. Tập nghiệm T của bất phương trình * là a  2 2 log 23 23 log 2 15 * a   19   17  A. T   ;    . B. T  1;   .
C. T  2;8 .
D. T  2;9 .  2   2  Lời giải Chọn D. x     2 x x     x     2 2 log 23 23 log 2 15 log 23 23 log x  2x 15 a a a a . 2 
23x  23  x  2x  15
Nếu a  1 ta có log x   x x      x a  23 23 loga  2 2 15 2 19 2
x  2x 15  0 .  Nếu 0  a  1 ta có 2
23x  23  x  2x 15 1   x  2 log x   x x     a  23 23 loga  2 2 15  23x  23  0 x  19 .   15 Mà x
là một nghiệm của bất phương trình. 2
Phân tích phương án nhiễu. 15
- A sai do quên nghiệm x  thuộc tập nghiệm. 2 15
- B sai chỉ đúng cho nghiệm x
còn sai trong các nghiệm khác. 2 - C sai do giải sai. ---------HẾT-----------
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 10/10 - Mã đề 002
TOÁN HỌC BẮC–TRUNG–NAM
KIỂM TRA CHƯƠNG 2 GIẢI TÍCH 12
Nhóm: THBTN – ĐỀ KIỂM TRA MÃ ĐỀ 003
(25 câu trắc nghiệm)
Thời gian làm bài: 45 phút, không kể thời gian phát đề. 2 2 Câu 1.
[2D2-1] Cho góc , giá trị của biểu thức sin cos 5 .5 bằng 2 2 A. 1. B. 5 . C. 25 . D. sin .cos 5 . Câu 2.
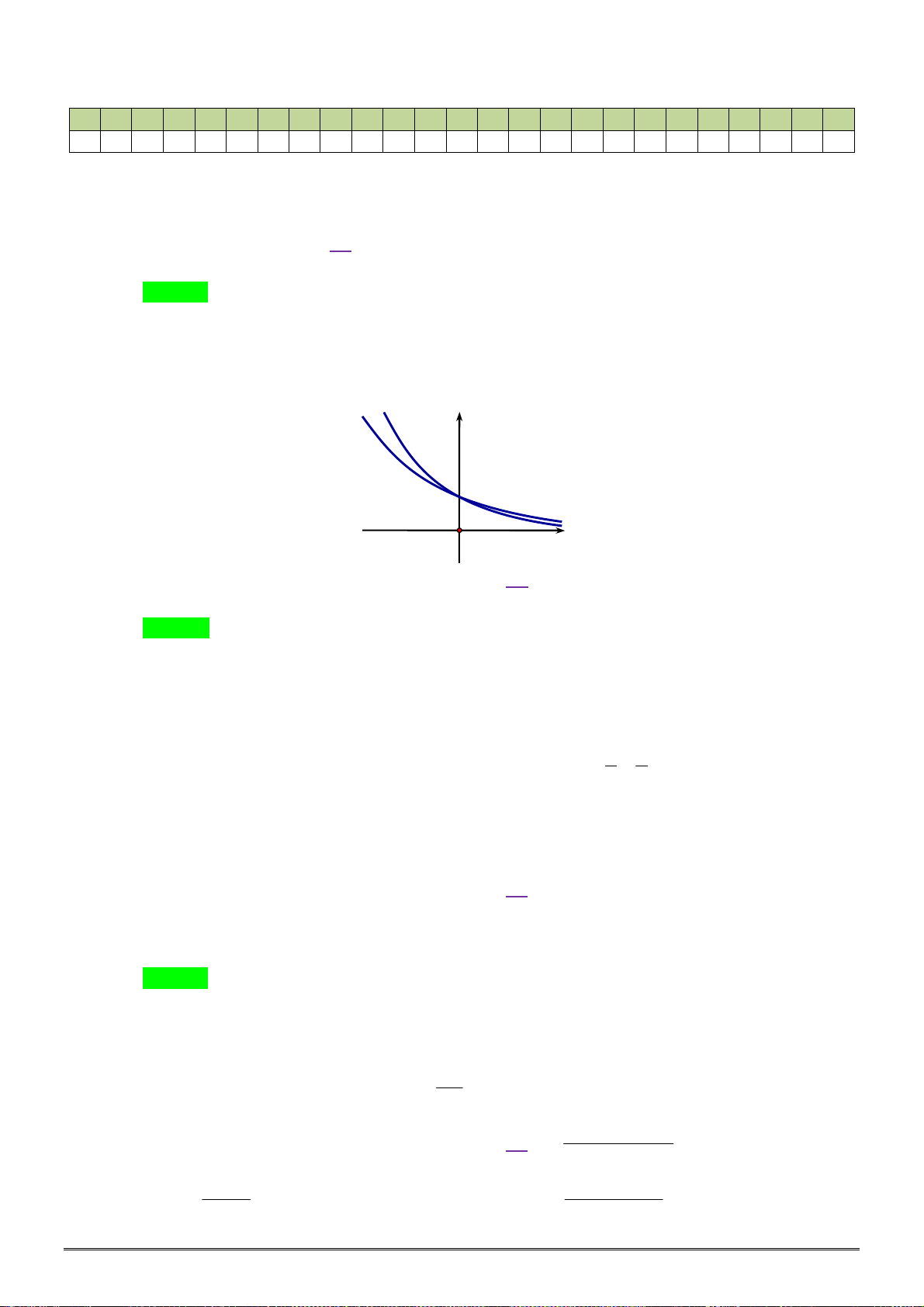
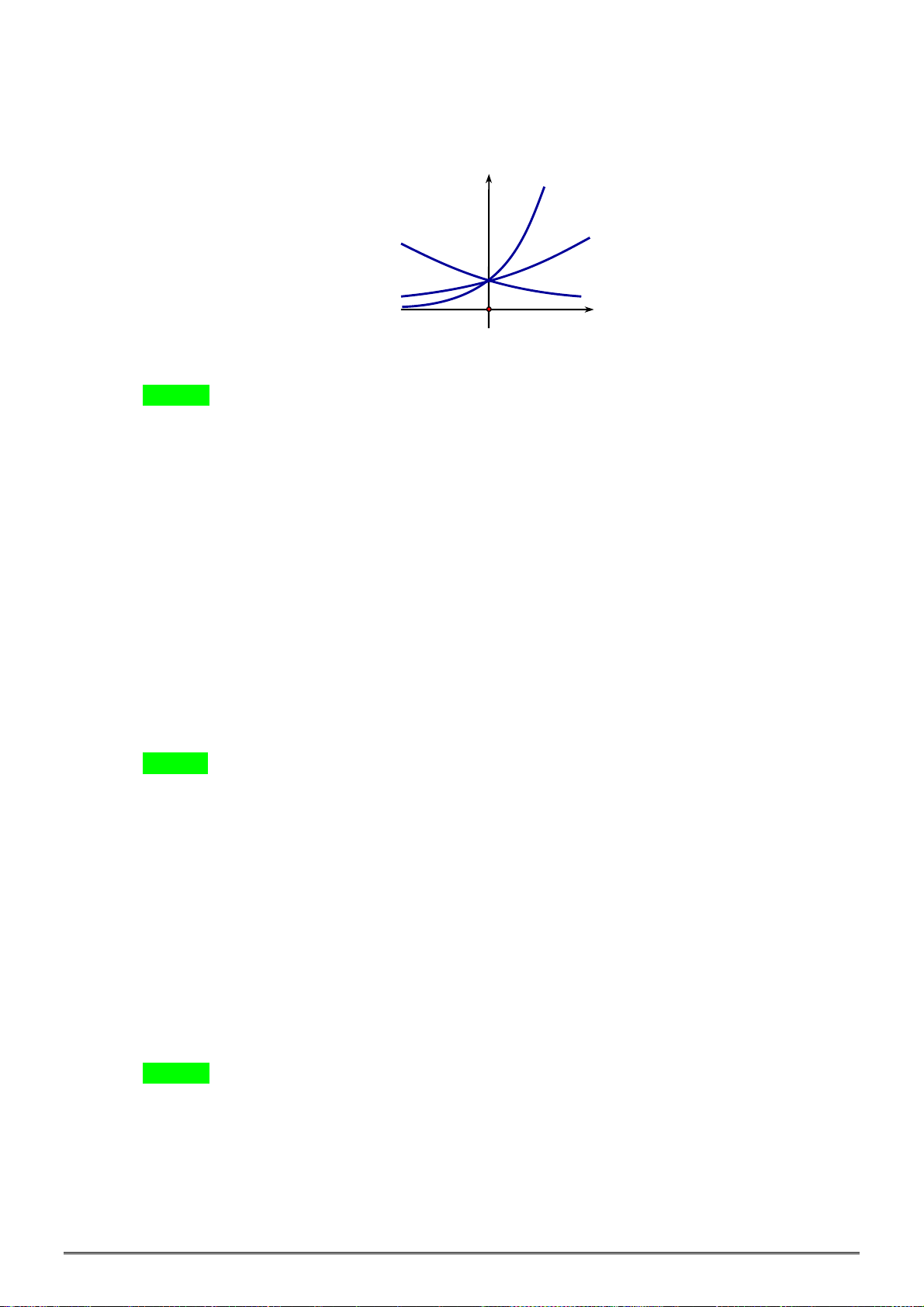
[2D2-2] Cho a , b là các số thực dương khác 1. Hình yC1
vẽ bên là đồ thị của 2 hàm số  : x C y a , 1  C2   : x C
y b . Mệnh đề nào sau đây là đúng? 2  1
A. b a  1 .
B. a b  1 .
C. a b  1.
D. b a  1. O xCâu 3.
[2D2-1] Tìm tập xác định D của hàm số y   x x   2 2 2 . A. D   .
B. D   \  1  ;  2 .
C. D   ;    1  2;  .
D. D  0;   . 13x Câu 4.
[2D2-2] Tính đạo hàm của hàm số y  . x
13x x ln13   1 A. 1 13x y    . B. y  . 2 x 13x 1 13x ln13   1 C. y  . D. y  . x . x ln13 2 x Câu 5.
[2D2-2] Cho hàm số y  ln x
1. Khẳng định nào sau đây là đúng. 2
A. Hàm số đồng biến trên khoảng 0;   .
B. Hàm số đạt cực tiểu tại x  1 .
C. Hàm số nghịch biến trên khoảng 0;  1 .
D. Hàm số đạt cực đại tại x  1 . Câu 6.
[2D2-1] Cho a  0 , a  1 và x , y là hai số dương. Mệnh đề nào sau đây là đúng?
A. log  x y  log x  log y . B. log x y x y . a   log .log a a a a a C. log  .
x y   log x  log y . D. log x y x y . a  .  log .log a a a a a 3 4 5 123 124 Câu 7.
[2D2-2] Đặt a  ln 3 , b  ln 5 . Tính S  ln  ln  ln  ...  ln  ln
theo a và b . 4 5 6 124 125
A. I a  2b .
B. I a  3b .
C. I a  2b .
D. I a  3b . Câu 8.
[2D2-2] Biết sin x  0 , cos x  0 và log sin x  log cos x  1  . Giá trị của 3   3   log
sin x  cos x bằng 3   1 1 A. 1  . B. . C. log 5 1 . D. log 5 1. 3  3 2 3 b b Câu 9.
[2D2-3] Cho a  0 , b  0 , c  0 là các số thực khác 0 thỏa 5a 15b 45c   . Tính T   . a c
A. T  log 5 . B. T  3. C. T  2 .
D. T  log 45 . 15 5
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 1/11 - Mã đề 003 1  2x
Câu 10. [2D2-3] Cho hàm số f x  log . 2   2  1 x   1   2   3   2015   2016 
Tính tổng: S fff  ...  ff           .  2017   2017   2017   2017   2017  A. 2017 . B. 2016 . C. 4032 . D. 1008 .
Câu 11. [2D2-1] Tìm tập xác định D của hàm số y  log  3
x  3x  2 . 0,5  A.  2  ;   . B. 0;  1 . C. 1;  . D.  2  ;   \   1 . x y  1  C4 
C1 C2 
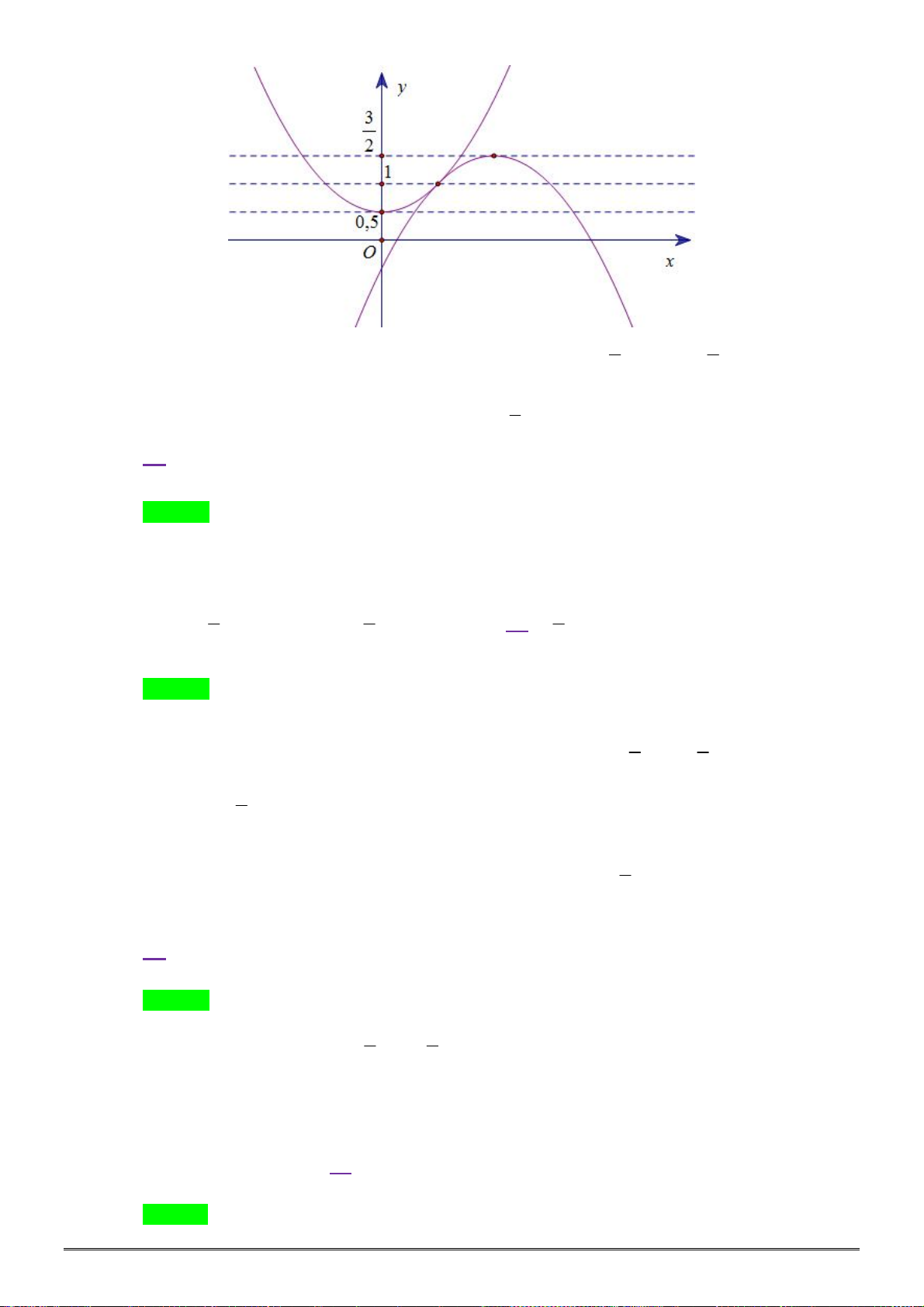
Câu 12. [2D2-2] Cho bốn hàm số y x     1 , y  3 2 ,  2  x  1  y x
  3 , y  4  4 và bốn đường cong C , 1  C3   2  1
C , C , C như hình vẽ bên. Đồ thị hàm số 4  3  2   
1 , 2 , 3 , 4 lần lượt là O x
A. C , C , C , C .
B. C , C , C , C . 3   2   4   1  1   2   3   4 
C. C , C , C , C .
D. C , C , C , C . 4   1   3   2  2   4   1   3 
Câu 13. [2D2-2] Tìm tất cả giá trị thực của tham số m để hàm số y   2
ln x  2mx m có tập xác định là  .
A. m  0 hoặc m  1.
B. 0  m  1 .
C. m  0 hoặc m  1.
D. 0  m  1 .
Câu 14. [2D2-3] Trong mặt phẳng tọa độ Oxy cho hình vuông ABCD có diện tích bằng 36 , đường
thẳng AB song song với trục Ox , các đỉnh A , B và C lần lượt nằm trên đồ thị của các hàm
số y  log x , y  log x , y  log
x và a là một số thực lớn hơn 1. Tìm a . a a 3 a A. a  3 . B. 3 a  6 . C. a  6 . D. 6 a  3 . 2a 4b  8
Câu 15. [2D2-4] Cho a , b là hai số thực dương thỏa mãn 
. Tính giá trị của biểu 2a  2b a  4b  8 2017a thức P  . 2017b A. 1. B. 2 2017 . C. 2017a . D. 2017b . x 1  2x  2   3 
Câu 16. [2D2-1] Tập nghiệm S của phương trình      là  3   2   1  A. S    1 .
B. S    .  3
C. S    1 . D. S    2 .
Câu 17. [2D2-2] Tìm tọa độ giao điểm của đồ thị hàm số 3 x y  
 2 và đường thẳng y  5 . A.  1  ;5 . B. 1;5 . C. 2;5 . D.  2  ;5 .
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 2/11 - Mã đề 003
Câu 18. [2D2-2] Biết rằng phương trình 2018 x log 9 8 3  2
 0 có nghiệm duy nhất x x . Khẳng định nào 0 sau đây là đúng?
A. x là số nguyên tố.
B. x là số chính phương. 0 0
C. x chia hết cho 3 .
D. x là một số chẵn. 0 0
Câu 19. [2D2-3] Tính tổng T tất cả các nghiệm của phương trình
x2   x   x2 3.25 3 10 .5  3  x  0 .  2 
A. T  4  log .
B. T  3  log 2 .
C. T  4  log 3 .
D. T  2  log 6 . 5   5 5 5  7 
Câu 20. [2D2-4] Tính tổng T tất cả các giá trị của tham số m để phương trình  x 2 1 2 log  2
x  2x  3  4 xm log
2 x m  2 có đúng ba nghiệm phân biệt. 2  2   A. T  1. B. T  2 . C. T  3. D. T  4 . x 1
Câu 21. [2D2-1] Tập nghiệm của bất phương trình 1 3  là 9 A.  3  ;    . B. 1;  . C.  ;    1 . D.  1  ;3 .
Câu 22. [2D2-2] Tập nghiệm của bất phương trình log x 1  2 là 0,5    5   5   5  A.  ;    . B. ;     . C. 1;   . D. 1;3 .  4   4   4  2 x3 2 x  1 
Câu 23. [2D2-2] Gọi S là tập nghiệm của bất phương trình 0, 25   
. Khi đó S có dạng  4 
a;b với a b . Tính P a b . A. 2 . B. 2  . C. 1. D. 0 .
Câu 24. [2D2-2] Có bao nhiêu số nguyên x thỏa mãn bất phương trình log  x  40  log 60  x  2 . A. 20 . B. 18 . C. 21 . D. 19 .
Câu 25. [2D2-4] Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng  2  018; 2018 để bất 2 2
phương trình 1 4x     1 4 9 20 .3  x m
 2m  5  0 có tập nghiệm  2  ; 2 . A. 2057 . B. 2060 . C. 2058 . D. 2056 .
----------HẾT----------
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 3/11 - Mã đề 003 ĐÁP ÁN 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
B C B B D C D C C D D B D D B B A C C C A C A B D HƯỚNG DẪN GIẢI 2 2 Câu 1.
[2D2-1] Cho góc , giá trị của biểu thức sin cos 5 .5 bằng 2 2 A. 1. B. 5 . C. 25 . D. sin .cos 5 . Lời giải Chọn B. 2 2 2 2
Ta có: sin x cos x sin xcos x 1 5 .5  5  5  5 . Câu 2.
[2D2-2] Cho a , b là các số thực dương khác 1. Hình vẽ bên là đồ thị của 2 hàm số  : x C y a ,  : x C
y b . Mệnh đề nào sau đây là đúng? 2  1  yC1 C2  1 O x
A. b a  1 .
B. a b  1 .
C. a b  1.
D. b a  1. Lời giải Chọn C. Đồ thị hàm số x y a và x
y b đi từ trái sang phải theo chiều hướng xuống nên là những hàm số nghịch biến 
a,b  1 . Loại A,B.
Từ đồ thị hàm số ta thấy tại cùng một giá trị x  0 thì đồ thị hàm số x
y a nằm trên đồ thị 0 x  0 x  1 1 1 hàm số x y b hay 0  
a b . Ví dụ: 0     a b . x x b a 1 1   ba b a
Vậy a b  1.  Câu 3.
[2D2-1] Tìm tập xác định D của hàm số y   x x   2 2 2 . A. D   .
B. D   \  1  ;  2 .
C. D   ;    1  2;  .
D. D  0;   . Lời giải Chọn B. x  1
Hàm số xác định khi và chỉ khi 2
x x  2  0     D   \  1  ;  2 . x  2  13x Câu 4.
[2D2-2] Tính đạo hàm của hàm số y  . x
13x x ln13   1 A. 1 13x y    . B. y  . 2 x 13x 1 13x ln13   1 C. y  . D. y  . x . x ln13
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 4/11 - Mã đề 003 Lời giải Chọn B. 13x
13x x ln13   1 Ta có: y    y  . 2 x x 2 x Câu 5.
[2D2-2] Cho hàm số y  ln x
1. Khẳng định nào sau đây là đúng. 2
A. Hàm số đồng biến trên khoảng 0;   .
B. Hàm số đạt cực tiểu tại x  1 .
C. Hàm số nghịch biến trên khoảng 0;  1 .
D. Hàm số đạt cực đại tại x  1 . Lời giải Chọn D.
Tập xác định D  0;   1  x  1 Đạo hàm: y   x   y  0   . x x  1   Bảng biến thiên: x  1  y  0  1 y 2  
Dựa vào bảng biến thiên, hàm số đạt cực đại tại x  1 . Câu 6.
[2D2-1] Cho a  0 , a  1 và x, y là hai số dương. Mệnh đề nào sau đây là đúng?
A. log  x y  log x  log y . B. log x y x y . a   log .log a a a a a C. log  .
x y   log x  log y . D. log x y x y . a  .  log .log a a a a a Lời giải Chọn C. 3 4 5 123 124 Câu 7.
[2D2-2] Đặt a  ln 3 , b  ln 5 . Tính S  ln  ln  ln  ...  ln  ln
theo a và b . 4 5 6 124 125
A. I a  2b .
B. I a  3b .
C. I a  2b .
D. I a  3b . Lời giải Chọn D. 3 4 123 124  3 4 123 124  3 Ta có: S  ln  ln  ...  ln  ln  ln . .... .  ln   4 5 124 125  4 5 124 125  125
 ln 3  ln125  ln 3  3ln 5  a  3b . Câu 8.
[2D2-2] Biết sin x  0 , cos x  0 và log sin x  log cos x  1  . Giá trị của 3   3   log
sin x  cos x bằng. 3   1 1 A. 1  . B. . C. log 5 1 . D. log 5 1. 3  3 2 3 Lời giải Chọn C.  1
Ta có: log sin x  log cos x  1   log sin . x cos x 1  log 3  sin . x cos x  . 3 3 3 3 3
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 5/11 - Mã đề 003 15    x x2 5 sin cos 
. Mà sin x  0, cos x  0 
 sin x  cos x  . 3 3 15 1
Do đó: log sin x  cos x  log  log 5 1 . 3   3  3  3 2 b b Câu 9.
[2D2-3] Cho a  0 , b  0 , c  0 là các số thực khác 0 thỏa 5a 15b 45c   . Tính T   . a c
A. T  log 5 . B. T  3. C. T  2 .
D. T  log 45 . 15 5 Lời giải Chọn C. a  log t 5 
Giả sử 5a  15b  45c t 
 b  log t . 15 c  log t  45 b b log t log t Ta có: 15 15 T    
 log 5  log 45  log 225  2 . 15 15 15 a c log t log t 5 45 1  2x
Câu 10. [2D2-3] Cho hàm số f x  log . Tính tổng: 2   2  1 x   1   2   3   2015   2016  S fff  ...  ff           .  2017   2017   2017   2017   2017  A. 2017 . B. 2016 . C. 4032 . D. 1008 . Lời giải Chọn D. 1  2x  1  21 x  1
Xét f x  f 1 x  log  log  log 4  1 2   2   2 2  1 x  2 x 2    1   2016   2   2015  Do đó: ff  1     , ff  1      2017   2017   2017   2017   1   2   2015   2016  Suy ra: S ff  ...  ff
 1 1 .. 11  1008         .  2017   2017   2017   2017 
Câu 11. [2D2-1] Tìm tập xác định D của hàm số y  log  3
x  3x  2 . 0,5  A.  2  ;   . B. 0;  1 . C. 1;  . D.  2  ;   \   1 . Lời giải Chọn D. m  2 
Hàm số xác định khi và chỉ khi 3
x  3x  2  0   . m  1  x x  1   1 
Câu 12. [2D2-2] Cho bốn hàm số y x x    
1 , y  3 2 , y    3 , y  4 4 và bốn đường  2   2 
cong C , C , C , C như hình vẽ bên. Đồ thị hàm số  
1 , 2 , 3 , 4 lần lượt là 4  3  2  1 
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 6/11 - Mã đề 003 yC4 
C1 C2  C3  1 O x
A. C , C , C , C .
B. C , C , C , C . 3   2   4   1  1   2   3   4 
C. C , C , C , C .
D. C , C , C , C . 4   1   3   2  2   4   1   3  Lời giải Chọn B.
Đồ thị hàm số C , C đi từ trái sang phải theo chiều hướng xuống nên là những hàm số 4  3  nghịch biến 
 C , C tương ứng với   1 hoặc 3 . 4  3 
Từ đồ thị hàm số ta thấy tại cùng một giá trị x  0 thì đồ thị hàm số C nằm trên đồ thị hàm 4  0 1 1   1   1 
số C . Chọn x  1  
. Do đó C  3 , C  1 . 3    4    3  0      2   2 
Tương tự: C  4 , C  2 . 2    1   
Câu 13. [2D2-2] Tìm tất cả giá trị thực của tham số m để hàm số y   2
ln x  2mx m có tập xác định là  .
A. m  0 hoặc m  1.
B. 0  m  1 .
C. m  0 hoặc m  1.
D. 0  m  1 . Lời giải Chọn D. YCBT 2 2
x  2mx m  0, x
      0  m m  0  0  m  1.
Câu 14. [2D2-3] Trong mặt phẳng tọa độ Oxy cho hình vuông ABCD có diện tích bằng 36 , đường
thẳng AB song song với trục Ox , các đỉnh ,
A B và C lần lượt nằm trên đồ thị của các hàm số
y  log x , y  log x , y  log
x và a là một số thực lớn hơn 1. Tìm a . a a 3 a
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 7/11 - Mã đề 003 A. a  3 . B. 3 a  6 . C. a  6 . D. 6 a  3 . Lời giải Chọn D. Do ,
A B thuộc đường thẳng song song trục Ox , giả sử ,
A B d : y  log m , m  0 . a   A ;
m log m , B m;log m , Mà S
 36  AB  6  m m  6   m  9 . a aABCD 6 a  3 
Suy ra: B 3;2 log 3 
C 3;3log a . Ta lại có: BC  6  log a  6  . a 3  3 1 a  6  3
Đối chiếu với điều kiện 6 a  1   a  3 . 2a 4b  8 Câu 15. [2D2-4] Cho ,
a b là hai số thực dương thỏa mãn 
. Tính giá trị của biểu thức 2a  2b a  4b  8 2017a P  . 2017b A. 1. B. 2 2017 . C. 2017a . D. 2017b . Lời giải Chọn B. 2a 4b  8 Ta có: 
 2a.a  2b b   a   b   . a b 4 8 a b 2 2 . 2 . 2   2  2 a  4b  8 Xét hàm số
   2t. ,  0 
    2t  2t f t t t f t
.t.ln 2  0, t  0
Suy ra hàm số đồng biến trên khoảng 0;   .
Do đó:   f a  f b  2  a b  2 . a b2 2017 2017 Vậy 2 P    2017 . 2017b 2017b x 1  2x  2   3 
Câu 16. [2D2-1] Tập nghiệm S của phương trình      là  3   2   1  A. S    1 .
B. S    .
C. S    1 . D. S    2 .  3 Lời giải Chọn B. x 1  2 xx 1  2 x  2   3   3   3  1 Ta có:   
 x 1  2x x           .  3   2   2   2  3
Câu 17. [2D2-2] Tìm tọa độ giao điểm của đồ thị hàm số 3 x y  
 2 và đường thẳng y  5 . A.  1  ;5 . B. 1;5 . C. 2;5 . D.  2  ;5 . Lời giải Chọn A.
Phương trình hoành độ giao điểm: 3x  2  5  3x  3  x  1.
Vậy tọa độ giao điểm là  1  ;5 .
Câu 18. [2D2-2] Biết rằng phương trình 2018 x log 9 8 3  2
 0 có nghiệm duy nhất x x . Khẳng định nào 0 sau đây là đúng.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 8/11 - Mã đề 003
A. x là số nguyên tố.
B. x là số chính phương. 0 0
C. x chia hết cho 3 .
D. x là một số chẵn. 0 0 Lời giải Chọn C. 2 2 x x.log 3 2 Ta có: 2018 x.log 9 8 2018 2018 3 3 3  2  0  2  3  3  3  x  3027 .
Câu 19. [2D2-3] Tính tổng T tất cả các nghiệm của phương trình
x2   x   x2 3.25 3 10 .5  3  x  0 .  2 
A. T  4  log .
B. T  3  log 2 .
C. T  4  log 3 .
D. T  2  log 6 . 5   5 5 5  7  Lời giải Chọn C. Đặt 2 5x t  
, t  0 . Phương trình trở thành: 2
3t  3x 10.t  3  x  0   1 .      x
2    x  x x    x  2 2 3 10 12 3 9 48 64 3 8 1   Phương trình  
1 có hai phân biệt t
hay t  3  x . 3 1 x 1 Với 2 t   5 
x  2  log 3 . 5 3 3 Với x2
t  3  x  5
 3  x  . VT f xx2  
f  xx2 5  5 ln 5  0   Hàm số
đồng biến, VP g x  3  x 
g  x  1   0 
 Hàm số nghịch biến.
Do đó:  có nghiệm duy nhất: x  2 . Tổng hai nghiệm là 4  log 3 . 5
Câu 20. [2D2-4] Tính tổng T tất cả các giá trị của tham số m để phương trình  x 2 1 2 log  2
x  2x  3  4 xm log
2 x m  2 có đúng ba nghiệm phân biệt. 2  2   A. T  1. B. T  2 . C. T  3. D. T  4 . Lời giải Chọn C. 2 x 1  2
Phương trình trở thành:   2 .log  x 1
 2  2 xm.log
2 x m  2   1 . 2   2 2     t t 2t
Xét hàm số f t  2 .log t  2 , t  0 
f t  2 .log t  2 ln 2   0, t  0 . 2     2   t  2ln 2 
 Hàm số đồng biến trên 0;   . 2  x 1 m    2x   2 2 2 2 Do đó:  
1  f  x  
1   f 2 x m    x   1
 2 x m    . 2    x 1 m   2 2  x 1   2x    2 2
Số nghiệm pt  là số giao điểm của đường thẳng y m và đồ thị hàm số y   . 2 x 1    2
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 9/11 - Mã đề 003 1 3
Dựa vào đồ thị hàm số:  có 3 nghiệm phân biệt   m  ; m  1; m  . 2 2 x 1
Câu 21. [2D2-1] Tập nghiệm của bất phương trình 1 3  là 9 A.  3  ;    . B. 1;  . C.  ;    1 . D.  1  ;3 . Lời giải Chọn A.
Bất phương trình trở thành: x 1  2 3  3
x 1  2  x  3 .
Câu 22. [2D2-2] Tập nghiệm của bất phương trình log x 1  2 là 0,5    5   5   5  A.  ;    . B. ;     . C. 1;   . D. 1;3 .  4   4   4  Lời giải Chọn C.
Điều kiện: x 1  0  x  1 1 5
Bất phương trình trở thành: log  x   1  log
0,52  x 1   x  . 0,5 0,5 4 4  5  Vậy: x  1;   .  4  2 x3 2 x  1 
Câu 23. [2D2-2] Gọi S là tập nghiệm của bất phương trình 0, 25   
. Khi đó S có dạng  4 
a;b với a b . Tính P a b . A. 2 . B. 2  . C. 1. D. 0 . Lời giải Chọn A. 2 x 2 x3  1   1 
Bất phương trình trở thành: 2 2 
x  2x  3  x  2x  3  0  1   x  3     .  4   4 
Vậy S  1;3 
a b  2 .
Câu 24. [2D2-2] Có bao nhiêu số nguyên x thỏa mãn bất phương trình log  x  40  log 60  x  2 . A. 20 . B. 18 . C. 21 . D. 19 . Lời giải Chọn B.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 10/11 - Mã đề 003
Điều kiện: 40  x  60 .
Bất phương trình trở thành:  x    x 2 log 40 60
 log100  x 100x  2500  0  x  50 .
Vậy S  40;60 \ 5  0 
 có 18 giá trị nguyên.
Câu 25. [2D2-4] Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng  2  018; 2018 để bất 2 2
phương trình 1 4x     1 4 9 20 .3  x m
 2m  5  0 có tập nghiệm  2  ; 2 . A. 2057 . B. 2060 . C. 2058 . D. 2056 . Lời giải Chọn D. Điều kiện: 2   x  2 . x
Xét hàm số f x 2
 1 4  x , x 2; 2  f  x  
f  x  0  x  0 . 2 4  x
Ta có: f 2  1, f 2  1, f 0  3 
1  f x  3 . 2 Đặt 1 4  3  x tt 3; 27 2 t  20t  5 Bất pt trở thành: 2
t  m  20 t  2m  5  0, t
 3; 27  m  , t  3; 27 . t  2 2 2 t  20t  5 t  4t  45 t  9
Xét hàm số f t  , t  3;27 
f t 
f t  0  . 2    t  2 t  2 t  5   Bảng biến thiên: t ∞ 3 9 27 _ f' t ( ) 0 + f t ( ) 74 1274 25 38
Dựa vào bảng biến thiên: m f t , t  3; 27  m  38 
m có 2056 giá trị nguyên.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 11/11 - Mã đề 003
TOÁN HỌC BẮC–TRUNG–NAM
KIỂM TRA CHƯƠNG 2 GIẢI TÍCH 12
Nhóm: THBTN – ĐỀ KIỂM TRA MÃ ĐỀ 004
(25 câu trắc nghiệm)
Thời gian làm bài: 45 phút, không kể thời gian phát đề. Câu 1. [2D2-1] Cho
. Kết luận nào sau đây là đúng?
A.  0 .
B. . 1.
C. .
D. . Câu 2.
[2D2-2] Cho biểu thức 3 2 5 3 P x
x x . Mệnh đề nào dưới đây đúng. 14 17 13 16 A. 15 P x . B. 36 P x . C. 15 P x . D. 15 P x .  Câu 3.
[2D2-1] Tìm tập xác định D của hàm số y   x   2 2 3 1  1   1 
A. D   \   . B. D    .  3   3   1   1   1 1  C. ;   ;      . D. D   ;   .  3   3   3 3  Câu 4.
[2D2-2] Đường cong ở hình bên là đồ thị của một hàm số trong y
bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây.
Hỏi hàm số đó là hàm số nào? 1 A. 2
y   x  2x  1. B. y  log x . 0,5 1 O x C. y  . D. 2x y  . 2x 1 Câu 5.
[2D2-1] Hàm số y   x  3 1 có đạo hàm là 1 1  x  2 3 1  x  3 1 A. y  . B. y  . C. y  . D. y  . 3  x  2 3 1 3  x  3 1 3 3 Câu 6.
[2D2-2] Cho a  log 3 và b  log 5 . Tính log 1350 theo a và b . 30 30 30
A. 1 2a b B. 1 2a  . b
C. 1 2a b D. 1
  2a b Câu 7.
[2D2-2] Nếu log x  5 log a  4 log b, (a,b  0) thì x bằng 2 2 2 A. 5 4 a b . B. 4 5 a b . C. 5a  4 . b D. 4a  5 . b 2 3 2 5 4 a . a . . a a Câu 8.
[2D2-2] Cho A  log
với a  0; a  1 . Giá trị A bằng a 3 a 16 67 22 62 A. B. C. D. 5 5 5 15 x y x Câu 9.
[2D2-3] Cho x , y là các số thực dương thỏa mãn log x  log y  log . Tính tỉ số . 9 6 4 6 y x x x x A.  3 . B.  5 . C.  2 . D.  4 . y y y y
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 1/9 - Mã đề 004
Câu 10. [2D2-3] Cho các số thực dương khác 1 là a , b , c . Rút gọn 2 log b.log c .log a ta được 2 a 2 b c m m ,  ,
m n N  , với
là phân số tối giản. Chọn khẳng định đúng. n 2 n
A. m  2n
B. m  2n  0
C. m  2n  0 D. 2 n  4m  0
Câu 11. [2D2-1] Đồ thị sau là của hàm số nào sau đây? y
A. y  log x . B. y  log 2x . 2   3
C. y  2 log x .
D. y  log x . O 1 x 3 5
Câu 12. [2D2-2] Hàm số y   2
ln x  2mx  4 có tập xác định D   khi:  m  2 A. m  2 . B.  . C. m  2 . D. 2   m  2 . m  2   2 ln x m
Câu 13. [2D2-3] Biết rằng giá trị lớn nhất của hàm số y  trên đoạn 3 1  ; e  M  trong đó x   là en
M , n là các số tự nhiên. Tính 2 3
S m  2n . A. S  22. B. S  24. C. S  32. D. S  135.
Câu 14. [2D2-1] Cho f x  x ln x . Đạo hàm cấp hai f e bằng: 1 A. 2. B. . C. 3. D. e . e ln x
Câu 15. [2D2-2] Đồ thị hàm số y
có tọa độ điểm cực đại là a;b . Khi đó ab bằng x A. e . B. 2e . C. 1  D. 1
Câu 16. [2D2-1] Tìm các nghiệm của phương trình x 1 3   27. A. x  9. B. x  3. C. x  4. D. x  10.
Câu 17. [2D2-1] Phương trình log  2
x  4x 12  2 . Chọn phương án đúng? 3 
A. Có hai nghiệm cùng dương.
B. Có hai nghiệm trái dấu.
C. Có hai nghiệm cùng âm. D. Vô nghiệm.
Câu 18. [2D2-2] Cho phương trình log
4.5x  2  x 1 có hai nghiệm là x , x . Tổng x x bằng 25   1 2 1 2 A. 50. B. log 100 C. 30. D. log 50. 5 5 x x
Câu 19. [2D2-2] Bất phương trình        2 2 3 2 3 có tập nghiệm là A.  1  ; . B.  ;    1 . C. (2; ). D. ( ;  2  ).
Câu 20. [2D2-2] Tập nghiệm của bất phương trình log
x  3 1  0 có dạng a;b . Khi đó giá trị 1   3
a  3b bằng 37 A. 15 . B. 13 . C. . D. 30 . 3
Câu 21. [2D2-2] Tìm số nghiệm nguyên của bất phương trình: log x 1  3 . 3   A. 7 . B. 26 . C. 15 . D. 27 .
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 2/9 - Mã đề 004
Câu 22. [2D2-2] Anh Nam vay tiền ngân hàng 1 tỷ đồng theo phương thức trả góp (chịu lãi số tiền chưa
trả) với lãi suất 0,5% /tháng. Nếu cuối mỗi tháng bắt đầu từ tháng thứ nhất anh Nam trả 30
triệu đồng. Hỏi sau bao nhiêu tháng anh Nam trả hết nợ? A. 35 tháng. B. 36 tháng. C. 37 tháng. D. 38 tháng. Câu 23. [2D2-3] Tìm tất cả các giá trị của tham số m để phương trình 2
log x m  2 log x  3m 1  0 có 2 nghiệm x , x sao cho x x  27 . 3   3 1 2 1 2 4 28 A. m  . B. m  25 . C. m  . D. m  1. 3 3
Câu 24. [2D2-4] Tìm tập hợp các giá trị của tham số thực m để phương trình 6x  3   2x mm  0 có
nghiệm thuộc khoảng 0;  1 . A. 3; 4 . B. 2; 4 . C. 2; 4 . D. 3; 4 . 2 2  b
Câu 25. [2D2-4] Tìm giá trị nhỏ nhất của biểu thức P   2 log b   6 log
 với a , b là các số a ba   a
thực thay đổi thỏa mãn b a  1. A. 30. B. 40. C. 50. D. 60.
----------HẾT----------
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 3/9 - Mã đề 004 ĐÁP ÁN 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
D A A C A B A D C A A D C B D C C D B B B C D C D HƯỚNG DẪN GIẢI Câu 1. [2D2-1] Cho
. Kết luận nào sau đây là đúng?
A.  0 .
B. . 1.
C. .
D. . Lời giải Chọn D.
Vì  1 nên
. Câu 2.
[2D2-2] Cho biểu thức 3 2 5 3 P x
x x . Mệnh đề nào dưới đây đúng. 14 17 13 16 A. 15 P x . B. 36 P x . C. 15 P x . D. 15 P x . Lời giải Chọn A. 1 1 1 1 3 1   3 2 1 3 2 1 1 14   2 3     Ta có 3 2 5 3 2 5 3 P x x x x x x     2  x  5 3 x x 2 3  2 5  3 6 10 15
  x . x . x
x .x .xx   .              Câu 3.
[2D2-1] Tìm tập xác định D của hàm số y   x   2 2 3 1  1   1 
A. D   \   . B. D    .  3   3   1   1   1 1  C. ;   ;      . D. D   ;   .  3   3   3 3  Lời giải Chọn A.  1 Vì 2
  0 nên y   x   2 2 3 1 xác định khi 2
3x 1  0  x   . 3 Câu 4.
[2D2-2] Đường cong ở hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn
phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào? y 1 O x 1 A. 2
y   x  2x  1. B. y  log x . C. y  . D. 2x y  . 0,5 2x Lời giải Chọn C.
Nhìn vào đồ thị ta thấy:.
+ Hàm số nghịch biến trên  . Nên loại đáp án A, D.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 4/9 - Mã đề 004
+ Hàm số xác định trên  nên loại đáp án B ( hàm số y  log
x xác định khi x  0 ) 0,5 1 Câu 5.
[2D2-1] Hàm số y   x  3 1 có đạo hàm là 1 1  x  2 3 1  x  3 1 A. y  . B. y  . C. y  . D. y  . 3  x  2 3 1 3  x  3 1 3 3 Lời giải Chọn A. 1 1 2 1  1  1
y   x   1
y   x   1   . x   1 3 3 1   x   3 1  . 3 3 3  x  2 3 1 Câu 6.
[2D2-2] Cho a  log 3 và b  log 5 . Tính log 1350 theo a và b . 30 30 30
A. 1 2a b B. 1 2a  . b
C. 1 2a b D. 1
  2a b Lời giải Chọn B. Ta có: 2
log 1350  log 30.3 .5  1 2 log 3  log 5  1 2a b . 30 30 30 30 Câu 7.
[2D2-2] Nếu log x  5 log a  4 log b, (a,b  0) thì x bằng 2 2 2 A. 5 4 a b . B. 4 5 a b . C. 5a  4 . b D. 4a  5 . b Lời giải Chọn A. 5 4 5 4 5 4
log x  5 log a  4 log b  log x  log a  log b  log x  log a .b x a .b . 2 2 2 2 2 2 2 2 2 3 2 5 4 a . a . . a a Câu 8.
[2D2-2] Cho A  log
với a  0; a  1 . Giá trị A bằng a 3 a 16 67 22 62 A. B. C. D. 5 5 5 15 Lời giải Chọn D. 2 3 2 5 4 62 a . a . . a a 62
Với 0  a  1 . Ta có: 15 A  log  log aa 3 a a 15 x y x Câu 9.
[2D2-3] Cho x , y là các số thực dương thỏa mãn log x  log y  log . Tính tỉ số . 9 6 4 6 y x x x x A.  3 . B.  5 . C.  2 . D.  4 . y y y y Lời giải Chọn C.  x  9t x y
Đặt t  log x  log y  log   y  6t 9 6 4 6  x y   4t  6 2t t t       x t t t 3 3 3  9  6  6.4    6   2         2   2   2  y
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 5/9 - Mã đề 004
Câu 10. [2D2-3] Cho các số thực dương khác 1 là a , b , c . Rút gọn 2 log b.log c .log a ta được 2 a 2 b c m m ,  ,
m n N  , với
là phân số tối giản. Chọn khẳng định đúng. n 2 n
A. m  2n
B. m  2n  0
C. m  2n  0 D. 2 n  4m  0 Lời giải Chọn A.    1   2  Ta có 2 log b.log c .log a  log b . log c . log a  2 a 2        2 a   2 b c b c   2  1 2  . . log b c a   m n a
.logb .logc  1, 2. 2 2 2 2 2
Câu 11. [2D2-1] Đồ thị sau là của hàm số nào sau đây? y O x 1
A. y  log x . 3 B. y  log 2x . 2  
C. y  2 log x . 3
D. y  log x . 5 Lời giải Chọn A.
Ta thấy đồ thị hàm số đi qua điểm 3; 
1 . Do đó ta loại các đáp án B, C, D.
Câu 12. [2D2-2] Hàm số y   2
ln x  2mx  4 có tập xác định D   khi:  m  2 A. m  2 . B.  . C. m  2 . D. 2   m  2 . m  2   Lời giải Chọn D. 2
  m  4  0
Hàm số có tập xác định 2
D    x  2mx  4  0, m     2  m  2 a  1  0  2 ln x m
Câu 13. [2D2-3] Biết rằng giá trị lớn nhất của hàm số y  trên đoạn 3 1  ; e M  trong đó x   là n e
M , n là các số tự nhiên. Tính 2 3
S m  2n . A. S  22. B. S  24. C. S  32. D. S  135. Lời giải Chọn C. 2 2 ln x 2 ln x  ln x ln x  0  x  1
y f x 
f   x 
f x  0   . 2     2 x x ln x  2  x e  4 9 4 mm  4 Ta có: f   1  0, f  2 e   , f  3 e  2 3     
S m  2n  32. 2 3 2 n e e e e n  2 
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 6/9 - Mã đề 004
Câu 14. [2D2-1] Cho f x  x ln x . Đạo hàm cấp hai f e bằng: 1 A. 2. B. . C. 3. D. . e e Lời giải Chọn B. 1 1
Ta có: f  x  ln x 1  f  x 
f  e  . x e ln x
Câu 15. [2D2-2] Đồ thị hàm số y
có tọa độ điểm cực đại là a;b . Khi đó ab bằng x A. . e B. 2 . e C. 1  D. 1 Lời giải Chọn D.  ln x   1 ln x Ta có y  
y  0  1 ln x  0  x e   2  x x  1 ln x  
x 2ln x  3 1 Mặt khác y  
y e    0  2  4   3  xx ea e  1  
Suy ra, hàm số đạt cực đại tại x e , suy ra tọa độ điểm cực đại là ; e     1  ab  1  e b    e
Câu 16. [2D2-1] Tìm các nghiệm của phương trình x 1 3   27. A. x  9. B. x  3. C. x  4. D. x  10. Lời giải Chọn C. Ta có x 1  3 3  3  x  4 .
Câu 17. [2D2-1] Phương trình log  2
x  4x 12  2 . Chọn phương án đúng? 3 
A. Có hai nghiệm cùng dương.
B. Có hai nghiệm trái dấu.
C. Có hai nghiệm cùng âm. D. Vô nghiệm. Lời giải Chọn C. Phương trình 2
x  4x 12  9  x  1  hoặc x  3  .
Vậy phương trình có hai nghiệm cùng âm.
Câu 18. [2D2-2] Cho phương trình log
4.5x  2  x 1 có hai nghiệm là x , x . Tổng x x bằng 25   1 2 1 2 A. 50. B. log 100 C. 30. D. log 50. 5 5 Lời giải Chọn D. log 4.5x  2 
1  5 x 100.5x x
 50  0  5x x  50 . 25   2 1 2 x x
Câu 19. [2D2-2] Bất phương trình        2 2 3 2 3 có tập nghiệm là A.  1  ; . B.  ;    1 . C. (2; ). D. ( ;  2  ). Lời giải Chọn B.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 7/9 - Mã đề 004  x x
Bất phương trình         2 2 3 2 3
 x x  2  x  1  .
Câu 20. [2D2-2] Tập nghiệm của bất phương trình log
x  3 1  0 có dạng a;b . Khi đó giá trị 1   3
a  3b bằng 37 A. 15 . B. 13 . C. . D. 30 . 3 Lời giải Chọn B. 1 10 log
x  3 1  0  log
x  3  1  0  x  3   3  x
. Do đó a  3b  13 1   1   3 3 3 3
Câu 21. [2D2-2] Tìm số nghiệm nguyên của bất phương trình: log x 1  3 . 3   A. 7 . B. 26 . C. 15 . D. 27 . Lời giải Chọn B. Ta có log
x 1  3  0  x  3  27  1  x  28 . 3  
Nghiệm nguyên của phương trình là 2 ; 3 ; 4 …, 26 ; 27 . Vậy có 26 nghiệm nguyên.
Câu 22. [2D2-2] Anh Nam vay tiền ngân hàng 1 tỷ đồng theo phương thức trả góp (chịu lãi số tiền chưa
trả) với lãi suất 0,5% /tháng. Nếu cuối mỗi tháng bắt đầu từ tháng thứ nhất anh Nam trả 30
triệu đồng. Hỏi sau bao nhiêu tháng anh Nam trả hết nợ? A. 35 tháng. B. 36 tháng. C. 37 tháng. D. 38 tháng. Lời giải Chọn C.
Gọi a là số tiền vay, r là lãi, m là số tiền hàng tháng trả.
Số tiền nợ sau tháng thứ nhất là N a 1 r m 1  
Số tiền nợ sau tháng thứ hai là
N  a 1 r   m  a 1 r   mr m a 1 r 2  m  1 r 1 2         ….  n  1 r  1   n  
Số tiền nợ sau n tháng là N a r m n 1  rn  1 r  1   n  
Sau n tháng anh Nam trả hết nợ: N a r m   n n 1  0 37 r
Vậy 37 tháng thì anh Nam trả hết nợ. Câu 23. [2D2-3] Tìm tất cả các giá trị của tham số m để phương trình 2
log x m  2 log x  3m 1  0 có 2 nghiệm x , x sao cho x x  27 . 3   3 1 2 1 2 4 28 A. m  . B. m  25 . C. m  . D. m  1. 3 3 Lời giải Chọn D.
Nếu đặt t  log x , khi đó ta tìm 3
t t  log x  log x  log x x  log 27  3  m  2  3  m  1. 1 2 3 1 3 2 3 1 2 3
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 8/9 - Mã đề 004
Câu 24. [2D2-4] Tìm tập hợp các giá trị của tham số thực m để phương trình 6x  3   2x mm  0 có
nghiệm thuộc khoảng 0;  1 . A. 3; 4 . B. 2; 4 . C. 2; 4 . D. 3; 4 . Lời giải Chọn C. x x 6x 3.2x
Ta có 6  3  m 2  m  0   m . 2x 1 6x  3.2x
Đặt f x  với x 0;  1 . 2x 1
6x ln 6  3.2x ln 22x  
1  6x  3.2x 2x ln 2
Ta có f  x  2x 1
6x2x ln 6  ln 2  6x ln 6  3.2x ln 2   0 x   0;1 2   2x   1
Suy ra f x đồng biến trên 0;  1 ta suy ra
yêu cầu bài toán tương đương với 2  m  4 . 2 2  b
Câu 25. [2D2-4] Tìm giá trị nhỏ nhất của biểu thức P   2 log b   6 log
 với a , b là các số a ba   a
thực thay đổi thỏa mãn b a  1. A. 30. B. 40. C. 50. D. 60. Lời giải Chọn D. 2   2 b b
Ta có P  2 log b  6 log . Đặt 2 x
 1  b a x . a b    2 a 2 aa  2 2 2 2  a x   1  Khi đó P   2 2 log a x    x   a  2 6 log 4(2 log ) 6 1  xa   a log x    a  2 2  1 
Đặt t  log x  log 1  0  P  4 t  2  6 t a a    t  2 2  1 
Xét hàm số f t   4t  2  6 t  
 với t 0;  .Ta có  t  12t   1
f t  8t  2   0  t  1 3 t
Suy ra f t  f   1  60 . Vậy 3 P
 60  log x  1  x a b a . min a
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 9/9 - Mã đề 004
TOÁN HỌC BẮC–TRUNG–NAM
KIỂM TRA CHƯƠNG 2 GIẢI TÍCH 12
Nhóm: THBTN – ĐỀ KIỂM TRA MÃ ĐỀ 005
(25 câu trắc nghiệm)
Thời gian làm bài: 45 phút, không kể thời gian phát đề. Câu 1. [2D2-1] Tính: 3 2 1 2 4 2 K  4 .2 : 2 , ta được A. 5 . B. 6 . C. 7 . D. 8 . 3 5 Câu 2.
[2D1-2] Với biểu thức  a  4   a  6 2 1 2 1
. Khi đó cơ số a phải thỏa điều kiện 1 A. a  1 .
B. 0  a  1. C. a  1. D. a  1 . 2  Câu 3.
[2D2-1] Hàm số y =  x   4 2 4 1 có tập xác định là  1 1   1 1  A.  . B. 0;  .
C.  \  ;  . D.  ;   .  2 2   2 2  e Câu 4.
[2D2-2] Tìm đạo hàm của hàm số y   2 x  2 1 trên  . e 1  
A. y  x  2 x  2 2 1 .
B. y  x x  e 2 2 e 1 . e e 1 e  C. y   2 x  2 1 .
D. y   2 x    2 2 1 ln x   1 . 2 e Câu 5.
[2D2-2] Tìm điểm cực trị của hàm số y   2 x  2 1 trên  . A. x  1  . B. x  0 . C. x  1 . D. x  2 . Lời giải Câu 6.
[2D2-1] Giá trị của biểu thức log2 3 A  4 bằng A. 6 . B. 2 . C. 12 . D. 9 . 27 Câu 7.
[2D2-2] Biết log 3  a , khi đó giá trị của log
được tính theo a là 5 3 25 3a  2 3a 3 a A. . B. . C. . D. . a 2 2a 3a  2 Câu 8.
[2D2-2] Nếu a  log 3 và b  log 5 thì 30 30
A. log 1350  2a b  2.
B. log 1350  a  2b  1. 30 30
C. log 1350  2a b  1.
D. log 1350  a  2b  2. 30 30 Câu 9.
[2D2-3] Giả sử ta có hệ thức 2 2
a b  7ab a,b  0. Hệ thức nào sau đây là đúng? a b a b A. 4 log
 log a  log b . B. log
 2 log a  log b . 2  2 2  2 2 2 6 3 a b C. 2 log
a b  log a  log b . D. 2 log
 log a  log b . 2   2 2 2 2 2 3
Câu 10. [2D2-3] Tìm tất cả các giá trị thực của tham số m để bất phương trình sau có nghiệm m log 3  x x x 12 . 3 4 x   A. m  2 3 . B. m  0 .
C. 2 3  m  12 log 5 .
D. m  12 log 5 . 3 3
Câu 11. [2D2-1] Tìm tập xác định D của hàm số y   2
log x  6x  5 .
A. D   ;   1  5;  .
B. D  1;5 .
C. D   ;   1  5;  .
D. D  1;5 .
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 1/10 - Mã đề 005
Câu 12. [2D2-2] Hàm số y =  2  2  2ex x x có đạo hàm là A. 2   ex y x . B.    2   4  4ex y x x .
C.   2 ex y x .
D.   2  2 ex y x . x  2
Câu 13. [2D2-3.2-2] Tính đạo hàm của hàm số y
tại điểm x  2 . 9x 1 1 1 1
A. y2  .
B. y2  .
C. y2  .
D. y2  . 3 5 9 2 9 2 x 3x
Câu 14. [2D2-3] Hàm số x 1 y e  
có giá trị lớn nhất trên đoạn 0;3 là: A. 2 e . B. 1. C. e . D. 3 e .
Câu 15. [2D2-4] Bạn Hùng trúng tuyển vào trường đại học A nhưng vì do không đủ nộp học phí nên
Hùng quyết định vay ngân hàng trong 4 năm mỗi năm vay 3.000.000 đồng để nộp học phí với
lãi suất 3% /năm. Sau khi tốt nghiệp đại học bạn Hùng phải trả góp hàng tháng số tiền T
(không đổi) cùng với lãi suất 0, 25% /tháng trong vòng 5 năm. Số tiền T hàng tháng mà bạn
Hùng phải trả cho ngân hàng (làm tròn đến kết quả hàng đơn vị) là: A. 309604 đồng. B. 232518 đồng. C. 232289 đồng. D. 215456 đồng. x 1
Câu 16. [2D2-1] Nghiệm của phương trình 2 1 2   0 là. 8 A. x  2 . B. x  2  . C. x  1 . D. x  1  .
Câu 17. [2D2-2] Tìm tập nghiệm S của phương trình log  2
x 10x  23  log x  5  0 . 0,5  2   A. S    7 .
B. S  2;  9 . C. S    9 .
D. S  4;  7 . x x
Câu 18. [2D2-2] Tìm tích các nghiệm của phương trình  2   1   2   1  2 2  0 . A. 0 . B. 2 . C. 1. D. 1  .
Câu 19. [2D2-3] Phương trình 3 log x  log 3x 1  0 có tổng các nghiệm bằng 3 3 A. 81. B. 3 . C. 78 . D. 84 . 2
Câu 20. [2D2-4] Tổng các nghiệm của phương trình  x   x x  2
x     x 1  2 1 .2 2 1 4 2  x  bằng A. 3 . B. 5 . C. 4 . D. 2 . 2x 1  2 x  4   4 
Câu 21. [2D2-1] Tập nghiệm của bất phương trình      là  5   5  A.  . B.  ;   1 . C. 3; . D. 1; .
Câu 22. [2D2-1] Tìm tập nghiệm của bất phương trình log  2
x  3x  2  1.  1  2 A. 0; 2 . B.  ;   1 . C. 0;  1  2;  3 .
D. 0; 2  3;7 . 2 x 3x 1  0 x2  1   1 
Câu 23. [2D2-2] Tìm số nghiệm nguyên của bất phương trình      .  3   3  A. 0 . B. 1. C. 9 . D. 11.
Câu 24. [2D2-2] Bất phương trình log x  log x  1 có nghiệm là 2 3 A. log log 6 log 2 2 6 x  3 . B. 3 x  2 . C. x  6 . D. 6 x  3 . 2 2 2
Câu 25. [2D2-4] Tìm tập hợp tất cả các giá trị của tham số m để bất phương trình sin x cos x cos 4  5  .7 x m có nghiệm. 6 6 6 6 A. m  . B. m  . C. m   . D. m   . 7 7 7 7
----------HẾT----------
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 2/10 - Mã đề 005 ĐÁP ÁN 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
D C C B B D A C D B C A D B C D A D D B D C C D A HƯỚNG DẪN GIẢI Câu 1. [2D2-1] Tính: 3 2 1 2 4 2 K  4 .2 : 2 , ta được A. 5 . B. 6 . C. 7 . D. 8 . Lời giải Chọn D. 2    3 2    2 3 2  1   2 4 2 3 2 1 2 4 2 1 2 4 2  K  4 .2 : 2  2 .2 : 2  2  8 . 3 5 Câu 2.
[2D1-2] Với biểu thức  a  4   a  6 2 1 2 1
. Khi đó cơ số a phải thỏa điều kiện 1 A. a  1 .
B. 0  a  1. C. a  1. D. a  1 . 2 Lời giải Chọn C. 3 5 1 Vì 
nên 0  2a 1  1   a  1. 4 6 2  Câu 3.
[2D2-1] Hàm số y =  x   4 2 4 1 có tập xác định là  1 1   1 1  A.  . B. 0;  .
C.  \  ;  . D.  ;   .  2 2   2 2  Lời giải Chọn C. 1
Vì hàm số xác định khi 2
4x 1  0  x   2  1 1 
Vậy TXĐ: D   \  ;  .  2 2  e Câu 4.
[2D2-2] Tìm đạo hàm của hàm số y   2 x  2 1 trên  . e e
A. y  x x   1 2 2 2 1 .
B. y  ex x   2 2 1 . e e eC. y  x   1 2 2 1 .
D. y   2 x    2 2 1 ln x   1 . 2 Lời giải Chọn B. ee e   1  1  e2 e Ta có: y   2 x    x  2 x    ex  2 x    ex  2 2 2 2 1 .2 1 1 x     1 . 2   e Câu 5.
[2D2-2] Tìm điểm cực trị của hàm số y   2 x  2 1 trên  . A. x  1  . B. x  0 . C. x  1 . D. x  2 . Lời giải Chọn B.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 3/10 - Mã đề 005 ee e   1  1  e2 e Ta có: y   2 x    x  2 x    ex  2 x    ex  2 2 2 2 1 .2 1 1 x     1 . 2  
y  0  x  0 Lập bảng xét dấu suy ra x  0 là điểm cực tiểu của hàm số. Câu 6.
[2D2-1] Giá trị của biểu thức log2 3 A  4 bằng A. 6 . B. 2 . C. 12 . D. 9 . Lời giải log2 3 2log2 3 log2 9 4  2  2  9 . 27 Câu 7.
[2D2-2] Biết log 3  a , khi đó giá trị của log
được tính theo a là 5 3 25 3a  2 3a 3 a A. . B. . C. . D. . a 2 2a 3a  2 Lời giải Chọn A. 27 2 3a  2 Ta có log
 log 27  log 25  3  2 log 5  3  
. Ta chọn đáp án A. 3 3 3 3 25 a a Câu 8.
[2D2-2] Nếu a  log 3 và b  log 5 thì 30 30
A. log 1350  2a b  2.
B. log 1350  a  2b  1. 30 30
C. log 1350  2a b  1.
D. log 1350  a  2b  2. 30 30 Lời giải Chọn C. log 1350  log  2
30.3 .5  1 2 log 3  log 5  1 2a  . b 30 30  30 30
Sử dụng Casio: *log 3  ; A log 5  . B 30 30
*log 1350  1 2a b . 30   Kết quả bằng 0. Chọn đáp án C. Câu 9.
[2D2-3] Giả sử ta có hệ thức 2 2
a b  7ab a,b  0. Hệ thức nào sau đây là đúng? a b a b A. 4 log
 log a  log b . B. log
 2 log a  log b . 2  2 2  2 2 2 6 3 a b C. 2 log
a b  log a  log b . D. 2 log
 log a  log b . 2   2 2 2 2 2 3 Lời giải Chọn D. Ta có: 2 2 a b  7 . a b .
 a b2  9ab  log a b2  log (9ab) 2 2 2 .  a b   a b   log  log (ab)  2 log
 log a  log b 2   2 2   2 2  3   3 
Câu 10. [2D2-3] Tìm tất cả các giá trị thực của tham số m để bất phương trình sau có nghiệm m log 3  x x x 12 . 3 4 x   A. m  2 3 . B. m  0 .
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 4/10 - Mã đề 005
C. 2 3  m  12 log 5 .
D. m  12 log 5 . 3 3 Lời giải Chọn B. 3   4  x  0  3   4  x  1 
Điều kiện: x  0  0  x  4 . x 12  0  4  x  0 
Nhận xét: 3  4  x  3  4  0  1  log 3  log 1  0 . 3 4 x 3 4x
x x x 12 m log 3  x x x   m
m x x x    x  x  12   12 .log 3 4 3 3 4   log 3 3 4 x
Đặt f x  x x x 12.log 3  4  x . 3    3 2  1
f  x  x
log 3  4  x x x x 12 .   3      2 2 x 12 
3 4 xln3.2 4 x
Vì f  x  0 , x
  0; 4  f x tăng trên 0; 4  tập giá trị của f x là 0;12 .
Bất phương trình có nghiệm  m  0 .
Câu 11. [2D2-1] Tìm tập xác định D của hàm số y   2
log x  6x  5 .
A. D   ;   1  5;  .
B. D  1;5 .
C. D   ;   1  5;  .
D. D  1;5 . Lời giải Chọn C. x  1 Biểu thức  2
log x  6x  5 xác định 2
x  6x  5  0   . x  5 
Câu 12. [2D2-2] Hàm số y =  2  2  2 x x x e có đạo hàm là A. 2 x y  x e . B.    2   4  4 x y x x e . C.   2 x y xe .
D.   2  2 x y x e . Lời giải Chọn A.    2 
  x   x  2    2     x x   2    2 2 2 2 2 2 2 2 2 x y x x e e x x x x e e x xx e . x  2
Câu 13. [2D2-3.2-2] Tính đạo hàm của hàm số y
tại điểm x  2 . 9x 1 1 1 1
A. y2  .
B. y2  .
C. y2  .
D. y2  . 3 5 9 2 9 Lời giải Chọn D. x  2
9x  9x.ln 9  x  2
1  x  2 ln 9 1 2  2 ln 9 1 y   y    y 2   . x 2 9 9 x 9x 2 2 9 9
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 5/10 - Mã đề 005 2 x 3x
Câu 14. [2D2-3] Hàm số x 1 y e  
có giá trị lớn nhất trên đoạn 0;3 là: A. 2 e . B. 1. C. e . D. 3 e . Lời giải Chọn B.
Tập xác định D   \   1 . 2 2 2  x 3x 2 x 3  x  3x x  2x  3 x Ta có x 1  x 1 y  .e  .e    . x 1    x  2 1 2 2 x 3xx  1 x 2x 3    0;  3 2 x 1 y  0  .e
 0  x  2x  3  0   .  x  2 1
x  30;  3  1 Mà y  
1  ; y 0  y 3  1. e 2 x 3x Vậy hàm số x 1 y e  
có giá trị lớn nhất trên đoạn 0;3 là 1.
Câu 15. [2D2-4] Bạn Hùng trúng tuyển vào trường đại học A nhưng vì do không đủ nộp học phí nên
Hùng quyết định vay ngân hàng trong 4 năm mỗi năm vay 3.000.000 đồng để nộp học phí với
lãi suất 3% /năm. Sau khi tốt nghiệp đại học bạn Hùng phải trả góp hàng tháng số tiền T
(không đổi) cùng với lãi suất 0, 25% /tháng trong vòng 5 năm. Số tiền T hàng tháng mà bạn
Hùng phải trả cho ngân hàng (làm tròn đến kết quả hàng đơn vị) là: A. 309604 đồng. B. 232518 đồng. C. 232289 đồng. D. 215456 đồng. Lời giải Chọn C.
Bạn Hùng nợ sau năm thứ nhất là:
3000000.1 0, 03  3000000.1, 03
Bạn Hùng nợ sau năm thứ hai là:       2
3000000 3000000.1, 03 . 1 0, 03  3000000.1, 03  3000000.1, 03
Bạn Hùng nợ sau năm thứ ba là: 2 3
3000000.1, 03  3000000.1, 03  3000000.1, 03
Bạn Hùng nợ sau năm thứ tư là: 2 3 4
3000000.1, 03  3000000.1, 03  3000000.1, 03  3000000.1, 03
Vậy sau 4 năm bạn Hùng nợ ngân hàng số tiền là: N  
4  3  2 3000000 1, 03
    12927407, 43 .  
Lúc này ta coi như bạn Hùng nợ ngân hàng khoản tiền ban đầu là 12.927.407, 43 đồng.
số tiền này bắt đầu được tính lãi và được trả góp trong 5 năm với lãi suất 0, 25% / tháng .
Tháng thứ nhất Hùng còn nợ ngân hàng là:
N.1 0, 0025  T N.1, 0025  T
Tháng thứ hai Hùng còn nợ ngân hàng là:  NT     2 .1, 0025
. 1 0, 0025  T N.1.0025  T.1, 0025  T
Tháng thứ ba Hùng còn nợ ngân hàng là:  2 NTT     3 2 .1.0025 .1, 0025
. 1 0, 0025  T N.1.0025  T .1, 0025  T .1, 0025  T
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 6/10 - Mã đề 005
Tháng thứ tư Hùng còn nợ ngân hàng là: 4 3 2
N.1.0025  T.1, 0025  T.1, 0025  T.1, 0025  T
………………………………
Tháng thứ sáu mươi Hùng còn nợ ngân hàng là: 60 59 2
N.1.0025  T.1, 0025 ..........  T .1, 0025  T .1, 0025  T
Vì Hùng trả dần trong 5 năm nên 60 tháng Hùng trả hết nợ do đó ta có: 60 59 2
N.1.0025  T.1, 0025 ..........  T .1, 0025  T .1, 0025  T  0 60 59 2  N.1.0025
T.1, 0025 ..........  T.1, 0025  T .1, 0025  T 60 1.0025 1 60  N.1.0025  T 1, 0025 1 60
N.1.0025 .1, 0025   1  T   60 1.0025   1  T  232289 . x 1
Câu 16. [2D2-1] Nghiệm của phương trình 2 1 2   0 là. 8 A. x  2 . B. x  2  . C. x  1 . D. x  1  . Lời giải Chọn D. x 1 Ta có 2 1 2 x 1  3 2   0  2  2  x  1 . 8
Câu 17. [2D2-2] Tìm tập nghiệm S của phương trình log  2
x 10x  23  log x  5  0 . 0,5  2   A. S    7 .
B. S  2;  9 . C. S    9 .
D. S  4;  7 . Lời giải Chọn A. 2
x 10x  23  0 Điều kiện:   x  5 . x  5  0 
Phương trình tương đương.  log  2
x 10x  23  log x  5  0 2  2  
 log  x  5  log  2 x 10x  23 2 2  2
x  5  x 10x  23 2
x 11x  28  0  x  4 (l)
 x  7 (n)  Vậy S    7 . x x
Câu 18. [2D2-2] Tìm tích các nghiệm của phương trình  2   1   2   1  2 2  0 . A. 0 . B. 2 . C. 1. D. 1  . Lời giải Chọn D.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 7/10 - Mã đề 005 x x x x Vì  2   1 . 2   1
 1 . Đặt t =  2  
1 ( t  0 ) suy ra:    1 2 1  . t 1
Khi đó, phương trình trở thành: t   2 2  0 . t  t    x 1   2   1 2 1 2 x  1        . t       x x  1 1 2 1 2  1 2  
Câu 19. [2D2-3] Phương trình 3 log x  log 3x 1  0 có tổng các nghiệm bằng 3 3 A. 81. B. 3 . C. 78 . D. 84 . Lời giải Chọn D. x  0 x  0 Điều kiện:     x  1 . log x  0 x  1  3 
3 log x  log 3x 1  0  3 log x  1 log x 1  0 . 3 3 3  3 
  log x  3 log x  2  0 . 3 3
Đặt t  log x t  0 . 3   t  1  log x  1   3 x 3 Ta có 2 t   3t  2  0       . t  2   x  81 log x  2   3
Vậy tổng các nghiệm bằng 84 . 2
Câu 20. [2D2-4] Tổng các nghiệm của phương trình  x   x x  2
x     x 1  2 1 .2 2 1 4 2  x  bằng A. 3 . B. 5 . C. 4 . D. 2 . Lời giải Chọn B.  2
x  2 x x  2
x     x 1  2 1 .2 2 1 4 2
x    x   x x  2 x   x 2 1 .2 2 1  2.2  4x . x   2    x x x   x  2 2 2 1 2.2 2 x 1 2x x   2
x x    x  2 2 2 1 2 x  2x   1 . 2
x  2x 1  0  1   . 2x  2x 2   x  1 2 PT   1   .  x  1 2 
PT 2 :2x  2     2x x f x  2x  0 . Xét hàm số    2x f x  2x .    2x f x ln 2  2 . x  2 
f  x  0  2 ln 2  2  0  x  log có 1 nghiệm. 2    ln 2 
f x  0 có không quá 2 nghiệm. Mà nhẩm thấy x  1, x  2 là 2 nghiệm của PT f x  0 .
Vậy tổng các nghiệm của phương trình đã cho là: 1 2 1 2 1 2  5 .
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 8/10 - Mã đề 005 2x 1  2 x  4   4 
Câu 21. [2D2-1] Tập nghiệm của bất phương trình      là  5   5  A.  . B.  ;   1 . C. 3; . D. 1; . Lời giải Chọn D. 2x 1  2 x  4   4  
 2x 1  2  x x  1     .  5   5 
Câu 22. [2D2-1] Tìm tập nghiệm của bất phương trình log  2
x  3x  2  1.  1  2 A. 0; 2 . B.  ;   1 . C. 0;  1  2;  3 .
D. 0; 2  3;7 . Lời giải Chọn C. 0  x  3 2 2 
x  3x  2  2 
x  3x  0  0  x  1 log  2
x  3x  2  1       x  1  1  2 2 
x  3x  2  0 
x  3x  2  0 2  x  3 2    x  2 
Vậy tập nghiệm của bất phương trình là: 0;  1  2;  3 . 2 x 3x 1  0 x2  1   1 
Câu 23. [2D2-2] Tìm số nghiệm nguyên của bất phương trình      .  3   3  A. 0 . B. 1. C. 9 . D. 11. Lời giải Chọn C. 2  2
x  3x 10  0 x 3x 1  0 x2  1   1   2   
x  3x 10  x  2      x  2  0  3   3 
x 3x 10    x  22 2  .
x  2  x  5   x  2  5  x  14 x  14 
Vì x nguyên nên x 5;6;7;8;9;10;11;12;1 
3 , do đó số nghiệm nguyên là 9.
Câu 24. [2D2-2] Bất phương trình log x  log x  1 có nghiệm là 2 3 A. log log 6 log 2 2 6 x  3 . B. 3 x  2 . C. x  6 . D. 6 x  3 . Lời giải Chọn D.
Ta có log x  log x  1  log x  log 2.log x  1. 2 3 2 3 2
 1 log 2 .log x  1. 3  2  log 6.log x  1. 3 2 1  log x   log 3 . 2 6 log 6 3  log 3 log 2 6 x  2  6 x  3 .
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 9/10 - Mã đề 005 2 2 2
Câu 25. [2D2-4] Tìm tập hợp tất cả các giá trị của tham số m để bất phương trình sin x cos x cos 4  5  .7 x m có nghiệm. 6 6 6 6 A. m  . B. m  . C. m   . D. m   . 7 7 7 7 Lời giải Chọn A. 2 2 cos x cos x 2 2 2 x x x  1   5  Ta có sin cos cos 4  5  . m 7  4    m     .  28   7  t t  1   5  Đặt 2 t  cos , x t 0;  1 thì BPT trở thành: 4    m     .  28   7  t t  1   5 
Xét f t   4.   
  là hàm số nghịch biến trên 0;  1 .  28   7  6 Suy ra: f  
1  f t   f 0 
f t   5 . 7 6
Từ đó BPT có nghiệm  m  . 7
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 10/10 - Mã đề 005
TOÁN HỌC BẮC–TRUNG–NAM
KIỂM TRA CHƯƠNG 2 GIẢI TÍCH 12
Nhóm: THBTN – ĐỀ KIỂM TRA MÃ ĐỀ 006
(25 câu trắc nghiệm)
Thời gian làm bài: 45 phút, không kể thời gian phát đề. Câu 1.
[2D2-1] Viết biểu thức a a a  0 về dạng lũy thừa của a là 5 1 3 1 A. 4 a . B. 4 a . C. 4 a . D. 2 a . Câu 2.
[2D2-2] Trong các khẳng định sau đây, khẳng định nào sai?  2  2  2  2 A. 0, 0  1  10 . B. 0, 0  1  10 . 2  2 C. 0,  1  10 . D. 0 a  1, a   0 . Câu 3.
[2D2-1] Tập xác định của hàm số 2017 y  (2x 1) là  1   1  1  A. D   . B. D  ;    . C. D  ;     . D. D  \    2   2   2  1 Câu 4.
[2D2-2] Hàm số y   x  3 1 có đạo hàm là 1 1  x  2 3 1  x  3 1 A. y  . B. y  . C. y  . D. y  3  x  2 3 1 3  x  3 1 3 3 ln x Câu 5.
[2D2-2] Đồ thị hàm số y
có tọa độ điểm cực đại là a;b . Khi đó ab bằng x A. e . B. 2e . C. 1. D. 1  . log 4 Câu 6.
[2D2-1] Cho a  0 , a  1, giá trị của biểu thức a a bằng bao nhiêu? A. 16 . B. 4 . C. 8 . D. 2 . Câu 7.
[2D2-2] Cho log 6  a . Khi đó giá trị của log 18 được tính theo a là 2 3 a 2a 1 A. a . B. . C. 2a  3 . D. . a 1 a 1 Câu 8.
[2D2-2] Cho log 5  a , log 5  b . Khi đó log 5 tính theo a và b là 2 3 6 1 ab A. . B. .
C. a b . D. 2 2 a b . a b a b Câu 9. [2D2-3] Cho , a b  0 và 2 2
a b  7ab . Khẳng định nào sau đây là khẳng định đúng?  a b
A. 2 log a b  log a  log b . B. 4 log
 log a  log b   .  6   a b  1  a b C. log   
log a  logb . D. log  3  
log a  log b .  3  2  3 
Câu 10. [2D2-3] Cho hàm số   2 2 x sin 2 .3 x f x
. Khẳng định nào sau đây là khẳng định đúng?
A. f x 2
 1  x ln 4  sin x ln 3  0 .
B. f x  1  2x  2sin x log 3  0 . 2
C. f x 2
 1  x log 2  sin x  0 .
D. f x 2
 1  2  x log 3  0 . 3 2
Câu 11. [2D2-1] Với giá trị nào của x thì biểu thức: f x  log  2 2x x xác định? 6 
A. 0  x  2 . B. x  2 . C. 1   x  1. D. x  3 .
Câu 12. [2D2-2] Đạo hàm của hàm số 2 4 x y  là A. 2 2.4 x y  ln 4 . B. 2 4 x y  .ln 2 . C. 2 4 x y  ln 4 . D. 2 2.4 x y  ln 2
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 1/9 - Mã đề 006
Câu 13. [2D2-2] Cho hàm số f x  log  2
x  2x . Tập nghiệm S của phương trình f  x  0 là 3  A. S    1 .
B. S  1 2 .
C. S  0;  2 .
D. S    1 .  1 
Câu 14. [2D2-3] Giá trị lớn nhất và giá trị nhỏ nhất của hàm số x 2
y  2xe  2x x trên đoạn  ; 2  là 2    max y  4e  8 max y  0 2 max y  4e  8 2 max y  4e  8  1   1   ;2   1  1    ;2         2   ;2  ;2  2         A.   2   2   . B.  .C.  . D.  . min y  0 1 5  min y    min y  0  min y  0   1   1  1    ;2    1    e 4  ;2  ;2 2    ;2         2   2 2     
Câu 15. [2D2-4] Bạn Duy Anh trúng tuyển vào đại học nhung vì không đủ nộp tiền học phí Duy Anh
quyết định vay ngân hàng trong 4 năm mỗi năm 3.000.000 đồng để nộp học với lãi suất
3% /năm. Sau khi tốt nghiệp đại học Duy Anh phải trả góp hàng tháng số tiền T (không đổi)
cùng với lãi suất 0, 25% /tháng trong vòng 5 năm. Số tiền T mà Duy Anh phải trả cho ngân
hàng (làm tròn đến hàng đơn vị) là A. 232518 đồng. B. 309604 đồng. C. 215456 đồng. D. 232289 đồng. 2
Câu 16. [2D2-1] Số nghiệm của phương trình 2x 7x5 2  1 là A. 2 . B. 0 . C. 3 . D. 1.
Câu 17. [2D2-2] Phương trình log  2
x  2x  3  2 log
x 1 có nghiệm là 2  4   A. x  4 . B. x  1 .
C. x  4; x  1 . D. x  2 .
Câu 18. [2D2-2] Phương trình 9x 3.3x
 2  0 có hai nghiệm x , x với x x . Giá trị A  2x  3x là 1 2 1 2 1 2 A. 2 log 3. B. 1. C. 3log 2 . D. 4 log 2 . 2 3 3 4 x
Câu 19. [2D2-3] Phương trình 2 2
log x  7 log 4x  10  0 có hai nghiệm x , x với x x . Giá trị 1 A  là 4 4 1 2 1 2 x2 1 1 A. . B. 16 . C. 64 . D. . 4 16 log 4 x2  3
Câu 20. [2D2-1] Biết rằng phương trình  x 2 2     
 4. x  2 có hai nghiệm x , x x x . 2  1 2  1
Tính 2x x . 1 2 A. 1. B. 3 . C. 5  . D. 1  . x 1
Câu 21. [2D2-1] Tìm tập nghiệm S của bất phương trình 1 5   0 . 5
A. S  1;   .
B. S  1;   . C. S   2  ;    .
D. S  ; 2 .
Câu 22. [2D2-1] Tập nghiệm của bất phương trình: log
x  3  1 có dạng a;b . Khi đó giá trị a  3b bằng 1   3 37 A. 15 . B. 13 . C. . D. 30 . 3 2 x 1  0 2 x x  1 
Câu 23. [2D2-2] Bất phương trình 3 4 2   
có bao nhiêu nghiệm nguyên dương?  2  A. 2 . B. 4 . C. 6 . D. 3 .
Câu 24. [2D2-2] Tập nghiệm của bất phương trình 2 log 4x  3  log 2x  3  2 là 3   1   3  3   3   3  A. S   ;3  .
B. S   ;3 .
C. S   ;  3 . D. S  ;3  . 8      8   4 
Câu 25. [2D2-3] Tìm m để bất phương trình 1 log  2 x   1  log  2
mx  4x m thỏa mãn với mọi x   . 5 5  A. 1   m  0 . B. 1   m  0 .
C. 2  m  3 .
D. 2  m  3 .
----------HẾT----------
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 2/9 - Mã đề 006 ĐÁP ÁN 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
C B A A C A D B C A A A A D D A A C C D C B D D C HƯỚNG DẪN GIẢI Câu 1.
[2D2-1] Viết biểu thức a a a  0 về dạng lũy thừa của a là 5 1 3 1 A. 4 a . B. 4 a . C. 4 a . D. 2 a . Lời giải Chọn C. 1 3 1 3 . 2 2 2 4 a a  . a a aa . Câu 2.
[2D2-2] Trong các khẳng định sau đây, khẳng định nào sai?  2  2  2  2 A. 0, 0  1  10 . B. 0, 0  1  10 . 2  2 C. 0,  1  10 . D. 0 a  1, a   0 . Lời giải Chọn B.  2 2 2  2 A đúng vì 0,  01  10  10 2 2  1   2 C đúng vì 0,  1   10    10  D đúng vì 0 a  1, a   0 . Câu 3.
[2D2-1] Tập xác định của hàm số 2017 y  (2x 1) là  1   1  1  A. D   . B. D  ;    . C. D  ;     . D. D  \    2   2   2  Lời giải Chọn A. Vì 2007 
  nên hàm số xác định với mọi x . 1 Câu 4.
[2D2-2] Hàm số y   x  3 1 có đạo hàm là 1 1  x  2 3 1  x  3 1 A. y  . B. y  . C. y  . D. y  3  x  2 3 1 3  x  3 1 3 3 Lời giải Chọn A. 1 1 2 1  1  1
y   x   1
y   x   1   . x   1 3 3 1   x   3 1  3 3 3  x  2 3 1 . ln x Câu 5.
[2D2-2] Đồ thị hàm số y
có tọa độ điểm cực đại là a;b . Khi đó ab bằng x A. e . B. 2e . C. 1. D. 1  . Lời giải Chọn C.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 3/9 - Mã đề 006 1 ln x y  2 x 1 1
y  0  x e y   . a b  . e  1 . e e log 4 Câu 6.
[2D2-1] Cho a  0, a  1 , giá trị của biểu thức a a bằng bao nhiêu? A. 16 . B. 4 . C. 8 . D. 2 . Lời giải Chọn A. log 4 1 2 log 4 a 2 2log 4 log 4 2 a a a aaaa  4  16. . Câu 7.
[2D2-2] Cho log 6  a . Khi đó giá trị của log 18 được tính theo a là 2 3 a 2a 1 A. a . B. . C. 2a  3 . D. . a 1 a 1 Lời giải Chọn D. 1
Ta có: a  log 6  log (2.3)  1 log 3  log 2  2 2 2 3 a 1 1 2a 1 Suy ra 2
log 18  log (2.3 )  log 2  2   2  . 3 3 3 a 1 a 1 Câu 8.
[2D2-2] Cho log 5  a , log 5  b . Khi đó log 5 tính theo a và b là 2 3 6 1 ab A. . B. .
C. a b . D. 2 2 a b . a b a b Lời giải Chọn B. 1 1 1 log 5.log 5 ab log 5    2 3   . 6 log 6 log (2.3) log 2  log 3 log 5  log 5 a b 5 5 5 5 2 3 Câu 9. [2D2-3] Cho , a b  0 và 2 2
a b  7ab . Khẳng định nào sau đây là khẳng định đúng?  a b
A. 2 log a b  log a  log b . B. 4 log
 log a  log b   .  6   a b  1  a b C. log   
log a  logb . D. log  3  
log a  log b .  3  2  3  Lời giải Chọn C.
a b ab  a b2  ab  a b2 2 2 7 9 log  log 9ab .  a b2 log
 log 9  log a  log b  a b2 log
 log 9  log a  log b 2  a b a b  log
 log a  log b    2 log
 log a  log b  3  3 a b 1  log 
log a  log b . 3 2
Câu 10. [2D2-3] Cho hàm số   2 2 x sin 2 .3 x f x
. Khẳng định nào sau đây là khẳng định đúng?
A. f x 2
 1  x ln 4  sin x ln 3  0 .
B. f x  1  2x  2sin x log 3  0 . 2
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 4/9 - Mã đề 006
C. f x 2
 1  x log 2  sin x  0 .
D. f x 2
 1  2  x log 3  0 . 3 2 Lời giải Chọn A.      2 2 x sin x f x  2 1 ln 2 .3
 ln1  x ln 4  sin x ln 3  0 .
Câu 11. [2D2-1] Với giá trị nào của x thì biểu thức: f x  log  2 2x x xác định? 6 
A. 0  x  2 . B. x  2 . C. 1   x  1. D. x  3 . Lời giải Chọn A.
f x  log  2 2x x xác định khi 2
2x x  0  0  x  2 . 6 
Câu 12. [2D2-2] Đạo hàm của hàm số 2 4 x y  là A. 2 2.4 x y  ln 4 . B. 2 4 x y  .ln 2 . C. 2 4 x y  ln 4 . D. 2 2.4 x y  ln 2 Lời giải Chọn A.    2x  2 4  2.4 x y ln 4 .
Câu 13. [2D2-2] Cho hàm số f x  log  2
x  2x . Tập nghiệm S của phương trình f  x  0 là 3  A. S    1 .
B. S  1 2 .
C. S  0;  2 .
D. S    1 . Lời giải Chọn A. 2x  2 y 
. y  0  2x  2  0  x  1.  2 x  2x ln 3  1 
Câu 14. [2D2-3] Giá trị lớn nhất và giá trị nhỏ nhất của hàm số x 2
y  2xe  2x x trên đoạn  ; 2  là 2   
max y  4e  8 max y  0 2
max y  4e  8 2
max y  4e  8  1   1   ;2   1  1    ;2         2   ;2  ;2  2         A.   2   2   . B.  .C.  . D.  . min y  0 1 5  min y    min y  0  min y  0   1   1  1    ;2    1    e 4  ;2  ;2 2    ;2         2   2 2      Lời giải Chọn D. Cách 1: Tự luận   2 x  2 x  2  2 x y e xe
x e 2  2x  2  2x
  2  2  x y x e   1  x   y 
   x x e   1 0 2 2 1  0   x  0  y 0  0  1  3 1 y   2 e     2  4 y   2 2  4e  8
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 5/9 - Mã đề 006 1
Cách 2: Sử dụng chức năng MODE 7 của máy tính Casio với thiết lập Start  End 2 Step 2 1 2  2 19
Quan sát bảng giá trị F X  ta thấy giá trị lớn nhất F X  có thể đạt được là f   2
2  21.556  4e  8.
Ta thấy giá trị nhỏ nhất F X  có thể đạt được là f   3 1.05  9.95.10  0. .
Câu 15. [2D2-4] Bạn Duy Anh trúng tuyển vào đại học nhung vì không đủ nộp tiền học phí Duy Anh
quyết định vay ngân hàng trong 4 năm mỗi năm 3.000.000 đồng để nộp học với lãi suất
3% /năm. Sau khi tốt nghiệp đại học Duy Anh phải trả góp hàng tháng số tiền T (không đổi)
cùng với lãi suất 0, 25% /tháng trong vòng 5 năm. Số tiền T mà Duy Anh phải trả cho ngân
hàng (làm tròn đến hàng đơn vị) là A. 232518 đồng. B. 309604 đồng. C. 215456 đồng. D. 232289 đồng. Lời giải Chọn D.
+ Tính tổng số tiền mà Duy Anh nợ sau 4 năm học:.
Sau 1 năm số tiền Duy Anh nợ là 3  3r  31 r  2
Sau 2 năm số tiền Duy Anh nợ là 31 r   31 r  .
Tương tự: Sau 4 năm số tiền Duy Anh nợ là
  r4    r3    r2 3 1 3 1 3 1
 31 r   12927407, 43  A .
+ Tính số tiền T mà Duy Anh phải trả trong 1 tháng:.
Sau 1 tháng số tiền còn nợ là A Ar T A1 r   T . 2
Sau 2 tháng số tiền còn nợ là A1 r   T   A1 r   T r T A1 r   T 1 r  T   . 60 59 58
Tương tự sau 60 tháng số tiền còn nợ là A1 r  T 1 r   T 1 r  T 1 r   T
Duy Anh trả hết nợ khi và chỉ khi.
A  r 60 T   r 59  T   r 58 1 1 1
 T 1 r   T  0
A   r 60 T   r 59    r 58 1 1 1
  1 r  1  0   60 1 r60 1
A1 r   T  0 1 r 1 60 1 r60 1
Ar 1 r 60
A1 r   T  0  T   T  232.289 . r 1 r60 1 2
Câu 16. [2D2-1] Số nghiệm của phương trình 2x 7x5 2  1 là A. 2 . B. 0 . C. 3 . D. 1. Lời giải Chọn A. x  1 2 2x 7 x5 2 2 1 2x 7x 5 0        5 .  x   2
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 6/9 - Mã đề 006
Câu 17. [2D2-2] Phương trình log  2
x  2x  3  2 log
x 1 có nghiệm là 2  4   A. x  4 . B. x  1 .
C. x  4; x  1 . D. x  2 . Lời giải Chọn A. 2
x  2x  3  0 Điều kiện   x  3 x  1  0  log  2
x  2x  3  2log  x   1  log  2
x  2x  3  log x  1 2 4 2  2   2 2
x  2x  3  x 1  x  3x  4  0  x  1  (L)   x  4 (N )   S    4 .
Câu 18. [2D2-2] Phương trình 9x 3.3x
 2  0 có hai nghiệm x , x với x x . Giá trị A  2x  3x là 1 2 1 2 1 2 A. 2 log 3. B. 1. C. 3log 2 . D. 4 log 2 . 2 3 3 Lời giải Chọn C. x  log 2 x x 2 3 9  3.3  2  0  
A  2x  3x  3log 2 . x  0 1 2 3  1
Câu 19. [2D2-3] Phương trình 2 2
log x  7 log 4x  10  0 có hai nghiệm x , x với x x . Giá trị 4 4 1 2 1 2 4 x1 A  là x2 1 1 A. . B. 16 . C. 64 . D. . 4 16 Lời giải Chọn C. 2 2
log x  7 log 4x  10  0 2
 4 log x  7 log x  3  0 4 4 4 4 log x  1 4  x  4 3   3   4
3  x  4 , x  4 .  1 2 log x   4 4  4 x  4  log 4 x2  3
Câu 20. [2D2-1] Biết rằng phương trình  x 2 2     
 4. x  2 có hai nghiệm x , x x x . 2  1 2  1
Tính 2x x . 1 2 A. 1. B. 3 . C. 5  . D. 1  . Lời giải Chọn D.
Điều kiện x  2 . log 4log x2 3
Phương trình thành  x  2 2 2 
  4.x  2   log x2
x  2  x  log2x 2   x  3 2 . 2 4.
2 hay  x  2 2
  4.x  2.
Lấy lôgarit cơ số 2 hai vế ta được log x  2 .log
x  2  log 4 x  2  2   2   2    
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 7/9 - Mã đề 006  5 log x  2  1  2   x  2 log x 2 2 log x 2          . 2   2   2 log x  2  2  2    x  6  5 5 Suy ra x
và x  6. Vậy 2x x  2.  6  1  . 1 2 2 1 2 2 x 1
Câu 21. [2D2-1] Tìm tập nghiệm S của bất phương trình 1 5   0 . 5
A. S  1;   .
B. S  1;   . C. S   2  ;    .
D. S  ; 2 . Lời giải Chọn C. x 1 1 x 1  1 5 0 5 5      x 1  1   x  2  . 5
Câu 22. [2D2-1] Tập nghiệm của bất phương trình: log
x  3  1 có dạng a;b . Khi đó giá trị a  3b 1   3 bằng 37 A. 15 . B. 13 . C. . D. 30 . 3 Lời giải Chọn B. x  3  0 x  3    10  log x  3  1    x  3; 1    1  10   x  3  x   3  3    3  3 a  3   
10  a  3b  13 . b    3 2 x 1  0 2 x x  1 
Câu 23. [2D2-2] Bất phương trình 3 4 2   
có bao nhiêu nghiệm nguyên dương?  2  A. 2 . B. 4 . C. 6 . D. 3 . Lời giải Chọn D. 2x 1  0 2 x x  1 3 4  2 2 2 
x  3x  4  10  2x x x  6  0  2  x  3   .  2  Do x
   x 1; 2;  3 .
Câu 24. [2D2-2] Tập nghiệm của bất phương trình 2 log 4x  3  log 2x  3  2 là 3   1   3  3   3   3  A. S   ;3  .
B. S   ;3 .
C. S   ;  3 . D. S  ;3  . 8      8   4  Lời giải Chọn D.  3 x  4x  3  0   4 3 Điều kiện:     x  2x  3  0  3  4 x     2
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 8/9 - Mã đề 006 4x  32
log 4x  32  log 2x  3  2  log  2 3 3   3 2x  3 2
16x  24x  9   9 2
 16x  24x  9  18x  27 2x  3  8 2 
 16x  42x 18  0  x   ;3  3     3  Kết luận: S  ;3  . 4   
Câu 25. [2D2-3] Tìm m để bất phương trình 1 log  2 x   1  log  2
mx  4x m thỏa mãn với mọi 5 5  x   . A. 1   m  0 . B. 1   m  0 .
C. 2  m  3 .
D. 2  m  3 . Lời giải Chọn C. 2
mx  4x m  0 
BPT thỏa mãn với mọi x      x   5   2 x   2
1  mx  4x m  m  0  m  0 m  2    2  
mx  4x m  0 2  16  4m  0   m  2     x         2  m  3 . 5  m 2
x  4x  5  m  0 5  m  0   m  5  16 
 4 5  m2  0   m  3   m  7 
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 9/9 - Mã đề 006
TOÁN HỌC BẮC–TRUNG–NAM
KIỂM TRA CHƯƠNG 2 GIẢI TÍCH 12
Nhóm: THBTN – ĐỀ KIỂM TRA MÃ ĐỀ 007
(25 câu trắc nghiệm)
Thời gian làm bài: 45 phút, không kể thời gian phát đề. 2 1    1  Câu 1.
[2D2-1] Cho a là số thực dương. Rút gọn biểu thức 2 2 P a .    2 1  a   A. 3 P a . B. 2 P a . C. 2 2 P a . D. 2 P a . Câu 2.
[2D2-2] Mệnh đề nào sau đây là đúng?  A.   1 1 1  1 . B. 0,5 0,5  e . C. 1 1   e . D.  3 0 2  0 . 1 Câu 3.
[2D2-1] Tập xác định của hàm số y    x3 1 2 là  1   1  A.  . B.  ;    . C. 0;   . D.  ;    .  2   2  4  Câu 4.
[2D2-2] Hàm số y   2  x  3 3
có đạo hàm trên khoảng  3; 3 là 7 4 7 8 A. y    2 3  x  3 . B. y x  2 3  x  3 . 3 3 7 8  7 4 C. y   x  2 3  x  3 . D. 2 y   x  2 3  x  3 3 3 Câu 5.
[2D2-2] Hàm số nào sau đây có cực trị? 1 A. 3 y x . B. 4 y x . C. 1 y x  . D. 3 y x . 0,3 10  aCâu 6.
[2D2-1] Với các số thực dương a , b bất kì, đặt M   
. Mệnh đề nào dưới đây đúng? 3 5  b  1 1 A. log M  3  log a  log b . B. log M  3  log a  log b . 2 2 C. log M  3
 log a  2 log b .
D. log M  3log a  2 log b . Câu 7.
[2D2-2] Cho log 5  a , log 6  b , log 22  c . Mệnh đề nào dưới đây đúng? 3 3 3  270   270  A. log
a 3b 2c . B. log  a 3b 2c . 3     3      121   121   270   270  C. log
a 3b 2c . D. log
a 3b 2c . 3     3      121   121  Câu 8.
[2D2-2] Với các số thực dương a , b bất kì. Mệnh đề nào dưới đây đúng? 3  a  ln b 3  a  3ln 3 A. log  log a  . B. log  log a  . 7 2   3   b 3ln 3 27 3   b ln b   3  a  ln b 3  a  3ln 3 C. log  log a  . D. log  log a  . 7 2   3   b 3ln 3 27 3   b ln b   Câu 9.
[2D2-3] Cho a , b , x là các số thực dương và khác 1 và các mệnh đề:  ab
log a  1 log x Mệnh đề (I) : log b x x . Mệnh đề (II) : log b b  . b loga a a    x  log a b
Khẳng định nào dưới đây là đúng ?
A. (II) đúng, (I) sai.
B. (I) đúng, (II) sai.
C. (I), (II) đều sai.
D. (I), (II) đều đúng.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 1/10 - Mã đề 007
Câu 10. [2D2-3] Cho hàm số   2 3x .4x f x
. Khẳng định nào sau đây sai?
A. f x 2
 9  x  2x log 2  2 .
B. f x 2
 9  x ln 3  x ln 4  2 ln 3 . 3
C. f x 2
 9  x log 3  2x  2 log 3 .
D. f x  9  2x log 3  x log 4  log 9 . 2 2
Câu 11. [2D2-1] Tìm tập xác định D của hàm số y  log  2 x  2x . 2 
A. D  0;  .
B. D   ;
 0  2;  .
C. D   ;  0 2; .
D. D   ;  0 2; .
Câu 12. [2D2-2] Đạo hàm của hàm số log ex y  1 là 2   ex 2x ln 2 2x ex ln 2 A. y  . B. y  . C. y  . D. y  . ex   1 ln 2 2x 1 2x   1 ln 2 ex 1
Câu 13. [2D2-2] Cho hàm số   2x.5x f x
. Tính giá trị của f 0 . 1
A. f 0  10 .
B. f 0  1.
C. f 0  .
D. f 0  ln10 . ln10  1 
Câu 14. [2D2-3] Cho ba số thực a , b , c  ;1   .  4   1   1   1 
Tìm giá trị nhỏ nhất P
của biểu thức P  log b   log c   log a  . min a        4 b   4 c   4  A. P  3 . B. P  6 . C. P  3 3 . D. P  1 . min min min min
Câu 15. [2D2-4] Bác Hiếu đầu tư 99 triệu đồng vào một công ty theo thể thức lãi kép với lãi suất
8, 25% một năm. Hỏi sau 5 năm mới rút tiền lãi thì bác Hiếu thu được bao nhiêu tiền lãi? (Giả
sử rằng lãi suất hàng năm không đổi). A. 48,155 triệu. B. 147,155 triệu. C. 58, 004 triệu. D. 8, 7 triệu.
Câu 16. [2D2-1] Tìm nghiệm của phương trình x 1  ln81 9  e . A. x  5 . B. x  4 . C. x  6 . D. x  17 .
Câu 17. [2D2-2] Phương trình 2 log x  log
9x  0 có 2 nghiệm là x , x ,  x x . Khi đó 3x x 1 2  3 3   1 2 1 2 bằng 28 8 A. . B. 3 . C. . D. 10 . 9 9
Câu 18. [2D2-2] Phương trình 3 log x  log 3x 1  0 có tổng các nghiệm bằng 3 3 A. 3 . B. 84 . C. 81. D. 78 .
Câu 19. [2D2-3] Phương trình log
3.2x 1  x 1 có hai nghiệm x , x thì tổng x x là 4   1 2 1 2 A. 4 . B. 2 . C. log 6  4 2 . D. 6  4 2 . 2  
Câu 20. [2D2-4] Tìm tập hợp tất cả các giá trị của tham số thực m đề phương trình log 5z 1 .log
2.5z  2  m có nghiệm thuộc khoảng 0; . 2   2    1   1  A.  ;    . B.  ;     . C.  ;
 0  2; . D. 0; 2 .  4   4 
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 2/10 - Mã đề 007 x
Câu 21. [2D2-1] Tìm tập nghiệm S của bất phương trình    1 3 1  4  2 3
A. S  1;  .
B. S  1;  .
C. S  ;  1 .
D. S   ;   1 .
Câu 22. [2D2-1] Tìm tập hợp nghiệm S của bất phương trình log    .  2 x  1
log2x 4 4 4 A. S   2  ;   1 .
B. S  2;  .
C. S  3;  2;   1 .
D. S  3; . x 1  x 1 
Câu 23. [2D2-2] Nghiệm của bất phương trình    x 1 5 2 5 2     là A. 2
  x  1 hoặc x  1. B. x  1. C. 2   x  1 . D. 3   x  1  .
Câu 24. [2D2-2] Nghiệm của bất phương trình 2 log x  log x  2  log 2x  3 là 2 1   2   2 3 3 A. x   . B. x   . 2 2 3 C. 1
  x  0 hoặc x  0 . D.   x  1  . 2
Câu 25. [2D2-4] Tìm tập hợp X gồm tất cả các giá trị của tham số thực m để bất phương trình 1 log  2 x   1  log  2
mx  4x m có tập nghiệm là .  5 5 
A. X  2;  3 .
B. X  3;5 .
C. X  2;  3 .
D. X  3;5.
----------HẾT----------
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 3/10 - Mã đề 007 ĐÁP ÁN 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
A B B B B A A A D D B A D B A A D B B D D C B C C HƯỚNG DẪN GIẢI 2 1    1  Câu 1.
[2D2-1] Cho a là số thực dương. Rút gọn biểu thức 2 2 P a .    2 1  a   A. 3 P a . B. 2 P a . C. 2 2 P a . D. 2 P a . Lời giải Chọn A. 2 1    1    P aa .      .   a   2 1   2 2 1 2 2 2 2 2 1 2 2 2 2 32 2 3 a .a a .a a 2 1  aCâu 2.
[2D2-2] Mệnh đề nào sau đây là đúng?  A.   1 1 1  1 . B. 0,5 0,5 e . C. 1 1   e . D.  3 0 2  0 . Lời giải Chọn B.
Hai đáp án A, D sai do không đúng định nghĩa lũy thừa. 1 Câu 3.
[2D2-1] Tập xác định của hàm số y    x3 1 2 là  1   1  A.  . B.  ;    . C. 0;   . D.  ;    .  2   2  Lời giải Chọn B. 1  1 
Hàm số xác định khi: 1 2x  0  x
. Vậy tập xác định là D   ;    . 2  2  4  Câu 4.
[2D2-2] Hàm số y   2  x  3 3
có đạo hàm trên khoảng  3; 3 là 7 4 7 8 A. y    2 3  x  3 . B. y x  2 3  x  3 . 3 3 7 8  7 4 C. y   x  2 3  x  3 . D. 2 y   x  2 3  x  3 3 3 Lời giải Chọn B. 4 4 7  1 4    1 4  8x
Ta có: y    2 3  x  . 2 3 3  x     2 3  x  3 . 2  x   2 3  x  3 . 3 3 3 Câu 5.
[2D2-2] Hàm số nào sau đây có cực trị? 1 A. 3 y x . B. 4 y x . C. 1 y x  . D. 3 y x . Lời giải Chọn B. 3 y x 2
y  3x  0 nên hàm số không có cực trị. 4 y x 3
y  4x có nghiệm x  0 và đạo hàm đổi dấu khi đi qua x  0 nên hàm số có cực trị
tại điểm x  0 .
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 4/10 - Mã đề 007 1  1 y x   y 
 0 nên hàm số không có cực trị. 2 x 1 2 1  1 3 y x 3  y  x
 0, x  0 nên hàm số không có cực trị. 2 3 3 3x 0,3 10  aCâu 6.
[2D2-1] Với các số thực dương a , b bất kì, đặt M   
. Mệnh đề nào dưới đây đúng? 3 5  b  1 1 A. log M  3  log a  log b . B. log M  3  log a  log b . 2 2 C. log M  3
 log a  2 log b .
D. log M  3log a  2 log b . Lời giải Chọn A. 0  ,3 0,3 10    a  10 a 3 a 3  a    1 M  3 0,5        log M  log
 log a  log b  3log a  log b   . 3 5 5 0,5 0,5  b    b b 2 3  b    Câu 7.
[2D2-2] Cho log 5  a , log 6  b , log 22  c . Mệnh đề nào dưới đây đúng? 3 3 3  270   270  A. log
a 3b 2c . B. log  a 3b 2c . 3     3      121   121   270   270  C. log
a 3b 2c . D. log
a 3b 2c . 3     3      121   121  Lời giải Chọn A. log 6  b  log
3.2  b  1 log 2  b  log 2  b 1 3 3   3 3
log 22  c  log 11.2  c  log 11 log 2  c 3 3   3 3
 log 11  c  log 2  c b 1 3 3  270  3  2.3 .5  log  log  log  3 2.3 .5  2 log 11 3  3   3   3    121  2 11  
 log 2  3  log 5  2 log 11 3 3 3
b 1 3  a  2c b   1
a  3b  2c . Câu 8.
[2D2-2] Với các số thực dương a , b bất kì. Mệnh đề nào dưới đây đúng? 3  a  ln b 3  a  3ln 3 A. log  log a  . B. log  log a  . 7 2   3   b 3ln 3 27 3   b ln b   3  a  ln b 3  a  3ln 3 C. log  log a  . D. log  log a  . 7 2   3   b 3ln 3 27 3   b ln b   Lời giải Chọn A. 3  a  ln b ln b 3 log
 log a  log b  log a   log a  . 3 3 27   3 3 3 3 3 b ln 3 3ln 3   Câu 9.
[2D2-3] Cho a , b , x là các số thực dương và khác 1 và các mệnh đề:
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 5/10 - Mã đề 007  ab
log a  1 log x Mệnh đề (I) : log b x x . Mệnh đề (II) : log b b  . b loga a a    x  log a b
Khẳng định nào dưới đây là đúng ?
A. (II) đúng, (I) sai.
B. (I) đúng, (II) sai.
C. (I), (II) đều sai.
D. (I), (II) đều đúng. Lời giải Chọn D. b 1 log x b x x  (I) đúng. b .log log a a a bab  logb    ab   x
log a  log b  log x
log a 1 log x log  b b b b b     (II) đúng. a    x  log a log a log a b b b
Câu 10. [2D2-3] Cho hàm số   2 3x .4x f x
. Khẳng định nào sau đây sai?
A. f x 2
 9  x  2x log 2  2 .
B. f x 2
 9  x ln 3  x ln 4  2 ln 3 . 3
C. f x 2
 9  x log 3  2x  2 log 3 .
D. f x  9  2x log 3  x log 4  log 9 . 2 2 Lời giải Chọn D.   2 2 2 9 3x .4x f x    9 x 2  4  3 x   x    2 log 4
log 3 x   x   2 log 4 2  x log 3 2
x log 3  x log 4  log 9 .
Câu 11. [2D2-1] Tìm tập xác định D của hàm số y  log  2 x  2x . 2 
A. D  0;  .
B. D   ;
 0  2;  .
C. D   ;  0 2; .
D. D   ;  0 2; . Lời giải. Chọn B. Hàm số xác định khi 2
x  2x  0  x  0  x  2 .
Vậy tập xác định của hàm số là D   ;
 0  2;  .
Câu 12. [2D2-2] Đạo hàm của hàm số  log x y e 1 là 2   x e 2x ln 2 2x x e ln 2 A. y  . B. y  . C. y  . D. y  .  x e   1 ln 2 2x 1 2x   1 ln 2 x e 1 Lời giải Chọn A. x e Ta có: y  .  x e   1 ln 2
Câu 13. [2D2-2] Cho hàm số   2x.5x f x
. Tính giá trị của f 0 . 1
A. f 0  10 .
B. f 0  1.
C. f 0  .
D. f 0  ln10 . ln10 Lời giải Chọn D.
  2x.5x 10x f x  
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 6/10 - Mã đề 007    10x f x .ln10 Vậy f   0 0  10 .ln10  ln10 .  1 
Câu 14. [2D2-3] Cho ba số thực a , b , c  ;1 
 . Tìm giá trị nhỏ nhất P của biểu thức min  4   1   1   1  P  log b   log c   log a  . a        4 b   4 c   4  A. P  3 . B. P  6 . C. P  3 3 . D. P  1 . min min min min Lời giải Chọn B. 2  1  1  1  1 Với mọi x  ; 1 2 2 
 ta có x x   x
 0  x x     4  4  2  4  1 
Lấy logarit 2 vế, ta được 2 log x  log x  (với t 0;  1 (*) t t    4   1 
Áp dụng BĐT (*) ta được: 2 log b
 log b  2 log b a    4 a a   1  2 log c
 log c  2 log c b    4 b b   1  2 log a
 log a  2 log a c    4 c c
Suy ra P  2log b  log c  log a 3  2.3 log . b log .
c log a  6  P . a b c a b c min
Câu 15. [2D2-4] Bác Hiếu đầu tư 99 triệu đồng vào một công ty theo thể thức lãi kép với lãi suất
8, 25% một năm. Hỏi sau 5 năm mới rút tiền lãi thì bác Hiếu thu được bao nhiêu tiền lãi? (Giả
sử rằng lãi suất hàng năm không đổi). A. 48,155 triệu. B. 147,155 triệu. C. 58, 004 triệu. D. 8, 7 triệu. Lời giải. Chọn A.
Áp dụng công thức lãi kép, số tiền thu được cả vốn lẫn lãi là   N T
A 1 r  , với tiền gửi : A  99 triệu đồng, lãi suất r  0, 0825 , N  5 kì. Ta được :
T  147,155 triệu đồng  số tiền lãi là T A  48,155 triệu đồng.
Câu 16. [2D2-1] Tìm nghiệm của phương trình 1  ln81 9 xe . A. x  5 . B. x  4 . C. x  6 . D. x  17 . Lời giải Chọn A.
Điều kiện : x  1. Ta có : x 1  ln81 x 1 9 e 9     81 
x 1  2  x  5 (t/m) .
Câu 17. [2D2-2] Phương trình 2 log x  log
9x  0 có 2 nghiệm là x , x ,  x x . Khi đó 3x x 1 2  3 3   1 2 1 2 bằng 28 8 A. . B. 3 . C. . D. 10 . 9 9 Lời giải
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 7/10 - Mã đề 007 Chọn D. x  0  1 x  0 x  2  log x  log 9x  0   1 
log x  1  3 . 3 3    2 3
log x  log x  2  0   3 3 log x  2 x  9  3  2 1 Khi đó 3.  9  10 . 3
Câu 18. [2D2-2] Phương trình 3 log x  log 3x 1  0 có tổng các nghiệm bằng 3 3 A. 3 . B. 84 . C. 81. D. 78 . Lời giải Chọn B. x  0 x  0 Điều kiện:     x  1 log x  0 x  1  3 
3 log x  log 3x 1  0  3 log x  1 log x 1  0 3 3 3  3 
  log x  3 log x  2  0 3 3
Đặt t  log x t  0 3   t  1  log x  1   3 x 3 Ta có 2 t   3t  2  0       t  2   x  81 log x  2   3
Vậy tổng các nghiệm bằng 84 .
Câu 19. [2D2-3] Phương trình log
3.2x 1  x 1 có hai nghiệm x , x thì tổng x x là 4   1 2 1 2 A. 4 . B. 2 . C. log 6  4 2 . D. 6  4 2 . 2   Lời giải Chọn B. x x x 1 log 3.2 1 1 3.2 1 4  2x 2 1 3.2x 1 0 2x x            6  4 2 . 4 4 Vậy x  log
6  4 2 . Ta có x x  log 6  4 2  log 6  4 2  2 . 1 2 2   2   2  
Câu 20. [2D2-4] Tìm tập hợp tất cả các giá trị của tham số thực m đề phương trình log 5z 1 .log
2.5z  2  m có nghiệm thuộc khoảng 0; . 2   2    1   1  A.  ;    . B.  ;     . C.  ;
 0  2; . D. 0; 2 .  4   4  Lời giải Chọn D.
Phương trình đã cho  log 5z 1 .log 2 5z 1   m 2   2      log 5z 1 1
  log 5z 1   . m 2   2       5z   1 5z  ln 5 Đặt log 5 z t  
1 với t  z  
 0 nên hàm t z nghịch biến. 2   5z   1 ln 2 5z   1 ln 2
m t t  
1  f t  .
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 8/10 - Mã đề 007 t   log 1  0 2 
Với z  0;  thì   t  0;1 . 0   t  log 5  1  1  2   
Khi đó YCBT  f 0  m f   1 hay 0  m  2. x
Câu 21. [2D2-1] Tìm tập nghiệm S của bất phương trình    1 3 1  4  2 3
A. S  1;  .
B. S  1;  .
C. S  ;  1 .
D. S   ;   1 . Lời giải Chọn D. x 1  x 1  2 Ta có  3   1
 4  2 3   3   1   3   1
x 1  2  x  1.
Vậy tập nghiệm của bất phương trình là S   ;   1 . .
Câu 22. [2D2-1] Tìm tập hợp nghiệm S của bất phương trình log    .  2 x  1
log2x 4 4 4 A. S   2  ;   1 .
B. S  2;  .
C. S  3;  2;   1 .
D. S  3; . Lời giải. Chọn C.
Điều kiện: 2x  4  0  x  2  . Bpt 2
x 1  2x  4 (do
 1 nên đổi chiều bất phương trình). 4 2
x  2x  3  0  x ; 
1  3;  , kết hợp với điều kiện: S  3;  2;   1 . x 1  x 1 
Câu 23. [2D2-2] Nghiệm của bất phương trình    x 1 5 2 5 2     là A. 2
  x  1 hoặc x  1. B. x  1. C. 2   x  1 . D. 3   x  1  . Lời giải Chọn B.
Điều kiện: x  1 1 Ta có 5  2  . 5  2 1 x 2  x  x x x
5  2 1   5  2 1 2 x 1   x 1    0  x  2  ;   1  1;  . x 1 x 1
Câu 24. [2D2-2] Nghiệm của bất phương trình 2 log x  log x  2  log 2x  3 là 2 1   2   2 3 3 A. x   . B. x   . 2 2 3 C. 1
  x  0 hoặc x  0 . D.   x  1  . 2 Lời giải Chọn C.  3 
TXĐ: D   ;  \     0 .  2 
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 9/10 - Mã đề 007 Khi đó, 2
log x  log  x  2  log 2x  3 2  log x  log x  2  log 2x  3 2 1 2 2   2   2 2 2
 log x  log 2x  3  log  x  2 2  log x  log
2x  3 . x  2 2 2 2 2 2     2 2 2
x  2x  7x  6  x  7x  6x  0  x   ;  7
   1;  .
So với điều kiện x  1;0  0;  .
Câu 25. [2D2-4] Tìm tập hợp X gồm tất cả các giá trị của tham số thực m để bất phương trình 1 log  2 x   1  log  2
mx  4x m có tập nghiệm là .  5 5 
A. X  2;  3 .
B. X  3;5 .
C. X  2;  3 .
D. X  3;5. Lời giải Chọn C. 1 log  2 x   1  log  2
mx  4x m 5 5   log 5 2 x   1   log  2
mx  4x m 5 5    2 
mx  4x m  0   2 2
5x  5  mx  4x m  2
mx  4x m  0    5  m 2
x  4x  5  m  0 
Để bất phương trình trên có tập nghiệm là  khi và chỉ khi: 2
mx  4x m  0 x      I  5  m 2
x  4x  5  m  0 x   
+ Trường hợp m  0 hoặc m  5 không thỏa  I  .
+ Với m  0 và m  5 m  0  0  m  5 2
  4  m  0    I   
 m  2  m  2  2  m  3 là giá trị cần tìm. 5  m  0 
m  3  m  7  
4  5  m2  0 
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 10/10 - Mã đề 007
TOÁN HỌC BẮC–TRUNG–NAM
KIỂM TRA CHƯƠNG 2 GIẢI TÍCH 12
Nhóm: THBTN – ĐỀ KIỂM TRA MÃ ĐỀ 008
(25 câu trắc nghiệm)
Thời gian làm bài: 45 phút, không kể thời gian phát đề. 5 Câu 1.
[2D2-1] Rút gọn biểu thức 3 3
Q a : a với a  0. 4 4 5 A. 3 Q a . B. 3 Q a . C. 9 Q a . D. 2 Q a . x y Câu 2.
[2D2-1] Nếu 2  3  2  3 thì kết luận nào sau đây đúng?
A. x y .
B. x y .
C. x y .
D. x y . Câu 3.
[2D2-1] Tìm tập xác định D của hàm số e y x .
A. D  ;0. B. D  . 
C. D  0;.
D. D   \   0 . Câu 4.
[2D2-2] Tính đạo hàm của hàm số 1 2x y   . x 1 2  A.      1 2x y x ln 2 . B. x 1 y 2    log 2 . C. y  . D. x 1 y 2    ln 2 . ln 2 Câu 5.
[2D2-2] Hình bên là đồ thị của ba hàm số x y a , x y b , y x y b x
y c 0  a,b, c  
1 được vẽ trên cùng một hệ trục tọa độ. x y c
Khẳng định nào sau đây là khẳng định đúng? x
A. b a c .
B. a b c . y a
C. a c b .
D. c b a 1 O x 2  a Câu 6.
[2D2-2] Cho a là số thực dương khác 2 . Tính I  log . a   4 2   1 1 A. I  . B. I  2 . C. I   . D. I  2  . 2 2 Câu 7. [2D2-2] Cho log 9  .
a Tính log 2 theo a . 6 3 a a  2 a  2 2  a A. . B. . C. . D. . 2  a a a a 1 Câu 8.
[2D2-2] Cho log a  2 và log b
. Tính I  2 log log 3a   log b 3 3   2 3 2 2 1   . 4 5 3 A. I  . B. I  4 . C. I  0 . D. I  . 4 2 Câu 9.
[2D2-3] Đường cong trong hình bên là đồ thị của một hàm số y
trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới 1
đây. Hỏi hàm số đó là hàm số nào? 2
A. y  log x .
B. y  log x . O x 2 1 2 1  C. y  log x . D. y  log 2x 2   2
Câu 10. [2D2-3] Cho a và b là hai số thực dương và a  1 . Mệnh đề nào sau đây là đúng? A. x
a b x  log a . B. x
a b x  log b . b a C. x
a b x  log b . D. x
a b  0  x  log b a a
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 1/9 - Mã đề 008
Câu 11. [2D2-1] Tìm tập xác định D của hàm số y  log  2
x  4x  3 . 3 
A. D  2  2;  1  3;2  2  .
B. D  1;3 .
C. D   ;   1  3; .
D. D   ;
 2  2  2  2; . 1
Câu 12. [2D2-2] Tính đạo hàm của hàm số y   2   4 1 x . 5 1  5 5  A. y   2 1 x  4 . B. y  x  2 1 x  4 . 4 2 5 5 5 1 C. y  x  2 1 x  4 . D. y  x  2 1 x  4 . 2 2
Câu 13. [2D2-2] Cho hàm số f x   2
ln x  2x . Chọn khẳng định đúng trong các khẳng định sau: 4 1 1
A. f  3  .
B. f 3  .
C. f 3  .
D. f 3  ln 3 3 12 3
Câu 14. [2D2-2] Cho hàm số x y ex e  
. Nghiệm của phương trình y  0 ? A. x  1  . B. x  1 . C. x  0 . D. x  ln 2 1 ab
Câu 15. [2D2-4] Xét các số thực dương a , b thỏa mãn log
 2ab a b  3 . Tìm giá trị nhỏ 2 a b nhất P
của P a  2b . min 2 10  3 2 10  5 3 10  7 2 10 1 A. P  . B. P  . C. P  . D. P  . min 2 min 2 min 2 min 2 2 xx  1 
Câu 16. [2D2-2] Gọi x , x là hai nghiệm của phương trình: 6 x 1  0  5
; khi đó x x bằng: 1 2  5  1 2   7 7 A. . B.  . C. 7  . D. 7 . 2 2
Câu 17. [2D2-2] Tìm nghiệm của phương trình log x  5  4 . 2   A. x  21. B. x  3 . C. x  11 . D. x  13 .
Câu 18. [2D2-3] Số nghiệm của phương trình x 1 9x 3    4  0 : A. n  1 . B. n  2 . C. n  3 . D. n  4 .
Câu 19. [2D2-2] Nghiệm nguyên nhỏ nhất của bất phương trình log 3  log 3  0 là: x x 3 A. x  3 . B. x  1 . C. x  2 . D. x  4 .
Câu 20. [2D2-3] Giá trị của m để phương trình x x 1 4 . m 2  
 2m  0 có hai nghiệm x , x thỏa mãn 1 2
x x  3 là 1 2 9 3 A. m  3 . B. 4 . C. m  . D. m  . 2 2 x 1
Câu 21. [2D2-1] Nghiệm của bất phương trình 2 3  là 9 A. x  4  . B. x  0 . C. x  0 . D. x  4 .
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 2/9 - Mã đề 008
Câu 22. [2D2-1] Tập nghiệm của bất phương trình 2 log x  1  là 1 2 A.  2;  . B.  2; 0  .  0; 2    C.  2; 2  . D. 0; 2 .   
Câu 23. [2D2-2] Tập nghiệm của bất phương trình x x 1  x x 1 2 2 3 3    
A. x 2;  .
B. x 2;  . C. x  ;  2 . D. 2;  .
Câu 24. [2D2-2] Bất phương trình log x  7  log
x 1 có tập nghiệm là 4   2   A. 1; 4 . B. 5; . C.  1  ; 2 . D.  ;   1 . 1
Câu 25. [2D2-4] Tìm tất cả các giá trị thực của tham số m để hàm số y   log x m 3 2m 1 x
xác định trên 2;3 .
A. 1  m  2 .
B. 1  m  2 . C. 1   m  2 . D. 1   m  2
----------HẾT----------
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 3/9 - Mã đề 008 ĐÁP ÁN 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
B A C D A B D D A B C D A A A D A A D B A B A C A LỜI GIẢI 5 Câu 1.
[2D2-1] Rút gọn biểu thức 3 3
Q a : a với a  0. 4 4 5 A. 3 Q a . B. 3 Q a . C. 9 Q a . D. 2 Q a . Lời giải Chọn B. 5 5 1 5 1 4  Ta có: 3 3 3 3 3 3 3
Q a : a a : a aa . x y Câu 2.
[2D2-1] Nếu 2  3  2  3 thì kết luận nào sau đây đúng?
A. x y .
B. x y .
C. x y .
D. x y . Lời giải Chọn A.
Vì 0  2  3  1 nên ta chọn đáp án A. Câu 3.
[2D2-1] Tìm tập xác định D của hàm số e y x .
A. D  ;0. B. D  . 
C. D  0;.
D. D   \   0 . Lời giải Chọn C.
Ta có hàm số xác định khi x  0. Câu 4.
[2D2-2] Tính đạo hàm của hàm số 1 2x y   . x 1 2  A.      1 2x y x ln 2 . B. x 1 y 2    log 2 . C. y  . D. x 1 y 2    ln 2 . ln 2 Lời giải Chọn D. Câu 5.
[2D2-2] Hình bên là đồ thị của ba hàm số x y a , x y b , x
y c 0  a,b, c   1 được vẽ trên
cùng một hệ trục tọa độ. Khẳng định nào sau đây là khẳng định đúng? y x y b x y c x y a 1 O x
A. b a c .
B. a b c .
C. a c b .
D. c b a Lời giải Chọn A. Do x y a và x
y b là hai hàm đồng biến nên , a b  1. Do x
y c nghịch biến nên c  1 . Vậy x bé nhất.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 4/9 - Mã đề 008 m  a y
Mặt khác: Lấy x m , khi đó tồn tại y , y  0 để 1 1 2  m b   y  2 Dễ thấy m m
y y a b a b ( Có thể so sánh ,
a b bằng cách kiểm tra tại x  1 đối với 1 2 hai hàm số x  , x y a y b )
Vậy b a c . 2  a Câu 6.
[2D2-2] Cho a là số thực dương khác 2 . Tính I  log . a   4 2   1 1 A. I  . B. I  2 . C. I   . D. I  2  . 2 2 Lời giải Chọn B. 2 2  a   a   a I  log  log  2 log  2 . a       4 a    2 a   2  2 2 2 Câu 7. [2D2-2] Cho log 9  .
a Tính log 2 theo a . 6 3 a a  2 a  2 2  a A. . B. . C. . D. . 2  a a a a Lời giải Chọn D. 2 2 2  a Ta có: log 9  2 log 3  a   log 2 1   log 2  . . 6 2.3 log 2.3 3 a 3 a 3 1 Câu 8.
[2D2-2] Cho log a  2 và log b
. Tính I  2 log log 3a   log b 3 3   2 3 2 2 1   . 4 5 3 A. I  . B. I  4 . C. I  0 . D. I  . 4 2 Lời giải Chọn D. 1 1 Ta có 2
log a  2  a  3  9 và 2 log b   b  2  2 . 3 2 2 1 3
I  2 log log 3.9  log    22  2  . 3 3 1 2 2 4 Câu 9.
[2D2-3] Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở
bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào? y 1 2 O x 1 
A. y  log x .
B. y  log x . C. y  log x . D. y  log 2x 2   2 1 2 2 Lời giải Chọn A.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 5/9 - Mã đề 008  1 
Nhận thấy đây là đồ thị hàm số y  log x . Điểm
; 1 thuộc đồ thị hàm số nên a    2  1  1 1 1 1 1   log  a   
a  2 . Hàm số là y  log x . a 2 2 a 2 2
Câu 10. [2D2-3] Cho a và b là hai số thực dương và a  1 . Mệnh đề nào sau đây là đúng? A. x
a b x  log a . b B. x
a b x  log b . a C. x
a b x  log b . a D. x
a b  0  x  log b a Lời giải Chọn B.
Câu 11. [2D2-1] Tìm tập xác định D của hàm số y  log  2
x  4x  3 . 3 
A. D  2  2;  1  3;2  2  .
B. D  1;3 .
C. D   ;   1  3; .
D. D   ;
 2  2  2  2; . Lời giải Chọn C. x  1 Điều kiện 2
x  4x  3  0   . x  3  1
Câu 12. [2D2-2] Tính đạo hàm của hàm số y   2   4 1 x . 5 1  5 5  A. y   2 1 x  4 . B. y  x  2 1 x  4 . 4 2 5 5 5 1 C. y  x  2 1 x  4 . D. y  x  2 1 x  4 . 2 2 Lời giải Chọn D.
Các hàm số đã cho có dạng y  u x 
 (với u x 2
 1 x và  1  / 4 ) 1  5 5      y   1 1 2 1 x     2 1 x   2
1 x   x  2 4 4 1 x  4 . 4 2  
Câu 13. [2D2-2] Cho hàm số f x   2
ln x  2x . Chọn khẳng định đúng trong các khẳng định sau: 4 1 1
A. f  3  .
B. f 3  .
C. f 3  .
D. f 3  ln 3 3 12 3 Lời giải Chọn A.  2  x  2x 2x  2 4
f  x    f  3  . 2 2 x  2x x  2x 3
Câu 14. [2D2-2] Cho hàm số x y ex e  
. Nghiệm của phương trình y  0 ? A. x  1  . B. x  1 . C. x  0 . D. x  ln 2
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 6/9 - Mã đề 008 Lời giải Chọn A. xx
y ex e
y  e e . Suy ra   0  x ye e  0  x  1 . 1 ab
Câu 15. [2D2-4] Xét các số thực dương a , b thỏa mãn log
 2ab a b  3 . Tìm giá trị nhỏ 2 a b nhất P
của P a  2b . min 2 10  3 2 10  5 3 10  7 2 10 1 A. P  . B. P  . C. P  . D. P  . min 2 min 2 min 2 min 2 Lời giải Chọn A.
Điều kiện: ab  1. 1 ab Ta có log
 2ab a b  3  log 2 1 ab   2 1 ab  log
a b a b * . 2 2       2      a b
Xét hàm số y f t   log t t trên khoảng 0;  . 2 1
Ta có f t   1  0, t
  0 .Suy ra hàm số f t  đồng biến trên khoảng 0;  . t.ln 2 b  2
Do đó, *  f 21 ab  f a b  21 ab  a b a 2b  
1  2  b a    . 2b  1 b  2
P a  2b
 2b g b . 2b  1 5 5 10 10  2 gb   2  0  2b 1   2b 1   b  (vì b  0 ). 2  2 2b   1 2 2 4  10  2  2 10  3
Lập bảng biến thiên ta được Pg    . min  4  2   2 xx  1 
Câu 16. [2D2-2] Gọi x , x là hai nghiệm của phương trình: 6 x 1  0  5
; khi đó x x bằng: 1 2  5  1 2   7 7 A. . B.  . C. 7  . D. 7 . 2 2 Lời giải Chọn D. 2 xx  1  6 x 1  0 2 b  5 x x 6 x 1  0   5  5  2
x  7x 10  0  x x    7 5  1 2   a
Câu 17. [2D2-2] Tìm nghiệm của phương trình log x  5  4 . 2   A. x  21. B. x  3 . C. x  11 . D. x  13 . Lời giải Chọn A.
Điều kiện: x  5 . Phương trình log
x  5  log 16  x  5  16  x  21. 2   2
Câu 18. [2D2-3] Số nghiệm của phương trình x 1 9x 3    4  0 : A. n  1 . B. n  2 . C. n  3 . D. n  4 .
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 7/9 - Mã đề 008 Lời giải Chọn A. 3x  1  x 1 9x 3    4  0  2 3 x 3.3x   4  0  x   3  4 . 3x  4 
Câu 19. [2D2-2] Nghiệm nguyên nhỏ nhất của bất phương trình log 3  log 3  0 là: x x 3 A. x  3 . B. x  1 . C. x  2 . D. x  4 . Lời giải Chọn D.
Cách 1: Điều kiện: x  0; x  1; x  3 1  log x  0 0  x  1 3 log 3  log 3  0   0   x x   log . x log x 1 log x  1 x  3 3 3  3   3  Cách 2:
Loại B, A vì x  1; x  3
Loại C vì x  2  log 3  log 3  0 Vậy chọn đáp án. D. 2 2 3
Câu 20. [2D2-3] Giá trị của m để phương trình x x 1 4 . m 2  
 2m  0 có hai nghiệm x , x thỏa mãn 1 2
x x  3 là 1 2 9 3 A. m  3 . B. 4 . C. m  . D. m  . 2 2 Lời giải Chọn B. Đặt 2x t
, điều kiện t  0 . Phương trình đã cho trở thành 2
t  2mt  2m  0 (1). Ta có 1xx2 2  8 1 x x2  2 .2  8 .
Vậy phương trình (1) phải có hai nghiệm dương t ,t sao cho t .t  8 . 1 2 1 2 2   0
m  2m  0   Điều kiện t
  t  0  2m  0  m  4 . 1 2 t  .t  8 2m  8  1 2  x 1
Câu 21. [2D2-1] Nghiệm của bất phương trình 2 3  là 9 A. x  4  . B. x  0 . C. x  0 . D. x  4 . Lời giải Chọn A. x 1 2 x2 2 3   3  3  x  2  2   x  4 . 9
Câu 22. [2D2-1] Tập nghiệm của bất phương trình 2 log x  1  là 1 2 A.  2;  . B.  2; 0  . C.  2; 2  . D. 0; 2 .  0; 2       Lời giải Chọn B .
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 8/9 - Mã đề 008 2 x  0  x  0 x  0  Ta có 2 1 log x  1       
x   2; 0  0; 2  . . 1  1 2  2    x x 2      2 x 2      2    2 
Câu 23. [2D2-2] Tập nghiệm của bất phương trình x x 1  x x 1 2 2 3 3    
A. x 2;  .
B. x 2;  . C. x   ;  2 . D. 2;  . Lời giải Chọn A. x  3  9 x 4 x x 1  x x 1 2 2 3 3     3.2 .3x        x  2 3  2  4
Câu 24. [2D2-2] Bất phương trình log x  7  log
x 1 có tập nghiệm là 4   2   A. 1; 4 . B. 5; . C.  1  ; 2 . D.  ;   1 . Lời giải Chọn C.
Điều kiện x  1 
Ta có log  x  7  log  x   1  log x  7  log x 1  log x  7  2 log x 1 2   2   2 4 2   2   2
 log  x  7  log  x  2 1
x  7   x  2 1 (do cơ số
a  2 lớn hơn 1, hàm số 2 2
y  log x đồng biến) a 2
x x  6  0  3  x  2
Kết hợp với điều kiện suy ra 1   x  2 . 1
Câu 25. [2D2-4] Tìm tất cả các giá trị thực của tham số m để hàm số y   log x m xác 3 2m 1 x định trên 2;3 .
A. 1  m  2 .
B. 1  m  2 . C. 1   m  2 . D. 1   m  2 Lời giải Chọn A.
2m 1 x  0 x  2m 1 Hàm số xác định     x m  0 x m  
Suy ra, tập xác định của hàm số là D   ; m 2m   1 , với m  1  . m  2 m  2
Hàm số xác định trên 2;3 suy ra 2;3  D     2m 1  3 m  1  
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 9/9 - Mã đề 008
TOÁN HỌC BẮC–TRUNG–NAM
KIỂM TRA CHƯƠNG 2 GIẢI TÍCH 12
Nhóm: THBTN – ĐỀ KIỂM TRA MÃ ĐỀ 008
(25 câu trắc nghiệm)
Thời gian làm bài: 45 phút, không kể thời gian phát đề. 1 4 4 1   3 3 3 3 a b a b     Câu 1.
[2D2-1] Cho các số thực dương a , b . Khi đó biểu thức bằng 3 3 a b 1 1 2 2
A. a b. B. 3 3 a b . C. a . b D. 3 3 a b . m n Câu 2.
[2D2-2] Cho m , n thoả mãn  5  2    5  2 . Khi đó ta có A. m  . n B. m  . n C. m  . n D. m  . n 1 Câu 3.
[2D2-1] Tập xác định của hàm số y   2  x 3 4 là A. 0; . B. . C.  2  ; 2. D.  ;  2. 4 Câu 4.
[2D2-2] Đạo hàm của hàm số y   2 x x  3 2 3 là 1 1 4 A.  2 x x  3 2 3 . B.  2
x  2x  33 . 3 1 4 1  8 C.  2
x  2x  3 3 .
D. x   1  2
x  2x  33 . 3 3 1 Câu 5.
[2D2-2] Số cực trị của hàm số 3
y x x là A. 0. B. 1. C. 2. D. 3. Câu 6.
[2D2-1] Cho 0  a  1, b   . Rút gọn biểu thức 2 4
log b  log b ta được 2 a a A. 4 log . b B. 6 log . b C. 4 log b . D. 6 log b . a a a a Câu 7.
[2D2-2] Biết a  log 3, khi đó log 27 bằng 5 15 3a 2a 4a 1 4a 1 A. . B. . C. . D. . 1 a 1 a 1 a 2a 1 Câu 8.
[2D2-2] Đặt a  log 3, b  log 5. Khi đó log 675 bằng 2 2 2 A. 3a  2 . b B. 2a  3 . b C. a  3 . b D. 3a  . b Câu 9.
[2D2-3] Cho các số thực dương a , b thỏa mãn a b và 2 2
a  3ab b  0. Trong các đẳng
thức sau, đẳng thức nào đúng ln a  ln b ln a  ln b
A. ln a b  .
B. ln a b  . 2 3 ln a  ln b ln a  ln b
C. ln 2a  2b  .
D. ln a b  . 2 2
Câu 10. [2D2-3] Cho hai số thực ,
m n thỏa mãn 2m 2n
. Khẳng định nào sau đấy đúng A. log  3
m  3m   log  3 n  3n . B. log  3
m  3m   log  3 n  3n . 1 1  1 1  2 2 2 2 C. log  3
m  3m   log  3 n  3n . D. log  3
m  3m   log  3 n  3n . 1 1  1 1  2 2 2 2
Câu 11. [2D2-1] Tập xác định của hàm số y  log  2 2x x là 5  A. 0; . B. . C. 0;2. D. 0; 2.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 1/8 - Mã đề 009
Câu 12. [2D2-2] Đạo hàm của hàm số  2x  .ex y x 2x A. x 1  x x 1 2 e . x e    .
B. 2x ln 2     1 ex x
. C. 2x     1 ex x . D.     1 ex x . ln 2
Câu 13. [2D2-2] Tìm tất cả các khoảng đồng biến của hàm số y  log  2 x  2x  3 2  A. 1; . B.  ;   1 . C. 0; . D.  ;  2.
Câu 14. [2D2-3] Gọi M , m lần lượt là giá trị lớn nhất, nhỏ nhất của hàm số 3 e x 3ex y    4 trên 1 
;1 . Khi đó M m bằng 1 3 A. 3 e  3e  4. B. 3 e  3e  6. C. 3 e  3e  2. D.   6. 3 e e
Câu 15. [2D2-4] Một người gửi ngân hàng 100 triệu đồng theo thể thức lãi kép định kì liên tục, với lãi
suất không đổi mỗi năm. Sau 5 năm thì thu được cả vốn lẫn lãi là 200 triệu đồng. Hỏi người
đó muốn thu được 300 triệu đồng khi gửi 100 triều đồng thì cần bao nhiêu năm A. 7. B. 8. C. 9. D. 10 2 1
Câu 16. [2D2-1] Số nghiệm của phương trình x 2  9 x là 3x A. 0. B. 1. C. 2. D. 3.
Câu 17. [2D2-2] Số nghiệm của phương trình log  x  
1  log  x  3 2 1 là 2 8 A. 0. B. 1. C. 2. D. 3.
Câu 18. [2D2-2] Tổng các nghiệm của phương trình 16x 10.4x  16  0 là A. 10. B. 16. C. 2. D. 6.
Câu 19. [2D2-3] Tích các nghiệm của phương trình log .
x log x  4  log x  4 log x là 2 3 3 2 A. 83. B. 54. C. 4. D. 60.
Câu 20. [2D2-4] Số nghiệm của phương trình 3   1 .2x x  3x 1 là A. 0. B. 1. C. 2. D. 3. 2 x x 1
Câu 21. [2D2-1] Tập nghiệm của bất phương trình 3 1 2  là 2 A. 1;2. B. 1;3. C.  
;1  2;. D. 2; .
Câu 22. [2D2-1] Tập nghiệm của bất phương trình log 2x  2  1  là 1   2 A.  1  ; 0. B. 0  ;1 . C.  ;  0. D.  1  ; . 2
Câu 23. [2D2-2] Tập nghiệm của bất phương trình x x2 x2 3  9 là A. 2;3. B.  2  ;3. C.  3  ; 2. D. 1;3.
Câu 24. [2D2-2] Khoảng  ;
a b là tập nghiệm của bất phương trình log x 1  log x  3 . Khi đó 5     5 2 2 a b bằng A. 29. B. 27. C. 34. D. 30.
Câu 25. [2D2-3] Tìm tất cả các giá trị của tham số m để bất phương trình  2
log x x  6  x < log  x  2  m có tập nghiệm chứa 3; 4 A. m  3 B. m  4 C. m  5 D. m  6
----------HẾT----------
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 2/8 - Mã đề 009 ĐÁP ÁN 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
A B C D B C A A A B D B A B B C B C B C C A A C B LỜI GIẢI 1 4 4 1   3 3 3 3 a b a b     Câu 1.
[2D2-1] Cho các số thực dương a , b . Khi đó biểu thức bằng 3 3 a b 1 1 2 2
A. a b. B. 3 3 a b . C. a . b D. 3 3 a b . Lời giải Chọn A. 1 4 4 1   3 3 3 3 1 1 a b a b   3 3 a b   a b   a b 1 1 3 3 a b 3 3 a b m n Câu 2.
[2D2-2] Cho m , n thoả mãn  5  2    5  2 . Khi đó ta có A. m  . n B. m  . n C. m  . n D. m  . n Lời giải Chọn B. m n
Ta có 0  5  2  1 nên  5  2    5  2  m n 1 Câu 3.
[2D2-1] Tập xác định của hàm số y   2  x 3 4 là A. 0; . B. . C.  2  ; 2. D.  ;  2. Lời giải Chọn C.
Hàm số trên xác định khi 2 4  x  0  2   x  2 4 Câu 4.
[2D2-2] Đạo hàm của hàm số y   2 x x  3 2 3 là 1 1 4 A.  2 x x  3 2 3 . B.  2
x  2x  33 . 3 1 4 1  8 C.  2
x  2x  3 3 .
D. x   1  2
x  2x  33 . 3 3 Lời giải Chọn D. 1 1 4  y   8 2
x  2x  3 . 2
x  2x  3   x   1  2 3
x  2x  33 3 3 1 Câu 5.
[2D2-2] Số cực trị của hàm số 3
y x x là A. 0. B. 1. C. 2. D. 3. Lời giải Chọn B. TXĐ: 0;
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 3/8 - Mã đề 009 2 1  1 3 y  1 x  1 3 2 3 3 x 1
y  0  x  3 3
Lập bảng xét dấu y 1 x 0  3 3 y  0 
Suy ra hàm số có một điểm cực trị Câu 6.
[2D2-1] Cho 0  a  1, b   . Rút gọn biểu thức 2 4
log b  log b ta được 2 a a A. 4 log . b B. 6 log . b C. 4 log b . D. 6 log b . a a a a Lời giải Chọn C. 4 2 4
log b  log b  2 log b
log b  4 log b 2 a a 2 a a a Câu 7.
[2D2-2] Biết a  log 3, khi đó log 27 bằng 5 15 3a 2a 4a 1 4a 1 A. . B. . C. . D. . 1 a 1 a 1 a 2a 1 Lời giải Chọn A. log 27 3log 3 3a 5 5 log 27    15 log 15 1 log 3 1 a 5 5 Câu 8.
[2D2-2] Đặt a  log 3, b  log 5. Khi đó log 675 bằng 2 2 2 A. 3a  2 . b B. 2a  3 . b C. a  3 . b D. 3a  . b Lời giải Chọn A. log 675  log  3 2 3 .5
 3log 3  2 log 5  3a  2b 2 2  2 2 Câu 9.
[2D2-3] Cho các số thực dương a , b thỏa mãn a b và 2 2
a  3ab b  0. Trong các đẳng
thức sau, đẳng thức nào đúng ln a  ln b ln a  ln b
A. ln a b  .
B. ln a b  . 2 3 ln a  ln b ln a  ln b
C. ln 2a  2b  .
D. ln a b  . 2 2 Lời giải Chọn A.
a ab b
 a b2  ab  a b2 2 2 3 0 ln  ln ab ln a  ln b
 2 ln a b  ln a  ln b  ln a b  2
Câu 10. [2D2-3] Cho hai số thực ,
m n thỏa mãn 2m 2n
. Khẳng định nào sau đấy đúng A. log  3
m  3m   log  3 n  3n . B. log  3
m  3m   log  3 n  3n . 1 1  1 1  2 2 2 2
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 4/8 - Mã đề 009 C. log  3
m  3m   log  3 n  3n . D. log  3
m  3m   log  3 n  3n . 1 1  1 1  2 2 2 2 Lời giải Chọn B.
2m  2n m n
Xét hàm số f t  3  t  3t f t 2
 3t  3  0 với t  
Suy ra hàm số f t  là hàm số đồng biến trên  ;  
Mà m n f m  f n 3 3
m  3m n  3n  log  3
m  3m  log  3 n  3n 1 1  2 2
Câu 11. [2D2-1] Tập xác định của hàm số y  log  2 2x x là 5  A. 0; . B. . C. 0;2. D. 0; 2. Lời giải Chọn D. Hàm số xác định khi 2
2x x  0  0  x  2
Câu 12. [2D2-2] Đạo hàm của hàm số  2x  . x y x e 2x A. x 1  x x 1 2 e . x e    .
B. 2x ln 2     1 x x
e . C. 2x     1 x x e . D.     1 x x e . ln 2 Lời giải Chọn B.
 2x ln 2   . x   2x ln   x  . x   2x ln 2     1 . x y x e x e x e x e
Câu 13. [2D2-2] Tìm tất cả các khoảng đồng biến của hàm số y  log  2 x  2x  3 2  A. 1; . B.  ;   1 . C. 0; . D.  ;  2. Lời giải Chọn A. TXĐ:  2x  2 y   2
x  2x  3ln 2
Hàm số đồng biến khi y '  0  x  1
Câu 14. [2D2-3] Gọi M , m lần lượt là giá trị lớn nhất, nhỏ nhất của hàm số 3x   3 x y e e  4 trên 1 
;1 . Khi đó M m bằng 1 3 A. 3 e  3e  4. B. 3 e  3e  6. C. 3 e  3e  2. D.   6. 3 e e Lời giải Chọn B.   Đặt x
t e x   1 1;1  t  ; ee   
Hàm số trở thành y f t  3
t  3t  4
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 5/8 - Mã đề 009  1  t  1 ;e   e    f t 2
 3t  3 ; f 't 0     1  t  1 ; e   e      1  1 3 f    4   3  e e e f e 3
e  3e  4 f   1  2 Suy ra 3
M e  3e  4, m  2
Câu 15. [2D2-4] Một người gửi ngân hàng 100 triệu đồng theo thể thức lãi kép định kì liên tục, với lãi
suất không đổi mỗi năm. Sau 5 năm thì thu được cả vốn lẫn lãi là 200 triệu đồng. Hỏi người
đó muốn thu được 300 triệu đồng khi gửi 100 triều đồng thì cần bao nhiêu năm A. 7. B. 8. C. 9. D. 10 Lời giải Chọn B.
Gọi r là lãi suất một năm
Số tiền người đó thu được khi gửi 100 triệu sau 5 năm là   5 100 1 r Ta có    r5 5 200 100. 1  r  2 1 n n
Số tiền người đó thu được sau n năm gửi 100 triệu vào ngân hàng là   r  5 100. 1 100. 2  n Theo giả thiết 5 100.
2   300  n  8 2 1
Câu 16. [2D2-1] Số nghiệm của phương trình x 2  9 x là 3x A. 0. B. 1. C. 2. D. 3. Lời giải Chọn C. x  0 2 2 1 x 2xx 2 x 4 x 2 2 9 3 3 x 2x 4x 2x 3x 0             x 3 3  x   2
Câu 17. [2D2-2] Số nghiệm của phương trình log  x  
1  log  x  3 2 1 là 2 8 A. 0. B. 1. C. 2. D. 3. Lời giải Chọn B. 2 x 1  0  ĐK :   x  1   x  3 1  0  log  x  
1  log  x  3 2 1  log  2 x 1  log x 1 2 8 2  2   x  1  2 2
x 1  x 1  x x  2  0   x  2 
Suy ra PT có một nghiệm x  2
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 6/8 - Mã đề 009
Câu 18. [2D2-2] Tổng các nghiệm của phương trình 16x 10.4x  16  0 là A. 10. B. 16. C. 2. D. 6. Lời giải Chọn C.  1 x x     x x      x 2 4 2 x 2 16 10.4 16 0 4 10.4 16  0     4x  8 3  x   2
Câu 19. [2D2-3] Tích các nghiệm của phương trình log .
x log x  4  log x  4 log x là 2 3 3 2 A. 83. B. 54. C. 4. D. 60. Lời giải Chọn B. ĐK: x  0 log x  1  x  2 log .
x log x  4  log x  4 log x  log x 1 log x  4  0 2   2 3 3 2  2  3    log x  3 x  27  3 
Câu 20. [2D2-4] Số nghiệm của phương trình 3   1 .2x x  3x 1 là A. 0. B. 1. C. 2. D. 3. Lời giải Chọn C. 1 Kiểm tra x
không phải là nghiệm của PT 3 1 Với x  3 x x x 3 1 3x  
1 .2  3x 1  2  3x 1  1   1  Hàm số 2x y
là hàm số đồng biến trên mỗi khoảng ;   và ;     3   3  3x 1  1   1  Hàm số y
là hàm số nghịch biến trên mỗi khoảng ;   và ;    3x 1  3   3   1   1 
Suy ra trên mỗi khoảng ;   và ;  
 PT có tối đa 1 nghiệm  3   3 
Ta thấy x  1 là nghiệm của PT
Vậy phương trình có 2 nghiệm x  1 2 x x 1
Câu 21. [2D2-1] Tập nghiệm của bất phương trình 3 1 2  là 2 A. 1;2. B. 1;3. C.  
;1  2;. D. 2; . Lời giải Chọn C. 2 2  x x x 1 1 3 1 x 3x 1  1 2 2 2   2  2
x  3x 1  1
  x  3x  2  0   2 x  2 
Câu 22. [2D2-1] Tập nghiệm của bất phương trình log 2x  2  1  là 1   2
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 7/8 - Mã đề 009 A.  1  ; 0. B. 0  ;1 . C.  ;  0. D.  1  ; . Lời giải Chọn A. log 2x  2  1
  0  2x  2  2  1   x  0 1   2 2
Câu 23. [2D2-2] Tập nghiệm của bất phương trình x x2 x2 3  9 là A. 2;3. B.  2  ;3. C.  3  ; 2. D. 1;3. Lời giải Chọn B. 2 2 x x2 x2 x x2 2 x4 2 2 3  9  3  3
x x  2  2x  4  x x  6  0  2   x  3
Câu 24. [2D2-2] Khoảng  ;
a b là tập nghiệm của bất phương trình log x 1  log x  3 . Khi đó 5     5 2 2 a b bằng A. 29. B. 27. C. 34. D. 30. Lời giải Chọn C. ĐK: x  3 log  x   1  log
x  3  log  x  
1  2 log  x  3  log  x  
1  log  x  32 5 5 5 5 5 5
x    x  2 2 1 3
x  7x 10  0  2  x  5
Kết hợp điều kiện, suy ra 3  x  5 Suy ra 2 2
a  3,b  5  a b  34
Câu 25. [2D2-3] Tìm tất cả các giá trị của tham số m để bất phương trình  2
log x x  6  x < log  x  2  m có tập nghiệm chứa 3; 4 A. m  3 B. m  4 C. m  5 D. m  6 Lời giải Chọn B. 2
x x  6  0 ĐK:   x  3 x  2  0  Với ĐK trên  2
x x    x
x     m   2 log 6 < log 2 m
log x x  6  log  x  2  x 2 x x  6  m  log
x m  log  x  3  x x  2
Đặt f x  log  x  3  x
BPT có tập nghiệm chứa 3; 4  m  log  x  3  x đúng với x   3;4
Xét hàm số f x  log  x  3  x trên khoảng 3; 4 1 f ' x  1  0 với x   3;4  x  3ln10
Suy ra hàm số f x  log  x  3  x đồng biến trên 3; 4
m f x đúng với x
  3;4  m f 4  4
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 8/8 - Mã đề 009
TOÁN HỌC BẮC–TRUNG–NAM
KIỂM TRA CHƯƠNG 2 GIẢI TÍCH 12
Nhóm: THBTN – ĐỀ KIỂM TRA MÃ ĐỀ 010
(25 câu trắc nghiệm)
Thời gian làm bài: 45 phút, không kể thời gian phát đề. Câu 1.
[2D2-1] Cho m là số nguyên dương, biểu thức nào sau đây sai? A. m 2 16 4 m  . B. m m  3 16 2 . 2 m   . C. 16m 4m.2m   . D. m 4 16 2 m  . 3 1  3 5
a .a b .b Câu 2.
[2D2-2] Với a  0, b  0 . Giá trị của biểu thức A  là:    . a b 2 :  . a b 3 2  b b a a a b A. A  .
B. A a 1. C. A  1. D. A  . a b b Câu 3.
[2D2-1] Tập xác định của hàm số y   x   3 3 1 là tập:  1   1  1  A.  3  ;  . B.  ;    . C.  ;    . D. \   .  3   3  3 Câu 4.
[2D2-2] Đạo hàm của hàm số y x x 3 4 3 3 A. y   . B. y  . C. y  . D. y  . 4 4 x 4 3 x 4 x 4 4 x Câu 5. [2D2-2] Hàm số   2   1 x y x
e có bao nhiêu cực trị? A. 0 . B. 1. C. 2 . D. 3 . Câu 6.
[2D2-1] Cho a  0 và a  1. Tìm mệnh đề đúng trong các mệnh đề sau:
A. log x có nghĩa với x  .
B. log 1  a và log a  0. a a a log x C. log x y D. log x y x
y (x  0, y  0). a  .  log log a   a . log y a a a Câu 7.
[2D2-2] Với m  0 , cho a  log m với. Tính P  log
27m theo a 3 m 6  2a 6  a A. P  .
B. P  6  a. . a C. P  .
D. A  6  2a. . a a a Câu 8.
[2D2-2] Đặt a  log 3, b  log 3. Hãy biểu diễn log 45 theo a và . b 2 5 6 a  2ab 2 2a  2ab A. log 45  . B. log 45  . 6 ab 6 ab a  2ab 2 2a  2ab C. log 45  . D. log 45  . 6 ab b 6 ab b Câu 9.
[2D2-3] Khẳng định nào sau đây đúng: 1 A. 2
log a  2 log a . B. 2 2 2
log a  4 log a . C. 2 2 2
log a  4 log a . D. 2 log a  log a . 3 3 3 3 3 3 3 3 2 2 2 3 4 Câu 10. [2D2-3] Nếu 3 2 aa và log  log
thì khẳng định nào sau đây đúng? b 4 b 5
A. 0  a  1 và 0  b  1.
B. 0  a  1 và b  1.
C. a  1 và 0  b  1.
D. a  1 và b  1.
Câu 11. [2D2-2] Tìm tập xác định D của hàm số y  log  2
x  2x  1 . 3 
A. D  ;  1 .
B. D  1;  .
C. D   ;    .
D. D   ;   1  1; .
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 1/9 - Mã đề 010
Câu 12. [2D2-1] Đạo hàm f  x của hàm số   2 e x f x   là 2e A.   2e x f x    . B.    2  ex f x .
C. f  x   . D.   2 2e x f x     . x
Câu 13. [2D2-2] Cho hàm số y x ln x , khi đó đạo hàm cấp hai tại x  e là ye có giá trị bằng bao nhiêu? 1 A. e . B. 2 . C. . D. 1. e
Câu 14. [2D2-3] Bác Anh đem gửi tiết kiệm ở ngân hàng với lãi suất là 12% một năm. Biết rằng cứ sau
mỗi một quý ( 3 tháng) thì lãi được cộng dồn vào gốc. Hỏi sau tối thiểu bao nhiêu năm thì Bác
Anh nhận lại được số tiền (cả vốn lẫn lãi) gấp ba số tiền ban đầu. A. 8 năm. B. 9 năm. C. 10 năm. D. 11 năm. 2 2
Câu 15. [2D2-4] Tìm giá trị lớn nhất của sin x cos 2 2 x y   A. 3 . B. 2 . C. 4 . D. 5 . 2
Câu 16. [2D2-1] Cho phương trình x 4x5 3
 9 tổng lập phương các nghiệm thực của phương trình là A. 28. B. 27. C. 26. D. 25.
Câu 17. [2D2-2] Gọi x , x là nghiệm của phương trình log 2  log x  0 . Khi đó giá trị 1 . 2 2x x bằng 1 2 x 16 A. 1  . B. 1. C. 2 . D. 2  . x3 x 1 
Câu 18. [2D2-2] Tổng các nghiệm của phương trình: x 1  x 1 2 5 2    là A. 0 . B. 2 . C. 2  . D. 4.
Câu 19. [2D2-3] Số nghiệm của phương trình log log x  log log x  2 là 4  2  2  4  A. 0 . B. 2 . C. 3 . D. 1. x 1 
Câu 20. [2D2-4] Biết phương trình 5x.8 x  500 hai nghiệm x , x . Tính 1 . 2 5x x P  . 1 2 1 1 A. P  8 . B. P  . C. P  3 . D. P  . 8 3 2 x 1  3x 1   3   3 
Câu 21. [2D2-1] Bất phương trình      có tập nghiệm là  2   2      A. (2;5) . B. 1;2. C.  1  ;  3 . D.  ;    1 .
Câu 22. [2D2-1] Tìm tập nghiệm S của bất phương trình log 4  3x  4  . 1   2  4   4 
A. S   ;  4  . B. S  ; 2 .   C. S   ;  .   D. S  .   3   3 
Câu 23. [2D2-2] Nghiệm của bất phương trình 2x4 x 2 x2 3  45.6  9.2  0 A. x  2 . B. x  2 . C. x  2  . D. x  2  .
Câu 24. [2D2-2] Có bao nhiêu giá trị nguyên dương của x thỏa mãn bất phương trình
log  x  40  log 60  x  2 . A. 10 . B. 19 . C. 18 . D. 20 .
Câu 25. [2D2-4] Tìm tất cả các giá trị thực của tham số
m để bất phương trình log 5x 1 .log
2.5x  2  m nghiệm đúng với mọi x  1. 2   2   A. m  6 . B. m  6 . C. m  6 . D. m  6 .
----------HẾT----------
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 2/9 - Mã đề 010 ĐÁP ÁN 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
C C B D 5 D A C B B D D C C A A C C D B B A D C C HƯỚNG DẪN GIẢI Câu 1.
[2D2-1] Cho m là số nguyên dương, biểu thức nào sau đây sai? A. m 2 16 4 m  . B. m m  3 16 2 . 2 m   . C. 16m 4m.2m   . D. m 4 16 2 m  . Lời giải Chọn C. n m Ta có:  m m.n m  4  4m m 3m m 3m 2 16 2 2 2 2 .2 4 m a a         m m 2m m 3 4 .2 2 .2 2 m   . Vậy C sai. 3 1  3 5
a .a b .b Câu 2.
[2D2-2] Với a  0, b  0 . Giá trị của biểu thức A  là:    . a b 2 :  . a b 3 2  b b a a a b A. A  .
B. A a 1. C. A  1. D. A  . a b b Lời giải Chọn C. 3 1  3 5 2 2
a .a b .b a b
a ba ba b a
Với a  0, b  0 . Xét A      1 .    . a b 2 :  . a b 3 2 2  b ab b
b a bb b Câu 3.
[2D2-1] Tập xác định của hàm số y   x   3 3 1 là tập:  1   1  1  A.  3  ;  . B.  ;    . C.  ;    . D. \   .  3   3  3 Lời giải Chọn B. 1 Ta có:
không nguyên nên đkxđ của hàm số là 3x 1  0  x   3 3  1 
Suy ra tập xác định: D   ;    .  3  Câu 4.
[2D2-2] Đạo hàm của hàm số y x x 3 4 3 3 A. y   . B. y  . C. y  . D. y  . 4 4 x 4 3 x 4 x 4 4 x Lời giải Chọn D.
Áp dụng công thức:  n u n 1  . n u .u  3 1 3  3 Suy ra: 4 4 y
x x x y  .x  . 4 4 4 x Câu 5. [2D2-2] Hàm số   2   1 x y x
e có bao nhiêu cực trị? A. 0 . B. 1. C. 2 . D. 3 . Lời giải
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 3/9 - Mã đề 010 Chọn A. Ta có:   2   x x   
  2   x   2 1 2 . 1 .  2   1 . x     1 . x y x e y x e x e x x e x e  0 với x   
Nên hàm số không có cực trị. Câu 6.
[2D2-1] Cho a  0 và a  1. Tìm mệnh đề đúng trong các mệnh đề sau:
A. log x có nghĩa với x  .
B. log 1  a và log a  0. a a a log x C. log x y D. log x y x
y (x  0, y  0). a  .  log log a   a . log y a a a Lời giải Chọn D.
Ta có: log x xác định khi x  0 nên A sai a
log 1  0 và log a  1 nên B sai a a C không tồn tại log  .
x y   log x  log y (x  0, y  0). Đúng. a a a Câu 7.
[2D2-2] Với m  0 , cho a  log m với. Tính P  log
27m theo a 3 m 6  2a 6  a A. P  .
B. P  6  a. . a C. P  .
D. A  6  2a. . a a a Lời giải Chọn A. 2.log 27m 2. 3  log m 6  2a 3    3  Ta có P  log 27m    . m log m log m a 3 2 Câu 8.
[2D2-2] Đặt a  log 3, b  log 3. Hãy biểu diễn log 45 theo a và . b 2 5 6 a  2ab 2 2a  2ab A. log 45  . B. log 45  . 6 ab 6 ab a  2ab 2 2a  2ab C. log 45  . D. log 45  . 6 ab b 6 ab b Lời giải Chọn C. log 3 a a Cách 1: Ta có 2 b  log 3    log 5  5 2 log 5 log 5 b 2 2 a  2 2 log 3 .5 a  log 45 2  2log 3 log 5 a  2ab 2 2 2  log 45 b      . 6 log 6 log 2.3 1 log 3 1 a ab b 2 2   2
Cách 2: Dùng Casio: Nếu A B A B  0.
Gán log 3  A ; log 3  B . Sau đó ta thử các các phương án. 2 5 A  2 AB 2 2 A  2 AB  log 45 
 0. suy ra A loại.  log 45   0. suy ra B loại. 6 AB 6 AB A  2 AB  log 45   0. suy ra chọn. C. 6 AB B Câu 9.
[2D2-3] Khẳng định nào sau đây đúng: 1 A. 2
log a  2 log a . B. 2 2 2
log a  4 log a . C. 2 2 2
log a  4 log a . D. 2 log a  log a . 3 3 3 3 3 3 3 3 2
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 4/9 - Mã đề 010 Lời giải Chọn B. Ta có: 2
log a  2 log a nên A sai 3 3
log a  log a 2  2log a 2 2 2 2 2
 4 log a . Vậy B đúng. 3 3 3 3 2 2 3 4 Câu 10. [2D2-3] Nếu 3 2 aa và log  log
thì khẳng định nào sau đây đúng? b 4 b 5
A. 0  a  1 và 0  b  1.
B. 0  a  1 và b  1.
C. a  1 và 0  b  1.
D. a  1 và b  1. Lời giải Chọn B.  2 2  3 4       4 5 Ta có 3 2 
 0  a  1 và   b  1 . 2 2  3 4 log  log 3 2 aab   4 b 5
Câu 11. [2D2-2] Tìm tập xác định D của hàm số y  log  2
x  2x  1 . 3 
A. D  ;  1 .
B. D  1;  .
C. D   ;    .
D. D   ;   1  1; . Lời giải Chọn D.
Hàm số y  log  2
x  2x  1 xác định khi 2
x  2x 1  0  x  1 3 
Vậy TXĐ là D   ;   1  1; .
Câu 12. [2D2-1] Đạo hàm f  x của hàm số   2 x f x e  là 2e A.   2 x f x e   .
B.    2 x f xe .
C. f  x   . D.   2 2 x f x e    . x Lời giải Chọn D. Ta có:      2x 2 2 .  2 x f x x ee .
Câu 13. [2D2-2] Cho hàm số y x ln x , khi đó đạo hàm cấp hai tại x e là ye có giá trị bằng bao nhiêu? 1 A. e . B. 2 . C. . D. 1. e Lời giải Chọn C. 1 1
Ta có: y   x .ln x  . x ln x 
 ln x 1  y 
y e  . x e
Câu 14. [2D2-3] Bác Anh đem gửi tiết kiệm ở ngân hàng với lãi suất là 12% một năm. Biết rằng cứ sau
mỗi một quý ( 3 tháng) thì lãi được cộng dồn vào gốc. Hỏi sau tối thiểu bao nhiêu năm thì Bác
Anh nhận lại được số tiền (cả vốn lẫn lãi) gấp ba số tiền ban đầu. A. 8 năm. B. 9 năm. C. 10 năm. D. 11 năm. Lời giải
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 5/9 - Mã đề 010 Chọn C.
Gọi số tiền Bác Anh gửi là A , lãi suất mỗi quý là 0, 03 . n
Sau n quý, tiền mà người đó nhận được là : A1 0, 03 . n
Yêu cầu bài toán  A1 0, 03  3A n  log 3  37,16 . 1,03
Suy ra số năm tổi thiểu xấp xỉ 9, 29 năm. Vậy sau 10 năm thì Bác Anh nhận lại được số tiền thỏa ycbt. 2 2
Câu 15. [2D2-4] Tìm giá trị lớn nhất của sin x cos 2 2 x y   A. 3 . B. 2 . C. 4 . D. 5 . Lời giải Chọn A. Xét    2 2 sin x cos  2  2 x y f x Đặt 2 t  sin , x t 0;  1 . Tìm GTLN của   t 1 2 2 t y f t     trên 0;  1 . tt 1 t 1 2 ln 2 2 t y     ln 2  0 1  2  2  t  . 2  1 
f (0)  3; f (1)  3; f  2 2   .  2  Vậy max y  3 . 0;  1 2
Câu 16. [2D2-1] Cho phương trình x 4x5 3
 9 tổng lập phương các nghiệm thực của phương trình là A. 28. B. 27. C. 26. D. 25. Lời giải Chọn A. 2 2  x  1
Ta có: x 4x5 x 4 x5 2 2 2 3  9  3
 3  x  4x  5  2  x  4x  3  0  .  x  3  Suy ra 3 3 1  3  28 .
Câu 17. [2D2-2] Gọi x , x là nghiệm của phương trình log 2  log x  0 . Khi đó giá trị 1 . 2 2x x bằng 1 2 x 16 A. 1  . B. 1. C. 2 . D. 2  . Lời giải Chọn C.
Điều kiện: 0  x  1
PT  log 2  log x  0  log 2  log x  0 4 x 16 x 2 1  log 2  log x  0 x 2 4  1 log 2   x  4 x 1 1         x 2 2 log 2 1 4 1  x   2 log 2   x  4  2 Vậy x .x 1 2 x .x  1  2  2 . 1 2 x3 x 1 
Câu 18. [2D2-2] Tổng các nghiệm của phương trình: x 1  x 1 2 5 2    là:
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 6/9 - Mã đề 010 A. 0 . B. 2 . C. 2  . D. 4. Lời giải Chọn C.
Điều kiện: x  1 2 2 2 1 1 2 Phương trình  x 1  x 1  x 1 2  5  2  2.2   5  2 x 1 2  t  2 2 2 Đặt x 1 t 2  
 0 phương trình trở thành: 2 2.t 5 2t 5t 2 0         1 tt   2 2 2 Với x 1 t 2 2     2 
 1  x 1  2  x  1 1 x 1 2 1  2 Với 1 x 1 t 2     2 
 1  x 1  2  x  3  2 2 x 1
Nên x x  1 3  2 . 1 2
Câu 19. [2D2-3] Số nghiệm của phương trình log log x  log log x  2 là 4  2  2  4  A. 0 . B. 2 . C. 3 . D. 1. Lời giải Chọn D. x  0  x  1 log x  0 2   PT    1  1 . log x 0   4 log log x  log log x  2 2  2  2    2   2  2  log log x  log log x  2 2  2  2 2  2 2   x  1 x  1     1 1  3 . log log x  log  log log x  2 log log x 1  2  2  2  2 2  2   2  2   2 2  2 x  1  x  1 x  1        x  16 . log log x  2 log x  4 x  16  2  2   2  x 1 
Câu 20. [2D2-4] Biết phương trình 5x.8 x  500 hai nghiệm x , x . Tính 1 . 2 5x x P  . 1 2 1 1 A. P  8 . B. P  . C. P  3 . D. P  . 8 3 Lời giải Chọn B.
Điều kiện: x  0  . x 1  3x3 3 x3   x x 3 2 5 .8  500  5 .2
 5 .2  log 5 .x x x 2 x   log  3 2 5 .2 5 5    3x  3  x  3 2  x
.log 2  3  2 log 2  x  log 2  3 x  3log 2  0  5 5  5  1 5  x x   log 2  2 5 3 x x   1 Vậy . 3.log 2 log 2 1 2 5 P  5  5   5 5  3  2  . 8
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 7/9 - Mã đề 010 2 x 1  3x 1   3   3 
Câu 21. [2D2-1] Bất phương trình      có tập nghiệm là  2   2      A. (2;5) . B. 1;2. C.  1  ;  3 . D.  ;    1 . Lời giải Chọn B. 2 x 1  3x 1   3   3  Ta có 2 2     
x 1  3x 1  x  3x  2  0  1  x  2 .  2   2     
Câu 22. [2D2-1] Tìm tập nghiệm S của bất phương trình log 4  3x  4  . 1   2  4   4 
A. S   ;  4  . B. S  ; 2 .   C. S   ;  .   D. S  .   3   3  Lời giải Chọn A. 4
Đk: 4  3x  0  x  3 4  1  Ta có: log 4  3x  4   4  3x
 4  3x  16  x  4  . 1      2  2 4
Kết hợp điều kiện ta có : 4   x  . 3
Câu 23. [2D2-2] Nghiệm của bất phương trình 2x4 x 2 x2 3  45.6  9.2  0 A. x  2 . B. x  2 . C. x  2  . D. x  2  . Lời giải Chọn D. 2x x xx xx x x  3   3  Ta có: 2 4 2 2 2 3  45.6  9.2
 0  81.3  45.6  36.4  0  81.  45.  36  0      2   2  x  3  Đặt t  ,t  0  
. Khi đó bất phương trình trở thành  2  x 4 4  3  4 2
81t  45t  36  0  1   t   0  t     x  2    . 9 9  2  9
Câu 24. [2D2-2] Có bao nhiêu giá trị nguyên dương của x thỏa mãn bất phương trình
log  x  40  log 60  x  2 . A. 10 . B. 19 . C. 18 . D. 20 . Lời giải Chọn C.
ĐK: 40  x  60.
Ta có: log  x  40  log 60  x  2  log  x  4060  x  2   xv4060  x  100 2
 x 100x  2500  0   x  2 50  0  x  50.
Số giá trị nguyên dương thỏa bpt là 59  41  1 1  18.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 8/9 - Mã đề 010
Câu 25. [2D2-4] Tìm tất cả các giá trị thực của tham số
m để bất phương trình log 5x 1 .log
2.5x  2  m nghiệm đúng với mọi x  1. 2   2   A. m  6 . B. m  6 . C. m  6 . D. m  6 . Lời giải Chọn C.
BPT  log 5x 1 .log 2 5x 1    log 5x 1 . 1   log 5x m 1   m 2   2   2   2       Đặt log 5x t
1 do x  1  t 2; 2  
Ta được t   t  2 1
m t t m f t   m Xét hàm số   2
f t t t , t 2; 
f t  2t 1  0 với t 2;  nên hàm đồng biến trên t 2; 
 min f t   f 2  6
Do đó để để bất phương trình log 5x 1 .log
2.5x  2  m nghiệm đúng với mọi x  1thì 2   2  
m  min f t  m  6 .
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 9/9 - Mã đề 010
TOÁN HỌC BẮC–TRUNG–NAM
KIỂM TRA CHƯƠNG 2 GIẢI TÍCH 12
Nhóm: THBTN – ĐỀ KIỂM TRA MÃ ĐỀ 011
(25 câu trắc nghiệm)
Thời gian làm bài: 45 phút, không kể thời gian phát đề. 1 Câu 1. [2D2-1] Biểu thức 4 3
27 a ( với a  0 ) viết dưới dạng lũy thừa với số mũ hữu tỉ là 3 1 1 1 1 1 1 1 A. 4 12 3 .a . B. 4 2 3 .a . C. 12 9.a . D. 4 3 3 .a 3 4 1 2 Câu 2.
[2D2-1] Cho a , b là các số thực dương thỏa mãn 4 5 a a và log  log . Mệnh đề nào b 2 b 3 sau đây đúng?
A. a  1,b  1 .
B. a  1, 0  b a .
C. 0  a  1, 0  b  1 . D. 0  a  1,b  1. 1 Câu 3.
[2D2-1] Tìm x để biểu thức  2 x  3 1 có nghĩa: A. x    ;   1  1; . B. x    ;    1  1;  . C. x    1  ;  1 . D. x    \   1 . 1 Câu 4.
[2D2-2] Đạo hàm của hàm số y   2 x x  3 5 2 là 10x 1 10x 1 A. y  . B. y  . 3 2 3 5x x  2 3 2 5x x  2 10x 1 1 C. y  . D. y  . 3 2
3 5x x  22 2 3 3 5x x  2 x Câu 5.
[2D2-2] Hàm số y   2
3a 10a  2 đồng biến trên  ;   khi:  1   1   1  A. a   ;    .
B. a 3;  . C. a   ;    . D. a  ;3   .  3   3  3  1 1 Câu 6. [2D2-1] Nếu 2 6 a a và 2 3 bb thì
A. a  1; 0  b  1.
B. a  1;b  1 .
C. 0  a  1;b  1.
D. a  1;0  b  1. 0  ,2 10  aCâu 7.
[2D2-2] Cho a  0 , b  0 . Nếu viết log
x log a y log b thì xy bằng bao nhiêu? 5   5 5 6 5  b  1 1 A. 3 . B. . C.  . D. 3  . 3 3 Câu 8.
[2D2-2] Cho x, y  0 và 2 2
x  4 y  12xy . Khẳng định nào sau đây là khẳng định đúng?
x  2 y  1 A. log
 log x  log y . B. log
x  2 y  2 
log x  log y . 2    2 2  2   2 2  4  2 C. log
x  2 y  log x  log y 1. D. 4 log
x  2 y  log x  log y . 2   2   2 2 2 2 Câu 9.
[2D2-2] Cho log 3  a , log 7  b . Tính log 2016 theo a và b . 2 2 2
A. 5  2a b .
B. 5  3a  2b .
C. 2  2a  3b .
D. 2  3a  2b .
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 1/10 - Mã đề 011
Câu 10. [2D2-3] Hình bên là đồ thị của ba hàm số x y a , y x y b , x
y c 0  a,b, c  
1 được vẽ trên cùng một hệ x y b
trục tọa độ. Khẳng định nào sau đây là khẳng định đúng? x y c
A. b a c . x y a
B. a b c .
C. a c b . 1
D. c b a . O x
Câu 11. [2D2-2] ] Cho a là số thực dương khác 1. Xét hai số thực x , x . Phát biểu nào sau đây là 1 2 đúng? A. Nếu 1 x 2 x
a a thì x x . B. Nếu 1 x 2 x
a a thì a  
1  x x  0 . 1 2  1 2 C. Nếu 1 x 2 x
a a thì a  
1  x x  0 . D. Nếu 1 x 2 x
a a thì x x . 1 2  1 2
Câu 12. [2D2-1] Hàm số y  log
x xác định khi và chỉ khi: x 1  x  1 A.  . B. x  1 . C. x  0 . D. x  2 x  2 
Câu 13. [2D2-1] Cho hàm số    ex f x x
. Gọi f  x là đạo hàm cấp hai của f x . Ta có f   1 bằng A. 3e . B. 2 3  e . C. 3 e . D. 2 5  e
Câu 14. [2D2-1] Cho hàm số e e x y x   
.Nghiệm của phương trình y  0 ? A. x  1  . B. x  1 . C. x  0 . D. x  ln 2
Câu 15. [2D2-2] Tính giá trị của biểu thức P  ln tan1°  ln  tan 2  ln tan 3  ...  ln tan 89 . 1 A. P  1. B. P  . C. P  0. D. P  2. 2
Câu 16. [2D2-3] Một người mỗi tháng đều đặn gửi vào ngân hàng một khoản tiền T theo hình thức lãi
kép với lãi suất 0, 6 % mỗi tháng. Biết sau 15 tháng người đó có số tiền là 10 triệu đồng.Hỏi số
tiền T gần với số tiền nào nhất trong các số sau? A. 535000 . B. 635000 . C. 613000 . D. 643000 .
Câu 17. [2D2-1] Nghiệm của phương trình x x 1  x x 1 2 2 3 3     là 3 2 A. x  log . B. x  1 . C. x  0 . D. x  log . 3 4 4 3 2 3
Câu 18. [2D2-1] Số nghiệm của phương trình log  2 x  3  log
6x 10 1  0 là 2  2   A. Vô nghiệm. B. 1. C. 2 . D. 3 .
Câu 19. [2D2-1] Phương trình 9x 5.3x
 6  0 có tổng các nghiệm là 2 3 A. log 6 . B. log . C. log . D.  log 6 . 3 3 3 3 2 3
Câu 20. [2D2-2] Tìm số nghiệm thực của phương trình log    .   3 2 2x 2x 3x 1 x 1  A. 0 . B. 1. C. 2 . D. 3 .
Câu 21. [2D2-3] Hỏi phương trình 3.2x 4.3x 5.4x 6.5x   
có tất cả bao nhiêu nghiệm thực? A. 2 . B. 4 . C. 1. D. 3 .
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 2/10 - Mã đề 011 3 2
Câu 22. [2D2-3] Phương trình 23x x x 3 2 2
.2 1024  23x  10x x có tổng các nghiệm gần nhất với số nào dưới đây A. 0,35. B. 0, 40. C. 0,50. D. 0, 45.
Câu 23. [2D2-3] Tìm m để phương trình 2 log
x  log x m  0 có nghiệm x  0;  1 ? 2 2 1 1 A. m  1. B. m  . C. m  . D. m  1. 4 4
Câu 24. [2D2-2] Cho hàm số   2 2 x sin 2 .3 x f x
. Khẳng định nào sau đây là khẳng định đúng?
A. f x 2
 1  x ln 4  sin x ln 3  0 .
B. f x  1  2x  2sin x log 3  0 . 2
C. f x 2
 1  x log 2  sin x  0 .
D. f x 2
 1  2  x log 3  0 . 3 2 3 e x    1 ex m 1   4 
Câu 25. [2D2-4] Cho hàm số y   
. Tìm m để hàm số đồng biến trên khoảng 1; 2 .  2017  A. 3 4
3e 1  m  3e  1. B. 4 m  3e 1 . C. 2 3
3e 1  m  3e  1. D. 2 m  3e 1 .
----------HẾT----------
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 3/10 - Mã đề 011 ĐÁP ÁN 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
A D B C D A C B A A B A A A C B A B A B C D C A B LỜI GIẢI 1 Câu 1. [2D2-1] Biểu thức 4 3
27 a ( với a  0 ) viết dưới dạng lũy thừa với số mũ hữu tỉ là 3 1 1 1 1 1 1 1 A. 4 12 3 .a . B. 4 2 3 .a . C. 12 9.a . D. 4 3 3 .a Lời giải Chọn A. 1 1 1 1 1 3 1 1  1 4 1 1 4   1 1 1  4 3 3 3 4 12 4 12 4 12 27 a  27.a  27a  27 a  3 a  3 .a   . 3 3 3 3   3 4 1 2 Câu 2.
[2D2-1] Cho a , b là các số thực dương thỏa mãn 4 5 a a và log  log . Mệnh đề nào b 2 b 3 sau đây đúng?
A. a  1,b  1 .
B. a  1, 0  b a .
C. 0  a  1, 0  b  1 . D. 0  a  1,b  1. Lời giải Chọn D. 3 4 3 4 Ta có   4 5
a a nên hàm số x
y a giảm. Suy ra 0  a  1. 4 5 1 2 1 2 Và   log  log
nên hàm số y  log x tăng. Suy ra b  1. 2 3 b 2 b 3 b 1 Câu 3.
[2D2-1] Tìm x để biểu thức  2 x  3 1 có nghĩa: A. x    ;   1  1; . B. x    ;    1  1;  . C. x    1  ;  1 . D. x    \   1 . Lời giải Chọn B. 1  x  1 Biểu thức  2 x  3 1 có nghĩa 2
x 1  0   . x  1   1 Câu 4.
[2D2-2] Đạo hàm của hàm số y   2 x x  3 5 2 là 10x 1 10x 1 A. y  . B. y  . 3 2 3 5x x  2 3 2 5x x  2 10x 1 1 C. y  . D. y  . 3 2
3 5x x  22 2 3 3 5x x  2 Lời giải Chọn C.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 4/10 - Mã đề 011 1  2   1  10x 1 Ta có: y   2
5x x  2   2 3
5x x  2 3 10x   1    3  
3 5x x  22 2 3 x Câu 5.
[2D2-2] Hàm số y   2
3a 10a  2 đồng biến trên  ;   khi:  1   1   1  A. a   ;    .
B. a 3;  . C. a   ;    . D. a  ;3   .  3   3  3  Lời giải Chọn D. x 1 Hàm số y   2
3a 10a  2 đồng biến trên  ;   khi 2 3
a 10a  2  1   a  3 . 3 1 1 Câu 6. [2D2-1] Nếu 2 6 a a và 2 3 bb thì
A. a  1; 0  b  1.
B. a  1;b  1 .
C. 0  a  1;b  1.
D. a  1;0  b  1 Lời giải Chọn A. 1 1 1 1 Do  nên 2 6
a a a  1 . 2 6 Vì 2  3 nên 2 3 bb  0  b  1. 0  ,2 10  aCâu 7.
[2D2-2] Cho a  0 , b  0 . Nếu viết log
x log a y log b thì xy bằng bao nhiêu? 5   5 5 6 5  b  1 1 A. 3 . B. . C.  . D. 3  . 3 3 Lời giải Chọn C. 0,2 10 1  a     1 1 Ta có: 2 6 log  log a .b  2  log a  log b  . x y   . 5   5   5 5 6 5 6 3  b    Câu 8.
[2D2-2] Cho x, y  0 và 2 2
x  4 y  12xy . Khẳng định nào sau đây là khẳng định đúng?
x  2 y  1 A. log
 log x  log y . B. log
x  2 y  2 
log x  log y . 2    2 2  2   2 2  4  2 C. log
x  2 y  log x  log y 1. D. 4 log
x  2 y  log x  log y . 2   2   2 2 2 2 Lời giải Chọn B. Ta có:
x  4 y  12xy   x  2 y2  16xy  log  x  2y2 2 2  log 16xy 2 2 1  2 log
x  2 y  4  log x  log y  log
x  2 y  2 
log x  log y . 2   2 2 2    2 2  2 Câu 9.
[2D2-2] Cho log 3  a , log 7  b . Tính log 2016 theo a và b . 2 2 2
A. 5  2a b .
B. 5  3a  2b .
C. 2  2a  3b .
D. 2  3a  2b . Lời giải Chọn A.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 5/10 - Mã đề 011
Ta có: log 2016  log  5 2 2 3 7 5 2
 log 2  log 3  log 7  5  2a b . 2 2  2 2 2
Câu 10. [2D2-3] Hình bên là đồ thị của ba hàm số x y a , x y b , x
y c 0  a,b, c   1 được vẽ trên
cùng một hệ trục tọa độ. Khẳng định nào sau đây là khẳng định đúng? y x y b x y c x y a 1 O x
A. b a c .
B. a b c .
C. a c b .
D. c b a . Lời giải Chọn A. Do x y a và x
y b là hai hàm đồng biến nên , a b  1. Do x
y c nghịch biến nên c  1 . Vậy x bé nhất. m  a y
Mặt khác: Lấy x m , khi đó tồn tại y , y  0 để 1 1 2  m b   y  2 Dễ thấy m m
y y a b a b 1 2
Vậy b a c .
Câu 11. [2D2-2] ] Cho a là số thực dương khác 1. Xét hai số thực x , x . Phát biểu nào sau đây là 1 2 đúng? A. Nếu 1 x 2 x
a a thì x x . B. Nếu 1 x 2 x
a a thì a  
1  x x  0 . 1 2  1 2 C. Nếu 1 x 2 x
a a thì a  
1  x x  0 . D. Nếu 1 x 2 x
a a thì x x . 1 2  1 2 Lời giải Chọn B. Xét 2 trường hợp:
+) TH1: a  1. Khi đó, x x 1 2 a a
x x x x  0. 1 2  1 2 
Mà a  1  a 1  0  a  
1  x x  0. 1 2 
+) TH1: 0  a  1. Khi đó, x x 1 2 a a
x x x x  0. 1 2  1 2 
Mà a  1  a 1  0  a  
1  x x  0. . 1 2 
Câu 12. [2D2-1] Hàm số y  log
x xác định khi và chỉ khi: x 1  x  1 A.  . B. x  1 . C. x  0 . D. x  2 x  2  Lời giải Chọn A. x  0 x  0   x  1 Hàm số y  log
x xác định khi x 1  0  x  1  . x 1  x  2    x 1  1 x  2  
Câu 13. [2D2-1] Cho hàm số   x
f x xe . Gọi f  x là đạo hàm cấp hai của f x . Ta có f   1 bằng
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 6/10 - Mã đề 011 A. 3e . B. 2 3  e . C. 3 e . D. 2 5  e Lời giải Chọn A.
   . x    x   . x    x x    . x f x x e f x e x e f x e e
x e f   1  3e .
Câu 14. [2D2-1] Cho hàm số x y ex e  
.Nghiệm của phương trình y  0 ? A. x  1  . B. x  1 . C. x  0 . D. x  ln 2 Lời giải Chọn A. xx
y ex e
y  e e . Suy ra   0  x ye e  0  x  1 .
Câu 15. [2D2-2] Tính giá trị của biểu thức P  ln tan1°  ln  tan 2  ln tan 3  ...  ln tan 89 . 1 A. P  1. B. P  . C. P  0. D. P  2. 2 Lời giải Chọn C.
P  ln tan1°  ln  tan 2  ln tan 3  ... ln tan 89  ln  tan1 .  tan 2 .  tan 3 .  ..tan 89  ln  tan1 .  tan 2 .  tan 3 .  ..tan 45 .  cot 44 .  cot 43...cot1
 ln  tan 45  ln1  0.(vì tan.cot 1).
Câu 16. [2D2-3] Một người mỗi tháng đều đặn gửi vào ngân hàng một khoản tiền T theo hình thức lãi
kép với lãi suất 0, 6 % mỗi tháng. Biết sau 15 tháng người đó có số tiền là 10 triệu đồng.Hỏi số
tiền T gần với số tiền nào nhất trong các số sau? A. 535000 . B. 635000 . C. 613000 . D. 643000 . Lời giải Chọn B.
Đầu mỗi tháng khách hàng gửi vào ngân hàng số tiền A đồng với lãi kép r% một tháng thì số A n
tiền khách hàng nhận được cả vốn lẫn lãi sau n tháng  *
n    là Sr      r n 1  1 1  r   T 15 Ta có: 10.000.000  
 1 0,6% 1.1 0,6%  T  635.000 . 0,6%  
Câu 17. [2D2-1] Nghiệm của phương trình x x 1  x x 1 2 2 3 3     là 3 2 A. x  log . B. x  1 . C. x  0 . D. x  log . 3 4 4 3 2 3 Lời giải Chọn A. x x xx xx x  3  3 3 1 1 2  2  3  3  3.2  4.3    x  log   . 3  2  4 4 2
Câu 18. [2D2-1] Số nghiệm của phương trình log  2 x  3  log
6x 10 1  0 là 2  2   A. Vô nghiệm. B. 1. C. 2 . D. 3 . Lời giải Chọn B.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 7/10 - Mã đề 011
Điều kiện: x  3 . 2 2 x  3 x  3 1  x  2 Phương trình 2  log  1   
x  3x  2  0  2  6x 10 6x 10 2 x  1 
So điều kiện nhận nghiệm x  2 nên phương trình có 1 nghiệm.
Câu 19. [2D2-1] Phương trình 9x 5.3x
 6  0 có tổng các nghiệm là 2 3 A. log 6 . B. log . C. log . D.  log 6 . 3 3 3 3 2 3 Lời giải Chọn A. 9x 5.3x   6  0   1 x 2    2 1 3  5.3x 6 0 3x  5.3x        6  0 1'
t  2  N  Đặt 3x t   0 . Khi đó: 1' 2
t  5t  6  0  
t  3  N   Với  2  3x t
 2  x  log 2 . 3 Với  3  3x t
 3  x  log 3  1 . 3
Suy ra 1 log 2  log 3  log 2  log 6 . 3 3 3 3
Câu 20. [2D2-2] Tìm số nghiệm thực của phương trình log    .   3 2 2x 2x 3x 1 x 1  A. 0 . B. 1. C. 2 . D. 3 . Lời giải Chọn B. x  1  Điều kiện: 
. Ta có phương trình tương đương x  0  3 2 3 2 3 2
2x  2x  3x 1  x  3x  3x 1  x x  6x  0  x  0  x  3  x  2  .
Kết hợp với điều kiện ta có nghiệm x  3 .
Câu 21. [2D2-3] Hỏi phương trình 3.2x 4.3x 5.4x 6.5x   
có tất cả bao nhiêu nghiệm thực? A. 2 . B. 4 . C. 1. D. 3 . Lời giải Chọn C. x x x  2   3   4  pt  3.  4.  5.  6  0        5   5   5  x x x  2   3   4 
Xét hàm số f x  3.  4.  5.  6       liên tục trên  .  5   5   5  x x x  2  2  3  3  4  4
Ta có: f  x  3  ln  4   ln  5   ln  0, x           5  5  5  5  5  5
Do đó hàm số luôn nghịch biến trên  mà f 0  6  0 , f 2  22  0 nên phương trình
f x  0 có nghiệm duy nhất. 3 2
Câu 22. [2D2-3] Phương trình 23x x x 3 2 2
.2 1024  23x  10x x có tổng các nghiệm gần nhất với số nào dưới đây
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 8/10 - Mã đề 011 A. 0,35. B. 0, 40. C. 0,50. D. 0, 45. Lời giải Chọn D. 3 2 3 2 Ta có 23x x x 3 2 23x x 3 10x 2 2
.2 1024  23x  10x x  2
 23x x  2 10x Hàm số    2t f t
t đồng biến trên  nên 3 2 5  2 23x x 3 10 x 2 3 2 2
 23x x  2
10x  23x x  10x x  0 hoặc x  23 10 Tổng các nghiệm bằng  0, 4347 . 23
Câu 23. [2D2-3] Tìm m để phương trình 2 log
x  log x m  0 có nghiệm x  0;  1 ? 2 2 1 1 A. m  1. B. m  . C. m  . D. m  1. 4 4 Lời giải Chọn C. Đặt 2
t  log x PT : t t m  0, do 0  x  1  log x  0  t  0 2 2
Để phương trình đã cho có nghiệm x 0;  1 thì phương trình 2
t t m  0 có nghiệm âm   0 1   4m  0 1      m S  0 1   0 4  
Câu 24. [2D2-2] Cho hàm số   2 2 x sin 2 .3 x f x
. Khẳng định nào sau đây là khẳng định đúng?
A. f x 2
 1  x ln 4  sin x ln 3  0 .
B. f x  1  2x  2sin x log 3  0 . 2
C. f x 2
 1  x log 2  sin x  0 .
D. f x 2
 1  2  x log 3  0 . 3 2 Lời giải Chọn A.      2 2 x sin x f x  2 1 ln 2 .3
 ln1  x ln 4  sin x ln 3  0 3 x    1 x e m e 1   4 
Câu 25. [2D2-4] Cho hàm số y   
. Tìm m để hàm số đồng biến trên khoảng 1; 2 .  2017  A. 3 4
3e 1  m  3e 1. B. 4 m  3e 1 . C. 2 3
3e 1  m  3e 1. D. 2 m  3e 1 . Hướng dẫn giải Chọn B. 3 x    1 x e m e 1   4   4        .ln  . 3x     1 x y e m e   1  2017   2017  3 x    1 x e m e 1   4   4  =     .ln  . 3 3 x     1 x y e m e   2017   2017 
Hàm số đồng biến trên khoảng 1;2 3 x    1 x e m e 1   4   4       .ln  . 3 3 x     1 x y e m e   0, x   1; 2 (*),  2017   2017 
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 9/10 - Mã đề 011 3 x    1 x e m e 1   4     0 , x     mà  2017   .   4  ln    0    2017  Nên (*)  3 3 x     1 x e m e  0, x   1; 2  2 3 x e 1  , m x   1; 2  Đặt   2  3 x g x e 1, x   1; 2 ,   2  3 x g x e .2  0, x   1;2 x 1 2 g x |  |
. Vậy (*) xảy ra khi m g 2  4 m  3e 1 . g x |  |
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 10/10 - Mã đề 011