Bộ Đề Kiểm Tra Cuối HK1 Toán 9 Cánh Diều Có Đáp Án Ma Trận Đặc Tả

ĐỀ KIỂM TRA HỌC KÌ I, MÔN TOÁN LỚP 9
Thời gian làm bài: 90 phút ĐỀ 1
PHẦN I. TRẮC NGHIỆM (3 điểm)
Khoanh tròn vào chữ cái đứng trước câu trả lời đúng nhất
Câu 1. Cho bất phương trình x + 2 > 0, đâu là nghiệm của bất phương trình: A. x > -2
B. x < -2 C. x >2 D. x < 2
Câu 2. Trong các bất phương trình sau, bất phương trình bậc nhất một ẩn là: A. x-1>3x2+1 B. 3x-1>0 C. 1 x −  0 D. 0x-5<0 x
Câu 3. Căn bậc hai của 25 là A. 5 B. -5 C. 5 và -5 D. 625 và -625
Câu 4. Căn bậc ba của -64 là A. 4 và -4 B. -4 C. 3 −4 D. 3 4
Câu 5. Biểu thức x − 3 có điều kiện xác định là
A. x  3. B. x  3. C. x  3. D. x  3.
Câu 6. Kết quả của (x − )3 3 1 là A. x −1 . B. 1 − 𝑥. C. 3(𝑥 − 1). D. x - 1 3
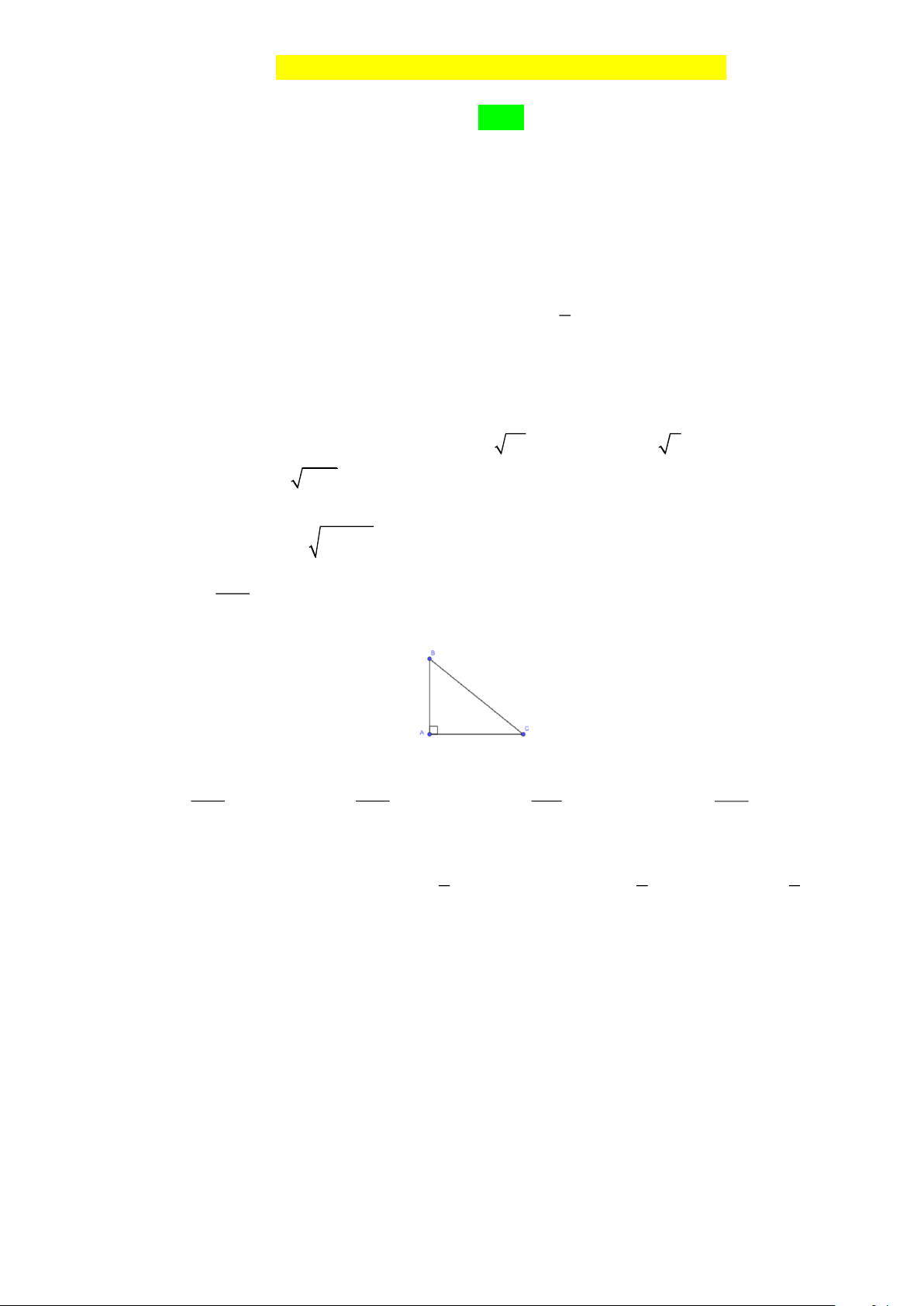
Dựa vào hình vẽ sau trả lời câu 7, câu 8:
Câu 7. Cho tam giác ABC vuông tại A, sin B là: BC AC AB AC A. . B. . C. . D. AC BC BC AB Câu 8. Cho A
 BC vuông tại A; AB = 8 và AC = 6. Khi đó 4 4 3 A. tan C = 0,75 B. tan C = D. 3 C. tan C = 5 tan C = 5
Câu 9. Khẳng định nào sau đây là đúng khi nói về trục đối xứng của đường tròn
A.Đường tròn không có trục đối xứng
B.Đường tròn có duy nhất một trục đối xứng là đường kính
C.Đường tròn có hai trục đối xứng là hai đường kính vuông góc với nhau
D.Đường tròn có vô số trục đối xứng là đường kính.
10. Số tâm đối xứng của đường tròn là: A.1 B.2 C.3 D.4
Câu 11. Trong đường tròn (O), AOB là Trang 1 A. góc nội tiếp B. góc ở tâm O C. góc tù B D. góc vuông. A
Câu 12. Khẳng định nào sau đây là sai?
A.Trong một đường tròn, góc nội tiếp chắn nửa đường tròn là góc vuông
B.Trong một đường tròn, hai góc nội tiếp bằng nhau chắn hai cung bằng nhau
C.Trong một đường tròn, hai góc nội tiếp cùng chắn một cung thì bằng nhau
D.Trong một đường tròn, hai góc nội tiếp bằng nhau thì cùng chắn một cung.
PHẦN II. TỰ LUẬN (7 điểm )
Câu 13. VDT (1,0 điểm). . Rút gọn biểu thức sau  x x  x − 9 P =  + . (x  0;x  9) x − 3 x + 3 9x  
Câu 14 (1,0 điểm). Tính a) NB. 3 81; 27
b) NB Đưa biểu thức sau ra ngoài dấu căn: 3 3 (x −1)
Câu 15. TH (1,0 điểm) Bạn Hoa có x quyển vở, bạn Lâm có y quyển vở.
Cô giáo tặng thêm mỗi bạn 10 quyển vở. Viết biểu thức biểu thị mối liên hệ số
quyển vở của hai bạn sau khi được cô giáo tặng, biết rằng ban đầu số vở bạn
Hoa nhiều hơn bạn Lâm.
Câu 16.VDT (1,0 điểm) Trục căn thức ở mẫu 7 a) (0,5 đ) 3 − 2 5 b)
với x.>0, x ≠9 (0,5 đ) x + 3
Câu 17 (1,0 điểm). VDC Hai bạn An và Bình đến một nhà sách để mua
bút và vở. Bạn An mua 5 chiếc bút và 10 quyển vở với tổng số tiền là 230 nghìn
đồng. Bạn Bình mua 10 chiếc bút và 8 quyển vở với tổng số tiền là 220 nghìn
đồng. Tính giá bán của mỗi chiếc bút và của mỗi quyển vở, biết rằng hai bạn An
và Bình mua cùng loại bút và vở. Câu 18 (1,0 điểm).
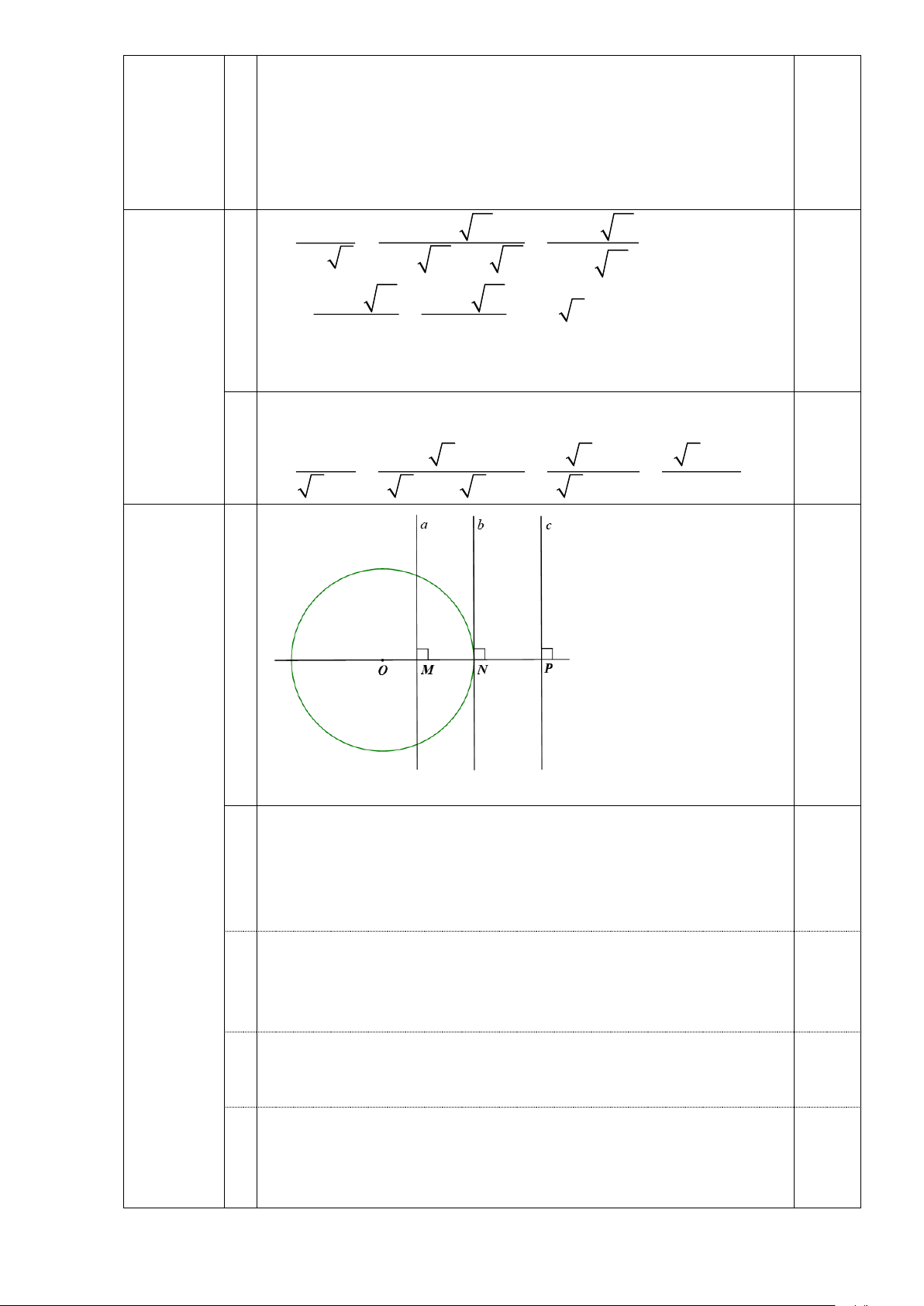
TH Cho bốn điểm O, M, N, P cùng nằm
trên một đường thẳng sao cho điểm M nằm giữa
hai điểm O và N; điểm N nằm giữa hai điểm M
và P. Gọi a, b, c lần lượt là các đường thẳng đi
qua M, N, P và vuông góc với đường thẳng OP.
Xác định vị trí tương đối của mỗi đường thẳng a,
b, c và đường tròn (O; ON). Câu 19 (1,0 điểm). Trang 2
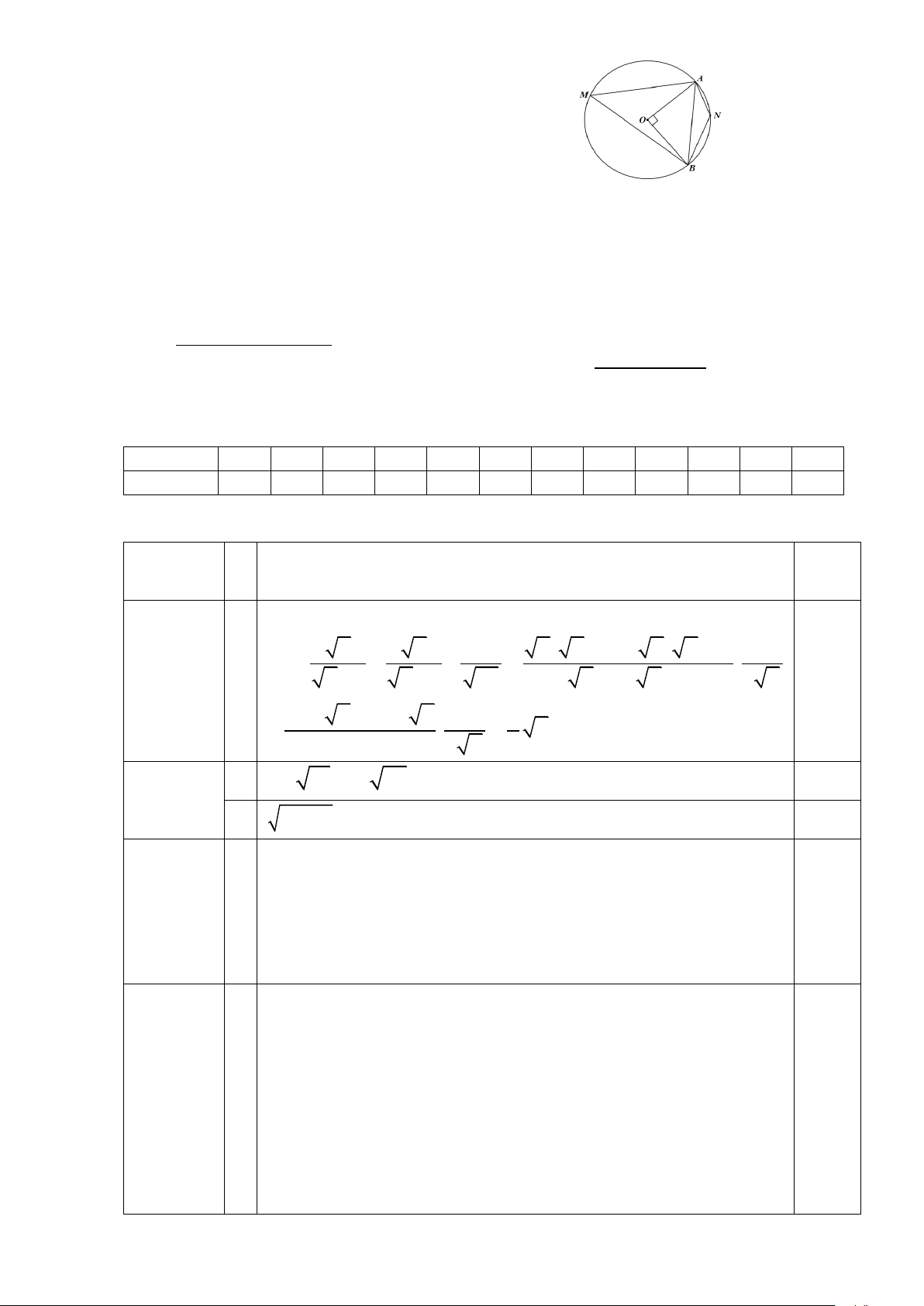
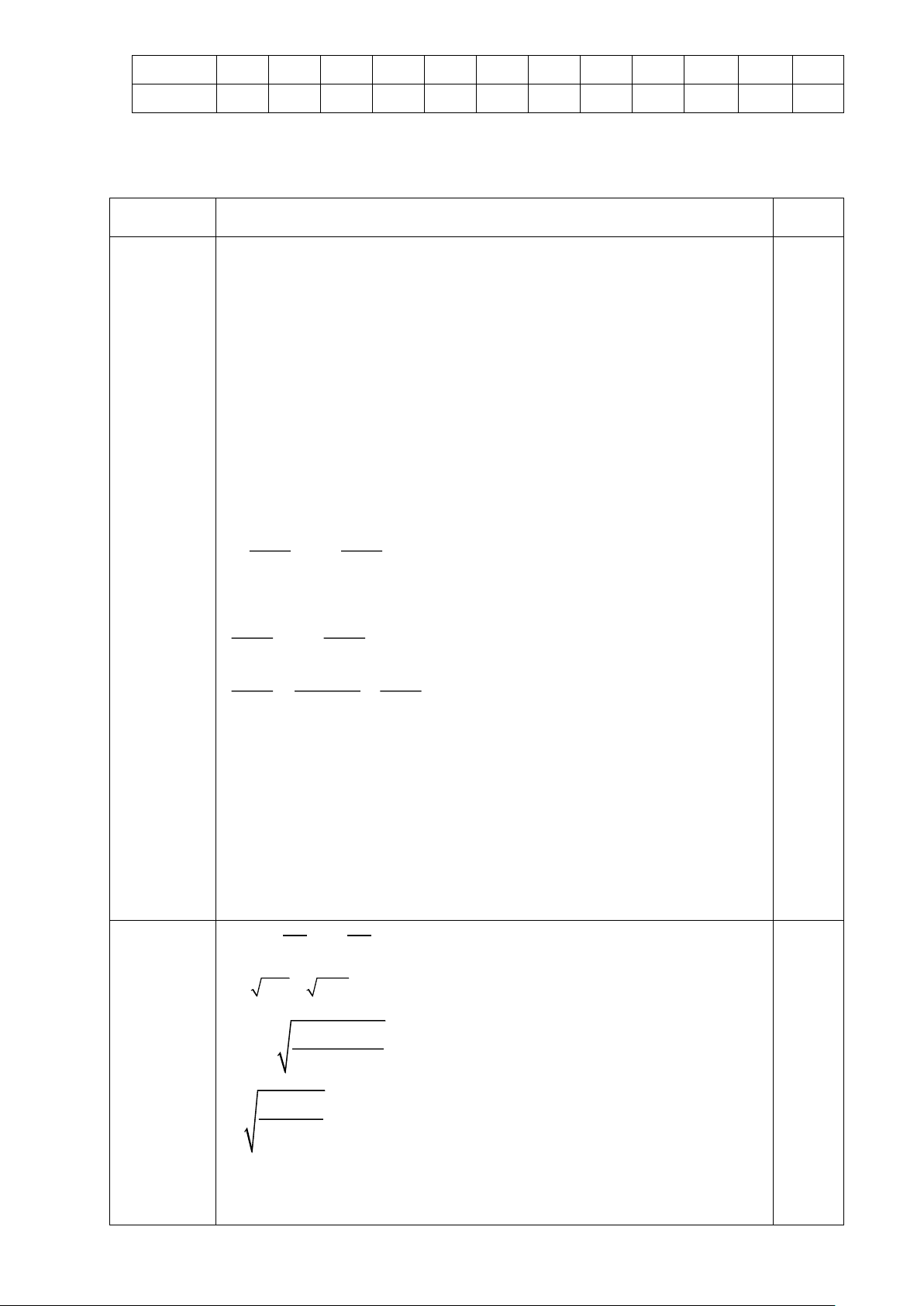
TH Cho đường tròn (O; R) và
dây AB sao cho AOB = 90°. Giả sử
M, N lần lượt là các điểm thuộc cung
lớn AB và cung nhỏ AB (M, N khác A và B) (Hình 1)
a. Tính số đo cung lớn AB
b. Tính số đo các góc AMB. AMB
----------- Hết ------
PHÒNG GD&ĐT THUẬN CHÂU
ĐÁP ÁN VÀ HƯỚNG DẪN CHẤM
TRƯỜNG THCS ……..
KIỂM TRA CUỐI HỌC KỲ I NĂM HỌC 2024-2025
MÔN: TOÁN, LỚP 9
I.TRẮC NGHIỆM (3,0 điểm): Mỗi câu đúng được 0,25 điểm Câu 1 2 3 4 5 6 7 8 9 10 11 12 Đáp án A B C D B D B B D A B D
II. TỰ LUẬN 7,0 điểm): Câu Ý Nội dung (Đáp án) Điểm (Bài)
Với: x  0; x  9 Câu 13  x x  x − 9
x ( x + 3) + x ( x − 3) x − 9 0,5 P =  + . = . (1,0 x − 3 x + 3 9x ( x + 3)( x − 3) 3 x   điểm) x + 3 x + x − 3 x x − 9 2 = . = x 0,5 x − 9 3 x 3 Câu 14 a 3 81 = 9; 27 = 3 0,5 (1,0điểm) b 3 3 (x −1) = x-1 0,5 Câu 15
- Vì số vở ban đầu của Hoa nhiều hơn số vở của Lâm nên ta 0,5 (1,0 có: x > y. điểm)
- Cố giáo tặng thêm mỗi bạn 10 quyển vở nên ta có biểu 0,5 thức: x + 10 > y +10 Câu 16
Gọi x (nghìn đồng), y (nghìn đồng) lần lượt là giá của mỗi 0,25 (1,0
chiếc bút và mỗi quyển vở. (x>0; y>0) điểm)
Vì An mua 5 chiếc bút và 10 quyển vở với tổng số tiền là
230 nghìn đồng nên ta có phương trình: 5x + 10y = 230 (1)
Vì Bình mua 10 chiếc bút và 8 quyển vở với tổng số tiền là
220 nghìn đồng nên ta có phương trình: 10x + 8y = 220 0,25 (2) Trang 3 5x +10y = 230
Từ (1) và (2) ta có hệ  1
 0x + 8y = 220. 0,25
Giải hệ này ta được nghiệm ( ; x y) = (6;20). 0,25
Vậy giá mỗi chiếc bút là 6 nghìn đồng, giá mỗi quyển vở là 20 nghìn đồng Câu 17 a 7 7(3 + 2) 7(3 + 2) 0,25 (1,0 = = 3 − 2 2 2 (3 − 2)(3 + 2) 3 − ( 2) điểm) 7(3 + 2) 7(3 + 2) = = = 3 + 2 0,25 9 − 2 7
b Với x > 0, x ≠ 9, ta có: 0,25 5 5( x − 3) 5 x −15 5 x −15 = = = 0,25 2 2
x + 3 ( x + 3)( x − 3) ( x) − 3 x − 9 Câu 18 (1,0 điểm)
– Vì điểm M nằm giữa hai điểm O và N nên OM < ON suy 0,25
ra khoảng cách từ O đến đường thẳng a nhỏ hơn bán kính
của đường tròn (O; ON). Vậy đường thẳng a và đường tròn (O; ON) cắt nhau.
– Vì khoảng cách từ O đến đường thẳng b (là ON) bằng 0,25
bán kính của đường tròn (O; ON). Vậy đường thẳng b và
đường tròn (O; ON) tiếp xúc nhau.
– Vì điểm M nằm giữa hai điểm O và N; điểm N nằm giữa 0,25
hai điểm M và P nên điểm N nằm giữa hai điểm O và P.
Suy ra OP > ON nên khoảng cách từ O đến đường thẳng c 0,25
lớn hơn bán kính của đường tròn (O; ON). Vậy đường
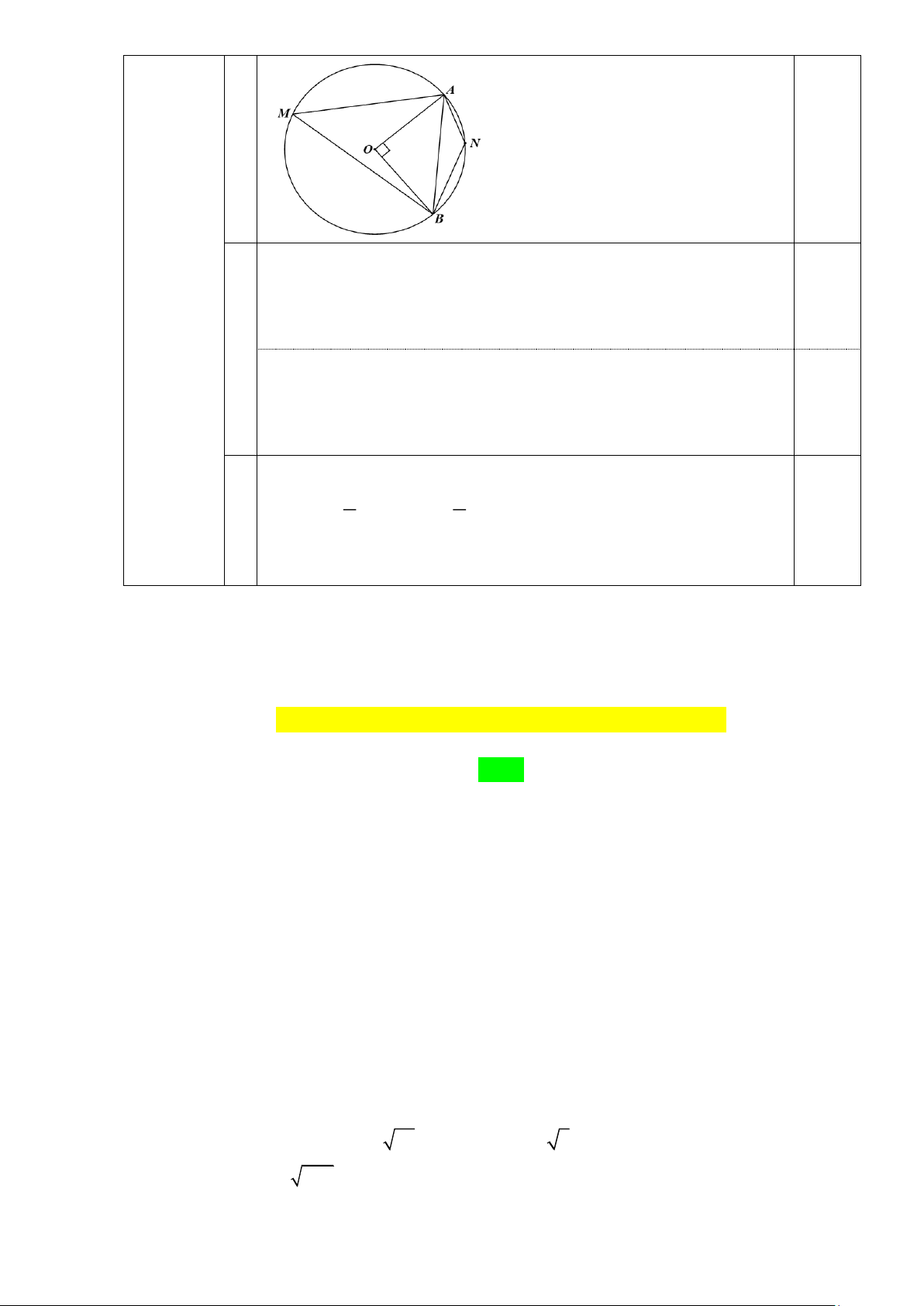
thẳng b và đường tròn (O; ON) không giao nhau. Trang 4 Câu 19 (1,0 điểm) a Ta có: 0,25
AOB = sđ ANB = 900 (Vì số đo của cung nhỏ bằng số đo của góc ở tâm)
sđ AMB = 3600 – 900 = 2700 (Vì số đo của cung lớn bằng
hiệu giữa 3600 và số đo của cung nhỏ có chung hai mút với cung lớn) 0,25 b Ta có 1 1
AMB = sđ AOB = . 900 = 450 (Vì số đo góc nội tiết 2 2
bằng nửa số đo góc ở tâm cùng chắn một cung) 0,5
Chú ý: - Mọi cách giải khác nếu đúng và đảm bảo tính khoa học cho điểm tối đa.
- Điểm bài thi được làm tròn đến chữ số thập phân thứ nhất
----------- HẾT-------------
ĐỀ KIỂM TRA HỌC KÌ I, MÔN TOÁN LỚP 9
Thời gian làm bài: 90 phút ĐỀ 2
PHẦN I. TRẮC NGHIỆM (3 điểm)
Khoanh tròn vào chữ cái đứng trước câu trả lời đúng nhất
NB.Câu 1. Hệ phương trình nào dưới đây là hệ hai phương trình bậc nhất hai ẩn?  x + y =1  x + 2y = 3 −x + y =1  x − y = 2     2
A.  y + z = 3;
− B. x − y = 1
− ; C.  2y =1; D. 0x +0y = 0.
Câu 2. Trong các hệ thức sau, hệ thức nào là bất phương trình bậc nhất một ẩn? A.2𝑥 + 3𝑦 ≤ −1. B. 3𝑥 + 2 = 6.
C. −6𝑥2 + 1 ≥ 0. D. −9𝑥 + 5 ≤ 0.
Câu 3. Căn bậc hai của 16 là B. 4 B. -4 C. 4 và -4 D.81 và -81
Câu 4. Căn bậc ba của -27 là B. 3 và -3 B. -3 C. 3 −3 D. 3 3
Câu 5. Biểu thức x −1 có điều kiện xác định là
B. x 1. B. x 1. C. x 1. D. x 1. Trang 5
Câu 6. Kết quả của (x − )3 3 2 là A. x − 2 . B. 2 − 𝑥. C. 3(𝑥 − 2). D. x - 2 3
Câu 7. Cho tam giác ABC vuông tại A, cos B là: BC AC AB AC A. B. C. D . AC BC BC AB
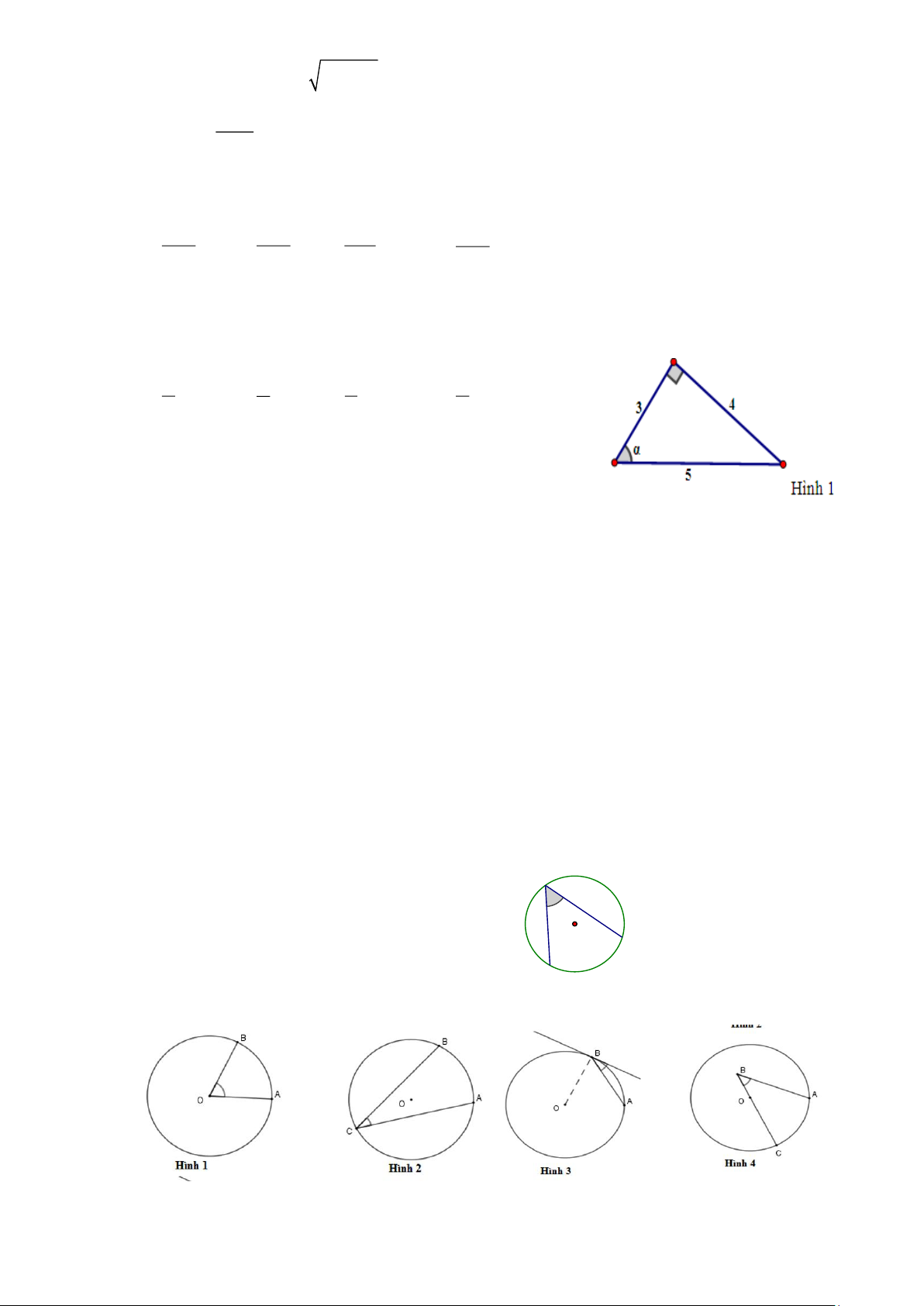
Câu 8. Trong hình 1, ta có cotα bằng 4 3 3 4 A. B. C. D. 3 4 5 5
Câu 9. Phát biểu nào sau đây không đúng?
A. Đường tròn có vô số tâm đối xứng.
B. Tâm đối xứng của đường tròn chính là tâm của đường tròn đó.
C. Đường tròn chỉ có duy nhất một tâm đối xứng.
D. Tâm đối xứng của đường tròn là giao điểm của hai đường kính bất kì của đường tròn đó.
Câu 10. Phát biểu nào sau đây đúng?
A. Đường tròn không có trục đối xứng nào.
B. Đường tròn có duy nhất một trục đối xứng.
C. Đường tròn chỉ có hai trục đối xứng.
D. Đường tròn có vô số trục đối xứng.
Câu 11. Trong đường tròn (O), BAC là A A. góc tù B. góc ở tâm O B C. góc nội tiếp D. góc vuông. C m
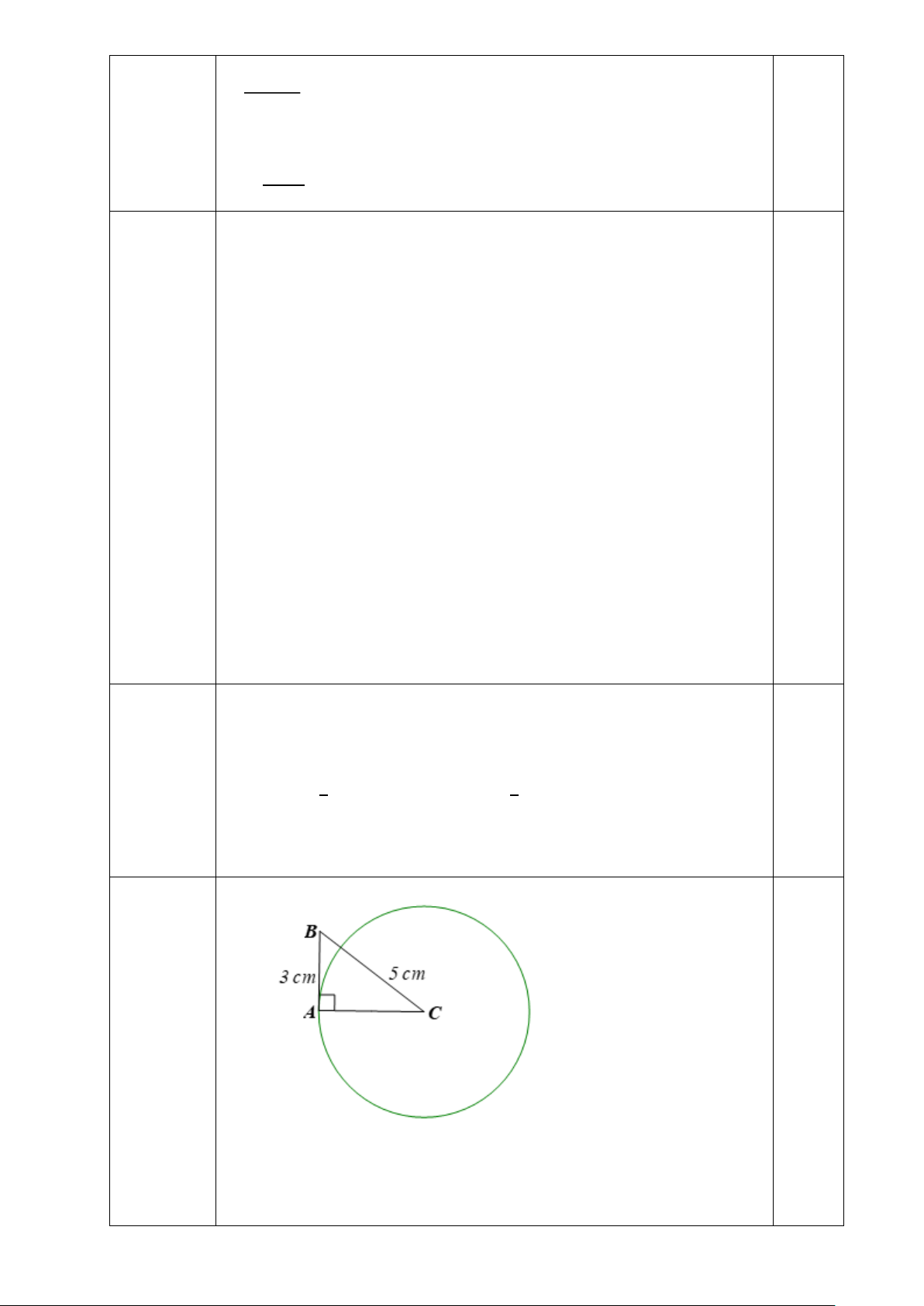
Câu 12. Hình nào dưới đây biểu diễn góc ở tâm ?
A. Hình 1 B. Hình 2 C. Hình 3 D. Hình 4 Trang 6
PHẦN II. TỰ LUẬN (7 điểm )
VD.Câu 13 (1,0 điểm). Giải phương trình sau:
a) (3x + 6)(x −8) = 0 b) 5x 10 = 7 + x − 2 x − 2 Câu 14 (2,0 điểm). TH. 1. Tính a) √81 + √49 b) 3 3 125 − 27 − 9
VDT.2. Cho biểu thức: A= với x  1 2 x − 2x +1
a) Rút gọn biểu thức A
b) Tính giá trị của A tại x = 4
VDC. Câu 15 (1,0 điểm). Tại một buổi biểu diễn nhằm gây quỹ từ thiện, ban tổ
chức đã bán được 500 vé. Trong đó có hai loại vé: vé loại I giá 100 000 đồng; vé
loại II giá 75 000 đồng. Tổng số tiền thu được từ bán vé là 44 500 000 đồng.
Tính số vé bán ra của mỗi loại.
Câu 16 (1,5 điểm). Cho hình vẽ bên, cho biết 0 ABC = 45 .
NB a) Chỉ ra 1 góc nội tiếp và 1 góc ở tâm cùng chắn cung nhỏ AC ?
TH b) Tính số cung nhỏ AC ?
TH c) Tính số đo góc AOC ?
TH. Câu 17 (1,5 điểm)
1. Cho tam giác ABC vuông tại A, AB = 3cm; BC = 5cm. Đường thẳng
AB có tiếp xúc với đường tròn (C; 4cm) hay không? Vì sao?
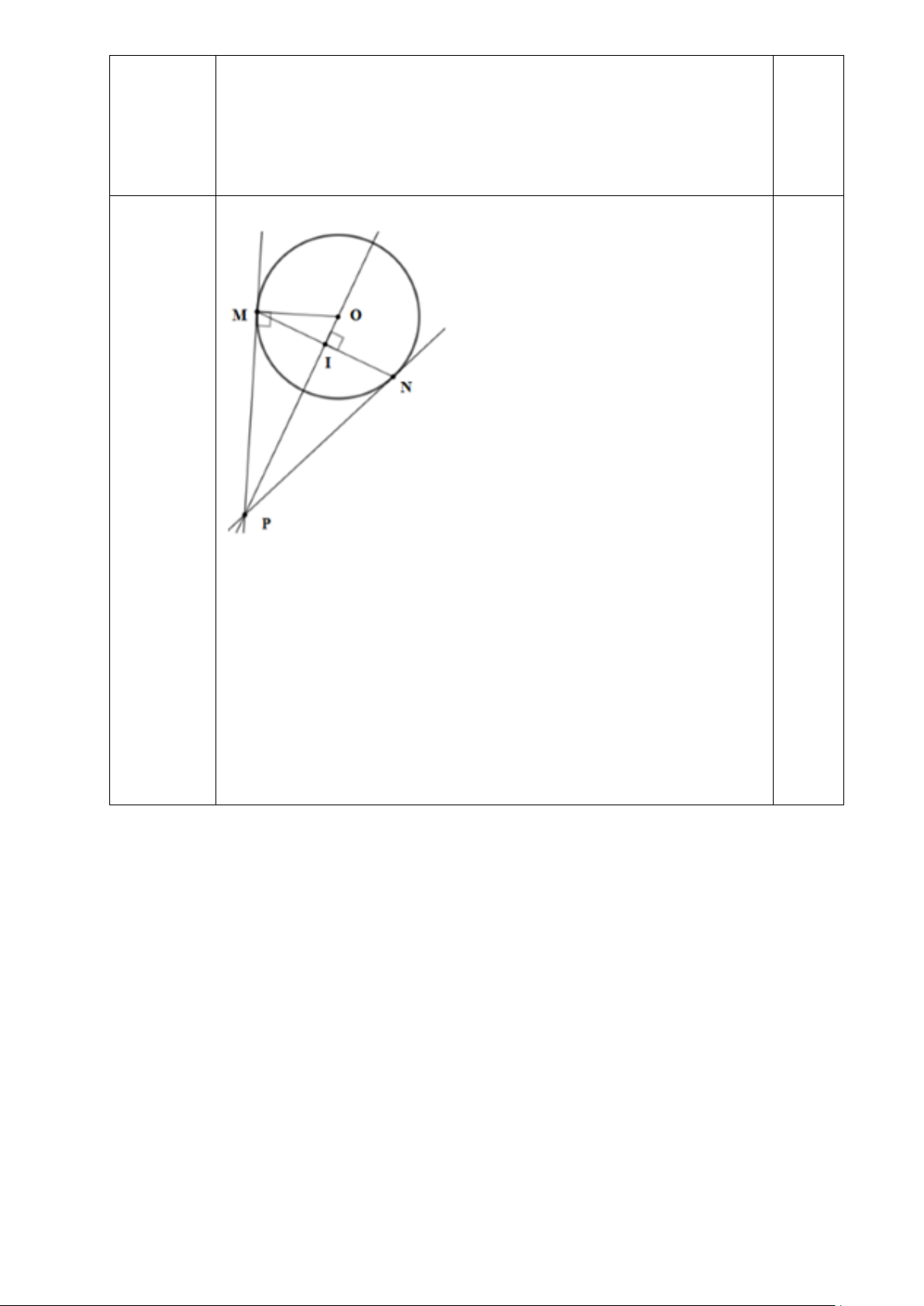
2. Cho đường tròn (O). Kẻ dây cung MN của đường tròn (không trùng với
đường kính). Từ O kẻ OI vuông góc với MN (I thuộc MN), đường thẳng OI cắt
tiếp tuyến tại M của đường tròn tại P. Giải thích vì sao NP cũng là tiếp tuyến
của đường tròn tại điểm N ?
---------------Hết---------------
HƯỚNG DẪN CHẤM BÀI KIỂM TRA HỌC KÌ I MÔN TOÁN LỚP 9
I. Phần trắc nghiệm: 3,0 điểm. (Mỗi câu đúng 0,25 điểm) Trang 7 Câu 1 2 3 4 5 6 7 8 9 10 11 12 Đáp án C D C B C D C B A D C A
II. Phần tự luận: 7,0 điểm. Câu Đáp án Điểm Câu 13 a)(3x + 6)(x − 8) = 0 (1,0 điểm)
Để giải phương trình đã cho, ta giải hai phương trình sau: *) 3x + 6 = 0 0,25 3x = -6 x = -2 *) x – 8 = 0 0,25 x = 8 b) 5x 10 = 7 + x − 2 x − 2
Điều kiện xác định: x ≠ 2. 5x 10 = 7 + x − 2 x − 2 5x 7(x − 2) 10 0,25 = + x − 2 x − 2 x − 2 5x = 7(x – 2) + 10 5x = 7x – 14 + 10 5x – 7x = –4 –2x = –4 x = 2.
Ta thấy x = 2 thỏa mãn điều kiện xác định của phương trình. 0,25
Vậy phương trình đã cho có nghiệm x = 2.
Câu 14(2 1. a) √81 + √49 = 9 + 7 = 16 0,5 điểm) 0,5 b) 3 3 125 − 27 − = 5 + 3 = 8 9 2. A= với x  1 2 x − 2x +1 9 = ( x − )2 1 0.5 0,25 Trang 8 3 = (x − ) 1 0,25
Thay x = 4 vào A biểu thức ta được A 3 = = 1 ( 4−1) Câu 15(1
Gọi số vé bán ra của vé loại I và vé loại II lần lượt là x, y (vé) 0,25
(0 < x < 500, 0 < y < 500). điểm)
Theo bài, ban tổ chức đã bán được 500 vé cả hai loại vé nên
ta có phương trình: x + y = 500.
Số tiền thu được khi bán ra x vé loại I là 100 000x (đồng). 2,25
Số tiền thu được khi bán ra y vé loại II là 75 000y (đồng).
Theo bài, tổng số tiền thu được từ bán vé là 44 500 000 đồng nên ta có phương trình: 0,25
100 000x + 75 000y = 44 500 000 hay 4x + 3y = 1 780. 0,25 Ta có hệ phương trình:  x + y = 500  (1) 4x + 3y =1780 0,25
Giải hệ phương trình (1) ta được x = 280; y = 220
Vậy vé loại I bán ra được 280 vé; Vé loại 2 bán ra được 220 0,25 vé. Câu
a) a) Góc AOC là góc ở tâm 0,25 16(1,5
Góc ABC là góc nội tiếp 0,25 b) b) Vì 0,25 điểm) 𝐴𝐵𝐶
̂ là góc nội tiếp chắn cung nhỏ AC nên 1 1 0,25 𝐴𝐵𝐶
̂ = 𝑠đ𝐴𝐶 suy ra sđ𝐴𝐶 = .450 = 900 2 2
c) c) Vì góc AOC là góc ở tâm chắn cung nhỏ AC nên 0,5 𝐴𝑂𝐶 ̂= sđAC = 900 Câu 17(1,5 điểm) 1.
Xét ∆ABC vuông tại A, theo định lí Pythagore, ta có: BC2 = AB2 + AC2
Suy ra AC2 = BC2 – AB2 = 52 – 32 = 16.
Do đó AC = 4 cm (AC > 0). 0,25 Trang 9
Vì CA ⊥ AB tại A nên khoảng cách từ điểm C đến đường thẳng AB bằng CA.
Mà AC = 4 cm nên khoảng cách từ tâm C của đường tròn (C; 4
cm) đến đường thẳng AB bằng bán kính của đường tròn.
Vậy đường thẳng AB tiếp xúc với đường tròn (C; 4 cm) 0,25 2. 0,25
Xét tam giác cân MON có OI ⊥ MN tại I ⇒ I là trung điểm của MN
Xét tam giác MNP có PI ⊥ MN ; MI = NI ⇒∆MNP cân tại P
Xét hai tam giác PMO và PNO có 0,25
OM = ON = R; PM = PN (cmt); PO là cạnh chung
Nên ΔPMO = ΔPNO (c.c.c) suy ra 𝑃𝑀𝑂 ̂ = 𝑃𝑁𝑂 ̂ = 900 (2 góc 0,25 tương ứng)
⇒ PN là tiếp tuyến của (O) tại N 0,25 Trang 10
MA TRẬN VÀ ĐẶC TẢ ĐỀ 1
KHUNG MA TRẬN ĐỀ KIỂM TRA CUỐI KỲ I
MÔN: TOÁN 9 - THỜI GIAN LÀM BÀI: 90 phút
Mức độ đánh giá Tổng %
Nội dung/Đơn vị kiến TT Chủ đề điểm thức Nhận biết Thông hiểu Vận dụng Vận dụng cao 0TNKQ TL TNKQ TL TNKQ TL TNKQ TL
Phương trình quy về phương
Chương I. Phương trình bậc nhất một ẩn 1
trình và hệ phương
Phương trình và hệ phương trình bậc nhất 1 (14t)
trình bậc nhất hai ẩn 1,0 25% Chương II. Bất
Bất đẳng thức. Bất phương đẳng thức. Bất
trình bậc nhất một ẩn 2 1 2 phương trình bậc nhất một ẩn 0,5 1,0 (10t) Chương III. Căn
Căn bậc hai và căn bậc ba 2 1 1 thức
của số thực 0,5 0,5 1,0 3 (16t) 40%
Căn thức bậc hai và căn thức 2 1 1
bậc ba của biểu thức đại số 0,5 0,5 1,0 Chương IV. Hệ
Tỉ số lượng giác của góc
nhọn. Một số hệ thức về cạnh 2 4 thức lượng trong tam giác vuông
và góc trong tam giác vuông 5% 0,5 (8t) 2 5
Chương V. Đường Đường tròn. Vị trí tương 30% tròn
đối của hai đường tròn 0,5 Trang 11 (12t)
Vị trí tương đối của đường
thẳng và đường tròn. Tiếp 1
tuyến của đường tròn 1,0
Góc ở tâm, góc nội tiếp 2 1 0,5 1,0 Tổng: Số câu 12 2 3 2 1 20 Điểm 3,0 1,0 3,0 2,0 1,0 10,0 Tỉ lệ % 40% 30% 20% 10% 100% Tỉ lệ chung 70% 30% 100% Ghi chú:
- Đề kiểm tra cuối học kì 1 dành khoảng 10% -30% số điểm để kiểm tra, đánh giá phần nội dung thuộc nửa đầu của học kì đó. Đề kiểm tra cuối
học kì 2 dành khoảng 10% -30% số điểm để kiểm tra, đánh giá phần nội dung từ đầu năm học đến giữa học kì 2.
- Tỉ lệ % số điểm của các chủ đề nên tương ứng với tỉ lệ thời lượng dạy học của các chủ đề đó.
- Tỉ lệ các mức độ đánh giá: Nhận biết khoảng từ 30-40%; Thông hiểu khoảng từ 30-40%; Vận dụng khoảng từ 20-30%; Vận dụng cao khoảng 10%.
- Tỉ lệ điểm TNKQ khoảng 30%, TL khoảng 70%.
- Số câu hỏi TNKQ 12 câu, mỗi câu 0,25 điểm. Trang 12
BẢN ĐẶC TẢ ĐỀ KIỂM TRA CUỐI KỲ I
MÔN: TOÁN 9 - THỜI GIAN LÀM BÀI: 90 phút
Số câu hỏi theo mức độ nhận thức TT
Chương/Chủ đề
Mứ c đô ̣đánh giá Thông Vận dụng Nhận biết Vận dụng hiểu cao ĐẠI SỐ Vận dụng:
Phương trình quy – Giải được phương trình tích có dạng (a1x +
về phương trình
b1).(a2x + b2) = 0.
bậc nhất một ẩn – Giải được phương trình chứa ẩn ở mẫu quy về phương trình bậc nhất. Nhâṇ biết :
– Nhận biết đươc ̣ khái niệm phương trình bậc nhất
hai ẩn, hệ hai phương trình bậc nhất hai ẩn.
Phương trình và hệ – Nhận biết được khái niệm nghiệm của hệ hai
phương trình bậc
phương trình bậc nhất hai ẩn. nhất hai ẩn Thông hiểu:
– Tính đươc ̣ nghiệm của hệ hai phương trình
bậc nhất hai ẩn bằng máy tính cầm tay. Trang 13 Chương I. Vận dụng: Phương trình và
– Giải đươc ̣ hệ hai phương trình bậc nhất hai ẩn. 1 hệ phương trình
- Giải quyết được môṭ số vấn đề thưc ̣ tiễn (đơn bậc nhất
giản, quen thuộc) gắn với hệ hai phương trình bậc
nhất hai ẩn (ví dụ: các bài toán liên quan đến cân
bằng phản ứng trong Hoá học,...). Vận dụng cao: 1 TL
– Giải quyết được môṭ số vấn đề thưc ̣ tiễn (phức (Câu 17)
hợp, không quen thuộc) gắn với hệ hai phương 1 điểm
trình bậc nhất hai ẩn. Nhận biết
– Nhận biết được thứ tự trên tập hợp các số thực. 2TN
– Nhận biết được bất đẳng thức. (Câu 1,2)
– Nhận biết đươc ̣ khái niệm bất phương trình bậc 0,5 điểm Chương II. Bất
nhất một ẩn, nghiệm của bất phương trình bậc nhất
Bất đẳng thức. Bất đẳng thức. Bất một ẩn. 2
phương trình bậc phương trình Thông hiểu
nhất một ẩn 1TL
bậc nhất một ẩn
– Mô tả được một số tính chất cơ bản của bất đẳng (Câu 15
thức (tính chất bắc cầu; liên hệ giữa thứ tự và phép 1 điểm cộng, phép nhân). Vâṇ dung
– Giải được bất phương trình bậc nhất một ẩn. Nhận biết: 2 TN
– Nhận biết được khái niệm về căn bậc hai của số (Câu 3,4) Chương III.
Căn bậc hai và căn thực không âm, căn bậc ba của một số thực. 0,5 điểm 3 Căn thức
bậc ba của số thực 1TL (Câu 14a) 0,5 điểm Trang 14 Thông hiểu:
– Tính được giá trị (đúng hoặc gần đúng) căn bậc
hai, căn bậc ba của một số hữu tỉ bằng máy tính cầm tay. Vận dụng:
– Thực hiện được một số phép tính đơn giản về
căn bậc hai của số thực không âm (căn bậc hai của 1 TL
một bình phương, căn bậc hai của một tích, căn (Câu 13)
bậc hai của một thương, đưa thừa số ra ngoài dấu 1 điểm
căn bậc hai, đưa thừa số vào trong dấu căn bậc hai). Nhận biết 2 TN
– Nhận biết được khái niệm về căn thức bậc hai và (Câu 5,6
căn thức bậc ba của một biểu thức đại số. 0,5 điểm) 1TL (Câu 14b
Căn thức bậc hai và 0,5 điểm)
căn thức bậc ba của Vận dụng
biểu thức đại số
– Thực hiện được một số phép biến đổi đơn giản 1TL
về căn thức bậc hai của biểu thức đại số (căn thức (Câu 16,
bậc hai của một bình phương, căn thức bậc hai của 1,0 điểm)
một tích, căn thức bậc hai của một thương, trục căn thức ở mẫu).
HÌNH HỌC VÀ ĐO LƯỜNG
Hình học phẳng Trang 15 Nhận biết 2 TN
– Nhận biết được các giá trị sin (sine), côsin (Câu 7,8
(cosine), tang (tangent), côtang 0,5 điểm)
(cotangent) của góc nhọn. Thông hiểu
– Giải thích được tỉ số lượng giác của các góc nhọn
đặc biệt (góc 30o, 45o, 60o) và của hai góc phụ nhau.
Tỉ số lượng giác Chương IV.
– Giải thích được một số hệ thức về cạnh và góc
của góc nhọn. Một Hệ thức lượng
trong tam giác vuông (cạnh góc vuông bằng cạnh 4
số hệ thức về cạnh trong tam giác
huyền nhân với sin góc đối hoặc nhân với côsin góc
và góc trong tam vuông
kề; cạnh góc vuông bằng cạnh góc vuông kia nhân giác vuông
với tang góc đối hoặc nhân với côtang góc kề).
– Tính được giá trị (đúng hoặc gần đúng) tỉ số
lượng giác của góc nhọn bằng máy tính cầm tay. Vận dụng
– Giải quyết được một số vấn đề thực tiễn gắn với
tỉ số lượng giác của góc nhọn (ví dụ: Tính độ dài
đoạn thẳng, độ lớn góc và áp dụng giải tam giác vuông,...). Nhận biết 2 TN
– Nhận biết được tâm đối xứng, trục đối xứng của (Câu 9,10
Đường tròn. Vị trí đường tròn. 0,5 điểm) Chương V. 5
tương đối của hai Thông hiểu Đường tròn đường tròn
– Mô tả được ba vị trí tương đối của hai đường tròn
(hai đường tròn cắt nhau, hai đường tròn tiếp xúc
nhau, hai đường tròn không giao nhau). Trang 16 Vận dụng
– So sánh được độ dài của đường kính và dây. Vận dụng cao
– Giải quyết được môṭ số vấn đề thưc ̣ tiễn (phức hợp,
không quen thuộc) gắn với đường tròn. Thông hiểu
– Mô tả được ba vị trí tương đối của đường thẳng
Vị trí tương đối
và đường tròn (đường thẳng và đường tròn cắt
của đường thẳng 1 TL
nhau, đường thẳng và đường tròn tiếp xúc nhau,
và đường tròn. (Câu 18
đường thẳng và đường tròn không giao nhau).
Tiếp tuyến của 1 điểm)
- Giải thích được dấu hiệu nhận biết tiếp tuyến đường tròn
của đường tròn và tính chất của hai tiếp tuyến cắt nhau. Nhâṇ biết 2 TN
– Nhâṇ biết được góc ở tâm, góc nội tiếp. (Câu 11,12 0,5 điểm)
Góc ở tâm, góc nội Thông hiểu tiếp
– Giải thích đươc ̣ mối liên hệ giữa số đo của cung 1 TL
với số đo góc ở tâm, số đo góc nội tiếp. (Câu 19
– Giải thích được mối liên hệ giữa số đo góc nội tiếp 1,0 điểm)
và số đo góc ở tâm cùng chắn một cung.
MA TRẬN VÀ ĐẶC TẢ ĐỀ 2
KHUNG MA TRẬN ĐỀ KIỂM TRA CUỐI KỲ I: NHÓM 2 Trang 17
MÔN: TOÁN 9 - THỜI GIAN LÀM BÀI: 90 phút
Mức độ đánh giá Tổng %
Nội dung/Đơn vị kiến TT Chủ đề điểm thức Nhận biết Thông hiểu Vận dụng Vận dụng cao TNKQ TL TNKQ TL TNKQ TL TNKQ TL
Phương trình quy về phương 2
Chương I. Phương trình bậc nhất một ẩn 1,0 1
trình và hệ phương
Phương trình và hệ phương trình bậc nhất 1 14T
trình bậc nhất hai ẩn 1 0,25 1,0 25% Chương II. Bất
Bất đẳng thức. Bất phương đẳng thức. Bất
trình bậc nhất một ẩn 1 2 phương trình bậc 0,25 nhất một ẩn 13T Chương III. Căn
Căn bậc hai và căn bậc ba của 2 1 thức số thực 0,5 0,5 3 17T 30%
Căn thức bậc hai và căn thức 2 1 2
bậc ba của biểu thức đại số 0,5 0,5 1,0 Chương IV. Hệ
Tỉ số lượng giác của góc 2 4 thức lượng trong
nhọn. Một số hệ thức về cạnh 5% tam giác vuông
và góc trong tam giác vuông 0,5 9T
Đường tròn. Vị trí tương 2 1
đối của hai đường tròn 0,5 0,5 Chương V. Đường 5
Vị trí tương đối của đường tròn 1 40% 19T
thẳng và đường tròn. Tiếp
tuyến của đường tròn 1,0
Góc ở tâm, góc nội tiếp 2 1 2 Trang 18 0,5 0,5 1,0 Tổng: Số câu 12 2 5 4 1 24 Điểm 3,0 1,0 3,0 2,0 1,0 10,0 Tỉ lệ % 40% 30% 20% 10% 100% Tỉ lệ chung 70% 30% 100% Ghi chú:
- Đề kiểm tra cuối học kì 1 dành khoảng 10% -30% số điểm để kiểm tra, đánh giá phần nội dung thuộc nửa đầu của học kì đó. Đề kiểm tra cuối
học kì 2 dành khoảng 10% -30% số điểm để kiểm tra, đánh giá phần nội dung từ đầu năm học đến giữa học kì 2.
- Tỉ lệ % số điểm của các chủ đề nên tương ứng với tỉ lệ thời lượng dạy học của các chủ đề đó.
- Tỉ lệ các mức độ đánh giá: Nhận biết khoảng từ 30-40%; Thông hiểu khoảng từ 30-40%; Vận dụng khoảng từ 20-30%; Vận dụng cao khoảng 10%.
- Tỉ lệ điểm TNKQ khoảng 30%, TL khoảng 70%.
- Số câu hỏi TNKQ 12 câu, mỗi câu 0,25 điểm. Trang 19
BẢN ĐẶC TẢ ĐỀ KIỂM TRA CUỐI KỲ I
MÔN: TOÁN 9 - THỜI GIAN LÀM BÀI: 90 phút
Số câu hỏi theo mức độ nhận thức TT
Chương/Chủ đề
Mứ c đô ̣đánh giá Thông Vận dụng Nhận biết Vận dụng hiểu cao ĐẠI SỐ Vận dụng:
Phương trình quy – Giải được phương trình tích có dạng (a1x + 2 TL
về phương trình
b1).(a2x + b2) = 0. (Câu 13
bậc nhất một ẩn – Giải được phương trình chứa ẩn ở mẫu quy về 1, 0 điểm) phương trình bậc nhất. Nhâṇ biết :
– Nhận biết đươc ̣ khái niệm phương trình bậc nhất 1 TN
hai ẩn, hệ hai phương trình bậc nhất hai ẩn. (Câu 1
Phương trình và hệ – Nhận biết được khái niệm nghiệm của hệ hai 0,25 điểm)
phương trình bậc
phương trình bậc nhất hai ẩn. nhất hai ẩn Thông hiểu:
– Tính đươc ̣ nghiệm của hệ hai phương trình
bậc nhất hai ẩn bằng máy tính cầm tay. Trang 20