











Preview text:
SÔÛ GD&ÑT TP HOÀ CHÍ MINH
ÑEÀ THAM KHAÛO TUYEÅN SINH 10
PHOØNG GÑ&ÑT QUAÄN 6 MÔN: TOÁN 9
Đê thi gồm 8 câu hỏi tự luận. MÃ Đ Đ Ề Ề T : H Quận Tân AM KH P Ả h O ú
Thời gian: 120 phút (không kể thời gian phát đề)
Câu 1. (1,5 điểm). Cho (P) 2
: y = −x và đường thẳng (d) : y = x − 2 .
a) Vẽ đồ thị (P) và (d) trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.
Câu 2. (1 điểm). Cho phương trình 2
2x − 3x − 4 = 0 có 2 nghiệm là x , x . Không giải phương 1 2 1 2 1 2
trình, hãy tính giá trị của biểu thức A = + x x 1 2
Câu 3. (1 điểm). Bác Hùng mua hai món hàng tại một cửa hàng món hàng thứ nhất có giá ghi là
400000 đồng và Bác được giảm 20% trên giá trị món hàng; món hàng thứ hai Bác được
giảm 30% trên giá trị món hàng. Tổng số tiền Bác phải thanh toán là 740000 đồng. Hỏi nếu
Bác mua thêm một món hàng thứ hai thì Bác được giảm tất cả bao nhiêu tiền?
Câu 4. (1 điểm). Một thùng chứa một lượng thể tích dung dịch cồn rửa tay 70 . Lần đầu người ta 1 1
sử dụng thể tích dung dịch; lần thứ hai người ta sử dụng
của thể tích dung dịch lần 6 2 1
đầu sử dụng; lần thứ ba người ta sử dụng thể tích dung dịch; lần thứ tư người ta sử 7 8
dụng nhiều hơn lần thứ nhất và lần thứ ba sử dụng
thể tích dung dịch; lúc này trong 42
thùng còn lại 0,9 lít dung dịch. Hỏi thể tích dung dịch có trong thùng là bao nhiêu lít?
Câu 5. (1 điểm). Để tìm hiểu về sự nở vì nhiệt của chất rắn, Bạn An đã
thực hiện một thí nghiệm đơn giản. Chuẩn bị một thanh kim loại
đồng chất, sau đó nung nóng thanh kim loại. Quan sát sự thay đổi
chiều dài của thanh kim loại theo nhiệt độ, bạn thấy rằng ban đầu khi ở nhiệt độ 0
40 thanh kim loại có chiều dài là 5 mét; khi nung
nóng thanh kim loại ở nhiệt độ 0
140 thì chiều dài của của nó tăng
thêm 6 mm. Mối liên hệ giữa chiều dài y (mét) của thanh kim và nhiệt độ ( 0
x C ) là một hàm số bậc nhất y = ax + b .
a. Xác định hệ số a và b .
b. Hãy tính chiều dài của thanh kim loại khi ở nhiệt độ 0 100 .
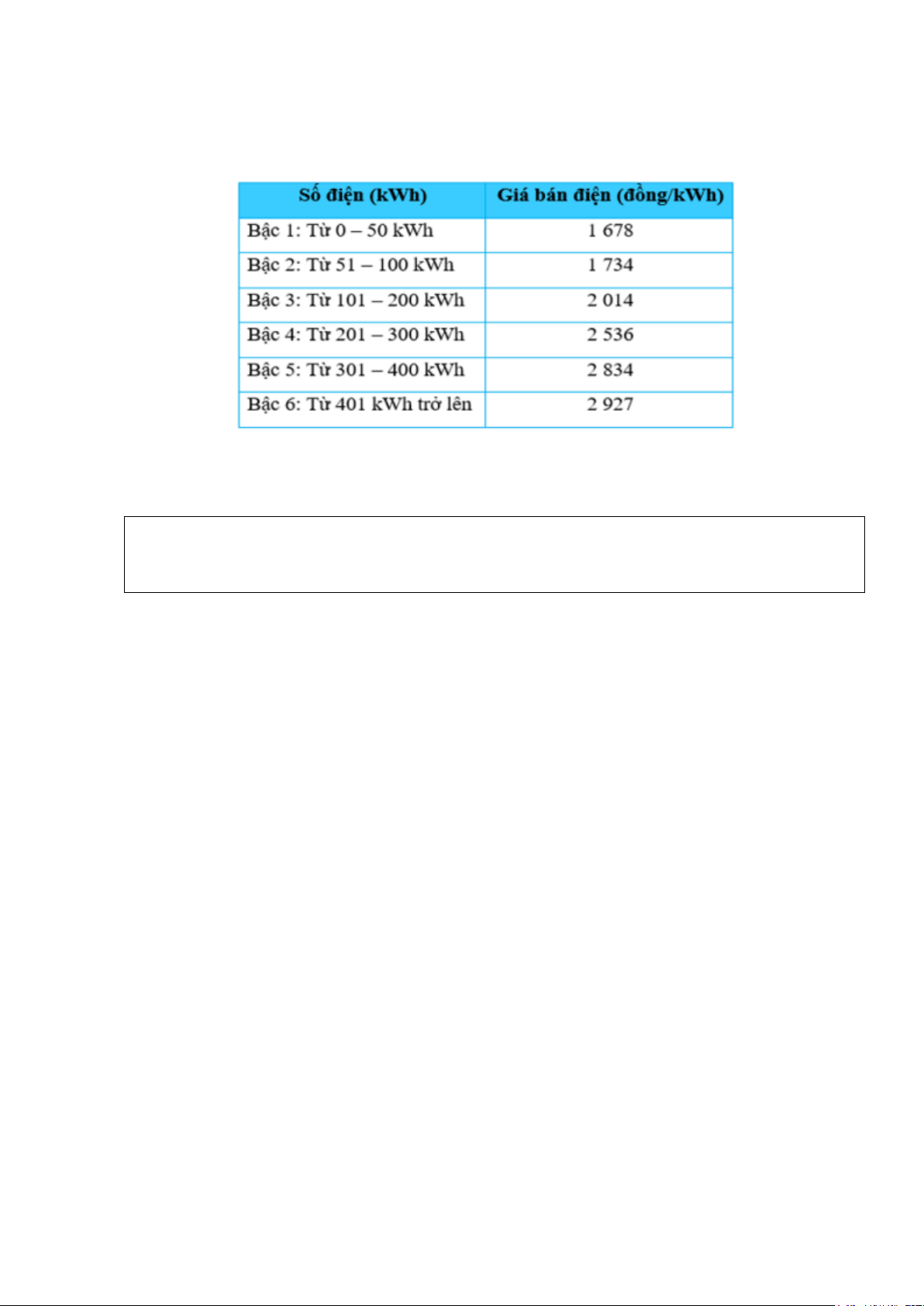
Câu 6. (1 điểm). Biểu giá bán lẻ điện sinh hoạt của khách hàng năm 2022 được áp dụng để tính
toán tiền sử dụng điện như sau: Trang 1
Như vậy, số điện tiêu thụ sinh hoạt hàng tháng càng cao thì mức giá tiền điện càng cao. Để
tính tiền điện hàng tháng được thực hiện theo công thức sau:
Tiền điện bậc i = (số kWh áp dụng giá bậc i) x (giá 1 kWh bậc i)
Tiền điện = tổng tiền điện các bậc
Ví dụ: nếu sử dụng hết 100kWh thì tiền điện là 50.1678 + 50.1734 = 170600 đồng
Ngoài ra, trên hóa đơn tiền điện người sử dụng điện còn phải trả thêm 8% thuế giá trị gia
tăng (VAT) trên số tiền điện.
a. Hãy tính số tiền điện khách hàng cần trả nếu sử dụng hết 200kWh điện (bao gồm cả VAT).
b. Trong tháng 4 / 2022 nhà cô Bình đã trả 336506,4 đồng cho hóa đơn tiền điện. Hỏi nhà
cô Bình tiêu thụ hết bao nhiêu kWh điện?
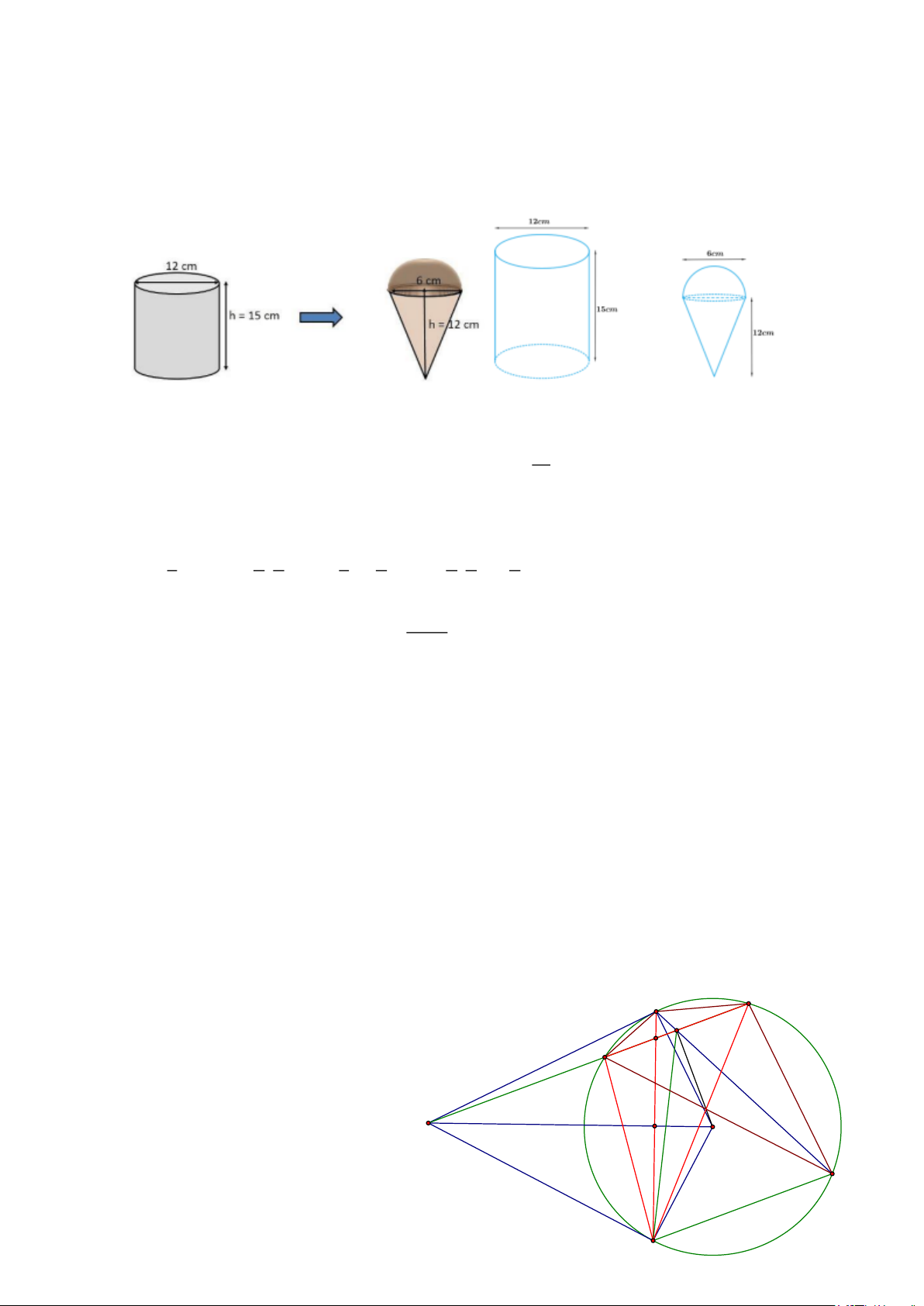
Câu 7. (0,75 điểm). Một hộp kem hình trụ có đường kính 12cm và chiều cao 15cm đựng đầy kem.
Kem sẽ được chia vào các bánh ốc quế hình nón có chiều cao 12cm và đường kính 6cm , có
hình bán cầu trên đỉnh như hình vẽ. Hãy tìm số que kem có thể chia được.
Câu 8. (3 điểm). Từ điểm A ở ngoài (O) vẽ 2 tiếp tuyến AB và AC ( B , C là 2 tiếp điểm) và cát
tuyến ADE( AD AE)
a) Chứng minh: OA ⊥ BC và tứ giác ABOC nội tiếp.
b) Đường thẳng đi qua điểm C , song song với DE và cắt đường tròn (O) tại F ( F khác C ).
Gọi I là giao điểm của BF và DE . Chứng minh: I là trung điểm của DE . c) Chứng minh: . BE EF + .
BD DF = BC.DE . ----HẾT--- Trang 2 Trang 3 HƯỚNG DẪN GIẢI
Câu 1. (1,5 điểm) Cho (P) 2
: y = −x và đường thẳng (d) : y = x − 2 .
a) Vẽ đồ thị (P) và (d) trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính. Lời giải
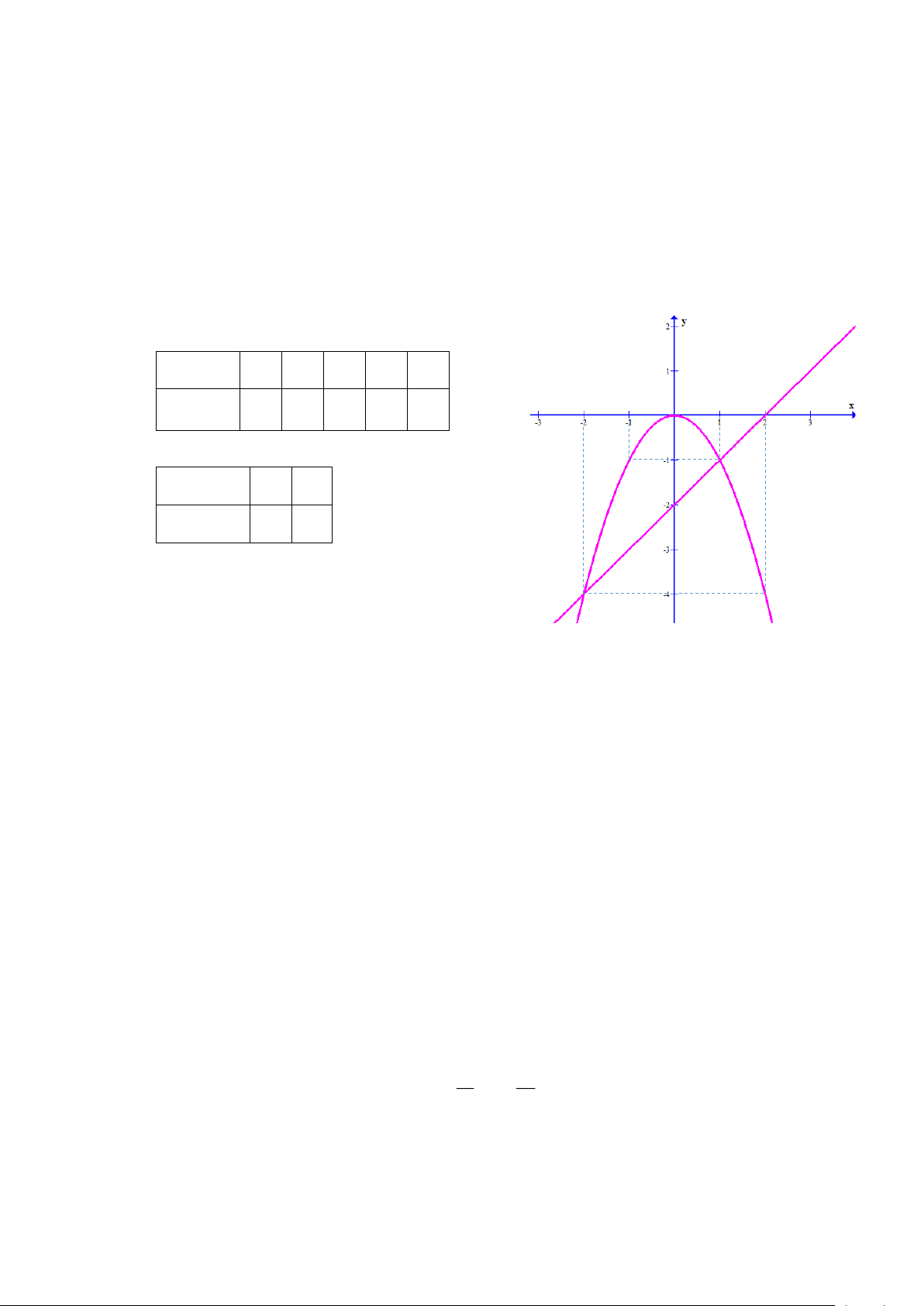
a. Vẽ đồ thị (P) và (d) trên cùng hệ trục tọa độ. BGT: x −2 1 − 0 1 2 2 y = −x −4 1 − 0 1 − −4 x 0 1 y = x − 2 −2 1 −
b. Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.
Phương trình hoành độ giao điểm của (P) và (d) : − 2 x = x − 2 2 x + x − 2 = 0 x = 1 x = − 2 Thay x = 1 vào 2
y = −x , ta được: 2 y = 1 − = −1 . 2 Thay x = −2 vào 2
y = −x , ta được: y = −(−2) = −4 .
Vậy (1; − 1) , (−2; − 4) là hai giao điểm cần tìm.
Câu 2. (1 điểm). Cho phương trình 2
2x − 3x − 4 = 0 có 2 nghiệm là x , x . Không giải phương 1 2 1 2 1 2
trình, hãy tính giá trị của biểu thức A = + x x 1 2 Lời giải 2 Vì = 2
b − 4ac = (−3) − 4.(−4).2 = 41 0 Trang 4
Nên phương trình có hai nghiệm phân biệt x ,x . 1 2 −b −(−3) 3
S = x + x = = = 1 2 a 2 2
Theo định lí Vi-et, ta có: c 4 −
P = x .x = = = −2 1 2 a 2 2 3 2 2 − 2. 2 − 2 2 2 ( ) 1 1 x + x S − 2P 2 25 1 2 A = + = = = = 2 2 2 x x x .x P 2 − 16 1 2 1 2 ( )2
Câu 3. (1 điểm). Bác Hùng mua hai món hàng tại một cửa hàng món hàng thứ nhất có giá ghi là
400000 đồng và Bác được giảm 20% trên giá trị món hàng; món hàng thứ hai Bác được
giảm 30% trên giá trị món hàng. Tổng số tiền Bác phải thanh toán là 740000 đồng. Hỏi nếu
Bác mua thêm một món hàng thứ hai thì Bác được giảm tất cả bao nhiêu tiền? Lời giải
Gọi x (đồng) là giá ban đầu của món hàng thứ hai ( x 0 )
Vì tổng số tiền thanh toán 740000 nên
400000.(1− 20%) + x(1− 30%) = 740000 x = 600000
Vậy số tiền Bác được giảm là : 20%.400000 + 30%.600000 = 260000 đồng.
Câu 4. (1 điểm). Một thùng chứa một lượng thể tích dung dịch cồn rửa tay 70 . Lần đầu người ta 1 1
sử dụng 6 thể tích dung dịch; lần thứ hai người ta sử dụng 2 của thể tích dung dịch lần 1
đầu sử dụng; lần thứ ba người ta sử dụng 7 thể tích dung dịch; lần thứ tư người ta sử 8
dụng nhiều hơn lần thứ nhất và lần thứ ba sử dụng
thể tích dung dịch; lúc này trong 42
thùng còn lại 0,9 lít dung dịch. Hỏi thể tích dung dịch có trong thùng là bao nhiêu lít? Lời giải
Gọi x (l) là thể tích dung dịch có trong thùng lúc đầu. ( x 0) 1 5
Số lít dung dịch lần đầu sử dụng: x − x = x (lít) 6 6 1 1 1
Số lít dung dịch lần thứ hai sử dụng: . x = x (lít) 2 6 12 Trang 5 1
Số lít dung dịch lần thứ ba sử dụng: x (lít) 7 1 1 8 1
Số lít dung dịch lần thứ tư sử dụng: x + x + x = x (lít) 6 7 42 2 1 1 1 1 3
Số lít dung dịch còn lại: x − x −
x − x − x = x (lít) 6 12 7 2 28 3 Ta có phương trình:
x = 0,9 x = 8, 4 (nhận) 28
Vậy thể tích dung dịch có trong thùng lúc đầu là 8, 4 lít.
Câu 5. (1 điểm). Để tìm hiểu về sự nở vì nhiệt của chất rắn, Bạn An đã
thực hiện một thí nghiệm đơn giản. Chuẩn bị một thanh kim loại
đồng chất, sau đó nung nóng thanh kim loại. Quan sát sự thay đổi
chiều dài của thanh kim loại theo nhiệt độ, bạn thấy rằng ban đầu khi ở nhiệt độ 0
40 thanh kim loại có chiều dài là 5 mét; khi nung
nóng thanh kim loại ở nhiệt độ 0
140 thì chiều dài của của nó tăng
thêm 6 mm. Mối liên hệ giữa chiều dài y (mét) của thanh kim và nhiệt độ ( 0 x C ) là một
hàm số bậc nhất y = ax + b .
a. Xác định hệ số a và b .
b. Hãy tính chiều dài của thanh kim loại khi ở nhiệt độ 0 100 . Lời giải
a. Xác định các hệ số a và b . ( ) 1 Theo đề bài, ta có: x = 40 Với 5 = 40.a + . ( ) 1 y = b 5 x = 140 Với 5.006 = 140.a + . 2 = b ( ) y 5 + 0,006 a + b = a = 3 40 5 Từ ( )
1 và (2) ta có hệ phương trình: . 140a + b = 50000 5,006 b = 4,9976 3 Vậy: a = 3
, b = 4,9976 và y = x + 4,9976 . 50000 50000
b. Chiều dài của thanh kim loại khi ở nhiệt độ 100 C 3 3
Thế x = 100 vào y = x + 4,9976 = .100 + 4,9976 = 5,0036 50000 50000 Trang 6
Vậy chiều dài của thanh kim loại của thanh kim loại khi ở nhiệt độ 0
100 C là 5,0036 m .
Câu 6. (1 điểm). Biểu giá bán lẻ điện sinh hoạt của khách hàng năm 2022 được áp dụng để tính
toán tiền sử dụng điện như sau:
Như vậy, số điện tiêu thụ sinh hoạt hàng tháng càng cao thì mức giá tiền điện càng cao. Để
tính tiền điện hàng tháng được thực hiện theo công thức sau:
Tiền điện bậc i = (số kWh áp dụng giá bậc i) x (giá 1 kWh bậc i)
Tiền điện = tổng tiền điện các bậc
Ví dụ: nếu sử dụng hết 100kWh thì tiền điện là 50.1678 + 50.1734 = 170600 đồng
Ngoài ra, trên hóa đơn tiền điện người sử dụng điện còn phải trả thêm 8% thuế giá trị gia
tăng (VAT) trên số tiền điện.
a. Hãy tính số tiền điện khách hàng cần trả nếu sử dụng hết 200kWh điện (bao gồm cả VAT).
b. Trong tháng 4 / 2022 nhà cô Bình đã trả 336506,4 đồng cho hóa đơn tiền điện. Hỏi nhà cô
Bình tiêu thụ hết bao nhiêu kWh điện? Lời giải
a. Số tiền điện khách hàng cần trả nếu sử dụng hết 200kWh điện là:
(50.1678+50.1734+100.2014).(1+8%) = 401760 đồng
b. Vì số tiền nhà cô Bình phải trả lớn hơn số tiền sử dụng 100kWh
Nên số kWh điện nhà cô Bình sử dụng ở bậc 3 .
Gọi x (kWh) là số kWh điện nhà cô Bình sử dụng.
Theo đề bài, ta có phương trình: 50.1678 + 50.1734 +
(x −100)2014.(1+8%) =336506,4
170600 + (x −100)2014 = 336506,4 x =170 Trang 7
Vậy nhà cô Bình tiêu thụ hết 170 kWh điện.
Câu 7. (0,75 điểm). Một hộp kem hình trụ có đường kính 12cm và chiều cao 15cm đựng đầy kem.
Kem sẽ được chia vào các bánh ốc quế hình nón có chiều cao 12cm và đường kính 6cm , có
hình bán cầu trên đỉnh như hình vẽ. Hãy tìm số que kem có thể chia được. Lời giải 2 12
Thể tích kem trong hộp hình trụ là: 2
V = R .h = .15 = 540 cm T T T ( 3) 2
Thể tích kem trong hộp hình trụ là: 2 3 1 1 4 1 6 1 4 6 2 3 V
= R .h + . R = .12 + . .. = 54 cm kem N N C ( 3) 3 2 3 3 2 2 3 2 540
Vậy số que kem có thể chia được là: =10 que. 54
Câu 8. (3 điểm). Từ điểm A ở ngoài (O) vẽ 2 tiếp tuyến AB và AC ( B , C là 2 tiếp điểm) và cát
tuyến ADE( AD AE)
a. Chứng minh: OA ⊥ BC và tứ giác ABOC nội tiếp.
b. Đường thẳng đi qua điểm C , song song với DE và cắt đường tròn (O) tại F ( F khác C ).
Gọi I là giao điểm của BF và DE . Chứng minh: I là trung điểm của DE . c. Chứng minh: . BE EF + .
BD DF = BC.DE . Lời giải E B I D A H O F Trang 8 C
a. Chứng minh: OA ⊥ BC và tứ giác ABOC nội tiếp. AB =
AC (2 tiep tuyen cat nhau) * OA = OB(= R)
Suy ra OA là đường trung trực của BC OA ⊥ BC
*Xét tứ giác ABOC có: 0
ABO = 90 (Vì AB là tiếp tuyến của (O) ) 0
ACO = 90 (Vì AC là tiếp tuyến của (O) ) ABO + ACO = 180
Vậy tứ giác ABOC là tứ giác nội tiếp.
b. Chứng minh: I là trung điểm của DE .
AIB = CFB ( AE / /CF )
Và CFB = ACB (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn 1 cung) 1 AIB = BOA = BOC 2
Suy ra tứ giác BIOA nội tiếp
Suy ra AIO = ABO = 90 ( 2 góc nội tiếp cùng chắn 1 cung)
OI ⊥ DE tại I
Suy ra I là trung điểm của DE (Quan hệ vuông góc giữa đường kính và dây cung) c. Chứng minh: . BE EF + .
BD DF = BC.DE .
* BEC = ACB (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn 1 cung BC )
Và EIF = BIA (đối đỉnh)
Mặt khác BIA = ACB ( 2 góc nội tiếp cùng chắn 1 cung của đường tròn đi qua 5 điểm ,
A B,O,C, I )
Suy ra BEC = EIF
* Xét BEC và EIF có :
+ BCE = BFE ( 2 góc nội tiếp cùng chắn 1 cung)
+ BEC = EIF (cmt) Trang 9 CE B ” F
IE (g − g) BE BC =
BE.FE = BC.IE ( ) 1 EI FE * DE / /CF (GT)
Suy ra tứ giác DEFC là hình thang
Mà DEFC nội tiếp (O)
Suy ra DEFC là hình thang cân Nên DC = EF DC = EF DBC = EDF
* Xét CBD và FDI có:
+ DCB = DFI ( 2 góc nội tiếp cùng chắn 1 cung BD )
+ DBC = IDF (cmt) CBD ” F
DI (g − g) CB BD = B .
D DF = BC.ID (2) DF DI * Từ ( ) 1 và (2) ta có: BE.EF + .
BD DF = BC.IE + BC.ID
BE.EF + B .
D DF = BC.(IE + ID) BE.EF + .
BD DF = BC.DE ----HẾT---
SÔÛ GD&ÑT TP HOÀ CHÍ MINH
ÑEÀ THAM KHAÛO TUYEÅN SINH 10
PHOØNG GÑ&ÑT QUAÄN 6
NAÊM HOÏC: 2023 - 2024 MÔN: TOÁN 9 ĐỀ TH AM KHẢO
Đê thi gồm 8 câu hỏi tự luận. MÃ ĐỀ: Quận 6 - 3
Thời gian: 120 phút (không kể thời gian phát đề) 1
Câu 1. (1,5 điểm). Cho parabol (P) 2 : y =
x và đường thẳng (d) 1 : y = x + 3 . 2 2
a) Vẽ đồ thị (P) và (d) trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính. Trang 10
Câu 2. (1,0 điểm). Cho phương trình 2
2x − 5x − 1 = 0 có hai nghiệm là x , x . Không giải phương 1 2
trình, hãy tính giá trị của biểu thức (2x − x
2x − x − 2023. 1 2 ) ( 2 1 )
Câu 3. (1,0 điểm). Công ty viễn thông có gói cước được tính như sau:
- Gói I : 2000 đồng/phút cho 30 phút đầu tiên; 1800 đồng/phút cho 30 phút tiếp theo; 1200
đồng/phút cho 30 phút tiếp theo nữa và 800 đồng/phút cho thời gian còn lại.
- Gói II : 1800 đồng/phút cho 60 phút đầu tiên; 1500 đồng/phút cho 60 phút tiếp theo và 1000
đồng/ phút cho thời gian còn lại.
a) Tính số tiền phải trả của gói I khi gọi 130 phút và gói II khi gọi 130 phút.
b) Bác An nhận thấy rằng mỗi tháng trung bình gọi chưa đến 904 phút. Sau khi cân nhắc
thì bác An chọn gói I vì sẽ tiết kiệm được 150000 đồng so với gói II . Hỏi trung bình
bác An gọi bao nhiêu phút mỗi tháng?
Câu 4. (0,75 điểm). Do ảnh hưởng của tình hình dịch bệnh, thu nhập của một công ty bị giảm dần
trong năm 2021. Các số liệu thống kê được thể hiện bằng đồ thị như hình vẽ.
a) Tìm hàm số thể hiện sự liên quan của đại lượng y (trăm triệu/ tháng) theo đại lượng x (tháng).
b) Biết một sản phẩm bán được thì công ty có lợi nhuận là 100 ngàn đồng, em hãy tính số
sản phẩm mà công ty bán được trong tháng 9 năm 2021 (làm tròn đến hàng đơn vị).
Câu 5. (1,0 điểm). Cửa hàng lấy một thùng nước ngọt ( 24 lon) của đại lý phân phối với giá 192000
đồng và bán lẻ với giá 10000 đồng một lon.
a) Hỏi khi bán hết một thùng nước ngọt đó thì cửa hàng thu được lãi bao nhiêu phần trăm so với giá gốc?
b) Trong đợt khuyến mãi, do đại lý phân phối giảm giá nên cửa hàng cũng giảm giá còn
9500 đồng một lon và thu được lãi suất như cũ. Hỏi trong đợt này cửa hàng đã mua
một thùng nước ngọt với giá bao nhiêu?
Câu 6. (1,0 điểm). Một bể chứa nước có dạng như hình vẽ.
a) Tính thể tích của bể (kết quả không làm tròn).
b) Ban đầu, bể không có nước. Sau đó người ta bơm nước vào
bể với tốc độ 1 lít/giây. Hỏi sau 20 phút kể từ khi bắt đầu Trang 11
bơm thì mực nước trong hồ cách miệng hồ bao nhiêu mét (làm tròn đến hàng phần 1
trăm)? Biết thể tích hình trụ là 2
V = r h và thể tích hình nón là 2 V = r . h 3
Câu 7. (1,0 điểm). Trước ngày kết thúc năm học tập thể các học sinh lớp 9A muốn mua quà tặng
cho các giáo viên giảng dạy lớp mình trong suốt năm học để tỏ lòng tri ân, mỗi món quà
tặng cho thầy với giá là 50 ngàn đồng, mỗi món quà tặng cho cô có giá là 65 ngàn đồng,
biết lớp tặng quà cho 15 giáo viên và tổng số tiền mà lớp mua quà là 870 ngàn đồng. Em
hãy tính số thầy giáo và số cô giáo lớp 9A dự định mua quà tặng.
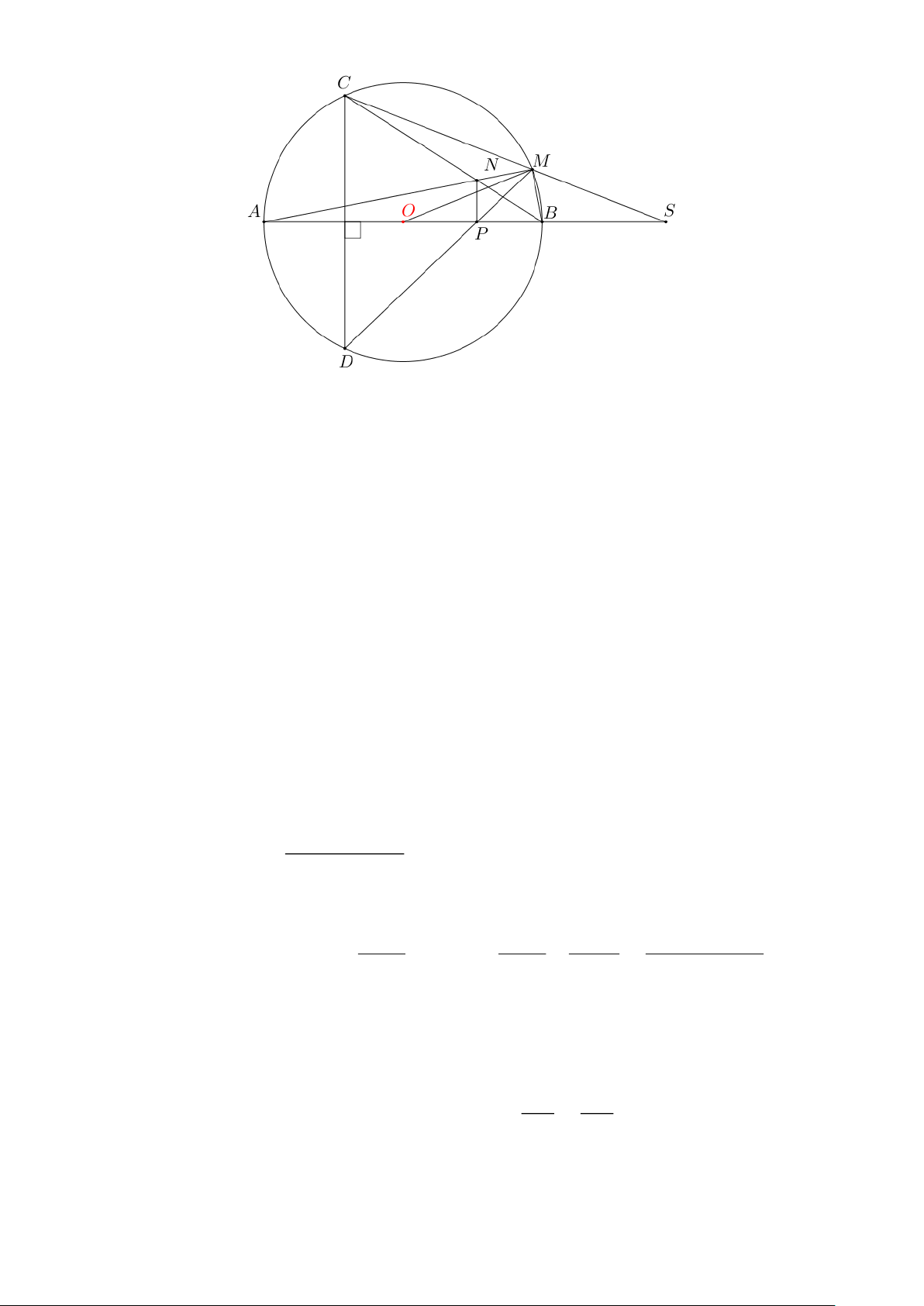
Câu 8. (3,0 điểm). Cho đường tròn (O) đường kính AB . Lấy điểm S tùy ý trên tia đối của tia BA .
Vẽ cát tuyến SMC của (O) . Vẽ dây cung CD của đường tròn (O) vuông góc với AB .
a) Chứng minh tam giác SMA đồng dạng với tam giác SBC .
b) Các dây cung AM, BC cắt nhau tại N ; các dây cung AB, DM cắt nhau tại P . Chứng
minh rằng tứ giác BMNP nội tiếp và NP song song với . CD c) Chứng minh 2
OP.OS = OM . ---- HẾT ---- Trang 12 HƯỚNG DẪN GIẢI 1 1
Câu 1 (1,5 điểm). Cho parabol (P ): y = x2 và đường thẳng (d): y = x + 3 . 2 2
a) Vẽ đồ thị (P ) và (d) trên cùng hệ trục tọa độ.
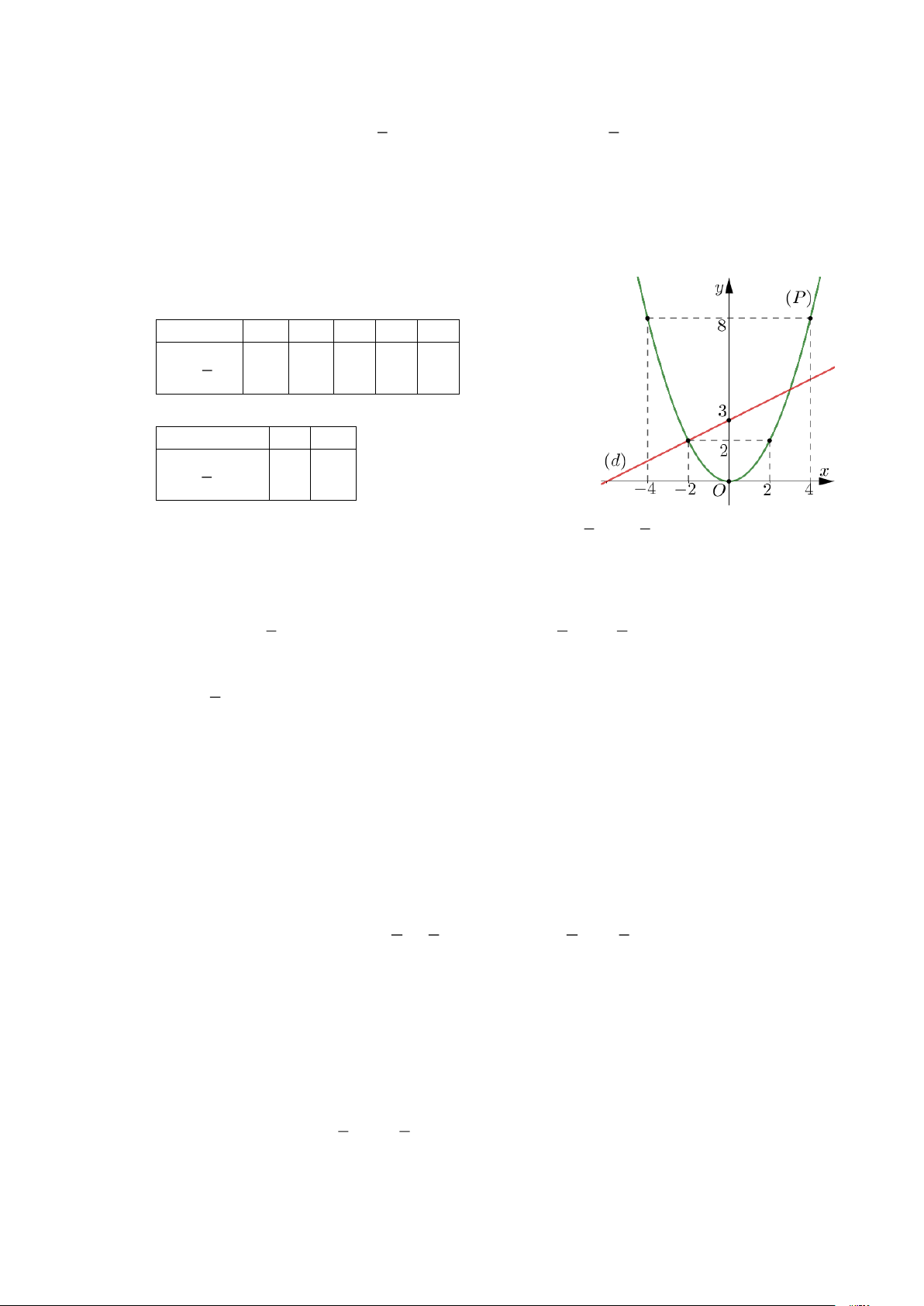
b) Tìm tọa độ giao điểm của (P ) và (d) bằng phép tính. Lời giải a) Bảng giá trị: x - 4 - 2 0 2 4 1 y = x 2 8 2 0 2 8 2 x 0 - 2 1 y = x + 3 3 2 2 1 1
b) Phương trình hoành độ giao điểm của (P ) và (d) là x2 = x + 3 2 2 x 2 Û
- x - 6 = 0 Û x = - 2 hoặc x = 3 . 1 1 9
Với x = - 2 ta được y = .(- )2 2 = .
2 Với x = 3 ta được 2 y = .3 = . 2 2 2 æ ö 9 Vậy (- ; 2 2) và ç ; ÷ 3 ç ÷ ç
÷ là tọa độ của hai giao điểm cần tìm. çè 2÷ø
Câu 2 (1,0 điểm). Cho phương trình x 2 2 - x
5 - 1 = 0 có hai nghiệm là x , x . Không giải phương trình, 1 2
hãy tính giá trị của biểu thức ( x 2 - x )( x 2 - x - 2023 1 2 2 1 ) . Lời giải
Vì a.c = 2.(- 1) = - 2 < 0 nên phương trình đã cho có hai nghiệm phân biệt x , x . 1 2 b 5 c 1
Theo định lý Viète, ta có S = x + x = - = và P = x x = = - . Khi đó 1 2 a 2 1 2 a 2
(2x - x )(2x - x ) 2 2
- 2023 = 4x x - 2x - 2x + x x - 2023 1 2 2 1 1 2 1 2 1 2 = 5x x - 2( 2 2 x + x - 2023 1 2 1 2 )
= 5x x - 2(x + x )2 + 4x x - 2023 1 2 1 2 1 2 2 = 9P - 2S - 2023 2 æ 1ö ç ÷ 5 æ ö = 9. - ç ÷- 2.ç ÷ ç ÷ - 2023 = - 2040. çè 2÷÷ ç ø è2÷÷ø
Câu 3 (1,0 điểm). Công ty viễn thông có gói cước được tính như sau: Trang 13
- Gói I : 2000 đồng/phút cho 30 phút đầu tiên; 1800 đồng/phút cho 30 phút tiếp theo; 1200 đồng/phút
cho 30 phút tiếp theo nữa và 800 đồng/phút cho thời gian còn lại.
- Gói II : 1800 đồng/phút cho 60 phút đầu tiên; 1500 đồng/phút cho 60 phút tiếp theo và 1000 đồng/
phút cho thời gian còn lại.
a) Tính số tiền phải trả của gói I khi gọi 130 phút và gói II khi gọi 130 phút.
b) Bác An nhận thấy rằng mỗi tháng trung bình gọi chưa đến 904 phút. Sau khi cân nhắc thì bác
An chọn gói I vì sẽ tiết kiệm được 150000 đồng so với gói II . Hỏi trung bình bác An gọi
bao nhiêu phút mỗi tháng? Lời giải
a) Số tiền phải trả của gói I khi gọi 130 phút là
2000´ 30 + 1800´ 30 + 1200´ 30 + 800´ (130 - 90) = 182000 (đồng).
Số tiền phải trả của gói II khi gọi 130 phút là
1800 ´ 60 + 1500´ 60 + 1000´ (130 - 120) = 208000 (đồng).
b) Gọi x (phút) là thời gian trung bình mà bác An gọi mỗi tháng và y (nghìn đồng) là số tiền
chênh lệch giữa gói I và gói II . Nhận xét rằng 60 < x £ 904 .
• Nếu 60 < x £ 90 thì y 1 é, 8 60 1, 5(x 60)ù 2 é 30 1, 8 30 1, 2(x 60)ù = ´ + - - ´ + ´ + - = 0, 3(x - 60) - 6 êë úû êë úû ,
do đó y = 150 Û x = 580 (không thỏa mãn).
• Nếu 90 < x £ 120 thì y 1 é, 8 60 1, 5(x 60)ù 2 é 30 1, 8 30 1, 2 30 0, 8 (x 90)ù = ´ + - - ´ + ´ + ´ + ´ - = 0, 7x - 60, êë úû êë úû
do đó y = 150 Û x = 300 (không thỏa mãn).
• Nếu x > 120 thì y 1
é, 8 60 1, 5 60 (x 120)ù 2 é 30 1, 8 30 1, 2 30 0, 8(x 90)ù = ´ + ´ + - - ´ + ´ + ´ + - = 0, 2x, êë úû êë úû
do đó y = 150 Û x = 750 (thỏa mãn).
Vậy trung bình mỗi tháng bác An gọi 750 phút.
Câu 4 (0,75 điểm). Do ảnh hưởng của tình hình dịch bệnh, thu nhập của một công ty bị giảm dần trong
năm 2021 . Các số liệu thống kê được thể hiện bằng đồ thị như hình vẽ. Trang 14
a) Tìm hàm số thể hiện sự liên quan của đại lượng y (trăm triệu/ tháng) theo đại lượng x (tháng).
b) Biết một sản phẩm bán được thì công ty có lợi nhuận là 100 ngàn đồng, em hãy tính số sản
phẩm mà công ty bán được trong tháng 9 năm 2021 (làm tròn đến hàng đơn vị). Lời giải a)
Gọi y = ax + b (a,b Î ¡ ) là hàm số bậc nhất thể hiện sự liên quan giữa đại lượng y theo x.
Vì các điểm (1;5) và (12;2) thuộc đồ thị hàm số trên nên ta có hệ phương trình ìï 3 ìï + = 5 ïïa a b = - ï ï 11 í Û í . ï 12a + b = 2 ï 58 ïî ïïb = ïïî 11 3 58
Vậy hàm số cần tìm có dạng y = - x + . 11 11 3 58 31
b) Thu nhập của công ty trong tháng 9 là - .9 + = (trăm triệu). 11 11 11 31
Số sản phẩm bán được trong tháng 9 là
: 0, 001 » 2818 (sản phẩm). 11
Câu 5 (1,0 điểm). Cửa hàng lấy một thùng nước ngọt ( 24 lon) của đại lý phân phối với giá 192000 đồng
và bán lẻ với giá 10000 đồng một lon.
a) Hỏi khi bán hết một thùng nước ngọt đó thì cửa hàng thu được lãi bao nhiêu phần trăm so với giá gốc?
b) Trong đợt khuyến mãi, do đại lý phân phối giảm giá nên cửa hàng cũng giảm giá còn 9500
đồng một lon và thu được lãi suất như cũ. Hỏi trong đợt này cửa hàng đã mua một thùng nước ngọt với giá bao nhiêu? Lời giải
a) Số tiền thu được khi bán hết thùng nước ngọt là 10000 ´ 24 = 240000 (đồng). 240000 - 192000
Phần trăm lãi so với giá gốc cửa hàng thu được là .10 % 0 = 2 % 5 . 192000
b) Số tiền thu được khi bán hết thùng nước ngọt với giá giảm là 9500 ´ 24 = 228000 (đồng).
Gọi x (đồng) là số tiền cửa hàng đã mua của đại lý trong đợt này (x > 0 ). Ta có phương trình
228000 - x = 0,25 Û 228000 = 1,25x Û x = 182400. x
Vậy trong đợt này cửa hàng đã mua của đại lý 182400 đồng.
Câu 6 (1,0 điểm). Một bể chứa nước có dạng như hình vẽ.
a) Tính thể tích của bể (kết quả không làm tròn). Trang 15
b) Ban đầu, bể không có nước. Sau đó người ta bơm nước vào bể với tốc độ 1 lít/giây. Hỏi sau
20 phút kể từ khi bắt đầu bơm thì mực nước trong hồ cách miệng hồ bao nhiêu mét (làm tròn 1
đến hàng phần trăm)? Biết thể tích hình trụ là 2
V = pr h và thể tích hình nón là 2 V = pr h. 3 Lời giải 1
a) Thể tích phần khối nón là 2
p.0, 7 .(1, 6 - 0, 7) = 0,147p 3 (m ) . 3
Thể tích phần khối trụ là 2
p.0, 7 .0, 7 = 0, 343p 3 (m ) .
Vậy thể tích của bể là 0,147p + 0, 343p = 0, 49p 3 (m ) .
b) Sau 20 phút thì thể tích nước trong bể là 1´ 20 ´ 60 = 1200 (lít) = 1, 2 3
(m ) > 0,147p 3 (m ) .
Do đó phần nước trong bể đầy kín khối nón và thể tích nước trong khối trụ là 1, 2 - 0,147p 3 (m ) , suy ra 1, 2 - 0,147p
chiều cao của mực nước trong hồ là (m) . 2 p.0, 7 1, 2 - 0,147p
Vậy mực nước trong hồ cách miệng hồ một khoảng là 0, 7 - » 0, 22 (m) . 2 p.0, 7
Câu 7 (1,0 điểm). Trước ngày kết thúc năm học tập thể các học sinh lớp 9A muốn mua quà tặng cho các
giáo viên giảng dạy lớp mình trong suốt năm học để tỏ lòng tri ân, mỗi món quà tặng cho thầy với giá là
50 ngàn đồng, mỗi món quà tặng cho cô có giá là 65 ngàn đồng, biết lớp tặng quà cho 15 giáo viên và
tổng số tiền mà lớp mua quà là 870 ngàn đồng. Em hãy tính số thầy giáo và số cô giáo lớp 9A dự định mua quà tặng. Lời giải
Gọi số thầy giáo và số cô giáo của lớp 9A dự định mua quà tặng lần lượt là x, y * (x, y Î ¥ ).
Vì lớp tặng quà cho 15 giáo viên và tổng số tiền mà lớp mua quà là 870 ngàn đồng nên từ đề bài ta có hệ phương trình ìï x + y = 15 ìï x = 7 ï ï í Û í .
ï 50x + 65y = 870 ï y = 8 ïî ïî
Vậy lớp 9A dự định mua quà tặng cho 7 thầy giáo và 8 cô giáo.
Câu 8 (3,0 điểm). Cho đường tròn (O) đường kính A B . Lấy điểm S tùy ý trên tia đối của tia BA . Vẽ
cát tuyến SMC của (O) . Vẽ dây cung CD của đường tròn (O) vuông góc với A B .
a) Chứng minh tam giác SMA đồng dạng với tam giác SBC .
b) Các dây cung A M , BC cắt nhau tại N ; các dây cung A B, DM cắt nhau tại P . Chứng
minh rằng tứ giác BMNP nội tiếp và NP song song với CD. c) Chứng minh 2
OP .OS = OM . Lời giải Trang 16
a) Xét D SMA và D SBC ta có µ
S là góc chung và · ·
SA M = SCB (hai góc nội tiếp (O) cùng chắn ¼ BM ).
Dẫn đến D SMA đồng dạng D SBC (góc-góc). b)
Chứng minh BMNP là tứ giác nội tiếp.
Xét đường tròn (O) đường kính A B có dây cung CD ^ A B , nên A là điểm chính giữa » CD . Dẫn đến ¼ ¼
A C = A D , do đó · ·
A BC = A MD (hai góc nội tiếp (O) chắn hai cung bằng nhau).
Vì thế tứ giác BMNP nội tiếp (do hai đỉnh kề B, M cùng nhìn NP dưới hai góc bằng nhau).
Chứng minh NP song song CD .
Vì tứ giác BMNP nội tiếp nên · ·
BMD = BNP (hai góc nội tiếp cùng chắn » BP ). Mặt khác, · ·
BMD = BCD (hai góc nội tiếp (O) cùng chắn » BD ). Suy ra · ·
BNP = BCD , mà hai góc này ở vị trí đồng vị, nên NP song song CD . ¼ ¼ sñA C - sñBM c) Xét (O) , có µ S =
(góc có đỉnh ở bên ngoài đường tròn). 2
Cũng xét (O) , lại có ¼ ¼ ¼ ¼ ¼ · · · sñA D · sñA D sñBM sñA D - sñBM
OMP = A MP - A MO = - MA O = - = . 2 2 2 2
(với lưu ý rằng D A MO cân tại O ). Mà ¼ ¼
A C = A D (chứng minh trên), nên µ · S = OMP .
Xét D OSM và D OMP có ·
MOS là góc chung và µ · S = OMP . OS OM
Dẫn đến D OSM đồng dạng với D OMP (góc-góc), suy ra 2 =
Û OP = OS .OM . OM OP ---- HẾT ---- Trang 17




