Bộ đề ôn tập giữa học kì 2 môn Toán 10 Kết Nối Tri Thức Với Cuộc Sống

Tài liệu gồm 70 trang, được biên soạn bởi thầy giáo Lê Bá Bảo, tuyển tập 05 đề ôn tập kiểm tra giữa học kì 2 môn Toán 10 bộ sách Kết Nối Tri Thức Với Cuộc Sống, có đáp án và lời giải chi tiết; thời gian làm bài 90 phút, mời bạn đọc đón xem

47 24 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề giữa HK2 Toán 10

Môn: Toán 10

Sách: Kết nối tri thức

Thông tin:

70 trang 6 tháng trước

Tác giả:

Profile Thanh Tâm
BỘ SÁCH
KẾT NỐI TRI THỨC VỚI CUỘC SỐNG
BỘ ĐỀ ÔN GIỮA KÌ 2
MÔN
TOÁN 10
Tác giả: LÊ BÁ BẢO
Trường THPT Đặng Huy Trứ, Huế
Admin CLB Giáo viên trẻ TP Huế
20
23
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
ĐỀ ÔN TẬP SỐ 01_TrNg 2023
¤N TËP GI÷A K× 2
Môn: TOÁN 10
SGK 2022 – Kết nối tri thức và cuộc sống
Líp To¸n thÇy L£ B¸ B¶O
Trưêng THPT §Æng Huy Trø S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch
, TP HuÕ
Trung t©m KM 10
Hương
Trà, HuÕ.
NỘI DUNG ĐỀ BÀI
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm)
Câu 1: Cho hàm số
2
y ax bx c
, với
0a
. Khẳng định nào sau đây sai?
A. Hàm số đồng biến trên khoảng
;
2
b
a




.
B. Hàm số nghịch biến trên khoảng
;
2
b
a




.
C. Hàm số nghịch biến trên khoảng
;
2
b
a




.
D. Đồ thị hàm số có trục đối xứng là đường thẳng
.
2

b
x
a
Câu 2: Trong mặt phẳng
,Oxy
cho hai điểm
1;3 , 2;7 .AB
Một vectơ chỉ phương của đường thẳng
AB
là
A.
1
4;1 .u 
B.
2
2;1 .u 
C.
3
3;2 .u 
D.
4
1;4 .u
Câu 3: Trong mặt phẳng
,Oxy
đường Elip
22
1
54
xy

có tiêu cự bằng
A.
2.
B.
4.
C.
9.
D.
1.
Câu 4: Nghiệm của phương trình
2 1 3xx
là
A.
3
4
x
. B.
2
3
x
. C.
4
3
x
. D.
3
2
x
.
Câu 5: Với
m
là tham số bất kì, biểu thức nào dưới đây là tam thức bậc hai?
A.
.ym
B.
.y mx
C.
22
1.y m x
D.
2
.y mx m
Câu 6: Trong mặt phẳng
,Oxy
đường tròn
22
: 4 6 12 0C x y x y
có tâm là
A.
2; 3I 
. B.
2;3I
. C.
4;6I
. D.
4; 6I 
.
Câu 7: Cho hàm số
2
31y x x
. Điểm nào sau đây thuộc đồ thị của hàm số?
A.
0 ; 2A
. B.
1; 5B
. C.
1; 3C
. D.
2; 4D 
.
Câu 8: Trong mặt phẳng
,Oxy
viết phương trình chính tắc của
2
2
22
:1
y
x
E
ab

có
2ab
và có tiêu cự
bằng
4 3.
A.
22
1
36 9

xy
. B.
22
1
36 24

xy
. C.
22
1
24 6

xy
. D.
22
1
16 4

xy
.
Câu 9: Trong mặt phẳng
,Oxy
phương trình đường tròn
C
có tâm
1;3I
và đi qua
3;1M
là
A.
22
1 3 8xy
. B.
22
1 3 10.xy
C.
22
3 1 10xy
. D.
22
3 1 8xy
.
Câu 10: Cho hàm số bậc hai
y f x
có đồ thị như hình bên dưới:
x
y
2
-1
O
1
Khẳng đinh nào dưới đây đúng?
A.
0, 0;2 .f x x
B.
0, 0;2 .f x x
C.
0, 1; .f x x 
D.
0, 0;2 .f x x


Câu 11: Trong mặt phẳng
,Oxy
với những giá trị nào của
m
thì đường thẳng
:4 3 0x y m
tiếp
xúc với đường tròn
22
: 9?C x y
A.
3.m
B.
3m
và
3.m
C.
45m
và
45.m
D.
15m
và
15.m
Câu 12: Trong các hàm số sau hàm số nào là hàm số bậc hai?
A.
2
2 3 5y x x
B.
3
2 3 5xx
y
x

. C.
23
2 3 5y x x
. D.
32yx
.
Câu 13: Cho hàm số
2
2 3.f x x x
Khẳng định nào dưới đây đúng?
A.
2 3.f
B.
3 4.f
C.
0 2.f
D.
4 5.f
Câu 14: Cho hàm số
2
3 4 3y x x
có đồ thị (P). Trục đối xứng của (P) là đường thẳng có phương
trình là
A.
2
3
x
. B.
2
3
x 
. C.
4
3
x
. D.
4
3
x 
Câu 15: Tam thức bậc hai nào dưới đây có bảng xét dấu như hình sau?
x

0
4

fx
0
0
A.
2
2.y x x
B.
2
2.y x x
C.
2
4.y x x
D.
2
4.y x x
Câu 16: Tìm tập xác định của hàm số
21
45

x
y f x
x
.
A.
D
. B.
4
\.
5



D
C.
5
;
4
D




. D.
5
\
4
D



.
Câu 17: Tìm tất cả giá trị tham số
m
để hàm số
2
12y x m x m
đồng biến trên
1; 
.
A.
3m 
. B.
3m 
. C.
3m 
. D.
3m 
.
Câu 18: Đỉnh của parabol
2
45 y x x
có toạ độ là
A.
0;2
. B.
1;2
. C.
2;0
. D.
2;1
.
Câu 19: Giá trị nhỏ nhất của hàm số
2
45y x x
là
A.
min
0y
. B.
min
2y 
. C.
min
2y
. D.
min
1y
.
Câu 20: Tam thức nào dưới đây luôn dương với mọi
?x
A.
2
1.y x x
B.
2
2 1.y x x
C.
2
1.y x x
D.
2
4.y x x
Câu 21: Trong mặt phẳng
,Oxy
cho đường thẳng


1
:.
23
xt
dt
yt
Điểm nào dưới đây nằm trên
đường thẳng
?d
A.
1;3 .M
B.
5;2 .N
C.
2;5 .P
D.
2;0 .Q
Câu 22: Số nghiệm của phương trình
2
4 1 3x x x
là
A. Vô số. B.
0.
C.
1.
D.
2.
Câu 23: Hàm số
1
1
x
y
xm

xác định trên
0;1
khi chỉ khi
A.
1m
. B.
1
2
m
m
. C.
1
2
m
m
. D.
12m
.
Câu 24: Trong mặt phẳng
,Oxy
cho đường thẳng
: 2 5 0.d x y
Vectơ nào dưới đây là một vectơ chỉ
phương của
?d
A.
1
1;2 .u
B.
2
2;1 .u 
C.
3
3;2 .u 
D.
4
2;3 .u
Câu 25: Phương trình
2 2 2
6 17 6x x x x x
có bao nhiêu nghiệm phân biệt?
A. 2. B. 1. C. 3. D. 4.
Câu 26: Trong mặt phẳng
,Oxy
phương trình nào sau đây là phương trình của đường tròn?
A.
22
2 4 8 1 0x y x y
. B.
22
4 6 12 0x y x y
.
C.
22
2 8 20 0x y x y
. D.
22
4 10 6 2 0x y x y
.
Câu 27: Trong mặt phẳng
,Oxy
cho hai điểm
1;1 , 2;4 .MN
Phương trình đường thẳng
MN
là
A.
1
.
3
xt
yt

B.
13
.
1
xt
yt


C.
1
.
3
xt
yt


D.
.
23
xt
yt
Câu 28: Cho
2
,0f x ax bx c a
và
2
4b ac
. Tìm điều kiện của
để
fx
cùng dấu với
hệ số
a
với mọi
x
.
A.
0
. B.
0
. C.
0
. D.
0
.
Câu 29: Trong mặt phẳng
,Oxy
cho hai đường thẳng
1
: 4 2 1 0d x y
và
2
: 2 3 0.d x y
Khẳng
định nào sau đây đúng?
A.
12
/ / .dd
B.
12
.dd
C.
1
d
,
2
d
cắt nhau và không vuông góc. D.
12
.dd
Câu 30: Tập nghiệm của bất phương trình
2
2 3 0xx
là
A.
1;3 .


B.
; 1 3; . 
C.
1;3 .
D.
; 1 3; .

 

Câu 31: Trong mặt phẳng
,Oxy
cho điểm
2; 3A
và đường thẳng
12
: , .
3
xt
dt
yt


Phương trình
đường thẳng
qua
A
và vuông góc với
d
là
A.
2 7 0.xy
B.
2 0.xy
C.
2 1 0.xy
D.
2 4 0.xy
Câu 32: Đường thẳng nào dưới đây là đường chuẩn của parabol
2
4y x
?
A.
1.x
B.
2.x
C.
1.x
D.
2.x
Câu 33: Tập nghiệm của phương trình
2
2 4 3 0x x x
là
A.
2;3S
. B.
2S
. C.
1;3S
. D.
1;2;3S
.
Câu 34: Trong mặt phẳng
,Oxy
cho điểm
1;2A
và đường thẳng
: 2 1 0.xy
Tính khoảng cách
từ điểm
A
đến đường thẳng
.
A.
5.
B.
5.
C.
25
D.
5
.
5
Câu 35: Trong mặt phẳng
,Oxy
hypebol
2
2
:1
16 9
y
x
H 
có hai tiêu điểm là
A.
1
5;0F
,
2
.5;0F
B.
1
2;0F
,
2
.2;0F
C.
1
3;0F
,
2
.3;0F
D.
1
4;0F
,
2
.4;0F
II. PHẦN TỰ LUẬN (03 câu – 3,0 điểm)
Câu 1: (1,0 điểm).
a) Tìm tập xác định của hàm số
2
21
.
4
x
y
x
b) Tìm
,ab
để parabol
2
:1P y ax bx
đi qua hai điểm
1;4A
và
2;9 .B
Câu 2: (1,0 điểm).
a) Giải phương trình
2
5 1 1.x x x
b) Tìm
m
để phương trình
22
2 2 3 1 0x x m m
có hai nghiệm dương phân biệt.
Câu 3: (1,0 điểm).
Trong mặt phẳng
,Oxy
cho hai đường thẳng
12
: 1 0, : 2 1 0d x y d x y
. Viết phương
trình đường thẳng đi qua
(1; 1)M
và cắt
12
,dd
tương ứng tại A, B sao cho
20MA MB
.
____________________HẾT____________________
Huế, 08h45’ Ngày 10 tháng 02 năm 2023
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
ĐỀ ÔN TẬP SỐ 01_TrNg 2023
¤N TËP GI÷A K× 2
Môn: TOÁN 10
SGK 2022 – Kết nối tri thức và cuộc sống
Líp To¸n thÇy L£ B¸ B¶O
Trưêng THPT §Æng Huy Trø S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch
, TP HuÕ
Trung t©m KM 10
Hương
Trà, HuÕ.
LỜI GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm)
Câu 1: Cho hàm số
2
y ax bx c
, với
0a
. Khẳng định nào sau đây sai?
A. Hàm số đồng biến trên khoảng
;
2
b
a




.
B. Hàm số nghịch biến trên khoảng
;
2
b
a




.
C. Hàm số nghịch biến trên khoảng
;
2
b
a




.
D. Đồ thị hàm số có trục đối xứng là đường thẳng
.
2

b
x
a
Câu 2: Trong mặt phẳng
,Oxy
cho hai điểm
1;3 , 2;7 .AB
Một vectơ chỉ phương của đường thẳng
AB
là
A.
1
4;1 .u 
B.
2
2;1 .u 
C.
3
3;2 .u 
D.
4
1;4 .u
Lời giải:
Ta có:
1;4 .AB
Các vectơ chỉ phương của đường thẳng
AB
có tọa độ
;4 , 0 .k k k
Chọn đáp án D.
Câu 3: Trong mặt phẳng
,Oxy
đường Elip
22
1
54
xy

có tiêu cự bằng
A.
2.
B.
4.
C.
9.
D.
1.
Lời giải:
Ta có
22
5 4 1 2 2c a b c
.
Chọn đáp án A.
Câu 4: Nghiệm của phương trình
2 1 3xx
là
A.
3
4
x
. B.
2
3
x
. C.
4
3
x
. D.
3
2
x
.
Lời giải:
Thay các nghiệm
x
vào phương trình thấy
4
3
x
là nghiệm.
Chọn đáp án C.
Câu 5: Với
m
là tham số bất kì, biểu thức nào dưới đây là tam thức bậc hai?
A.
.ym
B.
.y mx
C.
22
1.y m x
D.
2
.y mx m
Câu 6: Trong mặt phẳng
,Oxy
đường tròn
22
: 4 6 12 0C x y x y
có tâm là
A.
2; 3I 
. B.
2;3I
. C.
4;6I
. D.
4; 6I 
.
Câu 7: Cho hàm số
2
31y x x
. Điểm nào sau đây thuộc đồ thị của hàm số?
A.
0 ; 2A
. B.
1; 5B
. C.
1; 3C
. D.
2; 4D 
.
Câu 8: Trong mặt phẳng
,Oxy
viết phương trình chính tắc của
2
2
22
:1
y
x
E
ab

có
2ab
và có tiêu cự
bằng
4 3.
A.
22
1
36 9

xy
. B.
22
1
36 24

xy
. C.
22
1
24 6

xy
. D.
22
1
16 4

xy
.
Lời giải:
Theo giả thiết:
2ab
và
22 4 3 3c c
Khi đó:
2
2 2 2 2
2 12a b c b b
2
3 12 0b
2b
4a
.
Vậy phương trình chính tắc của Elip là:
22
1
16 4

xy
.
Chọn đáp án D.
Câu 9: Trong mặt phẳng
,Oxy
phương trình đường tròn
C
có tâm
1;3I
và đi qua
3;1M
là
A.
22
1 3 8xy
. B.
22
1 3 10.xy
C.
22
3 1 10xy
. D.
22
3 1 8xy
.
Lời giải:
Ta có:
2; 2 .IM 
Do điểm
3; 1M
thuộc đường tròn
C
nên
22R IM
.
Đường tròn
C
có tâm
1; 3I
và bán kính
22R
có phương trình là
22
: 1 3 8C x y
.
Chọn đáp án A.
Câu 10: Cho hàm số bậc hai
y f x
có đồ thị như hình bên dưới:
x
y
2
-1
O
1
Khẳng đinh nào dưới đây đúng?
A.
0, 0;2 .f x x
B.
0, 0;2 .f x x
C.
0, 1; .f x x 
D.
0, 0;2 .f x x


Câu 11: Trong mặt phẳng
,Oxy
với những giá trị nào của
m
thì đường thẳng
:4 3 0x y m
tiếp
xúc với đường tròn
22
: 9?C x y
A.
3.m
B.
3m
và
3.m
C.
45m
và
45.m
D.
15m
và
15.m
Lời giải:
Đường tròn
C
có tâm
0;0IO
và bán kính là
3R
.
tiếp xúc
C
,d I R
3
5
m
15
.
15

m
m
Chọn đáp án D.
Câu 12: Trong các hàm số sau hàm số nào là hàm số bậc hai?
A.
2
2 3 5y x x
B.
3
2 3 5xx
y
x

. C.
23
2 3 5y x x
. D.
32yx
.
Câu 13: Cho hàm số
2
2 3.f x x x
Khẳng định nào dưới đây đúng?
A.
2 3.f
B.
3 4.f
C.
0 2.f
D.
4 5.f
Câu 14: Cho hàm số
2
3 4 3y x x
có đồ thị (P). Trục đối xứng của (P) là đường thẳng có phương
trình là
A.
2
3
x
. B.
2
3
x 
. C.
4
3
x
. D.
4
3
x 
Lời giải:
Trục đối xứng của (P) là đường thẳng
42
2 6 3
b
x
a

.
Chọn đáp án B.
Câu 15: Tam thức bậc hai nào dưới đây có bảng xét dấu như hình sau?
x

0
4

fx
0
0
A.
2
2.y x x
B.
2
2.y x x
C.
2
4.y x x
D.
2
4.y x x
Lời giải:
Kiểm tra các sự kiện:
0a
và tam thức có hai nghiệm
0, 4.xx
Chọn đáp án C.
Câu 16: Tìm tập xác định của hàm số
21
45

x
y f x
x
.
A.
D
. B.
4
\.
5



D
C.
5
;
4
D




. D.
5
\
4
D



.
Lời giải:
Điều kiện :
5
4 5 0
4
xx
. Tập xác định của hàm số là
5
\
4
D



.
Chọn đáp án D.
Câu 17: Tìm tất cả giá trị tham số
m
để hàm số
2
12y x m x m
đồng biến trên
1; 
.
A.
3m 
. B.
3m 
. C.
3m 
. D.
3m 
.
Lời giải:
Hàm số đã cho xác định với mọi
x
.
Bảng biến thiên:
Dựa vào bảng biến thiên ta có hàm số đã cho đồng biến trên khoảng
1; 
khi
1
13
2
m
m
.
Chọn đáp án B.
Câu 18: Đỉnh của parabol
2
45 y x x
có toạ độ là
A.
0;2
. B.
1;2
. C.
2;0
. D.
2;1
.
Lời giải:
Đỉnh của parabol
2
45 y x x
có toạ độ là
2;1
.
Chọn đáp án D.
Câu 19: Giá trị nhỏ nhất của hàm số
2
45y x x
là
A.
min
0y
. B.
min
2y 
. C.
min
2y
. D.
min
1y
.
Lời giải:
Hàm số
2
45y x x
có
10a 
, do đó hàm số đạt giá trị nhỏ nhất tại
2
2
b
x
a

và
min
21yy
.
Chọn đáp án D.
Câu 20: Tam thức nào dưới đây luôn dương với mọi
?x
A.
2
1.y x x
B.
2
2 1.y x x
C.
2
1.y x x
D.
2
4.y x x
Lời giải:
Bảng xét dấu
2
1:y x x
x


y
Chọn đáp án A.
Câu 21: Trong mặt phẳng
,Oxy
cho đường thẳng


1
:.
23
xt
dt
yt
Điểm nào dưới đây nằm trên
đường thẳng
?d
A.
1;3 .M
B.
5;2 .N
C.
2;5 .P
D.
2;0 .Q
Lời giải:
Thay tọa độ điểm
P
vào phương trình
d
ta được:
21
1.
5 2 3
t
t
t



Chọn đáp án C.
Câu 22: Số nghiệm của phương trình
2
4 1 3x x x
là
A. Vô số. B.
0.
C.
1.
D.
2.
Lời giải:
Ta có:
2
4 1 3x x x
22
30
4 1 6 9
x
x x x x

3
1
x
x
(vô nghiệm).
Chọn đáp án B.
Câu 23: Hàm số
1
1
x
y
xm

xác định trên
0;1
khi chỉ khi
A.
1m
. B.
1
2
m
m
. C.
1
2
m
m
. D.
12m
.
Lời giải:
Điều kiện xác định:
1xm
.
Để hàm số đã cho xác định trên
0;1
thì
1 0 1
1 0;1
1 1 2
mm
m
mm
.
Chọn đáp án C.
Câu 24: Trong mặt phẳng
,Oxy
cho đường thẳng
: 2 5 0.d x y
Vectơ nào dưới đây là một vectơ chỉ
phương của
?d
A.
1
1;2 .u
B.
2
2;1 .u 
C.
3
3;2 .u 
D.
4
2;3 .u
Lời giải:
Các vectơ chỉ phương của
d
có tọa độ
2 ; , 0 .k k k
Chọn đáp án B.
Câu 25: Phương trình
2 2 2
6 17 6x x x x x
có bao nhiêu nghiệm phân biệt?
A. 2. B. 1. C. 3. D. 4.
Lời giải:
2 2 2 2 2
6 17 6 6 17 1 0x x x x x x x x
2
2
2
2
0( )
60
6( )
0
17 0
.
4
17
17 1
17 1
x TM
xx
xL
x
x
x
x
x
x





Vậy phương trình có 3 nghiệm phân biệt.
Chọn đáp án C.
Câu 26: Trong mặt phẳng
,Oxy
phương trình nào sau đây là phương trình của đường tròn?
A.
22
2 4 8 1 0x y x y
. B.
22
4 6 12 0x y x y
.
C.
22
2 8 20 0x y x y
. D.
22
4 10 6 2 0x y x y
.
Lời giải:
Để là phương trình đường tròn thì điều kiện cần là hệ số của
2
x
và
2
y
phải bằng nhau nên
loại được đáp án A và D.
Ta có:
22
22
2 8 20 0 1 4 3 0x y x y x y
vô lý.
Ta có:
22
22
4 6 12 0 2 3 25x y x y x y
là phương trình đường tròn tâm
2; 3I
, bán kính
5R
.
Chọn đáp án B.
Câu 27: Trong mặt phẳng
,Oxy
cho hai điểm
1;1 , 2;4 .MN
Phương trình đường thẳng
MN
là
A.
1
.
3
xt
yt

B.
13
.
1
xt
yt


C.
1
.
3
xt
yt


D.
.
23
xt
yt
Lời giải:
Ta có:
1;3 .MN
Đường thẳng
MN
qua
1;1M
và nhận
1;3MN
làm một vectơ chỉ phương.
Vậy
1
: , .
13
xt
MN t
yt


Test phương án D, thấy thỏa mãn.
Chọn đáp án D.
Câu 28: Cho
2
,0f x ax bx c a
và
2
4b ac
. Tìm điều kiện của
để
fx
cùng dấu với
hệ số
a
với mọi
x
.
A.
0
. B.
0
. C.
0
. D.
0
.
Câu 29: Trong mặt phẳng
,Oxy
cho hai đường thẳng
1
: 4 2 1 0d x y
và
2
: 2 3 0.d x y
Khẳng
định nào sau đây đúng?
A.
12
/ / .dd
B.
12
.dd
C.
1
d
,
2
d
cắt nhau và không vuông góc. D.
12
.dd
Lời giải:
Ta có:
4 2 1
2 1 3
1
d
và
2
d
song song.
Chọn đáp án A.
Câu 30: Tập nghiệm của bất phương trình
2
2 3 0xx
là
A.
1;3 .


B.
; 1 3; . 
C.
1;3 .
D.
; 1 3; .

 

Lời giải:
Bảng xét dấu
2
2 3 :f x x x
x

1
3

fx
0
0
Chọn đáp án B.
Câu 31: Trong mặt phẳng
,Oxy
cho điểm
2; 3A
và đường thẳng
12
: , .
3
xt
dt
yt


Phương trình
đường thẳng
qua
A
và vuông góc với
d
là
A.
2 7 0.xy
B.
2 0.xy
C.
2 1 0.xy
D.
2 4 0.xy
Lời giải:
Đường thẳng
d
có một vectơ chỉ phương là
2;1 .
d
u
Do
vuông góc với
d
nên
nhận
2;1
d
u
làm một vectơ pháp tuyến.
Vậy
: 2 2 1 3 0 2 7 0.x y x y
Chọn đáp án A.
Câu 32: Đường thẳng nào dưới đây là đường chuẩn của parabol
2
4y x
?
A.
1.x
B.
2.x
C.
1.x
D.
2.x
Lời giải:
Phương trình chính tắc của parabol
2
: 2Py px
2p
Phương trình đường chuẩn là
1
2
p
x
.
Chọn đáp án A.
Câu 33: Tập nghiệm của phương trình
2
2 4 3 0x x x
là
A.
2;3S
. B.
2S
. C.
1;3S
. D.
1;2;3S
.
Lời giải:
Điều kiện:
2 0 2xx
(*).
Với điều kiện (*), phương trình đã cho tương đương với
2
2
20
1
4 3 0
3
x
x
x
xx
x


.
So với điều kiện (*) chỉ có
2x
,
3x
thỏa mãn.
Vậy tập nghiệm của phương trình là
2;3S
.
Chọn đáp án A.
Câu 34: Trong mặt phẳng
,Oxy
cho điểm
1;2A
và đường thẳng
: 2 1 0.xy
Tính khoảng cách
từ điểm
A
đến đường thẳng
.
A.
5.
B.
5.
C.
25
D.
5
.
5
Lời giải:
Ta có:
2.1 2 1
; 5.
41
dA

Chọn đáp án A.
Câu 35: Trong mặt phẳng
,Oxy
hypebol
2
2
:1
16 9
y
x
H 
có hai tiêu điểm là
A.
1
5;0F
,
2
.5;0F
B.
1
2;0F
,
2
.2;0F
C.
1
3;0F
,
2
.3;0F
D.
1
4;0F
,
2
.4;0F
Lời giải:
Ta có :
2
2
2 2 2
16
9
25
a
b
c a b

4
3.
5
a
b
c
Vậy các tiêu điểm của
H
là
1
5;0F
,
2
.5;0F
II. PHẦN TỰ LUẬN (03 câu – 3,0 điểm)
Câu 1: (1,0 điểm).
a) Tìm tập xác định của hàm số
2
21
.
4
x
y
x
b) Tìm
,ab
để parabol
2
:1P y ax bx
đi qua hai điểm
1;4A
và
2;9 .B
Lời giải:
a) Hàm số xác định
2
2
4 0 .
2
x
x
x

Vậy tập xác định của hàm số là
\ 2;2 .D
b) Do
P
đi qua hai điểm
1;4A
và
2;9B
nên ta có:
1 4 3 1
.
4 2 1 9 4 2 8 2
a b a b a
a b a b b

Vậy
2
: 2 1.P y x x
Câu 2: (1,0 điểm).
a) Giải phương trình
2
5 1 1.x x x
b) Tìm
m
để phương trình
22
2 2 3 1 0x x m m
có hai nghiệm dương phân biệt.
Lời giải:
a) Ta có:
2
22
1
1 0 1
5 1 1 6.
0
5 1 1 6 0
6
x
xx
x x x x
x
x x x x x
x



Vậy phương trình có tập nghiệm là
6.S
b) Phương trình có hai nghiệm dương phân biệt khi
2
2
0 1 (2 3 1) 0
0 2 0,
0
2 3 1 0
mm
Sm
P
mm


2
2
31
00
2 3 0
22
.
13
2 3 1 0
11
22
mm
mm
mm
m m m





Câu 3: (1,0 điểm).
Trong mặt phẳng
,Oxy
cho hai đường thẳng
12
: 1 0, : 2 1 0d x y d x y
. Viết phương
trình đường thẳng đi qua
(1; 1)M
và cắt
12
,dd
tương ứng tại A, B sao cho
20MA MB
.
Lời giải:
Gọi
12
; 1 , ;2 1A a a d B b b d
. Ta có:
1; , 1;2MA a a MB b b
Theo giả thiết:
2 1 1 0
1 1; 2
20
2 2 0
1
ab
aA
MA MB
ab
b

Lúc đó, đường thẳng
d
cần tìm đi qua
1; 2A
và có 1 vectơ chỉ phương
0;1AM
nên
có phương trình là
1
:.
2
x
dt
xt
____________________HẾT____________________
Huế, 08h45’ Ngày 10 tháng 02 năm 2023
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
ĐỀ ÔN TẬP SỐ 02_TrNg 2023
¤N TËP GI÷A K× 2
Môn: TOÁN 10
SGK 2022 – Kết nối tri thức và cuộc sống
Líp To¸n thÇy L£ B¸ B¶O
Trưêng THPT §Æng Huy Trø S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch
, TP HuÕ
Trung t©m KM 10
Hương
Trà, HuÕ.
NỘI DUNG ĐỀ BÀI
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm)
Câu 1: Trong mặt phẳng
,Oxy
xác định tâm và bán kính của đường tròn
22
: 1 2 9.C x y
A. Tâm
1;2 ,I
bán kính
3R
. B. Tâm
1;2 ,I
bán kính
9R
.
C. Tâm
1; 2 ,I
bán kính
3R
. D. Tâm
1; 2 ,I
bán kính
9R
.
Câu 2: Điểm nào dưới đây không thuộc đồ thị hàm số
21
1
x
y
x
?
A.
0; 1 .P
B.
2;5 .N
C.
4;3 .Q
D.
2; 3 .M 
Câu 3: Trong mặt phẳng
,Oxy
phương trình nào sau đây là phương trình của một đường tròn?
A.
22
4 2 8 3 0x y xy x y
. B.
22
2 4 5 1 0x y x y
.
C.
22
14 2 2018 0x y x y
. D.
22
4 5 2 0x y x y
.
Câu 4: Trong mặt phẳng
,Oxy
cho đường thẳng
12
: , .
23
xt
dt
yt


Vectơ nào dưới đây là một
vectơ chỉ phương của
?d
A.
1
1;2 .u
B.
2
2;1 .u 
C.
3
3;2 .u 
D.
4
2;3 .u
Câu 5: Trong mặt phẳng
,Oxy
cho elip
22
:1
94
xy
E 
có hai tiêu điểm
1
F
,
2
F
. Gọi
M
là điểm
thuộc
,E
tính
12
MF MF
.
A.
5.
B.
6.
C.
3.
D.
2.
Câu 6: Cho hàm số bậc hai có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
2;
. B.
;2
. C.
2; 1
. D.
1;
.
Câu 7: Cặp điểm nào là các tiêu điểm của hypebol
22
1
95
xy

?
A.
4; 0
và
4; 0
. B.
14; 0
và
14; 0
.
C.
2; 0
và
2; 0
. D.
0; 14
và
0; 14
.
Câu 8: Trong mặt phẳng
,Oxy
đường tròn nào sau đây tiếp xúc với trục Ox?
A.
22
10 0x y x
. B.
22
50xy
.
C.
22
10 2 1 0x y x y
. D.
22
6 5 9 0x y x y
.
Câu 9: Đường thẳng nào dưới đây là đường chuẩn của parabol
2
3
?
2
yx
A.
3
.
4
x 
B.
3
.
4
x
C.
3
.
8
y
D.
3
.
8
x 
Câu 10: Trong mặt phẳng
,Oxy
cho hai đường thẳng
1
: 3 0d x y
và
2
: 2 3 0.d x y
Khẳng định
nào sau đây đúng?
A.
12
/ / .dd
B.
12
.dd
C.
1
d
,
2
d
cắt nhau và không vuông góc. D.
12
.dd
Câu 11: Tìm tất cả các giá trị của tham số
m
để biểu thức
2
2 5 9 f x m x x
là tam thức bậc hai.
A.
m
. B.
2m
. C.
2m
. D.
0m
.
Câu 12: Trong mặt phẳng
,Oxy
cho hai điểm
1;0 , 3;6 .AB
Phương trình đường thẳng trung trực
của đoạn thẳng
AB
là
A.
3 11 0xy
B.
3 11 0.xy
C.
3 9 0.xy
D.
3 7 0.xy
Câu 13: Tam thức bậc hai nào dưới đây có bảng xét dấu như hình vẽ?
x

0
2

fx
0
0
A.
2
2.y x x
B.
2
2.y x x
C.
2
4.y x x
D.
2
4.y x x
Câu 14: Trong mặt phẳng
,Oxy
cho đường thẳng
12
: , .
23
xt
dt
yt


Vectơ nào dưới đây là một
vectơ pháp tuyến của
?d
A.
1
1;2 .u
B.
2
2;1 .u 
C.
3
3;2 .u 
D.
4
2;3 .u
Câu 15: Trong mặt phẳng
,Oxy
viết phương trình chính tắc của Elip có tiêu cự bằng
6
và đi qua điểm
0;5A
.
A.
22
1
34 9
xy

. B.
22
1
34 25

xy
. C.
22
1
25 9

xy
. D.
22
1
25 16

xy
.
Câu 16: Trong mặt phẳng
,Oxy
cho hai điểm
1;1A
và
7;5B
. Phương trình đường tròn đường
kính
AB
là
A.
22
8 6 12 0x y x y
. B.
22
8 6 12 0x y x y
.
C.
22
8 6 12 0x y x y
. D.
22
8 6 12 0x y x y
.
Câu 17: Cho tam thức
2
3 2.f x x x
Khẳng định nào dưới đây đúng?
A.
0, 1;2 .f x x
B.
0, 1;2 .f x x
C.
0, ;1 2; .f x x  
D.
0, 1;2 .f x x


Câu 18: Trong mặt phẳng
,Oxy
cho đường thẳng
: , .
12
xt
dt
yt

Điểm nào dưới đây không
nằm trên đường thẳng
?d
A.
0;1 .M
B.
1;3 .N
C.
2;5 .P
D.
1;1 .Q
Câu 19: Tổng tất cả các nghiệm của phương trình và
2
3 2 2x x x
là
A.
3
. B.
4
. C.
1
. D.
3
.
Câu 20: Trong mặt phẳng
,Oxy
tìm giá trị tham số
n
để khoảng cách từ điểm
2;3I
đến đường
thẳng
: 1 2 0x ny n
bằng
1.
A.
0.n
B.
1.n
C.
1.n 
D.
2.n
Câu 21: Tìm
m
để parabol
2
( ): 2 3P y mx x
có trục đối xứng là đường thẳng
2x
.
A.
2m
. B.
1m 
. C.
1m
. D.
1
2
m
.
Câu 22: Trong mặt phẳng
,Oxy
cho điểm
2; 3A
và đường thẳng
12
: , .
3
xt
dt
yt


Phương trình
đường thẳng
qua
A
và song song với
d
là
A.
2 7 0.xy
B.
2 0.xy
C.
2 1 0.xy
D.
2 4 0.xy
Câu 23: Tập nghiệm của bất phương trình
2
2 1 0xx
là
A.
.
B. C.
1.
D.
\ 1 .
Câu 24: Số nghiệm của phương trình
2
3 2 3
0
1
x x x
x
là
A.
1
. B.
2
. C.
3
. D.
0
.
Câu 25: Cho hàm số
32f x x
. Giá trị của hàm số tại điểm
2x 
bằng
A.
1
. B.
3
. C.
7
. D.
7
.
Câu 26: Bảng biến thiên của hàm số
2
21y x x
là
A. . B. .
C. . D. .
Câu 27: Trong các hàm số sau, hàm số nào xác định trên ?
A.
1yx
. B.
1
2
y
x
. C.
3
1
1
y
x
. D.
2
1
1
y
x
.
Câu 28: Một nghiệm của phương trình
21xx
là
A.
2x
. B.
5x
. C.
1x
. D.
0x
.
Câu 29: Hàm số nào có đồ thị là đường parabol có đỉnh là
1;3 ?I
A.
2
2 4 3y x x
. B.
2
2 2 1y x x
. C.
2
2 4 5y x x
. D.
2
22y x x
.
Câu 30: Tìm tất các giá trị thực của tham số
m
để hàm số
2
2 3 2 1
x
y
x x m
xác định trên
.
A.
17
16
m
. B.
17
16
m
. C.
17
0
16
m
. D.
17
16
m
.
Câu 31: Tổng các nghiệm của phương trình
2
3 2 6 9x x x
bằng
A.
2
. B.
3
. C.
1
. D.
7
.
Câu 32: Tam thức nào dưới đây luôn âm với mọi
?x
A.
2
1.y x x
B.
2
1.y x x
C.
2
1.y x x
D.
2
4.y x x
Câu 33: Cho tam thức bậc hai
2
, ; ; , 0f x ax bx c a b c a
với
2
4.b ac
Mệnh đề nào dưới
đây đúng?
A.
0
0, .
0
a
f x x

B.
0
0, .
0
a
f x x

C.
0
0, .
0
a
f x x

D.
0
0, .
0
a
f x x

Câu 34: Gọi
M
là giá trị lớn nhất,
m
là giá trị nhỏ nhất của hàm số
2
42y x x
trên đoạn
0;3
.
Tính giá trị biểu thức
Mm
.
A.
1
. B.
4
. C.
0
. D.
1
.
Câu 35: Đồ thị hàm số:
2
y ax bx c
như hình vẽ bên dưới:
Trong các hệ số
,,abc
có bao nhiêu giá trị dương?
A.
1
.
B.
0
. C.
2
. D.
3
.
II. PHẦN TỰ LUẬN (03 câu – 3,0 điểm)
Câu 1: (1,0 điểm).
a) Tìm tập xác định của hàm số
2
5 4.y x x
b) Tìm
,ab
để parabol
2
:1P y ax bx
có đỉnh là
1;2 .I
Câu 2: (1,0 điểm).
a) Giải phương trình
2
3 17 23 3.x x x
b) Tìm
m
để các bất phương trình
2
2
5
17
2 3 2
x x m
xx


luôn đúng với mọi
.x
Câu 3: (1,0 điểm).
Trong mặt phẳng
,Oxy
viết phương trình đường thẳng
d
song song với
: 4 3 12 0xy
và
d
cách
một khoảng bằng
5.
____________________HẾT____________________
Huế, 08h45’ Ngày 10 tháng 02 năm 2023
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
ĐỀ ÔN TẬP SỐ 02_TrNg 2023
¤N TËP GI÷A K× 2
Môn: TOÁN 10
SGK 2022 – Kết nối tri thức và cuộc sống
Líp To¸n thÇy L£ B¸ B¶O
Trưêng THPT §Æng Huy Trø S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch
, TP HuÕ
Trung t©m KM 10
Hương
Trà, HuÕ.
LỜI GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm)
Câu 1: Trong mặt phẳng
,Oxy
xác định tâm và bán kính của đường tròn
22
: 1 2 9.C x y
A. Tâm
1;2 ,I
bán kính
3R
. B. Tâm
1;2 ,I
bán kính
9R
.
C. Tâm
1; 2 ,I
bán kính
3R
. D. Tâm
1; 2 ,I
bán kính
9R
.
Câu 2: Điểm nào dưới đây không thuộc đồ thị hàm số
21
1
x
y
x
?
A.
0; 1 .P
B.
2;5 .N
C.
4;3 .Q
D.
2; 3 .M 
Lời giải:
Với
2x 
ta có
2. 2 1
21
21
y


. Vậy điểm
2; 3M 
không thuộc đồ thị hàm số
21
1
x
y
x
.
Chọn đáp án D.
Câu 3: Trong mặt phẳng
,Oxy
phương trình nào sau đây là phương trình của một đường tròn?
A.
22
4 2 8 3 0x y xy x y
. B.
22
2 4 5 1 0x y x y
.
C.
22
14 2 2018 0x y x y
. D.
22
4 5 2 0x y x y
.
Câu 4: Trong mặt phẳng
,Oxy
cho đường thẳng
12
: , .
23
xt
dt
yt


Vectơ nào dưới đây là một
vectơ chỉ phương của
?d
A.
1
1;2 .u
B.
2
2;1 .u 
C.
3
3;2 .u 
D.
4
2;3 .u
Lời giải:
Các vectơ chỉ phương của
d
có tọa độ
2 ;3 , 0 .k k k
Chọn đáp án D.
Câu 5: Trong mặt phẳng
,Oxy
cho elip
22
:1
94
xy
E 
có hai tiêu điểm
1
F
,
2
F
. Gọi
M
là điểm
thuộc
,E
tính
12
MF MF
.
A.
5.
B.
6.
C.
3.
D.
2.
Lời giải:
Phương trình của
E
có dạng
22
22
1
xy
ab

(
2 2 2
a b c
). Suy ra
2
9a
3a
.
Do
M
thuộc
E
nên
12
2MF MF a
6
.
Chọn đáp án B.
Câu 6: Cho hàm số bậc hai có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
2;
. B.
;2
. C.
2; 1
. D.
1;
.
Lời giải:
Dựa vào bảng biến thiên ta có hàm số đồng biến trên
1;
.
Chọn đáp án D.
Câu 7: Cặp điểm nào là các tiêu điểm của hypebol
22
1
95
xy

?
A.
4; 0
và
4; 0
. B.
14; 0
và
14; 0
.
C.
2; 0
và
2; 0
. D.
0; 14
và
0; 14
.
Lời giải:
Ta có
22
9 5 14c a b
. Vậy cặp điểm
14; 0 , 14; 0
là các tiêu điểm của
hypebol.
Chọn đáp án B.
Câu 8: Trong mặt phẳng
,Oxy
đường tròn nào sau đây tiếp xúc với trục Ox?
A.
22
10 0x y x
. B.
22
50xy
.
C.
22
10 2 1 0x y x y
. D.
22
6 5 9 0x y x y
.
Lời giải:
Xét phương trình đường tròn
C
:
22
6 5 9 0x y x y
2
2
5 25
3.
24
xy



C
có tâm
5
3;
2
I




và bán kính
5
2
R
.
Ta có:
5
;
2
d I Ox R
. Vậy
C
tiếp xúc với trục Ox.
Chọn đáp án D.
Câu 9: Đường thẳng nào dưới đây là đường chuẩn của parabol
2
3
?
2
yx
A.
3
.
4
x 
B.
3
.
4
x
C.
3
.
8
y
D.
3
.
8
x 
Lời giải:
Phương trình chính tắc của parabol
2
: 2Py px
3
4
p
Phương trình đường chuẩn là
3
28
p
x
.
Chọn đáp án D.
Câu 10: Trong mặt phẳng
,Oxy
cho hai đường thẳng
1
: 3 0d x y
và
2
: 2 3 0.d x y
Khẳng định
nào sau đây đúng?
A.
12
/ / .dd
B.
12
.dd
C.
1
d
,
2
d
cắt nhau và không vuông góc. D.
12
.dd
Lời giải:
Đường thẳng
1
d
có một vectơ pháp tuyến là
1
1;1 .n
Đường thẳng
2
d
có một vectơ pháp tuyến là
2
2;1 .n
Ta có:
12
.0
11
21
nn
1
d
,
2
d
cắt nhau và không vuông góc.
Chọn đáp án C.
Câu 11: Tìm tất cả các giá trị của tham số
m
để biểu thức
2
2 5 9 f x m x x
là tam thức bậc hai.
A.
m
. B.
2m
. C.
2m
. D.
0m
.
Lời giải:
Biểu thức
2
2 5 9 f x m x x
là tam thức bậc hai khi:
20m
.
Suy ra
2m
.
Chọn đáp án C.
Câu 12: Trong mặt phẳng
,Oxy
cho hai điểm
1;0 , 3;6 .AB
Phương trình đường thẳng trung trực
của đoạn thẳng
AB
là
A.
3 11 0xy
B.
3 11 0.xy
C.
3 9 0.xy
D.
3 7 0.xy
Lời giải:
Ta có:
2;6 .AB
Gọi
I
là trung điểm
2;3 .AB I
Đường thẳng
qua
2;3I
và nhận
2;6AB
làm một vec tơ pháp tuyến.
Vậy
: 2 2 6 3 0 2 6 22 0 3 11 0.x y x y x y
Chọn đáp án B.
Câu 13: Tam thức bậc hai nào dưới đây có bảng xét dấu như hình vẽ?
x

0
2

fx
0
0
A.
2
2.y x x
B.
2
2.y x x
C.
2
4.y x x
D.
2
4.y x x
Lời giải:
Kiểm tra các sự kiện:
0a
và tam thức có hai nghiệm
0, 2.xx
Chọn đáp án B.
Câu 14: Trong mặt phẳng
,Oxy
cho đường thẳng
12
: , .
23
xt
dt
yt


Vectơ nào dưới đây là một
vectơ pháp tuyến của
?d
A.
1
1;2 .u
B.
2
2;1 .u 
C.
3
3;2 .u 
D.
4
2;3 .u
Lời giải:
Các vectơ pháp tuyến của
d
có tọa độ
3 ;2 , 0 .k k k
Chọn đáp án C.
Câu 15: Trong mặt phẳng
,Oxy
viết phương trình chính tắc của Elip có tiêu cự bằng
6
và đi qua điểm
0;5A
.
A.
22
1
34 9
xy

. B.
22
1
34 25

xy
. C.
22
1
25 9

xy
. D.
22
1
25 16

xy
.
Lời giải:
Phương trình chính tắc của elip có dạng
22
22
1 0
xy
ab
ab
.
Theo giả thiết:
2 6 3 cc
. Vì
0;5 A E
nên
22
22
05
15 b
ab
.
Khi đó:
2 2 2 2 2
5 3 34a b c
.
Vậy phương trình chính tắc của Elip là:
22
1
34 25

xy
.
Chọn đáp án B.
Câu 16: Trong mặt phẳng
,Oxy
cho hai điểm
1;1A
và
7;5B
. Phương trình đường tròn đường
kính
AB
là
A.
22
8 6 12 0x y x y
. B.
22
8 6 12 0x y x y
.
C.
22
8 6 12 0x y x y
. D.
22
8 6 12 0x y x y
.
Lời giải:
Gọi
I
là trung điểm của
AB
suy ra
4;3I
13.AI
Đường tròn đường kính
AB
nhận
4;3I
làm tâm và bán kính
13R AI
có phương trình:
22
22
4 3 13 8 6 12 0. x y x y x y
Chọn đáp án C.
Câu 17: Cho tam thức
2
3 2.f x x x
Khẳng định nào dưới đây đúng?
A.
0, 1;2 .f x x
B.
0, 1;2 .f x x
C.
0, ;1 2; .f x x  
D.
0, 1;2 .f x x


Lời giải:
Bảng xét dấu:
x

1
2

fx
0
0
Chọn đáp án B.
Câu 18: Trong mặt phẳng
,Oxy
cho đường thẳng
: , .
12
xt
dt
yt

Điểm nào dưới đây không
nằm trên đường thẳng
?d
A.
0;1 .M
B.
1;3 .N
C.
2;5 .P
D.
1;1 .Q
Lời giải:
Thay tọa độ điểm
Q
vào phương trình
1
:
1 1 2
t
d
t

(vô nghiệm).
Chọn đáp án D.
Câu 19: Tổng tất cả các nghiệm của phương trình và
2
3 2 2x x x
là
A.
3
. B.
4
. C.
1
. D.
3
.
Lời giải:
Ta có
2
22
2
22
3 2 2
0
3 2 2 4 0
4
x
xx
x x x
x
x x x x x
x



.
Vậy tập nghiệm của phương trình
0;4S
nên tổng các nghiệm là
4
.
Chọn đáp án B.
Câu 20: Trong mặt phẳng
,Oxy
tìm giá trị tham số
n
để khoảng cách từ điểm
2;3I
đến đường
thẳng
: 1 2 0x ny n
bằng
1.
A.
0.n
B.
1.n
C.
1.n 
D.
2.n
Lời giải:
Ta có:
2
2
2 3 1 2
; 1 1 1 0.
1
nn
d I n n n
n
Chọn đáp án A.
Câu 21: Tìm
m
để parabol
2
( ): 2 3P y mx x
có trục đối xứng là đường thẳng
2x
.
A.
2m
. B.
1m 
. C.
1m
. D.
1
2
m
.
Lời giải:
Vì
P
là parabol nên
0m
. Khi đó parabol
P
có trục đối xứng
21
2
xx
mm
Theo bài ra trục đối xứng
2x
nên
11
2
2
m
m
.
Chọn đáp án D.
Câu 22: Trong mặt phẳng
,Oxy
cho điểm
2; 3A
và đường thẳng
12
: , .
3
xt
dt
yt


Phương trình
đường thẳng
qua
A
và song song với
d
là
A.
2 7 0.xy
B.
2 0.xy
C.
2 1 0.xy
D.
2 4 0.xy
Lời giải:
Đường thẳng
d
có một vectơ chỉ phương là
2;1
d
u
nên
d
có một vectơ pháp tuyến là
1; 2 .
d
n 
Do
song song với
d
nên
nhận
1; 2
d
n 
làm một vectơ pháp tuyến.
Vậy
: 1 2 2 3 0 2 4 0.x y x y
Chọn đáp án D.
Câu 23: Tập nghiệm của bất phương trình
2
2 1 0xx
là
A.
.
B. C.
1.
D.
\ 1 .
Lời giải:
Bảng xét dấu
2
2 1:f x x x
x

1

y
0
Chọn đáp án C.
Câu 24: Số nghiệm của phương trình
2
3 2 3
0
1
x x x
x
là
A.
1
. B.
2
. C.
3
. D.
0
.
Lời giải:
Điều kiện:
3
3.
1

x
x
x
Khi đó pt
2
1
3 2 0
2
30
3
x
xx
x
x
x

.
Kết hợp với điều kiện suy ra phương trình có nghiệm duy nhất
3x
.
Chọn đáp án A.
Câu 25: Cho hàm số
32f x x
. Giá trị của hàm số tại điểm
2x 
bằng
A.
1
. B.
3
. C.
7
. D.
7
.
Câu 26: Bảng biến thiên của hàm số
2
21y x x
là
A. . B. .
C. . D. .
Lời giải:
Ta có:
2
21y x x
nên đỉnh của parabol là
1;2I
.
Do
10a
nên parabol có bề lõm xuống dưới.
Chọn đáp án A.
Câu 27: Trong các hàm số sau, hàm số nào xác định trên ?
A.
1yx
. B.
1
2
y
x
. C.
3
1
1
y
x
. D.
2
1
1
y
x
.
Câu 28: Một nghiệm của phương trình
21xx
là
A.
2x
. B.
5x
. C.
1x
. D.
0x
.
Câu 29: Hàm số nào có đồ thị là đường parabol có đỉnh là
1;3 ?I
A.
2
2 4 3y x x
. B.
2
2 2 1y x x
. C.
2
2 4 5y x x
. D.
2
22y x x
.
Câu 30: Tìm tất các giá trị thực của tham số
m
để hàm số
2
2 3 2 1
x
y
x x m
xác định trên
.
A.
17
16
m
. B.
17
16
m
. C.
17
0
16
m
. D.
17
16
m
.
Lời giải:
Điều kiện xác định của hàm số
2
2 3 2 1
x
y
x x m
là:
2
2 3 2 1 0x x m
.
Hàm số xác định trên
22
2 3 2 1 0, 2 3 2 1 0 x x m x x x m
vô nghiệm
2
17
3 4.2. 2 1 0
16
mm
.
Chọn đáp án D.
Câu 31: Tổng các nghiệm của phương trình
2
3 2 6 9x x x
bằng
A.
2
. B.
3
. C.
1
. D.
7
.
Lời giải:
Điều kiện:
2 6 0 3. xx
Ta có
2
3
3 2 6 9 3 2 6 3 0
2 6 3
x
x x x x x x
xx
.
Phương trình
2
2
30
3
2 6 3
4 3 0
2 6 3
x
x
xx
xx
xx



3
1
1
3
3
x
x
x
x
x






Vậy phương trình đã cho có ba nghiệm là
1, 3, 3x x x
.
Tổng các nghiệm của phương trình là
1 3 3 1
.
Chọn đáp án C.
Câu 32: Tam thức nào dưới đây luôn âm với mọi
?x
A.
2
1.y x x
B.
2
1.y x x
C.
2
1.y x x
D.
2
4.y x x
Lời giải:
Bảng xét dấu
2
1:y x x
x


y
Chọn đáp án C.
Câu 33: Cho tam thức bậc hai
2
, ; ; , 0f x ax bx c a b c a
với
2
4.b ac
Mệnh đề nào dưới
đây đúng?
A.
0
0, .
0
a
f x x

B.
0
0, .
0
a
f x x

C.
0
0, .
0
a
f x x

D.
0
0, .
0
a
f x x

Câu 34: Gọi
M
là giá trị lớn nhất,
m
là giá trị nhỏ nhất của hàm số
2
42y x x
trên đoạn
0;3
.
Tính giá trị biểu thức
Mm
.
A.
1
. B.
4
. C.
0
. D.
1
.
Lời giải:
Ta có bảng biến thiên của hàm số
2
42y x x
trên đoạn
0;3
:
Từ bảng biến thiên ta có
2; 2Mm
nên
0Mm
.
Chọn đáp án C.
Câu 35: Đồ thị hàm số:
2
y ax bx c
như hình vẽ bên dưới:
Trong các hệ số
,,abc
có bao nhiêu giá trị dương?
A.
1
.
B.
0
. C.
2
. D.
3
.
Lời giải:
Từ đồ thị hàm số ta có
0a
, hoành độ đỉnh của đồ thị hàm số là
0
00
2

a
b
xb
a
.
Giao điểm với trục tung có tung độ bằng
0c
.
Vậy các hệ số có giá trị dương là
,bc
.
Chọn đáp án C.
II. PHẦN TỰ LUẬN (03 câu – 3,0 điểm)
Câu 1: (1,0 điểm).
a) Tìm tập xác định của hàm số
2
5 4.y x x
b) Tìm
,ab
để parabol
2
:1P y ax bx
có đỉnh là
1;2 .I
Lời giải:
a) Hàm số xác định
2
5 4 0 ; 4 1; .x x x

 

Vậy tập xác định của hàm số là
; 4 1; .D

 

b) Do
P
có đỉnh là
1;2I
nên ta có:
12
11
.
2 0 2
1
2
ab
a b a
b
a b b
a




Vậy
2
: 2 1.P y x x
Câu 2: (1,0 điểm).
a) Giải phương trình
2
3 17 23 3.x x x
b) Tìm
m
để các bất phương trình
2
2
5
17
2 3 2
x x m
xx


luôn đúng với mọi
.x
Lời giải:
a) Ta có:
2
2 2 2
3 0 3
3 17 23 3
3 17 23 6 9 2 11 14 0
xx
x x x
x x x x x x





3
7
2
.
2
7
2
x
x
x
x
Vậy phương trình có tập nghiệm là
7
.
2
S



b) Ta có:
2
2 3 2 0,x x x
vì
70
.
20a

Khi đó bất phương trình trở thành:
2 2 2
2 3 2 5 7 2 3 2x x x x m x x
22
22
2 3 2 5
5 7 2 3 2
x x x x m
x x m x x
2
2
3 2 2 0
13 26 14 0
x x m
x x m
(1)
(2)
Xét
2
(1) : 3 2 2 0,x x m x
L3 0 :
5
1 3( 2) 0
3
a
m
m

Đ
Xét
2
(2) :13 26 14 0,x x m x
2
13 0
1.
13 13(14 ) 0
a
m
m

Vậy
5
;1 .
3
m



Câu 3: (1,0 điểm).
Trong mặt phẳng
,Oxy
viết phương trình đường thẳng
d
song song với
: 4 3 12 0xy
và
d
cách
một khoảng bằng
5.
Lời giải:
Vì
: 4 3 12 0d x y
nên
d
có dạng
: 4 3 0, ( 12).d x y m m
Chọn
(0;4) : 4 3 12 0.M x y
Khi đó
( , ) ( , ) 5d d d M d
22
4.0 3.4
5
4 ( 3)
m


12 25m
12 25 13
.
12 25 27
mm
mm




Vậy có hai đường thẳng thỏa mãn là
4 3 27 0xy
và
4 3 13 0.xy
____________________HẾT____________________
Huế, 08h45’ Ngày 10 tháng 02 năm 2023
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
ĐỀ ÔN TẬP SỐ 03_TrNg 2023
¤N TËP GI÷A K× 2
Môn: TOÁN 10
SGK 2022 – Kết nối tri thức và cuộc sống
Líp To¸n thÇy L£ B¸ B¶O
Trưêng THPT §Æng Huy Trø S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch
, TP HuÕ
Trung t©m KM 10
Hương
Trà, HuÕ.
NỘI DUNG ĐỀ BÀI
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm)
Câu 1: Cho hàm số
y f x
có đồ thị trên như hình vẽ. Mệnh đề nào sau đây sai?
A. Hàm số
y f x
đồng biến trên khoảng
;1
.
B. Hàm số
y f x
nghịch biến trên khoảng
1;2
.
C. Hàm số
y f x
nghịch biến trên khoảng
2; 
.
D. Hàm số
y f x
đồng biến trên khoảng
1;2
.
Câu 2: Trong mặt phẳng
,Oxy
phương trình nào dưới đây là phương trình đường tròn?
A.
22
2 4 11 0 x y x y
. B.
22
2 4 11 0 x y x y
.
C.
22
2 4 11 0 x y x y
. D.
22
2 2 4 11 0 x y x y
.
Câu 3: Trong mặt phẳng
,Oxy
xác định vị trí tương đối giữa hai đường thẳng
1
: 2 1 0 xy
và
2
: 3 6 10 0 xy
.
A. Cắt nhau và không vuông góc với nhau. B. Trùng nhau.
C. Vuông góc với nhau. D. Song song với nhau.
Câu 4: Cho hàm số
22
( ) 2f x mx x m m
(với
m
là tham số). Tất cả các giá trị của
m
để
20f
là
A. 1 và
4
. B.
4
. C. 1. D. 3.
Câu 5: Trong mặt phẳng
,Oxy
cho hai điểm
1;2A
,
3;1B
và đường thẳng
1
:
2
xt
yt


. Tọa độ
điểm
C
thuộc
để tam giác
ACB
cân tại
C
là
A.
7 13
;
66



. B.
7 13
;
66



. C.
7 13
;
66



. D.
13 7
;
66



.
Câu 6: Hai đồ thị hàm số
2
23y x x
và
21yx
có bao nhiêu điểm chung?
A.
2
. B.
1
. C.
0
. D.
3
.
Câu 7: Trong mặt phẳng
,Oxy
tâm
I
của đường tròn
C
có phương trình
22
4 3 1 0 x y x y
là
A.
3
2;
2



I
. B.
3
2;
2



I
. C.
4; 3I
. D.
4;3I
.
Câu 8: Cho hàm số bậc hai
2
y ax bx c
có đồ thị như hình vẽ bên dưới:
Tìm tất cả các giá trị của
x
để
0.y
A.
;0
. B.
3; 
. C.
0;3
. D.
0;3
.
Câu 9: Trong mặt phẳng
,Oxy
hypebol có hai tiêu điểm là
1
2;0F
và
2
2;0F
và một đỉnh
1;0A
có phương trình là chính tắc là
A.
2
2
1.
13
y
x

B.
2
2
1.
13
y
x

C.
2
2
1.
31
y
x

D.
2
2
1.
13
y
x

Câu 10: Trong mặt phẳng
,Oxy
cho đường thẳng
12
:,
23
xt
dt
yt


. Điểm nào sau đây thuộc đường
thẳng
d
.
A.
2; 3Q
. B.
3; 1M
. C.
1; 1N
. D.
1; 2P
.
Câu 11: Tập xác định
D
của hàm số
23
1
x
fx
x
là
A.
1;D
. B.
1;D
. C.
\ 1 .D
D.
\ 1;D
.
Câu 12: Đỉnh của parabol
2
45 y x x
có toạ độ là
A.
0;2
. B.
1;2
. C.
2;0
. D.
2;1
.
Câu 13: Cho hàm số bậc hai
2
, ; ;y ax bx c a b c
có đồ thị như hình bên dưới:
x
y
-1
3
-4
-3
O
1
Tính
2 2 2
.T a b c
A.
11.
B.
14.
C.
9.
D.
7.
Câu 14: Cho parabol
P
có phương trình chính tắc là
2
2y px
với
0p
. Phương trình đường
chuẩn của
P
là
A.
2
p
y 
. B.
2
p
x
. C.
2
p
y
. D.
2

p
x
.
Câu 15: Bất phương trình
2
23xx
có bao nhiêu nghiệm nguyên
?
A.
5
. B.
4
. C.
3
. D.
2
.
Câu 16: Hàm số
2
4 3 1y x x
có đồ thị là một trong bốn hình vẽ dưới đây. Đồ thị đó là đồ thị nào?
A. . B. . C. . D. .
Câu 17: Tam thức bậc hai nào dưới đây có bảng xét dấu như hình vẽ?
x

0
4

fx
0
0
A.
2
2.y x x
B.
2
2.y x x
C.
2
4.y x x
D.
2
4.y x x
Câu 18: Nghiệm của phương trình
2
7 10 4 x x x
thuộc tập nào dưới đây?
A.
4;5
. B.
5;6
. C.
5;6
. D.
5;6
.
Câu 19: Trong mặt phẳng
,Oxy
đường elip
22
1
16 7
xy

có tiêu cự bằng
A.
3
. B.
6
. C.
9
16
. D.
6
7
.
Câu 20: Tập xác định của hàm số
2
6
41

x
y
xx
là
A.
1; . D
B.
\ 2;1;2 .D
C.
1; \ 2 . D
D.
1; \ 2 . D
Câu 21: Khi đặt
1tx
thì phương trình
2 1 0xx
trở thành phương trình nào dưới đây?
A.
2
10tt
. B.
2
0tt
. C.
2
20tt
. D.
2
20tt
.
Câu 22: Trong mặt phẳng
,Oxy
viết phương trình chính tắc của elip có tiêu cự bằng
6
và đi qua điểm
0;5A
.
A.
22
1
100 81

xy
. B.
22
1
34 25

xy
. C.
22
1
25 9

xy
. D.
22
1
25 16

xy
.
Câu 23: Trong mặt phẳng
,Oxy
đường tròn
()C
tâm
(1; 4)I
và tiếp xúc với đườngthẳng
:4 3 4 0xy
có phương trình là
A.
22
( 1) ( 4) 17xy
. B.
22
( 1) ( 4) 16xy
.
C.
22
( 1) ( 4) 25xy
. D.
22
( 1) ( 4) 16xy
Câu 24: Tam thức bậc hai
2
56f x x x
nhận giá trị dương khi và chỉ khi
A.
;2 3; .  x
B.
2;3 .x
C.
;2 3; .  x
D.
2;3x
.
Câu 25: Trong mặt phẳng
,Oxy
cho đường tròn
22
( ): 4 2 20 0C x y x y
phương trình tiếp tuyến
của
C
vuông góc với đường thẳng
:3 4 9 0xy
là
A.
4 3 30 0xy
và
4 3 20 0xy
. B.
4 3 20 0xy
và
4 3 30 0xy
.
C.
4 3 30 0xy
và
4 3 20 0xy
. D.
4 3 20 0xy
và
4 3 30 0xy
.
Câu 26: Tổng tất cả các nghiệm của phương trình và
2
3 2 2x x x
là
A.
3
. B.
4
. C.
1
. D.
3
.
Câu 27: Xác định
2
:P y ax bx c
, biết
P
có đỉnh là
(1;3)I
và đi qua
(0;1)A
A.
2
2 3 1 y x x
. B.
2
2 4 1 y x x
. C.
2
2 4 1 y x x
. D.
2
2 4 1 y x x
.
Câu 28: Bất phương trình nào sau đây vô nghiệm?
A.
2
0x
. B.
2
0x
. C.
2
0x
. D.
2
0x
.
Câu 29: Trong mặt phẳng
,Oxy
đường tròn đi qua ba điểm
1;2A
,
5;2B
,
1; 3C
có phương trình
là.
A.
22
25 19 49 0x y x y
. B.
22
2 6 3 0x y x y
.
C.
22
6 1 0x y x y
. D.
22
6 1 0x y x xy
.
Câu 30: Tập nghiệm của phương trình
2
2 4 3 0x x x
là
A.
2;3S
. B.
2S
. C.
1;3S
. D.
1;2;3S
.
Câu 31: Trong mặt phẳng
,Oxy
xác định
a
để hai đường thẳng
1
: 3 – 4 0 d ax y
và
2
1
:
33
xt
d
yt

cắt nhau tại một điểm nằm trên trục hoành.
A.
–2a
. B.
2a
. C.
1a
. D.
–1a
.
Câu 32: Cho tam thức
22
0,Δ4f x ax bx c a b ac
. Tam thức
0fx
với
x
khi và
chỉ khi
A.
0
Δ0
a
. B.
0
Δ0
a
. C.
0
Δ0
a
. D.
0
Δ0
a
.
Câu 33: Trong mặt phẳng
,Oxy
cho hai điểm
1;2 , 3;0AB
và đường thẳng
: 3 5 0d x y
.
Phương trình đường thẳng
song song với
d
và đi qua trung điểm
M
của đoạn thẳng
AB
là
A.
3 2 0xy
. B.
3 4 0xy
. C.
3 1 0xy
D.
3 4 0xy
.
Câu 34: Tìm tất cả các giá trị của tham số
m
để bất phương trình
2
2 8 1 0x m x m
vô
nghiệm.
A.
0;28m
. B.
0;28m
.
C.
;0 28;m  
. D.
;0 28;m  
.
Câu 35: Trong mặt phẳng
,Oxy
cho hình bình hành
ABCD
có đỉnh
1;0A
, hai đường thẳng
,BC BD
lần lượt có phương trình là
20xy
và
2 3 8 0xy
. Tính độ dài cạnh
CD
.
A.
5
. B.
0
. C.
25
. D.
22
.
II. PHẦN TỰ LUẬN (03 câu – 3,0 điểm)
Câu 1: (1,0 điểm).
a) Tìm tập xác định của hàm số
2
1 2 4 .y x x
b) Tìm
,,a b c
để parabol
2
:P y ax bx c
đi qua ba điểm
1;3 , 1;1AB
và
2;7 .C
Câu 2: (1,0 điểm).
a) Giải phương trình
2
4 3 2 0.x x x
b) Tìm
m
để bất phương trình
2
( 1) 2( 1) 2 3 0m x m x m
vô nghiệm.
Câu 3: (1,0 điểm).
Trong mặt phẳng
,Oxy
cho hai đường thẳng
1
: 2 2 0,d x y
2
: 6 3 0d x y
và
(3;0).M
Viết phương trình đường thẳng
d
đi qua
M
và cắt
12
,dd
lần lượt tại hai điểm
,AB
sao cho
M
là trung điểm của
.AB
____________________HẾT____________________
Huế, 10h45’ Ngày 10 tháng 02 năm 2023
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
ĐỀ ÔN TẬP SỐ 03_TrNg 2023
¤N TËP GI÷A K× 2
Môn: TOÁN 10
SGK 2022 – Kết nối tri thức và cuộc sống
Líp To¸n thÇy L£ B¸ B¶O
Trưêng THPT §Æng Huy Trø S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch
, TP HuÕ
Trung t©m KM 10
Hương
Trà, HuÕ.
LỜI GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm)
Câu 1: Cho hàm số
y f x
có đồ thị trên như hình vẽ. Mệnh đề nào sau đây sai?
A. Hàm số
y f x
đồng biến trên khoảng
;1
.
B. Hàm số
y f x
nghịch biến trên khoảng
1;2
.
C. Hàm số
y f x
nghịch biến trên khoảng
2; 
.
D. Hàm số
y f x
đồng biến trên khoảng
1;2
.
Lời giải:
Dựa đồ thị ta thấy trên
1;1
đồ thị hàm số đi xuống, trên
1;2
đồ thị hàm số đi lên từ trái
sang phải. Do đó trên
1;2
hàm số đồng biến trên
1;2
và nghịch biến trên
1;1
.
Chọn đáp án B.
Câu 2: Trong mặt phẳng
,Oxy
phương trình nào dưới đây là phương trình đường tròn?
A.
22
2 4 11 0 x y x y
. B.
22
2 4 11 0 x y x y
.
C.
22
2 4 11 0 x y x y
. D.
22
2 2 4 11 0 x y x y
.
Lời giải:
Phương trình
22
2 4 11 0 x y x y
là phương trình đường tròn.
Vì
22
1 4 11 16 0 a b c
trong đó
1; 2; 11. a b c
Chọn đáp án A.
Câu 3: Trong mặt phẳng
,Oxy
xác định vị trí tương đối giữa hai đường thẳng
1
: 2 1 0 xy
và
2
: 3 6 10 0 xy
.
A. Cắt nhau và không vuông góc với nhau. B. Trùng nhau.
C. Vuông góc với nhau. D. Song song với nhau.
Lời giải:
Tọa độ giao điểm (nếu có) của
1
và
2
là nghiệm của hệ phương trình:
2 1 0
3 6 10 0
xy
xy
3 6 3 0
3 6 10 0
xy
xy
Hệ phương trình trên vô nghiệm nên hai đường thẳng
1
và
2
song song với nhau.
Cách khác: Do
1 2 1
3 6 10


nên hai đường thẳng
1
và
2
song song với nhau.
Chọn đáp án D.
Câu 4: Cho hàm số
22
( ) 2f x mx x m m
(với
m
là tham số). Tất cả các giá trị của
m
để
20f
là
A. 1 và
4
. B.
4
. C. 1. D. 3.
Lời giải:
Ta có:
20f
22
.2 2.2 0m m m
2
1
3 4 0
4
m
mm
m

.
Chọn đáp án A.
Câu 5: Trong mặt phẳng
,Oxy
cho hai điểm
1;2A
,
3;1B
và đường thẳng
1
:
2
xt
yt


. Tọa độ
điểm
C
thuộc
để tam giác
ACB
cân tại
C
là
A.
7 13
;
66



. B.
7 13
;
66



. C.
7 13
;
66



. D.
13 7
;
66



.
Lời giải:
C
B
A
M
d
Gọi
1 ;2 . C t t
Trung điểm của AB là
3
M 1; .
2



Tam giác ACB cân tại C nên
. 0(1)CM AB CM AB
.
Ta có
1
; ; (4; 1)
2
CM t t AB



1 1 7 13
(1) 4t ( t ) 0 ; .
2 6 6 6



tC
Chọn đáp án A.
Câu 6: Hai đồ thị hàm số
2
23y x x
và
21yx
có bao nhiêu điểm chung?
A.
2
. B.
1
. C.
0
. D.
3
.
Lời giải:
Xét phương trình:
22
2 3 2 1 4 4 0 2x x x x x x
.
Vì phương trình có một nghiệm nên hai đồ thị hàm số cắt nhau tại 1 điểm.
Chọn đáp án B.
Câu 7: Trong mặt phẳng
,Oxy
tâm
I
của đường tròn
C
có phương trình
22
4 3 1 0 x y x y
là
A.
3
2;
2



I
. B.
3
2;
2



I
. C.
4; 3I
. D.
4;3I
.
Lời giải:
Phương trình đường tròn đã cho có dạng:
22
2 2 0x y ax by c
.
Do đó,
2
24
3
23
2
1
1







a
a
bb
c
c
tâm
3
2;
2



I
.
Chọn đáp án A.
Câu 8: Cho hàm số bậc hai
2
y ax bx c
có đồ thị như hình vẽ bên dưới:
Tìm tất cả các giá trị của
x
để
0.y
A.
;0
. B.
3; 
. C.
0;3
. D.
0;3
.
Lời giải:
Dựa vào đồ thị ta có
0 ;0 3;yx  
và
0 0;3yx
.
Chọn đáp án D.
Câu 9: Trong mặt phẳng
,Oxy
hypebol có hai tiêu điểm là
1
2;0F
và
2
2;0F
và một đỉnh
1;0A
có phương trình là chính tắc là
A.
2
2
1.
13
y
x

B.
2
2
1.
13
y
x

C.
2
2
1.
31
y
x

D.
2
2
1.
13
y
x

Lời giải:
Ta có :
2 2 2
2
1
c
a
b c a

2
2
1
.
3
a
b
Phương trình
2
2
: 1.
13
y
x
H 
Chọn đáp án D.
Câu 10: Trong mặt phẳng
,Oxy
cho đường thẳng
12
:,
23
xt
dt
yt


. Điểm nào sau đây thuộc đường
thẳng
d
.
A.
2; 3Q
. B.
3; 1M
. C.
1; 1N
. D.
1; 2P
.
Câu 11: Tập xác định
D
của hàm số
23
1
x
fx
x
là
A.
1;D
. B.
1;D
. C.
\ 1 .D
D.
\ 1;D
.
Lời giải:
Hàm số xác định
1 0 1. xx
Vậy tập xác định của hàm số là
1; . D
Chọn đáp án B.
Câu 12: Đỉnh của parabol
2
45 y x x
có toạ độ là
A.
0;2
. B.
1;2
. C.
2;0
. D.
2;1
.
Câu 13: Cho hàm số bậc hai
2
, ; ;y ax bx c a b c
có đồ thị như hình bên dưới:
x
y
-1
3
-4
-3
O
1
Tính
2 2 2
.T a b c
A.
11.
B.
14.
C.
9.
D.
7.
Lời giải:
Dựa vào đồ thị, ta có hệ:
1
2 0 1
2
1 4 4 2.
33
03
b
a b a
a
y a b c b
cc
y




Vậy
2 2 2
14.T a b c
Chọn đáp án B.
Câu 14: Cho parabol
P
có phương trình chính tắc là
2
2y px
với
0p
. Phương trình đường
chuẩn của
P
là
A.
2
p
y 
. B.
2
p
x
. C.
2
p
y
. D.
2

p
x
.
Câu 15: Bất phương trình
2
23xx
có bao nhiêu nghiệm nguyên
?
A.
5
. B.
4
. C.
3
. D.
2
.
Lời giải:
22
2 3 2 3 0 1 3 x x x x x
Vì
0;1;2 xx
3 nghiệm nguyên.
Chọn đáp án C.
Câu 16: Hàm số
2
4 3 1y x x
có đồ thị là một trong bốn hình vẽ dưới đây. Đồ thị đó là đồ thị nào?
A. . B. . C. . D. .
Lời giải:
Từ hàm số
2
4 3 1y x x
ta có hệ số
1c
tọa độ giao điểm với trục
Oy
tại
0; 1
.
Mặt khác, trục đối xứng của parabol là
3
0.
8
x 
Chọn đáp án B.
Câu 17: Tam thức bậc hai nào dưới đây có bảng xét dấu như hình vẽ?
x

0
4

fx
0
0
A.
2
2.y x x
B.
2
2.y x x
C.
2
4.y x x
D.
2
4.y x x
Lời giải:
Kiểm tra các sự kiện:
0a
và tam thức có hai nghiệm
0, 4.xx
Chọn đáp án C.
Câu 18: Nghiệm của phương trình
2
7 10 4 x x x
thuộc tập nào dưới đây?
A.
4;5
. B.
5;6
. C.
5;6
. D.
5;6
.
Lời giải:
Ta có:
2
7 10 4 x x x
2
2
40
7 10 4

x
x x x
22
4
7 10 8 16
x
x x x x
4
6 5;6 .
6
x
x
x
Chọn đáp án D.
Câu 19: Trong mặt phẳng
,Oxy
đường elip
22
1
16 7
xy

có tiêu cự bằng
A.
3
. B.
6
. C.
9
16
. D.
6
7
.
Lời giải:
Phương trình chính tắc của elip có dạng
22
22
: 1 , 0
xy
E a b
ab
.
2
2
2 2 2
16
7
a
b
c a b


4
7
3
a
b
c

.
Vậy tiêu cự của elip là
12
2 2.3 6F F c
.
Chọn đáp án B.
Câu 20: Tập xác định của hàm số
2
6
41

x
y
xx
là
A.
1; . D
B.
\ 2;1;2 .D
C.
1; \ 2 . D
D.
1; \ 2 . D
Lời giải:
Điều kiện xác định:
2
1
10
2
40
2
x
x
x
x
x




1
2
x
x
.
Vậy tập xác định của hàm số là
1; \ 2 . D
Chọn đáp án D.
Câu 21: Khi đặt
1tx
thì phương trình
2 1 0xx
trở thành phương trình nào dưới đây?
A.
2
10tt
. B.
2
0tt
. C.
2
20tt
. D.
2
20tt
.
Lời giải:
Ta có:
2 1 0 1 1 1 0.x x x x
Đặt
2
1 1.t x t x
Vậy pt trở thành:
2
1 0.tt
Chọn đáp án A.
Câu 22: Trong mặt phẳng
,Oxy
viết phương trình chính tắc của elip có tiêu cự bằng
6
và đi qua điểm
0;5A
.
A.
22
1
100 81

xy
. B.
22
1
34 25

xy
. C.
22
1
25 9

xy
. D.
22
1
25 16

xy
.
Lời giải:
Phương trình chính tắc của elip có dạng
22
22
1 , 0
xy
ab
ab
.
Theo giả thiết:
2 6 3 cc
. Vì
0;5 A E
nên ta có phương trình:
22
22
05
15 b
ab
.
Khi đó:
2 2 2 2 2 2
53a b c a
2
34 34aa
.
Chọn đáp án B.
Câu 23: Trong mặt phẳng
,Oxy
đường tròn
()C
tâm
(1; 4)I
và tiếp xúc với đườngthẳng
:4 3 4 0xy
có phương trình là
A.
22
( 1) ( 4) 17xy
. B.
22
( 1) ( 4) 16xy
.
C.
22
( 1) ( 4) 25xy
. D.
22
( 1) ( 4) 16xy
Lời giải:
C
có bán kính
22
4.1 3.4 4
,4
34
R d I

.
Do đó,
C
có phương trình
22
( 1) ( 4) 16xy
.
Chọn đáp án B.
Câu 24: Tam thức bậc hai
2
56f x x x
nhận giá trị dương khi và chỉ khi
A.
;2 3; .  x
B.
2;3 .x
C.
;2 3; .  x
D.
2;3x
.
Lời giải:
Ta có:
2
5 6 0 2 3f x x x x
.
Vậy
2
56f x x x
nhận giá trị dương khi và chi khi
2;3x
.
Chọn đáp án D.
Câu 25: Trong mặt phẳng
,Oxy
cho đường tròn
22
( ): 4 2 20 0C x y x y
phương trình tiếp tuyến
của
C
vuông góc với đường thẳng
:3 4 9 0xy
là
A.
4 3 30 0xy
và
4 3 20 0xy
. B.
4 3 20 0xy
và
4 3 30 0xy
.
C.
4 3 30 0xy
và
4 3 20 0xy
. D.
4 3 20 0xy
và
4 3 30 0xy
.
Lời giải:
Đường tròn
C
có tâm
2;1I
và bán kính
22
2 1 20 5R
.
Đường thẳng d vuông góc với
:3 4 9 0xy
:4 3 0d x y m
.
d
là tiếp tuyến của
,C d I d R
2
2
4.2 3.1
5.
43
m


1
2
:4 3 20 0
5 25 20
5 25 30 :4 3 30 0



d x y
mm
m m d x y
.
Chọn đáp án B.
Câu 26: Tổng tất cả các nghiệm của phương trình và
2
3 2 2x x x
là
A.
3
. B.
4
. C.
1
. D.
3
.
Lời giải:
Ta có
2
22
2
22
3 2 2
0
3 2 2 4 0
4
x
xx
x x x
x
x x x x x
x



.
Vậy tập nghiệm của phương trình
0;4S
nên tổng các nghiệm là
4
.
Chọn đáp án B.
Câu 27: Xác định
2
:P y ax bx c
, biết
P
có đỉnh là
(1;3)I
và đi qua
(0;1)A
A.
2
: 2 3 1P y x x
. B.
2
: 2 4 1P y x x
.
C.
2
: 2 4 1P y x x
. D.
2
: 2 4 1P y x x
.
Lời giải:
Do
()P
có đỉnh là
1;3I
nên ta có hệ:
3
1
2
abc
b
a

(1)
Mặt khác,
()P
đi qua điểm
(0;1)A
nên
1c
thay vào (1) ta được
2; 4ab
.
Chọn đáp án B.
Câu 28: Bất phương trình nào sau đây vô nghiệm?
A.
2
0x
. B.
2
0x
. C.
2
0x
. D.
2
0x
.
Câu 29: Trong mặt phẳng
,Oxy
đường tròn đi qua ba điểm
1;2A
,
5;2B
,
1; 3C
có phương trình
là.
A.
22
25 19 49 0x y x y
. B.
22
2 6 3 0x y x y
.
C.
22
6 1 0x y x y
. D.
22
6 1 0x y x xy
.
Lời giải:
Gọi
C
là phương trình đường tròn đi qua ba điểm
,,A B C
với tâm
;I a b
C
có dạng:
22
2 2 0x y ax by c
. Vì đường tròn
C
đi qua qua ba điểm
,,A B C
nên ta có hệ phương trình:
3
1 4 2 4 0 2 4 5
1
25 4 10 4 0 10 4 29
2
1 9 2 6 0 2 6 10
1
a
a b c a b c
a b c a b c b
a b c a b c
c



.
Vậy phương trình đường tròn cần tìm là
22
6 1 0x y x y
.
Chọn đáp án C.
Câu 30: Tập nghiệm của phương trình
2
2 4 3 0x x x
là
A.
2;3S
. B.
2S
. C.
1;3S
. D.
1;2;3S
.
Lời giải:
Điều kiện:
2 0 2xx
(*).
Với điều kiện (*), phương trình đã cho tương đương với
2
2
20
1
4 3 0
3
x
x
x
xx
x


.
So với điều kiện (*) chỉ có
2x
,
3x
thỏa mãn.
Vậy tập nghiệm của phương trình là
2;3S
.
Chọn đáp án A.
Câu 31: Trong mặt phẳng
,Oxy
xác định
a
để hai đường thẳng
1
: 3 – 4 0 d ax y
và
2
1
:
33
xt
d
yt

cắt nhau tại một điểm nằm trên trục hoành.
A.
–2a
. B.
2a
. C.
1a
. D.
–1a
.
Lời giải:
Gọi
1 2 2
1 ;3 3M d d M t t d
Do
3 3 0 –1 2;0 . M Ox t t M
Mặt khác,
1
Md
2 3.0 – 4 0 –2 aa
.
Chọn đáp án A.
Câu 32: Cho tam thức
22
0,Δ4f x ax bx c a b ac
. Tam thức
0fx
với
x
khi và
chỉ khi
A.
0
Δ0
a
. B.
0
Δ0
a
. C.
0
Δ0
a
. D.
0
Δ0
a
.
Câu 33: Trong mặt phẳng
,Oxy
cho hai điểm
1;2 , 3;0AB
và đường thẳng
: 3 5 0d x y
.
Phương trình đường thẳng
song song với
d
và đi qua trung điểm
M
của đoạn thẳng
AB
là
A.
3 2 0xy
. B.
3 4 0xy
. C.
3 1 0xy
D.
3 4 0xy
.
Lời giải:
Trung điểm của đoạn
AB
là
1;1M
.
Vì
song song với đường thẳng
d
nên
có dạng:
30 x y m
.
Do
qua
M
nên
1 3.1 0 4 mm
.
Vậy phương trình đường thẳng
cần tìm là
3 4 0xy
.
Chọn đáp án B.
Câu 34: Tìm tất cả các giá trị của tham số
m
để bất phương trình
2
2 8 1 0x m x m
vô
nghiệm.
A.
0;28m
. B.
0;28m
.
C.
;0 28;m  
. D.
;0 28;m  
.
Lời giải:
Bất phương trình
2
2 8 1 0x m x m
vô nghiệm
2
2 8 1 0,x m x m x
.
Điều kiện:
2
2
0
2 4 8 1 0 28 0 0;28 .
0

a
m m m m m
Vậy
0;28 .m
Chọn đáp án B.
Câu 35: Trong mặt phẳng
,Oxy
cho hình bình hành
ABCD
có đỉnh
1;0A
, hai đường thẳng
,BC BD
lần lượt có phương trình là
20xy
và
2 3 8 0xy
. Tính độ dài cạnh
CD
.
A.
5
. B.
0
. C.
25
. D.
22
.
Lời giải:
A
B
D
C
Vì
B BC B D
nên tọa độ điểm
B
là nghiệm của hệ phương trình:
20
2 3 8 0
xy
xy

1
2
x
y


1; 2B
2;2BA
.
Suy ra
22
2 2 2 2 CD BA
.
Chọn đáp án D.
II. PHẦN TỰ LUẬN (03 câu – 3,0 điểm)
Câu 1: (1,0 điểm).
a) Tìm tập xác định của hàm số
2
1 2 4 .y x x
b) Tìm
,,a b c
để parabol
2
:P y ax bx c
đi qua ba điểm
1;3 , 1;1AB
và
2;7 .C
Lời giải:
a) Hàm số xác định
2
2;2
40
1;2 .
10
1
x
x
x
x
x









Vậy tập xác định của hàm số là
1;2 .D


b) Do
P
đi qua hai điểm
1;3 , 1;1AB
và
2;7C
nên ta có:
31
1 1.
4 2 7 1
a b c a
a b c b
a b c c





Vậy
2
: 1.P y x x
Câu 2: (1,0 điểm).
a) Giải phương trình
2
4 3 2 0.x x x
b) Tìm
m
để bất phương trình
2
( 1) 2( 1) 2 3 0m x m x m
vô nghiệm.
Lời giải:
a) Điều kiện:
2 0 2.xx
Ta có:
2
2
2
20
4 3 2 0 .
1
4 3 0
3
x
x
x x x
x
xx
x



Đối chiếu điều kiện, phương trình có tập nghiệm là
2;3 .S
b)
TH 1: 0 1 0 1.a m m
Bất phương trình trở thành:
5 0 :
vô nghiệm
nhận
1.m
TH 2 : 0 1 0 1.a m m
Ta có:
2
( 1) 2( 1) 2 3 0 :m x m x m
vô nghiệm
2
( 1) 2( 1) 2 3 0,m x m x m x
0
0
a

2
10
4( 1) 4.( 1)(2 3) 0
m
m m m

2
1
1
; 4 1;
4 12 16 0
m
m
m
mm




 

1.m
Kết luận:
1; .m

Câu 3: (1,0 điểm).
Trong mặt phẳng
,Oxy
cho hai đường thẳng
1
: 2 2 0,d x y
2
: 6 3 0d x y
và
(3;0).M
Viết phương trình đường thẳng
d
đi qua
M
và cắt
12
,dd
lần lượt tại hai điểm
,AB
sao cho
M
là trung điểm của
.AB
Lời giải:
Gọi
1
( ;2 2) : 2 2 0A a a d x y
và
2
( 6 3; ) : 6 3 0.B b b d x y
Theo đề bài,
M
là trung điểm
2
3 6 6
2 2 2 0
A B M
A B M
x x x
ab
AB
y y y a b



69
21
22
13
ab
a
ab


và
16
13
b 
21 16
;
13 13
A



và
57 16
;
13 13
B




Đường thẳng
d
qua điểm
(3;0)M
và có một VTCP là
36 32 4
; 9; 8
13 13 13
AB


Một VTPT của
d
là
8;9 : 8( 3) 9( 0) 0 : 8 9 24 0.
d
n d x y d x y
____________________HẾT____________________
Huế, 10h45’ Ngày 10 tháng 02 năm 2023
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
ĐỀ ÔN TẬP SỐ 04_TrNg 2023
¤N TËP GI÷A K× 2
Môn: TOÁN 10
SGK 2022 – Kết nối tri thức và cuộc sống
Líp To¸n thÇy L£ B¸ B¶O
Trưêng THPT §Æng Huy Trø S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch
, TP HuÕ
Trung t©m KM 10
Hương
Trà, HuÕ.
NỘI DUNG ĐỀ BÀI
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm)
Câu 1: Điểm
(0;1)I
thuộc đồ thị của hàm số nào dưới đây ?
A.
2
y x x
. B.
2
y x x
. C.
2
1y x x
. D.
2
1y x x
.
Câu 2: Trong mặt phẳng
,Oxy
cho đường thẳng
:2 3 4 0d x y
. Vectơ nào sau đây là một vectơ
chỉ phương của
d
?
A.
1
2;3u
. B.
2
3;2u
. C.
3
3; 2u
. D.
4
3; 2 u
.
Câu 3: Trong mặt phẳng
,Oxy
một tiêu điểm của elip (E):
22
1
25 9
xy

có tọa độ là
A.
4;0 .
B.
3;0 .
C.
16;0 .
D.
0; 4 .
Câu 4: Phương trình
13 xx
có tập nghiệm là
A.
5S
. B.
2;5S
. C.
2S
. D.
S
.
Câu 5: Tập nghiệm của bất phương trình
2
16 8xx
là
A.
4;
. B.
\4
. C. . D.
– ; 4
.
Câu 6: Phương trình
2
1 1 0x x x
có bao nhiêu nghiệm?
A.
2
. B.
1
. C.
0
. D.
3
.
Câu 7: Trong mặt phẳng
,Oxy
cho hai điểm
3;5A
và
2;7B
. Điểm nào sau đây thuộc đường
trung trực của đoạn
AB
?
A.
3
;1
2
M



. B.
5
1;
2
N



. C.
0; 1P
. D.
1
;4
2
Q



.
Câu 8: Toạ độ giao điểm của parabol
2
1
( ): 2 2 3P y x x
với parabol
2
2
( ): 6P y x x
là
A.
1;7
và
3;27
. B.
7;1
và
27;3
. C.
1;3
và
3;15
. D.
3; 1
và
15; 3
.
Câu 9: Trong mặt phẳng
,Oxy
cho elip
22
: 1
16 9
xy
E 
. Với
M
là điểm bất kì nằm trên
E
, khẳng
định nào sau đây là khẳng định đúng ?
A.
4 5.OM
B.
5.OM
C.
3.OM
D.
3 4.OM
Câu 10: Trong mặt phẳng
,Oxy
đường thẳng đi qua hai điểm
2;0A
và
0;3B
có phương trình là
A.
0
23
xy

. B.
1
23
xy

. C.
0
23
xy

. D.
1
23
xy

.
Câu 11: Cho phương trình
22
5 2 2 5 10 0x x x x
. Đặt
2
5 10t x x
thì phương trình trở
thành phương trình nào sau đây?
A.
2
2 10 0tt
. B.
2
2 2 0tt
. C.
2
2 8 0tt
. D.
2
2 8 0tt
.
Câu 12: Trong mặt phẳng
,Oxy
xác định vị trí tương đối của
2
đường thẳng
1
:
2 3 1 0xy
và
2
:
4 6 1 0xy
.
A. Song song. B. Trùng nhau.
C. Vuông góc. D. Cắt nhau nhưng không vuông góc nhau.
Câu 13: Bất phương trình nào dưới đây vô nghiệm?
A.
2
5 2 0.xx
B.
2
2 3 0.xx
C.
2
6 9 0.xx
D.
2
2 3 0.xx
Câu 14: Cho tam thức
2
3 2.f x x x
Khẳng định nào dưới đây đúng?
A.
0, 1;2 .f x x
B.
0, 1;2 .f x x
C.
0, ;1 2; .f x x  
D.
0, 1;2 .f x x


Câu 15: Trong mặt phẳng
,Oxy
cho đường thẳng
: 0 , , ; 4ax by c a b c b
vuông góc với
đường thẳng
: 3 4 0d x y
và
cách
1;3A
một khoảng
10
. Tính
T a b c
.
A.
10
. B.
11
. C.
4
. D.
9
.
Câu 16: Trong mặt phẳng
,Oxy
đường hyperbol
22
1
20 16
xy

có tiêu cự bằng
A.
12.
B.
2.
C.
4.
D.
6.
Câu 17: Tìm tập xác định của hàm số
2
2 5 2y x x
.
A.
1
;2 .
2



B.
1
; 2; .
2

 


C.
1
; 2;
2

 

. D.
1
;2
2



.
Câu 18: Cho
2
0 f x ax bx c a
có
2
4 b ac
. Điều kiện cần và đủ để
0, f x x
là
A.
0
0

a
. B.
0
0

a
. C.
0
0

a
. D.
0
0

a
.
Câu 19: Cho hàm số
y f x
có tập xác định
5;5
và đồ thị của nó được biểu diễn như hình dưới
đây:
x
y
4
5
1
2
3
1
2
1
5
O
1
Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên
2;2
. B. Hàm số đồng biến trên
5;5
.
C. Hàm số đồng biến trên
2; 3
. D. Hàm số đồng biến trên
5; 2
.
Câu 20: Tìm
m
để parabol
2
( ): 2 3P y mx x
có trục đối xứng là đường thẳng
2x
.
A.
2m
. B.
1m 
. C.
1m
. D.
1
2
m
.
Câu 21: Trong mặt phẳng
,Oxy
phương trình đường tròn có tâm
3;1I
và đi qua điểm
2; 1M
là
A.
22
3 1 5. xy
B.
22
3 1 5. xy
C.
22
3 1 5. xy
D.
22
3 1 5. xy
Câu 22: Tam thức nào dưới đây luôn âm với mọi
?x
A.
2
1.y x x
B.
2
1.y x x
C.
2
1.y x x
D.
2
4.y x x
Câu 23: Tập xác định của hàm số
34
45
x
y
x
là
A.
4
\.
5



D
B.
5
;
4
D




. C.
.D
D.
5
\
4
D



.
Câu 24: Cho hàm số bậc hai
2
, ; ;y ax bx c a b c
có đồ thị như hình bên dưới:
x
y
O
Khẳng định nào dưới đây đúng?
A.
0, 0, 0.a b c
B.
0, 0, 0.a b c
C.
0, 0, 0.a b c
D.
0, 0, 0.a b c
Câu 25: Trong mặt phẳng
,Oxy
đường tròn
22
: 4 6 12 0C x y x y
có tâm
I
và bán kính
R
lần
lượt là
A.
2; 3 , 5IR
. B.
2;3 , 5IR
. C.
4;6 , 5IR
. D.
2; 3 , 5 IR
.
Câu 26: Tìm tập hợp tất cả các giá trị của tham số
m
để hàm số
2
2 1 4y mx m x m
có tập xác
định là
.
A.
;1 .
B.
1; .
C.
1; .
D.
;1 .
Câu 27: Biết tập xác định của hàm số
3
2
5
x
yx
x
là nửa khoảng
;ab
. Khẳng định nào sau
đây đúng?
A.
27ab
. B.
21ab
. C.
3ab
. D.
26ab
.
Câu 28: Trong mặt phẳng
,Oxy
cho đường tròn
22
( ): 1 2 8C x y
. Phương trình tiếp tuyến
d
của
()C
tại điểm
3; 4M
là
A.
: 1 0d x y
. B.
: 2 11 0d x y
. C.
: 7 0d x y
. D.
: 7 0d x y
.
Câu 29: Cho hàm số
2
f x ax bx c
có đồ thị như hình bên dưới:
Giá trị của biểu thức:
2T a b c
bằng
A.
1.
B.
1.
C.
0.
D.
2.
Câu 30: Tập nghiệm của phương trình
32xx
là
A.
S 
. B.
1
2;
2
S




. C.
1
2
S



. D.
1
2
S




.
Câu 31: Trong mặt phẳng
,Oxy
điểm nào dưới đây thuộc đường tròn
22
: 1 2 25? C x y
A.
4;2M
. B.
2;4N
. C.
3;6P
. D.
4; 2Q
.
Câu 32: Biết parabol
2
:4 P y ax bx
có đỉnh là
1; 2 ,I
tính
3ab
.
A.
20
. B.
18
. C.
30
. D.
25.
Câu 33: Trong mặt phẳng
,Oxy
đường tròn có tâm
3;4I
tiếp xúc với đường thẳng
:3 4 10 0xy
thì có bán kính bằng
A.
5
3
. B.
5
. C.
3
. D.
3
5
.
Câu 34: Viết phương trình chính tắc của parabol đi qua điểm
5; 2 .Q
A.
2
3 12.xyx
B.
2
27.yx
C.
2
5 21.xy 
D.
2
4
.
5
y
x
Câu 35: Trong mặt phẳng
,Oxy
toạ độ hình chiếu
H
của điểm
4;1M
trên đường thẳng
: – 2 4 0xy
là
A.
14; 19 .
B.
2;3 .
C.
14 17
;
55



. D.
14 17
;
55



.
II. PHẦN TỰ LUẬN (03 câu – 3,0 điểm)
Câu 1: (1,0 điểm).
a) Tìm tập xác định của hàm số
2
2
41
.
43
x
y
xx


b) Tìm
m
để hàm số
2
2y x mx m
đồng biến trên
1; .
Lời giải:
Câu 2: (1,0 điểm).
a) Giải phương trình
2
1 3 3 4 5 2 0.x x x x
b) Tìm
m
để
22
2 4 3 0x mx m
nghiệm đúng với mọi
.x
Câu 3: (1,0 điểm).
Trong mặt phẳng
,Oxy
cho
(3; 1)M
và
: 3 4 12 0.d x y
Tìm hình chiếu
H
của điểm
M
lên
d
và
N
là điểm đối xứng của
M
qua
.d
____________________HẾT____________________
Huế, 10h45’ Ngày 10 tháng 02 năm 2023
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
ĐỀ ÔN TẬP SỐ 04_TrNg 2023
¤N TËP GI÷A K× 2
Môn: TOÁN 10
SGK 2022 – Kết nối tri thức và cuộc sống
Líp To¸n thÇy L£ B¸ B¶O
Trưêng THPT §Æng Huy Trø S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch
, TP HuÕ
Trung t©m KM 10
Hương
Trà, HuÕ.
LỜI GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm)
Câu 1: Điểm
(0;1)I
thuộc đồ thị của hàm số nào dưới đây ?
A.
2
y x x
. B.
2
y x x
. C.
2
1y x x
. D.
2
1y x x
.
Lời giải:
Xét hàm số:
2
1y x x
, tại
0x
ta có
2
0 0 1 1y
.
Chọn đáp án C.
Câu 2: Trong mặt phẳng
,Oxy
cho đường thẳng
:2 3 4 0d x y
. Vectơ nào sau đây là một vectơ
chỉ phương của
d
?
A.
1
2;3u
. B.
2
3;2u
. C.
3
3; 2u
. D.
4
3; 2 u
.
Lời giải:
Đường thẳng
:2 3 4 0d x y
có một véctơ pháp tuyến
2;3n
nên chọn một véctơ chỉ
phương của
d
là
3
3; 2u
.
Chọn đáp án C.
Câu 3: Trong mặt phẳng
,Oxy
một tiêu điểm của elip (E):
22
1
25 9
xy

có tọa độ là
A.
4;0 .
B.
3;0 .
C.
16;0 .
D.
0; 4 .
Lời giải:
Ta có:
2
2 2 2
2
25
16 4.
9
a
c a b c
b
 
Chọn đáp án A.
Câu 4: Phương trình
13 xx
có tập nghiệm là
A.
5S
. B.
2;5S
. C.
2S
. D.
S
.
Lời giải:
Ta có:
2
2
3
30
3
1 3 5.
2
7 10 0
13
5


x
x
x
x x x
x
xx
xx
x
Vậy tập nghiệm của phương trình là:
5S
.
Chọn đáp án A.
Câu 5: Tập nghiệm của bất phương trình
2
16 8xx
là
A.
4;
. B.
\4
. C. . D.
– ; 4
.
Lời giải:
2
16 8xx
2
40x
4x
.
Chọn đáp án B.
Câu 6: Phương trình
2
1 1 0x x x
có bao nhiêu nghiệm?
A.
2
. B.
1
. C.
0
. D.
3
.
Lời giải:
Điều kiện
1 0 1xx
.
Ta có
2
1 1 0x x x
2
0
0
1 0 1.
1 0 1
x
x
xx
xx
Đối chiếu điều kiện, tập nghiệm của bất phương trình là
1S
.
Chọn đáp án B.
Câu 7: Trong mặt phẳng
,Oxy
cho hai điểm
3;5A
và
2;7B
. Điểm nào sau đây thuộc đường
trung trực của đoạn
AB
?
A.
3
;1
2
M



. B.
5
1;
2
N



. C.
0; 1P
. D.
1
;4
2
Q



.
Lời giải:
Gọi
d
là đường trung trực của đoạn
AB
.
Gọi
I
là trung điểm của
AB
1
;6
2
I




.
Đường thẳng
d
đi qua
1
;6
2
I



và có VTPT là
5;2AB
do đó phương trình của
d
là:
1
5 2 6 0 10 4 19 0
2
x y x y



.
Kiểm tra được
3
;1
2



Md
.
Chọn đáp án A.
Câu 8: Toạ độ giao điểm của parabol
2
1
( ): 2 2 3P y x x
với parabol
2
2
( ): 6P y x x
là
A.
1;7
và
3;27
. B.
7;1
và
27;3
. C.
1;3
và
3;15
. D.
3; 1
và
15; 3
.
Lời giải:
Phương trình hoành độ giao điểm:
2 2 2
1
2 2 3 6 4 3 0
3
x
x x x x x x
x
Vậy có hai giao điểm cần tìm là
1;7
và
3;27
.
Chọn đáp án A.
Câu 9: Trong mặt phẳng
,Oxy
cho elip
22
: 1
16 9
xy
E 
. Với
M
là điểm bất kì nằm trên
E
, khẳng
định nào sau đây là khẳng định đúng ?
A.
4 5.OM
B.
5.OM
C.
3.OM
D.
3 4.OM
Lời giải:
Từ
22
: 1
16 9
xy
E 
, suy ra
4, 3ab
.
Với một điểm bất kì trên
E
, ta luôn có
3 4.b OM a OM
Chọn đáp án D.
Câu 10: Trong mặt phẳng
,Oxy
đường thẳng đi qua hai điểm
2;0A
và
0;3B
có phương trình là
A.
0
23
xy

. B.
1
23
xy

. C.
0
23
xy

. D.
1
23
xy

.
Lời giải:
Đường thẳng đi qua hai điểm
2;0A
và
0;3B
có phương trình đoạn chắn là
1
23
xy

.
Chọn đáp án D.
Câu 11: Cho phương trình
22
5 2 2 5 10 0x x x x
. Đặt
2
5 10t x x
thì phương trình trở
thành phương trình nào sau đây?
A.
2
2 10 0tt
. B.
2
2 2 0tt
. C.
2
2 8 0tt
. D.
2
2 8 0tt
.
Lời giải:
Ta có
2
5 10 0, x x x
.
Đặt
2
5 10, t x x
0t
22
5 10. t x x
Phương trình đã cho trở thành
2
2 8 0tt
.
Chọn đáp án C.
Câu 12: Trong mặt phẳng
,Oxy
xác định vị trí tương đối của
2
đường thẳng
1
:
2 3 1 0xy
và
2
:
4 6 1 0xy
.
A. Song song. B. Trùng nhau.
C. Vuông góc. D. Cắt nhau nhưng không vuông góc nhau.
Lời giải:
Xét:
2 3 1
4 6 1


nên hai đường thẳng song.
Chọn đáp án A.
Câu 13: Bất phương trình nào dưới đây vô nghiệm?
A.
2
5 2 0.xx
B.
2
2 3 0.xx
C.
2
6 9 0.xx
D.
2
2 3 0.xx
Câu 14: Cho tam thức
2
3 2.f x x x
Khẳng định nào dưới đây đúng?
A.
0, 1;2 .f x x
B.
0, 1;2 .f x x
C.
0, ;1 2; .f x x  
D.
0, 1;2 .f x x


Lời giải:
Bảng xét dấu:
x

1
2

fx
0
0
Chọn đáp án B.
Câu 15: Trong mặt phẳng
,Oxy
cho đường thẳng
: 0 , , ; 4ax by c a b c b
vuông góc với
đường thẳng
: 3 4 0d x y
và
cách
1;3A
một khoảng
10
. Tính
T a b c
.
A.
10
. B.
11
. C.
4
. D.
9
.
Lời giải:
Do
: 3 4 0 : 3 0d x y x y c
.
Ta có:
1 9 10
0
; 10 10 10
20
1 9 10
cc
c
d A c
c

Vì
c
nên
0c
. Suy ra
: 3 0xy
. Khi đó
1, 3, 0 4a b c T
.
Chọn đáp án C.
Câu 16: Trong mặt phẳng
,Oxy
đường hyperbol
22
1
20 16
xy

có tiêu cự bằng
A.
12.
B.
2.
C.
4.
D.
6.
Lời giải:
Ta có :
2
2
2 2 2
20
16
a
b
c a b
25
4
6
a
b
c
. Tiêu cự
2 12.c
Chọn đáp án A.
Câu 17: Tìm tập xác định của hàm số
2
2 5 2y x x
.
A.
1
;2 .
2



B.
1
; 2; .
2

 


C.
1
; 2;
2

 

. D.
1
;2
2



.
Lời giải:
Điều kiện
2
2
2 5 2 0
1
2
x
xx
x
.
Vậy tập xác định của hàm số là
1
; 2;
2

 

.
Chọn đáp án C.
Câu 18: Cho
2
0 f x ax bx c a
có
2
4 b ac
. Điều kiện cần và đủ để
0, f x x
là
A.
0
0

a
. B.
0
0

a
. C.
0
0

a
. D.
0
0

a
.
Câu 19: Cho hàm số
y f x
có tập xác định
5;5
và đồ thị của nó được biểu diễn như hình dưới
đây:
x
y
4
5
1
2
3
1
2
1
5
O
1
Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên
2;2
. B. Hàm số đồng biến trên
5;5
.
C. Hàm số đồng biến trên
2; 3
. D. Hàm số đồng biến trên
5; 2
.
Lời giải:
Hàm số đồng biến có đồ thị đi lên và hàm số nghịch biến có đồ thị đi xuống (từ trái sang
phải).
Chọn đáp án D.
Câu 20: Tìm
m
để parabol
2
( ): 2 3P y mx x
có trục đối xứng là đường thẳng
2x
.
A.
2m
. B.
1m 
. C.
1m
. D.
1
2
m
.
Lời giải:
Vì
P
là Parabol nên
0m
. Khi đó Parabol
P
có trục đối xứng
21
2
xx
mm
Theo bài ra trục đối xứng
2x
nên
11
2
2
m
m
.
Chọn đáp án D.
Câu 21: Trong mặt phẳng
,Oxy
phương trình đường tròn có tâm
3;1I
và đi qua điểm
2; 1M
là
A.
22
3 1 5. xy
B.
22
3 1 5. xy
C.
22
3 1 5. xy
D.
22
3 1 5. xy
Lời giải:
Ta có:
1; 2 .IM
Vì đường tròn có tâm
3;1I
và đi qua điểm
2; 1M
nên bán kính của đường tròn là
5R MI
.
Vậy phương trình đường tròn cần tìm là
22
3 1 5 xy
.
Chọn đáp án C.
Câu 22: Tam thức nào dưới đây luôn âm với mọi
?x
A.
2
1.y x x
B.
2
1.y x x
C.
2
1.y x x
D.
2
4.y x x
Lời giải:
Bảng xét dấu
2
1:y x x
x


y
Chọn đáp án C.
Câu 23: Tập xác định của hàm số
34
45
x
y
x
là
A.
4
\.
5



D
B.
5
;
4
D




. C.
.D
D.
5
\
4
D



.
Lời giải:
Điều kiện :
5
4 5 0
4
xx
. Tập xác định của hàm số là
5
\
4
D



.
Chọn đáp án D.
Câu 24: Cho hàm số bậc hai
2
, ; ;y ax bx c a b c
có đồ thị như hình bên dưới:
x
y
O
Khẳng định nào dưới đây đúng?
A.
0, 0, 0.a b c
B.
0, 0, 0.a b c
C.
0, 0, 0.a b c
D.
0, 0, 0.a b c
Lời giải:
Do đồ thị là parabol có bề lõm hướng xuống dưới nên
0a
.
Dựa vào đồ thị, ta có:
0
0 0.
2
a
b
b
a

Giao điểm của đồ thị với
Oy
có tọa độ
0; 0.cc
Vậy
0, 0, 0.a b c
Chọn đáp án B.
Câu 25: Trong mặt phẳng
,Oxy
đường tròn
22
: 4 6 12 0C x y x y
có tâm
I
và bán kính
R
lần
lượt là
A.
2; 3 , 5IR
. B.
2;3 , 5IR
. C.
4;6 , 5IR
. D.
2; 3 , 5 IR
.
Lời giải:
Phương trình
C
có tâm
2; 3I
và bán kính
2
2
2 3 12 5. R
Chọn đáp án A.
Câu 26: Tìm tập hợp tất cả các giá trị của tham số
m
để hàm số
2
2 1 4y mx m x m
có tập xác
định là
.
A.
;1 .
B.
1; .
C.
1; .
D.
;1 .
Lời giải:
Yêu cầu của bài toán tương đương với: Tìm m để
2
2 1 4 0,mx m x m x
(1)
TH 1: Xét
0m
, (1) trở thành
2 0,xx
, không thỏa mãn. Nên
0m
loại.
TH 2: Xét
0m
, (1) tương đương với
2
2
0
' 1 4 0
am
mm

2
0
0
1
3 2 1 0
1
3
m
m
m
mm
m




1m
.
Vậy
1.m
Chọn đáp án B.
Câu 27: Biết tập xác định của hàm số
3
2
5
x
yx
x
là nửa khoảng
;ab
. Khẳng định nào sau
đây đúng?
A.
27ab
. B.
21ab
. C.
3ab
. D.
26ab
.
Lời giải:
Điều kiện xác định:
2 0 2
5 0 5
xx
xx



Vậy
2;5D 
suy ra
2, 5ab
nên
21ab
.
Chọn đáp án B.
Câu 28: Trong mặt phẳng
,Oxy
cho đường tròn
22
( ): 1 2 8C x y
. Phương trình tiếp tuyến
d
của
()C
tại điểm
3; 4M
là
A.
: 1 0d x y
. B.
: 2 11 0d x y
. C.
: 7 0d x y
. D.
: 7 0d x y
.
Lời giải:
Đường tròn
()C
có tâm
(1; 2)I
.
Tiếp tuyến tại
M
có vectơ pháp tuyến là
(2; 2) n IM
Phương trình tiếp tuyến của đường tròn tại
M
là:
2( 3) 2( 4) 0 7 0x y x y
.
Chọn đáp án C.
Câu 29: Cho hàm số
2
f x ax bx c
có đồ thị như hình bên dưới:
Giá trị của biểu thức:
2T a b c
bằng
A.
1.
B.
1.
C.
0.
D.
2.
Lời giải:
Đồ thị cắt trục tung tại điểm có tung độ bằng
1
nên
1c 
. Suy ra
2
1y ax bx
Trục đối xứng
1 1 2 0
2
b
x a b
a
.
Khi đó
2 0 ( 1) 1.T a b c
Chọn đáp án A.
Câu 30: Tập nghiệm của phương trình
32xx
là
A.
S 
. B.
1
2;
2
S




. C.
1
2
S



. D.
1
2
S




.
Lời giải:
Ta có:
20
1
32
1
2
2
2
2
3
x
x
x
x
xx
x
x



.
Vậy tập nghiệm của phương trình là
1
2
S



.
Chọn đáp án C.
Câu 31: Trong mặt phẳng
,Oxy
điểm nào dưới đây thuộc đường tròn
22
: 1 2 25? C x y
A.
4;2M
. B.
2;4N
. C.
3;6P
. D.
4; 2Q
.
Lời giải:
Do
22
4 1 2 2 25
nên điểm
4; 2Q
thuộc đường tròn
C
.
Chọn đáp án D.
Câu 32: Biết parabol
2
:4 P y ax bx
có đỉnh là
1; 2 ,I
tính
3ab
.
A.
20
. B.
18
. C.
30
. D.
25.
Lời giải:
Do đồ thị hàm số
2
4y ax bx
có đỉnh là điểm
1; 2I
1
2
12
b
a
y

20
42
ab
ab

6
12
a
b

3 30ab
.
Chọn đáp án C.
Câu 33: Trong mặt phẳng
,Oxy
đường tròn có tâm
3;4I
tiếp xúc với đường thẳng
:3 4 10 0xy
thì có bán kính bằng
A.
5
3
. B.
5
. C.
3
. D.
3
5
.
Lời giải:
Đường tròn tâm
3;4I
tiếp xúc với đường thẳng
nên bán kính đường tròn là
22
3.3 4.4 10
15
,3
5
34
R d I

.
Chọn đáp án C.
Câu 34: Viết phương trình chính tắc của parabol đi qua điểm
5; 2 .Q
A.
2
3 12.xyx
B.
2
27.yx
C.
2
5 21.xy 
D.
2
4
.
5
y
x
Lời giải:
Phương trình chính tắc của parabol
2
: 2Py px
5; 2QP
4
2
5
p
Vậy phương trình
2
4
:
5
P y x
.
Chọn đáp án D.
Câu 35: Trong mặt phẳng
,Oxy
toạ độ hình chiếu
H
của điểm
4;1M
trên đường thẳng
: – 2 4 0xy
là
A.
14; 19 .
B.
2;3 .
C.
14 17
;
55



. D.
14 17
;
55



.
Lời giải:
H
M
Δ
Đường thẳng
có 1 vectơ pháp tuyến
1; 2n 
1 vectơ chỉ phương là
2;1 .u
Gọi
2 4;H t t
là hình chiếu của
4;1M
trên đường thẳng
.
Ta có:
2 8; 1 .MH t t
Do
MH 
nên
. 0 2 2 8 1 0MH u t t
17
5
t
14 17
;
55
H



.
Chọn đáp án D.
II. PHẦN TỰ LUẬN (03 câu – 3,0 điểm)
Câu 1: (1,0 điểm).
a) Tìm tập xác định của hàm số
2
2
41
.
43
x
y
xx


b) Tìm
m
để hàm số
2
2y x mx m
đồng biến trên
1; .
Lời giải:
a) Hàm số xác định
2
2
2;2
40
2;1 .
;1 3;
4 3 0
x
x
x
x
xx






 
Vậy tập xác định của hàm số là
2;1 .D

b) Hàm số
2
2y x mx m
đồng biến trên
;m 
(do
10a 
)
Yêu cầu bài toán
1; ; 1.mm  
Câu 2: (1,0 điểm).
a) Giải phương trình
2
1 3 3 4 5 2 0.x x x x
b) Tìm
m
để
22
2 4 3 0x mx m
nghiệm đúng với mọi
.x
Lời giải:
a) Ta có:
2 2 2
1 3 3 4 5 2 0 4 3 4 5 1 0x x x x x x x x
Đặt
2 2 2
4 5 0 4 5,x x t t x x t 
ta được phương trình:
(tháa m·n)
(lo¹i)
2
1
3 4 0
4
t
tt
t

Với
1,t
ta được
2 2 2
4 5 1 4 5 1 4 4 0 2.x x x x x x x
Vậy phương trình có tập nghiệm là
2.S
b) Yêu cầu bài toán
2
10
0
0
12 12 0
a
m



; 1 1; .m

 

Kết luận:
; 1 1; .m

 

Câu 3: (1,0 điểm).
Trong mặt phẳng
,Oxy
cho
(3; 1)M
và
: 3 4 12 0.d x y
Tìm hình chiếu
H
của điểm
M
lên
d
và
N
là điểm đối xứng của
M
qua
.d
Lời giải:
N
H
M
d
Phương trình đường thẳng
MH
qua
M
và vuông góc với
: 3 4 12 0d x y
có dạng
: 4 3 0.MH x y m
Vì
(3; 1) 4.3 3.( 1) 0 9.M MH m m
Suy ra
: 4 3 9 0.MH x y
Tọa độ hình chiếu
H
là nghiệm hệ
4 3 9 0
0;3 .
3 4 12 3
x y x
H
x y y




Do
N
là điểm đối xứng của
M
qua
d
nên
H
là trung điểm
MN
2 2.0 3 3
( 3;7).
2 2.3 ( 1) 7
N H M
N H M
x x x
N
y y y
____________________HẾT____________________
Huế, 10h45’ Ngày 10 tháng 02 năm 2023
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
ĐỀ ÔN TẬP SỐ 05_TrNg 2023
¤N TËP GI÷A K× 2
Môn: TOÁN 10
SGK 2022 – Kết nối tri thức và cuộc sống
Líp To¸n thÇy L£ B¸ B¶O
Trưêng THPT §Æng Huy Trø S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch
, TP HuÕ
Trung t©m KM 10
Hương
Trà, HuÕ.
NỘI DUNG ĐỀ BÀI
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm)
Câu 1: Đồ thị trong hình là đồ thị hàm số của một trong bốn hàm số được cho ở các phương án A, B,
C, D. Hỏi hàm số đó là hàm số nào?
x
y
-1
O
1
A.
2
2.y x x
B.
2
2 1.y x x
C.
2
2 4.y x x
D.
2
2.y x x
Câu 2: Trong mặt phẳng
,Oxy
đường tròn tâm
(3; 1)I
và bán kính
2R
có phương trình là
A.
22
( 3) ( 1) 4xy
. B.
22
( 3) ( 1) 4xy
.
C.
22
( 3) ( 1) 4xy
. D.
22
( 3) ( 1) 4xy
.
Câu 3: Trong mặt phẳng
,Oxy
đường thẳng đi qua
1;2A
, nhận
2; 4n 
làm vectơ pháp tuyến
có phương trình là
A.
2 5 0xy
. B.
2 4 0xy
. C.
40xy
. D.
2 4 0xy
.
Câu 4: Tìm tất cả các giá trị của tham số
m
để biểu thức
2
2 2 3f x m x x
là một tam thức
bậc hai.
A.
m
. B.
2m
. C.
2m
. D.
2m
.
Câu 5: Trong mặt phẳng
,Oxy
phương trình
22
2( 1) 2( 2) 6 7 0x y m x m y m
là phương trình
đường tròn khi và chỉ khi
A.
0.m
B.
1m
. C.
1m
. D.
1m 
hoặc
1m
.
Câu 6: Trong mặt phẳng
,Oxy
cho đường thẳng
:7 3 1 0d x y
. Vectơ nào sau đây là vectơ chỉ
phương của d?
A.
7;3u
. B.
3;7u
. C.
3;7u 
. D.
7; 3u
.
Câu 7: Tập nghiệm của phương trình
32xx
là
A.
S 
. B.
1
2;
2
S




. C.
1
2
S



. D.
1
2
S




.
Câu 8: Trong mặt phẳng
,Oxy
viết phương trình chính tắc của Parabol biết đường chuẩn có phương
trình
1
0.
4
x
A.
2
.y x
B.
2
.y x
C.
2
.
2
x
y
D.
2
2.y x
Câu 9: Trong mặt phẳng
,Oxy
đường tròn
()C
tâm
(4; 3)I
và tiếp xúc với đường thẳng
:3 4 5 0xy
có phương trình là
A.
22
( 4) ( 3) 1xy
. B.
22
( 4) ( 3) 1xy
.
C.
22
( 4) ( 3) 1xy
. D.
22
( 4) ( 3) 1xy
Câu 10: Trong mặt phẳng
,Oxy
đường thẳng
: 2 1 0d x y
song song với đường thẳng có phương
trình nào sau đây?
A.
2 1 0xy
. B.
20xy
. C.
2 1 0xy
. D.
2 4 1 0xy
.
Câu 11: Cho hàm số
y f x
có đồ thị như hình bên dưới.
Khẳng định nào sau đây đúng?
A. Hàm số
y
nghịch biến trên khoảng
0;3
. B. Hàm số
y
đồng biến trên khoảng
;1
.
C. Hàm số
y
nghịch biến trên khoảng
0;2
. D. Hàm số
y
đồng biến trên khoảng
;3
.
Câu 12: Trong mặt phẳng
,Oxy
phương trình chính tắc của
E
có tiêu cự bằng
6
và đi qua điểm
5;0A
là
A.
22
1
100 81
xy

. B.
22
1
15 16
xy

. C.
22
1
25 9
xy

. D.
22
1
25 16
xy

.
Câu 13: Bất phương trình
2
2 3 0xx
có tập nghiệm là
A.
; 1 3; 
. B.
1;3
. C.
1;3
. D.
3;1
.
Câu 14: Trong mặt phẳng
,Oxy
tính góc giữa hai đường thẳng
: 3 2 0xy
và
: 3 1 0xy
.
A.
90
. B.
120
. C.
60
. D.
30
.
Câu 15: Biết đồ thị hàm số
2
: 2, ; , 0P y ax bx a b a
qua hai điểm
1;4M
và
1;2 .N
Tính
22
.T a b
A.
10.
B.
5.
C.
1.
D.
2.
Câu 16: Đường Hyperbol
22
1
20 16
xy

có tiêu cự bằng
A.
12.
B.
2.
C.
4.
D.
6.
Câu 17: Tam thức nào dưới đây luôn dương với mọi giá trị của
x
?
A.
2
10 2xx
. B.
2
2 10xx
. C.
2
2 10xx
. D.
2
2 10xx
.
Câu 18: Cho hàm số bậc hai
2
, ; ;y ax bx c a b c
có đồ thị như hình bên dưới:
x
y
O
Khẳng định nào dưới đây đúng?
A.
0, 0, 0.a b c
B.
0, 0, 0.a b c
C.
0, 0, 0.a b c
D.
0, 0, 0.a b c
Câu 19: Tìm tất cả các giá trị của tham số
m
để phương trình
2
40x mx m
vô nghiệm.
A.
0 16m
. B.
44m
. C.
04m
. D.
0 16m
.
Câu 20: Tập xác định của hàm số
2
23
43
x
y
xx

là
A.
3
\ ;1;3
2
D


. B.
\1D
. C.
\3D
. D.
\ 1;3D
.
Câu 21: Tìm tập xác định của hàm số
2
2
2 5 2
1


xx
y
xx
.
A.
1
;2 .
2



D
B.
1
; 2; .
2




D
C.
1
; 2;
2



D
. D.
1
;2
2



D
.
Câu 22: Cho hàm số bậc hai
2
, ; ;y ax bx c a b c
có đồ thị như hình bên dưới:
x
y
-3
4
3
-1
O
1
Tính
.T abc
A.
6.
B.
6.
C.
5.
D.
4.
Câu 23: Hình vẽ dưới đây mô tả số người nhiễm Covid – 19 đang được điều trị ở Việt Nam tính từ
ngày 23/01/2020 đến ngày 13/02/2021.
Hỏi từ ngày 16/06/2020 đến ngày 27/01/2021, ngày nào Việt Nam có số người điều trị Covid-
19 nhiều nhất?
A.
16 /11/ 2020
. B.
17 / 08 / 2020
. C.
23/ 07 / 2020
. D.
13/ 02 / 2021
.
Câu 24: Cho
fx
và
gx
là các đa thức xác định trên
.
Mệnh đề nào dưới đây luôn đúng?
A.
2
.f x g x f x g x


B.
2
.
0
f x g x
f x g x
gx



C.
2
.
0
f x g x
f x g x
fx



D.



2
.
0
f x g x
f x g x
gx
Câu 25: Trong mặt phẳng
,Oxy
cho elip
E
có phương trình
22
1
36 16
xy

. Tìm tiêu cự của
E
.
A.
12
12.FF
B.
12
8.FF
C.
12
2 5.FF
D.
12
4 5.FF
Câu 26: Cho hàm số bậc hai
2
, ; ;y ax bx c a b c
có đồ thị như hình bên dưới:
x
y
-2
O
1
Tập hợp các giá trị của tham số
m
để phương trình
20f x m
có hai nghiệm phân biệt là
A.
2.m 
B.
4.m 
C.
2.m 
D.
4.m 
Câu 27: Trong mặt phẳng
,Oxy
cho đường thẳng
23
:
1
xt
yt

t
và điểm
1; 6M
. Phương
trình đường thẳng đi qua
M
và vuông góc với
là
A.
3 9 0xy
. B.
3 17 0xy
. C.
3 3 0xy
. D.
3 19 0xy
.
Câu 28: Với tất cả giá trị nào của
m
thì hàm số
2
21
23
x
y
x x m
xác định trên
?
A.
4m 
. B.
4m 
. C.
0m
. D.
4m
.
Câu 29: Trong mặt phẳng
,Oxy
đường tròn
()C
đi qua hai điểm
(1;3)A
,
(3;1)B
và có tâm nằm trên
đường thẳng
:2 7 0d x y
có phương trình là
A.
22
( 7) ( 7) 102xy
. B.
22
( 7) ( 7) 164xy
.
C.
22
( 3) ( 5) 25xy
. C.
22
( 3) ( 5) 25xy
.
Câu 30: Tích các nghiệm của phương trình
2
2 4 3 0x x x
bằng
A.
6.
B.
2.
C.
4.
D.
4.
Câu 31: Hệ bất phương trình
2
10
0


x
xm
có nghiệm khi và chỉ khi
A.
1m
. B.
1m
. C.
1m
. D.
1m
.
Câu 32: Tìm số giá trị của tham số m để đường thẳng
:1d y x
cắt parabol
2
:3P y x x m
tại 2
điểm phân biệt có hoành độ
12
,xx
sao cho
22
12
6xx
.
A.
0
. B.
1
. C.
2
. D.
4
.
Câu 33: Trong mặt phẳng
,Oxy
khoảng cách từ điểm
1(1; )M
đến đường thẳng
:3 4 0xy
là
A.
1
. B.
3 10
5
. C.
5
2
. D.
2 10
.
Câu 34: Có bao nhiêu giá trị nguyên của tham số m để phương trình
22
4 1 ( 1) 0x x m
có
nghiệm thuộc khoảng
0; 15 ?
A.
1
. B.
4
. C.
3
. D.
0.
Câu 35: Trong mặt phẳng
,Oxy
cho tam giác
ABC
với
2; 1 ; 4;5 ; 3;2A B C
. Phương trình tổng
quát của đường cao đi qua
A
của tam giác là
A.
3 7 1 0. xy
B.
7 3 13 0. xy
C.
3 7 13 0. xy
D.
7 3 11 0. xy
II. PHẦN TỰ LUẬN (03 câu – 3,0 điểm)
Câu 1: (1,0 điểm).
a) Tìm tập xác định của hàm số
2
2
4 3 7
.
2
xx
y
xx
b) Tìm
,,a b c
để parabol
2
:P y ax bx c
đi qua điểm
1;3A
và có đỉnh là
1; 1 .I
Câu 2: (1,0 điểm).
a) Tìm
m
để phương trình
2
1x x m x
có duy nhất một nghiệm.
b) Tìm
m
để phương trình
2
2 2 2 3 5 6 0m x m x m
có hai nghiệm trái dấu.
Câu 3: (1,0 điểm).
Trong mặt phẳng
,Oxy
cho đường thẳng
: 3 4 6 0.d x y
Viết phương trình đường tròn tâm
( 3;0)I
cắt
d
tại
,AB
sao cho
8.AB
____________________HẾT____________________
Huế, 08h45’ Ngày 13 tháng 02 năm 2023
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
ĐỀ ÔN TẬP SỐ 05_TrNg 2023
¤N TËP GI÷A K× 2
Môn: TOÁN 10
SGK 2022 – Kết nối tri thức và cuộc sống
Líp To¸n thÇy L£ B¸ B¶O
Trưêng THPT §Æng Huy Trø S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch
, TP HuÕ
Trung t©m KM 10
Hương
Trà, HuÕ.
LỜI GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm)
Câu 1: Đồ thị trong hình là đồ thị hàm số của một trong bốn hàm số được cho ở các phương án A, B,
C, D. Hỏi hàm số đó là hàm số nào?
x
y
-1
O
1
A.
2
2.y x x
B.
2
2 1.y x x
C.
2
2 4.y x x
D.
2
2.y x x
Lời giải:
Kiểm tra các sự kiện:
Đồ thị
P
có đỉnh
1; 1I
và đi qua
.O
Ta thấy hàm số ở phương án D thỏa mãn.
Chọn đáp án D.
Câu 2: Trong mặt phẳng
,Oxy
đường tròn tâm
(3; 1)I
và bán kính
2R
có phương trình là
A.
22
( 3) ( 1) 4xy
. B.
22
( 3) ( 1) 4xy
.
C.
22
( 3) ( 1) 4xy
. D.
22
( 3) ( 1) 4xy
.
Lời giải:
Phương trình đường tròn có tâm
3; 1I
, bán kính
2R
là:
22
3 1 4xy
.
Câu 3: Trong mặt phẳng
,Oxy
đường thẳng đi qua
1;2A
, nhận
2; 4n 
làm vectơ pháp tuyến
có phương trình là
A.
2 5 0xy
. B.
2 4 0xy
. C.
40xy
. D.
2 4 0xy
.
Lời giải:
Phương trình đường thẳng đi qua
1;2A
và
2; 4n 
là:
2 1 4 2 0 1 2 2 0 2 5 0x y x y x y
.
Chọn đáp án A.
Câu 4: Tìm tất cả các giá trị của tham số
m
để biểu thức
2
2 2 3f x m x x
là một tam thức
bậc hai.
A.
m
. B.
2m
. C.
2m
. D.
2m
.
Lời giải:
2
2 2 3f x m x x
là một tam thức bậc hai khi và chỉ khi:
2 0 2mm
.
Chọn đáp án B.
Câu 5: Trong mặt phẳng
,Oxy
phương trình
22
2( 1) 2( 2) 6 7 0x y m x m y m
là phương trình
đường tròn khi và chỉ khi
A.
0.m
B.
1m
. C.
1m
. D.
1m 
hoặc
1m
.
Lời giải:
Ta có:
22
2 2 2 2
22
22
2
2 1 2 2 6 7 0 1
2 1 1 2 2 2 1 2 6 7 0
1 2 2 2
x y m x m y m
x m x m y m y m m m m
x m y m m
Vậy điều kiện để (1) là phương trình đường tròn:
2
1
2 2 0
1
m
m
m

.
Chọn đáp án D.
Câu 6: Trong mặt phẳng
,Oxy
cho đường thẳng
:7 3 1 0d x y
. Vectơ nào sau đây là vectơ chỉ
phương của d?
A.
7;3u
. B.
3;7u
. C.
3;7u 
. D.
7; 3u
.
Lời giải:
Đường thẳng d có 1 VTPT là
7;3n
nên d có 1 VTCP là
3;7u 
.
Chọn đáp án C.
Câu 7: Tập nghiệm của phương trình
32xx
là
A.
S 
. B.
1
2;
2
S




. C.
1
2
S



. D.
1
2
S




.
Lời giải:
Ta có:
20
1
32
1
2
2
2
2
3
x
x
x
x
xx
x
x



.
Vậy tập nghiệm của phương trình là
1
2
S



.
Chọn đáp án C.
Câu 8: Trong mặt phẳng
,Oxy
viết phương trình chính tắc của Parabol biết đường chuẩn có phương
trình
1
0.
4
x
A.
2
.y x
B.
2
.y x
C.
2
.
2
x
y
D.
2
2.y x
Lời giải:
Phương trình chính tắc của parabol
2
: 2Py px
Parabol có đường chuẩn
1
0
4
x 
1
2
p
2
): yP x
.
Chọn đáp án A.
Câu 9: Trong mặt phẳng
,Oxy
đường tròn
()C
tâm
(4; 3)I
và tiếp xúc với đường thẳng
:3 4 5 0xy
có phương trình là
A.
22
( 4) ( 3) 1xy
. B.
22
( 4) ( 3) 1xy
.
C.
22
( 4) ( 3) 1xy
. D.
22
( 4) ( 3) 1xy
Lời giải:
C
có bán kính
2
2
3.4 4.3 5
,1
34
R d I


.
Do đó,
C
có phương trình
22
( 4) ( 3) 1xy
.
Chọn đáp án B.
Câu 10: Trong mặt phẳng
,Oxy
đường thẳng
: 2 1 0d x y
song song với đường thẳng có phương
trình nào sau đây?
A.
2 1 0xy
. B.
20xy
. C.
2 1 0xy
. D.
2 4 1 0xy
.
Lời giải:
Ta kiểm tra lần lượt các đường thẳng.
.+) Với
1
: 2 1 0d x y
có
12
12
d
cắt
1
d
.
.+) Với
2
: 2 0d x y
có
21
12
d

cắt
2
d
.
.+) Với
3
: 2 1 0d x y
có
1 2 1
1 2 1
d

trùng
3
d
.
.+) Với
4
: 2 4 1 0d x y
có
1 2 1
2 4 1
d


song song
4
d
.
Chọn đáp án D.
Câu 11: Cho hàm số
y f x
có đồ thị như hình bên dưới.
Khẳng định nào sau đây đúng?
A. Hàm số
y
nghịch biến trên khoảng
0;3
. B. Hàm số
y
đồng biến trên khoảng
;1
.
C. Hàm số
y
nghịch biến trên khoảng
0;2
. D. Hàm số
y
đồng biến trên khoảng
;3
.
Lời giải:
Trên khoảng
0;2
, đồ thị hàm số đi xuống từ trái sang phải nên hàm số nghịch biến.
Chọn đáp án C.
Câu 12: Trong mặt phẳng
,Oxy
phương trình chính tắc của
E
có tiêu cự bằng
6
và đi qua điểm
5;0A
là
A.
22
1
100 81
xy

. B.
22
1
15 16
xy

. C.
22
1
25 9
xy

. D.
22
1
25 16
xy

.
Lời giải:
Phương trình chính tắc của
E
là
22
22
: 1 0
xy
E a b
ab
.
Do
E
có tiêu cự bằng
6
nên
26c
3.c
Do
E
đi qua điểm
5;0A
nên
5a
2 2 2
25 9 16b a c
.
Vậy
22
:1
25 16
xy
E 
.
Chọn đáp án D.
Câu 13: Bất phương trình
2
2 3 0xx
có tập nghiệm là
A.
; 1 3; 
. B.
1;3
. C.
1;3
. D.
3;1
.
Lời giải:
Ta có:
2
2 3 0 1 3x x x
.
Chọn đáp án B.
Câu 14: Trong mặt phẳng
,Oxy
tính góc giữa hai đường thẳng
: 3 2 0xy
và
: 3 1 0xy
.
A.
90
. B.
120
. C.
60
. D.
30
.
Lời giải:
Đường thẳng
có vectơ pháp tuyến
1; 3n 
, đường thẳng
có vectơ pháp tuyến
1; 3n
.
Gọi
là góc giữa
,

, ta có:
13
1
cos cos , 60
2
1 3. 1 3


nn
.
Chọn đáp án C.
Câu 15: Biết đồ thị hàm số
2
: 2, ; , 0P y ax bx a b a
qua hai điểm
1;4M
và
1;2 .N
Tính
22
.T a b
A.
10.
B.
5.
C.
1.
D.
2.
Lời giải:
Do
1;4
2 4 2 1
.
2 2 0 1
1;2
MP
a b a b a
a b a b b
NP

Vậy
22
2.T a b
Chọn đáp án D.
Câu 16: Đường Hyperbol
22
1
20 16
xy

có tiêu cự bằng
A.
12.
B.
2.
C.
4.
D.
6.
Lời giải:
Ta có :
2
2
2 2 2
20
16
a
b
c a b
25
4
6
a
b
c
. Tiêu cự
2 12.c
Chọn đáp án A.
Câu 17: Tam thức nào dưới đây luôn dương với mọi giá trị của
x
?
A.
2
10 2xx
. B.
2
2 10xx
. C.
2
2 10xx
. D.
2
2 10xx
.
Lời giải:
Kiểm tra tam thức ở phương án C thỏa mãn
0
.
0

a
Chọn đáp án C.
Câu 18: Cho hàm số bậc hai
2
, ; ;y ax bx c a b c
có đồ thị như hình bên dưới:
x
y
O
Khẳng định nào dưới đây đúng?
A.
0, 0, 0.a b c
B.
0, 0, 0.a b c
C.
0, 0, 0.a b c
D.
0, 0, 0.a b c
Lời giải:
Do đồ thị là parabol có bề lõm hướng lên trên nên
0a
.
Dựa vào đồ thị, ta có:
0
0 0.
2
a
b
b
a

Giao điểm của đồ thị với
Oy
có tọa độ
0; 0.cc
Vậy
0, 0, 0.a b c
Chọn đáp án C.
Câu 19: Tìm tất cả các giá trị của tham số
m
để phương trình
2
40x mx m
vô nghiệm.
A.
0 16m
. B.
44m
. C.
04m
. D.
0 16m
.
Lời giải:
Phương trình
2
40x mx m
vô nghiệm khi
0
2
16 0mm
0 16m
.
Chọn đáp án A.
Câu 20: Tập xác định của hàm số
2
23
43
x
y
xx

là
A.
3
\ ;1;3
2
D


. B.
\1D
. C.
\3D
. D.
\ 1;3D
.
Lời giải:
Điều kiện
2
1
4 3 0
3
x
xx
x
.
Tập xác định của hàm số là
\ 1;3D
.
Chọn đáp án D.
Câu 21: Tìm tập xác định của hàm số
2
2
2 5 2
1


xx
y
xx
.
A.
1
;2 .
2



D
B.
1
; 2; .
2




D
C.
1
; 2;
2



D
. D.
1
;2
2



D
.
Lời giải:
Ta có:
2
1 0, x x x
vì có
0a
và
0.
Vậy hàm số xác định
2
2
2 5 2 0
1
2
x
xx
x
.
Suy ra, tập xác định của hàm số là
1
; 2;
2

 

D
.
Chọn đáp án C.
Câu 22: Cho hàm số bậc hai
2
, ; ;y ax bx c a b c
có đồ thị như hình bên dưới:
x
y
-3
4
3
-1
O
1
Tính
.T abc
A.
6.
B.
6.
C.
5.
D.
4.
Lời giải:
Dựa vào đồ thị, ta có hệ:
1
2 0 1
2
1 4 4 2.
33
03
b
a b a
a
y a b c b
cc
y



Vậy
6.T abc
Chọn đáp án B.
Câu 23: Hình vẽ dưới đây mô tả số người nhiễm Covid – 19 đang được điều trị ở Việt Nam tính từ
ngày 23/01/2020 đến ngày 13/02/2021.
Hỏi từ ngày 16/06/2020 đến ngày 27/01/2021, ngày nào Việt Nam có số người điều trị Covid-
19 nhiều nhất?
A.
16 /11/ 2020
. B.
17 / 08 / 2020
. C.
23/ 07 / 2020
. D.
13/ 02 / 2021
.
Câu 24: Cho
fx
và
gx
là các đa thức xác định trên
.
Mệnh đề nào dưới đây luôn đúng?
A.
2
.f x g x f x g x


B.
2
.
0
f x g x
f x g x
gx



C.
2
.
0
f x g x
f x g x
fx



D.



2
.
0
f x g x
f x g x
gx
Câu 25: Trong mặt phẳng
,Oxy
cho elip
E
có phương trình
22
1
36 16
xy

. Tìm tiêu cự của
E
.
A.
12
12.FF
B.
12
8.FF
C.
12
2 5.FF
D.
12
4 5.FF
Lời giải:
22
1
36 16
xy

6
4
a
b
2 2 2
c a b
20
25c
12
2 4 5F F c
.
Chọn đáp án D.
Câu 26: Cho hàm số bậc hai
2
, ; ;y ax bx c a b c
có đồ thị như hình bên dưới:
x
y
-2
O
1
Tập hợp các giá trị của tham số
m
để phương trình
20f x m
có hai nghiệm phân biệt là
A.
2.m 
B.
4.m 
C.
2.m 
D.
4.m 
Lời giải:
Ta có:
20
2
m
f x m f x
.
Số nghiệm của phương trình đã cho bằng số giao điểm của hai đồ thị
y f x
và
.
2
m
y
Yêu cầu bài toán
2 4.
2
m
m
Chọn đáp án B.
Câu 27: Trong mặt phẳng
,Oxy
cho đường thẳng
23
:
1
xt
yt

t
và điểm
1; 6M
. Phương
trình đường thẳng đi qua
M
và vuông góc với
là
A.
3 9 0xy
. B.
3 17 0xy
. C.
3 3 0xy
. D.
3 19 0xy
.
Lời giải:
có một vectơ chỉ phương
3;1u
.
Vì đường thẳng
d
vuông góc với
nên
d
có véctơ pháp tuyến
3;1nu
.
Phương trình tổng quát của đường thẳng
d
là
3 1 6 0 3 3 0x y x y
.
Chọn đáp án C.
Câu 28: Với tất cả giá trị nào của
m
thì hàm số
2
21
23
x
y
x x m
xác định trên
?
A.
4m 
. B.
4m 
. C.
0m
. D.
4m
.
Lời giải:
Hàm số
2
21
23
x
y
x x m
xác định trên khi phương trình
2
2 3 0x x m
vô nghiệm
Hay
4 0 4mm
.
Chọn đáp án B.
Câu 29: Trong mặt phẳng
,Oxy
đường tròn
()C
đi qua hai điểm
(1;3)A
,
(3;1)B
và có tâm nằm trên
đường thẳng
:2 7 0d x y
có phương trình là
A.
22
( 7) ( 7) 102xy
. B.
22
( 7) ( 7) 164xy
.
C.
22
( 3) ( 5) 25xy
. C.
22
( 3) ( 5) 25xy
.
Lời giải:
;I a b
là tâm của đường tròn
C
, do đó:
2 2 2 2
22
1 3 3 1 (1)AI BI a b a b a b
Mà
; :2 7 0 nên 2 7 0 (2)I a b d x y a b
.
Thay (1) vào (2) ta có:
22
7 7 164a b R AI
.
Vậy
22
: 7 7 164C x y
.
Chọn đáp án B.
Câu 30: Tích các nghiệm của phương trình
2
2 4 3 0x x x
bằng
A.
6.
B.
2.
C.
4.
D.
4.
Lời giải:
Điều kiện:
2 0 2xx
(*).
Ta có:
2
2
2
20
2 4 3 0 1
4 3 0
3

x
x
x x x x
xx
x
.
Đối chiếu điều kiện (*), tập nghiệm của phương trình là
2;3S
.
Chọn đáp án A.
Câu 31: Hệ bất phương trình
2
10
0


x
xm
có nghiệm khi và chỉ khi
A.
1m
. B.
1m
. C.
1m
. D.
1m
.
Lời giải:
Ta có:
2
11
10
0



x
x
xm
xm
.
Do đó hệ có nghiệm khi chỉ khi
1m
.
Chọn đáp án D.
Câu 32: Tìm số giá trị của tham số m để đường thẳng
:1d y x
cắt parabol
2
:3P y x x m
tại 2
điểm phân biệt có hoành độ
12
,xx
sao cho
22
12
6xx
.
A.
0
. B.
1
. C.
2
. D.
4
.
Lời giải:
Xét phương trình:
22
3 1 2 1 0x x m x x x m
(*)
Theo bài ra ta có:
12
12
2
12
12
2
22
12
1 2 1 2
2
' 1 1 0
2
2
2
0
1
1
( 2) 2( 1) 6
6
26
m
m
xx
xx
m
m
x x m
x x m
m
xx
x x x x






.
Chọn đáp án B.
Câu 33: Trong mặt phẳng
,Oxy
khoảng cách từ điểm
1(1; )M
đến đường thẳng
:3 4 0xy
là
A.
1
. B.
3 10
5
. C.
5
2
. D.
2 10
.
Lời giải:
Khoảng cách từ điểm
1(1; )M
đến đường thẳng
:3 4 0xy
là
22
3.1 1 4
6 3 10
;.
5
10
31
dM

Chọn đáp án B.
Câu 34: Có bao nhiêu giá trị nguyên của tham số m để phương trình
22
4 1 ( 1) 0x x m
có
nghiệm thuộc khoảng
0; 15 ?
A.
1
. B.
4
. C.
3
. D.
0.
Lời giải:
Ta có:
22
4 1 ( 1) 0x x m
22
1 4 1 0x x m
.
Đặt
2
1tx
. Với
0; 15x
thì
1;4t
.
Phương trình trở thành:
2
40t t m
2
4*m t t
.
Xét hàm số
2
( ) 4f t t t
với
1;4t
.
Ta có BBT:
Dựa vào BBT, suy ra phương trình đã cho có nghiệm thuộc khoảng
0; 15
.
Phương trình (*) có nghiệm thuộc khoảng
1;4t
40m
.
Vậy các giá trị nguyên
m
thỏa là
4; 3; 2; 1 m
.
Chọn đáp án B.
Câu 35: Trong mặt phẳng
,Oxy
cho tam giác
ABC
với
2; 1 ; 4;5 ; 3;2A B C
. Phương trình tổng
quát của đường cao đi qua
A
của tam giác là
A.
3 7 1 0. xy
B.
7 3 13 0. xy
C.
3 7 13 0. xy
D.
7 3 11 0. xy
Lời giải:
Đường cao
AH
của tam giác đi qua
2; 1A
và nhận
7;3n CB
làm VTPT.
:7 2 3 1 0 7 3 11 0.AH x y x y
Chọn đáp án C.
II. PHẦN TỰ LUẬN (03 câu – 3,0 điểm)
Câu 1: (1,0 điểm).
a) Tìm tập xác định của hàm số
2
2
4 3 7
.
2
xx
y
xx
b) Tìm
,,a b c
để parabol
2
:P y ax bx c
đi qua điểm
1;3A
và có đỉnh là
1; 1 .I
Lời giải:
a) Hàm số xác định
2
2
0
20
2 ;1 3; \ 0 .
4 3 0
;1 3;
x
xx
xx
xx
x

 

 
Vậy tập xác định của hàm số là
;1 3; \ 0 .D  
b) Do
P
đi qua điểm
1;3A
và có đỉnh là
1; 1I
nên ta có:
3 3 1
1 1 2.
2 0 0
1
2
a b c a b c a
a b c a b c b
b a b c
a






Vậy
2
: 2 .P y x x
Câu 2: (1,0 điểm).
a) Tìm
m
để phương trình
2
1x x m x
có duy nhất một nghiệm.
b) Tìm
m
để phương trình
2
2 2 2 3 5 6 0m x m x m
có hai nghiệm trái dấu.
Lời giải:
a) Ta có:
2
22
1 0 1
1.
1 2 1
xx
x x m x
x x m x m x x





Bảng biến thiên
2
21y x x
trên
1; :

x
1
1

y
2
2

Dựa vào bảng biến thiên, yêu cầu bài toán
; 2 2 .m 
b) Phương trình có hai nghiệm trái dấu
. 0 ( 2)(5 6) 0a c m m
2
6
5 16 12 0 2.
5
m m m
Câu 3: (1,0 điểm).
Trong mặt phẳng
,Oxy
cho đường thẳng
: 3 4 6 0.d x y
Viết phương trình đường tròn tâm
( 3;0)I
cắt
d
tại
,AB
sao cho
8.AB
Lời giải:
Ta có
22
3.( 3) 4.0 6 15
( , ) 3.
5
34
d I d
Gọi
H
là trung điểm của
AB
và do
8 4.AB HA
Tam giác
IHA
vuông tại
2 2 2
H IA IH HA
2
22
( , ) 5.R d I d AH R


Khi đó,
()C
có tâm
( 3;0),I
bán kính
5R
có dạng
22
( ) :( 3) 25.C x y
____________________HẾT____________________
Huế, 08h45’ Ngày 13 tháng 02 năm 2023
| 1/70
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

BỘ ĐỀ ÔN GIỮA KÌ 2 MÔN TOÁN 10 BỘ SÁCH
KẾT NỐI TRI THỨC VỚI CUỘC SỐNG 23 Tác giả: LÊ BÁ BẢO
Trường THPT Đặng Huy Trứ, Huế 20
Admin CLB Giáo viên trẻ TP Huế
Page: CLB GIÁO VIÊN TRẺ TP HUẾ ¤N TËP GI÷A K× 2 Môn: TOÁN 10
SGK 2022 – Kết nối tri thức và cuộc sống
ĐỀ ÔN TẬP SỐ 01_TrNg 2023 Líp To¸n thÇy L£ B¸ B¶O
Trưêng THPT §Æng Huy Trø
S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch, TP HuÕ Trung t©m KM 10 Hương Trà, HuÕ. NỘI DUNG ĐỀ BÀI
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm) Câu 1: Cho hàm số 2
y ax bx c , với a  0 . Khẳng định nào sau đây sai? b
A. Hàm số đồng biến trên khoảng  ;    .  2a   b
B. Hàm số nghịch biến trên khoảng  ;     .  2a   b
C. Hàm số nghịch biến trên khoảng ;    .  2a
D. Đồ thị hàm số có trục đối xứng là đường thẳng   b x . 2a
Câu 2: Trong mặt phẳng Oxy, cho hai điểm A1; 3 , B2;7. Một vectơ chỉ phương của đường thẳng AB là A. u  4  ;1 . B. u  2  ;1 . C. u  3;  2 .
D. u  1; 4 . 4   3   2   1   2 2 x y
Câu 3: Trong mặt phẳng Oxy, đường Elip  1 có tiêu cự bằng 5 4 A. 2. B. 4. C. 9. D.1.
Câu 4: Nghiệm của phương trình 2x 1  3  x là 3 2 4 3 A. x  . B. x  . C. x  . D. x  . 4 3 3 2
Câu 5: Với m là tham số bất kì, biểu thức nào dưới đây là tam thức bậc hai? A. y  . m
B. y m . x C. y   2 m   2 1 x . D. 2 y mx  . m
Câu 6: Trong mặt phẳng Oxy, đường tròn C 2 2
: x y  4x  6y  12  0 có tâm là A. I 2; 3  .
B. I 2; 3 .
C. I 4;6 . D. I 4; 6  . Câu 7: Cho hàm số 2
y x  3x 1 . Điểm nào sau đây thuộc đồ thị của hàm số?
A. A0 ; 2 .
B. B 1; 5 .
C. C 1;  3 .
D. D  2  ; 4 . 2 x y
Câu 8: Trong mặt phẳng Oxy, viết phương trình chính tắc của E 2 : 
 1 có a  2b và có tiêu cự 2 2 a b bằng 4 3. 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.  1. B.  1. C.  1. D.  1. 36 9 36 24 24 6 16 4
Câu 9: Trong mặt phẳng Oxy, phương trình đường tròn C  có tâm I 1;3 và đi qua M 3;  1 là 2 2 2 2 A.x  
1   y  3  8 . B.x   1
  y  3 10. 2 2 2 2
C.x  3   y   1  10 .
D.x  3   y   1  8.
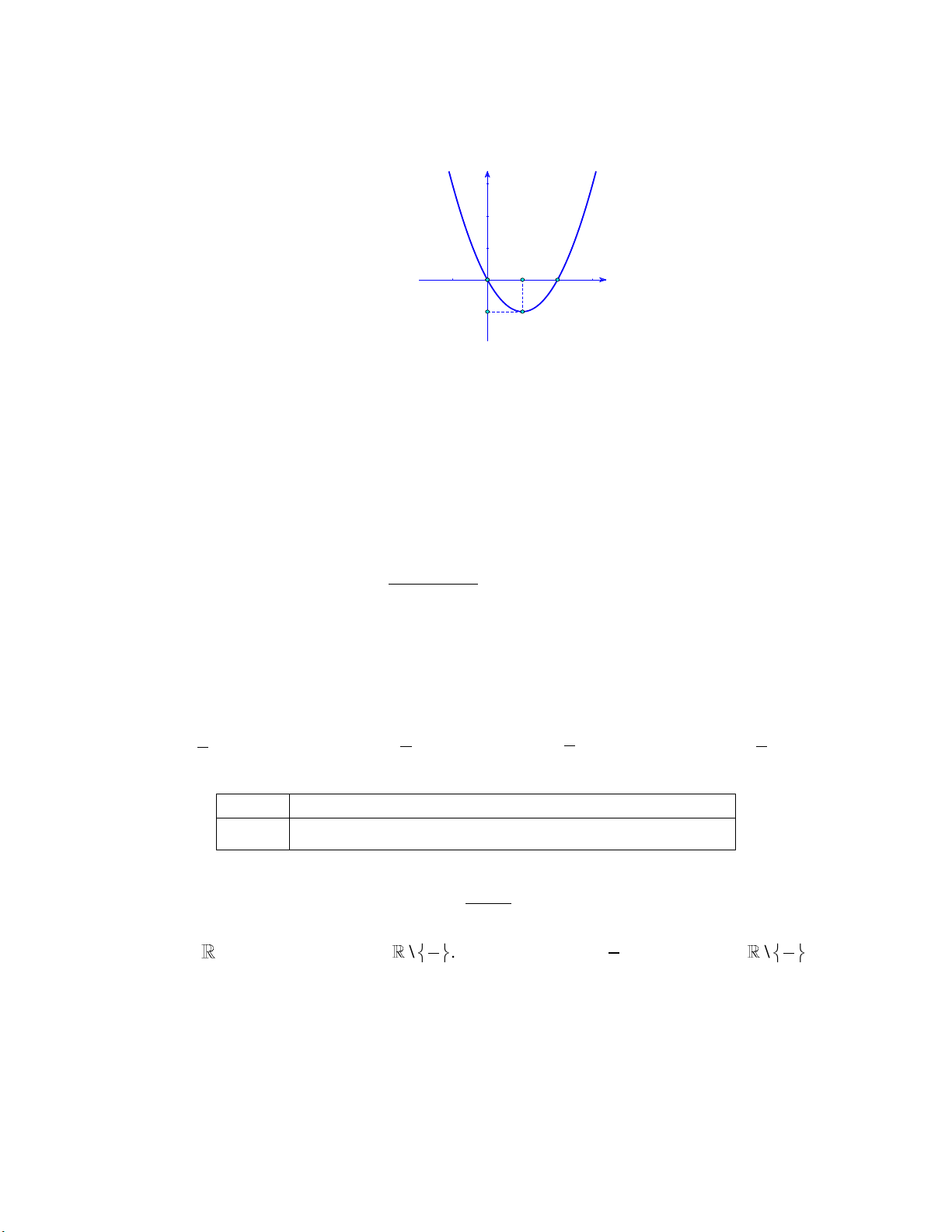
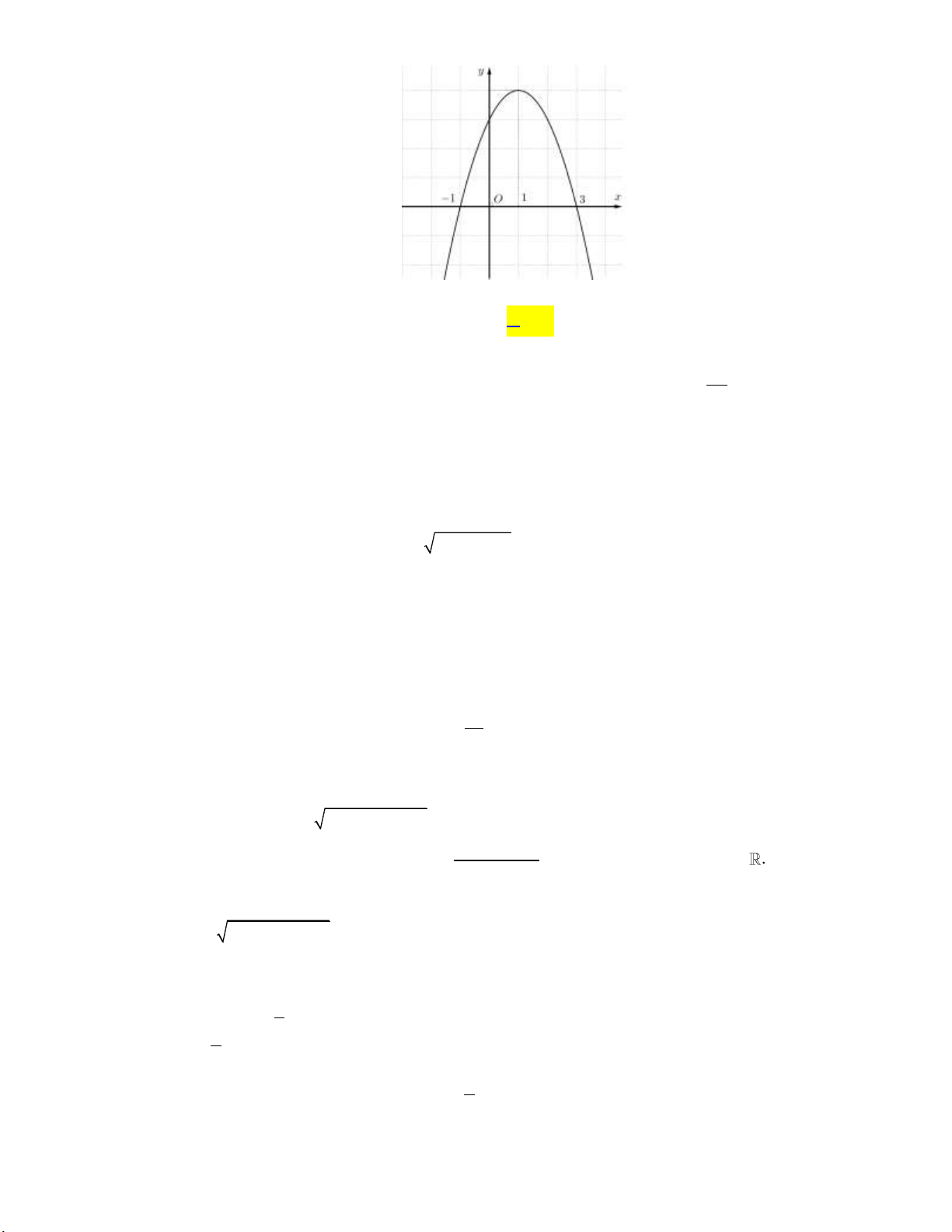
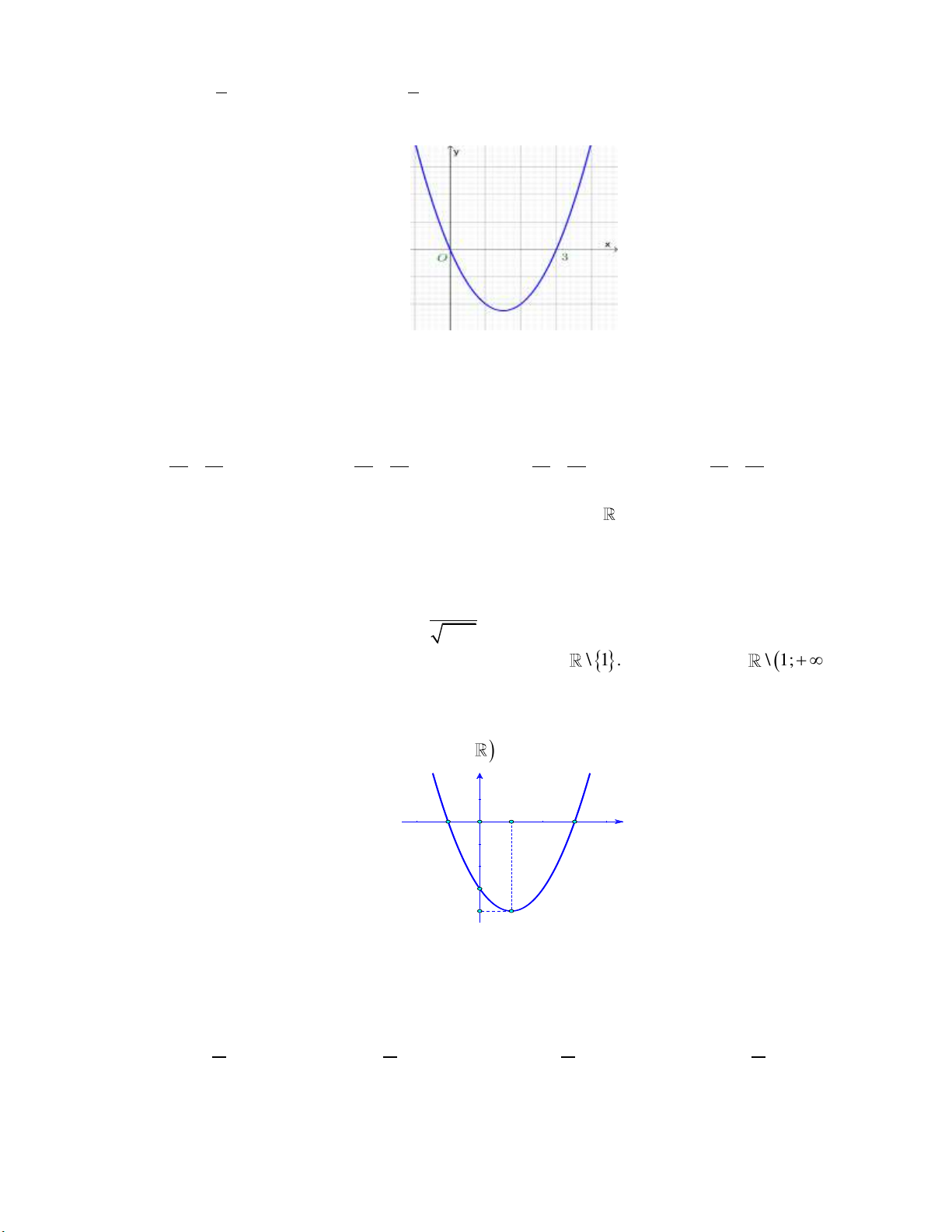
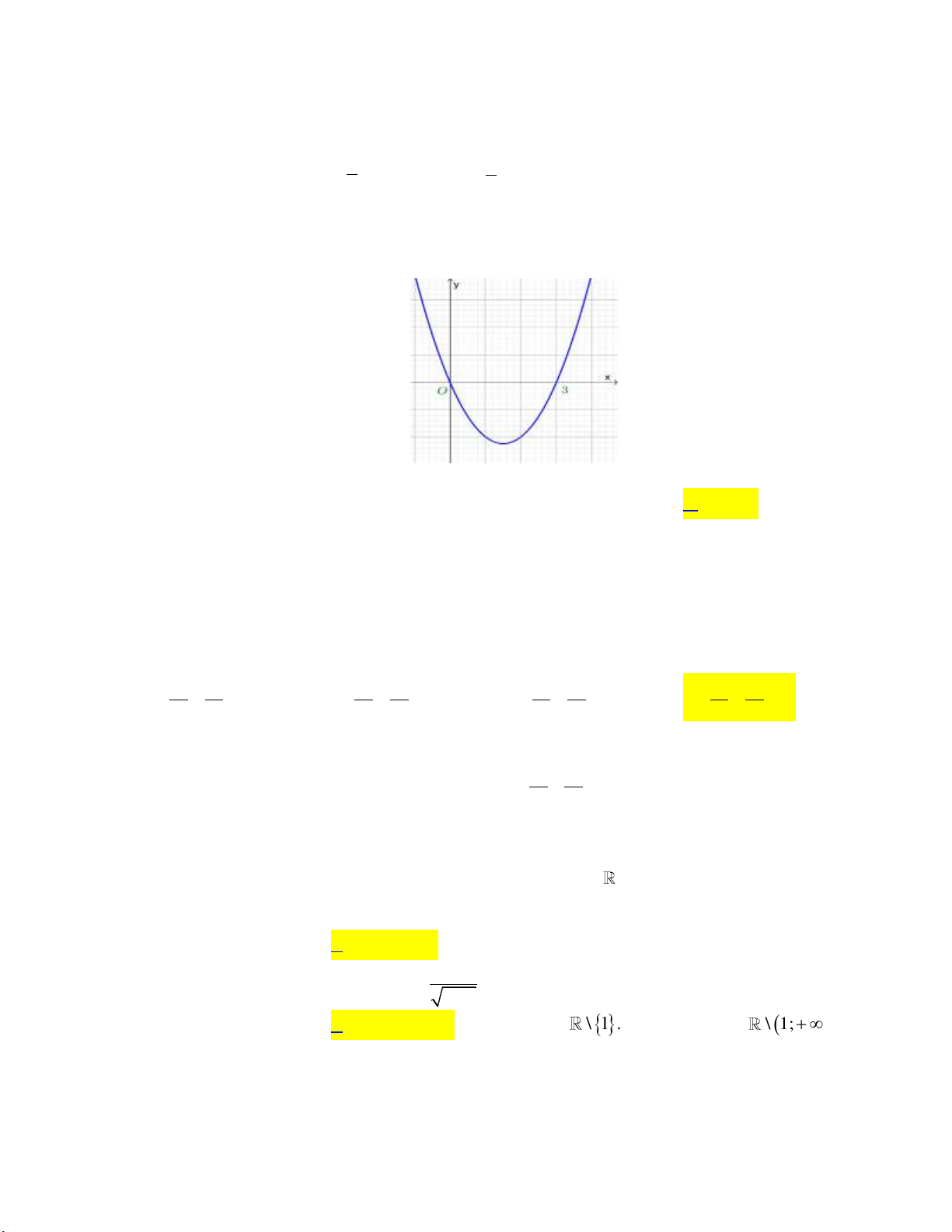
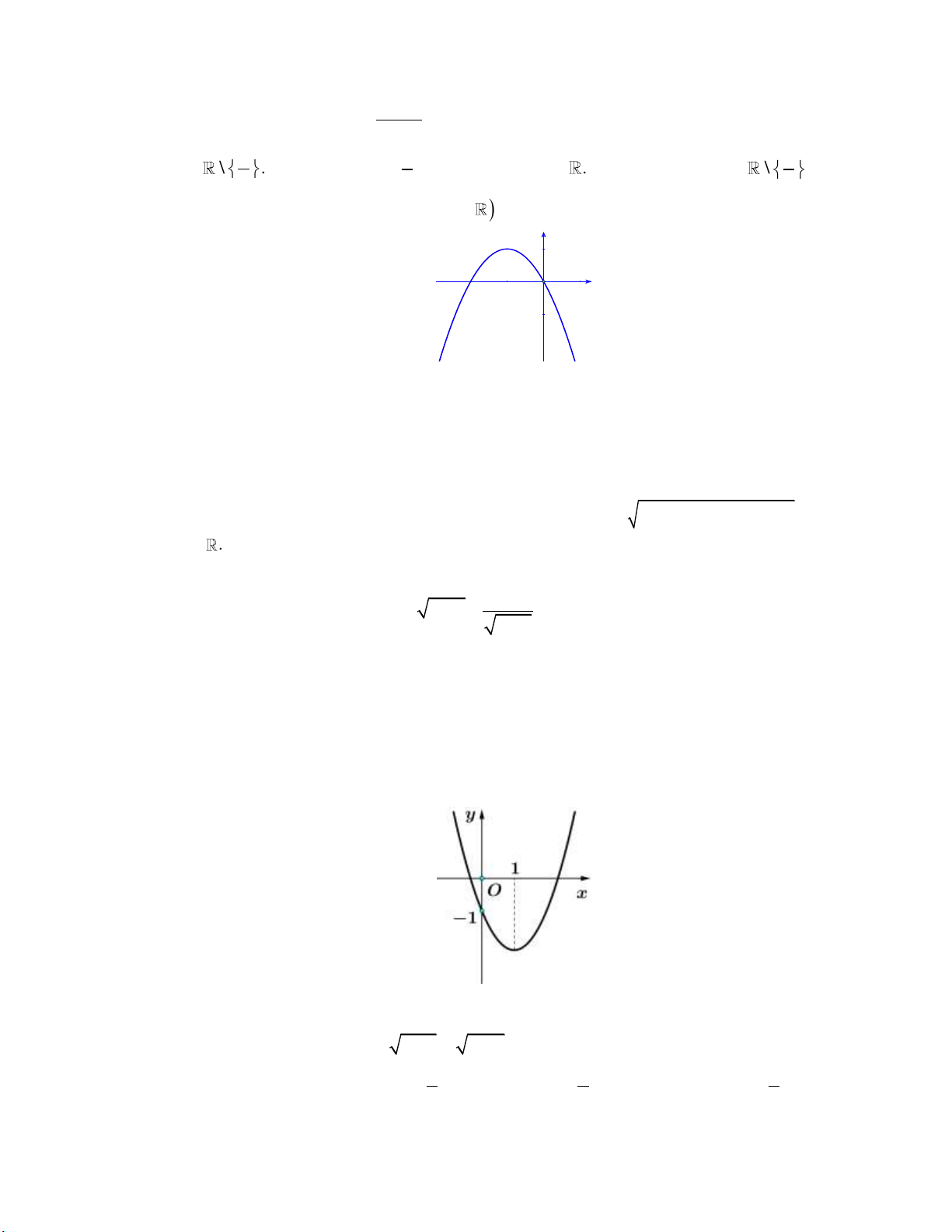
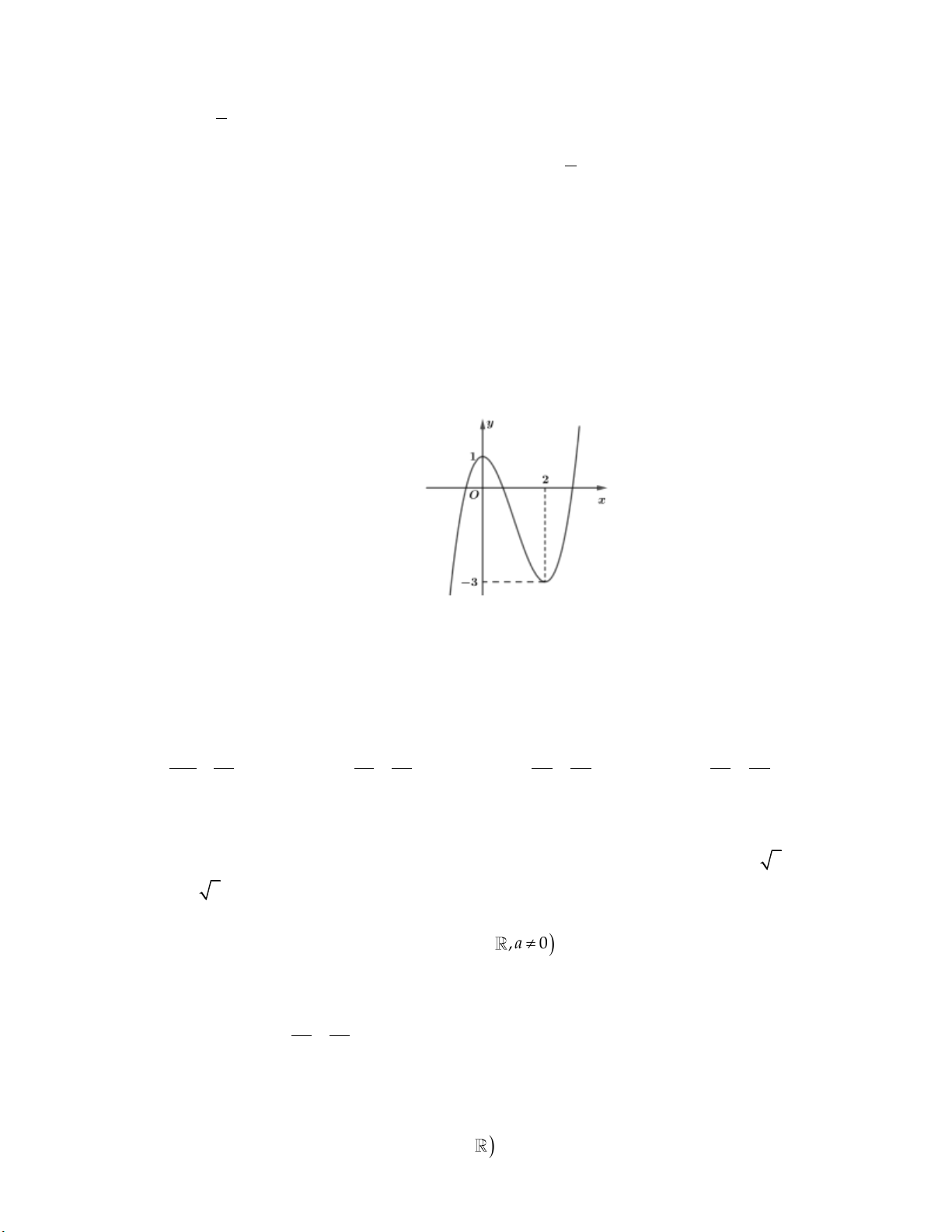
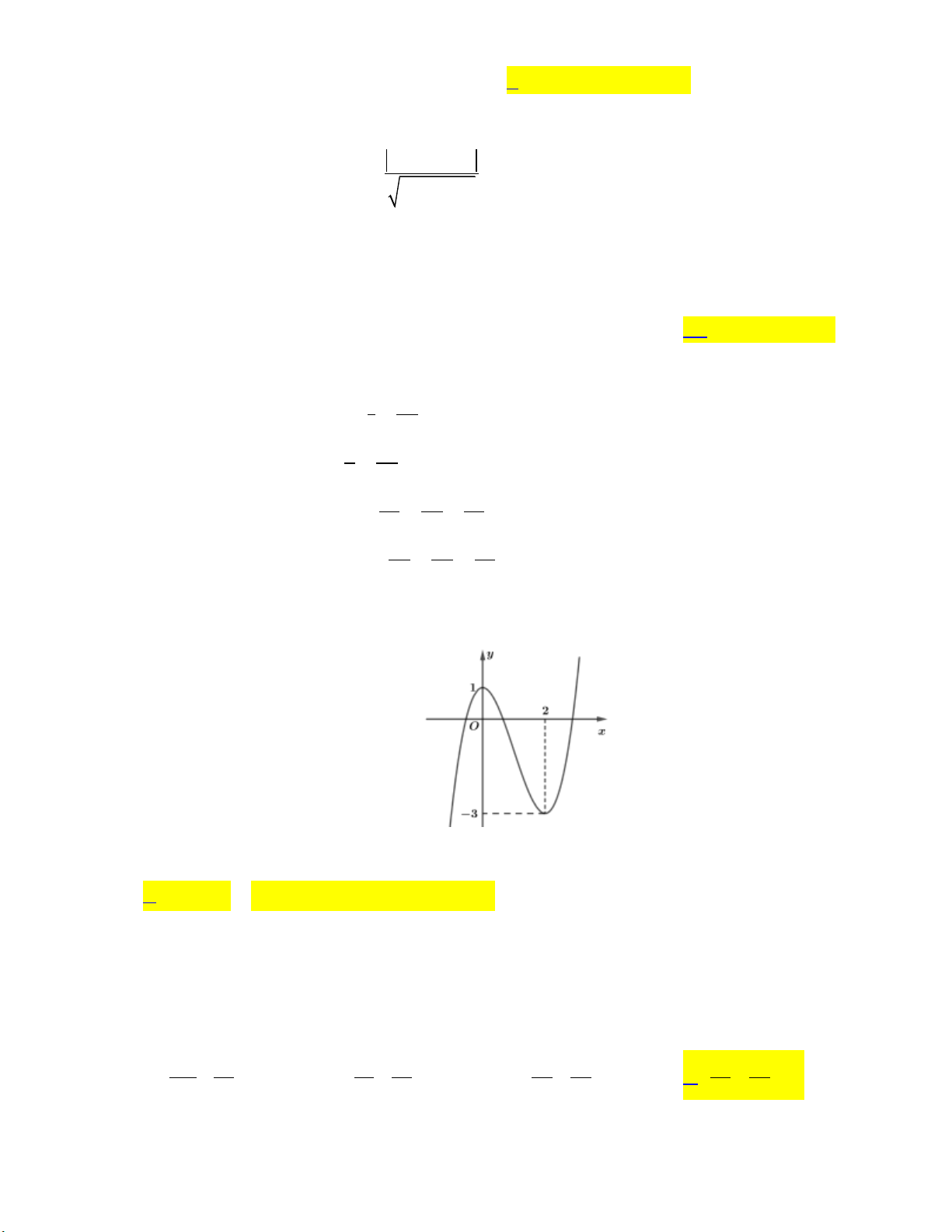
Câu 10: Cho hàm số bậc hai y f x có đồ thị như hình bên dưới: y 1 2 x O -1
Khẳng đinh nào dưới đây đúng?
A. f x  0, x  0;2.
B. f x  0, x  0;2.
C. f x  0, x  1;.
D. f x  0, x   0;2.  
Câu 11: Trong mặt phẳng Oxy, với những giá trị nào của m thì đường thẳng  : 4x  3y m  0 tiếp
xúc với đường tròn C  2 2
: x y  9 ? A. m  3.
B. m  3 và m  3.
C. m  45 và m  45. 
D. m  15 và m  15. 
Câu 12: Trong các hàm số sau hàm số nào là hàm số bậc hai? 3 2x  3x  5 A. 2
y  2x  3x  5 B. y  . C. 2 3
y  2x  3x  5 . D. y  3x  2 . x
Câu 13: Cho hàm số f x 2
x  2x  3. Khẳng định nào dưới đây đúng?
A. f 2  3.
B. f 3  4.
C. f 0  2.
D. f 4  5. Câu 14: Cho hàm số 2 y  3
x  4x  3 có đồ thị (P). Trục đối xứng của (P) là đường thẳng có phương trình là 2 2 4 4 A. x  .
B. x   . C. x  .
D. x   3 3 3 3
Câu 15: Tam thức bậc hai nào dưới đây có bảng xét dấu như hình sau? x  0 4  f x  0  0  A. 2 y x  2 . x B. 2 y x  2 . x C. 2 y x  4 . x D. 2
y  x  4 . x x
Câu 16: Tìm tập xác định của hàm số y f x 2 1  . 4x  5 4  5  5 A. D  . B. D  \  . C. D  ;    . D. D  \   . 5  4  4
Câu 17: Tìm tất cả giá trị tham số m để hàm số 2
y x  m  
1 x m  2 đồng biến trên 1;  .
A. m  3 .
B. m  3 .
C. m  3 . D. m  3 .
Câu 18: Đỉnh của parabol 2
y x  4x  5 có toạ độ là A. 0; 2 . B. 1; 2 . C. 2;0 . D. 2;  1 .
Câu 19: Giá trị nhỏ nhất của hàm số 2
y x  4x  5 là A. y  0. B. y  2 . C. y  2 . D. y  1. min min min min
Câu 20: Tam thức nào dưới đây luôn dương với mọi x  ? A. 2
y x x  1. B. 2
y x  2x  1. C. 2
y  x x  1. D. 2
y  x  4 . x x  1 t
Câu 21: Trong mặt phẳng Oxy, cho đường thẳng d : 
t  Điểm nào dưới đây nằm trên y  2  .  3t đường thẳng d?
A. M 1; 3.
B. N 5; 2.
C. P 2; 5.
D. Q2;0.
Câu 22: Số nghiệm của phương trình 2
x  4x 1  x  3 là A. Vô số. B. 0. C. 1. D. 2. x 1
Câu 23: Hàm số y  0;1 khi chỉ khi
x m  xác định trên   1  m 1  m 1
A. m  1. B.  . C.  .
D. 1  m  2 . m  2 m  2
Câu 24: Trong mặt phẳng Oxy, cho đường thẳng d : x  2y  5  0. Vectơ nào dưới đây là một vectơ chỉ phương của d?
A. u  1; 2 . B. u  2  ;1 . C. u  3;  2 .
D. u  2; 3 . 4   3   2   1  
Câu 25: Phương trình  2 x x 2 2 6
17  x x  6x có bao nhiêu nghiệm phân biệt? A. 2. B. 1. C. 3. D. 4.
Câu 26: Trong mặt phẳng Oxy, phương trình nào sau đây là phương trình của đường tròn? A. 2 2
x  2 y  4x  8 y 1  0 . B. 2 2
x y  4x  6 y 12  0 . C. 2 2
x y  2x  8 y  20  0 . D. 2 2
4x y 10x  6 y  2  0 .
Câu 27: Trong mặt phẳng Oxy, cho hai điểm M 1; 
1 , N 2; 4. Phương trình đường thẳng MN là x  1 tx  1 3tx  1 tx t A.  . B.  . C.  . D.  . y   3t y  1   t y  3   t y  2    3t
Câu 28: Cho f x 2
ax bx c,a  0 và 2
  b  4ac . Tìm điều kiện của  để f x cùng dấu với
hệ số a với mọi x  . A.   0 . B.   0 . C.   0 . D.   0 .
Câu 29: Trong mặt phẳng Oxy, cho hai đường thẳng d : 4x  2y  1  0 và d : 2x y  3  0. Khẳng 1 2
định nào sau đây đúng?
A. d / /d .
B. d d . 1 2 1 2
C. d , d cắt nhau và không vuông góc.
D. d d . 1 2 1 2
Câu 30: Tập nghiệm của bất phương trình 2
x  2x  3  0 là A. 1; 3.   B. ; 1
  3;. C. 1;3. D. ; 1    3;   . x  1 2t
Câu 31: Trong mặt phẳng Oxy, cho điểm A2; 3 và đường thẳng d : 
, t  . Phương trình y  3   t
đường thẳng  qua A và vuông góc với d là
A. 2x y  7  0.
B. 2x y  0.
C. x  2y  1  0.
D. x  2y  4  0.
Câu 32: Đường thẳng nào dưới đây là đường chuẩn của parabol 2 y  4x ?
A. x  1.
B. x  2.
C. x  1. D. x  2.
Câu 33: Tập nghiệm của phương trình x   2
2 x  4x  3  0 là
A. S  2;  3 . B. S    2 .
C. S  1;  3 .
D. S  1; 2;  3 .
Câu 34: Trong mặt phẳng Oxy, cho điểm A1; 2 và đường thẳng  : 2x y  1  0. Tính khoảng cách
từ điểm A đến đường thẳng . 5 A. 5. B. 5. C. 2 5 D. . 5 2 x y
Câu 35: Trong mặt phẳng Oxy, hypebol H 2 : 
 1 có hai tiêu điểm là 16 9
A. F  5;0 , F 5;0 .
B. F  2;0 , F 2;0 . 2   1  2   1 
C. F  3;0 , F 3;0 .
D. F  4;0 , F 4;0 . 2   1  2   1 
II. PHẦN TỰ LUẬN (03 câu – 3,0 điểm)
Câu 1: (1,0 điểm). 2x  1
a) Tìm tập xác định của hàm số y  . 2 x  4
b) Tìm a,b để parabol P 2
: y ax bx  1 đi qua hai điểm A1; 4 và B2;9.
Câu 2: (1,0 điểm). a) Giải phương trình 2
x  5x  1  x  1.
b) Tìm m để phương trình 2 2
x  2x  2m  3m  1  0 có hai nghiệm dương phân biệt.
Câu 3: (1,0 điểm).
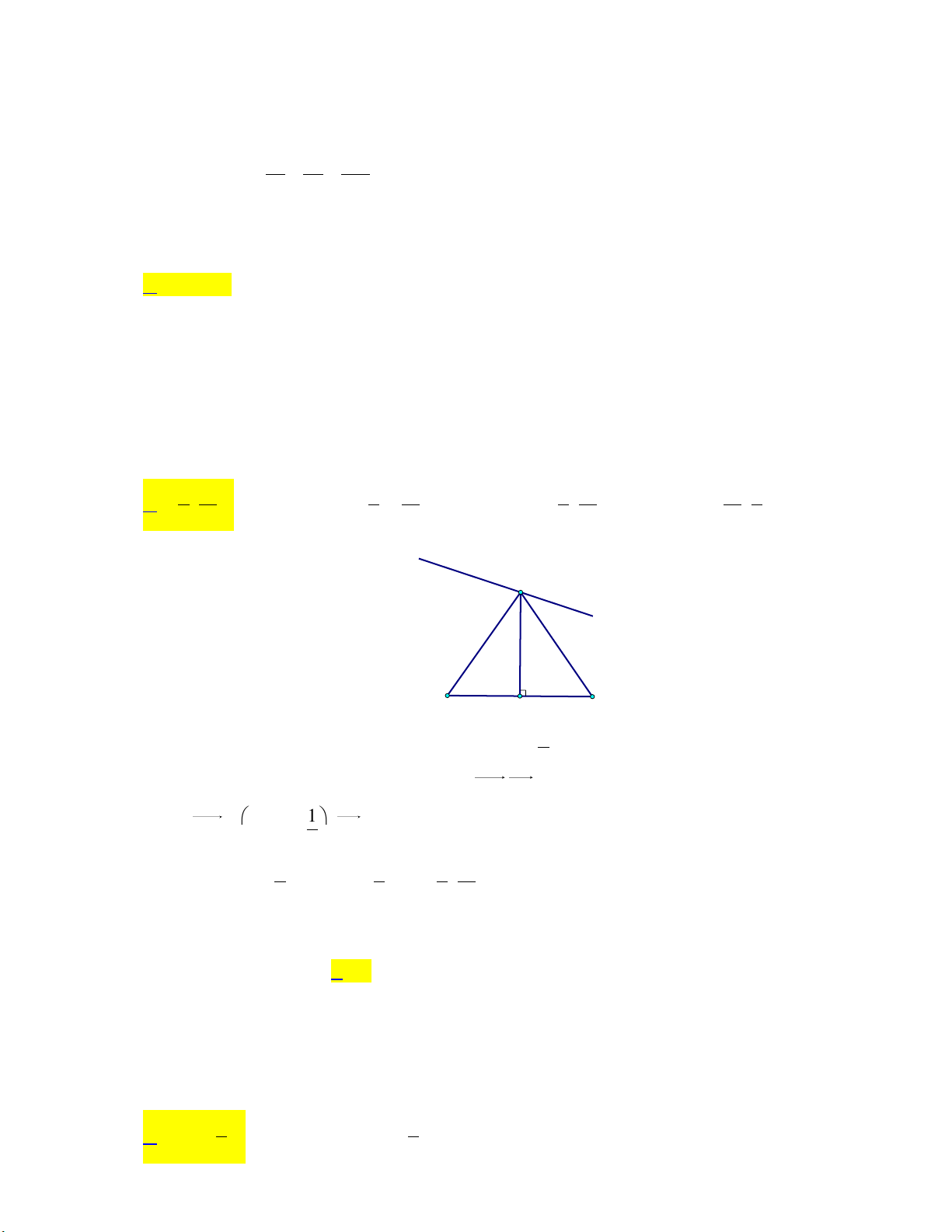
Trong mặt phẳng Oxy, cho hai đường thẳng d : x y  1  0, d : 2x y  1  0 . Viết phương 1 2
trình đường thẳng đi qua M(1; 1) và cắt d , d tương ứng tại A, B sao cho 2MA MB  0 . 1 2
____________________HẾT____________________
Huế, 08h45’ Ngày 10 tháng 02 năm 2023
Page: CLB GIÁO VIÊN TRẺ TP HUẾ ¤N TËP GI÷A K× 2 Môn: TOÁN 10
SGK 2022 – Kết nối tri thức và cuộc sống
ĐỀ ÔN TẬP SỐ 01_TrNg 2023 Líp To¸n thÇy L£ B¸ B¶O
Trưêng THPT §Æng Huy Trø
S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch, TP HuÕ Trung t©m KM 10 Hương Trà, HuÕ.
LỜI GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm) Câu 1: Cho hàm số 2
y ax bx c , với a  0 . Khẳng định nào sau đây sai? b
A. Hàm số đồng biến trên khoảng  ;    .  2a   b
B. Hàm số nghịch biến trên khoảng  ;     .  2a   b
C. Hàm số nghịch biến trên khoảng ;    .  2a
D. Đồ thị hàm số có trục đối xứng là đường thẳng   b x . 2a
Câu 2: Trong mặt phẳng Oxy, cho hai điểm A1; 3 , B2;7. Một vectơ chỉ phương của đường thẳng AB là A. u  4  ;1 . B. u  2  ;1 . C. u  3;  2 .
D. u  1; 4 . 4   3   2   1   Lời giải:
Ta có: AB  1; 4.
Các vectơ chỉ phương của đường thẳng AB có tọa độ k; 4k , k  0.
Chọn đáp án D. 2 2 x y
Câu 3: Trong mặt phẳng Oxy, đường Elip  1 có tiêu cự bằng 5 4 A. 2. B. 4. C. 9. D.1. Lời giải: Ta có 2 2 c
a b  5  4  1  2c  2 .
Chọn đáp án A.
Câu 4: Nghiệm của phương trình 2x 1  3  x là 3 2 4 3 A. x  . B. x  . C. x  . D. x  . 4 3 3 2 Lời giải: 4
Thay các nghiệm x vào phương trình thấy x  là nghiệm. 3
Chọn đáp án C.
Câu 5: Với m là tham số bất kì, biểu thức nào dưới đây là tam thức bậc hai? A. y  . m
B. y m . x C. y   2 m   2 1 x . D. 2 y mx  . m
Câu 6: Trong mặt phẳng Oxy, đường tròn C 2 2
: x y  4x  6y  12  0 có tâm là A. I 2; 3  .
B. I 2; 3 .
C. I 4;6 . D. I 4; 6  . Câu 7: Cho hàm số 2
y x  3x 1 . Điểm nào sau đây thuộc đồ thị của hàm số?
A. A0 ; 2 .
B. B 1; 5 .
C. C 1;  3 .
D. D  2  ; 4 . 2 x y
Câu 8: Trong mặt phẳng Oxy, viết phương trình chính tắc của E 2 : 
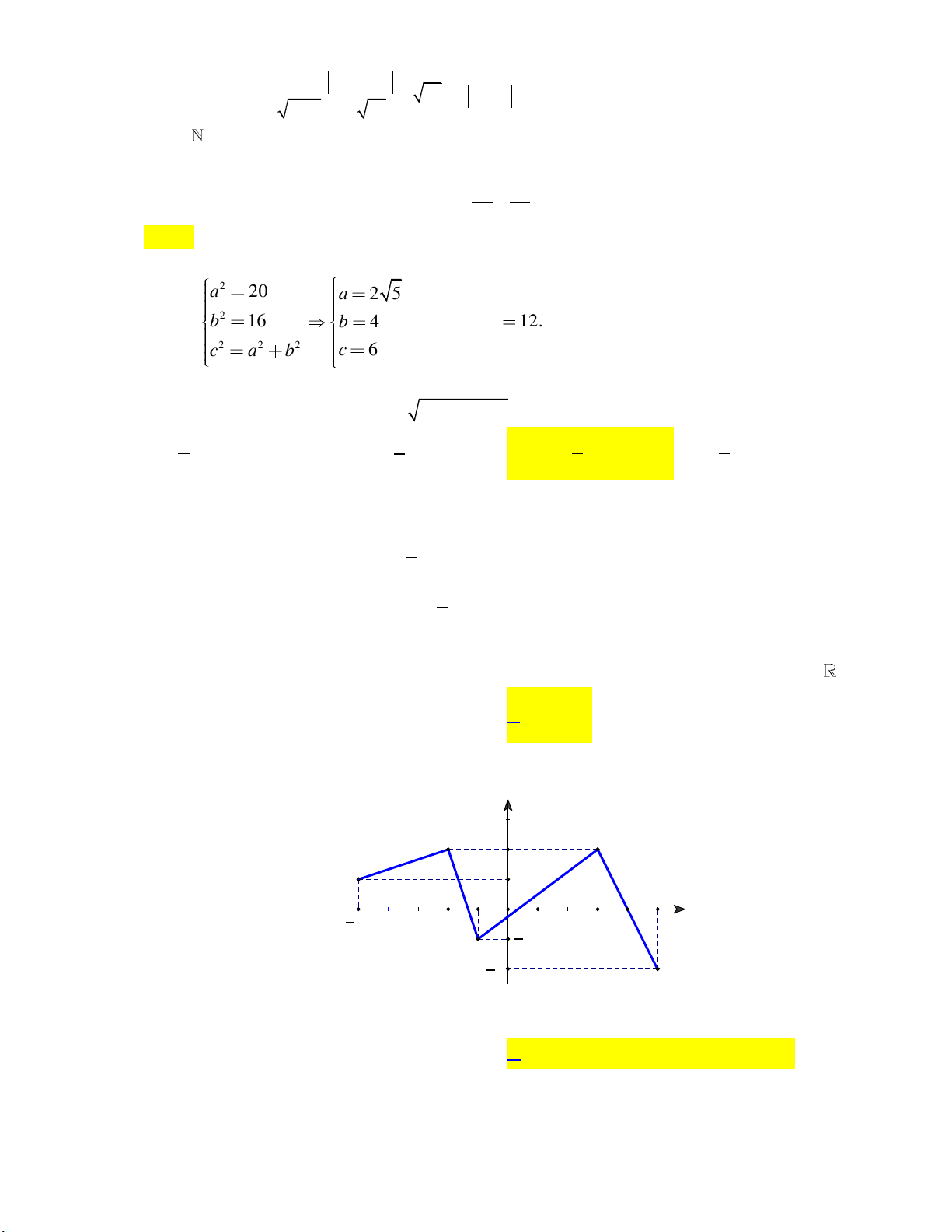
 1 có a  2b và có tiêu cự 2 2 a b bằng 4 3. 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.  1. B.  1. C.  1. D.  1. 36 9 36 24 24 6 16 4 Lời giải:
Theo giả thiết: a  2b và 2c  4 3  c  2 3
Khi đó: a b c   b2 2 2 2 2 2  b 12 2
 3b 12  0  b  2  a  4 . 2 2 x y
Vậy phương trình chính tắc của Elip là:  1. 16 4
Chọn đáp án D.
Câu 9: Trong mặt phẳng Oxy, phương trình đường tròn C  có tâm I 1;3 và đi qua M 3;  1 là 2 2 2 2 A.x  
1   y  3  8 . B.x   1
  y  3 10. 2 2 2 2
C.x  3   y   1  10 .
D.x  3   y   1  8. Lời giải:
Ta có: IM  2; 2  . Do điểm M 3; 
1 thuộc đường tròn C  nên R IM  2 2 .
Đường tròn C  có tâm I 1; 3 và bán kính R  2 2 có phương trình là
C x  2  y  2 : 1 3  8 .
Chọn đáp án A.
Câu 10: Cho hàm số bậc hai y f x có đồ thị như hình bên dưới: y 1 2 x O -1
Khẳng đinh nào dưới đây đúng?
A. f x  0, x  0;2.
B. f x  0, x  0;2.
C. f x  0, x  1;.
D. f x  0, x   0;2.  
Câu 11: Trong mặt phẳng Oxy, với những giá trị nào của m thì đường thẳng  : 4x  3y m  0 tiếp
xúc với đường tròn C  2 2
: x y  9 ? A. m  3.
B. m  3 và m  3.
C. m  45 và m  45. 
D. m  15 và m  15.  Lời giải:
Đường tròn C  có tâm I O 0;0 và bán kính là R  3 . m   m
tiếp xúc C   d I ,   R   3  15 .  5 m  15 
Chọn đáp án D.
Câu 12: Trong các hàm số sau hàm số nào là hàm số bậc hai? 3 2x  3x  5 A. 2
y  2x  3x  5 B. y  . C. 2 3
y  2x  3x  5 . D. y  3x  2 . x
Câu 13: Cho hàm số f x 2
x  2x  3. Khẳng định nào dưới đây đúng?
A. f 2  3.
B. f 3  4.
C. f 0  2.
D. f 4  5. Câu 14: Cho hàm số 2 y  3
x  4x  3 có đồ thị (P). Trục đối xứng của (P) là đường thẳng có phương trình là 2 2 4 4 A. x  .
B. x   . C. x  .
D. x   3 3 3 3 Lời giải: b  4 2 
Trục đối xứng của (P) là đường thẳng x    . 2a 6  3
Chọn đáp án B.
Câu 15: Tam thức bậc hai nào dưới đây có bảng xét dấu như hình sau? x  0 4  f x  0  0  A. 2 y x  2 . x B. 2 y x  2 . x C. 2 y x  4 . x D. 2
y  x  4 . x Lời giải:
Kiểm tra các sự kiện: a  0 và tam thức có hai nghiệm x  0, x  4.
Chọn đáp án C. x
Câu 16: Tìm tập xác định của hàm số y f x 2 1  . 4x  5 4  5  5 A. D  . B. D  \  . C. D  ;    . D. D  \   . 5  4  4 Lời giải: 5 5
Điều kiện : 4x  5  0  x D  \
4 . Tập xác định của hàm số là 4.  
Chọn đáp án D.
Câu 17: Tìm tất cả giá trị tham số m để hàm số 2
y x  m  
1 x m  2 đồng biến trên 1;  .
A. m  3 .
B. m  3 .
C. m  3 . D. m  3 . Lời giải:
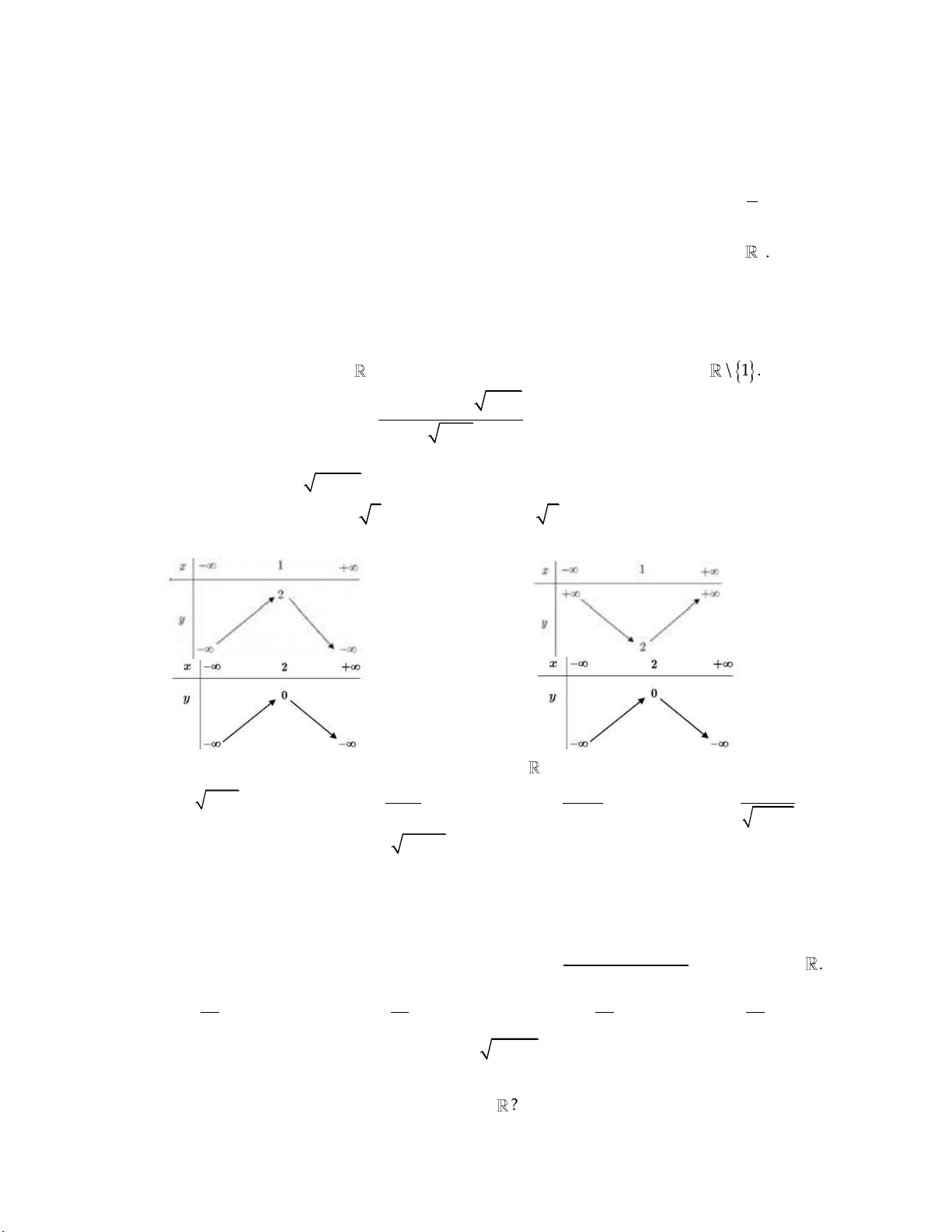
Hàm số đã cho xác định với mọi x  . Bảng biến thiên:
Dựa vào bảng biến thiên ta có hàm số đã cho đồng biến trên khoảng 1;  khi m 1  1  m  3  . 2
Chọn đáp án B.
Câu 18: Đỉnh của parabol 2
y x  4x  5 có toạ độ là A. 0; 2 . B. 1; 2 . C. 2;0 . D. 2;  1 . Lời giải: Đỉnh của parabol 2
y x  4x  5 có toạ độ là 2;  1 .
Chọn đáp án D.
Câu 19: Giá trị nhỏ nhất của hàm số 2
y x  4x  5 là A. y  0. B. y  2 . C. y  2 . D. y  1. min min min min Lời giải: b  Hàm số 2
y x  4x  5 có a  1  0 , do đó hàm số đạt giá trị nhỏ nhất tại x   2 và 2a yy 2  1. min  
Chọn đáp án D.
Câu 20: Tam thức nào dưới đây luôn dương với mọi x  ? A. 2
y x x  1. B. 2
y x  2x  1. C. 2
y  x x  1. D. 2
y  x  4 . x Lời giải: Bảng xét dấu 2
y x x  1 : x   y
Chọn đáp án A. x  1 t
Câu 21: Trong mặt phẳng Oxy, cho đường thẳng d : 
t  Điểm nào dưới đây nằm trên y  2  .  3t đường thẳng d?
A. M 1; 3.
B. N 5; 2.
C. P 2; 5.
D. Q2;0. Lời giải: 2  1 t
Thay tọa độ điểm P vào phương trình d ta được:   t  1. 5  2   3t
Chọn đáp án C.
Câu 22: Số nghiệm của phương trình 2
x  4x 1  x  3 là A. Vô số. B. 0. C. 1. D. 2. Lời giải: x  3  0 x  3 Ta có: 2
x  4x 1  x  3     2 2  (vô nghiệm).
x  4x 1  x  6x  9 x 1
Chọn đáp án B. x 1
Câu 23: Hàm số y  0;1 khi chỉ khi
x m  xác định trên   1  m 1  m 1
A. m  1. B.  . C.  .
D. 1  m  2 . m  2 m  2 Lời giải:
Điều kiện xác định: x m 1. m    m
Để hàm số đã cho xác định trên 0;  1 thì m    1 0 1 1 0;1     . m 1  1  m  2
Chọn đáp án C.
Câu 24: Trong mặt phẳng Oxy, cho đường thẳng d : x  2y  5  0. Vectơ nào dưới đây là một vectơ chỉ phương của d?
A. u  1; 2 . B. u  2  ;1 . C. u  3;  2 .
D. u  2; 3 . 4   3   2   1   Lời giải:
Các vectơ chỉ phương của d có tọa độ  2
k; k, k  0.
Chọn đáp án B.
Câu 25: Phương trình  2 x x 2 2 6
17  x x  6x có bao nhiêu nghiệm phân biệt? A. 2. B. 1. C. 3. D. 4. Lời giải:  2x x 2 2
x x x   2 x x 2 6 17 6 6
17  x  1  0
x  0(TM) 2
x  6x  0  
x  6(L) x  0 2   17    x  0     .   x  17  x  4  2  17  x  1  2 17  x   1
Vậy phương trình có 3 nghiệm phân biệt.
Chọn đáp án C.
Câu 26: Trong mặt phẳng Oxy, phương trình nào sau đây là phương trình của đường tròn? A. 2 2
x  2 y  4x  8 y 1  0 . B. 2 2
x y  4x  6 y 12  0 . C. 2 2
x y  2x  8 y  20  0 . D. 2 2
4x y 10x  6 y  2  0 . Lời giải:
Để là phương trình đường tròn thì điều kiện cần là hệ số của 2 x và 2
y phải bằng nhau nên
loại được đáp án A và D. 2 2 Ta có: 2 2
x y  2x  8y  20  0   x  
1   y  4  3  0 vô lý. 2 2 Ta có: 2 2
x y  4x  6 y 12  0   x  2   y  3  25 là phương trình đường tròn tâm I 2; 3
  , bán kính R  5.
Chọn đáp án B.
Câu 27: Trong mặt phẳng Oxy, cho hai điểm M 1; 
1 , N 2; 4. Phương trình đường thẳng MN là x  1 tx  1 3tx  1 tx t A.  . B.  . C.  . D.  . y   3t y  1   t y  3   t y  2    3t Lời giải:
Ta có: MN  1; 3.
Đường thẳng MN qua M 1;1 và nhận MN  1; 3 làm một vectơ chỉ phương. x  1 t Vậy MN :  , t  . y  1   3t
Test phương án D, thấy thỏa mãn.
Chọn đáp án D.
Câu 28: Cho f x 2
ax bx c,a  0 và 2
  b  4ac . Tìm điều kiện của  để f x cùng dấu với
hệ số a với mọi x  . A.   0 . B.   0 . C.   0 . D.   0 .
Câu 29: Trong mặt phẳng Oxy, cho hai đường thẳng d : 4x  2y  1  0 và d : 2x y  3  0. Khẳng 1 2
định nào sau đây đúng?
A. d / /d .
B. d d . 1 2 1 2
C. d , d cắt nhau và không vuông góc.
D. d d . 1 2 1 2 Lời giải: 4 2 1  Ta có:  
d và d song song. 2 1 3  1 2
Chọn đáp án A.
Câu 30: Tập nghiệm của bất phương trình 2
x  2x  3  0 là A. 1; 3.   B. ; 1
  3;. C. 1;3. D. ; 1    3;   . Lời giải:
Bảng xét dấu f x 2
x  2x  3 : x  1  3  f x  0  0 
Chọn đáp án B. x  1 2t
Câu 31: Trong mặt phẳng Oxy, cho điểm A2; 3 và đường thẳng d : 
, t  . Phương trình y  3   t
đường thẳng  qua A và vuông góc với d là
A. 2x y  7  0.
B. 2x y  0.
C. x  2y  1  0.
D. x  2y  4  0. Lời giải:
Đường thẳng d có một vectơ chỉ phương là u  2;1. d
Do  vuông góc với d nên  nhận u  2; 
1 làm một vectơ pháp tuyến. d
Vậy  : 2x  2  1y  3  0  2x y  7  0.
Chọn đáp án A.
Câu 32: Đường thẳng nào dưới đây là đường chuẩn của parabol 2 y  4x ?
A. x  1.
B. x  2.
C. x  1. D. x  2. Lời giải:
Phương trình chính tắc của parabol  P 2 : y  2 px   p
p  2  Phương trình đường chuẩn là x   1  . 2
Chọn đáp án A.
Câu 33: Tập nghiệm của phương trình x   2
2 x  4x  3  0 là
A. S  2;  3 . B. S    2 .
C. S  1;  3 .
D. S  1; 2;  3 . Lời giải:
Điều kiện: x  2  0  x  2 (*). x  2 x  2  0 
Với điều kiện (*), phương trình đã cho tương đương với   x  1 . 2 
x  4x  3  0 x  3 
So với điều kiện (*) chỉ có x  2 , x  3 thỏa mãn.
Vậy tập nghiệm của phương trình là S  2;  3 .
Chọn đáp án A.
Câu 34: Trong mặt phẳng Oxy, cho điểm A1; 2 và đường thẳng  : 2x y  1  0. Tính khoảng cách
từ điểm A đến đường thẳng . 5 A. 5. B. 5. C. 2 5 D. . 5 Lời giải:  
Ta có: dA  2.1 2 1 ;   5. 4  1
Chọn đáp án A. 2 x y
Câu 35: Trong mặt phẳng Oxy, hypebol H 2 : 
 1 có hai tiêu điểm là 16 9
A. F  5;0 , F 5;0 .
B. F  2;0 , F 2;0 . 2   1  2   1 
C. F  3;0 , F 3;0 .
D. F  4;0 , F 4;0 . 2   1  2   1  Lời giải:  2 a  16 a   4  Ta có :  2 b  9  b  3.   2 c  2 a  2 b   25 c   5
Vậy các tiêu điểm của H là F  5;0 , F 5;0 . 2   1 
II. PHẦN TỰ LUẬN (03 câu – 3,0 điểm)
Câu 1: (1,0 điểm). 2x  1
a) Tìm tập xác định của hàm số y  . 2 x  4
b) Tìm a,b để parabol P 2
: y ax bx  1 đi qua hai điểm A1; 4 và B2;9. Lời giải: x  2 a) Hàm số xác định 2
x  4  0   . x  2  
Vậy tập xác định của hàm số là D   \ 2  ;  2 .
a b  1  4 a b  3 a  1
b) Do P đi qua hai điểm A1; 4 và B2;9 nên ta có:      .
4a  2b  1  9 4a  2b  8 b     2 Vậy P 2
: y x  2x  1.
Câu 2: (1,0 điểm). a) Giải phương trình 2
x  5x  1  x  1.
b) Tìm m để phương trình 2 2
x  2x  2m  3m  1  0 có hai nghiệm dương phân biệt. Lời giải: x  1 x 1  0 x  1  a) Ta có: 2
x  5x  1  x  1    
 x  0  x  6. 2 2
x  5x  1  x  1
x  6x  0 x   6
Vậy phương trình có tập nghiệm là S    6 . 2   0 1
  (2m  3m  1)  0  
b) Phương trình có hai nghiệm dương phân biệt khi S
  0  2  0, m     2 P  0
2m  3m  1   0   3  1     2 0 m 0  2   3  0 m m m    2 2       . 2
2m  3m  1  0 1   3 m   m  1 1  m   2  2
Câu 3: (1,0 điểm).
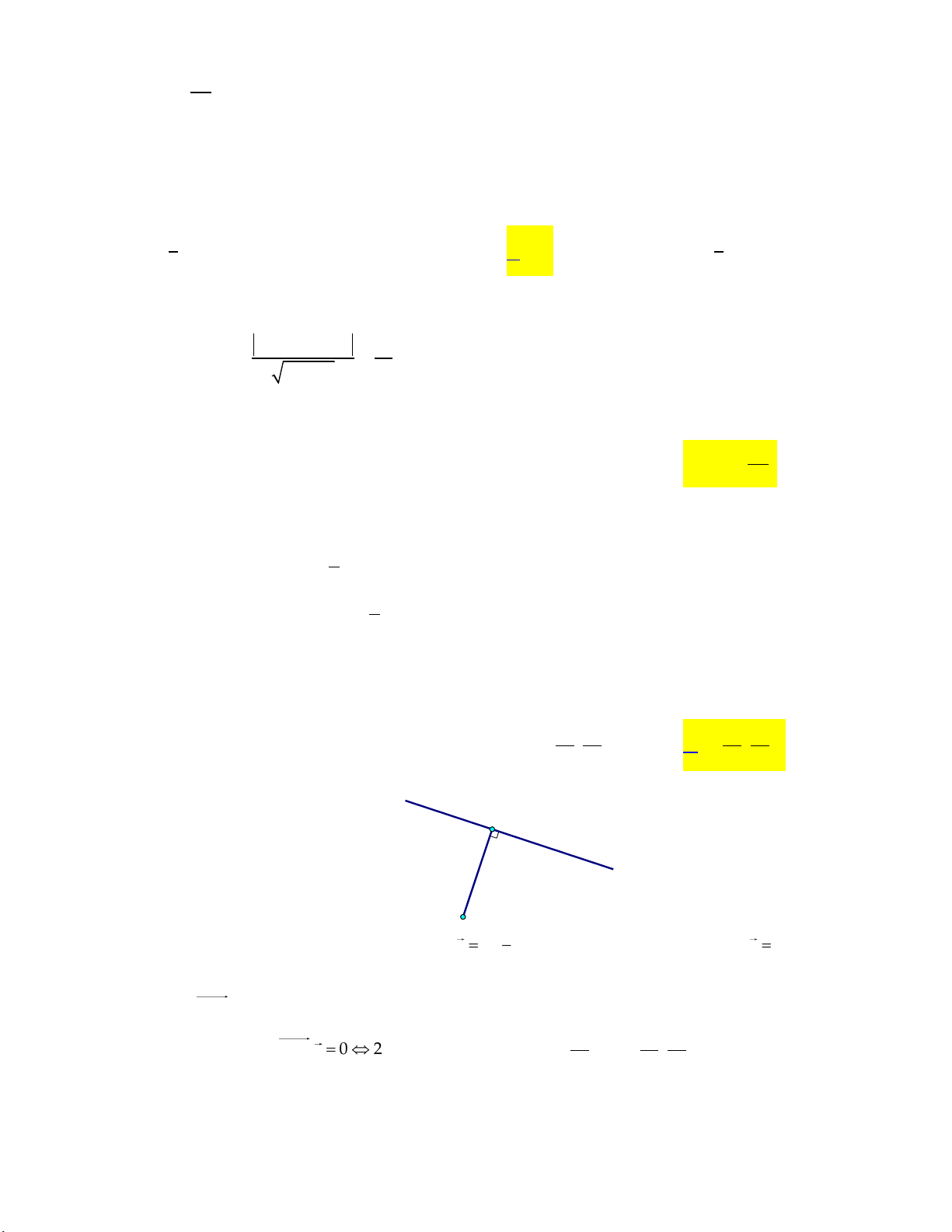
Trong mặt phẳng Oxy, cho hai đường thẳng d : x y  1  0, d : 2x y  1  0 . Viết phương 1 2
trình đường thẳng đi qua M(1; 1) và cắt d , d tương ứng tại A, B sao cho 2MA MB  0 . 1 2 Lời giải:
Gọi Aa; a  1d , B b; 2b  1 d . Ta có: MA  a  1; a , MB  b  1; 2b 1   2 2a   1  b   1  0
a  1 A1; 2  
Theo giả thiết: 2MA MB  0     2
 a  2b  0 b  1
Lúc đó, đường thẳng d cần tìm đi qua A1; 2 và có 1 vectơ chỉ phương AM  0;1 nên x  1
có phương trình là d :  t  . x  2    t
____________________HẾT____________________
Huế, 08h45’ Ngày 10 tháng 02 năm 2023
Page: CLB GIÁO VIÊN TRẺ TP HUẾ ¤N TËP GI÷A K× 2 Môn: TOÁN 10
SGK 2022 – Kết nối tri thức và cuộc sống
ĐỀ ÔN TẬP SỐ 02_TrNg 2023 Líp To¸n thÇy L£ B¸ B¶O
Trưêng THPT §Æng Huy Trø
S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch, TP HuÕ Trung t©m KM 10 Hương Trà, HuÕ. NỘI DUNG ĐỀ BÀI
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm)
Câu 1: Trong mặt phẳng 2 2
Oxy, xác định tâm và bán kính của đường tròn C  :  x   1
  y  2  9.
A. Tâm I 1; 2, bán kính R  3 .
B. Tâm I 1; 2, bán kính R  9 .
C. Tâm I 1; 2, bán kính R  3 .
D. Tâm I 1; 2, bán kính R  9 . 2x 1
Câu 2: Điểm nào dưới đây không thuộc đồ thị hàm số y  ? x 1
A. P 0;   1 .
B. N 2;5.
C. Q 4;3. D. M  2  ; 3  .
Câu 3: Trong mặt phẳng Oxy, phương trình nào sau đây là phương trình của một đường tròn? A. 2 2
x y  4xy  2x  8y  3  0 . B. 2 2
x  2y  4x  5y  1  0 . C. 2 2
x y  14x  2y  2018  0 . D. 2 2
x y  4x  5y  2  0 . x  1 2t
Câu 4: Trong mặt phẳng Oxy, cho đường thẳng d : 
,t  . Vectơ nào dưới đây là một y  2   3t
vectơ chỉ phương của d?
A. u  1; 2 . B. u  2  ;1 . C. u  3;  2 .
D. u  2; 3 . 4   3   2   1   2 2 x y
Câu 5: Trong mặt phẳng Oxy, cho elip  E  : 
1 có hai tiêu điểm F , F . Gọi M là điểm 1 2 9 4
thuộc  E , tính MF MF . 1 2 A. 5. B. 6. C. 3. D. 2.
Câu 6: Cho hàm số bậc hai có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A.  2;    .
B.  ; 2 . C. 2;   1 . D.  1;    . 2 2 x y
Câu 7: Cặp điểm nào là các tiêu điểm của hypebol  1? 9 5
A. 4; 0 và 4; 0 .
B.  14; 0 và  14; 0 .
C. 2; 0 và 2; 0 .
D. 0; 14  và 0;  14 .
Câu 8: Trong mặt phẳng Oxy, đường tròn nào sau đây tiếp xúc với trục Ox? A. 2 2
x y 10x  0 . B. 2 2
x y  5  0 . C. 2 2
x y 10x  2 y 1  0 . D. 2 2
x y  6x  5y  9  0 . 3
Câu 9: Đường thẳng nào dưới đây là đường chuẩn của parabol 2 y x ? 2 3 3 3 3
A. x   .
B. x  .
C. y   . D. x   . 4 4 8 8
Câu 10: Trong mặt phẳng Oxy, cho hai đường thẳng d : x y  3  0 và d : 2x y  3  0. Khẳng định 1 2 nào sau đây đúng?
A. d / /d .
B. d d . 1 2 1 2
C. d , d cắt nhau và không vuông góc.
D. d d . 1 2 1 2
Câu 11: Tìm tất cả các giá trị của tham số m để biểu thức f x  m   2
2 x  5x  9 là tam thức bậc hai. A. m  .
B. m  2 .
C. m  2 . D. m  0 .
Câu 12: Trong mặt phẳng Oxy, cho hai điểm A1;0 , B3;6. Phương trình đường thẳng trung trực
của đoạn thẳng AB là
A. x  3y  11  0
B. x  3y  11  0.
C. 3x y  9  0.
D. 3x y  7  0.
Câu 13: Tam thức bậc hai nào dưới đây có bảng xét dấu như hình vẽ? x  0 2  f x  0  0  A. 2 y x  2 . x B. 2
y  x  2 . x C. 2 y x  4 . x D. 2 y x  4 . x x  1 2t
Câu 14: Trong mặt phẳng Oxy, cho đường thẳng d : 
,t  . Vectơ nào dưới đây là một y  2   3t
vectơ pháp tuyến của d?
A. u  1; 2 . B. u  2  ;1 . C. u  3;  2 .
D. u  2; 3 . 4   3   2   1  
Câu 15: Trong mặt phẳng Oxy, viết phương trình chính tắc của Elip có tiêu cự bằng 6 và đi qua điểm A0;5 . 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.  1. B.  1. C.  1. D.  1. 34 9 34 25 25 9 25 16
Câu 16: Trong mặt phẳng Oxy, cho hai điểm A1; 
1 và B 7;5 . Phương trình đường tròn đường kính AB là A. 2 2
x y  8x  6 y 12  0 . B. 2 2
x y  8x  6 y 12  0 . C. 2 2
x y  8x  6 y 12  0 . D. 2 2
x y  8x  6 y 12  0 .
Câu 17: Cho tam thức f x 2
x  3x  2. Khẳng định nào dưới đây đúng?
A. f x  0, x  1;2.
B. f x  0, x  1;2.
C. f x  0, x
 ;1  2;.
D. f x  0, x   1  ;2.   x t
Câu 18: Trong mặt phẳng Oxy, cho đường thẳng d :
, t  . Điểm nào dưới đây không y  1   2t
nằm trên đường thẳng d?
A. M 0;1.
B. N 1; 3.
C. P 2; 5.
D. Q1;1.
Câu 19: Tổng tất cả các nghiệm của phương trình và 2
x  3x  2  x  2 là A. 3 . B. 4 . C. 1  . D. 3  .
Câu 20: Trong mặt phẳng Oxy, tìm giá trị tham số n để khoảng cách từ điểm I 2; 3 đến đường
thẳng  : x ny  1  2n  0 bằng 1.
A. n  0.
B. n  1.
C. n  1.
D. n  2.
Câu 21: Tìm m để parabol 2
(P) : y mx  2x  3 có trục đối xứng là đường thẳng x  2 . 1 A. m  2 .
B. m  1.
C. m  1. D. m  . 2 x  1 2t
Câu 22: Trong mặt phẳng Oxy, cho điểm A2; 3 và đường thẳng d : 
, t  . Phương trình y  3   t
đường thẳng  qua A và song song với d là
A. 2x y  7  0.
B. 2x y  0.
C. x  2y  1  0.
D. x  2y  4  0.
Câu 23: Tập nghiệm của bất phương trình 2
x  2x  1  0 là A. .  B. C.   1 . D.  \  1 .
 2x 3x2 x3
Câu 24: Số nghiệm của phương trình  0 là x 1 A. 1. B. 2 . C. 3 . D. 0 .
Câu 25: Cho hàm số f x  3  2x . Giá trị của hàm số tại điểm x  2 bằng A. 1. B. 3 . C. 7 . D. 7 .
Câu 26: Bảng biến thiên của hàm số 2
y  x  2x 1 là A. . B. . C. . D. .
Câu 27: Trong các hàm số sau, hàm số nào xác định trên ? 1 1 1
A. y x  1 . B. y  . C. y  . D. y  . x  2 3 x  1 2 x  1
Câu 28: Một nghiệm của phương trình 2x 1  x là A. x  2 . B. x  5 . C. x  1 . D. x  0 .
Câu 29: Hàm số nào có đồ thị là đường parabol có đỉnh là I  1  ;3? A. 2 y  2
x  4x  3. B. 2
y  2x  2x 1. C. 2
y  2x  4x  5 . D. 2
y  2x x  2 . x
Câu 30: Tìm tất các giá trị thực của tham số m để hàm số y  2
2x  3x  2m  xác định trên . 1 17 17 17 17 A. m  . B. m  . C. 0  m  . D. m  . 16 16 16 16
Câu 31: Tổng các nghiệm của phương trình  x   2 3
2x  6  x  9 bằng A. 2 . B. 3 . C. 1  . D. 7 .
Câu 32: Tam thức nào dưới đây luôn âm với mọi x  ? A. 2
y x x  1. B. 2
y  x x  1. C. 2
y  x x  1. D. 2
y  x  4 . x
Câu 33: Cho tam thức bậc hai f x 2
ax bx c,a;b;c ,a  0 với 2
  b  4ac. Mệnh đề nào dưới đây đúng? a  a
A. f x 0  0, x     .
B. f x 0       0, x  .  0    0 a  a
C. f x 0  0, x     .
D. f x 0       0, x  .  0    0
Câu 34: Gọi M là giá trị lớn nhất, m là giá trị nhỏ nhất của hàm số 2
y  x  4x  2 trên đoạn 0;  3 .
Tính giá trị biểu thức M m . A. 1. B. 4  . C. 0 . D. 1  .
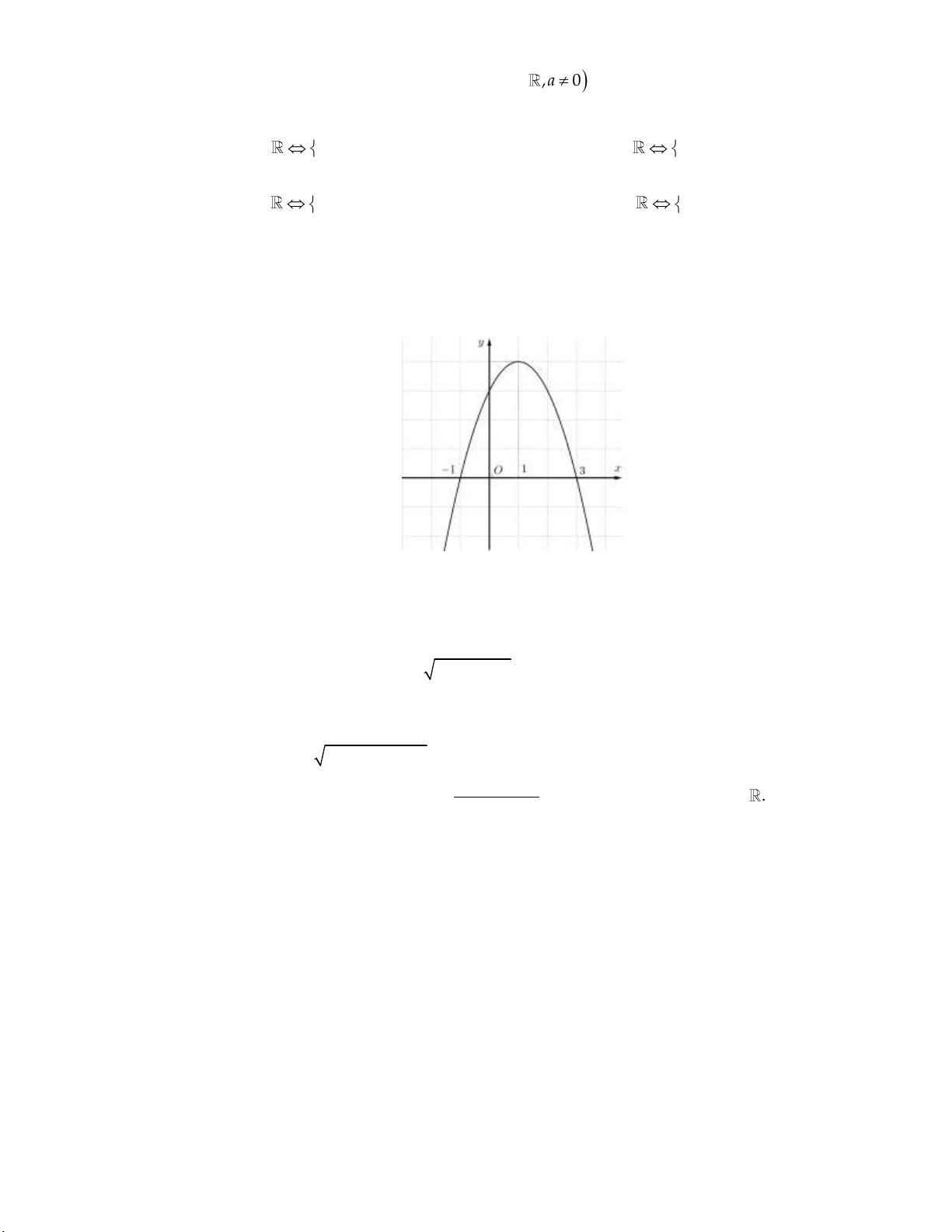
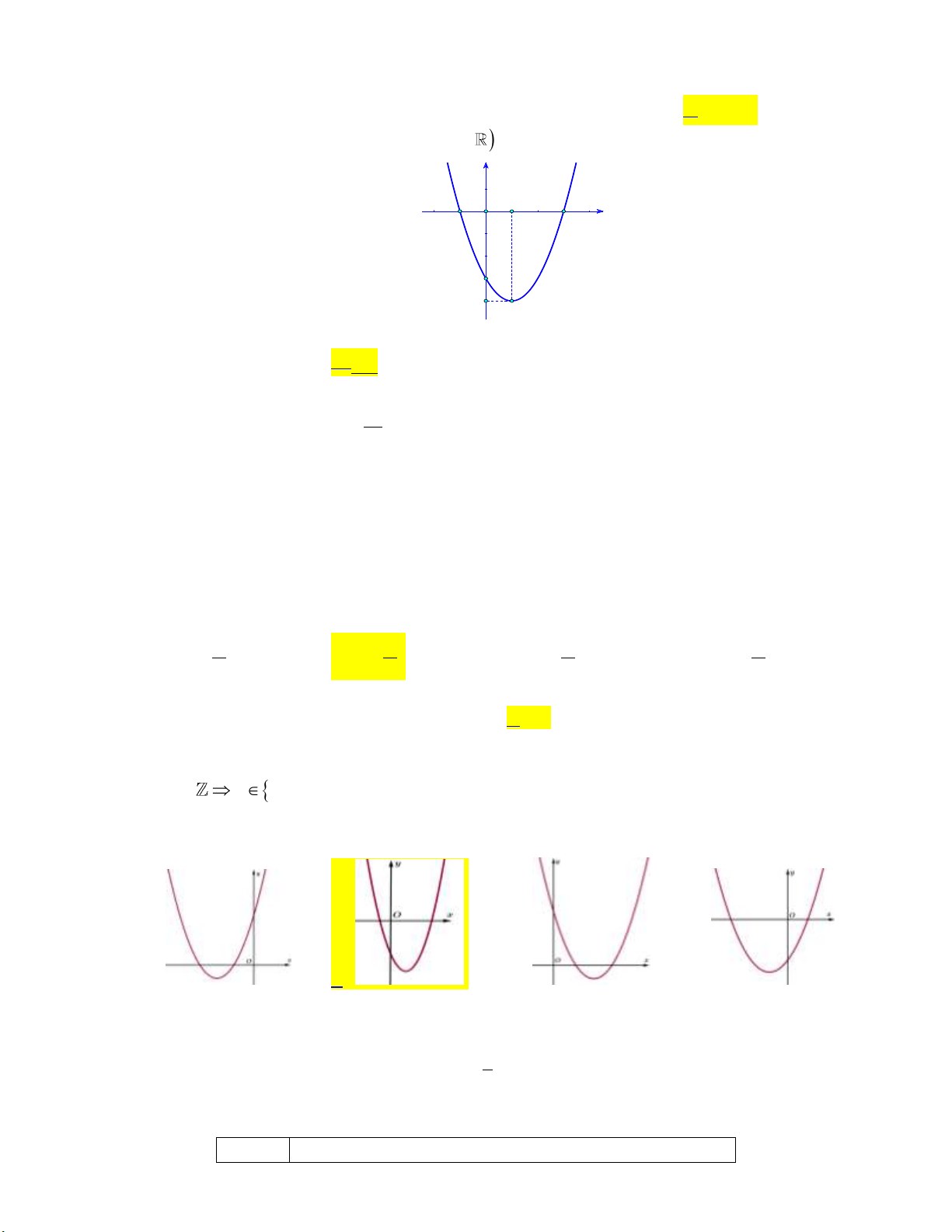
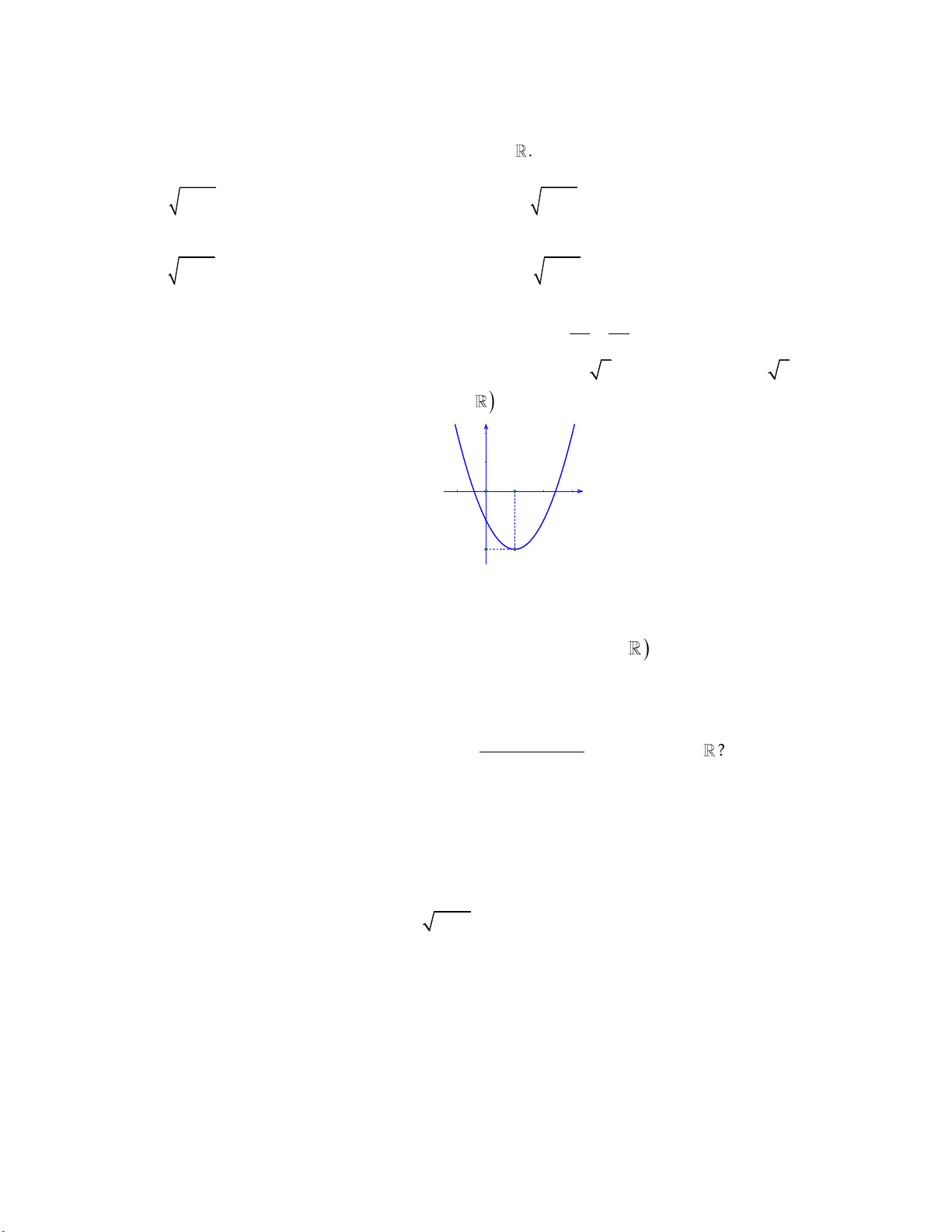
Câu 35: Đồ thị hàm số: 2
y ax bx c như hình vẽ bên dưới:
Trong các hệ số a, b, c có bao nhiêu giá trị dương? A. 1. B. 0 . C. 2 . D. 3 .
II. PHẦN TỰ LUẬN (03 câu – 3,0 điểm)
Câu 1: (1,0 điểm).
a) Tìm tập xác định của hàm số 2
y x  5x  4.
b) Tìm a,b để parabol P 2
: y ax bx  1 có đỉnh là I 1; 2.
Câu 2: (1,0 điểm). a) Giải phương trình 2
3x  17x  23  x  3. 2
x  5x m
b) Tìm m để các bất phương trình 1  
 7 luôn đúng với mọi x . 2 2x  3x  2
Câu 3: (1,0 điểm).
Trong mặt phẳng Oxy, viết phương trình đường thẳng d song song với  : 4x  3y  12  0 và
d cách  một khoảng bằng 5.
____________________HẾT____________________
Huế, 08h45’ Ngày 10 tháng 02 năm 2023
Page: CLB GIÁO VIÊN TRẺ TP HUẾ ¤N TËP GI÷A K× 2 Môn: TOÁN 10
SGK 2022 – Kết nối tri thức và cuộc sống
ĐỀ ÔN TẬP SỐ 02_TrNg 2023 Líp To¸n thÇy L£ B¸ B¶O
Trưêng THPT §Æng Huy Trø
S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch, TP HuÕ Trung t©m KM 10 Hương Trà, HuÕ.
LỜI GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm)
Câu 1: Trong mặt phẳng 2 2
Oxy, xác định tâm và bán kính của đường tròn C  :  x   1
  y  2  9.
A. Tâm I 1; 2, bán kính R  3 .
B. Tâm I 1; 2, bán kính R  9 .
C. Tâm I 1; 2, bán kính R  3 .
D. Tâm I 1; 2, bán kính R  9 . 2x 1
Câu 2: Điểm nào dưới đây không thuộc đồ thị hàm số y  ? x 1
A. P 0;   1 .
B. N 2;5.
C. Q 4;3. D. M  2  ; 3  . Lời giải: 2. 2  1
Với x  2 ta có y  2      1 M 2  ; 3
 không thuộc đồ thị hàm số 2   . Vậy điểm   1 2x 1 y  . x 1
Chọn đáp án D.
Câu 3: Trong mặt phẳng Oxy, phương trình nào sau đây là phương trình của một đường tròn? A. 2 2
x y  4xy  2x  8y  3  0 . B. 2 2
x  2y  4x  5y  1  0 . C. 2 2
x y  14x  2y  2018  0 . D. 2 2
x y  4x  5y  2  0 . x  1 2t
Câu 4: Trong mặt phẳng Oxy, cho đường thẳng d : 
,t  . Vectơ nào dưới đây là một y  2   3t
vectơ chỉ phương của d?
A. u  1; 2 . B. u  2  ;1 . C. u  3;  2 .
D. u  2; 3 . 4   3   2   1   Lời giải:
Các vectơ chỉ phương của d có tọa độ 2k; 3k, k  0.
Chọn đáp án D. 2 2 x y
Câu 5: Trong mặt phẳng Oxy, cho elip  E  : 
1 có hai tiêu điểm F , F . Gọi M là điểm 1 2 9 4
thuộc  E , tính MF MF . 1 2 A. 5. B. 6. C. 3. D. 2. Lời giải: 2 2 x y
Phương trình của  E  có dạng  1 ( 2 2 2
a b c ). Suy ra 2
a  9  a  3 . 2 2 a b
Do M thuộc  E  nên MF MF  2a  6 . 1 2
Chọn đáp án B.
Câu 6: Cho hàm số bậc hai có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A.  2;    .
B.  ; 2 . C. 2;   1 . D.  1;    . Lời giải:
Dựa vào bảng biến thiên ta có hàm số đồng biến trên  1;    .
Chọn đáp án D. 2 2 x y
Câu 7: Cặp điểm nào là các tiêu điểm của hypebol  1? 9 5
A. 4; 0 và 4; 0 .
B.  14; 0 và  14; 0 .
C. 2; 0 và 2; 0 .
D. 0; 14  và 0;  14 . Lời giải: Ta có 2 2 c
a b  9  5  14 . Vậy cặp điểm  14; 0,  14; 0 là các tiêu điểm của hypebol.
Chọn đáp án B.
Câu 8: Trong mặt phẳng Oxy, đường tròn nào sau đây tiếp xúc với trục Ox? A. 2 2
x y 10x  0 . B. 2 2
x y  5  0 . C. 2 2
x y 10x  2 y 1  0 . D. 2 2
x y  6x  5y  9  0 . Lời giải: 2 2  5  25
Xét phương trình đường tròn C  : 2 2
x y  6x  5y  9  0   x  3  y   .    2  4   5  5 C  có tâm I 3;   
 và bán kính R  .  2  2
Ta có: d I Ox 5 ;
  R . Vậy C tiếp xúc với trục Ox. 2
Chọn đáp án D. 3
Câu 9: Đường thẳng nào dưới đây là đường chuẩn của parabol 2 y x ? 2 3 3 3 3
A. x   .
B. x  .
C. y   . D. x   . 4 4 8 8 Lời giải:
Phương trình chính tắc của parabol  P 2 : y  2 px 3   p 3 p
 Phương trình đường chuẩn là x    . 4 2 8
Chọn đáp án D.
Câu 10: Trong mặt phẳng Oxy, cho hai đường thẳng d : x y  3  0 và d : 2x y  3  0. Khẳng định 1 2 nào sau đây đúng?
A. d / /d .
B. d d . 1 2 1 2
C. d , d cắt nhau và không vuông góc.
D. d d . 1 2 1 2 Lời giải:
Đường thẳng d có một vectơ pháp tuyến là n  1;1 . 1   1
Đường thẳng d có một vectơ pháp tuyến là n  2;1 . 2   2 n .n   0 1 2 Ta có:   1
d , d cắt nhau và không vuông góc.  1  1 2 2 1
Chọn đáp án C.
Câu 11: Tìm tất cả các giá trị của tham số m để biểu thức f x  m   2
2 x  5x  9 là tam thức bậc hai. A. m  .
B. m  2 .
C. m  2 . D. m  0 . Lời giải:
Biểu thức f x  m   2
2 x  5x  9 là tam thức bậc hai khi: m  2  0 . Suy ra m  2 .
Chọn đáp án C.
Câu 12: Trong mặt phẳng Oxy, cho hai điểm A1;0 , B3;6. Phương trình đường thẳng trung trực
của đoạn thẳng AB là
A. x  3y  11  0
B. x  3y  11  0.
C. 3x y  9  0.
D. 3x y  7  0. Lời giải:
Ta có: AB  2;6.
Gọi I là trung điểm AB I 2; 3.
Đường thẳng  qua I 2; 3 và nhận AB  2;6 làm một vec tơ pháp tuyến.
Vậy  : 2x  2  6y  3  0  2x  6y  22  0  x  3y  11  0.
Chọn đáp án B.
Câu 13: Tam thức bậc hai nào dưới đây có bảng xét dấu như hình vẽ? x  0 2  f x  0  0  A. 2 y x  2 . x B. 2
y  x  2 . x C. 2 y x  4 . x D. 2 y x  4 . x Lời giải:
Kiểm tra các sự kiện: a  0 và tam thức có hai nghiệm x  0, x  2.
Chọn đáp án B. x  1 2t
Câu 14: Trong mặt phẳng Oxy, cho đường thẳng d : 
,t  . Vectơ nào dưới đây là một y  2   3t
vectơ pháp tuyến của d?
A. u  1; 2 . B. u  2  ;1 . C. u  3;  2 .
D. u  2; 3 . 4   3   2   1   Lời giải:
Các vectơ pháp tuyến của d có tọa độ  3
k;2k, k  0.
Chọn đáp án C.
Câu 15: Trong mặt phẳng Oxy, viết phương trình chính tắc của Elip có tiêu cự bằng 6 và đi qua điểm A0;5 . 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.  1. B.  1. C.  1. D.  1. 34 9 34 25 25 9 25 16 Lời giải: 2 2 x y
Phương trình chính tắc của elip có dạng 
1 a b  0 . 2 2   a b 2 2 0 5
Theo giả thiết: 2c  6  c  3 . Vì A0;5  E  nên  1 b  5 . 2 2 a b Khi đó: 2 2 2 2 2
a b c  5  3  34 . 2 2 x y
Vậy phương trình chính tắc của Elip là:  1. 34 25
Chọn đáp án B.
Câu 16: Trong mặt phẳng Oxy, cho hai điểm A1; 
1 và B 7;5 . Phương trình đường tròn đường kính AB là A. 2 2
x y  8x  6 y 12  0 . B. 2 2
x y  8x  6 y 12  0 . C. 2 2
x y  8x  6 y 12  0 . D. 2 2
x y  8x  6 y 12  0 . Lời giải:
Gọi I là trung điểm của AB suy ra I 4;3  AI  13.
Đường tròn đường kính AB nhận I 4;3 làm tâm và bán kính R AI  13 có phương trình:
x  2  y  2 2 2 4 3
13  x y 8x  6y 12  0.
Chọn đáp án C.
Câu 17: Cho tam thức f x 2
x  3x  2. Khẳng định nào dưới đây đúng?
A. f x  0, x  1;2.
B. f x  0, x  1;2.
C. f x  0, x
 ;1  2;.
D. f x  0, x   1  ;2.   Lời giải:
Bảng xét dấu: x  1 2  f x  0  0 
Chọn đáp án B. x t
Câu 18: Trong mặt phẳng Oxy, cho đường thẳng d :
, t  . Điểm nào dưới đây không y  1   2t
nằm trên đường thẳng d?
A. M 0;1.
B. N 1; 3.
C. P 2; 5.
D. Q1;1. Lời giải: 1   t
Thay tọa độ điểm Q vào phương trình d :  (vô nghiệm). 1  1   2t
Chọn đáp án D.
Câu 19: Tổng tất cả các nghiệm của phương trình và 2
x  3x  2  x  2 là A. 3 . B. 4 . C. 1  . D. 3  . Lời giải: x  2   x  2   x  2   Ta có 2
x  3x  2  x  2      x  0 . 2 2
x  3x  2  x  2
x  4x  0  x  4
Vậy tập nghiệm của phương trình S  0; 
4 nên tổng các nghiệm là 4 .
Chọn đáp án B.
Câu 20: Trong mặt phẳng Oxy, tìm giá trị tham số n để khoảng cách từ điểm I 2; 3 đến đường
thẳng  : x ny  1  2n  0 bằng 1.
A. n  0.
B. n  1.
C. n  1.
D. n  2. Lời giải:
2  3n  1  2n
Ta có: dI; 2 
 1  1 n  1 n n  0. 2 1  n
Chọn đáp án A.
Câu 21: Tìm m để parabol 2
(P) : y mx  2x  3 có trục đối xứng là đường thẳng x  2 . 1 A. m  2 .
B. m  1.
C. m  1. D. m  . 2 Lời giải: 2  1
Vì  P là parabol nên m  0 . Khi đó parabol  P có trục đối xứng x    x  2m m 1 1
Theo bài ra trục đối xứng x  2 nên  2  m  . m 2
Chọn đáp án D.x  1 2t
Câu 22: Trong mặt phẳng Oxy, cho điểm A2; 3 và đường thẳng d : 
, t  . Phương trình y  3   t
đường thẳng  qua A và song song với d là
A. 2x y  7  0.
B. 2x y  0.
C. x  2y  1  0.
D. x  2y  4  0. Lời giải:
Đường thẳng d có một vectơ chỉ phương là u  2;1 nên d có một vectơ pháp tuyến là dn  1; 2  . d
Do  song song với d nên  nhận n  1; 2
 làm một vectơ pháp tuyến. d
Vậy  : 1x  2  2y  3  0  x  2y  4  0.
Chọn đáp án D.
Câu 23: Tập nghiệm của bất phương trình 2
x  2x  1  0 là A. .  B. C.   1 . D.  \  1 . Lời giải:
Bảng xét dấu f x 2
x  2x  1: x  1  y  0 
Chọn đáp án C.
 2x 3x2 x3
Câu 24: Số nghiệm của phương trình  0 là x 1 A. 1. B. 2 . C. 3 . D. 0 . Lời giải: x  3 Điều kiện:   x  3. x 1 x 1 2
x  3x  2  0  Khi đó pt    x  2  .  x 3  0 x  3 
Kết hợp với điều kiện suy ra phương trình có nghiệm duy nhất x  3 .
Chọn đáp án A.
Câu 25: Cho hàm số f x  3  2x . Giá trị của hàm số tại điểm x  2 bằng A. 1. B. 3 . C. 7 . D. 7 .
Câu 26: Bảng biến thiên của hàm số 2
y  x  2x 1 là A. . B. . C. . D. . Lời giải: Ta có: 2
y  x  2x 1 nên đỉnh của parabol là I 1; 2 .
Do a  1  0 nên parabol có bề lõm xuống dưới.
Chọn đáp án A.
Câu 27: Trong các hàm số sau, hàm số nào xác định trên ? 1 1 1
A. y x  1 . B. y  . C. y  . D. y  . x  2 3 x  1 2 x  1
Câu 28: Một nghiệm của phương trình 2x 1  x là A. x  2 . B. x  5 . C. x  1 . D. x  0 .
Câu 29: Hàm số nào có đồ thị là đường parabol có đỉnh là I  1  ;3? A. 2 y  2
x  4x  3. B. 2
y  2x  2x 1. C. 2
y  2x  4x  5 . D. 2
y  2x x  2 . x
Câu 30: Tìm tất các giá trị thực của tham số m để hàm số y  2
2x  3x  2m  xác định trên . 1 17 17 17 17 A. m  . B. m  . C. 0  m  . D. m  . 16 16 16 16 Lời giải: x
Điều kiện xác định của hàm số y  là: 2
2x  3x  2m 1  0 . 2
2x  3x  2m 1 Hàm số xác định trên 2 2
 2x  3x  2m 1  0, x   2x  3x  2m 1  0 vô nghiệm     2   m  17 3 4.2. 2 1  0  m  . 16
Chọn đáp án D.
Câu 31: Tổng các nghiệm của phương trình  x   2 3
2x  6  x  9 bằng A. 2 . B. 3 . C. 1  . D. 7 . Lời giải:
Điều kiện: 2x  6  0  x  3. x  3
Ta có x  3 2
2x  6  x  9   x  3 2x  6  x  3  0  .
 2x  6  x  3     x 3 x  3  0  x  3  x  1 
Phương trình 2x  6  x  3     x  1    2x  6   x 32 2
x  4x  3  0  x  3  x  3 
Vậy phương trình đã cho có ba nghiệm là x  1
 , x  3, x  3 .
Tổng các nghiệm của phương trình là 1 3  3  1 .
Chọn đáp án C.
Câu 32: Tam thức nào dưới đây luôn âm với mọi x  ? A. 2
y x x  1. B. 2
y  x x  1. C. 2
y  x x  1. D. 2
y  x  4 . x Lời giải: Bảng xét dấu 2
y  x x  1 : x   y
Chọn đáp án C.
Câu 33: Cho tam thức bậc hai f x 2
ax bx c,a;b;c ,a  0 với 2
  b  4ac. Mệnh đề nào dưới đây đúng? a  a
A. f x 0  0, x     .
B. f x 0       0, x  .  0    0 a  a
C. f x 0  0, x     .
D. f x 0       0, x  .  0    0
Câu 34: Gọi M là giá trị lớn nhất, m là giá trị nhỏ nhất của hàm số 2
y  x  4x  2 trên đoạn 0;  3 .
Tính giá trị biểu thức M m . A. 1. B. 4  . C. 0 . D. 1  . Lời giải:
Ta có bảng biến thiên của hàm số 2
y  x  4x  2 trên đoạn 0;  3 :
Từ bảng biến thiên ta có M  2; m  2 nên M m  0 .
Chọn đáp án C.
Câu 35: Đồ thị hàm số: 2
y ax bx c như hình vẽ bên dưới:
Trong các hệ số a, b, c có bao nhiêu giá trị dương? A. 1. B. 0 . C. 2 . D. 3 . Lời giải: b
Từ đồ thị hàm số ta có a  0 , hoành độ đỉnh của đồ thị hàm số là a0 x  
 0 b  0 . 2a
Giao điểm với trục tung có tung độ bằng c  0 .
Vậy các hệ số có giá trị dương là b, c .
Chọn đáp án C.
II. PHẦN TỰ LUẬN (03 câu – 3,0 điểm)
Câu 1: (1,0 điểm).
a) Tìm tập xác định của hàm số 2
y x  5x  4.
b) Tìm a,b để parabol P 2
: y ax bx  1 có đỉnh là I 1; 2. Lời giải:
a) Hàm số xác định 2
x  5x  4  0  x;4  1;   .
Vậy tập xác định của hàm số là D  ; 4     1  ;   .
a b  1  2  a b  1 a  1 
b) Do P có đỉnh là I 1; 2 nên ta có:      . b    1
2a b  0 b  2  2a Vậy P 2
: y  x  2x  1.
Câu 2: (1,0 điểm). a) Giải phương trình 2
3x  17x  23  x  3. 2
x  5x m
b) Tìm m để các bất phương trình 1  
 7 luôn đúng với mọi x . 2 2x  3x  2 Lời giải: x  3  0 x  3 a) Ta có: 2
3x  17x  23  x  3     2 2 2
3x 17x  23  x  6x  9
2x 11x  14  0 x  3 x  2 7    x  .   7 2 x    2 7 
Vậy phương trình có tập nghiệm là S   . 2    7   0 b) Ta có: 2
2x  3x  2  0, x   vì  . a  2   0
Khi đó bất phương trình trở thành:  2 x x   2
x x m   2 2 3 2 5
7 2x  3x  2    2
2x  3x  2 2
x  5x m 2       3x 2x m 2 0 (1)    2
x  5x m  7 2   2
2x  3x  2 1
 3x  26x m  14  0 (2) a  3  0 : Đ 5 Xét 2
(1) : 3x  2x m  2  0, x   L    m   
  1 3(m  2)   0 3 a  13  0 Xét 2
(2) : 13x  26x m  14  0, x      m  1. 2    13  13(14  ) m  0  5  Vậy m  ;1  .  3 
Câu 3: (1,0 điểm).
Trong mặt phẳng Oxy, viết phương trình đường thẳng d song song với  : 4x  3y  12  0 và
d cách  một khoảng bằng 5. Lời giải:
Vì d  : 4x  3y  12  0 nên d có dạng d : 4x  3y m  0, (m  12).
Chọn M(0; 4)  : 4x  3y  12  0. 4.0  3.4  m   m  m   Khi đó ( d d,)  ( d M,d)  5   5  12  m  12 25 13 25     . 2 2 4  ( 3  ) 12  m  2  5 m    27
Vậy có hai đường thẳng thỏa mãn là 4x  3y  27  0 và 4x  3y  13  0.
____________________HẾT____________________
Huế, 08h45’ Ngày 10 tháng 02 năm 2023
Page: CLB GIÁO VIÊN TRẺ TP HUẾ ¤N TËP GI÷A K× 2 Môn: TOÁN 10
SGK 2022 – Kết nối tri thức và cuộc sống
ĐỀ ÔN TẬP SỐ 03_TrNg 2023 Líp To¸n thÇy L£ B¸ B¶O
Trưêng THPT §Æng Huy Trø
S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch, TP HuÕ Trung t©m KM 10 Hương Trà, HuÕ. NỘI DUNG ĐỀ BÀI
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm) Câu 1:
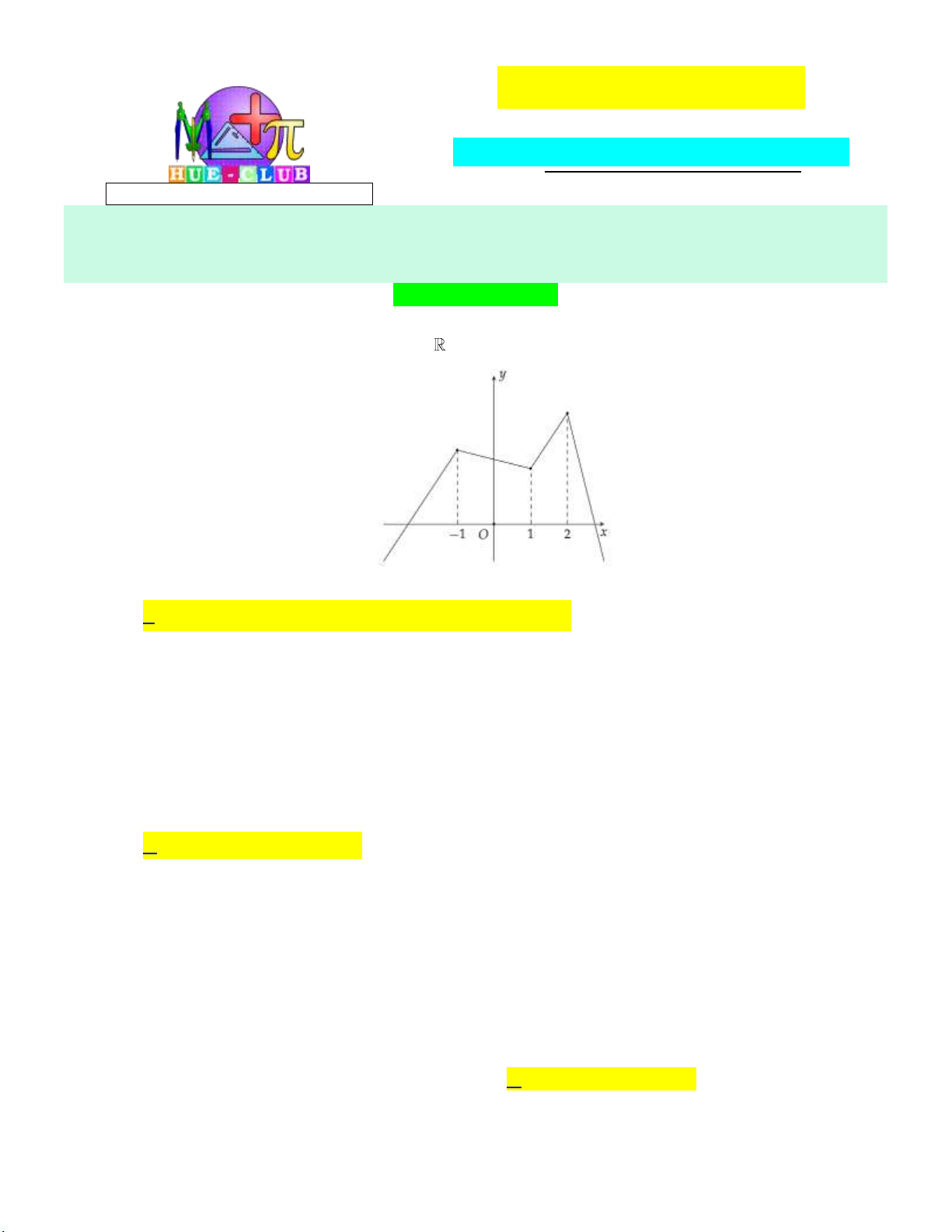
Cho hàm số y f x có đồ thị trên
như hình vẽ. Mệnh đề nào sau đây sai?
A. Hàm số y f x đồng biến trên khoảng  ;    1 .
B. Hàm số y f x nghịch biến trên khoảng 1; 2 .
C. Hàm số y f x nghịch biến trên khoảng 2;   .
D. Hàm số y f x đồng biến trên khoảng 1; 2 . Câu 2:
Trong mặt phẳng Oxy, phương trình nào dưới đây là phương trình đường tròn? A. 2 2
x y  2x  4 y 11  0 . B. 2 2
x y  2x  4 y 11  0 . C. 2 2
x y  2x  4 y 11  0 . D. 2 2
2x y  2x  4 y 11  0 . Câu 3:
Trong mặt phẳng Oxy, xác định vị trí tương đối giữa hai đường thẳng  : x  2 y 1  0 và 1
 : 3x  6y 10  0 . 2
A. Cắt nhau và không vuông góc với nhau.
B. Trùng nhau.
C. Vuông góc với nhau.
D. Song song với nhau. Câu 4: Cho hàm số 2 2
f (x)  mx  2x m m (với m là tham số). Tất cả các giá trị của m để f 2  0 là A. 1 và 4  . B. 4  . C. 1. D. 3.  x 1 t Câu 5:
Trong mặt phẳng Oxy, cho hai điểm A1; 2 , B 3; 
1 và đường thẳng  :  . Tọa độ y  2  t
điểm C thuộc  để tam giác ACB cân tại C là  7 13   7 13   7 13  13 7  A. ;   . B. ;    . C.  ;   . D. ;   .  6 6   6 6   6 6   6 6  Câu 6: Hai đồ thị hàm số 2
y x  2x  3 và y  2x 1 có bao nhiêu điểm chung? A. 2 . B. 1. C. 0 . D. 3 . Câu 7:
Trong mặt phẳng Oxy, tâm I của đường tròn C  có phương trình 2 2
x y  4x  3y 1  0 là  3   3  A. I 2;    .
B. I 2;    .
C. I 4; 3   .
D. I 4;3 .  2   2  Câu 8: Cho hàm số bậc hai 2
y ax bx c có đồ thị như hình vẽ bên dưới:
Tìm tất cả các giá trị của x để y  0. A.  ;  0.
B. 3;  . C. 0;  3 . D. 0;3 . Câu 9:
Trong mặt phẳng Oxy, hypebol có hai tiêu điểm là F 2; 0 và F 2; 0 và một đỉnh A1;0 2   1  
có phương trình là chính tắc là 2 2 y x 2 2 y x 2 2 x y 2 2 x y A.   1. B.   1. C.   1. D.   1. 1 3 1 3 3 1 1 3 x  1 2t
Câu 10: Trong mặt phẳng Oxy, cho đường thẳng d : 
,t   . Điểm nào sau đây thuộc đường y  2   3t thẳng d . A. Q 2; 3   .
B. M 3;   1 .
C. N  1;    1 .
D. P 1;  2 . x
Câu 11: Tập xác định D của hàm số f x 2 3  là x 1
A. D  1;   .
B. D  1;  . C. D  \   1 . D. D  \ 1;   .
Câu 12: Đỉnh của parabol 2
y x  4x  5 có toạ độ là A. 0; 2 . B. 1; 2 . C. 2;0 . D. 2;  1 .
Câu 13: Cho hàm số bậc hai 2
y ax bx c,a;b;c   có đồ thị như hình bên dưới: y 1 x -1 O 3 -3 -4 Tính 2 2 2
T a b c . A. 11. B. 14. C. 9. D. 7.
Câu 14: Cho parabol  P có phương trình chính tắc là 2 y  2
px với p  0 . Phương trình đường
chuẩn của  P là p A. y   . B.p x . C.p y . D.   p x . 2 2 2 2
Câu 15: Bất phương trình 2
x  2x  3 có bao nhiêu nghiệm nguyên ? A. 5 . B. 4 . C. 3 . D. 2 . Câu 16: Hàm số 2
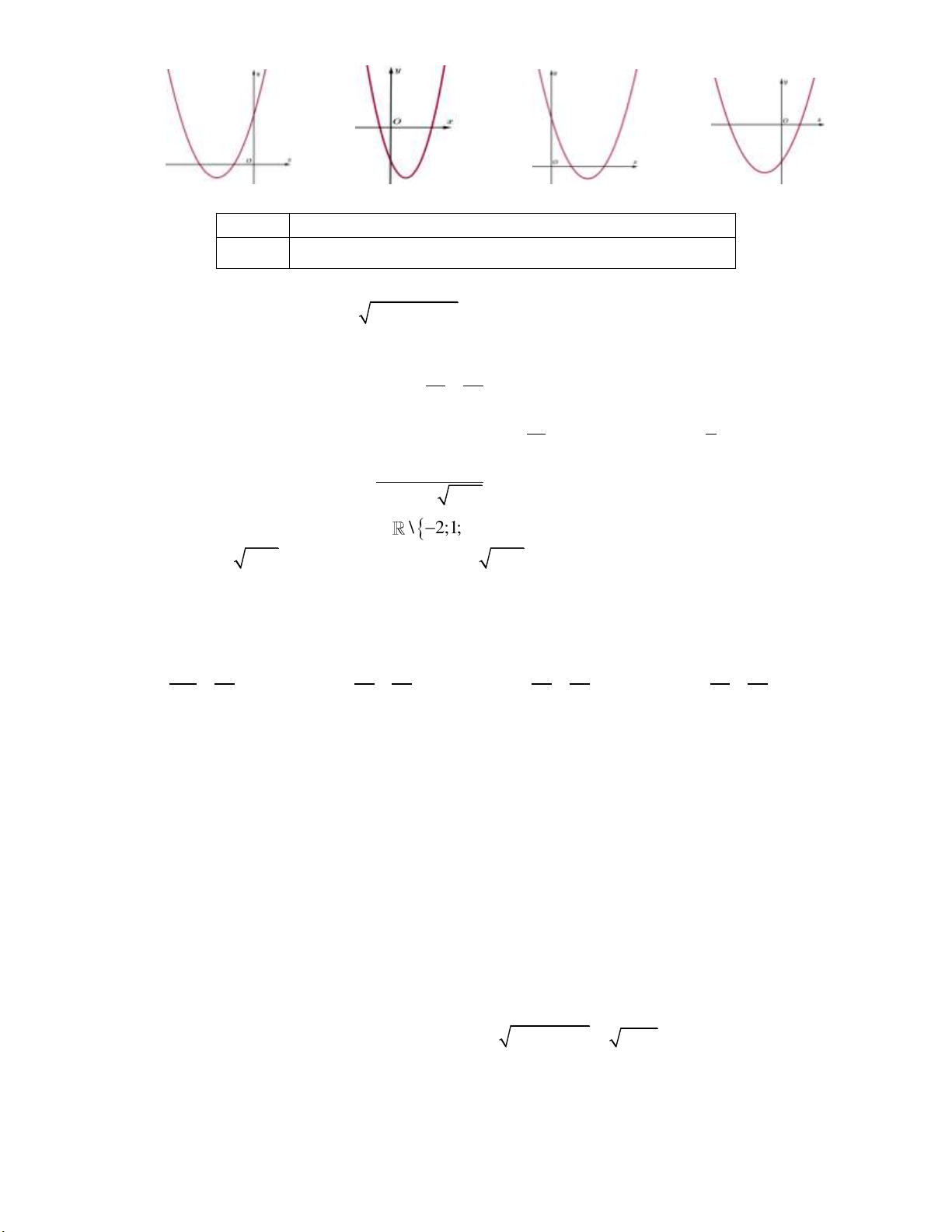
y  4x  3x 1 có đồ thị là một trong bốn hình vẽ dưới đây. Đồ thị đó là đồ thị nào? A. . B. . C. . D. .
Câu 17: Tam thức bậc hai nào dưới đây có bảng xét dấu như hình vẽ? x  0 4  f x  0  0  A. 2 y x  2 . x B. 2 y x  2 . x C. 2 y x  4 . x D. 2
y  x  4 . x
Câu 18: Nghiệm của phương trình 2
x  7x 10  x  4 thuộc tập nào dưới đây? A. 4;5 . B. 5;6 . C. 5;6 . D. 5;6 . 2 2 x y
Câu 19: Trong mặt phẳng Oxy, đường elip 
1 có tiêu cự bằng 16 7 9 6 A. 3 . B. 6 . C. . D. . 16 7 x  6
Câu 20: Tập xác định của hàm số y   là 2
x  4 x 1
A. D  1; . B. D  \  2  ;1; 
2 . C. D  1;  \  
2 . D. D  1;  \   2 .
Câu 21: Khi đặt t x 1 thì phương trình x  2  x 1  0 trở thành phương trình nào dưới đây? A. 2
t t 1  0 . B. 2 t t  0 . C. 2
t t  2  0 . D. 2
t  2t  0 .
Câu 22: Trong mặt phẳng Oxy, viết phương trình chính tắc của elip có tiêu cự bằng 6 và đi qua điểm A0;5 . 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.  1. B.  1. C.  1. D.  1 . 100 81 34 25 25 9 25 16
Câu 23: Trong mặt phẳng Oxy, đường tròn (C) tâm I (1; 4) và tiếp xúc với đườngthẳng
 : 4x  3y  4  0 có phương trình là A. 2 2
(x 1)  ( y  4)  17 . B. 2 2
(x 1)  ( y  4)  16 . C. 2 2
(x 1)  ( y  4)  25 . D. 2 2
(x 1)  ( y  4)  16
Câu 24: Tam thức bậc hai f x 2
 x  5x  6 nhận giá trị dương khi và chỉ khi
A. x  ; 2  3; .
B. x 2;  3 .
C. x   ;
 23;.
D. x 2;3 .
Câu 25: Trong mặt phẳng Oxy, cho đường tròn 2 2
(C) : x y  4x  2 y  20  0 phương trình tiếp tuyến
của C  vuông góc với đường thẳng  : 3x  4 y  9  0 là
A. 4x  3y  30  0 và 4x  3y  20  0 .
B. 4x  3y  20  0 và 4x  3y  30  0 .
C. 4x  3y  30  0 và 4x  3y  20  0 .
D. 4x  3y  20  0 và 4x  3y  30  0 .
Câu 26: Tổng tất cả các nghiệm của phương trình và 2
x  3x  2  x  2 là A. 3 . B. 4 . C. 1  . D. 3  .
Câu 27: Xác định  P 2
: y ax bx c , biết  P có đỉnh là I (1;3) và đi qua ( A 0;1) A. 2 y  2
x  3x 1. B. 2 y  2
x  4x 1. C. 2 y  2
x  4x 1. D. 2 y  2
x  4x 1.
Câu 28: Bất phương trình nào sau đây vô nghiệm? A. 2 x  0 . B. 2 x  0 . C. 2 x  0 . D. 2 x  0 .
Câu 29: Trong mặt phẳng Oxy, đường tròn đi qua ba điểm A1; 2 , B 5; 2 , C 1; 3 có phương trình là. A. 2 2
x y  25x 19 y  49  0 . B. 2 2
2x y  6x y  3  0 . C. 2 2
x y  6x y 1  0 . D. 2 2
x y  6x xy 1  0 .
Câu 30: Tập nghiệm của phương trình x   2
2 x  4x  3  0 là
A. S  2;  3 . B. S    2 .
C. S  1;  3 .
D. S  1; 2;  3 . x  1   t
Câu 31: Trong mặt phẳng Oxy, xác định a để hai đường thẳng d : ax  3y – 4  0 và d :  1 2 y  3 3t
cắt nhau tại một điểm nằm trên trục hoành. A. a  –2 .
B. a  2 .
C. a  1 .
D. a  –1 .
Câu 32: Cho tam thức f x 2
ax bx c a   2
0 , Δ  b  4ac . Tam thức f x  0 với x  khi và chỉ khi a  0 a  0 a  0 a  0 A.  . B.  . C.  . D.  . Δ  0 Δ  0 Δ  0 Δ  0
Câu 33: Trong mặt phẳng Oxy, cho hai điểm A1; 2, B  3
 ;0 và đường thẳng d : x 3y  5  0 .
Phương trình đường thẳng  song song với d và đi qua trung điểm M của đoạn thẳng AB là
A. 3x y  2  0 .
B. x  3y  4  0 .
C. x  3y 1  0
D. x  3y  4  0 .
Câu 34: Tìm tất cả các giá trị của tham số m để bất phương trình 2
x  m  2 x  8m 1  0 vô nghiệm.
A. m 0; 28 .
B. m 0; 28 .
C. m   ;
 0 28;. D. m  ;  028; .
Câu 35: Trong mặt phẳng Oxy, cho hình bình hành ABCD có đỉnh A1;0 , hai đường thẳng BC, BD
lần lượt có phương trình là 2x y  0 và 2x  3y  8  0 . Tính độ dài cạnh CD . A. 5 . B. 0 . C. 2 5 .
D. 2 2 .
II. PHẦN TỰ LUẬN (03 câu – 3,0 điểm)
Câu 1: (1,0 điểm).
a) Tìm tập xác định của hàm số 2
y x  1  2 4  x .
b) Tìm a,b,c để parabol P 2
: y ax bx c đi qua ba điểm A1; 3, B 1
 ;1 và C2;7.
Câu 2: (1,0 điểm).
a) Giải phương trình  2
x  4x  3 x  2  0.
b) Tìm m để bất phương trình 2
(m  1)x  2(m  1)x  2m  3  0 vô nghiệm.
Câu 3: (1,0 điểm).
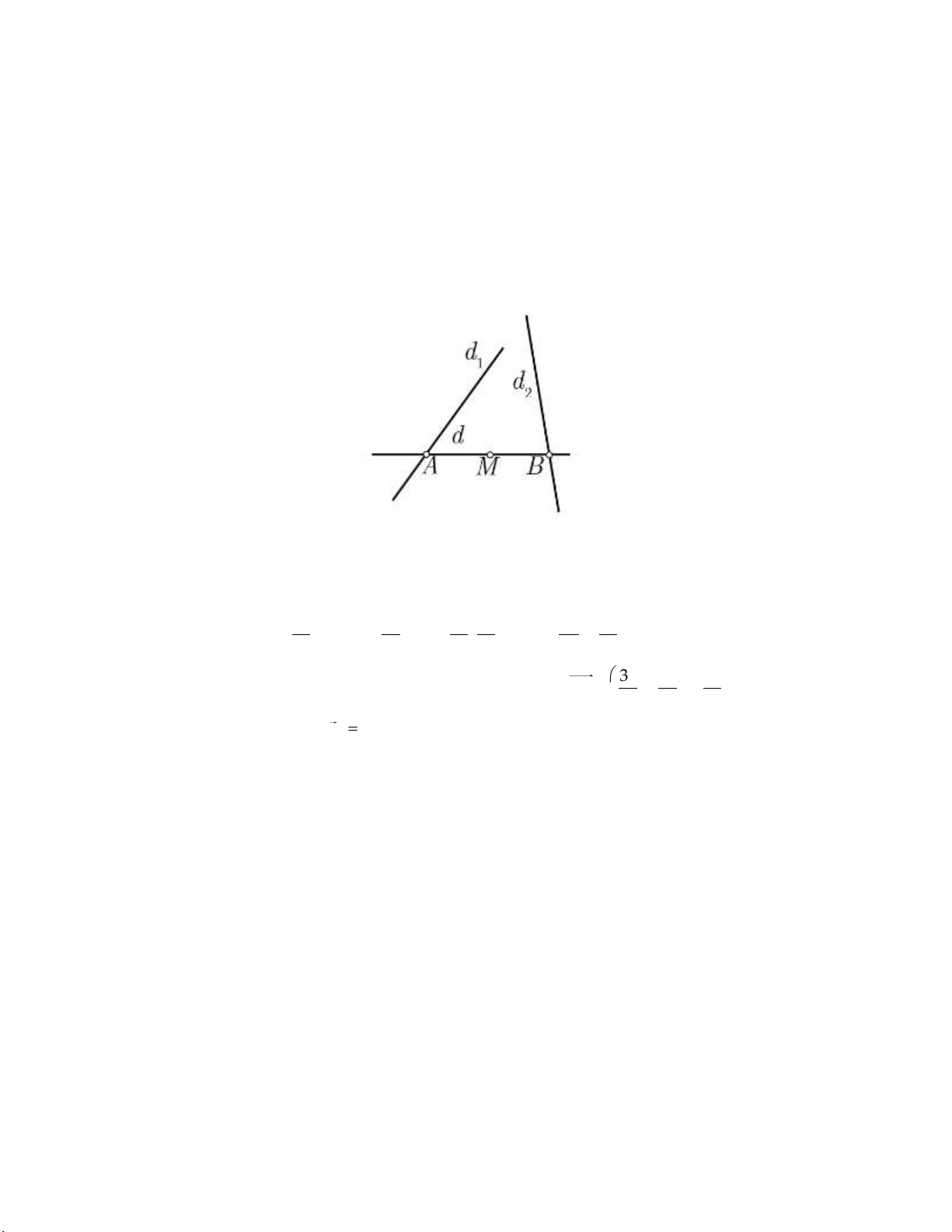
Trong mặt phẳng Oxy, cho hai đường thẳng d : 2x y  2  0, d : x  6y  3  0 và M(3; 0). 1 2
Viết phương trình đường thẳng d đi qua M và cắt d , d lần lượt tại hai điểm A, B sao cho 1 2
M là trung điểm của . AB
____________________HẾT____________________
Huế, 10h45’ Ngày 10 tháng 02 năm 2023
Page: CLB GIÁO VIÊN TRẺ TP HUẾ ¤N TËP GI÷A K× 2 Môn: TOÁN 10
SGK 2022 – Kết nối tri thức và cuộc sống
ĐỀ ÔN TẬP SỐ 03_TrNg 2023 Líp To¸n thÇy L£ B¸ B¶O
Trưêng THPT §Æng Huy Trø
S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch, TP HuÕ Trung t©m KM 10 Hương Trà, HuÕ.
LỜI GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm) Câu 1:
Cho hàm số y f x có đồ thị trên
như hình vẽ. Mệnh đề nào sau đây sai?
A. Hàm số y f x đồng biến trên khoảng  ;    1 .
B. Hàm số y f x nghịch biến trên khoảng 1; 2 .
C. Hàm số y f x nghịch biến trên khoảng 2;   .
D. Hàm số y f x đồng biến trên khoảng 1; 2 . Lời giải:
Dựa đồ thị ta thấy trên 1; 
1 đồ thị hàm số đi xuống, trên 1; 2 đồ thị hàm số đi lên từ trái
sang phải. Do đó trên 1; 2 hàm số đồng biến trên 1; 2 và nghịch biến trên 1;  1 .
Chọn đáp án B. Câu 2:
Trong mặt phẳng Oxy, phương trình nào dưới đây là phương trình đường tròn? A. 2 2
x y  2x  4 y 11  0 . B. 2 2
x y  2x  4 y 11  0 . C. 2 2
x y  2x  4 y 11  0 . D. 2 2
2x y  2x  4 y 11  0 . Lời giải: Phương trình 2 2
x y  2x  4 y 11  0 là phương trình đường tròn. Vì 2 2
a b c  1 4 11  16  0 trong đó a  1;b  2  ;c  11  .
Chọn đáp án A. Câu 3:
Trong mặt phẳng Oxy, xác định vị trí tương đối giữa hai đường thẳng  : x  2 y 1  0 và 1
 : 3x  6y 10  0 . 2
A. Cắt nhau và không vuông góc với nhau.
B. Trùng nhau.
C. Vuông góc với nhau.
D. Song song với nhau. Lời giải:
Tọa độ giao điểm (nếu có) của  và  là nghiệm của hệ phương trình: 1 2
x  2y 1  0 3
x  6y  3  0     3
x  6y 10  0 3
x  6y 10  0
Hệ phương trình trên vô nghiệm nên hai đường thẳng  và  song song với nhau. 1 2 1 2  1 Cách khác: Do  
nên hai đường thẳng  và  song song với nhau. 3  6 1  0 1 2
Chọn đáp án D. Câu 4: Cho hàm số 2 2
f (x)  mx  2x m m (với m là tham số). Tất cả các giá trị của m để f 2  0 là A. 1 và 4  . B. 4  . C. 1. D. 3. Lời giải: m 1 Ta có: f 2  0 2 2  .2 m
 2.2  m m  0 2
m  3m  4  0   . m  4 
Chọn đáp án A.x 1 t Câu 5:
Trong mặt phẳng Oxy, cho hai điểm A1; 2 , B 3; 
1 và đường thẳng  :  . Tọa độ y  2  t
điểm C thuộc  để tam giác ACB cân tại C là  7 13   7 13   7 13  13 7  A. ;   . B. ;    . C.  ;   . D. ;   .  6 6   6 6   6 6   6 6  Lời giải: C d A B M  3 
Gọi C 1 t; 2  t   .
 Trung điểm của AB là M 1; .    2 
Tam giác ACB cân tại C nên CM AB CM .AB  0 (1) .  1  Ta có CM t  ; t   ; AB  (4; 1  )    2  1 1  7 13  (1)  4
 t ( t )  0  t   C ; .   2 6  6 6 
Chọn đáp án A. Câu 6: Hai đồ thị hàm số 2
y x  2x  3 và y  2x 1 có bao nhiêu điểm chung? A. 2 . B. 1. C. 0 . D. 3 . Lời giải:
Xét phương trình: 2 2
x  2x  3  2x 1  x  4x  4  0  x  2 .
Vì phương trình có một nghiệm nên hai đồ thị hàm số cắt nhau tại 1 điểm.
Chọn đáp án B. Câu 7:
Trong mặt phẳng Oxy, tâm I của đường tròn C  có phương trình 2 2
x y  4x  3y 1  0 là  3   3  A. I 2;    .
B. I 2;    .
C. I 4; 3   .
D. I 4;3 .  2   2  Lời giải:
Phương trình đường tròn đã cho có dạng: 2 2
x y  2ax  2by c  0 . a  2 2a  4    3  3 
Do đó, 2b  3  b   tâm I 2;    . 2    2  c  1  c  1 
Chọn đáp án A. Câu 8: Cho hàm số bậc hai 2
y ax bx c có đồ thị như hình vẽ bên dưới:
Tìm tất cả các giá trị của x để y  0. A.  ;  0.
B. 3;  . C. 0;  3 . D. 0;3 . Lời giải:
Dựa vào đồ thị ta có
y  0  x   ;
 0 3; và y  0  x0;3 .
Chọn đáp án D. Câu 9:
Trong mặt phẳng Oxy, hypebol có hai tiêu điểm là F 2; 0 và F 2; 0 và một đỉnh A1;0 2   1  
có phương trình là chính tắc là 2 2 y x 2 2 y x 2 2 x y 2 2 x y A.   1. B.   1. C.   1. D.   1. 1 3 1 3 3 1 1 3 Lời giải: c  2  2 a  1 2 x y Ta có : a  1  
. Phương trình H 2 :   1.  2 b  3 1 3 2 2 2 b c   a
Chọn đáp án D.x  1 2t
Câu 10: Trong mặt phẳng Oxy, cho đường thẳng d : 
,t   . Điểm nào sau đây thuộc đường y  2   3t thẳng d . A. Q 2; 3   .
B. M 3;   1 .
C. N  1;    1 .
D. P 1;  2 . x
Câu 11: Tập xác định D của hàm số f x 2 3  là x 1
A. D  1;   .
B. D  1;  . C. D  \   1 . D. D  \ 1;   . Lời giải:
Hàm số xác định  x 1  0  x  1.
Vậy tập xác định của hàm số là D  1;  .
Chọn đáp án B.
Câu 12: Đỉnh của parabol 2
y x  4x  5 có toạ độ là A. 0; 2 . B. 1; 2 . C. 2;0 . D. 2;  1 .
Câu 13: Cho hàm số bậc hai 2
y ax bx c,a;b;c   có đồ thị như hình bên dưới: y 1 x -1 O 3 -3 -4 Tính 2 2 2
T a b c . A. 11. B. 14. C. 9. D. 7. Lời giải: b   1  2a
2a b  0 a  1   
Dựa vào đồ thị, ta có hệ: y1  4
  a b c  4  b  2.    y      c  3  c  3 0 3     Vậy 2 2 2
T a b c  14.
Chọn đáp án B.
Câu 14: Cho parabol  P có phương trình chính tắc là 2 y  2
px với p  0 . Phương trình đường
chuẩn của  P là p A. y   . B.p x . C.p y . D.   p x . 2 2 2 2
Câu 15: Bất phương trình 2
x  2x  3 có bao nhiêu nghiệm nguyên ? A. 5 . B. 4 . C. 3 . D. 2 . Lời giải: 2 2
x  2x  3  x  2x  3  0  1   x  3 Vì x   x 0;1;  2  3 nghiệm nguyên.
Chọn đáp án C. Câu 16: Hàm số 2
y  4x  3x 1 có đồ thị là một trong bốn hình vẽ dưới đây. Đồ thị đó là đồ thị nào? A. . B. . C. . D. . Lời giải: Từ hàm số 2
y  4x  3x 1 ta có hệ số c  1  tọa độ giao điểm với trục Oy tại 0;   1 . 3
Mặt khác, trục đối xứng của parabol là x   0. 8
Chọn đáp án B.
Câu 17: Tam thức bậc hai nào dưới đây có bảng xét dấu như hình vẽ? x  0 4  f x  0  0  A. 2 y x  2 . x B. 2 y x  2 . x C. 2 y x  4 . x D. 2
y  x  4 . x Lời giải:
Kiểm tra các sự kiện: a  0 và tam thức có hai nghiệm x  0, x  4.
Chọn đáp án C.
Câu 18: Nghiệm của phương trình 2
x  7x 10  x  4 thuộc tập nào dưới đây? A. 4;5 . B. 5;6 . C. 5;6 . D. 5;6 . Lời giải: x  4  0  Ta có: 2
x  7x 10  x  4  
x  7x 10   x  42 2 x  4 x   4   
x  65;6. 2 2
x  7x 10  x 8x 16 x 6
Chọn đáp án D. 2 2 x y
Câu 19: Trong mặt phẳng Oxy, đường elip 
1 có tiêu cự bằng 16 7 9 6 A. 3 . B. 6 . C. . D. . 16 7 Lời giải: 2 2 x y
Phương trình chính tắc của elip có dạng  E : 
1 a,b  0 . 2 2   a b 2 a 16 a  4   2  b   7  b   7 .   2 2 2
c a bc  3 
Vậy tiêu cự của elip là F F  2c  2.3  6 . 1 2
Chọn đáp án B. x  6
Câu 20: Tập xác định của hàm số y   là 2
x  4 x 1
A. D  1; . B. D  \  2  ;1; 
2 . C. D  1;  \  
2 . D. D  1;  \   2 . Lời giải: x  1  x 1  0  x 1
Điều kiện xác định: 
 x  2   . 2 x  4  0  x  2 x  2
Vậy tập xác định của hàm số là D  1;  \   2 .
Chọn đáp án D.
Câu 21: Khi đặt t x 1 thì phương trình x  2  x 1  0 trở thành phương trình nào dưới đây? A. 2
t t 1  0 . B. 2 t t  0 . C. 2
t t  2  0 . D. 2
t  2t  0 . Lời giải:
Ta có: x  2  x 1  0   x   1 
x 1 1  0. Đặt 2 t
x 1  t x 1. Vậy pt trở thành: 2
t t 1  0.
Chọn đáp án A.
Câu 22: Trong mặt phẳng Oxy, viết phương trình chính tắc của elip có tiêu cự bằng 6 và đi qua điểm A0;5 . 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.  1. B.  1. C.  1. D.  1 . 100 81 34 25 25 9 25 16 Lời giải: 2 2 x y
Phương trình chính tắc của elip có dạng 
1 a,b  0 . 2 2   a b 2 2 0 5
Theo giả thiết: 2c  6  c  3 . Vì A0;5  E  nên ta có phương trình:  1 b  5 . 2 2 a b Khi đó: 2 2 2 2 2 2
a b c a  5  3 2
a  34  a  34 .
Chọn đáp án B.
Câu 23: Trong mặt phẳng Oxy, đường tròn (C) tâm I (1; 4) và tiếp xúc với đườngthẳng
 : 4x  3y  4  0 có phương trình là A. 2 2
(x 1)  ( y  4)  17 . B. 2 2
(x 1)  ( y  4)  16 . C. 2 2
(x 1)  ( y  4)  25 . D. 2 2
(x 1)  ( y  4)  16 Lời giải:  4.1 3.4  4
C  có bán kính R d I,    4 . 2 2 3  4
Do đó, C  có phương trình 2 2
(x 1)  ( y  4)  16 .
Chọn đáp án B.
Câu 24: Tam thức bậc hai f x 2
 x  5x  6 nhận giá trị dương khi và chỉ khi
A. x  ; 2  3; .
B. x 2;  3 .
C. x   ;
 23;.
D. x 2;3 . Lời giải:
Ta có: f x 2
 x  5x  6  0  2  x  3. Vậy f x 2
 x  5x  6 nhận giá trị dương khi và chi khi x2;3 .
Chọn đáp án D.
Câu 25: Trong mặt phẳng Oxy, cho đường tròn 2 2
(C) : x y  4x  2 y  20  0 phương trình tiếp tuyến
của C  vuông góc với đường thẳng  : 3x  4 y  9  0 là
A. 4x  3y  30  0 và 4x  3y  20  0 .
B. 4x  3y  20  0 và 4x  3y  30  0 .
C. 4x  3y  30  0 và 4x  3y  20  0 .
D. 4x  3y  20  0 và 4x  3y  30  0 . Lời giải:
Đường tròn C  có tâm I 2;  1 và bán kính 2 2 R  2 1  20  5 .
Đường thẳng d vuông góc với  : 3x  4 y  9  0  d : 4x  3y m  0 . 4.2  3.1 m
d là tiếp tuyến của C   d I , d   R   5. 4  32 2 m  5  25 m  20
d : 4x  3y  20  0 1       . m  5  2  5 m  3  0
d : 4x  3y  30  0  2
Chọn đáp án B.
Câu 26: Tổng tất cả các nghiệm của phương trình và 2
x  3x  2  x  2 là A. 3 . B. 4 . C. 1  . D. 3  . Lời giải: x  2   x  2   x  2   Ta có 2
x  3x  2  x  2      x  0 . 2 2
x  3x  2  x  2
x  4x  0  x  4
Vậy tập nghiệm của phương trình S  0; 
4 nên tổng các nghiệm là 4 .
Chọn đáp án B.
Câu 27: Xác định  P 2
: y ax bx c , biết  P có đỉnh là I (1;3) và đi qua ( A 0;1) A. P 2 : y  2
x  3x 1. B. P 2 : y  2
x  4x 1. C. P 2 : y  2
x  4x 1. D. P 2 : y  2
x  4x 1. Lời giải:
a b c  3 
Do (P) có đỉnh là I 1;3 nên ta có hệ:  b   (1) 1  2a
Mặt khác, (P) đi qua điểm (
A 0;1) nên c  1 thay vào (1) ta được a  2;b  4 .
Chọn đáp án B.
Câu 28: Bất phương trình nào sau đây vô nghiệm? A. 2 x  0 . B. 2 x  0 . C. 2 x  0 . D. 2 x  0 .
Câu 29: Trong mặt phẳng Oxy, đường tròn đi qua ba điểm A1; 2 , B 5; 2 , C 1; 3 có phương trình là. A. 2 2
x y  25x 19 y  49  0 . B. 2 2
2x y  6x y  3  0 . C. 2 2
x y  6x y 1  0 . D. 2 2
x y  6x xy 1  0 . Lời giải:
Gọi C  là phương trình đường tròn đi qua ba điểm ,
A B, C với tâm I a;b
 C có dạng: 2 2
x y  2ax  2by c  0 . Vì đường tròn C  đi qua qua ba điểm , A B, C
nên ta có hệ phương trình: a  3 1
  4  2a  4b c  0  2
a  4b c  5      1
25  4 10a  4b c  0   1
 0a  4b c  2  9  b    . 2   
1 9  2a  6b c  0 2
a  6b c  1  0   c  1 
Vậy phương trình đường tròn cần tìm là 2 2
x y  6x y 1  0 .
Chọn đáp án C.
Câu 30: Tập nghiệm của phương trình x   2
2 x  4x  3  0 là
A. S  2;  3 . B. S    2 .
C. S  1;  3 .
D. S  1; 2;  3 . Lời giải:
Điều kiện: x  2  0  x  2 (*).
Với điều kiện (*), phương trình đã cho tương đương với x  2 x  2  0    x  1 . 2 
x  4x  3  0 x  3 
So với điều kiện (*) chỉ có x  2 , x  3 thỏa mãn.
Vậy tập nghiệm của phương trình là S  2;  3 .
Chọn đáp án A.x  1   t
Câu 31: Trong mặt phẳng Oxy, xác định a để hai đường thẳng d : ax  3y – 4  0 và d :  1 2 y  3 3t
cắt nhau tại một điểm nằm trên trục hoành. A. a  –2 .
B. a  2 .
C. a  1 .
D. a  –1 . Lời giải:
Gọi M d d M 1
  t;3  3t d 1 2   2
Do M Ox  3  3t  0  t  –1  M  2  ;0.
Mặt khác, M d a  2
   3.0 – 4  0  a  –2 . 1
Chọn đáp án A.
Câu 32: Cho tam thức f x 2
ax bx c a   2
0 , Δ  b  4ac . Tam thức f x  0 với x  khi và chỉ khi a  0 a  0 a  0 a  0 A.  . B.  . C.  . D.  . Δ  0 Δ  0 Δ  0 Δ  0
Câu 33: Trong mặt phẳng Oxy, cho hai điểm A1; 2, B  3
 ;0 và đường thẳng d : x 3y  5  0 .
Phương trình đường thẳng  song song với d và đi qua trung điểm M của đoạn thẳng AB là
A. 3x y  2  0 .
B. x  3y  4  0 .
C. x  3y 1  0
D. x  3y  4  0 . Lời giải:
Trung điểm của đoạn AB là M 1;  1 .
Vì  song song với đường thẳng d nên  có dạng: x  3y m  0 . Do  qua M nên 1
  3.1 m  0  m  4 .
Vậy phương trình đường thẳng  cần tìm là x  3y  4  0 .
Chọn đáp án B.
Câu 34: Tìm tất cả các giá trị của tham số m để bất phương trình 2
x  m  2 x  8m 1  0 vô nghiệm.
A. m 0; 28 .
B. m 0; 28 .
C. m   ;
 0 28;. D. m  ;  028; . Lời giải:
Bất phương trình 2
x  m  2 x  8m 1  0 vô nghiệm 2
x  m  2 x 8m 1  0, x   . a  0 2 Điều kiện: 
 m  2  48m   2
1  0  m  28m  0  m  0; 28.   0
Vậy m 0; 28.
Chọn đáp án B.
Câu 35: Trong mặt phẳng Oxy, cho hình bình hành ABCD có đỉnh A1;0 , hai đường thẳng BC, BD
lần lượt có phương trình là 2x y  0 và 2x  3y  8  0 . Tính độ dài cạnh CD . A. 5 . B. 0 . C. 2 5 .
D. 2 2 . Lời giải: A B D C
Vì B BC BD nên tọa độ điểm B là nghiệm của hệ phương trình:
2x y  0 x  1      B  1  ; 2
   BA  2;2.
2x  3y 8  0 y  2  Suy ra 2 2 CD BA  2  2  2 2 .
Chọn đáp án D.
II. PHẦN TỰ LUẬN (03 câu – 3,0 điểm)
Câu 1: (1,0 điểm).
a) Tìm tập xác định của hàm số 2
y x  1  2 4  x .
b) Tìm a,b,c để parabol P 2
: y ax bx c đi qua ba điểm A1; 3, B 1
 ;1 và C2;7. Lời giải: 2 4  x  0 x 2  ;2  
a) Hàm số xác định      x 1  ;2.   x 1  0 x  1
Vậy tập xác định của hàm số là D  1  ;2.  
a b c  3 a  1  
b) Do P đi qua hai điểm A1; 3 ,B1; 
1 và C 2;7 nên ta có: a b c  1  b  1.  
4a  2b c  7 c  1   Vậy P 2
: y x x  1.
Câu 2: (1,0 điểm).
a) Giải phương trình  2
x  4x  3 x  2  0.
b) Tìm m để bất phương trình 2
(m  1)x  2(m  1)x  2m  3  0 vô nghiệm. Lời giải:
a) Điều kiện: x  2  0  x  2. x  2 x  2  0  Ta có:  2
x  4x  3 x  2  0    x  1. 2
x  4x  3  0 x   3
Đối chiếu điều kiện, phương trình có tập nghiệm là S  2;  3 .
b) TH 1 : a  0  m  1  0  m  1.
Bất phương trình trở thành: 5  0 : vô nghiệm  nhận m  1.
TH 2 : a  0  m  1  0  m  1. Ta có: 2
(m  1)x  2(m  1)x  2m  3  0 : vô nghiệm 2
 (m  1)x  2(m  1)x  2m  3  0, x   a  0    m  1 m  1  m 1 0           0 2
4(m 1)  4.(m 1)(2m  3)  0 2  4
m  12m  16  0 m  ; 4    1  ;     m  1. Kết luận: m 1  ;  .
Câu 3: (1,0 điểm).
Trong mặt phẳng Oxy, cho hai đường thẳng d : 2x y  2  0, d : x  6y  3  0 và M(3; 0). 1 2
Viết phương trình đường thẳng d đi qua M và cắt d , d lần lượt tại hai điểm A, B sao cho 1 2
M là trung điểm của . AB Lời giải: Gọi (
A a; 2a  2) d : 2x y  2  0 và ( B 6
b  3;b)d : x  6y  3  0. 1 2
x x  2x
a  3  6b  6
Theo đề bài, M là trung điểm A B M AB    
y y  2y
2a  2  b  0 A B M
a  6b  9 21      16 57 16   a  và b   21 16
A ;  và B ;     2a b   2 13 13  13 13   13 13   36 32  4
Đường thẳng d qua điểm M(3;0) và có một VTCP là AB  ;   9; 8      13 13  13
 Một VTPT của d là n  8;9  d : 8(x  3)  9(y  0)  0  d : 8x  9y  24  0. d
____________________HẾT____________________
Huế, 10h45’ Ngày 10 tháng 02 năm 2023
Page: CLB GIÁO VIÊN TRẺ TP HUẾ ¤N TËP GI÷A K× 2 Môn: TOÁN 10
SGK 2022 – Kết nối tri thức và cuộc sống
ĐỀ ÔN TẬP SỐ 04_TrNg 2023 Líp To¸n thÇy L£ B¸ B¶O
Trưêng THPT §Æng Huy Trø
S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch, TP HuÕ Trung t©m KM 10 Hương Trà, HuÕ. NỘI DUNG ĐỀ BÀI
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm) Câu 1:
Điểm I (0;1) thuộc đồ thị của hàm số nào dưới đây ? A. 2
y x x . B. 2
y  x x . C. 2
y x x 1. D. 2
y  x x 1. Câu 2:
Trong mặt phẳng Oxy, cho đường thẳng d : 2x  3y  4  0 . Vectơ nào sau đây là một vectơ
chỉ phương của d ?
A. u  2;3 .
B. u  3; 2 .
C. u  3;  2 . D. u    4  3; 2 . 3   2   1   2 2 x y Câu 3:
Trong mặt phẳng Oxy, một tiêu điểm của elip (E): 
1 có tọa độ là 25 9 A. 4;0. B. 3;0. C. 16;0. D. 0; 4. Câu 4:
Phương trình x 1  x  3 có tập nghiệm là A. S    5 .
B. S  2;  5 . C. S    2 . D. S   . Câu 5:
Tập nghiệm của bất phương trình 2
x 16  8x là A. 4;  . B. \   4 . C. . D.  – ;  4 . Câu 6: Phương trình x  2 x   1
x 1  0 có bao nhiêu nghiệm? A. 2 . B. 1. C. 0 . D. 3 . Câu 7:
Trong mặt phẳng Oxy, cho hai điểm A3;5 và B 2;7 . Điểm nào sau đây thuộc đường
trung trực của đoạn AB ?  3   5   1  A. M ;1  . B. N 1;   .
C. P 0;   1 . D. Q  ; 4   .  2   2   2  Câu 8:
Toạ độ giao điểm của parabol 2
(P ) : y  2x  2x  3 với parabol 2
(P ) : y x  6x là 1 2
A. 1;7 và 3;27 . B. 7;  1 và 27;3 .
C. 1;3 và 3;15 . D. 3;  1 và 15;3 . x y Câu 9:
Trong mặt phẳng Oxy, cho elip  E 2 2 : 
1. Với M là điểm bất kì nằm trên E , khẳng 16 9
định nào sau đây là khẳng định đúng ?
A. 4  OM  5. B. OM  5. C. OM  3.
D. 3  OM  4.
Câu 10: Trong mặt phẳng Oxy, đường thẳng đi qua hai điểm A2;0 và B 0;3 có phương trình là x y x y x y x y A.   0 . B.  1. C.   0 . D.  1. 2 3 2 3 2 3 2 3
Câu 11: Cho phương trình 2 2
x  5x  2  2 x  5x 10  0 . Đặt 2 t
x  5x 10 thì phương trình trở
thành phương trình nào sau đây? A. 2
t  2t 10  0 . B. 2
t  2t  2  0 . C. 2
t  2t  8  0 . D. 2
t  2t  8  0 .
Câu 12: Trong mặt phẳng Oxy, xác định vị trí tương đối của 2 đường thẳng  : 2x  3y 1  0 và  : 1 2 4
x  6y 1  0 . A. Song song. B. Trùng nhau.
C. Vuông góc.
D. Cắt nhau nhưng không vuông góc nhau.
Câu 13: Bất phương trình nào dưới đây vô nghiệm? A. 2
x  5x  2  0. B. 2
x  2x  3  0. C. 2
x  6x  9  0. D. 2
x  2x  3  0.
Câu 14: Cho tam thức f x 2
x  3x  2. Khẳng định nào dưới đây đúng?
A. f x  0, x  1;2.
B. f x  0, x  1;2.
C. f x  0, x
 ;1  2;.
D. f x  0, x   1  ;2.  
Câu 15: Trong mặt phẳng Oxy, cho đường thẳng  : ax by c  0a,b,c  ;b  4 vuông góc với
đường thẳng d : 3x y  4  0 và  cách A1; 3 một khoảng 10 . Tính T a b c . A. 10 . B. 11 . C. 4 . D. 9 . 2 2 x y
Câu 16: Trong mặt phẳng Oxy, đường hyperbol  1 có tiêu cự bằng 20 16 A. 12. B. 2. C. 4. D. 6.
Câu 17: Tìm tập xác định của hàm số 2 y
2x  5x  2 .  1   1   1  1  A. ; 2 .   B.  ;  2;   . C.  ;  2;   . D. ;2 .     2   2   2  2 
Câu 18: Cho f x 2
ax bx c a  0 có 2
  b  4ac . Điều kiện cần và đủ để f x  0,x là a  0 a  0 a  0 a  0 A.  . B.  . C.  . D.  .   0   0   0   0
Câu 19: Cho hàm số y f x có tập xác định 5;5 và đồ thị của nó được biểu diễn như hình dưới đây: y 2 1 O 4 5 5 1 1 3 x 1 2
Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên 2; 2 .
B. Hàm số đồng biến trên 5;5 .
C. Hàm số đồng biến trên 2; 3 .
D. Hàm số đồng biến trên 5;  2 .
Câu 20: Tìm m để parabol 2
(P) : y mx  2x  3 có trục đối xứng là đường thẳng x  2 . 1 A. m  2 .
B. m  1.
C. m  1. D. m  . 2
Câu 21: Trong mặt phẳng Oxy, phương trình đường tròn có tâm I 3; 
1 và đi qua điểm M 2; 1  là 2 2 2 2
A. x  3   y   1  5.
B. x  3   y   1  5. 2 2 2 2
C. x  3   y   1  5.
D. x  3   y   1  5.
Câu 22: Tam thức nào dưới đây luôn âm với mọi x  ? A. 2
y x x  1. B. 2
y  x x  1. C. 2
y  x x  1. D. 2
y  x  4 . x 3x  4
Câu 23: Tập xác định của hàm số y  là 4x  5 4  5  5 A. D  \  . B. D  ;    .
C. D  . D. D  \   . 5  4  4
Câu 24: Cho hàm số bậc hai 2
y ax bx c,a;b;c   có đồ thị như hình bên dưới: y x O
Khẳng định nào dưới đây đúng?
A. a  0,b  0,c  0.
B. a  0,b  0,c  0.
C. a  0,b  0,c  0.
D. a  0,b  0,c  0.
Câu 25: Trong mặt phẳng Oxy, đường tròn C  2 2
: x y  4x  6 y 12  0 có tâm I và bán kính R lần lượt là A. I 2; 3  , R  5 .
B. I  2  ;3, R  5.
C. I  4
 ;6, R  5. D. I  2  ; 3  , R  5.
Câu 26: Tìm tập hợp tất cả các giá trị của tham số m để hàm số 2
y mx  2m  1 x  4m có tập xác định là . A.  ;   1 . B. 1; .
C. 1; . D.  ;   1 . x  3
Câu 27: Biết tập xác định của hàm số y x  2 
là nửa khoảng a;b . Khẳng định nào sau 5  x đây đúng?
A. 2a b  7 .
B. 2a b  1 .
C. a b  3 .
D. a  2b  6 . 2 2
Câu 28: Trong mặt phẳng Oxy, cho đường tròn (C) :  x  
1   y  2  8 . Phương trình tiếp tuyến d
của (C) tại điểm M 3;  4 là
A. d : x y 1  0 .
B. d : x  2 y 11  0 . C. d : x y  7  0 .
D. d : x y  7  0 .
Câu 29: Cho hàm số   2
f x ax bx c có đồ thị như hình bên dưới:
Giá trị của biểu thức: T  2a b c bằng A. 1. B. 1. C. 0. D. 2.
Câu 30: Tập nghiệm của phương trình 3  x x  2 là  1  1   1
A. S   . B. S   2;  .
C. S   .
D. S    .  2  2  2 2 2
Câu 31: Trong mặt phẳng Oxy, điểm nào dưới đây thuộc đường tròn C  : x  
1   y  2  25?
A. M 4; 2 .
B. N 2; 4 .
C. P 3;6 .
D. Q 4; 2 .
Câu 32: Biết parabol  P 2
: y ax bx  4 có đỉnh là I 1; 2, tính a  3b . A. 20 . B. 18 . C. 30 . D. 25.
Câu 33: Trong mặt phẳng Oxy, đường tròn có tâm I 3; 4 tiếp xúc với đường thẳng
 :3x  4y 10  0 thì có bán kính bằng 5 3 A. . B. 5 . C. 3 . D. . 3 5
Câu 34: Viết phương trình chính tắc của parabol đi qua điểm Q 5; 2  . 4x A. 2
y x  3x 12. B. 2
y x  27. C. 2
y  5x  21. D. 2 y  . 5
Câu 35: Trong mặt phẳng Oxy, toạ độ hình chiếu H của điểm M 4;1 trên đường thẳng
 : x – 2y  4  0 là  14 17   14 17  A. 14; 1  9. B. 2; 3. C.   ;  . D.  ;  .  5 5   5 5 
II. PHẦN TỰ LUẬN (03 câu – 3,0 điểm)
Câu 1: (1,0 điểm). 2 4  x  1
a) Tìm tập xác định của hàm số y  . 2 x  4x  3
b) Tìm m để hàm số 2
y x  2mx m đồng biến trên 1; . Lời giải:
Câu 2: (1,0 điểm).
a) Giải phương trình x  x   2 1
3  3 x  4x  5  2  0. b) Tìm m để 2 2
x  2mx  4m  3  0 nghiệm đúng với mọi x  .
Câu 3: (1,0 điểm).
Trong mặt phẳng Oxy, cho M(3; 1) và d : 3x  4y  12  0. Tìm hình chiếu H của điểm M lên
d và N là điểm đối xứng của M qua d.
____________________HẾT____________________
Huế, 10h45’ Ngày 10 tháng 02 năm 2023
Page: CLB GIÁO VIÊN TRẺ TP HUẾ ¤N TËP GI÷A K× 2 Môn: TOÁN 10
SGK 2022 – Kết nối tri thức và cuộc sống
ĐỀ ÔN TẬP SỐ 04_TrNg 2023 Líp To¸n thÇy L£ B¸ B¶O
Trưêng THPT §Æng Huy Trø
S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch, TP HuÕ Trung t©m KM 10 Hương Trà, HuÕ.
LỜI GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm) Câu 1:
Điểm I (0;1) thuộc đồ thị của hàm số nào dưới đây ? A. 2
y x x . B. 2
y  x x . C. 2
y x x 1. D. 2
y  x x 1. Lời giải: Xét hàm số: 2
y x x 1, tại x  0 ta có 2
y  0  0 1  1.
Chọn đáp án C. Câu 2:
Trong mặt phẳng Oxy, cho đường thẳng d : 2x  3y  4  0 . Vectơ nào sau đây là một vectơ
chỉ phương của d ?
A. u  2;3 .
B. u  3; 2 .
C. u  3;  2 . D. u    4  3; 2 . 3   2   1   Lời giải:
Đường thẳng d : 2x  3y  4  0 có một véctơ pháp tuyến n  2;3 nên chọn một véctơ chỉ
phương của d là u  3; 2  . 3  
Chọn đáp án C. 2 2 x y Câu 3:
Trong mặt phẳng Oxy, một tiêu điểm của elip (E): 
1 có tọa độ là 25 9 A. 4;0. B. 3;0. C. 16;0. D. 0; 4. Lời giải: 2 a  25 Ta có: 2 2 2  
c a b  16  c  4. 2 b  9
Chọn đáp án A. Câu 4:
Phương trình x 1  x  3 có tập nghiệm là A. S    5 .
B. S  2;  5 . C. S    2 . D. S   . Lời giải: x  3 x  3  0  x  3 
Ta có: x 1  x  3    
 x   x  x 1   x 3 2 5. 2 2
x  7x 10  0  x  5
Vậy tập nghiệm của phương trình là: S    5 .
Chọn đáp án A. Câu 5:
Tập nghiệm của bất phương trình 2
x 16  8x là A. 4;  . B. \   4 . C. . D.  – ;  4 . Lời giải: 2
x 16  8x   x  2 4  0  x  4 .
Chọn đáp án B. Câu 6: Phương trình x  2 x   1
x 1  0 có bao nhiêu nghiệm? A. 2 . B. 1. C. 0 . D. 3 . Lời giải:
Điều kiện x 1  0  x  1 . x  0 x  0   Ta có x  2 x   1 x 1  0 2
x 1  0  x  1  .   x 1 0 x 1  
Đối chiếu điều kiện, tập nghiệm của bất phương trình là S    1 .
Chọn đáp án B. Câu 7:
Trong mặt phẳng Oxy, cho hai điểm A3;5 và B 2;7 . Điểm nào sau đây thuộc đường
trung trực của đoạn AB ?  3   5   1  A. M ;1  . B. N 1;   .
C. P 0;   1 . D. Q  ; 4   .  2   2   2  Lời giải:
Gọi d là đường trung trực của đoạn AB .  1 
Gọi I là trung điểm của AB I  ;6   .  2   1 
Đường thẳng d đi qua I  ;6 
 và có VTPT là AB  5;2 do đó phương trình của d là:  2   1  5 x   2  
y 6  0 10x  4y 19  0 .  2   3  Kiểm tra được M ;1    d .  2 
Chọn đáp án A. Câu 8:
Toạ độ giao điểm của parabol 2
(P ) : y  2x  2x  3 với parabol 2
(P ) : y x  6x là 1 2
A. 1;7 và 3;27 . B. 7;  1 và 27;3 .
C. 1;3 và 3;15 . D. 3;  1 và 15;3 . Lời giải:
Phương trình hoành độ giao điểm: x 1 2 2 2
2x  2x  3  x  6x x  4x  3  0   x  3
Vậy có hai giao điểm cần tìm là 1;7 và 3; 27 .
Chọn đáp án A. x y Câu 9:
Trong mặt phẳng Oxy, cho elip  E 2 2 : 
1. Với M là điểm bất kì nằm trên E , khẳng 16 9
định nào sau đây là khẳng định đúng ?
A. 4  OM  5. B. OM  5. C. OM  3.
D. 3  OM  4. Lời giải: x y Từ  E 2 2 : 
1, suy ra a  4,b  3. 16 9
Với một điểm bất kì trên  E  , ta luôn có b OM a  3  OM  4.
Chọn đáp án D.
Câu 10: Trong mặt phẳng Oxy, đường thẳng đi qua hai điểm A2;0 và B 0;3 có phương trình là x y x y x y x y A.   0 . B.  1. C.   0 . D.  1. 2 3 2 3 2 3 2 3 Lời giải: x y
Đường thẳng đi qua hai điểm A2;0 và B 0;3 có phương trình đoạn chắn là  1. 2 3
Chọn đáp án D.
Câu 11: Cho phương trình 2 2
x  5x  2  2 x  5x 10  0 . Đặt 2 t
x  5x 10 thì phương trình trở
thành phương trình nào sau đây? A. 2
t  2t 10  0 . B. 2
t  2t  2  0 . C. 2
t  2t  8  0 . D. 2
t  2t  8  0 . Lời giải: Ta có 2
x  5x 10  0,  x  . Đặt 2 t
x  5x 10, t  0 2 2
t x  5x 10.
Phương trình đã cho trở thành 2
t  2t  8  0 .
Chọn đáp án C.
Câu 12: Trong mặt phẳng Oxy, xác định vị trí tương đối của 2 đường thẳng  : 2x  3y 1  0 và  : 1 2 4
x  6y 1  0 . A. Song song. B. Trùng nhau.
C. Vuông góc.
D. Cắt nhau nhưng không vuông góc nhau. Lời giải: 2 3  1 Xét:   4  6 1
 nên hai đường thẳng song.
Chọn đáp án A.
Câu 13: Bất phương trình nào dưới đây vô nghiệm? A. 2
x  5x  2  0. B. 2
x  2x  3  0. C. 2
x  6x  9  0. D. 2
x  2x  3  0.
Câu 14: Cho tam thức f x 2
x  3x  2. Khẳng định nào dưới đây đúng?
A. f x  0, x  1;2.
B. f x  0, x  1;2.
C. f x  0, x
 ;1  2;.
D. f x  0, x   1  ;2.   Lời giải:
Bảng xét dấu: x  1 2  f x  0  0 
Chọn đáp án B.
Câu 15: Trong mặt phẳng Oxy, cho đường thẳng  : ax by c  0a,b,c  ;b  4 vuông góc với
đường thẳng d : 3x y  4  0 và  cách A1; 3 một khoảng 10 . Tính T a b c . A. 10 . B. 11 . C. 4 . D. 9 . Lời giải:
Do   d : 3x y  4  0   : x  3y c  0 .   c c  c
Ta có: dA  1 9 10 0 ;  
 10  c  10  10   1  9 10 c  20 
Vì c  nên c  0 . Suy ra  : x  3y  0 . Khi đó a  1,b  3,c  0  T  4 .
Chọn đáp án C. 2 2 x y
Câu 16: Trong mặt phẳng Oxy, đường hyperbol  1 có tiêu cự bằng 20 16 A. 12. B. 2. C. 4. D. 6. Lời giải: 2 a 20 a 2 5 Ta có : 2 b 16 b 4 . Tiêu cự 2c 12. 2 2 2 c a b c 6
Chọn đáp án A.
Câu 17: Tìm tập xác định của hàm số 2 y
2x  5x  2 .  1   1   1  1  A. ; 2 .   B.  ;  2;   . C.  ;  2;   . D. ;2 .     2   2   2  2  Lời giải: x  2 Điều kiện 2 2x 5x 2 0      1  . x   2  1 
Vậy tập xác định của hàm số là  ;  2;    .  2 
Chọn đáp án C.
Câu 18: Cho f x 2
ax bx c a  0 có 2
  b  4ac . Điều kiện cần và đủ để f x  0,x là a  0 a  0 a  0 a  0 A.  . B.  . C.  . D.  .   0   0   0   0
Câu 19: Cho hàm số y f x có tập xác định 5;5 và đồ thị của nó được biểu diễn như hình dưới đây: y 2 1 O 4 5 5 1 1 3 x 1 2
Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên 2; 2 .
B. Hàm số đồng biến trên 5;5 .
C. Hàm số đồng biến trên 2; 3 .
D. Hàm số đồng biến trên 5;  2 . Lời giải:
Hàm số đồng biến có đồ thị đi lên và hàm số nghịch biến có đồ thị đi xuống (từ trái sang phải).
Chọn đáp án D.
Câu 20: Tìm m để parabol 2
(P) : y mx  2x  3 có trục đối xứng là đường thẳng x  2 . 1 A. m  2 .
B. m  1.
C. m  1. D. m  . 2 Lời giải: 2  1
Vì  P là Parabol nên m  0 . Khi đó Parabol  P có trục đối xứng x    x  2m m 1 1
Theo bài ra trục đối xứng x  2 nên  2  m  . m 2
Chọn đáp án D.
Câu 21: Trong mặt phẳng Oxy, phương trình đường tròn có tâm I 3; 
1 và đi qua điểm M 2;  1  là 2 2 2 2
A. x  3   y   1  5.
B. x  3   y   1  5. 2 2 2 2
C. x  3   y   1  5.
D. x  3   y   1  5. Lời giải:
Ta có: IM   1  ; 2  .
Vì đường tròn có tâm I 3; 
1 và đi qua điểm M 2; 1
 nên bán kính của đường tròn là
R MI  5 . 2 2
Vậy phương trình đường tròn cần tìm là  x  3   y   1  5 .
Chọn đáp án C.
Câu 22: Tam thức nào dưới đây luôn âm với mọi x  ? A. 2
y x x  1. B. 2
y  x x  1. C. 2
y  x x  1. D. 2
y  x  4 . x Lời giải: Bảng xét dấu 2
y  x x  1 : x   y
Chọn đáp án C. 3x  4
Câu 23: Tập xác định của hàm số y  là 4x  5 4  5  5 A. D  \  . B. D  ;    .
C. D  . D. D  \   . 5  4  4 Lời giải: 5 5
Điều kiện : 4x  5  0  x D  \
4 . Tập xác định của hàm số là 4.  
Chọn đáp án D.
Câu 24: Cho hàm số bậc hai 2
y ax bx c,a;b;c   có đồ thị như hình bên dưới: y x O
Khẳng định nào dưới đây đúng?
A. a  0,b  0,c  0.
B. a  0,b  0,c  0.
C. a  0,b  0,c  0.
D. a  0,b  0,c  0. Lời giải:
Do đồ thị là parabol có bề lõm hướng xuống dưới nên a  0 . b
Dựa vào đồ thị, ta có: a0 
 0 b  0. 2a
Giao điểm của đồ thị với Oy có tọa độ 0;c  c  0.
Vậy a  0,b  0,c  0.
Chọn đáp án B.
Câu 25: Trong mặt phẳng Oxy, đường tròn C  2 2
: x y  4x  6 y 12  0 có tâm I và bán kính R lần lượt là A. I 2; 3  , R  5 .
B. I  2  ;3, R  5.
C. I  4
 ;6, R  5. D. I  2  ; 3  , R  5. Lời giải:
Phương trình C  có tâm I 2; 3
  và bán kính R    2 2 2 3 12  5.
Chọn đáp án A.
Câu 26: Tìm tập hợp tất cả các giá trị của tham số m để hàm số 2
y mx  2m  1 x  4m có tập xác định là . A.  ;   1 . B. 1; .
C. 1; . D.  ;   1 . Lời giải:
Yêu cầu của bài toán tương đương với: Tìm m để 2
mx  2 m  
1 x  4m  0, x   (1)
TH 1: Xét m  0 , (1) trở thành 2  x  0, x
  , không thỏa mãn. Nên m  0 loại.
a m  0 
TH 2: Xét m  0 , (1) tương đương với   '   m  2 2 1  4m  0 m  0 m 0    m 1      m  1. 2   3
m  2m 1  0  1 m    3 Vậy m  1.
Chọn đáp án B. x  3
Câu 27: Biết tập xác định của hàm số y x  2 
là nửa khoảng a;b . Khẳng định nào sau 5  x đây đúng?
A. 2a b  7 .
B. 2a b  1 .
C. a b  3 .
D. a  2b  6 . Lời giải: x  2  0 x  2 
Điều kiện xác định:    5   x  0 x  5 Vậy D   2
 ;5 suy ra a  2,b  5 nên 2a b 1 .
Chọn đáp án B. 2 2
Câu 28: Trong mặt phẳng Oxy, cho đường tròn (C) :  x  
1   y  2  8 . Phương trình tiếp tuyến d
của (C) tại điểm M 3;  4 là
A. d : x y 1  0 .
B. d : x  2 y 11  0 . C. d : x y  7  0 .
D. d : x y  7  0 . Lời giải:
Đường tròn (C) có tâm I (1; 2) .
Tiếp tuyến tại M có vectơ pháp tuyến là n IM  (2;  2)
Phương trình tiếp tuyến của đường tròn tại M là: 2(x  3)  2( y  4)  0  x y  7  0 .
Chọn đáp án C.
Câu 29: Cho hàm số   2
f x ax bx c có đồ thị như hình bên dưới:
Giá trị của biểu thức: T  2a b c bằng A. 1. B. 1. C. 0. D. 2. Lời giải:
Đồ thị cắt trục tung tại điểm có tung độ bằng 1
 nên c  1. Suy ra 2
y ax bx 1 b
Trục đối xứng x  1  
1  2a b  0 . 2a
Khi đó T  2a b c  0  (1)  1.
Chọn đáp án A.
Câu 30: Tập nghiệm của phương trình 3  x x  2 là  1  1   1
A. S   . B. S   2;  .
C. S   .
D. S    .  2  2  2 Lời giải: x  2  x  2  0  1
Ta có: 3  x x  2     1  x  . 3
  x x  2 x  2  2 1 
Vậy tập nghiệm của phương trình là S   . 2
Chọn đáp án C. 2 2
Câu 31: Trong mặt phẳng Oxy, điểm nào dưới đây thuộc đường tròn C  : x  
1   y  2  25?
A. M 4; 2 .
B. N 2; 4 .
C. P 3;6 .
D. Q 4; 2 . Lời giải: 2 2 Do 4   1   2
  2  25 nên điểm Q4;2 thuộc đường tròn C .
Chọn đáp án D.
Câu 32: Biết parabol  P 2
: y ax bx  4 có đỉnh là I 1; 2, tính a  3b . A. 20 . B. 18 . C. 30 . D. 25. Lời giải:
Do đồ thị hàm số 2
y ax bx  4 có đỉnh là điểm I 1; 2  b   1
 2a b  0  a  6   2a    
a  3b  30 . 
a b  4  2  b   12  y    1  2
Chọn đáp án C.
Câu 33: Trong mặt phẳng Oxy, đường tròn có tâm I 3; 4 tiếp xúc với đường thẳng
 :3x  4y 10  0 thì có bán kính bằng 5 3 A. . B. 5 . C. 3 . D. . 3 5 Lời giải:
Đường tròn tâm I 3; 4 tiếp xúc với đường thẳng  nên bán kính đường tròn là  
R d I  3.3 4.4 10 15 ,    3 . 2 2  5 3 4
Chọn đáp án C.
Câu 34: Viết phương trình chính tắc của parabol đi qua điểm Q 5; 2  . 4x A. 2
y x  3x 12. B. 2
y x  27. C. 2
y  5x  21. D. 2 y  . 5 Lời giải:
Phương trình chính tắc của parabol  P 2 : y  2 px 4 Q 5; 2
 P  2p  5 4
Vậy phương trình  P 2 : y x . 5
Chọn đáp án D.
Câu 35: Trong mặt phẳng Oxy, toạ độ hình chiếu H của điểm M 4;1 trên đường thẳng
 : x – 2y  4  0 là  14 17   14 17  A. 14; 1  9. B. 2; 3. C.   ;  . D.  ;  .  5 5   5 5  Lời giải: H Δ M
Đường thẳng  có 1 vectơ pháp tuyến n  1; 2
   1 vectơ chỉ phương là u  2;1.
Gọi H 2t  4;t là hình chiếu của M 4;1 trên đường thẳng .
Ta có: MH  2t  8;t  1.  
Do MH   nên MH.u  0  22t  8  t  1  17 0  t  14 17  H  ; . 5  5 5 
Chọn đáp án D.
II. PHẦN TỰ LUẬN (03 câu – 3,0 điểm)
Câu 1: (1,0 điểm). 2 4  x  1
a) Tìm tập xác định của hàm số y  . 2 x  4x  3
b) Tìm m để hàm số 2
y x  2mx m đồng biến trên 1; . Lời giải: 2 4  x  0 x 2  ;2  
a) Hàm số xác định      x 2  ;1 .  2
x  4x  3  0 x 
; 13; 
Vậy tập xác định của hàm số là D   2  ;1  . b) Hàm số 2
y x  2mx m đồng biến trên m;  (do a  1  0 )
Yêu cầu bài toán  1;   ;
m   m  1.
Câu 2: (1,0 điểm).
a) Giải phương trình x  x   2 1
3  3 x  4x  5  2  0. b) Tìm m để 2 2
x  2mx  4m  3  0 nghiệm đúng với mọi x  . Lời giải:
a) Ta có: x  x   2 2 2 1
3  3 x  4x  5  2  0  x  4x  3 x  4x  5  1  0 Đặt 2
x x   t t   2 2 4 5 0 
x  4x t  5, ta được phương trình: t  1 (tháa m·n) 2
t  3t  4  0   t  4  (lo¹i)
Với t  1, ta được 2 2 2
x  4x  5  1  x  4x  5  1  x  4x  4  0  x  2.
Vậy phương trình có tập nghiệm là S    2 . a  0 1   0
b) Yêu cầu bài toán      m; 1    1  ;   . 2    0  1  2m  12  0
Kết luận: m; 1    1  ;   .
Câu 3: (1,0 điểm).
Trong mặt phẳng Oxy, cho M(3; 1) và d : 3x  4y  12  0. Tìm hình chiếu H của điểm M lên
d và N là điểm đối xứng của M qua d. Lời giải: M H d N
Phương trình đường thẳng MH qua M và vuông góc với d : 3x  4y  12  0 có dạng
MH : 4x  3y m  0. Vì M(3; 1
 ) MH  4.3  3.( 1
 )  m  0  m  9. 
Suy ra MH : 4x  3y  9  0.
4x  3y  9 x  0
Tọa độ hình chiếu H là nghiệm hệ     H 0;3. 3x  4y  1  2 y    3
Do N là điểm đối xứng của M qua d nên H là trung điểm MN
x  2x x  2.0  3  3  N H M    N( 3  ;7).
y  2y y  2.3  ( 1  )  7  N H M
____________________HẾT____________________
Huế, 10h45’ Ngày 10 tháng 02 năm 2023
Page: CLB GIÁO VIÊN TRẺ TP HUẾ ¤N TËP GI÷A K× 2 Môn: TOÁN 10
SGK 2022 – Kết nối tri thức và cuộc sống
ĐỀ ÔN TẬP SỐ 05_TrNg 2023 Líp To¸n thÇy L£ B¸ B¶O
Trưêng THPT §Æng Huy Trø
S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch, TP HuÕ Trung t©m KM 10 Hương Trà, HuÕ. NỘI DUNG ĐỀ BÀI
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm)
Câu 1: Đồ thị trong hình là đồ thị hàm số của một trong bốn hàm số được cho ở các phương án A, B,
C, D. Hỏi hàm số đó là hàm số nào? y 1 x O -1 A. 2
y  x  2 . x B. 2
y x  2x  1. C. 2
y x  2x  4. D. 2 y x  2 . x
Câu 2: Trong mặt phẳng Oxy, đường tròn tâm I (3; 1) và bán kính R  2 có phương trình là A. 2 2
(x  3)  ( y 1)  4 . B. 2 2
(x  3)  ( y 1)  4 . C. 2 2
(x  3)  ( y 1)  4 . D. 2 2
(x  3)  ( y 1)  4 .
Câu 3: Trong mặt phẳng Oxy, đường thẳng đi qua A1; 2 , nhận n  2; 4
  làm vectơ pháp tuyến có phương trình là
A. x  2 y  5  0 .
B. x  2 y  4  0 .
C. x y  4  0 .
D. x  2 y  4  0 .
Câu 4: Tìm tất cả các giá trị của tham số m để biểu thức f x  m   2
2 x  2x  3 là một tam thức bậc hai. A. m  .
B. m  2 .
C. m  2 .
D. m  2 .
Câu 5: Trong mặt phẳng Oxy, phương trình 2 2
x y  2(m 1)x  2(m  2) y  6m  7  0 là phương trình
đường tròn khi và chỉ khi A. m  0. B. m  1. C. m  1.
D. m  1 hoặc m  1.
Câu 6: Trong mặt phẳng Oxy, cho đường thẳng d : 7x  3y 1  0 . Vectơ nào sau đây là vectơ chỉ phương của d?
A. u  7;3 .
B. u  3;7 . C. u   3  ;7 . D. u   7  ; 3   .
Câu 7: Tập nghiệm của phương trình 3  x x  2 là  1  1   1
A. S   . B. S   2;  .
C. S   .
D. S    .  2  2  2
Câu 8: Trong mặt phẳng Oxy, viết phương trình chính tắc của Parabol biết đường chuẩn có phương 1 trình x   0. 4 x A. 2 y  . x B. 2 y   . x C. 2 y  . D. 2 y  2 . x 2
Câu 9: Trong mặt phẳng Oxy, đường tròn (C) tâm I (4; 3) và tiếp xúc với đường thẳng
 : 3x  4y  5  0 có phương trình là A. 2 2
(x  4)  ( y  3)  1. B. 2 2
(x  4)  ( y  3)  1. C. 2 2
(x  4)  ( y  3)  1 . D. 2 2
(x  4)  ( y  3)  1
Câu 10: Trong mặt phẳng Oxy, đường thẳng d : x  2 y 1  0 song song với đường thẳng có phương trình nào sau đây?
A. x  2 y 1  0 .
B. 2x y  0 .
C. x  2 y 1  0 . D. 2
x  4y 1  0 .
Câu 11: Cho hàm số y f x có đồ thị như hình bên dưới.
Khẳng định nào sau đây đúng?
A. Hàm số y nghịch biến trên khoảng 0; 3 . B. Hàm số y đồng biến trên khoảng ;1 .
C. Hàm số y nghịch biến trên khoảng 0; 2 . D. Hàm số y đồng biến trên khoảng ; 3 .
Câu 12: Trong mặt phẳng Oxy, phương trình chính tắc của  E có tiêu cự bằng 6 và đi qua điểm A5;0 là 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.  1. B.  1. C.  1. D.  1. 100 81 15 16 25 9 25 16
Câu 13: Bất phương trình 2
x  2x  3  0 có tập nghiệm là A.  ;   
1  3;  . B. 1;3 . C. 1;  3 . D. 3;  1 .
Câu 14: Trong mặt phẳng Oxy, tính góc giữa hai đường thẳng  : x  3y  2  0 và
 : x  3y 1  0 . A. 90 . B. 120 . C. 60 . D. 30 .
Câu 15: Biết đồ thị hàm số P 2
: y ax bx  2,a;b ,a  0 qua hai điểm M 1; 4 và N  1  ;2. Tính 2 2
T a b . A. 10. B. 5. C. 1. D. 2. 2 2 x y
Câu 16: Đường Hyperbol  1 có tiêu cự bằng 20 16 A. 12. B. 2. C. 4. D. 6.
Câu 17: Tam thức nào dưới đây luôn dương với mọi giá trị của x ? A. 2
x 10x  2 . B. 2
x  2x 10 . C. 2
x  2x 10 . D. 2
x  2x 10 .
Câu 18: Cho hàm số bậc hai 2
y ax bx c,a;b;c   có đồ thị như hình bên dưới: y x O
Khẳng định nào dưới đây đúng?
A. a  0,b  0,c  0.
B. a  0,b  0,c  0.
C. a  0,b  0,c  0.
D. a  0,b  0,c  0.
Câu 19: Tìm tất cả các giá trị của tham số m để phương trình 2
x mx  4m  0 vô nghiệm.
A. 0  m  16 .
B. 4  m  4 .
C. 0  m  4 .
D. 0  m  16 . 2x  3
Câu 20: Tập xác định của hàm số y  2
x  4x  là 3  3  A. D
\  ;1;3 . B. D  \   1 . C. D  \   3 . D. D  \ 1;  3 .  2  2 2x  5x  2
Câu 21: Tìm tập xác định của hàm số y  . 2 x x 1  1   1  A. D  ; 2 .   B. D   ;  2;   .  2   2   1  1  C. D   ;  2;    . D. D  ; 2 .    2  2 
Câu 22: Cho hàm số bậc hai 2
y ax bx c,a;b;c   có đồ thị như hình bên dưới: y 4 3 -3 1 x -1 O
Tính T abc. A. 6. B. 6. C. 5. D. 4.
Câu 23: Hình vẽ dưới đây mô tả số người nhiễm Covid – 19 đang được điều trị ở Việt Nam tính từ
ngày 23/01/2020 đến ngày 13/02/2021.
Hỏi từ ngày 16/06/2020 đến ngày 27/01/2021, ngày nào Việt Nam có số người điều trị Covid- 19 nhiều nhất? A. 16 / 11/ 2020 . B. 17 / 08 / 2020 . C. 23 / 07 / 2020 . D. 13 / 02 / 2021 .
Câu 24: Cho f x và gx là các đa thức xác định trên . Mệnh đề nào dưới đây luôn đúng? 2
 f x  g x
A. f x  gx  f x  g    x 2  . 
B. f x  gx       g  x .  0 2  2  
f x  g x
f x  g x
C. f xgx        
D. f xgx         .  f  x .  0
gx  0 2 2 x y
Câu 25: Trong mặt phẳng Oxy, cho elip  E có phương trình 
1 . Tìm tiêu cự của E . 36 16 A. F F 12. B. F F  8. C. F F  2 5. D. F F  4 5. 1 2 1 2 1 2 1 2
Câu 26: Cho hàm số bậc hai 2
y ax bx c,a;b;c   có đồ thị như hình bên dưới: y O 1 x -2
Tập hợp các giá trị của tham số m để phương trình 2 f x  m  0 có hai nghiệm phân biệt là A. m  2. B. m  4. C. m  2. D. m  4.
x  2  3t
Câu 27: Trong mặt phẳng Oxy, cho đường thẳng  : 
t   và điểm M  1  ; 6 . Phương y  1   t
trình đường thẳng đi qua M và vuông góc với  là
A. 3x y  9  0 .
B. x  3y 17  0 .
C. 3x y  3  0 .
D. x  3y 19  0 . 2x  1
Câu 28: Với tất cả giá trị nào của m thì hàm số y  xác định trên ? 2
x  2x  3  m
A. m  4 .
B. m  4 .
C. m  0 .
D. m  4 .
Câu 29: Trong mặt phẳng Oxy, đường tròn (C) đi qua hai điểm (
A 1;3) , B(3;1) và có tâm nằm trên
đường thẳng d : 2x y  7  0 có phương trình là A. 2 2
(x  7)  ( y  7)  102 . B. 2 2
(x  7)  ( y  7)  164 . C. 2 2
(x  3)  ( y  5)  25 . C. 2 2
(x  3)  ( y  5)  25 .
Câu 30: Tích các nghiệm của phương trình x   2
2 x  4x  3  0 bằng A. 6. B. 2. C. 4. D. 4. 2 x 1 0
Câu 31: Hệ bất phương trình 
có nghiệm khi và chỉ khi x m  0 A. m  1. B. m  1. C. m  1. D. m  1.
Câu 32: Tìm số giá trị của tham số m để đường thẳng d : y x 1 cắt parabol  P 2
: y x  3x m tại 2
điểm phân biệt có hoành độ x , x sao cho 2 2 x x  6 . 1 2 1 2 A. 0 . B. 1. C. 2 . D. 4 .
Câu 33: Trong mặt phẳng Oxy, khoảng cách từ điểm M (1; 1
 ) đến đường thẳng  :3x y  4  0 là 3 10 5 A. 1. B. . C. . D. 2 10 . 5 2
Câu 34: Có bao nhiêu giá trị nguyên của tham số m để phương trình 2 2
x  4 x 1  (m 1)  0 có
nghiệm thuộc khoảng 0; 15? A. 1. B. 4 . C. 3 . D. 0.
Câu 35: Trong mặt phẳng Oxy, cho tam giác ABC với A2; 
1 ; B 4;5;C  3
 ;2 . Phương trình tổng
quát của đường cao đi qua A của tam giác là
A. 3x  7 y 1  0.
B. 7x  3y 13  0. C. 3
x  7 y 13  0. D. 7x  3y 11  0.
II. PHẦN TỰ LUẬN (03 câu – 3,0 điểm)
Câu 1: (1,0 điểm). 2
x  4x  3  7
a) Tìm tập xác định của hàm số y  . 2 x  2x
b) Tìm a,b,c để parabol P 2
: y ax bx c đi qua điểm A1; 3 và có đỉnh là I 1; 1.
Câu 2: (1,0 điểm).
a) Tìm m để phương trình 2
x x m x  1 có duy nhất một nghiệm.
b) Tìm m để phương trình m   2
2 x  22m  3 x  5m  6  0 có hai nghiệm trái dấu.
Câu 3: (1,0 điểm).
Trong mặt phẳng Oxy, cho đường thẳng d : 3x  4y  6  0. Viết phương trình đường tròn tâm
I(3; 0) cắt d tại A, B sao cho AB  8.
____________________HẾT____________________
Huế, 08h45’ Ngày 13 tháng 02 năm 2023
Page: CLB GIÁO VIÊN TRẺ TP HUẾ ¤N TËP GI÷A K× 2 Môn: TOÁN 10
SGK 2022 – Kết nối tri thức và cuộc sống
ĐỀ ÔN TẬP SỐ 05_TrNg 2023 Líp To¸n thÇy L£ B¸ B¶O
Trưêng THPT §Æng Huy Trø
S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch, TP HuÕ Trung t©m KM 10 Hương Trà, HuÕ.
LỜI GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm)
Câu 1: Đồ thị trong hình là đồ thị hàm số của một trong bốn hàm số được cho ở các phương án A, B,
C, D. Hỏi hàm số đó là hàm số nào? y 1 x O -1 A. 2
y  x  2 . x B. 2
y x  2x  1. C. 2
y x  2x  4. D. 2 y x  2 . x Lời giải: Kiểm tra các sự kiện:
Đồ thị P có đỉnh I 1; 1 và đi qua O. Ta thấy hàm số ở phương án D thỏa mãn.
Chọn đáp án D.
Câu 2: Trong mặt phẳng Oxy, đường tròn tâm I (3; 1) và bán kính R  2 có phương trình là A. 2 2
(x  3)  ( y 1)  4 . B. 2 2
(x  3)  ( y 1)  4 . C. 2 2
(x  3)  ( y 1)  4 . D. 2 2
(x  3)  ( y 1)  4 . Lời giải: 2 2
Phương trình đường tròn có tâm I 3;  
1 , bán kính R  2 là:  x  3   y   1  4 .
Câu 3: Trong mặt phẳng Oxy, đường thẳng đi qua A1; 2 , nhận n  2; 4
  làm vectơ pháp tuyến có phương trình là
A. x  2 y  5  0 .
B. x  2 y  4  0 .
C. x y  4  0 .
D. x  2 y  4  0 . Lời giải:
Phương trình đường thẳng đi qua A1; 2 và n  2; 4   là: 2 x  
1  4 y  2  0   x  
1  2  y  2  0  x  2 y  5  0 .
Chọn đáp án A.
Câu 4: Tìm tất cả các giá trị của tham số m để biểu thức f x  m   2
2 x  2x  3 là một tam thức bậc hai. A. m  .
B. m  2 .
C. m  2 .
D. m  2 . Lời giải:
f x  m   2
2 x  2x  3 là một tam thức bậc hai khi và chỉ khi: m  2  0  m  2 .
Chọn đáp án B.
Câu 5: Trong mặt phẳng Oxy, phương trình 2 2
x y  2(m 1)x  2(m  2) y  6m  7  0 là phương trình
đường tròn khi và chỉ khi A. m  0. B. m  1. C. m  1.
D. m  1 hoặc m  1. Lời giải: Ta có: 2 2
x y  2m  
1 x  2m  2 y  6m  7  0   1
x  2m  
1 x  m  2
1  y  2 m  2 y  m  22  m  2 1  m  22 2 2  6m  7  0  x   m  2 1    y    m 2 2 2   2m  2  m  1 
Vậy điều kiện để (1) là phương trình đường tròn: 2 2m  2  0   .  m 1
Chọn đáp án D.
Câu 6: Trong mặt phẳng Oxy, cho đường thẳng d : 7x  3y 1  0 . Vectơ nào sau đây là vectơ chỉ phương của d?
A. u  7;3 .
B. u  3;7 . C. u   3  ;7 . D. u   7  ; 3   . Lời giải:
Đường thẳng d có 1 VTPT là n  7;3 nên d có 1 VTCP là u   3  ;7 .
Chọn đáp án C.
Câu 7: Tập nghiệm của phương trình 3  x x  2 là  1  1   1
A. S   . B. S   2;  .
C. S   .
D. S    .  2  2  2 Lời giải: x  2  x  2  0  1
Ta có: 3  x x  2     1  x  . 3
  x x  2 x  2  2 1 
Vậy tập nghiệm của phương trình là S   . 2
Chọn đáp án C.
Câu 8: Trong mặt phẳng Oxy, viết phương trình chính tắc của Parabol biết đường chuẩn có phương 1 trình x   0. 4 x A. 2 y  . x B. 2 y   . x C. 2 y  . D. 2 y  2 . x 2 Lời giải:
Phương trình chính tắc của parabol  P 2 : y  2 px 1
Parabol có đường chuẩn x   1 0  p  2
 P) : y  x . 4 2
Chọn đáp án A.
Câu 9: Trong mặt phẳng Oxy, đường tròn (C) tâm I (4; 3) và tiếp xúc với đường thẳng
 : 3x  4y  5  0 có phương trình là A. 2 2
(x  4)  ( y  3)  1. B. 2 2
(x  4)  ( y  3)  1. C. 2 2
(x  4)  ( y  3)  1 . D. 2 2
(x  4)  ( y  3)  1 Lời giải:  3.4  4.3  5
C  có bán kính R d I ,    1. 3  42 2
Do đó, C  có phương trình 2 2
(x  4)  ( y  3)  1.
Chọn đáp án B.
Câu 10: Trong mặt phẳng Oxy, đường thẳng d : x  2 y 1  0 song song với đường thẳng có phương trình nào sau đây?
A. x  2 y 1  0 .
B. 2x y  0 .
C. x  2 y 1  0 . D. 2
x  4y 1  0 . Lời giải:
Ta kiểm tra lần lượt các đường thẳng. 1 2
.+) Với d : x  2 y  1  0 có   d d . 1 1 2  cắt 1 2 1 
.+) Với d : 2x y  0 có   d d . 2 1 2  cắt 2 1  2 1
.+) Với d : x  2 y  1  0 có    d d . 3 1 2  1  trùng 3 1 2  1 
.+) Với d : 2x  4 y  1  0 có    d d . 4 2  4 1  song song 4
Chọn đáp án D.
Câu 11: Cho hàm số y f x có đồ thị như hình bên dưới.
Khẳng định nào sau đây đúng?
A. Hàm số y nghịch biến trên khoảng 0; 3 . B. Hàm số y đồng biến trên khoảng ;1 .
C. Hàm số y nghịch biến trên khoảng 0; 2 . D. Hàm số y đồng biến trên khoảng ; 3 . Lời giải:
Trên khoảng 0; 2 , đồ thị hàm số đi xuống từ trái sang phải nên hàm số nghịch biến.
Chọn đáp án C.
Câu 12: Trong mặt phẳng Oxy, phương trình chính tắc của  E  có tiêu cự bằng 6 và đi qua điểm A5;0 là 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.  1. B.  1. C.  1. D.  1. 100 81 15 16 25 9 25 16 Lời giải: 2 2 x y
Phương trình chính tắc của  E là  E : 
1 a b  0 . 2 2   a b
Do  E có tiêu cự bằng 6 nên 2c  6  c  3.
Do  E đi qua điểm A5;0 nên a  2 2 2
5  b a c  25  9  16 . x y Vậy  E 2 2 :  1. 25 16
Chọn đáp án D.
Câu 13: Bất phương trình 2
x  2x  3  0 có tập nghiệm là A.  ;   
1  3;  . B. 1;3 . C. 1;  3 . D. 3;  1 . Lời giải: Ta có: 2
x  2x  3  0  1   x  3 .
Chọn đáp án B.
Câu 14: Trong mặt phẳng Oxy, tính góc giữa hai đường thẳng  : x  3y  2  0 và
 : x  3y 1  0 . A. 90 . B. 120 . C. 60 . D. 30 . Lời giải:
Đường thẳng  có vectơ pháp tuyến n  1; 3 , đường thẳng  có vectơ pháp tuyến n  1; 3 . 
Gọi  là góc giữa ,  , ta có:   n n 1 3 1 cos cos ,      60 . 1 3. 1 3 2
Chọn đáp án C.
Câu 15: Biết đồ thị hàm số P 2
: y ax bx  2,a;b ,a  0 qua hai điểm M 1; 4 và N  1  ;2. Tính 2 2
T a b . A. 10. B. 5. C. 1. D. 2. Lời giải:
M1;4P
a b  2  4 a b  2 a  1 Do        N   1  ;2P .
a b  2  2 a b  0 b   1 Vậy 2 2
T a b  2.
Chọn đáp án D. 2 2 x y
Câu 16: Đường Hyperbol  1 có tiêu cự bằng 20 16 A. 12. B. 2. C. 4. D. 6. Lời giải: 2 a 20 a 2 5 Ta có : 2 b 16 b 4 . Tiêu cự 2c 12. 2 2 2 c a b c 6
Chọn đáp án A.
Câu 17: Tam thức nào dưới đây luôn dương với mọi giá trị của x ? A. 2
x 10x  2 . B. 2
x  2x 10 . C. 2
x  2x 10 . D. 2
x  2x 10 . Lời giải:   0
Kiểm tra tam thức ở phương án C thỏa mãn  . a  0
Chọn đáp án C.
Câu 18: Cho hàm số bậc hai 2
y ax bx c,a;b;c   có đồ thị như hình bên dưới: y x O
Khẳng định nào dưới đây đúng?
A. a  0,b  0,c  0.
B. a  0,b  0,c  0.
C. a  0,b  0,c  0.
D. a  0,b  0,c  0. Lời giải:
Do đồ thị là parabol có bề lõm hướng lên trên nên a  0 . b
Dựa vào đồ thị, ta có: a0 
 0 b  0. 2a
Giao điểm của đồ thị với Oy có tọa độ 0;c  c  0.
Vậy a  0,b  0,c  0.
Chọn đáp án C.
Câu 19: Tìm tất cả các giá trị của tham số m để phương trình 2
x mx  4m  0 vô nghiệm.
A. 0  m  16 .
B. 4  m  4 .
C. 0  m  4 .
D. 0  m  16 . Lời giải: Phương trình 2
x mx  4m  0 vô nghiệm khi   0 2
m 16m  0  0  m 16 .
Chọn đáp án A. 2x  3
Câu 20: Tập xác định của hàm số y  2
x  4x  là 3  3  A. D
\  ;1;3 . B. D  \   1 . C. D  \   3 . D. D  \ 1;  3 .  2  Lời giải: x  1 Điều kiện 2
x  4x  3  0   . x  3
Tập xác định của hàm số là D  \ 1;  3 .
Chọn đáp án D. 2 2x  5x  2
Câu 21: Tìm tập xác định của hàm số y  . 2 x x 1  1   1  A. D  ; 2 .   B. D   ;  2;   .  2   2   1  1  C. D   ;  2;    . D. D  ; 2 .    2  2  Lời giải: Ta có: 2
x x 1  0, x
vì có a  0 và   0. x  2 Vậy hàm số xác định 2 2x 5x 2 0       1  . x   2  1 
Suy ra, tập xác định của hàm số là D   ;  2;    .  2 
Chọn đáp án C.
Câu 22: Cho hàm số bậc hai 2
y ax bx c,a;b;c   có đồ thị như hình bên dưới: y 4 3 -3 1 x -1 O
Tính T abc. A. 6. B. 6. C. 5. D. 4. Lời giải: b   1   2a
2a b  0 a  1    
Dựa vào đồ thị, ta có hệ: y 1
   4  a b c  4  b  2
 . Vậy T abc  6.    y     c  3 c  3 0 3   
Chọn đáp án B.
Câu 23: Hình vẽ dưới đây mô tả số người nhiễm Covid – 19 đang được điều trị ở Việt Nam tính từ
ngày 23/01/2020 đến ngày 13/02/2021.
Hỏi từ ngày 16/06/2020 đến ngày 27/01/2021, ngày nào Việt Nam có số người điều trị Covid- 19 nhiều nhất? A. 16 / 11/ 2020 . B. 17 / 08 / 2020 . C. 23 / 07 / 2020 . D. 13 / 02 / 2021 .
Câu 24: Cho f x và gx là các đa thức xác định trên . Mệnh đề nào dưới đây luôn đúng? 2
 f x  g x
A. f x  gx  f x  g    x 2  . 
B. f x  gx       g  x .  0 2  2  
f x  g x
f x  g x
C. f xgx        
D. f xgx         .  f  x .  0
gx  0 2 2 x y
Câu 25: Trong mặt phẳng Oxy, cho elip  E có phương trình 
1 . Tìm tiêu cự của E . 36 16 A. F F 12. B. F F  8. C. F F  2 5. D. F F  4 5. 1 2 1 2 1 2 1 2 Lời giải: 2 2 x ya  6  1   2 2 2
c a b  20 c  2 5  F F  2c  4 5 . 1 2 36 16 b   4
Chọn đáp án D.
Câu 26: Cho hàm số bậc hai 2
y ax bx c,a;b;c   có đồ thị như hình bên dưới: y O 1 x -2
Tập hợp các giá trị của tham số m để phương trình 2 f x  m  0 có hai nghiệm phân biệt là A. m  2. B. m  4. C. m  2. D. m  4. Lời giải: m
Ta có: 2 f x  m  0  f x  . 2 m
Số nghiệm của phương trình đã cho bằng số giao điểm của hai đồ thị y f x và y  . 2 m Yêu cầu bài toán   2   m  4  . 2
Chọn đáp án B.
x  2  3t
Câu 27: Trong mặt phẳng Oxy, cho đường thẳng  : 
t   và điểm M  1  ; 6 . Phương y  1   t
trình đường thẳng đi qua M và vuông góc với  là
A. 3x y  9  0 .
B. x  3y 17  0 .
C. 3x y  3  0 .
D. x  3y 19  0 . Lời giải:
 có một vectơ chỉ phương u  3;  1 .
Vì đường thẳng d vuông góc với  nên d có véctơ pháp tuyến n u  3  ;1 .
Phương trình tổng quát của đường thẳng d là 3 x  
1   y  6  0  3x y  3  0 .
Chọn đáp án C. 2x  1
Câu 28: Với tất cả giá trị nào của m thì hàm số y  xác định trên ? 2
x  2x  3  m
A. m  4 .
B. m  4 .
C. m  0 .
D. m  4 . Lời giải: 2x  1 Hàm số y  xác định trên khi phương trình 2
x  2x  3  m  0 vô nghiệm 2
x  2x  3  m
Hay   m  4  0  m  4  .
Chọn đáp án B.
Câu 29: Trong mặt phẳng Oxy, đường tròn (C) đi qua hai điểm (
A 1;3) , B(3;1) và có tâm nằm trên
đường thẳng d : 2x y  7  0 có phương trình là A. 2 2
(x  7)  ( y  7)  102 . B. 2 2
(x  7)  ( y  7)  164 . C. 2 2
(x  3)  ( y  5)  25 . C. 2 2
(x  3)  ( y  5)  25 . Lời giải:
I a; b là tâm của đường tròn C  , do đó:
AI BI  a  2  b  2  a  2  b  2 2 2 1 3 3 1  a b (1) Mà I  ;
a b  d : 2x y  7  0 nên 2a b  7  0 (2) . Thay (1) vào (2) ta có: 2 2
a  7  b  7  R AI  164 . 2 2
Vậy C  :  x  7   y  7  164 .
Chọn đáp án B.
Câu 30: Tích các nghiệm của phương trình x   2
2 x  4x  3  0 bằng A. 6. B. 2. C. 4. D. 4. Lời giải:
Điều kiện: x  2  0  x  2 (*). x  2 x  2  0  Ta có: x  2  2
x  4x  3  0    x 1 . 2 
x  4x  3  0 x  3 
Đối chiếu điều kiện (*), tập nghiệm của phương trình là S  2;  3 .
Chọn đáp án A. 2 x 1 0
Câu 31: Hệ bất phương trình 
có nghiệm khi và chỉ khi x m  0 A. m  1. B. m  1. C. m  1. D. m  1. Lời giải: 2 x 1 0  1   x 1 Ta có:    . x m  0 x m
Do đó hệ có nghiệm khi chỉ khi m  1.
Chọn đáp án D.
Câu 32: Tìm số giá trị của tham số m để đường thẳng d : y x 1 cắt parabol  P 2
: y x  3x m tại 2
điểm phân biệt có hoành độ x , x sao cho 2 2 x x  6 . 1 2 1 2 A. 0 . B. 1. C. 2 . D. 4 . Lời giải: Xét phương trình: 2 2
x  3x m x 1  x  2x m 1  0 (*)
 '  1 m 1  0 m  2   x x  2  x x  2      1 2 m 2 1 2 Theo bài ra ta có:       m  0 . 2 x x m 1 x x m 1        1 2 1 2 ( 2) 2(m 1) 6 x x 6      x x  2 2 2  2x x  6 1 2 1 2 1 2
Chọn đáp án B.
Câu 33: Trong mặt phẳng Oxy, khoảng cách từ điểm M (1; 1
 ) đến đường thẳng  : 3x y  4  0 là 3 10 5 A. 1. B. . C. . D. 2 10 . 5 2 Lời giải:
Khoảng cách từ điểm M (1; 1
 ) đến đường thẳng  : 3x y  4  0 là  
d M  3.1 1 4 6 3 10 ;    . 2 2 3 1 10 5
Chọn đáp án B.
Câu 34: Có bao nhiêu giá trị nguyên của tham số m để phương trình 2 2
x  4 x 1  (m 1)  0 có
nghiệm thuộc khoảng 0; 15? A. 1. B. 4 . C. 3 . D. 0. Lời giải: Ta có: 2 2
x  4 x 1  (m 1)  0 2 2
x 1 4 x 1  m  0 . Đặt 2 t
x 1 . Với x 0; 15 thì t 1;4 .
Phương trình trở thành: 2
t  4t m  0 2
m t  4t * . Xét hàm số 2
f (t)  t  4t với t  1; 4 . Ta có BBT:
Dựa vào BBT, suy ra phương trình đã cho có nghiệm thuộc khoảng 0; 15 .
 Phương trình (*) có nghiệm thuộc khoảng t 1;4  4  m  0 .
Vậy các giá trị nguyên m thỏa là m  4  ; 3  ; 2  ;  1 .
Chọn đáp án B.
Câu 35: Trong mặt phẳng Oxy, cho tam giác ABC với A2; 
1 ; B 4;5;C  3
 ;2 . Phương trình tổng
quát của đường cao đi qua A của tam giác là
A. 3x  7 y 1  0.
B. 7x  3y 13  0. C. 3
x  7 y 13  0. D. 7x  3y 11  0. Lời giải:
Đường cao AH của tam giác đi qua A2; 
1 và nhận n CB  7;3 làm VTPT.
AH : 7x  2  3 y  
1  0  7x  3y 11  0.
Chọn đáp án C.
II. PHẦN TỰ LUẬN (03 câu – 3,0 điểm)
Câu 1: (1,0 điểm). 2
x  4x  3  7
a) Tìm tập xác định của hàm số y  . 2 x  2x
b) Tìm a,b,c để parabol P 2
: y ax bx c đi qua điểm A1; 3 và có đỉnh là I 1; 1. Lời giải: x  0 2
x  2x  0 
a) Hàm số xác định    x  2
x;1  3;  \  0 . 2
x  4x  3  0
x;13;  
Vậy tập xác định của hàm số là D  ;1  3;   \  0 .
b) Do P đi qua điểm A1; 3 và có đỉnh là I 1; 1 nên ta có: 
a b c  3
a b c  3 a  1   
a b c  1
  a b c  1  b  2.    b 2a b  0 c  0   1    2a Vậy P 2
: y x  2 . x
Câu 2: (1,0 điểm).
a) Tìm m để phương trình 2
x x m x  1 có duy nhất một nghiệm.
b) Tìm m để phương trình m   2
2 x  22m  3 x  5m  6  0 có hai nghiệm trái dấu. Lời giải: x  1 0 x  1  a) Ta có: 2
x x m x  1     . 2 2
x x m x  1
m  x  2x  1 Bảng biến thiên 2
y  x  2x  1 trên 1;   : x 1  1  2 y 2  
Dựa vào bảng biến thiên, yêu cầu bài toán  m; 2     2 .
b) Phương trình có hai nghiệm trái dấu  .
a c  0  (m  2)(5m  6)  0 2 6
 5m  16m  12  0   m  2. 5
Câu 3: (1,0 điểm).
Trong mặt phẳng Oxy, cho đường thẳng d : 3x  4y  6  0. Viết phương trình đường tròn tâm
I(3; 0) cắt d tại A, B sao cho AB  8. Lời giải: 3.( 3  )  4.0  6 1  5 Ta có ( d I,d)    3. 2 2  5 3 4
Gọi H là trung điểm của AB và do AB  8  HA  4.
Tam giác IHA vuông tại 2 2 2
H IA IH  2 HA 2 2  R   (
d I ,d)  AH R  5.  
Khi đó, (C) có tâm I(3; 0), bán kính R  5 có dạng 2 2
(C) : (x  3)  y  25.
____________________HẾT____________________
Huế, 08h45’ Ngày 13 tháng 02 năm 2023